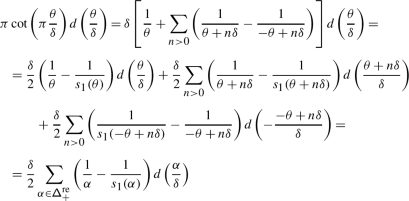Abstract
Let \(\mathfrak {g}\) be a symmetrisable Kac–Moody algebra and \(V\) an integrable \(\mathfrak {g}\)–module in category \(\mathcal {O}\). We show that the monodromy of the (normally ordered) rational Casimir connection on \(V\) can be made equivariant with respect to the Weyl group \(W\) of \(\mathfrak {g}\), and therefore defines an action of the braid group \(\mathcal {B}_{W}\) on \(V\). We then prove that this action is canonically equivalent to the quantum Weyl group action of \(\mathcal {B}_{W}\) on a quantum deformation of \(V\), that is an integrable, category \(\mathcal {O}\) module \(\mathcal {V}\) over the quantum group \(U_{\hbar }\mathfrak {g}\) such that \(\mathcal {V}/\hbar \mathcal {V}\) is isomorphic to \(V\). This extends a result of the second author which is valid for \(\mathfrak {g}\) semisimple.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1
Let \(\mathfrak {g}\) be a complex, semisimple Lie algebra, \((\cdot ,\cdot )\) an invariant inner product on \(\mathfrak {g}\), \(\mathfrak {h}\subset \mathfrak {g}\) a Cartan subalgebra, and  the corresponding root system. Set
the corresponding root system. Set  , and let \(V\) be a finite–dimensional representation of \(\mathfrak {g}\).
, and let \(V\) be a finite–dimensional representation of \(\mathfrak {g}\).
The Casimir connection of \(\mathfrak {g}\) is the flat connection on the holomorphically trivial vector bundle \(\mathbb{V}\) over \(\mathfrak {h}_{\scriptstyle {\operatorname {reg}}}\) with fibre \(V\) given by

Here, \(\mathsf {h}\) is a complex deformation parameter,  a chosen system of positive roots,Footnote 1 and \({\mathcal {K}}_{\alpha}\in U\mathfrak {g}\) the truncated Casimir operator of the three–dimensional subalgebra \(\mathfrak {sl}_{2}^{\alpha}\subset \mathfrak {g}\) corresponding to \(\alpha \) given by \({\mathcal {K}}_{\alpha}=x_{\alpha }x_{-\alpha}+x_{-\alpha} x_{\alpha}\), where \(x_{\pm \alpha}\in \mathfrak {g}_{\pm \alpha}\) are root vectors such that \((x_{\alpha}, x_{-\alpha})=1\) [29, 32, 30, 18].
a chosen system of positive roots,Footnote 1 and \({\mathcal {K}}_{\alpha}\in U\mathfrak {g}\) the truncated Casimir operator of the three–dimensional subalgebra \(\mathfrak {sl}_{2}^{\alpha}\subset \mathfrak {g}\) corresponding to \(\alpha \) given by \({\mathcal {K}}_{\alpha}=x_{\alpha }x_{-\alpha}+x_{-\alpha} x_{\alpha}\), where \(x_{\pm \alpha}\in \mathfrak {g}_{\pm \alpha}\) are root vectors such that \((x_{\alpha}, x_{-\alpha})=1\) [29, 32, 30, 18].
Although the Weyl group \(W\) of \(\mathfrak {g}\) does not act on \(V\) in general, the action of its Tits extension \(\widetilde {W}\) can be used to twist \((\mathbb{V},\nabla _{\mathcal {K}})\) into a \(W\)–equivariant, flat vector bundle \((\widetilde {\mathbb{V}},\widetilde {\nabla }_{\mathcal {K}})\) on \(\mathfrak {h}_{\scriptstyle {\operatorname {reg}}}\) [29, 32]. This gives rise to a one–parameter family of actions \(\mu _{\mathsf {h}}\) of the braid group \(\mathcal {B}_{W}=\pi _{1}(\mathfrak {h}_{\scriptstyle {\operatorname {reg}}}/W)\) on \(V\) which deforms the action of \(\widetilde {W}\).
A theorem of the second author, originally conjectured by De Concini around 1995 and independently in [32], asserts that the monodromy of \(\widetilde {\nabla }_{\mathcal {K}}\) is described by the quantum group \(U_{\hbar }\mathfrak {g}\), with deformation parameter given by \(\hbar =2\pi \sqrt{-1}\mathsf {h}\) [32–35]. Specifically, if \(\mathcal {V}\) is a quantum deformation of \(V\), that is a \(U_{\hbar }\mathfrak {g}\)–module which is topologically free over \(\mathbb{C}[\negthinspace [\hbar ]\negthinspace ]\) and such that \(\mathcal {V}/\hbar \mathcal {V}\cong V\) as \(U\mathfrak {g}\)–modules, the action of \(\mathcal {B}_{W}\) on \(V[\negthinspace [\hbar ]\negthinspace ]\) given by the formal Taylor series of \(\mu _{\mathsf {h}}\) at \(\mathsf {h}=0\) is equivalent to that on \(\mathcal {V}\) given by the quantum Weyl group operators of \(U_{\hbar }\mathfrak {g}\).
1.2
The goal of the present paper is to extend the description of the monodromy of the Casimir connection in terms of quantum Weyl groups to the case of an arbitrary symmetrisable Kac–Moody algebra \(\mathfrak {g}\). This extension requires several new ideas, which are described below. They lead to a far stronger result, even for a finite–dimensional \(\mathfrak {g}\), namely a constructive proof of the existence of a canonical equivalence between these representations.Footnote 2 We conjecture in fact that our equivalence can be specialised to non–rational values of \(\mathsf {h}\), and plan to return to this problem in future work.
1.3
When the root system is infinite, the sum in (1.1) does not converge. This is easily overcome, however, by replacing each Casimir by its normally ordered version
where \(\mathsf {m}_{\alpha}=\dim \mathfrak {g}_{\alpha}\), \(\{x_{\pm \alpha}^{(i)}\}_{i=1}^{\mathsf {m}_{\alpha}}\) are dual bases of the root spaces \(\mathfrak {g}_{\pm \alpha}\), and \(t_{\alpha}=\nu ^{-1}(\alpha )\), with \(\nu :\mathfrak {h}\to \mathfrak {h}^{*}\) the identification induced by the inner product. Although still infinite, the sum in

is now locally finite, provided the representation \(V\) lies in category \(\mathcal {O}\). Moreover, the connection \(\nabla _{:\mathcal {K}:}\) is flat [18] (we give an alternative proof of this, along the lines of its finite–dimensional counterpart, in Sect. 3).
1.4
Although it restores convergence, normal ordering breaks the \(W\)–equivariance of \(\nabla _{\mathcal {K}}\). If \(\mathfrak {g}\) is finite–dimensional, equivariance can be restored by reverting to the original connection (1.1), that is adding to \(\nabla _{:\mathcal {K}:}\) the \(\mathfrak {h}\)–valued, closed 1–form

Beyond finite type, it is therefore desirable to resum the divergent 1–formFootnote 3

Such an explicit resummation is carried out in the Appendix when \(\mathfrak {g}\) is affine. Its construction relies on the well–known resummation of the series \(\sum _{n\geqslant 0}(z+n)^{-1}\) via the logarithmic derivative \(\Psi \) of the Gamma function, through its expansion
1.5
At present, it is not clear how to carry out such a resummation for an arbitrary symmetrisable Kac–Moody algebra. We therefore opt for an alternative route: rather than altering \(\nabla _{:\mathcal {K}:}\), we modify its monodromy \(\mu _{:\mathcal {K}:}\) as follows.
The lack of equivariance of \(\mu _{:\mathcal {K}:}\) is measured by a 1–cocycle \(\mathcal {A}=\{\mathcal {A}_{w}\}\) on \(W\). We show in Sect. 4 that \(\mathcal {A}_{w}\) is the monodromy of the abelian connection \(d-a_{w}\), where

By relying on van der Lek’s presentation of the fundamental groupoid of the complexified Tits cone \(\mathsf {X}\subset \mathfrak {h}_{\scriptstyle {\operatorname {reg}}}\) [36], we then prove that \(\mathcal {A}\) is the coboundary of an explicit abelian cochain ℬ. As a consequence, the monodromy of \(\nabla _{:\mathcal {K}:}\) multiplied by ℬ gives rise to a canonical 1–parameter family of actions of the braid group \(\mathcal {B}_{W}=\pi _{1}(\mathsf {X}/W)\) on any integrable, category \(\mathcal {O}\) module \(V\).
We also prove that if \(b\) is a resummation of the divergent 1–form \(\widehat {b}\) (1.2), the cochain ℬ is the monodromy of the abelian connection \(d-\mathsf {h}b\), thus showing in particular that our two approaches coincide when \(\mathfrak {g}\) is finite–dimensional or affine.
1.6
Our main result can now be formulated as follows.
Theorem 1
The (\(W\)–equivariant) monodromy of \(\nabla _{:\mathcal {K}:}\) on a category \(\mathcal {O}\) integrable \(\mathfrak {g}\)–module \(V\) is canonically equivalent to the quantum Weyl group action of the braid group \(\mathcal {B}_{W}\) on a quantum deformation of \(V\).
Our strategy is patterned on that of [33–35], and hinges on the notion of braided Coxeter category developed in [2]. Informally speaking, such a category is a braided tensor category which carries commuting actions of Artin’s braid groups \(B_{n}\), and of a given generalised braid group \(\mathcal {B}_{W}\), on the tensor powers of its objects. For \(U_{\hbar }\mathfrak {g}\), such a structure arises on the category \(\mathcal {O}_{\hbar}^{{\scriptscriptstyle \operatorname {int}}}\) of integrable, highest weight modules from the \(R\)–matrix and quantum Weyl group operators.
For the category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) of integrable, highest weight \(\mathfrak {g}\)–modules, we prove in Sect. 13 that such a structure arises from the dynamical coupling of the KZ and Casimir connections of \(\mathfrak {g}\) [18]. This is analogous to the fact that the monodromy of the KZ equations gives rise to a braided tensor category structure on category \(\mathcal {O}\) [11], and the fact that the canonical fundamental solutions of the Casimir equations constructed by Cherednik and De Concini–Procesi [7, 9] give rise to a Coxeter structure on category \(\mathcal {O}\) [34]. One crucial difference, however, is that the joint Casimir–KZ system has irregular singularities when the differences \(z_{i}-z_{j}\) of the evaluation points tend to infinity. We address the corresponding Stokes phenomena by adapting the argument of [35], and construct canonical solutions of the joint KZ–Casimir system with prescribed asymptotics when \(z_{i}-z_{j}\to \infty \) for any \(i\neq j\).
1.7
Once the monodromy of the Casimir connection of \(\mathfrak {g}\) (resp. the quantum Weyl group operators of \(U_{\hbar }\mathfrak {g}\)) are understood as arising from a braided Coxeter structure on \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) (resp. \(\mathcal {O}_{\hbar}^{{\scriptscriptstyle \operatorname {int}}}\)), Theorem 1.6 is deduced by proving that \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) and \(\mathcal {O}_{\hbar}^{{\scriptscriptstyle \operatorname {int}}}\) are equivalent as braided Coxeter categories.
Such a statement presupposes in particular that \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) and \(\mathcal {O}_{\hbar}^{{\scriptscriptstyle \operatorname {int}}}\) are equivalent as abelian categories. When \(\mathfrak {g}\) is finite–dimensional, this follows from the fact that \(U\mathfrak {g}[\negthinspace [\hbar ]\negthinspace ]\) and \(U_{\hbar }\mathfrak {g}\) are isomorphic as algebras. While this is no longer true for an arbitrary \(\mathfrak {g}\), an equivalence of abelian categories can be obtained via Etingof–Kazhdan quantisation [15–17].
The EK equivalence relies on embedding category \(\mathcal {O}\) (resp. \(\mathcal {O}_{\hbar}\)) into the category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}\) of Drinfeld–Yetter modules over the negative Borel subalgebra \(\mathfrak {b}^{-}_{}\) (resp. the category \(\mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{}}\) of admissible Drinfeld–Yetter modules over \(U_{\hbar} \mathfrak {b}^{-}_{}\)), which follows from the fact that \(\mathfrak {g}\) is a quotient of the restricted Drinfeld double of \(\mathfrak {b}^{-}_{}\).
Given an associator \(\Phi \), Etingof–Kazhdan consider the braided tensor category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\Phi}\) with underlying abelian category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}\), and commutativity and associativity constraints given by \(e^{\hbar \Omega}\) and \(\Phi \). They construct a tensor functor \(\mathsf {f}_{ \mathfrak {b}^{-}_{}}:\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\Phi}\to \operatorname{{\mathsf{Vect}}}\), and prove that it lifts to an equivalence \(\widetilde {\mathsf {f}}_{ \mathfrak {b}^{-}_{}}: \mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\Phi}\to \mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{}}\) [16, 1].
1.8
An equivalence of braided Coxeter categories further requires that the EK equivalence be compatible with restriction to standard Levi subalgebras. To establish this, we constructed in [1] a relative version of Etingof–Kazhdan quantisation, which takes as input a pair of Lie bialgebras \(\mathfrak {a}\subseteq \mathfrak {b}\). This yields in particular a tensor functor \(\mathsf {f}_{\mathfrak {a},\mathfrak {b}}: \mathscr{DY}^{\Phi}_{\mathfrak {b}}\to \mathscr{DY}^{\Phi}_{\mathfrak {a}}\) which is isomorphic to restriction, is equal to \(\mathsf {f}_{\mathfrak {b}}\) when \(\mathfrak {a}=0\), and to the identity when \(\mathfrak {a}=\mathfrak {b}\). We also proved that \(\mathsf {f}_{\mathfrak {a},\mathfrak {b}}\) is compatible with the Tannakian equivalences \(\widetilde {\mathsf {f}}_{\mathfrak {a}}\), \(\widetilde {\mathsf {f}}_{\mathfrak {b}}\), in that there is a natural isomorphism \(v_{\mathfrak {a},\mathfrak {b}}\) which fits in the commutative diagram

In [2], we used the data \(\{\widetilde {\mathsf {f}}_{\mathfrak {b}},\mathsf {f}_{\mathfrak {a},\mathfrak {b}},v_{\mathfrak {a}\mathfrak {b}}\}\), where \(\mathfrak {a}\subseteq \mathfrak {b}\) range over the Borel subalgebras of all standard Levi subalgebras of \(\mathfrak {g}\), to transfer the braided Coxeter structure on \(\mathcal {O}_{\hbar}^{{\scriptscriptstyle \operatorname {int}}}\) arising from the \(R\)–matrix and quantum Weyl group to one on \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\).
1.9
To show that the transferred structure is equivalent to the one arising from the Casimir–KZ system, we rely on a rigidity result according to which there is, up to equivalence, a unique braided Coxeter structure on \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) with prescribed restriction functors, commutativity constraints, and local monodromies.
When \(\mathfrak {g}\) is finite–dimensional, rigidity is proved in [33, 34] by relying on the well–known computation of the Hochschild (coalgebra) cohomology of \(U \mathfrak {g}\) in terms of the exterior algebra of \(\mathfrak {g}\), as well as an appropriately defined Dynkin diagram cohomology designed to deal with secondary obstructions.
For an arbitrary \(\mathfrak {g}\), the cobar complex \(U\mathfrak {g}^{\otimes \bullet}\) needs to be replaced by its completion \(\mathcal {U}^{\bullet}_{\mathfrak {g}}\) with respect to category \(\mathcal {O}\). This is so because \(U\mathfrak {g}\) and \(U\mathfrak {g}^{\otimes 2}\) do not contain the Casimir operator \(C\) of \(\mathfrak {g}\) and the invariant tensor \(2\Omega =\Delta (C)-C\otimes 1-1\otimes C\) respectively, and are therefore not appropriate receptacles for the coefficients of the Casimir and KZ connections. Unfortunately, \(\mathcal {U}^{\bullet}_{\mathfrak {g}}\) has an unwieldy and, to the best of our knowledge, unknown Hochschild cohomology.
1.10
To remedy this, we replace \(\mathcal {U}^{\bullet}_{\mathfrak {g}}\) with a suitable cosimplicial subalgebra, which is big enough to contain the data describing the braided Coxeter structures coming from \(U_{\hbar }\mathfrak {g}\) and the Casimir–KZ connection, yet small enough to have a manageable Hochschild cohomology. This algebra is a refinement of Enriquez’s universal algebra [12] which we introduced in [3], and arises as follows.
We first embed category \(\mathcal {O}\) into the larger category of Drinfeld–Yetter modules over \(\mathfrak {b}^{-}_{}\), as explained in 1.7. This yields a smaller algebra of endomorphisms \(\mathcal {U}^{\bullet}_{ \mathfrak {b}^{-}_{}}\), together with a canonical map \(\mathcal {U}^{\bullet}_{ \mathfrak {b}^{-}_{}}\to \mathcal {U}^{\bullet}_{\mathfrak {g}}\). We then consider the subalgebra \(\mathbf {U}_{}^{\bullet}\subset \mathcal {U}^{\bullet}_{ \mathfrak {b}^{-}_{}}\) consisting of all universal endomorphisms, i.e., those obtained by compositions of iterated action and coaction maps. Finally, taking into account the root space decomposition of \(\mathfrak {b}^{-}_{}\), we consider the refinement  generated by the homogeneous components of universal endomorphisms.
generated by the homogeneous components of universal endomorphisms.
1.11
The Hoschschild cohomology of  can be computed via the calculus of Schur functors developed by Enriquez in [12], and shown to be given by a universal version of the exterior algebra of \(\mathfrak {g}\) [3]. In particular,
can be computed via the calculus of Schur functors developed by Enriquez in [12], and shown to be given by a universal version of the exterior algebra of \(\mathfrak {g}\) [3]. In particular,  behaves like an (uncompleted) enveloping algebra, with the added feature that it does not contain primitive elements. This leads to a strong rigidity statement, namely the fact that two braided Coxeter structures on \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) which are universal, that is such that their structure constants lie in
behaves like an (uncompleted) enveloping algebra, with the added feature that it does not contain primitive elements. This leads to a strong rigidity statement, namely the fact that two braided Coxeter structures on \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) which are universal, that is such that their structure constants lie in  , are uniquely equivalent. It also entirely bypasses the use of Dynkin diagram cohomology since the secondary obstructions are primitive, and therefore zero in
, are uniquely equivalent. It also entirely bypasses the use of Dynkin diagram cohomology since the secondary obstructions are primitive, and therefore zero in  .
.
1.12
To conclude the proof of Theorem 1.6, there remains to show that the braided Coxeter structures on \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) coming from the joint KZ–Coxeter system and the transfer from \(U_{\hbar }\mathfrak {g}\) are universal. The first statement is proved in Sects. 12, 16 and 22. It follows from the fact that an appropriate double holonomy algebra  underlying the KZ and Coxeter connections admits a map to
underlying the KZ and Coxeter connections admits a map to  .
.
The second statement is proved in Sect. 20. It follows from the construction of the transfer of braided Coxeter from \(\mathcal {O}_{\hbar}^{{\scriptscriptstyle \operatorname {int}}}\) to \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) described in 1.8. The latter implies that the structure constants of the transferred structure lie in a subalgebra  generated by the diagrammatic homogeneous components of universal endomorphisms. By definition, these are the components corresponding to the subalgebras of \(\mathfrak {b}^{-}_{}\) generated by \(\{h_{j},f_{j}\}_{j\in J}\), where \(J\) is a subset of the simple roots.
generated by the diagrammatic homogeneous components of universal endomorphisms. By definition, these are the components corresponding to the subalgebras of \(\mathfrak {b}^{-}_{}\) generated by \(\{h_{j},f_{j}\}_{j\in J}\), where \(J\) is a subset of the simple roots.
The following summarises the relations between the cosimplicial algebras described in Sections 1.9–1.12

1.13
In [4], we obtain an analogue of Theorem 1.6 for the actions of the pure braid group \(\mathcal {P}_{W}\subset \mathcal {B}_{W}\) on (not necessarily integrable) modules in \(\mathcal {O}\) and \(\mathcal {O}_{\hbar}\). Specifically, we show that the quantum Weyl group operators of \(U_{\hbar }\mathfrak {g}\) give rise to a canonical action of \(\mathcal {P}_{W}\) on any \(U_{\hbar }\mathfrak {g}\)–module \(\mathcal {V}\in \mathcal {O}_{\hbar}\). By relying on the methods developed in the present paper, we then show that this action describes the monodromy of \(\nabla _{:\mathcal {K}:}\) on the \(\mathfrak {g}\)–module \(V\in \mathcal {O}\) corresponding to \(\mathcal {V}\) under the Etingof–Kazhdan equivalence. We also extend these results to yield equivalent representations of parabolic pure braid groups on parabolic category \(\mathcal {O}\) for \(U_{\hbar }\mathfrak {g}\) and \(\mathfrak {g}\).
1.1 Outline of the paper
The paper is divided in four parts.
In Part I, we prove that the monodromy of the normally ordered Casimir connection can be modified by an abelian cochain to make it \(W\)–equivariant. We also review the definition of a Coxeter algebra following [34, 2]. By adapting the construction of fundamental solutions of the holonomy equations due to Cherednik and De Concini–Procesi [7, 9] to infinite hyperplane arrangements, we then show that this modified monodromy arises from a Coxeter algebra structure on the holonomy algebra  of the root arrangement of \(\mathfrak {g}\).
of the root arrangement of \(\mathfrak {g}\).
In Part II, we introduce the double holonomy algebra  of \(\mathfrak {g}\), a cosimplicial algebra which contains both
of \(\mathfrak {g}\), a cosimplicial algebra which contains both  and the tower of holonomy algebras of type \(\mathsf {A}_{n}\). We review the definition of a braided Coxeter algebra [34, 2], and show that the dynamical coupling of the Casimir and KZ equations gives rise to a braided Coxeter structure on
and the tower of holonomy algebras of type \(\mathsf {A}_{n}\). We review the definition of a braided Coxeter algebra [34, 2], and show that the dynamical coupling of the Casimir and KZ equations gives rise to a braided Coxeter structure on  .
.
In Part III, we review the definition of a braided Coxeter category following [2]. We show that a braided Coxeter structure on the double holonomy algebra  gives rise to a braided Coxeter structure on the category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) of integrable, highest weight modules over \(\mathfrak {g}\). By Part II, this implies that the coupled Casimir–KZ system yields a braided Coxeter category \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\) with underlying abelian category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\). We also point out that the quantum Weyl group operators and \(R\)–matrix of \(U_{\hbar }\mathfrak {g}\) give rise to a braided Coxeter category \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) with underlying abelian category \(\mathcal {O}_{\hbar}^{{\scriptscriptstyle \operatorname {int}}}\).
gives rise to a braided Coxeter structure on the category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\) of integrable, highest weight modules over \(\mathfrak {g}\). By Part II, this implies that the coupled Casimir–KZ system yields a braided Coxeter category \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\) with underlying abelian category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\). We also point out that the quantum Weyl group operators and \(R\)–matrix of \(U_{\hbar }\mathfrak {g}\) give rise to a braided Coxeter category \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) with underlying abelian category \(\mathcal {O}_{\hbar}^{{\scriptscriptstyle \operatorname {int}}}\).
The final Part IV contains the proof of our main result, namely the equivalence of the braided Coxeter categories \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\) and \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\). We first show that the braided Coxeter structure on \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\) can be extended to the category of Drinfeld–Yetter modules over \(\mathfrak {b}^{-}_{}\). The corresponding structure \(\mathscr{DY}_{ \mathfrak {b}^{-}_{},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}\) is universal, that is arises from a \(\mathsf {PROP}\)  describing a Lie bialgebra \([ \mathfrak {b}^{-}_{}]\) with the root decomposition of \(\mathfrak {b}^{-}_{}\). Specifically, we prove that the double holonomy algebra
describing a Lie bialgebra \([ \mathfrak {b}^{-}_{}]\) with the root decomposition of \(\mathfrak {b}^{-}_{}\). Specifically, we prove that the double holonomy algebra  maps to the endomorphisms of the tensor product of Drinfeld–Yetter modules over \([ \mathfrak {b}^{-}_{}]\).
maps to the endomorphisms of the tensor product of Drinfeld–Yetter modules over \([ \mathfrak {b}^{-}_{}]\).
In a parallel vein, we show that the braided Coxeter structure \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) can be extended to the category of admissible Drinfeld–Yetter modules over \(U_{\hbar} \mathfrak {b}^{-}_{}\) and then, using the 2–categorical extension of EK quantisation obtained in [1, 2], transferred to a braided Coxeter category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {\hbar ,{ \scriptscriptstyle \operatorname {int}}}}\) on integrable Drinfeld–Yetter modules over \(\mathfrak {b}^{-}_{}\). The latter is also universal in that it comes from a coarsening \({ \underline {\mathsf {LBA}}}_{\mathbb{D}}\) of the \(\mathsf {PROP}\) \({ \underline {\mathsf {LBA}}}_{\Delta}\), which only records the standard subalgebras of \(\mathfrak {b}^{-}_{}\) generated by simple root vectors. Finally, we use the rigidity of universal braided Coxeter algebra structures obtained in [3] to obtain the equivalence of \(\mathscr{DY}_{ \mathfrak {b}^{-}_{},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}\) and \(\mathscr{DY}_{ \mathfrak {b}^{-}_{},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {\hbar ,{ \scriptscriptstyle \operatorname {int}}}}\).
Part I. The Casimir connection
2 Kac–Moody algebras
2.1 Realisations of matrices
In Sects. 2.1–2.3, we mostly follow [21]. Let \(\mathbf {I}\) be a finite set, \(\mathsf {k}\) a field of characteristic zero, and \(\mathsf {A}=(a_{ij})_{i,j\in \mathbf {I}}\) a matrix with entries in \(\mathsf {k}\). A realisation of \(\mathsf {A}\) is a triple \((\mathfrak {h},\Pi ,\Pi ^{\vee})\), where
-
\(\mathfrak {h}\) is a finite–dimensional vector space over \(\mathsf {k}\)Footnote 4
-
\(\Pi =\{\alpha _{i}\}_{i\in \mathbf {I}}\) is a linearly independent subset of \(\mathfrak {h}^{*}\)
-
\(\Pi ^{\vee}=\{h_{i}\}_{i\in \mathbf {I}}\) is a linearly independent subset of \(\mathfrak {h}\)
-
\(\alpha _{i}(h_{j})=a_{ji}\) for any \(i,j\in \mathbf {I}\)
Given a realisation \((\mathfrak {h},\Pi ,\Pi ^{\vee})\) of \(\mathsf {A}\), we denote by
the \(|\mathbf {I}|\)–dimensional subspace and quotient of \(\mathfrak {h}\) determined by \(\Pi ^{\vee}\) and the annnihilator of \(\Pi \) respectively. Note that \(\mathfrak {h}'\), \(\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\) do not depend upon the choice of \(\mathfrak {h}\).
2.2 Kac–Moody algebras
Let \(\widetilde {\mathfrak {g}}\) be the Lie algebra generated by \(\mathfrak {h}\), \(\{e_{i}, f_{i}\}_{i\in \mathbf {I}}\) with relations \([h,h']=0\), for any \(h,h'\in \mathfrak {h}\), and
The Kac–Moody algebra corresponding to \(\mathsf {A}\) is the Lie algebra \(\mathfrak {g}=\widetilde {\mathfrak {g}}/\mathfrak {r}\), where \(\mathfrak {r}\) is the sum of all two–sided ideals in \(\widetilde {\mathfrak {g}}\) having trivial intersection with \(\mathfrak {h}\subset \widetilde {\mathfrak {g}}\). If \(\mathsf {A}\) is a generalised Cartan matrix (i.e., \(a_{ii}=2\), \(a_{ij}\in \mathbb{Z}_{\leqslant 0}\), \(i\neq j\), and \(a_{ij}=0\) implies \(a_{ji}=0\)), the ideal \(\mathfrak {r}\) is generated by the Serre relations \(\mathsf{ad}(e_{i})^{1-a_{ij}}(e_{j})=0=\mathsf{ad}(f_{i})^{1-a_{ij}}(f_{j})\) for any \(i\neq j\). The following is straightforward.
Lemma 1
-
(1)
The center of \(\mathfrak {g}\) is \(\mathfrak {z}(\mathfrak {g})=\Pi ^{\perp}\), and \(\dim \mathfrak {z}(\mathfrak {g})\cap \mathfrak {h}'=|\mathbf {I}|-\operatorname{rank}(\mathsf {A})\).
-
(2)
\(\mathfrak {h}'=\mathfrak {h}\cap [\mathfrak {g},\mathfrak {g}]\) and \(\mathfrak {h}^{\scriptstyle {\operatorname {e}}}=\mathfrak {h}/\mathfrak {z}(\mathfrak {g})\).
We refer to \(\mathfrak {h}'\) and \(\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\) as the derived and essential Cartan, respectively. Set \({\mathsf{Q}}_{+}=\bigoplus _{i\in \mathbf {I}}\mathbb{Z}_{\geqslant 0}{\alpha}_{i} \subseteq{ \mathfrak {h}}^{*}\), so that \(\mathfrak {g}\) has the root space decomposition \(\mathfrak {g}=\mathfrak {n}_{-}\oplus \mathfrak {h}\oplus \mathfrak {n}+\), where
Denote by  the set of positive roots of \({\mathfrak {g}}\) and set
the set of positive roots of \({\mathfrak {g}}\) and set  . For any root
. For any root  , the root multiplicity \(\mathsf {m}_{\alpha}= \dim \mathfrak {g}_{\alpha}\) is finite. Moreover, if \(\mathsf {A}\) is a generalised Cartan matrix, the Weyl group \(W\) of \(\mathfrak {g}\) preserves the root multiplicities, i.e., for any
, the root multiplicity \(\mathsf {m}_{\alpha}= \dim \mathfrak {g}_{\alpha}\) is finite. Moreover, if \(\mathsf {A}\) is a generalised Cartan matrix, the Weyl group \(W\) of \(\mathfrak {g}\) preserves the root multiplicities, i.e., for any  and \(w\in W\), \(\mathsf {m}_{\alpha}=\mathsf {m}_{w\alpha}\).
and \(w\in W\), \(\mathsf {m}_{\alpha}=\mathsf {m}_{w\alpha}\).
2.3 Symmetrisable Kac–Moody algebras
Let \(\mathsf {A}\) be a symmetrisable generalised Cartan matrix and fix a decomposition \(\mathsf {B}=\mathsf {DA}\), where \(\mathsf {D}=\operatorname {Diag}(\mathsf {d}_{i})_{i\in \mathbf {I}}\) is an invertible diagonal matrix with coprime entries \(\mathsf {d}_{i}\in \mathbb{Z}_{>0}\) such that \(\mathsf {B}\) is symmetric.
Let \(\langle \cdot ,\cdot \rangle \) be a symmetric, non–degenerate bilinear form on \(\mathfrak {h}\) such thatFootnote 5
Then, \(\langle \cdot ,\cdot \rangle \) uniquely extends to an invariant symmetric bilinear form on \(\widetilde {\mathfrak {g}}\), and \(\langle{e_{i}},{f_{j}}\rangle =\mathsf {d}_{i}^{-1}\delta _{ij}\). The kernel of this form is \(\mathfrak {r}\), so that \(\langle \cdot ,\cdot \rangle \) descends to a nondegenerate form on \(\mathfrak {g}\). Set  . The bilinear form induces a canonical isomorphism of graded vector spaces \(\mathfrak {b}^{+}_{}\simeq ( \mathfrak {b}^{-}_{})^{\star}\), where
. The bilinear form induces a canonical isomorphism of graded vector spaces \(\mathfrak {b}^{+}_{}\simeq ( \mathfrak {b}^{-}_{})^{\star}\), where  .
.
We denote by \(\nu :\mathfrak {h}\to \mathfrak {h}^{*}\) the isomorphism induced by \(\langle{\cdot},{\cdot}\rangle \) and, for any \(\beta \in \mathsf {Q}\), we set \(t_{\beta}=\nu ^{-1}(\beta )\). Recall that, by [21, Thm. 2.2], for any \(x\in \mathfrak {g}_{\alpha}\) and \(y\in \mathfrak {g}_{-\alpha}\), we have \([x,y]=\langle{x},{y}\rangle \cdot t_{\alpha}\).
2.4 Diagrammatic Kac–Moody algebras
Let \(\mathsf {A}\) be a generalised Cartan matrix and \(\mathbb{D}\) the Dynkin diagram of \(A\), i.e., the undirected graph having \(\mathbf {I}\) as its vertex set and an edge between \(i\neq j\) unless \(a_{ij}=0=a_{ji}\). For any subset of vertices \(B\subseteq \mathbb{D}\), let \(\mathsf {A}_{B}\) be the \(|B|\times |B|\) matrix \((a_{ij})_{i,j\in B}\), \(\Pi _{B}=\{\alpha _{i}\}_{i\in B}\subseteq \Pi \) and \(\Pi _{B}^{\vee}=\{\alpha _{i}^{\vee}\}_{i\in B}\subseteq \Pi ^{\vee}\).
Definition 1
-
(1)
A realisation \((\mathfrak {h},\Pi ,\Pi ^{\vee})\) of \(\mathsf {A}\) is diagrammatic if it is endowed with a collection of subspaces \(\{\mathfrak {h}_{B}\}_{B\subseteq \mathbb{D}}\) of \(\mathfrak {h}\) such that \(\mathfrak {h}_{\mathbb{D}}=\mathfrak {h}\), and the following holds
-
\(\Pi _{B}^{\vee}\subset \mathfrak {h}_{B}\) and \((\mathfrak {h}_{B}, \Pi _{B}|_{\mathfrak {h}_{B}},\Pi _{B}^{\vee})\) is a realisation of \(\mathsf {A}_{B}\) for any \(B\subseteq \mathbb{D}\)
-
\(\mathfrak {h}_{B'}\subseteq \mathfrak {h}_{B}\) whenever \(B'\subseteq B\)
-
\(\mathfrak {h}_{B_{1}\sqcup B_{2}}=\mathfrak {h}_{B_{1}}\oplus \mathfrak {h}_{B_{2}}\) and \(\mathfrak {h}_{B_{1}}\subseteq \Pi _{B_{2}}^{\perp}\) whenever \(B_{1}\perp B_{2}\).Footnote 6
-
-
(2)
If \(A\) is symmetrisable, a diagrammatic realisation \((\mathfrak {h},\Pi ,\Pi ^{\vee})\) is additionally required to be endowed with a non–degenerate symmetric bilinear form \(\langle \cdot ,\cdot \rangle \) such that (2.1) holds, and its restriction to each \(\mathfrak {h}_{B}\) is non–degenerate.Footnote 7
-
(3)
A (symmetrisable) Kac–Moody algebra is diagrammatic if the underlying realisation is.
Remark 1
-
(1)
Any symmetrisable generalised Cartan matrix \(\mathsf {A}\) has a diagrammatic realisation. Namely, if \(\mathsf {A}\) is of finite, affine or hyperbolic type, its minimal realisation is clearly diagrammatic. This is not always true for Cartan matrices of indefinite type. However, we proved in [2, Prop. 12.4] that a canonical (non–minimal) diagrammatic realisation with \(\dim \mathfrak {h}=2|\mathbf {I}|\) always exists.
-
(2)
Note that a diagrammatic symmetrisable Kac–Moody algebra \(\mathfrak {g}\) is naturally endowed with diagrammatic Lie subalgebras \(\mathfrak {g}_{B}=\langle \{e_{i},f_{i}\}_{i\in B}\), \(\mathfrak {h}_{B}\rangle \subseteq \mathfrak {g}\), \(B\subseteq \mathbb{D}\), such that \(\mathfrak {g}_{B'}\subseteq \mathfrak {g}_{B}\) if \(B'\subseteq B\) and \([\mathfrak {g}_{B_{1}},\mathfrak {g}_{B_{2}}]=0\) if \(B_{1}\perp B_{2}\). In particular, \(U\mathfrak {g}\) has a natural structure of diagrammatic algebra in the sense of Definition 6.1.
3 The Casimir connection
We review the definition of the Casimir connection of a symmetrisable Kac–Moody algebra, introduced by De Concini (cf. [30] where the Casimir connection is briefly mentioned in the introduction), Millson–Toledano Laredo [32, 29], and Felder–Markov–Tarasov–Varchenko [18], and provide an alternative proof of its flatness.
Henceforth, we fix a symmetrisable generalised Cartan matrix \(\mathsf {A}\), a diagrammatic realisation \((\mathfrak {h}_{\mathbb{R}, B},\Pi _{B}|_{\mathfrak {h}_{\mathbb{R},B}},\Pi _{B}^{\vee})_{B \subseteq \mathbb{D}}\) over ℝ, the diagrammatic realisation over ℂ given by its complexification \((\mathfrak {h}_{B},\Pi _{B}|_{\mathfrak {h}_{B}},\Pi _{B}^{\vee})_{B\subseteq \mathbb{D}}\), with \(\mathfrak {h}_{B}=\mathbb{C}\otimes _{\mathbb{R}}\mathfrak {h}_{\mathbb{R},B}\), the corresponding Kac–Moody algebra \(\mathfrak {g}\) over ℂ and the diagrammatic subalgebras \(\mathfrak {g}_{B}\subseteq \mathfrak {g}\), \(B\subseteq \mathbb{D}\).
3.1 Fundamental group of root system arrangements
Let \(\mathsf {A}\) be a symmetrisable generalised Cartan matrix, \((\mathfrak {h}_{\mathbb{R}},\Pi ,\Pi ^{\vee})\) a realisation of \(\mathsf {A}\) over ℝ, and \((\mathfrak {h}=\mathbb{C}\otimes _{\mathbb{R}}\mathfrak {h}_{\mathbb{R}},\Pi ,\Pi ^{\vee})\) its complexification. Let \(\Pi ^{\perp}\subset \mathfrak {h}\) be the annihilator of \(\Pi \), set \(\mathfrak {h}^{\scriptstyle {\operatorname {e}}}=\mathfrak {h}/\Pi ^{\perp}\), and note that \(\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\) is independent of the realisation of \(\mathsf {A}\). Let
be the fundamental Weyl chamber in \(\mathfrak {h}^{\scriptstyle {\operatorname {e}}}_{\mathbb{R}}\), and \({\mathsf{Y}}_{\mathbb{R}}=\bigcup _{w\in W}w(\overline {\mathcal {C}})\) the Tits cone. \({\mathsf{Y}}_{\mathbb{R}}\) is a convex cone, and the Weyl group \(W\) acts properly discontinuously on its interior \(\mathring{{\mathsf{Y}}}_{\mathbb{R}}\) and complexification \({\mathsf{Y}}=\mathring{{\mathsf{Y}}}_{\mathbb{R}}+\iota \mathfrak {h}^{\scriptstyle {\operatorname {e}}}_{\mathbb{R}}\subseteq \mathfrak {h}^{\scriptstyle {\operatorname {e}}}\), where \(\iota =\sqrt{-1}\) [26, 37]. The regular points of this action are given by

The action of \(W\) on \(\mathsf {X}\) is proper and free, and the space \(\mathsf {X}/W\) is a complex manifold.
Recall that the braid group of \(W\) is the group \(\mathcal {B}_{W}\) presented on the generators \(\mathscr{S}_{1},\dots , \mathscr{S}_{|\mathbf {I}|}\), with relations given by
for any \(i,j\in \mathbf {I}\) such that \(m_{ij}<\infty \), where \(m_{ij}\) is the order of \(s_{i}s_{j}\) in \(W\). The pure braid group \(\mathcal {P}_{W}\subset \mathcal {B}_{W}\) is the kernel of the standard projection \(\mathcal {B}_{W}\to W\).
The following result is due to van der Lek [36], and generalises Brieskorn’s Theorem [6] to the case of an arbitrary Weyl group.
Theorem 2
The fundamental groups of \(\mathsf {X}/W\) and \(\mathsf {X}\) are isomorphic to \(\mathcal {B}_{W}\) and \(\mathcal {P}_{W}\) respectively.
The generators \(\{\mathscr{S}_{i}\}_{i\in \mathbf {I}}\) of \(\mathcal {B}_{W}\) may be described as follows. Let \(p:\mathsf {X}\to \mathsf {X}/W\) be the canonical projection, fix a point \(x_{0}\in \mathcal {C}\) and use \([x_{0}]=p(x_{0})\) as a base point in \(\mathsf {X}/W\). For any \(i\in \mathbf {I}\), choose an open disk \(D_{i}\) in \(x_{0}+\mathbb{C}h_{i}\), centered in \(x_{0}-\frac{\alpha _{i}(x_{0})}{2}h_{i}\), and such that \(\overline {D}_{i}\) does not intersect any root hyperplane other than \(\operatorname{Ker}(\alpha _{i})\). Let \(\gamma _{i}:[0,1]\to x_{0}+\mathbb{C}h_{i}\) be the path from \(x_{0}\) to \(s_{i}(x_{0})\) in \(\mathsf {X}\) determined by \(\gamma _{i}\vert _{[0,1/3]\cup [2/3,1]}\) is affine and lies in \(x_{0}+\mathbb{R}h_{i}\setminus D_{i}\), the points \(\gamma _{i}(1/3)\), \(\gamma _{i}(2/3)\) are in \(\partial \overline {D}_{i}\), and \(\gamma _{i}|_{[1/3,2/3]}\) is a semicircular arc in \(\partial \overline {D}_{i}\), positively oriented with respect to the natural orientation of \(x_{0}+\mathbb{C}h_{i}\). Then, \(\mathscr{S}_{i}= p\circ \gamma _{i}\).
3.2 The Casimir connection
For any positive root \(\alpha \in \Delta _{+}\), let \(\{e_{\pm \alpha}^{(i)}\}_{i=1} ^{\mathsf {m}_{\alpha}}\) be bases of \(\mathfrak {g}_{\pm \alpha}\) which are dual with respect to \(\langle{\cdot},{\cdot}\rangle \), and
the corresponding truncated and normally ordered Casimir operator. Let \(V\) be a \(\mathfrak {g}\)–module in category \(\mathcal {O}\) and \(\mathbb{V}= \mathsf {X}\times V\) the holomorphically trivial vector bundle over \(\mathsf {X}\) with fibre \(V\) (cf. 15.1). Finally, let \(\mathsf {h}\in \mathbb{C}\) be a complex parameter.
Definition 2
The Casimir connection of \(\mathfrak {g}\) is the connection on \(\mathbb{V}\) given by

The Casimir connection for a semisimple Lie algebra was discovered by De Concini around ’95 (unpublished, though the connection is referenced in [30]) and, independently, Millson–Toledano Laredo [32, 29] and Felder–Markov–Tarasov–Varchenko [18]. In [18], the case of an arbitrary symmetrisable Kac–Moody algebra is considered. We give an alternative proof of flatness in this more general case, along the lines of [32, 29] in Sect. 3.4.
3.3 Local finiteness
The sum in (3.2) is locally finite even if  is infinite since, for any \(v\in V\), \({\mathcal {K}}_{\alpha}^{+} v=0\) for all but finitely many
is infinite since, for any \(v\in V\), \({\mathcal {K}}_{\alpha}^{+} v=0\) for all but finitely many  . Differently said, let \(\mathsf {ht}:\mathsf {Q}_{+}\to \mathbb{Z}_{\geqslant}\) be the height function on the positive root lattice given by \(\mathsf {ht}(\sum _{i\in \mathbf {I}}k_{i}\alpha _{i})=\sum _{i\in \mathbf {I}}k_{i}\). Then, \(\mathsf {ht}^{-1}(n)\) is finite for any \(n\in \mathbb{Z}_{\geqslant 0}\). Let \(\lambda _{1},\ldots ,\lambda _{p}\in \mathfrak {h}^{*}\) be such that the set of weights of \(V\) is contained in \(\bigcup _{i=1}^{p} D(\lambda _{i})\) where \(D(\lambda _{i})=\{\mu \in \mathfrak {h}^{*}|\mu \leqslant \lambda _{i}\}\) and \(\mu \leqslant \lambda \) iff \(\lambda -\mu \in \mathsf {Q}_{+}\). For \(n\in \mathbb{Z}_{>0}\), set
. Differently said, let \(\mathsf {ht}:\mathsf {Q}_{+}\to \mathbb{Z}_{\geqslant}\) be the height function on the positive root lattice given by \(\mathsf {ht}(\sum _{i\in \mathbf {I}}k_{i}\alpha _{i})=\sum _{i\in \mathbf {I}}k_{i}\). Then, \(\mathsf {ht}^{-1}(n)\) is finite for any \(n\in \mathbb{Z}_{\geqslant 0}\). Let \(\lambda _{1},\ldots ,\lambda _{p}\in \mathfrak {h}^{*}\) be such that the set of weights of \(V\) is contained in \(\bigcup _{i=1}^{p} D(\lambda _{i})\) where \(D(\lambda _{i})=\{\mu \in \mathfrak {h}^{*}|\mu \leqslant \lambda _{i}\}\) and \(\mu \leqslant \lambda \) iff \(\lambda -\mu \in \mathsf {Q}_{+}\). For \(n\in \mathbb{Z}_{>0}\), set
where \(V[\mu ]\) is the weight space of \(V\) of weight \(\mu \). Then, \(\displaystyle{V=\lim _{\longrightarrow}V^{n}}\), each \(V^{n}\) is invariant under the operators \({\mathcal {K}}_{\alpha}^{+}\), and \({\mathcal {K}}_{\alpha}^{+}\) acts as zero on \(V^{n}\) if \(\mathsf {ht}(\alpha )>n\). Thus, if \(\mathbb{V}^{n}= \mathsf {X}\times V^{n}\) is the trivial vector bundle over \(\mathsf {X}\) with fibre \(V^{n}\), then \(\displaystyle{ \mathbb{V}=\lim _{\longrightarrow} \mathbb{V}^{n}}\) and \(\displaystyle {\nabla _{\mathcal {K}}=\lim _{\longrightarrow} \nabla _{\mathcal {K}}^{n}}\) where

Note also that the pair \((\mathbb{V}^{n},\nabla _{\mathcal {K}}^{n})\) descends to a (trivial) vector bundle with connection on the complement \(\mathsf {X}^{n}\) of the hyperplanes \(\operatorname{Ker}(\alpha )\),  , in the finite–dimensional vector space
, in the finite–dimensional vector space

Remark 2
Let \({\mathcal {K}}_{\alpha}^{}=\sum _{i=1}^{\mathsf {m}_{\alpha}} e_{-\alpha}^{(i)}e_{\alpha}^{(i)}+ e_{\alpha}^{(i)}e_{-\alpha}^{(i)}\) be the truncated Casimir operator corresponding to \(\alpha \in \Delta _{+}\). Since \({\mathcal {K}}_{\alpha}^{}=2{\mathcal {K}}_{\alpha}^{+}+\mathsf {m}_{\alpha} t_{\alpha}\), the connection defined by \(\{{\mathcal {K}}_{\alpha}^{}\}_{\alpha \in \Delta _{+}}\) can be thought of as a Cartan extension of \(\nabla _{\mathcal {K}}\) since

However, if  , the second sum is not locally finite on category \(\mathcal {O}\) modules, in contrast with the case of \(\nabla _{\mathcal {K}}\).
, the second sum is not locally finite on category \(\mathcal {O}\) modules, in contrast with the case of \(\nabla _{\mathcal {K}}\).
3.4 Flatness
Theorem 3
The connection \(\nabla _{\mathcal {K}}\) is flat for any \(\mathsf {h}\in \mathbb{C}\).
Proof
It suffices to prove that the connection \(\nabla _{\mathcal {K}}^{n}\) defined by (3.3) is flat for any \(n\). Since \(\nabla _{\mathcal {K}}^{n}\) is pulled back from the finite–dimensional vector space \(\mathfrak {h}^{n}\) (3.4), Kohno’s lemma [23] implies that the flatness of \(\nabla _{\mathcal {K}}^{n}\) is equivalent to proving that, for any two–dimensional subspace \(U\subset \mathfrak {h}^{*}\) spanned by a subset of  , the following holds on \(V^{n}\) for any
, the following holds on \(V^{n}\) for any 

Since \({\mathcal {K}}_{\beta}^{+}\) acts as 0 on \(V^{n}\) if \(\mathsf {ht}(\beta )>n\), this amounts to proving that, on \(V^{n}\)

Let  be the subalgebra spanned by \(\mathfrak {h}\) and the root subspaces corresponding to the elements of
be the subalgebra spanned by \(\mathfrak {h}\) and the root subspaces corresponding to the elements of  . Then \(\mathfrak {g}_{U}\) is a generalized Kac–Moody algebra and, modulo terms in \(U\mathfrak {h}\), the operator
. Then \(\mathfrak {g}_{U}\) is a generalized Kac–Moody algebra and, modulo terms in \(U\mathfrak {h}\), the operator  is proportional to the Casimir operator. Since any element in \(U\mathfrak {h}\) commutes with \({\mathcal {K}}_{\alpha}^{+}\), the above commutator is therefore zero. □
is proportional to the Casimir operator. Since any element in \(U\mathfrak {h}\) commutes with \({\mathcal {K}}_{\alpha}^{+}\), the above commutator is therefore zero. □
3.5 Equivariance
It is well known that the Weyl group \(W\) of \(\mathfrak {g}\) does not act on an integrable \(\mathfrak {g}\)–module \(V\in \mathcal {O}\) in general, but that the triple exponentials
give rise to an action of an extension \(\widetilde {W}\) of \(W\) by the sign group \(\mathbb{Z}_{2}^{r}\), which is a quotient of \(\mathcal {B}_{W}\) [31].
However, the connection \(\nabla _{\mathcal {K}}\) is not \(\mathcal {B}_{W}\)–equivariant and therefore does not a priori yield a monodromy representation of \(\mathcal {B}_{W}\) on \(V\). Indeed, for any  , \(\widetilde {w}\in \mathcal {B}_{W}\) and \(w\in W\) such that \(\widetilde {w}\mapsto w\) under the morphism \(\mathcal {B}_{W}\to W\), we have
, \(\widetilde {w}\in \mathcal {B}_{W}\) and \(w\in W\) such that \(\widetilde {w}\mapsto w\) under the morphism \(\mathcal {B}_{W}\to W\), we have
where \(t_{\beta}=\nu ^{-1}(\beta )\in \mathfrak {h}'\) (cf. 2.3), and we used the fact that if  , then \(\alpha \) is real, and \(\mathsf {m}_{\alpha}=1\). The lack of equivariance of \(\nabla _{\mathcal {K}}\) will be addressed in Sect. 4.
, then \(\alpha \) is real, and \(\mathsf {m}_{\alpha}=1\). The lack of equivariance of \(\nabla _{\mathcal {K}}\) will be addressed in Sect. 4.
3.6 The holonomy algebra 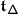
Let  be the free associative algebra with generators
be the free associative algebra with generators  . For any \(m\in \mathbb{Z}_{\geqslant 0}\), let
. For any \(m\in \mathbb{Z}_{\geqslant 0}\), let  be the two–sided ideal generated by \(\mathsf {t}_{\alpha}^{}\), with
be the two–sided ideal generated by \(\mathsf {t}_{\alpha}^{}\), with  , and set
, and set  . Note that
. Note that  is a well–defined element in
is a well–defined element in  .
.
Definition 3
The holonomy algebra  is the associative algebra given by the quotient of
is the associative algebra given by the quotient of  by the \(tt\)–relations
by the \(tt\)–relations

where  is any root subsystem of rank 2 containing \(\alpha \).
is any root subsystem of rank 2 containing \(\alpha \).
Remark 3
Let \(\widetilde {J}_{m}\) be the two sided ideal generated by \(J_{m}\) and the elements

where  is as before. Set
is as before. Set  . Then,
. Then,  is isomorphic to
is isomorphic to  .
.
3.7 The holonomy algebra 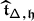
The holonomy algebra  is ℕ–graded by \(\deg (\mathsf {t}_{\alpha}^{})=1\),
is ℕ–graded by \(\deg (\mathsf {t}_{\alpha}^{})=1\),  . Let
. Let  be the completion of
be the completion of  with respect to the total grading.
with respect to the total grading.
The action of \(W\) on \(\mathfrak {h}'\) extends to one on  patterned on (3.6), by setting
patterned on (3.6), by setting
where \(w\in W\),  , and \(t_{w\alpha}=\nu ^{-1}(w\alpha )\in \mathfrak {h}'\) (cf. 2.3). Indeed, for \(u,v\in W\),
, and \(t_{w\alpha}=\nu ^{-1}(w\alpha )\in \mathfrak {h}'\) (cf. 2.3). Indeed, for \(u,v\in W\),  , one has
, one has
and therefore \(uv(\mathsf {t}_{\alpha}^{})=u(v(\mathsf {t}_{\alpha}^{}))\).
Remark 4
Note that any representation \(V\) of \(\mathfrak {g}\) and choice of \(\mathsf {h}\in \mathbb{C}\) give rise to an action

by \(\rho (\mathsf {t}_{\alpha}^{})=\mathsf {h}\cdot {\mathcal {K}}_{\alpha}^{+}\) and \(\rho (h)=\mathsf {h}\cdot h\) for  and \(h\in \mathfrak{h}\).
and \(h\in \mathfrak{h}\).
3.8 The universal Casimir connection
Definition 4
The universal Casimir connection is the formal connection on \(\mathsf {X}\)

The flatness of \(\nabla _{\mathsf {t}_{}^{}}\) is proved as in 3.4. Thus, any representation  gives rise to a flat connection
gives rise to a flat connection

on the trivial vector bundle over \(\mathsf {X}\) with fiber \(V\).
Remark 5
We shall consider only solutions of the holonomy equation

which are holomorphic functions in their domain of definition with values in  . The analytic computations performed with functions with values in
. The analytic computations performed with functions with values in  are justified by the fact that the latter is the inverse limit of the finite dimensional algebras
are justified by the fact that the latter is the inverse limit of the finite dimensional algebras  , where \(J_{k,n}\) is the ideal of the elements of degree \(\geqslant n\) in
, where \(J_{k,n}\) is the ideal of the elements of degree \(\geqslant n\) in  . In particular, a function \(G\) with values in
. In particular, a function \(G\) with values in  is determined by a sequence of compatible functions in the finite dimensional algebras
is determined by a sequence of compatible functions in the finite dimensional algebras  .
.
4 Equivariant monodromy
In this section, we prove that the monodromy of the universal Casimir connection can be made equivariant with respect to to the Weyl group by multiplying it by an explicit abelian cochain on \(W\), and that it then gives rise to a representation of the generalised braid group \(\mathcal {B}_{W}\).
4.1 The orbifold fundamental groupoid of \(\mathsf {X}\)
Let \(\mathbf {\Pi }_{1}{(}\mathsf {X};Wx_{0})\) be the fundamental groupoid of \(\mathsf {X}\) based at the \(W \)–orbit of \(x_{0}\). Then, \(\mathbf {\Pi }_{1}{(\mathsf {X}/W;[x_{0}])}\) is equivalent to the orbifold fundamental groupoid \(W\ltimes \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\), which is defined as follows.
-
Its set of objects is \(Wx_{0}\).
-
A morphism between \(x,y\in Wx_{0}\) is a pair \((w,\gamma )\), where \(w\in W\) and \(\gamma \) is a path in \(\mathsf {X}\) from \(x\) to \(w^{-1}y\).
-
The composition of \((w,\gamma ):x\to y\) and \((w',\gamma ') : y\to z\) is given by
$$ (w',\gamma ')\circ (w,\gamma )= (w'w, w^{-1}(\gamma ')\circ \gamma ):x \to z $$
The projection functor
given by \(P(wx_{0})=[x_{0}]\) and \(P(w,\gamma )=[\gamma ]\) is fully faithful since, for any given \(x,y\in Wx_{0}\), a loop \([\gamma ]\in \mathbf {\Pi }_{1}{(\mathsf {X}/W; [x_{0}])}\) lifts uniquely to a path \(\gamma : x\to w^{-1}y\), for a unique \(w\in W\). Any \(x\in Wx_{0}\) therefore determines a right inverse \(\mathcal {E}_{x}\) of \(P\) given by \(\mathcal {E}_{x}([x_{0}])=x\) and \(\mathcal {E}_{x}([\gamma ]) =(w,\gamma )\), where \(\gamma \) is the lift of \([\gamma ]\) through \(x\), and \(w\) is such that \(\gamma (1)=w^{-1}x\).
4.2 Obstruction to \(W\)–equivariance
In what follows, we shall repeatedly identify an algebra \(A\) such as \(\mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}}\), \(\mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}'}\) and their semi–direct product with \(W\), with the category with one object and morphisms given by \(A\), and abusively denote the latter by the same symbol.
The universal Casimir connection \(\nabla _{\mathsf {t}_{}^{}}\) gives rise to a functor
which maps a path \(\gamma \) to its parallel transport \(\mathscr{P}(\gamma )\). The lack of equivariance of \(\nabla _{\mathsf {t}_{}^{}}\) implies that of the functor \(\mathscr{P}\) with respect to the action of \(W\) on  defined in 3.7. Define the obstruction
defined in 3.7. Define the obstruction

for \(w\in W\) and \(\gamma \in \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\). The following shows that \(\mathscr{A}_{w}(\gamma )\) takes values in the abelian group  .
.
Lemma 2
For any \(\gamma \in \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\) and \(w\in W\), \(\mathscr{A}_{w}(\gamma )\in \exp (\mathfrak {h}')\).
Proof
\(w^{-1}(\mathscr{P}(w\gamma ))=w^{*}\mathscr{P}(\gamma )\) is the parallel transport of the connection

where the sum involves only real roots, since the set of positive imaginary roots is \(W\)–invariant [21, Prop. 5.2]. Since \(\nabla _{\mathsf {t}_{}^{}}\) and \(A_{w}\) commute, \(\mathscr{A}_{w}(\gamma )\) is the parallel transport along \(\gamma \) of the abelian connection
and therefore takes values in \(\exp (\mathfrak {h}')\) since \(t_{\alpha}=\nu ^{-1}(\alpha )\in \mathfrak {h}'\). □
4.3 Restoring equivariance
Let \(\mathsf {M}'\) be the abelian group defined by
and consider the action of \(W\) on \(\mathsf {M}'\) given by \((w\cdot f)(\gamma )=w(f(w^{-1}\gamma ))\).
Proposition 1
The following holds
-
(1)
\(\mathscr{A}=\{\mathscr{A}_{w}\}_{w\in W}\) is a 1–cocycle for \(W\) with values in \(\mathsf {M}'\), that is satisfies
$$ \mathscr{A}_{vw}=(w^{-1}\cdot \mathscr{A}_{v})\mathscr{A}_{w} $$(4.3) -
(2)
Assume that \(\mathscr{A}=d\mathscr{B}\mathcalligra{ }\) for some \(\mathscr{B}\mathcalligra{ }\in \mathsf {M}'\), where \(d\mathscr{B}\mathcalligra{ }_{w}=\mathscr{B}\mathcalligra{ }(w^{-1}\mathscr{B}\mathcalligra{ })^{-1}\). Then, there is a functor
$$ \mathscr{P}_{\mathscr{B}\mathcalligra{ }}:W\ltimes \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\to W\ltimes \mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}'}$$which is uniquely defined by
$$ w_{x}\to w\qquad \textit{and}\qquad \gamma \to \mathscr{P}(\gamma )\cdot \mathscr{B}\mathcalligra{ }(\gamma ) $$
Proof
(1) By Lemma 4.2, \(\mathscr{A}_{w}\) takes values in \(\exp (\mathfrak {h}')\) and satisfies \(\mathscr{A}_{w}(\gamma '\circ \gamma )=\mathscr{A}_{w}(\gamma ')\mathscr{A}_{w}(\gamma )\) since it is the monodromy of the connection (4.2). Moreover, for any \(v,w\in W\), and \(\gamma \) in \(\mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\)
as claimed.
(2) The restriction of \(\mathscr{P}_{\mathscr{B}\mathcalligra{ }}\) is a functor \(\mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\to \mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}'}\) for any \(\mathscr{B}\mathcalligra{ }\in \mathsf {M}'\) since \(\exp (\mathfrak {h}')\) lies in the center of  . Moreover, it is \(W\)–equivariant if and only if \(d\mathscr{B}\mathcalligra{ }=\mathscr{A}\) since, for any \(\gamma \in \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\) and \(w\in W\),
. Moreover, it is \(W\)–equivariant if and only if \(d\mathscr{B}\mathcalligra{ }=\mathscr{A}\) since, for any \(\gamma \in \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\) and \(w\in W\),
□
4.4 Natural transformations
Let \(\mathscr{B}\mathcalligra{ },\mathscr{B}\mathcalligra{ }'\in \mathsf {M}'\) be such that \(d\mathscr{B}\mathcalligra{ }=\mathscr{A}=d\mathscr{B}\mathcalligra{ }'\), and
be the corresponding functors. We shall consider natural isomorphisms \(\mathscr{P}_{\mathscr{B}\mathcalligra{ }}\Rightarrow \mathscr{P}_{\mathscr{B}\mathcalligra{ }'}\) which are given by a collection of elements \(c=\{c_{x}\}_{x\in Wx_{0}}\), with \(c_{x}\in \exp (\mathfrak {h}')\subset W\ltimes \mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}'}\). The relation
for any \((w,\gamma ):x\to y\) implies in particular that \(c_{wx_{0}}=w(c_{x_{0}})\), and therefore that \(c\) is uniquely determined by \(c_{x_{0}}\in \exp (\mathfrak {h}')\).
Proposition 2
An element \(\mathscr{C}\in \exp (\mathfrak {h}')\) determines an isomorphism \(\mathscr{P}_{\mathscr{B}\mathcalligra{ }}\Rightarrow \mathscr{P}_{\mathscr{B}\mathcalligra{ }'}\) if and only if \(\mathscr{B}\mathcalligra{ }'=\mathscr{B}\mathcalligra{ }\cdot d^{\operatorname {sing}}\mathscr{C}\), where \(d^{\operatorname {sing}}\mathscr{C}\in \mathsf {M}'\) is given byFootnote 8
for any \(\gamma :w_{1}x_{0}\to w_{2}x_{0}\).
Proof
If \(\mathscr{C}\in \exp (\mathfrak {h}')\) determines an isomorphism \(c\colon \mathscr{P}_{\mathscr{B}\mathcalligra{ }}\Rightarrow \mathscr{P}_{\mathscr{B}\mathcalligra{ }'}\), then, for \((\operatorname{id},\gamma ):x\to y\), the relation (4.4) gives \(\mathscr{B}\mathcalligra{ }'(\gamma )=\mathscr{B}\mathcalligra{ }(\gamma )c_{y}c_{x}^{-1}\). Thus, for any \(\gamma :w_{1}x_{0}\to w_{2}x_{0}\), one has \(\mathscr{B}\mathcalligra{ }'(\gamma )=\mathscr{B}\mathcalligra{ }(\gamma )w_{2}(\mathscr{C})w_{1}(\mathscr{C})^{-1}\), i.e., \(\mathscr{B}\mathcalligra{ }'=\mathscr{B}\mathcalligra{ }\cdot d^{\operatorname {sing}}\mathscr{C}\). The converse is clear. □
Remark 6
The assignment \((w,\gamma )\mapsto \mathscr{A}_{w}(\gamma )\) can equivalently be thought of as a 2–cocycle on the groupoid \(W\ltimes \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\) with values in \(\exp (\mathfrak {h}')\), which is normalised to vanish on \(W\) and \(\mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\). Similarly, ℬ and \(\mathscr{C}\) can be thought of as 1 and 0–cocycles, respectively. Then, the result above is simply stating that the equivalence classes of the representations \(\mathscr{P}_{\mathscr{B}\mathcalligra{ }}\) for \(\mathscr{B}\mathcalligra{ }\in \mathsf {M}'\) such that \(d\mathscr{B}\mathcalligra{ }=\mathscr{A}\) are controlled by the first cohomology group.
4.5 Presentation of \(\mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\)
Assume henceforth that the basepoint \(x_{0}\) lies in \(\imath \mathcal {C}\). For each \(i\in \mathbf {I}\), let \(\gamma _{i}\) be a fixed elementary path in \(\mathsf {X}\) from \(x_{0}\) to \(s_{i}(x_{0})\) above the wall \(\alpha _{i}=0\), i.e., is such that its real part lies in the half–space \(\{\alpha _{i}\geq 0\}\). For any \(i\in \mathbf {I}\) and \(w\in W\) set
Note that \(\mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\) is generated by \(\{\gamma _{w,i}\}_{w\in W,i\in \mathbf {I}}\). For instance, the elementary path from \(x_{0}\) to \(s_{i}x_{0}\) below the wall \(\alpha _{i}=0\) is given by \(\gamma _{s_{i}, i}^{-1}\).
We shall consider the following class of paths depending upon the choice of a reduced expression of a given element \(v\) in \(W\), which we refer to as minimal Tits paths. Let \(\underline {s}=(s_{i_{1}},\dots , s_{i_{\ell}})\) be a reduced expression of \(v\), set \(v_{k}^{}= s_{i_{1}}\cdots s_{i_{k}}\), \(1\leqslant k\leqslant \ell \), and denote by \(\gamma _{\underline {s}}\) the path

Then, a minimal Tits path is an element of the form \(\gamma _{w,\underline {s}}= w\gamma _{\underline {s}}\), where \(w\in W\) and \(\underline {s}\) is a reduced expression of some \(v\in W\). Note that two minimal Tits paths \(\gamma _{w,\underline {s}}\) and \(\gamma _{w',\underline {s}'}\) have the same endpoints if and only if \(w=w'\) and \(\underline {s}\), \(\underline {s}'\) are reduced expressions of the same element \(v\). The following is due to van der Lek [36].
Theorem 4
The homotopy relations in \(\mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\) are generated by the equivalence relation identifying minimal Tits paths with the same endpoints.
Proof
For the reader’s convenience, we provide a brief account of van der Lek’s proof. The latter hinges on the combinatorial description of \(\mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\) in terms of signed galleries in the root hyperplane arrangement (cf. [36, Thm. I-4.10]). A Tits gallery is a sequence of chambers \(\mathcal {C}_{0},\mathcal {C}_{1},\dots , \mathcal {C}_{\ell}\) such that, for any \(i=0,\dots , \ell -1\), \(\mathcal {C}_{i}\) and \(\mathcal {C}_{i+1}\) are separated by a single hyperplane \(M_{i}\). Let \(\mathcal {H}_{i}^{+}\), \(\mathcal {H}_{i}^{-}\) be the halfspaces determined by \(M_{i}\), with \(\mathcal {C}_{i}\subset \mathcal {H}_{i}^{+}\) and \(\mathcal {C}_{i+1}\subset \mathcal {H}_{i}^{-}\). Then, a signed gallery is a sequence \(\mathcal {C}_{0}^{\epsilon _{1}}\mathcal {C}_{1}^{\epsilon _{2}}\cdots \mathcal {C}_{\ell -1}^{ \epsilon _{\ell}} \mathcal {C}_{\ell}\), where \(\mathcal {C}_{0},\mathcal {C}_{1},\dots , \mathcal {C}_{\ell}\) is a Tits gallery and the signs \(\epsilon _{i}\in \{\pm \}\) denote a choice of the half–spaces \(\mathcal {H}_{i}^{\pm}\).
Chambers and signed galleries are interpreted, respectively, as the objects and the morphisms of the category \(\mathbf{Gal}(\mathsf {X};\Delta )\). Note that \(\mathbf{Gal}(\mathsf {X};\Delta )\) is naturally endowed with an action of \(W\).Footnote 9 Then, \(\mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\) is isomorphic to the quotient of \(\mathbf{Gal}(\mathsf {X};\Delta )\) by the following equivalence relations
-
Cancel relations. For any two adjacent chambers \(\mathcal {C}_{0}\), \(\mathcal {C}_{1}\), the signed gallery \(\mathcal {C}_{0}^{\pm} \mathcal {C}_{1}^{\mp} \mathcal {C}_{0}\) is equivalent to the gallery \(\mathcal {C}_{0}\).
-
Flip relations. Let \(\underline {\mathcal {C}}=\mathcal {C}_{0}^{\epsilon _{1}}\mathcal {C}_{1}^{\epsilon _{2}}\cdots \mathcal {C}_{ \ell -1}^{\epsilon _{\ell}} \mathcal {C}_{\ell}\) and \(\underline {\mathcal {D}}=\mathcal {D}_{0}^{\epsilon '_{1}}\mathcal {D}_{1}^{\epsilon '_{2}}\cdots \mathcal {D}_{ \ell -1}^{\epsilon '_{\ell}} \mathcal {D}_{\ell}\) be two minimal signed galleries such that \(\mathcal {C}_{0}=\mathcal {D}_{0}\) and \(\mathcal {C}_{\ell}=\mathcal {D}_{\ell}\) are opposite chambers with respect to a codimension 2 facet. Then, \(\underline {\mathcal {C}}\) and \(\underline {\mathcal {D}}\) are equivalent.
Note that, by [36, Rmk. I-5.3 and 5.4], the sequences of signs appearing in the flip relations must satisfy \(\epsilon _{i}=\epsilon '_{k-i+1}\) and admit at most one change of sign. It follows that is enough to consider only flip relations with \(\epsilon _{i}=+\) for any \(i\). Moreover, the minimal Tits galleries have a simple combinatorial description (cf. [36, Prop. II-2.16]). Let \(\mathcal {C}_{0}\) be a chamber and \(w_{0}\in W\) the unique element such that \(\mathcal {C}_{0}=w_{0}\mathcal {C}\). Then, for any \({w}\in W\), the minimal Tits gallery from \(\mathcal {C}_{0}\) to \({w}\mathcal {C}_{0}\) are in bijection with the reduced expressions of \(w_{0}^{-1}{w}w_{0}\), i.e., if \(\underline {s}=(s_{i_{1}},s_{i_{2}},\dots ,s_{i_{\ell}})\) is a reduced expression of \(w_{0}^{-1}{w}w_{0}\), the sequence
where \(w_{r}= s_{i_{1}}s_{i_{2}}\dots s_{i_{r}}\), is a minimal Tits gallery. Clearly, every minimal Tits gallery from \(\mathcal {C}_{0}\) to \(\widetilde {w}\mathcal {C}_{0}\) arises in this way and it is the image through \(w_{0}\) of a minimal Tits gallery starting in the fundamental chamber \(\mathcal {C}\).
Finally, the isomorphism between the two groupoids is induced by a \(W\)–equivariant full functor \(\phi :\mathbf{Gal}(\mathsf {X};\Delta )\to \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\) mapping the fundamental chamber to \(x_{0}\) and the step one galleries \(\mathcal {C}^{\pm}s_{i}\mathcal {C}\) to the elementary paths \(\gamma _{i}^{\pm}\), where \(\gamma _{i}^{+}=\gamma _{i}\) and \(\gamma _{i}^{-}=\gamma _{s_{i},i}^{-1}\) (cf. [36, Rmk. II-3.10]). The result follows. □
4.6 Normalised cochains
Let \(\mathsf {M}\supset \mathsf {M}'\) be the abelian group given by
Lemma 3
-
(1)
Let \(\mathscr{B}\mathcalligra{ }\in \mathsf {M}\) be such that \(d\mathscr{B}\mathcalligra{ }=1\). Then, ℬ is uniquely determined by the values \(\mathscr{B}\mathcalligra{ }(\gamma _{i})\in \exp (\mathfrak {h})\), \(i\in \mathbf {I}\).
-
(2)
For any collection of complex numbers \(\mathbf {a}=\{a_{i}\}_{i\in \mathbf {I}}\), there is a unique \(\mathscr{B}\mathcalligra{ }_{\mathbf {a}}\in \mathsf {M}'\) such that \(d\mathscr{B}\mathcalligra{ }_{\mathbf {a}}=1\) and \(\mathscr{B}\mathcalligra{ }_{\mathbf {a}}(\gamma _{i})=\exp (a_{i} t_{\alpha _{i}})\).
Proof
(1) follows from \(\mathscr{B}\mathcalligra{ }(\gamma '\circ \gamma )=\mathscr{B}\mathcalligra{ }(\gamma ')\mathscr{B}\mathcalligra{ }(\gamma )\), and the fact that the relation \(d\mathscr{B}\mathcalligra{ }=1\) reads \(\mathscr{B}\mathcalligra{ }(w\gamma )=w(\mathscr{B}\mathcalligra{ }(\gamma ))\).
(2) As above, the relation \(d\mathscr{B}\mathcalligra{ }_{\mathbf {a}}=1\) implies that, for any \(w\in W\) and \(i\in \mathbf {I}\), \(\mathscr{B}\mathcalligra{ }_{\mathbf {a}}(\gamma _{w,i})=w(\mathscr{B}\mathcalligra{ }_{\mathbf {a}}(\gamma _{i}))\). It is therefore sufficient to show that the assignment \(\gamma _{w,i}\mapsto \exp (a_{i}t_{w\alpha _{i}})\) is constant on minimal Tits paths with the same endpoints.
Let \(w,v\in W\), \(\underline {s}=(s_{i_{1}},\dots , s_{i_{\ell}})\) a reduced expression of \(v\), and set \(v_{k}^{ }=s_{i_{1}}\cdots s_{i_{k}}\), \(k\leqslant \ell \). Then,
where \(i_{\alpha}, \underline {s}\in \mathbf {I}\) is the unique index \(k\) such that \(\alpha =v_{k-1}^{}\alpha _{i_{k}}\). To check that this is independent of the reduced decomposition of \(v\), it is sufficient to consider the case when \(v\) is the longest element in a rank 2 Weyl group. If \(W\) is of Coxeter type \(\mathsf {A}_{1}\times \mathsf {A}_{1}\), \(\mathsf {B}_{2}\) or \(\mathsf {G}_{2}\), this follows because a given positive root \(\alpha \) is \(W \)–conjugate to a unique simple root \(\alpha _{i}\), namely the one of the same length of \(\alpha \). If \(W\) is of type \(\mathsf {A}_{2}\), with \(v=s_{1}s_{2}s_{1}=s_{2}s_{1}s_{2}\), the independence on the reduced decomposition amounts to the identity
which clearly holds. The uniqueness of \(\mathscr{B}\mathcalligra{ }_{\mathbf {a}}\) follows from (1). □
4.7 Triviality of the obstruction \(\mathscr{A}\)
Theorem 5
There is a unique \(\mathscr{B}\mathcalligra{ }\in \mathsf {M}'\) such that
for any \(i\in \mathbf {I}\).
Proof
The uniqueness of ℬ follows from Lemma 4.6. The relation \(d\mathscr{B}\mathcalligra{ }=\mathscr{A}\) together with the normalisation of ℬ are equivalent to the requirement that, for any \(w\in W\) and \(i\in \mathbf {I}\), \(\mathscr{B}\mathcalligra{ }(\gamma _{w,i})=w(\mathscr{A}_{w}(\gamma _{i}))^{-1}\). By 4.5, it is therefore sufficient to show that the assignment \(\gamma _{w,i}\mapsto w(\mathscr{A}_{w}(\gamma _{i}))^{-1}\) is constant on minimal Tits paths with the same endpoints.
Let \(w,v\in W\), \(\underline {s}=(s_{i_{1}},\dots , s_{i_{l}})\) a reduced expression of \(v\), set \(v_{k}^{ } =s_{i_{1}}\cdots s_{i_{k}}\), \(k\leqslant \ell \), and retain the notation used in (4.5). Note that, since \(\mathscr{A}\) satisfies the cocycle identity (4.3), one has
where the first equality follows from \(d\mathscr{A}=1\). Since \(\mathscr{A}_{w}\) is the parallel transport of the abelian connection (4.2), \(w(\mathscr{A}_{w}(\gamma _{\underline {s}}))\) only depends on the endpoints of \(\gamma _{\underline {s}}\), and is therefore independent of the reduced decomposition of \(v\). For the second factor, we can ignore \(w\) and consider
where \(I_{k-1}=\{\alpha >0\;|v_{k-1}^{ } \alpha <0\}\). Since \(s_{i_{k}}I_{k-1}=I_{k}\setminus \{\alpha _{i_{k}}\}\), this is equal to
It therefore remains to show that
is independent of the reduced expression of \(v\), where for each \(\alpha \in I_{\ell}\), \(i_{\alpha ,\underline {s}}\in \mathbf {I}\) is the unique index \(k\) such that \(\alpha =v_{k-1}^{}\alpha _{i_{k}}\). As in the proof of part (2) of Lemma 4.6, this reduces to the case when \(W\) is of type \(\mathsf {A}_{2}\), and \(v\) is the longest element of \(W\). In that case, \(\mathsf {s}=(1,2,1)\), \(\mathsf {s}'=(2,1,2)\), andFootnote 10
□
4.8 Monodromy representations of \(W\ltimes \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\)
Let \(\mathbf {a}=\{a_{i}\}_{i\in \mathbf {I}}\) be a collection of complex numbers, and \(\mathscr{B}\mathcalligra{ }_{\mathbf {a}},\mathscr{B}\mathcalligra{ }_{\mathscr{A}}\in \mathsf {M}'\) the elements determined by Lemma 4.6 and Theorem 4.7 respectively.
Since \(d\mathscr{B}\mathcalligra{ }_{\mathbf {a}}=1\) and \(d\mathscr{B}\mathcalligra{ }_{\mathscr{A}}=\mathscr{A}\), it follows from Proposition 4.3 (2) that there is a functor \(\mathscr{P}_{\mathbf {a}}:W\ltimes \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\to W\ltimes \mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}'}\) which is the identity on the morphisms \(\{w_{x}\}\), and maps a path \(\gamma \in \mathbf {\Pi }_{1}{(\mathsf {X};Wx_{0})}\) to
Proposition 3
For any collections \(\mathbf {a}\), \(\mathbf {a}'\), regard \(\mathscr{P}_{\mathbf {a}}\), \(\mathscr{P}_{\mathbf {a}'}\) as functors
via the embedding \(\mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}'}\subset \mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}}\). Then, there is an isomorphism \(\mathscr{P}_{\mathbf {a}}\Rightarrow \mathscr{P}_{\mathbf {a}'}\) determined by an element \(\mathscr{C}\in \exp (\mathfrak {h})\) (cf. 4.4).
Proof
Since \(\mathscr{B}\mathcalligra{ }_{\mathscr{A}}(\gamma _{i})=1\) for any \(i\in \mathbf {I}\), Proposition 4.4 implies that it is enough to find \(\mathscr{C}\in \exp (\mathfrak {h})\) such that \(\mathscr{B}\mathcalligra{ }_{\mathbf {a}'}(\gamma _{i})=\mathscr{B}\mathcalligra{ }_{\mathbf {a}}(\gamma _{i})\cdot s_{i}(\mathscr{C}) \cdot \mathscr{C}^{-1}\) for any \(i\in \mathbf {I}\). If we assume \(\mathscr{C}=\exp (c)\) for some \(c\in{ \mathfrak {h}}\), this condition reduces to the set of equations \(\alpha _{i}(c)=a_{i}-a_{i}'\), \(i\in \mathbf {I}\), which always possess a solution since \(\{\alpha _{i}\}\) are linearly independent in \(\mathfrak {h}^{*}\). □
4.9 Equivariance via resummation
We describe below an alternative way of restoring the equivariance of the universal Casimir connection \(\nabla _{\mathsf {t}_{}^{}}\) by resumming the formal \(\mathfrak {h}'\)–valued 1–form on \(\mathsf {X}\) given by

Definition 5
A resummation of \(\widehat {b}\) is a closed, holomorphic 1–form \(b\) on \(\mathsf {X}\) with values in \(\mathfrak {h}\supset \mathfrak {h}'\) such that
-
For any \(w\in W\),
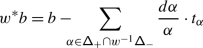
so that \(\nabla _{\mathsf {t}_{}^{}}-b\) is an integrable, \(W\)–equivariant connection.
-
For any \(i\in \mathbf {I}\), \(b\) has a logarithmic singularity on the hyperplane \(\alpha _{i}=0\), with residue \(t_{\alpha _{i}}/2\).
The existence of a resummation is clear if \(\mathfrak {g}\) is finite–dimensional, and is proved in the Appendix for \(\mathfrak {g}\) affine.Footnote 11
Proposition 4
Let \(b\) be a resummation of \(\widehat {b}\).
-
The parallel transport of the connection \(\nabla _{\mathsf {t}_{}^{}}-b\) is \(W\)–equivariant, and given on generators by
$$ \mathscr{P}_{\nabla _{\mathsf {t}_{}^{}}- b}(\gamma _{i}) = \mathscr{P}_{\nabla _{\mathsf {t}_{}^{}}}(\gamma _{i})\cdot \exp (a_{i}\cdot t_{\alpha _{i}}) $$for some complex numbers \(\{a_{i}\}\).
-
The corresponding functor
$$ \mathscr{P}_{\nabla _{\mathsf {t}_{}^{}}- b}:W\ltimes \mathbf {\Pi }_{1}{(\mathsf {X}; Wx_{0})}\to W\ltimes \mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}'}$$coincides with the functor \(\mathscr{P}_{\mathbf {a}}\) given by Proposition 4.8, with \(\mathbf {a}= \{a_{i}\}_{i\in \mathbf {I}}\).
Proof
The \(W\)–equivariance of \(\mathscr{P}_{\nabla _{\mathsf {t}_{}^{}}- b}\) follows from that of \({\nabla _{\mathsf {t}_{}^{}}- b}\). Moreover, if \(\mathscr{B}\mathcalligra{ }\in \mathsf {M}\) is the parallel transport of the connection \(d-b\) then, for any \(\gamma \in \Pi _{1}(\mathsf {X};Wx_{0})\), \(\mathscr{P}_{\nabla _{\mathsf {t}_{}^{}}- b}(\gamma )\) is equal to \(\mathscr{P}_{\nabla _{\mathsf {t}_{}^{}}}(\gamma )\cdot \mathscr{B}\mathcalligra{ }(\gamma )\). It follows that \(d\mathscr{B}\mathcalligra{ }=\mathscr{A}\), and therefore that ℬ is uniquely determined by the values \(\mathscr{B}\mathcalligra{ }(\gamma _{i})\) by Lemma 4.6. In particular, ℬ coincides with the cochain \(\mathscr{B}\mathcalligra{ }_{\mathscr{A}}(\gamma )\cdot \mathscr{B}\mathcalligra{ }_{\mathbf {b}}(\gamma )\) of Proposition 4.8 provided that, for any \(i\in \mathbf {I}\), \(\mathscr{B}\mathcalligra{ }(\gamma _{i})\) is of the form \(\exp (a_{i}\cdot t_{\alpha _{i}})\) for some \(a_{i}\in \mathbb{C}\).
Let \(b_{i}\) be the \(\mathfrak {h}\)–valued 1–form given by \(b_{i}=b-\frac{1}{2}d\log \alpha _{i}\cdot t_{\alpha _{i}}\). Clearly, \(\mathscr{B}\mathcalligra{ }(\gamma _{i})=\mathscr{B}\mathcalligra{ }_{i}(\gamma _{i})\cdot \exp (\iota \pi t_{\alpha _{i}}/2)\), where \(\mathscr{B}\mathcalligra{ }_{i}\) is the parallel transport of \(d-b_{i}\). Note that \(b_{i}\) is equivariant under \(s_{i}\) and regular on \(\operatorname{Ker}\alpha _{i}\). Let \(f\) be an \(\exp (\mathfrak {h})\)–valued fundamental solution of \(df=b_{i}f \). It suffices to show that \(g(x)=f(s_{i}x)\cdot f(x)^{-1}\) takes values in \(\exp (\mathbb{C}t_{\alpha _{i}})\). \(g\) satisfies
where the second identity follows from the \(s_{i}\)–equivariance of \(b_{i}\). Moreover, if \(x\) lies on \(\operatorname{Ker}\alpha _{i}\), then \(g(x)=1\), from which the conclusion follows. □
Remark 7
In the following, we shall need to further adjust the monodromy representations \(\mathscr{P}_{\mathbf {a}}\) by elements in \(S^{2}\mathfrak {h}\). More precisely, one checks easily that, for any \(W\)–invariant functions \(\mathbf {a}\), \(\mathbf {b}\), there is a unique solution of \(d\mathscr{B}\mathcalligra{ }=1\) such that \(\mathscr{B}\mathcalligra{ }(\gamma _{i})=\exp (a_{i}t_{\alpha _{i}}+b_{i}t_{\alpha _{i}}^{2})\), yielding a monodromy representation \(\mathscr{P}_{\mathbf {a},\mathbf {b}}\). Note that \(\mathscr{P}_{\mathbf {a},\mathbf {b}}\) and \(\mathscr{P}_{\mathbf {a}',\mathbf {b}'}\) are equivalent if and only if \(\mathbf {b}=\mathbf {b}'\).
4.10 Monodromy representations of \(\mathcal {B}_{W}\)
Denote by \(\mathscr{P}_{\mathbf {a}}^{x_{0}}\) the composition

where \(P_{x_{0}}\) is the restriction of the equivalence (4.1) to automorphisms of \(x_{0}\), and \(\mathscr{P}_{\mathbf {a}}\) the functor given by Proposition 4.8.
The homomorphism \(\mathscr{P}_{\mathbf {a}}^{x_{0}}\) is given by
where \(\widetilde {\gamma}:[0,1]\to \mathsf {X}\) is the unique lift of \(\gamma\) such that \(\widetilde {\gamma}(0)=x_{0}\), and \(w\in W\) the unique element such that \(\widetilde {\gamma}(1)=w^{-1}\widetilde {\gamma}(0)\). Moreover, any representation  gives rise to an action of the braid group \(\mathcal {B}_{W}\) on \(V\).
gives rise to an action of the braid group \(\mathcal {B}_{W}\) on \(V\).
4.11 Monodromy representations of \(\mathcal {B}_{W}\) on category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}\)
The above mechanism is not appropriate to construct representations of \(\mathcal {B}_{W}\) on integrable category \(\mathcal {O}\) modules, since \(W\) does not act on them. To remedy this, we introduce the following
Definition 6
The extended holonomy algebra is the semidirect product  , where the braid group \(\mathcal {B}_{W}\) acts on
, where the braid group \(\mathcal {B}_{W}\) acts on  through the morphism \(\mathcal {B}_{W}\to W\).
through the morphism \(\mathcal {B}_{W}\to W\).
Then, we simply lift

and use instead a representation of  . This yields the following.
. This yields the following.
Theorem 6
Let \(\mathbf {a}=\{a_{i}\}_{i\in \mathbf {I}}\) be a collection of complex numbers.
-
(1)
The parallel transport of the universal Casimir connection \(\nabla _{\mathsf {t}_{}^{}}\) gives rise to a homomorphism
$$\widetilde {\mathscr{P}}_{\mathbf {a}}^{x_{0}}:\mathcal {B}_{W}\to \mathcal {B}_{W}\ltimes \mathfrak {\widehat {t}}_{\Delta ,\mathfrak {h}'}\qquad\textit{given by}\qquad b\longrightarrow(b,\mathscr{P}_{\mathbf {a}}(\widetilde {b}))$$where \(\widetilde {b}\in \mathbf {\Pi }_{1}{(}X;Wx_{0})\) is the unique lift of \(b\) through \(x_{0}\), and
$$\mathscr{P}_{\mathbf {a}}(\widetilde {b})=\mathscr{P}(\widetilde {b})\cdot \mathscr{B}\mathcalligra{ }_{\mathscr{A}}(\widetilde {b})\cdot \mathscr{B}\mathcalligra{ }_{\mathbf {a}}(\widetilde {b})$$is defined in 4.8.
-
(2)
Let \(V\) be a category \(\mathcal {O}\) integrable \(\mathfrak {g}\)–module, equipped with the action of \(\mathcal {B}_{W}\) given by triple exponentials (cf. Remark 3.4). The parallel transport of the Casimir connection \(\nabla _{\mathcal {K}}\) gives rise to a a homomorphism \(\widetilde {\mathscr{P}}_{\mathbf {a},V}^{x_{0}}\colon \mathcal {B}_{W}\to\operatorname{GL}(V)\) given on generators by
$$ \widetilde {\mathscr{P}}_{\mathbf {a},V}^{x_{0}}(\mathscr{S}_{i})=\widetilde {s}_{i}\cdot \mathscr{P}({\gamma_{i}})\cdot\exp(a_{i}t_{\alpha_{i}}) $$(4.6)
4.12 Twisting
Let \(A\) be a resummation of the formal 1–form \(\widehat {A}\) (cf. 4.9). The representation \(\widetilde {\mathscr{P}}_{\mathbf {a},V}^{x_{0}}\) can be equivalently obtained from the following topological construction, twisting the \(\mathcal {B}_{W}\)–equivariant vector bundle \(\mathbb{V}\) into a \(W\)–equivariant vector bundle \(\widetilde {\mathbb{V}}\) on \(\mathsf {X}\) (cf. 3.2). Since \(\widetilde {W}\) is a quotient of the braid group \(\mathcal {B}_{W}\), the latter acts on the vector bundle \(p^{*}\mathbb{V}\) on \(\widetilde {\mathsf {X}}\). By definition, \(\widetilde {\mathbb{V}}\) is the quotient \(p^{*}\mathbb{V}/\mathcal {P}_{W}\), where \(\mathcal {P}_{W}\) is the pure braid group corresponding to \(W\), and carries a residual action of \(W=\mathcal {B}_{W}/\mathcal {P}_{W}\). As in Proposition 4.9, it follows that \(\widetilde {\mathscr{P}}_{\mathbf {a},V}^{x_{0}}\) coincides with the representation induced through parallel transport by the twisted connection on \(\widetilde {\mathbb{V}}\).
5 Diagrams and nested sets
In this section, we review the definition of (relative) nested sets on a diagram \(\mathbb{D}\) (cf. [9, 34]). We follow the exposition given in [2, Sect. 2].
5.1 Nested sets on diagrams
A diagram is an undirected graph \(\mathbb{D}\) with no multiple edges or loops. A subdiagram \(B\subseteq \mathbb{D}\) is a full subgraph of \(\mathbb{D}\), that is, a graph consisting of a (possibly empty) subset of vertices of \(\mathbb{D}\), together with all edges of \(\mathbb{D}\) joining any two elements of it. We will often identify \(B\) and its set of vertices, and denote by \(|B|\) the cardinality of the latter.
Two subdiagrams \(B_{1},B_{2}\subseteq \mathbb{D}\) are orthogonal if they have no vertices in common, and no two vertices \(i\in B_{1}\), \(j\in B _{2}\) are joined by an edge in \(\mathbb{D}\). We denote by \(B_{1}\sqcup B_{2}\) the disjoint union of orthogonal subdiagrams. Two subdiagrams \(B_{1}, B_{2}\subseteq \mathbb{D}\) are compatible if either one contains the other or they are orthogonal.
A nested set on \(\mathbb{D}\) is a collection ℋ of pairwise compatible, connected subdiagrams of \(\mathbb{D}\) which contains the empty subdiagram and \(\mathsf {conn}(\mathbb{D})\), where \(\mathsf {conn}(\mathbb{D})\) denotes the set of connected components of \(\mathbb{D}\). It is easy to see that the cardinality of any maximal nested set on \(\mathbb{D}\) is equal to \(|\mathbb{D}|+1\).
Let \(\mathsf {Ns}(\mathbb{D})\) be the set of nested sets on \(\mathbb{D}\), and \(\mathsf {Mns}(\mathbb{D})\) that of maximal nested sets. Every (maximal) nested set ℋ on \(\mathbb{D}\) is uniquely determined by a collection \(\{\mathcal {H}_{i}\}_{i=1}^{r}\) of (maximal) nested sets on the connected components \(\mathbb{D}_{i}\) of \(\mathbb{D}\). We therefore obtain canonical identifications
5.2 Relative nested sets
If \(B'\subseteq B\subseteq \mathbb{D}\) are two subdiagrams of \(\mathbb{D}\), a nested set on \(B\) relative to \(B'\) is a collection of subdiagrams of \(B\) which contains \(\mathsf {conn}(B)\) and \(\mathsf {conn}(B')\), and in which every element is compatible with, but not properly contained in any of the connected components of \(B'\). We denote by \(\mathsf {Ns}(B,B')\) and \(\mathsf {Mns}(B,B')\) the collections of nested sets and maximal nested sets on \(B\) relative to \(B'\). In particular,
Relative nested sets are endowed with the following operations, which preserve maximal nested sets.
-
(1)
Vertical union. For any \(B''\subseteq B' \subseteq B\), there is an embedding
$$\cup :\mathsf {Ns}(B,B')\times \mathsf {Ns}(B',B'')\to \mathsf {Ns}(B,B''), $$given by the union of nested sets. Its image is the collection \(\mathsf {Ns}_{B'}(B,B'')\subseteq \mathsf {Ns}(B,B'')\) of relative nested sets which contain \(\mathsf {conn}(B')\).
-
(2)
Orthogonal union. For any \(B_{1}'\subseteq B_{1}\perp B_{2}\supseteq B_{2}'\), there is a bijection
$$ \mathsf {Ns}(B_{1},B_{1}')\times \mathsf {Ns}(B_{2},B_{2}')\to \mathsf {Ns}(B_{1}\sqcup B_{2},B'_{1}\sqcup B_{2}'), $$mapping \((\mathcal {H}_{1},\mathcal {H}_{2})\mapsto \mathcal {H}_{1}\cup \mathcal {H}_{2}\).
5.3 Elementary sequences
Definition 7
-
(1)
Let \(B'\subseteq C'\subseteq C\subseteq B\), and \(\mathcal {F}\in \mathsf {Mns}(B,B')\) a maximal nested set such that \(\mathsf {conn}(C'), \mathsf {conn}(C)\subset \mathcal {F}\). The truncation of ℱ at \((C,C')\) is the element of \(\mathsf {Mns}(C,C')\) defined by
$$ { \mathcal {F}}^{C}_{C'}=\left \{C''\in \mathcal {F}\left |\right . C''\subseteq C\; \text{and}\; \forall \,\widetilde {C}\in \mathsf {conn}(C'),\; C''\not \subset \widetilde {C} \right \} $$We set \({ \mathcal {F}}^{C}_{}={ \mathcal {F}}^{C}_{B'}\) and \({ \mathcal {F}}^{}_{C}={ \mathcal {F}}^{B}_{C}\).
-
(2)
Let \(B'\subseteq B\), and \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\). The support and central support of the pair \((\mathcal {F},\mathcal {G})\) are the subdiagrams of \(B\) defined by
$$\begin{aligned} \operatorname {supp}(\mathcal {F},\mathcal {G})&=\min _{C}\{B'\subseteq C\subseteq B\;|\; \mathsf {conn}(C) \subseteq \mathcal {F}\cap \mathcal {G}, { \mathcal {F}}^{}_{C}={ \mathcal {G}}^{}_{C}\} \\ \operatorname {\mathfrak {z}supp}(\mathcal {F},\mathcal {G})&=\max _{C}\{B'\subseteq C\subseteq B\;|\; \mathsf {conn}(C) \subseteq \mathcal {F}\cap \mathcal {G}, { \mathcal {F}}^{C}_{}={ \mathcal {G}}^{C}_{}\} \end{aligned}$$ -
(3)
Two ordered pairs \((\mathcal {F},\mathcal {G})\), \((\mathcal {F}',\mathcal {G}')\) in \(\mathsf {Mns}(B,B')\) are equivalent if
$$ \mathcal {F}\setminus \mathcal {G}=\mathcal {F}'\setminus \mathcal {G}' \qquad \text{and}\qquad \mathcal {G}\setminus \mathcal {F}=\mathcal {G}' \setminus \mathcal {F}' $$If this is the case, then
$$ \operatorname {supp}(\mathcal {F},\mathcal {G})=\operatorname {supp}(\mathcal {F}',\mathcal {G}') \qquad \text{and}\qquad \operatorname {\mathfrak {z}supp}(\mathcal {F},\mathcal {G})=\operatorname {\mathfrak {z}supp}(\mathcal {F}', \mathcal {G}') $$ -
(4)
An ordered pair \((\mathcal {F},\mathcal {G})\) in \(\mathsf {Mns}(B,B')\) is elementary if ℱ and \(\mathcal {G}\) differ only by one element.
We shall make use of the following result [34, Prop. 3.26].Footnote 12
Proposition 5
-
(1)
For any \(B'\subseteq B\) and \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\), there is a sequence
$$ \mathcal {F}=\mathcal {H}_{1},\dots , \mathcal {H}_{l}=\mathcal {G}$$in \(\mathsf {Mns}(B,B')\) and the following holds for any \(i\)
-
\((\mathcal {H}_{i},\mathcal {H}_{i+1})\) is an elementary pair
-
\(\mathcal {F}\cap \mathcal {G}\subseteq \mathcal {H}_{i}\cap \mathcal {H}_{i+1}\)
-
\(\operatorname {supp}(\mathcal {H}_{i},\mathcal {H}_{i+1})\subseteq \operatorname {supp}(\mathcal {F},\mathcal {G})\)
-
For any component \(C\) of \(\operatorname {\mathfrak {z}supp}(\mathcal {F},\mathcal {G})\), either
$$ C\perp \operatorname {supp}(\mathcal {H}_{i},\mathcal {H}_{i+1})\qquad \textit{or}\qquad C\subseteq \operatorname {\mathfrak {z}supp}(\mathcal {H}_{i},\mathcal {H}_{i+1}) $$
-
-
(2)
If \((\mathcal {F},\mathcal {G})\), \((\mathcal {F}',\mathcal {G}')\) are equivalent pairs in \(\mathsf {Mns}(B,B')\), then the corresponding elementary sequences
$$ \mathcal {F}=\mathcal {H}_{1},\dots , \mathcal {H}_{l}=\mathcal {G}\qquad \textit{and}\qquad \mathcal {F}'=\mathcal {H}'_{1},\dots , \mathcal {H}'_{m}= \mathcal {G}' $$can be chosen such that \(l=m\) and, for any \(i=1,\dots , l-1\), \((\mathcal {H}_{i},\mathcal {H}_{i+1})\) is equivalent to \((\mathcal {H}'_{i}, \mathcal {H}'_{i+1})\).
6 Diagrammatic algebras
We review in this section the notions of diagrammatic and bidiagrammatic algebras, which are essential to the definition of a Coxeter algebra in Sect. 7.
6.1 Diagrammatic algebras
Let \(\mathbb{D}\) be a diagram. A diagrammatic structure of type \(\mathbb{D}\) on an algebra \(A\) is a collection of subalgebras \(A _{B}\subseteq A\) indexed by subdiagrams of \(\mathbb{D}\) which is compatible with nesting i.e., such that \(A_{B'}\subseteq A_{B}\) if \(B'\subseteq B\), and \([A_{B_{1}}, A_{B_{2}}]=0\) if \(B_{1}\perp B_{2}\) [34]. We formalise a slightly more general version as follows [2, Sect. 5].
Let \(\mathcal {P}(\mathbb{D})\) the category whose objects are the subdiagrams of \(\mathbb{D}\), and morphisms \(B'\to B\) the inclusions \(B'\subseteq B\). The union ⊔ of orthogonal diagrams is a (symmetric, strict) partial tensor product on \(\mathcal {P}(\mathbb{D})\), with the empty diagram \(\emptyset \) as unit object.
Recall that a lax monoidal structure on a functor \(F:\mathcal {C}\to \mathcal {D}\) between two monoidal categories is the datum of a morphism \(u: 1_{\mathcal {D}}\to F(1_{\mathcal {C}})\) and a natural transformation \(J: F(\cdot )\otimes _{\mathcal {D}} F(\cdot )\rightarrow F(\cdot \otimes _{\mathcal {C}}\cdot )\), which satisfies the cocycle identity and is compatible with the unit objects through \(u\). A monoidal structure is a lax monoidal structure with \(u\) and \(J\) invertible.
Definition 8
Let \(\mathsf {k}\) be a commutative unital ring and \((\mathsf{Alg(k)}, \otimes )\) the category of \(\mathsf {k}\)–algebras, with monoidal structure given by the tensor product and \(\mathsf {k}\) as unit object.
-
(1)
A (lax) diagrammatic algebra is a (lax) monoidal functor \(\mathcal {P}(\mathbb{D})\to \mathsf{Alg(k)}\).
-
(2)
A morphism of (lax) diagrammatic algebras is a natural transformation of the corresponding (lax) monoidal functors.
Note that for any lax monoidal functor \(F:\mathcal {P}(\mathbb{D})\to \mathsf{Alg(k)}\) the morphism \(u:\mathsf {k}\to F(\emptyset )\) is the unit of \(F(\emptyset )\).
6.2 Alternative description of diagrammatic algebras
The following gives a more concrete description of diagrammatic algebras [2, Prop. 5.14].
Proposition 6
-
(1)
A lax diagrammatic algebra \(\mathscr{A}_{}\) is the same as the datum of
-
for any \(B\subseteq \mathbb{D}\), a \(\mathsf {k}\)–algebra \(A_{B}\)
-
for any \(B'\subseteq B\), a morphism of algebras \(i_{BB'}:A_{B'}\to A_{B}\)
-
for any \(B_{1}\perp B_{2}\), a morphism of algebras \(j_{B_{1}B_{2}}:A_{B_{1}}\otimes A_{B_{2}}\to A_{B_{1}\sqcup B_{2}}\)
such that the following properties hold.
-
Normalisation. For any \(B\subseteq \mathbb{D}\), \(i_{BB}=\operatorname{id}_{A_{B}}\)
-
Composition. For any \(B''\subseteq B'\subseteq B\), \(i_{BB'}\circ i_{B'B''}=i_{BB''}\)
-
Naturality. For any \(B_{1}'\subseteq B_{1}\perp B_{2}\supseteq B_{2}'\), the following diagram is commutative
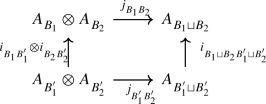
-
Associativity. For any pairwise orthogonal subdiagrams \(B_{1}\), \(B_{2}\), \(B_{3}\), the following diagram is commutative:
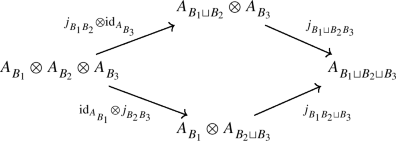
-
Unit. For any \(B\), \(j_{B \emptyset}|_{A_{B} \otimes 1}= \operatorname{id}_{A_{B}}= j_{\emptyset B}|_{1\otimes A_{B}}\).
-
-
(2)
\(\mathscr{A}_{}\) is diagrammatic if and only if the morphisms \({j}^{}_{B_{1}B_{2}}\) are invertible.
-
(3)
A morphism of lax diagrammatic algebras \(\varphi :\mathscr{A}_{}\to \mathscr{A}_{}'\) is the same as a collection of homomorphisms \(\varphi _{B}:{A}^{}_{B}\to {A'}^{}_{B}\) such that
$$ \varphi _{B}\circ {i}^{}_{BB'}={i'}^{}_{BB'}\circ \varphi _{B'} $$for any \(B'\subseteq B\), and
$$ \varphi _{B_{1}\sqcup B_{2}}\circ {j}^{}_{B_{1}B_{2}}= {j'}^{}_{B_{1}B_{2}}\circ \varphi _{B_{1}}\otimes \varphi _{B_{2}} $$for any \(B_{1}\perp B_{2}\).
Proof
A functor \(\mathscr{A}_{}:\mathcal {P}(\mathbb{D})\to \mathsf{Alg(k)}\) is the same as a collection of algebras \({A}^{}_{B}=\mathscr{A}_{}(B)\) and morphisms \({i}^{}_{BB'}=\mathscr{A}_{}(B'\subseteq B)\) which respect the composition of morphisms in \(\mathcal {P}(\mathbb{D})\). A lax monoidal structure on \(\mathscr{A}_{}\) is then a collection of morphisms \({j}^{}_{B_{1}B_{2}}\) which are natural with respect to the morphisms \({i}^{}_{BB'}\), associative as in the diagram above, and compatible with the unit \(u:\mathsf {k}\to {A}^{}_{\emptyset}\). □
6.3
Corollary 1
Let \(\mathscr{A}_{}\) be a lax diagrammatic algebra. For any \(B_{1}\perp B_{2}\),
where \(B=B_{1}\sqcup B_{2}\), and \(m_{B}\) denotes the product in \(A_{B}\). In particular, the images of \(A_{B_{1}}\) and \(A_{B_{2}}\) in \(A_{B}\) commute.
Proof
For any \((b_{1},b_{2})\in A_{B_{1}}\times A_{B_{2}}\), one has
where the second equality follows by naturality and compatibility with the unit. □
Remark 8
It follows from Corollary 6.3 that the morphisms \(j_{B_{1}B_{2}}\) are redundant. In fact, it is easy to see that the morphisms \(m_{B}\circ {i}^{}_{BB_{1}} \otimes {i}^{}_{BB_{2}}\) satisfy the properties of naturality, associativity, and unit listed above. We shall nevertheless retain the collection \(\{j_{B_{1}B_{2}}\}_{B_{1}\perp B_{2}}\) as part of datum since their redundancy does not hold in the bidiagrammatic case (cf. Corollary 6.5).
Example 1
Let \(\mathfrak {g}\) be a diagrammatic Kac–Moody algebra with Dynkin diagram \(\mathbb{D}\) and diagrammatic Lie subalgebras \(\mathfrak {g}_{B}\subseteq \mathfrak {g}\), \(B\subseteq \mathbb{D}\) (cf. 2.4). Then, the universal enveloping algebra \(A= U\mathfrak {g}\) is a diagrammatic algebra with \(A_{B}= U\mathfrak {g}_{B}\).
6.3 Bidiagrammatic algebras
We now refine a diagrammatic algebra by including, for any pair of subdiagrams \(C\subseteq B\), an algebra of invariants \({A}^{C}_{B}\) which maps to \(A_{B}\). In a number of relevant examples, \({A}^{C}_{B}\) is a subalgebra of the centraliser of \({i}^{}_{BC}(A_{C})\) in \(A_{B}\) (cf. Prop. 6.7), though this does not hold in general (cf. Example 6.7).
Let \(\mathcal {P}_{2}(\mathbb{D})\) be the category whose objects are pairs \((C,B)\) of subdiagrams of \(\mathbb{D}\) such that \(C\subseteq B\), and the morphisms \((C',B')\to (C,B)\) are given by inclusions of the form \(C\subseteq C' \subseteq B'\subseteq B\).
Two pairs \((C_{1},B_{1})\) and \((C_{2},B_{2})\) are orthogonal if \(B_{1}\perp B_{2}\). The componentwise union of orthogonal pairs is a (symmetric, strict) partial tensor product on \(\mathcal {P}_{2}(\mathbb{D})\), with \((\emptyset ,\emptyset )\) as unit object.
Definition 9
-
(1)
A (lax) bidiagrammatic algebra is a (lax) monoidal functor \(\mathcal {P}_{2}(\mathbb{D})\to \mathsf{Alg(k)}\).
-
(2)
A morphism of (lax) bidiagrammatic algebras is a natural transformation of the corresponding (lax) monoidal functors.
6.4 Alternative description of bidiagrammatic algebras
Proposition 7
-
(1)
A lax bidiagrammatic algebra \(\mathscr{A}_{}\) is the same as the datum of
-
for any \(C\subseteq B\subseteq \mathbb{D}\), a \(\mathsf {k}\)–algebra \({A}^{C}_{B}\)
-
for any \(C\subseteq C'\subseteq B'\subseteq B\), a morphism of algebras \({i}^{CC'}_{BB'}:{A}^{C'}_{B'}\to {A}^{C}_{B}\)
-
for any \(C_{1}\subseteq B_{1}\perp B_{2}\supseteq C_{2}\), a morphism of algebras
$$ {j}^{C_{1}C_{2}}_{B_{1}B_{2}}:{A}^{C_{1}}_{B_{1}}\otimes {A}^{C_{2}}_{B_{2}}\to {A}^{C_{1}\sqcup C_{2}}_{B_{1}\sqcup B_{2}} $$
such that the following properties hold.
-
Normalisation. For any \(C\subseteq B\subseteq \mathbb{D}\), \({i}^{CC}_{BB}=\operatorname{id}_{{A}^{C}_{B}}\)
-
Composition. For any
$$ C\subseteq C'\subseteq C''\subseteq B''\subseteq B'\subseteq B $$the following holds: \({i}^{CC'}_{BB'}\circ {i}^{C'C''}_{B'B''}= {i}^{CC''}_{BB''}\)
-
Naturality. For any
$$ C_{1}\subseteq C'_{1}\subseteq B'_{1}\subseteq B_{1}\perp B_{2} \supseteq B_{2}' \supseteq C'_{2}\supseteq C_{2} $$the following diagram is commutative
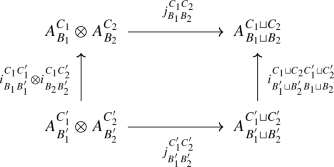
-
Associativity. For any pairwise orthogonal pairs \((C_{i},B_{i})\), \(1\leq i\leq 3\),
$$ {j}^{C_{1}\sqcup C_{2}C_{3}}_{B_{1}\sqcup B_{2}B_{3}}\circ {j}^{C_{1}C_{2}}_{B_{1}B_{2}}\otimes \operatorname{id}_{{A}^{C_{3}}_{B_{3}}}= {j}^{C_{1}C_{2}\sqcup C_{3}}_{B_{1}B_{2}\sqcup B_{3}}\circ \operatorname{id}_{ {A}^{C_{1}}_{B_{1}}}\otimes {j}^{C_{2}C_{3}}_{B_{2}B_{3}} $$as morphisms \({A}^{C_{1}}_{B_{1}}\otimes {A}^{C_{2}}_{B_{2}}\otimes {A}^{C_{3}}_{B_{3}}\to {A}^{C_{1}\sqcup C_{2}\sqcup C_{3}}_{B_{1}\sqcup B_{2}\sqcup B_{3}}\).
-
Unit. For any \(C\subseteq B\), \(j^{C \emptyset}_{B \emptyset}|_{A^{C}_{B}\otimes 1}=\operatorname{id}_{ A^{C}_{B}}= j^{\emptyset C}_{\emptyset B}|_{1\otimes A^{C}_{B}}\).
-
-
(2)
\(\mathscr{A}_{}\) is a bidiagrammatic algebra if and only if the morphisms \(j\)’s are invertible.
-
(3)
A morphism of lax bidiagrammatic algebras \(\varphi :\mathscr{A}_{}\to \mathscr{A}_{}'\) is a collection of homomorphisms \(\varphi _{B}^{C}:{A}^{C}_{B}\to {(A')}^{C}_{B}\) such that
$$ \varphi _{B}^{C}\circ {i}^{CC'}_{BB'}={(i')}^{CC'}_{BB'} \circ \varphi _{B'}^{C'} $$for any \(C\subseteq C'\subseteq B'\subseteq B\), and
$$ \varphi _{B_{1}\sqcup B_{2}}^{C_{1}\sqcup C_{2}}\circ {j}^{C_{1}C_{2}}_{B_{1}B_{2}}= {(j')}^{C_{1}C_{2}}_{B_{1}B_{2}}\circ \varphi _{B_{1}}^{C_{1}} \otimes \varphi _{B_{2}}^{C_{2}} $$for any \(C_{1}\subseteq B_{1}\perp B_{2}\supseteq C_{2}\).
The following is an analogue of Corollary 6.3. Note that, contrary to the diagrammatic case, the datum of the morphisms \(j\)’s is essential.
Corollary 2
Let \(\mathscr{A}_{}\) be a lax bidiagrammatic algebra. For any \(C_{1}\subseteq B_{1}\perp B_{2}\supseteq C_{2}\), set
Then,
where \(m^{C_{1}\sqcup C_{2}}_{B_{1}\sqcup B_{2}}\) denotes the product in \({A}^{C_{1}\sqcup C_{2}}_{B_{1}\sqcup B_{2}}\).
6.5 Remarks
-
(1)
There is a symmetric functor \(\mathcal {P}(\mathbb{D})\to \mathcal {P}_{2}(\mathbb{D})\) given by the assignment \(B\mapsto (\emptyset , B)\). This induces a forgetful functor \((-)^{{\scriptscriptstyle \operatorname {0}}}\) from the category of (lax) bidiagrammatic algebras to that of (lax) diagrammatic algebras. Explicitly, this maps \(\left ({A}^{C}_{B}, {i}^{CC'}_{BB'}, {j}^{C_{1}C_{2}}_{B_{1}B_{2}}\right )\) to \(\left ({A}^{{\scriptscriptstyle \operatorname {0}}}_{B},{i}^{{\scriptscriptstyle \operatorname {0}}}_{BB'}, {j}^{{\scriptscriptstyle \operatorname {0}}}_{B_{1}B_{2}}\right )\), where
$$ {A}^{{\scriptscriptstyle \operatorname {0}}}_{B}={A}^{\emptyset}_{B}\qquad {i}^{{\scriptscriptstyle \operatorname {0}}}_{BB'}=i^{\emptyset \emptyset}_{B B'} \qquad \text{and}\qquad {j}^{{\scriptscriptstyle \operatorname {0}}}_{B_{1}B_{2}}= j^{\emptyset \emptyset}_{B_{1} B_{2}} $$ -
(2)
Conversely, there is a symmetric functor \(\mathcal {P}_{2}(\mathbb{D})\to \mathcal {P}(\mathbb{D})\) given by the projection \((C,B)\mapsto B\). This induces a trivial extension functor \((-)^{{\scriptscriptstyle \operatorname {triv}}}\) from the category of (lax) diagrammatic algebras to that of (lax) bidiagrammatic algebras. This maps \(\left ({A}^{}_{B},{i}^{}_{BB'},{j}^{}_{B_{1}B_{2}} \right )\) to \(\left ({(A^{{\scriptscriptstyle \operatorname {triv}}})}^{C}_{B}, {(i^{{\scriptscriptstyle \operatorname {triv}}})}^{CC'}_{BB'}, {(j^{{\scriptscriptstyle \operatorname {triv}}})}^{C_{1}C_{2}}_{B_{1}B_{2}}\right )\) where
$$ {(A^{{\scriptscriptstyle \operatorname {triv}}})}^{C}_{B}={A}^{}_{B}\qquad {(i^{{\scriptscriptstyle \operatorname {triv}}})}^{CC'}_{BB'}= {i}^{}_{BB'} \qquad {(j^{{\scriptscriptstyle \operatorname {triv}}})}^{C_{1}C_{2}}_{B_{1}B_{2}}= {j}^{}_{B_{1}B_{2}} $$ -
(3)
Note that, for any diagrammatic algebra \(\mathscr{A}_{}\), \((\mathscr{A}_{}^{{\scriptscriptstyle \operatorname {triv}}})^{{\scriptscriptstyle \operatorname {0}}}=\mathscr{A}_{}\).
6.6 Invariant subalgebras
If \(\mathscr{A}_{}= ({A}^{}_{B},{i}^{}_{BB'}, {j}^{}_{B_{1}B_{2}})\) is a diagrammatic algebra, and \(C\subseteq B\), we denote by
the centraliser of \({i}^{}_{BC}(A_{C})\) in \(A_{B}\). The following result shows that \(\mathscr{A}_{}\) is endowed with a canonical bidiagrammatic structure.
Proposition 8
Set
Then \(\mathscr{A}_{}^{\flat}=\left ({(A^{\flat})}^{C}_{B}, {(i^{\flat})}^{CC'}_{BB'}, {(j^{\flat})}^{C_{1}C_{2}}_{B_{1}B_{2}}\right )\) is a bidiagrammatic algebra.
Proof
It is enough to check that the morphisms
are well–defined. The other properties are clear.
Note that \(i_{BB'}(A_{B'}^{A_{C'}})\subseteq A_{B}^{A_{C'}}\), since \(i_{BB'}\circ i_{B'C'}=i_{BC'}\), and \(A_{B}^{A_{C'}}\subseteq A_{B}^{A_{C}}\), since \(i_{C'C}(A_{C})\subseteq A_{C'}\). It follows that \({(i^{\flat})}^{CC'}_{BB'}\) is well–defined. Next, if \(C_{1}\subseteq B_{1}\perp B_{2}\supseteq C_{2}\) and \(B=B_{1} \sqcup B_{2}\), \(C=C_{1}\sqcup C_{2}\), the identity \({j}^{}_{BB_{1}}\circ {i}^{}_{C_{1}B_{1}}\otimes {i}^{}_{C_{2}B_{2}} ={i}^{}_{BC}\circ {j}^{}_{C_{1}C_{2}}\) implies that
The morphisms \({(j^{\flat})}^{C_{1}C_{2}}_{B_{1}B_{2}}\) are therefore well–defined and invertible. □
Remark 9
Note that the proof only relies on the surjectivity of the morphisms \({j}^{}_{B_{1}B_{2}}\), but not on their injectivity.
Example 2
Let \(\mathfrak {g}\) be a diagrammatic Kac–Moody algebra (cf. 2.4 and Example 6.3). Then, for any \(n\geq 0\), \(U\mathfrak {g}^{\otimes n}\) is bidiagrammatic with respect to the subalgebras \((U\mathfrak {g}_{B}^{\otimes n})^{\mathfrak {g}_{C}}\), \(C\subseteq B\subseteq \mathbb{D}\).
7 Coxeter algebras
In this section, we review the definition of a Coxeter structure on a bidiagrammatic algebra following [34, 2].
7.1 Generalised braid groups
Definition 10
A labeling \(\underline {m}\) of the diagram \(\mathbb{D}\) is the assignment of an integer \(m_{ij}\in \{2,3,\ldots ,\infty \}\) to any pair \(i\), \(j\) of distinct vertices of \(\mathbb{D}\) such that
The generalised braid group corresponding to \((\mathbb{D},\underline {m})\) is the group \(\mathcal {B}_{\mathbb{D}}^{\underline {m}}\) generated by th elements \(\mathscr{S}_{i}\), \(i\in \mathbb{D}\), with relations
Remark 10
Let \(\mathsf {A}\) be a symmetrisable Cartan matrix, \(\mathbb{D}\) its Dynkin diagram, and \(m_{ij}\) the order of the element \(s_{i}s_{j}\) in the Weyl group \(W\). We shall refer to \({\mathsf{Dyn}}=\{\mathsf{ord}(s_{i}s_{j})\}\) as the standard labeling on the Dynkin diagram \(\mathbb{D}\). Then, \(\mathcal {B}_{\mathbb{D}}^{{{\scriptscriptstyle \operatorname {\mathsf{Dyn}}}}}=\mathcal {B}_{W}\).
7.2 Coxeter algebras
Let \(\mathscr{A}_{}=\left ({A}^{C}_{B},{i}^{CC'}_{BB'}, {j}^{C'C''}_{B'B''}\right )\) be a (lax) bidiagrammatic algebra such that
Definition 11
-
(1)
A pre–Coxeter structure \((\Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})\) on \(\mathscr{A}_{}\) consists of the following data.
-
(a)
Generalised associators. For any \(B'\subseteq B\) and \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\), an invertible element \(\Upsilon _{\mathcal {G}\mathcal {F}}\in {A}^{B'}_{B}\) satisfying the following property.
-
Horizontal factorisation. For any \(\mathcal {F},\mathcal {G},\mathcal {H}\in \mathsf {Mns}(B,B')\),
$$ \Upsilon _{\mathcal {H}\mathcal {F}}=\Upsilon _{\mathcal {H}\mathcal {G}}\cdot \Upsilon _{\mathcal {G}\mathcal {F}} $$In particular, \(\Upsilon _{\mathcal {F}\mathcal {F}}=1\) and \(\Upsilon _{\mathcal {F}\mathcal {G}}=\Upsilon _{\mathcal {G}\mathcal {F}}^{-1}\).
-
Orthogonal factorisation. For any \(B_{1}^{\prime}\subseteq B_{1}\perp B_{2}\supseteq B'_{2}\), and pairs
$$ \begin{aligned} (\mathcal {G}_{1}, \mathcal {G}_{2}), (\mathcal {F}_{1},\mathcal {F}_{2})&\in \mathsf {Mns}(B_{1},B'_{1})\times \mathsf {Mns}(B_{2},B'_{2})\\&=\mathsf {Mns}(B_{1}\sqcup B_{2}, B'_{1}\sqcup B'_{2}) \end{aligned} $$the following holds
$$ \Upsilon _{(\mathcal {G}_{1},\mathcal {G}_{2})(\mathcal {F}_{1},\mathcal {F}_{2})} = {j}^{B_{1}'B_{2}'}_{B_{1}B_{2}}(\Upsilon _{\mathcal {G}_{1}\mathcal {F}_{1}}\otimes \Upsilon _{\mathcal {G}_{2}\mathcal {F}_{2}}) $$
-
-
(b)
Vertical joins. For any \(B''\subseteq B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B,B')\), and \(\mathcal {F}'\in \mathsf {Mns}(B', B'')\), an invertible element \(\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}\in {A}^{B''}_{B}\) satisfying the following properties.
-
Normalisation. For any \(\mathcal {F}\in \mathsf {Mns}(B,B')\),
$$ \mathsf {a}^{\mathcal {F}}_{B'}=1=\mathsf {a}^{B}_{\mathcal {F}} $$ -
Compatibility with \(\Upsilon _{}\) (vertical \(\Upsilon _{}\)–factorisation). For any \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B, B')\) and \(\mathcal {F}',\mathcal {G}'\in \mathsf {Mns}(B',B'')\),
$$ \Upsilon _{(\mathcal {G}\cup \mathcal {G}')(\mathcal {F}\cup \mathcal {F}')}\cdot \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}= \mathsf {a}^{\mathcal {G}}_{\mathcal {G}'}\cdot {i}^{B''B'}_{B\phantom{''}B\phantom{'}}( \Upsilon _{\mathcal {G}\mathcal {F}})\cdot {i}^{B''B''}_{B\phantom{''}B'\phantom{'}}( \Upsilon _{\mathcal {G}'\mathcal {F}'}) $$ -
Associativity. For any \(B'''\subseteq B''\subseteq B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B,B')\), \(\mathcal {F}'\in \mathsf {Mns}(B',B'')\), and \(\mathcal {F}''\in \mathsf {Mns}(B'',B''')\),
$$ \mathsf {a}^{\mathcal {F}'\cup \mathcal {F}}_{\mathcal {F}''}\cdot {i}^{B'''B''}_{B\phantom{'''}B\phantom{''}}(\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})= \mathsf {a}^{\mathcal {F}}_{\mathcal {F}''\cup \mathcal {F}'}\cdot {i}^{B'''B'''}_{B\phantom{'''}B'\phantom{''}}( \mathsf {a}^{\mathcal {F}'}_{\mathcal {F}''}) $$ -
Orthogonal factorisation. For any
$$\begin{gathered} B_{1}''\subseteq B_{1}^{\prime}\subseteq B_{1}\perp B_{2}\supseteq B'_{2} \supseteq B''_{2} \\ (\mathcal {F}_{1},\mathcal {F}_{2})\in \mathsf {Mns}(B_{1},B_{1}')\times \mathsf {Mns}(B_{2},B'_{2}) \\ (\mathcal {F}_{1}',\mathcal {F}_{2}')\in \mathsf {Mns}(B'_{1},B_{1}'')\times \mathsf {Mns}(B_{2}',B''_{2}) \end{gathered}$$the following holds
$$\begin{aligned} \mathsf {a}^{(\mathcal {F}_{1}, \mathcal {F}_{2})}_{(\mathcal {F}'_{1},\mathcal {F}'_{2})} =& {j}^{B_{1}''B_{2}''}_{B_{1}B_{2}}(\mathsf {a}^{\mathcal {F}_{1}}_{\mathcal {F}'_{1}} \otimes \mathsf {a}^{\mathcal {F}_{2}}_{\mathcal {F}'_{2}}) \end{aligned}$$
-
-
(a)
-
(2)
Let \(\underline {m}\) be a labelling of \(\mathbb{D}\). A Coxeter structure \((\Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}, S_{i})\) of type \((\mathbb{D},\underline {m})\) on \(\mathscr{A}_{}\) consists of a pre–Coxeter structure \((\Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})\) with the following additional data.
-
(a)
Local monodromies. For any vertex \(i\) of \(\mathbb{D}\), an invertible element \(S_{i }^{}\in {A}^{\emptyset}_{i}\) satisfying the following property.
-
Braid relations. For any \(B\subseteq \mathbb{D}\), \(i\neq j\in B\) and maximal nested sets \(\mathcal {K}[i]\), \(\mathcal {K}[j]\) on \(B\) with \(\{i\}\in \mathcal {K}[i]\), \(\{j\}\in \mathcal {K}[j]\), the following holds in \({A}^{\emptyset}_{B}\)
$$ \underbrace{\mathsf{Ad}\left (\Upsilon _{ji}\right )(S_{i }^{\mathsf {a}^{}_{}})\cdot S_{j }^{\mathsf {a}^{}_{}} \cdot \mathsf{Ad}\left (\Upsilon _{ji}\right )(S_{i }^{\mathsf {a}^{}_{}})\cdots}_{m_{ij}}= \underbrace{S_{j }^{\mathsf {a}^{}_{}}\cdot \mathsf{Ad}\left (\Upsilon _{ji}\right )(S_{i }^{\mathsf {a}^{}_{}})\cdot S_{j }^{\mathsf {a}^{}_{}}\cdots}_{m_{ij}} $$(7.3)where \(\Upsilon _{ji}=\Upsilon _{ \mathcal {K}[j] \mathcal {K}[i]}\), \(S_{i }^{\mathsf {a}^{}_{}}= \mathsf {Ad}(\mathsf {a}^{{ \mathcal {K}[i]}^{}_{i}}_{{ \mathcal {K}[i]}^{i}_{}})(S_{i }^{})\), and \({ \mathcal {K}[i]}^{}_{i}\) and \({ \mathcal {K}[i]}^{i}_{}\) are, respectively, the lower and upper truncations of \(\mathcal {K}[i]\) at \(\{i\}\).
-
-
(a)
Remark 11
Whenever clear from the context, we may omit the reference to the datum \((\mathbb{D},\underline {m})\) from the terminology.
7.3 Representations of generalised braid groups
Proposition 9
Let \(\mathscr{A}_{}\) be a Coxeter algebra.
-
(1)
There is a family of representations of generalised braid groups
$$ \lambda _{\mathcal {F}}:\mathcal {B}_{B}^{\underline {m}}\to ({A}^{\emptyset}_{B})^{\times} $$where \(B\subseteq \mathbb{D}\) and \(\mathcal {F}\in \mathsf {Mns}(B)\), which is uniquely determined by the conditions
-
(a)
\(\lambda _{\mathcal {F}}(\mathscr{S}_{i})= \mathsf {Ad}(\mathsf {a}^{{ \mathcal {F}}^{}_{i}}_{{ \mathcal {F}}^{i}_{}})(S_{i})\) if \(\{i\}\in \mathcal {F}\).
-
(b)
\(\lambda _{\mathcal {G}}=\mathsf {Ad}(\Upsilon _{\mathcal {G}\mathcal {F}})\circ \lambda _{\mathcal {F}}\).
-
(a)
-
(2)
For any \(B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B)\) with \(\mathsf {conn}(B')\subseteq \mathcal {F}\), and \(\mathcal {F}'\in \mathsf {Mns}(B')\), the diagram
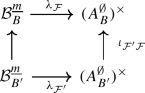
where the left vertical arrow is the canonical inclusion \(\mathcal {B}_{B'}^{\underline {m}}\subseteq \mathcal {B}_{B}^{\underline {m}}\) and
$$ \iota _{\mathcal {F}'\mathcal {F}}= \mathsf {Ad}(\mathsf {a}^{{ \mathcal {F}}^{}_{B'}}_{{ \mathcal {F}}^{B'}_{}}\cdot \Upsilon _{{ \mathcal {F}}^{B'}_{}\mathcal {F}'}) $$is commutative.
Proof
(1) For any \(i\in \mathbb{D}\), we choose \(\mathcal {K}[i]\in \mathsf {Mns}(B)\) such that \(\{i\}\in \mathcal {K}[i]\). We claim that the assignment
where \(S_{i }^{\mathsf {a}^{}_{}}= \mathsf {Ad}(\mathsf {a}^{{ \mathcal {K}[i]}^{}_{i}}_{{ \mathcal {K}[i]}^{i}_{}})(S_{i})\), provides a morphism of groups \(\lambda _{\mathcal {F}}:\mathcal {B}_{B}^{\underline {m}}\to ({A}^{B}_{\emptyset})^{\times}\). Moreover, this is independent of the chosen maximal nested sets \(\mathcal {K}[i]\)’s. Finally, we observe that the morphisms \(\{\lambda _{\mathcal {F}}\}_{\mathcal {F}\in \mathsf {Mns}(B)}\) satisfy the conditions (a), (b) and are uniquely determined by them.
-
\(\lambda _{\mathcal {F}}\) is a morphism of groups. We shall prove that the braid relations hold, i.e.,
$$ \begin{aligned} & \underbrace{ \mathsf{Ad}\left (\Upsilon _{\mathcal {F} \mathcal {K}[i]}\right )(S_{i }^{\mathsf {a}^{}_{}})\cdot \mathsf{Ad}\left (\Upsilon _{\mathcal {F} \mathcal {K}[j]}\right )(S_{j }^{\mathsf {a}^{}_{}}))\cdot \mathsf{Ad}\left (\Upsilon _{\mathcal {F} \mathcal {K}[i]}\right )(S_{i }^{\mathsf {a}^{}_{}}))\cdots}_{m_{ij}}= \\ &\qquad \qquad \qquad = \underbrace{ \mathsf{Ad}\left (\Upsilon _{\mathcal {F} \mathcal {K}[j]}\right )(S_{j }^{\mathsf {a}^{}_{}}))\cdot \mathsf{Ad}\left (\Upsilon _{\mathcal {F} \mathcal {K}[i]}\right )(S_{i }^{\mathsf {a}^{}_{}}))\cdot \mathsf{Ad}\left (\Upsilon _{\mathcal {F} \mathcal {K}[j]}\right )(S_{j }^{\mathsf {a}^{}_{}}))\cdots}_{m_{ij}} \end{aligned} $$(7.4)By horizontal factorisation \(\Upsilon _{ \mathcal {K}[j]\mathcal {F}}\Upsilon _{\mathcal {F} \mathcal {K}[j]}=1\) and \(\Upsilon _{ \mathcal {K}[j]\mathcal {F}}\Upsilon _{\mathcal {F} \mathcal {K}[i]}=\Upsilon _{ \mathcal {K}[j] \mathcal {K}[i]}\). Therefore, the equations (7.4) and (7.3) are equivalent and obtained from each other through \(\mathsf {Ad}(\Upsilon _{ \mathcal {K}[j]\mathcal {F}})\).
-
\(\lambda _{\mathcal {F}}\) does not depend on the choice of \(\mathcal {K}[i]\)’s. Indeed, let \(\mathcal {K}'[i]\in \mathsf {Mns}(B)\) be such that \(\{i\}\in \mathcal {K}'[i]\). Thus, \({ \mathcal {K}'[i]}^{i}_{}={ \mathcal {K}[i]}^{i}_{}\) and, by vertical factorisation,
$$ \Upsilon _{ \mathcal {K}'[i] \mathcal {K}[i]}\cdot \mathsf {a}^{{ \mathcal {K}[i]}^{}_{i}}_{{ \mathcal {K}[i]}^{i}_{}}= \mathsf {a}^{{ \mathcal {K}'[i]}^{}_{i}}_{{ \mathcal {K}'[i]}^{i}_{}}\cdot \Upsilon _{{ \mathcal {K}'[i]}^{}_{i}{ \mathcal {K}[i]}^{}_{i}} $$Since \(\Upsilon _{{ \mathcal {K}'[i]}^{}_{i}{ \mathcal {K}[i]}^{}_{i}}\in {A}^{\{i\}}_{B}\), it follows that \(\mathsf {Ad}(\Upsilon _{{ \mathcal {K}'[i]}^{}_{i}{ \mathcal {K}'[i]}^{}_{i}})(S_{i})=S_{i}\), and therefore
$$\begin{aligned} \mathsf {Ad}(\Upsilon _{\mathcal {F} \mathcal {K}[i]}) \mathsf {Ad}(\mathsf {a}^{{ \mathcal {K}[i]}^{}_{i}}_{{ \mathcal {K}[i]}^{i}_{}})(S_{i})=& \mathsf {Ad}(\Upsilon _{\mathcal {F} \mathcal {K}'[i]}) \mathsf {Ad}(\Upsilon _{ \mathcal {K}'[i] \mathcal {K}[i]}\cdot \mathsf {a}^{{ \mathcal {K}[i]}^{}_{i}}_{{ \mathcal {K}[i]}^{i}_{}})(S_{i}) \\ =&\mathsf {Ad}(\Upsilon _{\mathcal {F} \mathcal {K}'[i]}) \mathsf {Ad}(\mathsf {a}^{{ \mathcal {K}'[i]}^{}_{i}}_{{ \mathcal {K}'[i]}^{i}_{}}\cdot \Upsilon _{{ \mathcal {K}'[i]}^{}_{i}{ \mathcal {K}[i]}^{}_{i}})(S_{i}) \\ =&\mathsf {Ad}(\Upsilon _{\mathcal {F} \mathcal {K}'[i]}) \mathsf {Ad}(\mathsf {a}^{{ \mathcal {K}'[i]}^{}_{i}}_{{ \mathcal {K}'[i]}^{i}_{}})(S_{i}) \end{aligned}$$where the first and second equalities follows, respectively, from horizontal and vertical factorisations.
-
The morphisms \(\{\lambda _{\mathcal {F}}\}_{\mathcal {F}\in \mathsf {Mns}(B)}\) satisfy the conditions (a), (b). Let \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B)\). Then, \(\Upsilon _{\mathcal {G} \mathcal {K}[i]}=\Upsilon _{\mathcal {G}\mathcal {F}}\Upsilon _{\mathcal {F} \mathcal {K}[i]}\) and we get
$$ \mathsf {Ad}(\Upsilon _{\mathcal {G}\mathcal {F}})\circ \lambda _{\mathcal {F}}(\mathscr{S}_{i})= \mathsf {Ad}(\Upsilon _{\mathcal {G}\mathcal {F}}\cdot \Upsilon _{\mathcal {F} \mathcal {K}[i]})(S_{i }^{\mathsf {a}^{}_{}}) = \mathsf {Ad}(\Upsilon _{\mathcal {G} \mathcal {K}[i]})(S_{i }^{\mathsf {a}^{}_{}})=\lambda _{\mathcal {G}}( \mathscr{S}_{i}) $$Moreover, if \(\{i\}\in \mathcal {F}\), we can choose \(\mathcal {K}[i]=\mathcal {F}\), so that \(\lambda _{\mathcal {F}}(\mathscr{S}_{i})=S_{i }^{\mathsf {a}^{}_{}}= \mathsf {Ad}(\mathsf {a}^{{ \mathcal {F}}^{}_{i}}_{{ \mathcal {F}}^{i}_{}})(S_{i})\).
-
The morphisms \(\{\lambda _{\mathcal {F}}\}_{\mathcal {F}\in \mathsf {Mns}(B)}\) are uniquely determined by (a) and (b). Let \(\{\widetilde {\lambda}_{\mathcal {F}}\}_{\mathcal {F}\in \mathsf {Mns}(B)}\) be a collection of morphisms of groups satisfying (a), (b). Then, if we choose \(\mathcal {G}=\mathcal {K}[i]\), we get
$$ \widetilde {\lambda}_{\mathcal {F}}(\mathscr{S}_{i})\stackrel{(b)}{=} \mathsf {Ad}(\Upsilon _{\mathcal {F} \mathcal {K}[i]}) \circ \widetilde {\lambda}_{ \mathcal {K}[i]}(\mathscr{S}_{i})\stackrel{(a)}{=} \mathsf {Ad}(\Upsilon _{\mathcal {F} \mathcal {K}[i]})(S_{i }^{\mathsf {a}^{}_{}})= \lambda _{\mathcal {F}}( \mathscr{S}_{i}) $$
(2) Let \(B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B)\) with \(\mathsf {conn}(B')\subseteq \mathcal {F}\), and \(\mathcal {F}'\in \mathsf {Mns}(B')\). For any \(i\in B'\), let \(\mathcal {K}'[i]\in \mathsf {Mns}(B')\) be such that \(\{i\}\in \mathcal {K}'[i]\) and set \(\mathcal {K}[i]=\mathcal {K}'[i]\cup { \mathcal {F}}^{}_{B'}\in \mathsf {Mns}(B)\), so that \({ \mathcal {K}[i]}^{B'}_{}=\mathcal {K}'[i]\) and \({ \mathcal {K}[i]}^{}_{B'}={ \mathcal {F}}^{}_{B'}\). Note that \({ \mathcal {K}[i]}^{}_{i}= { \mathcal {K}'[i]}^{}_{i}\cup { \mathcal {F}}^{}_{B'}\) and \({ \mathcal {K}[i]}^{i}_{}={ \mathcal {K}'[i]}^{i}_{}\). Thus,
and one has
where the second equality follows by the invariance property \(\mathsf {a}^{{ \mathcal {F}}^{}_{B'}}_{{ \mathcal {K}'[i]}^{}_{i}}\in {A}^{\{i\}}_{B}\), the third one by the associativity of \(\mathsf {a}^{}_{}\), the fourth one by construction, the fifth one by vertical factorisation, and the sixth one by horizontal factorisation. □
7.4 Twisting and gauging of Coxeter structures
Definition 12
-
(1)
A twist \(u=\{u_{\mathcal {F}}\}\) in \(\mathscr{A}_{}\) is the datum, for any \(\mathcal {F}\in \mathsf {Mns}(B,B')\), of an invertible element \(u_{\mathcal {F}}\in {A}^{B'}_{B}\) such that, if \(B_{1}^{\prime}\subseteq B_{1}\perp B_{2}\supseteq B'_{2}\), \((\mathcal {F}_{1},\mathcal {F}_{2})\in \mathsf {Mns}(B_{1}\sqcup B_{2},B'_{1}\sqcup B'_{2})\),
$$\begin{aligned} u_{(\mathcal {F}_{1},\mathcal {F}_{2})} =& {j}^{B_{1}'B_{2}'}_{B_{1}B_{2}}(u_{\mathcal {F}_{1}} \otimes u_{\mathcal {F}_{2}}) \end{aligned}$$ -
(2)
The twisting of a Coxeter structure \(\mathbf {C}_{}=(\Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}, S_{i }^{})\) by a twist \(u=\{u_{\mathcal {F}}\}\) is the Coxeter structure
$$ \mathbf {C}_{u}=((\Upsilon _{\mathcal {F}\mathcal {G}})_{u}, (\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})_{u}, ( S_{i }^{})_{u}) $$given by
$$\begin{aligned} (\Upsilon _{\mathcal {F}\mathcal {G}})_{u} =&u_{\mathcal {F}}^{-1}\cdot \Upsilon _{\mathcal {F}\mathcal {G}}\cdot u_{\mathcal {G}} \\ (\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})_{u} =&u_{\mathcal {F}'\cup \mathcal {F}}^{-1}\cdot \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}\cdot u_{\mathcal {F}'} \cdot u_{\mathcal {F}} \\ (S_{i }^{})_{u} =& u_{\{i\}}^{-1}\cdot S_{i }^{}\cdot u_{\{i\}} \end{aligned}$$We denote by \(\mathscr{A}_{u}\) the Coxeter algebra with twisted structure \(\mathbf {C}_{u}\).
-
(3)
A gauge \({{a}}_{}=\{a_{B}\}\) in \(\mathscr{A}_{}\) consists of an invertible element \(a_{B}\in {A}^{B}_{B}\) for any \(B\subseteq \mathbb{D}\), satisfying
$$ a_{B_{1}\sqcup B_{2}}={j}^{B_{1}B_{2}}_{B_{1}B_{2}}(a_{B_{1}} \otimes a_{B_{2}}) $$ -
(4)
The gauging of a twist \(u=(u_{\mathcal {F}})\) by \(a\) is the twist \(u_{{{a}}_{}}=((u_{\mathcal {F}})_{{{a}}_{}})\) given by
$$\begin{aligned} (u_{\mathcal {F}})_{{{a}}_{}}&={i}^{B'B'}_{B\phantom{'}B'}(a_{B'})\cdot u_{ \mathcal {F}}\cdot {i}^{B'B}_{B\phantom{'}B}(a_{B})^{-1} \end{aligned}$$
The following is standard.
Proposition 10
Let \(\mathbf {C}_{}\) be a Coxeter structure on \(\mathscr{A}_{}\), \(u\) a twist and \(a\) a gauge. Then, \(\mathbf {C}_{u}=\mathbf {C}_{u_{{{a}}_{}}}\). Moreover, the representations of the braid group \(\lambda _{\mathcal {F}}^{\mathbf {C}_{}}\) and \(\lambda _{\mathcal {F}}^{\mathbf {C}_{u}}\), arising, respectively, from \(\mathbf {C}_{}\) and \(\mathbf {C}_{u}\), are equivalent.
7.5 Strict Coxeter structures
Let \(\mathscr{A}_{}\) be a Coxeter algebra. We say that
-
\(\mathscr{A}_{}\) is \(\Upsilon _{}\)–strict if \(\Upsilon _{\mathcal {F}\mathcal {G}}=1\) for any \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\)
-
\(\mathscr{A}_{}\) is \(\mathsf {a}^{}_{}\)–strict if \(\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}=1\) for any \(\mathcal {F}\in \mathsf {Mns}(B,B')\) and \(\mathcal {F}'\in \mathsf {Mns}(B',B'')\)
The following result shows that we can always restrict to either of these cases.
Proposition 11
-
(1)
\(\mathscr{A}_{}\) is twist equivalent to a \(\Upsilon _{}\)–strict Coxeter algebra.
-
(2)
\(\mathscr{A}_{}\) is canonically twist equivalent to an \(\mathsf {a}^{}_{}\)–strict Coxeter algebra.
Thanks to the condition (7.2), the proof is identical to that of [2, Prop. 9.10] and therefore omitted.
Remark 12
Note, however, that the latter result cannot be used to obtain a Coxeter structure which is both \(\Upsilon _{}\)–strict and \(\mathsf {a}^{}_{}\)–strict (cf. [2, Sect. 9.]).
8 Canonical fundamental solutions
We generalise to an arbitrary root system the construction of the fundamental solutions of the universal Casimir connection due to Cherednik [7, 8] and De Concini–Procesi [9]. More precisely, it is enough to observe that, by restriction to the truncated root system  (cf. 3.3 and Remark 3.6), the corresponding hyperplane arrangement is finite. Thus, the theory developed in [9] (see also [34, Sect. 1]) applies and can be extended by limit to the full root system. In the following, we describe the construction of the fundamental solutions in this context, omitting all proofs, which can be recovered verbatim from [9, 34].
(cf. 3.3 and Remark 3.6), the corresponding hyperplane arrangement is finite. Thus, the theory developed in [9] (see also [34, Sect. 1]) applies and can be extended by limit to the full root system. In the following, we describe the construction of the fundamental solutions in this context, omitting all proofs, which can be recovered verbatim from [9, 34].
8.1 Diagrammatic structure on 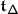
For any subdiagram \(B\subseteq \mathbb{D}\), we denote by  the corresponding root subsystem, and by \(\mathfrak {t}_{B}\) the holonomy algebra
the corresponding root subsystem, and by \(\mathfrak {t}_{B}\) the holonomy algebra  . For any \(B'\subseteq B\), the inclusion
. For any \(B'\subseteq B\), the inclusion  induces a morphism \(i_{BB'}:\mathfrak {t}_{B'}\to \mathfrak {t}_{B}\), mapping \(\mathsf {t}_{\alpha}^{} \in \mathfrak {t}_{B'}\) to the same symbol in \(\mathfrak {t}_{B}\).
induces a morphism \(i_{BB'}:\mathfrak {t}_{B'}\to \mathfrak {t}_{B}\), mapping \(\mathsf {t}_{\alpha}^{} \in \mathfrak {t}_{B'}\) to the same symbol in \(\mathfrak {t}_{B}\).
Lemma 4
The assignment

extends to a morphism of algebras \(p_{B'B}:\mathfrak {t}_{B}\to \mathfrak {t}_{B'}\) such that \(p_{B'B}\circ i_{BB'}=\operatorname{id}_{\mathfrak {t}_{B'}}\). In particular, \(i_{BB'}\) is injective.
Proof
It is enough to show that \(p_{B'B}\) preserves the \(tt\)–relations
where  and
and  is a subsystem of rank 2, which contains \(\alpha \). Denote by \(X\) the left–hand side, and consider the following cases.
is a subsystem of rank 2, which contains \(\alpha \). Denote by \(X\) the left–hand side, and consider the following cases.
-
If
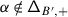 , then \(p_{B'B}(X)=0\).
, then \(p_{B'B}(X)=0\). -
If
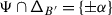 , then \(p_{B'B}(X)=[\mathsf {t}_{\alpha}^{},\mathsf {t}_{\alpha}^{}]=0\).
, then \(p_{B'B}(X)=[\mathsf {t}_{\alpha}^{},\mathsf {t}_{\alpha}^{}]=0\). -
If
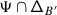 contains at least two linearly independent elements, then
contains at least two linearly independent elements, then 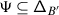 , and the \(tt\)–relations in \(\mathfrak {t}_{B'}\) imply that \(p_{B'B}(X)=0\).
, and the \(tt\)–relations in \(\mathfrak {t}_{B'}\) imply that \(p_{B'B}(X)=0\).
□
Finally, note that, if \(B_{1},B_{2}\subseteq B\) with \(B_{1}\perp B_{2}\), multiplication induces an isomorphism of algebras \({j}^{}_{B_{1}B_{2}}:\mathfrak {t}_{B_{1}}\otimes \mathfrak {t}_{B_{2}}\to \mathfrak {t}_{B_{1}\sqcup B_{2}}\), with inverse given by reordering. Thus, we have the followingFootnote 13
Proposition 12
\(\mathfrak {t}_{}=\{\mathfrak {t}_{B}\}\) is a split diagrammatic algebra with respect to the structural morphisms described above.
Remark 13
For any \(B'\subseteq B\), let \(\mathfrak {t}_{BB'}\) be the centraliser of \(\mathfrak {t}_{B'}\) in \(\mathfrak {t}_{B}\). Then, by Proposition 6.7, \(\mathfrak {t}_{}^{\flat}=\{\mathfrak {t}_{BB'}\}\) is a bidiagrammatic algebra.
If \(A=\bigoplus _{N\geqslant 0}A_{N}\) is an ℕ–graded algebra, we denote by \(\widehat {A}=\prod _{N\geqslant 0}A_{N}\) the completion of \(A\) with respect to its grading. For any \(B\subseteq \mathbb{D}\), let \(\widehat {\mathfrak {t}}_{B}\) be the completion of \(\mathfrak {t}_{B}\) with respect to the grading \(\deg (\mathsf {t}_{\alpha}^{})=1\),  , and \(\widehat {\mathfrak {t}}_{BB'}\) the centraliser of \(\mathfrak {t}_{B'}\) in \(\widehat {\mathfrak {t}}_{B}\), \(B'\subseteq B\). The results above extend to completions, in the sense that \(\widehat {\mathfrak {t}}_{}=\{ \widehat {\mathfrak {t}}_{B}\}\) and \(\widehat {\mathfrak {t}}_{}^{\flat}=\{ \widehat {\mathfrak {t}}_{BB'}\}\) are naturally lax diagrammatic and bidiagrammatic algebras, respectively.Footnote 14
, and \(\widehat {\mathfrak {t}}_{BB'}\) the centraliser of \(\mathfrak {t}_{B'}\) in \(\widehat {\mathfrak {t}}_{B}\), \(B'\subseteq B\). The results above extend to completions, in the sense that \(\widehat {\mathfrak {t}}_{}=\{ \widehat {\mathfrak {t}}_{B}\}\) and \(\widehat {\mathfrak {t}}_{}^{\flat}=\{ \widehat {\mathfrak {t}}_{BB'}\}\) are naturally lax diagrammatic and bidiagrammatic algebras, respectively.Footnote 14
Henceforth, we will identify \(\mathfrak {t}_{B}\) (resp. \(\widehat {\mathfrak {t}}_{B}\)) with the subalgebra in \(\mathfrak {t}_{}\) (resp. \(\widehat {\mathfrak {t}}_{}\)) topologically generated by the elements \(\mathsf {t}_{\alpha}^{}\),  .
.
8.2 Commutation relations
We say that  are strongly orthogonal, and we write \(\alpha \perp _{\mathbb{D}}\beta \), if the root system generated by \(\alpha \) and \(\beta \) is \(\{\pm \alpha ,\pm \beta \}\). Note that this condition is indeed stronger than \(\alpha \) and \(\beta \) being orthogonal with respect to the inner product on \(\mathfrak {h}^{*}\). However, it is equivalently stated in terms of orthogonality of subdiagrams, i.e., \(\alpha \perp _{\mathbb{D}}\beta \) if and only if \(\operatorname {supp}(\alpha )\perp \operatorname {supp}(\beta )\). Therefore, with a slight abuse of notation and terminology, in the following we shall simply say that two roots are orthogonal and write \(\alpha \perp \beta \). Moreover, we write \(\alpha \perp B\) if \(\operatorname {supp}(\alpha )\perp B\).
are strongly orthogonal, and we write \(\alpha \perp _{\mathbb{D}}\beta \), if the root system generated by \(\alpha \) and \(\beta \) is \(\{\pm \alpha ,\pm \beta \}\). Note that this condition is indeed stronger than \(\alpha \) and \(\beta \) being orthogonal with respect to the inner product on \(\mathfrak {h}^{*}\). However, it is equivalently stated in terms of orthogonality of subdiagrams, i.e., \(\alpha \perp _{\mathbb{D}}\beta \) if and only if \(\operatorname {supp}(\alpha )\perp \operatorname {supp}(\beta )\). Therefore, with a slight abuse of notation and terminology, in the following we shall simply say that two roots are orthogonal and write \(\alpha \perp \beta \). Moreover, we write \(\alpha \perp B\) if \(\operatorname {supp}(\alpha )\perp B\).
For any \(B\subseteq \mathbb{D}\), set

Proposition 13
The following holds.
-
(1)
If \(B_{1}\perp B_{2}\), then \([\mathsf {t}_{B_{1}}^{},\mathsf {t}_{B_{2}}^{}]=0\).
-
(2)
If
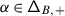 , then \([\mathsf {t}_{\alpha}^{}, \mathsf {t}_{B}^{}]=0\).
, then \([\mathsf {t}_{\alpha}^{}, \mathsf {t}_{B}^{}]=0\). -
(3)
If \(B'\subseteq B\), then \([\mathsf {t}_{B'}^{}, \mathsf {t}_{B}^{}]=0\).
Analogous results hold for the elements \(\mathsf {t}_{B}^{(m)}\) in \(\mathfrak {t}_{B}^{(m)}\).
Proof
(1) is clear and (3) follows from (2). Note that, if \(B_{1}\perp B_{2}\),then \(\mathsf {t}_{B_{1}\sqcup B_{2}}^{}=\mathsf {t}_{B_{1}}^{}+\mathsf {t}_{B_{2}}^{}\). Therefore, it is enough to prove \([\mathsf {t}_{\alpha}^{}, \mathsf {t}_{B}^{}]=0\) for \(B\) connected and  .
.
Let \(\mathsf{C}_{\alpha}\) be the set of equivalence classes in  with respect to the equivalence relation given by \(\beta \sim \gamma \) if they span the same line in \(\mathfrak {h}_{B}^{*}/\langle \alpha \rangle \). Then,
with respect to the equivalence relation given by \(\beta \sim \gamma \) if they span the same line in \(\mathfrak {h}_{B}^{*}/\langle \alpha \rangle \). Then,
By construction, the span of \(\alpha \) and \(\{\beta \;|\;\beta \in [\beta ]\}\) is two–dimensional, therefore
where the second equality follows from (3.7). The case \(\mathsf {t}_{}^{(m)}\) is identical. □
Remark 14
Note that the results above hold in greater generality. Let  be a subset of positive roots, \(\langle S\rangle \subseteq \mathfrak {h}^{*}\) the subspace spanned by \(S\). Set
be a subset of positive roots, \(\langle S\rangle \subseteq \mathfrak {h}^{*}\) the subspace spanned by \(S\). Set  and
and

Then, if  , one has \([\mathsf {t}_{\alpha}^{}, \mathsf {t}_{\langle S\rangle}^{}]=0\).
, one has \([\mathsf {t}_{\alpha}^{}, \mathsf {t}_{\langle S\rangle}^{}]=0\).
8.3 Blow–up coordinates on \(\mathsf {X}\)
Let \(\mathcal {F}\in \mathsf {Mns}(\mathbb{D})\) be a maximal nested set on \(\mathbb{D}\). For any  , let \(p_{\mathcal {F},\alpha}\) be the minimal element \(B\in \mathcal {F}\) such that \(\operatorname {supp}({\alpha})\subseteq B\). Then \(p_{\mathcal {F},\bullet}\) establishes a one to one correspondence between the simple roots \(\{\alpha _{1},\dots , \alpha _{n}\}\) and the elements in ℱ. For any \(B\in \mathcal {F}\), we denote by \(\alpha _{\mathcal {F},B}\) the simple root corresponding to \(B\) under \(p_{\mathcal {F},\bullet}\). For any \(B\in \mathcal {F}\), we denote by \(c_{\mathcal {F},B}\) the minimal element in ℱ which contains properly \(B\).
, let \(p_{\mathcal {F},\alpha}\) be the minimal element \(B\in \mathcal {F}\) such that \(\operatorname {supp}({\alpha})\subseteq B\). Then \(p_{\mathcal {F},\bullet}\) establishes a one to one correspondence between the simple roots \(\{\alpha _{1},\dots , \alpha _{n}\}\) and the elements in ℱ. For any \(B\in \mathcal {F}\), we denote by \(\alpha _{\mathcal {F},B}\) the simple root corresponding to \(B\) under \(p_{\mathcal {F},\bullet}\). For any \(B\in \mathcal {F}\), we denote by \(c_{\mathcal {F},B}\) the minimal element in ℱ which contains properly \(B\).
For any \(B\in \mathcal {F}\), set \(x_{B}=\sum _{i\in B}\alpha _{i}\). Then \(\{x_{B}\}_{B\in \mathcal {F}}\) defines a set of coordinates on \(\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\). Set \(U_{\mathcal {F}}=\mathbb{C}^{|\mathcal {F}|}\) with coordinates \(\{u_{\mathcal {F},B}\}_{B\in \mathcal {F}}\). Let \(\rho :U_{\mathcal {F}}\to \mathsf {X}\) be the map defined on the coordinates \(\{x_{B}\}\) by \(x_{B}=\prod _{B\subseteq C\in \mathcal {F}}u_{\mathcal {F},C}\). Then, \(\rho \) is birational with inverse
For any  set \(P_{\mathcal {F},\alpha}=\frac{\alpha}{x_{p_{\mathcal {F},\alpha}}}\).
set \(P_{\mathcal {F},\alpha}=\frac{\alpha}{x_{p_{\mathcal {F},\alpha}}}\).
Remark 15
In the case of affine root systems, it is convenient to impose \(x_{\mathbb{D}}=\sum _{i} a_{i}\alpha _{i}=\delta \).
8.4 Solutions of the Casimir connection
Following [7–9], we construct a collection of fundamental solutions of the universal Casimir connection (3.8), indexed by maximal nested sets on \(\mathbb{D}\).
Let \(m\geqslant 0\). For any \(\mathcal {F}\in \mathsf {Mns}(\mathbb{D})\) and \(B\in \mathcal {F}\), set  . Hence,
. Hence,

and finally
Let \(\mathcal {C}_{\mathbb{C}}\) be the complexification of the fundamental Weyl chamber. For any \(\mathcal {F}\in \mathsf {Mns}(\mathbb{D})\), let \(\mathcal {U}^{(m)}_{\mathcal {F}}\subset U\) be the complement of the zeros of the polynomials \(P_{\mathcal {F},\alpha}\),  , and \(\mathcal {D}^{(m)}\subset \mathcal {U}^{(m)}_{\mathcal {F}}\cap \mathcal {C}_{\mathbb{C}}\) a simply connected set with \(\mathsf {pt}_{\mathcal {F}}=\cap _{B\in \mathcal {F}}\{u_{\mathcal {F},B}=0\}\in \overline {\mathcal {D}^{(m)}}\). We have the following
, and \(\mathcal {D}^{(m)}\subset \mathcal {U}^{(m)}_{\mathcal {F}}\cap \mathcal {C}_{\mathbb{C}}\) a simply connected set with \(\mathsf {pt}_{\mathcal {F}}=\cap _{B\in \mathcal {F}}\{u_{\mathcal {F},B}=0\}\in \overline {\mathcal {D}^{(m)}}\). We have the following
Theorem 7
-
(1)
There is a unique holomorphic function
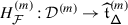 such that \(H^{(m)}_{\mathcal {F}}(\mathsf {pt}_{\mathcal {F}})=1\) and, for every determination of \(\log (x_{B})\), \(B\in \mathcal {F}\), the multivalued function $$ \Psi _{\mathcal {F}}^{(m)}= H^{(m)}_{\mathcal {F}}\prod _{B\in \mathcal {F}}x_{B}^{R^{(m)}_{\mathcal {F},B}}=H^{(m)}_{ \mathcal {F}}\prod _{B\in \mathcal {F}}u_{\mathcal {F},B}^{\mathsf {t}_{B}^{(m)}} $$
such that \(H^{(m)}_{\mathcal {F}}(\mathsf {pt}_{\mathcal {F}})=1\) and, for every determination of \(\log (x_{B})\), \(B\in \mathcal {F}\), the multivalued function $$ \Psi _{\mathcal {F}}^{(m)}= H^{(m)}_{\mathcal {F}}\prod _{B\in \mathcal {F}}x_{B}^{R^{(m)}_{\mathcal {F},B}}=H^{(m)}_{ \mathcal {F}}\prod _{B\in \mathcal {F}}u_{\mathcal {F},B}^{\mathsf {t}_{B}^{(m)}} $$is a solution of the holonomy equation \(dG=A^{(m)}G\), where
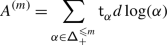
-
(2)
The sequence of solutions \(\{\Psi _{\mathcal {F}}^{(m)}\}_{m\geqslant 0}\) uniquely determines a multivalued function \(\Psi _{\mathcal {F}}\) with values in
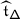 , satisfying the holonomy equation \(dG=AG\), where
, satisfying the holonomy equation \(dG=AG\), where 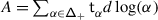 .
.
8.5 Asymptotics of the canonical solutions at infinity
We conclude this section with the study of the asymptotic behavior of fundamental solution \(\Psi _{\mathcal {F}}\) as \(\alpha _{i}\to \infty \) with \(\{i\}\in \mathcal {F}\), which is a straightforward generalisation of [35, Prop. 4.5, 4.6].
8.5.1
Fix \(i\in \mathbf {I}\), let  be the root system generated by the simple roots \(\{\alpha _{j}\}_{j\neq i}\), \({\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\subset \mathfrak {h}^{\scriptstyle {\operatorname {e}}}\) the corresponding essential Cartan subalgebra, and
be the root system generated by the simple roots \(\{\alpha _{j}\}_{j\neq i}\), \({\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\subset \mathfrak {h}^{\scriptstyle {\operatorname {e}}}\) the corresponding essential Cartan subalgebra, and  the holonomy algebra. The inclusion of root systems
the holonomy algebra. The inclusion of root systems  gives rise to a projection \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\) determined by the requirement that \(\alpha (\pi (h))=\alpha (h)\) for any
gives rise to a projection \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\) determined by the requirement that \(\alpha (\pi (h))=\alpha (h)\) for any  . The kernel of \(\pi \) is the line \(\mathbb{C}\lambda ^{\vee }_{i}\) spanned by the \(i\)th fundamental coweight of \(\mathfrak {h}\). We shall coordinatise the fibres of \(\pi \) by restricting the simple root \(\alpha _{i}\) to them. This amounts to trivialising the fibration \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to \overline {\mathfrak {h}}^{\scriptstyle {\operatorname {e}}}\) as \(\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\simeq \mathbb{C}\times \overline {\mathfrak {h}}^{\scriptstyle {\operatorname {e}}}\) via \((\alpha _{i},\pi )\). The inverse of this isomorphism is given by \((w,{\overline {\mu }})\to w\lambda ^{\vee }_{i}+\imath ({\overline {\mu }})\), where \(\imath :\overline{\mathfrak {h}}\to \mathfrak {h}\) is the embedding with image \(\ker (\alpha _{i})\) given by
. The kernel of \(\pi \) is the line \(\mathbb{C}\lambda ^{\vee }_{i}\) spanned by the \(i\)th fundamental coweight of \(\mathfrak {h}\). We shall coordinatise the fibres of \(\pi \) by restricting the simple root \(\alpha _{i}\) to them. This amounts to trivialising the fibration \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to \overline {\mathfrak {h}}^{\scriptstyle {\operatorname {e}}}\) as \(\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\simeq \mathbb{C}\times \overline {\mathfrak {h}}^{\scriptstyle {\operatorname {e}}}\) via \((\alpha _{i},\pi )\). The inverse of this isomorphism is given by \((w,{\overline {\mu }})\to w\lambda ^{\vee }_{i}+\imath ({\overline {\mu }})\), where \(\imath :\overline{\mathfrak {h}}\to \mathfrak {h}\) is the embedding with image \(\ker (\alpha _{i})\) given by
Let

be the universal Casimir operators in  and
and  , respectively.
, respectively.
Set \(\overline {\mathbb{D}}= \mathbb{D}\setminus \{i\}\). Fix \(\overline {\mu}\in \overline {\mathfrak {h}}^{\scriptstyle {\operatorname {e}}}=\mathfrak {h}_{\overline {\mathbb{D}}}^{\scriptstyle {\operatorname {e}}}\), and consider the fiber of \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\) at \({\overline {\mu }}\). Since the restriction of  to \(\pi ^{-1}({\overline {\mu }})\) is equal to \(\alpha (\lambda ^{\vee }_{i})\alpha _{i}+\alpha (\imath ({\overline {\mu }}))\), the restriction of the Casimir connection \(\nabla _{\mathcal {K}}\) to \(\pi ^{-1}({\overline {\mu }})\) is equal to
to \(\pi ^{-1}({\overline {\mu }})\) is equal to \(\alpha (\lambda ^{\vee }_{i})\alpha _{i}+\alpha (\imath ({\overline {\mu }}))\), the restriction of the Casimir connection \(\nabla _{\mathcal {K}}\) to \(\pi ^{-1}({\overline {\mu }})\) is equal to

where \(w_{\alpha}=-\alpha (\imath ({\overline {\mu }}))/\alpha (\lambda ^{\vee }_{i})\). Set  .
.
Proposition 14
-
(1)
For any \({\overline {\mu }}\in {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\), there is a unique holomorphic function
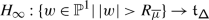
such that \(H_{\infty}(\infty )=1\) and, for any determination of \(\log (\alpha _{i})\), the function \(\Upsilon _{\infty}=H_{\infty}(\alpha _{i})\cdot \alpha _{i}^{\mathsf {t}_{}^{}-\overline {\mathsf {t}_{}^{}}}\) satisfies
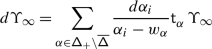
-
(2)
The function \(H_{\infty}(\alpha _{i},{\overline {\mu }})\) is holomorphic on the simply–connected domain \(\mathcal {D}_{\infty}=\{(w,\overline{\mu})|\,|w|>R_{{ \overline {\mu }}}\}\subset \mathbb{P}^{1}\times \overline {\mathfrak {h}}\) and, as a function on \(\mathcal {D}_{\infty}\), \(\Upsilon _{\infty}\) satisfies
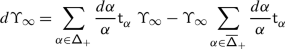
8.5.2
Let ℱ be a maximal nested set on \(\mathbb{D}\), set \(\overline {\mathcal {F}}=\mathcal {F}\setminus \{\mathbb{D}\}\) and \(\alpha _{i}=\alpha _{\mathcal {F},\mathbb{D}}\), i.e., \(\alpha _{i}\) is the only simple root whose support is not contained in the maximal elements of ℱ. Let

be the fundamental solutions of the Casimir connection for  and
and  corresponding to ℱ, \(\overline {\mathcal {F}}\) respectively, with blow-up coordinates \(\{x_{B}\}_{B\subseteq \mathbb{D}}\) (cf. 8.3). Regard \(\Psi _{ \overline {\mathcal {F}}}\) as being defined on \(\mathcal {C}\) via the projection \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\). The result below expresses \(\Psi _{\mathcal {F}}\) in terms of \(\Psi _{ \overline {\mathcal {F}}}\) and the solution \(\Upsilon _{\infty}\).
corresponding to ℱ, \(\overline {\mathcal {F}}\) respectively, with blow-up coordinates \(\{x_{B}\}_{B\subseteq \mathbb{D}}\) (cf. 8.3). Regard \(\Psi _{ \overline {\mathcal {F}}}\) as being defined on \(\mathcal {C}\) via the projection \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\). The result below expresses \(\Psi _{\mathcal {F}}\) in terms of \(\Psi _{ \overline {\mathcal {F}}}\) and the solution \(\Upsilon _{\infty}\).
Proposition 15
\(\Psi _{\mathcal {F}}= \Upsilon _{\infty}\cdot \Psi _{ \overline {\mathcal {F}}}\cdot x_{\mathbb{D}}( \lambda ^{\vee }_{i})^{\mathsf {t}_{}^{}-\overline {\mathsf {t}_{}^{}}}\).
Clearly, the same results holds for any \(\Psi _{\mathcal {F}}\) with \(\mathcal {F}\in \mathsf {Mns}(B)\) and \(B\subseteq \mathbb{D}\).
9 A Coxeter structure from holonomy
We prove that the monodromy of the Casimir connection defines a Coxeter structure on the holonomy algebra  of the root arrangement in \(\mathfrak {h}\).
of the root arrangement in \(\mathfrak {h}\).
9.1 De Concini–Procesi associators
Let \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(\mathbb{D})\) be two maximal nested sets and \(\Psi _{\mathcal {F}}\), \(\Psi _{\mathcal {G}}\) be the corresponding fundamental solutions given by Theorem 8.4. Define the De Concini–Procesi associator \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\) to be the invertible element of  defined by
defined by
where \(x\) lies in the fundamental Weyl chamber. The following summarises the essential properties of these associators.
Theorem 8
Let \(\mathcal {F},\mathcal {G},\mathcal {H}\in \mathsf {Mns}(\mathbb{D})\). Then, the following properties hold.
-
(1)
Transitivity: \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}=\Upsilon _{\mathcal {F}\mathcal {H}}^{\nabla} \Upsilon _{\mathcal {H}\mathcal {G}}^{\nabla}\).
-
(2)
Support: \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\in \widehat {\mathfrak {t}}_{\operatorname {supp}(\mathcal {F},\mathcal {G})}^{\;\operatorname {\mathfrak {z}supp}(\mathcal {F}, \mathcal {G})}\).
-
(3)
Forgetfulness: \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}=\Upsilon _{\mathcal {F}'\mathcal {G}'}^{\nabla}\) whenever \((\mathcal {F},\mathcal {G})\), \((\mathcal {F}',\mathcal {G}')\) are equivalent.
Proof
Transitivity follows directly from the definition of \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\). The proof of the properties of support and forgetfulness is identical to those in [9, Thm. 3.6] and [34, Thm. 1.33, Prop. 1.38] and is therefore omitted. □
9.2 Pre–Coxeter structure
By Proposition 8.1, the holonomy algebra gives rise to a diagrammatic algebra \(\mathfrak {t}_{}=\{\mathfrak {t}_{B}\}\) and a bidiagrammatic algebra \(\mathfrak {t}_{}^{\flat}=\{\mathfrak {t}_{BB'}\}\), where \(\mathfrak {t}_{BB'}\subseteq \mathfrak {t}_{B}\) is the centraliser of \(\mathfrak {t}_{B'}\). Both structures are compatible with the grading, and we denote by \(\widehat {\mathfrak {t}}_{}\) (resp. \(\widehat {\mathfrak {t}}_{}^{\flat}\)) the lax diagrammatic (resp. lax bidiagrammatic) algebras corresponding to the algebras \(\widehat {\mathfrak {t}}_{B}\) (resp. \(\widehat {\mathfrak {t}}_{BB'}\)).
Choose \(\mathcal {M}\in \mathsf {Mns}(\mathbb{D},B)\), \(\mathcal {M}'\in \mathsf {Mns}(B')\), and let
be the map defined by \({\mathcal {F}}^{\mathcal {M}}_{\mathcal {M}'}=\mathcal {M}\cup \mathcal {F}\cup \mathcal {M}'\). For any relative maximal nested sets \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\), we set \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}=\Upsilon _{ {\mathcal {F}}^{\mathcal {M}}_{\mathcal {M}'} {\mathcal {G}}^{\mathcal {M}}_{\mathcal {M}'}}^{\nabla}\), which we also refer to as a De Concini–Procesi associator, with a slight abuse of terminology. Note that, by the forgetfulness property, \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\) is independent of the choice of ℳ and \(\mathcal {M}'\), and it is therefore well–defined. Moreover, by the support property, \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\) is an invertible element in \(\widehat {\mathfrak {t}}_{BB'}\). Finally, the following holds by construction.
-
(a)
For any \(B'''\subseteq B''\subseteq B'\subseteq B\), \(\mathcal {M}\in \mathsf {Mns}(B,B')\), \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B',B'')\), \(\mathcal {M}''\in \mathsf {Mns}(B'',B''')\),
$$ \Upsilon _{(\mathcal {M}\cup \mathcal {F}\cup \mathcal {M}'')(\mathcal {M}\cup \mathcal {G}\cup \mathcal {M}'')}^{\nabla}= \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla} $$ -
(b)
For any \(B'\subseteq B\perp C\),
$$ \Upsilon _{(\mathcal {F}\cup \{C\})(\mathcal {G}\cup \{C\})}^{\nabla}= \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla} $$
Theorem 9
The collection of De Concini–Procesi associators \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\), for any \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\) with \(B'\subseteq B\subseteq \mathbb{D}\), defines an \(\mathsf {a}\)–strict pre–Coxeter structure on \(\widehat {\mathfrak {t}}_{}^{\flat}\).
Proof
We shall show that the associators \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\) satisfy the requirements of Definition 7.2.
-
Horizontal factorisation. This follows from transitivity.
-
Vertical factorisation. For any \(B''\subseteq B'\subseteq B\),
$$ \mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\qquad \text{and}\qquad \mathcal {F}',\mathcal {G}'\in \mathsf {Mns}(B',B'') $$one has
$$\begin{aligned} \Upsilon _{(\mathcal {G}\cup \mathcal {G}')(\mathcal {F}\cup \mathcal {F}')}^{\nabla}= \Upsilon _{(\mathcal {G}\cup \mathcal {G}')(\mathcal {F}\cup \mathcal {G}')}^{\nabla}\cdot \Upsilon _{(\mathcal {F}\cup \mathcal {G}')(\mathcal {F}\cup \mathcal {F}')}^{\nabla}= \Upsilon _{\mathcal {G}\mathcal {F}}^{\nabla}\cdot \Upsilon _{\mathcal {G}'\mathcal {F}'}^{\nabla} \end{aligned}$$where the first identity follows from transitivity and the second one from (a) above. Note that, since \(\Upsilon _{\mathcal {G}\mathcal {F}}^{\nabla}\in \widehat {\mathfrak {t}}_{BB'}\) and \(\Upsilon _{\mathcal {G}'\mathcal {F}'}^{\nabla}\in \widehat {\mathfrak {t}}_{B'}\), the order of factors does not matter.
-
Orthogonal factorisation. For any \(B_{1}^{\prime}\subseteq B_{1}\perp B_{2} \supseteq B'_{2}\), and pairs
$$\begin{gathered} (\mathcal {G}_{1}, \mathcal {G}_{2}), (\mathcal {F}_{1},\mathcal {F}_{2})\in \mathsf {Mns}(B_{1},B'_{1})\times \mathsf {Mns}(B_{2},B'_{2})=\mathsf {Mns}(B_{1}\sqcup B_{2},B'_{1}\sqcup B'_{2}) \end{gathered}$$one has \((\mathcal {G}_{1},\mathcal {G}_{2})=(\mathcal {G}_{1}, B_{2})\cup (B'_{1}, \mathcal {G}_{2})\) and \((\mathcal {F}_{1},\mathcal {F}_{2})=(\mathcal {F}_{1}, B_{2})\cup (B'_{1}, \mathcal {F}_{2})\), hence
$$ \Upsilon _{(\mathcal {G}_{1},\mathcal {G}_{2})(\mathcal {F}_{1},\mathcal {F}_{2})}^{\nabla}= \Upsilon _{(\mathcal {G}_{1}, B_{2})(\mathcal {F}_{1}, B_{2})}^{\nabla}\cdot \Upsilon _{(B'_{1}, \mathcal {G}_{2})(B'_{1},\mathcal {F}_{2})}^{\nabla} = \Upsilon _{\mathcal {G}_{1}\mathcal {F}_{1}}^{\nabla}\cdot \Upsilon _{\mathcal {G}_{2}\mathcal {F}_{2}}^{\nabla} $$where the first identity follows from vertical factorisation and the second one from (b) above. Therefore, orthogonal factorisation holds. Note that, since \([\mathfrak {t}_{B_{1}}, \mathfrak {t}_{B_{2}}]=0\), the order of factors does not matter.
□
9.3 Coxeter structure on 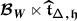
As for  and
and  , the extended holonomy algebra gives rise to a bidiagrammatic algebra, which we denote by
, the extended holonomy algebra gives rise to a bidiagrammatic algebra, which we denote by  and is described by the collection of algebras
and is described by the collection of algebras

where \(B'\subseteq B\subseteq \mathbb{D}\), \(\mathfrak {h}'_{B}=\mathsf{span}\{h_{i}\;|\; i\in B\}\), \(W_{B}=\langle s_{i}\;|\; i\in B\rangle \subseteq W\), and the action of \(\mathcal {B}_{W_{B}}\) is given by Definition 4.11. Indeed, it is enough to observe that, if \(B'\perp B''\), then \(\widehat {\mathfrak {t}}_{B'}\) is pointwise fixed by \(W_{B''}\). Finally, we have the following
Theorem 10
-
(1)
The De Concini–Procesi associators
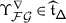 and the elements
and the elements 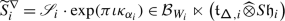
where \({\kappa }_{\alpha _{i}}=\mathsf {t}_{\alpha _{i}}^{}+t_{\alpha _{i}}/2\) define an \(\mathsf {a}\)–strict Coxeter structure \(\widetilde {\mathbf {C}_{}}\) on
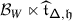 with respect to the standard labelling on \(\mathbb{D}\) (i.e., \(m_{ij}=\mathsf{ord}(s_{i}s_{j})\) in \(W\)).
with respect to the standard labelling on \(\mathbb{D}\) (i.e., \(m_{ij}=\mathsf{ord}(s_{i}s_{j})\) in \(W\)). -
(2)
The action of \(\mathcal {B}_{W}\) arising from \(\widetilde {\mathbf {C}_{}}\) coincides with the monodromy of the universal Casimir connection from Sect. 4, given in terms of the fundamental solutions \(\Psi _{\mathcal {F}}\).
Proof
Let \(\widetilde {\mathsf {X}}\stackrel{p}{\rightarrow} \mathsf {X}\) be the universal cover of \(\mathsf {X}\), fix a \(\widetilde {x}_{0}\in \widetilde {\mathsf {X}}\) which lifts \(x_{0}\in \mathsf {X}\) and a fundamental solution \(G\) of \(p^{*}\nabla _{\mathsf {t}_{}^{}}\) valued in  . Let
. Let  be its monodromy along the path \(\gamma \). Then, by Corollary 4.11 (1), for any \(W\)–invariant function \(\mathbf {a}\), we obtain a representation
be its monodromy along the path \(\gamma \). Then, by Corollary 4.11 (1), for any \(W\)–invariant function \(\mathbf {a}\), we obtain a representation  , given, for any \(\gamma :x_{0}\to w^{-1}x_{0}\), by
, given, for any \(\gamma :x_{0}\to w^{-1}x_{0}\), by
where \(\mu _{G,\mathbf {a}}(\gamma )=\mu _{G}(\gamma )\mathscr{B}\mathcalligra{ }_{\mathscr{A}}(\gamma )\mathscr{B}\mathcalligra{ }_{\mathbf {a}}( \gamma )\).
Let \(\mathcal {F}\in \mathsf {Mns}(B)\) with \(\{i\}\in \mathcal {F}\). Then, by choosing \(G=\Psi _{\mathcal {F}}\) and \(\mathbf {a}\) such that \(a_{i}=\pi \iota \), it follows from (4.6) that \(\mu ^{\sharp}_{\Psi _{\mathcal {F}}, \pi \iota}(s_{i}, \gamma _{i})= \widetilde {S}_{i }^{\nabla}\). Moreover, if \(\mathcal {G}\in \mathsf {Mns}(B)\) with \(\{j\}\in \mathcal {G}\), then
In particular, the elements \(\widetilde {S}_{i }^{\nabla}\) and the associators \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\) satisfy the braid relations (7.3) and define a Coxeter structure on  . The results follow. □
. The results follow. □
Remark 16
Following Remark 4.8 (2), we further adjust the monodromy operators by setting \(S_{i }^{\nabla}= \widetilde {S}_{i }^{\nabla}\cdot \exp (\pi \iota \mathsf {d}_{i}^{-1}t_{\alpha _{i}}^{2}/4)\). This yields another \(\mathsf {a}^{}_{}\)–strict Coxeter structure \(\mathbf {C}_{}=(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}, S_{i }^{\nabla})\) on  , encoding the monodromy representation \(\mu ^{\sharp}_{\Psi _{\mathcal {F}}, \pi \iota ,\pi \iota \langle{ \alpha _{i}},{\alpha _{i}}\rangle }\). Indeed, it is enough to observe that, since the associators \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\) are supported on
, encoding the monodromy representation \(\mu ^{\sharp}_{\Psi _{\mathcal {F}}, \pi \iota ,\pi \iota \langle{ \alpha _{i}},{\alpha _{i}}\rangle }\). Indeed, it is enough to observe that, since the associators \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\) are supported on  , the generalised braid relations (7.3) still hold. We shall show in Sect. 16 that, given a representation \(V\) of \(\mathfrak {g}\), the operator \(S_{i }^{\nabla}\) (resp. \(\widetilde {S}_{i }^{\nabla}\)) specialises on \(V\) to the local monodromy operators \(\widetilde {s}_{i}\cdot \exp (\pi \iota \mathsf {h}\cdot C_{i}/2)\) (resp. \(\widetilde {s}_{i}\cdot \exp (\pi \iota \mathsf {h}\cdot {\mathcal {K}}_{i}^{}/2)\)) where \(C_{i}\) denote the Casimir operator of \(U\mathfrak {sl}_{2}^{i}\) (resp. \({\mathcal {K}}_{i}^{}=C_{i}-\mathsf {d}_{i}^{-1}t_{\alpha _{i}}^{2}/2\)).
, the generalised braid relations (7.3) still hold. We shall show in Sect. 16 that, given a representation \(V\) of \(\mathfrak {g}\), the operator \(S_{i }^{\nabla}\) (resp. \(\widetilde {S}_{i }^{\nabla}\)) specialises on \(V\) to the local monodromy operators \(\widetilde {s}_{i}\cdot \exp (\pi \iota \mathsf {h}\cdot C_{i}/2)\) (resp. \(\widetilde {s}_{i}\cdot \exp (\pi \iota \mathsf {h}\cdot {\mathcal {K}}_{i}^{}/2)\)) where \(C_{i}\) denote the Casimir operator of \(U\mathfrak {sl}_{2}^{i}\) (resp. \({\mathcal {K}}_{i}^{}=C_{i}-\mathsf {d}_{i}^{-1}t_{\alpha _{i}}^{2}/2\)).
Part II. The KZ–Casimir connection
10 Cosimplicial diagrammatic algebras
We describe (bi)diagrammatic algebras endowed with a compatible cosimplicial structure.
10.1 Cosimplicial algebras
In the following, we shall consider a number of algebras, which are not bialgebras, but fit instead in the more general setting of cosimplicial algebras.
A cosimplicial algebra is a cosimplicial object in the category of algebras, i.e., the datum

of a collection of algebras \(\{A^{n}\}_{n\geqslant 0}\) endowed with face morphisms \(d^{n+1}_{i}: A^{n}\to A^{n+1}\), \(i=0, 1, \dots , n+1\), and degeneration morphisms \(\varepsilon ^{n}_{i}: A^{n}\to A^{n-1}\), \(i=1,\dots , n\), such that
Remarks 1
-
(1)
For any \(x\in A^{n}\), we write \(x_{1,\dots , ii+1, \dots , n+1}= d^{n+1}_{i}(x)\in A^{n+1}\), with \(i=1,\dots , n\). Moreover, for any \(m>0\), we denote by \(x_{1,\dots , n}\in A^{n+m}\) the element \(d_{n+m}^{n+m}\circ d_{n+m-1}^{n+m-1}\circ \cdots \circ d_{n+1}^{n+1}(x)\).
-
(2)
For any \(n\geqslant 1\), we consider denote by \(d^{(n)}: A^{1}\to A^{n}\) the canonical morphism recursively defined by \(d^{(1)}=\operatorname{id}_{A^{1}}\) and \(d^{(n)}= d^{n}_{1}\circ d^{(n-1)}\).
Henceforth, we shall further assume that \(A^{{\scriptscriptstyle \operatorname {\bullet}}}\) is endowed with an action of the symmetric group in each degree such that, for any \(x\in A^{n}\) and \(1\leqslant i\leqslant n-1\),
and
For \(x\in A^{n}\) and \(\sigma \in \mathfrak {S}_{n}\), we write \(x_{\sigma (1),\dots , \sigma (n)}=\sigma \cdot x\).
10.2 Examples
Let \(A\) be a bialgebra over a base ring \(\mathsf {k}\) with coproduct \(\Delta : A\to A^{\otimes 2}\) and counit \(\varepsilon : A\to \mathsf {k}\). We provide two basic examples of cosimplicial algebras associated to \(A\).
-
(1)
The tower of algebras \(A^{n}= A^{\otimes n}\), \(n\geqslant 0\), is a cosimplicial algebra with face morphisms
$$ d_{i}^{n+1} (x)= \left \{ \textstyle\begin{array}{c@{\quad}c} 1\otimes x & i=0 \\ \operatorname{id}_{A}^{\otimes i-1}\otimes \Delta \otimes \operatorname{id}_{A}^{\otimes n-i}(x) & 1 \leqslant i \leqslant n \\ x\otimes 1 & i=n+1 \end{array}\displaystyle \right . $$and degeneration morphisms
$$ \varepsilon ^{n}_{i}(x)=\operatorname{id}_{A}^{\otimes i-1}\otimes \varepsilon \otimes \operatorname{id}_{A}^{ \otimes n-i}(x) $$where \(x\in A^{\otimes n}\). In particular, \(d^{2}_{1}=\Delta \) and \(\varepsilon ^{1}_{1}=\varepsilon \).
-
(2)
Let \(\mathcal {C}\subseteq \operatorname{Rep}(A)\) be a tensor subcategory, and \(\mathsf {f}^{\boxtimes n}:\mathcal {C}^{\boxtimes n}\to \operatorname{{\mathsf{Vect}}}\) the \(n\)–fold forgetful functor given by \(\mathsf {f}^{\boxtimes n}(V_{1},\dots , V_{n})= V_{1}\otimes \cdots \otimes V_{n}\). The tower of algebras \(\mathcal {A}^{n}=\mathsf{End}\left (\mathsf{f}^{\boxtimes n}\right )\) gives rise to a cosimplicial algebra with face and degeneration morphisms induced by the tensor product and the unit of \(\mathcal {C}\) and defined as follows.
-
The face morphisms \(d_{i}^{n+1}:\mathsf{End}\left (\mathsf{f}^{\boxtimes n}\right )\to \mathsf{End}\left (\mathsf{f}^{\boxtimes n+1}\right )\), \(i=0,\dots , n+1\), are given by
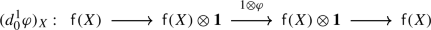

where \({\mathbf{1}}\) is the trivial module, \(X\in \mathcal {C}\), \(\varphi \in \mathsf {k}\), and,
$$ (d_{i}^{n+1} \varphi )_{X_{1},\dots , X_{n+1}}= \left \{ \textstyle\begin{array}{l@{\quad}l} \operatorname{id} \otimes \varphi _{X_{2},\dots , X_{n+1}} & i=0 \\ \varphi _{X_{1},\dots , X_{i}\otimes X_{i+1},\dots X_{n+1}} & 1 \leqslant i \leqslant n \\ \varphi _{X_{1},\dots , X_{n}}\otimes \operatorname{id}& i=n+1 \end{array}\displaystyle \right . $$where \(\varphi \in \mathsf{End}\left (\mathsf{f}^{\boxtimes n}\right )\), \(X_{j}\in \mathcal {C}\), \(j=1,\dots , n+1\).
-
The degeneration morphisms \(\varepsilon ^{n}_{i}:\mathsf{End}\left (\mathsf{f}^{\boxtimes n} \right )\to \mathsf{End}\left (\mathsf{f}^{\boxtimes n-1}\right )\), for \(i=1, \dots , n\), are
$$ (\varepsilon ^{n}_{i} \varphi )_{X_{1}, \dots , X_{n-1}}=\varphi _{X_{1}, \dots , X_{i-1}, {\mathbf{1}}, X_{i}, \dots , X_{n-1} } $$where \(\varphi \in \mathsf{End}\left (\mathsf{f}^{\boxtimes n}\right )\), \(X_{j}\in \mathcal {C}\), \(j=1,\dots , n-1\).
-
Remark 17
Note that there is a natural morphisms of cosimplicial algebras \(A^{{\scriptscriptstyle \operatorname {\otimes \bullet}}}\to \mathcal {A}^{{\scriptscriptstyle \operatorname {\bullet}}}\), so that the latter can be regarded as a topological completion of the former. However, in Sects. 12.2 and 19.9, we shall consider certain cosimplicial algebras which do not arise from topological bialgebras.
10.3 Cosimplicial diagrammatic algebras
A cosimplicial (lax) diagrammatic algebra is a cosimplicial object in the category of (lax) diagrammatic algebras, i.e., the datum of a collection of (lax) diagrammatic algebras \(\{A^{n}\}_{n\geqslant 0}\) endowed with the face and degeneration maps, which are further required to be morphisms of diagrammatic algebras.
Given a (lax) diagrammatic bialgebra \(\mathscr{A}_{}= ({A}^{}_{B}, {i}^{}_{BB'}, {j}^{}_{B'B''})\), it is clear that
is a (lax) diagrammatic algebra for any given \(n\geqslant 0\).Footnote 15 Moreover, the collection of morphisms \(\Delta _{B}:{A}^{}_{B}\to {A}^{\otimes 2}_{B}\) and \(\varepsilon _{B}:{A}^{}_{B}\to \mathsf {k}\), with \(B\subseteq \mathbb{D}\), define a cosimplicial structure on \(\{\mathscr{A}_{}^{\otimes n}\}_{n\geqslant 0}\), and we denote by \(\mathscr{A}_{}^{\otimes \bullet}\) the resulting cosimplicial diagrammatic algebra.
10.4 Cosimplicial bidiagrammatic algebras
Definition 13
A cosimplicial (lax) bidiagrammatic algebra is a cosimplicial object in the category of (lax) bidiagrammatic algebras such that, for any \(B,C\subseteq \mathbb{D}\), the map
is a morphism of algebras, where \(m\) is the multiplication in \({(A^{n+1})}^{\emptyset}_{B}\), \(i_{1}=(i^{n+1})^{\emptyset \emptyset}_{BC}\), \(i_{2}=(i^{n+1})^{\emptyset C}_{B B}\), and \(d^{(n)}_{C}: {(A^{1})}^{\emptyset}_{C}\to {(A^{n+1})}^{\emptyset}_{C}\) is defined as in Remark 10.1 (2).
The definition above generalises the following situation. Let \(A\) be a bialgebra with a distinguished subbialgebra \(A'\subseteq A\). By definition, the subalgebra \((A^{\otimes n})^{A'}\) of (diagonal) \(A'\)–invariants in \(A^{\otimes n}\) satisfies
Indeed, we have the following
Proposition 16
Let \(\mathscr{A}_{}=({A}^{}_{B},{i}^{}_{BB'}, {j}^{}_{B'B''})\) be a diagrammatic bialgebra.
-
(1)
For any \(n\geqslant 0\), set
$$\begin{aligned} {(A^{\otimes n, \flat})}^{C}_{B} =& (A^{\otimes n}_{B})^{A_{C}}\subseteq A^{ \otimes n}_{B} \\ {(i^{\otimes n, \flat})}^{CC'}_{BB'} =&{i}^{\otimes n}_{BB'}|_{( {A}^{\otimes n}_{B'})^{{A}^{}_{C'}}} \\ {(j^{\otimes n, \flat})}^{C'C''}_{B'B''} =& {j}^{\otimes n}_{B'B''}|_{({A}^{\otimes n}_{B'})^{{A}^{}_{C'}} \otimes ({A}^{\otimes n}_{B''})^{{A}^{}_{C''}}} \end{aligned}$$where we regard \(({A}^{\otimes n}_{B'})^{{A}^{}_{C'}}\otimes ({A}^{\otimes n}_{B''})^{ {A}^{}_{C''}}\) as a subalgebra in \(({A}^{}_{B'}\otimes {A}^{}_{B''})^{\otimes n}\). Then
$$ \mathscr{A}_{}^{\otimes n, \flat}=({(A^{\otimes n,\flat})}^{C}_{B}, {(i^{\otimes n, \flat})}^{CC'}_{BB'}, {(j^{\otimes n, \flat})}^{C'C''}_{B'B''}) $$is a bidiagrammatic algebra.
-
(2)
The morphisms \(\Delta _{B}:{A}^{}_{B}\to {A}^{\otimes 2}_{B}\) and \(\varepsilon _{B}:{A}^{}_{B}\to \mathsf {k}\), with \(B\subseteq \mathbb{D}\), define a cosimplicial structure on \(\{\mathscr{A}_{}^{\otimes n, \flat}\}_{n\geqslant 0}\), and we denote by \(\mathscr{A}_{}^{\otimes \bullet , \flat}\) the resulting cosimplicial bidiagrammatic algebra.
Remarks 2
-
Note that \(\mathscr{A}_{}^{\otimes n,\flat}\) contains, but does not coincide with, the bidiagrammatic algebra \((\mathscr{A}_{}^{\otimes n})^{\flat}\) defined using Proposition 6.7. The difference is the same as that between the subalgebras \((A^{\otimes n})^{A'}\) and \((A^{\otimes n})^{(A')^{\otimes n}}\) in \(A^{\otimes n}\) for any bialgebra \(A\) with a distinguished subbialgebra \(A'\).
-
Let \(A\) be a cocommutative bialgebra. The canonical action of the symmetric group \(\mathfrak {S}_{n}\) on \(A^{\otimes n}\) preserves the subalgebra \((A^{\otimes n})^{A'}\), since for any \(\sigma \in \mathfrak {S}_{n}\) it holds \(\sigma \circ \Delta ^{(n-1)}=\Delta ^{(n-1)}\). Similarly, whenever \(\mathscr{A}_{}\) is a bidiagrammatic cocommutative bialgebra, the symmetric group \(\mathfrak {S}_{n}\) acts on \(\mathscr{A}_{}^{\otimes n, \flat}\) by bidiagrammatic automorphisms.
Example 3
Let \(\mathfrak {g}\) be a diagrammatic Kac–Moody algebra (cf. 2.4). Then, \(U\mathfrak {g}\) is a lax diagrammatic Hopf algebra and \(\mathbf {U}_{\mathfrak {g}}^{\scriptscriptstyle {\bullet}}= U\mathfrak {g}^{\otimes \bullet , \flat}\) is the cosimplicial bidiagrammatic algebra with face/degeneration maps induced by the Hopf algebra structure on \(U\mathfrak {g}\) and bidiagrammatic subalgebras \((U\mathfrak {g}_{B}^{\otimes n})^{\mathfrak {g}_{C}}\), \(C\subseteq B\subseteq \mathbb{D}\).
11 Braided Coxeter algebras
The notion of a braided Coxeter algebra arises from the combination of a quasitriangular and a Coxeter structure on a cosimplicial bidiagrammatic algebra. In particular, it is naturally endowed with commuting actions of the (type \(\mathsf {A}\)) braid groups \(\mathcal {B}_{n}\) and a fixed generalised braid group \(\mathcal {B}_{W}\).
11.1 Braided Coxeter algebras
Let \((\mathbb{D},\underline {m})\) be a labelled diagram. Let \(\mathscr{A}_{}^{{\scriptscriptstyle \operatorname {\bullet}}}\) be a cosimplicial (lax) bidiagrammatic algebra, satisfying the condition (7.2) in degree one.
Definition 14
A braided Coxeter structure \(\mathbf {C}_{}=(\Phi _{B},R_{B}, J^{}_{\mathcal {F}},\Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}, S_{i }^{})\) on \(\mathscr{A}_{}^{{\scriptscriptstyle \operatorname {\bullet}}}\) consists of the following data.
-
(a)
Associators. For any \(B\subseteq \mathbb{D}\), an invertible element \(\Phi _{B}\in {(A^{3})}^{B}_{B}\) satisfying the following properties
-
Pentagon relation.
$$ (\Phi _{B})_{1,2,34}(\Phi _{B})_{12,3,4}=(\Phi _{B})_{2,3,4}(\Phi _{B})_{1,23,4}( \Phi _{B})_{1,2,3} $$ -
Degeneration. For \(i=1,2,3\), \(\varepsilon ^{3}_{i}(\Phi _{B})=1_{{(A^{2})}^{B}_{B}}\).
-
Orthogonal factorisation. If \(B_{1}\perp B_{2}\),
$$\begin{aligned} \Phi _{B_{1}\sqcup B_{2}} =& {(j^{3})}^{B_{1}B_{2}}_{B_{1}B_{2}}(\Phi _{B_{1}}\otimes \Phi _{B_{2}}) \end{aligned}$$
-
-
(b)
\(R\)–matrices. For any \(B\subseteq \mathbb{D}\), an invertible element \(R_{B}\in {(A^{2})}^{B}_{B}\) satisfying the following properties
-
Hexagon relations.
$$\begin{aligned} &(R_{B})_{12,3}=(\Phi _{B})_{3,1,2}(R_{B})_{13}(\Phi _{B})_{1,3,2}^{-1}(R_{B})_{23}( \Phi _{B})_{1,2,3} \\ &(R_{B})_{1,23}=(\Phi _{B})_{2,3,1}^{-1}(R_{B})_{13}(\Phi _{B})_{2,1,3}(R_{B})_{12}( \Phi _{B})_{1,2,3}^{-1} \end{aligned}$$ -
Degeneration. For \(i=1,2\), \(\varepsilon ^{2}_{i}(R_{B})=1_{{A}^{B}_{B}}\).
-
Orthogonal factorisation. If \(B_{1}\perp B_{2}\),
$$\begin{aligned} R_{B_{1}\sqcup B_{2}} =& {(j^{2})}^{B_{1}B_{2}}_{B_{1}B_{2}}(R_{B_{1}} \otimes R_{B_{2}}) \end{aligned}$$
-
-
(c)
Relative twists. For any \(B^{\prime}\subseteq B\) and maximal nested set \(\mathcal {F}\in \mathsf {Mns}(B,B^{\prime})\), an invertible element \(J^{}_{\mathcal {F}}\in {(A^{2})}^{B'}_{B}\) satisfying the following properties.
-
Compatibility with associators. The relative twist equation holds,
$$ J_{\mathcal {F}, 1,23}\cdot J_{\mathcal {F}, 23}\cdot \Phi _{B'} = \Phi _{B}\cdot J_{ \mathcal {F}, 12,3}\cdot J_{\mathcal {F}, 12} $$ -
Normalisation. For any \(B\subseteq D\), \(J_{B}=1_{{(A^{1})}^{B}_{B}}\).Footnote 16
-
Degeneration. For \(i=1,2\), \(\varepsilon _{i}^{2}(J^{}_{\mathcal {F}})=1_{{(A^{1})}^{B}_{B'}}\).
-
Orthogonal factorisation. If \(B_{1}^{\prime}\subseteq B_{1}\perp B_{2}\supseteq B'_{2}\), \((\mathcal {F}_{1},\mathcal {F}_{2})\in \mathsf {Mns}(B_{1}\sqcup B_{2},B'_{1}\sqcup B'_{2})\),
$$\begin{aligned} J_{(\mathcal {F}_{1},\mathcal {F}_{2})} =& {(j^{2})}^{B_{1}'B_{2}'}_{B_{1}B_{2}}(J_{ \mathcal {F}_{1}}\otimes J_{\mathcal {F}_{2}}) \end{aligned}$$
-
-
(d)
Generalised associators. For any \(B'\subseteq B\) and \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\), an invertible element \(\Upsilon _{\mathcal {G}\mathcal {F}}\in {(A^{1})}^{B'}_{B}\) satisfying the properties from Definition 7.2 and the following
-
Compatibility with \(J\). For any \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\),
$$ J^{}_{\mathcal {G}}=(\Upsilon _{\mathcal {G}\mathcal {F}})^{-1}_{12}\cdot J^{}_{\mathcal {F}}\cdot (\Upsilon _{\mathcal {G}\mathcal {F}})_{1}\cdot (\Upsilon _{\mathcal {G}\mathcal {F}})_{2} $$
-
-
(e)
Vertical joins. For any \(B''\subseteq B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B,B')\), and \(\mathcal {F}'\in \mathsf {Mns}(B',B'')\), an invertible element \(\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}\in {(A^{1})}^{B''}_{B}\) satisfying the same properties from Definition 7.2 and the following
-
Compatibility with \(J\) (vertical \(J\)–factorisation).
$$ J^{}_{\mathcal {F}'\cup \mathcal {F}}= (\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})_{12}\cdot {(i^{2})}^{B''B'}_{B\phantom{''}B}(J^{}_{\mathcal {F}})\cdot {(i^{2})}^{B''B''}_{B\phantom{''}B'}(J^{}_{\mathcal {F}'})\cdot (\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})_{1}^{-1}\cdot (\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})_{2}^{-1} $$
-
-
(f)
Local monodromies. For any vertex \(i\) of \(\mathbb{D}\), an invertible element \(S_{i}\in {(A^{1})}^{\emptyset}_{i}\) satisfying the braid relations (7.3) and the following
-
Coproduct identity. For any \(i\in D\),
$$ J_{i}^{-1}\cdot (S_{i})_{12}\cdot J_{i}= J_{i}^{-1}\cdot R_{i, 21} \cdot J_{i,21}\cdot (S_{i})_{1}\cdot (S_{i})_{2} $$(11.1)
-
Remarks 3
-
The relations above readily imply the following.
-
(1)
If \(B'\subseteq B\perp B''\) and \(\mathcal {F}\in \mathsf {Mns}(B,B')\),
$$\begin{aligned} J_{(\mathcal {F}, B'')} =&{(j^{2})}^{B'B''}_{B\phantom{'}B''}( J^{}_{\mathcal {F}}\otimes 1_{{(A^{2})}^{B''}_{B''}}) \\ \Upsilon _{(\mathcal {F}, B'')(\mathcal {G},B'')} =& {(j^{1})}^{B'B''}_{BB''}( \Upsilon _{\mathcal {F}\mathcal {G}}\otimes 1_{{(A^{1})}^{B''}_{B''}}) \end{aligned}$$ -
(2)
If \(B'_{1}\subseteq B_{1}\perp B_{2}\supseteq B'_{2}\), \(\mathcal {F}_{1}\in \mathsf {Mns}(B_{1},B'_{1})\), and \(\mathcal {F}_{2}\in \mathsf {Mns}(B_{2},B'_{2})\),
$$ \mathsf {a}^{(\mathcal {F}_{1},B_{2})}_{(B'_{1},\mathcal {F}_{2})}= 1_{ {(A^{1})}^{B_{1}'\sqcup B_{2}'}_{B_{1}\sqcup B_{2}}}= \mathsf {a}^{(B_{1},\mathcal {F}_{2})}_{(\mathcal {F}_{1},B'_{2})} $$
-
(1)
-
It is clear from the definition that a braided Coxeter algebra is a cosimplicial (lax) bidiagrammatic algebra with a Coxeter algebra in degree one and some further compatible data in degree two and three.
11.2 Representations of braid groups
Let \(\mathcal {B}_{n}\) be the braid group associated to \(\mathfrak {S}_{n}\), with generators \(\mathtt {\rho }_{1}, \dots , \mathtt {\rho }_{n-1}\), and \(\mathsf {br}_{n}\) the set of complete bracketing on the non–commutative monomial \(x_{1} x_{2}\cdots x_{n}\). The following is a straightforward generalisation of Proposition 7.3.
Proposition 17
Let \(\mathscr{A}_{}^{{\scriptscriptstyle \operatorname {\bullet}}}\) be a braided Coxeter algebra. Then, there is a family of representations
labelled by \(B\subseteq \mathbb{D}\), \(\mathcal {F}\in \mathsf {Mns}(B)\), and \(b\in \mathsf {br}_{n}\), which is uniquely determined by the conditions
-
(1)
\(\lambda _{\mathcal {F}, b}(\mathscr{S}_{i})= \mathsf {Ad}(\mathsf {a}^{{ \mathcal {F}}^{}_{i}}_{{ \mathcal {F}}^{i}_{}}) (S_{i }^{})_{1 \dots n}\) if \(\{i\}\in \mathcal {F}\).
-
(2)
\(\lambda _{\mathcal {G}, b}=\mathsf {Ad}(\Upsilon _{\mathcal {G}\mathcal {F}})_{1\dots n}\circ \lambda _{\mathcal {F}, b}\).
and
-
(3)
\(\lambda _{\mathcal {F}, b}(\mathtt {\rho }_{i})=(i\ i+1)\circ (R_{B})_{i,i+1}\) if \(b= x_{1}\cdots (x_{i}x_{i+1})\cdots x_{n}\).
-
(4)
\(\lambda _{\mathcal {F}, b'}=\mathsf {Ad}(\Phi _{B, b'b})\circ \lambda _{\mathcal {F}, b}\).
11.3 Twisting and gauging of braided Coxeter structures
The notions of twisting and gauging of braided Coxeter structure extends those introduced in 7.4.
Definition 15
-
(1)
A twist \({T}_{}=(u_{\mathcal {F}},K_{B})\) in \(\mathscr{A}_{}^{{\scriptscriptstyle \operatorname {\bullet}}}\) consists of the following data.
-
(a)
For any \(\mathcal {F}\in \mathsf {Mns}(B,B')\), an invertible element \(u_{\mathcal {F}}\in {(A^{1})}^{B'}_{B}\) such that \(\varepsilon ^{1}_{1}(u_{\mathcal {F}})=1\) and, if \(B_{1}^{\prime}\subseteq B_{1}\perp B_{2}\supseteq B'_{2}\), \((\mathcal {F}_{1},\mathcal {F}_{2})\in \mathsf {Mns}(B_{1}\sqcup B_{2},B'_{1}\sqcup B'_{2})\),
$$\begin{aligned} u_{(\mathcal {F}_{1},\mathcal {F}_{2})} =& {(j^{1})}^{B_{1}'B_{2}'}_{B_{1}B_{2}}(u_{ \mathcal {F}_{1}}\otimes u_{\mathcal {F}_{2}}) \end{aligned}$$ -
(b)
For any \(B\subseteq \mathbb{D}\), an invertible element \(K_{B}\in {(A^{1})}^{B}_{B}\) such that \((K_{B})_{21}=K_{B}\), \(\varepsilon ^{2}_{i}(K_{B})=1_{{(A^{1})}^{B}_{B}}\), \(i=1,2\), and, if \(B_{1}\perp B_{2}\),
$$\begin{aligned} K_{(B_{1},B_{2})} =& {(j^{2})}^{B_{1}B_{2}}_{B_{1}B_{2}}( K_{B_{1}}\otimes K_{B_{2}}) \end{aligned}$$
-
(a)
-
(2)
The twisting of a braided Coxeter structure \(\mathbf {C}_{}=(\Phi _{B},R_{B}, J^{}_{\mathcal {F}},\Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}, S_{i }^{})\) by a twist \({T}_{}=(u_{\mathcal {F}},K_{B})\) is the braided Coxeter structure
$$ \mathbf {C}_{{T}_{}}=((\Phi _{B})_{{T}_{}},(R_{B})_{{T}_{}}, (J^{}_{\mathcal {F}})_{ {T}_{}},(\Upsilon _{\mathcal {F}\mathcal {G}})_{{T}_{}}, (\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})_{{T}_{}}, (S_{i})_{ {T}_{}}) $$given by
$$\begin{aligned} (\Phi _{B})_{{T}_{}} =&{(K_{B})}_{23}^{-1}\cdot {(K_{B})}^{-1}_{1,23}\cdot \Phi _{B}\cdot {(K_{B})}_{12,3}\cdot {(K_{B})}_{12} \\ (R_{B})_{{T}_{}} =& {(K_{B})}_{21}^{-1}\cdot R_{B}\cdot (K_{B}) \\ (J^{}_{\mathcal {F}})_{{T}_{}} =& (u_{\mathcal {F}})^{-1}_{12}\cdot {i}^{B'B}_{BB}(K_{B})^{-1}\cdot J^{}_{\mathcal {F}}\cdot {i}^{B'B'}_{BB'}(K_{B'})\cdot (u_{\mathcal {F}})_{1}\cdot (u_{\mathcal {F}})_{2} \end{aligned}$$and
$$ \textstyle\begin{array}{r@{\quad}c@{\quad}c@{\quad}c@{\quad}r} (\Upsilon _{\mathcal {F}\mathcal {G}})_{{T}_{}} &=&u_{\mathcal {F}}^{-1}\cdot \Upsilon _{\mathcal {F}\mathcal {G}}\cdot u_{ \mathcal {G}} &=& (\Upsilon _{\mathcal {F}\mathcal {G}})_{u} \\ (\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})_{{T}_{}} &=&u_{\mathcal {F}'\cup \mathcal {F}}^{-1}\cdot \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}\cdot u_{\mathcal {F}'} \cdot u_{\mathcal {F}} &=& (\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})_{u} \\ (S_{i }^{})_{{T}_{}} &=& u_{\{i\}}^{-1}\cdot S_{i }^{}\cdot u_{ \{i\}} &=& (S_{i }^{})_{u} \end{array} $$We denote by \(\mathscr{A}_{{T}_{}}^{{\scriptscriptstyle \operatorname {\bullet}}}\) the braided Coxeter algebra with twisted structure \(\mathbf {C}_{{T}_{}}\).
-
(3)
A gauge \({{a}}_{}=\{a_{B}\}\) in \(\mathscr{A}_{}^{{\scriptscriptstyle \operatorname {\bullet}}}\) consists of an invertible element \(a_{B}\in {(A^{1})}^{B}_{B}\) for any \(B\subseteq \mathbb{D}\), satisfying \(\varepsilon _{1}^{1}(a_{B})=1\) and
$$ a_{B_{1}\sqcup B_{2}}={(j^{1})}^{B_{1}B_{2}}_{B_{1}B_{2}}(a_{B_{1}} \otimes a_{B_{2}}) $$ -
(4)
The gauging of a twist \({T}_{}=(u_{\mathcal {F}},K_{B})\) by \({{a}}_{}\) is the twist \({T}_{{{a}}_{}}=((u_{\mathcal {F}})_{{{a}}_{}},(K_{B})_{{{a}}_{}})\) given by
$$\begin{aligned} (u_{\mathcal {F}})_{{{a}}_{}}&={(i^{1})}^{B'B'}_{B\phantom{'}B'}(a_{B'}) \cdot u_{\mathcal {F}}\cdot {(i^{1})}^{B'B}_{B\phantom{'}B}(a_{B})^{-1} \\ (K_{B})_{{{a}}_{}} &=(a_{B})^{-1}_{12}\cdot K_{B}\cdot (a_{B})_{1}\cdot (a_{B})_{2} \end{aligned}$$
The following is standard.
Proposition 18
Let \(\mathbf {C}_{}\) be a braided Coxeter structure on \(\mathscr{A}_{}^{{\scriptscriptstyle \operatorname {\bullet}}}\), \({T}_{}\) a twist, and \(a\) a gauge. Then, \(\mathbf {C}_{{T}_{}}=\mathbf {C}_{{T}_{{{a}}_{}}}\). Moreover, the representations of the braid groups \(\lambda _{\mathcal {F},b}^{\mathbf {C}_{}}\) and \(\lambda _{\mathcal {F},b}^{\mathbf {C}_{{T}_{}}}\), arising from \(\mathbf {C}_{}\) and \(\mathbf {C}_{{T}_{}}\), respectively, are equivalent.
12 The double holonomy algebra
We proved in 9.3 that the holonomy algebra  of the Casimir connection \(\nabla_{\mathsf {C}}\) is a bidiagrammatic algebra, and that it can be endowed with a Coxeter structure encoding the monodromy of \(\nabla_{\mathsf {C}}\). In this section, we introduce the holonomy algebra
of the Casimir connection \(\nabla_{\mathsf {C}}\) is a bidiagrammatic algebra, and that it can be endowed with a Coxeter structure encoding the monodromy of \(\nabla_{\mathsf {C}}\). In this section, we introduce the holonomy algebra  of the joint KZ–Casimir system and describe its cosimplicial bidiagrammatic structure.
of the joint KZ–Casimir system and describe its cosimplicial bidiagrammatic structure.
12.1 The holonomy algebra of the KZ connection
Let \(n\geqslant 2\).
Definition 16
The holonomy algebra \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) is the associative algebra generated by the elements \(\{\mathsf {t}^{ij} \;|\; 1\leqslant i\neq j\leqslant n\}\) with the following relations.
-
Symmetry. For any \(i\neq j\), \(\mathsf {t}^{ij}=\mathsf {t}^{ji}\).
-
Locality. For any distinct \(i\), \(j\), \(k\), \(l\) \([\mathsf {t}^{ij},\mathsf {t}^{kl}]=0\).
-
KZ relations. For any distinct \(i\), \(j\), \(k\),
$$ [\mathsf {t}^{ij},\mathsf {t}^{ik}+\mathsf {t}^{jk}]=0 $$(12.1)
Remark 18
The algebra \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) is the holonomy algebra  of the root system of type \(\mathsf {A}_{n-1}\). Indeed, under the map \(\mathsf {t}^{ij}\mapsto \mathsf {t}_{\alpha _{i}+\cdots +\alpha _{j-1}}^{}\), \(i< j\), the relations (12.1) correspond precisely to the \(tt\)–relations (3.7). For instance, in \(\mathfrak {t}_{\mathsf {A}_{3}}\) one has
of the root system of type \(\mathsf {A}_{n-1}\). Indeed, under the map \(\mathsf {t}^{ij}\mapsto \mathsf {t}_{\alpha _{i}+\cdots +\alpha _{j-1}}^{}\), \(i< j\), the relations (12.1) correspond precisely to the \(tt\)–relations (3.7). For instance, in \(\mathfrak {t}_{\mathsf {A}_{3}}\) one has
The grading and the completion of \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) are therefore defined as in 8.1.
12.2 Cosimplicial structure on \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\)
Set \(\mathfrak {t}_{}^{\scriptscriptstyle {1}}=\mathsf {k}\). The tower of algebras \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}=\{\mathfrak {t}_{}^{\scriptscriptstyle {n}}\}_{n\geqslant 1}\) is a cosimplicial algebra (cf. 10.1), with the face morphisms \(d_{n}^{k}:\mathfrak {t}_{}^{\scriptscriptstyle {n}}\to \mathfrak {t}_{}^{\scriptscriptstyle {n+1}}\), \(k=0,1,\dots , n+1\), given by
and
while the degeneration homomorphisms \(\varepsilon _{n}^{k}:\mathfrak {t}_{}^{\scriptscriptstyle {n}}\to \mathfrak {t}_{}^{\scriptscriptstyle {n-1}}\), \(k=1,\dots , n\) are given by
We shall describe several refinements of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\), to which the cosimplicial structure naturally extend. Their mutual relations are described in Proposition 12.9 and diagram (12.16) below.
12.3 Diagrammatic refinement \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet, \mathbb{D}}}\) of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\)
Let \(\mathbb{D}\) be a diagram. We construct a cosimplicial diagrammatic algebra by gluing together a copy of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\) for any subdiagram \(B\subseteq \mathbb{D}\). The algebra \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet, \mathbb{D}}}\) allows to simultaneously describe the monodromy of the KZ equations corresponding to all diagrammatic subalgebras of a symmetrisable Kac–Moody algebra.
Definition 17
The algebra \(\mathfrak {t}_{}^{\scriptscriptstyle {n,\mathbb{D}}}\) is the associative algebra generated by the symbols \(\{\mathsf {t}_{B}^{ij}\;|\; 1\leqslant i\neq j\leqslant n,\; B\subseteq \mathbb{D}\}\) with the following relations.
-
Symmetry. For any \(i\neq j\), and \(B\subseteq \mathbb{D}\), \(\mathsf {t}_{B}^{ij}=\mathsf {t}_{B}^{ji}\).
-
Locality. For any distinct \(i\), \(j\), \(k\), \(l\), and \(B,B'\subseteq \mathbb{D}\)
$$ [\mathsf {t}_{B}^{ij}{},\mathsf {t}_{B'}^{kl}{}]=0 $$(12.2) -
KZ relations. For any distinct \(i\), \(j\), \(k\), and \(B'\subseteq B\subseteq \mathbb{D}\),
$$ [\mathsf {t}_{B}^{ij}{},\mathsf {t}_{B'}^{ik}{}+\mathsf {t}_{B'}^{jk}{}]=0 $$(12.3) -
Orthogonality. For any \(i\), \(j\), \(k\), \(l\) and \(B_{1}\perp B_{2}\),
$$ \mathsf {t}_{B_{1}\sqcup B_{2}}^{ij}{}=\mathsf {t}_{B_{1}}^{ij}{}+\mathsf {t}_{B_{2}}^{ij}{} \qquad \text{and}\qquad [\mathsf {t}_{B_{1}}^{ij}{},\mathsf {t}_{B_{2}}^{kl}{}]=0 $$(12.4)
Remark 19
Note that, by (12.4), it is enough to assume (12.2) and (12.3) for connected subdiagrams only.
12.4 Diagrammatic and cosimplicial structure
Proposition 19
-
(1)
For any \(B\subseteq \mathbb{D}\), there is an embedding \(\iota_{B}^{n}:\mathfrak {t}_{}^{\scriptscriptstyle {n}}\to \mathfrak {t}_{}^{\scriptscriptstyle {n,B}}\) given by \(\mathsf {t}_{}^{ij}\mapsto \mathsf {t}_{B}^{ij}{}\).
-
(2)
There is a unique cosimplicial structure on \(\mathfrak {t}_{}^{\scriptscriptstyle {n,B}}\) such that \(\{\iota_{B}^{n}\}\) is a morphism of cosimplicial algebras \(\iota_{B}\colon \mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\to \mathfrak {t}_{}^{\scriptscriptstyle {\bullet, \mathbb{D}}}\) for every \(B\subseteq \mathbb{D}\).
-
(3)
For any \(B\subseteq \mathbb{D}\), there is an embedding \(i_{B'B}^{n}:\mathfrak {t}_{}^{\scriptscriptstyle {n,B'}}\to \mathfrak {t}_{}^{\scriptscriptstyle {n,B}}\) given by \(\mathsf {t}_{B''}^{ij}\mapsto \mathsf {t}_{B''}^{ij}\) for any \(B''\subseteq B'\subseteq B\). Moreover, if \(B_{1}\perp B_{2}\), multiplication induces an isomorphism of algebras \(j_{B_{1}B_{2}}:\mathfrak {t}_{}^{\scriptscriptstyle {n,B_{1}}}\otimes \mathfrak {t}_{}^{\scriptscriptstyle {n,B_{2}}}\to \mathfrak {t}_{}^{\scriptscriptstyle {n,B_{1}\sqcup B_{2}}}\), so that
$$ \mathfrak {t}_{}^{\scriptscriptstyle {n,{\scriptscriptstyle \operatorname {\mathbb{D}}}}}=(\mathfrak {t}_{}^{\scriptscriptstyle {n,B}}, i_{B'B}^{n}) $$is a diagrammatic algebra.
-
(4)
The tower \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet ,{\scriptscriptstyle \operatorname {\mathbb{D}}}}}=\{\mathfrak {t}_{}^{\scriptscriptstyle {n,{\scriptscriptstyle \operatorname {\mathbb{D}}}}}\;|\; n \geqslant 1\}\) is a cosimplicial diagrammatic algebra.
12.5 Root refinement \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet,\Delta}}\) of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\)
Let \(\mathfrak {g}\) be a symmetrisable Kac–Moody algebra, \(\mathfrak {h}\) its Cartan subalgebra, and  its root system. We define a cosimplicial refinement of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\) controlled by
its root system. We define a cosimplicial refinement of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\) controlled by  , which is suitable to describe the monodromy of the dynamical KZ equations of \(\mathfrak {g}\).
, which is suitable to describe the monodromy of the dynamical KZ equations of \(\mathfrak {g}\).
Definition 18
The algebra  is the associative algebra generated by the symbols
is the associative algebra generated by the symbols  with the following relations.
with the following relations.
-
Symmetry. For any \(i\neq j\) and
 ,
, 
-
Locality. For any distinct \(i\), \(j\), \(k\), \(l\) and
 ,
, 
-
KZ relations. SetFootnote 17
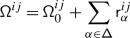 (12.5)
(12.5)Then, for any distinct \(i\), \(j\), \(k\),
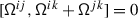 .
. -
Orthogonality. For any \(i\), \(j\), \(k\), \(l\), and \(\alpha \perp \beta \), \([\mathsf {r}^{ij}_{\alpha}, \mathsf {r}^{kl}_{\beta}]=0\).
-
Weight zero. For any \(i\), \(j\), \(k\), \(l\),
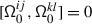 .
.
Note that locality implies that  for any distinct \(i\), \(j\), \(k\), \(l\).
for any distinct \(i\), \(j\), \(k\), \(l\).
Proposition 20
-
(1)
For every \(n\geq 2\), there is an embedding
 given by
given by 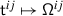 .
. -
(2)
The tower of algebras
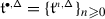 is endowed with a unique cosimplicial structure which extends that on \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\), and is given byFootnote 18$$ d_{n}^{k}(\mathsf {r}^{ij}_{\alpha})=\delta _{ki}(\mathsf {r}^{ij}_{\alpha}+ \mathsf {r}^{i+1,j}_{\alpha})+ \delta _{kj}(\mathsf {r}^{ij}_{\alpha}+ \mathsf {r}^{i,j+1}_{\alpha})\qquad k=1,\dots , n $$
is endowed with a unique cosimplicial structure which extends that on \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\), and is given byFootnote 18$$ d_{n}^{k}(\mathsf {r}^{ij}_{\alpha})=\delta _{ki}(\mathsf {r}^{ij}_{\alpha}+ \mathsf {r}^{i+1,j}_{\alpha})+ \delta _{kj}(\mathsf {r}^{ij}_{\alpha}+ \mathsf {r}^{i,j+1}_{\alpha})\qquad k=1,\dots , n $$
The algebra  is acted upon by \(\mathfrak {h}^{\oplus n}\). For any \(h\in \mathfrak {h}\) and \(1\leq k\leq n\), we set
is acted upon by \(\mathfrak {h}^{\oplus n}\). For any \(h\in \mathfrak {h}\) and \(1\leq k\leq n\), we set
Note that \(\mathfrak {h}^{\oplus n}\) does not preserve the elements  , and thus the image of \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) in
, and thus the image of \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) in  .
.
Remark 20
Let \(\mathbb{D}\) be the Dynkin diagram of  . For any \(B\subseteq \mathbb{D}\), consider the subsystem
. For any \(B\subseteq \mathbb{D}\), consider the subsystem  consisting of all
consisting of all  with \(\operatorname {supp}(\alpha )\subseteq B\) and define the subalgebra
with \(\operatorname {supp}(\alpha )\subseteq B\) and define the subalgebra  generated by the symbolsFootnote 19
generated by the symbolsFootnote 19

The cosimplicial structure on  restricts to one on
restricts to one on  and, for any \(B'\subseteq B\), we have
and, for any \(B'\subseteq B\), we have  .
.
Note, however, that this does not give rise to a diagrammatic structure on \(\mathfrak {t}_{}^{\scriptscriptstyle {n, \Delta}}\). Indeed, if \(B_{1}\perp B_{2}\),  and
and  do not commute in
do not commute in  since the elements
since the elements  do not distinguish between \(\alpha\in B_{1}\) or \(\alpha\in B_{2}\). In order to obtain a diagrammatic structure, we need to further refine the elements
do not distinguish between \(\alpha\in B_{1}\) or \(\alpha\in B_{2}\). In order to obtain a diagrammatic structure, we need to further refine the elements  in a way which is analogous to the refinement of the elements \(\mathsf {t}^{ij}\) into \(\mathsf {t}^{ij}_{B}\) in 12.3. We shall do so in the following section, integrating the diagrammatic and root refinements of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\) with the holonomy algebra
in a way which is analogous to the refinement of the elements \(\mathsf {t}^{ij}\) into \(\mathsf {t}^{ij}_{B}\) in 12.3. We shall do so in the following section, integrating the diagrammatic and root refinements of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\) with the holonomy algebra  .
.
12.6 The double holonomy algebra 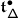
Retain the notation of 12.5.
Definition 19
For \(n\geqslant 1\), let \(\mathfrak {t}_{\Delta}^{\scriptscriptstyle {n}}\) be the ℂ–algebra generated by the elementsFootnote 20

with the following relations.
-
Symmetry. For any \(i\neq j\), \(B'\subseteq B\), and
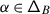 ,
, 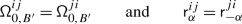 (12.6)
(12.6) -
Locality. For any distinct \(i\), \(j\), \(k\), \(l\), \(B,B'\subseteq \mathbb{D}\),
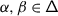 , and
, and 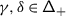
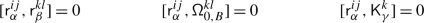 (12.7)
(12.7)and
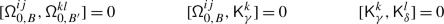 (12.8)
(12.8) -
KZ relations. For any distinct \(i\), \(j\), \(k\), and \(B'\subseteq B\subseteq \mathbb{D}\),
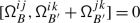 (12.9)
(12.9)where
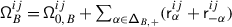 .
. -
Orthogonality. For any \(i\), \(j\), \(k\), \(l\), \(B_{1}\perp B_{2}\subseteq \mathbb{D}\),
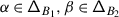 , and any
, and any 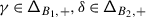 , $$\begin{aligned}{} [\mathsf {r}^{ij}_{\alpha}, \mathsf {r}^{kl}_{\beta}]=0 \qquad [\mathsf {r}^{ij}_{\alpha}, \mathsf {K}_{\gamma}^{k}]=0 \qquad [\mathsf {K}_{\gamma}^{k},\mathsf {K}_{\delta}^{l}]=0 \end{aligned}$$(12.10)
, $$\begin{aligned}{} [\mathsf {r}^{ij}_{\alpha}, \mathsf {r}^{kl}_{\beta}]=0 \qquad [\mathsf {r}^{ij}_{\alpha}, \mathsf {K}_{\gamma}^{k}]=0 \qquad [\mathsf {K}_{\gamma}^{k},\mathsf {K}_{\delta}^{l}]=0 \end{aligned}$$(12.10)and
 (12.11)
(12.11)together with
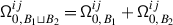 .
. -
Weight zero. For any \(i\), \(j\), \(k\), \(l\), and \(B,B'\subseteq \mathbb{D}\),
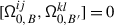 .
. -
Casimir relations. For any \(1\leqslant k\leqslant n\), rank 2 subsystem
 , and
, and 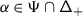 ,
, 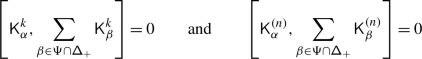 (12.12)
(12.12) -
Invariance relations. For any \(1\leqslant i\neq j\leqslant n\), \(B\subseteq \mathbb{D}\),
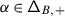 ,
, 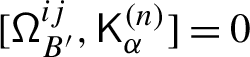 (12.13)
(12.13) -
Coproduct relation. For any
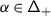 , $$ \mathsf {K}_{\alpha}^{(n)}=\sum _{i< j}(\mathsf {r}^{ij}_{\alpha}+\mathsf {r}^{ij}_{-\alpha})+ \sum _{k=1}^{n}\mathsf {K}_{\alpha ,k}^{} $$(12.14)
, $$ \mathsf {K}_{\alpha}^{(n)}=\sum _{i< j}(\mathsf {r}^{ij}_{\alpha}+\mathsf {r}^{ij}_{-\alpha})+ \sum _{k=1}^{n}\mathsf {K}_{\alpha ,k}^{} $$(12.14)
Remark 21
The coproduct relation (12.14) implies that the generators \(\mathsf {K}_{\alpha}^{(n)}\) are redundant. However, the relations (12.12) and (12.13) are easier to formulate in terms of \(\mathsf {K}_{\alpha}^{(n)}\) rather than the remaining generators. Note also that  is the holonomy algebra
is the holonomy algebra  introduced in 3.6.
introduced in 3.6.
12.7 Actions of \(\mathfrak {S}_{n}\) and \(\mathfrak {h}_{B}^{\oplus n}\)
The algebra \(\mathfrak {t}_{\Delta}^{\scriptscriptstyle {n}}\) is acted upon by \(\mathfrak {S}_{n} \ltimes \mathfrak {h}^{\oplus n}\). The action of \(\sigma \in \mathfrak {S}_{n}\) is defined by

The action of \(\mathfrak {h}^{\oplus n}\) is defined as follows. For any \(h\in \mathfrak {h}\), we set

and
Note that this is consistent with the relation (12.13). Moreover, the action of \(\mathfrak {h}^{\oplus n}\) on \(\mathfrak {t}_{\Delta}^{\scriptscriptstyle {n}}\) clearly factors through the essential Cartan \(({ \mathfrak {h}^{\scriptstyle {\operatorname {e}}}})^{\oplus n}\).
12.8 Cosimplicial structure on 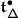
Set  . The tower of algebras \(\mathfrak {t}_{\Delta}^{\scriptscriptstyle {\bullet}}=\{\mathfrak {t}_{\Delta}^{\scriptscriptstyle {n}}\}\) is endowed with a natural cosimplicial structure. The face morphisms
. The tower of algebras \(\mathfrak {t}_{\Delta}^{\scriptscriptstyle {\bullet}}=\{\mathfrak {t}_{\Delta}^{\scriptscriptstyle {n}}\}\) is endowed with a natural cosimplicial structure. The face morphisms
are defined on  as in the case of
as in the case of  (see 12.5) and on \(\mathsf {K}_{\alpha}^{i}\) by
(see 12.5) and on \(\mathsf {K}_{\alpha}^{i}\) by
where \((\mathsf {K}_{\alpha}^{i})^{(2)}=\mathsf {r}^{i,i+1}_{\alpha}+\mathsf {r}^{i,i+1}_{-\alpha}+\mathsf {K}_{\alpha}^{i}+\mathsf {K}_{\alpha}^{i+1}\).
More generally, set
so that \((\mathsf {K}_{\alpha}^{1})^{(m)}=\mathsf {K}_{\alpha}^{(m)}\) and \((\mathsf {K}_{\alpha}^{k})^{(1)}=\mathsf {K}_{\alpha}^{k}\). Then, one has
Similarly, the degeneration morphisms \(\varepsilon^{n}_{k}:\mathfrak {t}_{\Delta}^{\scriptscriptstyle {n}}\to \mathfrak {t}_{\Delta}^{\scriptscriptstyle {n-1}}\), \(k=1,\dots, n\) are defined as in 12.5, together with the additional requirement that
12.9 Cosimplicial bidiagrammatic structures
For any \(B\subseteq \mathbb{D}\), we denote  by \(\mathfrak {t}_{B}^{\scriptscriptstyle {n}}\). The following result describes a bidiagrammatic structure on
by \(\mathfrak {t}_{B}^{\scriptscriptstyle {n}}\). The following result describes a bidiagrammatic structure on  and its relation with the diagrammatic and root refinements \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet, \mathbb{D}}}\), \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet,\Delta}}\) of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\) defined in 12.3 and 12.5.
and its relation with the diagrammatic and root refinements \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet, \mathbb{D}}}\), \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet,\Delta}}\) of \(\mathfrak {t}_{}^{\scriptscriptstyle {\bullet}}\) defined in 12.3 and 12.5.
Proposition 21
-
(1)
For any \(n\geq 2\), there is a morphism
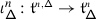 given by
given by 
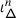 is \(\mathfrak {h}^{\oplus n}\)–equivariant, and gives rise to a morphism of cosimplicial algebras
is \(\mathfrak {h}^{\oplus n}\)–equivariant, and gives rise to a morphism of cosimplicial algebras  .
. -
(2)
For any \(B'\subseteq B\), there is an embedding \(i_{B'B}^{n}:\mathfrak {t}_{B'}^{\scriptscriptstyle {n}}\to \mathfrak {t}_{B}^{\scriptscriptstyle {n}}\), which maps every generator in \(\mathfrak {t}_{B'}^{\scriptscriptstyle {n}}\) to the same symbol in \(\mathfrak {t}_{B}^{\scriptscriptstyle {n}}\). Then,
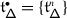 is a cosimplicial diagrammatic algebra.
is a cosimplicial diagrammatic algebra. -
(3)
For any \(n\geq 2\), there is a morphism
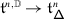 given by
given by 
give rise to a morphism of diagrammatic cosimplicial algebras \(\iota_{\mathbb{D}}\colon \mathfrak {t}_{}^{\scriptscriptstyle {\bullet, \mathbb{D}}}\to \mathfrak {t}_{\Delta}^{\scriptscriptstyle {\bullet}}\).
-
(4)
For any \(B'\subseteq B\subseteq \mathbb{D}\), let \(\mathfrak {t}_{BB'}^{\scriptscriptstyle {n}}\) be the subalgebra of \(\mathfrak {t}_{B'}\)–invariant elements in \(\mathfrak {t}_{B}^{\scriptscriptstyle {n}}\). Then,
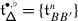 is a cosimplicial bidiagrammatic algebra, whose structure is obtained from
is a cosimplicial bidiagrammatic algebra, whose structure is obtained from  by restriction.
by restriction.
Proof
For (2) it is enough to observe that, if \(B'''\subseteq B''\subseteq B'\), clearly \(i_{B''B'}^{n}\circ i_{B'''B''}^{n}=i_{B'''B'}^{n}\). Moreover, if \(B',B''\subseteq B\) with \(B'\perp B''\), the multiplication induces an isomorphism of algebras \(j_{B_{1}B_{2}}:\mathfrak {t}_{B_{1}}^{\scriptscriptstyle {n}}\otimes \mathfrak {t}_{B_{2}}^{\scriptscriptstyle {n}}\to \mathfrak {t}_{B_{1}\sqcup B_{2}}^{\scriptscriptstyle {n}}\). (1) and (3) are clear. (4) follows as in Proposition 10.4. □
Remark 22
Combined with Propositions 12.4 and 12.5 and the fact that  , the result above yields the commutative diagram of holonomy algebras
, the result above yields the commutative diagram of holonomy algebras

12.10 Grading completions.
We denote by \(\widehat {\mathfrak {t}}_{B}^{\scriptscriptstyle {n}}\) the completion of \(\mathfrak {t}_{B}^{\scriptscriptstyle {n}}\) with respect to the grading  . Let \(\widehat {\mathfrak {t}}_{BB'}^{\scriptscriptstyle {n}}\) be the subalgebra of \(\mathfrak {t}_{B'}\)–invariant elements in \(\widehat {\mathfrak {t}}_{B}^{\scriptscriptstyle {n}}\). Note that, if \(B_{1}'\subseteq B_{1}\perp B_{2}\supseteq B_{2}'\), we get injective morphisms \(\widehat {\mathfrak {t}}_{B_{1}}^{\scriptscriptstyle {n}}\otimes \widehat {\mathfrak {t}}_{B_{2}}^{\scriptscriptstyle {n}}\to \widehat {\mathfrak {t}}_{B}^{\scriptscriptstyle {n}}\) and \(\widehat {\mathfrak {t}}_{B_{1}B_{1}'}^{\scriptscriptstyle {n}}\otimes \widehat {\mathfrak {t}}_{B_{2}B_{2}'}^{\scriptscriptstyle {n}}\to \widehat {\mathfrak {t}}_{BB'}^{\scriptscriptstyle {n}}\), where \(B= B_{1}\sqcup B_{2}\), \(B'= B'_{1}\sqcup B'_{2}\), and ⊗ denotes the completion of the tensor product with respect to the grading.
. Let \(\widehat {\mathfrak {t}}_{BB'}^{\scriptscriptstyle {n}}\) be the subalgebra of \(\mathfrak {t}_{B'}\)–invariant elements in \(\widehat {\mathfrak {t}}_{B}^{\scriptscriptstyle {n}}\). Note that, if \(B_{1}'\subseteq B_{1}\perp B_{2}\supseteq B_{2}'\), we get injective morphisms \(\widehat {\mathfrak {t}}_{B_{1}}^{\scriptscriptstyle {n}}\otimes \widehat {\mathfrak {t}}_{B_{2}}^{\scriptscriptstyle {n}}\to \widehat {\mathfrak {t}}_{B}^{\scriptscriptstyle {n}}\) and \(\widehat {\mathfrak {t}}_{B_{1}B_{1}'}^{\scriptscriptstyle {n}}\otimes \widehat {\mathfrak {t}}_{B_{2}B_{2}'}^{\scriptscriptstyle {n}}\to \widehat {\mathfrak {t}}_{BB'}^{\scriptscriptstyle {n}}\), where \(B= B_{1}\sqcup B_{2}\), \(B'= B'_{1}\sqcup B'_{2}\), and ⊗ denotes the completion of the tensor product with respect to the grading.
Corollary 3
-
(1)
For any \(n\geqslant 1\),
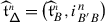 is a diagrammatic algebra. The face and degeneration morphisms of the cosimplicial structure on
is a diagrammatic algebra. The face and degeneration morphisms of the cosimplicial structure on 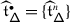 are morphisms of diagrammatic algebras. Thus,
are morphisms of diagrammatic algebras. Thus,  is a cosimplicial diagrammatic algebra.
is a cosimplicial diagrammatic algebra. -
(2)
 is a cosimplicial bidiagrammatic algebra, whose structure is obtained from
is a cosimplicial bidiagrammatic algebra, whose structure is obtained from 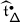 by restriction.
by restriction.
13 A braided Coxeter structure from double holonomy
We prove that the monodromy data of the KZ and Casimir connections, described in Sects. 9 and 12, are encoded by a braided Coxeter structure with relative twists arising from the monodromy of the dynamical KZ equations. The proof is a simple generalisation of [35] at the level of the double holonomy algebra, which in turn applies to the case of infinite–dimensional Kac–Moody algebras.
13.1 Monodromy of the KZ connection
We observed in Remark 12.1 that \(\mathfrak {t}_{}^{\scriptscriptstyle {3}}=\mathfrak {t}_{\mathsf {A}_{2}}\) and it is well–known that in this case the canonical solutions of the holonomy equation (3.9) are obtained by solving the \(\mathsf{KZ}_{3}\) equation
at \(u=0\) and \(u=1\). Therefore, let ℱ, \(\mathcal {G}\) be the only two elements of \(\mathsf {Mns}(\mathsf {A}_{2})\) with
and set \(\Phi ^{\nabla}=\Upsilon _{\mathcal {F}\mathcal {G}}\in \widehat {\mathfrak {t}}_{}^{\scriptscriptstyle {3}}\).
Definition 20
An invertible element \(\Phi \in \widehat {\mathfrak {t}}_{}^{\scriptscriptstyle {3}}\) is called a Lie associator if \(\Phi \) is the exponential of a formal Lie series in \(\mathsf {t}^{12}\) and \(\mathsf {t}^{23}\) and the following relations are satisfied.Footnote 21
-
Pentagon relation
$$ \Phi _{1,2,34}\Phi _{12,3,4}=\Phi _{2,3,4}\Phi _{1,23,4}\Phi _{1,2,3} $$ -
Hexagon relations
$$\begin{aligned} &e^{\mathsf {t}^{12,3}/2}=\Phi _{3,1,2}e^{\mathsf {t}^{13}/2}\Phi _{1,3,2}^{-1}e^{ \mathsf {t}^{23}/ 2}\Phi _{1,2,3} \\ &e^{\mathsf {t}^{1,23}/2}=\Phi _{2,3,1}^{-1}e^{\mathsf {t}^{13}/2}\Phi _{2,1,3}e^{ \mathsf {t}^{12}/ 2}\Phi _{1,2,3}^{-1} \end{aligned}$$ -
Duality
$$ \Phi _{3,2,1}=\Phi _{1,2,3}^{-1} $$ -
2–jet
$$ \Phi =1+\frac{1}{24}[\mathsf {t}^{12},\mathsf {t}^{23}]\qquad \mod(\; \widehat {\mathfrak {t}}_{}^{\scriptscriptstyle {3}})_{ \geqslant 3} $$
The following result is well–known and due to Drinfeld [11].
Theorem 11
The element \(\Phi ^{\nabla}\in \widehat {\mathfrak {t}}_{}^{\scriptscriptstyle {3}}\) is a Lie associator.
Remark 23
For any \(B\), set
The datum of \(\Phi ^{\nabla}_{B}\in \widehat {\mathfrak {t}}_{B}^{\scriptscriptstyle {3}}\) and \(R^{\nabla}_{B}\in \widehat {\mathfrak {t}}_{B}^{\scriptscriptstyle {2}}\) satisfies the properties of associators and \(R\)–matrices listed in Definition 11.1. Note, in particular, that since \(\Phi ^{\nabla}\) is a Lie associator, then the invariance and orthogonal factorisation property of \(\Phi ^{\nabla}_{B}\) follow, respectively, from (12.3) and (12.4).
13.2 A braided Coxeter structure on 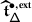
In analogy with 3.7 and 9.3, we extend the double holonomy algebra  with the parabolic braid groups \(\mathcal {B}_{W_{B}}\). This yields a cosimplicial bidiagrammatic algebra
with the parabolic braid groups \(\mathcal {B}_{W_{B}}\). This yields a cosimplicial bidiagrammatic algebra  where
where

\(B'\subseteq B\subseteq \mathbb{D}\), \(\mathfrak {h}'_{B}=\mathsf{span}\{h_{i}\;|\; i\in B\}\), \(W_{B}=\langle s_{i}\;|\; i\in B\rangle \subseteq W\), and the action of \(\mathcal {B}_{W_{B}}\) extends that on  . The goal of this section is to prove the following
. The goal of this section is to prove the following
Theorem 12
Let \((\Phi ^{\nabla}_{B}, R^{\nabla}_{B}, \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}, S_{i }^{\nabla})\) be the monodromy data of the KZ and Casimir connections defined in 12.3and 9.3, respectively. Then, the dynamical KZ equations give rise to a collection of relative twists \(J^{\nabla}_{\mathcal {F}}\in \widehat {\mathfrak {t}}_{B'B}^{\scriptscriptstyle {2}}\), \(\mathcal {F}\in \mathsf {Mns}(B,B')\) such that the datum of
defines an \(\mathsf {a}\)–strict braided Coxeter structure on the cosimplicial bidiagrammatic algebra  with respect to the standard labeling on \(\mathbb{D}\) (i.e., \(m_{ij}=\mathsf{ord}(s_{i}s_{j})\) in \(W\)).
with respect to the standard labeling on \(\mathbb{D}\) (i.e., \(m_{ij}=\mathsf{ord}(s_{i}s_{j})\) in \(W\)).
The proof closely follows [35, Sect. 3–7], and is outlined in this section. In 13.3–13.5, we introduce the notion of a differential twist with values in  . In 13.6–13.7, we show that a differential twist with the centraliser property induces a braided Coxeter structure on
. In 13.6–13.7, we show that a differential twist with the centraliser property induces a braided Coxeter structure on  compatible with the monodromy data of the KZ and Casimir connections. Finally, in 13.8–13.9, we show that such a differential twist can be obtained as a regularised holonomy of the dynamical KZ equations.
compatible with the monodromy data of the KZ and Casimir connections. Finally, in 13.8–13.9, we show that such a differential twist can be obtained as a regularised holonomy of the dynamical KZ equations.
13.3 Differential twist
Let \(\mathcal {C}_{\mathbb{R}}=\{h\in \mathfrak {h}^{\scriptstyle {\operatorname {e}}}_{\mathbb{R}}|\,\alpha _{i}(h)>0,\,\,\forall i\in \mathbf {I}\}\) be the fundamental chamber, and set \(\mathcal {C}=\mathcal {C}_{\mathbb{R}}+i\mathfrak {h}^{\scriptstyle {\operatorname {e}}}_{\mathbb{R}}\). Let  be the double holonomy algebra, and define
be the double holonomy algebra, and define  by
by

Definition 21
A differential twist is a holomorphic map  such that
such that
-
(1)
\(\varepsilon _{2}^{1}(F)=1=\varepsilon _{2}^{2}(F)\).
-
(2)
\((\Phi ^{\nabla}_{\mathbb{D}})_{F}=1\) in
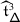 , where $$ (\Phi ^{\nabla}_{\mathbb{D}})_{F}={F}_{23}\cdot {F}_{1,23}\cdot \Phi\cdot {F}_{12,3}^{-1}\cdot {F}_{12}^{-1} $$
, where $$ (\Phi ^{\nabla}_{\mathbb{D}})_{F}={F}_{23}\cdot {F}_{1,23}\cdot \Phi\cdot {F}_{12,3}^{-1}\cdot {F}_{12}^{-1} $$ -
(3)
 , where
, where 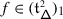 satisfies \(\operatorname {Alt}_{2} f=\widetilde {\mathsf {r}^{}_{}}\).
satisfies \(\operatorname {Alt}_{2} f=\widetilde {\mathsf {r}^{}_{}}\). -
(4)
F satisfies
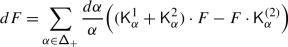
13.4 Compatibility with De Concini–Procesi associators
For any maximal nested set \(\mathcal {F}\in \mathsf {Mns}(\mathbb{D})\), let  be the fundamental solution of \(\nabla _{\mathcal {K}}\) corresponding to ℱ (cf. 8.4), and \(\Upsilon _{\mathcal {G}\mathcal {F}}^{\nabla}=\Psi _{\mathcal {G}}^{-1}\cdot \Psi _{\mathcal {F}}\) the corresponding associator. Let
be the fundamental solution of \(\nabla _{\mathcal {K}}\) corresponding to ℱ (cf. 8.4), and \(\Upsilon _{\mathcal {G}\mathcal {F}}^{\nabla}=\Psi _{\mathcal {G}}^{-1}\cdot \Psi _{\mathcal {F}}\) the corresponding associator. Let  be a differential twist, and set
be a differential twist, and set
The following is straightforward.
Lemma 5
-
(1)
\(\varepsilon _{2}^{1}(F_{\mathcal {F}})=1=\varepsilon _{2}^{2}(F_{\mathcal {F}})\)
-
(2)
\((\Phi ^{\nabla}_{\mathbb{D}})_{F_{\mathcal {F}}}=1\)
-
(3)
 , where
, where 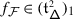 satisfies \(\operatorname {Alt}_{2} f_{\mathcal {F}}=\widetilde {\mathsf {r}^{}_{}}\).
satisfies \(\operatorname {Alt}_{2} f_{\mathcal {F}}=\widetilde {\mathsf {r}^{}_{}}\). -
(4)
\(F_{\mathcal {F}}\) is constant on \(\mathcal {C}\)
-
(5)
The following holds for any \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(\mathbb{D})\)
$$ F_{\mathcal {F}}=(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla})_{1}\cdot (\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla})_{2}\cdot F_{\mathcal {G}}\cdot (\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla})_{12}^{-1} $$
13.5 Relative differential twists
We recall the settings of Sect. 8.5. Fix \(i\in \mathbf {I}\), let  be the root subsystem generated by the simple roots \(\{\alpha _{j}\}_{j\neq i}\), \({\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\subset \mathfrak {h}^{\scriptstyle {\operatorname {e}}}\) and
be the root subsystem generated by the simple roots \(\{\alpha _{j}\}_{j\neq i}\), \({\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\subset \mathfrak {h}^{\scriptstyle {\operatorname {e}}}\) and  the corresponding essential Cartan and double holonomy subalgebras, respectively. Let \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\) be the projection determined by the requirement that \(\alpha (\pi (h))=\alpha (h)\) for any
the corresponding essential Cartan and double holonomy subalgebras, respectively. Let \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\) be the projection determined by the requirement that \(\alpha (\pi (h))=\alpha (h)\) for any  .
.
Let \(F\) be a differential twist and \(\Upsilon _{\infty}\) the solution of the Casimir equations given by Proposition 8.5.1 with respect to the simple root \(\alpha _{i}\), where we are using the standard determination of log. Define  by
by
Then, the following holds
-
(1)
\(\varepsilon _{2}^{1}(F_{\infty})=1=\varepsilon _{2}^{2}(F_{\infty})\)
-
(2)
\((\Phi ^{\nabla}_{\mathbb{D}})_{F_{\infty}}=1^{\otimes 3}\)
-
(3)
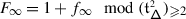 , where
, where 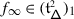 satisfies \(\operatorname {Alt}_{2} f_{\infty}=\overline {r}\).
satisfies \(\operatorname {Alt}_{2} f_{\infty}=\overline {r}\). -
(4)
\(F_{\infty}\) satisfies
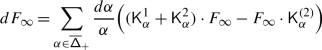
Let \(\overline {\mathcal {C}}\) be the complexified chamber of \({\overline {\mathfrak {g}}}\), and  a differential twist for
a differential twist for  . Since the projection \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\) maps \(\mathcal {C}\) to \(\overline {\mathcal {C}}\), we may regard \(\overline {F}\) as a function on \(\mathcal {C}\), and define
. Since the projection \(\pi :\mathfrak {h}^{\scriptstyle {\operatorname {e}}}\to {\overline {\mathfrak {h}}}^{\scriptstyle {\operatorname {e}}}\) maps \(\mathcal {C}\) to \(\overline {\mathcal {C}}\), we may regard \(\overline {F}\) as a function on \(\mathcal {C}\), and define  by
by
Proposition 22
Set \(\overline {\mathbb{D}}=\mathbb{D}\setminus \{i\}\). The following holds
-
(1)
\(\varepsilon _{2}^{1}(F'_{(\mathbb{D};\alpha _{i})})=1=\varepsilon _{2}^{2}(F'_{( \mathbb{D};\alpha _{i})})\)
-
(2)
\((\Phi ^{\nabla}_{\mathbb{D}})_{F'_{(\mathbb{D};\alpha _{i})}}=\Phi ^{\nabla}_{ \overline {\mathbb{D}}}\)
-
(3)
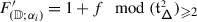 , where
, where 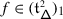 satisfies \(\operatorname {Alt}_{2} f=\widetilde {r}_{\mathbb{D}}-\widetilde {r}_{ \overline {\mathbb{D}}}\).
satisfies \(\operatorname {Alt}_{2} f=\widetilde {r}_{\mathbb{D}}-\widetilde {r}_{ \overline {\mathbb{D}}}\). -
(4)
\(F'_{(\mathbb{D};\alpha _{i})}\) satisfies
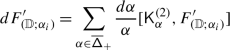
In particular, if \(F'_{(\mathbb{D};\alpha _{i})}\) is invariant under
 , then it is constant on \(\mathcal {C}\).
, then it is constant on \(\mathcal {C}\).
13.6 Centraliser property
Let \(\{F_{B}:\mathcal {C}_{B}\to \widehat {\mathfrak {t}}_{B}^{\scriptscriptstyle {2}}\}_{B\subseteq \mathbb{D}}\) be a factorisable collection of differential twists, i.e., such that \(F_{B}=\prod _{i} F_{B_{i}}\) if \(B\) has connected components \(\{B_{i}\}\).
Definition 22
The collection \(\{F_{B}\}\) has the centraliser property if, for any \(i \in B\subseteq \mathbb{D}\), the relative twist \(F'_{(B,\alpha _{i})}\) defined by (13.2) is invariant under \(\mathfrak {t}_{B\setminus \{i\}}\) and therefore constant.
Assume the centraliser property holds, let \(i\in B\subseteq \mathbb{D}\), and set
where \(\{x_{B}\}_{B\subseteq D}\) are the blow-up coordinates defined in 8.3. The (constant) twist \(F_{(B;\alpha _{i})}\) is invariant under \(\mathfrak {t}_{B\setminus \{i\}}\), and has the properties (1)–(3) given in Proposition 13.5. Moreover,

where  satisfies \(\operatorname {Alt}_{2} f=\widetilde {r}_{B}-\widetilde {r}_{B\setminus \alpha _{i}}\). The following is a direct consequence of Proposition 8.5.2.
satisfies \(\operatorname {Alt}_{2} f=\widetilde {r}_{B}-\widetilde {r}_{B\setminus \alpha _{i}}\). The following is a direct consequence of Proposition 8.5.2.
Lemma 6
Let ℱ be a maximal nested set on \(\mathbb{D}\), and \(F_{\mathcal {F}}\) the twist defined in (13.1). Then, the following holds
where the product is taken with \(F_{(B;\alpha _{\mathcal {F},B})}\) to the right of \(F_{(C;\alpha _{\mathcal {F},C})}\) if \(B\supset C\).Footnote 22
13.7 Braided Coxeter structure
The relative twists arising from a suitable collection of differential twists give rise to a braided Coxeter structure encoding the monodromy data of the KZ and Casimir connections. Specifically, we have the following
Proposition 23
Let \(\mathbf{F}=\{F_{B}:\mathcal {C}_{B}\to \widehat {\mathfrak {t}}_{B}^{\scriptscriptstyle {2}}\}\) be a factorisable collection of differential twists satisfying the centraliser property.
-
(1)
The elements \(\{F_{(B;\alpha _{i})}\}\) defined in (13.3) give rise to an \(\mathsf {a}^{}_{}\)–strict braided pre–Coxeter structure \((\Phi ^{\nabla}_{B}, R^{\nabla}_{B}, J^{\mathbf{F}}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla})\) on
 with relative twists $$ J^{\mathbf{F}}_{\mathcal {F}}= \stackrel{\longleftarrow}{\prod _{B\in \mathcal {F}}}F_{(B; \alpha _{\mathcal {F},B})}^{-1} $$
with relative twists $$ J^{\mathbf{F}}_{\mathcal {F}}= \stackrel{\longleftarrow}{\prod _{B\in \mathcal {F}}}F_{(B; \alpha _{\mathcal {F},B})}^{-1} $$where \(B'\subseteq B\) and \(\mathcal {F}\in \mathsf {Mns}(B,B')\).
-
(2)
Assume that, for any \(i\in \mathbf {I}\), the elementary differential twist \(F_{i}\) satisfies \(\mathsf {Ad}( \widetilde {s}_{i})(F_{i})=F_{i,21}\). Then, \(\mathbf {C}_{\mathbf{F}}=(\Phi ^{\nabla}_{B}, R^{\nabla}_{B}, J^{ \mathbf{F}}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}, S_{i }^{\nabla})\) is an \(\mathsf {a}^{}_{}\)–strict braided Coxeter structure on
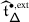 .
.
Proof
(1) is a direct consequence of 13.3, Proposition 13.5, and Lemma 13.6. (2) amounts to prove the coproduct identity (11.1). Namely, recall that \(S_{i }^{\nabla}= \widetilde {s}_{i}\exp (\pi \iota \mathsf{C}_{i})\) with \(\mathsf{C}_{i}=\mathsf {t}_{\alpha _{i}}^{+}t_{i}+\mathsf {d}_{i}^{-1}t_{i}^{2}/2\). Since

and \(\mathsf{C}_{i,1}\mathsf{C}_{i,2}\) is central in \(\widehat {\mathfrak {t}}_{i}^{\scriptscriptstyle {2}}\), the coproduct identity for \(\mathbf {C}_{\mathbf{F}}\) reduces to the condition \(\mathsf {Ad}( \widetilde {s}_{i})(J^{\mathbf{F}}_{i})=J^{\mathbf{F}}_{i,21}\), which then follows from the assumption on \(F_{i}\). □
13.8 The dynamical KZ equation
The dynamical KZ equation is the connection on the trivial bundle over \(\mathbb{C}^{\times}\) with fiber  given by
given by

It has a regular singularity at \(z=0\), and an irregular singularity at \(z=\infty \). We shall exploit these singularities to produce a collection of differential twists satisfying the assumptions of Theorem 13.7.
13.8.1 Canonical fundamental solution at \(z=0\)
Proposition 24
[35]
-
(1)
For any \(\mu \in \mathfrak {h}\), there is a unique holomorphic function
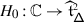 such that \(H_{0}(0,\mu )\equiv 1\) and, for any determination of \(\log (z)\), the \(\mathsf{End}\left (\widehat{\mathfrak{t}}_{{\Delta }}^{ \scriptscriptstyle{2}}\right )\)–valued function
such that \(H_{0}(0,\mu )\equiv 1\) and, for any determination of \(\log (z)\), the \(\mathsf{End}\left (\widehat{\mathfrak{t}}_{{\Delta }}^{ \scriptscriptstyle{2}}\right )\)–valued function 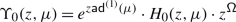
is a fundamental solution of the dynamical KZ equations.
-
(2)
\(H_{0}\) and \(\Upsilon _{0}\) are holomorphic functions of \(\mu \in \mathfrak {h}\), and \(\Upsilon _{0}\) satisfies
$$ d_{\mathfrak {h}}\Upsilon _{0}= \sum _{\alpha \in \Phi _{+}} \frac{d\alpha}{\alpha} \left [\mathsf {K}_{\alpha}^{(2)},\Upsilon _{0}\right ] +z \mathsf {ad}^{(1)}(d\mu) \Upsilon _{0} $$
13.8.2 Canonical fundamental solutions at \(z=\infty \)
Let \(\mathbb{H}_{\pm}=\{z\in \mathbb{C}|\,\operatorname {Im}(z)\gtrless 0\}\).
Theorem 13
[35]
-
(1)
For any \(\mu \in \mathcal {C}\), there is a unique holomorphic function
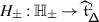 such that \(H_{\pm}(z)\) tends to 1 as $$ z\to \infty \quad \textit{with}\quad |\arg (z)|\in (\delta ,\pi -\delta ) $$
such that \(H_{\pm}(z)\) tends to 1 as $$ z\to \infty \quad \textit{with}\quad |\arg (z)|\in (\delta ,\pi -\delta ) $$\(\delta >0\), and, for any determination of \(\log (z)\), the \(\mathsf{End}\left (\widehat{\mathfrak{t}}_{{\Delta }}^{ \scriptscriptstyle{2}}\right )\)–valued function
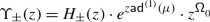
is a fundamental solution of the dynamical KZ equations.
-
(2)
\(H_{\pm}\) and \(\Upsilon _{\pm}\) are smooth functions of \(\mu \in \mathcal {C}\), and \(\Upsilon _{\pm}\) satisfies
$$ d_{\mathfrak {h}}\Upsilon _{\pm}= \sum _{\alpha \in \Phi _{+}} \frac{d\alpha}{\alpha} \left (\mathsf {K}_{\alpha}^{(2)}\Upsilon _{\pm }- \Upsilon _{\pm }(\mathsf {K}_{\alpha }^{1}+\mathsf {K}_{\alpha }^{2})\right ) +z \mathsf {ad}^{(1)}(d\mu)\Upsilon _{\pm} $$
13.9 Differential twist from the dynamical KZ equation
Fix henceforth the standard determination of \(\log z\) with a cut along the negative real axis, and let \(\Upsilon _{0}\), \(\Upsilon _{\pm}\) be the corresponding fundamental solutions of the dynamical KZ equations given in 13.8.1 and 13.8.2 respectively.
Let  be the smooth function defined by
be the smooth function defined by
where \(z\in \mathbb{C}\setminus \mathbb{R}_{\leq 0}\). \(F_{\pm}\) is a regularised holonomy of the dynamical KZ equations from \(z=0\) to \(z=\pm \iota \infty \). The form of \(\Upsilon _{0}\), \(\Upsilon _{\pm}(z)\) shows that
so that \(F_{\pm}\) acts by left multiplication. We henceforth identify \(F_{\pm}\) and \(F_{\pm}(1)\), and consider the former as taking values in  .
.
Theorem 14
[35]
\(F_{\pm}\) is a differential twist with values in  , which satisfies the centraliser property and the assumption of Proposition 13.7(2).
, which satisfies the centraliser property and the assumption of Proposition 13.7(2).
Part III. Braided Coxeter categories
14 Braided Coxeter categories
In this section, we briefly review the definition of a braided Coxeter category introduced in [2]. Roughly, this is a monoidal category carrying commuting actions of a generalised braid group \(\mathcal {B}_{\mathbb{D}}^{\underline {m}}\) and Artin’s braid groups \(\mathcal {B}_{n}\) on the tensor powers of its objects. Under the Tannakian formalism, a braided Coxeter category is the categorical counterpart of a braided Coxeter algebra.
14.1 Braided Coxeter categories
Let \(\mathbb{D}\) be a diagram with a labelling \(\underline {m}\). A braided Coxeter category of type \((\mathbb{D},\underline {m})\) is a tuple \(\mathscr{C}_{}=(\mathcal {C}_{B}, F_{\mathcal {F}}, \Upsilon _{\mathcal {G}\mathcal {F}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}, S_{i }^{})\) consisting of the following data.
-
Diagrammatic categories. For any subdiagram \(B\subseteq \mathbb{D}\), a braided monoidal category \(\mathcal {C}_{B}\).
-
Restriction functors. For any pair of subdiagrams \(B'\subseteq B\) and relative maximal nested set \(\mathcal {F}\in \mathsf {Mns}(B,B')\), a tensor functor \(F_{\mathcal {F}}:\mathcal {C}_{B}\to \mathcal {C}_{B'}\) (\(F_{\mathcal {F}}\) is not assumed to be braided).
-
Generalised associators. For any pair of subdiagrams \(B'\subseteq B\) and relative maximal nested sets \(\mathcal {F},G\in \mathsf {Mns}(B,B')\), an isomorphism of tensor functors \(\Upsilon _{\mathcal {G}\mathcal {F}}:F_{\mathcal {F}}\Rightarrow F_{\mathcal {G}}\).
-
Vertical joins. For any chain of inclusions \(B''\subseteq B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B,B')\), and \(\mathcal {F}'\in \mathsf {Mns}(B',B'')\), an isomorphism of tensor functors \(\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}: F_{\mathcal {F}'}\circ F_{\mathcal {F}} \Rightarrow F_{\mathcal {F}'\cup \mathcal {F}}\).
-
Local monodromies. For any vertex \(i\) of \(\mathbb{D}\) with corresponding restriction functor \(F_{\{i\}}:\mathcal {C}_{i}\to \mathcal {C}_{\emptyset}\), a distinguished automorphism \(S_{i }^{}\in \mathsf {Aut}(F_{\{i\}})\) (\(S_{i }^{}\) is not assumed to be a monoidal automorphism).
These data are assumed to satisfy the following properties.
-
Normalisation. If \(\mathcal {F}=\{B\}\) is the unique element in \(\mathsf {Mns}(B,B)\), then \(F_{\mathcal {F}}=\operatorname{id}_{\mathcal {C}_{\mathcal {F}}}\) with the trivial tensor structure.
-
Transitivity. For any \(B'\subseteq B\) and \(\mathcal {F},\mathcal {G}, \mathcal {H}\in \mathsf {Mns}(B,B')\), \(\Upsilon _{\mathcal {H}\mathcal {F}}=\Upsilon _{\mathcal {H}\mathcal {G}}\circ \Upsilon _{\mathcal {G}\mathcal {F}}\) as isomorphisms \(F_{\mathcal {F}}\Rightarrow F_{\mathcal {H}}\). In particular, \(\Upsilon _{\mathcal {F}\mathcal {F}} =\operatorname{id}_{F_{\mathcal {F}}}\) and \(\Upsilon _{\mathcal {G}\mathcal {F}}=\Upsilon _{\mathcal {F}\mathcal {G}}^{-1}\).
-
Associativity. For any \(B'''\subseteq B''\subseteq B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B,B')\), \(\mathcal {F}'\in \mathsf {Mns}(B',B'')\), and \(\mathcal {F}''\in \mathsf {Mns}(B'',B''')\),
$$ \mathsf {a}^{\mathcal {F}'\cup \mathcal {F}}_{\mathcal {F}''}\cdot \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}= \mathsf {a}^{\mathcal {F}}_{\mathcal {F}''\cup \mathcal {F}'}\cdot \mathsf {a}^{\mathcal {F}'}_{\mathcal {F}''} $$as isomorphisms \(F_{\mathcal {F}''}\circ F_{\mathcal {F}'}\circ F_{\mathcal {F}}\Rightarrow F_{\mathcal {F}''\cup \mathcal {F}' \cup \mathcal {F}}\).
-
Vertical factorisation. For any \(B''\subseteq B'\subseteq B\), \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\) and \(\mathcal {F}',\mathcal {G}'\in \mathsf {Mns}(B',B'')\),
$$ \Upsilon _{(\mathcal {G}'\cup \mathcal {G})(\mathcal {F}'\cup \mathcal {F})}\circ \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}= \mathsf {a}^{\mathcal {G}}_{\mathcal {G}'} \circ \left ( \textstyle\begin{array}{l} \Upsilon _{\mathcal {G}\mathcal {F}} \\ \phantom{00}\circ \\ \Upsilon _{\mathcal {G}'\mathcal {F}'}\end{array}\displaystyle \right ) $$as isomorphisms \(F_{\mathcal {F}'}\circ F_{\mathcal {F}}\Rightarrow F_{\mathcal {G}'}\circ F_{\mathcal {G}}\).
-
Generalised braid relations. For any \(B\subseteq \mathbb{D}\), \(i\neq j\in B\) and maximal nested sets \(\mathcal {K}[i]\), \(\mathcal {K}[j]\) on \(B\) such that \(\{i\}\in \mathcal {K}[i]\), \(\{j\}\in \mathcal {K}[j]\), the following holds in \(\mathsf {Aut}(F_{ \mathcal {K}[i]})\)
$$ \underbrace{\mathsf{Ad}\left (\Upsilon _{ij}\right )(S_{j }^{\mathsf {a}})\cdot S_{i }^{\mathsf {a}} \cdot \mathsf{Ad}\left (\Upsilon _{ij}\right )(S_{j }^{\mathsf {a}})\cdots}_{m_{ij}}= \underbrace{S_{i }^{\mathsf {a}}\cdot \mathsf{Ad} \left (\Upsilon _{ij}\right )(S_{j }^{\mathsf {a}})\cdot S_{i }^{\mathsf {a}}\cdots}_{m_{ij}} $$where \(\Upsilon _{ij}=\Upsilon _{ \mathcal {K}[i] \mathcal {K}[j]}\) and \(S_{i }^{\mathsf {a}}=\mathsf {Ad}(\mathsf {a}^{{ \mathcal {K}[i]}^{}_{i}}_{{ \mathcal {K}[i]}^{i}_{}})( S_{i }^{})\in \mathsf {Aut}(F_{ \mathcal {K}[i]})\).Footnote 23
-
Coproduct identity. For any \(i\in D\), the following holds in \(\mathsf {Aut}\left (F_{\{i\}}\otimes F_{\{i\}}\right )\)
$$ J_{i}^{-1}\circ F_{\{i\}}(c_{i})\circ \Delta (S_{i }^{})\circ J_{i}= c_{ \emptyset}\circ S_{i }^{}\otimes S_{i }^{} $$(14.1)where \(J_{i}\) is the tensor structure on \(F_{\{i\}}\) and \(c_{i}\), \(c_{\emptyset}\) are the opposite braidings in \(\mathcal {C}_{i}\) and \(\mathcal {C}_{\emptyset}\), respectively.Footnote 24 Specifically, the following diagram is commutative for any \(V,W\in \mathcal {C}_{i}\)

Remark 24
The identity (14.1) relates the failure of \((F_{i},J_{i})\) to be a braided monoidal functor and that of \(S_{i}\) to be a monoidal isomorphism. That is, if (14.1) holds, \(S_{i}\) is monoidal if and only if \(J_{i}\) is braided. Conversely, if \(S_{i}\) is monoidal and \(J_{i}\) is braided, then (14.1) automatically holds.
14.2 Morphisms
Let \(\mathscr{C}_{}\), \(\mathscr{C}_{}'\) be two braided Coxeter categories of type \((\mathbb{D},\underline {m})\). A 1–morphism \(\mathbf {H}_{}:\mathscr{C}_{}\to \mathscr{C}_{}'\) consists of the following data.
-
Horizontal functors. For any \(B\subseteq \mathbb{D}\), a braided tensor functor \(H_{B}: \mathcal {C}_{B}\to \mathcal {C}'_{B}\).
-
Diagonal isomorphisms. For any \(B'\subseteq B\subseteq \mathbb{D}\) and \(\mathcal {F}\in \mathsf {Mns}(B,B')\), an isomorphism of tensor functors
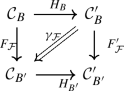
such that \(\Upsilon _{\mathcal {G}\mathcal {F}}^{} \circ \gamma _{\mathcal {F}}=\gamma _{\mathcal {G}}\circ ( \Upsilon _{\mathcal {G}\mathcal {F}}^{})'\) as isomorphisms \(F'_{\mathcal {F}}\circ H_{B}\Rightarrow H_{B'}\circ F_{\mathcal {G}}\).
These data are assumed to satisfy the following properties.
-
Normalisation. If \(\mathcal {F}=\{B\}\) is the unique element in \(\mathsf {Mns}(B,B)\), so that \(F_{\mathcal {F}}=\operatorname{id}_{\mathcal {C}_{B}}\) and \(F'_{\mathcal {F}}=\operatorname{id}_{\mathcal {C}'_{B}}\), then \(\gamma _{\mathcal {F}}=\operatorname{id}_{H_{B}}\).
-
Vertical factorisation. For any \(B''\subseteq B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B,B')\) and \(\mathcal {F}'\in \mathsf {Mns}(B', B'')\), the following equality holds
$$ \gamma _{\mathcal {F}'\cup \mathcal {F}}\circ (\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})'= \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'} \circ \left ( \textstyle\begin{array}{l} \gamma _{\mathcal {F}} \\ \phantom{0}\circ \\ \gamma _{\mathcal {F}'}\end{array}\displaystyle \right ) $$as isomorphisms \(F'_{\mathcal {F}'}\circ F'_{\mathcal {F}}\circ H_{B} \Rightarrow H_{B''}\circ F_{\mathcal {F}'} \circ F_{\mathcal {F}}\).
-
Generalised braid group invariance. The generalised braid group operator are preserved, i.e., for any \(i\in D\), \(S_{i }^{}\circ \gamma _{\emptyset i}=\gamma _{\emptyset i}\circ S_{i}'\) as isomorphisms \(F'_{i}\circ H_{i}\Rightarrow H_{\emptyset}\circ F_{i}\).
Finally, let \(\mathbf {H}_{}^{1}\), \(\mathbf {H}_{}^{2}\) be two 1–morphisms \(\mathscr{C}_{}\to \mathscr{C}_{}'\). A 2–morphism \(\mathbf {v}_{}: \mathbf {H}_{}^{1}\Rightarrow \mathbf {H}_{}^{2}\) is the datum, for any \(B\subseteq \mathbb{D}\), of a natural transformation of braided tensor functors \(v_{B}:H^{1}_{B}\Rightarrow H^{2}_{B}\) such that, for any \(B'\subseteq B\) and \(\mathcal {F}\in \mathsf {Mns}(B,B')\), \(\gamma _{\mathcal {F}}\circ v_{B}=v_{B'}\circ \gamma _{\mathcal {F}}\) as morphisms \(F'_{\mathcal {F}}\circ H^{1}_{B}\Rightarrow H^{2}_{B'}\circ F_{\mathcal {F}}\).
14.3 Coxeter algebras and Coxeter categories
The notion of braided Coxeter category is tailored to describe the category of representations of a braided Coxeter algebra. In particular, let \(\mathscr{A}_{}\) be a diagrammatic bialgebra and \(\mathscr{A}_{}^{\otimes \bullet , \flat}\) the corresponding cosimplicial bidiagrammatic algebra (cf. Proposition 10.4). We have the following
Proposition 25
-
(1)
Let \(\mathbf {C}_{}=(\Phi _{B},R_{B}, J^{}_{\mathcal {F}},\Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}, S_{i})\) be a braided Coxeter structure on \(\mathscr{A}_{}^{\otimes \bullet , \flat}\) (cf. Definition 11.1). Then, \(\mathbf {C}_{}\) gives rise to a braided Coxeter category \(\operatorname{Rep}_{\mathbf {C}_{}}(\mathscr{A}_{})\) given by the following data
-
for any \(B\subseteq \mathbb{D}\), the braided monoidal category \(\operatorname{Rep}({A}^{}_{B})\) with associativity and commutativity constraints given, respectively, by the action of \(\Phi _{B}\in {A}^{\otimes 3, B}_{B}\) and \(R_{B}\in {A}^{\otimes 2, B}_{B}\)
-
for any \(B'\subseteq B\) and \(\mathcal {F}\in \mathsf {Mns}(B,B')\), the tensor restriction functor \(\operatorname{Res}_{\mathcal {F}}: \operatorname{Rep}({A}^{}_{B})\to \operatorname{Rep}({A}^{}_{B'})\), with tensor structure given by the action of \(J^{}_{\mathcal {F}}\in {A}^{\otimes 2, B'}_{B}\)
-
for any \(B'\subseteq B\) and \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\), the natural isomorphism of tensor functors \(\operatorname{Res}_{\mathcal {G}}\Rightarrow \operatorname{Res}_{\mathcal {F}}\) given by the action of \(\Upsilon _{\mathcal {F}\mathcal {G}}\in A_{B}^{B'}\)
-
for any chain of inclusions \(B''\subseteq B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B,B')\), and \(\mathcal {F}'\in \mathsf {Mns}(B',B'')\), an isomorphism of tensor functors \(\operatorname{Res}_{\mathcal {F}'}\circ \operatorname{Res}_{\mathcal {F}} \Rightarrow \operatorname{Res}_{\mathcal {F}'\cup \mathcal {F}}\) given by the action of \(\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}\in A_{B}^{B''}\)
-
for any vertex \(i\) of \(\mathbb{D}\), the invertible operator in \(\mathsf {Aut}(F_{\{i\}})\) given by the action of \(S_{i}\in A_{i}\).
-
-
(2)
Let \({T}_{}=(u_{\mathcal {F}},K_{B})\) be a twist in \(\mathscr{A}_{}\) (cf. Definition 11.3). There is a canonical 1–isomorphism of braided Coxeter categories \(\mathbf {H}_{{T}_{}}:\operatorname{Rep}_{\mathbf {C}_{}}(\mathscr{A}_{}) \to \operatorname{Rep}_{\mathbf {C}_{{T}_{}}}( \mathscr{A}_{})\) given by the tensor equivalences \(H_{{T}_{},B}=(\operatorname{id}_{B},K_{B}): \operatorname{Rep}_{\mathbf {C}_{}}(A_{B}) \to \operatorname{Rep}_{ \mathbf {C}_{{T}_{}}}(A_{B})\), with tensor structure given by the action of \(K_{B}\in A_{B}^{\otimes 2,B}\), and the tensor isomorphisms \(\gamma _{{T}_{},\mathcal {F}}:H_{{T}_{},B'}\circ \operatorname{Res}_{\mathbf {C}_{}, \mathcal {F}} \Rightarrow \operatorname{Res}_{\mathbf {C}_{{T}_{}},\mathcal {F}}\circ H_{{T}_{},B}\), given by the action of \(u_{\mathcal {F}}\in A_{B}^{B'}\).
-
(3)
Let \(a=\{a_{B}\}\) be a gauge in \(\mathscr{A}_{}\). There is a canonical 2–isomorphism \(\mathbf {v}_{a}: \mathbf {H}_{{T}_{}}\Rightarrow \mathbf {H}_{{T}_{{{a}}_{}}}\) with natural braided tensor isomorphism \(v_{a,B}: H_{{T}_{},B}\Rightarrow H_{{T}_{{{a}}_{}}, B}\) given by the action of \(a_{B}\in A_{B}^{B}\).
14.4 Braid group representations
The following is a categorical analogue of Propositions 11.2 and 11.3.
Proposition 26
Let \(\mathscr{C}_{}=(\mathcal {C}_{B}, F_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}, S_{ i}^{})\) be a braided Coxeter category. Then, there is a family of representations
labelled by \(B\subseteq \mathbb{D}\), \(\mathcal {F}\in \mathsf {Mns}(B)\), and \(b\in \mathsf {br}_{n}\), which is uniquely determined by the conditions
-
\(\lambda ^{\mathscr{C}_{}}_{\mathcal {F}, b}(\mathscr{S}_{i})= \mathsf {Ad}(\mathsf {a}^{{ \mathcal {F}}^{}_{i}}_{{ \mathcal {F}}^{i}_{}}) (S_{i }^{})_{1 \dots n}\) if \(\{i\}\in \mathcal {F}\) and \(\lambda ^{\mathscr{C}_{}}_{\mathcal {G}, b}=\mathsf {Ad}(\Upsilon _{\mathcal {G}\mathcal {F}})_{1\dots n}\circ \lambda ^{\mathscr{C}_{}}_{\mathcal {F}, b}\).
-
\(\lambda ^{\mathscr{C}_{}}_{\mathcal {F}, b}(\mathtt {\rho }_{i})=(i\ i+1)\circ (R_{B})_{i,i+1}\) if \(b= x_{1}\cdots (x_{i}x_{i+1})\cdots x_{n}\) and \(\lambda ^{\mathscr{C}_{}}_{\mathcal {F}, b'}= \mathsf {Ad}(\Phi _{B, b'b})\circ \lambda ^{ \mathscr{C}_{}}_{\mathcal {F}, b}\).
Let \(\mathbf {H}_{}:\mathscr{C}_{}\to \mathscr{C}_{}'\) be a 1–isomorphism of braided Coxeter categories. Then, the representations \(\lambda ^{\mathscr{C}_{}}_{\mathcal {F}, b}\) and \(\lambda ^{\mathscr{C}_{}'}_{\mathcal {F}, b}\) are equivalent through the natural isomorphism \(\gamma _{\mathcal {F}}: F'_{\mathcal {F}}\circ H_{B}\Rightarrow F_{\mathcal {F}}\).
15 Braided Coxeter structures on Kac–Moody algebras
In this section, we describe the standard symmetric Coxeter category associated to a diagrammatic symmetrisable Kac–Moody algebra, and its deformations.
15.1 Category \(\mathcal {O}_{\infty }\) representations
Let \(\mathfrak {g}\) be a diagrammatic symmetrisable Kac–Moody algebra (cf. 2.4). If \(V\) is an \(\mathfrak {h}\)–module and \(\lambda \in \mathfrak {h}^{*}\), we denote the corresponding weight space of \(V\) by
and set \(P(V)=\{\lambda \in \mathfrak {h}^{*}|\,V{[\lambda ]}\neq 0\}\). Recall that a \(\mathfrak {g}\)–module \(V\) is
-
(C1)
a weight module if \(V=\bigoplus _{\lambda \in \mathfrak {h}^{*}} V{[\lambda ]}\).
-
(C2)
integrable if it is a weight module, and the elements \(\{e_{i}, f_{i}\}_{i\in \mathbf {I}}\) act locally nilpotently.
This implies that \(\lambda (h_{i})\in \mathbb{Z}\) for any \(\lambda \in P(V)\) and \(i\in \mathbf {I}\), and that \(V\) is completely reducible as a (possibly infinite) direct sum of simple finite–dimensional modules over \(\mathfrak {sl}_{2}^{\alpha _{i}}=\langle e_{i}, h_{i},f_{i}\rangle \subset \mathfrak {g}\).
-
(C3)
in category \(\mathcal {O}_{\infty ,\mathfrak {g}}\) if the action of \(\mathfrak {b}^{+}_{}\) is locally finite, i.e., any \(v\in V\) is contained in a finite–dimensional \(\mathfrak {b}^{+}_{}\)–submodule of \(V\). This is equivalent to \(V\) being the direct sum of its generalised weight spaces, together with
- (C3′):
-
for any \(v\in \mathcal {V}\), \((U \mathfrak {n}^{+}_{})_{\beta}v=0\) for all but finitely many \(\beta \in \mathsf {Q}_{+}\).
-
(C4)
in category \(\mathcal {O}_{\mathfrak {g}}\) if it is a weight module with finite–dimensional weight spaces, such that
$$ P(V)\subseteq D(\lambda _{1})\cup \cdots \cup D(\lambda _{m}) $$(15.1)for some \(\lambda _{1},\ldots ,\lambda _{m}\in \mathfrak {h}^{*}\), where \(D(\lambda )=\{\mu \in \mathfrak {h}^{*}\;|\;\mu \leqslant \lambda \}\) and \(\mu \leqslant \lambda \) iff \(\lambda -\mu \in \mathsf {Q}_{+}=\bigoplus _{i\in \mathbf {I}}\mathbb{N}\alpha _{i}\).
The categories \(\mathcal {O}_{\mathfrak {g}}\subset \mathcal {O}_{\infty ,\mathfrak {g}}\) are symmetric tensor categories. Let \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\mathfrak {g}}\subset \mathcal {O}_{\mathfrak {g}}\) and \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty ,\mathfrak {g}}\subset \mathcal {O}_{\infty ,\mathfrak {g}}\) be the full tensor subcategories of integrable representations. We have the following inclusions

Remarks 4
-
(1)
Category \(\mathcal {O}\) does not fit naturally within the framework of Coxeter categories, since condition (C4) is not stable under restriction to a diagrammatic Lie subalgebra \(\mathfrak {g}_{B}\). It is therefore convenient to consider instead the categories \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B}}\), \(B\subseteq \mathbb{D}\), with restriction functors \(\operatorname{Res}_{B'B}:\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B}}\to \mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B}'}\), \(B'\subseteq B\).
-
(2)
As pointed out in [2, Sect. 13.9], the lack of diagrammatic restriction functors at the level of categories \(\mathcal {O}\) can also be overcome by replacing the Lie subalgebras \(\mathfrak {g}_{B}\) with the Levi subalgebras \(\mathfrak{l}_{B}=\mathfrak {g}_{B}+\mathfrak {h}\). These, however, do not induce a diagrammatic structure on \(U\mathfrak {g}\) since \(\mathfrak{l}_{B'}\) and \(\mathfrak{l}_{B''}\) do not commute if \(B'\perp B''\), and require a further modification of the framework.
15.2 The symmetric Coxeter category \(\mathscr{O}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\)
Let \(W\) be the Weyl group of \(\mathfrak {g}\) with set of simple reflections \(\{s_{i}\}_{i\in \mathbf {I}}\subset W\). Set \(\underline {m}=(m_{ij})\), where \(m_{ij}\) is the order of \(s_{i}s_{j}\) in \(W\). Let
be the algebra of endomorphism of the forgetful functor. Then, it is well–known that \(U\mathfrak {g}\subset \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {int}},1}}\), i.e., the objects in \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty ,\mathfrak {g}}\) separate points in \(U\mathfrak {g}\), and \(\widetilde {s}_{i}\in (\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {int}},1}})^{\times}\) where \(\widetilde {s}_{i}=\exp (e_{i})\cdot \exp (-f_{i})\cdot \exp (e_{i})\). Since the triple exponential operators satisfy the generalised braid relations (7.1), we obtain a homomorphism \(\mathcal {B}_{W}\to \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {int}},1}}\) given by \(\mathscr{S}_{i}\mapsto \widetilde {s}_{i}\) (cf. Remarks 3.4 and 7.1). The following is straightforward.
Proposition 27
There is a canonical \((\mathsf {a}^{}_{},\Upsilon _{})\)–strict symmetric Coxeter category \(\mathscr{O}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) of type \((\mathbb{D},\underline {m})\) given by the following data.
-
For any \(B\subseteq \mathbb{D}\), the symmetric monoidal category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B}}\).
-
For any \(B'\subseteq B\), the restriction functor \(\operatorname{Res}_{B'B}:\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B}}\to \mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B'}}\) with the trivial tensor structure.
-
For any \(i\in \mathbb{D}\), the operator \(S_{i }^{\mathscr{O}_{}^{\scriptscriptstyle {}}}= \widetilde {s}_{i}\in (\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {int}},1}})^{\times}\).
Proof
It is enough to observe that the operator \(S_{i }^{\mathscr{O}_{}^{\scriptscriptstyle {}}}\) is group–like and therefore satisfies the coproduct identity (14.1), which for the symmetric category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{i}}\) reduces precisely to the condition \(\Delta (S_{i }^{\mathscr{O}_{}^{\scriptscriptstyle {}}})=S_{i }^{\mathscr{O}_{}^{\scriptscriptstyle {}}}\otimes S_{i }^{\mathscr{O}_{}^{\scriptscriptstyle {}}}\). □
15.3 Deformation category \(\mathcal {O}_{\infty }\) representations
We shall be interested in deformations of the symmetric Coxeter category \(\mathscr{O}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\). To this end, consider the deformation parameter \(\hbar \) and set \(\mathsf {h}=\hbar /2\pi \iota \) (cf. 3.2). Let \(\operatorname{{\mathsf{Vect}}}_{\hbar }\) be the category of topologically free \({ \mathbb{C}}[\negthinspace [\hbar ]\negthinspace ]\)–modules. A \(\mathfrak {g}\)–module \(\mathcal {V}\in \operatorname{{\mathsf{Vect}}}_{\hbar }\) is called
-
(D1)
a weight module if \(\mathcal {V}=\bigoplus _{\lambda \in \mathfrak {h}^{*}}\mathcal {V}[\lambda ]\),Footnote 25 where ⨁ is the direct sum in \(\operatorname{{\mathsf{Vect}}}_{\hbar }\), i.e., the completion of the algebraic direct sum in the \(\hbar \)–adic topology.
-
(D2)
integrable if it is a weight module and, for any \(i\in \mathbf {I}\) and \(v\in \mathcal {V}\), \(\lim _{n\to \infty}e_{i}^{n} v=0=\lim _{n\to \infty}f^{n}_{i}v\), where the limit is taken in the \(\hbar\)–adic topology.
This implies that \(\mathcal {V}\) is complete reducible as a (possibly infinite) direct sum of indecomposable finite–rank modules over \(\mathfrak {sl}_{2}^{\alpha _{i}}=\langle e_{i}, h_{i},f_{i}\rangle \).
-
(D3)
in category \(\mathcal {O}^{\hbar }_{\infty ,\mathfrak {g}}\) if the action of \(\mathfrak {b}^{+}_{}\) on \(\mathcal {V}/\hbar ^{n}\mathcal {V}\) is locally finite for any \(n\geqslant 0\). This is equivalent to \(\mathcal {V}\) being the \(\hbar\)–adic direct sum of its generalised weight spaces, and
- (D3′):
-
for any \(v\in \mathcal {V}\), \(\displaystyle \lim _{\operatorname {ht}(\beta )\to \infty}(U \mathfrak {n}^{+}_{})_{\beta}v=0\).
-
(D4)
in category \(\mathcal {O}^{\hbar }_{\mathfrak {g}}\) if it is a weight representation with finite–rank weight spaces, and such that \(P(\mathcal {V})\) satisfies (15.1).
It is easy to see that \(\mathcal {V}\) is a weight (resp. integrable, in category \(\mathcal {O}^{\hbar }_{\infty ,\mathfrak {g}}\)) module in \(\operatorname{{\mathsf{Vect}}}_{\hbar }\) if and only if \(\mathcal {V}/\hbar ^{n}\mathcal {V}\) is a weight (resp. integrable, in category \(\mathcal {O}_{\infty ,\mathfrak {g}}\)) module in \(\operatorname{{\mathsf{Vect}}}\) for any \(n\geq 0\).
We denote by \(\mathcal {O}^{\hbar ,{\scriptscriptstyle \operatorname {int}}}_{\mathfrak {g}}\subset \mathcal {O}^{\hbar }_{\mathfrak {g}}\) and \(\mathcal {O}^{\hbar ,{\scriptscriptstyle \operatorname {int}}}_{\infty ,\mathfrak {g}}\subset \mathcal {O}^{\hbar }_{\infty ,\mathfrak {g}}\) the full tensor subcategories of integrable representations. We shall describe the deformations of \(\mathscr{O}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) arising from braided Coxeter structures on the cosimplicial lax bidiagrammatic algebra \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) of endomorphisms of the forgetful functor from \(\mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty ,\mathfrak {g}}\) to \(\operatorname{{\mathsf{Vect}}}_{\hbar }\).
15.4 The cosimplicial algebra \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)
Let
be the forgetful functor and endomorphisms of its \(n\)th tensor power. By [4, Thm. 3.1] the category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty ,\mathfrak {g}}\) separates points in \(U\mathfrak {g}[\negthinspace [\hbar ]\negthinspace ]\). Thus, we get a natural embedding \({U\mathfrak {g}^{\otimes n}}[\negthinspace [\hbar ]\negthinspace ]\subset \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\). The tower of algebras \(\{\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\}_{n\geqslant 0}\) is a cosimplicial algebra with the face and degeneration morphisms described in 10.1. Moreover, there is a canonical embedding of cosimplicial algebras \({U \mathfrak {g}^{\otimes \bullet}} [\negthinspace [\hbar ]\negthinspace ]\subset \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\).
15.5 Bidiagrammatic structure on \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)
For \(B'\subseteq B\subseteq \mathbb{D}\) and \(n\geq 0\), let
be the restriction functor and the algebra of endomorphisms of its \(n\)th tensor power. In particular, we have \(\mathsf {f}_{\emptyset B}=\mathsf {f}_{B}\) and \(\mathcal {U}_{\mathfrak {g},B\emptyset}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}= \mathcal {U}_{\mathfrak {g}_{B}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\). Note that \({(U\mathfrak {g}_{B}^{\otimes n})^{\mathfrak {g}_{B'}}}[\negthinspace [\hbar ]\negthinspace ]\subset \mathcal {U}_{\mathfrak {g},BB'}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\). The collection of algebras \(\{\mathcal {U}_{\mathfrak {g},BB'}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\;|\; B'\subseteq B\}\) gives rise to a lax bidiagrammatic algebra (cf. 6.4 and [2, Sect. 8.6]) with the following structural morphisms.
-
For any \(C\subseteq B\), \(C'\subseteq B'\), with \(C\subseteq C'\subseteq B'\subseteq B\), the identity
$$ \mathsf {f}_{CC'}\circ \mathsf {f}_{C'B'}\circ \mathsf {f}_{B'B}=\mathsf {f}_{CB} $$induces a canonical morphism of algebras \(\mathcal {U}_{\mathfrak {g},B'C'}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\to \mathcal {U}_{\mathfrak {g},BC}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\).
-
For any \(C_{1}\subseteq B_{1}\perp B_{2}\supset C_{2}\), the identities \(\mathfrak {g}_{B_{1}\sqcup B_{2}}=\mathfrak {g}_{B_{1}}\oplus \mathfrak {g}_{B_{2}}\) and \(\mathfrak {g}_{C_{1}\sqcup C_{2}}=\mathfrak {g}_{C_{1}}\oplus \mathfrak {g}_{C_{2}}\) imply that the natural morphism \(\mathcal {U}_{\mathfrak {g},B_{1}C_{1}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\otimes \mathcal {U}_{\mathfrak {g},B_{2}C_{2}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\to \mathcal {U}_{\mathfrak {g},B_{1}\sqcup B_{2}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) factors through the image of \(\mathcal {U}_{\mathfrak {g},(B_{1}\sqcup B_{2})(C_{1}\sqcup C_{2})}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) in \(\mathcal {U}_{\mathfrak {g},B_{1}\sqcup B_{2}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\).
We denote by \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) the resulting lax bidiagrammatic cosimplicial algebra.
15.6 Braided Coxeter structures on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)
The following is an analogue of Proposition 14.3.
Proposition 28
-
(1)
Let \(\mathbf {C}_{}=(\Phi _{B},R_{B}, J^{}_{\mathcal {F}},\Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}, S_{i})\) be a braided Coxeter structure on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) (cf. Definition 11.1). Then, \(\mathbf {C}_{}\) gives rise to a Coxeter category \(\mathscr{O}_{\mathbf {C}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}}\) given by the following data
-
For any \(B\subseteq \mathbb{D}\), the braided monoidal category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B}}\) with associativity and commutativity constraints given, respectively, by \(\Phi _{B}\in \mathcal {U}_{\mathfrak {g},BB}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},3}}\) and \(R_{B}\in \mathcal {U}_{\mathfrak {g},BB}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},2}}\)
-
For any \(B'\subseteq B\) and \(\mathcal {F}\in \mathsf {Mns}(B,B')\), the restriction functor \(\operatorname{Res}_{\mathcal {F}}: \mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B}}\to \mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B'}}\) with tensor structure given by \(J^{}_{\mathcal {F}}\in \mathcal {U}_{\mathfrak {g},B'B}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},2}}\)
-
For any \(B'\subseteq B\) and \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\), the isomorphism of tensor functors \(\operatorname{Res}_{\mathcal {G}}\Rightarrow \operatorname{Res}_{\mathcal {F}}\) given by \(\Upsilon _{\mathcal {F}\mathcal {G}}\in \mathcal {U}_{\mathfrak {g},B'B}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\)
-
For any chain of inclusions \(B''\subseteq B'\subseteq B\), \(\mathcal {F}\in \mathsf {Mns}(B,B')\), and \(\mathcal {F}'\in \mathsf {Mns}(B',B'')\), the isomorphism of tensor functors \(\operatorname{Res}_{\mathcal {F}'}\circ \operatorname{Res}_{\mathcal {F}} \Rightarrow \operatorname{Res}_{\mathcal {F}'\cup \mathcal {F}}\) given by \(\mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}\in \mathcal {U}_{\mathfrak {g},B''B}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\)
-
For any vertex \(i\) of \(\mathbb{D}\), the invertible operator \(S_{i}\in \left(\mathcal {U}_{\mathfrak {g},\{i\}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\right)^{\times}\)
-
-
(2)
Let \({T}_{}=(u_{\mathcal {F}},K_{B})\) be a twist in \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) (cf. Definition 11.3). Then, \({T}_{}\) gives rise to a 1–isomorphism of braided Coxeter categories \(\mathbf {H}_{{T}_{}}:\mathscr{O}_{\mathbf {C}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}}\to \mathscr{O}_{\mathbf {C}_{{T}_{}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}}\) given by the tensor equivalences
$$ H_{{T}_{},B}=(\operatorname{id}_{B},K_{B}): \mathscr{O}_{\mathbf {C}_{}, B}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}} \to \mathscr{O}_{\mathbf {C}_{{T}_{}}, B'}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}} $$with tensor structure given by the action of \(K_{B}\in \mathcal {U}_{\mathfrak {g},BB}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},2}}\), and the tensor isomorphisms \(\gamma _{{T}_{},\mathcal {F}}:H_{{T}_{},B'}\circ \operatorname{Res}_{\mathbf {C}_{}, \mathcal {F}} \Rightarrow \operatorname{Res}_{\mathbf {C}_{{T}_{}},\mathcal {F}}\circ H_{{T}_{},B}\), given by the action of \(u_{\mathcal {F}}\in \mathcal {U}_{\mathfrak {g},BB'}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\).
-
(3)
Let \(a=\{a_{B}\}\) be a gauge in \(\mathscr{A}_{}\). Then, \(a\) gives rise to a 2–isomorphism \(\mathbf {v}_{a}: \mathbf {H}_{{T}_{}}\Rightarrow \mathbf {H}_{{T}_{{{a}}_{}}}\) with natural braided tensor isomorphism \(v_{a,B}: H_{{T}_{},B}\Rightarrow H_{{T}_{{{a}}_{}}, B}\) given by the action of \(a_{B}\in \mathcal {U}_{\mathfrak {g},BB}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\).
16 Double holonomy and the category \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\)
In this section. we prove that the braided Coxeter structure \(\mathbf {C}_{\nabla}\) on the extended double holonomy algebra  arising from the monodromy data of the KZ and Casimir connections (Theorem 13.2) gives rise to a braided Coxeter structure on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\), and therefore to a braided Coxeter category \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\).
arising from the monodromy data of the KZ and Casimir connections (Theorem 13.2) gives rise to a braided Coxeter structure on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\), and therefore to a braided Coxeter category \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\).
16.1 From the extended double holonomy algebra  to \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)
to \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)
Proposition 29
There is a canonical morphism of cosimplicial lax diagrammatic algebras  .
.
The construction of \(\xi \) is carried out in 16.1.1–16.1.4. Set \(\mathsf {h}=\hbar /2\pi \iota \).
16.1.1 The holonomy algebra  and \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\)
and \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\)
Let  be the root system of the diagrammatic Kac–Moody algebra \(\mathfrak {g}\) and
be the root system of the diagrammatic Kac–Moody algebra \(\mathfrak {g}\) and  the corresponding holonomy algebra with diagrammatic subalgebras
the corresponding holonomy algebra with diagrammatic subalgebras  , \(B\subseteq \mathbb{D}\) (cf. 3.6 and 8.1). Recall that \(U\mathfrak {g}\) naturally embeds in \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\). We have the following
, \(B\subseteq \mathbb{D}\) (cf. 3.6 and 8.1). Recall that \(U\mathfrak {g}\) naturally embeds in \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\). We have the following
Lemma 7
-
(1)
There is a morphism of algebras
 defined by
defined by 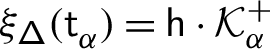
where \({\mathcal {K}}_{\alpha}^{+}=\sum_{i=1}^{\mathsf {m}_{\alpha}}e_{-\alpha}^{(i)}e_{\alpha}^{(i)}\) is the normally–ordered, truncated Casimir operator (3.1).
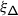 is compatible with the grading, and therefore extends to a morphism
is compatible with the grading, and therefore extends to a morphism 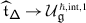 .
. -
(2)
For any \(B\subseteq \mathbb{D}\), the restriction of
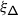 to
to  coincides with the morphism
coincides with the morphism 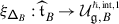 . In particular,
. In particular, 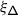 is a morphism of lax diagrammatic algebras.
is a morphism of lax diagrammatic algebras.
Proof
(1) follows from the commutation relations proved in 3.4. (2) is clear. □
16.1.2 The holonomy algebra \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) and \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\)
Let \(r\in \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},2}}\) be the classical \(r\)–matrix of \(\mathfrak {g}\), i.e., in the notation of 3.2.

where \(\{x_{j}\}\), \(\{x^{j}\}\) are dual bases of \(\mathfrak {h}\) with respect to the inner product \(\langle{\cdot},{\cdot}\rangle \). Note that, if  , \(r\notin U\mathfrak {g}^{\otimes 2}\). For any \(n\geqslant 2\) and \(1\leq i\neq j\leq n\), set
, \(r\notin U\mathfrak {g}^{\otimes 2}\). For any \(n\geqslant 2\) and \(1\leq i\neq j\leq n\), set
Let \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) be the holonomy algebra introduced in 12.1. The following result is well-known (see e.g., [13]).
Lemma 8
There is a morphism of algebras \(\xi ^{\scriptscriptstyle {n}}: \mathfrak {t}_{}^{\scriptscriptstyle {n}}\to \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) defined by
\(\xi ^{\scriptscriptstyle {n}}\) is compatible with the cosimplicial structure and the grading on \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) given by \(\deg \mathsf {t}^{ij}=1\), and therefore extends to a morphism of cosimplicial algebras \(\xi ^{\scriptscriptstyle {\bullet}}: \widehat {\mathfrak {t}}_{}^{\scriptscriptstyle {\bullet}} \to \mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\).
Remark 25
An element \(\varphi \in \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) is \(\mathfrak {g}\)–invariant if \([\varphi ,\Delta ^{(n)}(x)]=0\) for any \(x\in \mathfrak {g}\). In particular, since the elements \(\Omega^{ij}\) are \(\mathfrak {g}\)–invariant, it follows that \(\mathsf{im}(\xi ^{\scriptscriptstyle {n}})\subseteq (\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}})^{\mathfrak {g}}\).
16.1.3 The root refinement 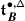 and \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)
and \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)
We now discuss the relation between the algebra  , which can be thought of as a root refinement of \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) (cf. 12.5), and the algebra \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\). For any
, which can be thought of as a root refinement of \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) (cf. 12.5), and the algebra \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\). For any  , we set
, we set
where \(\{(e_{-\alpha})_{a}\}\), \(\{(e_{\alpha})^{a}\}\) are dual bases of \(\mathfrak {g}_{-\alpha}\), \(\mathfrak {g}_{\alpha}\), and
where \(\{x_{a}\}\), \(\{x^{a}\}\) are dual bases of \(\mathfrak {h}\). The following is clear.
Lemma 9
There is a morphism of algebras  defined by
defined by

 is compatible with the cosimplicial structure and the natural grading on
is compatible with the cosimplicial structure and the natural grading on  , and therefore extends to a morphism of cosimplicial algebras
, and therefore extends to a morphism of cosimplicial algebras  .
.
16.1.4 The extended double holonomy algebra  and \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)
and \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)
Recall that, with respect to the root refinement  , the algebra
, the algebra  is endowed with additional generators
is endowed with additional generators  (cf. 12.6). These should be thought of as the elements of \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) given by, respectively
(cf. 12.6). These should be thought of as the elements of \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) given by, respectively
where \({\mathcal {K}}_{\alpha}^{+}\) is Casimir operator (3.1). Specifically, for any \(B\subseteq \mathbb{D}\), set
where \(\{x_{B,a}\},\{x_{B}^{a}\}\) are dual bases of \(\mathfrak {h}_{B}\). Then, the following holds
Lemma 10
-
(1)
There is a morphism of lax diagrammatic algebras
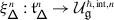 defined by
defined by 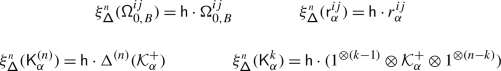
-
(2)
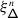 is compatible with the cosimplicial structure, the action of \(\mathfrak {S}_{n}\ltimes \mathfrak {h}^{\oplus n}\), and the grading on
is compatible with the cosimplicial structure, the action of \(\mathfrak {S}_{n}\ltimes \mathfrak {h}^{\oplus n}\), and the grading on  given by
given by  . It therefore extends to a morphism of cosimplicial lax diagrammatic algebras
. It therefore extends to a morphism of cosimplicial lax diagrammatic algebras  .
. -
(3)
The following holds
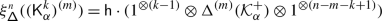
where \((\mathsf {K}_{\alpha}^{k})^{(m)}\) is defined in (12.15).
Proof
(1) The relations satisfied by  , follow from the commutativity of the diagram
, follow from the commutativity of the diagram

where the vertical arrow  is the natural morphism from \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) in
is the natural morphism from \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) in  . The relations (12.12) are satisfied by the elements \({\mathcal {K}}_{\alpha}^{+}\in \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) (cf. Theorem 3.4). The invariance relations
. The relations (12.12) are satisfied by the elements \({\mathcal {K}}_{\alpha}^{+}\in \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) (cf. Theorem 3.4). The invariance relations  (12.13) follow from the \(\mathfrak {g}\)–invariance of \(\Omega^{ij}=r^{ij}+r^{ji}\) in \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\).
(12.13) follow from the \(\mathfrak {g}\)–invariance of \(\Omega^{ij}=r^{ij}+r^{ji}\) in \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\).
The coproduct identity (12.14) holds in \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) since
where \({\mathcal {K}}_{\alpha}^{0}=\sum_{i=1}^{n}(1^{\otimes k-1}\otimes {\mathcal {K}}_{\alpha}^{+}\otimes 1^{\otimes n-k})\) is a weight zero element.
(2)–(3) are clear. □
Through the action of the braid group \(\mathcal {B}_{W_{B}}\) on any object in \(\mathcal {O}_{\infty ,B}^{{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}\), we readily lift the collection of the morphisms  , \(B\subseteq \mathbb{D}\) and \(n\geqslant 0\), to the extended double holonomy algebras (cf. 4.11, 9.3 and 13.2)
, \(B\subseteq \mathbb{D}\) and \(n\geqslant 0\), to the extended double holonomy algebras (cf. 4.11, 9.3 and 13.2)

and we obtain a morphism of cosimplicial lax diagrammatic algebras  .
.
16.2 The braided Coxeter category \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\)
Theorem 15
-
(1)
Let \(\mathbf {C}_{\nabla}=(\Phi ^{\nabla}_{B}, R^{\nabla}_{B}, J^{\nabla}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}, S_{i }^{\nabla})\) be the \(\mathsf {a}^{}_{}\)-strict braided Coxeter structure on
 given by Theorem 13.2. Then, then datum of $$ \mathbf {C}_{\nabla , \mathfrak {g}}=(\Phi ^{\nabla, \mathfrak {g}}_{B}, R^{\nabla, \mathfrak {g}}_{B}, J^{\nabla, \mathfrak {g}}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla, \mathfrak {g}}, S_{i }^{\nabla, \mathfrak {g}}) $$
given by Theorem 13.2. Then, then datum of $$ \mathbf {C}_{\nabla , \mathfrak {g}}=(\Phi ^{\nabla, \mathfrak {g}}_{B}, R^{\nabla, \mathfrak {g}}_{B}, J^{\nabla, \mathfrak {g}}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla, \mathfrak {g}}, S_{i }^{\nabla, \mathfrak {g}}) $$where
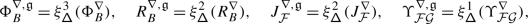
and \(S_{i }^{\nabla, \mathfrak {g}}=\xi ^{1}_{W}(S_{i }^{\nabla})\), is an \(\mathsf {a}^{}_{}\)–strict braided Coxeter structure on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\).
-
(2)
There is a braided Coxeter category \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\) with the following data.
-
For any \(B\subseteq \mathbb{D}\), the category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B}}\), \(B\subseteq \mathbb{D}\), with braided monoidal structure given by \(\Phi ^{\nabla, \mathfrak {g}}_{B}\) and \(R^{\nabla, \mathfrak {g}}_{B}\)
-
For any \(B'\subseteq B\) and \(\mathcal {F}\in \mathsf {Mns}(B,B')\), the standard restriction functor \(\operatorname{Res}_{\mathcal {F}}:\mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B}}\to \mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty , \mathfrak {g}_{B'}}\) with tensor structure given by \(J^{\nabla, \mathfrak {g}}_{\mathcal {F}}\).
-
For any \(B'\subseteq B\) and \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\), the natural isomorphism of tensor functors \(\operatorname{Res}_{\mathcal {G}}\Rightarrow \operatorname{Res}_{\mathcal {F}}\) given by the De Concini–Procesi associator \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla, \mathfrak {g}}\).
-
For any \(i\in \mathbb{D}\), the monodromy operator \(S_{i }^{\nabla, \mathfrak {g}}\).
-
Proof
We shall verify that \(\mathbf {C}_{\nabla ,\mathfrak {g}}\) satisfy the properties (a)–(e) of Definition 11.1 with respect to the cosimplicial lax bidiagrammatic structure on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\). By construction, \(\mathbf {C}_{\nabla ,\mathfrak {g}}\) is the image of a braided pre–Coxeter structure \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre}}}\) in  through the morphism
through the morphism  . Although
. Although  is a morphism of cosimplicial lax diagrammatic algebras, it does not preserve the invariant subalgebras, as the condition of being invariant in \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) is generally stronger than being invariant in
is a morphism of cosimplicial lax diagrammatic algebras, it does not preserve the invariant subalgebras, as the condition of being invariant in \(\mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) is generally stronger than being invariant in  . For instance, while the element \(\mathsf {K}_{\alpha _{i},1}^{}\) is obviously central in
. For instance, while the element \(\mathsf {K}_{\alpha _{i},1}^{}\) is obviously central in  , the normally ordered Casimir operator
, the normally ordered Casimir operator  is not \(\mathfrak {sl}_{2}^{\alpha _{i}}\)–invariant. Therefore, proving that \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre}}}\) is a braided pre–Coxeter structure in \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) reduces to showing that the defining elements of \(\mathbf {C}_{\nabla ,\mathfrak {g}}\) satisfy the necessary invariance properties in \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\).
is not \(\mathfrak {sl}_{2}^{\alpha _{i}}\)–invariant. Therefore, proving that \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre}}}\) is a braided pre–Coxeter structure in \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) reduces to showing that the defining elements of \(\mathbf {C}_{\nabla ,\mathfrak {g}}\) satisfy the necessary invariance properties in \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\).
Note that, for any \(B\subseteq \mathbb{D}\),
are clearly \(\mathfrak {g}_{B}\)–invariant since \(\Omega _{B}\in \mathcal {U}_{\mathfrak {g},BB}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},2}}\). It remains to prove that the relative twist \(J^{\nabla, \mathfrak {g}}_{\mathcal {F}}\) and the De Concini–Procesi associator \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla, \mathfrak {g}}\), corresponding to the maximal nested sets \(\mathcal {F},\mathcal {G}\in \mathsf {Mns}(B,B')\), are \(\mathfrak {g}_{B'}\)–invariant. To this end, it is enough to observe that the coefficients of the equations defining \(J^{\nabla, \mathfrak {g}}_{\mathcal {F}}\) and \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla, \mathfrak {g}}\) specialise to \(\mathfrak {g}_{B'}\)–invariant elements in \(\mathcal {U}_{\mathfrak {g},B}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},1}}\) and \(\mathcal {U}_{\mathfrak {g},B}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},2}}\), which follows as in [34, Thm. 1.33] and [35, App. B.4]. Finally, by Proposition 15.6, (2) follows from (1). □
Remark 26
Note that the operators \(\Phi ^{\nabla, \mathfrak {g}}_{B}\), \(R^{\nabla, \mathfrak {g}}_{B}\), \(J^{\nabla, \mathfrak {g}}_{\mathcal {F}}\), and \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla, \mathfrak {g}}\) are well–defined on category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules and therefore give rise to a braided pre–Coxeter category \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname { {\scriptscriptstyle \operatorname {\hbar }}}}}}\).
17 Quantum Kac–Moody algebras and the category \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\)
In this section, we describe the standard braided Coxeter category \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) associated to a quantised Kac–Moody algebra \(U_{\hbar} \mathfrak {g}\), which encodes the action of the universal \(R\)–matrix and Lusztig’s quantum Weyl group operators [27] on integrable highest weight \(U_{\hbar }\mathfrak {g}\)–modules. We then recall the main result of [2, Thm. 13.9], which provides a description of \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) in terms of integrable highest weight \(\mathfrak {g}\)–modules.
17.1 The Drinfeld–Jimbo quantum group [10, 20]
Let \(\mathfrak {g}\) be a symmetrisable Kac–Moody algebra. Set \(q=\exp (\hbar /2)\) and \(q_{i}= q^{\mathsf {d}_{i}}\), \(i\in \mathbf {I}\). The Drinfeld–Jimbo quantum group of \(\mathfrak {g}\) is the algebra \(U_{\hbar }{\mathfrak {g}}\) over \({ \mathbb{C}}[\negthinspace [\hbar ]\negthinspace ]\) topologically generated by \(\mathfrak {h}\) and the elements \(\{E_{i}, F_{i}\}_{ i\in \mathbf {I}}\), subject to the relations \([h,h']=0\),
for any \(h,h'\in \mathfrak {h}\), \(i,j\in \mathbf {I}\), and the \(q\)–Serre relations
for \(X=E,F\), \(i\neq j\in \mathbf {I}\), where \(\displaystyle [n]_{i}=\frac{q_{i}^{n}-q_{i}^{-n}}{q_{i}-q_{i}^{-1}}\) and, for any \(k\leqslant n\),
We consider on \(U_{\hbar }{\mathfrak {g}}\) the Hopf algebra structure with coproduct
counit \(\varepsilon (h)=\varepsilon (E_{i})=\varepsilon (F_{i})=0\), and antipode \(S(h)=-h\), \(S(E_{i})=- E_{i}q_{i}^{{-}h_{i}}\), and \(S(F_{i})=-q_{i}^{{}h_{i}}F_{i}\) for any \(h\in \mathfrak {h}\) and \(i\in \mathbf {I}\).
Define weight, integrable, category \(\mathcal {O}_{\infty }\) and \(\mathcal {O}\) modules for \(U_{\hbar }\mathfrak {g}\) in \(\operatorname{{\mathsf{Vect}}}_{\hbar }\) analogously to Sect. 15.3, and denote by
the subcategories of integrable modules.Footnote 26
17.2 The universal \(R\)–matrix
The Hopf algebra \(U_{\hbar }{\mathfrak {g}}\) is quasitriangular (cf. [10, 27]). Namely, let \(U_{\hbar }\mathfrak {n}^{+}\) (resp. \(U_{\hbar }\mathfrak {n}^{-}\)) be the subalgebra generated by \(E_{i}, i\in \mathbf {I}\) (resp. \(F_{i}, i\in \mathbf {I}\)), and set \(U_{\hbar }\mathfrak {b}^{\pm }_{}=U_{\hbar }\mathfrak {n}^{\pm }{}{U \mathfrak {h}}[\negthinspace [\hbar ]\negthinspace ]\). By [10], there is a unique non–degenerate Hopf pairing \(\langle{\cdot},{\cdot}\rangle _{\mathcal {D}}:U_{\hbar }\mathfrak {b}^{-}_{}\otimes U_{\hbar }\mathfrak {b}^{+}_{}\to \mathbb{C}(\negthinspace ( \hbar )\negthinspace )\) such that \(\langle{1},{1}\rangle _{\mathcal {D}}= 1\),
and zero otherwise. Let \(\{x_{a}\}, \{x^{a}\}\subset \mathfrak {h}\) be dual bases. Note that the pairing respects the weight decomposition in \(U_{\hbar }\mathfrak {b}^{\pm }_{}\). For any \(\mu \in \mathsf {Q}_{+}\), let \(\{X^{\pm}_{\mu ,p}\}_{p}\subset U_{\hbar }\mathfrak {n}^{\pm }[\pm \mu ]\) be dual bases with respect to \(\langle{\cdot},{\cdot}\rangle _{\mathcal {D}}\) and set \(\Theta _{\mu}=\sum _{p}X^{-}_{\mu ,p}\otimes X^{+}_{\mu ,p}\). Then, \(U_{\hbar }\mathfrak {g}\) is a quasitriangular Hopf algebra with \(R\)–matrix
where \(\Omega ^{0}=\sum _{a} x_{a}\otimes x^{a}\) and \(\Theta =\sum _{\mu >0}\Theta _{\mu}\), that is, \(\mathbf {R}\) satisfies the intertwining property \(\Delta ^{^{\scriptscriptstyle {\operatorname {op}}}}(x)=\mathbf {R}\cdot \Delta (x)\cdot \mathbf {R}^{-1}\), as well as the cabling identities
from which the Yang–Baxter equation \(\mathbf {R}_{12}\cdot \mathbf {R}_{13}\cdot \mathbf {R}_{23} = \mathbf {R}_{23}\cdot \mathbf {R}_{13} \cdot \mathbf {R}_{12}\) follows. The action of the \(R\)–matrix on a tensor product of representations in \(\mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}\) is well–defined and induces a braiding.
17.3 Quantum Weyl group operators
Let \(\mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}^{{\scriptscriptstyle \operatorname {int}}}\) be the category of integrable \(U_{\hbar }\mathfrak {g}\)–modules in category \(\mathcal {O}_{\infty }\), i.e., the action of the elements \(E_{i}\), \(F_{i}\), \(i\in \mathbf {I}\), is locally nilpotent mod \(\hbar^{n}\) for any \(n\geq 0\). Let \(V\in \mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}^{{\scriptscriptstyle \operatorname {int}}}\). For any \(i \in \mathbf {I}\), the operator \(\widetilde {\mathbf {S}}_{i}\) is defined on \(V\) as followsFootnote 27 [27, 22, 25]: for any \(v_{\mu}\in V[\mu ]\),
where \(X_{i}^{(a)}= X^{a}/[a]_{i}!\), \(X=E,F\). Clearly we have \(\widetilde {\mathbf {S}}_{i}(V[\mu ]) \subseteq V[s_{i}(\mu )]\). By [27, Sect. 39.4], the operators \(\widetilde {\mathbf {S}}_{i}\), \(i\in I\), induce an action of the generalised braid group \(\mathcal {B}_{W}\) on \(V\in \mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}^{{\scriptscriptstyle \operatorname {int}}}\), which recovers the action by triple exponentials described in 15.2 at \(\hbar =0\). By construction, \(\widetilde {\mathbf {S}}_{i}\) is an element of the completion of \(U_{\hbar }\mathfrak {g}\) with respect to the category \(\mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}^{{\scriptscriptstyle \operatorname {int}}}\), i.e., \(\widetilde {\mathbf {S}}_{i}\in \mathsf {Aut}(\mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}^{{\scriptscriptstyle \operatorname {int}}}\to \operatorname{{\mathsf{Vect}}}_{\hbar })\). By [27, Sect. 37.1], the action of the operators \(\widetilde {\mathbf {S}}_{i}\) induces an algebra automorphism of \(U_{\hbar }\mathfrak {g}\), which we denote by the same symbol, such that, for any \(u\in U_{\hbar }\mathfrak {g}\) and \(v\in V\in \mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}^{{\scriptscriptstyle \operatorname {int}}}\), one has \(\widetilde {\mathbf {S}}_{i}(u\cdot m)= \widetilde {\mathbf {S}}_{i}(u)\cdot \widetilde {\mathbf {S}}_{i}(m)\). Moreover, for any \(h\in \mathfrak {h}\), \(\widetilde {\mathbf {S}}_{i}(h)=s_{i}(h)\).
The operator \(\widetilde {\mathbf {S}}_{i}\) allows to recover the universal \(R\)–matrix as a multiplicative coboundary. Indeed, by [27, Sect. 5.3] (see also [5, Sect. 4.10] which follows our conventions), the operator \(\widetilde {\mathbf {S}}_{i}\) satisfies the coproduct identity
where \(\mathbf {R}_{i}\in U_{\hbar }\mathfrak {b}^{-}_{i}\widehat {\otimes }U_{\hbar }\mathfrak {b}^{+}_{i}\) is the universal \(R\)–matrix of the subalgebra \(U_{\hbar} \mathfrak {g}_{i}\) corresponding to the simple root \(\alpha _{i}\) and \(\mathbf {R}_{i}=q_{i}^{h_{i}\otimes h_{i}/2}\cdot \Theta _{i}\). Note that
Set \(\mathbf {S}_{i}= q_{i}^{{h_{i}^{2}}/{4}}\cdot \widetilde {\mathbf {S}}_{i}= \widetilde {\mathbf {S}}_{i}\cdot q_{i}^{{ h_{i}^{2}}/{4}}\). Note that the operators \(\mathbf {S}_{i}\), \(i\in \mathbf {I}\), also satisfy the generalised braid relations (7.1). Moreover, we have
Therefore, from the identity \(\Delta (\mathbf {S}_{i})=\mathbf {R}_{i,21}\cdot \Delta ^{^{\scriptscriptstyle {\operatorname {op}}}}(\mathbf {S}_{i})\cdot \mathbf {R}_{i,21}^{-1}\), we get the coproduct identity
We shall refer to both \(\widetilde {\mathbf {S}}_{i}\) and \(\mathbf {S}_{i}\) as the quantum Weyl group operators of \(U_{\hbar }\mathfrak {g}\).
Remark 27
By [27, Sect. 5.2], the squares of the operators \(\widetilde {\mathbf {S}}_{i}\) and \(\mathbf {S}_{i}\) are particularly simple and related to the quantum Casimir element of the quantum algebra \(U_{\hbar} \mathfrak {sl}_{2}^{\alpha _{i}}=\langle E_{i}, F_{i}, h_{i}\rangle \subset U_{\hbar} \mathfrak {g}\). Recall that, since \(\mathcal {O}_{\infty ,U_{\hbar} \mathfrak {sl}_{2}}^{{ \scriptscriptstyle \operatorname {int}}}\) is semisimple, an element in \(\mathsf {Aut}(\mathcal {O}_{\infty ,U_{\hbar} \mathfrak {sl}_{2}}^{{ \scriptscriptstyle \operatorname {int}}}\to \operatorname{{\mathsf{Vect}}}_{\hbar })\) is uniquely determined by its action on the indecomposable finite–rank representations. Let \({\mathcal {C}}_{\hbar ,i}\) be the quantum Casimir operator, acting on the irreducible representation of rank \(d+1\) as \(\mathsf {d}_{i}\cdot d\cdot (d+2)/2\), and set \({\mathcal {K}}_{\hbar , i}= {\mathcal {C}}_{\hbar ,i}-\mathsf {d}_{i}\cdot h_{i}^{2}/2\). Then, we have
Note that \(\exp (\pi \iota h_{i})\) is central, i.e., it commutes with the action of \(U_{\hbar} \mathfrak {g}_{i}\) and therefore so is \(\mathbf {S}_{i}^{2}\).
17.4 The braided Coxeter category \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\)
Integrable highest weight representations of quantum Kac–Moody algebras give rise to a braided Coxeter category. Namely, let \(\mathfrak {g}\) be a diagrammatic Kac–Moody algebra with labelled Dynkin diagram \((\mathbb{D},\underline {m})\) and Cartan subalgebras \(\mathfrak {h}_{B}\subseteq \mathfrak {h}\), \(B\subseteq \mathbb{D}\). The quantum group \(U_{\hbar }\mathfrak {g}\) is a bidiagrammatic Hopf algebra, with subalgebras
\(B\subseteq \mathbb{D}\), and the corresponding diagrammatic invariants. These induce restriction functors \(\operatorname{Res}^{\hbar }_{B'B}:\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , U_{\hbar }\mathfrak {g}_{B}}\to \mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , U_{\hbar }\mathfrak {g}_{B'}}\) with \(B'\subseteq B\), and yield the following analogue of Proposition 15.2.
Proposition 30
There is a canonical \((\mathsf {a}^{}_{},\Upsilon _{})\)–strict braided Coxeter category \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) of type \((\mathbb{D}, \underline {m})\) given by the following data.
-
For any \(B\subseteq \mathbb{D}\), the braided monoidal category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , U_{\hbar }\mathfrak {g}_{B}}\) with braiding induced by the action of the universal \(R\)–matrix \(\mathbf {R}_{B}\in U_{\hbar }\mathfrak {b}^{-}_{B}\widehat {\otimes }U_{\hbar }\mathfrak {b}^{+}_{B}\).
-
For any \(B'\subseteq B\), the restriction functor \(\operatorname{Res}^{\hbar }_{B'B}:\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , U_{\hbar }\mathfrak {g}_{B}}\to \mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , U_{\hbar }\mathfrak {g}_{B'}}\).
-
For any \(i\in \mathbb{D}\), the quantum Weyl group operator \(\mathbf {S}_{i}\in \mathsf {Aut}(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , U_{\hbar} \mathfrak {g}_{i}}\to \operatorname{{\mathsf{Vect}}}_{\hbar })\).
Proof
It is enough to observe that the quantum Weyl group operators \(\mathbf {S}_{i}\) satisfy the coproduct identity (14.1), which for the braided monoidal category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty , U_{\hbar} \mathfrak {g}_{i}}\) reduces precisely to the equation (17.1). □
Remark 28
Note that the action of the \(R\)–matrix on category \(\mathcal {O}_{\infty}\) modules, together with the corresponding restriction functors, gives rise to a braided pre–Coxeter category \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}}^{\scriptscriptstyle {}}\).
Part IV. The monodromy theorem
This final part is devoted to the proof of the main result of the paper. The material is organized as follows. In Sect. 18, we introduce the notions of a split diagrammatic Lie bialgebra \(\mathfrak {b}\), its Drinfeld–Yetter modules \(\mathsf {DY}_{{\mathfrak {b}}}^{}\), and the symmetric pre–Coxeter category \(\mathscr{DY}_{\mathfrak {b}}^{\scriptscriptstyle {}}\). In Sect. 19, we introduce the \(\mathsf {PROP}\) of universal Drinfeld–Yetter modules over a split diagrammatic Lie bialgebra and the universal algebra \(\mathbf {U}_{\mathbb{D}}^{\bullet}\) which controls the deformation of \(\mathscr{DY}_{\mathfrak {b}}^{\scriptscriptstyle {}}\) as a braided pre–Coxeter category. In Sect. 20, we describe similar results for split diagrammatic quantum enveloping algebras and their admissible Drinfeld–Yetter modules. We review the construction of an explicit equivalence of braided pre–Coxeter categories \(\mathscr{DY}_{\mathfrak {b}}^{\scriptscriptstyle {\Phi}}\to \mathscr{DY}_{\mathcal {Q}(\mathfrak {b})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\), given in [2, Thm. 10.10], where \(\mathfrak {b}\) is a split diagrammatic Lie bialgebra, \(\mathscr{DY}_{\mathfrak {b}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\Phi}}\) denotes a deformation of \(\mathscr{DY}_{\mathfrak {b}}^{\scriptscriptstyle {}}\) depending upon the choice of a Lie associator \(\Phi \), \(\mathcal {Q}(\mathfrak {b})\) is the Etingof–Kazhdan quantisation of \(\mathfrak {b}\) [15], and \(\mathscr{DY}_{\mathcal {Q}(\mathfrak {b})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) denotes the braided pre–Coxeter category arising from admissible Drinfeld–Yetter \(\mathcal {Q}(\mathfrak {b})\)–modules. In Sect. 21, we fix a diagrammatic Kac–Moody algebra \(\mathfrak {g}\) with root system  . We introduce the \(\mathsf {PROP}\) of universal Drinfeld–Yetter modules over a split diagrammatic Lie bialgebra graded over
. We introduce the \(\mathsf {PROP}\) of universal Drinfeld–Yetter modules over a split diagrammatic Lie bialgebra graded over  , modelled over \(\mathfrak {b}^{-}_{}\). Its universal algebra
, modelled over \(\mathfrak {b}^{-}_{}\). Its universal algebra  controls the deformation of \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {}}\). In Sect. 22, we prove that the monodromy data of the KZ and Casimir connections are encoded by a universal structure on
controls the deformation of \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {}}\). In Sect. 22, we prove that the monodromy data of the KZ and Casimir connections are encoded by a universal structure on  . We rely on the rigidity of
. We rely on the rigidity of  , proved in [3, Thm. 15.15], to obtain an equivalence of braided pre–Coxeter categories \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\Phi}}\to \mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\), which finally yields the equivalence \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\to \mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\).
, proved in [3, Thm. 15.15], to obtain an equivalence of braided pre–Coxeter categories \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\Phi}}\to \mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\), which finally yields the equivalence \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\to \mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\).
18 From category \(\mathcal {O}\) to Drinfeld–Yetter modules
We review the notion of diagrammatic Lie bialgebra introduced in [2], and the fact that their Drinfeld–Yetter modules give rise to a braided pre–Coxeter category. In the case of a diagrammatic Kac–Moody algebra, this recovers category \(\mathscr{O}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) as a full subcategory of Drinfeld–Yetter modules over its negative Borel subalgebra.
18.1 Lie bialgebras
A Lie bialgebra is a triple \((\mathfrak {b},[\,,\,]_{\mathfrak {b}}, \delta _{\mathfrak {b}})\) where \((\mathfrak {b},[\,,\,]_{\mathfrak {b}})\) is a Lie algebra, \((\mathfrak {b},\delta _{\mathfrak {b}})\) a Lie coalgebra, and the cobracket \(\delta _{\mathfrak {b}}:\mathfrak {b}\to \mathfrak {b}\otimes \mathfrak {b}\) satisfies the cocycle condition
18.2 Drinfeld double [10]
The Drinfeld double of a Lie bialgebra \((\mathfrak {b},[\,,\,]_{\mathfrak {b}},\delta _{\mathfrak {b}})\) is the Lie algebra \(\mathfrak {g}_{\mathfrak {b}}\) defined as follows. As a vector space, \(\mathfrak {g}_{\mathfrak {b}}=\mathfrak {b}\oplus \mathfrak {b}^{*}\). The duality pairing \(\mathfrak {b}^{*}\otimes \mathfrak {b}\to \mathsf {k}\) extends uniquely to a symmetric, non–degenerate bilinear form \(\langle{\cdot},{\cdot}\rangle \) on \(\mathfrak {g}_{\mathfrak {b}}\), with respect to which both \(\mathfrak {b}\) and \(\mathfrak {b}^{*}\) are isotropic subspaces. The Lie bracket on \(\mathfrak {g}_{\mathfrak {b}}\) is defined as the unique bracket which coincides with \([\,,\,]_{\mathfrak {b}}\) on \(\mathfrak {b}\), with \(\delta _{\mathfrak {b}}^{t}\) on \(\mathfrak {b}^{*}\), and is compatible with \(\langle{\cdot},{\cdot}\rangle \), i.e., satisfies \(\langle{[x,y]},{z}\rangle =\langle{x},{[y,z]}\rangle \) for all \(x,y,z\in \mathfrak {g}_{\mathfrak {b}}\). The mixed bracket of \(x\in \mathfrak {b}\) and \(\phi \in \mathfrak {b}^{*}\) is then given by
where \(\mathsf {ad}^{*}\) is the coadjoint action of \(\mathfrak {b}\) on \(\mathfrak {b}^{*}\). Note that \((\mathfrak {g}_{\mathfrak {b}},\mathfrak {b},\mathfrak {b}^{*})\) is a Manin triple [10, 15], and any such triple arises this way.
Similarly, if \(\mathfrak {b}\) is a Lie bialgebra which is ℕ–graded with finite–dimensional components, and such that the bracket and cobracket are homogeneous of degrees 0 and \(d\in \mathbb{Z}\) respectively,Footnote 28 the restricted double of \(\mathfrak {b}\) is defined as \(\mathfrak {g}_{\mathfrak {b}}^{\scriptscriptstyle \operatorname {res}}=\mathfrak {b}\oplus \mathfrak {b}^{\star}[d]\), where \(\mathfrak {b}^{\star}[d]_{n}=(\mathfrak {b}_{-n+d})^{*}\), and is a restricted Manin triple.
The restricted double \(\mathfrak {g}_{\mathfrak {b}}^{\scriptscriptstyle \operatorname {res}}\) (and, in particular, the double of a finite–dimensional Lie bialgebra) is additionally endowed with a Lie bialgebra structure, with cobracket
where \(r\) is the canonical element in \(\mathfrak {b}\widehat {\otimes} \mathfrak {b}^{\star}\), with \(\widehat {\otimes}\) the completion of the tensor product with respect to the grading, and \(\delta_{ \mathfrak {g}_{\mathfrak {b}}^{\scriptscriptstyle \operatorname {res}}}=\delta_{\mathfrak {b}}-\delta_{\mathfrak {b}^{\star}}\).
18.3 Drinfeld–Yetter modules [10, 16]
A Drinfeld–Yetter module over a Lie bialgebra \(\mathfrak {b}\) is a triple \((V,\pi _{V},\pi _{V}^{*})\), where \((V,\pi _{V})\) is a left \(\mathfrak {b}\)–module, \((V,\pi _{V}^{*})\) a right \(\mathfrak {b}\)–comodule, and the maps \(\pi _{V}:\mathfrak {b}\otimes V\to V\) and \(\pi _{V}^{*}:V\to \mathfrak {b}\otimes V\) satisfy the following compatibility in \(\operatorname{End}(\mathfrak {b}\otimes V)\)
The category \(\mathsf {DY}_{\mathfrak {b}}\) of such modules is a symmetric tensor category. For any \(V,W\in \mathsf {DY}_{\mathfrak {b}}\), the action and coaction on the tensor product \(V\otimes W\) are defined, respectively, by
The associativity constraints are trivial, and the braiding is defined by \(\beta _{VW}=(1\,2)\).
18.4 Representations of the Drinfeld double
The category \(\mathsf {DY}_{\mathfrak {b}}\) is canonically isomorphic to the category \(\mathcal {E}_{ \mathfrak {g}_{\mathfrak {b}}}\) of equicontinuous \(\mathfrak {g}_{\mathfrak {b}}\)–modules [15], i.e., those endowed with a locally finite \(\mathfrak {b}^{*}\)–action. This condition yields a functor \(E: \mathcal {E}_{ \mathfrak {g}_{\mathfrak {b}}} \to \mathsf {DY}_{\mathfrak {b}}\), which assigns to any \(V\in \mathcal {E}_{ \mathfrak {g}_{\mathfrak {b}}}\) the Drinfeld–Yetter \(\mathfrak {b}\)–module \((V,\pi ,\pi ^{*})\), where \(\pi \) is the restriction of the action of \(\mathfrak {g}_{\mathfrak {b}}\) to \(\mathfrak {b}\), and the coaction \(\pi ^{*}\) is given by
where \(\{b_{i}\}\), \(\{b^{i}\}\) are dual bases of \(\mathfrak {b}\) and \(\mathfrak {b}^{*}\). The inverse functor is obtained by letting \(\phi \in \mathfrak {b}^{*}\subset \mathfrak {g}_{\mathfrak {b}}\) act on \(V\in \mathsf {DY}_{\mathfrak {b}}\) by \(\phi \otimes \operatorname{id}_{V}\circ \pi ^{*}\).
If \(\mathfrak {b}\) is ℕ–graded with finite–dimensional homogeneous components, the formulae defining \(E\) similarly give rise to an isomorphism \(E^{\scriptscriptstyle \operatorname {res}}\) between the category \(\mathcal {E}_{ \mathfrak {g}_{\mathfrak {b}}^{\scriptscriptstyle \operatorname {res}}}\) of equicontinuous modules over the restricted double of \(\mathfrak {b}\) and \(\mathsf {DY}_{\mathfrak {b}}\). Moreover, the categories \(\mathcal {E}_{ \mathfrak {g}_{\mathfrak {b}}}\) and \(\mathcal {E}_{ \mathfrak {g}_{\mathfrak {b}}^{\scriptscriptstyle \operatorname {res}}}\) are isomorphic, since any locally finite action of \(\mathfrak {b}^{\star}\) extends uniquely to one of \(\mathfrak {b}^{*}\), and the following diagram is commutative

18.5 Symmetrisable Kac–Moody algebras
Let \(\mathfrak {g}\) be a symmetrisable Kac–Moody algebra with opposite Borel subalgebras \(\mathfrak {b}^{\pm }_{}\subset \mathfrak {g}\) (cf. 2.2). The identifications \(( \mathfrak {b}^{\mp }_{})^{\star}\simeq \mathfrak {b}^{\pm }_{}\) give rise to a Lie bialgebra structure on \(\mathfrak {b}^{\pm }_{}\) and \(\mathfrak {g}\), which is compatible with the grading. Specifically, consider the Lie algebra \(\mathfrak {g}^{(2)}=\mathfrak {g}\oplus \mathfrak {h}_{\mathfrak {z}}\), with \(\mathfrak {h}_{\mathfrak {z}}=\mathfrak {h}\), and endow it with the inner product
Let \(\pi _{0}:\mathfrak {g}\to \mathfrak {h}\) be the projection arising from the root space decomposition, and \(\mathfrak {b}^{(2)}_{\pm}\subset \mathfrak {g}^{(2)}\) the subalgebra
Note that the projection \(\mathfrak {g}^{(2)}\to \mathfrak {g}\) onto the first component restricts to an isomorphism \(\mathfrak {b}^{(2)}_{\pm}\to \mathfrak {b}^{\pm }_{}\) with inverse \(\mathfrak {b}^{\pm }_{}\ni X\to (X,\pm \pi _{0}(X))\in \mathfrak {b}^{(2)}_{\pm}\). The following is easily seen to hold (cf. [10, 17]).
Proposition 31
-
(1)
\((\mathfrak {g}^{(2)}, \mathfrak {b}^{(2)}_{-}, \mathfrak {b}^{(2)}_{+})\) is a restricted Manin triple. In particular, \(\mathfrak {b}^{(2)}_{\mp}\) and \(\mathfrak {g}^{(2)}\) are Lie bialgebras, with cobracket \(\delta _{\mathfrak {b}^{(2)}_{\mp}}=[\cdot ,\cdot ]_{\mathfrak {b}^{(2)}_{\pm}}^{t}\) and \(\delta _{ \mathfrak {g}^{(2)}}=\delta _{\mathfrak {b}^{(2)}_{-}}-\delta _{\mathfrak {b}^{(2)}_{+}}\).
-
(2)
The central subalgebra \(0\oplus \mathfrak {h}_{\mathfrak {z}}\subset \mathfrak {g}^{(2)}\) is a coideal, so that the projection \(\mathfrak {g}^{(2)}\to \mathfrak {g}\) induces a Lie bialgebra structure on \(\mathfrak {g}\) and \(\mathfrak {b}_{\mp}\).
-
(3)
The Lie bialgebra structure on \(\mathfrak {g}\) is given by
$$ \delta |_{\mathfrak {h}}=0 \qquad \delta (e_{i})=\mathsf {d}_{i} h_{i}\wedge e_{i} \qquad \delta (f_{i})=\mathsf {d}_{i} h_{i}\wedge f_{i} $$ -
(4)
The projection \(\mathfrak {g}^{(2)}\to \mathfrak {g}\) maps the canonical elements \(r_{ \mathfrak {g}^{(2)}}\in \mathfrak {b}^{(2)}_{-}\widehat {\otimes} \mathfrak {b}^{(2)}_{+}\) and \(\Omega_{ \mathfrak {g}^{(2)}}=r_{ \mathfrak {g}^{(2)}}+r_{ \mathfrak {g}^{(2)}}^{21}\in \mathfrak {g}^{(2)}\widehat {\otimes} \mathfrak {g}^{(2)}\) corresponding to the inner product \(\langle{\cdot},{\cdot}\rangle ^{(2)}\) to
$$ r_{\mathfrak {g}}=\sum_{i} x_{i}\otimes x^{i}+\frac {1}{2}\sum_{a} t_{a}\otimes t^{a} $$and the canonical element \(\Omega_{\mathfrak {g}}\in \mathfrak {g}\widehat {\otimes} \mathfrak {g}\) corresponding to \(\langle{\cdot},{\cdot}\rangle \), where \(\{x_{i}\},\{x^{i}\}\) are homogeneous dual bases of \(\mathfrak {n}_{-},\mathfrak {n}_{+}\), and \(\{t_{a}\},\{t^{a}\}\) are dual bases of \(\mathfrak {h}\).Footnote 29
18.6 From category \(\mathcal {O}\) to Drinfeld–Yetter modules
By Proposition 18.5 and 18.4, the category of Drinfeld–Yetter modules over \(\mathfrak {b}^{-}_{}\) is equivalent to the category \(\mathcal {E}_{ \mathfrak {g}^{(2)}}\) of \(\mathfrak {g}^{(2)}\)–modules which carry a locally finite action of \(\mathfrak {b}^{(2)}_{+}\subset \mathfrak {g}^{(2)}\). This implies the following, cf. [2, Prop. 12.8].
Proposition 32
-
(1)
Category \(\mathcal {O}_{\infty ,\mathfrak {g}}\) is isomorphic to the full tensor subcategory of \(\mathcal {E}_{ \mathfrak {g}^{(2)}}\) consisting of those modules carrying a trivial action of \(\mathfrak {h}_{\mathfrak {z}}\).
-
(2)
Under the equivalence \(\mathcal {E}_{ \mathfrak {g}^{(2)}}\simeq \mathsf {DY}_{ \mathfrak {b}^{-}_{}}\), \(\mathcal {O}_{\infty , \mathfrak {g}}\) is isomorphic to the full tensor subcategory of \(\mathsf {DY}_{ \mathfrak {b}^{-}_{}}\) consisting of those modules \(V\) such that the action \(\rho _{V}\) and the coaction \(\rho ^{*}_{V}\) of \(\mathfrak {h}\) on \(V\) coincide under \(\langle{\cdot},{\cdot}\rangle _{\mathfrak {h}}\), i.e.,
$$ \rho _{V}= \langle{\cdot},{\cdot}\rangle _{\mathfrak {h}}\otimes \operatorname{id}_{V}\circ \operatorname{id}_{\mathfrak {h}}\otimes \rho _{V}^{*} $$(18.1)
18.7 Split pairs and restriction functors
Drinfeld–Yetter modules cannot be pulled back under morphisms of Lie bialgebras since modules are contravariant and comodules are covariant with respect to such morphisms. This can be rectified, however, by considering a different notion of morphism of Lie bialgebras.
A split pair of Lie bialgebras \((\mathfrak {b},\mathfrak {a})\) [1] is the datum of two Lie bialgebras \(\mathfrak {a}\), \(\mathfrak {b}\), together with Lie bialgebra morphisms \(i:\mathfrak {a}\to \mathfrak {b}\) and \(p:\mathfrak {b}\to \mathfrak {a}\) such that \(p\circ i=\operatorname{id}_{\mathfrak {a}}\). For any split pair of Lie bialgebras \((\mathfrak {b},\mathfrak {a})\), there is a monoidal restriction functor \(\operatorname{Res}_{\mathfrak {a},\mathfrak {b}}:\mathsf {DY}_{\mathfrak {b}}\to \mathsf {DY}_{\mathfrak {a}}\) defined by
Moreover, if \(\mathfrak {a}\hookrightarrow \mathfrak {b}\hookrightarrow \mathfrak {c}\) is a chain of split embeddings, then \(\operatorname{Res}_{\mathfrak {a},\mathfrak {b}}\circ \operatorname{Res}_{\mathfrak {b},\mathfrak {c}}=\operatorname{Res}_{\mathfrak {a},\mathfrak {c}}\). Note that, under the identification of \(\mathsf {DY}_{\mathfrak {b}}\), \(\mathsf {DY}_{\mathfrak {a}}\) with the categories of equicontinuous modules over the doubles \(\mathfrak {g}_{\mathfrak {b}}\) and \(\mathfrak {g}_{\mathfrak {a}}\) respectively, \(\operatorname{Res}_{\mathfrak {a},\mathfrak {b}}\) coincides with the pullback functor corresponding to the morphism \(i\oplus p^{t}:\mathfrak {g}_{\mathfrak {a}}\to \mathfrak {g}_{\mathfrak {b}}\).
18.8 Diagrammatic Lie bialgebras [2]
By analogy with Sect. 6.1, a diagrammatic Lie (bi)algebra is a monoidal functor from \(\mathcal {P}(\mathbb{D})\) to the category of Lie bialgebras. Specifically, a diagrammatic Lie (bi)algebra \(\mathfrak {b}\) is the datum of
-
a diagram \(\mathbb{D}\)
-
for any \(B\subseteq \mathbb{D}\), a Lie (bi)algebra \(\mathfrak {b}_{B}\)
-
for any \(B'\subseteq B\), a Lie (bi)algebra morphism \(i_{BB'} :\mathfrak {b}_{B'}\to \mathfrak {b}_{B}\)
such that
-
for any \(B\subseteq \mathbb{D}\), \(i_{BB}=\operatorname{id}_{\mathfrak {b}_{B}}\)
-
for any \(B''\subseteq B'\subseteq B\), \(i_{BB'}\circ i_{B'B''}=i_{BB''}\)
-
for any \(B_{1}\perp B_{2}\),
$$ i_{(B_{1}\sqcup B_{2})B_{1}}+i_{(B_{1}\sqcup B_{2})B_{2}}:\mathfrak {b}_{B_{1}} \oplus \mathfrak {b}_{B_{2}}\to \mathfrak {b}_{B_{1}\sqcup B_{2}} $$is an isomorphism of Lie (bi)algebras.
The above properties imply in particular that \(\mathfrak {b}_{\emptyset}=0\), and that \(U\mathfrak {b}\) is a diagrammatic algebra, with \((U\mathfrak {b})_{B}=U\mathfrak {b}_{B}\) (cf. 6.2).
A morphism \(\varphi :\mathfrak {b}\to \mathfrak {c}\) of diagrammatic Lie (bi)algebras with the same underlying diagram \(\mathbb{D}\) is a collection of Lie (bi)algebra morphisms \(\varphi _{B}:\mathfrak {b}_{B}\to \mathfrak {c}_{B}\) labelled by the subdiagrams \(B\subseteq \mathbb{D}\) such that, for any \(B'\subseteq B\), \(\varphi _{B}\circ i^{\mathfrak {b}}_{BB'}= i^{\mathfrak {c}}_{BB'}\circ \varphi _{B'}\).
18.9 Split diagrammatic Lie bialgebras [2]
A diagrammatic Lie (bi)algebra \(\mathfrak {b}\) is split if there are Lie (bi)algebra morphisms \(p_{B'B}:\mathfrak {b}_{B}\to \mathfrak {b}_{B'}\) for any \(B'\subseteq B\), such that \(p_{B'B}\circ i_{BB'}=\operatorname{id}_{\mathfrak {b}_{B'}}\), and
-
for any \(B\subseteq D\), \(p_{BB}=\operatorname{id}_{\mathfrak {b}_{B}}\)
-
for any \(B''\subseteq B'\subseteq B\), \(p_{B''B'}\circ p_{B'B}=p_{B''B}\)
-
for any \(B_{1}\perp B_{2}\)
$$ p_{B_{1}(B_{1}\sqcup B_{2})}\oplus p_{B_{2}(B_{1}\sqcup B_{2})}:\mathfrak {b}_{B_{1} \sqcup B_{2}}\to \mathfrak {b}_{B_{1}}\oplus \mathfrak {b}_{B_{2}} $$is an isomorphism of Lie (bi)algebras, and is the inverse of \(i_{(B_{1}\sqcup B_{2})B_{1}}+i_{(B_{1}\sqcup B_{2})B_{2}}\).
A morphism \(\varphi :\mathfrak {b}\to \mathfrak {c}\) of split diagrammatic Lie (bi)algebras with the same underlying diagram is one of the underlying diagrammatic Lie (bi)algebras such that, for any \(B'\subseteq B\), \(p^{\mathfrak {c}}_{B'B}\circ \varphi _{B}=\varphi _{B'}\circ p^{\mathfrak {b}}_{B'B}\).
The following is clear.
Proposition 33
Let \(\mathfrak {b}\) be a split diagrammatic Lie bialgebra. Then, there is an \((\mathsf {a}^{}_{},\Upsilon _{})\)–strict symmetric pre–Coxeter category \(\mathscr{DY}_{\mathfrak {b}}^{\scriptscriptstyle {}}{}\) defined by the following data
-
For any \(B\subseteq \mathbb{D}\), the symmetric monoidal category \(\mathsf {DY}_{\mathfrak {b}_{B}}\).
-
For any \(B'\subseteq B\), the restriction functor \(\operatorname{Res}_{\mathfrak {b}_{B'},\mathfrak {b}_{B}}\).
Remark 29
A split diagrammatic Lie bialgebra \(\mathfrak {b}=\{b_{B}\}_{B\subseteq D}\) gives rise to a diagrammatic Manin triple \(\mathfrak {g}_{\mathfrak {b}}=\{\mathfrak {g}_{\mathfrak {b}_{B}}\}_{B\subseteq D}\), which will be referred to as the double of \(\mathfrak {b}\), and any such triple arises this way (cf. [2, Sect. 5]). Similarly, if \(\mathfrak {b}\) is an ℕ–graded split diagrammatic Lie bialgebra with finite–dimensional homogeneous components (i.e., for any \(B\subseteq D\), \(\mathfrak {b}_{B}\) is ℕ–graded, with finite–dimensional homogeneous components and, for any \(B'\subseteq B\), the morphisms \(i_{BB'}\) and \(p_{B'B}\) are homogeneous of degree 0), one can similarly define a diagrammatic Lie bialgebra \(\mathfrak {g}_{\mathfrak {b}}^{\scriptscriptstyle \operatorname {res}}\), with \((\mathfrak {g}_{\mathfrak {b}}^{\scriptscriptstyle \operatorname {res}})_{B}=\mathfrak {g}_{\mathfrak {b}_{B}}^{\scriptscriptstyle \operatorname {res}}\), endowed with a canonical morphism of diagrammatic Lie bialgebras \(\mathfrak {b}\to \mathfrak {g}_{\mathfrak {b}}^{\scriptscriptstyle \operatorname {res}}\).
18.10 Diagrammatic Kac–Moody algebras and split structures
Let \(\mathfrak {g}\) be a diagrammatic Kac–Moody algebra with Dynkin diagram \(\mathbb{D}\) and Cartan subalgebras \(\mathfrak {h}_{B}\), \(B\subseteq \mathbb{D}\) (cf. 2.4). Then \(\mathfrak {g}\) is a diagrammatic Lie bialgebra where, for any \(B\subseteq \mathbb{D}\), \(\mathfrak {g}_{B}=\langle e_{i}, f_{i}\), \(\mathfrak {h}_{B}\;|\; i\in B\rangle \).
The diagrammatic structure on \(\mathfrak {g}\) determines a split diagrammatic one on \(\mathfrak {b}^{\pm }_{}\) as follows. For any \(B \subseteq \mathbb{D}\), let \(\mathfrak {b}^{\pm }_{B}= \mathfrak {b}^{\pm }_{}\cap \mathfrak {g}_{B}\) be the subalgebras generated by \(\{\mathfrak {h}_{B},e_{i}\;|\; i\in B\}\) and \(\{\mathfrak {h}_{B},f_{i}\;|\; i\in B\}\) respectively. If \(B'\subseteq B\), let \(i_{\pm ,BB'}: \mathfrak {b}^{\pm }_{B'}\to \mathfrak {b}^{\pm }_{B}\) be the standard embedding, and regard \(p_{\pm ,B'B}=i_{\mp ,BB'}^{t}\) as a map \(\mathfrak {b}^{\pm }_{B}\to \mathfrak {b}^{\pm }_{B'}\) via the identifications \(( \mathfrak {b}^{\mp }_{C})^{\star}\cong \mathfrak {b}^{\pm }_{C}\) given by the inner product. Then, \(\ker (p_{\pm , B'B})\) is a Lie subalgebra in \(\mathfrak {b}^{\pm }_{B}\), and therefore \(\{p_{\pm ,B'B}\}\) give the required splitting of the Lie bialgebra \(\mathfrak {b}^{\pm }_{}\).
Note that the restriction of \(i_{\pm,BB'}\) to \(\mathfrak {h}_{B'}\) is the embedding \(\mathfrak {h}_{B'}\hookrightarrow \mathfrak {h}_{B}\), while \(p_{\pm,B'B}:\mathfrak {h}_{B}\to \mathfrak {h}_{B'}\) is the projection corresponding to the decomposition \(\mathfrak {h}_{B}=\mathfrak {h}_{B'}\oplus \mathfrak {h}_{B'}^{\perp}\).
18.11 The symmetric Coxeter category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\)
We describe the Drinfeld–Yetter analogue of the symmetric Coxeter category \(\mathscr{O}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) from 15.2. Let \(\mathsf {DY}_{{ \mathfrak {b}^{-}_{}}}^{{\scriptscriptstyle \operatorname {int}}}\) be the category of integrable Drinfeld–Yetter \(\mathfrak {b}^{-}_{}\)–modules, i.e., \(\mathfrak {h}\)–diagonalisable, endowed with a locally nilpotent action of the elements \(\{f_{i}\}_{i\in \mathbb{D}}\subseteq \mathfrak {b}^{-}_{}\), and satisfying (18.1), so as to give rise to integrable \(\mathfrak {g}\)–modules under the correspondence described in Proposition 18.6. Thus, the generalised braid group \(\mathcal {B}_{W}\) acts on the objects in \(\mathsf {DY}_{{ \mathfrak {b}^{-}_{}}}^{{\scriptscriptstyle \operatorname {int}}}\) via the triple exponential operators \(\widetilde {s}_{i}\), \(i\in \mathbf {I}\). Moreover, \(\mathcal {O}^{{ \scriptscriptstyle \operatorname {int}}}_{\infty ,\mathfrak {g}}\) identifies with a full braided tensor subcategory of \(\mathsf {DY}_{{ \mathfrak {b}^{-}_{}}}^{{\scriptscriptstyle \operatorname {int}}}\). The following is straightforward.
Proposition 34
There is a canonical \((\mathsf {a}^{}_{},\Upsilon _{})\)–strict symmetric Coxeter category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) of type \((\mathbb{D},\underline {m})\) given by the following data.
-
For any \(B\subseteq D\), the symmetric monoidal category \(\mathsf {DY}_{{ \mathfrak {b}^{-}_{B}}}^{{ \scriptscriptstyle \operatorname {int}}}\).
-
For any \(B'\subseteq B\), the restriction functor \(\operatorname{Res}_{B'B}:\mathsf {DY}_{{ \mathfrak {b}^{-}_{B}}}^{{\scriptscriptstyle \operatorname {int}}} \to \mathsf {DY}_{{ \mathfrak {b}^{-}_{B'}}}^{{\scriptscriptstyle \operatorname {int}}}\).
-
For any \(i\in D\), the operator \(S_{i }^{\mathscr{DY}_{}^{\scriptscriptstyle {}}}= \widetilde {s}_{i}\).
Moreover, \(\mathscr{O}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) naturally identifies with a subcategory in \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\).
18.12 Deformations of \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\)
We shall be interested in deformations of the symmetric Coxeter category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\). It is clear that the results of 15.3 extend from category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules to Drinfeld–Yetter \(\mathfrak {b}^{-}_{}\)–modules. Indeed, let \(\mathsf {DY}_{{ \mathfrak {b}^{-}_{}}}^{{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}\) denote the category of deformation integrable Drinfeld–Yetter \(\mathfrak {b}^{-}_{}\)–modules. Since \(\mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty ,\mathfrak {g}}\) identifies with a full braided tensor subcategory of \(\mathsf {DY}_{{ \mathfrak {b}^{-}_{}}}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}\), the algebra \(\mathcal {U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) of the endomorphisms of the forgetful functor \((\mathsf {DY}_{{ \mathfrak {b}^{-}_{}}}^{{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}})^{\boxtimes n}\to \operatorname{{\mathsf{Vect}}}_{\hbar }\) is endowed with a canonical morphism \(\mathcal {U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\to \mathcal {U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\).
Note that the restriction functors preserve the subcategories \(\mathcal {O}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}_{\infty ,\mathfrak {g}_{B}}\), \(B\subseteq \mathbb{D}\), therefore we obtain a cosimplicial lax bidiagrammatic algebra \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\). By restriction to category \(\mathcal {O}^{{\scriptscriptstyle \operatorname {int}}}_{\infty}\) modules, we obtain a canonical morphism \(\varphi ^{\scriptscriptstyle {\bullet}}_{\mathfrak {g}}:\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\to \mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\). This yields the following analogue of Proposition 15.6.
Proposition 35
-
(1)
Every braided Coxeter structure \(\mathbf {C}_{}\) on \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) gives rise to a canonical braided Coxeter category \(\mathscr{DY}_{\mathbf {C}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}}\) on deformation integrable Drinfeld–Yetter modules.
-
(2)
By restriction to integrable category \(\mathcal {O}_{\infty}\) modules, \(\mathbf {C}_{}\) defines a braided Coxeter structure on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\). The corresponding category \(\mathscr{O}_{\mathbf {C}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}}\), defined as in Proposition 15.6, identifies with a subcategory of \(\mathscr{DY}_{\mathbf {C}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}}\).
19 Universal pre–Coxeter structures on diagrammatic Lie bialgebras
We review the definition of the diagrammatic \(\mathsf {PROP}\)s \({ \underline {\mathsf {LBA}}}_{\mathbb{D}}\), \(\underline {\mathsf {DY}}_{\mathbb{D}}^{\scriptscriptstyle {n}}\) and the universal algebra \(\mathbf {U}_{\mathbb{D}}^{\bullet}\) introduced in [3]. The latter is a universal analogue of the cosimplicial bidiagrammatic algebra \(U\mathfrak {g}_{\mathfrak {b}}^{\otimes \bullet}\) given by the enveloping algebra of the double of a split diagrammatic Lie bialgebra.
19.1 \(\mathsf {PROP}\)s [24, 28, 14, 2]
A \(\mathsf {PROP}\) is a \(\mathsf {k}\)–linear, strict, symmetric monoidal category \({\mathsf {P}}\) whose objects are the non–negative integers, and such that \([n]\otimes [m]=[n+m]\). In particular, \([0]\) is the unit object and \([n]=[1]^{\otimes n}\) carries an action of the symmetric group \(\mathfrak {S}_{n}\). A morphism of \(\mathsf {PROP}\)s is a symmetric monoidal functor \(\mathcal {G}: {\mathsf {P}}\to \mathsf {Q}\) which is the identity on objects, and is endowed with the trivial tensor structure
Fix henceforth a complete bracketing \(b_{n}\) on \(n\) letters for any \(n\geqslant 2\), and set \(\mathbf {b}=\{b_{n}\}_{n\geqslant 2}\). A module over \({\mathsf {P}}\) in a symmetric monoidal category \(\mathcal {N}\) is a symmetric monoidal functor \((\mathcal {G},J):{\mathsf {P}}\to \mathcal {N}\) such thatFootnote 30
and the following diagram is commutative

where \(\Phi \) is the associativity constraint in \(\mathcal {N}\).
A morphism of modules over \({\mathsf {P}}\) is a natural transformation of functors. The category of \({\mathsf {P}}\)–modules in \(\mathcal {N}\) is denoted by \(\mathsf {Fun}_{\mathbf {b}}^{\otimes}({\mathsf {P}},\mathcal {N})\).
Example 4
Let \(\mathsf {LA}\) be the \(\mathsf {PROP}\) generated by a morphism \(\mu :[2]\to [1]\), subject to the relations
as morphisms \([2]\to [1]\) and \([3]\to [1]\) respectively. Let \(\mathsf {LA}(\mathsf {k})\) be the category of Lie algebras over a field \(\mathsf {k}\). Note that there is a canonical isomorphism of categories \(\mathsf {Fun}_{\mathbf {b}}^{\otimes }(\mathsf {LA},\operatorname{{\mathsf{Vect}}}_{\mathsf {k}})\to \mathsf {LA}(\mathsf {k})\), which assigns to a functor \(\mathcal {G}\) the Lie algebra \(\mathcal {G}([1])\) with bracket \(\mathcal {G}(\mu ):\mathcal {G}(1)\otimes \mathcal {G}([1])=\mathcal {G}([2])\to \mathcal {G}([1])\). We denote by \(\mathsf{LBA}\) the analogous \(\mathsf {PROP}\) corresponding to Lie bialgebras.
19.2 The Karoubi envelope
Recall that the Karoubi envelope of a category \(\mathcal {C}\) is the category \(\mathsf {Kar}(\mathcal {C})\) whose objects are pairs \((X,\pi )\), where \(X\in \mathcal {C}\) and \(\pi :X\to X\) is an idempotent. The morphisms in \(\mathsf {Kar}(\mathcal {C})\) are defined as
with \(\operatorname{id}_{(X,\pi )}=\pi \). In particular, \({\mathsf {Kar}(\mathcal {C})}((X,\operatorname{id}),(Y,\operatorname{id}))={\mathcal {C}}(X,Y)\), so that the functor \(\mathcal {C}\to \mathsf {Kar}(\mathcal {C})\) which maps \(X\mapsto (X,\operatorname{id})\) and \(f\mapsto f\) is fully faithful.
Every idempotent in \(\mathsf {Kar}(\mathcal {C})\) splits canonically. Namely, if \(q\in \mathsf {Kar}(\mathcal {C})((X,\pi ), (X,\pi ))\) satisfies \(q^{2}=q\), the maps
satisfy \(i\circ p=q\) and \(p\circ i=\operatorname{id}_{(X,q)}\).
If \({\mathsf {P}}\) is a \(\mathsf {PROP}\), we denote by \(\underline {{\mathsf {P}}}\) the closure under infinite direct sums of the Karoubi completion of \({\mathsf {P}}\). By a slight abuse of terminology, in the following we still refer to \(\underline {{\mathsf {P}}}\) as a \(\mathsf {PROP}\). If \(\mathcal {N}\) is a symmetric monoidal category, a module over \(\underline {{\mathsf {P}}}\) in \(\mathcal {N}\) is a symmetric monoidal functor \(\underline {{\mathsf {P}}}\to \mathcal {N}\) such that the composition \({\mathsf {P}}\to \underline {{\mathsf {P}}}\to \mathcal {N}\) is a module over \({\mathsf {P}}\). We denote the category of such modules by \(\mathsf {Fun}_{\mathbf {b}}^{\otimes}( \underline {{\mathsf {P}}},\mathcal {N})\). It is clear that, if \(\mathcal {N}\) is Karoubi complete and closed under infinite direct sums, the pull–back functor
is an equivalence of categories.
19.3 Colored \(\mathsf {PROP}\)s
A colored \(\mathsf {PROP}\) \(\mathsf{P}\) is a \(\mathsf {k}\)–linear, strict, symmetric monoidal category whose objects are finite sequences over a set \(\mathsf {A}\), i.e.,
with tensor product given by the concatenation of sequences, and tensor unit given by the empty sequence. Modules over a colored \(\mathsf {PROP}\) \(\mathsf{P}\) and its closure \(\underline {{\mathsf {P}}}\) are defined as in 19.1 and 19.2, respectively.
19.4 Diagrammatic \(\mathsf {PROP}\)s
Let \(\mathbb{D}\) be a non–empty diagram. We denote by \({ \underline {\mathsf {LBA}}}_{\mathbb{D}}\) the \(\mathsf {PROP}\) generated by a Lie bialgebra object \(([1],\mu ,\delta )\) with a Lie bialgebra idempotent \(\theta _{B}:[1]\to [1]\) for any \(B\subseteq \mathbb{D}\) subject to the relations
-
\(\theta _{\mathbb{D}}=\operatorname{id}_{[1]}\)
-
for any \(B'\subseteq B\), \(\theta _{B'}\circ \theta _{B}=\theta _{B'}=\theta _{B}\circ \theta _{B'}\)
-
for any \(B_{1}\perp B_{2}\), \(\theta _{B_{1}\sqcup B_{2}}=\theta _{B_{1}}+\theta _{B_{2}}\).
The above relations imply in particular that \(\theta _{\emptyset}=0\), and that \(\theta _{B'}\circ \theta _{B''}=0=\theta _{B''}\circ \theta _{B'}\) for any \(B'\perp B''\) since if \(p\), \(q\) are idempotents, \(p+q\) is an idempotent if and only if \(pq=0=qp\).
Remark 30
Note that a module over \(\mathsf{LBA}_{\mathbb{D}}\) in \(\mathcal {N}\) (or equivalently a module over its Karoubi completion \({ \underline {\mathsf {LBA}}}_{\mathbb{D}}\)) is the same as a split diagrammatic Lie bialgebra in \(\mathcal {N}\), as defined in 18.9.
19.5 Universal Drinfeld–Yetter modules
Given a diagram \(\mathbb{D}\) and \(n\geqslant 0\), the category \(\underline {\mathsf {DY}}_{\mathbb{D}}^{\scriptscriptstyle {n}}\) is the colored \(\mathsf {PROP}\) generated by \(n+1\) objects, \([1]\) and \(\{ \underline {\mathsf {V}}_{k}\}_{k=1}^{n}\), and morphisms
-
\(\theta _{B}:[1]\to [1]\), \(B\subseteq \mathbb{D}\)
-
\(\mu :[2]\to [1]\), \(\delta :[1]\to [2]\)
-
\(\pi _{k}:[1]\otimes \underline {\mathsf {V}}_{k}\to \underline {\mathsf {V}}_{k}\) and \(\pi _{k}^{*}: \underline {\mathsf {V}}_{k}\to [1]\otimes \underline {\mathsf {V}}_{k}\)
such that
-
\(([1],\{\theta _{B}\}_{B\subseteq \mathbb{D}},\mu ,\delta )\) is an \({ \underline {\mathsf {LBA}}}_{\mathbb{D}}\)–module in \(\underline {\mathsf {DY}}_{\mathbb{D}}^{\scriptscriptstyle {n}}\)
-
every \(( \underline {\mathsf {V}}_{k},\pi _{k},\pi _{k}^{*})\) is a Drinfeld–Yetter module over \([1]\)
In particular, \(\underline {\mathsf {DY}}_{\mathbb{D}}^{\scriptscriptstyle {0}}={ \underline {\mathsf {LBA}}}_{\mathbb{D}}\).
Remark 31
If \(\mathcal {N}\) is a \(k\)–linear symmetric monoidal category, \(\underline {\mathsf {DY}}_{\mathbb{D}}^{\scriptscriptstyle {n}}\)–modules in \(\mathcal {N}\) are isomorphic to the category whose objects are tuples \((\mathfrak {b};V_{1},\ldots ,V_{n})\) consisting of a split diagrammatic Lie bialgebra \(\mathfrak {b}\) in \(\mathcal {N}\), and \(n\) Drinfeld–Yetter modules \(V_{1},\ldots ,V_{n}\in \mathcal {N}\) over \(\mathfrak {b}\). For any such tuple, we shall refer to the corresponding functor \(\mathcal {G}_{(\mathfrak {b};V_{1},\ldots ,V_{n})}: \underline {\mathsf {DY}}_{\mathbb{D}}^{\scriptscriptstyle {n}}\to \mathcal {N}\) as its realisation functor.
19.6 Universal algebras
For \(B\subseteq \mathbb{D}\) and \(n\geqslant 0\), set
Let \(\mathfrak {b}\) be a split diagrammatic Lie bialgebra and \(\mathfrak {g}_{\mathfrak {b}}\) its Drinfeld double. The algebra \(\mathsf {U}_{B}^{n}\) is a universal analogue of \(U\mathfrak {g}_{B}^{\otimes n}\). Specifically, let \(\mathcal {U}_{\mathfrak {b}_{B}}^{\scriptscriptstyle {n}}\) be the algebra of endomorphisms of the forgetful functor \((\mathsf {DY}_{{\mathfrak {b}_{B}}}^{})^{\boxtimes n}\to \operatorname{{\mathsf{Vect}}}\), and \(\mathscr{U}_{\mathfrak {b}}^{\scriptscriptstyle {\bullet}}\) the corresponding cosimplicial lax bidiagrammatic algebra. Then, the following holds [2, Prop. 8.5 and 8.9].
Proposition 36
-
(1)
For any \(B'\subseteq B\), there is a canonical morphism of algebras \(\mathsf {i}_{BB'}^{n}:\mathsf {U}_{B'}^{n}\to \mathsf {U}_{B}^{n}\). The algebras \(\{\mathsf {U}_{B}^{n}\}_{B\subseteq \mathbb{D}}\) and morphisms \(\{\mathsf {i}_{BB'}^{n}\}_{B'\subseteq B\subseteq \mathbb{D}}\) give rise to a diagrammatic algebra \(\mathbf {U}_{\mathbb{D}}^{n}\) for any \(n\geq 0\).
-
(2)
For any \(B'\subseteq B\), there is a canonical invariant subalgebra \(\mathsf {U}_{BB'}^{n}\subset \mathsf {U}_{B}^{n}\), yielding a bidiagrammatic structure on \(\mathbf {U}_{\mathbb{D}}^{n}\).
-
(3)
For any \(B\subseteq \mathbb{D}\), there is a canonical cosimplicial structure on the tower of algebras \(\{\mathsf {U}_{B}^{n}\}_{n\geqslant 0}\), which is compatible with the morphisms \(\mathsf {i}_{BB'}^{n}\) and the invariant subalgebras, yielding a cosimplicial bidiagrammatic structure \(\mathbf {U}_{\mathbb{D}}^{\bullet}\).
-
(4)
Let \(\mathfrak {b}\) be a split diagrammatic Lie bialgebra. The realisation functors induce a canonical morphism of cosimplicial lax bidiagrammatic algebras \(\rho _{\mathfrak {b}}^{\bullet}: \mathbf {U}_{\mathbb{D}}^{\bullet}\to \mathscr{U}_{\mathfrak {b}}^{\scriptscriptstyle {\bullet}}\).
We describe the diagrammatic subalgebras and morphisms \(\mathsf {i}_{BB'}^{n}\) in 19.7, the subalgebras of invariants in 19.8, the cosimplicial structure in 19.9, and the morphisms \(\rho _{\mathfrak {b}}^{n}: \mathsf {U}_{B}^{n}\to \mathcal {U}_{\mathfrak {b}_{B}}^{\scriptscriptstyle {n}}\) in 19.10.
19.7 Diagrammatic subalgebras
For any \(B'\subseteq B\), there is a canonical realisation functor \(\underline {\mathsf {DY}}^{n}_{B'}\to \underline {\mathsf {DY}}^{n}_{B}\) which sends the object \([1]_{B'}\) in \(\underline {\mathsf {DY}}^{n}_{B'}\) to the Lie bialgebra \(\theta _{B'}([1]_{B})=([1]_{B},\theta _{B'})\) in \(\underline {\mathsf {DY}}^{n}_{B}\), and each \(( \underline {\mathsf {V}}_{B',k},\pi _{B',k},\pi _{B', k}^{*})\) to
where \(\theta _{B'}\) is regarded both as the split injection \(([1]_{B}, \theta _{B'})\to [1]_{B}\) and projection \([1]_{B}\to ([1]_{B},\theta _{B'})\) (cf. 19.2). The functor induces a homomorphism \(\mathsf {i}_{BB'}: \mathsf {U}_{B'}^{n}\to \mathsf {U}_{B}^{n}\), and it is clear that \(\mathsf {i}_{BB}= \operatorname{id}_{\mathsf {U}_{B}^{n}}\), and \(\mathsf {i}_{BB'}\circ \mathsf {i}_{B'B''}=\mathsf {i}_{BB''}\) for any \(B''\subseteq B'\subseteq B\).
Remark 32
We show in [3] that the homomorphism \(\mathsf {i}_{BB'}:\mathsf {U}_{B'}^{n}\to \mathsf {U}_{B}^{n}\) is injective. We shall therefore regard \(\mathsf {U}_{B'}^{n}\) as a subalgebra of \(\mathsf {U}_{B}^{n}\) and, for \(x\in \mathsf {U}_{B'}^{n}\), write \(x\in \mathsf {U}_{B}^{n}\) instead of \(\mathsf {i}_{BB'}(x)\in \mathsf {U}_{B}^{n}\). Moreover, \(\{\mathsf {U}_{B}^{n}\}_{B\subseteq \mathbb{D}}\) is a diagrammatic algebra, since multiplication induces an isomorphism \(\mathsf {U}_{B_{1}\sqcup B_{2}}^{n} \cong \mathsf {U}_{B_{1}}^{n}\otimes \mathsf {U}_{B_{2}}^{n}\) [3, Prop. 10.6 (4)].
19.8 Invariants
For any pair of subdiagrams \(B'\subseteq B\), denote by \(\mathsf {U}_{BB'}^{n}\subseteq \mathsf {U}_{B}^{n}\) the subalgebra of elements which commute with the diagonal action and coaction of \([\mathfrak {b}_{B'}]=([1],\theta _{B'})\) on \(\underline {\mathsf {V}}_{1}\otimes \cdots \otimes \underline {\mathsf {V}}_{n}\). Note that, by [2, Lemma 8.4], \(\mathsf {U}_{BB'}^{n}\) commutes with the diagonal action of \(\mathsf {U}_{B'}^{}\) on \(\underline {\mathsf {V}}_{1}\otimes \cdots \otimes \underline {\mathsf {V}}_{n}\), which is given by
19.9 Cosimplicial structure
For every \(B\subseteq \mathbb{D}\), \(n\geqslant 1\) and \(i=0,\dots , n+1\), there are faithful functors
mapping \([1]\) to \([1]\), and given by
for \(1\leqslant k\leqslant n\), and, for \(1\leqslant i\leqslant n\),
and \(\mathcal {E}_{n}^{(i)}: \underline {\mathsf {DY}}_{B}^{\scriptscriptstyle {n}}\to \underline {\mathsf {DY}}_{B}^{\scriptscriptstyle {n-1}}\)
where \(\mathbf {1}\) is the tensor unit in \(\underline {\mathsf {DY}}_{B}^{\scriptscriptstyle {n}}\), regarded as trivial Drinfeld–Yetter module. These induce algebra homomorphisms
which are universal analogues of the insertion/coproduct maps on \(U\mathfrak {g}_{\mathfrak {b}_{B}}^{\otimes n}\). They endow the tower \(\{\mathsf {U}_{B}^{n}\}_{n\geqslant 0}\) with the structure of a cosimplicial algebra, with Hochschild differential \(d^{n}=\sum _{i=0}^{n+1}(-1)^{i}\Delta _{i}^{n}:\mathsf {U}_{B}^{n}\to \mathsf {U}_{B}^{n+1}\). This structure is compatible with the maps \(\{\mathsf {i}_{BB'}\}_{B'\subseteq B \subseteq D}\) and invariants.
19.10 Realisation functors and endomorphisms
Let \(B\subseteq D\). For any \(n\)–tuple \(\{V_{k},\pi _{k},\pi _{k}^{*}\}_{k=1}^{n}\) of Drinfeld–Yetter modules over \(\mathfrak {b}_{B}\), let
be the corresponding realisation functor. We have the following [2, Prop. 8.7].
Proposition 37
-
(1)
There is an algebra homomorphism
$$ \rho ^{n}_{\mathfrak {b}_{B}}:\mathsf {U}_{B}^{n}\to \mathcal {U}_{\mathfrak {b}_{B}}^{\scriptscriptstyle {n}} $$which assigns to any \(T\in \mathsf {U}_{B}^{n}\), and any \(V_{1},\ldots ,V_{n}\in \mathsf {DY}_{\mathfrak {b}_{B}}\) the endomorphism \(\mathcal {G}_{(\mathfrak {b}_{B};V_{1},\dots , V_{n})}(T)\in \operatorname{End}_{\mathsf {k}}(V_{1} \otimes \cdots \otimes V_{n})\).
-
(2)
The collection of homomorphisms \(\{\rho ^{n}_{\mathfrak {b}_{B}}\}_{B\subseteq \mathbb{D}}\) is a morphism of cosimplicial bidiagrammatic algebras \(\rho ^{\bullet}_{\mathfrak {b}}:\mathbf {U}_{\mathbb{D}}^{\bullet}\to \mathscr{U}_{\mathfrak {b}}^{\scriptscriptstyle {\bullet}}\).
19.11 Gradings and completions
Let \(B\subseteq \mathbb{D}\). The \(\mathsf {PROP}\) \(\underline {\mathsf {DY}}_{B}^{\scriptscriptstyle {n}}\) has a natural ℕ–bigrading given by \(\deg (\sigma )=(0,0)=\deg (\theta _{B'})\) for any \(\sigma \in \mathfrak {S}_{N}\) and \(B'\subseteq B\),
for any \(1\leqslant k\leqslant n\). The algebra \(\mathsf {U}_{B}^{n}\) inherits this bigrading and is concentrated in bidegrees \((N,N)\), since a degree \((p,q)\) morphism with source \(\underline {\mathsf {V}}_{1}\otimes \cdots \otimes \underline {\mathsf {V}}_{n}\) is easily seen to map to \([1]^{\otimes (q-p)}\otimes \underline {\mathsf {V}}_{1}\otimes \cdots \otimes \underline {\mathsf {V}}_{n}\). For any \(a,b\in \mathbb{N}\), the corresponding ℕ–grading determined by mapping \((1,0)\), \((0,1)\) to \(a\), \(b\) respectively yields the same graded completion \(\widehat {\mathsf {U}}_{B}^{n}\) of \(\mathsf {U}_{B}^{n}\), so long as \(a+b>0\). For definiteness, we set \(a=0\) and \(b=1\).
Note that the morphisms \(\mathsf {i}_{BB'}^{n}\) and the cosimplicial structure are compatible with grading, thus yielding a cosimplicial lax bidiagrammatic algebra \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\) given by the collection of the invariant subalgebras \(\widehat {\mathsf {U}}_{BB'}^{n}\subseteq \widehat {\mathsf {U}}_{B}^{n}\), \(B'\subseteq B\), defined as in 19.8.
19.12 Universal pre–Coxeter structures
Let \(\mathfrak {b}\) be a split diagrammatic Lie bialgebra and \(\mathfrak {g}_{\mathfrak {b}}\) its Drinfeld double. By Proposition 19.6, \(\mathbf {U}_{\mathbb{D}}^{\bullet}\) can be thought of as a universal analogue of the cosimplicial bidiagrammatic algebra \(U\mathfrak {g}_{\mathfrak {b}}^{\otimes \bullet}\). In a similar vein, its completion \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\) is a universal analogue of the trivial deformation \({U \mathfrak {g}_{\mathfrak {b}}^{\otimes \bullet}} [\negthinspace [\hbar ]\negthinspace ]\). Namely, let \(\mathcal {U}_{\mathfrak {b}_{B}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},n}}\) be the algebra of endomorphisms of the forgetful functor \((\mathsf {DY}_{{\mathfrak {b}_{B}}}^{ {\scriptscriptstyle \operatorname {\hbar }}})^{\boxtimes n}\to{ \operatorname{{\mathsf{Vect}}}_{\hbar }}\) and \(\mathscr{U}_{\mathfrak {b}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\) the corresponding cosimplicial lax bidiagrammatic algebra. We have the following [2, Sect. 9.7 and Prop. 9.8].
Proposition 38
-
(1)
There is a canonical morphism of cosimplicial lax bidiagrammatic algebras \(\widehat {\rho}_{\mathfrak {b}}^{\bullet}: \widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\to \mathscr{U}_{\mathfrak {b}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\).
-
(2)
A braided pre–Coxeter structure \(\mathfrak {C}_{}=(\Phi _{B}, R_{B}, J_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})\) on \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\) is universal, i.e., for any split diagrammatic Lie bialgebra \(\mathfrak {b}\), it induces one on \(\mathscr{U}_{\mathfrak {b}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\) through \(\widehat {\rho}_{\mathfrak {b}}^{\bullet}\). We denote the resulting braided pre–Coxeter category by \(\mathscr{DY}_{\mathfrak {b},\mathfrak {C}_{}}^{\scriptscriptstyle {}}\).
For the reader’s convenience, we recall the construction of \(\widehat {\rho}_{\mathfrak {b}}^{\bullet}\) from [2, Sect. 9.7]. Let \(\mathfrak {c}\) be a Lie bialgebra and \(\mathsf {DY}_{{\mathfrak {c}}}^{ {\scriptscriptstyle \operatorname {\hbar }}}\) the category of Drinfeld–Yetter \(\mathfrak {c}\)–modules in \(\operatorname{{\mathsf{Vect}}}_{\hbar }\). Scaling the coaction on \(V\in \mathsf {DY}_{{\mathfrak {c}}}^{ {\scriptscriptstyle \operatorname {\hbar }}}\) by \(\hbar \) yields an isomorphism between \(\mathsf {DY}_{{\mathfrak {c}}}^{ {\scriptscriptstyle \operatorname {\hbar }}}\) and the category \(\mathsf {DY}_{{{ \mathfrak {c}}^{\hbar }}}^{ \scriptscriptstyle \operatorname {adm}}\) of Drinfeld–Yetter modules over the Lie bialgebra \({ \mathfrak {c}}^{\hbar }=({ \mathfrak {c}}[\negthinspace [\hbar ]\negthinspace ],[\cdot ,\cdot ],\hbar \delta )\), whose coaction is divisible by \(\hbar \). We denote by \(\mathcal {U}_{\mathfrak {c}}^{n}\) the algebra of endomorphisms of the \(n\)–fold tensor power of the forgetful functor \(\mathsf {f}_{\mathfrak {c}}:\mathsf {DY}_{{\mathfrak {c}}}^{ {\scriptscriptstyle \operatorname {\hbar }}}\to{ \operatorname{{\mathsf{Vect}}}_{\hbar }}\). Note that \(\mathcal {U}_{\mathfrak {c}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},n}}\) identifies canonically with the analogous completion defined for \(\mathsf {DY}_{{{ \mathfrak {c}}^{\hbar }}}^{ \scriptscriptstyle \operatorname {adm}}\).
In the case of the split diagrammatic Lie bialgebra \(\mathfrak {b}\), the realisation functors
corresponding to \(V_{1},\ldots ,V_{n}\in \mathsf {DY}_{{{ \mathfrak {b}}^{\hbar }_{B}}}^{ \scriptscriptstyle \operatorname {adm}}\cong \mathsf {DY}_{{\mathfrak {b}_{B}}}^{ {\scriptscriptstyle \operatorname {\hbar }}}\) induce a homomorphism \(\widehat {\rho}_{\mathfrak {b}}^{n}:\mathbf {U}_{\mathbb{D}}^{n}\to \mathcal {U}_{\mathfrak {b}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},n}}\) which naturally extends to \(\widehat {\mathbf {U}}_{\mathbb{D}}^{n}\). Finally, note that, if \(B'\subseteq B\), the subalgebra of \([\mathfrak {b}_{B'}]\)–invariants in \(\widehat {\mathsf {U}}_{BB'}^{n}\subset \widehat {\mathsf {U}}_{B}^{n}\) is mapped by \(\widehat {\rho}_{\mathfrak {b}_{B}}^{n}\) to elements in \(\mathcal {U}_{\mathfrak {b}_{B}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},n}}\) commuting with the diagonal (co)action of \(\mathfrak {b}_{B'}\).
19.13 Distinguished elements in \(\mathbf {U}_{\mathbb{D}}^{\bullet}\)
There are two distinguished families of elements in \(\mathbf {U}_{\mathbb{D}}^{n}\), namely
where \(1\leqslant i\neq j\leqslant n\) and \(B\subseteq \mathbb{D}\). Note that, for a split diagrammatic Lie bialgebra \(\mathfrak {b}\), under the equivalence between Drinfeld–Yetter \(\mathfrak {b}\)–modules and equicontinuous \(\mathfrak {g}_{\mathfrak {b}}\)–modules described in 18.4, one has
where \(\{b_{k}\}\), \(\{b^{k}\}\) are dual bases of \(\mathfrak {b}_{B}\) and \(\mathfrak {b}_{B}^{*}\). Therefore, the algebra \(\mathbf {U}_{\mathbb{D}}^{\bullet}\) contains the universal analogues of the \(r\)–matrices and the normally ordered Casimir elements of the Drinfeld doubles \(\mathfrak {g}_{\mathfrak {b}_{B}}\), \(B\subseteq \mathbb{D}\).
Set \(\boldsymbol {\Omega }^{ij}_{B}=\mathbf {r}^{ij}_{B}+\mathbf {r}^{ji}_{B}\). As in Lemma 16.1.2, we obtain a morphism of algebras \(\xi _{B}^{n}: \widehat {\mathfrak {t}}_{}^{\scriptscriptstyle {n}}\to \widehat {\mathbf {U}}_{B}^{n}\) given by the assignment \(\xi _{B}^{n}(\mathsf {t}^{ij})=\boldsymbol {\Omega }^{ij}_{B}\). Therefore, any universal associator \(\Phi \in \widehat {\mathfrak {t}}_{}^{\scriptscriptstyle {3}}\) is naturally realised in \(\widehat {\mathbf {U}}_{B}^{3}\) as \(\Phi _{B}=\xi _{B}^{3}(\Phi )\). Note also that, if \(\Phi \) is a Lie associator, then for any \(B_{1}\perp B_{2}\) one has \(\Phi _{B_{1}\sqcup B_{2}}=\Phi _{B_{1}}\cdot \Phi _{B_{2}}\). In the following, we shall be interested in braided pre–Coxeter structure on \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\) whose diagrammatic associators \(\Phi _{B}\) are uniformly determined by a fixed Lie associatorFootnote 31\(\Phi \in \widehat {\mathfrak {t}}_{}^{\scriptscriptstyle {3}}\) and \(R_{B}=\exp (\boldsymbol {\Omega }^{}_{B}/2)\).
20 Quantisation of diagrammatic Lie bialgebras
In this section, we review the notion of admissible Drinfeld–Yetter module over a quantised universal enveloping algebra (QUE) introduced in [1]. The category of such modules over a split diagrammatic QUE \(\mathfrak {B}\) gives rise to a braided pre–Coxeter category \(\mathscr{DY}_{\mathfrak {B}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\). When \(\mathfrak {B}\) is the Etingof–Kazhdan quantisation of a split diagrammatic Lie bialgebra \(\mathfrak {b}\), we outline the construction of a Tannakian equivalence between \(\mathscr{DY}_{\mathfrak {B}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) and a braided pre–Coxeter category of deformation Drinfeld–Yetter modules over \(\mathfrak {b}\) arising from the universal diagrammatic algebra \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\) obtained in [1, 2].
20.1 Drinfeld–Yetter modules over a Hopf algebra [16, 38]
A Drinfeld–Yetter module over a Hopf algebra \(\mathfrak {B}\) is a triple \((\mathcal {V},\pi _{\mathcal {V}},\pi _{\mathcal {V}}^{*}) \), where \((\mathcal {V},\pi _{\mathcal {V}})\) is a left \(\mathfrak {B}\)–module, \((\mathcal {V},\pi ^{*}_{\mathcal {V}})\) a right \(\mathfrak {B}\)–comodule, and the maps \(\pi _{\mathcal {V}}:\mathfrak {B}\otimes \mathcal {V}\to \mathcal {V}\) and \(\pi _{\mathcal {V}}^{*}:\mathcal {V}\to \mathfrak {B}\otimes \mathcal {V}\) satisfy the following compatibility condition:
where \(m^{(3)}:\mathfrak {B}^{\otimes 3}\to \mathfrak {B}\) and \(\Delta ^{(3)}:\mathfrak {B}\to \mathfrak {B}^{\otimes 3}\) are the iterated multiplication and comultiplication respectively, and \(S:\mathfrak {B}\to \mathfrak {B}\) is the antipode.
The category \(\mathsf {DY}_{\mathfrak {B}}\) of such modules is a braided monoidal category. For any \(\mathcal {V},\mathcal {W}\in \mathsf {DY}_{\mathfrak {B}}\), the action and coaction on the tensor product \(\mathcal {V}\otimes \mathcal {W}\) are defined by
The associativity constraints are trivial, and the braiding is \(\beta _{\mathcal {V}\mathcal {W}}= (1\,2)\circ R_{\mathcal {V}\mathcal {W}}\), where the \(R\)–matrix \(R_{\mathcal {V}\mathcal {W}}\in \operatorname{End}(\mathcal {V}\otimes \mathcal {W})\) is defined by
The linear map \(R_{\mathcal {V}\mathcal {W}}\) is invertible, with inverse
20.2 The finite quantum double [10]
Let \(\mathfrak {B}\) be a finite–dimensional Hopf algebra, and \(\mathfrak {B}^{\circ}\) the dual Hopf algebra \(\mathfrak {B}^{*}\) with opposite coproduct. The quantum double of \(\mathfrak {B}\) is the unique quasitriangular Hopf algebra \((D\mathfrak {B}, R)\) such that 1) \(D\mathfrak {B}= \mathfrak {B}\otimes \mathfrak {B}^{\circ}\) as vector spaces 2) \(\mathfrak {B}\) and \(\mathfrak {B}^{\circ}\) are Hopf subalgebras of \(D\mathfrak {B}\) and 3) \(R\) is the canonical element in \(\mathfrak {B}\otimes \mathfrak {B}^{\circ}\subset D\mathfrak {B}\otimes D\mathfrak {B}\). The category \(\operatorname{Rep}D \mathfrak {B}\) is readily seen to be canonically isomorphic, as a braided monoidal category, to \(\mathsf {DY}_{\mathfrak {B}}\) (see e.g., [1, Appendix A]).
20.3 Quantum double for QUEs
The construction of the quantum double can be adapted to quantised universal enveloping algebras (QUE). Recall that a QUE is a topological Hopf algebra \(\mathfrak {B}\) over \({ \mathbb{C}}[\negthinspace [\hbar ]\negthinspace ]\) which reduces modulo \(\hbar \) to an enveloping algebra \(U\mathfrak {b}\) for some Lie bialgebra \(\mathfrak {b}\), and is such that, for any \(x\in \mathfrak {b}\),
where \(\widetilde {x}\in \mathfrak {B}\) is any lift of \(x\). A QUE is of finite type if the underlying Lie bialgebra \(\mathfrak {b}\) is finite–dimensional. In this case, the dual \(\mathfrak {B}^{*}\) is a quantised formal series Hopf algebra (QFSH), i.e., a topological Hopf algebra over \({ \mathbb{C}}[\negthinspace [\hbar ]\negthinspace ]\) which reduces modulo \(\hbar \) to \(\widehat {S\mathfrak {b}}=\prod _{n}S^{n}\mathfrak {b}\). Conversely, the dual of a QFSH of finite type is a QUE (cf. [10, 19] or [1, Sect. 2.19]).
If \(\mathfrak {B}\) is a QUE, set
where \(\Delta ^{(n)}:\mathfrak {B}\to \mathfrak {B}^{\otimes n}\) is the iterated coproduct. Then, \(\mathfrak {B}'\) is a Hopf subalgebra of \(\mathfrak {B}\), and a QFSH. In particular, if \(\mathfrak {B}\) is of finite type, \(\mathfrak {B}^{\vee}=(\mathfrak {B}')^{*}\) is a QUE. As in 20.2, \((\mathfrak {B}, \mathfrak {B}^{\vee})\) is a matched pair of Hopf algebras [1, A.5]. The double cross product \(D\mathfrak {B}= \mathfrak {B}\negthinspace \triangleright \negthinspace \negthinspace \triangleleft \negthinspace \; \mathfrak {B}^{\vee}\) is a quasitriangular QUE, whose \(R\)–matrix is the canonical element \(R\in \mathfrak {B}'\otimes \mathfrak {B}^{\vee}\), and underlying Lie bialgebra the Drinfeld double \(\mathfrak {g}_{\mathfrak {b}}=\mathfrak {b}\oplus \mathfrak {b}^{*}\).
This construction extends to the case of finitely ℕ–graded QUEs, i.e., ℕ–graded Hopf algebras \(\mathfrak {B}=\bigoplus _{n\geqslant 0} \mathfrak {B}_{n}\) such that \(\mathfrak {B}_{0}\) is a QUE of finite type, and each \(\mathfrak {B}_{n}\) is a finitely generated \(\mathfrak {B}_{0}\)–module. Note that such a QUE is a quantisation of an ℕ–graded Lie bialgebra with finite–dimensional components and cobracket of degree \(d=0\) (cf. 18.2). Moreover, \(\mathfrak {B}'=\bigoplus _{n\geqslant 0}(\mathfrak {B}'\cap \mathfrak {B}_{n})\) is also graded, and its restricted dual \(\mathfrak {B}^{\star}=\bigoplus _{n\geqslant 0}(\mathfrak {B}'\cap \mathfrak {B}_{n})^{*}\) is a finitely ℕ–graded QUE quantising the restricted dual Lie bialgebra \(\mathfrak {b}^{\star}\). The double cross product \((D\mathfrak {B})^{\scriptscriptstyle \operatorname {res}}= \mathfrak {B}\;\negthinspace \triangleright \negthinspace \negthinspace \triangleleft \negthinspace \;\;\mathfrak {B}^{\star}\) is called the restricted quantum double of \(\mathfrak {B}\). \((D\mathfrak {B})^{\scriptscriptstyle \operatorname {res}}\) is a quasitriangular, finitely ℤ–graded QUE whose \(R\)–matrix is the canonical element in the graded completion of \(\mathfrak {B}'\otimes \mathfrak {B}^{\star}\), and underlying Lie bialgebra is the restricted Drinfeld double \(\mathfrak {g}_{\mathfrak {b}}^{\scriptscriptstyle \operatorname {res}}=\mathfrak {b}\oplus \mathfrak {b}^{\star}\).
Example 5
Let \(\mathfrak {g}\) be a symmetrisable Kac–Moody algebra. It is well–known (cf. [10] or [2, 13.1]) that the quantum group \(U_{\hbar }\mathfrak {g}\) is isomorphic to a quotient of the restricted quantum double of \(U_{\hbar }\mathfrak {b}^{-}_{}\). This isomorphism yields the universal \(R\)–matrix \(\mathbf {R}\in U_{\hbar }\mathfrak {b}^{-}_{}\widehat {\otimes }U_{\hbar }\mathfrak {b}^{+}_{}\) described in 17.2, and reduces modulo \(\hbar \) to the classical isomorphism described in Proposition 18.5.
20.4 Admissible Drinfeld–Yetter modules over a QUE [1]
If \(\mathfrak {B}\) is a QUE, the categories of Drinfeld–Yetter \(\mathfrak {B}\)–modules and modules over \((D\mathfrak {B})^{\scriptscriptstyle \operatorname {res}}\) are not equivalent, even when \(\mathfrak {B}\) is of finite type. This motivates the following definition, due to P. Etingof.
A Drinfeld–Yetter module \((\mathcal {V},\pi _{\mathcal {V}},\pi ^{*}_{\mathcal {V}})\) over \(\mathfrak {B}\) is admissible if the coaction \(\pi ^{*}_{\mathcal {V}}:\mathcal {V}\to \mathfrak {B}\otimes \mathcal {V}\) factors through \(\mathfrak {B}'\otimes \mathcal {V}\), where ⊗ is the \(\hbar \)–adic tensor product, and \(\mathfrak {B}'\) is endowed with topology induced by the \(\hbar \)–adic topology on \(\mathfrak {B}\), so that \(\mathfrak {B}'\otimes \mathcal {V}\subset \mathfrak {B}\otimes \mathcal {V}\).Footnote 32 We denote the category of such modules by \(\mathsf {DY}^{\scriptscriptstyle \operatorname {adm}}_{\mathfrak {B}}\). If ℬ is a quantisation of \(\mathfrak {b}\), the category \(\mathsf {DY}^{\scriptscriptstyle \operatorname {adm}}_{\mathfrak {B}}\) reduces modulo \(\hbar \) to \(\mathsf {DY}_{\mathfrak {b}}\). Moreover, we observe in [2, Sect. 6.4] that, if \(\mathfrak {B}\) is a finitely ℕ–graded QUE, there is a canonical isomorphism between \(\mathsf {DY}^{\scriptscriptstyle \operatorname {adm}}_{\mathfrak {B}}\) and the category of \((D\mathfrak {B})^{\scriptscriptstyle \operatorname {res}}\)–modules with a locally finite action of \(\mathfrak {B}^{\star}\).
Example 6
Let \(\mathfrak {g}\) be a symmetrisable Kac–Moody algebra. In analogy with Proposition 18.6, one can identify \(\mathcal {O}_{\infty , U_{\hbar }\mathfrak {g}}\) with a full tensor subcategory of \(\mathsf {DY}_{{U_{\hbar }\mathfrak {b}^{-}_{}}}^{ \scriptscriptstyle \operatorname {adm}}\) whose objects satisfy the condition (18.1). Similarly, \(\mathcal {O}_{\infty , U_{\hbar }\mathfrak {g}}^{{ \scriptscriptstyle \operatorname {int}}}\) identifies with a subcategory of integrable admissible Drinfeld–Yetter \(U_{\hbar }\mathfrak {b}^{-}_{}\)–modules (cf. [2, Sect. 13.3]).
20.5 Diagrammatic Hopf algebras [2]
By analogy with Sect. 6.1, a diagrammatic Hopf algebra is a monoidal functor from \(\mathcal {P}(\mathbb{D})\) to the category of Hopf bialgebras. Specifically, adiagrammatic Hopf algebra is the datum of
-
a diagram \(\mathbb{D}\)
-
for any \(B\subseteq \mathbb{D}\), a Hopf algebra \(\mathfrak {B}_{B}\)
-
for any \(B'\subseteq B\), a morphism of Hopf algebras \(i_{BB'}:\mathfrak {B}_{B'}\to \mathfrak {B}_{B}\)
such that
-
for any \(B\subseteq \mathbb{D}\), \(i_{BB}=\operatorname{id}_{\mathfrak {B}_{B}}\)
-
for any \(B''\subseteq B'\subseteq B\), \(i_{BB'}\circ i_{B'B''}=i_{BB''}\)
-
for any \(B_{1}\sqcup B_{2}\),
$$ m_{B_{1}\sqcup B_{2}}\circ i_{(B_{1}\sqcup B_{2})B_{1}}\otimes i_{(B_{1} \sqcup B_{2})B_{2}}:\mathfrak {B}_{B_{1}}\otimes \mathfrak {B}_{B_{2}}\to \mathfrak {B}_{B_{1} \sqcup B_{2}} $$is an isomorphism of Hopf algebras, where \(m_{B_{1}\sqcup B_{2}}\) is the multiplication of \(\mathfrak {B}_{B_{1}\sqcup B_{2}}\).
Diagrammatic QUEs are defined similarly.
20.6 Split diagrammatic Hopf algebras [2]
Recall that a split pair of Hopf algebras is the datum of two Hopf algebras \(\mathfrak {A}\), \(\mathfrak {B}\) together with Hopf algebra morphisms \(\mathfrak {A}\xrightarrow{i} \mathfrak {B}\xrightarrow {p}\mathfrak {A}\) such that \(p\circ i=\operatorname{id}_{\mathfrak {A}}\) [1, Sect. 4.6]. A split diagrammatic Hopf algebra is a diagrammatic Hopf algebra \(\mathfrak {B}=\{\mathfrak {B}_{B}\}_{B\subseteq D}\), together with Hopf algebra morphisms \(p_{B'B}:\mathfrak {B}_{B}\to \mathfrak {B}_{B'}\) for any \(B'\subseteq B\), such that \(p_{B'B}\circ i _{BB'}=\operatorname{id}_{\mathfrak {B}_{B'}}\) and
-
for any \(B\), \(p_{BB}=\operatorname{id}_{\mathfrak {b}_{B}}\)
-
for any \(B''\subseteq B'\subseteq B\), \(p_{B''B'}\circ p_{B'B}=p_{B''B}\)
-
for any \(B_{1}\perp B_{2}\), \(p_{B_{1}(B_{1}\sqcup B_{2})}\otimes p_{B_{2}(B_{1}\sqcup B_{2})}\circ \Delta _{B_{1}\sqcup B_{2}}:\mathfrak {B}_{B_{1}\sqcup B_{2}}\to \mathfrak {B}_{B_{1}} \otimes \mathfrak {B}_{B_{2}}\) is a morphism of Hopf algebras, and the inverse of \(m_{B_{1}\sqcup B_{2}}\circ i_{(B_{1}\sqcup B_{2})B_{1}}\otimes i_{(B_{1} \sqcup B_{2})B_{2}}\).
Split diagrammatic QUEs are defined similarly.
Remark 33
Note that, if \(\mathfrak {B}\) is a split diagrammatic Hopf algebra, where \(\mathfrak {B}_{B}\) are finitely ℕ–graded QUE, there is a diagrammatic QUE \((D\mathfrak {B})^{\scriptscriptstyle \operatorname {res}}\) with \((D\mathfrak {B})^{\scriptscriptstyle \operatorname {res}}_{B}=(D\mathfrak {B}_{B})^{\scriptscriptstyle \operatorname {res}}\), endowed with a canonical embedding of diagrammatic Hopf algebras \(\mathfrak {B}\to (D\mathfrak {B})^{\scriptscriptstyle \operatorname {res}}\).
Example 7
Let \(\mathfrak {g}\) be a diagrammatic Kac–Moody algebra. The algebra \(U_{\hbar }\mathfrak {b}^{-}_{}\) is a finitely ℕ–graded split diagrammatic QUE and therefore \(U_{\hbar }\mathfrak {g}\), as a quotient of \((DU_{\hbar }\mathfrak {b}^{-}_{})^{\scriptscriptstyle \operatorname {res}}\), is a finitely ℤ–graded diagrammatic QUE.
20.7 Drinfeld–Yetter modules over split diagrammatic Hopf algebras
If \(\mathfrak {A}\leftrightarrows \mathfrak {B}\) is a split pair of Hopf algebras, there is a monoidal restriction functor \(\operatorname{Res}_{\mathfrak {A},\mathfrak {B}}:\mathsf {DY}_{\mathfrak {B}}\to \mathsf {DY}_{\mathfrak {A}}\) given by
If \(\mathfrak {A}\), \(\mathfrak {B}\) are QUEs, \(\operatorname{Res}_{\mathfrak {A},\mathfrak {B}}\) restricts to a functor \(\mathsf {DY}^{\scriptscriptstyle \operatorname {adm}}_{\mathfrak {B}} \to \mathsf {DY}^{\scriptscriptstyle \operatorname {adm}}_{\mathfrak {A}}\).
Proposition 39
Let \(\mathfrak {B}\) be a split diagrammatic Hopf algebra. Then, there is an \((\mathsf {a}^{}_{},\Upsilon _{})\)–strict braided pre–Coxeter category \(\mathscr{DY}_{\mathfrak {B}}^{\scriptscriptstyle {}}\) defined by the following data
-
For any \(B\subseteq \mathbb{D}\), the braided monoidal category \(\mathsf {DY}_{\mathfrak {B}_{B}}\).
-
For any \(B'\subseteq B\), the restriction functor \(\operatorname{Res}_{\mathfrak {B}_{B'},\mathfrak {B}_{B}}:\mathsf {DY}_{\mathfrak {B}_{B}}\to \mathsf {DY}_{\mathfrak {B}_{B'}}\).
In the case of a split diagrammatic QUE, we have a braided pre–Coxeter subcategory \(\mathscr{DY}_{\mathfrak {B}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) given by admissible Drinfeld–Yetter modules.
20.8 Quantisation of diagrammatic Lie bialgebras
In [15, 16], Etingof and Kazhdan construct a quantisation functor \(\mathcal {Q}\) from the category of Lie bialgebras to the category of QUEs. We observe in [2, Prop. 6.8] that \(\mathcal {Q}\) respects direct sums, i.e., for any Lie bialgebras \(\mathfrak {a}\), \(\mathfrak {b}\), there is an isomorphism of Hopf algebras \(J_{\mathfrak {a},\mathfrak {b}}:\mathcal {Q}(\mathfrak {a})\otimes \mathcal {Q}(\mathfrak {b})\to \mathcal {Q}(\mathfrak {a}\oplus \mathfrak {b})\). It follows that the quantisation of a (split) diagrammatic Lie bialgebra is a (split) diagrammatic QUE. Thus, for any split diagrammatic Lie bialgebra \(\mathfrak {b}\), we have the braided pre–Coxeter category \(\mathscr{DY}_{\mathcal {Q}(\mathfrak {b})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\), which reduces modulo \(\hbar \) to the category \(\mathscr{DY}_{\mathfrak {b}}^{\scriptscriptstyle {}}\) defined in 18.9.
Example 8
Let \(\mathfrak {g}\) be a symmetrisable Kac–Moody algebra. By [17], there are isomorphisms \(\mathcal {Q}( \mathfrak {b}^{\pm }_{})\simeq U_{\hbar }\mathfrak {b}^{\pm }_{}\) and \(\mathcal {Q}(\mathfrak {g})\simeq U_{\hbar }\mathfrak {g}\). In [2, Prop. 13.6], we observe that, in the case of a diagrammatic Kac–Moody algebra, the isomorphisms preserve the (split) diagrammatic structure.
20.9 Universal structures arising from quantisation
Let \(\mathfrak {b}\) be a Lie bialgebra and \(\Phi \) a Lie associator. In [15], Etingof and Kazhdan define an equivalence of braided monoidal categories \(H_{\mathfrak {b}}:\mathsf {DY}_{{\mathfrak {b}}}^{\Phi}\to \mathsf {DY}^{\scriptscriptstyle \operatorname {adm}}_{\mathcal {Q}(\mathfrak {b})}\), where \(\mathsf {DY}_{{\mathfrak {b}}}^{\Phi}\) denotes the Drinfeld category, i.e., deformation Drinfeld–Yetter \(\mathfrak {b}\)–modules with associativity and commutativity constraints given by \(\Phi _{\mathfrak {b}}= \widehat {\rho}_{\mathfrak {b}}^{3}(\Phi )\) and \(R_{B}=\exp (\hbar /2\cdot \Omega _{B})\).
In [2], this result is extended to a split diagrammatic Lie bialgebra \(\mathfrak {b}\) with underlying diagram \(\mathbb{D}\). Specifically, the following holds.
Theorem 16
[2, Thm. 10.2 and 10.10]
-
(1)
Let \(\Phi \) be a Lie associator. There is a canonical \(\Upsilon _{}\)–strict braided pre–Coxeter structure
 on \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\) which is trivial in degree zero, and is such that \(\Phi _{B}=\xi _{B}^{3}(\Phi )\) for any \(B\subseteq \mathbb{D}\) (cf. Remark 19.12–(2)).
on \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\) which is trivial in degree zero, and is such that \(\Phi _{B}=\xi _{B}^{3}(\Phi )\) for any \(B\subseteq \mathbb{D}\) (cf. Remark 19.12–(2)). -
(2)
Set
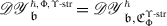 . There is a canonical equivalence of braided pre–Coxeter categories
. There is a canonical equivalence of braided pre–Coxeter categories 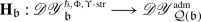
whose diagrammatic equivalences are given by the Etingof–Kazhdan functors \(H_{\mathfrak {b}_{B}}:\mathsf {DY}_{{\mathfrak {b}_{B}}}^{{\scriptscriptstyle \operatorname {\hbar }},\Phi _{B}}\to \mathsf {DY}^{\scriptscriptstyle \operatorname {adm}}_{\mathcal {Q}(\mathfrak {b}_{B})}\), \(B\subseteq D\).
Remark 34
The main ingredients of the pre–Coxeter structure  and equivalence \(\mathbf {H}_{\mathfrak {b}}\) are the following.
and equivalence \(\mathbf {H}_{\mathfrak {b}}\) are the following.
-
(1)
For any \(B'\subseteq B\), the tensor structure \(J_{B'B}^{\Phi}\) on the restriction functor \(\operatorname{Res}_{B'B}:\mathsf {DY}_{{\mathfrak {b}_{B}}}^{{\scriptscriptstyle \operatorname {\hbar }},\Phi _{B}}\to \mathsf {DY}_{{\mathfrak {b}_{B'}}}^{{\scriptscriptstyle \operatorname {\hbar }},\Phi _{B'}}\) and the vertical join \(\mathsf {a}^{B'}_{B''B}:\operatorname{Res}_{B''B'}\circ \operatorname{Res}_{B'B}\Rightarrow \operatorname{Res}_{B''B}\), are constructed in [1, Thm. 1.5], and determine the \(\Upsilon _{}\)–strict braided pre–Coxeter structure
 .
. -
(2)
The horizontal equivalences \(\mathsf {DY}_{{\mathfrak {b}_{B}}}^{{\scriptscriptstyle \operatorname {\hbar }},\Phi _{B}}\to \mathsf {DY}^{\scriptscriptstyle \operatorname {adm}}_{\mathcal {Q}(\mathfrak {b}_{B})}\) of braided tensor categories are the Etingof–Kazhdan Tannakian equivalences \(H_{\mathfrak {b}_{B}}\).
-
(3)
The diagonal isomorphism of tensor functors \(\gamma _{B'B}:H_{B'}\circ \operatorname{Res}_{B'B}\Rightarrow \operatorname{Res}_{B'B}^{\hbar} \circ H_{B}\), \(B'\subseteq B\), are constructed in [1, Thm. 1.7].
Note that, by Proposition 7.5, we obtain an \(\mathsf {a}^{}_{}\)–strict braided Coxeter structure  and the corresponding category
and the corresponding category  , which is canonically equivalent to
, which is canonically equivalent to  and therefore to \(\mathscr{DY}_{\mathcal {Q}(\mathfrak {b})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) via \(\mathbf {H}_{\mathfrak {b}}\).
and therefore to \(\mathscr{DY}_{\mathcal {Q}(\mathfrak {b})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) via \(\mathbf {H}_{\mathfrak {b}}\).
20.10 Universality
The category  is universal in that its essential data are described by the diagrammatic \(\mathsf {PROP}\)s \(\underline {\mathsf {DY}}_{\mathbb{D}}^{\scriptscriptstyle {n}}\), \(n\geqslant 0\). The category \(\mathscr{DY}_{\mathcal {Q}(\mathfrak {b})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) and the equivalence
is universal in that its essential data are described by the diagrammatic \(\mathsf {PROP}\)s \(\underline {\mathsf {DY}}_{\mathbb{D}}^{\scriptscriptstyle {n}}\), \(n\geqslant 0\). The category \(\mathscr{DY}_{\mathcal {Q}(\mathfrak {b})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) and the equivalence  are also universal as we briefly explain below. For further details, we refer the reader to [1, Sect. 6.17] and [2, Sect. 10.7].
are also universal as we briefly explain below. For further details, we refer the reader to [1, Sect. 6.17] and [2, Sect. 10.7].
Let \(\underline {\mathsf {DY}}_{\mathsf{QUE}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) be the \(\mathsf {PROP}\) describing an admissible Drinfeld–Yetter module over a QUE. The category \(\mathsf {DY}_{{\mathcal {Q}(\mathfrak {b})}}^{ \scriptscriptstyle \operatorname {adm}}\) is isomorphic to that of realisation functors from \(\underline {\mathsf {DY}}_{\mathsf{QUE}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) to \(\operatorname{{\mathsf{Vect}}}_{\hbar }\). It follows that the essential data defining the braided pre–Coxeter category \(\mathscr{DY}_{\mathcal {Q}(\mathfrak {b})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) is entirely encoded by the diagrammatic \(\mathsf {PROP}\)s \(\underline {\mathsf {DY}}_{\mathsf{QUE},\mathbb{D}}^{\scriptscriptstyle {n, \scriptscriptstyle \operatorname {adm}}}\) describing \(n\) admissible Drinfeld–Yetter modules over a split diagrammatic QUE. Therefore, the braided pre–Coxeter structure on \(\mathscr{DY}_{\mathcal {Q}(\mathfrak {b})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) is clearly universal, induced by the standard braided pre–Coxeter structure of the quantum universal diagrammatic algebra \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\hbar ,\bullet}\) naturally associated to \(\underline {\mathsf {DY}}_{\mathsf{QUE},\mathbb{D}}^{\scriptscriptstyle {\bullet , \scriptscriptstyle \operatorname {adm}}}\) (as in 19.6).
The universality of the equivalence  is more subtle. Roughly, this means that every datum listed in Remark 20.9 admits a suitable universal counterpart. For instance, the Etingof–Kazhdan functor \(H_{\mathfrak {b}}\) with its tensor structure arises as the pullback of a morphism of topological \(\mathsf {PROP}\)s \({\mathsf{H}}: \underline {\mathsf {DY}}_{\mathsf{QUE}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\to \widehat { \underline {\mathsf {DY}}_{}^{\scriptscriptstyle {}}}_{\mathsf{LBA}}\), where the latter is a graded completion of the \(\mathsf {PROP}\) \({ \underline {\mathsf {DY}}_{\mathsf{LBA}}^{\scriptscriptstyle {}}}\) describing a Drinfeld–Yetter module over a Lie bialgebra (cf. 19.5) and \(H\) depends upon the choice of a universal associator \(\Phi \) and a universal twist \(J^{\Phi}\).
is more subtle. Roughly, this means that every datum listed in Remark 20.9 admits a suitable universal counterpart. For instance, the Etingof–Kazhdan functor \(H_{\mathfrak {b}}\) with its tensor structure arises as the pullback of a morphism of topological \(\mathsf {PROP}\)s \({\mathsf{H}}: \underline {\mathsf {DY}}_{\mathsf{QUE}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\to \widehat { \underline {\mathsf {DY}}_{}^{\scriptscriptstyle {}}}_{\mathsf{LBA}}\), where the latter is a graded completion of the \(\mathsf {PROP}\) \({ \underline {\mathsf {DY}}_{\mathsf{LBA}}^{\scriptscriptstyle {}}}\) describing a Drinfeld–Yetter module over a Lie bialgebra (cf. 19.5) and \(H\) depends upon the choice of a universal associator \(\Phi \) and a universal twist \(J^{\Phi}\).
The restriction functors are similarly obtained through morphisms of \(\mathsf {PROP}\)s involving a universal split pair. Namely, let \(\underline {\mathsf {DY}}_{\mathsf{LBA, sp}}^{\scriptscriptstyle {}}\) (resp. \(\underline {\mathsf {DY}}_{\mathsf{QUE, sp}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\)) denote the \(\mathsf {PROP}\)s describing a Drinfeld–Yetter module over a split pair of Lie bialgebras \([\mathfrak {a}]\to [\mathfrak {b}]\) (resp. over a split pair of QUEs \([A]\to [B]\)). Given a split pair of Lie bialgebras \(\mathfrak {a}\to \mathfrak {b}\), we realise the restriction functor \(\mathsf {DY}_{{\mathfrak {b}}}^{{\scriptscriptstyle \operatorname {\hbar }},\Phi}\to \mathsf {DY}_{{\mathfrak {a}}}^{{\scriptscriptstyle \operatorname {\hbar }},\Phi}\) as a morphism of \(\mathsf {PROP}\)s \(\widehat { \underline {\mathsf {DY}}_{}^{\scriptscriptstyle {}}}_{\mathsf{LBA}}\to \widehat { \underline {\mathsf {DY}}_{}^{\scriptscriptstyle {}}}_{\mathsf{LBA,sp}}\) mapping the generating objects of \(\mathsf{LBA}\) to \([\mathfrak {a}]\), depending upon the upon the choice of a Lie associator \(\Phi \) and a universal relative twist \(J^{\Phi}_{[\mathfrak {a}],[\mathfrak {b}]}\). Finally, we prove that the natural isomorphism \(\gamma \) is also universal, i.e., it is induced by a natural isomorphism

Remark 35
Let \(\underline {\mathsf {DY}}_{\mathsf{UE_{cP}}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) be the \(\mathsf {PROP}\) describing an admissible Drinfeld–Yetter module over a co–Poisson universal enveloping algebra, so that the category \(\mathsf {DY}_{{\mathfrak {b}}}^{ {\scriptscriptstyle \operatorname {\hbar }}}\simeq \mathsf {DY}_{{{U \mathfrak {b}}[\negthinspace [\hbar ]\negthinspace ]}}^{ \scriptscriptstyle \operatorname {adm}}\) is equivalent to that of realisation functors from \(\underline {\mathsf {DY}}_{\mathsf{UE_{cP}}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) to \(\operatorname{{\mathsf{Vect}}}_{\hbar }\). Restricting the above constructions to \(\underline {\mathsf {DY}}_{\mathsf{UE_{cP}}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\), we obtained in [1, Sect. 6.17] an alternative proof of the invertibility of the Etingof–Kazhdan functor \(H_{\mathfrak {b}}\).
21 Universal Coxeter structures on Kac–Moody algebras
We enhance the results of Sect. 19 by introducing the \(\mathsf {PROP}\)  as a refinement of \({ \underline {\mathsf {LBA}}}_{\mathbb{D}}\) modelled over the set of non–negative roots of a Kac–Moody algebra. The corresponding universal algebra
as a refinement of \({ \underline {\mathsf {LBA}}}_{\mathbb{D}}\) modelled over the set of non–negative roots of a Kac–Moody algebra. The corresponding universal algebra  interpolates between \(\mathscr{O}_{\mathbf {R}{},\mathbf {S}_{}}^{\scriptscriptstyle {\hbar ,{ \scriptscriptstyle \operatorname {int}}}}\) and \(\mathscr{O}_{\nabla}^{\scriptscriptstyle {{ \scriptscriptstyle \operatorname {int}}}}\). Specifically, we will prove in Sect. 22 that it is endowed with morphisms
interpolates between \(\mathscr{O}_{\mathbf {R}{},\mathbf {S}_{}}^{\scriptscriptstyle {\hbar ,{ \scriptscriptstyle \operatorname {int}}}}\) and \(\mathscr{O}_{\nabla}^{\scriptscriptstyle {{ \scriptscriptstyle \operatorname {int}}}}\). Specifically, we will prove in Sect. 22 that it is endowed with morphisms  , and therefore contains the data defining both categories.
, and therefore contains the data defining both categories.
21.1
 –graded diagrammatic Lie bialgebras
–graded diagrammatic Lie bialgebras
Let \(\mathfrak {g}\) be a symmetrisable Kac–Moody algebra with Cartan subalgebra \(\mathfrak {h}\subset \mathfrak {g}\), Dynkin diagram \(\mathbb{D}\), and root system  . For any \(B\subseteq \mathbb{D}\), we denote by
. For any \(B\subseteq \mathbb{D}\), we denote by  the corresponding root subsystem. Recall that, for any
the corresponding root subsystem. Recall that, for any  and \(B\subseteq \mathbb{D}\), we write \(\alpha \perp B\) if \(\operatorname {supp}(\alpha )\perp B\).
and \(B\subseteq \mathbb{D}\), we write \(\alpha \perp B\) if \(\operatorname {supp}(\alpha )\perp B\).
Let  be the \(\mathsf {PROP}\) generated by a Lie bialgebra object \([1]\), i.e., a module over \({ \underline {\mathsf {LBA}}}_{}\) with bracket \(\mu :[2]\to [1]\) and cobracket \(\delta :[1]\to [2]\), and two sets of projectors
be the \(\mathsf {PROP}\) generated by a Lie bialgebra object \([1]\), i.e., a module over \({ \underline {\mathsf {LBA}}}_{}\) with bracket \(\mu :[2]\to [1]\) and cobracket \(\delta :[1]\to [2]\), and two sets of projectors
-
Weight projectors: a complete set of orthogonal idempotentsFootnote 33

-
Diagrammatic projectors: a family of idempotents
$$ \theta _{0,B}:[1]\to [1]\qquad B\subseteq \mathbb{D}$$
such that the following relations hold.
-
Normalisation: \(\theta _{0,\mathbb{D}}=\theta _{0}\).
-
 –grading: for any
–grading: for any 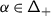 , $$\begin{aligned} \theta _{\alpha}\circ \mu =&\sum _{\beta +\gamma =\alpha}\mu \circ \theta _{\beta} \otimes \theta _{\gamma} \\ \delta \circ \theta _{\alpha} =&\sum _{\beta +\gamma =\alpha} \theta _{\beta} \otimes \theta _{\gamma}\circ \delta \end{aligned}$$
, $$\begin{aligned} \theta _{\alpha}\circ \mu =&\sum _{\beta +\gamma =\alpha}\mu \circ \theta _{\beta} \otimes \theta _{\gamma} \\ \delta \circ \theta _{\alpha} =&\sum _{\beta +\gamma =\alpha} \theta _{\beta} \otimes \theta _{\gamma}\circ \delta \end{aligned}$$where the sums run over all ordered pairs
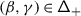 such that \(\beta +\gamma =\alpha \). Moreover, \(\theta _{0}\circ \mu =0=\mu \circ \theta _{0}\otimes \theta _{0}\) and \(\delta \circ \theta _{0}=0=\theta _{0}\circ \theta _{0}\circ \delta \).
such that \(\beta +\gamma =\alpha \). Moreover, \(\theta _{0}\circ \mu =0=\mu \circ \theta _{0}\otimes \theta _{0}\) and \(\delta \circ \theta _{0}=0=\theta _{0}\circ \theta _{0}\circ \delta \). -
Nestedness: for any \(B'\subseteq B\subseteq \mathbb{D}\),
$$ \theta _{0,B'}\circ \theta _{0,B}=\theta _{0,B'}=\theta _{0,B}\circ \theta _{0,B'} $$and, for any \(B_{1}\perp B_{2}\),
$$ \theta _{0,B_{1}\sqcup B_{2}}=\theta _{0,B_{1}}+\theta _{0,B_{2}} $$In particular, \(\theta _{0,\emptyset}=0\) and \(\theta _{0,B_{1}}\circ \theta _{0,B_{2}}=0=\theta _{0,B_{2}}\circ \theta _{0,B_{1}}\) for any \(B_{1}\perp B_{2}\).
-
Support: for any
 and \(B\subseteq \mathbb{D}\),
and \(B\subseteq \mathbb{D}\), 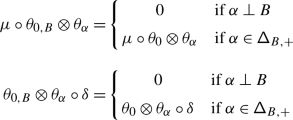
21.2 Remarks
-
(1)
In [3, Sect. 12.7], we introduced a refinement of the \(\mathsf {PROP}\) \(\mathsf{LBA}\) associated to a diagrammatic partial semigroup \(\mathsf {S}\) [3, Sect. 9].
 is a special case of this construction and arises when
is a special case of this construction and arises when  .
. -
(2)
A module over
 (in a Karoubi complete category) is a Lie bialgebra \((\mathfrak {c},[\cdot ,\cdot ], \delta )\) carrying some extra structure. The weight projectors induce a decomposition
(in a Karoubi complete category) is a Lie bialgebra \((\mathfrak {c},[\cdot ,\cdot ], \delta )\) carrying some extra structure. The weight projectors induce a decomposition  . This is compatible with the Lie algebra structure in that, for any
. This is compatible with the Lie algebra structure in that, for any 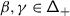 , \([\mathfrak {c}_{\beta}, \mathfrak {c}_{\gamma}]\subseteq \mathfrak {c}_{\beta +\gamma}\), whenever
, \([\mathfrak {c}_{\beta}, \mathfrak {c}_{\gamma}]\subseteq \mathfrak {c}_{\beta +\gamma}\), whenever 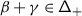 , and \([\mathfrak {c}_{\beta}, \mathfrak {c}_{\gamma}]=0\) otherwise. Moreover, \([\mathfrak {c}_{0},\mathfrak {c}_{\beta}]\subseteq \mathfrak {c}_{\beta}\) and \([\mathfrak {c}_{0},\mathfrak {c}_{0}]=0\). The compatibility with the Lie coalgebra structure is similar.
, and \([\mathfrak {c}_{\beta}, \mathfrak {c}_{\gamma}]=0\) otherwise. Moreover, \([\mathfrak {c}_{0},\mathfrak {c}_{\beta}]\subseteq \mathfrak {c}_{\beta}\) and \([\mathfrak {c}_{0},\mathfrak {c}_{0}]=0\). The compatibility with the Lie coalgebra structure is similar.The diagrammatic projectors lead instead to a split diagrammatic structure on \(\mathfrak {c}\). Indeed, note that, for any \(B\subseteq \mathbb{D}\), the morphism
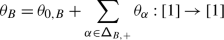 (21.1)
(21.1)is a Lie bialgebra idempotent i.e., \(\theta _{B}^{2}=\theta _{B}\),
$$ \theta _{B}\circ \mu =\mu \circ \theta _{B}\otimes \theta _{B} \qquad \text{and}\qquad \delta \circ \theta _{B}=\theta _{B}\otimes \theta _{B}\circ \delta $$In particular, \(\mathfrak {c}\) is a split diagrammatic Lie bialgebra with \(\mathfrak {c}_{B}=\theta _{B}(\mathfrak {c})\), \(B\subseteq \mathbb{D}\).
-
(3)
If \(\mathfrak {g}\) is a diagrammatic Kac–Moody algebra, the Borel subalgebras \(\mathfrak {b}^{\pm }_{}\) are modules over
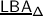 . Namely, for any \(B\subseteq \mathbb{D}\), the idempotent \(\theta _{0,B}\) corresponds to the splitting \(\mathfrak {h}=\mathfrak {h}_{B}\oplus \mathfrak {h}_{B}^{\perp}\), while the idempotents \(\theta _{\alpha}\),
. Namely, for any \(B\subseteq \mathbb{D}\), the idempotent \(\theta _{0,B}\) corresponds to the splitting \(\mathfrak {h}=\mathfrak {h}_{B}\oplus \mathfrak {h}_{B}^{\perp}\), while the idempotents \(\theta _{\alpha}\), 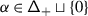 , arise from the root space decomposition
, arise from the root space decomposition 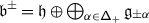 . In particular, for any \(B\subseteq \mathbb{D}\), we have \(\mathfrak {b}^{\pm }_{B}=\theta _{B}( \mathfrak {b}^{\pm }_{})\).
. In particular, for any \(B\subseteq \mathbb{D}\), we have \(\mathfrak {b}^{\pm }_{B}=\theta _{B}( \mathfrak {b}^{\pm }_{})\).
21.3 Universal Drinfeld–Yetter modules
Proceeding as in 19.5 and 19.6, we introduce the \(\mathsf {PROP}\)s of universal Drinfeld–Yetter modules  and the universal algebras
and the universal algebras  associated with
associated with  .
.
The category  , \(n\geqslant 0\), is the colored \(\mathsf {PROP}\) generated by \(n+1\) objects, \([1]\) and \(\{ \underline {\mathsf {V}}_{k}\}_{k=1}^{n}\), and morphisms
, \(n\geqslant 0\), is the colored \(\mathsf {PROP}\) generated by \(n+1\) objects, \([1]\) and \(\{ \underline {\mathsf {V}}_{k}\}_{k=1}^{n}\), and morphisms
-
\(\theta _{\alpha}: [1]\to [1]\),
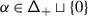 , and \(\theta _{0,B}:[1]\to [1]\), \(B\subseteq \mathbb{D}\)
, and \(\theta _{0,B}:[1]\to [1]\), \(B\subseteq \mathbb{D}\) -
\(\mu :[2]\to [1]\), \(\delta :[1]\to [2]\)
-
\(\pi _{k}:[1]\otimes \underline {\mathsf {V}}_{k}\to \underline {\mathsf {V}}_{k}\), \(\pi _{k}^{*}: \underline {\mathsf {V}}_{k}\to [1]\otimes \underline {\mathsf {V}}_{k}\)
such that
-
\(([1], \theta _{\alpha}, \theta _{0,B},\mu ,\delta )\) is an
 –module in
–module in 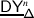
-
every \(( \underline {\mathsf {V}}_{k},\pi _{k},\pi _{k}^{*})\) is a Drinfeld–Yetter module over \([1]\)
In particular,  .
.
Similarly to 19.11, we consider on  the ℕ–grading given by \(\deg(\sigma)=0\) for any \(\sigma\in \mathfrak {S}_{N}\), \(\deg(\mu)=0=\deg(\pi_{ \underline {\mathsf {V}}_{k}})\) and \(\deg(\delta)=1=\deg(\pi_{ \underline {\mathsf {V}}_{k}}^{*})\) for any \(1\leqslant k\leqslant n\), and finally \(\deg(\theta _{\alpha})=0=\deg(\theta _{0,B})\), for any
the ℕ–grading given by \(\deg(\sigma)=0\) for any \(\sigma\in \mathfrak {S}_{N}\), \(\deg(\mu)=0=\deg(\pi_{ \underline {\mathsf {V}}_{k}})\) and \(\deg(\delta)=1=\deg(\pi_{ \underline {\mathsf {V}}_{k}}^{*})\) for any \(1\leqslant k\leqslant n\), and finally \(\deg(\theta _{\alpha})=0=\deg(\theta _{0,B})\), for any  and \(B\subseteq \mathbb{D}\). This yields the universal algebra
and \(B\subseteq \mathbb{D}\). This yields the universal algebra

and its completion  .
.
21.4 The universal algebra 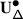
The algebra  has a canonical diagrammatic structure, arising from the projectors \(\{\theta _{B}\}_{B\subseteq \mathbb{D}}\) (21.1). Namely, for any \(B\subseteq \mathbb{D}\), we set
has a canonical diagrammatic structure, arising from the projectors \(\{\theta _{B}\}_{B\subseteq \mathbb{D}}\) (21.1). Namely, for any \(B\subseteq \mathbb{D}\), we set  and
and  . For any \(B\subseteq B'\), there is a canonical realisation functor
. For any \(B\subseteq B'\), there is a canonical realisation functor

which sends the object \([1]_{B}\) in  to the Lie bialgebra object \(\theta _{B}[1]_{B'}=([1]_{B'},\theta _{B})\) in
to the Lie bialgebra object \(\theta _{B}[1]_{B'}=([1]_{B'},\theta _{B})\) in  . This induces a morphism of algebras
. This induces a morphism of algebras  .
.
The following is an analogue of Proposition 19.6 (cf. [3, Prop. 12.4]).
Proposition 40
-
(1)
For any \(n\geqslant 0\), the algebras
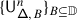 and morphisms
and morphisms 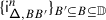 give rise to a diagrammatic algebra
give rise to a diagrammatic algebra  .
. -
(2)
The invariant subalgebras
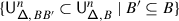 yield a bidiagrammatic structure on
yield a bidiagrammatic structure on 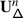 .
. -
(3)
For any \(B\subseteq \mathbb{D}\), there is a canonical cosimplicial structure on the tower of algebras
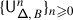 , which is defined as in 19.9, is compatible with the morphisms \(\mathsf {i}_{BB'}^{n}\) and preserves the invariant subalgebras, yielding a cosimplicial bidiagrammatic structure
, which is defined as in 19.9, is compatible with the morphisms \(\mathsf {i}_{BB'}^{n}\) and preserves the invariant subalgebras, yielding a cosimplicial bidiagrammatic structure 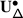 .
.
Remark 36
The morphisms  and the cosimplicial structure are compatible with grading, thus yielding a cosimplicial lax bidiagrammatic algebra
and the cosimplicial structure are compatible with grading, thus yielding a cosimplicial lax bidiagrammatic algebra  given by the collection of the invariant subalgebras
given by the collection of the invariant subalgebras  , \(B'\subseteq B\).
, \(B'\subseteq B\).
21.5 From \(\mathbf {U}_{\mathbb{D}}^{\bullet}\) to 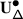
As pointed out in 21.2 (2), the generating object in  is a split diagrammatic Lie bialgebra, with diagrammatic structure given by the projectors \(\{\theta _{B}\}_{B\subseteq \mathbb{D}}\) (21.1). This yields canonical realisation functors
is a split diagrammatic Lie bialgebra, with diagrammatic structure given by the projectors \(\{\theta _{B}\}_{B\subseteq \mathbb{D}}\) (21.1). This yields canonical realisation functors

and morphisms of algebras  , \(n\geqslant 0\). One readily checks that these preserve the diagrammatic subalgebras, the invariant subalgebras, the cosimplicial structure, and the grading, thus giving rise to the morphisms of cosimplicial (lax) bidiagrammatic algebras
, \(n\geqslant 0\). One readily checks that these preserve the diagrammatic subalgebras, the invariant subalgebras, the cosimplicial structure, and the grading, thus giving rise to the morphisms of cosimplicial (lax) bidiagrammatic algebras  and
and  .
.
21.6 Universal pre–Coxeter structures for Kac–Moody algebras
Let \(\mathfrak {g}\) be a diagrammatic Kac–Moody algebra with root system  and Borel subalgebras \(\mathfrak {b}^{\pm }_{}\subseteq \mathfrak {g}\) and \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) the cosimplicial lax bidiagrammatic algebra arising from deformation category \(\mathcal {O}_{\infty}\) integrable \(\mathfrak {g}\)–modules defined in 15.3.
and Borel subalgebras \(\mathfrak {b}^{\pm }_{}\subseteq \mathfrak {g}\) and \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) the cosimplicial lax bidiagrammatic algebra arising from deformation category \(\mathcal {O}_{\infty}\) integrable \(\mathfrak {g}\)–modules defined in 15.3.
By 21.2 (3), the Lie bialgebras \(\mathfrak {b}^{\pm }_{}\) are modules over  . Therefore, for any \(n\)–tuple \(\{V_{k},\pi _{k},\pi _{k}^{*}\}_{k=1}^{n}\) of Drinfeld–Yetter \(\mathfrak {b}^{\pm }_{}\)–modules, there is a canonical realisation functor
. Therefore, for any \(n\)–tuple \(\{V_{k},\pi _{k},\pi _{k}^{*}\}_{k=1}^{n}\) of Drinfeld–Yetter \(\mathfrak {b}^{\pm }_{}\)–modules, there is a canonical realisation functor

sending \([1]\mapsto \mathfrak {b}^{\pm }_{}\), and \(\underline {\mathsf {V}}_{k}\mapsto V_{k}\).
Let \(\mathsf {DY}_{{ \mathfrak {b}^{\pm }_{}}}^{{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}\) be the category of deformation integrable Drinfeld–Yetter \(\mathfrak {b}^{\pm }_{}\)–modules as defined in 18.11. Let \(\mathcal {U}_{ \mathfrak {b}^{\pm }_{}}^{n}\) be the algebra of endomorphisms of the forgetful functor \((\mathsf {DY}_{{ \mathfrak {b}^{\pm }_{}}}^{{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}})^{\boxtimes n}\to \operatorname{{\mathsf{Vect}}}_{\hbar }\) and \(\mathcal {U}_{ \mathfrak {b}^{\pm }_{},\mathfrak {h}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\subseteq \mathcal {U}_{ \mathfrak {b}^{\pm }_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) the subalgebra of \(\mathfrak {h}\)–invariant (or weight–zero) elements. Proceeding as in 19.12, we obtain a canonical morphism of algebras  induced by the realisation functors \(\mathcal {G}_{( \mathfrak {b}^{\pm }_{},V_{1},\dots , V_{n})}\). We observed in [3, Remark 15.12] that the morphism \(\rho _{ \mathfrak {b}^{\pm }_{}}^{n}\) factors through the weight–zero subalgebra \(\mathcal {U}_{ \mathfrak {b}^{\pm }_{},\mathfrak {h}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\).
induced by the realisation functors \(\mathcal {G}_{( \mathfrak {b}^{\pm }_{},V_{1},\dots , V_{n})}\). We observed in [3, Remark 15.12] that the morphism \(\rho _{ \mathfrak {b}^{\pm }_{}}^{n}\) factors through the weight–zero subalgebra \(\mathcal {U}_{ \mathfrak {b}^{\pm }_{},\mathfrak {h}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\).
Let \(\mathscr{U}_{ \mathfrak {b}^{\pm }_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) be the cosimplicial lax bidiagrammatic algebra corresponding to \(\mathcal {U}_{ \mathfrak {b}^{\pm }_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},n}}\) (cf. 18.12). We have the following analogue of Proposition 19.12.
Proposition 41
Let \(\mathfrak {g}\) be a diagrammatic Kac–Moody algebra with root system  and Borel subalgebras \(\mathfrak {b}^{\pm }_{}\subseteq \mathfrak {g}\).
and Borel subalgebras \(\mathfrak {b}^{\pm }_{}\subseteq \mathfrak {g}\).
-
(1)
The realisation functors induce a canonical morphism of cosimplicial lax bidiagrammatic algebras
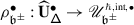 .
. -
(2)
Every braided pre–Coxeter structure \(\mathfrak {C}_{}=(\Phi _{B}, R_{B},J^{}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})\) on
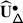 yields the following.
yields the following. -
(a)
A weight–zero braided pre–Coxeter structure \(\mathfrak {C}_{ \mathfrak {b}^{\pm }_{}}\) on \(\mathscr{U}_{{ \mathfrak {b}^{\pm }_{}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) through the morphism
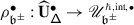 .
. -
(b)
A braided pre–Coxeter category \(\mathscr{DY}_{\mathfrak {C}_{}}^{\scriptscriptstyle {\pm}}\) on deformation integrable Drinfeld–Yetter \(\mathfrak {b}^{\pm }_{}\)–modules, defined by \(\mathfrak {C}_{ \mathfrak {b}^{\pm }_{}}\) through Proposition 18.12 (1).
-
(c)
A braided pre–Coxeter category \(\mathscr{O}_{\mathfrak {C}_{}}^{\scriptscriptstyle {}}\) on deformation integrable category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules, defined by \(\mathfrak {C}_{ \mathfrak {b}^{-}_{}}\) through Proposition 18.12 (2).
-
(a)
We say that a braided pre–Coxeter structure on \(\mathscr{U}_{{ \mathfrak {b}^{\pm }_{}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) is universal if it is lifted from one on  as in (2)–(a) above.
as in (2)–(a) above.
Remark 37
Note that elements in  act on any Drinfeld–Yetter \(\mathfrak {b}^{\pm }_{}\)–modules (in particular, category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules) without any requirement of integrability. Therefore, the categories from (b) and (c) above can be similarly defined without the requirement of integrability.
act on any Drinfeld–Yetter \(\mathfrak {b}^{\pm }_{}\)–modules (in particular, category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules) without any requirement of integrability. Therefore, the categories from (b) and (c) above can be similarly defined without the requirement of integrability.
21.7 Universal Coxeter structures for Kac–Moody algebras [3, Def. 15.12]
A braided Coxeter structure \(\mathbf {C}_{}=(\Phi _{B}, R_{B}, J^{}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'}, S_{i})\) of type \((\mathbb{D},\underline {m})\) on \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) (or equivalently on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\)) is universal if
-
(1)
\(\mathbf {C}_{}\) is supported on
 , i.e., the underlying braided pre–Coxeter structure \(\mathbf {C}_{}^{{\scriptscriptstyle \operatorname {pre}}}= (\Phi _{B}, R_{B}, J^{}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})\) arises from a braided pre-Cox structure on
, i.e., the underlying braided pre–Coxeter structure \(\mathbf {C}_{}^{{\scriptscriptstyle \operatorname {pre}}}= (\Phi _{B}, R_{B}, J^{}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}, \mathsf {a}^{\mathcal {F}}_{\mathcal {F}'})\) arises from a braided pre-Cox structure on  via Proposition 21.6
via Proposition 21.6 -
(2)
the local monodromies \(S_{i}\) have the form
$$ S_{i}= \widetilde {s}_{i}\cdot \underline {S}_{i} $$where \(\widetilde {s}_{i}=\exp (e_{i})\cdot \exp (-f_{i})\cdot \exp (e_{i})\), and \(\underline {S}_{i}\in {U\mathfrak {sl}_{2}^{\alpha _{i}}}[\negthinspace [\hbar ]\negthinspace ]\) is \(\mathfrak {h}\)–invariant with \(\underline {S}_{i}=1\mod\hbar\).
Remark 38
Note that, by 18.11, \(\widetilde {s}_{i}\) and \(\underline {S}_{i}\) act on integrable Drinfeld–Yetter \(\mathfrak {b}_{i}^{-}\)–modules.
22 Proof of the monodromy theorem
22.1
The following is the main result of this paper.
Theorem 17
Let \(\mathfrak {g}\) be a diagrammatic Kac–Moody algebra with negative Borel subalgebra \(\mathfrak {b}^{-}\).
-
(1)
The monodromy data of the joint KZ–Casimir connection gives rise to a braided Coxeter category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}\) on deformation integrable Drinfeld–Yetter modules over \(\mathfrak {b}^{-}_{}\), which extends the braided Coxeter category \(\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }}, { \scriptscriptstyle \operatorname {int}}}}}}\) given by Theorem 16.2.
-
(2)
The \(R\)–matrix and quantum Weyl group operators of \(U_{\hbar }\mathfrak {g}\) give rise to a braided Coxeter category \(\mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}}\) on integrable admissible Drinfeld–Yetter modules over \(U_{\hbar }\mathfrak {b}^{-}_{}\), which extends the braided Coxeter category \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {{ \scriptscriptstyle \operatorname {int}}}}\) given by Proposition 17.4.
-
(3)
There is a canonical equivalence of braided Coxeter categories
$$ \mathbf {H}_{ \mathfrak {b}^{-}_{}}:\mathscr{DY}_{ \mathfrak {b}^{-}_{},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}} \to \mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}} $$which preserves category \(\mathcal {O}_{\infty}\) modules, and restricts to an equivalence of braided Coxeter categories \(\mathbf {H}_{\mathfrak {g}}: \mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}}\to \mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {{ \scriptscriptstyle \operatorname {int}}}}\).
-
(4)
The equivalence \(\mathbf {H}_{ \mathfrak {b}^{-}_{}}\) is obtained as follows.
-
(a)
The structure \(\mathscr{DY}_{ \mathfrak {b}^{-}_{},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}\) is universal, that is arises from a canonical braided pre–Coxeter structure \(\mathbf {C}_{\nabla}\) on the universal root diagrammatic algebra
 introduced in 21.4, via the realisation morphism associated to \(\mathfrak {b}^{-}\).
introduced in 21.4, via the realisation morphism associated to \(\mathfrak {b}^{-}\). -
(b)
The structure \(\mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}}\) is universal, that is arises from the standard braided pre–Coxeter structure \(\mathbf {C}_{\mathbf {R},\mathbf {S}_{}}^{\hbar}\) on the quantum universal diagrammatic algebra \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\hbar ,\bullet}\) introduced in 20.10.
-
(c)
There is a canonical braided pre–Coxeter structure \(\mathbf {C}_{\mathbf {R},\mathbf {S}_{}}\) on the universal diagrammatic algebra \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\) introduced in 19.6, together with a canonical universal equivalence
$$ \mathbf {H}_{ \mathfrak {b}^{-}_{}}':\mathscr{DY}_{ \mathfrak {b}^{-}_{},\mathbf {C}_{\mathbf {R},\mathbf {S}_{}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}\to \mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{},\mathbf {C}_{\mathbf {R},\mathbf {S}_{}}^{\hbar}}^{\scriptscriptstyle {\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}} $$ -
(d)
The braided pre–Coxeter structures \(\mathbf {C}_{\nabla}\) and \(\mathbf {C}_{\mathbf {R},\mathbf {S}_{}}\) are related by a unique twist, which yields an equivalence
$$ \mathbf {H}_{ \mathfrak {b}^{-}_{}}'': \mathscr{DY}_{ \mathfrak {b}^{-}_{},\mathbf {C}_{\nabla}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}} \to \mathscr{DY}_{ \mathfrak {b}^{-}_{},\mathbf {C}_{\mathbf {R},\mathbf {S}_{}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}} $$ -
(e)
The equivalence \(\mathbf {H}_{ \mathfrak {b}^{-}_{}}\) is given by the composition
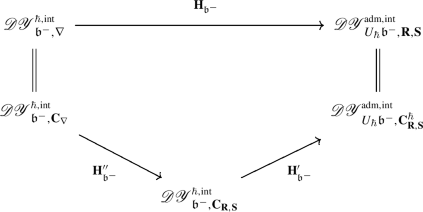
where the vertical equalities follow, respectively, from (a) and (b).
-
(a)
In particular, we obtain the following.
Theorem 18
Let \(V\) be an integrable category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–module, and \(\mathcal {V}\in \mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}^{{\scriptscriptstyle \operatorname {int}}}\) a quantum deformation of \(V\). Then, the \(W\)–equivariant monodromy of the Casimir connection on \({V} [\negthinspace [\hbar ]\negthinspace ]\) is equivalent to the quantum Weyl group action of the braid group \(\mathcal {B}_{W}\) on \(\mathcal {V}\).
22.2
Remark 39
As explained in 22.9, \(\mathbf {H}_{ \mathfrak {b}^{-}_{}}\) (resp. \(\mathbf {H}_{\mathfrak {g}}\)) hold more generally as equivalences of pre–Coxeter structures for arbitrary Drinfeld–Yetter \(\mathfrak {b}^{-}_{}\)–modules (resp. category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules) without any requirement on integrability.
The proof of Theorem 22.1 is carried out in rest of this section. In Sects. 22.3–22.6, we prove that the double holonomy algebra \(\widehat {\mathfrak {t}}_{\nabla}^{\scriptscriptstyle {\bullet}}\) maps to the universal algebra  . Then, (1) and (4a) are proved in Sect. 22.7; (2) and (4b) are proved in Sect. 22.8; (4c) and (4d) are proved in Sects. 22.9, and 22.10, respectively. Thus, (4e) and the first statement in (3) follow. Finally, the second statement in (3) is proved in 22.11.
. Then, (1) and (4a) are proved in Sect. 22.7; (2) and (4b) are proved in Sect. 22.8; (4c) and (4d) are proved in Sects. 22.9, and 22.10, respectively. Thus, (4e) and the first statement in (3) follow. Finally, the second statement in (3) is proved in 22.11.
22.1 From 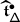 to
to 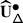
In Sect. 16.1, we constructed a morphism of cosimplicial lax diagrammatic algebras  and used it to define a braided Coxeter structure on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) encoding the monodromy data of the joint KZ–Casimir connection. We prove in Proposition 22.6 that
and used it to define a braided Coxeter structure on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) encoding the monodromy data of the joint KZ–Casimir connection. We prove in Proposition 22.6 that  factors through the universal algebra
factors through the universal algebra  introduced in 21.3, i.e., there is a canonical morphism
introduced in 21.3, i.e., there is a canonical morphism  which fits in a commutative diagram
which fits in a commutative diagram

where \(\rho ^{\scriptscriptstyle {\bullet}}_{ \mathfrak {b}^{-}_{}}\) is the realisation morphism from 21.6, and \(\varphi ^{\scriptscriptstyle {\bullet}}_{\mathfrak {g}}\) is given by restriction from Drinfeld–Yetter \(\mathfrak {b}^{-}_{}\)–modules to category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules, as described in 18.12.
22.2 Arc diagrams in 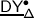
The elements in  may conveniently be represented in terms of string and arc diagrams, which we read as morphisms from left to right. In
may conveniently be represented in terms of string and arc diagrams, which we read as morphisms from left to right. In  , we represent \(\operatorname{id}_{[1]}\) with a line and each \(\operatorname{id}_{ \underline {\mathsf {V}}_{i}}\) with a bold line. The bracket \(\mu :[2]\to [1]\) and the cobracket \(\delta :[1]\to [2]\) are represented, respectively, by the diagrams
, we represent \(\operatorname{id}_{[1]}\) with a line and each \(\operatorname{id}_{ \underline {\mathsf {V}}_{i}}\) with a bold line. The bracket \(\mu :[2]\to [1]\) and the cobracket \(\delta :[1]\to [2]\) are represented, respectively, by the diagrams

Set \(\underline {\mathsf {V}}_{}= \underline {\mathsf {V}}_{1}\otimes \cdots \otimes \underline {\mathsf {V}}_{n}\). The action \(\pi _{ \underline {\mathsf {V}}_{i}}: [1]\otimes \underline {\mathsf {V}}_{}\to \underline {\mathsf {V}}_{}\) and coaction \(\pi ^{*}_{ \underline {\mathsf {V}}_{i}}: \underline {\mathsf {V}}_{}\to [1] \otimes \underline {\mathsf {V}}_{}\) on the \(i\)th component of \(\underline {\mathsf {V}}_{}\) are represented, respectively, by the diagrams

Finally, the idempotent \(\theta _{\star}:[1]\to [1]\), where the label ⋆ is either  or \((0,B)\) with \(B\subseteq \mathbb{D}\), is represented by the diagram
or \((0,B)\) with \(B\subseteq \mathbb{D}\), is represented by the diagram

22.3 Relations in 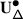
As in 19.13, there are two distinguished families of elements in  , namely
, namely
where \(1\leqslant i\neq j\leqslant n\), and ⋆ is either  or \((0,B)\) with \(B\subseteq \mathbb{D}\). These correspond, respectively, to the diagrams
or \((0,B)\) with \(B\subseteq \mathbb{D}\). These correspond, respectively, to the diagrams

Similarly to 19.13, it follows from the definition of \({\rho}^{\bullet}\) in 21.6 and Proposition 18.5 (4) that

where \(\{t_{k}\},\{t^{k}\}\) are dual bases of \(\mathfrak {h}_{B}\).
Lemma 11
The following holds.
-
(1)
For any \(B\subseteq \mathbb{D}\) and
 , \(\left [\boldsymbol {\kappa }^{i}_{0,B},\boldsymbol {\kappa }^{i}_{\alpha}\right ]=0\).
, \(\left [\boldsymbol {\kappa }^{i}_{0,B},\boldsymbol {\kappa }^{i}_{\alpha}\right ]=0\). -
(2)
For any \(B\subseteq \mathbb{D}\) and
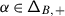 ,
, 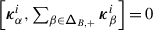 .
.
Proof
(1) follows from the identities

(2) Let  be the morphism defined in 21.4. Then, for any \(B\subseteq \mathbb{D}\), one has
be the morphism defined in 21.4. Then, for any \(B\subseteq \mathbb{D}\), one has

where \(\boldsymbol {\kappa }^{i}_{B}\in \mathsf {U}_{B}^{n}\) is defined in 19.13. In [3, Prop. 9.8], we proved that \(\sum_{i}\boldsymbol {\kappa }^{i}_{B}\) is central in \(\mathsf {U}_{B}^{n}\). The same proof applies to  in
in  . Then, the result follows from (1). □
. Then, the result follows from (1). □
Clearly, the identity (2) above can be regarded as a \(tt\)–relation (3.5) with respect to a diagrammatic root subsystem. Proceeding along the same lines, one shows the standard \(tt\)–relations hold in  .
.
Proposition 42
For any rank 2 subsystem  and \(\alpha \in \Psi \), \(\left [\boldsymbol {\kappa }^{i}_{\alpha}, \sum _{\beta \in \Psi} \boldsymbol {\kappa }^{i}_{\beta}\right ]=0\).
and \(\alpha \in \Psi \), \(\left [\boldsymbol {\kappa }^{i}_{\alpha}, \sum _{\beta \in \Psi} \boldsymbol {\kappa }^{i}_{\beta}\right ]=0\).
22.4 The morphism 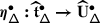
For any \(n\geq 2\) and \(1\leq i\neq j\leq n\), define  by \(\boldsymbol {\Omega }^{ij}_{\star}=\mathbf {r}^{ij}_{\star}+\mathbf {r}^{ji}_{\star}\).
by \(\boldsymbol {\Omega }^{ij}_{\star}=\mathbf {r}^{ij}_{\star}+\mathbf {r}^{ji}_{\star}\).
Proposition 43
The assignments

uniquely extends to a morphisms of algebras  compatible with the cosimplicial structure, the diagrammatic structure, and the natural ℕ–gradings.
compatible with the cosimplicial structure, the diagrammatic structure, and the natural ℕ–gradings.
The corresponding morphism of cosimplicial lax diagrammatic algebras  give rise to the commutative diagram
give rise to the commutative diagram

where  and \(\rho ^{\scriptscriptstyle {\bullet}}_{ \mathfrak {b}^{-}_{}}\) are the realisation morphism from 16.1and 19.10, respectively, and \(\varphi ^{\scriptscriptstyle {\bullet}}_{\mathfrak {g}}\) is given by the restriction from integrable Drinfeld–Yetter \(\mathfrak {b}^{-}_{}\)–modules to integrable category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules, described in 18.12.
and \(\rho ^{\scriptscriptstyle {\bullet}}_{ \mathfrak {b}^{-}_{}}\) are the realisation morphism from 16.1and 19.10, respectively, and \(\varphi ^{\scriptscriptstyle {\bullet}}_{\mathfrak {g}}\) is given by the restriction from integrable Drinfeld–Yetter \(\mathfrak {b}^{-}_{}\)–modules to integrable category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules, described in 18.12.
Remark 40
It is clear that, at this stage, it is not necessary to work with integrable modules. Namely, let \(\mathscr{U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\) and \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\) be, respectively, the completions with respect to deformation category \(\mathcal {O}_{\infty}\) \(\mathfrak {g}\)–modules and Drinfeld–Yetter \(\mathfrak {b}^{-}_{}\)–modules (cf. 15.3 and 18.12). Note that there are canonical maps \(\mathscr{U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\to \mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) and \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\to \mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\), given by restriction to integrable modules. One readily checks that the maps  , \(\rho ^{\scriptscriptstyle {\bullet}}_{ \mathfrak {b}^{-}_{}}\), \(\varphi ^{\scriptscriptstyle {\bullet}}_{\mathfrak {g}}\) factor through \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\) and \(\mathscr{U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\), yielding a commutative diagram as in (22.1).
, \(\rho ^{\scriptscriptstyle {\bullet}}_{ \mathfrak {b}^{-}_{}}\), \(\varphi ^{\scriptscriptstyle {\bullet}}_{\mathfrak {g}}\) factor through \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\) and \(\mathscr{U}_{\mathfrak {g}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},\bullet}}\), yielding a commutative diagram as in (22.1).
Proof
The commutativity of (22.1) is verified by direct inspection. Note that the scaling factor in the definition of  is chosen so to guarantee the commutativity of (22.1) and it is determined by the relation \(\hbar =2\pi \iota \mathsf {h}\). It remains to check that the linear map
is chosen so to guarantee the commutativity of (22.1) and it is determined by the relation \(\hbar =2\pi \iota \mathsf {h}\). It remains to check that the linear map  preserves the relations from Definition 12.6.
preserves the relations from Definition 12.6.
The symmetry and locality relations (12.6) and (12.7), (12.8), clearly holds in  , as they involve string diagrams insisting on distinct thick lines. The orthogonality relations (12.10) follow from the
, as they involve string diagrams insisting on distinct thick lines. The orthogonality relations (12.10) follow from the  –grading relations in
–grading relations in  (cf. 21.1). Indeed, it is enough to observe that, if \(\alpha \perp \beta \), one has
(cf. 21.1). Indeed, it is enough to observe that, if \(\alpha \perp \beta \), one has

Therefore, actions and coactions labelled by \(\alpha \) and \(\beta \) commute, i.e.,

and

It follows that any two arc diagrams labelled, respectively, by \(\alpha \) and \(\beta \) clearly commute. The orthogonality relations (12.11) are proved similarly, by relying on the nestedness and support relations in  .
.
The proof of the KZ relations (12.9) is standard. Let \(\underline {\mathsf {DY}}_{}^{\scriptscriptstyle {n}}\) the \(\mathsf {PROP}\) describing \(n\) Drinfeld–Yetter modules over a Lie bialgebra. One first observes that the operator

is invariant, i.e., it commutes with the action and the coaction on \(\underline {\mathsf {V}}_{1}\otimes \underline {\mathsf {V}}_{2}\)

Therefore, the operator \(\boldsymbol {\Omega }^{12}_{}\) on \(\underline {\mathsf {V}}_{1}\otimes \underline {\mathsf {V}}_{2}\otimes \underline {\mathsf {V}}_{3}\) commutes with \(\boldsymbol {\Omega }^{13}_{}+\boldsymbol {\Omega }^{23}_{}\), since the latter is the operator

For any \(B\subseteq \mathbb{D}\), we consider the canonical morphism of \(\mathsf {PROP}\)s  , mapping the Lie bialgebra object \([1]\) in \(\underline {\mathsf {DY}}_{}^{\scriptscriptstyle {n}}\) to the Lie bialgebra \(([1],\theta _{B})\) in
, mapping the Lie bialgebra object \([1]\) in \(\underline {\mathsf {DY}}_{}^{\scriptscriptstyle {n}}\) to the Lie bialgebra \(([1],\theta _{B})\) in  . This shows that \(\boldsymbol {\Omega }^{}_{B}\) commutes with the action and coaction of \([\mathfrak {b}_{B' }]\) for any \(B'\subseteq B\), and the diagrammatic KZ relations (12.9) follow.
. This shows that \(\boldsymbol {\Omega }^{}_{B}\) commutes with the action and coaction of \([\mathfrak {b}_{B' }]\) for any \(B'\subseteq B\), and the diagrammatic KZ relations (12.9) follow.
The weight zero relations follow from the fact that the Lie bialgebras \(([1],\theta _{0,B})\) are abelian.
By Lemma 22.5 (3), the operators \(\boldsymbol {\kappa }^{i}_{\alpha}\) and \(\Delta ^{(n)}(\boldsymbol {\kappa }^{}_{\alpha})\) satisfy the Casimir relations (12.12). Finally, it is clear that
so that (12.14) and (12.13) hold in  .
.
The algebra maps  clearly preserve the cosimplicial structure, the diagrammatic subalgebras, and the natural grading. The result follows. □
clearly preserve the cosimplicial structure, the diagrammatic subalgebras, and the natural grading. The result follows. □
22.5 Proof of Theorem 22.1 (1) and (3a)
We shall prove the following
Theorem 19
Let \(\mathbf {C}_{\nabla}=(\Phi ^{\nabla}_{B}, R^{\nabla}_{B}, J^{\nabla}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}, S_{i }^{\nabla})\) be the \(\mathsf {a}^{}_{}\)–strict braided Coxeter structure on the extended double holonomy algebra  defined in Theorem 13.2.
defined in Theorem 13.2.
-
(a)
The datum of
$$ \mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre,\eta}}}=(\Phi ^{\nabla,\eta}_{B}, R^{\nabla,\eta}_{B}, J^{\nabla,\eta}_{\mathcal {F}}, \Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla,\eta}) $$where
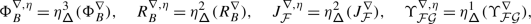
is a braided pre–Coxeter structure on
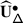 .
. -
(b)
Through the realisation morphisms
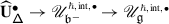 (cf. Sect. 22.6), \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre,\eta}}}\) induces on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) the braided Coxeter structure arising from the joint KZ–Casimir connection defined in Theorem 16.2.
(cf. Sect. 22.6), \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre,\eta}}}\) induces on \(\mathscr{U}_{{\mathfrak {g}}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\) the braided Coxeter structure arising from the joint KZ–Casimir connection defined in Theorem 16.2.
Proof
Part (b) follows from the commutativity of the diagram (22.1). For part (a), we proceed as in the proof of Theorem 16.2. We shall verify that \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre,\eta}}}\) satisfy the properties (a)–(e) from Definition 11.1 with respect to the cosimplicial bidiagrammatic structure on  . By construction, \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre,\eta}}}\) is the image of a braided pre–Coxeter structure \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre}}}\) in
. By construction, \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre,\eta}}}\) is the image of a braided pre–Coxeter structure \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre}}}\) in  through the morphism
through the morphism  defined in 22.6. Although
defined in 22.6. Although  is a morphism of cosimplicial diagrammatic algebras, it does not preserve the invariant subalgebras, as the condition of being invariant in
is a morphism of cosimplicial diagrammatic algebras, it does not preserve the invariant subalgebras, as the condition of being invariant in  is generally stronger than being invariant in
is generally stronger than being invariant in  . Therefore, proving that \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre,\eta}}}\) is a braided pre–Coxeter structure in
. Therefore, proving that \(\mathbf {C}_{\nabla}^{{\scriptscriptstyle \operatorname {pre,\eta}}}\) is a braided pre–Coxeter structure in  reduces to showing that the elements \(\Phi ^{\nabla,\eta}_{B}\), \(R^{\nabla,\eta}_{B}\), \(J^{\nabla,\eta}_{\mathcal {F}}\), and \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla,\eta}\) satisfy the necessary invariance properties.
reduces to showing that the elements \(\Phi ^{\nabla,\eta}_{B}\), \(R^{\nabla,\eta}_{B}\), \(J^{\nabla,\eta}_{\mathcal {F}}\), and \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla,\eta}\) satisfy the necessary invariance properties.
By definition,  and, by Theorem 13.1, the associator
and, by Theorem 13.1, the associator  is the exponential of a Lie series in \(\boldsymbol {\Omega }^{12}_{B}\) and \(\boldsymbol {\Omega }^{23}_{B}\). As observed in 22.6, the operator \(\boldsymbol {\Omega }^{i,i+1}_{B}\) is \([1]_{B}\)–invariant in
is the exponential of a Lie series in \(\boldsymbol {\Omega }^{12}_{B}\) and \(\boldsymbol {\Omega }^{23}_{B}\). As observed in 22.6, the operator \(\boldsymbol {\Omega }^{i,i+1}_{B}\) is \([1]_{B}\)–invariant in  , therefore so are
, therefore so are  and
and  . The invariance of the relative twists and the De Concini–Procesi associators is obtained as in [34, Thm. 1.33] and [35, App. B.4]. Namely, it is enough to observe that the relative Casimir operators, which provide the coefficients of the differential equations defining \(J^{\nabla}_{\mathcal {F}}\) and \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\) in
. The invariance of the relative twists and the De Concini–Procesi associators is obtained as in [34, Thm. 1.33] and [35, App. B.4]. Namely, it is enough to observe that the relative Casimir operators, which provide the coefficients of the differential equations defining \(J^{\nabla}_{\mathcal {F}}\) and \(\Upsilon _{\mathcal {F}\mathcal {G}}^{\nabla}\) in  , specialise in
, specialise in  to elements with the necessary invariant properties.
to elements with the necessary invariant properties.
For any \(B'\subseteq B\subseteq \mathbb{D}\), set  . We shall prove that \(\boldsymbol {\kappa }^{}_{BB'}\) commutes with the action and the coaction of the universal Lie subbialgebra \([1]_{B'}=([1],\theta _{B'})\). Note that the elements \(\boldsymbol {\kappa }^{}_{\beta}\) are weight zero, i.e., for any
. We shall prove that \(\boldsymbol {\kappa }^{}_{BB'}\) commutes with the action and the coaction of the universal Lie subbialgebra \([1]_{B'}=([1],\theta _{B'})\). Note that the elements \(\boldsymbol {\kappa }^{}_{\beta}\) are weight zero, i.e., for any  , we have
, we have

Let  and
and  . Note that \(\alpha -\beta \) is never a positive root and we have
. Note that \(\alpha -\beta \) is never a positive root and we have

where the second and third summands appear if and only if  . Summing over all positive roots
. Summing over all positive roots  , the first and third summands cancel out. Namely, if
, the first and third summands cancel out. Namely, if  , then the third summand in the equation (22.3) for \(\beta \) cancels out with the first summand in the equation (22.3) for \(\beta -\alpha \). On the other hand, assume that
, then the third summand in the equation (22.3) for \(\beta \) cancels out with the first summand in the equation (22.3) for \(\beta -\alpha \). On the other hand, assume that  . Then, the first summand in the equation (22.3) for \(\beta \) cancels out with the third summand in the equation (22.3) for \(\beta +\alpha \). Finally, if
. Then, the first summand in the equation (22.3) for \(\beta \) cancels out with the third summand in the equation (22.3) for \(\beta +\alpha \). Finally, if  , then
, then

Therefore, by (22.2), the operator \(\boldsymbol {\kappa }^{}_{BB'}\) commutes with the action of \([1]_{B'}\). The invariance of \(\boldsymbol {\kappa }^{}_{BB'}\) under the coaction of \([1]_{B'}\) is proved similarly. □
Therefore, \(\mathbf {C}_{\nabla}\) induces an \(\mathsf {a}^{}_{}\)–strict universal braided Coxeter structure on \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\), which we denote by  and, by Proposition 18.12, yields a braided Coxeter category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}\).
and, by Proposition 18.12, yields a braided Coxeter category \(\mathscr{DY}_{ \mathfrak {b}^{-}_{},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}\).
22.6 Proof of Theorem 22.1 (2) and (4b)
In Proposition 17.4, we described the \((\mathsf {a}^{}_{},\Upsilon _{})\)–strict braided Coxeter category \(\mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{ \scriptscriptstyle \operatorname {int}}}}}}\) arising from the action of the \(R\)–matrix and the quantum Weyl group operators of the quantum group \(U_{\hbar }\mathfrak {g}\) on category \(\mathcal {O}_{\infty}\) integrable \(U_{\hbar }\mathfrak {g}\)–modules. In analogy with the classical case (cf. 18.6 and 18.11), this extends to admissible Drinfeld–Yetter \(U_{\hbar }\mathfrak {b}^{-}_{}\)–modules. Namely, the quantum group \(U_{\hbar }\mathfrak {g}\) is isomorphic, as diagrammatic QUEs, to the quotient of the restricted quantum double of \(U_{\hbar }\mathfrak {b}^{-}_{}\). Therefore, any admissible Drinfeld–Yetter module \((V,\rho _{V},\rho _{V})\) satisfying
is naturally a module over \(U_{\hbar }\mathfrak {g}\). In particular, this allows to recover category \(\mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}\) as a braided tensor subcategory of \(\mathsf {DY}_{{U_{\hbar }\mathfrak {b}^{-}_{}}}^{ \scriptscriptstyle \operatorname {adm}}\). We say that a deformation Drinfeld–Yetter \(\mathfrak {b}^{-}_{}\)–module is integrable if it satisfies (22.4) and (D2) from 15.3. Similarly for \(U_{\hbar }\mathfrak {b}^{-}_{}\). Let \(\mathsf {DY}_{{U_{\hbar }\mathfrak {b}^{-}_{}}}^{\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}\) be the category of integrable admissible Drinfeld–Yetter \(U_{\hbar }\mathfrak {b}^{-}_{}\)–modules. Then, the generalised braid group \(\mathcal {B}_{W}\) acts on the objects in \(\mathsf {DY}_{{U_{\hbar }\mathfrak {b}^{-}_{}}}^{\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}\) via the quantum Weyl group operators \(\mathbf {S}_{i}\), \(i\in \mathbf {I}\). By elying on the split diagrammatic structure of \(U_{\hbar }\mathfrak {b}^{-}_{}\), we obtain the following extension of Proposition 17.4.
Proposition 44
There is a \((\mathsf {a}^{}_{},\Upsilon _{})\)–strict braided Coxeter category \(\mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}}\) of type \((\mathbb{D}, \underline {m})\) given by the following data.
-
For any \(B\subseteq \mathbb{D}\), the braided monoidal category \(\mathsf {DY}_{{U_{\hbar }\mathfrak {b}^{-}_{B}}}^{\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}\).
-
For any \(B'\subseteq B\), the restriction functor \(\operatorname{Res}^{\hbar }_{B'B}: \mathsf {DY}_{{U_{\hbar }\mathfrak {b}^{-}_{B}}}^{\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}\to \mathsf {DY}_{{U_{\hbar }\mathfrak {b}^{-}_{B'}}}^{\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}\).
-
For any \(i\in \mathbb{D}\), the quantum Weyl group operator \(\mathbf {S}_{i}\in \mathsf {Aut}(\mathsf {DY}_{{U_{\hbar }\mathfrak {b}^{-}_{i}}}^{\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}\to \operatorname{{\mathsf{Vect}}}_{\hbar })\).
Moreover, \(\mathscr{O}_{U_{\hbar }\mathfrak {b}^{-}_{},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {{ \scriptscriptstyle \operatorname {int}}}}\) naturally identifies with a subcategory of \(\mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{},\mathbf {R},\mathbf {S}_{}}^{\scriptscriptstyle {\scriptscriptstyle \operatorname {adm},{ \scriptscriptstyle \operatorname {int}}}}\).
Finally, it follows as in 20.10 that the braided pre–Coxeter structure \(\mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{},\mathbf {R}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\) is universal and induced by the standard braided pre–Coxeter structure on \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\hbar ,\bullet}\).
22.7 Proof of Theorem 22.1 (4c)
Let \(\Phi ^{\nabla}\) be the KZ associator. Since \(\Phi ^{\nabla}\) is a Lie associator by Theorem 13.1, Theorem 20.9 yields a universal braided pre–Coxeter structure  on \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\), and therefore an equivalence of braided pre–Coxeter categories
on \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\), and therefore an equivalence of braided pre–Coxeter categories

By [17] and [2, Prop. 13.6], the split diagrammatic QUEs \(\mathcal {Q}( \mathfrak {b}^{-}_{})\) and \(U_{\hbar }\mathfrak {b}^{-}_{}\) are isomorphic, thus yielding an equivalence of braided pre–Coxeter categories \(\mathscr{DY}_{\mathcal {Q}( \mathfrak {b}^{-}_{})}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\simeq \mathscr{DY}_{U_{\hbar }\mathfrak {b}^{-}_{},\mathbf {R}}^{\scriptscriptstyle { \scriptscriptstyle \operatorname {adm}}}\).
Lemma 12
The composite equivalence

preserves integrability.
Proof
Recall that, for \(\mathfrak {g}=\mathfrak{sl}_{2}\), integrability is equivalent to complete reducibility as a possibly infinite direct sum of (indecomposable) finite–rank modules. Since the equivalence commutes with direct sums and preserves the rank, the result is clear in this case.
For any \(i\in \mathbf {I}\), set \(\mathfrak {b}^{-}_{i}=\langle f_{i}, h_{i}\rangle \subset \mathfrak{sl}_{2}^{ \alpha _{i}}\). By [1, Thm. 1.7], there is a commutative diagram of functors

where the horizontal arrows are the Etingof–Kazhdan equivalences and the vertical arrows are restrictions. Then, the result follows, since restrictions preserve integrability and the isomorphism \(\mathcal {Q}( \mathfrak {b}^{-}_{})\simeq U_{\hbar }\mathfrak {b}^{-}_{}\) is split diagrammatic. □
This allows to enhance \(\mathbf {H}_{ \mathfrak {b}^{-}_{}}^{{\scriptscriptstyle \operatorname {pre}}}\) to an equivalence of braided Coxeter categories

where  is a universal braided Coxeter structure which extends
is a universal braided Coxeter structure which extends  , i.e.,
, i.e.,  .
.
22.8 Proof of Theorem 22.1 (4d)
By the discussion above, we now have an \(\mathsf {a}^{}_{}\)–strict universal braided Coxeter structure  , arising from the monodromy data and supported on
, arising from the monodromy data and supported on  , and a \(\Upsilon _{}\)–strict braided Coxeter structure
, and a \(\Upsilon _{}\)–strict braided Coxeter structure  , arising from the quantum group \(U_{\hbar }\mathfrak {g}\) and supported on \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\). Note that, by construction,
, arising from the quantum group \(U_{\hbar }\mathfrak {g}\) and supported on \(\widehat {\mathbf {U}}_{\mathbb{D}}^{\bullet}\). Note that, by construction,  and
and  already share the same associators and \(R\)–matrices. The proof of Theorem 22.1 (3b) amounts to showing that
already share the same associators and \(R\)–matrices. The proof of Theorem 22.1 (3b) amounts to showing that  and
and  are twist equivalent. More precisely, we prove the following
are twist equivalent. More precisely, we prove the following
Theorem 20
The universal structures  and
and  are twist equivalent (cf. 11.3) with respect to a twist of the form \({T}_{}={T}_{}'\cdot {T}_{}''\), where
are twist equivalent (cf. 11.3) with respect to a twist of the form \({T}_{}={T}_{}'\cdot {T}_{}''\), where
-
(1)
\({T}_{}'\) is uniquely determined by a tuple of grouplike elements in \(\widehat {S}\mathfrak {h}_{i}\), \(i\in \mathbb{D}\).
-
(2)
\({T}_{}''\) is a unique universal twist supported on
 .
.
This is achieved in two steps, which rely heavily on the fact that both structures are universal and supported on  . Indeed, we proved in [3] that braided pre–Coxeter structures on
. Indeed, we proved in [3] that braided pre–Coxeter structures on  are rigid. Specifically, we have the following
are rigid. Specifically, we have the following
Theorem 21
[3, Thm. 13.4] Let \(\mathfrak {C}_{k}\), \(k=1,2\), be two \(\mathsf {a}^{}_{}\)–strict braided pre–Coxeter structures on  . Then, there exists a twist \({T}_{}\) such that \(\mathfrak {C}_{2}=(\mathfrak {C}_{1})_{{T}_{}}\). Moreover, \({T}_{}\) is unique up to a unique gauge.
. Then, there exists a twist \({T}_{}\) such that \(\mathfrak {C}_{2}=(\mathfrak {C}_{1})_{{T}_{}}\). Moreover, \({T}_{}\) is unique up to a unique gauge.
Note that, by Proposition 7.5,  is canonically twist equivalent to an \(\mathsf {a}^{}_{}\)–strict universal braided Coxeter structure
is canonically twist equivalent to an \(\mathsf {a}^{}_{}\)–strict universal braided Coxeter structure  . Let
. Let  and
and  be the braided pre–Coxeter structures underlying
be the braided pre–Coxeter structures underlying  and
and  , respectively. The result above determines a universal twist \({T}_{}''\), unique up to a unique universal gauge, such that
, respectively. The result above determines a universal twist \({T}_{}''\), unique up to a unique universal gauge, such that  .
.
However, at the level of braided Coxeter structures, we need a further correction, since the local monodromy operators are determined by the underlying universal structure in  only up to a unique Cartan–valued gauge. More precisely, we have the following
only up to a unique Cartan–valued gauge. More precisely, we have the following
Proposition 45
[3, Cor. 15.13] Up to a unique gauge transformation determined by a tuple of grouplike elements in \({S\mathfrak {h}_{i}}[\negthinspace [\hbar ]\negthinspace ]\), \(i\in \mathbb{D}\), a braided pre–Coxeter structure on  can be lifted to at most one universal braided Coxeter structure on \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\).
can be lifted to at most one universal braided Coxeter structure on \(\mathscr{U}_{ \mathfrak {b}^{-}_{}}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {\hbar }},{\scriptscriptstyle \operatorname {int}},\bullet}}\).
Therefore, this yields a canonical twist \({T}_{}'\) such that  with \({T}_{}={T}_{}'\cdot {T}_{}''\). The twist \({T}_{}\) induces an equivalence of braided Coxeter categories
with \({T}_{}={T}_{}'\cdot {T}_{}''\). The twist \({T}_{}\) induces an equivalence of braided Coxeter categories  and therefore
and therefore
22.9 Proof of Theorem 22.1 (3)
There remains to show that the equivalence \(\mathbf {H}_{ \mathfrak {b}^{-}_{}}\) preserves category \(\mathcal {O}_{\infty}\) modules, and therefore restricts to an equivalence of braided Coxeter categories \(\mathbf {H}_{\mathfrak {g}}:\mathscr{O}_{\mathfrak {g},\nabla}^{\scriptscriptstyle {{\scriptscriptstyle \operatorname {{\scriptscriptstyle \operatorname {\hbar }},{ \scriptscriptstyle \operatorname {int}}}}}}\to \mathscr{O}_{U_{\hbar }\mathfrak {g},\mathbf {R}, \mathbf {S}_{}}^{\scriptscriptstyle {{ \scriptscriptstyle \operatorname {int}}}}\).
Lemma 13
The functor

restricts to an equivalence of categories \(\mathcal {O}^{\hbar }_{\infty ,\mathfrak {g}}\to \mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}\).
Proof
In analogy with Proposition 18.6, category \(\mathcal {O}^{\hbar }_{\infty ,\mathfrak {g}}\) identifies with the subcategory of deformation Drinfeld–Yetter modules over \(\mathfrak {b}^{-}_{}\) satisfying condition (18.1). An analogous characterization holds for \(\mathcal {O}_{\infty ,U_{\hbar }\mathfrak {g}}\). Since the equivalence (22.5) is the identity on Drinfeld–Yetter \(\mathfrak {h}\)–modules, condition (18.1) is automatically preserved, and the result follows. □
This concludes the proof of Theorem 22.1.
Notes
\(\nabla _{\mathcal {K}}\) is independent of the choice of
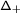 since \(d\log \alpha =d\log (-\alpha )\) and \({\mathcal {K}}_{\alpha}= {\mathcal {K}}_{-\alpha}\).
since \(d\log \alpha =d\log (-\alpha )\) and \({\mathcal {K}}_{\alpha}= {\mathcal {K}}_{-\alpha}\).The 1–form \(\widehat {b}\) may be thought of as a differential analogue of the half–sum \(\widehat {\rho}\) of all positive roots, and its resummation as parallel to Kac’s construction of an element \(\rho \in \mathfrak {h}\) with the same formal properties as \(\widehat {\rho}\). Note also that, since positive imaginary roots are invariant under \(W\), it is equivalent to resum \(\widehat {b}^{^{\operatorname {re}}}=\frac {1}{2}\sum d\log \alpha \,t_{\alpha}\), where the sum is restricted to positive real roots. Correspondingly, both \(\widehat {b}\) and \(\widehat {b}^{^{\operatorname {re}}}\) satisfy
 for any \(w\in W\).
for any \(w\in W\).Note that, unlike [21], we do not require \(\mathfrak {h}\) to be of (minimal) dimension \(2|\mathbf {I}|-\operatorname{rank}(\mathsf {A})\).
Such a form always exists, see e.g., [2, Prop. 11.4].
Two subdiagrams \(B_{1},B_{2}\subseteq \mathbb{D}\) are orthogonal if they have no vertices in common, and no two vertices \(i\in B_{1}\), \(j\in B _{2}\) are joined by an edge in \(\mathbb{D}\) (cf. 5.1).
Following [2, Sects. 5 and 9], one could consider a more general definition, where a diagrammatic realisation of \(\mathsf {A}\) is a collection of realisations \((\mathfrak {h}_{B}, \Pi _{B}, \Pi _{B}^{\vee})\) of \(\mathsf {A}_{B}\) (\(B\subseteq \mathbb{D}\)) equipped with a system of linear maps \(i_{BB'}\colon \mathfrak {h}_{B'}\to \mathfrak {h}_{B}\) (\(B'\subseteq B\)) satisfying natural compatibility conditions with respect to subdiagrams and orthogonal diagrams. When \(\mathsf {A}\) is symmetrisable, however, the maps \(i_{BB'}\) are required to be isometries, and thus embeddings. We have therefore opted to identify \(\mathfrak {h}_{B}\) with a subspace of \(\mathfrak {h}=\mathfrak {h}_{\mathbb{D}}\) in Definition 2.4.
Note that \(d(d^{\operatorname {sing}}\mathscr{C})=1\).
Indeed, note that, given a chamber \(\mathcal {C}\) with a wall \(M\), if \(\mathcal {H}_{M}(\mathcal {C})\) denotes the half–space determined by \(M\) and containing \(\mathcal {C}\), one has \(w(\mathcal {H}_{M}(\mathcal {C}))=\mathcal {H}_{w(M)}(w(\mathcal {C}))\) for any \(w\in W\). Therefore, \(W\) preserves the signs of the signed galleries.
Theorem 4.7 and Lemma 4.6 reduce to the same verification because they are special cases of the more general statement that, for any collection of complex numbers \(\mathbf {a}=\{a_{i}\}_{i\in \mathbf {I}}\), there is a (unique) \(\mathscr{B}\mathcalligra{ }_{\mathbf {a}}\in \mathsf {M}'\) such that \(d\mathscr{B}\mathcalligra{ }_{\mathbf {a}}=\mathscr{A}\) and \(\mathscr{B}\mathcalligra{ }_{\mathbf {a}}(\gamma _{i})=\exp (a_{i} t_{\alpha _{i}})\).
In that case, a resummation only exists if it is taken with values in \(\mathfrak {h}\) rather than \(\mathfrak {h}'\).
In [34], this result is proved only for elements in \(\mathsf {Mns}(\mathbb{D})\). However, it generalises immediately to the case of relative nested sets.
Henceforth, for simplicity, we will denote a (bi)diagrammatic algebra by the collection of its subalgebras only, omitting the structural morphisms \(i\) and \(j\).
The isomorphism \({j}^{}_{B_{1}B_{2}}:\mathfrak {t}_{B_{1}}\otimes \mathfrak {t}_{B_{2}}\to \mathfrak {t}_{B_{1}\sqcup B_{2}}\) extends to an injective, but not surjective, morphism \({ \widehat {j}}^{}_{B_{1}B_{2}}: \widehat {\mathfrak {t}}_{B_{1}}\otimes \widehat {\mathfrak {t}}_{B_{2}}\to \widehat {\mathfrak {t}}_{B_{1}\sqcup B_{2}}\). It is clear, however, that \(\widehat {\mathfrak {t}}_{}\) (resp. \(\widehat {\mathfrak {t}}_{}^{\flat}\)) is diagrammatic (resp. bidiagrammatic) with respect to the completed tensor product \(\mathbin {\hat {\otimes }}\).
More precisely, \({j}^{\otimes n}_{B_{1}B_{2}}:({A}^{}_{B_{1}}\otimes {A}^{}_{B_{2}})^{\otimes n}\to {A}^{\otimes n}_{B_{1}\sqcup B_{2}}\). By abuse of notation, we omit the identification \(({A}^{}_{B_{1}}\otimes {A}^{}_{B_{2}})^{\otimes n}\simeq {A}^{\otimes n}_{B_{1}}\otimes {A}^{\otimes n}_{B_{2}}\) and we denote by \({j}^{\otimes n}_{B_{1}B_{2}}\) the morphism \({A}^{\otimes n}_{B_{1}}\otimes {A}^{\otimes n}_{B_{2}}\to {A}^{\otimes n}_{B_{1}\sqcup B_{2}}\).
Here \(B\) is identified with the unique element in \(\mathsf {Mns}(B,B)\).
By convention, \(\mathsf {r}^{ii}_{\alpha}=0\).
Note that
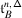 does not coincide with the root refinement of \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) corresponding to
does not coincide with the root refinement of \(\mathfrak {t}_{}^{\scriptscriptstyle {n}}\) corresponding to 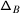 , since the operators
, since the operators 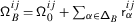 are not required to satisfy the KZ relations
are not required to satisfy the KZ relations 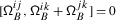 .
.The generators
 and \(\mathsf {K}_{\alpha}^{(n)}\) are included only if \(n\geqslant 2\).
and \(\mathsf {K}_{\alpha}^{(n)}\) are included only if \(n\geqslant 2\).We use the notation from 11.1.
\(\alpha _{\mathcal {F},B}\) denotes the only simple root whose support is not contained in any maximal element of \(\mathcal {F}^{B}\) (cf. 8.3).
\({ \mathcal {K}[i]}^{}_{i}\) and \({ \mathcal {K}[i]}^{i}_{}\) denote the truncations of \(\mathcal {K}[i]\) at \((\mathbb{D},\{i\})\) and \((\{i\},\emptyset)\), respectively, see Definition 5.3(1).
Given a braided monoidal category with braiding \(\beta \), we set \(\beta ^{\scriptscriptstyle \operatorname{op}}_{X,Y}:=\beta _{Y,X}^{-1}\).
Note that the eigenvalues of the action of \(\mathfrak {h}\) on \(\mathcal {V}\) are required to lie in \(\mathfrak {h}^{*}\subsetneq \mathfrak {h}^{*}[\negthinspace [\hbar ]\negthinspace ]\).
In particular a representation \(\mathcal {V}\) of \(U_{\hbar }\mathfrak {g}\) is in category \(\mathcal {O}_{\infty }\) if the action of \(U_{\hbar }\mathfrak {b}^{+}_{}\) on \(\mathcal {V}/\hbar ^{n}\mathcal {V}\) is locally finite for any \(n\geqslant 0\). Note that the analogue of the condition (D3′) from 15.3 holds.
The operators \(\widetilde {\mathbf {S}}_{i}\) are well–defined on any integrable \(U_{\hbar }\mathfrak {g}\)–module. Note that in the notation of [27, Sect. 5.2] \(\widetilde {\mathbf {S}}_{i}\) coincides with the operator \(T''_{i,+1}\).
In the sequel, we shall abusively refer to such a \(\mathfrak {b}\) as an ℕ–graded Lie bialgebra.
The \(\frac {1}{2}\) factor in \(r_{\mathfrak {g}}\) arises because if \(t,t'\in \mathfrak {h}\) and \(t_{+}=(t,t)\) and \(t'_{-}=(t',-t')\) are the corresponding elements of \(\mathfrak {b}^{(2)}_{\pm}\), then \(\langle{t_{+}},{t'_{-}}\rangle ^{(2)}=2\langle{t},{t'}\rangle \).
In a monoidal category \((\mathcal {C},\otimes )\), \(V^{\otimes n}_{b_{n}}\) denotes the \(n\)–fold tensor product of \(V\in \mathcal {C}\) bracketed according to \(b_{n}\). For example \(V^{\otimes 3}_{(\bullet \bullet )\bullet}=(V\otimes V)\otimes V\).
In [2, Sect. 10.1], we consider a larger class of factorisable associators.
Note that the induced topology on \(\mathfrak {B}'\) coincide with its QFSH topology.
If
 , the completeness relation
, the completeness relation 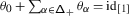 is imposed by considering an appropriate completion of the \(\mathsf {PROP}\) \(\underline {\mathsf {LBA}}\) (cf. [3, Sect. 9.1]).
is imposed by considering an appropriate completion of the \(\mathsf {PROP}\) \(\underline {\mathsf {LBA}}\) (cf. [3, Sect. 9.1]).In the case of \(\mathfrak {g}=\widehat {\mathfrak {sl}_{2}}\), one has
Similarly for higher rank \(\mathfrak {g}\) and \(w\in W\).
References
Appel, A., Toledano Laredo, V.: A 2–categorical extension of Etingof–Kazhdan quantisation. Sel. Math. New Ser. 24, 3529–3617 (2018)
Appel, A., Toledano Laredo, V.: Coxeter categories and quantum groups. Sel. Math. New Ser. 25, 97 pp (2019)
Appel, A., Toledano Laredo, V.: Uniqueness of Coxeter structures on Kac–Moody algebras. Adv. Math. 347, 1–104 (2019)
Appel, A., Toledano Laredo, V.: Pure braid group actions on category \(\mathcal {O}\) modules. Pure Appl. Math. Q. 20(1), 52 pp (2024, to appear)
Appel, A., Vlaar, B.: Universal K-matrices for quantum Kac–Moody algebras. Represent. Theory 26, 764–824 (2022)
Brieskorn, E.: Die Fundamentalgruppe des Raumes der regulären Orbits einer endlichen komplexen Spiegelungsgruppe. Invent. Math. 12, 57–61 (1971)
Cherednik, I.V.: Generalized braid groups and local r-matrix systems. Sov. Math. Dokl. 40(1), 43–48 (1990). Translated from Dokl. Akad. Nauk SSSR 307(1), 49–53 (1989)
Cherednik, I.V.: Monodromy representations for generalized Knizhnik–Zamolodchikov equations and Hecke algebras. Publ. Res. Inst. Math. Sci. 27(5), 711–726 (1991)
De Concini, C., Procesi, C.: Hyperplane arrangements and holonomy equations. Sel. Math. New Ser. 1(3), 495–535 (1995)
Drinfeld, V.G.: Quantum groups. In: Proceedings of the International Congress of Mathematicians (Berkeley, Calif., 1986), pp. 798–820. Am. Math. Soc., Providence (1987)
Drinfeld, V.G.: On quasitriangular quasi-Hopf algebras and on a group that is closely connected with \(Gal(\hat{\mathbb{Q}}/\mathbb{Q})\). Leningr. Math. J. 2(4), 829–860 (1991)
Enriquez, B.: On some universal algebras associated to the category of Lie bialgebras. Adv. Math. 164(1), 1–23 (2001)
Enriquez, B.: A cohomological construction of quantization functors of Lie bialgebras. Adv. Math. 197(2), 430–479 (2005)
Enriquez, B., Etingof, P.: On the invertibility of quantisation functors. J. Algebra 289(2), 321–345 (2005)
Etingof, P., Kazhdan, D.: Quantization of Lie bialgebras. I. Sel. Math. New Ser. 2(1), 1–41 (1996)
Etingof, P., Kazhdan, D.: Quantization of Lie bialgebras. II. Sel. Math. New Ser. 4(2), 213–231 (1998)
Etingof, P., Kazhdan, D.: Quantization of Lie bialgebras. VI. Quantization of generalized Kac-Moody algebras. Transform. Groups 13(3–4), 527–539 (2008)
Felder, G., Markov, Y., Tarasov, V., Varchenko, A.: Differential equations compatible with KZ equations. Math. Phys. Anal. Geom. 3(2), 139–177 (2000)
Gavarini, F.: The quantum duality principle. Ann. Inst. Fourier (Grenoble) 52, 809–834 (2002)
Jimbo, M.: A \(q\)–analog of \(U(\mathfrak{gl}(N +1))\), Hecke algebra, and the Yang–Baxter equation. Lett. Math. Phys. 11, 247–252 (1986)
Kac, V.G.: Infinite–Dimensional Lie Algebras, 3rd edn. Cambridge University Press, Cambridge (1990)
Kirillov, A.N., Reshetikhin, N.: \(q\)–Weyl group and a multiplicative formula for universal \(R\)-matrices. Commun. Math. Phys. 134(2), 421–431 (1990)
Kohno, T.: On the holonomy Lie algebra and the nilpotent completion of the fundamental group of the complement of hypersurfaces. Nagoya Math. J. 93, 21–37 (1983)
Lawvere, F.W.: Functorial semantics of algebraic theories. Proc. Natl. Acad. Sci. USA 50, 869–872 (1963)
Levendorskii, S.Z., Soibelman, Ya.S.: The quantum Weyl group and a multiplicative formula for the \(R\)-matrix of a simple Lie algebra. Funkc. Anal. Prilozh. 25(2), 73–76 (1991)
Looijenga, E.: Invariant theory for generalized root systems. Invent. Math. 61(1), 1–32 (1980)
Lusztig, G.: Introduction to Quantum Groups. Birkhäuser, Boston (1993)
MacLane, S.: Categorical algebra. Bull. Am. Math. Soc. 71, 40–106 (1965)
Millson, J.J., Toledano Laredo, V.: Casimir operators and monodromy representations of generalised braid groups. Transform. Groups 10, 217–254 (2005)
Procesi, C.: Complements of subspaces and conical singularities. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 7(2), 113–123 (1996)
Tits, J.: Normalisateurs de tores. I. Groupes de Coxeter étendus. J. Algebra 4, 96–116 (1966)
Toledano Laredo, V.: A Kohno–Drinfeld theorem for quantum Weyl groups. Duke Math. J. 112(3), 421–451 (2002)
Toledano Laredo, V.: Cohomological construction of relative twists. Adv. Math. 210, 375–403 (2007)
Toledano Laredo, V.: Quasi–Coxeter algebras, Dynkin diagram cohomology and quantum Weyl groups. Int. Math. Res. Pap. IMRP (2008)
Toledano Laredo, V.: Quasi–Coxeter quasitriangular quasibialgebras and the Casimir connection. arXiv:1601.04076
van der Lek, H.: The homotopy type of complex hyperplane complements. Ph.D. Thesis, University of Nijmegen (1983)
Vinberg, E.B.: Discrete linear groups that are generated by reflections. Izv. Akad. Nauk SSSR, Ser. Mat. 35, 1072–1112 (1971) (Russian)
Yetter, D.N.: Quantum groups and representations of monoidal categories. Math. Proc. Cambridge Philos. Soc. 108, 261–290 (1990)
Acknowledgements
It is a pleasure, as ever, to thank Pavel Etingof for his insightful comments and interest in the present work.
Funding
Open access funding provided by Northeastern University Library. The first author was partially supported by the ERC Grant 637618 and by the Programme FIL 2022 of the University of Parma and co-sponsored by Fondazione Cariparma. The second author was supported in part through the NSF grants DMS–1505305 and DMS–1802412.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: The \(W\)–equivariant Casimir connection of an affine Kac–Moody algebra
Appendix: The \(W\)–equivariant Casimir connection of an affine Kac–Moody algebra
In this appendix, we construct two explicit \(W\)–equivariant corrections of the Casimir connection

where  is the set of positive roots of an affine Lie algebra and \({\mathcal {K}}_{\alpha}^{+}\) is the normally ordered Casimir operator (cf. 3.2). These extensions provide an affine analogue of the \(W\)–equivariant Casimir connections \(\nabla =d-A_{{\mathcal {K}}_{}^{}}\) and \(\nabla =d-A_{C}\) with
is the set of positive roots of an affine Lie algebra and \({\mathcal {K}}_{\alpha}^{+}\) is the normally ordered Casimir operator (cf. 3.2). These extensions provide an affine analogue of the \(W\)–equivariant Casimir connections \(\nabla =d-A_{{\mathcal {K}}_{}^{}}\) and \(\nabla =d-A_{C}\) with

where  is the set of positive roots of a finite–dimensional simple Lie algebra and \({\mathcal {K}}_{\alpha}^{}\) (resp. \(C_{\alpha}\)) is the truncated (resp. full) Casimir element of \(\mathfrak {sl}_{2}^{\alpha}\). More precisely, we prove the following.
is the set of positive roots of a finite–dimensional simple Lie algebra and \({\mathcal {K}}_{\alpha}^{}\) (resp. \(C_{\alpha}\)) is the truncated (resp. full) Casimir element of \(\mathfrak {sl}_{2}^{\alpha}\). More precisely, we prove the following.
Theorem 22
Let \(\mathfrak {g}\) be an affine Lie algebra with Cartan subalgebra \(\mathfrak {h}\). Then, there are two explict closed 1–forms \(A_{\mathfrak {h}}\) and \(A_{S^{2}\mathfrak {h}}\) valued, respectively, in \(\mathfrak {h}\) and \(S^{2}\mathfrak {h}\), such that the following holds.
-
(1)
The connection \(\nabla =d-A_{{\mathcal {K}}_{}^{}}\), with \(A_{{\mathcal {K}}_{}^{}}= A+A_{\mathfrak {h}}\), is flat and \(W\)–equivariant. Moreover, for any \(i\in \mathbf {I}\), \(\operatorname{Res}_{\alpha _{i}=0}A_{{\mathcal {K}}_{}^{}}=\frac{\mathsf {h}}{2}\cdot {\mathcal {K}}_{i}^{}\), where \({\mathcal {K}}_{i}^{}\) is the truncated Casimir element of \(\mathfrak {sl}_{2}^{\alpha _{i}}\).
-
(2)
The connection \(\nabla =d-A_{C}\), with \(A_{C}= A +A_{\mathfrak {h}}+A_{S^{2}\mathfrak {h}}\), is flat and \(W\)–equivariant. Moreover, for any \(i\in \mathbf {I}\), \(\operatorname{Res}_{\alpha _{i}=0}A_{C}=\frac{\mathsf {h}}{2}\cdot C_{i}\), where \(C_{i}\) is the full Casimir element of \(\mathfrak {sl}_{2}^{\alpha _{i}}\).
The construction of the forms \(A_{\mathfrak {h}}\) and \(A_{S^{2}\mathfrak {h}}\) is given in A.1 and A.3, respectively. The proof of (1) and (2) is given in A.2 and A.4, respectively.
1.1 A.1 The form \(A_{\mathfrak {h}}\)
For any \(\delta \in \mathbb{C}^{\times}\), set
One verifies easily that \(\Psi ^{\pm}_{\delta}\) satisfies the following properties:
-
(i)
\(\Psi ^{\pm}_{\delta}(x)\) is holomorphic on \(\mathbb{C}\setminus \mathbb{Z}_{\neq 0}\delta \)
-
(ii)
\(\displaystyle \Psi ^{+}_{\delta}(x+\delta )=\Psi ^{+}_{\delta}(x)- \frac{1}{x+\delta}\)
-
(iii)
\(\displaystyle \Psi ^{-}_{\delta}(x+\delta )=\Psi ^{-}_{\delta}(x)- \frac{1}{x}\)
Set \(\Psi ^{\pm}=\Psi ^{\pm}_{1}\) and \(\Psi =\Psi ^{+}+\Psi ^{-}\).
Let \(\mathfrak {g}\) be an affine Kac–Moody of rank \(\ell +1\) associated to the minimal realisation, with Cartan subalgebra \(\mathfrak {h}\subset \mathfrak {g}\) and root system  . Let \(\mathring {\mathfrak {g}}\) be the corresponding finite dimensional Lie algebra with Cartan subalgebra \(\mathring {\mathfrak {h}}\subset \mathfrak {g}\) and root system
. Let \(\mathring {\mathfrak {g}}\) be the corresponding finite dimensional Lie algebra with Cartan subalgebra \(\mathring {\mathfrak {h}}\subset \mathfrak {g}\) and root system  , so that
, so that
where \(\mathring {\mathfrak {h}}\subset \mathring {\mathfrak {g}}\), \(c=\sum _{i=0}^{\ell} a_{i}^{\vee} h_{i}\) is the canonical central element and \(d\) satisfies \(\alpha _{i}(d)=\delta _{i,0}\). Let \(\langle{\cdot},{\cdot}\rangle \) be the normalized non–degenerate bilinear form on \(\mathfrak {h}\), and \(\nu :\mathfrak {h}\to \mathfrak {h}^{*}\) the isomorphism induced by \(\langle{\cdot},{\cdot}\rangle \) (cf. 2.2). Let \(\delta =\sum _{i=0}^{\ell }a_{i}\alpha _{i}\) be the minimal imaginary root. We set
where
and \(\rho ^{\vee}\in \mathfrak {h}\) is a fixed solution of
1.2 A.2 Proof of (1)
We shall prove that the form \(A+A_{\mathfrak {h}}\) defines a flat and \(W\)–equivariant connection with residues \(\operatorname{Res}_{\alpha _{i}=0}A+A_{\mathfrak {h}}=\mathsf {h}\cdot \left (f_{i}e_{i}+ \frac{1}{2}h_{i}\right )=\frac{\mathsf {h}}{2}\cdot {\mathcal {K}}_{i}^{}\). To this end, we explain below that the formula for \(A_{\mathfrak {h}}\) naturally arises by imposing the equivariance condition with respect to the extended Weyl group in the case of affine rank one, i.e., \(\mathfrak {g}=\widehat {\mathfrak {sl}_{2}}\), and then by extending it to the higher rank case. In A.2.1–A.2.6, we prove the case of affine rank one. The proof for the general case is carried out in A.2.7–A.2.10.
1.2.1 A.2.1 The case of affine rank one
Set \(\mathfrak {g}=\widehat {\mathfrak {sl}_{2}}\) and assume that \(A_{\mathfrak {h}}\) has the form
where \(\theta =\alpha _{1}\) and \(h=h_{1}\). In particular, \(A_{\mathfrak {h}}\) is closed.
Let \(W^{\scriptscriptstyle{\operatorname{ext}}}\) the extended Weyl group, i.e., \(W^{\scriptscriptstyle{\operatorname{ext}}}= W\rtimes \mathsf{Aut}( \mathbb{D})\), where \(\mathsf {Aut}(\mathbb{D})\) denotes the group of diagram automorphisms of the Dynkin diagram of \(\mathfrak {g}\). Then, the form \(A+A_{\mathfrak {h}}\) is \(W^{\scriptscriptstyle{\operatorname{ext}}}\)–equivariant if and only if
where \(s_{1}\) is the simple reflection on \(\theta \) and \(\gamma \) is induced by the symmetry of the Dynkin diagram of \(\widehat {\mathfrak {sl}_{2}}\). In particular, we have
A.2.2
Set \(z=\theta /\delta \). The condition (A.2) is equivalent to the system of equations
and
where the subscripts \(X_{(h)}\), \(X_{(c)}\) denote the components along \(h\) and \(c\), respectively.
A.2.3
If \(S(z)\), \(T(z)\) are functions satisfying (A.3), (A.4), (A.5), (A.6), then \(B(\delta )\) is bound to satisfy
The general solution is easily computed to be
where \(f(\delta )\) is any function in \(\delta \). In particular, the condition (A.1) is satisfied. Note however that \(B(\delta )\) is not supported in \(\mathfrak {h}'\) (cf. Theorem 4.8).
A.2.4
Let \(S(z)\) be a given function satisfying (A.3) and (A.5). We aim to find two polynomials \(p(z)\) and \(q(z)\) such that \(T'(z)= p(z)S(z)+q(z)\) satisfies (A.4), (A.6). In terms of \(p\) and \(q\), the latter conditions are equivalent to the system
A solution is given by \(p(z)=-z\) and \(q(z)=\frac{1}{2}-z\). Therefore, given \(S(z)\), the function \(T(z)\) has the form
where \(E(z)\) is any function satisfying \(E(-z)=-E(z)\) and \(E(z)=-E(1-z)\).
A.2.5
Finally, we need to solve the equations (A.3) and (A.5), which are equivalent to the system \(S(-z)=S(z)-\frac{1}{z}\) and \(S(z+1)=S(z)-\frac{1}{z}\). A particular solution is given by the function
Therefore, the general solution is given by the formula
where \(e(z)\) is any function satisfying \(e(-z)=e(z)\) and \(e(z+1)=e(z)\).
A.2.6
Setting \(e=E=f=0\), we get, for \(\mathfrak {g}=\widehat {\mathfrak {sl}_{2}}\),
and the resulting connection \(\nabla =d-(A+A_{\mathfrak {h}})\) is flat and \(W\)–equivariant. A simple computation shows that
1.2.2 A.2.7 The general case
Let now \(\mathfrak {g}\) be an affine Kac–Moody algebra and set
where
with \(t_{\beta}=\nu ^{-1}(\beta )\) and \(B\in \mathfrak {h}\). We shall prove that there exists \(B\in \mathfrak {h}\) such that \(A_{{\mathcal {K}}_{}^{}}=A+A_{\mathfrak {h}}\) satisfies (1). Note that the form \(A_{\beta}(\beta /\delta )\) satisfies
as proved in the case \(\mathfrak {g}=\widehat {\mathfrak {sl}_{2}}\).
A.2.8
For every \(i=1,\dots ,\ell \), the simple reflection \(s_{i}\) permutes the elements in \(\mathring {\mathsf {R}}_{+}\setminus \{\alpha _{i}\}\), and
where the second equality follows from (A.7). Therefore, the form \(A+A_{\mathfrak {h}}\) is \(\mathring{W}\)–equivariant if and only if \(s_{i}(B)=B-h_{i}\) and \(\alpha _{i}(B)=1\).
A.2.9
Let \(\beta \in \mathring {\mathsf {R}}_{+}\). It follows from (A.8) that
Therefore
Therefore, \(s_{0}^{*}(A+A_{\mathfrak {h}})=A+A_{\mathfrak {h}}\) if and only if \(s_{0}(B)=B-h_{0}\) and \(\alpha _{0}(B)=1\).
A.2.10
Finally, we conclude that, for any \(B\in \mathfrak {h}\) satisfying \(\alpha _{i}(B)=1\), \(i=0,1,\dots ,\ell \), there is a flat and \(W\)–equivariant connection \(A_{{\mathcal {K}}_{}^{}}=A+A_{\mathfrak {h}}\), where
Moreover, its residues \(\operatorname{Res}_{\alpha _{i}=0}A_{\kappa}=\frac{1}{2}{\mathcal {K}}_{i}^{}d\alpha _{i}\) are given by the truncated Casimir elements. This completes the proof of (1).
1.3 A.3 The form \(A_{S^{2}\mathfrak {h}}\)
We shall extend the \(W\)–equivariant connection \(\nabla =d-A_{{\mathcal {K}}_{}^{}}\) with a closed, \(W\)–equivariant form \(A_{S^{2}\mathfrak {h}}\) with values in \(S^{2}\mathfrak {h}\), so that
where \(A_{C}=A+A_{\mathfrak {h}}+A_{S^{2}\mathfrak {h}}\). This provides an affine analogue of the Casimir connection of a finite–dimensional simple Lie algebra with coefficients \(C_{\alpha}\). To this end, we set
1.4 A.4 Proof of (2)
As before, we first consider the case \(\mathfrak {g}=\widehat {\mathfrak {sl}_{2}}\). We have
Then, \(A_{S^{2}\mathfrak {h}}\) is closed with residues
Moreover, \(A_{S^{2}\mathfrak {h}}\) is \(W\)–equivariant since we have
and
Let now \(\mathfrak {g}\) be an affine Kac–Moody algebra and
Clearly, \(A_{S^{2}\mathfrak {h}}\) is closed with the required residues. Moreover, for any element of the Weyl group \(w\in W\), we haveFootnote 34

Remark 41
The expression of the form \(A_{S^{2}\mathfrak {h}}\) for \(\mathfrak {g}=\widehat {\mathfrak {sl}_{2}}\) has been computed as in A.2.1–A.2.6. We set
with \(A_{\theta}(\theta ,\delta )=S(\theta ,\delta )h^{2}+T(\theta , \delta )hc+U(\theta ,\delta )c^{2}\) and similarly for \(A_{\delta}\). By imposing the \(W\)–equivariance (for a fixed value \(\delta \in \mathbb{C}^{*}\)) we obtain a sistem of difference equation in \(\theta \) for the functions \(S\), \(T\), \(U\) which is easily solved with functions of the form \(p(z)\cot (z)\), where \(p\) is a polynomial. More specifically, \(S\), \(U\) are odd functions in \(\theta \) and \(T\) is an even function in \(\theta \) such that
The system above encodes the invariance with respect to the translation \(\theta \mapsto \theta -\delta \). Finally, the condition \(dA=0\) gives a formula for \(A_{\delta}\). Namely, we obtain to a general solution of the form
where \(B(\delta )\) is any \(W\)–equivariant function (which is therefore chosen to be equal to zero).
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Appel, A., Toledano Laredo, V. Monodromy of the Casimir connection of a symmetrisable Kac–Moody algebra. Invent. math. 236, 549–672 (2024). https://doi.org/10.1007/s00222-024-01242-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-024-01242-8



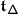
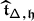
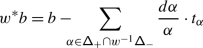




 , then
, then 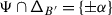 , then
, then 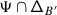 contains at least two linearly independent elements, then
contains at least two linearly independent elements, then 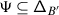 , and the
, and the 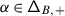 , then
, then 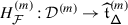 such that
such that 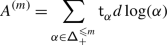
 , satisfying the holonomy equation
, satisfying the holonomy equation 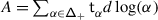 .
.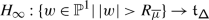
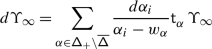
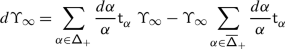
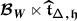
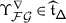 and the elements
and the elements 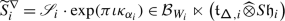
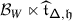 with respect to the standard labelling on
with respect to the standard labelling on 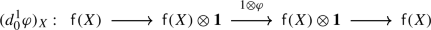

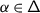 ,
, 
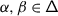 ,
, 
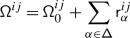
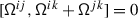 .
.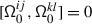 .
.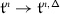 given by
given by 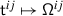 .
.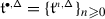 is endowed with a unique cosimplicial structure which extends that on
is endowed with a unique cosimplicial structure which extends that on 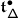
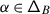 ,
, 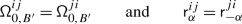
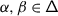 , and
, and 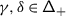
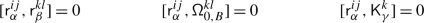
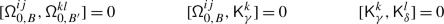
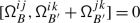
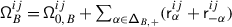 .
. , and any
, and any  ,
, 
 .
.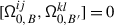 .
.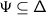 , and
, and 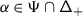 ,
, 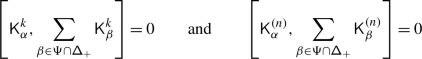
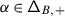 ,
, 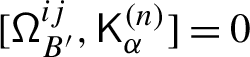
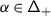 ,
, 
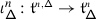 given by
given by 
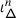 is
is  .
.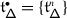 is a cosimplicial diagrammatic algebra.
is a cosimplicial diagrammatic algebra.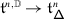 given by
given by 
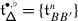 is a cosimplicial bidiagrammatic algebra, whose structure is obtained from
is a cosimplicial bidiagrammatic algebra, whose structure is obtained from 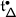 by restriction.
by restriction.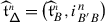 is a diagrammatic algebra. The face and degeneration morphisms of the cosimplicial structure on
is a diagrammatic algebra. The face and degeneration morphisms of the cosimplicial structure on 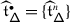 are morphisms of diagrammatic algebras. Thus,
are morphisms of diagrammatic algebras. Thus,  is a cosimplicial diagrammatic algebra.
is a cosimplicial diagrammatic algebra. is a cosimplicial bidiagrammatic algebra, whose structure is obtained from
is a cosimplicial bidiagrammatic algebra, whose structure is obtained from 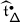 by restriction.
by restriction.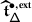
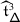 , where
, where  , where
, where 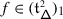 satisfies
satisfies 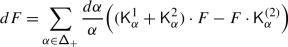
 , where
, where 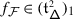 satisfies
satisfies 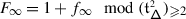 , where
, where 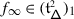 satisfies
satisfies 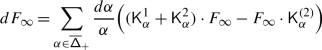
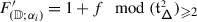 , where
, where  satisfies
satisfies 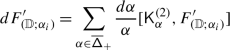
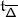 , then it is constant on
, then it is constant on 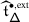 with relative twists
with relative twists 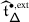 .
.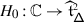 such that
such that 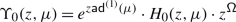
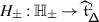 such that
such that 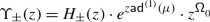


 to
to  and
and 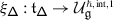 defined by
defined by 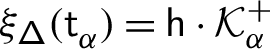
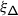 is compatible with the grading, and therefore extends to a morphism
is compatible with the grading, and therefore extends to a morphism 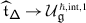 .
.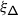 to
to  coincides with the morphism
coincides with the morphism 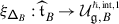 . In particular,
. In particular, 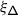 is a morphism of lax diagrammatic algebras.
is a morphism of lax diagrammatic algebras.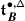 and
and  and
and 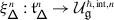 defined by
defined by 
 is compatible with the cosimplicial structure, the action of
is compatible with the cosimplicial structure, the action of  given by
given by 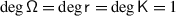 . It therefore extends to a morphism of cosimplicial lax diagrammatic algebras
. It therefore extends to a morphism of cosimplicial lax diagrammatic algebras  .
.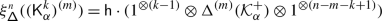
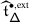 given by Theorem
given by Theorem 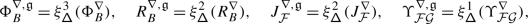
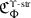 on
on 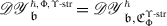 . There is a canonical equivalence of braided pre–Coxeter categories
. There is a canonical equivalence of braided pre–Coxeter categories 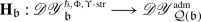
 .
. –graded diagrammatic Lie bialgebras
–graded diagrammatic Lie bialgebras
 –grading: for any
–grading: for any 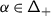 ,
, 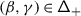 such that
such that  and
and 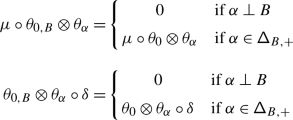
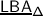 is a special case of this construction and arises when
is a special case of this construction and arises when 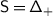 .
. (in a Karoubi complete category) is a Lie bialgebra
(in a Karoubi complete category) is a Lie bialgebra  . This is compatible with the Lie algebra structure in that, for any
. This is compatible with the Lie algebra structure in that, for any 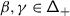 ,
, 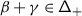 , and
, and 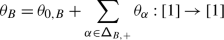
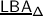 . Namely, for any
. Namely, for any 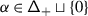 , arise from the root space decomposition
, arise from the root space decomposition 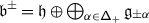 . In particular, for any
. In particular, for any 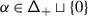 , and
, and 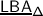 –module in
–module in 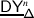
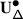
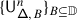 and morphisms
and morphisms 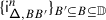 give rise to a diagrammatic algebra
give rise to a diagrammatic algebra  .
.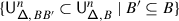 yield a bidiagrammatic structure on
yield a bidiagrammatic structure on 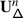 .
.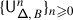 , which is defined as in
, which is defined as in 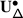 .
.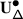
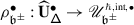 .
.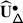 yields the following.
yields the following. 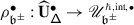 .
. , i.e., the underlying braided pre–Coxeter structure
, i.e., the underlying braided pre–Coxeter structure  via Proposition
via Proposition  introduced in
introduced in 
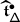 to
to 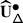
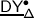
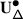
 ,
, 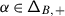 ,
, 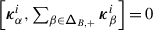 .
.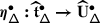
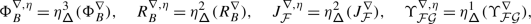
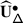 .
.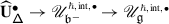 (cf. Sect.
(cf. Sect.  .
.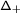 since
since  for any
for any  , then the relation (
, then the relation (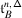 does not coincide with the root refinement of
does not coincide with the root refinement of 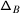 , since the operators
, since the operators 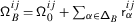 are not required to satisfy the KZ relations
are not required to satisfy the KZ relations 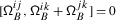 .
.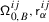 and
and  , the completeness relation
, the completeness relation 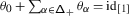 is imposed by considering an appropriate completion of the
is imposed by considering an appropriate completion of the