Skip to main content
SpringerLink
Log in

o-minimal GAGA and a conjecture of Griffiths

  • Published:
Inventiones mathematicae Aims and scope

Abstract

We prove a conjecture of Griffiths on the quasi-projectivity of images of period maps using algebraization results arising from o-minimal geometry. Specifically, we first develop a theory of analytic spaces and coherent sheaves that are definable with respect to a given o-minimal structure, and prove a GAGA-type theorem algebraizing definable coherent sheaves on complex algebraic spaces. We then combine this with algebraization theorems of Artin to show that proper definable images of complex algebraic spaces are algebraic. Applying this to period maps, we conclude that the images of period maps are quasi-projective and that the restriction of the Griffiths bundle is ample.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. It is important to include the natural scheme structure on the equivalence relation.

  2. Here we use \(|\cdot |\) to denote the vanishing locus as a definable topological space—that is, forgetting the sheaf of functions—rather than the underlying topological space as in Sect. 2.1.

  3. That is, the resulting map \(\text {Hom}(S,R)\rightarrow \text {Hom}(S,X)\times \text {Hom}(S,X)\) is the inclusion of a set-theoretic equivalence relation.

  4. That is, the image of the exceptional locus in \(X^{\textrm{def}}\).

  5. Note that Artin uses the notation

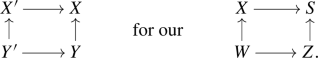
  6. Note that the analytifications of \({\mathcal {O}}_W,I\) as \({\mathcal {O}}_{W'}\)-modules are naturally the analytifications as \({\mathcal {O}}_W\)-modules.

  7. Recall this means that \(R\rightarrow {\mathcal {O}}_Z\) is a homomorphisms of sheaves of rings and that J with its induced ideal structure is of square zero.

  8. That is, a locally liftable map satisfying Griffiths transversality on the regular locus.

  9. The proof in the algebraic space case is the same as that of varieties, as it relies on the existence and uniqueness of the analytic extension and ordinary GAGA.

  10. Strictly speaking, pulling back from the stack. Alternatively, one can take a definable cover by simply-connected opens, lift to \(\Omega \), pull back and glue.

References

  1. Allcock, D., Carlson, J., Toledo, D.: The complex hyperbolic geometry of the moduli space of cubic surfaces. J. Algebr. Geom. 11(4), 659–724 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  2. Artin, M.: Algebraization of formal moduli II: existence of modifications. Ann. Math. (2) 91, 88–135 (1970)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bakker, B., Klingler, B., Tsimerman, J.: Tame topology of arithmetic quotients and algebraicity of Hodge loci. J. Am. Math. Soc. 33(4), 917–939 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bănică, C., Stănăşilă, O.: Algebraic Methods in the Global Theory of Complex Spaces. Editura Academiei, Bucharest (1976)

    MATH  Google Scholar 

  5. Benoist, O.: Séparation et propriété de Deligne–Mumford des champs de modules d’intersections complètes lisses. J. Lond. Math. Soc. (2) 87(1), 138–156 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  6. Benoist, O.: Quelques espaces de modules d’intersections complètes lisses qui sont quasi-projectifs. J. Eur. Math. Soc. (JEMS) 16(8), 1749–1774 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bierstone, E., Milman, P.: Semianalytic and subanalytic sets. Inst. Hautes Études Sci. Publ. Math. 67, 5–42 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  8. Borel, A.: Some metric properties of arithmetic quotients of symmetric spaces and an extension theorem. J. Differ. Geom. 6, 543–560 (1972)

    MathSciNet  MATH  Google Scholar 

  9. Boucksom, S.: On the volume of a line bundle. Int. J. Math. 13(10), 1043–1063 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  10. Brunebarbe, Y.: Semi-positivity from Higgs Bundles. arXiv:1707.08495

  11. Carlson, J., Müller-Stach, S., Peters, C.: Period Mappings and Period Domains. Cambridge Studies in Advanced Mathematics, vol. 168. Cambridge University Press, Cambridge (2017)

    Book  MATH  Google Scholar 

  12. Carlson, J., Toledo, D.: Compact quotients of non-classical domains are not Kähler, Hodge theory, complex geometry, and representation theory. Am. Math. Soc. 608, 51–57 (2014)

    MATH  Google Scholar 

  13. Cattani, E., Deligne, P., Kaplan, A.: On the locus of Hodge classes. J. Am. Math. Soc. 8(2), 483–506 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  14. Deligne, P.: La conjecture de Weil pour les surfaces K3. Invent. Math. 15, 206–226 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  15. Deligne, P.: Local behavior of Hodge structures at infinity. Mirror Symmetry II 1, 683–699 (1997)

    MathSciNet  MATH  Google Scholar 

  16. Demailly, J.-P.: Regularization of closed positive currents and intersection theory. J. Algebr. Geom. 1(3), 361–409 (1992)

    MathSciNet  MATH  Google Scholar 

  17. Douady, A.: Le problème des modules pour les sous-espaces analytiques compacts d’un espace analytique donné. Ann. Inst. Fourier (Grenoble) 16(fasc. 1), 1–95 (1966)

    Article  MathSciNet  MATH  Google Scholar 

  18. Edmundo, M., Jones, G., Peatfield, N.: Sheaf cohomology in o-minimal structures. J. Math. Log. 6(2), 163–179 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  19. Flenner, H.: The infinitesimal Torelli problem for zero sets of sections of vector bundles. Math. Z. 193(2), 307–322 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  20. Fujino, O., Fujisawa, T.: On semipositivity theorems. Math. Res. Lett. 26(5), 1359–1382 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  21. Fujita, T.: Vanishing theorems for semipositive line bundles. In: Algebraic geometry. Springer, Berlin (1982)

  22. Grauert, H., Remmert, R.: Coherent Analytic Sheaves. Grundlehren der Mathematischen Wissenschaften, vol. 265. Springer, Berlin (1984)

    MATH  Google Scholar 

  23. Griffiths, P.: Periods of integrals on algebraic manifolds: Summary of main results and discussion of open problems Bull. Am. Math. Soc. 75, 228–296 (1970)

    Article  MATH  Google Scholar 

  24. Griffiths, P.: Periods of integrals on algebraic manifolds III. Inst. Hautes Études Sci. Publ. Math. 38, 125–180 (1970)

    Article  MATH  Google Scholar 

  25. Griffiths, P., Robles, C., Toledo, D.: Quotients of non-classical flag domains are not algebraic. Algebr. Geom. 1(1), 1–13 (2014)

    MathSciNet  MATH  Google Scholar 

  26. Grothendieck, A.: Éléments de géométrie algébrique. II. Étude globale élémentaire de quelques classes de morphisme. I. Inst. Hautes Études Sci. Publ. Math. 8, 5–222 (1961)

    Article  Google Scholar 

  27. Grothendieck, A.: Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. I. Inst. Hautes Études Sci. Publ. Math. 32 (1967)

  28. Kaiser, T.: Piecewise Weierstrass preparation and division for o-minimal holomorphic functions. Proc. Am. Math. Soc. 145(9), 3887–3897 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  29. Kashiwara, M., Schapira, P.: Ind-sheaves, Astérisque No. 271 (2001)

  30. Keel, S., Mori, S.: Quotients by groupoids. Ann. Math. (2) 145(1), 193–213 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  31. Kollár, J.: Subadditivity of the Kodaira dimension: fibers of general type. In: Algebraic Geometry, Sendai, 1985. Adv. Stud. Pure Math., 10, pp. 361–398. North-Holland, Amsterdam (1987)

  32. Kresch, A., Vistoli, A.: On coverings of Deligne–Mumford stacks and surjectivity of the Brauer map. Bull. Lond. Math. Soc. 36(2), 188–192 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  33. Lazarsfeld, R.: Positivity in Algebraic Geometry. I, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 48, p. xviii+387. Springer, Berlin (2004)

    MATH  Google Scholar 

  34. Matsumura, H.: Commutative Algebra. Mathematics Lecture Note Series 56, 2nd edn. Springer, Berlin (1980)

    MATH  Google Scholar 

  35. Mok, N., Pila, J., Tsimerman, J.: Ax-Schanuel for Shimura varieties. Ann. Math. (2) 189(3), 945–978 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  36. Mumford, D., Fogarty, J., Kirwan, F.: Geometric Invariant Theory. Ergebnisse der Mathematik und ihrer Grenzgebiete (2), vol. 34, Third Springer, Berlin (1994)

    Book  MATH  Google Scholar 

  37. Petit, F.: Tempered Subanalytic Topology on Algebraic Varieties. arXiv:1703.00870v1

  38. Popp, H.: On moduli of algebraic varieties II. Compos. Math. 28(1), 51–81 (1974)

    MathSciNet  MATH  Google Scholar 

  39. Peterzil, Y., Starchenko, S.: Complex analytic geometry in a nonstandard setting. In: Model Theory with Applications to Algebra and Analysis London Mathematical Society. Lecture Note Series, 349, vol. 1, pp. 117–165. Cambridge University Press, Cambridge (2008)

  40. Peterzil, Y., Starchenko, S.: Complex analytic geometry and analytic-geometric categories. J. Reine Angew. Math. 626, 39–74 (2009)

    MathSciNet  MATH  Google Scholar 

  41. Schmid, W.: Variation of Hodge structure: the singularities of the period mapping. Invent. Math. 22, 211–319 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  42. Serre, J.-P.: Géométrie algébrique et géométrie analytique. Ann. Inst. Fourier 6, 1–42 (1956)

    Article  MATH  Google Scholar 

  43. Sommese, A.: Criteria for quasi-projectivity. Math. Ann. 217, 247–256 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  44. Sommese, A.: On the rationality of the period mapping. Ann. della Sc. Norm. Super. Pisa Classe Sci. 5(4), 683–717 (1978)

    MathSciNet  MATH  Google Scholar 

  45. The Stacks project authors. The Stacks project. https://stacks.math.columbia.edu (2021)

  46. Toën, B.: K-théorie et cohomologie des champs algébriques, Ph.D. Thesis. Université de Toulouse 3 (1999)

  47. van den Dries, L.: Tame Topology and O-minimal Structures. London Mathematical Society Lecture Note Series, vol. 48. Cambridge University Press, Cambridge (1998)

    Book  MATH  Google Scholar 

  48. van den Dries, L., Miller, C.: Geometric categories and o-minimal structures. Duke Math J. 84(2), 497–540 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  49. Viehweg, E.: Quasi-Projective Moduli for Polarized Manifolds. Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 30. Springer, Berlin (1995)

    Book  MATH  Google Scholar 

Download references

Acknowledgements

J.T. would like to thank Vivek Shende, Jonathan Pila, and Ryan Keast for useful conversations. B.B. would like to thank Valery Alexeev and Johan de Jong for useful conversations. Y.B. would like to thank Olivier Benoist, Patrick Brosnan, and Wushi Goldring for useful conversations. The authors would also like to thank Ariyan Javanpeykar for useful remarks, specifically regarding Sect. 7.1. This paper, and in particular Sect. 2 owes a lot to the works of Peterzil and Starchenko, who initiated the study of o-minimal complex geometry. B.B. was partially supported by NSF Grant DMS-1702149. The authors are indebted to the referees for their careful reading and for greatly improving the exposition.

Author information

Authors and Affiliations

  1. Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, USA

    Benjamin Bakker

  2. Department of Mathematics, University of Bordeaux, Talence, France

    Yohan Brunebarbe

  3. Department of Mathematics, University of Toronto, Toronto, Canada

    Jacob Tsimerman

Authors
  1. Benjamin Bakker
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yohan Brunebarbe
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jacob Tsimerman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yohan Brunebarbe.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bakker, B., Brunebarbe, Y. & Tsimerman, J. o-minimal GAGA and a conjecture of Griffiths. Invent. math. 232, 163–228 (2023). https://doi.org/10.1007/s00222-022-01166-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00222-022-01166-1

Search

Navigation