A proof of the instability of AdS for the Einstein-massless Vlasov system

Abstract

In recent years, the conjecture on the instability of Anti-de Sitter spacetime, put forward by Dafermos–Holzegel (Dynamic instability of solitons in 4 + 1 dimesnional gravity with negative cosmological constant, 2006. https://www.dpmms.cam.ac.uk/~md384/ADSinstability.pdf) and Dafermos (The Black Hole Stability problem, Talk at the Newton Institute, Cambridge, 2006. http://www-old.newton.ac.uk/webseminars/pg+ws/2006/gmx/1010/dafermos/) in 2006, has attracted a substantial amount of numerical and heuristic studies. Following the pioneering work (Phys Rev Lett 107(3):031102, 2011) of Bizon–Rostworowski, research efforts have been mainly focused on the study of the spherically symmetric Einstein-scalar field system. The first rigorous proof of the instability of AdS in the simplest spherically symmetric setting, namely for the Einstein-null dust system, was obtained in Moschidis (A proof of the instability of AdS for the Einstein-null dust system with an inner mirror, 2017. arXiv:1704.08681). In order to circumvent problems associated with the trivial break down of the Einstein-null dust system occuring at the center $r=0$, Moschidis (2017) studied the evolution of the system in the exterior of an inner mirror placed at $r=r_{0}$, $r_{0}>0$. However, in view of additional considerations on the nature of the instability, it was necessary for Moschidis (2017) to allow the mirror radius $r_{0}$ to shrink to 0 with the size of the initial perturbation; well-posedness in the resulting complicated setup (involving low-regularity estimates of uniform modulus with respect to $r_{0}$) was obtained in Moschidis (The Einstein-null dust system in spherical symmetry with an inner mirror: structure of the maximal development and Cauchy stability, 2017. arXiv:1704.08685). In this paper, we establish the instability of AdS for the Einstein-massless Vlasov system in spherical symmetry; this will be the first proof of the AdS instability conjecture for an Einstein-matter system which is well-posed for regular initial data in the standard sense, without the addition of an inner mirror. The necessary well-posedness results for this system are obtained in our companion paper (Moschidis in The characteristic initial-boundary value problem for the Einstein-massless Vlasov system in spherical symmetry, 2018. arXiv:1812.04274). Our proof utilises an instability mechanism based on beam interactions which is superficially similar to the one appearing in Moschidis (A proof of the instability of AdS for the Einstein-null dust system with an inner mirror, 2017. arXiv:1704.08681). However, new difficulties associated with the Einstein-massless Vlasov system (such as the need for control on the paths of non-radial geodesics in a large curvature regime) will force us to develop a different strategy of proof involving a novel configuration of beam interactions. One of the main novelties of our construction is the introduction of a multi-scale hierarchy of domains in phase space, on which the initial support of the Vlasov field f is localised. The propagation of this hierarchical structure of the support of f along the evolution will be crucial both for controlling the geodesic flow under minimal regularity assumptions and for guaranteeing the existence of the solution until the time of trapped surface formation.

1 Introduction

In the presence of a negative cosmological constant $\Lambda$, the maximally symmetric solution of the vacuum Einstein equations

$$\begin{aligned} Ric_{{{\upmu }{\upnu }}}-\frac{1}{2}Rg_{{{\upmu }{\upnu }}}+\Lambda g_{{{\upmu }{\upnu }}}=0 \end{aligned}$$

(1.1)

in $n+1$ dimensions, $n\ge 3$, is Anti-de Sitter spacetime $({\mathcal {M}}_{AdS},g_{AdS})$. Expressed in the standard polar coordinate chart on ${\mathcal {M}}_{AdS}\simeq {\mathbb {R}}^{n+1}$, the AdS metric $g_{AdS}$ takes the form

$$\begin{aligned} g_{AdS}= & {} -\big (1-\frac{2}{n(n-1)}\Lambda r^{2}\big )dt^{2}\nonumber \\{} & {} +\big (1-\frac{2}{n(n-1)}\Lambda r^{2}\big )^{-1}dr^{2}+r^{2}g_{{\mathbb {S}}^{n-1}}, \end{aligned}$$

(1.2)

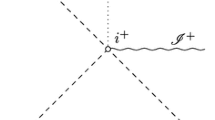
where $g_{{\mathbb {S}}^{n-1}}$ is the standard metric on the round sphere of radius 1. A conformal boundary ${\mathcal {I}}$ can be naturally attached to $({\mathcal {M}}_{AdS},g_{AdS})$ at $r=\infty$, with ${\mathcal {I}}$ having the conformal structure of a timelike hypersurface diffeomorphic to ${\mathbb {R}}\times {\mathbb {S}}^{n-1}$ (see Fig. 1).

Fig. 1

The AdS spacetime $({\mathcal {M}}_{AdS}^{n+1},g_{AdS})$ can be conformally identified with the interior of $({\mathbb {R}}\times {\mathbb {S}}_{+}^{n},g_{E}^{(\Lambda )})$, where ${\mathbb {S}}_{+}^{n}$ is the northern hemisphere of ${\mathbb {S}}^{n}$ and $g_{E}^{(\Lambda )}\doteq -dt^{2}+\Big (\frac{n(n-1)}{-2\Lambda }\Big )g_{{\mathbb {S}}_{+}^{n}}$ (with conformal factor $(1-\frac{2}{n(n-1)}\Lambda r^{2})^{-1}$ vanishing as $r\rightarrow \infty$). The timelike boundary ${\mathcal {I}}$ of $({\mathbb {R}}\times {\mathbb {S}}_{+}^{n},g_{E}^{(\Lambda )})$ corresponds to the conformal boundary of $({\mathcal {M}}_{AdS}^{n+1},g_{AdS})$ at infinity

More generally, a conformal boundary ${\mathcal {I}}$ with similar properties can be attached to any spacetime $({\mathcal {M}},g)$ which is merely asymptotically AdS, i.e. possesses an asymptotic region with geometry resembling that of (1.2) in the region $\{r\ge R_{0}\}$, $R_{0}\gg \frac{1}{\sqrt{-\Lambda }}$. For a more detailed exposition of the geometric properties associated to AdS asymptotics, see [33].

The hyperbolic nature of the system (1.1) and the timelike character of ${\mathcal {I}}$ imply that the right framework to study asymptotically AdS solutions of (1.1) is that of an initial-boundary value problem, with boundary conditions imposed asymptotically on ${\mathcal {I}}$. The well-posedness of the asymptotically AdS initial-boundary value problem for (1.1) was first addressed by Friedrich [28], who established the existence of solutions for a broad class of boundary conditions on ${\mathcal {I}}$, including examples both of reflecting and of dissipative conditions (see also the discussion in [29, 34], as well as [26, 27]). The formulation of appropriate boundary conditions for (1.1) on ${\mathcal {I}}$ and their effects on the spacetime geometry have also been investigated in the high energy physics literature; the recent surge of interest on these topics was sparked by the putative AdS/CFT correspondence, put forward by Maldacena [39], Gubser–Klebanov–Polyakov [31] and Witten [50] (see [1, 2, 32]).

The well-posedness of the initial-boundary value problem for (1.1) allows discussing the dynamics associated to families of asymptotically AdS initial data sets for (1.1). Thus, the question of stability of the trivial solution $({\mathcal {M}}_{AdS},g_{AdS})$ under perturbation of its initial data arises naturally in this context. When reflecting boundary conditions are imposed on ${\mathcal {I}}$, the possibility of non-linear instability for $({\mathcal {M}}_{AdS},g_{AdS})$ is already insinuated by the lack of asymptotic stability for solutions to linear toy-models for (1.1); this is already illustrated by the simple example of the conformally coupled Klein–Gordon equation

$$\begin{aligned} \square _{g_{AdS}}\varphi -\frac{2}{3}\Lambda \varphi =0 \end{aligned}$$

(1.3)

on $({\mathcal {M}}_{AdS}^{3+1},g_{AdS})$, where imposing Dirichlet conditions for $r\varphi$ on ${\mathcal {I}}$ results in the energy flux of $\varphi$ through the foliation $\{t=\tau \}$ to be constant in $\tau$, thus preventing any non-trivial solution $\varphi$ from decaying to 0 as $\tau \rightarrow +\infty$.¹ Motivated by additional considerations in the setting of the biaxial Bianchi IX symmetry class for (1.1) in $4+1$ dimensions, Dafermos and Holzegel [16, 17] in fact conjectured a stronger instability statement in 2006:

AdS instability conjecture There exist arbitrarily small perturbations to the initial data of AdS spacetime which, under evolution by the vacuum Einstein equations (1.1) with a reflecting boundary condition on ${\mathcal {I}}$, lead to the development of black hole regions. In particular, $({\mathcal {M}}_{AdS},g_{AdS})$ is non-linearly unstable.

The scenario proposed by the conjecture can be also viewed as a manifestation of gravitational turbulence: The formation of black hole regions signifies the emergence of non-trivial geometric structures at small scales, arising from the non-linear evolution of initial data which were almost trivial at the same spatial scales.

Remark

We should point out that the above formulation of the AdS instability conjecture is ambiguous with respect to the initial data norm $||\cdot ||_{data}$ measuring the “smallness” of the perturbations. A minimal requirement for $||\cdot ||_{data}$ is that perturbations of $({\mathcal {M}}_{AdS},g_{AdS})$ which are small with respect to $||\cdot ||_{data}$ should give rise to solutions g of (1.1) which exist (and remain close to $g_{AdS}$) for long time intervals $\{0\le t\le T_{*}\}$, i.e. that $({\mathcal {M}}_{AdS},g_{AdS})$ is Cauchy stable as a solution of the initial-boundary value problem for (1.1);² this condition implies, in particular, that the timescale of black hole formation tends to $+\infty$ as the size of the initial perturbation shrinks to 0. The requirement for long-time existence in fact imposes a condition on $||\cdot ||_{data}$ as a measure of regularity of initial data sets: The trapped surface formation results of [3, 13, 38] imply that there is no uniform time of existence for solutions to (1.1) in terms of initial data norms for which the vacuum equations are supercritical (such as norms of regularity below $||\cdot ||_{H^{\frac{3}{2}}}$ when $n=3$, as a corollary of [3]).

The choice of reflecting boundary conditions on ${\mathcal {I}}$ is also crucial for the validity of the conjecture: Assuming, instead, “optimally dissipative” conditions on ${\mathcal {I}}$, Holzegel–Luk–Smulevici–Warnick [34] showed that solutions to the linearized vacuum Einstein equations on $({\mathcal {M}}_{AdS},g_{AdS})$ decay at a superpolynomial rate in t, providing a strong indication of non-linear asymptotic stability for perturbations of $({\mathcal {M}}_{AdS},g_{AdS})$ in this setting.

The study of the AdS instability conjecture in $3+1$ dimensions has been mainly focused, so far, on Einstein-matter systems which admit non-trivial spherically symmetric dynamics (thus reducing the problem to the more tractable setting of $1+1$ dimensional hyperbolic systems), while still retaining many of the qualitative properties of the vacuum equations (1.1);³ a prominent example of such a model is provided by the Einstein–Klein–Gordon system

$$\begin{aligned} {\left\{ \begin{array}{ll} Ric_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }+\Lambda g_{\mu \nu }=8\pi T_{\mu \nu }[\varphi ],\\ \square _{g}\varphi -\mu \varphi =0,\\ T_{\mu \nu }[\varphi ]\doteq \partial _{\mu }\varphi \partial _{\nu }\varphi -\frac{1}{2}g_{\mu \nu }\partial ^{\alpha }\varphi \partial _{\alpha }\varphi . \end{array}\right. } \end{aligned}$$

(1.4)

In the case when the Klein–Gordon mass $\mu$ satisfies the so-called Breitenlohner–Freedman bound, well-posedness for the initial-boundary value problem for (1.4) in the spherically symmetric case was established, for a wide class of boundary conditions on ${\mathcal {I}}$, by Holzegel–Smulevici [35] and Holzegel–Warnick [36].⁴

The first numerical and heuristic study in the direction of establishing the AdS instability conjecture for (1.4) was carried out by Bizon–Rostworowski [11] in 2011. The numerical simulations of [11] verified the existence of spherically symmetric initial data sets for (1.4), with small initial size, the evolution of which (under Dirichlet conditions at ${\mathcal {I}}$) reaches the threshold of trapped surface formation after sufficiently long time. In addition, Bizoń and Rostworowski [11] was the first to propose a mechanism driving the initial stage of the instability: Analyzing perturbatively the interactions of different frequency modes of the scalar function $\varphi$, Bizoń and Rostworowski [11] suggested that the transfer of energy from low to high frequencies was propelled by a hierarchy of resonant interactions.

Following [11], a vast amount of numerical and heuristic works were dedicated to the study of the AdS instability conjecture for the spherically symmetric system (1.4), addressing, in addition, questions related to the long time dynamics of generic perturbations to $({\mathcal {M}}_{AdS},g_{AdS})$ and the possibility of existence of “islands of stability” in the moduli space of initial data for (1.4) close to $({\mathcal {M}}_{AdS},g_{AdS})$; see, e. g. [6, 9, 10, 12, 14, 15, 19, 20, 22,23,24, 30, 37, 40]. For works moving outside the realm of $1+1$ systems, see also [7, 21, 46]. Most of the aforementioned works utilised a frequency space analysis similar to the one introduced in [11], with the notable exception of [22]. A more detailed discussion on the numerics literature surrounding the AdS instability conjecture can be found in [41].

The first rigorous proof of the instability of AdS in a spherically symmetric setting was obtained in [41], for the case of the Einstein-null dust system with both ingoing and outgoing dust; this system can be formally viewed as a high frequency limit of (1.4) in spherical symmetry (see also the discussion in [44]). The proof of [41] uncovered and utilised an alternative instability mechanism at the level of position space: Arranging the null dust into a specific configuration of localised spherically symmetric beams, Moschidis [41] showed that successive reflections off ${\mathcal {I}}$ lead to the concentration of energy in the beam lying initially to the exterior of the rest. However, in order to circumvent a trivial break down of the Einstein-null dust system occuring once the dust reaches the center of symmetry, Moschidis [41] placed an inner mirror at a finite radius $r=r_{0}>0$ and studied the evolution restricted to the region $r>r_{0}$. Moreover, further considerations on the nature of the dynamics around $({\mathcal {M}}_{AdS},g_{AdS})$ necessitated that the mirror radius $r_{0}$ in [41] was allowed to shrink to 0 at a rate proportional to the size of the initial perturbation. Well-posedness for the initial-boundary value problem in this rather complicated setup, in an initial data topology allowing for estimates with uniform modulus with respect to $r_{0}$, was obtained in [42].

In this paper, we will prove the instability of $({\mathcal {M}}_{AdS}^{3+1},g_{AdS})$ for the Einstein-massless Vlasov system in spherical symmetry; this system is well-posed for regular initial data in the standard sense, without the addition of an inner mirror around the center of symmetry. Novel difficulties associated with the Einstein-massless Vlasov system (both at a technical and at a more conceptual level) will force us to depart from the main strategy of proof followed in [41], and develop a new physical space configuration of beam interactions, where the sizes of the phase-space domains corresponding to each beam are part of a complicated hierarchy of scales. It appears that the same ideas can also yield (after merely minor modifications) the instability of $({\mathcal {M}}_{AdS}^{n+1},g_{AdS})$ in the higher dimensional case $n\ge 3$; however, in order to avoid further complicating our exposition, we will restrict ourselves to the case $n=3$.

We will now proceed to review the main result of this paper in more detail; a discussion on the complications arising in the proof as well as a brief comparison with the methods of [41] will then follow in Sect. 1.2.

1.1 The main result: AdS instability for the spherically symmetric Einstein-massless Vlasov system

Let $({\mathcal {M}},g)$ be a $3+1$ dimensional, smooth Lorentzian manifold and let f be a non-negative measure on $T{\mathcal {M}}$ supported on the set of future directed null vectors. The Einstein-massless Vlasov system for $({\mathcal {M}},g;f)$ takes the form

$$\begin{aligned} {\left\{ \begin{array}{ll} Ric_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu }+\Lambda g_{\mu \nu }=8\pi T_{\mu \nu }[f],\\ {\mathcal {L}}^{(g)}f=0, \end{array}\right. } \end{aligned}$$

(1.5)

where ${\mathcal {L}}^{(g)}$ is the geodesic spray on $T{\mathcal {M}}$ (i.e. the Lagrangean vector field of ${\mathscr {L}}:T{\mathcal {M}}\rightarrow {\mathbb {R}}$, ${\mathscr {L}}(v) \doteq \frac{1}{2} g(v,v)$; see [45]) and $T_{\mu \nu }[f]$ is expressed in terms of f and g by (2.22). In the spherically symmetric setting, there is a unique reflecting boundary condition for (1.5) at conformal infinity ${\mathcal {I}}$; it is formulated simply as the requirement that the Vlasov field f is conserved along the reflection of null geodesics $\gamma$ off ${\mathcal {I}}$ (see Sect. 2.4).

The main result of this paper is the proof of the AdS instability conjecture for the system (1.5) in spherical symmetry:

Theorem 1

(rough version) There exists a one-parameter family of smooth, spherically symmetric, asymptotically AdS initial data ${\mathcal {D}}^{(\varepsilon )}$ for (1.5), $\varepsilon \in (0,1]$, satisfying the following properties:

• As $\varepsilon \rightarrow 0$, ${\mathcal {D}}^{(\varepsilon )}$ converge to the trivial data ${\mathcal {D}}^{(0)}$ of $({\mathcal {M}}_{AdS},g_{AdS};0)$ with respect to a suitable initial data norm $||\cdot ||_{data}$.

• For any $\varepsilon \in (0,1]$, the (unique) maximally extended solution $({\mathcal {M}},g;f)^{(\varepsilon )}$ of (1.5) arising from ${\mathcal {D}}^{(\varepsilon )}$ with reflecting boundary conditions on ${\mathcal {I}}$ contains a trapped sphere, and, hence, a black hole region.

In particular, $({\mathcal {M}}_{AdS},g_{AdS})$ is unstable as a solution of (1.5) under spherically symmetric perturbations which are small with respect to $||\cdot ||_{data}$.

For a more detailed statement of Theorem 1, see Sect. 4. For the definition the maximal future development $({\mathcal {M}},g;f)^{(\varepsilon )}$ of an initial data set ${\mathcal {D}}^{(\varepsilon )}$ and the notion of a trapped sphere, see Sect. 3.

Remark

The initial data norm $||\cdot ||_{data}$ appearing in the statement of Theorem 1 is a scale invariant norm that has just enough regularity to provide control of the integrals of the right hand sides of the constraint equations (2.38)–(2.39) in the evolution; a precise definition of the norm is given in Sect. 3.4 (see Definition 3.14), while a simple relation expressing the size of ${\mathcal {D}}^{(\epsilon )}$ with respect to $||\cdot ||_{data}$ is given by (1.36) (for a discussion on the scale invariance of $||\cdot ||_{data}$, see the remark below Definition 3.14). The necessary well-posedness results for the initial-boundary value problem for (1.5), as well as the crucial Cauchy stability statement for $({\mathcal {M}}_{AdS},g_{AdS})$ in the topology defined by $||\cdot ||_{data}$ (see the remark below the statement of the AdS instability conjecture), are obtained in our companion paper [43] and are also reviewed in Sect. 3.

We should point out that, switching to the case $\Lambda =0$, Minkowski spacetime $({\mathbb {R}}^{3+1},\eta )$ is non-linearly stable as a solution of (1.5) under spherically symmetric perturbations which are initially small with respect to the norm $||\cdot ||_{data}$ (suitably modified in the region $r\gg 1$ to accommodate for the change in the value of $\Lambda$). This result, which can be viewed as a straightforward corollary of our method of proof of Cauchy stability for $({\mathcal {M}}_{AdS},g_{AdS})$ and is discussed in more detail in Section 6 of [43], provides further justification for the use of the initial data norm $||\cdot ||_{data}$ in the study of the AdS instability conjecture.⁵ In the case $\Lambda <0$, a non-linear stability statement for AdS spacetime with respect to the initial data norm $||\cdot ||_{data}$ is also expected to hold when a maximally dissipative boundary condition is imposed for (1.5) on ${\mathcal {I}}$ (cf. [34]); in this case however, such a result would not be a direct consequence of our proof of Cauchy stability for $({\mathcal {M}}_{AdS},g_{AdS})$.

1.2 Sketch of the proof and further discussion

In this section, we will briefly sketch the proof of Theorem 1, highlighting the main technical complications and obstacles shaping our strategy. We will then comment on the relation between the proof of Theorem 1 and the ideas appearing in [41].

The proof of Theorem 1 is carried out in double null coordinates $(u,v,\theta ,\varphi )$, in which a general spherically symmetric metric g takes the form

$$\begin{aligned} g=-\Omega ^{2}(u,v)du\,dv+r^{2}(u,v)g_{{\mathbb {S}}^{2}} \end{aligned}$$

(1.6)

(see Sect. 2.1). The initial data family ${\mathcal {D}}^{(\varepsilon )}$ in the statement of Theorem 1 is then constructed as a family of characteristic smooth initial data prescribed at $u=0$; the necessary well-posedness results for the characteristic initial-boundary value problem in this setting are established in our companion paper [43] and are also reviewed in Sect. 3.

Fig. 2

The initial data family ${\mathcal {D}}^{(\epsilon )}$ gives rise to a large number ${\mathcal {N}}_{\epsilon }$ of spherically symmetric Vlasov beams, which are initially ingoing. The left part of the figure provides a schematic depiction of just three of these beams, projected onto the (u, v)-plane. Each successive beam is increasingly narrower compared to the previous ones in the configuration (as shown schematically on the right), and contains geodesics of increasingly smaller angular momenta

The family ${\mathcal {D}}^{(\varepsilon )}$ is constructed so that the physical space support of the corresponding Vlasov field $f_{\varepsilon }$ is initially separated into a large number $N_{\varepsilon }\gg 1$ of narrow ingoing beams (see Fig. 2), organised in terms of a particular multi-scale hierarchy, which we will now describe: Denoting with $\zeta _{i}$ the i-th Vlasov beam (with i increasing with the initial distance of the beam from $r=0$), the configuration of beams is set up so that, at $u=0$, $\zeta _{i}$ has physical space width ${{\Delta }}L_{i}$ satisfying

$$\begin{aligned} {{\Delta }}L_{i}\sim \varepsilon ^{(i)}(-\Lambda )^{-\frac{1}{2}}, \end{aligned}$$

(1.7)

where the hierarchy of small parameters $\{\varepsilon ^{(i)}\}_{i=0}^{N_{\varepsilon }}$ (each given by an explicit formula in terms of $\varepsilon$ and i) satisfies

$$\begin{aligned} \varepsilon ^{(i+1)}\ll \varepsilon ^{(i)}\text { and }\varepsilon ^{(i)}\xrightarrow {\varepsilon \rightarrow 0}0\text { for all }i=0,\ldots ,N_{\varepsilon }-1. \end{aligned}$$

(1.8)

The initial separation $d_{i}$ (with respect to the v coordinate) between the beams $\zeta _{i}$ and $\zeta _{i+1}$ is chosen to satisfy

$$\begin{aligned} {{\Delta }}L_{i}\ll d_{i}\ll {{\Delta }}L_{i-1}. \end{aligned}$$

(1.9)

(where we used the convention that ${{\Delta }}L_{-1}\doteq (-\Lambda )^{\frac{1}{2}}$).

The energy content ${\mathcal {E}}_{i}$ of the beam $\zeta _{i}$ at $u=0$ is defined as the difference of the renormalised Hawking mass

$$\begin{aligned} {\tilde{m}}\doteq \frac{r}{2}\Big (1-4\Omega ^{-2}\partial _{u}r\partial _{v}r\Big )-\frac{1}{6}\Lambda r^{3} \end{aligned}$$

between the inner and outer boundary of $\zeta _{i}$ at $u=0$, i.e.:

$$\begin{aligned} {\mathcal {E}}_{i}\doteq {\tilde{m}}(0,v_{i}^{+})-{\tilde{m}}(0,v_{i}^{-}) \end{aligned}$$

(where $\zeta _{i}\cap \{u=0\}=\{0\}\times [v_{i}^{-},v_{i}^{+}]$ in the (u, v)-plane). The Vlasov field $f_{\varepsilon }$ is chosen so that ${\mathcal {E}}_{i}$ satisfies

$$\begin{aligned} {\mathcal {E}}_{i}\sim a_{i}{{\Delta }}L_{i}, \end{aligned}$$

(1.10)

where the parameters $0\le a_{i}\ll 1$ are only fixed at a later stage in the proof (we will come back to this point later in the discussion).

Remark

In order to ensure the condition

$$\begin{aligned} ||{\mathcal {D}}^{(\varepsilon )}||_{data}\xrightarrow {\varepsilon \rightarrow 0}0 \end{aligned}$$

(1.11)

in the statement of Theorem 1, an additional smallness condition needs to be imposed on $\sum _{i=0}^{N_{\varepsilon }}a_{i}$; we refer the reader to the detailed construction of the initial data family in Sect. 6.2.

Regarding the momentum space conditions imposed on the beam configuration, the beam $\zeta _{i}$ is chosen to consist only of null geodesics $\gamma$ with angular momentum $l_i$ satisfying:⁶

$$\begin{aligned} \frac{l_i}{(E_{0})_i}\sim \varepsilon ^{(i)}(-\Lambda )^{-\frac{1}{2}}. \end{aligned}$$

(1.12)

As a result, the geodesics in the support of the Vlasov beam $f_{\varepsilon }$ are nearly radial when $\varepsilon \ll 1$.

Remark

For a null geodesic $\gamma$ in AdS spacetime $({\mathcal {M}}_{AdS},g_{AdS})$, the normalised angular momentum $\frac{l}{E_{0}}$ determines the minimum value of r along $\gamma$, with geodesics having smaller normalised angular momentum approaching closer to the center $r=0$; in the case when $\frac{l}{E_{0}}\ll (-\Lambda )^{-\frac{1}{2}}$, the following approximate relation holds on $({\mathcal {M}}_{AdS},g_{AdS})$ (see the relation A.2 in [43]):

$$\begin{aligned} \min _{\gamma }r\sim \frac{l}{E_{0}}. \end{aligned}$$

(1.13)

In the maximal future development $({\mathcal {M}}_{\varepsilon };f_{\varepsilon })$ of ${\mathcal {D}}^{(\varepsilon )}$, the Vlasov beams $\zeta _{i}$ are reflected off ${\mathcal {I}}$ multiple times (see Fig. 2); between any two successive reflections, the Vlasov beams $\zeta _{i}$ exchange energy through their non-linear interactions, possibly at a loss of coherence.⁷ The proof of Theorem 1 will consist of showing that, after a large number of reflections off ${\mathcal {I}}$, the non-linear interactions lead to the concentration of sufficient energy at the top beam $\zeta _{N_{\varepsilon }}$ so that a trapped surface can form as $\zeta _{N_{\varepsilon }}$ approaches the center $r=0$ for the last time.

Controlling the coherence of the Vlasov beams for sufficiently long time (ensuring, in particular, that the qualitative picture of the configuration is similar to the one depicted in Fig. 2) will constitute a major technical challenge of the proof, but the relevant details will be only briefly sketched in this discussion. The fact that, for $\Lambda =0$, the system (1.5) admits static solutions $({\mathcal {M}}_{st},g_{st};f_{st})$ with

$$\begin{aligned} \sup _{{\mathcal {M}}_{st}}\frac{2{\tilde{m}}}{r}>\frac{4}{5} \end{aligned}$$

(1.14)

(see [5])⁸ shows that, in general, when $\frac{2{\tilde{m}}}{r}$ exceeds a certain threshold in the evolution, the configuration of Vlasov beams cannot be expected to behave in a qualitatively similar fashion as on $({\mathcal {M}}_{AdS},g_{AdS})$ (i.e. approach $r=0$ only for a brief period of time separating an ingoing and an outgoing phase, like the beams depicted in Fig. 2).⁹ The additional flexibility provided by the freedom in the choice of the parameters $\varepsilon ^{(i)}$ in the multi-scale hierarchy of parameters (1.7)–(1.10) will be crucial for circumventing this obstacle.

The evolution of ${\mathcal {D}}^{(\varepsilon )}$ will be studied in two steps:

• 1. In the first step, we will show that a scale invariant norm measuring the concentration of energy of $({\mathcal {M}},g;f)^{(\varepsilon )}$ grows in time at a specific rate, driven by an instability mechanism based on the interactions of the beams similar to the one implemented in [41]. Provided the initial parameters $a_{i}$ in (1.10) are chosen appropriately, we will show that the beam interactions lead to the formation of a specific, predetermined profile ${\mathcal {S}}_{*}=(g;f)^{(\varepsilon )}|_{u=u_{*}}$ at a late enough retarded time $u=u_{*}(\varepsilon )\gg 1$. The freedom in the choice of the parameters $\varepsilon _{i}$ and a collection of robust estimates on the exchange of energy between the beams will enable us to control a priori for $0\le u\le u_{*}$

  $$\begin{aligned} \frac{2{\tilde{m}}}{r}\le \delta _{*} \end{aligned}$$

  (1.15)

  where $\delta _{*}\ll 1$ is fixed; the bound (1.15) will be crucial for controlling the paths of geodesics in the support of $f^{(\varepsilon )}$ for $u\in [0,u_{*}]$.

• 2. In a second step, we will show that the specific features of ${\mathcal {S}}_{*}$ (inherited by the properties of the multi-scale hierarchy (1.7)–(1.10)) imply that a trapped surface necessarily forms along $\zeta _{N_{\varepsilon }}\cap \{u=u_{\dagger }\}$ for some $u_{*}<u_{\dagger }\le u_{*}+O(1)$, i.e. that

  $$\begin{aligned} \sup _{\zeta _{N_{\varepsilon }}\cap \{u=u_{\dagger }\}}\frac{2{\tilde{m}}}{r}>1. \end{aligned}$$

  (1.16)

  It will thus follow that $({\mathcal {M}},g;f^{(\varepsilon )})$ contains a black hole region.

We will now proceed to discuss the above steps in more detail.

Remark

The first of the two steps described above already provides an orbital instability statement for AdS spacetime, since, once the profile ${\mathcal {S}}_*$ is formed, the size of the solution measured with respect to the norm $||\cdot ||_{data}$ at $u=u_*$ is large (see (1.39) below). In the simpler case where one would be interested in merely obtaining such an orbital instability statement, the precise form of the profile ${\mathcal {S}}_*$ would be less relevant; however, the conditions (1.8) and (1.9) on the hierarchy of scales $\epsilon ^{(i)}$, $\Delta L_i$ would still be necessary for our proof to carry over without major modifications.

1.2.1 First stage of the instability: growth of the scale invariant norm and formation of the intermediate profile

The first step in the proof of Theorem 1 will consist of showing that the interactions of the beams $\zeta _{i}$ lead to a gradual increase in the energy content of all beams $\zeta _{j}$ with $j\ge 1$ (implying the concentration of energy at finer scales, in view of the length-scale hierarchy (1.7)). In particular, our aim at this stage would be to show that there exists a time $u=u_{*}\gg 1$ (determined in terms of $\varepsilon$) at which the solution $(g;f)^{(\varepsilon )}|_{u=u_*}$ takes a specific form, characterized by the fact the energy contents ${\mathcal {E}}_{j}^{*}$ of the beams $\zeta _{j}$ at time $u=u_{*}$ satisfy

$$\begin{aligned} \frac{2{\mathcal {E}}_{j}^{*}}{d_{j}^{*}}\sim \frac{C}{N_{\varepsilon }}\exp \big (-2\frac{C}{N_{\varepsilon }}j\big )\quad \text { for all }1\le j\le N_{\varepsilon }-1 \end{aligned}$$

(1.17)

and,

$$\begin{aligned} {\mathcal {E}}_{N_{\varepsilon }}^{*}\sim \frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}, \end{aligned}$$

(1.18)

where $d_{j}^{*}$ is the distance between $\zeta _{j}\cap \{u=u_{*}\}$ and $\zeta _{j+1}\cap \{u=u_{*}\}$. For simplicity, for the rest of this discussion, we will refer to the initial data induced on $\{u=u_{*}\}$ by the solution $({\mathcal {M}},g;f)^{(\varepsilon )}$ simply as the intermediate profile ${\mathcal {S}}_{*}$. This step will in fact occupy the bulk of the proof of Theorem 1.

Estimates for the geodesic flow Obtaining estimates for the null geodesic flow on $({\mathcal {M}},g;f)^{(\varepsilon )}$ for sufficiently long times is a prerequisite for studying the interactions of the beams $\zeta _{i}$. More precisely, we would like to show that, at least until the formation of the intermediate profile ${\mathcal {S}}_{*}$, null geodesics in $({\mathcal {M}},g;f)^{(\varepsilon )}$ follow trajectories which are similar (in a certain sense) to the trajectories of null geodesics on $({\mathcal {M}}_{AdS},g_{AdS})$.

The only quantitative bound assumed on the initial data family is a smallness condition in terms of the low-regularity norm $||\cdot ||_{data}$. The well-posedness estimates established in our companion paper [43] imply that, for any fixed ${\bar{U}}>0$, if we define the scale-invariant norm

$$\begin{aligned} ||({\mathcal {M}},g;f)^{(\varepsilon )}||_{u\le {\bar{U}}}&\doteq \sup _{{\bar{u}}\le {\bar{U}}}\int _{\{u={\bar{u}}\}}r\Big (\frac{T_{vv}[f]}{\partial _{v}r}+\frac{T_{uv}[f]}{-\partial _{u}r}\Big ) ({\bar{u}},v)\,dv\nonumber \\&\quad \quad +\sup _{{\bar{v}}}\int _{\{v={\bar{v}}\}\cap \{u\le {\bar{U}}\}}r \Big (\frac{T_{uv}[f]}{\partial _{v}r}+\frac{T_{uu}[f]}{-\partial _{u}r}\Big )(u,{\bar{v}})\,du, \end{aligned}$$

(1.19)

then the following estimate holds for $({\mathcal {M}},g;f)^{(\varepsilon )}$ as $\varepsilon \rightarrow 0$:

$$\begin{aligned} ||({\mathcal {M}},g;f)^{(\varepsilon )}||_{u\le {\bar{U}}} \lesssim ||{\mathcal {D}}^{(\varepsilon )}||_{data}, \end{aligned}$$

(1.20)

where $T_{\mu \nu }[f]$ are the components of the energy momentum tensor of $f^{(\varepsilon )}$ and the constants implicit in the $\lesssim$ notation depend on ${\bar{U}}$ but are independent of $\epsilon$ (this can be viewed as a corollary of Proposition 3.15). However, for values of ${\bar{U}}$ which are comparable to $u_{*}$ (note that $u_*(\epsilon ) \xrightarrow {\epsilon \rightarrow 0} +\infty$), we will only be able to estimate

$$\begin{aligned} ||({\mathcal {M}},g;f)^{(\varepsilon )}||_{u\le {\bar{U}}}\le C \end{aligned}$$

(1.21)

for some absolute constant $C\gg 1$ (depending on the precise form of the profile ${\mathcal {S}}_*$). Therefore, it will be necessary for us to obtain sufficient control on the phase space trajectories of null geodesics $\gamma :[0,a)\rightarrow ({\mathcal {M}},g)^{(\varepsilon )}$ merely under the (rather weak) assumption that (1.21) and the a priori estimate (1.15) hold. To this end, we will rely crucially on a reformulation of the equations of motion for null geodesics, making use of the fact that $({\mathcal {M}},g;f)^{(\varepsilon )}$ satisfies (1.5), yielding identities such as the following:

$$\begin{aligned}&\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(s)-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(0)\nonumber \\&\quad = \int _{v(\gamma (0))}^{v(\gamma (s))}\int _{u_{1}(v)}^{u(\gamma (s_{v}))}\Big (\frac{1}{2}\frac{\frac{6{\tilde{m}}}{r}-1}{r^{2}}\Omega ^{2}-24\pi T_{uv}[f]\Big )\,du\,dv\nonumber \\&\qquad +\int _{v(\gamma (0))}^{v(\gamma (s))}\big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\big )(0,v)\,dv \end{aligned}$$

(1.22)

(assuming that the initial point $\gamma (0)$ of $\gamma$ belongs to $\{u=0\}$; see Fig. 3).¹⁰ In the above, ${\dot{\gamma }}^u$ denotes the u-component of the derivative ${\dot{\gamma }}$ of $\gamma$. We refer the reader to Sect. 5 for more details; for the rest of this discussion, we will suppress any technical issues related to the precise estimates on the geodesic flow on $({\mathcal {M}},g)^{(\varepsilon )}$.

Fig. 3

Schematic depiction of the domain of integration appearing in the right hand side of (1.22) for a null geodesic $\gamma$

Beam interactions and energy concentration Let us now proceed to consider a pair of beams $\zeta _{i}$ $\zeta _{j}$, with

$$\begin{aligned} 0\le i<j\le N_{\varepsilon } \end{aligned}$$

(the fact that i is smaller than j, i.e. that $\zeta _{i}$ initially lies in the interior of $\zeta _{j}$, will be crucial for this part of this discussion). The beams $\zeta _{i}$ and $\zeta _{j}$ will be successively reflected off ${\mathcal {I}}$ multiple times in the time interval $u\in [0,u_{*}]$, intersecting each other twice between each successive pair of reflections, in a pattern as depicted in Fig. 4. In particular, assuming that the geodesic flow on $({\mathcal {M}},g)^{(\varepsilon )}$ behaves in a similar fashion as on AdS spacetime $({\mathcal {M}}_{AdS},g_{AdS})$, the condition (1.9) on the initial separation of the beams implies that (with notations as in Fig. 4):

$$\begin{aligned} \varepsilon ^{(i)}(-\Lambda )^{-\frac{1}{2}}\ll \sup _{{\mathcal {R}}_{0}}r\sim d_{i} \end{aligned}$$

(1.23)

and

$$\begin{aligned} \inf _{{\mathcal {R}}_{\infty }}r\sim \frac{1}{\varepsilon ^{(i)}}(-\Lambda )^{-\frac{1}{2}}\gg \sup _{{\mathcal {R}}_{0}}r. \end{aligned}$$

(1.24)

Fig. 4

Any two beams $\zeta _i$ and $\zeta _j$, $0\le i< j\le N_{\epsilon }$, will intersect twice between each successive pair of reflections off conformal infinity; here, ${\mathcal {R}}_{0}$ denotes the intersection region closer to the axis, while ${\mathcal {R}}_{\infty }$ denotes the intersection region closer to conformal infinity. Note that, since $i<j$, the beam $\zeta _i$ lies initially in the interior of $\zeta _j$. As a result, $\zeta _i$ is outgoing at the first intersection ${\mathcal {R}}_0$, while $\zeta _j$ is ingoing

In view of the condition (1.12) on the angular momenta of the geodesics in the beams $\zeta _{i}$ and $\zeta _{j}$, the relations (1.23) and (1.24) imply that, on the intersection regions ${\mathcal {R}}_{0}$ and ${\mathcal {R}}_{\infty }$, the geodesics of $\zeta _{i}$ and $\zeta _{j}$ can be essentially viewed as purely radial (since their angular momentum is negligible compared to the sphere radius r in these regions, in view of (1.12) and (1.23), (1.24)). Therefore, it is reasonable to expect that the exchange of energy occuring between $\zeta _{i}$ and $\zeta _{j}$ is governed by the same mechanism as for beams of null dust, evolving according to the Einstein-null dust system; this is the mechanism employed in [41].

According to [41], when a localised, spherically symmetric and ingoing null-dust beam ${\bar{\zeta }}$ intersects a similar outgoing beam $\zeta$ over a region ${\mathcal {R}}$ (see Fig. 5), the energy contents ${\mathcal {E}}[{\bar{\zeta }}]$, ${\mathcal {E}}[\zeta ]$ of ${\bar{\zeta }},\zeta$, respectively, right before and right after the interaction are related by the following approximate formulas (assuming that ${\mathcal {E}}[\zeta ],{\mathcal {E}}[{\bar{\zeta }}]\ll r|_{{{\mathcal {R}}}}$ and that (1.15) holds):

$$\begin{aligned} {\mathcal {E}}_{+}[{\bar{\zeta }}]={\mathcal {E}}_{-}[{\bar{\zeta }}]\cdot \exp \Big (\frac{2{\mathcal {E}}_{-}[\zeta ]}{r|_{{\mathcal {R}}}}+\mathfrak {Err}\Big ) \end{aligned}$$

(1.25)

and

$$\begin{aligned} {\mathcal {E}}_{+}[\zeta ]={\mathcal {E}}_{-}[\zeta ]\cdot \exp \Big (-\frac{2{\mathcal {E}}_{-}[{\bar{\zeta }}]}{r|_{{\mathcal {R}}}}+\mathfrak {Err}\Big ), \end{aligned}$$

(1.26)

where ${\mathcal {E}}_{-}$ and ${\mathcal {E}}_{+}$ denote the energy contents of the beams before and after the interaction, respectively, defined by the difference in the values of the renormalised Hawking mass ${\tilde{m}}$ at the two vacuum regions bounding each beam before and right after the intersection (see Fig. 5); for the purpose of this discussion, we will assume that the error terms $\mathfrak {Err}$ in (1.25)–(1.26) are negligible and can be ignored. The formula (1.25) can be deduced by tracking the change in the mass difference around ${\bar{\zeta }}$ through the relation

$$\begin{aligned} \partial _{u}\partial _{v}{\tilde{m}}=2\pi \partial _{u}\Big (\frac{1-\frac{2m}{r}}{\partial _{v}r}r^{2}T_{vv}[f|_{{\bar{\zeta }}}]\Big ) \end{aligned}$$

(1.27)

(see the relation (6.57) in [41]) using the following facts:

• 1. The change in $\frac{1-\frac{2m}{r}}{\partial _{v}r}$ is determined in terms of $\zeta$ by the constraint equation (see (2.47))

  $$\begin{aligned} \partial _{u}\log \Big (\frac{\partial _{v}r}{1-\frac{2m}{r}}\Big )=-\frac{4\pi }{r}\frac{r^{2}T_{uu}[f]}{-\partial _{u}r}. \end{aligned}$$

  (1.28)

• 2. The quantity $r^{2}T_{vv}[f|_{{\bar{\zeta }}}]$ is constant in u as a consequence of the conservation of energy relation, i.e.:

  $$\begin{aligned} \partial _{u}\big (r^{2}T_{vv}[f|_{{\bar{\zeta }}}]\big )=0 \end{aligned}$$

  (1.29)

  (see the relation (2.38) in [41]).

The formula (1.26) is obtained by following the same procedure for $\zeta$ with the roles of u and v inverted (resulting in a change of sign in (1.28)). Note that (1.25)–(1.26) imply that the energy of the ingoing beam increases, while that of the outgoing beam decreases.

Fig. 5

Schematic depiction of a pair $\zeta$, ${\bar{\zeta }}$ of intersecting Vlasov beams supported on nearly radial null geodesics. Due to the non-linear interaction of the beams, the energy ${\mathcal {E}}[{\bar{\zeta }}]$ of the ingoing beam ${\bar{\zeta }}$ increases, while the energy ${\mathcal {E}}[\zeta ]$ of $\zeta$ decreases (the total energy being conserved during the interaction)

In this paper, we show that the formulas (1.25)–(1.26) also hold in the case when we are dealing with solutions of the system (1.5) instead of the Einstein-null dust system, under the condition the beams $\zeta$, ${\bar{\zeta }}$ consist of null geodesics which are nearly radial at their intersection region ${\mathcal {R}}$. In this case, the additional error terms appearing in the analogues of the relations (1.27) and (1.29) (see (7.45) and (7.49), respectively) can be eventually controlled; we should point out, however, that the error terms appearing in this case in (1.29) are of higher order in terms of derivatives of the metric, and are not controlled by the norm $||\cdot ||$ defined by (1.19); estimating their size requires a novel set of higher order bounds and precise control on the size of the interaction region in terms of the hierarchy $\varepsilon ^{(i)}$. We will suppress this technical issue here (for more details, see Sect. 7).

Let us now return to the interaction of the beams $\zeta _{i}$ and $\zeta _{j}$ in Fig. 4. Note that, for the interaction taking place in the region ${\mathcal {R}}_{0}$, $\zeta _{i}$ has the role of the outgoing beam $\zeta$ in (1.25)–(1.26), while $\zeta _{j}$ is the ingoing beam ${\bar{\zeta }}$; in the case of ${\mathcal {R}}_{\infty }$, these roles are inverted.

Remark

Note here the asymmetry between $\zeta _{i}$ and $\zeta _{j}$: For this part of the discussion, it is important that $i<j$, which is the order convention fixing $\zeta _{i}$ to be the outgoing beam in the region ${\mathcal {R}}_{0}$ closest to the axis.

In view of the relation (1.24) between $r|_{{\mathcal {R}}_{0}}$ and $r|_{{\mathcal {R}}_{\infty }}$, the formulas (1.25)–(1.26) imply that the loss of energy occuring for the beam $\zeta _{j}$ at ${\mathcal {R}}_{\infty }$ is negligible compared to the gain of energy for the same beam occuring earlier in the region ${\mathcal {R}}_{0}$; the opposite is true for $\zeta _{i}$. As a result, the net contribution for the energy ${\mathcal {E}}[\zeta _{j}]$ of $\zeta _{j}$ after the pair of interactions with the beam $\zeta _{i}$ between two successive reflections off ${\mathcal {I}}$ is strictly positive, i.e. ${\mathcal {E}}[\zeta _{j}]$ strictly increases, with the total energy gain estimated as follows:

$$\begin{aligned} {\mathcal {E}}_{after}[\zeta _{j}]= & {} {\mathcal {E}}_{before}[\zeta _{j}]\cdot \exp \Big (\frac{2{\mathcal {E}}_{before}[\zeta _{i}]}{r|_{{\mathcal {R}}_{0}}}+\mathfrak {Err}\Big )\nonumber \\> & {} {\mathcal {E}}_{before}[\zeta _{j}]. \end{aligned}$$

(1.30)

On the other hand, the energy of $\zeta _{i}$ strictly decreases as a result of this interaction:

$$\begin{aligned} {\mathcal {E}}_{after}[\zeta _{i}]= & {} {\mathcal {E}}_{before}[\zeta _{i}]\cdot \exp \Big (-\frac{2{\mathcal {E}}_{before}[\zeta _{j}]}{r|_{{\mathcal {R}}_{0}}}+\frac{2{\mathcal {E}}_{before}[\zeta _{j}]}{r|_{{\mathcal {R}}_{\infty }}}+\mathfrak {Err}\Big )\nonumber \\< & {} {\mathcal {E}}_{before}[\zeta _{i}]. \end{aligned}$$

(1.31)

However, using the fact that $\varepsilon ^{(i)}\gg \varepsilon ^{(j)}$ and assuming (in the context of a bootstrap argument) that the energy content of each beam $\zeta _k$ satisfies for $u\in [0,u_*]$ a bound of the form

$$\begin{aligned} \varepsilon ^{(k+1)} (-\Lambda )^{\frac{1}{2}} \ll {\mathcal {E}}[\zeta _k] \lesssim \varepsilon ^{(k)} (-\Lambda )^{\frac{1}{2}}, \end{aligned}$$

from (1.23)–(1.24) we deduce that

$$\begin{aligned} \begin{aligned} \frac{2{\mathcal {E}}_{before}[\zeta _{j}]}{r|_{{\mathcal {R}}_{0}}}&\lesssim \frac{\varepsilon ^{(j)}}{\varepsilon ^{(i)}}\ll \frac{2{\mathcal {E}}_{before}[\zeta _{i}]}{r|_{{\mathcal {R}}_{0}}} ,\\ \frac{2{\mathcal {E}}_{before}[\zeta _{j}]}{r|_{{\mathcal {R}}_{\infty }}}&\lesssim \varepsilon ^{(j)}\varepsilon ^{(i)} \ll \frac{2{\mathcal {E}}_{before}[\zeta _{i}]}{r|_{{\mathcal {R}}_{0}}} . \end{aligned} \end{aligned}$$

(1.32)

Substituting (1.32) in the formula (1.31), we infer that, during the interaction of $\zeta _{i}$ and $\zeta _{j}$, the relative change in the energy content of $\zeta _{i}$ is negligible compared to the corresponding change for $\zeta _{j}$, i.e.:

$$\begin{aligned} \frac{{\mathcal {E}}_{before}[\zeta _{i}]}{{\mathcal {E}}_{after}[\zeta _{i}]}-1 \ll \frac{{\mathcal {E}}_{after}[\zeta _{j}]}{{\mathcal {E}}_{before}[\zeta _{j}]}-1. \end{aligned}$$

(1.33)

To sum up, for any beam $\zeta _{i_{0}}$, $0\le i_{0}\le N_{\varepsilon }$, the energy content of $\zeta _{i_{0}}$ between two successive reflections off ${\mathcal {I}}$ changes according to the following rules:

• 1. The interaction of $\zeta _{i_{0}}$ with any beam $\zeta _{i_{1}}$ with $i_{1}<i_{0}$ results in an increase in the energy of $\zeta _{i_0}$, quantified by (1.30).

• 2. The interaction of $\zeta _{i_{0}}$ with any beam $\zeta _{i_{1}}$ with $i_{1}>i_{0}$ has virtually no effect on the energy content of $\zeta _{i_0}$.

• 3. The energy content of $\zeta _{i_{0}}$ before and after each reflection off ${\mathcal {I}}$ remains the same (as a consequence of the reflecting boundary conditions imposed on ${\mathcal {I}}$).

In particular, the energy content of each beam, except for $\zeta _{0}$, strictly increases with the number of reflections off ${\mathcal {I}}$.¹¹ See Proposition 7.6.

Formation of the intermediate profile ${\mathcal {S}}_{*}$. For any beam index $0\le i\le N_{\varepsilon }-1$, and any $n\in {\mathbb {N}}$ corresponding to a specific number of reflections of the beam $\zeta _{i}$ off ${\mathcal {I}}$, let us introduce the following dimensionless quantity:

$$\begin{aligned} \mu _{i}[n]\doteq \frac{2{\mathcal {E}}^{(n)}[\zeta _{i}]}{d_{i}^{(n)}}, \end{aligned}$$

(1.34)

where ${\mathcal {E}}^{(n)}[\zeta _{i}]$ is the energy of $\zeta _{i}$ after the n-th reflection off ${\mathcal {I}}$, while $d_{i}^{(n)}$ denotes the distance (defined in an appropriate sense) between the beams $\zeta _{i}$ and $\zeta _{i+1}$ after the same reflection. Using the relations (1.30) and (1.31), combined with an analogous set of estimates for the change in the separation of the beams over time, we will be able to infer that the quantities $\mu _{i}[n]$ satisfy the following recursive system of relations:

$$\begin{aligned} \mu _{i}[n]=\mu _{i}[n-1]\exp \Big (2\sum _{{\bar{i}}=0}^{i-1}\mu _{{\bar{i}}}[n]+\mathfrak {Err}\Big ), \end{aligned}$$

(1.35)

(see (7.150) and Proposition 7.6). Ignoring the error terms $\mathfrak {Err}$, the relation (1.35) can be readily solved inductively in i: For $i=0$, (1.35) implies that $\mu _{0}[n]\simeq \mu _{0}[0]$, for $i=1$ we infer that $\mu _{1}[n]\simeq \mu _{1}[0]e^{2n\mu _{0}[0]}$, and so on. In particular, all the quantities $\mu _{i}[n]$ except for $\mu _{0}[n]$ are strictly increasing in n.

Remark

When $n=0$, the definition of the initial data norm $||\cdot ||_{data}$ (see Definition 3.14) implies that

$$\begin{aligned} \sum _{i\ge 0}\mu _{i}[0] \sim ||{\mathcal {D}}^{(\varepsilon )}||_{data}. \end{aligned}$$

(1.36)

Therefore, while (1.35) implies a fast rate of growth for $\mu _{i}[n]$, $i\ge 1$, the smallness condition (1.11) on the initial data necessitates that, for any fixed value of n, $\max _{i}\mu _{i}[n]\rightarrow 0$ as $\varepsilon \rightarrow 0$; this is, of course, also implied by the Cauchy stability of the trivial solution $({\mathcal {M}}_{AdS},g_{AdS})$ with respect to $||\cdot ||_{data}$ (see Proposition 3.15).

Given any natural number $n_{*}$ and using the fact that (1.35) can be solved backwards in n, we can choose the initial data parameters $a_{i}$ in (1.10) so that the quantities $\mu _{j}[n_{*}]$, $0\le j\le N_{\varepsilon }-1$, obtained by solving (1.35) (with initial values $\mu _{j}[0]$ computed explicitly in terms of $a_{j}$), are equal to the right hand side of (1.17), i.e.

$$\begin{aligned} \mu _{j}[n_{*}]=\frac{C}{N_{\varepsilon }}\exp \big (-2\frac{C}{N_{\varepsilon }}j\big ). \end{aligned}$$

(1.37)

Similarly, using (1.30), $a_{N_{\varepsilon }}$ can be chosen so that the energy ${\mathcal {E}}^{(n_{*})}[\zeta _{N_{\varepsilon }}]$ of the last beam is equal to the right hand side of (1.18), i.e.:

$$\begin{aligned} {\mathcal {E}}^{(n_{*})}[\zeta _{N_{\varepsilon }}]=\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}. \end{aligned}$$

(1.38)

See Proposition 8.1 for a more detailed derivation. Provided $n_{*}$ is large enough in terms of $\varepsilon$, we can estimate a priori (using the explicit solution of (1.35) and the fast growth of $\mu _{i}[n]$ in n) that the aforementioned values of the parameters $a_{i}$ (which were defined in terms of $n_{*}$) are consistent with the initial smallness assumption (1.11). It can be then readily shown that, between the $n_{*}$-th and the $(n_{*}+1)$-th reflection of the beams off ${\mathcal {I}}$, there exists a time $u=u_{*}\sim n_{*}(-\Lambda )^{-\frac{1}{2}}$ such that the beam slices $\zeta _{i}\cap \{u=u_{*}\}$ satisfy (1.17) and (1.18); see Sect. 8.

Remark

At the time $u=u_{*}$ when the intermediate profile ${\mathcal {S}}_{*}$ is formed, the $||\cdot ||$-norm of the solution (defined by (1.19)) satisfies

$$\begin{aligned} ||({\mathcal {M}},g;f)^{(\varepsilon )}||_{u\le u_{*}}\gtrsim \sum _{i=0}^{N_{\varepsilon }-1}\mu _{i}[n_{*}]\gtrsim \sum _{i=0}^{N_{\varepsilon }-1}\frac{C}{N_{\varepsilon }}e^{-2\frac{C}{N_{\varepsilon }}i}\sim C\gg 1.\qquad \end{aligned}$$

(1.39)

As a result, the formation of ${\mathcal {S}}_{*}$ already provides an instability statement for $({\mathcal {M}}_{AdS},g_{AdS})$ with respect to the initial data norm $||\cdot ||_{data}$; for the proof of the AdS instability conjecture, however, it is necessary to move beyond $u=u_{*}$ and establish that, moreover, a trapped surface forms in $({\mathcal {M}},g;f)^{(\varepsilon )}$.

We should also point out that, as a consequence of the explicit formulas (1.17)–(1.18) for the energy content of $\zeta _{i}$ at $\{u=u_{*}\}$, we can trivially bound

$$\begin{aligned} \mu _{i}[n]\le \frac{C}{N_{\varepsilon }}\quad \text { for all }0\le i\le N_{\varepsilon }-1. \end{aligned}$$

Therefore, since (1.35) implies (ignoring once more the error terms) that $\mu _{i}[n]$ is non-decreasing in n, we can estimate a priori that, for all $0\le n\le n_{*}$:

$$\begin{aligned} \max _{0\le i\le N_{\varepsilon }-1}\mu _{i}[n]\le \frac{C}{N_{\varepsilon }}. \end{aligned}$$

(1.40)

Provided that the number $N_{\varepsilon }$ of beams is sufficiently large in terms of C and satisfies

$$\begin{aligned} \frac{N_{\varepsilon }}{C}\gg \max _{i}\frac{d_{i}}{\varepsilon ^{(i)}} \end{aligned}$$

(where $d_{i}$ is the initial separation between $\zeta _{i}$ and $\zeta _{i+1}$), the estimate (1.40) (combined with a number of technical lemmas related to the geodesic flow on $({\mathcal {M}},g)^{(\varepsilon )}$) allows us to obtain the crucial a priori bound (1.15) for $\frac{2{\tilde{m}}}{r}$ (see the relation (8.4) in the statement of Proposition 8.1). As mentioned earlier, this bound is fundamental for rigorously implementing the heuristic ideas discussed in this section.¹²

1.2.2 Second stage of the instability: trapped surface formation

The second step of the proof of Theorem 1 will consist of showing that a trapped surface (and, hence, a black hole region) is formed at a time $u=u_{\dagger }>u_{*}$ with $u_{\dagger }-u_{*}\lesssim 1$. More precisely, in Sect. 9, we will show that, in the development of the intermediate profile ${\mathcal {S}}_{*}$, the configuration of the beams $\zeta _{i}$, $0\le i\le N_{\varepsilon }$ behaves as follows (see Fig. 6):

• 1. For $0\le i\le N_{\varepsilon }-1$, the geodesics in the beams $\zeta _{i}$ obey dynamics which are qualitatively similar to those on AdS spacetime (albeit satisfying weaker bounds than in the region $u<u_{*}$; see (9.1) in Lemma 9.1). In particular, the beams $\zeta _{i}$ briefly approach the center $r=0$ before being deflected away, intersecting with each other, in the meantime, as depicted in Fig. 6. Up until the time $u=u'$ when the last intersection between these beams and the outermost beam $\zeta _{N_{\varepsilon }}$ occurs (see Fig. 6), the mass ratio $\frac{2{\tilde{m}}}{r}$ satisfies the smallness condition (1.15).

• 2. The final beam $\zeta _{N_{\varepsilon }}$, moving in the ingoing direction, interacts with all the beams $\zeta _{i}$, $i=0,\ldots ,N_{\varepsilon }-1$, increasing its energy content ${\mathcal {E}}[\zeta _{N_{\varepsilon }}]$. The increase in ${\mathcal {E}}[\zeta _{N_{\varepsilon }}]$ is sufficient for a trapped surface to form before $\zeta _{N_{\varepsilon }}$ has the chance to be deflected off to infinity again: There exists a point $p_{\dagger }\in \zeta _{N_{\varepsilon }}\cap \{u\ge u'\}$ (see Fig. 6) such that

  $$\begin{aligned} \frac{2{\tilde{m}}}{r}(p_{\dagger })>1. \end{aligned}$$

  (1.41)

Fig. 6

Schematic depiction of the evolution of the intermediate profile ${\mathcal {S}}_*$. After interacting with each other for one last time, the beams $\zeta _i$, $1\le i \le N_{\epsilon }-1$ gain a sufficient amount of energy so that, at the region of intersection of any of those beams with the last beam $\zeta _{N_{\epsilon }}$, the mass ratio $\frac{2{\tilde{m}}}{r}$ is proportional to the (small) constant $\frac{C}{N_{\epsilon }}$. In turn, $\zeta _{N_{\epsilon }}$ gains enough energy from those interactions, so that a trapped sphere $p_{\dagger }$ is created before $\zeta _{N_{\epsilon }}$ is deflected again to infinity

The first of the two statements above will be established in Sect. 9.1. In order to prove that the beams $\zeta _{i}$, $0\le i\le N_{\varepsilon }-1$ approximately obey the AdS dynamics in the region $\{u_{*}\le u\le u'\}$, we appeal to arguments similar to the ones implemented in the previous step. In this case, however, the estimates satisfied by the solution are in many respects weaker than those we obtained previously (crucially, (1.21) will no longer be true at this step; compare also the statements about the regions ${\mathcal {U}}^+_{\varepsilon }$ and ${\mathcal {T}}^+_{\varepsilon }$ in Lemma 7.8). It is the need to obtain control over quantities like the $||\cdot ||_{u\le u'}$ size of the solution at this step that enforces some of the complexity of the hierarchy of parameters introduced in Sect. 6.1.

More precisely, arguing similarly as for the proof of (1.35), we show that an analogous approximate formula holds for the energy content ${\mathcal {E}}^{*}[\zeta _{i}]$ of the beams $\zeta _{i}$, $0\le i\le N_{\varepsilon }-1$, right before their intersection with $\zeta _{N_{\varepsilon }}$ (see Fig. 6): Setting, for $0\le i\le N_{\varepsilon }-1$,

$$\begin{aligned} \mu _{i}^{*}\doteq \frac{2{\mathcal {E}}^{*}[\zeta _{i}]}{\sup _{\zeta _{i}\cap \zeta _{N_{\varepsilon }}}r}, \end{aligned}$$

the analogue of formula (1.35) reads

$$\begin{aligned} \mu _{i}^{*}=\mu _{i}[n_{*}]\exp \Big (2\sum _{{\bar{i}}=0}^{i-1}\mu _{{\bar{i}}}^{*}+\mathfrak {Err}\Big ), \end{aligned}$$

(1.42)

where the quantities $\mu _{i}[n_{*}]$ are given by (1.37) (the technical machinery for establishing this fact is contained in the second part of Proposition 7.6). We therefore readily deduce by substituting (1.37) in (1.42) (ignoring the error terms $\mathfrak {Err}$) that, for all $0\le i\le N_{\varepsilon }-1$:

$$\begin{aligned} \mu _{i}^{*}\sim \frac{C}{N_{\varepsilon }}. \end{aligned}$$

(1.43)

See Lemma 9.1 for more details.

Let us now move on to the statement of trapped surface formation along the beam $\zeta _{N_{\varepsilon }}$; the proof of this statement occupies Sect. 9.2. Using the formula (1.25) for $\zeta _{N_{\varepsilon }}$ at every intersection between $\zeta _{N_{\varepsilon }}$ and the beams $\zeta _{i}$, $0\le i\le N_{\varepsilon }-1$, we infer that the energy content ${\mathcal {E}}_{final}[\zeta _{N_{\varepsilon }}]$ of $\zeta _{N_{\varepsilon }}$ at $u=u'$ satisfies the following lower bound in terms of the associated energy ${\mathcal {E}}^{(n_{*})}[\zeta _{N_{\varepsilon }}]$ at $u=u_{*}$:

$$\begin{aligned} {\mathcal {E}}_{final}[\zeta _{N_{\varepsilon }}]\gtrsim {\mathcal {E}}^{(n_{*})}[\zeta _{N_{\varepsilon }}]\cdot \exp \Big (\sum _{i=0}^{N_{\varepsilon }-1}\mu _{i}^{*}\Big ). \end{aligned}$$

In view of the relations (1.38) and (1.43) for ${\mathcal {E}}^{(n_{*})}[\zeta _{N_{\varepsilon }}]$ and $\mu _{i}^{*}$, respectively, we thus deduce that

$$\begin{aligned} {\mathcal {E}}_{final}[\zeta _{N_{\varepsilon }}]\sim e^{C}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\gg \frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}. \end{aligned}$$

(1.44)

We will now argue that the lower bound (1.44) and the fact that the beam $\zeta _{N_{\varepsilon }}$ consists of geodesics satisfying initially the angular momentum condition

$$\begin{aligned} \frac{l}{E_{0}}\sim \frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }} \end{aligned}$$

(1.45)

(see (1.12)) imply that there exists a point $p_{\dagger }\in \zeta _{N_{\varepsilon }}\cap \{u\ge u'\}$ such that (1.41) holds. For any $u_0 \in [u', u'+O(1)]$, we can estimate from below

$$\begin{aligned} \sup _{\zeta _{N_{\varepsilon }}\cap \{u=u_{0}\}}\frac{2{\tilde{m}}}{r}\gtrsim \frac{2{\mathcal {E}}_{final}[\zeta _{N_{\varepsilon }}]}{\sup _{\zeta _{N_{\varepsilon }}\cap \{u=u_{0}\}}r}. \end{aligned}$$

Thus, in order to establish (1.41) and complete the proof of Theorem 1, it suffices to show that, as a corollary of (1.45), the beam slice $\zeta _{N_{\varepsilon }}\cap \{u=u_{\dagger }\}$ for a suitable $u_{\dagger }>u'$ satisfies

$$\begin{aligned} \sup _{\zeta _{N_{\varepsilon }}\cap \{u=u_{\dagger }\}}r \le r_0, \end{aligned}$$

(1.46)

where

$$\begin{aligned} r_{0}\doteq \frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}. \end{aligned}$$

(1.47)

Heuristically, on a spacetime where the geodesic flow behaves similarly as on $({\mathcal {M}}_{AdS},g_{AdS})$, the bound (1.46) would follow from the fact that, for every null geodesic $\gamma$ of $({\mathcal {M}}_{AdS},g_{AdS})$, the minimum value of r along $\gamma$ satisfies

$$\begin{aligned} \min _{\gamma }r\sim \frac{l}{E_{0}}. \end{aligned}$$

However, in our case, for $u\ge u'$, the spacetime metric g is no longer close to $g_{AdS}$; the fact that there exists a $u_{\dagger }$ such that (1.46) holds follows from a careful manipulation of the equations of the geodesic flow (in the regime where the condition (1.15) is violated), using in addition some of the monotonicity properties of the system (1.5) (see the proof of (9.32)), as well as the estimates on the geodesic flow for $u\le u_{*}$ obtained in the previous step. See Proposition 9.2.

Remark

A technical issue which was not highlighted so far in this discussion is the fact that the existence and smoothness of the development $({\mathcal {M}},g;f)^{(\varepsilon )}$ up to the time $u=u_{\dagger }$ of trapped surface formation (including, in particular, the statement that a naked singularity does not appear earlier in the evolution) is non-trivial. The Cauchy stability statement for $({\mathcal {M}}_{AdS},g_{AdS})$ guarantees the existence of $({\mathcal {M}},g;f)^{(\varepsilon )}$ only up to times U when

$$\begin{aligned} ||({\mathcal {M}},g;f)^{(\varepsilon )}||_{u\le U}\ll 1. \end{aligned}$$

Beyond that point, and up to time $u=u'$, we infer the existence and smoothness of $({\mathcal {M}},g;f)^{(\varepsilon )}$ using an extension principle established in our companion paper [43], guaranteeing the smooth extendibility of a development under the smallness condition (1.15) for $\frac{2{\tilde{m}}}{r}$. From $u=u'$ up to $u=u_{\dagger }$, the existence and smoothness of the solution follows from our explicit a priori estimates for the geodesics in the beam $\zeta _{N_{\varepsilon }}$ and the fact that, in the part of $\{u'\le u\le u_{\dagger }\}$ consisting of the past of the point $p_{\dagger }$, the spacetime is vacuum (and hence trivially extendible) outside $\zeta _{N_{\varepsilon }}$; for a review of the relevant extension principles, see Sect. 3, as well as Sect. 6.3.

1.2.3 Discussion: comparison with the case of the Einstein-null dust system with an inner mirror

In this section, we will highlight the differences between the strategy of proof of Theorem 1, sketched in the previous sections, and the one implemented in [41] for the case of the spherically symmetric Einstein-null dust system.

In [41], the instability of $({\mathcal {M}}_{AdS},g_{AdS})$ as a solution of the Einstein-null dust system with an inner mirror was established by setting up a family of initial data $(r,\Omega ^{2};{\bar{\tau }})^{(\varepsilon )}|_{u=0}$ which gave rise to a configuration of null dust beams $\zeta _{i}^{\prime }$, $0\le i\le N_{\varepsilon }$, of comparable size (see Fig. 7). These beams were successively reflected off an inner mirror at $r=r_{0}^{(\varepsilon )}$ (with $r_{0}^{(\varepsilon )}$ proportional to the total energy ${\tilde{m}}^{(\varepsilon )}|_{{\mathcal {I}}}$ of $(r,\Omega ^{2};{\bar{\tau }})^{(\varepsilon )}|_{u=0}$) and conformal infinity ${\mathcal {I}}$, exchanging energy through their non-linear interactions. Using the relations (1.27)–(1.29) and the fact that the beams $\zeta _{i}^{\prime }$ were initially comparable in size, it was shown in [41] that, for this family of configurations, the quantities

$$\begin{aligned} \mu _{n}\doteq \max _{\{U_{n}\le u\le U_{n+1}\}}\frac{2{\tilde{m}}}{r} \end{aligned}$$

and

$$\begin{aligned} \rho _{n}=r\text {-separation between }\zeta _{N_{\varepsilon }}^{\prime }\text { and }\zeta _{0}^{\prime }\text { in the region }\{U_{n}\le u\le U_{n+1}\} \end{aligned}$$

(where $U_{n}$ is the value of u at the point where the beam $\zeta _{0}^{\prime }$ is reflected off ${\mathcal {I}}$ for the n-th time¹³), satisfy the system of relations

$$\begin{aligned} {{\uprho }}_{n+1}&\le {{\uprho }}_{n}+C_{1}r_{0}^{(\varepsilon )}\log \big ((1-{{\upmu }}_{n})^{-1}+1\big ),\nonumber \\ {{\upmu }}_{n+1}&\ge {{\upmu }}_{n}\exp \big (\frac{c_{1}r_{0}^{(\varepsilon )}}{{{\uprho }}_{n+1}}\big ), \end{aligned}$$

(1.48)

for some $0<c_{1}<1<C_{1}$ (see the relation (6.165) in [41]). It was then shown that the system (1.48) guarantees the existence of some $n_{0}=n_{0}(\varepsilon )\in {\mathbb {N}}$ such that

$$\begin{aligned} \mu _{n_{0}}\ge 1-\delta _{\varepsilon } \end{aligned}$$

(1.49)

for some $\delta _{\varepsilon }\ll 1$. From (1.49), it was concluded using a suitable Cauchy stability statement that, by possibly perturbing the initial data set $(r,\Omega ^{2};{\bar{\tau }})^{(\varepsilon )}|_{u=0}$ ever so slightly (with the size of the perturbation determined by $\delta _{\varepsilon }$), one could in fact achieve

$$\begin{aligned} \mu _{n_{0}}>1. \end{aligned}$$

(1.50)

The lower bound (1.50) then implied the existence of a trapped sphere in the development of $(r,\Omega ^{2};{\bar{\tau }})^{(\varepsilon )}|_{u=0}$ at time $u\sim U_{n_{0}}+O(1)$; see [41].

Fig. 7

Schematic depiction of the configuration of beam interactions in the case of the Einstein-null dust system with an inner mirror (left), which was treated in [41], and the multi-scale configuration employed in this paper for the case of the Einstein-massless Vlasov system (right). For simplicity, only three beams are depicted in each case

The analysis of [41] leading to the recursive system of inequalities (1.48) relied crucially on the fact that the null-dust beams $\zeta _{i}^{\prime }$ consisted entirely of radial null geodesics, which, in a double null coordinate chart $(u,v,\theta ,\varphi )$, necessarily move along lines of the form $\{u=const\}$ or $\{v=const\}$ (see Fig. 7). This trivial a priori control on the paths of radial null geodesics in the (u, v)-plane implies, in particular, that the qualititative picture of beam interactions depicted in Fig. 7 remains valid even in the regime where $\frac{2{\tilde{m}}}{r}\sim 1$, i.e. in the last few reflections of the beams off $r=r_{0}^{(\varepsilon )}$ and ${\mathcal {I}}$ before a trapped surface is formed. Furthermore, the presence of an inner mirror at $r=r_{0}^{(\varepsilon )}>0$ in the setup of [41] guaranteed the absence of naked singularities in the evolution of the initial data family $(r,\Omega ^{2};{\bar{\tau }})^{(\varepsilon )}|_{u=0}$ (as a consequence of the results of [42]).

In contrast, in the case of the Einstein-massless Vlasov system (1.5), there is no useful general a priori estimate for the shape of beams consisting of non-radial geodesics in the regime where $\frac{2{\tilde{m}}}{r}\sim 1$ (as suggested already by the relation (1.22)). Therefore, in order to establish the formation of a trapped sphere in this setting, we were forced to design a configuration of interacting Vlasov beams with the property that all the beam interactions preceding the first point $p_{\dagger }$ where $\frac{2{\tilde{m}}}{r}=1$ lie in the regime $\frac{2{\tilde{m}}}{r}\ll 1$; in this regime, the qualititative picture of the (right half of) Fig. 7 can be shown to remain relevant (see Sect. 5). In particular, this was achieved by first identifying the profile ${\mathcal {S}}_{*}$ (described at the end of Sect. 1.2.1) as a useful intermediate step for trapped surface formation. In turn, the structure of ${\mathcal {S}}_{*}$ necessitated imposing the multi-scale hierarchy (1.7)–(1.10) on the construction of the initial data family ${\mathcal {D}}^{(\varepsilon )}$. It is a remarkable feature of the system (1.5) that the same hierarchy of scales greatly simplifies the formulas of energy exchange occuring between the Vlasov beams, resulting in the approximate monotonicity relations (1.35); the monotonicity properties of (1.35) are crucial for obtaining a priori control of $\frac{2{\tilde{m}}}{r}$ in the evolution until the formation of ${\mathcal {S}}_{*}$, thus ensuring the absence of naked singularities in the solution in view of results obtained in our companion paper [43].

1.3 Outline of the paper

The structure of the paper is as follows:

In Sect. 2, we will introduce the Einstein-massless Vlasov system (1.5) in spherical symmetry. In addition, we will state a number of notational conventions related to asymptotically AdS spacetimes and we will introduce the notion of a reflecing boundary condition for (1.5) on ${\mathcal {I}}$ .

In Sect. 3, we will introduce the asymptotically AdS characteristic initial-boundary value problem for (1.5) and present a number of well-posedness results in this context. These results will include a fundamental Cauchy stability statement for $({\mathcal {M}}_{AdS},g_{AdS})$ in a low regularity topology. The proofs of the results of Sect. 3 are obtained in our companion paper [43].

The main result of this paper, namely Theorem 1, will be presented in detail in Sect. 4.

The proof of Theorem 1 will occupy Sects. 5–9. In particular, the arguments sketched in Sect. 1.2.1 regarding the first stage of the instability will be presented in detail in Sects. 5–8 (with Sects. 5 and 7 devoted to the development of the necessary technical machinery); the proof of trapped surface formation (roughly discussed in Sect. 1.2.2) will then be presented in Sect. 9.

2 The Einstein-massless Vlasov system in spherical symmetry

In this section, we will introduce the spherically symmetric Einstein-massless Vlasov system in $3+1$ dimensions, expressed in a double null coordinate chart. We will also formulate the reflecting boundary condition for a massless Vlasov field at conformal infinity ${\mathcal {I}}$ in the asymptotically AdS setting. A more detailed statement of the notions and the results appearing in this section can be found in our companion paper [43].

2.1 Spherically symmetric spacetimes and double null coordinate pairs

In this paper, we will follow the same conventions regarding spherically symmetric double null coordinate charts as in our companion paper [43] (similar also to those of [41, 42]). Our assumptions on the topology and regularity of the underlying spacetimes will be satisfied by the solutions of the Einstein-massless Vlasov system (1.5) constructed in the proof of Theorem 1.

In particular, we will only consider smooth, connected and time oriented spacetimes $({\mathcal {M}}^{3+1},g)$ which are spherically symmetric with a non-empty axis ${\mathcal {Z}}$ (see [43]). We will further assume that ${\mathcal {Z}}$ is connected and that ${\mathcal {M}}\backslash {\mathcal {Z}}$ splits diffeomorphically under the action of SO(3) as

$$\begin{aligned} {\mathcal {M}}\backslash {\mathcal {Z}}\simeq {\mathcal {U}}\times {\mathbb {S}}^{2}. \end{aligned}$$

(2.1)

We will also restrict ourselves to spacetimes $({\mathcal {M}},g)$ such that the region ${\mathcal {M}}\backslash {\mathcal {Z}}$ is regularly foliated by the two families of spherically symmetric null hypersurfaces ${\mathcal {H}}=\big \{{\mathcal {C}}^{+}(p):\,p\in {\mathcal {Z}}\big \}$ and $\overline{{\mathcal {H}}}=\big \{{\mathcal {C}}^{-}(p):\,p\in {\mathcal {Z}}\big \}$, where ${\mathcal {C}}^{+}(p),{\mathcal {C}}^{-}(p)$ are the future and past light cones emanating from p, respectively. See [43] for a more detailed discussion on the properties of spacetimes $({\mathcal {M}},g)$ satisfying the aforementioned conditions.

A double null coordinate pair (u, v) on $({\mathcal {M}},g)$ will consist of a pair of continuous functions $u,v:{\mathcal {M}}\rightarrow {\mathbb {R}}$ which are a smooth parametrization of the foliations ${\mathcal {H}},\overline{{\mathcal {H}}}$, respectively, on ${\mathcal {M}}\backslash {\mathcal {Z}}$. Note that any choice of double null coordinate pair (u, v) on ${\mathcal {M}}$ fixes a smooth embedding $(u,v):{\mathcal {U}}\rightarrow {\mathbb {R}}^{2}$; from now on, we will identify ${\mathcal {U}}$ with its image in ${\mathbb {R}}^{2}$ associated to a given null coordinate pair.

Remark

We will only consider double null coordinate pairs (u, v) for which $\partial _{u}+\partial _{v}$ is a timelike and future directed vector field on ${\mathcal {M}}\backslash {\mathcal {Z}}$.

Given a double null coordinate pair (u, v), the metric g, restricted on ${\mathcal {M}}\backslash {\mathcal {Z}}$, is expressed as follows:

$$\begin{aligned} g=-\Omega ^{2}(u,v)du\,dv+r^{2}(u,v)g_{{\mathbb {S}}^{2}}, \end{aligned}$$

(2.2)

where $g_{{\mathbb {S}}^{2}}$ is the standard round metric on ${\mathbb {S}}^{2}$ and ${{\Omega }},r:{\mathcal {U}}\rightarrow (0,+\infty )$ are smooth functions, with r extending continuously to 0 on the axis ${\mathcal {Z}}$.

For any pair of smooth functions $h_{1},h_{2}:{\mathbb {R}}\rightarrow {\mathbb {R}}$ with $h_{1}^{\prime },h_{2}^{\prime }\ne 0$, we can define a new double null coordinate pair on ${\mathcal {M}}$ by the relation

$$\begin{aligned} ({\bar{u}},{\bar{v}})=(h_{1}(u),h_{2}(v)). \end{aligned}$$

(2.3)

In the new coordinates, the metric g takes the form

$$\begin{aligned} g=-\bar{{{\Omega }}}^{2}({\bar{u}},{\bar{v}})d{\bar{u}}d{\bar{v}}+r^{2}({\bar{u}},{\bar{v}})g_{{\mathbb {S}}^{2}}, \end{aligned}$$

(2.4)

where

$$\begin{aligned}{} & {} \bar{{{\Omega }}}^{2}({\bar{u}},{\bar{v}})=\frac{1}{h_{1}^{\prime }h_{2}^{\prime }}{{\Omega }}^{2}(h_{1}^{-1}({\bar{u}}),h_{2}^{-1}({\bar{v}})), \end{aligned}$$

(2.5)

$$\begin{aligned}{} & {} r({\bar{u}},{\bar{v}})=r(h_{1}^{-1}({\bar{u}}),h_{2}^{-1}({\bar{v}})). \end{aligned}$$

(2.6)

Remark

We will frequently make use of such coordinate transformations, without renaming the coordinates each time.

Let $(y^{1},y^{2})$ be a local coordinate chart on ${\mathbb {S}}^{2}$. Then, the non-zero Christoffel symbols $\Gamma _{\beta \gamma }^{\alpha }$ of (2.2) in the $(u,v,y^{1},y^{2})$ local coordinate chart on ${\mathcal {M}}\backslash {\mathcal {Z}}$ take the following form:

$$\begin{aligned}{} & {} \Gamma _{uu}^{u}=\partial _{u}\log ({{\Omega }}^{2}), \quad \Gamma _{vv}^{v}=\partial _{v}\log ({{\Omega }}^{2}),\nonumber \\{} & {} \Gamma _{uB}^{A}=r^{-1}\partial _{u}r\delta _{B}^{A},\quad \Gamma _{vB}^{A}=r^{-1}\partial _{v}r\delta _{B}^{A},\nonumber \\{} & {} \Gamma _{AB}^{u}={{\Omega }}^{-2}\partial _{v}(r^{2})(g_{{\mathbb {S}}^{2}})_{AB},\quad \Gamma _{AB}^{v}={{\Omega }}^{-2}\partial _{u}(r^{2})(g_{{\mathbb {S}}^{2}})_{AB},\nonumber \\{} & {} \Gamma _{BC}^{A}=(\Gamma _{{\mathbb {S}}^{2}})_{BC}^{A}. \end{aligned}$$

(2.7)

In the above, the latin indices A, B, C are associated to the spherical coordinates $y^{1},y^{2}$, $\delta _{B}^{A}$ is Kronecker delta and $\Gamma _{{\mathbb {S}}^{2}}$ are the Christoffel symbols of the round sphere in the $(y^{1},y^{2})$ coordinate chart.

We will define the Hawking mass $m:{\mathcal {M}}\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} m=\frac{r}{2}\big (1-g(\nabla r,\nabla r)\big ). \end{aligned}$$

(2.8)

Notice that, when viewed as a function on ${\mathcal {U}}$, the Hawking mass m is related to the metric coefficients $\Omega$ and r by the formula:

$$\begin{aligned} m=\frac{r}{2}\big (1+4\Omega ^{-2}\partial _{u}r\partial _{v}r\big )\Leftrightarrow \Omega ^{2}=\frac{4\partial _{v}r(-\partial _{u}r)}{1-\frac{2m}{r}}. \end{aligned}$$

(2.9)

Finally, on pure AdS spacetime $({\mathcal {M}}_{AdS}^{3+1},g_{AdS})$, where $g_{AdS}$ is defined by (1.2), we will fix a distinguished double null coordinate pair (u, v) by the relations

$$\begin{aligned} u=t-\sqrt{-\frac{3}{\Lambda }}\text {Arctan}\Big (\sqrt{-\frac{\Lambda }{3}}r\Big ), \nonumber \\ v=t+\sqrt{-\frac{3}{\Lambda }}\text {Arctan}\Big (\sqrt{-\frac{\Lambda }{3}}r\Big ). \end{aligned}$$

(2.10)

In the resulting double null coordinate chart, $g_{AdS}$ is expressed as

$$\begin{aligned} g_{AdS}=-\Omega _{AdS}^{2}\,du\,dv+r^{2}g_{{\mathbb {S}}^{2}}, \end{aligned}$$

(2.11)

where

$$\begin{aligned} r(u,v)&=\sqrt{-\frac{3}{\Lambda }}\tan \Big (\frac{1}{2}\sqrt{-\frac{\Lambda }{3}}(v-u)\Big ),\\ \Omega _{AdS}^{2}(u,v)&=1-\frac{1}{3}\Lambda r^{2}(u,v).\nonumber \end{aligned}$$

(2.12)

2.2 Asymptotically Anti-de Sitter spacetimes

In this section, we will introduce the class of asymptotically AdS spacetimes in spherical symmetry; the geometry of these spacetimes will resemble that of (2.11) in a neighborhood of $r=\infty$. In particular, in accordance with [43], we will adopt the following definition:

Definition 2.1

Let $({\mathcal {M}},g)$ be a spherically symmetric spacetime as in Sect. 2.1, with $\sup _{{\mathcal {M}}}r=+\infty$. We will say that $({\mathcal {M}},g)$ is asymptotically AdS if, for some $R_{0}\gg 1$, there exists a spherically symmetric double null coordinate pair (u, v) on ${\mathcal {M}}$ as in Sect. 2.1, such that the following conditions hold:

• 1. The region ${\mathcal {V}}_{as}$ has the form

  $$\begin{aligned} {\mathcal {V}}_{as}=\big \{ u_{1}<u<u_{2}\big \}\cap \big \{ u+v_{R_{0}}(u)\le v<u+v_{{\mathcal {I}}}\big \} \end{aligned}$$

  for some $u_{1}<u_{2}\in {\mathbb {R}}\cup \{\pm \infty \}$, $v_{{\mathcal {I}}}\in {\mathbb {R}}$ and $v_{R_{0}}:(u_{1},u_{2})\rightarrow {\mathbb {R}}$ with $v(u)<v_{{\mathcal {I}}}$.

• 2. The function $\frac{1}{r}$ on ${\mathcal {U}}$ extends smoothly (as a function on ${\mathbb {R}}^2$) on

  $$\begin{aligned} {\mathcal {I}}\doteq \big \{ u_{1}<u<u_{2}\big \}\cap \big \{ v=u+v_{{\mathcal {I}}}\big \}\subset clos({\mathcal {U}}) \end{aligned}$$

  (2.13)

  (where $clos({\mathcal {U}})$ denotes the closure of ${\mathcal {U}}$ with respect to the standard topology of the plane) and satisfies

  $$\begin{aligned} \frac{1}{r}\Big |_{{\mathcal {I}}}=0. \end{aligned}$$

  (2.14)

• 3. The function $\frac{\Omega ^{2}}{r^{2}}$ extends smoothly on ${\mathcal {I}}$, with

  $$\begin{aligned} \frac{\Omega ^{2}}{r^{2}}\Big |_{{\mathcal {I}}}\ne 0. \end{aligned}$$

  (2.15)

See [43] for further discussion on the above definition and its relation with the standard definition of asymptotically AdS spacetimes (appearing, e. g., in [28]). For a spherically symmetric, asymptotically AdS spacetime $({\mathcal {M}},g)$ as above, we will use the term conformal infinity both for the planar boundary curve ${\mathcal {I}}$ and for the spacetime conformal boundary ${\mathcal {I}}^{(2+1)}$ of $({\mathcal {M}},g)$ (Fig. 8).

Fig. 8

Schematic depiction of the asymptotic region ${\mathcal {V}}_{as}=\{r \ge R_0 \gg 1 \}$ of an asymptotically AdS spacetime

2.3 Properties of the null geodesic flow and the massless Vlasov equation

Let $({\mathcal {M}},g)$ be a time oriented, spherically symmetric spacetime as in Sect. 2.1. In this section, we will briefly review the properties of the geodesic flow on $({\mathcal {M}},g)$ and we will introduce the Vlasov field equations on $T{\mathcal {M}}$. We will use the same notations as those adopted in [43].

2.3.1 The geodesic flow on $({\mathcal {M}},g)$

The equations of motion for a geodesic of $({\mathcal {M}},g)$, expressed in a local coordinate chart $(x^{0},x^{1},x^{2},x^{3})$ on ${\mathcal {M}}$ with dual momentum coordinates $(p^{0},p^{1},p^{2},p^{3})$ on the fibers of $T{\mathcal {M}}$, takes the following form

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}^{\alpha }=p^{\alpha },\\ {\dot{p}}^{\alpha }+\Gamma _{\beta \gamma }^{\alpha }p^{\beta }p^{\gamma }=0, \end{array}\right. } \end{aligned}$$

(2.16)

where $\Gamma _{{{\upbeta }{\upalpha }}}^{{{\upgamma }}}$ are the Christoffel symbols of g with respect to the chart $(x^{0},x^{1},x^{2},x^{3})$. Fixing a non-vanishing future directed vector field Q on ${\mathcal {M}}$ (e. g. the vector field $\partial _{u}+\partial _{v}$ in the notation of Sect. 2.1), the set

$$\begin{aligned} {\mathcal {P}}^{+}\doteq \Big \{(x;p)\in T{\mathcal {M}}:\text { }g_{{{\alpha }{\upbeta }}}(x)p^{{{\alpha }}}p^{{{\upbeta }}}=0,\text { }g_{{{\alpha }{\upbeta }}}(x)p^{{{\upalpha }}}Q^{{{\upbeta }}}(x)\le 0\Big \},\qquad \end{aligned}$$

(2.17)

i.e. the set of future directed null vectors in $T{\mathcal {M}}$, is invariant under (2.16).

The angular momentum function $l:T{\mathcal {M}}\rightarrow [0,+\infty )$ is defined in a local coordinate chart $(u,v,y^{1},y^{2})$ as in Sect. 2.1 by

$$\begin{aligned} l^{2}\doteq r^{2}g_{AB}p^{A}p^{B}=r^{4}(g_{{\mathbb {S}}^{2}})_{AB}p^{A}p^{B} \end{aligned}$$

(2.18)

(note that l is in fact coordinate independent). The spherical symmetry of $({\mathcal {M}},g)$ implies that l is a constant of motion for the geodesic flow (2.16). As a result, (2.16) can be reduced to a system in terms only of u, v, $p^{u}$, $p^{v}$ and l. Reexpressed in terms of these variables, the null-shell relation defining ${\mathcal {P}}^{+}$ in (2.17) takes the form

$$\begin{aligned} \Omega ^{2}p^{u}p^{v}=\frac{l^{2}}{r^{2}},\quad \text { }p^{u}\ge 0 \end{aligned}$$

(2.19)

while relations (2.16) restricted on ${\mathcal {P}}^{+}$ is reduced (using the expressions (2.7) and (2.19)) to

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{du}{ds}=p^{u},\\ \frac{dv}{ds}=p^{v},\\ \frac{d}{ds}\big (\Omega ^{2}p^{u}\big )=\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )\frac{l^{2}}{r^{2}},\\ \frac{d}{ds}\big (\Omega ^{2}p^{v}\big )=\Big (\partial _{u}\log (\Omega ^{2})-2\frac{\partial _{u}r}{r}\Big )\frac{l^{2}}{r^{2}},\\ \frac{dl}{ds}=0. \end{array}\right. } \end{aligned}$$

(2.20)

Remark

Identifying a geodesic in $({\mathcal {M}},g)$ with its image in the planar domain ${\mathcal {U}}$, we will frequently refer to (2.20) simply as the equations of motion for a “geodesic in ${\mathcal {U}}$”. Let us also note that, on a smooth spacetime $({\mathcal {M}},g)$ as above, the relations (2.19) and (2.20) imply that a geodesic $\gamma$ with $l>0$ cannot cross the axis ${\mathcal {Z}}\equiv \{r=0\}$.

2.3.2 The Vlasov equation

We will adopt the following definition for a Vlasov field f on $T{\mathcal {M}}$:

Definition 2.2

A Vlasov field f is a non-negative measure on $T{\mathcal {M}}$ which is constant along the flow lines of (2.16). A Vlasov field f supported on (2.17) will be called a massless Vlasov field.

As a consequence of the above definition, in any local coordinate chart $(x^{\alpha };p^{\alpha })$ on $T{\mathcal {M}}$ (with $p^{\alpha }$ dual to $x^{a}$), f satisfies the following equation (refered to, from now on, as the Vlasov field equation)

$$\begin{aligned} p^{\alpha }\partial _{x^{\alpha }}f-{{\Gamma }}_{\beta \gamma }^{\alpha }p^{\beta }p^{\gamma }\partial _{p^{\alpha }}f=0. \end{aligned}$$

(2.21)

The energy momentum tensor of a Vlasov field f is a symmetric (0, 2)-form $T_{\alpha \beta }$ on ${\mathcal {M}}$ (possibly defined only in the sense of distributions), given by the expression

$$\begin{aligned} T_{\alpha \beta }(x)\doteq \int _{T_{x}{\mathcal {M}}}p_{\alpha }p_{\beta }f\,\sqrt{-det(g(x))}dp^{0}\cdots dp^{3}, \end{aligned}$$

(2.22)

where $T_{x}{\mathcal {M}}$ denotes the fiber of $T{\mathcal {M}}$ over $x\in {\mathcal {M}}$ and

$$\begin{aligned} p_{\gamma }=g_{\gamma \delta }(x)p^{\delta }. \end{aligned}$$

(2.23)

Equation (2.21) implies that

$$\begin{aligned} \nabla ^{\alpha }T_{\alpha \beta }=0, \end{aligned}$$

(2.24)

i.e. that $T_{\alpha \beta }$ is conserved.

Another conserved quantity associated to a Vlasov field f is a 1-form called the particle current, defined by the formula

$$\begin{aligned} N_{\alpha }(x)\doteq \int _{T_{x}{\mathcal {M}}}p_{\alpha }f\,\sqrt{-det(g(x))}dp^{0}\cdots dp^{3}. \end{aligned}$$

(2.25)

The Vlasov equation (2.21) readily implies that

$$\begin{aligned} \nabla ^{\alpha }N_{\alpha }=0. \end{aligned}$$

(2.26)

A spherically symmetric Vlasov field f, i.e. a Vlasov field which is invariant under the induced action of SO(3) on $T{\mathcal {M}}$, only depends on the u, v, $p^{u}$, $p^{v}$ and l variables. Assuming, in addition, that f is massless, it follows that f is conserved along the flow lines of the reduced system (2.20). The Vlasov field equation formally reduces, in this case, to (2.21):

$$\begin{aligned} p^{u}\partial _{u}f+p^{v}\partial _{v}f= & {} \Big (\partial _{u}\log (\Omega ^{2})(p^{u})^{2}+\frac{2}{r}\Omega ^{-2}\partial _{v}r\frac{l^{2}}{r^{2}}\Big )\partial _{p^{u}}f\nonumber \\{} & {} +\Big (\partial _{v}\log (\Omega ^{2})(p^{v})^{2}+\frac{2}{r}\Omega ^{-2}\partial _{u}r\frac{l^{2}}{r^{2}}\Big )\partial _{p^{v}}f\quad \end{aligned}$$

(2.27)

(note that (2.27) does not contain derivatives in l).

Remark

In this paper, we will only consider smooth spherically symmetric massless Vlasov fields f, i.e. f will be of the form

$$\begin{aligned} f(u,v;p^{u},p^{v},l)={\bar{f}}(u,v;p^{u},p^{v},l)\cdot \delta \big (\Omega ^{2}p^{u}p^{v}-\frac{l^{2}}{r^{2}}\big ), \end{aligned}$$

(2.28)

where ${\bar{f}}$ is smooth in its variables and $\delta$ is Dirac’s delta function. For a smooth and spherically symmetric massless Vlasov field f, we will frequently denote with ${\bar{f}}$ any smooth function for which (2.28) holds; note that ${\bar{f}}$ is uniquely determined only along the null set (2.17).

Moreover, we will only consider smooth Vlasov fields f which are compactly supported in the momentum coordinates $p^{\alpha }$ for any fixed x. Under this condition, it can be readily shown that $N_{\alpha }(x)$, $T_{\alpha \beta }(x)$ are smooth tensor fields on ${\mathcal {M}}$.

The energy-momentum tensor (2.22) associated to a smooth, spherically symmetric Vlasov field f takes the form

$$\begin{aligned} T=T_{uu}(u,v)du^{2}+2T_{uv}(u,v)du\,dv+T_{vv}(u,v)dv^{2}+T_{AB}(u,v)dy^{A}dy^{B}.\nonumber \\ \end{aligned}$$

(2.29)

In the case when f is in addition massless, the components of (2.29) can be expressed as

$$\begin{aligned} T_{uu}&=\frac{\pi }{2}r^{-2}\int _{0}^{+\infty }\int _{0}^{+\infty }\big (\Omega ^{2}p^{v}\big )^{2}{\bar{f}}(u,v;p^{u},p^{v},l)\Big |_{{\mathcal {P}}^+}\,\frac{dp^{u}}{p^{u}}ldl, \nonumber \\ T_{vv}&=\frac{\pi }{2}r^{-2}\int _{0}^{+\infty }\int _{0}^{+\infty }\big (\Omega ^{2}p^{u}\big )^{2}{\bar{f}}(u,v;p^{u},p^{v},l)\Big |_{{\mathcal {P}}^+}\,\frac{dp^{u}}{p^{u}}ldl,\nonumber \\ T_{uv}&=\frac{\pi }{2}r^{-2}\int _{0}^{+\infty }\int _{0}^{+\infty }\big (\Omega ^{2}p^{u}\big )\cdot \big (\Omega ^{2}p^{v}\big ){\bar{f}}(u,v;p^{u},p^{v},l)\Big |_{{\mathcal {P}}^+}\,\frac{dp^{u}}{p^{u}}ldl,\nonumber \\ g^{AB}T_{AB}&=4\Omega ^{-2}T_{uv}. \end{aligned}$$

(2.30)

Similarly, the particle current (2.25) associated to f is of the form

$$\begin{aligned} N=N_{u}du+N_{v}dv, \end{aligned}$$

(2.31)

where, in the case when f is in addition massless:

$$\begin{aligned} N_{u}&=\pi r^{-2}\int _{T_{x}{\mathcal {M}}\cap {\mathcal {P}}^+}\Omega ^{2}p^{v}{\bar{f}}(u,v;p^{u},p^{v},l)\Big |_{{\mathcal {P}}^+}\,\frac{dp^{u}}{p^{u}}ldl, \nonumber \\ N_{v}&=\pi r^{-2}\int _{T_{x}{\mathcal {M}}\cap {\mathcal {P}}^+}\Omega ^{2}p^{u}{\bar{f}}(u,v;p^{u},p^{v},l)\Big |_{{\mathcal {P}}^+}\,\frac{dp^{u}}{p^{u}}ldl. \end{aligned}$$

(2.32)

The following estimate of $T_{\mu \nu }$ in terms of $N_{\mu }$ will be useful later in the paper: In view of the expressions (2.9), (2.30) and (2.32), we can bound

$$\begin{aligned}{} & {} \frac{1-\frac{2m}{r}}{\partial _{v}r}T_{vv}(u,v)+\frac{1-\frac{2m}{r}}{-\partial _{u}r}T_{uv}(u,v)\nonumber \\{} & {} \quad \le 2\sup _{(p^u, p^v) \in supp\big (f(u,v;\cdot ,\cdot ,l)\big )}\Big (\partial _{v}r(u,v)p^{v}-\partial _{u}r(u,v)p^{u}\Big )\cdot N_{v}(u,v)\nonumber \\ \end{aligned}$$

(2.33)

and

$$\begin{aligned}{} & {} \frac{1-\frac{2m}{r}}{\partial _{v}r}T_{uv}(u,v)+\frac{1-\frac{2m}{r}}{-\partial _{u}r}T_{uu}(u,v)\nonumber \\{} & {} \quad \le 2\sup _{(p^u, p^v) \in supp\big (f(u,v;\cdot ,\cdot ,l)\big )}\Big (\partial _{v}r(u,v)p^{v}-\partial _{u}r(u,v)p^{u}\Big )\cdot N_{u}(u,v).\nonumber \\ \end{aligned}$$

(2.34)

2.4 The Einstein-massless Vlasov system

The Einstein-massless Vlasov system with cosmological constant $\Lambda$ takes the form

$$\begin{aligned} {\left\{ \begin{array}{ll} Ric_{\mu \nu }(g)-\frac{1}{2}R(g)g_{\mu \nu }+\Lambda g_{\mu \nu }=8\pi T_{\mu \nu }[f],\\ p^{\alpha }\partial _{x^{\alpha }}f-{{\Gamma }}_{\beta \gamma }^{\alpha }p^{\beta }p^{\gamma }\partial _{p^{\alpha }}f=0,\\ supp(f)\subset {\mathcal {P}}^{+} \end{array}\right. } \end{aligned}$$

(2.35)

where $({\mathcal {M}},g)$ is a Lorentzian manifold, f is a non-negative measure on $T{\mathcal {M}}$, $T_{\mu \nu }[f]$ is expressed in terms of f by (2.22) and ${\mathcal {P}}^{+}\subset T{\mathcal {M}}$ is defined by (2.17) (see also [18, 41, 42]). In this paper, we will only consider the case when the cosmological constant $\Lambda$ is negative.

Reduced to the case where $({\mathcal {M}},g)$ is a spherically symmetric spacetime (see Sect. 2.1) and f is a spherically symmetric massless Vlasov field (see Sect. 2.3), the system (2.35) is equivalent to the following set of relations for $(r,\Omega ^{2},f)$:

$$\begin{aligned} \partial _{u}\partial _{v}(r^{2})&= -\frac{1}{2}(1-\Lambda r^{2})\Omega ^{2}+8\pi r^{2}T_{uv}, \end{aligned}$$

(2.36)

$$\begin{aligned} \partial _{u}\partial _{v}\log (\Omega ^{2})&= \frac{\Omega ^{2}}{2r^{2}}\big (1+4\Omega ^{-2}\partial _{u}r\partial _{v}r\big )-8\pi T_{uv}-2\pi \Omega ^{2}g^{AB}T_{AB}, \end{aligned}$$

(2.37)

$$\begin{aligned} \partial _{u}(\Omega ^{-2}\partial _{u}r)&= -4\pi rT_{uu}\Omega ^{-2}, \end{aligned}$$

(2.38)

$$\begin{aligned} \partial _{v}(\Omega ^{-2}\partial _{v}r)&= -4\pi rT_{vv}\Omega ^{-2}, \end{aligned}$$

(2.39)

$$\begin{aligned} p^{\alpha }\partial _{x^{\alpha }}f&= {{\Gamma }}_{\beta \gamma }^{\alpha }p^{\beta }p^{\gamma }\partial _{p^{\alpha }}f, \end{aligned}$$

(2.40)

$$\begin{aligned} supp(f)\subseteq&\left\{ \Omega ^{2}(u,v)p^{u}p^{v}-\frac{l^{2}}{r^{2}(u,v)}=0,\text { }p^{u}\ge 0\right\} . \end{aligned}$$

(2.41)

Remark

In view of the relation $4\Omega ^{-2}T_{uv}=g^{AB}T_{AB}$ (following from the fact that f is supported on the null set ${\mathcal {P}}$) and the definition (2.9) of m, equation (2.37) is equivalent to

$$\begin{aligned} \partial _{u}\partial _{v}\log (\Omega ^{2})=4\frac{m}{r^{3}}\frac{(-\partial _{u}r)\partial _{v}r}{1-\frac{2m}{r}}-16\pi T_{uv}. \end{aligned}$$

(2.42)

It is useful, in general, to consider transformations of the double null coordinate pair (u, v) of the form $(u,v)\rightarrow (u',v')=(U(u),V(v))$ (see Sect. 2.1). Under such a gauge transformation, a solution $(r,\Omega ^{2},f)$ is transformed into a solution $(r',(\Omega ^{\prime })^{2},f')$ in the new coordinate system through the relations:

$$\begin{aligned} r^{\prime }(u',v')&\doteq r(u,v), \nonumber \\ (\Omega ^{\prime })^{2}(u',v')&\doteq \frac{1}{\frac{dU}{dv}(u)\cdot \frac{dV}{dv}(v)}\Omega ^{2}(u,v),\nonumber \\ f^{\prime }\left( u',v';\frac{dU}{du}(u)p^{u^{\prime }},\frac{dV}{dv}(v)p^{v^{\prime }},l\right)&\doteq f(u,v;p^{u},p^{v},l). \end{aligned}$$

(2.43)

Let us introduce the renormalised Hawking mass ${\tilde{m}}$ by the relation

$$\begin{aligned} {\tilde{m}}\doteq m-\frac{1}{6}\Lambda r^{3}, \end{aligned}$$

(2.44)

where m is defined by (2.9). Equations (2.36)–(2.39) yield (formally, at least) the following system for $(r,{\tilde{m}},f)$ on the subset of ${\mathcal {M}}$ where $1-\frac{2m}{r}>0$ and $\partial _{u}r<0<\partial _{v}r$:

$$\begin{aligned}&\partial _{u}\partial _{v}r = -\frac{2{\tilde{m}}-\frac{2}{3}\Lambda r^{3}}{r^{2}}\frac{(-\partial _{u}r)\partial _{v}r}{1-\frac{2m}{r}}+4\pi rT_{uv}, \end{aligned}$$

(2.45)

$$\begin{aligned}&\partial _{v}\log \big (\frac{-\partial _{u}r}{1-\frac{2m}{r}}\big ) = 4\pi r^{-1}\frac{r^{2}T_{vv}}{\partial _{v}r}, \end{aligned}$$

(2.46)

$$\begin{aligned}&\partial _{u}\log \big (\frac{\partial _{v}r}{1-\frac{2m}{r}}\big ) = -4\pi r^{-1}\frac{r^{2}T_{uu}}{-\partial _{u}r}, \end{aligned}$$

(2.47)

$$\begin{aligned}&\partial _{v}{\tilde{m}} = 2\pi \big (1-\frac{2m}{r}\big )\Big (\frac{r^{2}T_{vv}}{\partial _{v}r}+\frac{r^{2}T_{uv}}{-\partial _{u}r}\Big ), \end{aligned}$$

(2.48)

$$\begin{aligned}&\partial _{u}{\tilde{m}} = -2\pi \big (1-\frac{2m}{r}\big )\Big (\frac{r^{2}T_{uu}}{-\partial _{u}r}+\frac{r^{2}T_{uv}}{\partial _{v}r}\Big ). \end{aligned}$$

(2.49)

Useful relations for null-geodesics on solutions of the system (2.36)–(2.41)

We will now present a number of relations for null geodesics on solutions $({\mathcal {M}},g;f)$ of the system (2.36)–(2.41). These relations, appearing also in our companion paper [43], will be useful for the construction of localised Vlasov beams appearing in the proof of Theorem 1.

In particular, we will establish the following result:

Lemma 2.3

Let $u_1: {\mathbb {R}}\rightarrow {\mathbb {R}}$ be continuous and strictly increasing and, for some $a>0$, let $\gamma :[0,a)\rightarrow {\mathcal {U}}$ be a curve contained in the region $\{u\ge u_{1}(v)\}$ such that:

• $\gamma$ is the projection of a null geodesic in $({\mathcal {M}},g)$ with angular momentum $l>0$ and

• $\gamma (0)\in \{u=u_{1}(v)\}$

(see Fig. 9). Then, for all $s\in [0,a)$, the following relation holds for the tangent ${\dot{\gamma }}$ to $\gamma$:

$$\begin{aligned}&\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(s)-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(0) \nonumber \\&\quad = \int _{v(\gamma (0))}^{v(\gamma (s))}\int _{u_{1}(v)}^{u(\gamma (s_{v}))}\Big (\frac{1}{2}\frac{\frac{6{\tilde{m}}}{r}-1}{r^{2}}\Omega ^{2}-24\pi T_{uv}\Big )\,du\,dv\nonumber \\&\qquad +\int _{v(\gamma (0))}^{v(\gamma (s))}\big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\big )(u_{1}(v),v)\,dv, \end{aligned}$$

(2.50)

where $s_{{\bar{v}}}$ is defined as the value of the parameter s determined by the condition

$$\begin{aligned} v(\gamma (s_{{\bar{v}}}))={\bar{v}}, \end{aligned}$$

(2.51)

i.e. corresponding to the point of intersection between $\gamma$ and the line $v={\bar{v}}$.

Similarly, for any continuous and strictly increasing function $v_1: {\mathbb {R}} \rightarrow {\mathbb {R}}$ and any null geodesic $\gamma :[0,a)\rightarrow \{v\ge v_{1}(u)\}$ with $\gamma (0)\in \{v=v_{1}(u)\}$, we have

$$\begin{aligned} \log \big (\Omega ^{2}{\dot{\gamma }}^{v}\big )(s)-\log \big (\Omega ^{2}{\dot{\gamma }}^{v}\big )(0) =&\int _{u(\gamma (0))}^{u(\gamma (s))}\int _{v_{1}(u)}^{v(\gamma (s_{u}))}\Big (\frac{1}{2}\frac{\frac{6{\tilde{m}}}{r}-1}{r^{2}}\Omega ^{2}-24\pi T_{uv}\Big )\,dv\,du\nonumber \\&+\int _{u(\gamma (0))}^{u(\gamma (s))}\big (\partial _{u}\log (\Omega ^{2})-2\frac{\partial _{u}r}{r}\big )(u,v_{1}(u))\,du,\quad \end{aligned}$$

(2.52)

where $s_{{\bar{u}}}$ is defined by:

$$\begin{aligned} u(\gamma (s_{{\bar{u}}}))={\bar{u}}. \end{aligned}$$

(2.53)

Remark

In view of the relation (2.19), the projection $\gamma$ on ${\mathcal {U}}$ of a null geodesic in $({\mathcal {M}},g)$ with $l>0$ is a timelike curve in ${\mathcal {U}}$ with respect to the reference metric

$$\begin{aligned} g_{ref}=-du\,dv. \end{aligned}$$

(2.54)

Fig. 9

Formula (2.50) expresses the change in the magnitude of $\Omega ^{2}{\dot{\gamma }}^{u}$ for a future directed null geodesic $\gamma$ in terms of a spacetime integral over a region as depiced above

Proof

Using the equations of motion (2.20) combined with the null shell relation (2.19), we infer that, for all $s\in [0,a)$:

$$\begin{aligned}&\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(s)-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(0) \nonumber \\&\quad = \int _{{{\upalpha }}([0,s]))}\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )\,dv\nonumber \\&\quad = \int _{v(\gamma (0))}^{v(\gamma (s))}\int _{u_{1}(v)}^{u(\gamma (s_{v}))}\Big (\partial _{u}\partial _{v}\log (\Omega ^{2})-2\partial _{u}\frac{\partial _{v}r}{r}\Big )\,du\,dv\nonumber \\&\qquad +\int _{v(\gamma (0))}^{v(\gamma (s))}\big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\big )(u_{1}(v),v)\,dv \end{aligned}$$

(2.55)

(see also Fig. 9, as well as the remark above on why $\gamma$ is a timelike curve in ${\mathcal {U}}$). Therefore, substituting the relations (2.45) and (2.42) for $\partial _{u}\partial _{v}r$ and $\partial _{u}\partial _{v}\log \Omega ^{2}$ in the right hand side of (2.55) and recalling the definition (2.44) of ${\tilde{m}}$, we readily infer (2.50) from (2.55).

The proof of (2.52) follows in a similar way. $\square$

Asymptotically AdS solutions and the reflecting boundary condition at infinity Let $({\mathcal {M}},g;f)$ be a spherically symmetric solution of (2.35), such that, in addition, $({\mathcal {M}},g)$ is asymptotically AdS, in accordance with the Definition 2.1. In this case, the following quantities will be useful as renormalised substitutes of r, $\Omega ^{2}$ and $T_{\mu \nu }$ near conformal infinity (see Sect. 2.2):

$$\begin{aligned} \rho&\doteq \tan ^{-1}\big (\sqrt{-\frac{\Lambda }{3}}r\big ),\\ {\widetilde{\Omega }}^{2}&\doteq \frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}},\nonumber \\ \tau _{\mu \nu }&\doteq r^{2}T_{\mu \nu }.\nonumber \end{aligned}$$

(2.56)

From (2.45) and (2.42), it readily follows that $(\rho ,{\widetilde{\Omega }}^{2},\tau _{\mu \nu })$ satisfy the relations

$$\begin{aligned} \partial _{u}\partial _{v}\rho&=-\frac{1}{2}\sqrt{-\frac{\Lambda }{3}}\frac{{\tilde{m}}}{r^{2}}\frac{1-\frac{2}{3}\Lambda r^{2}}{1-\frac{1}{3}\Lambda r^{2}}{\widetilde{\Omega }}^{2}+4\pi \sqrt{-\frac{\Lambda }{3}}\frac{1}{r-\frac{1}{3}\Lambda r^{3}}\tau _{uv},\\ \partial _{u}\partial _{v}\log ({\widetilde{\Omega }}^{2})&=\frac{{\tilde{m}}}{r}\Big (\frac{1}{r^{2}}+\frac{1}{3}\Lambda \frac{\Lambda r^{2}-1}{1-\frac{1}{3}\Lambda r^{2}}\Big ){\widetilde{\Omega }}^{2}-16\pi \frac{1-\frac{1}{2}\Lambda r^{2}}{1-\frac{1}{3}\Lambda r^{2}}r^{-2}\tau _{uv}.\nonumber \end{aligned}$$

(2.57)

In the asymptotically AdS setting, it is natural to study the system (2.36)–(2.41) with boundary conditions imposed for f on ${\mathcal {I}}$. In this paper, we will consider the reflecting boundary condition. Defined in terms of the reflection of null geodesics off ${\mathcal {I}}^{(2+1)}$, the reflecting boundary condition can be formulated as follows (see [43] for more details):

Definition 2.4

Let $({\mathcal {M}},g)$ be as in Definition 2.1, and let f be a smooth massless Vlasov field on $T{\mathcal {M}}$, as defined in Sect. 2.3. We will say that f satisfies the reflecting boundary condition on conformal infinity if, for any pair of future directed null geodesics $\gamma :(a,+\infty )\rightarrow {\mathcal {M}}$ and $\gamma _{\models }:(-\infty ,b)\rightarrow {\mathcal {M}}$ such that $\gamma _{\models }$ is the reflection of $\gamma$ off conformal infinity ${\mathcal {I}}^{(2+1)}$, according to Definition 2.2 in [43], f satisfies

$$\begin{aligned} f|_{(\gamma ,{\dot{\gamma }})}=f|_{(\gamma _{\models },{\dot{\gamma }}_{\models })}, \end{aligned}$$

(2.58)

where $f|_{(\gamma ,{\dot{\gamma }})}$ is the (constant) value of f along the curve $(\gamma ,{\dot{\gamma }})$ in $T{\mathcal {M}}$.¹⁴

Remark

Equivalently, f satisfies the reflecting condition on ${\mathcal {I}}^{(3+1)}$ if f is constant along the trajectory of $(\gamma ,{\dot{\gamma }})$ for any future directed, affinely parametrized null geodesic $\gamma$ which is maximally extended through reflections, in accordance with Definition 2.3 in [43] (see also Fig. 10).

Fig. 10

Schematic depiction of the components $\gamma _n$ of a maximally extended geodesic $\gamma =\bigcup _{n=0}^{N}\gamma _n$ through reflections off conformal infinity, as defined in [43]. Each component $\gamma _n$ is the reflection off ${\mathcal {I}}$ of $\gamma _{n-1}$. A massless Vlasov field f satisfying the reflecting boundary condition on ${\mathcal {I}}$ is constant along any such maximally extended null geodesic

The following Lemma is a trivial corollary of the relations (2.49)–(2.48) for ${\tilde{m}}$, the condition (2.14) on conformal infinity ${\mathcal {I}}$ and the reflecting boundary condition (2.58) for f:

Lemma 2.5

Let $(r,\Omega ^{2},f)$ be an asymptotically AdS solution of (2.36)–(2.41) as above, satisfying on ${\mathcal {I}}$ the reflecting boundary condition, in accordance with Definition 2.4. Then, the renormalised Hawking mass ${\tilde{m}}$ is constant along ${\mathcal {I}}$, satisfying formally:

$$\begin{aligned} (\partial _{u}+\partial _{v}){\tilde{m}}|_{{\mathcal {I}}}=0. \end{aligned}$$

(2.59)

See also Lemma 2.1 in [43].

3 The asymptotically AdS characteristic initial-boundary value problem

In this section, we will review the well-posedness results regarding the characteristic-boundary initial value problem for (2.36)–(2.41) established in [43]. In particular, we will introduce the notion of a smoothly compatible, characteristic asymptotically AdS initial data set for the system (2.36)–(2.41) and we will present a result on the existence and uniqueness of a maximal future development for (2.36)–(2.41) when reflecting boundary conditions are imposed on ${\mathcal {I}}$. We will also state a few continuation criteria for smooth solutions of (2.36)–(2.41), which will be crucial for the constructions involved in the proof of Theorem 1. We will end this section by presenting a Cauchy stability statement for the trivial solution of (2.36)–(2.41) in a scale invariant initial data topology, which will later allow us to address the AdS instability conjecture in a low regularity setting in Sect. 4. The proofs of the results appearing in this section are presented in detail in our companion paper [43].

3.1 Smoothly compatible characteristic initial data sets for (2.36)–(2.41)

In this paper, the study of the dynamics of the system (2.36)–(2.41) in the asymptotically AdS setting will take place in the framework of the characteristic initial-boundary value problem, with initial data prescribed at $u=0$, satisfying the constraint equation (2.39). We will consider the following class of initial data which is compatible with smoothness of the associated development for (2.36)–(2.41) at the axis ${\mathcal {Z}}$ and at conformal infinity ${\mathcal {I}}$. In fact, this will be precisely the class of initial data giving rise to a smooth development for (2.36)–(2.41) and it will contain the initial data family of Theorem 1 (which will be constructed in Sect. 6.2); see also Definitions 3.4 and 3.5 in [43].

Definition 3.1

For a given $v_{{\mathcal {I}}}>0$, let $r_{/},\Omega _{/}:[0,v_{{\mathcal {I}}})\rightarrow [0,+\infty )$ and ${\bar{f}}_{/}:(0,v_{{\mathcal {I}}})\times [0,+\infty )^{2}\rightarrow [0,+\infty )$ be smooth functions. The quadruplet $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ (simplified to $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/})$ when the value of $v_{{\mathcal {I}}}$ is clear from the context) will be called a smoothly compatible asymptotically AdS initial data set for the system (2.36)–(2.41) if it satisfies the following conditions:

• 1. The functions $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/})$ satisfy on $(0,v_{{\mathcal {I}}})$ the constraint equation (2.39), with $T_{vv}$ is defined in terms of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/})$ by the second relation in (2.30) with ${\bar{f}}(u,v;p^{u},p^{v},l)\Big |_{\Omega ^{2}p^{u}p^{v}=\frac{l^{2}}{r^{2}}}$ replaced by ${\bar{f}}_{/}(v;p^{u},l)$.

• 2. At $v=0$, the functions $r_{/}$, $\Omega _{/}^{2}$ extend smoothly and satisfy

  $$\begin{aligned} \Omega _{/}^{2}(0)>0 \end{aligned}$$

  (3.1)

  and

  $$\begin{aligned} r_{/}(0)=0. \end{aligned}$$

  (3.2)

• 3. The functions $1/r_{/}$ and $r_{/}^{-2}\Omega _{/}^{2}$ extend smoothly on $v=v_{{\mathcal {I}}}$ and satisfy

  $$\begin{aligned}{} & {} 1/r_{/}(v_{{\mathcal {I}}})=0, \end{aligned}$$

  (3.3)
  $$\begin{aligned}{} & {} r_{/}^{-2}\Omega _{/}^{2}(v_{{\mathcal {I}}})>0, \end{aligned}$$

  (3.4)
  $$\begin{aligned}{} & {} \partial _{v}(1/r_{/})(v_{{\mathcal {I}}})<0. \end{aligned}$$

  (3.5)

  Furthermore, for any ${\bar{p}}\ge 0$ and $l\ge 0$, the function ${\bar{f}}_{/}(v;\Omega _{/}^{-2}(v){\bar{p}},l)$ extends smoothly on $v=v_{{\mathcal {I}}}$.

• 4. The functions $r_{/},\text { }\Omega _{/}^{2},\text { }{\bar{f}}_{/}$ satisfy Conditions 1–3 of Definition 3.5 of [43] on smooth compatibility at $v=0$ and $v=v_{{\mathcal {I}}}$.

Remark

The requirement that the functions $r_{/},\text { }\Omega _{/}^{2},\text { }{\bar{f}}_{/}$ satisfy Conditions 1–3 of Definition 3.5 of [43] corresponds to the statement that, roughly speaking, the initial data set $(r_{/},\text { }\Omega _{/}^{2},\text { }{\bar{f}}_{/})$, which is originally defined along $\{u=0\}$, can be smoothly extended as a triplet of functions $(r,\Omega ^2,{\tilde{f}})$ defined on an open neighborhood of $\{u=0\}$ in the region $\{u\le v < v+v_{{\mathcal {I}}}\}$, such that

• The spherically symmetric metric determined by the parameters $(r,\Omega ^2)$ is smooth and asymptotically AdS (with smooth axis and conformal infinity)

• The functions $(r,\Omega ^2,{\tilde{f}})$ satisfy the system (2.36)–(2.41) at $\{u=0\}$ at all orders.

See Definition 3.5 of [43].

We will also denote by ${\mathfrak {B}}_{0}$ the set of all smoothly compatible, asymptotically AdS initial data sets $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ for (2.36)–(2.41) which have bounded support in phase space, i.e. satisfy for every $v\in (0,v_{{\mathcal {I}}})$ and every $l\ge 0$:

$$\begin{aligned} \sup _{p^{u}\in supp(f_{/}(v;\cdot ,l))}\Big (\Omega _{/}^{2}\big (p^{u}+\frac{l^{2}}{\Omega _{/}^{2}r_{/}^{2}p^{u}}\big )\Big )\le C \end{aligned}$$

(3.6)

for some constant $C<+\infty$ independent of v, l.¹⁵

For a more detailed discussion on Definition 3.1 and the properties of initial data sets in ${\mathfrak {B}}_{0}$, see Definitions 3.4 and 3.5 in [43].

The following remarks regarding Definition 3.1 were also discussed in [43] (see Section 3.2 of [43]):

• Under a gauge transformation of the (u, v)-plane of the form $(u,v)\rightarrow (u',v')=(U(u),V(v))$, $\frac{dU}{du},\frac{dV}{dv}\ne 0$, solutions $(r,\Omega ^{2},f)$ to (2.36)–(2.41) transform according to (2.43). Considering the restriction of such a transformation with $U(0)=V(0)=0$ at the initial data $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/})$ induced on $\{u=0\}$, we infer that $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/})$ transform as follows:

  $$\begin{aligned} r_{/}^{\prime }(v')&\doteq r_{/}(v),\\ (\Omega _{/}^{\prime })^{2}(v')&\doteq \frac{1}{\frac{dU}{du}(0)\cdot \frac{dV}{dv}(v)}\Omega _{/}^{2}(v),\nonumber \\ {\bar{f}}_{/}^{\prime }(v';\frac{dU}{du}(0)\cdot p,l)&\doteq {\bar{f}}_{/}(v;p,l).\nonumber \end{aligned}$$

  (3.7)

• In this paper, following the conventions of [43], we will study asymptotically AdS solutions $(r,\Omega ^{2},f)$ of (2.36)–(2.41) under the gauge condition that $r=0$ on $\{u=v\}$ and $r=\infty$ on $\{u=v-v_{{\mathcal {I}}}\}$ (see Definition 3.5 in the next section). For a gauge transformation $(u,v)\rightarrow (U(u),V(v))$ to preserve this condition, it is necessary that

  $$\begin{aligned} U(v)=V(v)\text { and }U(v-v_{{\mathcal {I}}})=V(v)-v_{{\mathcal {I}}}. \end{aligned}$$

  (3.8)

  At the level of the initial data transformation at $u=0$ associated to the coordinate transformation $v\rightarrow V(v)$ and the parameter $\frac{dU}{du}(0)$, (3.8) implies that

  $$\begin{aligned} \frac{dU}{du}(0)=\frac{dV}{dv}(0)\quad \text {and}\quad V(0)=0\text {, }V(v_{{\mathcal {I}}})=v_{{\mathcal {I}}}. \end{aligned}$$

  (3.9)

  Note that, in general, the property of an initial data set $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ being smoothly compatible is gauge dependent. In particular, when the transformed initial data set $(r_{/}^{\prime },(\Omega _{/}^{\prime })^2,{\bar{f}}_{/}^{\prime };V(v_{{\mathcal {I}}}))$ is also smoothly compatible, Condition 4 of Definition 3.1 implies that a certain relation holds between $\frac{d^{k}V}{(dv)^{k}}(0)$ and $\frac{d^{k}V}{(dv)^{k}}(v_{{\mathcal {I}}})$ for all $k\in {\mathbb {N}}$; this relation does not hold, in general, for gauge transformations as above, even when V satisfies the (necessary) condition $V\in C^{\infty }([0,v_{{\mathcal {I}}}])$. However, under certain assumptions on the support of ${\bar{f}}$, an initial data set $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ satisfying Conditions 1–3 above can be gauge-transformed into a smoothly compatible initial data set. See Lemma 3.4, as well as the discussion in Section 3.2 of [43].

• Let $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\in {\mathfrak {B}}_{0}$. We will define the function $(\partial _{u}r)_{/}$ on $(0,v_{{\mathcal {I}}})$ (coinciding formally with $\partial _{u}r|_{u=0}$ in a development of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ solving (2.36)–(2.41) and satisfying $r=0$ on $\{u=v\}$) by integrating equation (2.36) in v. In particular:

  $$\begin{aligned} (\partial _{u}r)_{/}(v)\doteq \frac{1}{2r_{/}(v)}\int _{0}^{v}\Big (-\frac{1}{2}(1-\Lambda r_{/}^{2})\Omega _{/}^{2}+8\pi r_{/}^{2}(T_{/})_{uv}\Big )\,d{\bar{v}},\qquad \end{aligned}$$

  (3.10)

  where $(T_{uv})_{/}$ is defined in terms of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/})$ by (2.30) with $\frac{l^{2}}{\Omega _{/}^{2}r_{/}^{2}p^{u}}$ in place of $p^{v}$ and ${\bar{f}}_{/}\big (v;p^{u},l\big )$ in place of ${\bar{f}}(0,v;p^{u},p^{v},l)\Big |_{\Omega ^{2}p^{u}p^{v}=\frac{l^{2}}{r^{2}}}$. We will also define the functions $m_{/},{\tilde{m}}_{/}$ on $(0,v_{{\mathcal {I}}})$ through the relations (2.9), (2.44), as well as the energy-momentum components $(T_{/})_{\mu \nu }$ through the relation (2.30) (again, with $\frac{l^{2}}{\Omega _{/}^{2}r_{/}^{2}p^{u}}$ in place of $p^{v}$ and ${\bar{f}}_{/}\big (v;p^{u},l\big )$ in place of ${\bar{f}}(0,v;p^{u},p^{v},l)\Big |_{\Omega ^{2}p^{u}p^{v}=\frac{l^{2}}{r^{2}}}$).

• For $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\in {\mathfrak {B}}_{0}$ as above, the functions $(T_{/})_{\mu \nu }$, $m_{/}$ and ${\tilde{m}}_{/}$ extend smoothly on $v=0$, with

  $$\begin{aligned} m_{/},{\tilde{m}}_{/}=O(r_{/}^{3}). \end{aligned}$$

  Furthermore, the condition (3.6) implies that

  $$\begin{aligned} \lim _{v\rightarrow v_{{\mathcal {I}}}^{-}}{\tilde{m}}(v)<+\infty , \end{aligned}$$

  (3.11)

  while (2.39) and (3.5) imply that

  $$\begin{aligned} \inf _{v\in (0,v_{{\mathcal {I}}})}\partial _{v}r_{/}(v)>0 \end{aligned}$$

  (3.12)

  (see also Remark 2 in Section 3.2 of [43]).

The following normalised gauge condition for initial data sets $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ was introduced in [43] for the purpose of fixing a simple representation of the trivial initial data set $(r_{AdS/},\Omega _{AdS/}^{2},0;v_{{\mathcal {I}}})$ (see Definition 3.6 in [43]):

Definition 3.2

Let $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ be a smoothly compatible, asymptotically AdS initial data set for (2.36)–(2.41), as in Definition 3.1. Let also $v\rightarrow v'=V(v)$ (with $V\in C^{\infty }([0,v_{{\mathcal {I}}}])$), $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\rightarrow (r_{/}^{\prime },(\Omega _{/}^{\prime }),{\bar{f}}_{/}^{\prime };v_{{\mathcal {I}}})$, be a gauge transformation, defined by (3.7), satisfying the condition (3.9). We will say that $(r_{/}^{\prime },(\Omega _{/}^{\prime }),{\bar{f}}_{/}^{\prime };v_{{\mathcal {I}}})$ satisfies the normalised gauge condition if

$$\begin{aligned} \frac{\partial _{v}r_{/}^{\prime }}{1-\frac{1}{3}\Lambda (r_{/}^{\prime })^{2}}(v)=\frac{(\Omega _{/}^{\prime })^{2}}{4\partial _{v}r_{/}^{\prime }}(v)\quad \text { for }v\in (0,v_{{\mathcal {I}}}). \end{aligned}$$

(3.13)

In this case, we will say that $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\rightarrow (r_{/}^{\prime },(\Omega _{/}^{\prime }),{\bar{f}}_{/}^{\prime };v_{{\mathcal {I}}})$ is a gauge normalising transformation.

We should make the following remarks regarding Definition 3.2:

• It can be readily shown (see Lemma 3.2 in [43]) that, for any $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\in {\mathfrak {B}}_{0}$, there exists a unique gauge normalising transformation as in Definition 3.2. The trivial (normalised) initial data set $(r_{AdS/},\Omega _{AdS/}^{2},0;\sqrt{-\frac{3}{\Lambda }}\pi )$ is expressed as:

  $$\begin{aligned} r_{AdS/}(v)&=\sqrt{-\frac{3}{\Lambda }}\tan \Big (\frac{1}{2}\sqrt{-\frac{\Lambda }{3}}v\Big ),\\ \Omega _{AdS/}^{2}(v)&=1-\frac{1}{3}\Lambda r_{AdS}^{2}(v),\nonumber \end{aligned}$$

  (3.14)

  which are the data induced at $u=0$ by the AdS metric expressed in the standard double null coordinate chart (2.10). For different values of the endpoint parameter $v_{{\mathcal {I}}}>0$, we obtain by rescaling:

  $$\begin{aligned} r_{AdS/}^{(v_{{\mathcal {I}}})}(v)&=r_{AdS/}\Big (\sqrt{-\frac{3}{\Lambda }}\pi \frac{v}{v_{{\mathcal {I}}}}\Big ),\\ \big (\Omega _{AdS/}^{(v_{{\mathcal {I}}})}\big )^{2}(v)&=-\frac{3}{\Lambda }\frac{\pi ^{2}}{v_{{\mathcal {I}}}^{2}}\Omega _{AdS/}^{2}\Big (\sqrt{-\frac{3}{\Lambda }}\pi \frac{v}{v_{{\mathcal {I}}}}\Big ).\nonumber \end{aligned}$$

  (3.15)

• By integrating the constraint equation (2.39), we infer that the gauge condition (3.13) is equivalent to

  $$\begin{aligned} \frac{\partial _{v}r_{/}}{1-\frac{1}{3}\Lambda r_{/}^{2}}(v)=\frac{1}{2a}\exp \Big (4\pi \int _{0}^{v}\frac{r_{/}(T_{/})_{vv}}{(\partial _{v}r_{/})^{2}}({\bar{v}})\,(\partial _{v}r_{/})d{\bar{v}}\Big ), \end{aligned}$$

  (3.16)

  where

  $$\begin{aligned} a\doteq \sqrt{-\frac{\Lambda }{3}}\frac{1}{\pi }\int _{0}^{v_{{\mathcal {I}}}}\exp \Big (4\pi \int _{0}^{v}\frac{r_{/}(T_{/})_{vv}}{(\partial _{v}r_{/})^{2}}({\bar{v}})\,(\partial _{v}r_{/})d{\bar{v}}\Big )\,dv \end{aligned}$$

  (3.17)

  and $(T_{/})_{vv}$ is defined in terms of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/})$ by in (2.30) with ${\bar{f}}_{/}(v;p^{u},l)$ in place of ${\bar{f}}(u,v;p^{u},p^{v},l)\Big |_{\Omega ^{2}p^{u}p^{v}=\frac{l^{2}}{r^{2}}}$. Alternatively, the gauge condition (3.13) can be expressed as

  $$\begin{aligned} \frac{\partial _{v}r_{/}}{1-\frac{1}{3}\Lambda r_{/}^{2}}=-\frac{(\partial _{u}r)_{/}}{1-\frac{2m_{/}}{r_{/}}}. \end{aligned}$$

  (3.18)

A comparative advantage of considering the gauge condition (3.13) when constructing asymptotically AdS initial data sets $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ for (2.36)–(2.41) is that (3.13) allows one to completely determine $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ in terms of $v_{{\mathcal {I}}}$ and ${\bar{f}}_{/}$, which can be freely prescribed. In particular, the following result was established in [43]:

Lemma 3.3

(Lemma 3.1 in [43]). Let $v_{{\mathcal {I}}}>0$ and let $F:[0,v_{{\mathcal {I}}})\times [0,+\infty )^{2}\rightarrow [0,+\infty )$ be a smooth function such that $\text {supp}(F)$ is a compact subset of $(0,v_{{\mathcal {I}}})\times (0,+\infty )^{2}$. There exists a unique asymptotically AdS initial data set $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ for (2.36)–(2.41) satisfying Conditions 1–3 of Definition 3.1 and the gauge condition (3.13), such that

$$\begin{aligned} {\bar{f}}_{/}(v;p^{u},l)=F\big (v;\text { }\partial _{v}r_{/}(v)p^{u},\text { }l\big ). \end{aligned}$$

(3.19)

Assume, in addition, that F satisfies the smallness condition

$$\begin{aligned} {\mathcal {M}}[F]\doteq \int _{0}^{v_{{\mathcal {I}}}}\frac{r_{AdS/}^{(v_{{\mathcal {I}}})}(T_{AdS}^{(v_{{\mathcal {I}}})}[F])_{vv}}{\partial _{v}r_{AdS/}^{(v_{{\mathcal {I}}})}}({\bar{v}})\,d{\bar{v}}<c_{0}\ll 1, \end{aligned}$$

(3.20)

where $c_{0}>0$ is an absolute constant, $(T_{AdS}^{(v_{{\mathcal {I}}})}[F])_{vv}$ is defined by

$$\begin{aligned} (T_{AdS}^{(v_{{\mathcal {I}}})}[F])_{vv}(v)\doteq \frac{\pi }{2}\frac{1}{(r_{AdS/}^{(v_{{\mathcal {I}}})})^{2}(v)}\int _{0}^{+\infty }\int _{0}^{+\infty }p^{2}F(v;p,l)\,\frac{dp}{p}ldl\qquad \end{aligned}$$

(3.21)

and $r_{AdS/}^{(v_{{\mathcal {I}}})},\text { }(\Omega _{AdS/}^{(v_{{\mathcal {I}}})})^{2}$ are the rescaled AdS metric coefficients given by (3.15). Then, the following bounds hold:

$$\begin{aligned} \Big |\frac{\partial _{v}r_{/}}{1-\frac{1}{3}\Lambda r_{/}^{2}}(v)-\frac{\partial _{v}r_{AdS/}^{(v_{{\mathcal {I}}})}}{1-\frac{1}{3}\Lambda (r_{AdS/}^{(v_{{\mathcal {I}}})})^{2}}(v)\Big |\le C{\mathcal {M}}[F]\quad \text { for all }v\in (0,v_{{\mathcal {I}}})\nonumber \\ \end{aligned}$$

(3.22)

and

$$\begin{aligned} \int _{0}^{v_{{\mathcal {I}}}}\frac{r_{/}(T_{/})_{vv}}{\partial _{v}r_{/}}({\bar{v}})\,d{\bar{v}}\le C{\mathcal {M}}[F], \end{aligned}$$

(3.23)

where $C>0$ is an absolute constant and is $(T_{/})_{vv}$ is defined in terms of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ by the second relation in (2.30) with ${\bar{f}}(u,v;p^{u},p^{v},l)\Big |_\Omega ^{2}p^{u}p^{v}=\frac{l^{2}}{r^{2}}$ replaced by ${\bar{f}}_{/}(v;p^{u},l)$.

For the proof of Lemma 3.3, see [43].

In general, a gauge normalising transformation (as in Definition 3.2) is not smoothly compatible; that is to say, an initial data set $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ expressed in a gauge where (3.13) holds will not, in general, satisfy Condition 4 of Definition 3.1 (see also the more detailed discussion in Sections 3.2 and 3.3 in [43]).

Remark

For the trivial initial data set $(r_{AdS/},\Omega _{AdS/}^{2},0;\sqrt{-\frac{3}{\Lambda }}\pi )$, the gauge normalised form (3.14) is also smoothly compatible (see [43]).

The following lemma, which is established in [43], shows that any initial data set $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ which satisfies Conditions 1–3 of Definition 3.1 when expressed in a gauge where (3.13) holds can be gauge transformed into a smoothly compatible initial data set, provided ${\bar{f}}_{/}$ is supported away from $v=0,v_{{\mathcal {I}}}$ and $l=0$.

Lemma 3.4

(Lemma 3.3 in [43]). Let $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ satisfy Conditions 1–3 of Definition 3.1, as well as the normalised gauge condition (3.13). Assume that ${\bar{f}}_{/}$ is supported away from $v=0,v_{{\mathcal {I}}}$ and $l=0$, i.e. there exists some ${\bar{\delta }}>0$, such that ${\bar{f}}_{/}$ satisfies

$$\begin{aligned} {\bar{f}}_{/}(v;p,l)=0\quad \text { for }v\in (0,{\bar{\delta }}]\cup [v_{{\mathcal {I}}}-{\bar{\delta }},v_{{\mathcal {I}}}) \end{aligned}$$

(3.24)

and

$$\begin{aligned} {\bar{f}}_{/}(v;p,l)=0\quad \text { for }l\in [0,{\bar{\delta }}]. \end{aligned}$$

(3.25)

Then, there exists a gauge transformation $v\rightarrow v'(V)$, $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\rightarrow (r_{/}^{\prime },(\Omega _{/}^{\prime })^{2},{\bar{f}}_{/}^{\prime };v_{{\mathcal {I}}})$ (of the form (3.7)), satisfying $V\in C^{\infty }[0,+\infty )$, (3.9) and

$$\begin{aligned} V(v)=v\text { for }v\le v_{{\mathcal {I}}}-\frac{1}{2}{\bar{\delta }}, \end{aligned}$$

(3.26)

such that the transformed initial data set $(r_{/}^{\prime },(\Omega _{/}^{\prime })^{2},{\bar{f}}_{/}^{\prime };v_{{\mathcal {I}}})$ satisfies all of the Conditions 1–4 of Definition 3.1.

Furthermore, for any $\varepsilon _{0}\in (0,1)$, the gauge transformation can be chosen so that

$$\begin{aligned} 1-\varepsilon _{0}\le \frac{dV}{dv}(v)\le 1+\varepsilon _{0}\quad \text { for }v\in [0,v_{{\mathcal {I}}}] \end{aligned}$$

(3.27)

and

$$\begin{aligned} \max _{v\in [0,v_{{\mathcal {I}}}]}\Big |\frac{d^{2}V}{(dv)^{2}}(v)\Big |\le \int _{0}^{v_{{\mathcal {I}}}}\Big (\frac{1-\Lambda r_{/}^{2}}{1-\frac{1}{3}\Lambda r_{/}^{2}}(T_{/})_{vv}+3(T_{/})_{uv}\Big )(v)\,dv+\frac{\varepsilon _{0}}{v_{{\mathcal {I}}}},\nonumber \\ \end{aligned}$$

(3.28)

where $(T_{/})_{vv}$, $(T_{/})_{uv}$ are defined in terms of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/})$ by (2.30) with ${\bar{f}}_{/}(v;p^{u},l)$ in place of ${\bar{f}}(u,v;p^{u},p^{v},l)\Big |_{\Omega ^{2}p^{u}p^{v}=\frac{l^{2}}{r^{2}}}$ and $\frac{l^{2}}{\Omega _{/}^{2}r_{/}^{2}p^{u}}$ in place of $p^{v}$.

For the proof of Lemma 3.4, see [43].

Remark

The above lemma applies, in particular, to the normalised initial data sets $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ provided by Lemma 3.3 for any function F which is compactly supported in $(0,v_{{\mathcal {I}}})\times (0,+\infty )^{2}$.

3.2 Well-posedness of the characteristic initial-boundary value problem and the maximal future development

In this section, we will formulate the notion of a development of a smoothly compatible, asymptotically AdS initial data set (see Definition 3.1) with respect to the system (2.36)–(2.41), assuming the reflecting boundary condition on ${\mathcal {I}}$ (see Definition 2.4). We will then present a fundamental well-posedness result for the associated characteristic initial–boundary value problem for (2.36)–(2.41), culminating in the statement of the existence and uniqueness of a maximal future development for any given smoothly compatible, asymptotically AdS initial data set with bounded support in phase space. The proofs of the results presented in this section (together with a wider collection of well-posedness results) can be found in our companion paper [43].

The following class of domains in the (u, v)-plane will appear naturally as the class of domains of definition for solutions $(r,\Omega ^{2},f)$ to the characteristic initial-boundary value problem for (2.36)–(2.41); see also [43].

Definition 3.5

For any given $v_{{\mathcal {I}}}>0$, we will define ${\mathscr {U}}_{v_{{\mathcal {I}}}}$ to be the set of all connected open domains ${\mathcal {U}}$ of the (u, v)-plane with piecewise Lipschitz boundary $\partial {\mathcal {U}}$, with the property that

$$\begin{aligned} \partial {\mathcal {U}}={\mathcal {S}}_{v_{{\mathcal {I}}}}\cup \gamma _{{\mathcal {Z}}}\cup {\mathcal {I}}\cup clos(\zeta ), \end{aligned}$$

(3.29)

where, for some $u_{\gamma _{{\mathcal {Z}}}},u_{{\mathcal {I}}}\in (0,+\infty ]$,

$$\begin{aligned}{} & {} {\mathcal {S}}_{v_{{\mathcal {I}}}}=\{0\}\times [0,v_{{\mathcal {I}}}], \end{aligned}$$

(3.30)

$$\begin{aligned}{} & {} \gamma _{{\mathcal {Z}}}=\{u=v\}\cap \{0\le u<u_{\gamma _{{\mathcal {Z}}}}\}, \end{aligned}$$

(3.31)

$$\begin{aligned}{} & {} {\mathcal {I}}=\{u=v-v_{{\mathcal {I}}}\}\cap \{0\le u<u_{{\mathcal {I}}}\} \end{aligned}$$

(3.32)

and the Lipschitz curve $\zeta$ is achronal with respect to the reference Lorentzian metric

$$\begin{aligned} g_{ref}\doteq -du\,dv \end{aligned}$$

(3.33)

on ${\mathbb {R}}^{2}$. In particular, the case $\zeta =\emptyset$ is allowed.

Remark

In the case when $\zeta =\emptyset$ in (3.29), it is necessary that both ${{\upalpha }}_{{\mathcal {Z}}}$ and ${\mathcal {I}}$ extend all the way to $u+v=+\infty$.

We will define a future development of an asymptotically AdS characteristic initial data set for (2.36)–(2.41) with reflecting boundary conditions on ${\mathcal {I}}$ as follows:

Definition 3.6

For a given $v_{{\mathcal {I}}}>0$, let $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ be a smoothly compatible, asymptotically AdS initial data set for the system (2.36)–(2.41), as introduced by Definition 3.1. A future development of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ for (2.36)–(2.41) with reflecting boundary conditions on ${\mathcal {I}}$ will consist of a domain ${\mathcal {U}}\subset {\mathbb {R}}^{2}$ belonging to the class ${\mathscr {U}}_{v_{{\mathcal {I}}}}$ introduced in Definition 3.5, together with a solution $(r,\Omega ^{2},f)$ of the system (2.36)–(2.41) on ${\mathcal {U}}$, such that the following conditions hold:

• 1. $({\mathcal {U}};r,\Omega ^{2},f)$ is a smooth solution of (2.36)–(2.41) with smooth axis $\gamma _{{\mathcal {Z}}}$ and smooth conformal infinity ${\mathcal {I}}$, in accordance with Definitions 3.1 and 3.2 of [43].¹⁶

• 2. The solution $(r,\Omega ^{2},f)$ induces the initial data $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ at $u=0$:

  $$\begin{aligned} (r,\Omega ^{2})(0,v)=(r_{/},\Omega _{/}^{2})(v) \end{aligned}$$

  (3.34)

  and

  $$\begin{aligned} f(0,v;p^{u},p^{v},l)={\bar{f}}_{/}(v;p^{u},l)\cdot \delta \Big (\Omega _{/}^{2}(v)p^{u}p^{v}-\frac{l^{2}}{(r_{/}(v))^2}\Big ).\qquad \end{aligned}$$

  (3.35)

• 3. The reflecting boundary condition (2.58) is satisfied by f along conformal infinity ${\mathcal {I}}$ (Fig. 11).

Fig. 11

Depicted above is a typical domain ${\mathcal {U}}\in {\mathscr {U}}_{v_{{\mathcal {I}}}}$. In the case when the boundary set $\zeta$ is empty, it is necessary that both $\gamma _{{\mathcal {Z}}}$ and ${\mathcal {I}}$ are unbounded (i.e. extend all the way to $u+v=\infty$)

Remark

For any smooth development $({\mathcal {U}};r,\Omega ^{2},f)$ as in Definition 3.6, the fact that the vector field $\partial _{v}+\partial _{u}$ is tangential to $\gamma _{{\mathcal {Z}}}$, ${\mathcal {I}}$ implies that

$$\begin{aligned} \partial _{v}r|_{\gamma _{{\mathcal {Z}}}}&=-\partial _{u}r|_{\gamma _{{\mathcal {Z}}}}, \end{aligned}$$

(3.36)

$$\begin{aligned} \partial _{v}(\frac{1}{r})|_{{\mathcal {I}}}&=-\partial _{u}(\frac{1}{r})|_{{\mathcal {I}}}. \end{aligned}$$

(3.37)

Moreover, differentiating the formula (2.9) for $\Omega ^{2}$ and using equation (2.45) for $\partial _u \partial _v r$, the boundary condition (3.36) for r on $\gamma _{{\mathcal {Z}}}$ and the smoothness of $(r,\Omega ^{2},f)$ at $\gamma _{{\mathcal {Z}}}$ (implying, in particular, that $m=O(r^{3})$ as $r \rightarrow 0$), we calculate that

$$\begin{aligned} \partial _v \Omega ^2 |_{\gamma _{{\mathcal {Z}}}}&= 4 \frac{(-\partial _u \partial _v r) \partial _v r + (-\partial _u r) \partial _v^2 r}{1-\frac{2m}{r}} \Big |_{\gamma _{{\mathcal {Z}}}} + 4 \Big (\frac{(-\partial _u r) \partial _v r}{(1-\frac{2m}{r})^2} \partial _v \big (1-\frac{2m}{r}\big ) \Big )\Big |_{\gamma _{{\mathcal {Z}}}} \\&= \partial _v r \partial _v^2 r |_{\gamma _{{\mathcal {Z}}}} \end{aligned}$$

and, similarly:

$$\begin{aligned} \partial _u \Omega ^2 |_{\gamma _{{\mathcal {Z}}}} = \partial _u r \partial _u^2 r |_{\gamma _{{\mathcal {Z}}}} \end{aligned}$$

Thus, using once more (3.36) and the fact that $(\partial _u +\partial _v)^2 r |_{\gamma _{{\mathcal {Z}}}}=0$ (since $r\equiv 0$ on $\gamma _{{\mathcal {Z}}}$), we infer that $\Omega ^2$ satisfies the following Neuman-type boundary condition at $\gamma _{{\mathcal {Z}}}$:

$$\begin{aligned} (\partial _{v}-\partial _{u})\Omega ^{2}\Big |_{\gamma _{{\mathcal {Z}}}} =0. \end{aligned}$$

(3.38)

Arguing similarly at ${\mathcal {I}}$ (where $\frac{1}{r}\equiv 0$ and using (2.57) and (3.37) in place of (2.45) and (3.36), respectively, we also infer that:

$$\begin{aligned} (\partial _{v}-\partial _{u})\Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )\Bigg |_{{\mathcal {I}}} =0. \end{aligned}$$

(3.39)

Let us also point out that, for any smooth development $({\mathcal {U}};r,\Omega ^{2},f)$ as in Definition 3.6 and any $u_{*}\in [0,u_{\gamma _{{\mathcal {I}}}})$, the characteristic initial data set $(r_{/u_{*}},\Omega _{/u_{*}}^{2},{\bar{f}}_{/u_{*}};v_{{\mathcal {I}}})$ induced on the slice $\{u=u_{*}\}\cap {\mathcal {U}}$ by $(r,\Omega ^{2},f)$ is smoothly compatible, in accordance with Definition 3.1; see also the Discussion in Section 3.2 of [43].

The following proposition establishes the well-posedness of the initial-boundary value problem for (2.36)–(2.41) with reflecting boundary conditions on ${\mathcal {I}}$ in the class ${\mathfrak {B}}_{0}$ of smoothly compatible, asymptotically AdS initial data with bounded support in phase space, as introduced in Definition 3.1:

Proposition 3.7

(Theorem 4.1 of [43]). Let $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\in {\mathfrak {B}}_{0}$ (see Definition 3.1). Then, there exists a $u_{*}>0$ (depending on $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$) and a unique solution $(r,\Omega ^{2}f)$ of (2.36)–(2.41) on the domain

$$\begin{aligned} {\mathcal {U}}_{u_{*};v_{{\mathcal {I}}}}\doteq \big \{0\le u<u_{*}\big \}\cap \big \{ u<v<u+v_{{\mathcal {I}}}\big \}, \end{aligned}$$

(3.40)

such that $({\mathcal {U}}_{u_{*},v_{{\mathcal {I}}}};r,\Omega ^{2}f)$ is a future development of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ with reflecting boundary conditions on ${\mathcal {I}}$, in accordance with Definition 3.6.

For the proof of Proposition 3.7, see Section 4.3 of [43].

The existence of a unique maximal future development for smoothly compatible, asymptotically AdS characteristic initial data with bounded support in phase space was also established in [43]:

Proposition 3.8

(Corollary 4.2 of [43]). Let $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ be initial data set in ${\mathfrak {B}}_{0}$. Then there exists a unique future development $({\mathcal {U}}_{max};r,\Omega ^{2},f)$ of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ with reflecting boundary conditions on ${\mathcal {I}}$ having the following property: If $({\mathcal {U}}_{*};r_{*},\Omega _{*}^{2},f_{*})$ is any other future development of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ with reflecting boundary conditions on ${\mathcal {I}}$, then

$$\begin{aligned} {\mathcal {U}}_{*}\subseteq {\mathcal {U}}_{max} \end{aligned}$$

(3.41)

and

$$\begin{aligned} (r,\Omega ^{2},f)|_{{\mathcal {U}}_{*}}=(r_{*},\Omega _{*}^{2},f_{*}). \end{aligned}$$

(3.42)

The solution $({\mathcal {U}}_{max};r,\Omega ^{2},f)$ will be called the maximal future development of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ under the reflecting boundary condition on ${\mathcal {I}}$.

For a a more detailed presentation and a discussion on the proof of Proposition 3.8, see Section 4.2 of [43].

The following notions regarding conformal infinity for future developments of smoothly compatible, asymptotically AdS initial data set will be frequently used in this paper:

Definition 3.9

Let $({\mathcal {U}};r,\Omega ^{2},f)$ be a future development of a smoothly compatible, asymptotically AdS initial data set $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ for the system (2.36)–(2.41), and let $u_{{\mathcal {I}}}$ and ${\mathcal {I}}$ be defined according to Definition 3.5.

• The black hole region of $({\mathcal {U}};r,\Omega ^{2},f)$ will be defined as the set

  $$\begin{aligned} {\mathcal {B}}\doteq \{u\ge u_{{\mathcal {I}}}\}\cap {\mathcal {U}}. \end{aligned}$$

  (3.43)

  We will say that $({\mathcal {U}};r,\Omega ^{2},f)$ contains a black hole if ${\mathcal {B}}\ne \emptyset$.

• We will say that a point $p\in {\mathcal {U}}$ corresponds to a trapped sphere of $({\mathcal {U}};r,\Omega ^{2},f)$ if

  $$\begin{aligned} \frac{2m}{r}(p)>1. \end{aligned}$$

  (3.44)

• We will say that $({\mathcal {U}};r,\Omega ^{2},f)$ has future complete¹⁷ conformal infinity ${\mathcal {I}}$ if

  $$\begin{aligned} \int _{0}^{u_{{\mathcal {I}}}}\frac{\Omega }{\big (1-\frac{1}{3}\Lambda r^{2}\big )^{\frac{1}{2}}}(u,u+v_{{\mathcal {I}}})\,du=+\infty . \end{aligned}$$

  (3.45)

Remark

As a consequence of the relation (2.9) and the fact that $\partial _{u}r<0$ everywhere on ${\mathcal {U}}$ (following from (2.38) and the fact that $\partial _{u}r<0$ on $\{u=0\}\cup {\mathcal {I}}$), if $({\bar{u}},{\bar{v}})\in {\mathcal {U}}$ satisfies

$$\begin{aligned} \frac{2m}{r}({\bar{u}},{\bar{v}})\ge 1, \end{aligned}$$

then

$$\begin{aligned} \partial _{v}r({\bar{u}},{\bar{v}}) \le 0. \end{aligned}$$

Hence, as a consequence of (2.39):

$$\begin{aligned} \sup _{v\ge {\bar{v}}}\partial _{v}r({\bar{u}},v) \le 0. \end{aligned}$$

(3.46)

Therefore, in this case the function r is bounded from above along $\{u={\bar{u}}\}$ and hence the line $\{u={\bar{u}}\}$ does not intersect $\{r=\infty \}={\mathcal {I}}$, i.e. $({\bar{u}},{\bar{v}})$ is contained in the black hole region ${\mathcal {B}}$. Equivalently,

$$\begin{aligned} \frac{2m}{r}(u,v)<1\quad \text { for all }(u,v)\in \{u<u_{{\mathcal {I}}}\}\cap {\mathcal {U}}. \end{aligned}$$

(3.47)

For general initial data, we will not be able to show that the maximal future development of a smooth initial data set $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ has future complete conformal infinity ${\mathcal {I}}$.¹⁸ However, in the presence of a trapped sphere, the following statement holds:

Lemma 3.10

(Lemma B.1 in [43]) Let $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\in {\mathfrak {B}}_{0}$ and let $({\mathcal {U}}_{max};r,\Omega ^{2},f)$ be the maximal future development of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ with reflecting boundary conditions on ${\mathcal {I}}$. Assume that there exists a point $({\bar{u}},{\bar{v}})\in {\mathcal {U}}_{max}$ satisfying

$$\begin{aligned} \frac{2m}{r}({\bar{u}},{\bar{v}})>1. \end{aligned}$$

(3.48)

Then, $({\mathcal {U}}_{max};r,\Omega ^{2},f)$ has future complete conformal infinity ${\mathcal {I}}$, i.e. (3.45) holds.

For a proof of Lemma 3.10, see Section B of the Appendix of [43].

3.3 Continuation criteria for smooth solutions of (2.36)–(2.41)

In this section, we will state two criteria that will allow us to extend smooth solutions $(r,\Omega ^{2},f)$ of (2.36)–(2.41) beyond their original domain of definition. These criteria will be applied in our proof of Theorem 1 in Sects. 7–9. For a wider class of continuation criteria, as well as for a proof of the results of this section, see Section 5 of our companion paper [43].

The main extension principle of this section is the following:

Proposition 3.11

(Corollary 5.1 in [43]). For any $v_{{\mathcal {I}}}>0$ and $u_{1}>0$, let $(r,\Omega ^{2},f)$ be a smooth solution of the system (2.36)–(2.41) on the domain ${\mathcal {U}}_{u_{1};v_{{\mathcal {I}}}}$ (defined as in (3.40)), with smooth axis $\{u=v\}$ and smooth conformal infinity $\{u=v-v_{{\mathcal {I}}}\}$ (see Definitions 3.1–3.3 of [43]). Assume that $(r,\Omega ^{2},f)$ satisfies

$$\begin{aligned}{} & {} \sup _{{\mathcal {U}}_{u_{1};v_{{\mathcal {I}}}}}\frac{2m}{r}<1, \end{aligned}$$

(3.49)

$$\begin{aligned}{} & {} \limsup _{(u,v)\rightarrow (u_{1},u_{1})}\frac{2{\tilde{m}}}{r}\le \delta _{0}, \end{aligned}$$

(3.50)

where $\delta _{0}<1$ is a small absolute constant¹⁹ and, moreover, at $u=0$, we have

$$\begin{aligned} supp\Big (f(0,\cdot ;\cdot )\Big )\subset \Big \{\Omega ^{2}(p^{u}+p^{v})\le C_{0}\Big \}\quad \text { for some }C_{0}<+\infty .\qquad \end{aligned}$$

(3.51)

Then, there exists some ${\bar{u}}_{1}>u_{1}$, such that $(r,\Omega ^{2},f)$ extends on the whole of the domain ${\mathcal {U}}_{{\bar{u}}_{1};v_{{\mathcal {I}}}}\supset {\mathcal {U}}_{u_{1};v_{{\mathcal {I}}}}$ as a smooth solution of (2.36)–(2.41) with smooth axis $\{u=v\}$ and smooth conformal infinity $\{u=v+v_{{\mathcal {I}}} \}$.

For a proof of Proposition 3.11, see Section 5.3 in [43].

The next extension principle, which is also presented in [43], applies to the case of smooth solutions of (2.36)–(2.41), restricted to domains on which r is bounded away from 0 and $+\infty$:

Proposition 3.12

(Proposition 5.1 in [43]). For any $u_{1}<u_{2}$, any $v_{1}<v_{2}$ and any $\Lambda \in {\mathbb {R}}$, let $(r,\Omega ^{2},f)$ be a smooth solution of the system (2.36)–(2.41) on an open neighborhood ${\mathcal {V}}$ of the rectangular region

$$\begin{aligned} {\mathcal {R}}\doteq [u_{1},u_{2}]\times [v_{1},v_{2}]\backslash \{(u_{2},v_{2})\}, \end{aligned}$$

satisfying

$$\begin{aligned}{} & {} \inf _{{\mathcal {V}}}r>0, \end{aligned}$$

(3.52)

$$\begin{aligned}{} & {} \sup _{{\mathcal {V}}}r<+\infty , \end{aligned}$$

(3.53)

$$\begin{aligned}{} & {} \sup _{{\mathcal {V}}}{\tilde{m}}<+\infty , \end{aligned}$$

(3.54)

$$\begin{aligned}{} & {} \sup _{(\{u_{1}\}\times [v_{1},v_{2}])\cup ([u_{1},u_{2}]\times \{v_{1}\})}\partial _{u}r<0, \end{aligned}$$

(3.55)

and, for some $C<+\infty$:

$$\begin{aligned} supp\Big (f(u_{1},\cdot ;\cdot )\Big ),supp\Big (f(\cdot ,v_{1};\cdot )\Big )\subseteq \big \{\Omega ^{2}(p^{v}+p^{u})\le C\big \}. \end{aligned}$$

(3.56)

Then, $(r,\Omega ^{2},f)$ extends smoothly in a neighborhood of the whole rectangle $[u_1, u_2]\times [v_1, v_2]$ (i.e. including the corner $\{(u_{2},v_{2})\}$).

For a proof of Proposition 3.12, as well as a discussion on the connection between Proposition 3.12 and an analogous result established in [18], see [43]. Note that Proposition 3.12 applies to the system (2.36)–(2.41) for any value of the cosmological constant $\Lambda$.

3.4 Cauchy stability of $({\mathcal {M}}_{AdS},g_{AdS})$ for (2.36)–(2.41) in a low regularity topology

In this section, we will introduce a low regularity, scale invariant topology on the space ${\mathfrak {B}}_{0}$ of smoothly compatible, asymptotically AdS initial data of bounded support in phase space (see Definition 3.1). We will then formulate a Cauchy stability statement for the trivial solution $({\mathcal {M}}_{AdS},g_{AdS})$ in this topology. This statement will be crucial for addressing the AdS instability conjecture in the associated low regularity topology. A more detailed discussion on the results of this section can be found in our companion paper [43].

In accordance with [43], we will introduce the following map from ${\mathfrak {B}}_{0}$ to the space of smooth solutions of the (free) massless Vlasov equation (2.21) on AdS spacetime:

Definition 3.13

For any given $v_{{\mathcal {I}}}>0$, let $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ be an asymptotically AdS initial data set in the class ${\mathfrak {B}}_{0}$ (see Definition 3.1). Let also $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\rightarrow (r_{/}^{\prime },(\Omega _{/}^{\prime })^{2},{\bar{f}}_{/}^{\prime };v_{{\mathcal {I}}})$ be the (unique) gauge transformation such that $(r_{/}^{\prime },(\Omega _{/}^{\prime })^{2},{\bar{f}}_{/}^{\prime };v_{{\mathcal {I}}})$ satisfies the normalised gauge condition (3.13) (the existence of such a gauge transformation is guaranteed by Lemma 3.2 in [43]). Let us also define ${\bar{f}}_{/}^{(AdS)}:[0,\sqrt{-\frac{3}{\Lambda }}\pi )\times [0,+\infty )^{2}\rightarrow [0,+\infty )$ in terms of ${\bar{f}}_{/}^{\prime }$ by the expression

$$\begin{aligned} {\bar{f}}_{/}^{(AdS)}(v;\,p^{u},l)\doteq {\bar{f}}_{/}^{\prime }(\frac{\sqrt{-\frac{3}{\Lambda }}\pi }{v_{{\mathcal {I}}}}\cdot v;\,p^{u},l). \end{aligned}$$

We will define $f^{(AdS)}=f^{(AdS)}[{\bar{f}}_{/};v_{{\mathcal {I}}}]:T{\mathcal {M}}_{AdS}\rightarrow [0,+\infty )$ to be the unique solution of the massless Vlasov equation (2.21) on $({\mathcal {M}}_{AdS},g_{AdS})$ with initial conditions corresponding to ${\bar{f}}_{/}^{(AdS)}$, i.e. satisfying at $u=0$:

$$\begin{aligned}{} & {} f^{(AdS)}\left( 0,v;p^{u},\frac{l^{2}}{p^{u}\cdot \Omega _{AdS}^{2}r_{AdS}^{2}(0,v)},l\right) \nonumber \\{} & {} \quad ={\bar{f}}_{/}^{(AdS)}(v;\,p^{u},l)\cdot \delta \Big (\Omega _{AdS}^{2}(0,v)p^{u}p^{v}-\frac{l^{2}}{r_{AdS}^{2}(0,v)}\Big ), \end{aligned}$$

(3.57)

where $\Omega _{AdS}^{2}$, $r_{AdS}$ are the coefficients of $g_{AdS}$ given by (2.12). For any ${\bar{u}}\ge 0$ and ${\bar{v}}\in ({\bar{u}},{\bar{u}}+\sqrt{-\frac{3}{\Lambda }}\pi )$, we will also set

$$\begin{aligned} \Big [\frac{rT_{vv}}{\partial _{v}r}\Big ]^{(AdS)}({\bar{u}},{\bar{v}})\doteq \frac{r_{AdS}T_{vv}[f^{(AdS)}]}{\partial _{v}r_{AdS}}({\bar{u}},{\bar{v}}) \end{aligned}$$

(3.58)

(and similarly for $\Big [\frac{rT_{uv}}{-\partial _{u}r}\Big ]^{(AdS)}$, $\Big [\frac{rT_{uv}}{\partial _{v}r}\Big ]^{(AdS)}$ and $\Big [\frac{rT_{uu}}{-\partial _{u}r}\Big ]^{(AdS)}$), where the energy momentum components $T_{\alpha \beta }[f^{(AdS)}]$ are defined using the relations (2.30) with $\Omega _{AdS}^{2}$, $r_{AdS}$ in place of $\Omega ^{2}$, r.

Using the mapping $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\rightarrow f^{(AdS)}$ fixed in Definition 3.13, we will define the following positive definite functional on ${\mathfrak {B}}_{0}$ (see also Section 6.1 in [43]):

Definition 3.14

For any $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\in {\mathfrak {B}}_{0}$, we will define the norm $||(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})||$ of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ in terms of the free Vlasov field $f^{(AdS)}$ on $({\mathcal {M}}_{AdS},g_{AdS})$ as follows:

$$\begin{aligned}&||(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})||\nonumber \\&\quad \doteq \sup _{U_{*}\ge 0} \int _{U_{*}}^{U_{*}+\sqrt{-\frac{3}{\Lambda }}\pi }\Big (\Big [\frac{rT_{vv}}{\partial _{v}r}\Big ]^{(AdS)}(U_{*},v)+\Big [\frac{rT_{uv}}{-\partial _{u}r}\Big ]^{(AdS)}(U_{*},v)\Big )\,dv\nonumber \\&\qquad + \sup _{V_{*}\ge 0}\int _{\max \{0,V_{*}-\sqrt{-\frac{3}{\Lambda }}\pi \}}^{V_{*}}\Big (\Big [\frac{rT_{uu}}{-\partial _{u}r}\Big ]^{(AdS)}(u,V_{*})+\Big [\frac{rT_{uv}}{\partial _{v}r}\Big ]^{(AdS)}(u,V_{*})\Big )\,du\nonumber \\&\qquad +\sqrt{-\Lambda }{\tilde{m}}_{/}|_{v=v_{{\mathcal {I}}}}. \end{aligned}$$

(3.59)

Remark

The functional $||\cdot ||$ defined above is positive definite and measures the distance of an initial data set in ${\mathfrak {B}}_0$ from the trivial one with respect to an appropriate distance function (see also the remark below). However, strictly speaking, it is not a norm on ${\mathfrak {B}}_0$, since ${\mathfrak {B}}_0$ is not even a linear space. Despite this fact, in what follows, we will keep referring to $||\cdot ||$ as a norm on the space of initial data; see also the discussion in Section 6.1 of [43].

Let us also notice the following regarding the definition of $||\cdot ||$: As explained in Section 6.1 of [43], the quantity $||\cdot ||$ measures the concentration of energy occuring along the evolution of the free Vlasov field $f^{(AdS)}$ in $({\mathcal {M}}_{AdS},g_{AdS})$. However, it turns out that, for initial data which are small with respect to $||\cdot ||$, the evolution of f remains close (in a certain sense) to that of $f^{(AdS)}$ for a long time; thus, in this case, $||\cdot ||$ also measures the concentration of energy of f in the same time interval. This is the content of Proposition 3.15 below.

Given a smooth asymptotically AdS solution $(r,\Omega ^{2};f)$ of (2.36)–(2.41) on a domain ${\mathcal {U}}_{u_{1};v_{{\mathcal {I}}}}$ of the form (3.40) with axis $\{u=v\}$ and conformal infinity $\{u=v-v_{{\mathcal {I}}}\}$, we will similarly define the norm of the initial data induced by $(r,\Omega ^{2};f)$ on slices of the form $\{u=u_{*}\}\cap {\mathcal {U}}_{u_{1};v_{{\mathcal {I}}}}$ for any $u_{*}\in (0,u_{1})$ as follows:

$$\begin{aligned} ||(r,\Omega ^{2};f)|_{u=u_{*}}||\doteq ||(r_{/u_{*}},\Omega _{/u_{*}}^{2},{\bar{f}}_{/u_{*}};v_{{\mathcal {I}}})|| \end{aligned}$$

(3.60)

where

$$\begin{aligned} (r_{/u_{*}},\Omega _{/u_{*}}^{2})({\bar{v}})\doteq (r,\Omega ^{2})(u_{*},u_{*}+{\bar{v}}) \end{aligned}$$

and

$$\begin{aligned} {\bar{f}}_{/u_{*}}({\bar{v}};p,l) ={\bar{f}}\left( u_{*},u_{*}+{\bar{v}};p,\frac{l^{2}}{\Omega ^{2}r^{2}|_{(u_{*},u_{*}+{\bar{v}})}p},l\right) \end{aligned}$$

(where the function ${\bar{f}}$ is related to the distribution f by (2.28)).

Remark

The fact that $||\cdot ||$ takes finite values on ${\mathfrak {B}}_{0}$ follows readily from the condition (3.6) on the support of ${\bar{f}}_{/}$. Moreover, $||(r_{/},\Omega _{/}^{2},{\bar{f}}_{/})||=0$ if and only if ${\bar{f}}_{/}\equiv 0$; in this case, $(r_{/},\Omega _{/}^{2},0)$ can be identified through a gauge transformation with the rescaled trivial data

$$\begin{aligned} r_{AdS}^{(v_{{\mathcal {I}}})}(u,v)&=r_{AdS}\Big (\sqrt{-\frac{3}{\Lambda }}\pi \frac{u}{v_{{\mathcal {I}}}},\sqrt{-\frac{3}{\Lambda }}\pi \frac{v}{v_{{\mathcal {I}}}}\Big ),\\ \big (\Omega _{AdS}^{(v_{{\mathcal {I}}})}\big )^{2}(u,v)&=-\frac{3}{\Lambda }\frac{\pi ^{2}}{v_{{\mathcal {I}}}^{2}}\Omega _{AdS}^{2}\Big (\sqrt{-\frac{3}{\Lambda }}\pi \frac{u}{v_{{\mathcal {I}}}},\sqrt{-\frac{3}{\Lambda }}\pi \frac{v}{v_{{\mathcal {I}}}}\Big ).\nonumber \end{aligned}$$

(3.61)

Notice that $||\cdot ||$ is both gauge invariant and scale invariant, i.e. invariant under transformations of $(r_{/},\Omega _{/}^{2};{\bar{f}}_{/})$ of the form

$$\begin{aligned} r_{/}(v)\rightarrow & {} \lambda ^{-1}r_{/}(\lambda v),\\ \Omega _{/}^{2}(v)\rightarrow & {} \Omega _{/}^{2}(\lambda v),\\ {\bar{f}}_{/}(v;p^{v},l)\rightarrow & {} \lambda ^{2}(\lambda ')^{4}{\bar{f}}_{/}(\lambda v;\lambda 'p^{v},\lambda \cdot \lambda 'l),\\ \Lambda\rightarrow & {} \lambda ^{2}\Lambda , \end{aligned}$$

for any $\lambda ,\lambda '>0$. For a detailed discussion on the special properties and the scale-invariant character of $||\cdot ||$, see Section 6.1 of [43].

The following result provides a Cauchy stability statement for the trivial solution $({\mathcal {M}}_{AdS},g_{AdS})$ of (2.36)–(2.41) in the context of the initial data topology defined by (3.59) on ${\mathfrak {B}}_{0}$:

Proposition 3.15

(Theorem 6.1 in [43]). For any $v_{{\mathcal {I}}}>0$, any $U>0$ and any $C_{0}>0$, there exist $\varepsilon _{0}>0$ and $C_{1}>0$ such that the following statement holds: For any $0\le \varepsilon <\varepsilon _{0}$ and any smooth initial data set $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})\in {\mathfrak {B}}_{0}$ satisfying

$$\begin{aligned} ||(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})||<\varepsilon \end{aligned}$$

(3.62)

(where $||\cdot ||$ is defined by (3.59)) and the bound (3.6) with $C_{0}$ in place of C, the maximal future development $({\mathcal {U}}_{max};f,\Omega ^{2},f)$ of $(r_{/},\Omega _{/}^{2},{\bar{f}}_{/};v_{{\mathcal {I}}})$ under the reflecting boundary condition on ${\mathcal {I}}$ (see Proposition 3.8) satisfies

$$\begin{aligned} {\mathcal {U}}_{U;v_{{\mathcal {I}}}}\subset {\mathcal {U}}_{max} \end{aligned}$$

(where the domain ${\mathcal {U}}_{U;v_{{\mathcal {I}}}}\subset {\mathbb {R}}^{2}$ is defined in terms of U, $v_{{\mathcal {I}}}$ by (3.40)). Furthermore, $({\mathcal {U}}_{U;v_{{\mathcal {I}}}};r,\Omega ^{2},f)$ satisfies the following bounds:

$$\begin{aligned}{} & {} \sup _{u_{*}\in (0,U)}||(r,\Omega ^{2};f)|_{u=u_{*}}||\le C_{1}\varepsilon , \end{aligned}$$

(3.63)

$$\begin{aligned}{} & {} \sup _{(u,v)\in {\mathcal {U}}_{U;v_{{\mathcal {I}}}}}\Big (\sup _{p^{u},p^{v}\in supp(f(u,v;\cdot ,\cdot ,\cdot ))}\Big (\Omega ^{2}(u,v)\big (p^{u}+p^{v}\big )\Big )\Big )\le (1+C_{1}\varepsilon )C_{0},\nonumber \\ \end{aligned}$$

(3.64)

$$\begin{aligned}{} & {} \sup _{u\in (0,U)}\int _{u}^{u+v_{{\mathcal {I}}}}r\Big (\frac{T_{vv}[f]}{\partial _{v}r}+\frac{T_{uv}[f]}{-\partial _{u}r}\Big )(u,v)\,dv\nonumber \\{} & {} \quad +\sup _{v\in (0,U+v_{{\mathcal {I}}})}\int _{\max \{0,v-v_{{\mathcal {I}}}\}}^{\min \{v,U\}}r\Big (\frac{T_{uv}[f]}{\partial _{v}r}+\frac{T_{uu}[f]}{-\partial _{u}r}\Big )(u,v)\,du\le C_{1}\varepsilon , \end{aligned}$$

(3.65)

and

$$\begin{aligned} \sup _{{\mathcal {U}}_{U;v_{{\mathcal {I}}}}}\frac{2{\tilde{m}}}{r}<C_{1}\varepsilon . \end{aligned}$$

(3.66)

For the proof of Proposition 3.15, see Section 6.2 of [43].

4 Statement of the main result

In this section, we will present a detailed formulation of Theorem 1 on the instability of $({\mathcal {M}}_{AdS},g_{AdS})$ as a solution of the system (2.36)–(2.41). In particular, the main result of this paper can be stated as follows:

Theorem 1

(final version) There exists a 1-parameter family ${\mathcal {S}}^{(\varepsilon )}=(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$, $\varepsilon \in (0,1]$, of smoothly compatible, asymptotically AdS initial data sets for (2.36)–(2.41) with bounded support in phase space (see Definition 3.1), satisfying the following conditions:

• 1. ${\mathcal {S}}^{(\varepsilon )}$ converge to the trivial initial data as $\varepsilon \rightarrow 0$ with respect to the topology defined by (3.59), i.e.

  $$\begin{aligned} ||(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )||\xrightarrow {\varepsilon \rightarrow 0}0. \end{aligned}$$

  (4.1)

• 2. For any $\varepsilon \in (0,1]$, the corresponding maximal future development $({\mathcal {U}}_{max}^{(\varepsilon )};r_{\varepsilon },\Omega _{\varepsilon }^{2},f_{\varepsilon })$ of ${\mathcal {S}}^{(\varepsilon )}$ with reflecting boundary conditions on ${\mathcal {I}}$ contains a point $(u_{\dagger }^{(\varepsilon )},v_{\dagger }^{(\varepsilon )})$ such that

  $$\begin{aligned} \frac{2m_{\varepsilon }}{r_{\varepsilon }}(u_{\dagger }^{(\varepsilon )},v_{\dagger }^{(\varepsilon )})>1. \end{aligned}$$

  (4.2)

Remark

As a consequence of (3.47), the relation (4.2) implies that $({\mathcal {U}}_{max}^{(\varepsilon )};r_{\varepsilon },\Omega _{\varepsilon }^{2},f_{\varepsilon })$ contains a non-trivial black hole region for any $\varepsilon \in (0,1]$. Furthermore, Lemma 3.10 implies that, in this case, $({\mathcal {U}}_{max}^{(\varepsilon )};r_{\varepsilon },\Omega _{\varepsilon }^{2},f_{\varepsilon })$ possesses a complete null infinity ${\mathcal {I}}_{\varepsilon }$ for any $\varepsilon \in (0,1]$.

Using the estimates established in the proof of Theorem 1, it can be actually shown (although this is not carried out in this paper) that there exists an advanced time $v_{*}^{(\varepsilon )}>0$ satisfying

$$\begin{aligned} v_{\dagger }^{(\varepsilon )}<v_{*}^{(\varepsilon )}<u_{{\mathcal {I}}_{\varepsilon }}+\sqrt{-\frac{3}{\Lambda }}\pi \end{aligned}$$

such that, in the region ${\mathcal {V}}_{\infty }\doteq \{v\ge v_{*}^{(\varepsilon )}\}\cap {\mathcal {U}}_{max}^{(\varepsilon )}$, the Vlasov field $f^{(\varepsilon )}$ vanishes identically and the solution is locally isometric to a member of the Schwarzschild–AdS family. This fact implies, in particular, that $u_{{\mathcal {I}}}<+\infty$ and that the future boundary of ${\mathcal {U}}_{max}^{(\varepsilon )}$ is strictly spacelike in a neighborhood of “future timelike infinity” $(u_{{\mathcal {I}}_{\varepsilon }},u_{{\mathcal {I}}_{\varepsilon }}+\sqrt{-\frac{3}{\Lambda }}\pi )$. However, we are not able to rule out the possibility of the future boundary of ${\mathcal {U}}_{max}^{(\varepsilon )}$ containing a null segment emanating from $r=0$ and corresponding to a Cauchy horizon for the maximal future development $({\mathcal {U}}_{max}^{(\varepsilon )};r_{\varepsilon },\Omega _{\varepsilon }^{2},f_{\varepsilon })$ (note that the extension principle along $r=0$ provided by Theorem 5.1 in [43] only applies under the condition that $\frac{2{\tilde{m}}}{r}\ll 1$). We will not pursue this issue any further in this paper.

The proof of Theorem 1 will occupy Sects. 6–9. In particular, the construction of the initial data family ${\mathcal {S}}^{(\varepsilon )}$ will be presented in Sect. 6, with (4.1) established in Sect. 6.2 (see Lemma 6.5). The fact that the corresponding maximal developments $({\mathcal {U}}_{max}^{(\varepsilon )};r_{\varepsilon },\Omega _{\varepsilon }^{2},f_{\varepsilon })$ contain points where (4.2) holds will finally be established in Sect. 9, using the technical machinery developed in Sect. 7 and the fact that the specific choice of the initial data family leads to the formation of an intermediate profile with certain properties (see Sect. 8). For a sketch of the proof, see also Sect. 1.2 of the introduction.

Before proceeding to the proof of Theorem 1 and its related constructions, we will need to establish a number of fundamental estimates that will allow us to control the geodesic flow on solutions of (2.36)–(2.41) under minimal assumptions on their geometry; this will be achieved in Sect. 5.

5 Auxiliary estimates for the null geodesic flow in the case $2{\tilde{m}}/r\ll 1$

In this section, we will establish a number of estimates related to the paths of null geodesics on asymptotically AdS solutions $(r,\Omega ^{2},f)$ of (2.36)–(2.41), assuming, in addition, that the spacetimes under consideration satisfy the smallness condition

$$\begin{aligned} \frac{2{\tilde{m}}}{r}\le \delta _{0}\ll 1. \end{aligned}$$

The results of this section will be crucial for the proof of Theorem 1, since they will allow us to estimate the paths traced out by narrow Vlasov beams with minimal control on the spacetime geometry.

5.1 Geodesic paths under rough assumptions on the spacetime geometry

For any $U>0$ and $v_{{\mathcal {I}}}>0$, let ${\mathcal {U}}_{U;v_{{\mathcal {I}}}}$ be the domain in the (u, v)-plane defined by (3.40). Let also $(r,\Omega ^{2},f)$ be a smooth solution of (2.36)–(2.41) on ${\mathcal {U}}_{U;v_{{\mathcal {I}}}}$, with smooth axis $\{u=v\}$ and smooth conformal infinity $\{u=v-v_{{\mathcal {I}}}\}$, in accordance with to Definitions 3.1–3.3 of [43].

The following result provides quantitative bounds for the paths of null geodesics in ${\mathcal {U}}_{U;v_{{\mathcal {I}}}}$:

Lemma 5.1

Let $0<\delta _{0}\ll 1$ be a sufficiently small absolute constant, and let ${\mathcal {U}}_{U;v_{{\mathcal {I}}}}$ and $(r,\Omega ^{2},f)$ be as above. Assume that the following bounds are satisfied for some $C_{0}>100$:

$$\begin{aligned} \sup _{{\mathcal {U}}_{U;v_{{\mathcal {I}}}}}\Bigg (\Big |\log \Big (\frac{\partial _{v}r}{1-\frac{1}{3}\Lambda r^{2}}\Big )\Big |+\Big |\log \Big (\frac{-\partial _{u}r}{1-\frac{1}{3}\Lambda r^{2}}\Big )\Big |\Bigg )\le C_{0} \end{aligned}$$

(5.1)

and²⁰

$$\begin{aligned} \sup _{{\mathcal {U}}_{U;v_{{\mathcal {I}}}}}\Big (\frac{2{\tilde{m}}}{r}+\sqrt{-\Lambda }{\tilde{m}}\Big )\le \delta _{0}. \end{aligned}$$

(5.2)

Let $\gamma :[0,a)\rightarrow {\mathcal {U}}_{U;v_{{\mathcal {I}}}}$ (with $a\in (0,+\infty ]$) be a future inextendible, future directed, affinely parametrised null geodesic of $(r,\Omega ^{2})$ satisfying the following conditions:

• $\gamma$ is initially ingoing, i.e.

  $$\begin{aligned} {\dot{\gamma }}^{u}(0)>{\dot{\gamma }}^{v}(0), \end{aligned}$$

  (5.3)

• $\gamma$ has angular momentum l satisfying the bound

  $$\begin{aligned} 0<\frac{l}{E_{0}}\sqrt{-\Lambda }\le e^{-50C_{0}}, \end{aligned}$$

  (5.4)

  where

  $$\begin{aligned} E_{0}\doteq \frac{1}{2}\Big (\Omega ^{2}{\dot{\gamma }}^{u}+\Omega ^{2}{\dot{\gamma }}^{v}\Big )(0), \end{aligned}$$

  (5.5)

• $\gamma (0)$ satisfies

  $$\begin{aligned} r(\gamma (0))\ge e^{50C_{0}}\frac{l}{E_{0}}. \end{aligned}$$

  (5.6)

Then, the following statements hold for $\gamma$:

• 1. Setting

  $$\begin{aligned} (u_{0},v_{0})\doteq \gamma (0) \end{aligned}$$

  and

  $$\begin{aligned} {\mathcal {V}}_{\nwarrow }&=\left[ u_{0},v_{0}+e^{150C_{0}}\frac{l}{E_{0}}\right] \left[ v_{0}-e^{150C_{0}}\frac{l}{E_{0}},v_{0}+e^{150C_{0}}\frac{l}{E_{0}}\right] , \end{aligned}$$

  (5.7)
  $$\begin{aligned} {\mathcal {V}}_{\nearrow }&=\left[ v_{0}-e^{150C_{0}}\frac{l}{E_{0}},v_{0}+e^{150C_{0}}\frac{l}{E_{0}}\right] \nonumber \\ {}&\quad \times \left[ v_{0}-e^{150C_{0}}\frac{l}{E_{0}},v_{0}+v_{{\mathcal {I}}}+e^{150C_{0}}\frac{l}{E_{0}}\right] , \end{aligned}$$

  (5.8)

  the curve $\gamma$ is contained in the following region:

  $$\begin{aligned} \gamma \subset \Big \{ r\ge e^{-6C_{0}}\frac{l}{E_{0}}\Big \}\cap \Big ({\mathcal {V}}_{\nwarrow }\cup {\mathcal {V}}_{\nearrow }\Big )\cap {\mathcal {U}}_{U;v_{{\mathcal {I}}}} \end{aligned}$$

  (5.9)

  (see Fig. 12).

• 2. For any $s\in [0,a)$, we can estimate

  $$\begin{aligned} e^{-100C_{0}}E_{0}\le \frac{1}{2}\Big (\Omega ^{2}{\dot{\gamma }}^{u}(s)+\Omega ^{2}{\dot{\gamma }}^{v}(s)\Big )\le e^{e^{200C_{0}}}E_{0}. \end{aligned}$$

  (5.10)

• 3. Let $s_{c}\in (0,a]$ be defined as

  $$\begin{aligned} s_{c}=\sup \big \{ s\in (0,a):\text { }u(\gamma (s))+v(\gamma (s))\le u_{0}+v_{0}+v_{{\mathcal {I}}}\big \}.\qquad \end{aligned}$$

  (5.11)

  Then, for any $s\in [0,s_{c})$, we can bound

  $$\begin{aligned} \frac{{\dot{\gamma }}^{v}}{{\dot{\gamma }}^{u}}\le e^{e^{200C_{0}}}\frac{l^{2}}{E_{0}^{2}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Bigg |_{\gamma (s)} \end{aligned}$$

  (5.12)

  while, for any $s\in (s_{c},a)$, we have:²¹

  $$\begin{aligned} \frac{{\dot{\gamma }}^{u}}{{\dot{\gamma }}^{v}}(s)\le e^{e^{200C_{0}}}\frac{l^{2}}{E_{0}^{2}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Bigg |_{\gamma (s)}. \end{aligned}$$

  (5.13)

  In particular, $s=s_c$ roughly separates the ingoing from the outgoing part of the curve $\gamma$.

Fig. 12

Schematic depiction of the rectangular domains ${\mathcal {V}}_{\nwarrow }$ and ${\mathcal {V}}_{\nearrow }$ in the statement of Lemma 5.1

Remark

In the case when one considers future inextendible geodesics $\gamma$ in ${\mathcal {U}}_{U;v_{{\mathcal {I}}}}$ with future endpoints on conformal infinity, the statement of Lemma 5.1 can be readily generalised to the extension of such geodesics through their reflection off $\{u=v-v_{{\mathcal {I}}}\}$; see Corollary 5.2. Notice also that the condition (5.1) implies that $\frac{1}{10}e^{-C_{0}}\le \sqrt{-\Lambda }v_{{\mathcal {I}}}\le 10e^{C_{0}}$, i.e. that, in the class of spacetimes satisfying (5.1), $v_{{\mathcal {I}}}$ and $(-\Lambda )^{-\frac{1}{2}}$ can be used almost interchangeably as units of length with merely $O(e^{C_{0}})$ errors occuring in the transition. Let us also remark that Lemma 5.1 is also valid in the case when the initial point of $\gamma$ lies on ${\mathcal {I}}$, i.e. $\gamma (0)$ in the statement of the Lemma is replaced by $\gamma (-\infty )$, with $\gamma (-\infty )\in {\mathcal {I}}$, and (5.3) is replaced by $\frac{\Omega ^{2}{\dot{\gamma }}^{u}}{\Omega ^{2}{\dot{\gamma }}^{v}}(-\infty )>1$.

We should point out that Lemma 5.1 will be applied in situations where the smallness of $l/E_0$ dominates any constant depending on $C_0$ appearing above.

Proof

We will adopt the following convention regarding the parametrization of $\gamma$: We will denote with s the affine parametrization of $\gamma$ (and the corresponding derivative by $\dot{}$ ), while $\tau$ will denote the parameter corresponding to $u+v$. Let also $[\tau _{0},\tau _{1})$ be the parameter interval for $\gamma$ associated to the parameter $\tau$, i.e. $\tau _{0}=u_{0}+v_{0}$ and $\tau _{1}=\lim _{s\rightarrow a}\big (u(\gamma (s))+v(\gamma (s))\big )$.

In view of the formula (2.9), the bounds (5.1) and (5.2) imply that

$$\begin{aligned} \sup _{{\mathcal {U}}_{U;v_{{\mathcal {I}}}}}\Big |\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )\Big |\le 2C_{0}. \end{aligned}$$

(5.14)

Using (2.50) with

$$\begin{aligned} u_{1}(v)={\left\{ \begin{array}{ll} u_{0}, &{} v\le u_{0}+v_{{\mathcal {I}}},\\ v-v_{{\mathcal {I}}}, &{} v\ge u_{0}+v_{{\mathcal {I}}}, \end{array}\right. } \end{aligned}$$

(5.15)

and then using the relation (3.39) for $\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}$ along $\{u=v-v_{{\mathcal {I}}}\}$, we readily infer that, for any $\tau \in (\tau _{0},\tau _{1})$:

$$\begin{aligned}&\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau )- \log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau _{0})\nonumber \\&\quad =\int _{v_{0}}^{v(\gamma (\tau ))}\int _{u_{1}(v)}^{u(\gamma (\tau _{v}))}\Big (\frac{1}{2}\frac{\frac{6{\tilde{m}}}{r}-1}{r^{2}}\Omega ^{2}-24\pi T_{uv}\Big )\,du\,dv\nonumber \\&\qquad +\Big (\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\frac{1-\frac{1}{3}\Lambda r^{2}}{-\Lambda r^{2}}\Big )\big (u_{1}(v(\gamma (\tau ))),v(\gamma (\tau ))\big )\nonumber \\&\qquad -\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\frac{1-\frac{1}{3}\Lambda r^{2}}{-\Lambda r^{2}}\Big )(u_{0},v_{0})\Big ), \end{aligned}$$

(5.16)

where $\tau _{v}$ is defined by

$$\begin{aligned} v(\gamma (\tau _{{\bar{v}}}))={\bar{v}}. \end{aligned}$$

(5.17)

In view of the fact that the first term in the right hand side of (5.16) is non-positive (as a consequence of (5.2)), using (5.14), (5.3), (5.5) and the fact that

$$\begin{aligned} r(u_{1}(v(\gamma (\tau ))),v(\gamma (\tau )))\ge r(u_{0},v_{0}) \end{aligned}$$

(since $\gamma$ has a timelike projection on the (u, v)-plane and thus $v(\gamma (\tau ))\ge v_{0}$, while $r(u_{1}(v),v)=\infty$ if $u_{1}(v)\ne u_{0}$), we infer from (5.16) that, for any $\tau \in (\tau _{0},\tau _{1})$:

$$\begin{aligned} \Omega ^{2}{\dot{\gamma }}^{u}(\tau )\le e^{3C_{0}}\Omega ^{2}{\dot{\gamma }}^{u}(\tau _{0})\le 2e^{3C_{0}}E_{0}. \end{aligned}$$

(5.18)

For any $\tau \in (\tau _{0},\tau _{1})$ such that $\frac{d}{d\tau }r(\gamma (\tau ))\le 0$, i.e.

$$\begin{aligned} \partial _{v}r|_{\gamma (\tau )}{\dot{\gamma }}^{v}(\tau )\le -\partial _{u}r|_{\gamma (\tau )}{\dot{\gamma }}^{u}(\tau ), \end{aligned}$$

(5.19)

we can estimate from (2.19) using (5.1), (5.18) and (5.19):

$$\begin{aligned} \frac{\Omega ^{2}l^{2}}{r^{2}}\Big |_{\gamma (\tau )}&= (\Omega ^{2}|_{\gamma (\tau )}{\dot{\gamma }}^{u}(\tau ))\cdot (\Omega ^{2}|_{\gamma (\tau )}{\dot{\gamma }}^{v}(\tau ))\\&\le \sup _{{\mathcal {U}}_{U;v_{{\mathcal {I}}}}}\big (\frac{\partial _{v}r}{-\partial _{u}r}\big )(\Omega ^{2}|_{\gamma (\tau )}{\dot{\gamma }}^{u}(\tau ))^{2}\nonumber \\&\le 4e^{8C_{0}}E_{0}^{2}.\nonumber \end{aligned}$$

(5.20)

Since (5.20) holds whenever $\frac{d}{d\tau }r(\gamma (\tau ))\le 0$, using (5.14) we deduce that

$$\begin{aligned} \inf _{\gamma }r\ge \frac{1}{2}e^{-5C_{0}}\frac{l}{E_{0}}. \end{aligned}$$

(5.21)

The identity (5.16) implies, using the bound (5.2) for ${\tilde{m}}/r$, combined with the bound

$$\begin{aligned} T_{uv}\le e^{C_{0}}\frac{-\partial _{u}{\tilde{m}}}{r^{2}} \end{aligned}$$

(following readily from (2.49) and (5.1)), as well as the bounds (5.1) and (5.14), that the following estimate holds for any $\tau \in (\tau _{0},\tau _{1})$

$$\begin{aligned}&\Big |\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau )- \log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau _{0})\Big |\nonumber \\&\quad \le e^{4C_{0}}\int _{u_{0}+v_{{\mathcal {I}}}}^{v(\gamma (\tau ))}\int _{u_{1}(v)}^{u(\gamma (\tau _{v}))}\frac{(-\partial _{u}r)}{r^{2}}\,du\,dv\nonumber \\&\qquad +e^{2C_{0}}\int _{u_{1}(v)}^{v(\gamma (\tau ))}\int _{u_{1}(v)}^{u(\gamma (\tau _{v}))}(-\partial _{u}{\tilde{m}})\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\,du\,dv+2C_{0}\nonumber \\&\quad \le e^{4C_{0}}\Big (\sup _{v\in [v_{0},v(\gamma (\tau ))]}\int _{u_{1}(v)}^{u(\gamma (\tau _{v}))}\frac{(-\partial _{u}r)}{r^{2}}\,du\Big )\big (v(\gamma (\tau ))-v(\gamma (\tau _{0}))\big )\nonumber \\&\qquad +e^{2C_{0}}\int _{u_{1}(v)}^{v(\gamma (\tau ))}\int _{u_{1}(v)}^{u(\gamma (\tau _{v}))}4\frac{{\tilde{m}}}{r}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}(-\partial _{u}r)\,du\,dv \nonumber \\&\qquad +e^{2C_{0}}\int _{u_{1}(v)}^{v(\gamma (\tau ))}{\tilde{m}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Big |_{u=u_{1}(v)}\,dv\nonumber \\&\qquad -e^{2C_{0}}\int _{u_{1}(v)}^{v(\gamma (\tau ))}{\tilde{m}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Big |_{u=u(\gamma (\tau _{v}))}\,dv\nonumber \\&\quad \le e^{4C_{0}}\sup _{{\bar{\tau }}\in (\tau _{0},\tau )}\frac{1}{r(\gamma ({\bar{\tau }}))}\cdot \big (v(\gamma (\tau ))-v(\gamma (\tau _{0}))\big )+2C_{0}, \end{aligned}$$

(5.22)

where, in passing from the first to the second line in (5.22), we integrated in u for the $\partial _{u}{\tilde{m}}$ term. On the other hand, the identity (5.16) can also be used to similarly obtain an one-sided bound for $\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau )-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau _{0})$, using the fact that $T_{uv}\ge 0$:

$$\begin{aligned}&\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau )-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau _{0})\nonumber \\&\quad \le \int _{u_{0}+v_{{\mathcal {I}}}}^{v(\gamma (\tau ))}\int _{u_{1}(v)}^{u(\gamma (\tau _{v}))}\Big (\frac{1}{2}\frac{\frac{6{\tilde{m}}}{r}-1}{r^{2}}\Omega ^{2}\Big )\,du\,dv\\&\qquad +\Big (\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )\big (u_{1}(v(\gamma (\tau ))),v(\gamma (\tau ))\big )-\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )(u_{0},v_{0})\Big )\nonumber \\&\quad \le -e^{-4C_{0}}{\mathcal {B}}[\tau ]+2C_{0},\nonumber \end{aligned}$$

(5.23)

where

$$\begin{aligned} {\mathcal {B}}[\tau ]\doteq \int _{u_{1}(v)}^{v(\gamma (\tau ))}\int _{v-v_{{\mathcal {I}}}}^{u(\gamma (\tau _{v}))}\frac{(-\partial _{u}r)}{r^{2}}\,du\,dv. \end{aligned}$$

(5.24)

Therefore, in view of (5.5), (5.3):

$$\begin{aligned}{} & {} -e^{4C_{0}}\sup _{{\bar{\tau }}\in (\tau _{0},\tau )}\frac{1}{r(\gamma ({\bar{\tau }}))}\cdot \big (v(\gamma (\tau ))-v(\gamma (\tau _{0}))\big )-2C_{0}\nonumber \\{} & {} \quad \le \log \Big (\frac{\Omega ^{2}{\dot{\gamma }}^{u}(\tau )}{E_{0}}\Big )\le -e^{-4C_{0}}{\mathcal {B}}[\tau ]+2C_{0}. \end{aligned}$$

(5.25)

Let us define $\tau _{in}\in [\tau _{0},\tau _{1}]$ as follows:

$$\begin{aligned} \tau _{in}\doteq \sup \Big \{\tau \in (\tau _{0},\tau _{1}):\text { }r(\gamma ({\bar{\tau }}))\ge e^{30C_{0}}\frac{l}{E_{0}}\text { for all }{\bar{\tau }}\le \tau \Big \}. \end{aligned}$$

(5.26)

Our analysis of the path traced by $\gamma$ will be separated into two regimes: The ingoing interval $\tau \in [\tau _{0},\tau _{in})$ and the outgoing interval $\tau \in [\tau _{in},\tau _{1})$. Note that the latter interval will be trivial if $\tau _{in}=\tau _{1}$. However, in view of (5.6), it is necessary that the ingoing interval is non-trivial, i.e.:

$$\begin{aligned} \tau _{in}>\tau _{0}. \end{aligned}$$

(5.27)

The ingoing regime $\tau \in [\tau _{0},\tau _{in})$. Let us define $\tau _{*}\in (\tau _{0},\tau _{in}]$ by the relation:

$$\begin{aligned} \tau _{*}=\sup \Big \{\tau \in (\tau _{0},\tau _{c}):\text { }v(\gamma ({\bar{\tau }}))-v(\gamma (\tau _{0}))\le e^{20C_{0}}\frac{l}{E_{0}}\text { for all }{\bar{\tau }}\le \tau \Big \}.\nonumber \\ \end{aligned}$$

(5.28)

The estimate (5.25) implies, in view of the fact that $\text { }r(\gamma ({\bar{\tau }}))\ge e^{30C_{0}}\frac{l}{E_{0}}$ for $\tau <\tau _{in}$ (following from the definition (5.26) of $\tau _{in}$) and the definition (5.28) of $\tau _{*}$, that, for all $\tau \in [\tau _{0},\tau _{*})$:

$$\begin{aligned} \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau )\ge e^{-4C_{0}}E_{0}. \end{aligned}$$

(5.29)

Thus, in view of (2.19) and (5.14), we can bound for all $\tau \in [\tau _{0},\tau _{*})$:

$$\begin{aligned} (\Omega ^{2}{\dot{\gamma }}^{v})(\tau )\le e^{6C_{0}}\frac{l^{2}(1-\frac{1}{3}\Lambda r^{2})}{E_{0}r^{2}}\Big |_{\gamma (\tau )}. \end{aligned}$$

(5.30)

In view of (5.18), (5.21), (5.29), and (5.30), we therefore infer that, for all $\tau \in [\tau _{0},\tau _{*})$:

$$\begin{aligned} e^{-4C_{0}}E_{0}\le \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau )+\big (\Omega ^{2}{\dot{\gamma }}^{v}\big )(\tau )\le e^{10C_{0}}E_{0} \end{aligned}$$

(5.31)

and

$$\begin{aligned} \frac{(\Omega ^{2}{\dot{\gamma }}^{v})(\tau )}{\big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau )+(\Omega ^{2}{\dot{\gamma }}^{v})(\tau )}\le e^{10C_{0}}\frac{l^{2}(1-\frac{1}{3}\Lambda r^{2})}{E_{0}^{2}r^{2}}\Big |_{\gamma (\tau )}. \end{aligned}$$

(5.32)

Moreover, as a result of (5.1), (5.31), (5.32) and the definition (5.26) of $\tau _{in}$, as well as using assumption (5.4) for $\gamma$, we deduce that, for all $\tau \in [\tau _{0},\tau _{*})$:

$$\begin{aligned}{} & {} \frac{d}{d\tau }\Big (\tan ^{-1}\big (\sqrt{-\Lambda }r(\gamma (\tau ))\big )\Big )\nonumber \\{} & {} \quad \le -e^{-4C_{0}}\Big (1-e^{10C_{0}}\frac{l^{2}(1-\frac{1}{3}\Lambda r^{2})}{E_{0}^{2}r^{2}}\Big |_{\gamma (\tau )}\Big )\sqrt{-\Lambda }\nonumber \\{} & {} \quad \le -\frac{1}{2}e^{-4C_{0}}\sqrt{-\Lambda }. \end{aligned}$$

(5.33)

Integrating (5.32) over $\tau \in [\tau _{0},\tau _{*})$ and using (5.33) and (5.21), we infer that, for all $\tau \in [\tau _{0},\tau _{*})$:

$$\begin{aligned} v(\gamma (\tau ))-v_{0}\le \frac{1}{2}e^{20C_{0}}\frac{l}{E_{0}}. \end{aligned}$$

(5.34)

In view of (5.34), the definition (5.28) of $\tau _{*}$ implies (through a standard continuity argument) that

$$\begin{aligned} \tau _{*}=\tau _{in}. \end{aligned}$$

(5.35)

Therefore, the estimates (5.29)–(5.34)hold for all $\tau \in [\tau _{0},\tau _{in})$. Moreover, the bound (5.34) and the fact that $u\le v$ on ${\mathcal {U}}_{U;v_{{\mathcal {I}}}}$ implies that

$$\begin{aligned} \tau _{in}=\lim _{\tau \rightarrow \tau _{in}^{-}}\big (u(\gamma (\tau ))+v(\gamma (\tau ))\big )\le 2v_{0}+e^{20C_{0}}\frac{l}{E_{0}}. \end{aligned}$$

(5.36)

The outgoing regime $\tau \in [\tau _{in},\tau _{1})$. In the case when $\tau _{in}<\tau _{1}$ (which is necessarily the case, for instance, when $\tau _{1}>2v_{0}+e^{20C_{0}}\frac{l}{E_{0}}$, as a consequence of (5.36)), the definition (5.26) of $\tau _{in}$ implies that

$$\begin{aligned} r(\gamma (\tau _{in}))=e^{30C_{0}}\frac{l}{E_{0}} \end{aligned}$$

(5.37)

from which we obtain, in view of the bound (5.1) on $\partial _{v}r$ and the boundary condition $r|_{\{u=v\}}=0$, that

$$\begin{aligned} v(\gamma (\tau _{in}))-u(\gamma (\tau _{in}))\le e^{32C_{0}}\frac{l}{E_{0}}. \end{aligned}$$

(5.38)

The bounds (5.34) and (5.38) therefore yield:

$$\begin{aligned} u(\gamma (\tau _{in}))-v_{0}\le 2e^{32C_{0}}\frac{l}{E_{0}}. \end{aligned}$$

(5.39)

For any $\tau \in [\tau _{in},\tau _{1})$, the analogue of the identity (5.16) after replacing $u_{1}(v)$ with

$$\begin{aligned} u_{2}(v)={\left\{ \begin{array}{ll} u(\gamma (\tau _{in})), &{} v\le u(\gamma (\tau _{in}))+v_{{\mathcal {I}}},\\ v-v_{{\mathcal {I}}}, &{} v\ge u(\gamma (\tau _{in}))+v_{{\mathcal {I}}}, \end{array}\right. } \end{aligned}$$

is

$$\begin{aligned}&\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau )-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau _{in})\nonumber \\&\quad = \int _{v(\gamma (\tau _{in}))}^{v(\gamma (\tau ))}\int _{u_{2}(v)}^{u(\gamma (\tau _{v}))}\Big (\frac{1}{2}\frac{\frac{6{\tilde{m}}}{r}-1}{r^{2}}\Omega ^{2}-24\pi T_{uv}\Big )\,du\,dv\\&\qquad +\Big (\log \Big (\frac{\Omega ^{2}}{-\Lambda r^{2}}\Big )\big (u_{2}(v(\gamma (\tau ))),v(\gamma (\tau ))\big )\nonumber \\&\qquad -\log \Big (\frac{\Omega ^{2}}{-\Lambda r^{2}}\Big )(u(\gamma (\tau _{in})),v(\gamma (\tau _{in})))\Big ).\nonumber \end{aligned}$$

(5.40)

Using the fact that the first term in the right hand side of (5.40) is non-positive (in view of (5.2)), the bounds (5.14) for $\Omega ^{2}/(1-\frac{1}{3}\Lambda r^{2})$ and (5.18) for ${\dot{\gamma }}^{u}(\tau _{in})$ imply that, for any $\tau \in [\tau _{in},\tau _{1})$:

$$\begin{aligned}&\Omega ^{2}{\dot{\gamma }}^{u}(\tau ) \le \Omega ^{2}{\dot{\gamma }}^{u}(\tau _{in})\\&\qquad \times \exp \Bigg \{\log \big (\frac{1-\frac{1}{3}\Lambda r^{2}}{-\Lambda r^{2}}\big )\Big |_{(u_{2}(v(\gamma (\tau ))),v(\gamma (\tau )))}\nonumber \\&\qquad -\log \big (\frac{1-\frac{1}{3}\Lambda r^{2}}{-\Lambda r^{2}}\big )\Big |_{(u(\gamma (\tau _{in})),v(\gamma (\tau _{in})))}+4C_{0}\Bigg \}\nonumber \\&\quad \le 2e^{7C_{0}}\frac{r^{2}(u(\gamma (\tau _{in})),v(\gamma (\tau _{in})))}{r^{2}(u_{2}(v(\gamma (\tau ))),v(\gamma (\tau )))}\cdot \frac{\big (1-\frac{1}{3}\Lambda r^{2}\big )(u_{2}(v(\gamma (\tau ))),v(\gamma (\tau )))}{\big (1-\frac{1}{3}\Lambda r^{2}\big )(u(\gamma (\tau _{in})),v(\gamma (\tau _{in})))}E_{0}.\nonumber \end{aligned}$$

(5.41)

Using (5.4) and (5.37), the bound (5.41) yields for any $\tau \in [\tau _{in},\tau _{1})$:

$$\begin{aligned} \Omega ^{2}{\dot{\gamma }}^{u}(\tau )\le e^{70C_{0}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Big |_{\big (u_{2}(v(\gamma (\tau ))),v(\gamma (\tau ))\big )}\frac{l^{2}}{E_{0}}. \end{aligned}$$

(5.42)

The relation (2.19) implies, in view of (5.14), (5.42) and the fact that $\partial _{u}r<0$, that, for any $\tau \in [\tau _{in},\tau _{1})$:

$$\begin{aligned} \Omega ^{2}{\dot{\gamma }}^{v}(\tau )\ge e^{-72C_{0}}\frac{\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Big |_{\big (u(\gamma (\tau ))),v(\gamma (\tau ))\big )}}{\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Big |_{\big (u_{2}(v(\gamma (\tau ))),v(\gamma (\tau ))\big )}}E_{0}\ge e^{-72C_{0}}E_{0}.\qquad \end{aligned}$$

(5.43)

The estimates (5.42) and (5.43), combined with (5.1), (5.4) and (5.37), imply that, for any $\tau \in [\tau _{in},\tau _{1})$:

$$\begin{aligned} |u(\gamma (\tau ))-u(\gamma (\tau _{in}))|&=\int _{\tau _{in}}^{\tau }{\dot{\gamma }}^{u}({\bar{\tau }})\,d{\bar{\tau }}=\int _{v(\gamma (\tau _{in}))}^{v(\gamma (\tau ))}\frac{\Omega ^{2}{\dot{\gamma }}^{u}}{\Omega ^{2}{\dot{\gamma }}^{v}}({\bar{\tau }})\,dv(\gamma ({\bar{\tau }}))\\&\le e^{150C_{0}}\frac{l^{2}}{E_{0}^{2}}\int _{v(\gamma (\tau _{in}))}^{v(\gamma (\tau ))}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}(u_{2}(v),v)\,dv\nonumber \\&\le e^{160C_{0}}\frac{l^{2}}{E_{0}^{2}}\frac{1}{r(\gamma (\tau _{in}))}\nonumber \\&\le e^{130C_{0}}\frac{l}{E_{0}}.\nonumber \end{aligned}$$

(5.44)

Using (5.37) and (5.44) (as well as (5.1), (5.4) and (5.14)), we can estimate

$$\begin{aligned}&\int _{v(\gamma (\tau _{in}))}^{v(\gamma (\tau ))}\int _{u_{2}(v)}^{u(\gamma (\tau _{v}))}\frac{1}{r^{2}}\Omega ^{2}\,du\,dv\nonumber \\&\le \int _{\{r\ge r(\gamma (\tau _{in}))\}\cap \{|u-u(\gamma (\tau _{in}))|\le e^{130C_{0}}\frac{l}{E_{0}}\}}\frac{1}{r^{2}}\Omega ^{2}\,du\,dv\\&\le e^{150C_{0}}\frac{l}{E_{0}}\int _{r(\gamma (\tau _{in}))}^{\infty }\frac{1}{r^{2}}\,dr\le \nonumber \\&\le e^{120C_{0}}.\nonumber \end{aligned}$$

(5.45)

Similarly, in view of (2.48) and (5.2):

$$\begin{aligned}&\int _{v(\gamma (\tau _{in}))}^{v(\gamma (\tau ))}\int _{u_{2}(v)}^{u(\gamma (\tau _{v}))} T_{uv}\,du\,dv\\&\quad =\int _{v(\gamma (\tau _{in}))}^{v(\gamma (\tau ))}\int _{u_{2}(v)}^{u(\gamma (\tau _{v}))}\frac{\partial _{v}{\tilde{m}}}{8\pi r^{2}}\frac{\Omega ^{2}}{-\partial _{u}r}\,du\,dv\nonumber \\&\quad \le e^{4C_{0}}\int _{v(\gamma (\tau _{in}))}^{v(\gamma (\tau ))}\int _{u_{2}(v)}^{u(\gamma (\tau _{v}))}\frac{\partial _{v}{\tilde{m}}}{r^{2}}\,du\,dv\nonumber \\&\quad \le e^{4C_{0}}\Big (\int _{v(\gamma (\tau _{in}))}^{v(\gamma (\tau ))}\int _{u_{2}(v)}^{u(\gamma (\tau _{v}))}2\frac{{\tilde{m}}}{r}\frac{\partial _{v}r}{r^{2}}\,du\,dv\nonumber \\&\qquad +\int _{u_{2}(v(\gamma (\tau )))}^{u(v(\gamma (\tau )))}\frac{{\tilde{m}}}{r^{2}}(u,v(\gamma (\tau )))\,du\Big )\nonumber \\&\quad \le e^{10C_{0}}\delta _{0}\Big (\int _{v(\gamma (\tau _{in}))}^{v(\gamma (\tau ))}\int _{u_{2}(v)}^{u(\gamma (\tau _{v}))}\frac{\Omega ^{2}}{r^{2}}\,du\,dv\nonumber \\&\qquad +\int _{u_{2}(v(\gamma (\tau )))}^{u(v(\gamma (\tau )))}\frac{1}{r(\gamma (\tau _{1}))}\,du\Big )\nonumber \\&\quad \le e^{150C_{0}}\delta _{0}.\nonumber \end{aligned}$$

(5.46)

Using (5.2), (5.45) and (5.46), we infer from (5.40) that, for any $\tau \in [\tau _{in},\tau _{1})$:

$$\begin{aligned} \log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau )&-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )(\tau _{in}) \end{aligned}$$

(5.47)

$$\begin{aligned}&\ge -2e^{120C_{0}}+\Big (\log \Big (\frac{\Omega ^{2}}{-\Lambda r^{2}}\Big )\big (u_{2}(v(\gamma (\tau ))),v(\gamma (\tau ))\big )\nonumber \\&\quad -\log \Big (\frac{\Omega ^{2}}{-\Lambda r^{2}}\Big )(u(\gamma (\tau _{in})),v(\gamma (\tau _{in})))\Big ) \end{aligned}$$

(5.48)

and, therefore, in view of the bounds (5.14) for $\Omega ^{2}/(1-\frac{1}{3}\Lambda r^{2})$ and (5.29) for ${\dot{\gamma }}^{u}(\tau _{in})$:

$$\begin{aligned}&\Omega ^{2}{\dot{\gamma }}^{u}(\tau ) \ge \Omega ^{2}{\dot{\gamma }}^{u}(\tau _{in})\\&\qquad \times \exp \Bigg \{-e^{130C_{0}}+\log \big (\frac{1-\frac{1}{3}\Lambda r^{2}}{-\Lambda r^{2}}\big )\Big |_{(u_{2}(v(\gamma (\tau ))),v(\gamma (\tau )))}\nonumber \\&\qquad -\log \big (\frac{1-\frac{1}{3}\Lambda r^{2}}{-\Lambda r^{2}}\big )\Big |_{(u(\gamma (\tau _{in})),v(\gamma (\tau _{in})))}+4C_{0}\Bigg \}\le \nonumber \\&\quad \ge e^{-e^{140C_{0}}}\frac{r^{2}(u(\gamma (\tau _{in})),v(\gamma (\tau _{in})))}{r^{2}(u_{2}(v(\gamma (\tau ))),v(\gamma (\tau )))}\nonumber \\&\qquad \cdot \frac{\big (1-\frac{1}{3}\Lambda r^{2}\big )(u_{2}(v(\gamma (\tau ))),v(\gamma (\tau )))}{\big (1-\frac{1}{3}\Lambda r^{2}\big )(u(\gamma (\tau _{in})),v(\gamma (\tau _{in})))}E_{0}.\nonumber \end{aligned}$$

(5.49)

The estimate (5.49) implies, in view of (2.19), (5.4), (5.14), (5.21) and the fact that $\partial _{v}r>0$, that, for any $\tau \in [\tau _{in},\tau _{1})$:

$$\begin{aligned} \Omega ^{2}{\dot{\gamma }}^{v}(\tau )&\le e^{2C_{0}}l^{2}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Bigg |_{\gamma (\tau )}\frac{1}{\Omega ^{2}{\dot{\gamma }}^{u}(\tau )}\\&\le e^{e^{145C_{0}}}\frac{l^{2}}{E_{0}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Bigg |_{\gamma (\tau )}\nonumber \\&\qquad \cdot \frac{r^{2}}{\big (1-\frac{1}{3}\Lambda r^{2}\big )}\Bigg |_{(u_{2}(v(\gamma (\tau ))),v(\gamma (\tau )))}\cdot \frac{\big (1-\frac{1}{3}\Lambda r^{2}\big )}{r^{2}}\Bigg |_{\gamma (\tau _{in})}\nonumber \\&\le e^{e^{145C_{0}}}\frac{l^{2}}{E_{0}}\frac{1-\frac{1}{3}\Lambda (\inf _{\gamma }r)^{2}}{(\inf _{\gamma }r)^{2}}\nonumber \\&\le e^{e^{150C_{0}}}E_{0}.\nonumber \end{aligned}$$

(5.50)

The bounds (5.18), (5.43) and (5.50) therefore imply that, for any $\tau \in [\tau _{in},\tau _{1})$:

$$\begin{aligned} e^{-72C_{0}}E_{0}\le \Omega ^{2}{\dot{\gamma }}^{u}(\tau )+\Omega ^{2}{\dot{\gamma }}^{v}(\tau )\le e^{e^{200C_{0}}}E_{0}. \end{aligned}$$

(5.51)

The estimates we have established so far are sufficient to complete the proof of Lemma 5.1. In particular:

• The bound (5.9) follows readily from the bound (5.21) on $\inf _{\gamma }r$, the bounds (5.34) and (5.44) on the total change of u, v along the intervals $[\tau _{0},\tau _{in})$, $[\tau _{in},\tau _{1})$, respectively (in view also of (5.35)), and the bounds (5.38) and (5.39) on $\gamma (\tau _{in})$.

• The energy bound (5.10) follows immediately from (5.31) and (5.51).

• The estimates (5.12) and (5.13) follow readily from the bounds (5.29), (5.30) for $\tau \in [\tau _{0},\tau _{in})$ and the bounds (5.42), (5.43) for $\tau \in [\tau _{in},\tau _{1})$, as well as the fact that, for any $\tau \in [\tau _{0},\tau _{1})$ such that $r(\gamma (\tau ))\le e^{50C_{0}}\frac{l}{E_{0}}$, we can estimate as a consequence of (2.19), (5.14), (5.18), (5.31) and (5.51):

  $$\begin{aligned} \frac{{\dot{\gamma }}^{v}}{{\dot{\gamma }}^{u}}(\tau )=l^{2}\frac{\Omega ^{2}}{r^{2}}\Big |_{\gamma (\tau )}\frac{1}{(\Omega ^{2}{\dot{\gamma }}^{u})^{2}(\tau )}\ge e^{-60C_{0}} \end{aligned}$$

  (5.52)

  and

  $$\begin{aligned} \frac{{\dot{\gamma }}^{v}}{{\dot{\gamma }}^{u}}(\tau )=l^{-2}\frac{r^{2}}{\Omega ^{2}}\Big |_{\gamma (\tau )}(\Omega ^{2}{\dot{\gamma }}^{v})^{2}(\tau )\le e^{e^{200C_{0}}}. \end{aligned}$$

  (5.53)

$\square$

By applying Lemma 5.1 successively between the points of reflection off ${\mathcal {I}}$ of a maximally extended null geodesic $\gamma$, we obtain the following useful generalisation of Lemma 5.1:

Corollary 5.2

Let $0<\delta _{0}\ll 1$ be a sufficiently small absolute constant, and let ${\mathcal {U}}_{U;v_{{\mathcal {I}}}}$ and $(r,\Omega ^{2},f)$ be as in Lemma 5.1, satisfying (5.1) and (5.2) for some $C_{0}>100$. Let also $\gamma _{n}:(a_{n},b_{n})\rightarrow {\mathcal {U}}_{U;v_{{\mathcal {I}}}}$, $0\le n<N+1$ (for some $N\in {\mathbb {N}}\cup \{\infty \}$ and $-\infty \le a_{n}<b_{n}\le +\infty$ ), be a collection of future directed, affinely parametrized null geodesics in $({\mathcal {U}}_{U;v_{{\mathcal {I}}}};r,\Omega ^{2})$ with $a_{0}=0$ and $\gamma _{0}(0)\in \{u=0\}$, such that $\gamma _{n}$ is the reflection of $\gamma _{n-1}$ off ${\mathcal {I}}$; thus, $\gamma =\cup _{n=0}^{N}\gamma _{n}$ constitutes an affinely parametrised, maximally extended geodesic through reflections off ${\mathcal {I}}$, in accordance with Definition 2.3 in [43].

Assume that $\gamma _{0}$ satisfies initially the conditions (5.3), (5.6) and

$$\begin{aligned} 0<\frac{l}{E_{0}}\sqrt{-\Lambda }\le e^{-400(1+\lceil v_{{\mathcal {I}}}^{-1}U\rceil )C_{0}}, \end{aligned}$$

(5.54)

with $E_{0}$ defined by (5.5). Then, the following statements hold for the maximally extended geodesic $\gamma$:

• The curve $\gamma =\cup _{n=0}^{N}\gamma _{n}$ is contained in the region

  $$\begin{aligned} \gamma \subset \Big \{ r\ge e^{-e^{400C_{0}}(1+v_{{\mathcal {I}}}^{-1}U)}\frac{l}{E_{0}}\Big \}\cap \bigcup _{k=0}^{\lceil v_{{\mathcal {I}}}^{-1}U\rceil }\Big ({\mathcal {V}}_{\nwarrow }^{(k)}\cup {\mathcal {V}}_{\nearrow }^{(k)}\Big )\cap {\mathcal {U}}_{U;v_{{\mathcal {I}}}},\qquad \quad \end{aligned}$$

  (5.55)

  where, setting

  $$\begin{aligned} v_{0}\doteq v\big (\gamma _{0}(0)\big ), \end{aligned}$$

  the domains ${\mathcal {V}}_{\nwarrow }^{(k)}$, ${\mathcal {V}}_{\nearrow }^{(k)}$ are defined for any $k\in {\mathbb {N}}$ by

  $$\begin{aligned} {\mathcal {V}}_{\nwarrow }^{(k)}&=\left[ kv_{{\mathcal {I}}},v_{0}+kv_{{\mathcal {I}}}+e^{300(k+1)C_{0}}\frac{l}{E_{0}}\right] \nonumber \\&\quad \times \left[ v_{0}+kv_{{\mathcal {I}}}-e^{300(k+1)C_{0}} \frac{l}{E_{0}},v_{0}+kv_{{\mathcal {I}}}+e^{300(k+1)C_{0}}\frac{l}{E_{0}}\right] , \end{aligned}$$

  (5.56)
  $$\begin{aligned} {\mathcal {V}}_{\nearrow }^{(k)}&=\left[ v_{0}+kv_{{\mathcal {I}}}-e^{300(k+1)C_{0}}\frac{l}{E_{0}},v_{0}+kv_{{\mathcal {I}}}+e^{300(k+1)C_{0}}\frac{l}{E_{0}}\right] \\&\quad \times \left[ v_{0}+kv_{{\mathcal {I}}}-e^{300(k+1)C_{0}}\frac{l}{E_{0}},v_{0}+(k+1)v_{{\mathcal {I}}}+e^{300(k+1)C_{0}}\frac{l}{E_{0}}\right] .\nonumber \end{aligned}$$

  (5.57)

• Denoting by ${\dot{\gamma }}$ the derivative of $\gamma$ with respect to the affine parametrisation of the $\gamma _{n}$’s, we can estimate

  $$\begin{aligned} e^{-300C_{0}(1+v_{{\mathcal {I}}}^{-1}U)}E_{0}\le \Omega ^{2}({\dot{\gamma }}^{u}+{\dot{\gamma }}^{v})\le e^{e^{300C_{0}}(1+v_{{\mathcal {I}}}^{-1}U)}E_{0}. \end{aligned}$$

  (5.58)

• For any $0\le {\bar{u}}<U$, defining $n[{\bar{u}}]$ by the condition that $\gamma \cap \{u={\bar{u}}\}\in \gamma _{n[{\bar{u}}]}$, we can bound at the point $\gamma \cap \{u={\bar{u}}\}$:

  $$\begin{aligned}&\frac{{\dot{\gamma }}^{v}}{{\dot{\gamma }}^{u}}\Bigg |_{\gamma \cap \{u={\bar{u}}\}} \le e^{e^{300C_{0}}(1+v_{{\mathcal {I}}}^{-1}U)}\frac{l^{2}}{E_{0}^{2}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Bigg |_{\gamma \cap \{u={\bar{u}}\}}\nonumber \\&\quad \text { if }\gamma \cap \{u={\bar{u}}\}\in \cup _{k\in {\mathbb {N}}}{\mathcal {V}}_{\nwarrow }^{(k)}, \end{aligned}$$

  (5.59)
  $$\begin{aligned}&\frac{{\dot{\gamma }}^{u}}{{\dot{\gamma }}^{v}}\Bigg |_{\gamma \cap \{u={\bar{u}}\}} \le e^{e^{300C_{0}}(1+v_{{\mathcal {I}}}^{-1}U)}\frac{l^{2}}{E_{0}^{2}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Bigg |_{\gamma \cap \{u={\bar{u}}\}}\nonumber \\&\quad \text { if }\gamma \cap \{u={\bar{u}}\}\in \cup _{k\in {\mathbb {N}}}{\mathcal {V}}_{\nearrow }^{(k)}. \end{aligned}$$

  (5.60)

Proof

The proof of Corollary (5.2) follows by applying Lemma (5.1) successively on the curves $\gamma _{n}$, treating the cases $n\ge 1$ by considering the limit where the initial point of $\gamma$ in the statement of Lemma (5.1) is sent to ${\mathcal {I}}$ and establishing (as a consequence of (5.10)) the inductive bound

$$\begin{aligned} e^{-100C_{0}}E_{n-1}\le E_{n}\le e^{e^{200C_{0}}}E_{n-1} \end{aligned}$$

(5.61)

for the energy $E_{n}=\frac{1}{2}\Big (\Omega ^{2}{\dot{\gamma }}_{n}^{u}+\Omega ^{2}{\dot{\gamma }}_{n}^{v}\Big )\big |_{s=-\infty }$ of $\gamma _{n}$ at its initial point on ${\mathcal {I}}$. Following this procedure, (5.55) is inferred from (5.9), (5.58) is inferred from (5.61) and (5.59)–(5.60) are inferred from (5.12)–(5.13), using also that (5.58) and (2.19) imply that

$$\begin{aligned} e^{-e^{300C_{0}}(1+v_{{\mathcal {I}}}^{-1}U)}\frac{l^{2}}{E_{0}^{2}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\le \frac{{\dot{\gamma }}^{v}}{{\dot{\gamma }}^{u}}\le e^{e^{300C_{0}}(1+v_{{\mathcal {I}}}^{-1}U)}\frac{l^{2}}{E_{0}^{2}}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}} \end{aligned}$$

in the region $\cup _{k=0}^{\lceil v_{{\mathcal {I}}}^{-1}U\rceil }({\mathcal {V}}_{\nwarrow }^{(k)}\cap {\mathcal {V}}_{\nearrow }^{(k)})$. We will omit the trivial details. $\square$

6 Construction of the initial data and notation

In this section, we will construct the family of initial data $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )\in {\mathfrak {B}}_{0}$ appearing in the statement of Theorem 1. To this end, we will first introduce a hierarchy of parameters depending on $\varepsilon$, the precise choice of which will be crucial for the proof of Theorem 1. We will also introduce some shorthand notation associated to a few fundamental constructions on the maximal future development $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ of $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$.

6.1 The hierarchy of parameters

In this section, we will introduce a set of parameters that will be used in the construction of the family of initial data $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$.

We will first introduce the following hierarchy of parameters:

Definition 6.1

Let $0<\varepsilon _{1}\ll 1$ be a sufficiently small absolute constant. For any $\varepsilon \in (0,\varepsilon _{1})$, we will define the parameters $\delta _{\varepsilon },\rho _{\varepsilon },\sigma _{\varepsilon }$ through the following hierarchy of relations:

$$\begin{aligned} \varepsilon&=\exp \Big (-\exp (\rho _{\varepsilon }^{-10})\Big ),\\ \rho _{\varepsilon }&=\exp \Big (-\exp \big (\exp (\exp (\exp (\delta _{\varepsilon }^{-10})))\big )\Big ),\nonumber \\ \delta _{\varepsilon }&=\exp \Big (-\exp \big (\exp (\sigma _{\varepsilon }^{-10})\big )\Big ).\nonumber \end{aligned}$$

(6.1)

For $\varepsilon \in [\varepsilon _{1},1]$, we will define the parameters $\delta _{\varepsilon },\rho _{\varepsilon },\sigma _{\varepsilon }$ to be equal to $\delta _{\varepsilon _{1}},\rho _{\varepsilon _{1}},\sigma _{\varepsilon _{1}}$, respectively.

We will also set

$$\begin{aligned} N_{\varepsilon }\doteq \lceil \rho _{\varepsilon }^{-1}\exp \big (\exp (\delta _{\varepsilon }^{-15})\big )\rceil . \end{aligned}$$

(6.2)

Notice that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\delta _{\varepsilon }=\lim _{\varepsilon \rightarrow 0}\rho _{\varepsilon }=\lim _{\varepsilon \rightarrow 0}\sigma _{\varepsilon }=\lim _{\varepsilon \rightarrow 0}\frac{1}{N_{\varepsilon }}=0 \end{aligned}$$

(6.3)

and, as $\varepsilon \rightarrow 0$:

$$\begin{aligned} \varepsilon \ll \rho _{\varepsilon }\ll \delta _{\varepsilon }\ll \sigma _{\varepsilon }\ll 1. \end{aligned}$$

(6.4)

Finally, for any $\varepsilon \in (0,1]$ and any $0\le i\le N_{\varepsilon }$, we will define the parameter $\varepsilon ^{(i)}$ by the recursive relation

$$\begin{aligned} {\left\{ \begin{array}{ll} \varepsilon ^{(i+1)}=\exp \big (-\exp \big ((\varepsilon ^{(i)})^{-2}\big )\big ),\\ \varepsilon ^{(0)}=\varepsilon . \end{array}\right. } \end{aligned}$$

(6.5)

Note that, as $\varepsilon \rightarrow 0$:

$$\begin{aligned} 1\gg \varepsilon ^{(0)}\gg \varepsilon ^{(1)}\gg \ldots \gg \varepsilon ^{(N_{\varepsilon })}. \end{aligned}$$

(6.6)

Remark

In the rest of the paper, we will frequently use the relation (6.1) in order to bound an expression involving $\sigma _{\varepsilon },\delta _{\varepsilon },\rho _{\varepsilon }$ (appearing usually as an error term in some estimate) by a simpler one; for instance, (6.1) allows us to bound

$$\begin{aligned} \exp \big (\exp (e^{\delta _{\varepsilon }^{-6}})\big )\le \rho _{\varepsilon }^{\frac{1}{20}}. \end{aligned}$$

We will not always explicitly refer to (6.1) when using such bounds while passing from one line to the next in a complicated estimate.

6.2 The initial data family

In this section, we will define the initial data family $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ appearing in the statement of Theorem 1 in terms of the parameters introduced in the previous section. The construction of the initial data family will proceed in two steps: We will first obtain a gauge normalised expression for $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ (in accordance with Definition 3.2) by suitably prescribing the value of ${\bar{f}}_{/}^{(\varepsilon )}$ and using Lemma 3.3, and we will then obtain a smoothly compatible initial data set through the gauge transformation provided by Lemma 3.4.

Let us fix a smooth cut-off function $\chi :{\mathbb {R}}\rightarrow [0,1]$ such that $\chi |_{[-1,1]}=1$ and $\chi _{{\mathbb {R}}\backslash (-2,2)}=0$. The following functions will later be used to define the initial Vlasov field ${\bar{f}}_{/}^{(\varepsilon )}$:

Definition 6.2

For any $\varepsilon \in (0,\varepsilon _{1}]$, where $0<\varepsilon _{1}\ll 1$ is the constant appearing in Definition 6.1, we will define the following sequence of smooth functions $F_{i}^{(\varepsilon )}:[0,\sqrt{-\frac{3}{\Lambda }}\pi ]\times [0,+\infty )^{2}\rightarrow [0,+\infty )$ for any $0\le i\le N_{\varepsilon }$:

$$\begin{aligned} F_{i}^{(\varepsilon )}(v;p,l)\doteq \frac{1}{(\varepsilon ^{(i)})^{2}}\chi \Big (\frac{\sqrt{-\Lambda }(v-v_{\varepsilon ,i})}{\varepsilon ^{(i)}}\Big )\cdot \chi \big (p-3\big )\cdot \chi \Big (\frac{\sqrt{-\Lambda }l}{\varepsilon ^{(i)}}-4\Big ),\nonumber \\ \end{aligned}$$

(6.7)

where

$$\begin{aligned} v_{\varepsilon ,i}\doteq \sqrt{-\frac{3}{\Lambda }}\frac{\pi }{2}+\rho _{\varepsilon }^{-1}\sum _{j=0}^{i-1}\varepsilon ^{(j)}(-\Lambda )^{-1/2} \end{aligned}$$

(6.8)

and $\varepsilon ^{(i)}$, $\rho _{\varepsilon }$ are defined in terms of $\varepsilon$ by (6.1) and (6.5).

Remark

Note that, for any $\varepsilon \ll 1$ and any $0\le i\le N_{\varepsilon }$, direct computation shows that the functions $F_{i}^{(\varepsilon )}$ satisfy

$$\begin{aligned}{} & {} \int _{0}^{\sqrt{-\frac{3}{\Lambda }}\pi }\left( 1-\frac{1}{3}\Lambda r_{AdS/}^{2}\right) \Big (\frac{r_{AdS/}T_{vv}^{(AdS)}[F_{i}^{(\varepsilon )}]}{\partial _{v}r_{AdS/}}\nonumber \\{} & {} \quad +\frac{r_{AdS/}T_{uv}^{(AdS)}[F_{i}^{(\varepsilon )}]}{-(\partial _{u}r_{AdS})_{/}}\Big )(v)\,dv\le C\varepsilon ^{(i)}, \end{aligned}$$

(6.9)

for some absolute constant $C>0$, where $T_{\mu \nu }^{(AdS)}[F_{i}^{(\varepsilon )}]$ is defined by

$$\begin{aligned} T_{vv}^{(AdS)}[F_{i}^{(\varepsilon )}]&\doteq \frac{\pi }{2}r_{AdS/}^{-2}(v)\int _{0}^{+\infty }\!\!\int _{0}^{+\infty }\Big (\Omega _{AdS/}^{2}(v)p\Big )^{2}\cdot F_{i}^{(\varepsilon )}(v;p,l)\,\frac{dp}{p}ldl,\\ T_{uv}^{(AdS)}[F_{i}^{(\varepsilon )}]&\doteq \frac{\pi }{2}r_{AdS/}^{-2}(v)\int _{0}^{+\infty }\int _{0}^{+\infty }\frac{\Omega _{AdS/}^{2}(v)l^{2}}{r_{AdS/}^{2}(v)}\cdot F_{i}^{(\varepsilon )}(v;p,l)\,\frac{dp}{p}ldl \end{aligned}$$

and $r_{AdS/},\text { }\Omega _{AdS/}^{2}$ are given by (3.14). Note, in particular, that $T_{vv}^{(AdS)}[F_i^{(\varepsilon )}]$ and $T_{uv}^{(AdS)}[F_i^{(\varepsilon )}]$ are of size $\sim 1$ and supported in an interval of width $\sim \varepsilon ^{(i)}(-\Lambda )^{-\frac{1}{2}}$ centered around $v_{\epsilon ,i}\sim (-\Lambda )^{-\frac{1}{2}}$.

We will define the initial data family $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ in terms of $F_{i}^{(\varepsilon )}$ as follows:

Definition 6.3

Let $0<\varepsilon _{1}\ll 1$ be the constant appearing in Definition 6.1. For any $\varepsilon \in (0,\varepsilon _{1}]$ and any finite sequence of weights $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}\in (0,\sigma _{\varepsilon })$ satisfying the smallness condition

$$\begin{aligned} \sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}\le \rho _{\varepsilon }^{-1}\sigma _{\varepsilon }, \end{aligned}$$

(6.10)

we will define

$$\begin{aligned} F^{(\varepsilon )}(v;p,l)=\sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}F_{i}^{(\varepsilon )}(v;p,l), \end{aligned}$$

(6.11)

where $F_i^{(\varepsilon )}$ are given by (6.7). Let also $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ be the gauge normalised, asymptotically AdS initial data set provided by Lemma 3.3 for $F=F^{(\varepsilon )}$ and $v_{{\mathcal {I}}}=\sqrt{-\frac{3}{\Lambda }}\pi$; recall that, according to Lemma 3.3, ${\bar{f}}_{/}^{\prime (\varepsilon )}$ is related to $F^{(\varepsilon )}$ by

$$\begin{aligned} {\bar{f}}_{/}^{\prime (\varepsilon )}(v;p^{u},l)=F^{(\varepsilon )}\big (v;\text { }\partial _{v}r_{/}^{\prime (\varepsilon )}(v)p^{u},\text { }l\big ). \end{aligned}$$

(6.12)

For any $\varepsilon \in (0,\varepsilon _{1}]$, we will define $(r_{/}^{(\varepsilon )},\Omega _{/}^{(\varepsilon )},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ as the (unique) smoothly compatible, asymptotically AdS initial data set which is obtained from the gauge normalised initial data set $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ through the gauge transformation of Lemma 3.4 (note that the notation for $(r_{/}^{(\varepsilon )},\Omega _{/}^{(\varepsilon )},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ and $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ is inverted in Lemma 3.4), with $\varepsilon$ in place of $\varepsilon _{0}$ in (3.27)–(3.28) (see also Fig. 13).

For $\varepsilon \in (\varepsilon _{1},1]$, we will set

$$\begin{aligned} (r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )})\doteq (r_{/}^{(\varepsilon _{1})},(\Omega _{/}^{(\varepsilon _{1})})^{2},{\bar{f}}_{/}^{(\varepsilon _{1})}), \end{aligned}$$

(6.13)

(the precise defintion of the family of initial data away from $\varepsilon =0$ is irrelevant for us; we will only be interested in the behaviour of the development for $\varepsilon$ close to 0).

Remark

The fact that $F^{(\varepsilon )}$ is compactly supported in $(0,\sqrt{-\frac{3}{\Lambda }}\pi )\times (0,+\infty )^{2}$, satisfying in particular

$$\begin{aligned}{} & {} F^{(\varepsilon )}(v;p,l)=0\quad \text { for }v\in \left[ 0,v_{\varepsilon ,0}-2\frac{\varepsilon ^{(0)}}{\sqrt{-\Lambda }}\right] \cup [v_{\varepsilon ,N_{\varepsilon }}+2\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }},+\infty )\nonumber \\{} & {} \quad \text { or }l\in \left[ 0,2\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\right] \end{aligned}$$

(6.14)

(see (6.7) and (6.11)), allows us to apply Lemma 3.4 in the statement of Definition 6.3. In view of the fact that, as a consequence of (3.26), the gauge transformation provided by Lemma 3.4 is the identity when restricted to $v\in [0,v_{\varepsilon ,N_{\varepsilon }}+2\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}]$ (which includes the support of $F^{(\varepsilon )}$ in the v-variable), the following relations hold between $(r_{/}^{(\varepsilon )},\Omega _{/}^{(\varepsilon )},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ and $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$:

$$\begin{aligned} {\bar{f}}_{/}^{(\varepsilon )}={\bar{f}}_{/}^{\prime (\varepsilon )}\text { on }(0,\sqrt{-\frac{3}{\Lambda }}\pi )\times [0,+\infty )^{2} \end{aligned}$$

(6.15)

and

$$\begin{aligned} (r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2})(v)=(r_{/}^{\prime (\varepsilon )},(\Omega _{/}^{\prime (\varepsilon )})^{2})(v)\text { for }v\in \left[ 0,v_{\varepsilon ,N_{\varepsilon }}+2\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\right] .\nonumber \\ \end{aligned}$$

(6.16)

In particular, (6.11) and (6.12) imply that:

$$\begin{aligned} {\bar{f}}_{/}^{(\varepsilon )}(v;p^{u},l)=\sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}F_{i}^{(\varepsilon )}\big (v;\text { }\partial _{v}r_{/}^{\prime (\varepsilon )}(v)p^{u},\text { }l\big ). \end{aligned}$$

(6.17)

Fig. 13

Schematic depiction of the support in the (u, v)-plane of the Vlasov beams emanating from the initial data at $u=0$. The i-th beam in the picture corresponds to ${\bar{f}}_{i}^{(\varepsilon )}$, $0\le i\le N_{\varepsilon }$, and contains null geodesics with angular momenta $\sim \varepsilon ^{(i)}(-\Lambda )^{-1/2}$, i.e. proportional to the width of the beam

The estimates for the initial data family $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )})$ stated in the following lemma are an immediate consequence of the expression (6.7) for $F_{i}^{(\varepsilon )}$ and the quantitative bounds provided by Lemmas 3.3 and 3.4:

Lemma 6.4

There exists some $C>0$, such that, for all $\varepsilon \in (0,1)$, the initial data set $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ satisfies:

$$\begin{aligned}{} & {} \sup _{v\in (0,\sqrt{-\frac{3}{\Lambda }}\pi )}\Bigg (\Big |\frac{\partial _{v}r_{/}^{(\varepsilon )}}{1-\frac{1}{3}\Lambda (r_{/}^{(\varepsilon )})^{2}}-\frac{\partial _{v}r_{AdS/}}{1-\frac{1}{3}\Lambda r_{AdS/}^{2}}\Big |(v)\nonumber \\{} & {} \quad +\Big |\frac{(\Omega _{/}^{(\varepsilon )})^{2}}{1-\frac{1}{3}\Lambda (r_{/}^{(\varepsilon )})^{2}}-\frac{\Omega _{AdS/}^{2}}{1-\frac{1}{3}\Lambda r_{AdS/}^{2}}\Big |(v)\Bigg )\le C\varepsilon . \end{aligned}$$

(6.18)

Furthermore, for any $i=0,\ldots ,N_{\varepsilon }$, we can estimate on the support of $F_{i}^{(\varepsilon )}$:

$$\begin{aligned} \sup _{v\in (0,\sqrt{-\frac{3}{\Lambda }}\pi )}\Bigg [\!\Big |\partial _{v}\Big (\frac{\partial _{v}r_{/}^{(\varepsilon )}}{1\!-\!\frac{1}{3}\Lambda (r_{/}^{(\varepsilon )})^{2}}\Big )\Big |(v)+\Big |\partial _{v}\!\Big (\frac{(\Omega _{/}^{(\varepsilon )})^{2}}{1\!-\!\frac{1}{3}\Lambda (r_{/}^{(\varepsilon )})^{2}}\Big )\Big |(v)\Bigg ] \!\le C\sqrt{-\Lambda }.\nonumber \\ \end{aligned}$$

(6.19)

Finally, the following estimate holds:

$$\begin{aligned} \sup _{v\in (0,\sqrt{-\frac{3}{\Lambda }}\pi )}\frac{2{\tilde{m}}_{/}^{(\varepsilon )}}{r_{/}^{(\varepsilon )}}<C\varepsilon , \end{aligned}$$

(6.20)

where ${\tilde{m}}_{/}^{(\varepsilon )}$ is defined in terms of $r_{/}^{(\varepsilon )},\text { }(\Omega _{/}^{(\varepsilon )})^{2},\text { }{\bar{f}}_{/}^{(\varepsilon )}$ by (2.48), i.e. by the implicit relation

$$\begin{aligned} {\tilde{m}}_{/}^{(\varepsilon )}(v)= & {} 2\pi \int _{0}^{v}\Bigg (\big (1-\frac{2{\tilde{m}}_{/}^{(\varepsilon )}}{r_{/}^{(\varepsilon )}}-\frac{1}{3}\Lambda r_{/}^{(\varepsilon )}\big )\frac{(r_{/}^{(\varepsilon )})^{2}(T_{/}^{(\varepsilon )})_{vv}}{\partial _{v}r_{/}^{(\varepsilon )}}\nonumber \\{} & {} \quad +4\frac{\partial _{v}r_{/}^{(\varepsilon )}}{(\Omega _{/}^{(\varepsilon )})^{2}}(r_{/}^{(\varepsilon )})^{2}(T_{/}^{(\varepsilon )})_{uv}\Bigg )({\bar{v}})\,d{\bar{v}}. \end{aligned}$$

(6.21)

Proof

In view of (6.13), it suffices to establish (6.18)–(6.20) for $\varepsilon \in (0,\varepsilon _{1}]$. Furthermore, it suffices to establish the bounds (6.18)–(6.20) for the intermediate, gauge normalised initial data set $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ constructed in Definition 6.3. Since $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ is related to $(r_{/}^{(\varepsilon )},\Omega _{/}^{(\varepsilon )},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ by the gauge transformation of Lemma 3.4 with $\varepsilon$ in place of $\varepsilon _{0}$,²² the bounds (3.27), (3.28) and (6.9) imply (in view of the relation

$$\begin{aligned} r_{/}^{\prime (\varepsilon )}(V(v))&=r_{/}^{(\varepsilon )}(v),\\ (\Omega _{/}^{\prime (\varepsilon )})^{2}(V(v))&=\frac{1}{\frac{dV}{du}(0)\cdot \frac{dV}{dv}(v)}\Omega _{/}^{(\varepsilon )}(v),\nonumber \end{aligned}$$

(6.22)

between $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )})$ and $(r_{/}^{(\varepsilon )},\Omega _{/}^{(\varepsilon )})$) that if (6.18)–(6.19) hold for $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$, then they also hold for $(r_{/}^{(\varepsilon )},\Omega _{/}^{(\varepsilon )},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ with 2C in place of C. The bound (6.20), on the other hand, is gauge invariant.

The bound (6.18) for $r_{/}^{\prime (\varepsilon )}$ is a corollary of the gauge condition (3.13) relating $\Omega _{/}^{\prime (\varepsilon )}$ to $\partial _{v}r_{/}^{\prime (\varepsilon )}$ and Lemma 3.3 relating $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ to $F^{(\varepsilon )}$ (in particular, the estimate (3.22)), noting that the bound (3.20) for $F^{(\varepsilon )}$ is a direct consequence of (6.9) (assuming that $\varepsilon _{1}$ has been fixed smaller than $c_{0}$ in (3.20)).

We will now proceed to establish that

$$\begin{aligned} \sup _{v\in (0,v_{{\mathcal {I}}})}\Big |\partial _{v}\Big (\frac{\partial _{v}r_{/}^{\prime (\varepsilon )}}{1-\frac{1}{3}\Lambda (r_{/}^{\prime (\varepsilon )})^{2}}\Big )(v)\Big |\le C\sqrt{-\Lambda }. \end{aligned}$$

(6.23)

Note that, since $\Omega _{/}^{\prime (\varepsilon )}$ and $\partial _{v}r_{/}^{\prime (\varepsilon )}$ are related by the gauge normalising condition (3.13), the bounds (6.19)–(6.19) for $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )})$ follow immediately from (6.23) and (6.18).

The alternative form (3.16) of the gauge condition (3.13) for $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )})$ yields, after differentiating in v:

$$\begin{aligned} \partial _{v}\Big (\frac{\partial _{v}r_{/}^{\prime (\varepsilon )}}{1-\frac{1}{3}\Lambda (r_{/}^{\prime (\varepsilon )})^{2}}\Big )(v)=\Big (4\pi \frac{r_{/}^{\prime (\varepsilon )}(T_{/}^{\prime (\varepsilon )})_{vv}}{(\partial _{v}r_{/}^{\prime (\varepsilon )})}(v)\Big )\cdot \frac{\partial _{v}r_{/}^{\prime (\varepsilon )}}{1-\frac{1}{3}\Lambda (r_{/}^{\prime (\varepsilon )})^{2}},\qquad \end{aligned}$$

(6.24)

where, in view of the relation (6.12) between ${\bar{f}}_{/}^{\prime (\varepsilon )}$ and $F^{(\varepsilon )}$ and the gauge condition (3.13) for $(r_{/}^{\prime (\varepsilon )},\Omega _{/}^{\prime (\varepsilon )})$:

$$\begin{aligned} (T_{/}^{\prime (\varepsilon )})_{vv}(v)\doteq 8\pi \frac{(\partial _{v}r_{/}^{\prime (\varepsilon )})^{2}}{\big (r_{/}^{\prime (\varepsilon )}-\frac{1}{3}\Lambda (r_{/}^{\prime (\varepsilon )})^{3}\big )^{2}}(v)\int _{0}^{+\infty }\int _{0}^{+\infty }p^{2}F^{(\varepsilon )}(v;p,l)\,\frac{dp}{p}ldl.\nonumber \\ \end{aligned}$$

(6.25)

In view of (6.24) and (6.25), the bound (6.23) follows from the expression (6.7) for $F_{i}^{(\varepsilon )}$ and the fact that $F^{(\varepsilon )}=\sum _{i=0}^{N_{\varepsilon }}F_{i}^{(\varepsilon )}$.

The bound (6.20) follows readily by applying Gronwall’s inequality on the integral relation (6.21) for $\frac{2{\tilde{m}}_{/}^{(\varepsilon )}}{r_{/}^{(\varepsilon )}}$, using the estimates (6.9) and (6.18). $\square$

The initial data family $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )})$ satisfies the following smallness condition with respect to the initial data norm $||\cdot ||$ introduced by Definition 3.14:

Lemma 6.5

There exists some $C>0$, such that, for all $\varepsilon \in (0,1)$, the initial data set $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ satisfies:

$$\begin{aligned} ||(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )||\le C\sigma _{\varepsilon }, \end{aligned}$$

(6.26)

where $||\cdot ||$ is defined by (3.59). In particular, as a consequence of (6.3):

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}||(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )||=0. \end{aligned}$$

(6.27)

Proof

Since the bound (6.26) is non-trivial only in the limit $\varepsilon \rightarrow 0$, it suffices to establish it for $\varepsilon \in (0,\varepsilon _{1}]$.

Let $(r_{/}^{\prime (\varepsilon )},(\Omega _{/}^{\prime (\varepsilon )})^{2},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ be the gauge-normalised expression of $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$, constructed in Definition 6.3. Recall that $(r_{/}^{\prime (\varepsilon )},(\Omega _{/}^{\prime (\varepsilon )})^{2},{\bar{f}}_{/}^{\prime (\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ and $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ satisfy (6.15) and (6.16), i.e. coincide in the support of ${\bar{f}}_{/}^{(\varepsilon )}={\bar{f}}_{/}^{\prime (\varepsilon )}$.

For any $\varepsilon \in (0,\varepsilon _{1}]$ and $0\le i\le N_{\varepsilon }$, let us define $f_{\varepsilon ,i}^{(AdS)}$ and $\Big [\frac{rT_{\alpha \beta }}{\partial _{v}r}\Big ]_{\varepsilon ,i}^{(AdS)}$ in terms of $v_{{\mathcal {I}}}=\sqrt{-\frac{3}{\Lambda }}\pi$ and

$$\begin{aligned} {\bar{f}}_{i}^{(\varepsilon )}(v;p^{u},l)\doteq F_{i}^{(\varepsilon )}\big (v;\text { }\partial _{v}r_{/}^{\prime (\varepsilon )}(v)p^{u},\text { }l\big ) \end{aligned}$$

(6.28)

as in Definition 3.13; we will similarly define $f_{\varepsilon }^{(AdS)}$ and $\Big [\frac{rT_{\alpha \beta }}{\partial _{v}r}\Big ]_{\varepsilon }^{(AdS)}$ in terms of ${\bar{f}}_{/}^{\prime (\varepsilon )}={\bar{f}}_{/}^{(\varepsilon )}$ (see (6.15)). Note that the relations (6.12), (6.15) and (6.17) imply that

$$\begin{aligned} f_{\varepsilon }^{(AdS)}\doteq \sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}f_{\varepsilon ,i}^{(AdS)} \end{aligned}$$

(6.29)

and

$$\begin{aligned} \Big [\frac{rT_{\alpha \beta }}{\partial _{v}r}\Big ]_{\varepsilon }^{(AdS)}=\sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}\Big [\frac{rT_{\alpha \beta }}{\partial _{v}r}\Big ]_{\varepsilon ,i}^{(AdS)}. \end{aligned}$$

(6.30)

Note that, in view of (6.14) and (6.16), (6.28) implies that

$$\begin{aligned} {\bar{f}}_{i}^{(\varepsilon )}(v;p^{u},l)\doteq F_{i}^{(\varepsilon )}\big (v;\text { }\partial _{v}r_{/}^{(\varepsilon )}(v)p^{u},\text { }l\big ) \end{aligned}$$

(6.31)

From the expression (6.7) for $F_{i}^{(\varepsilon )}$, the relation (6.31) between ${\bar{f}}_{i}^{(\varepsilon )}$ and $F_{i}^{(\varepsilon )}$, the bound (6.18) for $r_{/}^{(\varepsilon )}$ and properties of the geodesic flow on AdS when $\frac{l}{E}\ll 1$ (see the relation A.10 in the Appendix of [43]), it readily follows that the support of $f_{\varepsilon ,i}^{(AdS)}$ satisfies (for some absolute constant $C>0$)

$$\begin{aligned} supp\big (f_{\varepsilon ,i}^{(AdS)}\big ){} & {} \subset \Bigg (\Big \{(u,v)\in {\mathcal {V}}_{\varepsilon ,i}^{(AdS)}\Big \}\cap \Big \{\Omega _{AdS}^{2}(u,v)\Big (p^{u}+p^{v}\Big )\le C\Big \}\nonumber \\{} & {} \cap \Big \{2\le \frac{\sqrt{-\Lambda }l}{\varepsilon ^{i+1}}\le 6\Big \}\Bigg ), \end{aligned}$$

(6.32)

where

$$\begin{aligned} {\mathcal {V}}_{\varepsilon ,i}^{(AdS)}&\doteq \bigcup _{k\in {\mathbb {Z}}}\Big (\Big \{\Big |v -v_{\varepsilon ,i}-k\sqrt{-\frac{3}{\Lambda }}\pi \Big |\le C\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big \}\nonumber \\&\quad \cup \Big \{\Big |u-v_{\varepsilon ,i}-k\sqrt{-\frac{3}{\Lambda }}\pi \Big |\le C\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big \}\Big )\\&\quad \cap \Big \{ r_{AdS}(u,v)\ge C^{-1}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big \}.\nonumber \end{aligned}$$

(6.33)

In view of (6.32), using (2.33) (with $r_{AdS}$ in place of r and $m_{AdS}=\frac{1}{6}\Lambda r_{AdS}^{3}$ in place of m), as well as the conservation (2.26) of the particle current $N_{\mu }[f_{\varepsilon ,i}^{(AdS)}]$ of $f_{\varepsilon ,i}^{(AdS)}$, we can readily calculate for any $\varepsilon \in (0,\varepsilon _{1}]$, any $U_{*}\ge 0$ and any $0\le i\le N_{\varepsilon }$:

$$\begin{aligned}&\int _{U_{*}}^{U_{*}+\sqrt{-\frac{3}{\Lambda }}\pi }\Big (\Big [\frac{rT_{vv}}{\partial _{v}r}\Big ]_{\varepsilon ,i}^{(AdS)}(U_{*},v)+\Big [\frac{rT_{uv}}{-\partial _{u}r}\Big ]_{\varepsilon ,i}^{(AdS)}(U_{*},v)\Big )\,dv\nonumber \\&\quad \le C\int _{U_{*}}^{U_{*}+\sqrt{-\frac{3}{\Lambda }}\pi }r(U_{*},v)\cdot N_{v}[f_{\varepsilon ,i}^{(AdS)}](U_{*},v)\,dv\\&\quad \le C\Big (\sup _{{\mathcal {V}}_{\varepsilon ,i}^{(AdS)}\cap \{u=U_{*}\}}\frac{1}{r_{AdS}}\Big )\cdot \int _{u=0}r_{AdS}^{2}N_{v}[f_{\varepsilon ,i}^{(AdS)}]\,dv\nonumber \end{aligned}$$

(6.34)

for some absolute constant $C>0$. Using the expression (2.32), the explicit formula (6.7) for $F_{i}^{(\varepsilon )}$ and the bound (6.18) (the latter used in order to estimate the term $\partial _{v}r_{/}^{(\varepsilon )}$ in the relation (6.31) between $F_{i}^{(\varepsilon )}$ and $f_{\varepsilon ,i}^{(AdS)}|_{u=0}$), we can readily estimate

$$\begin{aligned} \int _{u=0}r_{AdS}^{2}N_{v}[f_{\varepsilon ,i}^{(AdS)}]\,dv\le C\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}, \end{aligned}$$

(6.35)

thus obtaining from (6.34) that, for any $U_{*}\ge 0$ and any $0\le i\le N_{\varepsilon }$:

$$\begin{aligned}{} & {} \int _{U_{*}}^{U_{*}+\sqrt{-\frac{3}{\Lambda }}\pi }\Big (\Big [\frac{rT_{vv}}{\partial _{v}r}\Big ]_{\varepsilon ,i}^{(AdS)}(U_{*},v)+\Big [\frac{rT_{uv}}{-\partial _{u}r}\Big ]_{\varepsilon ,i}^{(AdS)}(U_{*},v)\Big )\,dv\nonumber \\{} & {} \quad \le C\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\sup _{{\mathcal {V}}_{\varepsilon ,i}^{(AdS)}\cap \{u=U_{*}\}}\frac{1}{r_{AdS}}. \end{aligned}$$

(6.36)

For any $\varepsilon \in (0,\varepsilon _{1}]$ and any $U_{*}\ge 0$, let us define $i_{\varepsilon }[U_{*}]$ to be the unique integer i in $[0,N_{\varepsilon }]$ for which

$$\begin{aligned} v_{\varepsilon ,i-1}+k\sqrt{-\frac{3}{\Lambda }}\pi +\rho _{\varepsilon }^{-\frac{1}{2}}\frac{\varepsilon ^{(i-1)}}{\sqrt{-\Lambda }}<U_{*}\le v_{\varepsilon ,i}+k\sqrt{-\frac{3}{\Lambda }}\pi +\rho _{\varepsilon }^{-\frac{1}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\nonumber \\ \end{aligned}$$

(6.37)

for some $k\in {\mathbb {Z}}$, with the convention that

$$\begin{aligned} v_{\varepsilon ,-1}\doteq v_{\varepsilon ,N_{\varepsilon }}-\sqrt{-\frac{3}{\Lambda }}\pi \end{aligned}$$

(6.38)

and

$$\begin{aligned} \varepsilon ^{(-1)}\doteq \varepsilon ^{(N_{\varepsilon })}. \end{aligned}$$

Then, in view of the bound (6.32) for the support of $f_{\varepsilon ,i}^{(AdS)}$, the definition (6.33) of the domains ${\mathcal {V}}_{\varepsilon ,i}^{(AdS)}$ (see also Fig. 14), the relation (6.8) defining $v_{\varepsilon ,i}$ and the relations (6.1) and (6.5) between $\varepsilon$, $\rho _{\varepsilon }$ and $\varepsilon ^{(i)}$, we infer that, given any $U_{*}\ge 0$, we can bound

$$\begin{aligned} {\left\{ \begin{array}{ll} \inf _{{\mathcal {V}}_{\varepsilon ,i}^{(AdS)}\cap \{u=U_{*}\}}r_{AdS}\ge c\varepsilon ^{(i)}(-\Lambda )^{-\frac{1}{2}}, &{} \text { for }i=i_{\varepsilon }[U_{*}],\\ \inf _{{\mathcal {V}}_{\varepsilon ,i}^{(AdS)}\cap \{u=U_{*}\}}r_{AdS}\ge \rho _{\varepsilon }^{-1}\varepsilon ^{(i)}(-\Lambda )^{-\frac{1}{2}}, &{} \text { for }i_{\varepsilon }[U_{*}]<i\le N_{\varepsilon },\\ \inf _{{\mathcal {V}}_{\varepsilon ,i}^{(AdS)}\cap \{u=U_{*}\}}r_{AdS}\ge c(-\Lambda )^{-\frac{1}{2}}, &{} \text { for }0\le i<i_{\varepsilon }[U_{*}], \end{array}\right. }\qquad \end{aligned}$$

(6.39)

for some absolute constant $c>0$. Multiplying (6.36) with $a_{\varepsilon i}$ and adding the resulting bounds for $0\le i\le N_{\varepsilon }$, we therefore infer using (6.39) (in view also of (6.30)) and (6.5) that, for any $\varepsilon \in (0,\varepsilon _{1}]$ and any $U_{*}\ge 0$:

$$\begin{aligned}{} & {} \int _{U_{*}}^{U_{*}+\sqrt{-\frac{3}{\Lambda }}\pi }\Big (\Big [\frac{rT_{vv}}{\partial _{v}r}\Big ]_{\varepsilon }^{(AdS)}(U_{*},v)+\Big [\frac{rT_{uv}}{-\partial _{u}r}\Big ]_{\varepsilon }^{(AdS)}(U_{*},v)\Big )\,dv\nonumber \\{} & {} \quad \le C\Big (\varepsilon +\max _{0\le i\le N_{\varepsilon }}a_{\varepsilon i}+\sum _{i=0}^{N_{\varepsilon }}\rho _{\varepsilon }a_{\varepsilon i}\Big ). \end{aligned}$$

(6.40)

Similarly, we can estimate for any $V_{*}\ge 0$:

$$\begin{aligned}{} & {} \int _{\max \{0,V_{*}-\sqrt{-\frac{3}{\Lambda }}\pi \}}^{V_{*}}\Big (\Big [\frac{rT_{uu}}{-\partial _{u}r}\Big ]_{\varepsilon }^{(AdS)}(u,V_{*})+\Big [\frac{rT_{uv}}{\partial _{v}r}\Big ]_{\varepsilon }^{(AdS)}(u,V_{*})\Big )\,du\nonumber \\{} & {} \quad \le C\Big (\varepsilon +\max _{0\le i\le N_{\varepsilon }}a_{\varepsilon i}+\sum _{i=0}^{N_{\varepsilon }}\rho _{\varepsilon }a_{\varepsilon i}\Big ). \end{aligned}$$

(6.41)

Fig. 14

Schematic depiction of the regions ${\mathcal {V}}_{\varepsilon ,i}^{(AdS)}$ bounding the trajectories of the geodesics in the support of $f_{\epsilon ,i}^{(AdS)}$, for $0\le i\le 2$. The region ${\mathcal {V}}_{\varepsilon ,i}^{(AdS)}$ has width proportional to $\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}$. The minimum value of r along ${\mathcal {V}}_{\varepsilon ,i}^{(AdS)}$ is also proportional to $\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}$. On the other hand, the separation of ${\mathcal {V}}_{\varepsilon ,i}^{(AdS)}$ from the rest of these regions when $u=0$ is proportional to $\rho _{\varepsilon }^{-1} \frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}$

Using the expression (2.30), the explicit formula (6.7) for $F_{i}^{(\varepsilon )}$ and the relation (6.31) between $F_{i}^{(\varepsilon )}$ for $f_{\varepsilon ,i}^{(AdS)}|_{u=0}$ (arguing similarly as for obtaining (6.35)), we can bound

$$\begin{aligned} \sqrt{-\Lambda }{\tilde{m}}_{\varepsilon }|_{{\mathcal {I}}}\le C\big (\max _{0\le i\le N_{\varepsilon }}a_{\varepsilon i}\big )\varepsilon . \end{aligned}$$

(6.42)

Therefore, for any $\varepsilon \in (0,\varepsilon _{1}]$, the following estimate for the size of $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ with respect to the norm (3.59) follows readily by adding (6.40), (6.41) and (6.42) and using (6.1), (6.10) and the assumption that $a_{\varepsilon i}\in (0,\sigma _{\varepsilon })$:

$$\begin{aligned} ||(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )||\le C\Big (\sigma _{\varepsilon }+\sum _{i=0}^{N_{\varepsilon }}\rho _{\varepsilon }a_{\varepsilon i}\Big )\le C\sigma _{\varepsilon }. \end{aligned}$$

(6.43)

In particular, (6.26) holds. $\square$

6.3 Notational conventions for domains and fundamental computations

For the rest of this paper, we will denote with $({\mathcal {U}}_{max}^{(\varepsilon )};r_{\varepsilon },\Omega _{\varepsilon }^{2},f_{\varepsilon })$ the maximal future development of the initial data set $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ (for the definition of the notion of a maximal future development for (2.36)–(2.41), see Proposition 3.8). We will also denote with ${\mathcal {I}}_{\varepsilon }$ and $\gamma _{{\mathcal {Z}}\varepsilon }$ the conformal infinity and axis, respectively, of $({\mathcal {U}}_{max}^{(\varepsilon )};r_{\varepsilon },\Omega _{\varepsilon }^{2},f_{\varepsilon })$, with corresponding endpoint parameters $u_{{\mathcal {I}}_{\varepsilon }}\in (0,+\infty ]$ and $u_{\gamma _{{\mathcal {Z}}\varepsilon }}\in (0,+\infty ]$, defined in accordance with Definition 3.5. Note that the proof of Theorem 1 will consist of showing that $u_{{\mathcal {I}}_{\varepsilon }}<+\infty$.

Remark

In order to simplify the heavy notation associated with all the parameters that will be introduced in the proof of Theorem 1, we will frequently drop the subscript $\varepsilon$ in $r_{\varepsilon }$, $\Omega _{\varepsilon }^{2}$, $m_{\varepsilon }$ and ${\tilde{m}}_{\varepsilon }$, but not in $f_{\varepsilon }$. Therefore, from now on we will almost always denote $({\mathcal {U}}_{max}^{(\varepsilon )};r_{\varepsilon },\Omega _{\varepsilon }^{2},f_{\varepsilon })$ as $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$.

For any $\delta \in (0,1]$ and any $\varepsilon \in (0,1]$, we will define $u_{\delta ;\varepsilon }^{+}\in [0,u_{{\mathcal {I}}_{\varepsilon }}]$ by

$$\begin{aligned} u_{\delta ;\varepsilon }^{+}\doteq \sup \Big \{{\bar{u}}\in [0,u_{{\mathcal {I}}_{\varepsilon }}):\text { }\frac{2{\tilde{m}}}{r}(u,v)< & {} \delta \text { for all }(u,v)\in {\mathcal {U}}_{max}^{(\varepsilon )}\nonumber \\{} & {} \quad \text { with }0<u<{\bar{u}}\Big \}. \end{aligned}$$

(6.44)

Similarly, we will define for any $K>0$ and any $\varepsilon \in (0,1]$:

$$\begin{aligned}&u_{K;\varepsilon }^{\sharp }\doteq \sup \Big \{{\bar{u}}\in [0,u_{{\mathcal {I}}_{\varepsilon }}):\text { }\sup _{u\in (0,{\bar{u}})}\int _{u}^{u+\sqrt{-\frac{3}{\Lambda }}\pi }r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,dv<K\\&\quad \text { and}\sup _{v\in (0,{\bar{u}}+\sqrt{-\frac{3}{\Lambda }}\pi )}\int _{\max \{0,v-\sqrt{-\frac{3}{\Lambda }}\pi \}}^{\min \{v,{\bar{u}}\}}r\Big (\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,du<K\Big \}.\nonumber \end{aligned}$$

(6.45)

We will define ${\mathcal {U}}_{K,\delta }^{(\varepsilon )}\subset {\mathcal {U}}_{max}^{(\varepsilon )}$ to be the open subset

$$\begin{aligned} {\mathcal {U}}_{K,\delta }^{(\varepsilon )}\doteq \big \{0<u<\min \{u_{\delta ;\varepsilon }^{+},\text { }u_{K;\varepsilon }^{\sharp }\big \}. \end{aligned}$$

(6.46)

Note that ${\mathcal {U}}_{K,\delta }^{(\varepsilon )}$ is non-empty if and only if $\delta$ and K satisfy in terms of the initial data:

$$\begin{aligned} \sup _{v\in (0,\sqrt{-\frac{3}{\Lambda }}\pi )}\frac{2{\tilde{m}}_{/}^{(\varepsilon )}}{r_{/}^{(\varepsilon )}}(v)<\delta \end{aligned}$$

(6.47)

and

$$\begin{aligned} \int _{0}^{\sqrt{-\frac{3}{\Lambda }}\pi }r_{/}^{(\varepsilon )}\Big (\frac{(T_{/}^{(\varepsilon )})_{vv}}{\partial _{v}r_{/}^{(\varepsilon )}}+\frac{(T_{/}^{(\varepsilon )})_{uv}}{-\partial _{u}r_{/}^{(\varepsilon )}}\Big )(v)\,dv<K. \end{aligned}$$

(6.48)

As a consequence of (6.27) and Lemma 6.4, given any $\delta \in (0,1)$ and $K>0$, there always exists an $\varepsilon _{0}\in (0,\varepsilon _{1}]$ such that (6.47) and (6.48) are satified for all $\varepsilon \in (0,\varepsilon _{0})$ (in particular, it suffices to choose any $\varepsilon _{0}$ for which $\sigma _{\varepsilon _{0}}\lesssim \min \{K,\delta \}$).

Remark

In the case when ${\mathcal {U}}_{K,\delta }^{(\varepsilon )}$ is non-empty, $({\mathcal {U}}_{K,\delta }^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ is a future development of $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$ for (2.36)–(2.41) with reflecting boundary conditions on conformal infinity, in accordance with Definition 3.6. Note also that

$$\begin{aligned} u_{1;\varepsilon }^{+}=u_{{\mathcal {I}}_{\varepsilon }} \end{aligned}$$

as a trivial consequence of (3.47).

Let

$$\begin{aligned} 0<\eta _{0}\ll 1 \end{aligned}$$

be a small absolute constant. For the rest of the paper, we will assume that $\eta _{0}$ has been fixed small enough in terms of the absolute constant $\delta _{0}$ appearing in the statements of Lemma 5.1 and Proposition 3.11.

The following domains in ${\mathcal {U}}_{max}^{(\varepsilon )}$ will be play a central role in the proof of Theorem 1:

Definition 6.6

We will define the domains ${\mathcal {U}}_{\varepsilon }^{+},{\mathcal {T}}_{\varepsilon }^{+}\subset {\mathcal {U}}_{max}^{(\varepsilon )}$ by

$$\begin{aligned} {\mathcal {U}}_{\varepsilon }^{+}\doteq {\mathcal {U}}_{\sigma _{\varepsilon }^{-1};\eta _{0}}^{(\varepsilon )}\cap \big \{ u<\frac{\sigma _{\varepsilon }^{-2}}{\sqrt{-\Lambda }}\big \} \end{aligned}$$

(6.49)

and

$$\begin{aligned} {\mathcal {T}}_{\varepsilon }^{+}\doteq {\mathcal {U}}_{\delta _{\varepsilon }^{-1};\eta _{0}}^{(\varepsilon )}\cap \big \{ u<\frac{\sigma _{\varepsilon }^{-2}}{\sqrt{-\Lambda }}\big \} \end{aligned}$$

(6.50)

where ${\mathcal {U}}_{\sigma _{\varepsilon }^{-1};\eta _{0}}^{(\varepsilon )}$, ${\mathcal {U}}_{\delta _{\varepsilon }^{-1};\eta _{0}}^{(\varepsilon )}$ are defined by (6.46).

Remark

Note that, since $\delta _{\varepsilon }\ll \sigma _{\varepsilon }$,

$$\begin{aligned} {\mathcal {U}}_{\varepsilon }^{+}\subseteq {\mathcal {T}}_{\varepsilon }^{+}. \end{aligned}$$

Let us define

$$\begin{aligned} u[{\mathcal {U}}_{\varepsilon }^{+}]\doteq \min \big \{ u_{\eta _{0};\varepsilon }^{+},\text { }u_{\sigma _{\varepsilon }^{-1};\varepsilon }^{\sharp },\frac{\sigma _{\varepsilon }^{-2}}{\sqrt{-\Lambda }}\big \} \end{aligned}$$

and

$$\begin{aligned} u[{\mathcal {T}}_{\varepsilon }^{+}]\doteq \min \big \{ u_{\eta _{0};\varepsilon }^{+},\text { }u_{\delta _{\varepsilon }^{-1};\varepsilon }^{\sharp },\frac{\sigma _{\varepsilon }^{-2}}{\sqrt{-\Lambda }}\big \}, \end{aligned}$$

so that

$$\begin{aligned} {\mathcal {U}}_{\varepsilon }^{+}&=\big \{0<u<u[{\mathcal {U}}_{\varepsilon }^{+}]\big \}\cap \big \{ u<v<u+\sqrt{-\frac{3}{\Lambda }}\pi \big \},\\ {\mathcal {T}}_{\varepsilon }^{+}&=\big \{0<u<u[{\mathcal {T}}_{\varepsilon }^{+}]\big \}\cap \big \{ u<v<u+\sqrt{-\frac{3}{\Lambda }}\pi \big \}.\nonumber \end{aligned}$$

(6.51)

As an immediate consequence of the extension principle of Proposition 3.11, we infer the following condition for the boundary of ${\mathcal {U}}_{\varepsilon }^{+}$ and ${\mathcal {T}}_{\varepsilon }^{+}$ in ${\mathcal {U}}_{max}^{(\varepsilon )}$ :

Lemma 6.7

For any $\varepsilon \in (0,\varepsilon _{1}]$,

$$\begin{aligned} u[{\mathcal {U}}_{\varepsilon }^{+}]<u[{\mathcal {T}}_{\varepsilon }^{+}]<u_{{\mathcal {I}}_{\varepsilon }}. \end{aligned}$$

(6.52)

In particular, there exists a $u_{0}>0$ such that

$$\begin{aligned} \big \{0<u<u[{\mathcal {T}}_{\varepsilon }^{+}]+u_{0}\big \}\subset {\mathcal {U}}_{max}^{(\varepsilon )}.\text { } \end{aligned}$$

(6.53)

Furthermore, in the case when

$$\begin{aligned} u[{\mathcal {U}}_{\varepsilon }^{+}]<\frac{\sigma _{\varepsilon }^{-2}}{\sqrt{-\Lambda }}, \end{aligned}$$

(6.54)

at least one of the following three conditions hold for the future boundary $\{u=u[{\mathcal {U}}_{\varepsilon }^{+}]\}$ of ${\mathcal {U}}_{\varepsilon }^{+}$:

$$\begin{aligned}{} & {} \limsup _{p\rightarrow \{u=u[{\mathcal {U}}_{\varepsilon }^{+}]\}}\frac{2{\tilde{m}}}{r}(p)=\eta _{0},\qquad \end{aligned}$$

(6.55)

$$\begin{aligned}{} & {} \lim \sup _{u\rightarrow u[{\mathcal {U}}_{\varepsilon }^{+}]}\int _{u}^{u+\sqrt{-\frac{3}{\Lambda }}\pi }r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,dv=\sigma _{\varepsilon }^{-1},\qquad \end{aligned}$$

(6.56)

or

$$\begin{aligned} \sup _{v\in (0,u[{\mathcal {U}}_{\varepsilon }^{+}]+\sqrt{-\frac{3}{\Lambda }}\pi )}\int _{\max \{0,v-\sqrt{-\frac{3}{\Lambda }}\pi \}}^{\min \{v,u[{\mathcal {U}}_{\varepsilon }^{+}]\}}r\Big (\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,du=\sigma _{\varepsilon }^{-1}.\nonumber \\ \end{aligned}$$

(6.57)

Similarly, the same condition holds on $\{u=u[{\mathcal {T}}_{\varepsilon }^{+}]\}$ for ${\mathcal {T}}_{\varepsilon }^{+}$, with $\delta _{\varepsilon }$ in place of $\sigma _{\varepsilon }$ in (6.56) and (6.57).

Proof

The proof of (6.52) and (6.53) follows immediately by applying Proposition 3.11 to ${\mathcal {T}}_{\varepsilon }^{+}$, using the fact that

$$\begin{aligned} \sup _{{\mathcal {T}}_{\varepsilon }^{+}}\frac{2{\tilde{m}}}{r}\le \eta _{0} \end{aligned}$$

(following from (6.44) and the definition of ${\mathcal {T}}_{\varepsilon }^{+}$), as well as the fact that the initial Vlasov field ${\bar{f}}_{/}^{(\varepsilon )}$ (introduced in Definition 6.3) is compactly supported in phase space.

In order to establish that at least one of the relations 6.55–6.57 hold for ${\mathcal {U}}_{\varepsilon }^{+}$, we will assume, for the sake of contradiction, that there exists a (possibly small)$\delta >0$

$$\begin{aligned}{} & {} \limsup _{p\rightarrow \{u=u[{\mathcal {U}}_{\varepsilon }^{+}]\}}\frac{2{\tilde{m}}}{r}(p)<\eta _{0}-\delta , \end{aligned}$$

(6.58)

$$\begin{aligned}{} & {} \lim \sup _{u\rightarrow u[{\mathcal {U}}_{\varepsilon }^{+}]}\int _{u}^{u+\sqrt{-\frac{3}{\Lambda }}\pi }r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,dv<\sigma _{\varepsilon }^{-1}-\delta \nonumber \\ \end{aligned}$$

(6.59)

and

$$\begin{aligned} \sup _{v\in (0,u[{\mathcal {U}}_{\varepsilon }^{+}]+\sqrt{-\frac{3}{\Lambda }}\pi )}\int _{\max \{0,v-\sqrt{-\frac{3}{\Lambda }}\pi \}}^{\min \{v,u[{\mathcal {U}}_{\varepsilon }^{+}]\}}r\Big (\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,du<\sigma _{\varepsilon }^{-1}-\delta .\nonumber \\ \end{aligned}$$

(6.60)

Then, we readily infer by continuity (using (6.53) and the fact that $r^{2}T_{\mu \nu }$ and ${\tilde{m}}$ extend continuously on ${\mathcal {I}}_{\varepsilon }$) that there exists some $0<u_{0}^{\prime }<\frac{\sigma _{\varepsilon }^{-2}}{\sqrt{-\Lambda }}-u[{\mathcal {U}}_{\varepsilon }^{+}]$ such that

$$\begin{aligned}{} & {} \sup _{\{0<u<u[{\mathcal {U}}_{\varepsilon }^{+}]+u_{0}^{\prime }\}}\frac{2{\tilde{m}}}{r}(p)<\eta _{0}-\frac{\delta }{2}, \end{aligned}$$

(6.61)

$$\begin{aligned}{} & {} \sup _{\{0<u<u[{\mathcal {U}}_{\varepsilon }^{+}]+u_{0}^{\prime }\}}\int _{u}^{u+\sqrt{-\frac{3}{\Lambda }}\pi }r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,dv<\sigma _{\varepsilon }^{-1}-\frac{\delta }{2}\nonumber \\ \end{aligned}$$

(6.62)

and

$$\begin{aligned}{} & {} \sup _{v\in (0,u[{\mathcal {U}}_{\varepsilon }^{+}]+u_{0}^{\prime }+\sqrt{-\frac{3}{\Lambda }}\pi )}\int _{\max \{0,v-\sqrt{-\frac{3}{\Lambda }}\pi \}}^{\min \{v,u[{\mathcal {U}}_{\varepsilon }^{+}]+u_{0}^{\prime }\}}r\Big (\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,du\nonumber \\{} & {} \quad <\sigma _{\varepsilon }^{-1}-\frac{\delta }{2}. \end{aligned}$$

(6.63)

Then, in view of the definition (6.46) and (6.49) of ${\mathcal {U}}_{\sigma _{\varepsilon }^{-1},\eta _{0}}^{(\varepsilon )}$ and ${\mathcal {U}}_{\varepsilon }^{+}$, as well as assumption (6.54), the bounds (6.61)–(6.63) imply that

$$\begin{aligned} \{0<u<u[{\mathcal {U}}_{\varepsilon }^{+}]+u_{0}^{\prime }\}\subset {\mathcal {U}}_{\varepsilon }^{+}, \end{aligned}$$

which is a contradiction, in view of (6.51). Therefore, 6.55–6.57 hold for ${\mathcal {U}}_{\varepsilon }^{+}$. The proof of the analogous relations for ${\mathcal {T}}_{\varepsilon }^{+}$ follows in exactly the same way. $\square$

For any $\varepsilon \in (0,1]$ and any $0\le i\le N_{\varepsilon }$, we will define $f_{\varepsilon i}$ to be the solution of the Vlasov equation (2.40) on $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2})$ satisfying at $u=0$:

$$\begin{aligned} f_{\varepsilon i}(0,v;p^{u},p^{v},l)=F_{i}^{(\varepsilon )}(v;\text { }\partial _{v}r_{/}^{(\varepsilon )}p^{u},\text { }l)\cdot \delta \Big (\Omega ^{2}(0,v)p^{u}p^{v}-\frac{l^{2}}{r^{2}(0,v)}\Big ),\nonumber \\ \end{aligned}$$

(6.64)

where $F_{i}^{(\varepsilon )}$ is given by (6.7) for $\varepsilon \in (0,\varepsilon _{1}]$, and $F_{i}^{(\varepsilon )}=F_{i}^{(\varepsilon _{1})}$ for $\varepsilon \in (\varepsilon _{1},1]$. Note that, as a consequence of (6.17), the total Vlasov field $f_{\varepsilon }$ is expressed as

$$\begin{aligned} f_{\varepsilon }=\sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}\cdot f_{\varepsilon i}. \end{aligned}$$

(6.65)

We will also define the functions ${\bar{f}}_{\varepsilon }$, ${\bar{f}}_{\varepsilon i}$ on the phase space over ${\mathcal {U}}_{max}^{(\varepsilon )}$, associated to the Vlasov distributions $f_{\varepsilon }$, $f_{\varepsilon i}$, respectively, as in Sect. 2.3, i.e. by the relation

$$\begin{aligned} f_{\varepsilon i}(u,v;p^{u},p^{v},l)\doteq {\bar{f}}_{\varepsilon i}(u,v;p^{u},p^{v},l)\cdot \delta \Big (\Omega ^{2}p^{u}p^{v}-\frac{l^{2}}{r^{2}}\Big ) \end{aligned}$$

(6.66)

and similarly for ${\bar{f}}_{\varepsilon }$, $f_{\varepsilon }$ in place of ${\bar{f}}_{\varepsilon i}$, $f_{\varepsilon i}$. Note that the relation 6.66 uniquely determines ${\bar{f}}_{\varepsilon i}$ only on the shell $\big \{\Omega ^{2}p^{u}p^{v}=\frac{l^{2}}{r^{2}}\big \}$; see Sect. 2.3. As a consequence of the Vlasov equation for (2.40), the functions ${\bar{f}}_{\varepsilon i}$ and ${\bar{f}}_{\varepsilon }$ are conserved along the integral curves of (2.20); since l is a constant of motion for (2.20), we can estimate using the explicit formula (6.7) for $F_{i}^{(\varepsilon )}$ and the bound (6.18) for $\partial _{v}r_{/}^{(\varepsilon )}$:

$$\begin{aligned}&\sup _{(u,v)\in {\mathcal {U}}_{max}^{(\varepsilon )},\text { }p^{u},p^{v}\in (0,+\infty )} \int _{0}^{+\infty }{\bar{f}}_{\varepsilon i}(u,v;p^{u},p^{v},l)|_{\Omega ^{2}p^{u}p^{v}=\frac{l^{2}}{r^{2}}}\,ldl\\&\quad =\sup _{v\in (0,\sqrt{-\frac{3}{\Lambda }}\pi ),\text { }p^{u}\in (0,+\infty )}\int _{0}^{+\infty }F_{i}^{(\varepsilon )}(v;\text { }\partial _{v}r_{/}^{(\varepsilon )}p^{u},\text { }l)\,ldl\le \nonumber \\&\quad \le 16.\nonumber \end{aligned}$$

(6.67)

In view of the formula (6.7) for $F_{i}^{(\varepsilon )}$, the bound (6.18) for $\partial _{v}r_{/}^{(\varepsilon )}$ and the form (6.17) of the initial Vlasov distribution ${\bar{f}}_{/}^{(\varepsilon )}$, we infer that the total renormalised Hawking mass ${\tilde{m}}|_{{\mathcal {I}}_{\varepsilon }}$ of $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ at ${\mathcal {I}}_{\varepsilon }$ (which is conserved, in view of the reflecting boundary condition on ${\mathcal {I}}$; see (2.59)) satisfies

$$\begin{aligned} \sqrt{-\Lambda }{\tilde{m}}|_{{\mathcal {I}}_{\varepsilon }}\sim \sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}\varepsilon ^{(i)}, \end{aligned}$$

(6.68)

where the constants implicit in the $\sim$ notation in (6.68) are independent of $\varepsilon$ and $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$. In particular, in view of (6.5) and the assumption $a_{\varepsilon i}\in [0,\sigma _{\varepsilon })$:

$$\begin{aligned} \sqrt{-\Lambda }{\tilde{m}}|_{{\mathcal {I}}_{\varepsilon }}\le \sigma _{\varepsilon }\varepsilon . \end{aligned}$$

(6.69)

As an immediate consequence of the definition (6.44) and (6.45) of $u_{\eta _{0};\varepsilon }^{+}$ and $u_{\sigma _{\varepsilon }^{-1};\varepsilon }^{\sharp }$, respectively, and the definition (6.49) of ${\mathcal {U}}_{\varepsilon }^{+}$, we can bound for any $\varepsilon \in (0,\varepsilon _{1}]$:

$$\begin{aligned} \sup _{{\mathcal {U}}_{\varepsilon }^{+}}\frac{2{\tilde{m}}}{r}\le \eta _{0}, \end{aligned}$$

(6.70)

$$\begin{aligned}&\sup _{U\ge 0}\int _{\{u=U\}\cap {\mathcal {U}}_{\varepsilon }^{+}}r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(U,v)\,dv\\&\quad +\sup _{V\ge 0}\int _{\{v=V\}\cap {\mathcal {U}}_{\varepsilon }^{+}}r\Big (\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,V)\,du \le 2\sigma _{\varepsilon }^{-1}\nonumber \end{aligned}$$

(6.71)

and

$$\begin{aligned} \sup _{{\mathcal {U}}_{\varepsilon }^{+}}(u+v)\le \frac{2}{\sqrt{-\Lambda }}\sigma _{\varepsilon }^{-2}+\sqrt{-\frac{3}{\Lambda }}\pi . \end{aligned}$$

(6.72)

In particular, integrating the constraint equations (2.45) and (2.45) along lines of the form $v=const$ and $u=const$, respectively, using also the boundary conditions (3.36) and (3.37) for $\partial _{v}r$, $\partial _{u}r$ on ${\mathcal {I}}_{\varepsilon }$ and $\gamma _{{\mathcal {Z}}_{\varepsilon }}$, we can estimate for any $\varepsilon \in (0,\varepsilon _{1}]$

$$\begin{aligned}&\sup _{{\mathcal {U}}_{\varepsilon }^{+}}\Bigg (\Big |\log \Big (\frac{\partial _{v}r}{1-\frac{2m}{r}}\Big )\Big |+\Big |\log \Big (\frac{-\partial _{u}r}{1-\frac{2m}{r}}\Big )\Big |\Bigg )\nonumber \\&\quad \le \big (\sup _{{\mathcal {U}}_{\varepsilon }^{+}}\sqrt{-\Lambda }(u+v)\big )\cdot \Bigg (\sup _{{\bar{v}}\ge 0}\int _{\{v={\bar{v}}\}\cap {\mathcal {U}}_{\varepsilon }^{+}}r\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}(u,{\bar{v}})\,du\\&\qquad +\sup _{{\bar{u}}\ge 0}\int _{\{u={\bar{u}}\}\cap {\mathcal {U}}_{\varepsilon }^{+}}r\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}({\bar{u}},v)\,dv\Bigg )\nonumber \\&\qquad +\sup _{v\in [0,\sqrt{-\frac{3}{\Lambda }}\pi )}\Big |\log \Big (\frac{\partial _{v}r_{/}^{(\varepsilon )}}{1-\frac{1}{3}\Lambda (r_{/}^{(\varepsilon )})^{2}}\Big )\Big |\nonumber \\&\quad \le 5\sigma _{\varepsilon }^{-3}\nonumber \end{aligned}$$

(6.73)

where, in passing from the second to the third line in (6.73), we made use of (6.71), (6.72) and Lemma 6.4. Notice that (6.73) implies, in particular, that

$$\begin{aligned} e^{-\sigma _\varepsilon ^-4} (v-u) \le r(u,v) \le e^{\sigma _\varepsilon ^-4} (v-u) \quad \text {on} \quad {\mathcal {U}}_\varepsilon ^+. \end{aligned}$$

(6.74)

Similarly, the (6.50) of ${\mathcal {T}}_{\varepsilon }^{+}$ yields for any $\varepsilon \in (0,\varepsilon _{1}]$:

$$\begin{aligned} \sup _{{\mathcal {T}}_{\varepsilon }^{+}}\frac{2{\tilde{m}}}{r}\le \eta _{0}, \end{aligned}$$

(6.75)

$$\begin{aligned}&\sup _{U\ge 0}\int _{\{u=U\}\cap {\mathcal {T}}_{\varepsilon }^{+}}r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(U,v)\,dv\\&\quad +\sup _{V\ge 0}\int _{\{v=V\}\cap {\mathcal {T}}_{\varepsilon }^{+}}r\Big (\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,V)\,du \le 2\delta _{\varepsilon }^{-1},\nonumber \end{aligned}$$

(6.76)

$$\begin{aligned} \sup _{{\mathcal {T}}_{\varepsilon }^{+}}(u+v)\le \frac{2}{\sqrt{-\Lambda }}\sigma _{\varepsilon }^{-2}+\sqrt{-\frac{3}{\Lambda }}\pi \end{aligned}$$

(6.77)

and, in analogy to (6.73):

$$\begin{aligned} \sup _{{\mathcal {T}}_{\varepsilon }^{+}}\Bigg (\Big |\log \Big (\frac{\partial _{v}r}{1-\frac{2m}{r}}\Big )\Big |+\Big |\log \Big (\frac{-\partial _{u}r}{1-\frac{2m}{r}}\Big )\Big |\Bigg )\le 5\sigma _{\varepsilon }^{-2}\delta _{\varepsilon }^{-1}\le \delta _{\varepsilon }^{-2}. \end{aligned}$$

(6.78)

6.4 Notational conventions for the beams and their intersection regions

In this Section we will introduce some shorthand notation for regions of the (u, v)-plane which, when intersected with the domain ${\mathcal {U}}_{max}^{(\varepsilon )}$ of the maximal future development of $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )};\sqrt{-\frac{3}{\Lambda }}\pi )$, will contain the support of the Vlasov beams emanating from the initial data on $u=0$.

Fig. 15

Schematic depiction of the domains ${\mathcal {V}}_{i\nwarrow }^{(n)}$ and ${\mathcal {V}}_{i\nearrow }^{(n)}$ for some $\varepsilon >0$ and some $0\le i \le N_{\varepsilon }$. For the definition of $v_{\varepsilon ,i}^{(n)}$, $h_{\varepsilon ,i}$ and $\alpha _{\varepsilon ,i}$, see the relation (6.79)

Using the shorthand notation

$$\begin{aligned} v_{\varepsilon ,i}^{(n)}&\doteq v_{\varepsilon ,i}+n\sqrt{-\frac{3}{\Lambda }}\pi ,\\ h_{\varepsilon ,i}&\doteq e^{\sigma _{\varepsilon }^{-6}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }},\nonumber \\ \beta _{\varepsilon ,i}&\doteq \exp \big (-\exp (\sigma _{\varepsilon }^{-4})\big )\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }},\nonumber \end{aligned}$$

(6.79)

we will define the following “narrow” sets for any $n\in {\mathbb {N}}$, any $\varepsilon \in (0,\varepsilon _{1}]$ and any integer $0\le i\le N_{\varepsilon }$:

$$\begin{aligned} {\mathcal {V}}_{i}^{(n)}\doteq \Big ({\mathcal {V}}_{i\nwarrow }^{(n)}\cup {\mathcal {V}}_{i\nearrow }^{(n)}\Big ), \end{aligned}$$

(6.80)

where (Fig. 15)

$$\begin{aligned} {\mathcal {V}}_{i\nwarrow }^{(n)}&\doteq \Big \{\Big |v-v_{\varepsilon ,i}^{(n)}\Big |\le h_{\varepsilon ,i}\Big \}\cap \Big \{\beta _{\varepsilon ,i}\le v-u\le \sqrt{-\frac{3}{\Lambda }}\pi \Big \},\\ {\mathcal {V}}_{i\nearrow }^{(n)}&\doteq \Big \{\Big |u-v_{\varepsilon ,i}^{(n)}\Big |\le h_{\varepsilon ,i}\Big \}\cap \Big \{\beta _{\varepsilon ,i}\le v-u\le \sqrt{-\frac{3}{\Lambda }}\pi \Big \}.\nonumber \end{aligned}$$

(6.81)

We will also set

$$\begin{aligned} {\mathcal {V}}_{i}\doteq \cup _{n\in {\mathbb {N}}}{\mathcal {V}}_{i}^{(n)}. \end{aligned}$$

Remark

As a consequence of the formula (6.7) for $F_{i}^{(\varepsilon )}$, the definition (6.64) of $f_{\varepsilon i}$ in terms of $F_{i}^{(\varepsilon )}$, the properties of the geodesic flow on AdS spacetime (see the relation A.10 in the Appendix of [43]) and the Cauchy stability statement 3.15 for (2.36)–(2.41), we readily infer that there exists some $C_{\varepsilon }>0$ with $C_{\varepsilon }\xrightarrow {\varepsilon \rightarrow 0}+\infty$ such that the Vlasov beam corresponding to $f_{\varepsilon i}$ is supported in ${\mathcal {V}}_{i}$ in the retarded time interval $0\le u\le C_{\varepsilon }$, i.e.

$$\begin{aligned} supp(f_{\varepsilon i})\cap \Big \{0\le u\le C_{\varepsilon }\Big \}\subset \Big \{(u,v)\in \bigcup _{n\in {\mathbb {N}}}{\mathcal {V}}_{i}^{(n)}\cap {\mathcal {U}}_{max}^{(\varepsilon )}\Big \}. \end{aligned}$$

(6.82)

In Sect. 7.1, we will establish a quantitative refinement of (6.82) (see Lemma 7.1) (Fig. 16).

Fig. 16

Schematic depiction of the intersection domains ${\mathcal {R}}_{i;j}^{(n)}$, ${\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)}$ and ${\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}$ for $i>j$

We will also define the intersection regions ${\mathcal {R}}_{i;j}^{(n)}$ for any $n\in {\mathbb {N}}$ and any integers $0\le i\ne j\le N_{\varepsilon }$ as follows:

$$\begin{aligned} {\mathcal {R}}_{i;j}^{(n)}\doteq {\left\{ \begin{array}{ll} {\mathcal {V}}_{i\nwarrow }^{(n)}\cap {\mathcal {V}}_{j\nearrow }^{(n)}, &{} \text { if }i>j,\\ {\mathcal {V}}_{i\nwarrow }^{(n+1)}\cap {\mathcal {V}}_{j\nearrow }^{(n)}, &{} \text { if }i<j. \end{array}\right. } \end{aligned}$$

(6.83)

The self-intersection regions ${\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)}$ and ${\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}$ will be defined for any $n\in {\mathbb {N}}$ and any $0\le i\le N_{\varepsilon }$ as

$$\begin{aligned} {\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)}\doteq {\mathcal {V}}_{i\nwarrow }^{(n)}\cap {\mathcal {V}}_{i\nearrow }^{(n)} \cap \Big \{ v-u\ge \beta _{\varepsilon ,i}\Big \} \end{aligned}$$

(6.84)

and

$$\begin{aligned} {\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}\doteq {\mathcal {V}}_{i\nwarrow }^{(n+1)}\cap {\mathcal {V}}_{i\nearrow }^{(n)} \cap \Big \{ v-u\le \sqrt{-\frac{3}{\Lambda }}\pi \Big \}. \end{aligned}$$

(6.85)

Remark

Note that the domains ${\mathcal {R}}_{i;j}^{(n)}$, ${\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)}$ and ${\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}$ can be also expressed as

$$\begin{aligned}{} & {} {\mathcal {R}}_{i;j}^{(n)}={\left\{ \begin{array}{ll} [v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}]\times [v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i},v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}], &{} \text { if }i>j,\\ {} [v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}]\times [v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i},v_{\varepsilon ,i}^{(n+1)}+h_{\varepsilon ,i}], &{} \text { if }i<j, \end{array}\right. }\nonumber \\ \end{aligned}$$

(6.86)

$$\begin{aligned}{} & {} {\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)}=[v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i},v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}]\times [v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i},v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}]\cap \big \{ v-u\ge \beta _{\varepsilon ,i}\big \}\nonumber \\ \end{aligned}$$

(6.87)

and

$$\begin{aligned} {\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}{} & {} =[v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i},v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}]\times [v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i},v_{\varepsilon ,i}^{(n+1)}+h_{\varepsilon ,i}]\nonumber \\{} & {} \cap \left\{ v-u\le \sqrt{-\frac{3}{\Lambda }}\pi \right\} . \end{aligned}$$

(6.88)

Fig. 17

Schematic depiction of the crooked lines $\zeta _{\nwarrow }[p]$ and $\zeta _{\nearrow }[p]$ emanating from a point $p\in {\mathcal {U}}^{(\epsilon )}_{max}$. The distance functions $dist_{\nwarrow }[p]$ and $dist_{\nearrow }[p]$ are defined as the infimum of the distance from the axis (measured by $v-u$) of the points on the intersection of the union of the beams ${\mathcal {V}}_{i}^{(n)}$ with $\zeta _{\nwarrow }[p]$ and $\zeta _{\nearrow }[p]$, respectively

For any point $p=({\bar{u}},{\bar{v}})\in {\mathcal {U}}_{max}^{(\varepsilon )}$, we will define the pair of crooked lines $\zeta _{\nwarrow }[p]$ and $\zeta _{\nearrow }[p]$ as follows (Fig. 17):

$$\begin{aligned} \zeta _{\nwarrow }[p]\doteq \bigcup _{k\in {\mathbb {N}}}\Big (\big \{ v={\bar{v}}-k\sqrt{-\frac{3}{\Lambda }}\pi \big \}\cup \big \{ u={\bar{v}}-(k+1)\sqrt{-\frac{3}{\Lambda }}\pi \big \}\Big )\cap {\mathcal {U}}_{max}^{(\varepsilon )}\nonumber \\ \end{aligned}$$

(6.89)

and

$$\begin{aligned} \zeta _{\nearrow }[p]\doteq \bigcup _{k\in {\mathbb {N}}}\Big (\big \{ u={\bar{u}}-k\sqrt{-\frac{3}{\Lambda }}\pi \big \}\cup \big \{ v={\bar{u}}-k\sqrt{-\frac{3}{\Lambda }}\pi \big \}\Big )\cap {\mathcal {U}}_{max}^{(\varepsilon )}.\nonumber \\ \end{aligned}$$

(6.90)

Among other things, the intersection of those lines with $\{u=0\}$ will help us detect the portion of the initial data that will mainly contribute to estimates involving quantities in a neighborhood of a point p, as well as keep track of the interactions of the Vlasov beams arriving at p with the rest of the Vlasov beams emanating from the intitial data. We will also define the following functions on ${\mathcal {U}}_{max}^{(\varepsilon )}$:

$$\begin{aligned} dist_{\nwarrow }[p]\doteq \inf _{\zeta _{\nwarrow }[p]\cap \big (\cup _{n\in {\mathbb {N}}}\cup _{i=0}^{N_{\varepsilon }}{\mathcal {V}}_{i}^{(n)}\big )}(v-u) \end{aligned}$$

(6.91)

and

$$\begin{aligned} dist_{\nearrow }[p]\doteq \inf _{\zeta _{\nearrow }[p]\cap \big (\cup _{n\in {\mathbb {N}}}\cup _{i=0}^{N_{\varepsilon }}{\mathcal {V}}_{i}^{(n)}\big )}(v-u). \end{aligned}$$

(6.92)

Remark

Notice that, if $p\in \cup _{n\in {\mathbb {N}}}{\mathcal {V}}_{i\nwarrow }^{(n)}$, then

$$\begin{aligned} dist_{\nwarrow }[p]=\beta _{\varepsilon ,i}. \end{aligned}$$

(6.93)

Similarly, if $p\in \cup _{n\in {\mathbb {N}}}{\mathcal {V}}_{i\nearrow }^{(n)}$:

$$\begin{aligned} dist_{\nearrow }[p]=\beta _{\varepsilon ,i}. \end{aligned}$$

(6.94)

For any $n\in {\mathbb {N}}$, any $\varepsilon \in (0,\varepsilon _{1}]$ and any integers $0\le i,j\le N_{\varepsilon }$, $i\ne j$, such that ${\mathcal {R}}_{i;j}^{(n)}\subset {\mathcal {U}}_{max}^{(\varepsilon )}$, we will introduce the following quantities related to the energy content of ${\mathcal {V}}_{i\nwarrow }^{(n)}$, ${\mathcal {V}}_{j\nearrow }^{(n)}$ before and after their intersection with the region ${\mathcal {R}}_{i;j}^{(n)}$:

$$\begin{aligned}&{\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j] \nonumber \\&\quad \doteq {\left\{ \begin{array}{ll} {\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}\Big )-{\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}\Big ), \text { if }i>j,\\ {\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n+1)}+h_{\varepsilon ,i}\Big )-{\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i}\Big ), \text { if }i<j, \end{array}\right. } \end{aligned}$$

(6.95)

$$\begin{aligned}&{\mathcal {E}}_{\nwarrow }^{(+)}[n;i,j] \nonumber \\&\quad \doteq {\left\{ \begin{array}{ll} {\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}\Big )-{\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}\Big ), \text { if }i>j,\\ {\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n+1)}+h_{\varepsilon ,i}\Big )-{\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i}\Big ), \text { if }i<j \end{array}\right. } \end{aligned}$$

(6.96)

and

$$\begin{aligned}&{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j] \nonumber \\&\quad \doteq {\left\{ \begin{array}{ll} {\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}\Big )-{\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}\Big ), \text { if }i>j,\\ {\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i}\Big )-{\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i}\Big ), \text { if }i<j, \end{array}\right. } \end{aligned}$$

(6.97)

$$\begin{aligned}&{\mathcal {E}}_{\nearrow }^{(+)}[n;i,j] \nonumber \\&\quad \doteq {\left\{ \begin{array}{ll} {\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}\Big )-{\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}\Big ), \text { if }i>j,\\ {\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n+1)}+h_{\varepsilon ,i}\Big )-{\tilde{m}}_{\varepsilon }\Big (v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j},\text { }v_{\varepsilon ,i}^{(n+1)}+h_{\varepsilon ,i}\Big ), \text { if }i<j, \end{array}\right. } \end{aligned}$$

(6.98)

For any $n\in {\mathbb {N}}$, any $\varepsilon \in (0,\varepsilon _{1}]$ and any integer $0\le i\le N_{\varepsilon }$ such that ${\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)}\subset {\mathcal {U}}_{max}^{(\varepsilon )}$ and ${\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}\subset {\mathcal {U}}_{max}^{(\varepsilon )}$, we will define, respectively,

$$\begin{aligned} {\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;i]\doteq {\tilde{m}}\Big (v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i},\text { }v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}\Big )-0, \end{aligned}$$

(6.99)

and

$$\begin{aligned} {\mathcal {E}}_{{\mathcal {I}}}[n;i]\doteq {\tilde{m}}|_{{\mathcal {I}}_{\varepsilon }}-{\tilde{m}}\Big (v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i},\text { }v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i}\Big ). \end{aligned}$$

(6.100)

Remark

When $i>j$, the quantity ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j]$ measures the energy content of the ingoing beam ${\mathcal {V}}_{i\nwarrow }^{(n)}$ right before entering the region ${\mathcal {R}}_{i;j}^{(n)}$, while ${\mathcal {E}}_{\nwarrow }^{(+)}[n;i,j]$ measures the energy content of ${\mathcal {V}}_{i\nwarrow }^{(n)}$ right after leaving ${\mathcal {R}}_{i;j}^{(n)}$ (when $i<j$, the same holds after replacing ${\mathcal {V}}_{i\nwarrow }^{(n)}$ with ${\mathcal {V}}_{i\nwarrow }^{(n+1)}$). Similarly, ${\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]$ and ${\mathcal {E}}_{\nearrow }^{(+)}[n;i,j]$ measure the energy content of the outgoing beam ${\mathcal {V}}_{j\nearrow }^{(n)}$ right before and right after, respectively, ${\mathcal {R}}_{j;i}^{(n)}$. Finally, ${\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;i]$ measures the energy content of ${\mathcal {V}}_{i}^{(n)}$ measured at the region ${\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)}$, while ${\mathcal {E}}_{{\mathcal {I}}}[n;i]$ measures the energy content of ${\mathcal {V}}_{i}^{(n)}$ at the region ${\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}$. For a schematic depiction of the definition of the above quantities, see Fig. 18.

Fig. 18

The quantities ${\mathcal {E}}_{\nwarrow }^{(\pm )}[n;i,j]$ and ${\mathcal {E}}_{\nearrow }^{(\pm )}[n;i,j]$ measure the energy content of the beams ${\mathcal {V}}_{i\nwarrow }^{(n)}$ (with $n+1$ in place of n when $i<j$) and ${\mathcal {V}}_{j\nearrow }^{(n)}$ right before and right after intersecting the region ${\mathcal {R}}_{i;j}^{(n)}$

For any $n\in {\mathbb {N}}$, any $\varepsilon \in (0,\varepsilon _{1}]$ and any integers $0\le i,j\le N_{\varepsilon }$ such that $i>0$ or $j>0$, we will introduce the following quantities measuring the separation of two successive beams of matter (defined when the corresponding regions of integration lie in the domain ${\mathcal {U}}_{max}^{(\varepsilon )}\cap \big \{\frac{2m}{r}<1\big \}$):

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]&\doteq {\left\{ \begin{array}{ll} \int _{\text { }v_{\varepsilon ,i-1}^{(n)}+(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,i-1}}^{\text { }v_{\varepsilon ,i}^{(n)}-(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,i-1}}\frac{\partial _{v}r}{1-\frac{2m}{r}}(v_{\varepsilon ,j}^{(n)}\pm h_{\varepsilon ,j},v)\,dv, &{} \text { if }i>j,\\ \int _{\text { }v_{\varepsilon ,i-1}^{(n+1)}+(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,i-1}}^{\text { }v_{\varepsilon ,i}^{(n+1)}-(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,i-1}}\frac{\partial _{v}r}{1-\frac{2m}{r}}(v_{\varepsilon ,j}^{(n)}\pm h_{\varepsilon ,j},v)\,dv, &{} \text { if }i\le j, \end{array}\right. } \end{aligned}$$

(6.101)

(well-defined when $i>0$) and

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]&\doteq {\left\{ \begin{array}{ll} \int _{\text { }v_{\varepsilon ,j-1}^{(n)}+(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,j-1}}^{\text { }v_{\varepsilon ,j}^{(n)}-(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,j-1}}\frac{-\partial _{u}r}{1-\frac{2m}{r}}(u,v_{\varepsilon ,i}^{(n)}\pm h_{\varepsilon ,i})\,du, \text { if }i\ge j,\\ \int _{\text { }v_{\varepsilon ,j-1}^{(n)}+(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,j-1}}^{\text { }v_{\varepsilon ,j}^{(n)}-(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,j-1}}\frac{-\partial _{u}r}{1-\frac{2m}{r}}(u,v_{\varepsilon ,i}^{(n+1)}\pm h_{\varepsilon ,i})\,du, \text { if }i<j. \end{array}\right. } \end{aligned}$$

(6.102)

(well-defined when $j>0$) (Fig. 19).

Remark

Notice that, when $\frac{2{\tilde{m}}}{r}\ll 1$ and $\frac{\partial _{v}r}{1-\frac{1}{3}\Lambda r^{2}},\frac{\partial _{u}r}{1-\frac{1}{3}\Lambda r^{2}}\ll \rho _{\varepsilon }^{-\delta }$, in the case when $i=j$ we have

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,i]\sim \max _{{\mathcal {R}}_{i-1;i}^{(n)}}\frac{1}{-\frac{1}{3}\Lambda r} \end{aligned}$$

(6.103)

and

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]\sim \min _{{\mathcal {R}}_{i;i-1}^{(n)}}r. \end{aligned}$$

(6.104)

Fig. 19

In the figure above, we present a schematic depiction of the configuration of neighboring beams when $i\ne j$, using the shorthand notation ${\bar{h}}_{\epsilon ,k}=\rho _{\epsilon }^{-\frac{7}{8}}h_{\epsilon ,k}$. The quantities ${\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j]$ and ${\mathfrak {D}}r_{\nearrow }^{(+)}[n;i,j]$ measure the geometric separation of the beams ${\mathcal {V}}_{j\nearrow }^{(n)}$ and ${\mathcal {V}}_{j-1\nearrow }^{(n)}$ right before and right after their intersection with ${\mathcal {V}}_{i\nwarrow }^{(n)}$ (or ${\mathcal {V}}_{i\nwarrow }^{(n+1)}$, when $i<j$), respectively. Similarly, ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j]$ and ${\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]$ measure the separation of ${\mathcal {V}}_{i\nwarrow }^{(n)}$ and ${\mathcal {V}}_{i-1\nwarrow }^{(n)}$ (or ${\mathcal {V}}_{i\nwarrow }^{(n+1)}$ and ${\mathcal {V}}_{i-1\nwarrow }^{(n+1)}$, when $i<j$) right before and right after their intersection with ${\mathcal {V}}_{j\nearrow }^{(n)}$, respectively

Finally, setting

$$\begin{aligned} {\tilde{h}}_{\varepsilon ,i}&\doteq e^{\delta _{\varepsilon }^{-6}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }},\\ {\tilde{\beta }}_{\varepsilon ,i}&\doteq \exp \big (-\exp (\delta _{\varepsilon }^{-4})\big )\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }},\nonumber \end{aligned}$$

(6.105)

(noting that ${\tilde{h}}_{\varepsilon ,i}$, ${\tilde{\beta }}_{\varepsilon ,i}$ are defined like $h_{\varepsilon ,i}$, $\beta _{\varepsilon ,i}$, albeit with $\delta _{\varepsilon }$ in place of $\sigma _{\varepsilon }$), we will define $\widetilde{{\mathcal {V}}}_{i}^{(n)}$, $\widetilde{{\mathcal {V}}}_{i\nwarrow }^{(n)}$ and $\widetilde{{\mathcal {V}}}_{i\nearrow }^{(n)}$ by (6.80)–(6.81) with ${\tilde{h}}_{\varepsilon ,i}$, ${\tilde{\beta }}_{\varepsilon ,i}$ in place of $h_{\varepsilon ,i}$, $\beta _{\varepsilon ,i}$, i.e.:

$$\begin{aligned} \widetilde{{\mathcal {V}}}_{i}^{(n)}\doteq \Big (\widetilde{{\mathcal {V}}}_{i\nwarrow }^{(n)}\cup \widetilde{{\mathcal {V}}}_{i\nearrow }^{(n)}\Big ), \end{aligned}$$

(6.106)

$$\begin{aligned} \widetilde{{\mathcal {V}}}_{i\nwarrow }^{(n)}&\doteq \Big \{\Big |v-v_{\varepsilon ,i}^{(n)}\Big |\le {\tilde{h}}_{\varepsilon ,i}\Big \}\cap \Big \{{\tilde{\beta }}_{\varepsilon ,i}\le v-u\le \sqrt{-\frac{3}{\Lambda }}\pi \Big \},\\ \widetilde{{\mathcal {V}}}_{i\nearrow }^{(n)}&\doteq \Big \{\Big |u-v_{\varepsilon ,i}^{(n)}\Big |\le {\tilde{h}}_{\varepsilon ,i}\Big \}\cap \Big \{{\tilde{\beta }}_{\varepsilon ,i}\le v-u\le \sqrt{-\frac{3}{\Lambda }}\pi \Big \}.\nonumber \end{aligned}$$

(6.107)

Similarly, we will define $\widetilde{{\mathcal {R}}}_{i;j}^{(n)}$, $\widetilde{{\mathcal {R}}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)}$, $\widetilde{{\mathcal {R}}}_{i;{\mathcal {I}}}^{(n)}$, $\widetilde{{\mathcal {E}}}_{\nwarrow }^{(\pm )}[n;i,j]$, $\widetilde{{\mathcal {E}}}_{\nearrow }^{(\pm )}[n;i,j]$, $\widetilde{{\mathfrak {D}}}r_{\nwarrow }^{(\pm )}[n;i,j]$ and $\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(\pm )}[n;i,j]$ by (6.86), (6.87), (6.88), (6.95)–(6.96), (6.97)–(6.98), (6.101) and (6.102), respectively (i.e. using the same definitions as for ${\mathcal {V}}_{i}^{(n)}$, ${\mathcal {R}}_{i;j}^{(n)}$, ${\mathcal {E}}_{\nwarrow }^{(\pm )}[n;i,j]$, ${\mathcal {E}}_{\nearrow }^{(\pm )}[n;i,j]$, ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]$ and ${\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]$), with ${\tilde{h}}_{\varepsilon ,i}$, ${\tilde{\beta }}_{\varepsilon ,i}$ in place of $h_{\varepsilon ,i}$, $\beta _{\varepsilon ,i}$.

Remark

Note that ${\mathcal {V}}_{i}^{(n)}\subset \widetilde{{\mathcal {V}}}_{i}^{(n)}$, and similarly for ${\mathcal {V}}_{i\nwarrow }^{(n)}$, ${\mathcal {V}}_{i\nearrow }^{(n)}$ and $\widetilde{{\mathcal {V}}}_{i\nwarrow }^{(n)}$, $\widetilde{{\mathcal {V}}}_{i\nearrow }^{(n)}$.

7 First steps for the proof of Theorem 1: beam interactions and energy concentration

This section will constitute the technical core of the proof of Theorem 1. First, in Sect. 7.1, we will obtain estimates controlling the geodesics in the support of the components $f_{\varepsilon i}$ constituting the total Vlasov field $f_{\varepsilon }$ (see the relation (6.65)) in the regions ${\mathcal {U}}_{\varepsilon }^{+},{\mathcal {T}}_{\varepsilon }^{+}\subset {\mathcal {U}}_{max}^{(\varepsilon )}$, showing that the supports of the $f_{\varepsilon i}$’s form a configuration of intersecting beams in physical space. Then, in Sects. 7.2–7.4, we will proceed to establish refined estimates for the exchange of energy occuring at the intersection of any two of those beams, as well as for the change in the geometric separation of the beams over time; these bounds will be used in Sects. 8–9 to show that, provided the initial data parameters $a_{\varepsilon i}$ in (6.17) are chosen appropriately, the total energy of $f_{\varepsilon }$ is eventually concentrated in regions of sufficiently small scale in phase space, resulting in the formation of a trapped sphere.

7.1 Control of the Vlasov beams and the spacetime geometry away from the trapped region

The following lemma will allow us to control the support of the Vlasov beams $f_{\varepsilon i}$ in the regions ${\mathcal {U}}_{\varepsilon }^{+}$ and ${\mathcal {T}}_{\varepsilon }^{+}$ introduced in Sect. 6.3.

Lemma 7.1

For any $\varepsilon \in (0,\varepsilon _{1}]$ and any $0\le i\le N_{\varepsilon }$, the support of the Vlasov field $f_{\varepsilon i}=f_{\varepsilon i}(u,v;p^{u},p^{v},l)$ on ${\mathcal {U}}_{\varepsilon }^{+}$ satisfies

$$\begin{aligned}{} & {} supp(f_{\varepsilon i})\cap \big \{(u,v)\in {\mathcal {U}}_{\varepsilon }^{+}\big \}\subset \Big \{(u,v)\in {\mathcal {V}}_{i}\Big \}\nonumber \\{} & {} \quad \cap \Big \{\exp (-\sigma _{\varepsilon }^{-6})\le \Omega ^{2}(p^{u}+p^{v})\le \exp \big (\exp (\sigma _{\varepsilon }^{-4})\big )\Big \}, \end{aligned}$$

(7.1)

where the regions ${\mathcal {V}}_{i}=\cup _{n}{\mathcal {V}}_{i}^{(n)}$ in the (u, v)-plane are defined by (6.80). Furthermore, if $\gamma \subset {\mathcal {U}}_{\varepsilon }^{+}$ is a future directed, affinely parametrised null geodesic in the support of $f_{\varepsilon i}$ which is maximally extended through reflections off ${\mathcal {I}}$ (see Definition 2.3 in [43], or Corollary 5.2) and p is any point on $\gamma$, then:

$$\begin{aligned} \frac{{\dot{\gamma }}^{v}}{{\dot{\gamma }}^{u}}\Big |_{p}\le \exp \big (\exp (\sigma _{\varepsilon }^{-4})\big )l^{2}\frac{1-\frac{1}{3}\Lambda r^{2}}{r^{2}}\Big |_{p}\text { if }p\in \cup _{n\in {\mathbb {N}}}{\mathcal {V}}_{i\nwarrow }^{(n)} \end{aligned}$$

(7.2)

and

$$\begin{aligned} \frac{{\dot{\gamma }}^{u}}{{\dot{\gamma }}^{v}}\Big |_{p}\le \exp \big (\exp (\sigma _{\varepsilon }^{-4})\big )l^{2}\frac{1-\frac{1}{3}\Lambda r^{2}}{ r^{2}}\Big |_{p}\text { if }p\in \cup _{n\in {\mathbb {N}}}{\mathcal {V}}_{i\nearrow }^{(n)}, \end{aligned}$$

(7.3)

where l is the angular momentum of $\gamma$.

Similarly, on ${\mathcal {T}}_{\varepsilon }^{+}$, the support of $f_{\varepsilon i}$ satisfies

$$\begin{aligned}{} & {} supp(f_{\varepsilon i})\cap \big \{(u,v)\in {\mathcal {T}}_{\varepsilon }^{+}\big \}\subset \Big \{(u,v)\in \widetilde{{\mathcal {V}}}_{i}\Big \}\nonumber \\{} & {} \quad \cap \Big \{\exp (-\delta _{\varepsilon }^{-6})\le \Omega ^{2}(p^{u}+p^{v})\le \exp \big (\exp (\delta _{\varepsilon }^{-4})\big )\Big \}, \end{aligned}$$

(7.4)

Furthermore, if $\gamma \subset {\mathcal {T}}_{\varepsilon }^{+}$ is a future directed, affinely parametrised null geodesic in the support of $f_{\varepsilon i}$ which is maximally extended through reflections and p is any point on $\gamma$, then (7.2)–(7.3) hold with $\delta _{\varepsilon }$ in place of $\sigma _{\varepsilon }$.

Remark

The bound (7.1) implies that the domains ${\mathcal {V}}_{i}$ (or $\widetilde{{\mathcal {V}}}_{i}$, in the case of (7.4)) strictly contain the Vlasov beams $\zeta _{i}$ appearing in the discussion of Sect. 1.2.

Proof

The proof of Lemma (7.1) will be a simple consequence of Corollary 5.2. In particular, let $\gamma \subset {\mathcal {U}}_{\varepsilon }^{+}$ is a future directed, affinely parametrised null geodesic in the support of $f_{\varepsilon i}$ which is maximally extended through reflections. Setting

$$\begin{aligned}{} & {} C_{0}\doteq 5\sigma _{\varepsilon }^{-3}, \end{aligned}$$

(7.5)

$$\begin{aligned}{} & {} v_{{\mathcal {I}}}\doteq \sqrt{-\frac{3}{\Lambda }}\pi \end{aligned}$$

(7.6)

and

$$\begin{aligned} U\doteq \sup _{{\mathcal {U}}_{\varepsilon }^{+}}u, \end{aligned}$$

(7.7)

we readily observe the following:

• Using the definition (6.49) of ${\mathcal {U}}_{\varepsilon }^{+}$, we can readily bound

  $$\begin{aligned} U\le \frac{\sigma _{\varepsilon }^{-2}}{\sqrt{-\Lambda }}. \end{aligned}$$

  (7.8)

• The bound (5.2) holds on ${\mathcal {U}}_{\varepsilon }^{+}\doteq {\mathcal {U}}_{U;v_{{\mathcal {I}}}}$, in view of (6.70) (using also the assumption that $\eta _{0}<\delta _{0}$). Moreover, the bound (5.1) follows from (7.8) and the estimate (6.73), assuming that $\varepsilon _{1}$ has been fixed small enough.

• As a consequence of the expression (6.7) for $F_{i}^{(\varepsilon )}$ and the relation (6.64) between $F_{i}^{(\varepsilon )}$ and $f_{\varepsilon i}$ (using also the bound (6.18) for $\partial _{v}r_{/}^{(\varepsilon )}$ in (6.64)), we can estimate for the angular momentum l and the initial energy $E_{0}$ of $\gamma$ (defined by (5.5)) that

  $$\begin{aligned} \frac{1}{10}\varepsilon ^{(i)}\le \sqrt{-\Lambda }l\le 10\varepsilon ^{(i)} \end{aligned}$$

  and

  $$\begin{aligned} \frac{1}{10}\le E_{0}\le 10, \end{aligned}$$

  as well as

  $$\begin{aligned} \frac{{\dot{\gamma }}^{v}}{{\dot{\gamma }}^{u}}\Big |_{u=0}<1. \end{aligned}$$

  Therefore, $\gamma$ satisfies the conditions (5.3), (5.6) and (5.54).

Hence, the conditions of Corollary 5.2 are satisfied for $\gamma$, provided $\varepsilon _{1}$ is chosen smaller than some absolute constant. As a result, (7.1) follows readily from (5.55) and (5.58), while (7.2) and (7.3) follow from 5.59–5.60.

The corresponding statements for $\gamma \subset {\mathcal {T}}_{\varepsilon }^{+}$ follow by exactly the same arguments, after replacing $\sigma _{\varepsilon }$ with $\delta _{\varepsilon }$ in (7.5) and using (6.78) in place of (6.73). $\square$

The following Lemma will allow us to control various quantities related to the geometry of $({\mathcal {U}}_{\varepsilon }^{+};r,\Omega ^{2})$ and $({\mathcal {T}}_{\varepsilon }^{+};r,\Omega ^{2})$, some of which are of higher regularity than that controlled by the norm 3.60. Effective control on such quantities will be obtained through the quantitative estimates provided by Lemma 7.1 on the support of the Vlasov fields $f_{\varepsilon i}$.

Lemma 7.2

For any $\varepsilon \in (0,\varepsilon _{1}]$ and any $0\le i\le N_{\varepsilon }$, the following estimate holds on ${\mathcal {U}}_{\varepsilon }^{+}$:

$$\begin{aligned} \Big |\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )\Big |\le 10\sigma _{\varepsilon }^{-3}, \end{aligned}$$

(7.9)

while the following estimates hold in the regions $\cup _{k\in {\mathbb {N}}}{\mathcal {V}}_{i}^{(k)}\cap {\mathcal {U}}_{\varepsilon }^{+}$:

$$\begin{aligned} \inf _{{\mathcal {V}}_{i}\cap {\mathcal {U}}_{\varepsilon }^{+}}r\ge \exp \big (-2\exp (\sigma _{\varepsilon }^{-4})\big )\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}, \end{aligned}$$

(7.10)

$$\begin{aligned} {\left\{ \begin{array}{ll} r^{2}T_{vv}[f_{\varepsilon i}](u,v)\le \exp \big (\exp (\sigma _{\varepsilon }^{-5})\big ), &{} \text {and}\\ r^{2}T_{uu}[f_{\varepsilon i}](u,v)\le \exp \big (\exp (2\sigma _{\varepsilon }^{-5})\big )\frac{(\varepsilon ^{(i)})^{4}}{r^{4}(u,v)}(-\Lambda )^{-2}, &{} \text { if }(u,v)\in \cup _{n\in {\mathbb {N}}}{\mathcal {V}}_{i\nwarrow }^{(n)}, \end{array}\right. }\nonumber \\ {\left\{ \begin{array}{ll} r^{2}T_{uu}[f_{\varepsilon i}](u,v)\le \exp \big (\exp (\sigma _{\varepsilon }^{-5})\big ), &{} \text {and}\\ r^{2}T_{vv}[f_{\varepsilon i}](u,v)\le \exp \big (\exp (2\sigma _{\varepsilon }^{-5})\big )\frac{(\varepsilon ^{(i)})^{4}}{r^{4}(u,v)}(-\Lambda )^{-2}, &{} \text { if }(u,v)\in \cup _{n\in {\mathbb {N}}}{\mathcal {V}}_{i\nearrow }^{(n)}, \end{array}\right. } \end{aligned}$$

(7.11)

and

$$\begin{aligned} r^{2}T_{uv}[f_{\varepsilon i}](u,v)\le \exp \big (\exp (\sigma _{\varepsilon }^{-5})\big )\cdot \frac{(\varepsilon ^{(i)})^{2}}{r^{2}(u,v)}(-\Lambda )^{-1}. \end{aligned}$$

(7.12)

Furthermore, we can estimate

$$\begin{aligned}&\sup _{(u,v)\in {\mathcal {U}}_{\varepsilon }^{+}}\Big |dist_{\nwarrow }[(u,v)]\cdot \partial _{v}\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )(u,v)\Big |\\&\quad +\sup _{(u,v)\in {\mathcal {U}}_{\varepsilon }^{+}}\Big |dist_{\nearrow }[(u,v)]\cdot \partial _{u}\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )(u,v)\Big |\le \exp \big (\exp (\sigma _{\varepsilon }^{-5})\big )\nonumber \end{aligned}$$

(7.13)

and

$$\begin{aligned}&\sup _{(u,v)\in {\mathcal {U}}_{\varepsilon }^{+}}\Big |dist_{\nwarrow }[(u,v)]\cdot \partial _{v}\Big (\frac{\partial _{v}r}{1-\frac{1}{3}\Lambda r^{2}}\Big )(u,v)\Big |\\&\quad +\sup _{(u,v)\in {\mathcal {U}}_{\varepsilon }^{+}}\Big |dist_{\nearrow }[(u,v)]\cdot \partial _{u}\Big (\frac{\partial _{u}r}{1-\frac{1}{3}\Lambda r^{2}}\Big )(u,v)\Big |\le \exp \big (\exp (\sigma _{\varepsilon }^{-5})\big ),\nonumber \end{aligned}$$

(7.14)

where the functions $dist_{\nwarrow }[\cdot ]$ and $dist_{\nearrow }[\cdot ]$ are defined by (6.91) and (6.92). Moreover, for any $n\in {\mathbb {N}}$ and $0\le i,j\le N_{\varepsilon }$, $i\ne j$, such that ${\mathcal {R}}_{i;j}^{(n)}\subset {\mathcal {U}}_{+}^{(\varepsilon )}$, the following estimates hold on ${\mathcal {R}}_{i;j}^{(n)}$, depending on whether $i>j$ or $i<j$:

• In the case $i>j$,

  $$\begin{aligned} \exp (-\sigma _{\varepsilon }^{-7})\rho _{\varepsilon }^{-1}\le \frac{\sqrt{-\Lambda }r|_{{\mathcal {R}}_{i;j}^{(n)}}}{\varepsilon ^{(j)}}\le \exp (\sigma _{\varepsilon }^{-7})\rho _{\varepsilon }^{-1} \end{aligned}$$

  (7.15)

  and

  $$\begin{aligned} \sup _{{\mathcal {R}}_{i;j}^{(n)}}r-\inf _{{\mathcal {R}}_{i;j}^{(n)}}r\le \frac{\exp (\sigma _{\varepsilon }^{-7})}{\sqrt{-\Lambda }}\varepsilon ^{(j)}. \end{aligned}$$

  (7.16)

• In the case $i<j$,

  $$\begin{aligned} \exp (-\sigma _{\varepsilon }^{-4})\rho _{\varepsilon }\frac{1}{\varepsilon ^{(i)}}\le \sqrt{-\Lambda }r|_{{\mathcal {R}}_{i;j}^{(n)}}\le \exp (\sigma _{\varepsilon }^{-4})\rho _{\varepsilon }\frac{1}{\varepsilon ^{(i)}} \end{aligned}$$

  (7.17)

  and

  $$\begin{aligned} \sup _{{\mathcal {R}}_{i;j}^{(n)}}\frac{1}{r}-\inf _{{\mathcal {R}}_{i;j}^{(n)}}\frac{1}{r}\le \exp (\sigma _{\varepsilon }^{-7})\sqrt{-\Lambda }\varepsilon ^{(i)}. \end{aligned}$$

  (7.18)

Replacing ${\mathcal {U}}_{\varepsilon }^{+}$ with ${\mathcal {T}}_{\varepsilon }^{+}$, the estimates (7.9)–(7.18) still hold with $\delta _{\varepsilon }$ in place of $\sigma _{\varepsilon }$, $\widetilde{{\mathcal {V}}}_{i}^{(n)}$ in place of ${\mathcal {V}}_{i}^{(n)}$ and $\widetilde{{\mathcal {R}}}_{i;j}^{(n)}$ in place of ${\mathcal {R}}_{i;j}^{(n)}$.

Remark

Note that, in view of the relations (6.93) and (6.94), the estimates (7.13) and (7.14) yield, as a special case, that, for any $0\le i\le N_{\varepsilon }$:

$$\begin{aligned}{} & {} \sup _{\cup _{k\in {\mathbb {N}}}{\mathcal {V}}_{i\nwarrow }^{(k)}\cap {\mathcal {U}}_{\varepsilon }^{+}}\Big |\partial _{v}\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )\Big |+\sup _{\cup _{k\in {\mathbb {N}}}{\mathcal {V}}_{i\nearrow }^{(k)}\cap {\mathcal {U}}_{\varepsilon }^{+}}\Big |\partial _{u}\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )\Big |\nonumber \\{} & {} \quad \le \exp \big (2\exp (\sigma _{\varepsilon }^{-5})\big )\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}} \end{aligned}$$

(7.19)

and

$$\begin{aligned}{} & {} \sup _{\cup _{k\in {\mathbb {N}}}{\mathcal {V}}_{i\nwarrow }^{(k)}\cap {\mathcal {U}}_{\varepsilon }^{+}}\Big |\partial _{v}\Big (\frac{\partial _{v}r}{1-\frac{1}{3}\Lambda r^{2}}\Big )\Big |+\sup _{\cup _{k\in {\mathbb {N}}}{\mathcal {V}}_{i\nearrow }^{(k)}\cap {\mathcal {U}}_{\varepsilon }^{+}}\Big |\partial _{u}\Big (\frac{\partial _{u}r}{1-\frac{1}{3}\Lambda r^{2}}\Big )\Big |\nonumber \\{} & {} \quad \le \exp \big (2\exp (\sigma _{\varepsilon }^{-5})\big )\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}} \end{aligned}$$

(7.20)

Notice that the left hand sides of (7.19) and (7.20) are not estimated by the low regularity norm (3.60). This loss of regularity is reflected in the fact that the right hand sides of (7.19) and (7.20) can not be bounded merely by terms of the form $(\exp (\exp (\sigma _{\varepsilon }^{-C}))$, but have additional $(\varepsilon ^{(i)})^{-1}$ terms which, in these cases, are optimal.

Proof

Let $\varepsilon \in (0,\varepsilon _{1}]$ and let $0\le i\le N_{\varepsilon }$. In view of the formula (2.9) and the bound (6.70) for $2{\tilde{m}}/r$, the estimate (6.73) readily implies (7.9).

Using the fact that

$$\begin{aligned} \inf _{{\mathcal {V}}_{i}}(v-u)=\exp \big (-\exp (\sigma _{\varepsilon }^{-4})\big )\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }} \end{aligned}$$

(following from the definition of (6.81)${\mathcal {V}}_{i\nwarrow }^{(n)},{\mathcal {V}}_{i\nearrow }^{(n)}$), the lower bound (7.10) for r follows readily after integrating $(\partial _{v}-\partial _{u})r$ in $\partial _{v}-\partial _{u}$ starting from $\gamma _{{\mathcal {Z}}_{\varepsilon }}$ and using the bound (6.73).

The estimates (7.11) and (7.12) for $T_{\mu \nu }[f_{\varepsilon i}]$ follow readily from the explicit formulas (2.30) for $T_{\mu \nu }[f_{\varepsilon i}]$, the estimates (7.1) and (7.2)–(7.3) for the support of $f_{\varepsilon i}$ in $p^{u}$, $p^{v}$, the fact that $f_{\varepsilon i}$ is supported on $\{2\le \frac{l\sqrt{-\Lambda }}{\varepsilon ^{(i)}}\le 6\}$ (in view of (6.7) and (6.64)), the bound (6.67), and the bounds (6.73), (7.9).

For any $({\bar{u}},{\bar{v}})\in {\mathcal {U}}_{\varepsilon }^{+}$, integrating the renormalised equation (2.57) for $\Omega$ in u along $\zeta _{\nwarrow }[({\bar{u}},{\bar{v}})]$ and in v along $\zeta _{\nearrow }[({\bar{u}},{\bar{v}})]$ (see (6.89) and (6.90) for the definition of $\zeta _{\nwarrow }[\cdot ]$ and $\zeta _{\nearrow }[\cdot ]$), making use of the boundary conditions (3.38)–(3.39) for $\Omega ^{2}$ at $\gamma _{{\mathcal {Z}}}$, ${\mathcal {I}}_{\varepsilon }$, we infer that:

$$\begin{aligned}&\Big |\partial _{v} \log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )({\bar{u}},{\bar{v}})\Big |\\&\quad \le \int _{\zeta _{\nwarrow }[({\bar{u}},{\bar{v}})]}\Big (\frac{{\tilde{m}}}{r}\Big (\frac{1}{r^{2}}+\frac{1}{3}\Lambda \frac{\Lambda r^{2}-1}{1-\frac{1}{3}\Lambda r^{2}}\Big )\cdot \frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\nonumber \\&\qquad -16\pi \frac{1-\frac{1}{2}\Lambda r^{2}}{1-\frac{1}{3}\Lambda r^{2}}\frac{1}{r^{2}}(r^{2}T_{uv}[f_{\varepsilon }])\Big )\,d(u+v)\nonumber \\&\qquad +\Big |\partial _{v}\log \Big (\frac{(\Omega _{/}^{(\varepsilon )})^{2}}{1-\frac{1}{3}\Lambda (r_{/}^{(\varepsilon )})^{2}}\Big )\Big |\Bigg |_{\{u=0\}\cap \zeta _{\nwarrow }[({\bar{u}},{\bar{v}})]}\nonumber \end{aligned}$$

(7.21)

and

$$\begin{aligned}&\Big |\partial _{u} \log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )({\bar{u}},{\bar{v}})\Big |\\&\quad \le \int _{\zeta _{\nearrow }[({\bar{u}},{\bar{v}})]}\Big (\frac{{\tilde{m}}}{r}\Big (\frac{1}{r^{2}}+\frac{1}{3}\Lambda \frac{\Lambda r^{2}-1}{1-\frac{1}{3}\Lambda r^{2}}\Big )\cdot \frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\nonumber \\&\qquad -16\pi \frac{1-\frac{1}{2}\Lambda r^{2}}{1-\frac{1}{3}\Lambda r^{2}}\frac{1}{r^{2}}(r^{2}T_{uv}[f_{\varepsilon }])\Big )\,d(u+v)\nonumber \\&\qquad +\Big |\partial _{v}\log \Big (\frac{(\Omega _{/}^{(\varepsilon )})^{2}}{1-\frac{1}{3}\Lambda (r_{/}^{(\varepsilon )})^{2}}\Big )\Big |\Bigg |_{\{u=0\}\cap \zeta _{\nearrow }[({\bar{u}},{\bar{v}})]}.\nonumber \end{aligned}$$

(7.22)

Making use of the following:

• The bounds (6.70) and (6.72) for $2{\tilde{m}}/r$ and $\sqrt{-\Lambda }(u+v)$ (the latter estimating the number of straight segments contained in $\zeta _{\nwarrow }[({\bar{u}},{\bar{v}})]$ and $\zeta _{\nearrow }[({\bar{u}},{\bar{v}})]$),

• The bounds (6.73) and (7.9) for $\frac{\partial _{v}r}{1-\frac{1}{3}\Lambda r^{2}}$, $\frac{\partial _{u}r}{1-\frac{1}{3}\Lambda r^{2}}$ and $\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}$

• The bound

  $$\begin{aligned} r^{2}T_{uv}[f_{\varepsilon }]\le \frac{1}{2\pi }\frac{-\partial _{u}r}{1-\frac{2m}{r}}\partial _{v}{\tilde{m}}\text { and }r^{2}T_{uv}[f_{\varepsilon }]\le \frac{1}{2\pi }\frac{\partial _{v}r}{1-\frac{2m}{r}}(-\partial _{u}{\tilde{m}})\qquad \end{aligned}$$

  (7.23)

  (following from (2.49)–(2.48))

• The fact that the support of ${\tilde{m}}|_{\zeta _{\nwarrow }[({\bar{u}},{\bar{v}})]}$, $T_{\mu \nu }|_{\zeta _{\nwarrow }[({\bar{u}},{\bar{v}})]}$ is contained in $\{v-u\ge dist_{\nwarrow }[({\bar{u}},{\bar{v}})]\}$ (and similarly for $\zeta _{\nearrow }[({\bar{u}},{\bar{v}})]$),

• The trivial estimates

  $$\begin{aligned}&\sup _{0\le {\hat{u}}\le {\bar{u}}}\int _{\{u={\hat{u}}\}\cap \{v-u\ge dist_{\nwarrow }[({\bar{u}},{\bar{v}})]\}}\frac{1}{r^{2}}(\partial _{v}r)\,dv\\&\quad +\sup _{0\le {\hat{v}}\le {\bar{v}}}\int _{\{v={\hat{v}}\}\cap \{v-u\ge dist_{\nwarrow }[({\bar{u}},{\bar{v}})]\}} \frac{1}{r^{2}}(-\partial _{u}r)\,du\le e^{\sigma _{\varepsilon }^{-4}}\frac{1}{dist_{\nwarrow }[({\bar{u}},{\bar{v}})]}\nonumber \end{aligned}$$

  (7.24)

  and

  $$\begin{aligned}&\sup _{0\le {\hat{u}}\le {\bar{u}}}\int _{\{u={\hat{u}}\}\cap \{v-u\ge dist_{\nearrow }[({\bar{u}},{\bar{v}})]\}}\frac{1}{r^{2}}(\partial _{v}r)\,dv\\&\quad +\sup _{0\le {\hat{v}}\le {\bar{v}}}\int _{\{v={\hat{v}}\}\cap \{v-u\ge dist_{\nearrow }[({\bar{u}},{\bar{v}})]\}} \frac{1}{r^{2}}(-\partial _{u}r)\,du\le e^{\sigma _{\varepsilon }^{-4}}\frac{1}{dist_{\nearrow }[({\bar{u}},{\bar{v}})]}\nonumber \end{aligned}$$

  (7.25)

  (following from (6.73)),

• The initial data estimates (6.18) and (6.19) for $\partial _{v}\log \Big (\frac{(\Omega _{/}^{(\varepsilon )})^{2}}{1-\frac{1}{3}\Lambda (r_{/}^{(\varepsilon )})^{2}}\Big )$,

we infer from (7.21)–(7.22) that

$$\begin{aligned} \Big |\partial _{v}\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )({\bar{u}},{\bar{v}})\Big |\le e^{2\sigma _{\varepsilon }^{-4}}\frac{1}{dist_{\nwarrow }[({\bar{u}},{\bar{v}})]}+C\sqrt{-\Lambda } \end{aligned}$$

(7.26)

and

$$\begin{aligned} \Big |\partial _{u}\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )({\bar{u}},{\bar{v}})\Big |\le e^{2\sigma _{\varepsilon }^{-4}}\frac{1}{dist_{\nearrow }[({\bar{u}},{\bar{v}})]}+C\sqrt{-\Lambda }. \end{aligned}$$

(7.27)

The bound (7.13) follows readily from (7.26)–(7.27).

The constraint equations (2.39) and (2.38) imply that

$$\begin{aligned} \partial _{v}\Big (\frac{\partial _{v}r}{1-\frac{1}{3}\Lambda r^{2}}\Big )=\partial _{v}\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )\cdot \frac{\partial _{v}r}{1-\frac{1}{3}\Lambda r^{2}}-\frac{4\pi }{1-\frac{1}{3}\Lambda r^{2}}\frac{1}{r}\cdot r^{2}T_{vv}[f_{\varepsilon }]\nonumber \\ \end{aligned}$$

(7.28)

and

$$\begin{aligned} \partial _{u}\Big (\frac{\partial _{u}r}{1-\frac{1}{3}\Lambda r^{2}}\Big )=\partial _{u}\log \Big (\frac{\Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}\Big )\cdot \frac{\partial _{u}r}{1-\frac{1}{3}\Lambda r^{2}}-\frac{4\pi }{1-\frac{1}{3}\Lambda r^{2}}\frac{1}{r}\cdot r^{2}T_{uu}[f_{\varepsilon }].\nonumber \\ \end{aligned}$$

(7.29)

The estimate (7.14) is obtained readily from the relations (7.28)–(7.29), the bound (7.13) for $\frac{\partial \Omega ^{2}}{1-\frac{1}{3}\Lambda r^{2}}$, the bound (6.73) for $\frac{\partial r}{1-\frac{1}{3}\Lambda r^{2}}$, the bounds (7.11) for $f_{\varepsilon i}$, the fact that $T_{\mu \nu }[f_{\varepsilon }]$ is supported only on $\cup _{i=0}^{N_{\varepsilon }}{\mathcal {V}}_{i}$ and the trivial estimate

$$\begin{aligned}&\sup _{(u,v)\in \cup _{n\in {\mathbb {N}}}\cup _{i=0}^{N_{\varepsilon }}{\mathcal {V}}_{i}^{(n)}}\Big (\frac{\max \{dist_{\nwarrow }[(u,v)],\text { }dist_{\nearrow }[(u,v)]\}}{r(u,v)}\Big )\\&\quad \le e^{\sigma _{\varepsilon }^{-4}}\sup _{(u,v)\in \cup _{n\in {\mathbb {N}}}\cup _{i=0}^{N_{\varepsilon }}{\mathcal {V}}_{i}^{(n)}}\Big (\frac{\max \{dist_{\nwarrow }[(u,v)],\text { }dist_{\nearrow }[(u,v)]\}}{v-u}\Big )\le e^{\sigma _{\varepsilon }^{-4}} \end{aligned}$$

(following from the bound (6.74) and the definition (6.91), (6.92) of $dist_{\nwarrow }[\cdot ]$, $dist_{\nearrow }[\cdot ]$).

Finally, let $n\in {\mathbb {N}}$ and $0\le i,j\le N_{\varepsilon }$, $i\ne j$, be such that ${\mathcal {R}}_{i;j}^{(n)}\subset {\mathcal {U}}_{+}^{(\varepsilon )}$. In view of the form (6.86) of ${\mathcal {R}}_{i;j}^{(n)}$, we infer the following:

• In the case $i>j$, integrating $(\partial _{v}-\partial _{u})r$ in $\partial _{v}-\partial _{u}$ from $(\frac{u+v}{2},\frac{u+v}{2})\in \gamma _{{\mathcal {Z}}_{\varepsilon }}$ up to $(u,v)\in {{\mathcal {R}}}_{i;j}^{(n)}$, using the bound (6.73) and the formulas (6.8) and (6.79) for $v_{i,\varepsilon }$ and $v_{i,\varepsilon }^{(n)}$, we obtain (7.15) and (7.16).

• In the case $i<j$, arguing similarly but integrating $(\partial _{v}-\partial _{u})\frac{1}{r}$ in $\partial _{v}-\partial _{u}$ from $(\frac{u+v}{2}-\frac{1}{2}\sqrt{-\frac{3}{\Lambda }}\pi ,\frac{u+v}{2}+\frac{1}{2}\sqrt{-\frac{3}{\Lambda }}\pi )\in {\mathcal {I}}_{\varepsilon }$ up to $(u,v)\in {{\mathcal {R}}}_{i;j}^{(n)}$, we obtain (7.17) and (7.18).

The proof of the analogous estimates for ${\mathcal {T}}_{\varepsilon }^{+}$ in place of ${\mathcal {U}}_{\varepsilon }^{+}$ (with $\delta _{\varepsilon }$, $\widetilde{{\mathcal {V}}}_{i}^{(n)}$, $\widetilde{{\mathcal {R}}}_{i;j}^{(n)}$ replacing $\sigma _{\varepsilon }$, ${\mathcal {V}}_{i}^{(n)}$, ${\mathcal {R}}_{i;j}^{(n)}$) follows in exactly the same way, using (6.78) in place of (6.73). $\square$

7.2 Interaction of the Vlasov beams: energy exchange and concentration

In this section, we will establish a number of results providing quantitative bounds on the change of the energy content (as measured by (6.95)–(6.98)) and the geometric separation (as measured by (6.101)–(6.102)) of the beams ${\mathcal {V}}_{i}^{(n)}$, before and after their pairwise intersections. As a corollary of these technical bounds, we will be able to estimate the total change of the energy content and the separation of the beams after each successive reflection off ${\mathcal {I}}_{\varepsilon }$ in the next section (see Proposition 7.6).

The next result provides an estimate for the change of the energy content of the beams ${\mathcal {V}}_{j\nearrow }^{(n)}$ and ${\mathcal {V}}_{i\nwarrow }^{(n)}$ (or ${\mathcal {V}}_{i\nwarrow }^{(n+1)}$, if $i<j$) before and after their intersection (recall the definition (6.1) of the hierarchy of parameters $\rho _{\varepsilon }, \delta _\varepsilon , \sigma _\varepsilon$).

Proposition 7.3

Let $\varepsilon \in (0,\varepsilon _{1}]$ and let $n\in {\mathbb {N}}$ and $0\le i,j\le N_{\varepsilon }$, $i\ne j$, be such that

$$\begin{aligned} {\mathcal {R}}_{i;j}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}. \end{aligned}$$

Let us also define

$$\begin{aligned} r_{n;i,j}\doteq \inf _{{\mathcal {R}}_{i;j}^{(n)}}r. \end{aligned}$$

(7.30)

Then the following relations hold for the change of the energy of the two Vlasov beams entering and leaving the intersection region ${\mathcal {R}}_{i;j}^{(n)}$:

• If $i>j$, then

  $$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(+)}[n;i,j]&={\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j]\cdot \exp \Big (\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+O(\rho _{\varepsilon }^{\frac{3}{2}})\Big )\nonumber \\&\quad +O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ), \end{aligned}$$

  (7.31)
  $$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(+)}[n;i,j]&={\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]\cdot \big (1+O(\varepsilon )\big )+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big ). \end{aligned}$$

  (7.32)

• If $i<j$, then

  $$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(+)}[n;i,j]&={\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j]\cdot \big (1+O(\varepsilon )\big )+O\Big (\varepsilon \frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ), \end{aligned}$$

  (7.33)
  $$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(+)}[n;i,j]&={\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]\cdot \big (1+O(\varepsilon )\big )+O\Big (\varepsilon \frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big ). \end{aligned}$$

  (7.34)

In the case when $\widetilde{{\mathcal {R}}}_{i;j}^{(n)}\subset {\mathcal {T}}_{\varepsilon }^{+}$, the relations (7.31)–(7.34) also hold for $\widetilde{{\mathcal {E}}}_{\nwarrow }^{(\pm )}[n;i,j]$, $\widetilde{{\mathcal {E}}}_{\nearrow }^{(\pm )}[n;i,j]$ in place of ${\mathcal {E}}_{\nwarrow }^{(\pm )}[n;i,j]$, ${\mathcal {E}}_{\nearrow }^{(\pm )}[n;i,j]$.

Proof

For the purpose of simplifying the expressions appearing in the proof of Proposition 7.3, let us introduce the shorthand notation

$$\begin{aligned} v_{n;i,j}^{(\pm )}&={\left\{ \begin{array}{ll} v_{\varepsilon ,i}^{(n)}\pm h_{\varepsilon ,i}, &{} \text { if }i>j,\\ v_{\varepsilon ,i}^{(n+1)}\pm h_{\varepsilon ,i} &{} \text { if }i<j, \end{array}\right. } \end{aligned}$$

(7.35)

$$\begin{aligned} u_{n;i,j}^{(\pm )}&=v_{\varepsilon ,j}^{(n)}\pm h_{\varepsilon ,j}. \end{aligned}$$

(7.36)

Note that, with this notation,

$$\begin{aligned} {\mathcal {R}}_{i;j}^{(n)}=[u_{n;i,j}^{(-)},u_{n;i,j}^{(+)}]\times [v_{n;i,j}^{(-)},v_{n;i,j}^{(+)}]. \end{aligned}$$

Let us introduce the following energy densities: On $\{v_{n;i,j}^{(-)}\le v\le v_{n;i,j}^{(+)}\}$, we will set

$$\begin{aligned} E_{\nwarrow }[n;i,j]\doteq 2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}r^{2}\cdot a_{\varepsilon i}T_{vv}[f_{\varepsilon i}], \end{aligned}$$

(7.37)

while on $\{u_{n;i,j}^{(-)}\le u\le u_{n;i,j}^{(+)}\}$ we will set

$$\begin{aligned} E_{\nearrow }[n;i,j]\doteq 2\pi \frac{1-\frac{2m}{r}}{-\partial _{u}r}r^{2}\cdot a_{\varepsilon j}T_{uu}[f_{\varepsilon j}]. \end{aligned}$$

(7.38)

We will also define the following energy-related quantities by integrating $E_{\nwarrow }[n;i,j]$ and $E_{\nearrow }[n;i,j]$ in directions transverse to the corresponding index arrow: On $\{v_{n;i,j}^{(-)}\le v\le v_{n;i,j}^{(+)}\}$, we will define

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }[n;i,j](u,v)\doteq \int _{v_{n;i,j}^{(-)}}^{v}E_{\nwarrow }[n;i,j](u,{\bar{v}})\,d{\bar{v}}, \end{aligned}$$

(7.39)

while on $\{u_{n;i,j}^{(-)}\le u\le u_{n;i,j}^{(+)}\}$ we will define

$$\begin{aligned} {\mathcal {E}}_{\nearrow }[n;i,j](u,v)\doteq \int _{u_{n;i,j}^{(-)}}^{u}E_{\nearrow }[n;i,j]({\bar{u}},v)\,d{\bar{u}}. \end{aligned}$$

(7.40)

In view of the fact that, among all the $f_{\varepsilon k}$’s, only $f_{\varepsilon i}$ and $f_{\varepsilon j}$ are supported on ${\mathcal {R}}_{i;j}^{(n)}$, the expression (6.65) for $f_{\varepsilon }$ implies that

$$\begin{aligned} T_{\mu \nu }[f_{\varepsilon }]|_{{\mathcal {R}}_{i;j}^{(n)}}=a_{\varepsilon i}T_{\mu \nu }[f_{\varepsilon i}]|_{{\mathcal {R}}_{i;j}^{(n)}}+a_{\varepsilon j}T_{\mu \nu }[f_{\varepsilon j}]|_{{\mathcal {R}}_{i;j}^{(n)}}. \end{aligned}$$

(7.41)

Notice that, in view of the fact that $T_{\mu \nu }[f_{\varepsilon i}]$ and $T_{\mu \nu }[f_{\varepsilon j}]$ are supported on ${\mathcal {V}}_{i}$ and ${\mathcal {V}}_{j}$, respectively (and hence vanish to infinite order on $v=v_{n;i,j}^{(\pm )}$ and $u=u_{n;i,j}^{(\pm )}$, respectively), the relation (7.41) implies (in view of the relations (2.49)–(2.48) for ${\tilde{m}}$, the definition (7.37)–(7.38) of $E_{\nwarrow }$, $E_{\nearrow }$ and the bounds (6.73) and (7.12) on $\partial r$, $T_{uv}$) that:

$$\begin{aligned}&{\tilde{m}}\big (u,v_{n;i,j}^{(+)}\big )-{\tilde{m}}\big (u,v_{n;i,j}^{(-)}\big )\nonumber \\&\quad ={\mathcal {E}}_{\nwarrow }[n;i,j](u,\text { }v_{n;i,j}^{(+)})+\mathfrak {Err}_{i,j\nwarrow }^{(n)}(u),\text { for any }u\in [u_{n;i,j}^{(-)},u_{n;i,j}^{(+)}],\\&{\tilde{m}}(u_{n;i,j}^{(-)},v)-{\tilde{m}}(u_{n;i,j}^{(+)},v) \nonumber \\&\quad ={\mathcal {E}}_{\nearrow }[n;i,j](u_{n;i,j}^{(+)},\text { }v)+\mathfrak {Err}_{i,j\nearrow }^{(n)}(v),\text { for any }v\in [v_{n;i,j}^{(-)},v_{n;i,j}^{(+)}],\nonumber \end{aligned}$$

(7.42)

where

$$\begin{aligned} |\mathfrak {Err}_{i,j\nwarrow }^{(n)}(u)|&\le \exp \big (\exp (2\sigma _{\varepsilon }^{-5})\big )\cdot \frac{(\varepsilon ^{(i)})^{2}}{(-\Lambda )(\inf _{{\mathcal {R}}_{i;j}^{(n)}}r)^{2}}\cdot \frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }},\\ |\mathfrak {Err}_{i,j\nearrow }^{(n)}(v)|&\le \exp \big (\exp (2\sigma _{\varepsilon }^{-5})\big )\cdot \frac{(\varepsilon ^{(j)})^{2}}{(-\Lambda )(\inf _{{\mathcal {R}}_{i;j}^{(n)}}r)^{2}}\cdot \frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}.\nonumber \end{aligned}$$

(7.43)

In particular, in view of the definition (6.95)–(6.98) of ${\mathcal {E}}_{\nwarrow }^{(\pm )}$, ${\mathcal {E}}_{\nearrow }^{(\pm )}$:

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(\pm )}[n;i,j]&={\mathcal {E}}_{\nwarrow }[n;i,j](u_{n;i,j}^{(\pm )},\text { }v_{n;i,j}^{(+)})+\mathfrak {Err}_{i,j\nwarrow }^{(n)}(u_{n;i,j}^{(\pm )}),\\ {\mathcal {E}}_{\nearrow }^{(\pm )}[n;i,j]&={\mathcal {E}}_{\nearrow }[n;i,j](u_{n;i,j}^{(+)},\text { }v_{n;i,j}^{(\pm )})+\mathfrak {Err}_{i,j\nearrow }^{(n)}(v_{n;i,j}^{(\pm )}).\nonumber \end{aligned}$$

(7.44)

The conservation of energy relation (2.24) for the Vlasov field $f_{\varepsilon i}$ reads (in view of the relation $T_{uv}[f_{\varepsilon i}]=\frac{1}{4}\Omega ^{2}g^{AB}T_{AB}[f_{\varepsilon i}]$ holding for all massless Vlasov fields):

$$\begin{aligned} \partial _{u}(r^{2}T_{vv}[f_{\varepsilon i}])&=-\partial _{v}(r^{2}T_{uv}[f_{\varepsilon i}])+\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon i}]), \end{aligned}$$

(7.45)

$$\begin{aligned} \partial _{v}(r^{2}T_{uu}[f_{\varepsilon i}])&=-\partial _{u}(r^{2}T_{uv}[f_{\varepsilon i}])+\Big (\partial _{u}\log (\Omega ^{2})-2\frac{\partial _{u}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon i}]) \end{aligned}$$

(7.46)

and similarly for $f_{\varepsilon j}$. Furthermore, Eqs. (2.46) and (2.47) readily yield:

$$\begin{aligned} \partial _{u}\Big (\frac{1-\frac{2m}{r}}{\partial _{v}r}\Big )&=\Big (4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}\Big )\cdot \frac{1-\frac{2m}{r}}{\partial _{v}r}, \end{aligned}$$

(7.47)

$$\begin{aligned} \partial _{v}\Big (\frac{1-\frac{2m}{r}}{-\partial _{u}r}\Big )&=\Big (-4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}\Big )\cdot \frac{1-\frac{2m}{r}}{-\partial _{u}r}. \end{aligned}$$

(7.48)

Differentiating (7.37) with resepect to $\partial _{u}$ and using (7.45) and (7.47), we obtain:

$$\begin{aligned} \partial _{u}E_{\nwarrow }[n;i,j]&= \Big (4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}\Big )\cdot E_{\nwarrow }[n;i,j]\\&\quad -a_{\varepsilon i}\Big \{2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}\partial _{v}(r^{2}T_{uv}[f_{\varepsilon i}])\nonumber \\&\quad +2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon i}])\Big \}.\nonumber \end{aligned}$$

(7.49)

Remark

Notice that the coefficient of $E_{\nwarrow }[n;i,j]$ in the right hand side of (7.49) is strictly positive. It is the sign of this coefficient that will lead to the increase of the energy quantity ${\mathcal {E}}_{\nwarrow }[n;i,j]$ as quantified by (7.31).

From (7.49), we obtain the following explicit formula for $E_{\nwarrow }[n;i,j](u,v)$ for $(u,v)\in {\mathcal {R}}_{i;j}^{(n)}$:

$$\begin{aligned}{} & {} E_{\nwarrow }[n;i,j](u,v)=\exp \Big (\int _{u_{n;i,j}^{(-)}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\bar{u}},v)\,d{\bar{u}}\Big )\nonumber \\{} & {} \quad \cdot E_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},v)-a_{\varepsilon i}\mathfrak {Err}_{\nwarrow }[n;i,j](u,v), \end{aligned}$$

(7.50)

where

$$\begin{aligned}&\mathfrak {Err}_{\nwarrow }[n;i,j](u,v)\nonumber \\&\doteq -\int _{u_{n;i,j}^{(-)}}^{u}\exp \Big (\int _{{\bar{u}}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\hat{u}},v)\,d{\hat{u}}\Big )\\&\quad \times \Bigg \{2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}\partial _{v}(r^{2}T_{uv}[f_{\varepsilon i}])\nonumber \\&\quad +2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon i}])\Bigg \}({\bar{u}},v)\,d{\bar{u}}.\nonumber \end{aligned}$$

(7.51)

Similarly, differentiating (7.38) with respect to $\partial _{v}$, we infer the following formula for $E_{\nearrow }[n;i,j](u,v)$ on ${\mathcal {R}}_{i;j}^{(n)}$:

$$\begin{aligned} E_{\nearrow }[n;i,j](u,v)= & {} \exp \Big (-\int _{v_{n;i,j}^{(-)}}^{v}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\bar{v}})\,d{\bar{v}}\Big )\nonumber \\{} & {} \cdot E_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})-a_{\varepsilon j}\mathfrak {Err}_{\nearrow }[n;i,j](u,v),\nonumber \\ \end{aligned}$$

(7.52)

where

$$\begin{aligned}&\mathfrak {Err}_{\nearrow }[n;i,j](u,v)\nonumber \\&\doteq -\int _{v_{n;i,j}^{(-)}}^{v}\exp \Big (-\int _{{\bar{v}}}^{v}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\hat{v}})\,d{\hat{v}}\Big )\\&\quad \times \Bigg \{2\pi \frac{1-\frac{2m}{r}}{-\partial _{u}r}\partial _{u}(r^{2}T_{uv}[f_{\varepsilon j}])\nonumber \\&\quad +2\pi \frac{1-\frac{2m}{r}}{-\partial _{u}r}\Big (\partial _{u}\log (\Omega ^{2})-2\frac{\partial _{u}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon j}])\Bigg \}(u,{\bar{v}})\,d{\bar{v}}.\nonumber \end{aligned}$$

(7.53)

In view of the relation (7.41) for $f_{\varepsilon }$, $f_{\varepsilon i}$ and $f_{\varepsilon j}$ on ${\mathcal {R}}_{i;j}^{(n)}$ and the definition (7.37)–(7.38) of $E_{\nwarrow }$, $E_{\nearrow }$, we have for any $(u,v)\in [u_{n;i,j}^{(-)},u_{n;i,j}^{(+)}]\times [v_{n;i,j}^{(-)},v_{n;i,j}^{(+)}]$:

$$\begin{aligned}{} & {} \int _{u_{n;i,j}^{(-)}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\bar{u}},v)\,d{\bar{u}}\nonumber \\{} & {} \quad =\int _{u_{n;i,j}^{(-)}}^{u}\Bigg \{\frac{2E_{\nearrow }[n;i,j]}{r}({\bar{u}},v)\nonumber \\{} & {} \qquad \cdot \Big (1-\frac{2m}{r}({\bar{u}},v)\Big )^{-1}+\frac{4\pi a_{\varepsilon i}}{r} \cdot \frac{r^{2}T_{uu}[f_{\varepsilon i}]}{-\partial _{u}r}({\bar{u}},v)\Bigg \}\,d{\bar{u}} \end{aligned}$$

(7.54)

and

$$\begin{aligned}{} & {} \int _{v_{n;i,j}^{(-)}}^{v}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\bar{v}})\,d{\bar{v}} =\int _{v_{n;i,j}^{(-)}}^{v}\Bigg \{\frac{2E_{\nwarrow }[n;i,j]}{r}(u,{\bar{v}})\nonumber \\{} & {} \qquad \cdot \Big (1-\frac{2m}{r}(u,{\bar{v}})\Big )^{-1}+\frac{4\pi a_{\varepsilon j}}{r}\cdot \frac{r^{2}T_{vv}[f_{\varepsilon j}]}{\partial _{v}r}(u,{\bar{v}})\Bigg \}\,d{\bar{v}}. \end{aligned}$$

(7.55)

Using (7.11) for $T_{uu}[f_{\varepsilon i}]$, $T_{vv}[f_{\varepsilon j}]$, recalling that ${\mathcal {R}}_{i;j}^{(n)}={\mathcal {V}}_{i\nwarrow }^{(n)}\cap {\mathcal {V}}_{j\nearrow }^{(n)}$, as well as the bound (6.73) and the assumption $a_{\varepsilon k}\in (0,\sigma _{\varepsilon }]$, the relations (7.54) and (7.55) yield:

$$\begin{aligned}{} & {} \int _{u_{n;i,j}^{(-)}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\bar{u}},v)\,d{\bar{u}}\nonumber \\{} & {} \quad =\int _{u_{n;i,j}^{(-)}}^{u}\Bigg \{\frac{2E_{\nearrow }[n;i,j]}{r\cdot \big (1-\frac{1}{3}\Lambda r^{2}-O(\mu _{i;j})\big )}({\bar{u}},v)\nonumber \\{} & {} \qquad +O\Big ((-\Lambda )^{-2}\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\frac{(\varepsilon ^{(i)})^{4}}{r^{5}({\bar{u}},v)}\Big )\Bigg \}\,d{\bar{u}} \end{aligned}$$

(7.56)

and

$$\begin{aligned}{} & {} \int _{v_{n;i,j}^{(-)}}^{v}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\bar{v}})\,d{\bar{v}}\nonumber \\{} & {} \quad =\int _{v_{n;i,j}^{(-)}}^{v}\Bigg \{\frac{2E_{\nwarrow }[n;i,j]}{r\cdot \big (1-\frac{1}{3}\Lambda r^{2}-O(\mu _{i;j})\big )}(u,{\bar{v}})\nonumber \\{} & {} \qquad +O\Big ((-\Lambda )^{-2}\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\frac{(\varepsilon ^{(j)})^{4}}{r^{5}(u,{\bar{v}})}\Big )\Bigg \}\,d{\bar{v}}, \end{aligned}$$

(7.57)

where

$$\begin{aligned} \mu _{i;j}\doteq \sup _{{\mathcal {R}}_{i;j}^{(n)}}\frac{2{\tilde{m}}}{r}. \end{aligned}$$

(7.58)

Note that

$$\begin{aligned} \mu _{i;j}=O(\eta _{0}), \end{aligned}$$

(7.59)

as a trivial consequence of (6.70).

For the rest of the proof of (7.31)–(7.34), we will consider the cases $i>j$ and $i<j$ separately.

The case $i>j$: Proof of (7.31) and (7.32). Integrating (2.48) in v from the axis $\gamma _{{\mathcal {Z}}_{\varepsilon }}$ up to ${\mathcal {R}}_{i;j}^{(n)}$, using the fact that, among all the $f_{\varepsilon k}$’s, only $f_{\varepsilon {\bar{j}}}$, $j\le {\bar{j}}\le i$ are supported on $\{u_{n;i,j}^{(-)}\le u\le u_{n;i,j}^{(+)}\}\cap \{v\le v_{n;i,j}^{(+)}\}$, we can readily estimate (using (6.73) and (7.11), (7.12)):

$$\begin{aligned} \sup _{{\mathcal {R}}_{i;j}^{(n)}}{\tilde{m}}\le \exp (\exp (\sigma _{\varepsilon }^{-6}))\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}. \end{aligned}$$

(7.60)

From (7.60) and the bound (7.15) for r on ${\mathcal {R}}_{i;j}^{(n)}$, we immediately infer that:

$$\begin{aligned} \mu _{i;j}=\sup _{{\mathcal {R}}_{i;j}^{(n)}}\frac{2{\tilde{m}}}{r}\le \exp (\exp (\sigma _{\varepsilon }^{-7}))\rho _{\varepsilon }\le \rho _{\varepsilon }^{\frac{3}{4}}. \end{aligned}$$

(7.61)

Using the bounds (7.61), (7.15) and (7.16) on ${\mathcal {R}}_{i;j}^{(n)}$ as well as (6.1) and (6.5), the relation (7.56) yields:

$$\begin{aligned}&\int _{u_{n;i,j}^{(-)}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\bar{u}},v)\,d{\bar{u}} =\int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{u}\Bigg \{\frac{2E_{\nearrow }[n;i,j]({\bar{u}},v)}{r_{n;i,j}}\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )\nonumber \\&\qquad +O\Big (\sqrt{-\Lambda }\rho _{\varepsilon }\exp (e^{\sigma _{\varepsilon }^{-8}})\frac{(\varepsilon ^{(i)})^{4}}{(\varepsilon ^{(j)})^{5}}\Big )\Bigg \}\,d{\bar{u}}\\&\quad =\frac{2{\mathcal {E}}_{\nearrow }[n;i,j](u,v)}{r_{n;i,j}}\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )+O\Big (\sqrt{-\Lambda }\rho _{\varepsilon }\exp (e^{\sigma _{\varepsilon }^{-8}})\frac{(\varepsilon ^{(i)})^{4}}{(\varepsilon ^{(j)})^{5}}h_{\varepsilon ,j}\Big )\nonumber \\&\quad =\frac{2{\mathcal {E}}_{\nearrow }[n;i,j](u,v)}{r_{n;i,j}}\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )+O\Big (\sqrt{-\Lambda }\rho _{\varepsilon }^{2}\exp (e^{\sigma _{\varepsilon }^{-8}})\frac{(\varepsilon ^{(i)})^{4}}{(\varepsilon ^{(j)})^{4}}\Big )\nonumber \\&\quad =\frac{2{\mathcal {E}}_{\nearrow }[n;i,j](u,v)}{r_{n;i,j}}\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )+O(\varepsilon ^{4})\nonumber \end{aligned}$$

(7.62)

(where we have used the bound $\frac{\varepsilon ^{(i)}}{\varepsilon ^{(j)}}\le \varepsilon$ when $i>j$). Similarly, (7.57) yields:

$$\begin{aligned}&\int _{v_{n;i,j}^{(-)}}^{v}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\bar{v}})\,d{\bar{v}} =\frac{2{\mathcal {E}}_{\nwarrow }[n;i,j](u,v)}{r_{n;i,j}}\nonumber \\&\qquad \cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )+O(\sqrt{-\Lambda }\rho _{\varepsilon }\exp (e^{\sigma _{\varepsilon }^{-8}})\frac{(\varepsilon ^{(j)})^{4}}{(\varepsilon ^{(j)})^{5}}h_{\varepsilon ,i}),\\&\quad =\frac{2{\mathcal {E}}_{\nwarrow }[n;i,j](u,v)}{r_{n;i,j}}\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )+O(\varepsilon ).\nonumber \end{aligned}$$

(7.63)

where $r_{n;i,j}$ is defined by (7.30).

Substituting (7.62) in (7.50) and integrating in v over $[v_{n;i,j}^{(-)},v]$, we obtain:

$$\begin{aligned}&{\mathcal {E}}_{\nwarrow }[n;i,j](u,v) =\int _{v_{n;i,j}^{(-)}}^{v}\Bigg \{\exp \Big (\frac{2{\mathcal {E}}_{\nearrow }[n;i,j](u,{\bar{v}})}{r_{n;i,j}}\nonumber \\&\qquad \cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )+O(\varepsilon )\Big )\cdot E_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},{\bar{v}})\Bigg \}\,d{\bar{v}}\\&\qquad -a_{\varepsilon i}\int _{v_{n;i,j}^{(-)}}^{v}\mathfrak {Err}_{\nwarrow }[n;i,j](u,{\bar{v}})\,d{\bar{v}}.\nonumber \end{aligned}$$

(7.64)

Integrating by parts in $\partial _{v}$ for the term $\partial _{v}(r^{2}T_{uv})$ in $\int _{v_{n;i,j}^{(-)}}^{v}\mathfrak {Err}_{\nwarrow }[n;i,j](u,{\bar{v}})\,d{\bar{v}}$ (see the expression (7.51)), and using the fact that $T_{uv}[f_{\varepsilon i}]$ is supported on ${\mathcal {V}}_{i}$ (and hence vanishes to infinite order on $v=v_{n;i,j}^{(\pm )}$), we calculate:

$$\begin{aligned}&\Big |\int _{v_{n;i,j}^{(-)}}^{v} \mathfrak {Err}_{\nwarrow }[n;i,j](u,{\bar{v}})\,d{\bar{v}}\Big |\\&\quad =\Bigg |\int _{v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}}^{v}\int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{u}\Bigg [\exp \Big (\int _{{\bar{u}}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\hat{u}},{\bar{v}})\,d{\hat{u}}\Big )\nonumber \\&\qquad \times \Bigg \{2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}\partial _{v}(r^{2}T_{uv}[f_{\varepsilon i}])\nonumber \\&\qquad +2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon i}])\Bigg \}\Bigg ]({\bar{u}},{\bar{v}})\,d{\bar{u}}d{\bar{v}}\Bigg |\nonumber \\&\quad =\Bigg |\int _{v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}}^{v}\int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{u}\Bigg [\exp \Big (\int _{{\bar{u}}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\hat{u}},{\bar{v}})\,d{\hat{u}}\Big )\nonumber \\&\qquad \cdot 2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}r^{2}T_{uv}[f_{\varepsilon i}]\nonumber \\&\qquad \times \Bigg \{-\int _{{\bar{u}}}^{u}\partial _{v}\Big (\frac{4\pi }{r(-\partial _{u}r)}\Big )\cdot r^{2}T_{uu}[f_{\varepsilon }]({\hat{u}},{\bar{v}})\,d{\hat{u}}\nonumber \\&\qquad -\int _{{\bar{u}}}^{u}\frac{4\pi }{r}\frac{1}{-\partial _{u}r}\partial _{v}(r^{2}T_{uu}[f_{\varepsilon }])({\hat{u}},{\bar{v}})\,d{\hat{u}}\nonumber \\&\qquad -\partial _{v}\log \Big (\frac{1-\frac{2m}{r}}{\partial _{v}r}\Big )+\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )\Bigg \}\Bigg ]({\bar{u}},{\bar{v}})\,d{\bar{u}}d{\bar{v}}\Bigg |.\nonumber \end{aligned}$$

(7.65)

We will estimate the right hand side of (7.65) in a number of steps:

• Using the bounds (6.70), (6.73), (7.11), (7.41), (7.15) and (7.16), we can estimate:

  $$\begin{aligned}&\sup _{(u,{\bar{v}})\in {\mathcal {R}}_{i;j}^{(n)},\text { }{\bar{u}}\in [v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},u]}\Big |\int _{{\bar{u}}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\hat{u}},{\bar{v}})\,d{\hat{u}}\Big |\nonumber \\&\quad \le \int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}}\exp \big (\exp (4\sigma _{\varepsilon }^{-5})\big )\cdot \frac{1}{r_{n;i,j}}\,du\\&\quad \le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\cdot \frac{h_{\varepsilon ,j}}{r_{n;i,j}}\nonumber \\&\quad \le 1.\nonumber \end{aligned}$$

  (7.66)

• Using the bounds (6.73), (7.12), (7.15) and (7.16), we can estimate:

  $$\begin{aligned} 2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}r^{2}T_{uv}[f_{\varepsilon i}]\le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\frac{(\varepsilon ^{(i)})^{2}}{r_{n;i,j}^{2}}(-\Lambda )^{-1}. \end{aligned}$$

  (7.67)

• Using equation (2.45) and the bounds (6.70), (6.73), (7.11), (7.12), (7.15) and (7.16) (as well as the relation (7.41) between $f_{\varepsilon }$, $f_{\varepsilon i}$ and $f_{\varepsilon j}$ on ${\mathcal {R}}_{i;j}^{(n)}$ and the bound $a_{\varepsilon k}\le 1$), we can estimate:

  $$\begin{aligned}&\sup _{(u,{\bar{v}})\in {\mathcal {R}}_{i;j}^{(n)},\text { }{\bar{u}}\in [v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},u]}\Big |\int _{{\bar{u}}}^{u} \partial _{v}\Big (\frac{4\pi }{r(-\partial _{u}r)}\Big )\cdot r^{2}T_{uu}[f_{\varepsilon }]({\hat{u}},{\bar{v}})\,d{\hat{u}}\Big |\nonumber \\&\quad =\sup _{(u,{\bar{v}})\in {\mathcal {R}}_{i;j}^{(n)}, \text { }{\bar{u}}\in [v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},u]} \nonumber \\&\qquad \Big |\int _{{\bar{u}}}^{u}4\pi \Big (-\frac{\partial _{v}r}{r^{2}(-\partial _{u}r)}+\frac{\partial _{u}\partial _{v}r}{r(-\partial _{u}r)^{2}}\Big )r^{2}T_{uu}[f_{\varepsilon }]({\hat{u}},{\bar{v}})\,d{\hat{u}}\Big |\nonumber \\&\quad =\sup _{(u,{\bar{v}})\in {\mathcal {R}}_{i;j}^{(n)},\text { }{\bar{u}}\in [v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},u]} \nonumber \\&\qquad \Big |\int _{{\bar{u}}}^{u}4\pi \Big (-\frac{\partial _{v}r}{r^{2}(-\partial _{u}r)}+\frac{\frac{2{\tilde{m}}}{r}-\frac{2}{3}\Lambda r^{2}}{r^{2}(1-\frac{2m}{r})}\frac{\partial _{v}r}{-\partial _{u}r}\nonumber \\&\qquad +\frac{4\pi r^{2}T_{uv}}{r^{2}(-\partial _{u}r)^{2}}\Big )r^{2}T_{uu}[f_{\varepsilon }]({\hat{u}},{\bar{v}})\,d{\hat{u}}\Big |\nonumber \\&\quad \le \int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}}\exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\frac{1}{r_{n;i,j}^{2}}\,du\nonumber \\&\quad \le 2\exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\frac{h_{\varepsilon ,j}}{r_{n;i,j}^{2}}\nonumber \\&\quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-9})\big )\rho _{\varepsilon }\frac{1}{r_{n;i,j}}\nonumber \\&\quad \le \rho _{\varepsilon }^{\frac{1}{2}}\frac{1}{r_{n;i,j}}. \end{aligned}$$

  (7.68)

• Using (7.46) for $f_{\varepsilon }$ in place of $f_{\varepsilon i}$ to express $\partial _{v}(r^{2}T_{uu}[f_{\varepsilon }])$ in terms of $\partial _{u}(r^{2}T_{uv}[f_{\varepsilon }])$ and integrating by parts in $\partial _{u}$, we calculate (in view of the bounds (6.70), (6.73), (7.12), (7.19) for $\partial _{u}\Omega ^{2}$ with j in place of i, (7.20) for $\partial _{u}^{2}r$ with j in place of i, (7.15) and (7.16)):

  $$\begin{aligned}&\sup _{(u,{\bar{v}})\in {\mathcal {R}}_{i;j}^{(n)},\text { }{\bar{u}}\in [v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},u]}\Big |\int _{{\bar{u}}}^{u}\frac{4\pi }{r}\frac{1}{-\partial _{u}r}\partial _{v}(r^{2}T_{uu}[f_{\varepsilon }])({\hat{u}},{\bar{v}})\,d{\hat{u}}\Big |\nonumber \\&\quad =\sup _{(u,{\bar{v}})\in {\mathcal {R}}_{i;j}^{(n)},\text { }{\bar{u}}\in [v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},u]}\Bigg |\int _{{\bar{u}}}^{u}\frac{4\pi }{r}\frac{1}{-\partial _{u}r}\Big (-\partial _{u}(r^{2}T_{uv}[f_{\varepsilon }])\nonumber \\&\qquad +\Big (\partial _{u}\log (\Omega ^{2})-2\frac{\partial _{u}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon }])\Big )({\hat{u}},{\bar{v}})\,d{\hat{u}}\Bigg |\nonumber \\&\quad =\sup _{(u,{\bar{v}})\in {\mathcal {R}}_{i;j}^{(n)},\text { }{\bar{u}}\in [v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j},u]}\Bigg |\int _{{\bar{u}}}^{u}4\pi \Big (\partial _{u}\big (\frac{1}{r(-\partial _{u}r)}\big )\cdot r^{2}T_{uv}[f_{\varepsilon }]\nonumber \\&\qquad +\frac{1}{r(-\partial _{u}r)}\Big (\partial _{u}\log (\Omega ^{2})-2\frac{\partial _{u}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon }])\Big )({\hat{u}},{\bar{v}})\,d{\hat{u}}\nonumber \\&\qquad +\frac{4\pi }{r}\frac{1}{-\partial _{u}r}\cdot r^{2}T_{uv}[f_{\varepsilon }]({\bar{u}},{\bar{v}})-\frac{4\pi }{r}\frac{1}{-\partial _{u}r}\cdot r^{2}T_{uv}[f_{\varepsilon }](u,{\bar{v}})\Bigg |\nonumber \\&\quad \le \int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}}\exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\nonumber \\&\qquad \times \frac{1}{r_{n;i,j}}\big (\frac{\sqrt{-\Lambda }}{\varepsilon ^{(j)}}+\frac{1}{r_{n;i,j}}\big )\frac{(\varepsilon ^{(j)})^{2}}{(-\Lambda )r_{n;i,j}^{2}}\,du\nonumber \\&\qquad +\exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\frac{1}{r_{n;i,j}}\frac{(\varepsilon ^{(j)})^{2}}{(-\Lambda )r_{n;i,j}^{2}}\nonumber \\&\quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-9})\big )\rho _{\varepsilon }^{2}\frac{1}{r_{n;i,j}}\nonumber \\&\quad \le \rho _{\varepsilon }\frac{1}{r_{n;i,j}}. \end{aligned}$$

  (7.69)

• Using the the relation (2.48) for $\partial _{v}{\tilde{m}}$, the estimate (7.20) for $\partial _{v}^{2}r$, as well as the bounds (6.73), (7.11), (7.12), (6.70), (7.15) and (7.16), we can estimate:

  $$\begin{aligned} \sup _{{\mathcal {R}}_{i;j}^{(n)}\text { }}\Big |\partial _{v}\log \Big (\frac{1-\frac{2m}{r}}{\partial _{v}r}\Big )\Big |\le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\Big (\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}+\frac{1}{r_{n;i,j}}\Big ).\qquad \end{aligned}$$

  (7.70)

• Using the estimate (7.19) for $\partial _{v}\Omega ^{2}$, as well as the bounds (6.73), (7.12), (7.15) and (7.16), we can estimate:

  $$\begin{aligned} \sup _{{\mathcal {R}}_{i;j}^{(n)}\text { }}\Big |\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big |\le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\Big (\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}+\frac{1}{r_{n;i,j}}\Big ).\qquad \end{aligned}$$

  (7.71)

Using the estimates (7.66)–(7.71) (together with the relation of the parameters $\varepsilon$, $\rho _{\varepsilon }$, $\delta _{\varepsilon }$ and $\sigma _{\varepsilon }$) to bound the right hand side of (7.65), we therefore obtain:

$$\begin{aligned}&\sup _{(u,v)\in {\mathcal {R}}_{i;j}^{(n)}}\Big |\int _{v_{n;i,j}^{(-)}}^{v}\mathfrak {Err}_{\nwarrow }[n;i,j](u,{\bar{v}})\,d{\bar{v}}\Big |\nonumber \\&\quad \le \int _{v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}}^{v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}}\int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}}\frac{(\varepsilon ^{(i)})^{2}}{r_{n;i,j}^{2}}\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )(-\Lambda )^{-1}\\&\qquad \times \Big (\exp \big (\exp (\sigma _{\varepsilon }^{-7})\big )\Big (\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}+\frac{1}{r_{n;i,j}}\Big )+2\rho _{\varepsilon }^{\frac{1}{2}}\frac{1}{r_{n;i,j}}\Big )\,d{\bar{u}}d{\bar{v}}\nonumber \\&\quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-7})\big )\rho _{\varepsilon }^{2}\frac{(\varepsilon ^{(i)})^{2}}{(\varepsilon ^{(j)})^{2}}\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}h_{\varepsilon ,i}h_{\varepsilon ,j}\nonumber \\&\quad \le \exp \big (\exp (\sigma _{\varepsilon }^{-8})\big )\rho _{\varepsilon }^{2}\frac{(\varepsilon ^{(i)})^{2}}{(\varepsilon ^{(j)})^{2}}\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}\varepsilon ^{(i)}\varepsilon ^{(j)}(-\Lambda )^{-1}\nonumber \\&\quad \le \rho _{\varepsilon }^{\frac{3}{2}}\varepsilon ^{(i)}(-\Lambda )^{-\frac{1}{2}}\nonumber \end{aligned}$$

(7.72)

where, in the last step in (7.72), we have used the bound $\varepsilon ^{(i)}<\varepsilon ^{(j)}$ (holding when $i>j$). Returning to (7.64) and using (7.72) to estimate the last term in the right hand side (using also the bound $a_{\varepsilon i}<\delta _{\varepsilon }\ll \exp \big (-\exp (\sigma _{\varepsilon }^{-8})\big )$), we infer that, for any $(u,v)\in {\mathcal {R}}_{i;j}^{(n)}$:

$$\begin{aligned}{} & {} {\mathcal {E}}_{\nwarrow }[n;i,j](u,v)\nonumber \\{} & {} \quad =\int _{v_{n;i,j}^{(-)}}^{v}\Bigg \{\exp \Big (\frac{2{\mathcal {E}}_{\nearrow }[n;i,j](u,{\bar{v}})}{r_{n;i,j}}\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )+O(\varepsilon )\Big )\nonumber \\{} & {} \qquad \cdot E_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},{\bar{v}})\Bigg \}\,d{\bar{v}}+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ). \end{aligned}$$

(7.73)

Similarly, substituting (7.63) in (7.52) and integrating in u over $[u_{n;i,j}^{(-)},u]$, estimating $\int _{u_{n;i,j}^{(-)}}^{u}\mathfrak {Err}_{\nearrow }[n;i,j]({\bar{u}},v)\,d{\bar{u}}$ in the same way as we did for (7.72), we obtain for any $(u,v)\in {\mathcal {R}}_{i;j}^{(n)}$:

$$\begin{aligned}{} & {} {\mathcal {E}}_{\nearrow }[n;i,j](u,v)\nonumber \\{} & {} \quad =\int _{u_{n;i,j}^{(-)}}^{u}\Bigg \{\exp \Big (-\frac{2{\mathcal {E}}_{\nwarrow }[n;i,j]({\bar{u}},v)}{r_{n;i,j}}\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )+O(\varepsilon )\Big )\nonumber \\{} & {} \qquad \cdot E_{\nearrow }[n;i,j]({\bar{u}},v_{n;i,j}^{(-)})\Bigg \}\,d{\bar{u}}+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big ). \end{aligned}$$

(7.74)

Using the bounds (6.73), (7.11), (7.15) and (7.16), we can trivially estimate

$$\begin{aligned}{} & {} \sup _{(u,v)\in {\mathcal {R}}_{i;j}^{(n)}}\frac{{\mathcal {E}}_{\nearrow }[n;i,j](u,v)}{r_{n;i,j}}\nonumber \\{} & {} \quad \le \frac{\int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}}\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\,du}{r_{n;i,j}}\nonumber \\{} & {} \quad \le 2\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\frac{h_{\varepsilon ,j}}{r_{n;i,j}}\le \rho _{\varepsilon }^{\frac{3}{4}}. \end{aligned}$$

(7.75)

Dividing (7.73) with $r_{n;i,j}$ and using (7.75) to estimate its right hand side, making also use of (6.73) and (7.11) to estimate $E_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},{\bar{v}})$, we obtain:

$$\begin{aligned}&\sup _{(u,v)\in {\mathcal {R}}_{i;j}^{(n)}}\frac{{\mathcal {E}}_{\nwarrow }[n;i,j](u,v)}{r_{n;i,j}} \nonumber \\&\quad \le \frac{\int _{v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}}^{v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}}\Big \{\exp (O(\rho _{\varepsilon }^{\frac{3}{4}}))E_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},{\bar{v}})+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\Big \}\,d{\bar{v}}+}{r_{n;i,j}}\\&\quad \le 2\int _{v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}}^{v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}}\frac{\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )}{r_{n;i,j}}\,d{\bar{v}}\nonumber \\&\quad \le 4\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\frac{h_{\varepsilon ,i}}{r_{n;i,j}}\nonumber \\&\quad \le \varepsilon ,\nonumber \end{aligned}$$

(7.76)

where, in passing from the third to the fourth line in (7.76), we made use of the bound $\frac{\varepsilon ^{(i)}}{\varepsilon ^{(j)}}\le \varepsilon$ and the approximate relation (7.15) between $\varepsilon ^{(j)}$ and $r_{n;i,j}$.

Returning to (7.74) and using the bound (7.76), we infer:

$$\begin{aligned}&{\mathcal {E}}_{\nearrow }[n;i,j](u,v)\nonumber \\&\quad =\int _{u_{n;i,j}^{(-)}}^{u}\Bigg \{\exp \Big (O(\varepsilon )\Big )\cdot E_{\nearrow }[n;i,j]({\bar{u}},v_{n;i,j}^{(-)})\Bigg \}\,d{\bar{u}}+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )\\&\quad =(1+O(\varepsilon ))\int _{u_{n;i,j}^{(-)}}^{u}E_{\nearrow }[n;i,j]({\bar{u}},v_{n;i,j}^{(-)})\,d{\bar{u}}+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )\nonumber \\&\quad =(1+O(\varepsilon )){\mathcal {E}}_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big ),\nonumber \end{aligned}$$

(7.77)

from which (7.32) follows by setting $u=u_{n;i,j}^{(+)}$ and $v=v_{n;i,j}^{(+)}$ and using (7.44). Returning, now, to (7.73) and using (7.77) to estimate the exponential in the right hand side, as well as the bound (7.75) to estimate the $\frac{2{\mathcal {E}}_{\nearrow }[n;i,j]}{r_{n;i,j}}\cdot O(\rho _{\varepsilon }^{\frac{3}{4}})$ error term, we obtain:

$$\begin{aligned}&{\mathcal {E}}_{\nwarrow } [n;i,j](u,v) \\&\quad =\int _{v_{n;i,j}^{(-)}}^{v}\Bigg \{\exp \Big (\frac{2{\mathcal {E}}_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})}{r_{n;i,j}}\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )+O(\rho _{\varepsilon }^{2})\Big )\nonumber \\&\qquad \cdot E_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},{\bar{v}})\Bigg \}\,d{\bar{v}}+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\nonumber \\&\quad =\exp \Big (\frac{2{\mathcal {E}}_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})}{r_{n;i,j}}+O(\rho _{\varepsilon }^{\frac{3}{2}})\Big )\nonumber \\&\qquad \cdot \int _{v_{n;i,j}^{(-)}}^{v}E_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},{\bar{v}})\,d{\bar{v}}+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\nonumber \\&\quad =\exp \Big (\frac{2{\mathcal {E}}_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})}{r_{n;i,j}}+O(\rho _{\varepsilon }^{\frac{3}{2}})\Big )\nonumber \\&\qquad \cdot {\mathcal {E}}_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},v)+O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ),\nonumber \end{aligned}$$

(7.78)

from which (7.31) follows by setting $u=u_{n;i,j}^{(+)}$ and $v=v_{n;i,j}^{(+)}$ and using (7.44).

Remark

More generally, setting $u=u_{n;i,j}^{(+)}$ in (7.77), $v=v_{n;i,j}^{(+)}$ in (7.78) and using (7.42), we obtain

$$\begin{aligned}{} & {} {\tilde{m}}(u_{n;i,j}^{(-)},v)-{\tilde{m}}(u_{n;i,j}^{(+)},v)\nonumber \\{} & {} \quad ={\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]\cdot \big (1+O(\varepsilon )\big )\nonumber \\{} & {} \qquad +O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )\text { for all }v\in [v_{n;i,j}^{(-)},v_{n;i,j}^{(+)}] \end{aligned}$$

(7.79)

and

$$\begin{aligned}{} & {} {\tilde{m}}\big (u,v_{n;i,j}^{(+)}\big )-{\tilde{m}}\big (u,v_{n;i,j}^{(-)}\big )\nonumber \\{} & {} \quad \le {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j]\cdot \exp \Big (\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+O(\rho _{\varepsilon }^{\frac{3}{2}})\Big )\nonumber \\{} & {} \qquad +O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\text { for all }u\in [u_{n;i,j}^{(-)},u_{n;i,j}^{(+)}]. \end{aligned}$$

(7.80)

The case $i<j$: Proof of (7.33) and (7.34). The proof of (7.33) and (7.34) will follow by the same arguments as the proof of (7.32) and (7.31), the main difference being that in this case, we will use (7.17) and (7.18) in place of (7.15) and (7.16), respectively. In particular, in this case, the fact that $r_{n;i,j}\gtrsim \frac{1}{\varepsilon }$ will actually render all the error terms appearing in the relevant computations of order $O(\varepsilon )$ or smaller, simplyfying the whole procedure substantially.

Using the bounds (6.73), (7.11), (7.17) and (7.18) on ${\mathcal {R}}_{i;j}^{(n)}$ as well as (6.1) and (6.5), we can estimate

$$\begin{aligned}&\int _{u_{n;i,j}^{(-)}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\bar{u}},v)\,d{\bar{u}} \nonumber \\&\quad =\int _{u_{n;i,j}^{(-)}}^{u}4\pi \frac{1}{r(1-\frac{1}{3}\Lambda r^{2})}\frac{1-\frac{1}{3}\Lambda r^{2}}{-\partial _{u}r}r^{2}T_{uu}[f_{\varepsilon }]({\bar{u}},v)\,d{\bar{u}}\\&\quad \le \exp (\exp (\sigma _{\varepsilon }^{-7}))\frac{1}{r_{n;i,j}^{3}}h_{\varepsilon ,j}(-\Lambda )^{-1}\le \varepsilon \nonumber \end{aligned}$$

(7.81)

and, similarly

$$\begin{aligned} \int _{v_{n;i,j}^{(-)}}^{v}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\bar{v}})\,d{\bar{v}}\le \varepsilon . \end{aligned}$$

(7.82)

Substituting (7.81) in (7.50) and integrating in v over $[v_{n;i,j}^{(-)},v]$, we obtain the following analogue of (7.64):

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }[n;i,j](u,v)&=\int _{v_{n;i,j}^{(-)}}^{v}\Bigg \{\exp \Big (O(\varepsilon )\Big )\cdot E_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},{\bar{v}})\Bigg \}\,d{\bar{v}}\nonumber \\&\qquad -a_{\varepsilon i}\int _{v_{n;i,j}^{(-)}}^{v}\mathfrak {Err}_{\nwarrow }[n;i,j](u,{\bar{v}})\,d{\bar{v}}\\&=(1+O(\varepsilon )){\mathcal {E}}_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},v)\nonumber \\&\qquad -a_{\varepsilon i}\int _{v_{n;i,j}^{(-)}}^{v}\mathfrak {Err}_{\nwarrow }[n;i,j](u,{\bar{v}})\,d{\bar{v}}.\nonumber \end{aligned}$$

(7.83)

Repeating the same procedure as for the proof of (7.72), but using (7.17) and (7.18) in place of (7.15) and (7.16), we can estimate:

$$\begin{aligned} \sup _{(u,v)\in {\mathcal {R}}_{i;j}^{(n)}}\Big |\int _{v_{n;i,j}^{(-)}}^{v}\mathfrak {Err}_{\nwarrow }[n;i,j](u,{\bar{v}})\,d{\bar{v}}\Big |\le \varepsilon \cdot \frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }} \end{aligned}$$

(7.84)

Therefore, from (7.83) we infer that

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }[n;i,j](u,v)=(1+O(\varepsilon )){\mathcal {E}}_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},v)+O\Big (\varepsilon \cdot \frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ),\nonumber \\ \end{aligned}$$

(7.85)

from which (7.33) follows by setting $u=u_{n;i,j}^{(+)}$ and $v=v_{n;i,j}^{(+)}$ and using (7.44). Similarly,

$$\begin{aligned} {\mathcal {E}}_{\nearrow }[n;i,j](u,v)=(1+O(\varepsilon )){\mathcal {E}}_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})+O\Big (\varepsilon \cdot \frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big ),\nonumber \\ \end{aligned}$$

(7.86)

from which the estimate (7.34) follows by setting $u=u_{n;i,j}^{(+)}$ and $v=v_{n;i,j}^{(+)}$.

Remark

Similarly as in the case $i>j$, from (7.85) and (7.85) (7.86), using (7.42), we obtain

$$\begin{aligned} {\tilde{m}}\big (u,v_{n;i,j}^{(+)}\big )-{\tilde{m}}\big (u,v_{n;i,j}^{(-)}\big )= & {} \big (1+O(\varepsilon )\big ){\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j]\nonumber \\{} & {} +O\Big (\varepsilon \frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\quad \text { for all }u\in [u_{n;i,j}^{(-)},u_{n;i,j}^{(+)}]\nonumber \\ \end{aligned}$$

(7.87)

and

$$\begin{aligned} {\tilde{m}}(u_{n;i,j}^{(-)},v)-{\tilde{m}}(u_{n;i,j}^{(+)},v)= & {} \big (1+O(\varepsilon )\big ){\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]\nonumber \\{} & {} +O\Big (\varepsilon \frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )\quad \text { for all }v\in [v_{n;i,j}^{(-)},v_{n;i,j}^{(+)}].\nonumber \\ \end{aligned}$$

(7.88)

The relations (7.31)–(7.34) for $\widetilde{{\mathcal {E}}}_{\nwarrow }^{(\pm )}[n;i,j]$, $\widetilde{{\mathcal {E}}}_{\nearrow }^{(\pm )}[n;i,j]$ in place of ${\mathcal {E}}_{\nwarrow }^{(\pm )}[n;i,j]$, ${\mathcal {E}}_{\nearrow }^{(\pm )}[n;i,j]$ follow in exactly the same way, after replacing $\sigma _{\varepsilon }$, $h_{\varepsilon ,i}$, ${\mathcal {V}}_{i}^{(n)}$, ${\mathcal {R}}_{i;j}^{(n)}$ with $\delta _{\varepsilon }$, ${\tilde{h}}_{\varepsilon ,i}$, $\widetilde{{\mathcal {V}}}_{i}^{(n)}$, ${\mathcal {R}}_{i;j}^{(n)}$ respectively, in all the expressions above and using (6.78) in place of (6.73). $\square$

The next result provides an estimate for the change of the geometric separation of the beams ${\mathcal {V}}_{i\nwarrow }^{(n)}$ and ${\mathcal {V}}_{i-1\nwarrow }^{(n)}$ before and after their intersection with ${\mathcal {V}}_{j\nearrow }^{(n)}$, as well as the change of the separation of ${\mathcal {V}}_{j\nearrow }^{(n)}$ and ${\mathcal {V}}_{j-1\nearrow }^{(n)}$before and after their intersection with ${\mathcal {V}}_{i\nwarrow }^{(n)}$ (with ${\mathcal {V}}_{i\nwarrow }^{(n+1)}$ and ${\mathcal {V}}_{i-1\nwarrow }^{(n+1)}$ in place of ${\mathcal {V}}_{i\nwarrow }^{(n)}$ and ${\mathcal {V}}_{i-1\nwarrow }^{(n)}$, if $i<j$).

Proposition 7.4

Let $\varepsilon \in (0,\varepsilon _{1}]$ and let $n\in {\mathbb {N}}$ and $0\le i,j\le N_{\varepsilon }$, $i\ne j$, be such that

$$\begin{aligned} {\mathcal {R}}_{i;j}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}. \end{aligned}$$

Let also $r_{n;i,j}$ be defined by (7.30). Then, the following relations hold regarding the change of the separation-measuring quantities ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]$, ${\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]$:

• In the case $i>j$, the quantities ${\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]$ (defined for $j>0$) satisfy

  $$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(+)}[n;i,j]={\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j]\cdot \big (1+O(\varepsilon )\big ), \end{aligned}$$

  (7.89)

  while for the quantities ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]$ the following hold:

  • If $i=j+1$,

    $$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big ). \end{aligned}$$

    (7.90)

  • If $i>j+1$,

    $$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j]\cdot \exp \Big (-\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+O(\rho _{\varepsilon }^{\frac{3}{2}})\Big ).\nonumber \\ \end{aligned}$$

    (7.91)

• In the case $i<j$, the quantities ${\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]$ satisfy

  $$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(+)}[n;i,j]={\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j]\cdot \big (1+O(\varepsilon )\big ), \end{aligned}$$

  (7.92)

  while the quantities ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]$ (defined for $i>0$) satisfy:

  $$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]&={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j]\cdot \big (1+O(\varepsilon )\big ). \end{aligned}$$

  (7.93)

In the case when

$$\begin{aligned} {\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)},{\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+} \end{aligned}$$

the following relations hold for ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,i]$, ${\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,i]$:

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,i]&={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,i]\cdot \big (1+O(\varepsilon )\big ), \end{aligned}$$

(7.94)

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(+)}[n;i,i]&={\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,i]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big ). \end{aligned}$$

(7.95)

Replacing ${\mathcal {U}}_{\varepsilon }^{+}$ with ${\mathcal {T}}_{\varepsilon }^{+}$ and ${\mathcal {V}}_{i}^{(n)}$ with $\widetilde{{\mathcal {V}}}_{i}^{(n)}$, the relations (7.89)–(7.95) also hold with $\widetilde{{\mathfrak {D}}}r_{\nwarrow }^{(\pm )}[n;i,j]$, $\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(\pm )}[n;i,j]$ in place of ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]$, ${\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]$.

Proof

In order to establish (7.89)–(7.95), we will assume without loss of generality that $i>0$ and $j>0$, so that both ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]$ and ${\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]$ are well defined. In the case when $i=0$ (when ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]$ is not defined), the proof of (7.92) follows exactly as in the case $i>0$, and similarly for the proof of (7.90)–(7.91) in the case $j=0$.

As we did in the proof of Proposition 7.3, we will use the shorthand notation $v_{n;i,j}^{(\pm )}$, $u_{n;i,j}^{(\pm )}$ for the expressions (7.35), (7.36), respectively. We will also define the energy quantities $E_{\nwarrow }[n;i,j](u,v)$, $E_{\nearrow }[n;i,j](u,v)$, ${\mathcal {E}}_{\nwarrow }[n;i,j](u,v)$ and ${\mathcal {E}}_{\nearrow }[n;i,j](u,v)$ by (7.37), (7.38), (7.39) and (7.40), respectively.

Let us define the domains

$$\begin{aligned} {\mathcal {W}}_{\nwarrow }[n;i,j]&\doteq [u_{n;i,j-1}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1},u_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}]\times [v_{n;i,j}^{(-)},v_{n;i,j}^{(+)}], \end{aligned}$$

(7.96)

$$\begin{aligned} {\mathcal {W}}_{\nearrow }[n;i,j]&\doteq [u_{n;i,j}^{(-)},u_{n;i,j}^{(+)}]\times [v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1},v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}], \end{aligned}$$

(7.97)

with the following convention for $v_{i-1,i-1}^{(+)}$ (recall that (7.35) defined $v_{n;i,j}^{(\pm )}$ only for $i\ne j$):

$$\begin{aligned} v_{n;i-1,i-1}^{(+)}&=v_{\varepsilon ,i-1}^{(n)}+h_{\varepsilon ,i-1}. \end{aligned}$$

(7.98)

Notice that the quantities ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]$ and ${\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]$ (given by (6.101) and (6.102)) are defined through integration on the $u=u_{n;i,j}^{(\pm )}$ and $v=v_{n;i,j}^{(\pm )}$ parts of the boundary of ${\mathcal {W}}_{\nearrow }[n;i,j]$ and ${\mathcal {W}}_{\nwarrow }[n;i,j]$, respectively. Note also that

$$\begin{aligned} {\mathcal {W}}_{\nwarrow }[n;i,j]\subset {\mathcal {V}}_{i\nwarrow }^{(n)} \end{aligned}$$

(with ${\mathcal {V}}_{i\nwarrow }^{(n+1)}$ in place of ${\mathcal {V}}_{i\nwarrow }^{(n)}$ if $i<j$) and

$$\begin{aligned} {\mathcal {W}}_{\nearrow }[n;i,j]\subset {\mathcal {V}}_{j\nearrow }^{(n)}, \end{aligned}$$

as well as (Fig. 20)

$$\begin{aligned} {\mathcal {W}}_{\nwarrow }[n;i,j]\cap {\mathcal {R}}_{i;j}^{(n)}={\mathcal {W}}_{\nearrow }[n;i,j]\cap {\mathcal {R}}_{i;j}^{(n)}=\emptyset . \end{aligned}$$

Fig. 20

Schematic depiction of the domains ${\mathcal {W}}_{\nwarrow }[n;i,j]$ and ${\mathcal {W}}_{\nearrow }[n;i,j]$

In view of the definition (6.91) and (6.92) of $dist_{\nwarrow }[\cdot ]$ and $dist_{\nearrow }[\cdot ]$, we can readily calculate that:

• For all $(u,v)\in {\mathcal {W}}_{\nwarrow }[n;i,j]$:

  $$\begin{aligned} dist_{\nwarrow }[(u,v)]=\exp \big (-\exp (\sigma _{\varepsilon }^{-4})\big )\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }} \end{aligned}$$

  (7.99)

  and²³

  $$\begin{aligned} dist_{\nearrow }[(u,v)]\ge e^{-\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }^{-\frac{7}{8}}\frac{\varepsilon ^{(j-1)}}{\sqrt{-\Lambda }}. \end{aligned}$$

  (7.100)

• For all $(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]$:

  $$\begin{aligned} dist_{\nearrow }[(u,v)]=\exp \big (-\exp (\sigma _{\varepsilon }^{-4})\big )\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }} \end{aligned}$$

  (7.101)

  and

  $$\begin{aligned} dist_{\nwarrow }[(u,v)]\ge e^{-\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }^{-\frac{7}{8}}\frac{\varepsilon ^{(i-1)}}{\sqrt{-\Lambda }}. \end{aligned}$$

  (7.102)

In view of the bound (7.1) on the support of $f_{\varepsilon i}$, we know that, among all the $f_{\varepsilon k}$’s, only $f_{\varepsilon i}$ is supported on ${\mathcal {W}}_{\nwarrow }[n;i,j]$, and only $f_{\varepsilon j}$ is supported on ${\mathcal {W}}_{\nearrow }[n;i,j]$. As a result,

$$\begin{aligned} T_{\mu \nu }[f_{\varepsilon }]\big |_{{\mathcal {W}}_{\nwarrow }[n;i,j]}&=a_{\varepsilon i}T_{\mu \nu }[f_{\varepsilon i}]\big |_{{\mathcal {W}}_{\nwarrow }[n;i,j]},\\ T_{\mu \nu }[f_{\varepsilon }]\big |_{{\mathcal {W}}_{\nearrow }[n;i,j]}&=a_{\varepsilon j}T_{\mu \nu }[f_{\varepsilon j}]\big |_{{\mathcal {W}}_{\nearrow }[n;i,j]}.\nonumber \end{aligned}$$

(7.103)

Furthermore, (6.73) and the definition (7.96), (7.97) of ${\mathcal {W}}_{\nwarrow }[n;i,j]$, ${\mathcal {W}}_{\nearrow }[n;i,j]$, readily yield the following lower bounds:

• When $i>j$:

  $$\begin{aligned} \inf _{{\mathcal {W}}_{\nwarrow }[n;i,j]}r\ge e^{-\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }^{-1}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\quad \text { and }\quad \inf _{{\mathcal {W}}_{\nearrow }[n;i,j]}r\ge e^{-\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }^{-\frac{7}{8}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}.\nonumber \\ \end{aligned}$$

  (7.104)

• When $i<j$:

  $$\begin{aligned} \inf _{{\mathcal {W}}_{\nwarrow }[n;i,j]}r\ge e^{-\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }\frac{1}{\varepsilon ^{(i)}\sqrt{-\Lambda }}\quad \text { and }\quad \inf _{{\mathcal {W}}_{\nearrow }[n;i,j]}r\ge e^{-\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }\frac{1}{\varepsilon ^{(i)}\sqrt{-\Lambda }}.\nonumber \\ \end{aligned}$$

  (7.105)

Integrating (2.47) from $u=u_{n;i,j}^{(-)}$ up to $u=u_{n;i,j}^{(+)}$, exponentiating the resulting expression and then integrating in $v\in [v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1},v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}]$, we readily obtain using the definition (6.101) of ${\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]$:

$$\begin{aligned}&{\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]=\int _{\text { }v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}^{\text { }v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}\nonumber \\&\qquad \exp \Big (-\int _{u_{n;i,j}^{(-)}}^{u_{n;i,j}^{(+)}}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\bar{u}},{\bar{v}})\,d{\bar{u}}\Big )\frac{\partial _{v}r}{1-\frac{2m}{r}}(u_{n;i,j}^{(-)},{\bar{v}})\,d{\bar{v}}. \end{aligned}$$

(7.106)

Similarly, after integrating (2.46):

$$\begin{aligned}&{\mathfrak {D}}r_{\nearrow }^{(+)}[n;i,j] =\int _{\text { }u_{n;i,j-1}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}^{\text { }u_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}\nonumber \\&\qquad \exp \Big (\int _{v_{n;i,j}^{(-)}}^{v_{n;i,j}^{(+)}}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}({\bar{u}},{\bar{v}})\,d{\bar{v}}\Big )\frac{-\partial _{u}r}{1-\frac{2m}{r}}({\bar{u}},v_{n;i,j}^{(-)})\,d{\bar{u}}. \end{aligned}$$

(7.107)

In view of (7.103), we readily infer (arguing exactly as in the proof of (7.56)–(7.57)) that, for all $(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]$,

$$\begin{aligned} \int _{u_{n;i,j}^{(-)}}^{u}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\bar{u}},v)\,d{\bar{u}}=\int _{u_{n;i,j}^{(-)}}^{u}\frac{2E_{\nearrow }[n;i,j]}{r\cdot \big (1-\frac{1}{3}\Lambda r^{2}-O(\mu _{\nearrow ij})\big )}({\bar{u}},v)\,d{\bar{u}}\nonumber \\ \end{aligned}$$

(7.108)

and, for all $(u,v)\in {\mathcal {W}}_{\nwarrow }[n;i,j]$,

$$\begin{aligned} \int _{v_{n;i,j}^{(-)}}^{v}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\bar{v}})\,d{\bar{v}}=\int _{v_{n;i,j}^{(-)}}^{v}\frac{2E_{\nwarrow }[n;i,j]}{r\cdot \big (1-\frac{1}{3}\Lambda r^{2}-O(\mu _{\nwarrow ij})\big )}(u,{\bar{v}})\,d{\bar{v}},\nonumber \\ \end{aligned}$$

(7.109)

where

$$\begin{aligned} \mu _{\nearrow ij}&\doteq \sup _{{\mathcal {W}}_{\nearrow }[n;i,j]}\frac{2{\tilde{m}}}{r},\\ \mu _{\nwarrow ij}&\doteq \sup _{{\mathcal {W}}_{\nwarrow }[n;i,j]}\frac{2{\tilde{m}}}{r}.\nonumber \end{aligned}$$

(7.110)

Note that

$$\begin{aligned} \mu _{\nearrow ij},\text { }\mu _{\nwarrow ij}=O(\eta _{0}), \end{aligned}$$

(7.111)

as a trivial consequence of (6.70).

Substituting (7.108) and (7.109) in (7.106) and (7.107), respectively, we obtain

$$\begin{aligned}&{\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]=\int _{\text { }v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}^{\text { }v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}\nonumber \\&\qquad \exp \Big (-\int _{u_{n;i,j}^{(-)}}^{u_{n;i,j}^{(+)}}\frac{2E_{\nearrow }[n;i,j]}{r\cdot \big (1-\frac{1}{3}\Lambda r^{2}-O(\mu _{\nearrow ij})\big )}({\bar{u}},{\bar{v}})\,d{\bar{u}}\Big )\nonumber \\&\qquad \cdot \frac{\partial _{v}r}{1-\frac{2m}{r}}(u_{n;i,j}^{(-)},{\bar{v}})\,d{\bar{v}} \end{aligned}$$

(7.112)

and

$$\begin{aligned}&{\mathfrak {D}}r_{\nearrow }^{(+)}[n;i,j]=\int _{\text { }u_{n;i,j-1}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}^{\text { }u_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}\nonumber \\&\qquad \exp \Big (\int _{v_{n;i,j}^{(-)}}^{v_{n;i,j}^{(+)}}\frac{2E_{\nwarrow }[n;i,j]}{r\cdot \big (1-\frac{1}{3}\Lambda r^{2}-O(\mu _{\nwarrow ij})\big )}({\bar{u}},{\bar{v}})\,d{\bar{v}}\Big )\nonumber \\&\qquad \cdot \frac{-\partial _{u}r}{1-\frac{2m}{r}}({\bar{u}},v_{n;i,j}^{(-)})\,d{\bar{u}}. \end{aligned}$$

(7.113)

From (7.49) (and the analogous equation for $\partial _{v}E_{\nearrow }[n;i,j](u,v)$), we obtain the following formulas (in analogy with (7.50) and (7.52)):

• For $(u,v)\in {\mathcal {W}}_{\nwarrow }[n;i,j]$,

  $$\begin{aligned}{} & {} E_{\nwarrow }[n;i,j](u,v)\nonumber \\{} & {} \quad =\exp \Big (-\int _{u}^{u_{n;i,j}^{(-)}}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\bar{u}},v)\,d{\bar{u}}\Big )\nonumber \\{} & {} \qquad \cdot E_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},v)-a_{\varepsilon i}\mathfrak {Err}_{\nwarrow }^{(0)}[n;i,j](u,v), \end{aligned}$$

  (7.114)

  where

  $$\begin{aligned}&\mathfrak {Err}_{\nwarrow }^{(0)}[n;i,j](u,v)\nonumber \\&\quad \doteq \int _{u}^{u_{n;i,j}^{(-)}}\exp \Big (-\int _{u}^{{\bar{u}}}4\pi \frac{rT_{uu}[f_{\varepsilon }]}{-\partial _{u}r}({\hat{u}},v)\,d{\hat{u}}\Big )\times \\&\qquad \times \Bigg \{2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}\partial _{v}(r^{2}T_{uv}[f_{\varepsilon i}])\nonumber \\&\quad \quad +2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon i}])\Bigg \}({\bar{u}},v)\,d{\bar{u}}.\nonumber \end{aligned}$$

  (7.115)

• For $(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]$,

  $$\begin{aligned}{} & {} E_{\nearrow }[n;i,j](u,v)\nonumber \\{} & {} \quad =\exp \Big (\int _{v}^{v_{n;i,j}^{(-)}}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\bar{v}})\,d{\bar{v}}\Big )\nonumber \\{} & {} \qquad \cdot E_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})-a_{\varepsilon j}\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j](u,v), \end{aligned}$$

  (7.116)

  where

  $$\begin{aligned}&\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j](u,v)\nonumber \\&\quad \doteq \int _{v}^{v_{n;i,j}^{(-)}}\exp \Big (-\int _{v}^{{\bar{v}}}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\hat{v}})\,d{\hat{v}}\Big )\times \\&\qquad \times \Bigg \{2\pi \frac{1-\frac{2m}{r}}{-\partial _{u}r}\partial _{u}(r^{2}T_{uv}[f_{\varepsilon j}])\nonumber \\&\quad +2\pi \frac{1-\frac{2m}{r}}{-\partial _{u}r}\Big (\partial _{u}\log (\Omega ^{2})-2\frac{\partial _{u}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon j}])\Bigg \}(u,{\bar{v}})\,d{\bar{v}}.\nonumber \end{aligned}$$

  (7.117)

We will now procced to treat the cases $i>j$ and $i<j$ separately.

The case $i>j$: Proof of (7.89)–(7.91). Integrating (2.48) in v from the axis $\gamma _{{\mathcal {Z}}_{\varepsilon }}$ up to ${\mathcal {W}}_{\nearrow }[n;i,j]$, ${\mathcal {W}}_{\nwarrow }[n;i,j]$, using the fact that, among all the $f_{\varepsilon k}$’s, only $f_{\varepsilon {\bar{j}}}$, $j\le {\bar{j}}\le i$ are supported on the domain

$$\begin{aligned} \left\{ \inf _{{\mathcal {W}}_{\nearrow }[n;i,j]}u\le u\le \sup _{{\mathcal {W}}_{\nearrow }[n;i,j]}u\right\} \cap \left\{ v\le \sup _{{\mathcal {W}}_{\nearrow }[n;i,j]}v\right\} \end{aligned}$$

(and the same for ${\mathcal {W}}_{\nwarrow }[n;i,j]$), we can readily estimate (using (6.73) and (7.11), (7.12)):

$$\begin{aligned} \sup _{{\mathcal {W}}_{\nearrow }[n;i,j]\cup {\mathcal {W}}_{\nwarrow }[n;i,j]}{\tilde{m}}\le \exp (\exp (\sigma _{\varepsilon }^{-6}))\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}. \end{aligned}$$

(7.118)

From (7.118) and the bound (7.104) for r on ${\mathcal {W}}_{\nearrow }[n;i,j]$, ${\mathcal {W}}_{\nwarrow }[n;i,j]$, we immediately infer that:

$$\begin{aligned} \mu _{\nearrow ij}+\mu _{\nwarrow ij}= & {} \sup _{{\mathcal {W}}_{\nearrow }[n;i,j]}\frac{2{\tilde{m}}}{r}+\sup _{{\mathcal {W}}_{\nwarrow }[n;i,j]}\frac{2{\tilde{m}}}{r}\nonumber \\\le & {} \exp (\exp (\sigma _{\varepsilon }^{-7}))\rho _{\varepsilon }^{\frac{7}{8}}\le \rho _{\varepsilon }^{\frac{3}{4}}. \end{aligned}$$

(7.119)

Using the fact that $T_{\mu \nu }[f_{\varepsilon }]=a_{\varepsilon j}T_{\mu \nu }[f_{\varepsilon j}]$ on ${\mathcal {W}}_{\nearrow }[n;i,j]$, the bound (7.11) for $T_{vv}[f_{\varepsilon j}]$ on ${\mathcal {W}}_{\nearrow }[n;i,j]\subset {\mathcal {V}}_{j\nearrow }^{(n)}$, combined with (6.73), implies that

$$\begin{aligned}&\sup _{(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]} \int _{v}^{v_{n;i,j}^{(-)}}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}(u,{\bar{v}})\,d{\bar{v}}\nonumber \\&\quad \le a_{\varepsilon j}\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )(-\Lambda )^{-2}\nonumber \\&\qquad \times \int _{r(u_{n;i,j}^{(+)},v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1})}^{r(u_{n;i,j}^{(-)},v_{n;i,j}^{(-)})}\frac{(\varepsilon ^{(j)})^{4}}{{\bar{r}}^{5}}\,d{\bar{r}}\nonumber \\&\quad \le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )(-\Lambda )^{-2}(\varepsilon ^{(j)})^{4}\nonumber \\&\qquad \times \frac{r(u_{n;i,j}^{(-)},v_{n;i,j}^{(-)})-r(u_{n;i,j}^{(+)},v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1})}{\big (r(u_{n;i,j}^{(+)},v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1})\big )^{5}}\nonumber \\&\quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-6})\big )(-\Lambda )^{-2}(\varepsilon ^{(j)})^{4}\nonumber \\&\qquad \times \frac{(u_{n;i,j}^{(+)}-u_{n;i,j}^{(-)})+(v_{n;i,j}^{(-)}-v_{n;i-1,j}^{(+)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1})}{(\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}+v_{n;i-1,j}^{(+)}-u_{n;i,j}^{(+)})^{5}}\nonumber \\&\quad \le \exp \big (\exp (\sigma _{\varepsilon }^{-7})\big )(\varepsilon ^{(j)})^{4}\nonumber \\&\qquad \times \frac{\varepsilon ^{(j)}+\rho _{\varepsilon }^{-1}\varepsilon ^{(i-1)}}{(\rho _{\varepsilon }^{-\frac{7}{8}}\varepsilon ^{(i-1)}+\text {sgn}(i-j-1)\cdot \rho _{\varepsilon }^{-1}\varepsilon ^{(j)})^{5}}\nonumber \\&\quad \le \rho _{\varepsilon }, \end{aligned}$$

(7.120)

where

$$\begin{aligned} \text {sgn}(i-j-1)={\left\{ \begin{array}{ll} 0, &{} i=j+1,\\ +1, &{} i>j+1 \end{array}\right. } \end{aligned}$$

and, in passing from the second to the third line in (7.120), we used the fact that $\partial _{u}r<0$ and $\partial _{v}r>0$ on ${\mathcal {U}}_{\varepsilon }^{+}$. Substituting the bound (7.120) in (7.116), we infer that, for any $(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]$:

$$\begin{aligned}{} & {} E_{\nearrow }[n;i,j](u,v)\nonumber \\{} & {} \quad =\big (1+O(\rho _{\varepsilon })\big )\cdot E_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})-a_{\varepsilon j}\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j](u,v).\nonumber \\ \end{aligned}$$

(7.121)

Dividing (7.121) with r and integrating in u, we infer that, for any $(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]$:

$$\begin{aligned}{} & {} \int _{u_{n;i,j}^{(-)}}^{u}\frac{E_{\nearrow }[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}}=\big (1+O(\rho _{\varepsilon })\big )\nonumber \\{} & {} \qquad \cdot \int _{u_{n;i,j}^{(-)}}^{u}\frac{E_{\nearrow }[n;i,j]({\bar{u}},v_{n;i,j}^{(-)})}{r({\bar{u}},v)}\,d{\bar{u}}-a_{\varepsilon j}\int _{u_{n;i,j}^{(-)}}^{u}\frac{\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}}.\nonumber \\ \end{aligned}$$

(7.122)

Using the bound

$$\begin{aligned} \sup _{v\ge 0}\Bigg (\sup _{(u_{1},v),(u_{2},v)\in {\mathcal {W}}_{\nearrow }[n;i,j]}\Big |\frac{r(u_{1},v)}{r(u_{2},v)}-1\Big |\Bigg )\le e^{\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }^{\frac{7}{8}}\le \rho _{\varepsilon }^{\frac{1}{2}}\qquad \end{aligned}$$

(7.123)

(following readily from (6.73) and the definition (7.97) of ${\mathcal {W}}_{\nearrow }[n;i,j]$), we readily infer from (7.122) that:

$$\begin{aligned}{} & {} \int _{u_{n;i,j}^{(-)}}^{u}\frac{E_{\nearrow }[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}} \nonumber \\{} & {} \quad =\big (1+O(\rho _{\varepsilon }^{\frac{1}{2}})\big )\cdot \frac{1}{r(u,v)}\int _{u_{n;i,j}^{(-)}}^{u}E_{\nearrow }[n;i,j]({\bar{u}},v_{n;i,j}^{(-)})\,d{\bar{u}}\\{} & {} \qquad -a_{\varepsilon j}\int _{u_{n;i,j}^{(-)}}^{u}\frac{\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}}\nonumber \\{} & {} \quad =\big (1+O(\rho _{\varepsilon }^{\frac{1}{2}})\big )\cdot \frac{{\mathcal {E}}_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})}{r(u,v)} -a_{\varepsilon j}\int _{u_{n;i,j}^{(-)}}^{u}\frac{\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}}.\nonumber \end{aligned}$$

(7.124)

Similarly, for any $(u,v)\in {\mathcal {W}}_{\nwarrow }[n;i,j]$:

$$\begin{aligned}{} & {} \int _{v_{n;i,j}^{(-)}}^{v}\frac{E_{\nwarrow }[n;i,j]}{r}(u,{\bar{v}})\,d{\bar{v}}\nonumber \\{} & {} \quad =\big (1+O(\rho _{\varepsilon }^{\frac{1}{2}})\big )\cdot \frac{{\mathcal {E}}_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},v)}{r(u,v)}\nonumber \\{} & {} \qquad -a_{\varepsilon i}\int _{v_{n;i,j}^{(-)}}^{v}\frac{\mathfrak {Err}_{\nwarrow }^{(0)}[n;i,j]}{r}(u,{\bar{v}})\,d{\bar{v}}. \end{aligned}$$

(7.125)

Arguing similarly as for the derivation of (7.65), integrating by parts in $\partial _{u}$ for the term $\partial _{u}(r^{2}T_{uv})$ in $\int _{u_{n;i,j}^{(-)}}^{u}\frac{\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}}$ (see the expression (7.117)), we calculate:

$$\begin{aligned}&\Big |\int _{u_{n;i,j}^{(-)}}^{u} \frac{\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}}\Big |\\&\quad =\Bigg |\int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{u}\int _{v}^{v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}}\frac{1}{r({\bar{u}},v)}\Bigg [\exp \Big (-\int _{v}^{{\bar{v}}}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}({\bar{u}},{\hat{v}})\,d{\hat{v}}\Big )\nonumber \\&\qquad \times \Bigg \{2\pi \frac{1-\frac{2m}{r}}{-\partial _{u}r}\partial _{u}(r^{2}T_{uv}[f_{\varepsilon j}])\nonumber \\&\qquad +2\pi \frac{1-\frac{2m}{r}}{-\partial _{u}r}\Big (\partial _{u}\log (\Omega ^{2})-2\frac{\partial _{u}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon j}])\Bigg \}({\bar{u}},{\bar{v}})\Bigg ]\,d{\bar{v}}d{\bar{u}}\Bigg |\nonumber \\&\quad =\Bigg |\int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{u}\int _{v}^{v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}}\Bigg (\frac{1}{r({\bar{u}},v)}\Bigg [\exp \Big (-\int _{v}^{{\bar{v}}}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}({\bar{u}},{\hat{v}})\,d{\hat{v}}\Big )\nonumber \\&\qquad \cdot 2\pi \frac{1-\frac{2m}{r}}{-\partial _{u}r}r^{2}T_{uv}[f_{\varepsilon j}]({\bar{u}},{\bar{v}})\nonumber \\&\qquad \times \Bigg \{\int _{v}^{{\bar{v}}}\partial _{u}\Big (\frac{4\pi }{r\partial _{v}r}\Big )r^{2}T_{vv}[f_{\varepsilon }]({\bar{u}},{\hat{v}})\,d{\hat{v}}+\int _{v}^{{\bar{v}}}\frac{4\pi }{r\partial _{v}r}\partial _{u}(r^{2}T_{vv}[f_{\varepsilon }])({\bar{u}},{\hat{v}})\,d{\hat{v}}\nonumber \\&\qquad -\partial _{u}\log \Big (\frac{1-\frac{2m}{r}}{-\partial _{u}r}\Big )({\bar{u}},{\bar{v}})+\Big (\partial _{u}\log (\Omega ^{2})-2\frac{\partial _{u}r}{r}\Big )({\bar{u}},{\bar{v}})\Bigg \}\Bigg ]\nonumber \\&\qquad +\frac{\partial _{u}r}{r^{2}}({\bar{u}},v)\exp \Big (-\int _{v}^{{\bar{v}}}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}({\bar{u}},{\hat{v}})\,d{\hat{v}}\Big )\nonumber \\&\qquad \cdot 2\pi \frac{1-\frac{2m}{r}}{-\partial _{u}r}r^{2}T_{uv}[f_{\varepsilon i}]({\bar{u}},{\bar{v}})\Bigg )\,d{\bar{v}}d{\bar{u}}\Bigg |.\nonumber \end{aligned}$$

(7.126)

We will estimate the right hand side of (7.126) similarly as we did for (7.65):

• Using the bounds (6.70), (6.73), (7.11), (7.103) (and the fact that $i\ge j+1$), we can estimate:

  $$\begin{aligned}&\sup _{(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j],\text { }({\bar{u}},{\bar{v}})\in [u_{n;i-1,j}^{(-)},u]\times [v,v_{n;i,j}^{(-)}]} \nonumber \\&\quad \Big |\int _{v}^{{\bar{v}}}4\pi \frac{rT_{vv}[f_{\varepsilon }]}{\partial _{v}r}({\bar{u}},{\hat{v}})\,d{\hat{v}}\Big |\\&\quad \le \int _{v_{n;i-1,j}^{(-)}+(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,i-1}}^{v_{n;i,j}^{(-)}}\exp \big (\exp (4\sigma _{\varepsilon }^{-5})\big )\cdot \frac{(\varepsilon ^{(j)})^{4}}{r^{5}(u_{n;i,j}^{(+)},v)}(-\Lambda )^{-2}\,dv\nonumber \\&\quad \le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\cdot \frac{(\varepsilon ^{(j)})^{4}}{r^{4}(u_{n;i,j}^{(+)},v_{n;i-1,j}^{(-)}+(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,i-1})}(-\Lambda )^{-2}\nonumber \\&\quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-6})\big )\cdot \rho _{\varepsilon }^{\frac{7}{2}}\nonumber \\&\quad \le 1.\nonumber \end{aligned}$$

  (7.127)

• Using the bounds (6.73) and (7.12), we can estimate:

  $$\begin{aligned}&\sup _{{\mathcal {W}}_{\nearrow }[n;i,j]}\Big (2\pi \frac{1-\frac{2m}{r}}{\partial _{v}r}r^{2}T_{uv}[f_{\varepsilon j}]\Big ) \nonumber \\&\quad \le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\sup _{{\mathcal {W}}_{\nearrow }[n;i,j]}\frac{(\varepsilon ^{(j)})^{2}}{r^{2}}(-\Lambda )^{-1}\nonumber \\&\quad \le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\frac{(\varepsilon ^{(j)})^{2}}{r^{2}(u_{n;i,j}^{(+)},v_{n;i-1,j}^{(-)}+(\rho _{\varepsilon }^{-\frac{7}{8}}+1)h_{\varepsilon ,i-1})}(-\Lambda )^{-1}\nonumber \\&\quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-6})\big )\rho _{\varepsilon }^{\frac{7}{4}}\le \rho _{\varepsilon }^{\frac{3}{2}}. \end{aligned}$$

  (7.128)

• Using equation (2.45) and the bounds (6.70), (6.73), (7.103), (7.11), (7.12), and (7.104) (as well as the trivial bound $a_{\varepsilon k}\le 1$), we can estimate for all $(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]$:

  $$\begin{aligned}&\sup _{({\bar{u}},{\bar{v}})\in [u_{n;i,j}^{(-)},u]\times [v,v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}]} \Big |\int _{v}^{{\bar{v}}} \partial _{u}\Big (\frac{4\pi }{r\partial _{v}r}\Big )r^{2}T_{vv}[f_{\varepsilon }]({\bar{u}},{\hat{v}})\,d{\hat{v}}\Big |\\&\quad =\sup _{({\bar{u}},{\bar{v}})\in [u_{n;i-,j}^{(-)},u]\times [v,v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}]}\nonumber \\&\qquad \Big |\int _{v}^{{\bar{v}}}4\pi \Big (-\frac{\partial _{u}r}{r^{2}\partial _{v}r}-\frac{\partial _{u}\partial _{v}r}{r(\partial _{v}r)^{2}}\Big )r^{2}T_{vv}[f_{\varepsilon }]({\bar{u}},{\hat{v}})\,d{\hat{v}}\Big |\nonumber \\&\quad =\sup _{({\bar{u}},{\bar{v}})\in [u_{n;i,j}^{(-)},u]\times [v,v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}]}\nonumber \\&\qquad \Big |\int _{v}^{{\bar{v}}}4\pi \Big (-\frac{\partial _{u}r}{r^{2}\partial _{v}r}+\frac{\frac{2{\tilde{m}}}{r}-\frac{2}{3}\Lambda r^{2}}{r^{2}(1-\frac{2m}{r})}\frac{-\partial _{u}r}{\partial _{v}r}+\frac{4\pi r^{2}T_{uv}}{r^{2}(\partial _{v}r)^{2}}\Big )r^{2}T_{vv}[f_{\varepsilon }]({\bar{u}},{\hat{v}})\,d{\hat{v}}\Big |\nonumber \\&\quad \le \int _{v}^{v_{n;i,j}^{(-)}}\exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\frac{1}{r^{2}(u,{\hat{v}})}\frac{(\varepsilon ^{(j)})^{4}}{r^{4}(u,{\hat{v}})}(-\Lambda )^{-2}\,d{\hat{v}}\nonumber \\&\quad \le \exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\frac{(\varepsilon ^{(j)})^{4}}{r^{5}(u,v)}(-\Lambda )^{-2}\nonumber \\&\quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-9})\big )\rho _{\varepsilon }^{\frac{7}{2}}\frac{1}{r(u,v)}.\nonumber \end{aligned}$$

  (7.129)

• Using (7.45) to express $\partial _{u}(r^{2}T_{vv}[f_{\varepsilon }])$ in terms of $\partial _{v}(r^{2}T_{uv}[f_{\varepsilon }])$ and integrating by parts in $\partial _{v}$, we calculate for any $(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]$ (in view of (7.103) and the bounds (6.70), (6.73), (7.103), (7.12), (7.104), (7.13) for $\partial _{v}\Omega ^{2}$, (7.14) for $\partial _{v}^{2}r$ and (7.102) for $dist_{\nwarrow }[\cdot ]$ on ${\mathcal {W}}_{\nearrow }[n;i,j]$):

  $$\begin{aligned}&\sup _{({\bar{u}},{\bar{v}})\in [u_{n;i,j}^{(-)},u]\times [v,v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}]}\Big |\int _{v}^{{\bar{v}}}\frac{4\pi }{r\partial _{v}r}\partial _{u}(r^{2}T_{vv}[f_{\varepsilon }])({\bar{u}},{\hat{v}})\,d{\hat{v}}\Big |\\&\quad =\sup _{({\bar{u}},{\bar{v}})\in [u_{n;i,j}^{(-)},u]\times [v,v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}]}\Big |\int _{v}^{{\bar{v}}}\frac{4\pi }{r}\frac{1}{\partial _{v}r}\Big (-\partial _{v}(r^{2}T_{uv}[f_{\varepsilon }])\nonumber \\&\qquad +\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon }])\Big )({\bar{u}},{\hat{v}})\,d{\hat{v}}\Big |\nonumber \\&\quad =\sup _{({\bar{u}},{\bar{v}})\in [u_{n;i,j}^{(-)},u]\times [v,v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}]}\Big |\int _{v}^{{\bar{v}}}4\pi \Big (\partial _{v}\big (\frac{1}{r\partial _{v}r}\big )\cdot r^{2}T_{uv}[f_{\varepsilon }]\nonumber \\&\qquad +\frac{1}{r\partial _{v}r}\Big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big )(r^{2}T_{uv}[f_{\varepsilon }])\Big )({\bar{u}},{\hat{v}})\,d{\hat{v}}\nonumber \\&\qquad +\frac{4\pi }{r}\frac{1}{\partial _{v}r}\cdot r^{2}T_{uv}[f_{\varepsilon }]({\bar{u}},{\bar{v}})-\frac{4\pi }{r}\frac{1}{\partial _{v}r}\cdot r^{2}T_{uv}[f_{\varepsilon }]({\bar{u}},v)\Big |\nonumber \\&\quad \le \int _{v}^{v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}\exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\frac{1}{r(u,{\hat{v}})}\nonumber \\&\qquad \big (\frac{1}{dist_{\nwarrow }[(u,{\hat{v}})]}+\frac{1}{r(u,{\hat{v}})}\big )\frac{(\varepsilon ^{(j)})^{2}}{(-\Lambda )r^{2}(u,{\hat{v}})}\,d{\hat{v}}\nonumber \\&\qquad +\exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\frac{1}{r(u,v)}\frac{(\varepsilon ^{(j)})^{2}}{(-\Lambda )r^{2}(u,v)}\nonumber \\&\quad \le \exp \big (2\exp (\sigma _{\varepsilon }^{-9})\big )\frac{1}{r(u,v)}\Big (1+\int _{v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}^{v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}\nonumber \\&\quad \frac{1}{dist_{\nwarrow }[(u,{\hat{v}})]}\,d{\hat{v}}\Big )\frac{(\varepsilon ^{(j)})^{2}}{(-\Lambda )r^{2}(u,{\hat{v}})}\nonumber \\&\qquad +\exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\frac{1}{r(u,v)}\frac{(\varepsilon ^{(j)})^{2}}{(-\Lambda )r^{2}(u,v)}\nonumber \\&\quad \le \exp \big (4\exp (\sigma _{\varepsilon }^{-9})\big )\frac{1}{r(u,v)}\Big (1+\exp (\sigma _{\varepsilon }^{-7})\rho _{\varepsilon }^{-\frac{1}{8}}\Big )\frac{(\varepsilon ^{(j)})^{2}}{(-\Lambda )r^{2}(u,{\hat{v}})}\nonumber \\&\qquad +\exp \big (\exp (\sigma _{\varepsilon }^{-9})\big )\frac{1}{r(u,v)}\frac{(\varepsilon ^{(j)})^{2}}{(-\Lambda )r^{2}(u,v)}\nonumber \\&\quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-9})\big )\rho _{\varepsilon }^{\frac{13}{8}}\frac{1}{r(u,v)}.\nonumber \end{aligned}$$

  (7.130)

• Using the the relation (2.49) for $\partial _{u}{\tilde{m}}$, the estimate (7.14) for $\partial _{u}^{2}r$, as well as the bounds (6.73), (7.11), (7.12) and (6.70), we can estimate for any $({\bar{u}},{\bar{v}})\in {\mathcal {W}}_{\nearrow }[n;i,j]$:

  $$\begin{aligned} \Big |\partial _{u}\log \Big (\frac{1-\frac{2m}{r}}{-\partial _{u}r}\Big )({\bar{u}},{\bar{v}})\Big |\le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\Big (\frac{1}{dist_{\nwarrow }[({\bar{u}},{\bar{v}})]}+\frac{1}{r({\bar{u}},{\bar{v}})}\Big ).\nonumber \\ \end{aligned}$$

  (7.131)

• Using the estimate (7.13) for $\partial _{u}\Omega ^{2}$, as well as the bound (6.73),, we can estimate for any $({\bar{u}},{\bar{v}})\in {\mathcal {W}}_{\nearrow }[n;i,j]$:

  $$\begin{aligned} \Big |\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\Big |({\bar{u}},{\bar{v}})\le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\Big (\frac{1}{dist_{\nwarrow }[({\bar{u}},{\bar{v}})]}+\frac{1}{r({\bar{u}},{\bar{v}})}\Big ).\nonumber \\ \end{aligned}$$

  (7.132)

Using the estimates (7.127)–(7.132) (together with (6.73), (7.12), (7.103), (7.102), (7.104) and the relation of the parameters $\varepsilon$, $\rho _{\varepsilon }$, $\delta _{\varepsilon }$ and $\sigma _{\varepsilon }$) to bound the right hand side of (7.126), we therefore obtain for any $(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]$:

$$\begin{aligned}&\Big |\int _{u_{n;i,j}^{(-)}}^{u} \frac{\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}}\Big |\\&\quad \le \int _{v_{\varepsilon ,j}^{(n)}-h_{\varepsilon ,j}}^{u}\int _{v}^{v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i-1}}\Bigg (\frac{1}{r({\bar{u}},v)}\rho _{\varepsilon }^{\frac{3}{2}}\Bigg \{\exp \big (\exp (2\sigma _{\varepsilon }^{-9})\big )\rho _{\varepsilon }^{\frac{7}{2}}\frac{1}{r(u,v)}\nonumber \\&\qquad +\exp \big (\exp (2\sigma _{\varepsilon }^{-9})\big )\rho _{\varepsilon }^{\frac{13}{8}}\frac{1}{r(u,v)}\nonumber \\&\qquad +\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\Big (\frac{1}{dist_{\nwarrow }[({\bar{u}},{\bar{v}})]}+\frac{1}{r({\bar{u}},{\bar{v}})}\Big )\Bigg \}+ e^{\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }^{\frac{3}{2}}\frac{1}{r^{2}({\bar{u}},v)}\Bigg )\,d{\bar{v}}d{\bar{u}}\nonumber \\&\quad \le \exp \big (\exp (3\sigma _{\varepsilon }^{-9})\big )\rho _{\varepsilon }^{\frac{3}{2}}h_{\varepsilon ,j}\cdot \rho _{\varepsilon }^{-1}h_{\varepsilon ,i-1}\cdot \Big (\rho _{\varepsilon }^{\frac{7}{8}}\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i-1)}}+\frac{1}{r(u,v)}\Big )\frac{1}{r(u,v)}\nonumber \\&\quad \le \exp \big (\exp (4\sigma _{\varepsilon }^{-9})\big )\rho _{\varepsilon }^{\frac{1}{2}}\varepsilon ^{(j)}\varepsilon ^{(i-1)}\cdot \Big (\rho _{\varepsilon }^{\frac{7}{8}}\frac{1}{\varepsilon ^{(i-1)}}+\rho _{\varepsilon }^{\frac{7}{8}}\frac{1}{\varepsilon ^{(j)}}\Big )(-\Lambda )^{-\frac{1}{2}}\frac{1}{r(u,v)}\nonumber \\&\quad \le \exp \big (\exp (4\sigma _{\varepsilon }^{-9})\big )\rho _{\varepsilon }^{\frac{11}{8}}\max \{\varepsilon ^{(i-1)},\varepsilon ^{(j)}\}(-\Lambda )^{-\frac{1}{2}}\frac{1}{r(u,v)}\nonumber \\&\quad \le \rho _{\varepsilon }^{\frac{5}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\frac{1}{r(u,v)}.\nonumber \end{aligned}$$

(7.133)

Returning to (7.124) and using (7.133) to estimate the last term in the right hand side, we infer that, for any $(u,v)\in {\mathcal {W}}_{\nearrow }[n;i,j]$:

$$\begin{aligned}{} & {} \int _{u_{n;i,j}^{(-)}}^{u}\frac{E_{\nearrow }[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}}\nonumber \\{} & {} \quad =\big (1+O(\rho _{\varepsilon }^{\frac{1}{2}})\big )\cdot \frac{{\mathcal {E}}_{\nearrow }[n;i,j](u,v_{n;i,j}^{(-)})+O\Big (\rho _{\varepsilon }^{\frac{5}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )}{r(u,v)}. \end{aligned}$$

(7.134)

Similarly, estimating $\int _{v_{n;i,j}^{(-)}}^{v}\frac{\mathfrak {Err}_{\nwarrow }^{(0)}[n;i,j]}{r}(u,{\bar{v}})\,d{\bar{v}}$ similarly as we did for $\int _{u_{n;i,j}^{(-)}}^{u}\frac{\mathfrak {Err}_{\nearrow }^{(0)}[n;i,j]}{r}({\bar{u}},v)\,d{\bar{u}}$, we infer from (7.125) that, for all $(u,v)\in {\mathcal {W}}_{\nwarrow }[n;i,j]$:

$$\begin{aligned} \int _{v_{n;i,j}^{(-)}}^{v}\frac{E_{\nwarrow }[n;i,j]}{r}(u,{\bar{v}})\,d{\bar{v}}=\big (1+O(\rho _{\varepsilon }^{\frac{1}{2}})\big )\cdot \frac{{\mathcal {E}}_{\nwarrow }[n;i,j](u_{n;i,j}^{(-)},v)+O\Big (\rho _{\varepsilon }^{\frac{5}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )}{r(u,v)}.\qquad \quad \end{aligned}$$

(7.135)

Substituting (7.134) in (7.112) and using (7.119), (7.44) and the fact that $\Lambda r^{2}=O(\varepsilon )$ on ${\mathcal {W}}_{\nearrow }[n;i,j]$ when $i>j$, we infer that

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]= & {} \int _{\text { }v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}^{\text { }v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}\nonumber \\{} & {} \times \exp \Bigg (-\big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )\cdot \frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]+O\Big (\rho _{\varepsilon }^{\frac{5}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )}{r(u_{n;i,j}^{(+)},{\bar{v}})}\Bigg )\nonumber \\{} & {} \cdot \frac{\partial _{v}r}{1-\frac{2m}{r}}(u_{n;i,j}^{(-)},{\bar{v}})\,d{\bar{v}}.\nonumber \\ \end{aligned}$$

(7.136)

Similarly, from (7.113) we infer that

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(+)}[n;i,j]= & {} \int _{\text { }u_{n;i,j-1}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}^{\text { }u_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}\nonumber \\{} & {} \exp \Big (\big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )\cdot \frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j]+O\Big (\rho _{\varepsilon }^{\frac{5}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )}{r({\bar{u}},v_{n;i,j}^{(-)})}\Big )\cdot \frac{-\partial _{u}r}{1-\frac{2m}{r}}({\bar{u}},v_{n;i,j}^{(-)})\,d{\bar{u}}.\nonumber \\ \end{aligned}$$

(7.137)

• In the case when $i=j+1$, using the bounds (6.73), (7.11) and (7.104), we can trivially estimate

  $$\begin{aligned}&\sup _{{\bar{v}}\in [v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1},v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}]} \frac{{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]+O\Big (\rho _{\varepsilon }^{\frac{5}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )}{r(u_{n;i,j}^{(+)},{\bar{v}})}\\&\quad \le \frac{\int _{u_{n;i,j}^{(-)}}^{u_{n;i,j}^{(+)}}\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\,du+O\Big (\rho _{\varepsilon }^{\frac{5}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )}{e^{-\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }^{-\frac{7}{8}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}}\nonumber \\&\quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-6})\big )\rho _{\varepsilon }^{\frac{7}{8}}\nonumber \\&\quad \le \rho _{\varepsilon }^{\frac{3}{4}}.\nonumber \end{aligned}$$

  (7.138)

  From (7.136), we therefore infer that

  $$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]&=\int _{\text { }v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}^{\text { }v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}\exp \big (O(\rho _{\varepsilon }^{\frac{3}{4}})\big )\cdot \frac{\partial _{v}r}{1-\frac{2m}{r}}(u_{n;i,j}^{(-)},{\bar{v}})\,d{\bar{v}}\\&=\int _{\text { }v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}^{\text { }v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}\big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )\frac{\partial _{v}r}{1-\frac{2m}{r}}(u_{n;i,j}^{(-)},{\bar{v}})\,d{\bar{v}}\nonumber \\&=\big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big ){\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j].\nonumber \end{aligned}$$

  (7.139)

  As a result, the relation (7.90) follows readily for $i=j+1$.

• In the case when $i>j+1$, we can trivially estimate (using (7.15) and the relation (6.5) between the $\varepsilon ^{(k)}$’s) that, for any ${\bar{v}}\in [v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1},v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}]$:

  $$\begin{aligned} 1-\frac{r(u_{n;i,j}^{(+)},{\bar{v}})}{r_{n;i,j}}=\frac{r(u_{n;i,j}^{(+)},v_{n;i,j}^{(-)})-r(u_{n;i,j}^{(+)},{\bar{v}})}{r(u_{n;i,j}^{(+)},v_{n;i,j}^{(-)})}=O(\varepsilon ). \end{aligned}$$

  (7.140)

  Thus, from (7.136), we infer that

  $$\begin{aligned}&{\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]\nonumber \\&\quad =\int _{\text { }v_{n;i-1,j}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}^{\text { }v_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}\nonumber \\&\quad \exp \Bigg (-\big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})+O(\varepsilon )\big )\cdot \frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]+O\Big (\rho _{\varepsilon }^{\frac{5}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )}{r_{n;i,j}}\Bigg )\times \\&\qquad \times \frac{\partial _{v}r}{1-\frac{2m}{r}}(u_{n;i,j}^{(-)},{\bar{v}})\,d{\bar{v}}=\nonumber \\&=\exp \Bigg (-\big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )\cdot \frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]+O\Big (\rho _{\varepsilon }^{\frac{5}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )}{r_{n;i,j}}\Bigg )\nonumber \\&\qquad \cdot {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j].\nonumber \end{aligned}$$

  (7.141)

  From (7.141) and (7.15) (as well as the upper bound (7.75) for $\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}$), the relation (7.91) follows readily for $i>j+1$.

• In all the cases when $i>j$, we can readily estimate using (6.73) and (7.11):

  $$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]\le \exp \big (\exp (2\sigma _{\varepsilon }^{-6})\big )\varepsilon ^{(i)}(-\Lambda )^{-\frac{1}{2}} \end{aligned}$$

  (7.142)

  and

  $$\begin{aligned} \inf _{{\bar{u}}\in [\text { }u_{n;i,j-1}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1},\text { }u_{n;i,j}^{(-)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}]}r({\bar{u}},v_{n;i,j}^{(-)})\ge e^{-\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }^{-\frac{7}{8}}\varepsilon ^{(j-1)}(-\Lambda )^{-\frac{1}{2}}.\nonumber \\ \end{aligned}$$

  (7.143)

  Thus, from (7.137) (and the relation (6.5) between the $\varepsilon ^{(k)}$’s) we infer that

  $$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(+)}[n;i,j]&=\int _{\text { }u_{n;i,j-1}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}^{\text { }u_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}\nonumber \\&\quad \exp \Big (O\Big (\frac{\exp \big (\exp (2\sigma _{\varepsilon }^{-6})\big )\varepsilon ^{(i)}}{e^{-\sigma _{\varepsilon }^{-6}}\rho _{\varepsilon }^{-\frac{7}{8}}\varepsilon ^{(j-1)}}\Big )\Big )\cdot \frac{-\partial _{u}r}{1-\frac{2m}{r}}({\bar{u}},v_{n;i,j}^{(-)})\,d{\bar{u}}\\&=\int _{\text { }u_{n;i,j-1}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}^{\text { }u_{n;i,j}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,j-1}}\exp \Big (O(\varepsilon )\Big )\cdot \frac{-\partial _{u}r}{1-\frac{2m}{r}}({\bar{u}},v_{n;i,j}^{(-)})\,d{\bar{u}}\nonumber \\&=(1+O(\varepsilon ))\cdot {\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j].\nonumber \end{aligned}$$

  (7.144)

  In particular, (7.89) follows from (7.144).

The case $i<j$: Proof of (7.92)–(7.93). In the case when $i<j$, the proof of (7.92)–(7.93) follows by repeating exactly the same steps as for the proof of (7.89)–(7.91), but using the bound (7.105) in place of (7.104). This results in several simplifications and improvements in the bounds of the various error terms (compare with the proof of (7.33)–(7.34) in relation to (7.31)–(7.32)): using (7.105), it readily follows that the first term in the right hand side of (7.124)–(7.125) is of order $O(\varepsilon ^{\frac{1}{2}})$, while the right hand side of (7.126) is of order $O(\varepsilon )$. As a result, using once more the bound (7.105) for the $\Lambda r^{2}$ terms, one infers that the arguments of the exponentials in (7.112)–(7.113) are of order $O(\varepsilon )$, therefore obtaining (7.92)–(7.93). We will omit the tedious details.

Proof of (7.94)–(7.95). The proof of (7.94) follows by repeating exactly the same steps as for the proof of (7.90), while the proof of (7.95) follows exactly in the same way as the proof of (7.93). We will omit the relevant details.

The relations (7.89)–(7.95) for $\widetilde{{\mathfrak {D}}}r_{\nwarrow }^{(\pm )}[n;i,j]$, $\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(\pm )}[n;i,j]$ in place of ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]$, ${\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]$ follow by repeating exactly the same steps, after replacing $\sigma _{\varepsilon }$, $h_{\varepsilon ,i}$, ${\mathcal {V}}_{i}^{(n)}$, ${\mathcal {R}}_{i;j}^{(n)}$ with $\delta _{\varepsilon }$, ${\tilde{h}}_{\varepsilon ,i}$, $\widetilde{{\mathcal {V}}}_{i}^{(n)}$, $\widetilde{{\mathcal {R}}}_{i;j}^{(n)}$ respectively, in all the expressions above and using (6.78) in place of (6.73). $\square$

7.3 The instability mechanism: energy growth for the Vlasov beams

In this section, we will use Propositions 7.3 and 7.4 in order to obtain quantitative control on the total change in the energy content and the geometric separation of the beams ${\mathcal {V}}_{i}^{(n)}$ between two successive reflections off ${\mathcal {I}}_{\varepsilon }$. To this end, we will first introduce the quantities $\mu _{i}[n]$, ${\mathcal {E}}_{i}[n]$ and $R_{i}[n]$, which are determined by a recursive system of relations and will be later shown to approximate sufficiently $\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]}$, ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]$ and ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]$, respectively:

Definition 7.5

For any $\varepsilon \in (0,\varepsilon _{1}]$, let us define the sequences $\mu _{i}:{\mathbb {N}}\rightarrow (0,+\infty )$, $0\le i\le N_{\varepsilon }-1$, by the recursive relations

$$\begin{aligned} \mu _{i}[n+1]=\mu _{i}[n]\cdot \exp \Big (2\sum _{j=0}^{i-1}\mu _{j}[n+1]\Big ), \end{aligned}$$

(7.145)

with initial conditions

$$\begin{aligned} \mu _{i}[0]=\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[0;i,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[0;i+1,0]}. \end{aligned}$$

(7.146)

We will also define ${\mathcal {E}}_{i}:{\mathbb {N}}\rightarrow (0,+\infty )$ (for $0\le i\le N_{\varepsilon }$) and $R_{i}:{\mathbb {N}}\rightarrow (0,+\infty )$ (for $1\le i\le N_{\varepsilon }$) by the following recursive system of relations:

$$\begin{aligned} {\mathcal {E}}_{i}[n+1]&={\mathcal {E}}_{i}[n]\cdot \exp \Big (\sum _{j=0}^{i-1}\mu _{j}[n+1]\Big ), \end{aligned}$$

(7.147)

$$\begin{aligned} R_{i}[n+1]&=R_{i}[n]\cdot \exp \Big (-\sum _{j=0}^{i-2}\mu _{j}[n+1]\Big ), \end{aligned}$$

(7.148)

with initial conditions

$$\begin{aligned} {\mathcal {E}}_{i}[0]&={\mathcal {E}}_{\nwarrow }^{(-)}[0;i,0],\\ R_{i}[0]&={\mathfrak {D}}r_{\nwarrow }^{(-)}[0;i,0].\nonumber \end{aligned}$$

(7.149)

Notice that the quantities $\mu _{i}[n]$, ${\mathcal {E}}_{i}[n]$ and $R_{i+1}[n]$ satisfy for all $0\le i\le N_{\varepsilon }-1$:

$$\begin{aligned} \frac{2{\mathcal {E}}_{i}[n]}{R_{i+1}[n]}=\mu _{i}[n]. \end{aligned}$$

(7.150)

Remark

The relations (7.145) and (7.146) uniquely determine $\mu _{i}[n]$ for all $0\le i\le N_{\varepsilon }-1$, $n\in {\mathbb {N}}$, as can be seen by arguing inductively on i: For $i=0$, (7.145) yields that $\mu _{0}[n]=\mu _{0}[0]$ for all $n\in {\mathbb {N}}$. Provided $\mu _{{\bar{i}}}:{\mathbb {N}}\rightarrow (0,+\infty )$ has been determined for $0\le {\bar{i}}\le i-1$, the relation (7.145) yields

$$\begin{aligned} \mu _{i}[n]=\mu _{i}[0]\cdot \exp \Big (2\sum _{{\bar{n}}=1}^{n}\sum _{j=0}^{i-1}\mu _{j}[{\bar{n}}]\Big ) \end{aligned}$$

(7.151)

for all $n\in {\mathbb {N}}$. In particular, note that, as a consequence of (7.151), for any $i>0$,

$$\begin{aligned} \mu _{i}[n]\xrightarrow {n\rightarrow \infty }+\infty . \end{aligned}$$

We will later show that the quantities $\mu _i [n]$ provide a good proxy for the evolution of the scale-invariant norm of the Vlasov beams after n successive reflections.

The following proposition is the main result of this section. It will provide us with useful approximate formulas for the total change of the energy content and the geometric separation of the beams between two successive reflections off ${\mathcal {I}}_{\varepsilon }$, expressed in terms of the quantities ${\mathcal {E}}_{i}[n]$ and $R_{i}[n]$. In particular, it will be readily inferred from these formulas that, for any $i>0$, the energy content of each beam ${\mathcal {V}}_{i}^{(n)}$ increases in n, while the geometric separation of the beams remains under control.²⁴

Proposition 7.6

Let $n\in {\mathbb {N}}$ be such that

$$\begin{aligned} \{0\le u\le v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0}\}\cap \big \{ u<v<u+\sqrt{-\frac{3}{\Lambda }}\pi \big \}\subset {\mathcal {U}}_{\varepsilon }^{+}. \end{aligned}$$

(7.152)

Then the following relations hold:

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]&={\mathcal {E}}_{i}[n]+O\Big (\rho _{\varepsilon }^{\frac{1}{16}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\quad \text { for all }0\le i\le N_{\varepsilon }, \end{aligned}$$

(7.153)

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]&=R_{i}[n]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{16}})\big )\quad \text { for all }1\le i\le N_{\varepsilon }, \end{aligned}$$

(7.154)

where the sequences ${\mathcal {E}}_{i}$ and $R_{i}$ were introduced in Definition 7.5.

In addition, for any $0\le j\le N_{\varepsilon }-1$ such that

$$\begin{aligned} \widetilde{{\mathcal {R}}}_{N_{\varepsilon };j}^{(n)}\subset {\mathcal {T}}_{\varepsilon }^{+}, \end{aligned}$$

(7.155)

we have

$$\begin{aligned} \widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },j]={\mathcal {E}}_{j}[n+1]+O\Big (\rho _{\varepsilon }^{\frac{1}{17}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big ) \end{aligned}$$

(7.156)

and, if $j\ge 1$:

$$\begin{aligned} \widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },j]=R_{j}[n+1]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{17}})\big ). \end{aligned}$$

(7.157)

Finally, if

$$\begin{aligned} \widetilde{{\mathcal {R}}}_{N_{\varepsilon };N_{\varepsilon }-1}^{(n)}\subset {\mathcal {T}}_{\varepsilon }^{+}, \end{aligned}$$

we have

$$\begin{aligned} \widetilde{{\mathcal {E}}}_{\nwarrow }^{(-)}[n;N_{\varepsilon },N_{\varepsilon }-1]={\mathcal {E}}_{N_{\varepsilon }}[n+1]+O\Big (\rho _{\varepsilon }^{\frac{1}{17}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\Big ). \end{aligned}$$

(7.158)

Proof

The proof of Proposition 7.6 will be separated in a number of steps. We will first establish a number of auxiliary relations and estimates, before proceeding with the proof of (7.153)–(7.154) and (7.156)–(7.158).

Auxiliary bounds and relations. In view of the fact that

$$\begin{aligned} supp(T_{\mu \nu }[f_{\varepsilon }])\cap {\mathcal {U}}_{\varepsilon }^{+}\subset \bigcup _{k=0}^{N_{\varepsilon }}{\mathcal {V}}_{k} \end{aligned}$$

(following readily from the bound (7.1) on the support of the $f_{\varepsilon k}$’s and the relation (6.65) between $f_{\varepsilon }$ and the $f_{\varepsilon k}$’s), we infer from equations (2.49) and (2.48) for ${\tilde{m}}$ that the function ${\tilde{m}}(u,v)$ is constant in every connected component of ${\mathcal {U}}_{\varepsilon }^{+}\backslash \bigcup _{n\in {\mathbb {N}}}\bigcup _{k=0}^{N_{\varepsilon }}{\mathcal {V}}_{k}^{(n)}$, i.e. in the regions between the beams ${\mathcal {V}}_{k}^{(n)}$. This fact immediately implies, in view of the definition (6.95)–(6.100) of the quantities ${\mathcal {E}}_{\nwarrow }^{(\pm )}$, ${\mathcal {E}}_{\nearrow }^{(\pm )}$, ${\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}$ and ${\mathcal {E}}_{{\mathcal {I}}}$, that, for all $n\in {\mathbb {N}}$ and all $0\le i,j\le N_{\varepsilon }$ with $i\ne j$:

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j]={\mathcal {E}}_{\nwarrow }^{(+)}[n;i,j-1] \end{aligned}$$

(7.159)

and

$$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]={\mathcal {E}}_{\nearrow }^{(+)}[n;i-1,j], \end{aligned}$$

(7.160)

where we have used the following index convention for (7.159) and (7.160):

• When $i=j-1$ or $j=i-1$:

  $$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,i]\doteq {\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;i],\\ {\mathcal {E}}_{\nearrow }^{(-)}[n;i,i]\doteq {\mathcal {E}}_{{\mathcal {I}}}[n;i], \nonumber \\ {\mathcal {E}}_{\nwarrow }^{(+)}[n;i,i]\doteq {\mathcal {E}}_{{\mathcal {I}}}[n;i]\nonumber \end{aligned}$$

  (7.161)

  and

  $$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(+)}[n;i,i]\doteq {\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;i]. \end{aligned}$$

  (7.162)

• When $j=-1$ or $i=-1$:

  $$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(+)}[n;i,-1]\doteq {\mathcal {E}}_{\nwarrow }^{(+)}[n-1;i,N_{\varepsilon }] \end{aligned}$$

  (7.163)

  and

  $$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(+)}[n;-1,j]\doteq {\mathcal {E}}_{\nearrow }^{(+)}[n;N_{\varepsilon },j] \end{aligned}$$

  (7.164)

The relations (7.159) and (7.160) also hold with $\widetilde{{\mathcal {E}}}_{\nwarrow }^{(\pm )}$, $\widetilde{{\mathcal {E}}}_{\nearrow }^{(\pm )}$ in place of ${\mathcal {E}}_{\nwarrow }^{(\pm )}$, ${\mathcal {E}}_{\nwarrow }^{(\pm )}$ (Fig. 21).

Fig. 21

The relations (7.153)–(7.154) provide approximate formulas for the incoming energy ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]$ of the i-th beam, as well as its geometric separation ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]$ from the $(i-1)$-th beam, as measured at $u=v_{\epsilon ,0}^{(n)}-h_{\epsilon ,0}$ (schematic depiction on the left). Similarly, the relations (7.156)–(7.157) provide approximate formulas for the outgoing energy of the i-th beam and its geometric separation from the $(i-1)$-th beam, as measured before its intersection with the $N_{\epsilon }$-th beam, i.e. at $v=v_{\epsilon ,N_{\epsilon }}^{(n)}-{\tilde{h}}_{\epsilon ,N_{\epsilon }}$ (schematic depiction on the right). The reason for using the ${\tilde{\cdot }}$ quantities (as well as the slightly larger beams $\widetilde{{\mathcal {V}}}_i$) in the latter case is that the relations (7.156)–(7.157) will later be used in a region of the maximal development domain ${\mathcal {U}}_{max}^{(\epsilon )}$ which is a subset of ${\mathcal {T}}^+_{\epsilon }$, but not a subset of ${\mathcal {U}}^+_{\epsilon }$; however, the analogous relations also hold (with exactly the same proof) for ${\mathcal {E}}_{\nearrow }^{(-)}[n;N_{\epsilon },j]$ and ${\mathfrak {D}}r_{\nearrow }^{(-)}[n;N_{\epsilon },j]$ in the region ${\mathcal {U}}^+_{\epsilon }$

By the same reasoning, the right hand side of the constraint equations (2.46) and (2.47) vanishes in every connected component of ${\mathcal {U}}_{\varepsilon }^{+}\backslash \bigcup _{k=0}^{N_{\varepsilon }}{\mathcal {V}}_{k}$; hence, it readily follows (by the definition (7.93)–(6.102) of ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}$, ${\mathfrak {D}}r_{\nearrow }^{(\pm )}$) that, for all $n\in {\mathbb {N}}$ and all $0\le i,j\le N_{\varepsilon }$, $i\ne j$:

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j]={\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j-1] \end{aligned}$$

(7.165)

and

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j]={\mathfrak {D}}r_{\nearrow }^{(+)}[n;i-1,j], \end{aligned}$$

(7.166)

where we have used the index convention

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,-1]\doteq {\mathfrak {D}}r_{\nwarrow }^{(+)}[n-1;i,N_{\varepsilon }] \end{aligned}$$

(7.167)

and

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(+)}[n;-1,j]\doteq {\mathfrak {D}}r_{\nearrow }^{(+)}[n;N_{\varepsilon },j]. \end{aligned}$$

(7.168)

Similarly for $\widetilde{{\mathfrak {D}}}r_{\nwarrow }^{(\pm )}$, $\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(\pm )}$ in place of ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}$, ${\mathfrak {D}}r_{\nearrow }^{(\pm )}$.

The following bounds will be useful for estimating the error terms appearing after repeated applications of the formulas (7.31)–(7.34): In view of the bounds (7.11) and (7.12) for the components of the energy momentum tensor, the bounds (6.73) and (7.15)–(7.18) for r on ${\mathcal {R}}_{i;j}^{(n)}$ and the relations (2.49)–(2.48) for ${\tilde{m}}$, we can readily bound for any $n\in {\mathbb {N}}$ and $0\le i,j\le N_{\varepsilon }$, $i\ne j$, such that ${\mathcal {R}}_{i;j}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}$:

$$\begin{aligned} \frac{{\mathcal {E}}_{\nwarrow }^{(\pm )}[n;i,j]}{r_{n;i,j}}+\frac{{\mathcal {E}}_{\nearrow }^{(\pm )}[n;i,j]}{r_{n;i,j}}\le \exp \big (\exp (2\sigma _{\varepsilon }^{-5})\big )\rho _{\varepsilon }. \end{aligned}$$

(7.169)

Moreover, in view of the definition (7.93)–(6.102) of ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}$, ${\mathfrak {D}}r_{\nearrow }^{(\pm )}$, the definition (6.8) of $v_{\varepsilon ,i}$ and the estimate (6.73), we infer that, for any $n\in {\mathbb {N}}$ and any $0\le i,j\le N_{\varepsilon }$, such that ${\mathcal {R}}_{i;j}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}$ if $i\ne j$ or ${\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)},{\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}$ if $i=j$:

$$\begin{aligned} e^{-\sigma _{\varepsilon }^{-4}}\rho _{\varepsilon }^{-1}\frac{\varepsilon ^{(i-1)}}{\sqrt{-\Lambda }}&\le {\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]\le e^{\sigma _{\varepsilon }^{-4}}\rho _{\varepsilon }^{-1}\frac{\varepsilon ^{(i-1)}}{\sqrt{-\Lambda }},\\ e^{-\sigma _{\varepsilon }^{-4}}\rho _{\varepsilon }^{-1}\frac{\varepsilon ^{(j-1)}}{\sqrt{-\Lambda }}&\le {\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]\le e^{\sigma _{\varepsilon }^{-4}}\rho _{\varepsilon }^{-1}\frac{\varepsilon ^{(j-1)}}{\sqrt{-\Lambda }}.\nonumber \end{aligned}$$

(7.170)

For any $0\le i\le N_{\varepsilon }-1$ such that ${\mathcal {R}}_{i+1;i}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}$, we can express $r_{n;i+1,i}$ by integrating $\partial _{v}r$ in v from $(u_{n;i+1,i}^{(+)},u_{n;i+1,i}^{(+)})\in \gamma _{{\mathcal {Z}}_{\varepsilon }}$ up to $(u_{n;i+1,i}^{(+)},v_{n;i+1,i}^{(-)})$ as follows (using the notational conventions (7.35)–(7.36) and (7.98), as well as the bounds (7.15)–(7.16), the fact that ${\tilde{m}}=0$ on $\{u_{n;i+1,i}^{(+)}\}\times [u_{n;i+1,i}^{(+)},v_{n;i+1,i}^{(-)}]$ and the bounds (6.73) and (7.170)):

$$\begin{aligned} r_{n;i+1,i}&=r(u_{n;i+1,i}^{(+)},v_{n;i+1,i}^{(-)})\\&=\int _{u_{n;i+1,i}^{(+)}}^{v_{n;i+1,i}^{(-)}}\partial _{v}r(u_{n;i+1,i}^{(+)},v)\,dv\nonumber \\&=\int _{u_{n;i+1,i}^{(+)}}^{v_{n;i+1,i}^{(-)}}\frac{\partial _{v}r}{1-\frac{2m}{r}}(u_{n;i+1,i}^{(+)},v)\cdot (1+O(\varepsilon ))\,dv\nonumber \\&=\int _{v_{n;i,i}^{(+)}+\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}^{v_{n;i+1,i}^{(-)}-\rho _{\varepsilon }^{-\frac{7}{8}}h_{\varepsilon ,i-1}}\frac{\partial _{v}r}{1-\frac{2m}{r}}(u_{n;i+1,i}^{(+)},v)\nonumber \\&\quad \cdot (1+O(\varepsilon ))\,dv+O\Big (\exp \big (\exp (2\sigma _{\varepsilon }^{-5})\big )\rho _{\varepsilon }^{-\frac{7}{8}}\frac{\varepsilon ^{(i-1)}}{\sqrt{-\Lambda }}\Big )\nonumber \\&=(1+O(\varepsilon )){\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i+1,i]+O\Big (\exp \big (\exp (2\sigma _{\varepsilon }^{-5})\big )\rho _{\varepsilon }^{-\frac{7}{8}}\frac{\varepsilon ^{(i-1)}}{\sqrt{-\Lambda }}\Big )\nonumber \\&={\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i+1,i]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{10}})\big ).\nonumber \end{aligned}$$

(7.171)

However, we can similarly express $r_{n;i+1,i}$ as an integral of $-\partial _{u}r$ in u (provided $(u_{n;i+1,i}^{(+)},v_{n;i+1,i}^{(-)})\times \{v_{n;i+1,i}^{(-)}\}\subset {\mathcal {U}}_{\varepsilon }^{+}$, which is necessarily true if ${\mathcal {R}}_{i+1;\gamma _{{\mathcal {Z}}}}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}$:

$$\begin{aligned} r_{n;i+1,i}&=\int _{u_{n;i+1,i}^{(+)}}^{v_{n;i+1,i}^{(-)}}(-\partial _{u}r)(u,v_{n;i+1,i}^{(-)})\,du=\\&={\mathfrak {D}}r_{\nearrow }^{(-)}[n;i+1,i+1]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{10}})\big ).\nonumber \end{aligned}$$

(7.172)

Arguing similarly (replacing $\sigma _{\varepsilon }$ with $\delta _{\varepsilon }$ and using (6.78) in place of (6.73)), we infer that, for any $0\le i\le N_{\varepsilon }-1$ such that $\widetilde{{\mathcal {R}}}_{i+1;\gamma _{{\mathcal {Z}}}}^{(n)}\subset {\mathcal {T}}_{\varepsilon }^{+}$, the relations (7.171) and (7.172) also hold with

$$\begin{aligned} {\tilde{r}}_{n;i+1,i}\doteq \inf _{\widetilde{{\mathcal {R}}}_{i+1;i}^{(n)}}r \end{aligned}$$

(7.173)

in place of $r_{n;i+1,i}$ and $\widetilde{{\mathfrak {D}}}r_{\nwarrow }^{(+)}[n;i+1,i]$, $\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;i+1,i+1]$ in place of ${\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i+1,i]$, ${\mathfrak {D}}r_{\nearrow }^{(-)}[n;i+1,i+1]$, respectively.

From (7.171) and (7.172), we immediately infer that, for all $0\le i\le N_{\varepsilon }-1$ such that ${\mathcal {R}}_{i+1;\gamma _{{\mathcal {Z}}}}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}$:

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(-)}[n;i+1,i+1]={\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i+1,i]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{10}})\big ). \end{aligned}$$

(7.174)

Similarly, expressing $\frac{1}{r_{n;i,i+1}}$ as an integral of $\partial _{v}(\frac{1}{r})$ and $\partial _{u}(\frac{1}{r})$ from ${\mathcal {I}}_{\varepsilon }$ up to $(u_{n;i,i+1}^{(+)},v_{n;i,i+1}^{(-)})$, we infer that, for all $0\le i\le N_{\varepsilon }-1$ such that ${\mathcal {R}}_{i+1;{\mathcal {I}}}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}$

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i+1,i+1]={\mathfrak {D}}r_{\nearrow }^{(+)}[n;i,i+1]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{10}})\big ). \end{aligned}$$

(7.175)

Proof of (7.153)–(7.154). In order to establish (7.153) and (7.154), we will first show that, for all $n\in {\mathbb {N}}$ such that

$$\begin{aligned} \{0\le u\le v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,0}\}\cap \left\{ u<v<u+\sqrt{-\frac{3}{\Lambda }}\pi \right\} \subset {\mathcal {U}}_{\varepsilon }^{+} \end{aligned}$$

(7.176)

and any $0\le i\le N_{\varepsilon }$:

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n+1;i,0]= & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]\cdot \exp \Big (\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[n+1;j,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n+1;j+1,0]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )\nonumber \\{} & {} +O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ) \end{aligned}$$

(7.177)

and, for all $1\le i\le N_{\varepsilon }$:

$$\begin{aligned}{} & {} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n+1;i,0]={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]\nonumber \\{} & {} \quad \cdot \exp \Big (-\sum _{j=0}^{i-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n+1;j+1,0]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big ). \end{aligned}$$

(7.178)

Note that the recursive system (7.177)–(7.178), modulo the $O(\cdot )$ error terms, is in fact the same as the recursive system (7.147)–(7.148) for ${\mathcal {E}}_{i}[n]$, $R_{i}[n]$, with the quantities ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]$, ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]$ and ${\mathcal {E}}_{i}[n]$, $R_{i}[n]$, respectively, satisfying the same initial conditions at $n=0$.

Let us first assume that (7.177)–(7.178) have been established. The relations (7.153) and (7.154) will then follow by showing that the quantities

$$\begin{aligned} e_{i}[n]&\doteq \frac{{\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]-{\mathcal {E}}_{i}[n]}{\varepsilon ^{(i)}}\sqrt{-\Lambda }\quad \text { for }0\le i\le N_{\varepsilon },\\ r_{i}[n]&\doteq \frac{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]}{R_{i}[n]}\quad \text { for }1\le i\le N_{\varepsilon },\\ {\bar{\mu }}_{i}[n]&\doteq \rho _{\varepsilon }^{-1}\Big (\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i+1,0]}-\mu _{i}[n]\Big )\quad \text { for }0\le i\le N_{\varepsilon }-1 \end{aligned}$$

satisfy

$$\begin{aligned} |e_{i}[n]|,\text { }|r_{i}[n]-1|,\text { }|{\bar{\mu }}_{i}[n]|\le \rho _{\varepsilon }^{\frac{1}{16}}. \end{aligned}$$

(7.179)

To this end, let $n^{*}$ be the maximum number in $\{0,1,\ldots ,n\}$ such that, for all $0\le {\bar{n}}\le n^{*}$:

$$\begin{aligned} |{\bar{\mu }}_{i}[{\bar{n}}]|\le \rho _{\varepsilon }^{\frac{1}{15}}\quad \text { for all }0\le i\le N_{\varepsilon }-1 \end{aligned}$$

(7.180)

(note that (7.180) is trivially true for ${\bar{n}}=0$, since ${\bar{\mu }}_{i}[0]=0$ by (7.149)). Assuming, for the sake of contradiction, that $n^{*}<n$, we will show that (7.180) also holds for $n^{*}+1$, hence contradicting the maximality of $n^{*}$. Note that, in view of the definition (6.49), it is necessary that

$$\begin{aligned} n^{*}<n\lesssim \sigma _{\varepsilon }^{-2} \end{aligned}$$

(7.181)

(otherwise, (7.176) cannot hold). We will argue inductively on i, assuming that, for all $0\le {\bar{i}}\le i-1$,

$$\begin{aligned} |{\bar{\mu }}_{{\bar{i}}}[{\bar{n}}]|\le \rho _{\varepsilon }^{\frac{1}{15}}\quad \text { for all }0\le {\bar{n}}\le n^{*}+1 \end{aligned}$$

(7.182)

and then showing that (7.182) also holds for ${\bar{i}}=i$. Note that (7.182) holds trivially for ${\bar{i}}=0$, since, in this case, (7.145), (7.177)–(7.178) and (7.181) imply that

$$\begin{aligned} \mu _{0}[{\bar{n}}]=\mu _{0}[0] \end{aligned}$$

(7.183)

and

$$\begin{aligned} \frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}};0,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[{\bar{n}};1,0]}=(1+O(\rho _{\varepsilon }^{\frac{1}{14}}))\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[0;0,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[0;1,0]}+O(\rho _{\varepsilon }^{1+\frac{1}{6}}), \end{aligned}$$

(7.184)

which yield (in view of our initial data bounds)

$$\begin{aligned} |{\bar{\mu }}_{0}[{\bar{n}}]|\le \rho _{\varepsilon }^{-1}\Big |O(\rho _{\varepsilon }^{\frac{1}{14}}))\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[0;0,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[0;1,0]}+O(\rho _{\varepsilon }^{1+\frac{1}{6}})\Big |\le \exp (\exp (\sigma _{\varepsilon }^{-9}))\rho _{\varepsilon }^{\frac{1}{14}}.\nonumber \\ \end{aligned}$$

(7.185)

In view of the relation (7.145) for $\mu _{i}[n]$ and the relations (7.177)–(7.178) for ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]$, ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i+1,0]$, we can readily calculate that, for $0\le {\bar{n}}\le n^{*}$:

$$\begin{aligned} \big |&{\bar{\mu }}_{i} [{\bar{n}}+1]\big |\\&=\rho _{\varepsilon }^{-1}\Bigg |\frac{{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}};i,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[{\bar{n}};i+1,0]}\exp \Big (2\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}}+1;j,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[{\bar{n}}+1;j+1,0]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )\nonumber \\&\quad +O(\rho _{\varepsilon }^{1+\frac{1}{6}})-\mu _{i}[{\bar{n}}]\exp \Big (2\sum _{j=0}^{i-1}\mu _{j}[{\bar{n}}+1]\Big )\Bigg |\nonumber \\&=\exp \Big (2\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}}+1;j,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[{\bar{n}}+1;j+1,0]}\Big )\rho _{\varepsilon }^{-1}\Bigg |\frac{{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}};i,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[{\bar{n}};i+1,0]}-\mu _{i}[{\bar{n}}]\nonumber \\&\quad \times \exp \Big (-2\rho _{\varepsilon }\sum _{j=0}^{i-1}{\bar{\mu }}_{j}[{\bar{n}}+1]\Big )+O(\rho _{\varepsilon }^{1+\frac{1}{13}})\Bigg |.\nonumber \end{aligned}$$

(7.186)

Note that we can estimate, in view of (7.169)–(7.170) and the fact that $N_{\varepsilon }=\rho _{\varepsilon }^{-1}\exp (e^{\delta _{\varepsilon }^{-15}})$:

$$\begin{aligned} \sum _{j=0}^{N_{\varepsilon }-1}\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[k;j,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[k;j+1,0]}\le \exp (\exp (2\delta _{\varepsilon }^{-15}))\quad \text { for all }0\le k\le n\qquad \end{aligned}$$

(7.187)

Thus, using also the the bounds (7.169)–(7.170), the bound

$$\begin{aligned} \sum _{j=0}^{i-1}{\bar{\mu }}_{j}[k]\le \rho _{\varepsilon }^{-1+\frac{1}{15}}\exp (\exp (\delta _{\varepsilon }^{-15}))\quad \text { for all }0\le k\le n^{*}+1\qquad \end{aligned}$$

(7.188)

(following from the inductive assumption (7.182)) and the bound (7.180), we obtain from (7.186) that, for $0\le {\bar{n}}\le n^{*}$:

$$\begin{aligned}&\big | {\bar{\mu }}_{i} [{\bar{n}}+1]\big |\\&\quad =\exp \Big (O(\exp (\exp (2\delta _{\varepsilon }^{-15})))\Big )\rho _{\varepsilon }^{-1}\Bigg |\frac{{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}};i,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[{\bar{n}};i+1,0]}\nonumber \\&\qquad -\mu _{i}[{\bar{n}}]\Big (1-2\rho _{\varepsilon }\sum _{j=0}^{i-1}{\bar{\mu }}_{j}[{\bar{n}}+1]+O(\rho _{\varepsilon }^{\frac{2}{15}}\delta _{\varepsilon }^{-4})\Big )+O(\rho _{\varepsilon }^{1+\frac{1}{13}})\Bigg |\nonumber \\&\quad \le \exp \Big (\exp \big (e^{\delta _{\varepsilon }^{-16}}\big )\Big )\cdot |{\bar{\mu }}_{i}[{\bar{n}}]|\nonumber \\&\qquad +\exp \Big (\exp \big (e^{\delta _{\varepsilon }^{-16}}\big )\Big )\rho _{\varepsilon }\sum _{j=0}^{i-1}|{\bar{\mu }}_{j}[{\bar{n}}+1]|+\rho _{\varepsilon }^{\frac{1}{14}}.\nonumber \end{aligned}$$

(7.189)

Applying (7.189) successively for ${\bar{n}}=0,\ldots n^{*}$, using also the bound (7.181) for $n^{*}<n$, we obtain

$$\begin{aligned} \max _{0\le {\bar{n}}\le n^{*}}\big |{\bar{\mu }}_{i}[{\bar{n}}+1]\big |&\le \exp \Big (n^{*}\exp \big (e^{\delta _{\varepsilon }^{-16}}\big )\Big )\nonumber \\&\quad \cdot \sum _{{\bar{n}}=0}^{n^{*}}\sum _{j=0}^{i-1}|{\bar{\mu }}_{j}[{\bar{n}}+1]|+\exp \Big (n^{*}\exp \big (e^{\delta _{\varepsilon }^{-16}}\big )\Big )\cdot \rho _{\varepsilon }^{\frac{1}{14}}\\&\le {\bar{\delta }}_{\varepsilon }^{-1}\rho _{\varepsilon }\sum _{j=0}^{i-1}\big (\max _{0\le {\bar{n}}\le n^{*}}{\bar{\mu }}_{j}[{\bar{n}}+1]\big )+{\bar{\delta }}_{\varepsilon }^{-1}\rho _{\varepsilon }^{\frac{1}{14}},\nonumber \end{aligned}$$

(7.190)

where

$$\begin{aligned} {\bar{\delta }}_{\varepsilon }\doteq \exp \Big (-\exp \big (2e^{\delta _{\varepsilon }^{-16}}\big )\Big ). \end{aligned}$$

(7.191)

Since (7.190) is similarly valid for any ${\bar{i}}$ with $0\le {\bar{i}}\le i$ in place of i, we infer from (7.190) after applying a discrete Gronwall-type argument in the i variable (using also the bound (7.185) for ${\bar{\mu }}_{0}$ and the fact that $i\le N_{\varepsilon }$):

$$\begin{aligned} \max _{0\le {\bar{n}}\le n^{*}}\big |{\bar{\mu }}_{i}[{\bar{n}}+1]\big |\le \exp (2{\bar{\delta }}_{\varepsilon }^{-1}\rho _{\varepsilon }N_{\varepsilon })\rho _{\varepsilon }^{\frac{1}{14}}\le \exp ({\bar{\delta }}_{\varepsilon }^{-2})\rho _{\varepsilon }^{\frac{1}{14}}, \end{aligned}$$

(7.192)

from which (7.182) for ${\bar{i}}=i$ follows, in view of the relation (6.1) between $\rho _{\varepsilon }$ and $\delta _{\varepsilon }$.

As a result, we have established inductively that (7.182) holds for any $0\le i\le N_{\varepsilon }-1$, and hence:

$$\begin{aligned} \max _{0\le i\le N_{\varepsilon }-1}\max _{0\le {\bar{n}}\le n}|{\bar{\mu }}_{i}[{\bar{n}}]|\le \rho _{\varepsilon }^{\frac{1}{15}}. \end{aligned}$$

(7.193)

From the relations (7.177)–(7.178) for ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]$, ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i+1,0]$ and (7.147)–(7.148) for ${\mathcal {E}}_{i}[n]$, $R_{i}[n]$, the bounds (7.169)–(7.170), the bound (7.187) and the bound (7.193), we obtain for any $0\le {\bar{n}}\le n-1$ and any $0\le i\le N_{\varepsilon }$:

$$\begin{aligned}&|e_{i} [{\bar{n}}+1]|\\&\quad =\Bigg |\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}};i,0]\cdot \exp \Big (\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}}+1;j,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[{\bar{n}}+1;j+1,0]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )\nonumber \\&\qquad +O(\rho _{\varepsilon }^{\frac{1}{4}})-\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}{\mathcal {E}}_{i}[{\bar{n}}]\cdot \exp \Big (\sum _{j=0}^{i-1}\mu _{j}[{\bar{n}}]\Big )\Bigg |\nonumber \\&\quad =\exp \Big (\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[n+1;j,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n+1;j+1,0]}\Big )\Bigg |(1+O(\rho _{\varepsilon }^{\frac{1}{12}}))\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}};i,0]\nonumber \\&\qquad -\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}{\mathcal {E}}_{i}[{\bar{n}}]\cdot \exp \Big (-\rho _{\varepsilon }\sum _{j=0}^{i-1}{\bar{\mu }}_{j}[{\bar{n}}+1]\Big )+O(\rho _{\varepsilon }^{\frac{1}{4}})\Bigg |\nonumber \\&\quad \le {\bar{\delta }}_{\varepsilon }^{-\frac{1}{2}}\Bigg |e_{i}[{\bar{n}}]+O(\rho _{\varepsilon }^{\frac{1}{12}})\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}};i,0]+O(\exp (\exp (\delta _{\varepsilon }^{-15}))\rho _{\varepsilon }^{\frac{1}{15}})\nonumber \\&\quad \frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}{\mathcal {E}}_{i}[{\bar{n}}]+O(\rho _{\varepsilon }^{\frac{1}{4}})\Bigg |\nonumber \\&\quad \le {\bar{\delta }}_{\varepsilon }^{-1}\Big (|e_{i}[{\bar{n}}]|+\rho _{\varepsilon }^{\frac{1}{15}}\Big )\nonumber \end{aligned}$$

(7.194)

and, for any $1\le i\le N_{\varepsilon }$:

$$\begin{aligned}&|r_{i}[{\bar{n}}+1]-1|\nonumber \\&\quad =\Bigg |\frac{{\mathfrak {D}}r_{\nwarrow }^{(-)}[{\bar{n}};i,0]\cdot \exp \Big (-\sum _{j=0}^{i-2}\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[{\bar{n}}+1;j,0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[{\bar{n}}+1;j+1,0]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )}{R_{i}[{\bar{n}}]\cdot \exp \Big (-\sum _{j=0}^{i-2}{\bar{\mu }}_{j}[{\bar{n}}+1]\Big )}-1\Bigg |\\&\quad =\Bigg |r_{i}[{\bar{n}}]\cdot \exp \Big (-\rho _{\varepsilon }\sum _{j=0}^{i-2}{\bar{\mu }}_{j}[{\bar{n}}+1]+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )-1\Bigg |\nonumber \\&\quad =\Bigg |r_{i}[{\bar{n}}]\cdot \exp \Big (O(\exp (\exp (\delta _{\varepsilon }^{-15}))\rho _{\varepsilon }^{\frac{1}{15}})\Big )-1\Bigg |\nonumber \\&\quad \le \big (1+\exp (\exp (\delta _{\varepsilon }^{-16}))\rho _{\varepsilon }^{\frac{1}{15}}\big )\cdot |r_{i}[{\bar{n}}+1]-1|+\exp (\exp (\delta _{\varepsilon }^{-15}))\rho _{\varepsilon }^{\frac{1}{15}}.\nonumber \end{aligned}$$

(7.195)

From (7.194) and (7.195), using also the initial conditions $e_{i}[0]=0$ and $r_{i}[0]=1$, we obtain (using also (7.181))

$$\begin{aligned} \max _{0\le i\le N_{\varepsilon }}\max _{0\le {\bar{n}}\le n}|e_{i}[{\bar{n}}+1]|\le \exp (n{\bar{\delta }}_{\varepsilon }^{-1}){\bar{\delta }}_{\varepsilon }^{-1}\rho _{\varepsilon }^{\frac{1}{15}}\le \rho _{\varepsilon }^{\frac{1}{16}} \end{aligned}$$

(7.196)

and

$$\begin{aligned} \max _{1\le i\le N_{\varepsilon }}\max _{0\le {\bar{n}}\le n}|r_{i}[{\bar{n}}]-1|\le {\bar{\delta }}_{\varepsilon }^{-1}n\rho ^{\frac{1}{15}}\le \rho _{\varepsilon }^{\frac{1}{16}}. \end{aligned}$$

(7.197)

From (7.193), (7.196) and (7.197), we therefore infer (7.179), thus obtaining (7.153) and (7.154) (assuming that (7.177) and (7.178) have been proven).

Proof of (7.177)–(7.178). We will now proceed with the proof of (7.177)–(7.178). Let $n\in {\mathbb {N}}$ be an integer satisfying (7.176) and let $0\le i\le N_{\varepsilon }$.

Fig. 22

For the proof of (7.177), we move along ${\mathcal {V}}_i$ in the direction of the red arrows in three steps: First, from $u=v_{\epsilon ,0}^{(n)}-h_{\epsilon ,i}$ up to $u=v_{\epsilon ,i}^{(n)}-h_{\epsilon ,i}$ (ingoing regime), then from $v=v_{\epsilon ,i}^{(n)}+h_{\epsilon ,i}$ up to $v=v_{\epsilon ,i}^{(n+1)}+h_{\epsilon ,i}$ (outgoing regime) and finally again from $u=v_{\epsilon ,i}^{(n)}+h_{\epsilon ,i}$ up to $u=v_{\epsilon ,0}^{(n+1)}-h_{\epsilon ,i}$ (ingoing regime). Along the way, we use the formulas (7.31)–(7.34) to calculate the change in the energy content of ${\mathcal {V}}_i$ after each intersection with one of the beams ${\mathcal {V}}_j$, $j\ne i$

• 1. First, moving along the beam ${\mathcal {V}}_{i\nwarrow }^{(n)}$ from $u=v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,i}$ up to $u=v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}$ (see Fig. 22) and calculating the differene between ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j]$ and ${\mathcal {E}}_{\nwarrow }^{(+)}[n;i,j]$ using (7.31) for all $0\le j<i$ (measuring the change in the energy content of ${\mathcal {V}}_{i\nwarrow }^{(n)}$ as it crosses each of the outgoing beams ${\mathcal {V}}_{j\nearrow }^{(n)}$, $j<i$), making also use of the equality (7.159) (expressing the conservation of the energy content of ${\mathcal {V}}_{i\nwarrow }^{(n)}$ in the region between two successive intersections with the outgoing beams) and the bound (7.169), we infer

  $$\begin{aligned}&{\mathcal {E}}_{\gamma _{{\mathcal {Z}}}} [n;i]\nonumber \\&\quad ={\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]\cdot \exp \Big (\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+\sum _{j=0}^{i-1}O(\rho _{\varepsilon }^{\frac{3}{2}})\Big )+\\&\qquad +\sum _{j=0}^{i-1}\Big \{\exp \Big (\sum _{k=0}^{j-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,k]}{r_{n;i.k}}+\sum _{k=0}^{j-1}O(\rho _{\varepsilon }^{\frac{3}{2}})\Big )\cdot O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\Big \}\nonumber \\&\quad ={\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]\cdot \exp \Big (\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+O(N_{\varepsilon }\rho _{\varepsilon }^{\frac{3}{2}})\Big )\nonumber \\&\qquad +O\Big (\exp \big (N_{\varepsilon }\exp \big (\exp (2\sigma _{\varepsilon }^{-5})\big )\rho _{\varepsilon }\big )\cdot N_{\varepsilon }\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\nonumber \\&\quad ={\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]\cdot \exp \Big (\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+O(\rho _{\varepsilon }^{\frac{1}{4}})\Big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ),\nonumber \end{aligned}$$

  (7.198)

  where, in passing from the second to the third line in (7.198), we have made use of the definition (6.2) of $N_{\varepsilon }$ and the relations (6.1) between $\rho _{\varepsilon }$, $\delta _{\varepsilon }$ and $\sigma _{\varepsilon }$.

• 2. Moving along ${\mathcal {V}}_{i\nearrow }^{(n)}$ from $v=v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}$ up to $v=v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i}$ (see Fig. 22), calculating the differene between ${\mathcal {E}}_{\nearrow }^{(-)}[n;j,i]$ and ${\mathcal {E}}_{\nearrow }^{(+)}[n;j,i]$ using (7.32) for $i<j\le N_{\varepsilon }$ and (7.34) for $0\le j<i$ (measuring the change in the energy content of ${\mathcal {V}}_{i\nearrow }^{(n)}$ as it crosses each of the ingoing beams ${\mathcal {V}}_{j\nwarrow }^{(n)}$, $1\le j\le N_{\varepsilon }$), making also use of the equality (7.160), we similarly infer that

  $$\begin{aligned} {\mathcal {E}}_{{\mathcal {I}}}[n;i]&={\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;i]\cdot \left( 1+\sum _{j=0}^{N_{\varepsilon }}O(\varepsilon )\right) +\sum _{j=0}^{i-1}O\Big (\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )\nonumber \\&+\sum _{j=i+1}^{N_{\varepsilon }}O\Big (\varepsilon \frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )\\&={\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;i]\cdot \big (1+O(N_{\varepsilon }\varepsilon )\big )+O\Big (N_{\varepsilon }(\rho _{\varepsilon }^{\frac{3}{2}}+\varepsilon )\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big )\nonumber \\&={\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;i]\cdot \big (1+O(\varepsilon ^{\frac{1}{2}})\big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big ).\nonumber \end{aligned}$$

  (7.199)

• 3. Finally, moving along ${\mathcal {V}}_{i\nwarrow }^{(n+1)}$ from $u=v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}$ up to $u=v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,i}$ (see Fig. 22), calculating the difference between ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j]$ and ${\mathcal {E}}_{\nwarrow }^{(+)}[n;i,j]$ using (7.33) for all $j>i$ (making use of the equality (7.159)), we obtain:

  $$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n+1;i,0]&={\mathcal {E}}_{{\mathcal {I}}}[n;i]\cdot \big (1+\sum _{j=i+1}^{N_{\varepsilon }}O(\varepsilon )\big )+\sum _{j=i+1}^{N_{\varepsilon }}O\Big (\varepsilon \frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\\&={\mathcal {E}}_{{\mathcal {I}}}[n;i]\cdot \big (1+O(\varepsilon ^{\frac{1}{2}})\big )+O\Big (\varepsilon ^{\frac{1}{2}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ).\nonumber \end{aligned}$$

  (7.200)

Combining (7.198), (7.199) and (7.200) and using the relations (6.1) between $\varepsilon$ and $\rho _{\varepsilon }$, we therefore infer that:

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n+1;i,0]= & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]\cdot \exp \Big (\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+O(\rho _{\varepsilon }^{\frac{1}{4}})\Big )\nonumber \\{} & {} +O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ). \end{aligned}$$

(7.201)

Using the estimates (7.15), (6.73), (6.70) and the fact that $\Lambda R^{2}=O(\varepsilon )$ on $\{u_{n;i,j}^{(+)}\}\times [v_{n;j+1,j}^{(-)},v_{n;i,j}^{(-)}]$, we can readily estimate:

$$\begin{aligned} \frac{r_{n;i,j}}{r_{n;j+1,j}}-1&=\frac{\int _{v_{n;j+1,j}^{(-)}}^{v_{n;i,j}^{(-)}}\partial _{v}r(u_{n;i,j}^{(+)},v)\,dv}{r_{n;j+1,j}}\\&\le \frac{1}{r_{n;j+1,j}}\sup _{\{u_{n;i,j}^{(+)}\}\times [v_{n;j+1,j}^{(-)},v_{n;i,j}^{(-)}]}(\partial _{v}r)\sum _{k=j+1}^{i-1}\rho _{\varepsilon }^{-1}\frac{\varepsilon ^{(k)}}{\sqrt{-\Lambda }}\nonumber \\&\le \exp (\exp (\sigma _{\varepsilon }^{-6}))\rho _{\varepsilon }^{-1}\frac{\sum _{k=j+1}^{i-1}\varepsilon ^{(k)}}{\varepsilon ^{(j)}}\nonumber \\&\le \varepsilon ^{\frac{1}{2}}.\nonumber \end{aligned}$$

(7.202)

Using the relation (7.172) and the bounds (7.169) and (7.202), from (7.201) we then infer that

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n+1;i,0]= & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]\cdot \exp \Big (\sum _{j=0}^{i-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;j+1,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )\nonumber \\{} & {} +O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ). \end{aligned}$$

(7.203)

Assuming that $1\le i\le N_{\varepsilon }$, we will now repeat the same procedure for the geometric separation ${\mathfrak {D}}r$ in place of the energy content ${\mathcal {E}}$ of the beams:

• 1. First, moving in the u direction along the strip

  $$\begin{aligned} {\mathcal {S}}_{i\nwarrow }^{(n)}\doteq \{v_{\varepsilon ,i-1}^{(n)}+(\rho _{\varepsilon }^{-1}+1)h_{\varepsilon ,i-1}\le v\le v_{\varepsilon ,i}^{(n)}-(\rho _{\varepsilon }^{-1}+1)h_{\varepsilon ,i-1}\}, \end{aligned}$$

  from $u=v_{\varepsilon ,0}^{(n)}$ up to the axis $\gamma _{{\mathcal {Z}}_{\varepsilon }}$, calculating the difference between ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j]$ and ${\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j]$ using (7.91) for all $0\le j\le i-1$ and (7.90) for $j=i-1$, making also use of the equality (7.165) between ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j]$ and ${\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,j-1]$, we infer

  $$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,i-1]&={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0] \nonumber \\&\quad \cdot \exp \Big (-\sum _{j=0}^{i-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+\sum _{j=0}^{i-2}O(\rho _{\varepsilon }^{\frac{3}{2}})+O(\rho _{\varepsilon }^{\frac{3}{4}})\Big )\\&={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]\nonumber \\&\quad \cdot \exp \Big (-\sum _{j=0}^{i-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+O(N_{\varepsilon }\rho _{\varepsilon }^{\frac{3}{2}})+O(\rho _{\varepsilon }^{\frac{3}{4}})\Big )\nonumber \\&={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0] \cdot \exp \Big (-\sum _{j=0}^{i-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+O(\rho _{\varepsilon }^{\frac{1}{4}})\Big ).\nonumber \end{aligned}$$

  (7.204)

• 2. Moving in the v direction along along the strip

  $$\begin{aligned} {\mathcal {S}}_{i\nearrow }^{(n)}\doteq \{v_{\varepsilon ,i-1}^{(n)}+(\rho _{\varepsilon }^{-1}+1)h_{\varepsilon ,i-1}\le u\le v_{\varepsilon ,i}^{(n)}-(\rho _{\varepsilon }^{-1}+1)h_{\varepsilon ,i-1}\}, \end{aligned}$$

  from the axis $\gamma _{{\mathcal {Z}}_{\varepsilon }}$ up to conformal infinity ${\mathcal {I}}_{\varepsilon }$, calculating the differene between ${\mathfrak {D}}r_{\nearrow }^{(-)}[n;j,i]$ and ${\mathfrak {D}}r_{\nearrow }^{(+)}[n;j,i]$ using (7.95) for $j=i$, (7.89) for $i<j\le N_{\varepsilon }$ and (7.92) for $0\le j<i$, making also use of the equality (7.166) as well as the approximate equality (7.174) between ${\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,i]$ and ${\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,i-1]$, we similarly infer that

  $$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(+)}[n;N_{\varepsilon },i]&={\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,i]\cdot \big (1+\sum _{j=0,j\ne i}^{N_{\varepsilon }}O(\varepsilon )+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )\\&={\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,i-1]\nonumber \\&\quad \cdot \big (1+O((N_{\varepsilon }-1)\varepsilon )+O(\rho _{\varepsilon }^{\frac{3}{4}})+O(\rho _{\varepsilon }^{\frac{1}{10}})\big )\nonumber \\&={\mathfrak {D}}r_{\nwarrow }^{(+)}[n;i,i-1]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{10}})\big ).\qquad \nonumber \end{aligned}$$

  (7.205)

• 3. Finally, moving in the u direction along ${\mathcal {S}}_{i\nwarrow }^{(n+1)}$ from ${\mathcal {I}}_{\varepsilon }$ up to $u=v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,i}$, calculating the difference between ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;j,i]$ and ${\mathfrak {D}}r_{\nwarrow }^{(+)}[n;j,i]$ using (7.94) for $j=i$ and (7.93) for all $j>i$, making use of the equality (7.165) and the approximate equality (7.175) between ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,i]$ and ${\mathfrak {D}}r_{\nearrow }^{(+)}[n;i-1,i]$, we obtain:

  $$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n+1;i,0]&={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,i]\cdot \big (1+\sum _{j=i}^{N_{\varepsilon }}O(\varepsilon )\big )=\\&={\mathfrak {D}}r_{\nearrow }^{(+)}[n;i-1,i]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{10}})\big ).\nonumber \end{aligned}$$

  (7.206)

Combining (7.204), (7.205) and (7.206), we obtain that

$$\begin{aligned}{} & {} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n+1;i,0]\nonumber \\{} & {} \quad ={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]\cdot \exp \Big (-\sum _{j=0}^{i-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{r_{n;i,j}}+O(\rho _{\varepsilon }^{\frac{1}{10}})\Big ). \end{aligned}$$

(7.207)

Using the relation (7.172) and the bounds (7.169) and (7.202), from (7.207) we then infer that

$$\begin{aligned}{} & {} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n+1;i,0]={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]\nonumber \\{} & {} \qquad \cdot \exp \Big (-\sum _{j=0}^{i-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;j+1,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big ). \end{aligned}$$

(7.208)

For any $n\in {\mathbb {N}}$ such that (7.176) is satisfied, arguing in exactly the same way as for the proof of (7.199), but moving along ${\mathcal {V}}_{j\nearrow }^{(n)}$ starting from $v=v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}$ (instead of $v=v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}$) up to $v=v_{\varepsilon ,j}^{(n+1)}-h_{\varepsilon ,j}$, we infer that, for any $0\le j\le i-1$:

$$\begin{aligned} {\mathcal {E}}_{{\mathcal {I}}}[n;j]={\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]\cdot \big (1+O(\varepsilon ^{\frac{1}{2}})\big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big ). \end{aligned}$$

(7.209)

Using (7.200) (for j in place of i) and (7.209), we therefore infer that

$$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]={\mathcal {E}}_{\nwarrow }^{(-)}[n+1;j,0]\cdot \big (1+O(\varepsilon ^{\frac{1}{2}})\big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\Big ).\qquad \end{aligned}$$

(7.210)

Similarly, using the first line of (7.205) and (7.206), we obtain:

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(+)}[n;j+1,j+1]={\mathfrak {D}}r_{\nwarrow }^{(-)}[n+1;j+1,0]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{10}})\big ).\qquad \end{aligned}$$

(7.211)

Substituting ${\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]$ and ${\mathfrak {D}}r_{\nearrow }^{(-)}[n;j+1,j+1]$ in the right hand side of (7.203) with (7.210) and (7.211), respectively, we therefore obtain (7.177). Similarly, from (7.208) we infer (7.178).

Remark

For any $0\le j_{1}\le i\le N_{\varepsilon }$ and $0\le j_{0}\le j_{1}$, it readily follows from the proof of (7.177) and (7.178) (after restricting ourselves to the interactions of the beams taking place only between $u=v_{j_{0},\varepsilon }^{(n)}-h_{\varepsilon ,j_{0}}$ and $v=v_{i,\varepsilon }^{(n)}-h_{\varepsilon ,i}$) that:

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j_{1}]= & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j_{0}]\nonumber \\{} & {} \cdot \exp \Big (\sum _{j=j_{0}}^{j_{1}-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ),\nonumber \\ \end{aligned}$$

(7.212)

$$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(-)}[n;i,j_{1}]= & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;j_{1},j_{0}]\nonumber \\{} & {} \cdot \exp \Big (\sum _{j=j_{0}}^{j_{1}-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(j_{1})}}{\sqrt{-\Lambda }}\Big )\nonumber \\ \end{aligned}$$

(7.213)

(with the convention that, when $i=j_{1}$, ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,i]={\mathcal {E}}_{\nwarrow }^{(-)}[n;i,i]={\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;i]$) and

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j_{1}]= & {} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j_{0}]\nonumber \\{} & {} \quad \cdot \exp \Big (-\sum _{j=j_{0}}^{j_{1}-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big ),\nonumber \\{} & {} \qquad \text { provided }i>0, \end{aligned}$$

(7.214)

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j_{1}]= & {} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;j_{1},j_{0}]\nonumber \\{} & {} \quad \cdot \exp \Big (-\sum _{j=j_{0}}^{j_{1}-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big ),\nonumber \\{} & {} \qquad \text { provided }j_{1}>0 \end{aligned}$$

(7.215)

(with the convention that, when $i=j_{1}$, ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,i]={\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j_{1}]$).

Similarly, for $0\le i\le j_{1}\le N_{\varepsilon }$ and $0\le j_{0}\le i$,

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j_{1}]= & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,j_{0}]\nonumber \\{} & {} \cdot \exp \Big (\sum _{j=j_{0}}^{i-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ),\nonumber \\ \end{aligned}$$

(7.216)

$$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(-)}[n;i,j_{1}]= & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;j_{1},j_{0}]\nonumber \\{} & {} \cdot \exp \Big (\sum _{j=j_{0}}^{j_{1}-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(j_{1})}}{\sqrt{-\Lambda }}\Big )\nonumber \\ \end{aligned}$$

(7.217)

(with the convention that, when $i=j_{1}$, ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,i]={\mathcal {E}}_{\nwarrow }^{(-)}[n;i,i]={\mathcal {E}}_{{\mathcal {I}}}[n;i]$) and

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j_{1}]= & {} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,j_{0}]\nonumber \\{} & {} \cdot \exp \Big (-\sum _{j=j_{0}}^{i-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big ),\text { provided }i>0,\nonumber \\ \end{aligned}$$

(7.218)

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j_{1}]= & {} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;j_{1},j_{0}]\nonumber \\{} & {} \cdot \exp \Big (-\sum _{j=j_{0}}^{j_{1}-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big ),\text { provided }j_{1}>0\nonumber \\ \end{aligned}$$

(7.219)

(with the convention that, when $i=j_{1}$, ${\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j_{1}]={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,i]$).

The same relations also hold for $\widetilde{{\mathcal {E}}}^{(\pm )}$, $\widetilde{{\mathfrak {D}}}r^{(\pm )}$ in place of ${\mathcal {E}}^{(\pm )}$, ${\mathfrak {D}}r^{(\pm )}$.

Proof of (7.156)–(7.158). In order to establish (7.156) and (7.157), we will use the fact that, for any $n\in {\mathbb {N}}$ and $0\le j\le N_{\varepsilon }-1$ such that (7.152) and (7.155) hold, we have for all $0\le {\bar{j}}\le j$

$$\begin{aligned} \widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}]= & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]\cdot \exp \Big (\sum _{k=0}^{{\bar{j}}-1}\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },k]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },k+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )\nonumber \\{} & {} +O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{({\bar{j}})}}{\sqrt{-\Lambda }}\Big ) \end{aligned}$$

(7.220)

and, for all $1\le {\bar{j}}\le j$

$$\begin{aligned}{} & {} \widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}]\nonumber \\{} & {} \quad ={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{j}},0] \cdot \exp \Big (-\sum _{k=0}^{{\bar{j}}-2}\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },k]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },k+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big ).\nonumber \\ \end{aligned}$$

(7.221)

Note that, if (7.152) holds, then it is also necessarily true that

$$\begin{aligned} \widetilde{{\mathcal {R}}}_{N_{\varepsilon };{\bar{j}}}^{(n)}\subset {\mathcal {T}}_{\varepsilon }^{+}\quad \text { for all }0\le {\bar{j}}\le j, \end{aligned}$$

(7.222)

and hence all the terms in the relations (7.220)–(7.221) are well defined. The relations (7.220) and (7.221) are immediate corollaries of (7.213) and (7.215) (for $\widetilde{{\mathcal {E}}}^{(\pm )}$, $\widetilde{{\mathfrak {D}}}r^{(\pm )}$ in place of ${\mathcal {E}}^{(\pm )}$, ${\mathfrak {D}}r^{(\pm )}$) with $i=N_{\varepsilon }$, $j_{1}={\bar{j}}$ and $j_{0}=0$, using also the fact that, since (7.152) holds,

$$\begin{aligned} \widetilde{{\mathcal {E}}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]&={\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]\quad \text { for all }0\le {\bar{j}}\le j\text { and }\\ \widetilde{{\mathfrak {D}}}r_{\nwarrow }^{(-)}[n;{\bar{j}},0]&={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{j}},0]\Big (1+O(\rho _{\varepsilon }^{\frac{1}{9}})\Big )\quad \text { for all }1\le {\bar{j}}\le j\nonumber \end{aligned}$$

(7.223)

(which is inferred from the definition of ${\mathcal {E}}_{\nwarrow }^{(-)}$, ${\mathfrak {D}}r_{\nwarrow }^{(-)}$, $\widetilde{{\mathcal {E}}}_{\nwarrow }^{(-)}$and $\widetilde{{\mathfrak {D}}}r_{\nwarrow }^{(-)}$ in Sect. 6.4, as well as the fact that

$$\begin{aligned} {\tilde{m}}(v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0},v_{\varepsilon ,{\bar{j}}}^{(n)}\pm h_{\varepsilon ,{\bar{j}}})={\tilde{m}}(v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0},v_{\varepsilon ,{\bar{j}}}^{(n)}\pm {\tilde{h}}_{\varepsilon ,{\bar{j}}}), \end{aligned}$$

since the support of $T_{\mu \nu }[f]$ in $\{0\le u\le v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0}\}\subset {\mathcal {U}}_{\varepsilon }^{+}$ is contained in $\cup _{k\in {\mathbb {N}}}\cup _{i=0}^{N_{\varepsilon }}{\mathcal {V}}_{i}^{(k)}$).

In order to infer (7.156)–(7.157) from (7.220)–(7.221), we will argue similarly as in the case of (7.153)–(7.154): Defining the quantities

$$\begin{aligned} {\tilde{e}}_{{\bar{j}}}[n+1]&\doteq \frac{\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}]-{\mathcal {E}}_{{\bar{j}}}[n+1]}{\varepsilon ^{({\bar{j}})}}\sqrt{-\Lambda }\quad \text { for }0\le {\bar{j}}\le j,\\ {\tilde{r}}_{{\bar{j}}}[n+1]&\doteq \frac{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}]}{R_{{\bar{j}}}[n+1]}\quad \text { for }1\le {\bar{j}}\le j,\\ {\tilde{\mu }}_{{\bar{j}}}[n+1]&\doteq \rho _{\varepsilon }^{-1}\Big (\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}+1]}-\mu _{{\bar{j}}}[n+1]\Big )\quad \text { for }0\le {\bar{j}}\le j, \end{aligned}$$

the relations (7.156) and (7.157) will follow by showing that

$$\begin{aligned} \max _{0\le {\bar{j}}\le j}\big |{\tilde{e}}_{{\bar{j}}}[n+1]\big |,\text { }\max _{1\le {\bar{j}}\le j}\big |{\tilde{r}}_{{\bar{j}}}[n+1]-1\big |,\text { }\max _{0\le {\bar{j}}\le j}\big |{\tilde{\mu }}_{{\bar{j}}}[n+1]\big |\le \rho _{\varepsilon }^{\frac{1}{17}}.\nonumber \\ \end{aligned}$$

(7.224)

We will argue by induction on ${\bar{j}}$: For any $0\le {\bar{j}}\le j$, we will show that, if

$$\begin{aligned} \max _{0\le k\le {\bar{j}}-1}\big |{\tilde{\mu }}_{k}[n+1]\big |\le \rho _{\varepsilon }^{\frac{1}{16}}, \end{aligned}$$

(7.225)

then

$$\begin{aligned} \big |{\tilde{\mu }}_{{\bar{j}}}[n+1]\big |\le \rho _{\varepsilon }^{\frac{1}{16}}. \end{aligned}$$

(7.226)

In view of the relations (7.220)–(7.221) for $\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}]$, $\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}]$ and the relation (7.145) for $\mu _{{\bar{j}}}[n]$, we infer using the bounds (7.169)–(7.170) (for $\widetilde{{\mathcal {E}}}^{(\pm )}$, $\mathfrak {{\widetilde{D}}}r^{(\pm )}$ and $\delta _{\varepsilon }$ in place of ${\mathcal {E}}^{(\pm )}$, ${\mathfrak {D}}r^{(\pm )}$ and $\sigma _{\varepsilon }$, respectively), the bound

$$\begin{aligned} \sum _{k=0}^{j-1}\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },k]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },k+1]}\le \exp (\exp (\delta _{\varepsilon }^{-6}))\quad \text { for all }0\le k\le n\qquad \end{aligned}$$

(7.227)

(following from (7.169)–(7.170) for $\widetilde{{\mathcal {E}}}^{(\pm )}$, $\mathfrak {{\widetilde{D}}}r^{(\pm )}$ and the fact that $N_{\varepsilon }=\rho _{\varepsilon }^{-1}\exp \big (e^{\delta _{\varepsilon }^{-15}}\big )$), the bound

$$\begin{aligned} \sum _{k=0}^{{\bar{j}}-1}{\tilde{\mu }}_{k}[n+1]\le \rho _{\varepsilon }^{-1+\frac{1}{16}}\exp \big (e^{\delta _{\varepsilon }^{-15}}\big ) \end{aligned}$$

(7.228)

(following from the inductive assumption (7.225)) and the estimate (7.193) for ${\bar{\mu }}_{{\bar{j}}}[n]$ established previously that:

$$\begin{aligned}&\big |{\tilde{\mu }}_{{\bar{j}}}[n+ 1]\big |\\&\quad =\rho _{\varepsilon }^{-1}\Bigg |\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{j}}+1,0]}\exp \Big (2\sum _{k=0}^{{\bar{j}}-1}\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },k]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },k+1]}\nonumber \\&\qquad +O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )+O(\rho _{\varepsilon }^{1+\frac{1}{6}})\nonumber \\&\qquad -\mu _{{\bar{j}}}[n]\exp \Big (2\sum _{k=0}^{{\bar{j}}-1}\mu _{k}[n+1]\Big )\Bigg |\nonumber \\&\quad =\exp \Big (2\sum _{k=0}^{{\bar{j}}-1}\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },k]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },k+1]}\Big )\rho _{\varepsilon }^{-1}\Bigg |\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{j}}+1,0]}(1+O(\rho _{\varepsilon }^{\frac{1}{12}}))\nonumber \\&\qquad -\mu _{{\bar{j}}}[n]\exp \Big (-2\rho _{\varepsilon }\sum _{k=0}^{{\bar{j}}-1}{\tilde{\mu }}_{k}[n+1]\Big )+O(\rho _{\varepsilon }^{1+\frac{1}{6}})\Bigg |\nonumber \\&\quad =\exp \big (O(\exp \big (2e^{\delta _{\varepsilon }^{-15}}\big ))\big )\Bigg |\rho _{\varepsilon }^{-1}\Big (\frac{2{\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]}{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{j}}+1,0]}\nonumber \\&\qquad -\mu _{{\bar{j}}}[n](1-2\rho _{\varepsilon }\sum _{k=0}^{{\bar{j}}-1}{\tilde{\mu }}_{k}[n+1]\Big )+O(\rho _{\varepsilon }^{\frac{1}{13}})\Bigg |\nonumber \\&\quad \le {\bar{\delta }}_{\varepsilon }^{-\frac{1}{2}}\Big \{|{\bar{\mu }}_{{\bar{j}}}[n]|+\rho _{\varepsilon }\sum _{k=0}^{{\bar{j}}-1}|{\tilde{\mu }}_{k}[n+1]|+O(\rho _{\varepsilon }^{\frac{1}{13}})\Big \}\nonumber \\&\quad \le {\bar{\delta }}_{\varepsilon }^{-1}\Big \{\rho _{\varepsilon }\sum _{k=0}^{{\bar{j}}-1}|{\tilde{\mu }}_{k}[n+1]|+\rho _{\varepsilon }^{\frac{1}{15}}\Big \},\nonumber \end{aligned}$$

(7.229)

where ${\bar{\delta }}_{\varepsilon }$ was defined in terms of $\delta _{\varepsilon }$ by (6.1). Note that, for ${\bar{j}}=0$, from (7.229) we infer that

$$\begin{aligned} \big |{\tilde{\mu }}_{0}[n+1]\big |\le {\bar{\delta }}_{\varepsilon }^{-1}\rho _{\varepsilon }^{\frac{1}{15}}. \end{aligned}$$

(7.230)

In general, for $0\le {\bar{j}}\le j$, applying a Gronwall-type inequality in the ${\bar{j}}$ variable, from (7.229) and (7.230) we infer that:

$$\begin{aligned} \big |{\tilde{\mu }}_{{\bar{j}}}[n+1]\big |\le \exp \Big ({\bar{\delta }}_{\varepsilon }^{-1}N_{\varepsilon }\rho _{\varepsilon }\Big )\rho _{\varepsilon }^{\frac{1}{15}}\le \rho _{\varepsilon }^{\frac{1}{16}}, \end{aligned}$$

(7.231)

thus establishing (7.226). As a result,

$$\begin{aligned} \max _{0\le {\bar{j}}\le j}\big |{\tilde{\mu }}_{{\bar{j}}}[n+1]\big |\le \rho _{\varepsilon }^{\frac{1}{16}}. \end{aligned}$$

(7.232)

From the relations (7.220)–(7.221) for $\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}]$, $\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },{\bar{j}}]$ and (7.147)–(7.148) for ${\mathcal {E}}_{{\bar{j}}}[n+1]$, $R_{{\bar{j}}}[n+1]$, in view of the bounds (7.169)–(7.170) (for $\widetilde{{\mathcal {E}}}^{(\pm )}$, $\widetilde{{\mathfrak {D}}}r^{(\pm )}$), the bound (7.227), the bound (7.232), as well as the approximate equalities (7.153) and (7.154) between ${\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]$, ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{j}},0]$ and ${\mathcal {E}}_{{\bar{j}}}[n]$, $R_{{\bar{j}}}[n]$, respectively, we can estimate for any $0\le {\bar{j}}\le j$ (arguing similarly as for the derivation of (7.194) and (7.195)):

$$\begin{aligned}&|{\tilde{e}}_{{\bar{j}}} [n+1]|\\&\quad =\Bigg |\frac{\sqrt{-\Lambda }}{\varepsilon ^{({\bar{j}})}}{\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]\cdot \exp \Big (\sum _{k=0}^{{\bar{j}}-1}\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },k]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },k+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )\nonumber \\&\qquad +O(\rho _{\varepsilon }^{\frac{1}{4}})-\frac{\sqrt{-\Lambda }}{\varepsilon ^{({\bar{j}})}}{\mathcal {E}}_{i}[n]\cdot \exp \Big (\sum _{k=0}^{{\bar{j}}-1}\mu _{k}[n+1]\Big )\Bigg |\nonumber \\&\quad =\exp \Big (\sum _{k=0}^{{\bar{j}}-1}\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },k]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },k+1]}\Big )\Bigg |(1+O(\rho _{\varepsilon }^{\frac{1}{12}}))\frac{\sqrt{-\Lambda }}{\varepsilon ^{({\bar{j}})}}{\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]\nonumber \\&\qquad -\frac{\sqrt{-\Lambda }}{\varepsilon ^{({\bar{j}})}}{\mathcal {E}}_{{\bar{j}}}[n]\cdot \exp \Big (-\rho _{\varepsilon }\sum _{k=0}^{{\bar{j}}-1}{\tilde{\mu }}_{{\bar{j}}}[{\bar{n}}+1]\Big )+O(\rho _{\varepsilon }^{\frac{1}{4}})\Bigg |\nonumber \\&\quad \le \exp \big (\exp (\exp (2\delta _{\varepsilon }^{-15}))\big )\Bigg |\frac{\sqrt{-\Lambda }}{\varepsilon ^{({\bar{j}})}}\Big ({\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]-{\mathcal {E}}_{{\bar{j}}}[n]\Big )\nonumber \\&\qquad +O(\rho _{\varepsilon }^{\frac{1}{12}})\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}{\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]+O(\rho _{\varepsilon }^{\frac{1}{15}})\frac{\sqrt{-\Lambda }}{\varepsilon ^{(i)}}{\mathcal {E}}_{i}[n]+O(\rho _{\varepsilon }^{\frac{1}{4}})\Bigg |\nonumber \\&\quad \le \exp \big (\exp (\exp (4\delta _{\varepsilon }^{-15}))\big )\Big (\rho _{\varepsilon }^{\frac{1}{16}}+\exp (\exp (\sigma _{\varepsilon }^{-6}))\rho _{\varepsilon }^{\frac{1}{15}}\Big )\nonumber \\&\quad \le {\bar{\delta }}_{\varepsilon }^{-1}\rho _{\varepsilon }^{\frac{1}{16}}\nonumber \end{aligned}$$

(7.233)

and, for any $1\le {\bar{j}}\le j$:

$$\begin{aligned}&|{\tilde{r}}_{i}[n+1]-1|\nonumber \\&\quad =\Bigg |\frac{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{i}},0]\cdot \exp \Big (-\sum _{k=0}^{{\bar{j}}-2}\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },k]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },k+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )}{R_{{\bar{j}}}[n]\cdot \exp \Big (-\sum _{k=0}^{{\bar{j}}-1}\mu _{k}[n+1]\Big )}-1\Bigg |\\&\quad =\Bigg |\frac{{\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{i}},0]}{R_{{\bar{j}}}[n]}\cdot \exp \Big (-\rho _{\varepsilon }\sum _{k=0}^{{\bar{j}}-1}{\tilde{\mu }}_{k}[n+1]+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )-1\Bigg |\nonumber \\&\quad =\Bigg |\Big (1+O(\rho _{\varepsilon }^{\frac{1}{16}})\Big )\cdot \exp \Big (O\big (\exp (e^{\delta _{\varepsilon }^{-15}})\rho _{\varepsilon }^{\frac{1}{15}}\big )\Big )-1\Bigg |\le \nonumber \\&\quad \le {\bar{\delta }}_{\varepsilon }^{-1}\rho _{\varepsilon }^{\frac{1}{16}}.\nonumber \end{aligned}$$

(7.234)

From (7.233), (7.234) and (7.232), in view of the relation (6.1) between $\rho _{\varepsilon }$, $\delta _{\varepsilon }$ and $\sigma _{\varepsilon }$, we readily obtain (7.224). Thus, we infer (7.156) and (7.157).

Using the relation (7.212) for $i=N_{\varepsilon }$, $j_{0}=0$, $j_{1}=N_{\varepsilon }-1$ with $\widetilde{{\mathcal {E}}}$, $\widetilde{{\mathfrak {D}}}r$ in place of ${\mathcal {E}}$, ${\mathfrak {D}}r$, the relation (7.31) for $i=N_{\varepsilon }$, $j=N_{\varepsilon }-1$ with $\widetilde{{\mathcal {E}}}$ in place of ${\mathcal {E}}$, as well as the relation (7.172) for $i=N_{\varepsilon }-1$ with ${\tilde{r}}_{n;i+1,i}$, $\widetilde{{\mathfrak {D}}}r$ in place of $r_{n;i+1,i}$, ${\mathfrak {D}}r$, we readily infer that:

$$\begin{aligned}{} & {} \widetilde{{\mathcal {E}}}_{\nwarrow }^{(+)}[n;N_{\varepsilon },N_{\varepsilon }-1]\nonumber \\{} & {} \quad =\widetilde{{\mathcal {E}}}_{\nwarrow }^{(-)}[n;N_{\varepsilon },0]\cdot \exp \Big (\sum _{j=0}^{N_{\varepsilon }-1}\frac{2\widetilde{{\mathcal {E}}}_{\nearrow }^{(-)}[n;N_{\varepsilon },j]}{\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(-)}[n;N_{\varepsilon },j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )\nonumber \\{} & {} \qquad +O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\Big ). \end{aligned}$$

(7.235)

The relation (7.158) now readily follows from (7.235) using (7.156), (7.157) and (7.223) for the right hand side of (7.235), as well as the relation (7.147) for ${\mathcal {E}}_{N_{\varepsilon }}[n+1]$ and the fact that (7.153) holds for ${\mathcal {E}}_{\nwarrow }^{(-)}[n;N_{\varepsilon },0]$. $\square$

7.4 Control of the evolution in terms of ${\mathcal {E}}_{i}[n]$, $R_{i}[n]$, $\mu _{i}[n]$

In this section, we will establish some additional bounds on various quantities related to the geometry of $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ in terms of the quantities ${\mathcal {E}}_{i}[n]$, $R_{i}[n]$ and $\mu _{i}[n]$. These bounds will enable us to obtain a priori control of the evolution of $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2},{\bar{f}}_{/}^{(\varepsilon )})$ by estimating the growth rate of solutions to the recursive systems 7.145 and 7.147–7.148.

The following result can be viewed as a supplement to Proposition 7.6, providing us with additional bounds on the energy content and the geometric separation of the beams on the regions ${\mathcal {R}}_{i;j}^{(n)}$ (not necessarily with $j=0$ or $i=N_{\varepsilon }$):

Lemma 7.7

For any $n\in {\mathbb {N}}$ such that

$$\begin{aligned} \{0\le u\le v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0}\}\cap \big \{ u<v<u+\sqrt{-\frac{3}{\Lambda }}\pi \big \}\subset {\mathcal {U}}_{\varepsilon }^{+} \end{aligned}$$

(7.236)

and any $0\le i,j\le N_{\varepsilon }$, such that ${\mathcal {R}}_{i;j}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}$, if $i\ne j$, and ${\mathcal {R}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)},{\mathcal {R}}_{i;{\mathcal {I}}}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}$, if $i=j$,²⁵ we can estimate:

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(\pm )}[n;i,j]&\le {\mathcal {E}}_{i}[n+1]+\rho _{\varepsilon }^{\frac{1}{18}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }},\\ {\mathcal {E}}_{\nearrow }^{(\pm )}[n;i,j]&\le {\mathcal {E}}_{j}[n+1]+\rho _{\varepsilon }^{\frac{1}{18}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\nonumber \end{aligned}$$

(7.237)

(if $i\ne j$),

$$\begin{aligned} {\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;i]&\le {\mathcal {E}}_{i}[n+1]+\rho _{\varepsilon }^{\frac{1}{18}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }},\\ {\mathcal {E}}_{{\mathcal {I}}}[n;i]&\le {\mathcal {E}}_{j}[n+1]+\rho _{\varepsilon }^{\frac{1}{18}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\nonumber \end{aligned}$$

(7.238)

(if $i=j)$ and

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(\pm )}[n;i,j]&\ge R_{i}[n+1]\cdot \big (1-\rho _{\varepsilon }^{\frac{1}{18}}\big ),\text { if }i>0,\\ {\mathfrak {D}}r_{\nearrow }^{(\pm )}[n;i,j]&\ge R_{j}[n+1]\cdot \big (1-\rho _{\varepsilon }^{\frac{1}{18}}\big ),\text { if }j>0.\nonumber \end{aligned}$$

(7.239)

Similarly, for any $0\le i,j\le N_{\varepsilon }$ such that $\widetilde{{\mathcal {R}}}_{i;j}^{(n)}\subset {\mathcal {T}}_{\varepsilon }^{+}$ if $i\ne j$, or $\widetilde{{\mathcal {R}}}_{i;\gamma _{{\mathcal {Z}}}}^{(n)},\widetilde{{\mathcal {R}}}_{i;{\mathcal {I}}}^{(n)}\subset {\mathcal {T}}_{\varepsilon }^{+}$, if $i=j$, the bounds (7.237)–(7.239) also hold with $\widetilde{{\mathcal {E}}}_{\nwarrow }^{(\pm )}$, $\widetilde{{\mathcal {E}}}_{\nearrow }^{(\pm )}$, $\widetilde{{\mathcal {E}}}_{\gamma _{{\mathcal {Z}}}}$, $\widetilde{{\mathcal {E}}}_{{\mathcal {I}}}$, $\widetilde{{\mathfrak {D}}}r_{\nwarrow }^{(\pm )}$ and $\widetilde{{\mathfrak {D}}}r_{\nearrow }^{(\pm )}$ in place of ${\mathcal {E}}_{\nwarrow }^{(\pm )}$, ${\mathcal {E}}_{\nearrow }^{(\pm )}$, ${\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}$, ${\mathcal {E}}_{{\mathcal {I}}}$, ${\mathfrak {D}}r_{\nwarrow }^{(\pm )}$ and ${\mathfrak {D}}r_{\nearrow }^{(\pm )}$, respectively.

Proof

Let $n\in {\mathbb {N}}$ be such that (7.236) is satisfied, and let $0\le i,j\le N_{\varepsilon }$, $i>j$, be such that

$$\begin{aligned} {\mathcal {R}}_{i;j}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}. \end{aligned}$$

(7.240)

Notice that (7.240) implies that

$$\begin{aligned} {\mathcal {R}}_{{\bar{i}};{\bar{j}}}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}\text { for all }0\le {\bar{i}}\le i,\text { }0\le {\bar{j}}\le j,\text { }{\bar{i}}\ne {\bar{j}} \end{aligned}$$

(7.241)

and

$$\begin{aligned} {\mathcal {R}}_{{\bar{i}};\gamma _{{\mathcal {Z}}}}^{(n)},{\mathcal {R}}_{{\bar{i}};{\mathcal {I}}}^{(n)}\subset {\mathcal {U}}_{\varepsilon }^{+}\text { for all }0\le {\bar{i}}\le j. \end{aligned}$$

(7.242)

Using (7.213) and (7.215) for $j_{0}=0$ and $j_{1}={\bar{j}}$, we obtain for any $0\le {\bar{j}}\le j$:

$$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(-)}[n;i,{\bar{j}}]= & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]\cdot \exp \Big (\sum _{k=0}^{{\bar{j}}-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,k]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,k+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )\nonumber \\{} & {} \quad +O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{({\bar{j}})}}{\sqrt{-\Lambda }}\Big ) \end{aligned}$$

(7.243)

and, provided ${\bar{j}}\ge 1$:

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,{\bar{j}}]\!=\!{\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{j}},0]\cdot \exp \Big (-\sum _{k=0}^{{\bar{j}}-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,k]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,k+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big ).\nonumber \\ \end{aligned}$$

(7.244)

Arguing exactly as in the proof of (7.156)–(7.157), by comparing the system (7.243)–(7.244) for ${\mathcal {E}}_{\nearrow }^{(-)}[n;i,{\bar{j}}]$, ${\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,{\bar{j}}]$ with the system (7.147)–(7.148) for ${\mathcal {E}}_{{\bar{j}}}[n+1]$, $R_{{\bar{j}}}[n+1]$, using also the approximate equalities (7.153)–(7.154) for ${\mathcal {E}}_{\nwarrow }^{(-)}[n;{\bar{j}},0]$, ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;{\bar{j}},0]$ and ${\mathcal {E}}_{{\bar{j}}}[n]$, $R_{{\bar{j}}}[n]$, respectively, we infer that

$$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(-)}[n;i,{\bar{j}}]&={\mathcal {E}}_{{\bar{j}}}[n+1]+O\Big (\rho _{\varepsilon }^{\frac{1}{16}}\frac{\varepsilon ^{({\bar{j}})}}{\sqrt{-\Lambda }}\Big )\quad \text { for all }0\le {\bar{j}}\le j, \end{aligned}$$

(7.245)

$$\begin{aligned} {\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,{\bar{j}}]&=R_{{\bar{j}}}[n+1]\cdot \big (1+O(\rho _{\varepsilon }^{\frac{1}{16}})\big )\quad \text { for all }1\le {\bar{j}}\le j. \end{aligned}$$

(7.246)

Using (7.212) and (7.214) for $j_{0}=0$ and $j_{1}={\bar{j}}$, we obtain for any $0\le {\bar{j}}\le j$:

$$\begin{aligned}{} & {} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,{\bar{j}}]\nonumber \\{} & {} \quad ={\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]\cdot \exp \Big (\sum _{k=0}^{{\bar{j}}-1}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,k]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,k+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big )\nonumber \\{} & {} \qquad +O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big ) \end{aligned}$$

(7.247)

and, provided ${\bar{j}}\ge 1$:

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,{\bar{j}}]={\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]\cdot \exp \Big (-\sum _{k=0}^{{\bar{j}}-2}\frac{2{\mathcal {E}}_{\nearrow }^{(-)}[n;i,j]}{{\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,j+1]}+O(\rho _{\varepsilon }^{\frac{1}{12}})\Big ).\nonumber \\ \end{aligned}$$

(7.248)

Using the approximate equalities (7.153)–(7.154) for ${\mathcal {E}}_{\nwarrow }^{(-)}[n;i,0]$, ${\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,0]$ and ${\mathcal {E}}_{i}[n]$, $R_{i}[n]$, respectively, as well as the approximate equalities (7.245)–(7.246) for ${\mathcal {E}}_{\nearrow }^{(-)}[n;i,{\bar{j}}]$, ${\mathfrak {D}}r_{\nearrow }^{(-)}[n;i,{\bar{j}}]$ and ${\mathcal {E}}_{{\bar{j}}}[n+1]$, $R_{{\bar{j}}}[n+1]$, respectively, and the bounds (7.169) and (7.170), we obtain from (7.247)–(7.248) that, for any $0\le {\bar{j}}\le j$:

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,{\bar{j}}]&={\mathcal {E}}_{i}[n]\cdot \exp \Big (\sum _{k=0}^{{\bar{j}}-1}\frac{2{\mathcal {E}}_{k}[n+1]}{R_{k+1}[n+1]}+O(\rho _{\varepsilon }^{\frac{1}{17}})\Big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\\&\le {\mathcal {E}}_{i}[n]\cdot \exp \Big (\sum _{k=0}^{i-1}\frac{2{\mathcal {E}}_{k}[n+1]}{R_{k+1}[n+1]}+O(\rho _{\varepsilon }^{\frac{1}{17}})\Big )+O\Big (\rho _{\varepsilon }^{\frac{1}{4}}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\Big )\nonumber \end{aligned}$$

(7.249)

and, provided $i\ge 1$:

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,{\bar{j}}]&=R_{i}[n]\cdot \exp \Big (-\sum _{k=0}^{{\bar{j}}-2}\frac{2{\mathcal {E}}_{k}[n+1]}{R_{k+1}[n+1]}+O(\rho _{\varepsilon }^{\frac{1}{17}})\Big )\\&\ge R_{i}[n]\cdot \exp \Big (-\sum _{k=0}^{i-2}\frac{2{\mathcal {E}}_{k}[n+1]}{R_{k+1}[n+1]}+O(\rho _{\varepsilon }^{\frac{1}{17}})\Big )\nonumber \end{aligned}$$

(7.250)

(where we have used the fact that $i\ge {\bar{j}}$). On the other hand, from (7.147)–(7.148) we obtain:

$$\begin{aligned} {\mathcal {E}}_{i}[n+1]={\mathcal {E}}_{i}[n]\cdot \exp \Big (\sum _{k=0}^{i-1}\frac{2{\mathcal {E}}_{k}[n+1]}{R_{k+1}[n+1]}\Big ) \end{aligned}$$

(7.251)

and, for $i\ge 1$:

$$\begin{aligned} R_{i}[n+1]=R_{i}[n]\cdot \exp \Big (-\sum _{k=0}^{i-2}\frac{2{\mathcal {E}}_{k}[n+1]}{R_{k+1}[n+1]}\Big ). \end{aligned}$$

(7.252)

Comparing (7.249)–(7.250) and (7.251)–(7.252), using also the bounds (7.169) and (7.170), we obtain

$$\begin{aligned} {\mathcal {E}}_{\nwarrow }^{(-)}[n;i,{\bar{j}}]&\le {\mathcal {E}}_{i}[n+1]+\rho _{\varepsilon }^{\frac{1}{18}}\text { for all }0\le {\bar{j}}\le j, \end{aligned}$$

(7.253)

$$\begin{aligned} {\mathfrak {D}}r_{\nwarrow }^{(-)}[n;i,{\bar{j}}]&\ge R_{i}[n+1]\Big (1-\rho _{\varepsilon }^{\frac{1}{18}}\Big )\text { for all }0\le {\bar{j}}\le j,\text { if }i\ge 1. \end{aligned}$$

(7.254)

From (7.245)–(7.246) and (7.253)–(7.254), we infer (7.237) and (7.239) in the case $i>j$. The proof of (7.237) and (7.239), when $i<j$, or (7.238) and (7.239), when $i=j$, follows in exactly the same way (using (7.216)–(7.219) in place of (7.212)–(7.215)), and hence the details will be omitted. $\square$

The following result will be useful in obtaining a priori control on the concentration of the energy of $f_{\varepsilon }$ on ${\mathcal {U}}_{\varepsilon }^{+}$ and ${\mathcal {T}}_{\varepsilon }^{+}$ in terms of the sequence $\mu _i[n]$:

Lemma 7.8

For any $n\in {\mathbb {N}}$ such that

$$\begin{aligned} \{0\le u\le v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0}\}\cap \big \{ u<v<u+\sqrt{-\frac{3}{\Lambda }}\pi \big \}\subset {\mathcal {U}}_{\varepsilon }^{+}, \end{aligned}$$

(7.255)

we can estimate on

$$\begin{aligned} {\mathcal {U}}_{\varepsilon ;n}^{+}\doteq {\mathcal {U}}_{\varepsilon }^{+}\cap \{v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0}\le u\le v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,0}\} \end{aligned}$$

(7.256)

(see Fig. 23) that:

$$\begin{aligned}&\sup _{V\ge 0}\int _{\{v=V\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big ) (u,V)\,du\\&\qquad +\sup _{U\ge 0}\int _{\{u=U\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+ \frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(U,v)\,dv\nonumber \\&\quad \le 8\sum _{i=0}^{N_{\varepsilon }-1}\mu _{i}[n+1]+\max _{0\le i\le N_{\varepsilon }}\big \{\big (\exp (e^{\sigma _{\varepsilon }^{-7}}\big )a_{\varepsilon i}\big \}+\rho _{\varepsilon }^{\frac{1}{19}}\nonumber \end{aligned}$$

(7.257)

(where $\mu _{i}[n]$ were introduced in Definition 7.5). Furthermore,

$$\begin{aligned} \sup _{{\mathcal {U}}_{\varepsilon ;n}^{+}}\frac{2{\tilde{m}}}{r}\le \max _{0\le i\le N_{\varepsilon }}\big \{\big (\exp (e^{\sigma _{\varepsilon }^{-8}}\big )a_{\varepsilon i}\big \}+\varepsilon ^{\frac{1}{2}} \end{aligned}$$

(7.258)

and, for any $0\le j\le N_{\varepsilon }$:

$$\begin{aligned} \sup _{{\mathcal {U}}_{\varepsilon ;n}^{+}\cap \{u\le v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}\}}\frac{2{\tilde{m}}}{r}\le \max _{0\le i\le j}\big \{\big (\exp (e^{\sigma _{\varepsilon }^{-8}}\big )a_{\varepsilon i}\big \}+\varepsilon ^{\frac{1}{2}}. \end{aligned}$$

(7.259)

Similarly, the estimates (7.257), (7.258) and (7.259) also hold on

$$\begin{aligned} {\mathcal {T}}_{\varepsilon ;n}^{+}\doteq {\mathcal {T}}_{\varepsilon }^{+}\cap \{v_{\varepsilon ,0}^{(n)}-{\tilde{h}}_{\varepsilon ,0}\le u\le v_{\varepsilon ,0}^{(n+1)}-{\tilde{h}}_{\varepsilon ,0}\}, \end{aligned}$$

(7.260)

with $\delta _{\varepsilon }$ and ${\tilde{h}}_{\varepsilon ,j}$ in place of $\sigma _{\varepsilon }$ and $h_{\varepsilon ,j}$, respectively.

Remark

Notice that ${\mathcal {U}}_{\varepsilon ;n}^{+}$ can be alternatively expressed as

$$\begin{aligned} {\mathcal {U}}_{\varepsilon ;n}^{+}=\big \{ v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0}\le u\le u_{\varepsilon ,n}^{+}\big \}\cap \left\{ u<v<u+\sqrt{-\frac{3}{\Lambda }}\pi \right\} , \end{aligned}$$

where

$$\begin{aligned} u_{\varepsilon ,n}^{+}\doteq \min \{v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,0},u[{\mathcal {U}}_{\varepsilon }^{+}]\} \end{aligned}$$

(7.261)

(see the relation (6.51) for ${\mathcal {U}}_{\varepsilon }^{+}$).

Proof

In order to show (7.257), we will first show that, for any $V\ge 0$,

$$\begin{aligned}{} & {} \int _{\{v=V\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\nonumber \\{} & {} \quad \le \frac{1}{2}\max _{0\le i \le N_{\varepsilon }} \big \{\big (\exp (e^{\sigma _{\varepsilon }^{-7}}\big )a_{\varepsilon i}\big \}+4\sum _{i=0}^{N_{\varepsilon }-1}\mu _{i}[n+1]+\frac{1}{2}\rho _{\varepsilon }^{\frac{1}{19}}\qquad \end{aligned}$$

(7.262)

Note that, in view of the definition (7.256) of ${\mathcal {U}}_{\varepsilon ;n}^{+}$, the inequality (7.262) is non trivial only when

$$\begin{aligned} v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0}<V<v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,0}+\sqrt{-\frac{3}{\Lambda }}\pi . \end{aligned}$$

In view of the relation (2.49) for $\partial _{u}{\tilde{m}}$, the linear relation (6.65) between $f_{\varepsilon }$ and $f_{\varepsilon i}$, as well as the bound (7.1) on the support of $f_{\varepsilon i}$, we have

$$\begin{aligned}{} & {} \int _{\{v=V\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\nonumber \\{} & {} \quad =\frac{1}{4\pi }\sum _{i=0}^{N_{\varepsilon }}\int _{\{v=V\}\cap ({\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i}^{(n+1)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}\big (1-\frac{2{\tilde{m}}}{r}-\frac{1}{3}\Lambda r^{2}\big )^{-1}\frac{-\partial _{u}{\tilde{m}}}{r}(u,V)\,du.\nonumber \\ \end{aligned}$$

(7.263)

We will proceed to establish (7.262) by considering the cases when $V^{(-)}\le V\le V^{(+)}$, $V<V^{(-)}$ and $V>V^{(+)}$ separately, where we have set

$$\begin{aligned} V^{(-)}&\doteq v_{\varepsilon ,N_{\varepsilon }}^{(n)}+h_{\varepsilon ,N_{\varepsilon }}, \end{aligned}$$

(7.264)

$$\begin{aligned} V^{(+)}&\doteq v_{\varepsilon ,N_{\varepsilon }}^{(n)}+\rho _{\varepsilon }^{-2}\frac{\varepsilon }{\sqrt{-\Lambda }} \end{aligned}$$

(7.265)

(see Fig. 23).

Fig. 23

Schematic depiction of the domain ${\mathcal {U}}_{\epsilon ;n}^{+}$ in the case when $v_{\epsilon ,0}^{(n+1)}-h_{\epsilon ,0}<u[{\mathcal {U}}_{\epsilon }^{+}]$. For simplicity, we have only depicted three of the beam domains ${\mathcal {V}}_i$

Case I: $V\in [V^{(-)},V^{(+)}]$. In this case, the bound (6.73) and the definition (7.265) of $V^{(+)}$ imply that

$$\begin{aligned} r|_{\{v=V\}\cap (\cup _{i=0}^{N_{\varepsilon }}({\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i}^{(n+1)}))\cap {\mathcal {U}}_{\varepsilon }^{+}}\le e^{\sigma _{\varepsilon }^{-4}}\rho _{\varepsilon }^{-2}\frac{\varepsilon }{\sqrt{-\Lambda }}. \end{aligned}$$

(7.266)

Furthermore, for any $0\le i\le N_{\varepsilon }$, we have

$$\begin{aligned} \{v=V\}\cap ({\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i}^{(n+1)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}=\{v=V\}\cap {\mathcal {V}}_{i\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}. \end{aligned}$$

(7.267)

Let us define $i_{+}$ as the maximum number in $\{0,1,\ldots ,N_{\varepsilon }\}$ such that

$$\begin{aligned} {\mathcal {V}}_{i\nearrow }^{(n)}\subset {\mathcal {U}}_{\varepsilon ;n}^{+}\text { for all }i<i_{+}. \end{aligned}$$

(7.268)

Note that, if $i_{+}<N_{\varepsilon }$, then it is necessary that ${\mathcal {V}}_{j\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon }^{+}=\emptyset$ for all $\iota _{+}<j\le N_{\varepsilon }$. Moreover, for any $i<i_{+}$:

$$\begin{aligned} \inf _{\{v=V\}\cap {\mathcal {V}}_{i\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}(v-u)\ge v_{n;N_{\varepsilon },i_{+}+1}^{(+)}-u_{n;N_{\varepsilon },i_{+}+1}^{(+)}\ge \rho _{\varepsilon }^{-1}\frac{\varepsilon ^{(i_{+}+1)}}{\sqrt{-\Lambda }}.\qquad \end{aligned}$$

(7.269)

Note that the above definition of $i_{+}$ implies that, in the extreme case when ${\mathcal {V}}_{j\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon }^{+}=\emptyset$ for all j, we have $i_{+}=0$.

Remark

In the case when $v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,0}=u[{\mathcal {U}}_{\varepsilon }^{+}]$ (and hence $u_{\varepsilon ,n}^{+}=v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,0}$ in (7.261)), such as the case depicted in Fig. 23, the parameter $i_{+}$ is equal to $N_{\varepsilon }$; similarly, in this case, for the parameters $i_{+}^{(1)},i_{+}^{(2)}$ defined by (7.278)–(7.279), we have $i_{+}^{(1)}=i_{+}^{(2)}=N_{\varepsilon }$. The parameters $i_{+}$, $i_{+}^{(1)}$ and $i_{+}^{(2)}$ are only introduced to treat the case when $u_{\varepsilon ,n}^{+}<v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,0}$ and $u=u_{\varepsilon ,n}^{+}$ intersects one of the outgoing beam components ${\mathcal {V}}_{i\nearrow }^{(n)}$, $0\le i\le N_{\varepsilon }$.

For any $i<i_{+}$, let us denote for simplicity

$$\begin{aligned} r_{min}^{(i)}(V)&=\inf _{\{v=V\}\cap {\mathcal {V}}_{i\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r=r\Big (v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i},V\Big ),\\ r_{max}^{(i)}(V)&=\sup _{\{v=V\}\cap {\mathcal {V}}_{i\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r=r\Big (v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i},V\Big ).\nonumber \end{aligned}$$

(7.270)

In view of the definition (6.80) of ${\mathcal {V}}_{i\nearrow }^{(n)}$, the bound (7.15) for $r_{n;N_{\varepsilon },i}$, the bound (6.73) on $\partial _{u}r$, the bounds (6.70), (7.266) on $\frac{2{\tilde{m}}}{r}$, r, the fact that $\partial _{v}r>0$ on ${\mathcal {U}}_{\varepsilon }^{+}$ and the lower bound (7.269), we have for any $i<i_{+}$:

$$\begin{aligned} \frac{r_{max}^{(i)}(V)-r_{min}^{(i)}(V)}{r_{min}^{(i)}(V)}\le & {} \frac{\int _{([v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i},v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}]\times \{V\})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}\big (-\partial _{u}r\big )\,du}{r_{min}^{(i)}(V^{(-)})}\nonumber \\\le & {} \frac{\exp (2\sigma _{\varepsilon }^{-6})\varepsilon ^{(i)}}{r_{n;N_{\varepsilon },i}}\le \rho _{\varepsilon }^{\frac{3}{4}}. \end{aligned}$$

(7.271)

Using (6.70), (7.266), (7.267) and (7.271), together with the fact that $\partial _{u}{\tilde{m}}\le 0$ on ${\mathcal {U}}_{\varepsilon }^{+}$, we infer that, for any $i<i_{+}$:

$$\begin{aligned}&\int _{\{v=V\}\cap ({\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i}^{(n+1)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}\big (1-\frac{2{\tilde{m}}}{r}- \frac{1}{3}\Lambda r^{2}\big )^{-1}\frac{-\partial _{u}{\tilde{m}}}{r}(u,V)\,du\\&\quad =\int _{\{v=V\}\cap {\mathcal {V}}_{i\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}(1+O(\eta _{0})+O(\varepsilon ))\frac{-\partial _{u}{\tilde{m}}}{r_{min}^{(i)}(V)\big (1+O(\rho _{\varepsilon }^{\frac{3}{4}})\big )}(u,V)\,du\nonumber \\&\quad \le \frac{2}{r_{min}^{(i)}(V)}\int _{\{v=V\}\cap {\mathcal {V}}_{i\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}(-\partial _{u}{\tilde{m}})(u,V)\,du.\nonumber \end{aligned}$$

(7.272)

Using the definition (6.98) of ${\mathcal {E}}_{\nearrow }^{(+)}[n;N_{\varepsilon },i]$, with the convention that

$$\begin{aligned} {\mathcal {E}}_{\nearrow }^{(+)}[n;N_{\varepsilon },N_{\varepsilon }]={\mathcal {E}}_{\gamma _{{\mathcal {Z}}}}[n;N_{\varepsilon }], \end{aligned}$$

as well as the fact that ${\tilde{m}}$ is constant on each connected component of ${\mathcal {U}}_{\varepsilon }^{+}\backslash \cup _{j=0}^{N_{\varepsilon }}{\mathcal {V}}_{j}$ and that $\partial _{v}r>0$, from (7.272) we obtain that, for any $i<i_{+}$:

$$\begin{aligned}&\int _{\{v=V\}\cap ({\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i}^{(n+1)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}\big (1-\frac{2{\tilde{m}}}{r}- \frac{1}{3}\Lambda r^{2}\big )^{-1}\frac{-\partial _{u}{\tilde{m}}}{r}(u,V)\,du\\&\quad \le \frac{2}{r_{min}^{(i)}(V^{(-)})}{\mathcal {E}}_{\nearrow }^{(+)}[n;N_{\varepsilon },i]\le \nonumber \\&\quad \le \frac{2}{r_{n;N_{\varepsilon },i}}{\mathcal {E}}_{\nearrow }^{(+)}[n;N_{\varepsilon },i].\nonumber \end{aligned}$$

(7.273)

Using the relations (7.172) and (7.202) (implying that $r_{n;N_{\varepsilon },i}={\mathfrak {D}}r_{\nearrow }^{(-)}[n;i+1,i+1]\big (1+O(\rho _{\varepsilon }^{\frac{1}{10}})\big )$), the bound (7.169) for ${\mathcal {E}}_{\nearrow }^{(\pm )}$ and the estimates (7.237)–(7.239) for ${\mathcal {E}}_{\nearrow }^{(\pm )}$, ${\mathfrak {D}}r_{\nearrow }^{(-)}$, we infer from (7.273) that, for any $i<i_{+}$:

$$\begin{aligned}&\int _{\{v=V\}\cap ({\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i}^{(n+1)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}\big (1-\frac{2{\tilde{m}}}{r}-\frac{1}{3}\Lambda r^{2}\big )^{-1}\frac{-\partial _{u}{\tilde{m}}}{r}(u,V)\,du \nonumber \\&\quad \le 4\frac{{\mathcal {E}}_{i}[n+1]}{R_{i}[n+1]}+O(\rho _{\varepsilon }^{1+\frac{1}{18}})\le \\&\quad \le 2\mu _{i}[n+1]+O(\rho _{\varepsilon }^{1+\frac{1}{18}}).\nonumber \end{aligned}$$

(7.274)

On the other hand, for $i=i_{+}$, using directly the bounds (6.73), (7.10), (7.11), (7.12) and the fact that

$$\begin{aligned} f_{\varepsilon }|_{{\mathcal {V}}_{j\nearrow }^{(n)}\cap \{V^{(-)}\le v\le V^{(+)}\}}=a_{\varepsilon j}f_{\varepsilon j}|_{{\mathcal {V}}_{j\nearrow }^{(n)}\cap \{V^{(-)}\le v\le V^{(+)}\}} \end{aligned}$$

(7.275)

(as a consequence of (6.65), (7.1) and the definition of $V^{(-)}$, $V^{(+)}$), we infer that

$$\begin{aligned}&\int _{\{v=V\}\cap ({\mathcal {V}}_{i_{+}}^{(n)}\cup {\mathcal {V}}_{i_{+}}^{(n+1)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}} \big (1-\frac{2{\tilde{m}}}{r}-\frac{1}{3}\Lambda r^{2}\big )^{-1}\frac{-\partial _{u}{\tilde{m}}}{r}(u,V)\,du\\&\quad =\int _{\{v=V\}\cap {\mathcal {V}}_{i_{+}\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\nonumber \\&\quad =a_{\varepsilon i_{+}}\int _{\{v=V\}\cap {\mathcal {V}}_{i_{+}\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon i_{+}}]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon i_{+}}]}{\partial _{v}r}\Big )(u,V)\,du\nonumber \\&\quad \le a_{\varepsilon i_{+}}\exp \big (\exp (3\sigma _{\varepsilon }^{-5})\big )\int _{\{v=V\}\cap {\mathcal {V}}_{i_{+}\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}\nonumber \\&\qquad \times \Big (\frac{(\varepsilon ^{(i_{+})})^{4}}{r^{5}(u,v)}(-\Lambda )^{-2}+\frac{(\varepsilon ^{(i_{+})})^{2}}{r^{3}(u,v)}(-\Lambda )^{-1}\Big )(u,V)\,du\nonumber \\&\quad \le a_{\varepsilon i_{+}}\exp \big (\exp (3\sigma _{\varepsilon }^{-5})\big )\Big (\frac{(\varepsilon ^{(i_{+})})^{4}}{(\min _{{\mathcal {V}}_{i_{+}\nearrow }^{(n)}}r)^{4}}(-\Lambda )^{-2}+\frac{(\varepsilon ^{(i_{+})})^{2}}{(\min _{{\mathcal {V}}_{i_{+}\nearrow }^{(n)}}r)^{2}}(-\Lambda )^{-1}\Big )\nonumber \\&\quad \le a_{\varepsilon i_{+}}\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big ).\nonumber \end{aligned}$$

(7.276)

From (7.263), (7.267), (7.274), (7.276) and the fact that

$$\begin{aligned} \sum _{i=0}^{N_{\varepsilon }}O(\rho _{\varepsilon }^{1+\frac{1}{18}})=O(N_{\varepsilon }\rho _{\varepsilon }^{1+\frac{1}{18}})=O(\rho _{\varepsilon }^{\frac{1}{19}}) \end{aligned}$$

and

$$\begin{aligned} {\mathcal {V}}_{j\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon }^{+}=\emptyset \text { for any }j>i_{+}, \end{aligned}$$

we immediately infer (7.262) in the case $V\in [V^{(-)},V^{(+)}]$.

Case II: $V\in [v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0},V^{(-)})$. In this case, the upper bound (7.266) for r still holds. However, for any $0\le i\le N_{\varepsilon }$, we now have

$$\begin{aligned} \{v=V\}\cap ({\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i+1}^{(n)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}=\{v=V\}\cap {\mathcal {V}}_{i}^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}. \end{aligned}$$

(7.277)

Let us define $i_{+}^{(1)}$ as the maximum number in the set $\{0,1,\ldots ,N_{\varepsilon }\}$ such that

$$\begin{aligned} \{v=V\}\cap {\mathcal {V}}_{i}^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}\ne \emptyset \text { for all }i\le i_{+}^{(1)} \end{aligned}$$

(7.278)

and let $i_{+}^{(2)}$ be the maximum number in $\{0,1,\ldots ,i_{+}^{(1)}\}$ such that

$$\begin{aligned} v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}<u_{\varepsilon ,n}^{+}\text { for all }i\le i_{+}^{(2)} \end{aligned}$$

(7.279)

(where $\{u=u_{n,\varepsilon }^{+}\}$ is the future boundary of ${\mathcal {U}}_{\varepsilon ;n}^{+}$). Note that the definition of $i_{+}^{(1)}$ implies that

$$\begin{aligned} \{v=V\}\cap {\mathcal {V}}_{i}^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}=\emptyset \quad \text { for all }i>i_{+}^{(1)} \end{aligned}$$

(7.280)

(which is a non-trivial statement only if $i_{+}^{(1)}<N_{\varepsilon }$) and that

$$\begin{aligned} V\ge v_{\varepsilon ,i_{+}^{(1)}}^{(n)}-h_{\varepsilon ,i_{+}^{(1)}}. \end{aligned}$$

(7.281)

Let us also remark that, trivially, in view of the form (6.80) of ${\mathcal {V}}_{i}^{(n)}={\mathcal {V}}_{i\nwarrow }^{(n)}\cup {\mathcal {V}}_{i\nearrow }^{(n)}$,

$$\begin{aligned}{} & {} i_{+}^{(2)}\nonumber \\{} & {} \quad ={\left\{ \begin{array}{ll} i_{+}^{(1)}-2, &{} \text {if }u_{\varepsilon ,n}^{+}\in [v_{\varepsilon ,i_{+}^{(1)}-1}^{(n)}-h_{\varepsilon ,i_{+}^{(1)}-1},v_{\varepsilon ,i_{+}^{(1)}-1}^{(n)}+h_{\varepsilon ,i_{+}^{(1)}-1}]\\ \qquad \text { and }V\le v_{\varepsilon ,i_{+}^{(1)}}^{(n)}+h_{\varepsilon ,i_{+}^{(1)}},\\ i_{+}^{(1)}-1, &{} \text { if }u_{\varepsilon ,n}^{+}\in [v_{\varepsilon ,i_{+}^{(1)}}^{(n)}-h_{\varepsilon ,i_{+}^{(1)}},v_{\varepsilon ,i_{+}^{(1)}}^{(n)}+h_{\varepsilon ,i_{+}^{(1)}}],\\ i_{+}^{(1)}, &{} \text { for all other values of }u_{\varepsilon ,n}^{+}\le v_{\varepsilon ,0}^{(n)}-h_{\varepsilon ,0}. \end{array}\right. } \end{aligned}$$

(7.282)

It can be readily inferred from (7.281) and the form (6.80) of ${\mathcal {V}}_{i}^{(n)}={\mathcal {V}}_{i\nwarrow }^{(n)}\cup {\mathcal {V}}_{i\nearrow }^{(n)}$ (and in particular, the fact that ${\mathcal {V}}_{i\nwarrow }^{(n)}\subset \{v\le v_{\varepsilon ,i_{+}^{(1)}}^{(n)}-h_{\varepsilon ,i_{+}^{(1)}}\}$ when $i<i_{+}^{(1)}$) that

$$\begin{aligned} \{v=V\}\cap {\mathcal {V}}_{i}^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}=\{v=V\}\cap {\mathcal {V}}_{i\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}\quad \text { for all }i<i_{+}^{(1)}\qquad \end{aligned}$$

(7.283)

and

$$\begin{aligned} \inf _{\{v=V\}\cap {\mathcal {V}}_{i}^{(n)}\cap {\mathcal {U}}_{\varepsilon }^{+}}(v-u)\ge \rho _{\varepsilon }^{-1}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}\quad \text { for all }i<i_{+}^{(1)}. \end{aligned}$$

(7.284)

From (7.266), (7.284), (6.73) and the fact that $\partial _{v}r>0$, we infer that, for any $i<i_{+}^{(2)}$, analogously to (7.271):

$$\begin{aligned} \frac{r_{max}^{(i)}(V)-r_{min}^{(i)}(V)}{r_{min}^{(i)}(V)}\le & {} \frac{\int _{([v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i},v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}]\times \{V\})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}\big (-\partial _{u}r\big )\,du}{r_{min}^{(i)}(v_{\varepsilon ,i_{+}^{(1)}}^{(n)}-h_{\varepsilon ,i_{+}^{(1)}})}\nonumber \\\le & {} \frac{\exp (2\sigma _{\varepsilon }^{-6})\varepsilon ^{(i)}}{r_{n;i_{+}^{(1)},i}}\le \rho _{\varepsilon }^{\frac{3}{4}}, \end{aligned}$$

(7.285)

where $r_{max}^{(i)}(V),$ $r_{min}^{(i)}(V)$ are defined by (7.270). Therefore, using (7.277) and (7.285) and arguing as in the proof of (7.272)–(7.274), using in addition the estimate

$$\begin{aligned} \int _{\{v=V\}\cap {\mathcal {V}}_{i\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}(-\partial _{u}{\tilde{m}})\,du\le {\mathcal {E}}_{\nearrow }^{(-)}[n;i_{+}^{(1)},i]\cdot \big (1+C\varepsilon \big )+C\rho _{\varepsilon }^{\frac{3}{2}}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }} \end{aligned}$$

(following from (7.79)) in the case when $V\in [v_{\varepsilon ,i_{+}^{(1)}}^{(n)}-h_{\varepsilon ,i_{+}^{(1)}},v_{\varepsilon ,i_{+}^{(1)}}^{(n)}+h_{\varepsilon ,i_{+}^{(1)}}]$, we obtain for any $i<i_{+}^{(2)}$:

$$\begin{aligned}{} & {} \int _{\{v=V\}\cap ({\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i}^{(n+1)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}\big (1-\frac{2{\tilde{m}}}{r}-\frac{1}{3}\Lambda r^{2}\big )^{-1}\frac{-\partial _{u}{\tilde{m}}}{r}(u,V)\,du\nonumber \\{} & {} \quad \le 2\mu _{i}[n+1]+O(\rho _{\varepsilon }^{1+\frac{1}{18}}) \end{aligned}$$

(7.286)

On the other hand, for $i_{+}^{(2)}\le i\le i_{+}^{(1)}$, using the relation

$$\begin{aligned}&\int _{\{v=V\}\cap {\mathcal {V}}_{i}^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}\backslash \cup _{j<i_{+}^{(2)}}{\mathcal {V}}_{j}^{(n)}}\big (1-\frac{2{\tilde{m}}}{r}- \frac{1}{3}\Lambda r^{2}\big )^{-1}\frac{-\partial _{u}{\tilde{m}}}{r}(u,V)\,du\\&\quad =a_{\varepsilon i}\int _{\{v=V\}\cap {\mathcal {V}}_{i\nearrow }^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}\backslash \cup _{j<i_{+}^{(2)}}{\mathcal {V}}_{j}^{(n)}}r\Big (\frac{T_{uu}[f_{\varepsilon i}]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon i}]}{\partial _{v}r}\Big )(u,V)\,du \end{aligned}$$

(following from (2.49), (6.65) and (7.1)), we infer by arguing exactly as in the proof of (7.276) that

$$\begin{aligned}{} & {} \sum _{i=i_{+}^{(2)}}^{i_{+}^{(1)}}\int _{\{v=V\}\cap {\mathcal {V}}_{i}^{(n)}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}\backslash \cup _{j<i_{+}^{(2)}}{\mathcal {V}}_{j}^{(n)}}\big (1-\frac{2{\tilde{m}}}{r}-\frac{1}{3}\Lambda r^{2}\big )^{-1}\frac{-\partial _{u}{\tilde{m}}}{r}(u,V)\,du\nonumber \\{} & {} \quad \le \sum _{i=i_{+}^{(2)}}^{i_{+}^{(1)}}a_{\varepsilon i_{+}}\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big ). \end{aligned}$$

(7.287)

From (7.263), (7.277), (7.280)(7.286), (7.287) and the fact that $|i_{+}^{(1)}-i_{+}^{(2)}|\le 2$, we readily infer (7.262) in the case $V<V^{(-)}$.

Case III: $V\in (V^{(+)},v_{\varepsilon ,0}^{(n+1)}-h_{\varepsilon ,0}+\sqrt{-\frac{3}{\Lambda }}\pi )$. In this case, we will split the left hand side of (7.263) as

$$\begin{aligned}&\int _{\{v=V\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\\&\quad = \int _{\{v=V\}\cap \{u\le U^{(+)}\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\nonumber \\&\qquad +\int _{\{v=V\}\cap \{u\ge U^{(+)}\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du,\nonumber \end{aligned}$$

(7.288)

where

$$\begin{aligned} U^{(+)}\doteq v_{\varepsilon ,0}^{(n+1)}-\rho _{\varepsilon }^{-2}\frac{\varepsilon }{\sqrt{-\Lambda }}, \end{aligned}$$

(7.289)

and we will estimate each term in the right hand side of (7.288) separately.

From the form (6.80) of ${\mathcal {V}}_{i}^{(n)}$ and the definitions (7.265), (7.289) of $V^{(+)}$, $U^{(+)}$, respectively, we infer that

$$\begin{aligned} \inf _{\{v\ge V^{(+)}\}\cap \{u\le U^{(+)}\}\cap (\cup _{i=0}^{N_{\varepsilon }}{\mathcal {V}}_{i}^{(n)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}(v-u)\ge \frac{1}{2}\rho _{\varepsilon }^{-2}\frac{\varepsilon }{\sqrt{-\Lambda }}. \end{aligned}$$

(7.290)

Thus, using (6.73), we infer that

$$\begin{aligned} \inf _{\{v\ge V^{(+)}\}\cap \{u\le U^{(+)}\}\cap (\cup _{i=0}^{N_{\varepsilon }}{\mathcal {V}}_{i}^{(n)})\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\ge e^{-\sigma _{\varepsilon }^{-4}}\rho _{\varepsilon }^{-2}\frac{\varepsilon }{\sqrt{-\Lambda }}. \end{aligned}$$

(7.291)

Using the relation (6.65) and the bounds (6.73), (7.11)–(7.12), from (7.291) we infer that

$$\begin{aligned}&\int _{\{v=V\}\cap \{u\le U^{(+)}\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}} r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\\&\quad =\sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}\int _{\{v=V\}\cap \{u\le U^{(+)}\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon i}]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon i}]}{\partial _{v}r}\Big )(u,V)\,du\nonumber \\&\quad \le \exp (\exp (\sigma _{\varepsilon }^{-6}))\sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}\int _{\{v=V\}\cap \{u\le U^{(+)}\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}\frac{1}{1-\frac{1}{3}\Lambda r^{2}}\Big (\frac{(\varepsilon ^{(i)})^{4}}{r^{5}}(-\Lambda )^{-1}\nonumber \\&\qquad +\frac{(\varepsilon ^{(i)})^{2}}{r^{3}}(-\Lambda )^{-1}\Big )(u,V)\,du\nonumber \\&\quad \le \exp (\exp (\sigma _{\varepsilon }^{-6}))\sum _{i=0}^{N_{\varepsilon }}a_{\varepsilon i}\Bigg \{\frac{1}{1-\frac{1}{3}\Lambda r^{2}}\Big (\frac{(\varepsilon ^{(i)})^{4}}{r^{4}}(-\Lambda )^{-1}\nonumber \\&\quad \quad +\frac{(\varepsilon ^{(i)})^{2}}{r^{2}}(-\Lambda )^{-1}\Bigg \}_{r=e^{-\sigma _{\varepsilon }^{-4}}\rho _{\varepsilon }^{-2}\frac{\varepsilon }{\sqrt{-\Lambda }}}\nonumber \\&\quad \le \rho _{\varepsilon }^{3}.\nonumber \end{aligned}$$

(7.292)

On the other hand, in the case when

$$\begin{aligned} \{v=V\}\cap \{u\ge U^{(+)}\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}\ne \emptyset , \end{aligned}$$

from the form (6.80) of ${\mathcal {V}}_{i}^{(n)}$ and the definitions (7.265), (7.289) of $V^{(+)}$, $U^{(+)}$, respectively, we infer that, depending on whether V belongs to $\cup _{i=0}^{N_{\varepsilon }}[v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i},v_{\varepsilon ,i}^{(n+1)}+h_{\varepsilon ,i}]$ or not:

• Either

  $$\begin{aligned} \{v=V\}\cap \{u\ge U^{(+)}\}\cap \big \{\cup _{i=0}^{N_{\varepsilon }}({\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i}^{(n+1)}\big \}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}=\emptyset , \end{aligned}$$

  in which case

  $$\begin{aligned} \int _{\{v=V\}\cap \{u\ge U^{(+)}\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du=0,\qquad \end{aligned}$$

  (7.293)

• or

  $$\begin{aligned}&\{v=V\}\cap \{u\ge U^{(+)}\}\cap \big \{\cup _{i=0}^{N_{\varepsilon }}( {\mathcal {V}}_{i}^{(n)}\cup {\mathcal {V}}_{i}^{(n+1)}\big \}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}=\\&= \{v=V\}\cap \{u\ge U^{(+)}\}\cap \{{\mathcal {V}}_{i_{0}\nwarrow }^{(n+1)}\big \}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}\quad \text { for some }0\le i_{0}\le N_{\varepsilon }, \end{aligned}$$

  in which case, using the bounds (6.73), (7.1), (7.10), (7.11) and the fact that the regions

  $$\begin{aligned} {\mathcal {V}}_{i\nwarrow }^{(n+1)}\cap \{U^{(+)}\le u\le u_{\varepsilon ,n}^{+}\} \end{aligned}$$

  are disjoint, we can estimate

  $$\begin{aligned}&\int _{\{v=V\}\cap \{u\ge U^{(+)}\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r \Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\\&\quad =a_{\varepsilon i_{0}}\int _{\{v=V\}\cap \{u\ge U^{(+)}\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon i_{0}}]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon i_{0}}]}{\partial _{v}r}\Big )(u,V)\,du\nonumber \\&\quad \le \exp (\exp (\sigma _{\varepsilon }^{-6}))a_{\varepsilon i_{0}}\int _{\inf _{{\mathcal {V}}_{i_{0}\nwarrow }^{(n+1)}}r}^{+\infty }\frac{1}{1-\frac{1}{3}\Lambda r^{2}}\Big (\frac{(\varepsilon ^{(i_{0})})^{4}}{r^{5}}(-\Lambda )^{-1}\nonumber \\&\qquad +\frac{(\varepsilon ^{(i_{0})})^{2}}{r^{3}}(-\Lambda )^{-1}\Big )\,dr\le \nonumber \\&\quad \le \frac{1}{2}\exp (\exp (\sigma _{\varepsilon }^{-7}))a_{\varepsilon i_{0}}.\nonumber \end{aligned}$$

  (7.294)

From (7.292), (7.293) and (7.294), we therefore infer (7.262) in the case $V>V^{(+)}$. Thus, we have established (7.262) for all values of V.

Arguing as for the proof of(7.262), we similarly obtain that, for all $U\ge 0$:

$$\begin{aligned}{} & {} \int _{\{u=U\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(U,v)\,dv\nonumber \\{} & {} \quad \le \frac{1}{2}\max _{0\le i\le N_{\varepsilon }}\big \{\big (\exp (e^{\sigma _{\varepsilon }^{-7}}\big )a_{\varepsilon i}\big \}+4\sum _{i=0}^{N_{\varepsilon }-1}\mu _{i}[n+1]+\frac{1}{2}\rho _{\varepsilon }^{\frac{1}{19}}.\qquad \end{aligned}$$

(7.295)

Thus, adding (7.262) and (7.295), we infer (7.257).

We will now proceed to establish (7.258). To this end, let us define the domains

$$\begin{aligned}{} & {} {\mathcal {Q}}_{i}^{(n)}=\Big (\big \{\{u\le v_{\varepsilon ,i}^{(n)}+h_{\varepsilon ,i}\}\cap \{v\ge v_{\varepsilon ,i}^{(n)}-h_{\varepsilon ,i}\}\big \}\nonumber \\{} & {} \quad \cup \big \{ v\ge v_{\varepsilon ,i}^{(n+1)}-h_{\varepsilon ,i}\big \}\Big )\cap \big \{ v-u\ge \beta _{\varepsilon ,i}\big \}\cap {\mathcal {U}}_{\varepsilon ,n}^{+}, \end{aligned}$$

(7.296)

where $\beta _{\varepsilon ,i}$ are defined by (6.79) (see Fig. 24).

Fig. 24

The domain ${\mathcal {Q}}^{(n)}_i$ is equal to the union of the beam ${\mathcal {V}}_i \cap {\mathcal {U}}_{\epsilon ,n}^{+}$ with the darker shaded region depicted above (where we assumed for simplicity that $v_{\epsilon ,0}^{(n+1)}-h_{\epsilon ,0}<u[{\mathcal {U}}_{\epsilon }^{+}]$)

Remark

Notice that, for any $0\le i\le N_{\varepsilon }$, the domain ${{\mathcal {Q}}}_{i}^{(n)}$ consists of the region “to the right” of the beam ${\mathcal {V}}_{i}$ (including ${\mathcal {V}}_{i}$), within the domain ${\mathcal {U}}_{\varepsilon ,n}^{+}$. Moreover, in view of (7.1), we have

$$\begin{aligned} {\tilde{m}}\equiv 0\text { on }{\mathcal {U}}_{\varepsilon ;n}^{+}\backslash \cup _{i=0}^{N_{\varepsilon }}{{\mathcal {Q}}}_{i}^{(n)}. \end{aligned}$$

(7.297)

(since ${\mathcal {U}}_{\varepsilon ;n}^{+}\backslash \cup _{i=0}^{N_{\varepsilon }}{{\mathcal {Q}}}_{i}^{(n)}$ consists of the single connected component of ${\mathcal {U}}_{\varepsilon ;n}^{+}\backslash \cup _{i=0}^{N_{\varepsilon }}{\mathcal {V}}_{i}$ containing $\gamma _{{\mathcal {Z}}}$).

As a corollary of the bound (6.73) for $\partial r$ and the definition (6.79) of $\beta _{\varepsilon ,i}$, we can bound for any $0\le i\le N_{\varepsilon }$:

$$\begin{aligned} \inf _{{{\mathcal {Q}}}_{i}^{(n)}}r\ge \exp (-\exp (\sigma _{\varepsilon }^{-5}))\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}. \end{aligned}$$

(7.298)

In view of the relation (6.65) between $f_{\varepsilon }$ and the $f_{\varepsilon j}$’s, the fact that $f_{\varepsilon j}$ is supported on $\cup _{k}{\mathcal {V}}_{j}^{(k)}$, the bound (6.73) for $\partial r$ and the bounds (7.11)–(7.12) on $T_{\mu \nu }[f_{\varepsilon j}]$, we obtain from the relations (2.49)–(2.48) for $\partial {\tilde{m}}$ (and the fact that ${\tilde{m}}|_{\gamma _{{\mathcal {Z}}}}=0$) that, for any $0\le i\le N_{\varepsilon }$:

$$\begin{aligned}{} & {} \sup _{{{\mathcal {Q}}}_{i}^{(n)}\backslash \cup _{j=0}^{i-1}{{\mathcal {Q}}}_{j}^{(n)}}{\tilde{m}}\le \exp (\exp (\sigma _{\varepsilon }^{-7}))\sum _{j=i}^{N_{\varepsilon }}a_{\varepsilon j}\frac{\varepsilon ^{(j)}}{\sqrt{-\Lambda }}\nonumber \\{} & {} \quad \le \exp (\exp (\sigma _{\varepsilon }^{-7}))a_{\varepsilon i}\frac{\varepsilon ^{(i)}}{\sqrt{-\Lambda }}+\exp (\exp (\sigma _{\varepsilon }^{-8}))\frac{\varepsilon ^{(i+1)}}{\sqrt{-\Lambda }}. \end{aligned}$$

(7.299)

Combining (7.298) and (7.299), we infer that, for any $0\le i\le N_{\varepsilon }$,

$$\begin{aligned} \sup _{{{\mathcal {Q}}}_{i}^{(n)}\backslash \cup _{j=0}^{i-1}{{\mathcal {Q}}}_{j}^{(n)}}\frac{2{\tilde{m}}}{r}\le \exp (\exp (\sigma _{\varepsilon }^{-8}))a_{\varepsilon i}+\varepsilon ^{\frac{1}{2}}. \end{aligned}$$

(7.300)

The upper bound (7.258) now follows readily from (7.300), (7.297) and the fact that

$$\begin{aligned} {\mathcal {U}}_{\varepsilon ;n}^{+}=\bigcup _{i=0}^{N_{\varepsilon }}\Big ({{\mathcal {Q}}}_{i}^{(n)}\backslash \cup _{j=0}^{i-1}{{\mathcal {Q}}}_{j}^{(n)}\Big )\cup \Big ({\mathcal {U}}_{\varepsilon ;n}^{+}\backslash \cup _{i=0}^{N_{\varepsilon }}{{\mathcal {Q}}}_{i}^{(n)}\Big ). \end{aligned}$$

(7.301)

The upper bound (7.259) follows similarly from (7.300) and (7.297), after noting that

$$\begin{aligned} ({{\mathcal {Q}}}_{i}^{(n)}\backslash \cup _{k=0}^{i-1}{{\mathcal {Q}}}_{k}^{(n)})\cap \{u\le v_{\varepsilon ,j}^{(n)}+h_{\varepsilon ,j}\}=\emptyset \text { for all }j<i\le N_{\varepsilon }. \end{aligned}$$

The proof of the estimates (7.257), (7.258) and (7.259) (with $\delta _{\varepsilon }$, ${\tilde{h}}_{\varepsilon ,j}$ in place of $\sigma _{\varepsilon }$, $h_{\varepsilon ,j}$) on ${\mathcal {T}}_{\varepsilon ;n}^{+}$ follows in exactly the same way, using (6.78) in place of (6.73) and replacing all the statements about ${\mathcal {V}}_{i}^{(n)}$, ${\mathcal {E}}^{(\pm )}$, ${\mathfrak {D}}r^{(\pm )}$ with the corresponding statements about $\widetilde{{\mathcal {V}}}_{i}^{(n)}$, $\widetilde{{\mathcal {E}}}^{(\pm )}$, $\widetilde{{\mathfrak {D}}}r^{(\pm )}$, respectively; we will omit the details. $\square$

8 The first stage of the instability

In this section, we will show that the parameters $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$, appearing in the definition of the initial data family $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2};{\bar{f}}_{/}^{(\varepsilon )})$, can be carefully chosen (without violating the smallness condition (6.10)) so that, after $\sim \sigma _{\varepsilon }^{-\frac{3}{2}}$ reflections off ${\mathcal {I}}_{\varepsilon }$, the Vlasov beams form a configuration of a particular form; this configuration will be shown in the next section to guarantee the formation of a trapped sphere in O(1) retarded time.

In particular, we will establish the following result (for the definition of $v_{\varepsilon ,i}^{(n)}$, $h_{\varepsilon ,i}$ and the domain ${\mathcal {U}}_{\varepsilon }^{+}\subset {\mathcal {U}}_{max}^{(\varepsilon )}$, see Sects. 6.3–6.4; for the definition of the sequences $\mu _{i}$, ${\mathcal {E}}_{i}$ and $R_{i}$, see Sect. 7.3):

Proposition 8.1

For any $\varepsilon \in (0,\varepsilon _{1}]$, there exists a finite sequence $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}\in (0,\sigma _{\varepsilon })$ satisfying (6.10),

$$\begin{aligned} \max _{0\le i\le N_{\varepsilon }-1}a_{\varepsilon i}<\exp (-\exp (\delta _{\varepsilon }^{-10})) \end{aligned}$$

(8.1)

and

$$\begin{aligned} a_{\varepsilon N_{\varepsilon }}<\exp (-\exp (\sigma _{\varepsilon }^{-9})), \end{aligned}$$

(8.2)

such that the following statements hold for the maximal future development $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ of the initial data set $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2};{\bar{f}}_{/}^{(\varepsilon )})$ associated to $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$ (see Definition 6.3):

• 1. Setting

  $$\begin{aligned} n_{+}\doteq \lceil \sigma _{\varepsilon }^{-\frac{3}{2}}\rceil , \end{aligned}$$

  (8.3)

  we have

  $$\begin{aligned} \big \{0<u\le v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\big \}\cap \left\{ u<v<u+\sqrt{-\frac{3}{\Lambda }}\pi \right\} \subset {\mathcal {U}}_{\varepsilon }^{+}. \end{aligned}$$

  (8.4)

• 2. The quantities $\mu _{i}[n_{+}]$ (introduced in Definition 7.5) satisfy, for all $0\le j\le N_{\varepsilon }-1$,

  $$\begin{aligned} \mu _{j}[n_{+}]=\frac{\delta _{\varepsilon }^{-\frac{3}{4}}}{N_{\varepsilon }}e^{-2\frac{j}{N_{\varepsilon }}\delta _{\varepsilon }^{-\frac{3}{4}}}, \end{aligned}$$

  (8.5)

  and, for $j=N_{\varepsilon }$:

  $$\begin{aligned} {\mathcal {E}}_{N_{\varepsilon }}[n_{+}]=\exp (-\exp (4\sigma _{\varepsilon }^{-9}))\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}. \end{aligned}$$

  (8.6)

Proof

Let us set for convenience

$$\begin{aligned} \mu _{N_{\varepsilon }}[n]\doteq 2\rho _{\varepsilon }{\mathcal {E}}_{N_{\varepsilon }}[n]\frac{\sqrt{-\Lambda }}{\varepsilon ^{(N_{\varepsilon })}} \end{aligned}$$

(8.7)

for any $n\in {\mathbb {N}}$. In this way, the quantities $\mu _{i}[n]$ are defined for all $0\le i\le N_{\varepsilon }$ (note that Definition 7.5 only defined $\mu _{i}[n]$ for $0\le i\le N_{\varepsilon }-1$). In particular, (8.6) becomes equivalent to

$$\begin{aligned} \mu _{N_{\varepsilon }}[n_{+}]=2\rho _{\varepsilon }\exp (-\exp (4\sigma _{\varepsilon }^{-9})). \end{aligned}$$

(8.8)

Note that (7.147) implies that

$$\begin{aligned} \mu _{N_{\varepsilon }}[n+1]=\mu _{N_{\varepsilon }}[n]\cdot \exp \Big (\sum _{j=0}^{N_{\varepsilon }-1}\mu _{j}[n+1]\Big ) \end{aligned}$$

(8.9)

for all $n\in {\mathbb {N}}$.

In view of the initial condition (7.146) for $\mu _{i}$ for $0\le i\le N_{\varepsilon }-1$ (which, in particular, expresses $\mu _{i}$ as a function of $T_{\mu \nu }$ and r along $u=v_{\varepsilon ,0}^{(0)}-h_{0,\varepsilon }$), the form (6.17) of ${\bar{f}}_{/}^{(\varepsilon )}$, the bound (6.26) and the Cauchy stability statement of Proposition 3.15 applied to $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2};{\bar{f}}_{/}^{(\varepsilon )})$ (implying, in particular, that $\frac{\partial _{v}r}{1-\frac{1}{3}\Lambda r^{2}}=\frac{1}{2}+O(\sigma _{\varepsilon })$ on $\{0\le u\le v_{\varepsilon ,0}^{(0)}-h_{0,\varepsilon }\}$), we readily infer that, for any $\varepsilon \in [0,\varepsilon _{1})$, the quantities $\{\mu _{i}[0]\}_{i=0}^{N_{\varepsilon }}$ uniquely determine $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$ and vice-versa and, moreover,

$$\begin{aligned} C_{1}\rho _{\varepsilon }a_{\varepsilon i}\le \mu _{i}[0]\le C_{2}\rho _{\varepsilon }a_{\varepsilon i}\quad \text { for all }0\le i\le N_{\varepsilon }, \end{aligned}$$

(8.10)

for some constants $C_{1},C_{2}>0$ independent of i, $\varepsilon$.

By solving the recursive relation (7.145) for $\mu _{i}[n]$ backwards in n, for $0\le i\le N_{\varepsilon }-1$,²⁶ and then solving (8.9) backwards in n for $i=N_{\varepsilon }$, we infer that, imposing (8.5) and (8.8) as initial conditions in the future, the values of $\{\mu _{i}[0]\}_{i=0}^{N_{\varepsilon }}$ are completely determined; thus, $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$ are also uniquely determined. For this reason, in order establish Proposition 8.1, it suffices to show the following (in view of (8.10)):

• The finite sequence $\{\mu _{i}[0]\}_{i=0}^{N_{\varepsilon }}$, fixed uniquely by the future conditions (8.5) and (8.8), satisfies

  $$\begin{aligned}{} & {} \mu _{i}[0]<\rho _{\varepsilon }\exp (-\exp (2\delta _{\varepsilon }^{-10}))\quad \text { for all }0\le i\le N_{\varepsilon }-1, \end{aligned}$$

  (8.11)
  $$\begin{aligned}{} & {} \mu _{N_{\varepsilon }}[0]<\rho _{\varepsilon }\exp (-\exp (2\sigma _{\varepsilon }^{-9})) \end{aligned}$$

  (8.12)

  and

  $$\begin{aligned} \sum _{i=0}^{N_{\varepsilon }}\mu _{i}[0]\le C_{1}\sigma _{\varepsilon }. \end{aligned}$$

  (8.13)

• The maximal future development $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ of the initial data set $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2};{\bar{f}}_{/}^{(\varepsilon )})$ associated to the finite sequence $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$ (uniquely determined by $\{\mu _{i}[0]\}_{i=0}^{N_{\varepsilon }}$) satisfies (8.4).

Step 1: Proof of (8.11)–(8.13). The relations (8.5) and (8.8) for $\mu _{i}[n_{+}]$ readily imply that

$$\begin{aligned} \frac{1}{4}\le \sum _{i=0}^{N_{\varepsilon }}\mu _{i}[n_{+}]\le 1. \end{aligned}$$

(8.14)

From (7.145) and (8.9) we infer that, for any $0\le i\le N_{\varepsilon }$:

$$\begin{aligned} \mu _{i}[n]\le \mu _{i}[n+1] \end{aligned}$$

(8.15)

(with equality only when $i=0$). In particular,

$$\begin{aligned} \mu _{i}[0]\le \mu _{i}[n_{+}]\quad \text { for all }0\le i\le N_{\varepsilon }. \end{aligned}$$

(8.16)

From (8.16), we infer, using (8.5) and (8.8), that

$$\begin{aligned} \mu _{i}[0]&\le N_{\varepsilon }^{-1}\delta _{\varepsilon }^{-\frac{3}{4}},\\ \mu _{N_{\varepsilon }}[0]&\le 2\rho _{\varepsilon }\exp (-\exp (4\sigma _{\varepsilon }^{-9})), \end{aligned}$$

from which (8.11) and (8.12) follow readily, in view of the fact that $\delta _{\varepsilon }\ll \sigma _{\varepsilon }\ll 1$ and $N_{\varepsilon }=\rho _{\varepsilon }^{-1}\exp (e^{\delta _{\varepsilon }^{-15}})$.

Let us define $i_{0}$ to be the minimum number in the set $\{0,1,\ldots ,N_{\varepsilon }\}$ such that

$$\begin{aligned} \sum _{i=0}^{i_{0}}\mu _{i}[0]\ge \frac{1}{2}C_{1}\sigma _{\varepsilon }. \end{aligned}$$

(8.17)

Notice that the definition of $i_{0}$ implies that

$$\begin{aligned} \sum _{i=0}^{i_{0}-1}\mu _{i}[0]<\frac{1}{2}C_{1}\sigma _{\varepsilon }. \end{aligned}$$

(8.18)

Note also that the bound (8.11) (which we already established) implies that, necessarily,

$$\begin{aligned} i_{0}\ge 1. \end{aligned}$$

For the proof of (8.13), we will consider two cases, depending on the value of $i_{0}$:

• In the case when $i_{0}=N_{\varepsilon }$, the bound (8.17) trivially implies (8.13).

• In the case when $i_{0}\le N_{\varepsilon }-1$, for any $i_{0}+1\le j\le N_{\varepsilon }-1$ and any $n\ge 0$, we can estimate using the recursive formula (7.145), the monotonicity property (8.15) and the lower bound (8.17):

  $$\begin{aligned} \mu _{j}[n+1]&=\mu _{j}[n]\exp \Big (2\sum _{k=0}^{j-1}\mu _{k}[n+1]\Big )\\&=\mu _{j}[0]\exp \Big (2\sum _{{\bar{n}}=0}^{n}\sum _{k=0}^{j-1}\mu _{k}[{\bar{n}}+1]\Big )\nonumber \\&\ge \mu _{j}[0]\exp \Big (2\sum _{{\bar{n}}=0}^{n}\sum _{k=0}^{i_{0}}\mu _{k}[{\bar{n}}+1]\Big )\nonumber \\&\ge \mu _{j}[0]\exp \Big (2\sum _{{\bar{n}}=0}^{n}\sum _{k=0}^{i_{0}}\mu _{k}[0]\Big )\nonumber \\&\ge \mu _{j}[0]\exp \Big (2\sum _{{\bar{n}}=0}^{n}(\frac{1}{2}C_{1}\sigma _{\varepsilon })\Big )\nonumber \\&=\mu _{j}[0]\exp \Big (C_{1}\sigma _{\varepsilon }n\Big ).\nonumber \end{aligned}$$

  (8.19)

  Similarly, for $j=N_{\varepsilon }$, we can estimate using (8.9) in place of (7.145):

  $$\begin{aligned} \mu _{N_{\varepsilon }}[n+1]&=\mu _{N_{\varepsilon }}[n]\exp \Big (\sum _{k=0}^{N_{\varepsilon }-1}\mu _{k}[n+1]\Big )\\&=\mu _{N_{\varepsilon }}[0]\exp \Big (\sum _{{\bar{n}}=0}^{n}\sum _{k=0}^{N_{\varepsilon }-1}\mu _{k}[{\bar{n}}+1]\Big )\nonumber \\&\ge \mu _{N_{\varepsilon }}[0]\exp \Big (\sum _{{\bar{n}}=0}^{n}\sum _{k=0}^{i_{0}}\mu _{k}[0]\Big )\nonumber \\&=\mu _{N_{\varepsilon }}[0]\exp \Big (\frac{1}{2}C_{1}\sigma _{\varepsilon }n\Big ).\nonumber \end{aligned}$$

  (8.20)

  From (8.19) and (8.20) for $n=n_{+}-1$, using also the definition (8.3) of $n_{+}$, the upper bound (8.14) and the fact that $C_{1}$ is an absolute constant, we obtain that (provided $\varepsilon _{1}$ has been fixed small enough)

  $$\begin{aligned} \sum _{j=i_{0}+1}^{N_{\varepsilon }}\mu _{j}[0]&\le \exp \Big (-\frac{1}{2}C_{1}\sigma _{\varepsilon }(n_{+}-1)\Big )\sum _{j=i_{0}+1}^{N_{\varepsilon }}\mu _{j}[n_{+}]\\&\le \exp \Big (-\frac{1}{2}C_{1}\sigma _{\varepsilon }(n_{+}-1)\Big )\nonumber \\&\le \exp \Big (-\frac{1}{2}C_{1}\sigma _{\varepsilon }^{-\frac{1}{2}}\Big )\nonumber \\&\le \exp \Big (-\sigma _{\varepsilon }^{-\frac{1}{4}}\Big ).\nonumber \end{aligned}$$

  (8.21)

  From (8.18), (8.11) and (8.21) (using also the relation (6.1) between $\rho _{\varepsilon }$, $\delta _{\varepsilon }$, $\sigma _{\varepsilon }$) , we therefore obtain that

  $$\begin{aligned} \sum _{j=0}^{N_{\varepsilon }}\mu _{j}[0]&=\sum _{j=0}^{i_{0}}\mu _{j}[0]+\mu _{i_{0}}[0]+\sum _{j=i_{0}+1}^{N_{\varepsilon }}\mu _{j}[0]\le \\&\le \frac{1}{2}C_{1}\sigma _{\varepsilon }+\rho _{\varepsilon }\exp (-\exp (2\delta _{\varepsilon }^{-10}))+\exp \Big (-\sigma _{\varepsilon }^{-\frac{1}{4}}\Big )\le \\&\le C_{1}\sigma _{\varepsilon }, \end{aligned}$$

  hence inferring (8.13).

Step 2: Proof of (8.4). The inclusion (8.4) is equivalent to the bound

$$\begin{aligned} v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}<u[{\mathcal {U}}_{\varepsilon }^{+}], \end{aligned}$$

(8.22)

in view of the form (6.51) of ${\mathcal {U}}_{\varepsilon }^{+}$. For the sake of contradiction, let us assume that

$$\begin{aligned} u[{\mathcal {U}}_{\varepsilon }^{+}]\le v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}. \end{aligned}$$

(8.23)

Notice that (8.23) implies (in view of (8.3)) that

$$\begin{aligned} u[{\mathcal {U}}_{\varepsilon }^{+}]\lesssim \frac{\sigma _{\varepsilon }^{-\frac{3}{2}}}{\sqrt{-\Lambda }}\ll \frac{\sigma _{\varepsilon }^{-2}}{\sqrt{-\Lambda }}. \end{aligned}$$

(8.24)

Hence, Lemma 6.7 implies that at least one of the relations (6.55), (6.56)and (6.57) holds.

In view of the bound (7.257), we can estimate (using the hypothesis (8.23)):

$$\begin{aligned}&\sup _{V\ge 0}\int _{\{v=V\}\cap {\mathcal {U}}_{\varepsilon }^{+}} r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\\&\qquad +\sup _{U\ge 0} \int _{\{u=U\}\cap {\mathcal {U}}_{\varepsilon }^{+}}r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(U,v)\,dv\nonumber \\&\quad = \max _{n\le n_{+}-1}\Bigg \{\sup _{V\ge 0}\int _{\{v=V\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\nonumber \\&\qquad +\sup _{U\ge 0}\int _{\{u=U\}\cap {\mathcal {U}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(U,v)\,dv\Bigg \}\nonumber \\&\quad \le \max _{n\le n_{+}-1}\Bigg \{8\sum _{i=0}^{N_{\varepsilon }-1}\mu _{i}[n+1]+\max _{0\le i\le N_{\varepsilon }}\big \{\big (\exp (e^{\sigma _{\varepsilon }^{-7}})\big )a_{\varepsilon i}\big \}+\rho _{\varepsilon }^{\frac{1}{19}}\Bigg \}.\nonumber \end{aligned}$$

(8.25)

Using the bounds (8.1) and (8.2) for $a_{\varepsilon i}$, the relation (8.5) for $\mu _{i}[n_{+}]$, as well as the fact that $\mu _{i}[n]$ is increasing in n for all $0\le i\le N_{\varepsilon }$, we infer from (8.25) that

$$\begin{aligned}&\sup _{V\ge 0}\int _{\{v=V\}\cap {\mathcal {U}}_{\varepsilon }^{+}} r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big )(u,V)\,du\\&\qquad +\sup _{U\ge 0} \int _{\{u=U\}\cap {\mathcal {U}}_{\varepsilon }^{+}}r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(U,v)\,dv\nonumber \\&\quad \le 8\sum _{i=0}^{N_{\varepsilon }-1} \left\{ \mu _{i}[n_{+}]+\exp (e^{\sigma _{\varepsilon }^{-7}}\big ) \cdot \exp (e^{-\sigma _{\varepsilon }^{-9}}\big )+\rho _{\varepsilon }^{\frac{1}{19}}\right\} \nonumber \\&\quad \le 8\sum _{i=0}^{N_{\varepsilon }-1}\frac{\delta _{\varepsilon }^{-\frac{3}{4}}}{N_{\varepsilon }}e^{-2\frac{j}{N_{\varepsilon }}\delta _{\varepsilon }^{-\frac{3}{4}}}+O(\sigma _{\varepsilon }) \le 20.\nonumber \end{aligned}$$

(8.26)

Furthermore, we infer from (7.258) (using the bounds (8.1) and (8.2) for $a_{\varepsilon i}$) that

$$\begin{aligned} \sup _{{\mathcal {U}}_{\varepsilon }^{+}}\frac{2{\tilde{m}}}{r}&\le \max _{n\le n_{+}-1}\Big \{\sup _{{\mathcal {U}}_{\varepsilon ;n}^{+}}\frac{2{\tilde{m}}}{r}\Big \}\\&\le \max _{0\le i\le N_{\varepsilon }}\big \{\big (\exp (e^{\sigma _{\varepsilon }^{-8}}\big )a_{\varepsilon i}\big \}+\varepsilon ^{\frac{1}{2}}\nonumber \\&\le \exp (e^{\sigma _{\varepsilon }^{-8}}\big )\cdot \exp (e^{-\sigma _{\varepsilon }^{-9}}\big )+\varepsilon ^{\frac{1}{2}}\nonumber \\&\le \frac{1}{2}\eta _{0}.\nonumber \end{aligned}$$

(8.27)

In view of the estimates 8.26 and 8.27, we therefore deduce that none of the relations (6.55), (6.56) and (6.57) can hold on ${\mathcal {U}}_{\varepsilon }^{+}$, which is a contradiction. Hence, (8.22) holds.

Therefore, the proof of Proposition 8.1 is complete. $\square$

9 The final stage of the instability: formation of a black hole region

In this section, we will show that, with the initial data parameters $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$ chosen as dictated by Proposition 8.1, the maximal future development $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ of the associated initial data set $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2};{\bar{f}}_{/}^{(\varepsilon )})$ satisfies (4.2). Since (4.1) was already established in Lemma 6.5, this section will complete the proof of Theorem 1.

9.1 Energy growth for the final beam

In order to complete the proof of Theorem 1, our aim is to show that a trapped sphere is formed along the beam ${\mathcal {V}}_{N_{\varepsilon }\nwarrow }^{(n_{+})}$, after its interaction with the beams ${\mathcal {V}}_{i\nearrow }^{(n_{+})}$, $i\le N_{\varepsilon }-1$. To this end, in this section, we will first establish the following result regarding the increase in the energy content of the $N_{\varepsilon }$-th Vlasov beam occuring through these interactions:

Lemma 9.1

For any $\varepsilon \in (0,\varepsilon _{1}]$, let $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$ and $n_{+}$ be as in Proposition 8.1, and let $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ be the maximal future development of the initial data set $(r_{/}^{(\varepsilon )},(\Omega _{/}^{(\varepsilon )})^{2};{\bar{f}}_{/}^{(\varepsilon )})$ associated to $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$. Then, the following (u, v)-region is contained in the domain ${\mathcal {T}}_{\varepsilon }^{+}\subset {\mathcal {U}}_{max}^{(\varepsilon )}$ (see Sect. 6.3 and, in particular, (6.50) for the definition of the domain ${\mathcal {T}}^+_{\varepsilon }$):

$$\begin{aligned} \big \{0<u\le v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\big \}\cap \left\{ u<v<u+\sqrt{-\frac{3}{\Lambda }}\pi \right\} \subset {\mathcal {T}}_{\varepsilon }^{+} \end{aligned}$$

(9.1)

(see (6.79) for the definition of $v^{(n)}_{\varepsilon ,i}$ and (6.105) for the definition of ${\tilde{h}}_{\varepsilon ,i}$.) Furthermore, we have

$$\begin{aligned} \widetilde{{\mathcal {E}}}_{\nwarrow }^{(+)}[n_{+};N_{\varepsilon },N_{\varepsilon }-1]\ge \delta _{\varepsilon }^{-\frac{1}{2}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}. \end{aligned}$$

(9.2)

Proof

Before establishing (9.1) and (9.2), we will first show that

$$\begin{aligned} \mu _{j}[n_{+}+1]=N_{\varepsilon }^{-1}\delta _{\varepsilon }^{-\frac{3}{4}}\text { for any }0\le j\le N_{\varepsilon }-1. \end{aligned}$$

(9.3)

The recursive formula (7.145) yields that, for all $0\le j\le N_{\varepsilon }-1$:

$$\begin{aligned} \mu _{j}[n_{+}+1]=\mu _{j}[n_{+}]\cdot \exp \Big (2\sum _{k=0}^{j-1}\mu _{k}[n_{+}+1]\Big ), \end{aligned}$$

(9.4)

while, in view of the relation (8.5), we have for all $0\le j\le N_{\varepsilon }-1$:

$$\begin{aligned} \mu _{j}[n_{+}]=\frac{\delta _{\varepsilon }^{-\frac{3}{4}}}{N_{\varepsilon }}e^{-2\frac{j}{N_{\varepsilon }}\delta _{\varepsilon }^{-\frac{3}{4}}}. \end{aligned}$$

(9.5)

We will show (9.3) by arguing inductively in j:

• For $j=0$, (9.4) and (9.5) imply that

  $$\begin{aligned} \mu _{0}[n_{+}+1]=\mu _{0}[n_{+}]=N_{\varepsilon }^{-1}\delta _{\varepsilon }^{-\frac{3}{4}}. \end{aligned}$$

• Assuming that, for some $1\le j_{0}\le N_{\varepsilon }-1$, the relation (9.3) holds for all $0\le j\le j_{0}-1$, we calculate from (9.4) and (9.5) for $j=j_{0}$ that

  $$\begin{aligned} \mu _{j_{0}}[n_{+}+1]&=\mu _{j_{0}}[n_{+}]\cdot \exp \Big (2\sum _{k=0}^{j_{0}-1}\mu _{k}[n_{+}+1]\Big )\\&=\frac{\delta _{\varepsilon }^{-\frac{3}{4}}}{N_{\varepsilon }}e^{-2\frac{j_{0}}{N_{\varepsilon }}\delta _{\varepsilon }^{-\frac{3}{4}}}\cdot \exp \Big (2\sum _{k=0}^{j_{0}-1}(N_{\varepsilon }^{-1}\delta _{\varepsilon }^{-\frac{3}{4}})\Big )\\&=\frac{\delta _{\varepsilon }^{-\frac{3}{4}}}{N_{\varepsilon }}e^{-2\frac{j_{0}}{N_{\varepsilon }}\delta _{\varepsilon }^{-\frac{3}{4}}}\cdot e^{+2\frac{j_{0}}{N_{\varepsilon }}\delta _{\varepsilon }^{-\frac{3}{4}}}\\&=\frac{\delta _{\varepsilon }^{-\frac{3}{4}}}{N_{\varepsilon }}, \end{aligned}$$

  i.e. (9.3) also holds for $j=j_{0}$. Therefore, (9.3) holds for all $0\le j\le N_{\varepsilon }-1$.

We will now proceed to show the inclusion (9.1). In view of the form (6.51) of the domain ${\mathcal {T}}_{\varepsilon }^{+}$, (9.1) is equivalent to the bound

$$\begin{aligned} v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}<u[{\mathcal {T}}_{\varepsilon }^{+}]. \end{aligned}$$

(9.6)

In order to establish (9.6), we will assume, for the sake of contradiction, that

$$\begin{aligned} u[{\mathcal {T}}_{\varepsilon }^{+}]\le v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}. \end{aligned}$$

(9.7)

In view of the inclusion (8.22) for ${\mathcal {U}}_{\varepsilon }^{+}$ and the fact that $u[{\mathcal {U}}_{\varepsilon }^{+}]<u[{\mathcal {T}}_{\varepsilon }^{+}]$, the bound (9.6) in fact implies that

$$\begin{aligned} v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}<u[{\mathcal {T}}_{\varepsilon }^{+}]\le v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}. \end{aligned}$$

(9.8)

In view of (9.7) and the definition (8.3) of $n_{+}$, we can bound

$$\begin{aligned} u[{\mathcal {T}}_{\varepsilon }^{+}]\ll \frac{\sigma _{\varepsilon }^{-2}}{\sqrt{-\Lambda }}. \end{aligned}$$

(9.9)

As a consequence of Lemma 6.7, we therefore infer that one of the following conditions holds:

$$\begin{aligned}{} & {} \limsup _{p\rightarrow \{u=u[{\mathcal {T}}_{\varepsilon }^{+}]\}}\frac{2{\tilde{m}}}{r}(p)=\eta _{0}, \end{aligned}$$

(9.10)

$$\begin{aligned}{} & {} \lim \sup _{u\rightarrow u[{\mathcal {T}}_{\varepsilon }^{+}]}\int _{u}^{u+\sqrt{-\frac{3}{\Lambda }}\pi }r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,dv=\delta _{\varepsilon }^{-1},\qquad \end{aligned}$$

(9.11)

or

$$\begin{aligned} \sup _{v\in (0,u[{\mathcal {T}}_{\varepsilon }^{+}]+\sqrt{-\frac{3}{\Lambda }}\pi )}\int _{\max \{0,v-\sqrt{-\frac{3}{\Lambda }}\pi \}}^{\min \{v,u[{\mathcal {T}}_{\varepsilon }^{+}]\}}r\Big (\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}+\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(u,v)\,du=\delta _{\varepsilon }^{-1}.\nonumber \\ \end{aligned}$$

(9.12)

In view of the bounds (9.8) and (8.1), Lemma 7.8 (and, in particular, the estimate (7.259) for ${\mathcal {T}}_{\varepsilon ;n}^{+}$, $\delta _{\varepsilon }$ in place of ${\mathcal {U}}_{\varepsilon ;n}^{+}$, $\sigma _{\varepsilon }$) implies that

$$\begin{aligned} \sup _{{\mathcal {T}}_{\varepsilon ;n_{+}}^{+}\cap \{u\le v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\}}\frac{2{\tilde{m}}}{r}\le & {} \max _{0\le i\le N_{\varepsilon }-1}\big \{\big (\exp (e^{\delta _{\varepsilon }^{-8}}\big )a_{\varepsilon i}\big \}\nonumber \\ {}{} & {} +\varepsilon ^{\frac{1}{2}}\le \exp (e^{-\delta _{\varepsilon }^{-9}}\big )\le \frac{1}{2}\eta _{0}. \end{aligned}$$

(9.13)

Furthermore, the bound (7.257) of Lemma 7.8 (with ${\mathcal {T}}_{\varepsilon ;n}^{+}$, $\delta _{\varepsilon }$ in place of ${\mathcal {U}}_{\varepsilon ;n}^{+}$, $\sigma _{\varepsilon }$), together with (8.1), (9.3) and the fact that $\mu _{i}[n]$ is increasing in n for all $0\le i\le N_{\varepsilon }-1$, imply that

$$\begin{aligned}&\sup _{V\ge 0}\int _{\{v=V\}\cap {\mathcal {T}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{uu}[f_{\varepsilon }]}{-\partial _{u}r}+\frac{T_{uv}[f_{\varepsilon }]}{\partial _{v}r}\Big ) (u,V)\,du\\&\qquad +\sup _{U\ge 0}\int _{\{u=U\}\cap {\mathcal {T}}_{\varepsilon ;n}^{+}}r\Big (\frac{T_{vv}[f_{\varepsilon }]}{\partial _{v}r}+ \frac{T_{uv}[f_{\varepsilon }]}{-\partial _{u}r}\Big )(U,v)\,dv\nonumber \\&\quad \le 8\sum _{i=0}^{N_{\varepsilon }-1}\mu _{i}[n_{+}+1]+\max _{0\le i\le N_{\varepsilon }}\big \{\big (\exp (e^{\delta _{\varepsilon }^{-7}}\big )a_{\varepsilon i}\big \}+\rho _{\varepsilon }^{\frac{1}{19}}\nonumber \\&\quad \le 8N_{\varepsilon }\cdot N_{\varepsilon }^{-1}\delta _{\varepsilon }^{-\frac{3}{4}}+\exp (e^{-\delta _{\varepsilon }^{-9}}\big )\nonumber \\&\quad \le \frac{1}{2}\delta _{\varepsilon }^{-1}.\nonumber \end{aligned}$$

(9.14)

The bounds (9.13) and (9.14) readily imply that none of the relations (9.10)–(9.12) can hold, which is a contradiction. Hence, (9.6) (and, therefore, (9.1)) holds.

We are finally ready to establish (9.2): From Proposition 7.6 (in particular, the relation (7.158)), the relations (8.6) for ${\mathcal {E}}_{N_{\varepsilon }}[n_{+}]$ and (9.3) for $\mu _{j}[n_{+}+1]$, as well as the recursive formula (7.147) for ${\mathcal {E}}_{N_{\varepsilon }}[n]$, we obtain that

$$\begin{aligned} \widetilde{{\mathcal {E}}}_{\nwarrow }^{(+)}[n_{+};N_{\varepsilon },N_{\varepsilon }-1]&={\mathcal {E}}_{N_{\varepsilon }}[n_{+}+1]+O\Big (\rho _{\varepsilon }^{\frac{1}{17}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\Big )\\&={\mathcal {E}}_{N_{\varepsilon }}[n_{+}]\cdot \exp \Big (\sum _{j=0}^{N_{\varepsilon }-1}\mu _{j}[n_{+}+1]\Big )+O\Big (\rho _{\varepsilon }^{\frac{1}{17}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\Big )\nonumber \\&=\exp (-\exp (4\sigma _{\varepsilon }^{-9}))\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\cdot \exp \Big (N_{\varepsilon }\cdot N_{\varepsilon }^{-1}\delta _{\varepsilon }^{-\frac{3}{4}}\Big )\nonumber \\&\quad +O\Big (\rho _{\varepsilon }^{\frac{1}{17}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\Big )\nonumber \\&=\Big (\exp \big (\delta _{\varepsilon }^{-\frac{3}{4}}-\exp (4\sigma _{\varepsilon }^{-9})\big )+O(\rho _{\varepsilon }^{\frac{1}{17}})\Big )\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}.\nonumber \end{aligned}$$

(9.15)

The bound (9.2) now follows readily from (9.15), in view of the relations (6.1) between $\rho _{\varepsilon }$, $\sigma _{\varepsilon }$ and $\delta _{\varepsilon }$. $\square$

9.2 Trapped surface formation and completion of the proof of Theorem 1

In this section, we will show that the energy content of the $N_{\varepsilon }$-th beam ${\mathcal {V}}_{N_{\varepsilon }\nwarrow }^{(n_{+})}$, after its interaction with the rest of the beams at the final step of the evolution (which was studied in the previous section), is sufficiently high for a trapped sphere to form before ${\mathcal {V}}_{N_{\varepsilon }\nwarrow }^{(n_{+})}$ reaches its minimum distance from the axis $\gamma _{{\mathcal {Z}}}$. This statement will thus conclude the proof of Theorem 1.

In particular, we will show the following:

Proposition 9.2

For any $\varepsilon \in (0,\varepsilon _{1}]$, let $\{a_{\varepsilon i}\}_{i=0}^{N_{\varepsilon }}$, $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ and $n_{+}$ be as in Proposition 8.1 and Lemma 9.1. Then, setting

$$\begin{aligned} {\mathcal {B}}_{\varepsilon }\doteq \big \{ v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}&+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\le u\le v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-\delta _{\varepsilon }^{-\frac{1}{4}}h_{\varepsilon ,N_{\varepsilon }}\big \}\\&\cap \big \{ v\le v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}+\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}\big \}\cap \big \{ u<v\big \}\nonumber \end{aligned}$$

(9.16)

(where $h_{\varepsilon ,N_{\varepsilon }}$ is defined by (6.79) and ${\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}$ is defined by (6.105)), there exists a point $(u_{\dagger },v_{\dagger })\in {\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}$ such that

$$\begin{aligned} \frac{2m}{r}(u_{\dagger },v_{\dagger })>1. \end{aligned}$$

(9.17)

In particular, $({\mathcal {U}}_{max}^{(\varepsilon )};r,\Omega ^{2},f_{\varepsilon })$ contains a trapped sphere.

Proof

In order to establish (9.17) for some $(u_{\dagger },v_{\dagger })\in {\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}$, we will assume for the sake of contradiction that

$$\begin{aligned} \frac{2m}{r}\le 1\quad \text { everywhere on }{\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}. \end{aligned}$$

(9.18)

Note that the bound (9.18) implies, in view of the inequality

$$\begin{aligned} \partial _{u}\Big (\frac{\Omega ^{2}}{-\partial _{u}r}\Big )\le 0 \end{aligned}$$

(9.19)

(following readily from the constraint equation (2.38)), the relation (2.9) and the fact that $\Omega ^{2}$ is smooth on ${\mathcal {U}}_{max}^{(\varepsilon )}$, that

$$\begin{aligned} \partial _{u}r<0\le \partial _{v}r\quad \text { on }{\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}. \end{aligned}$$

(9.20)

Furthermore, integrating the inequality (9.19) in u from $u=v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}$ and using (8.4) and (6.73) at $u=v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}$, we obtain the following one-sided bound:

$$\begin{aligned} \sup _{{\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}}\frac{\Omega ^{2}}{-\partial _{u}r}\le \max _{u=v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}}\frac{\Omega ^{2}}{-\partial _{u}r}\le e^{\sigma _{\varepsilon }^{-4}}. \end{aligned}$$

(9.21)

Note also that, in view of (9.20) and the bound (6.78) for $\{u=v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\}\cap {\mathcal {B}}_{\varepsilon }$ (which is contained in ${\mathcal {T}}_{\varepsilon }^{+}$, in view of (9.1)), we can estimate

$$\begin{aligned} \sup _{{\mathcal {B}}_{\varepsilon }}(-\Lambda r^{2})=-\Lambda r^{2}|_{(u,v)=\big (v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1},v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}\big )}\le \varepsilon \nonumber \\ \end{aligned}$$

(9.22)

and, hence, (9.18) also implies (in view of (2.44)) that

$$\begin{aligned} \frac{2{\tilde{m}}}{r}\le 1+\varepsilon \text { everywhere on }{\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}. \end{aligned}$$

(9.23)

Among all components $f_{\varepsilon i}$ of the Vlasov field $f_{\varepsilon }$ (see the relation (6.65)), only $f_{\varepsilon N_{\varepsilon }}$ has non-trivial support on $\{u=v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\}\cap {\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}$ (as a consequence of Lemma 7.1 on the support of $f_{\varepsilon i}$ and (9.1)). Hence, by the domain of dependence property, all the $f_{\varepsilon i}$’s for $i\ne N_{\varepsilon }$ vanish on ${\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}$, i.e.:

$$\begin{aligned} f_{\varepsilon }|_{{\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}}=a_{\varepsilon N_{\varepsilon }}f_{\varepsilon N_{\varepsilon }}|_{{\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}}. \end{aligned}$$

(9.24)

Fig. 25

In the figure above, the domain ${\mathcal {B}}_{\epsilon }$ consists of the two darker shaded regions ${\mathcal {B}}_{\epsilon } \setminus {\mathcal {B}}^{*}_{\epsilon }$ and ${\mathcal {B}}^{*}_{\epsilon }$, while th region ${\mathcal {D}}_{\epsilon }$ is the blue-shaded triangle (containing ${\mathcal {B}}_{\epsilon } \setminus {\mathcal {B}}^{*}_{\epsilon }$). A fundamental step in the proof of Proposition 9.2 consists of showing that the physical-space support of the Vlasov field $f_{\epsilon N_{\epsilon }}$ in the region $\big \{ r\ge \delta _{\epsilon }^{-\frac{1}{4}}\frac{\epsilon ^{(N_{\epsilon })}}{\sqrt{-\Lambda }}\big \}$ is contained in a domain ${\mathcal {B}}^{\sharp }_{\epsilon } \subset {\mathcal {B}}^{*}_{\epsilon }$ and that the region ${\mathcal {D}}_{\epsilon }$ is vacuum (colour figure online)

Let $\gamma \subset {\mathcal {U}}_{max}^{(\varepsilon )}$ be a future directed null geodesic which is maximally extended through reflections off ${\mathcal {I}}_{\varepsilon }$, in accordance with Definition 2.3 of [43] (see also the statement of Corollary 5.2), such that $(\gamma ,{\dot{\gamma }})$ lies in the support of $f_{\varepsilon N_{\varepsilon }}$ (where ${\dot{\gamma }}$ denotes the derivative with respect to the fixed affine parametrisation of each maximal geodesic component $\gamma _{n}$ of $\gamma =\cup _{n}\gamma _{n}$). In view of the bound (7.1) for the support of $f_{\varepsilon N_{\varepsilon }}$ and the inclusion (8.4), we can trivially estimate that, at the point of $\gamma$ where $u=v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}$:

$$\begin{aligned} v|_{\gamma \cap \{u=v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\}}\ge v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-h_{\varepsilon ,N_{\varepsilon }}. \end{aligned}$$

(9.25)

Since $\gamma$ traces out a causal curve in ${\mathcal {U}}_{max}^{(\varepsilon )}$ (and, in particular, the coordinate function v is non-decreasing along $\gamma$), we infer from (9.25) that

$$\begin{aligned} v|_{\gamma \cap {\mathcal {B}}_{\varepsilon }}\ge v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-h_{\varepsilon ,N_{\varepsilon }}. \end{aligned}$$

(9.26)

Therefore:

$$\begin{aligned} supp(f_{\varepsilon N_{\varepsilon }})\cap {\mathcal {B}}_{\varepsilon }\subset \{v\ge v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-h_{\varepsilon ,N_{\varepsilon }}\}. \end{aligned}$$

(9.27)

In view of(9.24) and (9.27), we obtain that

$$\begin{aligned} f_{\varepsilon }\equiv 0\text { on }\big ({\mathcal {B}}_{\varepsilon }\backslash {\mathcal {B}}_{\varepsilon }^{*}\big )\cap {\mathcal {U}}_{max}^{(\varepsilon )}, \end{aligned}$$

(9.28)

where

$$\begin{aligned} {\mathcal {B}}_{\varepsilon }^{*}\doteq \{v\ge v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-h_{\varepsilon ,N_{\varepsilon }}\}\cap {\mathcal {B}}_{\varepsilon } \end{aligned}$$

(see Fig. 25). By the domain of dependence property, we therefore infer that the solution $(r,\Omega ^{2},f_{\varepsilon })$ extends to the whole triangle

$$\begin{aligned} {\mathcal {D}}_{\varepsilon }\doteq \{v\le v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-h_{\varepsilon ,N_{\varepsilon }}\}\cap \{u\ge v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\}\cap \{u<v\}, \end{aligned}$$

i.e. that

$$\begin{aligned} {\mathcal {D}}_{\varepsilon }\subset {\mathcal {U}}_{max}^{(\varepsilon )}, \end{aligned}$$

and that ${\mathcal {D}}_{\varepsilon }$ is a vacuum region, i.e.

$$\begin{aligned} f_{\varepsilon }|_{{\mathcal {D}}_{\varepsilon }}=0. \end{aligned}$$

(9.29)

In view of (9.29), we readily infer that $\partial _{v}r>0$ on ${\mathcal {D}}_{\varepsilon }$, and, therefore:

$$\begin{aligned} \inf _{{\mathcal {B}}_{\varepsilon }^{*}\cap \{v=v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-h_{\varepsilon ,N_{\varepsilon }}\}}r>0. \end{aligned}$$

Thus, using (9.20), we infer that

$$\begin{aligned} 0<\inf _{{\mathcal {B}}_{\varepsilon }^{*}\cap \{v=v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-h_{\varepsilon ,N_{\varepsilon }}\}}&r\le r|_{{\mathcal {B}}_{\varepsilon }^{*}\cap {\mathcal {U}}_{max}^{(\varepsilon )}}\\&\le \max _{{\mathcal {B}}_{\varepsilon }^{*}\cap \{u=v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\}}r<+\infty .\nonumber \end{aligned}$$

(9.30)

The bounds (9.18) and (9.30) and the extension principle of Proposition 3.12 then readily imply that the solution extends on the whole of the domain ${\mathcal {B}}_{\varepsilon }^*$, i.e.

$$\begin{aligned} {\mathcal {B}}_{\varepsilon }^{*}\subset {\mathcal {U}}_{max}^{(\varepsilon )}. \end{aligned}$$

(9.31)

The following estimate for the support of the Vlasov field $f_{\varepsilon N_{\varepsilon }}$ will be crucial for the proof of Proposition 9.2:

$$\begin{aligned} supp(f_{\varepsilon N_{\varepsilon }})\cap {\mathcal {B}}_{\varepsilon }\cap \big \{ r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\big \}\subset \big \{(u,v)\in {\mathcal {B}}_{\varepsilon }^{\sharp }\big \}, \end{aligned}$$

(9.32)

where

$$\begin{aligned} {\mathcal {B}}_{\varepsilon }^{\sharp }\doteq \big \{ v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-h_{\varepsilon ,N_{\varepsilon }}&\le v\le v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}+\frac{1}{2}\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}\big \}\\&\cap \big \{ v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\le u\le v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-\delta _{\varepsilon }^{-\frac{1}{4}}h_{\varepsilon ,N_{\varepsilon }}\big \}\subset {\mathcal {B}}_{\varepsilon }^{*}.\nonumber \end{aligned}$$

(9.33)

This will be established by Lemma 9.3.

Remark

Note that the bound (9.32) does not follow from Lemma 7.1, since we do not expect the region ${\mathcal {B}}_{\varepsilon }^{\sharp }$ to lie within the domains ${\mathcal {U}}_{\varepsilon }^{+}$ or ${\mathcal {T}}_{\varepsilon }^{+}$, where $\frac{2m}{r}\le \eta _{0}$ (in fact, our aim is to show that $\frac{2m}{r}$ exceeds 1 at some point on ${\mathcal {B}}_{\varepsilon }^{\sharp }$). However, even when restricted to ${\mathcal {B}}_{\varepsilon }\cap \{u=v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\}$, (9.32) is a partial improvement of the bounds provided by Lemma 7.1, since ${\mathcal {B}}_{\varepsilon }\cap \{u=v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+{\tilde{h}}_{\varepsilon ,N_{\varepsilon }-1}\}$ is contained in ${\mathcal {T}}_{\varepsilon }^{+}$, but is not necessarily contained in ${\mathcal {U}}_{\varepsilon }^{+}$, and hence Lemma 7.1 can only guarantee bounds for $supp(f_{\varepsilon N_{\varepsilon }})$ in terms of ${\tilde{h}}_{\varepsilon N_{\varepsilon }}$.

Let us assume, for a moment, that Lemma 9.3 (and, thus, (9.32)) has been established, and let us set

$$\begin{aligned}{} & {} (u_{\star },v_{\star })\doteq \text {future endpoint of the curve }\big \{ v=v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+\frac{1}{2}\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}\big \}\nonumber \\{} & {} \quad \cap {\mathcal {B}}_{\varepsilon } \cap \big \{ r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\big \}. \end{aligned}$$

(9.34)

(see also Fig. 26).

Fig. 26

Schematic depiction of the domains ${\mathcal {D}}_{\epsilon }$ and ${\mathcal {B}}^{\sharp }_{\epsilon }\subset {\mathcal {B}}^{*}_{\epsilon }$. The timelike curve ${\mathcal {C}}_{\epsilon } \doteq \{r=\delta _{\epsilon }^{-\frac{1}{4}}\frac{\epsilon ^{(N_{\epsilon })}}{\sqrt{-\Lambda }}\}$ does not necessarily have to intersect the region ${\mathcal {B}}^{\sharp }_{\epsilon }$. In the case when the future boundary segment $\{u=v_{\epsilon ,N_{\epsilon }}^{(n_{+})}-\delta _{\epsilon }^{-\frac{1}{4}}h_{\epsilon ,N_{\epsilon }}\} \cap {\mathcal {B}}^{\sharp }_{\epsilon }$ of ${\mathcal {B}}^{\sharp }_{\epsilon }$ lies to the left of the curve ${\mathcal {C}}_{\epsilon }$, the point $(u_{\star }, v_{\star })$ lies on ${\mathcal {C}}_{\epsilon }$

In view of (9.24), the bound (9.32) on the support of $f_{\varepsilon N_{\varepsilon }}$ implies that

$$\begin{aligned} f_{\varepsilon }\equiv 0\text { on }\big \{ v\ge v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+\frac{1}{2}\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}\big \}\cap {\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}, \end{aligned}$$

and hence ${\tilde{m}}$ is constant on $\big \{ v\ge v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+\frac{1}{2}\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}\big \}\cap {\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}$. This fact, combined with (9.29) and the definition (6.96) of $\widetilde{{\mathcal {E}}}_{\nwarrow }^{(+)}[n_{+};N_{\varepsilon },N_{\varepsilon }-1]$ implies that

$$\begin{aligned} {\tilde{m}}(u_{\star },v_{\star })=\widetilde{{\mathcal {E}}}_{\nwarrow }^{(+)}[n_{+};N_{\varepsilon },N_{\varepsilon }-1]. \end{aligned}$$

(9.35)

The definition (9.34) of $(u_{\star },v_{\star })$ implies that:

• Either

  $$\begin{aligned} r(u_{\star },v_{\star })=\delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}, \end{aligned}$$

  (9.36)

• Or

  $$\begin{aligned} (u_{\star },v_{\star })=\Big (v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}-\delta _{\varepsilon }^{-\frac{1}{4}}h_{\varepsilon ,N_{\varepsilon }},v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+\frac{1}{2}\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}\Big ),\qquad \end{aligned}$$

  (9.37)

  in which case, by integrating the bound

  $$\begin{aligned} \partial _{v}r=\frac{\partial _{v}r}{1-\frac{2m}{r}}\cdot \big (1-\frac{2{\tilde{m}}}{r}-\frac{1}{3}\Lambda r^{2}\big )\le 2e^{\sigma _{\varepsilon }^{-4}} \end{aligned}$$

  (following from (9.21) and (9.22)) along $u=u_{\star }$ from $v=u_{\star }$ up to $v=v_{\star }$, we can estimate

  $$\begin{aligned} r(u_{\star },v_{\star })\le \exp (e^{\sigma _{\varepsilon }^{-8}})\delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}. \end{aligned}$$

  (9.38)

Since (9.38) is weaker than (9.36), we infer that, in any case, (9.38) always holds for $(u_{\star },v_{\star })$. Combining (9.35), (9.38), (9.22) and the lower bound (9.2) for $\widetilde{{\mathcal {E}}}_{\nwarrow }^{(+)}[n_{+};N_{\varepsilon },N_{\varepsilon }-1]$, we therefore calculate (using the relation (6.1) between $\sigma _{\varepsilon }$ and $\delta _{\varepsilon }$) that

$$\begin{aligned} \frac{2m}{r}(u_{\star },v_{\star })&=\big (\frac{2{\tilde{m}}}{r}-\frac{1}{3}\Lambda r^{2}\big )(u_{\star },v_{\star })\\&=\frac{2\widetilde{{\mathcal {E}}}_{\nwarrow }^{(+)}[n_{+};N_{\varepsilon },N_{\varepsilon }-1]}{r(u_{\star },v_{\star })}+O(\varepsilon )\\&\ge \frac{\delta _{\varepsilon }^{-\frac{1}{2}}}{\exp (e^{\sigma _{\varepsilon }^{-8}})\delta _{\varepsilon }^{-\frac{1}{4}}}+O(\varepsilon )\\&=\exp (-e^{\sigma _{\varepsilon }^{-8}})\delta _{\varepsilon }^{-\frac{1}{4}}+O(\varepsilon )\\&\ge \delta _{\varepsilon }^{-\frac{1}{8}}\\&>1, \end{aligned}$$

which is a contradiction, in view of our assumption (9.18). Thus, we infer that (9.18) cannot hold, i.e. that there exists some $(u_{\dagger },v_{\dagger })\in {\mathcal {B}}_{\varepsilon }\cap {\mathcal {U}}_{max}^{(\varepsilon )}$ for which (9.17) holds.

This completes the proof of Proposition 9.2. $\square$

Lemma 9.3

The support of the Vlasov field $f_{\varepsilon N_{\varepsilon }}$ inside the rectangle ${\mathcal {B}}_{\varepsilon }$ satisfies

$$\begin{aligned} supp(f_{\varepsilon N_{\varepsilon }}|_{{\mathcal {B}}_{\varepsilon }}) \cap \big \{ r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\big \}\subset \big \{(u,v)\in {\mathcal {B}}_{\varepsilon }^{\sharp }\big \}, \end{aligned}$$

(9.39)

Proof

Let $\gamma$ be any affinely parametrised, future directed, null geodesic $\gamma$ (which is maximally extended through reflections off ${\mathcal {I}}$) in the support of $f_{\varepsilon N_{\varepsilon }}$. The definition (6.7) of $F_{N_{\varepsilon }}^{(\varepsilon )}$ and the relation (6.64) between $F_{N_{\varepsilon }}^{(\varepsilon )}$ and the initial data for $f_{\varepsilon N_{\varepsilon }}$ implies that the angular momentum l of $\gamma$ satisfies

$$\begin{aligned} 2\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\le l\le 6\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}. \end{aligned}$$

(9.40)

In view of (9.27), in order to show (9.39), it suffices to show that (Fig. 27)

$$\begin{aligned}{} & {} \max \Big \{ v(p):\text { }p\in \gamma \cap {\mathcal {B}}_{\varepsilon }\cap \big \{ r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\big \}\Big \}\nonumber \\{} & {} \quad \le v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}+\frac{1}{2}\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}. \end{aligned}$$

(9.41)

Fig. 27

Schematic depiction of a null geodesic $\gamma$ in the support of $f_{\epsilon N_{\epsilon }}$. In order to establish the estimate (9.41), we will integrate the geodesic equation starting from the point $p_0$ (which lies in the region ${\mathcal {U}}^+_{\epsilon }$), i.e. before the last interaction of $\gamma$ with the beams ${\mathcal {V}}^{(n_+)}_{i\nearrow }$, $0\le i \le N_{\epsilon }-1$

Applying Lemma 7.1 for $i=N_{\varepsilon }$ and using (8.4) and (6.73) we infer that, at the point

$$\begin{aligned} p_{0}=(v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0},v_{0})\doteq \gamma \cap \{u=v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\}, \end{aligned}$$

we can estimate

$$\begin{aligned}{} & {} \big |v_{\varepsilon ,N_{\varepsilon }}^{(n_{+})}-v_{0}\big |\le h_{\varepsilon ,N_{\varepsilon }}, \end{aligned}$$

(9.42)

$$\begin{aligned}{} & {} \exp (-\sigma _{\varepsilon }^{-6})\le \Omega ^{2}({\dot{\gamma }}^{u}+{\dot{\gamma }}^{u})\big |_{p_{0}}\le \exp \big (\exp (\sigma _{\varepsilon }^{-4})\big ) \end{aligned}$$

(9.43)

and

$$\begin{aligned} \frac{{\dot{\gamma }}^{v}}{{\dot{\gamma }}^{u}}\Big |_{p_{0}}\le \exp \big (\exp (\sigma _{\varepsilon }^{-4})\big )\frac{2l^{2}}{r^{2}}\Big |_{p_{0}}\le \varepsilon ^{\frac{1}{2}} \end{aligned}$$

(9.44)

(where, for 9.44, we made use of the fact that $\varepsilon ^{(N_{\varepsilon })}/r|_{p_{0}}\lesssim \varepsilon ^{(N_{\varepsilon })}/\varepsilon ^{(0)}<\varepsilon$). Furthermore, using (6.73), (7.13) and the form (6.80) of ${\mathcal {V}}_{N_{\varepsilon }\nwarrow }^{(n_{+})}$, we can estimate for any ${\bar{v}}\in [v_{0},v_{0}+\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}]$:

$$\begin{aligned}{} & {} \Big |\int _{v_{0}}^{{\bar{v}}}\big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\big )(v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0},v)\,dv\Big |\nonumber \\{} & {} \quad \quad \le \exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\sqrt{-\Lambda }\frac{|{\bar{v}}-v_{0}|}{\varepsilon ^{(N_{\varepsilon })}}. \end{aligned}$$

(9.45)

We will establish (9.41) by continuity: We will show that, for any ${\bar{u}}\in [v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0},v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}-\delta _{\varepsilon }^{-\frac{1}{4}}h_{\varepsilon ,N_{\varepsilon }}]$ such that

$$\begin{aligned}{} & {} v(p)\le v_{0}+\frac{1}{4}\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}\quad \text { for all }p\in \gamma \cap \big \{ v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\le u\le {\bar{u}}\big \}\nonumber \\{} & {} \quad \quad \cap \big \{ r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\big \}\Big \} \end{aligned}$$

(9.46)

(note that (9.46) holds trivially when ${\bar{u}}=v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}$), the following stronger bound actually holds:

$$\begin{aligned}{} & {} v(p)\le v_{0}+\frac{1}{8}\exp (e^{\sigma _{\varepsilon }^{-7}})h_{\varepsilon ,N_{\varepsilon }}\text { for all }p\in \gamma \cap \big \{ v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\le u\le {\bar{u}}\big \}\nonumber \\{} & {} \quad \cap \big \{ r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\big \}\Big \}. \end{aligned}$$

(9.47)

Let ${\bar{u}}\in [v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0},v_{\varepsilon ,N_{\varepsilon }-1}^{(n_{+})}-\delta _{\varepsilon }^{-\frac{1}{4}}h_{\varepsilon ,N_{\varepsilon }}]$ satisfy (9.46). Then, for any $u'\in [v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0},{\bar{u}}]$, setting

$$\begin{aligned}{} & {} v'=\sup \Big \{ v(p):\text { }p\in \gamma \cap \big \{ v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\le u\le u'\big \}\nonumber \\{} & {} \quad \cap \big \{ r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\big \}\Big \} \end{aligned}$$

(9.48)

and applying (2.50) for $u_{1}(v)=v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}$, we obtain:

$$\begin{aligned}&\Big |\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )|_{v=v'}-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )|_{v=v_{0}}\Big | \nonumber \\&\quad \le \Big |\int _{v_{0}}^{v'}\int _{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}}^{u(\gamma (s_{v}))}\Big (\frac{1}{2}\frac{\frac{6{\tilde{m}}}{r}-1}{r^{2}}\Omega ^{2}-24\pi T_{uv}\Big )\,du\,dv\Big |\\&\qquad +\Big |\int _{v_{0}}^{v'}\big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\big )(u_{1}(v),v)\,dv\Big |.\nonumber \end{aligned}$$

(9.49)

In view of the relation (2.49) for ${\tilde{m}}$, the upper bound (9.21) and the fact that $\partial _{u}{\tilde{m}}\le 0$ (which follows readily from (2.49) and (9.20)), we can estimate on ${\mathcal {B}}_{\varepsilon }$:

$$\begin{aligned} 24\pi T_{uv}&\le 3\frac{\Omega ^{2}}{-\partial _{u}r}\frac{-\partial _{u}{\tilde{m}}}{r^{2}}\\&\le 3e^{\sigma _{\varepsilon }^{-4}}\frac{-\partial _{u}{\tilde{m}}}{r^{2}}\nonumber \\&=3e^{\sigma _{\varepsilon }^{-4}}\Big (-\partial _{u}\big (\frac{{\tilde{m}}}{r^{2}}\big )+2\frac{{\tilde{m}}}{r^{3}}(-\partial _{u}r)\Big ).\nonumber \end{aligned}$$

(9.50)

Furthermore, from the relation (2.9) and the upper bound (9.21), we can estimate on ${\mathcal {B}}_{\varepsilon }$:

$$\begin{aligned} \Omega ^{2}\le 4e^{\sigma _{\varepsilon }^{-4}}(-\partial _{u}r). \end{aligned}$$

(9.51)

Using the bounds (9.23), (9.45), (9.50) and (9.51) to estimate the right hand side of (9.49) (integrating, also, in u for the $\partial _{u}\big (\frac{{\tilde{m}}}{r^{2}}\big )$ term), we obtain:

$$\begin{aligned}&\Big |\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )|_{v=v'}-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )|_{v=v_{0}}\Big |\nonumber \\&\quad \le \int _{v_{0}}^{v'}\int _{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}}^{u(\gamma (s_{v}))}\Big (\frac{1}{2}\frac{\frac{6{\tilde{m}}}{r}+1}{r^{2}}\Omega ^{2}\Big )\,du\,dv+24\pi \int _{v_{0}}^{v'}\int _{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}}^{u(\gamma (s_{v}))}T_{uv}\,du\,dv\\&\qquad +\Big |\int _{v_{0}}^{v'}\big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\big )(u_{1}(v),v)\,dv\Big |\nonumber \\&\quad \le e^{\sigma _{\varepsilon }^{-5}}\int _{v_{0}}^{v'}\int _{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}}^{u(\gamma (s_{v}))}\frac{(-\partial _{u}r)}{r^{2}}\,du\,dv-3e^{\sigma _{\varepsilon }^{-4}}\int _{v_{0}}^{v'}\int _{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}}^{u(\gamma (s_{v}))}\partial _{u}\big (\frac{{\tilde{m}}}{r^{2}}\big )\,du\,dv\nonumber \\&\qquad +\Big |\int _{v_{0}}^{v'}\big (\partial _{v}\log (\Omega ^{2})-2\frac{\partial _{v}r}{r}\big )(u_{1}(v),v)\,dv\Big |\nonumber \\&\quad \le e^{\sigma _{\varepsilon }^{-5}}\frac{1}{r|_{\gamma \cap \{v=v'\}}}|v'-v_{0}|+\exp \big (\exp (\sigma _{\varepsilon }^{-6})\big )\sqrt{-\Lambda }\frac{|v'-v_{0}|}{\varepsilon ^{(N_{\varepsilon })}}.\nonumber \end{aligned}$$

(9.52)

In view of the definition (9.48) of $v'$ (and, in particular, the fact that $r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}$ at $\gamma \cap \{v=v'\}$), from (9.52) we obtain that:

$$\begin{aligned}{} & {} \Big |\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )|_{v=v'}-\log \big (\Omega ^{2}{\dot{\gamma }}^{u}\big )|_{v=v_{0}}\Big |\nonumber \\{} & {} \quad \le \exp \big (\exp (2\sigma _{\varepsilon }^{-6})\big )\sqrt{-\Lambda }\frac{|v'-v_{0}|}{\varepsilon ^{(N_{\varepsilon })}}. \end{aligned}$$

(9.53)

In view of (9.43) and assumption (9.46), from (9.53) we infer that

$$\begin{aligned} \Omega ^{2}{\dot{\gamma }}^{u}|_{v=v'}\ge \exp \Big (-\exp \big (\exp (\sigma _{\varepsilon }^{-8})\Big ). \end{aligned}$$

(9.54)

Furthermore, using the null-shell relation (2.19) for $\gamma$, the relation (2.9) for $\Omega ^{2}$, the upper bounds (9.18) and (9.21) and the lower bound (9.54), we can readily estimate (using also the fact that $r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}$ at $\gamma \cap \{v=v'\}$, as a consequence of (9.46)):

$$\begin{aligned} \frac{\partial _{v}r\cdot {\dot{\gamma }}^{v}}{-\partial _{u}r\cdot {\dot{\gamma }}^{u}}\big |_{v=v'}= & {} \frac{1}{4}\big (1-\frac{2m}{r})\Big (\frac{\Omega ^{2}}{-\partial _{u}r}\Big )^{2}\frac{l^{2}}{r^{2}}\frac{1}{(\Omega ^{2}{\dot{\gamma }}^{u})^{2}}\Big |_{v=v'}\nonumber \\\le & {} \exp \Big (\exp \big (\exp (\sigma _{\varepsilon }^{-9})\Big )\delta _{\varepsilon }^{\frac{1}{2}}\le \delta _{\varepsilon }^{\frac{1}{4}}. \end{aligned}$$

(9.55)

In particular, (9.55) implies that the integration forms dr and du along $\gamma$ satisfy at $v=v'$:

$$\begin{aligned} dr|_{\gamma \cap \{v=v'\}}= & {} \big (\partial _{u}r+\frac{{\dot{\gamma }}^{v}}{{\dot{\gamma }}^{u}}\partial _{v}r\big )du|_{\gamma \cap \{v=v'\}}\nonumber \\= & {} \partial _{u}r(1+O(\delta _{\varepsilon }^{\frac{1}{4}}))du|_{\gamma \cap \{v=v'\}}. \end{aligned}$$

(9.56)

Using the relation (2.19) for $\gamma$ as well as the bounds (9.21), (9.54), (9.55) and (9.56), we can readily estimate that, for all $p\in \gamma \cap \big \{ v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\le u\le {\bar{u}}\big \}\cap \big \{ r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}\big \}\Big \}$:

$$\begin{aligned} v(p)-v_{0}&\le \int _{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}}^{{\bar{u}}}\frac{\Omega ^{2}{\dot{\gamma }}^{v}}{\Omega ^{2}{\dot{\gamma }}^{u}}(s_{u})\,du\\&=\int _{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}}^{{\bar{u}}}\frac{\Omega ^{2}l^{2}}{r^{2}}\frac{1}{(\Omega ^{2}{\dot{\gamma }}^{u})^{2}}(s_{u})\,du\nonumber \\&\le \exp \Big (2\exp \big (\exp (\sigma _{\varepsilon }^{-8})\Big )\int _{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}}^{{\bar{u}}}\frac{\Omega ^{2}l^{2}}{r^{2}}\Big |_{\gamma (s_{u})}\,du\nonumber \\&\le \exp \Big (4\exp \big (\exp (\sigma _{\varepsilon }^{-8})\Big )\int _{\gamma \cap \{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\le u\le {\bar{u}}\}}\frac{l^{2}}{r^{2}}\frac{\Omega ^{2}}{-\partial _{u}r}\,dr\nonumber \\&\le \exp \Big (\exp \big (\exp (\sigma _{\varepsilon }^{-9})\Big )\int _{\gamma \cap \{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\le u\le {\bar{u}}\}}\frac{l^{2}}{r^{2}}\,dr\nonumber \\&\le \exp \Big (\exp \big (\exp (\sigma _{\varepsilon }^{-9})\Big )\frac{l^{2}}{\inf _{\gamma \cap \{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\le u\le {\bar{u}}\}}r}\nonumber \\&\le \delta _{\varepsilon }^{\frac{1}{8}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }},\nonumber \end{aligned}$$

(9.57)

where, in passing to the last line of (9.57), we made use of (9.40) and the bound $r\ge \delta _{\varepsilon }^{-\frac{1}{4}}\frac{\varepsilon ^{(N_{\varepsilon })}}{\sqrt{-\Lambda }}$ on $\gamma \cap \{v_{\varepsilon ,0}^{(n_{+})}-h_{\varepsilon ,0}\le u\le {\bar{u}}\}$ (following from (9.46)). From (9.57), the bound (9.47) follows readily, in view of the relation (6.1) between $\sigma _{\varepsilon }$ and $\delta _{\varepsilon }$. Thus, by continuity, we have established (9.41) and, therefore, (9.39). Thus, the proof of Lemma 9.3 (and, thus, Proposition 9.2) has been completed. $\square$