Abstract
We investigate both linear and nonlinear stability aspects of rigid motions (resp. Möbius transformations) of \({\mathbb {S}}^{n-1}\) among Sobolev maps from \({\mathbb {S}}^{n-1}\) into \({\mathbb {R}}^n\). Unlike similar in flavour results for maps defined on domains of \({\mathbb {R}}^n\) and mapping into \({\mathbb {R}}^n\), not only an isometric (resp. conformal) deficit is necessary in this more flexible setting, but also a deficit measuring the distortion of \({\mathbb {S}}^{n-1}\) under the maps in consideration. The latter is defined as an associated isoperimetric type of deficit. The focus is mostly on the case \(n=3\) (where it is explained why the estimates are optimal in their corresponding settings), but we also address the necessary adaptations for the results in higher dimensions. We also obtain linear stability estimates for both cases in all dimensions. These can be regarded as Korn-type inequalities for the combination of the quadratic form associated with the isometric (resp. conformal) deficit on \({\mathbb {S}}^{n-1}\) and the isoperimetric one.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we examine stability issues of isometric and conformal maps from \({\mathbb {S}}^{n-1}\) into \({\mathbb {R}}^n\) of relatively low regularity, focusing mostly, but not solely, on the case \(n=3\). Since the starting domain is of codimension 1 in \({\mathbb {R}}^n\), these maps exhibit of course more flexibility than their analogues from open subdomains of \({\mathbb {R}}^n\) into \({\mathbb {R}}^n\). On the one hand, isometric and conformal maps are actually rigid when considered from \({\mathbb {S}}^{n-1}\) into itself, as the following version of the well known theorem by J. Liouville asserts.
Theorem 1.1
(Liouville’s Theorem on \({\mathbb {S}}^{n-1}\))
-
(i)
Let \(n\ge 2\) and \(p\in [1,+\infty ]\). A generalized orientation-preserving \(\mathrm{(}\backslash \)-reversing) \(u\in W^{1,p}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) is isometric iff it is a rigid motion of \({\mathbb {S}}^{n-1}\), i.e., iff there exists \(O\in O(n)\) so that for every \(x\in {\mathbb {S}}^{n-1}\),
$$\begin{aligned} u(x)=Ox . \end{aligned}$$(1.1) -
(ii)
Let \(n\ge 3\). A generalized orientation-preserving \(\mathrm{(}\backslash \)-reversing) \(u\in W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) of degree 1 \(\mathrm{(}\backslash \)-1) is conformal iff it is a Möbius transformation of \({\mathbb {S}}^{n-1}\), i.e., iff there exist \(O\in O(n)\), \(\xi \in {\mathbb {S}}^{n-1}\) and \(\lambda >0\) so that for every \(x\in {\mathbb {S}}^{n-1}\),
$$\begin{aligned} u(x)=O\phi _{\xi ,\lambda }(x) . \end{aligned}$$(1.2)Here, \(\phi _{\xi ,\lambda }:=\sigma _\xi ^{-1} \circ i_\lambda \circ \sigma _\xi \), where \(\sigma _\xi \) is the stereographic projection of \({\mathbb {S}}^{n-1}\) onto \({T_\xi {\mathbb {S}}^{n-1}}\cup \{\infty \}\), and \(i_\lambda :T_\xi {\mathbb {S}}^{n-1}\mapsto T_\xi {\mathbb {S}}^{n-1}\) is the dilation in \(T_ \xi {\mathbb {S}}^{n-1}\) by factor \(\lambda >0\).
On the other hand however, there is a wide variety of such maps from \({\mathbb {S}}^{n-1}\) into \({\mathbb {R}}^n\). In contrast to the classical rigidity in the Weyl problem for isometric embeddings, according to which the only \(C^2\) (or even \(C^{1,\alpha }\) for \(\alpha >\frac{2}{3}\)) isometric embedding of \({\mathbb {S}}^{n-1}\) into \({\mathbb {R}}^n\) is the standard one modulo rigid motions (cf. [3, 8, 9, 14]), as a consequence of the celebrated Nash–Kuiper theorem (cf. [16, 20]), the following paradox happens for less regular, say \(C^1\) isometric embeddings.
Given any \(\delta \in (0,1)\), in an arbitrarily small \(C^0\)-neighbourhood of the short homothety \(u_\delta :{\mathbb {S}}^{n-1}\mapsto {\mathbb {R}}^n\), \(u_\delta (x):=\delta x\), there exist \(C^1\) isometric embeddings, which can be visualized as wrinkling isometrically \({\mathbb {S}}^{n-1}\) inside the small ball \(B_\delta (0)\) in a way that produces continuously changing tangent planes. For the more general case of conformal maps from \({\mathbb {S}}^{n-1}\) to \({\mathbb {R}}^n\), at least when \(n=3\), other examples that are not Möbius transformations are provided by the Uniformization Theorem and some of them have often been used in cartography, for instance the inverse of Jacobi’s conformal map projection that smoothly and conformally maps \({\mathbb {S}}^2\) onto the surface of an ellipsoid.
Therefore, Liouville’s rigidity theorem on \({\mathbb {S}}^{n-1}\) on the one hand, and the aforementioned flexibility phenomena on the other, indicate the following fact. When one seeks stability of the isometry (resp. the conformal) group of \({\mathbb {S}}^{n-1}\) among Sobolev maps \(u:{\mathbb {S}}^{n-1}\mapsto {\mathbb {R}}^n\), apart from an isometric (resp. conformal) deficit, an extra deficit measuring the deviation of \(u({\mathbb {S}}^{n-1})\) from being a round sphere is necessary. In this paper we make a connection between stability aspects for these two classes of mappings and the isoperimetric inequality, and this extra deficit should be interpreted in both cases as an isoperimetric type of deficit produced by the maps in consideration.
With the notations that we adopt in Sect. 2, our main result in the isometric case is the following.
Theorem 1.2
There exists \(c_1>0\) so that for every \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) there exists \(O\in O(3)\) such that

where \(0\le \sigma _1\le \sigma _{2}\) are the principal stretches of u, i.e., the eigenvalues of \(\sqrt{\nabla _{T}u^t \nabla _{T}u}\), and

The first term on the right hand side of (1.3) is an \(L^2\)-isometric deficit of u penalizing local stretches, while the second term (in the definition of which in (1.4) we use the identification between a 2-simple vector and its Hodge dual) represents in this setting the isoperimetric deficit of u. Since isometric maps preserve the surface area of \({\mathbb {S}}^{2}\), the latter reduces in this situtation to the positive part of the excess in the signed volume produced by u. The exact analogue of Theorem 1.2 holds true also in dimension \(n=2\) (see Proposition 3.2 in Sect. 3) and, as long as u satisfies an apriori bound on its homogeneous \(W^{1,2(n-2)}\)-seminorm, also in dimensions \(n\ge 4\), as stated in the following.
Theorem 1.3
Let \(n\ge 4\) and \(M>0\). There exists \(c_{n,M}>0\) so that for every \(u\in \dot{W}^{1,2(n-2)}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) with \(\Vert \nabla _{T}u\Vert _{L^{2(n-2)}({\mathbb {S}}^{n-1})}\le M\), there exists \(O\in O(n)\) such that

where \(0\le \sigma _1\le \dots \le \sigma _{n-1}\) are again the eigenvalues of \(\sqrt{\nabla _{T}u^t \nabla _{T}u}\), and the signed volume of u is now

Let us clarify that here we are using the identification
The constant in (1.5) depends in principle now both on the dimension and on the apriori bound in the \(L^{2(n-2)}\)-norm of the gradient. The reason why this particular condition is introduced will be explained in Sect. 3.4. As we also justify by examples in Remark 3.3, the estimate is optimal in this setting, in the sense that the exponents with which the two deficits appear cannot generically be improved.
For the conformal case, due to the scaling invariant nature of the problem, the correct notions for the average conformal deficit and the isoperimetric one can be combined together. The main result when \(n=3\) in this case is the following.
Theorem 1.4
There exists a constant \(c_2>0\) so that for every \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) with \(V_3(u)\ne 0\) there exist a Möbius transformation \(\phi \) of \({\mathbb {S}}^{2}\) and \(\lambda >0\) such that

where  is the Dirichlet energy of u, and \(V_3(u)\) is again its signed volume, as in (1.4).
is the Dirichlet energy of u, and \(V_3(u)\) is again its signed volume, as in (1.4).
Of course the question is void when \(n=2\), since conformality is a trivial notion for maps from \({\mathbb {S}}^1\) to \({\mathbb {R}}^2\). One can directly check that the estimate (1.8) is again optimal in its setting, by considering the sequence of maps \(u_{\sigma }(x):=A_\sigma x:{\mathbb {S}}^{2}\mapsto {\mathbb {R}}^3,\ \mathrm{where}\ A_\sigma :=\mathrm{diag}(1,1,1+\sigma )\in {\mathbb {R}}^{3\times 3}\) as \(\sigma \rightarrow 0^+\).
The use of this combined conformal-isoperimetric deficit is very natural in this framework. Indeed, generalizing to any dimension \(n\ge 3\) (for \(n=3\) cf. [25, Theorem 2.4]), for \(u\in W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) the following inequalities, sometimes referred to as Wente’s isoperimetric inequality for mappings, are known to hold.

where \(D_{n-1}(u)\), \(P_{n-1}(u)\) are the first two integral quantities in the first line of the above inequalities, i.e., the \((n-1)\)-Dirichlet energy and the generalized area produced by u respectively. The first inequality in (1.9) follows from the arithmetic mean-geometric mean inequality for the eigenvalues of \(\sqrt{\nabla _{T}u^t\nabla _{T}u}\) and equality is achieved iff these eigenvalues coincide for \({\mathcal {H}}^{n-1}\)-a.e. \(x\in {\mathbb {S}}^{n-1}\), or equivalently, iff
i.e., iff u is a generalized conformal map from \({\mathbb {S}}^{n-1}\) to \({\mathbb {R}}^n\). The second inequality in (1.9) is the functional form of the isoperimetric inequality (cf. [1, inequality (2)]), which can be proven first for smooth maps and can then be extended by density in \(W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\). Equality is achieved iff the image of u is another round sphere in the \({\mathcal {H}}^{n-1}\)-a.e. sense. In the case of a \(C^1\) embedding, the inequality reduces of course to the classical Euclidean isoperimetric inequality for the open bounded set in \({\mathbb {R}}^n\) whose boundary is \(u({\mathbb {S}}^{n-1})\).
Based on these simple observations, the combined conformal-isoperimetric deficit
considered among maps \(u\in W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) for which \(V_n(u)\ne 0\), provides a correct notion of deficit when one seeks stability of the conformal group of \({\mathbb {S}}^{n-1}\) among maps from \({\mathbb {S}}^{n-1}\) into \({\mathbb {R}}^n\). Indeed, it is immediate that \({\mathcal {E}}_{n-1}\) is translation, rotation and scaling invariant, as well as invariant under precompositions with Möbius transformations of \({\mathbb {S}}^{n-1}\). Moreover, as we have discussed above, \({\mathcal {E}}_{n-1}\) is nonnegative and vanishes iff u is a generalized conformal map from \({\mathbb {S}}^{n-1}\) onto another round sphere, which after translation and scaling can be taken to be \({\mathbb {S}}^{n-1}\) again. If \(d\in {\mathbb {Z}}\) would denote the degree of \(u\in W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) (following the definitions in [5]), then
Since the degree (for maps from \({\mathbb {S}}^{n-1}\) to itself) takes integer values, we would have that either \(d=0\) or \(d=\pm 1\), with the first case being excluded automatically, since by assumption \(V_n(u)\ne 0\). Hence, absolute minimizers of \({\mathcal {E}}_{n-1}\) are degree \(\pm 1\) conformal maps from \({\mathbb {S}}^{n-1}\) into itself, up to a translation vector and a scaling factor, i.e., according to Theorem 1.1, Möbius transformations of \({\mathbb {S}}^{n-1}\) up to translation and scaling. In this respect, Theorem 1.4 can be thought of as a sharp quantitative version of the previous statements for \(n=3\). At the core of its proof lies the study of the linearized version of the problem, since by the use of a contradiction\(\backslash \)compactness argument it is enough to show the theorem for maps that are sufficiently close to the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) in the \(W^{1,2}\)-topology. In this regime, and after a correct rescaling of u, if \(w:=u-\mathrm{id}_{{\mathbb {S}}^{2}}\) is the corresponding displacement field, one obtains the formal Taylor expansion

where \(Q_3(w)\) is the associated quadratic form, i.e., the second derivative of \({\mathcal {E}}_2\) at the \(\mathrm{id}_{{\mathbb {S}}^{2}}\), defined explicitely later in (4.7). The next and main step of the proof is to examine the coercivity properties of the quadratic form \(Q_3\). This is something that can actually be done in every dimension \(n\ge 3\), the main ingredient for doing so being the fine interplay between the Fourier decomposition of a \(W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\)-vector field into \({\mathbb {R}}^n\)-valued spherical harmonics and the properties of the linear first order differential operator associated to the second derivative of \(V_n\) at the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\).
To be more precise, as we thoroughly examine in Sect. 4.2 for the case \(n=3\), and in Sect. 5.1 for the higher dimensional case, if one rescales u properly, sets \(w:=u-\mathrm{id}_{{\mathbb {S}}^{n-1}}\) and expands \({\mathcal {E}}_{n-1}(u)\) in (1.10) around the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\), then the resulting quadratic form

has finite-dimensional kernel and its dimension actually coincides with that of the conformal group of \({\mathbb {S}}^{n-1}\). Moreover, when considered in the correct space (see the definitions of the spaces \(H_n\), \((H_{n,k,i})_{k\ge 1, i=1,2,3}\) in Eq. (4.15) and Theorem 4.7 in Sect. 4.2), the form \(Q_n\) satisfies the following coercivity estimate.
Theorem 1.5
Let \(n\ge 3\). There exists a constant \(C_n>0\) such that for every \(w\in H_n\),

where \(H_{n,0}:=H_{n,1,2}\oplus H_{n,2,3}\) is the kernel of \(Q_n\) in \(H_n\), and \(\Pi _{n,0}:H_n\mapsto H_{n,0}\) is the \(W^{1,2}\)-orthogonal projection of \(H_n\) onto \(H_{n,0}\).
When \(n=3\), the optimal constant in (1.13) can actually be calculated explicitely. Since \(H_{n,0}\) turns out to be isomorphic to the Lie algebra of infinitesimal Möbius transformations of \({\mathbb {S}}^{n-1}\), an application of the Inverse Function Theorem together with a topological argument (given in Lemma 4.13) will finally allow us to infer the nonlinear estimate (1.8) from the linear one (1.13) in the \(W^{1,2}\)-close to the \(\mathrm{id}_{{\mathbb {S}}^{2}}\)-regime, and hence conclude with Theorem 1.4.
It is maybe worth remarking here that in contrast to (1.11), in dimensions \(n\ge 4\) a formal expansion of the combined conformal-isoperimetric deficit around the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\) yields

Since the higher order term is now cubic in \(\nabla _{T}w\), the linear estimate (1.13) alone would only imply the nonlinear one (following exactly the same steps of proof as those described in Sects. 4.1, 4.3 and 4.4 for the case \(n=3\)) only in the \(W^{1,\infty }\)-close to the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\)-regime (see Remark 5.5), as stated in the following.
Corollary 1.6
Let \(n\ge 4\). There exist constants \(\theta \in (0,1)\) (sufficiently small) and \(c_{n-1}>0\) such that the following statement holds. For every \(u\in W^{1,\infty }({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) with \(\Vert \nabla _{T}u-P_T\Vert _{L^{\infty }({\mathbb {S}}^{n-1})}\le \theta \ll 1\), there exist a Möbius transformation \(\phi \) of \({\mathbb {S}}^{n-1}\) and \(\lambda >0\) such that

where \({\mathcal {E}}_{n-1}\) is defined in (1.10).
Remark 1.7
An interesting question would be if the local statement of the above Corollary can be improved to a global one, possibly via a PDE argument. However, in the case of maps \(u:{\mathbb {S}}^{n-1}\mapsto {\mathbb {R}}^n\), one cannot perform something like an n-harmonic replacement trick, as for instance in [21] (or F-harmonic, harmonic in the setting of [10, 11] respectively), since \({\mathbb {S}}^{n-1}\) is boundaryless, and there are of course no boundary conditions to relate to the replacement map. It seems that a penalization argument in the spirit of the selection principle devised in [7] (for the optimal quantitative isoperimetric inequality) could be more promising in that direction, which is an interesting question for future investigation.
As one can easily notice, and for convenience of the reader we provide the details in “Appendix B”,
where

is the quadratic form associated to the nonlinear conformal deficit \(\left[ \frac{D_{n-1}(u)}{P_{n-1}(u)}\right] ^{\frac{n}{n-1}} -1\ge 0\), and

is the one associated to the nonlinear isoperimetric deficit \(\frac{\big [P_{n-1}(u)\big ]^{\frac{n}{n-1}}}{|V_{n} (u)|}-1\ge 0\). Actually, an estimate like (1.13) holds true for every positive combination of the two forms \(Q_{n,\mathrm{conf}}\) and \(Q_{n,\mathrm{isop}}\).
Finally, as we mention in Sect. 5.3, a similar linear stability phenomenon holds true in the isometric case as well, namely one can prove the following.
Theorem 1.8
Let \(n\ge 2\). For every \(\alpha >0\) there exists a constant \(C_{n,\alpha }>0\) such that for every map \(w\in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\),

where

is the quadratic form associated to the full \(L^2\)-isometric deficit  , \(Q_{n,\mathrm{isop}}\) is as in (1.16), and \(w_h:\overline{B_1}\mapsto {\mathbb {R}}^n\) denotes the (componentwise) harmonic continuation of w in the interior of \(B_1\).
, \(Q_{n,\mathrm{isop}}\) is as in (1.16), and \(w_h:\overline{B_1}\mapsto {\mathbb {R}}^n\) denotes the (componentwise) harmonic continuation of w in the interior of \(B_1\).
The structure of the paper is the following. In Sect. 2 we introduce some notations that we are going to use in the subsequent sections. In Sect. 3 we give in steps the proof of Theorem 1.2 and remark on the adaptations needed to prove its generalization in higher dimensions, i.e., Theorem 1.3. In Sect. 4 we give again in steps the proof of Theorem 1.4. Building upon the analysis that we perform in Sect. 4.2, in Sect. 5 we prove the linear stability estimates stated in Theorems 1.5 and 1.8 in all dimensions. In “Appendix A” we first exhibit a short, intrinsic and to our knowledge, new proof of Liouville’s Theorem 1.1, as well as a related compactness result that can be proven by a slight perturbation of the idea. In “Appendix B” we include just for the convenience of the reader a detailed derivation of some integral identities for Jacobians, as well as the Taylor expansions of the geometric quantities that appear in the main body of the paper. Finally, in “Appendix C” we collect some basic facts from the theory of spherical harmonics that we are using.
2 Notation
The following standard notation will be adopted throughout the paper.
- \(\{e_i\}_{i=1}^n,\ \langle \cdot , \cdot \rangle ,\ |\cdot |\):
-
the Euclidean orthonormal basis, inner product, norm in \({\mathbb {R}}^n\)
- \(A^t\):
-
the transpose of a matrix or the adjoint of the corresponding linear map
- Sym(n), Skew(n):
-
the space of \(n\times n\) symmetric, skew-symmetric matrices respectively
- \(A_{\mathrm{sym}}\), \(A_{\mathrm{skew}}\):
-
the symmetric, skew-symmetric part of a matrix \(A\in {\mathbb {R}}^{n\times n}\) respectively
- \(\{\tau _1,\dots ,\tau _{n-1}\}\):
-
a positively oriented local orthonormal frame for \(T_x{\mathbb {S}}^{n-1}\), so that for every \(x\in {\mathbb {S}}^{n-1}\ \{\tau _1(x),\dots ,\tau _{n-1}(x),x\}\) is a positively oriented orthonormal system of n vectors in \({\mathbb {R}}^n\)
- \(\omega _n\):
-
the volume of the unit ball \(B_1\) in \({\mathbb {R}}^n\)
- \(dv_g\):
-
the standard \((n-1)\)-volume form on \({\mathbb {S}}^{n-1}\)
- \({\mathcal {H}}^k\):
-
the k-dimensional Hausdorff measure
- O(n), SO(n):
-
the orthogonal, special orthogonal group of \({\mathbb {R}}^n\) respectively
- \(Isom_{(+)}({\mathbb {S}}^{n-1})\):
-
the group of rigid motions of \({\mathbb {S}}^{n-1}\) (the orientation-preserving ones respectively)
- \(Conf_{(+)}({\mathbb {S}}^{n-1})\):
-
the group of Möbius transformations of \({\mathbb {S}}^{n-1}\) (the orientation-preserving ones respectively)
- \(I_x\):
-
the identity transformation on \(T_x{\mathbb {S}}^{n-1}\)
- \(\nabla _{T}u\):
-
the tangential gradient of \(u:{\mathbb {S}}^{n-1}\mapsto {\mathbb {R}}^n\), represented in local coordinates by the \(n\times (n-1)\) matrix with entries \((\nabla _{T}u)_{ij}=\langle \nabla _{T}u^i,\tau _j\rangle \)
- \(P_T\):
-
\(\nabla _{T}\mathrm{id}_{{\mathbb {S}}^{n-1}}\)
- \(d_x u\):
-
the intrinsic gradient of a map \(u:{\mathbb {S}}^{n-1}\mapsto {\mathbb {S}}^{n-1}\), viewed as a linear map \(d_x u:T_x{\mathbb {S}}^{n-1}\mapsto T_{u(x)}{\mathbb {S}}^{n-1}\) with respect to the frame \(\{\tau _1,\dots ,\tau _{n-1}\}\)
- \(\partial _{\mathbf {\nu }}f\):
-
the radial derivative of a map \(f:\overline{B_1}\mapsto {\mathbb {R}}^m\) on \({\mathbb {S}}^{n-1}\)
- \(\mathrm{div}_{{\mathbb {S}}^{n-1}}u\), \(\Delta _{{\mathbb {S}}^{n-1}}u\):
-
the tangential divergence, Laplace-Beltrami operator of a map \(u:{\mathbb {S}}^{n-1}\rightarrow {\mathbb {R}}^n\)
- \(C^k\):
-
the space of k-times continuously differentiable maps, \(k\in {\mathbb {N}}\)
- \(L^p, W^{1,p}\):
-
the standard Lebesgue or Sobolev spaces (on \({\mathbb {S}}^{n-1}\)) respectively, for \(1\le p<\infty \). The norms are taken with respect to the normalized \({\mathcal {H}}^{n-1}\)-measure, to simplify some dimensional constants appearing later in the content
- \(W^{1,\infty }({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\):
-
the space of Lipschitz maps from \({\mathbb {S}}^{n-1}\) to \({\mathbb {R}}^n\); \(\Vert u\Vert _{W^{1,\infty }}:=\mathrm{max} \left\{ \Vert u\Vert _{L^{\infty }},\Vert \nabla _{T}u\Vert _{L^{\infty }}\right\} \)
- \(\sim _{M_1,M_2,\dots }, \lesssim _{M_1,M_2,\dots }\):
-
the corresponding equality, inequality is valid up to a constant that is allowed to vary from line to line but depends only on the parameters \(M_1, M_2,\dots \), or only on the dimension when the subscripts are absent.
- \(c,C>0\):
-
universal constants whose value is allowed to vary from line to line and place to place but depend in any case only on the dimension.
3 The isometric case: Proof of Theorem 1.3
In what follows, the \(L^2\)-isometric deficit of a map \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) that we are using is denoted by
where \(0\le \sigma _1\le \sigma _{2}\) are the principal stretches of u, i.e., the eigenvalues of \(\sqrt{\nabla _{T}u^t \nabla _{T}u}\).
Note that \(\delta (u)=0\) whenever u is a short map, i.e., \(u\in W^{1,\infty }({\mathbb {S}}^{2};{\mathbb {R}}^3)\) with \(\nabla _{T}u^t\nabla _{T}u\le I_x\) , \({\mathcal {H}}^2\)-a.e. on \({\mathbb {S}}^{2}\) in the sense of quadratic forms. In general,
so that (having in mind the Nash–Kuiper Theorem, cf. [16, 20]) the deficit \(\delta (u)\) is sharper than the full \(L^2\)-isometric deficit
since it only penalizes local stretches under u. The isoperimetric deficit (or the positive part of the excess in volume) in this setting is denoted by
Before presenting the proof of the result, let us make some preliminary remarks.
Remark 3.1
- (i):
-
If \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) is a globally short map, then \(\delta (u)=0\). Moreover, since in this case \(|\partial _{\tau _1}u\wedge \partial _{\tau _2}u|\le 1\) and \(|\nabla _{T}u|\le \sqrt{2}\) \({\mathcal {H}}^2\)-a.e. on \({\mathbb {S}}^{2}\), by the Cauchy–Schwarz inequality and the sharp Poincare inequality on \({\mathbb {S}}^{2}\) (equality in which is achieved for restrictions on \({\mathbb {S}}^{2}\) of affine maps of \({\mathbb {R}}^3\), see (C.5) in “Appendix C”),
 (3.5)
(3.5)that is, \(\varepsilon (u)=1-|V_3(u)|\). This is something that could also be seen just by using the isoperimetric inequality in this case. Hence, for globally short maps only the excess in volume is present in the right hand side of the stability estimate (1.3).
- (ii):
-
On the other hand, if \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) is volume-increasing in the sense that \(|V_3(u)|\ge 1\), then \(\varepsilon (u)=0\), and only the isometric deficit \(\delta (u)\) is present in the right hand side of (1.3).
- (iii):
-
In all other cases, i.e., if \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) is not globally short and not volume-increasing, both deficits are present in the estimate. It is also immediate that one cannot have simultaneously a globally short map u that is volume-increasing, unless u is a rigid motion of \({\mathbb {S}}^{2}\), something that can be directly verified by checking the equality cases in (3.5).
As we also mentioned in the Introduction, (1.3) is optimal in the norm appearing on the left hand side and the deficits on the right hand side, i.e., the exponent 1 with which \(\delta (u)\) and \(\varepsilon (u)\) appear in the estimate cannot generically be improved. Examples showing the optimality of the exponents can easily be constructed even in dimension \(n=2\), where the exact analogue of Theorem 1.2 becomes
Proposition 3.2
There exists a constant \(c_0>0\) so that for every \(u\in W^{1,2}({\mathbb {S}}^1;{\mathbb {R}}^2)\) there exists \(O\in O(2)\) such that

Here, \(\partial _\tau u\) denotes the tangential derivative of u along \({\mathbb {S}}^1\). The previous proposition can be proven in exactly the same way as Theorem 1.2, following the arguments of the next subsections. As the reader might observe later, the Lipschitz truncation argument of Sect. 3.1 is even simpler in the case \(n=2\), because the signed volume  is of first order in \(\partial _\tau u\).
is of first order in \(\partial _\tau u\).
Keeping the notation \(\delta (u)\) and \(\varepsilon (u)\) for the isometric and the isoperimetric deficit also when \(n=2\), two instructive examples for the optimality of the exponents are given in the next remark.
Remark 3.3
- (i):
-
For \(0<\sigma \ll 2\pi \), let \(u_{\sigma }:{\mathbb {S}}^1\mapsto {\mathbb {R}}^2\) be defined in polar coordinates via
$$\begin{aligned} u_{\sigma }(\theta ):=\left\{ \begin{array}{lr} (\cos \theta ,\sin \theta );\quad 0\le \theta<\frac{3\pi }{2} -\frac{\sigma }{2} ,\\ \left( \cos \theta ,2\sin \left( \frac{3\pi }{2}-\frac{\sigma }{2}\right) -\sin \theta \right) ;\quad \frac{3\pi }{2}-\frac{\sigma }{2} \le \theta<\frac{3\pi }{2}+\frac{\sigma }{2}\ \\ (\cos \theta ,\sin \theta );\quad \frac{3\pi }{2} +\frac{\sigma }{2}\le \theta <2\pi \end{array}\right\} . \end{aligned}$$(3.7)For each \(\sigma \in [0,2\pi )\) the map \(u_{\sigma }\) is isometric, being essentially the identity transformation, except for a small circular arc of angle \(\sigma \), where it is a flip with respect to the horizontal line at height \(y_0=\sin \left( \frac{3\pi }{2}-\frac{\sigma }{2}\right) \). Hence, \(\delta (u_\sigma )=0\) for every \(\sigma \in [0,2\pi )\). Obviously, \(\partial _\tau u_{\sigma }\rightarrow \partial _\tau \mathrm{id}_{{\mathbb {S}}^1}\) strongly in \(L^2({\mathbb {S}}^1;{\mathbb {R}}^2)\) as \(\sigma \rightarrow 0^+\), and one can easily obtain that

On the other hand, using elementary plane-geometry formulas for the area of circular triangles, we can compute the area of the double arc-region of the unit disc missed by \(u_{\sigma }\), so that also
$$\begin{aligned} \varepsilon (u_{\sigma })=\frac{2}{\pi }\left( \pi \cdot \frac{\sigma }{2\pi }-\frac{1}{2}\sin {\sigma }\right)&=\frac{1}{\pi }(\sigma -\sin {\sigma })={\mathcal {O}} ({\sigma }^3), \\&\quad \mathrm{for}\ 0<\sigma \ll 2\pi , \end{aligned}$$which reveals the optimality of the exponent of \(\varepsilon (u)\) in the estimate (3.6).
- (ii):
-
Identify now \({\mathbb {S}}^1\) with the interval [0, 1] by identifying the endpoints. For \(0<\sigma \ll 1\), consider the maps \(f_{\sigma }:[0,1]\mapsto [0,1]\), defined as follows.
$$\begin{aligned} f_{\sigma }(t):=\left\{ \begin{array}{lr} t;\quad 0\le t<\sigma ,\\ 2{\sigma }-t; \quad \sigma \le t<2\sigma , \\ -\frac{2\sigma }{1-2\sigma }+\frac{1}{1-2\sigma }t;\quad 2\sigma \le t<1 \end{array}\right\} , \end{aligned}$$(3.8)and let \(u_{\sigma }:{\mathbb {S}}^1\mapsto {\mathbb {S}}^1\) be the corresponding maps defined on the unit circle. Obviously, \(\varepsilon (u_{\sigma })=0\) for every \(\sigma \in [0,2\pi )\). Geometrically, the maps \(u_{\sigma }\) travel back and forth, and produce a triple cover of a small \({\sigma }\)-arc, locally stretching \({\mathbb {S}}^1\). With similar calculations as before,

Moreover,
$$\begin{aligned} \delta ^2(u_{\sigma })&\sim \int _{0}^{1}\Big |\big (|f'_{\sigma }(t)|-1\big )_+ \Big |^2=\int _{2\sigma }^{1}\left( \frac{1}{1-2\sigma }-1\right) ^2 \sim \frac{4{\sigma }^2}{1-2{\sigma }}\\&\sim {\sigma }^2\big (1+{\mathcal {O}}(\sigma )\big )={\mathcal {O}} ({\sigma }^2), \quad \mathrm{for}\ 0<\sigma \ll 1 , \end{aligned}$$which reveals the optimality of the exponent of \(\delta (u)\) in the estimate (3.6) in the generic setting. The geometric reason behind this, is the fact that the deficit \(\delta (u)\) (as well as the full \(L^2\)-isometric deficit \(\delta _{\mathrm{isom}}(u)\)) does not penalize changes in the orientation neither extrinsically, i.e., flips in ambient space, nor intrinsically, when u is seen as a map from the sphere onto its image.
When \(n=3\) (and also in higher dimensions) one can construct similar examples as in (3.7), (3.8). For instance, in the first case one can consider maps that are the identity outside a small geodesic ball of \({\mathbb {S}}^{n-1}\) and inside being again flips in \({\mathbb {R}}^n\) with respect to the appropriate affine hyperplane. In the second case, one can rotate the previous one-dimensional example around a fixed axis.
We are now ready to present the proof of Theorem 1.2 in steps. For the most part, by straightforward modifications that mainly regard the change of some dimensional constants in the estimates and of some purely algebraic expressions, the arguments are valid in all dimensions, and can be used to prove Theorem 1.3 as well. We will come back to that issue in Sect. 3.4.
3.1 Reduction to Lipschitz mappings
As in the pioneering geometric rigidity result of G. Friesecke, R.D. James and S. Müller (cf. [11, Theorem 3.1]), the first step is to justify why it suffices to work with maps with a universal upper bound on their Lipschitz constant. This is achieved through the use of the following standard truncation lemma.
Lemma 3.4
There exists \(c>0\) so that for every \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) and every \(M>0\), there exists \(u_M\in W^{1,\infty }({\mathbb {S}}^{2};{\mathbb {R}}^3)\) such that
-
(i)
\(\Vert \nabla _{T}u_M\Vert _{L^{\infty }}\le cM\) ,
-
(ii)
\({\mathcal {H}}^{2}\big (\{x\in {\mathbb {S}}^{2}:u(x)\ne u_M(x)\}\big )\le \frac{c}{M^2}\int _{\{|\nabla _{T}u|>M\}}|\nabla _{T}u|^2\) ,
-
(iii)
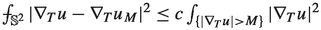 .
.
The proof of this lemma can be performed as for the corresponding statement in the bulk (cf. [11, Proposition A.1]), since it relies basically on a partition of unity argument. With the use of it we can now prove the following.
Lemma 3.5
For \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) let \(u_M\) be its Lipschitz truncation of Lemma 3.4 for \(M:=2\sqrt{2}\). Then,
Proof
If \(\delta (u)>1\), recalling the definitions of the deficits in (3.2)–(3.4), we trivially have

and
so we may assume without loss of generality that \(0\le \delta (u)\le 1\). With the notation we have employed in (3.1), \(|\nabla _{T}u|^2=\sigma _1^2+\sigma _2^2\le 2\sigma _2^2\), and therefore in this case we also have the upper bound

By a standard argument, using Lemma 3.4, we also obtain

Indeed, in the set \(\{x\in {\mathbb {S}}^2:|\nabla _{T}u(x)|>M:=2\sqrt{2}\}\) we have \(\sigma _2\ge \frac{1}{\sqrt{2}}|\nabla _{T}u|> 2\), so in this set we can estimate pointwise,
and then the final estimates in (3.11) follow immediately.
For the first estimate in (3.9) the argument is now elementary. Labelling \(0\le \sigma _{M,1}\le \sigma _{M,2}\) the eigenvalues of \(\sqrt{\nabla _{T}u_M^t\nabla _{T}u_M}\), using (3.11) and the fact that \(\{u_M=u\}\subseteq \{\nabla _{T}u_M=\nabla _{T}u\}\) in the \({\mathcal {H}}^2\)-a.e. sense, we can estimate
For the second desired estimate in (3.9) we observe that if \(\big |V_3(u_M)\big |>1\) then \(\varepsilon (u_M)=0\le \varepsilon (u)\), so we may assume without loss of generality that \(\big |V_3(u_M)\big |\le 1\). Then,
i.e., it suffices to control the absolute value of the difference between the corresponding signed volumes. Towards this end, denoting by

one can easily verify that
where

We can now estimate each term on the right hand side of (3.15) separately. For the first one, by the isoperimetric inequality (see (1.9) for \(n=3\)) and the second estimate in (3.11), we obtain

To estimate the terms \((R_i(u,u_M))_{i=1,\dots ,4}\) we can now use the properties of the Lipschitz truncation \(u_M\) provided by Lemma 3.4, the Cauchy–Schwarz inequality and the sharp Poincare inequality on \({\mathbb {S}}^{2}\) (see (C.5) in “Appendix C”), as well as the estimates (3.10) and (3.11), in order to estimate each of the remaining terms in (3.15) as follows.
By (3.16)–(3.18), and since we have assumed without loss of generality that \(0\le \delta (u)\le 1\), the expansion (3.15) implies that
and then (3.13) yields the desired estimate (3.9) for the isoperimetric deficit. \(\square \)
In view of Lemma 3.5, fixing from now on \(M:=2\sqrt{2}\), we easily see that if the estimate (1.3) holds true for the Lipschitz map \(u_M\) for some \(O\in O(3)\), then it also holds true for u with the same O, up to changing the constant in its right hand side. It therefore suffices to prove Theorem 1.2 for maps \(u\in W^{1,\infty }({\mathbb {S}}^{2};{\mathbb {R}}^3)\) whose Lipschitz constant is apriori bounded from above by cM, where \(c>0\) is the constant of Lemma 3.4.
3.2 Further reduction to maps \(W^{1,2}\)-close to the \(\mathrm{id}_{{\mathbb {S}}^{2}}\)
Having reduced our attention to maps that enjoy an apriori Lipschitz bound, we show in this subsection that for our purposes, we can further assume without loss of generality that the maps in consideration are sufficiently close to the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) in the \(W^{1,2}\)-topology. To do so, we first prove a qualitative analogue of Theorem 1.2. Recalling the notations introduced in (3.1), (3.4) and (3.14), we have.
Lemma 3.6
Let \((u_k)_{k\in {\mathbb {N}}}\subset W^{1,\infty }({\mathbb {S}}^{2};{\mathbb {R}}^3)\) be such that \(\underset{k\in {\mathbb {N}}}{\mathrm{sup}}\ \Vert \nabla _{T}u_k\Vert _{L^{\infty }}\le cM\), and suppose that
Then, there exists \(O\in O(3)\) so that up to a non-relabeled subsequence,
Proof
We can obviously assume without loss of generality that  for all \(k\in {\mathbb {N}}\). Hence, the sequence \((u_k)_{k\in {\mathbb {N}}}\) is uniformly bounded in \(W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\), and up to passing to a non-relabeled subsequence, converges weakly in \(W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) and also pointwise \({\mathcal {H}}^{2}\)-a.e. to a map \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) with \(\overline{u}=0\). By lower semicontinuity of the Dirichlet energy under weak \(W^{1,2}\)-convergence, we further have that
for all \(k\in {\mathbb {N}}\). Hence, the sequence \((u_k)_{k\in {\mathbb {N}}}\) is uniformly bounded in \(W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\), and up to passing to a non-relabeled subsequence, converges weakly in \(W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) and also pointwise \({\mathcal {H}}^{2}\)-a.e. to a map \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) with \(\overline{u}=0\). By lower semicontinuity of the Dirichlet energy under weak \(W^{1,2}\)-convergence, we further have that

The last inequality in (3.22) is justified by the following estimates.

In a similar manner, we can use again the assumption that \(\mathop {\mathrm{sup}}\nolimits _{k\in {\mathbb {N}}}\ \Vert \nabla _{T}u_k\Vert _{L^{\infty }}\le cM\), and the fact that the determinant is a Lipschitz function, to estimate also

Since \(0\le 1-\varepsilon (u_k)\le \big |V_3(u_k)\big |\) and \(\overline{u_k}=0\), by the sharp Poincare inequality on \({\mathbb {S}}^{2}\) (see again (C.5) in “Appendix C”) and the estimates (3.23), (3.24), we obtain

By the assumption (3.20), and since \(u_k\rightarrow u\) strongly in \(L^2({\mathbb {S}}^{2};{\mathbb {R}}^3)\), we can let \(k\rightarrow \infty \) in (3.25), to obtain

Hence, the limiting map u is such that  , and by (3.22) and (3.26) it also satisfies
, and by (3.22) and (3.26) it also satisfies

By the equality case in the sharp Poincare inequality on \({\mathbb {S}}^{2}\) (since the first nontrivial eigenfunctions of \(-\Delta _{{\mathbb {S}}^{2}}\) are the coordinate functions, cf. “Appendix C”), we deduce from (3.27) that \(u(x)=Ax\) for some \(A\in {\mathbb {R}}^{3\times 3}\) with \(|A|^2=3\). In particular, equalities are achieved in (3.22), and therefore \(u_k\rightarrow u:=A\mathrm{id}_{{\mathbb {S}}^{2}}\) in the strong \(W^{1,2}\)-topology.
To show that \(A\in O(3)\), we argue as follows. Having established the strong \(W^{1,2}\)-convergence of \((u_k)_{k\in {\mathbb {N}}}\) towards u, up to a further non-relabeled subsequence we can assume now that \(\nabla _{T}u_k\rightarrow \nabla _{T}u\) also pointwise \({\mathcal {H}}^{2}\)-a.e. on \({\mathbb {S}}^{2}\) and therefore, using the assumption that \(\Vert \nabla _{T}u_k\Vert _{L^\infty }\le cM\) for every \(k\in {\mathbb {N}}\),
Using a variant of Lebesgue’s Dominated Convergence Theorem in the assumption that \(\lim _{k\rightarrow \infty }\varepsilon (u_k)=0\) and (3.28), allows us to conclude. Indeed,

i.e., \(|\mathrm{det}A|\ge 1\). If we now perform the polar decomposition \(A=O\sqrt{A^tA}\), where \(O\in O(3)\), and label \(0\le \alpha _1\le \alpha _2\le \alpha _3\) the eigenvalues of \(\sqrt{A^tA}\), by the arithmetic mean-geometric mean inequality we get
and equality in this algebraic inequality implies that \(\alpha _1=\alpha _2=\alpha _3=1\), i.e., \(O:=A\in O(3)\). \(\square \)
As an immediate consequence of the Lemmata 3.5 and 3.6, we obtain the following.
Corollary 3.7
It suffices to prove Theorem 1.2 for maps

where \(c>0\) is the constant of Lemma 3.4, \(M:=2\sqrt{2}\) and \(0<\theta \ll 1\) is a sufficiently small constant that will be suitably chosen later.
Proof
The proof is a standard contradiction argument. Indeed, suppose that we have proven Theorem 1.2 for maps in \({\mathcal {A}}_{M,\theta }\) for some \(\theta \in (0,1)\) sufficiently small. According to the Lipschitz truncation argument provided by Lemma 3.5, for the general case it suffices to prove that

whenever the denominator above is non-zero. Arguing by contradiction, suppose that the latter is false. Then, for every \(k\in {\mathbb {N}}\) there exist \(u_k\) with mean value 0, Lipschitz norm bounded by cM, \(\delta (u_k)+\varepsilon (u_k)>0\), and  , such that
, such that

In particular,

and letting \(k\rightarrow \infty \) we see that along this sequence, \(\lim _{k\rightarrow \infty }(\delta (u_k)+\varepsilon (u_k))=0\). By Lemma 3.6 and up to passing to a subsequence, we can find \(O_0\in O(3)\) so that \(u_k\rightarrow O_0\mathrm{id}_{{\mathbb {S}}^{2}}\) strongly in \(W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\). Without loss of generality (up to considering \(O_0^tu_k\) instead of \(u_k\) if necessary) we can also suppose that \(O_0=I_3\), so there exists \(k_0:=k_0(\theta )\in {\mathbb {N}}\) such that
i.e., \(u_k\in {\mathcal {A}}_{M,\theta }\) for all \(k\ge k_0\). Therefore, by assumption, there should exist \((R_k)_{k\ge k_0}\subset O(3)\) (and actually in SO(3)) such that

which contradicts (3.30). \(\square \)
3.3 Proof of the local version of Theorem 1.2
By the reductions we have performed in the previous two subsections, we are left with proving a local version of Theorem 1.2. This will be done by perturbing quantitatively the idea of proof of Lemma 3.6.
Proposition 3.8
There exists a constant \(\theta \in (0,1)\) so that for every \(u\in {\mathcal {A}}_{M,\theta }\) (defined in (3.29)), there exists \(R\in SO(3)\) such that

Proof
First of all, it obviously suffices to prove (3.31) in the regime where both deficits are sufficiently small, say
for some absolute constants \(\delta _0, \varepsilon _0>0\) which will also be chosen sufficiently small later. By using (3.23) with u instead of \(u_k\), we have

and therefore (3.25), with u instead of \(u_k\), would now give us

Since by (C.5) we have  , we can rearrange the terms and use (3.32) to arrive at the estimate
, we can rearrange the terms and use (3.32) to arrive at the estimate

the first inequality in which, is justified as follows. Let \(u_h:\overline{B_1}\mapsto {\mathbb {R}}^3\) be the harmonic continuation of u in the interior of \(B_1\), being taken componentwise. The quantity in the middle of (3.33) is the deficit of u in the \(L^2\)-Poincare inequality for maps with zero average on \({\mathbb {S}}^{2}\). For every \(k\in {\mathbb {N}}\), let \(H_{k}\) be the subspace of \(W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) consisting of vector fields whose components are all k-th order spherical harmonics (see also “Appendix C”), so that one has the orthogonal (with respect to the \(W^{1,2}\)-inner product) decomposition \(W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)=\bigoplus _{k=0}^\infty H_{k}\). Let also \(\Pi _{k}\) be the corresponding orthogonal projection. In our case of consideration,  , and it is straightforward to check that \(\Pi _{1} u=\nabla u_h(0)x\). Since the first non-trivial eigenvalue of the Laplace-Beltrami operator on \({\mathbb {S}}^{2}\) is \(\lambda _{1}=2\) and the second one is \(\lambda _{2}=6\) (see (C.2)), by orthogonally decomposing \(u=\Pi _1u+(u-\Pi _1u)\), we have
, and it is straightforward to check that \(\Pi _{1} u=\nabla u_h(0)x\). Since the first non-trivial eigenvalue of the Laplace-Beltrami operator on \({\mathbb {S}}^{2}\) is \(\lambda _{1}=2\) and the second one is \(\lambda _{2}=6\) (see (C.2)), by orthogonally decomposing \(u=\Pi _1u+(u-\Pi _1u)\), we have

Hence, the only thing that is left to be justified in order to prove (3.31), is why in (3.33) the matrix
can be replaced by a matrix \(R\in SO(3)\). In that respect, observe that by the mean-value property of harmonic functions, the basic \(L^2\)-estimate C.6 (whose simple proof is given at the end of “Appendix C”) applied to the function \(u-\mathrm{id}_{{\mathbb {S}}^{2}}\), and (3.29), we obtain

In particular, if \(\theta \in (0,1)\) is sufficiently small, (3.36) directly implies that
Using the polar decomposition \(A=R_0\sqrt{A^tA}\) for some \(R_0\in SO(3)\), the last inequality in (3.37) (in particular the fact that \(\mathrm{det}A>0\)) and (3.36) yield
Labelling \(0<\alpha _1\le \alpha _2\le \alpha _3\) the eigenvalues of \(\sqrt{A^tA}\), and setting
the inequality (3.38) can be rewritten as
The key observation now is that when \(\theta \in (0,1)\) is sufficiently small, a map \(u\in {\mathcal {A}}_{M,\theta }\) satisfies the estimate
The proof of (3.41) is a bit more involved, and is therefore presented separately in Lemma 3.9. Let us assume for the moment its validity, and see how to finish the proof of (3.31). With the notations introduced in (3.35) and (3.39), we can write
expand the polynomial in the eigenvalues and use (3.40), to obtain
Since \(0<\tfrac{\theta }{3\sqrt{2}}<\tfrac{1}{3\sqrt{2}}<\tfrac{1}{4}\), after rearranging terms in (3.42) and using (3.41), we get
In order to handle the term \(\left( \lambda +\frac{\lambda ^2}{2}\right) \), we proceed as follows. Using again the mean value property of harmonic functions, (C.6) applied to u now, and the outcome of (3.23) with u instead of \(u_k\) here, we can estimate

With the notations introduced in (3.35) and (3.39) we have
and the last identity, together with (3.44), implies that
Since \(\lambda \) does not necessarily have a sign, we distinguish two cases:
- \(\mathrm{(i)}\):
-
In the case \(\lambda \le 0\), and since by (3.40) \(|\lambda |\le \sqrt{3}{\Lambda }\le \frac{3}{\sqrt{2}} \theta \ll 1\), the term in the first parenthesis on the right hand side of (3.43) is estimated by
$$\begin{aligned} \lambda +\frac{\lambda ^2}{2}\le \lambda +\frac{3\theta }{2\sqrt{2}}| \lambda |=\left( 1-\frac{3\theta }{2\sqrt{2}}\right) \lambda \le 0 , \end{aligned}$$since by choosing \(\theta \in (0,1)\) even smaller if necessary, we can also achieve \(1-\frac{3\theta }{2\sqrt{2}}>0\). The term \((\lambda +\frac{\lambda ^2}{2})\) is therefore nonpositive in this case, and (3.43) gives
$$\begin{aligned} \mathrm{dist}^2\big (A,SO(3)\big )=\Lambda ^2\le 4c\Big (\delta (u) +\varepsilon (u)\Big ). \end{aligned}$$ - \(\mathrm{(ii)}\):
-
In the case \(\lambda > 0\), by (3.45) we have \(0<\lambda \le c\delta (u)\), so again (3.43) together with (3.32) imply that
$$\begin{aligned} \mathrm{dist}^2\big (A,SO(3)\big )=\Lambda ^2 \lesssim \delta (u) +\delta ^2(u)+c\big (\delta (u)+\varepsilon (u)\big )\lesssim \delta (u)+\varepsilon (u) . \end{aligned}$$
In both cases, we obtain
and combining (3.46) with (3.33) allows us to deduce (3.31) with \(R:=R_0\in SO(3)\), and conclude. \(\square \)
To complete the arguments, we finally give the proof of the estimate (3.41), which for convenience of the reader we recall in the next lemma.
Lemma 3.9
Let \(u\in {\mathcal {A}}_{M,\theta }\), defined in (3.29). Then, the matrix \(A:=\nabla u_h(0)\) (see (3.35)) satisfies
where \(\delta (u)\) and \(\varepsilon (u)\) are as always defined by (3.1) and (3.4) respectively, and are here supposed to further satisfy (3.32) .
Proof
The main trick is to write the signed-volume in the isoperimetric deficit \(\varepsilon (u)\) as the corresponding bulk integral in \(B_1\). In particular, using the identity (B.1) (which we prove in “Appendix B”), we have

where
By the fact that \(u\in {\mathcal {A}}_{M,\theta }\) and (3.37), the map w also satisfies

and we will not distinguish further between the universal constants c and \(\tilde{c}\). Because of (3.33), (3.35) and (3.37), we actually get

Now, in the rightmost hand side of (3.48) we can use the expansion of the determinant around \(I_3\), i.e., the identity (B.2) which is proved in “Appendix B”, according to which,

where the quadratic form \(Q_{V_3}(w)\) is explicitly given in (B.3). Notice that the linear term is vanishing, because the definitions of \(A:=\nabla u_h(0)\) and w in (3.49), together with the mean value property of harmonic functions, imply that

For the higher order terms one can argue as follows. Recalling the notation \(\Pi _k\) for the projections onto the subspaces \(H_k\) of the k-th order spherical harmonics (see the comments after (3.33)), we note that (3.49) and (3.50) directly imply that \(\Pi _0w=\Pi _1w=0\). Hence, by the Cauchy–Schwarz inequality and the sharp Poincare inequality on \({\mathbb {S}}^{2}\) for w (see the comment just below (C.5)), we obtain

and by Wente’s isoperimetric inequality (see (1.9) for \(n=3\)),

Therefore, by (3.54), (3.55) and (3.51), together with the assumption (3.32), we estimate

In particular, since \(\mathrm{det}A>0\) (see (3.37)), by (3.48), the expansion in (3.52), (3.53) and (3.56), we deduce that \(V_3(u)>0\), and we can finally consider two cases:
- (i):
-
If \(V_3(u)>1\implies \varepsilon (u)=0\), then by combining (3.48) with (3.52) and (3.53), rearranging terms, and then using again (3.37), (3.56), the isoperimetric inequality and (3.23) with u instead of \(u_k\) here, we obtain the estimate

- (ii):
-
If \(0\le V_3(u)\le 1\), then we can again similarly estimate,

This finishes the proof of (3.47) in both cases, and allows us to conclude.
\(\square \)
3.4 The generalization to dimensions \(n\ge 4\): Proof of Theorem 1.3
By following closely the steps of proof of Theorem 1.2, one can also prove its generalization in dimensions \(n\ge 4\), i.e., Theorem 1.3. Regarding the extra assumption on an apriori bound in the \(L^{2(n-2)}\)-norm of \(\nabla _{T}u\) in the latter, let us first make the following short remark. When \(n=3\), \(n-1=2(n-2)=2\) and the assumption that \(\nabla _{T}u\) is apriori bounded in \(L^2\) is obsolete in this case, since we have anyway seen that it suffices to prove Theorem 1.2 for maps \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) for which \(0<\delta (u)\ll 1\), which trivially implies the bound \(\Vert \nabla _{T}u\Vert _{L^2}\le \sqrt{10}\) (recall (3.10)). In higher dimensions, the assumption is imposed by the growth behaviour of the signed-volume term with respect to \(\nabla _{T}u\).
Indeed, as we will see next, apart from the obvious differences in the proof due to the change in dimension, the only essential difference appears when we are trying to implement the Lipschitz truncation argument of Sect. 3.1, in order to control both the isometric and the isoperimetric deficit of the Lipschitz truncated map in terms of the ones of the original map u.
Proof of Theorem 1.3
Let \(n\ge 4\), \(M>0\) and \(u\in \dot{W}^{1,2(n-2)}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) with \(\Vert \nabla _{T}u\Vert _{L^{2(n-2)}}\le M\). Applying the analogue of Lemma 3.4 in \(W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) for \(M_n:=2\sqrt{n-1}\), we obtain again \(u_{M_n}\in W^{1,\infty }({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) with \(\Vert \nabla _{T}u_{M_n}\Vert _{L^\infty }\lesssim M_n\) and for which, exactly as in the estimates (3.12) (with \(\sigma _{M_n,n-1}\) in the place of \(\sigma _{M,2}\) now) and (3.13) of Lemma 3.5,
Since \(V_n\) is now of order \(n-1>2\) in \(\nabla _{T}u\), it is of course not expected that one can have an estimate of the form of (3.19) without any further assumption, since \(V_n(u)\) is not even finite if u does not belong to \(W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) at least. Nevertheless, under the imposed assumption that \(\Vert \nabla _{T}u\Vert _{L^{2(n-2)}}\le M\), the difference of the corresponding signed volumes in (3.57) can be controlled as follows. Assuming again without loss of generality that \(0<\delta (u)\le 1\), adopting the notation in (3.14) and using the fact that \(\Vert \nabla _{T}u_{M_n}\Vert _{L^\infty }\lesssim M_n:=2\sqrt{n-1}\), as well as (3.11) (in dimension \(n\ge 4\) now), we can estimate

where

By the Sobolev embedding and our assumption, we further have
Therefore, by the fact that \(\{u_{M_n}=u\}\subseteq \{\nabla _{T}u_{M_n}=\nabla _{T}u\}\) \({\mathcal {H}}^{n-1}\)-a.e., (3.60), the first inequality in (3.11) (in dimension \(n\ge 4\)), and the assumption that \(\Vert \nabla _{T}u\Vert _{L^{2(n-2)}}\le M\), the remainder term in (3.59) can be estimated further by
Therefore, under this extra assumption for \(n\ge 4\), in view of (3.58) and (3.61), (3.57) implies again that
Hence, under the assumption that \(\Vert \nabla _{T}u\Vert _{L^{2(n-2)}}\le M\) when \(n\ge 4\), we can again reduce to proving Theorem 1.3 for Lipschitz maps that enjoy an apriori dimensional upper bound on their Lipschitz constant. The proof can then be continued exactly as in Sects. 3.2 and 3.3, with the obvious modifications in the dimensional constants and the algebraic expressions involved.
For instance, and just for the sake of clarity, we note that in this higher dimensional setting,  should be replaced in the corresponding arguments by
should be replaced in the corresponding arguments by  , but the arguments go through exactly in the same way, since \(n-1\) is both the norm of the gradient of isometric maps from \({\mathbb {S}}^{n-1}\) to \({\mathbb {R}}^n\) and also the first nontrivial eigenvalue of \(-\Delta _{{\mathbb {S}}^{n-1}}\) (the second being 2n, see “Appendix C” and (3.34)). In this respect, the estimate (3.33) should of course be replaced by
, but the arguments go through exactly in the same way, since \(n-1\) is both the norm of the gradient of isometric maps from \({\mathbb {S}}^{n-1}\) to \({\mathbb {R}}^n\) and also the first nontrivial eigenvalue of \(-\Delta _{{\mathbb {S}}^{n-1}}\) (the second being 2n, see “Appendix C” and (3.34)). In this respect, the estimate (3.33) should of course be replaced by

and analogously to (3.52), the expansion of the signed-volume around the identity is now

Modulo these changes, the proof remains essentially unchanged, which is left to the reader to verify. \(\square \)
Remark 3.10
An interesting question would be whether for \(n\ge 4\) the apriori bound on the \(L^{2(n-2)}\)-norm of \(\nabla _{T}u\), imposed as an assumption in Theorem 1.3, can be replaced by one in an \(L^p\)-norm for some \(p\in (n-1,2(n-2))\). The previous approach indicates however that the exponent \(2(n-2)=(n-1)+(n-3)\) in the assumption is the sharpest one.
Indeed, let us assume that \(\left\| \nabla _{T}u\right\| _{L^{n-1 +\gamma }}\le M\) for some \(\gamma \in (0,n-3)\) and \(M>0\). Then, for \(\alpha \in (0,n-1)\) and \(p>1\), we can apply Hölder’s inequality and use again the analogues of the estimates in (3.11) for \(n\ge 4\), to deduce as before that
As long as \(\alpha p\le 2\), by Hölder’s inequality again,
and (3.11) (for \(n\ge 4\)) would finally give us
as long as \(1\le \frac{p(n-1-\alpha )}{p-1}\le n-1+\gamma \). Therefore, by (3.63) and following closely the estimates used to arrive at (3.58) and (3.61), we deduce that the optimal exponent with which \(\delta (u)\) can appear in (3.62) through these estimates is exactly
But this value should also satisfy the inequality \(\alpha p'\le 2\), which implies that
for \(0<\gamma <n-3\), i.e., the exponent of \(\delta (u)\) in (3.62) would become suboptimal.
4 Proof of Theorem 1.4
4.1 Reduction to maps \(W^{1,2}\)-close to the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) and linearization of the problem
We recall that for a map \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) with \(V_3(u)\ne 0\), its combined conformal-isoperimetric deficit is denoted by
where \(D_2(u)\), \(V_3(u)\) are as in the statement of Theorem 1.4, and that \({\mathcal {E}}_2(u)=0\) iff u is a Möbius transformation of \({\mathbb {S}}^{2}\), up to a translation vector and a dilation factor.
To pass from the nonlinear deficit \({\mathcal {E}}_2\) to its linearized version, we make use of the following compactness result, whose proof can be found for instance in [4] or [6, Lemma 2.1] (stated on \({\mathbb {R}}^2\) rather than \({\mathbb {S}}^{2}\) therein).
Lemma 4.1
Let \((u_k)_{k\in {\mathbb {N}}}\subset W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) be such that \(V_3(u_k)\ne 0\), and for which
Then, there exist Möbius transformations \((\phi _k)_{k\in {\mathbb {N}}}\) of \({\mathbb {S}}^{2}\), \((\lambda _k)_{k\in {\mathbb {N}}}\subset {\mathbb {R}}_+\) and \(O\in O(3)\), such that

Using this compactness lemma and the invariances of the combined conformal-isoperimetric deficit, with a contradiction argument as the one we used in the proof of Corollary 3.7, one can now prove the following.
Corollary 4.2
It suffices to prove the \(W^{1,2}\)-local version of Theorem 1.4, i.e., to prove it for maps

where \(\theta , \varepsilon _0\in (0,1)\) are sufficiently small constants that will be suitably chosen later.
Proof
The fact that without loss of generality we can assume (i) is obvious because (1.8) is translation invariant. That we can assume property (iii) is also immediate, because for every \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) with \(V_3(u)\ne 0\), choosing \(\lambda :=\Vert \nabla _{T}u\Vert _{L^2}>0\) and \(\phi :=\mathrm{id}_{{\mathbb {S}}^{2}}\) we have that  . Therefore, it suffices to prove the desired estimate in the small-deficit regime.
. Therefore, it suffices to prove the desired estimate in the small-deficit regime.
Suppose now that we have proven Theorem 1.4 for maps in \({\mathcal {B}}_{\theta ,\varepsilon _0}\), but for the sake of contradiction the theorem fails to hold globally. Then, for every \(k\in {\mathbb {N}}\) there exists \(u_k\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) with \(V_3(u_k)\ne 0\) such that for every pair \((\lambda ,\phi )\in {\mathbb {R}}_+\times Conf({\mathbb {S}}^{2})\);

Choosing \((\lambda ,\phi ):=(\Vert \nabla _{T}u_k\Vert _{L^2},\mathrm{id}_{{\mathbb {S}}^{2}})\) we obtain \({\mathcal {E}}_2(u_k)\le \frac{6}{k}\rightarrow 0\), as \(k\rightarrow \infty \). We can then use Lemma 4.1, and argue as in the end of the proof of Corollary 3.7, to arrive at a contradiction for the corresponding maps  . \(\square \)
. \(\square \)
Remark 4.3
Note that \(V_3(u)>0\) whenever \(u\in {\mathcal {B}}_{\theta ,\varepsilon _0}\) with \(\theta \in (0,1)\) sufficiently small. Indeed, recalling the expansions and the estimates (3.15)–(3.18), with the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) in place of \(u_M\) here, we can arrive exactly as in the second half of the proof of Lemma 3.4 (recall (3.19)) at the estimate
Having now reduced to showing Theorem 1.4 for mappings in \( {\mathcal {B}}_{\theta ,\varepsilon _0}\), where \(V_3(u)>0\), we can linearize the initial problem, by making use of the following two lemmata.
Lemma 4.4
Given \(\theta ,\varepsilon _0 \in (0,1)\) sufficiently small, there exists \(\tilde{\theta }\in (0,1)\) sufficiently small accordingly, so that after possibly replacing \(\theta \) with \(\tilde{\theta }\), we can assume that every \(u\in {\mathcal {B}}_{\theta ,\varepsilon _0}\) has the additional property that

Proof
Let \(u\in {\mathcal {B}}_{\theta ,\varepsilon _0}\) (defined in (4.2)) with \(0<\theta ,\varepsilon _0\ll 1\), and set

By the cancellation property  and the sharp Poincare inequality on \({\mathbb {S}}^{2}\) (see (C.5)) we have,
and the sharp Poincare inequality on \({\mathbb {S}}^{2}\) (see (C.5)) we have,

i.e.,
Hence, setting \(\tilde{u}:=\frac{u}{\lambda _u}\), by (4.2) and (4.4) we have

and by using (4.5),
Although the precise value of the new constant \(\tilde{\theta }>0\) is not of major importance, what is more important is that \(\lim _{\theta \rightarrow 0^+}\tilde{\theta } =0\), so that when we will finally choose \(\theta >0\) sufficiently small, \(\tilde{\theta }>0\) will be sufficiently small accordingly. \(\square \)
Lemma 4.5
There exists a constant \(\beta :=\beta (\theta ,\varepsilon _0)>0\) that tends to 0 as \((\theta ,\varepsilon _0)\rightarrow (0,0)\), such that the following holds. If \(u\in {\mathcal {B}}_{\theta ,\varepsilon _0}\) satisfies (4.3) and one sets \(w:=u-\mathrm{id}_{{\mathbb {S}}^{2}}\), then

where

Proof
For u as in the statement of the lemma, property (4.3) can be rewritten as

Then,

Since \(\frac{d^2}{dt^2}\Big |_{t=0}(1+t)^{\frac{3}{2}}=\frac{3}{4}\), we can take \(\theta \in (0,1)\) small enough so that (by (4.2)(ii)) the higher-order term in the expansion (4.9) is estimated by

Regarding the expansion of the signed volume term \(V_3(u)\), as we calculate in detail in Lemma B.1 and by using (4.8), we have
where

Hence, by using the expansions (4.9) and (4.11) in the definition (4.1) of the deficit, we obtain

and after rearranging terms,

Arguing exactly as in (3.54) (with the Poincare inequality being applied with constant \(\frac{1}{2}\) instead of \(\frac{1}{6}\) in this case) and (3.55), and using again (4.2)(ii), we have

Therefore, (4.13), the estimates (4.10) and (4.14) for the remainder terms, and (4.2)(iii) imply that

where the precise value of the constant is \(\beta :=\sqrt{\frac{27}{8}}\varepsilon _0+2^{-3/2} (1+\varepsilon _0)\theta + \frac{\theta ^2}{2}\). \(\square \)
In view of Lemma 4.5, if we thus choose \(\varepsilon _0\in (0,1)\) sufficiently small and then \(\theta \in (0,1)\) sufficiently small accordingly, the last term on the right hand side of (4.6) can be set to be a sufficiently small multiple of the Dirichlet energy of w. Therefore, we can move our focus of attention on the coercivity properties of the resulting quadratic form \(Q_3\) defined in (4.7), which is just the second derivative of the nonlinear combined conformal-isoperimetric deficit \({\mathcal {E}}_2(u)\) at the \(\mathrm{id}_{{\mathbb {S}}^{2}}\). This will be the content of the next subsection.
4.2 On the coercivity of the quadratic form \(Q_3\)
For the most part of this subsection the results hold true in every dimension \(n\ge 3\). Since we will use them also in Sect. 5, where we prove linear stability estimates in all dimensions, we also denote here the ambient dimension 3 with the general letter n (in order to avoid the repetition of the arguments in Sect. 5), and hope that no confusion will be caused to the reader. Our goal is to examine the coercivity properties of the quadratic form \(Q_n\) in (4.7). By the reductions we have performed (see (4.2) and (4.3)), this can be considered in the space

Similarly to the notation introduced in the proof of Proposition 3.8 in Sect. 3.3, for every \(k\ge 1\) we define \(H_{n,k}\) to be the linear subspace of \(H_n\) consisting of those maps in \(H_n\), all the components of which are k-th order spherical harmonics (cf. also “Appendix C”), and also define
so that \(\bigoplus \nolimits _{k=1}^{\infty } \tilde{H}_{n,k}\) is a \(W^{1,2}\)-orthogonal decomposition of the vector space of harmonic maps \(w_h:\overline{B_1}\mapsto {\mathbb {R}}^n\) for which \(w_h(0)=0\) and \(\mathrm{Tr}\nabla w_h(0)=0\), the last identities following immediately from their equivalent formulation on \({\mathbb {S}}^{n-1}\) in (4.15). Actually, for every \(k\ge 1\) we can further consider the \(W^{1,2}(B_1)\)-Helmholtz decomposition
where
and \(\tilde{H}_{n,k,\mathrm{sol}}^{\bot }\) is its orthogonal complement in \(W^{1,2}(B_1;{\mathbb {R}}^n)\). In view of the k-homogeneity of the maps in \(\tilde{H}_{n,k}\) in (4.16), we can write the equivalent to (4.17) \(W^{1,2}\)-decomposition also on \({\mathbb {S}}^{n-1}\), namely
where
and \(H_{n,k,\mathrm{sol}}^{\bot }\) is its \(W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\)-orthogonal complement. Hence, adopting from now on all these notations introduced in (4.15)–(4.20), let us also denote
so that \(N_{n,k}\ = N_{1,n,k}+N_{2,n,k}\).
Recall also that the second derivative of the signed-volume term \(V_n\) at the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\) corresponds to the bilinear form

where the associated linear first-order differential operator A is defined as
For \(n=3\), the expression (4.22) for the bilinear form \(Q_{V_n}(\cdot ,\cdot ):H_n\times H_n\mapsto {\mathbb {R}}\) is essentially derived in the proof of Lemma B.1, see (B.2),(B.3) and (B.9) therein. Another intrinsic calculation for its computation in any dimension is also given in Lemma B.3 at the end of “Appendix B”. The main feature that we are going to use in this subsection is the fine interplay between the operator A and the above defined spaces, as it is properly described in the following.
Lemma 4.6
For every \(k\ge 1\), the operator A defined in (4.23) is a linear self-adjoint isomorphism of the spaces \(H_{n,k,\mathrm{sol}}\) and \(H_{n,k,\mathrm{sol}}^{\bot }\) defined in and after (4.20), with respect to the \(W^{1,2}\)-inner product.
Proof
First of all, it is immediate that A is self-adjoint with respect to the \(L^2\)-inner product in \(H_n\), since it arises as the second derivative of \(V_n\) at the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\), but it is also easy to verify directly after integrating by parts that for any \(v,w\in H_n\),

Note also that, since \((H_{n,k,\mathrm{sol}})_{k\ge 1}\) and \((H_{n,k,\mathrm{sol}}^{\bot })_{k\ge 1}\) are subspaces of the k-th order spherical harmonics, the \(W^{1,2}\)- and the \(L^2\)-inner products restricted on these subspaces are equivalent (see (C.2)). It is also easy to check that for every \(k\ge 1\),
Indeed, as we mention in the beginning of “Appendix C”, for \(k\ge 1\) fixed and \(w \in H_{n,k}\), its harmonic extension \(w_h\) in \(\overline{B_1}\) is an \({\mathbb {R}}^n\)-valued homogeneous harmonic polynomial of degree k, and \( \forall j=1,2,\dots ,n\),
Therefore, the operator A can alternatively be rewritten as
Writing A in terms of the full gradient and divergence operators on \({\mathbb {S}}^{n-1}\) as in (4.25), we see that

and by (4.15),

It is also straightforward to verify that
so \([A(w)]_h\) is also an \({\mathbb {R}}^n\)-valued homogeneous harmonic polynomial of degree k, and therefore its restriction on \({\mathbb {S}}^{n-1}\) is an \({\mathbb {R}}^n\)-valued k-th order spherical harmonic. In total, (4.26)–(4.28) yield the implication in (4.24). Directly from (4.28) one can also verify that A leaves \(H_{n,k,\mathrm{sol}}\) invariant, i.e.,
as well. It remains to be checked that
Indeed, let \(w\in H_{n,k,\mathrm{sol}}\) be such that
Note that since \(w\in H_{n,k,\mathrm{sol}}\) is the restriction on \({\mathbb {S}}^{n-1}\) of an \({\mathbb {R}}^n\)-valued homogeneous harmonic polynomial of degree k (hence smooth up to the boundary), the above equation holds true in the classical sense. Hence, by orthogonality, both the normal and the tangential part of A(w) would have to vanish identically, namely,
By the definition of \(H_{n,k,\mathrm{sol}}\) in (4.20) we have that \(\mathrm{div}w_h\equiv 0\) in \(B_1\), and therefore (4.30) implies that
Testing now the second one of the equations in (4.30) with the vector field w itself, integrating by parts on \({\mathbb {S}}^{n-1}\) and using (4.31), we obtain

i.e., \(w\equiv 0\) on \({\mathbb {S}}^{n-1}\). This concludes the proof of (4.29), and thus the proof of the fact that A is a self-adjoint linear isomorphism of \(H_{n,k,\mathrm{sol}}\). Hence, A leaves \(H_{n,k,\mathrm{sol}}^{\bot }\) invariant as well, and is actually also an isomorphism of it, as we will see next. \(\square \)
As a consequence of Lemma 4.6, each one of the finite-dimensional subspaces \((H_{n,k,\mathrm{sol}})_{k\ge 1}\) and \((H_{n,k,\mathrm{sol}}^{\bot })_{k\ge 1}\) admit an eigenvalue decomposition with respect to A (cf. [17, Chapter 8, Theorem 4.3]).
Theorem 4.7
The following statements hold.
-
(i)
For every \(k\ge 1\), the subspace \(H_{n,k,\mathrm{sol}}\) in (4.20), has an eigenvalue decomposition with respect to the operator A, defined in (4.23), as
$$\begin{aligned} H_{n,k,\mathrm{sol}}=H_{n,k,1}\oplus H_{n,k,2} , \end{aligned}$$(4.33)where \(H_{n,k,1}\) is the eigenspace of A corresponding to the eigenvalue \(\sigma _{n,k,1}:=-k\) and \(H_{n,k,2}\) is the one corresponding to the eigenvalue \(\sigma _{n,k,2}:=1\).
-
(ii)
For every \(k\ge 1\), the subspace \(H_{n,k,3}:=H_{n,k,\mathrm{sol}}^{\bot }\) is an eigenspace with respect to A corresponding to the eigenvalue \(\sigma _{n,k,3}:=k+n-2\) .
Proof
As we have just remarked before the statement of Theorem 4.7, for every \(k\ge 1\) there exists a \(W^{1,2}\)-orthonormal basis of eigenfunctions \(\{w_{n,k,1},\dots ,w_{n,k,N_{1,n,k}}\}\) for the subspace \(H_{n,k,\mathrm{sol}}\) (see also (4.21)) and similarly, \(\{w_{n,k,N_{1,n,k}+1},\dots ,w_{n,k,N_{n,k}}\}\) for \(H_{n,k,\mathrm{sol}}^{\bot }\), i.e., for \(i=1,\dots ,N_{n,k}\), the map \(w_{n,k,i}\) satisfies the eigenvalue equation
For each such eigenvalue \(\sigma _{n,k,i}\) we denote its corresponding eigenspace by \(H_{n,k,i}\). If in (4.34) we take the inner product with the unit normal vector field on \({\mathbb {S}}^{n-1}\), we obtain further that each eigenfunction \(w_{n,k,i}\) satisfies the equation
which in terms of the full divergence can be rewritten as
We now fix the index \(k\ge 1\) and consider all the different possible cases that will allow us to find the eigenvalues of A in the invariant subspaces \(H_{n,k,\mathrm{sol}}\) and \(H_{n,k,\mathrm{sol}}^{\bot }\) respectively.
- (\(a_1\)):
-
Let w be a non-trivial eigenfunction of A in \(H_{n,k,\mathrm{sol}}\), so
$$\begin{aligned} \mathrm{div}w_h= 0 \ \mathrm{in}\ \overline{B_1} \ \ \iff \ \ \mathrm{div}w_h = 0 \ \ \mathrm{on} \ \ {\mathbb {S}}^{n-1}, \end{aligned}$$(4.37)due to (4.16), (4.18) and the \((k-1)\)-homogeneity of \(\mathrm{div}w_h\) in this case. By (4.36) we see that one possibility for (4.37) to hold, is for the eigenvalue \(\sigma =-k\). We thus set \(\sigma _{n,k,1}:=-k\) and label its corresponding eigenspace as
$$\begin{aligned} H_{n,k,1}:=\mathrm{span}\{w_{n,k,1},\dots ,w_{n,k,p_{n,k}}\} , \end{aligned}$$where \(p_{n,k}:=\mathrm{dim}H_{n,k,1}\).
- (\(a_2\)):
-
Let now w be a non-trivial eigenfunction of A in \(H_{n,k,\mathrm{sol}}\), with \(w\in H_{n,k,1}^{\bot }\). Then, in view of (4.36), the only possibility for (4.37) to hold is iff
$$\begin{aligned} \langle w, x \rangle \equiv 0 \ \ \mathrm{on}\ {\mathbb {S}}^{n-1}. \end{aligned}$$(4.38)In this case, w is a tangential vector field and by (4.35) and (4.38), we have \(\mathrm{div}_{{\mathbb {S}}^{n-1}}w\equiv 0\) on \({\mathbb {S}}^{n-1}\), as well. The eigenvalue equation (4.34) reduces then to
$$\begin{aligned} \sigma w=-\sum _{j=1}^n x_j\nabla _Tw^j \ \ \mathrm{on}\ {\mathbb {S}}^{n-1}. \end{aligned}$$(4.39)With the very same calculations that we performed in the proof of Lemma 4.6 (see (4.32)), we can test (4.39) with w, integrate by parts and use (4.38), to obtain

We label this eigenvalue \(\sigma _{n,k,2}:= 1\), and its corresponding eigenspace as
$$\begin{aligned} H_{n,k,2}:=\mathrm{span}\{w_{n,k,p_{n,k}+1},\dots , w_{n,k,N_{1,n,k}}\} , \end{aligned}$$and in this way we are led to the decomposition (4.33).
- (b):
-
Let us now look at eigenfunctions w of A in \(H_{n,k,\mathrm{sol}}^{\bot }\), where the divergence of \(w_h\in \tilde{H}_{n,k}\) in (4.16) does not vanish identically in \(\overline{B_1}\). Since \(w_h\) is an \({\mathbb {R}}^n\)-valued k-homogeneous harmonic polynomial, we have that \(\mathrm{div}w_h\) is a scalar \((k-1)\)-homogeneous harmonic polynomial, and therefore its restriction on \({\mathbb {S}}^{n-1}\) is a scalar \((k-1)\)-spherical harmonic. We can then apply the Laplace-Beltrami operator (see (C.1)) on both sides of (4.36) and use again (4.35), to obtain
$$\begin{aligned}&(k-1)(k+n-3)\mathrm{div}w_h\\&\quad = -\Delta _{{\mathbb {S}}^{n-1}}(\mathrm{div}w_h) = -(\sigma +k)\Delta _{{\mathbb {S}}^{n-1}}\big (\langle w,x\rangle \big )\\&\quad = (\sigma +k)\Big (\langle -\Delta _{{\mathbb {S}}^{n-1}} w,x\rangle -2 \nabla _{T}w:P_T+\langle w, -\Delta _{{\mathbb {S}}^{n-1}} x\rangle \Big )\\&\quad = \Big (k(k+n-2)-2\sigma +(n-1)\Big )(\sigma +k)\langle w, x\rangle \\&\quad = \Big (k(k+n-2)-2\sigma +(n-1)\Big )\mathrm{div}w_h \ \ \mathrm{on}\ {\mathbb {S}}^{n-1}. \end{aligned}$$Since in this case \(\mathrm{div}w_h\) does not vanish identically, we conclude that
$$\begin{aligned} k(k+n-2)-2\sigma +(n-1) = (k-1)(k+n-3)\iff \sigma = k+n-2. \end{aligned}$$We label this eigenvalue as \(\sigma _{n,k,3}:= k+n-2\) and its corresponding eigenspace as \(H_{n,k,3}\). In particular, we have found that \(H_{n,k,\mathrm{sol}}^{\bot }=H_{n,k,3}\).
\(\square \)
Remark 4.8
We have obtained in total the \(W^{1,2}\)-orthogonal decomposition of our space of interest into eigenspaces of A as
It is easy to construct examples showing that except for \(H_{n,1,3}\), none of these eigenspaces are apriori trivial. The triviality of \(H_{n,1,3}\) is a consequence of the fact that we had already scaled properly our initial maps u, so that the corresponding maps w satisfy  (recall (4.15)). Indeed, let \(w(x):=\Lambda x \in H_{n,1,3}\) for some \(\Lambda \in {\mathbb {R}}^{n\times n}\). By assumption,
(recall (4.15)). Indeed, let \(w(x):=\Lambda x \in H_{n,1,3}\) for some \(\Lambda \in {\mathbb {R}}^{n\times n}\). By assumption,

Therefore, \(\mathrm{div}w_h\equiv \mathrm{Tr}\Lambda \equiv 0\) in \(\overline{B_1}\), i.e., \(w\in H_{n,1,\mathrm{sol}}=H_{n,1,3}^{\bot }\), forcing \(w\equiv 0\), and thus, \(H_{n,1,3}=\{0\}\).
The eigenvalue decomposition (4.40) of \(H_n\) into eigenspaces of A is valid for every \(n\ge 3\). In the case of interest of this subsection, i.e., in dimension \(n=3\), it immediately gives the desired coercivity estimate for the quadratic form \(Q_3\) defined in (4.7), with optimal constant. For the rest of this subsection we switch back to denoting the ambient dimension by the number 3. As a consequence of Theorem 4.7, we have
Lemma 4.9
The following statements hold true.
-
(i)
The forms \(Q_{V_3}\) and \(Q_3\), defined in (4.12) and (4.7) respectively, diagonalize on each one of the subspaces \((H_{3,k,i})_{k\ge 1,i=1,2,3}\), i.e., there exist explicit constants \((c_{3,k,i})_{i=1,2,3}\) and \((C_{3,k,i})_{i=1,2,3}\) so that for every \(w\in H_{3,k,i}\),
 (4.41)
(4.41) -
(ii)
For every \(k,l\ge 1\) and \(i,j=1,2,3\) with \((k,i)\ne (l,j)\), the subspaces \(H_{3,k,i}\) and \(H_{3,l,j}\) are also \(Q_{V_3}\)- and \(Q_3\)-orthogonal, i.e., for every \(w_{k,i}\in H_{3,k,i}\) and \(w_{l,j}\in H_{3,l,j}\),
$$\begin{aligned} Q_{V_3}(w_{k,i},w_{l,j})=0 \quad \mathrm{and} \quad Q_3(w_{k,i},w_{l,j})=0. \end{aligned}$$(4.42)
Proof
The proof is immediate. For part (i) of the lemma, if we denote by \(\lambda _{3,k}:=k(k+1)\) the eigenvalues of \(-\Delta _{{\mathbb {S}}^{2}}\) (see (C.2)), then

In particular, for \(i=1,2,3\), if \(w\in H_{3,k,i}\), by the definition (4.22) (for \(n=3\)) and Theorem 4.7, we have

which is precisely the first identity in (4.41) for \(c_{3,k,i}:=\frac{3\sigma _{3,k,i}}{2\lambda _{3,k}}\), and then

where \(C_{3,k,i}:=\tfrac{3}{4}-c_{3,k,i}\). We list below the precise values of the constants, which are important in this case, since we will need to sum up the identities for \(Q_3\) in the subspaces \((H_{3,k,i})_{k\ge 1, i=1,2,3}\), in order to obtain an estimate on the full space \(H_3\).
Part (ii) of the lemma is immediate by the mutual \(W^{1,2}\)-orthogonality of \((H_{3,k,i})_{k\ge 1, i=1,2,3}\). \(\square \)
As an immediate consequence of Lemma 4.9 we obtain the desired estimate for the quadratic form \(Q_3\) defined in (4.7).
Theorem 4.10
For every \(w\in H_3\) (given in (4.15)), the following coercivity estimate holds.

where \(H_{3,0}:=H_{3,1,2}\oplus H_{3,2,3}\) is the kernel of \(Q_3\) in \(H_3\) and \(\Pi _{3,0}\) is the \(W^{1,2}\)-orthogonal projection of \(H_3\) onto \(H_{3,0}\). The constant \(\frac{1}{4}\) in the previous estimate is sharp.
Proof
Having the precise values of the constants \((C_{3,k,i})_{k\ge 1,i=1,2,3}\) in (4.43), we see that \(C_{3,1,2}=C_{3,2,3}=0\), but otherwise it is easy to verify that
Now we can express any \(w\in H_3\) as a Fourier series in terms of the eigenspace decomposition (4.40), i.e.,
Note that, as we have justified in Remark 4.8, \(w_{3,1,3}=0\). Expanding the quadratic form \(Q_3\), and using (4.41), (4.42) and (4.45), we indeed obtain

which finishes the proof of (4.44). \(\square \)
4.3 Proof of the local version of Theorem 1.4
The presence of the \(Q_3\)-degenerate space \(H_{3,0}\) in the coercivity estimate (4.44) is a small but natural obstacle to overcome in order to complete the proof of Theorem 1.4. As we mentioned after the statement of Theorem 1.5 in the Introduction, since \(H_{3,0}\) will eventually turn out to be isomorphic to the Lie algebra of infinitesimal Möbius transformations of \({\mathbb {S}}^{2}\), at an infinitesimal level this basically means the following. Although, by the reductions we have made, the map u is apriori supposed to be \(\theta \)-close to the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) in the \(W^{1,2}\)-topology (recall (4.2)(ii)), there might be another Möbius transformation of \({\mathbb {S}}^{2}\) that is also \(\theta \)-close to the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) and is a better candidate for the nearest Möbius map to u in terms of its combined conformal-isoperimetric deficit \({\mathcal {E}}_2(u)\) in (4.1). Similarly to [10, 21], an application of the Inverse Function Theorem and a topological argument will allow us to identify this more suitable candidate, see the details in the subsequent Lemma 4.13 and its proof. For this purpose, we will need the following characterization of the \(Q_3\)-degenerate subspace \(H_{3,0}\), which is valid in every dimension \(n\ge 3\), and that is why we now switch back to denoting the ambient dimension by n.
Lemma 4.11
The following statements hold true.
-
(i)
The subspace \(H_{n,1,2}\) in (4.33) can be characterized as
$$\begin{aligned} H_{n,1,2}=\big \{w\in H_n: w(x)=\Lambda x,\ \mathrm{where} \ \Lambda \in Skew(n)\big \} , \end{aligned}$$(4.47)and its dimension is \(\mathrm{dim}H_{n,1,2}=\frac{n(n-1)}{2}\). The projection on \(H_{n,1,2}\) is therefore characterized by
$$\begin{aligned} \Pi _{H_{n,1,2}}w=0\iff \nabla w_h(0)=\nabla w_h(0)^t . \end{aligned}$$(4.48) -
(ii)
The subspace \(H_{n,2,\mathrm{sol}}\) in (4.20) can be characterized as
$$\begin{aligned} H_{n,2,\mathrm{sol}}=\left\{ w\in H_n: \begin{array}{lr} \forall k=1,\dots ,n:\ \ w^k(x)=\langle \Lambda ^kx,x\rangle ,\\ \Lambda ^k\in Sym(n): \mathrm{Tr}\Lambda ^k=0,\ \sum _{l=1}^n\Lambda _{lk}^l=0 \end{array}\right\} , \end{aligned}$$(4.49)and thus
$$\begin{aligned} \mathrm{dim}H_{n,2,3}=\mathrm{dim}H_{n,2}-\mathrm{dim}H_{n,2,\mathrm{sol}}=n. \end{aligned}$$The projection on \(H_{n,2,3}\) is therefore characterized by
 (4.50)
(4.50)
Proof
For part (i) of the lemma, if \(w\in H_{n,1,2}\) we can write it as \(w(x)=\Lambda x\) for some \(\Lambda \in {\mathbb {R}}^{n\times n}\). In this space, recalling (4.38),
The characterization (4.48) of the projection \(\Pi _{H_{n,1,2}}\) is then immediate. For part (ii), let \(w\in H_{n,2,\mathrm{sol}}\). By (4.18) and (4.20), its harmonic extension is a homogeneous solenoidal harmonic polynomial of degree 2, so for each \(k=1,\dots ,n\), there exists \(\Lambda ^k\in Sym(n)\) such that
In particular, for each \(k,l=1,\dots ,n\), we can compute
so (4.49) follows directly from (4.51). For the last characterization, i.e., (4.50), we have
and by the mean value property of harmonic functions again, we can indeed equivalently write

\(\square \)
Remark 4.12
It is worth noticing here that simply by counting dimensions,
which is also the dimension of \(Conf({\mathbb {S}}^{2})\) (recall the notation in Sect. 2 and see also Remark A.1 for some more details on this Lie group and its corresponding Lie algebra). We therefore only need to verify that \(H_{3,0}\) (introduced after (4.44)) is actually isomorphic to the Lie algebra of infinitesimal Möbius transformations of \({\mathbb {S}}^{2}\), and then the Inverse Function Theorem can be applied. This is the context of the following.
Lemma 4.13
Given \(\theta , \varepsilon _0 \in (0,1)\) sufficiently small, there exists \(\tilde{\theta } \in (0,1)\) that depends only on \(\theta \) and is sufficiently small as well, so that for every \(u\in {\mathcal {B}}_{\theta ,\varepsilon _0}\) (as in (4.2)) there exists \(\phi \in Conf_+({\mathbb {S}}^{2})\) such that

Proof
Given \(u\in {\mathcal {B}}_{\theta ,\varepsilon _0}\), in view of the characterizations (4.48) and (4.50), let us introduce the map \(\Psi _u:Conf_+({\mathbb {S}}^{2})\mapsto {\mathbb {R}}^{6}\), via

Our goal for (4.52) is essentially to show that \(0\in \mathrm{Im}(\Psi _u)\). To simplify notation, let us also set
Clearly, \(\Psi (\mathrm{id}_{{\mathbb {S}}^{2}})=0\). In order to apply the Inverse Function Theorem, we look at the differential
and prove that it is a non-degenerate linear map. The differential of \(\Psi \) at the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) is easy to compute. Indeed, by the linearity of all the operations involved, for every \(Y \in T_{\mathrm{id}_{{\mathbb {S}}^{2}}}Conf_+({\mathbb {S}}^{2})\), defined via
(see (A.11) in Remark A.1 for the derivation of this representation), and with a slight abuse of notation in the domain of definition of \(\Psi \) in (4.54), we can calculate

It is clear that the harmonic extension in \(B_1\) of Y as in (4.55) is given by the vector field
In particular, (4.57) directly implies that

Therefore, in view of (4.56) and (4.58), we indeed obtain \(\mathrm{ker}(d\Psi |_{\mathrm{id}_{{\mathbb {S}}^{2}}})=\{0\}\), i.e.,
From now on, we denote by \(D_\sigma \) the open ball in the 6-dimensional vector space \(T_{\mathrm{id}_{{\mathbb {S}}^{2}}}Conf_+({\mathbb {S}}^{2})\), centered at 0 (or better said, at \(\mathrm{id}_{{\mathbb {S}}^{2}}\)) and of radius \(\sigma >0\). Since the exponential mapping \(\mathrm{exp}_{\mathrm{id}_{{\mathbb {S}}^{2}}}(\cdot )\) is a local diffeomorphism between a neighbourhood of 0 in \(T_{\mathrm{id}_{{\mathbb {S}}^{2}}}Conf_+({\mathbb {S}}^{2})\) and a neighbourhood of \(\mathrm{id}_{{\mathbb {S}}^{2}}\) in \(Conf_+({\mathbb {S}}^{2})\), we can use the Inverse Function Theorem to find a sufficiently small \(\sigma _0\in (0,1)\) such that for the open neighbourhood
of the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) in \(Conf_+({\mathbb {S}}^{2})\), the map
As a next step, we justify that \(\Psi \) is homotopic to \(\Psi _u\) in \({{\mathcal {U}}}_0\). Indeed, for every \(\phi \in {{\mathcal {U}}}_0\), we can estimate

In the last step of (4.61) we used the general estimate

the last inequality following from the second estimate in (C.7) which is proved in Lemma C.2. Note now that by the conformal invariance of the Dirichlet energy in two dimensions and (4.2)(ii),

By the change of variables formula, (4.2) again, and the Poincare inequality (C.5) (since  ), we also have
), we also have

where
The strict positivity of the constant \(C_1({{\mathcal {U}}}_0)\) in (4.64) is ensured by the fact that we can take the neighbourhood \({{\mathcal {U}}}_0\) to be sufficiently small around \(\mathrm{id}_{{\mathbb {S}}^{2}}\), which amounts to choosing \(\sigma _0\in (0,1)\) sufficiently small (see (4.59) and (4.60)). Hence, (4.61)–(4.64) imply that
We can now continue as in [10, Proposition 4.7]. For the sake of making the proof self-contained, we present the argument here, adapted to our setting.
Recalling the notation \(D_\sigma \) introduced before (4.59), let us consider the family \((\Gamma _s)_{s\in [0,1]}\) of closed hypersurfaces in \(Conf_+({\mathbb {S}}^{2})\), defined by
so that \(\Gamma _0=\{\mathrm{id}_{{\mathbb {S}}^{2}}\}\), and \(\Gamma _1\) is the topological boundary of \({{\mathcal {U}}}_0\) inside the manifold \(Conf_+({\mathbb {S}}^{2})\). Let us define
This is obviously a continuous function of s. Since \(\Psi |_{\Gamma _0}\equiv 0\) and (by (4.60)) \(\Psi |_{{{\mathcal {U}}}_0}\) is a homeomorphism onto its image, by (4.67) we deduce that
Notice that \(m(1)>0\) depends only on \({{\mathcal {U}}}_0\), or equivalently only on \(\sigma _0\). We can thus choose \(\theta \in (0,1)\) sufficiently small (depending on \(\sigma _0\)), so that for the constant \(C({{\mathcal {U}}}_0)\) of (4.65), there holds
and then define
By (4.67) and (4.69) it is clear that \(\lim _{\theta \rightarrow 0^+}s_{\theta }=0\). Let us now consider the linear homotopy between \(\Psi \) and \(\Psi _u\). For every \(t\in [0,1]\) and \(\phi \in \Gamma _{s_\theta }\subseteq {{\mathcal {U}}}_0\subseteq Conf_+({\mathbb {S}}^{2})\), by (4.67), (4.69) and (4.65), we have
In particular, by (4.70) we find that
Since the degree around 0 remains constant through this linear homotopy, if \({{\mathcal {U}}}_{s_\theta }\subseteq {{\mathcal {U}}}_{0}\) is the open neighbourhood around the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) in \(Conf_+({\mathbb {S}}^{2})\) with \(\partial {{\mathcal {U}}}_{s_\theta }=\Gamma _{s_\theta }\), i.e., \({{\mathcal {U}}}_{s_\theta }:=\mathrm{exp}_{\mathrm{id}_{{\mathbb {S}}^{2}}}(D_{s_\theta \sigma _0})\) (recall (4.66)), then
As a consequence of (4.71), (4.53) and the characterizations (4.48), (4.50), there exists a Möbius transformation \(\phi \in {{\mathcal {U}}}_{s_\theta }\subseteq Conf_+({\mathbb {S}}^{2})\), so that
In the same fashion as have estimated in (4.62), and by (4.2)(ii) again,

where
Since all topologies in the finite dimensional manifold \(Conf_+({\mathbb {S}}^{2})\) are equivalent and \(\lim _{\theta \rightarrow 0^+}s_{\theta }=0\), by (4.72) we also have that \(\lim _{\theta \rightarrow 0^+}C_{s_{\theta }}=0\). Hence, we can first take \(\sigma _0\in (0,1)\) small enough and then \(\theta \in (0,1)\) small enough (see also (4.68)), so that after replacing \(u\circ \phi \) with  if necessary to fix its mean value to 0, we have (by using again the conformal invariance of the deficit) that \(u\circ \phi \in {\mathcal {B}}_{\tilde{\theta },\varepsilon _0}\), where \(\tilde{\theta }:=\sqrt{2(\theta ^2+C_{s_\theta })}>0\) is again small accordingly. This finishes the proof of (4.52). \(\square \)
if necessary to fix its mean value to 0, we have (by using again the conformal invariance of the deficit) that \(u\circ \phi \in {\mathcal {B}}_{\tilde{\theta },\varepsilon _0}\), where \(\tilde{\theta }:=\sqrt{2(\theta ^2+C_{s_\theta })}>0\) is again small accordingly. This finishes the proof of (4.52). \(\square \)
4.4 Proof of Theorem 1.4
We can now combine all the previous steps to complete the proof of the main theorem for the conformal case in dimension 3.
Proof of Theorem 1.4
In view of Corollary 4.2, for \(\theta \in (0,1)\) and \(\varepsilon _0\in (0,1)\) that will be chosen sufficiently small in the end, let us consider a map \(u\in {\mathcal {B}}_{\theta ,\varepsilon _0}\). By first using Lemma 4.13 and then Lemma 4.4, we can find a Möbius transformation \(\phi \in Conf_+({\mathbb {S}}^{2})\) such that the map

has all the desired properties, i.e.,

where we have abused notation by not replacing \(\theta \) with \(\tilde{\theta }\). Setting \(\tilde{w}:=\tilde{u}-\mathrm{id}_{{\mathbb {S}}^{2}}\), we can again expand the deficit around the \(\mathrm{id}_{{\mathbb {S}}^{2}}\) and arrive at (4.6). This estimate, together with (4.44) and the fact that \(\tilde{w}\in H_3\) is such that \(\Pi _{3,0}\tilde{w}=0\) (by (4.15) and (4.73)) yield

By Lemma 4.5, we can then choose \(\varepsilon _0\in (0,1)\) small enough and subsequently \(\theta \in (0,1)\) small enough, so that \(\beta \le \frac{1}{8}\), in order to absorb the last term on the right hand side of (4.74) in the one on the left, and conclude for \(\phi \) as above and  . \(\square \)
. \(\square \)
5 Linear stability estimates for \(Isom({\mathbb {S}}^{n-1})\) and \(Conf({\mathbb {S}}^{n-1})\)
As we have seen in the Sect. 4, the key step in proving Theorem 1.4 consists in establishing the corresponding linear estimate, i.e., Theorem 4.10. What we would like to present in this section, is how the eigenvalue decomposition of \(H_n\) into eigenspaces of A, as provided by Theorem 4.7, which is valid in every dimension (actually even in dimension \(n=2\)), can be used to prove the analogous linear estimate for the quadratic form \(Q_n\) introduced in (1.12), also in dimensions \(n\ge 4\). As explained in the Introduction, this quadratic form is associated with the combined conformal-isoperimetric deficit \({\mathcal {E}}_{n-1}\) defined in (1.10) (cf. “Appendix B” for the precise calculations). We discuss in detail this case first, since the proof of the corresponding estimate for the isometric case, i.e., Theorem 1.8, is essentially the same and is discussed in Sect. 5.3.
5.1 Proof of Theorem 1.5
For \(n=3\), Theorem 1.5 is precisely Theorem 4.10, whose proof was given in Sect. 4.2, and actually the optimal constant for the linear estimate (4.44) was calculated. In the higher dimensional case \(n\ge 4\), the quadratic form \(Q_n\) in (1.12) has an extra  -term, and the study of its coercivity properties is slightly more complicated than before.
-term, and the study of its coercivity properties is slightly more complicated than before.
Remark 5.1
An abstract way to obtain the estimate (1.13) of Theorem 1.5 would be to identify the kernel of \(Q_n\) in \(H_n\) (see (4.15)) (and prove that it is exactly the subspace \(H_{n,0}\)) and then use a standard contradiction\(\backslash \)compactness argument (that we describe in Sect. 5.3 for the corresponding result in the isometric case). Notice that \(w\in H_n\) lies in the kernel of the nonnegative quadratic form \(Q_n\) iff \(Q_n(v,w)=0\ \ \forall v\in H_n\), i.e., iff \(w\in H_n\) lies in the kernel of the associated Euler–Lagrange operator
in the sense of distributions. When \(n=3\), the second term in (5.1) is dropping out, and since \({\mathcal {L}}\) leaves the subspaces \((H_{3,k,\mathrm{sol}})_{k\ge 1},(H_{3,k,\mathrm{sol}}^{\bot })_{k\ge 1}\) invariant in this case, the Euler–Lagrange equation can be solved explicitely, showing that \(\mathrm{ker}{\mathcal {L}}=H_{3,0}\) (as Theorem 4.10 describes quantitatively). Although in slightly hidden form, this was essentially the point of Lemma 4.6 and the subsequent results in Sect. 4.2.
In higher dimensions \(n\ge 4\), since the operator \(\big (\nabla _{T}\mathrm{div}_{{\mathbb {S}}^{n-1}}w-(n-1)(\mathrm{div}_{{\mathbb {S}}^{n-1}}w)x\big )\) neither commutes with A ((4.23)), nor leaves the subspaces \((H_{n,k,\mathrm{sol}})_{k\ge 1},(H_{n,k,\mathrm{sol}}^{\bot })_{k\ge 1}\) invariant, it is not clear if there is a straightforward argument to solve the equation \({\mathcal {L}}(w)=0\) explicitely, and show that indeed \(\mathrm{ker}{\mathcal {L}}=H_{n,0}\) in this case as well. In particular, (comparing with (4.46)), mixed terms of special type are expected to be present in the Fourier decomposition of \(Q_n\) into the eigenspaces of A, which were identified in Theorem 4.7. Nevertheless, it will turn out that we can still use the latter to show that the presence of the mixed divergence-terms is harmless, i.e., it does not produce any further zeros (other than \(H_{n,0}\)) in \(Q_n\). Simultaneously, we obtain the desired coercivity estimate (1.13) (with an explicit lower bound for the optimal constant) by examining how \(Q_n\) behaves in each one of the eigenspaces \((H_{n,k,i})_{k\ge , i=1,2,3}\) of A separately.
Following the notation we had in Sect. 4.2, we first present two auxiliary lemmata that entail most of the essential ingredients for the proof of Theorem 1.5 also in dimensions \(n\ge 4\).
Lemma 5.2
For \(n\ge 3\) and \(k\ge 1\), let us denote by \(\lambda _{n,k}:=k(k+n-2)\) the eigenvalues of \(-\Delta _{{\mathbb {S}}^{n-1}}\) (see (C.2)) and let \(i=1,2,3\). For every \(w\in H_{n,k,i}\) (as in Theorem 4.7), we have

Proof
The first identity is immediate from (4.22), (4.23), Theorem 4.7 and (C.3). For the second one, after integration by parts we see that the quadratic form \(Q_{V_n}\) can be equivalently rewritten as

Together with the first identity and (4.35), (5.3) yields the desired identity, and then the one for \(Q_n\) follows immediately by its definition in (1.12) and the two previous identities that we just checked. \(\square \)
Since they will again play an important role in the sequel (as it was the case for the constants in (4.43)), let us list below the precise values of the previous constants appearing in (5.2). The last set of constants in the following table is considered for \(k\ge 2\), because in any case \(\Pi _{H_{n,1,3}}w=0\) for every \(w\in H_n\), as we have justified in Remark 4.8.
The next ingredient we need is the following.
Lemma 5.3
The following statements hold true.
-
(i)
Let \(n\ge 3\). For every \(k,l\ge 1\) and \(i,j=1,2,3\) with \((k,i)\ne (l,j)\), the subspaces \(H_{n,k,i}\) and \(H_{n,l,j}\) (introduced in Theorem 4.7) are \(Q_{V_n}\)- and \(\widetilde{Q}_n\)-orthogonal, where
 (5.5)
(5.5)i.e., for every \(w_{n,k,i}\in H_{n,k,i}\) and \(w_{n,l,j}\in H_{n,l,j}\),
$$\begin{aligned} Q_{V_n}(w_{n,k,i},w_{n,l,j})=0 \ \ \ \mathrm{and} \ \ \ \widetilde{Q}_n(w_{n,k,i},w_{n,l,j})=0 . \end{aligned}$$(5.6) -
(ii)
Let \(n\ge 3\), \(w\in H_n\) written in Fourier series as \(w=\underset{\underset{(k,i)\ne (1,3)}{(k,i) \in {\mathbb {N}}^*\times \{1,2,3\}}}{\sum }w_{n,k,i}\), where \(w_{n,k,i}\in H_{n,k,i}\). Then,
 (5.7)
(5.7)
Remark 5.4
Before giving the proof of Lemma 5.3, let us point out an interesting feature in formula (5.7), which will be useful in the proof of Theorem 1.5, namely that the summation in the last term of the expression starts from \(k=3\). The reason for this is that in any case \(w_{n,1,3}\equiv 0\) whenever \(w\in H_n\) (see Remark 4.8), but one can also check that

In order to prove (5.8), recall that by definition (see (4.18), (4.20) and (4.33)), \(\mathrm{div} (w_{n,4,1})_h\equiv 0\) in \(\overline{B_1}\), and by also using (4.35) for \((k,i)=(2,3),(4,1)\) and the divergence theorem, we obtain

To justify that the last integral on the right hand side of (5.9) is zero, observe that

because  . Moreover, we observe that for every \(i=1,\dots ,n\),
. Moreover, we observe that for every \(i=1,\dots ,n\),
Since \((w_{n,2,3})_h\) is an \({\mathbb {R}}^n\)-valued 2nd-order homogeneous harmonic polynomial, \(\partial _i\mathrm{div}(w_{n,2,3})_h\) is simply a constant. But then, (5.11) implies that the function
is a homogeneous harmonic polynomial of degree 2, hence also \(L^2\)-orthogonal to \((w_{n,4,1})_h^i\). Thus,

where we used the fact that the function \((w_{n,4,1})_h^i|x|^2\) is 6-homogeneous, so that we can write its integral over \(B_1\) as an integral over \({\mathbb {S}}^{n-1}\), up to the correct multiplicative constant. The last integral in (5.12) is of course zero for every nontrivial spherical harmonic. Therefore, (5.9)–(5.12) imply (5.8). Note that the previous argument relies on the fact that \(\partial _i\mathrm{div}(w_{n,2,3})_h\) is constant, and of course cannot be implemented for the mixed terms of higher order.
Proof of Lemma 5.3
As in Lemma 4.9, part (i) is an immediate consequence of the fact that the subspaces \((H_{n,k,i})_{k\ge 1, i=1,2,3}\) are mutually orthogonal in \(W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\). For part (ii), having established that the form \(\widetilde{Q}_n\) in (5.5) splits completely in the eigenspaces \((H_{n,k,i})_{(k,i)\in {\mathbb {N}}^{*}\times \{1,2,3\}\setminus (1,3)}\), what remains to be checked is that whenever \(w_{n,k,i}\in H_{n,k,i}\) and \(w_{n,l,j}\in H_{n,l,j}\), there holds

for all pairs \(\{(k,i),(l,j)\}\in {\mathbb {N}}^{*} \times \{1,2,3\}\setminus (1,3)\) with \((k,i)\ne (l,j)\), except those of the form \(\{(k,1),(k+2,3)\}\) and \(\{(k,3),(k+2,1)\}\).
This can be checked again using the different equivalent formulas for \(Q_{V_n}\). Since \(\mathrm{div}_{{\mathbb {S}}^{n-1}}w\equiv 0\) whenever \(w\in H_{n,k,2}\) (see (4.35) and (4.38)), we may suppose without loss of generality that \(i,j\in \{1,3\}\), and then by (5.3) (written now in its bilinear expression),

Actually, as we verified in part (i), \(Q_{V_n}(w_{n,k,i}, w_{n,l,j})=0\), and in view of (4.35), (5.14) yields

i.e., (5.13) holds, unless the pairs \((k,i)\ne (l,j)\) are such that \(\sigma _{n,k,i}+\sigma _{n,l,j}=n\). In this respect,
which proves the desired claim and then the formula (5.7) for \(Q_n\) follows by the bilinearity of the expression, and the observation we made in Remark 5.4. \(\square \)
We now have all the necessary ingredients to prove Theorem 1.5. As a preliminary remark, let us note that by taking a closer look at the values of the constants (5.4) of Lemma 5.2, we see that in the case \(n\ge 4\) one cannot merely neglect the  -term and argue exactly as in the proof of Theorem 4.10 (\(n=3\)), something that was also indicated in Remark 5.1. Indeed, although the quadratic form \(\widetilde{Q}_n(w)\) in (5.5) is splitting among the eigenspaces \((H_{n,k,i})_{k\ge 1, i=1,2,3}\), for \(n\ge 4\) it does not have a sign. Actually, \(\widetilde{Q}_n(w)\) is negative in \(H_{n,k,3}\) for every \(k=2,\dots ,n-2\), zero in \(H_{n,1,2}, H_{n,n-1,3}\) and strictly positive in each one of the other eigenspaces. On the other hand, we see that the quadratic form \(Q_n\) vanishes again in the space \(H_{n,0}:=H_{n,1,2}\oplus H_{n,2,3}\). Proof of Theorem 1.5 (\(n\ge 4\)). For every \(k\ge 1\), we use the Cauchy–Schwartz inequality, the second identity in (5.2), the inequality
-term and argue exactly as in the proof of Theorem 4.10 (\(n=3\)), something that was also indicated in Remark 5.1. Indeed, although the quadratic form \(\widetilde{Q}_n(w)\) in (5.5) is splitting among the eigenspaces \((H_{n,k,i})_{k\ge 1, i=1,2,3}\), for \(n\ge 4\) it does not have a sign. Actually, \(\widetilde{Q}_n(w)\) is negative in \(H_{n,k,3}\) for every \(k=2,\dots ,n-2\), zero in \(H_{n,1,2}, H_{n,n-1,3}\) and strictly positive in each one of the other eigenspaces. On the other hand, we see that the quadratic form \(Q_n\) vanishes again in the space \(H_{n,0}:=H_{n,1,2}\oplus H_{n,2,3}\). Proof of Theorem 1.5 (\(n\ge 4\)). For every \(k\ge 1\), we use the Cauchy–Schwartz inequality, the second identity in (5.2), the inequality
with weight \(\varepsilon _{n,k}=\frac{k+n}{k}>0\), and (5.4), in order to estimate

For the last summand in (5.7), we shift the summation index to start from \(k=1\) and estimate as before,

Note that the choice of the weights \(\varepsilon _{n,k}\) was such that the second term in the last line of (5.15) coincides with the first term in the last equality in (5.16). The series appearing in (5.7) are all absolutely summable, \(Q_n(w_{n,1,2})=Q_n(w_{n,2,3})=0\), and using (5.15) and (5.16), we can estimate the form \(Q_n\) from below by

After rearranging terms in (5.17), we arrive at the estimate

where the new constants are defined as
By elementary algebraic calculations that we omit here for the sake of brevity, one can verify that
Indeed, for \(i=1,2,3\), one can write \(\tilde{C}_{n,k,i}:=\frac{p_{n,i}(k)}{q_{n,i}(k)}\), where \(p_{n,i}(k), q_{n,i}(k)\) are explicit polynomials of the same degree in k (of degree 3 when \(i=1\), and degree 2 when \(i=2,3\)) and verify algebraically that
Moreover, directly from (5.4) and (5.19), one sees that
and then (5.20) follows from (5.21) and (5.22). The precise values of the constants \(C_{n,i}\) could be calculated as well, by examining the monotonicity with respect to k of the sequences \((\tilde{C}_{n,k,i})\) respectively (or alternatively of the corresponding rational functions with respect to the continuum variable). Labelling
we can use (5.18)–(5.23), to further estimate from below,

which finishes the proof of (1.13). For \(n\ge 4\), the constant \(C_n\) in (5.23) provides an explicit lower bound for the value of the optimal constant for which (1.13) holds. \(\square \)
Remark 5.5
As we mentioned in the Introduction, the linear estimate (1.13) would then imply Corollary 1.6, by following exactly the same procedure as in Sect. 4. In this setting, one can of course reduce to showing 1.15 for maps \(u\in W^{1,\infty }({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) which satisfy the stronger conditions

With the aid of Lemma B.3 and Remark B.4, the reader can easily verify that the rest of the arguments in the proof of Theorem 1.4 carry over also in dimensions \(n\ge 4\), essentially unchanged.
5.2 Comparison of Theorem 1.5 with Korn’s inequality for the trace-free symmetrized gradient operator in the bulk
Let \(n\ge 3\) and U be an open bounded Lipschitz domain of \({\mathbb {R}}^n\). If \(v\in W^{1,n}(U;{\mathbb {R}}^n)\), then
with equality iff \(\nabla v\in {\mathbb {R}}_+SO(n)\) for a.e. \(x \in U\), i.e., according to Liouville’s theorem, iff v is the restriction of an orientation-preserving Möbius transformation on U. Setting again \(v:=w+\mathrm{id}|_U\), and expanding the deficit, one obtains formally
Another well known fact regarding the connection of the quadratic form in the right hand side of (5.24) to the geometry of \({\mathbb {R}}_+SO(n)\) is the following (see [22, Chapters 2 and 3], or [10] for more details). If \(T{\mathbb {R}}_+SO(n)\) stands for the tangent space to the conformal group \({\mathbb {R}}_+SO(n)\) at \(I_n\), it is immediate that
so that the function \(A\mapsto d(A):=\left| A_{\mathrm{sym}}-\frac{\mathrm{Tr}A}{n}I_n\right| \) is equivalent to the distance of A from \(T{\mathbb {R}}_+SO(n)\). Therefore, the linear subspace
can be viewed as the Lie algebra of the Möbius group of \(\overline{{\mathbb {R}}^n}\). If \(\Pi _{\Sigma _n}: W^{1,2}(U;{\mathbb {R}}^n)\mapsto \Sigma _n\) is the \(W^{1,2}\)-projection on this finite-dimensional subspace, the following variant of Korn’s inequality for the trace-free part of the symmetrized gradient is known to hold.
Theorem 5.6
(Reshetnyak, cf. [22, Theorem 3.3, Chapter 3]) Let \(n\ge 3\) and U be an open bounded Lipschitz domain of \({\mathbb {R}}^n\) that is starshaped with respect to a ball. There exists a constant \(C:=C(n,U)>0\) such that for every \(w\in W^{1,2}(U;{\mathbb {R}}^n)\),
In a certain sense, Theorem 1.5 is the analogue of Theorem 5.6 for maps from \({\mathbb {S}}^{n-1}\) to \({\mathbb {R}}^n\). In particular, as an upshot of it we have encountered the following fact. Although the kernels of the nonnegative quadratic forms arising as the second derivatives of the conformal deficit \(\big [D_{n-1}(u)\big ]^{\frac{n}{n-1}} -\big [P_{n-1}(u)\big ]^{\frac{n}{n-1}}\) and the isoperimetric deficit \(\big [P_{n-1}(u)\big ]^{\frac{n}{n-1}}-V_n(u)\) at the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\) are both infinite-dimensional, the intersection of the two kernels is finite-dimensional and actually isomorphic to the Lie algebra of infinitesimal Möbius transformations of \({\mathbb {S}}^{n-1}\).
Indeed, by the calculations that we exhibit in Lemma B.3 in “Appendix B”, we have that

and

The nonnegative quadratic form \(Q_{n,\mathrm{conf}}\) in (5.25) corresponds to the one associated to the conformal deficit in (5.24) for maps defined in the bulk, but the kernel of \(Q_{n,\mathrm{conf}}\) is infinite-dimensional. Intuitively, the underlying geometric reason behind this, is the abundance of \(C^2\) conformal maps from \({\mathbb {S}}^{n-1}\) into \({\mathbb {R}}^n\). Actually, we observe that for every \(\phi \in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}})\) with  and
and  , the map \(w_\phi (x):=\phi (x)x\) belongs to \(H_n\) (recall (4.15)) and one can easily verify that
, the map \(w_\phi (x):=\phi (x)x\) belongs to \(H_n\) (recall (4.15)) and one can easily verify that
Since the space of such \(\phi \) is infinite-dimensional, we have in particular that \(\mathrm{dim}(\mathrm{ker}(Q_{n,\mathrm{conf}}))=\infty \).
Regarding the quadratic form \(Q_{n,\mathrm{isop}}\) in (5.26), we have that it is also nonnegative and its kernel is also infinite-dimensional. In fact (with the notation of Theorem 4.7), one can directly check that
To verify (5.27) we use the following identity, referred to as Korn’s identity, that is interesting in its own right and whose derivation is a simple calculation which is also included at the end of “Appendix B”.
Lemma 5.7
(Korn’s identity on \({\mathbb {S}}^{n-1}\)). For every \(w\in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) the following identity holds

The interesting point of this identity is that when \(n\ge 3\), the quadratic form \(Q_{V_n}\) appears in the right hand side of (5.28) as some short of curvature contribution and it is really a surface identity, in the sense that the corresponding identity in the bulk is
but the last term on the right hand side of (5.29) should now be interpreted as a boundary-term contribution.
By using Korn’s identity, the form \(Q_{n,\mathrm{isop}}\) can be rewritten in a simpler form as

But if \(w\in H_{n,2}\), then \(-\sum _{j=1}^nx_j\nabla _{T}w^j=A(w)=w\) on \({\mathbb {S}}^{n-1}\) (recall that (4.34), (4.39) are then satisfied with \(\sigma =1\)), and therefore \(Q_{n,\mathrm{isop}}(w)=0\), which proves the implication in (5.27).
5.3 Proof of Theorem 1.8
As we have mentioned in the Introduction, if \(u\in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) and \(w:=u-\mathrm{id}_{{\mathbb {S}}^{n-1}}\), then the full \(L^2\)-isometric deficit of u is formally expanded around the identity as

where

For \(n=2\) we have that \(\mathrm{dim}(\mathrm{ker}(Q_{2,\mathrm{isom}})) =\infty \). Indeed, for \(v(x):=\psi (x)\tau (x)+\phi (x)x: {\mathbb {S}}^1\mapsto {\mathbb {R}}^2\), where \(\phi ,\psi \in C^{\infty }({\mathbb {S}}^1,{\mathbb {R}})\) and \(\tau (x):=(-x_2,x_1)\) is the unit tangent vector field on \({\mathbb {S}}^1\), it is an easy calculation to check that \( (P_T^t\nabla _{T}v)_{\mathrm{sym}}=\phi -\partial _{\tau }\psi \), i.e., for every \(\psi \in C^{\infty }({\mathbb {S}}^1;{\mathbb {R}})\) the map \(v_\psi (x):=\psi (x)\tau (x)+\partial _{\tau }\psi (x)x\) lies in the kernel of \( Q_{2,\mathrm{isom}}\).
For \(n\ge 3\), and unlike \(Q_{n,\mathrm{conf}}\), which as we have seen has infinite-dimensional kernel, \(Q_{n, \mathrm{isom}}\) has finite-dimensional kernel and actually
this fact being known as the infinitesimal rigidity of the sphere. The reader is referred to [23, Chapter 12] for a detailed discussion and further references regarding this well known geometric fact that is the linear analogue of the \(C^2\)-rigidity of the sphere in the Weyl problem.
Remark 5.8
Without referring to the classical proof of the infinitesimal rigidity of \({\mathbb {S}}^{n-1}\), it is very easy to deduce in particular that
Indeed, if \(w\in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) lies in the common null-space of these two nonnegative forms, we have
By taking the trace in the first equation in (5.32), we see that \(\mathrm{div}_{{\mathbb {S}}^{n-1}} w\equiv 0\) on \({\mathbb {S}}^{n-1}\), and then the second equation in (5.32), in view also of (5.26), reduces to

By the alternative formula (5.3), the Eq. (5.33) results in

Once again, the quantity in the parenthesis in (5.34) is nonnegative, being the \(L^2\)-Poincare deficit of w, and therefore the only solutions to (5.34) are maps w for which

Hence, by (5.35), \(\Lambda ^t=-\Lambda \) and reversely any map of the form \(w(x)=\Lambda x+b\), where \(\Lambda \in Skew(n), b\in {\mathbb {R}}^n\) is in the null-space of both quadratic forms. It would be interesting if by some algebraic manipulations one could directly prove that whenever \(n\ge 3\), \(Q_{n,\mathrm{isom}}(w)=0\implies Q_{n,\mathrm{isop}}(w)=0\). Combined with the argument just presented, this would give an alternative algebraic proof of the infinitesimal rigidity of the sphere, supplementing the differential-geometric one.
Remark 5.9
Even though for \(n\ge 3\) we have \(\mathrm{ker}(Q_{n,\mathrm{isom}})\simeq \mathfrak {so}(n)\), an estimate of the type

does not hold, the obstacle being (loosely speaking) the derivatives of the normal component of w. For example, if one considers purely normal displacements \(w_{\phi }(x):= \phi (x)x\) with \(\phi \in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}})\), then by a straightforward computation one can check that

whereas the full gradient of \(w_{\phi }\) also has derivatives of \(\phi \) in it. In coordinates,
so if the estimate above was to be valid, it would resemble some short of reverse-Poincare inequality, which is of course generically false. Combining additively \(Q_{n,\mathrm{isom}}\) and \(Q_{n,\mathrm{isop}}\) has though the merit of providing a Korn-type inequality in terms of the full gradient, as described in Theorem 1.8.
Proof of Theorem 1.8
For \(\alpha >0\) let us call
By looking at the formulas (5.26) and (5.30), and rearranging terms, (5.36) gives

With the notation we had introduced in Sect. 4.2, the estimate to be proven for \(Q_{n,\frac{n}{n-1}}\) reads

Once we have (5.38), the case of general \(\alpha >0\) is immediate, since:

The proof of (5.38) can now be performed by following exactly the same procedure as in the proof of Theorem 1.5 in Sect. 5.1. The latter could of course also be phrased in terms of any positive combination of \(Q_{n,\mathrm{conf}}\) in (5.25) and \(Q_{n,\mathrm{isop}}\) in (5.26), and not only of \(Q_n=Q_{n,\mathrm{conf}}+Q_{n,\mathrm{isop}}\), as in (1.12).
The arguments after Lemmata 5.2 and 5.3 (handling the mixed \(\mathrm{div}_{{\mathbb {S}}^{n-1}}\)-terms after the expansion in spherical harmonics as in (5.15)–(5.18)) are then modified accordingly. A last trivial comment in this case is that for \(k \ge 1\) and \(i= 1,2, 3\), if \(w\in H_{n,k,i}\) (recall Theorem 4.7 and Lemma 5.2),

Recalling the values of the constants from (5.2) and the table (5.4), we have that
So for the quadratic form in (5.37), one can directly check from (5.39) that \(C'_{n,1,2}=0\), but otherwise \(\mathop {\min }\nolimits _{(k,i)\ne (1,2)} C'_{n,k,i}>0\), which eventually leads to the desired coercivity estimate (5.38). \(\square \)
Remark 5.10
Since in this case we had an easy argument to infer that \(\mathrm{ker} (Q_{n,\mathrm{isom}})\cap \mathrm{ker}(Q_{n,\mathrm{isop}}) \simeq \mathfrak {so}(n)\) (see Remark 5.8), the proof of Theorem 1.8, for \(\alpha =\frac{n}{n-1}\) for example, could also be performed by a standard contradiction\(\backslash \)compactness argument, for an abstract constant though. Indeed, suppose that for \(\alpha :=\frac{n}{n-1}\) the estimate (1.17) (or equivalently (5.38)) is false. By translation and scaling invariance of the estimate, there exists a sequence \((w_k)_{k\in {\mathbb {N}}}\subset W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) such that for all \(k\in {\mathbb {N}}\),

and

in particular,
Up to a further nonrelabeled subsequence we can assume that there exists \(w\in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) with  such that \(w_k\rightharpoonup w\) in \(W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\), and also pointwise \({\mathcal {H}}^{n-1}\)-a.e. on \({\mathbb {S}}^{n-1}\). But then (recalling (4.22) and (4.23)),
such that \(w_k\rightharpoonup w\) in \(W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\), and also pointwise \({\mathcal {H}}^{n-1}\)-a.e. on \({\mathbb {S}}^{n-1}\). But then (recalling (4.22) and (4.23)),

since \(w_k\rightarrow w\) strongly in \(L^2({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) and \(A(w_k)\rightharpoonup A(w)\) weakly in \(L^2({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\). Thus, by lower semicontinuity of the first two terms in (5.37) under weak convergence in \(W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\), we obtain
i.e. \(Q_{n,\frac{n}{n-1}}(w)=0\) and therefore, by (5.31),
i.e., \(w\in H_{n,1,2}\). Moreover, being the (\({\mathcal {H}}^{n-1}\)-a.e.) pointwise limit of \((w_k)_{k\in {\mathbb {N}}}\subset H_{n,1,2}^{\bot }\), we must also have that \(w\in H_{n,1,2}^{\bot }\), since \(H_{n,1,2}\) is finite-dimensional and therefore its orthogonal complement in \(W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) is a closed subspace. This forces \(w\equiv 0\) on \({\mathbb {S}}^{n-1}\) and in particular, by (5.42),
But then (5.37), (5.41) and (5.43) imply that

contradicting the assumption in (5.40) that  . \(\square \)
. \(\square \)
Remark 5.11
As we had mentioned in Remark 5.1, the argument just described could have also been used to prove Theorem 1.5 if we knew already that the kernel of \(Q_n\) (defined in (1.12)) is finite-dimensional (and actually equal to \(H_{n,0}\)). Nevertheless, as we had remarked therein, there does not seem to be a direct argument to show this fact when \(n\ge 4\), neither by trying to solve the Euler–Lagrange equation associated to the operator \({\mathcal {L}}\) in (5.1) explicitely, nor by trying to argue as above.
Indeed, if \(w\in \mathrm{ker}(Q_n)\iff w\in \mathrm{ker}(Q_{n,\mathrm{conf}}) \cap \mathrm{ker}(Q_{n,\mathrm{isop}})\) (see (5.25), (5.26)), then again the following two equations must be satisfied simultaneously,
Because of the first equation in (5.44), the second one therein results in the equation

i.e., (5.45) ends up back to the original equation \(Q_n(w)=0\). Arguing directly with the eigenvalue decomposition with respect to A (recall Theorem 4.7) also has the extra benefit of showing explicitely how the form \(Q_n\) behaves in each one of the eigenspaces separately (see Lemma 5.2), and also gives an explicit lower bound (5.23) for the value of the optimal constant \(C_n\) in the coercivity estimate.
References
Almgren, F.: Optimal isoperimetric inequalities. Indiana Univ. Math. J. 35, 451–547 (1986)
Bernand-Mantel, A., Muratov, C.B., Simon, T.: A quantitative description of skyrmions in ultrathin ferromagnetic films and rigidity of degree \(\pm 1\) harmonic maps from \({\mathbb{R}}^2\) to \({\mathbb{S}}^2\). Arch. Ration. Mech. Anal. 239, 219–299 (2020)
Borisov, J.F.: On the connection between the spatial form of smooth surfaces and their intrinsic geometry. Vestnik Leningrad. Univ. 14, 20–26 (1959)
Brezis, H., Coron, J.M.: Convergence of solutions of H-systems or how to blow bubbles. Arch. Ration. Mech. Anal. 89, 21–56 (1985)
Brezis, H., Nirenberg, L.: Degree theory and BMO; part I: compact manifolds without boundaries. Sel. Math. New Ser. 1, 197–264 (1995)
Caldiroli, P., Musina, R.: The Dirichlet problem for H-systems with small boundary data: blowup phenomena and nonexistence results. Arch. Ration. Mech. Anal. 181, 1–42 (2006)
Cicalese, M., Leonardi, G.P.: A selection principle for the sharp quantitative isoperimetric inequality. Arch. Ration. Mech. Anal. 206(2), 617–643 (2012)
Cohn-Vossen, S.: Zwei Sätze über die Starrheit der Einflächen. Nachrichten Göttingen, 125–137 (1927)
Conti, S., De Lellis, C., Székelyhidi, L.: \(h\)-Principle and rigidity for \(C^{1,\alpha }\) isometric embeddings. Nonlinear Partial Differ. Equ. Abel Symp. 7, 83–116 (2012)
Faraco, D., Zhong, X.: Geometric rigidity of conformal matrices. Ann. Sc. Normale Super. Pisa-Classe di Sci. 4, 557–585 (2005)
Friesecke, G., James, R.D., Müller, S.: A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Commun. Pure Appl. Math. 55, 1461–1506 (2002)
Gallier, J.: Notes on Spherical Harmonics and Linear Representations of Lie Groups (2013)
Groemer, H.: Geometric Applications of Fourier Series and Spherical Harmonics, vol. 61. Cambridge University Press, Cambridge (1996)
Herglotz, G.: Über die Starrheit der Einflächen. Abh. Math. Semin. Univ. Hambg. 15, 127–129 (1943)
Hirsch, J., Zemas, K.: A simple proof of a rigidity estimate for degree \(\pm 1\) conformal maps on \({\mathbb{S}}^{2}\). Bull. LMS 54(1), 256–263 (2022)
Kuiper, N.H.: On \({C}^1\)-isometric imbeddings. I, II. Nederl. Akad. Wetensch. Proc. Ser. A. 58 Indag. Math. 17(545–556), 683–689 (1955)
Lang, S.: Linear Algebra, 3rd edn. Springer, Berlin (1987)
Lin, F.: Mapping problems, fundamental groups and defect measures. Acta Math. Sin. 15, 25–52 (1999)
Lions, P.L.: The concentration-compactness principle in the calculus of variations. The limit case, part 1. Rev. Math. Iberoam. 1, 145–201 (1985)
Nash, J.: \({C}^1\) isometric imbeddings. Ann. Math. (2)60, 383–396 (1954)
Reshetnyak, Y.G.: On stability bounds in the Liouville theorem on conformal mappings of multidimensional spaces. Sib. Math. J. 11, 833–846 (1970)
Reshetnyak, Y.G.: Stability Theorems in Geometry and Analysis, vol. 304. Springer, Berlin (2013)
Spivak, M.: A Comprehensive Introduction to Differential Geometry, vol. V. Publish or Perish, Berkeley (1979)
Topping, P.: A rigidity estimate for maps from \({\mathbb{S}}^2\) to \({\mathbb{S}}^2\) via the harmonic map flow. Bull. LMS (to appear) (2020). arXiv:2009.10459
Wente, H.C.: An existence theorem for surfaces of constant mean curvature. J. Math. Anal. Appl. 26, 318–344 (1969)
Acknowledgements
The second author is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics–Geometry–Structure and would also like to thank the Max Planck Institute for Mathematics in the Sciences in Leipzig, where his PhD project was carried out.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. A new simple proof of Liouville’s theorem on \({\mathbb {S}}^{n-1}\) and a qualitative analogue
Proof of Theorem 1.1
We present the proof in the case of generalized orientation-preserving maps, since the case of orienation-reversing ones is identical (or it can be retrieved by the former by composing with the flip \(x:=(x_1,\dots ,x_{n-1},x_n)\mapsto (x_1, \dots ,x_{n-1},-x_n)\)).
For part (i) of the theorem, we have that any map of the form \(u(x)=Rx\) with \(R\in SO(n)\) is of course an orientation-preserving isometry of \({\mathbb {S}}^{n-1}\). Conversely, let \(n\ge 2\), \(p\in [1,\infty ]\) and \(u\in W^{1,p}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) be a generalized orientation-preserving isometric map. By definition, this means that at \({\mathcal {H}}^{n-1}\)-a.e. \(x\in {\mathbb {S}}^{n-1}\) the intrinsic gradient of u is an orientation-preserving linear map between \(T_x{\mathbb {S}}^{n-1}\) and \(T_{u(x)}{\mathbb {S}}^{n-1}\), such that
or equivalently, in terms of the extrinsic gradient,
In particular, for \({\mathcal {H}}^{n-1}\)-a.e. \(x\in {\mathbb {S}}^{n-1}\) one has
By the change of variables formula applied to the vector-valued \((n-1)\)-form \(xdv_g\), we obtain

Hence, Poincare’s inequality (C.5) on \({\mathbb {S}}^{n-1}\), together with (A.1), (A.2), and the fact that \(|u|\equiv 1\), yield

As we have also encountered before (see also “Appendix C”), the equality case in the Poincare inequality implies that in the Fourier expansion of u in spherical harmonics, no other spherical harmonics except the first order ones should appear, hence \(u(x)=Rx\) for some \(R\in {\mathbb {R}}^{n\times n}\). But this linear map would transform \({\mathbb {S}}^{n-1}\) into the boundary of an ellipsoid, which after possibly an orthogonal change of coordinates is
where \(0\le \alpha _1 \le \dots \le \alpha _n\) are the eigenvalues of \(\sqrt{R^tR}\). By assumption, \(u({\mathbb {S}}^{n-1})\equiv {\mathbb {S}}^{n-1}\) and this forces \(\alpha _1=\dots =\alpha _n=1\), i.e., \(R\in O(n)\) and in particular, since u is assumed to be orientation-preserving, \(R\in SO(n)\).
For part (ii) we can argue similarly, after making use of the following useful fact.
Claim
Given \(u\in W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) of degree one, one can always find a Möbius transformation \(\phi _{\xi _0,\lambda _0}\) of \({\mathbb {S}}^{n-1}\) (see (1.2)) so that

Indeed, assume first that \(u\in C^{\infty }({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) and has degree one, in particular u is surjective. If  , there is nothing to prove. If \(b_u\ne 0\), consider the map \(F:{\mathbb {S}}^{n-1}\times [0,1]\mapsto \overline{B_1}\), defined as
, there is nothing to prove. If \(b_u\ne 0\), consider the map \(F:{\mathbb {S}}^{n-1}\times [0,1]\mapsto \overline{B_1}\), defined as

The map F is continuous with \(F(\xi ,0)=u(\xi )\) for every \(\xi \in {\mathbb {S}}^{n-1}\), i.e., \(F({\mathbb {S}}^{n-1},0)=u({\mathbb {S}}^{n-1})={\mathbb {S}}^{n-1}\), whereas \(F({\mathbb {S}}^{n-1},1)=\{b_u\}\). In other words, F is a continuous homotopy between \({\mathbb {S}}^{n-1}\) and the point \(b_u\in \overline{B_1}\setminus \{0\}\), and therefore there exists \(\lambda _0\in (0,1)\) such that \(0\in F({\mathbb {S}}^{n-1},\lambda _0)\), i.e., there exists also \(\xi _0\in {\mathbb {S}}^{n-1}\) such that \(F(\xi _0,\lambda _0)=0\).
In the general case of a map \(u\in W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) of degree 1, by the approximation property given in [5, Section I.4, Lemma 7], there exists a sequence \((u_j)_{j\in {\mathbb {N}}}\subset C^{\infty }({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) with the property that
Up to passing to a non-relabeled subsequence, we can without loss of generality also suppose that \(u_j\rightarrow u\) and \(\nabla _{T}u_j\rightarrow \nabla _{T}u\) pointwise \({\mathcal {H}}^{n-1}\)-a.e. on \({\mathbb {S}}^{n-1}\). Since the maps \((u_j)_{j\in \mathbb {N}}\) are smooth and surjective, by the previous argument there exist \((\xi _j)_{j\in {\mathbb {N}}}\subset {\mathbb {S}}^{n-1}\) and \((\lambda _j)_{j\in {\mathbb {N}}}\subset (0,1]\) so that for every \(j\in {\mathbb {N}}\),

Up to non-relabeled subsequences, we can suppose further that \(\xi _j\rightarrow \xi _0\in {\mathbb {S}}^{n-1}\) and \(\lambda _j\rightarrow \lambda _0 \in [0,1]\), thus \(\phi _{\xi _j,\lambda _j}\rightarrow \phi _{\xi _0,\lambda _0}\) pointwise \({\mathcal {H}}^{n-1}\)-a.e. on \({\mathbb {S}}^{n-1}\), and also weakly in \(W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\).
In fact \(\lambda _0\in (0,1]\), i.e., the Möbius transformations \((\phi _{\xi _j,\lambda _j})_{j\in {\mathbb {N}}}\) do not converge to the trivial map \(\phi _{\xi _0,0}(x)\equiv \xi _0\). Indeed, suppose that this was the case. Then \(u_j\circ \phi _{\xi _j,\lambda _j}\rightarrow u(\xi _0)\) pointwise \({\mathcal {H}}^{n-1}\)-a.e., and \(|u_j\circ \phi _{\xi _j,\lambda _j}|\equiv 1\), so we could use the Dominated Convergence Theorem and (A.4), to infer that

and derive a contradiction. Having justified that \(\lambda _0\in (0,1]\), what we actually obtain by the Dominated Convergence Theorem and (A.4) is that

Continuing with the proof of Theorem 1.1(ii), we of course have that all the maps given by (1.2) are orientation-preserving conformal diffeomorphisms of \({\mathbb {S}}^{n-1}\). Conversely, if \(u\in W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) is a generalized orientation-preserving conformal map, similarly to (i) we have that \({\mathcal {H}}^{n-1}\)-a.e. on \({\mathbb {S}}^{n-1}\),
or equivalently, in terms of the extrinsic gradient,
By taking the determinant in both sides of (A.6), we get that \({\mathcal {H}}^{n-1}\)-a.e. on \({\mathbb {S}}^{n-1}\),
Precomposing with the Möbius map \(\phi _{\xi _0,\lambda _0}\in Conf_+({\mathbb {S}}^{n-1})\) of the previous claim, we have that the map \(\tilde{u}:=u\circ \phi _{\xi _0,\lambda _0}\), whose mean value is 0 by (A.5), is also a generalized orientation-preserving conformal transformation of \({\mathbb {S}}^{n-1}\) of degree 1, and therefore by (A.7),
By approximation, the analytic formula for the degree in terms of integration of \((n-1)\)-forms on \({\mathbb {S}}^{n-1}\) holds true for \(\tilde{u}\) as well, i.e.,

We can now use (A.8), Jensen’s inequality, and the sharp Poincare inequality on \({\mathbb {S}}^{n-1}\) (C.5), to obtain the chain of inequalities

since  and \(|u|\equiv 1\) \({\mathcal {H}}^{n-1}\)-a.e. on \({\mathbb {S}}^{n-1}\). Arguing as in part (i), we deduce that \(\tilde{u}=R\mathrm{id}_{{\mathbb {S}}^{n-1}}\), i.e., \(u=R\phi _{\xi ,\lambda }\), where \(R\in SO(n)\), \(\xi :=\xi _0\in {\mathbb {S}}^{n-1}\) and \(\lambda :=\frac{1}{\lambda _0}>0\). \(\square \)
and \(|u|\equiv 1\) \({\mathcal {H}}^{n-1}\)-a.e. on \({\mathbb {S}}^{n-1}\). Arguing as in part (i), we deduce that \(\tilde{u}=R\mathrm{id}_{{\mathbb {S}}^{n-1}}\), i.e., \(u=R\phi _{\xi ,\lambda }\), where \(R\in SO(n)\), \(\xi :=\xi _0\in {\mathbb {S}}^{n-1}\) and \(\lambda :=\frac{1}{\lambda _0}>0\). \(\square \)
Remark A.1
The Möbius transformations of \({\mathbb {S}}^{n-1}\) given by (1.2) could of course alternatively be described by performing an inversion in \(\overline{T_\xi {\mathbb {S}}^{n-1}}\) with respect to some center, say the origin \(\xi \) of the affine hyperplane \(T_\xi {\mathbb {S}}^{n-1}\) of \({\mathbb {R}}^n\), and some radius, say \(\sqrt{\lambda }>0\). These maps however would correspond exactly to the Möbius transformations produced by dilation in \(T_\xi {\mathbb {S}}^{n-1}\) by factor \(\frac{1}{\lambda }\), composed finally with a flip in \({\mathbb {R}}^n\), i.e., an orthogonal map that would change back the orientation. By Liouville’s Theorem 1.1, the conformal group of the sphere is given by
and is a actually a Lie group, i.e., a differentiable manifold (of dimension \(\tfrac{n(n+1)}{2}\)) with a group structure, given by composition of maps. Analytically, the maps \((\phi _{\xi ,\lambda })_{\xi \in {\mathbb {S}}^{n-1},\lambda >0}\) are given by the formula
Using (A.10), the corresponding Lie algebra of infinitesimal Möbius transformations, i.e., the tangent space of \(Conf({\mathbb {S}}^{n-1})\) at the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\), can easily be identified. Indeed, it is then an elementary exercise in differential geometry to check that
which is the representation that we made use of in the proof of Lemma 4.13.
Remark A.2
In the conformal case, the argument for the proof of Theorem 1.1(ii) can easily be modified in order to give a compactness statement for sequences of orientation-preserving (resp. orientation-reversing) approximately conformal maps on \({\mathbb {S}}^{n-1}\) of degree 1 (resp. \(-1\)), see the subsequent Lemma A.3. When \(n=3\), the statement therein essentially reduces to a well known compactness result for harmonic maps of degree \(\pm 1\) on \({\mathbb {S}}^2\) (cf. [2, Theorem 2.4, Step 1 in the proof], as well as [18]), which was proven using a concentration-compactness argument in the spirit of P.L. Lions [19]. With the observation that the Möbius transformations can be used to “globally invert” a map from \({\mathbb {S}}^{n-1}\) to itself, in the sense of fixing its mean value to be 0, we can give a simpler and more elementary proof of this fact, which can be appropriately generalized in every dimension \(n\ge 3\). For further applications of this simple observation the interested reader is also referred to [15, 24] for two different and shorter proofs of [2, Theorem 2.4]. In the following lemma we present again for simplicity the case of orientation-preserving degree 1 maps.
Lemma A.3
Let \(n\ge 3\) and \((u_j)_{j\in {\mathbb {N}}}\subset W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\) be a sequence of generalized orientation-preserving maps of degree 1 which are approximately conformal, in the sense that

which as a condition is in this case equivalent to

Then, there exist Möbius transformations \((\phi _j)_{j\in {\mathbb {N}}}\subset Conf_+({\mathbb {S}}^{n-1})\) and \(R\in SO(n)\) so that up to a non-relabeled subsequence,
Proof
By the degree 1 condition, as in (A.3),we can again find \((\xi _j)_{j\in {\mathbb {N}}}\subset {\mathbb {S}}^{n-1}\) and \((\lambda _j)_{j\in {\mathbb {N}}}\subset (0,1]\), so that after setting \(\phi _j:=\phi _{\xi _j,\lambda _j}\in Conf_+({\mathbb {S}}^{n-1})\) and \(\tilde{u}_j:=u_j\circ \phi _j\), we have

Thanks to the conformal invariance of the \((n-1)\)-Dirichlet energy, (A.12) is left unchanged, i.e.,

Because of (A.14) and (A.15), the sequence \((\tilde{u}_j)_{j\in {\mathbb {N}}}\) is in particular uniformly bounded in \(W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\), hence up to a non-relabeled subsequence converges weakly in \(W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\), and up to a further one also pointwise \({\mathcal {H}}^{n-1}\)-a.e. to a map \(\tilde{u}\in W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\). Since \(\tilde{u}_j\rightarrow \tilde{u}\) strongly in \(L^{n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\), we obtain by (A.14) that in particular,

and by lower semicontinuity of the \((n-1)\)-Dirichlet energy under weak convergence and (A.15),

We can then apply the same argument as in (A.9) in the proof of Theorem 1.1(ii), to obtain the chain of inequalities

and with the same reasoning as in there, we conclude that \(\tilde{u}(x)=Rx\) for some \(R\in O(n)\). Finally, by (A.16)–(A.18) we actually obtain that \(\tilde{u}_j\rightarrow \tilde{u}\) strongly in \(W^{1,n-1}({\mathbb {S}}^{n-1};{\mathbb {S}}^{n-1})\). Since the degree is stable under this notion of convergence,

i.e., indeed \(R\in SO(n)\). \(\square \)
Appendix B. Integral identities for Jacobians, Taylor expansions of the deficits and proof of Korn’s identity
We start this appendix by collecting and proving some integral identities for Jacobians that we used in the bulk of the paper, and especially in the proof of Lemma 3.9.
Lemma B.1
Let \(u\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) and let \(u_h:\overline{B_1}\mapsto {\mathbb {R}}^3\) be as usual its harmonic continuation in \(B_1\), taken componentwise. Then (with the notation adopted in (1.7) for \(n=3\)),

Moreover, if \(w\in W^{1,2}({\mathbb {S}}^{2};{\mathbb {R}}^3)\) and \(w_h\) is defined analogously, then

where the quadratic form \(Q_{V_3}\) is defined as

Remark B.2
As the reader might already know from the theory of null-Lagrangians or notice from the next proof, the above formulas actually hold true with \(B_1\) being replaced by any other open bounded domain \(U\subset {\mathbb {R}}^3\) with sufficiently regular boundary, and \(u_h\) (resp. \(w_h\)) being replaced by any other interior extension of u (resp. w), for which the previous bulk integrals are well defined. Since we only used the expressions for the harmonic extension, which is smooth in the interior of the unit ball, we have preferred to state the previous lemma in this particular form.
Proof of Lemma B.1
Regarding the proof of the identity (B.1), the determinant of \(\nabla u_h:=(\partial _ju_h^i)_{1\le i,j\le 3}\) can be rewritten as
where \(a\times b\in {\mathbb {R}}^3\) denotes the exterior product of two vectors \(a,b\in {\mathbb {R}}^3\). Using the first identity in (B.4), and integrating by parts, we have
Here, we have used the vector calculus identities
and we have written the full gradients \(\nabla u_h^2\) and \(\nabla u_h^3\) on \({\mathbb {S}}^{2}\) in terms of the local orthonormal oriented frame \(\{\tau _1,\tau _2,x\}\) for \({\mathbb {S}}^{2}\), which is such that \(\tau _1\times \tau _2=x, \tau _2\times x=\tau _1, x\times \tau _1=\tau _2\). Using the other two expressions from (B.4) and arguing in the same manner, we also obtain
and
Therefore, summing (B.5)–(B.7), and recalling the notation (1.7) (for \(n=3\)), we arrive at (B.1). Regarding (B.2), the first equality is immmediate from the expansion of the determinant around the identity matrix \(I_3\). The expression in the second line of (B.2) follows from the fact that the resulting terms can be written as boundary integrals in the following fashion. Using again Stokes’ theorem, we can calculate

and
Subtracting the last two identities we arrive at

Hence, the second equality in (B.2) follows from (B.8), (B.9) and (B.1) for w in the place of u here. \(\square \)
Next, we calculate in detail the Taylor expansions up to second order of the geometric quantities that we used in the main body of the paper. The computations presented in the following lemma are formal, and we assume without further clarification that the maps in consideration are always regular enough so that we can perform the expansions. In the case \(n=3\), we had directly performed the expansion of the 2-Dirichlet energy of u around the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\) in the proof of Lemma 4.5, and the one for \(V_3(u)\) was performed in the previous Lemma B.1. Thus, the focus in the next lemma is mostly on the case \(n\ge 4\). Moreover, notice that in Sect. 4.2 we had already translated and scaled the initial map u properly (recall (4.2) and (4.3)), which we will also assume for convenience next.
Lemma B.3
Let \(n\ge 3\), \(u:{\mathbb {S}}^{n-1}\mapsto {\mathbb {R}}^n\) (be sufficiently regular) and as always, \(w:=u-\mathrm{id}_{{\mathbb {S}}^{n-1}}\). Assuming that  , and recalling the notation introduced in (1.9), we can formally write
, and recalling the notation introduced in (1.9), we can formally write
where the corresponding quadratic forms are given by the expressions

and the remainder terms \((R_{i,n}(w))_{i=1,2,3}\) are of higher order.
Proof
Regarding the expansion of the \((n-1)\)-Dirichlet energy, in the case \(n=3\) the calculation was performed in the proof of Lemma 4.5 (see (4.9)). For \(n\ge 4\), by using the fact that

we can formally calculate

Therefore, (B.13) gives the expansion (B.10)(i), with the formula (B.11)(i) for the quadratic term and the growth behaviour for the higher order term \(R_{1,n}(w)\). For the expansion of the generalized perimeter-term around the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\), for every \(n\ge 3\) we have

where
The Taylor expansion of the determinant around \(I_x\) gives
and since in our case,
by the identities (B.14)–(B.17), we obtain the formal expansion

where
Since \((\Theta (w))^2=4(\mathrm{div}_{{\mathbb {S}}^{n-1}}w)^2+{\mathcal {O}}(|\nabla _{T}w|^3)\), we can perform a Taylor expansion of the square root inside the integral in (B.18) and use (B.12), (B.19), to get

A final Taylor expansion of the function \(t\mapsto (1+t)^{\frac{n}{n-1}}\) around 0 gives,

Therefore, (B.20) gives the expansion (B.10)(ii), with the formula (B.11)(ii) for the corresponding quadratic term and the growth behaviour for the higher order term \(R_{2,n}(w)\).
The expansion of the generalized signed-volume \(V_n(u)\) in (1.6), (1.7) around the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\), for \(n=3\) was given in Lemma B.1. An intrinsic way to perform the calculation in every dimension \(n\ge 3\) is the following.

Here, we have used standard multiindex notation. For every \(k\in \{0,1,\dots ,n-1\}\) and for every multiindex \(\alpha :=(\alpha _1,\dots ,\alpha _k)\), where \((a_i)_{i=1,\dots ,k}\in {\mathbb {N}}\) with \(1\le \alpha _1<\dots <\alpha _k\le n-1\) we denote \(\bar{\alpha }\) its complementary multiindex (with its entries also in increasing order), \(\sigma (\alpha ,\bar{\alpha })\) the sign of the permutation that maps \((\alpha ,\bar{\alpha })\) to the standard ordering \((1,\dots ,n)\) and
We have also denoted by \((I_{n,i}(w))_{i=0,1,2}\) the zeroth, first and second order terms with respect to w and \(\nabla _{T}w\) in the expansion of \(V_n(u)\) around the \(\mathrm{id}_{{\mathbb {S}}^{n-1}}\) respectively, and by \(I_{n,3}(w)\) the remaining term which is a polynomial of order at least 3 and at most n in w and its first derivatives. Keeping in mind that \(\partial _{\tau _i}x=\tau _i\) for \(i=1,\dots ,n-1\) and that by an abuse of notation, \(\tau _1\wedge \dots \wedge \tau _{n-1}\equiv x\), we can compute each term separately.


the last equality following from (B.12). For the quadratic term, we can write it as

The change of sign in the last line of (B.25) is due to orientation reasons, since we have taken the local orthonormal basis \(\{ \tau _1,\dots ,\tau _{n-1}\}\) of \(T_x{\mathbb {S}}^{n-1}\) in such a way that at every \(x\in {\mathbb {S}}^{n-1}\) the set of vectors \(\{\tau _1(x),\dots ,\tau _{n-1} (x),x\}\) is a positively oriented frame of \({\mathbb {R}}^n\). Similarly,

After integrating by parts it is easy to see that the first term in the last line of (B.26) is

while the second one therein is

Subtracting (B.27) and (B.28) by parts, we infer that (B.26) implies

and therefore, (B.22)–(B.29) give the desired expansion (B.10)(iii), with the formula (B.11)(iii) for the corresponding quadratic term \(Q_{V_n}\). Regarding the remainder term \(R_{3,n}\) it is easy to see from (B.21) that it has the algebraic structure

where for each \(k=2,\dots ,n-1\), \(A_{n,k}\) is a nonlinear first order differential operator that is a homogeneous polynomial of order k in the first derivatives of w. \(\square \)
Remark B.4
From the growth behaviour of the higher order terms \((R_{i,n})_{i=1,2,3}\) in (B.10), as these can be derived from (B.13), (B.20) and (B.30), it is immediate to deduce the following simple fact. Even in the case \(n\ge 4\), if \(u\in W^{1,\infty }({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) is such that \(\Vert \nabla _{T}u-P_T\Vert _{L^{\infty }({\mathbb {S}}^{n-1})}\le \theta \) for some \(\theta \in (0,1)\) sufficiently small (as in the setting of Corollary 1.6, see also (1.14)), and moreover  , then for \(w:=u-\mathrm{id}_{{\mathbb {S}}^{n-1}}\), one has
, then for \(w:=u-\mathrm{id}_{{\mathbb {S}}^{n-1}}\), one has

for some constant \(c_\theta \in (0,1)\), such that \(c_\theta \rightarrow 0\) as \(\theta \rightarrow 0\).
Let us conclude this appendix by giving a proof of Korn’s identity on \({\mathbb {S}}^{n-1}\).
Proof of Lemma 5.7
We have

and recalling (B.26),

By the definition of \(Q_{V_n}(w)\) in (B.11)(iii) and (B.29) we have that \( I_{n,2,2}(w) =\frac{n-2}{n}Q_{V_n}(w)\), and Korn’s identity (5.7) follows immediately. \(\square \)
Appendix C. Spherical Harmonics
We first recall that in local coordinates, the spherical Laplace-Beltrami operator \(-\Delta _{{\mathbb {S}}^{n-1}}\) is given for every \(f\in C^2({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) through the expression
Here, \(g:=(g_{ij})_{i,j=1,\dots ,n-1}\) denotes the standard round metric on \({\mathbb {S}}^{n-1}\), \((g^{ij})_{i,j=1,\dots ,n-1}\) its inverse, and \(\{\tau _1,\dots ,\tau _{n-1}\}\) is the local orthonormal frame on \({\mathbb {S}}^{n-1}\) as introduced in Sect. 2. It is well known that \(L^2({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) admits an orthonormal basis consisting of eigenfunctions of \(-\Delta _{{\mathbb {S}}^{n-1}}\). In particular, for every \(k \in {\mathbb {N}}\) there exists a finite number (denoted by \(G_{n,k}\)) of mutually \(L^2\)- (and actually \(W^{1,2}\)-) orthogonal functions \((\psi _{n,k,j})_{j=1,\dots ,G_{n,k}}\subset W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\), which are called the vector valued k-th order spherical harmonics, are restrictions on \({\mathbb {S}}^{n-1}\) of (\({\mathbb {R}}^n\)-valued) homogeneous harmonic polynomials in \({\mathbb {R}}^n\) of degree k respectively, and satisfy
In particular,

In the scalar case, \(G_{n,0}=1\) (with trivial eigenfunction the constant 1), \(G_{n,1}=n\) (with the first order spherical harmonics being the coordinate functions \(\psi _{n,1,j}(x) :=\frac{x_j}{\sqrt{\omega _n}}\)), and \(G_{n,k} ={n+k-1}\atopwithdelims (){k}\)-\({n+k-3}\atopwithdelims (){k-2}\) for \(k\ge 2\). The reader can refer to [12, 13] for more information on spherical harmonics.
Remark C.1
The following Parseval identities on \({\mathbb {S}}^{n-1}\) hold true: If \(u \in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) with its Fourier expansion in spherical harmonics being \(u=\sum _{k=0}^{\infty }\sum _{j=1}^{G_{n,k}} \alpha _{n,k,j}\psi _{n,k,j}\), then
The sharp Poincare inequality for maps \(u\in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\) is then easily deduced. Since \(\lambda _{n,k}\ge n-1\) for every \(k\ge 1\), from (C.4) we obtain

Of course, depending on the number of vanishing first Fourier modes in the expansion of u, the constant in the above inequality can be improved in an obvious way. By expanding a function in spherical harmonics one can often obtain useful estimates. In the next lemma, we mention two of them that we have used earlier in the paper.
Lemma C.2
If \(u\in W^{1,2}({\mathbb {S}}^{n-1};{\mathbb {R}}^n)\), and \(u_h:\overline{B_1}\mapsto {\mathbb {R}}^n\) denotes its (componentwise) harmonic extension, the following estimates hold true:


Proof
Let us give the proof of these two simple estimates in the case that u is scalar-valued, the case of vector-valued u being an immediate consequence. We write again
and therefore, its harmonic extension can be written in polar coordinates \((r,\theta )\in [0,1]\times {\mathbb {S}}^{n-1}\) as
For C.6, we write

while for (C.7), we write

Since \(\frac{1}{n-1}\le \frac{k}{k+n-2}\le 1\) for every \(k\ge 1\), the desired estimates follows immediately by the above identities and (C.4). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Luckhaus, S., Zemas, K. Rigidity estimates for isometric and conformal maps from \({\mathbb {S}}^{n-1}\) to \({\mathbb {R}}^n\). Invent. math. 230, 375–461 (2022). https://doi.org/10.1007/s00222-022-01128-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-022-01128-7







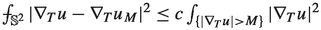 .
.





