Abstract
For an arbitrary Nakajima quiver variety X, we construct an analog of the quantum dynamical Weyl group acting in its equivariant K-theory. The correct generalization of the Weyl group here is the fundamental groupoid of a certain periodic locally finite hyperplane arrangement in \({{\,\mathrm{Pic}\,}}(X)\otimes {\mathbb {C}}\). We identify the lattice part of this groupoid with the operators of quantum difference equation for X. The cases of quivers of finite and affine type are illustrated by explicit examples.



Similar content being viewed by others
Notes
Here the threefold need not be Calabi–Yau, to point out a frequent misconception. For example, the equivariant Donaldson-Thomas theory of toric varieties is a very rich subject with many applications in mathematical physics.
\({\mathsf {S}}(u,z)\) is denoted by \({\mathsf {S}}_{\sigma }(u,z)\) in [47] for a shift \(u\rightarrow u q^{\sigma }\) by a specific \({\mathsf {A}}\)-character \(\sigma \).
See Theorem 9.3.1 in [37] for similar statement in the case of equivariant cohomology.
Note, that we use modified quantum parameter z which differs by a sign:
$$\begin{aligned} z^{{\mathsf {v}}} \mapsto (-1)^{\text {codim}/2} z^{{\mathsf {v}}}, \end{aligned}$$see Theorem 10.2.8 in [47]. Explicitly, this change of variables amounts to the following substitution of Kähler parameters:
$$\begin{aligned} z_i \mapsto (-1)^{2 \kappa _i } z_i \end{aligned}$$for canonical vector (81). To get rid of the minus sign, we will use modified notations in this paper. :
In this section we often switch from the variables z, denoting Kähler parameters, to their logarithms \(\lambda \) and back. The two are related via (72).
Note the substitution \(\hbar \rightarrow \hbar ^{2}\) on the left side of this equality which was introduced at the begining of Sect. 6.1.10. We have \(\hbar ^{2 \Omega }={{\,\mathrm{diag}\,}}(1,\hbar ,\hbar ,1)\) and \(\hbar ^{-H \otimes H/2}={{\,\mathrm{diag}\,}}(\hbar ^{-1/2},\hbar ^{1/2},\hbar ^{1/2},\hbar ^{-1/2})=\hbar ^{-1/2}\hbar ^{2 \Omega }\).
The factor 2 in \(\hbar ^{2\kappa }\) is from our conventions introduced at the beginning of Sect. 6.1.10.
This expectation is in agreement with explicit computations of capped vertex functions [47] for the first values of k and n.
Note that we need to substitute \(\hbar \rightarrow \hbar ^{2}\) in the geometric formulas to relate them to the action of \({{\mathscr {U}}_{\hbar }(\widehat{\mathfrak {gl}}_2)}\), as we explain in Sect. 6.1.10.
This expectation is in agreement with explicit computations of the capped vertex functions [47] for the first several values of n and r.
We use a Maple package, implemented by the second author, which computes the action of
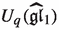 on the Fock space. The package is available from the author upon request.
on the Fock space. The package is available from the author upon request.
References
Aganagic, M., Okounkov, A.: Quasimap counts and Bethe eigenfunctions. Mosc. Math. J. 17(4), 565–600 (2017)
Aganagic, M., Okounkov, A.: Elliptic stable envelopes. J. Am. Math. Soc. 34(1), 79–133 (2021)
Arnaudon, D., Buffenoir, E., Ragoucy, E., Roche, P.: Universal solutions of quantum dynamical Yang–Baxter equations. Lett. Math. Phys. 44(3), 201–214 (1998)
Balagović, M.: Degeneration of trigonometric dynamical difference equations for quantum loop algebras to trigonometric Casimir equations for Yangians. Comm. Math. Phys. 334(2), 629–659 (2015)
Bezrukavnikov, R., Finkelberg, M.: Wreath Macdonald polynomials and the categorical McKay correspondence. Camb. J. Math. 2(2):163–190 (2014). With an appendix by Vadim Vologodsky
Bezrukavnikov, R., Kaledin, D.: Fedosov quantization in positive characteristic. J. Am. Math. Soc. 21(2), 409–438 (2008)
Bezrukavnikov, R., Losev, I.: Etingofs conjecture for quantized quiver varieties. Invent. Math. 223(3), 1097–1226 (2021)
Bezrukavnikov, R., Mirković, I.: Representations of semisimple Lie algebras in prime characteristic and the noncommutative Springer resolution. Ann. Math. (2) 178(3), 835–919 (2013)
Bezrukavnikov, R., Okounkov, A.: In preparation
Braverman, A., Maulik, D., Okounkov, A.: Quantum cohomology of the Springer resolution. Adv. Math. 227(1), 421–458 (2011)
Ciocan-Fontanine, I., Kim, B., Maulik, D.: Stable quasimaps to GIT quotients. J. Geom. Phys. 75, 17–47 (2014)
Cox, D.A., Katz, S.: Mirror symmetry and algebraic geometry. Mathematical Surveys and Monographs, vol. 68. American Mathematical Society, Providence, RI (1999)
Dinkins, H.: 3D mirror symmetry of the cotangent bundle of the full flag variety. arXiv e-prints, page arXiv:2011.08603 (2020)
Dinkins, H.: Elliptic stable envelopes of affine type \(A\) quiver varieties. arXiv e-prints, page arXiv:2107.09569 (2021)
Etingof, P.: Symplectic reflection algebras and affine Lie algebras. Mosc. Math. J. 12(3):543–565, 668–669 (2012)
Etingof, P., Schedler, T., Schiffmann, O.: Explicit quantization of dynamical \(r\)-matrices for finite dimensional semisimple Lie algebras. J. Am. Math. Soc. 13(3), 595–609 (2000)
Etingof, P., Varchenko, A.: Dynamical Weyl groups and applications. Adv. Math. 167(1), 74–127 (2002)
Frenkel, I.B., Reshetikhin, N.Y.: Quantum affine algebras and holonomic difference equations. Commun. Math. Phys. 146, 1–60 (1992)
Givental, A., Lee, Y.-P.: Quantum \(K\)-theory on flag manifolds, finite-difference Toda lattices and quantum groups. Invent. Math. 151(1), 193–219 (2003)
Givental, A., Tonita, V.: The Hirzebruch-Riemann-Roch theorem in true genus-0 quantum K-theory. In Symplectic, Poisson, and noncommutative geometry, vol. 62 of Mathematical Science and Research Institution of Publication, pp 43–91. Cambridge Univ. Press, New York (2014)
Haiman, M.: Notes on Macdonald polynomials and the geometry of Hilbert schemes. In Symmetric functions 2001: surveys of developments and perspectives, volume 74 of NATO Science Series II Mathematical Physics and Chemistry, pp 1–64. Kluwer Acad. Publ., Dordrecht (2002)
Kaledin, D.: Derived equivalences by quantization. Geom. Funct. Anal. 17(6), 1968–2004 (2008)
Khoroshkin, S.M., Tolstoy, V.N.: Universal \(R\)-matrix for quantized (super)algebras. Comm. Math. Phys. 141(3), 599–617 (1991)
Kononov, Y., Okounkov, A., Osinenko, A.: Correction to: The 2-leg vertex in K-theoretic DT theory. Comm. Math. Phys. 388(2), 1129 (2021)
Kononov, Y., Smirnov, A.: Pursuing quantum difference equations I: stable envelopes of subvarieties. arXiv e-prints, page arXiv:2004.07862 (2020)
Kononov, Y., Smirnov, A.: Pursuing quantum difference equations II: 3D-mirror symmetry. arXiv e-prints, page arXiv:2008.06309 (2020)
Koroteev, P., Pushkar, P.P., Smirnov, A.V., Zeitlin, A.M.: Quantum K-theory of quiver varieties and many-body systems. Selecta Math. (N.S.) 27(5), 40 (2021)
Koroteev, P., Zeitlin, A.M.: 3D Mirror Symmetry for Instanton Moduli Spaces. arXiv e-prints, page arXiv:2105.00588 (2021)
Li, J.: Stable morphisms to singular schemes and relative stable morphisms. J. Differ. Geom. 57(3), 509–578 (2001)
Li, J.: A degeneration formula of GW-invariants. J. Differ. Geom. 60(2), 199–293 (2002)
Li, J., Wu, B.: Good degeneration of Quot-schemes and coherent systems. Comm. Anal. Geom. 23(4), 841–921 (2015)
Majid, S.: Foundations of quantum group theory. Cambridge University Press, Cambridge (1995)
Maulik, D., Nekrasov, N., Okounkov, A., Pandharipande, R.: Gromov–Witten theory and Donaldson-Thomas theory. I. Compos. Math. 142(5), 1263–1285 (2006)
Maulik, D., Nekrasov, N., Okounkov, A., Pandharipande, R.: Gromov–Witten theory and Donaldson–Thomas theory. II. Compos. Math. 142(5), 1286–1304 (2006)
Maulik, D., Oblomkov, A.: Quantum cohomology of the Hilbert scheme of points on \(A_n\)-resolutions. J. Am. Math. Soc. 22(4), 1055–1091 (2009)
Maulik, D., Oblomkov, A., Okounkov, A., Pandharipande, R.: Gromov–Witten/Donaldson–Thomas correspondence for toric three-folds. Invent. Math. 186(2), 435–479 (2011)
Maulik, D., Okounkov, A.: Quantum groups and quantum cohomology. Astérisque, (408):ix+209 (2019)
McGerty, K., Nevins, T.: Kirwan surjectivity for quiver varieties. Invent. Math. 212(1) (2017)
Nakajima, H.: Instantons on ALE spaces, quiver varieties, and Kac–Moody algebras. Duke Math. J. 76(2), 365–416 (1994)
Nakajima, H.: Quiver varieties and Kac–Moody algebras. Duke Math. J. 91(3), 515–560 (1998)
Nakajima, H.: Quiver varieties and finite-dimensional representations of quantum affine algebras. J. Am. Math. Soc. 14(1), 145–238 (2001)
Neguţ, A.: The R-matrix of the quantum toroidal algebra. arXiv e-prints, page arXiv:2005.14182 (2020)
Negut, A.: Quantum algebras and cyclic quiver varieties. ProQuest LLC, Ann Arbor, MI (2015). Thesis (Ph.D.)–Columbia University
Nekrasov, N., Okounkov, A.: Membranes and sheaves. Algebr. Geom. 3(3), 320–369 (2016)
Nekrasov, N.A., Shatashvili, S.L.: Quantum integrability and supersymmetric vacua. Prog. Theor. Phys. Suppl. 177, 105–119 (2009)
Nekrasov, N.A., Shatashvili, S.L.: Supersymmetric vacua and Bethe ansatz. Nucl. Phys. B Proc. Suppl. 192(193), 91–112 (2009)
Okounkov, A.: Lectures on K-theoretic computations in enumerative geometry. In Geometry of moduli spaces and representation theory, volume 24 of IAS/Park City Mathematical Series, pp 251–380. American and Mathematical Society, Providence, RI (2017)
Okounkov, A.: Nonabelian stable envelopes, vertex functions with descendents, and integral solutions of \(q\)-difference equations. arXiv e-prints, page arXiv:2010.13217 (2020)
Okounkov, A.: Inductive construction of stable envelopes. Lett. Math. Phys. 111(6), 56 (2021)
Okounkov, A., Pandharipande, R.: The quantum differential equation of the Hilbert scheme of points in the plane. Transform. Groups 15(4), 965–982 (2010)
Pandharipande, R., Pixton, A.: Gromov–witten/pairs correspondence for the quintic three-fold. J. Am. Math. Soc. 30, 389–449 (2012)
Pushkar, P.P., Smirnov, A.V., Zeitlin, A.M.: Baxter \(Q\)-operator from quantum \(K\)-theory. Adv. Math. 360, 106919 (2020)
Reshetikhin, N.Y.: Quasitriangular Hopf algebras and invariants of links. Algebra i Analiz 1(2), 169–188 (1989)
Reshetikhin, N.Y., Takhtadzhyan, L.A., Faddeev, L.D.: Quantization of Lie groups and Lie algebras. Algebra i Analiz 1(1), 178–206 (1989)
Rimanyi, R., Rozansky, L.: New quiver-like varieties and Lie superalgebras. arXiv e-prints, page arXiv:2105.11499 (2021)
Rimányi, R., Smirnov, A., Varchenko, A., Zhou, Z.: Three-dimensional mirror self-symmetry of the cotangent bundle of the full flag variety. SIGMA Symm. Integrabil. Geom. Methods Appl. 15, 22 (2019)
Rimányi, R., Weber, A.: Elliptic classes on Langlands dual flag varieties. Commun. Contemp. Math. 24(1), 15 (2022)
Rimányi, R., Smirnov, A., Varchenko, A., Zhou, Z.: Three-dimensional mirror symmetry and elliptic stable envelopes. Int. Math. Res. Notices (2021). rnaa389
Schiffmann, O., Vasserot, E.: The elliptic Hall algebra and the \(K\)-theory of the Hilbert scheme of \(\mathbb{A}^2\). Duke Math. J. 162(2), 279–366 (2013)
Shou, Y.: Bow Varieties—Geometry, Combinatorics, Characteristic Classes. ProQuest LLC, Ann Arbor, MI, (2021). Thesis (Ph.D.)–The University of North Carolina at Chapel Hill
Smirnov, A.: On the Instanton R-matrix. Comm. Math. Phys. 345, 703–740 (2016)
Smirnov, A.: Elliptic stable envelope for Hilbert scheme of points in the plane. Selecta Math. (N.S.) 26(1), 57 (2020)
Smirnov, A.: Quantum differential and difference equations for \({{\rm Hilb}}^{n}({\mathbb{C}}^2)\). arXiv e-prints, page arXiv:2102.10726 (2021)
Smirnov, A., Zhou, Z.: 3D mirror symmetry and quantum \(K\)-theory of hypertoric varieties. Adv. Math. 395, 61 (2022)
Tarasov, V., Varchenko, A.: Difference equations compatible with trigonometric KZ differential equations. Internat. Math. Res. Notices 15, 801–829 (2000)
Tarasov, V., Varchenko, A.: Duality for Knizhnik–Zamolodchikov and dynamical equations. Acta Appl. Math. 73(1–2):141–154 (2002). The 2000 Twente Conference on Lie Groups (Enschede)
Tarasov, V., Varchenko, A.: Dynamical differential equations compatible with rational \(qKZ\) equations. Lett. Math. Phys. 71(2), 101–108 (2005)
Toledano Laredo, V.: The trigonometric Casimir connection of a simple Lie algebra. J. Algebra 329, 286–327 (2011)
Varagnolo, M.: Quiver varieties and Yangians. Lett. Math. Phys. 53(4), 273–283 (2000)
Acknowledgements
During our work on this project, we greatly benefited from interaction with M. Aganagic, R. Bezrukavnikov, H. Dinkins, S. Gautam, D. Maulik, S. Shakirov, V. Toledano Laredo and A. Oblomkov. We are particularly grateful to Pavel Etingof for his inspiration and guidance.
A.O. thanks the Simons foundation for being financially supported as a Simons investigator.
The work of A.S. was partially supported by NSF grant DMS-2054527 and by the RSF grant 19-11-00062.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Okounkov, A., Smirnov, A. Quantum difference equation for Nakajima varieties. Invent. math. 229, 1203–1299 (2022). https://doi.org/10.1007/s00222-022-01125-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-022-01125-w



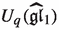 on the Fock space. The package is available from the author upon request.
on the Fock space. The package is available from the author upon request.