Supercritical percolation on nonamenable graphs: isoperimetry, analyticity, and exponential decay of the cluster size distribution

Abstract

Let G be a connected, locally finite, transitive graph, and consider Bernoulli bond percolation on G. We prove that if G is nonamenable and $p > p_c(G)$ then there exists a positive constant $c_p$ such that

$$\begin{aligned} \mathbf {P}_p(n \le |K| < \infty ) \le e^{-c_p n} \end{aligned}$$

for every $n\ge 1$, where K is the cluster of the origin. We deduce the following two corollaries:

• 1. Every infinite cluster in supercritical percolation on a transitive nonamenable graph has anchored expansion almost surely. This answers positively a question of Benjamini et al. (in: Random walks and discrete potential theory (Cortona, 1997), symposium on mathematics, XXXIX, Cambridge University Press, Cambridge, pp 56–84, 1999).

• 2. For transitive nonamenable graphs, various observables including the percolation probability, the truncated susceptibility, and the truncated two-point function are analytic functions of p throughout the supercritical phase.

Introduction

Let $G=(V,E)$ be a connected, locally finite graph. In Bernoulli bond percolation, we choose to either delete or retain each edge of G independently at random with retention probability $p\in [0,1]$ to obtain a random subgraph $\omega$ of G with law $\mathbf {P}_p=\mathbf {P}_p^G$. The connected components of $\omega$ are referred to as clusters, and we denote the cluster of v in $\omega$ by $K_v=K_v(\omega )$. Percolation theorists are particularly interested in the geometry of the open clusters, and how this geometry changes as the parameter p is varied. It is natural to break this study up into several cases according to the relationship between p and the critical probability

$$\begin{aligned} p_c=p_c(G) = \inf \bigl \{p \in [0,1] : \omega \text { has an infinite cluster } \mathbf {P}_p\text {-a.s.}\bigr \}, \end{aligned}$$

which always satisfies $0<p_c<1$ when G is transitive and has superlinear growth [21] (this result is easier and older if G has polynomial growth [47, Corollary 7.19] or exponential growth [34, 46]).

Among the different regimes this leads one to consider, the subcritical phase $0<p<p_c$ is by far the easiest to understand. Indeed, the basic features of subcritical percolation have been well understood since the breakthrough 1986 works of Menshikov [49] and Aizenman and Barsky [1] which, together with the work of Aizenman and Newman [4], establish in particular that if G is a connected, locally finite, transitive graph then

$$\begin{aligned} \zeta (p):= -\limsup _{n\rightarrow \infty } \frac{1}{n}\log \mathbf {P}_p(n \le |E(K_v)| < \infty ) >0 \end{aligned}$$

(1.1)

for every $0 \le p < p_c$, where we write $E(K_v)$ for the set of edges that have at least one endpoint in the cluster $K_v$. See also [22, 23, 39] for alternative proofs, and [16] for more refined results. Note that $\zeta (p)=\zeta (p,G)$ is well-defined for every $0<p<1$ and every connected, locally finite graph G, and in particular that the definition does not depend on the choice of the vertex v.

In contrast, the supercritical phase $p_c<p<1$ is rather more difficult to understand, and no good theory yet exists for supercritical percolation on general transitive graphs. A central role in the theory of this phase is played by the distribution of finite clusters. For $\mathbb {Z}^d$ with $d\ge 3$, most results concerning this distribution rely crucially on the

important and technically challenging work of Grimmett and Marstrand [28], which allowed in particular for a complete proof of the asymptotics

$$\begin{aligned}&\mathbf {P}_p\bigl (o \leftrightarrow \partial [-n,n]^d, |K_o|< \infty \bigr )&= \exp \left[ -\Theta _p(n)\right]&\quad \text { as } n \uparrow \infty \end{aligned}$$

(1.2)

$$\begin{aligned} \text {and}&\mathbf {P}_p\bigl (n \le |K_o| < \infty \bigr )&= \exp \left[ -\Theta _p\left( n^{\frac{d-1}{d}}\right) \right]&\quad \text { as } n \uparrow \infty . \end{aligned}$$

(1.3)

The upper bounds of (1.2) and (1.3) were proven by Chayes et al. [18] and by Kesten and Zhang [43] respectively, both conditional on the then-conjectural Grimmett–Marstrand theorem. All of these upper bounds rely essentially on renormalization, a technique that is unavailable outside the Euclidean setting. The lower bound of (1.2) is trivial, while the lower bound (1.3) was proven by Aizenman et al. [2]; see also [27, Sections 8.4–8.6]. The more refined properties of finite clusters in supercritical percolation on $\mathbb {Z}^d$ remain an area of active research, see e.g. [15, 17] and references therein. We note moreover that percolation in the slightly supercritical $(p \downarrow p_c)$ regime remains very poorly understood on $\mathbb {Z}^d$ even when d is large, in which case critical ($p=p_c$) percolation is now well understood following in particular the work of Hara and Slade [32]; See [33] for an overview of progress and problems in this direction.

In this paper, we develop a theory of supercritical percolation on nonamenable transitive graphs, studying in particular the distribution of finite clusters, the geometry of the infinite clusters, and the regularity of the dependence of various observables on p.

Our main result, from which various corollaries will be derived, is the following theorem. An extension of the theorem to the quasi-transitive case is given in Sect. 4.

Theorem 1.1

Let $G=(V,E)$ be a connected, locally finite, nonamenable, transitive graph. Then $\zeta (p)>0$ for every $p_c < p \le 1$.

We stress that our methods are completely different to those used in the Euclidean context. We also note that we do not study the question of the (non)uniqueness of the infinite cluster, which remains completely open at this level of generality. We refer the interested reader to [35, 40] and references therein for an up-to-date account of what is known regarding this question and the closely related problem of understanding critical percolation on nonamenable transitive graphs.

Here, we recall that a locally finite graph G is said to be nonamenable if its Cheeger constant

$$\begin{aligned} \Phi _E(G)=\inf \left\{ \frac{|\partial _E K|}{\sum _{v\in K} \deg (v)} : K \subseteq V \text { finite}\right\} \end{aligned}$$

is positive, where for each set $K \subset V$ we write $\partial _E K$ for the set of edges with one endpoint in K and the other outside of K.

For example, Euclidean lattices such as $\mathbb {Z}^d$ are amenable, while regular trees of degree at least three and transitive tessellations of hyperbolic spaces are nonamenable. Previously, Theorem 1.1 was known only for $p > (1-\Phi _E(G))/(1+\Phi _E(G))$, where it follows by a simple counting argument [12, Theorem 2] and does not require transitivity. We believe that the full conclusions of Theorem 1.1 were only previously known for trees. Note that the theorem fails without the assumption of transitivity: For example, the graph obtained by attaching a 3-regular tree and a 4-regular tree by a single edge between their respective origins has $p_c=1/3$ and $\zeta (1/2)=0$.

It was observed in [8] that the argument of [2] can be generalized to prove that $\zeta (p)=0$ for every $p>p_c$ whenever G is a Cayley graph of a finitely presented amenable group. In Corollary 3.5 we prove via a different argument that in fact $\zeta (p)=0$ for every amenable transitive graph and every $p_c \le p <1$. This gives a converse to Theorem 1.1, so that, combining both results, we obtain the following appealing percolation-theoretic characterization of nonamenability for transitive graphs:

Corollary 1.2

Let G be a connected, locally finite, transitive graph. The following are equivalent:

• 1. G is nonamenable.

• 2. $p_c(G)<1$ and $\zeta (p)>0$ for every $p\in (p_c,1)$.

• 3. $p_c(G)<1$ and $\zeta (p)>0$ for some $p\in (p_c,1)$.

We note in particular that Theorem 1.1 and Corollary 1.2 resolve several questions raised by Bandyopadhyay et al. [8, Questions 1 and 2 and Conjecture 1].

Analyticity

One nice corollary of Theorem 1.1 is that many quantities including the percolation probability $\theta (p)=\mathbf {P}_p(|K_v|=\infty )$, the truncated susceptibility $\chi ^f(p)=\mathbf {E}_p |K_v| \mathbb {1}(|K_v|<\infty )$, the free energy $\kappa (p)=\mathbf {E}_p |K_v|^{-1}$, and the truncated two-point function $\tau ^f_p(u,v) = \mathbf {P}_p(u \leftrightarrow v, |K_v|<\infty )$ all depend analytically on p throughout the entire supercritical phase. The regularity properties of these functions have historically been a subject of great importance in percolation, motivated in part by the still uncompleted project to rigorize the heuristic computation of $p_c$ for various planar lattices by Sykes and Essam [55]. See e.g. [25, 27, 41] for further background.

Let us now state our general analyticity result.

Let $\mathscr {H}_v$ denote the set of finite connected subgraphs of G containing v, and say that a function $F : \mathscr {H}_v \rightarrow \mathbb {C}$ has subexponential growth if $\limsup _{n\rightarrow \infty } \frac{1}{n} \log \sup \{ |F(H)| : H \in \mathscr {H}_v,\, |E(H)| \le n \} \le 0$. It is an observation essentially due to Kesten [41, 42], and a consequence of Morera’s Theorem and the Weierstrass M-test, that if $F:\mathscr {H}_v \rightarrow \mathbb {C}$ has subexponential growth then the function

$$\begin{aligned} \mathbf {E}_p\left[ F(K_v) \mathbb {1}(|K_v| < \infty ) \right] = \sum _{H \in \mathscr {H}_v} F(H) \mathbf {P}_p(K_v=H) \end{aligned}$$

is analytic in p on the set $\{p\in (0,1) : \zeta (p)>0\}$, which always contains $(0,p_c)$ when G is transitive as discussed above. More precisely, this means that for every $p_0 \in (0,1)$ with $\zeta (p_0)>0$ there exists $\varepsilon >0$ and a complex analytic function on the complex ball of radius $\varepsilon$ around $p_0$ whose restriction to $(p_0-\varepsilon ,p_0+\varepsilon )$ agrees with the function under consideration. See Proposition 3.1 for details. Thus, Theorem 1.1 has the following corollary.

Corollary 1.3

Let $G=(V,E)$ be a connected, locally finite, nonamenable, transitive graph, let $v \in V$ and let $F:\mathscr {H}_v \rightarrow \mathbb {C}$ have subexponential growth. Then $\mathbf {E}_p\left[ F(K_v) \mathbb {1}(|K_v| < \infty ) \right]$ is an analytic function of p on $(0,p_c) \cup (p_c,1)$.

Previously, it was not even known that $\theta (p)$ was differentiable on $(p_c,1)$ under the same hypotheses. On the other hand, it is an immediate consequence of the mean-field lower bound on $\theta (p_c+\varepsilon )$ [23, Theorem 1.1] that the percolation probability $\theta (p)$ is always non-differentiable at $p_c$ when G is transitive, so that Corollary 1.3 is best-possible in this case. (Note that analyticity of $\theta (p)$ follows from Corollary 1.3 by taking $F \equiv 1$.) It remains open to prove that the free energy (a.k.a. open-clusters-per-vertex) $\kappa (p)=\mathbf {E}_p |K_v|^{-1}$ is not analytic at $p_c$.

We remark that in amenable transitive graphs, subexponential decay of the cluster volume distribution makes analyticity in the supercritical phase a much more delicate issue. Indeed, while infinite differentiability of $\theta (p)$, $\chi ^f(p)$, $\kappa (p)$, and $\tau _p^f(u,v)$ in the supercritical phase of $\mathbb {Z}^d$ is an easy consequence of superpolynomial decay [27, Theorem 8.92], the analyticity of these functions was settled only in the very recent work of Georgakopoulos and Panagiotis [25, 26].

Isoperimetry and random walk

In this section, we discuss applications of Theorem 1.1 to the isoperimetry of infinite percolation clusters on nonamenable transitive graphs. It is easily seen that percolation clusters cannot be nonamenable when $p<1$, since infinite clusters will always contain arbitrarily large isoperimetrically ‘bad regions’, such as long paths. Nevertheless, one has the intuition that supercritical percolation clusters on nonamenable transitive graphs ought to be ‘essentially nonamenable’ in some sense. With the aim of making this intuition precise, Benjamini et al. [10] defined the anchored Cheeger constant of a connected, locally finite graph $G=(V,E)$ to be

$$\begin{aligned} \Phi ^*_E(G):=\lim _{n\rightarrow \infty }\inf \left\{ \frac{|\partial _E K|}{\sum _{u\in K} \deg (u)} : K \subseteq V \text { connected},\, v\in K,\, \text { and } n\le |K|<\infty \right\} , \end{aligned}$$

where v is a vertex of G whose choice does not affect the value obtained, and said that G has anchored expansion if $\Phi _E^*(G)>0$. They asked [10, Question 6.5] whether every infinite cluster in supercritical Bernoulli bond percolation on G has anchored expansion whenever G is transitive¹ and nonamenable. (See also [47, Question 6.49].) Partial progress on this question was made by Chen et al. [19], who proved in particular that every infinite cluster has anchored expansion a.s. for p sufficiently close to 1. Their result does not require transitivity. Their paper also treats some other related models, most notably establishing anchored expansion for supercritical Galton–Watson trees. Anchored expansion has subsequently been established for various other random graph models, see [7, 11, 20].

Applying Theorem 1.1 together with the argument of [19, Theorem A.1], we are able to give a complete solution to [10, Question 6.5].

Corollary 1.4

Let G be a connected, locally finite, nonamenable, transitive graph, and let $p_c<p \le 1$. Then every infinite cluster in Bernoulli-p bond percolation on G has anchored expansion almost surely.

Corollary 1.4 also allows us to analyze the behaviour of the simple random walk on the infinite clusters of Bernoulli percolation under the same hypotheses. Indeed, it is a theorem of Virág [57, Theorem 1.2] that if G is a bounded degree graph with anchored expansion then there exists a positive constant c such that the simple random walk return probabilities on G satisfy the inequality $p_n(v,v) \le C_v e^{-cn^{1/3}}$ for every vertex v of G, where $C_v$ is a v-dependent constant. In Sect. 3.3 we establish that a matching lower bound also holds in our setting, thereby deducing the following corollary. We write $p_n^\omega (v,v)$ for the n-step return probability of simple random walk from v on the percolation configuration $\omega$.

Corollary 1.5

Let G be a connected, locally finite, nonamenable, transitive graph, let $p_c<p < 1$, and let v be a vertex of G. Then

$$\begin{aligned} 0< \liminf _{n\rightarrow \infty }\frac{-\log p_{2n}^\omega (v,v)}{n^{1/3}} \le \limsup _{n\rightarrow \infty } \frac{-\log p_{2n}^\omega (v,v)}{n^{1/3}} < \infty \end{aligned}$$

almost surely on the event that the cluster of v is infinite.

Remark 1.6

Virág [57, Theorem 1.1] also established that anchored expansion implies positive speed of the random walk on bounded degree graphs. For supercritical percolation on unimodular transitive nonamenable graphs, positive speed of the random walk was already proven to hold by Benjamini et al. [10, Theorem 1.3]. Combining Corollary 1.4 with the aforementioned result of Virág allows us to extend this result to the nonunimodular case. The resulting fact that every cluster is transient in supercritical percolation on nonunimodular transitive graphs was first proven by Tang [56].

The same $\exp (-\Theta (n^{1/3}))$ return probability asymptotics given by Corollary 1.5 also appear in many other random graph models of nonamenable flavour [7, 53].

For results on isoperimetry and random walks in supercritical percolation on $\mathbb {Z}^d$, see e.g. [9, 51] and references therein.

About the proof and organization The proof of the main theorem, Theorem 1.1, is given in Sect. 2. The starting point of the proof is to use Russo’s formula to express the p-derivative of the truncated exponential moment $\mathbf {E}_{p}[e^{t|E(K_v)|}\mathbb {1}(|E(K_v)|<\infty )]$ as the sum of a positive term, which corresponds to the cluster growing while remaining finite, and a negative term, which corresponds to the finite cluster becoming infinite. (To do this rigorously we instead truncate at a large finite volume.) The proof then hinges on two key ideas, each of which allows us to bound the absolute value of one of these two terms. The bounds on the negative term work by re-purposing ideas from the Burton–Keane proof that there is at most one infinite cluster in percolation on amenable transitive graphs [14]. We use here the fact that supercritical percolation on a nonamenable transitive graph always stochastically dominates an invariant percolation process with trifurcation points (Lemma 2.5), which is a sort of weak converse to Burton–Keane and is due in the unimodular case to Benjamini et al. [10]. Meanwhile, for the positive term, we first bound the derivative in terms of certain ‘skinny trees of bridges’, and then bound the resulting expression using an inductive argument. This is the most technical part of the paper. Finally, the derivative itself, which is the difference of these two terms, can be bounded using martingale methods. Once these three bounds are in hand, the finiteness of $\mathbf {E}_{p}[e^{t|E(K_v)|}\mathbb {1}(|E(K_v)|<\infty )]$ follows easily.

We then apply Theorem 1.1 to deduce Corollaries 1.2–1.5 in Sect. 3, generalize Theorem 1.1 to the quasi-transitive case in Sect. 4, and give closing remarks and open problems in Sect. 5.

Remark 1.7

An interesting feature of our proof is that, although we rely on an equality (2.3) obtained by expressing the derivative of $\mathbf {E}_{p}[e^{t|E(K_v)|}\mathbb {1}(|E(K_v)|\le n)]$ in two different ways, we do not use the fact that this equality is related to the derivative. In particular, we do not integrate any differential inequality nor use any sprinkling, in contrast with the classical results mentioned above. Speculatively, this may mean that some of the techniques we develop here have applications to critical percolation on amenable transitive graphs under the (presumably contradictory) assumption that there is an infinite cluster at $p_c$.

Proof of the main theorem

In this section we prove Theorem 1.1.

Let $G=(V,E)$ be a connected, locally finite graph, and let v be a vertex of G. For each $\omega \in \{0,1\}^E$ we write $K_v(\omega )$ for the cluster of v in $\omega$, and write $E_v(\omega ) = |E(K_v(\omega ))|$ for the number of edges touching $K_v(\omega )$. We will usually take $\omega$ be an instance of Bernoulli-p bond percolation on G, in which case we write $K_v=K_v(\omega )$ and $E_v=E_v(\omega )$ when there is no risk of confusion. Recall that $\mathscr {H}_v$ denotes the set of all finite connected subgraphs of G containing v. Given a function $F: \mathscr {H}_v \rightarrow \mathbb {R}$, we write

$$\begin{aligned}&\mathbf {E}_{p,n}[F(K_v)] := \mathbf {E}_p\left[ F(K_v)\mathbb {1}(E_v \le n)\right] \quad \text { and } \\&\quad \mathbf {E}_{p,\infty }[F(K_v)] := \mathbf {E}_p\left[ F(K_v)\mathbb {1}(E_v < \infty )\right] \end{aligned}$$

for every $p\in [0,1]$ and $n \ge 1$. To prove Theorem 1.1, it suffices to prove that if G is transitive and nonamenable then for every $p_c(G)<p<1$ there exists $t>0$ such that $\mathbf {E}_{p,\infty }[E_v e^{t E_v}] < \infty$.

Given $F: \mathscr {H}_v \rightarrow \mathbb {R}$ and $n\ge 1$, the truncated expectation $\mathbf {E}_{p,n}[F(K_v)]$ is a polynomial in p and is therefore differentiable. We begin our analysis by expressing the p-derivative of $\mathbf {E}_{p,n}[F(K_v)]$ in two different ways. The first way to express the derivative is in terms of the fluctuation in the number of open edges in the cluster of v, which we now introduce. For each finite subgraph H of G, we define E(H) to be the set of edges of G with at least one endpoint in the vertex set of H, define $E_o(H)$ to be the edges of H, and define $\partial H$ to be $E(H) {\setminus } E_o(H)$. (Note that $\partial H$ is not always the same thing as the edge boundary $\partial _E V(H)$ of the vertex set V(H) of H, and it is possible for edges of $\partial H$ to have both endpoints in the vertex set of H.) For each $p\in [0,1]$ we also define the fluctuation

$$\begin{aligned} h_p(H)=p|\partial H|-(1-p)|E_o(H)|. \end{aligned}$$

(2.1)

Then for every $n \ge 1$, $p\in (0,1)$, and $F: \mathscr {H}_v \rightarrow \mathbb {R}$ we may compute that

$$\begin{aligned}&\frac{d}{dp} \mathbf {E}_{p,n} \left[ F(K_v) \right] \nonumber \\&\quad = \sum _{H \in \mathscr {H}_v} \frac{d}{dp} p^{|E_o(H)|}(1-p)^{|\partial H|} F(H) \mathbb {1}(|E(H)|\le n) \nonumber \\&\quad = -\frac{1}{p(1-p)}\sum _{H \in \mathscr {H}_v} h_p(H) p^{|E_o(H)|}(1-p)^{|\partial H|} F(H) \mathbb {1}(|E(H)|\le n) \nonumber \\&\quad = -\frac{1}{p(1-p)}\mathbf {E}_{p,n} \left[ h_p(K_v) F(K_v)\right] =: -\mathbf {M}_{p,n}[F(K_v)]. \end{aligned}$$

(2.2)

In many situations, it is fruitful to bound the absolute value of this expression by viewing $h_p(K_v)$ as the final value of a certain martingale (indeed, a stopped random walk) that arises when exploring the cluster of v one step at a time. We will apply this strategy to bound the absolute value of the derivative $\frac{d}{dp}\mathbf {E}_{p,n} \left[ e^{tE_v} \right]$ in Sect. 2.2.

Next, we apply Russo’s formula to give an alternative expression for the derivative in terms of pivotal edges. For each $\omega \in \{0,1\}^E$ and $e \in E$, let $\omega ^e = \omega \cup \{e\}$ and let $\omega _e = \omega {\setminus } \{e\}$. (Here and elsewhere we abuse notation to identify elements of $\{0,1\}^E$ with subsets of E whenever it is convenient to do so. This should not cause any confusion.) Russo’s formula [27, Theorem 2.32] states that if $X:\{0,1\}^E\rightarrow \mathbb {R}$ depends on at most finitely many edges, then

$$\begin{aligned} \frac{d}{dp}\mathbf {E}_p \left[ X(\omega )\right] = \sum _{e\in E} \mathbf {E}_p\left[ X(\omega ^e)-X(\omega _e) \right] . \end{aligned}$$

Applying this formula to X of the form $X(\omega )=F(K_v)\mathbb {1}(E_v\le n)$ for $F:\mathscr {H}_v \rightarrow \mathbb {R}$, we deduce that

$$\begin{aligned} \frac{d}{dp}\mathbf {E}_{p,n} \left[ F(K_v)\right]= & {} \sum _{e\in E} \mathbf {E}_p\left[ \left( F\left[ K_v(\omega ^e)\right] -F\left[ K_v(\omega _e)\right] \right) \mathbb {1}\left( E_v(\omega ^e) \le n \right) \right] \\&-\sum _{e\in E} \mathbf {E}_p\left[ F\left[ K_v(\omega _e)\right] \mathbb {1}\bigl (E_v(\omega _e) \le n < E_v(\omega ^e)\bigr ) \right] . \end{aligned}$$

We denote the two terms appearing on the right hand side of this expression by

$$\begin{aligned} \mathbf{U}_{p,n}\left[ F(K_v)\right]&:= \sum _{e\in E} \mathbf {E}_p\left[ \left( F\left[ K_v(\omega ^e)\right] -F\left[ K_v(\omega _e)\right] \right) \mathbb {1}\left( E_v(\omega ^e) \le n \right) \right] \\&= {\frac{1}{p}} \sum _{e\in E} \mathbf {E}_{p,n}\left[ \left( F\left[ K_v\right] -F\left[ K_v(\omega _e)\right] \right) \mathbb {1}\bigl (\omega (e)=1\bigr ) \right] \end{aligned}$$

and

$$\begin{aligned} \mathbf{D}_{p,n}\left[ F(K_v)\right]&:= \sum _{e\in E} \mathbf {E}_p\left[ F\left[ K_v(\omega _e)\right] \mathbb {1}\bigl (E_v(\omega _e) \le n< E_v(\omega ^e)\bigr ) \right] \\&= {\frac{1}{1-p}}\sum _{e\in E} \mathbf {E}_p\left[ F(K_v) \mathbb {1}\bigl (\omega (e)=0,\, E_v \le n < E_v(\omega ^e)\bigr ) \right] , \end{aligned}$$

so that

$$\begin{aligned} -\mathbf {M}_{p,n}[F(K_v)] = \frac{d}{dp}\mathbf {E}_{p,n} \left[ F(K_v)\right] = \mathbf {U}_{p,n}[F(K_v)]-\mathbf {D}_{p,n}[F(K_v)] \end{aligned}$$

(2.3)

for every $F:\mathscr {H}_v \rightarrow \mathbb {R}$, every $p\in (0,1)$, and every $n\ge 1$. Note that $\mathbf {M}_{p,n}[F(K_v)]$, $\mathbf {U}_{p,n}[F(K_v)]$, and $\mathbf {D}_{p,n}[F(K_v)]$ all depend linearly on $F:\mathscr {H}_v \rightarrow \mathbb {R}$ for fixed $p \in (0,1)$ and $n\ge 1$, that $\mathbf {D}_{p,n}[F(K_v)]$ is nonnegative if F is nonnegative and that $\mathbf {U}_{p,n}[F(K_v)]$ is nonnegative if F is increasing.

Our strategy will be to use the equality (2.3) to obtain bounds on moments of certain random variables. In the remainder of this section we carry this out conditional on three supporting propositions, each of which gives control of one of the three quantities $\mathbf {M}_{p,n}[e^{t E_v}]$, $\mathbf {U}_{p,n}[e^{t E_v}]$, or $\mathbf {D}_{p,n}[e^{t E_v}]$, and which will be proved in the following three subsections. We begin by stating the following proposition, which is proven in Sect. 2.1.

Proposition 2.1

Let G be a connected, locally finite, nonamenable, transitive graph. Then for every $p_0>p_c(G)$ there exists a constant $c_{p_0}=c_{p_0}(G,p)$ such that

$$\begin{aligned} \mathbf {D}_{p,n}\left[ F(K_v)\right] \ge \frac{c_{p_0}}{1-p} \mathbf {E}_{p,n}\left[ E_v \cdot F(K_v)\right] \end{aligned}$$

for every nonnegative function $F: \mathscr {H}_v \rightarrow [0,\infty )$, every $p_0 \le p < 1$, and every $n\ge 1$.

We remark that the complementary inequality $\mathbf {D}_{p,n}\left[ F(K_v)\right] \le \frac{1}{1-p} \mathbf {E}_{p,n}\left[ E_v \cdot F(K_v)\right]$ always holds trivially on every connected, locally finite graph.

Applying Proposition 2.1 to the function $F(K_v) = e^{t E_v}$, we obtain that for every $p_c<p<1$ there exists a positive constant $c_p$ such that

$$\begin{aligned} \frac{c_{p}}{1-p} \mathbf {E}_{p,n}\left[ E_v e^{t E_v}\right] \le \mathbf {D}_{p,n}\left[ e^{t E_v}\right] = \mathbf {U}_{p,n}\left[ e^{t E_v}\right] + \mathbf {M}_{p,n}\left[ e^{t E_v}\right] \end{aligned}$$

(2.4)

for every $n\ge 1$, and $t\ge 0$. We want to show that if $t>0$ is sufficiently small then the expectation on the left is bounded uniformly in n.

To do this, we bound each term on the right hand side by the sum of a term that can be absorbed into the left hand side and a term that we will show is bounded as $n\rightarrow \infty$ for sufficiently small values of $t>0$. For the second term, this is quite straightforward to carry out using the bound

$$\begin{aligned} \mathbf {M}_{p,n}\left[ e^{t E_v}\right]\le & {} \frac{c_p}{4(1-p)} \mathbf {E}_{p,n}\left[ E_v e^{t E_v}\right] \nonumber \\&+ \frac{1}{p(1-p)} \mathbf {E}_{p,n}\left[ |h_p(K_v)| e^{t E_v} \mathbb {1}\left( |h_p(K_v)| \ge \frac{pc_p}{4}E_v\right) \right] .\nonumber \\ \end{aligned}$$

(2.5)

The term on the second line can readily be shown to be bounded as $n\rightarrow \infty$ for sufficiently small t via a martingale analysis, as summarized by the following proposition which is proven in Sect. 2.2.

Proposition 2.2

Let $\alpha >0$. Then

$$\begin{aligned} \mathbf {E}^G_p\left[ |h_p(K_v)| e^{t E_v } \mathbb {1}\left( \alpha E_v \le |h_p(K_v)|<\infty \right) \right] < \infty \end{aligned}$$

for every locally finite graph $G=(V,E)$, every $v\in V$, every $p\in [0,1]$, and every $0 \le t < \alpha ^2/2$.

Bounding $\mathbf {U}_{p,n}[e^{t E_v}]$ is rather more complicated. Let H be a finite connected graph. For each edge e of H, let $H_e$ denote the subgraph of H spanned by all edges of H other than e. Given a vertex v and a set W of vertices in H, we write ${\text {Piv}}(H,v,W)$ for the set of edges e such that there exists $w \in W$ such that v is not connected to w in $H_e$, and define

$$\begin{aligned} {\text {Br}}_k(H,v) = \max \Bigl \{|{\text {Piv}}(H,v,W)| : |W| \le k \Bigr \}. \end{aligned}$$

We will use these quantities to bound $\mathbf {U}_{p,n}[e^{tE_v}]$. To do this, we first write

$$\begin{aligned}&\mathbf {U}_{p,n}\left[ E_v^k\right] \\&\quad = \frac{1}{p} \sum _{e\in E} \mathbf {E}_{p,n}\left[ \left( E_v^k-E_v(\omega _e)^k\right) \mathbb {1}\bigl (\omega (e)=1\bigr ) \right] \\&\quad = \frac{1}{p} \sum _{a_1,\ldots ,a_k\in E} \sum _{e\in E} \mathbf {P}_p\biggl ( \{a_1,\ldots ,a_k\}\\&\subseteq E(K_v),\, \{a_1,\ldots ,a_k\} \not \subseteq E(K_v(\omega _e)), \omega (e)=1,\text { and } E_v \le n \biggr ) \end{aligned}$$

for each $k\ge 1$. Let $A \subseteq E(K_v)$ have $|A| \le k$ and for each edge $e \in A$ let w(e) be an endpoint of e in $K_v$, and let $W=W(A) = \{w(e) : e \in A\}$. Then we have that

$$\begin{aligned} \sum _{e\in E} \mathbb {1}\biggl ( A \not \subseteq E(K_v(\omega _e)) \text { and }\omega (e)=1 \biggr ) \le |{\text {Piv}}(K_v,v,W)| \le {\text {Br}}_k(K_v,v). \end{aligned}$$

Since this inequality holds for every set $A \subseteq E$ with $|A|\le k$, we deduce that

$$\begin{aligned} \mathbf {U}_{p,n}\left[ E_v^k\right]&\le \frac{1}{p} \sum _{a_1,\ldots ,a_k\in E} \mathbf {E}_{p,n}\biggl [ {\text {Br}}_k(K_v,v) \mathbb {1}\left( \{a_1,\ldots ,a_k\} \subseteq E(K_v)\right) \biggr ]\nonumber \\&= \frac{1}{p}\mathbf {E}_{p,n}\left[ {\text {Br}}_k(K_v,v) E_v^k \right] \end{aligned}$$

(2.6)

for every $p\in (0,1)$ and $k\ge 1$.

Summing over k, we obtain that

$$\begin{aligned} \mathbf {U}_{p,n}\left[ e^{tE_v}\right] = \sum _{k = 0}^\infty \frac{t^k}{k!} \mathbf {U}_{p,n}\left[ E_v^k \right] \le \frac{1}{p}\sum _{k = 1}^\infty \frac{t^k}{k!}\mathbf {E}_{p,n}\left[ {\text {Br}}_k(K_v,v) E_v^k \right] \end{aligned}$$

(2.7)

for every $t>0$. Similarly to (2.5), we can bound this expression by

$$\begin{aligned} \mathbf {U}_{p,n}\left[ e^{t E_v}\right]\le & {} \frac{c_p}{4(1-p)} \mathbf {E}_{p,n}\left[ E_v e^{t E_v}\right] \nonumber \\&+ \frac{1}{p} \sum _{k = 1}^\infty \frac{t^k}{k!}\mathbf {E}_{p,n}\left[ {\text {Br}}_k(K_v,v) E_v^k \mathbb {1}\left( {\text {Br}}_k(K_v,v) \ge \frac{pc_p}{4(1-p)} E_v \right) \right] . \nonumber \\ \end{aligned}$$

(2.8)

The second term is dealt with by the following proposition, which is proven in Sect. 2.3.

Proposition 2.3

Let $\alpha >0$ and $p\in (0,1)$. Then there exists $t_{\alpha ,p} >0$ such that

$$\begin{aligned} \sum _{k=1}^\infty \frac{t^k}{k! }\mathbf {E}^G_p\left[ {\text {Br}}_k(K_v,v) E_v^k \mathbb {1}\left( \alpha E_v \le {\text {Br}}_k(K_v,v)<\infty \right) \right] < \infty \end{aligned}$$

for every locally finite graph $G=(V,E)$, every $v\in V$ and every $0 \le t < t_{\alpha ,p}$.

Let us now see how the proof of Theorem 1.1 can be concluded given Propositions 2.1–2.3.

Proof of Theorem 1.1

Let G be a connected, locally finite, transitive, nonamenable graph, and let $p>p_c(G)$. Letting $c_p$ be the constant from Proposition 2.1, we deduce from (2.4), (2.5), and (2.8) that

$$\begin{aligned}&\frac{c_p}{2(1-p)} \mathbf {E}_{p,n}\left[ E_v e^{tE_v}\right] \\&\quad \le \frac{1}{p} \sum _{k = 1}^\infty \frac{t^k}{k!}\mathbf {E}_{p,n}\left[ {\text {Br}}_k(K_v,v) E_v^k \mathbb {1}\left( {\text {Br}}_k(K_v,v) \ge \frac{pc_p}{4(1-p)} E_v \right) \right] \\&\qquad +\frac{1}{p(1-p)} \mathbf {E}_{p,n}\left[ |h_p(K_v)| e^{t E_v} \mathbb {1}\left( |h_p(K_v)| \ge \frac{pc_p}{4}E_v\right) \right] \end{aligned}$$

for every $n\ge 1$ and $t\ge 0$. Taking limits as $n\uparrow \infty$ we obtain that

$$\begin{aligned}&\frac{c_p}{2(1-p)} \mathbf {E}_{p,\infty }\left[ E_v e^{tE_v}\right] \\&\quad \le \frac{1}{p} \sum _{k =1}^\infty \frac{t^k}{k!}\mathbf {E}_{p,\infty }\left[ {\text {Br}}_k(K_v,v) E_v^k \mathbb {1}\left( {\text {Br}}_k(K_v,v) \ge \frac{pc_p}{4(1-p)} E_v \right) \right] \\&\qquad +\frac{1}{p(1-p)} \mathbf {E}_{p,\infty }\left[ |h_p(K_v)| e^{t E_v} \mathbb {1}\left( |h_p(K_v)| \ge \frac{pc_p}{4}E_v\right) \right] \end{aligned}$$

for every $t\ge 0$. Propositions 2.2 and 2.3 imply that there exists $t_0=t_0(p,c_p)>0$ such that the right hand side is finite for every $0\le t < t_0$, completing the proof. $\square$

It now remains to prove Propositions 2.1–2.3.

Bounding the negative term

In this section we prove Proposition 2.1. Note that the proof of this proposition is the only place where the assumption of nonamenability and transitivity are used in the proof of Theorem 1.1. The proof is also ineffective in the sense that it does not yield any explicit lower bound on the constant $c_{p_0}$, and is in fact the only ineffective step in the proof of Theorem 1.1.

Let $G=(V,E)$ be a locally finite graph, let $\omega \in \{0,1\}^E$, and let S be a finite subset of V. We define the quantity

$$\begin{aligned} \mathscr {P}_\omega (S \rightarrow \infty ) = \min \Bigl \{ |C| : C \subseteq E,\, S \text { not connected to } \infty \text { in } \omega {\setminus } C \Bigr \}. \end{aligned}$$

By Menger’s Theorem [31], this quantity is equal to the maximum size of a set of edge-disjoint paths from S to $\infty$ in the subgraph of G spanned by $\omega$. Note in particular that $\mathscr {P}_\omega (S \rightarrow \infty )$ is an increasing function of $\omega \in \{0,1\}^E$. Proposition 2.1 will be deduced from the following proposition.

Proposition 2.4

Let G be a connected, locally finite, nonamenable, transitive graph. Then for every $p>p_c(G)$ there exists a positive constant $c_{p}$ such that

$$\begin{aligned} \mathbf {E}_p\left[ \mathscr {P}_\omega (S \rightarrow \infty )\right] \ge c_{p}|E(S)| \end{aligned}$$

(2.9)

for every $S \subset V$ finite.

The proof of Proposition 2.4 uses elements of the Burton–Keane [14] argument, which is usually used to establish uniqueness of the infinite cluster in percolation on amenable transitive graphs. This argument in fact establishes that the inequality (2.9) holds when there are infinitely many infinite clusters for percolation with parameter p. (In the amenable case one can then prove by contradiction that such p do not exist, since the left hand side of (2.9) is at most $|\partial _E S|$.) To apply this argument in our setting, since we are not assuming that there are infinitely many infinite clusters in Bernoulli-p percolation, we will first need to find an appropriate automorphism-invariant percolation process that has infinitely many infinite connected components each of which is infinitely ended and which is stochastically dominated by Bernoulli p-percolation. We do this by a case analysis according to whether or not G is unimodular, applying the results of [10] in the unimodular case and of [40] in the nonunimodular case.

We will borrow in particular from the presentation of the Burton-Keane argument given in [47, Theorem 7.6]. Let $G=(V,E)$ be a graph and let $\eta \in \{0,1\}^E$. We say that a vertex v is a furcation of $\eta$ if closing all edges incident to v would split the component of v in $\eta$ into at least three distinct infinite connected components.

Lemma 2.5

Let $G=(V,E)$ be a connected, locally finite, nonamenable, transitive graph, and let $p_c(G)<p \le 1$. Then there exists an automorphism-invariant percolation process $\eta$ on G such that the following hold:

• 1. The origin is a furcation of $\eta$ with positive probability.

• 2. The process $\eta$ is stochastically dominated by Bernoulli-p bond percolation on G.

Here, we recall that if G is a connected, locally finite, transitive graph, a random variable $\eta$ taking values in $\{0,1\}^E$ is an automorphism-invariant percolation process if its law is invariant under the automorphisms of G. See e.g. [10, 47] for background on general automorphism-invariant percolation processes.

Before beginning the proof of this lemma, let us briefly introduce the notion of unimodularity. We refer the reader to [47, Chapter 8] for further background. Let $G=(V,E)$ be a connected, locally finite, transitive graph with automorphism group ${\text {Aut}}(G)$. The modular function $\Delta : V^2 \rightarrow \mathbb {R}$ of G is defined to be $\Delta (u,v) = |{\text {Stab}}_v u |/|{\text {Stab}}_u v|$, where ${\text {Stab}}_v = \{ \gamma \in {\text {Aut}}(G) : \gamma v = v \}$ is the stabilizer of v in ${\text {Aut}}(G)$ and ${\text {Stab}}_v u = \{\gamma u : \gamma \in {\text {Stab}}_v\}$ is the orbit of u under ${\text {Stab}}_v$. We say that G is unimodular if $\Delta (u,v) \equiv 1$ and that G is nonunimodular otherwise. Most graphs occurring in examples are unimodular, including all Cayley graphs of finitely generated groups and all transitive amenable graphs [54].

Proof of Lemma 2.5

Recall the definition of the uniqueness threshold $p_u=p_u(G)=\inf \{ p\in [0,1] : \omega$ has a unique infinite cluster $\mathbf {P}_p$-a.s.$\}$. The usual Burton-Keane argument implies that if $q\in (p_c,p_u)$ then the origin is a furcation for Bernoulli-q percolation with positive probability; See in particular the proof of [47, Theorem 7.6]. Thus, if $p_c(G)<p_u(G)$ we may take $\eta$ to be Bernoulli-q percolation for some $p_c< q < p_u \wedge p$. The main result of [40] states that $p_c(G)<p_u(G)$ if G is nonunimodular (or more generally if G has a nonunimodular transitive subgroup of automorphisms), which completes the proof in this case. Now suppose that G is unimodular. A result of Benjamini et al. [10, Lemma 3.8 and Theorem 3.10] states that for every $p\in (p_c,1]$, Bernoulli-p bond percolation on G stochastically dominates an automorphism-invariant percolation process that is almost surely a forest all of whose components are infinitely-ended (see also [5, Theorem 8.13]). More precisely, [10, Theorem 3.10] implies that this is the case² when there is uniqueness at p, while [10, Lemma 3.8] implies that this is the case when there is non-uniqueness at p. (Here, we recall that a locally finite tree is infinitely-ended if it contains infinitely many disjoint infinite simple paths.) Any such automorphism-invariant process clearly has furcations, and so meets the conditions required by the lemma. $\square$

The rest of the proof of Proposition 2.4 is very similar to the Burton-Keane argument as presented in [47, Section 7.3]; we include the details for completeness. We will use the following elementary combinatorial lemma.

Lemma 2.6

Let $T=(V_T,E_T)$ be a tree in which every vertex has degree at least two. If $A \subseteq V_T$ is a finite set of vertices in T, then there exists a set of $\sum _{v\in A} (\deg (v)-2)$ edge-disjoint paths from A to $\infty$ in T.

Proof

We may assume that A is non-empty, the claim being trivial otherwise. Let $\Gamma$ be the smallest connected subtree of T containing A, so that $\Gamma$ is the union of all finite simple paths beginning and ending in A. Let I be the set of edges that are incident to a vertex of A but do not belong to $\Gamma$, and observe that the maximum number of edge-disjoint paths from A to infinity is at least |I|. (In fact this is an equality.) Indeed, for each element e of I we can choose an infinite simple path from A to $\infty$ in T with first edge e that does not revisit $\Gamma$, and any choice of such a path for each $e\in I$ will result in a collection of paths that are mutually edge-disjoint. Let W be the set of vertices that belong to $\Gamma$. The definition of $\Gamma$ ensures that every vertex $w \in W {\setminus } A$ has degree at least 2 in $\Gamma$. Writing $\deg _T$ and $\deg _\Gamma$ for degrees in T and $\Gamma$ and $E_\Gamma$ for the edge set of $\Gamma$, we deduce that

$$\begin{aligned} \sum _{v\in A} \deg _\Gamma (v) + 2 |W{\setminus } A|\le & {} \sum _{v\in A} \deg _\Gamma (v) + \sum _{v\in W {\setminus } A} \deg _\Gamma (v) = \sum _{v\in W} \deg _\Gamma (v) \\= & {} 2 |E_\Gamma | = 2 |W|-2 \end{aligned}$$

and hence that

$$\begin{aligned} |I|=\sum _{v\in A}(\deg _T(v)-\deg _{\Gamma }(v))\ge & {} \sum _{v\in A} \deg _T(v) - 2|A| + 2 \\= & {} 2+\sum _{v\in A} (\deg (v)-2), \end{aligned}$$

completing the proof. $\square$

Proof of Proposition 2.4

Let G be a connected, locally finite, transitive, nonamenable graph, and let o be a fixed root vertex of G. Let $p_c<p \le 1$, let $\omega$ be Bernoulli-p bond percolation, and let $\eta$ be as in Lemma 2.5. Let $\Lambda$ be the set of furcation points of $\eta$. Since $\omega$ stochastically dominates $\eta$ we have that $\mathbf {E}_p \mathscr {P}_\omega (S \rightarrow \infty ) \ge \mathbb {E}\mathscr {P}_\eta (S \rightarrow \infty )$ for every $S \subseteq V$ finite, and so it suffices to prove that

$$\begin{aligned} \mathbb {E}\mathscr {P}_\eta (S \rightarrow \infty ) \ge \mathbb {P}( o \in \Lambda ) |S| \ge \frac{\mathbb {P}( o \in \Lambda )}{\deg (o)} |E(S)| \end{aligned}$$

(2.10)

for every $S \subseteq V$ finite. Since $\eta$ is automorphism-invariant and G is transitive, it suffices to prove the deterministic statement

$$\begin{aligned} \mathscr {P}_\eta (S \rightarrow \infty ) \ge |\Lambda \cap S |, \end{aligned}$$

(2.11)

since (2.10) follows from (2.11) by taking expectations.

To prove (2.11), pick a spanning tree of each infinite cluster of $\eta$ and let F be the union of all of these spanning trees. For each connected component T of F, let $\Lambda _T$ be the set of furcations of T, and note that $\Lambda$ is contained in the disjoint union of the sets $\Lambda _T$. For each component T of F, let $T'$ be obtained from T by iteratively deleting all vertices of degree at most 1, and note that the set of furcations of $T'$ coincides with the set of furcations of T. Since every vertex in $\Lambda _T$ has degree at least 3 in $T'$, it follows from Lemma 2.6 that

$$\begin{aligned} \mathscr {P}_T(S \rightarrow \infty ) \ge |\Lambda _T \cap S|. \end{aligned}$$

Since the components of F are disjoint, we deduce that

$$\begin{aligned} \mathscr {P}_\eta (S \rightarrow \infty ) \ge \mathscr {P}_F(S \rightarrow \infty ) = \sum _T \mathscr {P}_T(S \rightarrow \infty ) \ge \sum _T |\Lambda _T \cap S| \ge |\Lambda \cap S| \end{aligned}$$

as claimed, where the sums are over the connected components of F. $\square$

Proof of Proposition 2.1

Fix a vertex v of G. Let $\omega _1,\omega _2$ be independent copies of Bernoulli-p bond percolation on G, and let $\omega \in \{0,1\}^E$ be defined by

$$\begin{aligned} \omega (e) = {\left\{ \begin{array}{ll} \omega _1(e) &{}\quad \text { if } e \in E(K_v(\omega _1))\\ \omega _2(e) &{}\quad \text { if } e \notin E(K_v(\omega _1)). \end{array}\right. } \end{aligned}$$

Since we can explore $K_v(\omega _1)$ without revealing the status of any edge in $E {\setminus } E(K_v(\omega _1))$, the configuration $\omega$ is also distributed as Bernoulli-p bond percolation on G. If $K_v(\omega )=K_v(\omega _1)$ is finite then any path from $K_v(\omega _1)$ to $\infty$ in $\omega _2$ must pass through the set $\left\{ e \in E : \omega (e)=0, \text { and } E_v(\omega ^e) = \infty \right\}$, and we deduce that

$$\begin{aligned} \#\left\{ e \in E : \omega (e)=0, E_v(\omega ^e) = \infty \right\}\ge & {} \mathscr {P}_{\omega _2}(K_v(\omega ) \rightarrow \infty ) \\= & {} \mathscr {P}_{\omega _2}(K_v(\omega _1) \rightarrow \infty ) \end{aligned}$$

when $K_v(\omega )$ is finite. Taking expectations on both sides and using that $\omega _1$ and $\omega _2$ are independent, we deduce from Proposition 2.4 that

$$\begin{aligned}&\mathbb {E}\left[ \#\left\{ e \in E : \omega (e)=0,\, E_v(\omega ) \le n < E_v(\omega ^e)\right\} \mid K_v(\omega ) \right] \\&\quad \ge c_p E_v(\omega ) \mathbb {1}(E_v(\omega ) \le n) \end{aligned}$$

where $c_p>0$ is the constant from Proposition 2.4. Using the standard fact that $\mathbb {E}[XY |\mathcal {F}] = X \mathbb {E}[Y |\mathcal {F}]$ whenever X and Y are bounded random variables and $\mathcal {F}$ is a $\sigma$-algebra such that X is $\mathcal {F}$-measurable, we deduce immediately that if $F:\mathscr {H}_v \rightarrow [0,\infty )$ is nonnegative then

$$\begin{aligned}&\frac{1}{1-p}\sum _{e\in E} \mathbb {E}\left[ F(K_v(\omega )) \mathbb {1}\bigl (\omega (e)=0,\, E_v(\omega ) \le n < E_v(\omega ^e)\bigr ) \mid K_v(\omega ) \right] \\&\quad \ge \frac{c_p}{1-p} E_v(\omega ) F(K_v(\omega )) \mathbb {1}(E_v(\omega ) \le n), \end{aligned}$$

and the claim follows by taking expectations over $K_v(\omega )$. $\square$

Bounding the total derivative

In this section we prove Proposition 2.2. This is the easiest of the three propositions used in the proof of Theorem 1.1; The methods used are completely standard and go back to some of the earliest work on percolation, see e.g. [24, 44] and [3, Section 3].

Proof of Proposition 2.2

Let $G=(V,E)$ be a connected, locally finite graph, let $v\in V$, and let $p\in (0,1)$. Let $(X_i)_{i\ge 1}$ be a sequence of i.i.d. mean-zero random variables with $\mathbf {P}(X_i=1-p)=p$ and $\mathbf {P}(X_i=-p)=1-p$, and let $Z_n = \sum _{i=1}^n X_i$. Exploring the cluster of v one edge at a time leads to a coupling of percolation on G with the sequence $(X_i)_{i\ge 1}$ and a stopping time T such that $E_v = T$ and if $E_v< \infty$ then $h_p(K_v)= -Z_T$; See e.g. [38, Section 3] for details. Using this coupling, we can write

$$\begin{aligned}&\mathbf {E}^G_p\left[ |h_p(K_v)| e^{t E_v } \mathbb {1}\left( \alpha E_v \le |h_p(K_v)|<\infty \right) \right] \\&\quad = \mathbb {E}\left[ |Z_T| e^{tT} \mathbb {1}(\alpha T \le |Z_T| < \infty ) \right] \end{aligned}$$

for each $t,\alpha >0$. Since $|Z_n|\le n$ for each $n \ge 0$, we also have that

$$\begin{aligned} \mathbb {E}\left[ |Z_T| e^{tT} \mathbb {1}(\alpha T \le |Z_T| < \infty ) \right]&\le \sum _{n=1}^\infty ne^{tn} \mathbb {P}(T=n, |Z_n| \ge \alpha n)\nonumber \\&\le \sum _{n=1}^\infty ne^{tn} \mathbb {P}(|Z_n| \ge \alpha n) \end{aligned}$$

(2.12)

for each $t,\alpha >0$. Finally, since $|X_i|\le 1$ for every $i \ge 1$, we deduce from Azuma’s inequality that

$$\begin{aligned} \mathbb {P}(|Z_n| \ge \alpha n) \le 2 \exp \left[ -\frac{\alpha ^2}{2} n \right] , \end{aligned}$$

for every $n \ge 1$ and $\alpha >0$, so that the right hand side of (2.12) is finite whenever $t<\alpha ^2/2$. $\square$

Bounding the positive term

In this section we prove Proposition 2.3. This is the most difficult of the three propositions going into the proof of Theorem 1.1. The basic idea is to control the probability $\mathbf {P}_p(E_v = n, {\text {Br}}_k(K_v,v) \ge \alpha E_v)$ by induction on k. The proof will (implicitly) establish the explicit moment estimate

$$\begin{aligned} \mathbf {E}_p^G\left[ E_v^{k+1} \mathbb {1}(\alpha E_v \le {\text {Br}}_k(K_v,v) <\infty )\right] \le k! \left( \frac{2^{18} e^{2}}{\alpha ^3 (1-p)^{96/\alpha }}\right) ^k, \end{aligned}$$

(2.13)

which holds for every countable, locally finite graph $G=(V,E)$, $v\in V$, $p\in [0,1)$, $k\ge 1$, and $0<\alpha \le 1$. It will be important for us to work on arbitrary graphs in this section to facilitate the induction. Indeed, working on arbitrary graphs (or arbitrary subgraphs of a given graph) in this way is a useful trick to avoid non-monotonicity problems in inductive analyses of percolation, which we believe was first used by Kozma and Nachmias in [45] following a suggestion of Peres.

We begin with the base case $k=1$. Note that ${\text {Br}}_1(K_v,v)$ is bounded from above by the intrinsic radius $R_v$ of $K_v$, i.e., the maximal graph distance in $K_v$ of a vertex from v. It will therefore be relevant to bound the probability of having a large skinny cluster, whose intrinsic radius is of the same order as its volume; think of m below as being at least $\alpha n$ in the following lemma.

Lemma 2.7

Let $G=(V,E)$ be a locally finite graph and let v be a vertex of G. Then the bound

$$\begin{aligned} \mathbf {P}^G_p(R_v \ge m \text { and } E_{v} \le n) \le \exp \left[ -\frac{1}{2}(1-p)^{4n/m}m\right] \end{aligned}$$

holds for every $p\in [0,1)$ and $n \ge m \ge 0$.

Proof

Consider exploring the cluster of v as follows: at stage i, expose the value of those edges that touch $\partial B_{\mathrm {int}}(v,i-1)$, the set of vertices with intrinsic distance exactly $i-1$ from v, and have not yet been exposed. Stop when $\partial B_{\mathrm {int}}(v,i)=\emptyset$. If $R_v \ge m$ and $E_v\le n$, there must exist at least m/2 stages $i\in \{1,\ldots ,m\}$ where the sum of degrees in G of the vertices in $\partial B_\mathrm {int}(v,i-1)$ is at most 4n/m. At each such stage, the conditional probability that $\partial B_\mathrm {int}(v,i)\ne \emptyset$ given everything that has happened up to stage $i-1$ is at most $1-(1-p)^{4n/m}$. We deduce that

$$\begin{aligned} \mathbf {P}^G_p\bigl ( R_v \ge m \text { and } E_{v} \le n\bigr ) \le \left( 1-(1-p)^{4n/m}\right) ^{m/2} \le \exp \left[ -\frac{1}{2}(1-p)^{4n/m}m\right] \end{aligned}$$

as claimed, where the inequality $1-x \le e^{-x}$ has been used in the second inequality. $\square$

Remark 2.8

Using Lemma 2.7, we can already conclude the proof of the weaker statement that the intrinsic radius of a finite cluster has an exponential tail in supercritical percolation on a nonamenable transitive graph. This can be done via the same strategy used for the volume, but using Lemma 2.7 instead of Proposition 2.3 to bound the term $\mathbf {U}_{p,n}[e^{tR_v}]$, which is easily seen to be at most $\frac{1}{p}\mathbf {E}_{p,n}[R_v e^{tR_v}]$.

We now introduce the notation that we will use to set up our induction. Let H be a finite connected graph. Recall that two vertices u, v of H are said to be (edge) 2-connected to each other if there exist two edge-disjoint paths in H from u to v. Being 2-connected is an equivalence relation, so that H can be decomposed into a collection of 2-connected components. An edge e of H is said to be a bridge if its endpoints are in different 2-connected components of H, or equivalently if the subgraph of H spanned by all edges other than e is disconnected. We define ${\text {Tr}}(H)$ to be the finite graph whose vertices are the 2-connected components of H and where two 2-connected components A and B of H are connected in ${\text {Tr}}(H)$ if there is an edge of H with one endpoint in A and the other in B. It follows readily from the definitions that the edges of ${\text {Tr}}(H)$ are naturally in bijection with the bridges of H and that ${\text {Tr}}(H)$ is a tree (hence the notation).

Now let H be a finite connected graph, let v be a vertex of H, and let $k\ge 1$. Write $[v]^2_H$ for the 2-connected component of v in H. We define ${\text {Lf}}_k(H,v)$ to be the maximum number of edges in a subgraph of ${\text {Tr}}(H)$ spanned by the union of the geodesics between $[v]^2_H$ and exactly k leaves of the tree ${\text {Tr}}(H)$. (By a leaf we mean a degree one vertex distinct from the root $[v]_H^2$.) If ${\text {Tr}}(H)$ has fewer than k leaves we set ${\text {Lf}}_k(H,v)=0$. Note that

$$\begin{aligned} {\text {Br}}_k(H,v) = \max \left\{ {\text {Lf}}_\ell (H,v) : 1 \le \ell \le k \right\} . \end{aligned}$$

(2.14)

For each $k\ge 1$ and $n,m \ge 0$ we define the quantity

$$\begin{aligned} Q_k(p,n,m)= & {} \sup \Bigl \{ \mathbf {P}^G_p\bigl ( {\text {Lf}}_k(K_v,v)= m, E_{v} = n\bigr ) : \\&G=(V,E) \text { countable, locally finite, } v\in V \Bigr \}. \end{aligned}$$

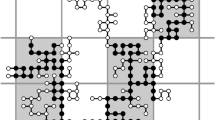
Note that $Q_k(p,n,m)$ is trivially equal to zero when $0< m < k$ or $n < m$ but that $Q_k(p,n,0)$ can be positive. We will prove Proposition 2.3 by analysis of the following inductive inequality (Fig. 1).

Fig. 1

Illustration of the notions used in the proof of Lemma 2.9. Left: a finite subgraph H of a graph G (in this case $G=\mathbb {Z}^2$) with 2-connected components represented by blue shaded regions. Edges of H are represented by solid lines, while edges of $\partial H$ are represented by dotted lines. Centre: the tree ${\text {Tr}}(H)$, together with a distinguished set of leaves (drawn as squares) obtaining the maximum in the definition of ${\text {Lf}}_3(H,v)$. Purple lines denote edges of ${\text {Tr}}(H)$ lying in the tree S spanned by the union of the geodesics between the root $o=[v]^2_H$ and this distinguished set of leaves. Double purple lines represent those edges that are also last-branching edges of S. Right: cutting H into two-components (green and yellow) by removing a last-branching bridge (red). The other two last-branching bridges associated to the distinguished set of leaves are in blue (colour figure online)

Lemma 2.9

The inequality

$$\begin{aligned} Q_{k+1}(p,n,m) \le \frac{2e n}{k+1}\sum _{m_1=1}^{m-1}\sum _{n_1=1}^{n} Q_{k}\left( pe^{-1/n},n_{1},m_{1} \right) Q_1(p,n-n_1,m-m_1-1) \end{aligned}$$

(2.15)

holds for every $p\in [0,1]$, $k\ge 1$, and $n,m\ge 1$.

Proof of Lemma 2.9

Let $G=(V,E)$ be countable and locally finite and let $v \in V$. Let $(U_e:e \in E)$ be i.i.d. Uniform[0, 1] random variables. We say that an edge e is q-open if $U_e \le q$, and otherwise that it is q-closed, so that the subgraph $\omega _q$ of G spanned by the q-open edges is distributed as Bernoulli-q bond percolation on G. We write $K_v(q) =K_v^G(q)$ for the cluster of v in $\omega _q$, write $E_v(q) = E^G_v(q)$ for the number of edges of G that $K^G_v(q)$ touches, and write $T_v(q)=T_v^G(q)= {\text {Tr}}(K^G_v(q))$. Write $\mathbb {P}=\mathbb {P}^G$ for the law of the collection of random variables $(U_e : e \in E)$.

Fix $p\in [0,1]$, $k\ge 1$, and $n,m\ge 1$, and consider the event $\mathscr {A}=\{E^G_v(p)=n$, ${\text {Lf}}_{k+1}(K^G_v(p),v)=m\}$. It suffices to prove that

$$\begin{aligned} \mathbf {P}^G_p(\mathscr {A})\le \frac{2e n}{k+1}\sum _{m_1=1}^{m-1}\sum _{n_1=1}^{n} Q_{k}\left( pe^{-1/n},n_{1},m_{1} \right) Q_1(p,n-n_1,m-m_1-1). \end{aligned}$$

We may assume that v has degree at least 1, since the claim is trivial otherwise. Suppose that the event $\mathscr {A}$ holds, and let $u_1,\ldots ,u_{k+1}$ be a collection of leaves of $T_v^G(p)={\text {Tr}}(K_v^G(p))$ attaining the maximum in the definition of ${\text {Lf}}_{k+1}(K_v^G(p),v)$. (Note that this collection is not unique, but that the choice will not matter. In particular, we can and do choose $u_1,\ldots ,u_{k+1}$ to be a measurable function of the cluster $K^G_v(p)$.) Let S be the subtree of $T_v^G(p)$ spanned by the union of the geodesics connecting $u_1,\ldots ,u_{k+1}$ and the root $o:=[v]^2_{K^G_v(p)}$. We say that an edge e of S is a last-branching edge if deleting it from S results in two connected components $S_1,S_2$, where $S_1$ contains the root and the following conditions hold:

• $S_2$ is either a path or an isolated vertex;

• The endpoint of e that belongs to $S_1$ is either equal to o or has degree at least three in S.

Observe that every last-branching edge of S is naturally associated both to a leaf of S and to a bridge of $K^G_v(p)$, which we call a last-branching bridge. In particular, we may enumerate the last-branching bridges of $K^G_v(p)$ by $e_1,\ldots ,e_{k+1}$ in such a way that for each $1 \le i \le k+1$ the geodesic from o to $u_i$ in S passes through the edge corresponding to $e_i$ but does not pass through the edge of S corresponding to $e_j$ for any $j \ne i$. Write $L=\{e_1,\ldots ,e_{k+1}\}$.

As the form of the recursion (2.15) suggests, we will perform surgery to a random edge in L. Write $p':=pe^{-1/n}$, and consider the event

$$\begin{aligned} \mathscr {B}=\mathscr {A}\cap \bigl \{\text {exactly one } p\text {-open edge } \text { in } K_v^G(p)\text { is } p'\text {-closed, and this edge belongs to } L \bigr \}. \end{aligned}$$

Since $|L|=k+1$ and there are at most n p-open edges in $K_v^G(p)$ on the event $\mathscr {A}$, we may compute that

$$\begin{aligned} \mathbb {P}( \mathscr {B}\mid \mathscr {A})\ge & {} (k+1)\left( \frac{p'}{p}\right) ^{n-1}\left( 1-\frac{p'}{p}\right) = (k+1) e^{-(n-1)/n} (1-e^{-1/n}) \\\ge & {} \frac{k+1}{2en}, \end{aligned}$$

where we have used that $1-e^{-x} \ge \frac{x}{2}$ for every $x\in [0,1]$ in the final inequality, and hence that

$$\begin{aligned} \mathbb {P}(\mathscr {A}) \le \frac{2en}{k+1}\mathbb {P}(\mathscr {B}). \end{aligned}$$

(2.16)

Write $H_v=H^G_v(p')$ for the subgraph of G spanned by those edges of G that do not touch $K_v^G(p')$. To bound $\mathbb {P}(\mathscr {B})$ we now argue that

$$\begin{aligned} \mathscr {B}= \bigcup _{b=1}^{m-1} \bigcup _{a=1}^n \mathscr {C}_{a,b}, \end{aligned}$$

(2.17)

where $\mathscr {C}_{a,b}$ is the event that the following conditions all hold:

• (i) $E^G_v(p')=a$ and ${\text {Lf}}_{k}(K^G_v(p'),v)=b$.

• (ii) There is exactly one p-open edge e touched by $K^G_v(p')$ that is not $p'$-open, and this edge lies in the set L. In particular, this edge has an endpoint x that does not lie in $K^G_v(p')$.

• (iii) The p-cluster $K^{H_v}_{x}(p)$ of x in the graph $H_v$ touches $n-a$ edges of $H_v$.

• (iv) Every p-open edge in the p-cluster $K^{H_v}_{x}(p)$ is also $p'$-open.

• (v) ${\text {Lf}}_{1}(K_{x}^{H_v}(p),x)=m-b-1$.

It may seem that the unions in (2.17) should begin at $b=0$, $a=0$ rather than $b=1$, $a=1$. What is written is correct, however: $E_v^G(p')$ is positive by the assumption that v has degree at least 1 in G, while $b=0$ would mean by (i) that $T_v^G(p')$ has fewer than k leaves, which is incompatible with the conditions that (ii) holds and that ${\text {Lf}}_{k+1}(K_v^G(p))=m>0$.

The only other part of the claim (2.17) that merits explanation is the implicit claim that if (ii) holds then

$$\begin{aligned} {\text {Lf}}_{1}\bigl (K_{x}^{H_v}(p),x\bigr )+{\text {Lf}}_{k}\bigl (K^G_v(p'),v\bigr )={\text {Lf}}_{k+1}\bigl (K^G_v(p),v\bigr )-1. \end{aligned}$$

Without loss of generality assume that $e=e_{k+1} \in L$. Consider the subgraph $S'$ of $T_v^G(p')$ spanned by the union of the geodesics between $u_1,\ldots ,u_k$ and the root. Since $e=e_{k+1}$ is the last-branching bridge associated to $u_{k+1}$, the tree $S'$ contains one of the endpoints of the edge corresponding to e and we therefore observe that

$$\begin{aligned} {\text {Lf}}_{k}\bigl (K_v(p'),v\bigr ) \ge \#\{\text {edges of }S'\} = {\text {Lf}}_{k+1}\bigl (K_v(p),v\bigr )-1-{\text {Lf}}_{1}\bigl (K_{x}^{H_v}(p),x\bigr ), \end{aligned}$$

where the $-1$ term corresponds to the edge e itself. On the other hand, suppose that $v_1,\ldots ,v_{k}$ are leaves of $T_v^G(p')$ attaining the maximum in the definition of ${\text {Lf}}_{k}(K^G_v(p'),v)$ and let $r \ge 0$ be the distance in $T_v^G(p')$ from e to the subgraph of $T_v^G(p')$ spanned by the union of the geodesics between the leaves $v_1,\ldots ,v_k$ and the root. Then considering the subgraph of $T_v^G(p)$ spanned by the union of the geodesics between the leaves $v_1,\ldots ,v_k$, the leaf $u_{k+1}$, and the root yields that

$$\begin{aligned} {\text {Lf}}_{k+1}\bigl (K^G_v(p),v\bigr ) \ge {\text {Lf}}_{1}\bigl (K_{x}^{H_v}(p),x\bigr )+{\text {Lf}}_{k}\bigl (K^G_v(p'),v\bigr )+1 +r \end{aligned}$$

(again, the $+1$ term corresponds to the edge e itself) and hence that

$$\begin{aligned} {\text {Lf}}_{k}\bigl (K^G_v(p'),v\bigr )\le & {} {\text {Lf}}_{k+1}\bigl (K^G_v(p),v\bigr )-1-{\text {Lf}}_{1}\bigl (K_{x}^{H_v}(p),x\bigr ) -r \\\le & {} {\text {Lf}}_{k+1}\bigl (K^G_v(p),v\bigr )-1-{\text {Lf}}_{1}\bigl (K_{x}^{H_v}(p),x\bigr ) \end{aligned}$$

as claimed.

It remains to estimate the probability of the event $\mathscr {C}_{a,b}$. Let $\mathscr {D}_{a,b} \supseteq \mathscr {C}_{a,b}$ be the simpler event that the following conditions hold:

• (ib) $E^G_v(p')=a$ and ${\text {Lf}}_{k}(K^G_v(p'),v)=b$.

• (iib) There is exactly one p-open edge e touched by $K^G_v(p')$ that is not $p'$-open, and this edge has an endpoint x that does not lie in $K^G_v(p')$.

• (iiib) The p-cluster $K^{H_v}_{x}(p)$ of x in the graph $H_v$ touches $n-a$ edges of $H_v$.

• (vb) ${\text {Lf}}_{1}(K_{x}^{H_v}(p),x)=m-b-1$.

By definition, the probability that the condition (ib) holds is at most $Q_k(p',a,b)$. On the other hand, the conditional probability that (iiib) and (vb) hold given both that (ib) and (iib) hold and given the cluster $K^G_v(p')$ and the edge e is equal to

$$\begin{aligned} \mathbb {P}^{H_v}\Bigl (E_x^{H_v}(p) = n-a \text { and } {\text {Lf}}_{1}\bigl (K_{x}^{H_v}(p),x\bigr )=m-b-1\Bigr ) \end{aligned}$$

which is at most $Q_1(p,n-a,m-b-1)$ since $Q_1$ was defined by taking a supremum over all graphs. Thus, we have that

$$\begin{aligned} \mathbb {P}^G(\mathscr {C}_{a,b}) \le \mathbb {P}^G(\mathscr {D}_{a,b}) \le Q_k(p',a,b)Q_1(p,n-a,m-b-1) \end{aligned}$$

for every $1 \le a \le n$ and $1\le b \le m-1$. Since G was arbitrary, the claim now follows from (2.16) and (2.17). $\square$

We now apply Lemmas 2.7 and 2.9 to prove Proposition 2.3 via a generating function analysis.

Proof of Proposition 2.3

In order to analyze the inductive inequality of Lemma 2.9, we introduce for each $p \in [0,1]$ and $k\ge 1$ the function $\mathscr {G}_{p,k}:\mathbb {R}^2 \rightarrow [0,\infty ]$ given by

$$\begin{aligned} \mathscr {G}_{p,k}(s,t) = \sum _{n =1}^\infty \sum _{m=1}^\infty \frac{e^{sn+tm}}{n^{k-1}} \sup _{q \le p} Q_k(q,n,m), \end{aligned}$$

which is a sort of multivariate generating function. Lemma 2.9 implies the inductive inequality

$$\begin{aligned} \mathscr {G}_{p,k+1}(s,t)&\le \frac{2e}{k+1} \sum _{n=1}^\infty \sum _{m=1}^\infty \sum _{n_1 =1}^n \sum _{m_1=1}^{m-1} \frac{e^{sn+tm}}{n^{k-1}} \\&\quad \sup _{q \le p} \left[ Q_{k}(q e^{-1/n},n_1,m_1) Q_{1}(q,n-n_1,m-m_1-1) \right] \\&\le \frac{2e}{k+1} \sum _{n=1}^\infty \sum _{m=1}^\infty \sum _{n_1 =1}^n \sum _{m_1=1}^{m-1} \frac{e^{sn+tm}}{n_1^{k-1}}\\&\quad \sup _{q \le p} Q_{k}(q,n_1,m_1) \sup _{q \le p} Q_{1}(q,n-n_1,m-m_1-1), \end{aligned}$$

and using the change of variables $n_2=n-n_1$ and $m_2=m-m_1-1$ yields that

$$\begin{aligned} \mathscr {G}_{p,k+1}(s,t)&\le \frac{2e^{t+1}}{k+1} \sum _{n_1 =1}^\infty \sum _{m_1=1}^\infty \frac{e^{sn_1+tm_1}}{n_1^{k-1}} \nonumber \\&\quad \sup _{q \le p} Q_{k}(q,n_1,m_1) \sum _{n_2=0}^\infty \sum _{m_2=0}^\infty e^{sn_2+tm_2} \sup _{q \le p} Q_{1}(q,n_2,m_2) \nonumber \\&=\frac{2e^{t+1}}{k+1} \mathscr {G}_{p,k}(s,t) \sum _{n_2=0}^\infty \sum _{m_2=0}^\infty e^{sn_2+tm_2} \sup _{q \le p} Q_{1}(q,n_2,m_2) \end{aligned}$$

(2.18)

for every $k \ge 1$, $p\in [0,1]$, and $s,t \in \mathbb {R}$. (Note that both sides of this inequality could be equal to $+\infty$, but this will not cause us any problems.) On the other hand, Lemma 2.7 implies that

$$\begin{aligned}&Q_1(p,n,m) \nonumber \\&\quad \le \sup \Bigl \{ \mathbf {P}^G_p\bigl (E_{v} = n, R_v \ge m\bigr ) : G=(V,E) \text { countable, locally finite, } v\in V \Bigr \}\nonumber \\&\quad \le \exp \left[ -\frac{1}{2}(1-p)^{4n/m}m\right] \end{aligned}$$

(2.19)

for every $p\in [0,1)$ and $n,m \ge 0$, and since the right hand side of (2.19) is increasing in p it follows that

$$\begin{aligned} \sum _{n =0}^\infty \sum _{m=0}^\infty e^{sn+tm} \sup _{q \le p} Q_1(q,n,m) \le \sum _{n =0}^\infty \sum _{m=0}^\infty \exp \left[ sn+tm-\frac{1}{2}(1-p)^{4n/m}m\right] \end{aligned}$$

for every $p\in [0,1]$ and $s,t\in \mathbb {R}$. If $0\le p <1$, $0 < \alpha \le 1$, and $0 < 4t \le (1-p)^{12/\alpha }$ then separate consideration of the two cases $3m \le \alpha n$ and $3m \ge \alpha n$ yields that

$$\begin{aligned} -\alpha tn + tm - \frac{1}{2}(1-p)^{4n/m} m \le -\frac{1}{2}\alpha tn - \frac{1}{2} tm \end{aligned}$$

for every $n,m \ge 0$, and hence that

$$\begin{aligned} \mathscr {G}_{p,1}(-\alpha t,t)\le & {} \sum _{n =0}^\infty \sum _{m=0}^\infty e^{sn+tm} \sup _{q \le p} Q_1(q,n,m) \nonumber \\\le & {} \sum _{n =0}^\infty \sum _{m=0}^\infty \exp \left[ -\frac{1}{2}\alpha t n- \frac{1}{2}tm\right] \nonumber \\= & {} \frac{e^{\alpha t/2}}{e^{\alpha t/2}-1} \frac{e^{t/2}}{e^{t/2}-1} \le \frac{16}{\alpha t^2} \end{aligned}$$

(2.20)

for every $0\le p < 1$, $0 <\alpha \le 1$, and $0 < 4t \le (1-p)^{8/\alpha } \le 1$, where we used that $e^x/(e^x-1) \le 2/x$ for every $x>0$. Substituting (2.20) into (2.18) and inducting over $k\ge 1$ yields that

$$\begin{aligned} \mathscr {G}_{p,k}(-\alpha t,t) \le \frac{1}{k!} \left( \frac{32e^{2}}{\alpha t^2}\right) ^k \end{aligned}$$

(2.21)

for every $k\ge 1$, $0\le p < 1$, $0 <\alpha \le 1$, and $0 < 4t \le (1-p)^{12/\alpha } \le 1$.

We now apply (2.21) to conclude the proof. Let $G=(V,E)$ be a countable, locally finite graph and let $v\in V$. Note that

$$\begin{aligned}&\mathbf {E}^G_p\left[ E_v^{k+1}\mathbb {1}\left( 2\alpha E_v \le {\text {Lf}}_\ell (K_v,v)<\infty \right) \right] \\&\quad \le \frac{(k+\ell )!}{(\alpha t)^{k+\ell }} \mathbf {E}^G_p\left[ E_v^{-\ell +1} e^{\alpha t E_v} \mathbb {1}\left( 2\alpha E_v \le {\text {Lf}}_\ell (K_v,v) <\infty \right) \right] \end{aligned}$$

for every $k\ge \ell \ge 1$, $0\le p < 1$, and $\alpha ,t>0$. Since

$$\begin{aligned} e^{\alpha t E_v} \mathbb {1}\left( 2\alpha E_v \le {\text {Lf}}_\ell (K_v,v)<\infty \right) \le e^{-\alpha t E_v + t{\text {Lf}}_\ell (K_v,v) }\mathbb {1}(E_v<\infty ) \end{aligned}$$

for each $\alpha ,t>0$ and $\ell \ge 1$, it follows that

$$\begin{aligned}&\mathbf {E}^G_p\left[ E_v^{k+1}\mathbb {1}\left( 2\alpha E_v \le {\text {Lf}}_\ell (K_v,v)<\infty \right) \right] \nonumber \\&\quad \le \frac{(k+\ell )!}{(\alpha t)^{k+\ell }} \mathbf {E}^G_p\left[ E_v^{-\ell +1} e^{-\alpha t E_v + t{\text {Lf}}_\ell (K_v,v) } \mathbb {1}(E_v<\infty )\right] \nonumber \\&\quad \le \frac{(k+\ell )!}{(\alpha t)^{k+\ell }}\mathscr {G}_{p,\ell }(-\alpha t, t) \le \frac{(k+\ell )!}{\ell !} \left( \frac{32 e^{2}}{\alpha ^2 t^3}\right) ^\ell \frac{1}{(\alpha t)^k} \end{aligned}$$

(2.22)

for every $k\ge \ell \ge 1$, $0\le p < 1$, $0 <\alpha \le 1$, and $0 < 4t \le (1-p)^{12/\alpha } \le 1$, where we used (2.21) in the final inequality. Using that ${\text {Br}}_k(K_v,v) \le E_v$, we deduce that

$$\begin{aligned}&\sum _{k=1}^\infty \frac{\lambda ^k}{k! }\mathbf {E}^G_p\left[ {\text {Br}}_k(K_v,v) E_v^k \mathbb {1}\left( 2\alpha E_v \le {\text {Br}}_k(K_v,v)<\infty \right) \right] \nonumber \\&\quad \le \sum _{k=1}^\infty \frac{\lambda ^k}{k! } \sum _{\ell =1}^k \mathbf {E}^G_p\left[ E_v^{k+1} \mathbb {1}\left( 2\alpha E_v \le {\text {Lf}}_\ell (K_v,v) <\infty \right) \right] \nonumber \\&\quad \le \sum _{k=1}^\infty \sum _{\ell =1}^k\left( {\begin{array}{c}k+\ell \\ \ell \end{array}}\right) \left( \frac{32 e^{2}}{\alpha ^2 t^3}\right) ^\ell \left( \frac{\lambda }{\alpha t}\right) ^k \end{aligned}$$

(2.23)

for every $\lambda >0$, $0\le p < 1$, $0 <\alpha \le 1$, and $0 < 4t \le (1-p)^{12/\alpha } \le 1$. It follows in particular that

$$\begin{aligned}&\sum _{k=1}^\infty \frac{\lambda ^k}{k! }\mathbf {E}^G_p\left[ {\text {Br}}_k(K_v,v) E_v^k \mathbb {1}\left( 2\alpha E_v \le {\text {Br}}_k(K_v,v) <\infty \right) \right] \nonumber \\&\quad \le \sum _{k=1}^\infty \sum _{\ell =1}^k\left( {\begin{array}{c}2k\\ \ell \end{array}}\right) \left( \frac{32 e^{2}}{\alpha ^2 t^3}\right) ^k \left( \frac{\lambda }{\alpha t}\right) ^k \le \sum _{k=1}^\infty \left( \frac{128 e^{2} \lambda }{\alpha ^3 t^4}\right) ^k \end{aligned}$$

(2.24)

for every $\lambda >0$, $0\le p < 1$, $0 <\alpha \le 1$, and $0 < 4t \le (1-p)^{12/\alpha } \le 1$. (A similar computation yields (2.13).) Taking $t=(1-p)^{12/\alpha }/4$, it follows that for each $0<\alpha \le 1$ and $0 \le p < 1$ there exists

$$\begin{aligned} \lambda (\alpha ,p)= \frac{\alpha ^3(1-p)^{48/\alpha }}{2^{16}e^2}>0 \end{aligned}$$

such that

$$\begin{aligned} \sum _{k=1}^\infty \frac{\lambda (\alpha ,p) ^k}{k! }\mathbf {E}^G_p\left[ {\text {Br}}_k(K_v,v) E_v^k \mathbb {1}\left( 2\alpha E_v \le {\text {Br}}_k(K_v,v) <\infty \right) \right] \le \sum _{k=1}^\infty 2^{-k} = 1 \end{aligned}$$

(2.25)

for every $0\le p < 1$ and $0 <\alpha \le 1$. This clearly implies the claim. $\square$

Proofs of corollaries

In this section we apply Theorem 1.1 to deduce Corollaries 1.2–1.5.

Analyticity

In this section, we apply the following proposition to deduce Corollary 1.3 from Theorem 1.1.

Proposition 3.1

Let G be a connected, locally finite graph, let $v \in V$ and let $F:\mathscr {H}_v \rightarrow \mathbb {C}$ have subexponential growth. Then $\mathbf {E}_p\left[ F(K_v) \mathbb {1}(|K_v| < \infty ) \right]$ is an analytic function of p on $\{p \in (0,1) : \zeta (p) > 0\}$.

Although the statement is more general, the proof of this proposition is essentially identical to the original argument of Kesten [42, pp. 250–251]. Many further results on analyticity can be found in the works of Georgakopoulos and Panagiotis [25, 26]. (Indeed, Corollary 4.14 of [25] can be seen to imply Proposition 3.1, but we prefer to give a direct proof since that result is rather technical.)

Proof

Let $F:\mathscr {H}_v \rightarrow \mathbb {C}$ have subexponential growth. We wish to show that for each $p_0 \in \{p \in (0,1) : \zeta (p) >0\}$ there exists $\varepsilon >0$ and an analytic function $f : B(p_0,\varepsilon ) \rightarrow \mathbb {C}$ such that

$$\begin{aligned} f(p) = \mathbf {E}_p\left[ F(K_v) \mathbb {1}(|K_v|<\infty )\right] = \sum _{H \in \mathscr {H}_v} F(H) p^{|E_o(H)|}(1-p)^{|\partial H|} \end{aligned}$$

for every $p\in (p_0-\varepsilon ,p_0+\varepsilon )$. By Morera’s Theorem, it suffices to prove that for every $p_0 \in \{p \in (0,1) : \zeta (p) >0\}$ there exists $\varepsilon >0$ such that the series $\sum _{H \in \mathscr {H}_v} F(H) q^{|E_o(H)|}(1-q)^{|\partial H|}$ converges uniformly in $q \in B(p_0,\varepsilon )$. To prove this, it suffices by the Weierstrass M-test to prove that for each $p_0 \in \{p \in (0,1) : \zeta (p) >0\}$ there exists $\varepsilon >0$ such that

$$\begin{aligned} \sum _{H \in \mathscr {H}_v} \sup _{|h| \le \varepsilon } \left| F(H) (p_0+h)^{|E_o(H)|}(1-p_0-h)^{|\partial H|}\right| < \infty . \end{aligned}$$

(3.1)

We stress that the supremum in this expression is taken over complex h with $|h|\le \varepsilon$. To prove eq. (3.1), we observe that

$$\begin{aligned}&\left| F(H) (p_0+h)^{|E_o(H)|}(1-p_0-h)^{|\partial H|}\right| \\&\quad = |F(H)| p_0^{|E_o(H)|}(1-p_0)^{|\partial H|}\left| \frac{p_0+h}{p_0}\right| ^{|E_o(H)|}\left| \frac{1-p_0-h}{1-p_0}\right| ^{|\partial H|}\\&\quad \le |F(H)| p_0^{|E_o(H)|}(1-p_0)^{|\partial H|}\left( 1+\frac{|h|}{p_0(1-p_0)}\right) ^{|E(H)|} \end{aligned}$$

for every $p\in (0,1)$ and $h \in \mathbb {C}$, and hence that

$$\begin{aligned}&\sum _{H \in \mathscr {H}_v} \sup _{|h| \le \varepsilon } \left| F(H) (p_0+h)^{|E_o(H)|}(1-p_0-h)^{|\partial H|}\right| \\&\quad \le \mathbf {E}_{p_0}\left[ |F(K_v)| \left( 1+\frac{\varepsilon }{p_0(1-p_0)}\right) ^{|E(H)|} \right] \end{aligned}$$

for every $p_0 \in (0,1)$ and $\varepsilon >0$. The right hand side is finite if $\varepsilon < p_0(1-p_0) (e^{\zeta (p_0)}-1)$, concluding the proof. $\square$

Proof of Corollary 1.3

This is immediate from Theorem 1.1 and Proposition 3.1. $\square$

Remark 3.2

One can strengthen the conclusions of Proposition 3.1 to give analyticity at $p=0$ and $p=1$ using the methods of [25].

Anchored expansion

The following proposition, which allows us to deduce Corollary 1.4 from Theorem 1.1, is implicit in the proof of [19, Theorem A.1]. We give a proof both for completeness and to stress that the argument does not require any isoperimetric assumptions on the ambient graph G.

Proposition 3.3

Let $G=(V,E)$ be a connected, locally finite graph. Let $p_c<p < 1$ and suppose that $\zeta (p)>0$. Then every infinite cluster K of Bernoulli-p bond percolation on G has anchored expansion with anchored Cheeger constant

$$\begin{aligned}&\Phi ^*_E(K) \ge \frac{1}{2}\alpha (p)\\&\quad := \frac{1}{2}\sup \left\{ \alpha \in [0,p] : \alpha ^{-\alpha }(1-\alpha )^{-(1-\alpha )} \left[ \frac{p}{1-p}\right] ^{\alpha } < e^{\zeta (p)} \right\} > 0 \end{aligned}$$

almost surely.

Before beginning the proof, let us note that if G is a connected locally finite graph then

$$\begin{aligned}&\Phi ^*_E(G)\nonumber \\&\quad :=\lim _{n\rightarrow \infty }\inf \left\{ \frac{|\partial _E K|}{\sum _{u\in K} \deg (u)} : K \subseteq V \text { connected},\, v\in K,\, \text { and } n\le |K|<\infty \right\} \nonumber \\&\quad \ge \lim _{n\rightarrow \infty }\inf \left\{ \frac{|\partial H|}{2 |E(H)|} : H \text { a connected subgraph of } G\text { containing } v\text { with } n\le |E(H)|<\infty \right\} \end{aligned}$$

(3.2)

for each vertex v of G. Indeed, if K is any finite set of vertices in G and H is the subgraph of G induced by K then $\partial H=\partial _E K$ and $\sum _{u \in K} \deg (u) \le 2|E(H)|$, so that $|\partial _E K|/\sum _{u \in K} \deg (u) \ge |\partial H| / (2|E(H)|)$.

Proof

Fix a vertex v of G. For each $n\ge 1$, let $\mathscr {H}_v^n$ be the set of connected subgraphs of G containing v that touch exactly n edges. Given $\omega$, for each $H \in \mathscr {H}_v$, let $\partial _\omega H = \partial H \cap \{e \in E: \omega (e) =1\}$ be the set of open edges in $\partial H$, where we recall that $\partial H = E(H) {\setminus } E_o(H)$ is the set of edges that touch but do not belong to H. For each $n,m\ge 1$, we define $\mathscr {A}_{n,m}$ to be the event that there exists a subgraph $H \in \mathscr {H}_v^n$ such that $H\subseteq K_v$ (equivalently, every edge of H is open in $\omega$) and $|\partial _\omega H| = m$. By (3.2), the anchored Cheeger constant satisfies $\Phi ^*_E(K_v) \ge \alpha /2$ on the event $\{|K_v|=\infty \} {\setminus } (\cap _{N\ge 1}\cup _{n \ge N} \cup _{m \le \alpha n} \mathscr {A}_{n,m})$. Thus, to prove the claim it suffices to prove that if $\zeta (p)>0$ then

$$\begin{aligned} \sum _{n=1}^\infty \sum _{m=1}^{\lfloor \alpha n \rfloor } \sum _{H \in \mathscr {H}_v^n} \mathbf {P}_p\left( H \subseteq K_v,\, |\partial _\omega H| =m\right) < \infty \end{aligned}$$

(3.3)

for every $\alpha <\alpha (p)$, since Markov’s inequality will then imply that $\lim _{N\rightarrow \infty }\mathbf {P}_p\left( \cup _{n \ge N} \cup _{m \le \alpha n} \mathscr {A}_{n,m}\right) =0$ for every $\alpha <\alpha (p)$ as desired. To prove (3.3), first observe that if $H\in \mathscr {H}_v$ and $S \subseteq \partial H$ then

$$\begin{aligned} \mathbf {P}_p(H \subseteq K_v \text { and } \partial _\omega H = S)= & {} \mathbf {P}_p( E_o(H) \cup S \subseteq \omega , (\partial H {\setminus } S) \cap \omega = \emptyset ) \\= & {} p^{|E_o(H)|+|S|}(1-p)^{|\partial H|-|S|}. \end{aligned}$$

Summing over the possible choices of S with $S \subseteq E(H)$ and $|S|=m$, we deduce that if $H \in \mathscr {H}_v^n$ then

$$\begin{aligned} \mathbf {P}_p(H \subseteq K_v \text { and } |\partial _\omega H | =m)= & {} \left( {\begin{array}{c}|\partial H|\\ m\end{array}}\right) \left[ \frac{p}{1-p}\right] ^m \mathbf {P}_p(K_v=H)\\\le & {} \left( {\begin{array}{c}n\\ m\end{array}}\right) \left[ \frac{p}{1-p}\right] ^m \mathbf {P}_p(K_v=H) \end{aligned}$$

and hence that

$$\begin{aligned}&\sum _{n=1}^\infty \sum _{m=1}^{\lfloor \alpha n \rfloor } \sum _{H \in \mathscr {H}_v^n} \mathbf {P}_p\left( H \subseteq K_v,\, |\partial _\omega H| =m\right) \nonumber \\&\quad \le \mathbf {E}_p\left[ \sum _{m=1}^{\lfloor \alpha E_v \rfloor }\left( {\begin{array}{c}E_v \\ m\end{array}}\right) \left( \frac{p}{1-p}\right) ^m\mathbb {1}(E_v < \infty )\right] . \end{aligned}$$

(3.4)

To conclude, simply note that if $0<\alpha \le p$ then $\left( \frac{p}{1-p}\right) ^m \left( \frac{\alpha }{1-\alpha }\right) ^{-m}$ is increasing in m, so that

$$\begin{aligned} \sum _{m=1}^{\lfloor \alpha n \rfloor } \left( {\begin{array}{c}n\\ m\end{array}}\right) \left( \frac{p}{1-p}\right) ^m&\le \left( \frac{p}{1-p}\right) ^{\alpha n} \left( \frac{\alpha }{1-\alpha }\right) ^{-\alpha n} \sum _{m=1}^{\lfloor \alpha n \rfloor } \left( {\begin{array}{c}n\\ m\end{array}}\right) \left( \frac{\alpha }{1-\alpha }\right) ^m\\&\le \left( \frac{p}{1-p}\right) ^{\alpha n} \left( \frac{\alpha }{1-\alpha }\right) ^{-\alpha n} \sum _{m=0}^{n} \left( {\begin{array}{c}n\\ m\end{array}}\right) \left( \frac{\alpha }{1-\alpha }\right) ^m\\&= \left( \frac{p}{1-p}\right) ^{\alpha n} \left( \frac{\alpha }{1-\alpha }\right) ^{-\alpha n} \left( 1+\frac{\alpha }{1-\alpha }\right) ^n \\&= \alpha ^{-\alpha n} (1-\alpha )^{-(1-\alpha )n}\left( \frac{p}{1-p}\right) ^{\alpha n}. \end{aligned}$$

If $0<\alpha <\alpha (p) \le p$ then $\alpha ^{-\alpha }(1-\alpha )^{-(1-\alpha )}(p/(1-p))^{\alpha }<e^{\zeta (p)}$ by definition of $\alpha (p)$, and it follows that the right hand side of (3.4) is finite for $0<\alpha <\alpha (p)$ as claimed. $\square$

Remark 3.4

When G is transitive, it is a consequence of indistinguishability [29, 48] that for each $p_c<p \le 1$ there exists a deterministic constant $\phi ^*_E(p)$ such that every infinite cluster has anchored Cheeger constant equal to $\phi ^*_E(p)$ almost surely.

We now turn to Corollary 1.2. It is a result of Häggström et al. [30] (see also [47, Corollary 8.38]) that if G is an amenable transitive graph and $\omega$ is an automorphism-invariant percolation process on G, then every cluster K of $\omega$ has $\Phi _E^*(K)=0$ almost surely. Thus, as discussed in the introduction, Proposition 3.3 has the following corollary.

Corollary 3.5

Let $G=(V,E)$ be a connected, locally finite, transitive graph. If G is amenable then $\zeta (p)=0$ for every $p_c \le p < 1$.

Proof of Corollary 1.2

This is immediate from Theorem 1.1 and Corollary 3.5. $\square$

Remark 3.6

Consider the graph G formed by attaching a binary tree to each vertex of $\mathbb {Z}^3$. This graph is nonamenable, has bounded degrees, and satisfies $p_c(G)=p_c(\mathbb {Z}^3)<1/2$. Moreover, if $p_c(G)<p < 1/2$, then Bernoulli-p percolation on G has a unique infinite cluster almost surely, which is distributed as the graph obtained by taking the unique infinite cluster of percolation on $\mathbb {Z}^3$ and attaching an independent subcritical Galton-Watson tree to each vertex. This graph clearly has subexponential growth, and consequently does not have anchored expansion. This example shows that Theorem 1.1 cannot be extended to arbitrary connected, bounded degree, nonamenable graphs, and therefore gives a negative answer to [10, Question 6.5] as originally stated.

Random walk analysis

Proof of Corollary 1.5

As discussed in the introduction, it is a theorem of Virág [57, Theorem 1.2] that if H is a bounded degree graph with anchored expansion then there exists a positive constant c such that the simple random walk return probabilities on H satisfy the inequality $p_n(v,v) \le C_v e^{-cn^{1/3}}$ for every vertex v of H, where $C_v$ is a v-dependent constant. This theorem together with Corollary 1.4 yield the desired upper bound. Thus, it suffices to prove that for each $p_c<p<1$ we have that

$$\begin{aligned} \liminf _{ n\rightarrow \infty } -n^{-1/3}\log p_{2n}^\omega (v,v) > 0 \end{aligned}$$

(3.5)

almost surely on the event that the cluster of v is infinite. We call a path in $K_v$ a pipe if all of its internal vertices have degree two in $K_v$. The estimate (3.5) will be deduced as a consequence of the following geometric claim:

$$\begin{aligned} \begin{array}{l} \text {There exists a constant } c>0\text { such that the intrinsic } n\text {-ball around } v\text { contains a pipe }\\ \text {of length } \lceil cn \rceil \text { for every } n\text { sufficiently large a.s. on the event that } K_v\text { is infinite.} \end{array} \end{aligned}$$

(3.6)

We now prove this claim. Fix $p_c<p<1$ and $v\in V$. Write $B_\mathrm {int}(v,n)$ for the intrinsic ball of radius n around v in $K_v$, and $\partial B_\mathrm {int}(v,n)$ for the set of vertices with intrinsic distance exactly n from v. Since $K_v$ has anchored expansion a.s. on the event that it is infinite by Corollary 1.4, it must trivially also have exponential growth a.s. on the event that it is infinite. Indeed, it follows from Theorem 1.1 and Proposition 3.3 that there exists a constant $g_1>1$ and a random variable $N_1$ that is almost surely finite on the event that $K_v$ is infinite such that $\# \partial B_\mathrm {int}(v,n)\ge g_1^n$ for every $n\ge N_1$. On the other hand, since the cardinality of the intrinsic n-ball of any vertex is deterministically at most $M^n$, where M is the maximum degree of G, it follows that

$$\begin{aligned}&\#\{u \in \partial B_\mathrm {int}(v,n) : u \text { lies on an intrinsic geodesic from } v\text { to } \partial B_\mathrm {int}(v,n+m) \} \\&\quad \ge M^{-m} \#\partial B_\mathrm {int}(v,n+m) \ge M^{-m}g_1^{n+m} \end{aligned}$$

for every $n\ge N_1$ and $m\ge 0$ almost surely on the event that $K_v$ is infinite. It follows in particular that there exist constants $c_1>0$ and $g_2>1$ such that

$$\begin{aligned}&\#\{u \in \partial B_\mathrm {int}(v,n) : u \text { lies on an intrinsic geodesic from } v\\&\quad \text { to } \partial B_\mathrm {int}(v, n+\lceil c_1 n\rceil ) \} \ge g_2^n \end{aligned}$$

for every $n\ge N_1$ almost surely on the event that the cluster of v is infinite. Let $A_{n,m}$ be the set of vertices u in $\partial B_\mathrm {int}(v,n)$ such that there exists a not necessarily open path of length m in G starting at u that does not visit any vertex of $B_\mathrm {int}(v,n)$ other than at its starting point, so that

$$\begin{aligned}&\# A_{n,\lceil c_1 n \rceil } \ge \#\{u \in \partial B_\mathrm {int}(v,n) : u \text { lies on an intrinsic geodesic from } v\\&\quad \text { to } \partial B_\mathrm {int}(v,n+\lceil c_1 n\rceil )\} \ge g_2^n \end{aligned}$$

for every $n\ge N_1$ almost surely on the event that the cluster of v is infinite. Moreover, choosing points greedily shows that for every $n,m \ge 1$ and $r \ge 1$ there exists a subset $A_{n,m,r}$ of $A_{n,m}$ with cardinality at least $M^{-r} \# A_{n,m}$ such that any two distinct points in $A_{n,m,r}$ have distance at least r in G. Furthermore, we can and do choose $A_{n,m,r}$ in such a way that it is a measurable function of $B_\mathrm {int}(v,n)$. (This property is crucial to the argument of the next paragraph. It is very important here that the definitions of $A_{n,m}$ and $A_{n,m,r}$ do not require the path of length m to be open; the argument would not work otherwise.) Putting the above facts together, we deduce that there exist constants $c_2>0$ and $g_3>1$ such that

$$\begin{aligned} \# A_{n,\lceil c_2 n\rceil , \lceil c_2 n \rceil } \ge g_3^n \end{aligned}$$

(3.7)

for every $n\ge N_1$ almost surely on the event that the cluster of v is infinite.

Let $k\ge 1$ and let $\mathscr {A}_{n,k}$ be the event that $B_\mathrm {int}(v,n+ k)$ contains a pipe of length k. Let $m \ge 2(k +1)$. For each element u of $A_{n,m,m}$, the conditional probability given $B_\mathrm {int}(v,n)$ that $K_v$ contains a pipe of length k starting at u is at least $[p(1-p)^{M-1}]^{k}$, since we can take a path of the required length starting at u that is disjoint from $B_\mathrm {int}(v,n)$ other than at u, find all of its edges to be open, and find to be closed all the edges that touch a vertex of the path other than u but are not included in the path. On the other hand, the separation between the points of $A_{n,m,m}$ makes all of these events independent from each other, and we deduce that

$$\begin{aligned} \mathbf {P}_p\bigl (\mathscr {A}_{n,k} \mid B_\mathrm {int}(v,n)\bigr ) \ge 1-(1-[p(1-p)^{M-1}]^{k})^{\# A_{n,m,m}} \end{aligned}$$

(3.8)

for every $n,k \ge 1$ and $m\ge 2(k+1)$. Choosing

$$\begin{aligned} c= \min \left\{ \frac{\log g_3}{-2\log (p(1-p)^{M-1})},\, \frac{c_2}{2}\right\} >0 \end{aligned}$$

and using the inequality $((x-1)/x)^x \le e^{-1}$ yields that

$$\begin{aligned} \mathbf {P}_p\Bigl (\mathscr {A}_{n, \lceil c n \rceil } \cup \{ \# A_{n,\lceil 2cn \rceil , \lceil 2cn \rceil } < g_3^n \} \mid B_\mathrm {int}(v,n)\Bigr ) \ge 1-\bigl (1-g_3^{-n/2}\bigr )^{g_3^n} \ge 1-e^{-g_3^{n/2}}. \end{aligned}$$

(3.9)

Thus, it follows by Borel–Cantelli that there exists an almost surely finite $N_2$ such that the event $\mathscr {A}_{n, \lceil c n \rceil } \cup \{ \# A_{n,\lceil 2cn \rceil , \lceil 2cn \rceil } < g_3^n \}$ occurs for every $n \ge N_2$ almost surely. Together with (3.7), this shows that the event $\mathscr {A}_{n, \lceil c n \rceil }$ holds for every $n \ge N_1 \vee N_2$ almost surely on the event that $K_v$ is infinite. This completes the proof of (3.6).

It remains to deduce (3.5) from (3.6). This argument is well-known and appears in e.g. [57, Example 6.1], so we will keep the discussion brief. Let $c>0$ and $N<\infty$ be random variables such that $B_\mathrm {int}(v,\lceil n^{1/3}\rceil )$ contains a pipe of length $\lceil c n^{1/3} \rceil$ for every $n \ge N$. Pick one such pipe, call it the n-pipe, and let w(n) be the vertex of the n-pipe at minimal intrinsic distance from v. In time 2n, the random walk on G can return to v using the following strategy: Walk to w(n) in exactly $d_\mathrm {int}(v,w(n))=O(n^{1/3})$ steps, spend the following $2n-2d_\mathrm {int}(v,w(n))=\Theta (n)$ steps performing an excursion from w(n) to itself inside the n-pipe, then return to v in the final $d_\mathrm {int}(v,w(n))=O(n^{1/3})$ steps. Each of these three stages has probability at least $e^{-C n^{1/3}}$ to occur for an appropriate choice of constant C, concluding the proof. $\square$

Extension to quasi-transitive graphs

Recall that a graph is said to be quasi-transitive if the action of its automorphism group on its vertex set has at most finitely many orbits. Theorems concerning percolation on transitive graphs can almost always be generalized to the quasi-transitive case, and ours are no exception.

Theorem 4.1

Let $G=(V,E)$ be a connected, locally finite, nonamenable, quasi-transitive graph. Then $\zeta (p)>0$ for every $p_c < p \le 1$.

Once this theorem is established, extensions of Corollaries 1.3–1.5 to the quasi-transitive case follow by essentially the same proofs as in the transitive case.

Let $G=(V,E)$ be a connected, locally finite, nonamenable, quasi-transitive graph, and let v be a vertex of G. The only place in the proof of Theorem 1.1 where transitivity is used is in the proof of Proposition 2.1. Thus, to prove Theorem 4.1, it suffices to prove that for every $p_c<p<1$ there exist positive constants $t_0,c$ and C such that

$$\begin{aligned} \mathbf {D}_{p,n}\left[ e^{t E_v}\right] \ge c \mathbf {E}_{p,n}\left[ E_v e^{tE_v} \right] - C \end{aligned}$$

(4.1)

for every $n\ge 1$ and $0 < t \le t_0$. Indeed, once this is established the proof may be concluded in a very similar way to the transitive case.

Let $V_1,\ldots ,V_k$ be the orbits of the action of ${\text {Aut}}(G)$ on V. The proof of Lemma 2.5 generalizes to show that for every $p_c<p<1$, there exists an automorphism-invariant percolation process $\eta$ such that $\eta$ has furcations almost surely and $\eta$ is stochastically dominated by Bernoulli-p bond percolation on G. Thus, the proof of Proposition 2.4 yields that there exists $1 \le i_0 \le k$ and a positive constant $c_p$ such that

$$\begin{aligned} \mathbf {E}_p\left[ \mathscr {P}_\omega (S \rightarrow \infty )\right] \ge c_p |S \cap V_{i_0}| \end{aligned}$$

(4.2)

for every finite set $S \subseteq V$. The proof of Proposition 2.1 then yields that

$$\begin{aligned} \mathbf {D}_{p,n}\left[ e^{t E_v}\right] \ge \frac{c_p}{1-p} \mathbf {E}_{p,n}\left[ |K_v \cap V_{i_0}| e^{tE_v} \right] \end{aligned}$$

(4.3)

for every $t>0$ and $n\ge 1$. In order to deduce an inequality of the form (4.1) from (4.3), it suffices to prove the following lemma.

Lemma 4.2

Let $G=(V,E)$ be a connected, locally finite, quasi-transitive graph with maximum degree M, let $0<p<1$, and let $V_1\ldots ,V_k$ be the orbits of the action of ${\text {Aut}}(G)$ on V. Then for every $0<p<1$ there exist positive constants $\alpha =\alpha (p,k,M)$ and $t_0=t_0(p,k,M)$ such that

$$\begin{aligned} \mathbf {P}_p\left( n \le E_v <\infty ,\, |K_v \cap V_{i}| \le \alpha E_v\right) \le e^{-2t_0 n} \end{aligned}$$

(4.4)

for every $n\ge 1$ and $1 \le i \le k$.

Proof of Lemma 4.2

It suffices to prove the claim for $i=1$. Fix $0<p<1$. Since G is connected, we may reorder $V_2,V_3,\ldots ,V_k$ so that $V_j$ is adjacent to $\bigcup _{\ell =1}^{j-1} V_\ell$ for every $2 \le j \le k$. Since ${\text {Aut}}(G)$ acts transitively on $V_\ell$ for each $1 \le \ell \le k$, every vertex in $V_m$ must be adjacent to at least one vertex in $\cup _{\ell =1}^{m-1} V_\ell$ for each $2 \le m \le k$. Let M be the maximum degree of G, and write $K_v^m = K_v \cap \cup _{\ell =1}^m V_\ell$ for each $1 \le m \le k$. We first claim that there exists a positive constant $c=c(p,M)$ such that for each $2 \le m \le k$ we have that

$$\begin{aligned}&\mathbf {P}_p\left( s \le \bigl |K_v^m\bigr |< \infty \text { and } \bigl |K_v^{m-1} \bigr | \le \frac{p}{p+2M} \bigl |K_v^m\bigr | \right) \nonumber \\&\quad \le \mathbf {P}_p\left( \frac{2Ms}{p+2M} \le \bigl |K_v \cap V_m \bigr | <\infty \text { and } \bigl |K_v^{m-1} \bigr | \le \frac{p}{2M} \bigl |K_v \cap V_m\bigr | \right) \le e^{-c s} \nonumber \\ \end{aligned}$$

(4.5)

for every $s>0$. The first inequality is trivial. For the second, consider exploring $K_v$ one edge at a time. On the event under consideration, we must query some number $N \ge |K_v \cap V_m| \ge 2M s/(p+2M)$ edges with one endpoint in $V_m$ and the other in $\bigcup _{\ell =1}^{m-1} V_\ell$ and find that at most pN/2 of these edges are open. Since $p/2<p$, the claimed inequality (4.5) follows by standard large deviation estimates for Binomial random variables.

To conclude, we note that we trivially have $|K_v^k|=|K_v| \ge E_v /M$, and apply (4.5) and a union bound to deduce that

$$\begin{aligned}&\mathbf {P}_p\left( n \le E_v<\infty ,\, |K_v \cap V_1| \le \left[ \frac{p}{p+2M}\right] ^{k-1} \frac{E_v}{M} \right) \\&\quad \le \sum _{m=2}^{k} \mathbf {P}_p\left( \left[ \frac{p}{p+2M}\right] ^{k-m} \frac{n}{M} \le \bigl |K_v^{m}\bigr | < \infty \text { and } \bigl |K_v^{m-1}\bigr | \le \frac{p}{p+2M} \bigl |K_v^{m}\bigr | \right) \\&\quad \le (k-1) \exp \left[ -\left[ \frac{p}{p+2M}\right] ^{k-1}\frac{cn}{M}\right] \end{aligned}$$

for every $n\ge 1$. This immediately implies the claim. $\square$

Proof of Theorem 4.1

Let $t_0=t_0(p,k,M)$ and $\alpha =\alpha (p,k,M)$ be as in Lemma 4.2, and note that (4.3) implies that

$$\begin{aligned} \mathbf {D}_{p,n}\left[ e^{t E_v}\right] \ge \frac{c_p \alpha }{1-p} \mathbf {E}_{p,n}\left[ E_v e^{tE_v} \right] - \frac{c_p}{1-p}\mathbf {E}_p\left[ E_v e^{t_0 E_v} \mathbb {1}\left( |K_v \cap V_{i}| \le \alpha E_v\right) \right] \end{aligned}$$

(4.6)

for every $n\ge 1$ and $t\le t_0$. The second term on the right is finite by Lemma 4.2, so that (4.6) is of the form required by (4.1). Thus, the proof of Theorem 4.1 may be concluded in a very similar manner to the proof of Theorem 4.1 as discussed above. $\square$

Closing remarks and open problems

Analyticity at the uniqueness threshold

The analyticity of $\theta (p)$ and $\tau ^f_p(x,y)$ throughout the entire supercritical phase $(p_c,1)$ established by Corollary 1.3 is in stark contrast to the behaviour of the untruncated two-point function $\tau _p(x,y)=\mathbf {P}_p(x \leftrightarrow v)$, which can be discontinuous on the same interval under the same hypotheses.

Indeed, it is known that there exists a unimodular transitive graph G for which $p_c<p_u$ and for which there are infinitely many infinite clusters in Bernoulli-$p_u$ percolation almost surely. The most easily understood example with these properties is probably the product $T \times T$ of two three-regular trees, which is treated by the results of [36, 50]. We claim that for such a graph G, there must exist vertices x and y such that $\tau _p(x,y)$ is discontinuous at $p_u$. Indeed, it is a theorem of Lyons and Schramm [48, Theorem 4.1] that if G is transitive and unimodular and $p\in (0,1)$ is such that there are infinitely many infinite clusters $\mathbf {P}_p$-a.s. then $\inf _{x,y} \tau _p(x,y) = 0$ (see also [56] for the nonunimodular case). Thus, it follows by our assumptions that there exist $x,y \in V$ with $\tau _{p_u}(x,y) \le \frac{1}{2}\theta (p_u)^2$. On the other hand, the Harris-FKG inequality implies that $\tau _p(x,y) \ge \mathbf {P}_p(x,y$ both in the infinite cluster$) \ge \theta (p)^2 \ge \theta (p_u)^2$ for every $p_u<p\le 1$, so that $\tau _p(x,y)$ must have a jump discontinuity at $p_u$ as claimed. (The fact that the qualitative change in behaviour at $p_u$ is not necessarily reflected in any failure of regularity of $\theta (p)$ at $p_u$ was also remarked on in [25].)

Intrinsic geodesics in the hyperbolic plane

Theorem 4.1 also has consequences for the geometry of intrinsic geodesics in percolation in the hyperbolic plane. Indeed, let M be a locally finite, quasi-transitive, simply connected, nonamenable planar map with locally finite dual $M^\dagger$, which is also quasi-transitive and nonamenable. Every edge e of M has a corresponding dual edge $e^\dagger$. (See e.g. [6, Section 2.1] for detailed definitions.) If $\omega$ is Bernoulli-p bond percolation on M then the configuration $\omega ^\dagger$ defined by $\omega ^\dagger (e^\dagger ) = 1-\omega (e)$ is distributed as Bernoulli-$(1-p)$ bond percolation on $M^\dagger$, and it follows from the results of [13] that $p_u(M)=1-p_c(M^\dagger )$, so that $p_u$-percolation on M is dual to $p_c$-percolation on $M^\dagger$.

Suppose that e is an edge of M with endpoints x and y, and let f and g be the two faces incident to e. Let $\omega$ be Bernoulli-p bond percolation on M and let $K_1$ and $K_2$ be the clusters of f and g in $\omega ^\dagger {\setminus } \{e^\dagger \}$. If e is closed and x is connected to y in $\omega$ then at least one of $K_1$ or $K_2$ must be finite. Moreover, if x is connected to y and $K_i$ is finite then the collection of edges other than e whose duals are in the boundary of $K_i$ must contain an open path from x to y, so that

$$\begin{aligned} d_\mathrm {int}(x,y) \le \min \{ |E(K_1)|,|E(K_2)|\}. \end{aligned}$$

Thus, it follows from sharpness of the phase transition (1.1) and Theorem 4.1 that for every $p\in (0,p_u) \cup (p_u,1)$ there exists a constant $c_p>0$ such that

$$\begin{aligned} \mathbf {P}_{p}\bigl [ d_\mathrm {int}(x,y) \ge n \mid x \leftrightarrow y \bigr ] \le e^{-c_p n} \end{aligned}$$

(5.1)

for every pair of adjacent vertices x and y of M and every $n\ge 1$. (With a little more work one can also obtain similar bounds for non-neighbouring pairs of vertices.) This contrasts the behaviour at $p_u$, where it is proven in [37, Theorem 6.1] that, under the same assumptions, $\mathbf {P}_{p_u}\bigl [ d_\mathrm {int}(x,y) \ge n \mid x \leftrightarrow y \bigr ] \asymp n^{-1}$ for some neighbouring pairs of vertices.

Conjectures for amenable graphs

We end with some conjectures concerning supercritical percolation on general transitive graphs that could potentially unify our results with those from the Euclidean case [2, 18, 43, 51]. We expect that these conjectures have been around for some time as folklore. We recall that if G is a connected, locally finite graph, the isoperimetric profile of G is defined to be

$$\begin{aligned} \psi (t)=\psi (G,t) = \inf \Bigl \{ |\partial _E K| : K \subseteq V,\, t \le \sum _{v\in K} \deg (v) < \infty \Bigr \}. \end{aligned}$$

Conjecture 5.1

Let $G=(V,E)$ be an infinite, connected, locally finite, transitive graph. Then for every $p_c<p<1$ there exist positive constants $c_p$ and $C_p$ such that

$$\begin{aligned} \exp \left[ - C_p \psi ( C_p n) \right] \le \mathbf {P}_p(n \le |K_v| < \infty ) \le \exp \left[ -c_p \psi (c_p n) \right] \quad \text {for every } n \ge 1. \end{aligned}$$

Note that the nonamenable case of Coonjecture 5.1 is exactly Theorem 1.1, and that the case $G=\mathbb {Z}^d$ is covered by (1.3). In the case that G is a Cayley graph of a one-ended finitely presented group, the lower bound of Coonjecture 5.1 is implicit in the proof of [8, Theorem 3]. For the same class of graphs and for p sufficiently close to 1 one can also establish the upper bound of Coonjecture 5.1 via a Peierls argument.

Let us also draw attention to the following much weaker question, which also remains open.

Conjecture 5.2

Let $G=(V,E)$ be an infinite, connected, locally finite, transitive graph. Then the truncated susceptibility $\mathbf {E}_p |K_v| \mathbb {1}(|K_v|<\infty )$ is finite for every $p_c<p \le 1$.

In contrast to the volume, we expect that the radius of a finite supercritical cluster has an exponential tail on every transitive graph. Similar statements should also hold for the intrinsic radius. The nonamenable case of this conjecture is implied by Theorem 1.1, while the case $G=\mathbb {Z}^d$ was proven by Chayes et al. [18].

Conjecture 5.3

Let $G=(V,E)$ be an infinite, connected, locally finite, transitive graph. Then for every $p_c<p<1$ there exists a positive constant $c_p$ such that

$$\begin{aligned} \mathbf {P}_p(K_v \leftrightarrow \partial B(v,n), |K_v|<\infty ) \le e^{-c_p n} \quad \text {for every } n \ge 1. \end{aligned}$$

Finally, we conjecture that the infinite clusters in supercritical percolation on G always inherit an anchored version of any isoperimetric inequality satisfied by G.

Conjecture 5.4

Let $G=(V,E)$ be an infinite, connected, locally finite, transitive graph, and let $p_c<p \le 1$. Then there exists a positive constant $c_p$ such that

$$\begin{aligned}&\lim _{n\rightarrow \infty } \inf \left\{ \frac{|\partial _\omega H|}{\psi (G, c_p n)} : H \text { a connected subgraph of } K_v\text { containing } v\right. \\&\quad \left. \text { with } n\le |E(H)|<\infty \right\} >0 \end{aligned}$$

almost surely on the event that $K_v$ is infinite.

The nonamenable case of this conjecture is implied by Corollary 1.4, while the case $G=\mathbb {Z}^d$ was established by Pete [51]. Similarly to above, for Cayley graphs of one-ended, finitely presented groups and p close to 1 the conjecture may be established via a Peierls argument, see [51, Theorem 1.5]. We remark that Conjectures 5.1 and 5.4 are also closely related to Pete’s exponential cluster repulsion conjecture [52, Conjecture 12.32].

Other models

It would be very interesting (and seemingly non-trivial) to extend our analysis to dependent percolation models such as the random cluster model. One can also wonder whether our main theorems hold for an arbitrary automorphism-invariant percolation process that is subjected to Bernoulli noise.

Question 5.5

Let $G=(V,E)$ be an infinite, connected, locally finite, nonamenable transitive graph. Let $\omega \in \{0,1\}^E$ be an ergodic, automorphism-invariant percolation process on G, let $\eta \in \{0,1\}^E$ be an independent Bernoulli process in which each edge is included independently at random with probability $\varepsilon >0$, and suppose that the symmetric difference $\omega \Delta \eta$ has infinite clusters almost surely.

• 1. Is the origin exponentially unlikely to be in a large finite cluster of $\omega \Delta \eta$?

• 2. Does every infinite cluster of $\omega \Delta \eta$ have anchored expansion almost surely?

Note that most of our analysis extends straightforwardly to such a model; it seems that the only part of our proof that breaks down badly is in the proof of Proposition 2.1, where we use that conditioning on $K_v$ does not affect the distribution of the restriction of the process to the complement of $E(K_v)$.