Abstract
For a classical group over a non-archimedean local field of odd residual characteristic p, we prove that two cuspidal types, defined over an algebraically closed field \({\mathbf {C}}\) of characteristic different from p, intertwine if and only if they are conjugate. This completes work of the first and third authors who showed that every irreducible cuspidal \({\mathbf {C}}\)-representation of a classical group is compactly induced from a cuspidal type. We generalize Bushnell and Henniart’s notion of endo-equivalence to semisimple characters of general linear groups and to self-dual semisimple characters of classical groups, and introduce (self-dual) endo-parameters. We prove that these parametrize intertwining classes of (self-dual) semisimple characters and conjecture that they are in bijection with wild Langlands parameters, compatibly with the local Langlands correspondence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1. One approach to study smooth representations of a reductive p-adic group on modules over a commutative ring intrinsically is by restriction to compact open subgroups. For p-adic general linear groups this has yielded detailed classification results, for example Bushnell and Kutzko’s monograph [12] for complex representations and its subsequent partial generalizations to other coefficient rings, see for example [23, 28, 44].
At the base of the work of Bushnell and Kutzko is an explicit construction of characters of compact open pro-p subgroups of p-adic general linear groups called simple characters, constructed from certain arithmetic data. However, there is a lot of flexibility in the choice of arithmetic data leading to, for example, simple characters contained in isomorphic cuspidal representations. Moreover, there are functorial relations between simple characters defined on compact open subgroups of different rank p-adic general linear groups. To control this flexibility and encapsulate these relations, Bushnell and Henniart [8] collected simple characters into families called ps-characters and introduced an equivalence relation on ps-characters called endo-equivalence.
Endo-classes (endo-equivalence classes of ps-characters) have subsequently been extended to inner forms of general linear groups [5], and have proved fundamental in understanding fine properties of the local Langlands correspondence [10, 11] and the Jacquet–Langlands correspondence [19, 37], as well as in the study of Galois-distinguished cuspidal representations [1, 33] and in Bernstein decompositions of the category of smooth representations over fields of positive characteristic [36].
1.2. Let \(\mathrm{G}^{\mathsf {o}}\) be a p-adic classical group: that is, the group of \(\mathrm{F}_{\mathsf {o}}\)-points of a unitary, symplectic, or special orthogonal group defined over a non-archimedean local field \(\mathrm{F}_{\mathsf {o}}\) of odd residual characteristic p. Let \({\mathbf {C}}\) be an algebraically closed field of characteristic different from p.
Building on the work of Bushnell and Kutzko, all cuspidal representations of \(\mathrm{G}^{\mathsf {o}}\) on \({\mathbf {C}}\)-vector spaces have been constructed in [26, 43], and for complex representations types have been constructed for all Bernstein components [29]. Fundamental to this approach are the self-dual semisimple characters of compact open pro-p subgroups of \(\mathrm{G}^{\mathsf {o}}\) constructed in [42].Footnote 1 There are functorial relations between the self-dual semisimple characters of different p-adic classical groups, and their definition is cursed by the same flexibility as for general linear groups.
In this article, we generalize Bushnell and Henniart’s notions of ps-character and endo-equivalence to self-dual pss-characters and endo-equivalence for p-adic classical groups, and along the way to the semisimple setting of pss-characters and endo-equivalence for p-adic general linear groups. We then prove two applications.
-
(i)
We complete the classification of isomorphism classes of cuspidal (smooth) representations of \(\mathrm{G}^{\mathsf {o}}\) on \({\mathbf {C}}\)-vector spaces by conjugacy classes of cuspidal types, following the exhaustive constructions of [26, 43].
-
(ii)
We parametrize the intertwining classes of self-dual semisimple characters by self-dual endo-parameters.
1.3. We expect self-dual endo-parameters to have a natural interpretation via the local Langlands correspondence in terms of the restriction to wild inertia of (extended) Langlands parameters, generalizing Bushnell and Henniart’s ramification theorem [10, 6.1 Theorem] to classical groups and refining work of the third author with Blondel and Henniart [4, Theorem 7.1]. See the end of the introduction for a precise conjecture. The added complexity in endo-parameters for p-adic classical groups in comparison to p-adic general linear groups is explained in the parametrization of L-indistinguishable representations.
Another application of endo-parameters is found in current work of the first and third authors which gives a decomposition of the category of all smooth \({\mathbf {C}}\)-representations of \(\mathrm{G}^{\mathsf {o}}\) by self-dual endo-parameters, refining the decomposition by depth [44, II 5.8]. This decomposition is particularly interesting when \({\mathbf {C}}\) has positive characteristic where a block decomposition of the category is not yet known, but where there has been recent progress in depth zero [27]. We expect using endo-parameters that there is a reduction of the block decomposition for \(\mathrm{G}^{\mathsf {o}}\) to the depth zero block decompositions of twisted Levi subgroups of \(\mathrm{G}^{\mathsf {o}}\). This fits with work of Chinello for general linear groups [15] and with general predictions of Dat [17] .
1.4. We now state our results precisely. Henceforth, all representations are assumed to be smooth. We assume that \(\mathrm{G}^{\mathsf {o}}\) is not isomorphic to \({\text {SO}}(1,1)(\mathrm{F}_{\mathsf {o}})\simeq \mathrm{F}_{\mathsf {o}}^\times \), whose representation theory, in any case, is well-known.
In [43] for complex representations, extended to representations on \({\mathbf {C}}\) vector spaces in [26], an explicit list of pairs \((\mathrm{J},\lambda )\), called cuspidal types, are constructed consisting of a compact open subgroup \(\mathrm{J}\) of \(\mathrm{G}^{\mathsf {o}}\) and an irreducible representation \(\lambda \) of \(\mathrm{J}\) such that the induced representation \({\text {ind}}_{\mathrm{J}}^{\mathrm{G}^{\mathsf {o}}}\lambda \) is irreducible and cuspidal. The main results of the cited works say that every irreducible cuspidal representation \(\pi \) of \(\mathrm{G}^{\mathsf {o}}\) contains a cuspidal type \((\mathrm{J},\lambda )\), i.e. it is compactly induced \(\pi \simeq {\text {ind}}_{\mathrm{J}}^{\mathrm{G}^{\mathsf {o}}} \lambda \). In other words, this gives an explicit model of \(\pi \) in terms of the cuspidal type \((\mathrm{J},\lambda )\).
There is a precise recipe to construct cuspidal types whence cuspidal representations, however it is a recipe which requires many choices and it is far from clear when the procedure results in isomorphic representations. We prove the following intertwining implies conjugacy result:
Theorem
(Theorem 11.9). For \(i=1,2\), let \((\mathrm{J}_i,\lambda _i)\) be cuspidal types and put \(\pi _i\simeq {\text {ind}}_{\mathrm{J}_i}^{\mathrm{G}^{\mathsf {o}}} \lambda _i\). Then \(\pi _1\simeq \pi _2\) if and only if there exists \(g\in \mathrm{G}^{\mathsf {o}}\) such that \(\mathrm{J}_1^g=\mathrm{J}_2\) and \(\lambda _1^g\simeq \lambda _2\).
Here \(\lambda _1^g\) is the representation of \(\mathrm{J}_1^g=g^{-1}\mathrm{J}_1 g\) defined by \(\lambda _1^g(j)=\lambda _1(gjg^{-1})\) for all \(j\in \mathrm{J}_1^g\). This result is not unexpected, by analogy with results for inner forms of general linear groups [12, 34], but the proof for classical groups requires considerably more technical machinery. A major reason for this added complexity can be interpreted via the local Langlands correspondence: L-packets for classical groups are not singletons.
A special case of Theorem 11.9, where the self-dual semisimple characters underlying the cuspidal types are assumed to be closely related, is proved in [26]. The proof of Theorem 11.9 combines the work of this paper to control the choice in arithmetic data in the construction of cuspidal representations, together with an intertwining implies conjugacy result for semisimple characters of [39], to show that it is always possible to arrange for this to be the case.
1.5. In the main theme of this paper, we generalize Bushnell and Henniart’s theory of potential simple character and endo-equivalence, originally defined in [8], to potential semisimple characters and semisimple endo-equivalence for general linear groups, and to self-dual potential semisimple characters and self-dual semisimple endo-equivalence for classical groups. As well as appearing in an essential way in our proof of Theorem 11.9, this theory warrants independent study and forms a key part of our parametrization of intertwining classes of (self-dual) semisimple characters via endo-parameters which we introduce at the end of the paper.
1.6. To proceed further, we need to introduce more notation. First we realize our classical group as a subgroup of the group of isometries of a signed hermitian form.
Let \(\Sigma =\langle \sigma \rangle \) denote an abstract finite group of order two. Let \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) be a quadratic or trivial extension of non-archimedean local fields of odd residual characteristic p, and let  denote the generator of \({\text {Gal}}(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\). Let \(\mathrm{V}\) be an \(\mathrm{F}\)-vector space and \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_\mathrm{F}(\mathrm{V})\). Let \(\varepsilon =\pm 1\) and \(h:\mathrm{V}\times \mathrm{V}\rightarrow \mathrm{F}\) be an \(\varepsilon \)-hermitian form defining a unitary, symplectic or orthogonal group \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\):
denote the generator of \({\text {Gal}}(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\). Let \(\mathrm{V}\) be an \(\mathrm{F}\)-vector space and \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_\mathrm{F}(\mathrm{V})\). Let \(\varepsilon =\pm 1\) and \(h:\mathrm{V}\times \mathrm{V}\rightarrow \mathrm{F}\) be an \(\varepsilon \)-hermitian form defining a unitary, symplectic or orthogonal group \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\):
where \(\sigma \) acts on \({{\widetilde{\mathrm{G}}}}\) by the inverse of the adjoint anti-involution of h.
We let \(\mathrm{G}^{\mathsf {o}}\) denote \(\mathrm{G}\) in the unitary and symplectic cases, and the subgroup of all isometries of determinant one in the orthogonal case; we call \(\mathrm{G}^{\mathsf {o}}\) a classical group. We fix a non-trivial character \(\psi _{\mathsf {o}}\) of the additive group of \(\mathrm{F}_{\mathsf {o}}\), of level one, and put \(\psi =\psi _{\mathsf {o}}\circ {\text {Tr}}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}\).
We consider our sign \(\varepsilon \) and extension \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) fixed. However, we will vary our \(\mathrm{F}\)-vector space \(\mathrm{V}\) and \(\varepsilon \)-hermitian form \(h:\mathrm{V}\times \mathrm{V}\rightarrow \mathrm{F}\). Indeed, this flexibility will be one of the charms of the theory of endo-equivalence. We still use the notation \({{\widetilde{\mathrm{G}}}}={\text {GL}}_\mathrm{F}(\mathrm{V})\), \(\mathrm{G}\) for the group of isometries of h, and \(\mathrm{G}^{\mathsf {o}}\) its classical subgroup. While the notation \({{\widetilde{\mathrm{G}}}}\) does not specify \(\mathrm{V}\), nor \(\mathrm{G}\) or \(\mathrm{G}^{\mathsf {o}}\) specify h, we trust this will cause no confusion. Indeed, non-isometric \(\varepsilon \)-hermitian forms can define the same isometry group up to isomorphism.
1.7. We now introduce an abstraction of the data underlying the construction of semisimple characters, following Bushnell and Henniart in the simple case [8]. Let \((k,\beta )\) be a semisimple pair, that is \(\mathrm{E}=\mathrm{F}[\beta ]\) is a sum \(\bigoplus _{i\in \mathrm{I}}\mathrm{E}_i\) of field extensions \(\mathrm{E}_i\) of \(\mathrm{F}\) and k is an integer satisfying a certain technical bound (see Definition 9.1). We call \(\mathrm{I}\) the indexing set.
We let \({\mathscr {Q}}(k,\beta )\) denote the class of all quadruples \((\mathrm{V},\varphi ,\Lambda ,r)\) consisting of an \(\mathrm{F}\)-vector space \(\mathrm{V}\), an embedding \(\varphi :\mathrm{E}\rightarrow {\text {End}}_\mathrm{F}(\mathrm{V})\), a \(\varphi ({\mathfrak {o}}_\mathrm{E})\)-lattice sequence \(\Lambda \) in \(\mathrm{V}\), and an integer r closely related to k, see Sect. 9.
Using work of Bushnell–Kutzko [12] and the third author [42], to \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\) we associate a set \({\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) of semisimple characters (which depend on our initial fixed character \(\psi \)) of a compact open subgroup \({\mathrm {H}}^{r+1}(\varphi (\beta ),\Lambda )\) of \(\mathrm{G}\). In the special case where \(\mathrm{E}\) is a field we call the characters in \({\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) simple characters.
Corresponding to the decomposition \(\beta =\sum _{i\in \mathrm{I}}\beta _i\) of \(\beta \) in \(\bigoplus _{i\in \mathrm{I}}\mathrm{E}_i\), we have decompositions \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and \(\Lambda =\bigoplus _{i\in \mathrm{I}}\Lambda ^i\). Moreover, there are a natural embedding
which we write \(\theta \mapsto \theta _i\). Thus from a semisimple character \(\theta \) we get a collection of simple characters \(\theta _i\), for \(i\in \mathrm{I}\), which we call its simple block restrictions.
1.8. Let \((k,\beta )\) and \((k,\beta ')\) be semisimple pairs with indexing sets \(\mathrm{I}\) and \(\mathrm{I}'\) respectively, \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\) and \((\mathrm{V},\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta ')\) with \(\Lambda \) and \(\Lambda '\) of the same period as \({\mathfrak {o}}_\mathrm{F}\)-lattice sequences.
Suppose we have semisimple characters \(\theta \in {\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) and \(\theta '\in {\mathscr {C}}(\Lambda ',r',\varphi '(\beta '))\) which intertwine in \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_\mathrm{F}(\mathrm{V})\). The matching theorem of the second and third authors [39, Theorem 10.1], tells us that there exists a unique bijection \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) and \(g\in {{\widetilde{\mathrm{G}}}}\) such that \(g\mathrm{V}^i=\mathrm{V}^{\zeta (i)}\) and  and \(\theta _{\zeta (i)}'\) intertwine in \({\text {Aut}}_\mathrm{F}(\mathrm{V}^{\zeta (i)})\). In this case, we say that \(\theta \) intertwines with \(\theta '\) with matching \(\zeta \).
and \(\theta _{\zeta (i)}'\) intertwine in \({\text {Aut}}_\mathrm{F}(\mathrm{V}^{\zeta (i)})\). In this case, we say that \(\theta \) intertwines with \(\theta '\) with matching \(\zeta \).
1.9. There are natural (bijective) transfer maps between the sets of semisimple characters defined by a pair of quadruples in \({\mathscr {Q}}(k,\beta )\) (see Lemma 9.3). Following the methodology of Bushnell and Henniart [8], we collect together the semisimple characters related by transfer, into pss-characters: a pss-character \(\Theta \) supported on \((k,\beta )\) is a function from \({\mathscr {Q}}(k,\beta )\) to the class of all semisimple characters, such that \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\), whose values are related by transfer.
We call a value of a pss-character a realization of the pss-character. Thus, by definition, a pss-character is determined by any one of its realizations. This definition generalizes the definition of [8] of ps-characters - which forms the special case where \(\mathrm{F}[\beta ]\) is a field. The degree of a pss-character \(\Theta \) supported on \((k,\beta )\) is \(\deg (\Theta )=[\mathrm{F}[\beta ]:\mathrm{F}]\).
A pss-character \(\Theta \) supported on \((k,\beta )\) with index set \(\mathrm{I}\) gives rise to a collection of ps-characters \(\Theta _i\), for \(i\in \mathrm{I}\), supported on simple pairs \((k_i,\beta _i)\), which we call its component ps-characters. See Lemma 9.6 for more details on this decomposition and Definition 9.1 for the definition of \(k_i\).
Our next step is to generalize Bushnell and Henniart’s notion of endo-equivalence from ps-characters to pss-characters. Let \(\Theta \) be a pss-character supported on the semisimple pair \((k,\beta )\) and \(\Theta '\) be a pss-character supported on the semisimple pair \((k',\beta ')\). We say that \(\Theta \) and \(\Theta '\) are endo-equivalent, written \(\Theta \approx \Theta '\), if
-
(i)
\(k=k'\) and \(\deg (\Theta )= \deg (\Theta ')\); and
-
(ii)
there exist realizations on a common \(\mathrm{F}\)-vector space \(\mathrm{V}\) which intertwine in \({{\widetilde{\mathrm{G}}}}={\text {GL}}_\mathrm{F}(\mathrm{V})\).
We relate endo-equivalence of pss-characters with endo-equivalence of their component ps-characters:
Theorem
(Part of Theorem 9.9). Let \(\Theta \) and \(\Theta '\) be pss-characters supported on semisimple pairs \((k,\beta )\) and \((k,\beta ')\) respectively, with index sets \(\mathrm{I}\) and \(\mathrm{I}'\) respectively.
-
(i)
We have \(\Theta \approx \Theta '\) if and only if there is a bijection \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) such that, for all \(i\in \mathrm{I}\), the component ps-characters \(\Theta _i\) and \(\Theta _{\zeta (i)}\) are endo-equivalent. Moreover, if \(\Theta \approx \Theta '\) then the map \(\zeta \) is uniquely determined.
-
(ii)
Suppose that \(\Theta \approx \Theta '\) and let \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) be the bijection of (i). Let \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\) and \((\mathrm{V},\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta ')\). If \({\text {dim}}_\mathrm{F}(\mathrm{V}^i)={\text {dim}}_\mathrm{F}(\mathrm{V}^{\zeta (i)})\), for all \(i\in \mathrm{I}\), then \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\Theta '(\mathrm{V},\varphi ',\Lambda ',r')\) intertwine in \({{\widetilde{\mathrm{G}}}}\) with matching \(\zeta \).
-
(iii)
Endo-equivalence of pss-characters is an equivalence relation.
We call the endo-equivalence classes of pss-characters semisimple endo-classes. Given endo-equivalent pss-characters as in Theorem 9.9, we call the map \(\zeta \) of (i) a matching. The condition, \({\text {dim}}_\mathrm{F}(\mathrm{V}^i)={\text {dim}}_\mathrm{F}(\mathrm{V}^{\zeta (i)})\) for all \(i\in \mathrm{I}\), in (ii) is necessary, as follows from [39, Theorem 10.1]. In the special case of ps-characters, of course, this condition is automatic.
1.10. Now we turn to the analogous constructions for our classical group \(\mathrm{G}\), so consider the action of the involution \(\sigma \) on the data involved. Let \((k,\beta )\) be a semisimple pair with indexing set \(\mathrm{I}\) and \(\mathrm{E}=\mathrm{F}[\beta ]\). We call \((k,\beta )\) self-dual if the Galois involution generating \({\text {Gal}}(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) extends to a Galois involution on \(\mathrm{E}\) sending \(\beta \) to \(-\beta \); in this case we call the \(\mathrm{F}\)-algebra \(\mathrm{E}=\mathrm{F}[\beta ]\) self-dual (though self-duality is really a property of the pair \((\mathrm{E},\beta )\)). In this case, the Galois involution induces an action of \(\sigma \) on the indexing set \(\mathrm{I}\), which decomposes as \(\mathrm{I}=\mathrm{I}_+\cup \mathrm{I}_0\cup \mathrm{I}_-\) with \(\mathrm{I}_0\) the \(\sigma \)-fixed indices, \(\mathrm{I}_+\) a set of representatives for the orbits of size 2 and \(\mathrm{I}_-=\sigma (\mathrm{I}_+)\).
Suppose that \((k,\beta )\) is self-dual. We let \({\mathscr {Q}}_-(k,\beta )\) denote the class of all quadruples \(((\mathrm{V},h),\varphi ,\Lambda ,r)\) such that \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\), the \(\mathrm{F}\)-vector space \(\mathrm{V}\) is equipped with an \(\varepsilon \)-hermitian form \(h:\mathrm{V}\times \mathrm{V}\rightarrow \mathrm{F}\) and \(\varphi ,\Lambda \) are self-dual. If \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) then \({\mathrm {H}}^{r+1}(\beta ,\Lambda )\) is \(\Sigma \)-stable and \(\Sigma \) acts on \({\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) with fixed points \({\mathscr {C}}^\Sigma (\Lambda ,r,\varphi (\beta ))\), where as before \(\sigma \) acts via the inverse of the adjoint anti-involution of h. We set \({\mathrm {H}}^{r+1}_-(\beta ,\Lambda )={\mathrm {H}}^{r+1}(\beta ,\Lambda )^\Sigma \) and define the set of self-dual semisimple characters \({\mathscr {C}}_-(\Lambda ,r,\varphi (\beta ))\) of \({\mathrm {H}}^{r+1}_-(\beta ,\Lambda )\) by restriction from \({\mathscr {C}}^\Sigma (\Lambda ,r,\varphi (\beta ))\). By the Glauberman correspondence, this restriction is injective and, given \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\varphi (\beta ))\) we call the unique semisimple character in \({\mathscr {C}}^\Sigma (\Lambda ,r,\varphi (\beta ))\) whose restriction is \(\theta _-\) its lift.
1.11. Since, for self-dual semisimple pairs, the transfer maps commute with the action of \(\sigma \), there are natural (bijective) transfer maps between the sets of self-dual semisimple characters defined by a pair of quadruples in \({\mathscr {Q}}_-(k,\beta )\) (see Sect. 9.2). Thus we can follow the methodology of Bushnell and Henniart [8] once more.
A self-dual pss-character, supported on a self-dual semisimple pair \((k,\beta )\), is a function \(\Theta _-\) from \({\mathscr {Q}}_-(k,\beta )\) to the class of all self-dual semisimple characters, such that \(\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {C}}_-(\Lambda ,r,\varphi (\beta ))\), whose values are related by transfer. We call a value of a self-dual pss-character a self-dual realization of the self-dual pss-character. Thus a self-dual pss-character is determined by any one of its self-dual realizations.
A pss-character \(\Theta \) supported on the self-dual semisimple pair \((k,\beta )\) is called \(\sigma \)-invariant if, for any (or equivalently, some) \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_{-}(k,\beta )\) the realization \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) is \(\sigma \)-invariant. By the Glauberman correspondence, a self-dual pss-character \(\Theta _-\) comes uniquely from the restriction of a \(\sigma \)-invariant pss-character \(\Theta \) (see Sect. 9.3 for the precise statement), which we call its lift, and we set \(\deg (\Theta _-)=\deg (\Theta )\).
Let \(\Theta _-\) be a self-dual pss-character supported on the self-dual semisimple pair \((k,\beta )\) and \(\Theta '_-\) be a self-dual pss-character supported on the self-dual semisimple pair \((k',\beta ')\). We say that \(\Theta _-\) and \(\Theta '_-\) are endo-equivalent if
-
(i)
\(k=k'\) and \(\deg (\Theta _-)=\deg (\Theta '_-)\); and
-
(ii)
there exist self-dual realizations on a common \(\varepsilon \)-hermitian \(\mathrm{F}\)-space \((\mathrm{V},h)\) which intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\).
1.12. Let \((k,\beta )\) be a self-dual simple pair, \(\Theta _-\) a self-dual ps-character supported on \((k,\beta )\), and
It follows from [39, Theorem 5.2] that \(\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\) intertwines with \(\Theta _-((\mathrm{V},h),\varphi ',\Lambda ',r')\) in \(\mathrm{G}\) if and only if \(\varphi \) and \(\varphi '\) are conjugate in \(\mathrm{G}\). However, to develop endo-equivalence of self-dual pss-characters—where we may be dealing with embeddings of non-isomorphic fields—we need a more general notion than conjugacy. With this in mind, in Sect. 3 we go back to the start and the theory of \(\varepsilon \)-hermitian spaces and Witt groups.
We introduce an equivalence relation, which we call concordance, on the set of self-dual embeddings of self-dual field extensions into \({\text {End}}_\mathrm{F}(\mathrm{V})\) (where the embedding is self-dual with respect to a hermitian form on \(\mathrm{V}\)), see Definition 3.25; more precisely, this is a relation on pairs \((\beta ,\varphi )\). This relation generalizes conjugacy: if \(\varphi ,\varphi ':\mathrm{F}[\beta ]\hookrightarrow {\text {End}}_\mathrm{F}(\mathrm{V})\) are self-dual embeddings, then \((\beta ,\varphi )\) and \((\beta ,\varphi ')\) are concordant if and only if \(\varphi (\beta )\) and \(\varphi '(\beta )\) are conjugate in \(\mathrm{G}\), see Remark 3.26.
1.13. We carry concordance through the construction of self-dual simple characters, leading to the following result:
Proposition
(Proposition 6.10). Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\varphi (\beta ))\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',r,\varphi '(\beta '))\) be self-dual simple characters, and suppose that the periods of \(\Lambda \) and \(\Lambda '\) as sequences of \({\mathfrak {o}}_\mathrm{F}\)-lattices coincide. Then \(\theta _-\) and \(\theta '_-\) intertwine in \(\mathrm{G}\) if and only if their lifts intertwine in \({{\widetilde{\mathrm{G}}}}\) and the pairs \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are concordant.
In fact, the additional concordance hypothesis is only necessary in the symplectic case when \(\varepsilon =-1\) and \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\); it is implied by the intertwining of the lifts in all other cases.
1.14. In Definition 9.15, we extend our notion of concordance to self-dual embeddings of self-dual \(\mathrm{F}\)-algebras. Let \((k,\beta )\) and \((k,\beta ')\) be self-dual semisimple pairs with indexing sets \(\mathrm{I}\) and \(\mathrm{I}'\) respectively, and \(\mathrm{E}=\mathrm{F}[\beta ]\), \(\mathrm{E}'=\mathrm{F}[\beta ']\). Let \((\mathrm{V},h)\) be an \(\varepsilon \)-hermitian space and \(\varphi :\mathrm{E}\hookrightarrow {\text {End}}_\mathrm{F}(\mathrm{V})\) and \(\varphi ':\mathrm{E}'\hookrightarrow {\text {End}}_\mathrm{F}(\mathrm{V})\) self-dual \(\mathrm{F}\)-algebra embeddings. Suppose we have a bijection \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\). We say that \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are \(\zeta \)-concordant if, for all \(i\in \mathrm{I}_0\), the restrictions of \((\beta ,\varphi )\) and \((\beta ,\varphi ')\) to \(\mathrm{E}_i\) and \(\mathrm{E}'_{\zeta (i)}\) respectively are concordant.
1.15. We can now state our main result on endo-equivalence of self-dual pss-characters:
Theorem
(Theorem 9.16) Let \(\Theta _-\) and \(\Theta '_-\) be self-dual pss-characters supported on \((k,\beta )\) and \((k,\beta ')\), respectively, and \(\Theta \) and \(\Theta '\) their respective lifts. Then, the following assertions are equivalent:
-
(i)
The self-dual pss-characters \(\Theta _-\) and \(\Theta '_-\) are endo-equivalent;
-
(ii)
The lifts \(\Theta \) and \(\Theta '\) are endo-equivalent.
-
(iii)
\(\deg (\Theta _-)=\deg (\Theta '_-)\) and there is a bijection \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) which commutes with \(\sigma \) with the following property: if \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta ')\) are such that \((\varphi ,\beta )\) and \((\varphi ',\beta ')\) are \(\zeta \)-concordant and \({\text {dim}}_\mathrm{F}\mathrm{V}^i={\text {dim}}_\mathrm{F}\mathrm{V}'^{\zeta (i)}\), for \(i\in \mathrm{I}\), then the realizations \(\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\) and \(\Theta '_-((\mathrm{V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\) with matching \(\zeta \).
As a consequence of Theorems 9.9 and 9.16, we obtain that endo-equivalence of self-dual pss-characters is an equivalence relation.
1.16. We turn now to the notion of endo-parameter. We call a semisimple character full if it lies in a set of semisimple characters \({\mathscr {C}}(\Lambda ,0,\beta )\), and we call an endo-class full if it contains a pss-character supported on a semisimple pair \((0,\beta )\). Likewise, we call a self-dual pss-character, endo-class or semisimple character full if the corresponding lift is full. Every smooth representation of \({{\widetilde{\mathrm{G}}}}\) (respectively \(\mathrm{G}^{\mathsf {o}}\)) contains a full (respectively, full self-dual) semisimple character by [16, Propositions 7.5,8.5].
We call full (self-dual) semisimple characters endo-equivalent if they are realizations of endo-equivalent full (self-dual) pss-characters. By [9, Intertwining Theorem], full simple characters of \({{\widetilde{\mathrm{G}}}}\) intertwine if and only if they are endo-equivalent. This not only implies that intertwining of full simple characters is transitive, it also shows that the simple endo-classes of degree dividing \({\text {dim}}_\mathrm{F}(\mathrm{V})\) parametrize the intertwining classes of simple characters of \({{\widetilde{\mathrm{G}}}}\). In the final section we prove a broad generalization of this result to semisimple and self-dual semisimple characters, introducing endo-parameters to parametrize the intertwining classes.
First we recall, in the special case of full characters, the transitivity of intertwining statements obtained from Theorems 9.9 and 9.16:
Proposition
-
(i)
Suppose \(\theta ^{(l)}\in {\mathscr {C}}(\Lambda ^{(l)},0,\beta ^{(l)})\), for \(l=1,2,3\), are semisimple characters such that \(\theta ^{(1)}\) intertwines with \(\theta ^{(2)}\), and \(\theta ^{(2)}\) intertwines with \(\theta ^{(3)}\), and \([\mathrm{F}[\beta ^{(l)}]:\mathrm{F}]\) is independent of l. Then \(\theta ^{(1)}\) and \(\theta ^{(3)}\) intertwine.
-
(ii)
Suppose \(\theta ^{(l)}_-\in {\mathscr {C}}_-(\Lambda ^{(l)},0,\beta ^{(l)})\), for \(l=1,2,3\), are self-dual semisimple characters such that \(\theta ^{(1)}_-\) intertwines with \(\theta ^{(2)}_-\) in \(\mathrm{G}\), and \(\theta ^{(2)}_-\) intertwines with \(\theta ^{(3)}_-\) in \(\mathrm{G}\), and \([\mathrm{F}[\beta ^{(l)}]:\mathrm{F}]\) is independent of l. Then \(\theta ^{(1)}_-\) and \(\theta ^{(3)}_-\) intertwine in \(\mathrm{G}\).
In Corollary 10.3 we prove the analogous transitivity statement for intertwining of self-dual semisimple characters in \(\mathrm{G}^{\mathsf {o}}\) for special orthogonal groups. This transitivity of intertwining reflects the structure in the collection of semisimple characters.
1.17. Let \({\mathscr {E}}\) denote the set of all endo-classes of full ps-characters. An endo-parameter is a function \({{\mathfrak {f}}}\) from the set \({\mathscr {E}}\) to the set \({\mathbb {N}}_0\) of non-negative integers, with finite support. We define the degree of an endo-parameter \({{\mathfrak {f}}}\) by
Our main theorem on endo-parameters for general linear groups is then:
Theorem
(Theorem 12.9). The set of intertwining classes of full semisimple characters for \({{\widetilde{\mathrm{G}}}}={\text {GL}}_\mathrm{F}(\mathrm{V})\) is in canonical bijection with the set of endo-parameters \({{\mathfrak {f}}}\) of degree \({\text {dim}}_\mathrm{F}(\mathrm{V})\).
See the statement of Theorem 12.9 for the description of this map.
1.18. The definition of endo-parameters for classical groups is more intricate. Let \((0,\beta )\) and \((0,\beta ')\) be self-dual simple pairs, and \(\Theta _-\) and \(\Theta '_-\) be self-dual ps-characters supported on \((0,\beta )\) and \((0,\beta ')\) respectively. If \(\Theta _-\) and \(\Theta '_-\) are endo-equivalent then:
-
(i)
the extensions \(\mathrm{F}[\beta ]/\mathrm{F}\) and \(\mathrm{F}[\beta ']/\mathrm{F}\) share many arithmetic invariants—in particular, by Corollary 7.12, the extensions are similar, in the sense of Definition 3.33;
-
(ii)
if \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(0,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_-(0,\beta ')\), then \(\Theta _{-}((\mathrm{V},h),\varphi ,\Lambda ,r)\) and \(\Theta '_{-}((\mathrm{V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\) if and only if \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are concordant, (Proposition 7.10).
Thus, by (ii) to parametrize the \(\mathrm{G}\)-intertwining class of a self-dual simple character we need to take into account the concordance class of the embedding for which it is a realization of a self-dual ps-character and not just the self-dual endo-class of the ps-character. Moreover, by (i) we only need to consider similar extensions.
Our involutions induce an action of \(\Sigma \) on \({\mathscr {E}}\) , see Definition 12.13, and we denote by \({\mathscr {E}}/\Sigma \) the set of orbits. Note that orbits of length one correspond precisely to (the lifts of) endo-classes of self-dual simple ps-characters, but there are also orbits of length two. Using the theory of concordance, we attach to an element of \({\scriptstyle {{\mathcal {O}}}}\in {\mathscr {E}}/\Sigma \) a set \(\mathrm {WT}({\scriptstyle {{\mathcal {O}}}})\) of invariants to carry this concordance information, which we call the set of Witt types for \({\scriptstyle {{\mathcal {O}}}}\). When \({\scriptstyle {{\mathcal {O}}}}\) has cardinality one, so corresponds to the endo-class of a self-dual simple ps-character supported on some \((0,\beta )\) with \(\mathrm{E}=\mathrm{F}[\beta ]\), the set \(\mathrm {WT}({\scriptstyle {{\mathcal {O}}}})\) is in bijection with the Witt group of \(\varepsilon \)-hermitian forms over \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\); on the other hand, when \({\scriptstyle {{\mathcal {O}}}}\) has cardinality two, \(\mathrm {WT}({\scriptstyle {{\mathcal {O}}}})\) is a singleton. A self-dual endo-parameter \({{\mathfrak {f}}}_-\) is then a section of the map
with finite support. Attached to \({{\mathfrak {f}}}_-\), we have its degree \(\deg ({{\mathfrak {f}}}_-)\) and an element \({\text {herm}}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}({{\mathfrak {f}}}_-)\) of the Witt group of \(\varepsilon \)-hermitian forms over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) (see Sect. 12.4).
We denote by \(\mathrm {EP}(h,\mathrm{G})\) the set of self-dual endo-parameters with \({\text {herm}}_{\mathrm{F}/\mathrm{F}_0}({{\mathfrak {f}}}_-)=[h]\) and \(\deg ({{\mathfrak {f}}}_-)={\text {dim}}_\mathrm{F}\mathrm{V}\), and we call it the set of endo-parameters for \((h,\mathrm{G})\). Note that these depend not only on the isomorphism class of \(\mathrm{G}\), but on the isometry class of the hermitian form h too. Our main theorem on endo-parameters for \(\mathrm{G}\) is then:
Theorem
(Theorem 12.29) The set of intertwining classes of full self-dual semisimple characters for \(\mathrm{G}\) is in canonical bijection with the set \(\mathrm {EP}(h,\mathrm{G})\).
See the statement of Theorem 12.29 for the description of this map, which depends on the hermitian form h, not only on its isometry class.
1.19. In the case that \(\mathrm{G}^{\mathsf {o}}\) is a special orthogonal group, the partition of the set of all self-dual semisimple characters for \(\mathrm{G}\) into \(\mathrm{G}^{\mathsf {o}}\)-intertwining classes is in general finer than the partition into \(\mathrm{G}\)-intertwining classes (see Theorem 10.2). It is therefore necessary to augment the set of self-dual endo-parameters of Theorem 12.29: in Sect. 12.5 we define a set \(\mathrm {EP}(h,\mathrm{G}^{\mathsf {o}})\) of endo-parameters for \((h,\mathrm{G}^{\mathsf {o}})\) and prove that it is in canonical bijection with the set of \(\mathrm{G}^{\mathsf {o}}\)-intertwining classes of full self-dual semisimple characters (Corollary 12.34).
1.20. We now conjecture a Galois-theoretic interpretation of endo-parameters via the conjectural local Langlands correspondence. Although our results are for arbitrary classical groups and we expect a similar picture in that situation, we only make a precise conjecture in the case of a quasi-split classical group \(\mathrm{G}\).
Let \(\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}\) denote the Weil group of \(\mathrm{F}_{\mathsf {o}}\) with inertia subgroup \(\mathrm{I}_{\mathrm{F}_{\mathsf {o}}}\). Let \(\mathrm{P}_{\mathrm{F}_{\mathsf {o}}}\) denote the wild inertia subgroup of \(\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}\), that is the pro-p Sylow subgroup of \(\mathrm{I}_{\mathrm{F}_{\mathsf {o}}}\). Let \(\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}'=\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}\times {\text {SL}}_2({\mathbb {C}})\) denote the Weil–Deligne group, and let  the Langlands dual group of \(\mathrm{G}^{\mathsf {o}}\) over the complex numbers. For a group \({\mathrm {H}}\) we write \(\mathrm{Z}({\mathrm {H}})\) for its centre and \(\mathrm{C}_{\mathrm {H}}(\mathrm{X})\) for the centralizer in \({\mathrm {H}}\) of a subgroup \(\mathrm{X}\) of \({\mathrm {H}}\).
the Langlands dual group of \(\mathrm{G}^{\mathsf {o}}\) over the complex numbers. For a group \({\mathrm {H}}\) we write \(\mathrm{Z}({\mathrm {H}})\) for its centre and \(\mathrm{C}_{\mathrm {H}}(\mathrm{X})\) for the centralizer in \({\mathrm {H}}\) of a subgroup \(\mathrm{X}\) of \({\mathrm {H}}\).
Let \(({\varrho },\chi _{{\varrho }})\) be an (extended) Langlands parameter for \(\mathrm{G}^{\mathsf {o}}\). As these appear in various guises in the literature, we recall one formulation:
-
(i)
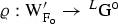 is a continuous homomorphism such that
is a continuous homomorphism such that -
(a)
\({\varrho }(\mathrm{I}_{\mathrm{F}_{\mathsf {o}}})\) is finite, \({\varrho }\) is Frobenius-semisimple, and \({\varrho }:{{\text {SL}}_2({\mathbb {C}})}\rightarrow \widehat{\mathrm{G}^{\mathsf {o}}}\) is algebraic,
-
(b)
the composition
 is the identity;
is the identity;
-
(a)
-
(ii)
\(\chi _{{\varrho }}\) is an irreducible complex representation of the group
$$\begin{aligned} {{\mathcal {S}}_{{\varrho }}:= \mathrm{C}_{\widehat{\mathrm{G}^{\mathsf {o}}}}({\varrho }(\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}'))/\mathrm{C}_{\widehat{\mathrm{G}^{\mathsf {o}}}}({\varrho }(\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}'))^\circ \mathrm{Z}(\widehat{\mathrm{G}^{\mathsf {o}}})^{\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}}.} \end{aligned}$$
We write \(\mathrm {Lang}(\mathrm{G}^{\mathsf {o}})\) for the set of equivalence classes of (extended) Langlands parameters for \(\mathrm{G}^{\mathsf {o}}\) under \(\widehat{\mathrm{G}^{\mathsf {o}}}\)-conjugacy.
The local Langlands correspondence for \(\mathrm{G}^{\mathsf {o}}\) predicts a natural bijection (dependent on fixing a non-degenerate character of the unipotent radical of a Borel subgroup of \(\mathrm{G}^{\mathsf {o}}\))
where \({\text {Irr}}(\mathrm{G}^{\mathsf {o}})\) denotes the set of isomorphism classes of irreducible smooth representations of \(\mathrm{G}^{\mathsf {o}}\) on complex vector spaces. When \(\mathrm{F}_{\mathsf {o}}\) has characteristic zero, \(\mathrm {LL}\) is known for tempered representations of split classical groups [2] and quasi-split unitary groups [30]. There is also work in progress in a generalization to inner forms of unitary groups [25]. When \(\mathrm{F}_{\mathsf {o}}\) has positive characteristic, Arthur’s results for split classical groups have been extended in some characteristics [21].
1.21. Let \({\rho }\) be a wild inertial parameter for \(\mathrm{G}^{\mathsf {o}}\), that is a homomorphism  which extends to a Langlands parameter
which extends to a Langlands parameter  . Set
. Set

As in [18], we notice that  which implies that
which implies that

as the centre of \(\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}\) is trivial and \({\varrho }({\text {SL}}_2({\mathbb {C}}))\subseteq \mathrm{C}_{\widehat{\mathrm{G}^{\mathsf {o}}}}({\rho })\). We set

By (1.1), we thus have a map from representations of \({\mathcal {S}}_{{\varrho }}\) to representations of \({\mathcal {S}}_{\rho }\) by considering a representation of \({\mathcal {S}}_{{\varrho }}\) as a representation of \(\mathrm{C}_{\widehat{\mathrm{G}^{\mathsf {o}}}}({\varrho }(\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}'))\) (trivial on \(\mathrm{C}_{\widehat{\mathrm{G}^{\mathsf {o}}}}({\varrho }(\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}'))^\circ \mathrm{Z}(\widehat{\mathrm{G}^{\mathsf {o}}})^{\mathrm{W}_{\mathrm{F}_{\mathsf {o}}}}\)) and restricting to  .
.
An extended wild inertial parameter for \(\mathrm{G}^{\mathsf {o}}\) is a pair \(({\rho },\chi _{{\rho }})\) such that  is a homomorphism and \(\chi _{{\rho }}\) is a representation of \({\mathcal {S}}_{\rho }\) such that there is an extended Langlands parameter \(({\varrho },\chi _{{\varrho }})\) with
is a homomorphism and \(\chi _{{\rho }}\) is a representation of \({\mathcal {S}}_{\rho }\) such that there is an extended Langlands parameter \(({\varrho },\chi _{{\varrho }})\) with  . We write \(\mathrm {Wild}(\mathrm{G}^{\mathsf {o}})\) for the set of equivalence classes of extended wild inertial parameters for \(\mathrm{G}^{\mathsf {o}}\) under \(\widehat{\mathrm{G}^{\mathsf {o}}}\)-conjugacy. Thus we have a well-defined restriction map \({\text {Res}}:\mathrm {Lang}(\mathrm{G}^{\mathsf {o}})\rightarrow \mathrm {Wild}(\mathrm{G}^{\mathsf {o}})\) given by
. We write \(\mathrm {Wild}(\mathrm{G}^{\mathsf {o}})\) for the set of equivalence classes of extended wild inertial parameters for \(\mathrm{G}^{\mathsf {o}}\) under \(\widehat{\mathrm{G}^{\mathsf {o}}}\)-conjugacy. Thus we have a well-defined restriction map \({\text {Res}}:\mathrm {Lang}(\mathrm{G}^{\mathsf {o}})\rightarrow \mathrm {Wild}(\mathrm{G}^{\mathsf {o}})\) given by  .
.
Let \(\mathrm {EP}(h,\mathrm{G}^{\mathsf {o}})\) denote the set of self-dual endo-parameters for \(\mathrm{G}^{\mathsf {o}}\subseteq \mathrm{U}(\mathrm{V},h)\). We have a map \(\vartheta :{\text {Irr}}(\mathrm{G}^{\mathsf {o}})\rightarrow \mathrm {EP}(h,\mathrm{G}^{\mathsf {o}})\) which takes \(\pi \in {\text {Irr}}(\mathrm{G}^{\mathsf {o}})\) to the self-dual endo-parameter attached to the intertwining class of any full self-dual semisimple character contained in \(\pi \), we note that this map depends on the hermitian form h.
Conjecture
(Wild local Langlands) There is a unique bijection
compatible with the local Langlands correspondence; that is, the following diagram commutes

In the special case of cuspidal representations of symplectic groups, and assuming \(\mathrm {LL}\), work of the third author with Blondel and Henniart [4, Theorem 7.6] (together with Theorem 12.29 to define the map \(\vartheta \) as above) shows that if we further project from the set of endo-parameters for \(\mathrm{G}^{\mathsf {o}}\) by forgetting their Witt type data and further project from \(\mathrm {Wild}(\mathrm{G}^{\mathsf {o}})\) to the set of (non-extended) wild parameters for \(\mathrm{G}^{\mathsf {o}}\), then we get a bijection for which the resulting diagram commutes.
1.22. In an orthogonal direction to Bushnell and Kutzko’s generalization [12] of Howe’s construction of cuspidal representations of p-adic general linear groups in the tame case [24], Yu constructed cuspidal representations of a broad class of p-adic connected reductive groups \({\mathrm {H}}\) defined over \(\mathrm{F}_{\mathsf {o}}\) [45], a construction which Fintzen recently proved exhausts all cuspidal representations whenever the residual characteristic of \(\mathrm{F}_{\mathsf {o}}\) does not divide the order of the Weyl group of \({\mathrm {H}}\) [20]. Hakim and Murnaghan [22] considered the flexibility in the data defining Yu’s cuspidal representations and developed a refactorization procedure to classify isomorphism classes of Yu’s cuspidal representations by equivalence classes of these data. It would be interesting to develop notions of pss-characters, endo-equivalence, and endo-parameters in this setting of more general groups \({\mathrm {H}}\).
2 Notation
Let \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) be an extension of locally compact nonarchimedean local fields of odd residual characteristic p, of degree at most two, and denote by \(x\mapsto {\overline{x}}\) the generator of \({\text {Gal}}(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\). For \(\mathrm{E}/\mathrm{F}_{\mathsf {o}}\) any finite extension, we use the usual notation: \({\mathfrak {o}}_\mathrm{E}\) its ring of integers, \({\mathfrak {p}}_E\) its maximal ideal, \(\mathrm {k}_\mathrm{E}\) its residue field, \({\text {val}}_\mathrm{E}\) the additive valuation on \(\mathrm{E}\) with image \({\mathbb {Z}}\). We also set \(\mathrm{U}^n_\mathrm{E}=1+{\mathfrak {p}}_\mathrm{E}^n\), for \(n\geqslant 1\). If \(\mathrm{E}/\mathrm{L}\) is any finite extension of fields, we usually write \(\mathrm{N}_{\mathrm{E}/\mathrm{L}}\) for the norm map and \(\mathrm{T}_{\mathrm{E}/\mathrm{L}}\) for the trace map; if the fields are nonarchimedean local then we write \(e(\mathrm{E}/\mathrm{L})\) for the ramification index and \(f(\mathrm{E}/\mathrm{L})\) for the residue degree.
Let \({\mathbf {C}}\) be an algebraically closed field of characteristic \(\ell \ne p\). Throughout, we consider smooth representations of locally compact topological groups on vector spaces over \({\mathbf {C}}\).
Let \(\mathrm{G}\) be a locally compact topological group, and let \({\mathrm {H}}\) and \({\mathrm {H}}'\) be compact open subgroups of \(\mathrm{G}\). Let \(\rho \) and \(\rho '\) be representations of \({\mathrm {H}}\) and \({\mathrm {H}}'\) respectively. For \(g\in \mathrm{G}\), we define \(\mathrm{I}_g(\rho ,\rho ')\) to be the \({\mathbf {C}}\)-vector space

where  and
and  is the representation of
is the representation of  defined by
defined by  for all
for all  . Moreover, we set
. Moreover, we set
We say that g intertwines \(\rho \) with \(\rho '\) if \(\mathrm {I}_g(\rho ,\rho ')\ne 0\), and that \(\rho \) intertwines with \(\rho '\) in \(\mathrm{G}\) if \(\mathrm{I}_\mathrm{G}(\rho ,\rho ')\ne \emptyset \). If \({\mathbf {C}}={\mathbb {C}}\) or \(\rho \) and \(\rho '\) are characters, then the definition is symmetric, because then the map \(g\mapsto g^{-1}\) restricts to a bijection from \(\mathrm{I}_\mathrm{G}(\rho ,\rho ')\) to \(\mathrm{I}_\mathrm{G}(\rho ',\rho )\). In this case, we just say that \(\rho \) and \(\rho '\) intertwine in \(\mathrm{G}\). When \(\rho '=\rho \) we abbreviate \(\mathrm{I}_\mathrm{G}(\rho )=\mathrm{I}_\mathrm{G}(\rho ,\rho )\).
Finally, we denote by \(\Sigma =\{1,\sigma \}\) an abstract group of order two, which will act on various objects.
3 Witt groups and transfer
In this section we cover the necessary background for our results from the theory of signed hermitian spaces and introduce a new notion: concordance of self-dual embeddings of field extensions.
3.1 Self-dual extensions
We begin with some basic results on quadratic extensions. For \(\mathrm{E}\) a finite extension of \(\mathrm{F}_{\mathsf {o}}\), we write
Lemma 3.1
Suppose \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic. Then,
In particular:
-
(i)
\(-1\in (\mathrm{F}^\times )^2\) if and only if \(-1\in \mathrm{N}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}(\mathrm{F}^\times )\);
-
(ii)
if \(-1\in (\mathrm{F}^\times )^2\) then \(\mathrm{N}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}(\mathrm{F}^\times )=(\mathrm{F}^\times )^2\cap \mathrm{F}_{\mathsf {o}}^\times \);
-
(iii)
if \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is unramified then \(\mathrm{N}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}(\mathrm{F}^\times )=\mathrm{F}_{\mathsf {o}}^{\mathsf {even}}\).
Proof
The assertions (i)–(iii) are immediate consequences of (3.2). We first prove
Since \(1+{\mathfrak {p}}_{\mathrm{F}_{\mathsf {o}}}\) is a subset of \(({\mathfrak {o}}_{\mathrm{F}_{\mathsf {o}}}^\times )^2\), by Hensel’s lemma, it suffices to show
Writing also \(\mathrm{N}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}\) for the map on the residue field \(\mathrm {k}_\mathrm{F}\) induced by the norm, this is equivalent to
If \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is unramified then both sides are equal to \(\mathrm {k}_{\mathrm{F}_{\mathsf {o}}}^\times \), while if \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is ramified, then both sides are \((\mathrm {k}_{\mathrm{F}_{\mathsf {o}}}^\times )^2\). Thus we have proved (3.3).
Now both sides of (3.2) are subgroups of \(\mathrm{F}_{\mathsf {o}}^\times \), containing the subgroup in (3.3). If \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is unramified then \((-(\mathrm{F}^\times )^2)\cap \mathrm{F}_{\mathsf {o}}^{\mathsf {odd}}\) is empty and both sides of (3.2) are generated by the square of a uniformizer of \(\mathrm{F}_{\mathsf {o}}\) and (3.3), If \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is ramified then, if \(\varpi _\mathrm{F}\) is a uniformizer of \(\mathrm{F}\) satisfying \({\overline{\varpi _\mathrm{F}}}=-\varpi _\mathrm{F}\), then both sides of (3.2) are generated by \(-\varpi _\mathrm{F}^2\) and (3.3). This completes the proof. \(\square \)
Let \(\mathrm{E}=\mathrm{F}[\beta ]\) be a field extension of \(\mathrm{F}\) with a distinguished generator \(\beta \). If the generator for \({\text {Gal}}(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) extends to an involution on \(\mathrm{E}\) which maps \(\beta \) to \(-\beta \) then we say the pair \((\mathrm{E},\beta )\) is a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\). We again denote by \(x\mapsto {\overline{x}}\) this involution on \(\mathrm{E}\), and by \(\mathrm{E}_{\mathsf {o}}\) the subfield of fixed points. Note that, provided \(\beta \ne 0\), the extension \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\) is always quadratic, since \(\beta \not \in \mathrm{E}_{\mathsf {o}}\).
Corollary 3.4
If \((\mathrm{E},\beta )\) is a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) with \(\beta \ne 0\), then \(-1\in (\mathrm{E}^\times )^2\) if and only if \(\beta ^2\in \mathrm{N}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}(\mathrm{E}^\times )\).
Proof
By Lemma 3.1(ii), if \(-1\in (\mathrm{E}^\times )^2\) then \(\beta ^2\in \mathrm{N}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}(\mathrm{E}^\times )\). Conversely, if \(-1\not \in (\mathrm{E}^\times )^2\) then \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\) is ramified and \({\text {val}}_\mathrm{E}(\beta )\) is odd since \({\overline{\beta }}=-\beta \). Hence \({\text {val}}_{\mathrm{E}_{\mathsf {o}}}(\beta ^2)\) is odd, and it follows from (3.2) that \(\beta ^2\not \in \mathrm{N}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}(\mathrm{E}^\times )\). \(\square \)
We will also need the following lemma on norms through self-dual extensions.
Lemma 3.5
Suppose \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic. Let \(\mathrm{E}_{\mathsf {o}}/\mathrm{F}_{\mathsf {o}}\) be a finite extension in an algebraic closure of \(\mathrm{F}\) which does not contain \(\mathrm{F}\) and set \(\mathrm{E}=\mathrm{F}\mathrm{E}_{\mathsf {o}}\). Then
We note also that, in the situation of the lemma, for \(\alpha \in \mathrm{E}_{\mathsf {o}}\), we have \(\mathrm{N}_{\mathrm{E}_{\mathsf {o}}/\mathrm{F}_{\mathsf {o}}}(\alpha )=\mathrm{N}_{\mathrm{E}/\mathrm{F}}(\alpha )\), since any \(\mathrm{F}_{\mathsf {o}}\)-basis for \(\mathrm{E}_{\mathsf {o}}\) is also an \(\mathrm{F}\)-basis for \(\mathrm{E}=\mathrm{F}\mathrm{E}_{\mathsf {o}}\).
Proof
We denote the right hand side of the asserted equation by \(\mathrm{R}_{\mathrm{E}/\mathrm{F}}\). If \(\mathrm{L}/\mathrm{F}\) is a subextension of \(\mathrm{E}\) and \(\mathrm{L}_{\mathsf {o}}=\mathrm{L}\cap \mathrm{E}_{\mathsf {o}}\) then we have
so the lemma follows from the special cases where \(\mathrm{E}/\mathrm{F}\) is separable or purely inseparable.
Suppose first that \(\mathrm{E}/\mathrm{F}\) is purely inseparable, so has odd degree. Then any element of \(\mathrm{F}^\times _{\mathsf {o}}\) which is not in the image of \(\mathrm{N}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}\) lies in \(\mathrm{E}_{\mathsf {o}}\) but not in \(\mathrm{R}_{\mathrm{E}/\mathrm{F}}\); in particular \(\mathrm{R}_{\mathrm{E}/\mathrm{F}}\ne \mathrm{E}^\times _{\mathsf {o}}\). Since certainly \(\mathrm{N}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}(\mathrm{E}^\times )\subseteq \mathrm{R}_{\mathrm{E}/\mathrm{F}}\subseteq \mathrm{E}^\times _{\mathsf {o}}\), while \(\mathrm{N}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}(\mathrm{E}^\times )\) has index two in \(\mathrm{E}^\times _{\mathsf {o}}\), it follows that \(\mathrm{E}^\times _{\mathsf {o}}\ne \mathrm{R}_{\mathrm{E}/\mathrm{F}}=\mathrm{N}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}(\mathrm{E}^\times )\).
Now suppose \(\mathrm{E}/\mathrm{F}\) is separable, so the same is true of \(\mathrm{E}_{\mathsf {o}}/\mathrm{F}_{\mathsf {o}}\). By local class field theory, for any finite abelian extension of local fields \(\mathrm{L}/\mathrm{K}\) (contained in a given separable closure) we have the Artin reciprocity isomorphism
Applying this to the extensions \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\) and \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), the base change property of class field theory implies that on \(\mathrm{E}_{\mathsf {o}}^\times /\mathrm{N}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}(\mathrm{E}^\times )\) we have
The restriction map induces an isomorphism \({\text {Gal}}(\mathrm{E}/\mathrm{E}_{\mathsf {o}})\rightarrow {\text {Gal}}(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) and the Artin reciprocity maps are isomorphisms so we see that \({\text {Art}}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}\) is trivial on the class of \(\alpha \in \mathrm{E}_{\mathsf {o}}^\times \) if and only if \({\text {Art}}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}\) is trivial on the class of \(\mathrm{N}_{\mathrm{E}_{\mathsf {o}}/\mathrm{F}_{\mathsf {o}}}(\alpha )\), and the claim follows. \(\square \)
Finally, we have the following result on ramification indices.
Lemma 3.6
Suppose \((\mathrm{E},\beta )\) is a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) with \(\beta \ne 0\) and ramification index \(e(\mathrm{E}/\mathrm{E}_{\mathsf {o}})=2\). Then \({\text {val}}_\mathrm{E}(\beta )\) is odd and either
-
(i)
\(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\); or
-
(ii)
\(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic ramified and the ramification index \(e(\mathrm{E}/\mathrm{F})\) is odd.
Proof
Since \(\beta =-{\overline{\beta }}\) and \(e(\mathrm{E}/\mathrm{E}_{\mathsf {o}})=2\), the first assertion is clear. If \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic unramified then there is a unit \(\zeta \in {\mathfrak {o}}_\mathrm{F}^\times \) such that \({\overline{\zeta }}=-\zeta \); since \(\zeta \in {\mathfrak {o}}_\mathrm{E}^\times \), this contradicts the assumption that \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\) is ramified. For the final assertion, suppose \(e(\mathrm{E}/\mathrm{F})=e(\mathrm{E}_{\mathsf {o}}/\mathrm{F}_{\mathsf {o}})=2r\) is even, let \(\varpi _{\mathsf {o}}\) be a uniformizer of \(\mathrm{E}_{\mathsf {o}}\) and let \(\varpi _\mathrm{F}\) be a uniformizer of \(\mathrm{F}\) such that \({\overline{\varpi _\mathrm{F}}}=-\varpi _\mathrm{F}\); then \(\zeta =\varpi _\mathrm{F}\varpi _{\mathsf {o}}^{-r}\) is a unit of \(\mathrm{E}^\times \) satisfying \({\overline{\zeta }}=-\zeta \), again contradicting the assumption that \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\) is ramified. \(\square \)
3.2 Hermitian spaces
Let \(\varepsilon =\pm 1\). By an \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), we mean a finite-dimensional \(\mathrm{F}\)-vector space \(\mathrm{V}\) equipped with a non-degenerate \(\varepsilon \)-hermitian form \(h:\mathrm{V}\times \mathrm{V}\rightarrow \mathrm{F}\), that is, a non-degenerate sesquilinear form (linear in the second variable) such that
Given two such spaces \((\mathrm{V}_i,h_i)\), for \(i=1,2\), for the same \(\varepsilon \), we can form their orthogonal direct sum, which is the space \(\mathrm{V}=\mathrm{V}_1\oplus \mathrm{V}_2\) equipped with the form \(h=h_1\oplus h_2\) defined by
If \((\mathrm{V},h)\) and \((\mathrm{V}',h')\) are \(\varepsilon \)-hermitian spaces over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), then an isometry from \((\mathrm{V},h)\) to \((\mathrm{V}',h')\) is an \(\mathrm{F}\)-linear isomorphism \(f:\mathrm{V}\rightarrow \mathrm{V}'\) such that
When there is such an isometry, we say that \((\mathrm{V},h)\) and \((\mathrm{V}',h')\) are isometric, and write \((\mathrm{V},h)\cong (\mathrm{V}',h')\), or just \(h\cong h'\) for short. Note that orthogonal direct sums behave well with respect to isometry: that is, if \(h_1\cong h'_1\) and \(h_2\cong h'_2\) then \(h_1\oplus h'_1\cong h_2\oplus h'_2\).
We write \({\mathcal {H}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) for the set of isometry classes of \(\varepsilon \)-hermitian spaces over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\). It is a monoid with the operation induced by the orthogonal direct sum and identity element the (class of the) zero space.
The Gram matrix of an \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) with respect to a basis \({\mathrm v}_1,\ldots ,{\mathrm v}_n\) is the \(n\times n\) matrix J whose (i, j)-entry is \(h({\mathrm v}_i,{\mathrm v}_j)\). This is an \(\varepsilon \)-hermitian matrix: that is \(J^T=\varepsilon {\overline{J}}\), where \(J^T\) denotes the transpose of J and \({\overline{J}}\) denotes the matrix obtained by applying the Galois involution \(x\mapsto {\overline{x}}\) to each entry. The Gram matrix of \((\mathrm{V},h)\) with respect to any other basis takes the form \({\overline{B}}^TJB\), where B is the change of basis matrix to \({\mathrm v}_1,\ldots ,{\mathrm v}_n\). The determinant \(\det (J)\) of the Gram matrix satisfies \({\overline{\det (J)}}=\varepsilon ^{{\text {dim}}_\mathrm{F}V}\det (J)\).
The determinant \(\det (\mathrm{V})\) (or \(\det (h)\)) of an \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) is defined to be the class in \(\mathrm{F}^\times /\mathrm{N}_\mathrm{F}\) of the determinant of any Gram matrix for \((\mathrm{V},h)\), where
This is well-defined and moreover depends only on the isometry class of \((\mathrm{V},h)\). Thus we get a morphism of monoids
An \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) is called isotropic if there is a non-zero \({\mathrm v}\in \mathrm{V}\) such that \(h({\mathrm v},{\mathrm v})=0\), and anisotropic otherwise. (Note that the zero space is anisotropic.) In particular, we have the smallest isotropic \(\varepsilon \)-hermitian space, the hyperbolic plane \(({\mathrm {H}},h_{\mathrm {H}})\): it is two-dimensional with basis \({\mathrm e}_{-1},{\mathrm e}_1\) such that
Thus the Gram matrix of \({\mathrm {H}}\) with respect to the basis \({\mathrm e}_{-1},{\mathrm e}_1\) is
so that \(\det ({\mathrm {H}})=(-\varepsilon )\mathrm{N}_\mathrm{F}\). Up to isometry, \({\mathrm {H}}\) is the unique two-dimensional isotropic \(\varepsilon \)-hermitian space. For \(n\geqslant 0\) an integer, we write \(n({\mathrm {H}},h_{\mathrm {H}})\) for the orthogonal sum of n copies of \(({\mathrm {H}},h_{\mathrm {H}})\). An \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) isometric to \(n({\mathrm {H}},h_{\mathrm {H}})\) for some n is called a hyperbolic space; these spaces possess a complete polarization, i.e. a direct sum decomposition
with totally isotropic spaces \(\mathrm{V}^{1}\) and \(\mathrm{V}^{-1}\).
Remark 3.7
The notation \(({\mathrm {H}},h_{\mathrm {H}})\) for hyperbolic plane does not specify either the extension \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) or \(\varepsilon \), which will be left implicit. We trust this will cause no confusion, even where it is used for different fields.
At the opposite extreme, we have the smallest non-trivial anisotropic spaces, which are one-dimensional when they exist. (There are no non-trivial anisotropic spaces when \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) and \(\varepsilon =-1\), the symplectic case.) They are given by a single element \(\alpha \in \mathrm{F}^\times \) such that \({\overline{\alpha }}=\varepsilon \alpha \), and we denote the corresponding space (or its isometry class) by \(\langle \alpha \rangle \): it has a basis with Gram matrix \((\alpha )\).
Remark 3.8
Again, the notation \(\langle \alpha \rangle \), while standard, does not specify \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), and for example we consider \(\langle 1\rangle \) as a \((+1)\)-hermitian space over different fields.
The isometry class of \(\langle \alpha \rangle \) is determined precisely by the coset of \(\alpha \) in \(\mathrm{F}^\times /\mathrm{N}_\mathrm{F}\). Thus we have the following isometry classes of one-dimensional spaces in \({\mathcal {H}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\):
-
if \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic, \(\beta \in \mathrm{F}^\times \) satisfies \({\overline{\beta }}=-\beta \) and \(\alpha \in \mathrm{F}_{\mathsf {o}}^\times \setminus \mathrm{N}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}(\mathrm{F}^\times )\), then
$$\begin{aligned}&\langle 1\rangle \text { and }\langle \alpha \rangle ,\,\qquad \text {if }\varepsilon =1, \\&\langle \beta \rangle \text { and }\langle \beta \alpha \rangle ,\quad \ \text {if }\varepsilon =-1; \end{aligned}$$ -
if \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) has uniformizer \(\varpi \), and \(\alpha \) is a non-square unit of \(\mathrm{F}^\times \), then
$$\begin{aligned} \langle 1\rangle ,\ \langle \alpha \rangle ,\ \langle \varpi \rangle ,\text { and }\langle \varpi \alpha \rangle . \end{aligned}$$
Any anisotropic space is an orthogonal direct sum of one-dimensional anisotropic subspaces so, with respect to a suitable basis, has a diagonal Gram matrix.
Remark 3.9
Up to isomorphism, there is a unique maximal anisotropic \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\). More precisely, and with the notation above, it is
By Witt’s Theorem, for any \(\varepsilon \)-hermitian space \((\mathrm{V},h)\), we have an isometry
with \((\mathrm{V}_{\mathsf {an}},h_{\mathsf {an}})\) an anisotropic space; moreover, the Witt index n and the isometry class of \((\mathrm{V}_{\mathsf {an}},h_{\mathsf {an}})\) are uniquely determined by \((\mathrm{V},h)\). We write [h] for the isometry class of \((\mathrm{V}_{\mathsf {an}},h_{\mathsf {an}})\) and call it the anisotropic class of \((\mathrm{V},h)\). We also write \({\mathrm {dim}}_{\mathrm {an}}(\mathrm{V})={\text {dim}}_{\mathrm{F}}(\mathrm{V}_{\mathsf {an}})\) and call it the anisotropic dimension of \((\mathrm{V},h)\).
Remark 3.10
If \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic, the isometry class of an \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) is uniquely determined by the pair \(({\text {dim}}(\mathrm{V}),\det (\mathrm{V}))\). If \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) and \(\varepsilon =-1\) (the symplectic case) then the isometry class of an \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) is uniquely determined by \({\text {dim}}(\mathrm{V})\), which is necessarily even.
3.3 Unitary groups
Let \((\mathrm{V},h)\) be an \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\). The ring \({\text {End}}_\mathrm{F}(\mathrm{V})\) is equipped with the adjoint anti-involution \(a\mapsto {\overline{a}}\) induced by h, defined by
We set
which is the group of all isometries from \(\mathrm{V}\) to itself. This is the group of \(\mathrm{F}_{\mathsf {o}}\)-points of a reductive group defined over \(\mathrm{F}_{\mathsf {o}}\): more precisely, it is a unitary group if \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic, a symplectic group if \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) and \(\varepsilon =-1\), and a full orthogonal group if \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) and \(\varepsilon =1\).
Remark 3.11
If \((\mathrm{V},h)\) and \((\mathrm{V}',h')\) are isometric \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) then the isometry induces an isomorphism \(\mathrm{U}(\mathrm{V},h)\simeq \mathrm{U}(\mathrm{V}',h')\). The converse, however, is false: for example, if \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\) and n is odd then there are two isometry classes of n-dimensional hermitian spaces over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) but their isometry groups are isomorphic.
We introduce the following useful technique which will sometimes allow us to reduce to cases which are easier to treat (in particular, the non-symplectic case). Given an element \(a\in {\text {End}}_\mathrm{F}(\mathrm{V}) \) such that \({\overline{a}}=\eta a\), with \(\eta =\pm \), we define the twisted form \(a^*(h)\) on \(\mathrm{V}\) by
If a is invertible then \((\mathrm{V},a^*(h))\) is an \(\eta \varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\). Moreover, the adjoint anti-involution on \({\text {End}}_\mathrm{F}(\mathrm{V})\) induced by the form \(a^*(h)\) is given by \(b\mapsto a^{-1}{\overline{b}}a\), for \(b\in {\text {End}}_\mathrm{F}(\mathrm{V})\).
A particular case of this twisting occurs when \(a=\gamma \in \mathrm{F}^\times \) satisfies \({\overline{\gamma }}=\eta \gamma \). Given such a \(\gamma \), the twisted form \(\gamma ^*(h)\) makes sense for any \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\).
3.4 Witt groups
The Witt group \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) is defined to be the set of isometry classes of anisotropic \(\varepsilon \)-hermitian spaces over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), equipped with the operation induced by taking the orthogonal sum, that is, the unique (well-defined) operation such that the following commutes:

where the map \({\mathcal {H}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\rightarrow {\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) sends the isometry class of \((\mathrm{V},h)\) to its anisotropic class [h]. We will sometimes refer to elements of the Witt group as Witt towers: that is, we will identify an element of \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) with its fibre under the map \({\mathcal {H}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\rightarrow {\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\). Note that \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) is an abelian group, and the inverse of the isometry class of an anisotropic space \((\mathrm{V},h)\) is given by the class of \((\mathrm{V},-h)\). We write \(\varvec{0}\) for the identity in \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\), which is the Witt tower of sums of hyperbolic planes \(n{\mathrm {H}}\).
The structure of the Witt group is given by the following proposition, where \(\mathrm{C}_n\) denotes the cyclic group of order n.
Proposition 3.12
-
(i)
Unitary case: if \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic then \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) is of order 4 and
$$\begin{aligned} {\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}}) \simeq {\left\{ \begin{array}{ll} \mathrm{C}_2\times \mathrm{C}_2 \quad &{}\text { if }-1\in \mathrm{N}_\mathrm{F},\\ \mathrm{C}_4 &{}\text { otherwise.} \end{array}\right. } \end{aligned}$$ -
(ii)
Symplectic case: if \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) and \(\varepsilon =-1\) then \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) is trivial.
-
(iii)
Orthogonal case: if \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) and \(\varepsilon =1\) then \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) is of order 16 and
$$\begin{aligned} {\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}}) \simeq {\left\{ \begin{array}{ll} \mathrm{C}_2\times \mathrm{C}_2\times \mathrm{C}_2\times \mathrm{C}_2 \quad &{}\text { if }-1\in \mathrm{N}_\mathrm{F},\\ \mathrm{C}_4\times \mathrm{C}_4 &{}\text { otherwise.} \end{array}\right. } \end{aligned}$$
The Witt group is generated by (the classes of) one-dimensional anisotropic spaces \(\langle \alpha \rangle \) and we use the same notation to represent the class in \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\). For example, we see that \(\langle 1\rangle \oplus \langle 1\rangle =\varvec{0}\) in \({\mathcal {W}}_1(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) if and only if \(-1\in \mathrm{N}_\mathrm{F}\). We also call the (class of) the unique maximal anisotropic \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) the maximal element of \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\), or the Witt tower of maximal anisotropic dimension. (See Remark 3.9 above for an explicit description of this maximal element.)
If \(\gamma \in \mathrm{F}^\times \) satisfies \({\overline{\gamma }}=\eta \gamma \), with \(\eta =\pm \), and \((\mathrm{V},h)\) is an \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), then we defined the twisted form \(\gamma ^*(h)\) on \(\mathrm{V}\) in the previous subsection so that \((\mathrm{V},\gamma ^*(h))\) is an \(\eta \varepsilon \)-hermitian space. Twisting by \(\gamma \) preserves orthogonal direct sums, isometries and hyperbolic spaces and thus induces a homomorphism
which is an isomorphism since it has inverse \((\gamma ^{-1})^*\).
3.5 Transfer
Let \((\mathrm{E},\beta )\) be a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) and set \(n=[\mathrm{E}:\mathrm{F}]\). Let \(\lambda :\mathrm{E}\rightarrow \mathrm{F}\) be any non-zero \(\mathrm{F}\)-linear form on \(\mathrm{E}\) which is Galois-equivariant, that is
Such forms always exist and we have the particular \(\mathrm{F}\)-linear form \(\lambda _\beta \) given by setting
Moreover, every such form can be written uniquely as \(\lambda (x)=\lambda _\beta (\gamma x)\), for some \(\gamma \in \mathrm{E}_{\mathsf {o}}^\times \): indeed, every non-trivial \(\mathrm{F}\)-linear form can be written in this way for some \(\gamma \in \mathrm{E}^\times \), and the Galois-equivariance implies that \(\gamma \in \mathrm{E}_{\mathsf {o}}\).
Now suppose \(\mathrm{E}/\mathrm{F}\) is any finite extension of degree n to which the Galois involution on \(\mathrm{F}\) extends, with fixed field \(\mathrm{E}_{\mathsf {o}}\). Let \((\mathrm{V},h)\) be an \(\varepsilon \)-hermitian space over \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\) and let \(\lambda :\mathrm{E}\rightarrow \mathrm{F}\) be a non-zero Galois-equivariant \(\mathrm{F}\)-linear form on \(\mathrm{E}\). Then it is easy to check that \((\mathrm{V},\lambda \circ h)\) is an \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), called the transfer \((\mathrm{V},\lambda ^* h)\) of \((\mathrm{V},h)\). Transfer preserves orthogonal direct sums and isometries, so induces a morphism of monoids
Moreover, we have \(\lambda ^*({\mathrm {H}})=n{\mathrm {H}}\), so it also induces a group homomorphism of Witt groups
This map depends on the choice of \(\lambda \) but nonetheless all these maps share some properties.
Proposition 3.13
-
(i)
The image \(\lambda ^*({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}}))\) is independent of the choice of \(\lambda \).
-
(ii)
The map \(\lambda ^*\) sends the maximal element of \({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) to the maximal element of \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\).
Proof
For arbitrary choices \(\lambda \) and \(\lambda '\), we know that \(\lambda (x)=\lambda '(\gamma x)\), for some \(\gamma \in \mathrm{E}_{\mathsf {o}}^\times \), so that \(\lambda ^*=\lambda '^*\circ \gamma ^*\). Now (i) follows since \(\gamma ^*\) is an isomorphism. On the other hand, (ii) is given by [39, Theorem 4.4] for a particular linear form, and follows in general by the proof of (i) since \(\gamma ^*\) maps the maximal element to itself. \(\square \)
The transfer map \(\lambda ^*\) is in general neither injective nor surjective, as can be seen by taking \(\mathrm{E}/\mathrm{F}\) of even degree. However, we have the following rather surprising result. We write \({\mathcal {W}}^\mathsf {even}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) for the subgroup of \({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) consisting of Witt towers of even anisotropic dimension; if \({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) is non-trivial then it is a subgroup of index two, and we write \({\mathcal {W}}^\mathsf {odd}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) for its non-identity coset, consisting of Witt towers of odd anisotropic dimension.
Proposition 3.14
Let \((\mathrm{E},\beta )\) be a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) and suppose we are not in the symplectic case: \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic or \(\varepsilon =1\). Then the restrictions of \(\lambda ^*\) to \({\mathcal {W}}^\mathsf {even}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) and to \({\mathcal {W}}^\mathsf {odd}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) are both injective.
Proof
Note that by the choice of \(\mathrm{E}\) we have \(\beta =0\) or \(\mathrm{E}\ne \mathrm{E}_{\mathsf {o}}\). The proof of Proposition 3.13 also shows that \(\lambda ^*({\mathcal {W}}^\mathsf {even}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}}))\) and \(\lambda ^*({\mathcal {W}}^\mathsf {odd}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}}))\) do not depend on the choice of \(\lambda \) so it is sufficient to prove the result for a single choice of \(\lambda \).
If \(\beta =0\) then \(\lambda _\beta ^*\) is the identity, and the result is immediate. If \(\mathrm{E}\ne \mathrm{E}_{\mathsf {o}}\) then \({\mathcal {W}}^\mathsf {even}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) and \({\mathcal {W}}^\mathsf {odd}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) each contain two elements, whose difference is always the maximal element of \({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\); injectivity follows, since the image of this maximal element is non-zero, by Proposition 3.13(ii). \(\square \)
We will also need more precise information on the transfer map in particular instances.
Proposition 3.15
Let \((\mathrm{E},\beta )\) be a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) and set \(n=[\mathrm{E}:\mathrm{F}]\).
-
(i)
For \((\mathrm{V},h)\) an \(\varepsilon \)-hermitian space over \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\), we have
$$\begin{aligned} \det (\lambda ^*(\mathrm{V}))=\det (\lambda ^*\langle 1\rangle )^{{\text {dim}}_\mathrm{E}(\mathrm{V})} \mathrm{N}_{\mathrm{E}/\mathrm{F}}(\det (\mathrm{V})). \end{aligned}$$ -
(ii)
In \({\mathcal {W}}_1(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\), we have:
$$\begin{aligned} \lambda _\beta ^*(\langle 1\rangle ) = {\left\{ \begin{array}{ll} \langle 1\rangle &{}\text { if} ~n \, \text {is odd,} \\ \langle 1\rangle \oplus \langle (-1)^{\frac{n}{2}+1}\mathrm{N}_{\mathrm{E}/\mathrm{F}}(\beta )\rangle \quad &{}\text { otherwise,} \end{array}\right. } \end{aligned}$$and, if \(\beta \) is non-zero, in \({\mathcal {W}}_{-1}(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\):
$$\begin{aligned} \lambda _\beta ^*(\langle \beta \rangle ) = {\left\{ \begin{array}{ll} \langle (-1)^{\frac{n-1}{2}}\mathrm{N}_{\mathrm{E}/\mathrm{F}}(\beta )\rangle &{}\text { if}~ n \, \text {is odd,} \\ \varvec{0} \quad &{}\text { otherwise.} \end{array}\right. } \end{aligned}$$
Proof
The analogue of these statements for the transfer of quadratic forms are proved by Scharlau in [31, Lemma 5.8, Theorem 5.12]. The hermitian case follows mutatis mutandis, taking care of the extra signs which appear; for this reason, we sketch the proof of (ii). Suppose \(\beta \) has minimal polynomial \(X^n+b_{n-1}X^{n-1}+\cdots +b_1X+b_0\). Then we can easily calculate the Gram matrix of the \(\varepsilon \)-hermitian space \(\lambda _\beta ^*(\langle 1\rangle )\) with respect to the basis \(1,\beta ,\ldots ,\beta ^{n-1}\), which looks like

If \(n=[\mathrm{E}:\mathrm{F}]\) is odd then the space \(\lambda _\beta ^*(\langle 1\rangle )\) is the orthogonal direct sum of the subspace \(\langle 1\rangle \) spanned by 1 and the subspace X spanned by \(\beta ,\beta ^2,\ldots ,\beta ^{n-1}\); but X has a totally isotropic subspace of half its dimension, generated by \(\beta ,\beta ^2,\ldots ,\beta ^{\frac{n-1}{2}}\), hence is hyperbolic. Thus \(\lambda _\beta ^*(\langle 1\rangle )\cong \frac{n-1}{2}{\mathrm {H}}\oplus \langle 1\rangle \).
Similarly, if \(n=[\mathrm{E}:\mathrm{F}]\) is even then we find that \(\lambda _\beta ^*(\langle 1\rangle )\cong \frac{n-2}{2}{\mathrm {H}}\oplus \langle 1\rangle \oplus \langle \gamma \rangle \), where \(\gamma =(-1)^{\frac{n}{2}+1}\mathrm{N}_{\mathrm{E}/\mathrm{F}}(\beta )\). The proof of the second assertion in (ii) is similar. \(\square \)
Remark 3.16
In the case that \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) is quadratic, since the isometry class of an \(\varepsilon \)-hermitian space is determined by its dimension and its determinant modulo the norm group \(\mathrm{N}_\mathrm{F}\), Proposition 3.15 completely characterizes the standard transfer map \(\lambda _\beta ^*\), for \((\mathrm{E},\beta )\) a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\).
3.6 Embeddings
Eventually, we will need to make comparisons of Witt towers for different self-dual extensions. In a first instance, we begin by considering the case of the same extension but embedded in different ways. Thus let \((\mathrm{E},\beta )\) be a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), and fix a non-zero Galois-equivariant \(\mathrm{F}\)-linear form \(\lambda \) as in the previous subsection.
Let \((\mathrm{V},h)\) be an \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) and let \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\). We say that an embedding \(\varphi :\mathrm{E}\hookrightarrow \mathrm{A}\) is self-dual if
where we recall that \(x\mapsto {\overline{x}}\) denotes the Galois involution on \(\mathrm{E}\), while, on the right hand side, \(a\mapsto {\overline{a}}\) is the adjoint anti-involution on \(\mathrm{A}\). Such an embedding gives \(\mathrm{V}\) the structure of an \(\mathrm{E}\)-vector space, and we write \(\mathrm{V}_\varphi \) when we want to emphasize that we are considering \(\mathrm{V}\) as an \(\mathrm{E}\)-vector space via \(\varphi \) in this way. The \(\mathrm{F}\)-linear map
is an isomorphism of \(\mathrm{F}\)-vector spaces. For each \({\mathrm v}\in \mathrm{V}\), there is a unique \(\mathrm{E}\)-linear map \(\psi _{{\mathrm v}}\in {\text {Hom}}_\mathrm{E}(\mathrm{V}_\varphi ,\mathrm{E})\) such that \(h({\mathrm v},-)=\lambda \circ \psi _{{\mathrm v}}\) and we define \(h_\varphi :\mathrm{V}_\varphi \times \mathrm{V}_\varphi \rightarrow \mathrm{E}\) by
Lemma 3.17
[6, Lemma 5.3] The map \(h_\varphi :\mathrm{V}_\varphi \times \mathrm{V}_\varphi \rightarrow \mathrm{E}\) is a nondegenerate \(\varepsilon \)-hermitian form. Moreover, it is the unique \(\varepsilon \)-hermitian form on \(\mathrm{V}_\varphi \) such that \(h({\mathrm v},{\mathrm w})=\lambda (h_\varphi ({\mathrm v},{\mathrm w}))\), for all \({\mathrm v},{\mathrm w}\in \mathrm{V}\).
Suppose now that we have a second self-dual embedding \(\varphi ':\mathrm{E}\hookrightarrow \mathrm{A}\) and let \((\mathrm{V}_{\varphi '},h_{\varphi '})\) be the corresponding \(\varepsilon \)-hermitian space over \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\). We have the following useful corollary of Lemma 3.17.
Corollary 3.18
[38, Proposition 1.3] The \(\varepsilon \)-hermitian spaces \((\mathrm{V}_{\varphi },h_{\varphi })\) and \((\mathrm{V}_{\varphi '},h_{\varphi '})\) over \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\) are isometric if and only if the embeddings \(\varphi ,\varphi '\) are conjugate in \(\mathrm{U}(\mathrm{V},h)\).
Proof
Any isometry from \((\mathrm{V}_{\varphi },h_{\varphi })\) to \((\mathrm{V}_{\varphi '},h_{\varphi '})\) is an element of \(\mathrm{U}(\mathrm{V},h)\) which conjugates \(\varphi \) to \(\varphi '\). Conversely, an element g of \(\mathrm{U}(\mathrm{V},h)\) conjugating \(\varphi \) to \(\varphi '\) is an isometry from \((\mathrm{V}_{\varphi },h_{\varphi })\) to \((\mathrm{V}_{\varphi '},h_{\varphi '})\), because \(h_{\varphi '}\circ (g\times g)\) and \(h_{\varphi }\) coincide by the uniqueness part of Lemma 3.17. \(\square \)
Remark 3.19
Suppose we have a self-dual embedding \(\varphi \) of \(\mathrm{E}\) into \(\mathrm{A}\). Since \({\text {dim}}_\mathrm{E}\mathrm{V}_\varphi \) is independent of the embedding, Corollary 3.18 implies that the \(\mathrm{U}(\mathrm{V},h)\)-orbits of self-dual embeddings of \(\mathrm{E}\) are in bijection with the set of classes in the fibre of the transfer map \(\lambda ^*\) above [h] which have dimension of the same parity as \({\text {dim}}_\mathrm{E}\mathrm{V}_\varphi \). In particular, Proposition 3.14 then implies the following:
-
(i)
Provided we are not in the symplectic case, there is a unique \(\mathrm{U}(\mathrm{V},h)\)-orbit of self-dual embeddings of \(\mathrm{E}\);
-
(ii)
In the symplectic case there are precisely two orbits of embeddings if \(\beta \ne 0\).
It will be useful also to observe the relationship between this lifting process of forms and the twisting of forms introduced previously. The following lemma comes immediately from the definitions and the uniqueness in Lemma 3.17.
Lemma 3.20
Let \((\mathrm{V},h)\) be an \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), let \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\) and let \(\varphi :\mathrm{E}\hookrightarrow \mathrm{A}\) be a self-dual embedding. Then
Note that this asserts the equality of two \((-\varepsilon )\)-hermitian \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\)-forms on the space \(V_\varphi \).
3.7 Comparison
We suppose now that we are given two self-dual extensions \((\mathrm{E},\beta )\) and \((\mathrm{E}',\beta ')\) of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), so that we have Witt groups \({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) and \({\mathcal {W}}_\varepsilon (\mathrm{E}'/\mathrm{E}'_{\mathsf {o}})\). We assume moreover that \(\beta ,\beta '\) are both non-zero, so that these Witt groups are both of order four. There are then unique bijections
which preserve anisotropic dimension and such that
We will use these maps \({\mathsf {w}}_{\varepsilon ,\beta ',\beta }\) to compare self-dual embeddings of \(\mathrm{E}\) and of \(\mathrm{E}'\) in \(\varepsilon \)-hermitian \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\)-spaces. It is useful to notice that the maps are related via twisting:
We will sometimes skip the subscripts \(\beta ,\beta '\) and just write \({\mathsf {w}}_\varepsilon \) if \(\beta ,\beta '\) are fixed.
Remark 3.22
Since there are two bijections \({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}}) \rightarrow {\mathcal {W}}_\varepsilon (\mathrm{E}'/\mathrm{E}'_{\mathsf {o}})\) which preserve anisotropic dimension, the choice for \({\mathsf {w}}_{\varepsilon ,\beta ',\beta }\) made above may seem arbitrary—for example, in the case \(\varepsilon =1\) one could instead have chosen the bijection sending \(\langle 1\rangle \) to \(\langle 1\rangle \). However, we will see that this choice is better suited to compatibility with the distinguished transfer maps \(\lambda _\beta ^*\) and \(\lambda _{\beta '}^*\).
The relationship between \({\mathsf {w}}_{\varepsilon ,\beta ',\beta }\) and the bijection sending \(\langle 1\rangle \) to \(\langle 1\rangle \) will prove to be an important consideration. As an immediate consequence of Corollary 3.4, we have:
Lemma 3.23
In the situation above, the following are equivalent:
-
(i)
\({\mathsf {w}}_{1,\beta ',\beta }(\langle 1\rangle )=\langle 1\rangle \);
-
(ii)
either \(-1\) belongs to both \((\mathrm{E}^\times )^2\) and \((\mathrm{E}'^\times )^2\) or it belongs to neither of them;
-
(iii)
\(-1\in (\mathrm{F}^\times )^2\) or the residue class degrees \(f(\mathrm{E}/\mathrm{F}),f(\mathrm{E}'/\mathrm{F})\) have the same parity.
In the case \(\beta =\beta '=0\) which we have so far excluded, we define \({\mathsf {w}}_{\varepsilon ,0,0}\) to be the identity on \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\). In both cases, we now have the following maps of Witt groups:

Remark 3.24
Suppose \(f:\mathrm{E}'\rightarrow \mathrm{E}\) is an \(\mathrm{F}\)-linear isomorphism of fields such that \(f(\beta ')=\beta \). From the definitions, we see that \(\lambda _{\beta '}=\lambda _\beta \circ f\) and that the map \({\mathsf {w}}_{\varepsilon ,\beta ',\beta }\) is likewise induced by composition with f: that is, it is induced by the map
Moreover, if \((\mathrm{V},h)\) is an \(\varepsilon \)-hermitian \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\)-space and \(\varphi :\mathrm{E}\hookrightarrow {\text {End}}_\mathrm{F}(\mathrm{V})\) is a self-dual embedding, then checking the definitions from the previous subsection shows that
so that \({\mathsf {w}}_{\varepsilon ,\beta ',\beta }([h_\varphi ])=[h_{\varphi \circ f}]\).
Suppose now we are given \(\varepsilon \)-hermitian \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\)-spaces \((\mathrm{V},h)\) and \((\mathrm{V}',h')\) which are isometric. Set \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\) and \(\mathrm{A}'={\text {End}}_\mathrm{F}(\mathrm{V}')\), suppose we have self-dual embeddings \(\varphi :\mathrm{E}\hookrightarrow \mathrm{A}\) and \(\varphi ':\mathrm{E}'\hookrightarrow \mathrm{A}'\). Then we get elements \([h_\varphi ]\) and \([h_{\varphi '}]\) of the respective Witt groups such that \(\lambda _\beta ^*([h_\varphi ])=[h]=[h']=\lambda _{\beta '}^*([h'_{\varphi '}])\), as in the previous subsection.
Definition 3.25
The pairs \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are \((h,h')\)-concordant (or just concordant if \(h=h'\) and the form is clear from context), if \(\beta \) and \(\beta '\) are either both zero or both non-zero, and \({\mathsf {w}}_{\varepsilon ,\beta ',\beta }([h_\varphi ])=[h'_{\varphi '}]\).
Remarks 3.26
-
(i)
It is immediate from the definition that concordance is an equivalence relation.
-
(ii)
In the special case that \(\beta =\beta '\), so that \({\mathsf {w}}_{\varepsilon ,\beta ,\beta }\) is the identity map, and \(h=h'\), it follows from Corollary 3.18 that \((\beta ,\varphi )\) and \((\beta ,\varphi ')\) are concordant if and only if \(\varphi (\beta )\) and \(\varphi '(\beta )\) are conjugate by an element of \(\mathrm{U}(\mathrm{V},h)\).
-
(iii)
If we have an isomorphism \(f:\mathrm{E}'\rightarrow \mathrm{E}\) such that \(f(\beta ')=\beta \), Remark 3.24 shows that \((\beta ,\varphi )\) and \((\beta ',\varphi \circ f)\) are concordant. Putting this together with (ii), we see that the pairs \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are \((h,h')\)-concordant if and only if there is an isometry from \((\mathrm{V},h)\) to \((\mathrm{V}',h')\) which conjugates \(\varphi (\beta )\) to \(\varphi '(\beta ')\).
Using the previous remarks, together with Lemma 3.20, we can use twisting to relate concordance in a symplectic space to concordance in orthogonal spaces obtained by twisting.
Lemma 3.27
Suppose that \((\mathrm{V},h)\) is a skew-hermitian \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\)-space, that \(\beta \) and \(\beta '\) are both non-zero, and that the spaces \((\mathrm{V},\beta ^*h)\) and \((\mathrm{V},\beta '^*h)\) are isometric. Then the following are equivalent:
-
(i)
\((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are concordant.
-
(ii)
\((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are \((\beta ^*h,\beta '^*h)\)-concordant.
We will be able to use this whenever we have additional information on \(\beta ,\beta '\) which enables us to see that the spaces \((\mathrm{V},\beta ^*h)\) and \((\mathrm{V},\beta '^*h)\) are isometric.
Proof
If \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are concordant then, from Lemma 3.20 and (3.21) we get
Thus \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are \((\beta ^*h,\beta '^*h)\)-concordant. Since the map \(\beta '^*\) is injective, the converse follows immediately. \(\square \)
3.8 Concordance in the non-symplectic case
We now look more closely at the non-symplectic case: indeed, Lemma 3.27 allows us to relate the skew-hermitian case to the hermitian case. Suppose we are given \(\varepsilon \)-hermitian \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\)-spaces \((\mathrm{V},h)\) and \((\mathrm{V}',h')\) which are isometric, and set \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\) and \(\mathrm{A}'={\text {End}}_\mathrm{F}(\mathrm{V}')\). Let \((\mathrm{E},\beta )\), \((\mathrm{E}',\beta ')\) be self-dual extensions with \(\beta ,\beta '\) non-zero, and suppose we have self-dual embeddings \(\varphi :\mathrm{E}\hookrightarrow \mathrm{A}\) and \(\varphi ':\mathrm{E}'\hookrightarrow \mathrm{A}'\). We prove the following first result on concordance in the case \(\varepsilon =1\).
Proposition 3.28
In the situation above, with \(\varepsilon =1\), suppose that \({\text {dim}}_\mathrm{E}\mathrm{V}_\varphi \) and \({\text {dim}}_{\mathrm{E}'}\mathrm{V}'_{\varphi '}\) have the same parity and moreover that either
-
(i)
this common parity is even; or
-
(ii)
this common parity is odd, \({\mathsf {w}}_1(\langle 1\rangle )=\langle 1\rangle \) and one of the following conditions is satisfied:
-
(a)
\({\text {dim}}_\mathrm{F}\mathrm{V}\) is odd;
-
(b)
\(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) and there exist an extension \(\mathrm{K}/\mathrm{F}\) contained in \(\varphi (\mathrm{E})\) which is invariant under the adjoint anti-involution on \(\mathrm{A}\) but not fixed pointwise, and an isometry \(g:\mathrm{V}\rightarrow \mathrm{V}'\) such that \(g\mathrm{K}g^{-1}\subseteq \varphi '(\mathrm{E}')\).
-
(a)
Then the pairs \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are \((h,h')\)-concordant.
In order to prove this we notice that, whenever we are in the non-symplectic case, concordance is related to the diagrams

and

If \({\text {dim}}_\mathrm{E}\mathrm{V}_\varphi \) and \({\text {dim}}_{\mathrm{E}'}\mathrm{V}'_{\varphi '}\) have the same parity then \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are concordant if and only if the diagram of the corresponding parity commutes: this follows because, in both diagrams, the maps \(\lambda _\beta ^*\) and \(\lambda _{\beta '}^*\) are injective by Proposition 3.14. Therefore we analyze cases when these diagrams are commutative.
Lemma 3.31
Suppose that \(\varepsilon =1\) and that \(\beta \) and \(\beta '\) are non-zero.
-
(i)
The diagram (3.30) is always commutative.
-
(ii)
Suppose that \({\mathsf {w}}_1(\langle 1\rangle )=\langle 1\rangle \) , that \([\mathrm{E}:\mathrm{F}]\) and \([\mathrm{E}':\mathrm{F}]\) have the same parity, and that one of the following conditions is satisfied:
-
(a)
\(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\) and \([\mathrm{E}:\mathrm{F}]\) is odd.
-
(b)
\(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) and there exist extensions \(\mathrm{K}/\mathrm{F}\) and \(\mathrm{K}'/\mathrm{F}\) contained in \(\mathrm{E}\) and \(\mathrm{E}'\) respectively, which are invariant under the Galois involution but not fixed pointwise, such that \([\mathrm{E}:\mathrm{K}]\) and \([\mathrm{E}':\mathrm{K}']\) have the same parity and there is a Galois-equivariant \(\mathrm{F}\)-linear field isomorphism from \(\mathrm{K}\) to \(\mathrm{K}'\).
Then the diagram (3.29) is commutative.
-
(a)
Proof
Diagram (3.30) is commutative because the maximal anisotropic class is mapped to the maximal anisotropic class, by Proposition 3.13(ii).
We now suppose that \({\mathsf {w}}_1(\langle 1\rangle )=\langle 1\rangle \) and that \([\mathrm{E}:\mathrm{F}]\) and \([\mathrm{E}':\mathrm{F}]\) have the same parity, and consider diagram (3.29), recalling that all maps in it are injective. Write
Then, since \(\langle a\rangle - \langle 1\rangle \) is the maximal element of \({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\), it follows from Proposition 3.13(ii) that \(\lambda _\beta ^*(\langle a\rangle ) - \lambda _\beta ^*(\langle 1\rangle )\) is the maximal element of \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\). The same applies to \(\lambda _{\beta '}^*(\langle a'\rangle ) - \lambda _{\beta '}^*(\langle 1\rangle )\) so that
Thus it is enough to check that \(\lambda _\beta ^*(\langle 1\rangle )=\lambda _{\beta '}^*(\langle 1\rangle )\) to prove commutativity of (3.29).
In the situation of (a), we have \(\lambda _\beta ^*(\langle 1\rangle )=\langle 1\rangle =\lambda _{\beta '}^*(\langle 1\rangle )\), by Proposition 3.15(ii). In case (b), again by Proposition 3.15(ii), we have
for some integers \(m,m'\) whose values are not needed for the proof. In particular, these both have anisotropic dimension at most two so cannot be the Witt tower of maximal anisotropic dimension.
If \([\mathrm{E}:\mathrm{K}]\) and \([\mathrm{E}':\mathrm{K}']\) are even, then the images of \(\lambda _\beta ^*\) and \(\lambda _{\beta '}^*\) consist of \(\varvec{0}\) and the maximal element. Since (3.32) shows that neither is maximal, we have \(\lambda _\beta ^*(\langle 1\rangle )=\varvec{0}=\lambda _{\beta '}^*(\langle 1\rangle )\).
Suppose now \([\mathrm{E}:\mathrm{K}]\) and \([\mathrm{E}':\mathrm{K}']\) are odd and denote by \(\mathrm{K}_{\mathsf {o}}\) the fixed field of \(\mathrm{K}\) under the Galois involution on \(\mathrm{E}\), so that \(\mathrm{K}/\mathrm{K}_{\mathsf {o}}\) is quadratic. Given \(\lambda :\mathrm{E}\rightarrow \mathrm{K}\) a non-zero Galois-equivariant \(\mathrm{K}\)-linear form, the induced transfer map \(\lambda ^*:{\mathcal {W}}_1(\mathrm{E}/\mathrm{E}_{\mathsf {o}})\rightarrow {\mathcal {W}}_1(\mathrm{K}/\mathrm{K}_{\mathsf {o}})\) is then bijective. It follows from Proposition 3.13(i) that the image of \(\lambda _\beta ^*\) coincides with that of \(\lambda _\mathrm{K}^*\), for any non-zero Galois-equivariant \(\mathrm{F}\)-linear form \(\lambda _\mathrm{K}:\mathrm{K}\rightarrow \mathrm{F}\). Since there is a Galois-equivariant \(\mathrm{F}\)-linear field isomorphism from \(\mathrm{K}\) to \(\mathrm{K}'\), this also coincides with the image of \(\lambda _{\mathrm{K}'}^*\), for any non-zero Galois-equivariant \(\mathrm{F}\)-linear form \(\lambda _{\mathrm{K}'}:\mathrm{K}'\rightarrow \mathrm{F}\). In particular, the images of \(\lambda _\beta ^*\) and \(\lambda _{\beta '}^*\) in \({\mathcal {W}}_1(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\) coincide.
If this image has order two then it consists of \(\varvec{0}\) and the maximal element, and we again have \(\lambda _\beta ^*(\langle 1\rangle )=\varvec{0}=\lambda _{\beta '}^*(\langle 1\rangle )\). Otherwise, it has order 4 and, since \({\mathcal {W}}_1(\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) and \({\mathcal {W}}_1(\mathrm{E}'/\mathrm{E}'_{\mathsf {o}})\) also have order 4, the transfer maps \(\lambda _\beta ^*\) and \(\lambda _{\beta '}^*\) are injective. We set \(\varvec{a}=\lambda _\beta ^*(\langle 1\rangle )\) and \(\varvec{b}=\lambda _{\beta '}^*(\langle 1\rangle )\), which are neither \(\varvec{0}\) nor the maximal element, by injectivity. Assume for contradiction that \(\varvec{a} \ne \varvec{b}\) so that (3.32) implies that \(\varvec{a}-\varvec{b}\) is also neither \(\varvec{0}\) nor maximal. Thus \(\varvec{a} -\varvec{b}\) is either \(\varvec{a}\) or \(\varvec{b}\), therefore \(\varvec{a}=2\varvec{b}\), as \(\varvec{b}\) is non-zero. By symmetry, we also have \(\varvec{b}=2\varvec{a}\) and it follows that \(\varvec{a}=\varvec{b}=\varvec{0}\), which is absurd. \(\square \)
Proof of Proposition 3.28
The three parts follow immediately from the corresponding parts of Lemma 3.31, once we notice, in (b), that \([\mathrm{E}:\mathrm{K}]\) and \([\mathrm{E}':\mathrm{K}']\) have the same parity as \({\text {dim}}_\mathrm{K}\mathrm{V}={\text {dim}}_{\mathrm{K}'}\mathrm{V}'\). \(\square \)
In order to go further than this, we need to add some conditions on \(\beta ,\beta '\); in particular, we will require them to be related in some way.
3.9 Similar extensions
We now introduce a notion of similarity on self-dual extensions. We fix a uniformizer \(\varpi _\mathrm{F}\) of \(\mathrm{F}\); if \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\) then we assume further that \({\overline{\varpi _\mathrm{F}}}=-\varpi _\mathrm{F}\). For \((\mathrm{E},\beta )\) a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) with \(\beta \ne 0\), we write \(y_\beta \) for the image of \(\varpi _\mathrm{F}^{n/g}\beta ^{e/g}\) in the residue field \(\mathrm {k}_\mathrm{E}\), where \(e=e(\mathrm{E}/\mathrm{F})\) is the ramification index, \(n=-{\text {val}}_\mathrm{E}(\beta )\), and \(g={\text {gcd}}(n,e)\). We also set \(y_0=0\) in \(k_\mathrm{F}\).
Definition 3.33
We say that self-dual extensions \((\mathrm{E},\beta )\) and \((\mathrm{E}',\beta ')\) of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) are similar if:
-
(i)
\(f(\mathrm{E}/\mathrm{F})=f(\mathrm{E}'/\mathrm{F})\), \(e(\mathrm{E}/\mathrm{F})=e(\mathrm{E}'/\mathrm{F})\) and \(e(\mathrm{E}/\mathrm{E}_{\mathsf {o}})=e(\mathrm{E}'/\mathrm{E}'_{\mathsf {o}})\);
-
(ii)
\({\text {val}}_\mathrm{E}(\beta )={\text {val}}_{\mathrm{E}'}(\beta ')\); and
-
(iii)
there is a \(\mathrm {k}_\mathrm{F}\)-linear field isomorphism from \(\mathrm {k}_\mathrm{E}\) to \(\mathrm {k}_{\mathrm{E}'}\) which sends \(y_\beta \) to \(y_{\beta '}\).
Note that the notion of similarity is independent of the choice of uniformizer \(\varpi _\mathrm{F}\). In the end we will mostly be concerned about concordance in cases where we already know that the extensions are similar.
Suppose, as before, we are given hermitian \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\)-spaces \((\mathrm{V},h)\) and \((\mathrm{V}',h')\) which are isometric, and set \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\) and \(\mathrm{A}'={\text {End}}_\mathrm{F}(\mathrm{V}')\). We also have \((\mathrm{E},\beta )\) and \((\mathrm{E}',\beta ')\), self-dual extensions with \(\beta ,\beta '\) non-zero, and we suppose we have self-dual embeddings \(\varphi :\mathrm{E}\hookrightarrow \mathrm{A}\) and \(\varphi ':\mathrm{E}'\hookrightarrow \mathrm{A}'\). We have the following result.
Lemma 3.34
Suppose that \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\) and that the self-dual extensions \((\mathrm{E},\beta )\) and \((\mathrm{E}',\beta ')\) are similar.
-
(i)
\(\varpi _\mathrm{F}^{-1}\beta \in \mathrm{N}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}(\mathrm{E}^\times )\) if and only \(\varpi _\mathrm{F}^{-1}\beta '\in \mathrm{N}_{\mathrm{E}'/\mathrm{E}'_{\mathsf {o}}}(\mathrm{E}'^\times )\).
- (ii)
-
(iii)
The pairs \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are \((h,h')\)-concordant.
We will see later (see Corollary 5.20) that (ii) is in fact also true without the hypothesis \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\).
Proof
We set \(e=e(\mathrm{E}/\mathrm{F})=e(\mathrm{E}'/\mathrm{F})\), \(e_{\mathsf {o}}=e(\mathrm{E}/\mathrm{E}_{\mathsf {o}})=e(\mathrm{E}'/\mathrm{E}'_{\mathsf {o}})\) and \(d=[\mathrm{E}:\mathrm{F}]=[\mathrm{E}':\mathrm{F}]\). We also set \(n=-{\text {val}}_\mathrm{E}(\beta )=-{\text {val}}_{\mathrm{E}'}{(\beta ')}\) and observe that \(\varpi _\mathrm{F}^{-1}\beta \) is fixed by the involution.
(i) If \(e_{\mathsf {o}}=2\) then both e and n are odd, by Lemma 3.6. Hence Hensel’s Lemma implies that \(\varpi _\mathrm{F}^{-1}\beta \) is a square in \(\mathrm{E}\) if and only if \(y_\beta \) is a square in \(\mathrm {k}_\mathrm{E}\), and similarly for \(\varpi _\mathrm{F}^{-1}\beta '\). On the other hand \(y_\beta \) is a square in \(\mathrm {k}_\mathrm{E}\) if and only if \(y_{\beta '}\) is a square in \(\mathrm {k}_{\mathrm{E}'}\), because we have a \(\mathrm {k}_\mathrm{F}\)-linear field isomorphism from \(\mathrm {k}_\mathrm{E}\) to \(\mathrm {k}_{\mathrm{E}'}\) which sends \(y_\beta \) to \(y_{\beta '}\). The result now follows from the description of norms in Lemma 3.1.
If \(e_{\mathsf {o}}=1\) then \(\varpi _\mathrm{F}^{-1}\beta \in \mathrm{N}_{\mathrm{E}/\mathrm{E}_{\mathsf {o}}}(\mathrm{E}^\times )\) if and only if \(\varpi _\mathrm{F}^{-1}\beta \) has even valuation, by Lemma 3.1. Since it has the same valuation as \(\varpi _\mathrm{F}^{-1}\beta '\), the result follows.
(iii) follows immediately from (ii), while the commutativity of (3.30) is immediate since the maximal element is mapped to the maximal element. To complete the proof of (ii), we need to prove that the diagram (3.29) is commutative. Since \(f(\mathrm{E}/\mathrm{F})=f(\mathrm{E}'/\mathrm{F})\), Lemma 3.23 implies that \({\mathsf {w}}_{1}(\langle 1\rangle )=\langle 1\rangle \) so that we only need to prove that \(\lambda _\beta ^*(\langle 1\rangle )=\lambda _{\beta '}^*(\langle 1\rangle )\) (for the case \(\varepsilon =1\)) and \(\lambda _\beta ^*(\langle \beta \rangle )=\lambda _{\beta '}^*(\langle \beta '\rangle )\) (for the case \(\varepsilon =-1\)). Now Lemma 3.5 and (i) imply that \(\mathrm{N}_{\mathrm{E}/\mathrm{F}}(\varpi _\mathrm{F}^{-1}\beta )=\varpi _\mathrm{F}^{-d}\mathrm{N}_{\mathrm{E}/\mathrm{F}}(\beta )\) lies in \(\mathrm{N}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}(\mathrm{F}^\times )\) if and only if \(\varpi _\mathrm{F}^{-d}\mathrm{N}_{\mathrm{E}'/\mathrm{F}}(\beta ')\) does also. The result now follows by applying Proposition 3.15(ii). \(\square \)
4 Classical groups
Let \((\mathrm{V},h)\) be an \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), and put \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\) and \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_\mathrm{F}(\mathrm{V})\). The ring \(\mathrm{A}\) is equipped with the adjoint anti-involution \(a\mapsto {\overline{a}}\) induced by h. We let our abstract group \(\Sigma =\{1,\sigma \}\) act both on \({{\widetilde{\mathrm{G}}}}\), with \(\sigma (g)=({\overline{g}})^{-1}\) for \(g\in {{\widetilde{\mathrm{G}}}}\), and on \(\mathrm{A}\), with \(\sigma (a)=-{\overline{a}}\) for \(a\in \mathrm{A}\).
We set \(\mathrm{G}:={{\widetilde{\mathrm{G}}}}^\Sigma =\mathrm{U}(\mathrm{V},h)\). We write \(\mathrm{G}^{\mathsf {o}}\) for the group of \(\mathrm{F}_{\mathsf {o}}\)-points of the connected component of the underlying reductive group, so that \(\mathrm{G}^{\mathsf {o}}=\mathrm{G}\) except in the orthogonal case when it is the special orthogonal group. We call the group \(\mathrm{G}^{\mathsf {o}}\) a classical group.
For \(\mathrm{J}\) a \(\sigma \)-stable subgroup of \({{\widetilde{\mathrm{G}}}}\), we will write \(\mathrm{J}_-=\mathrm{J}^\Sigma =\mathrm{J}\cap \mathrm{G}\). Similarly, if \(\mathrm{X}\) is any \(\sigma \)-stable \({\mathfrak {o}}_\mathrm{F}\)-submodule of \(\mathrm{A}\) then we write
for the set of skew-symmetric (respectively, symmetric) elements of \(\mathrm{X}\). Note that \(\mathrm{A}_-\) is the Lie algebra of \(\mathrm{G}\) (and \(\mathrm{G}^{\mathsf {o}}\)).
5 Simple strata and concordance
In this section, we investigate intertwining of self-dual pure strata and introduce concordance of self-dual pure strata (Definition 5.7). The main result is Proposition 5.19.
5.1 Lattice sequences and parahoric subgroups
We recall that an \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence in \(\mathrm{V}\) is a map \(\Lambda \) from \({\mathbb {Z}}\) to the set of \({\mathfrak {o}}_\mathrm{F}\)-lattices in \(\mathrm{V}\) which is decreasing and periodic; that is,
-
(i)
\(\Lambda (k+1)\subseteq \Lambda (k)\), for all \(k\in {\mathbb {Z}}\);
-
(ii)
there is a positive integer \(e=e(\Lambda )=e(\Lambda |{\mathfrak {o}}_\mathrm{F})\) such that \({\mathfrak {p}}_\mathrm{F}\Lambda (k)=\Lambda (k+e)\), for all \(k\in {\mathbb {Z}}\).
The integer e is called the \({\mathfrak {o}}_\mathrm{F}\)-period of \(\Lambda \). If \({\text {dim}}_{\mathrm {k}_\mathrm{F}}(\Lambda (k)/\Lambda (k+1))\) is independent of \(k\in {\mathbb {Z}}\) we say that \(\Lambda \) is regular. We call \(\Lambda \) strict if \(\Lambda (k+1)\subsetneq \Lambda (k)\), for all \(k\in {\mathbb {Z}}\). For \(a,b\in {\mathbb {Z}}\), \(a>0\), we let \(a\Lambda +b\) denote the \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence in \(\mathrm{V}\) defined by
We call \(a\Lambda +b\) an affine translation of \(\Lambda \) and say that lattice sequences \(\Lambda ,\Lambda '\) are in the same affine class if they have a common affine translation.
The direct sum of \({\mathfrak {o}}_\mathrm{F}\)-lattice sequences \(\Lambda \) and \(\Lambda '\) of the same \({\mathfrak {o}}_\mathrm{F}\)-period is defined by
An \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence \(\Lambda \) in \(\mathrm{V}\) defines an \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence in \(\mathrm{A}\), by setting
for \(n\in {\mathbb {Z}}\). The \({\mathfrak {o}}_\mathrm{F}\)-lattice \({\mathfrak {a}}_0(\Lambda )\) is a hereditary \({\mathfrak {o}}_\mathrm{F}\)-order in \(\mathrm{A}\) with Jacobson radical \({\mathfrak {a}}_1(\Lambda )\). Note that a strict \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence \(\Lambda \) is regular if and only if \({\mathfrak {a}}_0(\Lambda )\) is a principal order. We also get a valuation map \({\text {val}}_\Lambda \) on \(\mathrm{A}\) by setting
with the understanding that \({\text {val}}_\Lambda (0)=\infty \).
The normalizer in \({\text {Aut}}_\mathrm{F}(\mathrm{V})\) of \(\Lambda \) is a compact mod-centre subgroup
The restriction of the valuation map to \({\mathfrak {K}}(\Lambda )\) defines a group homomorphism \({\text {val}}_{\Lambda }:{\mathfrak {K}}(\Lambda )\rightarrow {\mathbb {Z}}\). The kernel of which is a compact open subgroup \(\mathrm{P}(\Lambda )\) of \({\text {Aut}}_\mathrm{F}(\mathrm{V})\) which coincides with the group of units of the order \({\mathfrak {a}}_0(\Lambda )\). This subgroup has a decreasing filtration by compact open pro-p subgroups, given by \(\mathrm{P}^n(\Lambda )=1+{\mathfrak {a}}_n(\Lambda )\), for \(n\geqslant 1\).
For \(\mathrm{L}\) an \({\mathfrak {o}}_\mathrm{F}\)-lattice in \(\mathrm{V}\), we define the dual lattice
For \(\Lambda \) an \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence in \(\mathrm{V}\) we define the dual lattice sequence \(\Lambda ^\#\) in \(\mathrm{V}\) by
for all \(r\in {\mathbb {Z}}\), and we call \(\Lambda \) self-dual if \(\Lambda ^\#=\Lambda +d\), for some \(d\in {\mathbb {Z}}\). If \(\Lambda \) is self-dual then the lattices \({\mathfrak {a}}_n(\Lambda )\) are fixed by the adjoint anti-involution on \(\mathrm{A}\), and we put
Note that while \(\mathrm{P}(\Lambda )\) is a parahoric subgroup of \({{\widetilde{\mathrm{G}}}}\) in the sense of Bruhat–Tits, \(\mathrm{P}_-(\Lambda )\) is not always a parahoric subgroup: it is the full stabilizer of a point in the Bruhat–Tits building of \(\mathrm{G}\). See Sect. 11 below for the definition of parahoric subgroup for \(\mathrm{G}^{\mathsf {o}}\), when we will need it.
Finally in this subsection, suppose that \(\mathrm{E}\) is a subfield of \(\mathrm{A}\) containing \(\mathrm{F}\). Then we can consider \(\mathrm{V}\) as an \(\mathrm{E}\)-vector space, so we have the notion of \({\mathfrak {o}}_\mathrm{E}\)-lattice sequence in \(\mathrm{V}\); these are in fact \({\mathfrak {o}}_\mathrm{F}\)-lattice sequences which are normalized by \(\mathrm{E}^\times \). We have the following elementary but useful lemma on the existence of lattice sequences with prescribed properties.
Lemma 5.1
Let \(\mathrm{E},\mathrm{E}'\) be subfields of \(\mathrm{A}\) containing \(\mathrm{F}\), such that \(e(\mathrm{E}/\mathrm{F})=e(\mathrm{E}'/\mathrm{F})\) and \(f(\mathrm{E}/\mathrm{F})=f(\mathrm{E}'/\mathrm{F})\), and let \(\Lambda \) be an \({\mathfrak {o}}_\mathrm{E}\)-lattice sequence in \(\mathrm{V}\). Then there exist an \({\mathfrak {o}}_{\mathrm{E}'}\)-lattice sequence \(\Lambda '\) in \(\mathrm{V}\) and \(g\in {{\widetilde{\mathrm{G}}}}\) such that \(g\Lambda '=\Lambda \).
Proof
There is an \(\mathrm{F}\)-linear isomorphism from \(\mathrm{E}\) to \(\mathrm{E}'\) which maps \({\mathfrak {p}}_\mathrm{E}^n\) to \({\mathfrak {p}}_{\mathrm{E}'}^n\), for each \(n\in {\mathbb {Z}}\). Now we choose an \(\mathrm{E}\)-basis of \(\mathrm{V}\) which splits \(\Lambda \) and map it to an \(\mathrm{E}'\)-basis of \(\mathrm{V}\), using this \(\mathrm{F}\)-linear isomorphism, and the image of \(\Lambda \) has the required property. \(\square \)
5.2 A self-dual \(\dag \)-construction
We recall briefly the \(\dag \)-construction of [26, §4], which is a useful way of generalizing results originally proved only for strict lattice sequences to the general case, and introduce a self-dual version.
Let \(\Lambda \) be an \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence in \(\mathrm{V}\) of \({\mathfrak {o}}_F\)-period \(e=e(\Lambda )\). Let \(\mathrm{V}^\dag =\mathrm{V}\oplus \cdots \oplus \mathrm{V}\) (e times) and define the \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence \(\Lambda ^\dag \) in \(\mathrm{V}^\dag \) by
Then \(\Lambda ^\dag \) is a strict regular \({\mathfrak {o}}_F\)-lattice sequence in \(\mathrm{V}^\dag \) of period e. We denote by \({\mathcal {M}}^\dag \) the Levi subalgebra of \(\mathrm{A}^\dag ={\text {End}}_\mathrm{F}(\mathrm{V}^\dag )\) which is the stabilizer of the decomposition \(\mathrm{V}^\dag =\mathrm{V}\oplus \cdots \oplus \mathrm{V}\). Any \(\beta \in \mathrm{A}\) then induces an element \(\beta ^\dag =\beta \oplus \cdots \oplus \beta \) in \({\mathcal {M}}^\dag \). We write \({{\widetilde{\mathrm{M}}}}^\dag \) for the group of units of \({\mathcal {M}}^\dag \), which is a Levi subgroup of \({{\widetilde{\mathrm{G}}}}^\dag ={\text {Aut}}_\mathrm{F}(\mathrm{V}^\dag )\). Then \(\mathrm{P}(\Lambda ^\dag )\cap \mathrm{M}^\dag \simeq \mathrm{P}(\Lambda )\times \cdots \times \mathrm{P}(\Lambda )\), and similarly for \(\mathrm{P}^n(\Lambda ^\dag )\), while the \({{\widetilde{\mathrm{G}}}}^\dag \)-conjugacy class of \(\mathrm{P}(\Lambda ^\dag )\) is independent of \(\Lambda \), depending only on the period e, see [7, 1.5.2(ii)].
Now we introduce a self-dual variant. We will again use the notation \(\dag \); when we use it, we will make it clear when we are applying this self-dual version. Let \(\Lambda \) be a self-dual lattice sequence in \(\mathrm{V}\) with \(e=e(\Lambda )\). Let \(\mathrm{V}^\dag =\mathrm{V}\oplus \cdots \oplus \mathrm{V}\) (2e times, indexed by \(j\in \{\pm 1,\ldots ,\pm e\}\)) and write vectors \({\mathrm v}\in \mathrm{V}^\dag \) as tuples: \({\mathrm v}=\left( v_j\right) _{j=-e}^e\), where we understand that 0 is omitted and \(v_j\) is in the j-th copy of \(\mathrm{V}\). We define the form \(h^\dag \) on \(\mathrm{V}^\dag \) by
so that each copy of \(\mathrm{V}\) is isotropic: indeed, the space \((\mathrm{V}^\dag ,h^\dag )\) is hyperbolic. Now we define the \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence \(\Lambda ^\dag \) in \(\mathrm{V}^\dag \) by
where we understand that \(\Lambda -j\) is in the j-th copy of \(\mathrm{V}\), and \((\Lambda -j)^\#\) in the \((-j)\)-th copy. Then \(\Lambda ^\dag \) is a regular strict lattice sequence in \(\mathrm{V}^\dag \) and is self-dual with respect to \(h^\dag \); indeed \((\Lambda ^\dag )^\#=\Lambda ^\dag \). We again set \(\mathrm{A}^\dag ={\text {End}}_\mathrm{F}(\mathrm{V}^\dag )\) and \({{\widetilde{\mathrm{G}}}}^\dag ={\text {Aut}}_\mathrm{F}(\mathrm{V}^\dag )\), and denote by \({\mathcal {M}}^\dag \) the Levi subalgebra of \(\mathrm{A}^\dag \) which is the stabilizer of the decomposition \(\mathrm{V}^\dag =\mathrm{V}\oplus \cdots \oplus \mathrm{V}\). As above, any \(\beta \in \mathrm{A}\) induces an element \(\beta ^\dag \) in \({\mathcal {M}}^\dag \), which is skew whenever \(\beta \) is skew. We also set \(\mathrm{G}^\dag =\mathrm{U}(\mathrm{V}^\dag ,h^\dag )\) and note that the map \(g\mapsto g^\dag \) defines an embedding of \(\mathrm{G}\) in \(\mathrm{G}^\dag \).
This construction becomes particularly useful when applied to two self-dual lattice sequences \(\Lambda ,\Lambda '\) with \(e(\Lambda )=e(\Lambda ')\) (which we can always ensure by an affine translation) but with \(\Lambda ,\Lambda '\) possibly not \(\mathrm{G}\)-conjugate. The lattice sequences \(\Lambda ^\dag ,\Lambda '^\dag \), as they are self-dual, regular and strict of the same \({\mathfrak {o}}_\mathrm{F}\)-period, are conjugate in \(\mathrm{G}^\dag \) by [38, Proposition 5.2].
5.3 Strata
A stratum in \(\mathrm{A}\) is a 4-tuple \([\Lambda ,n,r,\beta ]\) where
-
(i)
\(\Lambda \) is an \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence in \(\mathrm{V}\);
-
(ii)
\(n\geqslant r\geqslant 0\) are integers;
-
(iii)
\(\beta \in {\mathfrak {a}}_{-n}(\Lambda )\).
The fraction \(\max \{-{\text {val}}_\Lambda (\beta ),r\}/{e(\Lambda )}\) is called the depth of the stratum. We call the stratum \([\Lambda ,r,r,0]\) a null stratum. Two strata \([\Lambda ,n,r,\beta _i]\), for \(i=1,2\), are called equivalent if
An element \(g\in {{\widetilde{\mathrm{G}}}}\) intertwines strata \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) if
For a subgroup \(\mathrm{J}\) of \({{\widetilde{\mathrm{G}}}}\), we say \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) intertwine in \(\mathrm{J}\) if there exists an element of \(\mathrm{J}\) which intertwines the strata. We say that \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) are conjugate in \(\mathrm{J}\) if \(n=n'\), \(r=r'\) and there exists \(g\in \mathrm{J}\) such that
An affine translation of a stratum \([\Lambda ,n,r,\beta ]\) is a stratum \([\Lambda ',n',r',\beta ]\) such that there exist \(a,b\in {\mathbb {Z}}\), \(a>0\), with \(\Lambda '=a\Lambda +b\), \(n'=an\) and \(\lfloor r'/a\rfloor = r\). We say that two strata are in the same affine class if they have affine translations which are equal. As we shall see, many objects we later associate to a stratum are in fact shared by all strata in the same affine class.
We can also make a \(\dag \)-construction for strata. If \([\Lambda ,n,r,\beta ]\) is a stratum in \(\mathrm{A}\) then we have the lattice sequence \(\Lambda ^\dag \) in \(\mathrm{V}^\dag \) and the element \(\beta ^\dag \) of \(\mathrm{A}^\dag \), giving us a new stratum \([\Lambda ^\dag ,n,r,\beta ^\dag ]\). This process behaves well with respect to intertwining: if \(g\in {{\widetilde{\mathrm{G}}}}\) intertwines two strata \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) then the element \(g^\dag \in {{\widetilde{\mathrm{G}}}}^\dag \) intertwines \([\Lambda ^\dag ,n,r,\beta ^\dag ]\) and \([\Lambda '^\dag ,n',r',\beta '^\dag ]\).
We fix a uniformizer \(\varpi _\mathrm{F}\) of \(\mathrm{F}\). Given a stratum \([\Lambda ,n,r,\beta ]\) with \(r<n\), we write \(y_\beta \) for the image of \(\varpi _F^{n/g}\beta ^{e/g}\) in \({\mathfrak {a}}_0(\Lambda )/{\mathfrak {a}}_1(\Lambda )\), where \(e=e(\Lambda )\) and \(g={\text {gcd}}(n,e)\). The characteristic polynomial of \(y_\beta \) (in \(\mathrm {k}_\mathrm{F}[X]\)) is called the characteristic polynomial of the stratum \([\Lambda ,n,r,\beta ]\), while its minimal polynomial is called the minimal polynomial of the stratum \([\Lambda ,n,r,\beta ]\). These depend only on the equivalence class of the stratum \([\Lambda ,n,n-1,\beta ]\) (and the choice of uniformizer). A stratum \([\Lambda ,n,n-1,\beta ]\) is called fundamental if its characteristic polynomial is not a power of X; this property is independent of the choice of uniformizer.
A stratum \([\Lambda ,n,r,\beta ]\) is called pure if either it is null or the following three conditions are satisfied:
-
(i)
\(\mathrm{E}=\mathrm{F}[\beta ]\) is a field;
-
(ii)
\(\Lambda \) is an \({\mathfrak {o}}_\mathrm{E}\)-lattice sequence in \(\mathrm{V}\);
-
(iii)
\({\text {val}}_{\Lambda }(\beta )=-n\).
We call \([\mathrm{E}:\mathrm{F}]\) the degree of such a stratum, and write \(\mathrm{B}\) for the centralizer in \(\mathrm{A}\) of \(\beta \) and \({\mathfrak {b}}_n(\Lambda )={\mathfrak {a}}_n(\Lambda )\cap \mathrm{B}\), for \(n\in {\mathbb {Z}}\). We set
and define the critical exponent \(k_0(\beta ,\Lambda )\) by
For \(\mathrm{E}=\mathrm{F}[\beta ]\) a finite extension of \(\mathrm{F}\), we set
where \({\mathfrak {p}}_\mathrm{E}^{\mathbb {Z}}\) denotes the \({\mathfrak {o}}_F\)-lattice sequence in \(\mathrm{E}\) (considered as an \(\mathrm{F}\)-vector space) given by \(i\mapsto {\mathfrak {p}}_E^i\), \(i\in {\mathbb {Z}}\). Note that, our definition of \(k_\mathrm{F}(\beta )\) differs from that in [8, (1.4)] by the normalization \(1/e(\mathrm{E}/\mathrm{F})\). By [40, Lemma 5.6], we have
A pure stratum \([\Lambda ,n,r,\beta ]\) is called simple if \(k_0(\beta ,\Lambda )<-r\); in particular, a pure stratum \([\Lambda ,n,n,\beta ]\) is simple if and only if it is the null stratum \([\Lambda ,n,n,0]\). A particularly nice case occurs when \(r=n-1\) (see [12, 1.4.15]): a pure stratum \([\Lambda ,n,n-1,\beta ]\) is simple if and only if \(\beta \) is minimal over \(\mathrm{F}\), that is:
-
(i)
\({\text {val}}_\mathrm{E}(\beta )\) is prime to \(e(\mathrm{E}/\mathrm{F})\);
-
(ii)
\(\beta ^{e(\mathrm{E}/\mathrm{F})}\varpi _\mathrm{F}^{-{\text {val}}_\mathrm{E}(\beta )}+{\mathfrak {p}}_\mathrm{E}\) generates the residue field \(\mathrm {k}_{\mathrm{E}}\) over \(\mathrm {k}_\mathrm{F}\).
We observe that the notions of pure and simple behave well under the \(\dag \)-construction: if \([\Lambda ,n,r,\beta ]\) is pure then \([\Lambda ^\dag ,n,r,\beta ^\dag ]\) is also pure, since \(\mathrm{F}[\beta ]\simeq \mathrm{F}[\beta ^\dag ]\); and if \([\Lambda ,n,r,\beta ]\) is simple then the same applies to \([\Lambda ^\dag ,n,r,\beta ^\dag ]\), since \(k_\mathrm{F}(\beta )=k_\mathrm{F}(\beta ^\dag )\).
When pure strata intertwine, they share several invariants, and we also get a certain isomorphism between subextensions of the residue fields which is important for concordance in the unitary case (see Lemma 3.34).
Lemma 5.2
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) be non-null pure strata, with \(r<n\) and \(r'<n'\), which intertwine in \({{\widetilde{\mathrm{G}}}}\), and put \(\mathrm{E}=\mathrm{F}[\beta ]\) and \(\mathrm{E}'=\mathrm{F}[\beta ']\). Then
-
(i)
the strata have the same depth, \(n/e(\Lambda )=n'/e(\Lambda ')\);
-
(ii)
if both strata are simple and \(r/e(\Lambda )=r'/e(\Lambda ')\) then \(e(\mathrm{E}/\mathrm{F})=e(\mathrm{E}'/\mathrm{F})\) and \(f(\mathrm{E}/\mathrm{F})=f(\mathrm{E}'/\mathrm{F})\);
-
(iii)
the strata have the same characteristic and minimal polynomials;
-
(iv)
there is a \(\mathrm {k}_\mathrm{F}\)-linear field isomorphism from \(\mathrm {k}_{\mathrm{F}}[y_\beta ]\) to \(\mathrm {k}_{\mathrm{F}}[y_{\beta '}]\) which sends \(y_\beta \) to \(y_{\beta '}\).
Proof
(i) is given by [39, Proposition 6.9]. For (ii), by a \(\dag \)-construction, we can assume that \(\Lambda \) and \(\Lambda '\) are regular strict and of the same period, hence conjugate; then [12, Theorem 2.6.1] implies that the strata are conjugate up to equivalence, and the result follows from [12, Theorem 2.4.1(ii)]. Finally, for (iii) and (iv), conjugating by an element which intertwines, we may assume the strata are intertwined by the identity, in which case \(y_\beta ^i=y_{\beta '}^i\) in \(({\mathfrak {a}}_0(\Lambda )+{\mathfrak {a}}_0(\Lambda '))/({\mathfrak {a}}_1(\Lambda )+{\mathfrak {a}}_1(\Lambda '))\), for all \(i\geqslant 0\), and the results follow. \(\square \)
We also note that, under modest conditions, null strata and non-null simple strata do not intertwine.
Lemma 5.3
[39, Proposition 6.9] Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',n',0]\) be simple strata, with \(\beta \ne 0\), and suppose that \(n'/e(\Lambda ')<n/e(\Lambda )\). Then the strata do not intertwine in \({{\widetilde{\mathrm{G}}}}\).
A stratum \([\Lambda ,n,r,\beta ]\) is called self-dual if \(\Lambda \) is a self-dual \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence and \(\beta \in \mathrm {A}_{-}\). Note that, this is a slight change of terminology: In [43, Definition 2.1] these strata are called skew strata; we reserve skew for certain self-dual strata which satisfy an additional condition, see Definition 8.3.
A self-dual stratum \([\Lambda ,n,r,\beta ]\) is called standard if \(\Lambda \) has even \(\mathfrak {o}_{\text {F}}\)-period and \(\Lambda =\Lambda ^\#\). Any self-dual stratum has an affine translation which is standard self-dual. Note also that self-dual strata \([\Lambda ,n,r,\beta ]\) behave well with respect to the self-dual \(\dag \)-construction: that is, if \([\Lambda ,n,r,\beta ]\) is (standard) self-dual then the stratum \([\Lambda ^\dag ,n,r,\beta ^\dag ]\) obtained by the self-dual \(\dag \)-construction is (standard) self-dual with respect to \(h^\dag \). Again, the self-dual \(\dag \)-construction behaves well with respect to intertwining: if \(g\in \mathrm{G}\) intertwines two self-dual strata \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) then the element \(g^\dag \in \mathrm{G}^\dag \) intertwines \([\Lambda ^\dag ,n,r,\beta ^\dag ]\) and \([\Lambda '^\dag ,n',r',\beta '^\dag ]\).
An important application of this shows that equivalent self-dual simple strata have an additional invariant:
Lemma 5.4
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ']\) be self-dual simple strata which intertwine in \(\mathrm{G}\), and suppose \(e(\Lambda )=e(\Lambda ')\). Put \(\mathrm{E}=\mathrm{F}[\beta ]\), \(\mathrm{E}'=\mathrm{F}[\beta ']\). Then we have an equality of ramification indices \(e(\mathrm{E}/\mathrm{E}_{\mathsf {o}})=e(\mathrm{E}'/\mathrm{E}'_{\mathsf {o}})\).
Proof
By a self-dual \(\dag \)-construction, without loss of generality we can assume that \(\Lambda ,\Lambda '\) are regular standard self-dual, so conjugate in \(\mathrm{G}\). Then [39, Theorem 8.5] implies that the strata are conjugate up to equivalence in \(\mathrm{G}\) so, by conjugating, we may assume they are equivalent. Then, by [13, 5.2(i)] the residue fields of \(\mathrm{E}\) and \(\mathrm{E}'\) coincide in \({\mathfrak {a}}_0(\Lambda )/{\mathfrak {a}}_1(\Lambda )\) and thus the induced action of the adjoint anti-involution on the residue fields coincides, which finishes the proof. \(\square \)
Many results concerning simple strata are proved “by induction along r”: that is, they are proved for minimal strata first, when \(r=n-1\) and then in general using the following fundamental approximation result.
Proposition 5.5
([12, Theorem 2.4.1], [41, Proposition 1.10]) Let \([\Lambda ,n,r,\beta ]\) be a pure stratum. Then there is a simple stratum \([\Lambda ,n,r,\gamma ]\) equivalent to it and, for any such stratum,
Moreover, if \([\Lambda ,n,r,\beta ]\) is self-dual then \([\Lambda ,n,r,\gamma ]\) may be taken to be self-dual also.
Finally in this subsection, we introduce concordance of pure strata. We introduce the following notation:
Notation 5.6
For \(\beta \in \mathrm{A}\) with \(\mathrm{E}=\mathrm{F}[\beta ]\) a field, we denote by \({\varphi _\beta }\) the canonical embedding of \(\mathrm{E}\) in \(\mathrm{A}\).
If \([\Lambda ,n,r,\beta ]\) is a self-dual pure stratum with \(\mathrm{E}=\mathrm{F}[\beta ]\), then \((\mathrm{E},\beta )\) is a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) and the canonical embedding \({\varphi _\beta }\) is a self-dual embedding.
Definition 5.7
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) be self-dual pure strata in \(\mathrm{A}\). We say that they are concordant if the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant.
If two self-dual pure strata are conjugate in \(\mathrm{G}\) then they are concordant (see Remark 3.26(ii)). The purpose of this section is to investigate the relationship between intertwining of self-dual strata and concordance.
One particular case where we get concordance for free is by using the self-dual \(\dag \)-construction. If \([\Lambda ,n,r,\beta ]\) is a self-dual pure stratum with \(\mathrm{E}=\mathrm{F}[\beta ]\) and we write \(\varphi _\beta \) also for the canonical embedding of \(\mathrm{E}\) in \(\mathrm{A}^\dag \) then \([h^\dag _{\varphi _\beta }]\) is always the trivial class. Thus we get the following result:
Lemma 5.8
If \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) are non-null self-dual pure strata with \(e(\Lambda )=e(\Lambda ')\), then \([\Lambda ^\dag ,n,r,\beta ^\dag ]\) and \([\Lambda '^\dag ,n',r',\beta '^\dag ]\) are concordant.
5.4 Minimal elements and tamely ramified extensions
We will need the following lemmas on minimal elements and tamely ramified extensions:
Lemma 5.9
Suppose \(\mathrm{E}_1=\mathrm{F}[\beta _1]\) is a tamely ramified finite extension, with \(\beta _1\) a minimal element, and \(\mathrm{E}_2/\mathrm{F}\) is another finite extension, with \(\beta _2\in \mathrm{E}_2^\times \). For \(i=1,2\), write \(e_i=e(\mathrm{E}_i/\mathrm{F})\) for the ramification index and \(n_i={\text {val}}_{\mathrm{E}_i}(\beta _i)\), and suppose that
-
(i)
\(n_1/e_1=n_2/e_2\), and
-
(ii)
\(\beta _1^{e_1}\varpi _\mathrm{F}^{-n_1}+{\mathfrak {p}}_{\mathrm{E}_1}\) and \(\beta _2^{e_1}\varpi _\mathrm{F}^{-n_{1}}+{\mathfrak {p}}_{\mathrm{E}_2}\) have the same minimal polynomial over \(\mathrm {k}_\mathrm{F}\).
Then, there is a unique \(\mathrm{F}\)-embedding \(\phi :\mathrm{E}_1\rightarrow \mathrm{E}_2\) such that
Furthermore, if \((\mathrm{E}_1,\beta _1)\) and \((\mathrm{E}_2,\beta _2)\) are self-dual field extensions of \(\mathrm{F}\), then \(\phi \) is  -equivariant.
-equivariant.
Proof
Let \({\mathsf {p}}(X)\in \mathrm {k}_\mathrm{F}[X]\) denote the common minimal polynomial of \(\beta _1^{e_1}\varpi _\mathrm{F}^{-n_1}\bmod {{\mathfrak {p}}_{\mathrm{E}_1}}\) and \(\beta _2^{e_1}\varpi _\mathrm{F}^{-n_1}\bmod {{\mathfrak {p}}_{\mathrm{E}_2}}\) over \(\mathrm {k}_\mathrm{F}\). We take a monic polynomial \(P(X)\in {\mathfrak {o}}_\mathrm{F}[X]\) whose reduction modulo \({\mathfrak {p}}_\mathrm{F}\) is \({\mathsf {p}}(X)\). By Hensel’s Lemma, for \(i=1,2\), we have roots \(\gamma _i\in \mathrm{E}_i\) of P(X) satisfying \(\gamma _i\equiv \beta _i^{e_1}\varpi _\mathrm{F}^{-n_1}\bmod {{\mathfrak {p}}_{\mathrm{E}_i}}\). There is an \(\mathrm{F}\)-monomorphism from \(\mathrm{E}_1\) into a separable closure of \(\mathrm{E}_2\) which maps \(\gamma _1\) to \(\gamma _2\). Thus we can assume that \(\mathrm{E}_1/\mathrm{F}\) is totally ramified and \(\gamma _1=\gamma _2\).
We may suppose that the uniformizer \(\varpi _\mathrm{F}\) is an \(e_1\)-th power in \(\mathrm{E}_1\), so that \(\beta _1^{e_1}\varpi _\mathrm{F}^{-n_1}\) is also an \(e_1\)-th power. The latter is equal to \(\beta _2^{e_1}\varpi _\mathrm{F}^{-n_1}\bmod {{\mathfrak {p}}_{\mathrm{E}_2}}\) and Hensel’s Lemma provides \(e_1\)-th roots \(\xi _i\in E_i^\times \) of \(\beta _i^{e_1}\varpi _\mathrm{F}^{-n_1}\) such that \(\xi _1\bmod {{\mathfrak {p}}_{\mathrm{E}_1}}\) is equal to \(\xi _2\bmod {{\mathfrak {p}}_{\mathrm{E}_2}}\) as elements of \(\mathrm {k}_\mathrm{F}\). Then \(\beta _i\xi _i^{-1}\), for \(i=1,2\), are roots of the polynomial \(X^{e_1}-\varpi _\mathrm{F}^{n_1}\), which is irreducible over \(\mathrm{F}\) because \(\beta _1\xi _1^{-1}\) generates \(\mathrm{E}_1\). The \(\mathrm{F}\)-monomorphism \(\phi \) which maps \(\beta _1\xi _1^{-1}\) to \(\beta _2\xi _2^{-1}\) then satisfies (5.10).
We now prove the uniqueness of \(\phi \). First observe that (5.10) implies that the map on \(\mathrm {k}_{\mathrm{E}_1}\) induced by \(\phi \) sends \(\beta _1^{e_1}\varpi _\mathrm{F}^{-n_1}+{\mathfrak {p}}_{\mathrm{E}_1}\) to \(\beta _2^{e_1}\varpi _\mathrm{F}^{-n_{{1}}}+{\mathfrak {p}}_{\mathrm{E}_2}\). Since \(\beta _1^{e_1}\varpi _\mathrm{F}^{-n_1}+{\mathfrak {p}}_{\mathrm{E}_1}\) generates the residue field of \(\mathrm{E}_1\), we see that \(\phi \) is uniquely determined on the maximal unramified subextension of \(\mathrm{E}_1\) and, as above, we can assume without loss of generality that \(\mathrm{E}_1/\mathrm{F}\) is totally ramified. Again, we may suppose that the uniformizer \(\varpi _\mathrm{F}\) is an \(e_1\)-th power in \(\mathrm{E}_1\).
By Bézout’s Lemma, there are integers r, s such that \(\varpi _1=\beta _1^r\varpi _\mathrm{F}^s\) is a uniformizer of \(\mathrm{E}_1\), and we set \(\varpi _2=\beta _2^r\varpi _\mathrm{F}^s\) (which is not necessarily a uniformizer of \(\mathrm{E}_2\)). Then (5.10) implies that \(\phi (\varpi _1)\varpi _2^{-1}\) is an element of \(\mathrm{U}^1_{\mathrm{E}_2}\). Therefore, if \(\phi '\) also satisfies (5.10), then \(\phi (x)\phi '(x)^{-1}\) is an element of \(\mathrm{U}^1_{\mathrm{E}_2}\), for all \(x\in \mathrm{E}_1^\times \). In particular, if x is an \(e_1\)-th root of \(\varpi _\mathrm{F}\), then \(\phi (x)\phi '(x)^{-1}\) is an \(e_1\)-th root of unity in \(\mathrm{U}^1_{\mathrm{E}_2}\) and thus equal to 1, since p does not divide \(e_1\). This completes the proof of uniqueness.
The equivariance assertion follows from the uniqueness since \(\phi \) and  both satisfy (5.10). \(\square \)
both satisfy (5.10). \(\square \)
Lemma 5.11
Suppose \(\beta \) is a minimal element of an algebraic closure of \(\mathrm{F}\) and set \(\mathrm{E}=\mathrm{F}[\beta ]\). Let \(\mathrm{F}_{\mathsf {tame}}/\mathrm{F}\) be the maximal tamely ramified field extension of \(\mathrm{E}/\mathrm{F}\) and set \(e_p:=[\mathrm{E}:\mathrm{F}]/[\mathrm{F}_{\mathsf {tame}}:\mathrm{F}]\), the wild ramification index of \(\mathrm{E}/\mathrm{F}\).
-
(i)
There is a non-zero element \(\beta _{\mathsf {tame}}\) of \(\mathrm{F}_{\mathsf {tame}}\) such that \(\beta ^{e_p}(\beta _{\mathsf {tame}})^{-1}\in \mathrm{U}_\mathrm{E}^1\).
-
(ii)
Any element \(\beta _{\mathsf {tame}}\) as in (i) is minimal over \(\mathrm{F}\) and generates \(\mathrm{F}_{\mathsf {tame}}\) over \(\mathrm{F}\).
Proof
We set \(n={\text {val}}_\mathrm{E}(\beta )\).
-
(i)
Take a uniformizer \(\varpi _{\mathsf {tame}}\) of \(\mathrm{F}_{\mathsf {tame}}\). Then \({\text {val}}_{\mathrm{E}}(\varpi _{\mathsf {tame}})=e_p\) and there is a unit x of \(\mathrm{F}_{\mathsf {tame}}\) such that \(\beta ^{e_p}(\varpi _{\mathsf {tame}})^{-n}x^{-1}\) belong to \(\mathrm{U}_\mathrm{E}^1\). The element \(\beta _{\mathsf {tame}}:=(\varpi _{\mathsf {tame}})^{n}x\) satisfies the assertion.
-
(ii)
We take an element \(\beta _{\mathsf {tame}}\) as in (i). It generates a sub-extension \(\mathrm{L}/\mathrm{F}\) of \(\mathrm{F}_{\mathsf {tame}}/\mathrm{F}\). Set \(e=e(\mathrm{E}/\mathrm{F})\), \(e_{\mathsf {tame}}=e(\mathrm{F}_{\mathsf {tame}}/\mathrm{F})\) and \(n_{\mathsf {tame}}={\text {val}}_{\mathrm{F}_{\mathsf {tame}}}(\beta _{\mathsf {tame}})\). Then \(n=n_{\mathsf {tame}}\) and there is an element \(u\in \mathrm{U}^1_\mathrm{E}\) such that
$$\begin{aligned} \beta ^{e}\varpi _\mathrm{F}^{-n}u=(\beta _{\mathsf {tame}})^{e_{\mathsf {tame}}}\varpi _\mathrm{F}^{-n_{\mathsf {tame}}}. \end{aligned}$$Thus, by the minimality of \(\beta \), we obtain that the residue class of
$$\begin{aligned} (\beta _{\mathsf {tame}})^{e_{\mathsf {tame}}}\varpi _\mathrm{F}^{-n_{\mathsf {tame}}} \end{aligned}$$(5.12)generates the residue field extension \(\mathrm {k}_{\mathrm{E}}/\mathrm {k}_\mathrm{F}\). Thus \(\mathrm {k}_\mathrm{L}=\mathrm {k}_{\mathrm{E}}\), and \(\mathrm{E}\) contains the maximal unramified sub-extension of \(\mathrm{E}/\mathrm{F}\). Further \(n_{\mathsf {tame}}\) is prime to the ramification index \(e_{\mathsf {tame}}\), since \(e_{\mathsf {tame}}\) divides e and \(\beta \) is minimal. Thus
$$\begin{aligned} {\mathbb {Z}}\cup \{\infty \}={\text {val}}_{\mathrm{F}_{\mathsf {tame}}}(\mathrm{F}_{\mathsf {tame}})={\text {val}}_{\mathrm{F}_{\mathsf {tame}}}(\mathrm{L}), \end{aligned}$$and therefore \(\mathrm{F}_{\mathsf {tame}}=\mathrm{L}\). So \(\beta _{\mathsf {tame}}\) generates \(\mathrm{F}_{\mathsf {tame}}\) and the minimality follows.
\(\square \)
5.5 Tame subextensions
Lemma 5.13
Let \([\Lambda ,n,n-1,\beta ]\) be a self-dual pure stratum, and \([\Lambda ',n,n-1,\gamma ]\) be a self-dual simple stratum, in \(\mathrm{A}\), which intertwine in \(\mathrm{G}\). Let \(\mathrm{F}_{\mathsf {tame}}\) denote the maximal tamely ramified subextension of \(\mathrm{F}[\gamma ]/\mathrm{F}\) and set \(\mathrm{E}=\mathrm{F}[\beta ]\).
-
(i)
There exists \(g\in \mathrm{G}\) such that \(g\mathrm{F}_{\mathsf {tame}}g^{-1}\subseteq \mathrm{E}\).
-
(ii)
If \(\Lambda '=\Lambda \), then there exists \(g\in \mathrm{P}_-(\Lambda )\) such that \(g\mathrm{F}_{\mathsf {tame}}g^{-1}\subseteq \mathrm{E}\).
Proof
Set \(e_p=[\mathrm{F}[\gamma ]:\mathrm{F}_{\mathsf {tame}}]\). By Lemma 5.11, there is an element \(\gamma _{\mathsf {tame}}\) in \(\mathrm{F}_{\mathsf {tame}}\) such that \(\gamma _{\mathsf {tame}}\gamma ^{-e_p}\in \mathrm{U}^1_{\mathrm{F}[\gamma ]}\); since \(\gamma \) is skew and \(e_p\) is odd, we can choose \(\gamma _{\mathsf {tame}}\) to be skew, and it is also minimal.
The strata \([\Lambda ',ne_p,ne_p-1,\gamma ^{e_p}]\) and \([\Lambda ',ne_p,ne_p-1,\gamma _{\mathsf {tame}}]\) are then equivalent. Thus the pure strata \([\Lambda ,ne_p,ne_p-1,\beta ^{e_p}]\) and \([\Lambda ',ne_p,ne_p-1,\gamma _{\mathsf {tame}}]\) intertwine, so have a common characteristic polynomial and a common minimal polynomial, by Lemma 5.2. Thus we can apply Lemma 5.9 with \(\beta _1=\gamma _{\mathsf {tame}}\) and \(\beta _2=\beta ^{e_p}\) to deduce that there is an equivariant monomorphism \(\phi :\mathrm{F}_{\mathsf {tame}}\rightarrow \mathrm{E}\) such that \(\phi (\gamma _{\mathsf {tame}})\beta ^{-e_p} \in \mathrm{U}^1_\mathrm{E}\). Then the strata \([\Lambda ,ne_p,ne_p-1,\phi (\gamma _{\mathsf {tame}})]\) and \([\Lambda ,ne_p,ne_p-1,\beta ^{e_p}]\) are equivalent.
It follows that the simple strata \([\Lambda ',ne_p,ne_p-1,\gamma _{\mathsf {tame}}]\) and \([\Lambda ,ne_p,ne_p-1,\phi (\gamma _{\mathsf {tame}})]\) intertwine. Then [39, Theorem 5.2] implies the existence of an element of \(\mathrm{G}\) which conjugates \(\gamma _{\mathsf {tame}}\) to \(\phi (\gamma _{\mathsf {tame}})\). Thus we have found \(g\in \mathrm{G}\) such that \(g\mathrm{F}_{\mathsf {tame}}g^{-1}=\phi (\mathrm{F}_{\mathsf {tame}})\subseteq \mathrm{E}\).
Finally, if \(\Lambda '=\Lambda \) then [38, Theorem 1.2] implies that the element conjugating \(\gamma _{\mathsf {tame}}\) to \(\phi (\gamma _{\mathsf {tame}})\) can be chosen to be in \(\mathrm{P}_-(\Lambda )\). \(\square \)
Now let \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ',n,n-1,\beta ']\) be self-dual pure strata in \(\mathrm{A}\) which intertwine in \(\mathrm{G}\), and put \(\mathrm{E}=\mathrm{F}[\beta ],\mathrm{E}'=\mathrm{F}[\beta ']\). Let \([\Lambda ,n,n-1,\gamma ]\) and \([\Lambda ',n,n-1,\gamma ']\) be self-dual simple strata in \(\mathrm{A}\), respectively equivalent to \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ',n,n-1,\beta ']\).
Corollary 5.14
With the notation above, there exists \(g\in \mathrm{G}\) such that \(\mathrm{E}\cap g\mathrm{E}'g^{-1}\) contains a tamely ramified extension \(\mathrm{K}/\mathrm{F}\) which is stable under the adjoint anti-involution but is not fixed pointwise. Moreover, \(\mathrm{K}\) can be chosen to be \(\mathrm{P}_-(\Lambda )\)-conjugate to the maximal tamely ramified subextension of \(\mathrm{F}[\gamma ]/\mathrm{F}\). Furthermore, if \(\Lambda =\Lambda '\) then we can take \(g\in \mathrm{P}_-(\Lambda )\).
Proof
Let \(\mathrm{F}_{\mathsf {tame}}\) and \(\mathrm{F}'_{\mathsf {tame}}\) denote the maximal tamely ramified subextensions of \(\mathrm{F}[\gamma ]/\mathrm{F}\) and \(\mathrm{F}[\gamma ']/\mathrm{F}\) respectively. We apply Lemma 5.13 several times to find elements \(x\in \mathrm{P}_-(\Lambda )\), \(x'\in \mathrm{P}_-(\Lambda ')\) and \(y\in \mathrm{G}\) such that
Then \(\mathrm{K}=x\mathrm{F}_{\mathsf {tame}}x^{-1}\) and \(g=xyx'\) are as required. Moreover, if \(\Lambda =\Lambda '\) then y can be chosen in \(\mathrm{P}_-(\Lambda )\), by Lemma 5.13(ii), and then \(g\in \mathrm{P}_-(\Lambda )\) as required. \(\square \)
5.6 Concordance in the symplectic case
Using the technique of twisting, we now get an analogue of Proposition 3.28 for the symplectic case, when we have an additional hypothesis on intertwining of strata.
Lemma 5.15
Suppose that \(\varepsilon =-1\) and \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\). Let \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ',n,n-1,\beta ']\) be self-dual pure strata in \(\mathrm{A}\) which intertwine in \(\mathrm{G}\), and put \(\mathrm{E}=\mathrm{F}[\beta ],\mathrm{E}'=\mathrm{F}[\beta ']\). Suppose further that \({\text {dim}}_\mathrm{E}\mathrm{V},{\text {dim}}_{\mathrm{E}'}\mathrm{V}\) have the same parity, and either
-
(i)
this common parity is even; or
-
(ii)
this common parity is odd and \({\mathsf {w}}_1(\langle 1\rangle )=\langle 1\rangle \).
Then the strata are concordant.
Proof
Conjugating by an element of \(\mathrm{G}\) (which does not affect concordance, by Remark 3.26), we can assume that the strata are intertwined by the identity. Then [39, Lemma 5.3] applied twice (as in the proof of [39, Theorem 5.2]) implies that the spaces \((\mathrm{V},\beta ^*h)\) and \((\mathrm{V},\beta '^*h)\) are isometric (by an element of \(\mathrm{P}^1(\Lambda ')\mathrm{P}^1(\Lambda )\)).
Now Corollary 5.14 implies that the hypotheses of Proposition 3.28 are satisfied so that the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are \((\beta ^*h,\beta '^*h)\)-concordant, and it follows from Lemma 3.27 that our original strata are concordant. \(\square \)
The following Lemma will be useful when we need to understand whether concordance is preserved when we pass from pure strata to equivalent simple strata.
Lemma 5.16
Suppose that \(\varepsilon =-1\) and \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\). Let \([\Lambda ,n,n-1,\beta ],~[\Lambda ,n,n-1,\beta ']\) be self-dual pure strata in \(\mathrm{A}\) which intertwine in \(\mathrm{G}\) and put \(\mathrm{E}=\mathrm{F}[\beta ]\) and \(\mathrm{E}'=\mathrm{F}[\beta ']\). Suppose further that \({\text {dim}}_\mathrm{E}\mathrm{V}\) is odd, \({\text {dim}}_{\mathrm{E}'}\mathrm{V}\) is even and \([\Lambda ,n,n-1,\beta ']\) is simple. Then \(h_{{\varphi _{\beta '}}}\) is hyperbolic if and only if \([\beta ^*(h_{{\varphi _\beta }})]=\langle 1\rangle \).
Note that the condition \([\beta ^*(h_{{\varphi _\beta }})]=\langle 1\rangle \) can be translated into a condition on \(h_{\varphi _\beta }\), using Corollary 3.4: either \([h_{{\varphi _\beta }}]=\langle \beta \rangle \) and \(-1\) is a square in \(\mathrm{E}\), or \([h_{{\varphi _\beta }}]\ne \langle \beta \rangle \) and \(-1\) is a non-square in \(\mathrm{E}\).
Proof
The stratum \([\Lambda ,n,n-1,\beta ]\) is equivalent to a self-dual simple stratum \([\Lambda ,n,n-1,\gamma ]\) in \(\mathrm{A}\), which also intertwines \([\Lambda ,n,n-1,\beta ']\). By [39, 8.5], this implies that \([\Lambda ,n,n-1,\gamma ]\) is, up to equivalence, conjugate to \([\Lambda ,n,n-1,\beta ']\) in \(\mathrm{G}\) and, replacing \([\Lambda ,n,n-1,\beta ']\) by its conjugate, we may assume that \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ,n,n-1,\beta ']\) are equivalent. Then \((\mathrm{V},\beta ^*(h))\) is isometric to \((\mathrm{V},\beta '^*(h))\) by an element \(u\in \mathrm{P}^1(\Lambda )\) by [39, Lemma 5.3].
We show first that \(\lambda _\beta ^*(\langle 1\rangle )=\varvec{0}\). By Corollary 5.14 we can choose u such that \(u^{-1}\mathrm{E}' u\cap \mathrm{E}\) contains a Galois-invariant subfield \(\mathrm{K}\) with \(\mathrm{K}\ne \mathrm{K}_{\mathsf {o}}\). The assumptions imply that \([\mathrm{E}:\mathrm{K}]\) is even, since \({\text {dim}}_\mathrm{E}\mathrm{V}\) is odd while \({\text {dim}}_\mathrm{K}\mathrm{V}\) is even because \(\mathrm{K}\) is contained in \(u^{-1}\mathrm{E}' u\).
Choose non-zero Galois-equivariant linear forms
Then \(\lambda _\beta ^*\) and \(\lambda _{\mathrm{K}/\mathrm{F}}^*\circ \lambda _{\mathrm{E}/\mathrm{K}}^*\) on \({\mathcal {W}}_1(\mathrm{E}/\mathrm{E}_{\mathsf {o}})\) have the same image, by Proposition 3.13(i). Now the image of \(\lambda _{\mathrm{E}/\mathrm{K}}^*\) is contained in \({\mathcal {W}}_1^\mathsf {even}(\mathrm{K}/\mathrm{K}_{\mathsf {o}})\), so consists of \(\varvec{0}\) and the maximal element. Then, by Proposition 3.13, the image of \(\lambda _\beta ^*\) also consists of \(\varvec{0}\) and the maximal element (which has anisotropic dimension four). However, \(\lambda _\beta ^*(\langle 1\rangle )\) has anisotropic dimension at most 2, by Proposition 3.15(ii), so \(\lambda _\beta ^*(\langle 1\rangle )=\varvec{0}\).
Now, since \({\text {dim}}_\mathrm{E}\mathrm{V}\) is odd, the class \([\beta ^*(h_{\varphi _\beta })]\) is that of a 1-dimensional anisotropic space. Since \([\beta ^*h] = \lambda _\beta ^*([\beta ^*(h_{\varphi _\beta })])\) and \(\lambda _\beta ^*\) is injective on the 1-dimensional anisotropic spaces, it follows that \(\beta ^*h\) is hyperbolic if and only if \([\beta ^*(h_{\varphi _\beta })]=\langle 1\rangle \).
On the other hand, since \({\text {dim}}_{\mathrm{E}'}\mathrm{V}\) is even, the class \([\beta '^*h]\) is either \(\varvec{0}\) or maximal. By injectivity of \(\lambda _{\beta '}^*\) on \({\mathcal {W}}_1^\mathsf {even}(\mathrm{E}'/\mathrm{E}'_{\mathsf {o}})\) and Proposition 3.13(ii), we deduce that \(\beta '^*h\) is hyperbolic if and only if \(\beta '^*(h_{{\varphi _{\beta '}}})\) is hyperbolic, which occurs if and only if \(h_{{\varphi _{\beta '}}}\) is hyperbolic since \(\beta '^*\) is an isomorphism.
Putting together the results of the last two paragraphs, since \((\mathrm{V},\beta ^*h)\) and \((\mathrm{V},\beta '^*h)\) are isometric we see that \(h_{{\varphi _{\beta '}}}\) is hyperbolic if and only if \([\beta ^*(h_{\varphi _\beta })]=\langle 1\rangle \), as required. \(\square \)
5.7 Concordance of intertwining simple strata
We are now in a position to prove that self-dual simple strata which intertwine in \(\mathrm{G}\) are concordant. In fact, we deduce it from the following numerical criterion for concordance of pure strata.
Lemma 5.17
Let \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ',n,n-1,\beta ']\) be self-dual pure strata which intertwine in \(\mathrm{G}\). Setting \(\mathrm{E}=\mathrm{F}[\beta ]\) and \(\mathrm{E}'=\mathrm{F}[\beta ']\), suppose further that
Then the strata are concordant.
Proof
It follows from the assumptions and Lemma 5.2 that \(e(\Lambda )=e(\Lambda ')\) and \({\text {val}}_\mathrm{E}(\beta )={\text {val}}_{\mathrm{E}'}(\beta ')\), while there is a \(\mathrm {k}_\mathrm{F}\)-linear field isomorphism between \(\mathrm {k}_\mathrm{E}\) and \(\mathrm {k}_{\mathrm{E}'}\) which sends \(y_\beta \) to \(y_{\beta '}\). Thus the self-dual extensions \((\mathrm{E},\beta )\) and \((\mathrm{E}',\beta ')\) are similar, in the sense of Definition 3.33.
The result now follows from Lemma 5.15 when \(\mathrm{G}\) is symplectic, from Proposition 3.28 together with Corollary 5.14 when \(\mathrm{G}\) is orthogonal, and from Lemma 3.34 when \(\mathrm{G}\) is unitary. \(\square \)
Corollary 5.18
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ']\) be self-dual simple strata which intertwine in \(\mathrm{G}\). Then they are concordant.
Proof
If \(r=n\) then both strata are null so there is nothing to prove. Otherwise, the elements \(\beta \) and \(\beta '\) are necessarily both non-zero by the definition of simple stratum, because the third parameter r is smaller than n. Put \(\mathrm{E}=\mathrm{F}[\beta ]\) and \(\mathrm{E}'=\mathrm{F}[\beta ']\). Then Lemmas 5.2 and 5.4 imply that \(e(\Lambda )=e(\Lambda ')\) and that
and the result follows from Lemma 5.17. \(\square \)
5.8 Intertwining of concordant pure strata
Finally in this section, we consider the \(\mathrm{G}\)-intertwining of self-dual pure strata which intertwine in \({{\widetilde{\mathrm{G}}}}\):
Proposition 5.19
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ']\) be self-dual pure strata in \(\mathrm{A}\) which intertwine in \({{\widetilde{\mathrm{G}}}}\).
-
(i)
If \(\varepsilon =1\) or \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\) then they intertwine in \(\mathrm{G}\).
-
(ii)
If the strata are simple and concordant then they intertwine in \(\mathrm{G}\).
Note that, together with Corollary 5.18, this implies that, in the non-symplectic case, self-dual simple strata which intertwine in \({{\widetilde{\mathrm{G}}}}\) are automatically concordant; this is not true in the symplectic case.
Proof
If \(r=n\) then all strata are null and there is nothing to prove, so we assume \(r<n\). As the strata intertwine in \({{\widetilde{\mathrm{G}}}}\), the stratum \([\Lambda \oplus \Lambda ',n,r,\beta +\beta ']\) is equivalent to a simple stratum \([\Lambda \oplus \Lambda ',n,r,\gamma ]\) in \({\text {End}}_{\mathrm{F}}(\mathrm{V}\oplus \mathrm{V})\) by [39, Proposition 7.1]. By [39, Theorem 6.16], we can moreover take \([\Lambda \oplus \Lambda ',n,r,\gamma ]\) to be self-dual with respect to \(h\oplus h\) and \(\gamma =(\gamma _1,\gamma _2)\in \mathrm{A}\oplus \mathrm{A}\). Replacing \(\beta ,\beta '\) with \(\gamma _1,\gamma _2\), we can therefore assume that \(\beta ,\beta '\in \mathrm{A}_-\) have the same minimal polynomial over \(\mathrm{F}\). In the situation of (ii), Corollary 5.18 ensures that the strata are still concordant so this replacement is possible.
Now (i) follows from [39, Corollary 5.1], while (ii) follows from Remark 3.26(ii). \(\square \)
For later use, we also get the following corollary on similar self-dual extensions.
Corollary 5.20
Suppose \((\mathrm{E},\beta )\) and \((\mathrm{E}',\beta ')\) are similar self-dual extensions with non-zero \(\beta \) and \(\beta ^{\prime }\). Then the diagrams (3.29) and (3.30) are commutative.
Proof
There is nothing to prove in the symplectic case, while the result is given by Lemma 3.34(ii) if \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\). Thus we suppose we are in the orthogonal case: \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\) and \(\varepsilon =1\). Replacing \(\beta ,\beta '\) by \(\varpi _\mathrm{F}^{2k}\beta ,\varpi _\mathrm{F}^{2k}\beta '\) respectively, for suitable \(k<0\), we may assume that \({\text {val}}_\mathrm{E}(\beta )={\text {val}}_{\mathrm{E}'}(\beta ')<0\).
Let \((\mathrm{V},h_\mathrm{E})\) be a 2-dimensional hyperbolic space over \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\) and \(\Lambda \) a strict self-dual \({\mathfrak {o}}_\mathrm{E}\)-lattice sequence in \(\mathrm{V}\) of \({\mathfrak {o}}_\mathrm{E}\)-period 2 such that \(\Lambda (0)^{\#_{h_\mathrm{E}}}=\Lambda (0)\). By [6, Lemma 5.5], we can choose a non-zero Galois-equivariant \(\mathrm{F}\)-linear map \(\lambda :\mathrm{E}\rightarrow \mathrm{F}\) such that, setting \(h:=\lambda \circ h_\mathrm{E}\), we have
In particular, \(\Lambda (0)^{\#_{h}}=\Lambda (0)\). Doing the same with \(\mathrm{E}'/\mathrm{E}'_{\mathsf {o}}\), we obtain a space \((\mathrm{V}',h')\) isometric to \((\mathrm{V},h)\) and a regular self-dual \({\mathfrak {o}}_{\mathrm{E}'}\)-lattice sequence \(\Lambda '\) with \(e(\Lambda |{\mathfrak {o}}_\mathrm{F})=~e(\Lambda '|{\mathfrak {o}}_\mathrm{F})\) and \(\Lambda '(0)^{\#_{h'}}=\Lambda '(0)\). By [38, Proposition 5.2], there is an isometry from \((\mathrm{V},h)\) to \((\mathrm{V}',h')\) which sends \(\Lambda \) to \(\Lambda '\) so we may assume \((\mathrm{V},h)=(\mathrm{V}',h')\) and \(\Lambda =\Lambda '\).
Now \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ,n,n-1,\beta ']\) are self-dual pure strata, where \(n=-{\text {val}}_{\Lambda }(\beta )=-{\text {val}}_{\Lambda }(\beta ')\). By [12, 2.5.8,2.5.11] both strata are equivalent to simple strata in \(\gamma \)-standard form for the same \(\gamma \), since \(y_\beta ,y_{\beta '}\) have the same minimal polynomial. Thus the strata intertwine in \({{\widetilde{\mathrm{G}}}}\), and Proposition 5.19 implies that they intertwine in \(\mathrm{G}\). Now Corollary 5.14 implies that there is a \(g\in \mathrm{G}\) and an extension \(\mathrm{K}/\mathrm{F}\) contained in \(\mathrm{E}\cap g\mathrm{E}'g^{-1}\) which is stable under the adjoint anti-involution but is not fixed pointwise. Moreover, since \(\mathrm{E}/\mathrm{F}\) and \(\mathrm{E}'/\mathrm{F}\) have the same residue degree, Lemma 3.23 implies that \({\mathsf {w}}_1(\langle 1\rangle )=\langle 1\rangle \). Thus the hypotheses of Lemma 3.31 are satisfied and we conclude that the diagrams commute as required. \(\square \)
6 Self-dual simple characters: intertwining and concordance
In this section, we investigate intertwining of self-dual simple characters and concordance of their underlying simple strata. The main result is Proposition 6.10.
In previous works on self-dual simple characters it is often assumed that the characters take values in the complex numbers \({\mathbb {C}}\), for example in [42]. However, as they are characters of pro-p groups and \({\mathbf {C}}\) contains a complete set of p-power roots of unity, all of the results apply equally well over \({\mathbf {C}}\), and often we just refer to the results over \({\mathbb {C}}\).
For the rest of the paper, we fix a non-trivial character \(\psi _{{\mathsf {o}}}:\mathrm{F}_{\mathsf {o}}\rightarrow {\mathbf {C}}^\times \) of conductor \({\mathfrak {p}}_{\mathrm{F}_{\mathsf {o}}}\), and define \(\psi :\mathrm{F}\rightarrow {\mathbf {C}}^\times \) by \(\psi =\psi _{\mathsf {o}}\circ \mathrm{T}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}\).
6.1 Simple characters
Let \([\Lambda ,n,r,\beta ]\) be a non-zero simple stratum in \(\mathrm{A}\). Associated to \([\Lambda ,n,r,\beta ]\) is an \({\mathfrak {o}}_{\mathrm{F}}\)-order \({\mathfrak {H}}(\beta ,\Lambda )\) in \(\mathrm{A}\) defined inductively, see [12, §3.1] for the original definition when \(\Lambda \) is strict and [14, §5] in general. For \(m\geqslant 1\), we put
a compact open subgroup of \({{\widetilde{\mathrm{G}}}}\).
Also associated to \([\Lambda ,n,r,\beta ]\), and our fixed character \(\psi \), is a set \({\mathscr {C}}(\Lambda ,r,\beta )\) of simple characters of \({\mathrm {H}}^{r+1}(\beta ,\Lambda )\), defined in [12, §3.2] when \(\Lambda \) is strict and in [14, §5] in general. In the case of a zero simple stratum \([\Lambda ,n,n,0]\) we put \({\mathrm {H}}^{n+1}(0,\Lambda )=\mathrm{P}^{n+1}(\Lambda )\) and define the associated set of simple characters to be \({\mathscr {C}}(\Lambda ,n,0)=\{1_{\mathrm{P}^{n+1}(\Lambda )}\}\).
Given two simple strata \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ]\) in \(\mathrm{A}\), with \(\mathrm{E}=\mathrm{F}[\beta ]\), such that \(\left\lfloor \frac{r}{e(\Lambda |{\mathfrak {o}}_\mathrm{E})}\right\rfloor =\left\lfloor \frac{r'}{e(\Lambda '|{\mathfrak {o}}_\mathrm{E})}\right\rfloor \), there is a canonical bijection \(\tau _{\Lambda ',\Lambda ,\beta }:{\mathscr {C}}(\Lambda ,r,\beta )\rightarrow {\mathscr {C}}(\Lambda ',r',\beta )\) called transfer, see [12, 3.6.1], [42, Section 2.1] and [32, Section 3.1]; if \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) then \(\tau _{\Lambda ',\Lambda ,\beta }(\theta )\) is the unique simple character \(\theta '\in {\mathscr {C}}(\Lambda ',r',\beta )\) such that \(1\in {{\widetilde{\mathrm{G}}}}\) intertwines \(\theta \) with \(\theta '\). Note that, although we omit it from our notation, the transfer map depends on the integers \((r,r')\).
In general intertwining between simple characters does not imply intertwining between underlying strata, but we still have the following important implication: Suppose that \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) are simple strata and g is an element of \({{\widetilde{\mathrm{G}}}}\) which intertwines a character in \({\mathscr {C}}(\Lambda ,r,\beta )\) with a character in \({\mathscr {C}}(\Lambda ',r',\beta ')\). Then g intertwines \([\Lambda ,n,\max (n-1,r),\beta ]\) with \([\Lambda ',n',\max (n'-1,r'),\beta ']\), noting that every element of \({\mathscr {C}}(\Lambda ,r,\beta )\) and \({\mathscr {C}}(\Lambda ',r',\beta ')\) restricts to the character attached to \([\Lambda ,n,\max (n-1,r),\beta ]\) and \([\Lambda ',n',\max (n'-1,r'),\beta ']\), respectively, see [43, 2.1] and [39, 9.5].
By induction on \(k_\mathrm{F}(\beta )\), the groups and sets of simple characters only depend on the affine class of the strata:
Proposition 6.1
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ]\) be simple strata in the same affine class. Then
and the transfer map \(\tau _{\Lambda ',\Lambda ,\beta }:{\mathscr {C}}(\Lambda ,r,\beta )\rightarrow {\mathscr {C}}(\Lambda ',r',\beta )\) is the identity.
The next proposition shows how intertwining of simple characters interacts with certain arithmetic invariants of the underlying simple strata:
Proposition 6.2
(cf. [12, 3.5.1]) Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) be simple strata in \(\mathrm{A}\) satisfying \(e(\Lambda )=e(\Lambda ')\). Suppose that one of the following two conditions is satisfied:
-
(i)
\(r=r'\) and there are simple characters \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ',r,\beta ')\) which intertwine in \({{\widetilde{\mathrm{G}}}}\);
-
(ii)
\({\mathscr {C}}(\Lambda ,r,\beta )\) and \({\mathscr {C}}(\Lambda ',r',\beta ')\) intersect non-trivially.
Then, we have
Note that in the second part we allow \(r\ne r'\). The condition \(e(\Lambda )=e(\Lambda ')\) can always be obtained by changing the strata in their affine classes.
Proof
Suppose that condition (i) holds. If \(\theta \) is trivial then the first stratum is null, but then the other stratum is also null (since otherwise \([\Lambda ,r,r,0]\) would intertwine with \([\Lambda ',n',n'-1,\beta ']\), which is impossible by Lemma 5.3) and the result follows. Otherwise, both characters are non-trivial and the strata are non-null. Furthermore, by a \(\dag \)-construction we can assume that the lattice sequences are strict and regular, of the same period. Then there is an element of \({{\widetilde{\mathrm{G}}}}\) which maps \(\Lambda \) to \(\Lambda '\) so, by [12, Theorem 3.5.11], the simple characters are conjugate, and the result then follows from [12, Proposition 3.5.1].
Suppose that condition (ii) holds, and let \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\cap {\mathscr {C}}(\Lambda ',r',\beta ')\). Without loss of generality we assume that \(r\le r'\). Let \({\widetilde{\theta }}\in {\mathscr {C}}(\Lambda ',r,\beta ')\) be an extension of \(\theta \) (cf. [12, (3.2.5)]). Then \({\tilde{\theta }}\) intertwines with \(\theta \) and condition (i) holds, and we conclude by the last case. \(\square \)
The degree of a simple character \(\theta \) is the index \([\mathrm{F}[\beta ]:\mathrm{F}]\) for a stratum \([\Lambda ,n,r,\beta ]\) such that \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\); by Proposition 6.2 this is well-defined, i.e. it is independent of the choice of the stratum.
In order to prove results by induction along r, we also need to know what happens when we restrict a simple character.
Proposition 6.3
([12, Corollary 3.3.20, 3.2.5], [42, Remarks 3.14]) Let \([\Lambda ,n,r,\beta ]\) be a simple stratum and let \([\Lambda ,n,r+1,\gamma ]\) be a simple stratum equivalent to \([\Lambda ,n,r+1,\beta ]\). Then \({\mathrm {H}}^{r+1}(\beta ,\Lambda )={\mathrm {H}}^{r+1}(\gamma ,\Lambda )\) and restriction to \({\mathrm {H}}^{r+2}(\beta ,\Lambda )\) induces a surjective map \({\mathscr {C}}(\Lambda ,r,\beta )\rightarrow {\mathscr {C}}(\Lambda ,r+1,\gamma )\). Moreover, the assignment
defines a bijection \({\mathscr {C}}(\Lambda ,r,\gamma )\rightarrow {\mathscr {C}}(\Lambda ,r,\beta )\).
Let \([\Lambda ,n,r,\beta ]\) be a simple stratum and let \([\Lambda ,n,r+1,\gamma ]\) be a simple stratum equivalent to \([\Lambda ,n,r+1,\beta ]\). In this situation, we will write \(\mathrm{B}_\gamma ={\text {End}}_{\mathrm{F}[\gamma ]}(\mathrm{V})\) and \({{\widetilde{\mathrm{G}}}}_\gamma =\mathrm{B}_\gamma ^\times \). Associated to the field \(\mathrm{F}[\gamma ]\), there is a map \(s_\gamma :\mathrm{A}\rightarrow \mathrm{B}_\gamma \), called a tame corestriction (see [12, Definition 1.3.3] and [39, Definition 6.12]). If \(\theta \) belongs to \({\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta _0\in {\mathscr {C}}(\Lambda ,r,\gamma )\) is any extension of \(\theta |_{{\mathrm {H}}^{r+2}(\beta ,\Lambda )}\), then we can write \(\theta =\theta _0\psi _{\beta -\gamma +c}\), for some \(c\in {\mathfrak {a}}_{-(r+1)}(\Lambda )\). The stratum
is called a derived stratum in \(\mathrm{B}_\gamma \); this derived stratum is equivalent to a simple stratum [39, Theorem 6.14].
6.2 Self-dual simple characters
Let \([\Lambda ,n,r,\beta ]\) be a self-dual simple stratum in \(\mathrm{A}\). Then the subgroup \({\mathrm {H}}^{r+1}(\beta ,\Lambda )\) together with the set of simple characters \({\mathscr {C}}(\Lambda ,r,\beta )\) are stable under the involution \(\sigma \), and we define
Thus \({\mathrm {H}}^{r+1}_-(\beta ,\Lambda )\) is a compact open subgroup of \(\mathrm{G}\), and we have a set of self-dual simple characters of \({\mathrm {H}}^{r+1}_-(\beta ,\Lambda )\) defined by restriction:
This restriction of characters coincides with the Glauberman correspondence (see [41, §2]), and defines a bijection \({\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\rightarrow {\mathscr {C}}_-(\Lambda ,r,\beta )\). Given \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) we will call the unique \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) such that \(\theta \mid _{{\mathrm {H}}^{r+1}_-(\beta ,\Lambda )}=\theta _-\) the lift of \(\theta _-\) with respect to \((\Lambda ,r,\beta )\). (Below, we will simply write lift of \(\theta _-\), because the stratum will be given implicitly.) We also define the degree of a self-dual simple character to be the degree of any of its lift. This is well-defined by Proposition 6.2(i) and the following proposition:
A consequence of the Glauberman correspondence, see [41, 2.5], is the following proposition:
Proposition 6.4
Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',r',\beta ')\) be self-dual simple characters with lifts \(\theta \) and \(\theta '\) respectively. Then an element of \(\mathrm{G}\) intertwines \(\theta \) with \(\theta '\) if and only if it intertwines \(\theta _-\) with \(\theta _-'\).
When we restrict self-dual simple characters, as in Proposition 6.3, we may do so relative to a self-dual simple approximation \([\Lambda ,n,r+1,\gamma ]\) of our stratum. In particular, when only self-dual simple characters are considered, the derived strata we obtain will also be self-dual. Writing \(\varphi _\gamma \) for the canonical embedding of \(\mathrm{F}[\gamma ]\) in \(\mathrm{A}\) as usual, we also write \(\mathrm{G}_\gamma \) for the unitary group of the form \(h_{\varphi _\gamma }\) (defined relative to the standard linear form \(\lambda _\gamma \)).
We also have a self-dual \(\dag \)-construction for self-dual simple characters. Since self-dual simple characters are in bijection with \(\sigma \)-stable characters via Glauberman, we describe it for these. Let \([\Lambda ,n,r,\beta ]\) be a self-dual simple stratum and \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\), and denote by \(\mathrm{M}^\dag \) the Levi subgroup of \(\mathrm{G}^\dag \) which stabilizes the decomposition \(\mathrm{V}^\dag =\mathrm{V}\oplus \cdots \oplus \mathrm{V}\). There is a unique simple character \(\theta ^\dag \in {\mathscr {C}}(\Lambda ^\dag ,r,\beta ^\dag )\) whose restriction to \({\mathrm {H}}^{r+1}(\beta ^\dag ,\Lambda ^\dag )\) has the form \(\theta \otimes \cdots \otimes \theta \) (see [5, Lemma 2.7]). Moreover, by uniqueness \(\theta ^\dag \in {\mathscr {C}}^\Sigma (\Lambda ^\dag ,r,\beta ^\dag )\). If we have two self-dual simple characters \(\theta ,\theta '\) and \(g\in \mathrm{G}\) intertwines \(\theta \) with \(\theta '\) then \(g^\dag \in \mathrm{G}^\dag \) intertwines \(\theta ^\dag \) with \(\theta '^\dag \), by [26, Lemma 4.4].
6.3 Lemmas
In this subsection, we prove some partial results towards the main result in the next subsection. Let \([\Lambda ,n,r,\beta ],[\Lambda ',n,r,\beta ]\) be self-dual simple strata in \(\mathrm{A}\), put \(\mathrm{E}=\mathrm{F}[\beta ]\) and \(\mathrm{E}'=\mathrm{F}[\beta ']\). The first lemma we prove gives a strong “intertwining implies conjugacy” result in the non-symplectic case: one does not even need to assume that the intertwining takes place in \(\mathrm{G}\).
Lemma 6.5
Suppose that we are in the non-symplectic case, and let \(\theta _{-}\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_{-}\in {\mathscr {C}}_-(\Lambda ,r,\beta ')\) be self-dual simple characters with lifts \(\theta \) and \(\theta '\), respectively. Suppose that \(\theta \) and \(\theta '\) intertwine in \({{\widetilde{\mathrm{G}}}}\), then \(\theta _-\) and \(\theta '_-\) are conjugate in \(\mathrm{P}_-(\Lambda )\).
Proof
There is nothing to show if both strata are null. The proof is by induction along r. For the base case \(r=n-1\), Proposition 5.19(i) implies that the strata intertwine in \(\mathrm{G}\), and then [39, Theorem 8.5] implies that they are conjugate in \(\mathrm{P}_-(\Lambda )\). Assume now that \(r<n-1\). Since \(\theta |_{{\mathrm {H}}^{r+2}(\beta ,\Lambda )}\) and \(\theta '|_{{\mathrm {H}}^{r+2}(\beta ',\Lambda )}\) are simple characters by Proposition 6.3 (for approximations \([\Lambda ,n,r+1,\gamma ]\) and \([\Lambda ,n,r+1,\gamma ']\) of the strata with \(\beta \) and \(\beta '\) respectively), by the inductive hypothesis they are conjugate by an element of \(\mathrm{P}_-(\Lambda )\); conjugating by this element, we can assume that they are equal, so that
by [39, Proposition 9.23]. Then, by [39, Theorem 9.26], there is a self-dual simple stratum \([\Lambda ,n,r,\beta '']\) such that
Replacing \(\beta '\) by \(\beta ''\), we may therefore assume that \(\gamma '=\gamma \); that is, \([\Lambda ,n,r+1,\gamma ]\) is equivalent to both \([\Lambda ,n,r+1,\beta ]\) and \([\Lambda ,n,r+1,\beta ']\). Thus there are a skew-symmetric element c of \({\mathfrak {a}}_{-(r+1)}(\Lambda )\) and a simple character \(\theta _0\in {\mathscr {C}}^\Sigma (\Lambda ,r,\gamma )\) such that \(\theta =\theta _0\psi _{\beta -\gamma +c}\) and \(\theta '=\theta _0\psi _{\beta '-\gamma }\). Now [39, Proposition 9.17(i)] implies that the derived strata \([\Lambda ,r+1,r,s_\gamma (\beta -\gamma +c)]\) and \([\Lambda ,r+1,r,s_\gamma (\beta '-\gamma )]\) intertwine in the centralizer \({{\widetilde{\mathrm{G}}}}_\gamma \), whence also in \(\mathrm{G}_\gamma \) by the base case. But then [39, Proposition 9.27(ii)] implies that \(\theta \) and \(\theta '\) intertwine in \(\mathrm{G}\) and the result then follows from [39, Theorem 10.3]. \(\square \)
Lemma 6.6
Let \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ',r,\beta ')\) be simple characters which intertwine in \({{\widetilde{\mathrm{G}}}}\), and suppose that \(e(\Lambda )=e(\Lambda ')\). If \(\mathrm{G}\) is symplectic suppose further that \(\theta \) and \(\theta '\) intertwine in \(\mathrm{G}\). Then
-
(i)
\(e(\mathrm{E}/\mathrm{E}_{\mathsf {o}})=e(\mathrm{E}'/\mathrm{E}'_{\mathsf {o}})\);
-
(ii)
the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant.
Proof
We first prove the equality in (i). By a self-dual \(\dagger \)-construction we can reduce to the case of standard strict regular lattice sequences of the same period. By [38, Proposition 5.2] there is then an element of \(\mathrm{G}\) which maps \(\Lambda \) to \(\Lambda '\). Thus \(\theta \) and \(\theta '\) intertwine by an element of \(\mathrm{G}\), in the symplectic case by assumption and in the non-symplectic case by Lemma 6.5. Then by [39, Theorem 10.3] there is an element of \(\mathrm{G}\) which conjugates \(\theta \) to \(\theta '\) and, by [12, Theorem 3.5.8], we can conjugate to assume that both strata define the same set of simple characters. We now conclude as in the proof of Lemma 5.4, by looking at the image of the residue fields \(\mathrm {k}_\mathrm{E}\), \(\mathrm {k}_{\mathrm{E}'}\) in \({\mathfrak {a}}_0(\Lambda )/{\mathfrak {a}}_1(\Lambda )\).
We now turn to (ii). If either character is trivial then, since they intertwine, both are by Lemma 5.3; then \(\beta \) and \(\beta '\) vanish, and the result follows. Otherwise, both characters are non-trivial and both strata are non-null. From the intertwining of the two characters we find
-
\([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ',n,n-1,\beta ']\) intertwine in \(\mathrm{G}\), by restriction;
-
\(e(\mathrm{E}/\mathrm{F})=e(\mathrm{E}'/\mathrm{F})\) and \(f(\mathrm{E}/\mathrm{F})=f(\mathrm{E}'/\mathrm{F})\), by Proposition 6.2(i);
-
\(e(\mathrm{E}/\mathrm{E}_0)=e(\mathrm{E}'/\mathrm{E}'_0)\), by (i).
The result now follows from Lemma 5.17. \(\square \)
Lemma 6.7
Let \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ',r,\beta ')\) be simple characters which intertwine in \({{\widetilde{\mathrm{G}}}}\) and suppose that \(e(\Lambda )=e(\Lambda ')\). If \(\mathrm{G}\) is symplectic suppose further that the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant. Let \([\Lambda ,n,r+1,\gamma ]\) and \([\Lambda ',n,r+1,\gamma ']\) be self-dual simple strata equivalent to \([\Lambda ,n,r+1,\beta ]\) and \([\Lambda ',n,r+1,\beta ']\) respectively. Then the pairs \((\gamma ,{\varphi _\gamma })\) and \((\gamma ',{\varphi _{\gamma '}})\) are concordant.
Proof
Since the restrictions \(\theta |_{{\mathrm {H}}^{r+2}(\beta ,\Lambda )}\) and \(\theta '|_{{\mathrm {H}}^{r+2}(\beta ',\Lambda ')}\) are simple characters for \(\gamma ,\gamma '\) respectively which intertwine in \({{\widetilde{\mathrm{G}}}}\), in the non-symplectic case the result follows from Lemma 6.6. Suppose now that we are in the symplectic case. If \(r=n-1\) then \(\gamma ,\gamma '\) are both zero and there is nothing to prove, so we suppose \(r<n-1\).
If \({\text {dim}}_{\mathrm{F}[\beta ]}(\mathrm{V})\) and \({\text {dim}}_{\mathrm{F}[\gamma ]}(\mathrm{V})\) have the same parity then \((\beta ,{\varphi _\beta })\) and \((\gamma ,{\varphi _\gamma })\) are concordant, by Lemma 5.15. (Note that, since \(f(\mathrm{F}[\gamma ]/\mathrm{F})\) divides \(f(\mathrm{F}[\beta ]/\mathrm{F})\) and \(e(\mathrm{F}[\gamma ]/\mathrm{F})\) divides \(e(\mathrm{F}[\beta ]/\mathrm{F})\), if the common parity is odd then \(f(\mathrm{F}[\gamma ]/\mathrm{F})\) and \(f(\mathrm{F}[\beta ]/\mathrm{F})\) have the same 2-power divisor so \({\mathsf {w}}_{1,\gamma ,\beta }(\langle 1\rangle )=\langle 1\rangle \), by Lemma 3.23.) Since the invariants for \(\beta ',\gamma '\) are the same as for \(\beta ,\gamma \) respectively (by Proposition 6.2), we also have that \((\beta ',{\varphi _{\beta '}})\) and \((\gamma ',{\varphi _{\gamma '}})\) are concordant, and the result follows by transitivity of concordance.
Otherwise, \({\text {dim}}_{\mathrm{F}[\beta ]}(\mathrm{V})\) is odd and \({\text {dim}}_{\mathrm{F}[\gamma ]}(\mathrm{V})\) is even. Let \([\Lambda ,n,n-1,\gamma _0]\) be a simple stratum equivalent to \([\Lambda ,n,n-1,\gamma ]\), so that \({\text {dim}}_{\mathrm{F}[\gamma _0]}(\mathrm{V})\) is also even. As in the previous case, the pairs \((\gamma ,{\varphi _\gamma })\) and \((\gamma _0,\varphi _{\gamma _0})\) are concordant. Using analogous notation for \(\beta ',\gamma '\), we also have concordant pairs \((\gamma ',{\varphi _{\gamma '}})\) and \((\gamma '_0,\varphi _{\gamma '_0})\). Finally, since \(-1\) is a square in \(\mathrm{F}[\beta ]\) if and only if it is a square in \(\mathrm{F}[\beta ']\), it follows from Lemma 5.16 (see also the remark following that lemma) and the fact that \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant that \((\gamma _0,\varphi _{\gamma _0})\) and \((\gamma '_0,\varphi _{\gamma '_0})\) are also concordant. The result again follows by transitivity. \(\square \)
6.4 Intertwining self-dual simple characters
In the main result of the section, Proposition 6.10 below, we investigate the relation between \(\mathrm{G}\)-intertwining of self-dual simple characters and \({{\widetilde{\mathrm{G}}}}\)-intertwining of their lifts. This improves Lemma 6.5 in the non-symplectic case to allow for non-conjugate lattice sequences, and proves the analogue in the symplectic case using concordance. We start with the case of the same lattice sequence:
Proposition 6.8
Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ,r,\beta ')\) be self-dual simple characters with lifts \(\theta \) and \(\theta '\) respectively. Then the following assertions are equivalent:
-
(i)
\(\theta _-\) and \(\theta '_-\) are conjugate in \(\mathrm{P}_-(\Lambda )\).
-
(ii)
\(\theta _-\) and \(\theta '_-\) intertwine in \(\mathrm{G}\).
-
(iii)
\(\theta \) and \(\theta '\) are conjugate in \(\mathrm{P}(\Lambda )\) and the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant.
-
(iv)
\(\theta \) and \(\theta '\) intertwine in \({{\widetilde{\mathrm{G}}}}\) and the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant.
Proof
The first equivalence (i)\(\Leftrightarrow \)(ii) and the last equivalence (iii)\(\Leftrightarrow \)(iv) follow from [39, Theorem 10.2 and 10.3]. So we only have to prove the second equivalence (ii)\(\Leftrightarrow \)(iii).
If \(\theta _-\) and \(\theta '_-\) intertwine in \(\mathrm{G}\), then their lifts intertwine in \(\mathrm{G}\) and hence are conjugate by an element of \(\mathrm{P}(\Lambda )\), by [39, Theorem 10.2] (see also [12, 3.5.11] when \(\Lambda \) is strict). Moreover, by Lemma 6.6, the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant.
We prove the converse by induction along r. If \(r=n-1\) then the simple characters \(\theta ,\theta '\) (that is, the strata \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ,n,n-1,\beta ']\)) intertwine in \(\mathrm{G}\) by Proposition 5.19. The proof of the inductive step is now identical to that in Lemma 6.5, with two small additional arguments: first we use Lemma 6.7 and the induction hypothesis to conjugate \(\theta |_{{\mathrm {H}}^{r+2}(\beta ,\Lambda )}\) to \(\theta '|_{{\mathrm {H}}^{r+2}(\beta ',\Lambda )}\); secondly, when we obtain derived strata \([\Lambda ,r+1,r,s_\gamma (\beta -\gamma +c)]\) and \([\Lambda ,r+1,r,s_\gamma (\beta '-\gamma )]\) which intertwine in the centralizer \({{\widetilde{\mathrm{G}}}}_\gamma \), Proposition 5.19(i) implies that, since \(\mathrm{G}_\gamma \) is a unitary group, these strata intertwine in \(\mathrm{G}_\gamma \). \(\square \)
From Proposition 6.8 we now get a strengthening (in the symplectic case) of Lemma 6.6(i).
Corollary 6.9
Let \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ',r,\beta ')\) be simple characters which intertwine in \({{\widetilde{\mathrm{G}}}}\), and suppose that \(e(\Lambda )=e(\Lambda ')\). Then \((\mathrm{E},\beta )\) and \((\mathrm{E}',\beta ')\) are similar self-dual extensions (see Definition 3.33).
Proof
We already know, by Proposition 6.2, that \(\mathrm{E}/\mathrm{F}\) and \(\mathrm{E}'/\mathrm{F}'\) have the same ramification index and residue class degree, and, by Lemma 5.2 applied to the pure strata \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ',n,n-1,\beta ']\), that the elements \(y_\beta \) and \(y_{\beta '}\) have the same (irreducible) minimal polynomial over \(\mathrm {k}_\mathrm{F}\). Since \({\text {val}}_\mathrm{E}(\beta )=-n e(\mathrm{E}/\mathrm{F})/e(\Lambda )={\text {val}}_{\mathrm{E}'}(\beta ')\), it only remains to show that \(e(\mathrm{E}/\mathrm{E}_{\mathsf {o}})=e(\mathrm{E}'/\mathrm{E}'_{\mathsf {o}})\).
For this, by a self-dual \(\dag \)-construction, we may assume further that the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant, by Lemma 5.8. The proof is now the same as that of Lemma 6.6(i), except that we use Proposition 6.8 to obtain that the characters \(\theta ^\dag \) and \(\theta '^\dag \) intertwine in \(\mathrm{G}^\dag \). \(\square \)
Proposition 6.10
Let \(\theta _-\in {\mathscr {C}}_{-}(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_{-}(\Lambda ',r,\beta ')\) be self-dual simple characters of \(\mathrm{G}\), and suppose that \(e(\Lambda )=e(\Lambda ')\). Then \(\theta _-\) and \(\theta '_-\) intertwine in \(\mathrm{G}\) if and only if their lifts intertwine in \({{\widetilde{\mathrm{G}}}}\) and the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant.
We remark that, in the non-symplectic case the hypothesis on concordance is in fact not necessary: if the lifts of \(\theta _-\) and \(\theta '_-\) intertwine in \({{\widetilde{\mathrm{G}}}}\) then, by Lemma 6.6, the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are automatically concordant.
To prove Proposition 6.10, we will need the following lemma:
Lemma 6.11
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ']\) be self-dual simple strata and let \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ',r,\beta ')\). Suppose that \(\theta ,\theta '\) intertwine in \({{\widetilde{\mathrm{G}}}}\) and that the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant. Then, there are self-dual simple strata \([\Lambda ,n,r,\beta _1]\) and \([\Lambda ',n,r,\beta '_1]\) such that \(\beta _1\) and \(\beta '_1\) have the same characteristic polynomial, \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta _1)\) and \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ',r,\beta '_1)\). Moreover, for any such \(\beta _1,\beta '_1\), the pairs \((\beta _1,\varphi _{\beta _1})\) and \((\beta '_1,\varphi _{\beta '_1})\) are concordant.
Granting this, we complete the proof of Proposition 6.10:
Proof
Let \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ',r,\beta ')\) denote the lifts of \(\theta _-\) and \(\theta '_-\), respectively. Suppose first that \(\theta \) and \(\theta '\) intertwine by an element of \(\mathrm{G}\). Then they intertwine by an element of \({{\widetilde{\mathrm{G}}}}\) and, by Lemma 6.6(ii), the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant.
Suppose now that \(\theta \) and \(\theta '\) intertwine by an element of \({{\widetilde{\mathrm{G}}}}\) and the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant. By Lemma 6.11 we can assume that \(\beta \) and \(\beta '\) have the same characteristic polynomial and the pairs \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are still concordant; thus, by Remark 3.26(ii), they are conjugate by an element \(g\in \mathrm{G}\). The characters \(\theta \) and \(\theta '':=\tau _{g\Lambda ,\Lambda ',\beta '}(\theta ')\) intertwine by an element of \({{\widetilde{\mathrm{G}}}}\) by [5, Theorem 1.11]. Thus \(\theta \) and \(\theta ''\) are conjugate by an element of \(\mathrm{G}\), by Proposition 6.8. We deduce that \(\theta \) and \(\theta '\) intertwine in \(\mathrm{G}\), since \(\theta '\) and \(\theta ''\) are intertwined by 1. \(\square \)
It remains only to prove Lemma 6.11:
Proof
The proof is by induction along r. There is nothing to show if both strata are null so we assume that they are both non-null; in particular both characters are non-trivial.
The base case is \(r=n-1\). Applying [39, Proposition 7.1], as in the proof of Proposition 5.19, we can replace \(\beta \) and \(\beta '\) by elements \(\beta _1\) and \(\beta '_1\) without changing the equivalence classes of the simple self-dual strata and such that \(\beta _1\) and \(\beta '_1\) have the same minimal polynomial. Proposition 5.19(ii) also implies that the strata intertwine in \(\mathrm{G}\). Thus the pairs \((\beta _1,\varphi _{\beta _1})\) and \((\beta '_1,\varphi _{\beta '_1})\) are concordant by Corollary 5.18.
Suppose now that \(r<n-1\) and let \([\Lambda ,n,r+1,\gamma ]\) and \([\Lambda ',n,r+1,\gamma ']\) be self-dual simple strata equivalent to \([\Lambda ,n,r+1,\beta ]\) and \([\Lambda ',n,r+1,\beta ']\) respectively. Note that the pairs \((\gamma ,{\varphi _\gamma })\) and \((\gamma ',{\varphi _{\gamma '}})\) are concordant, by Lemma 6.7. By the induction hypothesis there are concordant self-dual simple strata \([\Lambda ,n,r+1,\gamma _1]\) and \([\Lambda ',n,r+1,\gamma '_1]\), such that \({\mathscr {C}}(\Lambda ,r+1,\gamma )={\mathscr {C}}(\Lambda ,r+1,\gamma _1)\) and \({\mathscr {C}}(\Lambda ',r+1,\gamma ')={\mathscr {C}}(\Lambda ',r+1,\gamma '_1)\) and such that the minimal polynomials of \(\gamma _1\) and \(\gamma '_1\) coincide. By Remark 3.26(ii), concordance provides an element g of \(\mathrm{G}\) such that \(g\gamma _1g^{-1}=\gamma '_1\). Now, \(\theta |_{{\mathrm {H}}^{r+2}(\gamma _1,\Lambda )}\) and \(\tau _{g\Lambda ,\Lambda ',\gamma '_1}(\theta '|_{{\mathrm {H}}^{r+2}(\gamma '_1,\Lambda ')})\) intertwine by an element of \({{\widetilde{\mathrm{G}}}}\) by [5, Theorem 1.11], so Proposition 6.8 implies they are conjugate by an element of \(\mathrm{G}\) which maps \(\Lambda \) to \(g\Lambda \). Thus, conjugating by this element, we can assume that \(\theta |_{{\mathrm {H}}^{r+2}(\gamma _1,\Lambda )}=\tau _{\Lambda ,\Lambda ',\gamma '_1}(\theta '|_{{\mathrm {H}}^{r+2}(\gamma '_1,\Lambda ')})\) and that \(\gamma _1=\gamma '_1\).
By [39, Theorem 9.26], there is a self-dual simple stratum \([\Lambda ,n,r,\beta _0]\) such that
moreover, the pairs \((\beta ,{\varphi _\beta })\) and \((\beta _0,\varphi _{\beta _0})\) are concordant, by Lemma 6.6. Thus we may replace \(\beta \) by \(\beta _0\) and assume that \(\gamma =\gamma _1\). By the same argument for \(\beta '\), we see that we may assume \(\gamma =\gamma '\). Then there are a character \(\theta _0\in {\mathscr {C}}^\Sigma (\Lambda ,r,\gamma )\) with transfer \(\theta '_0\in {\mathscr {C}}^\Sigma (\Lambda ',r,\gamma )\) and an element \(c\in {\mathfrak {a}}^-_{-(1+r)}(\Lambda ')\) such that
By a self-dual \(\dag \)-construction we obtain characters
which intertwine in \({{\widetilde{\mathrm{G}}}}^\dag \). Moreover, there exists an element \(g\in {{\widetilde{\mathrm{G}}}}^\dag _{\gamma ^\dag }\) such that \(g\Lambda ^\dag =\Lambda '^\dag \); then \(^g\theta _0^\dag =\theta '^\dag _0\), because \(\tau _{\Lambda '^\dag ,\Lambda ^\dag ,\gamma ^\dag }(\theta _0^\dag )=\theta '^\dag _0\) (as, by its definition, the \(\dag \)-construction commutes with transfer). Writing s for a tame corestriction with respect to \(\gamma ^\dag \), the strata \([g\Lambda ^\dag ,r+1,r,s(g\beta ^\dag g^{-1}-\gamma ^\dag )]\) and \([\Lambda '^\dag ,r+1,r,s(\beta '^\dag -\gamma ^\dag +c^\dag )]\) intertwine by an element of \({{\widetilde{\mathrm{G}}}}^\dag _{\gamma ^\dag }\), by [39, Proposition 9.17(i)]. Conjugating by this element, we may apply [39, Proposition 7.6], which then implies that the strata \([\Lambda ^\dag ,n,r,\beta ^\dag ]\) and \([\Lambda '^\dag ,n,r,\beta '^\dag +c^\dag ]\) intertwine.
Since \(\psi _{c^\dag }\) is intertwined by \({{\widetilde{\mathrm{G}}}}_\gamma \), it follows from [12, 2.4.11] that \(s(c^\dag )\) is congruent to an element of \(\mathrm{F}[\gamma ]\) modulo \({\mathfrak {a}}_{-r}(\Lambda '^\dag )\). Thus \([\Lambda '^\dag ,n,r,(\beta '+c)^\dag ]\) is equivalent to a simple stratum by [39, Proposition 6.14]. Since it intertwines with \([\Lambda ^\dag ,n,r,\beta ^\dag ]\), the stratum \([\Lambda ^\dag \oplus \Lambda '^\dag ,n,r,\beta ^\dag +(\beta '+c)^\dag ]\) is also equivalent to a simple stratum, by [39, Proposition 7.1]. Then [39, Theorem 6.16] implies that it is moreover equivalent to a simple stratum which is split by the decomposition \(\mathrm{V}^\dag \oplus \mathrm{V}^\dag =\mathrm{V}\oplus \cdots \oplus \mathrm{V}\). In particular, restricting to two copies of \(\mathrm{V}\), we see that \([\Lambda \oplus \Lambda ',n,r,\beta +(\beta '+c)]\) is equivalent to a simple stratum, and again, by [39, Theorem 6.16], to a self-dual simple stratum \([\Lambda \oplus \Lambda ',n,r,\beta _1+\beta '_1]\) split by \(\mathrm{V}\oplus \mathrm{V}\).
Thus we have found self-dual simple strata \([\Lambda ,n,r,\beta _1]\) and \([\Lambda ',n,r,\beta '_1]\) equivalent to \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta '+c]\) respectively, such that \(\beta _1\) and \(\beta '_1\) have the same minimal polynomial. Then \({\mathscr {C}}(\Lambda ,r,\beta )\) and \({\mathscr {C}}(\Lambda ,r,\beta _1)\) coincide, while
so we are done.
Finally, we prove that the pairs \((\beta _1,\varphi _{\beta _1})\) and \((\beta '_1,\varphi _{\beta '_1})\) are concordant. Since \(\theta \) lies in \({\mathscr {C}}(\Lambda ,r,\beta )\) and in \({\mathscr {C}}(\Lambda ,r,\beta _1)\), Proposition 6.6(ii) implies that \((\beta ,{\varphi _\beta })\) and \((\beta _1,\varphi _{\beta _1})\) are concordant; similarly \((\beta ',{\varphi _{\beta '}})\) and \((\beta '_1,\varphi _{\beta '_1})\) are concordant. Since \((\beta ,{\varphi _\beta })\) and \((\beta ',{\varphi _{\beta '}})\) are concordant by assumption, the result follows by transitivity of concordance. \(\square \)
7 Self-dual ps-characters and simple endo-classes
In this section we consider the collection of all self-dual simple characters while varying our \(\varepsilon \)-hermitian space, for fixed \(\varepsilon \) and \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\). We first recall results of Bushnell and Henniart [8], and their extensions to non-strict lattice sequences which are special cases of results in [5], on the foundational theory of ps-characters and simple endo-classes. Then we develop the theory in the presence of an \(\varepsilon \)-hermitian form over \(\mathrm{F}\).
For the remainder, while our \(\mathrm{F}\)-vector space \(\mathrm{V}\) and \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) over \(\mathrm{F}\) may be varying, we still use the notation \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_\mathrm{F}(\mathrm{V})\) and \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\).
7.1 Ps-characters
A simple pair over \(\mathrm{F}\) is a pair \((k,\beta )\) consisting of an element \(\beta \) of some finite field extension of \(\mathrm{F}\) and an integer k satisfying \(0\leqslant k<-k_\mathrm{F}(\beta )e(\mathrm{F}[\beta ]/\mathrm{F})\). For \((k,\beta )\) a simple pair, we write \(\mathrm{E}=\mathrm{F}[\beta ]\) and denote by \({\mathscr {Q}}(k,\beta )\) the class of all quadruples \((\mathrm{V},\varphi ,\Lambda ,r)\) consisting of
-
(i)
a finite dimensional \(\mathrm{F}\)-vector space \(\mathrm{V}\);
-
(ii)
an embedding \(\varphi :\mathrm{E}\hookrightarrow \mathrm{A}\), where \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\);
-
(iii)
an \({\mathfrak {o}}_{\varphi (\mathrm{E})}\)-lattice sequence \(\Lambda \) in \(\mathrm{V}\);
-
(iv)
and an integer r such that \(\left\lfloor r/e(\Lambda |{\mathfrak {o}}_{\varphi (\mathrm{E})})\right\rfloor =k\).
In this situation, we will abuse notation and write \(e(\Lambda |{\mathfrak {o}}_\mathrm{E})\) for \(e(\Lambda |{\mathfrak {o}}_{\varphi (\mathrm{E})})\), the period of \(\Lambda \) as an \({\mathfrak {o}}_{\varphi (\mathrm{E})}\)-lattice sequence. We will also abbreviate \(e(\Lambda )=e(\Lambda |{\mathfrak {o}}_\mathrm{F})\) for the period of \(\Lambda \) as an \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence.
Given \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\), we set
we then obtain a simple stratum \([\Lambda ,n,r,\varphi (\beta )]\) in \(\mathrm{A}\) which we call a realization of the simple pair \((k,\beta )\). It is simple because \(k_0(\beta ,\Lambda )=e(\Lambda |{\mathfrak {o}}_\mathrm{E})e(\mathrm{E}/\mathrm{F})k_\mathrm{F}(\beta )\) by [12, 1.4.13] (see also [14, 5.1]).
We let \({\mathfrak {C}}(k,\beta )\) denote the collection of all simple characters defined by a realization of a simple pair \((k,\beta )\):
Given two realizations \([\Lambda ,n,r,\varphi (\beta )]\) and \([\Lambda ',n',r',\varphi '(\beta )]\) of a simple pair \((k,\beta )\) there is a canonical bijection
defined in [12, 3.6.14], [42, Section 2.1] and [32, Section 3.1(53)], called transfer, and generalizing the transfer recalled in the previous section. Although the transfer depends on \(r,r'\), we do not include them in our notation; indeed, we will usually omit \(\varphi ',\varphi \) also and just write \(\tau _{\Lambda ',\Lambda ,\beta }\), as is usual in the literature.
We recall briefly some of the main properties of transfer. Given realizations \([\Lambda ,n,r,\varphi (\beta )]\), \([\Lambda ',n',r',\varphi '(\beta )]\), and \([\Lambda '',n'',r'',\varphi ''(\beta )]\) of a simple pair \((k,\beta )\), the associated transfer maps satisfy the following:
-
(symmetry) \(\tau _{\Lambda ,\Lambda ',\beta }=\tau _{\Lambda ',\Lambda ,\beta }^{-1}\);
-
(transitivity) \(\tau _{\Lambda '',\Lambda ,\beta }=\tau _{\Lambda '',\Lambda ',\beta }\circ \tau _{\Lambda ',\Lambda ,\beta }\);
-
(intertwining) suppose the embeddings \(\varphi ,\varphi '\) have image in the endomorphisms of the same space \(\varphi ,\varphi ':\mathrm{E}\hookrightarrow {\text {End}}_\mathrm{F}(\mathrm{V})\), and let \(\theta \in {\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\); then \(\tau _{\Lambda ',\Lambda ,\beta }(\theta )\) is the unique simple character \(\theta '\in {\mathscr {C}}(\Lambda ',r',\varphi '(\beta ))\) such that \(\theta \) is intertwined with \(\theta '\) by an element of \({{\widetilde{\mathrm{G}}}}\) which conjugates \(\varphi \) to \(\varphi '\).
In the final property, in fact every element of \({{\widetilde{\mathrm{G}}}}\) which conjugates \(\varphi \) to \(\varphi '\) also intertwines \(\theta \) with its transfer \(\tau _{\Lambda ',\Lambda ,\beta }(\theta )\).
It is also possible to describe the transfer map explicitly in terms of restrictions. Suppose we are given realizations \([\Lambda ,n,r,\varphi (\beta )]\) and \([\Lambda ',n',r',\varphi '(\beta )]\) of a simple pair \((k,\beta )\) on spaces \(\mathrm{V},\mathrm{V}'\) respectively, and \(\Lambda ,\Lambda '\) have the same period (so that also \(n'=n\)). We set \(\mathrm{V}''=\mathrm{V}\oplus \mathrm{V}'\) so that we have an embedding \(\varphi ''=\varphi +\varphi '\) of \(\mathrm{E}\) in \({\text {End}}_\mathrm{F}(\mathrm{V}'')\); we also set \(\Lambda ''=\Lambda \oplus \Lambda '\) and \(r''=\min \{r,r'\}\). Then we get a further realization \([\Lambda '',n,r'',\varphi ''(\beta )]\) on \(\mathrm{V}''\). Now, given a simple character \(\theta \in {\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) there is a unique simple character \(\theta ''\in {\mathscr {C}}(\Lambda '',r'',\varphi ''(\beta ))\) such that \(\theta \) is the restriction of \(\theta ''\) to \({\mathrm {H}}^{r+1}(\varphi ''(\beta ),\Lambda '')\cap {\text {Aut}}_\mathrm{F}(\mathrm{V})\). Then the transfer \(\theta '=\tau _{\Lambda ',\Lambda ,\beta }(\theta )\) is the restriction of \(\theta ''\) to \({\mathrm {H}}^{r'+1}(\varphi ''(\beta ),\Lambda '')\cap {\text {Aut}}_\mathrm{F}(\mathrm{V}')\).
A potential simple character, or ps-character, supported on the simple pair \((k,\beta )\) is a function \(\Theta :{\mathscr {Q}}(k,\beta )\rightarrow {\mathfrak {C}}(k,\beta )\) such that
-
(i)
\(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\), for \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\);
-
(ii)
\(\Theta (\mathrm{V}',\varphi ',\Lambda ',r')=\tau _{\Lambda ',\Lambda ,\beta }(\Theta (\mathrm{V},\varphi ,\Lambda ,r)),\) for \((\mathrm{V},\varphi ,\Lambda ,r),(\mathrm{V}',\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta )\).
For \((\mathrm{V},\varphi ,\Lambda ,r) \in {\mathscr {Q}}(k,\beta )\), we call \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) a realization of \(\Theta \). Thus, by property (ii), a ps-character is determined by any one of its realizations. We define the degree of \(\Theta \) to be \(\deg (\Theta )=[\mathrm{F}[\beta ]:\mathrm{F}]\).
Let \(\Theta ,\Theta '\) be ps-characters supported on the simple pairs \((k,\beta ),(k',\beta ')\) respectively.
Definition 7.1
We say that \(\Theta \) and \(\Theta '\) are endo-equivalent, denoted \(\Theta \approx \Theta '\), if
-
(i)
\(\deg (\Theta )=\deg (\Theta ')\);
-
(ii)
\(k=k'\);
-
(iii)
there exist realizations on a common \(\mathrm{F}\)-vector space which intertwine, i.e. there exist a finite dimensional \(\mathrm{F}\)-vector space \(\mathrm{V}\) and quadruples \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\) and \((\mathrm{V},\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k',\beta ')\), such that \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\Theta '(\mathrm{V},\varphi ',\Lambda ',r')\) intertwine in \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_\mathrm{F}(\mathrm{V})\).
Note that the formulation of endo-equivalence in [8, 8.6] and [5, 1.10] differs mildly from the above. In particular they do not consider ps-characters with a trivial character in the image. Therefore we need the following remarks.
Remarks 7.2
-
(i)
In Definition 7.1(iii), we could impose that \(\Lambda =\Lambda '\) and that \(\Lambda \) is strict without changing the relation. Indeed, suppose that \(\Lambda \ne \Lambda '\) or \(\Lambda \) is not strict. By changing the lattice sequences in their affine classes, we can assume that \(e(\Lambda )=e(\Lambda ')\). Then, performing a \(\dag \)-construction, there exists \(g\in {{\widetilde{\mathrm{G}}}}^\dag \) such that \(g\Lambda ^\dag =\Lambda '^\dag \), and the characters \(^g\theta ^\dag =\tau _{g\Lambda ^\dag , ^g\varphi ^\dag ,\Lambda ,\varphi ,\beta }(\theta )\) and \(\theta '^\dag =\tau _{\Lambda '^\dag ,\varphi '^\dag ,\Lambda ',\varphi ',\beta }(\theta ')\) intertwine in \({{\widetilde{\mathrm{G}}}}^\dag \), because \(\theta \) and \(\theta '\) intertwine in \({{\widetilde{\mathrm{G}}}}\).
-
(ii)
For every non-negative integer k we have exactly one ps-character supported on (k, 0), which we call the zero ps-character \(\mathbf{0}_k\). It is not endo-equivalent to any other ps-character, which can be seen as follows. Suppose \(\Theta \) is a ps-character supported on \((k,\beta )\), with \(\beta \ne 0\), which is endo-equivalent to \(\mathbf{0}_k\). Then \(\mathrm{F}[\beta ]=\mathrm{F}\) and there are realizations \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) of \(\Theta \) and \(\theta '\in {\mathscr {C}}(\Lambda ',r',0)\) of \(\mathbf{0}_k\) on the same vector space such that \(e(\Lambda )=e(\Lambda ')\) and \(\theta ,\theta '\) intertwine. We then get
$$\begin{aligned} \left\lfloor r'/e(\Lambda )\right\rfloor =k<\frac{-k_0(\beta ,\Lambda )}{e(\Lambda )}=\frac{-{\text {val}}_{\Lambda }(\beta )}{e(\Lambda )}\in {\mathbb {Z}}, \end{aligned}$$but this contradicts Lemma 5.3.
-
(iii)
It follows from the previous remarks and [8, Corollary 8.10] that endo-equivalence is indeed an equivalence relation.
We can now state some initial results on endo-equivalence of ps-characters from [8].
Proposition 7.3
(cf. [8, 8.4, 8.10]). Let \(\Theta ,\Theta '\) be ps-characters supported on the simple pairs \((k,\beta ),(k,\beta ')\) respectively, and put \(\mathrm{E}=\mathrm{F}[\beta ]\) and \(\mathrm{E}'=\mathrm{F}[\beta ']\). Suppose that \(\Theta \approx \Theta '\). Then:
-
(i)
We have \(e(\mathrm{E}/\mathrm{F})=e(\mathrm{E}'/\mathrm{F})\), \(f(\mathrm{E}/\mathrm{F})=f(\mathrm{E}'/\mathrm{F})\) and \(k_\mathrm{F}(\beta )=k_\mathrm{F}(\beta ')\).
-
(ii)
If \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\), \((\mathrm{V},\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta ')\) and \(e(\Lambda )=e(\Lambda ')\) then we have \((\mathrm{V},\varphi ,\Lambda ,r')\in {\mathscr {Q}}(k,\beta )\), i.e. \(\left\lfloor \frac{r'}{e(\Lambda |{\mathfrak {o}}_\mathrm{E})}\right\rfloor =k\).
Proof
If \(\Theta \) is zero then \(\Theta '=\Theta \) by Remark 7.2(ii), and the result follows, so we suppose both \(\Theta ,\Theta '\) are non-zero. Then (i) follows from Remark 7.2(i) and [8, Proposition 8.4]. By (i) we have \(e(\Lambda |{\mathfrak {o}}_\mathrm{E})=\frac{e(\Lambda )}{e(\mathrm{E}/\mathrm{F})}=e(\Lambda '|{\mathfrak {o}}_{\mathrm{E}'})\) and thus
which proves (ii). \(\square \)
Definition 7.4
We call the equivalence classes of ps-characters under endo-equivalence simple endo-classes. We define the degree of a simple endo-class to be the degree of any ps-character in the equivalence class.
A miracle of the theory is that, while endo-equivalence is defined via the existence of realizations on a common vector space which intertwine (property (iii) of the definition), all realizations of endo-equivalent ps-characters on common vector spaces intertwine:
Theorem 7.5
(cf. [5, Theorem 1.11] and [8, Corollary 8.7]) Let \(\Theta ,\Theta '\) be endo-equivalent ps-characters supported on the simple pairs \((k,\beta ),(k,\beta ')\) respectively. Let \(\theta ,\theta '\) be realizations of \(\Theta ,\Theta '\) respectively, on the same vector space \(\mathrm{V}\). Then, \(\theta \) and \(\theta '\) intertwine in \({{\widetilde{\mathrm{G}}}}\).
Proof
Without loss of generality, we can assume \(\theta \in {\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) and \(\theta '\in {\mathscr {C}}(\Lambda ',r',\varphi '(\beta '))\), for simple strata \([\Lambda ,n,r,\varphi (\beta )]\) and \([\Lambda ',n',r',\varphi '(\beta ')]\) with \(e(\Lambda )=e(\Lambda ')\) by adjusting the strata in their affine classes. If one of the ps-characters is zero then \(\theta \) and \(\theta '\) are trivial and therefore intertwine. Thus we assume that both ps-characters are non-zero.
We first consider the case \(r=r'\). By Proposition 7.3(i) we can apply Lemma 5.1 to find an \({\mathfrak {o}}_{\varphi '(\mathrm{E}')}\)-lattice sequence \(\Lambda ''\) in \(\mathrm{V}\) and an element \(g\in {{\widetilde{\mathrm{G}}}}\) such that \(g\Lambda ''=\Lambda \). Then \(\theta \) and  are conjugate in \({{\widetilde{\mathrm{G}}}}\) by [5, 1.13]. Thus \(\theta \) and \(\Theta '(\mathrm{V},\varphi ',\Lambda '',r')\) are conjugate and hence, as the latter is intertwined with \(\theta '\) by 1, we see that \(\theta \) and \(\theta '\) intertwine.
are conjugate in \({{\widetilde{\mathrm{G}}}}\) by [5, 1.13]. Thus \(\theta \) and \(\Theta '(\mathrm{V},\varphi ',\Lambda '',r')\) are conjugate and hence, as the latter is intertwined with \(\theta '\) by 1, we see that \(\theta \) and \(\theta '\) intertwine.
We now assume, without loss of generality, that \(r\le r'\). The quadruple \((\mathrm{V},\varphi ',\Lambda ',r)\) is an element of \({\mathscr {Q}}(k,\beta )\) by Proposition 7.3(ii), and by the \(r=r'\) case the characters \(\theta \) and \(\Theta '(\mathrm{V},\varphi ',\Lambda ',r)\) intertwine. Thus \(\theta \) and \(\theta '\) intertwine because \(\theta '\) is the restriction of \(\Theta '(\mathrm{V},\varphi ',\Lambda ',r)\). \(\square \)
That endo-equivalence is a transitive relation leads to the following transitivity of intertwining statement for simple characters:
Theorem 7.6
Let \(\theta _i\in {\mathscr {C}}(\Lambda _i,r_i,\beta _i)\), for \(i=1,2,3\). Suppose that \(\theta _1\) and \(\theta _2\) intertwine in \({{\widetilde{\mathrm{G}}}}\), \(\theta _2\) and \(\theta _3\) intertwine in \({{\widetilde{\mathrm{G}}}}\), and that either
-
(i)
\(\left\lfloor \frac{r_1}{e(\Lambda _1|{\mathfrak {o}}_{\mathrm{E}_1})}\right\rfloor = \left\lfloor \frac{r_2}{e(\Lambda _2|{\mathfrak {o}}_{\mathrm{E}_2})}\right\rfloor = \left\lfloor \frac{r_3}{e(\Lambda _3|{\mathfrak {o}}_{\mathrm{E}_3})}\right\rfloor \) and \(\theta _1,\theta _2\) and \(\theta _3\) have the same degree; or
-
(ii)
\(e(\Lambda _1)=e(\Lambda _2)=e(\Lambda _3)\) and \(r_1=r_2=r_3\).
Then \(\theta _1\) and \(\theta _3\) intertwine in \({{\widetilde{\mathrm{G}}}}\).
Proof
In case (i), let \(\Theta _i\) be the ps-character with realization \(\theta _i\) in \({\mathscr {C}}(\Lambda _i,r_i,\beta _i)\), for \(i=1,2,3\). We have \(\Theta _1\approx \Theta _2\) and \(\Theta _2\approx \Theta _3\) by assumption, and thus \(\Theta _1\approx \Theta _3\) by transitivity, and therefore \(\theta _1\) and \(\theta _3\) intertwine by Theorem 7.5. Case (ii) follows from case (i) by Proposition 6.2(i). \(\square \)
7.2 Self-dual ps-characters
We fix the extension \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), as usual let  denote the generator of \({\text {Gal}}(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\), and fix a sign \(\varepsilon =\pm 1\). In this section we introduce the theory of endo-class for self-dual simple characters under an \(\varepsilon \)-hermitian form over \(\mathrm{F}\).
denote the generator of \({\text {Gal}}(\mathrm{F}/\mathrm{F}_{\mathsf {o}})\), and fix a sign \(\varepsilon =\pm 1\). In this section we introduce the theory of endo-class for self-dual simple characters under an \(\varepsilon \)-hermitian form over \(\mathrm{F}\).
A simple pair \((k,\beta )\) over \(\mathrm{F}\) is called self-dual if \((\mathrm{E},\beta )\) is a self-dual extension of \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\). For \((k,\beta )\) a self-dual simple pair, we denote by \({\mathscr {Q}}_-(k,\beta )\) the class of all quadruples \(((\mathrm{V},h),\varphi ,\Lambda ,r)\) consisting of
-
(i)
a finite-dimensional \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\);
-
(ii)
a self-dual embedding \(\varphi :\mathrm{E}\rightarrow \mathrm{A}\), where \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\);
-
(iii)
a self-dual \({\mathfrak {o}}_{\varphi (\mathrm{E})}\)-lattice sequence \(\Lambda \) in \(\mathrm{V}\);
-
(iv)
and an integer r such that \(\left\lfloor r/e(\Lambda |{\mathfrak {o}}_{\varphi (\mathrm{E})})\right\rfloor =k\).
In particular, we then have \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\). Given \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) we obtain a self-dual simple stratum \([\Lambda ,n,r,\varphi (\beta )]\) which we call a self-dual realization of the simple pair \((k,\beta )\).
Let \((k,\beta )\) be a self-dual simple pair. By [42, Proposition 2.12], if we have self-dual realizations \([\Lambda ,n,r,\varphi (\beta )]\) and \([\Lambda ',n',r',\varphi '(\beta )]\) of \((k,\beta )\), then the transfer map \(\tau _{\Lambda ',\Lambda ,\beta }\) commutes with the involutions defined on \({\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) and \({\mathscr {C}}(\Lambda ',r',\varphi '(\beta ))\) and restricts to give a bijection
We let \({\mathfrak {C}}_-(k,\beta )\) denote the collection of all self-dual simple characters defined by a realization of the self-dual simple pair \((k,\beta )\):
Definition 7.7
Let \((k,\beta )\) be a self-dual simple pair.
-
(i)
A ps-character \(\Theta \) supported on \((k,\beta )\) is called \(\sigma \)-invariant if, for all quadruples \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\), \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) is \(\sigma \)-invariant with respect to \((\mathrm{V},h)\).
-
(ii)
A self-dual ps-character supported on \((k,\beta )\) is a function, \(\Theta _-:{\mathscr {Q}}_{-}(k,\beta )\rightarrow { {\mathfrak {C}}_{-}(k,\beta )}\) such that, for all \(((\mathrm{V},h),\varphi ,\Lambda ,r),((\mathrm{V}',h'),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_{-}(k,\beta )\),
$$\begin{aligned}&\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {C}}_{-}(\Lambda ,r,\varphi (\beta ));\\&\Theta _-((\mathrm{V}',h'),\varphi ',\Lambda ',r')=\tau _{\Lambda ',\Lambda ,\beta }(\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)). \end{aligned}$$
We call a value of a self-dual ps-character, a self-dual realization of the self-dual ps-character. Thus, again, a self-dual ps-character is determined by any one of its self-dual realizations. By the Glauberman correspondence, every self-dual ps-character arises uniquely by restriction from of a \(\sigma \)-invariant ps-character.
More precisely, for a self-dual ps-character \(\Theta _-\) supported on \((k,\beta )\), there is a unique \(\sigma \)-invariant ps-character \(\Theta \), supported on \((k,\beta )\), such that the following diagram commutes:

where the vertical arrow is the forgetful map \(((\mathrm{V},h),\varphi ,\Lambda ,r)\mapsto (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\mathrm {Gl}\ \circ \ \Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\) is the Glauberman lift in \({\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) of \(\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {C}}_-(\Lambda ,r,\varphi (\beta ))\). We call \(\Theta \) the lift of \(\Theta _-\). We also define the degree of \(\Theta _-\) to be the degree of its lift, so \(\deg (\Theta _-)=[\mathrm{F}[\beta ]:\mathrm{F}]\).
Let \(\Theta _-,\Theta '_-\) be self-dual ps-characters supported on the self-dual simple pairs \((k,\beta ),(k',\beta ')\) respectively.
Definition 7.8
We say that \(\Theta _-\) and \(\Theta '_-\) are endo-equivalent, denoted \(\Theta _-\approx \Theta '_-\), if
-
(i)
\(\deg (\Theta _-)=\deg (\Theta '_-)\);
-
(ii)
\(k=k'\);
-
(iii)
there exist realizations on a common \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) over \(\mathrm{F}\) which intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\), i.e. there exist a finite-dimensional \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) and quadruples \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_-(k',\beta ')\), such that \(\Theta _-({(\mathrm{V},h)},\varphi ,\Lambda ,r)\) and \(\Theta '_-({(\mathrm{V},h)},\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}\).
We can now prove our main result on endo-equivalence of self-dual ps-characters.
Theorem 7.9
Let \(\Theta _-,\Theta '_-\) be self-dual ps-characters supported on the self-dual simple pairs \((k,\beta ),(k,\beta ')\) respectively. Denote by \(\Theta ,\Theta '\) the lifts of \(\Theta _-,\Theta '_-\) respectively. Suppose that \(\deg (\Theta _-)=\deg (\Theta '_-)\). Then the following assertions are equivalent:
-
(i)
\(\Theta \) and \(\Theta '\) are endo-equivalent;
-
(ii)
\(\Theta _-\) and \(\Theta '_-\) are endo-equivalent;
-
(iii)
for all \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_-(k,\beta ')\) with \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) concordant the realizations \(\Theta _{-}((\mathrm{V},h),\varphi ,\Lambda ,r)\) and \(\Theta '_{-}((\mathrm{V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\);
-
(iv)
there are \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_-(k,\beta ')\) with \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) concordant such that \(\Theta _{-}((\mathrm{V},h),\varphi ,\Lambda ,r)\) and \(\Theta '_{-}((\mathrm{V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\).
Suppose further that \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\) or \(\varepsilon =1\). Then these four assertions are equivalent to:
-
(v)
for all \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_-(k,\beta ')\) the realizations \(\Theta _{-}((\mathrm{V},h),\varphi ,\Lambda ,r)\) and \(\Theta '_{-}((\mathrm{V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\).
Indeed, we will see in the proof that, in the non-symplectic case (i.e. \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\) or \(\varepsilon =1\)), if \(\Theta \) and \(\Theta '\) are endo-equivalent then, for any two self-dual embeddings \(\varphi ,\varphi '\) of \(\beta ,\beta '\) respectively into any \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\), the pairs \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are concordant.
Proof
Certainly (ii) follows from (iv), and (i) follows from (ii), by definition and Proposition 6.4. Clearly (iii) follows from (v).
Suppose now that \(\Theta ,\Theta '\) are endo-equivalent and we have \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_-(k,\beta ')\). Replacing \(\Lambda ,\Lambda '\) by an affine translation, which does not affect the realization, we can assume \(e(\Lambda )=e(\Lambda ')\); moreover, by Proposition 7.3(ii) we may replace \(r,r'\) by \(\min \{r,r'\}\) and hence assume they are equal. Note that these changes do not affect the concordance of \((\beta ,\varphi )\) and \((\beta ',\varphi ')\). Then \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\Theta '(\mathrm{V},\varphi ',\Lambda ',r)\) intertwine by Theorem 7.5 and, further, when \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\) or \(\varepsilon =1\), the pairs \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are automatically concordant by Lemma 6.6(ii). Then, provided we have concordant pairs \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) in the symplectic case, Proposition 6.10 implies that \(\Theta _{-}((\mathrm{V},h),\varphi ,\Lambda ,r)\) and \(\Theta '_{-}((\mathrm{V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\). Thus (i) implies (iii), and (i) implies (v) when \(\mathrm{F}\ne \mathrm{F}_{\mathsf {o}}\) or \(\varepsilon =1\).
Now suppose the two ps-characters satisfy (iii). In order to show (iv), we have to find elements of \({\mathscr {Q}}_-(k,\beta )\) and \({\mathscr {Q}}_-(k,\beta ')\) defined on the same \(\varepsilon \)-hermitian space with concordant pairs. Let \(h_\mathrm{E}\) and \(h_{\mathrm{E}'}\) be hyperbolic \(\varepsilon \)-hermitian spaces over \(\mathrm{E}\) and \(\mathrm{E}'\), respectively, of the same dimension, and recall that \([\mathrm{E}:\mathrm{F}]=[\mathrm{E}':\mathrm{F}]\), since \(\Theta _-,\Theta '_-\) have the same degree. Then (in the notation of Sect. 3.5) \(\lambda _\beta ^*(h_\mathrm{E})\) and \(\lambda _{\beta '}^*(h_{\mathrm{E}'})\) are hyperbolic spaces over \(\mathrm{F}\) of the same dimension; hence they are isometric and we can assume without loss of generality that they are the same space \((\mathrm{V},h)\). The pairs \((\beta ,\varphi _\beta )\) and \((\beta ',\varphi _{\beta '})\) are then concordant, because \(h_\mathrm{E}\) and \(h_{\mathrm{E}'}\) are hyperbolic. Now, for any self-dual \({\mathfrak {o}}_\mathrm{E}\)-lattice sequence \(\Lambda \) in \(\mathrm{V}\) and self-dual \({\mathfrak {o}}_{\mathrm{E}'}\)-lattice sequence \(\Lambda '\) in \(\mathrm{V}\), we have \(((\mathrm{V},h),\varphi ,\Lambda ,ke(\Lambda |{\mathfrak {o}}_\mathrm{E}))\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',ke(\Lambda '|{\mathfrak {o}}_{\mathrm{E}'}))\in {\mathscr {Q}}_-(k,\beta ')\). \(\square \)
In fact, concordance exactly determines whether realizations of endo-equivalent self-dual ps-characters intertwine:
Proposition 7.10
Let \(\Theta _-,\Theta '_-\) be endo-equivalent self-dual ps-characters supported on the self-dual simple pairs \((k,\beta ),(k,\beta ')\) respectively. Let \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_-(k,\beta ')\). Then the realizations \(\Theta _{-}((\mathrm{V},h),\varphi ,\Lambda ,r)\) and \(\Theta '_{-}((\mathrm{V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\) if and only if \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are concordant.
Proof
Suppose \(\theta _- =\Theta _{-}((\mathrm {V},h),\varphi ,\Lambda ,r)\) and \(\theta '_-=\Theta '_{-}((\mathrm {V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\). Replacing \(\Lambda ,\Lambda '\) by an affine translation, which does not affect the realization, we can assume \(e(\Lambda )=e(\Lambda ')\); moreover, by Proposition 7.3(ii) we may replace \(r,r'\) by \(\max \{r,r'\}\) (which is equivalent to restricting \(\theta _- ,\theta _- '\) to subgroups) and hence assume they are equal. Then Proposition 6.10 implies that \((\beta ,\varphi )\) and \((\beta ',\varphi ')\) are concordant. The converse is given by Theorem 7.9. \(\square \)
As endo-equivalence of ps-characters for general linear groups is an equivalence relation, from Theorem 7.9 we deduce the corresponding result for self-dual ps-characters:
Corollary 7.11
Endo-equivalence defines an equivalence relation on the class of self-dual ps-characters.
We also deduce that endo-equivalent self-dual ps-characters must be supported on similar self-dual extensions (see Definition 3.33).
Corollary 7.12
Let \(\Theta _-,\Theta '_-\) be endo-equivalent self-dual ps-characters supported on the self-dual simple pairs \((k,\beta ),(k,\beta ')\) respectively and put \(\mathrm{E}=\mathrm{F}[\beta ]\) and \(\mathrm{E}'=\mathrm{F}[\beta ']\). Then the self-dual extensions \((\mathrm{E},\beta )\) and \((\mathrm{E}',\beta ')\) are similar.
Proof
Denote by \(\Theta ,\Theta '\) the lifts of \(\Theta _-,\Theta '_-\) respectively; they are endo-equivalent by Theorem 7.9. We choose self-dual realizations of \(\Theta _-,\Theta '_-\) on a common space \(\mathrm{V}\) for which the lattice sequences have the same period. Then their lifts are realizations of the endo-equivalent \(\Theta ,\Theta '\) so intertwine in \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_\mathrm{F}(\mathrm{V})\) by Theorem 7.5. Then Corollary 6.9 says that the extensions \((\mathrm{E},\beta )\) and \((\mathrm{E}',\beta ')\) are similar. \(\square \)
We call the equivalence classes of self-dual ps-characters under endo-equivalence self-dual simple endo-classes. We also obtain the self-dual version of Theorem 7.6, the transitivity of intertwining of self-dual simple characters:
Corollary 7.13
Let \(\theta _{i,-}\in {\mathscr {C}}_-(\Lambda _i,r_i,\beta _i)\) be self-dual simple characters, for \(i=1,2,3\). Suppose that \(\theta _{1,-}\) and \(\theta _{2,-}\) intertwine in \(\mathrm{G}\), \(\theta _{2,-}\) and \(\theta _{3,-}\) intertwine in \(\mathrm{G}\), and that either
-
(i)
\(\left\lfloor \frac{r_1}{e(\Lambda _1|{\mathfrak {o}}_{\mathrm{E}_1})}\right\rfloor = \left\lfloor \frac{r_2}{e(\Lambda _2|{\mathfrak {o}}_{\mathrm{E}_2})}\right\rfloor = \left\lfloor \frac{r_3}{e(\Lambda _3|{\mathfrak {o}}_{\mathrm{E}_3})}\right\rfloor \) and \(\theta _{1,-},\theta _{2,-}\) and \(\theta _{3,-}\) have the same degree; or
-
(ii)
\(e(\Lambda _1)=e(\Lambda _2)=e(\Lambda _3)\) and \(r_1=r_2=r_3\).
Then \(\theta _{1,-}\) and \(\theta _{3,-}\) intertwine in \(\mathrm{G}\).
Proof
In case (i), let \(\Theta _{i-}\) be the ps-character with realization \(\theta _{i,-}\) in \({\mathscr {C}}_-(\Lambda _i,r_i,\beta _i)\), for \(i=1,2,3\). We have \(\Theta _{1,-}\approx \Theta _{2,-}\) and \(\Theta _{2,-}\approx \Theta _{3,-}\) by assumption, and thus \(\Theta _{1,-}\approx \Theta _{3,-}\) by Corollary 7.11. We abbreviate \(\varphi _i\) for the canonical embedding of \(\beta _i\) in \(\mathrm{A}\). Then \((\beta _1,\varphi _1)\) and \((\beta _2,\varphi _2)\) are concordant, by Proposition 7.10, and likewise \((\beta _2,\varphi _2)\) and \((\beta _3,\varphi _3)\) are concordant. Thus \((\beta _1,\varphi _1)\) and \((\beta _3,\varphi _3)\) are concordant, by transitivity of concordance, and \(\theta _{1,-}\) and \(\theta _{3,-}\) intertwine in \(\mathrm{G}\) by Proposition 7.10 again. Case (ii) follows from case (i) by Proposition 6.2(i). \(\square \)
8 Self-dual semisimple characters: intertwining and concordance
In this section we recall, from [29, 42], the basic properties of semisimple strata and characters, and of their self-dual versions. We also recall from [39] how the intertwining of semisimple characters induces a matching between their splittings, and use this to deduce both results on concordance and Skolem–Noether type results.
8.1 Semisimple strata
Suppose that \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}} \mathrm{V}^i\) is a decomposition into \(\mathrm{F}\)-subspaces. For \(\mathrm{J}\) any subset of \(\mathrm{I}\), we write \(\mathrm{V}^\mathrm{J}=\bigoplus _{i\in \mathrm{J}}\mathrm{V}^i\) and \({\mathbf {e}}^\mathrm{J}:\mathrm{V}\rightarrow \mathrm{V}^\mathrm{J}\) for the projection with kernel \(\bigoplus _{j\in \mathrm{I}\setminus \mathrm{J}}\mathrm{V}^j\). We also set \(\mathrm{A}^\mathrm{J}={\text {End}}_\mathrm{F}(\mathrm{V}^\mathrm{J})\) and \({{\widetilde{\mathrm{G}}}}_\mathrm{J}={\text {Aut}}_\mathrm{F}(\mathrm{V}^\mathrm{J})\). When \(\mathrm{J}=\{i\}\) is a singleton, then we will write \(\mathrm{A}^i\) rather than \(\mathrm{A}^{\{i\}}\), etc.
Now let \([\Lambda ,n,r,\beta ]\) be a stratum in \(\mathrm{A}\). For \(\mathrm{J}\) a subset of \(\mathrm{I}\), we set \(\Lambda ^\mathrm{J}=\Lambda \cap \mathrm{V}^\mathrm{J}\) and \(\beta _\mathrm{J}={\mathbf {e}}^\mathrm{J}\beta {\mathbf {e}}^\mathrm{J}\), and \(n_\mathrm{J}=\max \{-{\text {val}}_{\Lambda ^\mathrm{J}}(\beta _\mathrm{J}),r\}\), so that \([\Lambda ^\mathrm{J},n_\mathrm{J},r,\beta _\mathrm{J}]\) is a stratum in \(\mathrm{V}^\mathrm{J}\). The decomposition \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}} \mathrm{V}^i\) of \(\mathrm{V}\) is called a splitting of \([\Lambda ,n,r,\beta ]\) if \(\beta =\sum _{i\in \mathrm{I}}\beta _i\) and \(\Lambda (k)=\bigoplus _{i\in \mathrm{I}}\Lambda ^i(k)\), for all \(k\in {\mathbb {Z}}\).
Definition 8.1
A stratum \([\Lambda ,n,r,\beta ]\) in \(\mathrm{A}\) is called semisimple if it is a null stratum or if \({\text {val}}_{\Lambda }(\beta )=-n\) and there exists a splitting \(\bigoplus _{i\in \mathrm{I}} \mathrm{V}^i\) for \([\Lambda ,n,r,\beta ]\) such that
-
(i)
for \(i\in \mathrm{I}\), the stratum \([\Lambda ^i,n_i,r,\beta _i]\) in \({\text {End}}_\mathrm{F}(\mathrm{V}^i)\) is simple;
-
(ii)
for \(i,j\in \mathrm{I}\) with \(i\ne j\), the stratum \([\Lambda ^{\{i,j\}},n_{\{i,j\}},r,\beta _{\{i,j\}}]\) is not equivalent to a simple stratum in \({\text {End}}_\mathrm{F}(\mathrm{V}^{\{i,j\}})\).
Let \([\Lambda ,n,r,\beta ]\) be a semisimple stratum in \(\mathrm{A}\). We write \(\mathrm{E}=\mathrm{F}[\beta ]\) and \(\mathrm{E}_i=\mathrm{F}[\beta _i]\), so that \(\mathrm{E}=\bigoplus _{i\in \mathrm{I}}\mathrm{E}_i\) is a sum of fields, and set \(\mathrm{B}_\beta =\mathrm{C}_\mathrm{A}(\beta )\) and \({{\widetilde{\mathrm{G}}}}_\beta =\mathrm{B}_\beta ^\times \). By abuse of notation, we call an \({\mathfrak {o}}_\mathrm{F}\)-lattice sequence which is a sum of \({\mathfrak {o}}_{\mathrm{E}_i}\)-lattice sequences in \(\mathrm{V}^i\) an \({\mathfrak {o}}_\mathrm{E}\)-lattice sequence; thus \(\Lambda \) is an \({\mathfrak {o}}_\mathrm{E}\)-lattice sequence. We also call \([\mathrm{E}:\mathrm{F}]={\text {dim}}_\mathrm{F}\mathrm{E}\) the degree of the semisimple stratum.
For \([\Lambda ,n,0,\beta ]\) a non-null semisimple stratum in \(\mathrm{A}\), we let
denote the critical exponent of \([\Lambda ,n,0,\beta ]\) and set \(k_\mathrm{F}(\beta )=\frac{1}{e(\Lambda )}k_0(\beta ,\Lambda )\); by [42, §3.1], this is independent of \(\Lambda \). For null strata we put \(k_0(0,\Lambda )=k_\mathrm{F}(0)=-\infty \).
It is possible to generalize the critical exponent to all pairs \((\beta ,\Lambda )\) where \(\beta \) generates a product of fields, and \(\Lambda \) is an \({\mathfrak {o}}_{\mathrm{E}}\)-lattice sequence as follows. We set \(n=-{\text {val}}_\Lambda (\beta )\) and \(e=e(\Lambda )\).
Lemma 8.2
With the notation above, if \(\beta \) is non-zero then, for any sufficiently large integer l, the stratum \([\Lambda ,n+le,0,\varpi _\mathrm{F}^{-l}\beta ]\) is semisimple.
We can then define
for any integer l such that \([\Lambda ,n+le,0,\varpi _\mathrm{F}^{-l}\beta ]\) is semisimple; this is independent of the choice of l. We also set \(k_\mathrm{F}(\beta )=\frac{1}{e}k_0(\beta ,\Lambda )\), which is again independent of \(\Lambda \).
Proof
Replacing \(\beta \) by \(\varpi _\mathrm{F}^{-l}\beta \) for sufficiently large l, we can assume that \(k_\mathrm{F}(\beta _i)<0\) for all \(i\in \mathrm{I}\), in which case n is positive. We need only show that there is an integer l such that \([\Lambda ,n+le,0,\varpi _\mathrm{F}^{-l}\beta ]\) is semisimple so we suppose for contradiction that there is no such integer. From the definition of semisimple stratum, it is sufficient to consider the case that \(\mathrm{I}\) has cardinality two. For each \(l\geqslant 0\) there is then by [39, Theorem 6.16] a simple stratum \([\Lambda ,n+le,0,\gamma ^{(l)}]\) equivalent to \([\Lambda ,n+le,0,\varpi _\mathrm{F}^{-l}\beta ]\) with \(\gamma ^{(l)}\in \bigoplus _{i\in \mathrm{I}}\mathrm{A}^i\). Restricting these to the ith block (where both strata are simple), we see that \(k_\mathrm{F}(\gamma ^{(l)})= k_\mathrm{F}(\varpi _\mathrm{F}^{-l}\beta _i)\); in particular, \(k_\mathrm{F}(\varpi _\mathrm{F}^l\gamma ^{(l)})=k_\mathrm{F}(\beta _i)<0\) so that \([\Lambda ,n,0,\varpi _\mathrm{F}^l\gamma ^{(l)}]\) is a simple stratum. But then \(\varpi _\mathrm{F}^l\gamma ^{(l)}\) converges to \(\beta \) as \(l\rightarrow \infty \) so [41, Proposition 1.9] implies that \([\Lambda ,n,0,\beta ]\) is simple. In particular, \(\mathrm{F}[\beta ]\) is a field, which contradicts the fact that \(\mathrm{I}\) has cardinality two. \(\square \)
Now we turn to the self-dual case. If \([\Lambda ,n,r,\beta ]\) is self-dual and semisimple with associated splitting \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) then, for each \(i\in \mathrm{I}\), there exists a unique \(\sigma (i)=j\in \mathrm{I}\) such that \({\overline{\beta _i}}=-\beta _j\). We set \(\mathrm{I}_0=\{i\in \mathrm{I}:\sigma (i)=i\}\) and choose a set of representatives \(\mathrm{I}^+\) for the orbits of \(\sigma \) in \(\mathrm{I}\setminus \mathrm{I}_0\). Then we let \(\mathrm{I}_{-}=\sigma (\mathrm{I}_{+})\) so that we have a disjoint union \(\mathrm{I}=\mathrm{I}_+\cup \mathrm{I}_0\cup \mathrm{I}_{-}\). If \(\mathrm{J}\) is a \(\sigma \)-stable subset of \(\mathrm{I}\), then we write \(h_\mathrm{J}\) for the restriction of the form h to \(\mathrm{V}^\mathrm{J}\), so that \((\mathrm{V}^\mathrm{J},h_\mathrm{J})\) is an \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\); this applies in particular when \(\mathrm{J}\) is a singleton subset of \(\mathrm{I}_0\).
Definition 8.3
A semisimple stratum \([\Lambda ,n,r,\beta ]\) in \(\mathrm{A}\) is called skew if it is self-dual and the associated splitting \(\bigoplus _{i\in \mathrm{I}} \mathrm{V}^i\) is orthogonal with respect to the \(\varepsilon \)-hermitian form h, i.e. \(\mathrm{I}=\mathrm{I}_0\) in the notation above.
In particular, a self-dual simple stratum is automatically skew. At the start of the appendix, there is a brief discussion on the roles of skew and non-skew self-dual semisimple objects.
As in the simple case, many results concerning semisimple strata are proved “by induction along r” using the following fundamental approximation result.
Proposition 8.4
([42, Proposition 3.4], [29, Lemma 3.1]) Let \([\Lambda ,n,0,\beta ]\) be a non-null semisimple stratum with associated splitting \(\bigoplus _{i\in \mathrm{I}} \mathrm{V}^i\) and let \(0<r\leqslant n\). Then there is a semisimple stratum \([\Lambda ,n,r,\gamma ]\) equivalent to \([\Lambda ,n,r,\beta ]\) with \(\gamma \in \bigoplus _{i\in \mathrm{I}}\mathrm{A}^i\). Moreover, if \([\Lambda ,n,0,\beta ]\) is self-dual then \([\Lambda ,n,r,\gamma ]\) may be taken to be self-dual also.
8.2 Semisimple characters
Let \([\Lambda ,n,r,\beta ]\) be a semisimple stratum in \(\mathrm{A}\). Associated to it are an \({\mathfrak {o}}_{\mathrm{F}}\)-order \({\mathfrak {H}}(\beta ,\Lambda )\) in \(\mathrm{A}\) defined inductively (see [42, Section 3.2]) and, for \(m\geqslant 1\), the compact open subgroups \({\mathrm {H}}^{m}(\beta ,\Lambda )={\mathfrak {H}}(\beta ,\Lambda )\cap \mathrm{P}^{m}(\Lambda )\) of \({{\widetilde{\mathrm{G}}}}\). We also have a set \({\mathscr {C}}(\Lambda ,r,\beta )\) of characters of \({\mathrm {H}}^{r+1}(\beta ,\Lambda )\) called semisimple characters (which depend on our fixed choice of additive character \(\psi \)). For each subset \(\mathrm{J}\) of \(\mathrm{I}\), there is a natural embedding \({\mathrm {H}}^{r+1}(\beta _\mathrm{J},\Lambda ^\mathrm{J})\hookrightarrow {\mathrm {H}}^{r+1}(\beta ,\Lambda )\) and hence a map \({\mathscr {C}}(\Lambda ,r,\beta )\rightarrow {\mathscr {C}}(\Lambda ^\mathrm{J},r,\beta _\mathrm{J})\) which we write \(\theta \mapsto \theta _\mathrm{J}\). In the case when \(\mathrm{J}=\{i\}\) is a singleton, we call \(\theta _i\) a simple block restriction of \(\theta \).
As in the simple case we have a notion of transfer for semisimple characters. We define \(e(\Lambda _\mathrm{E})\) to be the greatest common divisor of the integers \(e(\Lambda ^i|{\mathfrak {o}}_{\mathrm{E}_i})\), for \(i\in \mathrm{I}\). Given two semisimple strata \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ]\) in \(\mathrm{A}\), which satisfy \(\left\lfloor \frac{r}{e(\Lambda _\mathrm{E})}\right\rfloor =\left\lfloor \frac{r'}{e(\Lambda '_{\mathrm{E}'})}\right\rfloor \), there is a canonical bijection \(\tau _{\Lambda ',\Lambda ,\beta }:\ {\mathscr {C}}(\Lambda ,r,\beta )\rightarrow {\mathscr {C}}(\Lambda ',r',\beta )\) called transfer (see [42, Proposition 3.26] and [43, Remark 3.3]): if \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) then \(\tau _{\Lambda ',\Lambda ,\beta }(\theta )\) is the unique semisimple character \(\theta '\in {\mathscr {C}}(\Lambda ',r',\beta )\) such that \(1\in {{\widetilde{\mathrm{G}}}}\) intertwines \(\theta \) with \(\theta '\). Again, despite the dependence of the bijection on \((r,r')\) we omit it from our notation.
Now suppose that \([\Lambda ,n,r,\beta ]\) is also self-dual. Then the subgroup \({\mathrm {H}}^{r+1}(\beta ,\Lambda )\) and the set \({\mathscr {C}}(\Lambda ,r,\beta )\) of semisimple characters are stable under \(\sigma \) (see [42, §3.6] and [29, §3.6]), and we set
As in the simple setting, \({\mathrm {H}}_-^{r+1}(\beta ,\Lambda )\) is a compact open subgroup of \(\mathrm{G}\), and we define the set of self-dual semisimple characters of \({\mathrm {H}}_-^{r+1}(\beta ,\Lambda )\) by restriction:
This restriction coincides with the Glauberman correspondence. By the Glauberman correspondence, if \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) then there is a unique \(\theta \in {\mathscr {C}}^{\Sigma }(\Lambda ,r,\beta )\) whose restriction to \({\mathrm {H}}^{r+1}_{-}(\beta ,\Lambda )\) is \(\theta _-\); we call \(\theta \) the lift of \(\theta _-\) with respect to \((\Lambda ,r,\beta )\). (As before, we will simply write lift of \(\theta _-\), since the stratum will be given implicitly.)
A self-dual semisimple character \(\theta _-\) is called skew semisimple if there is a skew semisimple stratum \([\Lambda ,n,r,\beta ]\) such that \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\).
If we have two self-dual semisimple strata \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ]\) in \(\mathrm{A}\), which satisfy \(\left\lfloor \frac{r}{e(\Lambda _\mathrm{E})}\right\rfloor =\left\lfloor \frac{r'}{e(\Lambda '_{\mathrm{E}'})}\right\rfloor \), then the transfer map \(\tau _{\Lambda ',\Lambda ,\beta }\) commutes with the involution \(\sigma \) (see [42, Proposition 3.32] and [29, §3.7]). In particular it restricts to a bijection \(\tau _{\Lambda ',\Lambda ,\beta }:{\mathscr {C}}_-(\Lambda ,r,\beta )\rightarrow {{\mathscr {C}}_-(\Lambda ',r',\beta )}\).
8.3 Matching splittings, intertwining and conjugacy
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n',r',\beta ']\) be semisimple strata in \(\mathrm{A}\) with associated splittings \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}'}\mathrm{V}'^i\), respectively. The starting point for this section is the Matching Theorem of the second and third authors.
Definition 8.5
Let \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ',r',\beta ')\) be semisimple characters and suppose there are a bijection \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) and \(g\in {\text {Aut}}_\mathrm{F}(\mathrm{V})\) such that, for each \(i\in \mathrm{I}\), we have:
-
(i)
\(g \mathrm{V}^i=\mathrm{V}'^{\zeta (i)}\);
-
(ii)
 and \(\theta _{\zeta (i)}'\) intertwine in \({\text {Aut}}_\mathrm{F}(\mathrm{V}'^{\zeta (i)})\).
and \(\theta _{\zeta (i)}'\) intertwine in \({\text {Aut}}_\mathrm{F}(\mathrm{V}'^{\zeta (i)})\).
Then we say that \(\zeta \) is a matching from \((\theta ,\beta )\) to \((\theta ',\beta ')\), and that \(\theta \) intertwines \(\theta '\) in \({\text {Aut}}_\mathrm{F}(\mathrm{V})\) with matching \(\zeta \).
The use of the terminology “intertwines with matching \(\zeta \)” is justified by the following result.
Proposition 8.6
Let \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ',r',\beta ')\) be semisimple characters in \({{\widetilde{\mathrm{G}}}}\), and suppose \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) is a bijection between their index sets. For \(i\in \mathrm{I}\), write \(\mathrm{I}(\theta _i,\theta '_{\zeta (i)})\) for the set of isomorphisms \(g\in {\text {Hom}}_\mathrm{F}(\mathrm{V}^i,\mathrm{V}'^{\zeta (i)})\) such that  is intertwined with \(\theta '_{\zeta (i)}\) by the identity. Then
is intertwined with \(\theta '_{\zeta (i)}\) by the identity. Then
Proof
It is clear that the left hand side of (8.7) is contained in the right hand side. Conversely, if \(g_i\in \mathrm{I}(\theta _i,\theta '_{\zeta (i)})\), for \(i\in \mathrm{I}\), then \(g=\sum _{i\in \ I}g_i\) intertwines \(\theta \) with \(\theta '\), by the Iwahori decomposition of semisimple characters. \(\square \)
For the matching theorem we restrict to the case \(r=r'\) and \(e(\Lambda )=e(\Lambda ')\), though we will see later that these hypotheses could be relaxed somewhat.
Theorem 8.8
[39, Theorem 10.1] Suppose that \(e(\Lambda )=e(\Lambda ')\, \text {and} \,r=r',\) and let \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ',r,\beta ')\) be semisimple characters which intertwine in \({{\widetilde{\mathrm{G}}}}\). Then there is a unique matching \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) from \((\theta ,\beta )\) to \((\theta ',\beta ')\). Moreover, if \(g\in {{\widetilde{\mathrm{G}}}}\) satisfies \(g \mathrm{V}^i=\mathrm{V}'^{\zeta (i)}\) for \(i\in \mathrm{I}\), then  and \(\theta _{\zeta (i)}'\) intertwine in \({\text {Aut}}_\mathrm{F}(\mathrm{V}'^{\zeta (i)})\).
and \(\theta _{\zeta (i)}'\) intertwine in \({\text {Aut}}_\mathrm{F}(\mathrm{V}'^{\zeta (i)})\).
In particular, under the notation of the theorem we have \(e(\mathrm{E}_i/\mathrm{F})=e(\mathrm{E}'_{\zeta (i)}/\mathrm{F})\), \(f(\mathrm{E}_i/\mathrm{F})=f(\mathrm{E}'_{\zeta (i)}/\mathrm{F})\), and \(k_0(\beta _i,\Lambda ^i)=k_0(\beta '_{{\zeta (i)}},\Lambda '^{{\zeta (i)}})\) by Proposition 6.2.
Remark 8.9
Suppose \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ']\) are self-dual semisimple strata and \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',r,\beta ')\) are self-dual semisimple characters, with lifts \(\theta ,\theta '\) respectively. If \(\theta _-,\theta '_-\) intertwine in \(\mathrm{G}\) then the lifts intertwine so we have a matching \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) from \((\theta ,\beta )\) to \((\theta ',\beta ')\). Moreover, by uniqueness of matchings, \(\zeta \) is \(\sigma \)-equivariant. We will also say that \(\zeta \) is a matching from \((\theta _-,\beta )\) to \((\theta '_-,\beta )\).
Remark 8.10
It follows from the \(\sigma \)-equivariance of the matching that if \(\theta _-\) is a skew semisimple character and \([\Lambda ,n,r,\beta ]\) is any self-dual semisimple stratum such that \(\theta _-\in {\mathscr {C}}(\Lambda ,r,\beta )\) then the stratum \([\Lambda ,n,r,\beta ]\) is in fact skew semisimple.
Corollary 8.11
Under the assumptions of Theorem 8.8, suppose that there exists \(g\in {{\widetilde{\mathrm{G}}}}\) such that \(g\beta g^{-1}=\beta '\) and  . Then \(\beta _i\) and \(\beta '_{\zeta (i)}\) have the same characteristic polynomial, for all \(i\in \mathrm{I}\).
. Then \(\beta _i\) and \(\beta '_{\zeta (i)}\) have the same characteristic polynomial, for all \(i\in \mathrm{I}\).
Proof
By conjugating by g we reduce to the case that \(\beta =\beta '\). As \(\theta '=\tau _{\Lambda ',\Lambda ,\beta }(\theta )\) we have \(1\in \mathrm{I}_{{\widetilde{\mathrm{G}}}}(\theta ,\theta ')\). The identity map \(\mathrm{I}\rightarrow \mathrm{I}\) is then a matching from \((\theta ,\beta )\) to \((\theta ',\beta ')\) so the uniqueness in Theorem 8.8 implies that \(\zeta \) is the trivial permutation of the index set, which finishes the proof. \(\square \)
Remark 8.12
If the semisimple characters are not related by transfer, then the conclusion of Corollary 8.11 need not hold, as the following example shows. Suppose the characteristic of \(\mathrm{F}\) is p and set \(\mathrm{I}=\{0,\ldots ,p-1\}\). Take an element \(\beta _0\in \mathrm{F}\) of negative even valuation, and a regular lattice sequence \(\Lambda ^0\). Set \(n=-{\text {val}}_\Lambda (\beta _0)\) and \(r=\frac{n}{2}\), both of which are non-zero multiples of \(e(\Lambda ^0)\). Take an element \(\lambda \in (\mathrm{F}\cap {\mathfrak {a}}_{-r}(\Lambda ^0))\setminus {\mathfrak {a}}_{-r+1}(\Lambda ^0)\) and set \(\beta _i=\beta _0+i\lambda \), for \(i\in \mathrm{I}\). Then, putting \(\beta =\sum _{i\in \mathrm{I}}\beta _i\) and \(\Lambda =\bigoplus _{i\in \mathrm{I}} \Lambda ^0\), the stratum \([\Lambda ,n,0,\beta ]\) is semisimple.
By the results of [12, §3.5], the sets \({\mathscr {C}}(\Lambda ^0,r-1,\beta _i)\) coincide, so multiplication by \(\psi _\lambda \) induces a permutation of \({\mathscr {C}}(\Lambda ^0,r-1,\beta _0)\). Choosing any \(\theta _0\in {\mathscr {C}}(\Lambda ^0,r-1,\beta _0)\), there are unique semisimple characters \(\theta ,\theta '\in {\mathscr {C}}(\Lambda ,r-1,\sum _{i\in \mathrm{I}}\beta _i)\) whose ith simple block restrictions are \(\theta _0\psi _{i\lambda }\) and \(\theta _0\psi _{(i+1)\lambda }\) respectively. Then the matching from \((\theta ,\beta )\) to \((\theta ',\beta )\) is a cyclic permutation, not the identity, but \(\beta _i,\beta _{i+1}\) do not have the same characteristic polynomial.
We need a description of the intertwining of transfers, which generalizes [42, Theorem 3.22] and which we prove in the appendix (as Proposition A.10). The statement involves a particular subgroup \(\mathrm {S}_r(\beta ,\Lambda )\) of \(\mathrm{P}^1(\Lambda )\) associated to the semisimple stratum \([\Lambda ,n,r,\beta ]\), which normalizes every character in \({\mathscr {C}}(\Lambda ,r,\beta )\) and is defined in [42, Section 3.2], where it is denoted \(\Gamma _r(\beta ,\Lambda )\) (see also [39, Proposition 9.8], and [12, (3.5.1)] for the simple case).
Proposition 8.13
Suppose \(e(\Lambda )=e(\Lambda '),\,r=r'\) and \(\beta '=\beta \).
-
(i)
Let \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '=\tau _{\Lambda ',\Lambda ,\beta }(\theta )\). Then
$$\begin{aligned} \mathrm{I}_{{{\widetilde{\mathrm{G}}}}}(\theta ,\theta ')=\mathrm {S}_{r}(\beta ,\Lambda '){{\widetilde{\mathrm{G}}}}_{\beta } \mathrm {S}_r(\beta ,\Lambda ). \end{aligned}$$ -
(ii)
Suppose \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ]\) are self-dual and let \(\theta _- \in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-=\tau _{\Lambda ',\Lambda ,\beta }(\theta _-)\). Then
$$\begin{aligned} \mathrm{I}_\mathrm{G}(\theta _-,\theta '_-)=(\mathrm{S}_{r}(\beta ,\Lambda ')\cap \mathrm{G}) \mathrm{G}_{\beta } (\mathrm{S}_r(\beta ,\Lambda )\cap \mathrm{G}). \end{aligned}$$
We also have the following intertwining implies conjugacy theorem. In the case of semisimple characters and skew semisimple characters, this is [39, Theorems 10.2,10.3] respectively; we prove the case of self-dual semisimple characters in the appendix (as Theorem A.13). The condition on a matching \(\zeta \) which allows one to deduce conjugacy is
Theorem 8.15
Suppose that \(\Lambda =\Lambda '\text { and }r=r'\).
-
(i)
Let \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ,r,\beta ')\) be semisimple characters which intertwine, such that the matching \(\zeta \) from \((\theta ,\beta )\) to \((\theta ',\beta ')\) satisfies (8.14). Then there is an element of \(\mathrm{P}(\Lambda )\cap \prod _{i\in \mathrm{I}}{\text {Hom}}_\mathrm{F}(\mathrm{V}^i,\mathrm{V}'^{\zeta (i)})\) which conjugates \(\theta \) to \(\theta '\).
-
(ii)
Suppose \([\Lambda ,n,r,\beta ]\) and \([\Lambda ,n,r,\beta ' ]\) are self-dual and let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ,r,\beta ')\) be self-dual semisimple characters which intertwine in \(\mathrm{G}\), such that the matching \(\zeta \) from \((\theta _-,\beta )\) to \((\theta '_-,\beta ')\) satisfies (8.14). Then there is an element of \(\mathrm{P}_-(\Lambda )\cap \prod _{i\in \mathrm{I}}{\text {Hom}}_\mathrm{F}(\mathrm{V}^i,\mathrm{V}'^{\zeta (i)})\) which conjugates \(\theta _-\) to \(\theta '_-\).
From these results we get the following important corollaries.
Corollary 8.16
Suppose that \(e(\Lambda )=e(\Lambda ')\, \text {and}\,r=r',\) and let \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ',r,\beta ')\) be semisimple characters which intertwine in \({{\widetilde{\mathrm{G}}}}\), and let \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) be the matching from \((\theta ,\beta )\) to \((\theta ',\beta ')\). Then
Suppose further that \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ']\) are self-dual and that we have a partition \({\mathcal {P}}\) of \(\mathrm{I}\) into \(\sigma \)-stable subsets such that for each \(\mathrm{J}\in {\mathcal {P}}\) the hermitian spaces \((\mathrm{V}^\mathrm{J},h_\mathrm{J})\) and \((\mathrm{V}'^{\zeta (\mathrm{J})},h_{\zeta (\mathrm{J})})\) are isometric. Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}(\Lambda ',r,\beta ')\) be self-dual semisimple characters which intertwine in \(\mathrm{G}\) . Then
Proof
Let \(g\in {{\widetilde{\mathrm{G}}}}\) be an element inducing the matching, that is, satisfying the conditions in Theorem 8.8. For each index i the field extensions \(\mathrm{E}_i/\mathrm{F}\) and \(\mathrm{E}'_{\zeta (i)}/\mathrm{F}\) have equal ramification indices and inertia degrees, by Proposition 6.2; thus, by Lemma 5.1, there is an \({\mathfrak {o}}_{\mathrm{E}_i}\)-lattice sequence \(\Lambda ''^i\) in \(\mathrm{V}^i\) which is conjugate in \({{\widetilde{\mathrm{G}}}}_i\) to \(g^{-1}\Lambda '^{\zeta (i)}\). In particular, \(\Lambda ''=\bigoplus _{i\in \mathrm{I}}\Lambda ''^i\) is then an \({\mathfrak {o}}_\mathrm{E}\)-lattice sequence in \(\mathrm{V}\) which is \({{\widetilde{\mathrm{G}}}}\)-conjugate to \(\Lambda '\) by an element which maps \(\Lambda ''^i\) to \(\Lambda '^{\zeta (i)}\).
Let \(\theta ''=\tau _{\Lambda '',\Lambda ,\beta }(\theta )\) be the transfer of \(\theta \) to \({\mathscr {C}}(\Lambda '',r,\beta )\). Applying Theorem 7.6 to the simple block restrictions of \(\theta '',\theta ,\theta '\) and Proposition 8.13, we see that \(\theta ''\) intertwines with \(\theta '\). Then Theorem 8.15(i) implies that \(\theta ''\) is conjugate to \(\theta '\) by an element \(g\in {{\widetilde{\mathrm{G}}}}\) which maps \(\Lambda ''^i\) to \(\Lambda '^{\zeta (i)}\).
Conjugating by this element, we can assume we are in the case \(\theta ''=\theta '\), \(\Lambda ''=\Lambda '\) and \(\mathrm{V}^i=\mathrm{V}'^{\zeta (i)}\) for all \(i\in \mathrm{I}\). We can then identify the index sets so that \(\zeta \) is the identity. We have \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ',r,\beta )\cap {\mathscr {C}}(\Lambda ',r,\beta ')\) so that
Then Proposition 8.13 implies
since \({{\widetilde{\mathrm{G}}}}_\beta \) and \({{\widetilde{\mathrm{G}}}}_{\beta '}\) are both contained in \(\prod _i {{\widetilde{\mathrm{G}}}}_{i}\). The final assertion now follows from a standard cohomology argument as in [42, 4.14] (cf. also [26, 2.4]). \(\square \)
8.4 Concordance and Skolem–Noether
We now prove a conjecture of the second and third authors, [39, Conjecture 10.4]. We let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ']\) be self-dual semisimple strata in \(\mathrm{A}\), with \(e(\Lambda )=e(\Lambda ')\) and with associated splittings \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}'}\mathrm{V}'^i\), respectively. We will write \(\varphi _i\) for the canonical embedding of \(\mathrm{E}_i=\mathrm{F}[\beta _i]\) in \(\mathrm{A}^i\), and similarly \(\varphi '_i\). For \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\), we write \(\theta \) for its lift and \(\theta _i\) for the simple block restrictions of \(\theta \); if \(i\in \mathrm{I}_0\) then \(\theta _i\) is \(\sigma \)-invariant and we write \(\theta _{-,i}\) for its restriction in \({\mathscr {C}}_-(\Lambda ^i,r,\beta _i)\). We use similar notation for \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',r,\beta ')\). When we write about a matching from \((\theta _-,\beta )\) to \((\theta '_-,\beta ')\), we mean a matching from \((\theta ,\beta )\) to \((\theta ',\beta ')\).
Theorem 8.17
Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',r,\beta ')\) be self-dual semisimple characters which intertwine in \(\mathrm{G}\) and let \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) be the matching from \((\theta _-,\beta )\) to \((\theta '_-,\beta ')\). Then, for \(i\in \mathrm{I}_0\), the spaces \((\mathrm{V}^i,h_i)\) and \((\mathrm{V}'^{\zeta (i)},h'_{\zeta (i)})\) are isometric and the characters \(\theta _{-,i}\) and \(\theta '_{-,\zeta (i)}\) intertwine by an isometry from \((\mathrm{V}^i,h_i)\) to \((\mathrm{V}'^{\zeta (i)},h'_{\zeta (i)})\). Moreover, the pairs \((\beta _i,\varphi _i)\) and \((\beta '_{\zeta (i)},\varphi '_{\zeta (i)})\) are \((h_i,h'_{\zeta (i)})\)-concordant.
In the proof of the theorem (and the subsequent corollaries), we abbreviate \(\mathrm{V}_0\) for \(\mathrm{V}^{\mathrm{I}_0}\), so that \(\mathrm{V}_0^\perp =\mathrm{V}^{\mathrm{I}_+\cup \mathrm{I}_-}\), and similarly \(\mathrm{V}'_0,\mathrm{V}_0'^\perp \). We also write \(\theta ,\theta '\) for the lifts of \(\theta _-,\theta '_-\) respectively.
Proof
Since the spaces \(\mathrm{V}_0^\perp \) and \(\mathrm{V}_0'^\perp \) have the same \(\mathrm{F}\)-dimension and are hyperbolic, they are isometric \(\varepsilon \)-hermitian spaces over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\); thus \(\mathrm{V}_0\) and \(\mathrm{V}'_0\) are also isometric and Corollary 8.16 then reduces us to the case \(\mathrm{I}=\mathrm{I}_0\). Moreover, the final assertion follows from the first and Proposition 6.10 so, by Corollary 8.16 again, it is enough to show that \(\mathrm{V}^i\) is isometric to \(\mathrm{V}'^{\zeta (i)}\) for all \(i\in \mathrm{I}\).
We proceed by induction along r. When \(r=n\), both characters are trivial so there is nothing to show, while the case \(r=n-1\) is given by [39, Proposition 7.10]. Suppose now that \(r<n-1\) and let \([\Lambda ,n,r+1,\gamma ]\) and \([\Lambda ',n,r+1,\gamma ']\) be self-dual semisimple strata equivalent to \([\Lambda ,n,r+1,\beta ]\) and \([\Lambda ',n,r+1,\beta ']\), respectively, such that \(\gamma \in \prod _{i\in \mathrm{I}}\mathrm{A}^{i}\) and \(\gamma '\in \prod _{j\in \mathrm{I}'}\mathrm{A}'^{j}\). By the induction hypothesis and Corollary 8.16 it is sufficient to assume that \(\gamma \) and \(\gamma '\) generate field extensions of \(\mathrm{F}\). Then Lemma 6.6(ii) and Lemma 6.11 imply that there exist simple self-dual strata \([\Lambda ,n,r+1,{\tilde{\gamma }}]\) and \([\Lambda ',n,r+1,{\tilde{\gamma }}']\) such that \({\tilde{\gamma }}\) and \({\tilde{\gamma }}'\) have the same minimal polynomial, their canonical embeddings are concordant, and
In particular, there is an element g in \(\mathrm{G}\) such that \(g{\tilde{\gamma }}g^{-1}={\tilde{\gamma }}'\). The characters \(\theta |_{{\mathrm {H}}^{r+2}({\tilde{\gamma }},\Lambda )}\) and \(\tau _{g\Lambda ,\Lambda ',{\tilde{\gamma }}'}(\theta '|_{{\mathrm {H}}^{r+2}({\tilde{\gamma }}',\Lambda ')})\) intertwine by an element of \(\mathrm{G}\), by Corollary 7.13, and therefore are conjugate by an element \(g'\in \mathrm{G}\) which maps \(\Lambda \) to \(g\Lambda \), by Proposition 6.8. Thus
and we can replace \({\tilde{\gamma }}\) by \({\tilde{\gamma }}'^{g'}\); that is, we can assume without loss of generality that \({\tilde{\gamma }}={\tilde{\gamma }}'^{g'}\). We only need to prove the result for  and \(\theta '\) so we can assume further that \({\tilde{\gamma }}={\tilde{\gamma }}'\) and \(g'=1\), that is, \(\theta |_{{\mathrm {H}}^{r+2}(\Lambda ,{\tilde{\gamma }})}\) is the transfer of \(\theta '|_{{\mathrm {H}}^{r+2}(\Lambda ',{\tilde{\gamma }}')}\) from \(\Lambda '\) to \(\Lambda \).
and \(\theta '\) so we can assume further that \({\tilde{\gamma }}={\tilde{\gamma }}'\) and \(g'=1\), that is, \(\theta |_{{\mathrm {H}}^{r+2}(\Lambda ,{\tilde{\gamma }})}\) is the transfer of \(\theta '|_{{\mathrm {H}}^{r+2}(\Lambda ',{\tilde{\gamma }}')}\) from \(\Lambda '\) to \(\Lambda \).
By the translation principle [39, Theorem 9.26] there are a skew semisimple stratum \([\Lambda ,n,r,{\tilde{\beta }}]\), such that \([\Lambda ,n,r+1,{\tilde{\beta }}]\) is equivalent to \([\Lambda ,n,r+1,{\tilde{\gamma }}]\), and \(u\in \mathrm{P}^1_-(\Lambda )\), which normalizes \([\Lambda ,n,r+1,{\tilde{\gamma }}]\) up to equivalence, such that
where \(\mathrm{V}=\bigoplus _{i\in {\tilde{\mathrm{I}}}}\mathrm{V}^i\) is the splitting of \([\Lambda ,n,r,{\tilde{\beta }}]\). If we denote by \(\tau \) the matching between \((\theta ,\beta )\) and \((\theta ,{{\tilde{\beta }}})\) then Proposition A.9(ii) implies that \(\mathrm{V}^i\) is isometric to \(\mathrm{V}^{\tau (i)}\) for all \(i\in \mathrm{I}\) and there is an element of the normalizer of \(\theta \) in \(\mathrm{G}\) which realizes this matching. Analogously, we have a skew semisimple stratum \([\Lambda ',n,r,{\tilde{\beta }}']\), such that \([\Lambda ',n,r+1,{\tilde{\beta }}']\) is equivalent to \([\Lambda ',n,r+1,{\tilde{\gamma }}]\), and \(u'\in \mathrm{P}^1_-(\Lambda ')\), and a matching \(\tau '\) between \((\theta ',\beta ')\) and \((\theta ',{\tilde{\beta }}')\). Thus we need only show that \(\mathrm{V}^{\tau (i)}\) and \(\mathrm{V}^{\tau '\zeta (i)}\) are isometric. Since matchings are unique, \(\tau '\zeta \tau ^{-1}\) is the matching between \((\theta ,{{\tilde{\beta }}})\) and \((\theta ',{{\tilde{\beta }}}')\), and we are thus reduced to the case \(\beta ={{\tilde{\beta }}}\) and \(\beta '={\tilde{\beta }}'\).
Now \([\Lambda ,n,r+1,u^{-1}\beta u]\) has splitting \(\bigoplus _{i\in \mathrm{I}} u^{-1}\mathrm{V}^i\) and is equivalent to \([\Lambda ,n,r+1,{\tilde{\gamma }}]\), with \({\tilde{\gamma }}\in \prod _{i\in \mathrm{I}} u^{-1}\mathrm{A}^i u\), and \(\theta ^u|_{{\mathrm {H}}^{r+2}({\tilde{\gamma }},\Lambda )}=\theta |_{{\mathrm {H}}^{r+2}({\tilde{\gamma }},\Lambda )}\). Since \(u^{-1}\mathrm{V}^i\) is isometric to \(\mathrm{V}^i\), if we replace \((\theta ,\beta )\) by \((\theta ^u,u^{-1}\beta u)\) we reduce further to the case \({{\tilde{\gamma }}}=\gamma \). Similarly, replacing \((\theta ',\beta ')\) by \((\theta '^{u'},u'^{-1}\beta ' u')\) we see that we may assume \(\gamma ={\tilde{\gamma }}={\tilde{\gamma }}'=\gamma '\).
Now we take \(\theta '_0\in {\mathscr {C}}(\Lambda ',r,\gamma )\) such that \(\theta '=\theta '_0\psi _{\beta '-\gamma }\). If we set \(\theta _0=\tau _{\Lambda ,\Lambda ',\gamma }(\theta '_0)\) then the restrictions of \(\theta \) and \(\theta _0\) coincide on \({\mathrm {H}}^{r+2}(\gamma ,\Lambda )\)) so there exists \(c\in (\prod _i \mathrm{A}^{i})_-\cap {\mathfrak {a}}_{-r-1}\) such that \(\theta =\theta _0\psi _{\beta -\gamma +c}\). Moreover, since then \(\theta _0\) and \(\theta _0\psi _c\) are both simple characters in \({\mathscr {C}}(\Lambda ,r,\gamma )\), the character \(\psi _c\) is intertwined by all of \({{\widetilde{\mathrm{G}}}}_\gamma \) and, writing \(s_\gamma \) for an equivariant tame corestriction with respect to \(\gamma \), it follows from [35, Lemma 3.10] that \(s_\gamma (c)\) is congruent to an element of \(\mathrm{F}[\gamma ]\) modulo \({\mathfrak {a}}_{-r}\).
Now Lemma A.12 implies that the self-dual strata \([\Lambda ,r+1,r,s_\gamma (\beta -\gamma +c)]\) and \([\Lambda ',r+1,r,s_\gamma (\beta '-\gamma )]\) intertwine in \(\mathrm{G}\); moreover, these strata are equivalent to self-dual semisimple strata with splittings \(\mathrm{V}=\oplus _i\mathrm{V}^i\) and \(\mathrm{V}=\oplus _{i\in \mathrm{I}'}\mathrm{V}'^{i}\), respectively, by [39, Theorem 6.15]. The matching between these latter strata is still \(\zeta \). Indeed, by [39, Proposition 7.1] there are a bijection \(\xi :\mathrm{I}\rightarrow \mathrm{I}'\) and an element \({\tilde{g}}\in {{\widetilde{\mathrm{G}}}}_\gamma \) which intertwines \([\Lambda ,r+1,r,s_\gamma (\beta -\gamma +c)]\) with \([\Lambda ',r+1,r,s_\gamma (\beta '-\gamma )]\) and satisfies \({\tilde{g}}\mathrm{V}^i=\mathrm{V}'^{\xi (i)}\). Then \({\text {id}}_{\mathrm{V}^i}\) intertwines \([\Lambda ^i,r+1,r,s_\gamma (\beta -\gamma +c)|_{\mathrm{V}^i}]\) with \([{\tilde{g}}^{-1}\Lambda '^{\xi (i)},r+1,r,s_\gamma ({\tilde{g}}^{-1}\beta '_{\xi (i)}{\tilde{g}}-\gamma )]\), for each \(i\in \mathrm{I}\). Thus \(\theta _i\) and \(\theta _{\xi (i)}'^{{\tilde{g}}}\) intertwine, by Lemma A.11(ii), and the uniqueness of the matching implies that \(\xi =\zeta \). Finally, the base case implies that there is an element \(g\in \mathrm{G}_\gamma \) such that \(g\mathrm{V}^i=\mathrm{V}'^{\zeta (i)}\), for all \(i\in \mathrm{I}\), which gives the required isometry. \(\square \)
Finally, we deduce from Theorem 8.17 a semisimple Skolem–Noether result:
Corollary 8.18
Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',r,\beta ')\) be self-dual semisimple characters which intertwine in \(\mathrm{G}\), let \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) be the matching from \((\theta _-,\beta )\) to \((\theta '_-,\beta ')\), and suppose that \(\beta _i\) and \(\beta '_{\zeta (i)}\) have the same characteristic polynomial for all indices i. Then \(\beta \) and \(\beta '\) are conjugate in \(\mathrm{G}\).
Proof
By Theorem 8.17, we can assume that the matching \(\zeta \) is the identity of \(\mathrm{I}\). Now, the characters \(\theta _i\) and \(\theta '_i\) intertwine in \(\mathrm{G}_i\) for all \(i\in \mathrm{I}_0\). Hence, by [39, Theorem 5.2], \(\beta _i\) and \(\beta '_i\) are conjugate by an element of \(\mathrm{U}(\mathrm{V}^i,h_i)\), \(i\in \mathrm{I}_0\). Thus \(\beta \) and \(\beta '\) are conjugate in \(\mathrm{G}\). \(\square \)
For Theorem 11.9 below, the following generalization of Lemma 6.11 is crucial: it allows us, when we have self-dual semisimple characters which intertwine, to find strata giving rise to these characters whose defining elements are conjugate.
Corollary 8.19
Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',r,\beta ')\) be self-dual semisimple characters which intertwine by an element of \(\mathrm{G}\), and let \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) be the matching from \((\theta _-,\beta )\) to \((\theta '_-,\beta ')\). Then there exist self-dual semisimple strata \([\Lambda ,n,r,{\tilde{\beta }}]\) and \([\Lambda ',n,r,{\tilde{\beta }}']\) with splittings \(\mathrm{V}=\oplus _{i\in \mathrm{I}}\mathrm{V}^i\) and \(\mathrm{V}=\oplus _{i\in \mathrm{I}'}\mathrm{V}'^i\) respectively, such that \({\mathscr {C}}(\Lambda ,r,\beta )={\mathscr {C}}(\Lambda ',r,{\tilde{\beta }})\) and \({\mathscr {C}}(\Lambda ,r,\beta ')={\mathscr {C}}(\Lambda ',r,{\tilde{\beta }}')\), and such that, for all \(i\in \mathrm{I}\), the characteristic polynomials of \({\tilde{\beta }}_i\) and \({\tilde{\beta }}'_{\zeta (i)}\) coincide. Moreover, \({\tilde{\beta }}\) and \({\tilde{\beta }}'\) are conjugate by an element of \(\mathrm{G}\).
Note that the final claim of the theorem is immediate from Corollary 8.18.
Proof
The proof is by induction along r. In the case of trivial characters we can just take \({\tilde{\beta }}\) and \({\tilde{\beta }}'\) to be zero. The case \(r=n-1\) is the case of self-dual semisimple strata. By [39, Proposition 7.1] we have, for all \(i\in \mathrm{I}_0\cup \mathrm{I}_+\), that \([\Lambda ^i\oplus \Lambda '^{\zeta (i)},n,r,\beta _i\oplus \beta '_{\zeta (i)}]\) is equivalent to a simple stratum \([\Lambda ^i\oplus \Lambda '^{\zeta (i)},n,r,{\tilde{\beta }}_i\oplus {\tilde{\beta }}'_{\zeta (i)}]\) split by \(\mathrm{V}^i\oplus \mathrm{V}'^{\zeta (i)}\); moreover, for \(i\in \mathrm{I}_0\), this can be chosen self-dual by [39, Theorem 6.16]. We set \({\tilde{\beta }}_i:=-{\overline{{\tilde{\beta }}_{\sigma (i)}}}\) for \(i\in \mathrm{I}_-\) and \({\tilde{\beta }}:=\sum _i{\tilde{\beta }}_i\) and we define \({\tilde{\beta }}'\) analogously. They satisfy the requirements.
We now come to the induction step. We consider self-dual semisimple strata \([\Lambda ,n,r+1,\gamma ]\) equivalent to \([\Lambda ,n,r+1,\beta ]\), and \([\Lambda ,n,r+1,\gamma ']\) equivalent to \([\Lambda ,n,r+1,\beta ']\), such that \(\gamma \in \prod _{i\in \mathrm{I}}\mathrm{A}^{i}\) and \(\gamma '\in \prod _{i\in \mathrm{I}'}\mathrm{A}^{i}\). We first show that we can assume that \(\gamma =\gamma '\).
We denote the splittings of \(\gamma \) and \(\gamma '\) by \(\mathrm{V}=\oplus _{j\in \mathrm{J}}\mathrm{V}^j\) and \(\mathrm{V}=\oplus _{j\in \mathrm{J}'}\mathrm{V}'^j\), respectively. Now the semisimple characters \(\theta |_{{\mathrm {H}}^{r+2}(\gamma ,\Lambda )}\) and \(\theta '|_{{\mathrm {H}}^{r+2}(\gamma ',\Lambda )}\) intertwine. Then, denoting by \(\xi : \mathrm{J}\rightarrow \mathrm{J}'\) their matching, the induction hypothesis implies that there are self-dual semisimple strata \([\Lambda ,n,r+1,{\tilde{\gamma }}]\) and \([\Lambda ',n,r+1,{\tilde{\gamma }}']\), with splittings \(\mathrm{V}=\oplus _{j\in \mathrm{J}}\mathrm{V}^j\) and \(\mathrm{V}=\oplus _{j\in \mathrm{J}'}\mathrm{V}'^j\) respectively, such that \({\mathscr {C}}(\Lambda ,r+1,\gamma )={\mathscr {C}}(\Lambda ,r+1,{\tilde{\gamma }})\) and \({\mathscr {C}}(\Lambda ',r+1,\gamma ')={\mathscr {C}}(\Lambda ',r+1,{\tilde{\gamma }}')\), and such that \(\tilde{\gamma } _j\) and \(\tilde{\gamma } '_{\xi (j)}\) have the same characteristic polynomial. By Corollary 8.18 there is then an element \(g\in \mathrm{G}\) such that \(^g{\tilde{\gamma }}={\tilde{\gamma }}'\). We write \(\theta _\gamma ,\theta '_{\gamma '}\) and \(\theta ''_{{\tilde{\gamma }}'}\) for the characters \(\theta |_{{\mathrm {H}}^{r+2}(\gamma ,\Lambda )},\theta '|_{{\mathrm {H}}^{r+2}(\gamma ',\Lambda ')}\) and the transfer \(\tau _{g\Lambda ,\Lambda ',{\tilde{\gamma }}'}(\theta '|_{{\mathrm {H}}^{r+2}(\gamma ',\Lambda ')})\), respectively. By Theorem 8.8, for \(j\in \mathrm{J}_+\) there exists an \(\mathrm{F}\)-linear isomorphism \(\mathrm{V}^j\rightarrow \mathrm{V}'^{\xi (j)}\) which intertwines \(\theta _{\gamma ,j}\) and \(\theta '_{\gamma ',\xi (j)}\); since \(\theta '_{\gamma '}\) and \(\theta ''_{{\tilde{\gamma }}'}\) are intertwined by the identity (so also \(\theta '_{\gamma ',\xi (j)}\) and \(\theta ''_{{\tilde{\gamma }}',\xi (j)}\) are intertwined by the identity), Theorem 7.6 implies that there is an isomorphism \(g_j:\mathrm{V}^j\rightarrow \mathrm{V}'^{\xi (j)}\) which intertwines \(\theta _{\gamma ,j}\) and \(\theta ''_{{\tilde{\gamma }}',\xi (j)}\). By the same argument, using Theorem 8.17 and Corollary 7.13, for each \(j\in \mathrm{J}_{\mathsf {o}}\) there is an isometry \(g_j:\mathrm{V}^j\rightarrow \mathrm{V}'^{\xi (j)}\) which intertwines \(\theta _{\gamma ,j}\) and \(\theta ''_{{\tilde{\gamma }}',\xi (j)}\). Finally, we put \(g_j={\overline{g_{-j}}}^{\,-1}\), for \(j\in \mathrm{J}_-\), and \(g=\sum _{j\in \mathrm{J}} g_j\). Then Proposition 8.6 implies that g is an element of \(\mathrm{G}\) which intertwines \(\theta _\gamma \) and \(\theta ''_{{\tilde{\gamma }}'}\) with matching \(\xi \).
Now Theorem 8.15 implies that there is an element of \(\mathrm{G}\) which conjugates \(\theta |_{{\mathrm {H}}^{r+2}(\gamma ,\Lambda )}\) to \(\tau _{g\Lambda ,\Lambda ',{\tilde{\gamma }}'}(\theta '|_{{\mathrm {H}}^{r+2}(\gamma ',\Lambda ')})\), and conjugates their splittings. Conjugating by this element, we are reduced to the situation that \(\theta |_{{\mathrm {H}}^{r+2}(\gamma ,\Lambda )}\) and \(\theta '|_{{\mathrm {H}}^{r+2}(\gamma ',\Lambda ')}\) intertwine by the identity, there exists an element \({\tilde{\gamma }}'\) such that the strata \([\Lambda ,n,r+1,{\tilde{\gamma }}']\) and \([\Lambda ',n,r+1,{\tilde{\gamma }}']\) are self-dual semisimple with \({\mathscr {C}}(\Lambda ,r,\gamma )={\mathscr {C}}(\Lambda ,r,{\tilde{\gamma }}')\) and \({\mathscr {C}}(\Lambda ',r,\gamma ')={\mathscr {C}}(\Lambda ',r,{\tilde{\gamma }}')\), and the splittings for \(\gamma \), \(\gamma '\) and \({\tilde{\gamma }}'\) coincide. Finally, applying the translation principle Theorem A.1 and Proposition A.9(ii), as in the proof of Theorem 8.17, we reduce to the case that \(\gamma =\gamma '={\tilde{\gamma }}'\) and \(\xi \) is the identity map.
Now we take \(\theta '_0\in {\mathscr {C}}(\Lambda ',r,\gamma )\) such that \(\theta '=\theta '_0\psi _{\beta '-\gamma }\). If we set \(\theta _0=\tau _{\Lambda ,\Lambda ',\gamma }(\theta '_0)\) then the restrictions of \(\theta \) and \(\theta _0\) coincide on \({\mathrm {H}}^{r+2}(\gamma ,\Lambda )\)) so there exists \(c\in (\prod _i \mathrm{A}^{i})_-\cap {\mathfrak {a}}_{-r-1}\) such that \(\theta =\theta _0\psi _{\beta -\gamma +c}\). By Corollary 8.16 the characters \(\theta _j\) and \(\theta '_j\) intertwine (and by an isometry if \(j\in \mathrm{J}_0\)). Writing \(s_{\gamma _j}\) for an equivariant tame corestriction with respect to \(\gamma _j\), Lemmas A.11 and A.12 imply that the strata \([\Lambda ^j,r+1,r,s_{\gamma _j}(\beta _j-\gamma _j+c_j)]\) and \([\Lambda '^j,r+1,r,s_{\gamma _j}(\beta '_j-\gamma _j)]\) intertwine (by an element of \(\mathrm{G}_{\gamma _j}\) if \(j\in \mathrm{J}_0\)). Thus [39, Proposition 7.6] implies that \([\Lambda ^j,n,r,\beta _j+c_j]\) and \([\Lambda '^j,n,r,\beta '_j]\) intertwine (by an element of \(\mathrm{G}\cap {\text {Aut}}_\mathrm{F}(\mathrm{V}^j)\) if \(j\in \mathrm{J}_0\)) and moreover that \([\Lambda ,n,r,\beta +c]\) and \([\Lambda ',n,r,\beta ']\) intertwine by an element of \(\mathrm{G}\). Furthermore \([\Lambda ,n,r,\beta +c]\) is equivalent to a semisimple stratum whose splitting is a coarsening of the splitting of \(\beta \) by [39, Theorem 6.15]. In fact the splitting cannot be a proper coarsening by [39, Proposition 7.1], because \([\Lambda ,n,r,\beta +c]\) intertwines with \([\Lambda ,n,r,\beta ']\) which has the same number of blocks as \(\beta \). Now we proceed as in the base case to obtain skew elements \({\tilde{\beta }}\) and \({\tilde{\beta }}'\) such that \([\Lambda ,n,r,\beta +c]\) is equivalent to \([\Lambda ,n,r,{\tilde{\beta }}]\) and \([\Lambda ',n,r,{\tilde{\beta }}']\) is equivalent to \([\Lambda ',n,r,\beta ']\). We further have
so that \({\mathscr {C}}(\Lambda ,r,{\tilde{\beta }})={\mathscr {C}}(\Lambda ,r,\beta )\), and also \({\mathscr {C}}(\Lambda ',r,{\tilde{\beta }}')={\mathscr {C}}(\Lambda ',r,\beta ')\), as required. \(\square \)
9 Self-dual semisimple endo-classes
In this section, we introduce one of the central concepts of the article, self-dual semisimple endo-equivalence. We generalize the previous notions of (self-dual) simple endo-equivalence to the semisimple setting and, via the Matching Theorem, reduce the fundamental properties of (self-dual) semisimple endo-equivalence to the (self-dual) simple setting we treated in Sect. 7.
9.1 Self-dual semisimple pairs
Definition 9.1
A semisimple pair is a pair \((k,\beta )\) consisting of an element \(\beta \) of a finite-dimensional semisimple commutative \(\mathrm{F}\)-algebra and an integer k such that, writing \(\mathrm{E}=\mathrm{F}[\beta ]=\bigoplus _{i\in \mathrm{I}} \mathrm{E}_i\) as a sum of fields, we have
where \(e_\mathrm{E}={\text {lcm}}_{i\in \mathrm{I}}e_i\) is the lowest common multiple of the ramification indices \(e_i=e(\mathrm{E}_i/\mathrm{F})\). (See after Lemma 8.2 for the definition of \(k_\mathrm{F}(\beta )\) in this generality.) We say that \(\mathrm{I}\) is the index set of \((k,\beta )\). Writing \(\beta =\sum _{i\in \mathrm{I}}\beta _i\) for the decomposition of \(\beta \) in \(\mathrm{E}=\bigoplus _{i\in \mathrm{I}} \mathrm{E}_i\) and setting \(k_i=\left\lfloor \frac{ke_i}{{e_\mathrm{E}}}\right\rfloor \), each \((k_i,\beta _i)\) is a simple pair, because \(k_\mathrm{F}(\beta _i)\le k_\mathrm{F}(\beta )\), and we call these the component simple pairs of \((k,\beta )\). More generally, if \(\mathrm{J}\) is a non-empty subset of \(\mathrm{I}\) and we set \(\beta _\mathrm{J}=\sum _{j\in \mathrm{J}}\beta _j\) and \(k_\mathrm{J}=\left\lfloor \frac{ke_\mathrm{J}}{e_\mathrm{E}}\right\rfloor \), where \(e_\mathrm{J}={\text {lcm}}_{j\in \mathrm{J}} e_j\), then \((k_\mathrm{J},\beta _\mathrm{J})\) is a semisimple pair.
A semisimple pair \((k,\beta )\) is called self-dual if there exists an extension of the Galois involution \(x\mapsto {\overline{x}}\) on \(\mathrm{F}\) to an involution on \(\mathrm{E}=\mathrm{F}[\beta ]\) such that \({\overline{\beta }}=-\beta \).
Let \((k,\beta )\) be a self-dual semisimple pair, and write the minimal polynomial of \(\beta \) as \(\Psi (X)=\prod _{i\in \mathrm{I}}\Psi _i(X)\) with \(\Psi _i(X)\) irreducible, so that \(\mathrm{E}_i\simeq \mathrm{F}[X]/(\Psi _i(X))\). The action of \(x\mapsto {\overline{x}}\) on the primitive idempotents of \(\mathrm{E}\) defines an action of \(\sigma \) on \(\mathrm{I}\). We let \(\mathrm{I}_0=\{i\in \mathrm{I}:\sigma (i)=i\}\), and choose a set of representatives \(\mathrm{I}^+\) for the orbits of \(\sigma \) in \(\mathrm{I}\backslash \mathrm{I}_0\). Then we let \(\mathrm{I}_{-}=\sigma (\mathrm{I}_+)\) so that we have a disjoint union \(\mathrm{I}=\mathrm{I}_+\cup \mathrm{I}_0\cup \mathrm{I}_-\).
Definition 9.2
A self-dual semisimple pair \((k,\beta )\) is called skew if \(\mathrm{I}=\mathrm{I}_0\) in the notation above.
Let \((k,\beta )\) be a semisimple pair, and let \({\mathscr {Q}}(k,\beta )\) denote the class of quadruples \((\mathrm{V},\varphi ,\Lambda ,r)\) consisting of:
-
(i)
a finite dimensional \(\mathrm{F}\)-vector space \(\mathrm{V}\);
-
(ii)
an embedding \(\varphi :\mathrm{E}\hookrightarrow \mathrm{A}\), where \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\);
-
(iii)
an \({\mathfrak {o}}_{\varphi (\mathrm{E})}\)-lattice sequence \(\Lambda \) in \(\mathrm{V}\);
-
(iv)
and an integer r such that \(\left\lfloor r/e(\Lambda _\mathrm{E})\right\rfloor =k\), where we recall that \(e(\Lambda _\mathrm{E})=e(\Lambda |{\mathfrak {o}}_\mathrm{F})/e_\mathrm{E}\) is the greatest common divisor of the \(e(\Lambda ^i|{\mathfrak {o}}_{\varphi (\mathrm{E}_i)})\).
Given \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\), setting \(n=\max \{r,-{\text {val}}_{\Lambda }(\varphi (\beta ))\}\) we obtain a semisimple stratum \([\Lambda ,n,r,\varphi (\beta )]\) with splitting \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}} \mathrm{V}^i\), where \(\mathrm{V}^i={\text {ker}}(\Psi _i(\varphi (\beta )))\), which we call a realization of the semisimple pair \((k,\beta )\). Note also that, since \(\varphi \) is an embedding, the spaces \(\mathrm{V}^i\) are all non-zero.
We let \({\mathfrak {C}}(k,\beta )\) denote the class of all semisimple characters defined by a realization of the semisimple pair \((k,\beta )\):
Now let \((k,\beta )\) be a self-dual semisimple pair. Let \((\mathrm{V},h)\) be a finite-dimensional \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) and \(\mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\). We say that an embedding \(\varphi :\mathrm{E}\hookrightarrow \mathrm{A}\) is self-dual if \(\varphi ({\overline{x}})={\overline{\varphi (x)}}\), for all \(x\in \mathrm{E}\). Let \({\mathscr {Q}}_-(k,\beta )\) denote the class of quadruples \(((\mathrm{V},h),\varphi ,\Lambda ,r)\) where
-
(i)
\((\mathrm{V},h)\) is a finite-dimensional \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\);
-
(ii)
\((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\);
-
(iii)
and \(\varphi \) and \(\Lambda \) are self-dual.
Given such a quadruple \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\), the realization \([\Lambda ,n,r,\varphi (\beta )]\) is a self-dual semisimple stratum, which we call a self-dual realization of \((k,\beta )\).
We let \({\mathfrak {C}}_-(k,\beta )\) denote the class of all self-dual semisimple characters defined by a realization of the self-dual semisimple pair \((k,\beta )\):
9.2 Transfer of semisimple characters
Let \((k,\beta )\) be a semisimple pair with index set \(\mathrm{I}\), and let \((\mathrm{V},\varphi ,\Lambda ,r),(\mathrm{V}',\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta )\). Let \(\theta \in {\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) and let \({{\widetilde{\mathrm{M}}}}\) denote the Levi subgroup of \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_\mathrm{F}(\mathrm{V})\) associated to the decomposition \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\). Then
with \(\theta _i\in {\mathscr {C}}(\Lambda _i,r,\varphi (\beta _i))\) simple characters. Put \(\theta '_i=\tau _{\Lambda '^i,\Lambda ^i,\beta }(\theta _i)\) and also write \({{\widetilde{\mathrm{M}}}}'\) for the Levi subgroup of \({{\widetilde{\mathrm{G}}}}'={\text {Aut}}_\mathrm{F}(\mathrm{V}')\) which is the stabilizer of \(\mathrm{V}'=\bigoplus _{i\in \mathrm{I}}\mathrm{V}'^i\).
Lemma 9.3
There is a unique semisimple character \(\theta '\in {\mathscr {C}}(\Lambda ',r',\varphi '(\beta ))\) satisfying
Writing \(\tau _{\Lambda ',\Lambda ,\beta }(\theta )\) for the character given by the lemma, this then defines a bijection
which we call transfer.
Proof
If \({{\widetilde{\mathrm{P}}}}'\) is any parabolic subgroup of \({{\widetilde{\mathrm{G}}}}'\) with Levi factor \({{\widetilde{\mathrm{M}}}}'\) and unipotent radical \({{\widetilde{\mathrm{U}}}}'\) then \({\mathrm {H}}^{r'+1}(\varphi '(\beta ),\Lambda ')\) has an Iwahori decomposition with respect to \(({{\widetilde{\mathrm{M}}}}',{{\widetilde{\mathrm{P}}}}')\) and the restriction to \({\mathrm {H}}^{r'+1}(\varphi '(\beta ),\Lambda ')\cap {{\widetilde{\mathrm{U}}}}'\) of any semisimple character in \({\mathscr {C}}(\Lambda ',r',\varphi '(\beta ))\) is trivial by [42, Lemma 3.15]. Uniqueness is then immediate so it only remains to prove existence.
Passing to an affine translation of \([\Lambda ,n,r,\varphi (\beta )]\), we can assume that \(e(\Lambda |{\mathfrak {o}}_\mathrm{F})>{\text {dim}}_\mathrm{F}\mathrm{V}'\). Then, by the \(\dag \)-construction, we obtain \(\theta ^\dag \in {\mathscr {C}}(\Lambda ^\dag ,r,\varphi (\beta )^\dag )\) (see [26, Lemma 3.3]), where \(\mathrm{V}^\dag =\bigoplus _{i\in \mathrm{I}}(\mathrm{V}^i)^\dag \) and \(\theta ^\dag \mid _{{\mathrm {H}}^{r+1}(\beta _i^\dag ,(\Lambda ^i)^\dag )}=\theta _i^\dag \). Moreover,
Hence, as \(\theta _i^\dag \) is the transfer of \(\theta _i\) to \((\Lambda ^i)^\dag \) and the transfer for simple characters is transitive, by replacing \(\theta \) with \(\theta ^\dag \) we can assume \({\text {dim}}_\mathrm{F}\mathrm{V}^i\ge {\text {dim}}_\mathrm{F}\mathrm{V}'^i\) for each \(i\in \mathrm{I}\). Then there are an \(\mathrm{E}_i\)-linear monomorphism \(g_i:\mathrm{V}'^i\rightarrow \mathrm{V}^i\) and an \(\mathrm{E}_i\)-subspace \(\mathrm{W}^i\) of \(\mathrm{V}^i\) such that \(\mathrm{W}^i\oplus g_i\mathrm{V}'^i=\mathrm{V}^i\) splits \(\Lambda ^i\). Write g for the direct sum of the \(g_i\) so that we have
Let \({\tilde{\theta }}\) be the transfer of \(\theta \mid _{{\mathrm {H}}^{r+1}(\varphi (\beta )|_{g\mathrm{V}'},\Lambda \cap g\mathrm{V}')}\) from \(\Lambda \cap g\mathrm{V}'\) to \(g\Lambda '\), see [42, Proposition 3.26]. Then \( ^{g^{-1}}{\tilde{\theta }}\) satisfies the desired properties. \(\square \)
Now suppose \((k,\beta )\) is a self-dual semisimple pair and \([\Lambda ,n,r,\varphi (\beta )]\) and \([\Lambda ',n',r',\varphi '(\beta )]\) are self-dual realizations. Then, as in [42, Proposition 3.32], the bijection \(\tau _{\Lambda ',\Lambda ,\beta }\) commutes with the restrictions of the actions of the adjoint involutions of h and \(h'\) on \({\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) and \({\mathscr {C}}(\Lambda ',r',\varphi '(\beta ))\), respectively. Thus it restricts to give a bijection
Thanks to this result and with the definition of semisimple pairs, we can now define (self-dual) potential semisimple characters.
9.3 Self-dual pss-characters
Let \((k,\beta )\) be a semisimple pair.
Definition 9.4
A potential semisimple character, or pss-character, supported on \((k,\beta )\) is a function \(\Theta :{\mathscr {Q}}(k,\beta )\rightarrow {\mathfrak {C}}(k,\beta )\) such that
-
(i)
for all \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\), we have \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\);
-
(ii)
and, for all pairs \((\mathrm{V},\varphi ,\Lambda ,r),(\mathrm{V}',\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta )\), we have
$$\begin{aligned} \Theta (\mathrm{V}',\varphi ',\Lambda ',r')=\tau _{\Lambda ',\Lambda ,\beta }(\Theta (\mathrm{V},\varphi ,\Lambda ,r)). \end{aligned}$$
We call the values of a pss-character its realizations; by definition a pss-character is determined by any one of its realizations. We also define the degree of a pss-character \(\Theta \) supported on \((k,\beta )\) to be \(\deg (\Theta )=[\mathrm{F}[\beta ]:\mathrm{F}]\).
Definition 9.5
Let \((k,\beta )\) be a self-dual semisimple pair.
-
(i)
A pss-character \(\Theta \) supported on \((k,\beta )\) is called \(\sigma \)-invariant if, for any (or equivalently, some) \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_{-}(k,\beta )\) the realization \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) is \(\sigma \)-invariant.
-
(ii)
A self-dual pss-character supported on \((k,\beta )\) is a function \(\Theta _-:{\mathscr {Q}}_-(k,\beta )\rightarrow {{\mathfrak {C}}_-(k,\beta )}\) such that, for all \(((\mathrm{V},h),\varphi ,\Lambda ,r),((\mathrm{V}',h'),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_{-}(k,\beta )\),
$$\begin{aligned}&\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {C}}_{-}(\Lambda ,r,\varphi (\beta ));\\&\Theta _-((\mathrm{V}',h'),\varphi ',\Lambda ',r')=\tau _{\Lambda ',\Lambda ,\beta }(\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)). \end{aligned}$$
We call the values of a self-dual pss-character its self-dual realizations; by definition a self-dual pss-character is determined by any one of its realizations. As in the simple setting, by the Glauberman correspondence, every self-dual pss-character comes uniquely from the restriction of a \(\sigma \)-invariant pss-character. More precisely, for a self-dual pss-character \(\Theta _-\) supported on \((k,\beta )\), there is a unique \(\sigma \)-invariant pss-character \(\Theta \), supported on \((k,\beta )\), such that the following diagram commutes:

where the vertical arrow is the forgetful map \(((\mathrm{V},h),\varphi ,\Lambda ,r)\mapsto (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\mathrm {Gl}\ \circ \ \Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\) is the Glauberman lift in \({\mathscr {C}}(\Lambda ,r,\varphi (\beta ))\) of \(\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {C}}_-(\Lambda ,r,\varphi (\beta ))\).
We call \(\Theta \) the lift of \(\Theta _-\). We also define the degree of \(\Theta _-\) to be the degree of its lift, so \(\deg (\Theta _-)=[\mathrm{F}[\beta ]:\mathrm{F}]\). We now see how a pss-character determines a set of ps-characters. Suppose we are given a semisimple character \(\theta \in {\mathscr {C}}_-(\Lambda ,r,\beta )\), whose index set splits as a disjoint union \(\mathrm{I}=\mathrm{I}_+\cup \mathrm{I}_0\cup \mathrm{I}_-\) as above; then we have
Moreover, writing \(\mathrm{M}\) for the subgroup of \(\mathrm{G}\) stabilizing this decomposition, which is the intersection with \(\mathrm{G}\) of the Levi subgroup \({{\widetilde{\mathrm{M}}}}\) of \({{\widetilde{\mathrm{G}}}}\) stabilizing the decomposition, we have
by applying [43, Proposition 5.4] to \({\mathrm {H}}^{r+1}(\beta ,\Lambda )\cap {{\widetilde{\mathrm{M}}}}\) and intersecting with \(\mathrm{G}\). Then, after identifying \({\mathrm {H}}^{r+1}_-(\beta ,\Lambda )\cap \mathrm{M}\) with the decomposition above we have
with \(\theta _i\in {\mathscr {C}}(\Lambda ^i,r,\beta _i),\ i\in \mathrm{I}_+\) and \(\theta _{i,-}\in {\mathscr {C}}_-(\Lambda ^i,r,\beta _i),\ i\in \mathrm{I}_0\), by applying [43, Proposition 5.5]. Moreover, as in [3, 4.3 Lemma 1], for \(i\in \mathrm{I}_+\) we have
The above decomposition generalizes to pss-characters as follows:
Lemma 9.6
Let \((k,\beta )\) be a semisimple pair with index set \(\mathrm{I}\) and component simple pairs \((k_i,\beta _i)\).
-
(i)
Let \(\Theta \) be a pss-character supported on \((k,\beta )\) and let \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\).
For each \(\mathrm{J}\subseteq \mathrm{I}\) there is a unique pss-character \(\Theta _\mathrm{J}\) supported on \((k_\mathrm{J},\beta _\mathrm{J})\) such that
$$\begin{aligned} \Theta (\mathrm{V},\varphi ,\Lambda ,r)\mid _{{\mathrm {H}}^{r+1}(\varphi (\beta _\mathrm{J}),\Lambda ^\mathrm{J})}= \Theta _\mathrm{J}(\mathrm{V}^\mathrm{J},\varphi |_{\mathrm{E}_\mathrm{J}},\Lambda ^\mathrm{J},r). \end{aligned}$$(9.7)Moreover, the pss-character \(\Theta _\mathrm{J}\) does not depend on the choice of \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\).
-
(ii)
If \(\Theta \) is a pss-character supported on \((k,\beta )\) and, for \(i\in \mathrm{I}\), we write \(\Theta _i\) for the ps-character given by (i), then the \(\Theta _i\) are pairwise endo-inequivalent.
-
(iii)
Suppose that \((k,\beta )\) is self-dual. Let \(\Theta _-\) be a self-dual pss-character supported on \((k,\beta )\) with lift \(\Theta \). For \(\mathrm{J}\subseteq \mathrm{I}\), write \(\Theta _\mathrm{J}\) for the pss-character given by (i).
Let \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\).
-
(a)
For all \(\sigma \)-stable \(\mathrm{J}\subseteq \mathrm{I}\), there is a unique self-dual pss-character \(\Theta _{\mathrm{J},-}\) supported on \((k_\mathrm{J},\beta _\mathrm{J})\) such that
$$\begin{aligned} \Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\mid _{{\mathrm {H}}^{r+1}_-(\varphi (\beta _\mathrm{J}),\Lambda ^\mathrm{J})}= \Theta _{\mathrm{J},-}((\mathrm{V}^\mathrm{J},h|_{\mathrm{V}^\mathrm{J}}),\varphi |_{\mathrm{E}_\mathrm{J}},\Lambda ^\mathrm{J},r). \end{aligned}$$Moreover, \(\Theta _\mathrm{J}\) is the lift of \(\Theta _{\mathrm{J},-}\).
-
(b)
For all \(i\in \mathrm{I}_+\), the map \(\Theta _i^2\) is the unique ps-character supported on \((k_i,2\beta _i)\) such that
$$\begin{aligned} \Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\mid _{{\mathrm {H}}^{r+1}(\varphi (\beta _i),\Lambda ^i)}= \Theta ^2_i(V^i,\varphi |_{\mathrm{E}_i},\Lambda ^i,r). \end{aligned}$$
-
(a)
Proof
Note first that all uniqueness statements follow from the compatibility with transfer. So we concentrate on the remaining parts of the assertions. For (i) we define \(\Theta _\mathrm{J}\) by (9.7) and transfer; it does not depend on the choice of \((\mathrm{V},\varphi ,\Lambda ,r)\) by Lemma 9.3. The same strategy works for the construction of \(\Theta _{\mathrm{J}.-}\) in (a); but then the values of \(\Theta _{\mathrm{J}.-}\) are the restrictions of the corresponding values of \(\Theta _\mathrm{J}\), which proves both that the definition is independent of the choice of \(((\mathrm{V},h),\varphi ,\Lambda ,r)\) and that \(\Theta _\mathrm{J}\) is the lift of \(\Theta _{\mathrm{J},-}\). Finally, for \(i\in \mathrm{I}_+\), once one has checked that \(\Theta _i^2\) is a ps-character supported on \((k_i,2\beta _i)\), the same argument proves (b).
It remains to prove (ii). Suppose for contradiction that there are distinct \(i,j\in \mathrm{I}\) such that \(\Theta _i\approx \Theta _j\) and let \(\zeta :\mathrm{I}\rightarrow \mathrm{I}\) be the transposition which exchanges i and j. Let \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\) be such that \({\text {dim}}_\mathrm{F}\mathrm{V}^i={\text {dim}}_\mathrm{F}\mathrm{V}^j\) and consider \(\theta =\Theta (\mathrm{V},\varphi ,\Lambda ,r)\), which has simple block restrictions \(\theta _i,\theta _j\). If \(g:\mathrm{V}^i\rightarrow \mathrm{V}^j\) is any isomorphism then, since \(\Theta _i,\Theta _j\) are endo-equivalent, the simple characters  and \(\theta _j\) intertwine in \({\text {Aut}}_\mathrm{F}(\mathrm{V}^j)\); replacing g if necessary, we can assume that
and \(\theta _j\) intertwine in \({\text {Aut}}_\mathrm{F}(\mathrm{V}^j)\); replacing g if necessary, we can assume that  and \(\theta _j\) are intertwined by the identity. In particular, we see that \(\mathrm{I}(\theta _i,\theta _{\zeta (i)})\ne \emptyset \), in the notation of Proposition 8.6. By symmetry we also have \(\mathrm{I}(\theta _j,\theta _{\zeta (j)})\ne \emptyset \). Since the identity lies in \(\mathrm{I}(\theta _l,\theta _{\zeta (l)})\), for any \(l\ne i,j\), Proposition 8.6 implies that \(\theta \) is intertwined with itself by an element of \({\text {Aut}}_\mathrm{F}(\mathrm{V})\) with matching \(\zeta \). However, this contradicts the uniqueness of matchings in Theorem 8.8, since the identity certainly intertwines \(\theta \) with itself, with matching the identity. \(\square \)
and \(\theta _j\) are intertwined by the identity. In particular, we see that \(\mathrm{I}(\theta _i,\theta _{\zeta (i)})\ne \emptyset \), in the notation of Proposition 8.6. By symmetry we also have \(\mathrm{I}(\theta _j,\theta _{\zeta (j)})\ne \emptyset \). Since the identity lies in \(\mathrm{I}(\theta _l,\theta _{\zeta (l)})\), for any \(l\ne i,j\), Proposition 8.6 implies that \(\theta \) is intertwined with itself by an element of \({\text {Aut}}_\mathrm{F}(\mathrm{V})\) with matching \(\zeta \). However, this contradicts the uniqueness of matchings in Theorem 8.8, since the identity certainly intertwines \(\theta \) with itself, with matching the identity. \(\square \)
This lemma shows that we can identify the index set of a semisimple pair \((k,\beta )\) with the index set of any realization of any pss-character supported on \((k,\beta )\). Given a pss-character \(\Theta \) supported on \((k,\beta )\), we call the ps-characters \(\Theta _i\) supported on \((k_i,\beta _i)\) given by the lemma the component ps-characters of \(\Theta \).
9.4 Semisimple endo-classes
Let \(\Theta \) be a pss-character supported on the semisimple pair \((k,\beta )\), and let \(\Theta '\) be a pss-character supported on the semisimple pair \((k',\beta ')\).
Definition 9.8
We say that \(\Theta \) and \(\Theta '\) are endo-equivalent, denoted \(\Theta \approx \Theta '\), if
-
(i)
\(\deg (\Theta )=\deg (\Theta ')\);
-
(ii)
\(k=k'\);
-
(iii)
there exist realizations on a common \(\mathrm{F}\)-vector space which intertwine, i.e. there exist a finite-dimensional \(\mathrm{F}\)-vector space \(\mathrm{V}\) and quadruples \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\) and \((\mathrm{V},\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k',\beta ')\) such that \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\Theta '(\mathrm{V},\varphi ',\Lambda ',r')\) intertwine in \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_{\mathrm{F}}(\mathrm{V})\).
Theorem 9.9
Let \(\Theta \) and \(\Theta '\) be pss-characters supported on semisimple pairs \((k,\beta )\) and \((k,\beta ')\) respectively.
-
(i)
We have \(\Theta \approx \Theta '\) if and only if there is a bijection \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) such that, for all \(i\in \mathrm{I}\), the component ps-characters \(\Theta _i\) and \(\Theta _{\zeta (i)}\) are endo-equivalent. Moreover, if \(\Theta \approx \Theta '\) then the map \(\zeta \) is uniquely determined.
-
(ii)
Suppose that \(\Theta \approx \Theta '\) and let \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) be the bijection of (i). Let \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\) and \((\mathrm{V}',\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta ')\).
-
(a)
For all \(i\in \mathrm{I}\), we have
$$\begin{aligned} e(\mathrm{E}_i|\mathrm{F})= & {} e(\mathrm{E}'_{\zeta (i)}|\mathrm{F}),\ f(\mathrm{E}_i|\mathrm{F})=f(\mathrm{E}'_{\zeta (i)}|\mathrm{F}),\ \nonumber \\ k_\mathrm{F}(\beta _i)= & {} k_\mathrm{F}(\beta '_{\zeta (i)}). \end{aligned}$$(9.10) -
(b)
If \(e(\Lambda )=e(\Lambda ')\) then \((\mathrm{V},\varphi ,\Lambda ,r')\in {\mathscr {Q}}(k,\beta )\).
-
(c)
If \(\mathrm{V}=\mathrm{V}'\) and \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\Theta '(\mathrm{V},\varphi ',\Lambda ',r')\) intertwine in \({{\widetilde{\mathrm{G}}}}\) with matching \(\xi \), then \(\xi =\zeta \).
-
(d)
If \(\mathrm{V}=\mathrm{V}'\) and \({\text {dim}}_\mathrm{F}(\mathrm{V}^i)={\text {dim}}_\mathrm{F}(\mathrm{V}'^{\zeta (i)})\), for all \(i\in \mathrm{I}\), then \(\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\Theta '(\mathrm{V},\varphi ',\Lambda ',r')\) intertwine in \({{\widetilde{\mathrm{G}}}}\) with matching \(\zeta \).
-
(a)
-
(iii)
Endo-equivalence of pss-characters is an equivalence relation.
Proof
Note first that (iii) follows from (i) and Remark 7.2(iii). Moreover, the uniqueness statement in (i) follows immediately from Lemma 9.6(ii) and the transitivity of endo-equivalence for ps-characters.
Suppose that \(\xi :\mathrm{I}\rightarrow \mathrm{I}'\) is a bijection such that \(\Theta _i\approx \Theta '_{\xi (i)}\), for all \(i\in \mathrm{I}\). From Proposition 7.3(i) it follows that \(\Theta \) and \(\Theta '\) have the same degree. Let \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\) and \((\mathrm{V},\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta ')\) be such that \(\mathrm{V}^i\) and \(\mathrm{V}'^{\xi (i)}\) have the same dimension for all \(i\in \mathrm{I}\), and set \(\theta =\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\theta '=\Theta '(\mathrm{V},\varphi ',\Lambda ',r')\). Then the simple block restrictions \(\theta _i\) and \(\theta '_{\xi (i)}\) intertwine by an \(\mathrm{F}\)-linear isomorphism from \(\mathrm{V}^i\) to \(\mathrm{V}'^{\xi (i)}\), for all \(i\in \mathrm{I}\), by Theorem 7.5. Then \(\theta \) and \(\theta '\) intertwine in \({\text {Aut}}_\mathrm{F}(\mathrm{V})\) with matching \(\xi \), by Proposition 8.6, so \(\Theta \approx \Theta '\). This proves one direction of (i), and also that (d) follows from (i).
Conversely, suppose that we have \((\mathrm{V},\varphi ,\Lambda ,r)\in {\mathscr {Q}}(k,\beta )\) and \((\mathrm{V},\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k,\beta ')\) such that \(\theta =\Theta (\mathrm{V},\varphi ,\Lambda ,r)\) and \(\theta '=\Theta '(\mathrm{V},\varphi ',\Lambda ',r')\) intertwine in \({{\widetilde{\mathrm{G}}}}={\text {Aut}}_\mathrm{F}(\mathrm{V})\). Replacing \(\Lambda ,\Lambda '\) in their affine classes, we can assume that \(\Lambda \) and \(\Lambda '\) have the same \({\mathfrak {o}}_\mathrm{F}\)-period and, exchanging them if necessary, that \(r\le r'\). To ease notation, we will identify \(\beta ,\beta '\) with their images under the embeddings \(\varphi ,\varphi '\) respectively.
Suppose for contradiction that \([\Lambda ,n,r',\beta ]\) is not semisimple and let \([\Lambda ,n,r',\gamma ]\) be a semisimple stratum equivalent to it such that \(\gamma \in \prod _i\mathrm{A}^{i}\). By Theorem 8.8 and Proposition 6.2 the algebras \(\mathrm{F}[\gamma ]\) and \(\mathrm{E}'=\mathrm{F}[\beta ']\) have the same degree and \(e_{\mathrm{E}'}=e_{\mathrm{F}[\gamma ]}\). As the pss-characters are endo-equivalent \(\mathrm{F}[\gamma ]\) also has the same \(\mathrm{F}\)-degree as \(\mathrm{E}=\mathrm{F}[\beta ]\). If \(\mathrm{J}\) is the index set for \(\gamma \), then \(\#\mathrm{J}\le \#\mathrm{I}\) and, for \(i\in \mathrm{I},j\in \mathrm{J}\) with \(\mathrm{V}^i\subseteq \mathrm{V}^j\), we have \(e(\mathrm{F}[\gamma _j]/\mathrm{F}) \mid e(\mathrm{F}[\beta _i]/\mathrm{F})\) and \(f(\mathrm{F}[\gamma _j]/\mathrm{F}) \mid f(\mathrm{F}[\beta _i]/\mathrm{F})\). Thus the equality \([\mathrm{F}[\gamma ]:\mathrm{F}]=[\mathrm{F}[\beta ]:\mathrm{F}]\) implies that \(\#\mathrm{J}=\#\mathrm{I}\), so we can identify \(\mathrm{J}\) with \(\mathrm{I}\), and that \(e(\mathrm{F}[\gamma _i]/\mathrm{F}) = e(\mathrm{F}[\beta _i]/\mathrm{F})\) and \(f(\mathrm{F}[\gamma _i]/\mathrm{F}) = f(\mathrm{F}[\beta _i]/\mathrm{F})\). In particular, we deduce that \(e_{\mathrm{E}}=e_{\mathrm{F}[\gamma ]}=e_{\mathrm{E}'}\).
Since \([\Lambda ,n,r',\beta ]\) is not semisimple, there must then be a (unique) index \(i_0\) with \(\gamma _{i_0}=0\) and \(\beta _{i_0}\in \mathrm{F}^\times \), by [39, 6.4, 6.1]. This implies that \(k_0(\beta ,\Lambda )=k_0(\beta _{i_0},\Lambda ^{i_0})\) is a multiple of \(e(\Lambda ^{i_0}|{\mathfrak {o}}_{\mathrm{E}_{i_0}})=e(\Lambda |{\mathfrak {o}}_F)\), so that
with the middle term an integer. In particular, we deduce that
But
which contradicts the previous inequality since \(e(\Lambda |{\mathfrak {o}}_\mathrm{F})=e(\Lambda '|{\mathfrak {o}}_\mathrm{F})\).
Thus \([\Lambda ,n,r',\beta ]\) is semisimple. Now \(\theta |_{{\mathrm {H}}^{r'+1}(\beta ,\Lambda )}\) and \(\theta '\) intertwine in \({{\widetilde{\mathrm{G}}}}\) as \(\theta \) and \(\theta '\) do, Theorem 8.8 provides a matching \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\), and (9.10) follows from Proposition 6.2. Note also that if we had started with a matching \(\xi :\mathrm{I}\rightarrow \mathrm{I}'\) from \((\beta ,\theta )\) to \((\beta ',\theta ')\) then we would obtain \(\xi =\zeta \) by restriction.
We see that:
-
the field extensions \(\mathrm{E}_i/\mathrm{F}\) and \(\mathrm{E}_{\zeta (i)}/\mathrm{F}\) have the same degree;
-
we have \(e(\Lambda ^i|{\mathfrak {o}}_{\mathrm{E}_i})=e(\Lambda '^{\zeta (i)}|{\mathfrak {o}}_{\mathrm{E}'_{\zeta (i)}})\) and \(e(\Lambda _\mathrm{E})=e(\Lambda '_{\mathrm{E}'})\) so, setting \(q=\frac{e(\Lambda ^i|{\mathfrak {o}}_{\mathrm{E}_i})}{e(\Lambda _\mathrm{E})}\), we obtain
$$\begin{aligned} \left\lfloor \frac{r}{e(\Lambda ^i|{\mathfrak {o}}_{\mathrm{E}_i})}\right\rfloor = \left\lfloor \frac{k}{q}\right\rfloor =\left\lfloor \frac{r'}{e(\Lambda '^{\zeta (i)}|{\mathfrak {o}}_{\mathrm{E}'_{\zeta (i)}})}\right\rfloor , \end{aligned}$$which integer we denote by \(k_i\);
-
we have \((\mathrm{V}^i,\varphi _i,\Lambda ^i,r')\in {\mathscr {Q}}(k_i,\beta _i)\), while \(\theta _i|_{{\mathrm {H}}^{r'+1}(\beta ,\Lambda )}\) and \(\theta '_{\zeta (i)}\) intertwine.
Thus the ps-characters \(\Theta _i\) and \(\Theta '_{\zeta (i)}\) are endo-equivalent. This completes the proof of the converse direction of (i), and also that of (a) and (c).
Finally, assertion (b) follows as in the proof of Proposition 7.3(ii). \(\square \)
We call the equivalence classes of pss-characters under endo-equivalence semisimple endo-classes.
Definition 9.11
Given endo-equivalent pss-characters \(\Theta \) and \(\Theta '\) we call the bijection \(\zeta \) of Theorem (i) the matching \(\zeta _{\Theta ',\Theta }\) from \(\Theta \) to \(\Theta '\).
The uniqueness statement in Theorem 9.9(i) immediately gives us:
Corollary 9.12
Let \(\Theta \) and \(\Theta '\) and \(\Theta ''\) be pss-characters such that \(\Theta \approx \Theta '\approx \Theta ''\). Then \(\zeta _{\Theta '',\Theta }=\zeta _{\Theta '',\Theta '}\circ \zeta _{\Theta ',\Theta }\).
We obtain, as another consequence, that intertwining is an equivalence relation for semisimple characters with the same degree and the same parameter k (cf. Theorem 7.6).
Corollary 9.13
Suppose \(\theta ^{(l)}\in {\mathscr {C}}(\Lambda ^{(l)},r^{(l)},\beta ^{(l)})\), for \(l=1,2,3\), are semisimple characters of the same degree such that \(\theta ^{(1)}\) intertwines with \(\theta ^{(2)}\), and \(\theta ^{(2)}\) intertwines with \(\theta ^{(3)}\). Suppose that \(\left\lfloor \frac{r^{(l)}}{e(\Lambda ^{(l)}_{{\mathrm{E}^{(l)}}})}\right\rfloor \) is independent of l. Then \(\theta ^{(1)}\) and \(\theta ^{(3)}\) intertwine.
9.5 Self-dual semisimple endo-classes
Let \(\Theta _-\) be a self-dual pss-character supported on the self-dual semisimple pair \((k,\beta )\), and let \(\Theta '_-\) be a self-dual pss-character supported on the self-dual semisimple pair \((k',\beta ')\).
Definition 9.14
We say that \(\Theta _-\) and \(\Theta '_-\) are endo-equivalent, denoted \(\Theta _- \approx \Theta '_-\), if
-
(i)
\(\deg (\Theta _-)=\deg (\Theta '_-)\);
-
(ii)
\(k=k'\);
-
(iii)
there exist self-dual realizations on a common \(\varepsilon \)-hermitian space which intertwine, i.e. there exist \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm{V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}(k',\beta ')\) such that \(\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\) and \(\Theta '_-((\mathrm{V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\).
Given two endo-equivalent self-dual pss-characters \(\Theta _-\) and \(\Theta '_-\) with lifts \(\Theta \) and \(\Theta '\) respectively, then \(\Theta \approx \Theta '\) by the Glauberman correspondence, and the matching from \(\Theta \) to \(\Theta '\) will also be written as the matching \(\zeta _{\Theta '_-,\Theta _-}\) from \(\Theta _-\) to \(\Theta '_-\). This matching is \(\sigma \)-equivariant because it is also the matching between any intertwining realizations of \(\Theta _-\) and \(\Theta '_-\), by Theorem 9.9(c).
We need to generalize the notion of concordance to embeddings of semisimple algebras over \(\mathrm{F}\).
Definition 9.15
Let \((k,\beta )\) and \((k,\beta ')\) be self-dual semisimple pairs with index sets \(\mathrm{I}\) and \(\mathrm{I}'\) respectively. Suppose that \((\mathrm{V},h)\) and \((\mathrm{V}',h')\) are isometric \(\varepsilon \)-hermitian spaces and \(\varphi :\mathrm{E}\hookrightarrow {\text {End}}_\mathrm{F}(\mathrm{V})\) and \(\varphi ':\mathrm{E}'\hookrightarrow {\text {End}}_{\mathrm{F}}(\mathrm{V}')\) are self-dual \(\mathrm{F}\)-algebra embeddings. Let \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) be a bijection. We say that \((\varphi ,\beta )\) and \((\varphi ',\beta ')\) are \(\zeta \)-concordant if, for all \(i\in \mathrm{I}_0\), the spaces \((\mathrm{V}^i,h_i)=(\mathrm{V}'^{\zeta (i)},h'_{\zeta (i)})\) are isometric and \((\varphi |_{\mathrm{E}_i},\beta _i)\) and \((\varphi '|_{\mathrm{E}'_{\zeta (i)}},\beta '_{\zeta (i)})\) are \((h_i,h'_{\zeta (i)})\)-concordant.
Now we can gather all the results of the previous sections to get the following:
Theorem 9.16
Let \(\Theta _-\) and \(\Theta '_-\) be self-dual pss-characters supported on \((k,\beta )\) and \((k,\beta ')\), respectively, and \(\Theta \) and \(\Theta '\) their respective lifts. Then, the following assertions are equivalent:
-
(i)
The self-dual pss-characters \(\Theta _-\) and \(\Theta '_-\) are endo-equivalent;
-
(ii)
The lifts \(\Theta \) and \(\Theta '\) are endo-equivalent.
-
(iii)
\(\deg (\Theta _-)=\deg (\Theta '_-)\) and there is a bijection \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) which commutes with \(\sigma \) with the following property: if \(((\mathrm{V},h),\varphi ,\Lambda ,r)\in {\mathscr {Q}}_-(k,\beta )\) and \(((\mathrm {V},h),\varphi ',\Lambda ',r')\in {\mathscr {Q}}_-(k,\beta ')\) are such that \((\varphi ,\beta )\) and \((\varphi ',\beta ')\) are \(\zeta \)-concordant and \({\text {dim}}_\mathrm{F}\mathrm{V}^i={\text {dim}}_\mathrm{F}\mathrm{V}'^{\zeta (i)}\), for \(i\in \mathrm{I}\), then the realizations \(\Theta _-((\mathrm{V},h),\varphi ,\Lambda ,r)\) and \(\Theta '_-((\mathrm{V},h),\varphi ',\Lambda ',r')\) intertwine in \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\) with matching \(\zeta \).
Proof
If \(\Theta _-\) and \(\Theta '_-\) are endo-equivalent then so are \(\Theta \) and \(\Theta '\) by the Glauberman correspondence, i.e. (i)\(\Rightarrow \)(ii).
We have (iii) \(\Rightarrow \)(i) because we can find realizations of the semisimple pairs such that, for all indices \(i\in \mathrm{I}_0\), the forms \(h_{i,\varphi (\beta _i)}\) and \(h_{\zeta (i),\varphi '(\beta '_{\zeta (i)})}\) are hyperbolic so that, in particular, \((\varphi |_{\mathrm{E}_i},\beta _i)\) and \((\varphi '|_{\mathrm{E}'_{\zeta (i)}},\beta '_{\zeta (i)})\) are \((h_i,h'_{\zeta (i)})\)-concordant.
It remains to show that (ii)\(\Rightarrow \)(iii), so suppose that \(\Theta \) and \(\Theta '\) are endo-equivalent. Let \(\zeta \) be the matching from \(\Theta \) to \(\Theta '\). Take realizations \(\theta _-=\Theta _-((V,h),\varphi ,\Lambda ,r)\) and \(\theta '_-=\Theta '_-((V,h),\varphi ',\Lambda ',r')\), such that for all \(i\in \mathrm{I}\) the \(\mathrm{F}\)-vector spaces \(\mathrm{V}^i\) and \(\mathrm{V}'^{\zeta (i)}\) have the same dimension. Let \(\theta \) and \(\theta '\) be the lifts of \(\theta _-\) and \(\theta '_-\). Then \(\theta \) and \(\theta '\) intertwine with matching \(\zeta \) by Theorem 9.9(d). Now suppose that \(\varphi \) and \(\varphi '\) are \(\zeta \)-concordant. Since \(\Theta _i\) and \(\Theta '_{\zeta (i)}\) are endo-equivalent, \(\theta _i\) and \(\theta '_{\zeta (i)}\) intertwine by an \(\mathrm{F}\)-linear isomorphism \(g_i\in {\text {Hom}}_\mathrm{F}(\mathrm{V}^i,\mathrm{V}'^{\zeta (i)})\) by Theorem 7.5. For \(i\in \mathrm{I}_-\) we can replace \(g_i\) by \({\overline{g_{-i}}}^{-1}\); moreover, for \(i\in \mathrm{I}_0\) we may assume that \(g_i\) is an isometry from \((V^i,h_i)\) to \((V'^{\zeta (i)},h_{\zeta (i)})\) which intertwines \(\theta _{i,-}\) with \(\theta '_{\zeta (i),-}\), by Proposition 6.10 (since the embeddings are \(\zeta \)-concordant). In particular, the element \(g=\sum _{i\in \mathrm{I}} g_i\) is then in \(\mathrm{G}\) and intertwines \(\theta \) with \(\theta '\) with matching \(\zeta \), by Proposition 8.6. \(\square \)
One consequence of Theorems 9.16, 9.9(iii) and Corollary 9.12 is:
Corollary 9.17
Endo-equivalence of self-dual pss-characters is an equivalence relation and, for self-dual pss-characters \(\Theta _-\approx \Theta '_-\approx \Theta ''_-\), we have \(\zeta _{\Theta ''_-,\Theta '_-}\circ \zeta _{\Theta '_-,\Theta _-}=\zeta _{\Theta ''_-,\Theta _-}\).
Definition 9.18
We call the equivalence classes of self-dual pss-characters under endo-equivalence self-dual semisimple endo-classes.
As another corollary of Theorems 9.16 and 8.17, we see the remarkable result that, for self-dual semisimple characters of same degree and with the same k, intertwining is an equivalence relation.
Corollary 9.19
Suppose \(\theta ^{(l)}_-\in {\mathscr {C}}_-(\Lambda ^{(l)},r^{(l)},\beta ^{(l)})\), for \(l=1,2,3\), are self-dual semisimple characters of the same degree such that \(\theta ^{(1)}_-\) intertwines with \(\theta ^{(2)}_-\) in \(\mathrm{G}\), and \(\theta ^{(2)}_-\) intertwines with \(\theta ^{(3)}_-\) in \(\mathrm{G}\). Suppose that \(\left\lfloor \frac{r^{(l)}}{e(\Lambda ^{(l)}_{{\mathrm{E}^{(l)}}})}\right\rfloor \) is independent of l. Then \(\theta ^{(1)}_-\) and \(\theta ^{(3)}_-\) intertwine in \(\mathrm{G}\).
Proof
Let \(\Theta ^{(l)}_-\) be the self-dual pss-character supported on \((k,\beta ^{(l)})\) with realization \(\theta ^{(l)}_-\). Now \(\Theta ^{(1)}_-\approx \Theta ^{(2)}_-\) and \(\Theta ^{(2)}_-\approx \Theta ^{(3)}_-\) and thus \(\Theta ^{(1)}_-\approx \Theta ^{(3)}_-\), by Corollary 9.17. Let \(\varphi ^{(l)}\) be the canonical embedding of \(\mathrm{E}^{(l)}\) into \(\mathrm{A}\). We need to show that \((\varphi ^{(1)},\beta ^{(1)})\) and \((\varphi ^{(3)},\beta ^{(3)})\) are \(\zeta _{\Theta ^{(3)}_-,\Theta ^{(1)}_-}\)-concordant. Without loss of generality we can assume that \(e(\Lambda ^{(l)})\) is independent of l, and by Theorem 9.9(b) we can assume without loss of generality that \(r^{(l)}\) is independent of l. By the Glauberman correspondence and Corollary 9.13, the lifts of \(\theta ^{(1)}_-\) and \(\theta ^{(3)}_-\) intertwine in \({{\widetilde{\mathrm{G}}}}\) and, by Theorem 9.9(c), they do so with matching \(\zeta :=\zeta _{\Theta ^{(1)}_-,\Theta ^{(3)}_-}\); in particular, \({\text {dim}}_\mathrm{F}\mathrm{V}^i={\text {dim}}_\mathrm{F}\mathrm{V}^{\zeta (i)}\), for \(i\in \mathrm{I}\). By Theorem 8.17 we have that \((\varphi ^{(1)},\beta ^{(1)})\) and \((\varphi ^{(2)},\beta ^{(2)})\) are \(\zeta _{\Theta ^{(2)}_-,\Theta ^{(1)}_-}\)-concordant, and that \((\varphi ^{(2)},\beta ^{(2)})\) and \((\varphi ^{(3)},\beta ^{(3)})\) are \(\zeta _{\Theta ^{(3)}_-,\Theta ^{(2)}_-}\)-concordant. Now the transitivity of concordance and Corollary 9.17 finish the proof. \(\square \)
10 Intertwining and conjugacy for special orthogonal groups
We now investigate intertwining and conjugacy of semisimple characters of special orthogonal groups, so for this section we suppose that \((\mathrm{V},h)\) is a 1-hermitian space with \(\mathrm{F}=\mathrm{F}_{\mathsf {o}}\), so that \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\) is an orthogonal group and \(\mathrm{G}^{\mathsf {o}}\) is its special orthogonal subgroup.
10.1 Intertwining self-dual semisimple characters
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ']\), be self-dual semisimple strata in \(\mathrm{A}\), with associated splittings \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}'}\mathrm{V}'^i\).
Lemma 10.1
Suppose that \(\beta \) and \(\beta '\) are non-zero. Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',r,\beta ')\) be self-dual semisimple characters which intertwine in \(\mathrm{G}\). Suppose also that \(\beta \) normalizes \(\Lambda \). Then \(\theta _-\) and \(\theta '_-\) intertwine in \(\mathrm{G}^{\mathsf {o}}\) (respectively in \(\mathrm{G}\setminus \mathrm{G}^{\mathsf {o}}\)) if and only if the symplectic spaces \((\mathrm{V},\beta ^*(h))\) and \((\mathrm{V},\beta '^*(h))\) are isometric by an automorphism of \(\mathrm{V}\) of determinant congruent to 1 modulo \({\mathfrak {p}}_\mathrm{F}\) (respectively, to \(-1\) modulo \({\mathfrak {p}}_\mathrm{F}\)).
Proof
By hypothesis, there is an element \(g\in \mathrm{G}\) which intertwines \(\theta _-\) with \(\theta '_-\). Then the fundamental strata \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ',n,n-1,\beta ']\) are intertwined by g so, by [39, Proposition 6.9], have the same level. In particular, we deduce that \(e(\Lambda )=e(\Lambda ')\). Moreover, writing \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) for the matching from \((\theta _-,\beta )\) to \((\theta '_-,\beta ')\), Theorem 8.8 and [39, Proposition 6.9] together imply that \(\nu _{\Lambda '}(\beta '_{\zeta (i)})=-n\) for all \(i\in \mathrm{I}\) also. In particular, this implies that \(\beta '\) normalizes \(\Lambda '\) also.
By the intertwining of the fundamental strata, there are skew elements \(c\in \beta +{\mathfrak {a}}_{1-n}^-\) and \(c'\in \beta '+{\mathfrak {a}}_{1-n}'^-\) such that \(gcg^{-1}=c'\), and g then gives an isometry from \(c^*(h)\) to \(c'^*(h)\). Then [39, Lemma 5.3] implies that there is an \(\mathrm{F}\)-linear isometry \(u\in \mathrm{P}^1(\Lambda )\) from \(\beta ^*(h)\) to \(c^*(h)\); similarly, there is an \(\mathrm{F}\)-linear isometry \(u'\in \mathrm{P}^1(\Lambda ')\) from \(c'^*(h)\) to \(\beta '^*(h)\). Thus \(u'gu\) is an isometry from \(\beta ^*(h)\) to \(\beta '^*(h)\), and \(\det (u'gu)\equiv \det (g) \pmod {{\mathfrak {p}}_\mathrm{F}}\). Since any isometry of a symplectic space has determinant 1, there cannot be isometries from \(\beta ^*(h)\) to \(\beta '^*(h)\) with determinant congruent to both \(\pm 1\) modulo \({\mathfrak {p}}_\mathrm{F}\) and the result follows. \(\square \)
Theorem 10.2
Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',r,\beta ')\) be self-dual semisimple characters which intertwine in \(\mathrm{G}\).
-
(i)
Suppose that there is \(i_0\in \mathrm{I}\) such that \(\beta _{i_0}=0\). Then, \(\theta _-\) and \(\theta '_-\) intertwine by an element of \(\mathrm{G}^{\mathsf {o}}\) and by an element of \(\mathrm{G}\setminus \mathrm{G}^{\mathsf {o}}\).
-
(ii)
If \(\beta \) has no zero component, then \(\theta _-\) and \(\theta '_-\) intertwine under an element of \(\mathrm{G}^{\mathsf {o}}\) if and only if \((\mathrm{V},\beta ^*(h))\) and \((\mathrm{V},\beta '^*(h))\) are isometric by an automorphism of \(\mathrm{V}\) of determinant congruent to 1 modulo \({\mathfrak {p}}_\mathrm{F}\). In this case every element of \(\mathrm{G}\) intertwining \(\theta _-\) and \(\theta '_-\) is in \(\mathrm{G}^{\mathsf {o}}\).
Note that the statement in (ii) is equivalent to saying that \(\theta _-\) and \(\theta '_-\) intertwine under an element of \(\mathrm{G}\setminus \mathrm{G}^{\mathsf {o}}\) if and only if \((\mathrm{V},\beta ^*(h))\) and \((\mathrm{V},\beta '^*(h))\) are isometric by an automorphism of \(\mathrm{V}\) of determinant congruent to \(-1\) modulo \({\mathfrak {p}}_\mathrm{F}\), in which case every element of \(\mathrm{G}\) intertwining \(\theta _-\) and \(\theta '_-\) is in \(\mathrm{G}\setminus \mathrm{G}^{\mathsf {o}}\).
Proof
Write \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) for the matching from \((\theta _-,\beta )\) to \((\theta '_-,\beta ')\). By Theorem 8.17, for \(i\in \mathrm{I}_+\) we can choose an isomorphism \(g_i:\mathrm{V}^i\rightarrow \mathrm{V}'^{\zeta (i)}\), and by Theorem 8.17, for \(i\in \mathrm{I}_0\) we can find an isometry \(g_i\) from \((\mathrm{V}^i,h_i)\) to \((\mathrm{V}'^{\zeta (i)},h'_{\zeta (i)})\). For \(i\in \mathrm{I}_-\) we set \(g_i={\overline{g_{-i}}}^{-1}\), so that \(g=\sum _{i\in \mathrm{I}}g_i\) is an element of \(\mathrm{G}\) which conjugates the splittings. Conjugating by this element g (which may have determinant \(-1\)), we reduce to the case that the characters have the same splitting and the matching is the identity map.
-
(i)
The characters \(\theta _{i_0}\) and \(\theta '_{i_0}\) are trivial, and therefore intertwine under any element of the group \(\mathrm{U}(\mathrm{V}^{i_0},h_{i_0})\), in particular by an element of determinant 1 and by an element of determinant \(-1\). The result follows immediately by applying Proposition 8.6 to the lifts of \(\theta _-,\theta '_-\).
-
(ii)
We write \(\mathrm{I}=\bigcup _{\mathrm{J}\in {\mathcal {P}}} \mathrm{J}\) in the coarsest way such that, for each \(\mathrm{J}\), all elements \(\beta _j\) with \(j\in \mathrm{J}\) have the same valuation with respect to \(\Lambda \). By Corollary 8.16, there are \(g_{\mathrm{J}}\in \mathrm{U}(\mathrm{V}^{\mathrm{J}},h_{\mathrm{J}})\) such that \(g=\sum _{\mathrm{J}\in {\mathcal {P}}} g_{\mathrm{J}}\) is an element of \(\mathrm{G}\) which intertwines \(\theta \) with \(\theta '\); then \(g_{\mathrm{J}}\) intertwines \(\theta _{\mathrm{J}}\) with \(\theta '_{\mathrm{J}}\). Applying Lemma 10.1 to \(\theta _{\mathrm{J},-}\) and \(\theta '_{\mathrm{J},-}\), we see that \(\beta _{\mathrm{J}}^*(h)\) is isometric to \(\beta _{\mathrm{J}}'^*(h)\) by an element of determinant congruent to \(\det (g_\mathrm{J})\) modulo \({\mathfrak {p}}_\mathrm{F}\). Summing the blocks, \(\beta ^*(h)\) is isometric to \(\beta '^*(h)\) by an element of determinant congruent to \(\det (g)\) modulo \({\mathfrak {p}}_\mathrm{F}\). The result now follows since \(\beta ^*(h)\) and \(\beta '^*(h)\) are symplectic forms and any isometry of a symplectic space has determinant 1.
\(\square \)
We deduce an analogue of Corollary 9.19 (transitivity of intertwining) for special orthogonal groups.
Corollary 10.3
Suppose \(\theta ^{(l)}_-\in {\mathscr {C}}_-(\Lambda ^{(l)},r^{(l)},\beta ^{(l)})\), for \(l=1,2,3\), are self-dual semisimple characters of the same degree such that \(\theta ^{(1)}_-\) intertwines with \(\theta ^{(2)}_-\) in \(\mathrm{G}^{\mathsf {o}}\), and \(\theta ^{(2)}_-\) intertwines with \(\theta ^{(3)}_-\) in \(\mathrm{G}^{\mathsf {o}}\). Suppose that \(\left\lfloor \frac{r^{(l)}}{e(\Lambda ^{(l)}_{{\mathrm{E}^{(l)}}})}\right\rfloor \) is independent of l. Then \(\theta ^{(1)}_-\) and \(\theta ^{(3)}_-\) intertwine in \(\mathrm{G}^{\mathsf {o}}\).
Proof
Changing the lattice sequences in their affine class, we can assume that they all have the same \({\mathfrak {o}}_\mathrm{F}\)-period; then Theorem 9.9(a) implies that \(e(\Lambda ^{(l)}_{{\mathrm{E}^{(l)}}})\) is also independent of l. Set \(r_{\min }=\min \{r_i\mid i=1,2,3\}\) and \(r_{\max }=\max \{r_i\mid i=1,2,3\}\), so that we can restrict the characters to \({\mathscr {C}}_-(\Lambda ^{(l)},r_{\max },\beta ^{(l)})\) and extend them uniquely to \({\mathscr {C}}_-(\Lambda ^{(l)},r_{\min },\beta ^{(l)})\) without changing endo-class (i.e. we pass to their transfers). Moreover, by Corollary 9.19, any two of these intertwine by an element of \(\mathrm{G}\). Then, if any \(\beta ^{(l)}\) has a zero component, then \(\theta _-^{(1)}\) and \(\theta _-^{(3)}\) intertwine by an element of \(\mathrm{G}^{\mathsf {o}}\) by Theorem 10.2(i).
Suppose now that none of the \(\beta ^{(l)}\) has a zero component. Applying Theorem 10.2(ii) to the restrictions to \({\mathscr {C}}_-(\Lambda ^{(l)},r_{\max },\beta ^{(l)})\), we have that
by isometries of determinant congruent to 1 modulo \({\mathfrak {p}}_F\). Then, by Theorem 10.2(ii) again, the extensions to \({\mathscr {C}}_-(\Lambda ^{(l)},r_{\min },\beta ^{(l)})\) all intertwine by an element of \(\mathrm{G}^{\mathsf {o}}\). In particular, their restrictions \(\theta _-^{(1)}\) and \(\theta _-^{(3)}\) intertwine by an element of \(\mathrm{G}^{\mathsf {o}}\). \(\square \)
10.2 Conjugacy of self-dual semisimple characters
There exist self-dual semisimple characters for \(\mathrm{G}^{\mathsf {o}}\) which intertwine in \(\mathrm{G}^{\mathsf {o}}\), are conjugate in \(\mathrm{G}\), but are not conjugate in \(\mathrm{G}^{\mathsf {o}}\). For example, let \([\Lambda ,n,r,\beta ]\) be a self-dual semisimple stratum in \(\mathrm{A}\) with associated splitting \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and let \(\theta \in {\mathscr {C}}^{\Sigma }(\Lambda ,r,\beta )\) be a semisimple character. Suppose there exists \(i_0\in \mathrm{I}\) with \(\beta _{i_0}=0\), such that \({\mathrm{P}_-(\Lambda ^{i_0})}\) has no element of determinant \(-1\) in its normalizer. Take an element \(g_{i_0}\) of determinant \(-1\) in \(\mathrm{U}(\mathrm{V}^{i_0},h_{i_0})\) and \(g_i={\text {id}}\) for \(i\ne i_0\), and put \(g=\sum _{i\in \mathrm{I}} g_i\). Then \(\theta \) and  intertwine by an element of \(\mathrm{G}^{\mathsf {o}}\) by Theorem 10.2, but they are not conjugate by an element of \(\mathrm{G}^{\mathsf {o}}\) by an exercise using Theorem 10.2 and Proposition A.9(ii).
intertwine by an element of \(\mathrm{G}^{\mathsf {o}}\) by Theorem 10.2, but they are not conjugate by an element of \(\mathrm{G}^{\mathsf {o}}\) by an exercise using Theorem 10.2 and Proposition A.9(ii).
Nonetheless, we do have the following intertwining implies conjugacy theorem.
Theorem 10.4
Suppose that \(e(\Lambda )=e(\Lambda ')\), let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ']\) be self-dual semisimple strata in \(\mathrm{A}\) with splittings \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}'}\mathrm{V}'^i\), and let \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ',r,\beta ')\) be semisimple characters which intertwine in \(\mathrm{G}^{\mathsf {o}}\) with matching \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\). Suppose there exists \(g\in \mathrm{G}\) such that \(g\Lambda ^i=\Lambda '^{\zeta (i)}\), for all \(i\in \mathrm{I}\), and
one of the following two assertions:
-
(i)
there is an \(i_0\) such that \(\beta _{i_0}=0\), and \(\mathrm{P}_-(\Lambda ^{i_0})\) contains an element of determinant \(-1\); or
-
(ii)
\(\beta _i\ne 0\), for all \(i\in \mathrm{I}\).
Then \(\theta \) is conjugate to \(\theta '\) by an element of \(\mathrm {G}^{\mathsf {o}}\cap g\mathrm {P}_-(\Lambda )\).
Remark 10.5
If \(\Lambda \) is a self-dual lattice sequence which corresponds to a vertex in the Bruhat–Tits building of \(\mathrm{G}\), then there is an element of \(\mathrm{G}\setminus \mathrm{G}^{\mathsf {o}}\) in the normalizer of \(\Lambda \). In particular, in the situation of Theorem 10.4, if \(\mathrm{P}^{\mathsf {o}}_-(\Lambda ^{i_0})\) is a maximal parahoric subgroup of \(\mathrm{U}(\mathrm{V}^{i_0},h_{i_0})\), then condition (i) is satisfied so \(\theta \) is conjugate to \(\theta '\) by an element \(g\in \mathrm{G}^{\mathsf {o}}\) such that \(g\Lambda =\Lambda '\).
Proof of Theorem 10.4
By Theorem 8.15(ii), there is a \(y\in \mathrm{G}\) which conjugates \(\theta \) to \(\theta '\).
-
(i)
If \(g_{i_0}\in \mathrm{P}_-(\Lambda ^{i_0})\) has determinant \(-1\), put \(g_i={\text {id}}\), for \(i\ne i_0\), and \(g=\sum _{i\in \mathrm{I}} g_i\). Then g is an element of determinant \(-1\) which normalizes \(\theta \). Then y and yg both conjugate \(\theta \) to \(\theta '\) and one of them lies in \(\mathrm{G}^{\mathsf {o}}\).
-
(ii)
Since y intertwines \(\theta \) with \(\theta '\), it lies in \(\mathrm{G}^{\mathsf {o}}\) by Theorem 10.2(ii).
\(\square \)
11 Intertwining implies conjugacy for cuspidal types
We recall the construction of cuspidal types for \(\mathrm{G}^{\mathsf {o}}\) of [43], or more precisely its extension to representations over \({\mathbf {C}}\) in [26], and then prove that two cuspidal types for \(\mathrm{G}^{\mathsf {o}}\) intertwine in \(\mathrm{G}^{\mathsf {o}}\) if and only if they are conjugate in \(\mathrm{G}^{\mathsf {o}}\). This completes the classification by types of the irreducible cuspidal representations of \(\mathrm{G}^{\mathsf {o}}\). In the whole section we assume that \(\mathrm{G}^{\mathsf {o}}\) has compact centre, i.e. that \(\mathrm{G}\) is not \(\mathrm{F}\)-isomorphic to \(\mathrm{O}(1,1)(\mathrm{F})\).
Let \([\Lambda ,n,0,\beta ]\) be a skew semisimple stratum with index set \(\mathrm{I}=\mathrm{I}_0\), and \(\mathrm{E}=\mathrm{F}[\beta ]=\bigoplus _{i\in \mathrm{I}}\mathrm{E}_i\). We write \({\mathfrak {b}}_n={\mathfrak {b}}_n(\Lambda )\) for the intersection of the \({\mathfrak {o}}_\mathrm{F}\)-lattice \({\mathfrak {a}}_n={\mathfrak {a}}_n(\Lambda )\) with the centralizer \(\mathrm{B}=\mathrm{B}_\beta \) of \(\beta \), so that \({\mathfrak {b}}_n=\bigoplus _{i\in \mathrm{I}}{\mathfrak {b}}^i_n\). The quotient \(\mathrm{P}_-(\Lambda _\mathrm{E})/\mathrm{P}^1_-(\Lambda _\mathrm{E})\) is the set of rational points of the reductive group (defined over \(\mathrm {k}_{\mathsf {o}}\))

where  is the reductive group defined by the anti-involution which is the restriction of
is the reductive group defined by the anti-involution which is the restriction of  to \({\mathfrak {b}}_0^i/{\mathfrak {b}}_1^i\) and \({\text {Res}}_{\mathrm {k}_{\mathrm{E}_{i,{\mathsf {o}}}}|\mathrm {k}_{\mathsf {o}}}\) is the Weil restriction. Recall that the parahoric group \(\mathrm{P}^{{\mathsf {o}}}_-(\Lambda _\mathrm{E})\) is the pre-image of the set of \(\mathrm {k}_{\mathsf {o}}\)-rational points of the neutral component of (11.1).
to \({\mathfrak {b}}_0^i/{\mathfrak {b}}_1^i\) and \({\text {Res}}_{\mathrm {k}_{\mathrm{E}_{i,{\mathsf {o}}}}|\mathrm {k}_{\mathsf {o}}}\) is the Weil restriction. Recall that the parahoric group \(\mathrm{P}^{{\mathsf {o}}}_-(\Lambda _\mathrm{E})\) is the pre-image of the set of \(\mathrm {k}_{\mathsf {o}}\)-rational points of the neutral component of (11.1).
We note also that \((\mathrm{G}^{\mathsf {o}})_\beta =(\mathrm{G}_\beta )^{\mathsf {o}}\), since there is at most a single \(i\in \mathrm{I}\) such that \(\beta _i=0\); we may therefore unambiguously denote this group by \(\mathrm{G}^{\mathsf {o}}_\beta \).
Definition 11.2
A skew semisimple stratum \([\Lambda ,n,0,\beta ]\) is called cuspidal if \(\mathrm{G}^{{\mathsf {o}}}_\beta \) has compact centre and \(\mathrm{P}^{{\mathsf {o}}}_-(\Lambda _\mathrm{E})\) is a maximal parahoric subgroup in \(\mathrm{G}_\beta ^{\mathsf {o}}\).
The property of being cuspidal depends only on the equivalence class of the stratum and we have the following stronger result.
Proposition 11.3
Suppose \([\Lambda ,n,0,\beta ]\) and \([\Lambda ,n,0,\beta ']\) are skew semisimple strata such that \({\mathscr {C}}(\Lambda ,0,\beta )={\mathscr {C}}(\Lambda ,0,\beta ')\). Then \([\Lambda ,n,0,\beta ]\) is cuspidal if and only if \([\Lambda ,n,0,\beta ']\) is cuspidal.
We need the following straightforward result on algebraic groups.
Lemma 11.4
Let \(\mathrm {k}\) be a finite field of odd characteristic p, with involution  on \(\mathrm {k}\) with fixed point set \(\mathrm {k}_{\mathsf {o}}\). Let \({\mathbb {H}}\) be an algebraic group defined over \(\mathrm {k}_{\mathsf {o}}\) and \(\mathrm {k}_{\mathsf {o}}\)-isomorphic to a symplectic, a unitary or an orthogonal group over \(\mathrm {k}_{\mathsf {o}}\). Suppose \({\mathbb {H}}(\mathrm {k}_{\mathsf {o}})\) is isomorphic to \(\mathrm{O}(1,1)(\mathrm {k})\) as an abstract group. Then \(\mathrm {k}=\mathrm {k}_{\mathsf {o}}\) and \({\mathbb {H}}\) is \(\mathrm {k}\)-isomorphic to \(\mathrm{O}(1,1)\).
on \(\mathrm {k}\) with fixed point set \(\mathrm {k}_{\mathsf {o}}\). Let \({\mathbb {H}}\) be an algebraic group defined over \(\mathrm {k}_{\mathsf {o}}\) and \(\mathrm {k}_{\mathsf {o}}\)-isomorphic to a symplectic, a unitary or an orthogonal group over \(\mathrm {k}_{\mathsf {o}}\). Suppose \({\mathbb {H}}(\mathrm {k}_{\mathsf {o}})\) is isomorphic to \(\mathrm{O}(1,1)(\mathrm {k})\) as an abstract group. Then \(\mathrm {k}=\mathrm {k}_{\mathsf {o}}\) and \({\mathbb {H}}\) is \(\mathrm {k}\)-isomorphic to \(\mathrm{O}(1,1)\).
Proof
Put \(q=|\mathrm {k}|\) and \(q_{\mathsf {o}}=|\mathrm {k}_{\mathsf {o}}|\) . If \({\mathbb {H}}\) is isotropic and not \(\mathrm {k}_{\mathsf {o}}\)-isomorphic to \(\mathrm{O}(1,1)\) then the cardinality of \({\mathbb {H}}(\mathrm {k}_{\mathsf {o}})\) is divisible by p, because the latter contains a unipotent group of cardinality p, so we are left with the cases \(\mathrm{U}(1)\), \(\mathrm{O}(2)\), \(\mathrm{O}(1)\) and \(\mathrm{O}(1,1)\). But \(\mathrm{U}(1)(\mathrm {k}/\mathrm {k}_{\mathsf {o}})\) is cyclic while \(\mathrm{O}(1,1)(\mathrm {k})\) is not; and the groups \(\mathrm{O}(2)({\mathrm {k}_{\mathsf {o}}})\) and \(\mathrm{O}(1)({\mathrm {k}_{\mathsf {o}}})\) have cardinalities \(2({q_{\mathsf {o}}}+1)\) and 2 which both differ from the cardinality \(2(q-1)\) of \(\mathrm{O}(1,1)(\mathrm {k})\). Thus \({\mathbb {H}}\) is \(\mathrm {k}_{\mathsf {o}}\)-isomorphic to \(\mathrm{O}(1,1)\) and, comparing cardinalities, \(\mathrm {k}=\mathrm {k}_{\mathsf {o}}\). \(\square \)
For the proof of Proposition 11.3 we need to recall some more of the data attached to a semisimple stratum \([\Lambda ,n,0,\beta ]\), in particular the \({\mathfrak {o}}_\mathrm{F}\)-order \({\mathfrak {J}}(\beta ,\Lambda )\) (see [39, Section 9.1] and [12, 3.1.8]). It is the additive group generated by the intersection of \({\mathfrak {a}}_0\) with the \({{\widetilde{\mathrm{G}}}}\)-intertwining of any semisimple character \(\theta \in {\mathscr {C}}(\Lambda ,0,\beta )\); it contains \({\mathfrak {b}}_1\) and, writing \({\mathfrak {J}}^1(\beta ,\Lambda )\) for its intersection with \({\mathfrak {a}}_1\), we have a canonical isomorphism \({\mathfrak {J}}(\beta ,\Lambda )/{\mathfrak {J}}^1(\beta ,\Lambda )\simeq {\mathfrak {b}}_0(\Lambda )/{\mathfrak {b}}_1(\Lambda )\). We have a chain of compact open subgroups of \(\mathrm{G}\)
with the first two defined as the intersection of \({\mathfrak {J}}(\beta ,\Lambda )\) with \(\mathrm{G}\) and \(\mathrm{G}^{\mathsf {o}}\) respectively, \(\mathrm{J}^1_-(\beta ,\Lambda )\) its intersection with \(\mathrm{P}^1_-(\Lambda )\), and \(\mathrm{J}^{\mathsf {o}}_-(\beta ,\Lambda )=\mathrm{P}^{{\mathsf {o}}}_-(\Lambda _\mathrm{E})\mathrm{J}^1_-(\beta ,\Lambda )\); this is the inverse image in \(\mathrm{J}^+_-(\beta ,\Lambda )\) of the connected component of
Proposition 11.3 is an immediate consequence of the following lemma, in which we consider the reduced Bruhat–Tits building \({\mathfrak {B}}_{{\text {red}}}(\mathrm{G}_\beta )\) (the product of the buildings \({\mathfrak {B}}_{{\text {red}}}(\mathrm{G}^i_{\beta _i})\)) with its weak simplicial structure, i.e. the facets of \({\mathfrak {B}}_{{\text {red}}}(\mathrm{G}^i_{\beta _i})\) are the intersection of the facets of \({\mathfrak {B}}_{{\text {red}}}({{\widetilde{\mathrm{G}}}}^i_{\beta _i})\) with \({\mathfrak {B}}_{{\text {red}}}(\mathrm{G}^i_{\beta _i})\).
Lemma 11.5
Let \([\Lambda ,n,0,\beta ]\) and \([\Lambda ,n,0,\beta ']\) be skew semisimple strata such that \({\mathscr {C}}(\Lambda ,0,\beta )={\mathscr {C}}(\Lambda ,0,\beta ')\).
-
(i)
\({\mathfrak {J}}(\beta ,\Lambda )={\mathfrak {J}}(\beta ',\Lambda )\) and we have a canonical isomorphism \(\mathrm{P}_-(\Lambda _\mathrm{E})/\mathrm{P}^1_-(\Lambda _\mathrm{E})\simeq \mathrm{P}_-(\Lambda _{\mathrm{E}'})/\mathrm{P}^1_-(\Lambda _{\mathrm{E}'})\).
-
(ii)
\(\mathrm{G}_\beta ^{\mathsf {o}}\) has compact centre if and only if \(\mathrm{G}_{\beta '}^{\mathsf {o}}\) has compact centre.
-
(iii)
Suppose \(\mathrm{G}_\beta ^{\mathsf {o}}\) has compact centre; then \(\Lambda _\mathrm{E}\) corresponds to a vertex of \({\mathfrak {B}}_{{\text {red}}}(\mathrm{G}_\beta )\) if and only if \(\Lambda _{\mathrm{E}'}\) corresponds to a vertex of \({\mathfrak {B}}_{{\text {red}}}(\mathrm{G}_{\beta '})\).
-
(iv)
Suppose \(\mathrm{G}_\beta ^{\mathsf {o}}\) has compact centre and \(\Lambda _\mathrm{E}\) corresponds to a vertex of \({\mathfrak {B}}_{{\text {red}}}(\mathrm{G}_\beta )\); then \(\mathrm{P}^{\mathsf {o}}_-(\Lambda _\mathrm{E})\) is a maximal parahoric subgroup of \(\mathrm{G}_\beta \) if and only if \(\mathrm{P}^{\mathsf {o}}_-(\Lambda _{\mathrm{E}'})\) is a maximal parahoric subgroup of \(\mathrm{G}_{\beta '}\).
-
(v)
Let \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) be the matching from \((\theta ,\beta )\) to \((\theta ,\beta ')\) for some semisimple character \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,0,\beta )\). Then \(\mathrm {k}_{\mathrm{E}_i}\) and \(\mathrm {k}_{\mathrm{E}'_{\zeta (i)}}\) coincide in \({\mathfrak {a}}_0/{\mathfrak {a}}_1\) and the canonical map from (i) is a product of algebraic isomorphisms
$$\begin{aligned} \mathrm{P}_-(\Lambda ^i_{\mathrm{E}_i})/\mathrm{P}^1_-(\Lambda ^i_{\mathrm{E}_i})\rightarrow \mathrm{P}_- (\Lambda ^{\zeta (i)}_{\mathrm{E}'_{\zeta (i)}})/\mathrm{P}^1_-(\Lambda ^{\zeta (i)}_{\mathrm{E}'_{\zeta (i)}}) \end{aligned}$$defined over \(\mathrm {k}_{\mathrm{E}_{i,{\mathsf {o}}}}\).
Proof
Assertion (i) follows immediately from the description of \({\mathfrak {J}}(\beta ,\Lambda )\) as the additive group generated by the intersection of \({\mathfrak {a}}_0\) with the \({{\widetilde{\mathrm{G}}}}\)-intertwining of any semisimple character in \({\mathscr {C}}(\Lambda ,0,\beta )\). The centre of \(\mathrm{G}_\beta ^{\mathsf {o}}\) is non-compact if and only if there is an index \(i\in \mathrm{I}\) such that \(\beta _i=0\), \({\text {dim}}_\mathrm{F}\mathrm{V}^i=2\) and the restriction \(h|_{\mathrm{V}^i}\) is isotropic and orthogonal. By Theorem 8.17, this is equivalent to \(\mathrm{G}_{\beta '}^{\mathsf {o}}\) having non-compact centre, proving (ii).
We now assume that the centre of \(\mathrm{G}_\beta ^{\mathsf {o}}\) is compact. By Proposition A.9 we can conjugate by some \(g\in \mathrm{G}\) which normalizes every character in \({\mathscr {C}}(\Lambda ,0,\beta )\) to reduce to the case where the splittings of \(\beta \) and \(\beta '\) coincide; thus we are in fact reduced to the case that \(\beta \) and \(\beta '\) are simple. We have the canonical maps
induced by the inclusions, which have the same image so we get an isomorphism
The anti-involution of h restricts to the anti-involution of the form \(h_\beta \) defining \(\mathrm{G}_\beta \). The lattice sequence \(\Lambda _\mathrm{E}\) corresponds to a vertex if and only if \({\mathfrak {b}}_0(\Lambda )/{\mathfrak {b}}_1(\Lambda )\) has at most two central idempotents and they are fixed (not permuted) by the adjoint anti-involution on \({\mathfrak {a}}_0/{\mathfrak {a}}_1\). Then (iii) follows because \(\Psi \) is an equivariant ring isomorphism. Now to prove assertion (iv), suppose \(\Lambda _\mathrm{E}\) and \(\Lambda _{\mathrm{E}'}\) correspond to vertices. Then \(\mathrm{P}^{\mathsf {o}}_-(\Lambda _\mathrm{E})\) is not a maximal parahoric subgroup of \(\mathrm{G}_\beta \) if and only if, for one of the central idempotents \({{\mathfrak {e}}}\) of \({\mathfrak {b}}_0(\Lambda )/{\mathfrak {b}}_1(\Lambda )\) the corresponding factor of \(\mathrm{P}_-(\Lambda _\mathrm{E})/\mathrm{P}^1_-(\Lambda _\mathrm{E})\) is given by the algebraic group \(\mathrm{O}(1,1)\) defined over \(\mathrm {k}_\mathrm{E}\); in that case the algebraic group defining the factor of \(\mathrm{P}_-(\Lambda _{\mathrm{E}'})/\mathrm{P}^1_-(\Lambda _{\mathrm{E}'})\) corresponding to \(\Psi ({{\mathfrak {e}}})\) must be \(\mathrm{O}(1,1)\) by Lemma 11.4, since \(\mathrm {k}_\mathrm{E}=\mathrm {k}_{\mathrm{E}'}\) by Proposition 6.2.
For the final assertion (v), first the canonical embeddings of \(\mathrm {k}_\mathrm{E}\) and \(\mathrm {k}_{\mathrm{E}'}\) into \({\mathfrak {a}}_0/{\mathfrak {a}}_1\) have the same image by [13, 5.2]. Further \(\mathrm{P}_-(\Lambda _\mathrm{E})/\mathrm{P}^1_-(\Lambda _\mathrm{E})\) is the set of rational points of the reductive group defined over \(\mathrm {k}_{\mathrm{E}_{\mathsf {o}}}\) defined by the anti-involution  on \({\mathfrak {b}}_0(\Lambda )/{\mathfrak {b}}_1(\Lambda )\). The map from (i) is \(\mathrm {k}_\mathrm{E}\)-linear and preserves
on \({\mathfrak {b}}_0(\Lambda )/{\mathfrak {b}}_1(\Lambda )\). The map from (i) is \(\mathrm {k}_\mathrm{E}\)-linear and preserves  , so it is an algebraic isomorphism defined over \(\mathrm {k}_{\mathrm{E}_{\mathsf {o}}}\). \(\square \)
, so it is an algebraic isomorphism defined over \(\mathrm {k}_{\mathrm{E}_{\mathsf {o}}}\). \(\square \)
Now let \([\Lambda ,n,0,\beta ]\) be a cuspidal skew semisimple stratum and let \(\theta _-\in {\mathscr {C}}_{-}(\Lambda ,0,\beta )\) be a skew semisimple character. By [42, Corollary 3.29], there exists a unique irreducible representation \(\eta \) of \(\mathrm{J}^1_-(\beta ,\Lambda )\) containing \(\theta _-\). The representation \(\eta \) extends to \(\mathrm{J}_-(\beta ,\Lambda )\) and we call such an extension \(\kappa \) a \(\beta \)-extension if it extends further to \(\mathrm{J}^+_-(\beta ,\Lambda )\) and its restriction to a pro-p-Sylow subgroup of \(\mathrm{J}_-(\beta ,\Lambda )\) is intertwined by all of \(\mathrm{I}_\mathrm{G}(\theta _-)\) (see [43, after Theorem 4.1] and [26, §6], where it is the extensions to \(\mathrm{J}^+_-(\beta ,\Lambda )\) which are called \(\beta \)-extensions).
Definition 11.6
A cuspidal type for \(\mathrm{G}^{\mathsf {o}}\) is a pair \((\mathrm{J},\lambda )\) such that there exist a cuspidal skew semisimple stratum \([\Lambda ,n,0,\beta ]\) and \(\theta _-\in {\mathscr {C}}_-(\Lambda ,0,\beta )\), such that \(\mathrm{J}=\mathrm{J}_-(\beta ,\Lambda )\) and \(\lambda =\kappa \otimes \tau \), with \(\kappa \) a \(\beta \)-extension of the unique irreducible representation of \(\mathrm{J}^1_-(\beta ,\Lambda )\) containing \(\theta _-\), and \(\tau \) an irreducible representation of \(\mathrm{J}_-(\beta ,\Lambda )/\mathrm{J}^1_-(\beta ,\Lambda )\) with cuspidal restriction to \(\mathrm{J}^{\mathsf {o}}_-(\beta ,\Lambda )/\mathrm{J}^1_-(\beta ,\Lambda )\).
Proposition 11.7
Let \((\mathrm{J},\lambda )\) be a cuspidal type for \(\mathrm{G}^{\mathsf {o}}\) defined via a cuspidal stratum \([\Lambda ,n,0,\beta ]\), with \(\lambda =\kappa \otimes \tau \). Suppose \([\Lambda ,n,0,\beta ']\) is a skew semisimple stratum such that \({\mathscr {C}}(\Lambda ,0,\beta )={\mathscr {C}}(\Lambda ,0,\beta ')\). Then \([\Lambda ,n,0,\beta ']\) is cuspidal, \(\mathrm{J}_-(\beta ',\Lambda )=\mathrm{J}\), \(\kappa \) is a \(\beta '\)-extension and the restriction of \(\tau \) to \(\mathrm{P}^{\mathsf {o}}_-(\Lambda _{\mathrm{E}'})\) is cuspidal.
Proof
The stratum \([\Lambda ,n,0,\beta ']\) is cuspidal by Proposition 11.3, while \(\mathrm{J}_-(\beta ',\Lambda )=\mathrm{J}\) by Lemma 11.5(i). Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,0,\beta )={\mathscr {C}}_-(\Lambda ,0,\beta ')\) be a skew semisimple character contained in \(\lambda \); then the characterization of \(\beta \)-extensions in terms of the intertwining of \(\theta _-\) implies that \(\kappa \) is also a \(\beta '\)-extension. Moreover, the restriction of \(\tau \) to \(\mathrm{P}^{\mathsf {o}}_-(\Lambda _{\mathrm{E}'})\) is cuspidal by Lemma 11.5(v). \(\square \)
The main result of [26], generalizing the main result of [43] in the case \({\mathbf {C}}={\mathbb {C}}\) (see also [29, Appendix A] for a correction to the definition of cuspidal type given in [43]), can be stated as follows.
Theorem 11.8
[26, Theorems 12.1, 12.2] Let \((\mathrm{J},\lambda )\) be a cuspidal type for \(\mathrm{G}^{\mathsf {o}}\). Then the representation \({\text {ind}}_\mathrm{J}^{\mathrm{G}^{\mathsf {o}}}(\lambda )\) is irreducible and cuspidal. Moreover, every irreducible cuspidal representation of \(\mathrm{G}^{\mathsf {o}}\) appears this way.
Thus, it remains to determine when cuspidal types \((\mathrm{J},\lambda )\) and \((\mathrm{J}',\lambda ')\) induce isomorphic cuspidal representations. Notice that conjugate cuspidal types induce equivalent representations and if \({\text {ind}}_\mathrm{J}^{\mathrm{G}^{\mathsf {o}}}(\lambda )\simeq {\text {ind}}_{\mathrm{J}'}^{\mathrm{G}^{\mathsf {o}}}(\lambda ')\) then \((\mathrm{J},\lambda )\) and \((\mathrm{J}',\lambda ')\) intertwine in \(\mathrm{G}^{\mathsf {o}}\). Hence the following result completes the classification in terms of conjugacy classes of cuspidal types.
Theorem 11.9
Let \((\mathrm{J},\lambda )\) and \((\mathrm{J},\lambda ')\) be cuspidal types for \(\mathrm{G}^{\mathsf {o}}\) which intertwine in \(\mathrm{G}^{\mathsf {o}}\). Then they are conjugate in \(\mathrm{G}^{\mathsf {o}}\).
Proof
As \(\lambda \) and \(\lambda '\) intertwine by an element of \(\mathrm{G}^{\mathsf {o}}\), the underlying skew semisimple characters \(\theta _-\in {\mathscr {C}}_-(\Lambda ,0,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',0,\beta ')\) intertwine by the same element, and we denote by \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) the matching from \((\theta _-,\beta )\) to \((\theta '_-,\beta ')\). By Corollary 8.19 we can replace the underlying strata so that there is an element \(g\in \mathrm{G}\) such that \(\beta _i^{g^{-1}}=\beta '_{\zeta (i)}\), for all \(i\in \mathrm{I}\), and by Proposition 11.7 these new strata are also cuspidal. Now \(\theta _-\) intertwines with \(\tau _{g\Lambda ,\Lambda ',\beta '}(\theta '_-)\) by an element of \(\mathrm{G}^{\mathsf {o}}\) by Corollaries 9.19 and 10.3. Thus, by [39, Theorem 10.3], Theorem 10.4 and Remark 10.5, there is an element \(g_1\in \mathrm{G}^{\mathsf {o}}\) such that
Then, using Proposition 11.7 again, we can assume that \(\theta '_-\) is the transfer of \(\theta _-\) to \(\Lambda '\) with respect to \(\beta '\), and the result now follows from [26, Theorem 12.3]. \(\square \)
Remark 11.10
The proof of Proposition 11.7 could have been given without using Proposition 11.3, using [29, Proposition 4.4] instead (and its analogue when \({\mathbf {C}}\) has positive characteristic \(\ell \ne p\)); however, this uses the full strength of the exhaustion proof in [43, Section 7], [29, Appendix A] and [26, Theorem 12.2], while our approach here is more direct, and independent of the proof of exhaustion.
12 Endo-parameters
In this section we are only interested in semisimple characters which are defined on \({\mathrm {H}}^1(\beta ,\Lambda )\)—we call such semisimple characters full. We parametrize the set of intertwining-classes of (self-dual) semisimple characters for \({{\widetilde{\mathrm{G}}}}\) (and for \(\mathrm{G}\)) by arithmetic parameters which we call endo-parameters. The restriction to full semisimple characters is natural because every smooth representation of \(\mathrm{G}^{\mathsf {o}}\) contains a full self-dual semisimple character [16, Proposition 8.5], though more refined arithmetic information could be sought by looking more generally (cf. [11]).
12.1 Endo-parameters for \({{\widetilde{\mathrm{G}}}}\)
Here we parametrize \({{\widetilde{\mathrm{G}}}}\)-intertwining classes for full semisimple characters for \({{\widetilde{\mathrm{G}}}}\). First we state the definition of full precisely.
Definition 12.1
-
(i)
A semisimple character \(\theta \) is called full if there exists a semisimple stratum \([\Lambda ,n,0,\beta ]\) such that \(\theta \in {\mathscr {C}}(\Lambda ,0,\beta )\).
-
(ii)
A pss-character is called full if it is supported on a semisimple pair of the form \((0,\beta )\).
-
(iii)
An endo-class of pss-characters is called full if it consists of full pss-characters; note that this includes the full zero endo-class \({\mathbf {0}}\).
Note that any non-trivial full semisimple character \(\theta \) is a realization of different pss-characters: for example, if \(\theta \) is a realization of a pss-character supported on a semisimple pair \((0,\beta )\), then it is also a realization (on the same lattice sequence) of a pss-character supported on the semisimple pair \((0,\beta +\varpi _\mathrm{F})\). Moreover, \(\theta \) can be a realization of different pss-characters supported on the same semisimple pair: for example, if \(\theta ,\theta '\in {\mathscr {C}}(\Lambda ,0,\beta )\) are as in Remark 8.12, then \(\theta \) is conjugate to \(\theta '\) by an element of \(\mathrm{P}(\Lambda )\), by Theorem 8.15(i); then the pss-characters \(\Theta \) and \(\Theta '\), supported on \((0,\beta )\), with realizations \(\theta \) and \(\theta '\) at \((\mathrm{V},{\text {id}}_{\mathrm{F}[\beta ]},\Lambda ,0)\), respectively, both attain \(\theta \).
Nonetheless, any full semisimple character determines a full endo-class. We will therefore say that two full semisimple characters are endo-equivalent if they determine the same full endo-class.
Since every ps-character is a pss-character, we can also make the following definition.
Definition 12.2
We let \({\mathscr {E}}\) denote the set of all full endo-classes of ps-characters, and let \({\mathscr {E}}^{\mathrm {fin}}\) denote the set of finite subsets of \({\mathscr {E}}\).
We know that we can decompose pss-characters into ps-characters via Lemma 9.6. This extends to give us a bijection between full semisimple endo-classes and \({\mathscr {E}}^{\mathrm {fin}}\).
Proposition 12.3
The map \({\mathcal {F}}\) from the set of all full semisimple endo-classes to \({\mathscr {E}}^{\mathrm {fin}}\), defined by
is well-defined and bijective where the \(\Theta _i\) are defined in Lemma 9.6.
For the proof (of surjectivity) we need the following lemmas.
Lemma 12.4
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ,n,r+1,{\tilde{\gamma }}]\) be semisimple strata split by \(\mathrm{V}={\mathrm{V}'}\oplus {\mathrm{V}''}\) such that \([\Lambda ,n,r+1,\beta ]\) is equivalent to \([\Lambda ,n,r+1,{\tilde{\gamma }}]\). Put \({\Lambda '}=\Lambda \cap {\mathrm{V}'}\) and \({\beta '}=\beta |_{\mathrm{V}'}\), and similarly for \(\Lambda '',\beta ''\). Given \({\tilde{\theta }}\in {{\mathscr {C}}(\Lambda ,r+1,{\tilde{\gamma }})}\) and an extension \({\theta '}\in {\mathscr {C}}({\Lambda '},r,{\beta '})\) of \({\tilde{\theta }}|_{{\mathrm {H}}^{r+2}({\beta '},{\Lambda '})}\) there is a semisimple character \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) such that the restriction to \({\mathrm {H}}^{r+1}({\beta '},{\Lambda '})\) is \({\theta '}\) and the restriction to \({\mathrm {H}}^{r+2}(\beta ,\Lambda )\) is \({\tilde{\theta }}\).
Proof
By induction on the number of simple blocks of \([{\Lambda ''},{n''},r,{\beta ''}]\), we are reduced to the case where \([{\Lambda ''},{n''},r,{\beta ''}]\) is simple. The proof proceeds by induction along the critical exponent \(k_0=k_0(\beta ,\Lambda )\). If \(\beta =0\) then we take \(\theta \) the trivial character of \(\mathrm{P}^{r+1}(\Lambda )\). Thus we can assume \(\beta \ne 0\); in particular \(-k_0\le n\). Write \(\mathrm{V}'=\bigoplus _{i\in \mathrm{I}'}\mathrm{V}'^i\) for the splitting of \([{\Lambda '},{n'},r,{\beta '}]\); then the splitting of \([\Lambda ,n,r,\beta ]\) is either \(\mathrm{V}=\mathrm{V}''\oplus \bigoplus _{i\in \mathrm{I}'}\mathrm{V}'^i\) (if \(\beta ''\) is a simple block of \(\beta \)) or \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}'}\mathrm{V}^i\), where
for some (unique) value \(i_0\in \mathrm{I}'\).
First we consider the case where \(r<\lfloor \frac{-k_0}{2}\rfloor \). If \(\beta ''\) is a simple block of \(\beta \) then [42, Lemma 3.15] says that there exists \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) whose simple block restrictions are an extension of \({\tilde{\theta }}|_{{\mathrm {H}}^{r+2}(\beta '',\Lambda '')}\) to \({\mathrm {H}}^{r+1}(\beta '',\Lambda '')\), and the simple block restrictions of \(\theta '\); since a semisimple character is determined by its simple block restrictions, we are done.
Otherwise we are in the second case (12.5) above, and \(\beta '_{i_0}\) and \(\beta ''\) have the same minimal polynomial over\(~\mathrm{F}\). If we denote by \(\theta ''\in {\mathscr {C}}(\Lambda '',r,\beta '')\) the transfer of the simple block restriction \(\theta '_{i_0}\), then the transfer of \(\theta '_{i_0}\) to \({\mathscr {C}}(\Lambda '^{i_0}\oplus \Lambda '',r,\beta '_i+\beta '')\) restricts to \(\theta '_{i_0}\otimes \theta ''\) on \({\mathrm {H}}^{r+1}(\beta '_{i_0},\Lambda '^{i_0})\times {\mathrm {H}}^{r+1}(\beta '',\Lambda '')\). Applying [42, Lemma 3.15] as above, we find a semisimple character as required.
Now suppose \(r\ge \lfloor \frac{-k_0}{2}\rfloor \). Then we take a semisimple stratum \([\Lambda ,n,-k_0,\gamma ]\) equivalent to \([\Lambda ,n,-k_0,\beta ]\) which is split under the decomposition \(\mathrm{V}''\oplus \bigoplus _{i\in \mathrm{I}'}\mathrm{V}'^i\). We write \(\gamma '\) for \(\gamma |_{\mathrm{V}'}\). Since \(k_0(\gamma ,\Lambda )<k_0(\beta ,\Lambda )\), we can apply the inductive hypothesis to find a common extension \(\theta _\gamma \in {\mathscr {C}}(\Lambda ,r,\gamma )\) of \(\theta '\psi _{\gamma '-\beta '}\) and \({\tilde{\theta }}\psi _{\gamma -\beta }\) to \({\mathrm {H}}^{r+1}(\beta ,\Lambda )={\mathrm {H}}^{r+1}(\gamma ,\Lambda )\). Then the character \(\theta =\theta _\gamma \psi _{\beta -\gamma }\) is as required. \(\square \)
Lemma 12.6
Let \([\Lambda ',n',r,\beta ']\) be a semisimple stratum in \(\mathrm{V}'\) and let \([\Lambda '',n'',r,\beta '']\) be a simple stratum in \(\mathrm{V}''\) such that \(e(\Lambda ')=e(\Lambda '')\). Set \(\mathrm{V}=\mathrm{V}'\oplus \mathrm{V}''\), \(\Lambda =\Lambda '\oplus \Lambda ''\) and \(n=\max \{n',n''\}\). Then there exists \({{\tilde{\beta }}}''\in {\text {End}}_\mathrm{F}(\mathrm{V}'')\) such that \([\Lambda '',n'',r,{{\tilde{\beta }}}'']\) is simple and equivalent to \([\Lambda '',n'',r,\beta '']\), and \([\Lambda ,n,r,\beta '\oplus {{\tilde{\beta }}}'']\) is semisimple.
Proof
Suppose \([\Lambda ,n,r,\beta ]\) is not semisimple. Then, using notation as in the previous proof, there is an index \(i_0\in \mathrm{I}'\) such that the stratum \([\Lambda '^{i_0}\oplus \Lambda '',\max \{n_{i_0},n''\},r,\beta '_{i_0}\oplus \beta '']\) is equivalent to a simple stratum. We only need to find \({\tilde{\beta }}''\) such that \([\Lambda '^{i_0}\oplus \Lambda '',\max \{n_{i_0},n''\},r,\beta '_{i_0}\oplus {\tilde{\beta }}'']\) is simple and we may therefore assume \(|\mathrm{I}'|=1\), that is \(\beta '=\beta _i\). Then \(\mathrm{F}[\beta ']/\mathrm{F}\) has the same ramification index and inertia degree as \(\mathrm{F}[\beta '']/\mathrm{F}\). (This follows from [39, Theorem 6.16] and [12, Theorem 2.4.1] when the lattice sequences are strict, and in general via a \(\dag \)-construction.) Thus there is an embedding \(\varphi :\mathrm{F}[\beta ']\rightarrow {\text {End}}_\mathrm{F}\mathrm{V}''\) such that \(\mathrm{F}[\varphi (\beta ')]^\times \) normalizes \(\Lambda ''\).
We set \(m'={\text {dim}}_\mathrm{F}\mathrm{V}'\) and \(m''={\text {dim}}_\mathrm{F}\mathrm{V}''\) and identify \(\mathrm{V}'^{\oplus m''}\) with \(\mathrm{V}''^{\oplus m'}\). Then the strata
intertwine, while the latter is equivalent to a simple stratum by [39, Theorem 6.16]. Since the first is certainly equivalent to a semisimple stratum, the matching of [39, Proposition 7.1] implies that it must be equivalent to a simple stratum. Therefore
is equivalent to a simple stratum ([39, Theorem 6.16] again) so that \([\Lambda '',n,r,\beta '']\) and \([\Lambda '',n,r,\varphi (\beta ')]\) intertwine. Then [39, Theorem 8.1] implies that there exists \(g\in \mathrm{P}(\Lambda '')\) such that \([\Lambda '',n,r,g\varphi (\beta ')g^{-1}]\) is equivalent to \([\Lambda '',n,r,\beta '']\) and the element \({\tilde{\beta }}'':=g\varphi (\beta ')g^{-1}\) satisfies the assertion. \(\square \)
Lemma 12.7
Let \(\theta '\in {\mathscr {C}}(\Lambda ',r,\beta ')\) and \(\theta ''\in {\mathscr {C}}(\Lambda '',r,\beta '')\) be semisimple characters in \({\text {Aut}}_\mathrm{F}(\mathrm{V}')\) and \({\text {Aut}}_\mathrm{F}(\mathrm{V}'')\) respectively, and suppose that \(e(\Lambda ')=e(\Lambda '')\). Set \(\mathrm{V}=\mathrm{V}'\oplus \mathrm{V}''\), \(\Lambda =\Lambda '\oplus \Lambda ''\) and \(n=\max \{n',n''\}\). Then there exist a semisimple stratum \([\Lambda '',n'',r,{{\tilde{\beta }}}'']\), such that \({\mathscr {C}}(\Lambda '',r,{{\tilde{\beta }}}'')={\mathscr {C}}(\Lambda '',r,\beta '')\) and \([\Lambda ,n,r,\beta '\oplus {{\tilde{\beta }}}'']\) is semisimple, and \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta '\oplus {{\tilde{\beta }}}'')\) such that \(\theta |_{{\mathrm {H}}^{r+1}(\beta ',\Lambda ')}=\theta '\) and \(\theta |_{{\mathrm {H}}^{r+1}(\beta '',\Lambda '')}=\theta ''\).
Proof
We begin by reducing to the case that \(\theta ''\) is a simple character. Indeed, the general case proceeds from this case by induction on the number of simple blocks of \([\Lambda '',n'',r,\beta '']\) as follows: Suppose this stratum has splitting \(\mathrm{V}''=\bigoplus _{i\in \mathrm{I}}\mathrm{V}''^i\) and \(\mathrm{I}=\mathrm{J}\cup \{i_0\}\) (disjoint union). Applying the inductive hypothesis to \(\theta '\) and \(\theta ''_\mathrm{J}\), we have a semisimple stratum \([\Lambda ''^\mathrm{J},n''_\mathrm{J},r,{{\tilde{\beta }}}''_\mathrm{J}]\), such that \({\mathscr {C}}(\Lambda ''^\mathrm{J},r,{{\tilde{\beta }}}''_\mathrm{J})={\mathscr {C}}(\Lambda ''^\mathrm{J},r,\beta ''_\mathrm{J})\) and \([\Lambda '\oplus \Lambda ''^\mathrm{J},n_\mathrm{J},r,\beta '\oplus {{\tilde{\beta }}}''_\mathrm{J}]\) is semisimple, and \(\theta _\mathrm{J}\in {\mathscr {C}}(\Lambda '\oplus \Lambda ''^\mathrm{J},r,\beta '\oplus {{\tilde{\beta }}}''_\mathrm{J})\) with \(\theta _\mathrm{J}|_{{\mathrm {H}}^{r+1}(\beta ',\Lambda ')}=\theta '\) and \(\theta _\mathrm{J}|_{{\mathrm {H}}^{r+1}(\beta ''_\mathrm{J},\Lambda ''^\mathrm{J})}=\theta ''_\mathrm{J}\). Then the simple case applied to \(\theta _\mathrm{J}\) and the simple block restriction \(\theta ''_{i_0}\) give a (semi)simple stratum \([\Lambda ''^{i_0},n''_{i_0},r,{{\tilde{\beta }}}''_{i_0}]\) and semisimple character \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta '\oplus {{\tilde{\beta }}}''_\mathrm{J}\oplus {{\tilde{\beta }}}''_{i_0})\) such that \(\theta |_{{\mathrm {H}}^{r+1}(\beta '\oplus {{\tilde{\beta }}}''_\mathrm{J},\Lambda '\oplus \Lambda ''^\mathrm{J})}=\theta _\mathrm{J}\) and \(\theta |_{{\mathrm {H}}^{r+1}(\beta ''_{i_0},\Lambda ''^{i_0})}=\theta ''_{i_0}\). Putting \({{\tilde{\beta }}}''={{\tilde{\beta }}}''_\mathrm{J}\oplus {{\tilde{\beta }}}''_{i_0}\), we see that \(\theta |_{{\mathrm {H}}^{r+1}(\beta '',\Lambda '')}\) is a semisimple character in \({\mathscr {C}}(\Lambda '',r,{{\tilde{\beta }}}'')\) whose restriction to any \({\mathrm {H}}^{r+1}(\beta ''_i,\Lambda ''^i)\) is \(\theta ''_i\), for \(i\in \mathrm{I}\). It follows from Corollary A.8 that \(\theta |_{{\mathrm {H}}^{r+1}(\beta '',\Lambda '')}=\theta ''\) and \({\mathscr {C}}(\Lambda '',r,{{\tilde{\beta }}}'')={\mathscr {C}}(\Lambda '',r,\beta '')\), as required.
So now we assume that \(\theta ''\) is simple, and prove the statement by induction on r. If \(r=n\) then we take \(\theta \) to be the trivial character. If \(r<n\) then let \([\Lambda ',n',r+1,\gamma ']\) be a semisimple stratum which is equivalent to \([\Lambda ',n',r+1,\beta ']\) and split with respect to the splitting of \(\beta '\), and let \([\Lambda '',n'',r+1,\gamma '']\) be a simple stratum equivalent to \([\Lambda '',n'',r+1,\beta '']\). By the inductive hypothesis, there are a simple stratum \([\Lambda '',n'',r+1,{{\tilde{\gamma }}}'']\) and a character \(\theta _\gamma \in {\mathscr {C}}(\Lambda ,r+1,\gamma '\oplus {{\tilde{\gamma }}}'')\) with restrictions \(\theta '|_{{\mathrm {H}}^{r+2}(\beta ',\Lambda ')}\) and \(\theta ''|_{{\mathrm {H}}^{r+2}(\beta '',\Lambda '')}\). By the translation principle [39, Theorem 9.16], there is a simple stratum \([\Lambda '',n'',r,{{\hat{\beta }}}'']\) such that \({\mathscr {C}}(\Lambda '',r,\beta '')={\mathscr {C}}(\Lambda '',r,{{\hat{\beta }}}'')\) and \([\Lambda '',n'',r+1,{{\hat{\beta }}}'']\) is equivalent to \([\Lambda '',n'',r+1,{{\tilde{\gamma }}}'']\). Moreover, Lemma 12.6 implies that we can replace \([\Lambda '',n'',r,{{\hat{\beta }}}'']\) by an equivalent simple stratum so that \([\Lambda ,n,r,\beta '\oplus {{\hat{\beta }}}'']\) is itself semisimple.
Now Lemma 12.4 provides a semisimple character \({{\tilde{\theta }}}\in {\mathscr {C}}(\Lambda ,r,\beta '\oplus {{\hat{\beta }}}'')\) with restrictions \(\theta '\) on \({\mathrm {H}}^{r+1}(\beta ',\Lambda ')\) and \(\theta _\gamma \) on \({\mathrm {H}}^{r+2}(\beta '\oplus {{\hat{\beta }}}'',\Lambda )\). Thus there is an element \(a\in {\mathfrak {a}}''_{-1-r}\) such that \(\theta ''={{\tilde{\theta }}}\psi _a|_{{\mathrm {H}}^{r+1}(\beta '',\Lambda '')}\); moreover, \([\Lambda '',n'',r,{{\hat{\beta }}}''+a]\) is equivalent to a simple stratum by Lemma A.7(i). Applying Lemma 12.6 again, there is a simple stratum \([\Lambda '',n'',r,{{\tilde{\beta }}}'']\) equivalent to \([\Lambda '',n'',r,{{\hat{\beta }}}''+a]\) such that \([\Lambda ,n,r,\beta '\oplus {{\tilde{\beta }}}'']\) is semisimple. Finally, setting \(\theta ={{\tilde{\theta }}}\psi _a\in {\mathscr {C}}(\Lambda ,r,\beta '\oplus {{\tilde{\beta }}}'')\), we are done. \(\square \)
Proof of Proposition 12.3
Let \(\Theta \) be a full pss-character supported on \((0,\beta )\), with index set \(\mathrm{I}\), and write \([\Theta ]\) for the endo-class of \(\Theta \). Then Theorem 9.9(i) shows that \({\mathcal {F}}([\Theta ])\) is well-defined and \(|\mathrm{I}|=|{\mathcal {F}}([\Theta ])|\), and also that the map \({\mathcal {F}}\) is injective. For surjectivity, suppose we are given a finite set \(\{[\Theta _i]:i\in \mathrm{I}\}\) of full simple ps-characters and, for each \(i\in \mathrm{I}\), choose a realization \(\theta _i\) of \(\Theta _i\). Then Lemma 12.7 and induction on \(|\mathrm{I}|\) give a full semisimple character \(\theta \) which has simple character restrictions \(\theta _i\). The corresponding pss-character \(\Theta \) has simple block restrictions which must be \(\Theta _i\), by Lemma 9.6, and \({\mathcal {F}}([\Theta ])=\{[\Theta _i]:i\in \mathrm{I}\}\), as required. \(\square \)
Recall that the degree of a full simple character \(\theta \in {\mathscr {C}}(\Lambda ,0,\beta )\) is defined to be \([\mathrm{F}[\beta ]:\mathrm{F}]\), and is independent of intertwining between full simple characters and transfer, and that the degree of a simple endo-class \(c\in {\mathscr {E}}\) is defined to be the common degree of the values of the ps-characters in c, which we denote by \(\deg (c)\).
Definition 12.8
An endo-parameter is a function \({{\mathfrak {f}}}\) from the set \({\mathscr {E}}\) to the set \({\mathbb {N}}_0\) of non-negative integers, with finite support. We define the degree of an endo-parameter \({{\mathfrak {f}}}\) by
Given a full semisimple character \(\theta \in {\mathscr {C}}(\Lambda ,0,\beta )\), let \(\Theta \) be the pss-character supported on \((0,\beta )\) with \(\Theta (\mathrm{V},\varphi _{\beta },\Lambda ,0)=\theta \), where \(\varphi _\beta \) denotes the canonical embedding of \(\mathrm{F}[\beta ]\) as usual, and \(c_i\) be the endo-classes of its simple block restrictions; we define the endo-parameter \({{\mathfrak {f}}}_\theta \) to be the map with support \({\mathcal {F}}([\Theta ])\), and such that \({{\mathfrak {f}}}_\theta (c_i):=\frac{{\text {dim}}_\mathrm{F}\mathrm{V}^i}{\deg (c_i)}\), for \(i\in \mathrm{I}\).
Theorem 12.9
There is a canonical bijection from the set of intertwining classes of full semisimple characters for \({{\widetilde{\mathrm{G}}}}={\text {GL}}_\mathrm{F}(\mathrm{V})\) to the set of endo-parameters \({{\mathfrak {f}}}\) of degree \({\text {dim}}_\mathrm{F}(\mathrm{V})\), defined by mapping the intertwining class of a full semisimple character \(\theta \) to the endo-parameter \({{\mathfrak {f}}}_\theta \).
Proof
Suppose \(\theta \in {\mathscr {C}}(\Lambda ,0,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ',0,\beta ')\) are semisimple characters with index sets \(\mathrm{I},\mathrm{I}'\) respectively. By changing lattice sequences in their affine class, we may and do assume \(e(\Lambda )=e(\Lambda ')\). Let \(\Theta \) be the pss-character supported on \((0,\beta )\) with value \(\theta \) at \((\mathrm{V},\varphi _\beta ,\Lambda ,0)\), and similarly \(\Theta '\) the pss-character supported on \((0,\beta ')\) with value \(\theta '\) at \((\mathrm{V},\varphi _{\beta '},\Lambda ',0)\).
First we prove that the map described is well-defined (on intertwining classes). Suppose \(\theta \) and \(\theta '\) intertwine in \({{\widetilde{\mathrm{G}}}}\). Then Theorem 8.8 gives a matching \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) between index sets, and \(\zeta _{\Theta ',\Theta }=\zeta \) by Theorem 9.9(c). Since \({\text {dim}}_\mathrm{F}\mathrm{V}^i={\text {dim}}_\mathrm{F}\mathrm{V}'^{\zeta (i)}\) (from Theorem 8.8 again), it follows that \({{\mathfrak {f}}}_\theta ={{\mathfrak {f}}}_{\theta '}\).
Conversely, suppose that \({{\mathfrak {f}}}_\theta ={{\mathfrak {f}}}_{\theta '}\). Then, by comparing the support, we have \({\mathcal {F}}([\Theta ])={\mathcal {F}}([\Theta '])\), so \(\Theta \approx \Theta '\) by Proposition 12.3 and we have a matching \(\zeta _{\Theta ',\Theta }:\mathrm{I}\rightarrow \mathrm{I}'\), by Theorem 9.9(i). In particular, the simple components \([\Theta _i]=[\Theta '_{\zeta (i)}]\) have the same degree so it follows from \({{\mathfrak {f}}}_\theta ={{\mathfrak {f}}}_{\theta '}\) that \({\text {dim}}_\mathrm{F}\mathrm{V}^i={\text {dim}}_\mathrm{F}\mathrm{V}^{\zeta (i)}\), for all \(i\in \mathrm{I}\). Finally Theorem 9.9(d) implies that \(\theta \) and \(\theta '\) intertwine. Thus the map is injective.
Finally we prove surjectivity, so let \({{\mathfrak {f}}}\) be an endo-parameter of degree \({\text {dim}}_\mathrm{F}(\mathrm{V})\). By Proposition 12.3, there is a full pss-character \(\Theta \), supported on some \((0,\beta )\), such that \({\text {supp}}({{\mathfrak {f}}})={\mathcal {F}}([\Theta ])=\{[\Theta _i]\mid i\in \mathrm{I}\}\); further, each \(\Theta _i\) is supported on the simple pair \((0,\beta _i)\). For \(i\in \mathrm{I}\), we choose \((\mathrm{V}^i,\varphi _i,\Lambda ^i,0)\in {\mathscr {Q}}(0,\beta _i)\) with \({\text {dim}}_\mathrm{F}\mathrm{V}^i=\deg ([\Theta _i]) {{\mathfrak {f}}}([\Theta _i])\). Replacing the \(\Lambda ^i\) in their affine classes, we may and do assume that \(e(\Lambda ^i)\) is independent of i. Since \({{\mathfrak {f}}}\) has degree \({\text {dim}}_\mathrm{F}(\mathrm{V})\), there is an isomorphism between \(\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and \(\mathrm{V}\); replacing the \(\mathrm{V}^i\) by their images, we may assume this isomorphism is an equality. Then \((\mathrm{V},\bigoplus _{i\in \mathrm{I}}\varphi _i,\bigoplus _{i\in \mathrm{I}}\Lambda ^i,0)\in {\mathscr {Q}}(0,\beta )\) and \({{\mathfrak {f}}}={{\mathfrak {f}}}_{\theta }\) for \(\theta =\Theta (\mathrm{V},\bigoplus _{i\in \mathrm{I}}\varphi _i,\bigoplus _{i\in \mathrm{I}}\Lambda ^i,0)\). \(\square \)
12.2 The classical involution on \({\mathscr {E}}\)
We return to the classical setting so that we have an extension \(\mathrm{F}/\mathrm{F}_{{\mathsf {o}}}\) of degree at most two, whose Galois group is generated by \(x\mapsto {\overline{x}}\). We fix an algebraic closure \(\mathrm{F}^{\mathsf {alg}}\) of \(\mathrm{F}\) and denote by \({\text {Ps}}(\mathrm{F}^{\mathsf {alg}})\) be the set of full ps-characters supported on simple pairs \((0,\beta )\) such that \(\mathrm{F}[\beta ]\) is contained in \(\mathrm{F}^{\mathsf {alg}}\).
We choose an automorphism f of \(\mathrm{F}^{\mathsf {alg}}\) extending the map \(x\mapsto {\overline{x}}\) on \(\mathrm{F}\) and a sign \(\varepsilon \). We are going to define a map \(\Theta \mapsto \Theta ^f\) on \({\text {Ps}}(\mathrm{F}^{\mathsf {alg}})\) which, a priori, depends on many choices we will make. In the end we will find that it is in fact independent of these choices and, moreover, it induces an involution on the set \({\mathscr {E}}\) of endo-classes over \(\mathrm{F}\) which is independent of the choices of f, \(\varepsilon \) and \(\mathrm{F}^{\mathsf {alg}}\).
Definition 12.10
Given \(\Theta \in {\text {Ps}}(\mathrm{F}^{\mathsf {alg}})\) supported on a simple pair \((0,\beta )\), we set \(\mathrm{E}=\mathrm{F}[\beta ]\) and choose the following:
-
a finite-dimensional \(\mathrm{F}\)-vector space \(\mathrm{V}\) such that \([\mathrm{E}:\mathrm{F}]\) divides \({\text {dim}}_\mathrm{F}\mathrm{V}\);
-
an \(\mathrm{F}\)-linear field embedding \(\varphi :\mathrm{E}\rightarrow \mathrm{A}={\text {End}}_\mathrm{F}(\mathrm{V})\);
-
a hyperbolic \(\varepsilon \)-hermitian space \((\mathrm{V}_h,h)\) over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) with a complete polarization \(\mathrm{V}_h=\mathrm{V}\oplus \mathrm{V}^{\#}\);
-
an \({\mathfrak {o}}_\mathrm{E}\)-lattice sequence \(\Lambda \) in \(\mathrm{V}\).
In particular, the adjoint anti-involution of h defines a map from \({\text {End}}_\mathrm{F}(\mathrm{V})\) to \({\text {End}}_\mathrm{F}(\mathrm{V}^\#)\). Then \((0,-f(\beta ))\) is a simple pair and we set \(\mathrm{E}^\#=f(\mathrm{E})\), define the lattice sequence \(\Lambda ^\#\) in \(\mathrm{V}^\#\) by
and denote by \(\varphi ^\#:\mathrm{E}^\#\hookrightarrow {\text {End}}_\mathrm{F}(\mathrm{V}^\#)\) the embedding \(\varphi ^\#(x)={\overline{\varphi (f^{-1}(x))}}\), for \(x\in \mathrm{E}^\#\), where  here denotes the adjoint anti-involution on \(\mathrm{V}_h\). Then \((\mathrm{V}^\#,\varphi ^\#,\Lambda ^\#,0)\in {\mathscr {Q}}(0,-f(\beta ))\) and we define \(\Theta ^f\) to be the unique full ps-character supported on \((0,-f(\beta ))\) such that
here denotes the adjoint anti-involution on \(\mathrm{V}_h\). Then \((\mathrm{V}^\#,\varphi ^\#,\Lambda ^\#,0)\in {\mathscr {Q}}(0,-f(\beta ))\) and we define \(\Theta ^f\) to be the unique full ps-character supported on \((0,-f(\beta ))\) such that
Note that we are defining \(\Theta ^f\) by its single value at \((\mathrm{V}^\#,\varphi ^\#,\Lambda ^\#,0)\in {\mathscr {Q}}(0,-f(\beta ))\), and its value at other elements of \({\mathscr {Q}}(0,-f(\beta ))\) is then given by transfer; it is for this reason that the definition appears to depend on the choices of \(\mathrm{V},\varphi ,(\mathrm{V}_h,h),\mathrm{V}^\#,\Lambda \). Note also that the value \(\Theta ^f(\mathrm{V}^\#,\varphi ^\#,\Lambda ^\#,0)\) is in fact independent of the automorphism f: the group \({\mathrm {H}}^1(\varphi ^\#(-f(\beta )),\Lambda ^\#)={\mathrm {H}}^1(-{\overline{\varphi (\beta )}},\Lambda ^\#)\) does not depend on f and the formula (12.11) is clearly independent of f. However, the ps-character \(\Theta ^f\) does depend on f since the simple pair \((0,-f(\beta ))\) on which it is supported does.
Proposition 12.12
Let \(\Theta ,\Theta '\) be elements of \({\text {Ps}}(\mathrm{F}^{\mathsf {alg}})\).
-
(i)
\(\Theta ^f\) is well-defined, i.e. is independent of the choices made.
-
(ii)
\((\Theta ^f)^f\) is endo-equivalent to \(\Theta \).
-
(iii)
If \(\Theta \) is endo-equivalent to \(\Theta '\) then \(\Theta ^f\) is endo-equivalent to \(\Theta '^f\).
-
(iv)
The endo-class of \(\Theta ^f\) does not depend on f or \(\varepsilon \).
Proof
We start with assertion (i). Suppose we have chosen \((\mathrm{V}_i,\varphi _i,(\mathrm{V}_{h_i},h_i),\mathrm{V}_i^\#,\Lambda _i)\), for \(i=1,2\), as in Definition 12.10. In order to show that these give rise to the same ps-character \(\Theta ^f\), we need to show that the characters \(\theta ^\#_i\) given by \(y\mapsto \left( \Theta (\mathrm{V}_i,\varphi _i,\Lambda _i,0)({\overline{y}})\right) ^{-1}\) are related by transfer (from \((\Lambda _1^\#,\varphi _1^\#)\) to \((\Lambda _2^\#,\varphi _2^\#)\)). Since the self-dual \(\dag \)-construction commutes with transfer, we can perform such a construction to reduce to the case where \((\mathrm{V}_{h_1},h_1)\) and \((\mathrm{V}_{h_2},h_2)\) are isometric; conjugating then by a suitable isometry, we can assume
Now, \(\Theta (\mathrm{V},\varphi _1,\Lambda _1,0)\) and \(\Theta (\mathrm{V},\varphi _2,\Lambda _2,0)\) are intertwined by an element \(g\in {\text {Aut}}_\mathrm{F}(\mathrm{V})\) which conjugates \(\varphi _1\) to \(\varphi _2\), because these characters are related by transfer (from \((\Lambda _1,\varphi _1)\) to \((\Lambda _2,\varphi _2)\)). Thus \({\bar{g}}^{-1}\) intertwines \(\theta ^\#_1\) with \(\theta ^\#_2\) and conjugates \(\varphi ^\#_1\) to \(\varphi ^\#_2\), i.e. they are transfers as required.
Now assertion (ii) follows immediately because, if the tuple \((\mathrm{V},\varphi ,(\mathrm{V}_h,h),\mathrm{V}^\#,\Lambda )\) is used to define \(\Theta ^f\) then \((\mathrm{V}^\#,\varphi ^\#,(\mathrm{V}_h,h),\mathrm{V},\Lambda ^\#)\) can be used to define \((\Theta ^f)^f\) so we see that \(\Theta (\mathrm{V},\varphi ,\Lambda ,0)=(\Theta ^f)^f(\mathrm{V},\varphi ^{\#\#},\Lambda ,0)\); thus the intersection of the images of \(\Theta \) and \((\Theta ^f)^f\) is non-empty and they are endo-equivalent. Similarly, if \(\Theta \) and \(\Theta '\) are endo-equivalent then they have a common value \(\Theta (\mathrm{V},\varphi ,\Lambda ,0)=\Theta '(\mathrm{V},\varphi ',\Lambda ,0)\) by Lemma 5.1, Theorems 7.5 and 8.15(i); using this (together with a choice of \(\mathrm{V}_h,\mathrm{V}^\#\)), it follows immediately from (12.11) that \(\Theta ^f,\Theta '^f\) have a common realization so are endo-equivalent, and (iii) follows.
We are left with assertion (iv). That \([\Theta ^f]\) is independent of f is clear from the formula (12.11) (which is independent of f). To see that \([\Theta ^f]\) is independent of \(\varepsilon \), we can replace h by the twist \({(\varphi (\beta )-{\overline{\varphi (\beta )}})}^*(h)\) (which is a \(-\varepsilon \)-hermitian form over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\)) in the construction; this replaces \(\Lambda ^\#\) by a translate, which affects nothing, so that the formula (12.11) remains the same. Thus the image of the resulting ps-character has a non-trivial intersection with the image of \(\Theta ^f\), and they are endo-equivalent. \(\square \)
The last proposition allows us to define an involution on \({\mathscr {E}}\).
Definition 12.13
We define an action of \(\Sigma \) on \({\mathscr {E}}\) by \(\sigma ([\Theta ]):=[\Theta ^f]\), for \(\Theta \in {\text {Ps}}(\mathrm{F}^{\mathsf {alg}})\).
Note that it also follows from Proposition 12.12 that this involution (defined on the set \({\mathscr {E}}\), which does not depend on the choice of \(\mathrm{F}^{\mathsf {alg}}\)) does not in fact depend on the choice of algebraic closure.
12.3 Orbits and self-dual endo-classes
We fix \(\varepsilon \), \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) and \(\mathrm{F}^{\mathsf {alg}}\) as in the previous subsection. We want to compare orbits of \({\mathscr {E}}\) with self-dual endo-classes. We therefore introduce the notion of full self-dual endo-classes. We call a self-dual pss-character or endo-class full if the corresponding lift is full and we call a self-dual semisimple character full if it is contained in \({\mathscr {C}}_-(\Lambda ,0,\beta )\) for some self-dual semisimple stratum \([\Lambda ,n,0,\beta ]\). Let \((0,\beta )\) be a self-dual semisimple pair. Recall that, attached to \(\beta \) is an index set \(\mathrm{I}\) together with an action of \(\sigma \), and we choose a set \(\mathrm{I}_0\cup \mathrm{I}_+\) of representatives for the orbits of \(\sigma \), where \(\mathrm{I}_0\) is the set of \(\sigma \)-fixed points, \(\mathrm{I}_+\) is a section through the orbits of length two, and we put \(\mathrm{I}_-:=\sigma (\mathrm{I}_+)\). Analogously to the previous subsection, we denote by \({\text {Ps}}_-(\mathrm{F}^{\mathsf {alg}})\) the set of full self-dual pss-characters \(\Theta _-\) such that the attached semisimple pair \((0,\beta )\) satisfies
and such that \(\mathrm{E}\) is a subset of \(\oplus _{i\in \mathrm{I}}\mathrm{F}^{\mathsf {alg}}\); in the case \(\mathrm{I}_+\ne \emptyset \), we will usually write \(\mathrm{I}_+=\{+1\}\) and \(\mathrm{I}_-=\{-1\}\), and write \(\Theta _{\pm 1}\) for the simple block restrictions of the lift \(\Theta \) of \(\Theta _-\). We denote by \({\mathscr {E}}_-\) the set of endo-classes of elements of \({\text {Ps}}_-(\mathrm{F}^{\mathsf {alg}})\).
Lemma 12.14
Suppose \(\Theta \) is a lift of a full self-dual pss-character \(\Theta _-\in {\text {Ps}}_-(\mathrm{F}^{\mathsf {alg}})\) supported on \((0,\beta )\).
-
(i)
If \(\Theta \) is not simple then \([\Theta _{{1}}]\ne [\Theta _{-1}]=\sigma ([\Theta _{{1}}])\).
-
(ii)
If \(\Theta \) is simple then \([\Theta ]=\sigma ([\Theta ])\).
Proof
We first prove (i). Take \(((\mathrm{V},h),\varphi ,\Lambda ,0)\in {\mathscr {Q}}_-(0,\beta )\) so that \(\mathrm{V}\), \(\beta \) and \(\varphi \) decompose as
Following Definition 12.10 using the data \((\mathrm{V}^{{1}},\varphi _{{1}},(\mathrm{V},h),\mathrm{V}^{-1},\Lambda ^{{1}})\) and taking \(f:\mathrm{F}^{\mathsf {alg}}\rightarrow \mathrm{F}^{\mathsf {alg}}\) to be an extension of the map \(x\mapsto {\overline{x}}\) on \(\mathrm{F}\) such that \(f(\beta _{{1}})=-\beta _{-1}\), we compute
Thus \(\Theta _{{1}}^f\) and \(\Theta _{-1}\) have a common value. They are already full and have the same degree so \([\Theta _{-1}]=\sigma ([\Theta _{{1}}])\). The inequality of (i) is a consequence of 9.6(ii).
The proof of (ii) is similar. We choose \(((\mathrm{V},h),\varphi ,\Lambda ,0)\in {\mathscr {Q}}_-(0,\beta )\) and f an extension of the generator of \({\text {Gal}}(\mathrm{E}/\mathrm{E}_{\mathsf {o}})\). We define an \(\varepsilon \)-hermitian form \({\tilde{h}}\) on \({{\tilde{\mathrm{V}}}}=\mathrm{V}\oplus \mathrm{V}\) by
Then \(\Lambda \oplus \Lambda \) is self-dual with respect to \({\tilde{h}}\). Applying the definition with \((\mathrm {V}\oplus 0,\varphi \oplus 0,({{\tilde{\mathrm {V}}}},{\tilde{h}}),0\oplus \mathrm {V},\Lambda \oplus 0)\), we obtain:
The third and the final equality follow from the fact that \(\Theta \) respects transfers, while the fourth follows from self-duality. \(\square \)
Using the notation of Lemma 12.14 we define a map \(\Phi \) from \({\mathscr {E}}_-\) to \({\mathscr {E}}/\Sigma \), the set of orbits of simple endo-classes, by
This map is well-defined and injective by Theorems 9.9 and 9.16. We now state the converse of Lemma 12.14.
Theorem 12.16
The map \(\Phi \) is surjective.
The key idea for the proof of the theorem is enclosed in the following lemma:
Lemma 12.17
Let \((\mathrm{V},h)\) be an \(\varepsilon \)-hermitian space over \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) with a complete polarization
Suppose \([\Lambda ,n,r,\beta ]\) is a semisimple stratum split by (12.18) such that \(\Lambda \) is self-dual and
and such that \([\Lambda ^{1},n,r,\beta _{1}]\) is simple. Then there exists a self-dual semisimple stratum \([\Lambda ,n,r,\beta ']\) split by (12.18) such that
Proof
We prove the statement by induction along r. If \(n=r\) then we choose \(\beta '=0\) so suppose now \(r<n\). We choose a semisimple approximation \([\Lambda ,n,r+1,\gamma ]\) of \([\Lambda ,n,r+1,\beta ]\) split by (12.18). Then by the induction hypothesis there is a self-dual semisimple stratum \([\Lambda ,n,r+1,\gamma ']\) split by (12.18) with the same set of semisimple characters as \([\Lambda ,n,r+1,\gamma ]\). By [39, Theorem 9.16] there is a simple stratum \([\Lambda ^{1},n,r,\beta '_{1}]\) such that \([\Lambda ^{1},n,r+1,\beta '_{1}]\) is equivalent to \([\Lambda ^{1},n,r+1,\gamma '_{1}]\) and
We choose \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) and \(\theta _0\in {\mathscr {C}}^\Sigma (\Lambda ,r,\gamma ')\) which coincide on \({\mathrm {H}}^{r+2}(\beta ,\Lambda )={\mathrm {H}}^{r+2}(\gamma ',\Lambda )\). Then there exists an element \(a_{1}\in {\mathfrak {a}}^{1}_{-r-1}\) such that
Lemma A.7(i) applied to \(\psi _{\beta '_1-\gamma '_1}\theta _{0,1}\) (with \(|K|=1\)) implies that \([\Lambda ^{1},n,r,\beta '_1+a_1]\) is equivalent to a semisimple stratum \([\Lambda ^{1},n,r,\beta ''_{1}]\), and Lemma A.7(ii) then implies
In particular \([\Lambda ^{1},n,r,\beta ''_{1}]\) is simple by Theorem 8.8 and therefore \([\Lambda ^{-1},n,r,-{\overline{\beta ''_{1}}}]\) is simple by duality. We put \(\beta '':=\beta _{1}''-{\overline{\beta _{1}''}}\). Then:
-
if \([\Lambda ,n,r,\beta '']\) is not equivalent to a simple stratum, then it is semisimple (and already self-dual);
-
if \([\Lambda ,n,r,\beta '']\) is equivalent to a simple stratum, then it is equivalent to a self-dual simple stratum split by (12.18), by [41, 1.10].
In any case \([\Lambda ,n,r,\beta '']\) is equivalent to a self-dual semisimple stratum \([\Lambda ,n,r,\beta ''']\) split by (12.18). Further we have:
Applying Corollary A.8 to the pair \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\psi _{\beta '''-\gamma '}\theta _{0}\in {\mathscr {C}}(\Lambda ,r,\beta ''')\), we obtain the desired equality
\(\square \)
Proof of Theorem 12.16
Let \([\Theta ]\) be a non-zero full simple endo-class and choose \((\mathrm{V},\varphi ,(\mathrm{V}_h,h),\mathrm{V}^\#,\Lambda )\) as in Definition 12.10. Let \(\theta =\Theta (\mathrm{V},\varphi ,\Lambda ,0)\), a simple character in \({\mathscr {C}}(\Lambda ,0,\varphi (\beta ))\), and define \(\theta ^\#\in {\mathscr {C}}(\Lambda ^\#,0,-{\overline{\varphi (\beta )}})\) by
Setting \(n=-v_\Lambda (\varphi (\beta ))\), the strata \([\Lambda ,n,0,\varphi (\beta )]\) and \([\Lambda ^\#,n,0,-{\overline{\varphi (\beta )}}]\) are simple, and therefore \([\Lambda \oplus \Lambda ^\#,n,0,\varphi (\beta )\oplus (-{\overline{\varphi (\beta )}})]\) is equivalent to a semisimple stratum split by \(\mathrm{V}\oplus \mathrm{V}^\#\). Lemma 12.7 provides us with a semisimple stratum \([\Lambda \oplus \Lambda ^\#,n,0,{\tilde{\beta }}]\) split by \(\mathrm{V}\oplus \mathrm{V}^\#\) and a semisimple character \({\tilde{\theta }}\in {\mathscr {C}}(\Lambda \oplus \Lambda ^\#,n,0,{\tilde{\beta }})\) with restrictions \(\theta \) and \(\theta ^\#\). Note that \([\Lambda ,n,0,{\tilde{\beta }}|_\mathrm{V}]\) and \([\Lambda ^\#,n,0,{\tilde{\beta }}|_{\mathrm{V}^\#}]\) are simple strata: they are certainly semisimple and, since \({\mathscr {C}}(\Lambda ,0,{\tilde{\beta }}|_\mathrm{V})={\mathscr {C}}(\Lambda ,0,\varphi (\beta ))\), the matching of Theorem 8.8 implies that \([\Lambda ,n,0,{\tilde{\beta }}|_\mathrm{V}]\) is simple. We have \({\tilde{\theta }}={\tilde{\theta }}^\sigma \) by Corollary A.8, and therefore by Lemma 12.17 we can choose \([\Lambda \oplus \Lambda ^\#,n,0,{\tilde{\beta }}]\) to be self-dual. Let \({\tilde{\Theta }}_-\) be the self-dual pss-character supported on \((0,{\tilde{\beta }})\) whose lift \({\tilde{\Theta }}\) takes value \({\tilde{\theta }}\) at \((\mathrm{V}_h,{\varphi _{{\tilde{\beta }}}},\Lambda \oplus \Lambda ^\#,0)\). Then
\(\square \)
Let us illustrate the two cases which occur at the end of (the proof of) Theorem 12.16. If the lift \({\tilde{\Theta }}\) is simple then \({\tilde{\Theta }}\) and \(\Theta \) are endo-equivalent and we have
so that \(\Phi ([{\tilde{\Theta }}_-])=\{[\Theta ]\}\). Otherwise, the lift \({\tilde{\Theta }}\) is not simple, the endo-classes \([\Theta ]\) and \(\sigma ([\Theta ])\) are the non-endo-equivalent simple block restrictions of \([{\tilde{\Theta }}]\), and \(\Phi ([{\tilde{\Theta }}_-])\) consists of two elements.
12.4 Endo-parameters for \((h,\mathrm{G})\)
We now fix \(\mathrm{F}/\mathrm{F}_{\mathsf {o}}\) and \(\varepsilon \), and our \(\varepsilon \)-hermitian space \((\mathrm{V},h)\) over \(\mathrm{F}\). In this section, we parametrize the \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\)- and \(\mathrm{G}^{\mathsf {o}}\)-intertwining classes of full self-dual semisimple characters (i.e. supported on a self-dual semisimple pair of the form \((0,\beta )\)).
One invariant of an intertwining class of skew semisimple characters comes from the theory of concordant pairs: if two skew semisimple characters \(\theta _-\in {\mathscr {C}}_-(\Lambda ,0,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ,0,\beta ')\) intertwine by an element of \(\mathrm{G}\) then the underlying simple block strata are concordant (see Theorem 8.17). We now encode this into invariants in the following way.
Definition 12.19
Consider the class of pairs \((\beta ,{{\mathfrak {t}}})\) where \((0,\beta )\) is a self-dual simple pair and \({{\mathfrak {t}}}\) is an element of \({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\), where \(\mathrm{E}=\mathrm{F}[\beta ]\) as usual. Two pairs \((\beta ,{{\mathfrak {t}}})\) and \((\beta ',{{\mathfrak {t}}}')\) are equivalent if
-
(i)
\((\mathrm{F}[\beta ],\beta )\) and \((\mathrm{F}[\beta '],\beta ')\) are similar self-dual extensions (see Definition 3.33); and
-
(ii)
\({\mathsf {w}}_{\varepsilon ,\beta ',\beta }({{\mathfrak {t}}})={{\mathfrak {t}}}'\).
This is clearly an equivalence relation. We call the equivalence classes Witt types and we denote the Witt type associated to a pair \((\beta ,{{\mathfrak {t}}})\) by \([\beta ,{{\mathfrak {t}}}]\).
Remarks 12.20
-
(i)
Note that the diagrams (3.29) and (3.30) commute by similarity of \((\mathrm{F}[\beta ],\beta )\) and \((\mathrm{F}[\beta '],\beta ')\) and Corollary 5.20. Therefore, in the non-symplectic case, the condition (ii) is equivalent to the anisotropic dimensions of \({{\mathfrak {t}}}\) and \({{\mathfrak {t}}}'\) having the same parity, together with \(\lambda ^*_{\beta }({{\mathfrak {t}}})=\lambda ^*_{\beta '}({{\mathfrak {t}}}')\).
-
(ii)
Given a self-dual field extension \((\mathrm{E},\beta )\), the set of all possible Witt types \([\beta ,{{\mathfrak {t}}}]\) is in bijection with \({\mathcal {W}}_\varepsilon (\mathrm{E}/\mathrm{E}_{\mathsf {o}})\).
We are going to attach Witt types to elements of \({\mathscr {E}}_-\). Throughout this section we identify \({\mathscr {E}}_-\) with \({\mathscr {E}}/\Sigma \), a consequence of Theorem 12.16 and (12.15); we will usually use \({\scriptstyle {{\mathcal {O}}}}\in {\mathscr {E}}/\Sigma \) and write \([\Theta _-]=\Phi ^{-1}({\scriptstyle {{\mathcal {O}}}})\) for the corresponding element of \({\mathscr {E}}_-\). We will write \(\deg ({\scriptstyle {{\mathcal {O}}}})=\deg (\Theta _-)\) so that, if \(\Theta _{\scriptscriptstyle {{\mathcal {O}}}}\) is any pss-character whose endo-class is in the orbit \({\scriptstyle {{\mathcal {O}}}}\), we have \(\deg ({\scriptstyle {{\mathcal {O}}}})=|{\scriptstyle {{\mathcal {O}}}}|\deg (\Theta _{\scriptscriptstyle {{\mathcal {O}}}})\).
Not all Witt types are suitable for a given \({\scriptstyle {{\mathcal {O}}}}\in {\mathscr {E}}/\Sigma \). We therefore define
In the non-simple case \(|{\scriptstyle {{\mathcal {O}}}}|=2\) there is only one Witt type because all realizations of a corresponding \(\Theta _-\) use a hyperbolic space over \(\mathrm{F}\).
Remark 12.21
If \({\scriptstyle {{\mathcal {O}}}}\in {\mathscr {E}}/\Sigma \) is an orbit of cardinality one and we choose a self-dual ps-character \(\Theta _-\) supported on the self-dual pair \((0,\beta )\) with \(\Phi ([\Theta _-])={\scriptstyle {{\mathcal {O}}}}\), then the map
is a bijection. Indeed, if \(\Theta '_-\) is another self-dual ps-character, supported on the self-dual pair \((0,\beta ')\) and with \(\Phi ([\Theta '_-])={\scriptstyle {{\mathcal {O}}}}\) then, since \(\Theta _-\) and \(\Theta '_-\) are endo-equivalent, Corollary 7.12 implies that the self-dual extensions \((\mathrm{F}[\beta ],\beta )\) and \((\mathrm{F}[\beta '],\beta ')\) are similar.
If we have self-dual semisimple characters \(\theta _-\in {\mathscr {C}}_-(\Lambda ,0,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',0,\beta ')\) which intertwine in \(\mathrm{G}\) with matching \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) then, for \(i\in \mathrm{I}\), the dimensions \({\text {dim}}_{\mathrm{E}_i}\mathrm{V}^i\) and \({\text {dim}}_{\mathrm{E}'_{\zeta (i)}}\mathrm{V}^{\zeta (i)}\) must coincide and, for \(i\in \mathrm{I}_0\), the forms \(h_{\beta _i}\) and \(h_{\beta _{\zeta (i)}}\) must have the same Witt index. We need invariants taking this into account.
We define the set of possible endo-parameters for \({\scriptstyle {{\mathcal {O}}}}\in {\mathscr {E}}/\Sigma \) to be
Definition 12.22
Let \({\scriptstyle {{\mathcal {O}}}}\in {\mathscr {E}}/\Sigma \) and let \({{\mathfrak {z}}}=([\alpha ,{{\mathfrak {t}}}],n)\) be an endo-parameter for \({\scriptstyle {{\mathcal {O}}}}\). We define
-
\({\mathrm {dim}}_{\mathrm {an}}({{\mathfrak {z}}}):={\mathrm {dim}}_{\mathrm {an}}({{\mathfrak {t}}})\), the anisotropic dimension of \({{\mathfrak {z}}}\),
-
\(\deg ({{\mathfrak {z}}}):=(2n+{\mathrm {dim}}_{\mathrm {an}}({{\mathfrak {z}}}))\frac{\deg ({\scriptscriptstyle {{\mathcal {O}}}})}{|{\scriptscriptstyle {{\mathcal {O}}}}|}\), the degree of \({{\mathfrak {z}}}\),
-
\({\text {herm}}_{\mathrm{F}/\mathrm{F}_{\mathsf {o}}}({{\mathfrak {z}}}):=\lambda _{\alpha }^*({{\mathfrak {t}}})\), an element of the Witt group \({\mathcal {W}}_\varepsilon (\mathrm{F}/\mathrm{F}_{\mathsf {o}})\).
We are now able to define the parameters for the classification of intertwining classes of self-dual semisimple characters.
Definition 12.23
A self-dual endo-parameter (with respect to \((\mathrm{F}/\mathrm{F}_{\mathsf {o}},\varepsilon )\)) is a section \({{\mathfrak {f}}}_-\) of
with finite support \({\text {supp}}({{\mathfrak {f}}}_-)=\{{\scriptstyle {{\mathcal {O}}}}\in {\mathscr {E}}/\Sigma \mid \deg ({{\mathfrak {f}}}_-({\scriptstyle {{\mathcal {O}}}}))\ne 0\}\). For \({{\mathfrak {f}}}_-\) a self-dual endo-parameter, we define its degree by
and also set
Notice then that the endo-parameters for \({\scriptstyle {{\mathcal {O}}}}\) are just the endo-parameters with support contained in the singleton \(\{{\scriptstyle {{\mathcal {O}}}}\}\).
Remark 12.24
A self-dual endo-parameter \({{\mathfrak {f}}}_-\) defines a \({\text {GL}}\)-endo-parameter \({{\mathfrak {f}}}:{\mathscr {E}}\rightarrow {\mathbb {N}}_0\) by setting
We have \(\deg ({{\mathfrak {f}}})=\deg ({{\mathfrak {f}}}_-)\).
Recall that Proposition 12.3 gives us a canonical bijection \({\mathcal {F}}\) from the set of all full semisimple endo-classes to \({\mathscr {E}}^{\mathrm {fin}}\). We write \(({\mathscr {E}}/\Sigma )^{\mathrm {fin}}\) for the set of all finite subsets of \({\mathscr {E}}/\Sigma \), and we have:
Proposition 12.25
There is a canonical bijection \({\mathcal {F}}_-\) from the set of all full self-dual endo-classes to \(({\mathscr {E}}/\Sigma )^{\mathrm {fin}}\), defined by mapping a full self-dual endo-class \([\Theta _-]\) with lift \([\Theta ]\) to \({\mathcal {F}}([\Theta ])/\Sigma \), the set of orbits of elements of \({\mathcal {F}}([\Theta ])\).
The proof mimics that of Proposition 12.3. First we have an analogue of Lemma 12.4:
Lemma 12.26
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ,n,r+1,\gamma ]\) be self-dual semisimple strata which are split by  and such that \([\Lambda ,n,r+1,\beta ]\) is equivalent to \([\Lambda ,n,r+1,\gamma ]\). Put \(\Lambda '=\Lambda \cap \mathrm{V}'\) and \(\beta '=\beta |_{\mathrm{V}'}\), and similarly for \(\Lambda '',\beta ''\). Given \({\tilde{\theta }}\in {{\mathscr {C}}^\Sigma (\Lambda ,r+1,\gamma )}\) and an extension \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ',r,\beta ')\) of \({\tilde{\theta }}|_{{\mathrm {H}}^{r+2}(\beta ',\Lambda ')}\), there is a semisimple character \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) such that the restriction to \({\mathrm {H}}^{r+1}(\beta ',\Lambda ')\) is \(\theta '\) and the restriction to \({\mathrm {H}}^{r+2}(\beta ,\Lambda )\) is \({\tilde{\theta }}\).
and such that \([\Lambda ,n,r+1,\beta ]\) is equivalent to \([\Lambda ,n,r+1,\gamma ]\). Put \(\Lambda '=\Lambda \cap \mathrm{V}'\) and \(\beta '=\beta |_{\mathrm{V}'}\), and similarly for \(\Lambda '',\beta ''\). Given \({\tilde{\theta }}\in {{\mathscr {C}}^\Sigma (\Lambda ,r+1,\gamma )}\) and an extension \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ',r,\beta ')\) of \({\tilde{\theta }}|_{{\mathrm {H}}^{r+2}(\beta ',\Lambda ')}\), there is a semisimple character \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) such that the restriction to \({\mathrm {H}}^{r+1}(\beta ',\Lambda ')\) is \(\theta '\) and the restriction to \({\mathrm {H}}^{r+2}(\beta ,\Lambda )\) is \({\tilde{\theta }}\).
We could prove this in a similar way to Lemma 12.4, but the group action of \(\Sigma \) provides a significant simplification.
Proof
By the definition of semisimple character, in particular see [39, Definition 9.5], we have that for any three characters \(\theta _0,\theta _1,\theta _2\in {\mathscr {C}}(\Lambda ,r,\beta )\) the character \(\theta _0\theta _1\theta _2^{-1}\) is also an element of \({\mathscr {C}}(\Lambda ,r,\beta )\). Thus for \(\theta '_1\in {\mathscr {C}}(\Lambda ',r,\beta ')\) and \({\tilde{\theta }}_1\in {\mathscr {C}}(\Lambda ,r+1,\gamma )\) coinciding on \({\mathrm {H}}^{r+2}(\beta ',\Lambda ')\), since there always is an extension to \({\mathscr {C}}(\Lambda ,r,\beta )\) by Lemma 12.4, the number of such extensions does not depend on the choice of \((\theta '_1,{\tilde{\theta }}_1)\) and therefore it is a divisor of the cardinality of \({\mathscr {C}}(\Lambda ,r,\beta )\). The cardinality of \({\mathscr {C}}(\Lambda ,r,\beta )\) is odd, and therefore the number of extensions of \((\theta ',{\tilde{\theta }})\) is odd; thus \(\Sigma \) has a fixed point which extends \(\theta '\) and \({\tilde{\theta }}\). \(\square \)
The analogue of Lemma 12.7 needs more subtle modifications.
Lemma 12.27
Let \((\mathrm{V}',h')\) and \((\mathrm{V}'',h'')\) be \(\varepsilon \)-hermitian spaces and let \(\theta '\in {\mathscr {C}}^{\Sigma '}(\Lambda ',r,\beta ')\) and \( \theta ''\in {\mathscr {C}}^{\Sigma ''}(\Lambda '',r,\beta '')\) be characters for self-dual semisimple strata in \(\mathrm{V}'\) and \(\mathrm{V}''\) respectively, such that \(e(\Lambda ')=e(\Lambda '')\). Set  , \(\Lambda =\Lambda '\oplus \Lambda ''\) and \(n=\max \{n',n''\}\). Then there exist self-dual semisimple strata \([\Lambda ',n',r,{\tilde{\beta }}']\) and \([\Lambda '',n'',r,{\tilde{\beta }}'']\) in \(\mathrm{V}'\) and \(\mathrm{V}''\) respectively, such that \([\Lambda ,n,r,{\tilde{\beta }}'\oplus {\tilde{\beta }}'']\) is self-dual semisimple and such that there is a character \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,{\tilde{\beta }}'\oplus {\tilde{\beta }}'')\) with restrictions \(\theta |_{{\mathrm {H}}^{r+1}({\tilde{\beta }}',\Lambda ')}=\theta '\) and \(\theta |_{{\mathrm {H}}^{r+1}({\tilde{\beta }}'',\Lambda '')}=\theta ''\). Moreover, we can choose \({\tilde{\beta }}'\) and \({\tilde{\beta }}''\) with the same associated splittings as \(\beta '\) and \(\beta ''\), respectively.
, \(\Lambda =\Lambda '\oplus \Lambda ''\) and \(n=\max \{n',n''\}\). Then there exist self-dual semisimple strata \([\Lambda ',n',r,{\tilde{\beta }}']\) and \([\Lambda '',n'',r,{\tilde{\beta }}'']\) in \(\mathrm{V}'\) and \(\mathrm{V}''\) respectively, such that \([\Lambda ,n,r,{\tilde{\beta }}'\oplus {\tilde{\beta }}'']\) is self-dual semisimple and such that there is a character \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,{\tilde{\beta }}'\oplus {\tilde{\beta }}'')\) with restrictions \(\theta |_{{\mathrm {H}}^{r+1}({\tilde{\beta }}',\Lambda ')}=\theta '\) and \(\theta |_{{\mathrm {H}}^{r+1}({\tilde{\beta }}'',\Lambda '')}=\theta ''\). Moreover, we can choose \({\tilde{\beta }}'\) and \({\tilde{\beta }}''\) with the same associated splittings as \(\beta '\) and \(\beta ''\), respectively.
Note that, contrary to the case in Lemma 12.7, we do not claim that we can take \({\tilde{\beta }}'=\beta '\). We cannot give a proof mutatis mutandis to that of loc.cit., because we would need to join non-skew self-dual characters. Instead, the proof uses the full strength of the translation principle A.1.
Proof
We proceed by induction along r. If \(r=n\) then \(\beta '\) and \(\beta ''\) vanish, and we put \({\tilde{\beta }}'\) and \({\tilde{\beta }}''\) as zero, so suppose \(r<n\). We choose approximations \([\Lambda ',n',r+1,\gamma ']\) and \([\Lambda '',n'',r+1,\gamma '']\) for the strata with \(\beta '\) and \(\beta ''\), respectively. By the induction hypothesis we can find self-dual semisimple strata \([\Lambda ',n',r+1,{\tilde{\gamma }}']\) and \([\Lambda '',n'',r+1,{\tilde{\gamma }}'']\), with the same associated splittings as \(\gamma '\) and \(\gamma ''\) respectively, such that their direct sum is semisimple and such that there is a character \(\theta _\gamma \in {\mathscr {C}}^\Sigma (\Lambda ,{r+1},{\tilde{\gamma }})\) with restrictions \(\theta '|_{{\mathrm {H}}^{r+2}(\beta ',\Lambda ')}\) and \(\theta ''|_{{\mathrm {H}}^{r+2}(\beta '',\Lambda '')}\).
Using Theorem A.1 we find a self-dual semisimple stratum \([\Lambda ',n',r,\delta ']\) and \(u'\in \mathrm{P}^1_-(\Lambda ')\) which normalizes every element of \({\mathscr {C}}(\Lambda ',r+1,{{\tilde{\gamma }}}')\), such that \({\mathscr {C}}(\Lambda ',r,\delta ')={\mathscr {C}}(\Lambda ',r,\beta ')\) and \([\Lambda ',n',r+1,\delta ']\) is equivalent to \([\Lambda ',n',r+1,{{\tilde{\gamma }}}']\), and \({{\tilde{\gamma }}}'\) respects the splitting of \(u\delta 'u^{-1}\). Moreover, replacing \({{\tilde{\gamma }}}'\) by \(u^{-1}{{\tilde{\gamma }}}'u\), we can assume that \({{{\tilde{\gamma }}}'}\) respects the splitting of \(\delta '\); that is, \([\Lambda ',n',r,\delta ']\) has an approximation given by \({{\tilde{\gamma }}}'\). Similarly, we have a self-dual semisimple stratum \([\Lambda '',n'',r,\delta '']\) with approximation \({\tilde{\gamma }}''\) such that \({\mathscr {C}}(\Lambda '',r,\delta '')={\mathscr {C}}(\Lambda '',r,\beta '')\).
The stratum \([\Lambda ,n,r,\delta '\oplus \delta '']\) is equivalent to a semisimple stratum and therefore, by [39, Theorem 6.16], to a self-dual semisimple stratum respecting the splittings of \(\delta ',\delta ''\) and  ; thus we may assume \([\Lambda ,n,r,\delta ]\) is self-dual semisimple, where \(\delta :=\delta '\oplus \delta ''\). We apply Lemma 12.26 to find a character \(\theta _\delta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\delta )\) with restrictions \(\theta ',\ \theta _\gamma \). Then there is a skew \(a''\in {\mathfrak {a}}_{-(r+1)}''\) split by the splitting of \(\delta ''\) such that
; thus we may assume \([\Lambda ,n,r,\delta ]\) is self-dual semisimple, where \(\delta :=\delta '\oplus \delta ''\). We apply Lemma 12.26 to find a character \(\theta _\delta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\delta )\) with restrictions \(\theta ',\ \theta _\gamma \). Then there is a skew \(a''\in {\mathfrak {a}}_{-(r+1)}''\) split by the splitting of \(\delta ''\) such that
The stratum \([\Lambda ,n,r,\delta +a'']\) is equivalent to a semisimple stratum by Lemma A.7 and therefore to a self-dual semisimple stratum \([\Lambda ,n,r,{\tilde{\beta }}]\) split by the splittings of \(\delta ',\delta ''\) and  . Thus \({\tilde{\beta }}={\tilde{\beta }}'\oplus {\tilde{\beta }}'' \) and \(\theta =\theta _\delta \psi _{a''}\) satisfy the first part of the lemma. Finally Proposition A.9(ii) states that we can conjugate \({\tilde{\beta }}'\) and \({\tilde{\beta }}''\) to the splittings of \(\beta '\) and \(\beta ''\), which completes the proof. \(\square \)
. Thus \({\tilde{\beta }}={\tilde{\beta }}'\oplus {\tilde{\beta }}'' \) and \(\theta =\theta _\delta \psi _{a''}\) satisfy the first part of the lemma. Finally Proposition A.9(ii) states that we can conjugate \({\tilde{\beta }}'\) and \({\tilde{\beta }}''\) to the splittings of \(\beta '\) and \(\beta ''\), which completes the proof. \(\square \)
Proof of Proposition 12.25
Let \(\Theta _-,\Theta '_-\) be self-dual pss-characters, with lifts \(\Theta ,\Theta '\) and index sets \(\mathrm{I}=\mathrm{I}_0\cup \mathrm{I}_-\cup \mathrm{I}_+\) and \(\mathrm{I}'\) respectively. If \([\Theta _-]\) and \([\Theta '_-]\) are mapped to the same set, then \({\mathcal {F}}([\Theta ])/\Sigma ={\mathcal {F}}_-([\Theta _-]) = {\mathcal {F}}_-([\Theta '_-]) ={\mathcal {F}}([\Theta '])/\Sigma \). It follows that \({\mathcal {F}}([\Theta ])\) and \({\mathcal {F}}([\Theta '])\) coincide because both sets are union of orbits; indeed, \(\sigma ([\Theta _i])=[\Theta _i]\) for \(i\in \mathrm{I}_0\) and \(\sigma ([\Theta _i])=[\Theta _{-i}]\) for \(i\in \mathrm{I}_+\), by Lemma 9.6(a) and then Lemma 12.14 applied to \(\Theta _{\{\pm i\}}\). Thus \(\Theta \) and \(\Theta '\) are endo-equivalent by Proposition 12.3 and therefore \(\Theta _-,\Theta '_-\) are endo-equivalent by Theorem 9.16. The surjectivity follows inductively as in the case of Proposition 12.3, using Lemma 12.27. \(\square \)
We are finally ready to define endo-parameters for \((h,\mathrm{G})\); note that these depend not only on the group \(\mathrm{G}\) but also on the isometry class of the form h.
Definition 12.28
We denote by \(\mathrm {EP}(h,\mathrm{G})\) the set of those self-dual endo-parameters with \({\text {herm}}_{\mathrm{F}/\mathrm{F}_0}({{\mathfrak {f}}}_-)=[h]\) and \(\deg ({{\mathfrak {f}}}_-)={\text {dim}}_\mathrm{F}\mathrm{V}\), and we call it the set of endo-parameters for \((h,\mathrm{G})\).
Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,0,\beta )\) be a self-dual semisimple character, let \(\Theta _-\) be the self-dual pss-character supported on \((0,\beta )\) with value \(\theta _-\) at \(((\mathrm{V},h),\varphi _\beta ,\Lambda ,0)\), and let \(\Theta \) be its lift, with index set \(\mathrm{I}=\mathrm{I}_0\cup \mathrm{I}_+\cup \mathrm{I}_-\). We have
where \({\scriptstyle {{\mathcal {O}}}}_i\) is the orbit associated to the block restriction \([\Theta _i]\). For each \(i\in \mathrm{I}_0\), we have the \(\varepsilon \)-hermitian form \(h_{{\text {id}}_{\mathrm{E}_i}}\) given by Lemma 3.17. We attach to \(\theta _-\) the endo-parameter with support \({\mathcal {F}}_-([\Theta _-])\) given by
where \(m_i\) denotes the Witt index of \(h_{{\text {id}}_{\mathrm{E}_i}}\) when \(i\in \mathrm{I}_0\), and \(m_i={\text {dim}}_{\mathrm{E}_i}(\mathrm{V}^i)\) for \(i\in \mathrm{I}_+\). Note that the map \(\theta _-\mapsto {{\mathfrak {f}}}_{\theta _-}\) depends on h (not just the isometry class of h), which is why we have included h in the notation \(\mathrm {EP}(h,\mathrm{G})\).
Theorem 12.29
There is a canonical bijection from the set of intertwining classes of full self-dual semisimple characters for \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)\) to the set of self-dual endo-parameters \(\mathrm {EP}(h,\mathrm{G})\), defined by mapping the intertwining class of a full self-dual semisimple character \(\theta _-\) to the self-dual endo-parameter \({{\mathfrak {f}}}_{\theta _-}\).
Before starting the proof, we give an example illustrating the dependence on h. Suppose that \(-1\) is not a square in \(\mathrm{F}\), that \((\mathrm{V},h)\) is a symplectic space, and that \(\varphi :\mathrm{E}\hookrightarrow {\text {End}}_\mathrm{F}(\mathrm{V})\) is a self-dual embedding of a self-dual extension \((\mathrm{E},\beta )\) such that \({\text {dim}}_\mathrm{E}\mathrm{V}\) is odd. Consider a self-dual simple character \(\theta _-\in {\mathscr {C}}_-(\Lambda ,0,\varphi (\beta ))\). Note that we have \(\mathrm{G}=\mathrm{U}(\mathrm{V},h)=\mathrm{U}(\mathrm{V},-h)\) so that we also have \(\mathrm {EP}(h,\mathrm{G})=\mathrm {EP}(-h,\mathrm{G})\). However, \([h_{\varphi }]\ne [-h_{\varphi }]=[(-h)_{\varphi }]\), if \(-1\not \in \mathrm{N}_{\mathrm{E}/\mathrm{E}_o}(\mathrm{E})\). Therefore, in that case, the \(\mathrm{G}\)-intertwining class of \(\theta _-\) is attached to a different self-dual endo-parameter in \(\mathrm {EP}(h,\mathrm{G})\) than in \(\mathrm {EP}(-h,\mathrm{G})\).
The reason for this phenomenon is that the notion of self-dual endo-parameter is equivariant with respect to isometries: in the above example, an isometry g from \((\mathrm{V},h)\) to \((\mathrm{V},-h)\) maps the intertwining class of \(\theta _-\) to the intertwining class of \({}^g\theta _-\); and \(\theta _-\) is not intertwined with \({}^g\theta _-\) by any element of \(\mathrm{G}\), only by an isometry from h to \(-h\).
Proof
We need to show that the map described is well-defined, injective and surjective. Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,0,\beta )\) and \(\theta '_-\in {\mathscr {C}}_-(\Lambda ',0,\beta ')\) be self-dual semisimple characters in \(\mathrm{G}\) with corresponding pss-characters \(\Theta _-\), \(\Theta '_-\) and lifts \(\theta ,\theta ',\Theta ,\Theta '\). Denote by \(\mathrm{I},\mathrm{I}'\) the corresponding index sets and decompose them \(\mathrm{I}=\mathrm{I}_0\cup \mathrm{I}_+\cup \mathrm{I}_-\) as usual, similarly for \(\mathrm{I}'\). For \(i\in \mathrm{I}\), we put \(\mathrm{E}_i=\mathrm{F}[\beta _i]\) as usual, \([\Theta _i]\) for the simple endo-classes corresponding to \(\Theta _i\), and \({\scriptstyle {{\mathcal {O}}}}_i\) for the orbit of \([\Theta _i]\) in \({\mathscr {E}}/\Sigma \), with similar notation \(\mathrm{E}'_{i'}\), \(\Theta '_{i'}\) and \({\scriptstyle {{\mathcal {O}}}}'_{i'}\), for \(i'\in \mathrm{I}'\).
Suppose first that \(\theta _-\) and \(\theta '_-\) intertwine by an element of \(\mathrm{G}=~\mathrm{U}(\mathrm{V},h)\), with matching \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\). In particular, the self-dual pss-characters \(\Theta _-,\Theta '_-\) are endo-equivalent so \({\mathcal {F}}_-([\Theta _-])={\mathcal {F}}_-([\Theta '_-])\) and the endo-parameters \({{\mathfrak {f}}}_{\theta _-},{{\mathfrak {f}}}_{\theta '_-}\) have the same support. Then, for all \(i\in \mathrm{I}\), we have:
-
\(\zeta \) commutes with \(\sigma \), by Remark 8.9, and \(\Theta _i\) is endo-equivalent to \(\Theta '_{\zeta (i)}\) so \({\scriptstyle {{\mathcal {O}}}}_i={\scriptstyle {{\mathcal {O}}}}'_{\zeta (i)}\);
-
\({\text {dim}}_\mathrm{F}\mathrm{V}^i={\text {dim}}_\mathrm{F}\mathrm{V}'^{\zeta (i)}\);
-
if \(i\in \mathrm{I}_0\) then the self-dual field extensions \((\mathrm{E}_i,\beta _i)\) and \((\mathrm{E}'_{\zeta (i)},\beta '_{\zeta (i)})\) are similar, by Corollary 7.12;
-
the pairs \((\beta _i,{\text {id}}_{\mathrm{E}_i})\) and \((\beta '_{\zeta (i)},{\text {id}}_{\mathrm{E}'_{\zeta (i)}})\) are \((h_i,h_{\zeta (i)})\)-concordant, by Theorem 8.17.
The final two points imply that the pairs \((\beta _i,[h_{{\text {id}}_{\mathrm{E}_i}}])\) and \((\beta '_{\zeta (i)},[h_{{\text {id}}_{\mathrm{E}'_{\zeta (i)}}}])\) are equivalent, for \(i\in \mathrm{I}_0\); then \((\mathrm{V}^i,h_{{\text {id}}_{\mathrm{E}_i}})\) and \((\mathrm{V}'^{\zeta (i)},h_{{\text {id}}_{\mathrm{E}'_{\zeta (i)}}})\) have the same anisotropic dimension and the same dimension so also the same Witt index. This implies \({{\mathfrak {f}}}_{\theta _-}({\scriptstyle {{\mathcal {O}}}}_i)={{\mathfrak {f}}}_{\theta '_-}({\scriptstyle {{\mathcal {O}}}}_i)\), for \(i\in \mathrm{I}_0\), while the same is true for \(i\in \mathrm{I}_+\) simply by the comparison of dimensions. Thus \({{\mathfrak {f}}}_{\theta _-}={{\mathfrak {f}}}_{\theta '_-}\), as required.
Conversely, suppose \({{\mathfrak {f}}}_{\theta _-}={{\mathfrak {f}}}_{\theta '_-}\) and let \({{\mathfrak {f}}}:{\mathscr {E}}\rightarrow {\mathbb {N}}_0\) be the corresponding \({\text {GL}}\)-endo-parameter (see Remark 12.24). Then \({{\mathfrak {f}}}_\theta ={{\mathfrak {f}}}={{\mathfrak {f}}}_{\theta '}\) by Theorem 12.9 and, applying the same theorem again, the characters \(\theta ,\theta '\) intertwine by an element of \({\text {Aut}}_\mathrm{F}(\mathrm{V})\) with a matching \(\zeta \); thus \(\Theta _i\) and \(\Theta '_{\zeta (i)}\) are endo-equivalent and \({\scriptstyle {{\mathcal {O}}}}_i={\scriptstyle {{\mathcal {O}}}}_{\zeta (i)}\) for all indices \(i\in \mathrm{I}\). The fact that \({{\mathfrak {f}}}_{\theta _-}({\scriptstyle {{\mathcal {O}}}}_i)={{\mathfrak {f}}}_{\theta '_-}({\scriptstyle {{\mathcal {O}}}}_i)\) says that \({\text {dim}}_\mathrm{F}\mathrm{V}^i={\text {dim}}_\mathrm{F}\mathrm{V}'^{\zeta (i)}\), for \(i\in \mathrm{I}\), and that the pairs \((\beta _i,{\text {id}}_{\mathrm{E}_i})\) and \((\beta '_{\zeta (i)},{\text {id}}_{\mathrm{E}'_{\zeta (i)}})\) are \((h_i,h'_{\zeta (i)})\)-concordant, for \(i\in \mathrm{I}_0\). Therefore \(\theta _-\) and \(\theta '_-\) intertwine in \(\mathrm{G}\), by Theorem 9.16.
It remains to prove surjectivity. Let \({{\mathfrak {f}}}_-\) be a self-dual endo-parameter for \((h,\mathrm{G})\) so that we need to construct a semisimple character \(\theta _-\) for \(\mathrm{G}\) satisfying \({{\mathfrak {f}}}_{\theta _-}={{\mathfrak {f}}}_-\). In fact it is enough to study endo-parameters supported on a single orbit in \({\mathscr {E}}/\Sigma \), since Lemma 12.27 then allows us to construct self-dual semisimple characters in general. So we suppose \({\text {supp}}({{\mathfrak {f}}}_-)=\{{\scriptstyle {{\mathcal {O}}}}\}\) and consider the two cases for the cardinality of the orbit separately.
Suppose first that \(|{\scriptstyle {{\mathcal {O}}}}|=1\) and \({{\mathfrak {f}}}_-({\scriptstyle {{\mathcal {O}}}})=([\beta ,{{\mathfrak {t}}}],m)\). Let \(\Theta _-\) be a self-dual ps-character supported on \((0,\beta )\) such that \(\Phi ([\Theta _-])={\scriptstyle {{\mathcal {O}}}}\), and set \(\mathrm{E}=\mathrm{F}[\beta ]\). We choose \(({\tilde{\mathrm{V}}},{\tilde{h}})\), an \(\varepsilon \)-hermitian space over \(\mathrm{E}/\mathrm{E}_{\mathsf {o}}\), such that \([{\tilde{h}}]={{\mathfrak {t}}}\) and with Witt index m, and a self-dual \({\mathfrak {o}}_{\mathrm{E}}\)-lattice sequence \(\Lambda \) in \({\tilde{\mathrm{V}}}\). Then \(\lambda ^*_\beta ({\tilde{h}})\) is isometric to h, as \(\lambda ^*_\beta ({{\mathfrak {t}}})=[h]\) and \({\text {dim}}_\mathrm{F}{\tilde{\mathrm{V}}}=\deg ({{\mathfrak {f}}}_-)={\text {dim}}_\mathrm{F}\mathrm{V}\). We identify \(\lambda ^*_\beta ({\tilde{h}})\) with h via an isometry and then the character
satisfies \({{\mathfrak {f}}}_{\theta _-}={{\mathfrak {f}}}_-\).
Finally, suppose \(|{\scriptstyle {{\mathcal {O}}}}|=2\) and \({{\mathfrak {f}}}_-({\scriptstyle {{\mathcal {O}}}})=([0,\varvec{0}],m)\). Let \(\Theta _-\) be a self-dual pss-character supported at some pair \((0,\beta _{1}\oplus \beta _{-1})\) such that \(\Phi ([\Theta _-])={\scriptstyle {{\mathcal {O}}}}\), and write \(\mathrm{E}_{1}=\mathrm{F}[\beta _{1}]\) and \(\mathrm{E}_{-1}=\mathrm{F}[\beta _{-1}]\). We take an m-dimensional \(\mathrm{E}_{1}\)-vector space \(\mathrm{W}\), which we consider as an \(\mathrm{F}\)-vector space and identify with a maximal totally isotropic space of \(\mathrm{V}\) as part of a complete polarization \((\mathrm{W},\mathrm{W}^\#)\). We choose an \({\mathfrak {o}}_{\mathrm{E}_{1}}\)-lattice sequence \(\Lambda \) in \(\mathrm{W}\) so that the stratum \([\Lambda ,n,0,\beta _{1}]\) is simple, for an appropriate integer n. Since \(\beta _{-1}\) and \(-{\overline{\beta _{1}}}\) have the same minimal polynomial over \(\mathrm{F}\), there is an embedding \(\varphi _{-1}:\mathrm{E}_{-1}\rightarrow {\text {End}}_\mathrm{F}(\mathrm{W}^\#)\) which maps \(\beta _{-1}\) to \(-{\overline{\beta _{1}}}\). Then the character
satisfies \({{\mathfrak {f}}}_{\theta _-}={{\mathfrak {f}}}_-\). \(\square \)
Let \(\theta \in {\mathscr {C}}(\Lambda ,0,\beta )\) be the lift of a self-dual semisimple character \(\theta _-\in {\mathscr {C}}(\Lambda ,0,\beta )\). Then Theorem 12.29, combined with Theorem 12.9, provides a way to count the number of \(\mathrm{G}\)-intertwining classes of full self-dual semisimple characters whose lift is in the \({{\widetilde{\mathrm{G}}}}\)-intertwining class of \(\theta \), by counting the number of endo-parameters \({{\mathfrak {f}}}_-\) which give the same \({\text {GL}}\)-endo-parameter (see Remark 12.24). We denote this number by \({\mathcal {N}}(\theta _-,{{\widetilde{\mathrm{G}}}},\mathrm{G})\). Write

Then we obtain
Note that the reason for the difference in the symplectic case lies in Proposition 6.10 and the remark following it: concordance is implied by intertwining in \({{\widetilde{\mathrm{G}}}}\) in the non-symplectic case, but not in the symplectic case. The difference in the orthogonal case comes from the fact that, when \(\mathrm{V}^{i_0}\) is small, there is no orthogonal space \((\mathrm{V}',h')\) such that \({\text {dim}}_\mathrm{F}\mathrm{V}^{i_0}={\text {dim}}_\mathrm{F}\mathrm{V}'\) and \([h_{i_0}]-[h']\) is the maximal element of the Witt group \({\mathcal {W}}_1(\mathrm{F}/\mathrm{F}_0)\).
12.5 Special orthogonal groups
We conclude with the parametrization of the \(\mathrm{G}^{\mathsf {o}}\)-intertwining classes of full self-dual semisimple characters in the orthogonal case (\(\sigma =1\), \(\varepsilon =1\)). The partition of the set of full self-dual semisimple characters for \(\mathrm{G}\) into \(\mathrm{G}^{\mathsf {o}}\)-intertwining classes is in general finer than the partition into \(\mathrm{G}\)-intertwining classes so it is necessary to augment the self-dual endo-parameters. This will of course only happen when \(\mathrm{V}\) is even-dimensional (since there is an element of determinant \(-1\) in the centre in the odd-dimensional case), and will indeed only occur when the zero endo-class is not in the support of the endo-parameter, by Theorem 10.2(i).
Definition 12.30
Two symplectic forms over \(\mathrm{F}\) on an even-dimensional \(\mathrm{F}\)-vector space \(\mathrm{V}\) are \((1+{\mathfrak {p}}_\mathrm{F})\)-equivalent if they are isometric by an automorphism of determinant in \(1+{\mathfrak {p}}_\mathrm{F}\). We write \([h']_{1+{\mathfrak {p}}_\mathrm{F}}\) for the \((1+{\mathfrak {p}}_\mathrm{F})\)-equivalence class of a symplectic form \(h'\) on \(\mathrm{V}\).
Now let \({{\mathfrak {f}}}_-\) be an endo-parameter for \((h,\mathrm{G})\), and let \(\Theta _-\) be a self-dual pss-character supported on some pair \((0,\beta )\) such that \({\mathcal {F}}_-([\Theta _-])\) is the support of \({{\mathfrak {f}}}_-\). As usual, let \(\mathrm{I}=\mathrm{I}_+\cup \mathrm{I}_0\cup \mathrm{I}_-\) be the corresponding index set, put \(\mathrm{E}=\mathrm{F}[\beta ]\), and write \({\mathcal {F}}_-([\Theta _-])=\{{\scriptstyle {{\mathcal {O}}}}_i\mid i\in \mathrm{I}_0\cup \mathrm{I}_+\}\).
Definition 12.31
For \(\varphi :\mathrm{E}\rightarrow {\text {End}}_\mathrm{F}\mathrm{V}\) a self-dual embedding with corresponding decomposition \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\), denote by \({{\mathfrak {f}}}_{\varphi ,-}\) the endo-parameter for \((h,\mathrm{G})\) with support \({\mathcal {F}}_-([\Theta _-])\) such that
where \(m_i\) denotes the Witt index of \(h_{i,\varphi _i}\) when \(i\in \mathrm{I}_0\), and \(m_i={\text {dim}}_{\mathrm{E}_i}(\mathrm{V}^i)\) for \(i\in \mathrm{I}_+\). We say that \(\varphi \) is adapted to \({{\mathfrak {f}}}_-\) if \({{\mathfrak {f}}}_-={{\mathfrak {f}}}_{\varphi ,-}\).
We are interested in the following classes of symplectic forms if the support of \({{\mathfrak {f}}}_-\) does not contain the zero endo-class:
If the support of \({{\mathfrak {f}}}_-\) contains the zero endo-class, then we formally just put \({{\mathcal {H}}}({{\mathfrak {f}}}_-):=\{0\}\). We need to prove that \({{\mathcal {H}}}({{\mathfrak {f}}}_-)\) is well-defined—that is, independent of the choice of self-dual pss-character \(\Theta _-\).
Lemma 12.32
The definition of \({{\mathcal {H}}}({{\mathfrak {f}}}_-)\) does not depend on the choice of \(\Theta _-\).
Proof
If the support of \({{\mathfrak {f}}}_-\) contains the zero endo-class then there is nothing to prove, so we suppose otherwise. Let \(\Theta '_-\) be a self-dual pss-character endo-equivalent to \(\Theta _-\) and supported on \((0,\beta ')\) and take embeddings \(\varphi ,\varphi '\), of \(\mathrm{E},\mathrm{E}'\) respectively, which are adapted to \({{\mathfrak {f}}}_-\). Take any self-dual \({\mathfrak {o}}_{\varphi (\mathrm{E})}\) (respectively \({\mathfrak {o}}_{\varphi '(\mathrm{E}')}\))-lattice sequence \(\Lambda \) (respectively \(\Lambda '\)) in \(\mathrm{V}\). The characters
intertwine in \(\mathrm{G}\) by Theorem 12.29, because \({{\mathfrak {f}}}_{\theta _-}={{\mathfrak {f}}}_{\theta '_-}={{\mathfrak {f}}}_-\). Thus \(\varphi (\beta )^*h\) is isometric to \(\varphi '(\beta ')^*h\) by an element of determinant congruent to \(\pm 1\pmod {{\mathfrak {p}}_\mathrm{F}}\) (and both are possible), by Lemma 10.1. \(\square \)
It follows moreover from the proof that \({{\mathcal {H}}}({{\mathfrak {f}}}_-)\) has cardinality two whenever it is non-trivial. We are now able to define the endo-parameters for \((h,\mathrm{G}^{\mathsf {o}})\).
Definition 12.33
The set
is called the set of endo-parameters for \((h,\mathrm{G}^{\mathsf {o}})\).
Let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,0,\beta )\) be a self-dual semisimple character. We attach to \(\theta _-\) the pair \(({{\mathfrak {f}}}_{\theta _-},{{\mathfrak {h}}}_{\theta _-})\in \mathrm {EP}(h,\mathrm{G}^{\mathsf {o}})\), where
Corollary 12.34
There is a canonical bijection from the set of \(\mathrm{G}^{\mathsf {o}}\)-intertwining classes of full self-dual semisimple characters to \(\mathrm {EP}(h,\mathrm{G}^{\mathsf {o}})\), defined by mapping the \(\mathrm{G}^{\mathsf {o}}\)-intertwining class of a full self-dual semisimple character \(\theta _-\) to the endo-parameter \(({{\mathfrak {f}}}_{\theta _-},{{\mathfrak {h}}}_{\theta _-})\).
Proof
It follows immediately from Theorems 12.29 and 10.2 that the map is well-defined and injective. For surjectivity, we only need to consider a pair \(({{\mathfrak {f}}}_-,{{\mathfrak {h}}})\in \mathrm {EP}(h,\mathrm{G}^{\mathsf {o}})\) such that the zero endo-class is not contained in the support of \({{\mathfrak {f}}}_-\). By Theorem 12.29 there is some \(\theta _-\in {\mathscr {C}}_-(g \Lambda ,0,\beta )\) such that \({{\mathfrak {f}}}_{\theta _-}={{\mathfrak {f}}}_-\). We are done, if \({{\mathfrak {h}}}_{\theta _-}={{\mathfrak {h}}}\); if not, then we conjugate \(\theta _-\) by any \(g\in \mathrm{G}\setminus \mathrm{G}^{\mathsf {o}}\) to find  while
while  , because \({{\mathcal {H}}}({{\mathfrak {f}}}_-)\) consists of only two elements. \(\square \)
, because \({{\mathcal {H}}}({{\mathfrak {f}}}_-)\) consists of only two elements. \(\square \)
Notes
In previous works, including [42], only semisimple characters valued in \({\mathbb {C}}\) are considered. However, the constructions and results also apply to characters valued in \({\mathbf {C}}\) because semisimple characters are (smooth) characters of pro-p groups and \({\mathbf {C}}\) contains a full set of p-power roots of unity.
References
Anandavardhanan, U.K., Kurinczuk, R., Matringe, N., Sécherre, V., Stevens, S.: Galois self-dual cuspidal types and Asai local factors. J. Eur. Math. Soc. (to appear)
Arthur, J.: The endoscopic classification of representations. In: American Mathematical Society Colloquium Publications, vol. 61. Orthogonal and symplectic groups. American Mathematical Society, Providence (2013)
Blondel, C.: \(\text{ SP }(2N)\)-covers for self-contragredient supercuspidal representations of \(\text{ GL }(N)\). Ann. Sci. École Norm. Sup. (4) 37(4), 533–558 (2004)
Blondel, C., Henniart, G., Stevens, S.: Jordan blocks of cuspidal representations of symplectic groups. Algebra Number Theory 12(10), 2327–2386 (2018)
Broussous, P., Sécherre, V., Stevens, S.: Smooth representations of \({\text{ GL }}_m(D)\) V: endo-classes. Doc. Math. 17, 23–77 (2012)
Broussous, P., Stevens, S.: Buildings of classical groups and centralizers of Lie algebra elements. J. Lie Theory 19(1), 55–78 (2009)
Bushnell, C.J., Fröhlich, A.: Non-abelian congruence gauss sums and \(p\)-adic simple algebras. Proc. Lond. Math. Soc. (3) 50, 207–264 (1985)
Bushnell, C.J., Henniart, G.: Local tame lifting for \(\text{ GL }(N)\). I. Simple characters. Inst. Hautes Études Sci. Publ. Math. 83, 105–233 (1996)
Bushnell, C.J., Henniart, G.: Intertwining of simple characters in \(\text{ GL }(n)\). Int. Math. Res. Not. 17, 3977–3987 (2013)
Bushnell, C.J., Henniart, G.: To an effective local Langlands correspondence. Mem. Am. Math. Soc. 231(1087), v+88 (2014)
Bushnell, C.J., Henniart, G.: Higher ramification and the local Langlands correspondence. Ann. Math. (2) 185(3), 919–955 (2017)
Bushnell, C.J., Kutzko, P.C.: The admissible dual of \(\text{ GL }(N)\) via compact open subgroups. In: Cafarelli, L.A., Mather, J.N., Stein, E.M. (eds.) Stein Annals of Mathematics Studies, vol. 129. Princeton University Press, Princeton (1993)
Bushnell, C.J., Kutzko, P.C.: Simple types in \(\text{ GL }(N)\): computing conjugacy classes. In: Gindikin, S., Goodman, R., Greenleaf, F.P., Sally Jr., P.J. (eds.) Representation Theory and Analysis on Homogeneous Spaces (New Brunswick, NJ, 1993), Contemporary Mathematics, vol. 177, pp. 107–135. American Mathematical Society, Providence (1994)
Bushnell, C.J., Kutzko, P.C.: Semisimple types in \({\text{ GL }}_n\). Compos. Math. 119(1), 53–97 (1999)
Chinello, G.: Blocks of the category of smooth \(\ell \)-modular representations of \(\text{ GL }(n, F)\) and its inner forms: reduction to level 0. Algebra Number Theory 12(7), 1675–1713 (2018)
Dat, J.-F.: Finitude pour les représentations lisses de groupes \(p\)-adiques. J. Inst. Math. Jussieu 8(2), 261–333 (2009)
Dat, J.-F.: A functoriality principle for blocks of \(p\)-adic linear groups. In: Brumley, F., Gómez Aparicio, M.P., Mínguez, A. (eds.) Around Langlands correspondences, Contemporary Mathematics, vol. 691, pp. 103–131. American Mathematical Society, Providence (2017)
Dat, J.-F., Helm, D., Kurinczuk, R., Moss, G.: Moduli of langlands parameters (2020). arXiv:2009.06708
Dotto, A.: The inertial Jacquet–Langlands correspondence (2018). arXiv:1707.00635
Fintzen, J.: Types for tame \(p\)-adic groups (2018). arXiv:1810.04198
Ganapathy, R., Varma, S.: On the local Langlands correspondence for split classical groups over local function fields. J. Inst. Math. Jussieu 16(5), 987–1074 (2017)
Hakim, J., Murnaghan, F.: Distinguished tame supercuspidal representations. Int. Math. Res. Pap. 2, 166 (2008)
Helm, D.: The Bernstein center of the category of smooth \(W(k)[{\text{ GL }}_n(F)]\)-modules. Forum Math. Sigma 4, e11, 98 (2016)
Howe, R.E.: Tamely ramified supercuspidal representations of \({\text{ Gl }}_{n}\). Pac. J. Math. 73(2), 437–460 (1977)
Kaletha, T., Minguez, A., Shin, S.W., White, P.-J.: Endoscopic classification of representations: inner forms of unitary groups (2014). arXiv:1409.3731
Kurinczuk, R., Stevens, S.: Cuspidal \(\ell \)-modular representations of \(p\)-adic classical groups. J. Reine Angew. Math. 764, 23–69 (2020)
Lanard, T.: Sur les \(\ell \)-blocs de niveau zéro des groupes \(p\)-adiques. Compos. Math. 154(7), 1473–1507 (2018)
Mínguez, A., Sécherre, V.: Types modulo \(\ell \) pour les formes intérieures de \({\text{ GL }}_n\) sur un corps local non archimédien. Proc. Lond. Math. Soc. (3) 109(4), 823–891 (2014). With an appendix by Vincent Sécherre et Shaun Stevens
Miyauchi, M., Stevens, S.: Semisimple types for \(p\)-adic classical groups. Math. Ann. 358(1–2), 257–288 (2014)
Mok, C.P.: Endoscopic classification of representations of quasi-split unitary groups. Mem. Am. Math. Soc. 235(1108), vi+248 (2015)
Scharlau, W.: Quadratic and Hermitian forms. In: Berger, M., Eckmann, B., Varadhan. S.R.S. et al., (eds.) Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 270. Springer, Berlin (1985)
Sécherre, V.: Représentations lisses de \(\text{ GL }(m, D)\). I. Caractères simples. Bull. Soc. Math. France 132(3), 327–396 (2004)
Sécherre, V.: Supercuspidal representations of \({\text{ GL }}_n(\text{ F})\) distinguished by a Galois involution. Algebra Number Theory 13(7), 1677–1733 (2019)
Sécherre, V., Stevens, S.: Représentations lisses de \({\text{ GL }}_m(D)\). IV. Représentations supercuspidales. J. Inst. Math. Jussieu 7(3), 527–574 (2008)
Sécherre, V., Stevens, S.: Smooth representations of \(GL_m(D)\) VI: semisimple types. Int. Math. Res. Not. 13, 2994–3039 (2012)
Sécherre, V., Stevens, S.: Block decomposition of the category of \(\ell \)-modular smooth representations of \({\text{ GL }}_n(\text{ F})\) and its inner forms. Ann. Sci. Éc. Norm. Supér. (4) 49(3), 669–709 (2016)
Sécherre, V., Stevens, S.: Towards an explicit local Jacquet–Langlands correspondence beyond the cuspidal case. Compos. Math. 155, 1853–1887 (2019)
Skodlerack, D.: Field embeddings which are conjugate under a p-adic classical group. Manuscr. Math. 144(1–2), 277–301 (2013)
Skodlerack, D., Stevens, S.: Intertwining semisimple characters for \(p\)-adic classical groups. Nagoya Math. J. 238, 137–205 (2020)
Stevens, S.: Double coset decompositions and intertwining. Manuscr. Math. 106(3), 349–364 (2001)
Stevens, S.: Intertwining and supercuspidal types for \(p\)-adic classical groups. Proc. Lond. Math. Soc. (3) 83(1), 120–140 (2001)
Stevens, S.: Semisimple characters for \(p\)-adic classical groups. Duke Math. J. 127(1), 123–173 (2005)
Stevens, S.: The supercuspidal representations of \(p\)-adic classical groups. Invent. Math. 172(2), 289–352 (2008)
Vignéras, M.-F.: Représentations \(l\)-modulaires d’un groupe réductif \(p\)-adique avec \(l\ne p\). In: Bass, H., Oesterlé, J., Alan Weinstein, A. (eds.) Progress in Mathematics, vol. 137. Birkhäuser Boston Inc., Boston (1996)
Yu, J.-K.: Construction of tame supercuspidal representations. J. Am. Math. Soc. 14(3), 579–622 (2001). (electronic)
Acknowledgements
This work was supported by the Engineering and Physical Sciences Research Council (EP/H00534X/1 and EP/M029719/1), the Heilbronn Institute for Mathematical Research, Imperial College London, ShanghaiTech University, and University of East Anglia. We thank Colin Bushnell and Marie-France Vignéras for their interest in this work, Jean-François Dat for sharing details of his current work, and David Helm and Guy Henniart for helpful conversations. Finally, we thank the referees for very helpful comments and suggestions, which have greatly improved the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: From skew to self-dual semisimple characters
Appendix A: From skew to self-dual semisimple characters
In this appendix, we generalize several previous results which are needed in the main body of the paper, in particular to extend them from the case of skew semisimple characters [39] (where the index set is pointwise fixed by the involution) to the case of self-dual semisimple characters.
Every cuspidal representation of \(\mathrm{G}^{\mathsf {o}}\) contains a skew semisimple character by [42, Theorem 5.1] so, for cuspidal representations, it suffices to only consider skew semisimple characters; thus many results were originally only proved in the skew case. However, to consider the category of all smooth representations of \(\mathrm{G}^{\mathsf {o}}\), it is necessary also to consider the broader class of self-dual semisimple characters: indeed, every smooth representation contains a full self-dual semisimple character by [16, Proposition 8.5], and every self-dual semisimple character is contained in some irreducible representation; moreover, if an irreducible representation contains two full self-dual semisimple characters then these characters are endo-equivalent. In particular, skew semisimple characters do not suffice to study the category of all smooth representations. For this reason, in the main text, we need to consider non-skew self-dual semisimple characters and pss-characters.
In this highly technical appendix, we extend the results of [39] we need to the self-dual case, relying heavily on (and assuming knowledge from) [39]. We will use the notation introduced in the main body of the paper freely, in particular that in Sect. 8, though not, of course, any results from the main paper.
1.1 A. 1. The translation principle for self-dual semisimple characters
We first generalize the translation principle of the second and third authors [39, Theorem 9.26]. Let \([\Lambda ,n,r,\beta ]\) be a non-null semisimple stratum and put \(k_0=k_0(\beta ,\Lambda )\). We write \({\mathfrak {m}}_r(\beta ,\Lambda )\) for the \({\mathfrak {o}}_\mathrm{F}\)-lattice
where \({\mathfrak {n}}_{-r}(\beta ,\Lambda )=\{a\in {\mathfrak {a}}\mid \beta a-a\beta \in {\mathfrak {a}}_{-r}\}\). The pro-p subgroup \({1+{\mathfrak {m}}_r(\beta ,\Lambda )}\) of \({\mathrm{P}^{-k_0-r}(\Lambda )}\) normalizes the equivalence class of the stratum, and every character in \({\mathscr {C}}(\Lambda ,r,\beta )\); indeed, the group
also normalizes every character in \({\mathscr {C}}(\Lambda ,r,\beta )\), by [42, Lemma 3.16].
Theorem A.1
Let \([\Lambda ,n,r+1,\gamma ]\) and \([\Lambda ,n,r+1,\gamma ']\) be self-dual semisimple strata with the same associated splitting \(\mathrm{V}=\bigoplus _{j\in \mathrm{J}}\mathrm{V}^j\) such that
Let \([\Lambda ,n,r,\beta ]\) be a self-dual semisimple stratum, with associated splitting \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\), such that \([\Lambda ,n,r+1,\beta ]\) is equivalent to \([\Lambda ,n,r+1,\gamma ]\) and \(\gamma \) is an element of \(\prod _{i\in \mathrm{I}} \mathrm{A}^{i}\). Then, there exist a self-dual semisimple stratum \([\Lambda ,n,r,\beta ']\), with splitting \(\mathrm{V}=\bigoplus _{i'\in \mathrm{I}'}\mathrm{V}^{i'}\) and an element u of \((1+{\mathfrak {m}}_{r+1}(\gamma ,\Lambda ))\cap \prod _{j\in \mathrm{J}}\mathrm{A}^{j}\cap \mathrm{G}\), such that \([\Lambda ,n,r+1,\beta ']\) is equivalent to \([\Lambda ,n,r+1,\gamma ']\), with \(u\gamma 'u^{-1}\in \prod _{i'\in \mathrm{I}'}\mathrm{A}^{i'}\) and
The proof will take the next few subsections
1.2 A. 2. Idempotents and self-dual minimal strata
Let \(({\mathfrak {k}}_r)_{r\geqslant 0}\) be a decreasing sequence of \(\sigma \)-invariant \({\mathfrak {o}}_\mathrm{F}\)-lattices in \(\mathrm{A}\) such that \({\mathfrak {k}}_r{\mathfrak {k}}_s\subseteq {\mathfrak {k}}_{r+s}\), for all \(r,s\geqslant 0\), and \(\bigcap _{r\geqslant 1}{\mathfrak {k}}_r = \{0\}\).
Lemma A.2
[39, Lemma 7.13] Suppose that there is an element \(\alpha \) of \({\mathfrak {k}}_0\) which satisfies \(\alpha ^2-\alpha \in {\mathfrak {k}}_1\). Then there is an idempotent \({\tilde{\alpha }}\in \alpha + {\mathfrak {k}}_1\). Moreover, if \({\overline{\alpha }}=\alpha \) then we can choose \({\tilde{\alpha }}\) such that \({\overline{{{\tilde{\alpha }}}}}={{\tilde{\alpha }}}\).
For the self-dual setting we also consider idempotents \(e\in \mathrm{A}\) which satisfy \({\overline{e}}e=0\).
Lemma A.3
Suppose that there is an element \(\alpha \) of \({\mathfrak {k}}_0\) which satisfies \(\alpha ^2- \alpha \in {\mathfrak {k}}_1\) and \({\overline{\alpha }}\alpha ,\alpha {\overline{\alpha }}\in {{\mathfrak {k}}_1}\). Then there is a idempotent \({\tilde{\alpha }} \in \alpha +{\mathfrak {k}}_1\) such that \({\overline{{\tilde{\alpha }}}}{\tilde{\alpha }}={\tilde{\alpha }}{\overline{{\tilde{\alpha }}}}=0\).
Proof
Lemma A.2 provides a symmetric idempotent e congruent to \(\alpha +{\overline{\alpha }}\) modulo \({\mathfrak {k}}_{1}\). Then the element \(\alpha '=e\left( \frac{1+\alpha -{\overline{\alpha }}}{2}\right) e\) satisfies \(\alpha '+{\overline{\alpha '}}=e\). We follow now the idea of the proof of Lemma [39, Lemma 7.13]. It is easy to check that \(\alpha '':=3\alpha '^2-2\alpha '^3\) also satisfies \(\alpha ''+{\overline{\alpha ''}}=e\) and the result follows in the same way as in loc. cit.. \(\square \)
Corollary A.4
Suppose that \(\alpha _1,\ldots ,\alpha _l\) are elements of \({\mathfrak {k}}_0\) such that \(\alpha _i^2-\alpha _i,\alpha _i\alpha _j\in {\mathfrak {k}}_1\), for all i, j with \(i\ne j\). Suppose further that \(\sum _i\alpha _i - 1\in {\mathfrak {k}}_1\) and that there is an action of \(\sigma \) on \(\mathrm{I}=\{1,\ldots ,l\}\) such that \({\overline{\alpha _i}}-\alpha _{\sigma (i)}\in {\mathfrak {k}}_1\), for all indices \(i\in \mathrm{I}\). Then there are idempotents \({\tilde{\alpha }}_i\in \alpha _i+{\mathfrak {k}}_1\) which are pairwise orthogonal and such that \(\sum _i{\tilde{\alpha }}_i=1\) and \({\overline{{\tilde{\alpha }}_i}}={\tilde{\alpha }}_{\sigma (i)}\) for all \(i\in \mathrm{I}\).
Proof
This follows from Lemmas A.2 and A.3, cf. [39, Corollary 7.14]. \(\square \)
Recall that, whenever we have a splitting \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\), we have the associated idempotents \({{\mathfrak {e}}}_i\) with image \(\mathrm{V}^i\) and kernel \(\bigoplus _{j\ne i}\mathrm{V}^j\).
Corollary A.5
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ,n,r,\beta ']\) be equivalent self-dual semisimple strata. Suppose that \([\Lambda ,n,r,\beta ]\) is split by \(\mathrm{V}=\oplus _{k\in \mathrm{K}}\mathrm{V}^k\) and suppose that the set of idempotents of this splitting is invariant under  . Then there is an element \(u\in (1+{\mathfrak {m}}_r(\beta ,\Lambda ))\cap \mathrm{G}\) such that \(u\beta 'u^{-1}\in \prod _{k\in \mathrm{K}}\mathrm{A}^{k}\).
. Then there is an element \(u\in (1+{\mathfrak {m}}_r(\beta ,\Lambda ))\cap \mathrm{G}\) such that \(u\beta 'u^{-1}\in \prod _{k\in \mathrm{K}}\mathrm{A}^{k}\).
Proof
The action of  on the idempotents gives a sum \(1=\sum _{k\in \mathrm{K}_0}{{\mathfrak {e}}}^k+\sum _{k\in \mathrm{K}_+}({{\mathfrak {e}}}^k+{\overline{{{\mathfrak {e}}}}}^k)\) and by [39, Lemma 9.25] there is an element g of \((1+{\mathfrak {m}}_r(\beta ,\Lambda ))\cap \mathrm{G}\) such that \(g\beta 'g^{-1}\) is split by \(\bigoplus _{[i]\in {\mathrm{K}}/\Sigma }V^{[i]}\), where \({\mathrm{K}}/\Sigma \) denotes the set of \(\Sigma \)-orbits in \({\mathrm{K}}\). Thus we only need to consider the case where \(\mathrm{K}\) is one orbit with two elements. In this case \(\mathrm{K}=\{+,-\}\), and we take idempotents \({{\mathfrak {e}}}'_+ \in {{\mathfrak {e}}}_+ + {\mathfrak {m}}_r(\beta ,\Lambda )\) and \({{\mathfrak {e}}}'_-\) commuting with \(\beta '\) such that \({\overline{{{\mathfrak {e}}}'_+}}={{\mathfrak {e}}}'_-\) and \({{\mathfrak {e}}}'_++{{\mathfrak {e}}}'_-=1\), which exist by Corollary A.4 and comparison of the descriptions of the intertwining of \([\Lambda ,n,r,\beta ]\) in terms of \(\beta \) and \(\beta '\). This case follows now from [39, Lemma 9.15] which provides an element \(g=(g_+,g_-)\) of \(({\text{ End }}_\mathrm {F}(\mathrm {V}'^+,\mathrm {V}^+)\times {\text{ End }}_\mathrm {F}(\mathrm {V}'^-,\mathrm {V}^-))\cap (1+{\mathfrak {m}}_r(\beta ,\Lambda ))\) such that \(g\beta 'g^{-1}\in \prod _{k\in \mathrm{K}}\mathrm{A}^{k}\), and we take the element \(u=(g_+,{\overline{g}}^{-1}_+)\in (1+{\mathfrak {m}}_r(\beta ,\Lambda ))\cap \mathrm{G}\). \(\square \)
on the idempotents gives a sum \(1=\sum _{k\in \mathrm{K}_0}{{\mathfrak {e}}}^k+\sum _{k\in \mathrm{K}_+}({{\mathfrak {e}}}^k+{\overline{{{\mathfrak {e}}}}}^k)\) and by [39, Lemma 9.25] there is an element g of \((1+{\mathfrak {m}}_r(\beta ,\Lambda ))\cap \mathrm{G}\) such that \(g\beta 'g^{-1}\) is split by \(\bigoplus _{[i]\in {\mathrm{K}}/\Sigma }V^{[i]}\), where \({\mathrm{K}}/\Sigma \) denotes the set of \(\Sigma \)-orbits in \({\mathrm{K}}\). Thus we only need to consider the case where \(\mathrm{K}\) is one orbit with two elements. In this case \(\mathrm{K}=\{+,-\}\), and we take idempotents \({{\mathfrak {e}}}'_+ \in {{\mathfrak {e}}}_+ + {\mathfrak {m}}_r(\beta ,\Lambda )\) and \({{\mathfrak {e}}}'_-\) commuting with \(\beta '\) such that \({\overline{{{\mathfrak {e}}}'_+}}={{\mathfrak {e}}}'_-\) and \({{\mathfrak {e}}}'_++{{\mathfrak {e}}}'_-=1\), which exist by Corollary A.4 and comparison of the descriptions of the intertwining of \([\Lambda ,n,r,\beta ]\) in terms of \(\beta \) and \(\beta '\). This case follows now from [39, Lemma 9.15] which provides an element \(g=(g_+,g_-)\) of \(({\text{ End }}_\mathrm {F}(\mathrm {V}'^+,\mathrm {V}^+)\times {\text{ End }}_\mathrm {F}(\mathrm {V}'^-,\mathrm {V}^-))\cap (1+{\mathfrak {m}}_r(\beta ,\Lambda ))\) such that \(g\beta 'g^{-1}\in \prod _{k\in \mathrm{K}}\mathrm{A}^{k}\), and we take the element \(u=(g_+,{\overline{g}}^{-1}_+)\in (1+{\mathfrak {m}}_r(\beta ,\Lambda ))\cap \mathrm{G}\). \(\square \)
Proposition A.6
(cf. [39, Lemma 7.19]). Let \([\Lambda ,n,n-1,\alpha ]\) be a self-dual stratum which is equivalent to a semisimple stratum. Then it is equivalent to a self-dual semisimple stratum.
Proof
The stratum \([\Lambda ,n,n-1,\alpha ]\) is equivalent to a semisimple stratum \([\Lambda ,n,n-1,\beta ]\) with associated splitting \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and idempotents \({{\mathfrak {e}}}_i\), for \(i\in \mathrm{I}\). The skew-symmetry of \(\alpha \) implies that the strata \([\Lambda ,n,n-1,\beta ]\) and \([\Lambda ,n,n-1,-{\overline{\beta }}]\) are equivalent and thus by [39, Lemma 7.17] the idempotents are permuted by  modulo \({\mathfrak {a}}_1\); this defines an action of \(\sigma \) on \(\mathrm{I}\). Corollary A.4 provides pairwise orthogonal idempotents \({{\mathfrak {e}}}'_i\) congruent to \({{\mathfrak {e}}}_i\) modulo \({\mathfrak {a}}_1\) which sum to 1 and satisfy \({\overline{{{\mathfrak {e}}}}}'_i={{\mathfrak {e}}}'_{\sigma (i)}\). The map \(g=\sum _i {{\mathfrak {e}}}'_i{{\mathfrak {e}}}_i\in {\mathrm{P}^1(\Lambda )} \) conjugates \([\Lambda ,n,n-1,\beta ]\) to a semisimple stratum which is split by \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}'^i\), where \(\mathrm{V}'^i={\text {im}}({{\mathfrak {e}}}'_i)\). For the indices i fixed by \(\sigma \) we put \(\beta '_i=g\beta _ig^{-1}\) and then the stratum \([\Lambda ,n,n-1,\beta _i']\) is equivalent to a self-dual stratum and to a simple stratum, so to a self-dual simple stratum by [41, Proposition 1.10]; thus we may assume it is itself self-dual simple. For the remaining indices we take a section \(\mathrm{I}_+\) through the non-singleton orbits and define \(\beta '_i=g\beta _ig^{-1}\) and \(\beta '_{\sigma (i)}=-{\overline{\beta '_i}}\) for all \(i\in \mathrm{I}_+\). Then setting \(\beta '=\sum _{i\in \mathrm{I}}\beta '_i\), we have found a self-dual semisimple stratum \([\Lambda ,n,n-1,\beta ']\) equivalent to \([\Lambda ,n,n-1,\alpha ]\). \(\square \)
modulo \({\mathfrak {a}}_1\); this defines an action of \(\sigma \) on \(\mathrm{I}\). Corollary A.4 provides pairwise orthogonal idempotents \({{\mathfrak {e}}}'_i\) congruent to \({{\mathfrak {e}}}_i\) modulo \({\mathfrak {a}}_1\) which sum to 1 and satisfy \({\overline{{{\mathfrak {e}}}}}'_i={{\mathfrak {e}}}'_{\sigma (i)}\). The map \(g=\sum _i {{\mathfrak {e}}}'_i{{\mathfrak {e}}}_i\in {\mathrm{P}^1(\Lambda )} \) conjugates \([\Lambda ,n,n-1,\beta ]\) to a semisimple stratum which is split by \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}'^i\), where \(\mathrm{V}'^i={\text {im}}({{\mathfrak {e}}}'_i)\). For the indices i fixed by \(\sigma \) we put \(\beta '_i=g\beta _ig^{-1}\) and then the stratum \([\Lambda ,n,n-1,\beta _i']\) is equivalent to a self-dual stratum and to a simple stratum, so to a self-dual simple stratum by [41, Proposition 1.10]; thus we may assume it is itself self-dual simple. For the remaining indices we take a section \(\mathrm{I}_+\) through the non-singleton orbits and define \(\beta '_i=g\beta _ig^{-1}\) and \(\beta '_{\sigma (i)}=-{\overline{\beta '_i}}\) for all \(i\in \mathrm{I}_+\). Then setting \(\beta '=\sum _{i\in \mathrm{I}}\beta '_i\), we have found a self-dual semisimple stratum \([\Lambda ,n,n-1,\beta ']\) equivalent to \([\Lambda ,n,n-1,\alpha ]\). \(\square \)
1.3 A. 3. Equal sets of semisimple characters
Lemma A.7
(cf. [39, Lemma 9.13]). Suppose that \(\mathrm{V}=\bigoplus _{k\in \mathrm{K}}\mathrm{V}^k\) is a splitting which refines the associated splitting of a semisimple stratum \([\Lambda ,n,r,\beta ]\); denote by \({{\mathfrak {e}}}_k\) the idempotents of the decomposition and \(\beta _k={{\mathfrak {e}}}_k\beta _k{{\mathfrak {e}}}_k\). Let \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) with restrictions \(\theta _k\in {\mathscr {C}}(\Lambda ^k,r,\beta _k)\) and, for \(k\in \mathrm{K}\), let \(a_k\in {\mathfrak {a}}_{-r-1}\cap \mathrm{A}^{k}\) be such that \(\theta _k\psi _{a_k}\in {\mathscr {C}}(\Lambda ^k,r,\beta _k)\). Put \(a=\sum _{k\in \mathrm{K}}a_k\).
-
(i)
\([\Lambda ,n,r,\beta +a]\) is equivalent to a semisimple stratum \([\Lambda ,n,r,\beta ']\) which is split by \(\mathrm{V}=\bigoplus _{k\in \mathrm{K}}\mathrm{V}^k\), and the sets \({\mathscr {C}}(\Lambda ,r,\beta ')\) and \(\psi _a{\mathscr {C}}(\Lambda ,r,\beta )\) coincide.
-
(ii)
Suppose \([\Lambda ,n,r,\beta '']\) is a semisimple stratum whose associated splitting is refined by \(\mathrm{V}=\bigoplus _{k\in \mathrm{K}}\mathrm{V}^k\), such that \({\mathrm {H}}^{r+2}(\beta ,\Lambda )={\mathrm {H}}^{r+2}(\beta '',\Lambda )\) and such that there is a semisimple character \(\theta ''\in {\mathscr {C}}(\Lambda ,r,\beta '')\) with \(\theta ''_k=\theta _k\psi _{a_k}\) for all \(k\in \mathrm{K}\). Then \(\theta \psi _a=\theta ''\) and \({\mathscr {C}}(\Lambda ,r,\beta '')={\mathscr {C}}(\Lambda ,r,\beta ')\).
Proof
Although the statement is slightly different, the proof is the same as that of [39, Lemma 9.13]. \(\square \)
Corollary A.8
[39, Corollary 9.14] Suppose that \(\mathrm{V}=\bigoplus _k\mathrm{V}^k\) is a splitting which refines the associated splittings of two semisimple strata \([\Lambda ,n,r,\beta ]\) and \([\Lambda ,n,r,\beta ']\), and suppose that there are characters \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ,r,\beta ')\) such that \(\theta _k\) and \(\theta '_k\) coincide, for all k. Then \(\theta =\theta '\) and \({\mathscr {C}}(\Lambda ,r,\beta )={\mathscr {C}}(\Lambda ,r,\beta ')\).
The following result shows that, if \({\mathscr {C}}(\Lambda ,r,\beta )\cap {\mathscr {C}}(\Lambda ,r,\beta ')\) is non-empty (or, equivalently, these sets are equal) then there is an element of \(\mathrm{S}_r(\beta ,\Lambda )\) which maps the splitting of \(\beta \) to the splitting of \(\beta '\).
Proposition A.9
([39, Proposition 9.9(iv)], cf. [39, 9.23(iii)]) Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ,n,r,\beta ']\) be semisimple strata with associated splittings \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and \(\mathrm{V}=\bigoplus _{i'\in \mathrm{I}'}\mathrm{V}'^{i'}\) respectively, with corresponding idempotents \({{\mathfrak {e}}}_i\) and \({{\mathfrak {e}}}'_{i'}\). Suppose that \({\mathscr {C}}(\Lambda ,r,\beta )={\mathscr {C}}(\Lambda ,r,\beta ')\), and let \(\tau :\mathrm{I}\rightarrow \mathrm{I}'\) be the bijection of [39, Proposition 9.9], such that \({{\mathfrak {e}}}_i\equiv {{\mathfrak {e}}}'_{\tau (i)}\pmod {{\mathfrak {a}}_1(\Lambda )}\), for all \(i\in \mathrm{I}\).
-
(i)
There is an element \(g\in \mathrm{S}_r(\beta ,\Lambda )\) such that \(g{{\mathfrak {e}}}_i g^{-1}={{\mathfrak {e}}}'_{\tau (i)}\).
-
(ii)
If \([\Lambda ,n,r,\beta ]\) and \([\Lambda ,n,r,\beta ']\) are also self-dual then there exists \(g\in \mathrm{S}_r(\beta ,\Lambda )\cap \mathrm{G}\) such that \(g{{\mathfrak {e}}}_i g^{-1}={{\mathfrak {e}}}'_{\tau (i)}\).
Notice that the element g in Proposition A.9 normalizes every element of \({\mathscr {C}}(\Lambda ,r,\beta )\). We denote the normalizer of a character \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) by \({\mathfrak {n}}(\theta )\). Note that all elements of \({\mathscr {C}}(\Lambda ,r,\beta )\) have the same normalizer, because they have the same set of intertwining elements.
Proof
Part (i) is given by [39, Proposition 9.9(iv)] so we prove (ii). Take a decomposition \(\mathrm{I}=\mathrm{I}_0\cup \mathrm{I}_+\cup \mathrm{I}_-\) as usual, which gives a decomposition into idempotents \(1={{\mathfrak {e}}}_0+{{\mathfrak {e}}}_++{{\mathfrak {e}}}_-\), and the same for \(\mathrm{I}'=\mathrm{I}'_0\cup \mathrm{I}'_+\cup \mathrm{I}'_-\) with \(\mathrm{I}'_+\) chosen to coincide with \(\tau (\mathrm{I}_+)\). Then \({{\mathfrak {e}}}_0\equiv {{\mathfrak {e}}}'_0\), \({{\mathfrak {e}}}_+\equiv {{\mathfrak {e}}}'_+\) and \({{\mathfrak {e}}}_-\equiv {{\mathfrak {e}}}'_-\) modulo \(\mathrm{S}_r(\beta ,\Lambda )-1\) by [39, Proposition 9.9(iv)]. By [39, Proposition 9.23(iii)] there is an element \(g\in {\mathrm{P}^1_-(\Lambda )}\cap {\mathfrak {n}}(\theta )\) which sends \(\mathrm{V}_0\) to \(\mathrm{V}'_0\). Thus by Corollary A.8 we only have to prove the proposition for the cases where \(\mathrm{I}_0\) or \(\mathrm{I}_+\) is empty. The case where \(\mathrm{I}_+\) is empty is [39, Proposition 9.23(iii)] so let us assume that \(\mathrm{I}_0\) is empty. By [39, Proposition 9.9(iv)] there is an element \(g=(g_+,g_-)\in \mathrm{S}_r(\beta ,\Lambda )\) which maps \(\mathrm{V}^i\) to \(\mathrm{V}'^{\tau (i)}\) for all \(i\in \mathrm{I}\); then \(u=(g_+,{\overline{g}}_+^{-1})\in {\mathrm{P}^1_-(\Lambda )}\) also maps \(\mathrm{V}^i\) to \(\mathrm{V}'^{\tau (i)}\).
Take a character \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )={\mathscr {C}}^\Sigma (\Lambda ,r,\beta ')\), so that \(\theta ^{u^{-1}}_{i}=\theta _{\tau (i)}\) for all \(i\in \mathrm{I}_+\); since \(u\in \mathrm{G}\) and \(\theta \) is self-dual, this equality holds for all \(i\in \mathrm{I}\). Then Corollary A.8 implies that the sets \({\mathscr {C}}(\Lambda ,r,u\beta u^{-1})\) and \({\mathscr {C}}(\Lambda ,r,\beta ')\) are the same and indeed that  . Since \(\mathrm{P}^1_-(\Lambda )\cap {\mathfrak {n}}(\theta )=(\mathrm{S}_r(\beta ,\Lambda )\cap \mathrm{G})\mathrm{P}^1_-(\Lambda _\mathrm{E})\) and \(\mathrm{P}^1_-(\Lambda _\mathrm{E})\) commutes with \(\beta \), this finishes the proof. \(\square \)
. Since \(\mathrm{P}^1_-(\Lambda )\cap {\mathfrak {n}}(\theta )=(\mathrm{S}_r(\beta ,\Lambda )\cap \mathrm{G})\mathrm{P}^1_-(\Lambda _\mathrm{E})\) and \(\mathrm{P}^1_-(\Lambda _\mathrm{E})\) commutes with \(\beta \), this finishes the proof. \(\square \)
1.4 A. 4. Proof of the translation principle
Here we prove Theorem A.1, granted that we have already the Theorem for the skew case [39, Theorem 9.26] and the \({{\widetilde{\mathrm{G}}}}\)-case [39, Theorem 9.16]. Let \(\mathrm{J}=\mathrm{J}_0\cup \mathrm{J}_+\cup \mathrm{J}_-\) be a partition with respect to the action of \(\sigma \) as usual, and write \(\mathrm{J}_{+-}=\mathrm{J}_+\cup \mathrm{J}_-\).
-
(i)
First we assume that \(\mathrm{J}_0\) is empty. By [39, Theorem 9.16] (the \({{\widetilde{\mathrm{G}}}}\)-case) there is a semisimple stratum \([\Lambda ^{\mathrm{J}_+},n,r,\beta '_{\mathrm{J}_+}]\) such that \({\mathscr {C}}(\Lambda ^{\mathrm{J}_+},r,\beta _{\mathrm{J}_+})={\mathscr {C}}(\Lambda ^{\mathrm{J}_+},r,\beta '_{\mathrm{J}_+})\) and such that \(\gamma '_{\mathrm{J}_+}\) satisfies the desired conjugation property. Setting \(\beta '=\beta '_{\mathrm{J}_+}-{\overline{\beta '_{\mathrm{J}_+}}}\), we deduce that \([\Lambda ,n,r,\beta ']\) is a self-dual stratum whose set of semisimple characters coincides on the blocks of \(\mathrm{V}^{\mathrm{J}_+}\) and \(\mathrm{V}^{\mathrm{J}_-}\) with the corresponding restrictions of characters in \({\mathscr {C}}(\Lambda ,r,\beta )\), and such that \(\gamma '=\gamma '_{\mathrm{J}_+\cup \mathrm{J}_-}\) satisfies the desired conjugation property. Take \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) and an extension \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta ')\) of \(\theta |_{{\mathrm {H}}^{r+2}(\beta ,\Lambda )}\). By Proposition A.9(i), conjugating \(\beta \) with an element of \(\mathrm{S}_r(\beta ,\Lambda )\cap \mathrm{G}\), we can assume that \(\beta \) and \(\beta '\) have the same associated splitting. Take a skew-symmetric \(a\in {\mathfrak {a}}_{-r-1}\cap \prod _{i\in \mathrm{I}} \mathrm{A}^{i}\) such that \(\theta =\theta '\psi _a\). Then by Lemma A.7 the stratum \([\Lambda ,n,r,\beta '+a]\) is equivalent to a self-dual semisimple stratum \([\Lambda ,n,r,\beta '']\) with the same associated splitting as \(\beta '\) and such that \({\mathscr {C}}(\Lambda ,r,\beta '')={\mathscr {C}}(\Lambda ,r,\beta )\).
-
(ii)
Now we reduce to the case where \(\mathrm{J}\) is a singleton, so suppose we have proven the theorem in that case. By (i) and the singleton case we find \([\Lambda ,n,r,\beta ']\) such that \({\mathscr {C}}(\Lambda ,r,\beta ')\) coincides with \({\mathscr {C}}(\Lambda ,r,\beta )\) on every simple block for \(j\in \mathrm{J}_0\) and on the block corresponding to \(\mathrm{J}_{+-}\) (and the conjugation property is satisfied). Using Proposition A.9 we can assume that \(\beta \) and \(\beta '\) have the same associated splitting and we finish the proof using Lemma A.7 in the same manner as at the end of (i).
-
(iii)
Finally we prove the case where \(\mathrm{J}\) is a singleton. We follow the step (iv) of the proof of [39, Theorem 9.16]. Note that, by Corollary A.5, we are free to replace \([\Lambda ,n,r+1,\gamma ']\) by any equivalent stratum. Thus, by [39, Proposition 9.24], we can assume that \({\mathscr {C}}(\Lambda ,r,\gamma )={\mathscr {C}}(\Lambda ,r,\gamma ')\). Take tame corestrictions s and \(s'\), for \(\gamma \) and \(\gamma '\) respectively, which commute with the adjoint anti-involution and which satisfy the assertions of [13, Lemma 5.2]; in particular \(s(x)\equiv s'(x) \pmod {{\mathfrak {a}}_l}\), for all \(x\in {\mathfrak {a}}_{l-1}\) and all integers l. The stratum \([\Lambda ,r,r+1,s(\beta -\gamma )]\) is equivalent to a semisimple stratum, by [39, Corollary 6.15], and as in step (iv) of the proof of [39, Theorem 9.16] it follows that \([\Lambda ,r,r+1,s'(\beta -\gamma )]\) is equivalent to a semisimple stratum; further, \(s'(\beta -\gamma )\) is skew-symmetric and, by Proposition A.6, this stratum is equivalent to a self-dual semisimple stratum, say with associated splitting \(\mathrm{V}=\bigoplus _{i''\in \mathrm{I}''}\mathrm{V}^{i''}\) and corresponding idempotents \({{\mathfrak {e}}}_{i''}\). Thus \([\Lambda ,n,r,\gamma '+\sum _{i''\in \mathrm{I}''}{{\mathfrak {e}}}_{i''}(\beta -\gamma ){{\mathfrak {e}}}_{i''}]\) is equivalent to a self-dual semisimple stratum \([\Lambda ,n,r,\beta '']\) with associated splitting \(\mathrm{V}=\bigoplus _{i''\in \mathrm{I}''}\mathrm{V}^{i''}\) by [39, Corollary 6.15] and [41, Proposition 1.10]. Finally, by [39, Proposition 7.6] there is an element \(u\in (1+{\mathfrak {m}}_{r+1}(\gamma ',\Lambda ))\cap \mathrm{G}\) such that \(\beta ':=u\beta ''u^{-1}\) is congruent to \(\gamma '+\beta -\gamma \) modulo \({\mathfrak {a}}_{-r}\). This element \(\beta '\) is as required.
1.5 A. 5. Asymmetric statements
We now prove some asymmetric versions of results already in the literature.
Proposition A.10
Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ]\) be semisimple strata with \(e(\Lambda )=e(\Lambda ')\).
-
(i)
Let \(\theta \in {\mathscr {C}}(\Lambda ,r,\beta )\) and \(\theta '=\tau _{\Lambda ',\Lambda ,\beta }(\theta )\). Then
$$\begin{aligned} \mathrm{I}_{{{\widetilde{\mathrm{G}}}}}(\theta ,\theta ')=\mathrm {S}_{r}(\beta ,\Lambda ') {{\widetilde{\mathrm{G}}}}_\beta \mathrm {S}_r(\beta ,\Lambda ). \end{aligned}$$ -
(ii)
Suppose \([\Lambda ,n,r,\beta ]\) and \([\Lambda ',n,r,\beta ]\) are self-dual and let \(\theta _-\in {\mathscr {C}}_-(\Lambda ,r,\beta )\) and \(\theta '_-=\tau _{\Lambda ',\Lambda ,\beta }(\theta _-)\). Then
$$\begin{aligned} \mathrm{I}_\mathrm{G}(\theta _-,\theta '_-)=(\mathrm{S}_{r}(\beta ,\Lambda ')\cap \mathrm{G}) \mathrm{G}_\beta (\mathrm{S}_r(\beta ,\Lambda )\cap \mathrm{G}). \end{aligned}$$
Proof
The proof is analogous to that of [26, Theorems 4.9, 4.10].
-
(i)
Let us at first assume that both lattice sequences are block-wise regular strict. There is an element \(g\in {{\widetilde{\mathrm{G}}}}_\beta \) such that \(g\Lambda \) is equal to \(\Lambda '\) and the conjugation with g realizes the transfer from \({\mathscr {C}}(\Lambda ,r,\beta )\) to \({\mathscr {C}}(\Lambda ',r,\beta )\). Thus we can reduce to the case where \(\theta \) is equal to \(\theta '\) which follows from [42, Theorem 3.22] (see also [39, Proposition 9.8] and the paragraph following it).
We now consider the general case. Applying the \(\dag \)-construction, we obtain semisimple characters \(\theta ^\dag \in {\mathscr {C}}(\Lambda ^\dag ,r,\beta ^\dag )\) and \(\theta '^\dag \in {\mathscr {C}}(\Lambda '^\dag ,r,\beta ^\dag )\), where \(\Lambda ^\dag \) and \(\Lambda '^\dag \) are strict and regular of the same block size. From the first case, we have the formula (i) for \(\mathrm{I}_{{{\widetilde{\mathrm{G}}}}^\dag }(\theta ^\dag ,\theta '^\dag )\). Moreover, exactly as in the proof of [26, Lemma 4.6], we have the simple intersection property
$$\begin{aligned} \mathrm{S}_{r}(\beta ^\dag ,\Lambda '^\dag )x \mathrm{S}_{r}(\beta ^\dag ,\Lambda ^\dag )\cap {{\widetilde{\mathrm{G}}}}_{\beta ^\dag }= (\mathrm{S}_{r}(\beta ^\dag ,\Lambda '^\dag )\cap {{\widetilde{\mathrm{G}}}}_{\beta ^\dag }) x (\mathrm{S}_{r}(\beta ^\dag ,\Lambda ^\dag )\cap {{\widetilde{\mathrm{G}}}}_{\beta ^\dag }), \end{aligned}$$for all \(x\in {{\widetilde{\mathrm{G}}}}_{\beta ^\dag }\). As in [40, Corollary 4.14], it follows from [26, Theorem 4.10] that the intertwining formula behaves well under intersection with the Levi group \(\mathrm{M}^\dag \) attached to the \(\dag \)-construction, i.e.
$$\begin{aligned} \mathrm{I}_{{{\widetilde{\mathrm{G}}}}^\dag }(\theta ^\dag ,\theta '^\dag )\cap \mathrm{M}^\dag =(\mathrm{S}_{r}(\beta ^\dag ,\Lambda '^\dag )\cap \mathrm{M}^\dag )({{\widetilde{\mathrm{G}}}}_{\beta ^\dag } \cap \mathrm{M}^\dag )(\mathrm{S}_{r}(\beta ^\dag ,\Lambda ^\dag )\cap \mathrm{M}^\dag ). \end{aligned}$$Finally, we restrict to the first block of \(\mathrm{M}^\dag \) to obtain the desired description of \(\mathrm{I}_{{{\widetilde{\mathrm{G}}}}}(\theta ,\theta ')\).
-
(ii)
This follows from (i) and a standard cohomology argument [26, Theorem 2.12], as in the proof of [26, Theorem 4.10].
\(\square \)
The proofs of the following two lemmas are mutatis mutandis to the proofs of [39, Proposition 9.17] and [39, Proposition 9.27] respectively, except that one uses Proposition A.10 instead of [39, Propositions 9.8,9.22].
Lemma A.11
(cf. [39, Proposition 9.17]). Suppose \(m<q-1\) and let \([\Lambda ,q,m,\beta ]\) and \([\Lambda ',q,m,\beta ']\) be semisimple strata with \(e(\Lambda )=e(\Lambda ')\), and with splitting \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}}\mathrm{V}^i\) and \(\mathrm{V}=\bigoplus _{i\in \mathrm{I}'}\mathrm{V}'^{i}\). Suppose that \([\Lambda ,q,m+1,\gamma ]\) and \([\Lambda ',q,m+1,\gamma ]\) are non-null simple strata equivalent to \([\Lambda ,q,m+1,\beta ]\) and \([\Lambda ',q,m+1,\beta ']\) respectively, and that \(\gamma \) lies in both \(\bigoplus _{i\in \mathrm{I}}\mathrm{A}^i\) and \(\bigoplus _{i'\in \mathrm{I}'}\mathrm{A}^{i'}\). Let \(\theta _0\in {\mathscr {C}}(\Lambda ,m,\gamma )\) and set \(\theta '_0=\tau _{\Lambda ',\Lambda ,\gamma }(\theta _0)\in {\mathscr {C}}(\Lambda ',m,\gamma )\). Let \(\theta \in {\mathscr {C}}(\Lambda ,m,\beta )\) and \(\theta '\in {\mathscr {C}}(\Lambda ',m,\beta ')\) be semisimple characters which satisfy
for some \(c\in {\mathfrak {a}}_{-(m+1)}\). Let \(s_\gamma \) be a tame corestriction with respect to \(\gamma \). Then we have:
-
(i)
For any \(g\in \mathrm{I}_{{{\widetilde{\mathrm{G}}}}}(\theta ,\theta ')\) there are elements \(x\in \mathrm{S}_{m+1}(\gamma ,\Lambda ')\) and \(y\in \mathrm{S}_{m+1}(\gamma ,\Lambda )\) and \(g'\in {{\widetilde{\mathrm{G}}}}_\gamma \) such that \(g=xg'y\); moreover, \(g'\) intertwines \([\Lambda ,m+1,m,s_\gamma (\beta -\gamma +c)]\) with \([\Lambda ',m+1,m,s_\gamma (\beta '-\gamma )]\).
-
(ii)
For any \(g'\in {{\widetilde{\mathrm{G}}}}_\gamma \) which intertwines \([\Lambda ,m+1,m,s_\gamma (\beta -\gamma +c)]\) with \([\Lambda ',m+1,m,s_\gamma (\beta '-\gamma )]\), there are elements \(x\in 1+{\mathfrak {m}}_{m+1}(\gamma ,\Lambda ')\) and \(y\in 1+{\mathfrak {m}}_{m+1}(\gamma ,\Lambda )\) such that \(xg'y\) intertwines \(\theta \) with \(\theta '\).
Lemma A.12
(cf. [39, Proposition 9.27]). In the situation of Lemma A.11, suppose additionally that all strata are self-dual, all semisimple characters are \(\sigma \)-invariant, \(c\in {\mathfrak {a}}_{-(m+1)}^-\), and \(s_\gamma \) commutes with the adjoint anti-involution.
-
(i)
For any \(g\in \mathrm{I}_\mathrm{G}(\theta ,\theta ')\) there are elements \(x\in \mathrm{S}_{m+1}(\gamma ,\Lambda ')\cap \mathrm{G}\) and \(y\in \mathrm{S}_{m+1}(\gamma ,\Lambda )\cap \mathrm{G}\) and \(g'\in \mathrm{G}_\gamma \) such that \(g=xg'y\); moreover, \(g'\) intertwines \([\Lambda ,m+1,m,s_\gamma (\beta -\gamma +c)]\) with \([\Lambda ',m+1,m,s_\gamma (\beta '-\gamma )]\).
-
(ii)
For any \(g'\in \mathrm{G}_\gamma \) which intertwines \([\Lambda ,m+1,m,s_\gamma (\beta -\gamma +c)]\) with \([\Lambda ',m+1,m,s_\gamma (\beta '-\gamma )]\), there are elements \(x\in (1+{\mathfrak {m}}_{m+1}(\gamma ,\Lambda '))\cap \mathrm{G}\) and \(y\in (1+{\mathfrak {m}}_{m+1}(\gamma ,\Lambda ))\cap \mathrm{G}\) such that \(xg'y\) intertwines \(\theta \) with \(\theta '\).
1.6 A. 6. Intertwining and conjugacy for self-dual semisimple characters
In this final subsection, we prove an intertwining implies conjugacy theorem for self-dual semisimple characters, which generalizes a result of the second and third authors [39, 10.2,10.3] for skew semisimple characters. Let \([\Lambda ,n,r,\beta ]\) and \([\Lambda ,n,r,\beta ']\) be self-dual semisimple strata in \(\mathrm{A}\).
Theorem A.13
Let \(\theta \in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta )\) and \(\theta '\in {\mathscr {C}}^\Sigma (\Lambda ,r,\beta ')\) be self-dual semisimple characters which intertwine in \(\mathrm{G}\) and such that the matching \(\zeta :\mathrm{I}\rightarrow \mathrm{I}'\) of [39, Theorem 10.1] satisfies
for all indices \(i\in \mathrm{I}\) and all integers j. Then there is an element of \({\mathrm{P}_-(\Lambda )}\cap \prod _{i\in \mathrm{I}}{\text {Hom}}_\mathrm{F}(\mathrm{V}^i,\mathrm{V}'^{\zeta (i)})\) which conjugates \(\theta \) to \(\theta '\).
Proof
The involution \(\sigma \) acts on the index sets \(\mathrm{I}\) and \(\mathrm{I}'\) and this action commutes with the map \(\zeta \) by the matching theorem [39, Theorem 10.1]. We write \(\mathrm{I}=\mathrm{I}_0\cup \mathrm{I}_+\cup \mathrm{I}_-\) as usual, and similarly for \(\mathrm{I}'\). We deduce that \(\zeta \) sends \(\mathrm{I}_0\) to \(\mathrm{I}'_0\) and \(\mathrm{I}_{+}\cup \mathrm{I}_-\) to \(\mathrm{I}'_{+}\cup \mathrm{I}'_-\). We abbreviate \(\mathrm{V}_0=\mathrm{V}^{\mathrm{I}_0}\) so that \(\mathrm{V}_0^\perp =\mathrm{V}^{\mathrm{I}_{+}\cup \mathrm{I}_-}\), and similarly \(\mathrm{V}'_0\).
The hyperbolic spaces \(\mathrm{V}_0^\perp \) and \(\mathrm{V}'^\perp _0\) are isometric since they have the same dimension, so \(\mathrm{V}_0\) and \(\mathrm{V}'_0\) are isometric. Take an isometry g of \((\mathrm{V},h)\) which sends \(\mathrm{V}_0\) to \(\mathrm{V}'_0\) and \(\mathrm{V}^\perp _0\) to \(\mathrm{V}'^\perp _0\). By [38, Proposition 5.2] we can modify g such that g is an element of \({\mathrm{P}_-(\Lambda )}\). Conjugating \(\theta \) by g, we may assume without loss of generality that \(\mathrm{V}_0\) and \(\mathrm{V}'_0\) coincide.
We show next that there is an element of \(\mathrm{G}\cap ({\text {Aut}}_\mathrm{F}(\mathrm{V}_0)\times {\text {Aut}}_\mathrm{F}(\mathrm{V}_0^\perp ))\) which intertwines \(\theta \) with \(\theta '\). By Theorem [39, Theorem 10.2] there is an element \({\tilde{g}}\in \mathrm{P}(\Lambda ) \cap \prod _{i\in \mathrm{I}} {\text {Hom}}_\mathrm{F}(\mathrm{V}^i,\mathrm{V}'^{\zeta (i)})\) which conjugates \(\theta \) to \(\theta '\). Taking the intertwining formula of Proposition A.10 and conjugating back with \({\tilde{g}}\) we obtain
By a standard cohomology argument, as in [40, Corollary 4.14], we see that
and thus we obtain that the restrictions of \(\theta \) and \(\theta '\) on \(\mathrm{V}_0\) and on \(\mathrm{V}_0^\perp \) intertwine by an element of \(\mathrm{U}(\mathrm{V}_0)\) and \(\mathrm{U}(\mathrm{V}_0^\perp )\) respectively. Thus, by Corollary A.8 we can restrict to the cases where \(\mathrm{I}=\mathrm{I}_0\) or \(\mathrm{I}=\mathrm{I}_{+-}\). The first case is precisely [39, Theorem 10.3] and the second case is an easy exercise using Theorem [39, Theorem 10.2] (for \(\mathrm{V}_+=\mathrm{V}^{\mathrm{I}_+}\) and \(\mathrm{V}'_+=\mathrm{V}^{\mathrm{I}'_+}\)) and Corollary A.8. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kurinczuk, R., Skodlerack, D. & Stevens, S. Endo-parameters for p-adic classical groups. Invent. math. 223, 597–723 (2021). https://doi.org/10.1007/s00222-020-00997-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-020-00997-0



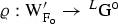 is a continuous homomorphism such that
is a continuous homomorphism such that  is the identity;
is the identity; and
and