Existence and uniqueness of the Liouville quantum gravity metric for $\gamma \in (0,2)$

Abstract

We show that for each $\gamma \in (0,2)$, there is a unique metric (i.e., distance function) associated with $\gamma$-Liouville quantum gravity (LQG). More precisely, we show that for the whole-plane Gaussian free field (GFF) h, there is a unique random metric $D_h$ associated with the Riemannian metric tensor “$e^{\gamma h} (dx^2 + dy^2)$” on ${\mathbb {C}}$ which is characterized by a certain list of axioms: it is locally determined by h and it transforms appropriately when either adding a continuous function to h or applying a conformal automorphism of $\mathbb {C}$ (i.e., a complex affine transformation). Metrics associated with other variants of the GFF can be constructed using local absolute continuity. The $\gamma$-LQG metric can be constructed explicitly as the scaling limit of Liouville first passage percolation (LFPP), the random metric obtained by exponentiating a mollified version of the GFF. Earlier work by Ding et al. (Tightness of Liouville first passage percolation for $\gamma \in (0,2)$, 2019. arXiv:1904.08021) showed that LFPP admits non-trivial subsequential limits. This paper shows that the subsequential limit is unique and satisfies our list of axioms. In the case when $\gamma = \sqrt{8/3}$, our metric coincides with the $\sqrt{8/3}$-LQG metric constructed in previous work by Miller and Sheffield, which in turn is equivalent to the Brownian map for a certain variant of the GFF. For general $\gamma \in (0,2)$, we conjecture that our metric is the Gromov–Hausdorff limit of appropriate weighted random planar map models, equipped with their graph distance. We include a substantial list of open problems.

1 Introduction

1.1 Overview

Fix $\gamma \in (0,2)$, let $U\subset \mathbb {C}$ be an open domain, and let h be the Gaussian free field (GFF) on U, or some minor variant thereof. The $\gamma$-Liouville quantum gravity (LQG) surface described by (U, h) is formally the random two-dimensional Riemannian manifold with metric tensor

$$\begin{aligned} e^{\gamma h}\, (dx^2 +dy^2), \end{aligned}$$

(1.1)

where $dx^2+dy^2$ is the Euclidean Riemannian metric tensor.

LQG surfaces were first introduced non-rigorously in the physics literature by Polyakov [73, 74] as a canonical model of a random Riemannian metric on U. Another motivation to study LQG surfaces is that they describe the scaling limit of random planar maps. The special case when $\gamma =\sqrt{8/3}$ (called “pure gravity”) corresponds to uniformly random planar maps, including uniform triangulations, quadrangulations, etc. Other values of $\gamma$ (sometimes referred to as “gravity coupled to matter”) correspond to random planar maps weighted by the partition function of an appropriate statistical mechanics model on the map, for example the uniform spanning tree for $\gamma =\sqrt{2}$ or the Ising model for $\gamma =\sqrt{3}$.

The definition (1.1) of LQG does not make literal sense since h is only a distribution, not a function, so it does not have well-defined pointwise values and cannot be exponentiated. Nevertheless, it is known that one can make sense of the associated volume form $\mu _h = e^{\gamma h(z)} \,dz$ (where dz denotes Lebesgue measure) as a random measure on U via various regularization procedures [27, 51, 76]. One such regularization procedure is as follows. For $s > 0$ and $z,w\in \mathbb {C}$, let $p_s (z,w) = \frac{1}{2\pi s} \exp \left( - \frac{|z-w|^2}{2s} \right)$ be the heat kernel, and note that $p_s (z,\cdot )$ approximates a point mass at z when s is small. For $\varepsilon >0$, we define a mollified version of the GFF by

$$\begin{aligned} h_\varepsilon ^*(z) := (h*p_{\varepsilon ^2/2})(z) = \int _{U} h(w) p_{\varepsilon ^2/2} (z,w) \, dw ,\quad \forall z\in U , \end{aligned}$$

(1.2)

where the integral is interpreted in the sense of distributional pairing. One can then define the $\gamma$-LQG measure $\mu _h$ as the a.s. weak limit [9, 27, 51, 76, 79]

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \varepsilon ^{\gamma ^2/2} e^{\gamma h_\varepsilon ^*(z)} \,dz . \end{aligned}$$

(1.3)

By [27, Proposition 2.1], the measure $\mu _h$ is conformally covariant: if $\phi : \widetilde{U} \rightarrow U$ is a conformal map and we set

$$\begin{aligned} \widetilde{h} := h\circ \phi + Q\log |\phi '|, \quad \text {where} \quad Q = \frac{2}{\gamma } + \frac{\gamma }{2} , \end{aligned}$$

(1.4)

then a.s. $\mu _h(\phi (A)) = \mu _{\widetilde{h}}(A)$ for each Borel set $A\subset \mathbb {C}$. This leads one to define a $\gamma$-LQG surface as an equivalence class of pairs (U, h), with two such pairs (U, h) and $(\widetilde{U} , \widetilde{h})$ declared to be equivalent if there is a conformal map $\phi : \widetilde{U} \rightarrow U$ for which h and $\widetilde{h}$ are related as in (1.4). We think of two equivalent pairs as representing different parameterizations of the same random surface. The conformal covariance property of $\mu _h$ says that this measure is intrinsic to the quantum surface—it does not depend on the particular equivalence class representative.

In order for $\gamma$-LQG to be a reasonable model of a “random two-dimensional Riemannian manifold”, one also needs a random metric¹ (distance function) $D_h$ on U which is in some sense obtained by exponentiating h and which satisfies a conformal covariance property analogous to that of the $\gamma$-LQG area measure. Moreover, this metric should be the scaling limit of the graph distance on random planar maps with respect to the Gromov–Hausdorff topology. Constructing a metric on $\gamma$-LQG is a much more difficult problem than constructing the measure $\mu _h$. Indeed, any natural regularization scheme for LQG distances involves minimizing over a large collection of paths, which results in a substantial degree of non-linearity.

Prior to this work, a $\gamma$-LQG metric has only been constructed in the special case when $\gamma = \sqrt{8/3}$ in a series of works by Miller and Sheffield [64, 65, 72]. In this case, for certain special choices of the pair (U, h), the random metric space $(U,D_h)$ agrees in law with a Brownian surface, such as the Brownian map [57, 59] or the Brownian disk [10]. These Brownian surfaces are continuum random metric spaces which arise as the scaling limits of uniform random planar maps with respect to the Gromov–Hausdorff topology. Miller and Sheffield’s construction of the $\sqrt{8/3}$-LQG metric does not use a direct regularization of the field h. Instead, they first construct a candidate for $\sqrt{8/3}$-LQG metric balls using a process called quantum Loewner evolution, which is built out of the Schramm-Loewner evolution with parameter $\kappa =6$ (${\text {SLE}}_6$), then show that there is a metric which corresponds to these balls.

In this paper, we will construct a $\gamma$-LQG metric for all $\gamma \in (0,2)$ via an explicit regularization procedure analogous to (1.3). We will also show that this metric is uniquely characterized by a list of natural properties that any reasonable notion of a metric on $\gamma$-LQG should satisfy, so is in some sense the only “correct” metric on $\gamma$-LQG. For simplicity, we will mostly restrict attention to the whole-plane case, but metrics associated with GFF’s on other domains can be easily constructed via restriction and/or absolute continuity (see Remark 1.5). In contrast to [64, 65, 72], the present work will make no use of ${\text {SLE}}$. Furthermore, we do not a priori have an ambient metric space to compare to (such as the Brownian map in the case $\gamma =\sqrt{8/3}$) and we do not have any sort of exact solvability, i.e., we do not know the exact laws of any observables related to the metric.

We now describe how our metric is constructed. It is shown in [20], building on [30, 33], that for each $\gamma \in (0,2)$, there is an exponent $d_\gamma > 2$ which describes distances in various discrete approximations of $\gamma$-LQG. A posteriori, once the $\gamma$-LQG metric is constructed, one can show that $d_\gamma$ is its Hausdorff dimension [43]. The value of $d_\gamma$ is not known explicitly except in the case when $\gamma = \sqrt{8/3}$, in which case we know that $d_{\sqrt{8/3}}=4$ (see Problem 7.1). We refer to [20, 42] for bounds for $d_\gamma$ and some speculation about its possible value. For $\gamma \in (0,2)$, we define

$$\begin{aligned} \xi = \xi _\gamma := \frac{\gamma }{d_\gamma } . \end{aligned}$$

(1.5)

We say that a random distribution h on $\mathbb {C}$ is a whole-plane GFF plus a continuous function if there exists a coupling of h with a random continuous function $f : \mathbb {C}\rightarrow \mathbb {R}$ such that the law of $h-f$ is that of a whole-plane GFF. We similarly define a whole-plane GFF plus a bounded continuous function, except we require that f is bounded.² Note that the whole-plane GFF is defined only modulo a global additive constant, but these definitions do not depend on the choice of additive constant. By definition, a whole-plane GFF plus a continuous function is well-defined as a distribution, not just modulo additive constant. For example, a whole-plane GFF with a particular choice of additive constant can be viewed as a whole-plane GFF plus a continuous function.

If h is a whole-plane GFF plus a bounded continuous function, we define $h^*_\varepsilon (z)$ for $\varepsilon > 0$ and $z\in \mathbb {C}$ as in (1.2) for our given choice of h. For $z,w\in \mathbb {C}$ and $\varepsilon > 0$, we define the $\varepsilon$-LFPP metric by

$$\begin{aligned} D_h^\varepsilon (z,w) := \inf _{P : z\rightarrow w} \int _0^1 e^{\xi h_\varepsilon ^*(P(t))} |P'(t)| \,dt\quad \end{aligned}$$

(1.6)

where the infimum is over all piecewise continuously differentiable paths from z to w. One should think of LFPP as the metric analog of the approximations of the LQG measure in (1.3).³ The intuitive reason why we look at $e^{\xi h_\varepsilon ^*(z)}$ instead of $e^{\gamma h_\varepsilon ^*(z)}$ to define the metric is as follows. By (1.3), we can scale LQG areas by a factor of $C>0$ by adding $\gamma ^{-1}\log C$ to the field. By (1.6), this results in scaling distances by $C^{\xi /\gamma } = C^{1/d_\gamma }$, which is consistent with the fact that the “dimension” should be the exponent relating the scaling of areas and distances.

Let $\mathfrak a_\varepsilon$ be the median of the $D_h^\varepsilon$-distance between the left and right boundaries of the unit square in the case when h is a whole-plane GFF normalized so that its circle average⁴ over $\partial \mathbb {D}$ is zero. We do not know the value of $\mathfrak a_\varepsilon$ explicitly, but see Corollary 1.11. It was shown by Ding, Dubédat, Dunlap, and Falconet [16] that the laws of the metrics $\mathfrak a_\varepsilon ^{-1} D_h^\varepsilon$ are tight w.r.t. the local uniform topology on $\mathbb {C}\times \mathbb {C}$, and every possible subsequential limit induces the Euclidean topology on $\mathbb {C}$ (see also the earlier tightness results for small $\gamma > 0$ [15, 17] and for Liouville graph distance, a related model, for all $\gamma \in (0,2)$ [14]). Subsequently, it was shown by Dubédat, Falconet, Gwynne, Pfeffer, and Sun [18], using [38, Corollary 1.8] (a general criterion for a local metric to be determined by the GFF), that every subsequential limit can be realized as a measurable function of h, so in fact the metrics $\mathfrak a_\varepsilon ^{-1} D_h^\varepsilon$ admit subsequential limits in probability. One of the main results of this paper gives the uniqueness of this subsequential limit.

Theorem 1.1

(Convergence of LFPP) The random metrics $\mathfrak a_\varepsilon ^{-1} D_h^\varepsilon$ converge in probability w.r.t. the local uniform topology on $\mathbb {C}\times \mathbb {C}$ to a random metric on $\mathbb {C}$ which is a.s. determined by h.

It is natural to define the limiting metric from Theorem 1.1 to be the $\gamma$-LQG metric associated with h. However, this definition is not entirely satisfactory since it is a priori possible that there are other natural ways to construct a metric on $\gamma$-LQG which do not yield the same result as the one in Theorem 1.1. For example, Theorem 1.1 does not yet tell us that the limit of LFPP coincides with the metric of [64, 65, 72] in the case when $\gamma =\sqrt{8/3}$.

We will therefore define a $\gamma$-LQG metric in terms of a list of axioms (see Sect. 1.2 just below). We will show that (a) the metric of Theorem 1.1 satisfies these axioms and (b) there is at most one metric satisfying these axioms for each $\gamma \in (0,2)$. Taken together, these statements tell us that the metric of Theorem 1.1 is the only reasonable metric that one can put on $\gamma$-LQG.

An important feature of our proofs is that they can be read with essentially no knowledge of the (substantial) existing literature on LQG. Aside from basic properties of the GFF (as discussed, e.g., in [80] and the introductory sections of [66, 70, 83]), the only prior works which this paper relies on are [16, 18, 36, 38]. All of the results which we need from these papers are reviewed in Sect. 2.

Our results open up many important new research directions in the theory of LQG. We have included in Sect. 7 a substantial list of open problems related to the $\gamma$-LQG metric.

1.2 Axiomatic characterization of the $\gamma$-LQG metric

To state our list of axioms precisely, we will need some preliminary definitions concerning metric spaces. In what follows, we let $(X,{{\mathfrak {d}}})$ be a metric space.

For $A,B\subset X$, we define

$$\begin{aligned} {{\mathfrak {d}}}(A,B) := \inf _{x\in A , y\in B} {{\mathfrak {d}}}(x,y) . \end{aligned}$$

A curve in X is a continuous function $P : [a,b] \rightarrow X$. For a curve P, the ${{\mathfrak {d}}}$-length of P is defined by

$$\begin{aligned} {\text {len}}\left( P ; {{\mathfrak {d}}}\right) := \sup _{T} \sum _{i=1}^{\# T} {{\mathfrak {d}}}(P(t_i) , P(t_{i-1})) \end{aligned}$$

where the supremum is over all partitions $T : a= t_0< \cdots < t_{\# T} = b$ of [a, b]. Note that the ${{\mathfrak {d}}}$-length of a curve may be infinite.

For $Y\subset X$, the internal metric of ${{\mathfrak {d}}}$ on Y is defined by

$$\begin{aligned} {{\mathfrak {d}}}(x,y ; Y) := \inf _{P \subset Y} {\text {len}}\left( P ; {{\mathfrak {d}}}\right) ,\quad \forall x,y\in Y \end{aligned}$$

(1.7)

where the infimum is over all paths P in Y from x to y. Then ${{\mathfrak {d}}}(\cdot ,\cdot ; Y)$ is a metric on Y, except that it is allowed to take infinite values.

We say that $(X,{{\mathfrak {d}}})$ is a length space if for each $x,y\in X$ and each $\varepsilon > 0$, there exists a curve of ${{\mathfrak {d}}}$-length at most ${{\mathfrak {d}}}(x,y) + \varepsilon$ from x to y.

A continuous metric on an open domain $U\subset \mathbb {C}$ is a metric ${{\mathfrak {d}}}$ on U which induces the Euclidean topology on U, i.e., the identity map $(U,|\cdot |) \rightarrow (U,{{\mathfrak {d}}})$ is a homeomorphism. We equip the space of continuous metrics on U with the local uniform topology for functions from $U\times U$ to $[0,\infty )$ and the associated Borel $\sigma$-algebra. We allow a continuous metric to satisfy ${{\mathfrak {d}}}(u,v) = \infty$ if u and v are in different connected components of U. In this case, in order to have ${{\mathfrak {d}}}^n\rightarrow {{\mathfrak {d}}}$ w.r.t. the local uniform topology we require that for large enough n, ${{\mathfrak {d}}}^n(u,v) = \infty$ if and only if ${{\mathfrak {d}}}(u,v)=\infty$.

Let $\mathcal D'(\mathbb {C})$ be the space of distributions (generalized functions) on $\mathbb {C}$, equipped with the usual weak topology. For $\gamma \in (0,2)$, a (strong) $\gamma$-Liouville quantum gravity (LQG) metric is a measurable function $h\mapsto D_h$ from $\mathcal D'(\mathbb {C})$ to the space of continuous metrics on $\mathbb {C}$ such that the following is true whenever h is a whole-plane GFF plus a continuous function.

• I. Length space Almost surely, $(\mathbb {C} , D_h)$ is a length space, i.e., the $D_h$-distance between any two points of $\mathbb {C}$ is the infimum of the $D_h$-lengths of $D_h$-continuous paths (equivalently, Euclidean continuous paths) between the two points.

• II. Locality Let $U\subset \mathbb {C}$ be a deterministic open set. The internal metric $D_h(\cdot ,\cdot ; U)$ is a.s. determined by $h|_U$.

• III. Weyl scaling Let $\xi$ be as in (1.5) and for each continuous function $f : \mathbb {C}\rightarrow \mathbb {R}$, define

  $$\begin{aligned} (e^{\xi f} \cdot D_h) (z,w) := \inf _{P : z\rightarrow w} \int _0^{{\text {len}}(P ; D_h)} e^{\xi f(P(t))} \,dt , \quad \forall z,w\in \mathbb {C} ,\qquad \end{aligned}$$

  (1.8)

  where the infimum is over all continuous paths from z to w parameterized by $D_h$-length. Then a.s. $e^{\xi f} \cdot D_h = D_{h+f}$ for every continuous function $f : \mathbb {C}\rightarrow \mathbb {R}$.

• IV. Coordinate change for translation and scaling For each fixed deterministic $r > 0$ and $z\in \mathbb {C}$, a.s.

  $$\begin{aligned}&D_h \left( ru + z , r v + z \right) = D_{h(r\cdot + z) +Q\log r}(u,v) , \, \forall u,v\in \mathbb {C} \nonumber \\&\quad \text {where} \quad Q =\frac{2}{\gamma } + \frac{\gamma }{2} . \end{aligned}$$

  (1.9)

Let us briefly discuss why the above axioms are natural. Recall that $\gamma$-LQG should be the random Riemannian metric with metric tensor $e^{\gamma h} (dx^2+dy^2)$. Axiom I is simply the LQG analog of the statement that for a true Riemannian metric, the distance between two points can be defined as the infima of the lengths of paths connecting them. In a similar vein, Axiom II corresponds to the fact that for a smooth Riemannian metric, the lengths of paths are determined locally by the Riemannian metric tensor. Axiom III is just expressing the fact that the metric is obtained by exponentiating $\xi h$, so adding a continuous function f to h results in re-scaling the metric length measure on paths by $e^{\xi f}$.

Axiom IV is the metric analog of the conformal coordinate change formula (1.4) for the $\gamma$-LQG area measure, but restricted to translations and scalings. This axiom together with Corollary 1.3 says that $D_h$ depends only on the LQG surface $(\mathbb {C} , h)$, not on the particular choice of parameterization. We will prove a conformal covariance property for the $\gamma$-LQG metric w.r.t. conformal automorphisms between arbitrary domains, directly analogous to the conformal covariance of the $\gamma$-LQG area measure, in [37].

Theorem 1.2

(Existence and uniqueness of the LQG metric) Fix $\gamma \in (0,2)$. There is a $\gamma$-LQG metric D such that the limiting metric of Theorem 1.1 is a.s. equal to $D_h$ whenever h is a whole-plane GFF plus a bounded continuous function. Furthermore, the $\gamma$-LQG metric is unique in the following sense. If D and $\widetilde{D}$ are two $\gamma$-LQG metrics, then there is a deterministic constant $C>0$ such that if h is a whole-plane GFF plus a continuous function, then a.s. $D_h = C \widetilde{D}_h$.

Theorem 1.2 justifies us in referring to the $\gamma$-LQG metric. Technically speaking there is a one-parameter family of such metrics, which differ by a global deterministic multiplicative constant. But, one can fix the constant in various ways to get a single canonically defined metric. For example, we can require that the median distance between the left and right boundaries of the unit square is 1 for the metric associated with a whole-plane GFF normalized so that its circle average over $\partial \mathbb {D}$ is zero (the limiting metric in Theorem 1.1 has this normalization).

Theorem 1.2 is related to Shamov’s axiomatic characterization of Gaussian multiplicative chaos (GMC) measures, such as the $\gamma$-LQG measure [79, Corollary 5]. Shamov’s result says that a subcritical GMC measure associated with a field X is uniquely characterized by how it transforms when we add to X a function in the Cameron–Martin space. Weyl scaling (Axiom III) is the metric analog of this property. Unlike in Shamov’s characterization we need other properties besides just Weyl scaling to characterize the LQG metric, most notably some sort of uniform control of the metric at different Euclidean scales (in the above list of axioms this is provided by Axiom IV, but this axiom can be weakened, see Sect. 1.4).

In Axiom IV in the definition of a strong $\gamma$-LQG metric, we did not require that the metric is invariant under rotations of $\mathbb {C}$. It turns out that rotational invariance is implied by the other axioms. See Remark 1.6 below for an intuitive explanation of why this is the case.

Corollary 1.3

(Rotational invariance) If $\gamma \in (0,2)$ and D is a $\gamma$-LQG metric then D is rotationally invariant, i.e., if $\omega \in \mathbb {C}$ with $|\omega | =1$ and h is a whole-plane GFF plus a continuous function, then a.s. $D_h(u,v) = D_{h(\omega \cdot )}(\omega ^{-1} u ,\omega ^{-1} v)$ for all $u,v\in \mathbb {C}$.

Proof

Define $D_h^{(\omega )}(u,v) := D_{h(\omega \cdot )}(\omega ^{-1} u ,\omega ^{-1} v)$. It is easily verified that $D^{(\omega )}$ is a strong LQG metric, so Theorem 1.2 implies that there is a deterministic constant $C >0$ such that a.s. $D^{(\omega )}_h = C D_h$ whenever h is a whole-plane GFF plus a continuous function. To check that $C = 1$, consider a whole-plane GFF h normalized so that its circle average over $\partial \mathbb {D}$ is 0. Then the law of h is rotationally invariant, so $\mathbb {P}[D_h(0,\partial \mathbb {D})> R] = \mathbb {P}[D_h^{(\omega )}(0,\partial \mathbb {D}) > R]$ for every $R > 0$. Therefore $C =1$. $\square$

It is easy to check that the metric constructed in [64, 65, 72] satisfies the axioms for a $\sqrt{8/3}$-LQG metric; see [41, Section 2.5] for a careful explanation of why this is the case. Consequently, Theorem 1.2 implies the following.

Corollary 1.4

(Equivalence with the construction of [64, 65, 72]) The $\sqrt{8/3}$-LQG metric constructed in [64, 65, 72] agrees with the limiting metric of Theorem 1.1 (equivalently, the metric of Theorem 1.2) up to a deterministic global scaling factor.

The present work does not use the results of [64, 65, 72], but also does not supersede these results. Indeed, without these works it is not at all clear how to link the $\sqrt{8/3}$-LQG metric constructed in the present article to Brownian surfaces, and thereby to uniform random planar maps.

There are a number of properties of the $\gamma$-LQG metric which are already known. It is shown in [18, Section 3.1] that one has superpolynomial concentration for the $D_h$-distance between two disjoint compact, connected sets which are not singletons (e.g., the inner and outer boundaries of an annulus or two opposite sides of a rectangle). Building on this, [18] computes the optimal Hölder exponents between $D_h$ and the Euclidean metric, in both directions, and establishes moment bounds for various distance quantities (see also Sect. 2.4). Confluence properties for $D_h$-geodesics analogous to the ones known for the Brownian map [56] are proven in [36] (see also Sect. 2.5). It is shown in [62] that $D_h$-geodesics are conformally removable and their laws are mutually singular with respect to Schramm-Loewner evolution curves. After the appearance of this paper, the work [43] proved that $D_h$ satisfies a version of the KPZ formula [27, 53] and the work [1] proved a concentration result for the LQG mass of a $D_h$-metric ball.

Remark 1.5

(Metrics associated with other fields) Theorem 1.2 gives us a canonical $\gamma$-LQG metric associated with a whole-plane GFF plus a continuous function. It is not hard to see that one can also define the metric if h is equal to a whole-plane GFF plus a continuous function plus a finite number of logarithmic singularities of the form $-\alpha \log |\cdot - z|$ for $z\in \mathbb {C}$ and $\alpha < Q$; see [18, Theorem 1.10 and Proposition 3.17].

We can also define metrics associated with GFF’s on proper sub-domains of $\mathbb {C}$. To this end, let $U\subset \mathbb {C}$ be open and let h be a whole-plane GFF. Due to Axiom II, we can define for each open set $U\subset \mathbb {C}$ the metric $D_{h|_U} := D_h(\cdot ,\cdot ;U)$ as a measurable function of $h|_U$. We can write $h|_U = \mathring{h}^U + \mathfrak h^U$, where $\mathring{h}^U$ is a zero-boundary GFF on U and $\mathfrak h^U$ is a random harmonic function on U independent from $\mathring{h}^U$. In the notation (1.8), we define

$$\begin{aligned} D_{\mathring{h}^U} := e^{-\xi \mathfrak h^U} \cdot D_{h|_U} . \end{aligned}$$

(1.10)

Note that this is well-defined even though $\mathfrak h^U$ does not extend continuously to $\partial U$, since the definition of $D_{h|_U}$ involves only paths contained in U. It is easily seen from Axioms II (locality) and III (Weyl scaling) that $D_{\mathring{h}^U}$ is a measurable function of $\mathring{h}^U$: indeed, if we are given an open set $V\subset U$ with $\overline{V}\subset U$, choose a smooth compactly supported bump $f : U\rightarrow [0,1]$ which is identically equal to 1 on V. Then Axiom II applied to the field $h - f \mathfrak h^U$ implies that the internal metric of $D_{\mathring{h}^U}$ on V, which equals $D_{h-f\mathfrak h^U}(\cdot ,\cdot ; V)$, is determined by $(h-f\mathfrak h^U)|_V = \mathring{h}^U|_V$. Letting V increase to all of U gives the desired measurability of $D_{\mathring{h}^U}$ w.r.t. $\mathring{h}^U$. This defines the $\gamma$-LQG metric for a zero-boundary GFF.

By Axiom III, we can also define the metric $D_{\widetilde{h}}$ in the case when $\widetilde{h} = \mathring{h}^U + f$ is a zero-boundary GFF plus a continuous function on U, namely $D_{\widetilde{h}} := e^{\xi f} D_{\mathring{h}^U}$. It is shown in [37] that this metric satisfies a conformal coordinate change relation analogous to the one satisfied by the $\gamma$-LQG measure (as discussed just below (1.4)).

We expect that for a fixed proper subdomain $U\subset \mathbb {C}$ there is an analogous formulation and characterization of the LQG metric on U. However, we will not formulate such a result here. We emphasize that the LQG metric on U is determined by the LQG metric on $\mathbb {C}$, and moreover the LQG metric on U determines the LQG metric on $\mathbb {C}$ due to Axiom II (locality) and the local absolute continuity between GFF’s on different domains. It is not hard to show using the results of [16] that for, say, a zero-boundary GFF $\mathring{h}^U$ on U, the metric $D_{\mathring{h}^U}$ is the limit in law of LFPP on U w.r.t. the topology of uniform convergence on compact subsets of $U\times U$: see, e.g., the arguments of [18, Section 2.2].

Remark 1.6

(Why rotational invariance is unnecessary) At a first glance, it may seem surprising that one does not need rotational invariance to uniquely characterize the LQG metric in Theorem 1.2. Indeed, one can define variants of LFPP which are not rotationally invariant by working with a stretched version of the Euclidean metric. For example, for a given $A > 1$ one can replace (1.6) by

$$\begin{aligned} D_{h,A}^\varepsilon (z,w) := \inf _{P : z\rightarrow w} \int _0^1 e^{\xi h_\varepsilon ^*(P(t))} \sqrt{P_1'(t)^2 + A P_2'(t)^2} \,dt \end{aligned}$$

(1.11)

where the infimum is over all piecewise continuously differentiable paths $P = (P_1,P_2)$ from z to w. The arguments of this paper and its predecessors apply verbatim with $D_{h,A}^\varepsilon$ in place of $D_h^\varepsilon$. In particular, $D_{h,A}^\varepsilon$ converges in probability to (a deterministic constant times) the $\gamma$-LQG metric and hence satisfies the rotational invariance property of Corollary 1.3. This is despite the fact that the metrics (1.11) do not satisfy this rotational invariance property.

Here is an intuitive explanation for this phenomenon. First, we note that $D_{h,A}^\varepsilon$ is bi-Lipschitz equivalent with respect to $D_{h,1}^\varepsilon = D_h^\varepsilon$ for each $\varepsilon > 0$, with a deterministic bi-Lipschitz constants. Therefore in a subsequential limit as $\varepsilon \rightarrow 0$, we obtain two metrics $D_{h,A}$ and $D_h = D_{h,1}$ which are bi-Lipschitz equivalent with deterministic bi-Lipschitz constants. Suppose that P is a $D_h$-geodesic connecting z and w. Using the confluence of geodesics results from [36], one can show that (very roughly speaking) for distinct times $s,t\in [0,D_h(z,w)]$, the restrictions of h to small neighborhoods of P(s) and P(t) are approximately independent; see the outline of Sect. 4 in Sect. 1.5 below for details. Moreover, since P is a fractal type curve, it has no local notion of direction, so one expects that the law of h restricted to a small neighborhood of P(t) does not depend very strongly on t or on the endpoints z, w of P. If we fix $n \in \mathbb {N}$ and let $0 = t_0 < \cdots t_n = D_h(z,w)$ be equally spaced times, we can approximate the $D_{h,A}$-length of P by

$$\begin{aligned} \sum _{j=1}^n D_{h,A}(P(t_{j-1}),P(t_j) ). \end{aligned}$$

The above considerations suggest that each of the random variables $D_{h,A}(P(t_{j-1}),P(t_j))$ has approximately the same distribution and is bounded above and below by deterministic constants times $t_j-t_{j-1}$. From law of large numbers type considerations, it follows that the $D_{h,A}$-length of P is a deterministic constant times the $D_h$-length of P, where the constant does not depend on the endpoints of P.

Knowing that the $D_{h,A}$-length of every $D_h$ geodesic is a constant times its $D_h$-length (and vice-versa) does not immediately imply that $D_h$ is equal to a constant times $D_{h,A}$. This is because if $P_n$ is a sequence of paths which converge uniformly to P, then it is not necessarily true that ${\text {len}}(P_n;D_{h,A})$ converges to ${\text {len}}(P;D_{h,A})$. For this and other reasons, we will argue in a somewhat different manner than we have indicated above, though our arguments will still be based on the bi-Lipschitz equivalence of metrics and approximate independence statements for the local behavior of a geodesic at different times. We will explain the general strategy in Sect. 1.5 in more detail.

1.3 Conjectured random planar map connection

As noted above, the $\gamma$-LQG metric should describe the large scale behavior of the graph metric for random planar maps. Since our $\gamma$-LQG metric is in some sense canonical, it is natural to make the following conjecture.

Conjecture 1.7

For each $\gamma \in (0,2)$, random planar maps in the $\gamma$-LQG universality class, equipped with their graph distance, converge in the scaling limit with respect to the Gromov–Hausdorff topology to $\gamma$-LQG surfaces equipped with the $\gamma$-LQG metric constructed in Theorem 1.1 (see also Remark 1.5).

Examples of planar map models to which Conjecture 1.7 should apply include random planar maps weighted by the number of spanning trees ($\gamma = \sqrt{2}$), the Ising model partition function ($\gamma =\sqrt{3}$), the number of bipolar orientations ($\gamma =\sqrt{4/3}$; [52]), or the Fortuin-Kasteleyn model partition function ($\gamma \in (\sqrt{2} , 2)$; [82]). Another class of models is the so-called mated-CRT maps, which are defined for all $\gamma \in (0,2)$; see [23, 33, 40].

For $\gamma =\sqrt{8/3}$, Conjecture 1.7 has already been proven for many different uniform-type random planar maps. The reason for this is that we know that our $\sqrt{8/3}$-LQG metric is equivalent to the metric of [64, 65, 72] (Corollary 1.4); which in turn is equivalent to a Brownian surface, such as the Brownian map, for certain special $\sqrt{8/3}$-LQG surfaces [64, Corollary 1.5]; which in turn is the scaling limit of uniform random planar maps of various types [57, 59].

Conjecture 1.7 has not been proven for any random planar map model for $\gamma \not =\sqrt{8/3}$. However, we already have a relationship between the continuum LQG metric and graph distances in random planar maps at the level of exponents for all $\gamma \in (0,2)$. Indeed, the quantity $d_\gamma$ appearing in (1.5) describes several exponents associated with random planar maps, such as the ball volume exponent [20, 33] and the displacement exponent for simple random walk on the map [31, 35]. It is proven in [43] that $d_\gamma$ is the Hausdorff dimension of $D_h$.

Conjecture 1.7 can be made somewhat more precise by specifying exactly what type of $\gamma$-LQG surface should arise in the scaling limit. For random planar maps with the topology of the sphere (resp. disk, plane, half-plane) this surface should be the quantum sphere (resp. quantum disk, $\gamma$-quantum cone, $\gamma$-quantum wedge). See [23] for precise definitions of these quantum surfaces. Equivalent definitions of the quantum sphere and quantum disk, respectively, can be found in [22, 50] (see [2, 12] for a proof of the equivalence). Some planar map models have been proven to converge to these quantum surfaces, for general $\gamma \in (0,2)$, with respect to topologies which do not encode the metric structure explicitly. Examples of such topologies include convergence in the so-called peanosphere sense [23, 82] and convergence of the counting measure on vertices to the $\gamma$-LQG measure when the planar map is embedded appropriately into the plane [40].

1.4 Weak LQG metrics and a stronger uniqueness statement

We will prove Theorem 1.1 and 1.2 simultaneously by establishing a uniqueness statement for metrics under a weaker list of axioms, which are satisfied for both the strong LQG metrics considered in Sect. 1.2 and for subsequential limits of LFPP (as is shown in [16, 18]).

Let $\mathcal D'(\mathbb {C})$ be the space of distributions as in Sect. 1.2. A weak $\gamma$-LQG metric is a measurable function $h\mapsto D_h$ from $\mathcal D'(\mathbb {C})$ to the space of continuous metrics on $\mathbb {C}$ such that the following is true whenever h is a whole-plane GFF plus a continuous function.

• I. Length space Almost surely, $(\mathbb {C} , D_h)$ is a length space, i.e., the $D_h$-distance between any two points of $\mathbb {C}$ is the infimum of the $D_h$-lengths of $D_h$-continuous paths (equivalently, Euclidean continuous paths) between the two points.

• II. Locality Let $U\subset \mathbb {C}$ be a deterministic open set. The internal metric $D_h(\cdot ,\cdot ; U)$ is a.s. determined by $h|_U$.

• III. Weyl scaling If we define $e^{\xi f} \cdot D_h$ as in (1.8), then a.s. $e^{\xi f} \cdot D_h = D_{h+f}$ for every continuous function $f : \mathbb {C}\rightarrow \mathbb {R}$.

• IV. Translation invariance For each fixed deterministic $z \in \mathbb {C}$, a.s. $D_{h(\cdot + z)} = D_h(\cdot + z , \cdot +z)$.

• V. Tightness across scales Suppose h is a whole-plane GFF and for $z\in \mathbb {C}$ and $r>0$ let $h_r(z)$ be the average of h over the circle $\partial B_r(z)$. For each $r > 0$, there is a deterministic constant $\mathfrak c_r > 0$ such that the set of laws of the metrics $\mathfrak c_r^{-1} e^{-\xi h_r(0)} D_h (r \cdot , r\cdot )$ for $r > 0$ is tight (w.r.t. the local uniform topology). Furthermore, the closure of this set of laws w.r.t. the Prokhorov topology is contained in the set of laws on continuous metrics on $\mathbb {C}$ (i.e., every subsequential limit of the laws of the metrics $\mathfrak c_r^{-1} e^{-\xi h_r(0)} D_h (r \cdot , r \cdot )$ is supported on metrics which induce the Euclidean topology on $\mathbb {C}$). Finally, there exists $\Lambda > 1$ such that for each $\delta \in (0,1)$,

  $$\begin{aligned} \Lambda ^{-1} \delta ^\Lambda \le \frac{\mathfrak c_{\delta r}}{\mathfrak c_r} \le \Lambda \delta ^{-\Lambda } ,\quad \forall r > 0. \end{aligned}$$

  (1.12)

Axioms I through III for a weak LQG metric are identical to the corresponding axioms for a strong LQG metric. Axiom IV for a weak LQG metric is equivalent to Axiom IV (coordinate change) for a strong LQG metric with $r=1$. Axiom V for a weak $\gamma$-LQG metric is a substitute for the exact scale invariance property given by Axiom IV for a strong LQG metric. This axiom implies the tightness of various functionals of $D_h$. For example, if $U\subset \mathbb {C}$ is open and $K\subset U$ is compact, then the laws of

$$\begin{aligned} \left( \mathfrak c_r^{-1} e^{-\xi h_r(0)} D_h (r K , r\partial U) \right) ^{-1} \quad \text {and} \quad \mathfrak c_r^{-1} e^{-\xi h_r(0)} \sup _{u,v\in r K} D_h ( u , v ; r U )\nonumber \\ \end{aligned}$$

(1.13)

as r varies are tight. It is shown in [18, Theorem 1.5] that for any weak $\gamma$-LQG metric, one in fact has the following stronger version of (1.12):

$$\begin{aligned} \frac{\mathfrak c_{\delta r}}{\mathfrak c_r} = \delta ^{\xi Q + o_\delta (1)}, \quad \text { uniformly over all } r>0. \end{aligned}$$

(1.14)

By the scale invariance of the law of the whole-plane GFF, modulo additive constant, Axiom IV for a strong LQG metric immediately implies Axiom V for a weak LQG metric with $\mathfrak c_r = r^{\xi Q }$, for Q as in (1.4). Indeed, using Axiom IV and then Axiom III for a strong $\gamma$-LQG metric shows that

$$\begin{aligned} r^{-\xi Q} e^{-\xi h_r(0)} D_h (r \cdot , r\cdot ) = r^{-\xi Q} e^{-\xi h_r(0)} D_{h(r\cdot ) +Q\log r} = D_{h(r\cdot ) - h_r(0)} \overset{d}{=}D_h .\nonumber \\ \end{aligned}$$

(1.15)

Hence every strong $\gamma$-LQG metric is a weak $\gamma$-LQG metric.

It is shown in [18, Theorem 1.2] that every subsequential limit in probability of the LFPP metrics $D_h^\varepsilon$ of (1.6) is of the form $D_h$ where D is a weak $\gamma$-LQG metric. Consequently, the following theorem contains both Theorem 1.1 and Theorem 1.2.

Theorem 1.8

(Strong uniqueness of weak LQG metrics) Let $\gamma \in (0,2)$. Every weak $\gamma$-LQG metric is a strong $\gamma$-LQG metric. In particular, by Theorem 1.2, such a metric exists for each $\gamma \in (0,2)$ and if D and $\widetilde{D}$ are two weak $\gamma$-LQG metrics, then there is a deterministic constant $C>0$ such that if h is a whole-plane GFF plus a continuous function, then a.s. $D_h = C \widetilde{D}_h$.

It turns out that all of our main results are easy consequences of the following statement, which superficially seems to be weaker that Theorem 1.8.

Theorem 1.9

(Weak uniqueness of weak LQG metrics) Let $\gamma \in (0,2)$ and let D and $\widetilde{D}$ be two weak $\gamma$-LQG metrics which have the same values of $\mathfrak c_r$ in Axiom V. There is a deterministic constant $C > 0$ such that if h is a whole-plane GFF plus a continuous function, then a.s. $D_h = C \widetilde{D}_h$.

Most of the paper is devoted to the proof of Theorem 1.9. Let us now explain how Theorem 1.9 implies the other main theorems stated above. We first establish the first statement of Theorem 1.8.

Lemma 1.10

Every weak $\gamma$-LQG metric is a strong $\gamma$-LQG metric.

Proof of Lemma 1.10 assuming Theorem 1.9

Suppose that D is a weak $\gamma$-LQG metric. For $b >0$, we define

$$\begin{aligned} D^{(b)}_h(\cdot ,\cdot ) := D_{h(\cdot /b)} (b\cdot , b\cdot ) . \end{aligned}$$

(1.16)

We claim that $D^{(b)}$ is a weak $\gamma$-LQG metric with the same scaling constants $\mathfrak c_r$ as D. It is easily verified that $D^{(b)}$ satisfies Axioms I through IV in the definition of a weak $\gamma$-LQG metric. To check Axiom V (tightness across scales), we compute for $r>0$:

$$\begin{aligned} \mathfrak c_r^{-1} e^{-\xi h_r(0)} D^{(b)}_h (r \cdot , r\cdot )&= \mathfrak c_r^{-1} e^{-\xi h_r(0)} D_{h(\cdot /b)} ( b r \cdot , b r \cdot ) \nonumber \\&= \left( \frac{\mathfrak c_{b r}}{\mathfrak c_r} e^{-\xi ( h_r(0) - h_{b r}(0) )} \right) \mathfrak c_{b r}^{-1} e^{-\xi h_{b r}(0)} D_{h(\cdot /b)} ( b r \cdot , b r \cdot ) . \end{aligned}$$

In the case when h is a whole-plane GFF, the random variable $h_r(0) - h_{b r}(0)$ is centered Gaussian with variance $\log b^{-1}$ [27, Section 3.1]. By (1.12), $\mathfrak c_{b r}/\mathfrak c_r$ is bounded above by a constant depending only on b (not on r). Axiom V (tightness across scales) for D applied with $h(\cdot /b)$ in place of h and br in place of r therefore implies that the laws of the metrics $\mathfrak c_r^{-1} e^{-\xi h_r(0)} D^{(b)}_h (r \cdot , r\cdot )$ are tight in the case when h is a whole-plane GFF, and that every subsequential limit of the laws of these metrics is supported on metrics (not pseudometrics).

Hence we can apply Theorem 1.9 with $\widetilde{D} = D^{(b)}$ to get that for each $b >0$, there is a deterministic constant $\mathfrak k_b >0$ such that whenever h is a whole-plane GFF plus a continuous function, a.s. $D_h^{(b)} = \mathfrak k_b D_h$. We now argue that $\mathfrak k_b$ is a power of b.

For $b_1,b_2 > 0$, we have $D^{(b_1b_2)} = ( D^{(b_1)} )^{(b_2)}$, which implies that a.s. $D_h^{(b_1b_2)} = \mathfrak k_{b_2} D_h^{(b_1)} = \mathfrak k_{b_1} \mathfrak k_{b_2} D_h$. Therefore,

$$\begin{aligned} \mathfrak k_{b_1b_2} = \mathfrak k_{b_1} \mathfrak k_{b_2} . \end{aligned}$$

(1.17)

It is also easy to see that $\mathfrak k_b$ depends continuously on b. Indeed, by Axiom III (Weyl scaling) and since $h(\cdot /b) - h_{1/b}(0) \overset{d}{=}h$, we have $e^{-\xi h_{1/b}(0)} D_h^{(b)}(\cdot /b,\cdot /b) \overset{d}{=}D_h$. By the continuity of $(z,w) \mapsto D_h(z,w)$ and $r\mapsto h_r(0)$, it follows that $D_h^{(b)} \rightarrow D_h$ in law as $b\rightarrow 1$. This gives the continuity of $b\mapsto \mathfrak k_b$ at $b = 1$. Using (1.17) then gives the desired continuity in general.

The relation (1.17) and the continuity of $b\mapsto \mathfrak k_b$ (actually, just Lebesgue measurability is enough) imply that $\mathfrak k_b = b^\alpha$ for some $\alpha \in \mathbb {R}$. Equivalently, for $b > 0$, a.s.

$$\begin{aligned} D_h(b\cdot , b\cdot ) = b^{-\alpha } D_{h(b\cdot )}(\cdot ,\cdot ) . \end{aligned}$$

(1.18)

For a whole-plane GFF, $h(b\cdot ) - h_b(0) \overset{d}{=}h$. By Axiom III (Weyl scaling) and the definition of $\mathfrak k_b$,

$$\begin{aligned} b^\alpha e^{-\xi h_b(0)} D_h(b\cdot ,b\cdot ) = D_{h(b\cdot ) - h_b(0)} \overset{d}{=}D_h . \end{aligned}$$

(1.19)

Therefore, Axiom V holds for D with $\mathfrak c_r = r^{-\alpha }$. By (1.14), we get that $\alpha = -\xi Q$. Hence for $b > 0$, we have (using Axiom III in the first equality)

$$\begin{aligned} D_{h(\cdot /b) + Q\log (1/b)}(b\cdot , b\cdot ) = b^{-\xi Q} D_h^{(b)} = D_h . \end{aligned}$$

(1.20)

Therefore, D is a strong LQG metric. $\square$

Proof of Theorems 1.1, 1.2, and 1.8 assuming Theorem 1.9

By Lemma 1.10, every weak $\gamma$-LQG metric is a strong $\gamma$-LQG metric. By (1.15), every strong LQG metric satisfies the axioms in the definition of a weak $\gamma$-LQG metric with $\mathfrak c_r = r^{\xi Q}$. We can therefore apply Theorem 1.9 to get that there is at most one strong LQG metric. This completes the proof of the uniqueness parts of Theorems 1.2 and 1.8.

As for existence, we recall that [18, Theorem 1.2] (building on [16]) shows that for every sequence of $\varepsilon$’s tending to zero, there is a weak $\gamma$-LQG metric D and a subsequence along which the re-scaled LFPP metrics $\mathfrak a_\varepsilon ^{-1} D_h^\varepsilon$ converge in probability to $D_h$, whenever h is a whole-plane GFF plus a bounded continuous function. By the uniqueness part of Theorem 1.8, D is in fact a strong $\gamma$-LQG metric and any two different subsequential limiting metrics differ by a deterministic multiplicative constant factor. Recall that $\mathfrak a_\varepsilon$ is the median $D_h^\varepsilon$-distance between the left and right boundaries of the unit square in the case when h is a whole-plane GFF normalized so that $h_1(0) = 0$. Hence for any subsequential limiting metric the median $D_h$-distance between the left and right boundaries of the unit square is 1. Therefore, the multiplicative constant factor is 1, so the subsequential limit of $D_h^\varepsilon$ in probability is unique. This gives Theorem 1.1 and the existence parts of Theorems 1.2 and 1.8 . $\square$

Finally, we note that our results give non-trivial information about the approximating LFPP metrics from (1.6). Indeed, let $\{\mathfrak a_\varepsilon \}_{\varepsilon > 0}$ be the scaling constants from Theorem 1.1. It is shown in [20, Theorem 1.5] that $\mathfrak a_\varepsilon = \varepsilon ^{1-\xi Q + o_\varepsilon (1)}$. Using Theorem 1.1, we obtain the following stronger form of this relation.

Corollary 1.11

The function $\varepsilon \mapsto \mathfrak a_\varepsilon$ is regularly varying with exponent $1-\xi Q$, i.e., for every $C > 0$ one has $\lim _{\varepsilon \rightarrow 0} \mathfrak a_{C\varepsilon }/\mathfrak a_\varepsilon = C^{ 1-\xi Q }$.

We expect, but do not prove here, that in fact Theorem 1.1 holds with $\mathfrak a_\varepsilon = \varepsilon ^{1-\xi Q}$.

Proof of Corollary 1.11

It is shown in [18, Lemma 2.14] that for any sequence of $\varepsilon$’s tending to zero along which the re-scaled LFPP metrics $\mathfrak a_\varepsilon ^{-1} D_h^\varepsilon$ converge in law, also $\mathfrak a_{C\varepsilon }/\mathfrak a_\varepsilon$ converges (the limit is $C \mathfrak c_{1/C}$, with $\mathfrak c_{1/C}$ as in Axiom V (tightness across scales) for the limiting weak $\gamma$-LQG metric). By Theorem 1.1, $\mathfrak a_\varepsilon ^{-1} D_h^\varepsilon$ converges in probability as $\varepsilon \rightarrow 0$, so in fact $\mathfrak a_{C\varepsilon }/\mathfrak a_\varepsilon$ converges, not just subsequentially. This means that $\mathfrak a_{C\varepsilon }$ is regularly varying with some exponent $\alpha > 0$. Since $\mathfrak a_\varepsilon = \varepsilon ^{1-\xi Q +o_\varepsilon (1)}$, we must have $\alpha =1-\xi Q$. $\square$

1.5 Outline

As explained above, to prove our main results it remains only to prove Theorem 1.9. We emphasize that unlike many results in the theory of LQG, this paper does not build on a large amount of external input. Rather, we will only use some results from the papers [16, 18, 36, 38], which can be taken as black boxes. All of the externally proven results which we will use are reviewed in Sect. 2.

Throughout this outline and the rest of the paper, we will use (without comment) the following two basic facts about $D_h$-geodesics when D is a weak $\gamma$-LQG metric and h is a whole-plane GFF.

• Almost surely, for every $z,w\in \mathbb {C}$, there is at least one $D_h$-geodesic from z to w. This follows from [6, Corollary 2.5.20] and the fact that $(\mathbb {C} , D_h)$ is a boundedly compact length space (i.e., closed bounded subsets are compact; see [18, Lemma 3.8]).

• For each fixed $z,w\in \mathbb {C}$, the $D_h$-geodesic from z to w is a.s. unique. This follows from, e.g., the proof of [62, Theorem 1.2] (see also [36, Lemma 2.2]).

In the remainder of this section we give a very rough idea of the proof of Theorem 1.9. There are a number of technicalities involved, which we will gloss over in order to make the central ideas as transparent as possible. Consequently, some of the statements in this subsection are not exactly accurate without additional caveats. More detailed (and more precise) outlines can be found at the beginnings of the individual sections and subsections.

We first comment briefly on the role of the axioms in the proof. Axiom II (locality) shows that the metric is compatible with the long-range independence and domain Markov properties of the GFF. These properties will be used in several places of our proofs (see Sect. 2.3). Axiom III (Weyl scaling) has two main uses. First, it implies that adding a constant C to the field scales distances by a factor of $e^{\xi C}$. This is important since the law of the GFF is only scale and translation invariant modulo additive constant. Second, it allows us to show that certain distance-related events occur with positive probability by adding a smooth bump function h and noting that this affects the law of the GFF in an absolutely continuous way (see the outline of Section 5 below). Axioms IV (translation invariance) and V (tightness across scales) are often used together to get estimates for the restriction of the metric to the Euclidean ball of radius r centered at z which are uniform over all possible points z and radii r. We will sometimes also use Axiom IV by itself, with r fixed, when we need more precise information than just up-to-constants estimates.

Main idea of the proof Suppose D and $\widetilde{D}$ are two weak $\gamma$-LQG metrics as in Theorem 1.9 and let h be a whole-plane GFF. As explained in Proposition 2.2, it follows from a general theorem for local metrics of the Gaussian free field [38, Theorem 1.6] that $D_h$ and $\widetilde{D}_h$ are bi-Lipschitz equivalent, i.e.,

$$\begin{aligned}&c_* := \inf \left\{ \frac{\widetilde{D}_h(u,v)}{D_h(u,v)} : u,v\in \mathbb {C} ,\, u\not =v\right\} > 0 \quad \text {and} \nonumber \\&\quad C_* := \sup \left\{ \frac{\widetilde{D}_h(u,v)}{D_h(u,v)} : u,v\in \mathbb {C} ,\, u\not = v\right\} < \infty . \end{aligned}$$

(1.21)

It is easily seen that $c_*$ and $C_*$ are a.s. equal to deterministic constants (Lemma 3.1). We identify $c_*$ and $C_*$ with these constants (which amounts to re-defining $c_*$ and $C_*$ on an event of probability zero). To prove Theorem 1.9 we will show that $c_* = C_*$.

The basic idea of the proof of this fact is as follows. Suppose by way of contradiction that $c_* < C_*$. Then for any $c' \in (c_* , C_*)$ there a.s. exist distinct points $u,v\in \mathbb {C}$ such that $\widetilde{D}_h(u,v) \le c' D_h(u,v)$. In Sect. 3 (see outline below), using translation invariance of the GFF, modulo additive constant, and the local independence properties of the GFF, we will deduce from this that the following is true. There exists $\underline{\beta }, \underline{p}\in (0,1)$, depending only on the laws of $D_h$ and $\widetilde{D}_h$, such that for each $c' \in (c_* , C_*)$ there are many small values of $r> 0$ (how small depends on $c'$) for which

$$\begin{aligned} \mathbb {P}\left[ \exists u, v \in B_{r }(0) \text { s.t. }\ |u - v | \ge \underline{\beta }r \text { and } \widetilde{D}_h(u,v) \le c' D_h(u,v) \right] \ge \underline{p} ,\nonumber \\ \end{aligned}$$

(1.22)

where $B_{r }(0)$ is the Euclidean ball of radius r centered at 0. By interchanging the roles of $D_h$ and $\widetilde{D}_h$, we can similarly find $\overline{\beta }, \overline{p}\in (0,1)$, depending only on the laws of $D_h$ and $\widetilde{D}_h$, such that for each $C' \in (c_* , C_*)$, there are many small values of $r>0$ (how small depends on $C'$) for which

$$\begin{aligned} \mathbb {P}\left[ \exists u, v \in B_{r }(0)\text { s.t. }\ |u - v | \ge \overline{\beta }r\text { and } \widetilde{D}_h(u,v) \ge C' D_h(u,v) \right] \ge \overline{p} .\nonumber \\ \end{aligned}$$

(1.23)

See Sect. 3 for precise statements. The reason why the bounds only hold for “many” choices of $r > 0$, instead of for all $r > 0$, is that we only have tightness across scales (Axiom V), not exact scale invariance. We will use (1.22) to deduce a contradiction to (1.23).

Consider a $D_h$-geodesic P between two fixed points $\mathbb {z} , \mathbb {w} \in \mathbb {C}$. Using (1.22) and a local independence argument for different segments of P (which is explained in the outlines of Sects. 4 and 5 below), one can show that it holds with superpolynomially high probability as $\delta \rightarrow 0$ (i.e., except on an event of probability decaying faster than any positive power of $\delta$), at a rate which is uniform over the choice of $\mathbb {z}$ and $\mathbb {w}$, that the following is true. There are times $0< s< t < D_h(\mathbb {z},\mathbb {w})$ such that $\widetilde{D}_h(P(s) , P(t)) \le c' (t-s)$ and $D_h(P(s) ,P(t)) \ge \delta D_h(\mathbb {z},\mathbb {w})$. By the definition (1.21) of $C_*$, the $\widetilde{D}_h$-distance from $\mathbb {z}$ to P(s) is at most $C_* s$ and the $\widetilde{D}_h$-distance from P(t) to $\mathbb {w}$ is at most $C_* (D_h(\mathbb {z},\mathbb {w}) -t)$. Combining these facts shows that with superpolynomially high probability as $\delta \rightarrow 0$,

$$\begin{aligned} \widetilde{D}_h(\mathbb {z}, \mathbb {w}) \le (C_* - (C_*-c') \delta ) D_h(\mathbb {z}, \mathbb {w}) . \end{aligned}$$

(1.24)

We now let $\overline{\beta }$ be as in (1.23) and fix a large constant $q > 1$. For any $r > 0$, we can take a union bound to get that with probability tending to 1 as $\delta \rightarrow 0$, at a rate which is uniform in r, the bound (1.24) holds simultaneously for all $\mathbb {z} ,\mathbb {w} \in \left( \delta ^q r \mathbb {Z}^2\right) \cap B_{r }(0)$. Now consider an arbitrary pair of points $\mathbb {z} , \mathbb {w} \in B_{r }(0)$ with $|\mathbb {z} - \mathbb {w}| \ge \overline{\beta }r$. Let $\mathbb {z}' ,\mathbb {w}' \in \left( r \delta ^q \mathbb {Z}^2\right) \cap B_{r }(0)$ be the points closest to $\mathbb {z}$ and $\mathbb {w}$, respectively. By the bi-Hölder continuity of $D_h$ and $\widetilde{D}_h$ w.r.t. the Euclidean metric [18, Theorem 1.7], if we choose q sufficiently large, in a manner depending only on the Hölder exponents (i.e., only on $\gamma$), then $|D_h(\mathbb {z} , \mathbb {w}) - D_h(\mathbb {z}' ,\mathbb {w}')|$ and $|\widetilde{D}_h(\mathbb {z} ,\mathbb {w}) - \widetilde{D}_h(\mathbb {z}' ,\mathbb {w}')|$ are much smaller than $\delta D_h(\mathbb {z},\mathbb {w})$. From this, we infer that with probability tending to 1 as $\delta \rightarrow 0$, at a rate which is uniform in r, the bound (1.24) holds simultaneously for all $\mathbb {z},\mathbb {w} \in B_{r }(0)$ with $|\mathbb {z}-\mathbb {w}| \ge \overline{\beta }r$. If $\delta$ is chosen sufficiently small so that this probability is at least $1 - \overline{p}/2$, we get a contradiction to (1.23) with $C ' = C_* - (C_*-c') \delta$.

The purpose of Sects. 3, 4, and 5 is to fill in the details of the above argument. These three sections are mostly independent from one another: only the main theorem/proposition statements at the beginning of each section are used in later sections.

Section 3: bounds for ratios of distances at many scales The purpose of Sect. 3 is to prove (more quantitative versions of) the bounds (1.22) and (1.23) stated above. Since we are only working with a weak $\gamma$-LQG metric, not a strong $\gamma$-LQG metric, we do not have exact scale invariance, just tightness across scales (Axiom V). Consequently, if $c' \in (c_* , C_*)$, then we cannot necessarily say that pairs of points u, v for which $\widetilde{D}_h(u,v) \le c' D_h(u,v)$ exist with uniformly positive probability over different Euclidean scales. That is, it could in principle be that for every small fixed $\underline{\beta }> 0$, the probability that there exists $u,v\in B_{r }(0)$ with $\widetilde{D}_h(u,v) \le c' D_h(u,v)$ and $|u-v| \ge \underline{\beta }r$ is very small for some values of $r > 0$. However, we can say that such pairs of points exist with uniformly positive probability for a suitably “dense” set of scales r via an argument which proceeds (very roughly) as follows.

Let $\underline{\beta }, \underline{p} \in (0,1)$ be small and suppose by way of contradiction that there is a sequence $r_k \rightarrow 0$ such that $r_{k+1} / r_k$ is bounded above and below by deterministic constants and the following is true. For each k, it holds with probability at least $1-\underline{p}$ that $\widetilde{D}_h(u,v) \ge c' D_h(u,v)$ for every pair of points $u,v\in B_{r_k }(0)$ for which $|u-v| \ge \underline{\beta }r_k$. Using the translation invariance of the metric (Axiom IV) and the local independence properties of the GFF (in particular, Lemma 2.6 below), we see that if $\underline{\beta },\underline{p}$ are sufficiently small (how small depends only on the laws of $D_h$ and $\widetilde{D}_h$, not on $c'$ or $r_k$), then the following is true. We can cover any fixed compact subset of $\mathbb {C}$ by Euclidean balls of the form $B_{r_k}(z)$ with the property that $\widetilde{D}_h(u,v) \ge c' D_h(u,v)$ for every pair of points $u \in \partial B_{(1-\underline{\beta })r_k}(z)$ and $v \in \partial B_{r_k}(z)$. By considering the times when a $\widetilde{D}_h$-geodesic between two fixed points of $\mathbb {C}$ crosses an annulus $B_{r_k}(z) {\setminus } B_{(1-\underline{\beta })r_k}(z)$ for z as above, we get that a.s. $\inf _{z,w\in \mathbb {C}} \widetilde{D}_h(z,w) / D_h(z,w) \ge c''$ for a constant $c'' \in (c_* ,c')$. This contradicts the definition (1.21) of $c_*$.

Hence the set of “bad” scales r for which points $u,v \in B_{r }(0)$ with $|u-v| \ge \underline{\beta }r$ and $\widetilde{D}_h(u,v) \le c' D_h(u,v)$ are unlikely to exist cannot be too large, which means that the complementary set of “good” scales for which such points exist with probability at least $\underline{p}$ has to be reasonably dense. This leads to (1.22). The bound (1.23) follows by interchanging the roles of $D_h$ and $\widetilde{D}_h$.

Fig. 1

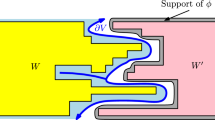
Illustration of the main ideas in Sect. 4. Using results on confluence of geodesics from [36], we can show that there are many times t at which the $D_h$-geodesic P is stable, in the sense that changing the behavior of the field in a small Euclidean ball around P(t) does not result in a macroscopic change to the $D_h$-geodesic (the precise condition is given in (4.11)). In particular, to produce such stable times we consider the metric ball growth started from $\mathbb {z}$ and use the confluence across a metric annulus from [36, Theorem 3.9] at a large number of evenly spaced radii. In fact, using the results of Sect. 3, we can arrange that there are many such stable times whose corresponding balls contain a pair of points u, v such that $\widetilde{D}_h(u,v) \le c' D_h(u,v)$ and $|u-v|$ is comparable to the Euclidean radius of the ball. These pairs of points and the $\widetilde{D}_h$-geodesics between them are shown in blue. Using the results of Sect. 5, we can show that for each of these stable times, it holds with positive conditional probability given the past that P gets close to the corresponding pair of points u, v. By a standard concentration inequality for Bernoulli sums, applied at the stable times, this shows that P has to get close to at least one such pair of points u, v with extremely high probability

Section 4: independence along an LQG geodesic Once we know that there are many pairs of points u, v with $\widetilde{D}_h(u,v) \le c' D_h(u,v)$, we want to use some sort of local independence to say that a $D_h$-geodesic P is extremely likely to get close to at least one such pair of points (i.e., we need the $D_h$-distance from P to each of u and v to be much smaller than $D_h(u,v)$). However, $D_h$-geodesics are highly non-local functionals of the field and do not satisfy any reasonable Markov property. So, techniques for obtaining local independence which may be familiar from the theory of SLE/GFF couplings [23, 28, 66,67,68, 70, 81, 83] do not apply in our setting.

Instead we need to develop a new set of techniques to obtain local independence at different points of $D_h$-geodesics. See Fig. 1 for an illustration. In fact, we will prove a general theorem (Theorem 4.1) which roughly speaking says the following. Suppose we are given events $\mathfrak E_r^{\mathbb {z} , \mathbb {w}}(z)$ for $z , \mathbb {z} , \mathbb {w} \in \mathbb {C}$ and $r > 0$ with the following properties. The event $\mathfrak E_r^{\mathbb {z} ,\mathbb {w}}(z)$ is determined by $h|_{B_r(z)}$ and the part of the $D_h$-geodesic $P^{\mathbb {z},\mathbb {w}}$ from $\mathbb {z}$ to $\mathbb {w}$ which is contained in $B_r(z)$. Moreover, for each $z , \mathbb {z} ,\mathbb {w} \in \mathbb {C}$, the conditional probability of $\mathfrak E_r^{\mathbb {z} , \mathbb {w}}(z)$ given $h|_{\mathbb {C}{\setminus } B_r(z)}$ and the event $\{ P^{\mathbb {z},\mathbb {w}} \cap B_r(z)\not =\emptyset \}$ is a.s. bounded below by a deterministic constant. Then when r is small it is very likely that for nearly every choice of $\mathbb {z}, \mathbb {w} \in \mathbb {C}$, the event $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ occurs for at least one ball $B_r(z)$ hit by $P^{\mathbb {z},\mathbb {w}}$.

We will eventually apply this theorem with $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ given by, roughly speaking, the event that $P^{\mathbb {z},\mathbb {w}}$ gets close to a pair of points $u,v \in B_r(z)$ with $\widetilde{D}_h(u,v) \le c' D_h(u,v)$ and $|u-v| \ge {\text {const}} \times r$. This together with the triangle inequality and the bi-Hölder continuity of $D_h$ and $\widetilde{D}_h$ w.r.t. the Euclidean metric (to transfer from $|u-v| \ge {\text {const}} \times r$ to a lower bound for $D_h(u,v)$) will lead to (1.24).

We will prove the above “independence along a geodesic” theorem using the results on confluence of $D_h$-geodesics established in [36]. These results tell us that if $\mathbb {z} \in \mathbb {C}$ is fixed and $\mathbb {w}_1, \mathbb {w}_2 \in \mathbb {C}$ are close together, then the $D_h$-geodesics $P_1$ from $\mathbb {z}$ to $\mathbb {w}_1$ and $P_2$ from $\mathbb {z}$ to $\mathbb {w}_2$ typically agree until they get close to $\mathbb {w}_1$ and $\mathbb {w}_2$, i.e., $P_1|_{[0,\tau ]} = P_2|_{[0,\tau ]}$ for a time $\tau$ which is close to $D_h(\mathbb {z},\mathbb {w}_1)$ (equivalently, to $D_h(\mathbb {z}, \mathbb {w}_2)$) when $D_h(\mathbb {w}_1,\mathbb {w}_2)$ is small. Note that this property is not true for geodesics for a smooth Riemannian metric, but it is true for geodesics in the Brownian map [56].

Now fix $\mathbb {z} , \mathbb {w}$ and consider the $D_h$-geodesic $P = P^{\mathbb {z},\mathbb {w}}$ from $\mathbb {z}$ to $\mathbb {w}$. The above confluence property applied with $\mathbb {w}_1 = P(t)$ for a typical time $t \in [0,D_h(\mathbb {z},\mathbb {w})]$ and $\mathbb {w}_2$ a point near P(t) will allow us to show that with extremely high probability, there are many times $t\in [0, D_h(\mathbb {z} , \mathbb {w})]$ at which P is “stable” in the following sense. If we make a small modification to h in a neighborhood of P(t), then we will not change $P|_{[0,\tau ]}$ for a time $\tau$ a little bit less than t. This allows us to say that events depending on the field in a small neighborhood of P(t) have positive conditional probability given an initial segment of P. Applying this at a large number of evenly spaced times $t \in [0,D_h(\mathbb {z},\mathbb {w})]$ will show that it is extremely likely that the event $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ discussed above occurs for at least one Euclidean ball $B_r(z)$ hit by P.

Section 5: an LQG geodesic gets close to a shortcut with positive probability Fix $\mathbb {z},\mathbb {w}\in \mathbb {C}$ and let $P = P^{\mathbb {z},\mathbb {w}}$ be the $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$. By (1.22) and translation invariance (Axiom IV) we know that there exists $\underline{\beta },\underline{p}\in (0,1)$ such that if $c' \in (c_* , C_*)$, then there are many values of $r >0$ such that (1.22) holds with z in place of 0 (actually, we will use a variant of (1.22) which gives more precise information about the locations of u and v; see Proposition 3.5). In light of the results of Sect. 4, we want to show that if we condition on $\{P\cap B_r(z) \not =\emptyset \}$, then the conditional probability that P gets close to a pair of points u, v as in (1.22) (with z in place of 0) is bounded below by a positive deterministic constant which does not depend on r or z.

For a deterministic open set $U \subset \mathbb {C}$, one can prove that the $D_h$-geodesic P enters U with positive probability as follows. Consider a deterministic path from $\mathbb {z}$ to $\mathbb {w}$ and let $\phi$ be a smooth bump function which takes large values in a narrow “tube” around this path and which vanishes outside a slightly larger tube. By Weyl scaling (Axiom III), $D_{h-\phi }$ distances in the tube are much shorter than distances anywhere else. Hence the $D_{h-\phi }$-geodesic from $\mathbb {z}$ to $\mathbb {w}$ has to stay in the tube and hence has to enter U. Since the laws of h and $h-\phi$ are absolutely continuous, we get that the $D_h$-geodesic enters U with positive probability.

We will use a similar strategy to show that P has positive conditional probability given $\{P\cap B_r(z)\not =\emptyset \}$ to get near a pair of points $u,v \in B_r(z)$ with $\widetilde{D}_h(u,v) \le c' D_h(u,v)$ and $|u-v| \ge \underline{\beta }r$. However, additional complications arise. For example, the region we want P to enter (a small neighborhood of either u or v) is random, which will be resolved by choosing a deterministic region which contains the $\widetilde{D}_h$-geodesic between u and v with positive probability. We also need to ensure that the condition $\widetilde{D}_h(u,v) \le c' D_h(u,v)$ is not destroyed when we add our bump function. To do this, we will need to make sure that the $\widetilde{D}_h$-geodesic between u and v is contained in the region where the bump function attains its largest possible value. Another issue is that we need the bump function $\phi$ to be supported on a region of diameter of order $r \approx |u-v|$, so that its Dirichlet energy is bounded independently of r. In particular, this support cannot contain the starting and ending points $\mathbb {z}$ and $\mathbb {w}$ of the $D_h$-geodesic. This will be resolved by growing the $D_h$-metric balls from $\mathbb {z}$ and $\mathbb {w}$ until they hit $B_{3r}(z)$ and choosing a bump function whose support approximates a path between the hitting points.

In Sect. 6, we combine all of the above ingredients to conclude the proof of Theorem 1.9, following the argument in the “main ideas” section above. Section 7 contains a list of open problems.

Remark 1.12

(Proof for strong LQG metrics) As explained above, we prove Theorem 1.9 instead of just proving Theorem 1.2 since subsequential limits of LFPP are only known to be weak LQG metrics, not strong LQG metrics. If we only wanted to prove Theorem 1.2, we could make only a few minor simplifications to our proofs. The most significant simplifications would be in Sect. 3. In particular, similar arguments to the ones in Sect. 3 would give points u, v such that $\widetilde{D}_h(u,v) = C_* D_h(u,v)$ instead of just $\widetilde{D}_h(u,v) \ge C' D_h(u,v)$ for $C'$ slightly less than $C_*$. Additionally, all of the results in Sect. 3 which are currently only proven to hold for “at least $\mu \log _8 \varepsilon ^{-1}$ scales” could instead be shown to hold for all scales. This would allow us to eliminate the parameters $\mu ,\nu ,$ and $C'$ throughout the paper. We could of course also replace $\mathfrak c_r$ by $r^{\xi Q}$ and eliminate the “scale parameter” $\mathbb {r}$ throughout. This results in cosmetic simplifications in Sects. 4, 5 and 6.

Remark 1.13

(Relationship to [57, 59]) It is natural to ask how our proof compares to the proofs of the Gromov–Hausdorff convergence of uniform quadrangulations to the Brownian map in [57, 59]. Both this paper and [57, 59] start from a tightness result and seek to show that the limiting object is unique. Moreover, all three papers rely crucially on confluence of geodesics (in the Brownian map setting, tightness is proven in [55] and confluence is proven in [56]). However, this is about the extent of the similarities.

In the Brownian map setting, one has an explicit a priori description of the conjectural limiting metric space $(X,{{\mathfrak {d}}})$ in terms of the Brownian snake. In particular, there is a marked point $x_* \in X$ (which is a uniform sample from the area measure on the Brownian map) such that ${{\mathfrak {d}}}(x_* , x)$ can be described explicitly in terms of the Brownian snake. Due to the convergence of discrete snakes to the Brownian snake and the Schaeffer bijection [13, 78], one gets that any possible subsequential limit of uniform quadrangulations can be represented by a metric $\widetilde{{{\mathfrak {d}}}}$ on X such that $\widetilde{{{\mathfrak {d}}}} \le {{\mathfrak {d}}}$ and $\widetilde{{\mathfrak {d}}}(x_* , x) = {{\mathfrak {d}}}(x_*,x)$ for every $x \in X$ (see [60]). The heart of the proof in each of [56, 59] consists of using confluence to approximate a $\widetilde{{\mathfrak {d}}}$-geodesic by a concatenation of segments of $\widetilde{{\mathfrak {d}}}$-geodesics started from $x_*$ (the method of approximation in the two papers is quite different).

In our setting, we do not have an a priori construction of the limiting object and we do not know a priori that any quantities related to two different weak LQG metrics are exactly equal. Instead, we have a coupling of our weak LQG metric to the GFF. We use confluence together with the Markov property of the GFF to get that far-away geodesic segments are nearly independent from each other.

2 Preliminaries

In this subsection, we first introduce some basic (mostly standard) notation. We then review all of the results from [18, 36, 38] which we will need for the proof of Theorem 1.9. On a first read, the reader may wish to read only Sects. 2.1 (which introduces notation) and 2.2 (which proves the bi-Lipschitz equivalence of the metrics $D_h$ and $\widetilde{D}_h$ in Theorem 2.5) then refer back to the other subsections as needed.

2.1 Basic notation and terminology

2.1.1 Integers

We write $\mathbb {N} = \{1,2,3,\ldots \}$ and $\mathbb {N}_0 = \mathbb {N} \cup \{0\}$. For $a < b$, we define $[a,b]_{\mathbb {Z}}:= [a,b]\cap \mathbb {Z}$.

2.1.2 Asymptotics

If $f :(0,\infty ) \rightarrow \mathbb {R}$ and $g : (0,\infty ) \rightarrow (0,\infty )$, we say that $f(\varepsilon ) = O_\varepsilon (g(\varepsilon ))$ (resp. $f(\varepsilon ) = o_\varepsilon (g(\varepsilon ))$) as $\varepsilon \rightarrow 0$ if $f(\varepsilon )/g(\varepsilon )$ remains bounded (resp. tends to zero) as $\varepsilon \rightarrow 0$. We say that

$$\begin{aligned} f(\varepsilon ) = o_\varepsilon ^\infty (\varepsilon ) \quad \text {if and only if} \quad f(\varepsilon ) = o_\varepsilon (\varepsilon ^p) ,\, \forall p > 0. \end{aligned}$$

(2.1)

We similarly define $O(\cdot )$ and $o(\cdot )$ errors as a parameter goes to infinity.

If $f,g : (0,\infty ) \rightarrow [0,\infty )$, we say that $f(\varepsilon ) \preceq g(\varepsilon )$ if there is a constant $C>0$ (independent from $\varepsilon$ and possibly from other parameters of interest) such that $f(\varepsilon ) \le C g(\varepsilon )$. We write $f(\varepsilon ) \asymp g(\varepsilon )$ if $f(\varepsilon ) \preceq g(\varepsilon )$ and $g(\varepsilon ) \preceq f(\varepsilon )$.

We often specify requirements on the dependencies on rates of convergence in $O(\cdot )$ and $o(\cdot )$ errors, implicit constants in $\preceq$, etc., in the statements of lemmas/propositions/theorems, in which case we implicitly require that errors, implicit constants, etc., in the proof satisfy the same dependencies.

The parameter $\gamma$ is fixed throughout the paper. All implicit constants and rates of convergence are allowed to depend on $\gamma$, and this will not be stated explicitly.

2.1.3 Balls and annuli

For $z\in \mathbb {C}$ and $r>0$, we write $B_r(z)$ for the Euclidean ball of radius r centered at z. We also define the open annulus

$$\begin{aligned} \mathbb {A}_{r_1,r_2}(z) := B_{r_2}(z) {\setminus } \overline{B_{r_1}(z)} ,\quad \forall 0< r_r< r_2 < \infty . \end{aligned}$$

(2.2)

For a metric space $(X,{{\mathfrak {d}}})$ and $r>0$, we write $\mathcal B_r(A;{{\mathfrak {d}}})$ for the open ball consisting of the points $x\in X$ with ${{\mathfrak {d}}}(x,A) < r$. If $A = \{y\}$ is a singleton, we write $\mathcal B_r(\{y\};{{\mathfrak {d}}}) = \mathcal B_r(y;{{\mathfrak {d}}})$.

For a metric ${{\mathfrak {d}}}$ on $\mathbb {C}$, $r>0$, and $z\in \mathbb {C}$ we write $\mathcal B_r^\bullet (z;{{\mathfrak {d}}})$ for the filled metric ball which is the union of $\overline{\mathcal B_r(z;{{\mathfrak {d}}})}$ and the bounded connected components of $\mathbb {C}{\setminus } \overline{\mathcal B_r(z;{{\mathfrak {d}}})}$.

2.1.4 Local sets

Following [83, Lemma 3.9], if (h, A) is a coupling of a whole-plane GFF and random compact set $A \subset \mathbb {C}$, we say that A is a local set for h if for each open set $U\subset \mathbb {C}$, the event $\{A\cap U \not =\emptyset \}$ is conditionally independent from $h|_{\mathbb {C}{\setminus } U}$ given $h|_U$. If A is determined by h (which will be the case for all of the local sets we consider), this is equivalent to the statement that A is determined by $h|_U$ on the event $\{A\subset U\}$. The following lemma is a re-statement of [36, Lemma 2.1].

Lemma 2.1

[36] Let D be a weak $\gamma$-LQG metric and let h be a whole-plane GFF. Also let $z\in \mathbb {C}$ and let $\tau$ be a stopping time for the filtration generated by $(\mathcal B_s^\bullet (z;D_h), h|_{\mathcal B_s^\bullet (z;D_h)})$. Then $\mathcal B_\tau ^\bullet (z;D_h)$ is a local set for h. The same is true with closures of ordinary $D_h$-metric balls in place of filled $D_h$-metric balls.

2.1.5 General notational conventions

We make some comments about how various symbols are used in order to help the reader follow the paper (we will not make any precise definitions here).

We use the symbols $\mathbb {z},\mathbb {w},z,w,u,v$ for points in $\mathbb {C}$. Typically, $\mathbb {z},\mathbb {w}$ are fixed (often the endpoints of a geodesic), z and w are allowed to vary (e.g., over some open set) or are random, and u, v are dummy variables appearing, e.g., in suprema/infima.

We use the symbols p and $\mathbb {p}$ for probabilities. Typically, $\mathbb {p}$ is fixed throughout several lemmas, whereas p is allowed to change more frequently.

The symbols r and $\mathbb {r}$ denote Euclidean radii. Typically, $\mathbb {r}$ represents a fixed Euclidean scale. The reason why we need this is that we do not have exact scale invariance, only tightness across scales, so we often need to prove things at an arbitrary Euclidean scale, rather than just considering a single scale and then re-scaling. The symbol r is used for other Euclidean radii, which may depend on $\mathbb {r}$ and/or be random. We use s and t for LQG radii.

The symbol $\varepsilon$ typically denotes a small parameter which is independent from the Euclidean scale $\mathbb {r}$ (so $\varepsilon \rightarrow 0$ at a rate which does not depend on $\mathbb {r}$). The symbols $\mu$ and $\nu$ will always carry the same meaning as in the proposition statements in Sect. 3: namely, we require that for any fixed $\mathbb {r}$ and any small enough $\varepsilon$, there are at least $\mu \log _8 \varepsilon ^{-1}$ “good” scales $r\in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]$.

2.2 Bi-Lipschitz equivalence of weak LQG metrics

In this subsection we explain why the results of [38] imply that any two weak $\gamma$-LQG metrics with the same scaling constants are bi-Lipschitz equivalent.

Proposition 2.2

Let h be a whole-plane GFF, let $\gamma \in (0,2)$, and let D and $\widetilde{D}$ be two weak $\gamma$-LQG metrics, with the same scaling constants $\mathfrak c_r$. There is a deterministic constant $C>0$ such that a.s.

$$\begin{aligned} C^{-1} D_h(z,w) \le \widetilde{D}_h(z,w) \le C D_h(z,w) ,\quad \forall z,w\in \mathbb {C} . \end{aligned}$$

(2.3)

Proposition 2.2 is a special case of a general theorem from [38] which tells us when two random metrics coupled with the same GFF are bi-Lipschitz equivalent. To state the theorem, we first recall some definitions.

Definition 2.3

(Jointly local metrics) Let $(h,D_1,\ldots ,D_n)$ be a coupling of the GFF h with n random continuous length metrics. We say that $D_1,\ldots ,D_n$ are jointly local metrics for h if for any open set $V\subset \mathbb {C}$, the collection of internal metrics $\{ D_j(\cdot ,\cdot ; V) \}_{j = 1,\ldots ,n}$ is conditionally independent from $(h|_{\mathbb {C}{\setminus } V} , \{ D_j(\cdot ,\cdot ; U{\setminus } \overline{V}) \}_{j = 1,\ldots ,n} )$ given $h|_V$.

In the setting of Proposition 2.2, the metrics $D_h$ and $\widetilde{D}_h$ are each local for h due to Axiom II. Since these metrics are each determined by h, they are conditionally independent given h. Therefore, we can apply [38, Lemma 1.4] to get that $D_h$ and $\widetilde{D}_h$ are jointly local for h.

Definition 2.4

(Additive local metrics) Let $(h,D_1,\ldots ,D_n)$ be a coupling of h with n random continuous length metric which are jointly local for h. For $\xi \in \mathbb {R}$, we say that $D_1,\ldots ,D_n$ are $\xi$-additive for h if for each $z\in \mathbb {C}$ and each $r> 0$ such that $B_r(z) \subset U$, the metrics $(e^{-\xi h_r(z)} D_1,\ldots , e^{-\xi h_r(z)} D_n)$ are jointly local metrics for $h - h_r(z)$.

By Axiom III (Weyl scaling), it follows that our metrics $D_h$ and $\widetilde{D}_h$ are jointly local for h. The following theorem is a special case of [38, Theorem 1.6].

Theorem 2.5

[38] Let $\xi \in \mathbb {R}$, let h be a whole-plane GFF normalized so that $h_1(0) = 0$, and let $(h,D_h ,\widetilde{D}_h)$ be a coupling of h with two random continuous metrics on $\mathbb {C}$ which are jointly local and $\xi$-additive for h. There is a universal constant $p \in (0,1)$ such that the following is true. Suppose there is a constant $C>0$ such that (using the notation for annuli from (2.2)), we have

$$\begin{aligned}&\mathbb {P}\left[ \sup _{u,v \in \partial B_r(z)} \widetilde{D}_h\left( u,v; \mathbb {A}_{r/2,2r}(z) \right) \le C D_h(\partial B_{r/2}(z) , \partial B_r(z) ) \right] \ge p ,\quad \forall z\in \mathbb {C} , \quad \nonumber \\&\qquad \forall r > 0 .\nonumber \\ \end{aligned}$$

(2.4)

Then a.s. $\widetilde{D}(z,w) \le C D(z,w)$ for all $z,w\in \mathbb {C}$.

Proof of Proposition 2.2

By Axioms IV and V for each of $D_h$ and $\widetilde{D}_h$, for any $p\in (0,1)$ we can find a constant $C_p > 1$ such that for each $z\in \mathbb {C}$ and each $r>0$, it holds with probability at least p that

$$\begin{aligned}&\sup _{u,v \in \partial B_r(z)} D_h\left( u,v; \mathbb {A}_{r/2,2r}(z) \right) \le C_p \mathfrak c_r e^{\xi h_r(z)} , \quad D_h(\partial B_{r/2}(z) , \partial B_r(z) )\nonumber \\&\qquad \ge C_p^{-1} \mathfrak c_r e^{\xi h_r(z)} ,\nonumber \\ \end{aligned}$$

(2.5)

and the same is true with $\widetilde{D}_h$ in place of h. Therefore, (2.4) holds with $C = C_p^2$ for each of the pairs $(D_h,\widetilde{D}_h)$ and $(\widetilde{D}_h , D_h)$. Theorem 2.5 therefore implies Proposition 2.2 with $C=C_p^2$, where p is as in Theorem 2.5. $\square$

2.3 Local independence for the GFF

In many places throughout the paper, we will estimate various probabilities using the local independence properties of the GFF. We will do this using two different lemmas, which we state in this section. The first is a restatement of part of [38, Lemma 3.1].

Lemma 2.6

(Iterating events in nested annuli) Fix $0< s_1<s_2 < 1$. Let $\{r_k\}_{k\in \mathbb {N}}$ be a decreasing sequence of positive numbers such that $r_{k+1} / r_k \le s_1$ for each $k\in \mathbb {N}$ and let $\{E_{r_k} \}_{k\in \mathbb {N}}$ be events such that $E_{r_k} \in \sigma \left( (h-h_{r_k}(0)) |_{\mathbb {A}_{s_1 r_k , s_2 r_k}(0) } \right)$ for each $k\in \mathbb {N}$. For $K\in \mathbb {N}$, let N(K) be the number of $k\in [1,K]_{\mathbb {Z}}$ for which $E_{r_k}$ occurs. For each $a > 0$ and each $b\in (0,1)$, there exists $p = p(a,b,s_1,s_2) \in (0,1)$ and $c = c(a,b,s_1,s_2) > 0$ such that if

$$\begin{aligned} \mathbb {P}\left[ E_{r_k} \right] \ge p , \quad \forall k\in \mathbb {N} , \end{aligned}$$

(2.6)

then

$$\begin{aligned} \mathbb {P}\left[ N(K) < b K\right] \le c e^{-a K} ,\quad \forall K \in \mathbb {N}. \end{aligned}$$

(2.7)

We will only ever apply Lemma 2.6 to say that $N(K) \ge 1$ with high probability, i.e., the choice of b in (2.7) will not matter for our purposes.

Lemma 2.7

(Iterating events in disjoint balls) Let h be a whole-plane GFF and fix $s > 0$. Let $n\in \mathbb {N}$ and let $\mathcal Z$ be a collection of $\#\mathcal Z = n$ points in $\mathbb {C}$ such that $|z-w| \ge 2(1+s)$ for each distinct $z,w\in \mathcal Z$. For $z\in \mathcal Z$, let $E_z$ be an event which is determined by $(h - h_{1+s}(z)) |_{B_1(z)}$. For each $p , q \in (0,1)$, there exists $n_* = n_*(s,p,q) \in \mathbb {N}$ such that if $\mathbb {P}[E_z] \ge p$ for each $z\in \mathcal Z$, then

$$\begin{aligned} \mathbb {P}\left[ \bigcup _{z\in \mathcal Z} E_z \right] \ge q ,\quad \forall n \ge n_* . \end{aligned}$$

Proof

Let $U := \bigcup _{z\in \mathcal Z} B_{1+s}(z)$ and let $\mathfrak h$ be the harmonic part of $h|_{U}$. Since the balls $B_{1+ s}(z)$ for $z\in \mathcal Z$ are disjoint, the Markov property of h implies that the fields $(h-h_{1+s}(z))|_{B_{1+s}(z)}$ for $z\in \mathcal Z$, and hence also the events $E_z$, are conditionally independent given $h|_{\mathbb {C}{\setminus } U}$ (equivalently, given $\mathfrak h$).

We will now compare the conditional law given $h|_{\mathbb {C}{\setminus } U}$ to the unconditional law. For $z\in \mathcal Z$, let

$$\begin{aligned} \mathfrak M_z := \sup _{u \in B_{1+s/2}(z)} |\mathfrak h(u) - \mathfrak h(z)| . \end{aligned}$$

(2.8)

By a standard Radon-Nikodym derivative calculation for the GFF (see, e.g., [62, Lemma 4.1]) and the translation and scale invariance of the law of h, modulo additive constant, for each $\alpha >0$ there is a constant $C = C(\alpha ,s) > 0$ such that the following is true. The conditional law given of $(h - h_{1+s}(z))|_{B_1(z)}$ given $h|_{\mathbb {C}{\setminus } U}$ is absolutely continuous with respect to its marginal law and if $H_z$ denotes the Radon-Nikodym derivative of the conditional law with respect to the marginal law, then a.s.

$$\begin{aligned} \max \left\{ \mathbb {E}\left[ H_z^{ \alpha } \,|\, h|_{\mathbb {C}{\setminus } U} \right] , \, \mathbb {E}\left[ H_r^{-\alpha } \,|\, h|_{\mathbb {C}{\setminus } U} \right] \right\} \le C \exp \left( C \mathfrak M_z^2 \right) . \end{aligned}$$

(2.9)

Each $\mathfrak M_z$ is an a.s. finite random variable. By the translation invariance of the law of h, modulo additive constant, the law of $\mathfrak M_z$ does not depend on z. So, we can find a constant $A = A(s,q) > 0$ such that $\mathbb {P}[\mathfrak M_z \le A ] \ge 1 - (1-q)/4$ for each $z \in \mathcal Z$. Then $\mathbb {E}[\#\{z\in \mathcal Z : \mathfrak M_z > A\}] \le (1-q) n / 4$ so

$$\begin{aligned} \mathbb {P}\left[ \#\{z\in \mathcal Z : \mathfrak M_z \le A\} \ge n/2 \right] \ge 1 - \frac{1-q}{2} . \end{aligned}$$

(2.10)

Since $E_z$ is determined by $(h - h_{1+s}(z))|_{B_1(z)}$ and $\mathbb {P}[E_z] \ge p$ for each $z\in \mathcal Z$, (2.9) implies that there exists $\widetilde{p} = \widetilde{p}(p, A) > 0$ such that on the event $\{\mathfrak M_z \le A\}$ (which is determined by $h|_{\mathbb {C}{\setminus } U}$), a.s.

$$\begin{aligned} \mathbb {P}\left[ E_z \,|\, h|_{\mathbb {C}{\setminus } U} \right] \ge \widetilde{p}. \end{aligned}$$

(2.11)

Since the $E_z$’s are conditionally independent given $h|_{\mathbb {C}{\setminus } U}$, we see that a.s.

$$\begin{aligned} \mathbb {P}\left[ \bigcup _{z\in \mathcal Z} E_z \,|\, h|_{\mathbb {C}{\setminus } U} \right] \ge 1 - \widetilde{p}^{\#\{z\in \mathcal Z : \mathfrak M_z \le A\}} . \end{aligned}$$

(2.12)

We now choose $n_*$ large enough that $1 - \widetilde{p}^{n_*/2} \ge 1 - (1-q)/2$ and combine (2.10) with (2.12). $\square$

2.4 Estimates for weak LQG metrics

In this subsection we review results from [18] which we will need for the proofs of our main theorems. Throughout, D denotes a weak $\gamma$-LQG metric and h denotes a whole-plane GFF. In particular, we state a bi-Hölder continuity bound for $D_h$ and the Euclidean metric (Lemma 2.8), a bound for the $D_h$-diameters of squares (Lemma 2.9), and bounds which prevent a $D_h$-geodesic from spending a long time near a line (Lemma 2.10), a circle (Lemma 2.11), or the boundary of a $D_h$-metric ball (Lemma 2.12).

All of the results which we state in this subsection involve a parameter $\mathbb {r}$, which controls the “Euclidean scale” at which we are working. This parameter is necessary since we are only assuming tightness across scales (Axiom V) instead of exact scale invariance. All estimates are required to be uniform in the choice of $\mathbb {r}$. Our first result, which follows from [18, Lemmas 3.20 and 3.22], is a form of local Hölder continuity for the identity map $(\mathbb {C} , |\cdot |) \rightarrow (\mathbb {C} , D_h)$ and its inverse.

Lemma 2.8

(Hölder continuity) Fix a compact set $K\subset \mathbb {C}$ and exponents $\chi \in (0,\xi (Q-2))$ and $\chi ' > \xi (Q+2)$. For each $\mathbb {r} > 0$, it holds with probability tending to 1 as $a \rightarrow 0$, at a rate which is uniform in $\mathbb {r}$, that for each $u,v\in \mathbb {r} K$ with $|u-v| \le a \mathbb {r}$,

$$\begin{aligned} D_h\left( u,v \right) \ge \mathfrak c_{\mathbb {r}} e^{ \xi h_{\mathbb {r}}(0)} \left| \frac{u-v}{\mathbb {r}} \right| ^{\chi '} \quad \text {and} \end{aligned}$$

(2.13)

$$\begin{aligned} D_h\left( u,v ; B_{2|u-v|}(u) \right) \le \mathfrak c_{\mathbb {r}} e^{ \xi h_{\mathbb {r}}(0)} \left| \frac{u-v}{\mathbb {r}} \right| ^\chi . \end{aligned}$$

(2.14)

We note that (2.14) gives an upper bound for the $D_h$-distance from u to v along paths which stay in $B_{2|u-v|}(u)$. This is slightly stronger than just an upper bound for $D_h(u,v)$. In Sect. 5, we will also need the following variant of (2.14) which gives an upper bound for the $D_h$-internal diameters of Euclidean squares and is proven in [18, Lemma 3.20].

Lemma 2.9

(Internal diameters of Euclidean squares) Let K and $\chi$ be as in Lemma 2.8. For each $\chi \in (0,\xi (Q-2))$ and each $\mathbb {r} > 0$, it holds with probability tending to 1 as $\varepsilon \rightarrow 0$, at a rate which is uniform in $\mathbb {r}$, that for each $k\in \mathbb {N}_0$ and each $2^{-k}\varepsilon \mathbb {r} \times 2^{-k}\varepsilon \mathbb {r}$ square S with corners in $2^{-k}\varepsilon \mathbb {r} \mathbb {Z}^2$ which intersects $\mathbb {r} K$,

$$\begin{aligned} \sup _{u,v \in S} D_h\left( u,v ; S \right) \le \mathfrak c_{\mathbb {r}} e^{ \xi h_{\mathbb {r}}(0)} (2^{-k} \varepsilon )^\chi . \end{aligned}$$

(2.15)

In several places throughout the paper, we will want to prevent a $D_h$-geodesic from staying in small neighborhood of a fixed Euclidean path. The following lemma, which is a restatement of [18, Proposition 4.1], will allow us to do this.

Lemma 2.10

(Lower bound for distances in a narrow tube) Let $L\subset \mathbb {C}$ be a compact set which is either a line segment or an arc of a circle and fix $b > 0$. For each $\mathbb {r} > 0$ and each $q > 0$, it holds with probability at least $1 - \varepsilon ^{q^2/(2\xi ^2) + o_\varepsilon (1)}$ that

$$\begin{aligned}&\inf \left\{ D_h\left( u,v ; B_{\varepsilon \mathbb {r}}(\mathbb {r} L ) \right) : u,v \in B_{\varepsilon \mathbb {r}}(\mathbb {r} L ) , |u-v| \ge b\mathbb {r} \right\} \nonumber \\&\qquad \ge \varepsilon ^{ q + \xi Q - 1-\xi ^2/2 } \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)} , \end{aligned}$$

(2.16)

where the rate of the $o_\varepsilon (1)$ depends on L, b, q but not on $\mathbb {r}$.

By [4, Theorem 1.9], for each $\gamma \in (0,2)$ we have $1-\xi Q \ge 0$, and hence $\xi Q - 1 - \xi ^2/2 < 0$. Therefore, the power of $\varepsilon$ on the right side of (2.16) is negative for small enough q. Hence, Lemma 2.10 implies that when $\varepsilon$ is small and $u,v\in B_{\varepsilon \mathbb {r}}(\mathbb {r} L)$ with $|u-v| \ge b\mathbb {r}$, it holds with high probability that $D_h\left( u,v; B_{\varepsilon \mathbb {r}}(\mathbb {r}L)\right)$ is much larger than $D_h(u,v)$. In particular, a $D_h$-geodesic from u to v cannot stay in $B_{\varepsilon \mathbb {r}}(L)$. Lemma 2.10 has the following useful corollary. For the statement, we recall the notation for Euclidean annuli from (2.2).

Lemma 2.11

(Lower bound for distances in a narrow annulus) For each $S> s > 0$ and each $p\in (0,1)$, there exists $\alpha _* = \alpha _*(s,S,p) \in (1/2,1)$ such that for each $\alpha \in [\alpha _*,1)$, each $z\in \mathbb {C}$, and each $\mathbb {r} > 0$,

$$\begin{aligned}&\mathbb {P}\left[ \inf \left\{ D_h\left( u , v ; \mathbb {A}_{\alpha \mathbb {r} , \mathbb {r}}(z) \right) : u , v \in \mathbb {A}_{\alpha \mathbb {r} ,\mathbb {r} }(z) , D_h(u,v) \ge s \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(z)} \right\} \right. \nonumber \\&\qquad \left. \ge S \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(z)} \right] \ge p . \end{aligned}$$

(2.17)

Proof

By Weyl scaling (Axiom III), the event in (2.17) does not depend on the choice of additive constant for h. By Axiom IV (translation invariance) and the translation invariance of the law of h modulo additive constant, the probability of this event does not depend on z. By Axiom V (tightness across scales), we can find $b = b(s) > 0$ such that with probability at least $1-(1-p)/2$, any points $u,v\in B_{\mathbb {r}}(0)$ with $D_h(u,v) \ge s \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)}$ satisfy $|u-v| \ge b \mathbb {r}$. Combining with Lemma 2.10 (with $\varepsilon = 1-\alpha$ and $L =\partial \mathbb {D}$) concludes the proof. $\square$

Finally, we record a lemma which prevents $D_h$-geodesics from spending a long time near the boundary of a $D_h$-metric ball which is needed in Sect. 4.2. The lemma is a re-statement of [18, Proposition 4.3].

Lemma 2.12

(Geodesics cannot spend a long time near metric ball boundary) For each $M > 0$ and each $\mathbb {r} >0$, it holds with probability $1-o_\varepsilon ^\infty (\varepsilon )$ as $\varepsilon \rightarrow 0$, at a rate which is uniform in the choice of $\mathbb {r}$, that the following is true. For each $s > 0$ for which $\mathcal B_s(0;D_h)\subset B_{\varepsilon ^{-M} \mathbb {r}}(0)$ and each $D_h$-geodesic P from 0 to a point outside of $\mathcal B_s(0;D_h)$,

$$\begin{aligned} {\text {area}}\left( B_{\varepsilon \mathbb {r}}(P) \cap B_{\varepsilon \mathbb {r}}\left( \partial \mathcal B_s(0;D_h) \right) \right) \le \varepsilon ^{2 - 1/ M} \mathbb {r}^2, \end{aligned}$$

(2.18)

where ${\text {area}}$ denotes 2-dimensional Lebesgue measure.

2.5 Confluence of geodesics

In this subsection we will review some facts about $D_h$-geodesics which are proven in [36]. These facts are used only in Sect. 4.4. For $z\in \mathbb {C}$, $r >0$, and $n\in \mathbb {N}$ we define the radii $\rho _r^n(z)$ as in [36, Equation (3.13)]. The radius $\rho _r^n(z)$ is the nth smallest $t \in \{2^k r\}_{k\in \mathbb {N}}$ for which a certain event in $\sigma ( (h-h_{6r}(z))|_{\mathbb {A}_{2r,5r}(z)})$ occurs. Roughly speaking, the event in question tells us that if we fix $\mathbb {z} \in \mathbb {C}$ and $t > 0$ such that the filled LQG metric ball $\mathcal B_t^\bullet (\mathbb {z} ;D_h)$ intersects $B_r(z)$, then with constant-order conditional probability given $(\mathcal B_t^\bullet (\mathbb {z} ;D_h) , h|_{\mathcal B_t^\bullet (\mathbb {z} ;D_h)})$, no $D_h$-geodesic from outside of $\mathcal B_t^\bullet (\mathbb {z} ;D_h) \cup B_{5r}(z)$ can enter $B_r(z)$ before hitting $\mathcal B_t^\bullet (\mathbb {z} ; D_h)$ (the precise definition of the event is given in [36, Section 3.2]). We will not need the precise definition of $\rho _r^n(z)$ here, only a few facts which we will review in this subsection.

We have $\rho _r^n(z) \ge 6r$ and $\rho _r^n(z)$ is a stopping time for the filtration generated by $h|_{B_{6 t}(z)}$ for $t\ge r$. The following is immediate from [36, Lemma 3.4], the translation invariance of the law of h, modulo additive constant, and Axiom IV (translation invariance).

Lemma 2.13

(Bounds for radii used to control geodesics) There is a constant $\eta > 0$ depending only on the choice of metric such that the following is true. If we abbreviate

$$\begin{aligned} \rho _{ \mathbb {r} , \varepsilon }(z) := \rho _{\varepsilon \mathbb {r}}^{\lfloor \eta \log \varepsilon ^{-1} \rfloor }(z) , \end{aligned}$$

(2.19)

then for each compact set $K\subset \mathbb {C}$, each $\mathbb {r} > 0$, and each $\mathbb {z}\in \mathbb {C}$, it holds with probability $1 - O_\varepsilon (\varepsilon ^2)$ (at a rate depending on K, but not on $\mathbb {r}$ or $\mathbb {z}$) that

$$\begin{aligned} \rho _{ \mathbb {r} , \varepsilon }(z) \le \varepsilon ^{1/2} \mathbb {r} , \quad \forall z\in \left( \frac{\varepsilon \mathbb {r}}{4} \mathbb {Z}^2 \right) \cap B_{\varepsilon \mathbb {r}}( \mathbb {r} K + \mathbb {z}) . \end{aligned}$$

(2.20)

Henceforth fix $\eta$ as in Lemma 2.13 and let $\rho _{\mathbb {r},\varepsilon }(z)$ be as in (2.19). For $\mathbb {r} > 0$, $\varepsilon > 0$, and a compact set $K\subset \mathbb {C}$, we define

$$\begin{aligned} R_{\mathbb {r}}^\varepsilon (K) := 6 \sup \left\{ \rho _{\mathbb {r},\varepsilon }(z) : z\in \left( \frac{\varepsilon \mathbb {r}}{4} \mathbb {Z}^2 \right) \cap B_{\varepsilon \mathbb {r}}\left( K \right) \right\} +\varepsilon \mathbb {r} . \end{aligned}$$

(2.21)

Since $\rho _{\mathbb {r},\varepsilon }(z)$ is a stopping time for the filtration generated by $h|_{B_{6 t}(z)}$ for $t\ge r$, each $\rho _{\mathbb {r},\varepsilon }(z)$ for $z\in \left( \frac{\varepsilon \mathbb {r}}{4} \mathbb {Z}^2 \right) \cap B_{\varepsilon \mathbb {r}}\left( K \right)$ is a.s. determined by $R_{\mathbb {r}}^\varepsilon (K)$ and the restriction of h to $B_{R_{\mathbb {r}}^\varepsilon (K)}(K)$. Lemma 2.13 shows that for each fixed choice of K, $\mathbb {P}[ R_{\mathbb {r}}^\varepsilon (\mathbb {r} K + \mathbb {z}) \le (6\varepsilon ^{1/2} +\varepsilon ) \mathbb {r} ]$ tends to 1 as $\varepsilon \rightarrow 0$, uniformly over all $\mathbb {z}\in \mathbb {C}$ and $\mathbb {r} >0$.

Recall from Sect. 2.1 that $\mathcal B_s^\bullet (\mathbb {z} ; D_h)$ for $\mathbb {z} \in \mathbb {C}$ and $s > 0$ denotes the filled $D_h$-ball of radius s centered at $\mathbb {z}$. Throughout the rest of this subsection we fix $\mathbb {z} \in \mathbb {C}$ and abbreviate $\mathcal B_s^\bullet := \mathcal B_s^\bullet (\mathbb {z}; D_h)$. For $s >0$, define

$$\begin{aligned} \sigma _{s,\mathbb {r}}^\varepsilon = \sigma _{s,\mathbb {r}}^\varepsilon (\mathbb {z}) := \inf \left\{ s' > s : B_{R_{\mathbb {r}}^\varepsilon (\mathcal B_s^\bullet )}(\mathcal B_s^\bullet ) \subset \mathcal B_{s'}^\bullet \right\} . \end{aligned}$$

(2.22)

We observe that if $\tau$ is a stopping time for $\left\{ \left( \mathcal B_t^\bullet , h|_{\mathcal B_t^\bullet } \right) \right\} _{t\ge 0}$, then so is $\sigma _{\tau , \mathbb {r} }^\varepsilon$. The following lemma is used to prevent $D_h$-geodesics from getting near a specified boundary point of a $D_h$-metric ball. It is an immediate consequence of [36, Lemma 3.6] (which is the case when $\mathbb {z} = 0$) together with the translation invariance of the law of h, modulo additive constant, and Axiom IV (translation invariance).

Lemma 2.14

(Geodesics are unlikely to get near a specified point of $\partial \mathcal B_\tau ^\bullet$) There exists $\alpha >0$, depending only on the choice of metric, such that the following is true. Let $r > 0$, let $\tau$ be a stopping time for the filtration generated by $\left\{ \left( \mathcal B_s^\bullet , h|_{\mathcal B_s^\bullet } \right) \right\} _{s \ge 0}$, and let $x\in \partial \mathcal B_\tau ^\bullet$ and $\varepsilon \in (0,1)$ be chosen in a manner depending only on $( \mathcal B_\tau ^\bullet , h|_{\mathcal B_\tau ^\bullet } )$. There is an event $G_x^\varepsilon \in \sigma \left( \mathcal B_{ \sigma _{\tau ,r}^\varepsilon }^\bullet , h|_{B_{ \sigma _{\tau ,r}^\varepsilon }^\bullet } \right)$ with the following properties.

• A. If $R_r^\varepsilon (\mathcal B_\tau ^\bullet ) \le {\text {diam}} \mathcal B_\tau ^\bullet$ and $G_x^\varepsilon$ occurs, then no $D_h$-geodesic from $\mathbb {z}$ to a point in $\mathbb {C}{\setminus } \mathcal B_{\sigma _{\tau ,\mathbb {r}}^\varepsilon }^\bullet$ can enter $B_{\varepsilon r}(x) {\setminus } \mathcal B_\tau ^\bullet$.

• B. There is a deterministic constant $C_0 > 1$ depending only on the choice of metric such that a.s. $\mathbb {P}\left[ G_x^\varepsilon \,|\, \mathcal B_\tau ^\bullet , h|_{\mathcal B_\tau ^\bullet } \right] \ge 1 - C_0 \varepsilon ^\alpha$.

We will now state a confluence property for LQG geodesics started from $\mathbb {z}$. Each point $x\in \partial \mathcal B_s^\bullet$ lies at $D_h$-distance exactly s from $\mathbb {z}$, so every $D_h$-geodesic from $\mathbb {z}$ to x stays in $\mathcal B_s^\bullet$. For some atypical points x there might be many such $D_h$-geodesics. But, it is shown in [36, Lemma 2.4] that there is always a distinguished $D_h$-geodesic from $\mathbb {z}$ to x, called the leftmost geodesic, which lies (weakly) to the left of every other $D_h$-geodesic from $\mathbb {z}$ to x if we stand at x and look outward from $\mathcal B_s^\bullet$. The following is [36, Theorem 1.4].

Theorem 2.15

(Confluence of geodesics across a metric annulus) Almost surely, for each $0< t< s < \infty$ there is a finite set of $D_h$-geodesics from $\mathbb {z}$ to $\partial \mathcal B_t^\bullet$ such that every leftmost $D_h$-geodesic from $\mathbb {z}$ to $\partial \mathcal B_s^\bullet$ coincides with one of these $D_h$-geodesics on the time interval [0, t]. In particular, there are a.s. only finitely many points of $\partial \mathcal B_t^\bullet$ which are hit by leftmost $D_h$-geodesics from $\mathbb {z}$ to $\partial \mathcal B_s^\bullet$.

Combined with [36, Lemma 2.7], Theorem 2.15 tells us that we can decompose $\partial \mathcal B_s^\bullet$ into a finite union of boundary arcs such that for any points $x,y\in \partial \mathcal B_s^\bullet$ which lie in the same arc, the leftmost $D_h$-geodesics from $\mathbb {z}$ to x and from $\mathbb {z}$ to y coincide in the time interval [0, t]. We will need a more quantitative version of Theorem 2.15 which gives us stretched exponential concentration for the number of such arcs if we truncate on a certain high-probability regularity event. To this end, we define

$$\begin{aligned} \tau _r(\mathbb {z}) := D_h(\mathbb {z} , \partial B_r(\mathbb {z}) ) = \inf \left\{ s> 0 : \mathcal B_s^\bullet \not \subset B_r(\mathbb {z}) \right\} ,\quad \forall r > 0 . \end{aligned}$$

(2.23)

We also fix $\chi \in (0, \xi (Q-2))$, chosen in a manner depending only on $\xi$ and Q, so that by Lemma 2.8$D_h$ is a.s. locally $\chi$-Hölder continuous w.r.t. the Euclidean metric. For $\mathbb {r} >0$ and $a \in (0,1)$, we define $\mathcal E_{\mathbb {r}}^{\mathbb {z}}(a)$ to be the event that the following is true.

• 1. (Comparison of $D_h$-balls and Euclidean balls) $B_{a \mathbb {r}}(\mathbb {z}) \subset \mathcal B_{\tau _{\mathbb {r}}}^\bullet$ and $\tau _{3\mathbb {r}} - \tau _{2\mathbb {r}} \ge a \mathfrak c_{\mathbb {r}} e^{ \xi h_{\mathbb {r}}(0)}$.

• 2. (One-sided Hölder continuity) $\mathfrak c_{\mathbb {r}}^{-1} e^{-\xi h_r(0)} D_h(u,v) \le \left( \frac{ |u - v| }{\mathbb {r}} \right) ^\chi$ for each $u,v \in B_{4 \mathbb {r}}(0)$ with $|u-v|/\mathbb {r} \le a$.

• 3. (Bounds for radii used to control geodesics) The radii of Lemma 2.13 satisfy $\rho _{\mathbb {r},\varepsilon }(z) \le \varepsilon ^{1/2}\mathbb {r}$ for each $z\in \left( \frac{\varepsilon \mathbb {r}}{4} \mathbb {Z}^2 \right) \cap B_{4 \mathbb {r}}(\mathbb {z})$ and each dyadic $\varepsilon \in (0,a]$.

It is easy to see that $\mathbb {P}[\mathcal E_{\mathbb {r}}^{\mathbb {z}}(a)] \rightarrow 1$ as $a\rightarrow 0$, uniformly over the choice of $\mathbb {r}$ and $\mathbb {z}$: in particular, this follows from [36, Lemma 3.8] (which is the case when $\mathbb {z}=0$) and Axiom IV. We will in fact show in Sect. 4.3 that with high probability, $\mathcal E_{\mathbb {r}}^{\mathbb {z}}(a)$ occurs simultaneously for all $\mathbb {z}$ in a fixed bounded open subset of $\mathbb {C}$. The following more quantitative version of Theorem 2.15 is [36, Theorem 3.9].

Theorem 2.16

(Quantitative confluence of geodesics) For each $a \in (0,1)$, there is a constant $b_0 > 0$ depending only on a and constants $b_1 , \beta > 0$ depending only on the choice of metric D such that the following is true. For each $\mathbb {z}\in \mathbb {C}$, each $\mathbb {r} >0$, each $N\in \mathbb {N}$, and each stopping time $\tau$ for $\{(\mathcal B_s^\bullet , h|_{\mathcal B_s^\bullet })\}_{s\ge 0}$ with $\tau \in [\tau _{\mathbb {r}}(\mathbb {z}) ,\tau _{2\mathbb {r}}(\mathbb {z}) ]$ a.s., the probability that $\mathcal E_{\mathbb {r}}^{\mathbb {z}}(a)$ occurs and there are more than N points of $\partial \mathcal B_{\tau }^\bullet$ which are hit by leftmost $D_h$-geodesics from $\mathbb {z}$ to $\partial \mathcal B_{\tau + N^{-\beta } \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})} }^\bullet$ is at most $b_0 e^{-b_1 N^\beta }$.

3 The optimal bi-Lipschitz constant

Throughout this section, we assume that we are in the setting of Theorem 1.9, so that D and $\widetilde{D}$ are two weak $\gamma$-LQG metrics with the same scaling constants. We also let h be a whole-plane GFF. We know from Proposition 2.2 that $D_h$ and $\widetilde{D}_h$ are a.s. bi-Lipschitz equivalent. We define the optimal bi-Lipschitz constants $c_*$ and $C_*$ as in (1.21). Since $D_h$ and $\widetilde{D}_h$ are a.s. bi-Lipschitz equivalent (Proposition 2.2), a.s. $0< c_* \le C_* < \infty$.

Lemma 3.1

Each of $c_*$ and $C_*$ is a.s. equal to a deterministic constant.

Proof

We will prove the statement for $C_*$; the statement for $c_*$ is proven in an identical manner. Suppose $C > 0$ is such that $\mathbb {P}[C_*>C] > 0$. We will show that in fact $\mathbb {P}[C_* >C] = 1$.

There is some large deterministic $R > 0$ such that with positive probability, there are points $u,v\in B_R(0)$ such that $\widetilde{D}_h(u,v) / D_h(u,v) > C$. Since each of $D_h$ and $\widetilde{D}_h$ induces the Euclidean topology on $\mathbb {C}$, after possibly increasing R, we can arrange that with positive probability, there are points $u,v\in B_R(0)$ such that

$$\begin{aligned}&\widetilde{D}_h(u,v) / D_h(u,v) > C , \quad D_h(u,v) \le D_h(u,\partial B_R(0)) ,\quad \nonumber \\&\qquad \text {and} \quad \widetilde{D}_h(u,v) \le \widetilde{D}_h(u,\partial B_R(0)) . \end{aligned}$$

(3.1)

The condition that $D_h(u,v) \le D_h(u,\partial B_R(0))$ is equivalent to the condition that v is contained in the $D_h$-metric ball of radius $D_h(u,\partial B_R(0))$ centered at u. By Axiom II (locality), it follows that $h|_{B_R(0)}$ a.s. determines $D_h(u,\partial B_R(0))$ for every $u\in B_R(0)$ and hence also $h|_{B_R(0)}$ determines all of the $D_h$-metric balls of radius $D_h(u,\partial B_R(0))$ centered at points of $B_R(0)$. Similar considerations hold with $\widetilde{D}_h$ in place of $D_h$. Therefore, the event that there exist $u,v\in B_R(0)$ such that (3.1) holds is determined by $h|_{B_R(0)}$. In fact, by Axiom III (Weyl scaling) this event is determined by $h|_{B_R(0)}$ viewed modulo additive constant, since adding a constant to h results in scaling $D_h$ and $\widetilde{D}_h$ by the same constant factor.

For $z\in \mathbb {C}$, let E(z) be the event that there exist points $u,v\in B_R(z)$ such that (3.1) holds with $B_R(z)$ in place of $B_R(0)$. Then E(z) is determined by $h|_{B_R(z)}$, viewed modulo additive constant. By Axiom IV (translation invariance) and the translation invariance of the law of h, modulo additive constant, the probability of E(z) does not depend on z. The event that E(z) occurs for infinitely many $z\in \mathbb {Z}^2$ is determined by the tail $\sigma$-algebra generated by $h|_{\mathbb {C}{\setminus } B_r(z)}$, viewed modulo additive constant, as $r\rightarrow \infty$. This tail $\sigma$-algebra is trivial, so we get that a.s. E(z) occurs for infinitely many $z\in \mathbb {C}$. This means that in fact $\mathbb {P}[C_* > C] = 1$, so $C_*$ is a.s. equal to a deterministic constant. $\square$

We henceforth re-define each of $c_*$ and $C_*$ on an event of probability zero so that they are deterministic. The main goal of this section is to show that there are many values of $r > 0$ for which it holds with uniformly positive probability that there are points $\mathbb {z}, \mathbb {w} \in \mathbb {C}$ such that $|\mathbb {z}| , |\mathbb {w}|,$ and $|\mathbb {z} - \mathbb {w}|$ are all of order r and $\widetilde{D}_h(\mathbb {z} ,\mathbb {w}) /D_h(\mathbb {z} , \mathbb {w})$ is close to $C_*$ (resp. $c_*$). To quantify this, we introduce the following events. For $r > 0$, $C' \in (0,C_*]$, and $\beta \in (0,1)$, define

$$\begin{aligned} \overline{G}_r(C',\beta ) := \left\{ \exists \mathbb {z} , \mathbb {w} \in B_{r }(0)\hbox { s.t. }\ |\mathbb {z} - \mathbb {w} | \ge \beta r \hbox { and }\widetilde{D}_h(\mathbb {z} , \mathbb {w} ) \ge C' D_h(\mathbb {z} , \mathbb {w} ) \right\} .\nonumber \\ \end{aligned}$$

(3.2)

For $c' \ge c_*$, we similarly define

$$\begin{aligned} \underline{G}_r(c',\beta ) := \left\{ \exists \mathbb {z} , \mathbb {w} \in B_{r }(0)\hbox { s.t. }\ |\mathbb {z} - \mathbb {w} | \ge \beta r\hbox { and }\widetilde{D}_h(\mathbb {z} , \mathbb {w} ) \le c' D_h(\mathbb {z} , \mathbb {w} ) \right\} .\nonumber \\ \end{aligned}$$

(3.3)

It is easy to see from the definition (1.21) of $C_*$ that for each fixed $r > 0$ and $C' \in (0,C_*)$, there exists $p , \beta \in (0,1)$ (allowed to depend on $C'$ and r) such that $\mathbb {P}[\overline{G}_r(C',\beta )]\ge p$.⁵ Since we are working with weak LQG metrics, which are not known to be exactly invariant under spatial scaling, it is not clear a priori that p and $\beta$ can be taken to be uniform in the choice of r. It is also not clear a priori that p and $\beta$ can be chosen independently of $C'$. Similar considerations apply for $\underline{G}_r(c',\beta )$. We will establish that one can choose p and $\beta$ independently of $C'$ and r provided r is restricted to lie in a suitably “dense” subset of (0, 1), in the following sense.

Proposition 3.2

For each $0< \mu< \nu < 1$, there exists $\overline{\beta }= \overline{\beta }(\mu ,\nu ) \in (0,1)$ and $\overline{p} = \overline{p}(\mu ,\nu ) \in (0,1)$ such that for each $C' \in (0,C_*)$ and each sufficiently small $\varepsilon > 0$ (depending on $C'$), there are at least $\mu \log _8\varepsilon ^{-1}$ values of $r \in [\varepsilon ^{1+\nu } ,\varepsilon ] \cap \{8^{-k} : k\in \mathbb {N}\}$ for which $\mathbb {P}[\overline{G}_r(C' , \overline{\beta })] \ge \overline{p}$.

Proposition 3.3

For each $0< \mu< \nu < 1$, there exists $\underline{\beta }= \underline{\beta }(\mu ,\nu ) \in (1/2,1)$ and $\underline{p} = \underline{p}(\mu ,\nu ) \in (0,1)$ such that for each $c' > c_*$ and each sufficiently small $\varepsilon > 0$ (depending on $c'$), there are at least $\mu \log _8\varepsilon ^{-1}$ values of $r \in [\varepsilon ^{1+\nu } ,\varepsilon ] \cap \{8^{-k} : k\in \mathbb {N}\}$ for which $\mathbb {P}[\underline{G}_r(c' , \underline{\beta })] \ge \underline{p}$.

We emphasize that the parameters $\overline{\beta },\overline{p}$ in Proposition 3.2 (resp. the parameters $\underline{\beta },\underline{p}$ in Proposition 3.3) do not depend on $C'$ (resp. $c'$). The only thing which depends on $C'$ (resp. $c'$) is how small $\varepsilon$ has to be in order for the conclusion of the proposition statement to hold.

3.1 Quantitative versions of Propositions 3.2 and 3.3

We will need more quantitative versions of Propositions 3.2 and 3.3 which differ from the original proposition statements in two important ways. First, instead of starting at a constant-order scale, we will start at some given scale $\mathbb {r} > 0$ for which we have an a priori lower bound on $\mathbb {P}[\overline{G}_{\mathbb {r}}(C'',\beta )]$ for some $C'' \in (0,C_*)$ and $\beta \in (0,1)$ (or $\mathbb {P}[\underline{G}_{\mathbb {r}}(c'',\beta )]$ for some $c'' > c_*$ and $\beta \in (0,1)$). We will then produce many radii in $[\varepsilon ^{1+\nu }\mathbb {r}, \varepsilon \mathbb {r}]$ instead of in $[\varepsilon ^{1+\nu } , \varepsilon ]$. The reason for introducing $\mathbb {r}$ is that we only have tightness across scales (Axiom V) instead of true scale invariance. Second, instead of just lower bounding the probability of $\overline{G}_r(C' , \beta )$ or $\underline{G}_r(c',\beta )$, we will obtain a lower bound for the probability of a smaller event which is more complicated, but also more useful. Let us begin by stating a more quantitative version of Proposition 3.2.

Proposition 3.4

For each $0< \mu< \nu < 1$, there exists $\alpha _* = \alpha _*(\mu ,\nu ) \in (1/2,1)$ and $p = p(\mu ,\nu ) \in (0,1)$ such that for each $\alpha \in [\alpha _*,1)$ and each $C' \in (0,C_*)$, there exists $C'' = C''(\alpha ,C',\mu ,\nu ) \in (C' , C_*)$ such that for each $\beta \in (0,1)$, there exists $\varepsilon _0 = \varepsilon _0(\beta ,\alpha ,C',\mu ,\nu ) > 0$ such that the following holds for each $\mathbb {r} > 0$ for which $\mathbb {P}[\overline{G}_{\mathbb {r}}(C'',\beta )] \ge \beta$ and each $\varepsilon \in (0,\varepsilon _0]$.

• (A) There are at least $\mu \log _8\varepsilon ^{-1}$ values of $r \in [\varepsilon ^{1+\nu } \mathbb {r} ,\varepsilon \mathbb {r} ] \cap \{8^{-k} \mathbb {r} : k\in \mathbb {N}\}$ for which the following holds with probability at least p. There exists $u \in \partial B_{\alpha r}(0)$ and $v \in \partial B_r(0)$ such that

  $$\begin{aligned} \widetilde{D}_h(u,v) \ge C' D_h(u,v) \end{aligned}$$

  (3.4)

  and the $D_h$-geodesic from u to v is unique and is contained in $\overline{\mathbb {A}_{\alpha r , r}(0)}$.

The event described in (A) is contained in $\overline{G}_r(C' , 1-\alpha )$, so if (A) holds for some $\mathbb {r} > 0$ then there are at least $\mu \log _8 \varepsilon ^{-1}$ values of $r \in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}] \cap \{8^{-k} : k\in \mathbb {N}\}$ such that

$$\begin{aligned} \mathbb {P}[\overline{G}_r(C' , 1 - \alpha )] \ge p . \end{aligned}$$

Furthermore, as explained in Footnote 5, the definition (1.21) of $C_*$ implies that for any $C'' \in (0,C_*)$, there exists some $\beta \in (0,1)$ such that $\mathbb {P}[\overline{G}_1(C'',\beta )] \ge \beta$. Therefore, Proposition 3.4 applied with $\mathbb {r} =1$ implies Proposition 3.2 with $\overline{\beta }=1-\alpha$ and $\overline{p} = p$.

By the symmetry between our hypotheses on $\widetilde{D}_h$ and $D_h$, Proposition 3.4 implies the analogous statement with the roles of $D_h$ and $\widetilde{D}_h$ interchanged, which reads as follows.

Proposition 3.5

For each $0< \mu< \nu < 1$, there exists $\alpha _* = \alpha _*(\mu ,\nu ) \in (1/2,1)$ and $p = p(\mu ,\nu ) \in (0,1)$ such that for each $\alpha \in [\alpha _*,1)$ and each $c' > c_*$, there exists $c'' = c''(\alpha ,c',\mu ,\nu ) \in (c_* , c')$ such that for each $\beta \in (0,1)$, there exists $\varepsilon _0 = \varepsilon _0(\alpha ,\beta ,c',\mu ,\nu ) > 0$ such that the following holds for each $\mathbb {r} > 0$ for which $\mathbb {P}[\underline{G}_{\mathbb {r}}(c'',\beta )] \ge \beta$ and each $\varepsilon \in (0,\varepsilon _0]$.

• (A’) There are at least $\mu \log _8\varepsilon ^{-1}$ values of $r \in [\varepsilon ^{1+\nu } \mathbb {r} ,\varepsilon \mathbb {r} ] \cap \{8^{-k} \mathbb {r} : k\in \mathbb {N}\}$ for which it holds with probability at least p that the following is true. There exists $u \in \partial B_{\alpha r}(0)$ and $v \in \partial B_r(0)$ such that

  $$\begin{aligned} \widetilde{D}_h(u,v) \le c' D_h(u,v) \end{aligned}$$

  (3.5)

  and the $\widetilde{D}_h$-geodesic from u to v is unique and is contained in $\overline{\mathbb {A}_{\alpha r , r}(0)}$.

As in the case of Proposition 3.4, Proposition 3.5 immediately implies Proposition 3.3.

To prove Proposition 3.4, we will (roughly speaking) prove the contrapositive.

Proposition 3.6

For each $0< \mu< \nu < 1$, there exists $\alpha _* = \alpha _*(\mu ,\nu ) \in (1/2,1)$ and $p = p(\mu ,\nu ) \in (0,1)$ such that for each $\alpha \in [\alpha _*,1)$ and each $C' \in (0,C_*)$, there exists $C'' = C''(\alpha ,C',\mu ,\nu ) \in (C' , C_*)$ such that for each $\beta \in (0,1)$, there exists $\varepsilon _0 = \varepsilon _0(\alpha ,\beta ,C',\mu ,\nu ) > 0$ such that if $\mathbb {r} > 0$ and there exists $\varepsilon \in (0,\varepsilon _0]$ satisfying the condition (B) just below, then $\mathbb {P}[\overline{G}_{\mathbb {r}}(C'',\beta ) ] < \beta$.

• (B) There are at least $(\nu -\mu ) \log _8\varepsilon ^{-1}$ values of $r \in [\varepsilon ^{1+\nu } \mathbb {r} ,\varepsilon \mathbb {r} ] \cap \{8^{-k} \mathbb {r} : k\in \mathbb {N}\}$ for which it holds with probability at least $1- p$ that the following is true. For each $u\in \partial B_{\alpha r}(0)$ and $v\in \partial B_r(0)$ for which the $D_h$-geodesic from u to v is unique and is contained in $\overline{\mathbb {A}_{\alpha r , r}(0)}$, one has

  $$\begin{aligned} \widetilde{D}_h(u,v) \le C' D_h(u,v) . \end{aligned}$$

  (3.6)

Proof of Proposition 3.4, assuming Proposition 3.6

Assume we are given $0<\mu<\nu <1$ and let $\alpha _* , p$ be chosen as in Proposition 3.6. Also fix $\alpha \in [\alpha _*,1)$, $C' \in (0,C_*)$, and $\beta \in (0,1)$ and let $C''$ and $\varepsilon _0$ be chosen as in Proposition 3.6. For $\mathbb {r}, \varepsilon > 0$, let $\mathcal K_{\mathbb {r}}^\varepsilon := [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}] \cap \left\{ 8^{-k} \mathbb {r} : k\in \mathbb {N} \right\}$ and note that $\#\mathcal K_{\mathbb {r}}^\varepsilon = \lfloor \nu \log _8 \varepsilon ^{-1} \rfloor$.

If (A) does not hold for some $\mathbb {r} > 0$ and $\varepsilon \in (0,\varepsilon _0]$, then there are fewer than $\mu \log _8 \varepsilon ^{-1}$ values of $k\in \mathcal K_{\mathbb {r}}^{\varepsilon }$ for which the last sentence of (A) holds with probability at least p. For such a choice of $\mathbb {r}$ and $\varepsilon$, there are at least $(\nu -\mu )\log _8\varepsilon ^{-1}$ values of $k\in \mathcal K_{\mathbb {r}}^{\varepsilon }$ for which the last sentence of (B) holds with probability at least $1-p$. That is, (B) holds for the pair $(\mathbb {r} , \varepsilon )$. By Proposition 3.6, this means that $\mathbb {P}[\overline{G}_{\mathbb {r}}(C'',\beta ) ] < \beta$. Hence we have proven the contrapositive of Proposition 3.4. $\square$

3.2 Proof of Proposition 3.6

As explained in Sect. 3.1, to prove all of the propositions statements from earlier in this section it remains only to prove Proposition 3.6. The basic idea of the proof is as follows. If we assume that (B) holds for a small enough choice of $p\in (0,1)$ (depending only on $\mu$ and $\nu$), then we can use Lemma 2.6 to cover space by Euclidean balls of the form $B_{r/2}(z)$ for $r\in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]$ with the following property. For each $u \in \partial B_{\alpha r}(z)$ and each $v\in \partial B_{r}(z)$ such that the $D_h$-geodesic from u to v is unique and is contained in $\overline{\mathbb {A}_{\alpha r , r}(z)}$, we have $\widetilde{D}_h(u,v) \le C' D_h(u,v)$. By considering the times when a $D_h$-geodesic between two fixed points $\mathbb {z} , \mathbb {w} \in \mathbb {C}$ crosses the annulus $\mathbb {A}_{\alpha r , r}(z)$ for such a z and r, we will be able to show that $\widetilde{D}_h(\mathbb {z} , \mathbb {w}) \le C'' D_h(\mathbb {z},\mathbb {w})$ for a suitable constant $C'' \in (C' , C_*)$. Applying this to an appropriate $\beta$-dependent collection of pairs of points $(\mathbb {z}, \mathbb {w})$ will show that $\mathbb {P}[\overline{G}_{\mathbb {r}}(C'',\beta ) ] < \beta$. The reason why we need to make $\alpha$ close to 1 is to ensure that the events we consider depend on h in a sufficiently “local” manner (see the discussion just after the definition of ${\mathsf {E}}_r(z)$ below).

Let us now define the events to which we will apply Lemma 2.6. For $z \in \mathbb {C}$, $r > 0$, and parameters $\alpha \in (1/2,1)$, $A > 1$ and $C' \in (0,C_*)$, let ${\mathsf {E}}_r(z) = {\mathsf {E}}_r(z; \alpha ,A,C')$ be the event that the following is true.

• 1. (Comparison of $D_h$ and $\widetilde{D}_h$) For each $u \in \partial B_{\alpha r}(z)$ and each $v\in \partial B_{r}(z)$ such that the $D_h$-geodesic from u to v is unique and is contained in $\overline{\mathbb {A}_{\alpha r , r}(z)}$, we have $\widetilde{D}_h(u,v) \le C' D_h(u,v)$.

• 2. (Lower bound for paths in $\mathbb {A}_{\alpha r , r}(z)$) If $u \in \partial B_{\alpha r}(z)$ and $v\in \partial B_r(z)$ are such that either $D_h(u,v) > D_h(u , \partial \mathbb {A}_{r/2,2r}(z))$ or $\widetilde{D}_h(u,v) > \widetilde{D}_h(u , \partial \mathbb {A}_{r/2,2r}(z))$, then each path from u to v which stays in $\overline{\mathbb {A}_{\alpha r , r}(z)}$ has $D_h$-length strictly larger than $D_h\left( u , v ; \mathbb {A}_{r/2,2r}(z) \right)$.

• 3. (Distance around $\mathbb {A}_{\alpha r , r}(z)$) There is a path in $\mathbb {A}_{\alpha r , r}(z)$ which disconnects the inner and outer boundaries of $\mathbb {A}_{\alpha r , r}(z)$ and has $D_h$-length at most $A D_h\left( \partial B_{\alpha r}(z) , \partial B_{ r}(z) \right)$.

Condition 1 is the main point of the event ${\mathsf {E}}_r(z)$, as discussed just above. The purpose of condition 2 is to ensure that ${\mathsf {E}}_r(z)$ is determined by $h|_{\mathbb {A}_{r/2,2r}(z)}$. Without this condition, we would not necessarily be able to tell whether a path in $\overline{\mathbb {A}_{\alpha r ,r}(z)}$ is a $D_h$-geodesic without seeing the field outside of $\mathbb {A}_{r/2,2r}(z)$ (see Lemma 3.7). The purpose of condition 3 is as follows. If a $D_h$-geodesic between two points outside of $B_r(z)$ enters $B_{\alpha r}(z)$, then it must cross the path from condition 3 twice. This means that it can spend at most $A D_h\left( \partial B_{\alpha r}(z) , \partial B_{ r}(z) \right)$ units of time in $B_{\alpha r}(z)$ since otherwise the path from condition 3 would provide a shortcut, which would contradict the definition of a geodesic. If we assume (B), this fact will eventually allow us to force a $D_h$-geodesic to spend a positive fraction of its time tracing segments between points u, v with $\widetilde{D}_h(u,v) \le C' D_h(u,v)$.

We want to use Lemma 2.6 to argue that if (B) holds, then with high probability there are many values of $z\in \mathbb {C}$ such that ${\mathsf {E}}_r(z)$ occurs for some $r\in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]$. We first check the measurability condition in Lemma 2.6

Lemma 3.7

For each $z\in \mathbb {C}$ and $r>0$,

$$\begin{aligned} {\mathsf {E}}_r(z) \in \sigma \left( (h-h_{4r}(z)) |_{ \mathbb {A}_{r/2,2r}(z) } \right) . \end{aligned}$$

(3.7)

Proof

By Axiom III (Weyl scaling) subtracting $h_{4r}(0)$ from h results in scaling $D_h$ and $\widetilde{D}_h$ by the same factor, so does not affect the occurrence of ${\mathsf {E}}_r(z)$. Hence it suffices to prove (3.7) with $h|_{\mathbb {A}_{r/2,2r}(z)}$ in place of $(h-h_{4r}(z)) |_{ \mathbb {A}_{r/2,2r}(z) }$. From Axiom III, it is obvious that condition 3 in the definition of ${\mathsf {E}}_r(z)$ (distance around $\mathbb {A}_{\alpha r , r}(z)$) is determined by $h |_{ \mathbb {A}_{r/2,2r}(z) }$.

For $u \in \partial B_{\alpha r}(z)$ and $v\in \partial B_{r}(z)$, we can determine whether $D_h(u,v) > D_h(u , \partial \mathbb {A}_{r/2,2r}(z))$ from the internal metric $D_h\left( \cdot ,\cdot ;\mathbb {A}_{r/2,2r}(z) \right)$: indeed, $D_h(u , \partial \mathbb {A}_{r/2,2r}(z))$ is clearly determined by this internal metric and $D_h(u,v) \le D_h(u , \partial \mathbb {A}_{r/2,2r}(z))$ if and only if v is contained in the $D_h$-ball of radius $D_h(u , \partial \mathbb {A}_{r/2,2r}(z))$ centered at v, which is contained in $\overline{\mathbb {A}_{r/2,2r}(z)}$. Similar considerations hold with $\widetilde{D}_h$ in place of $D_h$. Hence condition 2 in the definition of ${\mathsf {E}}_r(z)$ (lower bound for paths in $\mathbb {A}_{\alpha r , r}(z)$) is determined by $h|_{\mathbb {A}_{r/2,2r}(z)}$.

If P is a path from $u \in \partial B_{\alpha r}(z)$ to $v\in \partial B_r(z)$ which stays in $\overline{\mathbb {A}_{\alpha r ,r}(z)}$, then P is a $D_h$-geodesic if and only if ${\text {len}}(P ; D_h) = D_h(u,v)$. Hence if condition 2 holds, then P cannot be a $D_h$-geodesic unless $D_h(u,v) \le D_h(u , \partial \mathbb {A}_{r/2,2r}(z) )$ and $\widetilde{D}_h(u,v) \le \widetilde{D}_h(u , \partial \mathbb {A}_{r/2,2r}(z) )$ (note that $D_h(u,v ; \mathbb {A}_{r/2,2r}(z)) \ge D_h(u,v)$), in which case we can tell whether P is a $D_h$-geodesic from the restriction of h to the $D_h$-metric ball of radius $D_h(u , \partial \mathbb {A}_{r/2,2r}(z) )$ centered at u, which in turn is determined by $h|_{\mathbb {A}_{r/2,2r}(z)}$. Furthermore, on the event that $D_h(u,v) \le D_h(u , \partial \mathbb {A}_{r/2,2r}(z) )$ and $\widetilde{D}_h(u,v) \le \widetilde{D}_h(u , \partial \mathbb {A}_{r/2,2r}(z) )$, both $D_h(u,v)$ and $\widetilde{D}_h(u,v)$ are determined by $h|_{\mathbb {A}_{r/2,2r}(z)}$. Therefore, the intersection of conditions 1 (comparison of $D_h$ and $\widetilde{D}_h$) and 2 in the definition of ${\mathsf {E}}_r(z)$ is determined by $h|_{\mathbb {A}_{r/2,2r}(z)}$. Hence we have proven (3.7). $\square$

We now show that (B) implies a lower bound for $\mathbb {P}[{\mathsf {E}}_r(z)]$ for some values of $r \in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]$.

Lemma 3.8

For each $0< \mu< \nu < 1$ and each $q > 0$, there exists $\alpha _* \in (1/2,1)$ and $p\in (0,1)$ depending only on $q , \mu ,\nu$ such that for each $\alpha \in [\alpha _*,1)$, there exists $A = A(\alpha ,q,\mu ,\nu ) > 1$ such that the following is true for each $C'\in (0,C_*)$. If $\mathbb {r} > 0$ and $\varepsilon \in (0,1)$ such that (B) holds for the above choice of $p,\alpha , C'$, then

$$\begin{aligned}&\mathbb {P}\left[ {\mathsf {E}}_r(z)\text { occurs for at least one } r\in [\varepsilon ^{1+\mu } \mathbb {r} , \varepsilon \mathbb {r}] \cap \{8^{-k} \mathbb {r} :k\in \mathbb {N}\} \right] \nonumber \\&\quad \ge 1 - O_\varepsilon (\varepsilon ^q ) ,\quad \forall z \in \mathbb {C} , \end{aligned}$$

(3.8)

at a rate which is uniform over the choices of z and $\mathbb {r}$.

Proof

Assume (B) is satisfied for some choice of $\mathbb {r} ,\varepsilon , p , \alpha ,C'$ and let $r_1,\ldots ,r_K \in [\varepsilon ^{1+\mu } \mathbb {r} , \varepsilon \mathbb {r}] \cap \{8^{-k} \mathbb {r} :k\in \mathbb {N}\}$ be the values of r from (B), enumerated in decreasing order. Note that $K\ge (\nu -\mu ) \log _8\varepsilon ^{-1}$ by assumption. By Lemma 3.7, we can apply Lemma 2.6 to find that there exists $\widetilde{p} = \widetilde{p}(q,\mu , \nu ) \in (0,1)$ such that if

$$\begin{aligned} \mathbb {P}[{\mathsf {E}}_{r_k}(z)] \ge \widetilde{p} ,\quad \forall z\in \mathbb {C} , \quad \forall k\in [1,K ]_{\mathbb {Z}} , \end{aligned}$$

(3.9)

then (3.8) holds. It therefore suffices to choose p, $\alpha _*$, and A in an appropriate manner depending on $\widetilde{p}$ so that if (B) holds, then (3.9) holds.

By tightness across scales (Axiom V), we can find $S> s > 0$ depending on $\widetilde{p}$ such that for each $z\in \mathbb {C}$ and $r>0$, it holds with probability at least $1 - (1-\widetilde{p})/4$ that

$$\begin{aligned}&D_h\left( \partial B_r(z) , \partial \mathbb {A}_{r/2 , 2r}(z) \right) \ge s \mathfrak c_r e^{\xi h_r(z)} \quad \text {and} \quad \nonumber \\&\quad \sup _{u,v\in \mathbb {A}_{3 r /4 , r}(z)} D_h\left( u ,v ; \mathbb {A}_{r/2,2r}(z)\right) \le S \mathfrak c_r e^{\xi h_r(z)} , \end{aligned}$$

(3.10)

and the same is true with $\widetilde{D}_h$ in place of $D_h$. Since $\mathbb {A}_{\alpha r , r}(z) \subset \mathbb {A}_{3 r /4 , r}(z)$ for any choice of $\alpha \in [3/4,1)$, Lemma 2.11 with the above choice of s and S gives an $\alpha _* \in [3/4,1)$ depending on $\widetilde{p}$ such that for each $\alpha \in [\alpha _*,1)$, $z \in \mathbb {C}$, and $r>0$, condition 2 (lower bound for paths in $\mathbb {A}_{\alpha r , r}(z)$) in the definition of ${\mathsf {E}}_r(z)$ holds with probability at least $1-(1-\widetilde{p})/3$.

Now suppose $\alpha \in [\alpha _*,1)$. We can again apply Axiom V (tightness across scales) to find that there exists $A > 1$ depending on $\alpha$ and $\widetilde{p}$ such that for each $z\in \mathbb {C}$ and $r>0$, condition 3 (distance around $\mathbb {A}_{\alpha r , r}(z)$) in the definition of ${\mathsf {E}}_r(z)$ occurs with probability at least $1 - (1 - \widetilde{p})/3$.

If (B) holds for the above choice of $\alpha$ and with $p < (1-\widetilde{p})/3$, then for each $z\in \mathbb {C}$ and each $k\in [1,K ]_{\mathbb {Z}}$, condition 1 (comparison of $D_h$ and $\widetilde{D}_h$) in the definition of ${\mathsf {E}}_{r_k }(z)$ holds with probability at least $1- (1-\widetilde{p})/3$. Combining the three preceding paragraphs shows that (3.9) holds. $\square$

Lemma 3.9

There is a $q>1$ depending only on $\mu ,\nu$ such that if $p,\alpha _*$, $\alpha \in [\alpha _*,1)$, and A is chosen as in Lemma 3.8 for this choice of q, then the following is true for each $C'\in (0,C_*)$. If (B) holds for some $\mathbb {r} > 0$ and $\varepsilon \in (0,1)$ and for this choice of $p,\alpha ,C'$, then for each open set $U\subset \mathbb {C}$, it holds with probability tending to 1 as $\varepsilon \rightarrow 0$ (at a rate which is uniform in $\mathbb {r}$) that for $z\in \mathbb {r} U$, there exists $r \in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]\cap \{8^{-k} \mathbb {r} :k\in \mathbb {N}\}$ and $w\in \left( \frac{\varepsilon ^{1+\nu } \mathbb {r}}{100} \mathbb {Z}^2 \right) \cap (\mathbb {r} U)$ such that $z\in B_{r/2}(w)$ and ${\mathsf {E}}_r(w)$ occurs.

Proof

Upon choosing q sufficiently large, this follows from Lemma 3.8 and a union bound over all $w \in \left( \frac{\varepsilon ^{1+\nu } \mathbb {r}}{100} \mathbb {Z}^2 \right) \cap (\mathbb {r} U)$. $\square$

Fig. 2

Illustration of the proof of Proposition 3.6. The $D_h$-geodesic P from $\mathbb {z}$ to $\mathbb {w}$ along with one of the balls $B_{r_j}(w_j)$ hit by P for which ${\mathsf {E}}_{r_j}(w_j)$ occurs are shown. The time $t_j$ is the first time that P exits $B_{r_j}(w_j)$ after time $t_{j-1}$ and the time $s_j$ is the last time before $t_j$ at which P hits $\partial B_{\alpha r_j}(w_j)$. Condition 1 in the definition of ${\mathsf {E}}_{r_j}(w_j)$ shows that $\widetilde{D}_h(P(s_j) , P(t_j)) \le C' (t_j - s_j)$. The orange path comes from condition 3 in the definition of ${\mathsf {E}}_{r_j}(w_j)$, and its $D_h$-length is at most $A D_h(\partial B_{\alpha r_j}(w_j) , \partial B_{r_j}(w_j)) \le A (t_j - s_j)$. Since P crosses this orange path both before time $t_{j-1}$ and after time $s_j$ and P is a $D_h$-geodesic, we have that $s_j - t_{j-1} \le A (t_j - s_j)$. This shows that the intervals $[s_j , t_j]$ occupy a uniformly positive fraction of the total $D_h$-length of P, which in turn allows us to show that $\widetilde{D}_h(\mathbb {z} , \mathbb {w}) \le C'' D_h(\mathbb {z} ,\mathbb {w})$ for a constant $C'' \in (C' , C_*)$ depending only on $C' , A$

Proof of Proposition 3.6

See Fig. 2 for an illustration of the proof.

Step 1: setup Let $p, \alpha _*$, $\alpha \in [\alpha _*,1)$, and $A > 1$ be chosen as in Lemma 3.9. Also fix

$$\begin{aligned} C'' \in \left( C' + \frac{A}{ A+1 }(C_* - C') , C_* \right) , \end{aligned}$$

(3.11)

and note that we can choose $C''$ in a manner depending only on $\alpha ,C',\mu ,\nu$ (since A depends only on $\alpha ,\mu ,\nu$).

We will show that there exists $\varepsilon _0 = \varepsilon _0(\beta ,\alpha ,C',\mu ,\nu ) > 0$ such that if $\mathbb {r} > 0$, $\varepsilon \in (0,\varepsilon _0]$, and (B) holds for these values of $\mathbb {r} , \varepsilon ,p,\alpha$, then with probability greater than $1 - \beta$,

$$\begin{aligned} \widetilde{D}_h(\mathbb {z} , \mathbb {w}) \le C'' D_h(\mathbb {z},\mathbb {w}) \quad \forall \mathbb {z},\mathbb {w} \in B_{\mathbb {r} }(0)\text { with } |\mathbb {z}-\mathbb {w}| \ge \beta \mathbb {r}. \end{aligned}$$

(3.12)

In other words, $\mathbb {P}[\overline{G}_{\mathbb {r}}(C'',\beta )^c] > 1 - \beta$, as required.

By Axiom V (tightness across scales), there is some large bounded open set $U\subset \mathbb {C}$ depending only on $\beta$ such that for each $\mathbb {r} >0$, it holds with probability at least $1-\beta /2$, the $D_h$-diameter of $B_{\mathbb {r}}(0)$ is smaller than the $D_h$-distance from $B_{\mathbb {r}}(0)$ to $\partial (\mathbb {r} U)$, in which case every $D_h$-geodesic between points of $B_{\mathbb {r}}(0)$ is contained in $\mathbb {r} U$. Henceforth fix such a choice of U. Let $F_{\mathbb {r}}^\varepsilon$ be the event that every $D_h$-geodesic between points of $B_{\mathbb {r}}(0)$ is contained in $\mathbb {r} U$ and the event of Lemma 3.9 with the above choices of $\alpha ,A,C',$ and U, so that $\mathbb {P}[F^\varepsilon ] \ge 1 - \beta / 2 - o_\varepsilon (1)$, uniformly in $\mathbb {r}$, under the assumption (B).

Step 2: covering a $D_h$-geodesic with paths of short $\widetilde{D}_h$-length To prove (3.12), we consider points $\mathbb {z},\mathbb {w} \in B_{\mathbb {r}}(0) \cap \mathbb {Q}^2$ with $|\mathbb {z}-\mathbb {w}| \ge \beta \mathbb {r}$ and let $P : [0,D_h(\mathbb {z} , \mathbb {w} )] \rightarrow \mathbb {C}$ be the (a.s. unique) $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$. Let $t_0 = 0$ and inductively let $t_j$ for $j\in \mathbb {N}$ be the smallest time $t \ge t_{j-1}$ at which P exits a Euclidean ball of the form $B_{r}(w)$ for $w\in \left( \frac{\varepsilon ^{1+\nu } \mathbb {r}}{100} \mathbb {Z}^2 \right) \cap (\mathbb {r} U)$ and $r\in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}] \cap \{8^{-k} \mathbb {r} :k\in \mathbb {N}\}$ such that $P(t_{j-1}) \in B_{r/2}(w)$ and ${\mathsf {E}}_r(w)$ occurs; or let $t_j = D_h(\mathbb {z} , \mathbb {w} )$ if no such t exists. If $t_j < D_h(\mathbb {z} , \mathbb {w} )$, let $w_j$ and $r_j$ be the corresponding values of w and r. Also let $s_j$ be the last time before $t_j$ at which P hits $\partial B_{\alpha r_j}(w)$, so that $s_j \in [t_{j-1} , t_j]$ and $P([s_j , t_j]) \subset \overline{ \mathbb {A}_{\alpha r_j , r_j}(w_j)}$. Finally, define

$$\begin{aligned} \underline{J}:= & {} \max \left\{ j\in \mathbb {N} : |\mathbb {z} - P(t_{j-1} )|< 2 \varepsilon \mathbb {r} \right\} \quad \text {and} \quad \nonumber \\ \overline{J}:= & {} \min \left\{ j\in \mathbb {N} : |\mathbb {w} - P(t_{j+1} )| < 2 \varepsilon \mathbb {r} \right\} . \end{aligned}$$

(3.13)

The reason for the definitions of $\underline{J}$ and $\overline{J}$ is that $\mathbb {z} , \mathbb {w} \notin B_{ r_j}(w_j)$ for $j \in [\underline{J} , \overline{J}]_{\mathbb {Z}}$ (since $r_j \le \varepsilon \mathbb {r}$ and $P(t_j) \in B_{r_j}(w_j)$). By the definition of $F_{\mathbb {r}}^\varepsilon$, on this event we have $t_j < D_h(\mathbb {z},\mathbb {w})$ and $|P(t_{j-1}) - P(t_j)| \le 2 \varepsilon \mathbb {r}$ whenever $|\mathbb {w} - P(t_{j-1})| \ge \varepsilon \mathbb {r}$. Therefore, on $F_{\mathbb {r}}^\varepsilon$,

$$\begin{aligned} P(t_{\underline{J}}) \in B_{4\varepsilon \mathbb {r}}(\mathbb {z}) \quad \text {and} \quad P(t_{\overline{J}}) \in B_{4\varepsilon \mathbb {r}}(\mathbb {w}) . \end{aligned}$$

(3.14)

Since P is a $D_h$-geodesic, for $j\in [\underline{J} , \overline{J}]_{\mathbb {Z}}$ also $P|_{[s_j , t_j]}$ is a $D_h$-geodesic from $P(s_j) \in \partial \mathcal B_{\alpha r_j}(w_j)$ to $P(t_j) \in \partial B_{r_j}(w_j)$ and by definition this $D_h$-geodesic stays in $\overline{\mathbb {A}_{\alpha r_j , r_j}(w_j)}$. Moreover, $P|_{[s_j,t_j]}$ is the only $D_h$-geodesic from $P(s_j)$ to $P(t_j)$ since otherwise we could re-route P along another such $D_h$-geodesic to contradict the uniqueness of the $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$.

Combining this with condition 1 in the definition of ${\mathsf {E}}_{r_j}(w_j)$ (comparison of $D_h$ and $\widetilde{D}_h$), applied with $u = P(s_j)$ and $v = P(t_j)$, and the definition (1.21) of $C_*$, we find that

$$\begin{aligned}&\widetilde{D}_h\left( P(s_j) , P(t_j) \right) \le C' (t_j - s_j) \quad \text {and} \quad \widetilde{D}_h\left( P(t_{j-1}) , P(s_j) \right) \nonumber \\&\quad \le C_* (s_j - t_{j-1} ) ,\quad \forall j \in [\underline{J} ,\overline{J}]_{\mathbb {Z}}. \end{aligned}$$

(3.15)

We will now argue that $s_j - t_{j-1}$ is not too much larger than $t_j - s_j$. If $j \in [\underline{J} , \overline{J}]_{\mathbb {Z}}$, then since $r_j \le \varepsilon \mathbb {r}$ and $|P(t_j) -\mathbb {z}| \wedge |P(t_j) - \mathbb {w}| \ge 2\varepsilon \mathbb {r}$, the $D_h$-geodesic P must cross the annulus $\mathbb {A}_{\alpha r_j,r_j}(w_j)$ at least once before time $t_{j-1}$ and at least once after time $s_j$. By condition 3 in the definition of ${\mathsf {E}}_{r_j}(w_j)$, there is a path disconnecting the inner and outer boundaries of this annulus with $D_h$-length at most $A D_h\left( \partial B_{\alpha r_j}(w_j) , \partial B_{ r_j}(w_j) \right)$. The geodesic P must hit this path at least once before time $t_{j-1}$ and at least once after time $s_j$. Since P is a geodesic and $P(s_j) \in \partial B_{\alpha r_j}(w_j)$, $P(t_j) \in \partial B_{ r_j}(w_j)$, it follows that

$$\begin{aligned} s_j - t_{j-1} \le A D_h\left( \partial B_{\alpha r_j}(w_j) , \partial B_{ r_j}(w_j) \right) \le A (t_j - s_j) . \end{aligned}$$

Adding $A (s_j - t_{j-1})$ to both sides of this inequality, then dividing by $A+1$, gives

$$\begin{aligned} s_j - t_{j-1} \le \frac{A}{A+1} (t_j - t_{j-1}) . \end{aligned}$$

(3.16)

Step 3: upper bound for $\widetilde{D}_h$ By combining the above relations, we get that on $F_{\mathbb {r}}^\varepsilon$,

$$\begin{aligned}&\widetilde{D}_h\left( B_{4 \varepsilon \mathbb {r}}(\mathbb {z}) , B_{4 \varepsilon \mathbb {r}}(\mathbb {w}) \right) \nonumber \\&\quad \le \sum _{j=\underline{J}+1}^{\overline{J}} \left( \widetilde{D}_h\left( P(t_{j-1}) , P(s_j) \right) + \widetilde{D}_h\left( P(s_j) , P(t_j) \right) \right) \quad \text {(by }(3.14)) \nonumber \\&\quad \le \sum _{j=\underline{J}+1}^{\overline{J}} \left( C_*( s_j - t_{j-1}) + C' (t_j - s_j) \right) \quad \text {(by } (3.15)) \nonumber \\&\quad = \sum _{j=\underline{J}+1}^{\overline{J}} \left( C' (t_j - t_{j-1} ) + (C_* - C') (s_j - t_{j-1}) \right) \nonumber \\&\quad \le \left( C' + \frac{A}{A+1}(C_* - C') \right) \sum _{j=\underline{J}+1}^{\overline{J}} (t_j - t_{j-1} ) \quad \text {(by } (3.16)) \nonumber \\&\quad \le \left( C' + \frac{A}{A+1}(C_* - C') \right) D_h(\mathbb {z},\mathbb {w}). \end{aligned}$$

(3.17)

By (3.11), Axiom V (tightness across scales) for D and $\widetilde{D}$, and the triangle inequality, it holds with probability tending to 1 as $\varepsilon \rightarrow 0$, uniformly in r, that

$$\begin{aligned}&\left| \widetilde{D}_h(\mathbb {z},\mathbb {w}) - \widetilde{D}_h\left( B_{4 \varepsilon \mathbb {r}}(\mathbb {z}) , B_{4 \varepsilon \mathbb {r}}(\mathbb {w}) \right) \right| \nonumber \\&\quad \le \frac{1}{100} \left( C'' - \left( C' + \frac{A}{A+1}(C_* - C') \right) \right) D_h(\mathbb {z},\mathbb {w}) \end{aligned}$$

(3.18)

simultaneously for all $\mathbb {z},\mathbb {w}\in B_{ \mathbb {r} }(0)$ with $|\mathbb {z}-\mathbb {w}| \ge \beta \mathbb {r}$. By combining this with (3.17) and recalling that $\mathbb {P}[F_{\mathbb {r}}^\varepsilon ] = 1-\beta /2 - o_\varepsilon (1)$ uniformly in $\mathbb {r}$ if (B) holds, we get that if $\varepsilon _0$ is chosen to be sufficiently small, in a manner which does not depend on $\mathbb {r}$, then if (B) holds for $\mathbb {r} > 0$ and $\varepsilon \in (0 , \varepsilon _0]$, then it holds with probability at least $1-\beta$ that (3.12) holds simultaneously for each $\mathbb {z},\mathbb {w}\in B_{ \mathbb {r}}(0) \cap \mathbb {Q}^2$ with $|\mathbb {z}-\mathbb {w}| \ge \beta \mathbb {r}$. By the continuity of $D_h$ and $\widetilde{D}_h$, we can remove the requirement that $\mathbb {z},\mathbb {w}\in \mathbb {Q}^2$ (which was only used to get the uniqueness of the $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$). $\square$

4 Independence along a geodesic

Let h be a whole-plane GFF and let D be a weak $\gamma$-LQG metric. The goal of this section is to prove the following general “local independence” type result for events depending on a small segment of a $D_h$-geodesic. We will first state a simplified version of our result which is easier to parse (Theorem 4.1), then state the full version (Theorem 4.2).

Theorem 4.1

Suppose we are given events $\mathfrak E_r^{\mathbb {z} , \mathbb {w}}(z) \in \sigma (h)$ for $z\in \mathbb {C}$, $r > 0$, and $\mathbb {z} ,\mathbb {w} \in \mathbb {C}$ and a deterministic constant $\Lambda > 1$ which satisfy the following properties, where here $P = P^{\mathbb {z},\mathbb {w}}$ denotes the (a.s. unique) $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$.

• 1. (Measurability) The event $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ is determined by $h|_{ B_r(z)}$ and the geodesic P stopped at the last time it exists $B_r(z)$.

• 2. (Lower bound for $\mathbb {P}[\mathfrak E_r^{\mathbb {z}, \mathbb {w}}(z)]$) If $\mathbb {z},\mathbb {w}\in \mathbb {C}{\setminus } B_r(z)$, then a.s.

  $$\begin{aligned} \mathbb {P}\left[ \mathfrak E_r^{\mathbb {z}, \mathbb {w}}(z) \,\big |\, h|_{\mathbb {C}{\setminus } B_{ r}(z)} , \{P \cap B_{ r}(z)\not =\emptyset \} \right] \ge \Lambda ^{-1} . \end{aligned}$$

  (4.1)

For each $\nu \in (0,1)$, $q > 0$, $\ell \in (0,1)$, and bounded open set $U\subset \mathbb {C}$, it holds with probability tending to 1 as $\varepsilon \rightarrow 0$, at a rate depending only on $U,q,\ell ,\Lambda$, that for each $\mathbb {z} , \mathbb {w} \in \left( \varepsilon ^q \mathbb {Z}^2 \right) \cap U$ with $|\mathbb {z}-\mathbb {w}|\ge \ell$, there exists $z\in \mathbb {C}$ and $r\in [\varepsilon ^{1+\nu } , \varepsilon ]$ such that $P^{\mathbb {z},\mathbb {w}} \cap B_{ r}(z)\not =\emptyset$ and $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ occurs.

We think of the parameter $q > 0$ in Theorem 4.1 as large, so the conclusion of the theorem holds for all pairs $(\mathbb {z} , \mathbb {w})$ in a fine mesh of U.

Intuitively, the reason why Theorem 4.1 is true is as follows. The geodesic segments $P\cap B_r(z)$ and $P\cap B_r(w)$ are approximately independent from one another when $|z-w|$ is much larger than r. When r is small, we can cover P by a large number of balls $B_r(z)$ whose corresponding center points z lie at Euclidean distance much further than r from one another. Using (4.1) and a general concentration inequality for independent random variables, one gets that for each fixed pair $(\mathbb {z},\mathbb {w})$, with high probability there exists $z\in \mathbb {C}$ such that $P^{\mathbb {z},\mathbb {w}} \cap B_{ r}(z)\not =\emptyset$ and $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ occurs. One then takes a union bound over all pairs $\mathbb {z} , \mathbb {w} \in \left( r^q \mathbb {Z}^2 \right) \cap U$.

The above heuristic is not quite right since $D_h$-geodesics do not depend locally on the field, so $P\cap B_r(z)$ and $P\cap B_r(w)$ are not approximately independent when $|z-w|$ is much greater than r. Indeed, it is possible that changing what happens in $B_r(z)$ could affect the behavior of P macroscopically even when r is very small. As a substitute for this lack of long-range independence, we will use the confluence of geodesics results from [36], as discussed in Sect. 1.5, and only make changes to the field at places where the geodesics are “stable” in the sense that a microscopic change does not lead to macroscopic changes to P. The reason why we only get a statement which holds with probability tending to 1 as $r\rightarrow 0$ at the end of Theorem 4.1 is that we need to truncate on a global regularity event in order to make confluence hold with high probability.

We will actually prove (and use) a more general version of Theorem 4.1 which differs from Theorem 4.1 in the following respects.

• We allow for more flexibility in the Euclidean radii involved in the various conditions, which is represented by constants $\{\lambda _i\}_{i =1,\ldots ,5}$ (for our particular application, the constants are chosen explicitly in (5.11)).

• We introduce events $E_r(z)$ which are determined by the restriction of h to an annulus $\mathbb {A}_{\lambda _1 r , \lambda _4 r}(z)$ (for constants $\lambda _1 < \lambda _4$) and which are required to have probability close to 1. We replace (4.1) by a comparison between the conditional probabilities of $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ and $E_r(z)$ given $h|_{\mathbb {C}{\setminus } B_{\lambda _3 r}(z)}$, for another constant $\lambda _3$. The occurrence of $E_r(z)$ can be thought of as the statement that “$h|_{\mathbb {A}_{\lambda _1 r , \lambda _4 r}(z)}$ is sufficiently well behaved that $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ has a chance to occur”.

• We do not require our events to be defined for all $r>0$, but rather only for values of r in a suitably “dense” set $\mathcal R \subset (0,\infty )$. The reason why we need to allow for this is that the results of Sect. 3 only hold for values of r in a suitably dense set.

• We work with a given “base scale” $\mathbb {r} > 0$ (e.g., we consider points in $\mathbb {r} U$ instead of in U) and we require our estimates to be uniform in the choice of $\mathbb {r}$. The reason for this is that we have only assumed tightness across scales (Axiom V) instead of exact scale invariance.

Theorem 4.2

There exists $\nu _* \in (0,1)$ depending only on the choice of metric D such that for each $0< \mu < \nu \le \nu _*$ and each $0< \lambda _1< \lambda _2 \le \lambda _3 \le \lambda _4 < \lambda _5$, there exists $\mathbb {p} \in (0,1)$ such that the following is true. Suppose $\mathbb {r} > 0$ and we are given a small number $\varepsilon _0 > 0$; a deterministic set of radii $\mathcal R\subset (0,\varepsilon _0]$; events $E_r(z) \in \sigma (h)$ for $z\in \mathbb {C}$ and $r\in \mathcal R$; events $\mathfrak E_r^{\mathbb {z} , \mathbb {w}}(z) \in \sigma (h)$ for $z\in \mathbb {C}$, $r\in \mathcal R$, and $\mathbb {z} ,\mathbb {w} \in \mathbb {C}$; and a deterministic constant $\Lambda > 1$ which satisfy the following properties.

• 1. (Density of $\mathcal R$) For each $\varepsilon \in (0,\varepsilon _0]$, there exist $\lfloor \mu \log _8 \varepsilon ^{-1} \rfloor$ radii $r_1^\varepsilon , \ldots , r_{\lfloor \mu \log _8\varepsilon ^{-1} \rfloor }^\varepsilon \in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]\cap \mathcal R$ such that $r_k^\varepsilon /r_{k-1}^\varepsilon \ge \lambda _4/\lambda _1$ for each $k=2,\ldots ,\lfloor \mu \log _8\varepsilon ^{-1} \rfloor$.

• 2. (Measurability) For each $z\in \mathbb {C}$ and $r\in \mathcal R$, $E_r(z)$ is determined by $(h - h_{\lambda _5 r}(z)) |_{\mathbb {A}_{\lambda _1 r , \lambda _4 r}(z)}$ for each $\mathbb {z} ,\mathbb {w} \in \mathbb {C}$, and $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ is determined by $h|_{ B_{\lambda _4 r}(z) }$ and the (a.s. unique) $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$ stopped at the last time it exists $B_{\lambda _4 r}(z)$.

• 3. (Lower bound for $\mathbb {P}[E_r(z)]$) For each $z\in \mathbb {C}$ and $r\in \mathcal R$, we have $\mathbb {P}[E_r(z)] \ge \mathbb {p}$.

• 4. (Comparison of $E_r(z)$ and $\mathfrak E_r^{\mathbb {z}, \mathbb {w}}(z)$) Suppose $z\in \mathbb {C}$, $r\in \mathcal R$, $\mathbb {z} , \mathbb {w}$ are distinct points of $\mathbb {C}{\setminus } B_{\lambda _4 r}(z)$, and $P = P^{\mathbb {z} , \mathbb {w}}$ is the $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$. Then a.s.

  $$\begin{aligned}&\Lambda ^{-1} \mathbb {P}\left[ E_r(z) \cap \{P \cap B_{\lambda _2 r}(z)\not =\emptyset \} \,\big |\, h|_{\mathbb {C}{\setminus } B_{\lambda _3 r}(z)} \right] \nonumber \\&\qquad \le \mathbb {P}\left[ \mathfrak E_r^{\mathbb {z}, \mathbb {w}}(z) \cap \{P \cap B_{\lambda _2 r}(z)\not =\emptyset \} \,\big |\, h|_{\mathbb {C}{\setminus } B_{\lambda _3 r}(z)} \right] . \end{aligned}$$

  (4.2)

Under the above hypotheses, for each $q > 0$, $\ell \in (0,1)$, and bounded open set $U\subset \mathbb {C}$, it holds with probability tending to 1 as $\varepsilon \rightarrow 0$, at a rate depending only on $U,q,\ell ,\mu ,\nu , \{\lambda _i\}_{i=1,\ldots ,5} ,\varepsilon _0,\Lambda$, that for each $\mathbb {z} , \mathbb {w} \in \left( \varepsilon ^q \mathbb {r} \mathbb {Z}^2 \right) \cap \left( \mathbb {r} U\right)$ with $|\mathbb {z}-\mathbb {w}|\ge \ell \mathbb {r}$, there exists $z\in \mathbb {C}$ and $r \in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]$ such that $P^{\mathbb {z} , \mathbb {w}} \cap B_{\lambda _2 r}(z) \not =\emptyset$ and $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ occurs.

Theorem 4.1 is the special case of Theorem 4.2 where $\mathcal R = (0,\infty )$; $\lambda _2 = \lambda _3 = \lambda _4 = 1$; $E_r(z)$ is the whole probability space; and $\mathbb {r} =1$. The parameter $\mathbb {p}$ in Theorem 4.2 will eventually be chosen to be sufficiently close to 1 that we can apply Lemma 2.6 to cover a large region of space by balls $B_{\lambda _1 r}(z)$ for pairs (z, r) such that $E_r(z)$ occurs (see Lemma 4.11). The events $E_r(z)$ and $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ play very different roles in the statement of Theorem 4.2. The event $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ is the main event that we are interested in, and concerns a segment of the $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$. The event $E_r(z)$ is locally determined by h, has probability close to 1, and can be thought of as the event that the restriction of h to the annulus $\mathbb {A}_{\lambda _1 r , \lambda _4 r}(z)$ is sufficiently regular that $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ has a chance to occur.

The statement of Theorem 4.2 is easier to understand if one thinks of the particular setting in which we will apply it. Recall the optimal bi-Lipschitz constants from (1.21). For us, $E_r(z)$ will be the event that there exists a pair of points $u,v \in \mathbb {A}_{\lambda _1 r,\lambda _2 r}(z)$ at Euclidean distance of order r from each other for which $\widetilde{D}_h(u,v) \le c_2' D_h(u,v)$ for a constant $c_2' \in (c_* , C_*)$; and some regularity conditions hold which are needed to ensure that conditions 2 and 4 in the theorem statement are satisfied. We will only be able to show that $\mathbb {P}[E_r(z)]$ is bounded below for a “dense” set of scales $\mathcal R$ as in condition 1 due to the results in Sect. 3. The event $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ will be the event that, roughly speaking, the $D_h$-geodesic $P^{\mathbb {z},\mathbb {w}}$ gets close to u, v and hence (by the triangle inequality) hits a pair of points P(s), P(t) at Euclidean distance of order r from each other for which $\widetilde{D}_h(P(s) , P(t) ) \le c_2' D_h(P(s) , P(t) )$. More precisely, we will prove the following statement in Sect. 5.

Proposition 4.3

Assume (by way of eventual contradiction) that $c_* < C_*$. Let $0< \mu < \nu \le \nu _*$ and $c_*< c_1'< c_2' < C_*$. There exist universal constants $\{\lambda _i\}_{i=1,\ldots ,5}$ and parameters $b , \rho \in (0,1)$ depending only on $\mu ,\nu$ such that the following is true. Let $\mathbb {p}$ be as in Theorem 4.2 for the above choice of $\mu ,\nu ,\{\lambda _i\}_{i=1,\ldots ,5}$ and let $c'' =c''(c_1',\mu ,\nu ) > c_*$ be as in Proposition 3.5 with $c' = c_1'$. If $\beta \in (0,1)$ and $\mathbb {r} > 0$ are such that $\mathbb {P}[\underline{G}_{\mathbb {r}}(c'' , \beta )] \ge \beta$ (in the notation (3.3)), then there exists $\varepsilon _0 = \varepsilon _0(\beta ,c_1' , c_2',\mu ,\nu ) \in (0,1)$, a deterministic set of radii $\mathcal R\subset (0,\varepsilon _0]$, events $E_r(z)$ and $\mathfrak E_r^{\mathbb {z} , \mathbb {w}}(z)$, and a deterministic constant $\Lambda = \Lambda (c_1' , c_2',\mu ,\nu ) > 1$ which satisfy the hypotheses of Theorem 4.2 with $\rho ^{-1} \mathbb {r}$ in place of $\mathbb {r}$ and have the following additional property. Suppose $z \in \mathbb {C}$, $r \in \mathcal R$, and $\mathbb {z} , \mathbb {w} \in \mathbb {C}{\setminus } B_{\lambda _4 r}(z)$, and let $P = P^{\mathbb {z},\mathbb {w}}$ be the $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$. If $\mathfrak E_r^{\mathbb {z} , \mathbb {w}}(z)$ occurs, then there are times $0< s< t < |P|$ such that

$$\begin{aligned}&P([s,t]) \subset B_{\lambda _2 r}(z) ,\quad |P(s) - P(t)| \ge b r ,\quad \text {and} \quad \widetilde{D}_h(P(s) , P(t)) \nonumber \\&\quad \le c_2' D_h(P(s) , P(t)) . \end{aligned}$$

(4.3)

Roughly speaking, Proposition 4.3 combined with Theorem 4.2 implies that the pairs of points (u, v) such that $\widetilde{D}_h(u,v) \le c_2' D_h(u,v)$ and $|u-v|$ is not too small are sufficiently dense that a typical $D_h$-geodesic is extremely likely to get close to such a pair of points. This will be applied in Sect. 6 to derive a contradiction to the definition (1.21) of $C_*$ if we assume that $c_* < C_*$, and thereby to show that $c_* = C_*$.

Remark 4.4

The reason for the parameter $\rho$ in Proposition 4.3 is as follows. If $\mathbb {P}[\underline{G}_{\mathbb {r}}(c'' , \beta )] \ge \beta$, then Proposition 3.5 gives us a parameter $p = p(\mu ,\nu ) \in (0,1)$ such that there are many values of $r \in [\varepsilon ^{1+\nu } \mathbb {r}, \varepsilon \mathbb {r}]$ for which a certain event occurs with probability at least p. In Sect. 5, we will use the event of Proposition 3.5 to build the event $E_r(z)$. In order to make $E_r(z)$ occur with probability at least $\mathbb {p}$ (which can be arbitrarily close to 1) instead of just probability p, we will consider lots of small Euclidean balls and argue (using Lemma 2.7) that with probability at least $\mathbb {p}$ the event of Proposition 3.5 occurs for at least one of these balls. In order to do this, we need the radius of the annulus involved in the definition of $E_r(z)$ to be a large deterministic constant factor times the radius of the balls involved in the event of Proposition 3.5 (so that we can fit many such balls in the annulus). This factor is $\rho ^{-1}$.

4.1 Setup and outline

Assume that we are in the setting of Theorem 4.2 for some $\mathbb {r} >0$. To lighten notation, we will also impose the assumption that $\lambda _3 = 1$ (the proof when $\lambda _3\not =1$ is identical, just with extra factors of $\lambda _3$ in various subscripts). Let $U\subset \mathbb {C}$ be open and bounded and let $\ell > 0$, as in the conclusion of Theorem 4.2. Also fix $\varepsilon \in (0,\varepsilon _0]$ and distinct points $\mathbb {z} , \mathbb {w} \in \mathbb {r} U$ with $|\mathbb {z}- \mathbb {w}|\ge 4 \ell \mathbb {r}$ (the reason for the factor of 4 here is to reduce factors of 4 elsewhere). Let

$$\begin{aligned} P = P^{\mathbb {z},\mathbb {w}} := \left( D_h\text {-geodesic from} \mathbb {z} \text { to } \mathbb {w} \right) . \end{aligned}$$

(4.4)

To lighten notation, throughout the rest of this section we will not include the parameters $\mathbb {r} , \varepsilon , \mathbb {z} ,\mathbb {w}$ in the notation. But, we will always require that all estimates are uniform in the choice of $\mathbb {r}$, $\mathbb {z}$, and $\mathbb {w}$ (we will typically be sending $\varepsilon \rightarrow 0$). Since we will commonly be growing metric balls starting from $\mathbb {z}$, we also introduce the following abbreviations for $z\in \mathbb {C}$ and $r,s>0$:

$$\begin{aligned}&\mathfrak E_r(z) = \mathfrak E_r^{\mathbb {z},\mathbb {w}}(z) ,\quad \mathcal B_s^\bullet := \mathcal B_s^\bullet (\mathbb {z} ; D_h) \quad \text {and} \quad \nonumber \\&\quad \tau _r := \tau _r(\mathbb {z}) = \inf \{s > 0 : \mathcal B_s^\bullet \not \subset B_r(\mathbb {z})\}, \end{aligned}$$

(4.5)

where here we recall that $\mathcal B_s^\bullet (\mathbb {z} ;D_h)$ is the filled metric ball.

Fig. 3

Illustration of the objects defined in Sect. 4.1. The two filled LQG metric balls $\mathcal B_{s_k}^\bullet \subset \mathcal B_{t_k}^\bullet$ centered at $\mathbb {z}$ are shown, along with the set of points $\mathrm {Conf}_k \subset \partial \mathcal B_{s_k}^\bullet$ hit by leftmost $D_h$-geodesics from $\mathbb {z}$ to $\partial \mathcal B_{t_k}^\bullet$ (alternating blue and purple) and the set of arcs ${{\mathcal {I}}}_k$ of $\partial \mathcal B_{t_k}^\bullet$ consisting of points whose leftmost $D_h$-geodesics hit the same point of $\mathrm {Conf}_k$. Several representative leftmost $D_h$-geodesics are shown for each such arc. We have also shown in green several of the balls $B_r(z)$ for $(z,r) \in \mathcal Z_k$. Each such ball has radius in $[\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]$ and its Euclidean distance from $\mathcal B_{t_k}^\bullet$ is of order $\varepsilon$. We have highlighted examples of one such ball $B_r(z)$ for which the event $\mathrm {Stab}_{k,r}(z)$ of (4.11) occurs (light green), i.e., each of the red $D_h(\cdot ,\cdot ;\mathbb {C}{\setminus } \overline{B_r(z)})$-geodesics from $\mathbb {z}$ to points of $\partial B_r(z)$ hit the same arc of ${{\mathcal {I}}}_k$ (we have only shown the segments of these geodesics after they exit $\mathcal B_{t_k}^\bullet$). We have also highlighted one ball for which $\mathrm {Stab}_{k,r}(z)$ does not occur (pink) (color figure online)

We now define several objects which we will work with throughout the rest of this section. See Fig. 3 for an illustration. Fix $\beta \in (0,1)$ to be chosen later, in a manner depending only on D. Define

$$\begin{aligned}&s_k := \tau _{\ell \mathbb {r}} + k \varepsilon ^\beta \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})} \quad \text {and} \quad t_k := s_k + \varepsilon ^{2\beta } \nonumber \\&\quad \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})} \in [s_k ,s_{k+1}] , \quad \forall k \in \mathbb {N}_0 . \end{aligned}$$

(4.6)

By Theorem 2.15, it is a.s. the case that for each $k\in \mathbb {N}_0$ there are only finitely many points of $\partial \mathcal B_{s_k }^\bullet$ which are hit by leftmost $D_h$-geodesics from $\mathbb {z}$ to $\partial \mathcal B_{t_k}^\bullet$. Let $\mathrm {Conf}_k \subset \partial \mathcal B_{s_{k} }^\bullet$ be the set of such points and let ${{\mathcal {I}}}_{k}$ be the set of subsets of $\partial \mathcal B_{t_k}^\bullet$ of the form

$$\begin{aligned}&\left\{ y\in \partial \mathcal B_{t_k}^\bullet : \text {leftmost } D_h\text {-geodesic from } \mathbb {z} \text { to } y\text { passes through } x\right\} \quad \nonumber \\&\quad \text {for} \quad x\in \mathrm {Conf}_{k}. \end{aligned}$$

(4.7)

By [36, Lemma 2.7], ${{\mathcal {I}}}_{k}$ is a collection of disjoint arcs of $\partial \mathcal B_{t_k}^\bullet$ whose union is all of $\partial \mathcal B_{t_k}^\bullet$. We also note that by Axiom II (locality), ${{\mathcal {I}}}_k$ is determined by $\mathcal B_{t_k}^\bullet$ and $h|_{\mathcal B_{t_k}^\bullet }$.

For much of this section, we will work with the increasing filtration

$$\begin{aligned} \mathcal F_k := \sigma \left( \mathcal B_{t_k}^\bullet ,h|_{\mathcal B_{t_k}^\bullet } , P|_{[0,s_k]} \right) ,\quad \forall k\in \mathbb {N}_0. \end{aligned}$$

(4.8)

Conditioning on all of $P|_{[0,s_k]}$ may seem rather extreme, but thanks to the confluence of geodesics this conditioning is a equivalent to a much tamer looking conditioning.

Lemma 4.5

We have the equivalent representation

$$\begin{aligned} \mathcal F_k = \sigma \left( \mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet } , \text {arc of } {{\mathcal {I}}}_k\text { which contains } P(t_k)\right) . \end{aligned}$$

(4.9)

Proof

On the event that the target point $\mathbb {w}$ of P lies in $\mathcal B_{t_k}^\bullet$, the path $P|_{[0,s_k]}$ is determined by $(\mathcal B_{t_k}^\bullet ,h|_{\mathcal B_{t_k}^\bullet })$. On the complementary event $\{\mathbb {w} \notin \mathcal B_{t_k}^\bullet \}$, we have $P(s_k ) \in \partial \mathcal B_{s_k}^\bullet$ and $P|_{[0,s_k]}$ is the a.s. unique $D_h(\cdot ,\cdot ; \mathcal B_{t_k}^\bullet )$-geodesic from $\mathbb {z}$ to $P(s_k)$. Hence, on this event $P|_{[0,s_k]}$ is determined by $(\mathcal B_{s_k }^\bullet ,h|_{\mathcal B_{s_k }^\bullet } , P(s_k))$. Moreover, $P|_{[0,t_k]}$ is a.s. the unique (hence also leftmost) $D_h$-geodesic from $\mathbb {z}$ to $P(t_k)$, hence $P(s_{k} )$ is one of the points of $\mathrm {Conf}_{k}$. By the definition of ${{\mathcal {I}}}_k$, this point is determined by which arc of ${{\mathcal {I}}}_k$ contains $P(t_k)$. $\square$

We now introduce the set of Euclidean balls $B_r(z)$ which we will consider when trying to produce a ball for which $\mathfrak E_r(z)$ occurs. With $r_1^\varepsilon , \ldots , r_{\lfloor \mu \log _8\varepsilon ^{-1} \rfloor }^\varepsilon \in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]\cap \mathcal R$ as in condition 1 from Theorem 4.2, let $\mathcal Z_k$ for $k\in \mathbb {N}$ be the set of pairs (z, r) such that

$$\begin{aligned}&z\in \left( \frac{\lambda _1 \varepsilon ^{1+\nu } \mathbb {r} }{4} \mathbb {Z}^2 \right) {\setminus } \mathcal B_{t_k}^\bullet , \quad r \in \left\{ r_1^\varepsilon , \ldots , r_{\lfloor \mu \log _8\varepsilon ^{-1} \rfloor }^\varepsilon \right\} , \quad \nonumber \\&\quad \text {and} \quad {\text {dist}}\left( z , \partial \mathcal B_{t_k}^\bullet \right) \in [ \lambda _4 \varepsilon \mathbb {r} , 2 \lambda _4 \varepsilon \mathbb {r}] . \end{aligned}$$

(4.10)

Note that $\mathcal Z_k \in \sigma \left( \mathcal B_{t_k}^\bullet \right)$.

We want to say that with extremely high probability, there are many values of $k\in \mathbb {N}_0$ for which the event $\mathfrak E_r(z)$ occurs for some $(z,r)\in \mathcal Z_k$ such that $P\cap B_{\lambda _2 r}(z) \not =\emptyset$. We will do this by lower-bounding the conditional probability given $\mathcal F_k$ that $\mathfrak E_r(z)$ occurs for at least one $(z,r)\in \mathcal Z_k$, then considering a polynomial (in $\varepsilon$) number of values of k and applying a standard concentration inequality for binomial random variables.

In order to say something useful about the conditional law given $\mathcal F_k$ of what happens in one of the balls $B_r(z)$ for $(z,r)\in \mathcal Z_k$, we need to know that making a small change to what happens in $B_r(z)$ does not affect which arc of ${{\mathcal {I}}}_k$ contains $P(t_k)$. For $z\in \mathbb {C}$ and $r>0$, we therefore let $\mathrm {Stab}_{k,r}(z)$ be the event that $(z,r) \in \mathcal Z_k$ and

$$\begin{aligned}&\text {Each } D_h(\cdot ,\cdot ; \mathbb {C}{\setminus }\overline{ B_r(z)})\text {-geodesic from } \mathbb {z}\text { to a point of } \partial B_r(z)\text { hits }\partial \mathcal B_{t_k}^\bullet \nonumber \\&\quad \text { in the same arc of } {{\mathcal {I}}}_k . \end{aligned}$$

(4.11)

Here, by a $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)} )$-geodesic from $\mathbb {z}$ to a point $x \in \partial B_r(z)$ we mean a path from $\mathbb {z}$ to x in $\mathbb {C}{\setminus } B_r(z)$ which has minimal $D_h$-length among all such paths and which does not hit $\partial B_r(z)$ except at x. Note that such a geodesic need not exist for every point of $\partial B_r(z)$. However, if P is a $D_h$ geodesic started from $\mathbb {z}$ which enters $B_r(z)$, then P, stopped at the first time when it enters $B_r(z)$, is a $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)} )$-geodesic from $\mathbb {z}$ to a point of $\partial B_r(z)$.

In Sect. 4.4, we will use various quantitative results on confluence of geodesics from [36] to show that with high probability $\mathrm {Stab}_{k,r}(z)$ occurs for most of the pairs $(z,r)\in \mathcal Z_k$ such that P enters $B_{\lambda _2 r}(z)$. The reason why the events $\mathrm {Stab}_{k,r}(z)$ are useful is the following lemma, which is used only in Sect. 4.2.

Lemma 4.6

For each $z\in \mathbb {C}$, $r>0$, and $k\in \mathbb {N}_0$ the event $\mathrm {Stab}_{k,r}(z)$ of (4.11) is a.s. determined by $h|_{\mathbb {C}{\setminus } B_r(z)}$. Furthermore, on the event $\mathrm {Stab}_{k,r}(z) \cap \{P\cap B_r(z) \not =\emptyset \}$, both $(\mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet })$ and the arc of ${{\mathcal {I}}}_k$ which contains $P(t_k)$ are a.s. determined by $h|_{\mathbb {C}{\setminus } B_r(z)}$ and the indicator $\mathbb {1}_{\mathrm {Stab}_{k,r}(z) \cap \{P\cap B_r(z) \not =\emptyset \}}$. In particular, for any event $F\in \mathcal F_k$ the event $F\cap \mathrm {Stab}_{k,r}(z) \cap \{P\cap B_r(z) \not =\emptyset \}$ is a.s. determined by $h|_{\mathbb {C}{\setminus } B_r(z)}$ and the indicator $\mathbb {1}_{\mathrm {Stab}_{k,r}(z) \cap \{P\cap B_r(z) \not =\emptyset \}}$.

Proof

Since $\mathcal B_{t_k}^\bullet$ is a local set for h (Lemma 2.1) and since balls $B_r(z)$ for $(z,r) \in \mathcal Z_k$ are disjoint from $\mathcal B_{t_k}^\bullet$, we find that $\{(z,r) \in \mathcal Z_k\}$ is determined by $h|_{\mathbb {C}{\setminus } B_r(z)}$. Furthermore, $\left( \mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet } \right)$ and hence also ${{\mathcal {I}}}_k$ is determined by $h|_{\mathbb {C}{\setminus } B_r(z)}$ on the event $\{(z,r)\in \mathcal Z_k\}$. By Axiom II (locality), it then follows that $\mathrm {Stab}_{k,r}(z)$ is determined by $h|_{\mathbb {C}{\setminus } B_r(z)}$.

Since $\mathrm {Stab}_{k,r}(z) \subset \{(z,r) \in \mathcal Z_k\}$, we already know that $\left( \mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet } \right)$ is a.s. determined by $h|_{\mathbb {C}{\setminus } B_r(z)}$ on the event $\mathrm {Stab}_{k,r}(z)$. On the event $\{P\cap B_r(z) \not =\emptyset \}$, the $D_h$-geodesic P stopped at the first time it enters $B_r(z)$ is a $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus }\overline{ B_r(z)})$-geodesic from $\mathbb {z}$ to a point of $\partial B_r(z)$. If $\mathrm {Stab}_{k,r}(z)$ occurs, then every such $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus }\overline{ B_r(z)})$-geodesic passes through the same arc of ${{\mathcal {I}}}_k$, and we can see which arc this is by observing $h|_{\mathbb {C}{\setminus } B_r(z)}$. Therefore, on $\mathrm {Stab}_{k,r}(z) \cap \{P\cap B_r(z) \not =\emptyset \}$, the arc of ${{\mathcal {I}}}_k$ which contains $P(t_k)$ is a.s. determined by $h|_{\mathbb {C}{\setminus } B_r(z)}$ and $\mathbb {1}_{\mathrm {Stab}_{k,r}(z) \cap \{P\cap B_r(z) \not =\emptyset \}}$.

The last statement of the lemma follows from the second statement and Lemma 4.5. $\square$

We define the set of “good” pairs

$$\begin{aligned} \mathcal Z_k^E := \left\{ (z,r) \in \mathcal Z_k : E_r(z) \cap \mathrm {Stab}_{k,r}(z) \cap \{P\cap B_{\lambda _2 r}(z) \not =\emptyset \} \, \text {occurs} \right\} \nonumber \\ \end{aligned}$$

(4.12)

and the set of “very good” pairs

$$\begin{aligned} \mathcal Z_k^{\mathfrak E} := \left\{ (z,r) \in \mathcal Z_k : \mathfrak E_r(z) \cap \mathrm {Stab}_{k,r}(z) \cap \{P\cap B_{\lambda _2 r}(z) \not =\emptyset \} \, \text {occurs} \right\} .\nonumber \\ \end{aligned}$$

(4.13)

The proof of Theorem 4.1 is based on lower-bounding the conditional probability that $\mathcal Z_k^{\mathfrak E} \not =\emptyset$ given $\mathcal F_k$, which allows us to say that the number of k for which $\mathcal Z_k^{\mathfrak E} \not =\emptyset$ stochastically dominates a binomial random variable. To lower-bound $\mathbb {P}[\mathcal Z_k^{\mathfrak E}\not =\emptyset \,|\, \mathcal F_k]$, we will first establish a lower bound for $\mathbb {P}[\mathcal Z_k^{\mathfrak E}\not =\emptyset \,|\, \mathcal F_k]$ in terms of $\mathbb {P}[\mathcal Z_k^{ E}\not =\emptyset \,|\, \mathcal F_k]$ using condition 4 in Theorem 4.2 (Sect. 4.2). We will then show that it is very likely that $\mathcal Z_k^E \not =\emptyset$ for many values of k (Sect. 4.4). This will imply that it is very likely that there are many values of k for which $\mathbb {P}[\mathcal Z_k^{ E}\not =\emptyset \,|\, \mathcal F_k]$ is bounded below, and hence there are many values of k for which $\mathbb {P}[\mathcal Z_k^{\mathfrak E}\not =\emptyset \,|\, \mathcal F_k]$ is bounded below (Sect. 4.5). We will now outline the rest of the proof of Theorem 4.2. See Fig. 4 for a schematic illustration of how the various results in this section fit together.

Fig. 4

Schematic outline of Sect. 4. An arrow between two sections/results means that the first is used in the proof of the second. Note that Proposition 4.3 is proven in Sect. 5 and Theorem 1.9 is proven in Sect. 6

In Sect. 4.2, we show that for each $k\in \mathbb {N}$, $\mathbb {P}[\mathcal Z_k^{\mathfrak E} \not =\emptyset | \mathcal F_k]$ is bounded below by $\varepsilon ^{2\nu +o_\varepsilon (1)} \mathbb {P}[\mathcal Z_k^E\not =\emptyset |\mathcal F_k]$, minus a small error. The reason why this is true is that (4.2) together with Lemma 4.6 allows us to lower-bound $\mathbb {E}[\#\mathcal Z_k^{\mathfrak E} \,|\, \mathcal F_k]$ in terms of $\mathbb {E}[\#\mathcal Z_k^E \,|\, \mathcal F_k]$. Then, Lemma 2.12 along with a Paley-Zygmund type argument allows us to transfer from a lower bound for $\mathbb {E}[\#\mathcal Z_k^{\mathfrak E} \,|\, \mathcal F_k]$ to a lower bound for $\mathbb {P}[\mathcal Z_k^{\mathfrak E} \not =\emptyset \,|\, \mathcal F_k]$. Here, one should think of $\nu$ as being small (relative to $\beta$), so that $\varepsilon ^{2\nu + o_\varepsilon (1)}$ is not too much different from $\varepsilon ^{o_\varepsilon (1)}$.

In Sect. 4.3, we define a global regularity event $\mathcal E_{\mathbb {r}}$ which we will truncate on for most of the rest of the proof and show that it occurs with high probability. This event includes various bounds for $D_h$-distances (e.g., Hölder continuity), but the most important condition is that $E_r(z)$ occurs for many pairs (z, r). To make the latter condition occur with high probability, we will make $\mathbb {p}$ sufficiently close to 1 to allow us to apply Lemma 2.6 and a union bound.

In Sect. 4.4, we show that if we truncate on $\mathcal E_{\mathbb {r}}$, then with very high probability there are many values of k for which $\mathcal Z_k^E\not =\emptyset$. Since the definition of $\mathcal E_{\mathbb {r}}$ already includes the condition that $E_r(z)$ occurs for many pairs $(z,r) \in \mathcal Z_k$, the main difficulty here is showing that $\mathrm {Stab}_{k,r}(z)$ occurs for most of the pairs (z, r) such that $P\cap B_{\lambda _2 r}(z)\not =\emptyset$. This will be accomplished by applying the results on confluence of geodesics from [36], as reviewed in Sect. 2.5, and multiplying over k to get concentration. We will choose the parameter $\beta$ from (4.6) to be small so that we have enough “room” between $\partial \mathcal B_{s_k}^\bullet$ and $\partial \mathcal B_{t_k}^\bullet$ for various confluence effects to occur.

In Sect. 4.5, we will transfer from the statement that “$\mathcal Z_k^E\not =\emptyset$ for many values of k” to the statement that “$\mathcal Z_k^{\mathfrak E}\not =\emptyset$ for many values of k”. This will be accomplished using the result of Sect. 4.2 and an elementary probabilistic lemma (Lemma 4.18) which allows us to convert between conditional and unconditional probabilities. We will then complete the proof of Theorem 4.2 by truncating on $\mathcal E_{\mathbb {r}}$ and then taking a union bound over many pairs of initial and terminal points $\mathbb {z}, \mathbb {w}$.

In Sect. 4.6, we collect the proofs of some geometric lemmas which are stated in Sects. 4.4 and 4.5 , but whose proofs are postponed to avoid distracting from the core of the argument. These geometric lemmas are used to control the behavior of $D_h$-geodesics on the regularity event $\mathcal E_{\mathbb {r}}$.

4.2 Comparison of $E_r(z)$ and $\mathfrak E_r(z)$

Recall the definitions of the filtration $\{\mathcal F_k\}_{k\ge 0}$ from (4.8), the set of “good” pairs $\mathcal Z_k^E$ from (4.12), and the set of “very good” pairs $\mathcal Z_k^{\mathfrak E}$ from (4.13). The events $E_r(z)$ are easier to work with than the events $\mathfrak E_r(z)$ since $E_r(z)$ has high probability and is determined locally by h. The goal of this subsection is to prove the following lemma, which will eventually allow us to transfer from a lower bound for the probability that $\mathcal Z_k^E \not =\emptyset$ to a lower bound for the probability that $\mathcal Z_k^{\mathfrak E} \not =\emptyset$.

Lemma 4.7

Let $M >0$. On the event $\{ \mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M}}(\mathbb {z}) \} \cap \{\mathbb {w} \notin B_{ 3\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )\}$, it holds except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ that

$$\begin{aligned} \mathbb {P}\left[ \mathcal Z_k^{\mathfrak E}\not =\emptyset \,|\, \mathcal F_k \right] \ge \varepsilon ^{2\nu + o_\varepsilon (1)} \mathbb {P}\left[ \mathcal Z_k^E \not = \emptyset \,|\, \mathcal F_k \right] - o_\varepsilon ^\infty (\varepsilon ) , \end{aligned}$$

(4.14)

where the rates of the $o_\varepsilon (1)$ and $o_\varepsilon ^\infty (\varepsilon )$ are deterministic and depend only on $M,\mu ,\nu ,\{\lambda _i\}_{i=1,\ldots ,5}$.

Nothing from this section besides Lemma 4.7 is used in subsequent subsections. Lemma 4.7 will eventually be a consequence of condition 4 of Theorem 4.2, which together with Lemma 4.6 allows us to compare the conditional expectations of $\#\mathcal Z_k^{E}$ and $\#\mathcal Z_k^{\mathfrak E}$ given $\mathcal F_k$. To transfer from a lower bound for the conditional expectation of $\#\mathcal Z_k^{\mathfrak E}$ to a lower bound for the probability that $\mathcal Z_k^{\mathfrak E}\not =\emptyset$, we will use a Paley-Zygmund type argument. For this purpose we need the following upper bound for $\#\mathcal Z_k^{\mathfrak E}$, which comes from Lemma 2.12 and Markov’s inequality (to transfer from unconditional to conditional probability).

Lemma 4.8

Let $M > 0$ and $\zeta \in (0,1)$. Also let

$$\begin{aligned} \mathcal Z_k(P) := \left\{ (z,r) \in \mathcal Z_k : P\cap B_r(z) \not =\emptyset \right\} , \end{aligned}$$

so that $\mathcal Z_k^{\mathfrak E} \subset \mathcal Z_k^E \subset \mathcal Z_k(P)$. On the event $\{\mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M} \mathbb {r}}(\mathbb {z})\}$, it holds except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ as $\varepsilon \rightarrow 0$ that

$$\begin{aligned} \mathbb {E}\left[ \#\mathcal Z_k(P) \mathbb {1}_{(\#\mathcal Z_k(P) > \varepsilon ^{-2\nu -\zeta })} \,|\, \mathcal F_k \right] = o_\varepsilon ^\infty (\varepsilon ) , \end{aligned}$$

(4.15)

where the rate of the $o_\varepsilon ^\infty (\varepsilon )$ depends only on $M,\zeta ,\mu ,\nu ,\{\lambda _i\}_{i=1,\ldots ,5}$.

Proof

By Lemma 2.12 (applied with $M\vee (2/\zeta )$ in place of M and $4\lambda _4\varepsilon$ in place of $\varepsilon$), on the event $\{\mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M} \mathbb {r}}(\mathbb {z})\}$ it is extremely unlikely that P spends a long time near $\partial \mathcal B_{t_k}^\bullet$: more precisely, it holds except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ as $\varepsilon \rightarrow 0$ that

$$\begin{aligned} {\text {area}}\left( B_{4\lambda _4 \varepsilon \mathbb {r}}(P) \cap B_{4\lambda _4\varepsilon \mathbb {r}}\left( \partial \mathcal B_{t_k}^\bullet \right) \right) \le \varepsilon ^{2 - \zeta /2} \mathbb {r}^2 . \end{aligned}$$

(4.16)

By (4.10), each ball $B_r(z)$ for $(z,r) \in \mathcal Z_k$ is contained in $B_{4\lambda _4 \varepsilon \mathbb {r}}\left( \partial \mathcal B_{t_k}^\bullet \right)$ and the maximal number of such balls which contain any given point of $\mathbb {C}$ is at most a constant (depending only on $M,\mu ,\nu ,\{\lambda _i\}_{i=1,\ldots ,5}$) times $\varepsilon ^{-2\nu } \log _8 \varepsilon ^{-1}$. By the definition of $\mathcal Z_k(P)$, each ball $B_r(z)$ for $(z,r) \in \mathcal Z_k(P)$ is contained in $B_{4\lambda _4 \varepsilon \mathbb {r}}(P)$. Therefore, the left side of (4.16) is at least a constant times $\varepsilon ^{2 + 2\nu } (\log _8\varepsilon ^{-1})^{-1} \mathbb {r}^2 \# \mathcal Z_k(P)$. From (4.16), we now get that

$$\begin{aligned} \mathbb {P}\left[ \# \mathcal Z_k(P) > \varepsilon ^{-2\nu -\zeta } ,\, \mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M} \mathbb {r}}(\mathbb {z}) \right] = o_\varepsilon ^\infty (\varepsilon ) . \end{aligned}$$

(4.17)

Since $\{\mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M} \mathbb {r}}(\mathbb {z})\}\subset \mathcal F_k$, we can apply Markov’s inequality to deduce from (4.17) that with probability $1-o_\varepsilon ^\infty (\varepsilon )$,

$$\begin{aligned} \mathbb {P}\left[ \# \mathcal Z_k(P) > \varepsilon ^{-2\nu -\zeta } \,|\, \mathcal F_k \right] \mathbb {1}_{(\mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M} \mathbb {r}}(\mathbb {z}))} = o_\varepsilon ^\infty (\varepsilon ) . \end{aligned}$$

(4.18)

If $\mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M} \mathbb {r}}(\mathbb {z})$, then (4.10) implies that for each $(z,r) \in \mathcal Z_k$,

$$\begin{aligned} z\in \mathcal Z_k \subset B_{(\varepsilon ^{-M} + 2\lambda _4\varepsilon ) \mathbb {r}}(\mathbb {z}) \cap \left( \frac{\lambda _1 \varepsilon ^{1+\nu }}{4} \mathbb {Z}^2\right) . \end{aligned}$$

Since there are at most $\mu \log _8 \varepsilon ^{-1}$ possibilities for r, on the event $\{\mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M} \mathbb {r}}(\mathbb {z})\}$, we have the trivial upper bound

$$\begin{aligned} \# \mathcal Z_k(P) \le \#\mathcal Z_k \le O_\varepsilon \left( \varepsilon ^{-2M(1+\nu )} \log _8 \varepsilon ^{-1} \right) . \end{aligned}$$

(4.19)

Combining (4.18) and (4.19) gives (4.15). $\square$

We will also need the following elementary probabilistic lemma which will be used in conjunction with Lemma 4.6 to transfer from conditional probabilities given $h|_{\mathbb {C}{\setminus } B_r(z)}$ to conditional probabilities given $\mathcal F_k$.

Lemma 4.9

Let $(\Omega ,\mathcal M , \mathbb {P})$ be a probability space. Let $\mathcal F , \mathcal G\subset \mathcal M$ be sub-$\sigma$-algebras. Let $E \in \mathcal M$ be an event such that $F\cap E \in \mathcal G \vee \sigma (E)$ for each $F\in \mathcal F$. Also let $G\in \mathcal F\cap \mathcal G$. Suppose $H_1,H_2 \in \mathcal M$ are events and $\Lambda >0$ is a deterministic constant such that a.s.

$$\begin{aligned} \mathbb {P}\left[ H_1 \cap E \,|\, \mathcal G\right] \mathbb {1}_G \le \Lambda \mathbb {P}\left[ H_2 \cap E \,|\, \mathcal G \right] \mathbb {1}_G . \end{aligned}$$

(4.20)

Then a.s.

$$\begin{aligned} \mathbb {P}\left[ H_1 \cap E \,|\, \mathcal F\right] \mathbb {1}_G \le \Lambda \mathbb {P}\left[ H_2 \cap E \,|\, \mathcal F \right] \mathbb {1}_G . \end{aligned}$$

(4.21)

Proof

Let $\mathcal G' := \mathcal G\vee \sigma (E)$. On the event that $\mathbb {P}[E \,|\, \mathcal G] > 0$, for any $H\in \mathcal M$,

$$\begin{aligned} \mathbb {P}\left[ H \cap E \,|\, \mathcal G' \right] = \frac{ \mathbb {P}\left[ H \cap E \,|\, \mathcal G \right] }{ \mathbb {P}\left[ E \,|\, \mathcal G \right] } \mathbb {1}_{E} . \end{aligned}$$

(4.22)

On the event that $\mathbb {P}[E \,|\, \mathcal G] = 0$, we instead have $\mathbb {P}\left[ H \cap E \,|\, \mathcal G' \right] = 0$.

Applying (4.22) with $H=H_1$ and with $H=H_2$ and plugging the results into (4.20) shows that a.s.

$$\begin{aligned} \mathbb {P}\left[ H_1 \cap E \,|\, \mathcal G' \right] \mathbb {1}_G \le \Lambda \mathbb {P}\left[ H_2 \cap E \,|\, \mathcal G' \right] \mathbb {1}_G . \end{aligned}$$

(4.23)

We claim that for any $H\in \mathcal M$, a.s.

$$\begin{aligned} \mathbb {E}\left[ \mathbb {P}\left[ H \cap E \,|\, \mathcal G' \right] \,|\, \mathcal F \right] \mathbb {1}_G = \mathbb {P}\left[ H \cap E \,|\, \mathcal F \right] \mathbb {1}_G . \end{aligned}$$

(4.24)

Once (4.24) is proven, we can take the conditional expectations given $\mathcal F$ of both sides of (4.23) to get (4.21). To prove (4.24), let $F\in \mathcal F$. By hypothesis, $F\cap E \in \mathcal G'$. Therefore,

$$\begin{aligned}&\mathbb {E}\left[ \mathbb {E}\left[ \mathbb {P}\left[ H \cap E \,|\, \mathcal G' \right] \,|\, \mathcal F \right] \mathbb {1}_G \mathbb {1}_F \right] \nonumber \\&\quad = \mathbb {E}\left[ \mathbb {P}\left[ H\cap E \,|\, \mathcal G' \right] \mathbb {1}_{F\cap G} \right] \quad \text {(since } F \cap G \in \mathcal F) \nonumber \\&\quad = \mathbb {E}\left[ \mathbb {E}\left[ \mathbb {1}_{H\cap E} \,|\, \mathcal G' \right] \mathbb {1}_{F\cap G\cap E} \right] \quad \text {(since } E\in \mathcal G'\text { and } \mathbb {1}_E\mathbb {1}_E = \mathbb {1}_E) \nonumber \\&\quad = \mathbb {E}\left[ \mathbb {1}_{H\cap E} \mathbb {1}_{F\cap G\cap E} \right] \quad \text {since } F\cap G \cap E \in \mathcal G' \nonumber \\&\quad = \mathbb {P}\left[ H\cap F \cap G \cap E \right] . \end{aligned}$$

(4.25)

By the definition of conditional expectation, this implies (4.24). $\square$

Proof of Lemma 4.7

Recall that we are assuming that $\lambda _3 = 1$, so that our hypothesis (4.2) says that for $(z,r) \in \mathbb {C} \times \mathcal R$ such that $\mathbb {z} , \mathbb {w} \notin B_{ \lambda _4 r}(z)$,

$$\begin{aligned}&\mathbb {P}\left[ E_r(z) \cap \left\{ P \cap B_{\lambda _2 r}(z)\not =\emptyset \right\} \,\big |\, h|_{\mathbb {C}{\setminus } B_{ r}(z)} \right] \nonumber \\&\quad \le \Lambda \mathbb {P}\left[ \mathfrak E_r(z) \cap \left\{ P \cap B_{\lambda _2 r}(z)\not =\emptyset \right\} \,\big |\, h|_{\mathbb {C}{\setminus } B_{ r}(z)} \right] . \end{aligned}$$

(4.26)

Since $\mathrm {Stab}_{k,r}(z) \in \sigma \left( h|_{\mathbb {C}{\setminus } B_r(z)} \right)$ (Lemma 4.6), we infer from (4.26) and the definitions (4.12) and (4.13) of $\mathcal Z_k^E$ and $\mathcal Z_k^{\mathfrak E}$ that for each $(z,r) \in \mathbb {C}\times \mathcal R$ such that $\mathbb {z} ,\mathbb {w} \notin B_{\lambda _4 r}(z)$, a.s.

$$\begin{aligned} \mathbb {P}\left[ (z,r) \in \mathcal Z_k^E \,\big |\, h|_{\mathbb {C}{\setminus } B_r(z)} \right] \le \Lambda \mathbb {P}\left[ (z,r) \in \mathcal Z_k^{\mathfrak E} \,\big |\, h|_{\mathbb {C}{\setminus } B_r(z)} \right] . \end{aligned}$$

(4.27)

We will now deduce from (4.27) and Lemma 4.9 that on $\{(z,r) \in \mathcal Z_k\}\cap \{\mathbb {w} \notin B_{ 3\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )\}$, a.s.

$$\begin{aligned} \mathbb {P}\left[ (z,r) \in \mathcal Z_k^E \,\big |\, \mathcal F_k \right] \le \Lambda \mathbb {P}\left[ (z,r) \in \mathcal Z_k^{\mathfrak E} \,\big |\, \mathcal F_k \right] . \end{aligned}$$

(4.28)

In particular, we will apply Lemma 4.9 with $\mathcal F = \mathcal F_k$, $\mathcal G = \sigma \left( h|_{\mathbb {C}{\setminus } B_r(z)}\right)$, $E = \mathrm {Stab}_{k,r}(z) \cap \{P\cap B_r(z)\not =\emptyset \}$, $G = \{(z,r) \in \mathcal Z_k\}\cap \{\mathbb {w} \notin B_{ 3\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )\}$, $H_1 = \{(z,r) \in \mathcal Z_k^E \}$, and $H_2 = \{(z,r) \in \mathcal Z_k^{\mathfrak E}\}$.

We check the hypotheses of Lemma 4.9 with the above choice of parameters, starting with the requirement that the event G defined above belongs to $\mathcal F_k \cap \sigma \left( h|_{\mathbb {C}{\setminus } B_r(z)} \right)$. Indeed, it is clear from the definition (4.10) of $\mathcal Z_k$ that $G\in \sigma (\mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet })$. By the definition (4.9) of $\mathcal F_k$, we have $G \in \mathcal F_k$. By the definition (4.10) of $\mathcal Z_k$ and the locality of $\mathcal B_{t_k}^\bullet$ (Lemma 2.1), also $G\in \sigma \left( h|_{\mathbb {C}{\setminus } B_r(z)} \right)$. By the definition (4.10) of $\mathcal Z_k$, if G occurs with positive probability then $\mathbb {z} ,\mathbb {w} \notin B_{\lambda _4 r}(z)$, so in particular (4.27) holds a.s. on G. By Lemma 4.6, the intersection of any event in $\mathcal F_k$ with $\mathrm {Stab}_{k,r}(z) \cap \{P\cap B_{ r}(z)\not =\emptyset \}$ is a.s. determined by $h|_{\mathbb {C}{\setminus } B_r(z)}$ and $\mathbb {1}_{\mathrm {Stab}_{k,r}(z) \cap \{P\cap B_{ r}(z)\not =\emptyset \}}$. We may therefore apply Lemma 4.9 to deduce (4.28) from (4.27).

Summing (4.28) over all $(z,r)\in \mathcal Z_k$ gives that on $\{\mathbb {w} \notin B_{ 3\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )\}$,

$$\begin{aligned} \mathbb {E}\left[ \# \mathcal Z_k^{\mathfrak E} \,|\, \mathcal F_k \right] \ge \Lambda ^{-1} \mathbb {E}\left[ \# \mathcal Z_k^E \,|\, \mathcal F_k \right] \ge \Lambda ^{-1} \mathbb {P}\left[ \mathcal Z_k^E \not =\emptyset \,|\, \mathcal F_k \right] . \end{aligned}$$

(4.29)

By Lemma 4.8, for each $\zeta \in (0,1)$, on the event $\{ \mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M}}(\mathbb {z}) \}$, it holds except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ that

$$\begin{aligned} \mathbb {E}\left[ \# \mathcal Z_k^{\mathfrak E} \,|\, \mathcal F_k \right]&\le \varepsilon ^{-2\nu -\zeta } \mathbb {P}\left[ 0 < \# \mathcal Z_k^{\mathfrak E} \le \varepsilon ^{-2\nu -\zeta } \,|\, \mathcal F_k \right] \nonumber \\&\quad + \mathbb {E}\left[ \#\mathcal Z_k^{\mathfrak E} \mathbb {1}_{(\# \mathcal Z_k^{\mathfrak E} > \varepsilon ^{-2\nu -\zeta })} \,|\, \mathcal F_k \right] \nonumber \\&\le \varepsilon ^{-2\nu -\zeta } \mathbb {P}\left[ \mathcal Z_k^{\mathfrak E} \not =\emptyset \,|\, \mathcal F_k \right] + o_\varepsilon ^\infty (\varepsilon ) . \end{aligned}$$

(4.30)

Combining (4.29) and (4.30) gives that on the event $\{ \mathcal B_{t_k}^\bullet \subset B_{\varepsilon ^{-M}}(\mathbb {z}) \} \cap \{\mathbb {w} \notin B_{ 3\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )\}$, it holds except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ that

$$\begin{aligned} \varepsilon ^{-2\nu -\zeta } \mathbb {P}\left[ \mathcal Z_k^{\mathfrak E} \not =\emptyset \,|\, \mathcal F_k \right] + o_\varepsilon ^\infty (\varepsilon ) \ge \Lambda ^{-1} \mathbb {P}\left[ \mathcal Z_k^E \not =\emptyset \,|\, \mathcal F_k \right] . \end{aligned}$$

(4.31)

Re-arranging this inequality and then sending $\zeta \rightarrow 0$ sufficiently slowly as $\varepsilon \rightarrow 0$ gives (4.14). $\square$

4.3 Global regularity event

Throughout most of the rest of the proof of Theorem 4.2, we will truncate on a global regularity event which we define in this subsection. The parameter $\mathbb {p} \in (0,1)$ of Theorem 4.2 has to be chosen sufficiently close to 1 to allow us to apply Lemma 2.6 to make the probability of one of the conditions in the event as close to 1 as we like. We emphasize that our global regularity event does not depend on the particular choice of $\mathbb {z},\mathbb {w}$ in (4.4).

Fix bounded, connected open sets $U \subset V \subset \mathbb {C}$ and parameters $\nu , \ell > 0$ ($\nu$, U, and $\ell$ are the parameters from Theorem 4.2). Also fix, once and for all, parameters $\chi \in (0,\xi (Q-2))$ and $\chi ' > \xi (Q+2)$ as in Lemma 2.8, chosen in a manner which depends only on $\gamma$ (we will not make the dependence on these parameters explicit). For $\mathbb {r} > 0$ and $a \in (0,1)$, let $\mathcal E_{\mathbb {r}} = \mathcal E_{\mathbb {r}}(a , \nu , \ell , U , V )$ be the event that the following is true.

• 1. (Comparison of domains) $\sup _{z,w\in \mathbb {r} U} D_h(z,w) \le D_h(\mathbb {r} U , \mathbb {r} \partial V)$.

• 2. (Comparison of $D_h$-balls and Euclidean balls) For each $z \in \mathbb {C}$ and $r>0$, let $\tau _r(z)$ be the smallest $t > 0$ for which the filled $D_h$-metric ball $B_t^\bullet (z;D_h)$ intersects $\partial B_r(z)$, as in (2.23). Then for each $z\in B_{4\ell \mathbb {r}}(\mathbb {r} V)$, we have $B_{a\mathbb {r}}(z) \subset \mathcal B_{\tau _{\ell \mathbb {r}}(z)}^\bullet (z ; D_h)$ and

  $$\begin{aligned} \min \left\{ \tau _{2 \ell \mathbb {r}}(z) - \tau _{ \ell \mathbb {r}}(z) , \tau _{3 \ell \mathbb {r}}(z) - \tau _{2\ell \mathbb {r}}(z) \right\} \ge a \max \left\{ \mathfrak c_{ \mathbb {r}} e^{\xi h_{\mathbb {r}}(z)} , \mathfrak c_{ \ell \mathbb {r}} e^{\xi h_{\ell \mathbb {r}}(z)} \right\} .\nonumber \\ \end{aligned}$$

  (4.32)

• 3. (Hölder continuity) For each $z,w\in B_{4\ell \mathbb {r}}(\mathbb {r} V)$ with $|z-w| \le a \mathbb {r}$,

  $$\begin{aligned}&\mathfrak c_{\mathbb {r}}^{-1} e^{-\xi h_{\mathbb {r}}(0)} D_h(z,w) \ge \left| \frac{z-w}{\mathbb {r}} \right| ^{\chi '} \quad \text {and} \quad \nonumber \\&\quad \mathfrak c_{\mathbb {r}}^{-1} e^{-\xi h_{\mathbb {r}}(0)} D_h\left( z , w ; B_{2|z-w|}(z) \right) \le \left| \frac{z-w}{\mathbb {r}} \right| ^\chi . \end{aligned}$$

  (4.33)

• 4. (Comparison of circle averages) We have

  $$\begin{aligned} \sup _{z\in \mathbb {r} V} |h_{\mathbb {r}}(z) - h_{\mathbb {r}}(0)| \le a^{-1} . \end{aligned}$$

  (4.34)

• 5. (Existence of good annuli) Define $r_1^\varepsilon , \ldots , r_{\lfloor \mu \log _8 \varepsilon ^{-1} \rfloor }^\varepsilon \in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}]\cap \mathcal R$ as in condition 1 from Theorem 4.2. For each $\varepsilon \in (0,a \mathbb {r}] \cap \{2^{-n}\mathbb {r}\}_{n\in \mathbb {N}}$ and each $z\in \left( \frac{\lambda _1 \varepsilon ^{1+\nu } \mathbb {r}}{4} \mathbb {Z}^2 \right) \cap B_{4\ell \mathbb {r}}(\mathbb {r} V)$, there exists at least one $r \in \{r_1^\varepsilon ,\ldots ,r_{\lfloor \mu \log _8\varepsilon ^{-1} \rfloor } \}$ for which $E_r(z)$ occurs.

• 6. (Bounds for radii used to control geodesics) Define the radii $\rho _{\mathbb {r},\varepsilon }(z)$ for $\varepsilon > 0$ and $z\in \mathbb {C}$ as in Lemma 2.13 and the discussion just preceding it. For each $\varepsilon \in (0,a ] \cap \{2^{-n} \}_{n\in \mathbb {N}}$ and each $z\in \left( \frac{\varepsilon ^{1+\nu } \mathbb {r}}{4} \mathbb {Z}^2 \right) \cap B_{4\ell \mathbb {r}}(\mathbb {r} V)$, we have $\rho _{\mathbb {r},\varepsilon }(z) \le \varepsilon ^{1/2} \mathbb {r}$.

We note that the upper bound in (4.33) uses $D_h\left( z , w ; B_{2|z-w|}(z) \right) \ge D_h(z,w)$ instead of $D_h(z,w)$. We will need this slightly stronger upper bound for $D_h$-distances in the proof of Lemma 4.19 below.

Remark 4.10

Due to conditions 2, 3, and 6 , and since $\ell \in (0,1)$, for each $\mathbb {z}\in \mathbb {r} U$ the event $\mathcal E_{\mathbb {r}}$ defined just above is contained in the event $\mathcal E_{\ell \mathbb {r}}^{\mathbb {z}}(a )$ as defined just above Theorem 2.16 with $\ell \mathbb {r}$ in place of $\mathbb {r}$.

Lemma 4.11

There exists $\mathbb {p} \in (0,1)$ depending only on $\mu ,\nu , \{\lambda _i\}_{i=1,\ldots ,5}$ such that under the hypotheses of Theorem 4.2, the following is true. For each bounded open set $U\subset \mathbb {C}$, $\nu ,\ell \in (0,1)$, and $p\in (0,1)$, there exists a bounded open set $V\supset U$ and a parameter $a\in (0,1)$, depending only $U,\nu ,\ell , p$, such that $\mathbb {P}[\mathcal E_{\mathbb {r}}] \ge p$ for each $\mathbb {r} > 0$.

Proof

By Axiom V (tightness across scales), we can find a bounded open set $V\supset U$, depending only on U, such that condition 1 (comparison of domains) in the definition of $\mathcal E_{\mathbb {r}}$ holds with probability at least $1-(1-p)/6$. Again using Axiom V, we can find a small enough $a \in (0,1)$, depending on $\ell , V , p$, such that condition 2 (comparison of balls) holds with probability at least $1-(1-p)/6$. By Lemma 2.8, after possibly shrinking a we can further arrange that condition 3 (Hölder continuity) holds with probability at least $1-(1-p)/6$. By the continuity of the circle average process and the scale invariance of the law of h, modulo additive constant, after possibly further shrinking a we can arrange that condition 4 (comparison of circle averages) holds with probability at least $1- (1-p)/6$. By Lemma 2.6, conditions 2 and 3 of Theorem 4.2, and a union bound over all $z \in \left( \frac{\lambda _1 \varepsilon ^{1+\nu } \mathbb {r}}{4} \mathbb {Z}^2 \right) \cap V$, if $\mathbb {p}$ is chosen sufficiently close to 1, in a manner depending only on $\mu ,\nu$, and $\{\lambda _i\}_{i=1,\ldots ,5}$, then the probability of condition 5 (existence of good annuli) in the definition of $\mathcal E_{\mathbb {r}}$ tends to 1 as $a \rightarrow 0$, uniformly over the choice of $\mathbb {r}$. Therefore, after possibly further shrinking a, we can arrange that condition 5 in the definition of $\mathcal E_{\mathbb {r}}$ holds with probability at least $1 - (1-p)/6$. By Lemma 2.13 and a union bound over values of $\varepsilon \in (0,a ] \cap \{2^{-n} \}_{n\in \mathbb {N}}$, after possibly further shrinking a we can also arrange that condition 6 (bounds for $\rho _{\mathbb {r},\varepsilon }(z)$) in the definition of $\mathcal E_{\mathbb {r}}$ holds with probability at least $1-(1-p)/6$. $\square$

4.4 Geodesic stability event occurs at many times

Henceforth fix $p\in (0,1)$ (which we will eventually send to 1), a bounded open set $U\subset \mathbb {C}$, and $\ell \in (0,1)$ and let V, a be as in Lemma 4.11 for this choice of $p,U,\ell$ and the given values of $\mu ,\nu$ from Theorem 4.2. Let $\mathcal E_{\mathbb {r}}$ be the event of Sect. 4.3 with this choice of parameters, so that $\mathbb {P}[\mathcal E_{\mathbb {r}}] \ge p$. Define

$$\begin{aligned} K := \lfloor a \varepsilon ^{-\beta } \rfloor -1 , \end{aligned}$$

(4.35)

where $\beta$ is as in (4.6). The significance of the value K is that condition 2 (comparison of balls) in the definition of $\mathcal E_{\mathbb {r}}$ implies that, in the notation (4.6),

$$\begin{aligned} s_{K+1} \le \tau _{2 \ell \mathbb {r}} ,\quad \text {on } \mathcal E_{\mathbb {r}}. \end{aligned}$$

(4.36)

Recalling the parameter $\beta$ from (4.6) and the parameters $\chi <\chi '$ as in condition 3 (Hölder continuity) in the definition of $\mathcal E_{\mathbb {r}}$, we henceforth impose the requirement that

$$\begin{aligned} \beta \in (0, \chi / \chi ') . \end{aligned}$$

(4.37)

We will make our final choice of $\beta$ in Proposition 4.12 just below.

Let $\mathcal Z_k^E$ be as in (4.12) and let K be as in (4.35). The goal of this section is to show that with high probability there are many values of $k\in [0,K]_{\mathbb {Z}}$ for which $\mathcal Z_k^E \not =\emptyset$. In the next subsection, we will combine this with Lemma 4.7 to show that there are many values of $k\in [0,K]_{\mathbb {Z}}$ for which $\mathcal Z_k^{\mathfrak E}\not =\emptyset$. The following proposition is the main result of this subsection and is the only statement from this subsection which is referenced in Sect. 4.5.

Proposition 4.12

There are small constants $\beta ,\theta \in (0,1)$ depending only on the choice of metric D such that if we use this choice of $\beta$ in (4.6), then on $\mathcal E_{\mathbb {r}}$ it holds except on an event of probability decaying faster than any positive power of $\varepsilon$, at a rate which is uniform in $\mathbb {r}, \mathbb {z} ,\mathbb {w}$, that there are at least $(1-\varepsilon ^\theta ) K$ values of $k \in [0,K]_{\mathbb {Z}}$ for which $\mathcal Z_k^E \not =\emptyset$.

Fig. 5

Illustration of the proof of Proposition 4.12. The points in the set $\mathrm {EndPts}_k$ of endpoints of arcs in ${{\mathcal {I}}}_k$ are shown in red. We first use Theorem 2.16 to bound $\#\mathrm {EndPts}_k = \#\mathrm {Conf}_k$. Lemma 4.14 allows us to choose for each $y\in \mathrm {EndPts}_k$ a point $z_y \in \partial \mathcal B_{t_k}^\bullet$ (not shown) such that an arc of $B_{16\varepsilon ^\kappa \mathbb {r}} (z_y)$ disconnects the set $\mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$ (defined just after Lemma 4.14) from $\infty$ in $\mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet$. The set which this arc disconnects from $\infty$, which contains $\mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$, is shown in pink. Note that the sets $\mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$ for different choices of y are allowed to overlap. Lemma 2.14 and a union bound over $y\in \mathrm {EndPts}_k$ shows that with high probability, for each $y\in \mathrm {EndPts}_k$, no $D_h$-geodesic from $\mathbb {z}$ to $\partial \mathcal B_{s_{k+1}}^\bullet$ can enter any of the $\mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$’s. This together with Lemma 4.13 allows us to show that $\mathrm {Stab}_{k,r}(z)$ occurs for each $(z,r) \in \mathcal Z_k$ such that $P\cap B_r(z)\not =\emptyset$. One such ball $B_r(z)$ is shown in green and several segments of $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesics from $\mathbb {z}$ to points of $\partial B_r(z)$ are shown in red (color figure online)

By condition 5 (existence of good annuli) in the definition of $\mathcal E_{\mathbb {r}}$, we already know that on this event, for each $k\in [0,K]_{\mathbb {Z}}$ there are many pairs $(z,r) \in \mathcal Z_k$ for which $P\cap B_{\lambda _2 r}(z) \not =\emptyset$ and $E_r(z)$ occurs. The main point of this subsection is to show that there are many such pairs for which also the event $\mathrm {Stab}_{k,r}(z)$ of (4.11) occurs. Roughly speaking, the idea of the proof is as follows; see Fig. 5 for an illustration. If P enters $B_r(z)$ but $\mathrm {Stab}_{k,r}(z)$ fails to occur, then P has to get “close” in some sense to one of the endpoints of one of the arcs in ${{\mathcal {I}}}_k$.⁶ Indeed, otherwise Hölder continuity allows us to force all of the $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesics from $\mathbb {z}$ to points of $\partial B_r(z)$ to hit the same arc of ${{\mathcal {I}}}_k$ as P. This is explained in Lemma 4.13.

On the other hand, if we choose $\beta$ sufficiently small then results from [36] (in particular, Theorem 2.16) show that $\#{{\mathcal {I}}}_k$ is extremely likely to be of smaller order than $\varepsilon ^{-\alpha }$, where $\alpha$ is the exponent from Lemma 2.14. We can therefore apply that lemma once for each of the endpoints of the ${{\mathcal {I}}}_k$’s and take a union bound to say that with polynomially high probability given $(\mathcal B_{t_k}^\bullet ,h|_{\mathcal B_{t_k}^\bullet })$, no $D_h$-geodesic from $\mathbb {z}$ to a point at macroscopic distance from $\partial \mathcal B_{s_k}^\bullet$ can get near any of the endpoints of the ${{\mathcal {I}}}_k$’s (Lemma 4.15). The claimed superpolynomial concentration when we truncate on $\mathcal E_{\mathbb {r}}$ comes from a standard concentration bound for independent Bernoulli random variables, provided we choose $\theta$ to be sufficiently small relative to $\alpha$.

In order to quantify how close $D_h$-geodesics get to the endpoints of the ${{\mathcal {I}}}_k$’s, we will need some deterministic definitions. Let $U\subset \mathbb {C}$ be a connected domain such that $\mathbb {C}{\setminus } U$ is compact and connected. View $\partial U$ as a collection of prime ends. If $X\subset U$, we define the prime end closure ${\text {Cl}}'(X)$ to be the set of points in $z\in U\cup \partial U$ with the following property: if $\phi : U \cup \partial U \rightarrow \mathbb {C}{\setminus } \mathbb {D}$ is a conformal map, then $\phi (z)$ lies in $\overline{\phi (X)}$. Following [36, Equation (2.19)], for $z,w\in U\cup \partial U$ we define

$$\begin{aligned}&d^U(z,w) \nonumber \\&\quad = \inf \left\{ {\text {diam}}(X) : X\text { is a connected subset of } U \text { with } z,w\in {\text {Cl}}'(X) \right\} ,\nonumber \\ \end{aligned}$$

(4.38)

where here ${\text {diam}}$ denotes the Euclidean diameter. Then $d^U$ is a metric on $U \cup \partial U$ which is bounded below by the Euclidean metric on $\mathbb {C}$ restricted to $U \cup \partial U$ and bounded above by the internal Euclidean metric on $U \cup \partial U$. Note that $d^U$ is not a length metric.

Fig. 6

Illustration of the statement and proof of Lemma 4.13. If P gets $d^{\mathbb {C}{\setminus }\mathcal B_s^\bullet }$-close to $\partial \mathcal B_s^\bullet {\setminus } I$, then there is a set $X_0$ of small Euclidean diameter which intersects P and $\partial \mathcal B_s^\bullet {\setminus } I$. Moreover the Hölder continuity condition in the definition of $\mathcal E_{\mathbb {r}}$ implies that the Euclidean diameter of the segment of P between s and the first time it hits $X_0$ is small. The union X of this segment and $X_0$ disconnects one of the endpoints of I from $\infty$

Lemma 4.13

Almost surely, if $\mathcal E_{\mathbb {r}}$ occurs then the following is true for every $s \in [0,\tau _{3\ell \mathbb {r}}]$, every $\varepsilon \in (0,a]$, and every non-trivial proper connected arc $I \subset \partial \mathcal B_s^\bullet$ (i.e., I is the image of an arc of $\partial \mathbb {D}$ which is not a singleton or all of $\partial \mathbb {D}$ under a conformal map $\mathbb {C}{\setminus } \overline{\mathbb {D}} \rightarrow \mathbb {C}{\setminus } \mathcal B_s^\bullet$). Let P be a $D_h$-geodesic from $\mathbb {z}$ to a point outside of $\mathcal B_s^\bullet$ which passes through I and suppose that in the notation (4.38), we have $d^{\mathbb {C}{\setminus } \mathcal B_s^\bullet }(P , \partial \mathcal B_s^\bullet {\setminus } I) \le \varepsilon \mathbb {r}$. There is a connected set $X\subset \mathbb {C}{\setminus } \mathcal B_s^\bullet$ with Euclidean diameter at most $2 \varepsilon ^{\chi /\chi '} \mathbb {r}$ such that P(s) and at least one of the two endpoints of I both lie in the prime end closure of the same bounded connected component of $\mathbb {C}{\setminus } (\mathcal B_s^\bullet \cup X)$.

Proof

See Fig. 6 for an illustration of the statement and proof of the lemma. Assume that $\mathcal E_{\mathbb {r}}$ occurs and let $s , I ,\varepsilon$, and P be as in the lemma statement. By hypothesis, for each $\delta \in (0,1)$ there is a connected set $X_0 \subset \mathbb {C}{\setminus } \mathcal B_s^\bullet$ which has Euclidean diameter at most $(\varepsilon +\delta )\mathbb {r}$ and which satisfies $P\cap X_0\not =\emptyset$ and ${\text {Cl}}'(X_0) \cap (\partial \mathcal B_s^\bullet {\setminus } I) \not =\emptyset$. By possibly shrinking $X_0$, we can assume without loss of generality that ${\text {Cl}}'(X_0) \cap (\partial \mathcal B_s^\bullet {\setminus } I)$ is a single prime end, which is necessarily in $\mathcal B_s^\bullet {\setminus } I$.

Let t be the first time after s at which P hits $X_0$. By the upper bound in condition 3 (Hölder continuity) in the definition of $\mathcal E_{\mathbb {r}}$, the $D_h$-diameter of $X_0$ is at most $(\varepsilon +\delta )^{\chi } \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)}$. Since P is a $D_h$-geodesic, $P(t) \in X_0$, and ${\text {Cl}}'(X_0)$ contains a point of $\partial \mathcal B_s^\bullet$ (which implies that $D_h(X_0, \partial \mathcal B_s^\bullet ) = 0$), it follows that $t-s \le (D_h\text {-diameter of } X_0) \le (\varepsilon +\delta )^{ \chi } \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)}$. By the lower bound in condition 3 (Hölder continuity) in the definition of $\mathcal E_{\mathbb {r}}$, the Euclidean diameter of P([s, t]) is at most $(\varepsilon +\delta )^{ \chi / \chi '} \mathbb {r}$. The set $X := X_0 \cup P((s,t])$ has Euclidean diameter at most $((\varepsilon +\delta )^{\chi / \chi '} + \varepsilon + \delta ) \mathbb {r}$ and its prime end closure contains both the point $P(s) \in I$ and a point of $\partial \mathcal B_s^\bullet {\setminus } I$. Hence one of the connected components V of $\mathbb {C}{\setminus } (\mathcal B_s^\bullet \cup X)$ is bounded and contains an endpoint of I. Since ${\text {Cl}}'(X)$ intersects I only at P(s) (here we use that ${\text {Cl}}'(X_0) \cap \partial \mathcal B_s^\bullet$ is a single point), it follows that also $P(s) \in \partial V$. We now conclude the proof by choosing $\delta$ to be sufficiently small (depending on $\varepsilon$) so that $(\varepsilon +\delta )^{\chi / \chi '} + \varepsilon + \delta \le 2\varepsilon ^{\chi /\chi '}$. $\square$

We will eventually apply the contrapositive of Lemma 4.13, i.e., we will say that if P does not enter a region which contains one of the endpoints of I and which is disconnected from $\infty$ in $\mathbb {C}{\setminus } \mathcal B_s^\bullet$ by a set of small diameter, then $d^{\mathbb {C}{\setminus } \mathcal B_s^\bullet }(P ; \partial \mathcal B_s^\bullet {\setminus } I)$ is bounded below. The following elementary deterministic lemma will be used in conjunction with Lemma 2.14 to prevent P from entering such a region (we will apply the lemma with $\mathcal K = \mathcal B_{t_k}^\bullet$).

Lemma 4.14

Let $\mathcal K \subset \mathbb {C}$ be a compact connected set such that $\mathbb {C}{\setminus } \mathcal K$ is connected and view $\partial \mathcal K$ as a collection of prime ends. For $y\in \partial \mathcal K$ and $\varepsilon > 0$, let $\mathcal C_y^\varepsilon$ be the set of points in $z \in \mathbb {C}{\setminus } \mathcal K$ such that the following is true. There is a connected set $X\subset \mathbb {C}{\setminus } \mathcal K$ (allowed to depend on z and $y,\varepsilon$) with Euclidean diameter at most $\varepsilon$ such that z and y lie in the prime end closure of the same bounded connected component of $\mathbb {C}{\setminus } (X\cup \mathcal K)$. Then there is a compact connected set $Y_y^\varepsilon \subset \mathbb {C}{\setminus } \mathcal K$ of Euclidean diameter at most $16\varepsilon$ (depending only on $y,\varepsilon$) such that $\mathcal C_y^\varepsilon$ is contained in the prime end closure of a single bounded connected component of $\mathbb {C}{\setminus } (Y_y^\varepsilon \cup \mathcal K)$.

The proof of Lemma 4.14 is straightforward, but it takes a few paragraphs so we postpone it until Sect. 4.6 to avoid interrupting the proof of Theorem 4.2. The reader may want to refer to Fig. 7 for an illustration of the definition of $\mathcal C_y^\varepsilon$.

Returning now to the setting of Proposition 4.12, for $k\in [0,K]_{\mathbb {Z}}$ let $\mathrm {EndPts}_k$ be the set of endpoints of the arcs in ${{\mathcal {I}}}_k$. As in Lemma 4.14, for $\delta >0$ and $y\in \partial \mathcal B_{t_k}^\bullet$, we let $\mathcal C_y^\delta$ be the set of points $z\in (\mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet ) \cup \partial \mathcal B_{t_k}^\bullet$ with the following property: there is a compact connected set $X\subset \overline{\mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet }$ with Euclidean diameter at most $\delta$ such that z and y lie in the closure of the same bounded connected component of $\mathbb {C}{\setminus } (\mathcal B_{t_k}^\bullet \cup X)$.

Lemma 4.15

Fix $\kappa \in (0,1)$. If $\beta ,\theta \in (0,1)$ are chosen sufficiently small, in a manner depending only on $\kappa$ and the choice of metric D, then on $\mathcal E_{\mathbb {r}}$ it holds except on an event of probability decaying faster than any positive power of $\varepsilon$, at a rate which is uniform in $\mathbb {r}$, that there are at least $(1-\varepsilon ^\theta ) K$ values of $k \in [0,K]_{\mathbb {Z}}$ for which the following is true. In the notation introduced just above, no $D_h$-geodesic from $\mathbb {z}$ to $\partial \mathcal B_{s_{k+1}}^\bullet$ can enter $\bigcup _{y\in \mathrm {EndPts}_k} \mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$.

Proof

Fix parameters $\theta , \omega \in (0,1)$ to be chosen later, in a manner depending only on D. We will first choose $\beta$ in a manner depending on $\omega ,D$ and then choose $\omega$ in a manner depending on $\kappa , D$, and then choose $\theta$ in a manner depending on $\beta ,\omega$. In particular, we will take $\omega < \alpha \kappa /2$ and $\theta < \min \{\omega , \beta /2 \}$. The parameter $\kappa$ will be chosen in a manner depending only on D in the proof of Proposition 4.12 below.

We will first show, using Theorem 2.16, that if $\beta$ is chosen to be sufficiently small (depending on $\omega ,D$) then with extremely high probability on $\mathcal E_{\mathbb {r}}$ one has for each $k\in [0,K]_{\mathbb {Z}}$ that $\#\mathrm {Conf}_k \le \varepsilon ^{-\omega }$, which implies that $\#\mathrm {EndPts}_k \le \varepsilon ^{-\omega }$. We then show using Lemma 2.14 and a union bound over at most $\varepsilon ^{-\omega }$ elements of $\mathrm {EndPts}$ that if $\omega$ is chosen to be sufficiently small (depending on the parameter $\alpha$ of Lemma 2.14, which depends only on D), then for each k it holds with conditional probability at least $1-\varepsilon ^\omega$ given $\mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet }$ that no $D_h$-geodesic from $\mathbb {z}$ to $\partial \mathcal B_{s_{k+1}}^\bullet$ can enter $\bigcup _{y\in \mathrm {EndPts}_k} \mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$. Finally, we will use the Markovian structure of the GFF together with a standard concentration inequality for Bernoulli random variables to show that if $\theta$ is chosen to be sufficiently small then with extremely high probability this happens for at least $(1-\varepsilon ^\theta )K$ values of $k\in [0,K]_{\mathbb {Z}}$.

Step 1: bounding the number of confluence points Recall from Sect. 4.1 that $t_k = s_k + \varepsilon ^{2\beta } \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)}$ and $\mathrm {Conf}_k$ is the set of points of $\partial \mathcal B_{s_k}^\bullet$ which are hit by leftmost $D_h$-geodesics from $\mathbb {z}$ to $\partial \mathcal B_{t_k}^\bullet$. Due to Remark 4.10, we can apply Theorem 2.16 (with $N = \lfloor \varepsilon ^{-\omega } \rfloor$ and $\tau = s_k$) to get that if $\beta$ is chosen sufficiently small, in a manner depending only on $\omega$ and D, then for each $k\in [0,K]_{\mathbb {Z}}$, the probability that $\mathcal E_{\mathbb {r}}$ occurs and $\#\mathrm {Conf}_k > \varepsilon ^{-\omega }$ decays faster than any positive power of $\varepsilon$. By a union bound over k,

$$\begin{aligned} \mathbb {P}\left[ \mathcal E_{\mathbb {r}} ,\, \max _{k\in [0,K]_{\mathbb {Z}}} \#\mathrm {Conf}_k > \varepsilon ^{-\omega } \right] = o_\varepsilon ^\infty (\varepsilon ) . \end{aligned}$$

(4.39)

Step 2: bounding the parameters from Lemma 2.14 Recall the radii $\rho _{\mathbb {r},\varepsilon }(z)$, which appear in Lemma 2.13 and condition 6 (bounds for $\rho _{\mathbb {r},\varepsilon }(z)$) in the definition of $\mathcal E_{\mathbb {r}}$ (the precise definition of these radii is not needed here, only their role in Lemma 2.14). To lighten notation, for $k\in [0,K]_{\mathbb {Z}}$ we define

$$\begin{aligned} R_k&:= R_{\mathbb {r}}^{\varepsilon ^\kappa }(\mathcal B_{t_k}^\bullet ) = 6 \max \left\{ \rho _{\mathbb {r},\varepsilon ^\kappa }(z) : z\in \left( \frac{\varepsilon ^\kappa \mathbb {r}}{4} \mathbb {Z}^2 \right) \cap B_{\varepsilon ^\kappa \mathbb {r}}\left( \mathcal B_{t_k}^\bullet \right) \right\} \nonumber \\&\quad +\varepsilon \mathbb {r} ,\quad \text {as in}~(2.21) \text { and} \nonumber \\ \sigma _k&:= \sigma _{t_k,\mathbb {r}}^{\varepsilon ^\kappa } = \inf \left\{ s' > s : B_{R_k}(\mathcal B_{t_k}^\bullet ) \subset \mathcal B_{s'}^\bullet \right\} , \quad \text {as in}~(2.22) . \end{aligned}$$

(4.40)

Note that we use (2.21) and (2.22) with $\varepsilon ^\kappa$ in place of $\varepsilon$.

On $\mathcal E_{\mathbb {r}}$, we have $\mathcal B_{t_k}^\bullet \subset \mathcal B_{\tau _{2\ell \mathbb {r}}}^\bullet \subset B_{2\ell \mathbb {r}}(\mathbb {z}) \subset B_{4\ell \mathbb {r}}(\mathbb {r} V)$ for each $k\in [0,K]_{\mathbb {Z}}$ (see (4.36)). Hence we can apply condition 6 (bounds for $\rho _{\mathbb {r},\varepsilon }(z)$) in the definition of $\mathcal E_{\mathbb {r}}$ and the definition (4.40) of $R_k$ to get that if $\varepsilon$ is chosen sufficiently small, depending on a and $\kappa$, then on $\mathcal E_{\mathbb {r}}$, we have $R_k \le (6\varepsilon ^{\kappa /2} + \varepsilon ^{\kappa /2}) \mathbb {r} \le 7\varepsilon ^{\kappa /2} \mathbb {r}$ for each $k\in [0,K]_{\mathbb {Z}}$. By combining this with the upper bound for $D_h$-distances from condition 3 (Hölder continuity) in the definition of $\mathcal E_{\mathbb {r}}$, we get that $B_{R_k}(\mathcal B_{t_k}^\bullet ) \subset \mathcal B_{t_k + 7^{\chi } \varepsilon ^{\kappa \chi /2} \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)}}^\bullet$. By this together with the definition of $\sigma _k$ and condition 4 (comparison of circle averages) in the definition of $\mathcal E_{\mathbb {r}}$ (to replace $h_{\mathbb {r}}(0)$ with $h_{\mathbb {r}}(\mathbb {z})$), on $\mathcal E_{\mathbb {r}}$ we have $\sigma _k \le t_k + A \varepsilon ^{\kappa \chi /2} \mathfrak c_{\mathbb {r}} e^{\xi h_{ \mathbb {r} }(\mathbb {z})}$, where $A = 7^\chi e^{\xi /a}$ is an unimportant constant.

We henceforth assume that $\beta < \kappa \chi /2$, so that by the conclusion of the preceding paragraph and the definition (4.6) of $t_k$ and $s_{k+1}$, for small enough $\varepsilon \in (0,1)$ (how small depends only on $a , \beta ,\kappa$),

$$\begin{aligned} \sigma _k \le t_k + ( \varepsilon ^\beta - \varepsilon ^{2\beta } ) \mathfrak c_{ \mathbb {r} } e^{\xi h_{ \mathbb {r} }(\mathbb {z})} = s_{k+1} ,\quad \forall k \in [0,K]_{\mathbb {Z}} ,\quad \text {on } \mathcal E_{\mathbb {r}} . \end{aligned}$$

(4.41)

Step 3: killing off geodesics near the endpoints with polynomially high probability Recall that $\mathrm {EndPts}_k$ denotes the set of endpoints of arcs in ${{\mathcal {I}}}_k$. We have $\#\mathrm {EndPts}_k = \#{{\mathcal {I}}}_k$. By Lemma 4.14, each of the sets $\mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$ can be disconnected from $\infty$ in $\mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet$ by a connected subset of $\mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet$ of Euclidean diameter at most $16\varepsilon ^\kappa \mathbb {r}$. By an argument as in (4.41), if $\varepsilon \in (0,1)$ is chosen sufficiently small (how small depends only on $\beta ,\kappa$), then $B_{16\varepsilon ^\kappa \mathbb {r}}(\mathcal B_{t_k}^\bullet ) \subset \mathcal B_{s_{k+1}}^\bullet$. We may therefore choose for each $y\in \mathrm {EndPts}_k$ a point $z_y \in \partial \mathcal B_{t_k}^\bullet$, in a manner depending only on $(\mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet })$, with the following property.

• (*) Every path in $\mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet$ from $\mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$ to $\mathbb {C}{\setminus } \mathcal B_{s_{k+1}}^\bullet$ must enter $B_{16\varepsilon ^\kappa \mathbb {r}}(z_y)$.

By Lemma 2.14 (applied with $\tau = t_k$ and $16\varepsilon ^\kappa$ in place of $\varepsilon$), there are constants $C_0 > 1$ and $\alpha > 0$, depending only on the choice of metric, and an event $G_y$ for each $y\in \mathrm {EndPts}_k$ such that $G_y \in \sigma \left( \mathcal B_{\sigma _k}^\bullet , h|_{\mathcal B_{\sigma _k}^\bullet } \right)$ and the following is true.

• A. If $R_k \le {\text {diam}}(\mathcal B_{t_k}^\bullet )$ and $G_y$ occurs, then no $D_h$-geodesic from $\mathbb {z}$ to a point of $\mathbb {C}{\setminus } \mathcal B_{\sigma _k}^\bullet$ can enter $B_{16\varepsilon ^\kappa \mathbb {r} }(z_y) {\setminus } \mathcal B_{t_k}^\bullet$.

• B. Almost surely, $\mathbb {P}[G_y | \mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet } ] \ge 1 - C_0 \varepsilon ^{\alpha \kappa }$.

Henceforth assume that $\omega \in (0,\alpha \kappa /2)$. On the event $\{\#\mathrm {Conf}_k \le \varepsilon ^{-\omega }\}$ (which is in $\sigma ( \mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet })$ and has high probability by (4.39) and the fact that $\mathcal E_{\mathbb {r}}$ has high probability), we can take a union bound over at most $\varepsilon ^{-\omega }$ elements of $\mathrm {EndPts}_k$ to get

$$\begin{aligned} \mathbb {P}\left[ \bigcap _{y\in \mathrm {EndPts}_k} G_y \bigg | \mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet } \right] \ge 1 - C_0 \varepsilon ^{\alpha \kappa -\omega } . \end{aligned}$$

(4.42)

Since $\omega < \alpha \kappa /2$, the right side of (4.42) is at least $1-\varepsilon ^\omega$ for small enough $\varepsilon \in (0,1)$ (how small depends only on $\alpha ,\kappa ,\omega ,C_0$). This implies that for each such $\varepsilon$,

$$\begin{aligned} \mathbb {P}\left[ \left( \bigcap _{y\in \mathrm {EndPts}_k} G_y \right) ^c ,\, \sigma _k \le s_{k+1} ,\, \#\mathrm {Conf}_k \le \varepsilon ^{-\omega } \bigg | \mathcal B_{t_k}^\bullet , h|_{\mathcal B_{t_k}^\bullet } \right] \le \varepsilon ^{ \omega } .\nonumber \\ \end{aligned}$$

(4.43)

Note that we have added the additional event $\{\sigma _k \le s_{k+1}\}$, for reasons which will become apparent just below.

Step 4: independence across radii to get concentration The radius $\sigma _k$ is a stopping time for $\{(\mathcal B_s^\bullet , h|_{\mathcal B_s^\bullet })\}_{s\ge 0}$, so the event inside the conditional probability in (4.43) belongs to $\sigma \left( \mathcal B_{s_{k+1}}^\bullet , h|_{\mathcal B_{s_{k+1}}^\bullet } \right)$. Since $t_{k+1} \ge s_{k+1}$, it therefore follows from (4.43) that the number of $k \in [0,K]_{\mathbb {Z}}$ for which either $\bigcap _{y\in \mathrm {EndPts}_k} G_y$ occurs, $\sigma _k > s_{k+1}$, or $\#\mathrm {Conf}_k > \varepsilon ^{-\omega }$ stochastically dominates a binomial distribution with K trials and success probability $1 - \varepsilon ^{\omega }$. By Hoeffding’s inequality, for any choice of $\theta \in (0,1)$ the probability that there are fewer than $(1-\varepsilon ^{\theta }) K$ such values of k is at most

$$\begin{aligned} \exp \left( - 2 (\varepsilon ^\theta - \varepsilon ^{\omega })^2 K \right) . \end{aligned}$$

Since $K = \lfloor a \varepsilon ^{-\beta } \rfloor -1$ by (4.35), this last quantity decays faster than any positive power of $\varepsilon$ provided we take $\theta \in (0 , \min \{\omega , \beta /2\})$.

By (4.41), on $\mathcal E_{\mathbb {r}}$ we have $\sigma _k \le s_{k+1}$ for each $k\in [0,K]_{\mathbb {Z}}$. By (4.39), if $\mathcal E_{\mathbb {r}}$ occurs then except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ we have $\#\mathrm {Conf}_k \le \varepsilon ^{-\omega }$ for each $K\in [0,K]_{\mathbb {Z}}$. Combining these observations with the preceding paragraph shows that

$$\begin{aligned} \mathbb {P}\left[ \mathcal E_{\mathbb {r}} ,\, \#\left\{ k \in [0,K]_{\mathbb {Z}} : \bigcap _{y\in \mathrm {EndPts}_k} G_y \, \text {occurs} \right\} < (1-\varepsilon ^{\theta }) K \right] = o_\varepsilon ^\infty (\varepsilon ) .\nonumber \\ \end{aligned}$$

(4.44)

Recall that $R_k \le 7 \varepsilon ^{\kappa /2} \mathbb {r}$ on $\mathcal E_{\mathbb {r}}$ (see this discussion just after (4.40)). As $t_k \ge \tau _{\ell \mathbb {r}}$ we have that ${\text {diam}} \mathcal B_{t_k}^\bullet \ge \ell \mathbb {r}$. By choosing $\varepsilon > 0$ sufficiently small we can arrange so that $\ell \mathbb {r} \ge 7 \varepsilon ^{\kappa /2} \mathbb {r}$. That is, $R_k \le {\text {diam}}\mathcal B_{t_k}^\bullet$ on $\mathcal E_{\mathbb {r}}$ provided $\varepsilon$ is chosen sufficiently small (in a manner depending only on $\kappa$ and $\ell$). Consequently, (4.44) together with property A of $G_y$ show that on $\mathcal E_{\mathbb {r}}$, it holds except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ that there are at least $(1-\varepsilon ^\theta ) K$ values of $k \in [0,K]_{\mathbb {Z}}$ for which no $D_h$-geodesic from $\mathbb {z}$ to a point outside of $\mathcal B_{\sigma _k}^\bullet$ can enter $\bigcup _{y\in \mathrm {EndPts}_k} B_{16\varepsilon ^\kappa \mathbb {r} }(z_y) {\setminus } \mathcal B_{t_k}^\bullet$. By (4.41), this holds in particular for each $D_h$-geodesic from $\mathbb {z}$ to $\partial \mathcal B_{s_{k+1}}^\bullet$.

A $D_h$-geodesic started from $\mathbb {z}$ can hit $\partial \mathcal B_{t_k}^\bullet$ at most once. Therefore, the defining property ($*$) of $z_y$, applied to the path $P|_{(t_k , |P|]}$, shows that for each k as in the preceding paragraph, no $D_h$-geodesic from $\mathbb {z}$ to $\partial \mathcal B_{s_{k+1}}^\bullet$ can enter $\bigcup _{y\in \mathrm {EndPts}_k} \mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$. $\square$

To deduce Proposition 4.12 from Lemma 4.15, we need some quantitative control on the $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesics appearing in the definition (4.11) of $\mathrm {Stab}_{k,r}(z)$. The needed control is provided by the following lemma.

Lemma 4.16

If $\mathcal E_{\mathbb {r}}$ occurs, then for each $k\in [0,K]_{\mathbb {Z}}$, each $(z,r) \in \mathcal Z_k$, and each $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesic $P' : [0,|P'|] \rightarrow \mathbb {C} {\setminus } B_r(z)$ from $\mathbb {z}$ to a point of $\partial B_r(z)$, we have

$$\begin{aligned} {\text {diam}} P'([t_k , |P'|]) \preceq \varepsilon ^{\chi /\chi '} \mathbb {r} , \end{aligned}$$

(4.45)

with a deterministic implicit constant depending only on a and $\lambda _4$, where ${\text {diam}}$ denotes Euclidean diameter.

Lemma 4.16 is a straightforward consequence of the definition of $\mathcal E_{\mathbb {r}}$. We postpone the proof until Sect. 4.6.

Proof of Proposition 4.12

Let $\chi , \chi '$ be the Hölder exponents from condition 3 in the definition of $\mathcal E_{\mathbb {r}}$ and let $\beta ,\theta \in (0,1)$ be chosen so that the conclusion of Lemma 4.15 holds with $\kappa = \frac{1}{2} (\chi /\chi ')^2$. By Lemma 4.15, we only need to prove that if $\mathcal E_{\mathbb {r}}$ occurs and $\varepsilon \in (0,1)$ is chosen to be sufficiently small (in a deterministic manner which does not depend on k or $\mathbb {r}$), then the following is true. If $k\in [0,K]_{\mathbb {Z}}$ is such that no $D_h$-geodesic from $\mathbb {z}$ to $\partial \mathcal B_{s_{k+1}}^\bullet$ can enter $\bigcup _{y\in \mathrm {EndPts}_k} \mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$, then $\mathcal Z_k^E \not =\emptyset$.

Henceforth assume that $\mathcal E_{\mathbb {r}}$ occurs and k is as above. Recall the definition (4.10) of $\mathcal Z_k$. By condition 5 (existence of good annuli) in the definition of $\mathcal E_{\mathbb {r}}$, each point of $\partial B_{ 2\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )$ is contained in a Euclidean ball $B_{\lambda _2 r}(z)$ for some $(z,r) \in \mathcal Z_k$ for which $E_r(z)$ occurs. By the definition (4.10), each of these Euclidean balls has radius $r \le \varepsilon \mathbb {r}$, so is contained in $B_{4\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )$.

Since $t_k \le s_{k+1} \le \tau _{3\ell \mathbb {r}}$ (by (4.36)) and $|\mathbb {z} - \mathbb {w}| \ge 4\ell \mathbb {r}$, if $\varepsilon$ is sufficiently small then the union of these Euclidean balls disconnects $\partial \mathcal B_{t_k}^\bullet$ from $\mathbb {w}$. Therefore, P must enter $B_{\lambda _2 r}(z)$ for some $(z,r) \in \mathcal Z_k$ such that $E_r(z)$ occurs.

We will now conclude the proof by showing that, in the notation (4.11),

$$\begin{aligned} \mathrm {Stab}_{r,k}(z) \text { occurs for every } (z,r) \in \mathcal Z_k \text { with } P\cap B_r(z) \not =\emptyset . \end{aligned}$$

(4.46)

Recall that we are assuming that k is such that no $D_h$-geodesic from $\mathbb {z}$ to $\partial \mathcal B_{s_{k+1}}^\bullet$ can enter $\bigcup _{y\in \mathrm {EndPts}_k} \mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$. Since $s_{k+1} \le \tau _{3\ell \mathbb {r}} \le \tau _{|\mathbb {z}-\mathbb {w}|}$ we must have $|P| \ge s_{k+1}$, so P passes through $\partial \mathcal B_{s_{k+1}}^\bullet$. Hence $P|_{[0,s_{k+1}]}$ cannot enter $\bigcup _{y\in \mathrm {EndPts}_k} \mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$. Since P does not re-enter $\mathcal B_{s_{k+1}}^\bullet$ after time $s_{k+1}$ and $\bigcup _{y\in \mathrm {EndPts}_k} \mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}\subset \mathcal B_{s_{k+1}}^\bullet$, also P cannot enter $\bigcup _{y\in \mathrm {EndPts}_k} \mathcal C_y^{\varepsilon ^\kappa \mathbb {r}}$. From this and Lemma 4.13 (applied in the contrapositive direction with $(\varepsilon ^\kappa /2)^{ \chi '/\chi }$ in place of $\varepsilon$ and $I_k$ in place of I), we infer that if $I_k \in {{\mathcal {I}}}_k$ is chosen so that $P(t_k) \in I_k$, then

$$\begin{aligned} d^{\mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet }\left( P , \partial \mathcal B_{t_k}^\bullet {\setminus } I_k \right) \ge (\varepsilon ^\kappa /2)^{\chi '/\chi } \mathbb {r} . \end{aligned}$$

(4.47)

Now let $(z,r) \in \mathcal Z_k$ with $P\cap B_r(z) \not =\emptyset$ and let $P' : [0,|P'|] \rightarrow \mathbb {C}{\setminus } B_r(z)$ be a $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)} )$-geodesic from $\mathbb {z}$ to a point of $\partial B_r(z)$. We will show that $P'(t_k) \in I_k$ for any possible choice of $P'$, which by definition implies that $\mathrm {Stab}_{r,k}(z)$ occurs. By Lemma 4.16,

$$\begin{aligned} {\text {diam}}\left( P'([t_k , |P'|] )\right) \preceq \varepsilon ^{\chi /\chi '} \mathbb {r} \end{aligned}$$

(4.48)

with a deterministic implicit constant depending only on a and $\lambda _4$.

Since $B_r(z) \subset \mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet$, the definition (4.38) of $d^{\mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet }$ implies that the $d^{\mathbb {C}{\setminus } \mathcal B_{t_k}^\bullet }$-diameter of $B_r(z)$ is the same as its Euclidean diameter, which is $2\varepsilon \mathbb {r}$. Since $P\cap B_r(z) \not =\emptyset$ and $P'(|P'|) \in \partial B_r(z)$, it follows from (4.48) and the triangle inequality that for small enough $\varepsilon \in (0,1)$,

$$\begin{aligned} d^{\mathbb {C}{\setminus }\mathcal B_{t_k}^\bullet }(P , P'(t_k) ) \preceq \varepsilon \mathbb {r} + \varepsilon ^{\chi /\chi '} \mathbb {r} \preceq \varepsilon ^{\chi /\chi '} \mathbb {r} . \end{aligned}$$

(4.49)

Since $\kappa < (\chi /\chi ')^2$, we infer that the left side of (4.49) is strictly smaller than $(\varepsilon ^\kappa /2)^{\chi '/\chi } \mathbb {r}$ for small enough $\varepsilon \in (0,1)$ (depending only on a and $\lambda _4$). By combining (4.47) and (4.49) we infer that $P'(t_k) \notin \partial \mathcal B_{t_k}^\bullet {\setminus } I_k$. Hence $P'(t_k) \in I_k$. Since this holds for every choice of $P'$, we get that $\mathrm {Stab}_{r,k}(z)$ occurs, as required. $\square$

4.5 Transferring from $E_r(z)$ to $\mathfrak E_r(z)$

We now want to combine Lemma 4.7 and Proposition 4.12 to say that with high probability, there are many values of $k\in [0,K]_{\mathbb {Z}}$ for which there exists $(z,r)\in \mathcal Z_k$ for which $\mathfrak E_r(z)$ occurs. In particular, we will establish the following statement.

Proposition 4.17

Let $\beta ,\theta \in (0,1)$ be as in Proposition 4.12 and suppose we have chosen $\nu$ sufficiently small that $4\nu < \beta \wedge \theta$. Also let $\zeta \in (0,1)$ be a small “error” parameter. If $\mathcal E_{\mathbb {r}}$ occurs, then except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$, at a rate which is uniform in the choice of $\mathbb {r},\mathbb {z},\mathbb {w}$, there are at least $\varepsilon ^{2\nu +\zeta } K$ values of $k\in [0,K]_{\mathbb {Z}}$ for which $\mathcal Z_k^{\mathfrak E}\not =\emptyset$.

Lemma 4.7 gives a comparison of the conditional probabilities given $\mathcal F_k$ of $\{\mathcal Z_k^E\not =\emptyset \}$ and $\{\mathcal Z_k^{\mathfrak E}\not =\emptyset \}$ (the reason why we have this comparison is that condition 4 in Theorem 4.2 has a comparison of conditional probabilities). On the other hand, Propositions 4.12 and 4.17 give statements which hold with high unconditional probability. To transfer between conditional and unconditional probabilities we will use the following elementary lemma.

Lemma 4.18

Let $K \in \mathbb {N}$ and let $E_0,\ldots ,E_K$ be events (not necessarily independent). Also let $\mathcal F_1 \subset \mathcal F_1\subset \cdots \subset \mathcal F_K$ be $\sigma$-algebras such that $E_k \in \mathcal F_{k+1}$ for each $k\in [0,K-1]_{\mathbb {Z}}$. For $\alpha \in (0,1)$, $\delta \in (0,\alpha )$, and $m\in \mathbb {N}$,

$$\begin{aligned} \mathbb {P}\left[ \sum _{k=0}^K \mathbb {1}_{\left( \mathbb {P}[E_k \,|\, \mathcal F_k] \ge \alpha \right) } \le K - m ,\, \sum _{k=0}^K \mathbb {1}_{E_k} \ge K - (1 - \alpha -\delta ) m \right] \le e^{-2 \delta ^2 m} .\nonumber \\ \end{aligned}$$

(4.50)

Proof

For $j \in \mathbb {N}$, let $\tau _j$ be the jth smallest $k \in [0 , K ]_{\mathbb {Z}}$ for which $\mathbb {P}[E_k \,|\, \mathcal F_k] < \alpha$, or $\tau _j = K+1$ if no such j exists. Then $\{\tau _j = k\} \in \mathcal F_k$ for each $k \in [0 ,K]_{\mathbb {Z}}$ and

$$\begin{aligned}&\left\{ \sum _{k=0}^K \mathbb {1}_{\left( \mathbb {P}[E_k \,|\, \mathcal F_{k}] \ge \alpha \right) } \le K - m \right\} = \left\{ \sum _{k=0}^K \mathbb {1}_{\left( \mathbb {P}[E_k \,|\, \mathcal F_{k}] < \alpha \right) } \ge m + 1 \right\} \nonumber \\&\quad = \{ \tau _{m+1} \le K \} . \end{aligned}$$

(4.51)

By the definition of the $\tau _j$’s, for each $j \in \mathbb {N}$,

$$\begin{aligned} \mathbb {P}\left[ E_{\tau _j}^c \,|\, \mathcal F_{\tau _j} \right] \ge 1 - \alpha . \end{aligned}$$

(4.52)

Since $E_{\tau _{j'}} \in \mathcal F_{\tau _{j-1}}$ for each $j' \le j-1$, it follows that $\sum _{j=1}^{m+1} \mathbb {1}_{E_{\tau _j}^c}$ stochastically dominates a binomial distribution with $m+1$ trials and success probability $1-\alpha$. By Hoeffding’s inequality, for $m \in \mathbb {N}$ the probability that the number of $j \in [1,m+1]_{\mathbb {Z}}$ for which $E_{\tau _j}^c$ occurs is smaller than $(1 - \alpha - \delta ) m$ is at most $e^{-2\delta ^2 m}$. Therefore,

$$\begin{aligned} \mathbb {P}\left[ \tau _{m+1} \le K , \sum _{j=0}^K \mathbb {1}_{E_j} \ge K - (1 - \alpha -\delta ) m \right] \le e^{-2\delta ^2 m} . \end{aligned}$$

(4.53)

Combining this with (4.51) gives (4.50). $\square$

We want to apply Lemma 4.18 to the events $\{\mathcal Z_k^E \not =\emptyset \}$ and $\{\mathcal Z_k^{\mathfrak E} \not =\emptyset \}$. However, these events are not $\mathcal F_{k+1}$-measurable since for $(z,r) \in \mathcal Z_k$, the ball $B_r(z)$ and the $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesics from $\mathbb {z}$ to $\partial B_r(z)$ are not necessarily contained in $\mathcal B_{s_{k+1}}^\bullet$. To get around this, we need to instead work with a slightly modified event which is $\mathcal F_{k+1}$-measurable. In particular, we will intersect each of $\{\mathcal Z_k^E \not =\emptyset \}$ and $\{\mathcal Z_k^{\mathfrak E} \not =\emptyset \}$ with the event $F_k$ of the following lemma.

Lemma 4.19

For each $k\in [0,K]_{\mathbb {Z}}$, there is an event $F_k \in \sigma \left( \mathcal B_{s_{k+1}}^\bullet , h|_{\mathcal B_{s_{k+1}}^\bullet } \right)$ with the following properties. If $\varepsilon$ is sufficiently small (how small depends only on a, $\lambda _4$), then whenever $\mathcal E_{\mathbb {r}}$ occurs also $\bigcap _{k=0}^K F_k$ occurs. Moreover, if $F_k$ occurs then $s_{k+1} \le \tau _{2 \ell \mathbb {r}}$ and for each $(z,r) \in \mathcal Z_k$ we have $B_{\lambda _4 r}(z) \subset \mathcal B_{s_{k+1}}^\bullet$ and the set of $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesics from $\mathbb {z}$ to points of $\partial B_r(z)$ is determined by $(\mathcal B_{s_{k+1}}^\bullet , h|_{\mathcal B_{s_{k+1}}^\bullet })$.

Lemma 4.19 is a relatively straightforward consequence of the definition of $\mathcal E_{\mathbb {r}}$. The proof is postponed until Sect. 4.6. The event $F_k$ is defined explicitly in Lemma 4.22 below, but only the properties of the event given in Lemma 4.19 are important for our purposes.

Lemma 4.20

Let $F_k$ for $k\in [0,K]_{\mathbb {Z}}$ be the event of Lemma 4.19 and let $\mathcal F_k$ be the $\sigma$-algebra from (4.8). Then for $k\in \mathbb {N}$,

$$\begin{aligned} \left\{ \mathcal Z_k^E \not =\emptyset \right\} \cap F_k \in \mathcal F_{k+1} \quad \text {and} \quad \left\{ \mathcal Z_k^{\mathfrak E} \not =\emptyset \right\} \cap F_k \in \mathcal F_{k+1} . \end{aligned}$$

(4.54)

Proof

By Lemma 4.19, we have $F_k \in \mathcal F_{k+1}$. By the definition (4.10) we also have $\mathcal Z_k \in \mathcal F_k \subset \mathcal F_{k+1}$.

We now argue that on $F_k$, the set $\mathcal Z_k^E$ is determined by $\mathcal F_{k+1}$. Since there are only countably many pairs $(z,r) \in \mathbb {C}\times (0,\infty )$ which can possibly belong to $\mathcal Z_k^E$, it suffices to show that the event $\{(z,r) \in \mathcal Z_k^E\} \cap F_k$ is $\mathcal F_{k+1}$-measurable for each such pair (z, r). Recall from (4.12) that $\mathcal Z_k^E$ is the set of $(z,r) \in \mathcal Z_k$ for which $E_r(z) \cap \mathrm {Stab}_{r,k}(z) \cap \{P\cap B_{\lambda _2 r}(z) \not =\emptyset \}$ occurs. By Lemma 4.19, if $F_k$ occurs then $B_{\lambda _4 r}(z) \subset \mathcal B_{s_{k+1}}^\bullet$ for each $(z,r) \in \mathcal Z_k$. Since $E_r(z)$ is determined by $h|_{B_{\lambda _4 r}(z)}$ (condition 2), it follows that $F_k \cap E_r(z) \cap \{(z,r) \in \mathcal Z_k\} \in \mathcal F_{k+1}$ for each $(z,r) \in \mathbb {C}\times (0,\infty )$. Moreover, since $P|_{[0,s_{k+1}]} \in \mathcal F_{k+1}$ and P does not re-enter $\mathcal B_{s_{k+1}}^\bullet$ after time $s_{k+1}$, we have $F_k \cap \{P\cap B_{\lambda _2 r}(z) \not =\emptyset \} \cap \{(z,r) \in \mathcal Z_k\} \in \mathcal F_{k+1}$ for each (z, r). By (4.11), each of the events $\mathrm {Stab}_{r,k}(z)$ for $(z,r) \in \mathcal Z_k$ is determined by $\mathcal F_k$ and the set of $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesics from $\mathbb {z}$ to points of $\partial B_r(z)$. By Lemma 4.19, it therefore follows that $F_k \cap \mathrm {Stab}_{r,k}(z) \in \mathcal F_{k+1}$ for each $(z,r) \in \mathcal Z_k$. Combining these statements shows that $\{\mathcal Z_k^E\not =\emptyset \} \cap F_k \in \mathcal F_{k+1}$.

Using condition 2 from Theorem 4.2, we similarly obtain that $\left\{ \mathcal Z_k^{\mathfrak E} \not =\emptyset \right\} \cap F_k \in \mathcal F_{k+1}$. $\square$

Lemma 4.21

Let $\theta$ be as in Proposition 4.12 and let $F_k$ for $k\in \mathbb {N}$ be as in Lemma 4.19. If $\mathcal E_{\mathbb {r}}$ occurs, then except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ there are at least $(1 - 4\varepsilon ^\theta )K$ values of $k\in [0,K]_{\mathbb {Z}}$ for which

$$\begin{aligned} \mathbb {P}\left[ \left\{ \mathcal Z_k^E \not =\emptyset \right\} \cap F_k \,\big | \, \mathcal F_k \right] \ge \frac{1}{2} \end{aligned}$$

(4.55)

and

$$\begin{aligned} \mathbb {P}\left[ \mathcal Z_k^{\mathfrak E} \not =\emptyset \,\big | \, \mathcal F_k \right] \ge \varepsilon ^{2\nu + o_\varepsilon (1)} , \end{aligned}$$

(4.56)

where the rate of the $o_\varepsilon (1)$ in (4.56) is deterministic and depends only on $\nu$ and the choice of metric D.

Proof

For $k\in \mathbb {N}$, let $E_k := \left\{ \mathcal Z_k^E \not =\emptyset \right\} \cap F_k$. By Lemma 4.20, we have $E_k \in \mathcal F_{k+1}$. We may therefore apply Lemma 4.18 with $m = \lfloor 4 \varepsilon ^{\theta } K \rfloor$, $\alpha =1/2$, and $\delta =1/4$ to get that

$$\begin{aligned} \mathbb {P}\left[ \sum _{k=0}^K \mathbb {1}_{\left( \mathbb {P}[E_k \,|\, \mathcal F_{k}] \ge 1/2 \right) } \le (1- 4\varepsilon ^{\theta } ) K ,\, \sum _{k=0}^K \mathbb {1}_{E_k} \ge (1 - \varepsilon ^\theta ) K \right] = o_\varepsilon ^\infty (\varepsilon ) .\nonumber \\ \end{aligned}$$

(4.57)

By Proposition 4.12 and Lemma 4.19, on $\mathcal E_{\mathbb {r}}$ it holds except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ that $\sum _{k=1}^K \mathbb {1}_{E_k} \ge (1 - \varepsilon ^\theta ) K$. Combining this with (4.57) shows that if $\mathcal E_{\mathbb {r}}$ occurs, then except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ there are at least $(1-4\varepsilon ^\theta )K$ values of $k\in [0,K]_{\mathbb {Z}}$ for which (4.55) holds.

On $\mathcal E_{\mathbb {r}}$, for each $k\in [0,K]_{\mathbb {Z}}$ we have $\mathcal B_{t_k}^\bullet \subset B_{3\ell \mathbb {r}}(\mathbb {z})$ (by (4.36)) and $\mathbb {w} \notin B_{3\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )$ (since $|\mathbb {z} - \mathbb {w}| \ge 4\ell \mathbb {r}$). By Lemma 4.7, whenever these latter conditions hold it holds except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ that

$$\begin{aligned} \mathbb {P}\left[ \mathcal Z_k^{\mathfrak E} \not =\emptyset \,\big | \, \mathcal F_k \right] \ge \varepsilon ^{2\nu + o_\varepsilon (1)} \mathbb {P}\left[ \mathcal Z_k^E \not =\emptyset \,\big | \, \mathcal F_k \right] - o_\varepsilon ^\infty (\varepsilon ) . \end{aligned}$$

Combining this with (4.55) shows that if $\mathcal E_{\mathbb {r}}$ occurs, then except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ there are at least $(1 - 4\varepsilon ^\theta )K$ values of $k\in [0,K]_{\mathbb {Z}}$ for which (4.55) and (4.56) both hold. $\square$

We now apply the estimate (4.56) to deduce Proposition 4.17.

Proof of Proposition 4.17

Let $F_k$ be the event of Lemma 4.19, so that by Lemma 4.20 we have $\left\{ \mathcal Z_k^{\mathfrak E} =\emptyset \right\} \cap F_k \in \mathcal F_{k+1}$. By Lemma 4.21, if $\mathcal E_{\mathbb {r}}$ occurs then except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$ there are at least $(1-4\varepsilon ^\theta ) K$ values of $k\in [0,K]_{\mathbb {Z}}$ for which

$$\begin{aligned} \mathbb {P}\left[ \left\{ \mathcal Z_k^{\mathfrak E} = \emptyset \right\} \cap F_k \,|\,\mathcal F_k \right] \le 1 - \varepsilon ^{2\nu + \zeta /2} , \end{aligned}$$

(4.58)

equivalently, there are at most $4\varepsilon ^\theta K$ values of $k\in [0,K]_{\mathbb {Z}}$ for which

$$\begin{aligned} \mathbb {P}\left[ \left\{ \mathcal Z_k^{\mathfrak E} = \emptyset \right\} \cap F_k \,|\,\mathcal F_k \right] \ge 1 - \varepsilon ^{2\nu + \zeta /2} . \end{aligned}$$

By Lemma 4.18 applied with $E_k = \left\{ \mathcal Z_k^{\mathfrak E} =\emptyset \right\} \cap F_k$, $m = \lfloor (1- 4\varepsilon ^\theta ) K \rfloor$, $\alpha = 1 - \varepsilon ^{2\nu + \zeta /2}$, and $\delta = \varepsilon ^{2\nu + \zeta /2}/2$, it follows that if $\mathcal E_{\mathbb {r}}$ occurs and $\varepsilon$ is sufficiently small, then except on an event of probability at most

$$\begin{aligned} \exp \left( - \frac{1}{2} \varepsilon ^{4\nu + \zeta } \lfloor (1-4\varepsilon ^\theta ) K \rfloor \right) \end{aligned}$$

(4.59)

there are at most

$$\begin{aligned} K - (1-\alpha -\delta ) m \le \left( 1 - \varepsilon ^{2\nu + \zeta /2} (1-4\varepsilon ^\theta )/ 2 \right) K \le (1 - \varepsilon ^{2\nu +\zeta }) K \end{aligned}$$

values of $k \in [0,K]_{\mathbb {Z}}$ for which $E_k$ occurs. Equivalently, there are at least $\varepsilon ^{2\nu +\zeta } K$ values of $k\in [0,K]_{\mathbb {Z}}$ for which either $\mathcal Z^{\mathfrak E} \not = \emptyset$ or $F_k$ does not occur. By Lemma 4.19, on $\mathcal E_{\mathbb {r}}$ the event $F_k$ occurs for every $k\in [0,K]_{\mathbb {Z}}$. Since $K \asymp \varepsilon ^{-\beta }$ (by (4.35)), if $4\nu < \beta$ then for a small enough choice of $\zeta \in (0,1)$, the quantity (4.59) is of order $o_\varepsilon ^\infty (\varepsilon )$. The proposition now follows. $\square$

Proof of Theorem 4.2

Assume we are in the setting of the theorem statement with $\nu _* = \frac{1}{8}(\beta \wedge \theta )$. Fix $q > 0$. Recall that we have been fixing $\mathbb {z},\mathbb {w} \in \mathbb {r} U$ with $|\mathbb {z} - \mathbb {w}| \ge 4\ell \mathbb {r}$ throughout this section. Proposition 4.17 implies that if $\mathcal E_{\mathbb {r}}$ occurs, then for each fixed choice of $\mathbb {z} , \mathbb {w} \in \left( \varepsilon ^q \mathbb {r} \mathbb {Z}^2 \right) \cap \left( \mathbb {r} U\right)$ with $|\mathbb {z} -\mathbb {w}| \ge 4\ell \mathbb {r}$, it holds except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$, at a rate which does not depend on $\mathbb {z} , \mathbb {w}$, or $\mathbb {r}$, that there exists $k\in [0,K]_{\mathbb {Z}}$ for which the corresponding set $\mathcal Z_k^{\mathfrak E}$ of (4.13) is non-empty. By (4.13), this means that there exists $z\in \mathbb {C}$ and $r \in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}] \cap \mathcal R$ such that $P^{\mathbb {z} , \mathbb {w}} \cap B_{\lambda _2 r}(z) \not =\emptyset$ and $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ occurs.

Since the definition of $\mathcal E_{\mathbb {r}}$ does not depend on $\mathbb {z},\mathbb {w}$, we can truncate on $\mathcal E_{\mathbb {r}}$, then take a union bound over all pairs $\mathbb {z} , \mathbb {w} \in \left( \varepsilon ^q \mathbb {r} \mathbb {Z}^2 \right) \cap \left( \mathbb {r} U\right)$ with $|\mathbb {z} -\mathbb {w} | \ge 4 \ell \mathbb {r}$, to get that if $\mathcal E_{\mathbb {r}}$ occurs then the following is true except on an event of probability $o_\varepsilon ^\infty (\varepsilon )$. For each such pair $\mathbb {z},\mathbb {w}$ that there exists $z\in \mathbb {C}$ and $r \in [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}] \cap \mathcal R$ such that $P^{\mathbb {z} , \mathbb {w}} \cap B_{\lambda _2 r}(z) \not =\emptyset$ and $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ occurs.

Since the parameters in the definition of $\mathcal E_{\mathbb {r}}$ can be chosen so as to make $\mathbb {P}[\mathcal E_{\mathbb {r}}]$ as close to 1 as we like (Lemma 4.11), we obtain the theorem statement with $4\ell$ in place of $\ell$, which is sufficient since $\ell$ is arbitrary. $\square$

4.6 Proofs of geometric lemmas

In this section we prove the geometric lemmas stated in Sects. 4.4 and 4.5 whose proofs were postponed to avoid distracting from the main argument, namely Lemmas 4.14, 4.16, and 4.19 . The arguments in this section use only the definitions in Sects. 4.1 and 4.3 . In particular, we do not use any of the results in Sects. 4.4 or 4.5.

Fig. 7

Illustration of the proof of Lemma 4.14. The set $\mathcal C_y^\varepsilon$ is shown in pink. We have shown the boundary of a (non-maximal) ball $B\in \mathcal B$ as a dashed line and the associated arc $Y_B\subset \partial B{\setminus } K$ in purple. Each set X as in the lemma statement is contained in such a ball B and lies in the bounded connected component $U_B$ of $\mathbb {C}{\setminus } (Y_B\cup K)$. Several arcs $Y_B$ for maximal balls $B\in \mathcal B_*$ are shown in various colors. Any two such arcs must intersect each other, so the Euclidean diameter of their union is at most $8\varepsilon$. The set $Y_y^\varepsilon$ (green) in the lemma statement is chosen so as to disconnect this union from $\infty$ in $\mathbb {C}{\setminus } K$ (color figure online)

Proof of Lemma 4.14

See Fig. 7 for an illustration. The proof consists of two main steps.

• 1. We show that there is a finite collection of connected sets $X\subset \mathbb {C}{\setminus } \mathcal K$ with Euclidean diameter at most $4\varepsilon$ such that each point of $\mathcal C_y^\varepsilon$ is contained in the bounded connected component of $\mathbb {C}{\setminus } ( \mathcal K \cup X)$ for one of these sets X. The sets X can be taken to be appropriate boundary arcs of Euclidean balls of radius $2\varepsilon$.

• 2. We consider the maximal elements of our finite collection, i.e., those which do not lie in a bounded connected component of any other set in the collection. We show that any two maximal elements have to intersect, so the union of the maximal elements has Euclidean diameter at most $8\varepsilon$. We then choose a single connected set (which can be taken to be an arc of a Euclidean ball of radius $8\varepsilon$) which disconnects the union of the maximal elements from $\infty$ in $\mathbb {C}{\setminus } \mathcal K$.

Step 1: reducing to finitely many arcs of Euclidean balls We will first reduce to considering only a finite collection of sets X as in the statement of the lemma by looking at arcs of Euclidean balls. Let $\mathcal B$ be the set of closed Euclidean balls of the form $B = \overline{B_{2\varepsilon }(z)}$ for $z\in \frac{\varepsilon }{4} \mathbb {Z}^2$ with the following properties: $B \cap \partial \mathcal K\not =\emptyset$ and every unbounded connected subset of $\mathbb {C}{\setminus } \mathcal K$ whose prime end closure contains y has to intersect B. Since $\mathcal K$ is compact, $\mathcal B$ is a finite set.

For $B\in \mathcal B$, the set $\partial B{\setminus } \mathcal K$ is a countable union of open arcs of $\partial B$. Each such arc divides $\mathbb {C}{\setminus } \mathcal K$ into a bounded connected component and an unbounded connected component. There is one such arc $Y_B$ with the property that y lies on the boundary of the bounded connected component of $\mathbb {C}{\setminus } (\mathcal K\cup Y_B )$ and $Y_B$ is not contained in the bounded connected component of $\mathbb {C}{\setminus } (\mathcal K\cup X)$ for any other such arc $X\not =Y_B$. Note that since B has radius $2\varepsilon$, the arc $Y_B$ is connected and has Euclidean diameter at most $4\varepsilon$.

For $B\in \mathcal B$, let $U_B$ be the bounded connected component of $\mathbb {C}{\setminus } (\mathcal K\cup Y_B)$ so that $y\in \partial U_B$. We claim that

$$\begin{aligned} \forall z\in \mathcal C_y^\varepsilon , \quad \exists B\in \mathcal B \quad \text {such that} \quad z \in U_B . \end{aligned}$$

(4.60)

Indeed, let X be as in the definition of $\mathcal C_y^\varepsilon$ for our given z and let $V_X$ be the bounded connected component of $\mathbb {C}{\setminus } X$ with y on its boundary. Since X has Euclidean diameter at most $\varepsilon$, we can find $B\in \mathcal B$ such that X is contained in the interior of B. We claim that $V_X\subset U_B$, and hence $z\in U_B$. Since X is connected and $X\cap Y_B\subset X\cap \partial B=\emptyset$, it follows that X is either entirely contained in $U_B$ or X is entirely contained in the unbounded connected component of $\mathbb {C}{\setminus } (\mathcal K\cup Y_B)$. We claim that X cannot be entirely contained in the unbounded connected component of $\mathbb {C}{\setminus } (\mathcal K\cup U_B)$. Indeed, by the definition of X, each unbounded connected subset of $\mathbb {C}{\setminus } \mathcal K$ with y on its boundary must intersect X. Since $X \cap U_B =\emptyset$ and $y\in \partial U_B$, each unbounded connected subset of $\mathbb {C}{\setminus } \mathcal K$ which intersects $U_B$ must intersect X. This implies that $U_B\subset V_X$, but this cannot happen since $X\subset B$ and by the definition of $Y_B$. Therefore $X\subset U_B$, so $V_X\subset U_B$, so (4.60) holds.

Step 2: maximal elements of $\mathcal B$ We define a partial order on $\mathcal B$ by declaring that $B\preceq B'$ if and only if $U_B\subset U_{B'}$. Let $\mathcal B_*$ be the set of maximal elements of $\mathcal B$, i.e., $B_* \in \mathcal B_*$ if and only if there is no $B \in \mathcal B {\setminus } \{B_*\}$ such that $B_* \preceq B$. Since $\mathcal B$ is a finite set, for every $B\in \mathcal B$ there exists $B_* \in \mathcal B_*$ satisfying $B\preceq B_*$.

We claim that if $B_1,B_2 \in \mathcal B_*$, then $Y_{B_1}\cap Y_{B_2}\not =\emptyset$. Indeed, if $Y_{B_1}\cap Y_{B_2} =\emptyset$ then $Y_{B_1}$ is contained in either $U_{B_2}$ or in the unbounded connected component of $\mathbb {C}{\setminus } ( Y_{B_2} \cup \mathcal K)$. By the maximality of $B_1$, $Y_{B_1}$ must be contained in the unbounded connected component of $\mathbb {C}{\setminus } (\mathcal K\cup Y_{B_2})$. We will now argue that $U_{B_2} \subset U_{B_1}$, which will contradict the maximality of $B_2$. Indeed, by the definition of $Y_{B_1}$, every unbounded connected subset of $\mathbb {C}{\setminus } \mathcal K$ whose prime end closure contains y has to intersect $Y_{B_1}$. Since $Y_{B_1}$ is disjoint from $U_{B_2}$ and $y\in {\text {Cl}}'( U_{B_2})$, it follows that every unbounded connected subset of $\mathbb {C}{\setminus } \mathcal K$ which intersects $U_{B_2}$ has to intersect $Y_{B_1}$. Therefore, $U_{B_2} \subset U_{B_1}$, which gives the desired contradiction.

Since each set $Y_B$ for $B\in \mathcal B$ has Euclidean diameter at most $4\varepsilon$, the preceding paragraph implies that the set $\widetilde{Y}_y^\varepsilon := \overline{\bigcup _{B_* \in \mathcal B_*} Y_{B_*}}$ is connected and has Euclidean diameter at most $8\varepsilon$. Choose a Euclidean ball $\widetilde{B}$ of radius at most $8\varepsilon$ which contains $\widetilde{Y}_y^\varepsilon$. As in Step 1, there is a unique connected arc $Y_y^\varepsilon$ of $\partial \widetilde{B}{\setminus } \mathcal K$ with the property that y lies on the boundary of the bounded connected component of $\mathbb {C}{\setminus } (\mathcal K\cup Y_y^\varepsilon )$ and $Y_y^\varepsilon$ is not contained in the bounded connected component of $\mathbb {C}{\setminus } (\mathcal K\cup X)$ for any other such arc X. This arc $Y_y^\varepsilon$ has Euclidean diameter at most $16\varepsilon$. Then each $Y_{B_*}$ for $B_*\in \mathcal B_*$, and hence also each $U_{B_*}$ for $B_*\in \mathcal B_*$, is contained in the bounded connected component of $\mathbb {C}{\setminus } (\mathcal K\cup Y_y^\varepsilon )$. Since each $z\in \mathcal C_y^\varepsilon$ is contained in $U_B$ for some $B\in \mathcal B$, and hence in $U_{B_*}$ for some $B_*\in \mathcal B_*$, we get that $Y_y^\varepsilon$ satisfies the desired property. $\square$

We now turn our attention to Lemmas 4.16 and 4.19 . Both lemmas will be proven using the following statement, which in particular gives an explicit definition of the event $F_k$ of Lemma 4.19.

Fig. 8

Illustration of the statement and proof of Lemma 4.22. In order to upper-bound $\sup _{u \in \partial B_{2\lambda _4 \varepsilon \mathbb {r}}(z)} D_h\left( \mathbb {z} , u ; \mathcal B_{s_{k+1}}^\bullet {\setminus } \overline{B_{\varepsilon \mathbb {r}}(z)} \right)$, we cover $\partial B_{2\lambda _4 \varepsilon \mathbb {r}}(z)$ by Euclidean balls of radius $\varepsilon \mathbb {r}/2$ (orange) and upper-bound the $D_h$-diameters of these balls using condition 3 (Hölder continuity) in the definition of $\mathcal E_{\mathbb {r}}$. Each of these balls is disjoint from $B_{\varepsilon \mathbb {r}}(z)$ and is contained in $\mathcal B_{s_{k+1}}^\bullet$, which leads to (4.61). Using Lemma 4.22 we get an upper bound for the $D_h$-length of the segment of a $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesic from $\mathbb {z}$ to a point of $\partial B_r(z)$ (such as the one shown in red) stopped at the last time it hits $\partial B_{2\lambda _4 \varepsilon \mathbb {r}}(z)$. This upper bound allows us to prevent such a $D_h$-geodesic from exiting $\mathcal B_{s_{k+1}}^\bullet$. These considerations lead to the proofs of Lemmas 4.16 and 4.19 (color figure online)

Lemma 4.22

For $k\in [0,K]_{\mathbb {Z}}$, let $F_k$ be the event that the following is true. We have $s_{k+1} \le \tau _{2 \ell \mathbb {r}}$ and for each $z \in B_{2\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet ) {\setminus } B_{\lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )$,

$$\begin{aligned} \sup _{u \in \partial B_{2\lambda _4 \varepsilon \mathbb {r}}(z)} D_h\left( \mathbb {z} , u ; \mathcal B_{s_{k+1}}^\bullet {\setminus } \overline{B_{ \varepsilon \mathbb {r}}(z)} \right) \le t_k +c \varepsilon ^\chi \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})} , \end{aligned}$$

(4.61)

where $\lambda _4$ is the constant from Theorem 4.2, $\chi$ is as in condition 3 (Hölder continuity) in the definition of $\mathcal E_{\mathbb {r}}$, and $c > 0$ is constant depending only on $a , \lambda _4$ (which we do not make explicit). If $\mathcal E_{\mathbb {r}}$ occurs and $\varepsilon$ is sufficiently small (how small depends only on $a, \lambda _4$), then $F_k$ occurs for each $k\in [0,K]_{\mathbb {Z}}$.

The reason why we use internal distances in $\mathcal B_{s_{k+1}}^\bullet {\setminus } \overline{B_{\varepsilon \mathbb {r}}(z)}$ in (4.61) is as follows. Such distances are bounded above by $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-distances if $r \le \varepsilon \mathbb {r}$ (which is the case if $(z,r) \in \mathcal Z_k$), which will be important for controlling $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesics. Furthermore, such distances are determined by $(\mathcal B_{s_{k+1}}^\bullet , h|_{\mathcal B_{s_{k+1}^\bullet }})$ by Axiom II (locality), which will be important for the proof of Lemma 4.19. We also emphasize that the right side of (4.61) is smaller than $s_{k+1} = t_k + (\varepsilon ^\beta -\varepsilon ^{2\beta })\mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})}$ if $\varepsilon$ is small since $\beta < \chi$.

Proof of Lemma 4.22

See Fig. 8 for an illustration of the statement and proof. Assume that $\mathcal E_{\mathbb {r}}$ occurs. By (4.36), we have $s_{k+1} \le \tau _{2\ell \mathbb {r}}$. Hence we just need to check (4.61). By the definition (4.6) of $t_k$ and $s_{k+1}$ and since $\beta<\chi /\chi ' < \chi$ (by (4.37)), it holds for small enough $\varepsilon \in (0,1)$ that

$$\begin{aligned} D_h(\partial \mathcal B_{t_k}^\bullet , \partial \mathcal B_{s_{k+1}}^\bullet ) \ge (\varepsilon ^\beta - \varepsilon ^{2\beta }) \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})} > \varepsilon ^\chi \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})} . \end{aligned}$$

(4.62)

Note that $\chi ' > \xi (Q+2) \ge 1$, where the last inequality follows, e.g., from the fact that $1 - \xi Q \le 2\xi$, which is obvious from the definition of LFPP and an estimate for the maximum of $h_\varepsilon ^*$ on a bounded open set.

For $z \in B_{2 \lambda _4 \varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet ) {\setminus } B_{\lambda _4\varepsilon \mathbb {r}}(\mathcal B_{t_k}^\bullet )$, the Euclidean circle $\partial B_{2\lambda _4 \varepsilon \mathbb {r}}(z)$ intersects $\partial \mathcal B_{t_k}^\bullet$. We can cover $\partial B_{2 \lambda _4 \varepsilon \mathbb {r}}(z)$ by a $\lambda _4$-dependent constant number of Euclidean balls of the form $B_{\varepsilon \mathbb {r}/2}(w)$ for $w\in \partial B_{2\lambda _4 \varepsilon \mathbb {r}}(z)$. Note that since $\lambda _4 \ge 1$, the corresponding balls $B_{\varepsilon \mathbb {r}}(w)$ are disjoint from $B_{\lambda _4\varepsilon \mathbb {r}}(z) \supset B_{\varepsilon \mathbb {r}}(z)$. By the upper bound for $D_h$-distances from condition 3 in the definition of $\mathcal E_{\mathbb {r}}$ and then condition 4 (comparison of circle averages) in the definition of $\mathcal E_{\mathbb {r}}$, each such ball satisfies

$$\begin{aligned} \sup _{u,v\in B_{\varepsilon \mathbb {r}/2}(w)} D_h(u,v ; B_{\varepsilon \mathbb {r}}(w)) \le 2(\varepsilon /2)^\chi \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)} \preceq \varepsilon ^\chi \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})} ,\quad \quad \end{aligned}$$

(4.63)

with the implicit constant depending only on a.

By summing (4.63) over all such balls $B_{\varepsilon \mathbb {r}/2}(w)$, using that $\partial B_{2\lambda _4 \varepsilon \mathbb {r}}(z) \cap \partial \mathcal B_{t_k}^\bullet \not =\emptyset$, and comparing to (4.62), we get that for small enough $\varepsilon$ each such ball $B_{\varepsilon \mathbb {r}}(w)$ is contained in $\mathcal B_{s_{k+1}}^\bullet {\setminus } \overline{B_{\varepsilon \mathbb {r}}(z)}$. We deduce that the $D_h\left( \cdot ,\cdot ; \mathcal B_{s_{k+1}}^\bullet {\setminus } \overline{B_{\varepsilon \mathbb {r}}(z)} \right)$-diameter of $\partial B_{2 \lambda _4 \varepsilon \mathbb {r}}(z)$ is at most a $a,\lambda _4$-dependent constant times $\varepsilon ^\chi \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})}$. Since $\partial B_{2 \lambda _4 \varepsilon \mathbb {r}}(z)\cap \partial \mathcal B_{t_k}^\bullet \not =\emptyset$, we get that the left side of (4.61) is at most $t_k + c \varepsilon ^\chi \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})}$ for an appropriate constant c. $\square$

Proof of Lemma 4.16

Assume that $\mathcal E_{\mathbb {r}}$ occurs and let $P'$ be a $D_h(\cdot ,\cdot ; \overline{B_r(z)})$-geodesic from $\mathbb {z}$ to a point of $\partial B_r(z)$, as in the statement of the lemma. Let $t' \in [t_k , |P'|]_{\mathbb {Z}}$ be the last time that $P'$ hits $\partial B_{2 \lambda _4 \varepsilon \mathbb {r}}(z)$. Since $\overline{B_r(z)}$ is disjoint from $\mathcal B_{t_k}^\bullet$, the segment $P'|_{[0,t_k]}$ is a $D_h$-geodesic and $P'$ does not re-enter $\mathcal B_{t_k}^\bullet$ after time $t_k$. By (4.61) of Lemma 4.19 and since $P'$ is $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesic, it follows that the $D_h$-length of $P'|_{[0,t']}$ (which equals $t'$) is at most $t_k + c \varepsilon ^\chi \mathfrak c_r e^{\xi h_r(\mathbb {z})}$. Therefore, the $D_h$-length of $P'([t_k ,t'])$ is at most $c\varepsilon ^\chi \mathfrak c_r e^{\xi h_r(\mathbb {z})}$. By conditions 3 (Hölder continuity) and 4 (comparison of circle averages) in the definition of $\mathcal E_{\mathbb {r}}$, the Euclidean diameter of $P'([t_k,t'])$ is at most a $a,\lambda _4$-dependent constant times $\varepsilon ^{\chi /\chi '}\mathbb {r}$. Since $P'([t',|P'|])\subset B_{2\lambda _4 \varepsilon \mathbb {r}}(z)$, we obtain (4.45). $\square$

Proof of Lemma 4.19

Define $F_k$ as in Lemma 4.22. That lemma tells us that $\mathcal E_{\mathbb {r}} \subset \bigcap _{k=0}^K F_k$ for small enough $\varepsilon \in (0,1)$ (depending only on $a,\lambda _4$). Furthermore, it is clear from the definition of $F_k$ and Axiom II (locality) that $F_k \in \sigma \left( \mathcal B_{s_{k+1}}^\bullet , h|_{\mathcal B_{s_{k+1}}^\bullet } \right)$. Now assume that $F_k$ occurs. By definition, we have $s_k \le \tau _{2\ell \mathbb {r}}$. We consider $(z,r) \in \mathcal Z_k$ and check that if $\varepsilon \in (0,1)$ is small enough, then $B_{\lambda _4 r}(z) \subset \mathcal B_{s_{k+1}}^\bullet$ and the set of $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesics from $\mathbb {z}$ to points of $\partial B_r(z)$ is determined by $(\mathcal B_{s_{k+1}}^\bullet , h|_{\mathcal B_{s_{k+1}}^\bullet })$.

Note that the right side of (4.61) satisfies $t_k + c \varepsilon ^\chi \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})} \le s_{k+1}$. Since the left side of (4.61) is an upper bound for $\sup _{u\in \partial B_{2 \lambda _4 \varepsilon \mathbb {r}}(z)} D_h(\mathbb {z},u)$, it follows that $\partial B_{2 \lambda _4 \varepsilon \mathbb {r}}(z) \subset \mathcal B_{s_{k+1}}^\bullet$. Since $B_{\lambda _4 r}(z) \subset B_{\lambda _4 \varepsilon \mathbb {r}}(z)$ (by (4.10)) and $\mathcal B_{s_{k+1}}^\bullet$ contains every point which it disconnects from $\infty$, we therefore have $B_{\lambda _4 r}(z) \subset \mathcal B_{s_{k+1}}^\bullet$.

Finally, we claim that a $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesic from $\mathbb {z}$ to a point of $\partial B_r(z)$ is the same as a $D_h(\cdot ,\cdot ; \mathcal B_{s_{k+1}}^\bullet {\setminus } \overline{B_r(z)})$-geodesic from $\mathbb {z}$ to a point of $\partial B_r(z)$, which gives the desired measurability statement due to Axiom II for $D_h$. To see this, it suffices to show that if $P'$ is a $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesic from $\mathbb {z}$ to a point of $\partial B_r(z)$, then $P' \subset \mathcal B_{s_{k+1}}^\bullet$.

To this end, let t be the last time that $P'$ hits $\partial B_{2 \lambda _4 \varepsilon \mathbb {r}}(z)$. By (4.61) and since $P'$ is a $D_h(\cdot ,\cdot ; \mathbb {C}{\setminus } \overline{B_r(z)})$-geodesic, it follows that the $D_h$-length of $P'|_{[0,t]}$ (which equals t) is at most $t_k +c \varepsilon ^\chi \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(\mathbb {z})} < s_{k+1}$. Consequently, $P'$ cannot exit $\mathcal B_{s_{k+1}}^\bullet$ before time t. Since t is the last time that $P'$ hits $\partial B_{2 \lambda _4 \varepsilon \mathbb {r}}(z)$ and the terminal point of $P'$ is contained in $\partial B_r(z) \subset B_{ \varepsilon \mathbb {r}}(z)$, $P'$ cannot exit $\mathcal B_{s_{k+1}}^\bullet$ after time t, either. $\square$

5 Forcing a geodesic to take a shortcut

The goal of this section is to prove Proposition 4.3. Throughout, we assume that we are in the setting of Theorem 1.9, so D and $\widetilde{D}$ are two weak $\gamma$-LQG metrics with the same scaling constants. We also let h be a whole-plane GFF and we implicitly assume (by way of eventual contradiction) that the optimal bi-Lipschitz constants $c_*$ and $C_*$ of (1.21) satisfy $c_* < C_*$.

With $\nu _*$ as in Theorem 4.2, fix $0< \mu < \nu \le \nu _*$ and let $\alpha _* \in (1/2,1)$ and $p_0 \in (0,1)$ be the parameters from Proposition 3.5 for this choice of $\mu$ and $\nu$ (we write $p_0$ instead of p to avoid confusion with another parameter called p below). Also fix $\alpha \in [\alpha _* ,1)$ (to be chosen in Lemma 5.5 just below) and parameters $c_1' ,c_2'$ such that $c_*< c_1'< c_2' < C_*$.

Let $\mathcal R_0$ be the set of $r > 0$ for which it holds with probability at least $p_0$ that the following is true. There exists $u \in \partial B_{\alpha r}(0)$ and $v \in \partial B_r(0)$ such that

$$\begin{aligned} \widetilde{D}_h(u,v) \le c_1' D_h(u,v) \end{aligned}$$

(5.1)

and the $\widetilde{D}_h$-geodesic from u to v is unique and is contained in $\overline{\mathbb {A}_{\alpha r , r}(0)}$. We note that Proposition 3.4 implies in particular that for each $\mathbb {r} >0$ one has $\#(\mathcal R_0\cap [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}] \cap \{8^{-k} \mathbb {r}\}_{k\in \mathbb {N}}) \ge \mu \log _8\varepsilon ^{-1}$ for small enough $\varepsilon \in (0,1)$.

5.1 Outline of the proof of Proposition 4.3

The main task in the proof of Proposition 4.3 is to define the event $E_r(0)$ (which we abbreviate as $E_r$ throughout most of this section). The other events $E_r(z)$ for $z\in \mathbb {C}$ will be defined by translation.

Main ideas The basic idea to define $E_r$ is as follows. We will define for each pair of points $x' , y' \in \partial B_{3r}(0)$ a deterministic smooth bump function $\phi$ which takes a large (but independent of $r,x',y'$) value in a long, narrow “tube” contained in $B_{3r}(0)$ which (almost) contains a path from $x'$ to $y'$ and which vanishes outside of a small neighborhood of this tube. Roughly speaking, $E_r$ will be the event that, simultaneously for every choice of $x'$ and $y'$, this tube contains a pair of points u, v such that $\widetilde{D}_h(u,v) \le c_1' D_h(u,v)$ and $|u-v| \asymp r$; and several regularity conditions hold. We will show using Proposition 3.2 and basic estimates for LQG distances that when $\rho \in (0,1)$ is small (but independent of r), $\mathbb {P}[E_r]$ is close to 1 for all $r\in \rho ^{-1} \mathcal R_0$ (Lemma 5.10).

We will then consider a fixed pair of points $\mathbb {z},\mathbb {w} \in \mathbb {C} {\setminus } B_{4r}(0)$ and let $x'$ and $y'$ be the first points of $\partial B_{3r}(0)$ hit by the $D_h$-metric balls grown from $\mathbb {z}$ and $\mathbb {w}$, respectively. This choice of $x'$ and $y'$ (and hence also the corresponding bump function $\phi$) are random, but are determined by $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$. We will show that if $E_r$ occurs and the $D_h$-geodesic between $\mathbb {z}$ and $\mathbb {w}$ enters $B_{2r}(0)$, then the $D_{h-\phi }$-geodesic between $\mathbb {z}$ and $\mathbb {w}$ has to stay close to the long narrow tube where $\phi$ is large, and hence has to get close to points u, v with $\widetilde{D}_h(u,v) \le c_1' D_h(u,v)$ and $|u-v| \asymp r$. Essentially, this is because Axiom III (Weyl scaling) implies that subtracting $\phi$ makes distances inside the tube much shorter than distances outside. If we let $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(0)$ be the event that the $D_h$-geodesic gets close to such points u, v, then since the conditional laws of $h-\phi$ and h given $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$ are mutually absolutely continuous (and we can add regularity conditions to $E_r$ to control the Radon-Nikodym derivative), we get condition 4 in Theorem 4.2 (with $\lambda _3 = 3$).

We emphasize that the event $E_r$ does not include the condition that P stays in the long narrow tube where $\phi$ is large. Indeed, $E_r$ cannot include any conditions which depend on P since $E_r$ needs to be locally determined by h. Rather, as explained in the preceding paragraph, if $E_r$ occurs then we can force P to stay in the tube by subtracting the bump function $\phi$ from h.

Section 5.2. We give a precise statement of the properties that we need the event $E_r$ and the bump function $\phi$ described above to satisfy. We then assume the existence of these objects and deduce Proposition 4.3. Condition 1 of Theorem 4.2 (with $\mathcal R = \rho ^{-1}\mathcal R_0$) is true in our framework by the definition of $\mathcal R_0$ and Proposition 3.4. Conditions 2 and 3 are true by assumption (these conditions will be clear from the construction of $E_r$ and $\phi$). Condition 4 is proven by comparing the conditional laws of h and $h-\phi$ given $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$, as discussed above. The rest of the section is devoted to constructing the event $E_r$ and the bump functions $\phi$.

Section 5.3. We first show that for any $z\in \mathbb {C}$ and $r\in \mathcal R_0$, we can find a deterministic open “tube” $V_r(z) \subset B_{3r}(z)$ such that with uniformly positive probability over the choice of z and r, there are points $u,v \in V_r(z)$ with the following properties. We have $\widetilde{D}_h(u,v) \le c_1' D_h(u,v)$, $|u-v|\asymp r$, the $\widetilde{D}_h$-geodesic from u to v is contained in $V_r(z)$, and any path in $V_r(z)$ between $z-2r$ and $z+2r$ has to get close to each of u and v (Lemma 5.6). This is illustrated in Fig. 10.

To do this, we start with a pair of points u, v as in the definition of $\mathcal R_0$, but with z in place of 0. Such a pair of points exists with probability at least $p_0$ by Axiom IV (translation invariance). We then extend the $\widetilde{D}_h$-geodesic $\widetilde{P}$ from u to v to a path $\widetilde{P}'$ from $z-2r$ to $z+2r$ by concatenating $\widetilde{P}$ with smooth paths. For this purpose, the fact that $\widetilde{P}$ is contained in $\overline{\mathbb {A}_{\alpha r , r}(z)}$ is useful to ensure that the extra smooth paths intersect $\widetilde{P}$ only at u and v. We consider the set of squares in a fine grid which intersect $\widetilde{P}'$. Since there are only finitely many possibilities for this set of squares, there has to be a deterministic set of squares which equals the set of squares which intersect $\widetilde{P}'$ with uniformly positive probability. We define $V_r(z)$ to be the interior of the union of the squares in this set.

Section 5.4. We now have an event which satisfies many of the conditions which we are interested in, but it holds only with uniformly positive probability, not with probability close to 1. To get an event which holds with probability close to 1, we consider a small but fixed $\rho \in (0,1)$ and a radius $r\in \rho ^{-1}\mathcal R_0$. We can find a large number of disjoint balls of the form $B_{\rho r}(z)$ contained in $B_{2r}(0)$ (note that $\rho r\in \mathcal R_0$). By the spatial independence properties of the GFF (Lemma 2.7), if we make $\rho$ sufficiently small then it holds with high probability that the event of the preceding subsection occurs for a large number of these balls $B_{\rho r}(z)$. We then link up the corresponding sets $V_{\rho r}(z)$ by deterministic paths of squares to find a deterministic open “tube” $U_r^{x,y}$ joining any two given points of $x,y\in \partial B_{2r}(0)$ with the following property. With probability close to 1, there are points $u,v \in U_r^{x,y}$ such that $\widetilde{D}_h(u,v) \le c_1' D_h(u,v)$, $|u-v|\asymp r$, the $\widetilde{D}_h$-geodesic from u to v is contained in $U_r^{x,y}$, and any path in $U_r^{x,y}$ between x and y has to get close to each of u and v (Lemma 5.8). See Fig. 11 for an illustration of this part of the argument.

Section 5.5. Taking Lemma 5.8 as our starting point, we then build the high-probability event $E_r$ in Proposition 4.3 for $r\in \rho ^{-1} \mathcal R_0$. In addition to the aforementioned conditions on the tube $U_r^{x,y}$, we also include extra regularity conditions which will eventually be used to prevent $D_h$-geodesics from staying close to the boundary of $U_r^{x,y}$ without entering it, to get geodesics from $\partial B_{3r}(0)$ to $\partial B_{2r}(0)$, and to control the Radon-Nikodym derivative between the conditional law of h and $h-\phi$ (where $\phi$ is the bump function mentioned above) given $h|_{\mathbb {C} {\setminus } B_{3r}(0)}$. We also give a precise definition of the bump function $\phi$ which we will subtract from the field: it is equal to a large positive constant on the long narrow tube $U_r^{x,y}$, it is equal to an even larger constant on even narrower tubes which approximate each of the segments [x, 3x/2] and [y, 3y/2], and it vanishes outside of a small neighborhood of the union of $U_r^{x,y}$ and these two narrower tubes. The definitions of these objects are illustrated in Fig. 12.

Section 5.6. We prove that a $D_{h-\phi }$-geodesic is likely to get near points u, v satisfying (5.1), using the definition of $E_r(0)$ and deterministic arguments to compare various distances. A key point here is that we have set things up so that on $E_r$, the $\widetilde{D}_h$-geodesic from u to v is contained in $U_r^{x,y}$ and is far away from the narrow tubes where $\phi$ is larger than it is on $U_r^{x,y}$. This allows us to show that subtracting $\phi$ does not change the fact that $\widetilde{D}_h(u,v) \le c_1' D_h(u,v)$.

Remark 5.1

Our proof only shows that the $D_h$-geodesic P gets close to each of the points u and v from (5.1) with positive probability (we then use the triangle inequality to compare the $D_h$-length of a segment of P to $D_h(u,v)$). We do not show that P actually merges into the $D_h$-geodesic from u to v. We believe that it should be possible to show that P merges into this $D_h$-geodesic, but doing so is highly non-trivial. Indeed, this is closely related to the problem of showing that there are no “ghost geodesics” for $D_h$ which do not merge into any other $D_h$-geodesics; see [3, Section 1.4] for some discussion about the analogous problem in the setting of the Brownian map. Because we do not show that P merges into the $D_h$-geodesic from u to v, the arguments of this section do not immediately imply other statements of the form “if an event occurs for some (random) geodesic with high probability, then with high probability it occurs somewhere along the $D_h$-geodesic between two fixed points”.

5.2 Proof of Proposition 4.3 assuming the existence of events and functions

In this subsection, we assume the existence of an event $E_r = E_r(0)$ and a collection $\mathcal G_r$ of smooth bump functions $\phi$ which satisfy a few simple properties and deduce Proposition 4.3 from the existence of these objects. The later subsections are devoted to constructing these objects. In particular, we will deduce Proposition 4.3 from the following proposition.

Proposition 5.2

Let $0<\mu < \nu \le \nu _*$ be as above and let $\mathbb {p} \in (0,1)$. There exists $\rho \in (0,1)$, depending only on $\mathbb {p} , \mu , \nu$, such that for each $r \in \rho ^{-1} \mathcal R_0$, there is an event $E_r$ and a finite collection $\mathcal G_r$ of smooth bump functions, each of which is supported on a compact subset of $\mathbb {A}_{r/4,3r}(0)$, with the following properties.

• (A) (Measurability and high probability) We have $E_r \in \sigma ( (h - h_{5r}(0) )|_{\mathbb {A}_{r/4,4r}(0)})$ and $\mathbb {P}[E_r] \ge \mathbb {p}$.

• (B) (Bound for Dirichlet inner products) There is a deterministic constant $\Lambda _0 > 0$ depending only on $\mathbb {p} , \mu , \nu ,c_1',c_2'$ such that, writing $(\cdot ,\cdot )_\nabla$ for the Dirichlet inner product, it holds on $E_r$ that

  $$\begin{aligned} |(h,\phi )_\nabla | + \frac{1}{2} (\phi , \phi )_\nabla \le \Lambda _0 ,\quad \forall \phi \in \mathcal G_r . \end{aligned}$$

  (5.2)

• (C) (Subtracting a bump function forces a geodesic to take a shortcut) Suppose we are given points $\mathbb {z} , \mathbb {w} \in \mathbb {C}{\setminus } B_{4r}(0)$. There is a random $\phi \in \mathcal G_r$ depending only on $\mathbb {z}$, $\mathbb {w}$, and $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$ such that the following is true. Let P (resp. $P^\phi$) be the a.s. unique $D_h$- (resp. $D_{h-\phi }$-) geodesic from $\mathbb {z}$ to $\mathbb {w}$. There is a deterministic constant $b_0 >0$ depending only on $\mathbb {p} , \mu , \nu ,c_1',c_2'$ such that if $P\cap B_{2r}(0) \not =\emptyset$ and $E_r$ occurs, then there are times $0< s< t < D_{h - \phi }(\mathbb {z}, \mathbb {w})$ and such that

  $$\begin{aligned}&P^\phi (s) , P^\phi (t) \in B_{3r/2}(0) , \quad |P^\phi (s) - P^\phi (t)| \ge b_0 r , \nonumber \\&\qquad \widetilde{D}_{h-\phi }\left( P^\phi (s) , P^\phi (t)\right) \le c_2' D_{h- \phi }\left( P^\phi (s) , P^\phi (t)\right) ,\quad \text {and} \nonumber \\&\qquad \widetilde{D}_{h- \phi }\left( P^\phi (s) , P^\phi (t)\right) \le (c_* / C_*) \widetilde{D}_{h-\phi }\left( P^\phi (s) , \partial B_{3r}(0) \right) . \end{aligned}$$

  (5.3)

The event $E_r$ and the collection of functions $\mathcal G_r$ will be defined explicitly in Sect. 5.5; see Sect. 5.1 for an overview of the definitions. The reason why we are able to restrict to a finite collection $\mathcal G_r$ of bump functions $\phi$ is that we will break up space into a fine grid and require that the “tube” where $\phi$ is very large (as referred to in Sect. 5.1) is a finite union of squares in the grid. As explained in Lemma 5.4 just below, Properties (B) and (C) are used to check condition 4 in Theorem 4.2. The purpose of Property (B) is to control the Radon-Nikodym derivative between the conditional laws of h and $h-\phi$ given $h|_{\mathbb {C} {\setminus } B_{3r}(0)}$.

We now explain how to conclude the proof of Proposition 4.3 assuming Proposition 5.2. Fix points $\mathbb {z},\mathbb {w}\in \mathbb {C}{\setminus } B_{4r}(0)$ and let P be the $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$, as in Property (C). We first define the event $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(0)$ appearing in Proposition 4.3. Let $\mathfrak E_r = \mathfrak E_r^{\mathbb {z} , \mathbb {w}}(0)$ be the event that there are times $0< s< t < D_{h }(\mathbb {z}, \mathbb {w})$ such that

$$\begin{aligned}&P (s) , P (t) \in B_{3r/2}(0) , \quad |P (s) - P (t)| \ge b_0 r , \nonumber \\&\qquad \widetilde{D}_h(P(s) , P(t)) \le c_2' D_h(P (s) , P (t)) ,\quad \text {and} \nonumber \\&\qquad \widetilde{D}_h(P(s) , P(t)) \le (c_*/C_*) \widetilde{D}_h(P (s) , \partial B_{3r}(0) ), \end{aligned}$$

(5.4)

and

$$\begin{aligned} \exp \left( - (h ,\phi )_\nabla +\frac{1}{2} (\phi , \phi )_\nabla \right) \le \Lambda , \quad \forall \phi \in \mathcal G_r ,\quad \text {where} \quad \Lambda := e^{\Lambda _0} , \end{aligned}$$

(5.5)

where $\Lambda _0$ is the constant from Property (B) and $b_0$ is the constant from Property (C). We note that (5.4) is the same as (5.3) from Property (C), but with h instead of $h-\phi$. This condition is the main point of the definition of $\mathfrak E_r$. The extra condition (5.5) is only included to control a Radon-Nikodym derivative when we compare the conditional probabilities of $\mathfrak E_r$ and $E_r$ given $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$.

Lemma 5.3

The event $\mathfrak E_r$ is a.s. determined by $h|_{B_{3r}(0)}$ and the $D_h$-geodesic P stopped at its last exit time from $B_{3r}(0)$.

Proof

Recall that each of the functions $\phi \in \mathcal G_r$ is supported on $\mathbb {A}_{r/4,3r}(0)$. Since $\mathcal G_r$ is a finite set, it is clear that the condition (5.5) is determined by $h|_{B_{3r}(0)}$.

To deal with (5.4), we first observe that the set of pairs of times $s ,t \in [0, D_h(\mathbb {z} , \mathbb {w})]$ satisfying $\widetilde{D}_h(P(s) , P(t)) \le (c_*/C_*) \widetilde{D}_h(P (s) , \partial B_{3r}(0) )$ is determined by P stopped at its last exit time from $B_{3r}(0)$ and the internal metric $\widetilde{D}_h(\cdot ,\cdot ; B_{3r}(0))$. Indeed, a pair (s, t) belongs to this set if and only if P(t) is contained in the $\widetilde{D}_h$-metric ball of radius $(c_* / C_*) \widetilde{D}_h(P (s) , \partial B_{3r}(0) )$ centered at P(s). For each such pair of times s, t, we have $\widetilde{D}_h(P(s) , P(t)) = \widetilde{D}_h(P(s) , P(t) ; B_{3r}(0))$. Since P is a $D_h$-geodesic, the points P(s) , P(t) and the distance $D_h(P(s) , P(t)) = t-s$ for each such pair of points s, t is determined by P stopped at its last exit time from $B_{3r}(0)$. Since $\widetilde{D}_h(\cdot ,\cdot ; B_{3r}(0))$ is determined by $h|_{B_{3r}(0)}$ (Axiom II) we get that the event that there exists times $s ,t \in [0, D_h(\mathbb {z} , \mathbb {w})]$ satisfying (5.4) is determined by $h|_{B_{3r}(0)}$ and P stopped at its last exit time from $B_{3r}(0)$. $\square$

We can now check condition 4 of Theorem 4.2 for the above definitions of $E_r = E_r(0)$ and $\mathfrak E_r = \mathfrak E_r^{\mathbb {z},\mathbb {w}}(0)$ using the mutual absolute continuity of the laws of h and $h-\phi$.

Lemma 5.4

Assume Proposition 5.2. With $\Lambda$ as in (5.5), it is a.s. the case that

$$\begin{aligned}&\mathbb {P}\left[ E_r \cap \{P\cap B_{2r}(0) \not =\emptyset \} \,|\, h|_{\mathbb {C}{\setminus } B_{3r}(0)} \right] \nonumber \\&\quad \le \Lambda \mathbb {P}\left[ \mathfrak E_r \cap \{P \cap B_{2r}(0)\not =\emptyset \} \,|\, h|_{\mathbb {C}{\setminus } B_{3r}(0)} \right] . \end{aligned}$$

(5.6)

Proof

The occurrence of the events $E_r$ and $\mathfrak E_r$ is unaffected by adding a constant to h, so we can assume without loss of generality that h is normalized so that its circle average over $\partial B_{4r}(0)$, say, is zero. By the Markov property of h, under the conditional law given $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$, we can decompose $h|_{B_{3r}(0)}$ as the sum of a harmonic function which is determined by $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$ and a zero-boundary GFF on $B_{3r}(0)$ which is independent from $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$.

Let $\phi \in \mathcal G_r$ be the smooth bump function from Property (C), which is determined by $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$. By a standard Radon-Nikodym derivative calculation for the GFF, if we condition $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$ then the conditional law of $h-\phi$ is a.s. absolutely continuous with respect to the conditional law of h, and the Radon-Nikodym derivative of the former w.r.t. the latter is

$$\begin{aligned} M_h = \exp \left( - (h ,\phi )_\nabla - \frac{1}{2} (\phi , \phi )_\nabla \right) . \end{aligned}$$

(5.7)

Note that since $\phi$ is supported on $B_{3r}(0)$, the Radon-Nikodym derivative $M_h$ depends only on the zero-boundary part of $h|_{B_{3r}(0)}$.

Define the $D_{h-\phi }$-geodesic $P^\phi$ from $\mathbb {z}$ to $\mathbb {w}$ and the event $\mathfrak E_r^\phi$ in the same manner as P and $\mathfrak E_r$ but with $h-\phi$ in place of h. By (5.5), on $\mathfrak E_r$, we have $M_h \le \Lambda$. Therefore,

$$\begin{aligned}&\mathbb {P}\left[ \mathfrak E_r^\phi \cap \{P^\phi \cap B_{2r}(0)\not =\emptyset \} \,|\, h|_{\mathbb {C}{\setminus } B_{3r}(0)} \right] \nonumber \\&\quad = \mathbb {E}\left[ M_h \mathbb {1}_{\mathfrak E_r \cap \{P \cap B_{2r}(0)\not =\emptyset \}} \,|\, h|_{\mathbb {C}{\setminus } B_{3r}(0)} \right] \nonumber \\&\quad \le \Lambda \mathbb {P}\left[ \mathfrak E_r \cap \{P \cap B_{2r}(0)\not =\emptyset \} \,|\, h|_{\mathbb {C}{\setminus } B_{3r}(0)}\right] . \end{aligned}$$

(5.8)

We now claim that

$$\begin{aligned} E_r \cap \{P\cap B_{2r}(0) \not =\emptyset \} \subset \mathfrak E_r^\phi \cap \{P^\phi \cap B_{2r}(0) \not =\emptyset \} . \end{aligned}$$

(5.9)

Indeed, Property (C) (subtracting a bump function) says that the main condition (5.4) in the definition of $\mathfrak E_r$ is satisfied with $h-\phi$ in place of h whenever $E_r \cap \{P\cap B_{2r}(0) \not =\emptyset \}$ occurs, which implies in particular that $P^\phi \cap B_{2r}(0) \not =\emptyset$ whenever $E_r \cap \{P\cap B_{2r}(0) \not =\emptyset \}$ occurs. Furthermore, Property (B) (bound for Dirichlet inner products) implies that the Dirichlet energy condition (5.5) in the definition of $\mathfrak E_r$ holds with $h-\phi$ in place of h whenever $E_r$ occurs. Thus (5.9) holds.

As an immediate consequence of (5.9), a.s.

$$\begin{aligned}&\mathbb {P}\left[ E_r \cap \{P\cap B_{2r}(0) \not =\emptyset \} \,|\, h|_{\mathbb {C}{\setminus } B_{3r}(0)} \right] \nonumber \\&\quad \le \mathbb {P}\left[ \mathfrak E_r^\phi \cap \{P^\phi \cap B_{2r}(0)\not =\emptyset \} \,|\, h|_{\mathbb {C}{\setminus } B_{3r}(0)} \right] . \end{aligned}$$

(5.10)

Combining (5.8) and (5.10) gives (5.6). $\square$

Proof of Proposition 4.3, assuming Proposition 5.2

Let $\mathbb {p}$ be as in Theorem 4.2 with our given choice of $0< \mu < \nu \le \nu _*$ and with the constants

$$\begin{aligned} \lambda _1 := 1/4 ,\quad \lambda _2 := 2,\quad \lambda _3 := 3, \quad \lambda _4 := 4,\quad \text {and} \quad \lambda _5 :=5. \end{aligned}$$

(5.11)

For $z\in \mathbb {C}$, $r \in \rho ^{-1} \mathcal R_0$, and $\mathbb {z},\mathbb {w}\in \mathbb {C}{\setminus } B_{4r}(z)$, let $E_r(z)$ (resp. $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$) be the event $E_r$ of Proposition 5.2 (resp. the event and $\mathfrak E_r^{\mathbb {z} +z , \mathbb {w} + z}$ defined above) with the field $h(\cdot +z) - h_1(z)\overset{d}{=}h$ in place of h.

Let $c'' = c''(\alpha ,c_1',\mu ,\nu ) \in (c_* , c_1')$ be chosen as in Proposition 3.5 with $\alpha$ as in Lemma 5.5 and $c_1'$ in place of $c'$. Also let $\mathcal R_0$ be defined as in the discussion surrounding (5.1) and let $\mathcal R := \rho ^{-1} \mathcal R_0$. By the definition of $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ (in particular, (5.4)), the conditions (4.3) hold on $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ with $b = b_0$.

If $\mathbb {r} >0$ such that $\mathbb {P}[\underline{G}_{\mathbb {r}}(c'', \beta ) ] \ge \beta$, then Proposition 3.4 implies that there exists $\varepsilon _0 = \varepsilon _0(\beta ,c_1',\mu ,\nu ) > 0$ such that for each $\varepsilon \in (0,\varepsilon _0]$,

$$\begin{aligned} \#(\mathcal R_0 \cap [\varepsilon ^{1+\nu } \mathbb {r} , \varepsilon \mathbb {r}] \cap \{8^{-k} \mathbb {r}\}_{k\in \mathbb {N}}) \ge \mu \log _8 \varepsilon ^{-1} , \end{aligned}$$

(5.12)

equivalently,

$$\begin{aligned} \#( \mathcal R\cap [\varepsilon ^{1+\nu } \rho ^{-1} \mathbb {r} , \varepsilon \rho ^{-1} \mathbb {r}] \cap \{8^{-k} \rho ^{-1}\mathbb {r} \}_{k\in \mathbb {N}}) \ge \mu \log _8 \varepsilon ^{-1} . \end{aligned}$$

(5.13)

This shows that condition 1 of Theorem 4.2 is satisfied with $\rho ^{-1} \mathbb {r}$ in place of $\mathbb {r}$. By Property (A) (measurability and high probability) and Lemma 5.3, conditions 2 and 3 of Theorem 4.2 are satisfied for the events $E_r(z)$ and $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ above. By Lemma 5.4, condition 4 of Theorem 4.2 is also satisfied. $\square$

5.3 Building a tube which contains a shortcut with positive probability

Fig. 9

Illustration of the statement of Lemma 5.5. The lemma asserts that with probability at least $p_0/8$, there is a $D_h$-geodesic (red) between points u and v in the inner and outer boundaries, resp., of the pink half-annulus $H_r(z)$ which is contained in $\overline{H_r(z)}$ and satisfies $\widetilde{D}_h(u,v) \le c_1' D_h(u,v)$. The main task of Sect. 5 is to force a $D_h$-geodesic between two far away points to get near a $\widetilde{D}_h$-geodesic like the red one in the picture (color figure online)

We now turn our attention to constructing the event $E_r$ and the collection of functions $\mathcal G_r$ of Proposition 5.2, following the strategy outlined in Sect. 5.1. Recall that $\alpha _* \in (1/2,1)$ and $p_0 \in (0,1)$ are the parameters from Proposition 3.5 with $\mu$ and $\nu$ as in Proposition 4.3.

Our goal is to define for each $z\in \mathbb {C}$ and each $r\in \mathcal R_0$ a deterministic open “tube” $V_r(z) \subset B_{3r}(z)$ and an event $F_r(z)$ such that $\mathbb {P}[F_r(z)]$ is bounded below uniformly over z and r, $F_r(z) \in \sigma \left( (h-h_{4r}(z)) |_{B_{3r}(z)} \right)$, and on $F_r(z)$ there are points $u,v\in V_r(z)$ which satisfy (5.1) plus some additional conditions. We will define $V_r(z)$ and $F_r(z)$ and prove a lower bound for $\mathbb {P}[F_r(z)]$ in Lemma 5.6, with Lemma 5.5 as an intermediate step. We will prove the required measurability in Lemma 5.7.

We define a half-annulus of an annulus A to be the intersection of A with a half-plane whose boundary passes through the center of A. It is easier for us to work with a $\widetilde{D}_h$-geodesic which is constrained to stay in a half-annulus rather than a whole annulus. The reason for this is that it allows us to easily find paths from each of the endpoints of the geodesic to points far away from the half-annulus which do not get near the geodesic except at their endpoints (this might be trickier if the geodesic wraps around the whole annulus). The following lemma, which is a slight improvement on the condition in the definition of $\mathcal R_0$, will allow us to work with a half-annulus rather than a whole annulus.

Lemma 5.5

There exists $\alpha \in [\alpha _* ,1)$ depending only on $\mu ,\nu$ such that for each $r\in \mathcal R_0$ and each $z\in \mathbb {C}$, there is a deterministic half-annulus $H_r(z) \subset \mathbb {A}_{\alpha r , r}(z)$ such that with probability at least $p_0/8$, there exists $u \in \partial B_{\alpha r}(z)$ and $v \in \partial B_r(z)$ with the following properties.

• 1. $\widetilde{D}_h(u,v) \le c_1' D_h(u,v)$.

• 2. The $\widetilde{D}_h$-geodesic from u to v is unique and is contained in $\overline{H_r(z)}$.

• 3. $\widetilde{D}_h(u,v) \le (c_*/C_*)^{2} \widetilde{D}_h\left( \mathbb {A}_{\alpha r , r}(z) , \partial B_{2r}(z) \right)$, where $c_*$ and $C_*$ are as in (1.21).

Proof

By Axioms IV and V , we can find $S> s > 0$ depending only on $p_0$ (and hence only on $\mu ,\nu$) such that for each $r>0$, it holds with probability at least $1 - p_0/2$ that the following is true.

• Any two points of $\mathbb {A}_{3r/4, r}(z)$ which are not contained in a single quarter-annulus of $\overline{\mathbb {A}_{3r/4,r}(z)}$ lie at $\widetilde{D}_h$-length at least $s \mathfrak c_r e^{\xi h_r(z)}$ from each other.

• $(c_*/C_*)^{2} \widetilde{D}_h\left( \mathbb {A}_{3 r/4 , r}(z) , \partial B_{2r}(z) \right) \ge s \mathfrak c_r e^{\xi h_r(z)}$.

• $\widetilde{D}_h(u,v) \le S \mathfrak c_r e^{\xi h_r(z)}$ for each $u,v\in \overline{\mathbb {A}_{3r/4,r}(z)}$.

Since $\mathbb {A}_{\alpha r ,r}(z) \subset \mathbb {A}_{3r/4,r}(z)$ for each $\alpha \in [3/4,1)$, Lemma 2.11 applied with the above choice of s and S gives an $\alpha \in [(3/4)\vee \alpha _* ,1)$ depending on $p_0$ and $\alpha _*$ such that for each $r > 0$ it holds with probability at least $1-p_0/2$ that the following is true. For each pair of points $u,v\in \overline{\mathbb {A}_{\alpha r , r}(z)}$ such that $\widetilde{D}_h(u,v; \mathbb {A}_{\alpha r ,r}(0 ) ) = \widetilde{D}_h(u,v)$, it holds that u and v are contained in a single quarter-annulus of $\overline{\mathbb {A}_{\alpha r , r}(z)}$ and $\widetilde{D}(u,v) \le \widetilde{D}_h\left( \mathbb {A}_{\alpha r , r}(z) , \partial B_{2r}(z) \right)$. This happens in particular if there is a $\widetilde{D}_h$-geodesic from u to v contained in $\overline{\mathbb {A}_{\alpha r ,r}(z)}$.

Combining this with translation invariance (Axiom IV) and the definition of $\mathcal R_0$ shows that for $r\in \mathcal R_0$, it holds with probability at least $p_0/2$ that the conditions in the lemma statement hold but with a random quarter-annulus in place of a deterministic half-annulus. This random quarter annulus is a.s. contained in one of four possible deterministic half-annuli, so must be contained in one of these four half-annuli with probability at least $p_0/8$. We therefore obtain that for an appropriate choice of $H_r(z)$, it holds with probability at least $p_0/8$ that all of the conditions in the lemma statement hold. $\square$

Fig. 10

Illustration of the statement and proof of Lemma 5.6. Building on the setting of Fig. 9, we show that there is a deterministic long narrow “tube” $V_r(z)$ (light green), which is the interior of the set of $\varepsilon _1r\times \varepsilon _1r$ squares with corners in $\varepsilon _1r \mathbb {Z}^2$ which intersect a certain path from $z-2r$ to $z + 2r$, with the following property. With positive probability, every path in the tube from a point near $z-2r$ to a point near $z+2r$ has to get near a pair of points u, v in the tube for which $\widetilde{D}_h(u,v) \le c_1' D_h(u,v)$. We will eventually add a bump function to h which takes a very negative value in such a tube in order to force a geodesic between points which are far away from $B_{2r}(z)$ to get near u and v (color figure online)

We henceforth assume that $\alpha \in [\alpha _*,1)$ is chosen so that the conclusion of Lemma 5.5 is satisfied. In order to construct deterministic “tubes” as described in Sect. 5.1, we will look at unions of squares in a fine grid. For $\varepsilon > 0$ and $X\subset \mathbb {C}$, let

$$\begin{aligned} \mathcal S_\varepsilon (X) := \left\{ \text {closed } \varepsilon \times \varepsilon \text { squares with corners in } \varepsilon \mathbb {Z}^2\text { which intersect } X \right\} .\nonumber \\ \end{aligned}$$

(5.14)

Recall that we have fixed $c_2'> c_1' > c_*$. Choose, in a manner depending only on $c_1',c_2',c_*,C_*$, a small parameter $\eta \in (0,1)$ such that

$$\begin{aligned} \frac{ c_1' (1+2\eta ) }{ 1 - 2 c_*^{-1} C_* \eta }< c_2' \quad \text {and} \quad 1+2\eta < C_* / c_* . \end{aligned}$$

(5.15)

The particular choice of $\eta$ in (5.15) will not be used until (5.49) below. For now, the reader should just think of it as a small constant depending on $c_1',c_2'$. We also note that $\eta$ is fixed in a way that depends only on $c_1',c_2',c_*,C_*$ (hence only on $c_1',c_2'$ and the choice of $D,\widetilde{D}$), so we do not need to explicitly mention the dependence on $\eta$ in what follows. The following lemma gives us the basic “building blocks” which will be used to construct $E_r$ in the next two subsections.

Lemma 5.6

There exist small parameters $b_1, p_1\in (0,1/100)$ depending only on $\mu ,\nu$ and a parameter $\varepsilon _1\in (0,b_1/100)$ depending only on $c_1',c_2',\mu ,\nu$ such that for each $z\in \mathbb {C}$ and each $r\in \mathcal R_0$, there exists a deterministic connected open set $V_r(z) \subset B_{(2+ 2\varepsilon _1)r}(z)$ with the following properties. The set $V_r(z)$ is the interior of a finite union of squares in $\mathcal S_{\varepsilon _1r}(B_{2r}(z))$, $z-2r, z + 2r \in V_r$, and we have $\mathbb {P}[F_r(z)] \ge p_1$, where $F_r(z)$ is the event that the following is true. There are points $u,v\in V_r(z)\cap \overline{B_r(z)}$ with the following properties.

• 1. (Existence of a shortcut) We have

  $$\begin{aligned} |u-v|\ge & {} b_1r,\quad \widetilde{D}_h(u , v ) \le c_1' D_h(u ,v ) ,\quad \widetilde{D}_h(u,v)\nonumber \\\le & {} (c_*/C_*)^{2} \widetilde{D}_h\left( u , \partial B_{2r}(z) \right) , \end{aligned}$$

  (5.16)

  and the $\widetilde{D}_h$-geodesic from u to v is unique and is contained in $V_r(z) \cap \overline{B_r(z)}$.

• 2. (Removing neighborhoods of u, v disconnects $V_r(z)$) Let $O_u$ be the connected component of $V_r(z) \cap B_{20\varepsilon _1r}(u)$ which contains u and similarly define $O_v$ with v in place of u. The connected component of $V_r(z) {\setminus } O_u$ which contains $z-2r$ lies at Euclidean distance at least $\varepsilon _1r$ from the union of the other connected components of $V_r(z) {\setminus } O_u$. The same is true with v in place of u and $z+2r$ in place of $z-2r$.

• 3. (Upper bound for internal diameters of neighborhoods of u and v) Each point of $O_u$ lies at $\widetilde{D}_h(\cdot ,\cdot ; V_r(z))$-distance at most $\eta \widetilde{D}_h(u,v)$ from u, and the same is true with v in place of u (here $\eta$ is as in (5.15)).

Proof

Let $\alpha$ be as in Lemma 5.5 and set $b_1:= 1-\alpha$. On the event that points $u \in \partial B_{\alpha r}(z)$ and $v\in \partial B_r(z)$ satisfying the conditions on Lemma 5.5 exist (which happens with probability at least $p_0/8$), choose one such pair of points (u, v) in some measurable manner. Otherwise, let $u = v = 0$. On the event $\{u \not =0\}$, let $\widetilde{P}$ be the unique $\widetilde{D}_h$-geodesic from u to v and let $H_r(z) \subset \mathbb {A}_{\alpha r , r}(z)$ be the half-annulus with $\widetilde{P} \subset \overline{H_r(z)}$ as in Lemma 5.5.

We will now extend $\widetilde{P}$ to a path $\widetilde{P}'$ in $B_{2r}(z)$ from $z-2r$ to $z+2r$ (which will no longer be a $\widetilde{D}_h$-geodesic). To this end, we first let $v' := (3/2)(v - z) +z \in \partial B_{3r/2}(z)$ and we let $L_-$ (resp. $L_+$) be the linear segment from z to u (resp. v to $v'$). We note that the Euclidean distance between $L_-$ and $L_+$ is at least $b_1r$. We can choose a path $\pi _-$ from $z-2r$ to z and a path $\pi _+$ from $v'$ to $z+2r$ in $B_{2r}(z)$ such that the Euclidean distances from $\pi _-\cup \pi _+$ to $H_r(z)$ and from $\pi _- \cup L_-$ to $\pi _+ \cup L_+$ are each at least $b_1r$. Let $\widetilde{P}'$ be the concatenation of $\pi _- , L_- , \widetilde{P} , L_+ , \pi _+$.

Since $|u-v| \ge b_1r$ on the event $\{u\not =0\}$, Axiom V (tightness across scales) together with Lemma 2.9 imply that we can find $\varepsilon _1\in (0,b_1/100)$ depending only on $c_1',c_2',\mu ,\nu$ such that with probability at least $p_0/9$, the event of Lemma 5.5 occurs (i.e., $u\not =0$) and also

$$\begin{aligned} \sup _{S\in \mathcal S_{\varepsilon _1r}(B_{2r}(z))} \sup _{w_1,w_2 \in S} \widetilde{D}_h(w_1,w_2; S) \le \frac{\eta }{100} \widetilde{D}_h(u,v) . \end{aligned}$$

(5.17)

The number of subsets of $\mathcal S_{\varepsilon _1r}(B_{2r}(z))$ is bounded above by a deterministic constant depending only on $\varepsilon _1$. Consequently, we can choose $p_1\in (0,1)$ depending only on $\mu ,\nu ,D$ and a deterministic $\mathcal K_r(z) \subset \mathcal S_{\varepsilon _1r}(B_{2r}(z))$ such that with probability at least $p_1$, the events of Lemma 5.5 and (5.17) occur and also

$$\begin{aligned} \mathcal K_r(z) = \left\{ S \in \mathcal S_{\varepsilon _1r}(B_{2r}(z)) : S\cap \widetilde{P}' \not =\emptyset \right\} . \end{aligned}$$

(5.18)

Let $V_r(z)$ be the interior of the union of the squares in $\mathcal K_r(z)$. Since $z-2r ,z + 2r \in \widetilde{P}'$ and $\widetilde{P}'$ is connected, it follows that $V_r(z)$ is connected and contains $z-2r$ and $z+ 2r$.

Henceforth assume that the events of Lemma 5.5, (5.17), and (5.18) occur. We will check the conditions in the lemma statement with $V_r(z)$ as above.

Condition 1 This is immediate from the conditions on u and v from Lemma 5.5.

Condition 2 By the above definitions of $\pi _-$ and $L_-$, the Euclidean $\varepsilon _1r$-neighborhood of each square of $\mathcal S_{\varepsilon _1r}$ which intersects both $B_{2\varepsilon _1r} ( \pi _- \cup L_-)$ and $B_{2\varepsilon _1r}( H_r(z) )$ must be contained in $B_{10\varepsilon _1r}(u)$. Furthermore, using that $L_-$ is a linear segment, we get that the $\varepsilon _1$-neighborhood of each such square which intersects $B_{2\varepsilon _1r} ( \pi _- \cup L_-)$ and belongs to $\mathcal K_r(z)$ (as defined in (5.18)) must be contained in $\overline{O_u}$, with $O_u$ as in the lemma statement. Since the Euclidean distance between $\pi _- \cup L_-$ and $\pi _+ \cup L_+$ is at least $b_1r \ge 100 \varepsilon _1r$ and $\widetilde{P} \subset H_r(z)$, we see that removing $O_u$ disconnects $V_r(z)$ into at least two connected components, and the Euclidean distance between the connected component which contains $z - 2r$ and the union of the other connected components is at least $\varepsilon _1r$. A similar argument applies with v in place of u.

Condition 3 Each point of $O_u$ is contained in a square of $\mathcal K_r(z)$ which lies at graph distance at most 40 from a square which contains u in the adjacency graph of squares of $\mathcal K_r(z)$. The same is true with v in place of u. It therefore follows from (5.17) that condition 3 in the lemma statement is satisfied. $\square$

For $z\in \mathbb {C}$ and $r>0$, let $F_r(z)$ be as in Lemma 5.6. In the next subsection, we will use the local independence properties of the GFF (in the form of Lemma 2.7) to argue that for a small enough $\rho \in (0,1)$ and for all $r\in \rho ^{-1}\mathcal R_0$, it is very likely that $F_{\rho r}(z)$ occurs for many points $z\in B_r(0)$. To apply the lemma, we will need the following measurability statement.

Lemma 5.7

For each $z\in \mathbb {C}$ and $r>0$, the event $F_r(z)$ is a.s. determined by $(h-h_{4r}(z)) |_{B_{3r}(z)}$.

Proof

First note that the occurrence of $F_r(z)$ is unaffected by scaling each of $D_h$ and $\widetilde{D}_h$ by the same constant factor. Therefore, Axiom III (Weyl scaling) implies that $F_r(z)$ is determined by h, viewed modulo additive constant. So, we only need to show that $F_r(z) \in \sigma \left( h|_{B_{3r}(z)} \right)$.

We first observe that for $u,v \in \overline{B_r(z)}$, we have $\widetilde{D}_h(u,v) \le (c_*/C_*)^{2} \widetilde{D}_h\left( u , \partial B_{2r}(z) \right)$ if and only if v is contained in the $\widetilde{D}_h$-metric ball of radius $(c_*/C_*)^{2} \widetilde{D}_h\left( u , \partial B_{2r}(z) \right)$ centered at v. Since this $\widetilde{D}_h$-metric ball is contained in $B_{2r}(z)$, we infer from the locality of $\widetilde{D}_h$ that the set of $u,v \in B_{2r}(z)$ for which $\widetilde{D}_h(u,v) \le (c_*/C_*)^{2} \widetilde{D}_h\left( u , \partial B_{2r}(z) \right)$ is determined by $h|_{B_{3r}(z)}$. If $\widetilde{D}_h(u,v) \le (c_*/C_*)^{2} \widetilde{D}_h\left( u , \partial B_{2r}(z) \right)$, then each $\widetilde{D}_h$-geodesic from u to v is contained in $B_{2r}(z)$, so the set of $\widetilde{D}_h$-geodesics from u to v is the same as the set of $\widetilde{D}_h(\cdot ,\cdot ; B_{2r}(z))$-geodesics from u to v.

Furthermore, by the definition (1.21) of $c_*$ and $C_*$, we see that

$$\begin{aligned} \widetilde{D}_h(u,v)\le & {} (c_*/C_*)^{2} \widetilde{D}_h\left( u , \partial B_{2r}(z) \right) \Rightarrow D_h(u,v) \nonumber \\\le & {} (c_*/C_*) D_h\left( u , \partial B_{2r}(z) \right) , \end{aligned}$$

(5.19)

so $D_h(u,v) =D_h(u,v ; \partial B_{2r}(z))$ whenever $\widetilde{D}_h(u,v) \le (c_*/C_*)^{2} \widetilde{D}_h\left( u , \partial B_{2r}(z) \right)$.

By combining these observations with the locality of the metrics $D_h$ and $\widetilde{D}_h$, it follows that $F_r(z)$ is determined by $h|_{B_{3r}(z)}$. $\square$

5.4 Building a tube which contains a shortcut with high probability

Fig. 11

Illustration of the statement and proof of Lemma 5.8. To get an event with probability close to 1, instead of just an event with uniformly positive probability, we consider a large number of disjoint balls $B_{\rho r}(z)$ centered at a finite set of points $\mathcal Z\subset \partial B_r(0)$ and use Lemma 2.7 to argue that with high probability, the event $F_{\rho r}(z)$ of Lemma 5.6 occurs for a suitably “dense” set of points $z\in \mathcal Z$. Then, we link up the tubes $V_{\rho r}(z)$ for $z\in \mathcal Z$ (light green) via deterministic paths $L_k$ (blue). For a given choice of points $x,y\in \partial B_{2r}(0)$ with $|x-y|\ge \delta r$, we define $U_r^{x,y}$ to be the union of the sets $V_{\rho r}(z)$ for points $z \in \mathcal Z$ along the counterclockwise arc of $\partial B_r(0)$ from x/2 to y/2, the squares of $\mathcal S_{\varepsilon _1\rho r}(B_r(0))$ which intersect the deterministic paths joining these sets $V_{\rho r}(z)$, and paths of squares starting from each of x and y (light blue). The sets $O_u$ and $O_v$ from assertion B are shown in yellow (color figure online)

In the rest of this section, unlike in Sect. 5.3, our events will no longer depend on a parameter z. Rather, we will only define events for Euclidean balls centered at 0. We will now prove a variant of Lemma 5.6 which holds with probability close to 1, not just with uniformly positive probability. This will be accomplished as follows. We fix a small parameter $\rho > 0$ and consider a large number of radius-$\rho r$ balls $B_{\rho r}(z)$ contained in $B_{2r}(0)$ for which the event $F_{\rho r}(z)$ of Lemma 5.6 occurs with positive probability. We join up the “tubes” $V_{\rho r}(z)$ for the individual balls into a single large tube, which we will denote by $U_r^{x,y}$. We use Lemma 2.7 to say that with high probability the event $F_{\rho r}(z)$ occurs for at least one of the small balls, which means that with high probability the tube $U_r^{x,y}$ contains a pair of points u, v as in (5.1). See Fig. 11 for an illustration.

Lemma 5.8

For each $p , \delta \in (0,1)$, there exists $b , \rho \in (0,1/100)$ depending only on $p ,\delta , \mu ,\nu$ and $\varepsilon _0 \in (0,b/100)$ depending only on $c_1',c_2' , p,\delta ,\mu ,\nu$ such that for each $r\in \rho ^{-1} \mathcal R_0$ and each $x,y \in \partial B_{2r}(0)$ with $|x-y| \ge \delta r$, there exists a deterministic connected open set $U_r^{x,y} \subset B_{3r}(0)$ with the following properties. The set $U_r^{x,y}$ is the interior of a finite union of squares in $\mathcal S_{\varepsilon _0 r}(\mathbb {A}_{ r/2, 2r}(0) )$, $x,y\in U_r^{x,y}$. Moreover, with probability at least p, it holds simultaneously for each $x,y\in \partial B_{2r}(0)$ with $|x-y| \ge \delta r$ that there are points $u,v\in \mathbb {A}_{(1-4\rho ) r, (1+4\rho ) r}(0)\cap U_r^{x,y}$ with the following properties.

• A. (Existence of a shortcut) We have

  $$\begin{aligned}&|u-v| \ge b r,\quad \widetilde{D}_h(u , v ) \le c_1' D_h(u ,v ) ,\quad \widetilde{D}_h(u,v) \nonumber \\&\quad \le (c_*/C_*)^2 \widetilde{D}_h\left( u , \partial B_{4\rho r}(u) \right) , \end{aligned}$$

  (5.20)

  and the $\widetilde{D}_h$-geodesic from u to v is unique and is contained in $U_r^{x,y}$.

• B. (Removing neighborhoods of u, v disconnects $U_r^{x,y}$) Let $O_u$ be the connected component of $U_r^{x,y} \cap B_{20\varepsilon _0 r}(u)$ which contains u and define $O_v$ similarly with v in place of u. The connected component of $U_r^{x,y} {\setminus } O_u$ which contains x lies at Euclidean distance at least $\varepsilon _0 r$ from the union of the other connected components, and the same is true with v in place of u and y in place of x.

• C. (Upper bound for internal diameters of neighborhoods of u and v) Each point of $O_u$ lies at $\widetilde{D}_h(\cdot ,\cdot ;U_r^{x,y} )$-distance at most $\eta \widetilde{D}_h(u,v)$ from u, and the same is true with v in place of u (here $\eta$ is as in (5.15)).

Proof

Define the event $F_{\rho r}(z)$ for $z\in \mathbb {C}$ and $r\in \rho ^{-1} \mathcal R_0$ as in Lemma 5.6.

Step 1: $F_{\rho r}(z)$ occurs for many points $z\in B_{2r}(0)$ Let $n_* \in \mathbb {N}$ be chosen so that the conclusion of Lemma 2.7 is satisfied with $s = 1/3$, $p_1$ in place of p, and $1 - \delta (1-p)/100$ in place of q. Let $\rho := (500 n_*)^{-1} \delta$ and define the set of points

$$\begin{aligned} \mathcal Z := \left\{ r \exp \left( \frac{2\pi \mathbb {i} \delta k }{ 100 n_* } \right) : k \in [1, 100 n_* \delta ^{-1}]_{\mathbb {Z}} \right\} \subset \partial B_r(0) . \end{aligned}$$

(5.21)

Then the balls $B_{4\rho r}(z)$ for $z\in \mathcal Z$ are disjoint and each such ball is contained in $\mathbb {A}_{(1-4\rho ) r , (1+4\rho ) r}(0)$.

By Lemmas 5.6 and 5.7 , if $r \in \rho ^{-1} \mathcal R_0$, then each of the events $F_{\rho r}(z)$ for $z\in \mathcal Z$ has probability at least $p_1$ and is determined by $(h-h_{4\rho r}(z)) |_{B_{3\rho r}(z)}$. Each arc $I\subset \partial B_r(0)$ with Euclidean length at least $\delta r/4$ satisfies $\#(\mathcal Z\cap I) \ge n_*$. Therefore, Lemma 2.7 (applied with the whole-plane GFF $h(\cdot /(3\rho r))$ in place of h) implies that for each such arc I,

$$\begin{aligned} \mathbb {P}\left[ \exists z\in \mathcal Z \cap I \text { such that } F_{\rho r}(z)\text { occurs} \right] \ge 1 - \frac{\delta (1-p)}{100 } . \end{aligned}$$

(5.22)

We can choose at most $4\pi \delta ^{-1}$ arcs of $\partial B_r(0)$ with Euclidean length $\delta r/4$ in such a way that each arc of $\partial B_r(0)$ with Euclidean length at least $\delta r/2$ contains one of these arcs. By a union bound, we therefore get that with probability at least $1-(1-p)/4$,

$$\begin{aligned}&\text {Each arc of } \partial B_r(0) \text { with length at least } \delta r/2 \text { contains a point } z\in \mathcal Z\text { s.t. }\nonumber \\&\quad F_{\rho r}(z)\text { occurs.} \end{aligned}$$

(5.23)

We will show that the statement of the lemma is satisfied with

$$\begin{aligned} \varepsilon _0 = \varepsilon _1\rho \quad \text {and} \quad b = b_1\rho . \end{aligned}$$

(5.24)

Step 2: defining $U_r^{x,y}$ Enumerate $\mathcal Z = \{z_1,\ldots ,z_{N} \}$, where $N := \lfloor 100 n_*\delta ^{-1} \rfloor$ and $z_k := r \exp \left( \frac{2\pi \mathbb {i} \delta k }{ 100 n_* } \right)$. Also set $z_0 := z_N$. We now join up the balls $B_{2\rho r}(z_k)$, in a manner which is illustrated in Fig. 11. For $k \in [1,N]_{\mathbb {Z}}$, choose in a deterministic manner a piecewise linear path $L_k$ from $z_{k-1} + 2\rho r$ to $z_k - 2\rho r$ which is contained in $\mathbb {A}_{(1-4\rho )r , (1+4\rho )r}(0)$. We can choose the paths $L_k$ in such a way that the $L_k$’s do not intersect any of the balls $B_{2\rho r}(z)$ for $z\in \mathcal Z$ and lie at Euclidean distance at least $\rho r$ from one another.

Now consider points $x,y\in \partial B_{2r}(0)$ with $|x-y| \ge \delta r$. By possibly re-labeling, we can assume without loss of generality that the counterclockwise arc of $\partial B_{2r}(0)$ from x to y is shorter than the clockwise arc. Let $J \subset \partial B_r(0)$ by the counterclockwise arc from x/2 to y/2, so that J has length at least $\delta r/2$. Let $k_x , k_y \in [1,N]_{\mathbb {Z}}$ be chosen so that $J \cap \mathcal Z = \{z_{k_x} ,\ldots , z_{k_y}\}$. Let $\widehat{L}_x$ (resp. $\widetilde{L}_y$) be a smooth path from x to $z_{k_y} - 2r$ (resp. from $z_{k_y} + 2r$ to y) which does not intersect any of the $B_{2\rho r}(z)$’s for $z\in \mathcal Z$ and such that $\widehat{L}_x$ and $\widehat{L}_y$ lie Euclidean distance at least $\rho r$ from each other and from each $L_k$ for $k\in [k_x+1,k_y]_{\mathbb {Z}}$.

Recall that for $X\subset \mathbb {C}$, $\mathcal S_{\varepsilon _1\rho r}(X)$ denotes the set of closed Euclidean squares of side length $\varepsilon _1\rho r$ with corners in $\varepsilon _1\rho r\mathbb {Z}^2$ which intersect X. With $V_{\rho r}(z)$ as in the definition of $F_{\rho r}(z)$, we define

$$\begin{aligned} \overline{ U_r^{x,y} } := \bigcup _{k = k_x}^{k_y} \overline{V_{\rho r}(z_k)} \cup \bigcup \mathcal S_{\varepsilon _1\rho r}\left( \widehat{L}_x \cup \widehat{L}_y \cup \bigcup _{k=k_x+1}^{k_y} L_k \right) \end{aligned}$$

(5.25)

and we let $U_r^{x,y}$ be the interior of $\overline{U_r^{x,y}}$. Since each $V_r(z_k)$ is the interior of a finite union of squares in $\mathcal S_{\varepsilon _1\rho r}(B_{\rho r}(z_k))$, it follows that $U_r^{x,y}$ is the interior of a finite union of squares $\mathcal S_{\varepsilon _1\rho r}(\mathbb {A}_{r/2,2r}(0) )$. Since the $V_r(z_k)$’s are connected, it is clear that $U_r^{x,y}$ is connected and contains x, y. We also note that $U_r^{x,y}$ is deterministic.

Step 3: checking the conditions for u and v On the event that (5.23) holds, there is a random $k \in [k_x , k_y]_{\mathbb {Z}}$ for which $F_{\rho r}(z_k)$ occurs. If this is the case, choose such a k and point $u,v \in V_{\rho r}(z_k) \cap \overline{B_{\rho r}(z_k)}$ as in the definition of $F_{\rho r}(z_k)$ in some measurable manner. We will show that for $\varepsilon _0 , b$ as in (5.24), the conditions in the lemma statement hold whenever (5.23) holds.

Condition A Since $B_{2\rho r}(z_k) \subset B_{4\rho r}(u)$ and $V_{\rho r}(z_k) \subset U_r^{x,y}$, it is immediate from Condition 1 in the definition of $F_{\rho r}(z_k)$ that this condition holds with $b = b_1\rho$ whenever (5.23) holds.

Condition B Assume (5.23). Let

$$\begin{aligned}&\overline{W_k(x)} := \bigcup _{j = k_x}^{k-1} \overline{V_{\rho r}(z_j)} \cup \bigcup \mathcal S_{\varepsilon _1\rho r}\left( \widehat{L}_x \cup \bigcup _{j=k_x+1}^{k} L_j \right) \quad \text {and} \nonumber \\&\qquad \overline{W_k(y)} := \bigcup _{j = k+1}^{k_y} \overline{V_{\rho r}(z_j)} \cup \bigcup \mathcal S_{\varepsilon _1\rho r}\left( \widehat{L}_y \cup \bigcup _{j=k+1}^{k_y} L_j \right) \end{aligned}$$

(5.26)

and let $W_k(x)$ and $W_k(y)$ be the interiors of $W_k(x)$ and $W_k(y)$, respectively. By (5.25), $\overline{U_r^{x,y}} = \overline{W_k(x)} \cup \overline{W_k(y)} \cup \overline{V_{\rho r}(z_k)}$. Since $\widehat{L}_x$, $\widehat{L}_y$, and the $L_k$’s for $k\in [k_x+1,k_y]_{\mathbb {Z}}$ each lie at Euclidean distance at least $\rho r$ from one another and do not intersect the interiors of the balls $B_{\rho r}(z)$ for $z\in \mathcal Z$ and $\varepsilon _1< 1/100$, the sets $W_k(x)$ and $W_k(y)$ lie at Euclidean distance at least $\rho r/2$ from each other and from $B_{\rho r}(z_k)$.

We have

$$\begin{aligned} U_r^{x,y} \cap B_{20 \varepsilon _1\rho r}(u) = V_{\rho r}(z_k) \cap B_{20 \varepsilon _1\rho r}(u) , \end{aligned}$$

(5.27)

so the definition of $O_u$ is unaffected if we replace $U_r^{x,y}$ by $V_{\rho r}(z_k)$. Furthermore, the connected component of $U_r^{x,y} {\setminus } O_u$ which contains x is the same as the union of $W_k(x)$ and the connected component of $V_{\rho r}(z_k) {\setminus } O_u$ which contains $z_k-2 \rho r$; and the union of the other connected components of $U_r^{x,y} {\setminus } O_u$ is the same as the union of $W_k(y))$ and the connected components of $V_{\rho r}(z_k) {\setminus } O_u$ which do not contain $z_k + 2 \rho r$. By condition 2 in the definition of $F_{\rho r}(z_k)$, we find that these two sets lie at Euclidean distance at least $\varepsilon _1\rho r$ from one another.

Condition C By (5.27), condition 3 in the definition of $F_{\rho r}(z_k)$ implies that each point of $O_u$ lies at $D_h(\cdot ,\cdot ; U_r^{x,y} )$-distance at most $\eta \widetilde{D}_h(u,v)$ from u. The same is true with v in place of u. $\square$

5.5 Definition of the event $E_r$ and the bump functions $\mathcal G_r$

The goal of this subsection is to define the event $E_r$ and the collection of smooth bump functions $\mathcal G_r$ appearing in Proposition 5.2. We will also check Properties (A) and (B) from that proposition (measurability and high probability and bounds for Dirichlet inner products). Property (C) (subtracting a bump function) will be checked in Sect. 5.6.

Fig. 12

Left: Illustration of the definition of the event $E_r$. The blue set in the middle is the set $U_r^{x,y}$ of Lemma 5.8. The light blue region surrounding it is $B_{\zeta r}(U_r^{x,y})$, which is the support of the bump function $f_r^{x,y}$. The yellow regions are the supports of the bump functions $g_r^x$ and $g_r^y$, which are used to force $D_h$-geodesics started from points outside of $B_{3r}(0)$ to enter $B_{\zeta r}(U_r^{x,y})$. The figure shows the relevant set for one pair of points $x,y\in \partial B_{2r}(0)$, but all of the conditions in the event $E_r$ are required to hold simultaneously for all pairs of points $x,y\in \partial B_{2r}(0)$ with $|x-y|\ge \delta r$. This is important since in Sect. 5.6 we will take $x' = (3/2) x$ and $y' =(3/2) y$ to be the random points where the metric balls based at the starting and ending points of a given geodesic (here shown in grey) first hit $\partial B_{3r}(0)$. Right: schematic diagram of how the various quantities in the definitions of $E_r$ and $\mathcal G_r$ are chosen. An arrow between two parameters indicates that one is chosen in a way which depends directly on the other. The colors indicate where the choice is made. Most of the choices in the figure depend on $\mathbb {p}$, but this is not illustrated. In the end, all of the parameters depend only on $\mathbb {p} , \mu , \nu$ (and the choice of metric) (color figure online)

The definitions in this section are illustrated in Fig. 12, left. Before proceeding with the details, we briefly discuss the main ideas involved. Following Sect. 5.1, we want to define $\mathcal G_r$ to include for each $x,y \in \partial B_{3r}(0)$ a function $\phi$ which is equal to a large positive constant on the region $U_r^{x,y}$ of Lemma 5.8 and which is supported on the union of a small neighborhood of $U_r^{x,y}$ and two even narrower “tubes” which approximate the segments [x, 3x/2] and [y, 3y/2] (shown in yellow in the figure). The event $E_r$ will consist of the conditions of Lemma 5.8 plus several regularity conditions discussed below.

We will eventually consider a fixed pair of points $\mathbb {z},\mathbb {w} \in \mathbb {C} {\setminus } B_{4r}(0)$ and choose $x,y\in \partial B_{2r}(0)$ in such a way that $x' := 3x/2$ and $y' := 3y/2$ are the first points of $\partial B_{3r}(0)$ hit by the $D_h$-metric balls grown from $\mathbb {z}$ and $\mathbb {w}$, respectively. Since these points are random, it is important that the conditions in our event hold simultaneously for all possible choices of x and y. We will show in Sect. 5.6 that on $E_r$, subtracting a suitable $\phi \in \mathcal G_r$ from the field makes distances in the support of $\phi$ much shorter than distances outside, so the $D_{h-\phi }$-geodesic has to travel through the support of $\phi$ and hence has to get close to the points u, v of Lemma 5.8.

There are several subtleties involved in this argument which are dealt with via regularity conditions in the definition of $E_r$. For example, Lemma 5.8 requires that $|x-y| \ge \delta r$, so we need to ensure that our random metric ball hitting points $x',y'$ are separated. This is the purpose of condition 4 in the definition of $E_r$. Another difficulty is that it is relatively straightforward to get $D_{h-\phi }$-geodesics into the support of $\phi$, but we want such geodesics to actually enter the region $U_r^{x,y}$ where $\phi$ is equal to a large positive constant. The reason for this is that we will be comparing ratios of distances via Weyl scaling (Axiom III) and it could be that $\phi$ is much smaller on some parts of its support than it is on $U_r^{x,y}$. To deal with this, we will include a condition to the effect that paths which stay in a small neighborhood of $\partial U_r^{x,y}$ without entering $U_r^{x,y}$ are very long (condition 6). We also need functions in $\mathcal G_r$ to be supported on $\mathbb {A}_{r,3r}(0)$ so we need to make the yellow tubes in Fig. 12 very close to $x'$ and $y'$ without actually allowing these tubes to contain $x'$ and $y'$ (condition 8). The choice of constants involved in these conditions is somewhat delicate, so the event $E_r$ will include several parameters.

We now commence with the definitions. Fix a parameter $\delta \in (0,1)$, to be chosen in a manner depending only on $\mathbb {p}$ in Lemma 5.10 below. Let $\rho , b , \varepsilon _0$ be as in Lemma 5.8 for this choice of $\delta$ and with $p = 1-(1-\mathbb {p})/2$, so that $\rho ,b,\varepsilon _0$ depend only on $\delta ,\mathbb {p} , \mu , \nu$. The definitions of $E_r$ and $\mathcal G_r$ involve several additional small parameters $\Delta \in (0,1)$ and $\zeta , a,\theta \in (0,\varepsilon _0)$ and large parameters $A, M,\Lambda _0 >1$ which we will choose in Lemma 5.10 below, in a manner depending only on $\mathbb {p} , \mu , \nu$. See Fig. 12, right for a schematic illustration of how the parameters are chosen.

5.5.1 Definition of $\mathcal G_r$

We first give the definition of $\mathcal G_r$ in terms of the above parameters. For each $x,y\in \partial B_{2r}(0)$ with $|x-y| \ge \delta r$, choose in a deterministic manner depending only on $U_r^{x,y}$ (not on the particular values of x and y) a smooth, compactly supported bump function $f_r^{x,y} : \mathbb {C}\rightarrow [0,1]$ which is identically equal to 1 on $U_r^{x,y}$ and vanishes outside of $B_{ \zeta r}(U_r^{x,y} )$.

Since each $U_r^{x,y}$ is the interior of a finite union of squares in $\mathcal S_{\varepsilon _0 r}(B_{2r}(0))$, there are at most a finite, r-independent number of possibilities for $U_r^{x,y}$ as x and y vary. From this and the scale invariance of Dirichlet energy (i.e., $(f(r\cdot ), f(r\cdot ))_\nabla = (f,f)_\nabla$) it follows that we can arrange that the Dirichlet energy $(f_r^{x,y} , f_r^{x,y})_\nabla$ is bounded above by a constant depending only on $\varepsilon _0,\zeta$.

If we subtract a large constant multiple of $f_r^{x,y}$ from h, then LQG geodesics for the resulting field between points of $U_r^{x,y}$ will tend to stay in $U_r^{x,y}$. However, we also need to get geodesics between points of $\mathbb {C}{\setminus } B_{4r}(0)$ into $U_r^{x,y}$. For this purpose, we will also subtract even larger constant multiples of bump functions $g_r^x$ and $g_r^y$ which are supported in narrow tubes which approximate the segments [x, 3x/2] and [y, 3y/2]. The supports of these bump functions are shown in yellow in Fig. 12.

To define these bump functions, we first define for $x\in \partial B_{2r}(0)$ the set

$$\begin{aligned} W_r^x = W_r^x(\theta ) := \left( \text {Interior of } \bigcup _{S\in \mathcal S_{\theta r} ( [x , (3/2-\theta ) x])} S \right) \subset \mathbb {A}_{r,3r}(0) \end{aligned}$$

(5.28)

where here we recall from (5.14) that $\mathcal S_{\theta r}([x , (3/2-\theta ) x])$ is the set of $\theta r \times \theta r$ squares with corners in $\theta r \mathbb {Z}^2$ which intersect $[x , (3/2-\theta ) x]$. Let $g_r^x : \mathbb {C}\rightarrow [0,1]$ be a smooth compactly supported function which is identically equal to 1 on $W_r^x$ and is identically equal to 0 outside of $B_{\theta ^2 r}(W_r^x) \subset B_{3r}(0)$. As in the case of $f_r^{x,y}$ (see the paragraph just above (5.29)), we can arrange that the Dirichlet energy of $g_r^x$ is bounded above by a constant depending only on $\theta ,\mathbb {p}$.

We define the large constants

$$\begin{aligned} K_f := \frac{1}{\xi } \log \left( \frac{100 A}{a\Delta } \right) \quad \text {and} \quad K_g := K_f + \frac{1}{\xi } \log \left( M\right) . \end{aligned}$$

(5.29)

For each $x,y\in \partial B_{2r}(0)$ with $|x-y| \ge \delta r$, we define

$$\begin{aligned} \phi _r^{x,y} := K_f f_r^{x,y} + K_g(g_r^x + g_r^y) . \end{aligned}$$

(5.30)

Since each of $f_r^{x,y}, g_r^x,g_r^y$ is supported on $\mathbb {A}_{r/4,3r}(0)$, so is $\phi _r^{x,y}$. We set

$$\begin{aligned} \mathcal G_r := \left\{ \phi _r^{x,y} : x,y\in \partial B_{2r}(0) ,\, |x-y| \ge \delta r \right\} \cup \{\text {zero function}\} . \end{aligned}$$

(5.31)

We emphasize that the definition of $\mathcal G_r$ does not depend on the parameter $\Lambda _0$. This will be important when we choose $\Lambda _0$ in Lemma 5.10 below.

Recall from the above discussion that the number of possibilities for each of $f_r^{x,y} , g_r^x , g_r^y$ as x and y vary and the Dirichlet energies of each of these functions is bounded above by a constant which does not depend on r, x, or y. Consequently, each of

$$\begin{aligned} \#\mathcal G_r \quad \text {and} \quad \max _{\phi \in \mathcal G_r} (\phi ,\phi )_\nabla \end{aligned}$$

(5.32)

is bounded above by a constant which does not depend on r, x, or y.

5.5.2 Definition of $E_r$

We now define the event $E_r$ appearing in Proposition 5.2.

We encourage the reader to skim the list of conditions on a first read and refer back to them as they are used while reading the proof of Lemma 5.11 below.

With the parameters $\delta , \Delta , A, \zeta ,a,\theta ,M,\Lambda _0$ as above, we define $E_r$ to be the event that the following is true. For each $x,y\in \partial B_{2r}(0)$ with $|x-y| \ge \delta r$, there exists $u,v\in \mathbb {A}_{(1-4\rho )r,(1+4\rho )r}(0)$ satisfying the three numbered conditions of Lemma 5.8 and moreover the following additional conditions hold.

• 4. For each $x,y\in \partial B_{2r}(0)$ with $|x -y | < \delta r$,

  $$\begin{aligned}&D_h\left( x',y' ; \mathbb {A}_{ r , 4r} (0) \right) \le \Delta \mathfrak c_r e^{\xi h_r(0)} \\&\quad \le D_h\left( \partial B_{2r}(0), \partial B_{3r}(0) \right) ,\quad \text {where} \quad x' = \frac{3}{2} x \, \text {and}\, y' =\frac{3}{2} y. \end{aligned}$$

• 5. For each $x,y \in \partial B_{2r}(0)$ with $|x-y| \ge \delta r$ the $D_h$-internal diameter of $U_r^{x,y}$ satisfies

  $$\begin{aligned} \sup _{w_1,w_2 \in U_r^{x,y} } D_h\left( w_1,w_2 ; U_r^{x,y} \right) \le A\mathfrak c_r e^{\xi h_r(0)} . \end{aligned}$$

• 6. For each $x,y \in \partial B_{2r}(0)$ with $|x-y| \ge \delta r$, the $D_h$-length of every continuous path of Euclidean diameter at least $\varepsilon _0 r/100$ which is contained in $B_{2\zeta r}(\partial U_r^{x,y})$ is at least $100 A\mathfrak c_r e^{\xi h_r(0)}$.

• 7. For each $z_1,z_2 \in \mathbb {A}_{r/4,4r}(0)$ such that $|z_1-z_2| \ge \zeta r$,

  $$\begin{aligned} D_h\left( z_1, z_2 ; \mathbb {A}_{r/4,4r}(0) \right) \ge a\mathfrak c_r e^{\xi h_r(0)} . \end{aligned}$$

• 8. With $K_f$ as in (5.29),

  $$\begin{aligned} D_h\left( 3x/2, (3/2-\theta ) x ; \mathbb {A}_{r,4r}(0) \right) \le e^{-\xi K_f} \mathfrak c_r e^{\xi h_r(0)} , \quad \forall x\in \partial B_{2r}(0) . \end{aligned}$$

• 9. If we let $W_r^x \subset \mathbb {A}_{r,3r}(0)$ be the long narrow tube as in (5.28), then

  $$\begin{aligned} \sup _{w_1,w_2 \in W_r^x} D_h(w_1,w_2 ; W_r^x) \le M\mathfrak c_r e^{\xi h_r(0)} . \end{aligned}$$

• 10. With $\mathcal G_r$ as in (5.31), we have $(h,\phi )_\nabla + \frac{1}{2} |(\phi ,\phi )_\nabla | \le \Lambda _0$ for each $\phi \in \mathcal G_r$.

The conditions in the definition of $E_r$ are numbered in such a way that the new parameters involved in each condition depend only on the parameters from the previous conditions. We now comment briefly on the purpose of each of the conditions. As discussed in Sect. 5.1, to prove Property (C) (subtracting a bump function) of Proposition 5.2, we will grow the $D_h$-metric balls started from $\mathbb {z}$ and $\mathbb {w}$ until they hit $B_{3r}(0)$. We will let $\mathbb {x}'$ and $\mathbb {y}'$ be their respective hitting points, and we will apply the above conditions with $x = \mathbb {x} := (2/3) \mathbb {x}'$ and $y = \mathbb {y} = (2/3)\mathbb {y}'$ (note that $\mathbb {x},\mathbb {y}\in \partial B_{2r}(0)$).

Condition 4 is used to ensure that if P hits $B_{2r}(0)$, then $|\mathbb {x} - \mathbb {y}| \ge \delta r$ (see Lemma 5.12). Condition 5 gives us a deterministic upper bound for the $D_h$-diameter of $U_r^{\mathbb {x} , \mathbb {y}}$ before we subtract the bump function $\phi$. This allows us say that the $D_{h-\phi }$-diameter of $U_r^{x,y}$ is very small, which is what forces the $D_{h-\phi }$-geodesic $P^\phi$ to enter $U_r^{\mathbb {x} , \mathbb {y}}$. Condition 6 prevents $P^\phi$ from staying close to $\partial U_r^{\mathbb {x} , \mathbb {y}}$ (in the region where $\phi$ positive, but does not attain its largest possible value) without entering $U_r^{x,y}$ itself. Condition 7 is used to prevent $P^\phi$ from exiting $B_{\zeta r} ( U_r^{\mathbb {x} , \mathbb {y}})$ prematurely. Conditions 8 and 9 concern the yellow tubes in Fig. 12. These conditions are used to force $P^\phi$ to enter and exit $U_r^{\mathbb {x} , \mathbb {y}}$ at points near $\mathbb {x}$ and $\mathbb {y}$, respectively. Condition 10 is used to prove Property (B) (bounds for Dirichlet inner products) of Proposition 5.2.

5.5.3 Proof of Properties (A) and (B)

It is immediate from condition 10 in the definition of $E_r$ that Property (B) (bounds for Dirichlet inner products) of Proposition 5.2 is satisfied. In the next two lemmas we check the two assertions of Property (A) (measurability and high probability).

Lemma 5.9

The event $E_r$ is determined by $(h-h_{5r}(0)) |_{\mathbb {A}_{r/4,4r}(0)}$

Proof

By Axiom III (Weyl scaling), the occurrence of $E_r$ is unaffected by adding a real number to h, so we only need to show $E_r \in \sigma \left( h|_{\mathbb {A}_{r/4,4r}(0)} \right)$. The measurability of condition A follows from exactly the same argument used in the proof of Lemma 5.7 (this can also be seen from Lemma 5.7 and the proof of Lemma 5.6). Since $U_r^{x,y} , W_r^x , W_r^y \subset \mathbb {A}_{(1/2 - 2\varepsilon _0) r , 3 r}(0)$ and $D_h$ and $\widetilde{D}_h$ are local metrics for h, the measurability of the other conditions in the definition of $E_r$ follows by inspection and Axiom II (locality). $\square$

Lemma 5.10

We can choose the parameters $\delta , \Delta , A, \zeta ,a,\theta ,M,\Lambda _0$ in a manner depending only on $\mathbb {p} , \mu ,\nu ,c_1',c_2'$ in such a way that $\mathbb {P}[E_r] \ge \mathbb {p}$ for each $r\in \rho ^{-1}\mathcal R_0$.

Proof

By tightness across scales (Axiom V), we can choose $\Delta$ and then $\delta$ in such a way that condition 4 holds with probability at least $1-(1-\mathbb {p})/100$. As above, we choose $b,\rho ,\varepsilon _0$ as in Lemma 5.8 with the above choice of $\delta$ and with $p = 1-(1-\mathbb {p})/100$ (so that $b,\rho$ depend only on $\mathbb {p},\mu ,\nu$ and $\varepsilon _0$ depends only on $\mathbb {p} , \mu ,\nu ,c_1', c_2'$) and define $U_r^{x,y}$ for $x,y \in \partial B_{2r}(0)$ with $|x-y| \ge \delta r$ as in that lemma. Then the first four conditions (including the three from Lemma 5.8) in the definition of $E_r$ occur simultaneously with probability at least $1-2(1-\mathbb {p})/100$.

We will now choose the parameters so as to lower-bound the probabilities of the other conditions in the definition of $E_r$ in numerical order. By Lemma 2.9, we can find $C> 0$ depending only on $\varepsilon _0$ (and hence only on $p ,\mu ,\nu ,c_1',c_2'$) such that with probability at least $1- (1-\mathbb {p})/100$, we have, with $\mathcal S_{\varepsilon _0 r}(\cdot )$ as in (5.14),

$$\begin{aligned} \sup _{S\in \mathcal S_{\varepsilon _0 r}(B_{2r}(0))} \sup _{w_1,w_2 \in S} D_h(w_1,w_2 ; S) \le C \mathfrak c_r e^{\xi h_r(0)} . \end{aligned}$$

(5.33)

The total number of squares of $\mathcal S_{\varepsilon _0 r}(B_{2r}(0))$ is at bounded above by a constant depending only on $\varepsilon _0$ (and hence only on $\mathbb {p},\mu ,\nu ,c_1',c_2'$). Since each $U_r^{x,y}$ is connected and is the interior of a finite union of such squares, the triangle inequality shows that there is an $A>1$ depending only on $\mathbb {p} ,\mu ,\nu$ such that whenever (5.33) holds, also condition 5 holds. Hence the probability of condition 5 is at least $1-(1-\mathbb {p})/100$.

The set $\partial U_r^{x,y}$ is the union of some subset of the set of sides of squares in $\mathcal S_{\varepsilon _0 r}(B_{2r}(0))$. By Lemma 2.10 (applied with $\zeta$ in place of $\varepsilon$) and a union bound over all of the sides of all of the squares in $\mathcal S_{\varepsilon _0 r}(B_{2r}(0))$, we can choose $\zeta \in (0,\varepsilon _0/100)$ depending only on $\mathbb {p} , \varepsilon _0 , A$ (and hence only on $\mathbb {p} , \mu , \nu ,c_1',c_2'$) such that condition 6 holds with probability at least $1 - (1-\mathbb {p})/100$.

Since $D_h$ induces the Euclidean topology, we can find $a\in (0,1)$ depending only on $\mathbb {p} , \zeta$ (and hence only on $\mathbb {p} , \mu , \nu ,c_1',c_2'$) such that condition 7 holds with probability at least $1- (1-\mathbb {p})/100$.

Since the constant $K_f$ of (5.29) depends only on $A, \Delta ,a$, which have already been chosen in a manner depending only on $\mathbb {p} , \mu , \nu ,c_1',c_2'$, we can find a small enough $\theta \in (0,\zeta /100)$ depending only on $\mathbb {p} , \mu , \nu ,c_1',c_2'$ such that condition 8 holds with probability at least $1-(1-\mathbb {p})/100$.

Recall from (5.28) that $W_r^x$ is the interior of the union of a set of squares in $\mathcal S_{\theta r}(B_{3r}(0))$. By Axiom V (tightness across scalings) and Lemma 2.9, we can find a sufficiently large $M> 0$ depending only $\theta$ (hence only on $\mathbb {p} ,\mu ,\nu ,c_1',c_2'$) such that condition 9 holds with probability at least $1-(1-\mathbb {p})/100$.

The definition of the set of bump functions $\mathcal G_r$ above does not use the parameter $\Lambda _0$. As discussed just after (5.32), the number of functions in $\mathcal G_r$ and the Dirichlet energies of these functions are each bounded above by constants which depend only on $\mathbb {p} ,\mu , \nu ,c_1',c_2'$ and the other parameters which we have already chosen in a manner depending only on $\mathbb {p} , \mu , \nu ,c_1',c_2'$. Consequently, we can find a constant $\Lambda _0 > 0$ depending only on $\mathbb {p},\mu ,\nu ,c_1',c_2'$ such that condition 10 holds with probability at least $1- (1-\mathbb {p})/100$. Combining our above estimates gives the statement of the lemma. $\square$

5.6 Subtracting a bump function to move a geodesic

To prove Proposition 5.2, it remains to check Property (C) (subtracting a bump function) for the event $E_r$ and the collection of smooth bump functions $\mathcal G_r$ defined above. To this end, fix distinct points $\mathbb {z} , \mathbb {w} \in \mathbb {C}{\setminus } B_{4r}(0)$ and let $P = P^{\mathbb {z},\mathbb {w}}$ be the (a.s. unique) $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$. We first grow the $D_h$-metric balls until they hit $\partial B_{3r}(0)$. Let $\sigma _r$ (resp. $\widehat{\sigma }_r$) be the smallest $s > 0$ for which the $D_h$-metric ball $\mathcal B_s(\mathbb {z} ;D_h)$ (resp. $\mathcal B_s(\mathbb {w} ; D_h)$) intersects $\overline{B_{3r}(0)}$. Also let $\mathbb {x}'$ (resp. $\mathbb {y}'$) be a point of $\partial B_{3r}(0) \cap \mathcal B_{\sigma _r}(\mathbb {z} ; D_h)$ (resp. $\mathcal B_{\widehat{\sigma }_r}(\mathbb {w} ;D_h)$), chosen in some manner depending only on the appropriate $D_h$-metric ball,⁷ and define the points of $\partial B_{2r}(0)$

$$\begin{aligned} \mathbb {x} := (2/3) \mathbb {x}' \quad \text {and} \quad \mathbb {y} := (2/3) \mathbb {y} ' . \end{aligned}$$

(5.34)

Note that $\mathbb {x} , \mathbb {y} \in \sigma \left( h|_{\mathbb {C}{\setminus } B_{3r}(0)} \right)$.

In the notation (5.30), we set

$$\begin{aligned} \phi = {\left\{ \begin{array}{ll} \phi _r^{\mathbb {x} , \mathbb {y}} , \quad &{}\text {if } |\mathbb {x}-\mathbb {y}| \ge \delta r \\ 0 ,\quad &{}\text {otherwise} . \end{array}\right. } \end{aligned}$$

(5.35)

Then $\phi \in \mathcal G_r$, as defined in (5.31), and $\phi$ is determined by $\mathbb {x} , \mathbb {y}$ and hence by $h|_{\mathbb {C}{\setminus } B_{3r}(0)}$. Hence to prove Property (C) it remains only to prove the following.

Lemma 5.11

Let $P^\phi$ be the (a.s. unique) $D_{h - \phi }$-geodesic from $\mathbb {z}$ to $\mathbb {w}$. If $P\cap B_{2r}(0) \not =\emptyset$ and $E_r$ occurs, then there are times $0< s< t < D_{h - \phi }(\mathbb {z}, \mathbb {w})$ such that

$$\begin{aligned}&P^\phi (s) , P^\phi (t) \in B_{3r/2}(0) , \quad |P^\phi (s) - P^\phi (t)| \ge (b - 40 \varepsilon _0) r , \nonumber \\&\qquad \widetilde{D}_{h-\phi }\left( P^\phi (s) , P^\phi (t)\right) \le c_2' D_{h- \phi }\left( P^\phi (s) , P^\phi (t)\right) ,\quad \text {and} \nonumber \\&\qquad \widetilde{D}_{h- \phi }\left( P^\phi (s) , P^\phi (t)\right) \le (c_* / C_*) \widetilde{D}_{h-\phi }\left( P^\phi (s) , \partial B_{3r}(0) \right) . \end{aligned}$$

(5.36)

The rest of this section is devoted to the proof of Lemma 5.11. To lighten notation, write

$$\begin{aligned} U = U_r^{\mathbb {x},\mathbb {y}} \quad \text {and} \quad \mathcal W = B_{\theta ^2 r} ( W_r^{\mathbb {x}}) \cup B_{\theta ^2 r}( W_r^{\mathbb {y}} ) . \end{aligned}$$

(5.37)

Throughout, we assume that $E_r$ occurs and $P\cap B_{2r}(0)\not =\emptyset$. The proof is an elementary (though somewhat technical) deterministic argument using the conditions in the definition of $E_r$, and is divided into several lemmas.

Lemma 5.12

We have $|\mathbb {x} - \mathbb {y}| \ge \delta r$.

Lemma 5.12 allows us to apply all of the conditions in the definition of $E_r$ with $x = \mathbb {x}$ and $y=\mathbb {y}$ (note that these conditions hold for all $x,y\in \partial B_{2r}(0)$ with $|x-y|\ge \delta r$ simultaneously). We will use this fact without comment throughout the rest of the proof.

Proof of Proposition 4.3, assuming Proposition 5.2

Since P is a $D_h$-geodesic, the $D_h$-distance between the metric balls $\mathcal B_{\sigma _r}(\mathbb {z} ; D_h)$ and $\mathcal B_{\widehat{\sigma }_r}(\mathbb {w} ;D_h)$ is equal to the $D_h$-distance traveled by P between the times when it hits these two metric balls. Since P enters $B_{2r}(0)$, it must cross between the inner and outer boundaries of $\mathbb {A}_{2r,3r}(0)$ at least twice between hitting these two metric balls, so the $D_h$-distance between $\mathcal B_{\sigma _r}(\mathbb {z} ; D_h)$ and $\mathcal B_{\widehat{\sigma }_r}(\mathbb {w} ;D_h)$ must be at least $2 D_h(\partial B_{2r}(0) , \partial B_{3r}(0))$. Condition 4 in the definition of $E_r$ implies that if $|\mathbb {x} - \mathbb {y}| < \delta r$ then $D_h(\partial B_{2r}(0), \partial B_{3r}(0)) \ge D_h(\mathbb {x}', \mathbb {y}' ; \mathbb {A}_{r,4r}(0))$ which is at least the $D_h$-distance between $\mathcal B_{\sigma _r}(\mathbb {z} ; D_h)$ and $\mathcal B_{\widehat{\sigma }_r}(\mathbb {w} ;D_h)$. This is a contradiction and therefore $|\mathbb {x} - \mathbb {y}| \ge \delta r$. $\square$

We now prove an upper bound for $D_{h-\phi }(\mathbb {x}',\mathbb {y}')$. Since $P^\phi$ is a $D_{h-\phi }$-geodesic, this upper bound will allow us to constrain the behavior of $P^\phi$ since $P^\phi$ cannot have any segment whose $D_{h-\phi }$-length is larger than $D_{h-\phi }(\mathbb {x}',\mathbb {y}')$ (see Lemma 5.14 below).

Lemma 5.13

We have

$$\begin{aligned} D_{h-\phi }\left( \mathbb {x}' , \mathbb {y}' \right) \le e^{- \xi K_f} (A+4) \mathfrak c_r e^{\xi h_r(0)} . \end{aligned}$$

(5.38)

Proof

By condition 8 in the definition of $E_r$ and since $D_{h-\phi } \le D_h$,

$$\begin{aligned} D_{h-\phi }\left( \mathbb {x}' , W_r^{\mathbb {x}} \right) \le e^{-\xi K_f} \mathfrak c_r e^{\xi h_r(0)} \quad \text {and} \quad D_{h-\phi }\left( \mathbb {y}' , W_r^{\mathbb {y}} \right) \le e^{-\xi K_f} \mathfrak c_r e^{\xi h_r(0)} .\nonumber \\ \end{aligned}$$

(5.39)

By condition 9, Axiom III (Weyl scaling), and since $\phi \ge K_g$ on each of $W_r^{\mathbb {x}}$ and $W_r^{\mathbb {y}}$ (with $K_g$ as in (5.29)),

$$\begin{aligned}&\text {The internal } D_{h-\phi }\text {-diameters of } W_r^{\mathbb {x}}\text { and } W_r^{\mathbb {y}} \text { are each } \le e^{-\xi K_g} M\mathfrak c_r e^{ \xi h_r(0)} \nonumber \\&\quad \le e^{-\xi K_f} \mathfrak c_r e^{\xi h_r(0)}. \end{aligned}$$

(5.40)

By condition 5, Axiom III, and since $\phi \ge K_f$ on U,

$$\begin{aligned} \sup _{w_1,w_2 \in U } D_{h-\phi }\left( w_1,w_2 ; U \right) \le e^{-\xi K_f} A\mathfrak c_r e^{\xi h_r(0)} . \end{aligned}$$

(5.41)

Since $W_r^{\mathbb {x}}$ and $W_r^{\mathbb {y}}$ each intersect U, we can combine (5.39), (5.40), and (5.41) and use the triangle inequality to get (5.38). $\square$

Lemma 5.14

To lighten notation, let

$$\begin{aligned} \overline{P}^\phi := P^\phi {\setminus } \left( \mathcal B_{\sigma _r}(\mathbb {z} ; D_h) \cup \mathcal B_{\widehat{\sigma }_r}(\mathbb {w} ;D_h) \right) . \end{aligned}$$

In the notation (5.37), $\overline{P}^\phi$ is contained in $B_{2\zeta r}(U \cup \mathcal W)$. Furthermore, there is no segment of $\overline{P}^\phi$ of Euclidean diameter $\ge \varepsilon _0 r/100$ which is contained in $B_{2\zeta r}(\partial U) {\setminus } \mathcal W$.

Proof

Since $\phi$ is supported on $B_{3r}(0)$, the definitions of $\sigma _r$, $\widehat{\sigma }_r$, $\mathcal B_{\sigma _r}(\mathbb {z} ; D_h)$, and $\mathcal B_{\widehat{\sigma }_r}(\mathbb {w} ;D_h)$ are unaffected if we replace h by $h-\phi$. Since $\overline{P}^\phi$ is the $D_{h-\phi }$-shortest path between these metric balls, Lemma 5.13 implies that

$$\begin{aligned} \left( D_{ h-\phi }\text {-length of } \overline{P}^\phi \right) \le e^{- \xi K_f} (A+4) \mathfrak c_r e^{\xi h_r(0)} . \end{aligned}$$

(5.42)

We will now explain how (5.42) together with the definition of $E_r$ allows us to constrain the behavior of $\overline{P}^\phi$.

As in the proof of Lemma 5.12, condition 4 in the definition of $E_r$ implies that the $D_h$-distance between $\mathcal B_{\sigma _r}(\mathbb {z} ; D_h)$, and $\mathcal B_{\widehat{\sigma }_r}(\mathbb {w} ;D_h)$ is at least $2 \Delta \mathfrak c_r e^{\xi h_r(0)}$, which is larger than $e^{- \xi K_f} (A+4) \mathfrak c_r e^{\xi h_r(0)}$ by the definition (5.29) of $K_f$. If $\overline{P}^\phi$ did not enter the support $B_{\zeta r}(U) \cup \mathcal W$ of $\phi$, then the $D_{h-\phi }$-length of $\overline{P}^\phi$ would be the same as its $D_h$-length, which must be at least $2 \Delta \mathfrak c_r e^{\xi h_r(0)}$. Hence (5.42) implies that $\overline{P}^\phi$ must enter $B_{\zeta r}(U) \cup \mathcal W$.

Since $\phi \le K_f$ outside of $\mathcal W$, Axiom III (Weyl scaling) together with condition 6 in the definition of $E_r$ implies that the $D_{h - \phi }$-length of every continuous path of Euclidean diameter at least $\varepsilon _0 r/100$ which is contained in $B_{2\zeta r}(\partial U) {\setminus } \mathcal W$ is at least $100 e^{-\xi K_f} A\mathfrak c_r e^{\xi h_r(0)}$.

It therefore follows from (5.42) that the second assertion of the lemma holds.

We now prove the first assertion of the lemma. Since $\phi$ is identically equal to 0 on $\mathbb {C}{\setminus } (B_{\zeta r}(U) \cup \mathcal W)$, condition 7 in the definition of $E_r$ implies that the $D_{h- \phi }$-length of any curve which is contained in $\mathbb {A}_{r/4,4r}(0) {\setminus } (B_{\zeta r}(U) \cup \mathcal W)$ and has Euclidean diameter at least $\zeta r$ is at least $a\mathfrak c_r e^{\xi h_r(0)}$. This last quantity is strictly larger than the right side of (5.42) by the definition (5.29) of $K_f$. It follows that there is no segment of $\overline{P}^\phi$ of Euclidean diameter at least $\zeta r$ which is contained in $\mathbb {A}_{r/4,4r}(0) {\setminus } (B_{\zeta r}(U) \cup \mathcal W)$. Each path from $B_{\zeta r}(U) \cup \mathcal W$ to a point outside of $B_{2\zeta r}(U \cup \mathcal W)$ has a sub-path which is contained in $\mathbb {A}_{r/4,4r}(0) {\setminus } (B_{\zeta r}(U) \cup \mathcal W)$ and has Euclidean diameter at least $\zeta r$. Since we know that $\overline{P}^\phi$ has to hit $B_{\zeta r}(U) \cup \mathcal W$, we infer that $\overline{P}^\phi$ is contained in $B_{2\zeta r}(U) \cup \mathcal W)$. $\square$

We now produce the points $0< s< t < D_{h - \phi }(\mathbb {z}, \mathbb {w})$ from Lemma 5.11 and check all of the conditions of the lemma except $\widetilde{D}_{h-\phi }\left( P^\phi (s) , P^\phi (t)\right) \le c_2' D_{h- \phi }\left( P^\phi (s) , P^\phi (t)\right)$ (we will check this last condition in the proof of Lemma 5.11 just below).

Lemma 5.15

There are times $0< s< t < D_{h - \phi }(\mathbb {z}, \mathbb {w})$ such that $P^\phi (s) , P^\phi (t) \in B_{3r/2}(0)$, $|P^\phi (s) - P^\phi (t)| \ge (b - 40 \varepsilon _0) r$, and

$$\begin{aligned} \widetilde{D}_{h-\phi }(P^\phi (s) , P^\phi (t) ) \le (c_*/C_*) \widetilde{D}_{h -\phi }\left( P^\phi (s) , \partial B_{3r}(0) \right) . \end{aligned}$$

(5.43)

Proof

Recall the points $u,v \in \mathbb {A}_{(1-4\rho )r,(1 + 4\rho ) r}(0)$ from condition A in the definition of $E_r$. That condition says that the $\widetilde{D}_h$-geodesic $\widetilde{P}$ from u to v is contained in U and its $\widetilde{D}_h$-length is at most $(c_*/C_*)^2 \widetilde{D}_h(u , \partial B_{4\rho r}(u))$. The idea of the proof is to use Lemma 5.14 to force $P^\phi$ to get close to each of u and v, and then to take s and t to be the times at which it does so. Since $\phi$ attains its largest possible value on $B_{4\rho r}(u)$ (namely, $K_f$) at every point of $B_{4\rho r}(u) \cap U$ (here we note that $\mathcal W$ is disjoint from $B_{3r/2}(0) \supset B_{4\rho r}(u)$), it follows that $\widetilde{P}(e^{\xi K_f}\cdot )$ is a $\widetilde{D}_{h-\phi }$-geodesic from u to v and

$$\begin{aligned} \widetilde{D}_{h - \phi }(u,v) = \widetilde{D}_{h - \phi }\left( u,v ; U \cap B_{4\rho r}(u) \right) = e^{-\xi K_f} \widetilde{D}_h(u,v) . \end{aligned}$$

(5.44)

Recall from condition B in the definition of $E_r$ that $O_u$ (resp. $O_v$) is the connected component of $U\cap B_{20\varepsilon _0 r}(u)$ which contains u. Since $B_{20\varepsilon _0 r}(u)$ is contained in $B_{3r/2}(0)$, so is disjoint from $\mathcal W$, that condition tells us that the connected component of $(U \cup \mathcal W ){\setminus } O_u$ which contains $\mathbb {x}'$ lies at Euclidean distance at least $\varepsilon _0 r$ from the union of the other connected components of $(U\cup \mathcal W) {\setminus } O_u$. Since $\zeta < \varepsilon _0/100$, the $2\zeta r$-neighborhoods of these two sets lie at Euclidean distance at least $\varepsilon _0 r/2$ from one another. By Lemma 5.14, $\overline{P}^\phi = P^\phi {\setminus } \left( \mathcal B_{\sigma _r}(\mathbb {z} ; D_h) \cup \mathcal B_{\widehat{\sigma }_r}(\mathbb {w} ;D_h) \right)$ cannot exit $B_{2\zeta r}(U \cup \mathcal W)$, so $\overline{P}^\phi$ must have a segment of Euclidean diameter at least $\varepsilon _0 r/2$ which is contained in

$$\begin{aligned} B_{2\zeta r}(O_u) \subset O_u \cup \left( B_{2\zeta r}(\partial U) {\setminus } \mathcal W \right) . \end{aligned}$$

By the other assertion of Lemma 5.14, this segment cannot be entirely contained in $B_{2\zeta r}(\partial U) {\setminus } \mathcal W$, so $P^\phi$ must enter $O_u$. Similarly, $P^\phi$ must enter $O_v$ (and must do so at some time after it enters $O_u$).

Choose times $0< s< t < |P^\phi |$ such that $P^\phi (s) \in O_u$ and $P^\phi (t) \in O_v$. Then $|P^\phi (s) - u| \le 20 \varepsilon _0 r$ and $|P^\phi (t) - v| \le 20 \varepsilon _0 r$, By condition C in the definition of $E_r$, (5.44), and the fact that $\phi \equiv K_f$ on $U {\setminus } \mathcal W$, we get that

$$\begin{aligned}&\widetilde{D}_{h-\phi }\left( P^\phi (s) , u ; U \right) \le \eta \widetilde{D}_{h-\phi }(u,v) \quad \text {and} \quad \nonumber \\&\widetilde{D}_{h-\phi }\left( P^\phi (t) , v ; U \right) \le \eta \widetilde{D}_{h-\phi }(u,v) . \end{aligned}$$

(5.45)

Since $|u-v| \ge b r$, we have $|P^\phi (s) - P^\phi (t) | \ge (b- 40 \varepsilon _0) r$ and since $u,v \in \overline{B_r(0)}$ we have $P^\phi (s) , P^\phi (t) \in B_{3r/2}(0)$.

It remains to check the condition (5.43). Recall that $\widetilde{D}_h(u,v) \le (c_*/C_*)^2 \widetilde{D}_h(u , \partial B_{4\rho r}(u))$ and the $\widetilde{D}_h$-geodesic from u to v is contained in U. Since $\phi \equiv K_f$ on U and $\phi \le K_f$ on $B_{4\rho r}(u)$, it follows that

$$\begin{aligned} \widetilde{D}_{h-\phi }(u,v)\le & {} (c_*/C_*)^2 \widetilde{D}_{h-\phi }(u , \partial B_{4\rho r}(u)) \\\le & {} (c_*/C_*)^2 \widetilde{D}_{h -\phi }\left( P^\phi (s) , \partial B_{3r}(0) \right) . \end{aligned}$$

By (5.45) and the triangle inequality,

$$\begin{aligned}&\widetilde{D}_{h-\phi }\left( P^\phi (s) , P^\phi (t) \right) \le (1+2\eta ) \widetilde{D}_{h-\phi }(u,v) \\&\quad \le (1+2\eta )(c_*/C_*)^2 \widetilde{D}_{h-\phi }\left( P^\phi (s) , \partial B_{3r}(0) \right) , \end{aligned}$$

which is bounded above by the right side of (5.43) by the definition (5.15) of $\eta$. $\square$

Proof of Lemma 5.11

Let s and t be as in Lemma 5.15. By that lemma, it remains only to check that

$$\begin{aligned} \widetilde{D}_{h-\phi }\left( P^\phi (s) , P^\phi (t)\right) \le c_2' D_{h- \phi }\left( P^\phi (s) , P^\phi (t)\right) . \end{aligned}$$

By (5.45) and the definitions of $c_*$ and $C_*$,

$$\begin{aligned} D_{h - \phi }\left( P^\phi (s) , u ; U \right)\le & {} c_*^{-1} C_* \eta D_{h - \phi }(u,v) \quad \text {and} \quad D_{h - \phi }\left( P^\phi (t) , v ; U \right) \nonumber \\\le & {} c_*^{-1} C_* \eta D_{h - \phi }(u,v) . \end{aligned}$$

(5.46)

By the triangle inequality, (5.46) implies that

$$\begin{aligned} D_{h - \phi }(u,v)&\le D_{h - \phi }\left( P^\phi (s) , P^\phi (t) \right) + D_{h - \phi }\left( P^\phi (s) , u \right) + D_{h - \phi }\left( P^\phi (t) , v \right) \nonumber \\&\le D_{h - \phi }\left( P^\phi (s) , P^\phi (t) \right) + 2 c_*^{-1} C_* \eta D_{h - \phi }(u,v) \end{aligned}$$

which re-arranges to give

$$\begin{aligned} D_{h - \phi }(u,v) \le \left( 1 - 2 c_*^{-1} C_* \eta \right) ^{-1} D_{h - \phi }\left( P^\phi (s) , P^\phi (t) \right) . \end{aligned}$$

(5.47)

Recall that $\phi \le K_f$ on $\mathbb {C}{\setminus } \mathcal W$ and by the last condition in (5.20) we have $D_h(u,v) \le D_h(u,\mathcal W)$. It follows from this that each $D_{h-\phi }$-geodesic from u to v is disjoint from $\mathcal W$ and $D_{h- \phi }(u,v) \ge e^{-\xi K_f} D_h(u,v)$. By combining this with (5.44) and condition A in the definition of $E_r$, we get

$$\begin{aligned} \widetilde{D}_{h - \phi }(u,v) \le c_1' D_{h - \phi }(u,v) . \end{aligned}$$

(5.48)

By the triangle inequality,

$$\begin{aligned}&\widetilde{D}_{h - \phi }\left( P^\phi (s) , P^\phi (t) ; U \right) \nonumber \\&\quad \le \widetilde{D}_{h- \phi }(u, v ; U) + \widetilde{D}_{h - \phi }\left( P^\phi (s) , u ; U \right) + \widetilde{D}_{h - \phi }\left( v , P^\phi (t) ; U \right) \nonumber \\&\quad \le (1+2\eta ) \widetilde{D}_{h- \phi }(u, v ) \quad \text {(by } (5.44) \text { and } (5.45)) \nonumber \\&\quad \le c_1' (1+2\eta ) D_{h- \phi }(u, v ) \quad \text {(by } (5.48)) \nonumber \\&\quad \le \frac{ c_1' (1+2\eta ) }{ 1 - 2 c_*^{-1} C_* \eta } D_{h - \phi }\left( P^\phi (s) , P^\phi (t) \right) \quad \text {(by } (5.47)) \nonumber \\&\quad \le c_2' D_{h-\phi }(P^\phi (s) , P^\phi (t)) \quad \text {(by the definition}~(5.15) \text { of } \eta ) . \end{aligned}$$

(5.49)

$\square$

6 Proof of Theorem 1.9

Assume we are in the setting of Theorem 1.9 and let h be a whole-plane GFF. Also recall the definitions of the optimal bi-Lipschitz constants $c_*$ and $C_*$ from (1.21) and the events $\overline{G}_r(C' , \beta )$ and $\underline{G}_r(c',\beta )$ from (3.2) and (3.3). We want to show that $c_* = C_*$. To do this we will assume that $c_* <C_*$ and derive a contradiction. The following proposition will be used in conjunction with Proposition 3.3 to tell us that there are many scales for which the following is true: the pairs (u, v) such that $\widetilde{D}_h(u,v) / D_h(u,v)$ is close to $C_*$ are very sparse.

Proposition 6.1

Assume that $c_* < C_*$. Then there exists $c'' > c_*$, depending only on the values of $c_*$ and $C_*$, such that the following is true. If $\beta \in (0,1)$ and $\mathbb {r} > 0$ are such that $\mathbb {P}[\underline{G}_{\mathbb {r}}(c'',\beta )] \ge \beta$, then for every choice of $\overline{\beta }\in (0,1)$, one has

$$\begin{aligned} \lim _{\delta \rightarrow 0} \mathbb {P}\left[ \overline{G}_{\mathbb {r}}(C_* - \delta , \overline{\beta }) \right] = 0 \end{aligned}$$

(6.1)

at a rate depending only on $\beta ,\overline{\beta }$ (not on $\mathbb {r}$).

Proof

Assume $c_* < C_*$. Let $\nu _*$ be as in Theorem 4.2 and fix parameters $0< \mu < \nu \le \nu _*$ and $c_*< c_1'< c_2' < C_*$ chosen in a manner depending only on $c_*$ and $C_*$. The proof follows the strategy outlined in the “main idea” part of the outline in Sect. 1.5. Theorem 4.2 and Proposition 4.3 will allow us to show that if $q > 0$ is fixed, then with probability tending to 1 as $\varepsilon \rightarrow 0$, the following is true. For every pair of points $\mathbb {z},\mathbb {w} \in (\varepsilon ^q \mathbb {r} \mathbb {Z}^2) \cap B_{\mathbb {r}}(0)$ with $|\mathbb {z} - \mathbb {w} | \ge \overline{\beta }\mathbb {r}$, the $D_h$-geodesic P from $\mathbb {z}$ to $\mathbb {w}$ has to hit a pair of points P(s) , P(t) such that $|P(s) - P(t)| \ge {\text {const}} \times \varepsilon ^{1+\nu } \mathbb {r}$ and $\widetilde{D}_h(P(s) , P(t)) \le c_2' D_h(P(s) , P(t))$. This allows us to show that $\widetilde{D}_h(\mathbb {z},\mathbb {w}) / D_h(\mathbb {z},\mathbb {w})$ is bounded above by $C_*$ minus a $\gamma$-dependent power of $\varepsilon$ for all such pairs of points $\mathbb {z},\mathbb {w}$. We can then use Hölder continuity to get the same statement for all pairs of points $\mathbb {z},\mathbb {w} \in B_{\mathbb {r}}(0)$ with $|\mathbb {z} - \mathbb {w}|\ge \overline{\beta }\mathbb {r}$ simultaneously. Choosing $\varepsilon$ to be an appropriate $\gamma$-dependent power of $\delta$ then gives (6.1).

Step 1: setup and regularity events Let $c'' = c''(c_1', \mu ,\nu )$, $b = b( \mu ,\nu ) \in (0,1)$, and $\rho = \rho (\mu ,\nu ) \in (0,1)$ be as in Proposition 4.3 with the above choice of $\mu ,\nu ,c_1',c_2'$. Also fix $q > 0$ to be chosen later in a manner depending on $\beta ,\overline{\beta }$.

By Theorem 4.2 applied to the objects of Proposition 4.3 and with the above choice of q, $\rho ^{-1} \mathbb {r}$ in place of $\mathbb {r}$, $U = B_2(0)$, and $\ell = \rho \overline{\beta }$, we get the following. If $\mathbb {r} > 0$ is such that $\mathbb {P}[\underline{G}_{\mathbb {r}}(c'',\beta )] \ge \beta$, then it holds with probability tending to 1 as $\varepsilon \rightarrow 0$, at a rate depending only on $q,\overline{\beta },\beta ,c_1',c_2',\mu ,\nu$, that the following is true. Let $\mathbb {z} , \mathbb {w} \in \left( \varepsilon ^q \rho ^{-1} \mathbb {r} \mathbb {Z}^2 \right) \cap B_{2\mathbb {r}}\left( 0 \right)$ with $|\mathbb {z}-\mathbb {w}|\ge \overline{\beta }\mathbb {r}$ and let $P = P^{\mathbb {z},\mathbb {w}}$ be the $D_h$-geodesic from $\mathbb {z}$ to $\mathbb {w}$. Then there exists times $0< s< t < |P |$ such that

$$\begin{aligned} |P (s) - P (t) | \ge b \varepsilon ^{1+\nu } \rho ^{-1} \mathbb {r} \quad \text {and} \quad \widetilde{D}_h\left( P (s) , P (t)\right) \le c_2' D_h\left( P(s) , P (t)\right) \nonumber \\ \end{aligned}$$

(6.2)

(in particular, the times s, t arise from a radius $r\in [\varepsilon ^{1+\nu } \rho ^{-1} \mathbb {r}, \varepsilon \rho ^{-1} \mathbb {r}]$ and a point $z\in \mathbb {C}$ for which $\mathfrak E_r^{\mathbb {z},\mathbb {w}}(z)$ occurs). Henceforth assume that (6.2) holds for every $\mathbb {z} , \mathbb {w} \in \left( \varepsilon ^q \rho ^{-1} \mathbb {r} \mathbb {Z}^2 \right) \cap B_{2\mathbb {r}}\left( 0 \right)$ with $|\mathbb {z}-\mathbb {w}|\ge \overline{\beta }\mathbb {r}$.

Fix $\chi \in (0,\xi (Q-2))$ and $\chi ' > \xi (Q+2)$, as in Lemma 2.8. By Axiom V (tightness across scales), for each $p\in (0,1)$ we can find a bounded open set $U \subset \mathbb {C}$ which contains $B_2(0)$ such that $\mathbb {P}[\sup _{u,v\in B_{2\mathbb {r}}(0) } D_h(u,v) < D_h( B_{2\mathbb {r}}( 0 ) , \mathbb {r} \partial U )] \ge p$ for every $\mathbb {r} >0$. On the event of the preceding sentence, every $D_h$-geodesic between two points of $B_{2\mathbb {r}}(0)$ is contained in $\mathbb {r} U$. By applying Lemma 2.8 with $K= \overline{U}$ and then sending $p\rightarrow 1$, we get that with probability tending to 1 as $\varepsilon \rightarrow 0$, at a rate which is uniform in $\mathbb {r}$, for any two points $z,w\in \mathbb {C}$ with $|z-w| \le (\varepsilon ^q \vee (b \varepsilon ^{1+\nu }))\rho ^{-1} \mathbb {r}$ which are either contained in $B_{2\mathbb {r}}( 0 )$ or which lie on a $D_h$-geodesic between two points of $B_{2\mathbb {r}}(0)$,

$$\begin{aligned} \left| \frac{z-w}{\mathbb {r}} \right| ^{\chi '} \le \mathfrak c_{\mathbb {r}}^{-1} e^{-\xi h_{\mathbb {r}}(0)} D_h(z,w) \le \left| \frac{z-w}{\mathbb {r}} \right| ^\chi . \end{aligned}$$

(6.3)

Henceforth assume that this is the case.

Step 2: bounding $\widetilde{D}_h(\mathbb {z},\mathbb {w})/D_h(\mathbb {z},\mathbb {w})$ for points in a fine mesh By (6.2) and (6.3), the times s and t from (6.2) satisfy

$$\begin{aligned} t-s = D_h\left( P (s) , P (t)\right) \ge (b/\rho )^{\chi '} \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)} \varepsilon ^{(1+\nu )\chi '} . \end{aligned}$$

(6.4)

By the definition (1.21) of $C_*$, the $\widetilde{D}_h$-lengths of the segments $P|_{[0,s]}$ and $P|_{[t,|P|]}$ are bounded above by $C_* s$ and $C_* (|P|-t)$, respectively. Therefore, for each $\mathbb {z} , \mathbb {w} \in \left( \varepsilon ^q \rho ^{-1} \mathbb {r} \mathbb {Z}^2 \right) \cap B_{2\mathbb {r}}(0)$ with $|\mathbb {z}-\mathbb {w}|\ge \overline{\beta }\mathbb {r}$,

$$\begin{aligned} \widetilde{D}_h(\mathbb {z},\mathbb {w})&\le C_* \left( |P| - t + s \right) + \widetilde{D}_h\left( P (s) , P (t)\right) \nonumber \\&\le C_* \left( |P| - t + s \right) + c_2' (t-s) \quad \text {(by}~(6.2)) \nonumber \\&\le C_* D_h(\mathbb {z} , \mathbb {w}) - (C_* - c_2') (t-s) \nonumber \\&\le C_* D_h(\mathbb {z} , \mathbb {w}) - (C_* - c_2')(b/\rho )^{\chi '} \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)} \varepsilon ^{(1+\nu )\chi '} \quad \text {(by}~(6.4)) . \end{aligned}$$

(6.5)

Step 3: transferring from points in a fine mesh to general points If $z,w\in B_{\mathbb {r}}(0)$ with $|z-w| \ge \overline{\beta }\mathbb {r}$, then we can find $\mathbb {z} , \mathbb {w} \in \left( \varepsilon ^q \mathbb {r} \mathbb {Z}^2 \right) \cap B_{2\mathbb {r}}\left( 0\right)$ such that $|\mathbb {z}-\mathbb {w}|\ge \overline{\beta }\mathbb {r}$ and $\max \{|z-\mathbb {z}| , |w-\mathbb {w}|\} \le 2\varepsilon ^q \rho ^{-1} \mathbb {r}$. By (6.3) and the triangle inequality,

$$\begin{aligned} |D_h(\mathbb {z} , \mathbb {w}) - D_h(z,w)| \le 2^{2+\chi } \rho ^{-\chi } \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)} \varepsilon ^{q \chi } , \end{aligned}$$

(6.6)

and the same is true with $\widetilde{D}_h$ in place of $D_h$. If we choose $q > \chi '(1+\nu )/\chi$, then (6.6) and (6.5) together imply that for each $z,w\in B_{\mathbb {r}}(0)$ with $|z-w| \ge \overline{\beta }\mathbb {r}$ and each small enough $\varepsilon$,

$$\begin{aligned}&\widetilde{D}_h(z,w) \le C_* D_h(z,w) - a \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)} \varepsilon ^{(1+\nu )\chi '} ,\quad \nonumber \\&\quad \forall z,w\in B_{\mathbb {r}}(0) \quad \text {s.t.} \quad |z-w| \ge \overline{\beta }\mathbb {r} . \end{aligned}$$

(6.7)

where $a > 0$ is a constant depending only on $q,\overline{\beta },c_1',c_2',\mu ,\nu$.

Step 4: choosing $\varepsilon$ By Axiom V (tightness across scales), it holds with probability tending to 1 as $\varepsilon \rightarrow 0$, uniformly over all $\mathbb {r} > 0$, that $D_h(z,w) \le \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)} \varepsilon ^{-\chi '}$ for each $z,w\in B_{\mathbb {r}}(0)$. If this is the case then $a \mathfrak c_{\mathbb {r}} e^{\xi h_{\mathbb {r}}(0)} \varepsilon ^{(1+\nu )\chi '} \ge a \varepsilon ^{(2+\nu )\chi '} D_h(z,w)$. Hence (6.7) implies that with probability tending to 1 as $\varepsilon \rightarrow 0$, at a rate depending only on $q,\overline{\beta }, c',\mu ,\nu$,

$$\begin{aligned}&\widetilde{D}_h(z,w) \le \left( C_* - a \varepsilon ^{(2+\nu ) \chi '} \right) D_h(z,w) ,\quad \nonumber \\&\quad \forall z,w\in B_{\mathbb {r}}(0) \quad \text {s.t.}\quad |z-w| \ge \overline{\beta }\mathbb {r}. \end{aligned}$$

(6.8)

Recalling the definition (3.2) of $\overline{G}_{\mathbb {r}}(C_*-\delta ,\overline{\beta })$, we can choose $\varepsilon$ so that $a\varepsilon ^{(2+\nu ) \chi '} =\delta$ to get the proposition statement. $\square$

Proof of Theorem 1.9

Let D and $\widetilde{D}$ be as in Theorem 1.9, let h be a whole-plane GFF, and define the maximal and minimal ratios $c_*$ and $C_*$ as in (1.21). We claim that $c_* = C_*$, i.e., a.s. $\widetilde{D}_h = c_* D_h$. This gives the theorem statement in the case of a whole-plane GFF, which in turn implies the theorem statement for a whole-plane GFF plus a continuous function due to Axiom III (Weyl scaling).

It remains to prove that $c_* = C_*$. By Proposition 3.2 applied with $C' = C_* -\delta$, there exists $\overline{\beta }= \overline{\beta }(\mu ,\nu ) \in (0,1)$ and $\overline{p} = \overline{p}(\mu ,\nu ) \in (0,1)$ with the following property. For each $\delta \in (0,1)$, there exists $\varepsilon _0 = \varepsilon _0(\delta ,\mu ,\nu ) > 0$ such that for each $\varepsilon \in (0,\varepsilon _0]$, there are at least $\mu \log _8 \varepsilon ^{-1}$ values of $\mathbb {r} \in [\varepsilon ^{1+\nu } ,\varepsilon ] \cap \{8^{-k} : k\in \mathbb {N}\}$ for which

$$\begin{aligned} \mathbb {P}\left[ \overline{G}_{\mathbb {r}}(C_*-\delta , \overline{\beta })\right] \ge \overline{p} . \end{aligned}$$

(6.9)

We emphasize that $\overline{\beta }$ and $\overline{p}$ do not depend on $\delta$.

We now assume by way of contradiction that $c_* < C_*$ and show that this assumption is incompatible with the conclusion of the preceding paragraph. To this end, let $c'' \in (c_* , C_*)$ be as in Proposition 6.1, so that $c''$ depends only on the choice of metrics D and $\widetilde{D}$. Proposition 3.3 applied with $c''$ in place of $c'$ shows that there exists $\underline{\beta }= \underline{\beta }(\mu ,\nu ) \in (0,1)$, $\underline{p} = \underline{p}(\mu ,\nu ) \in (0,1)$, and $\varepsilon _1 = \varepsilon _1(\mu ,\nu ) > 0$ such that for each $\varepsilon \in (0,\varepsilon _1]$, there are at least $\mu \log _8 \varepsilon ^{-1}$ values of $\mathbb {r} \in [\varepsilon ^{1+\nu } ,\varepsilon ] \cap \{8^{-k} : k\in \mathbb {N}\}$ for which $\mathbb {P}[\underline{G}_{\mathbb {r}}(c'',\underline{\beta })] \ge \underline{p}$.

Proposition 6.1 applied with $\beta =\underline{\beta }\wedge \underline{p}$ therefore implies that there exists $\delta = \delta (\mu ,\nu ) \in (0,1)$ such that for each $\varepsilon \in (0,\varepsilon _1]$, there are at least $\mu \log _8 \varepsilon ^{-1}$ values of $\mathbb {r} \in [\varepsilon ^{1+\nu } ,\varepsilon ] \cap \{8^{-k} : k\in \mathbb {N}\}$ for which $\mathbb {P}\left[ \overline{G}_{\mathbb {r}}(C_* - \delta , \overline{\beta }) \right] \le \overline{p}/2$. If we take $\mu > \nu /2$, then this is incompatible with (6.9) whenever $\varepsilon \in (0, \varepsilon _0 \wedge \varepsilon _1)$, so we have obtained the desired contradiction. $\square$

7 Open problems

7.1 Dimension calculations

An important remaining question concerning the LQG metric is the following.

Problem 7.1

(Hausdorff dimension of $\gamma$-LQG) Compute the exponent $d_\gamma$ appearing in (1.5), which is the Hausdorff dimension of $\mathbb {C}$ with respect to the $\gamma$-LQG metric (this is proven in [43]).

Since $\xi = \gamma /d_\gamma$ and $Q=2/\gamma +\gamma /2$, Problem 7.1 is equivalent to determining the relationship between these two parameters. The only case in which $d_\gamma$ is known is when $\gamma =\sqrt{8/3}$, in which case $d_{\sqrt{8/3}}=4$. Due to existing results in the literature, $d_\gamma$ can equivalently be defined in a large number of other equivalent ways, e.g., the following.

• 1. For a large class of infinite-volume random planar maps in the $\gamma$-LQG universality class, the number of vertices in the graph distance ball of radius r centered at the root vertex is of order $r^{d_\gamma +o_r(1)}$ [20, Theorem 1.6] and the graph distance traveled by a simple random walk started from the root vertex and run for n steps is of order $n^{1/d_\gamma + o_n(1)}$ [31, 35].

• 2. For fixed distinct points $z,w\in \mathbb {C}$, the Liouville heat kernel (as constructed in [45]) satisfies ${\mathsf {p}}_t^\gamma (z,w) = \exp \left( - t^{-\frac{1}{d_\gamma -1} + o_t(1)} \right)$ as $t\rightarrow 0$ [30, Theorem 1.1].

• 3. The optimal Hölder exponent for the $\gamma$-LQG metric w.r.t. the Euclidean metric is $\frac{\gamma }{d_\gamma }(Q-2)$ and the optimal Hölder exponent for the Euclidean metric w.r.t. the $\gamma$-LQG metric is $\frac{d_\gamma }{\gamma }(Q+2)^{-1}$ [18, Theorem 1.7].

The best-known physics prediction for the value of $d_\gamma$ is the Watabiki prediction [85],

$$\begin{aligned} d_\gamma = 1 + \frac{\gamma ^2}{4} + \frac{1}{4} \sqrt{(4+\gamma ^2)^2 + 16\gamma ^2} . \end{aligned}$$

(7.1)

However, this prediction is known to be false at least for small values of $\gamma$ due to the results of Ding-Goswami [19]. See [20, 42] for rigorous upper and lower bounds for $d_\gamma$ as well as additional discussion about various possibilities for its value. In addition to $d_\gamma$, there are a number of other interesting dimensions related to $\gamma$-LQG which have not yet been computed, for example the following.

Problem 7.2

(Geodesic dimension) Compute the Euclidean Hausdorff dimension of the $\gamma$-LQG geodesic between two typical points of $\mathbb {C}$.

Problem 7.3

(Ball boundary dimension) Compute the $\gamma$-LQG Hausdorff dimension and the Euclidean Hausdorff dimension of the boundary of a filled $\gamma$-LQG metric ball $\mathcal B_s^\bullet (0;D_h)$.

In the setting of Problem 7.2, the $\gamma$-LQG Hausdorff dimension of a $\gamma$-LQG geodesic is trivially equal to 1. The Euclidean dimensions of $\gamma$-LQG geodesics and filled metric ball boundaries are unknown even for $\gamma =\sqrt{8/3}$ and there are not even any conjectures as to their values. The $\sqrt{8/3}$-LQG dimension of the outer boundary of a filled $\sqrt{8/3}$-LQG metric ball is 2 [64], but this quantity is not known (even heuristically) for any other value of $\gamma$. See [43] for upper bounds for the Euclidean Hausdorff dimension of a $\gamma$-LQG geodesic and for the outer boundary of a filled $\sqrt{8/3}$-LQG metric ball.

Currently, no explicit lower bounds for any of these quantities are known, although we expect it is not hard to show that they are strictly larger than 1; c.f. [29].

Another natural random fractal associated with the LQG metric is the boundary of a (non-filled) LQG metric ball (note that this boundary is typically not connected). It is shown in [44, 48] that a.s. the Hausdorff dimension of the LQG metric ball boundary w.r.t. the Euclidean (resp. LQG) metric is $2-\xi Q + \xi ^2/2$ (resp. $d_\gamma -1$). It is also shown in [44] that a.s. the Hausdorff dimension of the boundary of a filled metric ball w.r.t. the Euclidean (resp. LQG) metric is strictly smaller than this quantity.

The “quantum dimension” part of Problem 7.3 is closely related to the following question.

Problem 7.4

($\gamma$-LQG boundary length of metric balls) Is there a natural LQG length measure on the boundary of a filled $\gamma$-LQG metric ball?

In the case when $\gamma =\sqrt{8/3}$, for $s > 0$ the field $h|_{\mathbb {C}{\setminus }\mathcal B_s(0;D_h)}$ locally looks like a free-boundary GFF near $\partial \mathcal B_s(0;D_h)$. This allows one to define the $\gamma$-LQG boundary length measure on $\partial \mathcal B_s(0;D_h)$ in the manner of [27, Section 6]. Alternatively, the length measure on $\partial \mathcal B_s(0;D_h)$ can equivalently be constructed using Brownian surface theory; see [58, 63]. For general $\gamma \in (0,2)$, it is not expected that $h|_{\mathbb {C}{\setminus }\mathcal B_s(0;D_h)}$ locally looks like a free-boundary GFF near $\partial \mathcal B_s(0;D_h)$. Indeed, if this were the case then the heuristic argument in [69, Section 3.3] would imply that the dimension of $\gamma$-LQG is given by Watabiki’s prediction (7.1), which we know is false, at least for small $\gamma$, by the results of [19]. Hence new ideas are required to construct a natural length measure on $\partial \mathcal B_s(0;D_h)$ in this case.

7.2 Discrete approximations

Another interesting open problem is to connect the $\gamma$-LQG metric to its discrete counterparts.

Problem 7.5

(Scaling limit of random planar maps) Prove Conjecture 1.7, which asserts that random planar maps, equipped with their graph distance, converge to the $\gamma$-LQG surface, equipped with the $\gamma$-LQG metric, w.r.t. the Gromov–Hausdorff topology.

One possible approach to Problem 7.5 is to first prove a scaling limit result for the so-called mated-CRT maps, as studied, e.g., in [33, 34, 40] using their direct connection to Liouville quantum gravity. One could then try to transfer to other random planar map models by improving on the strong coupling techniques used in [33], which currently only give estimates for distances up to polylogarithmic multiplicative errors. We emphasize, however, that both of these steps are highly non-trivial and are likely to require substantial new ideas. Another possible approach would be to find some sort of “combinatorial miracle” which allows one to analyze distances in weighted random planar maps directly (analogous to the Schaeffer bijection [7, 13, 78] for uniform random planar maps).

A likely easier scaling limit problem is to show universality of the $\gamma$-LQG metric across different approximation schemes. One of the most natural approximation schemes is Liouville graph distance (LGD), whereby the distance between two points $z,w\in \mathbb {C}$ is defined to be the minimal number of Euclidean balls of $\gamma$-LQG mass $\varepsilon$ whose union contains a path from z to w.

Problem 7.6

(Other approximation schemes) Show that the LGD metrics, appropriately re-scaled, converge in law to the $\gamma$-LQG metric as $\varepsilon \rightarrow 0$.

We expect that the difficulties involved in solving Problem 7.6 are similar to the difficulties involved in showing that the mated-CRT map converges to $\gamma$-LQG in the metric sense, due to the SLE/LQG representation of the mated-CRT map (see [33, 40]).

It is shown in [14] that LGD, re-scaled by the median distance across a square, is tight and each subsequential limit induces the Euclidean topology. We expect that it is not hard to check that these subsequential limits satisfy Axioms I, II, and IV in the definition of the $\gamma$-LQG metric (the latter is just a consequence of the coordinate change formula for the LQG area measure [27, Proposition 2.1]). One can also obtain a much weaker version of Weyl scaling analogous to the “tightness across scales” condition (Axiom V) used in our definition of a weak $\gamma$-LQG metric, where one requires that the metrics obtained by adding different constants to the field, then re-scaling appropriately, are tight.

Hence one possible approach to Problem 7.6 is to adapt the arguments of this paper and its predecessors to the case when we know that our metric satisfies the coordinate change formula for translations and scalings, but we do not know that it satisfies Weyl scaling. However, our arguments are in some ways optimized to work for subsequential limits of LFPP, so there may also be an entirely different argument which is more appropriate for subsequential limits of LGD.

Theorem 1.1 says that the LFPP metrics converge in probability, unlike the case of various approximations of the LQG measure which are known to converge a.s. [27, 76, 84].

Problem 7.7

(Almost sure convergence of LFPP) Can the convergence $\mathfrak a_\varepsilon ^{-1} D_h^\varepsilon \rightarrow D_h$ in Theorem 1.1 be improved from convergence in probability to a.s. convergence?

7.3 Metric space structure versus quantum surface structure

In [65], it is shown that a $\sqrt{8/3}$-LQG surface is a.s. determined by its structure as a metric measure space, i.e., the metric measure space $(\mathbb {C} , \mu _h , D_h)$ a.s. determines its embedding into $\mathbb {C}$ and the associated GFF h (modulo conformal automorphisms). Our next problem asks for an extension of this result to the case when $\gamma \in (0,2)$.

Problem 7.8

(Metric measure space structure determines the field) Show that the field h is a.s. determined (modulo rotation and scaling) by the pointed $\gamma$-LQG metric measure space $(\mathbb {C} , 0 , \mu _h, D_h)$.

Likely the easiest approach to Problem 7.8 is to adapt the arguments of [41], which gives for $\gamma =\sqrt{8/3}$ an explicit way of re-constructing h from $(\mathbb {C} ,0, \mu _h , D_h)$ using the adjacency graph of a fine mesh of Poisson-Voronoi cells. The arguments of [41] are not very specific to the case when $\gamma =\sqrt{8/3}$. The main missing ingredient to extend these arguments to general values of $\gamma$ is the following estimate of independent interest.

Problem 7.9

(Concentration of areas of LQG metric balls) Show that the $\gamma$-LQG area of a $\gamma$-LQG metric ball has superpolynomial concentration, i.e., show that for $C > 1$,

$$\begin{aligned} \mathbb {P}\left[ C^{-1} \le \mu _h\left( \mathcal B_1(0;D_h) \right) \le C \right] = 1 - O_C(C^{-p}) ,\quad \forall p > 0 . \end{aligned}$$

(7.2)

Problem 7.9 in the case when $\gamma =\sqrt{8/3}$ follows from known estimates for the Brownian map; see [56, Corollary 6.2] and [41, Section 4.3].

Update Problems 7.8 and 7.9 are solved in [1].

It is shown in [11] that the LQG measure a.s. determines the GFF. It is also natural to try to recover the LQG measure (and thereby the GFF) from the LQG metric.

Problem 7.10

Does the LQG metric a.s. determine the LQG measure? More concretely, can the LQG measure be recovered as some sort of Minkowski content measure w.r.t. the LQG metric?

In this paper, we gave a characterization of the $\gamma$-LQG metric in terms of its coupling with the GFF. In light of Problem 7.8, it is natural to ask if there is also a characterization solely in terms of the metric space structure, which does not require reference to the GFF. Such a characterization of the Brownian map (equivalently, the $\sqrt{8/3}$-LQG sphere) is proven in [71]. A purely metric characterization of $\gamma$-LQG could potentially play an important role in a solution to Problem 7.5.

Problem 7.11

(Metric space characterization) Is there a characterization of $(\mathbb {C} , D_h )$ as a metric space (or of $(\mathbb {C} , \mu _h, D_h)$ as a metric measure space), without reference to the GFF and the embedding of this metric space into $\mathbb {C}$?

It is likely that the most natural setting to consider in Problem 7.11 is the one where h the field corresponding to a quantum cone or quantum sphere (as defined in [23]) rather than a whole-plane GFF.

7.4 Additional properties of the LQG metric

The construction of the $\sqrt{8/3}$-LQG metric in [64, 65, 72] yields many special properties of the metric in this case which are not known (and in many cases not expected to hold) for general $\gamma \in (0,2)$. For example, one has $d_{\sqrt{8/3}} =4$. Moreover, in the case when h is the GFF associated with a quantum sphere or $\sqrt{8/3}$-quantum wedge, the quantum surfaces obtained by restricting h to the complementary connected components of a $\sqrt{8/3}$-LQG metric ball are conditionally independent quantum disks given their boundary lengths. Many further properties can be obtained using the equivalence of $\sqrt{8/3}$-LQG surfaces and Brownian surfaces. However, there is nothing obviously special about $\gamma =\sqrt{8/3}$ from either of the definitions of the LQG metric given in this paper (the limit of LFPP or the axiomatic definition).

Problem 7.12

Can one prove that $d_{\sqrt{8/3}}=4$, the independence properties for complementary connected components of a $\sqrt{8/3}$-LQG metric ball, or any other special property of the $\sqrt{8/3}$-LQG metric directly from the LFPP definition or the axiomatic definition?

There has been a recent proliferation of exact formulas for quantities related to the $\gamma$-LQG area and boundary length measures for general $\gamma \in (0,2)$, proven using ideas from conformal field theory: see, e.g., [54, 75, 77]. In the special case when $\gamma =\sqrt{8/3}$, exact formulas for various quantities associated with the $\sqrt{8/3}$-LQG metric can be obtained using its connection to the Brownian surfaces. Exact formulas for the $\gamma$-LQG metric, if they can be found, could be very useful in attempts to solve most of the other problems listed above.

Problem 7.13

(Exact formulas) Are there exact formulas for any objects related to the $\gamma$-LQG metric for general $\gamma \in (0,2)$?

Problem 7.14

(Topology of geodesics) For a general value of $\gamma \in (0,2)$, what is the maximal possible number of $\gamma$-LQG geodesics joining two points in $\mathbb {C}$? Is this number finite, and, if so, does it depend on $\gamma$? More generally, can one prove results about the possible topologies of the set of $\gamma$-LQG geodesics joining two points in $\mathbb {C}$ analogous to the results for the Brownian map in [3]?

Update This problem is solved for $\gamma =\sqrt{8/3}$ in [61] using Brownian map based techniques. Substantial progress on Problem 7.14 is made in [47], where it is shown that the results about geodesic networks from [3] extend verbatim to the case of general $\gamma \in (0,2)$ and that the maximal number of LQG geodesics joining any two points is a.s. finite. It is also conjectured in [47] that the maximal number of geodesics is 9, regardless of the value of $\gamma$.

Liouville Brownian motion [8, 46] is the natural “quantum time” parameterization of Brownian motion on an LQG surface. If we condition Liouville Brownian motion to travel a macroscopic distance (e.g., from the origin to the unit circle) in a short amount of time, then it is natural to expect that it would roughly follow a path of minimal LQG length.

Problem 7.15

(Liouville Brownian motion and LQG geodesics) Does Liouville Brownian motion conditioned to travel a macroscopic (Euclidean or quantum) distance in a short amount of time approximate an LQG geodesic?

There is a one-parameter family of infinite-volume $\gamma$-LQG surfaces with boundary called quantum wedges, which can be indexed by the weight parameter $\mathfrak w > 0$. See [23] for details. In [23], building on [81], it is shown that one can conformally weld together a weight-$\mathfrak w_1$ quantum wedge and a weight-$\mathfrak w_2$ quantum wedge according to the quantum length measure along their boundaries to get a weight-$\mathfrak w_1 + \mathfrak w_2$ quantum wedge decorated by an SLE$_\kappa (\mathfrak w_1-2;\mathfrak w_2-2)$ curve which corresponds to the gluing interface. In [39], it is shown that in the special case when $\gamma =\sqrt{8/3}$, this conformal welding is compatible with the $\sqrt{8/3}$-LQG metric in the following sense: the weight-$(\mathfrak w_1+\mathfrak w_2)$ quantum wedge, equipped with its $\sqrt{8/3}$-LQG metric, is the metric space quotient of the weight-$\mathfrak w_1$ and weight-$\mathfrak w_2$ quantum wedges, equipped with their $\sqrt{8/3}$-LQG metrics, under the same equivalence relation used to define the conformal welding.

Problem 7.16

(Metric gluing of $\gamma$-LQG surfaces) Prove metric gluing statements for quantum wedges analogous to the ones in [39] for general $\gamma \in (0,2)$.

The main missing ingredient needed to solve Problem 7.16 is suitable estimates for distances between points of $\partial \mathbb {D}$ with respect to the $\gamma$-LQG metric induced by a free-boundary GFF on $\mathbb {D}$ (or a variant thereof, like the quantum disk). For $\gamma =\sqrt{8/3}$, the needed estimates are proven in [39, Section 3.2] using results for the Brownian disk.

7.5 Extensions of the theory

Throughout this paper, we have neglected the critical case when $\gamma =2$.

Problem 7.17

(Critical LQG metric) Construct a metric on $\gamma$-LQG when $\gamma =2$.

See [25, 26] for a construction of the $\gamma$-LQG measure for $\gamma =2$. One possible approach to Problem 7.17 is to try to take a limit of the $\gamma$-LQG metrics as $\gamma$ increases to 2 (it is shown that the 2-LQG measure is the $\gamma \nearrow 2$ limit of the $\gamma$-LQG measures, appropriately renormalized, in [5]). Another (likely more involved) possibility is to adapt the arguments of this paper and its predecessors [18, 36, 38] to the critical case, corresponding to LFPP with parameter $\xi = 2/d_2$. A major difficulty in the critical case is that the 2-LQG metric is not expected to be Hölder continuous w.r.t. the Euclidean metric (indeed, the optimal Hölder exponent from [18, Theorem 1.7] converges to zero as $\gamma \rightarrow 2^-$), so more refined estimates for the continuity of the metric and for LFPP are likely to be required.

Recall that our metric for $\gamma \in (0,2)$ is constructed as the limit of LFPP with parameter $\xi = \gamma /d_\gamma$. Extending further, it is natural to ask what happens when $\xi > 2/d_2$ (it is shown in [20, Proposition 1.7] that $\gamma \mapsto \gamma /d_\gamma$ is increasing, so $\gamma /d_\gamma < 2/d_2$). Very recently, it was shown in [21] that LFPP is tight w.r.t. the topology on lower semicontinuous functions for all $\xi > 0$. For $\xi > 2/d_2$ every possible subsequential limit is a metric on $\mathbb {C}$ which does not induce the Euclidean topology. Rather, there is an uncountable, dense, fractal set of “singular points” whose distance to every other point is infinite. These singular points arise from the thick points of the GFF [49].

Problem 7.18

(LFPP with $\xi >2/d_2$) Show that LFPP with parameter $\xi >2/d_2$ converges in law to a limiting metric w.r.t. the topology of [21].

This metric of Problem 7.18 should be related to Liouville quantum gravity with central charge ${\mathbf {c}} \in (1,25)$. Note that the central charge associated with $\gamma$-LQG for $\gamma \in (0,2]$ is ${\mathbf {c}} = 25 -6(2/\gamma +\gamma /2)^2 \in (-\infty ,1]$. We refer to [21, 32] and the references therein for more on LQG with ${\mathbf {c}} \in (1,25)$.

The $\gamma$-LQG measure is a special case of a more general theory of random measures called Gaussian multiplicative chaos (GMC) [51, 76], which studies limits of regularized versions of “$e^{\gamma X} \,dz$” for certain Gaussian random distributions X. Here, X is a random distribution on $\mathbb {R}^n$ for some $n\in \mathbb {N}$ and dz denotes Lebesgue measure on $\mathbb {R}^n$.

Problem 7.19

(More general random metrics) Is there a more general theory of random metrics associated with log-correlated random Gaussian distributions analogous to GMC? In particular, can one construct metrics with similar properties to the $\gamma$-LQG metric in higher dimensions?

Some of the arguments in the construction of the LQG metric, in this paper as well as [16, 18, 36, 38] are specific to the two-dimensional case. The following seem to be the places where the use of two-dimensionality is the most fundamental.

• The construction of the LQG metric makes extensive use of the Markov property of the GFF: for an open set $U\subset \mathbb {C}$, $h|_U$ decomposes as a zero-boundary GFF in U plus an independent random harmonic function on U. This property is not satisfied for log-correlated fields in dimension $\ge 3$, see, e.g., [24] (note that the GFF is only log-correlated in dimension 2).

• The proof of tightness in [16], as well as several proofs in [18], use RSW-type arguments which are based on the fact that one can force two paths to intersect each other in dimension 2.

• The proof of confluence in [36] is based on a decomposition of the boundary of a filled LQG metric ball into arcs of topological dimension 1, together with an iterative argument where one “kills off” all but one of the arcs by preventing LQG geodesics from passing through them. In higher dimensions, the boundary of an LQG metric ball cannot be decomposed into sets of dimension 1. In fact, it is plausible that confluence fails in higher dimensions since there is more “room” for geodesics to move around.