The space of stability conditions on abelian threefolds, and on some Calabi-Yau threefolds

Abstract

We describe a connected component of the space of stability conditions on abelian threefolds, and on Calabi-Yau threefolds obtained as (the crepant resolution of) a finite quotient of an abelian threefold. Our proof includes the following essential steps:

• 1. We simultaneously strengthen a conjecture by the first two authors and Toda, and prove that it follows from a more natural and seemingly weaker statement. This conjecture is a Bogomolov-Gieseker type inequality involving the third Chern character of “tilt-stable” two-term complexes on smooth projective threefolds; we extend it from complexes of tilt-slope zero to arbitrary tilt-slope.

• 2. We show that this stronger conjecture implies the so-called support property of Bridgeland stability conditions, and the existence of an explicit open subset of the space of stability conditions.

• 3. We prove our conjecture for abelian threefolds, thereby reproving and generalizing a result by Maciocia and Piyaratne.

Important in our approach is a more systematic understanding on the behaviour of quadratic inequalities for semistable objects under wall-crossing, closely related to the support property.

1 Introduction

In this paper, we determine the space of Bridgeland stability conditions on abelian threefolds and on Calabi-Yau threefolds obtained either as a finite quotient of an abelian threefold, or as the crepant resolution of such a quotient. More precisely, we describe a connected component of the space of stability conditions for which the central charge only depends on the degrees $H^{3-i} \mathop {\mathrm {ch}}\nolimits _i(\underline{\,\,})$, $i = 0, 1, 2, 3$, of the Chern character¹ with respect to a given polarization H, and that satisfy the support property.

1.1 Stability conditions on threefolds via a conjectural Bogomolov-Gieseker type inequality

The existence of stability conditions on three-dimensional varieties in general, and more specifically on Calabi-Yau threefolds, is often considered the biggest open problem in the theory of Bridgeland stability conditions. Until recent work by Maciocia and Piyaratne [29, 30], they were only known to exist on threefolds whose derived category admits a full exceptional collection. Possible applications of stability conditions range from modularity properties of generating functions of Donaldson-Thomas invariants [43, 45] to Reider-type theorems for adjoint linear series [6].

In [11], the first two authors and Yukinobu Toda, also based on discussions with Aaron Bertram, proposed a general approach towards the construction of stability conditions on a smooth projective threefold X. The construction is based on the auxiliary notion of tilt-stability for two-term complexes, and a conjectural Bogomolov-Gieseker type inequality for the third Chern character of tilt-stable objects; we review these notions in Sect. 2 and the precise inequality in Conjecture 2.4. It depends on the choice of two divisor classes $\omega , B \in \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$ with $\omega$ ample. It was shown that this conjecture would imply the existence of Bridgeland stability conditions,² and, in the companion paper [6], a version of an open case of Fujita’s conjecture, on the very ampleness of adjoint line bundles on threefolds.

Our first main result is the following, generalizing the result of [29, 30] for the case when X has Picard rank one:

Theorem 1.1

The Bogomolov-Gieseker type inequality for tilt-stable objects, Conjecture 2.4, holds when X is an abelian threefold, and $\omega$ is a real multiple of an integral ample divisor class.

There are Calabi-Yau threefolds that admit an abelian variety as a finite étale cover; we call them Calabi-Yau threefolds of abelian type. Our result applies similarly in these cases:

Theorem 1.2

Conjecture 2.4 holds when X is a Calabi-Yau threefold of abelian type, and $\omega$ is a real multiple of an integral ample divisor class.

Combined with the results of [11], these theorems imply the existence of Bridgeland stability conditions in either case. There is one more type of Calabi-Yau threefolds whose derived category is closely related to those of abelian threefolds: namely Kummer threefolds, that are obtained as the crepant resolution of the quotient of an abelian threefold X by the action of a finite group G. Using the method of “inducing” stability conditions on the G-equivariant derived category of X and the BKR-equivalence [8], we can also treat this case. Overall this leads to the following result (which we will make more precise in Theorem 1.4).

Theorem 1.3

Bridgeland stability conditions on X exist when X is an abelian threefold, or a Calabi-Yau threefold of abelian type, or a Kummer threefold.

1.2 Support property

The notion of support property of a Bridgeland stability condition is crucial in order to apply the main result of [13], namely that the stability condition can be deformed; moreover, it ensures that the space of such stability conditions satisfies well-behaved wall-crossing.

In order to prove the support property, we first need a quadratic inequality for all tilt-stable complexes, whereas Conjecture 2.4 only treats complexes E with tilt-slope zero. We state such an inequality in Conjecture 4.1 for the case where $\omega , B$ are proportional to a given ample class H:

Conjecture 4.1 Let (X, H) be a smooth polarized threefold, and $\omega = \sqrt{3} \alpha H$, $B = \beta H$, for $\alpha >0$, $\beta \in \mathbb {R}$. If $E\in \mathrm {D}^{b}(X)$ is tilt-semistable with respect to $\omega , B$, then

$$\begin{aligned}&\alpha ^2 \Bigl ( \left( H^2\mathop {\mathrm {ch}}\nolimits _1^B(E)\right) ^2 - 2 H^3 \mathop {\mathrm {ch}}\nolimits _0^B(E) H\mathop {\mathrm {ch}}\nolimits _2^B(E)\Bigr ) + 4 \left( H \mathop {\mathrm {ch}}\nolimits _2^B(E)\right) ^2\\&\quad -\, 6 H^2 \mathop {\mathrm {ch}}\nolimits _1^B(E) \mathop {\mathrm {ch}}\nolimits _3^B(E) \ge 0, \end{aligned}$$

where $\mathop {\mathrm {ch}}\nolimits ^B := e^{-B}\mathop {\mathrm {ch}}\nolimits$.

In Theorem 4.2, we prove that this generalized conjecture is in fact equivalent to the original Conjecture 2.4. Moreover, in Theorem 8.7 we prove that it implies a similar quadratic inequality for objects that are stable with respect to the Bridgeland stability conditions constructed in Theorem 1.3, thereby obtaining a version of the support property.

To be precise, we consider stability conditions whose central charge $Z :K(X) \rightarrow \mathbb {C}$ factors via

$$\begin{aligned} v_H:K(X) \rightarrow \mathbb {Q}^4, \quad E \mapsto \left( H^3 \mathop {\mathrm {ch}}\nolimits _0(E), H^2 \mathop {\mathrm {ch}}\nolimits _1(E), H \mathop {\mathrm {ch}}\nolimits _2(E), \mathop {\mathrm {ch}}\nolimits _3(E)\right) . \end{aligned}$$

(1)

(In the case of Kummer threefolds, we apply the BKR-equivalence before taking the Chern character.) We prove the support property with respect to $v_H$; this shows that a stability condition deforms along a small deformation of its central charge, if that deformation still factors via $v_H$.

We discuss the relation between support property, quadratic inequalities for semistable objects and deformations of stability conditions systematically in Appendix 1. In particular, we obtain an explicit open subset of stability conditions whenever Conjecture 4.1 is satisfied, see Theorem 8.2.

1.3 The space of stability conditions

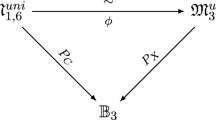
In each of the cases of Theorem 1.3, we show moreover that this open subset is a connected component of the space of stability conditions. We now give a description of this component.

Inside the space $\mathop {\mathrm {Hom}}\nolimits (\mathbb {Q}^4, \mathbb {C})$, consider the open subset $\mathfrak V$ of linear maps Z whose kernel does not intersect the (real) twisted cubic $\mathfrak C\subset \mathbb {P}^3(\mathbb {R})$ parametrized by $(x^3, x^2y, \frac{1}{2} xy^2, \frac{1}{6} y^3)$; it is the complement of a real hypersurface. Such a linear map Z induces a morphism $\mathbb {P}^1(\mathbb {R}) \cong \mathfrak C\rightarrow \mathbb {C}^*/\mathbb {R}^* = \mathbb {P}^1(\mathbb {R})$; we define $\mathfrak P$ be the component of $\mathfrak V$ for which this map is an unramified cover of topological degree $+3$ with respect to the natural orientations. Let $\widetilde{\mathfrak P}$ be its universal cover.

We let $\mathop {\mathrm {Stab}}\nolimits _H(X)$ be the space of stability conditions for which the central charge factors via the map $v_H$ as in equation (1) (and satisfying the support property).

Theorem 1.4

Let X be an abelian threefold, or a Calabi-Yau threefold of abelian type, or a Kummer threefold. Then $\mathop {\mathrm {Stab}}\nolimits _H(X)$ has a connected component isomorphic to $\widetilde{\mathfrak P}$.

1.4 Approach

We will now explain some of the key steps of our approach.

1.4.1 Reduction to a limit case

The first step applies to any smooth projective threefold. Assume that $\omega , B$ are proportional to a given ample polarization H of X. We reduce Conjecture 4.1 to a statement for objects E that are stable in the limit as $\omega (t) \rightarrow 0$ and $\nu _{\omega (t), B(t)}(E) \rightarrow 0$; if $\overline{B} := \lim B(t)$, the claim is that

$$\begin{aligned} \int _X e^{-\overline{B}}\mathop {\mathrm {ch}}\nolimits (E) \le 0. \end{aligned}$$

(2)

The reduction is based on the methods of [26]: as we approach this limit, either E remains stable, in which case the above inequality is enough to ensure that E satisfies our conjecture everywhere. Otherwise, E will be strictly semistable at some point; we then show that all its Jordan-Hölder factors have strictly smaller “H-discriminant” (which is a variant of the discriminant appearing in the classical Bogomolov-Gieseker inequality). This allows us to proceed by induction.

1.4.2 Abelian threefolds

In the case of an abelian threefold, we make extensive use of the multiplication by m map $\underline{m}:X \rightarrow X$ in order to establish inequality (2). The key fact is that if E is tilt-stable, then so is $\underline{m}^*E$.

To illustrate these arguments, assume that $\overline{B}$ is rational. Via pull-back we can then assume that $\overline{B}$ is integral; by tensoring with $\mathcal O_X(\overline{B})$ we reduce to the case of $\overline{B} = 0$. We then have to prove that $\mathop {\mathrm {ch}}\nolimits _3(E) \le 0$; in other words, we have to prove an inequality of the Euler characteristic of E. To obtain a contradiction, assume that $\mathop {\mathrm {ch}}\nolimits _3(E) > 0$, and consider further pull-backs:

$$\begin{aligned} \chi (\mathcal O_X, \underline{m}^*E) = \mathop {\mathrm {ch}}\nolimits _3(\underline{m}^*E) = m^6 \mathop {\mathrm {ch}}\nolimits _3(E) \ge m^6. \end{aligned}$$

(3)

However, by stability we have $\mathop {\mathrm {Hom}}\nolimits (\mathcal O_X(H), \underline{m}^*E) = 0$; moreover, if $D \in \left|H\right|$ is a general element of the linear system of H, classical arguments, based on the Grauert-Mülich theorem and bounds for global sections of slope-semistable sheaves, give a bound of the form

$$\begin{aligned} h^0(\underline{m}^*E) \le h^0((\underline{m}^*E)|_D) = O(m^4) \end{aligned}$$

Similar bounds for $h^2$ lead to a contradiction to (3).

1.4.3 Support property

As pointed out by Kontsevich and Soibelman in [21, Sect. 2.1], the support property is equivalent to the existence of a real quadratic form $Q :\mathbb {Q}^4 \rightarrow \mathbb {R}$ such that

• (a) The kernel of the central charge (as a subspace of $\mathbb {R}^4$) is negative definite with respect to Q, and

• (b) Every semistable object E satisfies $Q(v_H(E)) \ge 0$.

The inequality in Conjecture 4.1 precisely gives such a quadratic form. We therefore need to show that this inequality is preserved when we move from tilt-stability to actual Bridgeland stability conditions.

We establish a more basic phenomenon of this principle in Appendix 1, which may be of independent interest: if a stability condition satisfies the support property with respect to Q, and if we deform along a path for which the central charges all satisfy condition (a), then condition (b) remains preserved under this deformation, i.e., it is preserved under wall-crossing. The essential arguments involve elementary linear algebra of quadratic forms.

Tilt-stability can be thought of as a limiting case of a path in the set of stability conditions we construct. In Sect. 8 we show that the principle described in the previous paragraph similarly holds in this case: we show that a small perturbation of the quadratic form in Conjecture 4.1 is preserved under the wall-crossings between tilt-stability and any of our stability conditions, thereby establishing the desired support property.

1.4.4 Connected component

In Appendix 1, we also provide a more effective version of Bridgeland’s deformation result. In particular, the proof of the support property yields large open sets of stability conditions, which combine to cover the manifold $\widetilde{\mathfrak P}$ described above.

In Sect. 9, we show that this set is in fact an entire component. The proof is based on the observation that semi-homogeneous vector bundles E with $c_1(E)$ proportional to H are stable everywhere on $\mathfrak P$; their Chern classes (up to rescaling) are dense in $\mathfrak C$.

This fact is very unique to varieties admitting étale covers by abelian threefolds. In particular, while Conjecture 4.1 implies that $\widetilde{\mathfrak P}$ is a subset of the space of stability conditions, one should in general expect the space to be much larger than this open subset.

1.5 Applications

Our work has a few immediate consequences unrelated to derived categories. Although these are fairly specific, they still serve to illustrate the power of Conjecture 4.1.

Corollary 1.5

Let X be a Calabi-Yau threefold of abelian type. Given $\alpha \in \mathbb {Z}_{>0}$, let L be an ample line bundle on X satisfying

• $L^3 > 49\alpha$,

• $L^2 D \ge 7\alpha$ for every integral divisor class D with $L^2 D > 0$ and $L D^2 < \alpha$, and

• $L.C \ge 3\alpha$ for every curve $C \subset X$.

Then $H^1(L \otimes I_Z) = 0$ for every 0-dimensional subscheme $Z \subset X$ of length $\alpha$.

In addition, if $L = A^{\otimes 5}$ for an ample line bundle A, then L is very ample.

Proof

Since Conjecture 2.4 holds for X by our Theorem 1.2, we can apply Theorem 4.1 and Remark 4.3 of [6]. $\square$

Setting $\alpha = 2$ we obtain a Reider-type criterion for L to be very ample. The statement for $A^{\otimes 5}$ confirms (the very ampleness case of) Fujita’s conjecture for such X. The best known bounds for Calabi-Yau threefolds say that $A^{\otimes 8}$ is very ample if $L^3 > 1$ [18, Corollary 1], $A^{\otimes 10}$ is very ample in general, and that $A^{\otimes 5}$ induces a birational map [33, Theorem  I]. For abelian varieties, much stronger statements are known, see [37, 38].

Corollary 1.6

Let X be one of the following threefolds: projective space, the quadric in $\mathbb {P}^4$, an abelian threefold, or a Calabi-Yau threefold of abelian type. Let H be a polarization, and let $c \in \mathbb {Z}_{>0}$ be the minimum positive value of $H^2 D$ for integral divisor classes D. If E is a sheaf that is slope-stable with respect to H, and with $H^2 c_1(E) = c$, then

$$\begin{aligned} 3 c \mathop {\mathrm {ch}}\nolimits _3(E) \le 2 \left( H \mathop {\mathrm {ch}}\nolimits _2(E)\right) ^2. \end{aligned}$$

The assumptions hold when $\mathop {\mathrm {NS}}\nolimits (X)$ is generated by H, and $c_1(E) = H$. We refer to Example 4.4 and Remark 4.5 for a proof and more discussion. Even for vector bundles on $\mathbb {P}^3$, this statement was not previously known for rank bigger than three.

It is a special case of Conjecture 4.1. Even when X is a complete intersection threefold and $E = I_C \otimes L$ is the twist of an ideal sheaf of a curve C, this inequality is not known, see [49].

1.6 Open questions

1.6.1 General proof of Conjecture 4.1

While Conjecture 4.1 for arbitrary threefolds remains elusive, our approach seems to get a bit closer: in our proof of Theorem 1.1 (in Sects. 2, 3, 4, 5, 6, 7), only Sect. 7 is specific to abelian threefolds. One could hope to generalize our construction by replacing the multiplication map $\underline{m}$ with ramified coverings. This would immediately yield the set $\widetilde{\mathfrak P}$ as an open subset of the space of stability conditions.

1.6.2 Strengthening of Conjecture 4.1

In order to construct a set of stability conditions of dimension equal to the rank of the algebraic cohomology of X, we would need a stronger Bogomolov-Gieseker type inequality, depending on $\mathop {\mathrm {ch}}\nolimits _1$ and $\mathop {\mathrm {ch}}\nolimits _2$ directly, not just on $H^2 \mathop {\mathrm {ch}}\nolimits _1$ and $H \mathop {\mathrm {ch}}\nolimits _2$. We point out that the obvious guess, namely to replace $\left( H^2 \mathop {\mathrm {ch}}\nolimits _1\right) ^2$ by $H \mathop {\mathrm {ch}}\nolimits _1^2 \cdot H^3$, and $\left( H \mathop {\mathrm {ch}}\nolimits _2\right) ^2$ by an appropriate quadratic form on $H^4(X)$, does not work in general: for $\alpha \rightarrow +\infty$, such an inequality fails for torsion sheaves supported on a divisor D with $H D^2 < 0$.

1.6.3 Higher dimension

Our work also clarifies the expectations for higher dimensions. The definition of $\mathfrak P$ directly generalizes to dimension n in an obvious way, by replacing the twisted cubic with the rational normal curve $\left( x^n, x^{n-1}y, \frac{1}{2} x^{n-2}y^2, \dots , \frac{1}{n!} y^n\right)$. Let $\widetilde{\mathfrak P}_n \rightarrow \mathfrak P_n$ denote the corresponding universal covering.

Conjecture 1.7

Let (X, H) be a smooth polarized n-dimensional variety. Its space $\mathop {\mathrm {Stab}}\nolimits _H(X)$ of stability conditions contains an open subset $\widetilde{\mathfrak P}_n$, for which skyscraper sheaves of points are stable. In the case of abelian varieties, $\widetilde{\mathfrak P}_n \subset \mathop {\mathrm {Stab}}\nolimits _H(X)$ is a connected component.

Such stability conditions could be constructed by an inductive procedure; the i-th induction step would be an auxiliary notion of stability with respect to a weak notion of central charge $Z_i$ depending on $H^n \mathop {\mathrm {ch}}\nolimits _0, H^{n-1} \mathop {\mathrm {ch}}\nolimits _1, \dots , H^{n-i} \mathop {\mathrm {ch}}\nolimits _i$. Semistable objects would have to satisfy a quadratic inequality $Q_i$ involving $\mathop {\mathrm {ch}}\nolimits _{i+1}$. The precise form of $Q_i$ would depend on the parameters of the stability condition; it would always be contained in the defining ideal of the rational normal curve, and the kernel of $Z_i$ would be semi-negative definite with respect to $Q_i$.

One could hope to prove such inequalities for $i < n$ using a second induction by dimension: for example, an inequality for $\mathop {\mathrm {ch}}\nolimits _3$ for stable objects on a fourfold would follow from a Mehta-Ramanathan type restriction theorem, showing that such objects restrict to semistable objects on threefolds. As a first test case, one should try to prove that a given tilt-stable object on a threefold restricts to a Bridgeland-stable object on a divisor of sufficiently high degree.

1.7 Related work

As indicated above, the first breakthrough towards constructing stability conditions on threefolds (without using exceptional collections) is due to Maciocia and Piyaratne, who proved Theorem 1.1 in the case of principally polarized abelian varieties of Picard rank one in [29, 30]. Their method is based on an extensive analysis of the behavior of tilt-stability with respect to Fourier-Mukai transforms; in addition to constructing stability conditions, they show their invariance under Fourier-Mukai transforms.

Our approach is very different, as it only uses the existence of the étale self-maps given by multiplication with m. Nevertheless, there are some similarities. For example, a crucial step in their arguments uses restriction to divisors and curves to control a certain cohomology sheaf of the Fourier-Mukai transform of E, see the proof of [29, Proposition 4.15]; in Sect. 7 we use restriction of divisors explicitly and to curves implicitly (when we use Theorem 7.2) to control global sections of pull-backs of E.

As mentioned earlier, it is easy to construct stability conditions on any variety admitting a complete exceptional collection; however, it is still a delicate problem to relate them to the construction proposed in [11]. This was done in [11, 26] for the case of $\mathbb {P}^3$, and in [39] for the case of the quadric in $\mathbb {P}^4$; these are the only other cases in which Conjecture 2.4 is known.

There is an alternative conjectural approach towards stability conditions on the quintic hypersurface in $\mathbb {P}^4$ via graded matrix factorizations, proposed by Toda [46, 47]. It is more specific, but would yield a stability condition that is invariant under certain auto-equivalences; it would also lie outside of our set $\widetilde{\mathfrak P}$. His approach would require a stronger Bogomolov-Gieseker inequality already for slope-stable vector bundles, and likely lead to very interesting consequences for generating functions of Donaldson-Thomas invariants.

Conjecture 2.4 can be specialized to certain slope-stable sheaves, similar to Corollary 1.6; see [11, Conjecture 7.2.3]. This statement was proved by Toda for certain Calabi-Yau threefolds, including the quintic hypersurface, in [48]. Another case of that conjecture implies a certain Castelnuovo-type inequality between the genus and degree of curves lying on a given threefold; see [49] for its relation to bounds obtained via classical methods.

Our results are at least partially consistent with the expectations formulated in [36]; in particular, semi-homogeneous bundles are examples of the Lagrangian-invariant objects considered by Polishchuk, are semistable for our stability conditions, and their phases behave as predicted.

1.8 Plan of the paper

Appendix 1 may be of independent interest. We review systematically the relation between support property, quadratic inequalities for semistable objects and deformations of stability conditions, and their behaviour under wall-crossing.

Sections 2 and 3 and Appendix 2 review basic properties of tilt-stabilty, its deformation properties (fixing a small inaccuracy in [11]), the conjectural inequality proposed in [11] and variants of the classical Bogomolov-Gieseker inequality satisfies by tilt-stable objects.

In Sect. 4 we show that a more general form of Conjecture 2.4 is equivalent to the original conjecture, whereas Sect. 5 shows that both conjectures follows from a special limiting case.

This limiting case is proved for abelian threefolds in Sect. 7; in the following Sect. 8 we show that this implies the existence of the open subset $\widetilde{\mathfrak P}$ of stabilty conditions described above. Section 9 shows that in the case of abelian threefolds, $\widetilde{\mathfrak P}$ is in fact a connected component, and Sect. 10 extends these results to (crepant resolutions) of quotients of abelian threefolds.

1.9 Update (March 2016)

Counterexamples due to Schmidt [40] and Martinez [27] indicate that Conjectures 2.4 and 4.1 need to be modified in the case of a threefold obtained as the blowup at a point of another threefold; on the other hand, they have been verified for all Fano threefolds of Picard rank one [23].

2 Review: tilt-stability and the conjectural BG inequality

In this section, we review the notion of tilt-stability for threefolds introduced in [11]. We then recall the conjectural Bogomolov-Gieseker type inequality for tilt-stable complexes proposed there; see Conjecture 2.4 below.

2.1 Slope-stability

Let X be a smooth projective complex variety and let $n\ge 1$ be its dimension. Let $\omega \in \mathrm {NS}(X)_\mathbb {R}$ be a real ample divisor class.

For an arbitrary divisor class $B \in \mathrm {NS}(X)_\mathbb {R}$, we will always consider the twisted Chern character $\mathop {\mathrm {ch}}\nolimits ^B(E) = e^{-B} \mathop {\mathrm {ch}}\nolimits (E)$; more explicitly, we have

$$\begin{aligned} \begin{aligned}&\mathop {\mathrm {ch}}\nolimits ^B_0=\mathop {\mathrm {ch}}\nolimits _0= \mathrm {rank} \quad \mathop {\mathrm {ch}}\nolimits ^B_2=\mathop {\mathrm {ch}}\nolimits _2-B \mathop {\mathrm {ch}}\nolimits _1+\frac{B^2}{2} \mathop {\mathrm {ch}}\nolimits _0 \\&\mathop {\mathrm {ch}}\nolimits ^B_1=\mathop {\mathrm {ch}}\nolimits _1-B\mathop {\mathrm {ch}}\nolimits _0 \quad \mathop {\mathrm {ch}}\nolimits ^B_3=\mathop {\mathrm {ch}}\nolimits _3-B\mathop {\mathrm {ch}}\nolimits _2+\frac{B^2}{2} \mathop {\mathrm {ch}}\nolimits _1-\frac{B^3}{6} \mathop {\mathrm {ch}}\nolimits _0. \end{aligned} \end{aligned}$$

(4)

We define the slope $\mu _{\omega , B}$ of a coherent sheaf E on X by

$$\begin{aligned} \mu _{\omega , B}(E) = {\left\{ \begin{array}{ll} + \infty , &{} \quad \text { if }\mathop {\mathrm {ch}}\nolimits ^B_0(E)=0,\\ \frac{\omega ^{n-1} \mathop {\mathrm {ch}}\nolimits ^B_1(E)}{\omega ^n \mathop {\mathrm {ch}}\nolimits ^B_0(E)}, &{}\quad \text { otherwise.} \end{array}\right. } \end{aligned}$$

When $B=0$, we will often write $\mu _\omega$.

Definition 2.1

A coherent sheaf E is slope-(semi)stable (or $\mu _{\omega , B}$-(semi)stable) if, for all non-zero subsheaves $F \hookrightarrow E$, we have

$$\begin{aligned} \mu _{\omega , B}(F) < (\le ) \mu _{\omega , B}(E/F). \end{aligned}$$

Observe that if a sheaf is slope-semistable, then it is either torsion-free or torsion. Harder-Narasimhan filtrations (HN-filtrations, for short) with respect to slope-stability exist in $\mathop {\mathrm {Coh}}\nolimits (X)$: given a non-zero sheaf $E\in \mathop {\mathrm {Coh}}\nolimits (X)$, there is a filtration

$$\begin{aligned} 0=E_0 \subset E_1 \subset \dots \subset E_m=E \end{aligned}$$

such that: (i) $A_i := E_i/E_{i-1}$ is slope-semistable, and (ii) $\mu _{\omega , B}(A_1)> \dots > \mu _{\omega , B}(A_m)$. We set $\mu ^+_{\omega , B}(E):=\mu _{\omega , B}(A_1)$ and $\mu ^-_{\omega , B}(E):=\mu _{\omega , B}(A_m)$.

2.2 The tilted category

Let X be a smooth projective threefold. As above, let $\omega , B$ be real divisor classes with $\omega$ ample. There exists a torsion pair $(\mathcal T_{\omega , B}, \mathcal F_{\omega , B})$ in $\mathop {\mathrm {Coh}}\nolimits (X)$ defined as follows:

$$\begin{aligned} \mathcal T_{\omega , B}&= \left\{ E \in \mathop {\mathrm {Coh}}\nolimits (X)\,:\,\text {any quotient }E \twoheadrightarrow G\text { satisfies }\mu _{\omega , B}(G)> 0\right\} \\&= \left\{ E\,:\,\mu _{\omega , B}^-(E) > 0\right\} \\ \mathcal F_{\omega , B}&= \left\{ E \in \mathop {\mathrm {Coh}}\nolimits (X)\,:\,\text {any subsheaf }F \hookrightarrow E\text { satisfies }\mu _{\omega , B}(F) \le 0\right\} \\&= \left\{ E\,:\,\mu _{\omega , B}^+(E) \le 0\right\} \end{aligned}$$

Equivalently, $\mathcal T_{\omega , B}$ and $\mathcal F_{\omega , B}$ are the extension-closed subcategories of $\mathop {\mathrm {Coh}}\nolimits (X)$ generated by slope-stable sheaves of positive and non-positive slope, respectively.

Definition 2.2

We let $\mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X) \subset \mathrm {D}^{b}(X)$ be the extension-closure

$$\begin{aligned} \mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X) = \langle \mathcal T_{\omega , B}, \mathcal F_{\omega , B}[1] \rangle . \end{aligned}$$

By the general theory of torsion pairs and tilting [20], $\mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$ is the heart of a bounded t-structure on $\mathrm {D}^{b}(X)$; in particular, it is an abelian category.

2.3 Tilt-stability and the main conjecture

We now define the following slope function, called tilt, on the abelian category $\mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$: for an object $E \in \mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$, its tilt $\nu _{\omega , B}(E)$ is defined by

$$\begin{aligned} \nu _{\omega , B}(E) = {\left\{ \begin{array}{ll} + \infty , &{}\quad \text { if }\omega ^{2} \mathop {\mathrm {ch}}\nolimits ^B_1(E) = 0,\\ \frac{\omega \mathop {\mathrm {ch}}\nolimits ^B_2(E) - \frac{1}{6} \omega ^3 \mathop {\mathrm {ch}}\nolimits ^B_0(E)}{\omega ^{2} \mathop {\mathrm {ch}}\nolimits ^B_1(E)}, &{}\quad \text { otherwise.} \end{array}\right. } \end{aligned}$$

We think of this as induced by the “reduced” central charge

$$\begin{aligned} \overline{Z}_{\omega , B}(E) = \omega ^2 \mathop {\mathrm {ch}}\nolimits ^B_1(E) + i \omega \left( \mathop {\mathrm {ch}}\nolimits ^B_2(E) - \frac{1}{6} \omega ^2 \mathop {\mathrm {ch}}\nolimits ^B_0(E) \right) ; \end{aligned}$$

(5)

indeed, if $\overline{Z}_{\omega , B}(E) \ne 0$, then the tilt $\nu _{\omega , B}(E)$ of E agrees with the slope of that complex number; otherwise it is $+\infty$.

Definition 2.3

An object $E \in \mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$ is tilt-(semi)stable if, for all non-trivial subobjects $F \hookrightarrow E$, we have

$$\begin{aligned} \nu _{\omega , B}(F) < (\le ) \nu _{\omega , B}(E/F). \end{aligned}$$

Tilt-stability gives a notion of stability, in the sense that Harder-Narasimhan filtrations exist.

The following conjecture is the main topic of [11]:

Conjecture 2.4

[11, Conjecture 1.3.1] For any $\nu _{\omega ,B}$-semistable object $E\in \mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$ satisfying $\nu _{\omega , B}(E) = 0$, we have the following generalized Bogomolov-Gieseker inequality

$$\begin{aligned} \mathop {\mathrm {ch}}\nolimits ^B_3(E) \le \frac{\omega ^2}{18}\mathop {\mathrm {ch}}\nolimits ^B_1(E). \end{aligned}$$

(6)

2.4 Properties of tilt-stability

We will often fix B and vary $\omega$ along a ray in the ample cone via

$$\begin{aligned} \omega = \sqrt{3} \alpha H \end{aligned}$$

for some given integral ample class $H \in \mathop {\mathrm {NS}}\nolimits (X)$.³

To prove that tilt-stability is a well-behaved property, one needs to use variants of the classical Bogomolov-Gieseker inequality for slope-semistable sheaves; in particular, this leads to the following statements:

Remark 2.5

• (a) Tilt-stability is an open property. More precisely, assume that $E\in \mathrm {D}^{b}(X)$ is $\nu _{\omega , B}$-stable with $\omega = \sqrt{3}\alpha H$. Then the set of pairs $(\alpha ', B') \in \mathbb {R}_{>0} \times \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$ such that E is $\nu _{\sqrt{3}\alpha 'H, B'}$-stable is open.

• (b) The boundary of the above subset of $\mathbb {R}_{>0} \times \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$ where $E \in \mathrm {D}^{b}(X)$ is tilt-stable is given by a locally finite collection of walls, i.e., submanifolds of real codimension one.

Unfortunately, a slightly stronger statement was claimed in [11, Corollary 3.3.3], but (as noted first by Yukinobu Toda) the proof there only yields the above claims. We will therefore review these statements in more detail in Sect. 3 and Appendix 2; one can also deduce them with the same arguments as in the surface case, treated in detail in [44, Sect. 3].

Remark 2.6

It can be helpful to distinguish between two types of walls for tilt-stability, see Proposition 12.5. Locally, a wall for tilt-stability of E is described by the condition $\nu _{\omega , B}(F) = \nu _{\omega , B}(E)$ for a destabilizing subobject F. This translates into the condition that either

• (a) $\overline{Z}_{\omega , B}(F)$ and $\overline{Z}_{\omega , B}(E)$ are linearly dependent, or that

• (b) $\nu _{\omega , B}(E) = +\infty$.

In the limit $\omega \rightarrow +\infty \cdot H$, tilt-stability becomes closely related to slope-stability:

Lemma 2.7

Let H, B be fixed divisor classes with H ample, and let $\omega = \sqrt{3}\alpha H$ for $\alpha \in \mathbb {R}_{>0}$. Then

• (a) The category $\mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$ is independent of $\alpha$.

• (b) Moreover, its subcategory of objects E with $\nu _{\omega , B}(E) = +\infty$ is independent of $\alpha$.

• (c) If $E \in \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)$ is $\nu _{\omega , B}$-semistable for $\alpha \gg 0$, then it satisfies one of the following conditions:

  • (i) $H^{-1}(E) = 0$ and $H^0(E)$ is a $\mu _{\omega ,B}$-semistable torsion-free sheaf.

  • (ii) $H^{-1}(E) = 0$ and $H^0(E)$ is a torsion sheaf.

  • (iii) $H^{-1}(E)$ is a $\mu _{\omega ,B}$-semistable sheaf and $H^0(E)$ is either 0, or supported in dimension $\le 1$.

  Conversely, assume $E \in \mathop {\mathrm {Coh}}\nolimits (X)$ is a $\mu _{\omega ,B}$-stable torsion-free sheaf.

  • (i) If $H^2\mathop {\mathrm {ch}}\nolimits _1^B(E)>0$, then $E\in \mathop {\mathrm {Coh}}\nolimits ^{H,B}(X)$ and it is $\nu _{\omega , B}$-stable for $\alpha \gg 0$.

  • (ii) If $H^2\mathop {\mathrm {ch}}\nolimits _1^B(E)\le 0$, then $E[1]\in \mathop {\mathrm {Coh}}\nolimits ^{H,B}(X)$; if moreover E is a vector bundle, then it is $\nu _{\omega , B}$-stable for $\alpha \gg 0$.

Proof

The first two statements are immediate to see. The arguments for part (c) are completely analogous to the case of Bridgeland stable objects on surfaces, first treated in [14, Proposition  14.2]; see also [11, Proposition  7.2.1] for the first part. $\square$

3 Classical Bogomolov-Gieseker type inequalities

In this section, we review a result from [11] that shows that tilt-stable objects on X satisfy variants of the classical Bogomolov-Gieseker inequality.

We continue to assume that X is a smooth projective threefold. Throughout this section, let $H \in \mathop {\mathrm {NS}}\nolimits (X)$ be a polarization, $\omega = \sqrt{3} \alpha H$ for $\alpha > 0$, and $B \in \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$ arbitrary.

First we recall the classical Bogomolov-Gieseker inequality:

Definition 3.1

The discriminant of E with respect to H is defined by

$$\begin{aligned} \Delta _H(E):= & {} H \left( \mathop {\mathrm {ch}}\nolimits _1(E)^2 - 2 \mathop {\mathrm {ch}}\nolimits _0(E) \mathop {\mathrm {ch}}\nolimits _2(E)\right) \\= & {} H \left( \mathop {\mathrm {ch}}\nolimits _1^B(E)^2 - 2 \mathop {\mathrm {ch}}\nolimits ^B_0(E) \mathop {\mathrm {ch}}\nolimits ^B_2(E)\right) . \end{aligned}$$

Theorem 3.2

(Bogomolov, Gieseker) Assume that E is a $\mu _{H}$-semistable torsion-free sheaf on X. Then $\Delta _H(E) \ge 0$.

However, a sheaf F supported on a divisor $D \subset X$ does not necessarily satisfy $\Delta _H(F) \ge 0$ (even if it is the push-forward of a slope-stable sheaf); indeed, we may have $H D^2 < 0$. This leads us to modify the inequality to a form that also holds for torsion sheaves, and in consequence for tilt-stable objects. We first need the following easy observation (see, for example, the proof of [11, Corollary 7.3.3]):

Lemma 3.3

There exists a constant $C_H\ge 0$ such that for every effective divisor $D \subset X$, we have

$$\begin{aligned} C_H \left( H^2 D\right) ^2 + H.D^2 \ge 0. \end{aligned}$$

(Note that for abelian threefolds, we may take $C_H = 0$.)

Definition 3.4

We define the H-discriminant as the following quadratic form:

$$\begin{aligned} \overline{\Delta }_H^B := \left( H^2 \mathop {\mathrm {ch}}\nolimits _1^B\right) ^2 - 2 H^3 \mathop {\mathrm {ch}}\nolimits _0^B H.\mathop {\mathrm {ch}}\nolimits _2^B. \end{aligned}$$

(7)

For the second definition, choose a rational non-negative constant $C_H$ satisfying the conclusion of Lemma 3.3. Then

$$\begin{aligned} \Delta _{H, B}^C := \Delta _H + C_H \left( H^2 \mathop {\mathrm {ch}}\nolimits _1^B\right) ^2. \end{aligned}$$

(8)

Theorem 3.5

[11, Theorem 7.3.1, Corollaries 7.3.2, 7.3.3] Let X be a smooth projective threefold with ample polarization $H \in \mathop {\mathrm {NS}}\nolimits (X)$. Assume that E is $\nu _{\omega , B}$-semistable for $\omega = \sqrt{3}\alpha H$ and $B \in \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$. Then

$$\begin{aligned} \overline{\Delta }_H^B(E) \ge 0 \quad \text {and} \quad \Delta _{H, B}^C(E) \ge 0. \end{aligned}$$

This was proved for rational B in [11]; we will give a self-contained proof of the rational case with a slightly different presentation below, and extend it to arbitrary B in Appendix 2.

We think of $\Delta _{H, B}^C$ as the composition

$$\begin{aligned} K(X) \xrightarrow {v_H^B} H^0(X, \mathbb {R}) \oplus \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}\oplus \mathbb {R}\xrightarrow {q_H^B} \mathbb {R}\end{aligned}$$

where the first map is given by

$$\begin{aligned} v_H^B(E) = \left( \mathop {\mathrm {ch}}\nolimits _0^B(E), \mathop {\mathrm {ch}}\nolimits _1^B(E), H \mathop {\mathrm {ch}}\nolimits _2^B(E)\right) \end{aligned}$$

and where $q_H^B$ is the quadratic form

$$\begin{aligned} \left( r, c, d\right) \mapsto H c^2 +C_H \left( H^2 c\right) ^2 - 2rd. \end{aligned}$$

If B is rational, then the image of $v_H^B$ (and of $\overline{v}_H^B$, defined in Remark 3.8 below) is a finite rank lattice.

Notice that $\overline{Z}_{\omega , B}$ as defined in equation (5) factors via $v_H^B$. Its relation to $q_H^B$ is controlled by the following immediate consequences of the Hodge index theorem:

Lemma 3.6

The quadratic form $q_H^B$ has signature $(2, \rho (X))$.

The kernel of $\overline{Z}_{\omega , B}$ is negative definite with respect to $q_H^B$.

This makes our situation analogous to the one in Appendix 1; in particular, Theorem 3.5 implies a version of the support property for tilt-stable objects.

Lemma 3.7

Let $\nu \in \mathbb {R}\cup \{+\infty \}$. Then there exists a half-space

$$\begin{aligned} \mathbb {H}_{\omega , B, \nu } \subset H^0(X, \mathbb {R}) \oplus \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}\oplus \mathbb {R}\end{aligned}$$

of codimension one with the following properties:

• (a) For any object $E \in \mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$ with $\nu _{\omega , B}(E) = \nu$, we have

  $$\begin{aligned} v_H^B(E) \in \mathbb {H}_{\omega , B, \nu }. \end{aligned}$$

• (b) The intersection of $\mathbb {H}_{\omega , B, \nu }$ with the set defined by $q_H^B(\underline{\,\,}) \ge 0$ is a real convex cone.

Proof

We define $\mathbb {H}_{\omega , B, \nu }$ as the preimage under $\overline{Z}_{\omega , B}$ of the ray in the complex plane that has slope $\nu$, starting at the origin; this ensures the first claim. The second claim is a general fact about quadratic forms, see Lemma 11.7. $\square$

Note that by definition, a half-space is closed; indeed, we may have $v_H^B(E) = 0$ iff $\nu = +\infty$.

Remark 3.8

If we replace $v_H^B$ with the map

$$\begin{aligned} K(X) \xrightarrow {\overline{v}_H^B} \mathbb {R}^3, \quad \overline{v}_H^B(E) = \left( H^3 \mathop {\mathrm {ch}}\nolimits _0^B(E), H^2 \mathop {\mathrm {ch}}\nolimits _1^B(E), H \mathop {\mathrm {ch}}\nolimits _2^B(E)\right) \end{aligned}$$

and $q_H^B$ with the obvious quadratic form $\overline{q}_H^B$ on $\mathbb {R}^3$, then $\overline{\Delta }_H^B= \overline{q}_H^B \circ \overline{v}_H^B$ and the analogues of Lemmas 3.6 and 3.7 hold.

Proof of Theorem 3.5, case $H^2B \in \mathbb {Q}$   We prove the statement for $\Delta _{H, B}^C$ under the assumption that $H^2B$ is rational. The proof for $\overline{\Delta }_H^B$ follows similarly due to Remark 3.8, and the non-rational case will be treated in Appendix 2.

We proceed by induction on $H^2 \mathop {\mathrm {ch}}\nolimits _1^B(E)$, which by our assumption is a non-negative function with discrete values on objects of $\mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)$.

We start increasing $\alpha$. If E remains stable as $\alpha \rightarrow +\infty$, we apply Lemma 2.7, (c); by Theorem 3.2 (for torsion-free slope-semistable sheaves) and Lemma 3.3 (for torsion sheaves) one easily verifies that E satisfies the conclusion in any of the possible cases.

Otherwise, E will get destabilized. Note that as $\alpha$ increases, all possible destabilizing subobjects and quotients have strictly smaller $H^2 \mathop {\mathrm {ch}}\nolimits _1^B$, which satisfy the desired inequality by our induction assumption. This is enough to ensure that E satisfies well-behaved wall-crossing: following the argument of [14, Proposition 9.3] it is enough to know a support property type statement for all potentially destabilizing classes.

Hence there will be a wall $\alpha = \alpha _W$ where E is strictly $\nu _{\sqrt{3}\alpha _W H, B}$-semistable; let

$$\begin{aligned} 0\rightarrow E_1 \rightarrow E \rightarrow E_2 \rightarrow 0 \end{aligned}$$

be a short exact sequence where both $E_1$ and $E_2$ have the same tilt as E. Then both $E_1$ and $E_2$ have strictly smaller $H^2 \mathop {\mathrm {ch}}\nolimits _1^B$; so they satisfy the inequality $\Delta _{H, B}^C (E_i) \ge 0$ by the induction assumption. In other words, $v_H^B(E_i)$ are contained in the cone described in Lemma 3.7, (b); by convexity, the same holds for

$$\begin{aligned} v_H^B(E) = v_H^B(E_1) + v_H^B(E_2). \end{aligned}$$

$\square$

We now turn to some consequences of Theorem 3.5.

Lemma 3.9

Let Q be a quadratic form of signature (1, r). Let $\mathcal C^+$ be the closure of one of the two components of the positive cone given by $Q(x) > 0$. Assume that $x_1, \dots , x_m \in \mathcal C^+$, and let $x := x_1 + \dots , x_m$. Then

$$\begin{aligned} Q(x_i) \le Q(x) \quad \text {for all }i, \end{aligned}$$

with equality if and only if for all i, we have that $x_i$ is proportional to x and $Q(x_i) = Q(x) = 0$.

Proof

This follows immediately from the easy fact that if $x, y \in \mathcal C^+ - \{0\}$, then the bilinear form associated to Q satisfies $(x,y) \ge 0$, with equality if and only if x, y are proportional with $Q(x)= Q(y) = 0$. $\square$

Corollary 3.10

Assume that E is strictly $\nu _{\omega , B}$-semistable with $\nu _{\omega , B}(E) \ne +\infty$. Let $E_i$ be the Jordan-Hölder factors of E. Then

$$\begin{aligned} \overline{\Delta }_H^B(E_i) \le \overline{\Delta }_H^B(E) \quad \text {for all }i. \end{aligned}$$

Equality holds if and only if all $\overline{v}_H^B(E_i)$ are proportional to $\overline{v}_H^B(E)$ and satisfy $\overline{\Delta }_H^B(E_i) = \overline{\Delta }_H^B(E) = 0$. In particular, if E is $\nu _{\omega ', B'}$-stable for some $\omega ', B'$ with $\omega '$ proportional to $\omega$, then the inequality is strict.

The same statements hold with $\overline{\Delta }_H^B$ and $\overline{v}_H^B$ replaced by $\Delta _{H, B}^C$ and $v_H^B$, respectively.

The case $\nu = +\infty$ is excluded as in that case we may have $\overline{v}_H^B(E_i) = 0$ or $\overline{v}_H^B(E_i) = \overline{v}_H^B(E)$.

Proof

Let $x_i := \overline{v}_H^B(E_i)$ and $x := \overline{v}_H^B(E)$. By Lemmas 3.6 and 3.7, they satisfy the assumptions of Lemma 3.9, which then implies our claim. $\square$

As another application, one obtains the tilt-stability of certain slope-stable sheaves (see also [11, Proposition 7.4.1]):

Corollary 3.11

• (a) Let F be a $\mu _{H,B}$-stable vector bundle with $\Delta _{H, B}^C (F) = 0$ or $\overline{\Delta }_H^B(F) = 0$. Then F or F[1] is a $\nu _{\omega , B}$-stable object of $\mathop {\mathrm {Coh}}\nolimits ^{H,B}(X)$.

• (b) In particular, if L is a line bundle, and if in addition either $c_1(L) - B$ is proportional to H, or we can choose the constant $C_H$ of Lemma 3.3 to be zero, then L or L[1] is $\nu _{\omega , B}$-stable.

• (c) Conversely, consider an object $E \in \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)$ that is $\nu _{\omega , B}$-stable with $\Delta _{H, B}^C (E) = 0$ or $\overline{\Delta }_H^B(E) = 0$. Then either $E = H^0(E)$ is a $\mu _H$-semistable sheaf, or $E = H^0(E)$ is supported in dimension $\le 2$, or $H^{-1}(E) \ne 0$ is a $\mu _H$-semistable sheaf and $H^0(E)$ has zero-dimensional support. In addition, E is $\nu _{\omega ', B}$-stable for all $\omega '$ proportional to H.

Note that the choice $C_H = 0$ in particular applies to abelian threefolds (or more generally any threefold whose group of automorphisms acts transitively on closed points), or to any threefold of Picard rank one.

Proof

Consider an object E that is $\nu _{\omega , B}$-stable with $\overline{\Delta }_H^B(E) = 0$ or $\Delta _{H, B}^C (E) = 0$. By Corollary 3.10, E can never become strictly semistable with respect to $\nu _{\omega ', B'}$ as long as $\omega '$ is proportional to $\omega$. Combined with Lemma 2.7, (c) this implies all our claims. $\square$

The analogue to the case $C_H = 0$ of part (b) for Bridgeland stability on surfaces is due to Arcara and Miles, see [2, Theorem  1.1], with a very different proof.

Proposition 3.12

Assume that B is rational, and let $E \in \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)$ be a $\nu _{\omega , B}$-stable object with $\overline{\Delta }_H^B(E) = 0$ and $\nu _{\omega ,B}(E)=0$. Then E satisfies Conjecture 2.4.

Proof

If F is a $\mu _{\omega ,B}$-semistable reflexive sheaf on X with $\overline{\Delta }_H^B(F) = 0$, then F is a vector bundle by [24, Proposition  3.12], Further, if E is $\nu _{\omega ,B}$-semistable with $\nu _{\omega ,B}(E)<+\infty$, then $H^{-1}(E)$ is reflexive by [24, Proposition 3.1]. Hence, the case $H^{-1}(E) \ne 0$ of part (c) in Corollary 3.11 can actually be made much more precise: in this case, $H^0(E) = 0$ and $H^{-1}(E)$ is a vector bundle. In the other case, if $\nu _{\omega ,B}(E)=0$, $\overline{\Delta }_H^B(E)=0$, and $H^{-1}(E)=0$, then $H^0(E)$ is a torsion-free sheaf and its double-dual is again locally-free with $\overline{\Delta }_H^B=0$. In either case, a classical result of Simpson (see [41, Theorem 2] and [22, Theorem  4.1]) implies that E satisfies Conjecture 2.4; see [11, Proposition 7.4.2]. $\square$

4 Generalizing the main conjecture

For this and the following section, we assume that $\omega$ and B are proportional to a given ample class $H \in \mathop {\mathrm {NS}}\nolimits (X)$:

$$\begin{aligned} \omega = \sqrt{3}\alpha H, \quad B = \beta H. \end{aligned}$$

(9)

We will abuse notation and write $\mathop {\mathrm {ch}}\nolimits _i^\beta$ instead of $\mathop {\mathrm {ch}}\nolimits _i^{\beta H}$, $\mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ instead of $\mathop {\mathrm {Coh}}\nolimits ^{H,\beta H}(X)$, and $\nu ^H_{\alpha , \beta }$ or $\nu _{\alpha , \beta }$ to abbreviate

$$\begin{aligned} \nu _{\alpha , \beta } = \sqrt{3} \alpha \nu _{\sqrt{3}\alpha H, \beta H} = \frac{H \mathop {\mathrm {ch}}\nolimits _2^\beta - \frac{1}{2} \alpha ^2 H^3 \mathop {\mathrm {ch}}\nolimits _0^\beta }{H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta }. \end{aligned}$$

We will also write $\overline{\Delta }_H$ instead of $\overline{\Delta }_H^B$, as it is independent of the choice of $\beta$.

The goal of this section is to generalize Conjecture 2.4 to arbitrary tilt-semistable objects, not just those satisfying $\nu _{\alpha , \beta } = 0$. This generalization relies on the structure of walls for tilt-stability in $\mathbb {R}_{>0}\times \mathbb {R}$; it is completely analogous to the case of walls for Bridgeland stability on surfaces, treated most systematically in [25].

Conjecture 4.1

Let X be a smooth projective threefold, and $H \in \mathop {\mathrm {NS}}\nolimits (X)$ an ample class. Assume that E is $\nu ^H_{\alpha , \beta }$-semistable. Then

$$\begin{aligned} \alpha ^2 \overline{\Delta }_H(E) + 4 \left( H \mathop {\mathrm {ch}}\nolimits _2^\beta (E)\right) ^2 - 6 H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta (E) \mathop {\mathrm {ch}}\nolimits _3^\beta (E) \ge 0. \end{aligned}$$

(10)

Theorem 4.2

Let X be a smooth projective threefold, and $H \in \mathop {\mathrm {NS}}\nolimits (X)$ an ample class. Then Conjecture 4.1 holds if and only if Conjecture 2.4 holds for all $\omega , B$ proportional to H.

We begin with the following aspect of “Bertram’s Nested Wall Theorem” [25, Theorem 3.1]:

Lemma 4.3

Assume the situation and notation of Conjecture 4.1 with $\nu _{\alpha , \beta }(E) \ne +\infty$. Then the object E is $\nu _{\alpha , \beta }$-semistable along the semicircle $\mathcal C_{\alpha , \beta }(E)$ in the $(\alpha , \beta )$-plane $\mathbb {R}_{>0}\times \mathbb {R}$ with center $(0, \beta + \nu _{\alpha , \beta }(E))$ and radius $\sqrt{\alpha ^2 + \nu _{\alpha , \beta }(E)^2}$.

Proof

We have to show that $\mathcal C_{\alpha , \beta }(E)$ does not intersect any wall for tilt-stability, which are described in Remark 2.6 or Proposition 12.5. In our situation, all reduced central charges $\overline{Z}_{\alpha , \beta }$ factor via the map

$$\begin{aligned} \overline{v}_H :K(X) \rightarrow \mathbb {Q}^3, \quad w \mapsto \left( H^3 \mathop {\mathrm {ch}}\nolimits _0(w), H^2 \mathop {\mathrm {ch}}\nolimits _1(w), H \mathop {\mathrm {ch}}\nolimits _2(w)\right) . \end{aligned}$$

(11)

The first type of wall, case (a) in Proposition 12.5, can thus equivalently be described as the set of $(\alpha ', \beta ')$ for which $\overline{v}_H(F)$ (for some destabilizing subobject $F \hookrightarrow E$) is contained in the two-dimensional subspace of $\mathbb {Q}^3$ spanned by $\overline{v}_H(E)$ and the kernel of $\overline{Z}_{\alpha ', \beta '}$.

However, this two-dimensional subspace does not vary as $(\alpha ', \beta ')$ move within $\mathcal C_{\alpha , \beta }(E)$: the kernel of $\overline{Z}_{\alpha ', \beta '}$ is spanned by $\left( 1, \beta ', \frac{1}{2} (\alpha '^2 + \beta '^2)\right)$, and the the vectors

$$\begin{aligned}&\left( H^3 \mathop {\mathrm {ch}}\nolimits _0(E), H^2 \mathop {\mathrm {ch}}\nolimits _1(E), H \mathop {\mathrm {ch}}\nolimits _2(E)\right) ,\\&\quad \left( 1, \beta , \frac{1}{2} (\alpha ^2 + \beta ^2)\right) \quad \left( 1, \beta ', \frac{1}{2} (\alpha '^2 + \beta '^2)\right) \end{aligned}$$

are linearly dependent if and only if $(\alpha ', \beta ')$ is contained in $\mathcal C_{\alpha , \beta }(E)$.

In addition, a simple computation shows $H^2 \mathop {\mathrm {ch}}\nolimits _1^{\beta '}(E) > 0$ for $(\alpha ', \beta ') \in \mathcal C_{\alpha , \beta }(E)$; therefore, the semicircle cannot intersect a wall given by $\nu _{\alpha ', \beta '}(E) = +\infty$ either. $\square$

Proof of Theorem 4.2

We first note that due to Theorem 3.5, Conjecture 4.1 holds for all objects E with $H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta (E) = 0$. We may therefore assume $\nu _{\alpha , \beta }(E) \ne +\infty$ throughout the proof.

As an auxiliary step, consider the following statement:

• (*) Assume that E is $\nu _{\alpha , \beta }$-stable with $\nu _{\alpha , \beta }(E) \ne +\infty$. Let $\beta ':= \beta + \nu _{\alpha , \beta }(E)$. Then

  $$\begin{aligned} \mathop {\mathrm {ch}}\nolimits ^{\beta '}_3(E) \le \frac{1}{6} \left( \alpha ^2 + \nu _{\alpha , \beta }(E)^2\right) H^2\mathop {\mathrm {ch}}\nolimits _1^{\beta '}(E). \end{aligned}$$

  (12)

Evidently, Conjecture 2.4 (for the case of $\omega , B$ proportional to H) is a special case of (*). Conversely, consider the assumptions of (*). By Lemma 4.3, E is $\nu _{\alpha ', \beta '}$-semistable, where $\beta '$ is as above, and $\alpha '^2 = \alpha ^2 + \nu _{\alpha , \beta }(E)^2$. Moreover, a simple computation shows $\nu _{\alpha ', \beta '}(E) = 0$. Therefore, Conjecture 2.4 implies the statement (*).

Finally, a straightforward computation shows that the inequalities (12) and (10) are equivalent; for this purpose, let us use the abbreviations $e_i := H^{3-i}\mathop {\mathrm {ch}}\nolimits _i^\beta (E)$ for $0 \le i \le 3$. Note that by our assumptions, $e_1 > 0$. With this notation, expanding inequality (12) yields:

$$\begin{aligned}&e_3 - \nu _{\alpha , \beta }e_2 + \frac{1}{2} \nu _{\alpha , \beta }^2 e_1 - \frac{1}{6} \nu _{\alpha , \beta }^3 e_0\\&\quad \le \frac{1}{6} \alpha ^2 e_1 + \frac{1}{6} \nu _{\alpha , \beta }^2 e_1 - \frac{1}{6} \alpha ^2 \nu _{\alpha , \beta }e_0 - \frac{1}{6} \nu _{\alpha , \beta }^3 e_0 \end{aligned}$$

Collecting related terms, substituting $\nu _{\alpha , \beta } = \frac{-\frac{1}{2} \alpha ^2 e_0 + e_2}{e_1}$ and multiplying with $6e_1$ yields:

$$\begin{aligned} 0\le & {} -6e_1 e_3 + 3e_2 \left( - \alpha ^2 e_0 + 2e_2\right) - 2 \left( -\frac{1}{2} \alpha ^2 e_0 + e_2\right) ^2 \\&+\,\alpha ^2 e_1^2 - \alpha ^2 \left( -\frac{1}{2} \alpha ^2 e_0 + e_2\right) e_0 \end{aligned}$$

This simplifies to (10). $\square$

Example 4.4

Assume that E is a slope-stable sheaf such that $c:=H^2 c_1(E)$ is the minimum positive integer of the form $H^2 F$ for integral divisor classes F; for example, this is the case when $\mathop {\mathrm {NS}}\nolimits (X) = \mathbb {Z}\cdot H$ and $c_1(E) = H$. Then E is $\nu _{\alpha , 0}$-stable for all $\alpha > 0$ by [11, Lemma 7.2.2]. Hence in that case, Conjecture 4.1 claims that

$$\begin{aligned} 3 c \mathop {\mathrm {ch}}\nolimits _3(E) \le 2 \left( H \mathop {\mathrm {ch}}\nolimits _2(E)\right) ^2. \end{aligned}$$

(13)

This generalizes [11, Conjecture 7.2.3]. In particular, let $C \subset X$ be a curve of genus g and degree $d = H C$; then $E = I_C \otimes \mathcal O(H)$ is supposed to satisfy (13). Let $K \in \mathbb {Z}$ such that the canonical divisor class $K_X = K H$. By the Hirzebruch-Riemann-Roch Theorem, we have

$$\begin{aligned} 1 - g = \chi (\mathcal O_C) = \mathop {\mathrm {ch}}\nolimits _3(\mathcal O_C) - \frac{1}{2} K d. \end{aligned}$$

Since

$$\begin{aligned} \mathop {\mathrm {ch}}\nolimits (I_C \otimes \mathcal O(H)) = \left( 1, H, \frac{1}{2} H^2 - C, \frac{1}{6} H^3 - d - \mathop {\mathrm {ch}}\nolimits _3(\mathcal O_C)\right) , \end{aligned}$$

the inequality (13) specializes to the following Castelnuovo type inequality between genus and degree of the curve (where $D = H^3$ is the degree of the threefold):

$$\begin{aligned} g \le \frac{2 d^2}{3D} + \frac{5 + 3K}{6} d + 1 \end{aligned}$$

(14)

Even for complete intersection threefolds, this inequality does not follow from existing results; see [49, Sect.  3] for progress in that direction.

Remark 4.5

The inequality (13) holds when X is an abelian threefold, or a Calabi-Yau threefold of abelian type. Moreover, since Conjecture 4.1 is equivalent to Conjecture 2.4, and since the latter has been verified for $\mathbb {P}^3$ in [11, 26], and for the quadric threefold in [39], it also applies in these two cases.

The inequality is new even in the case of $\mathbb {P}^3$: for sheaves of rank three, it is slightly weaker than classically known results, see [16, Theorem 4.3] and [31, Theorem  1.2], but no such results are known for higher rank.

5 Reduction to small $\alpha$

The goal of this section is to reduce Conjecture 4.1 to a more natural inequality, that can be interpreted as an Euler characteristic in the case of abelian threefolds, and which considers the limit as $\alpha \rightarrow 0$ and $\nu _{\alpha , \beta } \rightarrow 0$.

We continue to assume that X is a smooth projective threefold with an ample polarization $H \in \mathop {\mathrm {NS}}\nolimits (X)$. To give a slightly better control over the limit $\alpha \rightarrow 0$, we will modify the definition of the reduced central charge of (5) to the following form (which is equivalent for $\alpha \ne 0$):

$$\begin{aligned} \overline{Z}_{\alpha , \beta } = H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta + i \left( H \mathop {\mathrm {ch}}\nolimits _2^\beta - \frac{1}{2} \alpha ^2 H^3 \mathop {\mathrm {ch}}\nolimits _0^\beta \right) \end{aligned}$$

(15)

It factors via the map $\overline{v}_H$ of (11). Also, as observed in Remark 3.8, the H-discriminant can be written as the composition $\overline{\Delta }_H= \overline{q} \circ \overline{v}_H$ where $\overline{q}$ is the quadratic form on $\mathbb {Q}^3$ given by

$$\begin{aligned} (r, c, d) \mapsto c^2 - 2rd. \end{aligned}$$

Given any $E \in \mathop {\mathrm {Coh}}\nolimits ^\beta (X)$, we define $\overline{\beta }(E)$ as follows:

$$\begin{aligned} \overline{\beta }(E) := {\left\{ \begin{array}{ll} \frac{H\mathop {\mathrm {ch}}\nolimits _2(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1(E)} &{}\quad \text {if }\mathop {\mathrm {ch}}\nolimits _0(E) = 0, \\ \frac{H^2\mathop {\mathrm {ch}}\nolimits _1(E) - \sqrt{\overline{\Delta }_H(E)}}{H^3\mathop {\mathrm {ch}}\nolimits _0(E)}&{}\quad \text {if }\mathop {\mathrm {ch}}\nolimits _0(E) \ne 0. \end{array}\right. } \end{aligned}$$

(16)

The motivation behind this definition is that $\overline{\beta }(E)$ is the limit of a curve $(\alpha (t), \beta (t)) \in \mathbb {R}_{>0} \times \mathbb {R}$ for which both $\alpha (t) \rightarrow 0$ and $\nu _{\alpha (t), \beta (t)}(E) \rightarrow 0$; in other words, for which the right-hand-side of the inequality (12) goes to zero: this follows from

$$\begin{aligned} H\mathop {\mathrm {ch}}\nolimits _2^{\overline{\beta }(E)}(E) = 0. \end{aligned}$$

(17)

We also point out that $H^2 \mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }(E)}(E) > 0$ unless $\overline{\Delta }_H(E) = 0$.

The other motivation for the definition of $\bar{\beta }$ lies in the following observations, extending Lemma 3.6.

Lemma 5.1

The kernel of $\overline{Z}_{0, \overline{\beta }(E)}$ (as a subspace of $\mathbb {R}^3$) is contained in the quadric $\overline{q} =0$, and the map $(\alpha , \beta ) \rightarrow \mathop {\mathrm {Ker}}\nolimits \overline{Z}_{\alpha , \beta }$ extends to a continuous map from of $\mathbb {R}_{\ge 0} \times \mathbb {R}$ to the projectivization $\mathcal C^-/\mathbb {R}^*$ of the cone $\mathcal C^- \subset \mathbb {R}^3$ given by $\overline{q} \le 0$.

Moreover, if $\overline{\Delta }_H(E) > 0$, then the quadratic form $\overline{q}$ is positive semi-definite on the 2-plane spanned by $\overline{v}_H(E)$ and the kernel of $\overline{Z}_{0, \overline{\beta }(E)}$.

In other words, the vector $\overline{v}_H(E)$ is contained in the tangent plane to the quadric $\overline{q} = 0$ at the kernel of $\overline{Z}_{0, \overline{\beta }(E)}$; see Fig. 1.

Remark 5.2

The map $(\alpha , \beta ) \mapsto \mathop {\mathrm {Ker}}\nolimits \overline{Z}_{\alpha , \beta }$ gives a homeomorphism from $\mathbb {R}_{\ge 0} \times \mathbb {R}$ onto its image in the closed unit disc $\mathcal C^-/\mathbb {R}^*$. This can be a helpful visualization, as a central charge is, up to the action of $\mathop {\mathrm {GL}}\nolimits _2(\mathbb {R})$, determined by its kernel.

Fig. 1

A section of the negative cone $\overline{q}\le 0$ and the tangent plane passing through $\overline{v}_H(E)$ and $\ker \overline{Z}_{0,\overline{\beta }(E)}$. The other planes through $\overline{v}_H(E)$ intersecting $\overline{q}<0$ correspond to walls of stability for $\overline{v}_H(E)$

Proof of Lemma 5.1

The kernel of $\overline{Z}_{\alpha , \beta }$ is spanned by the vector $\big (1, \beta , \frac{1}{2} (\alpha ^2 + \beta ^2)\big )$, which has H-discriminant $q_H(1, \beta , \frac{1}{2} (\alpha ^2 + \beta ^2))= -\alpha ^2$. This proves the first claim.

For the second claim, we just observe that $\left( 1, \overline{\beta }(E), \frac{1}{2} \overline{\beta }(E)^2\right)$ and $\overline{v}_H(E)$ are orthogonal with respect to the bilinear form on $\mathbb {R}^3$ associated to $\overline{q}$. $\square$

The following is a limit case of Conjecture 4.1.

Conjecture 5.3

Let $E \in \mathrm {D}^{b}(X)$ be an object with the following property: there exists an open neighborhood $U \subset \mathbb {R}^2$ of $(0, \overline{\beta }(E))$ such that for all $(\alpha , \beta ) \in U$ with $\alpha > 0$, either E or E[1] is a $\nu _{\alpha , \beta }$-stable object of $\mathop {\mathrm {Coh}}\nolimits ^\beta (X)$. Then

$$\begin{aligned} \mathop {\mathrm {ch}}\nolimits _3^{\overline{\beta }(E)}(E) \le 0. \end{aligned}$$

(18)

Unless $\overline{\Delta }_H(E) = 0$, we can always make U small enough such that $H^2\mathop {\mathrm {ch}}\nolimits _1^\beta (E) > 0$ for $(\alpha , \beta ) \in U$; then E itself is an object of $\mathop {\mathrm {Coh}}\nolimits ^\beta (X)$.

A strengthening of the methods of [26] leads to the main result of this section:

Theorem 5.4

Conjectures 5.3 and 4.1 are equivalent.

Lemma 5.5

Let $E \in \mathrm {D}^{b}(X)$ be an object with $\overline{\Delta }_H(E) > 0$ that is $\nu _{\alpha ,\beta }$-stable for some $(\alpha , \beta ) \in \mathbb {R}_{>0}\times \mathbb {R}$. The point $(0, \overline{\beta }(E))$ cannot be an endpoint of a wall of tilt-stability for E. Moreover, each of the semicircles of Lemma 4.3 (along which E has to remain stable) contains $(0, \overline{\beta }(E))$ in its interior.

Proof

Recall the description of walls in Remark 2.6. As $\overline{\Delta }_H(E) > 0$ implies $H^2\mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }(E)}(E) > 0$, we can exclude the possibility of a wall given by $\nu _{\omega , B}(E) = +\infty$. The other type of walls can equivalently be defined by the property that the kernel of $\overline{Z}_{\alpha , \beta }(E)$ is contained in the 2-plane $\Pi \subset \mathbb {R}^3$ spanned by $\overline{v}_H(F)$ and $\overline{v}_H(E)$, for some destabilizing subobject $F \hookrightarrow E$. The signature of $\overline{q}$ restricted to $\Pi$ has to be (1, 1) (as it contains $\overline{v}_H(E)$ and the kernel of $\overline{Z}_{\alpha , \beta }$ for some $\alpha > 0$). If $(0, \overline{\beta }(E))$ was an endpoint of this wall, then by Lemma 5.1 the kernel of $Z_{0, \overline{\beta }(E)}$ would also be contained in $\Pi$; this is a contradiction to the second assertion of Lemma 5.1.

For the second claim, recall that the semicircles of Lemma 4.3 do not intersect. (For example, in Fig.  1, they are given by the condition that $\mathop {\mathrm {Ker}}\nolimits \overline{Z}_{\alpha , \beta }$ is contained in a given plane through $\overline{v}_H(E)$.) As we shrink the radius of the circles, their center has to converge to the point with $\alpha = 0$ and $\nu _{\alpha , \beta }(E) = 0$.

$\square$

Lemma 5.6

Objects with $\overline{\Delta }_H(E) = 0$ satisfy both Conjectures 4.1 and 5.3.

Proof

Proposition 3.12 combined with Theorem 4.2 ensures that such an object satisfies Conjecture 4.1. If E in addition satisfies the assumptions of Conjecture 5.3, we consider inequality (10) nearby $(0, \overline{\beta }(E))$. The first term vanishes identically, the second vanishes to second order at $(0, \overline{\beta }(E))$. Therefore, we must have $\mathop {\mathrm {ch}}\nolimits _3^{\overline{\beta }(E)} (E)= 0$; otherwise the third term would only have a simple zero, in contradiction to Conjecture 4.1. $\square$

Proof of Theorem 5.4

By the previous lemma, we can restrict to the case $\overline{\Delta }_H(E) > 0$ throughout. First assume that Conjecture 4.1 holds. Let E be an object as in the assumptions of Conjecture 5.3 and consider the limit of (10) as $(\alpha , \beta ) \rightarrow (0, \overline{\beta })$. Evidently the first term $\alpha ^2 \overline{\Delta }_H(E)$ goes to zero; by equation (17), the same holds for the second term $(H \mathop {\mathrm {ch}}\nolimits _2^\beta (E))^2$. Since $H^2 \mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }(E)}> 0$, the limit yields exactly (18).

For the converse, we start with three observations on inequality (10).

• (a) Consider a semicircle given by Lemma 4.3. By the proof of Theorem 4.2, inequality (10) either holds for all points on the semicircle, or it is violated for all such points; indeed, it is equivalent to inequality (12), which is just the original Conjecture 2.4 applied at the point where this semicircle intersects the curve given by $\nu _{\alpha , \beta }(E) = 0$.

• (b) Once we fix $\beta$, it is clear from Theorem 3.5 that if (10) holds for a given $\alpha _0$, then it holds for all $\alpha \ge \alpha _0$.

• (c) Finally, if we consider the semicircles of Lemma 4.3 at all points $(\alpha , \beta )$ with $\alpha > 0, \beta = \overline{\beta }(E)$, then by Lemma 5.5 they fill up all points of $\mathbb {R}_{>0} \times \mathbb {R}$ with $H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta (E) > 0$.

Now assume that Conjecture 5.3 holds. We proceed by induction on $\overline{\Delta }_H(E)$ (recall that $\overline{\Delta }_H$ only obtains non-negative integers for tilt-stable objects E).

For contradiction, let E be an object that is $\nu _{\alpha , \beta }$-stable, with $\overline{\Delta }_H(E) > 0$, and that violates conjecture (10) at this point. By Lemma 5.5 and observation (a) above, we may assume $\beta = \overline{\beta }(E)$.

Now fix $\beta = \overline{\beta }(E)$ and start decreasing $\alpha$. Since we assume (10) to be violated, we must have $\mathop {\mathrm {ch}}\nolimits _3^{\overline{\beta }(E)}(E) > 0$. If E were to remain stable as $\alpha \rightarrow 0$, then by Lemma 5.5 it would be stable in a neighborhood of $(0, \overline{\beta }(E))$ as in the conditions of Conjecture 5.3; this is a contradiction.

Therefore there must be a point $\alpha _0$ where E is strictly $\nu _{\alpha _0,\overline{\beta }(E)}$-semistable; let $E_i$ be the list of its Jordan-Hölder factors. By observation (b), E still violates Conjecture (10) at $(\alpha _0, \overline{\beta }(E))$. On the other hand, by Corollary 3.10, $\overline{\Delta }_H(E_i) < \overline{\Delta }_H(E)$ for each i; by the induction assumption, $E_i$ satisfies Conjecture 4.1.

Now the conclusion follows just as in Lemma 11.6: consider the left-hand-side of (10) as a quadratic form on $\mathbb {R}^4$ with coordinates $(H^3 \mathop {\mathrm {ch}}\nolimits _0^\beta , H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta , H \mathop {\mathrm {ch}}\nolimits _2^\beta , \mathop {\mathrm {ch}}\nolimits _3^\beta )$. The kernel of $\overline{Z}_{\alpha , \beta }$, considered as a subspace of $\mathbb {R}^4$, is negative semi-definite with respect to the quadratic form. Therefore, the claim follows from Lemma 11.7. $\square$

6 Tilt stability and étale Galois covers

Consider an étale Galois cover $f :Y \rightarrow X$ with covering group G; in other words, G acts freely on Y with quotient $X = Y/G$. In this section, we will show that tilt-stability is preserved under pull-back by f.

For this section, we again let $\omega , B \in \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$ be arbitrary classes with $\omega$ a positive real multiple of an ample.

Proposition 6.1

If $E \in \mathrm {D}^{b}(X)$, then

• (a) $E\in \mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$ if and only if $f^*E\in \mathop {\mathrm {Coh}}\nolimits ^{f^*\omega , f^*B}(Y)$, and

• (b) E is $\nu _{\omega ,B}$-semistable if and only if $f^*E$ is $\nu _{f^*\omega ,f^*B}$-semistable.

Proof

The pull-back formula for Chern characters immediately gives

$$\begin{aligned} \mu _{f^*\omega ,f^*B}(f^*F)= \mu _{\omega , B}(F) \quad \text {and} \quad \nu _{f^*\omega ,f^*B}(f^*E)= \nu _{\omega , B}(E). \end{aligned}$$

By [19, Lemma 3.2.2], a torsion-free sheaf F is $\mu _{\omega ,B}$-semistable if and only if $f^*F$ is $\mu _{f^*\omega ,f^*B}$-semistable, which directly implies (a).

Now consider $E \in \mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$. Part (a) and the above computation shows that if E is tilt-unstable, then so is $f^*E$. Conversely, assume that $f^*E$ is tilt-unstable. Let $F \hookrightarrow f^*E$ be the first step in its Harder-Narasimhan filtration with respect to $\nu _{f^*\omega , f^*B}$. Since $f^*E$ is G-equivariant, and since the HN filtration is unique and functorial, the object F must also be G-equivariant. Hence it is the pull-back of an object $F'$ in $\mathrm {D}^{b}(X)$. Using part (a) again, we see that $F'$ must be an object of $\mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$. Applying the same arguments to the quotient $f^*E/F$, we see that $F'$ is a destabilizing subobject of E in $\mathop {\mathrm {Coh}}\nolimits ^{\omega , B}(X)$. $\square$

Example 6.2

Let $n\in \mathbb {Z}_{>0}$. Let $X=Y$ be an abelian threefold and let $\underline{n}:X\rightarrow X$ be the multiplication by n map. Then $\underline{n}$ has degree $n^6$, and $\underline{n}^*H=n^2 H$ for any class $H\in \mathrm {NS}(X)$; see e.g. [9, Corollary 2.3.6 and Chapter  16].

We also obtain directly the following consequence:

Proposition 6.3

If Conjecture 2.4 holds for tilt-stability with respect to $\nu _{f^*\omega , f^*B}$ on Y, then it also holds for tilt-stability with respect to $\nu _{\omega , B}$ on X.

7 Abelian threefolds

Let (X, H) be a polarized abelian threefold. In this section we prove Theorem 1.1.

Most of this section will be concerned with proving Conjecture 5.3, the case where $\omega$ and B are proportional to H. For $(\alpha ,\beta )\in \mathbb {R}_{>0}\times \mathbb {R}$, we let $\omega =\sqrt{3} \alpha H$ and $B = \beta H$. We can also assume that H is the class of a very ample divisor, which, by abuse of notation, will also be denoted by H.

We let $E\in \mathrm {D}^{b}(X)$ be an object satisfying the assumptions of Conjecture 5.3. By Lemma 5.6, we can also assume $\overline{\Delta }_H(E)>0$, and so $H^2\mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }(E)}(E)>0$. We proceed by contradiction, and assume that

$$\begin{aligned} \mathop {\mathrm {ch}}\nolimits _3^{\overline{\beta }(E)}(E) >0. \end{aligned}$$

7.1 Idea of the proof

Consider the Euler characteristic of the pull-backs

$$\begin{aligned} \underline{n}^* \left( E(-\overline{\beta }(E)H)\right) \end{aligned}$$

via the multiplication by n map. If we pretend that $E(-\overline{\beta }(E)H)$ exists, this Euler characteristic grows proportional to $n^6$; we will show a contradiction via restriction of sections to divisors.

The proof naturally divides into two cases: if $\overline{\beta }(E)$ is rational, then $\underline{n}^* \left( E(-\overline{\beta }(E)H)\right)$ exists when n is sufficiently divisible, and the above approach works verbatim; otherwise, we need to use Diophantine approximation of $\overline{\beta }(E)$.

7.2 Proof of Conjecture 5.3, rational case

We assume that $\overline{\beta }(E)$ is a rational number.

7.2.1 Reduction to $\overline{\beta }(E)=0$

Let $q \in \mathbb {Z}_{>0}$ such that $q \overline{\beta }(E) \in \mathbb {Z}$, and consider the multiplication map $\underline{q}:X\rightarrow X$. By Proposition 6.1, $\underline{q}^*E$ still violates Conjecture 5.3. By definition, we have

$$\begin{aligned} \overline{\beta }({{\underline{q}}^*E}) = q^2 \overline{\beta }(E) \in \mathbb {Z}. \end{aligned}$$

Replacing E with $\underline{q}^*E$, we may assume that $\overline{\beta }(E)$ is an integer. Replacing E again with $E\otimes \mathcal O_X(-\overline{\beta }(E) H)$, we may assume that E satisfies the assumptions of Conjecture 5.3, as well as

• $\overline{\beta }(E)=0$, and so $H.\mathop {\mathrm {ch}}\nolimits _2(E)=0$, and

• $\mathop {\mathrm {ch}}\nolimits _3(E)>0$, and so $\mathop {\mathrm {ch}}\nolimits _3(E)\ge 1$.

7.2.2 Asymptotic Euler characteristic

We look at $\chi (\mathcal O_X,\underline{n}^*E)$, for $n\rightarrow \infty$. By the Hirzebruch-Riemann-Roch Theorem, we have

$$\begin{aligned} \chi (\mathcal O_X,\underline{n}^*E) = n^6 \mathop {\mathrm {ch}}\nolimits _3(E) \ge n^6. \end{aligned}$$

(19)

The goal is to bound $\chi (\mathcal O_X,\underline{n}^*E)$ from above with a lower order in n.

7.2.3 First bound

We claim that

$$\begin{aligned} \chi (\mathcal O_X,\underline{n}^*E) \le \hom (\mathcal O_X,\underline{n}^*E) + \mathop {\mathrm {ext}}\nolimits ^2(\mathcal O_X,\underline{n}^*E). \end{aligned}$$

(20)

Indeed, both $\underline{n}^*E$ and $\mathcal O_X[1]$ are objects of $\mathop {\mathrm {Coh}}\nolimits ^{\beta =0}(X)$. Hence, for all $k\in \mathbb {Z}_{>0}$, we have

$$\begin{aligned} \hom ^{-k-1}(\mathcal O_X,\underline{n}^*E)&=\hom ^{-k}(\mathcal O_X[1],\underline{n}^*E)=0,\\ \hom ^{k+2}(\mathcal O_X,\underline{n}^*E)&=\hom ^{k+3}(\mathcal O_X[1],\underline{n}^*E)=\hom ^{-k}(\underline{n}^*E,\mathcal O_X[1]) =0. \end{aligned}$$

7.2.4 Hom-vanishing from stability

To bound the above cohomology groups, we use Hom-vanishing between line bundles and $\underline{n}^*E$. By Corollary 3.11, all objects of $\mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ of the form $\mathcal O_X(uH)$ and $\mathcal O_X(-uH)[1]$ are $\nu _{\alpha ,\beta }$-stable, for all $u>0$ and $\beta$ close to 0. For $(\beta ,\alpha )\rightarrow (0,0)$, we have

$$\begin{aligned}&\nu _{\alpha ,\beta }(\mathcal O_X(uH)) \rightarrow \frac{u}{2} >0\nonumber \\&\nu _{\alpha ,\beta }(\mathcal O_X(-uH)[1]) \rightarrow -\frac{u}{2} <0\nonumber \\&\nu _{\alpha ,\beta }(\underline{n}^*E) \rightarrow 0, \end{aligned}$$

(21)

and therefore

$$\begin{aligned} \nu _{\alpha ,\beta }(\mathcal O_X(H))> \nu _{\alpha ,\beta }(\underline{n}^*E) > \nu _{\alpha ,\beta }(\mathcal O_X(-H)[1]). \end{aligned}$$

Applying the standard Hom-vanishing between stable objects and Serre duality, we conclude

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (\mathcal O_X(H),\underline{n}^*E)=0 \quad \text { and }\quad \mathop {\mathrm {Ext}}\nolimits ^2(\mathcal O_X(-H),\underline{n}^*E)=0. \end{aligned}$$

(22)

7.2.5 Restriction to divisors

We will use this Hom-vanishing to restrict sections to divisors; we will repeatedly apply the following immediate observation.

Lemma 7.1

Let $F_1, \dots , F_m$ be a finite collection of sheaves. Then any globally generated linear system contains an open subset of divisors D with

$$\begin{aligned} \mathop {\mathrm {Tor}}\nolimits ^i(\mathcal O_D, F_j) = 0 \end{aligned}$$

for all $i > 0$ and $j = 1, \dots , m$.

Proof

We choose D such that it does not contain any of the associated points of $F_j$, i.e., such that the natural map $F_j(-D) \rightarrow F_j$ is injective. $\square$

In particular, for general D, a finite number of short exact sequences restrict to exact sequences on D, and taking cohomology sheaves of a complex E commutes with restriction to D.

7.2.6 Bound on $\hom (\mathcal O_X,\underline{n}^*E)$

We want to show

$$\begin{aligned} \hom (\mathcal O_X,\underline{n}^*E) = O(n^4). \end{aligned}$$

(23)

We consider the exact triangle in $\mathrm {D}^{b}(X)$

$$\begin{aligned} \underline{n}^*E \otimes \mathcal O_X(-H) \rightarrow \underline{n}^*E \rightarrow (\underline{n}^*E)\otimes \mathcal O_D, \end{aligned}$$

where D is a general smooth linear section of H. By (22), we have

$$\begin{aligned} \hom (\mathcal O_X,\underline{n}^*E) \le \hom (\mathcal O_X,(\underline{n}^*E)\otimes \mathcal O_D). \end{aligned}$$

We consider the cohomology sheaves of E and the exact triangle in $\mathrm {D}^{b}(X)$

$$\begin{aligned} H^{-1}(E)[1] \rightarrow E \rightarrow H^0(E). \end{aligned}$$

Since D is general, Lemma 7.1 gives

$$\begin{aligned} \hom \bigl (\mathcal O_X,(\underline{n}^*E)\otimes \mathcal O_D\bigr )\le h^0\bigl (D,(\underline{n}^*H^{0}(E))|_D\bigr ) + h^1\bigl (D,(\underline{n}^*H^{-1}(E))|_D\bigr ). \end{aligned}$$

The bound (23) will then follow from Lemma 7.3 below. We first recall a general bound on global sections of sheaves restricted to hyperplane sections, which is due to Simpson and Le Potier, and can be deduced as a consequence of the Grauert-Mülich Theorem:

Theorem 7.2

[19, Corollary 3.3.3] Let Y be a smooth projective complex variety of dimension $n\ge 1$ and let H be a very ample divisor on Y. Let $F\in \mathop {\mathrm {Coh}}\nolimits (Y)$ be a torsion-free sheaf. Then, for a general sequence of hyperplane section $D_1,\dots ,D_n\in |H|$ and for all $d=1,\dots ,n$, we have

$$\begin{aligned} h^0(Y_d,F |_{Y_d}) \le {\left\{ \begin{array}{ll} \frac{\mathop {\mathrm {ch}}\nolimits _0(F)H^n}{d!} \left( \mu _H^{+}(F) + \frac{\mathop {\mathrm {ch}}\nolimits _0(F)-1}{2} + d\right) ^d &{}\quad \text { if } \mu _{H}^{+}(F)\ge 0 \\ 0 &{}\quad \text { if } \mu _{H}^{+}(F)<0 \end{array}\right. }, \end{aligned}$$

where $Y_n=Y$ and $Y_d:=D_1\cap \dots \cap D_{n-d}$.

Notice that in the actual statement of [19, Corollary   3.3.3] there is a factor $H^n$; this is already included in our definition of slope.

Lemma 7.3

Let Q be a sheaf on X and let L be a line bundle. For all $i=0,1,2$ and for D a smooth very general surface in the linear system |H|, we have

$$\begin{aligned} h^i(D, (\underline{n}^*Q \otimes L) |_D) = O(n^4). \end{aligned}$$

Proof

We assume first that Q is torsion-free. Notice that the multiplication map $\underline{n}$ preserves slope-stability and the rank. Therefore, by Theorem 7.2, we have

$$\begin{aligned} h^0(D,(\underline{n}^*Q \otimes L)|_D)&\le \frac{\mathop {\mathrm {ch}}\nolimits _0(Q) H^3}{2} \left( \mu _H^{+}(\underline{n}^*Q \otimes L) + \frac{\mathop {\mathrm {ch}}\nolimits _0(Q)-1}{2} + 2\right) ^2\\&= \frac{\mathop {\mathrm {ch}}\nolimits _0(Q) H^3}{2} \left( \mu _H^+(Q)\right) ^2 n^4 + O(n^3). \end{aligned}$$

The $h^2$-estimate follows similarly, by using Serre Duality on D. Finally, the Hirzebruch-Riemann-Roch Theorem on D gives

$$\begin{aligned} h^1 (D,(\underline{n}^*Q \otimes L)|_D)&= -\chi (D,(\underline{n}^*Q \otimes L)|_D) + h^0(D,(\underline{n}^*Q \otimes L)|_D)\\&\quad + h^2(D,(\underline{n}^*Q \otimes L)|_D)\\&= O(n^4). \end{aligned}$$

This finishes the proof in the torsion-free case.

For a general sheaf Q, we take a resolution

$$\begin{aligned} 0 \rightarrow M \rightarrow N \rightarrow Q \rightarrow 0, \end{aligned}$$

with N locally-free and M torsion-free. Since D is very general, Lemma 7.1 applies, giving

$$\begin{aligned} h^i(D,(\underline{n}^*Q \otimes L)|_D) \le h^i(D,(\underline{n}^*N \otimes L)|_D) + h^{i+1}(D,(\underline{n}^*M \otimes L)|_D). \end{aligned}$$

Hence the result follows from the previous case. $\square$

7.2.7 Bound on $\mathop {\mathrm {ext}}\nolimits ^2(\mathcal O_X,\underline{n}^*E)$

This is similar to the previous case. We consider the exact triangle

$$\begin{aligned} \underline{n}^*E \rightarrow \underline{n}^*E \otimes \mathcal O_X(H) \rightarrow (\underline{n}^*E\otimes \mathcal O_X (H)) \otimes \mathcal O_D. \end{aligned}$$

Again, we apply (22), Lemmas 7.1 and 7.3 and reach

$$\begin{aligned} \mathop {\mathrm {ext}}\nolimits ^2(\mathcal O_X,\underline{n}^*E)&\le \mathop {\mathrm {ext}}\nolimits ^1(\mathcal O_X,(\underline{n}^*E\otimes \mathcal O_X(H)) \otimes \mathcal O_D)\nonumber \\&\le h^1(D,(\underline{n}^*H^0(E) \otimes \mathcal O_X(H))|_D) \nonumber \\&\quad + h^2(D,(\underline{n}^*H^{-1}(E) \otimes \mathcal O_X(H))|_D)\nonumber \\&= O(n^4). \end{aligned}$$

(24)

7.2.8 Conclusion

By (19), (20), (23), and (24), we have

$$\begin{aligned} n^6 \le \chi (\mathcal O_X,\underline{n}^*E) = O(n^4), \end{aligned}$$

which gives a contradiction for n sufficiently large.

7.3 Proof of Conjecture 5.3, irrational case

Now assume that $\overline{\beta }(E)\in \mathbb {R}{\setminus }\mathbb {Q}$ is an irrational number. As a consequence $\mathop {\mathrm {ch}}\nolimits _0(E)\ne 0$ and, for all $\beta \in \mathbb {Q}$, $H\mathop {\mathrm {ch}}\nolimits _2^\beta (E)\ne 0$.

By assumption, there exists $\epsilon >0$ such that E is $\nu _{\alpha ,\beta }$-stable for all $(\alpha ,\beta )$ in

$$\begin{aligned} V_\epsilon := \left\{ (\alpha ,\beta )\in \mathbb {R}_{>0}\times \mathbb {R}\,:\, 0< \alpha<\epsilon ,\, \overline{\beta }(E)-\epsilon<\beta <\overline{\beta }(E)+\epsilon \right\} . \end{aligned}$$

By the Dirichlet approximation theorem, there exists a sequence $\left\{ \beta _n=\frac{p_n}{q_n}\right\} _{n\in \mathbb {N}}$ of rational numbers such that

$$\begin{aligned} \left| \overline{\beta }(E) - \frac{p_n}{q_n} \right|< \frac{1}{q_n^2}< \epsilon \end{aligned}$$

(25)

for all n, and with $q_n \rightarrow +\infty$ as $n\rightarrow +\infty$.

7.3.1 The Euler characteristic

The function $f(\beta ) = \mathop {\mathrm {ch}}\nolimits _3^\beta (E)$ has derivatives $f'(\beta ) = -H \mathop {\mathrm {ch}}\nolimits _2^\beta (E)$ and $f''(\beta ) = H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta (E)$; since $H \mathop {\mathrm {ch}}\nolimits _2^{\overline{\beta }}(E) = 0$ and $H^2 \mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }}(E) > 0$, the point $\beta = \overline{\beta }(E)$ is a local minimum. Thus, for large n, we have

$$\begin{aligned} \mathop {\mathrm {ch}}\nolimits _3^{\beta _n}(E)> \mathop {\mathrm {ch}}\nolimits _3^{\overline{\beta }(E)}(E)>0. \end{aligned}$$

Consider the multiplication map $\underline{q_n}:X\rightarrow X$. We let

$$\begin{aligned} F_n:= \underline{q_n}^*E \otimes \mathcal O_X(-p_nq_nH). \end{aligned}$$

By Lemma 6.1, $F_n$ is $\nu _{\alpha ,0}$-stable, for all $\alpha >0$ sufficiently small. We have

$$\begin{aligned} \chi (\mathcal O_X,F_n) = \mathop {\mathrm {ch}}\nolimits _3(F_n) = q_n^6 \mathop {\mathrm {ch}}\nolimits _3^{\beta _n}(E) > q_n^6 \mathop {\mathrm {ch}}\nolimits _3^{\overline{\beta }(E)}(E). \end{aligned}$$

(26)

By (20), it is again enough to bound both $\hom (\mathcal O_X,F_n)$ and $\mathop {\mathrm {ext}}\nolimits ^2(\mathcal O_X,F_n)$ from above.

7.3.2 Hom-vanishing

As $\alpha \rightarrow 0$, we have

$$\begin{aligned} \nu _{\alpha ,0}(F_n) \rightarrow q_n^2 \frac{H\mathop {\mathrm {ch}}\nolimits _2^{\beta _n}(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1^{\beta _n}(E)}. \end{aligned}$$

We can bound this term as follows:

$$\begin{aligned}&\left|q_n^2 \frac{H\mathop {\mathrm {ch}}\nolimits _2^{\beta _n}(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1^{\beta _n}(E)}\right|\\&\quad = q_n^2 \left| \frac{ H\mathop {\mathrm {ch}}\nolimits _2^{\overline{\beta }}(E) - (\beta _n-\overline{\beta }) H^2\mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }}(E) + \frac{1}{2} (\beta _n - \overline{\beta })^2 H^3 \mathop {\mathrm {ch}}\nolimits _0(E)}{H^2\mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }}(E) - (\beta _n - \overline{\beta }) H^3 \mathop {\mathrm {ch}}\nolimits _0(E)}\right| \\&\quad = q_n^2 \left| \beta _n - \overline{\beta }\right| \left| \frac{H^2 \mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }}(E) - \frac{1}{2} (\beta _n - \overline{\beta })H^3 \mathop {\mathrm {ch}}\nolimits _0(E)}{H^2 \mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }}(E) - (\beta _n - \overline{\beta })H^3 \mathop {\mathrm {ch}}\nolimits _0(E)}\right| \\&\quad \le 1 \cdot \left( 1 + \left|\frac{\frac{1}{2} (\beta _n - \overline{\beta })H^3 \mathop {\mathrm {ch}}\nolimits _0(E)}{H^2 \mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }}(E) - (\beta _n - \overline{\beta })H^3 \mathop {\mathrm {ch}}\nolimits _0(E)}\right| \right) \rightarrow 1. \end{aligned}$$

Here we used $H^2 \mathop {\mathrm {ch}}\nolimits _2^{\overline{\beta }(E)}(E) = 0$ in the second equality, and $H^2 \mathop {\mathrm {ch}}\nolimits _1^{\overline{\beta }(E)}(E) > 0$ in the limit.

By comparison with (21), it follows that

$$\begin{aligned} \nu _{\alpha , \beta _n} (\mathcal O_X(3H))> \nu _{\alpha ,\beta _n}(F_n) > \nu _{\alpha ,\beta }(\mathcal O_X(-3H)[1]) \end{aligned}$$

for $\alpha \rightarrow 0$ and n sufficiently large; therefore

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (\mathcal O_X(3H),F_n)=0 \quad \text { and }\quad \mathop {\mathrm {Ext}}\nolimits ^2(\mathcal O_X(-3H),F_n)=0. \end{aligned}$$

(27)

7.3.3 Bound on $\hom (\mathcal O_X,\underline{m}^*F_n)$ and conclusion

Proceeding as in the rational case, we consider the exact triangle

$$\begin{aligned} F_n\otimes \mathcal O_X(-3H) \rightarrow F_n \rightarrow F_n\otimes \mathcal O_D, \end{aligned}$$

where D is a general smooth surface in the linear system |3H|. By (27), we have

$$\begin{aligned} \hom (\mathcal O_X,F_n)&\le \hom (\mathcal O_X,F_n\otimes \mathcal O_D)\\&\le h^0(D,H^0(F_n)|_D) + h^1(D,H^{-1}(F_n)|_D). \end{aligned}$$

The following is the analogue of Lemma 7.3:

Lemma 7.4

Let Q be a sheaf on X and let L be a line bundle. Then

$$\begin{aligned} h^i(D, (\underline{q_n}^* Q(-p_nq_n H) \otimes L)|_D) = O(q_n^4), \end{aligned}$$

for all i, and for D a general smooth surface in |3H|.

Proof

By the same argument as in the proof of Lemma 7.3, we may assume that Q is torsion-free. Applying Theorem 7.2 in our case we obtain, for general D,

$$\begin{aligned}&h^0\left( D,(\underline{q_n}^* Q(-p_nq_n H) \otimes L)|_D\right) \\&\quad \le \frac{\mathop {\mathrm {ch}}\nolimits _0(Q)(3H)^3}{2} \left( \mu _{3H}^{+}(\underline{q_n}^* Q(-p_nq_n H) \otimes L) + \frac{\mathop {\mathrm {ch}}\nolimits _0(Q)-1}{2} + 2\right) ^2\\&\quad = \frac{3 \mathop {\mathrm {ch}}\nolimits _0(Q) H^3}{2} \left( \mu _{H,\beta _n}^+(Q)\right) ^2 q_n^4 + O(q_n^3)\\&\quad = \frac{3 \mathop {\mathrm {ch}}\nolimits _0(Q) H^3}{2} \left( \mu _{H,\overline{\beta }(E)}^+(Q)\right) ^2 q_n^4 + O(q_n^3), \end{aligned}$$

The $h^1$ and $h^2$ bounds follow from Serre duality and the Riemann-Roch Theorem. $\square$

Applying Lemma 7.4 to the cohomology sheaves of E in combination with Lemma 7.1, we get

$$\begin{aligned} \hom (\mathcal O_X,F_n) = O(q_n^4). \end{aligned}$$

The same argument gives a similar bound on $\mathop {\mathrm {ext}}\nolimits ^2(\mathcal O_X,F_n)$ and a contradiction to (26). This completes the proof of Conjecture 5.3, and therefore Conjecture 4.1, for abelian threefolds.

7.4 Proof of Theorem 1.1

Let now $B\in \mathrm {NS}(X)_\mathbb {R}$ be an arbitrary divisor class and $\omega$ a positive multiple of H. In the abelian threefold case, we can use Conjecture 5.3 to deduce Conjecture 2.4 in this more general case.

We let $E\in \mathop {\mathrm {Coh}}\nolimits ^{\omega ,B}(X)$ be as in Conjecture 2.4. We first assume that $B\in \mathrm {NS}(X)_\mathbb {Q}$ is rational. Then, by Proposition 6.1, we can assume B integral. By taking the tensor product with $\mathcal O_X(-B)$, we can then assume E is $\nu _{\omega ,0}$-semistable. Conjecture 2.4 then follows directly from Conjecture 4.1 and Theorem 5.4.

Finally, we take B irrational. Since (6) is additive, by considering its Jordan-Hölder factors we can assume E is $\nu _{\omega ,B}$-stable. By using Theorem 3.5 and Remark 2.5, we can deform $(\omega , B)$ to $(\omega ', B')$ with $B'$ rational (and $\omega '$ still proportional to H), such that E is still $\nu _{\omega ',B'}$-stable with $\nu _{\omega ', B'}(E) = 0$. But, if (6) does not hold for $(\omega , B)$, then it does not hold for $(\omega ', B')$ sufficiently close, giving a contradiction to what we just proved.

8 Construction of Bridgeland stability conditions

It was already established in [11] that Conjecture 2.4 implies the existence of Bridgeland stability conditions on X, except that the notion of support property was ignored. This property ensures that stability conditions deform freely, and exhibit well-behaved wall-crossing.

In this section, we show that the equivalent Conjecture 4.1 is in fact strong enough to deduce the support property, and to construct an explicit open subset of the space of stability conditions. In the following section, we will show that in the case of abelian threefolds, this open set is in fact an entire component of the space of stability conditions.

8.1 Statement of results

Fix a threefold X with polarization H; we assume throughout this section that Conjecture 4.1 is satisfied for the pair (X, H). We consider the lattice $\Lambda _H\cong \mathbb {Z}^4$ generated by vectors of the form

$$\begin{aligned} \left( H^3 \mathop {\mathrm {ch}}\nolimits _0(E), H^2\mathop {\mathrm {ch}}\nolimits _1(E), H\mathop {\mathrm {ch}}\nolimits _2(E), \mathop {\mathrm {ch}}\nolimits _3(E) \right) \in \mathbb {Q}^4 \end{aligned}$$

together with the obvious map $v_H:K(X) \rightarrow \Lambda _H$.

We refer to Appendix 1 for the definition of stability conditions on $\mathrm {D}^{b}(X)$ with respect to $(\Lambda _H, v_H)$; it is given by a pair $\sigma = (Z, \mathcal P)$, where $\mathcal P$ is a slicing, and the central charge Z is a linear map $Z :\Lambda _H \rightarrow \mathbb {C}$. The main result of [13] shows that the space $\mathop {\mathrm {Stab}}\nolimits _H(X)$ of such stability conditions is a four-dimensional complex manifold such that

$$\begin{aligned} \mathcal Z:\mathop {\mathrm {Stab}}\nolimits _H(X) \rightarrow \mathop {\mathrm {Hom}}\nolimits (\Lambda _H, \mathbb {C}), \quad (Z, \mathcal P) \mapsto Z \end{aligned}$$

is a local isomorphism. In Proposition 11.5 we make this deformation result more effective. This result will be essential in the following, where we will construct an explicit open subset of this manifold. We let $\mathfrak C\subset \Lambda _H \otimes \mathbb {R}\cong \mathbb {R}^4$ be the cone over the twisted cubic

$$\begin{aligned} \mathfrak C= \left\{ \left( x^3, x^2y, \frac{1}{2} xy^2, \frac{1}{6} y^3\right) \,:\,x, y \in \mathbb {R}\right\} , \end{aligned}$$

which contains $v_H(\mathcal O_X(uH))$ for all $u \in \mathbb {Z}$.

Definition 8.1

Consider the open subset $\mathfrak V\subset \mathop {\mathrm {Hom}}\nolimits (\Lambda _H, \mathbb {C})$ of central charges whose kernel intersects $\mathfrak C$ only at the origin. We let $\mathfrak P\subset \mathfrak V$ be the connected component containing $Z_H^{\mathrm {basic}}$ defined by

$$\begin{aligned} Z_H^{\mathrm {basic}}(E) = \left[ - \mathop {\mathrm {ch}}\nolimits _3(E) + \frac{1}{2} H^2 \mathop {\mathrm {ch}}\nolimits _1(E) \right] + i \left[ H \mathop {\mathrm {ch}}\nolimits _2(E) - \frac{1}{6} H^3 \mathop {\mathrm {ch}}\nolimits _0(E) \right] . \end{aligned}$$

(28)

Let $\widetilde{\mathfrak P}$ be its universal covering.

The goal of this section is the following precise version of Theorem 1.3:

Theorem 8.2

Let (X, H) be a polarized threefold for which Conjecture 4.1 is satisfied. Then there is an open embedding $\widetilde{\mathfrak P} \subset \mathop {\mathrm {Stab}}\nolimits _H(X)$ for which the following diagram commutes:

We will prove this theorem by constructing an explicit family of stability conditions following the construction of [11], and then applying the deformation arguments of Proposition 11.5.

8.2 Alternative description of $\mathfrak P$

We will need a more explicit description of the set $\mathfrak P$ before proceeding to prove our main result.

The group $\mathop {\mathrm {GL}}\nolimits _2^+(\mathbb {R})$ of $2 \times 2$-matrices with positive determinant acts on $\mathfrak P$ on the left by post-composing a central charge with the induced $\mathbb {R}$-linear map of $\mathbb {R}^2 \cong \mathbb {C}$. There is also an action of $\mathbb {R}$ on $\mathfrak P$ on the right: for $\beta \in \mathbb {R}$, the multiplication by $e^{-\beta H}$ in $K(\mathrm {D}^{b}(X))$ corresponds to a linear selfmap of $\Lambda _H \otimes \mathbb {R}$ which leaves $\mathfrak C$ invariant; therefore we can act on $\mathfrak P$ by pre-composing with this linear map.

Lemma 8.3

There is a slice of $\mathfrak P$ with respect to the $\mathop {\mathrm {GL}}\nolimits _2^+(\mathbb {R})$-action given by central charges of the form

$$\begin{aligned} Z_{\alpha , \beta }^{a, b} := \left[ -\mathop {\mathrm {ch}}\nolimits ^\beta _3 + b H \mathop {\mathrm {ch}}\nolimits ^\beta _2 + a H^2 \mathop {\mathrm {ch}}\nolimits ^\beta _1 \right] + i \left[ H \mathop {\mathrm {ch}}\nolimits ^\beta _2 - \frac{1}{2} \alpha ^2 H^3 \mathop {\mathrm {ch}}\nolimits ^\beta _0 \right] \end{aligned}$$

for all $\alpha , \beta , a, b \in \mathbb {R}$ satisfying $\alpha > 0$ and

$$\begin{aligned} a > \frac{1}{6} \alpha ^2 + \frac{1}{2} \left|b\right| \alpha . \end{aligned}$$

(29)

This slice is simply-connected.

It follows that it is simultaneously a slice of the $\widetilde{\mathop {\mathrm {GL}}\nolimits }_2^+(\mathbb {R})$-action on $\widetilde{\mathfrak P}$.

Proof

Consider a central charge $Z \in \mathfrak P$. Since $Z(0, 0, 0, 1) \ne 0$ by definition of $\mathfrak P$, we may use the action of rotations and dilations to normalize to the assumption $Z(0, 0, 0, 1) = -1$. Now consider the functions

$$\begin{aligned} r(x):= & {} \mathfrak {R}Z\left( 1, x, \frac{1}{2} x^2, \frac{1}{6} x^3\right) = - \frac{1}{6} x^3 + O(x^2) \quad \text {and}\\ i(x):= & {} \mathfrak {I}Z\left( 1, x, \frac{1}{2} x^2, \frac{1}{6} x^3\right) = O(x^2) \end{aligned}$$

for $Z \in \mathfrak P$ normalized as above; their coefficients vary continuously with Z. They can never vanish simultaneously, by definition of $\mathfrak P$. In the case of $Z_H^{\mathrm {basic}}$, the function $r(x) = -\frac{1}{6} x^3 + \frac{1}{2} x$ has zeros as $x = - \sqrt{3}$, $x = 0$, $x = \sqrt{3}$, whereas $i(x) = \frac{1}{2} x^2 - \frac{1}{6}$ has zeros at $x = \pm \sqrt{\frac{1}{3}}$. This configuration of zeros on the real line will remain unchanged as Z varies: r(x) will always have three zeros, and i(x) will have two zeros lying between the first and second, and the second and third zero of r(x), respectively.

We now use the action of $\mathbb {R}$ on $\mathfrak P$ from the right to ensure that $x = 0$ is always the midpoint of the two zeros of i(x). The sign of the leading coefficient of i(x) must remain constant as Z varies; therefore, we can use vertical rescaling of $\mathbb {R}^2$ to normalize it to be $+\frac{1}{2}$. Since the sign of $i(0) = \mathfrak {I}Z(\mathcal O_X)$ is constant within this slice, it has to be negative; hence there exists a unique $\alpha \in \mathbb {R}_{>0}$ such that $i(0) = - \frac{1}{2} \alpha ^2$.

On the slice we have constructed thus far, we still have the action of $\mathbb {R}$ given by sheerings of $\mathbb {R}^2 \cong \mathbb {C}$ that leave the real line fixed. Since $\mathfrak {I}Z(\mathcal O_X) = i(0) < 0$, there is a unique such sheering that forces $Z(\mathcal O_X)$ to be real. Summarizing, we have constructed a slice in which all central charges are of the form

$$\begin{aligned} Z_{\alpha , \beta = 0}^{a, b} := \left[ -\mathop {\mathrm {ch}}\nolimits _3 + b H \mathop {\mathrm {ch}}\nolimits _2 + a H^2 \mathop {\mathrm {ch}}\nolimits _1 \right] + i \left[ H \mathop {\mathrm {ch}}\nolimits _2 - \frac{1}{2} \alpha ^2 H^3 \mathop {\mathrm {ch}}\nolimits _0 \right] . \end{aligned}$$

In this form, the zeros of $i(x) = \frac{1}{2} x^2 - \frac{1}{2}\alpha ^2$ are $x = \pm \alpha$; thus the kernel of Z intersects the twisted cubics if and only if

$$\begin{aligned} a = \frac{1}{6} \alpha ^2 \pm \frac{1}{2} b \alpha . \end{aligned}$$

In the case of $Z_H^{\mathrm {basic}}$, we have $\alpha = \sqrt{\frac{1}{3}}$, $b = 0$ and $a = \frac{1}{2}$, which is bigger than the right-hand-side. It follows that the inequality (29) holds in the whole connected component of our slice.

Conversely, given a central charge $Z_{\alpha , \beta }^{a, b}$ as described in the lemma, we can first use the action of $\mathbb {R}$ to reduce to the case $\beta = 0$. The coefficients of the linear functions $\mathfrak {I}Z, \mathfrak {R}Z$ are in one-to-one correspondence with the coefficients of r(x) and i(x), respectively; these are, up to scaling, uniquely determined by the configurations of zeros of r(x) and i(x) on the real line. But our conditions ensure that we can continuously deform the configuration of zeros into the one corresponding to $Z_H^{\mathrm {basic}}$. $\square$

Remark 8.4

From the proof of the lemma one can also deduce the following more intrinsic description of the set $\mathfrak P$. Consider the twisted cubic $\overline{\mathfrak C}$ in projective space $\mathbb {P}^3(\mathbb {R})$. There is an open subset of central charges Z with the following properties: the hyperplanes $\mathfrak {I}Z = 0$ and $\mathfrak {R}Z = 0$ both intersect $\overline{\mathfrak C}$ in three distinct points; moreover, their configuration on $\overline{\mathfrak C} \cong S^1$ are such that the zeros of the two functions alternate. This open set has two components: one of them is $\mathfrak P$, the other is obtained from $\mathfrak P$ by composing central charges with complex conjugation.

Moreover, one can also deduce the description given in the introduction.

Recall the H-discriminant

$$\begin{aligned} \overline{\Delta }_H= \left( H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta \right) ^2 - 2 H^3 \mathop {\mathrm {ch}}\nolimits _0^\beta H \mathop {\mathrm {ch}}\nolimits ^\beta _2. \end{aligned}$$

defined in (7), Let us also introduce a notation of the remainder term of (10):

$$\begin{aligned} \overline{\nabla }_H^\beta := 4 \left( H \mathop {\mathrm {ch}}\nolimits _2^\beta (E)\right) ^2 - 6 H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta (E) \mathop {\mathrm {ch}}\nolimits _3^\beta (E). \end{aligned}$$

Lemma 8.5

There is an open interval $I_{\alpha }^{a, b} \subset \mathbb {R}_{>0}$ such that the kernel of $Z_{\alpha , \beta }^{a, b}$ is negative definite with respect to the quadratic form $K \overline{\Delta }_H+ \overline{\nabla }_H^\beta$ for all $K \in I_{\alpha }^{a, b}$. In case $b = 0$, the interval is given by $I_{\alpha }^{a, b} = (\alpha ^2, 6a)$. In case $b \ne 0$, it is a subinterval of $(\alpha ^2, 6a)$ satisfying $\frac{1}{2} \left( \alpha ^2 + 6a\right) \in I_{\alpha }^{a, b}$ for all b, and

$$\begin{aligned} I_{\alpha }^{a, b'} \subset I_{\alpha }^{a, b} \end{aligned}$$

whenever $\left|b'\right| > \left|b\right|$.

Proof

Let us use the coordinates $e_i := H^{3-i}\mathop {\mathrm {ch}}\nolimits _i^\beta$ on $\Lambda _H \otimes \mathbb {R}$. In these coordinates, the kernel of $Z_{\alpha , \beta }^{a, b}$ is generated by the vectors $(1, 0, \frac{1}{2} \alpha ^2, \frac{1}{2} b\alpha ^2)$ and (0, 1, 0, a). The intersection matrix for the symmetric pairing associated to $K \overline{\Delta }_H+ \overline{\nabla }_H^\beta$ is

$$\begin{aligned} \begin{pmatrix} - K \alpha ^2 + \alpha ^4 &{} \quad -3 b \alpha ^2 \\ - 3b \alpha ^2 &{} \quad K - 6a \end{pmatrix}. \end{aligned}$$

The diagonal entries are negative for $K \in (\alpha ^2, 6a)$ (which is non-empty by the assumptions on a). In case $b \ne 0$, we additionally need to ensure that the determinant

$$\begin{aligned} \alpha ^2 \left( -K^2 + 6a K + K\alpha ^2 - 6a \alpha ^2 - 9 b^2 \alpha ^2\right) \end{aligned}$$

is positive. Solving the quadratic equation, one obtains a subinterval of $(\alpha ^2, 6a)$ symmetric around the midpoint $K = \frac{1}{2} \left( \alpha ^2 + 6a\right)$ with the properties as claimed. $\square$

8.3 Review: construction of stability conditions

We will use [13, Proposition 5.3] to construct stability conditions. It says that a stability condition is equivalently determined by a pair $\sigma =(Z,\mathcal A)$, where $Z:\Lambda _H\rightarrow \mathbb {C}$ is a group homomorphism (called central charge) and $\mathcal A\subset \mathrm {D}^{b}(X)$ is the heart of a bounded t-structure, which have to satisfy the following three properties:

• (a) For any $0 \ne E\in \mathcal A$ the central charge $Z(v_H(E))$ lies in the following semi-closed upper half-plane:

  $$\begin{aligned} Z(v_H(E)) \in \mathbb {R}_{>0} \cdot e^{(0,1]\cdot i\pi } \end{aligned}$$

  (30)

  We can use $\mathfrak {R}Z$ and $\mathfrak {I}Z$ to define a notion of slope-stability on the abelian category $\mathcal A$ via the slope function $\lambda _\sigma (E)= -\frac{\mathfrak {R}Z(v_H(E))}{\mathfrak {I}Z(v_H(E))}$

• (b) With this notion of slope-stability, every object in $E \in \mathcal A$ has a Harder-Narasimhan filtration $0 = E_0 \hookrightarrow E_1 \hookrightarrow \dots \hookrightarrow E_n = E$ such that each $E_i/E_{i-1}$ is $\lambda _\sigma$-semistable, with $\lambda _\sigma (E_1/E_0)> \lambda _\sigma (E_2/E_1)> \dots > \lambda _\sigma (E_n/E_{n-1})$.

• (c) (support property) There is a constant $C>0$ such that, for all $\lambda _\sigma$-semistable object $E\in \mathcal A$, we have

  $$\begin{aligned} ||v_H(E) ||\le C |Z(v_H(E)) |, \end{aligned}$$

  where $||\underline{\,\,}||$ is a fixed norm on $\Lambda _H\otimes \mathbb {R}\cong \mathbb {R}^4$.

For brevity, we will write Z(E) instead of $Z(v_H(E))$. Shifts of $\lambda _\sigma$-(semi)stable objects are called $\sigma$-(semi)stable.

8.4 Explicit construction of stability conditions

We start by reviewing (a slightly generalized version of) the construction of stability conditions in [11].

We define a heart $\mathcal A^{\alpha ,\beta }(X)\subset \mathrm {D}^{b}(X)$ as a tilt of $\mathop {\mathrm {Coh}}\nolimits ^{\beta }(X)$: we let

$$\begin{aligned} \mathcal T_{\alpha , \beta }'&= \left\{ E \in \mathop {\mathrm {Coh}}\nolimits ^{\beta } (X)\,:\,\text {any quotient }E \twoheadrightarrow G\text { satisfies }\nu _{\alpha ,\beta }(G) > 0\right\} \\ \mathcal F_{\alpha ,\beta }'&= \left\{ E \in \mathop {\mathrm {Coh}}\nolimits ^{\beta } (X)\,:\,\text {any subobject }F \hookrightarrow E\text { satisfies }\nu _{\alpha ,\beta }(F) \le 0\right\} \end{aligned}$$

and define

$$\begin{aligned} \mathcal A^{\alpha ,\beta }(X) = \langle \mathcal T_{\alpha ,\beta }', \mathcal F_{\alpha ,\beta }'[1] \rangle . \end{aligned}$$

Theorem 8.6

[11] Let (X, H) be a polarized threefold for which Conjecture  4.1 holds. Assume that $\alpha , \beta \in \mathbb {Q}$, and that $\alpha , \beta , a, b$ satisfy (29). Then the pair $\sigma = \left( Z_{\alpha , \beta }^{a, b}, \mathcal A^{\alpha , \beta }(X)\right)$ satisfy conditions (a) and (b) above.

Proof

The case $b = 0$ is [11, Corollary 5.2.4], and the same arguments apply here; let us review them briefly.

The construction of the heart directly ensures that if $E \in \mathcal A^{\alpha , \beta }(X)$, then $\mathfrak {I}Z_{\alpha , \beta }^{a, b} \ge 0$. Moreover, if $E\in \mathcal A^{\alpha ,\beta }(X)$ is such that $\mathfrak {I}Z_{\alpha ,\beta ,s}(E)=0$, then E fits into an exact triangle $F[1] \rightarrow E \rightarrow T$ where

• T is a zero-dimensional torsion sheaf, and

• $F\in \mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ is $\nu _{\alpha ,\beta }$-semistable with $\nu _{\alpha ,\beta }(E)=0$ (in particular, $H^2\mathop {\mathrm {ch}}\nolimits _1^{\beta }(F)> 0$).

We have $Z_{\alpha , \beta }^{a, b}(T) = - \mathrm {length}(T) < 0$ if T is non-trivial. To treat F[1], observer that $\nu _{\alpha , \beta }(F) = 0$ implies

$$\begin{aligned} \frac{1}{2} \alpha ^2 H^3 \mathop {\mathrm {ch}}\nolimits _0^\beta (F) = H \mathop {\mathrm {ch}}\nolimits _2^\beta (F). \end{aligned}$$

Therefore we can use Conjecture 4.1 and Theorem 3.5 to estimate

$$\begin{aligned} \begin{aligned} Z_{\alpha , \beta }^{a, b}(F[1])&= \mathop {\mathrm {ch}}\nolimits _3^\beta (F) - b H\mathop {\mathrm {ch}}\nolimits _2^\beta (F) - a H^2 \mathop {\mathrm {ch}}\nolimits _1(F) \\&\le \frac{1}{6} \alpha ^2 H^2 \mathop {\mathrm {ch}}\nolimits _1(F) + \left|b\right| \frac{1}{2} \alpha ^2 H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta (F) - a H^2 \mathop {\mathrm {ch}}\nolimits _1(F) < 0. \end{aligned} \end{aligned}$$

By [11, Proposition 5.2.2], the category $\mathcal A^{\alpha ,\beta }(X)$ is noetherian. Since $\mathfrak {I}Z_{\alpha ,\beta ,s}$ is a discrete subset of $\mathbb {R}$, we can apply [10, Proposition 12.2] to deduce the existence of Harder-Narasimhan filtrations. $\square$

8.5 Support property

The next step towards proving Theorem 8.2 is to establish the support property for the stability conditions constructed in Theorem 8.6. Our overall goal is the following analogue of Theorem 3.5.

Let $\sigma = (Z, \mathcal A) \in \widetilde{\mathfrak P} \subset \mathop {\mathrm {Stab}}\nolimits _H(X)$ be a stability condition in the open subset given in Theorem 8.6. We may assume that $Z = Z_{\alpha , \beta }^{a, b}$ is of the form given in Lemma 8.3. We also choose a constant $K \in I_{\alpha }^{a, b}$ in accordance with Lemma 8.5.

Theorem 8.7

Under the assumptions above, every $\sigma$-semistable object E satisfies

$$\begin{aligned} Q_K^\beta (E) : = K \overline{\Delta }_H(E) + \overline{\nabla }_H^\beta (E) \ge 0. \end{aligned}$$

(31)

Moreover, up to shift the heart $\mathcal A$ is of the form $\mathcal A= \mathcal A^{\alpha , \beta }(X)$.

We will treat only the case $b = 0$; then $I_{\alpha }^{a, b} = (\alpha ^2, 6a)$. We will also shorten notation and write $Z_{\alpha , \beta }^a$ instead of $Z_{\alpha , \beta }^{a, 0}$, and $I_{\alpha }^a$ instead of $I_{\alpha }^{a,0}$. The case $b\ne 0$ will then follow directly by Proposition 11.5.

The analogy between Theorems 3.5 and 8.7 is reflected also in their proof. We first treat the rational case:

Lemma 8.8

Let (X, H) be a polarized threefold and $(\alpha ,\beta )\in \mathbb {Q}_{>0}\times \mathbb {Q}$. Assume that Conjecture 4.1 holds for this pair $(\alpha ,\beta )$. Then for any $a > \frac{1}{6} \alpha ^2$, the pair $\sigma _{\alpha ,\beta }^a=(Z_{\alpha ,\beta }^a,\mathcal A^{\alpha ,\beta }(X))$ satisfies the support property; more precisely, the inequality (31) holds for all $\sigma _{\alpha ,\beta }^a$-semistable objects E and all $K \in I_{\alpha }^a$.

We first need an analogue of Lemma 2.7.

Let us denote by $H_\beta ^i$ the i-th cohomology object with respect to the t-structure $\mathop {\mathrm {Coh}}\nolimits ^{\beta }(X)$.

Lemma 8.9

Let $E\in \mathcal A^{\alpha ,\beta }(X)$ be a $\sigma _{\alpha ,\beta }^a$-semistable object, for all $a \gg 1$ sufficiently big. Then it satisfies one of the following conditions:

• (a) $H^{-1}_\beta (E)=0$ and $H^0_\beta (E)$ is $\nu _{\alpha ,\beta }$-semistable;

• (b) $H^{-1}_\beta (E)$ is $\nu _{\alpha ,\beta }$-semistable and $H^0_\beta (E)$ is either 0 or supported in dimension 0.

Proof

Consider the exact sequence

$$\begin{aligned} 0 \rightarrow H^{-1}_\beta (E)[1] \rightarrow E \rightarrow H^0_\beta (E) \rightarrow 0. \end{aligned}$$

in $\mathcal A^{\alpha ,\beta }(X)$. For $a\rightarrow +\infty$, we have

$$\begin{aligned} \mathfrak {R}Z_{\alpha , \beta }^a\left( H^{-1}_\beta (E)[1]\right) = -a H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta (H^{-1}_\beta (E)) + \mathrm {const} \rightarrow -\infty \end{aligned}$$

unless $H^{-1}_\beta (E) = 0$, and

$$\begin{aligned} \mathfrak {R}Z_{\alpha , \beta }^a\left( H^0_\beta (E)\right) = a H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta \left( H^0_\beta (E)\right) - \mathop {\mathrm {ch}}\nolimits _3^\beta \left( H^0_\beta (E)\right) \ge -\mathop {\mathrm {ch}}\nolimits _3^\beta \left( H^0_\beta (E)\right) . \end{aligned}$$

Their imaginary parts are constant, with $\mathfrak {I}Z_{\alpha , \beta }^a\left( H^0_\beta (E)\right) \ne 0$ unless $H^0_\beta (E)$ is supported in dimension zero. This means that E is $\sigma _{\alpha , \beta }^a$-unstable for $a \gg 0$ unless $H^{-1}_\beta (E) = 0$, or $H^0_\beta (E)$ is a zero-dimensional torsion sheaf, or $H^0_\beta (E) = 0$.

In the limit $a \rightarrow +\infty$, we have $Z_{\alpha , \beta }^a \rightarrow \overline{Z}_{\alpha , \beta }$ up to rescaling of the real part; this implies the $\nu _{\alpha , \beta }$-semistability of the cohomology objects in both cases.

$\square$

We have already proved the analogue of Lemma 3.6, as part of Lemma 8.5. This also enables us to use the result from Appendix 1.

Proof of Lemma 8.8

Throughout the proof, we fix $\alpha$ and $\beta$.

If E is strictly $\sigma _{\alpha ,\beta }^a$-semistable, and if (31) holds for all of the Jordan-Hölder factors $E_i$ of E, then by Lemma 11.6, it also holds for E. We may therefore assume that E is stable.

We also notice that if $F\in \mathop {\mathrm {Coh}}\nolimits ^{\beta }(X)$ is $\nu _{\alpha ,\beta }$-semistable, then Conjecture 4.1 and Theorem 3.5 show that in particular, it satisfies $Q_K^\beta (F) \ge 0$ for every $K > \alpha ^2$.

We proceed by induction on $f(E):=H\mathop {\mathrm {ch}}\nolimits _2^\beta (E) - \frac{\alpha ^2 \, H^3}{2} \mathop {\mathrm {ch}}\nolimits _0^\beta (E) = \mathfrak {I}Z_{\alpha , \beta }^a(E)$, which is a non-negative function on $\mathcal A^{\alpha , \beta }(X)$ with discrete values.

We fix $a_0 > \frac{1}{6} \alpha ^2$ and $K \in (\alpha ^2, 6a_0)$. Let E be a $\sigma _{\alpha ,\beta }^{a_0}$-stable object in $\mathcal A^{\alpha ,\beta }(X)$.

If E remains $\sigma _{\alpha ,\beta }^a$-semistable, for all $a > a_0$, then by Lemma 8.9 either $E=H_\beta ^0(E)$ is $\nu _{\alpha ,\beta }$-semistable, or $H_\beta ^{-1}(E)$ is $\nu _{\alpha ,\beta }$-semistable and $H^0(E)$ is either 0 or supported in dimension 0. In the first case, we already pointed out above that E satisfies (31). In the second case, $H^2\mathop {\mathrm {ch}}\nolimits _1^\beta (E)=H^2\mathop {\mathrm {ch}}\nolimits _1^\beta (H_\beta ^{-1}(E)[1])<0$ and $\mathop {\mathrm {ch}}\nolimits _3^\beta (H_\beta ^0(E))\ge 0$. Therefore $\overline{\Delta }_H(E) = \overline{\Delta }_H(H_\beta ^{-1}(E))$ and

$$\begin{aligned} \overline{\nabla }_H^\beta (E)= & {} \overline{\nabla }_H^\beta (H^{-1}_\beta (E)) - 6 H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta (H^{-1}_\beta (E)[1]) \mathop {\mathrm {ch}}\nolimits _3^\beta (H^0_\beta (E)) \\\ge & {} \overline{\nabla }_H^\beta (H^{-1}_\beta (E)). \end{aligned}$$

Since (31) holds for $H_\beta ^{-1}(E)$, it holds also for E.

Otherwise, E will be unstable for a sufficiently big. Every possibly destabilizing subobject or quotient F has $f(F) < f(E)$ (since f is non-negative, and since the subcategory of objects $F \in \mathcal A^{\alpha , \beta }(X)$ with $f(F) = 0$ has maximum possible slope with respect to $Z_{\alpha , \beta }^a$ for all a).

Therefore they obey the induction assumption; since $K \in (\alpha ^2, 6a_0) \subset (\alpha ^2, 6a)$, this means that all these possible subobject or quotients satisfy (31) with respect to our choice of K. Since $Z_{\alpha , \beta }^a$ has negative definite kernel with respect to $Q_K^\beta$ for all $a \ge a_0$, this is equivalent to a support property type statement, see Appendix 1. It follows that E satisfies well-behaved wall-crossing along our path. Hence, there will exist $a_1> a_0$ such that E is strictly $\sigma _{\alpha ,\beta }^{a_1}$-semistable. But all the Jordan-Hölder factors $E_i$ of E have strictly smaller f. Using the induction assumption again, we see that they satisfy $Q_K^\beta (E_i) \ge 0$; therefore, we can again apply Lemma 11.6 to deduce the same claim for E. $\square$

The combination of Lemma 8.3, Theorem 8.6 and Lemma 8.8 together with Proposition 11.5 leads to the following result: for each tuple $\alpha , \beta , a, b$ as in Theorem 8.6 (in particular $\alpha , \beta \in \mathbb {Q}$), we obtain an open subset $U(\alpha , \beta , a, b) \subset \mathop {\mathrm {Stab}}\nolimits _H(X)$ of stability conditions by deforming the pair $(Z_{\alpha , \beta }^{a, b}, \mathcal A^{\alpha , \beta }(X))$. The associated open subsets $\mathcal Z(U(\alpha , \beta , a, b))$ of central charges combine to cover the set $\mathfrak P$. To conclude the proof of Theorems 8.2 and 8.7, we need to show that the sets $U(\alpha , \beta , a, b)$ glue to form a continuous family covering $\widetilde{\mathfrak P}$.

This is done by the following analogue of Proposition 12.2.

Proposition 8.10

There is a continuous family of Bridgeland stability conditions in ${\mathop {\mathrm {Stab}}\nolimits }_H(X)$, parameterized by the set

$$\begin{aligned} (\alpha , \beta , a) \in \mathbb {R}_{>0}\times \mathbb {R}\times \mathbb {R}, \quad a > \frac{1}{6} \alpha ^2 \end{aligned}$$

via

$$\begin{aligned} (\alpha ,\beta , a) \mapsto \sigma ^a_{\alpha , \beta } := \left( Z_{\alpha , \beta }^a, \mathcal A^{\alpha , \beta }(X)\right) . \end{aligned}$$

Indeed, deformations of the central charge $Z_{\alpha , \beta }^{a, b}$ for $b \ne 0$ (while keeping $\alpha , \beta , a$ fixed) do not change the heart, as modifying b only affects the real part of the central charge. Acting on these stability conditions by $\mathop {\mathrm {GL}}\nolimits _2^+(\mathbb {R})$ produces the entire set $\widetilde{\mathfrak P}$.

To prove Proposition 8.10, we need a few preliminary results. We will use the notion of a pre-stability condition, which is a stability condition that does not necessarily satisfy the support property; see Appendix 1. The first result already appears implicitly in [14, Sect. 10].

Lemma 8.11

Assume that $\sigma _1 = (Z, \mathcal A_1)$ and $\sigma _2 = (Z, \mathcal A_2)$ are two pre-stability conditions with the following properties:

• (a) Their central charges agree.

• (b) There exists a heart $\mathcal B$ of a bounded t-structure such that each $\mathcal A_i$ can be obtained as a tilt of $\mathcal B$:

  $$\begin{aligned} \mathcal A_1, \mathcal A_2 \subset \langle \mathcal B, \mathcal B[1] \rangle . \end{aligned}$$

Then $\sigma _1 = \sigma _2$.

Proof

By [35, Lemma 1.1.2], for $i=1,2$, $\mathcal A_i$ is a tilt of $\mathcal B$ with respect to the torsion pair

$$\begin{aligned} \mathcal T_i := \mathcal B\cap \mathcal A_i \quad \text { and } \quad \mathcal F_i := \mathcal B\cap \mathcal A_i[-1]. \end{aligned}$$

We need to show that $\mathcal T_1=\mathcal T_2$ and $\mathcal F_1=\mathcal F_2$; in fact, since $\mathcal F_i = \mathcal T_i^\perp$, it is enough to show $\mathcal T_1 = \mathcal T_2$. Observe that, since the central charges agree, we have $\mathcal T_2 \cap \mathcal F_1 = \{0\} = \mathcal T_1 \cap \mathcal F_2$.

We let $T\in \mathcal T_2$. Consider the exact sequence in $\mathcal B$

$$\begin{aligned} 0 \rightarrow T_1 \rightarrow T \rightarrow F_1 \rightarrow 0, \end{aligned}$$

with $T_1\in \mathcal T_1$ and $F_1\in \mathcal F_1$. Since the torsion part of any torsion pair is closed under quotients, $F_1\in \mathcal T_2$, contradicting the observation above. Hence, $T\in \mathcal T_1$, and so $\mathcal T_2\subseteq \mathcal T_1$. The reverse inclusion follows similarly. $\square$

Lemma 8.12

There exists a continuous positive function $\epsilon (\alpha , \beta , a) > 0$ with the following property: if $E \in \mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ is $\nu _{\alpha , \beta }$-stable with

$$\begin{aligned} \left|\nu _{\alpha , \beta }(E)\right| < \epsilon (\alpha , \beta , a), \end{aligned}$$

then $\mathfrak {R}Z_{\alpha , \beta }^a(E) > 0$.

Proof

We first apply Conjecture 4.1, rewriting (10) as

$$\begin{aligned} 6 \mathop {\mathrm {ch}}\nolimits _3(E) \le \alpha ^2 H^2\mathop {\mathrm {ch}}\nolimits _1^\beta (E) + 4 H \mathop {\mathrm {ch}}\nolimits _2^\beta (E) \nu _{\alpha , \beta }(E). \end{aligned}$$

(32)

Now we apply Theorem 3.5. First of all, we can rewrite $\overline{\Delta }_H(E) \ge 0$ as

$$\begin{aligned} \left( H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta \right) ^2 + \frac{1}{\alpha ^2} \left( H \mathop {\mathrm {ch}}\nolimits _2^\beta - \frac{\alpha ^2}{2} H^3 \mathop {\mathrm {ch}}\nolimits _0^\beta \right) ^2 - \frac{1}{\alpha ^2} \left( H \mathop {\mathrm {ch}}\nolimits _2^\beta + \frac{\alpha ^2}{2} H^3 \mathop {\mathrm {ch}}\nolimits _0^\beta \right) ^2 \ge 0. \end{aligned}$$

By assumption,

$$\begin{aligned} \left|H \mathop {\mathrm {ch}}\nolimits _2^\beta - \frac{\alpha ^2}{2} H^3 \mathop {\mathrm {ch}}\nolimits _0^\beta \right| < \epsilon H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta \end{aligned}$$

and therefore

$$\begin{aligned} \left|H \mathop {\mathrm {ch}}\nolimits _2^\beta + \frac{\alpha ^2}{2} H^3 \mathop {\mathrm {ch}}\nolimits _0^\beta \right| < \sqrt{\alpha ^2 + \epsilon ^2}H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta . \end{aligned}$$

Summing up the last two equations we obtain

$$\begin{aligned} \left|H \mathop {\mathrm {ch}}\nolimits _2^\beta \right| \le \frac{\epsilon + \sqrt{\alpha ^2 + \epsilon ^2}}{2}H^2 \mathop {\mathrm {ch}}\nolimits _1^\beta . \end{aligned}$$

Plugging this into (32), we obtain the desired claim. $\square$

Lemma 8.13

We keep the notation as in the previous lemma. If $E \in \mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ is $\nu _{\alpha , \beta }$-stable with $\left|\nu _{\alpha , \beta }(E)\right| < \epsilon$, then $E \in \mathcal P_{\alpha , \beta }^{a}((-\frac{1}{2}, \frac{1}{2}))$.

Proof

We consider just the case $0 < \nu _{\alpha , \beta }(E)$; the opposite case follows from dual arguments.

By construction we know $E \in \mathcal A^{\alpha , \beta } = \mathcal P_{\alpha , \beta }^{a}((0,1])$. Let A be the HN-filtration factor of E with respect to $\sigma _{\alpha , \beta }^a$ and with the largest phase, and consider the associated short exact sequence $A \hookrightarrow E \twoheadrightarrow B$ in $\mathcal A^{\alpha , \beta }$. The associated long exact cohomology with respect to $\mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ shows that $A \in \mathop {\mathrm {Coh}}\nolimits ^\beta (X) \cap \mathcal A^{\alpha , \beta } = \mathcal T'_{\alpha , \beta }$; moreover, there is a sequence $H^{-1}(B) \hookrightarrow A \rightarrow E$ exact on the left with $H^{-1}(B) \in \mathcal F'_{\alpha , \beta }$.

Now consider the slopes appearing in the Harder-Narasimhan filtration of A for tilt-stability with respect to $\nu _{\alpha , \beta }$. By standard arguments using the observations in the previous paragraph, all these slopes lie in the interval $(0, \epsilon )$. Lemma 8.12 then implies $\mathfrak {R}Z_{\alpha , \beta }^a(A) > 0$, and therefore $E \in \mathcal P_{\alpha , \beta }^a((0, \frac{1}{2}))$ as we claimed. $\square$

Proof of Proposition 8.10

Consider a stability condition $\sigma _0 = (Z_0, \mathcal P_0) := \sigma _{\alpha _0, \beta _0}^{a_0}$. Let $\epsilon := \epsilon (\alpha _0, \beta _0, a_0)$ be as in Lemmas 8.12 and 8.13. Consider $(\alpha , \beta , a)$ sufficiently close to $(\alpha _0, \beta _0, a_0)$ (which we will make precise shortly). Let $\sigma _1 := \sigma _{\alpha , \beta }^{a}$, and let $\sigma _2 = (Z_{\alpha , \beta }^a, \mathcal P_2)$ be the stability condition with central charge $Z_{\alpha , \beta }^{a}$ obtained by deforming $\sigma _0$. We want to apply Lemma 8.11 with $\mathcal B= \mathcal P_0((-\frac{1}{2}, \frac{1}{2}])$.

By the support property for $\sigma _0$, and the analogous property for tilt-stability, we can require “sufficiently close” to mean that:

• If E is $\sigma _2$-stable of phase $\phi$, then $E \in \mathcal P_0((\phi -\epsilon , \phi +\epsilon ))$, and

• The analogous statement for tilt-stability with respect to $\nu _{\alpha , \beta }$ and $\nu _{\alpha _0, \beta _0}$, respectively. This means that if $E \in \mathop {\mathrm {Coh}}\nolimits ^{\beta }(X)$ is $\nu _{\alpha , \beta }$-semistable, and if $A_1, \dots , A_m$ are the Harder-Narasimhan filtration factors of E for tilt-stability with respect to $\nu _{\alpha _0, \beta _0}$, then the phases of $\overline{Z}_{\alpha _0, \beta _0}(A_i)$ differs by at most $\epsilon$ from the phase of $\overline{Z}_{\alpha , \beta }(E)$,

The first assumption implies that

$$\begin{aligned} \mathcal P_2((0,1]) \subset \mathcal P_0((-\epsilon , 1+ \epsilon ]) \subset \langle \mathcal B, \mathcal B[1] \rangle . \end{aligned}$$

The second assumption implies that if E is tilt-stable with respect to $\nu _{\alpha , \beta }$ and $\nu _{\alpha , \beta } > 0$, then all HN filtration factors $A_i$ of E with respect to $\nu _{\alpha _0, \beta _0}$ satisfy $\nu _{\alpha _0, \beta _0}(A_i) > - \epsilon$. In case $\nu _{\alpha _0, \beta _0}(A_i) > 0$ this implies $A_i \in \mathcal A^{\alpha _0, \beta _0} = \mathcal P_0((0, 1])$. Otherwise, if $- \epsilon< \nu _{\alpha _0, \beta _0}(A_i) < 0$, then Lemma 8.13 shows $A_i \in \mathcal P_0\big (\big (-\frac{1}{2}, \frac{1}{2}\big ]\big )$; overall we obtain

$$\begin{aligned} E \in \mathcal P_0\Big (\Big (-\frac{1}{2}, 1\Big ]\Big )\subset \langle \mathcal B, \mathcal B[1] \rangle . \end{aligned}$$

A similar argument implies that if E is tilt-stable with $\nu _{\alpha , \beta }\le 0$, then $E[1] \in \langle \mathcal B, \mathcal B[1] \rangle$. Combined, these two facts show that $\mathcal A^{\alpha , \beta } \subset \langle \mathcal B, \mathcal B[1] \rangle$.

We have verified all the assumptions of Lemma 8.11, which implies $\sigma _1 = \sigma _2$.

$\square$

Let us also mention the following property:

Proposition 8.14

[29, Proposition 2.1] Skyscraper sheaves are stable for all $\sigma \in \widetilde{\mathfrak P}$.

Proof (sketch)

Using the long exact cohomology sequence with respect to the heart $\mathop {\mathrm {Coh}}\nolimits (X)$, one sees that k(x) is a minimal object of $\mathop {\mathrm {Coh}}\nolimits ^\beta (X)$: otherwise, there would be a short exact sequence $E \hookrightarrow k(x) \twoheadrightarrow F[1]$ in $\mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ coming from a short exact sequence $F \hookrightarrow E \twoheadrightarrow k(x)$ of sheaves; this is a contradiction to $\mu _{H, \beta }(F) < 0$ and $\mu _{H, \beta }(E) \ge 0$. Similarly, taking the long exact cohomology sequence with respect to $\mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ of short exact sequences in $\mathcal A^{\alpha , \beta }(X)$, we see that k(x) is a minimal object of $\mathcal A^{\alpha , \beta }(X)$. $\square$

9 The space of stability conditions on abelian threefolds

In this section we prove the following:

Theorem 9.1

Let (X, H) be a polarized abelian threefold. Then $\widetilde{\mathfrak P} \hookrightarrow \mathop {\mathrm {Stab}}\nolimits _H(X)$ is a connected component of the space of stability conditions.

The fundamental reason behind Theorem 9.1 is the abundance of projectively flat vector bundles on abelian threefolds; their Chern classes are dense in the projectivization of the twisted cubic $\mathfrak C$.

Consider a slope $\mu = \frac{p}{q} \in \mathbb {Q}$ with p, q coprime and $q > 0$. Then there exists a family of simple vector bundles $E_{p/q}$ that are semi-homogeneous in the sense of Mukai, have slope ${\frac{p}{q}}$ and Chern character

$$\begin{aligned} \mathop {\mathrm {ch}}\nolimits (E_{p/q}) = r \cdot e^{\frac{pH}{q}}, \end{aligned}$$

see [32, Theorem 7.11]. They can be constructed as the push-forward of line bundles via an isogeny $Y \rightarrow X$ [32, Theorem 5.8], and are slope-stable [32, Proposition 6.16].

The above theorem is essentially based on the following result:

Proposition 9.2

The semi-homogeneous vector bundle $E_{p/q}$ is $\sigma$-stable for every $\sigma \in \widetilde{\mathfrak P}$.

Proof

As mentioned above, $E_{p/q}$ is slope-stable. By Corollary 3.11, either $E_{p/q}$ or $E_{p/q}[1]$ is a $\nu _{\alpha , \beta }$-stable object of $\mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ for all $\alpha > 0, \beta \in \mathbb {R}$.

Also observe that for all $K, \beta \in \mathbb {R}$, we have

$$\begin{aligned} \overline{\Delta }_H(E_{p/q}) = \overline{\nabla }_H^\beta (E_{p/q}) = 0 \Rightarrow Q_K^\beta (E_{p/q}) = 0. \end{aligned}$$

The open subsets of $\mathfrak P$ where the central charges are negative definite with respect to $Q_K^\beta = K \overline{\Delta }_H+ \overline{\nabla }_H^\beta$ for some $K, \beta$ form a covering of $\mathfrak P$; by Proposition 11.8, it is therefore enough to find a single stability condition $\sigma \in \widetilde{\mathfrak P}$ for which $E_{p/q}$ is $\sigma$-stable.

One can prove in general that $\nu _{\alpha , \beta }$-stable vector bundles are $\sigma _{\alpha , \beta }^{a, b}$-stable for $a \gg 0$; but in our situation one can argue more easily as follows. Choose $\alpha , \beta$ with $\beta < \frac{p}{q}$ (and therefore $E_{p/q} \in \mathop {\mathrm {Coh}}\nolimits ^\beta (X)$) and $\nu _{\alpha , \beta }(E) = 0$. Then $E[1] \in \mathcal A^{\alpha , \beta }(X)$ with $\mathfrak {I}Z_{\alpha , \beta }^{a, b} = 0$ for all a, b, i.e. it has maximal possible slope; therefore it is $\sigma _{\alpha , \beta }^{a, b}$-semistable. By Lemma 11.7, it must actually be strictly stable. $\square$

Proof of Theorem 9.1

Assume for a contradiction that there is a stability condition $\sigma = (Z, \mathcal P) \in \partial \widetilde{\mathfrak P}$ in the boundary of $\widetilde{\mathfrak P}$ inside $\mathop {\mathrm {Stab}}\nolimits _H(X)$. Since $\widetilde{\mathfrak P} \rightarrow \mathfrak P$ is a covering map, the central charge Z must be in the boundary $\partial \mathfrak P$ of $\mathfrak P\subset \mathop {\mathrm {Hom}}\nolimits (\Lambda _H, \mathbb {C})$; by definition, this means that there is a point $(x^3, x^2y, \frac{1}{2} xy^2, \frac{1}{6} y^3)$ on the twisted cubic $\mathfrak C$ that is contained in the kernel of Z.

If $\mu := \frac{y}{x} = \frac{p}{q}$ is rational, then we observe that every semi-homogeneous bundle $E_{p/q}$ is $\sigma$-semistable, because being $\sigma$-semistable is a closed condition on $\mathop {\mathrm {Stab}}\nolimits _H(X)$. This is an immediate contradiction, as $Z\left( E_{p/q}\right) = 0$. Similarly, if $x = 0$, we get $Z(\mathcal O_x) = 0$; yet skyscraper sheaves of points are $\sigma$-semistable by 8.14.

Otherwise, if $\mu \in \mathbb {R}{\setminus } \mathbb {Q}$, consider a sequence $(p_n, q_n)$ with

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{p_n}{q_n} = \mu , \end{aligned}$$

let $E_n := E_{{p_n}/{q_n}}$, and let $r_n = \mathop {\mathrm {rk}}E_n$. Then

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{1}{r_n} v_H(E_n) = \left( 1, \mu , \frac{1}{2} \mu ^2, \frac{1}{6} \mu ^3\right) \end{aligned}$$

and thus

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{\left|Z\left( v_H(E_n\right) \right|}{\Vert v_H(E) \Vert } = \lim _{n \rightarrow \infty } \frac{\left|Z\left( \frac{1}{r_n} v_H(E_n)\right) \right|}{\left\| \frac{1}{r_n} v_H(E) \right\| } = \frac{\left|Z\left( 1, \mu , \frac{1}{2} \mu ^2, \frac{1}{6} \mu ^3\right) \right|}{\left\| \left( 1, \mu , \frac{1}{2} \mu ^2, \frac{1}{6} \mu ^3\right) \right\| } = 0. \end{aligned}$$

This is a contradiction to the condition that $\sigma$ satisfies the support property.

$\square$

10 The space of stability conditions on some Calabi-Yau threefolds

Let X be a projective threefold with an action of a finite group G. In this section, we recall the main result of [28], which induces stability conditions on the G-equivariant derived category from G-invariant stability conditions on X; similar results are due to Polishchuk, see [35, Sect. 2.2]. We use it to construct stability conditions on Calabi-Yau threefolds that are (crepant resolutions of) quotients of abelian threefolds, thus proving Theorems 1.2, 1.3 and 1.4.

10.1 The equivariant derived category

We let $\mathop {\mathrm {Coh}}\nolimits ([X/G])$ be the abelian category of G-equivariant coherent sheaves on X, and $\mathrm {D}^{b}([X/G]):=\mathrm {D}^{b}(\mathop {\mathrm {Coh}}\nolimits ([X/G]))$. As explained in [17], the category $\mathrm {D}^{b}([X/G])$ is equivalent to the category of the G-equivariant objects in $\mathrm {D}^{b}(X)$.

The étale morphism $f :X \rightarrow [X/G]$ of Deligne-Mumford stacks induces a faithful pull-back functor

$$\begin{aligned} f^* :\mathrm {D}^{b}([X/G])\rightarrow \mathrm {D}^{b}(X). \end{aligned}$$

Let $H\in \mathop {\mathrm {NS}}\nolimits (X)$ be an ample G-invariant divisor class. We consider the space $\mathop {\mathrm {Stab}}\nolimits _H(X)$ of stability conditions on $\mathrm {D}^{b}(X)$ with respect to the lattice $\Lambda _H$ as in Sect.  8; for $\mathrm {D}^{b}([X/G])$ we use the same lattice, and the map

$$\begin{aligned} v_H^G :K(\mathrm {D}^{b}([X/G])) \rightarrow \Lambda _H, \quad v_H^G(E):=v_H(f^*(E)). \end{aligned}$$

By mild abuse of notation, we will write $\mathop {\mathrm {Stab}}\nolimits _H([X/G])$ for the space of stability conditions on $\mathrm {D}^{b}([X/G])$ satisfying the support property with respect to $(\Lambda _H, v_H^G)$. We will construct components of $\mathop {\mathrm {Stab}}\nolimits _H([X/G])$ from G-invariant components of $\mathop {\mathrm {Stab}}\nolimits _H(X)$.

10.2 Inducing stability conditions

Following [28], we consider

$$\begin{aligned} \mathop {\mathrm {Stab}}\nolimits _H^G(X) := \left\{ \sigma \in {\mathop {\mathrm {Stab}}\nolimits }_H(X)\,:\,g^*\sigma =\sigma \text {,\quad for any }g\in G\right\} . \end{aligned}$$

Here the action of g on $\mathop {\mathrm {Stab}}\nolimits _H(X)$ is given by

$$\begin{aligned} g^* (Z, \mathcal A) = \left( Z \circ (g^*)^{-1}, g^*(\mathcal A)\right) . \end{aligned}$$

For any $\sigma =(Z,\mathcal A)\in \mathop {\mathrm {Stab}}\nolimits _H^G(X)$, we define

$$\begin{aligned} (f^*)^{-1}(\sigma ):=(Z',\mathcal A') \end{aligned}$$

where

$$\begin{aligned}&Z':=Z \circ v_H^G, \\&\mathcal A':=\{E\in \mathrm {D}^{b}([X/G]) :f^*(E)\in \mathcal A\}. \end{aligned}$$

Theorem 10.1

[28] Let (X, H) be a polarized threefold with an action by a finite group G fixing the polarization. Then $\mathop {\mathrm {Stab}}\nolimits _H^G(X) \subset \mathop {\mathrm {Stab}}\nolimits _H(X)$ is a union of connected components.

Moreover, the pull-back $f^*$ induces an embedding

$$\begin{aligned} (f^*)^{-1} :\mathop {\mathrm {Stab}}\nolimits _H^G(X) \hookrightarrow \mathop {\mathrm {Stab}}\nolimits _H([X/G]) \end{aligned}$$

whose image is again a union of connected components.

Proof

The theorem is essentially a reformulation of Theorem 1.1 in [28] but some subtle issues have to be clarified. First of all, Theorem 1.1 in [28] deals with stability conditions whose central charge is defined on the Grothendieck group K(X) rather than on the lattice $\Lambda _H$. On the other hand, the same argument as in [28, Remark  2.18] shows that all the results in [28, Sect.  2.2], with the obvious changes in the statements and in the proofs, hold true if we consider pre-stability conditions as in Definition 11.1 with respect to the lattice $\Lambda _H$. Thus we will freely quote the results there.

We now observe that if $\sigma$ is a G-invariant pre-stability condition on $\mathrm {D}^{b}(X)$, then $\sigma$ satisfies the support property with respect to $v_H$ if and only if $(f^*)^{-1}(\sigma )$ satisfies the support property with respect to $v_H^G$. This is rather obvious, given the definition of $(f^*)^{-1}(\sigma )$ above, the fact that $\Lambda _H$ is invariant under the action of G and that the semistable objects in $(f^*)^{-1}(\sigma )$ are the image under $f^*$ of the semistable objects in $\sigma$ (see [28, Theorem 1.1]). Hence [28, Proposition 2.17] applies and $(f^*)^{-1}$ yields a well-defined and closed embedding.

It remains to point out that $\mathop {\mathrm {Stab}}\nolimits _H^G(X)$ is a union of connected components of $\mathop {\mathrm {Stab}}\nolimits _H(X)$. This is clear in view of the arguments in [28, Lemma 2.15] and, again, of the fact that $\Lambda _H$ is invariant under the action of G. Thus the image of $(f^*)^{-1}$ is a union of connected components as well. $\square$

An immediate consequence of the results of Sect.  8 and Theorem 10.1 is the following, which completes the proof of Theorem 1.3 (see also Examples 10.4, 10.5 below):

Proposition 10.2

Let (X, H) be a smooth polarized threefold with an action of a finite group G fixing the polarization. Assume that Conjecture 4.1 holds for (X, H). Then, given $\alpha , \beta \in \mathbb {R}$ and $\alpha , \beta , a, b$ satisfying (29), the stability condition $(Z_{\alpha , \beta }^{a, b}, \mathcal A^{\alpha , \beta }(X))$ is in $\mathop {\mathrm {Stab}}\nolimits _H^G(X)$, and $(f^*)^{-1}(\mathop {\mathrm {Stab}}\nolimits _H^G(X))$ is a non-empty union of connected components of $\mathop {\mathrm {Stab}}\nolimits _H([X/G])$.

Proof

Given Theorem 10.1, the result will follow once we prove that $(Z_{\alpha , \beta }^{a, b}, \mathcal A^{\alpha , \beta }(X))$ is in $\mathop {\mathrm {Stab}}\nolimits _H^G(X)$. Since slope-stability with respect to H is preserved by the group action, we have $g^* \mathop {\mathrm {Coh}}\nolimits ^\beta (X) = \mathop {\mathrm {Coh}}\nolimits ^\beta (X)$ for all $g \in G$. The same argument holds for tilt-stability, as

$$\begin{aligned} \nu _{\alpha ,\beta }(g^*E)=\nu _{\alpha ,\beta }(E) \end{aligned}$$

for all $g\in G$ and $E\in \mathop {\mathrm {Coh}}\nolimits ^\beta (X)$; therefore $A^{\alpha , \beta }(X)$ is G-invariant as well. Since the central charge $Z_{\alpha , \beta }^{a, b}$ is similarly preserved by G, this shows the claim. $\square$

As an immediate consequence we get the following.

Corollary 10.3

Let (X, H) be a polarized abelian threefold with an action of a finite group G fixing the polarization. Then $(f^*)^{-1}(\widetilde{\mathfrak P})$ is a connected component of $\mathop {\mathrm {Stab}}\nolimits _H([X/G])$.

Proof

By Theorem 9.1, the open subset $\widetilde{\mathfrak P}$ is a connected component of $\mathop {\mathrm {Stab}}\nolimits _H(X)$. By Proposition 10.2, we have that $\widetilde{\mathfrak P}\cap \mathop {\mathrm {Stab}}\nolimits _H^G(X)$ is not empty. Since $\mathop {\mathrm {Stab}}\nolimits _H^G(X)$ is a union of connected components of $\mathop {\mathrm {Stab}}\nolimits _H(X)$ (see Theorem 10.1), we get that $\widetilde{\mathfrak P}$ is a connected component of $\mathop {\mathrm {Stab}}\nolimits _H^G(X)$. Again by Theorem 10.1, we conclude that $(f^*)^{-1}(\widetilde{\mathfrak P})$ is a connected component of $\mathop {\mathrm {Stab}}\nolimits _H([X/G])$. $\square$

10.3 Applications

When the action of the finite group G is free, the quotient $Y=X/G$ is smooth and $\mathrm {D}^{b}(Y)\cong \mathrm {D}^{b}([X/G])$. In this case, an ample class H on X induces an ample class $H_Y$ on Y. If we take B on X to be G-invariant as well, and write $B_Y$ for the induced class on $\mathop {\mathrm {NS}}\nolimits (Y)_\mathbb {R}$, we then have, by Proposition 6.3, that Conjecture 2.4 holds for $\nu _{\sqrt{3}\alpha H_Y, B_Y}$-stability on Y if it holds for $\nu _{\sqrt{3}\alpha H, B}$-stability on X.

Here is a list of examples where X is an abelian threefold and this discussion can be implemented, concluding the proof of Theorems 1.2 and 1.4.

Example 10.4

(i) A Calabi-Yau threefold of abelian type is an étale quotient $Y=X/G$ of an abelian threefold X by a finite group G acting freely on X such that the canonical line bundle of Y is trivial and $H^1(Y,\mathbb {C})=0$. In [34, Theorem  0.1], those Calabi-Yau manifolds are classified; the group G can be chosen to be $(\mathbb {Z}/2)^{\oplus 2}$ or $D_8$, and the Picard rank of Y is 3 or 2, respectively. The following concrete example is usually referred to as Igusa’s example (see Example 2.17 in [34]). Take three elliptic curves $E_{1}$, $E_{2}$ and $E_{3}$ and set $X = E_{1} \times E_{2} \times E_{3}$. Pick three non-trivial elements $\tau _{1}$, $\tau _2$ and $\tau _3$ in the 2-torsion subgroups of $E_{1}$, $E_{2}$ and $E_{3}$, respectively. Then we define two automorphisms a and b of X by setting

$$\begin{aligned}&a(z_{1}, z_{2}, z_{3}) = (z_{1} + \tau _{1}, -z_{2}, -z_{3}) \quad \text { and }\\&b(z_{1}, z_{2}, z_{3}) = (-z_{1}, z_{2} + \tau _{2}, -z_{3} + \tau _{3}). \end{aligned}$$

By taking $G:=\langle a, b \rangle$, the quotient $Y=X/G$ is a Calabi-Yau threefold of abelian type.

(ii) Let A be an abelian surface and let E be an elliptic curve. We write $X:= A \times E$. Consider a finite group G acting on A and E, where the action on E is given by translations. Then the diagonal action on X is free, but it may have non-trivial (torsion) canonical bundle. The easiest example is by taking A as the product $E_1\times E_2$ of two elliptic curve, and the action of G only on the second factor so that $E_2/G\cong \mathbb {P}^1$. Then $Y=E_1 \times S$, where S is a bielliptic surface.

Let us now assume that X is an abelian threefold, that G acts faithfully, and that the dualizing sheaf is locally trivial as a G-equivariant sheaf. By [8], the quotient X / G admits a crepant resolution Y with an equivalence $\Phi _{\mathrm {BKR}} :\mathrm {D}^{b}(Y)\rightarrow \mathrm {D}^{b}([X/G])$. By a slightly more serious abuse of notation, we will continue to write $\mathop {\mathrm {Stab}}\nolimits _H(Y)$ for the space of stability conditions with respect to the lattice $\Lambda _H$ and the map $v_H^G \circ (\Phi _{\mathrm {BKR}})_* :K(Y) \rightarrow \Lambda _H$. By Corollary 10.3, we obtain a connected component as $\left( \Phi _{\mathrm {BKR}}\right) ^* (f^*)^{-1} \left( \widetilde{\mathfrak P}\right) \subset \mathop {\mathrm {Stab}}\nolimits _H(Y)$.

Example 10.5

We say that a Calabi-Yau threefold is of Kummer type if it is obtained as a crepant resolution of a quotient X / G of an abelian threefold X. Skyscraper sheaves will be semistable but not stable with respect to the stability conditions induced from X. We mention a few examples.

• (i) Let E be an elliptic curve, and let $X=E\times E\times E$. We consider a finite subgroup $G\subset \mathrm {SL}(3,\mathbb {Z})$ and let it act on X via the identification $X=\mathbb {Z}^3\otimes _\mathbb {Z}E$. These examples were studied in [3] and classified in [15]; there are 16 examples, and G has size at most 24. The singularities of the quotient X / G are not isolated.

• (ii) Let E be the elliptic curve with an automorphism of order 3, and let $X=E\times E\times E$. We can take $G=\mathbb {Z}/3\mathbb {Z}$ acting on X via the diagonal action. Then the crepant resolution Y of X / G is a simply connected rigid Calabi-Yau threefold containing 27 planes, see [7, Sect. 2].

  One can also take $G \subset (\mathbb {Z}/3\mathbb {Z})^3$ to be the subgroup of order 9 preserving the volume form. These examples were influential at the beginning of mirror symmetry, see [5] and references therein.

• (iii) Let X be the Jacobian of the Klein quartic curve. The group $G=\mathbb {Z}/7\mathbb {Z}$ acts on X, and again the crepant resolution Y of X / G is a simply connected rigid Calabi-Yau threefold.

• (iv) We can also provide easy examples involving three non-isomorphic elliptic curves $E_1$, $E_2$ and $E_3$. Indeed, take the involutions $\iota _i :E_i\rightarrow E_i$ such that $\iota _i(e)=-e$, for $i=1,2,3$, and set $G:=\langle \iota _1\times \iota _2\times \mathop {\mathrm {id}}\nolimits _{E_3}, \iota _1\times \mathop {\mathrm {id}}\nolimits _{E_2}\times \iota _3\rangle$. The quotient $(E_1\times E_2\times E_3)/G$ admits a crepant resolution Y which is a Calabi-Yau threefold. This is a very simple instance of the so called Borcea-Voisin construction (see [12, 50]). This yields smooth projective Calabi-Yau threefolds as crepant resolutions of the quotient $(S\times E)/G$, where S is a K3 surface, E is an elliptic curve and G is the group generated by the automorphism $f\times \iota$ of $S\times E$, with f an antisymplectic involution on S and $\iota$ the natural involution on E above. Example 2.32 in [34] is yet another instance of this circle of ideas.

Appendices

Appendix 1: Support property via quadratic forms

In this appendix, we clarify the relation between support property, quadratic inequalities for Chern classes of semistable objects, and effective deformations of Bridgeland stability conditions.

1.1 Equivalent definitions of the support property

Let $\mathcal D$ be a triangulated category, for which we fix a finite rank lattice $\Lambda$ with a surjective map $v :K(\mathcal D) \twoheadrightarrow \Lambda$. We recall the main definition of [13] with a slight change of terminology: a stability condition not necessarily satisfying the support property will be called a pre-stability condition:

Definition 11.1

A pre-stability condition on $\mathcal D$ is a pair $(Z, \mathcal P)$ where

• The central charge Z is a linear map $Z :\Lambda \rightarrow \mathbb {C}$, and

• $\mathcal P$ is a collection of full subcategories $\mathcal P(\phi ) \subset \mathcal D$ for all $\phi \in \mathbb {R}$,

such that

• (a) $\mathcal P(\phi + 1) = \mathcal P(\phi )[1]$;

• (b) For $\phi _1 > \phi _2$, we have $\mathop {\mathrm {Hom}}\nolimits (\mathcal P(\phi _1), \mathcal P(\phi _2)) = 0$;

• (c) For $0 \ne E \in \mathcal P(\phi )$, we the complex number Z(v(E)) is contained in the ray $\mathbb {R}_{>0} \cdot e^{i \pi \phi }$; and

• (d) Every E admits an HN-filtration.

  

  with $A_i \in \mathcal P(\phi _i)$ and $\phi _1> \phi _2> \dots > \phi _m$.

We write $\phi _{\sigma }^+(E) := \phi _1$ and $\phi _{\sigma }^-(E) := \phi _m$ for the maximal and minimum phase appearing in the HN filtration. The mass is defined by $m_\sigma (E) := \sum _{i=1}^m \left|Z(A_i)\right|$.

Recall the definition of the “support property” introduced by Kontsevich and Soibelman:

Definition 11.2

[21, Sect. 1.2] Pick a norm $\Vert \underline{\,\,}\Vert$ on $\Lambda \otimes \mathbb {R}$. The pre-stability condition $\sigma = (Z, \mathcal P)$ satisfies the support property if there exists a constant $C > 0$ such that for all $\sigma$-semistable objects $0 \ne E \in \mathrm {D}^{b}(X)$, we have

$$\begin{aligned} \Vert v(E) \Vert \le C \left|Z(v(E))\right| \end{aligned}$$

(33)

This notion is equivalent to $\sigma$ being “full” in the sense of [14], see [10, Proposition 12.4]. The definition is quite natural: it implies that if W is in an $\epsilon$-neighborhood of Z with respect to the operator norm on $\mathop {\mathrm {Hom}}\nolimits (\Lambda _\mathbb {R}, \mathbb {C})$ induced by $\Vert \underline{\,\,}\Vert$ and the standard norm on $\mathbb {C}$, then W(E) is in a disc of radius $\epsilon C \left|Z(E)\right|$ around Z(E) for all semistable objects E; in particular, we can bound the difference of the arguments of the complex numbers Z(E) and W(E).

Moreover, it is equivalent to the following notion; we follow Kontsevich-Soibelman and also call it “support property”:

Definition 11.3

The pre-stability condition $\sigma = (Z, \mathcal P)$ satisfies the support property if there exists a quadratic form Q on the vector space $\Lambda _\mathbb {R}$ such that

• The kernel of Z is negative definite with respect to Q, and

• For any $\sigma$-semistable object $E \in \mathrm {D}^{b}(X)$, we have

  $$\begin{aligned} Q(v(E)) \ge 0. \end{aligned}$$

Lemma 11.4

[21, Sect. 2.1] Definitions 11.2 and 11.3 are equivalent.

Proof

If $\sigma = (Z, \mathcal P)$ satisfies Definition 11.2, then the quadratic form

$$\begin{aligned} Q(w) := C^2 \left|Z(w)\right|^2 - \Vert w\Vert ^2 \end{aligned}$$

evidently satisfies both properties of Definition 11.3. Conversely, assume we are given a quadratic form Q as in Definition 11.3. The non-negative quadratic form $\left|Z(w)\right|^2$ is strictly positive on the set where $-Q(w) \le 0$; by compactness of the unit ball, there exists a constant C such that

$$\begin{aligned} C^2 \left|Z(w)\right|^2 - Q(w) \end{aligned}$$

is a positive definite quadratic form. Then Z clearly satisfies (33) with respect to the induced norm on $\Lambda _\mathbb {R}$. $\square$

1.2 Statement of deformation properties

By $\mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$ we denote the space of stability conditions satisfying the support property with respect to $(\Lambda ,v)$. By the main result of [13], the forgetful map

$$\begin{aligned} \mathcal Z:\mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D) \rightarrow \mathop {\mathrm {Hom}}\nolimits (\Lambda , \mathbb {C}), \quad (Z, \mathcal P) \mapsto Z \end{aligned}$$

is a local homeomorphism. The following result is the main purpose of this appendix:

Proposition 11.5

Assume that $\sigma = (Z, \mathcal P)\in \mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$ satisfies the support property with respect to a quadratic form Q on $\Lambda _\mathbb {R}$. Consider the open subset of $\mathop {\mathrm {Hom}}\nolimits (\Lambda , \mathbb {C})$ consisting of central charges whose kernel is negative definite with respect to Q, and let U be the connected component containing Z. Let $\mathcal U\subset \mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$ be the connected component of the preimage $\mathcal Z^{-1}(U)$ containing $\sigma$.

• (a) The restriction $\mathcal Z|_\mathcal U:\mathcal U\rightarrow U$ is a covering map.

• (b) Any stability condition $\sigma ' \in \mathcal U$ satisfies the support property with respect to the same quadratic form Q.

In other words, this proposition gives an effective version of Bridgeland’s deformation result [13, Theorem 1.2], and shows that Chern classes of semistable objects for varieties continue to satisfy the same inequalities within this class of deformations.

1.3 The quadratic form and wall-crossing

We start with the observation that the quadratic form is preserved by wall-crossing:

Lemma 11.6

Let Q be a quadratic form on $\Lambda _\mathbb {R}$. Assume that $\sigma = (Z, \mathcal P)$ is a pre-stability condition such that the kernel of Z is negative semi-definite with respect to Q. If E is strictly $\sigma$-semistable with Jordan-Hölder factors $E_1, \dots , E_m$, and if $Q(E_i) \ge 0$ for all $i =1, \dots , m$, then $Q(E) \ge 0$.

Proof

Let $\mathbb {H}_E \subset \Lambda _\mathbb {R}$ be the half-space of codimension one given as the preimage of the ray $\mathbb {R}_{\ge 0} \cdot Z(E)$, and let $\mathcal C^+ \subset \mathbb {H}_E$ be the subset defined by $Q \ge 0$. By the following Lemma, $\mathcal C^+$ is a convex cone, implying the claim. $\square$

Lemma 11.7

Let Q be a quadratic form an a real vector space V, and let $Z :V \rightarrow \mathbb {C}$ be a linear map such that the kernel of Z is semi-negative definite with respect to Q. Let $\rho$ be a ray in the complex plane starting at the origin. Then the intersection

$$\begin{aligned} \mathcal C^+ = Z^{-1}(\rho ) \cap \left\{ Q(\underline{\,\,}) \ge 0\right\} \end{aligned}$$

is a convex cone.

Moreover, if we assume that Q has signature $(2, \mathop {\mathrm {dim}}\nolimits V -2)$, and that the kernel of Z is negative definite, then any vector $w \in \mathcal C^+$ with $Q(w) = 0$ generates an extremal ray of $\mathcal C^+$.

Proof

To prove convexity we just need to show that if $w_1, w_2 \in \mathcal C^+$, then $Q(w_1 + w_2) \ge 0$. According to the taste of the reader, this can either be seen by drawing a picture of 2-plane $\Pi$ spanned by $w_1, w_2$—the only interesting case being where $Q|_{\Pi }$ has signature (1, 1)—, or by the following algebraic argument. Assume that $Q(w_1 + w_2) < 0$. Since $w_1, w_2 \in Z^{-1}(\rho )$, there exists $\lambda > 0$ such that $w_1 - \lambda w_2$ is in the kernel of Z. We therefore have

$$\begin{aligned} Q(w_1 - \lambda w_2) \le 0, \quad Q(w_1) \ge 0, \quad Q(w_1 + w_2) < 0, \quad \text {and} \quad Q(w_2) \ge 0. \end{aligned}$$

This configuration is impossible, since the quadratic function $f(x) := Q(w_1 + x w_2)$ would have too many sign changes.

To prove the second statement, observe that under these stronger assumptions and for $w_1, w_2, \lambda$ as above, we have $Q(w_1 - \lambda w_2) < 0$. This implies $Q(w_1+ w_2) >0$, from which the claim follows. $\square$

Before returning to the proof of Proposition 11.5, let us add one additional consequence:

Proposition 11.8

Assume that the quadratic form Q has signature $(2, \mathop {\mathrm {rk}}\Lambda _H -2)$. Let $U \subset \mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$ be a path-connected set of stability conditions that satisfy the support property with respect to Q. Let $E \in \mathrm {D}^{b}(X)$ be an object with $Q(E) = 0$ that is $\sigma$-stable for some $\sigma \in U$. Then E is $\sigma '$-stable for all $\sigma ' \in U$.

Proof

Otherwise there would be a wall at which E becomes strictly semi-stable. However, by the previous Lemma, $v_H(E)$ is an extremal ray of the cone $\mathcal C^+$. Therefore, all the Jordan-Hölder factors $E_i$ must have $v_H(E_i)$ proportional to $v_H(E)$, in contradiction to E being strictly stable for some nearby central charges. $\square$

1.4 Proof of the deformation property

In a sense, Lemma 11.6 is the key observation in the proof of Proposition 11.5; the remainder boils down to a careful application of local finiteness of wall-crossing, and of the precise version of the deformation result proved by Bridgeland.

To this end, we need to recall the definition of the metric on $\mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$.

Definition 11.9

[13, Proposition 8.1] The following is a generalized metric on $\mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$:

$$\begin{aligned} d(\sigma _1, \sigma _2):= & {} \sup _{0 \ne E \in \mathcal D} \Big \{ \left|\phi _{\sigma _2}^-(E) - \phi _{\sigma _1}^-(E)\right|, \left|\phi _{\sigma _2}^+(E) - \phi _{\sigma _1}^+(E)\right|, \\&\left|\log m_{\sigma _2}(E) - \log m_{\sigma _2}(E)\right| \Big \} \end{aligned}$$

Bridgeland’s proof of the deformation result in fact proves the following stronger statement:

Theorem 11.10

[13, Sects. 6, 7] Assume that $\sigma = (Z, \mathcal P)$ is a stability condition on $\mathcal D$, and let $C>0$ be a constant with respect to which $\sigma$ satisfies the support property condition (33). Let $\epsilon < \frac{1}{8}$, and consider the neighborhood $B_{\frac{\epsilon }{C}}(Z)$ of Z taken with respect to the operator norm on $\mathop {\mathrm {Hom}}\nolimits (\Lambda , \mathbb {C})$. Then there exists an open neighborhood $U \subset \mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$ containing $\sigma$, such that $\mathcal Z$ restricts to a homeomorphism

$$\begin{aligned} \mathcal Z|_U :U \rightarrow B_{\frac{\epsilon }{C}}(Z). \end{aligned}$$

Therefore, $\mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$ is a complex manifold; moreover, the generalized metric of Definition 11.9 is finite on every connected component of $\mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$.

Proof of Proposition 11.5

Consider the subset $\mathcal V\subset \mathcal U$ of stability conditions that do not satisfy the second claim; we want to prove that $\mathcal V$ is empty, thereby establishing the second claim.

Given $\sigma ' \in \mathcal V$, there exists a $\sigma '$-semistable object E with with $Q(v(E)) < 0$; by Lemma 11.6, we may assume that E is stable. By openness of stability of E, there exists a neighborhood of $\sigma '$ contained in $\mathcal V$; therefore, $\mathcal V\subset \mathcal U$ is open.

We claim that $\mathcal V\subset \mathcal U$ is also a closed subset; since $\mathcal U$ is a manifold and $\mathcal V\subset \mathcal U$ is open, it is enough to show that if $\sigma :[0,1] \rightarrow \mathcal U$ is a piece-wise linear path with $\sigma (t) \in \mathcal V$ for $0 \le t < 1$, then $\sigma (1) \in \mathcal V$. By the definition of $\mathcal V$ and Lemma 11.6 there exists an object $E_0$ that is $\sigma (0)$-stable with $Q(v(E_0)) < 0$. Since $\sigma (1) \notin \mathcal V$, there must be $0< t_1 < 1$ such that $E_0$ is strictly semistable; applying Lemma 11.6 again, it must have a Jordan-Hölder factor $\sigma (t_1)$-stable factor $E_1$ with $Q(v(E_1)) < 0$. Proceeding by induction, we obtain an infinite sequence $0=t_0<t_1< t_2< t_3< \dots < 1$ of real numbers and objects $E_i$ such that $E_i$ is $\sigma (t)$-stable for $t_i \le t < t_{i+1}$, strictly semistable with respect to $\sigma (t_{i+1})$ (having $E_{i+1}$ as a Jordan-Hölder factor), and satisfies $Q(v(E_i)) < 0$. This is a contradiction by Lemma 11.11 below.

Therefore, since $\mathcal V\subset \mathcal U$ is both open and closed, and does not contain $\sigma$, it must be empty.

It remains to prove the first claim. By Theorem 11.10, it is enough to show that there is a continuous function $C :U \rightarrow \mathbb {R}_{>0}$ such that every $\sigma \in \mathcal U$ satisfies the support property with respect to $C(\mathcal Z(\sigma ))$. This is evident from the second claim and the proof of Lemma 11.4. $\square$

Lemma 11.11

Let $\sigma :[0,1] \rightarrow \mathop {\mathrm {Stab}}\nolimits _\Lambda (\mathcal D)$ be a piece-wise linear path in the space of stability condition satisfying the support property. Assume there is a sequence $0 = t_0< t_1< t_2< \dots < 1$ of real numbers and a sequence of objects $E_0, E_1, E_2, \dots$ with the following properties:

• $E_i$ is $\sigma (t_i)$-stable.

• $E_{i}$ is $\sigma (t_{i+1})$-semistable, and $E_{i+1}$ is one of its Jordan-Hölder factors.

Such a sequence always terminates.

Proof

Assume we are given an infinite such sequence. Let $d_i := d(\sigma (t_i), \sigma (t_{i+1}))$; the assumptions imply that $\sigma$ is a path of bounded length, and hence that

$$\begin{aligned} D:= \sum _i d_i < +\infty . \end{aligned}$$

On the other hand, if we write $Z_i$ for the central charge of $\sigma (t_i)$, then

$$\begin{aligned} \left|Z_{i+1}\left( E_{i+1}\right) \right| < \left|Z_{i+1}\left( E_{i}\right) \right| = m_{\sigma (t_{i+1})}(E_i) \le e^{d_i} m_{\sigma (t_{i})}(E_i) = e^{d_i} \left|Z_{i}\left( E_{i}\right) \right|; \end{aligned}$$

using induction we deduce that the mass of all objects $E_i$ is bounded:

$$\begin{aligned} m_{\sigma (0)}(E_i) \le e^D m_{\sigma (t_i)}(E_i) = e^D \left|Z_{i}\left( E_{i}\right) \right| \le e^{2D} \left|Z_{0}\left( E_{0}\right) \right|. \end{aligned}$$

By [14, Sect. 9], this implies that there is a locally finite collection of walls of semistability for all $E_i$. Since our path is compact, it intersects only finitely many walls; since it is piece-wise linear, it intersects every wall only finitely many times. $\square$

Appendix 2: Deforming tilt-stability

The purpose of this appendix is to establish rigorously the deformation and wall-crossing properties of tilt-stability, in particular correcting [11, Corollary 3.3.3]. This will lead to variants of the results of Appendix 1 in this context. We assume that the reader of this appendix is familiar with the notion of tilt-stability as reviewed in Sects. 2 and 3, as well as with the proof of Bridgeland’s deformation result for stability conditions in [13, Sects. 6, 7].

Let X be a smooth projective threefold with polarization H; the role of $\Lambda$ and v in the previous appendix will be played by

$$\begin{aligned} \begin{aligned}&\Lambda = H^0(X, \mathbb {Z}) \oplus \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {Z}\oplus \frac{1}{2} \mathbb {Z}\\&v_H :K(X) \rightarrow \Lambda , \quad v_H(E) = \left( \mathop {\mathrm {ch}}\nolimits _0(E), \mathop {\mathrm {ch}}\nolimits _1(E), H \mathop {\mathrm {ch}}\nolimits _2(E)\right) . \end{aligned} \end{aligned}$$

We will use a variant of the notion of “weak stability” of [42], adapted to our situation:

Definition 12.1

A very weak stability condition on X is a pair $\sigma = (Z, \mathcal A)$, where $\mathcal A$ is the heart of a bounded t-structure on $\mathrm {D}^{b}(X)$, and $Z :\Lambda \rightarrow \mathbb {C}$ is a group homomorphism such that

• Z satisfies the following weak positivity criterion for every $E \in \mathcal A$:

  $$\begin{aligned} \mathfrak {R}Z(v_H(E)) \ge 0 \quad \text {and} \quad \mathfrak {R}Z(v_H(E)) = 0 \Rightarrow \mathfrak {I}Z(v_H(E)) \ge 0 \end{aligned}$$

• If we let $\nu _{Z, \mathcal A} :\mathcal A\rightarrow \mathbb {R}\cup {+\infty }$ be the induced slope function, then HN filtrations exist in $\mathcal A$ with respect to $\nu _{Z, \mathcal A}$-stability.

By induced slope function we mean that $\nu _{Z, \mathcal A}(E)$ is the usual slope $\frac{\mathfrak {I}}{\mathfrak {R}}$ of the complex number $Z(v_H(E))$ if its real part is positive, and $\nu _{Z, \mathcal A}(E) = +\infty$ if $Z(v_H(E))$ is purely imaginary or zero. The crucial difference to a Bridgeland stability condition is that $Z(v_H(E)) = 0$ is allowed for non-zero objects $E \in \mathcal A$.

Given a very weak stability condition, one can define a slicing $\mathcal P= \{\mathcal P(\phi ) \subset \mathrm {D}^{b}(X) \}_{\phi \in \mathbb {R}}$ just as in the case of a proper stability condition constructed from a heart of a t-structure: for $-\frac{1}{2} < \phi \le \frac{1}{2}$, we let $\mathcal P(\phi ) \subset \mathcal A$ be the subcategory of $\nu _{Z, \mathcal A}$-semistable objects with slope corresponding to the ray $\mathbb {R}_{>0} \cdot e^{i \pi \phi }$; this gets extended to all $\phi \in \mathbb {R}$ via $\mathcal P(\phi + n) = \mathcal P(\phi )[n]$ for $n \in \mathbb {Z}$.

This allows one to define a topology on the set of very weak stability conditions; it is the coarsest topology such that the maps $\sigma \mapsto Z$ and $\sigma \mapsto \phi _{\sigma }^\pm (E)$ are continuous, for all $E \in \mathrm {D}^{b}(X)$. Our first goal is to show tilt-stability conditions vary continuously; note that we use a slightly different normalization of the central charge than in Sect. 2:

Proposition 12.2

There is a continuous family of very weak stability conditions parameterized by $\mathbb {R}_{>0} \times \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$ given by

$$\begin{aligned} \left( \alpha , B \right) \mapsto \left( \overline{Z}_{\alpha , B}, \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)\right) \end{aligned}$$

where

$$\begin{aligned} \overline{Z}_{\alpha , B} = H^2 \mathop {\mathrm {ch}}\nolimits _1^B + i \left( H \mathop {\mathrm {ch}}\nolimits _2^B - \frac{1}{2} \alpha ^2 H^3 \mathop {\mathrm {ch}}\nolimits _0^B\right) . \end{aligned}$$

For rational B, this stability condition can be constructed by proving directly that the pair $\left( \overline{Z}_{\alpha , B}, \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)\right)$ admits Harder-Narasimhan filtrations, see [11, Lemma 3.2.4]. We will extend this to arbitrary B by deformations, and show simultaneously that these deformations glue to give a single family of very weak stability conditions.

Let us first indicate the key difficulty that prevents us from applying the methods of [13, Sects. 6, 7] directly. Let I be a small interval containing $\frac{1}{2}$; then the quasi-abelian category $\mathcal P(I)$ is not Artinian: if $x \in X$ lies on a curve $C \subset X$, then $\dots \hookrightarrow \mathcal O_C(-2x) \hookrightarrow \mathcal O_C(-x) \hookrightarrow \mathcal O_C$ is an infinite chain of strict subobjects of $\mathcal O_C$ in $\mathcal P(\frac{1}{2}) \subset \mathcal P(I)$. Therefore, the proof of [13, Lemma 7.7] does not carry over.

We now explain how to circumvent this problem. Fix $\alpha , B$ with B rational; we will use $Z := \overline{Z}_{\alpha , B}$ for the corresponding central charge. By the rational case of Theorem 3.5, proved in Sect. 3, the central charge Z satisfies the support property.⁴ Let $C > 0$ be the constant appearing in the support property; we also write $\mathcal P$ for the associated slicing.

Now consider a central charge $W := \overline{Z}_{\alpha ', B'}$, where $\alpha ',B'$ are sufficiently close to $\alpha ,B$ such that W satisfies $\Vert W - Z\Vert < \frac{\epsilon }{C}$, for some sufficiently small $\epsilon > 0$; recall that this implies that the phases of $\sigma$-semistable object change by at most $\epsilon$. We choose $\epsilon < \frac{1}{8}$ and small enough such that $\left|H^2(B'-B)\right| < \alpha H^3$ is automatically satisfied. For simplicity we also assume that $H^2(B' - B) < 0$; the other case can be dealt with analogously.

Let $I = (a, b)$ be a small interval with $a +\epsilon< \frac{1}{2} < b - \epsilon$; the key problem is to construct Harder-Narasimhan filtrations of objects in $\mathcal P(I)$ with respect to W. Our first observation is that due to our assumption $H^2(B' - B) < 0$, central charges of objects in $\mathcal P(I)$ can only “move to the left”; this is again based on the Bogomolov-Gieseker inequality for $\sigma$-stability:

Lemma 12.3

If $E \in \mathcal P((a, b))$ is $\sigma$-semistable with $\mathfrak {R}Z(E) < 0$, then also $\mathfrak {R}W(E) < 0$.

Note that the assumption is equivalent to $E \in \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)[1] \cap \mathcal P((a, b)) = \mathcal P((\frac{1}{2}, b))$.

Proof

By assumption we have $\mathfrak {R}Z(E) = H^2 \mathop {\mathrm {ch}}\nolimits _1^B (E)< 0$ and

$$\begin{aligned} \mathfrak {R}W(E) = \mathfrak {R}Z(E) - H^2(B'-B) \mathop {\mathrm {ch}}\nolimits _0(E). \end{aligned}$$

The case $\mathop {\mathrm {ch}}\nolimits _0(E) \le 0$ is trivial due to the assumption $H^2(B'-B) < 0$. Otherwise, note that $\mathfrak {I}Z(E) \ge 0$ implies

$$\begin{aligned} 2 H \mathop {\mathrm {ch}}\nolimits _2^B(E) H^3 \mathop {\mathrm {ch}}\nolimits _0(E) - \alpha ^2 \left( H^3 \mathop {\mathrm {ch}}\nolimits _0(E)\right) ^2 \ge 0. \end{aligned}$$

By using Theorem 3.5, applied to the rational class B, we also have

$$\begin{aligned}&2 H \mathop {\mathrm {ch}}\nolimits _2^B(E) H^3 \mathop {\mathrm {ch}}\nolimits _0(E) - \alpha ^2 \left( H^3 \mathop {\mathrm {ch}}\nolimits _0(E)\right) ^2\\&\quad \le \left( H^2 \mathop {\mathrm {ch}}\nolimits _1^B(E)\right) ^2- \alpha ^2 \left( H^3 \mathop {\mathrm {ch}}\nolimits _0(E)\right) ^2. \end{aligned}$$

Therefore, we deduce

$$\begin{aligned} H^2 \mathop {\mathrm {ch}}\nolimits _1^B (E) \le -\alpha H^3 \mathop {\mathrm {ch}}\nolimits _0(E). \end{aligned}$$

Using $\left|H^2(B'-B) \right| < \alpha H^3$, this implies the claim. $\square$

As in [13, Sect. 7], we define the set of semistable objects $\mathcal Q(\phi )$ to be objects of $\mathcal P((\phi -\epsilon , \phi +\epsilon ))$ that are W-semistable in a slightly larger category, e.g. in $\mathcal P((\phi - 2 \epsilon , \phi + 2\epsilon ))$. The key lemma overcoming the indicated difficulty above is the following:

Lemma 12.4

Given $E \in \mathcal P((a, b))$, there exists a filtration $0 = E_0 \hookrightarrow E_1 \hookrightarrow E_2 \hookrightarrow E_3$ such that

• $E_1 \in \mathop {\mathrm {Coh}}\nolimits ^{H, B'}(X)[1]$ and $E_1$ has no quotients $E_1 \twoheadrightarrow N$ in $\mathcal P((a, b))$ with $\mathfrak {R}W(N) \ge 0$;

• $E_2/E_1 \in \mathop {\mathrm {Coh}}\nolimits ^{H, B'}(X)$ is W-semistable in $\mathcal P((a, b))$ with $\mathfrak {R}W(E_2/E_1) = 0$;

• $E_3/E_2 \in \mathop {\mathrm {Coh}}\nolimits ^{H, B'}(X)$ and $E_3/E_2$ has no subobjects $M \hookrightarrow E_3/E_2$ in $\mathcal P((a, b))$ with $\mathfrak {R}W(M) \le 0$.

Proof

The t-structure associated to $\mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)$ gives a short exact sequence $E' \hookrightarrow E \twoheadrightarrow E''$ in $\mathcal P((a, b))$ with $E' \in \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)[1]$ and $E'' \in \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)$. Any quotient $E' \twoheadrightarrow N$ would necessarily satisfy $N \in \mathcal P((\frac{1}{2}, b))$; by Lemma 12.3, this implies $\mathfrak {R}W(N) < 0$. Thus, given a filtration as in the claim for $E''$, its preimage in E will still satisfy all the claims.

We may therefore assume $E \in \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)$. Note that $\mathop {\mathrm {Coh}}\nolimits ^{H, B'}(X)$ can be obtained as a tilt of $\mathop {\mathrm {Coh}}\nolimits ^{H, B}(X)$: there exists a a torsion pair

$$\begin{aligned} \mathcal T= \mathop {\mathrm {Coh}}\nolimits ^{H, B'}(X)[1] \cap \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X),\quad \mathcal F= \mathop {\mathrm {Coh}}\nolimits ^{H, B'}(X) \cap \mathop {\mathrm {Coh}}\nolimits ^{H, B}(X). \end{aligned}$$

Moreover,

$$\begin{aligned} T \in \mathcal T\Rightarrow \mathfrak {R}W(T) < 0 \quad \text {and} \quad F \in \mathcal F\Rightarrow \mathfrak {R}W(T) \ge 0. \end{aligned}$$

Let $E_1 \hookrightarrow E \twoheadrightarrow F$ be the short exact sequence associated to E via this torsion pair. Since $\mathcal T$ is closed under quotients, $E_1$ satisfies all the claims in the lemma; similarly, B only has subobjects with $\mathfrak {R}W(\underline{\,\,}) \ge 0$.

The existence of $E_2$ now follows from the fact that $\mathop {\mathrm {Coh}}\nolimits ^{H, B'}(X)$ admits a torsion pair whose torsion part is given by objects with $\mathfrak {R}W(\underline{\,\,}) = 0$; this is shown in the first paragraph of the proof of [11, Lemma 3.2.4], which does not use any rationality assumptions. $\square$

The existence of Harder-Narasimhan filtrations of $E_1$ and $E_3/E_2$ can now be proved with the same methods as in [13, Sect. 7]; the same goes for any $E \in \mathcal P((a, b))$ when (a, b) is an interval not intersecting the set $\frac{1}{2} + \mathbb {Z}$; this is enough to conclude the existence of HN filtrations for arbitrary $E \in \mathrm {D}^{b}(X)$, see the arguments at the end of Sect. 7 in [13]. Similar arguments apply in the case $H^2(B'-B) > 0$.

We have thus proved the claim that the tilt-stability condition $\sigma$ deforms to a very weak stability condition $\sigma '$ with central charge W. Moreover, by the construction in Lemma 12.4, its associated t-structure is exactly $\mathop {\mathrm {Coh}}\nolimits ^{H, B'}(X)$; this finishes the proof of Proposition 12.2.

Let us also observe that for $\phi \in \frac{1}{2} + \mathbb {Z}$, the subcategory $\mathcal P(\phi ) \cap \left\{ E \in \mathrm {D}^{b}(X)\,:\,v_H(E) = 0\right\}$ is unchanged under deformations: it consists of 0-dimensional torsion sheaves, shifted by $\phi - \frac{1}{2}$. These are the only semistable objects with central charge equal to zero; we will use this fact to show that tilt-stability conditions satisfy well-behaved wall-crossing:

Proposition 12.5

Fix a class $c \in \Lambda$. There exists a wall-and-chamber structure given by a locally finite set of walls in $\mathbb {R}_{>0} \times \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$ such that for an object E with $v_H(E) = c$, tilt-stability is unchanged as $(\alpha , B)$ vary within a chamber. Each of the walls is locally given by one of the following conditions on $Z = \overline{Z}_{\alpha , B}$:

• (a) Z(F) is proportional to Z(E) for some destabilizing subobject $F \hookrightarrow E$ with $v_H(F) \ne 0 \ne v_H(E/F)$, or

• (b) Z(E) is purely imaginary (if there exists a subobject or quotient F with $v_H(F) = 0$).

Proof

As indicated above, the second type of walls corresponds to the case where E has a shift of a zero-dimensional torsion sheaf as a subobject or quotient. Otherwise, any possibly destabilizing short exact sequence $F \hookrightarrow E \twoheadrightarrow E/F$ must have the properties given in (a), to which the usual arguments (e.g. in [14, Sect.   9]) based on support property apply. $\square$

This allows us to complete the proof of the Bogomolov-Gieseker type inequalities:

Proof of Theorem 3.5,

case $H^2B$ non-rational.  Consider a $\nu _{\omega ,B}$-semistable object E. We may assume have $H^2\mathop {\mathrm {ch}}\nolimits _1^B(E)\ne 0$. Using Lemma 3.7, we can assume that E is in fact $\nu _{\omega , B}$-stable. By Proposition 12.5, there is an open chamber in $\mathbb {R}_{>0} \times \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$ in which E is tilt-stable; this chamber contains points with rational B; therefore, our claim $\Delta _{H, B}^C (E) \ge 0$ follows from case $H^2B$ rational proved in Sect. 3. $\square$

Remark 12.6

(a) Alternatively, the statements of this appendix could be proved via the relation of tilt-stability to a certain polynomial stability condition (in the sense of [4]); see Sects. 4 and 5 of [11], in particular Proposition 5.1.3. The advantage is that the slicing associated to this polynomial stability condition is locally finite.

(b) Let us also explain precisely the problem with the statement of [11, Corollary 3.3.3]: if we allow arbitrary deformations of $\omega \in \mathop {\mathrm {NS}}\nolimits (X)_\mathbb {R}$, rather than just those proportional to a given polarization H, we would need to prove the support property for tilt-stable objects with respect to a non-degenerate quadratic form on the lattice

$$\begin{aligned} \Lambda = H^0(X) \oplus \mathop {\mathrm {NS}}\nolimits (X) \oplus \frac{1}{2} N_1(X), \quad v(E) = \left( \mathop {\mathrm {ch}}\nolimits _0(E), \mathop {\mathrm {ch}}\nolimits _1(E), \mathop {\mathrm {ch}}\nolimits _2(E)\right) . \end{aligned}$$

However, none of the variants of the classical Bogomolov-Gieseker inequality discussed in Sect. 3 give such a quadratic form, as they only depend on $H \mathop {\mathrm {ch}}\nolimits _2$ rather than $\mathop {\mathrm {ch}}\nolimits _2$ directly.