Abstract
In previous research, direction detection thresholds have been measured and successfully modeled by exposing participants to sinusoidal acceleration profiles of different durations. In this paper, we present measurements that reveal differences in thresholds depending not only on the duration of the profile, but also on the actual time course of the acceleration. The measurements are further explained by a model based on a transfer function, which is able to predict direction detection thresholds for all types of acceleration profiles. In order to quantify a participant’s ability to detect the direction of motion in the horizontal plane, a four-alternative forced-choice task was implemented. Three types of acceleration profiles (sinusoidal, trapezoidal and triangular) were tested for three different durations (1.5, 2.36 and 5.86 s). To the best of our knowledge, this is the first study which varies both quantities (profile and duration) in a systematic way within a single experiment. The lowest thresholds were found for trapezoidal profiles and the highest for triangular profiles. Simulations for frequencies lower than the ones actually measured predict a change from this behavior: Sinusoidal profiles are predicted to yield the highest thresholds at low frequencies. This qualitative prediction is only possible with a model that is able to predict thresholds for different types of acceleration profiles. Our modeling approach represents an important advancement, because it allows for a more general and accurate description of perceptual thresholds for simple and complex translational motions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In order to best simulate self-motion in virtual environments and to assess disorders of the vestibular system early on, it is important that we better understand the way in which we perceive self-motion. The majority of studies that have investigated direction detection thresholds for self-motion perception in humans have presented their participants with sinusoidal acceleration stimuli of different durations to investigate the influence of motion frequency on detection ability. Sinusoidal accelerations are used because they allow for an analysis within the framework of linear time-invariant (LTI) systems (see the Appendix). However, while we often experience sinusoidal acceleration motion, we also experience non-sinusoidal motion and thus in this paper we propose a model that is also able to predict direction detection thresholds for any (e.g., non-sinusoidal) translational motion. The proposed model is based on a description of otolith afferent firing rate. This is a reasonable approach, since the perception of self-motion without visual feedback is mainly governed by the vestibular system (Walsh 1961).
A prominent description of dynamic otolithic behavior is provided by Fernandez and Goldberg (1976). They directly measured the discharge rate of peripheral otolith neurons in response to sinusoidal accelerations of different frequencies in squirrel monkeys. Using Bode plots that show the gain and phase behavior of the measured output relative to the input stimulus, Fernandez and Goldberg developed a transfer function model describing the data. A transfer function is a complex-valued function describing the gain and the phase shift an LTI system performs on a sinusoidal input signal of a particular frequency (see the Appendix). As their transfer function model was also able to predict the dynamic behavior of the otolith discharge rate in response to non-sinusoidal acceleration stimuli, we hypothesized that the transfer function approach might also be well suited to describe direction detection thresholds for translational movements.
Describing perceptual thresholds in humans with a similar approach is not so straightforward: indeed, the available measurement (the threshold) is not a continuous function of time, as is the case for otolith discharge rate in monkeys. In order to identify a gain and phase relation between an input and an output signal, both signals must normally be continuous in time. This is possible, for example, when measuring eye movements as a function of acceleration inputs to the head (Robinson 1981). However, since eye movements are reflexive, they do not provide a direct measure of the perception of the human as thresholds would.
In order to still be able to relate a threshold measurement to a transfer function gain, one possible approach is to consider the inverse value of the threshold that represents a measure of the sensitivity (i.e., the gain) of the system. However, such an indirect identification approach of the system gain is only valid if sinusoidal accelerations are used and does not provide any phase information. Nevertheless, this method still allows inferring some properties of the system from the overall gain plot (see the Appendix).
The idea of identifying the gain as the inverse of thresholds was previously exploited by Benson et al. (1986). Benson measured direction detection thresholds for different frequencies and found that an increase in the frequency of a sinusoidal stimulus also leads to an increase in the gain level—corresponding to a decrease in the threshold level (Fig. 1). This indicates a sensitivity of the otolith organs not only to acceleration but also to jerk, the rate of change of acceleration with respect to time (see the Appendix for explanation). The exact opposite behavior was found in a motion detection study by Mah et al. (1989): the acceleration threshold decreased as the period of the stimulus increased, suggesting velocity sensitivity. However, in these measurements the stimuli were of higher frequency than in Benson’s study.
Data from previous motion and direction detection studies together with an illustrative model description (AP: anteroposterior). The data were offset adjusted along the y-axis so that the data points for the lowest frequencies coincide. This was done in order to highlight the qualitatively similar behaviors over certain frequency ranges which were found in different studies
While a transfer function model, based on the anatomy and physiology of the otolith organs, can explain both of these gain behaviors within a single framework, neither Benson nor Mah proposed an explicit model describing the relation between the perceptual gain and the stimulus frequency. However, Hosman and van der Vaart (1978) used a transfer function model proposed by Young and Meiry (1968) to describe thresholds for sinusoidal translational movements as a function of frequency. The gain of this model was computed based on the equations provided by Young and Meiry (1968) and fit to the inverse thresholds.
This model predicts different types of gain behavior depending on the frequency and can explain both Benson’s and Mah’s data in a single formulation. Starting from low frequencies, the gain of the model rises with increasing frequency, thus corresponding to a decrease in the detection threshold (Fig. 1). For medium frequencies, the gain remains nearly constant. For high frequencies, experimental data are lacking, but it is reasonable to assume that the sensitivity of the system decreases again, because of the physical limitations of the system. At very high frequencies, the otoconia cannot follow the accelerations anymore and the system might even be damaged.
More recently, two translational motion detection studies were published (Zaichik et al. 1999; Heerspink et al. 2005), which capture a broader range of frequencies and thereby unify Benson’s and Mah’s experiments and can also be described within a framework based on Young and Meiry’s model structure, thus confirming the power of describing perceptual thresholds with transfer functions.
To summarize, the state of the art in modeling perceptual thresholds for translational motions of sinusoidal accelerations is a transfer function model that fits the inverse of the thresholds to the gain of the model. This allows predicting direction detection thresholds for arbitrary sinusoidal motion profiles.
To the best of our knowledge, the possibility of predicting perceptual direction detection thresholds for non-sinusoidal motion profiles with a transfer function approach has not been addressed in previous studies.
Fernandez and Goldberg (1976) successfully described vestibular-related response dynamics on the neuronal level in monkeys with a linear system model. Since perception must be based on this neuronal activity, the approach to describe also the perceptual response with a transfer function model remains reasonable. Moreover, several studies concerning the vestibulo-ocular reflex (Furman et al. 1979; Buizza et al. 1985; Bouveresse et al. 1998) provide evidence for the appropriateness of a transfer function description.
The problem faced in attempting this modeling approach with humans is the following: usually the continuous output of a transfer function model given an arbitrary input stimulus represents the same physical quantity measured and used during the model identification process, e.g., eye movements or neuronal discharge rates. In the case of perceptual thresholds, the transfer function is identified by comparing the gain of the model to the inverse of the measured thresholds at some specific frequencies. Therefore, it is not clear a priori what the output of this transfer function represents. The output is not a single threshold value, but a time-varying signal, which is related to perceptual thresholds. The threshold for a sinusoidal acceleration input of a certain frequency can be predicted by simply looking at the gain of the system for that frequency and computing the inverse, but this does not easily extend to non-sinusoidal accelerations. In view of this, our proposal is to still interpret the output of the transfer function model as a function of the firing rate. This assumption, validated by the experimental results, will allow using the transfer function model output to predict thresholds also for any non-sinusoidal profile.
Methods
Participants
Six participants (3 women and 3 men) took part in the study. They were 27–31 years old and reported no vestibular problems. The participants were paid a standard fee. They did not receive any feedback about their performance during the study. The experiment was conducted in accordance with the requirements of the Helsinki Declaration.
Motion stimuli
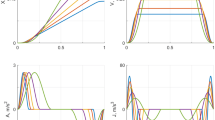
Three different types of motion profiles were used in this study. They all consisted of a translation with duration T, but the time course of the individual accelerating and braking phases was different from case to case. The profiles were named according to the shape of their accelerations: sinusoidal, triangular, and trapezoidal (Fig. 2). The ideal desired shape for the third profile should have been a rectangular one, because this would have been the profile with the steepest possible change in acceleration. However, a step in acceleration is physically impossible, and therefore a trapezoidal shape was chosen. The acceleration of the trapezoidal profile rises in dt seconds to its peak level, where \( dt = T/9.91 \). The deceleration starts at \( T/2 - dt \) and the second part of the profile (after T/2) is the mirrored version of the first part. The specific value of 9.91 was decided in pilot studies according to the capabilities of our motion simulator.
The sinusoidal profile is also known as the raised cosine bell profile (referring to its shape in the velocity domain). Since it has been used in previous studies on a similar task (Benson et al. 1986), it will allow a comparison between our results and previous findings.
The three profiles were tested for three different durations T: 1.5, 2.36 and 5.86 s, for a total of nine conditions. In order to apply these motion stimuli to the participants, we used the Max Planck Institute CyberMotion Simulator. This motion simulator is based on an anthropomorphic robot arm and can provide a large variety of motion stimuli. Further details on its hardware and software specifications are available (Robocoaster, KUKA Roboter GmbH, Germany; Teufel et al. 2007).
Experimental procedures
A four-alternative forced-choice (4AFC) task was used to find the acceleration thresholds for direction detection in the horizontal plane. Previous studies showed that the thresholds are similar for lateral and anteroposterior motions (Benson et al. 1986). Therefore, it is valid to compare all four directions in a single experiment. This also makes the task more difficult. In preliminary experiments, participants reported the perception of diagonal movements, although the true movement was lateral or anteroposterior. If a two-alternative forced-choice task had been used, they could still have given the correct answer even if perceiving a diagonal movement. That is because in a discrimination task between forward and backward, a perceived left-forward motion would be correctly reported as forward. With a 4AFC task, this resolution becomes more difficult and therefore the threshold levels are expected to be higher. This is advantageous for our experiment, because very low accelerations are difficult to produce with the simulator.
Participants initiated a trial with a button press and, after a one-second pause, the movement began. They were moved either forward, backward, left or right and were instructed to indicate the direction of their movement as fast as possible via a button press. After the answer was given, they were moved back to the starting position along the reverse path. No feedback was given to them about their performance.
A within-participants design was employed, so that every participant was tested in every condition. In order to counterbalance possible learning effects, the presentation sequence of the conditions was randomized with the constraint that the same profile type was never presented consecutively. The participants were seated in a chair with a 5-point harness. They wore light-proof goggles and the surrounding was completely dark. Acoustic white noise was played back during the movements, and a fan was installed to mask possible air movement cues during the motion of the simulator. Participants were tested in two sessions of approximately 3 h each on two different days. After a maximum of 20 min, a break was scheduled in order to prevent fatigue.
Threshold estimation
During the experiment, the peak acceleration of the tested profile was varied in order to measure a psychometric function (Wichmann and Hill 2001). Since a 4AFC task was used, the chance level of correctly detecting the direction of motion was 25% correct answers. Therefore, the inflection point of the psychometric function is located at \( (100\% - 25\% )/2 + 25\% = 62.5\% \). The peak acceleration needed to detect the correct direction of motion in 62.5% of all trials was defined as the detection threshold.
The psychometric function was modeled as a cumulative normal distribution in the logarithmic stimulus space. The mean of the underlying normal distribution coincides with the 62.5% point.
A Bayesian adaptive procedure, based on the method proposed by Kontsevich and Tyler (1999), was used to estimate the thresholds (Tanner 2008). The basic idea behind the method is to fit online a psychometric function after each newly acquired data point to the whole data set. Simulating the answer of the next trial for each possible acceleration stimulus allows to calculate for which stimulus the fit of the psychometric function would change the most. This stimulus is considered the most informative and is used for the next real trial. Making use of this method allows for a fast and accurate estimation of the threshold.
A lapse parameter was included into the fit to take into account the possibility of accidentally pressing the wrong button even if the direction was correctly perceived. It has been shown that this can significantly improve the fit (Wichmann and Hill 2001).
Twenty stimulus intensities (peak accelerations) were placed with a logarithmic spacing between \( 0.001\,{\text{m}}/{\text{s}}^{2} \) and \( 0.18\,{\text{m}}/{\text{s}}^{2} \). After each trial, the Bayesian adaptive method provides an estimate of the threshold and the variance of the estimate. To determine the threshold of a profile, participants were tested until the variance of the estimate was below a previously defined value—the break value—for 20 consecutive trials and until at least 80 trials were performed.
The predefined break value was chosen based on knowledge from similar, previously run, experiments with 300 trials per profile (Soyka et al. 2009). The estimated threshold after 300 trials was taken as ground truth. We compared the estimate after each trial to this ground truth and chose the break value in such a way that the absolute difference between the ground truth and the estimated threshold of the sample data, after the method had stopped, was smaller than \( 0.01\,{\text{m}}/{\text{s}}^{2} \).
Statistical tests
All statistical tests were performed with SPSS Statistics 17 on the threshold data expressed in logarithmic units. The experiment used a within-participants design to analyze the 2 factors (profile and duration) with 3 levels each. For the profiles, these were: triangular, sinusoidal, trapezoidal, and for the durations: 1.5, 2.36, 5.86 s.
Repeated-measures ANOVA was applied to test for main effects of the factors. Furthermore, post hoc tests with Bonferroni correction were conducted to also test for simple main effects.
Effects are referred to as significant if their P value is <0.05.
Modeling direction detection thresholds for non-sinusoidal accelerations
As discussed in the introduction, the current state of the art in modeling direction detection thresholds is the description of thresholds for translational motions of sinusoidal accelerations. This is achieved through the constraint that the gain of a transfer function model at a particular frequency should match the inverse of the threshold measured using a sinusoidal motion. This allows to predict direction detection thresholds for sinusoidal motion profiles of various frequencies using the gain of the transfer function. However, this approach does not make use of the output of the underlying transfer function and is not able to predict thresholds for non-sinusoidal accelerations.
In the following, we will present a model able to predict thresholds for an arbitrary motion profile based on the output of a suitable transfer function. To this end, we will first discuss the underlying transfer function structure in order to clarify the meaning assigned to its output.
The transfer function model and its interpretation
The transfer function used in this work is based on the structure proposed by Young and Meiry (1968), which has been successfully utilized to describe thresholds for translational movements with sinusoidal accelerations (Hosman and van der Vaart 1978; Hosman 1996; Heerspink et al. 2005):
(For a short introduction to transfer functions, see the Appendix).
The influence of the two terms in the denominator of the transfer function can be interpreted as representing the behavior (relative displacement) of two masses coupled by a spring/damper under the influence of external accelerations. This is a simple description of an accelerometer and can represent the basic functionality of the otoliths. One mass represents the human’s head and the other mass the otolith particles. The spring/damper describes the coupling between the otolith particles (otoconia) and the head through the otolith membrane, in which the stereocilia of the hair cells are imbedded. A relative displacement of the otoconia with respect to the head causes the stereocilia to bend and the hair cell to respond.
The term in the numerator takes into account the presence of two types of hair cells (Fernandez and Goldberg 1976). One type responds to the relative displacement due to acceleration (described by the denominator terms), and the other responds to the rate of change of that displacement—and therefore provides jerk sensitivity (described by the numerator term). A review of several transfer function models was provided by Mayne (1974).
This interpretation of the model parameters shows that the output can be thought of as a quantity closely related to the firing rate of otolith neurons. This fact will be instrumental to understand the ideas behind our modeling approach.
Using the transfer function output to predict detection thresholds
The simplest model of a detection process assumes a transduced signal and a constant level of noise. If the intensity of the signal becomes larger than the noise level, the signal can be detected. The same idea forms the basis of our model.
The intensity of the signal is represented as the output of the transfer function—the “firing rate”. In order to be able to detect the correct direction of motion in 62.5% of all trials, which is the definition of the perceptual threshold, the absolute peak output of the transfer function must overcome the noise level.
The peak output of a transfer function for a given acceleration profile can simply be calculated, but a reasonable value for the noise level must be found. In the following, we will motivate a numerical value for the noise level allowing us to model the detection process.
For a purely sinusoidal input signal at threshold level with amplitude \( A_{\text{threshold}} \), the gain of the transfer function is \( c \times {\frac{1}{{A_{{{\text{threshold}}}} }}} \) (Benson et al. 1986). Usually, the proportionality constant c is assumed to be equal to one. This is justified by the fact that the only effect of a different value for c would be a change in the parameter K of the model (Eq. 1), which, in turn, would result in a constant offset of the gain along the y-axis of the Bode plot. Since neither c nor K can be known, they are both treated as a scaling factor and c is conventionally set to one.
The output of an ideal transfer function model to a sinusoidal signal with an amplitude \( A_{\text{threshold}} \) (the threshold level) is a sinusoidal signal with an amplitude of one. This can be seen by multiplying the input amplitude by the gain of the ideal model \( {\frac{1}{{A_{\text{threshold}} }}} \). Thus, we can define the noise level which all sinusoidal signals must exceed for detection. The noise level has to be one, because a signal which is just detectable produces an output—a “firing rate”—with a peak amplitude equal to one.
Assuming that the noise level is independent of the profile shape, which is the simplest assumption, also implies a noise level of one for non-sinusoidal profiles. This allows predicting the threshold amplitude \( A_{\text{threshold}} \) for an arbitrary motion profile by finding the input stimulus amplitude A, which yields an absolute peak output of one (Fig. 3).
Example of an input profile (solid black curve), for which the amplitude is at threshold level. The corresponding output of the transfer function model has a maximum absolute value of one (black circle). The solid gray input curve is just below threshold level, because the output does not reach a maximum value of one
The threshold amplitude, \( A_{\text{threshold}} \), can be easily found in an algorithmic way due to the linearity of the model, i.e., by computing the output for a profile (“lsim” function, MATLAB, MathWorks, MA, USA) with an arbitrary input amplitude \( A_{\text{max,in}} \), and by finding the maximum absolute amplitude of the output \( A_{\text{max,out}} \). The predicted direction detection threshold level of the input profile is then given by:
Fitting the parameters of the transfer function
Using this model allows finding the parameters of the transfer function by optimally fitting the model predictions to the measured data. Generally speaking, the parameter optimization starts from a reasonable estimate of certain initial parameters K, τ 1, τ N , computes the predictions for the thresholds and then calculates the sum of the squared differences between measurements and predictions, i.e., a measure of the error of the predictions. This process can be repeated with different parameter estimates until the set that yields the lowest error locally (within a certain tolerance level) is found. This search was implemented with the Nelder-Mead non-linear optimization method (“fminsearch” function, MATLAB, MathWorks, MA, USA).
The parameter τ 2 was not included in the fit. In order to explain why, a closer look at the influence of each of the model parameters (Eq. 1) is necessary. The parameter K, the so-called static gain, acts as an offset factor that shifts the gain of the transfer function along the y-axis, but does not change the shape of the gain or the phase. The parameter τ N influences the frequency at which the gain starts increasing, while τ 1 influences the frequency at which the gain shows a plateau (canceling the influence of τ N ). The value of τ 2 influences the frequency at which the gain starts decreasing again (compare to the model example in Fig. 1).
Since no data were obtained for high frequencies, it was not possible to determine τ 2 reliably. Therefore, the parameter τ 2 was excluded from the fit, resulting in only three free parameters for the model instead of four. To test the influence of τ 2 on the fit, the fitting was also performed with τ 2 as an additional parameter. However, compared to the fit without τ 2, no significant differences for the other estimated parameters were found.
Nevertheless, all our plots were based on a model which included τ 2 for completeness, because, due to physical limits of the otoliths, the gain is expected to decrease at high frequencies (technically equivalent to the properness of the transfer function). We used the specific value \( \tau_{2} = 0.016\,{\text{s}} \) taken from Hosman (1996).
Transient versus steady state response of the system
It is important to realize that the output of a transfer function given a sinusoidal input consists of two parts: an initial transient response followed by the steady state response of the system.
In the ideal case, a sinusoidal input signal is infinitely long in time, but in reality a signal has finite starting and stopping times. The initial/transient response to an incipient sinusoidal signal is then different from the response of the system under the action of a sustained sinusoidal signal (i.e., with the starting time infinitely far in the past). In the latter case, the system will be in a steady state condition in which the response to a sinusoidal input is a sinusoidal output with the same frequency.
When the detection process consists of a stimulus with a single cycle, as it was the case of this study, the transient response of the system is still dominant. This fact can be appreciated in Fig. 3: being in the transient phase, the output to the sinusoidal input has not reached a constant amplitude or definite frequency yet. This initial behavior would expire as the sinusoidal input persists in time.
Notice that, for the present model, the absolute peak output during the transient response, which is the key point of our threshold prediction, is higher than it would be during the steady state phase. Therefore, a steady-state-only analysis would require a higher input peak amplitude to reach the same output level of one.
Taking the transient response into account constitutes another important advantage of this modeling approach over fitting the gain to the inverse of the thresholds for sinusoidal profiles. The latter implicitly assumes that the threshold is based on the steady state response, because the inverse of the threshold represents the steady state gain. However, as it can be seen from Fig. 3, this is not always the case: the threshold prediction is rather based on the transient response of the system.
This implies that even if only thresholds obtained for sinusoidal accelerations are used when fitting a model leads to different values of the optimal parameters depending on the modeling approach (i.e., if considering the transient response or not). The parameters identified with our approach are better in the sense that the actual profile length (a single cycle) is taken into account.
Results
The measured threshold estimates were averaged on a logarithmic scale, but for convenience are reported in m/s2 (Table 1). On average, it took 98 trials per profile until the variance of the estimate dropped below the break value and the threshold estimate could be determined. The maximum number of trials needed for one profile was 200.
The thresholds for the sinusoidal profiles decrease with increasing frequency. This finding indicates jerk sensitivity (see the Appendix) and, for this frequency range, is in accordance with previous findings (Benson et al. 1986; Zaichik et al. 1999; Heerspink et al. 2005; Fig. 1). Fitting a linear function in a double logarithmic plot to the thresholds for the sinusoidal profiles yields a slope of −0.40 logunits per decade, which is slightly different than the value of −0.26 reported by Benson et al. (1986), and indicates higher jerk sensitivity in our experiments. In general, the thresholds found are smaller than those reported by Benson et al. (1986). This might be attributed to the different simulators employed in the experiments, but nevertheless the results agree qualitatively, which allows comparison of our data to data found in the literature.
The transfer function model was fit to the 9 data points (Fig. 4.). The best model parameters (Eq. 1) found from the fit were \( K = 1.53\,,\;\tau_{N} = 22.05\,{\text{s}},\;\tau_{1} = 0.62\,{\text{s}} \). The mean absolute error was \( 0.001\,{\text{m}}/{\text{s}}^{2} \), which is less than 5% of the average threshold. This is a remarkable accuracy and shows that the model is able to explain the data very well.
Discussion
The main research question of this paper addresses the possibility of generalizing the modeling of direction detection thresholds to arbitrary non-sinusoidal profiles. Our results indicate that this is indeed possible, despite the simplifying assumptions considered for the model. The proposed transfer function is based on a simple anatomical and physiological description of the otoliths and provides a measure of how the firing rate of vestibular neurons might change due to acceleration stimuli. Together with the model of a signal detection process in a noisy environment, this approach is able to accurately describe perceptual thresholds measured with a psychophysical task.
Resolvability between profile types
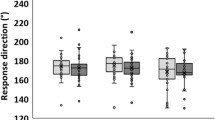
One important prerequisite for this study was the ability to resolve the differences (if any) in perception for the three profile types. As the results show (Table 1), the differences were small, especially for short duration profiles.
Previous direction detection experiments by Gianna et al. (1995, 1996) could reveal differences in thresholds between a parabolic acceleration profile and a trapezoidal acceleration profile, but no differences between a parabolic and a linearly rising acceleration profile could be found. Since the profiles which they compared differed in duration, their study did not provide information about the resolvability between different profiles with the same duration as it was needed in our work.
Another motion detection study (Richerson et al. 2003) could not find differences in thresholds between a trapezoidal and a sinusoidal acceleration profile for short movements of 4 or 20 mm. To our knowledge, no significant differences between profiles with the same duration have been measured so far.
To test the influence of the two factors (profile and frequency) on the thresholds, a repeated-measures ANOVA was applied to the data. The factor profile had a significant effect: \( F(2,10) = 43.1,\,P < 0.001,\,\eta_{p}^{2} = 0.90 \), as well as the factor frequency: \( F(2,10) = 24.3,\,P < 0.001,\,\eta_{p}^{2} = 0.83 \). Post hoc tests with Bonferroni correction, comparing the marginal means, revealed significant differences at the 0.05 level between all profile pairs (marginalized over the frequencies) and all frequency pairs (marginalized over profiles) apart from the 1.5–2.36 s pair (Table 2). However, for this frequency pair, no differences were expected, because in this frequency range the gain of the system is very similar.
Testing for differences between profile pairs with the same duration (repeated-measures ANOVA with only the factor profile) reveals significant differences for 4 out of 9 profile pairs (Table 3).
It was not known a priori if perceptual differences between profile pairs with the same duration could be expected. The fact that differences can be found shows how sensitive the otoliths are to small changes in acceleration profiles. For example, there was a significant difference between the 2.36 s triangular and the 2.36 s sinusoidal profile. The peak acceleration at threshold level only differed by \( 6.1\,{\text{mm}}/{\text{s}}^{2} \) and both profiles covered about the same distance (approximately \( 17\,{\text{mm}} \)), but still the participants could perceive them differently. Since there are differences in the perception, modeling this ability to discern these differences is important. The ability to detect the differences, despite the usually rather large variance obtained during psychophysical measurements, can partly be attributed to the use of the Bayesian adaptive measurement procedure, which yields an optimal estimate with respect to the amount of trials being run.
Predicting thresholds
The best model fit has a mean absolute error (MAE) less than 5% with respect to the average threshold. This fit was obtained by taking into account all measured data points.
In order to determine the ability of the model to not only fit measurements, but also predict them, the model was also fit to only part of the data points and used to predict the remaining ones. This methodology is commonly referred to as bootstrapping. Model fits were performed for all possible sets of n data points chosen from the nine measurements, where n was varied from 8 to 2.
A model fit was considered able to predict the data if its MAE, computed by taking into account all data points, was below 10% of the average threshold. The percentage of models which had a MAE of less than 10% was calculated and is reported in Table 4.
It can be seen that, by even using only five data points for the fitting, the model is still able to describe the whole data set adequately. This emphasizes the power of the model and also shows that it is not overfitting but instead able to predict measurements.
Comparison of the model parameters to previous research
The following parameters were found for the model fit by taking into account all measurements: \( K = 1.53\,,\;\tau_{N} = 22.05\,{\text{s}},\;\tau_{1} = 0.62\,{\text{s}} \).
Model fits based on the identification between the inverse of the measured thresholds and the gain of the model for data taken from Zaichik et al. (1999) and Heerspink et al. (2005) together with the parameters proposed by Hosman (1996) are given in Table 5.
It should be noted that, in all these studies, the experimental tasks, as well as the presented motion profiles, are slightly different. However, since the otoliths provide the relevant signals for detecting the motion, it is still possible to compare the different gain behaviors as a function of frequency.
The values for τ1 are all in a similar range, but for τ N a discrepancy appears. Hosman (1996) in his thesis already pointed out that there is no agreement on τ N yet. This is due to the fact that τ N can be correctly determined only by measuring the transition from a constant gain to an increasing gain for low frequencies (Fig. 1). Data characterized by this transition yield a low value for τ N , otherwise they yield a high value. However, it is not known if such a transition exists at all: for instance, by looking at Fernandez and Goldberg’s work (1976), the gain of the firing rate for the irregular units keeps decreasing down to frequencies of around \( 0.006\,{\text{Hz}} \) without showing a transition to a constant gain.
Due to the uncertainty about the parameter τ N , we discuss its influence on the model in more detail in the following section.
A closer look at the parameter τ N
In order to test the influence of the parameter τ N , model fits only adjusting K were calculated for two different values of τ N (\( \tau_{N} = 1\,{\text{s}} \) and \( \tau_{N} = 22\,{\text{s,}}\;\tau_{1} = 0.62\,{\text{s}},\;\tau_{2} = 0.016\,{\text{s}} \)), and model predictions were extrapolated to lower frequencies (Fig. 5).
Comparison of predictions calculated with a model which had a high value for τ N versus a model which had a low value. Both models show a crossover between the lines describing the thresholds for the triangular and the sinusoidal profile (black circles). For the model with τN = 1 the crossover occurs in the frequency range measured, but only one participant actually showed a crossover
The threshold predictions for the triangular and the sinusoidal profile for \( \tau_{N} = 1\,{\text{s}} \) are very similar. This shows that the parameter τ N also influences the separation between different profile types. Therefore, one can draw the conclusion that, in order to optimally identify our transfer function, one needs to measure different profile types so that this influence can also be taken into account.
Further analysis reveals that both models show a crossover between the lines representing the thresholds for a triangular and a sinusoidal profile. This implies that, below a certain frequency, the threshold for the triangular profile should become smaller than the threshold for the sinusoidal profile. This is an interesting qualitative prediction which could be tested experimentally in future studies.
In the model with \( \tau_{N} = 1 \), the crossover already occurs in the frequency range that was measured in our experiments. Looking at the individual participant’s threshold data, only one out of the six participants showed a lower threshold for the 5.86 s triangular profile compared to the sinusoidal profile. This is another indication that a model with a higher τ N might yield better predictions.
There certainly is a need for future experiments measuring thresholds for lower frequency movements in order to better determine the value of τ N . Measurements for both a triangular and a sinusoidal profile, together with the prediction of the crossover between the profiles, would provide an additional criterion to distinguish between different model types.
In order to perform experiments for lower frequencies, test setups that are capable of moving over a larger linear range are needed, both because the thresholds are expected to be higher, but also because lower frequencies require larger displacements for a given acceleration.
Furthermore, measurements for higher frequencies would also be very helpful to quantify the value of τ 2 for which experimental data is lacking.
Conclusions
Summary
In this paper, we addressed the problem of modeling direction detection thresholds for arbitrary acceleration profiles. In the existing literature, mathematical models of thresholds did not take into account the actual time course of the motion, implicitly assuming a sinusoidal shape. Here, we proposed a model based on a transfer function description of the otoliths able to characterize the changes in thresholds due to differences in the acceleration profiles with any shape (i.e., not only sinusoidal).
To verify this model, we measured direction detection thresholds for three different acceleration profiles and frequencies. Significant differences between thresholds for different profiles with the same duration could be measured and the proposed model was able to accurately fit the data. Furthermore, by considering only a subset of the data, the model was also able to correctly predict the remaining data. This further proves the validity of the model.
Threshold predictions for profiles with lower frequencies than those considered in this work were calculated. These predictions show very distinct differences depending on the actual value of one parameter of the model which could not be accurately identified. Therefore, our model could assist future studies aimed at determining the numerical value of the parameter.
The proposed model represents an important contribution to the field of vestibular mediated perception, because it allows for a more general and accurate description of direction detection thresholds. Apart from advancing our basic understanding of the vestibular system, a better modeling stage could also be exploited in more applied contexts such as in the diagnosis of people with vestibular-related complaints (Merfeld et al. 2010).
Future work
Measurements with different profile types for lower and higher frequencies than those investigated in this work would obviously be beneficial for modeling purposes. In addition, it would also be interesting to measure direction detection thresholds for superior-inferior (vertical when upright) movements. It has been shown that thresholds are higher for upright vertical movements compared to horizontal ones (Benson et al. 1986). Furthermore, Jones and Young (1978) reported the ability to detect the correct direction of upright vertical movements performed with a square pulse acceleration profile. Their participants were able to detect the correct direction of motion, independent of the peak acceleration of the presented profile, in approximately 70% of all trials. This indicates that the perception of upright vertical movements is somehow different compared to horizontal movements, perhaps due to normally experiencing a sustained background acceleration of one g along this axis.
It would be interesting to describe thresholds for upright vertical up/down movements within our theoretical framework and afterward measure thresholds for diagonal movements in the vertical plane, e.g. leftward-up/down versus rightward-up/down. This would represent a combination of both horizontal and vertical movements, and a model combing the findings for the previously tested conditions might be able to describe the results also in this case.
Furthermore, the framework presented to predict thresholds for non-sinusoidal profiles based on a transfer function description of the system can easily be adapted to the case of rotational movements. A transfer function describing the semi-circular canals together with a review of related literature can be found in the report by Hosman and van der Vaart (1978), for example. Threshold measurements for rotational thresholds over a large frequency range were among others performed by Heerspink et al. (2005) or more recently by Grabherr et al. (2008). They measured direction detection thresholds for yaw rotations around an earth vertical axis with a sinusoidal profile. This could be extended to include measurements for non-sinusoidal profiles in order to verify that our framework still applies, i.e., by replacing the transfer function of the otoliths with one describing the semi-circular canals.
Thresholds for roll or pitch rotations while seated upright might be influenced by signals coming from the otoliths, since during such rotations the orientation of the body with respect to gravity and therefore also the otolith stimulation changes. However, threshold measurements for roll and pitch rotations, while seated upright, for several frequencies performed by Heerspink et al. (2005) show that the threshold behavior for roll and pitch as a function of frequency is very similar compared to the behavior for yaw rotations. This indicates that within the frequency range measured, the detection process is dominated by the semi-circular canals and is influenced little by the otoliths.
If the framework turned out to be able to describe also rotations in a similar manner, a next step could be to measure thresholds describing the ability to discriminate between curved pathways, which would simultaneously stimulate both the otoliths and the semi-circular canals.
Including additional, very dim, visual stimuli would make the task multisensory. It has been shown by Benson and Brown (1989) that a dim light lowers the detection threshold for angular motion but not for translation. He tested a sinusoidal profile for one frequency. This experiment could be extended to more frequencies in order to test if the detection process is still dominated by the vestibular system. If the thresholds as a function of frequency showed a distinctly different behavior from what was found in darkness this would hint at the detection process being influenced by the visual signal.
Our immediate next step will be to investigate whether the modeling approach presented is also able to predict direction detection thresholds for arbitrary rotational motion profiles.
References
Benson AJ, Brown SF (1989) Visual display lowers detection threshold of angular, but not linear, whole-body motion stimuli. Aviat Space Environ Med 60(7):629–633
Benson AJ, Spencer M, Stott J (1986) Thresholds for the detection of the direction of whole-body, linear movement in the horizontal plane. Aviat Space Environ Med 57(11):1088–1096
Bouveresse A, Kalfane K, Gentine A, Eichhorn JL, Kopp C (1998) Pseudorandom rotational stimuli of the vestibulo-ocular reflex in humans: Normal values of the transfer function. Acta Otorhinolaryngol Belg 52(3):207–214
Buizza A, Castelnuovo P, Mevio E, Mira E (1985) Harmonic versus impulsive acceleration testing of the vestibulo-ocular reflex in normal humans. Acta Otolaryngol 100(1–2):106–111
DiStefano JJ, Stubberud AR, Williams IJ (1994) Schaum’s outline of feedback and control systems, 2nd edition edn. McGraw, Hill
Fernandez C, Goldberg J (1976) Physiology of peripheral neurons innervating otolith organs of squirrel monkey 3. Response dynamics. J Neurophysiol 39(5):996–1008
Furman JM, O’Leary DP, Wolfe JW (1979) Application of linear system analysis to the horizontal vestibulo-ocular reflex of the alert rhesus monkey using pseudorandom binary sequence and single frequency sinusoidal stimulation. Biol Cybern 33(3):159–165
Gianna C, Heimbrand S, Nakamura T, Gresty M (1995) Thresholds for perception of lateral motion in normal participants and patients with bilateral loss of vestibular function. Acta Oto-Laryngologica (Part 2 Suppl 520):343–346, 18th Barany-Society meeting on vestibular and equilibrium research—basic and clinical implications, Uppsala, Sweden, Jun 06–08, 1994
Gianna C, Heimbrand S, Gresty M (1996) Thresholds for detection of motion direction during passive lateral whole-body acceleration in normal participants and patients with bilateral loss of labyrinthine function. Brain Res Bull 40(5–6):443–447
Grabherr L, Nicoucar K, Mast FW, Merfeld DM (2008) Vestibular thresholds for yaw rotation about an earth-vertical axis as a function of frequency. Exp Brain Res 186(4):677–681
Heerspink HM, Berkouwer WR, Stroosma O, van Paassen MM, Mulder M, Mulder JA (2005) Evaluation of vestibular thresholds for motion detection in the Simona research simulator. In: Proceedings of the AIAA modeling and simulation technologies conference and exhibit, San Francisco (CA), AIAA-2005-6502
Hosman R (1996) Pilot’s perception and control of aircraft motions. PhD thesis, TU Delft
Hosman R, van der Vaart JC (1978) Vestibular models and thresholds of motion perception. Results of tests in a flight simulator. Techreport LR-265, TU Delft
Jones GM, Young LR (1978) Subjective detection of vertical acceleration: a velocity-dependent response? Acta Otolaryngol 85(1–2):45–53
Kontsevich L, Tyler C (1999) Bayesian adaptive estimation of psychometric slope and threshold. Vision Res 39(16):2729–2737
Mah RW, Young LR, Steele CR, Schubert ED (1989) Thresholds for the perception of whole-body linear sinusoidal motion in the horizontal plane. In: AIAA flight simulation technologies conference and exhibit, AIAA 89–3273
Mayne R (1974) A systems concept of the vestibular organs. In: Handbook of sensory physiology. Vestibular system. Part 2. Springer-Verlag, New York, pp 493–580
Merfeld DM, Priesol A, Lee D, Lewis RF (2010) Potential solutions to several vestibular challenges facing clinicians. J Vestib Res 20:71–77
Richerson S, Faulkner L, Robinson C, Redfern M, Purucker M (2003) Acceleration threshold detection during short anterior and posterior perturbations on a translating platform. Gait Posture 18(2):11–19
Robinson DA (1981) The use of control systems analysis in the neurophysiology of eye movements. Annu Rev Neurosci 4(1):463–503
Soyka F, Teufel HJ, Beykirch KA, Robuffo Giordano P, Butler JS, Nieuwenuizen FM, Bülthoff HH (2009) Does jerk have to be considered in linear motion simulation? In: Proceedings of the AIAA modeling and simulation technologies conference and exhibit, Chicago (IL), AIAA-2009-6245
Tanner T (2008) Generalized adaptive procedure for psychometric measurement. Perception 37 ECVP Abstract Supplement:93
Teufel H, Nusseck HG, Beykirch K, Butler J, Kerger M, Bülthoff H (2007) MPI motion simulator: Development and analysis of a novel motion simulator. In: AIAA modeling and simulation technologies conference and exhibit, AIAA 2007-6476
Walsh E (1961) Role of vestibular apparatus in perception of motion on a parallel swing. J Physiol 155(3):506
Wichmann F, Hill N (2001) The psychometric function: I. fitting, sampling, and goodness of fit. Percept psychophys 63(8):1293–1313
Young L, Meiry J (1968) A revised dynamic otolith model. Aerosp Med 39(6):606
Zaichik L, Rodchenko V, Rufov I, Yashin Y, White A (1999) Acceleration perception. In: AIAA modeling and simulation technologies conference—a collection of technical papers. Portland, OR, pp 512–520
Acknowledgments
This research was supported by a stipend from the Max Planck Society and by the WCU (World Class University) program through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology (R31–10008). The authors wish to thank Michael Kerger, Dr. Harald Teufel and Dr. Michael Barnett-Cowan for their intensive technical support and helpful discussions.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
This appendix provides a brief introduction to the framework of linear time-invariant (LTI) systems and explains how this framework can help to describe vestibular-related perception. For further details on LTI system, we refer the reader to the many textbooks on system theory, including an overview by DiStefano et al. (1994).
An LTI system can typically be defined as an input–output relation governed by a time-invariant linear differential equation. The property of being time-invariant refers to the independence of the output with respect to the absolute time the input is acting on the system (only the relative time with respect to an arbitrary initial time \( t_{0} \) is relevant). A very important property of an LTI system is that the output y(t) of the system given a sinusoidal input \( u(t) = A_{\rm in} \sin (\omega t) \), with amplitude \( A_{\rm in} \) and frequency \( \omega = 2\pi f \), will also be a sinusoidal function \( y(t) = A_{\rm out} \sin (\omega t + \varphi ) \) with amplitude \( A_{\text{out}} \), the same frequency ω, and a possible phase shift φ. This implies that the effect of the system on a sinusoidal input of frequency ω can be described by only two numbers: the ratio \( {\frac{{A_{\text{out}} }}{{A_{\text{in}} }}} \), referred to as the gain, and the phase shift φ.
Another important property of an LTI system is that if \( \left( {u_{1} (t),y_{1} (t)} \right) \) and \( \left( {u_{2} (t),y_{2} (t)} \right) \) are two input/output pairs of a system, then also \( \left( {au_{1} (t) + bu_{2} (t),ay_{1} (t) + by_{2} (t)} \right) \) will be a valid input/output pair owing to the system linearity. This is important because it allows breaking down a complex input stimulus into sub signals and determining the effect of the system on these sub signals. The effect of the original stimulus can afterward be calculated by looking at the responses of the system to each of the sub signals.
This property, together with the tool of Fourier analysis, that allows decomposing an arbitrary—non-sinusoidal periodic signal into a (possibly infinite) sum of sinusoidal signals, allows prediction of the effect of an LTI system on any kind of periodic signal by just measuring the effect (the output-input amplitude ratio and the phase shift) of the system on sinusoidal inputs of various frequencies. Therefore, to visualize the effect of an LTI system, it is sufficient to present the so-called Bode plot which shows the behavior of the two variables, the gain and phase of the system as a function of the input frequency ω. The gain is represented with a log scale, either graphically or often with a log unit, the decibel (dB), calculated as shown:
A transfer function is a complex-valued function usually referred to as \( H({\text{s}}) \) describing the gain and phase behavior of an LTI system. In the general case \( {\text{s}} = a + ib \), where i is the imaginary value \( i = \sqrt { - 1} \). To identify the frequency response (i.e., gain and phase) of a system, the complex variable s can be simplified to \( {\text{s}} = i\omega \). The magnitude of H(s) equals the real-valued gain G(ω) at the frequency ω, and the argument of H(s) equals the real-valued phase φ(ω).
An expression like \( H({\text{s}}) = K \times {\frac{{(1 + \tau_{N} {\text{s}})}}{{(1 + \tau_{1} {\text{s}})(1 + \tau_{2} {\text{s}})}}} \) describes the gain \( mag(H({\text{s}})) \) and the phase behavior \( \arg (H({\text{s}})) \) of the system at different frequencies in a closed-form with a set of parameters \( K,\,\tau_{1} ,\,\tau_{2} ,\,\tau_{N} \). Knowing that \( H(s) = {\frac{{{\text{Out}}({\text{s}})}}{{{\text{In}}({\text{s}})}}} \) allows calculation of the output \( {\text{Out}}({\text{s}}) = H({\text{s}}) \times In({\text{s}}) \) of the system for any given input \( {\rm In}({\text{s}}) \). Therefore, the input, as well as the output, must be converted into functions of the simplified frequency parameter \( s = i\omega \), as can be achieved with a Fourier transform, a special case of the more general Laplace transform.
If one can only measure the gain of the system for different frequencies, but the analytic expression of H(s) is known, one can often identify the parameters by comparing the measurements to \( mag(H({\text{s}})) \).
However, if the gain is identified indirectly, for example, through the inverse of threshold measurements, one cannot assume linearity of the system. The linearity is usually verified by testing whether the output to a sinusoidal input is also sinusoidal with the same frequency as the input. However, this is impossible for a discrete output like a threshold measurement. In the case of an indirect measurement of the gain, the assumption of linearity can be verified indirectly by testing if the predictions from a linear model for non-sinusoidal inputs are correct.
Inferring system properties from the sole gain
A system is referred to as being sensitive to acceleration for a specific frequency range if the input of the system is expressed in terms of acceleration and the gain of the system remains constant for the specified frequency range. If the input is expressed in terms of velocity and the gain is constant, the system would be referred to as being sensitive to velocity and so forth. The input signal can also be expressed in terms of velocity instead of acceleration, but then the gain would not be constant anymore as it would show an increase of 20 dB/decade in the Bode plot. This property stems from the fact that the gain is defined as the ratio between output and input amplitude of a sinusoidal signal. If the input profile in terms of acceleration is \( u_{acc} (t) = A_{\rm in} \sin (\omega t) \), then the same input profile in terms of velocity is the integral over time \( u_{vel} (t) = - {\frac{{A_{\rm in} }}{\omega }}\sin (\omega t + pi/2) \) plus an integration constant. Comparing the gain \( G_{acc} (\omega ) = 20\log_{10} \left( {{\frac{{A_{\text{out}} }}{{A_{\text{in}} }}}} \right) \) in terms of acceleration which was assumed to be constant for a certain frequency range to the gain in terms of velocity:
It can be seen that the gain expressed in terms of velocity increases with the frequency ω with a slope of 20 dB/decade. This shows that a system, which is sensitive to acceleration, will exhibit an increase in gain with increasing frequency if the input is expressed in terms of velocity. The inverse reasoning applies if we express the input in terms of jerk—the time derivative of acceleration. A system which is sensitive to acceleration would show a 20 dB/decade decrease in gain if the input is expressed in terms of jerk. The same can also be restated in terms of acceleration: a system which is sensitive to jerk shows an increase in gain with frequency if the input is expressed in terms of acceleration, and a system which is sensitive to velocity will show a decrease in gain if the input is expressed in terms of acceleration. The “amount of sensitivity” depends on the slope of the change. Therefore, it is possible to infer the sensitivity of a system for a given frequency range by just looking at the gain behavior. It is, of course possible, that for some frequencies a system is sensitive to velocity, whereas for a different frequency range it is sensitive to acceleration or jerk.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Soyka, F., Robuffo Giordano, P., Beykirch, K. et al. Predicting direction detection thresholds for arbitrary translational acceleration profiles in the horizontal plane. Exp Brain Res 209, 95–107 (2011). https://doi.org/10.1007/s00221-010-2523-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00221-010-2523-9