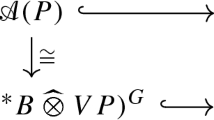Differential Calculi on Quantum Principal Bundles Over Projective Bases

Abstract

We propose a sheaf-theoretic approach to the theory of differential calculi on quantum principal bundles over non-affine bases. After recalling the affine case we define differential calculi on sheaves of comodule algebras as sheaves of covariant bimodules together with a morphism of sheaves -the differential- such that the Leibniz rule and surjectivity hold locally. The main class of examples is given by covariant calculi over quantum flag manifolds, which we provide via an explicit Ore extension construction. In a second step we introduce principal covariant calculi by requiring a local compatibility of the calculi on the total sheaf, base sheaf and the structure Hopf algebra in terms of exact sequences. In this case Hopf–Galois extensions of algebras lift to Hopf–Galois extensions of exterior algebras with compatible differentials. In particular, the examples of principal (covariant) calculi on the quantum principal bundles $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and $\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$ over the projective space $\textrm{P}^1(\mathbb {C})$ are discussed in detail.

1 Introduction

While in classical differential geometry there is a canonical (functorial) construction of the differential calculus on a differentiable manifold, a main feature of noncommutative differential geometry is the non uniqueness of the calculus. Even on quantum groups and requiring (co)invariance conditions there are interesting different calculi [47]. In this perspective, the definition of a noncommutative geometry requires also a characterization of its differential calculus structure. Going beyond quantum groups we have quantum homogeneous spaces and quantum principal bundles. Their study has been very active in the last three decades when the base space is a noncommutative deformation of an affine variety. In this case, as usual in noncomutative geometry, the affine geometric objects are replaced by a deformation of the algebra of functions on them. The case of bundles on projective varieties is intrinsically more difficult since it requires patching affine opens. In noncommutative geometry, when it is necessary to go beyond the affine setting, we must take the ringed space approach as expressed by Grothendieck: to do geometry one does not need the space itself, but only the category of sheaves on that would-be space (see [18] and also [44] with refs. therein for more insight on this point of view).

In this paper we propose an approach to noncommutative differential geometry which employs the sheaf-theoretic language developed in [4]. This does not only cover the established affine theory but also allows to consider differential structures for quantum principal bundles over non-affine bases.

Important steps towards a sound foundation of noncommutative algebraic geometry were taken in the works [1, 27, 38, 45]. In [1], quantum projective schemes are understood as the category of modules associated with a given graded noncommutative algebra, while in [38], an affine quantum space is viewed as the spectrum of a noncommutative ring and quantum projective schemes are defined accordingly with a gluing procedure in analogy with the classical $\textrm{Proj}$ construction. Indeed this is our perspective on non-affine noncommutative spaces: we shall define, following [4], a quantum space as a locally ringed space and then build quantum principal bundles over quantum spaces as sheaves with suitable (co)invariant properties with respect to a fixed quantum structure group.

While we have extensive studies on quantum principal bundles in the affine setting (see e.g. [6, 7, 12, 19]), the more general non-affine case (considered e.g. in [43]) lacks a comprehensive and exhaustive treatment. In [4] we study this more general setting combining the sheaf approach to principal bundles with affine bases of [35] (see also [11] and [3]) with the quantum projective homogeneous spaces construction of [10, 16], where a graded quantum ring is built out of the key notion of quantum section, associated to a quantum line bundle, with a gluing procedure similar to the classical $\textrm{Proj}$ one in [38]. In particular, we study the important example of quantum principal bundles on quantum flags of algebraic groups, the total space algebra being a quantum group.

More specifically, the main construction is based on quantizations of the classical principal bundle $G \rightarrow G/P$, where G is a semisimple complex algebraic group and P a parabolic subgroup, so that G/P is a projective variety. In this case the P-invariant ring $\mathcal {O}(G/P)$, i.e., the $\mathcal {O}(P)$-coaction invariant (for short coinvariant) ring $\mathcal {O}(G/P)$ is trivially $\mathbb {C}$ and is then replaced by the homogeneous coordinate ring ${\tilde{\mathcal {O}}}(G/P)$ of G/P with respect to a chosen projective embedding, associated with a very ample line bundle $\mathcal {L}$. This line bundle ${\mathcal {L}}$ can be recovered more algebraically via a character $\chi$ of P; the corresponding sections are the $\mathcal {O}(P)$-semi-coinvariant elements of $\mathcal {O}(G)$ with respect to $\chi$ and generate the homogeneous coordinate ring ${\tilde{\mathcal {O}}}(G/P)$ of G/P. The relation between this latter and the structure sheaf $\mathcal {O}_{G/P}$ of G/P is then as usual by considering projective localizations (zero degree subalgebras of the localizations) of ${\tilde{\mathcal {O}}}( G / P )$.

Let $\mathcal {O}_q(G)$ be a quantum deformation of G and $\mathcal {O}_q(P)$ a quantum deformation of a parabolic subgroup; both $\mathcal {O}_q(G)$ and $\mathcal {O}_q(P)$ are Hopf algebras (see [10] Sect. 3 and [4]). Via the datum of a quantum section $s\in \mathcal {O}_q(G)$, quantum version of the lift to $\mathcal {O}(G)$ of the character $\chi$ of P defining the line bundle $\mathcal {L}$, we obtain a quantization of ${\mathcal {L}}$. Indeed, through the quantum section we define a graded algebra ${\tilde{\mathcal {O}}}_q(G/P)$ (quantum homogeneous coordinate ring): each graded component consists of the elements of $\mathcal {O}_q(G)$, which are not coinvariant, but transform according to powers of the projection of s on $\mathcal {O}_q(P)$. Furthermore, the quantum section s allows to define two sheaves $\mathcal {F}_G$ and $\mathcal {O}_M$ on $M=G/P$ and in [4] we prove that $\mathcal {F}_G$ is a sheaf of $\mathcal {O}_q(P)$-comodule algebras on the quantum ringed space $(M,\mathcal {O}_M)$. Given the locally principal comodule algebra property (or faithfully flatness property) of $\mathcal {F}_G$, then this is a quantum principal bundle. In particular the (coproduct of the) quantum section determines an open cover $\{V_i\}$ of G. The projected open cover $\{U_i:=p(V_i)\}$ of M (where $p:G\rightarrow M=G/P$) then lead to the intersections $U_I:=U_{i_1} \cap \dots \cap U_{i_r}$, $I=(i_1,\dots , i_r)$ which form the basis $\mathcal {B}$ for the topology used to define both the sheaves $\mathcal {F}_G$ and $\mathcal {O}_M$.

In the present paper we develop a theory of differential calculi on sheaves which is suited but not limited to affine and non-affine examples such as quantum flags for quantum algebraic groups. In particular we construct first order differential calculi on the quantum principal bundles $\mathcal {F}_G$ that are canonically given once a calculus on $\mathcal {O}_q(G)$ is chosen. For a different approach to quantum differential calculi on quantum flags we refer to [21, 22, 34].

We start with the discussion of first order differential calculus in the affine setting, that is, when the base and total spaces are affine. Our focus is on the construction and induction of differential structures: via tensor products, algebra homomorphisms and quotients. This also on the level of covariant and bicovariant first order differential calculi. In particular, we recall the construction of covariant calculi on smash product algebras from [36], where a calculus on a module algebra and a bicovariant calculus on the structure Hopf algebra shape the so-called smash product calculus. This affine framework has been fruitfully investigated in a series of works, including [7, 13, 25, 29, 33, 36].

We conclude our discussion of the affine setting with a treatment of principal covariant calculi. Associated with a commutative principal bundle we canonically have the exact sequence of horizontal forms into forms on the total space onto vertical forms. Even for principal comodule algebras (faithfully flat Hopf–Galois extensions) exactness of this sequence in the noncommutative case is an extra requirement. It is known that the exterior algebra $\Omega ^\bullet _H$ of a bicovariant calculus on a quantum group H is a graded Hopf algebra. We here for simplicity study the quotient algebra $\Omega ^{\leqslant 1}_H=H\oplus \Gamma _H$ where forms of degree 2 and higher are set to zero. Similarly we can study when the (truncated) exterior algebra $\Omega ^{\leqslant 1}_A=A\oplus \Gamma _A$ is a $\Omega ^{{\scriptstyle {\leqslant }} 1}_H$-comodule algebra, and we can study the induced module of one forms $\Gamma _B$ on the subalgebra $B=A^{\textrm{co}H}\subseteq A$ of coinvariants. It was shown in [39, 40] that exactness of the sequence of modules

$$\begin{aligned} 0\rightarrow A\otimes _B\Gamma _B\longrightarrow \Gamma _A \longrightarrow A\square _H\Gamma _H\rightarrow 0 \end{aligned}$$

(where the cotensor product $A\square _H\Gamma _H$ equals $A\otimes {}^{\textrm{co}H}\Gamma _H$, with ${}^{\textrm{co}H}\Gamma _H$ the module of left coinvariant one-forms on the quantum group H) is equivalent to principality of the graded Hopf–Galois extension $(\Omega ^{\leqslant 1}_A)^{\textrm{co}\,\! \Omega ^{\leqslant 1}_H}\subseteq \Omega ^{\leqslant 1}_A$. We revisit these results considering differential graded algebras, where the above sequence becomes that of noncommutative horizontal forms, forms on A, vertical forms. The sequence then defines a principal covariant calculus on A. We show that these calculi correspond to graded Hopf–Galois extensions where the $\Omega ^{\leqslant 1}_H$-coaction is differentiable (compatible with the differentials on A and on $A\otimes H$). The main examples of differential calculi on sheaves we shall encounter satisfy such an exact sequence locally. In this section dedicated to the affine setting we further clarify the relation of principal covariant calculi to quantum principal bundles as pioneered in [7].

Building on the affine case results we proceed to introduce the sheaf approach to first order differential calculi. Namely, we define a first order differential calculus $(\Upsilon ,\textrm{d})$ on a sheaf $\mathcal {F}$ of comodule algebras as a sheaf $\Upsilon$ of covariant $\mathcal {F}$-bimodules together with a morphism $\textrm{d}:\mathcal {F}\rightarrow \Upsilon$ of sheaves of comodules. We demand the Leibniz rule and surjectivity of the $\mathcal {F}$-linear span of the differential only locally on stalks. These are the two characterizing properties of a first order differential calculus, and their holding true on stalks goes along with the property that stalks of a quantum principal bundle are principal comodule algebras.

The following result, proven in Theorem 4.16, shows that the construction of the sheaf $\mathcal {F}_G$ from the Hopf algebra $\mathcal {O}_q(G)$ developed in [4] (with G a semisimple complex algebraic group, P a parabolic subgroup) extends to the level of first order differential calculi.

Theorem 1.1

Let $(\Gamma ,\textrm{d})$ be a right covariant first order differential calculus on the Hopf algebra $\mathcal {O}_q(G)$.

• (i) The assignment

  $$\begin{aligned} \Upsilon _G: U_I\mapsto \Upsilon _G(U_I):= \mathcal {F}_G(U_I) \otimes _{\mathcal {O}_q(G)} \Gamma \otimes _{\mathcal {O}_q(G)} \mathcal {F}_G(U_I) \end{aligned}$$

  with $\textrm{d}: U_I\mapsto$ $(\textrm{d}_I:\mathcal {F}(U_I)\rightarrow \Upsilon _G(U_I))$ induced by Ore extensions, defines a right $\mathcal {O}_q(P)$-covariant first order differential calculus on the sheaf $\mathcal {F}_G$.

• (ii) The first order differential calculus $(\Upsilon _G,\textrm{d})$ on the sheaf $\mathcal {F}_G$ induces a first order differential calculus $(\Upsilon _M,\textrm{d}_M)$ on the sheaf $\mathcal {O}_M=\mathcal {F}_G^{\textrm{co}\!\, \mathcal {O}_q(P)}$.

• (iii) If $\mathcal {F}_G$ is a quantum principal bundle, the sheaf of base forms is isomorphic, as a sheaf of $\mathcal {O}_M$-bimodules, to the intersection of that of horizontal and $\mathcal {O}_q(P)$-coinvariant forms: $\Upsilon ^{}_M\cong \Upsilon _G^{\textrm{co}_{\,\!}\mathcal {O}_q(P)}\cap \Upsilon _G^{\textrm{hor}}$.

For the sheaf $\mathcal {F}_G$, which is obtained from the Hopf algebra $\mathcal {O}_q(G)$, the definition of the calculus on $\mathcal {O}_q(G)$ uniquely determines the quotient calculus on $\mathcal {O}_q(P)$, and from Theorem 4.16, the Ore extended calculus on $\mathcal {F}_G$ and that on the coinvariant subsheaf $\mathcal {O}_M=\mathcal {F}_G^{\textrm{co}\!\, \mathcal {O}_q(P)}$. Thus, despite non uniqueness of the noncommutative differential calculus, once defined the calculus on $\mathcal {O}_q(G)$ the other calculi are canonically obtained.

We next proceed to extend our sheaf-theoretic treatment to the notion of principal covariant calculus on a quantum principal bundle, which accounts for compatibility of the calculus $(\Upsilon ,\textrm{d})$ on the total sheaf $\mathcal {F}$, the calculus $(\Upsilon _M,\textrm{d}_M)$ on the base sheaf $\mathcal {O}_M$ and a bicovariant calculus $(\Gamma _H,\textrm{d}_H)$ on the structure Hopf algebra H. For a principal covariant calculus we demand the sequence of stalks

$$\begin{aligned} 0\rightarrow \mathcal {F}_p\otimes _{(\mathcal {O}_M)^{}_p}(\Upsilon _M)^{}_p \rightarrow \Upsilon _p\longrightarrow \mathcal {F}_p\square _H \Gamma _H\rightarrow 0 \end{aligned}$$

(1.1)

to be exact for every $p\in M$, and the calculus on H to be bicovariant, cf. equation (4.14).

The rest of the article is devoted to providing three explicit examples of this canonical construction. We study calculi on the quantum principal bundles $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and $\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$, both over $\textbf{P}^1(\mathbb {C})$. The first example is based on a 4D bicovariant differential calculus on $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$. The associated sequence (1.1) is well-defined but not exact. Despite the base sheaf $\mathcal {O}_{\textbf{P}^1(\mathbb {C})}$ being commutative the resulting calculus is noncommutative (the bimodule of one forms is noncommutative).

The second example is based on a 3D calculus on $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and the associated sequence is exact but not a principal covariant sequence since the induced calculus on the quantum parabolic subgroup $\mathcal {O}_q(\textrm{P})$ ($\textrm{P}\subseteq \textrm{SL}_2$ being the Borel subgroup of upper triangular matrices) is not bicovariant.

The third example has total space algebra $\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$ with a 4D bicovariant calculus. This induces a principal covariant calculus on the quantum principal bundle $\mathcal {F}_{\textrm{GL}_q}$ over the base sheaf $\mathcal {O}_{\textbf{P}^1(\mathbb {C})}$. Even though the sheaf $\mathcal {F}_{\textrm{GL}_q}$ is locally trivial, i.e., on an open cover $\{U_i\}$ of ${\textbf{P}^1(\mathbb {C})}$ the algebras $\mathcal {F}_{\textrm{GL}_q}(U_i)$ are isomorphic to smash product algebras, the associated smash product calculi do not give a first order differential calculus on the sheaf $\mathcal {F}_{\textrm{GL}_q}$. This is an instance where, while the sheaf defining the quantum principal bundle is locally trivial, the sheaf of one forms is not.

2 Preliminary Concepts

In this section we establish our notation and provide the key results we will need in the sequel. Though most of the material of this section is known, we include it by completeness, so that the reader has readily available the results in the form we need them later on.

2.1 Notation on modules and comodules

Let $\Bbbk$ be a commutative unital ring (in later sections specialized to $\mathbb {C}[q,q^{-1}]$ and to a field) and let $\otimes$ be the tensor product of $\Bbbk$-modules. Algebras over $\Bbbk$ will be associative and unital. Let H be a Hopf algebra over $\Bbbk$. Throughout this paper we denote the coproduct of H by $\Delta$ and its counit by $\epsilon$. Recall that those are algebra homomorphisms $\Delta : H\rightarrow H\otimes H$ and $\epsilon : H\rightarrow \Bbbk$ such that $(\Delta \otimes \textrm{id}_H)\circ \Delta =(\textrm{id}_H\otimes \Delta )\circ \Delta$ (coassociativity) and $(\epsilon \otimes \textrm{id}_H)\circ \Delta =(\textrm{id}_H\otimes \epsilon )\circ \Delta =\textrm{id}_H$ (counitality) hold. We employ Sweedler’s notation $\Delta (h)=h_1\otimes h_2$ for the coproduct of an element $h\in H$, i.e. we omit summation symbols and summation indices. By the coassociativity we write

$$\begin{aligned} h_1\otimes h_2\otimes h_3:=(\Delta \otimes \textrm{id}_H)(\Delta (h)) =(\textrm{id}_H\otimes \Delta )(\Delta (h)) \end{aligned}$$

for all $h\in H$ and similarly for higher coproducts. The antipode $S: H\rightarrow H$ of H is an anti-bialgebra homomorphism, namely $S(hh')=S(h')S(h)$, $S(1)=1$, $\Delta (S(h))=S(h_2)\otimes S(h_1)$, $\epsilon \circ S=\epsilon$, and furthermore we have $S(h_1)h_2=\epsilon (h)1=h_1S(h_2)$ for all $h,h'\in H$. We always assume that H has invertible antipode and denote its inverse by $\overline{S}: H\rightarrow H$. The latter is an anti-bialgebra homomorphism such that $\overline{S}(h_2)h_1=\epsilon (h)1=h_2\overline{S}(h_1)$ for all $h\in H$.

A right H-comodule is a $\Bbbk$-module M, together with a $\Bbbk$-linear map $\Delta _R: M\rightarrow M\otimes H$ such that

$$\begin{aligned} (\Delta _R\otimes \textrm{id}_H)\circ \Delta _R =(\textrm{id}_M\otimes \Delta )\circ \Delta _R \end{aligned}$$

(2.1)

and $(\textrm{id}_M\otimes \epsilon )\circ \Delta _R=\textrm{id}_M$, while a left H-comodule is a $\Bbbk$-module M with a $\Bbbk$-linear map $\Delta _L: M\rightarrow H\otimes M$ such that

$$\begin{aligned} (\textrm{id}_H\otimes \Delta _L)\circ \Delta _L =(\Delta \otimes \textrm{id}_M)\circ \Delta _L \end{aligned}$$

(2.2)

and $(\epsilon \otimes \textrm{id}_M)\circ \Delta _L=\textrm{id}_M$. The maps $\Delta _R$ and $\Delta _L$ are called right and left H-coaction, respectively. We use the Sweedler’s like notations $\Delta _R(m)=m_0\otimes m_1$ and $\Delta _L(m)=m_{-1}\otimes m_0$, where $m\in M$. In case M is a right H-comodule, we denote the $\Bbbk$-submodule of right H-coaction invariant elements, simply called H-coinvariant elements, by

$$\begin{aligned} M^{\textrm{co}H}:=\{m\in M~|~\Delta _R(m)=m\otimes 1\} \end{aligned}$$

Similarly, if M is a left H-comodule, ${}^{\textrm{co}H}M:=\{m\in M~|~\Delta _L(m)=1\otimes m\}$ is the $\Bbbk$-submodule of left H-coinvariant elements. Accordingly to (2.1) and (2.2), we further use the notations

$$\begin{aligned} m_0\otimes m_1\otimes m_2:=(\Delta _R\otimes \textrm{id}_H)(\Delta _R(m)) =(\textrm{id}_M\otimes \Delta )(\Delta _R(m)), \end{aligned}$$

$m_{-2}\otimes m_{-1}\otimes m_0:=(\textrm{id}_H\otimes \Delta _L)(\Delta _L(m)) =(\Delta \otimes \textrm{id}_M)(\Delta _L(m))$ and similarly for higher coactions. A right H-comodule M which is also a left H-comodule is said to be an H-bicomodule if $\Delta _R$ and $\Delta _L$ are commuting coactions, i.e.,

$$\begin{aligned} (\Delta _L\otimes \textrm{id}_H)\circ \Delta _R =(\textrm{id}_H\otimes \Delta _R)\circ \Delta _L. \end{aligned}$$

In Sweedler’s like notation this commutativity reads $m_{-1}\otimes (m_0\otimes m_1)=(m_{-1}\otimes m_0)\otimes m_1$, and hence we simply write $m_{-1}\otimes m_0\otimes m_1$. If M is an H-bicomodule then $M^{\textrm{co}H}$ and $^{\textrm{co}H}M$ are left and right H-subcomodules, respectively. A right H-comodule morphism is a $\Bbbk$-linear map $\phi : M\rightarrow N$ between right H-comodules $(M,\Delta _M)$ and $(N,\Delta _N)$ such that $\Delta _N\circ \phi =(\phi \otimes \textrm{id}) \circ \Delta _M\,$, i.e.,

$$\begin{aligned} \phi (m)_0\otimes \phi (m)_1 =\phi (m_0)\otimes m_1 \end{aligned}$$

(2.3)

for all $m\in M$. A $\Bbbk$-linear map satisfying (2.3) is also called right H-colinear. Similarly, left H-colinear and H-bicolinear maps are defined.

2.2 Covariant bimodules

Algebras in the category of comodules have a multiplication and unit that are compatible with the coaction. Since we are encountering several different coactions in the course of this section we utilize the convention to denote the right H-coaction on a right H-comodule algebra A by $\delta _R: A\rightarrow A\otimes H$.

Definition 2.1

A right H-comodule algebra is a right H-comodule $(A,\delta _R)$ together with an associative product $\mu : A\otimes A\rightarrow A$ and a unit $\eta :\Bbbk \rightarrow A$, such that

$$\begin{aligned} \delta _R\circ \mu =(\mu \otimes \mu _H)\circ (\textrm{id}_A\otimes \tau _{H,A}\otimes \textrm{id}_H) \circ (\delta _R\otimes \delta _R) \end{aligned}$$

and $\delta _R\circ \eta =\eta \otimes \eta _H$, where $\tau _{H,A}: H\otimes A \rightarrow A\otimes H$, $h\otimes a\mapsto a\otimes h$ denotes the flip of $\Bbbk$-modules and $(\mu _H,\eta _H)$ is the algebra structure of H. Using the previously introduced short notation, the compatibility conditions read

$$\begin{aligned} \delta _R(aa') =(aa')_0\otimes (aa')_1 =a_0a'_0\otimes a_1a'_1 =\delta _R(a)\delta _R(a') \end{aligned}$$

for all $a,a'\in A$ and $\delta _R(1)=1_0\otimes 1_1=1\otimes 1_H$. A right H-comodule algebra homomorphism is a right H-comodule homomorphism which is also an algebra homomorphism. Similarly, one defines left H-comodule algebras and H-bicomodule algebras and their morphisms.

Fix a right H-comodule algebra $(A,\delta _R)$ in the following. We now introduce A-bimodules in the category of right H-comodules.

Definition 2.2

An A-bimodule M is called a right H-covariant A-bimodule if there is a right H-comodule action $\Delta _R: M\rightarrow M\otimes H$ on M, such that

$$\begin{aligned} \Delta _R(a\cdot m\cdot a') =\delta _R(a)\Delta _R(m)\delta _R(a'), \end{aligned}$$

or equivalently, in short notation, $(a\cdot m\cdot a')_0\otimes (a\cdot m\cdot a')_1 =a_0\cdot m_0\cdot a'_0\otimes a_1m_1a'_1$ for all $a,a'\in A$ and $m\in M$. A right H-covariant right (resp. left) A-module is a right (resp. left) A-module, where we only ask compatibility of a right H-coaction with the right (resp. left) A-module structure. Similarly, left H-covariant A-modules and H-bicovariant A-bimodules are defined, if A is a left H-comodule algebra or an H-bicomodule algebra, respectively.

We are particularly interested in the case $A=H$, since H is naturally a right and a left H-comodule algebra with respect to the coactions given by the coproduct.

Definition 2.3

A bicovariant H-bimodule is an H-bimodule and an H-bicomodule M, such that

$$\begin{aligned} \Delta _R(h\cdot m\cdot h') =\Delta (h)\Delta _R(m)\Delta (h') \text { and } \Delta _L(h\cdot m\cdot h') =\Delta (h)\Delta _L(m)\Delta (h') \end{aligned}$$

for all $h,h'\in H$ and $m\in M$.

For H-covariant H-modules there is the following fundamental theorem (c.f. [31] Thm. 1.9.4, [41]).

Proposition 2.4

For any right H-covariant right H-module M, there is an isomorphism

$$\begin{aligned} M\rightarrow M^{\textrm{co}H}\otimes H,~~ m\mapsto m_0S(m_1)\otimes m_2, \end{aligned}$$

(2.4)

of right H-covariant right H-modules. If M is a bicovariant H-bimodule, (2.4) extends to an isomorphism of bicovariant H-bimodules.

If M is a left H-covariant left H-module, there is an isomorphism

$$\begin{aligned} M\rightarrow H\otimes {}^{\textrm{co}H}M,~~ m\mapsto m_{-2}\otimes S(m_{-1})m_0, \end{aligned}$$

(2.5)

of left H-covariant left H-modules. If M is a bicovariant H-bimodule, (2.5) extends to an isomorphism of bicovariant H-bimodules.

Note that in (2.4) the tensor product $M^{\textrm{co}H}\otimes H$ is a right H-covariant right H-module with respect to the diagonal coaction and the right H-action $(\overline{m}\otimes h)\cdot h':=\overline{m}\otimes (hh')$, where $\overline{m}\in M^{\textrm{co}H}$ and $h,h'\in H$. If M is furthermore a bicovariant H-bimodule we endow $M^{\textrm{co}H}\otimes H$ with the diagonal left H-coaction and the left H-action $h\cdot (\overline{m}\otimes h'):=h_1\overline{m}S(h_2)\otimes h_3h'$. Similarly in (2.5), $H\otimes {}^{\textrm{co}H}M$ becomes a left H-covariant left H-module via the diagonal coaction and the left H-action given by $h\cdot (h'\otimes \overline{m}):=(hh')\otimes \overline{m}$, where $h,h'\in H$ and $\overline{m}\in {}^{\textrm{co}H}M$. If M is furthermore a bicovariant H-bimodule we endow $H\otimes {}^{\textrm{co}H}M$ with the diagonal right H-coaction and the right H-action $(h\otimes \overline{m})\cdot h':=hh'_1\otimes S(h'_2)\overline{m}h'_3$.

Using the inverse $\overline{S}$ of the antipode S there are analogous isomorphism of right H-covariant left H-modules and left H-covariant right H-modules, respectively. The fundamental theorem allows us to write any element m of a bicovariant H-bimodule as $m=a_im^i$, where $\{m^i\}_i\in I\subseteq {}^{\textrm{co}H}M$ is a basis of (left) coinvariant elements and $a_i$ are coefficients in H. This is particularly useful when one is dealing with H-linear maps of bicovariant bimodules. Then, it is sufficient to specify properties on coinvariant elements.

2.3 Hopf–Galois extensions

In this section H denotes a Hopf algebra and A a right H-comodule algebra with right H-comodule action $\delta _R: A\rightarrow A\otimes H$. In particular H is a right H-comodule algebra with coaction $\Delta$.

Definition 2.5

The algebra extension $B:=A^{\textrm{co}H}\subseteq A$ is said to be

• (i) a Hopf–Galois extension, if the $\Bbbk$-linear map

  $$\begin{aligned} \chi := (\mu \otimes \text {id}_H)\circ (\text {id}_A\otimes _B\delta _R): A\otimes _BA&\rightarrow A\otimes H, \\ a\otimes _B a'&\mapsto \chi (a\otimes _Ba')= aa'_0\otimes a'_1 \end{aligned}$$

  is a bijection, where $\mu : A\otimes _B A\rightarrow A$ is the product of A induced on the balanced tensor product $A\otimes _B A$.

• (ii) a cleft extension, if there is a $\Bbbk$-linear map $j: H\rightarrow A$, the cleaving map, such that

  • (1) j is right H-colinear, i.e., $j(h)_0\otimes j(h)_1=j(h_1)\otimes h_2$ for all $h\in H$,

  • (2) j is convolution invertible, i.e., there is a $\Bbbk$-linear map $j^{-1}: H\rightarrow A$ such that $j(h_1)j^{-1}(h_2)=\epsilon (h)1=j^{-1}(h_1)j(h_2)$ for all $h\in H$,

  • (3) j respects the units, i.e., $j(1_H)=1$.

• (iii) a trivial extension, if there is a right H-comodule algebra homomorphism $j: H\rightarrow A$.

A trivial extension $A^{\textrm{co}H}\subseteq A$ is automatically a cleft extension since an H-comodule algebra map $j: H\rightarrow A$ is right H-colinear and unital by assumption and its convolution inverse is $j^{-1}=j\circ S$. This trivially implies that the composition $j^{-1}\circ \overline{S}: H\rightarrow A$ is right H-colinear. In the following lemma we prove that this H-colinearity property holds for any cleft extension.

Lemma 2.6

The inverse of the cleaving map satisfies

$$\begin{aligned} \delta _R\circ j^{-1} =(j^{-1}\otimes S)\circ \tau _{H,H}\circ \Delta , \end{aligned}$$

(2.6)

where $\tau _{H,H}$ is the flip. In particular, $j^{-1}\circ \overline{S}$ is right H-colinear.

Proof

Equation (2.6) is proven in [31] Lem. 7.2.6, 1). Then,

$$\begin{aligned} \delta _R(j^{-1}(\overline{S}(h)))&=j^{-1}(\overline{S}(h)_2)\otimes S(\overline{S}(h)_1) =j^{-1}(\overline{S}(h_1))\otimes S(\overline{S}(h_2))\\ {}&=j^{-1}(\overline{S}(h_1))\otimes h_2\end{aligned}$$

for all $h\in H$, where we used that $\overline{S}$ is an anti-bialgebra homomorphism. $\square$

To complete the hierarchy of Definition 2.5, we note that cleft extensions are in particular Hopf–Galois extensions. We shall frequently call them cleft Hopf–Galois extensions.

Proposition 2.7

$B:=A^{\textrm{co}H}\subseteq A$ is a cleft extension if and only if $B\subseteq A$ is a Hopf–Galois extension and there is a left B-module and right H-comodule isomorphism $B\otimes H\cong A$.

The proof of this proposition (see e.g. [31] Thm. 8.2.4) relies on the construction of the following left B-module and right H-comodule map

$$\begin{aligned} \theta : B\otimes H \rightarrow A,\,\,\,\, b\otimes h\mapsto bj(h) \end{aligned}$$

with inverse given by

$$\begin{aligned} \theta ^{-1}: A\rightarrow B \otimes H,\,\,\,\, a\mapsto a_0j^{-1}(a_1)\otimes a_2. \end{aligned}$$

Note that $\theta ^{-1}$ is well-defined, i.e. $a_0j^{-1}(a_1)\in B$, since

$$\begin{aligned} \delta _R(a_0j^{-1}(a_1))&=a_0j^{-1}(a_2)_0 \otimes a_1j^{-1}(a_2)_1 =a_0j^{-1}(a_3)\otimes a_1S(a_2) \\&=a_0j^{-1}(a_2) \otimes \epsilon (a_1)1 =a_0j^{-1}(a_1)\otimes 1, \end{aligned}$$

where we employed Lemma 2.6 (see also [31] Lem. 7.2.6, 2.).

We conclude this section by recalling the notion of principal comodule algebra from [12] and (part of) Schneider theorem for faithfully flat Hopf–Galois extensions.

Definition 2.8

A right H-comodule algebra A is said to be a principal comodule algebra if $B:=A^{\textrm{co}H}\subseteq A$ is a Hopf–Galois extension and if A is right H-equivariantly projective as a left B-module. The latter means that there exists a left B-linear and right H-colinear map $s: A\rightarrow B\otimes A$ such that $m\circ s=\textrm{id}_A$, where $m: B\otimes A\rightarrow A$ denotes the restricted product of A.

Any cleft extension is a principal comodule algebra with section $s: A\rightarrow B\otimes A$, $a\mapsto s(a)=a_0j^{-1}(a_1)\otimes j(a_2)$. Let $B:=A^{\textrm{co}H}\subseteq A$ be a Hopf–Galois extension. If $\Bbbk$ is a field, and recalling that we always consider Hopf algebras H with invertible antipode, the right H-equivariant projectivity of A is equivalent to the existence of a strong connection, it is also equivalent to faithfully flatness of A as a left B-module, see e.g. [8] Part VII, Thm. 6.16, 6.19, 6.20. For faithfully flat Hopf–Galois extensions we will later use the following main result which is an immediate consequence of Schneider [42, Thm. 1] by considering that categorical equivalences are adjoint equivalences and that adjoint functors are unique up to natural isomorphism.

Theorem 2.9

Let $B:=A^{\textrm{co}H}\subseteq A$ be a faithfully flat Hopf–Galois extension. We have the equivalence of categories via the following inverse functors:

$$\begin{aligned} \begin{array}{c} \Phi :{}_B\mathcal {M} \longrightarrow {}_A\mathcal {M}^H, \quad \Phi (M)=A\otimes _BM; \qquad \Psi :{}_A\mathcal {M}^H \longrightarrow {}_B\mathcal {M}, \qquad \Psi (N)=N^{\textrm{co}H} \end{array} \end{aligned}$$

where ${}_A\mathcal {M}^H$ denotes the category of right H-covariant left A-modules and ${}_B\mathcal {M}$ the category of left B-modules.

2.3.1 Smash products

A left H-module algebra $(B,\rhd )$ is a left H-module structure $\rhd : H\otimes B\rightarrow B$ on an algebra B such that $h\rhd (bb')=(h_1\rhd b)(h_2\rhd b')$ and $h\rhd 1_B=\epsilon (h)1_B$ for all $h\in H$ and $b,b'\in B$.

Definition 2.10

For a left H-module algebra $(B,\rhd )$ the smash product $B\# H$ is defined as the $\Bbbk$-module $B\otimes H$ endowed with the multiplication

$$\begin{aligned} (b\otimes h)\cdot _{\#}(b'\otimes h'):=b(h_1\rhd b')\otimes h_2h' \end{aligned}$$

for all $b,b'\in B$ and $h,h'\in H$.

In the following we write $b\# h$ instead of $b\otimes h$ if we want to view $b\otimes h$ as an element of $B\# H$. Moreover, we set $(b\# h)(b'\# h'):=(b\otimes h)\cdot _{\#}(b'\otimes h')$. The algebra $B \# H$ is naturally endowed with the right H-comodule structure

$$\begin{aligned} B\# H\rightarrow B\# H\otimes H,~~b\# h\mapsto (b\# h_1)\otimes h_2. \end{aligned}$$

The compatibility of this coaction with the product $\cdot _\#$ is easily checked and thus $B\# H$ is a right H-comodule algebra (see also [31] Sect. 4.1). The smash product algebra $B\# H$ is the trivial Hopf–Galois extension $B=(B\# H)^{\textrm{co}H}\subseteq B\# H$ with cleaving map defined by the algebra inclusion $H\rightarrow B\# H$. Vice versa trivial Hopf–Galois extensions are isomorphic (as H-comodule algebras) to smashed products.

For a trivial Hopf Galois extension $B=A^{co H}\subseteq A$, conjugation via the cleaving map $j: H\rightarrow A$ defines the left H-module algebra action on B

$$\begin{aligned} h\rhd b:=j(h_1)bj^{-1}(h_2). \end{aligned}$$

This is easily verified using that j is an algebra map and that its convolution inverse $j^{-1}=j\circ S$ is an anti-algebra map. Furthermore, $j(h_1)bj^{-1}(h_2)\in B$ follows from the right H-colinearity of j and Lemma 2.6. The compatibility of $\rhd$ with the algebra structure holds because $j^{-1}$ is the convolution inverse of j and j is unital.

Proposition 2.11

If $B:=A^{\textrm{co}H}\subseteq A$ is a trivial extension the map $\theta : B\# H\rightarrow A$, $\theta (b\# h):=bj(h)$ is an isomorphism of right H-comodule algebras. The inverse is $\theta ^{-1}(a)=a_0j^{-1}(a_1)\# a_2$.

Proof

In Proposition 2.7 it has been proven that $\theta$ is an isomorphism of right H-comodules. It remains to prove that $\theta$ is an algebra homomorphism. Trivially we have $\theta (1_B\# 1_H)=1_A$ and also

$$\begin{aligned} \theta ((b\# h)(b'\# h'))&=\theta (b(h_1\rhd b')\# h_2h') =b(h_1\rhd b')j(h_2h') =bj(h_1)b'j^{-1}(h_2)j(h_3)j(h')\\&=bj(h)b'j(h') =\theta (b\# h)\theta (b'\# h'), \end{aligned}$$

which concludes the proof. $\square$

3 Covariant Differential Calculi on Hopf–Galois Extensions

We begin this section with the definition of the category of noncommutative differential calculi and discuss pullback and quotient calculi. We then specialize to covariant differential calculi and bicovariant calculi, building on previous works of [23] and [47]. Examples of (bi)covariant calculi on the quantum groups $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and $\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$ are recalled and the induced calculi on their parabolic quantum subgroups are presented. We next revisit a result of Pflaum and Schauenburg [36], where an H-module calculus and a bicovariant calculus merge to the smash product calculus: a covariant calculus on the smash product algebra. This latter is a trivial principal bundle and the smash product calculus is a FODC on it.

In Sect. 3.5 we show that for right H-covariant FODCi on principal comodule algebras base forms are the intersection of horizontal and coinvariant forms. Furthermore, when the injection of horizontal forms into total space forms is completed in an exact sequence with vertical forms, we obtain a graded Hopf–Galois extension with compatible differentials on the total space algebra and on the quantum structure group.

3.1 Noncommutative differential calculi

In this section we give the definition and some results on noncommutative differential calculi. Though this material is well established in the context of bicovariant calculi on Hopf algebras, since we take a slightly more general point of view, we prefer to review the main points. We refer the reader to [47, 26, Chpt. 12], [5, Chpt. 2] for more details.

We give the definition of a differential calculus.

Definition 3.1

A first order differential calculus (FODC) on a (noncommutative) algebra A is a couple $(\Gamma ,\textrm{d})$, where

• (i) $\Gamma$ is an A-bimodule,

• (ii) $\textrm{d}: A\rightarrow \Gamma$ is a $\Bbbk$-linear map which satisfies the Leibniz rule $\textrm{d}(ab)=(\textrm{d}a)b+a\textrm{d}b$ for all $a,b\in A$,

• (iii) $\Gamma =A\textrm{d}A:=\textrm{span}_\Bbbk \{a\textrm{d}b~|~a,b\in A\}$.

We say that $\Gamma$ is generated (as a left A-module) by exact forms and refer to (iii) as the surjectivity property of the FODC. A morphism between a FODC $(\Gamma ,\textrm{d})$ on A and a FODC $(\Gamma ',\textrm{d}')$ on another algebra $A'$ is a couple $(\phi ,\Phi )$, where $\phi : A\rightarrow A'$ is an algebra homomorphism and $\Phi :\Gamma \rightarrow \Gamma '$ is a $\Bbbk$-linear map such that

$$\begin{aligned} \Phi (a\cdot \omega \cdot b) =\phi (a)\cdot '\Phi (\omega )\cdot '\phi (b) \end{aligned}$$

and

$$\begin{aligned} \Phi \circ \textrm{d}=\textrm{d}'\circ \phi \end{aligned}$$

for all $a,b\in A, \omega \in \Gamma$. Two FODCi are called equivalent if there is an isomorphism of FODCi between them.

The classical example of a FODC comes from differential geometry. Given a smooth manifold M, the $C^\infty (M)$-bimodule $\Omega ^1(M)$ of differential 1-forms on M together with the de Rham differential is a FODC on $C^\infty (M)$. On any algebra A there is the so-called universal FODC $(\Gamma _u,\textrm{d}_u)$, where $\Gamma _u:=\ker \mu _A\subseteq A\otimes A$ is the kernel of the multiplication $\mu _A: A\otimes A\rightarrow A$ and $\textrm{d}_ua:=1\otimes a-a\otimes 1$ for all $a\in A$. The left and right A-module action on $\Gamma _u$ is given by the multiplication on the first and the second tensor factor, respectively. This FODC is universal in the sense that every FODC on A is isomorphic to a quotient of $(\Gamma _u,\textrm{d}_u)$. (c.f. e.g. [47]).

It is well-known that the tensor product $A\otimes A'$ of two algebras A and $A'$ is an algebra with associative product $(a\otimes a')(b\otimes b') =ab\otimes a'b'$ and unit $1_A\otimes 1_{A'}$. This construction extends to the level of FODCi (see also [36] Thm. 2.2).

Proposition 3.2

Given a FODC $(\Gamma ,\textrm{d})$ on A and a FODC $(\Gamma ',\textrm{d}')$ on $A'$, there is a FODC $(\Gamma _{A\otimes A'},\textrm{d}_{A\otimes A'})$ on $A\otimes A'$, where $\Gamma _{A\otimes A'}=\Gamma \otimes A'\oplus A\otimes \Gamma '$ and

$$\begin{aligned} \textrm{d}_{A\otimes A'}: A\otimes A'\rightarrow \Gamma _{A\otimes A'},~~a\otimes a'\mapsto \textrm{d}a\otimes a'+a\otimes \textrm{d}'a'. \end{aligned}$$

(3.1)

The $A\otimes A'$-bimodule structure on $\Gamma _{A\otimes A'}$ is

$$\begin{aligned} (a\otimes a')\cdot (\omega \otimes b'+b\otimes \omega ')\cdot (c\otimes c') =a\omega c\otimes a'b'c'+abc\otimes a'\omega 'c', \end{aligned}$$

(3.2)

where $a,b,c\in A$, $a',b',c'\in A'$, $\omega \in \Gamma$ and $\omega '\in \Gamma '$. This construction is associative, i.e. $(\Gamma _{(A\otimes A')\otimes A''}, \textrm{d}_{(A\otimes A')\otimes A''})=(\Gamma _{A\otimes (A'\otimes A'')}, \textrm{d}_{A\otimes (A'\otimes A'')})$ for another algebra $A''$.

Proof

Clearly, (3.2) defines an $A\otimes A'$-bimodule structure and (3.1) a $\Bbbk$-linear map. This latter satisfies the Leibniz rule

$$\begin{aligned} \textrm{d}_{A\otimes A'}((a\otimes a')(b\otimes b'))&=\textrm{d}_{A\otimes A'}(ab\otimes a'b')\\&=\textrm{d}(ab)\otimes a'b'+ab\otimes \textrm{d}'(a'b')\\&=(\textrm{d}a)b\otimes a'b'+a\textrm{d}b\otimes a'b' +ab\otimes (\textrm{d}'a')b'+ab\otimes a'\textrm{d}'b'\\&=(\textrm{d}a\otimes a'+a\otimes \textrm{d}'a')\cdot (b\otimes b') +(a\otimes a')\cdot (\textrm{d}b\otimes b'+b\otimes \textrm{d}'b')\\&=\textrm{d}_{A\otimes A'}(a\otimes a')\cdot (b\otimes b') +(a\otimes a')\cdot \textrm{d}_{A\otimes A'}(b\otimes b') \end{aligned}$$

for all $a,b\in A$ and $a',b'\in A'$. Furthermore, $\Gamma _{A\otimes A'}$ is generated by $A\otimes A'$ and $\textrm{d}_{A\otimes A'}$, since

$$\begin{aligned} (A\otimes A')\cdot \textrm{d}_{A\otimes A'}(A\otimes A')&=(A\otimes A')\cdot (\textrm{d}A\otimes A'\oplus A\otimes \textrm{d}'A')\\&=A\textrm{d}A\otimes A'\oplus A\otimes A'\textrm{d}'A'\\&=\Gamma \otimes A'\oplus A\otimes \Gamma '\\&=\Gamma _{A\otimes A'} \end{aligned}$$

as an equality of sets. Finally, associativity follows from the equality of $A\otimes A'\otimes A''$-bimodules

$$\begin{aligned} \Gamma _{(A\otimes A')\otimes A''}&=\Gamma _{A\otimes A'}\otimes A'' \oplus (A\otimes A')\otimes \Gamma ''\\&=(\Gamma \otimes A'\oplus A\otimes \Gamma ')\otimes A'' \, \oplus \, A\otimes A'\otimes \Gamma ''\\&=\Gamma \otimes A'\otimes A'' \, \oplus \, A\otimes \Gamma '\otimes A''\,\oplus \,A\otimes A'\otimes \Gamma ''\\&=\Gamma \otimes (A'\otimes A'') \oplus A\otimes \Gamma _{A'\otimes A''}\\&=\Gamma _{A\otimes (A'\otimes A'')} \end{aligned}$$

and from $\textrm{d}_{(A\oplus A')\oplus A''}= \textrm{d}_{A\oplus ( A'\oplus A'')}$. $\square$

Remark 3.3

In other words, Proposition 3.2 proves that FODCi form a monoidal category. The monoidal product is

$$\begin{aligned} (\Gamma ,\textrm{d},A)\otimes (\Gamma ',\textrm{d}',A'):=(\Gamma _{A\otimes A'},\textrm{d}_{A\otimes A'},A\otimes A') \end{aligned}$$

and the monoidal unit is the trivial calculus $(\Gamma =\{0\},\textrm{d}=0)$ on the algebra $A=\Bbbk$.

Given a FODC on A we can induce a FODC on any subalgebra and quotient algebra of A. For a surjective algebra map $\pi : A\rightarrow A'$, we identify $A'$ with A/I where $I:=\ker \pi$ and denote by $[a]:=a+I$ the class of $a\in A$.

Proposition 3.4

Let $(\Gamma ,\textrm{d})$ be a FODC on A.

• (i) An algebra map $\iota : A'\rightarrow A$ induces a FODC $(\Gamma _\iota ,\textrm{d}_\iota )$ on $A'$, where

  $$\begin{aligned} \Gamma _\iota :=\iota (A')\textrm{d}\iota (A')\subseteq \Gamma \end{aligned}$$

  (3.3)

  and $\textrm{d}_\iota :=\textrm{d}\circ \iota : A'\rightarrow \Gamma _\iota$, $a'\mapsto \textrm{d}\iota (a')$.

• (ii) A surjective algebra map $\pi : A\rightarrow A'$ induces a FODC $(\Gamma _\pi ,\textrm{d}_\pi )$ on $A'$, where the $A'$-bimodule

  $$\begin{aligned} \Gamma _\pi :=\Gamma /\Gamma _I \end{aligned}$$

  is the quotient with $\Gamma _I:=I\textrm{d}A+A\textrm{d}I$, where $I:=\ker \pi \subseteq A$ and $\textrm{d}_\pi : A'\rightarrow \Gamma _\pi , \pi (a)\mapsto [\textrm{d}a]$.

• (iii) If the exact sequence of algebras $0\rightarrow \ker \pi \rightarrow A{\mathop {\rightarrow }\limits ^{\pi }}A'\rightarrow 0$ splits via $\iota : A'\rightarrow A$, so that $\pi \circ \iota =\textrm{id}_{A'}$, then $(\Gamma _\iota ,\textrm{d}_\iota )$ is equivalent to $(\Gamma _\pi ,\textrm{d}_\pi )$ with isomorphism $(\phi ,\Phi )$ given by

  $$\begin{aligned} \phi =\textrm{id}_{A'},~~~~ \Phi :\Gamma _\iota \rightarrow \Gamma _\pi ,~\omega \mapsto [\omega ]. \end{aligned}$$

  (3.4)

Proof

(i) The $\Bbbk$-submodule $\Gamma _\iota$ in (3.3) is structured as an $A'$-bimodule via

$$\begin{aligned} a'\cdot \omega \cdot b':=\iota (a')\omega \iota (b') \end{aligned}$$

(3.5)

for all $a',b'\in A'$ and $\omega \in \Gamma _\iota \subseteq \Gamma$. To see this, we first verify that the maps defined in (3.5) close in $\Gamma _\iota$. By definition, any $\omega \in \Gamma _\iota$ is a finite sum $\omega =\iota (a'^i)\textrm{d}\iota (b'_i)$, for $a'^i,b'_i\in A'$. Then, for all $a',b'\in A'$,

$$\begin{aligned} a'\cdot \omega \cdot b'&=\iota (a')\iota (a'^i)(\textrm{d}\iota (b'_i))\iota (b')\\&=\iota (a'a'^i)(\textrm{d}(\iota (b'_i)\iota (b'))-\iota (b'_i)\textrm{d}\iota (b'))\\&=\iota (a'a'^i)\textrm{d}\iota (b'_ib')-\iota (a'a'^ib'_i)\textrm{d}\iota (b') \in \Gamma _\iota , \end{aligned}$$

where we used that $\iota$ is an algebra map. The maps in (3.5) are left and right $A'$-actions because $\iota$ is an algebra map. They are trivially commuting. Next, the $\Bbbk$-linear map $\textrm{d}_\iota$ satisfies the Leibniz rule

$$\begin{aligned} \text {d}_\iota (a'b') =\text {d}\iota (a'b') =\text {d}(\iota (a')\iota (b')) =(\text {d}\iota (a'))\iota (b')+\iota (a')\text {d}\iota (b') =(\text {d}_\iota a')\!\!\,\cdot b'+a'\!\!\,\cdot \text {d}_\iota b' \end{aligned}$$

for all $a',b'\in A'$. Since by definition of $\Gamma _\iota$ any $\omega \in \Gamma _\iota$ is of the form $\omega =\iota (a'^i)\textrm{d}\iota (b'_i)$ for some $a'^i,b'_i\in A'$ (finite sum understood), we have $\omega =\iota (a'^i)\textrm{d}\iota (b'_i)=a'^i\cdot \textrm{d}_\iota b'_i$, proving that $(\Gamma _\iota ,\textrm{d}_\iota )$ is a FODC on $A'$.

(ii) Since $I=\ker \pi \subseteq A$ is an ideal, by the Leibniz rule of $\textrm{d}$ it immediately follows that $\Gamma _I =I\textrm{d}A+A\textrm{d}I\subseteq \Gamma$ is an A-subbimodule. Hence, $\Gamma /\Gamma _I$ is an A-bimodule. Since $I\cdot \Gamma \subseteq \Gamma _I$, $\Gamma \cdot I\subseteq \Gamma _I$, the A-actions on $\Gamma$ descend to $A'=A/I$-actions on $\Gamma /\Gamma _I$,

$$\begin{aligned} \pi (a)\cdot [\omega ]\cdot \pi (b):=[a\omega b] \end{aligned}$$

for all $a,b\in A$ and $\omega \in \Gamma$. It follows that the map $\textrm{d}$ induced on the quotient, $\textrm{d}_\pi : A'\rightarrow \Gamma _\pi , \pi (a)\mapsto [\textrm{d}a]$, is $\Bbbk$-linear and satisfies the Leibniz rule:

$$\begin{aligned} \textrm{d}_\pi (\pi (a)\pi (b))&=\textrm{d}_\pi (\pi (ab)) =[\textrm{d}(ab)] =[(\textrm{d}a)b+a\textrm{d}b]\\&=[\textrm{d}a]\cdot \pi (b)+\pi (a)\cdot [\textrm{d}b] =(\textrm{d}_\pi \pi (a))\cdot \pi (b)+\pi (a)\cdot \textrm{d}_\pi (\pi (b)) \end{aligned}$$

for all $a,b\in A$. Finally, since any $\omega \in \Gamma$ is of the form $\omega =a^i\textrm{d}b_i$ (sum understood) we have $[\omega ]=[a^i\textrm{d}b_i]=\pi (a^i)\cdot \textrm{d}_\pi (\pi (b_i))$ so that $\Gamma _\pi = A'\textrm{d}_\pi A'$. We conclude that $(\Gamma _\pi ,\textrm{d}_\pi )$ is a FODC on $A'$.

(iii) According to (i) and (ii) $(\Gamma _\iota ,\textrm{d}_\iota )$ and $(\Gamma _\pi ,\textrm{d}_\pi )$ are FODCi on $A'$. The splitting $\iota :A'\rightarrow A$ of the exact sequence $0\rightarrow \ker \pi \rightarrow A{\mathop {\rightarrow }\limits ^{\pi }}A'\rightarrow 0$ implies the direct sum of $A'$-bimodules $A=\iota (A')\oplus I$ where the $A'$-action is via the algebra embedding $A'\rightarrow \iota (A')\subseteq A$. This induces the direct sum of $A'$-bimodules

$$\begin{aligned} \Gamma =A\textrm{d} A=\iota (A')\textrm{d}\iota (A')\oplus \big (I\textrm{d}A+A\textrm{d}I\big )=\Gamma _\iota \oplus \Gamma _I. \end{aligned}$$

Considering the quotient with respect to $\Gamma _I$ gives the isomorphism $\Gamma _\iota \rightarrow \Gamma /\Gamma _I$, $\omega \mapsto \pi (\omega )$, which equals the $\Phi$ morphism defined in (3.4). We are left to prove the compatibility of $(\phi =\textrm{id}_{A'},\Phi )$ with the exterior derivatives, for all $a'\in A'$

$$\begin{aligned} \Phi ( \textrm{d}_\iota a')= \Phi ( \textrm{d} \iota (a'))=[ \textrm{d} \iota (a')]=\textrm{d}_\pi \pi (\iota (a'))= \textrm{d}_\pi a'=\textrm{d}_\pi \phi (a'). \end{aligned}$$

$\square$

We call $(\Gamma _\iota ,\textrm{d}_\iota )$ the pullback calculus, while we call $(\Gamma _\pi ,\textrm{d}_\pi )$ the quotient calculus. The above proposition provides a useful tool to produce examples of noncommutative differential calculi. In the context of Drinfel’d twist deformation quantization it has been employed to describe noncommutative differential geometry on submanifolds of $\mathbb {R}^n$ given by generators and relations [15]. More abstractly, the braided Cartan calculus of a braided commutative algebra with triangular Hopf algebra symmetry is related to the braided Cartan calculus on a submanifold algebra in the above sense [46].

3.2 Covariant calculi on comodule algebras

In this section we discuss the theory for covariant calculi on comodule algebras, following the perspectives of [23, 47] and [36]. Let H be a Hopf algebra.

Definition 3.5

• (i) A FODC $(\Gamma ,\textrm{d})$ on a right H-comodule algebra $(A,\delta _R)$ is said to be right H-covariant if

  $$\begin{aligned} a\textrm{d}b\mapsto a_0\textrm{d}b_0\otimes a_1b_1, \end{aligned}$$

  (3.6)

  for all $a,b\in A$, extends to a well-defined $\Bbbk$-linear map $\Gamma \rightarrow \Gamma \otimes H$.

• (ii) A FODC $(\Gamma ,\textrm{d})$ on a left H-comodule algebra $(A,\delta _L)$ is said to be left H-covariant if

  $$\begin{aligned} a\textrm{d}b\mapsto a_{-1}ab_{-1}\otimes a_0\textrm{d}b_0, \end{aligned}$$

  (3.7)

  for all $a,b\in A$, extends to a well-defined $\Bbbk$-linear map $\Gamma \rightarrow H\otimes \Gamma$.

• (iii) A FODC $(\Gamma ,\textrm{d})$ on an H-bicomodule algebra $(A,\delta _R,\delta _L)$ is said to be H-bicovariant if it is right and left H-covariant.

If $A=H$ is an H-comodule algebra with respect to the coproduct we call an H-covariant FODC simply covariant. We recall the following proposition.

Proposition 3.6

([47])

• (i) A FODC $(\Gamma ,\textrm{d})$ on a right H-comodule algebra $(A,\delta _R)$ is right H-covariant if and only if $(\Gamma ,\Delta _R)$ is a right H-covariant A-bimodule and $\textrm{d}$ is right H-colinear. In this case $\Delta _R$ is determined by (3.6).

• (ii) A FODC $(\Gamma ,\textrm{d})$ on a left H-comodule algebra $(A,\delta _L)$ is left H-covariant if and only if $(\Gamma ,\Delta _L)$ is a left H-covariant A-bimodule and $\textrm{d}$ is left H-colinear. In this case $\Delta _L$ is determined by (3.7).

• (iii) A FODC $(\Gamma ,\textrm{d})$ on an H-bicomodule algebra $(A,\delta _R,\delta _L)$ is an H-bicovariant FODC if and only if $(\Gamma ,\Delta _R,\Delta _L)$ is an H-bicovariant A-bimodule and $\textrm{d}$ is H-bicolinear.

We define a morphism of right/left/bi H-covariant FODCi $(\Gamma ,\textrm{d})$ and $(\Gamma ',\textrm{d}')$ on right/left/bi H-comodule algebras $A,A'$ to be a morphism $(\phi ,\Phi )$ between FODCi such that $\phi$ and $\Phi$ are right/left/bi H-colinear maps. Since $\Phi$, if it exists, is determined by $\phi$ via $\Phi (a^i\textrm{d}b_i)=\phi (a^i)\textrm{d}\phi (b_i)$ for $a^i, b_i\in A$ (finite sum understood), we see that the FODC morphism $(\phi ,\Phi )$ is right/left/bi H-colinear if and only if $\phi :A\rightarrow A'$ is right/left/bi H-colinear, indeed, for all $a\in A$,

$$\begin{aligned} \Delta _R(\Phi (\text {d}a))&= {} \Delta _R\text {d}\phi (a)=\text {d}\phi (a)_0 \otimes \phi (a)_1\\{}&= {} \text {d}\phi (a_0)\otimes a_1=\Phi (\text {d}a_0)\otimes a_1=(\Phi \otimes \text {id}_H) \Delta _R(\text {d}a). \end{aligned}$$

The natural question arises if Proposition 3.4 generalizes to the H-covariant setting.

Proposition 3.7

Let $(\Gamma ,\textrm{d})$ be a right H-covariant FODC on a right H-comodule algebra A.

• (i) If $\iota : A'\rightarrow A$ is a right H-comodule algebra homomorphism the pullback calculus $(\Gamma _\iota ,\textrm{d}_\iota )$ is a right H-covariant FODC on $A'$.

• (ii) If $\pi : A\rightarrow A'$ is a surjective right H-comodule algebra homomorphism the quotient calculus $(\Gamma _\pi ,\textrm{d}_\pi )$ is a right H-covariant FODC on $A'$.

• (iii) If the exact sequence of H-comodule algebras $0\rightarrow \ker \pi \rightarrow A{\mathop {\rightarrow }\limits ^{\pi }}A'\rightarrow 0$ splits via $\iota : A'\rightarrow A$, then $(\Gamma _\iota ,\textrm{d}_\iota )$ is equivalent to $(\Gamma _\pi ,\textrm{d}_\pi )$ as a right H-covariant FODC.

Analogous statements hold for left H-covariant and H-bicovariant FODCi on left H-comodule algebras and H-bicomodule algebras, respectively.

Proof

From Proposition 3.4 it follows that $(\Gamma _\iota ,\textrm{d}_\iota )$ and $(\Gamma _\pi ,\textrm{d}_\pi )$ are FODCi on $A'$. We prove (i) by observing that for all $a^i,b^i\in A$ (and understanding finite sums on the indices i)

$$\begin{aligned} \iota (a^i)_0\textrm{d}(\iota (b^i)_0)\otimes \iota (a^i)_1\iota (b^i)_1 =\iota (a^i_0)\textrm{d}(\iota (b^i_0))\otimes a^i_1b^i_1 \in \Gamma _\iota \otimes H \end{aligned}$$

by the right H-colinearity of $\iota$. Thus, the right H-coaction $\Delta _R:\Gamma \rightarrow \Gamma \otimes H$ restricts to a $\Bbbk$-linear map $\Delta _R|_{\Gamma _\iota }:\Gamma _\iota \rightarrow \Gamma _\iota \otimes H$ and consequently $(\Gamma _\iota ,\textrm{d}_\iota )$ is a right H-covariant FODC. For (ii) we first note that $I=\ker \pi \subseteq A$ satisfies $\delta _R(I)\subseteq I\otimes H$ since $\pi$ is right H-colinear. Then, by the right H-covariance of $(\Gamma ,\textrm{d})$ we have that $\Gamma _I\subseteq \Gamma$ is a right H-subcomodule: $\Delta _R(\Gamma _I)\subseteq \Gamma _I\otimes H$, so that $\Delta _R:\Gamma \rightarrow \Gamma \otimes H$ induces a well-defined right H-coaction on $\Gamma _\pi$, which reads

$$\begin{aligned} \Delta _R([a\textrm{d}b])=[a_0\textrm{d}b_0]\otimes a_1ab_1 =\pi (a_0)\cdot \textrm{d}_\pi \pi (b_0)\otimes a_1b_1 \end{aligned}$$

for all $a,b\in A$. This shows that $(\Gamma _\pi ,\textrm{d}_\pi )$ is right H-covariant. The third statement trivially holds recalling that for the morphism $(\phi ,\Phi )$ of FODCi $\Phi$ is H-colinear if $\phi$ is H-colinear, which is the case since $\phi =\textrm{id}_{A'}$. $\square$

We have the following corollary of Proposition (3.7) (ii).

Corollary 3.8

Let $\pi : A\rightarrow H$ be a Hopf algebra epimorphism. Any right/left/bicovariant FODC $(\Gamma ,\textrm{d})$ on the Hopf algebra A gives a right/left H-covariant or H-bicovariant FODC on A and projects to a right/left/bicovariant FODC $(\Gamma _\pi ,\textrm{d}_\pi )$ on the Hopf algebra H.

Proof

Here we prove the case of a bicovariant FODC $(\Gamma ,\textrm{d})$ on A. The others are similarly proven. The left and right H-coactions on A defined by

$$\begin{aligned} \begin{aligned} \delta _L&:=(\pi \otimes \textrm{id}_A)\circ \Delta : A\rightarrow H\otimes A,~ a\mapsto a_{-1}\otimes a_0:=[a_1]\otimes a_2\\ \delta _R&:=(\textrm{id}_A\otimes \pi )\circ \Delta : A\rightarrow A\otimes H,~ a\mapsto a_0\otimes a_1:=a_1\otimes [a_2] \end{aligned} \end{aligned}$$

and those on $\Gamma$ defined by

$$\begin{aligned} \begin{aligned} \Delta ^H_L:=(\pi \otimes \textrm{id}_A)\circ \Delta _L&:\Gamma \rightarrow H\otimes \Gamma , ~ a\textrm{d}b\mapsto a_{-1}b_{-1}\otimes a_0\textrm{d}b_0 \\ \Delta ^H_R:=(\textrm{id}_A\otimes \pi ) \circ \Delta _R&:\Gamma \rightarrow \Gamma \otimes H, ~ a\textrm{d}b\mapsto a_0\textrm{d}b_0\otimes a_1b_1,\\ \end{aligned} \end{aligned}$$

where $a,b\in A$, structure $(\Gamma , \textrm{d}_\pi )$ as an H-bicovariant FODC on A. The projection $\pi :A\rightarrow H$ is left and right H-colinear so that from Proposition (3.7) the induced FODC $(\Gamma _\pi , \textrm{d}_\pi )$ on H is H-bicovariant with H-coaction given by the H-coproduct. $\square$

3.3 Examples of covariant calculi

In this section we describe covariant calculi on the quantum groups $\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$, $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and on their parabolic subalgebras.

Example 3.9

(4D calculus on $\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$) Let $q\in \mathbb {C}$ be a non-zero complex number which is not a root of unity. The free $\mathbb {C}$-algebra $\mathbb {C}\langle \alpha ,\beta , \gamma ,\delta \rangle$ generated by indeterminates $\alpha ,\beta ,\gamma , \delta$ modulo the relations

$$\begin{aligned} \begin{array}{c} \alpha \beta =q^{-1}\beta \alpha , \quad \alpha \gamma =q^{-1}\gamma \alpha , \quad \beta \delta =q^{-1}\delta \beta , \quad \gamma \delta =q^{-1}\delta \gamma , \\ \\ \beta \gamma =\gamma \beta , \qquad \alpha \delta -\delta \alpha =(q^{-1}-q)\beta \gamma \end{array}\nonumber \\ \end{aligned}$$

(3.8)

is denoted by $\mathcal {O}_q(\textrm{M}_2(\mathbb {C})):=\mathbb {C}\langle \alpha ,\beta , \gamma ,\delta \rangle /I_M$, where $I_M$ is the ideal in $\mathbb {C}\langle \alpha ,\beta , \gamma ,\delta \rangle$ generated by the (3.8). The quotient algebra $\mathcal {O}_q(\textrm{M}_2(\mathbb {C}))$ is a bialgebra with coalgebra structure

$$\begin{aligned} \Delta \begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix} =\begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix}\dot{\otimes }\begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix},~ \epsilon \begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix} =\begin{pmatrix} 1 &{} 0\\ 0 &{} 1 \end{pmatrix}, \end{aligned}$$

(3.9)

where $\dot{\otimes }$ denotes the tensor product and matrix multiplication. Furthermore, there is a central element $\textrm{det}_q:=\alpha \delta -q^{-1}\beta \gamma \in \mathcal {O}_q(\textrm{M}_2(\mathbb {C}))$, satisfying $\Delta (\textrm{det}_q)=\textrm{det}_q\otimes \textrm{det}_q$ and $\epsilon (\textrm{det}_q)=1$. On the quotient algebra $\mathcal {O}_q(\textrm{GL}_2(\mathbb {C})):= \mathcal {O}_q(\textrm{M}_2(\mathbb {C}))[r]/\langle r~\textrm{det}_q-1\rangle$ we induce a Hopf algebra structure by (3.9) and $\Delta (r)=r\otimes r$, $\epsilon (r)=1$, together with the antipode

$$\begin{aligned} S\begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix} =r\begin{pmatrix} \delta &{} -q\beta \\ -q^{-1}\gamma &{} \alpha \end{pmatrix},~~~~~~~~~~ S(r)=\textrm{det}_q. \end{aligned}$$

(3.10)

On the quantum group $A:=\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$ there is a 4-dimensional bicovariant FODC $(\Gamma _{\textrm{GL}},\textrm{d}_{\textrm{GL}})$ which we are going to describe following the explicit exposition of [2].¹$\Gamma$ is a free left A-module generated by a basis $\{\omega ^1,\omega ^2,\omega ^3,\omega ^4\}$ of left coinvariant 1-forms obeying the commutation relations

$$\begin{aligned} \begin{aligned} \omega ^1\alpha&=q\alpha \omega ^1,\\ \omega ^2\alpha&=\alpha \omega ^2,\\ \omega ^3\alpha&=-q^{-1}\lambda \beta \omega ^1+\alpha \omega ^3,\\ \omega ^4\alpha&=-\lambda \beta \omega ^2+q^{-1}\alpha \omega ^4,\\ \omega ^1\gamma&=q\gamma \omega ^1,\\ \omega ^2\gamma&=\gamma \omega ^2,\\ \omega ^3\gamma&=\gamma \omega ^3-q^{-1}\lambda \delta \omega ^1,\\ \omega ^4\gamma&=-\lambda \delta \omega ^2+q^{-1}\gamma \omega ^4, \end{aligned} ~~~\begin{aligned} \omega ^1\beta&=q^{-1}\beta \omega ^1,\\ \omega ^2\beta&=-q^{-1}\lambda \alpha \omega ^1+\beta \omega ^2,\\ \omega ^3\beta&=\beta \omega ^3,\\ \omega ^4\beta&=q^{-1}\lambda ^2\beta \omega ^1-\lambda \alpha \omega ^3 +q\beta \omega ^4,\\ \omega ^1\delta&=q^{-1}\delta \omega ^1,\\ \omega ^2\delta&=\delta \omega ^2-q^{-1}\lambda \gamma \omega ^1,\\ \omega ^3\delta&=\delta \omega ^3,\\ \omega ^4\delta&=q^{-1}\lambda ^2\delta \omega ^1-\lambda \gamma \omega ^3 +q\delta \omega ^4 \end{aligned}\nonumber \\ \end{aligned}$$

(3.11)

with $\lambda :=q^{-1}-q$. The differential is given in terms of this basis by

$$\begin{aligned} \begin{array}{rcl} \textrm{d}_{\textrm{GL}} \alpha &{}=&{}\frac{q-1}{\lambda }\, \alpha \omega ^1 +\frac{q^{-1}-1}{\lambda }\,\alpha \omega ^4-\beta \omega ^2 \\ \textrm{d}_{\textrm{GL}} \beta &{}=&{}Q \beta \omega ^1 +\frac{q-1}{\lambda } \,\beta \omega ^4-\alpha \omega ^3\\ \textrm{d}_{\textrm{GL}} \gamma &{}=&{}\frac{q-1}{\lambda } \,\gamma \omega ^1 +\frac{q^{-1}-1}{\lambda }\, \gamma \omega ^4-\delta \omega ^2 \\ \textrm{d}_{\textrm{GL}} \delta &{}=&{}Q \delta \omega ^1 +\frac{q-1}{\lambda }\, \delta \omega ^4-\gamma \omega ^3, \end{array}\nonumber \\ \end{aligned}$$

(3.12)

where $Q:=\frac{q^{-1}(\lambda ^2+1)-1}{\lambda }=\frac{q^2+q+1}{q^2(q+1)}-1$. The basis 1-forms are then expressed explicitly as

$$\begin{aligned} \omega ^1&=Q'\bigg ((q^{-2}-q^{-1})(S(\alpha )\text {d}_{\text {GL}}\alpha +S(\beta )\text {d}_{\text {GL}}\gamma ) +q^{-2}(q^{-1}-1)(S(\gamma )\text {d}_{\text {GL}}\delta +S(\delta )\text {d}_{\text {GL}}\delta )\bigg )\nonumber \\ \omega ^2&=-q^2(S(\gamma )\text {d}_{\text {GL}}\alpha +S(\delta )\text {d}_{\text {GL}}\gamma )\nonumber \\ \omega ^3&=-q^2(S(\alpha )\text {d}_{\text {GL}}\beta +S(\beta )\text {d}_{\text {GL}}\delta )\nonumber \\ \omega ^4&=Q'\bigg ((q^{-5}-q^{-3}-q^{-2}+q^{-1}) (S(\alpha )\text {d}_{\text {GL}}\alpha +S(\beta )\text {d}_{\text {GL}}\gamma )\nonumber \\ {}&\qquad \qquad ~~~~~~\quad +(q^{-2}-q^{-1})(S(\gamma )\text {d}_{\text {GL}}\delta +S(\delta )\text {d}_{\text {GL}}\delta )\bigg ), \end{aligned}$$

(3.13)

where $Q':=\frac{1}{q^{-5}-q^{-4}-q^{-2}+q^{-1}}$.

We now construct a bicovariant FODC $(\Gamma _{P_{\textrm{GL}}},\textrm{d}_{P_{\textrm{GL}}})$ on $\mathcal {O}_q(P_{\textrm{GL}}):=A/\langle \gamma \rangle$. This is done via the Hopf algebra quotient $\pi _{P_{\textrm{GL}}}: A\rightarrow \mathcal {O}_q(P_{\textrm{GL}}),~ a\mapsto \pi _{P_{\textrm{GL}}}(a)=:[a]$, using Corollary 3.8. We recall that $\Gamma _{P_{\textrm{GL}}}:=\Gamma _{\textrm{GL}}/\Gamma _{I_\gamma }$, where $\Gamma _{I_\gamma }:=A\cdot \textrm{d}_{\textrm{GL}}\langle \gamma \rangle +\langle \gamma \rangle \textrm{d}_{\textrm{GL}}A\subseteq \Gamma _{\textrm{GL}}$. Writing $[\omega ]$ for the equivalence class of $\omega \in \Gamma _{\textrm{GL}}$ on the quotient $\pi ^\Gamma _{P_{\textrm{GL}}}:\Gamma _{\textrm{GL}}\rightarrow \Gamma _{P_{\textrm{GL}}}$, the differential on $\Gamma _{P_{\textrm{GL}}}$ is defined by $\textrm{d}_{P_{\textrm{GL}}}:\mathcal {O}_q(P_{\textrm{GL}}) \rightarrow \Gamma _{P_{\textrm{GL}}}$, $\textrm{d}_{P_{\textrm{GL}}}[a]:= [\textrm{d}_{\textrm{GL}}a]$ for all $a\in \mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$. As a free left $H:=\mathcal {O}_q(P_{\textrm{GL}})$-module $\Gamma _{P_{\textrm{GL}}}$ is 3-dimensional with basis $\{[\omega ^1],[\omega ^3],[\omega ^4]\}$.² Denoting the projected generators by

$$\begin{aligned} \pi _{P_{\textrm{GL}}}\begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix}=: \begin{pmatrix} t &{} p\\ 0 &{} s \end{pmatrix},~~~~~\pi _{\textrm{GL}}(r)=:r', \end{aligned}$$

the right H-action and differential are explicitly given by

$$\begin{aligned} \begin{array}{l} {[}\omega ^1]t=qt[\omega ^1],\\ {[}\omega ^3]t=-q^{-1}\lambda p[\omega ^1]+t[\omega ^3],\\ {[}\omega ^4]t=q^{-1}t[\omega ^4], \end{array} \quad \begin{array}{l} {[}\omega ^1]p=q^{-1}p[\omega ^1],\\ {[}\omega ^3]p=p[\omega ^3],\\ {[}\omega ^4]p=q^{-1}\lambda ^2p[\omega ^1]-\lambda t[\omega ^3] +qp[\omega ^4], \end{array}, \quad \begin{array}{l} {[}\omega ^1]s=q^{-1}s[\omega ^1],\\ {[}\omega ^3]s=s[\omega ^3],\\ {[}\omega ^4]s=q^{-1}\lambda ^2s[\omega ^1]+qs[\omega ^4] \end{array} \nonumber \\ \end{aligned}$$

(3.14)

and

$$\begin{aligned}{} & {} \textrm{d}_{P_{\textrm{GL}}}t=\frac{q-1}{\lambda }t[\omega ^1]+\frac{q^{-1}-1}{\lambda }t[\omega ^4],\nonumber \\{} & {} \textrm{d}_{P_{\textrm{GL}}}p=Qp[\omega ^1]+\frac{q-1}{\lambda }p[\omega ^4]-t[\omega ^3],~~ \textrm{d}_{P_{\textrm{GL}}}s=Qs[\omega ^1]+\frac{q-1}{\lambda }s[\omega ^4].\qquad \qquad \end{aligned}$$

(3.15)

Example 3.10

(Bicovariant FODC on $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and its parabolic quotient) Consider the quotient Hopf algebra $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C})):=\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))/\langle \textrm{det}_q-1\rangle$ with coalgebra structure and antipode induced from (3.9) and (3.10). We denote the associated Hopf algebra map projection by $\textrm{pr}_{\textrm{SL}}:\mathcal {O}_q(\textrm{GL}_2(\mathbb {C})) \rightarrow \mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$. The quantum group $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ is the Manin deformation (see [30]) of the ring of algebraic functions on the complex special linear group $\textrm{SL}_2(\mathbb {C})$. It is the deformed algebra of regular functions on the complex special linear group $\textrm{SL}_2(\mathbb {C})$. Let $\mathcal {O}_q(P)$ be the deformed algebra of functions on the Borel subgroup $P\subset \textrm{SL}_2(\mathbb {C})$. We identify it with the quotient $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))/I_P$ where $I_P\subseteq \mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ is the Hopf ideal generated by the element $\gamma$. On generators the Hopf algebra projection is given by

$$\begin{aligned} \pi _P:\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))\rightarrow \mathcal {O}_q(P),~~~~~ \begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix} \mapsto \begin{pmatrix} t &{} p\\ 0 &{} t^{-1} \end{pmatrix} \end{aligned}$$

(3.16)

or, in other words, $\mathcal {O}_q(P) =\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))/I_P =\mathbb {C}\langle t, t^{-1}, p \rangle /\langle tp-q^{-1}pt\rangle$. Note that $\mathcal {O}_q(P)=\mathcal {O}_q(P_{\textrm{GL}})/\langle \textrm{det}_q-1\rangle \cong \mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))/\langle \gamma ,\textrm{det}_q\rangle$ and the corresponding projection $\textrm{pr}_P: \mathcal {O}_q(P_{\textrm{GL}})\rightarrow \mathcal {O}_q(P)$ makes the diagram

(3.17)

commute.

There are bicovariant FODCi $(\Gamma ^+_{\textrm{SL}},\textrm{d}^+_{\textrm{SL}})$ on $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and $(\Gamma ^+_P,\textrm{d}_P^+)$ on $\mathcal {O}_q(P)$ induced from Example 3.9 as the quotient calculi

By the commutativity of the square diagram in (3.17) and recalling that the modules of 1-forms are generated by the algebras and differentials we obtain the commutative cube

To be more explicit, the bicovariant FODC $(\Gamma ^+_{\textrm{SL}},\textrm{d}^+_{\textrm{SL}})$ on $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ is 4-dimensional with basis of left coinvariant 1-forms $\{\omega ^1,\omega ^2, \omega ^3,\omega ^4\}$. Up to the identification $\textrm{det}_q=1$ the commutation relations and differentials coincide with (3.11) and (3.12). The bicovariant calculus $\Gamma ^+_P$ is only 2-dimensional: one of the three basis vectors $[\omega ^1],[\omega ^3], [\omega ^4]$ of $\Gamma _{P_{\textrm{GL}}}$ vanishes on $\Gamma ^+_P$, namely $[\omega ^1]$. Indeed, denoting equivalence classes on $\Gamma ^+_P$ under $\textrm{pr}^\Gamma _P:\Gamma _{P_{\textrm{GL}}}\rightarrow \Gamma ^+_P$ by $[\cdot ]'$ and using (3.8) and (3.12) we obtain

$$\begin{aligned} 0=[\textrm{d}(\alpha \delta )]' =[\textrm{d}(\alpha )\delta ]'+[\alpha \textrm{d}\delta ]' =\bigg [\bigg (\frac{q-1}{\lambda }+qQ\bigg )\omega ^1\bigg ]', \end{aligned}$$

which implies $[\omega ^1]'=0$. Then, the commutation relations (3.14) and the differentials (3.15) project to

$$\begin{aligned} \begin{aligned} \,[\omega ^3]' t&=t[{\omega }^3]',\,\, [{\omega }^3]' p=p[{\omega }^3]',\,\,[{\omega }^4]' t=q^{-1}t[{\omega }^4]',\,\,[{\omega }^4]'p=qp[{\omega }^4]'-\lambda t[{\omega }^3]',\\ \textrm{d}^+_P t&={\frac{q^{-1}-1}{\lambda }} \,t\,[{\omega }^4]',\,\,\,\, \textrm{d}^+_P p=-t \,[{\omega }^3]'+{\frac{q-1}{\lambda }}\,p\,[{\omega }^4]'~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned} \end{aligned}$$

on $\mathcal {O}_q(P)$, where we identified t, p as generators in $\mathcal {O}_q(P)$.

Example 3.11

(3-dim calculus on $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and its parabolic quotient $\mathcal {O}_q(P)$) Let $A:=\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and $H:=\mathcal {O}_q(P)$ be the Hopf algebras from Example 3.10. There is a 3-dimensional left covariant FODC $(\Gamma _{\textrm{SL}},\textrm{d}_{\textrm{SL}})$ on A described in [26] Sect. 14.1.4. $\Gamma _{\textrm{SL}}$ is the free left A-module generated by the basis $\{\omega ^0,\omega ^1,\omega ^2\}$ of left coinvariant 1-forms with commutation relations

$$\begin{aligned} \begin{aligned}&\omega ^j\alpha =q^3\alpha \omega ^j,~~~~~ \omega ^j\beta =q^{-3}\beta \omega ^j,\\&\omega ^j\gamma =q^3\gamma \omega ^j,~~~~~ \omega ^j\delta =q^{-3}\delta \omega ^j, \end{aligned} \end{aligned}$$

(3.18)

for $j=0,2$ and

$$\begin{aligned} \begin{aligned}&\omega ^1\alpha =q^2\alpha \omega ^1+(q^2-1)\beta \omega ^2,~~~~~ \omega ^1\beta =q^{-2}\beta \omega ^1+(q^2-1)\alpha \omega ^0,\\&\omega ^1\gamma =q^2\gamma \omega ^1+(q^2-1)\delta \omega ^2,~~~~~~ \omega ^1\delta =q^{-2}\delta \omega ^1+(q^2-1)\gamma \omega ^0. \end{aligned} \end{aligned}$$

(3.19)

The differential $\textrm{d}_{\textrm{SL}}: A \rightarrow \Gamma _{\textrm{SL}}$ is determined by

$$\begin{aligned} \begin{aligned}&\textrm{d}_{\textrm{SL}}\alpha =\alpha \omega ^1+\beta \omega ^2,~~~~~ \textrm{d}_{\textrm{SL}}\beta =\alpha \omega ^0-q^{-2}\beta \omega ^1,\\&\textrm{d}_{\textrm{SL}}\gamma =\gamma \omega ^1+\delta \omega ^2,~~~~~~ \textrm{d}_{\textrm{SL}}\delta =\gamma \omega ^0-q^{-2}\delta \omega ^1 \end{aligned} \end{aligned}$$

and thus

$$\begin{aligned} \begin{aligned} \omega ^0=\delta \textrm{d}_{\textrm{SL}}\beta -q\beta \textrm{d}_{\textrm{SL}}\delta ,~~~~~ \omega ^1=\delta \textrm{d}_{\textrm{SL}}\alpha -q\beta \textrm{d}_{\textrm{SL}}\gamma ,~~~~~ \omega ^2=-q^{-1}\gamma \textrm{d}_{\textrm{SL}}\alpha +\alpha \textrm{d}_{\textrm{SL}}\gamma . \end{aligned} \end{aligned}$$

As in Example 3.10 elements in the equivalence class H are denoted by $[\omega ]$ with a representative $\omega \in \Gamma _{\textrm{SL}}$. The induced quotient calculus $(\Gamma _P,\textrm{d}_P)$ on H is the 2-dimensional left covariant FODC with $\Gamma _P$ being the free left H-module generated by the basis $\{[\omega ^0],[\omega ^1]\}$ of left coinvariant elements (notice that $[\omega ^2]=0$, while $[\omega ^0],[\omega ^1]$ are linearly independent). The resulting commutation relations are

$$\begin{aligned} \begin{aligned}&[\omega ^0]t=q^3t[\omega ^0],~~~~~~~ [\omega ^0]p=q^{-3}p[\omega ^0],\\&[\omega ^1]t=q^2t[\omega ^1],~~~~~~~ [\omega ^1]p=q^{-2}p[\omega ^1]+(q^2-1)t[\omega ^0] \end{aligned} \end{aligned}$$

and the differential reads

$$\begin{aligned} \textrm{d}_Pt=t[\omega ^1],~~~~~ \textrm{d}_Pp=t[\omega ^0]-q^{-2}p[\omega ^1],~~~~~ \textrm{d}_Pt^{-1}=-q^{-2}t^{-1}[\omega ^1]. \end{aligned}$$

3.4 The smash product calculus

In this section we recall the construction of a covariant differential calculus on the smash product algebra $B\#H$ from an H-module calculus on an H-module algebra B and a bicovariant calculus on the Hopf algebra H, given in [36]. If the H-action on B is trivial we recover the tensor product differential calculus on $B\otimes H$ described in Proposition 3.2.

Let B be a left H-module algebra, with action $\rhd : H\otimes B\rightarrow B$. Let M be a B-bimodule, with actions $\cdot : B\otimes M\rightarrow M$, $\cdot : M\otimes B\rightarrow M$, and a left H-module with action that with slight abuse we denote $\rhd : H\otimes M\rightarrow M$. We say that M is a relative H-module B-bimodule if the H and B actions have the compatibility, for all $h\in H, b,b'\in B$, $m\in M$,

$$\begin{aligned} h\rhd (b \cdot m\cdot b')=(h_1\rhd b)\cdot (h_2\rhd m)\cdot (h_3\rhd b'). \end{aligned}$$

Similar definitions are given if M is just a left or a right B-module.

Definition 3.12

Let B be a left H-module algebra with action $\rhd : H\otimes B\rightarrow B$. A FODC $(\Gamma _B,{\textrm{d}_B})$ on B is said to be an H-module FODC if for any $b^i,b_i\in B$, $i=1,2,...n$, ($n\in \mathbb {N}$) and $h\in H$ we have

$$\begin{aligned} \sum _ib^i\textrm{d}_Bb_i=0 \,\Rightarrow \, \sum _i(h_1\rhd b^i)\textrm{d}_B(h_2\rhd b_i)=0 . \end{aligned}$$

(3.20)

The rationale of this definition is in the following proposition.

Proposition 3.13

$(\Gamma _B,{\textrm{d}_B})$ is an H-module FODC if and only if $\Gamma _B$ is a relative H-module B-bimodule and $\textrm{d}_B: B\rightarrow \Gamma _B$ is an H-module map: for all $h\in H$, $b\in B$, $h\rhd \textrm{d}_Bb=\textrm{d}_B(h\rhd b)$.

Proof

Since (3.20) holds we have a well-defined H-action given by,

$$\begin{aligned} H\otimes \Gamma _B\rightarrow \Gamma _B ,~~ h\rhd \sum _i(b^i\textrm{d}_Bb_i):=\sum _i(h_1\rhd b^i)\textrm{d}_B(h_2\rhd b_i) \end{aligned}$$

where we used that $\Gamma _B=B\textrm{d}_BB$, so that $\sum _i b^i\textrm{d}_Bb_i$ is a generic element of $\Gamma _B$. Trivially $\textrm{d}_B: B\rightarrow \Gamma _B$ is an H-module map. Compatibility of this action with the left B-action is immediate. Compatibility with the right B-action: $h\rhd ((\sum _i b^i\textrm{d}_Bb_i) b)=(h_1\rhd \sum _i b^i\textrm{d}_Bb_i)(h_2\rhd b)$, follows writing $(\sum _i b^i\textrm{d}_Bb_i) b=\sum _i b^i\textrm{d}_B(b_i b)-\sum _i b^ib_i\textrm{d}_Bb$.

Vice versa, if $\Gamma _B$ is a relative H-module B-bimodule and $\textrm{d}_B: B\rightarrow \Gamma _B$ is an H-module map, the implication (3.20) follows from its equivalence with $\sum _ib^i\textrm{d}_Bb_i=0 \,\Rightarrow \, h\rhd \sum _i(b^i\textrm{d}_Bb_i)=0$. $\square$

Given an H-module algebra B and a FODC $(\Gamma _{B},\textrm{d}_B)$ and a left covariant FODC $(\Gamma _{H},\textrm{d}_H)$, we consider the $\Bbbk$-module

$$\begin{aligned} \Gamma _\#:=\Gamma _B\otimes H\,\oplus \, B\otimes \Gamma _H~ \end{aligned}$$

(3.21)

and study when there is a FODC $(\Gamma _\#,\textrm{d}_\#)$ on $B\#H$. The $\Bbbk$-module $\Gamma _\#$ in (3.21) is a direct sum of tensor products of left H-modules hence it carries a left H-action canonically induced from the H-actions on the H-modules $\Gamma _B$, H, B, $\Gamma _H$: for all $h\in H$, $\omega _B\otimes h'+b'\otimes \omega _H\in \Gamma _\#$,

$$\begin{aligned} h\cdot (\omega _B\otimes h'+b'\otimes \omega _H)=h_1\rhd \omega _B\otimes h_2h'+h_1\rhd b'\otimes h_2\omega _H, \end{aligned}$$

extended linearly to all $\Gamma _\#$. Defining the left B-action on $\Gamma _\#$ as the B-action on the first factors in the tensor products $\Gamma _B\otimes H$ and $B\otimes \Gamma _H$ we obtain the left $B\#H$-action on $\Gamma _\#$ using that $b\# h=(b\# 1_H)(1_B\# h)$:

$$\begin{aligned} (b\# h)\cdot (\omega _B\otimes h'+b'\otimes \omega _H):=b(h_1\rhd \omega _B)\otimes h_2h'+b(h_1\rhd b)'\otimes h_2\omega _H. \end{aligned}$$

(3.22)

The proof that this indeed defines an action of the algebra $B\#H$ on $\Gamma _\#$, actually a $B\#H$-action on the submodules $\Gamma _B\otimes H$ and $B\otimes \Gamma _H$, uses the same steps of the proof of associativity of the multiplication in $B\#H$. We define

$$\begin{aligned} (\omega _B\otimes h'+b'\otimes \omega _H)\cdot b:= \omega _B(h'_1\rhd b)\otimes h'_2+b'((\omega _H)^{}_{-1}\rhd b)\otimes (\omega _H)^{}_{0} \end{aligned}$$

and extend it linearly to all $\Gamma _\#$. It is easy to prove that this is a right B-action on $\Gamma _\#$. Defining the right H-action on $\Gamma _\#$ as the right H-action on the second factors in the tensor products $\Gamma _B\otimes H$ and $B\otimes \Gamma _H$ we obtain the right $B\#H$-action on $\Gamma _\#$

$$\begin{aligned} (\omega _B\otimes h'+b'\otimes \omega _H)\cdot (b\#h):= \omega _B(h'_1\rhd b)\otimes h'_2h + b'((\omega _H)^{}_{-1}\rhd b)\otimes (\omega _H)^{}_{0}h.\nonumber \\ \end{aligned}$$

(3.23)

We prove commutativity of the left and right $B\#H$-actions on $\Gamma _B\otimes H$:

$$\begin{aligned} \begin{aligned} (b\# h)\cdot ((\omega _B\otimes h')\cdot ({\tilde{b}}\# {\tilde{h}}))&= (b\# h)\cdot (\omega _B( h'_1\rhd {\tilde{b}})\otimes h'_2{\tilde{h}})\\&= b\cdot (h_1\rhd (\omega _B( h'_1\rhd {\tilde{b}}))\otimes h_2h'_2{\tilde{h}})\\&=b(h_1\rhd \omega _B) (h_2 h'_1\rhd {\tilde{b}})\otimes h_3h'_2{\tilde{h}}\\&=(b(h_1\rhd \omega _B) \otimes h_2 h')\cdot ({\tilde{b}}\# {\tilde{h}})\\&=((b\# h)\cdot (\omega _B\otimes h'))\cdot ({\tilde{b}}\# {\tilde{h}}). \end{aligned} \end{aligned}$$

Commutativity of the left and right $B\#H$-actions on $B\otimes \Gamma _H$ is similarly proven using the left H-comodule structure of $\Gamma _H$. This shows that $\Gamma _\#$ is a $B\#H$-bimodule. We sometimes write $\Gamma _B\#H$ and $B\#\Gamma _H$ in order to stress that we consider them as bimodules over $B\#H$ instead of $B\otimes H$. As in [36] Thm. 2.7 we have a FODC on $B\#H$ with $B\#H$-bimodule $\Gamma _\#$.

Theorem 3.14

Let H be a Hopf algebra and B a left H-module algebra. Given an H-module FODC $(\Gamma _B,\textrm{d}_B)$ on B and a left covariant FODC $(\Gamma _H,\textrm{d}_H)$ on H there is a FODC $(\Gamma _\#,\textrm{d}_\#)$ on $B\#H$, where the $\Bbbk$-module $\Gamma _\#:=\Gamma _B\otimes H\oplus B\otimes \Gamma _H$ is endowed with the $B\#H$-bimodule actions (3.22), (3.23) and the exterior derivative $\textrm{d}_\#: B\#H\rightarrow \Gamma _\#$ is defined by

$$\begin{aligned} \textrm{d}_\#(b\#h):=\textrm{d}_Bb\otimes h+b\otimes \textrm{d}_Hh \end{aligned}$$

for all $b\in B$ and $h\in H$.

Proof

We show that $\textrm{d}_\#: B\#H\rightarrow \Gamma _\#$ satisfies the Leibniz rule:

$$\begin{aligned} \text {d}_\#((b\#h)(b'\#h'))&=\text {d}_\#(b(h_1\rhd b')\#h_2h')\\ {}&=\text {d}_B(b(h_1\rhd b'))\otimes h_2h' +b(h_1\rhd b')\otimes \text {d}_H(h_2h')\\ {}&=(\text {d}_Bb)(h_1\rhd b')\otimes h_2h' +\,b\!\;\text {d}_B(h_1\rhd b')\otimes h_2h'\\ {}&\quad ~ +b(h_1\rhd b')\otimes (\text {d}_Hh_2)h' \,+\, b(h_1\rhd b')\otimes h_2\!\,\text {d}_Hh'\\ {}&=\text {d}_\#(b\#h)\cdot (b'\#h') +(b\#h)\cdot \text {d}_\#(b'\#h') \end{aligned}$$

for all $b,b'\in B$ and $h,h'\in H$. We are left to prove that $\Gamma _\#=(B\#H)\cdot \textrm{d}_\#(B\#H)$. Let $b,b'\in B$ and $h,h'\in H$. Then

$$\begin{aligned} b\!\;\text {d}_Bb'\otimes h {}&{} =b\!\;\text {d}_Bb'\otimes h +bb'\otimes \text {d}_Hh -bb'\otimes \text {d}_Hh\\{}&{} =(b\#1)\cdot \text {d}_\#(b'\#h)-(bb'\#1)\cdot \text {d}_\#(1\#h) \end{aligned}$$

and $b\otimes h\!\,\textrm{d}_Hh'=(b\#h)\cdot \textrm{d}_\#(1\#h')$ establish the equality in question. $\square$

The smash product construction of differential calculi is compatible with right H-coactions.

Corollary 3.15

Let H be a Hopf algebra, B a left H-module algebra, $(\Gamma _B,\textrm{d}_B)$ an H-module FODC on B and $(\Gamma _H,\textrm{d}_H)$ a bicovariant FODC on H. The FODC $(\Gamma _\#,\textrm{d}_\#)$ of Theorem 3.14 is then right H-covariant.

Proof

Define a right H-coaction on $\Gamma _\#$ via

$$\begin{aligned} \begin{aligned} \Gamma _\#&\xrightarrow {\Delta _\#}\Gamma _\#\otimes H\\ \omega _B\otimes h+b\otimes \omega _H&\,\!\longmapsto \,\omega _B\otimes h_1\otimes h_2 +b\otimes (\omega _H)^{}_0\otimes (\omega _H)^{}_1. \end{aligned} \end{aligned}$$

We prove that the calculus is right H-covariant by showing right H-colinearity of the differential, cf. Proposition 3.6 (i). For all $b\#h\in B\# H$,

$$\begin{aligned} \Delta _\#(\textrm{d}_\#(b\#h))&=\Delta _\#(\textrm{d}_Bb\otimes h +b\otimes \textrm{d}_Hh)\\&=\textrm{d}_Bb\otimes h_1\otimes h_2 +b\otimes \textrm{d}_Hh_1\otimes h_2\\&=\textrm{d}_\#(b\#h_1)\otimes h_2\\&=(\textrm{d}_\#\otimes \textrm{id}_A)\Delta _\#(b\#h). \end{aligned}$$

$\square$

3.5 Base forms, horizontal forms and principal covariant calculi

In this section we study differential calculi on noncommutative principal bundles over affine bases. We assume the ground ring $\Bbbk$ to be a field and recall that the Hopf algebra (quantum structure group) H is assumed to have invertible antipode. We have seen that in this setting a principal comodule algebra $B=A^{\textrm{co}H}\subseteq A$ is equivalently a faithfully flat Hopf Galois extension $B=A^{\textrm{co}H}\subseteq A$.

Definition 3.16

Let $(\Gamma _A, \mathrm d_A)$ be a FODC on a right H-comodule algebra A. We call the pullback calculus $(\Gamma _B,\textrm{d}_B):=(B\textrm{d}_A|^{}_BB,\textrm{d}_A|^{}_B)$ on $B:=A^{\textrm{co}H}\subseteq A$ the FODC of base forms. We further call $\Gamma ^{\textrm{hor}}:=A\Gamma _B$, the (A, B)-bimodule of horizontal forms.

If $(\Gamma _A,\textrm{d}_A)$ is a right H-covariant FODC, base and horizontal forms can be further characterized.

Theorem 3.17

Let A be a principal comodule algebra, $B:=A^{\textrm{co}H}$ and $(\Gamma _A,\textrm{d}_A)$ a right H-covariant FODC on A. The natural map $A \otimes _B \Gamma _B \rightarrow \Gamma _A,~ a \otimes \omega \mapsto a\omega$ is injective and gives the left A-module isomorphism

$$\begin{aligned} A \otimes _B\Gamma _B\cong A\Gamma _B . \end{aligned}$$

The B-bimodule of base forms is the intersection of those of horizontal and coinvariant forms

$$\begin{aligned} \Gamma _B=\Gamma _A^{\textrm{hor}}\cap \Gamma _A^{\textrm{co}H}. \end{aligned}$$

Proof

The inclusion $A\Gamma _B \subseteq \Gamma _A$ implies $(A\Gamma _B)^{\textrm{co}H} \subseteq (\Gamma _A)^{\textrm{co}H}$ and, since A is a flat B-module, we have the inclusion

$$\begin{aligned} A \otimes _B (A\Gamma _B)^{\textrm{co}H} \longrightarrow A \otimes _B (\Gamma _A)^{\textrm{co}H} \cong \Gamma _A \end{aligned}$$

(3.24)

where for the isomorphism $A \otimes _B (\Gamma _A)^{\textrm{co}H}\cong \Gamma _A$ we used Theorem 2.9. The inclusion $\Gamma _B \subseteq (A\Gamma _B)^{\textrm{co}H}\,$ and flatness of A over B imply the inclusion

$$\begin{aligned} A \otimes _B \Gamma _B \longrightarrow A \otimes _B (A\Gamma _B)^{\textrm{co}H} \end{aligned}$$

(3.25)

that composed with (3.24) gives injectivity of the natural map $A \otimes _B \Gamma _B \rightarrow \Gamma _A$ and hence the isomorphism $A \otimes _B \Gamma _B\cong A\Gamma _B$.

From Theorem 2.9 we then have $\Gamma _B\cong (A \otimes _B \Gamma _B)^{\textrm{co}H}\cong (A\Gamma _B)^{\textrm{co}H}$, that is, $\Gamma _B=\Gamma _A^{\textrm{hor}}\cap \Gamma _A^{\textrm{co}H}$. $\square$

We now consider a FODC $(\Gamma _H,\textrm{d}_H)$ on H, with $(\Gamma _A,\textrm{d}_A)$ that is not necessarily right H-covariant.

Definition 3.18

A FODC $(\Gamma _A,\textrm{d}_A)$ on a principal comodule algebra A together with a left covariant FODC $(\Gamma _H,\textrm{d}_H)$ on H, is called a principal calculus on A if we have the short exact sequence

$$\begin{aligned} 0\rightarrow A\otimes _B\Gamma _B\rightarrow \Gamma _A\xrightarrow {\textrm{ver}} A\square _H\Gamma _H\rightarrow 0 \end{aligned}$$

(3.26)

where $A\square _H\Gamma _H:=\{ a_\ell \otimes \omega _\ell ^H\in A\otimes \Gamma _H~|~\delta _A(a_\ell )\otimes \omega _\ell ^H =a_\ell \otimes \Delta _L^{\Gamma _H}(\omega _\ell ^H)\}$ (sum over $\ell$ understood) is the cotensor product of A and $\Gamma _H$, and the vertical map $\textrm{ver}:\Gamma _A\rightarrow A\square _H\Gamma _H$ is well-defined as a $\Bbbk$-linear map by

$$\begin{aligned} \textrm{ver}(a\textrm{d}_Aa'):=a_0a'_0\otimes a_1\textrm{d}_Ha'_1. \end{aligned}$$

(3.27)

If, in addition, the FODC $(\Gamma _A,\textrm{d}_A)$ is right H-covariant and the FODC $(\Gamma _H,\textrm{d}_H)$ is bicovariant, we say we have a principal covariant calculus on the principal comodule algebra A.

We can easily check that $\textrm{ver}$, if it is well-defined, it satisfies

$$\begin{aligned} \textrm{ver}(a\cdot \omega \cdot a') =\delta _A(a)\textrm{ver}(\omega )\delta _A(a') \end{aligned}$$

(3.28)

for all $a,a'\in A$ and $\omega \in \Gamma _A$. The sequence is therefore a sequence of left A-modules right B-modules.

The following lemma provides a sufficient condition for the existence of the vertical map.

Lemma 3.19

Let $\pi : A\rightarrow H$ be a Hopf algebra quotient and A be a principal comodule algebra. For any left covariant calculus $(\Gamma _A,\textrm{d}_A)$ on A and induced left covariant quotient calculus $(\Gamma _H,\textrm{d}_H)$ on H the vertical map is well-defined.

Proof

Let us denote the left A-coaction on $\Gamma _A$ by $\Delta _L^{\Gamma _A}:\Gamma _A\rightarrow A\otimes \Gamma _A$, $\omega ^A\mapsto \omega ^A_{-1}\otimes \omega ^A_0$, and the quotient map of forms by $\pi _\Gamma :\Gamma _A\rightarrow \Gamma _H$. Then

$$\begin{aligned} \begin{aligned} (\textrm{id}_A\otimes \pi _\Gamma )\circ \Delta _L^{\Gamma _A}:\Gamma _A&\rightarrow A\otimes \Gamma _H\\ \omega ^A&\mapsto \omega ^A_{-1}\otimes [\omega ^A_0] \end{aligned} \end{aligned}$$

is a well-defined map. We prove that this map coincides with $\textrm{ver}$. Recall that the induced right H-coaction on A is given by $\delta _A:=(\textrm{id}_A\otimes \pi )\circ \Delta : A\rightarrow A\otimes H$, $a\mapsto a_0\otimes a_1:=a_1\otimes [a_2]$. For $a,a'\in A$ we obtain by the left covariance of $(\Gamma _A,\textrm{d}_A)$

$$\begin{aligned} (\text {id}_A\otimes \pi _\Gamma )(\Delta _L^{\Gamma _A}(a\text {d}_Aa'))&=(a\text {d}_Aa')_{-1}\otimes [(a\text {d}_Aa')_0]=a_1a'_1 \otimes [a_2\text {d}_Aa'_2] \\ {}&=a_1a'_1\otimes [a_2]\text {d}_H[a'_2] =a_0a'_0\otimes a_1\text {d}_Ha'_1, \end{aligned}$$

i.e. $(\textrm{id}_A\otimes \pi _\Gamma )\circ \Delta _L^{\Gamma _A}=\textrm{ver}$, as claimed. $\square$

For a right H-covariant calculus on a principal comodule algebra the second arrow in (3.26) is injective by Theorem 3.17. In this context of principal comodule algebras the notion of principal covariant calculus of Definition 3.18 is then equivalent to that of strong quantum principal bundle in [7] Def. 4.9 and [5] Sect. 5.4. This follows from the canonical identifications $A \otimes _B\Gamma _B\cong A\Gamma _B$, cf. Theorem 3.17, and $A\square _H\Gamma _H\cong A\otimes {}^{\textrm{co}H}\Gamma _H$, where ${}^{\textrm{co}H}\Gamma _H$ denotes the module of left coinvariant one forms characterizing the covariant FODC $(\Gamma _H,\textrm{d}_H)$ (see [47]). In this light Theorem 3.17, which does not assume an exact sequence, can be read as generalizing the conditions of [5] Cor. 5.53 for the equality $\Gamma _B=\Gamma _A^{\textrm{hor}}\cap \Gamma _A^{\textrm{co}H}$ to hold true.

We present two examples of principal covariant calculus, further examples including a principal calculus are in Sect. 4.5.

Example 3.20

(Smash product calculus) Let $(\Gamma _H,\textrm{d}_H)$ be a bicovariant FODC on a Hopf algebra H and $(\Gamma _B,\textrm{d}_B)$ an H-module FODC on a left H-module algebra B. Then, the smash product calculus $(\Gamma _\#,\textrm{d}_\#)$ of Sect. 3.4 is a principal covariant calculus on $B\#H$.

Proof

Recall from Sect. 2.3.1 that $B=(B\#H)^{\textrm{co}H}\subseteq B\#H$ is a trivial Hopf–Galois extension. We show that the sequence in (3.26) is equivalent to the exact sequence

$$\begin{aligned} 0\rightarrow \Gamma _B\#H\rightarrow \Gamma _B\#H\oplus B\#\Gamma _H\xrightarrow {\textrm{pr}}B\#\Gamma _H\rightarrow 0. \end{aligned}$$

From [36] Thm. 4.1 and Lem. 4.2 we have the isomorphisms of right H-covariant $B\#H$-bimodules

$$\begin{aligned} \begin{aligned} (B\#H)\otimes _B\Gamma _B\cong \Gamma _B\#H,~~~~~~~~&(b\#h)\otimes _B\omega ^B\mapsto b(h_1\rhd \omega ^B)\#h_2,\\ (B\#H)\square _H\Gamma _H\cong B\#\Gamma _H,~~~~~~~~&(b\#h)\otimes \omega ^H\mapsto b\#\epsilon (h)\omega ^H. \end{aligned} \end{aligned}$$

(3.29)

Their inverses are given by $\omega ^B\#h\mapsto (1\#h_2)\otimes _B( \overline{S}(h_1)\rhd \omega ^B)$ and $b\#\omega ^H\mapsto (b\#\omega ^H_{-1})\otimes \omega ^H_0$, respectively. Under this first isomorphism the second arrow in (3.26) becomes the inclusion $\Gamma _B\#H\rightarrow \Gamma _B\#H\oplus B\#\Gamma _H$. Finally, the vertical map equals the projection $\textrm{pr}:\Gamma _B\#H\oplus B\#\Gamma _H\rightarrow B\#\Gamma _H$ up to the second isomorphism in (3.29) (cf. e.g. [36] Thm. 2.9). $\square$

Example 3.21

(3D calculus on the q-monopole fibration) Consider $A=\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ (q real, $q\not =\pm 1$) with the Hopf algebra quotient

$$\begin{aligned} \pi : A\rightarrow H,~~~~~~ \begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix}\mapsto \begin{pmatrix} \alpha &{} 0\\ 0 &{} \delta \end{pmatrix} =\begin{pmatrix} \phi &{} 0\\ 0 &{} \phi ^{-1} \end{pmatrix}. \end{aligned}$$

The projection $\pi$ induces a right H-coaction:

$$\begin{aligned} \delta _A:=(\textrm{id}\otimes \pi )\circ \Delta : A\rightarrow A\otimes H,~~~~~~~ \begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix} \mapsto \begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix}\dot{\otimes }\begin{pmatrix} \phi &{} 0\\ 0 &{} \phi ^{-1} \end{pmatrix}. \end{aligned}$$

The subalgebra $B:=A^{\textrm{co}H}$ of coinvariants is given by the (complex) Podleś sphere $\mathcal {O}_q(\mathbb {S}^2)$ with generators $B_-=\alpha \beta$, $B_+=\gamma \delta$, $B_0=\beta \gamma$ and commutation relations

$$\begin{aligned} B_\pm B_0=q^{\pm 2}B_0B_\pm ,~~~~~~ B_-B_+=q^{-2}B_+B_-+q^{-2}(q^{-1}-q)B_0^2. \end{aligned}$$

(see [37] and refs. therein). It is known that $B\subseteq A$ is a faithfully flat Hopf–Galois extension, i.e. that A is a principal comodule algebra [32], (cf. also [8] Ex. 6.26). The 3-dimensional left covariant FODC on A introduced in [48] is H-bicovariant. It induces a 2-dimensional FODC on B via the algebra embedding $B\rightarrow A$ and a 1-dimensional bicovariant FODC on H via the quotient map $\pi$. This data is a principal covariant calculus on A, see [5] Ex. 5.51.

We next show that for a principal covariant calculus on a principal comodule algebra A the Hopf–Galois extension $B=A^{\textrm{co}H}\subseteq A$ lifts to a Hopf–Galois extension of graded algebras. Recall that for a bicovariant H-bimodule $\Gamma _H$ we obtain a graded Hopf algebra $\Omega ^{\leqslant 1}_H:=H\oplus \Gamma _H$. The multiplication is given by that in H and by the H-module structure, while the product of degree one elements is trivial. The comultiplication $\Delta _{\Omega ^{\leqslant 1}_H}:\Omega ^{\leqslant 1}_H\rightarrow \Omega ^{\leqslant 1}_H\otimes \Omega ^{\leqslant 1}_H$ has components on degree zero and one $\Delta ^0:=\Delta : H\rightarrow H\otimes H$ and

$$\begin{aligned} \Delta ^1:=\Delta _R^{\Gamma _H}+\Delta _L^{\Gamma _H}:\Gamma _H\rightarrow \Gamma _H\otimes H\oplus H\otimes \Gamma _H. \end{aligned}$$

The antipode $S_{\Omega ^{\leqslant 1}_H}:\Omega ^{\leqslant 1}_H\rightarrow \Omega ^{\leqslant 1}_H$ has components $S^0=S: H\rightarrow H$ and

$$\begin{aligned} \begin{aligned} S^1:\Gamma _H&\rightarrow \Gamma _H\\ \omega&\mapsto -S(\omega _{-1})\omega _0S(\omega _1). \end{aligned} \end{aligned}$$

Lemma 3.22

Consider a principal comodule algebra A with a principal covariant calculus $(\Gamma _A,\textrm{d}_A)$. The graded algebra $\Omega ^{\leqslant 1}_A:=A\oplus \Gamma _A$ is a graded right $\Omega ^{\leqslant 1}_H$-comodule algebra with right coaction $\Delta _{\Omega ^{\leqslant 1}_A}: \Omega ^{\leqslant 1}_A\rightarrow \Omega ^{\leqslant 1}_A\otimes \Omega ^{\leqslant 1}_H$ given by its components $\Delta _{\Omega ^{\leqslant 1}_A}^0:=\delta _A: A\rightarrow A\otimes H$ and

$$\begin{aligned} \Delta _{\Omega ^{\leqslant 1}_A}^1:=\Delta _R^{\Gamma _A}+\textrm{ver}:\Gamma _A\rightarrow \Gamma _A\otimes H\oplus A\otimes \Gamma _H. \end{aligned}$$

(3.30)

Defining $\Omega ^{\leqslant 1}_B:=B\oplus \Gamma _B\subseteq \Omega ^{\leqslant 1}_A$, we further have that $\Omega ^{\leqslant 1}_B=(\Omega ^{\leqslant 1}_A)^{\textrm{co}\Omega ^{\leqslant 1}_H}$ is the subalgebra of $\Omega ^{\leqslant 1}_H$-coinvariants.

Proof

By assumption $\Delta _{\Omega ^{\leqslant 1}_A}^0=\delta _A: A\rightarrow A\otimes H \subseteq A\otimes \Omega ^{\leqslant 1}_H$ is a right $\Omega ^{\leqslant 1}_H$-coaction and an algebra map. Similarly also $\Delta _{\Omega ^{\leqslant 1}_A}$ is an $\Omega ^{\leqslant 1}_H$-coaction and an algebra map. For the coaction property we just have to prove $(\Delta _{\Omega ^{\leqslant 1}_A}\otimes \textrm{id})\circ \Delta _{\Omega ^{\leqslant 1}_A}=( \textrm{id}\otimes \Delta _{\Omega ^{\leqslant 1}_H}) \circ \Delta _{\Omega ^{\leqslant 1}_A}$ on 1-forms. This is a straightforward computation using the right H-covariance of $(\Gamma _A,\textrm{d}_A)$, the definition of the vertical map and the bicovariance of $(\Gamma _H,\textrm{d}_H)$. The coaction $\Delta _{\Omega ^{\leqslant 1}_A}$ is an algebra map because for all $a,a'\in A$ and $\omega \in \Gamma _A$ we have

$$\begin{aligned} \Delta _{\Omega ^{\leqslant 1}_A}(a\cdot \omega \cdot a') =\delta _A(a)\Delta _{\Omega ^{\leqslant 1}_A}(\omega )\delta _A(a') =\Delta _{\Omega ^{\leqslant 1}_A}(a)\Delta _{\Omega ^{\leqslant 1}_A}(\omega ) \Delta _{\Omega ^{\leqslant 1}_A}(a'), \end{aligned}$$

where we used that $\Gamma _A$ is a right H-covariant A-bimodule and that the vertical map satisfies the compatibility condition (3.28).

The algebra inclusion $B\subseteq A$ implies the graded algebra one $\Omega ^{\leqslant 1}_B=B\oplus \Gamma _B\subseteq \Omega ^{\leqslant 1}_A$. The equality $\Omega ^{\leqslant 1}_B=(\Omega ^{\leqslant 1}_A)^{\textrm{co}\Omega ^{\leqslant 1}_H}$ is obvious in degree zero. In degree one, recalling definition (3.30) and that the codomain of $\Delta _{\Omega ^{\leqslant 1}_A}$ is a direct sum, the coinvariance condition $\Delta _{\Omega ^{\leqslant 1}_A}(\omega )=\omega \otimes 1$ implies $\Delta _R^{\Gamma _A}(\omega )=\omega \otimes 1$ and $\textrm{ver}(\omega )=0$. These equalities respectively imply $\omega \in \Gamma _A^{\textrm{co}H}$ and $\omega \in \Gamma _A^{\textrm{hor}}$, this latter condition following from exactness of the sequence (3.26). Then, from Theorem 3.17 we obtain $\Gamma _B=\Gamma ^{\textrm{hor}}\cap \Gamma ^{\textrm{co}H}$, which implies $(\Gamma _A)^{\textrm{co}\Omega ^{\leqslant 1}_H} =\Gamma _B$. In conclusion, $(\Omega ^{\leqslant 1}_A)^{\textrm{co}\Omega ^{\leqslant 1}_H} =\Omega ^{\leqslant 1}_B$. $\square$

In the following we prove that principal covariant calculi are equivalent to graded Hopf–Galois extensions with compatible differentials.

Theorem 3.23

Let A be a principal comodule algebra and $(\Gamma _A,\textrm{d}_A)$ a principal covariant calculus on A, with corresponding bicovariant FODC $(\Gamma _H,\textrm{d}_H)$ on H. Then

$$\begin{aligned} \Omega ^{\leqslant 1}_B=(\Omega ^{\leqslant 1}_A)^{\textrm{co} \Omega ^{\leqslant 1}_H} \subseteq \Omega ^{\leqslant 1}_A \end{aligned}$$

(3.31)

is a faithfully flat Hopf–Galois extension of graded algebras. Moreover we have the following commutative diagram

(3.32)

where we endow $A\otimes H$ with the tensor product calculus $(\Gamma _{A\otimes H},\textrm{d}_{A\otimes H})$.

Conversely, if $(\Gamma _A,\textrm{d}_A)$ is a FODC on a right H-comodule algebra A and $(\Gamma _H,\textrm{d}_H)$ a bicovariant FODC on H such that (3.31) is a faithfully flat Hopf–Galois extension of graded algebras and the diagram in (3.32) commutes, then A is a principal comodule algebra and $(\Gamma _A,\textrm{d}_A)$ a principal covariant calculus on A.

Proof

If $(\Gamma _A,\textrm{d}_A)$ is a principal covariant calculus on A, $B=A^{\text {co}H}\subseteq A$ is a faithfully flat Hopf–Galois extension, the sequence (3.26) is exact and by Lemma 3.22$\Omega ^{\leqslant 1}_A$ is a graded right $\Omega ^{\leqslant 1}_H$-comodule algebra. Then from [40] Cor. 5.9, $\Omega ^{\leqslant 1}_B=(\Omega ^{\leqslant 1}_A)^{\textrm{co}\Omega ^{\leqslant 1}_H} \subseteq \Omega ^{\leqslant 1}_A$ is a Hopf–Galois extension which is faithfully flat as a left $\Omega ^{\leqslant 1}_B$-module. Moreover, the diagram (3.32) commutes by the right H-covariance of $(\Gamma _A,\textrm{d}_A)$ and the definition (3.27) of the vertical map.

Conversely, if A is a right H-comodule algebra with a FODC $(\Gamma _A,\textrm{d}_A)$ and a bicovariant FODC $(\Gamma _H,\textrm{d}_H)$ on H such that (3.31) is a faithfully flat Hopf–Galois extension (so that in particular $B\subseteq A$ is a faithfully flat Hopf–Galois extension) then from [40] Cor. 5.9 the sequence

$$\begin{aligned} 0\rightarrow A\otimes _B\Gamma _B\rightarrow \Gamma _A\xrightarrow {\Theta } A\square _H\Gamma _H\rightarrow 0 \end{aligned}$$

(3.33)

is exact, where $\Theta$ is the projection of $\Delta ^1_{\Omega ^{\leqslant 1}_A}: \Gamma _A\rightarrow \Omega ^{\leqslant 1}_A\otimes \Omega ^{\leqslant 1}_H$ to $A\otimes \Gamma _H$. If we assume commutativity of the diagram in (3.32) it follows that

$$\begin{aligned} \Delta _R^{\Gamma _A}(\textrm{d}_Aa) +\Theta (\textrm{d}_Aa) =\textrm{d}_A(a_0)\otimes a_1 +a_0\otimes \textrm{d}_Ha_1 \end{aligned}$$

for all $a\in A$, which implies $\Delta _R^{\Gamma _A}(\textrm{d}_Aa)=\textrm{d}_A(a_0)\otimes a_1$ and $\Theta (\textrm{d}_Aa)=a_0\otimes \textrm{d}_Ha_1$ for all $a\in A$. Since $\Theta$ and $\Delta _R^{\Gamma _A}$ are A-bilinear (where $A\otimes H$ is an A-bimodule via $\delta _A$) the first equality implies that $(\Gamma _A,\textrm{d}_A)$ is a right H-covariant calculus, the second one that $\Theta$ is the vertical map. Thus (3.33) is the exact sequence showing the principality of the differential calculus $(\Gamma _A,\textrm{d}_A)$. $\square$

4 A Sheaf-Theoretic Approach to Noncommutative Calculi

In this section we introduce differential calculi on quantum principal bundles in a two-step process. First we define a covariant calculus on a sheaf of comodule algebras $\mathcal {F}$ as a sheaf $\Upsilon$ of $\mathcal {F}$-bimodules together with a morphism $\textrm{d}:\mathcal {F}\rightarrow \Upsilon$ of sheaves, requiring locally Leibniz rule and a surjectivity condition. In case $\mathcal {F}$ is a quantum principal bundle we demand an additional local compatibility of the calculi on the total sheaf, the base sheaf and the structure Hopf algebra.

4.1 Quantum principal bundles as sheaves

We start by recalling the main notions and results of [4]. Those concern the (function) algebra level. In the remaining sections we generalize the definitions and findings to FODCi.

A quantum ringed space $(M, \mathcal {O}_M)$ is a pair consisting of a classical topological space M and a sheaf $\mathcal {O}_M$ on M of noncommutative algebras. We call a sheaf of H-comodule algebras $\mathcal {F}$ an H-principal bundle or quantum principal bundle (QPB) over $(M,\mathcal {O}_M)$ if there exists an open covering $\{U_i\}$ of M such that:

• (i) $\mathcal {F}(U_i)^{\textrm{co}H}=\mathcal {O}_M(U_i)$,

• (ii) $\mathcal {F}$ is locally principal, that is, $\mathcal {O}_M(U_i)\subseteq \mathcal {F}(U_i )$ is a principal comodule algebra.

If the base ring is a field local principality is equivalent to faithfully flatness of the local Hopf–Galois extensions. If these Hopf–Galois extensions on the open cover $\{U_i\}$ are cleft or trivial we say that the QPB is locally cleft or locally trivial, respectively.

Remark 4.1

(Principal comodule algebras restrict locally) In [11] Lem. 4.1 it is shown that the pushforward of a strong connection $\ell : H\rightarrow A\otimes A$ by a comodule algebra map $\phi : A\rightarrow A'$ is a strong connection $(\phi \otimes \phi )\circ \ell$ on $A'$. Recalling that if the base ring $\Bbbk$ is a field there is a bijective correspondence of strong connections on comodule algebras with principal comodule algebras (cf. the paragraph after Definition 2.8) it follows that the existence of a comodule algebra map $\phi : A\rightarrow A'$ implies that if A is a principal comodule algebra, so is $A'$.

Since $\mathcal {F}$ is a sheaf of H-comodule algebras, for any inclusion $U\subset U_i$ of an open U of the topology of M in an open $U_i$ of the covering $\{U_i\}$, the restriction $r^{}_{U U_i}:\mathcal {F}(U_i)\rightarrow \mathcal {F}(U)$, which by definition is a comodule algebra map, then implies that $\mathcal {F}(U)$ is a principal comodule algebra.

Let now $\mathcal {F}_p$ be the stalk of $\mathcal {F}$ at $p\in M$. Choosing $U_i$ such that $p\in U_i$ and considering the canonical map $\mathcal {F}(U_i)\rightarrow \mathcal {F}_p$ of right H-comodule algebras, defined by $s\mapsto [(U_i,s)]_p$, where the equivalence class $[(U_i,s)]_p\in \mathcal {F}_p$ is the germ at p of the section $s\in \mathcal {F}(U_i)$, we obtain that the stalk $\mathcal {F}_p$ is a principal comodule algebra.

Our main examples of QPBs have a quantum group as total space. Let G be a complex semisimple algebraic group and P a parabolic subgroup. The quotient G/P is a projective variety and the projection $G \longrightarrow G/P$ is a principal bundle. Let $\mathcal {O}_q(G)$ and $\mathcal {O}_q(P)=\mathcal {O}_q(G)/I_P$ be Hopf algebras over $\mathbb {C}_q:=\mathbb {C}[q,q^{-1}]$, quantizations of $\mathcal {O}(G)$ and $\mathcal {O}(P)$, the coordinate algebras of G and P, respectively (see [4] Sect. 3, [10] Sect. 3). We shall later specialize q to a complex number in order to consider Hopf–Galois extensions with $\mathbb {C}$ the base ring. Once we fix a projective embedding for G/P, obtained through the global sections of a very ample line bundle $\mathcal {L}$, we have the graded algebra $\mathcal {O}(G/P)$. We say that $s\in \mathcal {O}_q(G)$ is a quantum section if

$$\begin{aligned} (\textrm{id} \otimes \pi ) \Delta (s) = s \otimes \pi (s), \qquad s \equiv t \quad \hbox {mod} \, (q-1), \end{aligned}$$

where $\pi : \mathcal {O}_q(G) \longrightarrow \mathcal {O}_q(P)$, $\Delta$ is the coproduct of $\mathcal {O}_q(G)$ and t is a classical section, that is, it lifts to $\mathcal {O}(G)$ the character of P defining $\mathcal {L}$ (see [4] Def. 3.6).

Denote by $\{s_i\}_{i\in \mathcal {I}}$ a choice of linearly independent elements in $\Delta (s)=\sum _{i\in \mathcal {I}} s^i \otimes s_i$, that we assume to generate the homogeneous coordinate ring $\mathcal {O}_q(G/P)$ quantization of the commutative homogeneous coordinate ring $\mathcal {O}(G/P)$ ($\mathcal {L}$ is very ample). Assume furthermore that $S_i=\{s_i^r, r \in \mathbb {Z}_{\ge 0}\}$ is Ore, denote by $\mathcal {O}_q(G)S_i^{-1}$ the Ore localization, and assume that subsequent Ore localizations do not depend on the order. In the specialization for $q=1$, the $s_i$’s define an open cover of G, whose projection on $M=G/P$ gives an open cover $\{U_i\}$ of M (see [4], Sect. 4 for more details). Let us define the open sets

$$\begin{aligned} U_I:= U_{i_1} \cap \dots \cap U_{i_r}, \qquad I=(i_1, \dots , i_r) \end{aligned}$$

with $r=0,1,2,\ldots n$ (here n is the cardinality of $\mathcal {I}$ and the empty set $\varnothing$ corresponds to $r=0$). We consider on M the topology generated by the open sets $U_I$, which hence form a basis ${\mathcal {B}}=\{U_I\}_{I\in \mathcal{I}\mathcal{I}}$, where $\mathcal{I}\mathcal{I}$ is the set of ordered multi-indices $I=(i_1,\dots , i_r)$, $1\le i_1< \dots < i_r \le n$ with $r=1,2,\ldots n$ (and we also consider the case $r=0$ corresponding to the empty set).

The main result in [4] is Theorem 4.8 that states the following.

Theorem 4.2

Let the notation be as above. Then

• (i) the assignment

  $$\begin{aligned} U_I \mapsto \mathcal {O}_M(U_I)\nonumber&:= {\mathbb {C}}_q[s_{k_1}s_{i_1}^{-1}, \dots , s_{k_r}s_{i_r}^{-1}; 1\le k_1\le n,\ldots 1\le k_r\le n]\\ {}&~\subset \mathcal {O}_q(G)S_{i_1}^{-1}\dots S_{i_r}^{-1} \end{aligned}$$

  (4.1)

  defines a sheaf $\mathcal {O}_M$ on $M=G/P$,

• (ii) the assignment

  $$\begin{aligned} U_I \mapsto \mathcal {F}_G(U_I):=\mathcal {O}_q(G)S_{i_1}^{-1} \dots S_{i_r}^{-1},\ \qquad I=(i_1, \dots , i_r) \end{aligned}$$

  (4.2)

  defines a sheaf $\mathcal {F}_G$ of right $\mathcal {O}_q(P)$-comodule algebras on the topological space M,

• (iii) $\mathcal {F}_G^{\textrm{co}\mathcal {O}_q(P)}=\mathcal {O}_M$, i.e., the subsheaf $\mathcal {F}_G^{\textrm{co}\mathcal {O}_q(P)}: U\rightarrow \mathcal {F}_G(U)^{\textrm{co}\mathcal {O}_q(P)}\subset \mathcal {F}_G(U)$ is canonically isomorphic to the sheaf $\mathcal {O}_M$.

Remark 4.3

We clarify the sheafification implicitly understood in [4] Thm. 4.8. The restriction morphisms

$$\begin{aligned} \begin{aligned} r^M_{IJ}:&\mathcal {O}_M(U_J)\rightarrow \mathcal {O}_M(U_I)\\ r_{IJ}:&\mathcal {F}_G(U_J)\rightarrow \mathcal {F}_G(U_I), \end{aligned} \end{aligned}$$

(4.3)

$U_I\subseteq U_J$ (i.e. $J\subseteq I$), for $\mathcal {O}_M$ and $\mathcal {F}_G$ are given by the natural morphisms. Thus, (4.1) and (4.2) determine presheaves $\mathcal {O}_M$ and $\mathcal {F}_G$ on the basis $\mathcal {B}$.

Define $\mathcal {F}_G^{\textrm{co}\mathcal {O}_q(P)}(U_I):=\mathcal {F}_G(U_I)^{\textrm{co}\mathcal {O}_q(P)}$ for all I and define the restriction morphisms

$$\begin{aligned} r^{\textrm{co}H}_{IJ}:=r_{IJ}|_{\mathcal {F}_G^{\textrm{co}H}(U_J)}:\mathcal {F}_G^{\textrm{co}H}(U_J) \rightarrow \mathcal {F}_G^{\textrm{co}H}(U_I), \end{aligned}$$

(4.4)

which are well-defined because H-colinearity of the $r_{IJ}$ in (4.3) implies $r_{IJ}(\mathcal {F}_G^{\textrm{co}H}(U_J))\subseteq \mathcal {F}_G^{\textrm{co}H}(U_I)$. The restriction morphisms $r^{\textrm{co}H}_{IJ}$ inherit the $\mathcal {B}$-presheaf properties from the $r_{IJ}$, so that $\mathcal {F}_G^{\textrm{co}\mathcal {O}_q(P)}$ is a $\mathcal {B}$-presheaf. Using the technique of [4] Prop. 4.7, one can prove the $\mathcal {B}$-presheaf equality $\mathcal {F}_G^{\textrm{co}\mathcal {O}_q(P)} =\mathcal {O}_M$. Using the following observation these $\mathcal {B}$-presheaves are extended to sheaves on the full topological space, these are the sheaves of Theorem 4.2.

Observation 4.4

If we have a presheaf $\mathcal {G}_\mathcal {B}$ defined on a basis $\mathcal {B}$ for the topology, we can always extend it to the presheaf $\mathcal {G}$, where $\mathcal {G}(U):=\varprojlim \mathcal {G}_\mathcal {B}(V)$ for $V \subset U$, $V \in \mathcal {B}$, provided the target category admit inverse limits (see [17] Chpt. 0, Sect. 3.2.1). If $\mathcal {B}$ is finite the existence of $\varprojlim \mathcal {G}_\mathcal {B}(V)$ is granted. Then, once we have a presheaf, we can always proceed to the sheafification and obtain a sheaf on the topology with the same target category (groups, H-comodule algebras, etc). By universality, a morphism of presheaves on a basis will extend uniquely first to a morphisms of presheaves and then to a morphisms of their sheafification (cf. [20] Chpt. 2 and also [14] for more details on this standard construction). To ease the notation, we shall use the same letter to denote a presheaf on $\mathcal {B}$, its extension to a presheaf and the sheafification.

The topology of M used in Theorem 4.2 is finite since it is induced by a finite cover $\{U_i\}_{i\in \mathcal {I}}$ of M via the finite basis $\mathcal {B}=\{U_I\}^{}_{I\in \mathcal {I}\mathcal {I}}$. We can then define the minimal opens

$$\begin{aligned} U_p:={\bigcap ^{}_{U_I\ni p\,}}U_I\in \mathcal {B}. \end{aligned}$$

(4.5)

Given a presheaf $\mathcal {F}$ on M, its stalk at $p\in M$ coincides with its sections on $U_p$, i.e. $\mathcal {F}_p=\mathcal {F}(U_p)$. This is immediate from the definition of stalk since any open neighbourhood of p includes $U_p$. Now the stalks of the sheafification of $\mathcal {F}$ coincide with the stalks of the initial presheaf, and so $\mathcal {F}$ coincides with its sheafification on the opens $U_p$.

4.2 Covariant calculi on sheaves of comodule algebras

We now give the definition of a covariant FODC on a sheaf of comodule algebras. The bimodule property is entirely captured in a sheaf-theoretic language, while we demand the Leibniz rule and surjectivity property of the differential on stalks. To account for coinvariance we have to consider the differential as a morphism of sheaves of comodules. We give some fundamental examples of covariant FODCi on sheaves and discuss the sheafs of base forms, horizontal forms and coinvariant forms.

Given a morphism $\varphi :\mathcal {F}\rightarrow \mathcal {G}$ of sheaves on M we denote the induced morphism on the stalks at $p\in M$ by $\varphi _p:\mathcal {F}_p\rightarrow \mathcal {G}_p$. We also recall that, for $\mathcal {F}$ a sheaf of algebras on a topological space M, a sheaf of $\mathcal {F}$-modules associates to each open U in M an $\mathcal {F}(U)$-module with compatible restriction maps.

Definition 4.5

Let $\mathcal {F}$ be a sheaf of algebras on a topological space M. A FODC on $\mathcal {F}$ is a sheaf $\Upsilon$ of $\mathcal {F}$-bimodules on M with a morphism

$$\begin{aligned} \textrm{d}:\mathcal {F}\longrightarrow \Upsilon \end{aligned}$$

of sheaves, such that for all $p\in M$ the induced maps on stalks $\textrm{d}_p:\mathcal {F}_p\rightarrow \Upsilon _p$ satisfy

(i):

the Leibniz rule $\textrm{d}_p(fg)=(\textrm{d}_pf)g+f\textrm{d}_pg\hbox { for all } f,g\in \mathcal {F}_p$

(ii):

the surjectivity condition $\Upsilon _p=\mathcal {F}_p\textrm{d}_p\mathcal {F}_p$.

If H is a Hopf algebra and $\mathcal {F}$ a sheaf of right H-comodule algebras over M we call a FODC $(\Upsilon ,\textrm{d})$ on $\mathcal {F}$ right H-covariant if $\Upsilon$ is a sheaf of right H-covariant $\mathcal {F}$-bimodules and $\textrm{d}$ is a morphism of sheaves of right H-comodules.

Similarly one defines left H-covariant and H-bicovariant FODCi on sheaves of left H-comodule algebras and H-bicomodule algebras, respectively.

Example 4.6

• (i) Let M be an algebraic variety and G an (affine) algebraic group acting on M. Then, $\mathcal {O}_M$, the structural sheaf of M, carries an $H=\mathcal {O}(G)$ coaction, where $\mathcal {O}(G)$ denotes the global sections of the structural sheaf of G, which carries a natural Hopf algebra structure. Define $\Omega$ as the sheaf of Kähler differentials with $\textrm{d}:\mathcal {O}_M \longrightarrow \Omega$ as in [20], Sec. 8, II. As one can readily check, using the results in [20], $(\Omega ,\textrm{d})$ is a FODC on $\mathcal {O}_M$.

• (ii) Let the algebraic variety $M=G$ be a simple complex algebraic group and let P be a parabolic subgroup of G. We can view the principal bundle $\pi : G \longrightarrow G/P$ in the sheaf-theoretic language. An example of FODC is again given by the sheaf of Kähler differentials on G. Since G is a principal bundle, we can also define base forms as the differential forms over G/P: they are obtained by considering horizontal forms invariant under the natural P action. We are going to give a quantum version of this Kähler differential construction in Sect. 4.4. The explicit example of $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ is discussed in Sect. 4.5.

We now turn to examine base, horizontal and coinvariant forms in the sheaf-theoretic context.

Let $\mathcal {F}$ be a sheaf of right H-comodule algebras. As for the $\mathcal {B}$-presheaf $\mathcal {F}_G^{\textrm{co}\mathcal {O}_q(P)}$, we define the presheaf $\mathcal {F}^{\textrm{co}H}$ of algebras by assigning to every open U of M the algebra $\mathcal {F}^{\textrm{co}H}(U):= \mathcal {F}(U)^{\textrm{co}H}$ with restriction morphisms, cf. (4.4),

$$\begin{aligned} r^{\textrm{co}H}_{VU}:=r_{VU}|_{\mathcal {F}^{\textrm{co}H}(U)}:\mathcal {F}^{\textrm{co}H}(U) \rightarrow \mathcal {F}^{\textrm{co}H}(V). \end{aligned}$$

(4.6)

The presheaf $\mathcal {F}^{\textrm{co}H}$ is a subsheaf of $\mathcal {F}$, indeed it is the kernel of the sheaf morphism $\delta _R-\textrm{id}\otimes 1_H: \mathcal {F}\rightarrow \mathcal {F}\otimes H$.

Definition 4.7

Let $(\Upsilon ,\textrm{d})$ be a FODC on a sheaf $\mathcal {F}$ of right H-comodule algebras over M. For U open in M we define the $\mathcal {F}^{\textrm{co}H}(U)$-subbimodules of

$$\begin{aligned}&\textit{base forms} \qquad \qquad \Upsilon _M(U) :=\mathcal {F}^{\textrm{co}H}(U)\textrm{d} \mathcal {F}^{\textrm{co}H}(U),\\&\textit{horizontal forms} \qquad \qquad \Upsilon ^{\textrm{hor}}(U) :=\mathcal {F}(U) \Upsilon _M (U). \end{aligned}$$

If $(\Upsilon ,\textrm{d})$ is a right H-covariant FODC on $\mathcal {F}$ we define the $\mathcal {F}^{\textrm{co}H}(U)$-subbimodule of

$$\begin{aligned} \textit{right}\ H-\textit{coinvariant forms} \qquad \Upsilon ^{\textrm{co}H} (U):=\{\omega \in \Upsilon (U) ~|~\Delta _R^{U}(\omega )=\omega \otimes 1\}, \end{aligned}$$

where $\Delta _R^{U}:\Upsilon (U) \rightarrow \Upsilon (U)\otimes H$ is the right H-coaction on $\Upsilon (U)$.

Proposition 4.8

The assignments

$$\begin{aligned} \Upsilon _M: U\mapsto \Upsilon _M(U), \qquad \Upsilon ^{\textrm{hor}}: U\mapsto \Upsilon ^{\textrm{hor}}(U), \qquad \Upsilon ^{\textrm{co}H}: U\mapsto \Upsilon ^{\textrm{co}H}(U), \end{aligned}$$

with restriction morphisms

$$\begin{aligned} \begin{aligned} r^{\Upsilon _M}_{VU}&:=r^\Upsilon _{VU}|_{\Upsilon _M(U)}:\Upsilon _M(U)\rightarrow \Upsilon _M(V),\\ r^{\textrm{hor}}_{VU}&:=r^\Upsilon _{VU}|_{\Upsilon ^{\textrm{hor}}(U)}:\Upsilon ^{\textrm{hor}}(U)\rightarrow \Upsilon ^{\textrm{hor}}(V),\\ r^{\Upsilon ^{\textrm{co}H}}_{VU}&:=r^\Upsilon _{VU}|_{\Upsilon ^{\textrm{co}H}(U)}:\Upsilon ^{\textrm{co}H}(U)\rightarrow \Upsilon ^{\textrm{co}H}(V), \end{aligned}\nonumber \\ \end{aligned}$$

(4.7)

where $r^\Upsilon _{VU}:\Upsilon (U)\rightarrow \Upsilon (V)$ denotes the restriction morphism of $\Upsilon$, define sheaves of $\mathcal {F}^{\textrm{co}H}$-bimodules.

Proof

We first prove that the maps in (4.7) are well-defined, that is they map in the claimed codomains (which are submodules of $\Upsilon (V)$). We show for example $r^{\Upsilon _M}_{VU}(\Upsilon _M(U))\subseteq \Upsilon _M(V)$. Let $f^i,g_i\in \mathcal {F}^{\textrm{co}H}(U)\subseteq \mathcal {F}(U)$ we have

$$\begin{aligned} r^{\Upsilon _M}_{VU}(f^i\textrm{d}_Ug_i) =r^{\Upsilon }_{VU}(f^i\textrm{d}_Ug_i) =r_{VU}(f^i)r^{\Upsilon }_{VU}(\textrm{d}_Ug_i) =r_{VU}^{\textrm{co}H}(f^i)\textrm{d}_Vr_{VU}^{\textrm{co}H}(g_i) \in \Upsilon _M(V), \end{aligned}$$

where we used that $r^\Upsilon$ is left $\mathcal {F}$-linear, $\textrm{d}$ is a morphism of sheaves and (4.6). Similarly $r^{\textrm{hor}}_{VU}$ is well-defined. The proof for $r^{\Upsilon ^{\textrm{co}H}}_{VU}$ is straightforward from H-colinearity of $r^{\Upsilon }_{VU}$. The maps in (4.7) are $\mathcal {F}^{\textrm{co}H}(U)$-bimodule maps (the $\mathcal {F}^{\textrm{co}H}(U)$-bimodule structure on the images being given via $r^{\textrm{co}H}_{VU}$) because they are restrictions of the $\mathcal {F}(U)$-bimodule map $r^\Upsilon _{VU}$. Finally, the morphisms in (4.7) for V, U open in M define the presheaves $\Upsilon _M$, $\Upsilon ^{\textrm{hor}}$, $\Upsilon ^{\textrm{co}H}$ since they are restrictions of the morphisms $r^\Upsilon _{VU}$ defining the presheaf $\Upsilon$. Since $\Upsilon ^{\textrm{co}H}$ is the kernel of the sheaf morphism $\Delta _R-\textrm{id}\otimes 1_H:\Upsilon \rightarrow \Upsilon \otimes H$, it is a sheaf. By common abuse of notation we shall denote by $\Upsilon _M$ and $\Upsilon ^{\textrm{hor}}$ the sheafifications of the corresponding presheaves. These are sheaves in the category of $\mathcal {F}^{\textrm{co}H}$-bimodules. $\square$

Corollary 4.9

Let $(\Upsilon ,\textrm{d})$ be a FODC on a sheaf $\mathcal {F}$ of right H-comodule algebras over M. Then $(\Upsilon _M,\textrm{d}_M)$ with $\textrm{d}_M:=\textrm{d}|_{\mathcal {F}^{\textrm{co}H}}:\mathcal {F}^{\textrm{co}H}\rightarrow \Upsilon _M$ is a FODC on $\mathcal {F}^{\textrm{co}H}$.

Proof

We already noted that the presheaf $\mathcal {F}^{\textrm{co}H}$ is a subsheaf of $\mathcal {F}$. Since $\textrm{d}_M$ is the restriction of $\textrm{d}:\mathcal {F}\rightarrow \Upsilon$ to $\mathcal {F}^{\textrm{co}H}$ it is a morphism of sheaves and satisfies the Leibniz rule on stalks. On the level of presheaves we have the surjectivity condition on stalks $\mathcal {F}^{\textrm{co}H}_p\, (\textrm{d}_M)^{}_p\!\,\mathcal {F}^{\textrm{co}H}_p=(\Upsilon _M)_p$, for any $p\in M$. Since the stalks of the presheaf coincide with the stalks of its sheafification we conclude that the surjectivity condition of the sheaf morphism $\textrm{d}_M$ is satisfied (cf. the analogue of (ii) in Definition 4.5). $\square$

Let $\Upsilon ^{\textrm{co}H}\cap \Upsilon ^{\textrm{hor}}$ denote the sheafification of the presheaf obtained intersecting the subsheaves $\Upsilon ^{\textrm{co}H}$ and $\Upsilon ^{\textrm{hor}}$ of $\Upsilon$.

Theorem 4.10

Let the base ring $\Bbbk$ be a field. For any right H-covariant FODC $(\Upsilon ,\textrm{d})$ on a QPB $\mathcal {F}$ we have an isomorphism

$$\begin{aligned} \Upsilon _M\cong \Upsilon ^{\textrm{co}H}\cap \Upsilon ^{\textrm{hor}} \end{aligned}$$

of sheaves of $\mathcal {O}_M$-bimodules.

Proof

The natural inclusion $\Upsilon _M\rightarrow \Upsilon ^{\textrm{co}H}\cap \Upsilon ^{\textrm{hor}}$ (by which we mean the sheafification of the corresponding morphism of presheaves) is a morphism of sheaves. Recalling from Remark 4.1 that stalks are principal comodule algebras, the induced inclusion on stalks, $(\Upsilon _M)^{}_p\rightarrow \Upsilon ^{\textrm{co}H}_p\cap \Upsilon ^{\textrm{hor}}_p$, is an isomorphism thanks to Theorem 3.17. Thus $\Upsilon _M\rightarrow \Upsilon ^{\textrm{co}H}\cap \Upsilon ^{\textrm{hor}}$ is an isomorphism of sheaves. $\square$

4.3 Ore extension of covariant calculi

As a tool for the following sections, we now discuss the Ore extension of covariant calculi. We recall that if $a \in A$ is a (right) Ore element, we denote by $AS^{-1}$ or by $A[a^{-1}]$ the Ore localization of A at the multiplicative right Ore set $S=\{a^m\}_{m \in \mathbb {Z}_\ge 0}$ (for more details see [28] Chpt. 4, Sect. 10 and [24] Sect. I.7.).

Let $(\Gamma ,\textrm{d})$ be a FODC on an algebra A. Let a be an Ore element in A. We define the $A[a^{-1}]$-bimodule

$$\begin{aligned} \Gamma _a:=A[a^{-1}] \, \Gamma \, A[a^{-1}]:=A[a^{-1}]\otimes _A\Gamma \otimes _AA[a^{-1}] \end{aligned}$$

(4.8)

and the $\Bbbk$-linear map

$$\begin{aligned} \textrm{d}_a:A[a^{-1}] \longrightarrow \Gamma _a, \qquad \textrm{d}_a(a')={\left\{ \begin{array}{ll} \textrm{d}a' &{} a' \in A \\ -a^{-1}\, \textrm{d}a \, a^{-1} &{} a'=a^{-1} \end{array}\right. }, \end{aligned}$$

(4.9)

where we extend $\textrm{d}_a$ to $A[a^{-1}]$ by the Leibniz rule.

Lemma 4.11

$(\Gamma _a,\textrm{d}_a)$ is a FODC on $A[a^{-1}]$.

Proof

We need to verify the properties of Definition 3.1. The first two properties are satisfied by definition. Moreover by the equality

$$\begin{aligned} a'\,\textrm{d}a''\,a^{-n}=a' \,\textrm{d}_a(a''a^{-n})-a' \, a'' \, \textrm{d}_a(a^{-n}), \end{aligned}$$

where $a',a''\in A$ and $n\in \mathbb {N}$, we see that we can express any element of $\Gamma _a$ as an element in $A[a^{-1}] \, \textrm{d}_a A[a^{-1}]$. $\square$

With a slight abuse of terminology, we call $(\Gamma _a,\textrm{d}_a)$ the localization of $(\Gamma ,\textrm{d})$ via the Ore element $a\in A$.

We now show that the covariant properties of the FODC $\Gamma$ are preserved under localization.

Lemma 4.12

Let $(\Gamma ,\textrm{d})$ be a right H-covariant FODC on a right H-comodule algebra $(A,\delta _R)$ and $a\in A$ an Ore element. Assume that $\delta _R(a)\in A\otimes H$ is invertible. Then

• (i) $\delta _R$ extends to a right H-coaction $\delta ^a_R: A[a^{-1}]\rightarrow A[a^{-1}]\otimes H$, structuring $(A[a^{-1}],\delta _R^a)$ as a right H-comodule algebra;

• (ii) the FODC $(\Gamma _a,\textrm{d}_a)$ on $(A[a^{-1}],\delta _R^a)$ is right H-covariant;

Proof

• (i) We set $\delta _R^a(a'):=\delta _R(a')$ for all $a'\in A$, furthermore $\delta _R^a(a^{-1}):=\delta _R(a)^{-1}$ and extend $\delta _R^a$ as an algebra homomorphism to $A[a^{-1}]$. From the coaction properties of $\delta _R$ it follows that $\delta _R^a$ is a right H-coaction on $A[a^{-1}]$ and by construction it is compatible with the algebra structure of $A[a^{-1}]$.

• (ii) There is a canonical right H-coaction $\Delta _R^a$ on $\Gamma _a:=A[a^{-1}]\otimes _A\Gamma \otimes _AA[a^{-1}]$ given by the diagonal coaction. We show that $\Delta _R^a$ structures $\Gamma _a$ as a right H-covariant $A[a^{-1}]$-bimodule such that $\textrm{d}_a$ is right H-colinear. The claim that $(\Gamma _a,\textrm{d}_a)$ is a right H-covariant FODC on $A[a^{-1}]$ then follows from Proposition 3.6. Consider an arbitrary element $b^i\otimes _A\omega ^i\otimes _Ac^i\in \Gamma _a$ with $b^i,c^i\in A[a^{-1}]$ and $\omega ^i\in \Gamma$, sum over i understood. Since, according to (i), $\delta _R^a$ is an algebra homomorphism, we obtain

  $$\begin{aligned} \Delta _R^a(b\cdot (b^i\otimes _A\omega ^i\otimes _Ac^i)\cdot c)&=(bb^i)_0\otimes _A\omega ^i_0\otimes _A(c^ic)_0\otimes (bb^i)_1\omega ^i_1(c^ic)_1\\&=b_0(b^i_0\otimes _A\omega ^i_0\otimes _Ac^i_0)c_0\otimes b_1(b^i_1\omega ^i_1c^i_1)c_1\\&=\delta _R^a(b)\Delta _R^a(b^i\otimes _A\omega ^i\otimes _Ac^i)\delta _R^a(c) \end{aligned}$$

  for all $b,c\in A[a^{-1}]$. That is $\Gamma _a$ is a right H-covariant $A[a^{-1}]$-bimodule. Next, applying $\textrm{d}_a\otimes \textrm{id}_H$ to the equation $1_A\otimes 1_H=\delta _R(a)\delta _R^a(a^{-1})$ we obtain

  $$\begin{aligned} 0&=(\textrm{d}a_0\otimes a_1)\cdot \delta _R^a(a^{-1}) +\delta _R^a(a)\cdot (\textrm{d}_aa^{-1}_0\otimes a^{-1}_1)\\&=\Delta _R(\textrm{d}a)\cdot \delta _R^a(a^{-1}) +\delta _R^a(a)\cdot (\textrm{d}_aa^{-1}_0\otimes a^{-1}_1), \end{aligned}$$

  where in the last expression we used right H-colinearity of $\textrm{d}$. This implies

  $$\begin{aligned} \textrm{d}_aa^{-1}_0\otimes a^{-1}_1= & {} -\delta _R^a(a^{-1})\cdot \Delta _R(\textrm{d}a)\cdot \delta _R^a(a^{-1}) =-\Delta _R^a(a^{-1}\textrm{d}(a)a^{-1})\nonumber \\= & {} \Delta _R^a(\textrm{d}_a(a^{-1})). \end{aligned}$$

  (4.10)

  The Leibniz rule of $\textrm{d}_a$, the algebra homomorphism property of $\delta _R^a$, the A-bilinearity of $\Delta _R^a$ and (4.10) then imply that $\textrm{d}_a$ is right H-colinear on any power of $a^{-1}$ and furthermore on any element of $A[a^{-1}]$.

$\square$

Let A be an algebra, $a_i\in A$, $i=1,\ldots ,n$ be Ore elements and $S_{i}=\{a^r_{i}, r\in \mathbb {Z}_{\ge 0}\}$. For a multi-index $I=(i_1,\ldots ,i_k)\in \{1,\ldots ,n\}^k$ we use the notation $A_I=AS_{i_1}^{-1}\ldots S_{i_k}^{-1}$, or equivalently the notation

$$\begin{aligned} A_I=A_{(i_1,\ldots ,i_k)}:=A[a_{i_1}^{-1},\ldots ,a_{i_k}^{-1}]:=(\cdots (A[a_{i_1}^{-1}]) \cdots )[a_{i_k}^{-1}] \end{aligned}$$

for the k-fold Ore localization. Given a FODC $(\Gamma ,\textrm{d})$ on A we similarly define the k-fold Ore localization of the A-bimodule $\Gamma$ by

and of the exterior derivative by

$$\begin{aligned} \textrm{d}_I=\textrm{d}_{(i_1,\ldots ,i_k)}:=(\cdots (\textrm{d}_{a_{i_1}})_{a_{i_2}}\cdots )_{a_{i_k}}: A_{I}~ \rightarrow \Gamma _{I}. \end{aligned}$$

(4.11)

Lemma 4.13

Let A be an algebra and $a_i\in A$, $i=1,\ldots ,n$ be Ore elements such that subsequent localizations do not depend on the order. Then, subsequent localizations of a FODC on A are independent of the order, as well.

Proof

Consider a FODC $(\Gamma ,\textrm{d})$ on A. For two Ore elements $a_i,a_j\in A$, using that $A_{(i,j)}=A_{(j,i)}$ we have

$$\begin{aligned} (\Gamma _{a_i})_{a_j}&=A_{(i,j)}\otimes _{A_i}(A_i\otimes _{A}\Gamma \otimes _{A}A_i)\otimes _{A_i}A_{(i,j)}\\&=A_{(i,j)}\otimes _A\Gamma \otimes _AA_{(i,j)}\\&=A_{(j,i)}\otimes _{A_j}(A_j\otimes _A\Gamma \otimes _AA_j)\otimes _{A_j}A_{(j,i)}\\&=(\Gamma _{a_j})_{a_i} \end{aligned}$$

as an equation of $A_{(i.j)}$-bimodules. In particular,

$$\begin{aligned} \textrm{d}_{(i,j)}, \textrm{d}_{(j,i)}: A_{(i.j)} \rightarrow \Gamma _{(i,j)} \end{aligned}$$

have the same domain and codomain. They coincide on A and by definition (4.9) they also agree on $a_i^{-1}$ and $a_j^{-1}$. Both differentials are extended by the Leibniz rule, therefore $\textrm{d}_{(i,j)}=\textrm{d}_{(j,i)}$. An easy inductive argument on the number of Ore localization then proves the lemma. $\square$

This lemma shows in particular that the k-fold Ore localization of the A-bimodule $\Gamma$ is $\Gamma _I=A_I\otimes _A\Gamma \otimes _AA_I$, that for short we frequently write as $\Gamma _I=A_I\Gamma A_I$. Recalling also Lemma 4.12 the following proposition is straightforward.

Proposition 4.14

Let $(\Gamma ,\textrm{d})$ be a FODC on a right H-comodule algebra $(A,\delta _R)$ and $a_i\in A$, $i=1,\ldots ,n$ be Ore elements such that $\delta _R(a_i)$ are invertible elements of $A_i\otimes H$. Then

$$\begin{aligned} \Gamma _I=A_I\otimes _A\Gamma \otimes _AA_I, \qquad \textrm{d}_I: A_I\rightarrow \Gamma _I \end{aligned}$$

is a right H-covariant FODC on $A_I$. If subsequent Ore localizations of A are independent on the order also the subsequent localizations of the FODC $(\Gamma , d)$ are order independent.

Remark 4.15

We have considered FODCi on Ore extended algebras. In Sect. 3.5, associated with a FODC $(\Gamma _A,\textrm{d}_A)$ there is the graded algebra of 0- and 1-forms $\Omega ^{\leqslant 1}_A=A\oplus \Gamma _A$. It is natural to consider also Ore extensions of this graded algebra (which are necessarily by degree zero elements). In this case an Ore element a is in particular Ore in the zero degree subalgebra A and we also require to be able to order on the right (and on the left) of 1-forms the negative powers a. Thus, if $a\in A$ is Ore in $\Omega ^{\leqslant 1}_A$ the graded algebra $A_a\oplus \Gamma _a$ with $\Gamma _a$ defined in (4.8) is the Ore extension of $A\oplus \Gamma$ corresponding to a. This Ore condition on 1-forms is met in the examples we shall consider.

4.4 Covariant differential calculi on sheaves over quantum projective varieties

In this section we consider all modules over the complex numbers $\mathbb {C}$. When considering the quantizations $\mathcal {O}_q(G)$, $\mathcal {O}_q(P)$ we therefore specialize q to be in $\mathbb {C}$. Fix a complex semisimple algebraic group G with parabolic subgroup P, quantizations $\mathcal {O}_q(G)$, $\mathcal {O}_q(P)$ and the sheaves $\mathcal {F}_G$ and $\mathcal {O}_M$ as in Theorem 4.2, where the QPB property of $\mathcal {F}_G$ is with respect to the finite open cover $\{U_i\}_{i\in \mathcal {I}}$, $\mathcal {I}=\{1,\dots ,n\}$ determined by a quantum section. Consider the (finite) topology generated by the open cover; it will have topological basis ${\mathcal {B}}=\{U_I\}_{I\in \mathcal{I}\mathcal{I}}$, where we recall that $\mathcal{I}\mathcal{I}$ is the set of ordered multi-indices $I=(i_1,\dots , i_r)$, $1\le i_1< \dots < i_r \le n$ with $r=1,2,\ldots n$ (and we also consider the case $r=0$ corresponding to the empty set) and $U_I:=\cap _{i \in I} U_i$.

Given a right $\mathcal {O}_q(P)$-covariant FODC $(\Gamma ,\textrm{d})$ on $\mathcal {O}_q(G)$ we induce a $\mathcal {O}_q(P)$-covariant FODC on $\mathcal {F}$ according to Sect. 4.3 as follows. We set on the basis $\mathcal {B}$ of open sets $U_I$

$$\begin{aligned} \Upsilon _G(U_I):= \mathcal {F}_G(U_I)\otimes _{{\mathcal {O}_q(G)}} \Gamma \otimes _{{\mathcal {O}_q(G)}}\mathcal {F}_G(U_I), \end{aligned}$$

(4.12)

and define restriction morphisms $r^\Upsilon _{JI}:\Upsilon _G(U_I)\rightarrow \Upsilon _G(U_J)$ for all $U_J\subseteq U_I$ by

$$\begin{aligned} r^\Upsilon _{JI}(f\otimes _{{\mathcal {O}_q(G)}} \omega \otimes _{{\mathcal {O}_q(G)}}g):=r_{JI}(f)\otimes _{{\mathcal {O}_q(G)}} \omega \otimes _{{\mathcal {O}_q(G)}}r_{JI}(g), \end{aligned}$$

(4.13)

where $f,g\in \mathcal {F}_G(U_I)$ and $\omega \in \Gamma$. Since $r_{JI}$ are algebra homomorphisms which are the identity on $\mathcal {O}_q(G)$ the expression (4.13) is well-defined on the algebraic tensor product. The right $\mathcal {O}_q(P)$-comodule algebra map $r_{JI}$ defines an $\mathcal {F}_G(U_I)$-bimodule structure on $\Upsilon _G(U_J)$ and $r^\Upsilon _{JI}:\Upsilon _G(U_I)\rightarrow \Upsilon _G(U_J)$ is a map of right $\mathcal {O}_q(P)$-covariant $\Upsilon _G(U_J)$-bimodules, i.e., it is $\mathcal {O}_q(P)$-colinear and $r^\Upsilon _{JI}(f\cdot \theta \cdot g) =r_{JI}(f)r^\Upsilon _{JI}(\theta )r_{JI}(g)$ for all $f,g\in \mathcal {F}_G(U_I)$ and $\theta \in \Upsilon _G(U_I)$. The equality $r^\Upsilon _{KJ}\circ r^\Upsilon _{JI}=r^\Upsilon _{KI}$ for any three opens $U_K\subseteq U_J\subseteq U_I$ then follows from that for the restriction morphisms of $\mathcal {F}_G$. We have defined the $\mathcal {B}$-presheaf $\Upsilon _G$ of right $\mathcal {O}_q(P)$-covariant $\mathcal {F}_G$-bimodules. We denote its sheafification by the same symbol $\Upsilon _G$.

Theorem 4.16

(Induced calculus on the sheaf $\mathcal {F}_G$) Let $(\Gamma ,\textrm{d})$ be a right covariant FODC on the Hopf algebra $\mathcal {O}_q(G)$ and $\mathcal {F}_G$, $\Upsilon _G$ the sheaves of right $\mathcal {O}_q(P)$-comodule algebras and of right $\mathcal {O}_q(P)$-covariant $\mathcal {F}_G$-bimodules defined above.

• (i) The linear maps

  $$\begin{aligned} {\textrm{d}}_I:\mathcal {F}_G(U_I) \longrightarrow \Upsilon _G(U_I), \end{aligned}$$

  defined in (4.11) for $A_I=\mathcal {F}_G(U_I)$ and $\Gamma _I=\Upsilon _G(U_I)$, define a morphism of sheaves of right $\mathcal {O}_q(P)$-comodules $\textrm{d}: \mathcal {F}_G\rightarrow \Upsilon _G$. This gives a right $\mathcal {O}_q(P)$-covariant FODC $(\Upsilon _G,\textrm{d})$ on the sheaf $\mathcal {F}_G$.

• (ii) The FODC $(\Upsilon _G,\textrm{d})$ on the sheaf $\mathcal {F}_G$ induces a FODC $(\Upsilon _M,\textrm{d}_M)$ on the sheaf $\mathcal {F}_G^{\textrm{co}\mathcal {O}_q(P)}=\mathcal {O}_M$.

• (iii) If $\mathcal {F}_G$ is a QPB the sheaf of base forms is isomorphic, as a sheaf of $\mathcal {O}_M$-bimodules, to the intersection of that of horizontal and H-coinvariant forms: $\Upsilon ^{}_M\cong \Upsilon _G^{\textrm{hor}} \cap \Upsilon _G^{\textrm{co}\,\!\mathcal {O}_q(P)}$.

Proof

Let $\mathcal {F}_G$ be the $\mathcal {B}$-presheaf defined in (4.2) and $\Upsilon _G$ the $\mathcal {B}$-presheaf defined in (4.12), (4.13). We show that the assignment $U_I\mapsto {\textrm{d}_I}$ defines a morphism of $\mathcal {B}$-presheaves $\textrm{d}:\mathcal {F}_G\rightarrow \Upsilon _G$. That is, $\textrm{d}_J(r_{JI}(f))= r^\Upsilon _{JI}(\textrm{d}_If)$ for all $f\in \mathcal {F}_G(U_I)$ and $U_J\subseteq U_I$. This is clear if $f\in \mathcal {O}_q(G)\subseteq \mathcal {F}_G(U_I)$. Also for $f=s_{i_\ell }^{-1}$, where $1\le \ell \le n$, $i_\ell \in I=(i_1,\ldots ,i_r)$, we obtain

$$\begin{aligned} r^\Upsilon _{JI}(\textrm{d}_Is_{i_\ell }^{-1})&=-r^\Upsilon _{JI}(s_{i_\ell }^{-1}\otimes _{\mathcal {O}_q(G)} \textrm{d}s_{i_\ell }\otimes _{\mathcal {O}_q(G)}s_{i_\ell }^{-1})\\&=-r_{JI}(s_{i_\ell }^{-1})\otimes _{\mathcal {O}_q(G)} \textrm{d}s_{i_\ell }\otimes _{\mathcal {O}_q(G)}r_{JI}(s_{i_\ell }^{-1})\\&=-s_{i_\ell }^{-1}\otimes _{\mathcal {O}_q(G)} \textrm{d}s_{i_\ell }\otimes _{\mathcal {O}_q(G)}s_{i_\ell }^{-1}\\&= ~\textrm{d}_J(s_{i_\ell }^{-1})\\&= ~\textrm{d}_J(r_{JI}(s_{i_\ell }^{-1}))\,. \end{aligned}$$

By the Leibniz rule, cf. Proposition 4.14, this $\mathcal {B}$-presheaf property extends to any element $f\in \mathcal {F}_G(U_I)$, $\textrm{d}_J(r_{JI}(f))= r^\Upsilon _{JI}(\textrm{d}_If)$.

Recalling from Proposition 4.14 that $(\Upsilon _G(U_I), \textrm{d}_I)$ is a right $\mathcal {O}_q(P)$-covariant FODC and that $\mathcal {F}_G$ and $\Upsilon _G$ are $\mathcal {B}$-presheaves of right $\mathcal {O}_q(P)$-comodules, we see that the $\mathcal {B}$-presheaf morphism $\textrm{d}:\mathcal {F}_G\rightarrow \Upsilon _G$ is compatible with the right $\mathcal {O}_q(P)$-comodule structure. Furthermore, the Leibniz rule and surjectivity condition are satisfied for all opens $U_I$ in $\mathcal {B}$. We sheafify according to Observation 4.4 and obtain the sheaf $\Upsilon _G$ of right $\mathcal {O}_q(P)$-covariant $\mathcal {F}_G$-bimodules with the sheaf morphism $\textrm{d}:\mathcal {F}_G\rightarrow \Upsilon _G$. Recalling that stalks are preserved under sheafification and that the stalks at p are respectively $(\mathcal {F}_G)_p =\mathcal {F}_G(U_p)$, $(\Upsilon _G)_p=\Upsilon _G(U_p)$ we infer that the Leibniz rule and the surjectivity condition for the sheafified morphism $\textrm{d}:\mathcal {F}_G\rightarrow \Upsilon _G$ are satisfied on the stalks. This proves (i). Recalling that the sheaf equality $\mathcal {F}_G^{\textrm{co}\mathcal {O}_q(P)}=\mathcal {O}_M$ was proven in Theorem 4.2 we have that (ii) follows directly from Corollary 4.9. The last point (iii) follows from Theorem 4.10. $\square$

4.5 Principal covariant calculi on quantum principal bundles

A principal covariant calculus on a QPB $\mathcal {F}$ is a right H-covariant FODC $(\Upsilon ,\textrm{d})$ on the sheaf $\mathcal {F}$ (see Definition 4.5) with an exact sequence on the stalks.

Definition 4.17

Consider a QPB $\mathcal {F}$ on a quantum ringed space $(M,\mathcal {O}_M)$ and a FODC $(\Upsilon ,\textrm{d})$ on $\mathcal {F}$. Given a left covariant FODC $(\Gamma _H,\textrm{d}_H)$ on H we call $(\Upsilon ,\textrm{d})$ a principal calculus on $\mathcal {F}$ if for all $p\in M$ we have the exact sequence of stalks

$$\begin{aligned} 0\rightarrow \mathcal {F}_p\otimes _{(\mathcal {O}_M)^{}_p}(\Upsilon _M)^{}_p \rightarrow \Upsilon _p\xrightarrow {\textrm{ver}_p} \mathcal {F}_p\square _H \Gamma _H\rightarrow 0, \end{aligned}$$

(4.14)

where $\textrm{ver}_p$ is the vertical map defined in Sect. 3.5 and $\Upsilon _M$ denotes the sheaf of base forms defined in Proposition 4.8. If, in addition, $(\Upsilon ,\textrm{d})$ is right H-covariant and $(\Gamma _H,\textrm{d}_H)$ is bicovariant, we say that $(\Upsilon ,\textrm{d})$ is a principal covariant calculus on the sheaf $\mathcal {F}$.

We next apply Theorem 4.16 and consider three FODCi on QPBs over $\textbf{P}^1(\mathbb {C})$, the second one being a principal calculus and the third one a principal covariant calculus. The first two have total space algebra $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ with total space calculus the 4D and 3D ones of Examples 3.10 and 3.11. The third example has total space algebra $\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$ with total space calculus the 4D one of Example 3.9.

4.5.1 First order differential calculus via ore localization of 4D calculus on $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$

Consider the principal bundle $\wp : \textrm{SL}_2(\mathbb {C}) \longrightarrow \textrm{SL}_2(\mathbb {C})/P \simeq \textbf{P}^1(\mathbb {C})$, where P is the upper Borel in $\textrm{SL}_2(\mathbb {C})$. Take $V_i$ to be the subset of matrices in $\textrm{SL}_2 (\mathbb {C})$ with entry (i, 1) not equal to zero. We observe that $\{V_1,V_2\}$ is an open cover of $\textrm{SL}_2 (\mathbb {C})$. Define $U_i=\wp (V_i)$ and observe that $\{U_1,U_2\}$ is an open cover of $\textbf{P}^1(\mathbb {C})$ since $\wp$ is an open map. This is the cover obtained via the quantum section $\alpha \in \mathcal {O}(\textrm{SL}_2(\mathbb {C}))$ with coproduct $\Delta (\alpha )=\alpha \otimes \alpha + \beta \otimes \gamma .$ In fact $V_1=\{g \in \textrm{SL}_2(\mathbb {C}) \,|\, \alpha (g) \ne 0\}$ and $V_2=\{g \in \textrm{SL}_2(\mathbb {C}) \,|\, \gamma (g) \ne 0\}$. Explicitly, $U_1,U_2$ are the opens obtained by removing the north or south pole. The coaction

$$\begin{aligned} \delta _R:\mathcal {O}(\textrm{SL}_2(\mathbb {C}))\rightarrow \mathcal {O}(\textrm{SL}_2(\mathbb {C}))\otimes \mathcal {O}(P),~~~~~~ \begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix}\mapsto \begin{pmatrix} \alpha &{} \beta \\ \gamma &{} \delta \end{pmatrix}\dot{\otimes }\begin{pmatrix} t &{} p\\ 0 &{} t^{-1} \end{pmatrix} \end{aligned}$$

uniquely extends to coactions on the localizations $\mathcal {O}(\textrm{SL}_2)[\alpha ^{-1}]$ and $\mathcal {O}(\textrm{SL}_2)[\gamma ^{-1}]$ by defining $\delta _R \alpha ^{-1}=\alpha ^{-1}\otimes t^{-1}$ and $\delta _R \gamma ^{-1}=\gamma ^{-1}\otimes t^{-1}$, respectively. The coinvariant subalgebras for $\mathcal {O}(\textrm{SL}_2)[\alpha ^{-1}]$ and $\mathcal {O}(\textrm{SL}_2)[\gamma ^{-1}]$ respectively are isomorphic to $\mathbb {C}[u]$ and $\mathbb {C}[v]$ with $u:=\alpha ^{-1}\gamma$ and $v:=\alpha \gamma ^{-1}$ and they are the coordinate rings of the affine algebraic varieties corresponding to the opens $U_1, U_2$ in $\textrm{SL}_2(\mathbb {C})/P\simeq \textbf{P}^1(\mathbb {C})$.

The quantum deformation of this construction has been studied in [4] as an example of QPB over projective base. In summary, starting with the Hopf algebra $A:=\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ and its parabolic quotient Hopf algebra $H:=\mathcal {O}_q(P)$ as in (3.16) we define the noncommutative localizations $A_{1}:=A[\alpha ^{-1}]$ and $A_2:=A[\gamma ^{-1}]$ and structure them as right H-comodule algebras in complete analogy to the classical setting. The subalgebras of right H-coinvariants are given by

$$\begin{aligned} B_1=\mathbb {C}_q[\gamma \alpha ^{-1}] \simeq \mathbb {C}_q[u], \qquad B_2=\mathbb {C}_q[\alpha \gamma ^{-1}] \simeq \mathbb {C}_q[v]~ \end{aligned}$$

and the ringed space $(\textbf{P}^1(\mathbb {C}), \mathcal {O}_{\textbf{P}^1(\mathbb {C})})$ can then be constructed as

$$\begin{aligned} \mathcal {O}_{\textbf{P}^1(\mathbb {C})}(U_i):=B_{i},~~\mathcal {O}_{\textbf{P}^1(\mathbb {C})}(U_{12}):=B_{12}:=B_{1}[u^{-1}],~~\mathcal {O}_{\textbf{P}^1(\mathbb {C})}(\textbf{P}^1(\mathbb {C})):=\mathbb {C},\qquad \qquad \end{aligned}$$

(4.15)

$i\in \{1,2\}$, with the only non-trivial restriction map given by $r_{{12},2}:B_{\,2}\rightarrow B_{12}$, $v\mapsto u^{-1}$. Moreover we observe that

$$\begin{aligned} \mathcal {F}_{\text {SL}_q}(U_i)&:= {} A_{i}, \quad \mathcal {F}_{\text {SL}_q}(U_{12}):=A_{12}:=A_{1}[\gamma ^{-1}]=A_{2}[\alpha ^{-1}], \\ \mathcal {F}_{\text {SL}_q}({\textbf {P}}^1(\mathbb {C}))&:=A,\quad \!\,\quad \mathcal {F}_{\text {SL}_q}(\emptyset ):= {} \{0\}, \end{aligned}$$

$i\in \{1,2\}$, defines a sheaf of right $\mathcal {O}_q(P)$-comodule algebras on $\textbf{P}^1(\mathbb {C})$, which we denote by $\mathcal {F}_{\textrm{SL}_q}$. Endowed with the cleaving maps,

$$\begin{aligned} {}&{} j_1: H\rightarrow A_1,~~~~\begin{pmatrix} t &{}{} \quad p\\ 0 &{}{} \quad t^{-1} \end{pmatrix}\mapsto \begin{pmatrix} \alpha &{}{}\quad \beta \\ 0 &{}{} \quad \alpha ^{-1} \end{pmatrix},\nonumber \\{}&{} j_2: H\rightarrow A_2,~~~~\begin{pmatrix} t &{}{}\quad p\\ 0 &{}{}\quad t^{-1} \end{pmatrix}\mapsto \begin{pmatrix} \gamma &{}{}\quad \delta \\ 0 &{}{}\quad \gamma ^{-1} \end{pmatrix}, \end{aligned}$$

(4.16)

$\mathcal {F}_{\textrm{SL}_q}$ becomes a QPB on $\textbf{P}^1(\mathbb {C})$ (on $A_{12}$ we can choose $j_{12}=j_1: H\rightarrow A_1\subset A_{12}$ as a cleaving map or alternatively $j_2$). Notice that the stalk $(\mathcal {F}_{\textrm{SL}_q})_p$ of $\mathcal {F}_{\textrm{SL}_q}$ at $p\in \textbf{P}^1(\mathbb {C})$ equals $\mathcal {F}_{\textrm{SL}_q}(U_{12})$ if $p\in U_{12}$ and $\mathcal {F}_{\textrm{SL}_q}(U_i)$ if $p\in U_i\setminus U_{12}$. Further notice that $\mathcal {B}=\{\emptyset ,U_1,U_2,U_{12}\}$. Recalling the induced calculus on a sheaf of Theorem 4.16 we have

Proposition 4.18

Let $(\Gamma ,\textrm{d}):=(\Gamma ^+_{\textrm{SL}},\textrm{d}^+_{\textrm{SL}})$ be the 4-dimensional bicovariant FODC on $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ of Example 3.10. The induced right $\mathcal {O}_q(P)$-covariant FODC $(\Upsilon _{\textrm{SL}_q},\textrm{d})$ on $\mathcal {F}_{\textrm{SL}_q}$ is a free left $\mathcal {F}_{\textrm{SL}_q}$-module of dimension 4.

Proof

The $A_I$-bimodules $\Upsilon _{\textrm{SL}_q}(U_I)=\Gamma _I=A_I\Gamma A_I$ of the induced calculus of Theorem 4.16 are constructed in Proposition 4.14. We show that $\Gamma _I=A_I\Gamma$. The proof then follows using that $\Gamma$ is a free left A-module and ordering the invertible elements of $A_I$ on the left. The only nontrivial cases are $\Gamma _i$, $i\in \{1,2\}$, and $\Gamma _{12}$. From the commutation relations (3.11) (recall that the differential and the bimodule structure of the 4-dimensional bicovariant calculi on $\textrm{SL}_q(2)$ and $\textrm{GL}_q(2)$ coincide up to the identification $\textrm{det}_q=1$) it immediately follows that

$$\begin{aligned} \begin{aligned}&\omega ^1\alpha ^{-1}=q^{-1}\alpha ^{-1}\omega ^1, \qquad \qquad \qquad \qquad ~~~~~\omega ^2\alpha ^{-1}=\alpha ^{-1}\omega ^2,\\&\omega ^3\alpha ^{-1}=\alpha ^{-1}\omega ^3 +q^{-3}\lambda \alpha ^{-2}\beta \omega ^1, \qquad ~~~~\omega ^4\alpha ^{-1}=q\alpha ^{-1}\omega ^4 +\lambda \alpha ^{-2}\beta \omega ^2 \end{aligned} \end{aligned}$$

(4.17)

in $\Gamma _1$ and

$$\begin{aligned} \begin{aligned}&\omega ^1\gamma ^{-1}=q^{-1}\gamma ^{-1}\omega ^1,\qquad \qquad \qquad ~~~~~\, \omega ^2\gamma ^{-1}=\gamma ^{-1}\omega ^2,\\&\omega ^3\gamma ^{-1}=\gamma ^{-1}\omega ^3 +q^{-3}\lambda \gamma ^{-2}\delta \omega ^1,\qquad \omega ^4\gamma ^{-1}=q\gamma ^{-1}\omega ^4 +\lambda \gamma ^{-2}\delta \omega ^2 \end{aligned} \end{aligned}$$

(4.18)

in $\Gamma _2$. Recalling that a general element of $A_1$ is of the form $\sum _ja^j\alpha ^{-n_j}\in A_1$ for $n_j\in \mathbb {N}$, $a^j\in A$ and that $\Gamma$ is an A-bimodule which is freely generated as a left A-module by $\omega ^1, \omega ^2, \omega ^3, \omega ^4$, the commutation relations (4.17) imply $\Gamma A_1 \subseteq A_1\Gamma$. Thus, $\Gamma _1=A_1\Gamma A_1\subseteq A_1\Gamma$ which gives $\Gamma _1=A_1\Gamma$ (the inclusion $\Gamma _1\supseteq A_1\Gamma$ being trivial). Similarly we prove $\Gamma _2=A_2\Gamma$, and $\Gamma _{12}=A_{12}\Gamma$ using both (4.17) and (4.18). $\square$

In the proof of Proposition 4.18 it was shown that for all $U_I\in \mathcal {B}$ the right H-covariant $A_I$-bimodule $\Upsilon _{\textrm{SL}_q}(U_I) =\textrm{span}_{A_I}\{\omega ^1,\omega ^2,\omega ^3,\omega ^4\}$ is freely generated from the left. This implies that $\Upsilon _{\textrm{SL}_q}(U_1\cup U_2)=\Gamma$, i.e. that the presheaf constructed by the Ore extensions is already a sheaf and there is no sheafification required.

Proposition 4.19

The induced FODC $(\Upsilon _{\textbf{P}^1(\mathbb {C})},\textrm{d}_{\textbf{P}^1(\mathbb {C})})$ of base forms on $\mathcal {O}_q(\textbf{P}^1(\mathbb {C}))$ (described in Corollary 4.9) is determined by

$$\begin{aligned} \begin{aligned}&\Upsilon _{\textbf{P}^1(\mathbb {C})}(U_1):=\Gamma _{B_1}= B_1\textrm{d}_1B_1=\textrm{span}_\mathbb {C}\{u^k\textrm{d}_1u~|~k\in \mathbb {N}\},\\&\Upsilon _{\textbf{P}^1(\mathbb {C})}(U_2):=\Gamma _{B_2}= B_2\textrm{d}_2B_2= \textrm{span}_\mathbb {C}\{v^k\textrm{d}_2v~|~k\in \mathbb {N}\},\\&\Upsilon _{\textbf{P}^1(\mathbb {C})}(U_{12}):=\Gamma _{B_{12}}= B_{12}\textrm{d}_{12}B_{12}= \textrm{span}_\mathbb {C}\{u^k\textrm{d}_{12}u~|~k\in \mathbb {Z}\}. \end{aligned}\nonumber \\ \end{aligned}$$

(4.19)

Moreover, $\Gamma _{B_1}=\textrm{span}_{B_1}\{\alpha ^{-2}\omega ^2\}$, $\Gamma _{B_2}=\textrm{span}_{B_2}\{\gamma ^{-2}\omega ^2\}$ and $\Gamma _{B_{12}}=\textrm{span}_{B_{12}}\{\alpha ^{-2}\omega ^2\}$ are free left modules and we have the sheaf isomorphism

$$\begin{aligned} \Upsilon _{\textbf{P}^1(\mathbb {C})}\cong \Upsilon _{\textrm{SL}_q}^{\textrm{co}H}\cap \Upsilon _{\textrm{SL}_q}^{\textrm{hor}}. \end{aligned}$$

(4.20)

Proof

Using (3.12), (4.17) and $\delta =\alpha ^{-1}+q^{-1}\alpha ^{-1}\beta \gamma$ we obtain

$$\begin{aligned} \text {d}_1u&=\text {d}_1(\gamma \alpha ^{-1})\\ {}&=\text {d}(\gamma )\alpha ^{-1}-\gamma \alpha ^{-1}\text {d}(\alpha )\alpha ^{-1}\\ {}&=\bigg (\frac{q-1}{\lambda }\gamma \omega ^1+\frac{q^{-1}-1}{\lambda }\gamma \omega ^4 -\delta \omega ^2\bigg )\alpha ^{-1}\\ {}&~\quad -\gamma \alpha ^{-1}\bigg (\frac{q-1}{\lambda }\alpha \omega ^1 +\frac{q^{-1}-1}{\lambda }\alpha \omega ^4-\beta \omega ^2 \bigg )\alpha ^{-1}\\ {}&=-\delta \omega ^2\alpha ^{-1}+\gamma \alpha ^{-1}\beta \omega ^2\alpha ^{-1}\\ {}&=-\alpha ^{-2}\omega ^2-q^{-1}\alpha ^{-1}\beta \gamma \alpha ^{-1}\omega ^2 +\gamma \alpha ^{-1}\beta \alpha ^{-1}\omega ^2\\ {}&=-\alpha ^{-2}\omega ^2. \end{aligned}$$

Similarly $\textrm{d}_2v=\textrm{d}_2(\alpha \gamma ^{-1})=-\gamma ^{-2}\omega ^2$. The generators $u=\gamma \alpha ^{-1}$ and $v=\alpha \gamma ^{-1}$ of $B_1$ and $B_2$ have therefore the commutation relations

$$\begin{aligned} (\textrm{d}_1u)u=q^2u\textrm{d}_1u,~~~~~ (\textrm{d}_2v)v=q^{-2}v\textrm{d}_2v. \end{aligned}$$

(4.21)

Then the equalities in (4.19) follow, the last one also recalling that $v=u^{-1}$ in $B_{12}$.

From $\textrm{d}_1u=-\alpha ^{-2}\omega ^2$, $\textrm{d}_2v=-\gamma ^{-2}\omega ^2$ and the freeness of the left modules $\Gamma _1$, $\Gamma _2$ and $\Gamma _{12}$ it further follows that $\Gamma _{B_1}=\textrm{span}_{B_1}\{\alpha ^{-2}\omega ^2\}$, $\Gamma _{B_2}=\textrm{span}_{B_2}\{\gamma ^{-2}\omega ^2\}$ and $\Gamma _{B_{12}}=\textrm{span}_{B_{12}}\{\alpha ^{-2}\omega ^2\}$ are free left modules. The sheaf equality (4.20) follows directly from Theorem 4.10. $\square$

Note that the commutation relations (4.21) agree with those obtained by Chu, Ho and Zumino in [9].

Remark 4.20

Consider the right H-covariant FODC $(\Upsilon _{\textrm{SL}_q},\textrm{d})$ on $\mathcal {F}_{\textrm{SL}_q}$ together with the bicovariant quotient calculus $(\Gamma _H,\textrm{d}_H)$ on H induced from the 4-dimensional bicovariant FODC $(\Gamma ,\textrm{d})$ on A. The sequences

$$\begin{aligned} 0\rightarrow A_I\otimes _{B_I}\Gamma _{B_I}\rightarrow \Gamma _{I} \xrightarrow {\textrm{ver}_I}A_I\square _H\Gamma _H \rightarrow 0 \end{aligned}$$

(4.22)

are well-defined for all $U_I\in \mathcal {B}$ with the vertical map given by $\textrm{ver}_I:\Gamma _{I} \rightarrow A_I\square _H\Gamma _H$, $a^i\omega ^i\mapsto a^i_0\otimes a^i_1[\omega ^i]$ for all $a^i\in A_I$ (the proof is as in Lemma 3.19). However $(\Upsilon _{\textrm{SL}_q},\textrm{d})$ is not a principal calculus on the QPB $\mathcal {F}_{\textrm{SL}_q}$. For example the sequence (4.22) for $I=1$ is not exact. Indeed first observe that, since $\Gamma _1$ and $\Gamma _{B_1}$ are free modules, $\omega ^1\notin A_1\Gamma _{B_1}=\textrm{span}_{A_1}\{\omega ^2\}$. Then, since $\omega ^1$ is in the kernel of the projection $\Gamma \rightarrow \Gamma _H$ it follows that $\textrm{ver}_1(\omega ^1)=1\otimes [\omega ^1]=0$ and therefore $A_1\Gamma _{B_1}\subsetneq \ker \textrm{ver}_1$.

4.5.2 Principal calculus via ore localization of 3D calculus on $\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$

In this section we show that the failure of (4.22) to be an exact sequence can be cured by considering a 3-dimensional left covariant FODC instead of a 4-dimensional bicovariant FODC on $A=\mathcal {O}_q(\textrm{SL}_2(\mathbb {C}))$ as the global calculus of $\mathcal {F}_{\textrm{SL}_q}$. We choose a left covariant calculus on A so to canonically obtain a left covariant calculus on the quotient $H=\mathcal {O}_q(P)$. As in the previous section we consider the QPB $\mathcal {F}_{\textrm{SL}_q}$ with the cleaving maps (4.16).

Lemma 4.21

Let $(\Gamma ,\textrm{d})=(\Gamma _{\textrm{SL}},\textrm{d}_{\textrm{SL}})$ be the 3-dimensional left covariant FODC on A of Example 3.11. The induced FODC $(\Upsilon _{\textrm{SL}_q},\textrm{d})$ on $\mathcal {F}_{\textrm{SL}_q}$ is a free left $\mathcal {F}_{\textrm{SL}_q}$-module of dimension 3.

Proof

We first provide the commutation relations of $\alpha ^{-1}$ and $\gamma ^{-1}$ with the basis $\{\omega ^0,\omega ^1,\omega ^2\}$ of the free A-module $\Gamma$. From those in (3.19) we deduce

$$\begin{aligned}&\omega ^0\alpha ^{-1}=q^{-3}\alpha ^{-1}\omega ^0, \qquad \qquad \omega ^1\alpha ^{-1}=q^{-2}\alpha ^{-1}\omega ^1 +(q^{-6}-q^{-4})\alpha ^{-2}\beta \omega ^2,\nonumber \\ {}&\omega ^2\alpha ^{-1}=q^{-3}\alpha ^{-1}\omega ^2\,, \! \qquad \qquad \omega ^0\gamma ^{-1}=q^{-3}\gamma ^{-1}\omega ^0,\nonumber \\ {}&\omega ^1\gamma ^{-1}=q^{-2}\gamma ^{-1}\omega ^1 +(q^{-6}-q^{-4})\gamma ^{-2}\delta \omega ^2,\nonumber \\ {}&\omega ^2\gamma ^{-1}=q^{-3}\gamma ^{-1}\omega ^2. \end{aligned}$$

(4.23)

Then, proceeding as in the proof of Proposition 4.18, we conclude that $\Gamma _I=A_I\Gamma$ is a free left module (with $I=1,2,12$). $\square$

As in Proposition 4.19 the sheaf of base forms $(\Upsilon _M,\textrm{d}_M)$ is determined by the free left modules

$$\begin{aligned} \Gamma _{B_1}&=B_1\textrm{d}_1B_1=\textrm{span}_{B_1}\{\alpha ^{-2}\omega ^2\}\,,~~ \Gamma _{B_2}=B_2\textrm{d}_2B_2=\textrm{span}_{B_2}\{\gamma ^{-2}\omega ^2\}\,,\\ \Gamma _{B_{12}}&=B_{12}\textrm{d}_{12}B_{12}=\textrm{span}_{B_{12}}\{\alpha ^{-2}\omega ^2\}\,. \end{aligned}$$

With $u=\gamma \alpha ^{-1}\in B_1$ and $v=\alpha \gamma ^{-1}\in B_2$ we have $\textrm{d}_1u=q^{-3}\alpha ^{-2}\omega ^2$ and $\textrm{d}_2v=-q^{-2}\gamma ^{-2}\omega ^2$. The $\Gamma _{B_I}$ bimodule relations are then determined by

$$\begin{aligned} (\textrm{d}_1u)u=q^2u\,\!\textrm{d}_1u,~~~~~ (\textrm{d}_2v)v=q^{-2}v\textrm{d}_2v. \end{aligned}$$

We prove for example the properties of $\Gamma _{B_1}$. We have

$$\begin{aligned} \begin{aligned} \textrm{d}_1u&= \textrm{d}_1(\gamma \alpha ^{-1})\\&=(\textrm{d}\gamma )\alpha ^{-1} -\gamma \alpha ^{-1}\textrm{d}(\alpha )\alpha ^{-1}\\&=\gamma \omega ^1\alpha ^{-1}+\delta \omega ^2\alpha ^{-1} -\gamma \alpha ^{-1}(\alpha \omega ^1+\beta \omega ^2)\alpha ^{-1}\\&=q^{-3}(\delta \alpha ^{-1}-\gamma \alpha ^{-1}\beta \alpha ^{-1})\omega ^2\\&=q^{-3}\alpha ^{-2}\omega ^2 \end{aligned} \end{aligned}$$

where we used (3.18), (4.23) and $\delta \alpha ^{-1}-q^{-1}\alpha ^{-1}\beta \gamma \alpha ^{-1}=\alpha ^{-2}$. Again by (4.23) the commutation relation

$$\begin{aligned} (\textrm{d}_1u)u =q^{-3}\alpha ^{-2}\omega ^2\gamma \alpha ^{-1} =q^{-3}\alpha ^{-2}\gamma \alpha ^{-1}\omega ^2 =q^{-1}\gamma \alpha ^{-3}\omega ^2 =q^2u\textrm{d}_1u \end{aligned}$$

follows. Thus, $\Gamma _{B_1}=B_1\textrm{d}_1B_1=\textrm{span}_{B_1}\{\alpha ^{-2}\omega ^2\}$. Similarly for $\Gamma _{B_2}$ and $\Gamma _{B_{12}}$.

Proposition 4.22

Let $(\Upsilon _{\textrm{SL}_q},\textrm{d})$ be the FODC on the locally trivial QPB $\mathcal {F}_{\textrm{SL}_q}$ of Lemma 4.21. Let $(\Gamma _H,\textrm{d}_H)$ be the left covariant FODC on H induced from the 3-dimensional left covariant FODC $(\Gamma ,\textrm{d})$ on A of Example 3.11. The sequences

$$\begin{aligned} \qquad \qquad 0\rightarrow A_I\otimes _{B_I}\Gamma _{B_I}\rightarrow \Gamma _{I} \xrightarrow {\textrm{ver}_I}A_I\square _H\Gamma _H \rightarrow 0, \quad \quad U_I\in \mathcal {B}=\{\emptyset ,U_1,U_2,U_{12}\}\nonumber \\ \end{aligned}$$

(4.24)

are exact and $(\Upsilon _{\textrm{SL}_q},\textrm{d})$ is a principal calculus on $\mathcal {F}_{\textrm{SL}_q}$.

Proof

Recalling Lemma 3.19, that $\Gamma _I$ are free left $A_I$-modules and the left linearity of the vertical map (3.28), we see that the vertical maps in (4.24) are given by $\textrm{ver}_I:\Gamma _{I} \rightarrow A_I\square _H\Gamma _H$, $a^\ell \omega ^\ell \mapsto a^\ell _0\otimes a^\ell _1[\omega ^\ell ]$, where $a^\ell \in A_I$. In particular, they are well-defined. We first show that the second arrow in (4.24) is injective in the case of $U_1$. The results for the other opens in $\mathcal {B}$ follow analogously. Recall that $\Gamma _{B_1}$ is generated as a left $B_1$-module by $\alpha ^{-2}\omega ^2$ (cf. the discussion following Lemma 4.21). An arbitrary element of $A_1\otimes _{B_1}\Gamma _{B_1}$ is therefore of the form $a^i\otimes _{B_1}b^i\alpha ^{-2}\omega ^2$ with $a^i\in A_1$ and $b^i\in B_1$ (sum understood). Since, by Lemma 4.21, $\Gamma _1$ is a free left $A_1$-module with basis $\{\omega ^0,\omega ^1,\omega ^2\}$, it follows that $a^ib^i\alpha ^{-2}\omega ^2=0$ if and only if $a^ib^i\alpha ^{-2}=0$, i.e., if and only if, $a^ib^i=0$, which proves injectivity. We next prove exactness in $\Gamma _{I}$. The condition $0=\textrm{ver}_I(a^\ell \omega ^\ell ) =a^\ell _0\otimes a^\ell _1[\omega ^\ell ]$ (sum understood) holds if and only if $a^0=a^1=0$, indeed $[\omega ^2]=0$, while $[\omega ^0]$ and $[\omega ^1]$ form a basis of the free left H-module $\Gamma _H$, cf. Example 3.11. This proves $\ker \textrm{ver}_I=\mathrm{{span}}_{A_I}\{\omega _2\}=A_I\Gamma _{B_I}$. In order to prove surjectivity of $\textrm{ver}_I: \Gamma _{I}\rightarrow A_I\square _H\Gamma _H$ let $a^{i\ell }\otimes h^i[\omega ^\ell ]$ (sums understood) be an arbitrary element in $A_I\square _H\Gamma _H$. Since the forms $[\omega ^\ell ]$ are left H-coinvariant, by definition of cotensor product we have $a^{i\ell }_0\otimes a^{i\ell }_1 \otimes h^i=a^{i\ell }\otimes h^i_1\otimes h^i_2$. Then

$$\begin{aligned} \textrm{ver}_I(a^{i\ell }\epsilon (h^i)\omega ^\ell ) =a^{i\ell }_0\otimes a^{i\ell }_1\epsilon (h^i)[\omega ^\ell ] =a^{i\ell }\otimes h^i[\omega ^\ell ] \end{aligned}$$

and the sequences in (4.24) are exact. $\square$

As in the previous section the freeness of the presheaf $\Upsilon _{\textrm{SL}_q}$ implies that there is no sheafification required and in particular $\Upsilon _{\textrm{SL}_q}(\textbf{P}^1(\mathbb {C}))=\Gamma$.

We have seen that the differential calculus $(\Upsilon _{\textrm{SL}_q},\textrm{d})$ is principal. Note that it is not principal covariant since the induced left covariant FODC $(\Gamma _H,\textrm{d}_H)$ on H is not bicovariant. This is the case because the ideal $I=\textrm{span}_H\{(t-1)(t-q^2), p^2,(t-q^2)p\}$ characterizing $(\Gamma _H,\textrm{d}_H)$ is not closed under the adjoint right coaction, e.g. $\textrm{Ad}_R(p^2)\notin I\otimes H$ (it contains a polinomial in t with roots different from 1 and $q^2$. See [47] for the classification of bicovariant FODCi on Hopf algebras in terms of ideals closed under the right adjoint coaction).

4.5.3 Principal covariant calculus via ore localization of 4D calculus on $\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$

Consider the principal bundle $\textrm{GL}_2(\mathbb {C})\rightarrow \textrm{GL}_2(\mathbb {C})/P_{\textrm{GL}}\cong \textbf{P}^1(\mathbb {C})$ with $P_{\textrm{GL}}$ the upper Borel in $\textrm{GL}_2(\mathbb {C})$. As before, localizing with respect to $\alpha$ and $\gamma$ gives the opens $U_1$ and $U_2$ with corresponding topology $\{\emptyset ,U_1,U_2,U_{12},\textbf{P}^1(\mathbb {C})\}$ on $\textbf{P}^1(\mathbb {C})$. Although $\textrm{GL}_2(\mathbb {C})$ is not semisimple, a quantum deformation of this bundle, which is a QPB $\mathcal {F}_{\textrm{GL}_q}$ on $\textbf{P}^1(\mathbb {C})$, is obtained via Ore extensions of the quantum group $A=\mathcal {O}_q(\textrm{GL}_2(\mathbb {C}))$. Explicitly, we define the sheaf of algebras by $\mathcal {F}_{\textrm{GL}_q}(\emptyset ):=\{0\}$, $\mathcal {F}_{\textrm{GL}_q}(\textbf{P}^1(\mathbb {C})):=A$,

$$\begin{aligned} \mathcal {F}_{\textrm{GL}_q}(U_1):= & {} A_1:=A[\alpha ^{-1}],~~~ \mathcal {F}_{\textrm{GL}_q}(U_2):=A_2:=A[\gamma ^{-1}],~~~\\ \mathcal {F}_{\textrm{GL}_q}(U_1\cap U_2):= & {} A_{12}:=A[\alpha ^{-1},\gamma ^{-1}]. \end{aligned}$$

The Hopf algebra quotient $A\rightarrow H=\mathcal {O}_q(P_{\textrm{GL}})=A/\langle \gamma \rangle$ defined from Example 3.9 induces a natural comodule algebra structure on $\mathcal {F}_{\textrm{GL}_q}$. This is a locally trivial QPB with cleaving maps $j_1: H\rightarrow A_1$, $j_2: H\rightarrow A_2$ and $j_{12}=j_1: H\rightarrow A_1\subset A_{12}$ given by

$$\begin{aligned}&j_1\begin{pmatrix} t &{}{}\quad p\\ 0 &{}{}\quad s \end{pmatrix} =\begin{pmatrix} \alpha &{}{}\quad \beta \\ 0 &{}{}\quad \alpha ^{-1}\text {det}_q \end{pmatrix},~~~ j_2 \begin{pmatrix} t &{}{}\quad p\\ 0 &{}{}\quad s \end{pmatrix} =\begin{pmatrix} \gamma &{}{}\quad \delta \\ 0 &{}{} \quad \gamma ^{-1}\text {det}_q \end{pmatrix},\nonumber \\ {}&j_1(r')=r,\qquad \qquad ~~~\quad \quad \qquad \qquad \quad j_2(r')=r, \end{aligned}$$

(4.25)

where $r\in A$ and $r'\in H$ are the inverses of the quantum determinants. It is straightforward to verify that the sheaf $\mathcal {O}_{\textbf{P}^1(\mathbb {C})}$ of coinvariants of the QPB $\mathcal {F}_{\textrm{GL}_q}$ coincides with the one defined in (4.15).

Proposition 4.23

The Ore extension of the bicovariant 4-dimensional FODC $(\Gamma ,\textrm{d}):=(\Gamma _{\textrm{GL}},\textrm{d}_{\textrm{GL}})$ of Example 3.9 gives a right H-covariant FODC $(\Upsilon _{\textrm{GL}_q},\textrm{d})$ on the QPB $\mathcal {F}_{\textrm{GL}_q}$. Explicitly, the sheaf $\Upsilon _{\textrm{GL}_q}$ of right H-covariant $\mathcal {F}_{\textrm{GL}_q}$-bimodules is defined by $\Upsilon _{\textrm{GL}_q}(\emptyset )=\{0\}$, $\Upsilon _{\textrm{GL}_q}(\textbf{P}^1(\mathbb {C}))=\Gamma$ and

$$\begin{aligned}{} & {} \Upsilon _{\textrm{GL}_q}(U_1)=A_1\otimes _A\Gamma \otimes _AA_1,~~~ \Upsilon _{\textrm{GL}_q}(U_2)=A_2\otimes _A\Gamma \otimes _AA_2,\nonumber \\{} & {} \Upsilon _{\textrm{GL}_q}(U_1\cap U_2)= A_{12}\otimes _A\Gamma \otimes _AA_{12}. \end{aligned}$$

(4.26)

Together with the pullback calculus on the sheaf $\mathcal {O}_{\textbf{P}^1(\mathbb {C})}$ of coinvariants and the bicovariant quotient calculus on H this gives a principal covariant calculus on $\mathcal {F}_{\textrm{GL}_q}$.

Proof

Clearly (4.26) defines a presheaf $\Upsilon _{\textrm{GL}_q}$ of right H-covariant $\mathcal {F}_{\textrm{GL}_q}$-bimodules with restriction morphisms as in (4.13). Repeating the computations of Proposition 4.18 and Proposition 4.19 one shows that

• (i) $\Upsilon _{\textrm{GL}_q}(U_I)$ is a free left $\mathcal {F}_{\textrm{GL}_q}(U_I)$-module generated by $\{\omega ^1,\omega ^2,\omega ^3,\omega ^4\}$,

• (ii) the base forms $(\Upsilon _{\textbf{P}^1(\mathbb {C})},\textrm{d}_{\textbf{P}^1(\mathbb {C})})$ are determined by $\Gamma _{B_1}=\textrm{span}_{B_1}\{-\alpha ^{-2}\omega ^2\}$, $\Gamma _{B_2}=\textrm{span}_{B_2}\{-\gamma ^{-2}\omega ^2\}$ and $\Gamma _{B_{12}}=\textrm{span}_{B_{12}}\{-\alpha ^{-2}\omega ^2\}$.

Using the freeness of the presheaf $\Upsilon _{\textrm{GL}_q}$ it is not hard to check that $\Upsilon _{\textrm{GL}_q}(U_1\cup U_2)=\Upsilon _{\textrm{GL}_q}(\textbf{P}^1(\mathbb {C}))$, proving that $\Upsilon _{\textrm{GL}_q}$ is a sheaf of right H-covariant $\mathcal {F}_{\textrm{GL}_q}$-bimodules. By Proposition 4.14 the extended differential $\textrm{d}_I: A_I \rightarrow \Upsilon _{\textrm{GL}_q}(U_I)$ defines a right H-covariant FODC for each open $U_I\in \mathcal {B}$ and it is straightforward to verify that this determines a morphism $\textrm{d}:\mathcal {F}_{\textrm{GL}_q}\rightarrow \Upsilon _{\textrm{GL}_q}$ of sheaves of right H-comodules.

We next prove that the sequences

$$\begin{aligned} 0\rightarrow A_I\otimes _A\Gamma _{B_I}\rightarrow \Gamma _{I} \xrightarrow {\textrm{ver}_I}A_I\square _H\Gamma _H\rightarrow 0 \end{aligned}$$

(4.27)

are exact for all $U_I\in \mathcal {B}$. From Theorem 3.17 we have injectivity of the second arrow. Recall from Example 3.9 that the bicovariant quotient calculus $(\Gamma _H,\textrm{d}_H)$ on H is 3-dimensional (instead of 2-dimensional in the framework of Proposition 4.18) with left coinvariant basis $\{[\omega ^1],[\omega ^3],[\omega ^4]\}$ and that by Lemma 3.19 the vertical map $\textrm{ver}_I:\Gamma _I\rightarrow A_I\square _H\Gamma _H$ is well-defined for all $U_I\in \mathcal {B}$. Now take an arbitrary element $a^\ell \omega ^\ell \in \Gamma _I$ (sum understood). Because of freeness $0=\textrm{ver}_I(a^\ell \omega ^\ell )=a^\ell _0\otimes a^\ell _1[\omega ^\ell ]$ if and only if $a^1=a^3=a^4=0$. Thus $\ker \textrm{ver}_I=\textrm{span}_{A_I}\{\omega ^2\}=A_I\Gamma _{B_I}$. Surjectivity of $\textrm{ver}_I$ is verified as in Proposition 4.22. Hence the sequences (4.27) are exact and $(\Upsilon _{\textrm{GL}_q},\textrm{d})$ is a principal covariant calculus on $\mathcal {F}_{\textrm{GL}_q}$. $\square$

As a corollary, applying Theorem 4.10 we have that $\Upsilon _{\textbf{P}^1(\mathbb {C})}\cong \Upsilon _{\textrm{GL}_q}^{\textrm{co}H}\cap \Upsilon _{\textrm{GL}_q}^{\textrm{hor}}$ are isomorphic sheaves.

The sheaf $\mathcal {F}_{\textrm{GL}_q}$ is locally trivial since $A_I\cong B_I\# H$ according to (4.25). Considering the FODC on $(\Upsilon _{\textbf{P}^1(\mathbb {C})},\textrm{d}_{\textbf{P}^1(\mathbb {C})})$ and the bicovariant calculus $(\Gamma _H,\textrm{d}_H)$ on H, we can construct locally the smash product calculus $(\Gamma _{B_I\#H}, \textrm{d}_{B_I\#H})$ of Sect. 3.4, which can be pulled back to $A_I$ via $\varphi _I:A_I\rightarrow B_I\# H$ (the module of one forms being $\Gamma _{B_I\#H}$ since $\varphi _I$ are isomorphisms). However this local data does not give a FODC on $\mathcal {F}_{\textrm{GL}_q}$. Indeed for that to be the case the restriction morphisms $r_{IJ}^{\!\Upsilon _\#}$ of the would be sheaf ${\Upsilon _\#}$ of covariant $\mathcal {F}_{\textrm{GL}_q}$-bimodules would have to be left $\mathcal {F}_{\textrm{GL}_q}$-linear and compatible with the differentials: $\textrm{d}_{B_I\#H}\circ \varphi _I\circ r_{IJ}= r_{IJ}^{\!\Upsilon _\#}\circ \textrm{d}_{B_J\#H}\circ \varphi _J$. Recalling that $\Gamma _{B_I\#H}$ are free left ${B_I\#H}$-bimodules it follows form straightforward computations that there is not such map $r_{12,2}^{\!\Upsilon _\#}:\Gamma _{B_2\#H}\rightarrow \Gamma _{B_{12}\#H}$.

As a consequence we have that in this example the Ore extended differential calculi $(\Gamma _{A_I}, \textrm{d}_I)$ on $A_I\cong B_I\#H$ are not isomorphic to the smash product calculi $(\Gamma _{B_I\#H}, \textrm{d}_{B_I\#H})$. While the latter, from a bottom up approach, could seem to be the canonical choice, it turns out that it is the first one to provide a FODC on the sheaf $\mathcal {F}_{\textrm{GL}_q}$. This is yet another instance of the non uniqueness of the differential calculus construction.