Abstract
Here \({\underline{M}}\) denotes a pair (M, A) of a manifold and a subset (e.g. \(A=\partial M\) or \(A=\varnothing \)). We construct for each \({\underline{M}}\) its motion groupoid \(\textrm{Mot}_{{\underline{M}}}\), whose object set is the power set \( {{\mathcal {P}}}M\) of M, and whose morphisms are certain equivalence classes of continuous flows of the ‘ambient space’ M, that fix A, acting on \({{\mathcal {P}}}M\). These groupoids generalise the classical definition of a motion group associated to a manifold M and a submanifold N, which can be recovered by considering the automorphisms in \(\textrm{Mot}_{{\underline{M}}}\) of \(N\in {{\mathcal {P}}}M\). We also construct the mapping class groupoid \(\textrm{MCG}_{{\underline{M}}}\) associated to a pair \({\underline{M}}\) with the same object class, whose morphisms are now equivalence classes of homeomorphisms of M, that fix A. We recover the classical definition of the mapping class group of a pair by taking automorphisms at the appropriate object. For each pair \({\underline{M}}\) we explicitly construct a functor \({\textsf{F}}:\textrm{Mot}_{{\underline{M}}} \rightarrow \textrm{MCG}_{{\underline{M}}}\), which is the identity on objects, and prove that this is full and faithful, and hence an isomorphism, if \(\pi _0\) and \(\pi _1\) of the appropriate space of self-homeomorphisms of M are trivial. In particular, we have an isomorphism in the physically important case \({\underline{M}}=([0,1]^n, \partial [0,1]^n)\), for any \(n\in {\mathbb {N}}\). We show that the congruence relation used in the construction \(\textrm{Mot}_{{\underline{M}}}\) can be formulated entirely in terms of a level preserving isotopy relation on the trajectories of objects under flows—worldlines (e.g. monotonic ‘tangles’). We examine several explicit examples of \(\textrm{Mot}_{{\underline{M}}}\) and \(\textrm{MCG}_{{\underline{M}}}\) demonstrating the utility of the constructions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The paper is about constructing algebraic structures that capture (in a broad sense) topological aspects of particle motion. Although we eventually construct groupoids, these are neither a convenient starting point, nor close in any absolute sense to the underlying physics. (The convenience of groupoids as an endpoint lies in the relatively well-developed state of their own representation theory; and the fact that eventually one must give a scheme for predicting results of physical measurement—i.e. pass to linear operators and their spectra, and so, in the algebraic language, pass to \({\textbf{Vect}}{}\), where the images of our constructions are indeed categories.) More natural are structures that, like categories, have partial compositions, but where (for quite different reasons) both the unit and the associativity conditions are relaxed. Here our starting points are ‘engines’ that take a manifold M as input—the choice of ambient space; and produce, as output for each M, a ‘magmoid’ (a triple of objects, morphisms and a partial composition with no conditions). In each case, the object class is \({\textsf{Set}}(M,\{0,1\}) \;\) (as a point of reference, note that if object \(f\in {\textsf{Set}}(M,\{0,1\} )\) has finite support then it is a ‘collection of point particles’, and endomorphisms are called braids). The main remaining step is to construct congruences on these magmoids that wash out irrelevant detail from particle motion, while retaining useful features... and yielding quotient groupoids.
To facilitate our main Introduction, we begin with a prelude summarizing some key constructions of engines and congruences. We postpone proofs and explanations, but we are explicit. This will allow us to be technically specific even in our Introduction.
Let \({\textbf{Top}}\) denote the category of topological spaces and continuous maps, and \({\textbf{Top}}^h\) the subcategory of homeomorphisms. Then let \({\textbf{TOP}}^h(X,Y)\) denote the space with underlying set \({\textbf{Top}}^h(X,Y)\) and the compact open topology. For example, Fig. 1 indicates a sequence of self-homeomorphisms of the disk such that successive terms are close in \({\textbf{TOP}}^h(D^2,D^2)\). Let \({{\mathbb {I}}}=[0,1]\subset {{\mathbb {R}}}\) with the usual topology. Fixing, for now, a manifold-subset pair \({\underline{M}}=(M,\varnothing )\), so writing simply M for \({\underline{M}}\),
– a set of gradual deformations of M over some standard unit of time. Thus Fig. 1 indicates sequential points on a path in \(\textrm{Flow}_{D^2}\). For \((f,g)\in \textrm{Flow}_{M}\times \textrm{Flow}_{M}\), note that \(g*f\) given by
is in \(\textrm{Flow}_{M}\); as is \({\bar{f}}\) given by \( {\bar{f}}_t \;=\; f_{(1-t)}\circ f_1^{-1}. \) Thus \((\textrm{Flow}_{M},*)\) is a magma.
A magma action of a magma P on a set S is a map \(\alpha : P\times S \rightarrow S\) with \(q(ps)=(qp)s\) (denoting the composition in P of a pair (p, q) as qp, and the image \(\alpha (p,s)\) as ps). Given such a magma action \(\alpha \), the action magmoid \(\varvec{\mu }_\alpha \) is a triple consisting of objects S, morphisms which are triples \((p,s,p s) \in P \times S \times S\), and a partial composition \(((p,s,ps),(q,ps,qps))\mapsto (qp,s,qps)\).
Fix a manifold M. Let \(\Sigma \) be a space. A \(\Sigma \)-field configuration is a function in \({\textbf{Top}}(M,\Sigma )\). There is a magma action \(\blacktriangleright \) of \((\textrm{Flow}_{M},*)\) on M given by \(\blacktriangleright (f, m) = f_1(m)\); and on \({\textbf{Top}}(M,\Sigma )\) given by \(\chi \mapsto \chi \circ f_1^{-1}\). In particular on the power set \({{\mathcal {P}}}M \cong {\textbf{Top}}(M,{{\mathbb {Z}}}_2)\) (\(\Sigma = {{\mathbb {Z}}}_2\) with the indiscrete topology), the action is denoted \(\triangleright \), so \(\triangleright (f, N) = f_1(N)\). The action magmoid \(\varvec{\mu }_{\triangleright }\) is denoted \(\textrm{Mt}_M^* \; =\; ( {{\mathcal {P}}}M, \textrm{Mt}_M^*(-,-), * )\). A morphism \((f,N,N')\) here is a gradual deformation of M that carries the initial object subset to the final object subset: \(f_1(N)=N'\), hence called a motion. The motion magmoid \(\textrm{Mt}_M^*\) is large, but amenable to various natural quotients, as we shall see.
Let X be a space. Paths \(\gamma ,\gamma '\in {\textbf{Top}}({{\mathbb {I}}},X)\) are path homotopic if \( {\textbf{Top}}({{\mathbb {I}}},X)({\gamma })({\gamma '}) \ne \varnothing \) where
Letting \(X={\textbf{TOP}}^h(M,M)\), path homotopy gives a congruence on \((\textrm{Flow}_{M},*)\) (with group quotient). But alternatively with f, g flows and \(N,N' {\subset M}\) subsets, let
Theorem 1.1
For M a manifold, there is a congruence on \(\textrm{Mt}_M^*\) given by the relation  if \({\textbf{Top}}({{\mathbb {I}}}^2,{\textbf{TOP}}^h(M,M))(f^{N'}_{N}\!g) \ne \varnothing \). The quotient is a groupoid—the motion groupoid
if \({\textbf{Top}}({{\mathbb {I}}}^2,{\textbf{TOP}}^h(M,M))(f^{N'}_{N}\!g) \ne \varnothing \). The quotient is a groupoid—the motion groupoid

Now let \(\textrm{Homeo}_{M}\) denote the action groupoid of the group action of \({\textbf{Top}}^h(M,M)\) on \({{\mathcal {P}}}M\) given by \(\mathfrak {f}\triangleright N = \mathfrak {f}(N)\). Let \(N,N' \in {{\mathcal {P}}}M\) and \(\mathfrak {f},\mathfrak {g}\in \textrm{Homeo}_{M}(N,N')\). Then define
The relation \(\mathfrak {f}{\mathop {\sim }\limits ^{i}}\mathfrak {g}\in \textrm{Homeo}_{M}(N,N')\) if \( {\textbf{Top}}({{\mathbb {I}}}, {\textbf{TOP}}^h(M,M))\!(\! {\tiny \mathfrak {f}}^{N'}_{N}\!\! {\tiny \mathfrak {g}} ) \ne \varnothing \) gives a congruence on \(\textrm{Homeo}_{M}\). The mapping class groupoid \(\textrm{MCG}_{M}\) is the quotient \(\textrm{Homeo}_{M}/{\mathop {\sim }\limits ^{i}}\). A functor
is given by ‘forgetting’ \([f]_{\text{ rp }}\mapsto [f_1]_{\text{ i }}\).
Finally in this pre-Introduction, we introduce one more ‘engine’ creating a power-set magmoid from each manifold; and, for this construction, one more type of congruence. For M a manifold and N a subset let \({\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\) be the subset of elements \(f \in {\textbf{Top}}(N\times {{\mathbb {I}}},M)\) such that \( f(-,t)\) is an embedding for each t, \(f(n,0)=n\) for all \(n \in N\), and \(f(N,1)=N'\). One indeed obtains another power-set magmoid for M upon noting that the formula

gives a composition \({\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\times {\textbf{Top}}_{{\textbf{B}}{},M}[N',N''] \rightarrow {\textbf{Top}}_{{\textbf{B}}{},M}[N,N'']\). Define
Then \(f {\mathop {\sim }\limits ^{fk}}f'\) if \({\textbf{Top}}( (N\times {{\mathbb {I}}})\times {{\mathbb {I}}}, M)[N^{f}_{f'} N']\ne \varnothing \). This defines a congruence, thus yielding the fake motion groupoid \(\; \textrm{FMot}_{M}\). A functor
is given by sending \([(f,N,N')]_{\text{ m }}\) to the class of the map \((n,t)\mapsto f_t(n)\), where \(n\in N\).
The engines \(\textrm{Mot}_{-}\), \(\textrm{MCG}_{-}\) and \(\textrm{FMot}_{-}\) all specialise when considering with \(M={{\mathbb {R}}}^2\) and \(N=N'\) finite, to constructions isomorphic to the braid group. However in general they differ from each other in a number of beautiful, intriguing and useful ways, as we shall see.
Main Introduction. We will show that embedding the various groups \(\textrm{Mot}_{M}(N,N)\) (motion groups, generalising [Dah62, Gol81]) into the groupoid \(\textrm{Mot}_{M}\) yields several significant benefits. By way of introduction, we now discuss these (in no particular order).
Left: A flow f in \(M=D^2\subset {{\mathbb {R}}}^2\) (from Fig. 1) as a level-preserving homeomorphism in \(M\times {{\mathbb {I}}}\). Middle: Induced motion of two point particles as induced by the flow f, drawn as paths in \(M\times {{\mathbb {I}}}\). Right: Induced motion of a line and a point particle as induced by the flow f
Firstly, the groupoid formalism allows us to study the set of objects in a unified way. The reader should think of finite sets passing to braids; compact manifolds passing to generalised loop-braids; hybrids passing to some beautiful new algebraic structures; and non-compact manifolds and various other generalisations passing to structures depending heavily on details of the embedding. This facility has many aspects—leading to monoidal structures, and vast generalisations thereof, as well as to other higher categorical formalisms; and, as we will consider here, different but often equivalent notions of congruence. Together these lead in turn to the question of non-isomorphims such as particle fusion, and hence to generalised tangle categories (cf. [BD95, Pic97]). In this direction we go little further than framing the construction. We do, however, make significant progress on the connection between isomorphisms in generalised tangle categories, and motion groupoids by realising motion equivalence in terms of a level preserving isotopy relation on ‘worldlines’ of motions.
Another benefit lies in object-changing morphisms themselves. Equipped with these, motions can be factored into compositions of simpler motions in many more ways. This is advantageous, for example, for giving generating sets of morphisms in motion subgroupoids. It is an extension of something that can already be seen in the classical setting of braid groups, in the sense that the Artin presentation of the braid group has fewer generators than the usual presentation of the pure braid group, where each individual point must return to its starting position.
Moreover, depending on the object N, in the group setting it is typically true that there exists an open neighbourhood of the identity homeomorphism such that all motions realised by a flow staying in this neighbourhood are identified with the identity: for instance for finite N all non-trivial flows connecting the same object are at positive “distance" from the identity. Thus Lie-theory/Lie-algebra-like linearisation strategies are hard to access. In contrast in the groupoid setting, even a flow very close to the identity can change the object, and then of course is not identified with the identity motion. It follows that morphisms of the groupoid can be obtained as a composition of arbitrarily “small” motions. A range of powerful techniques thus become accessible. This will be explored for example when proving the relation between motion groupoids and Artin braid groups in §5.
We will see here that motion groupoids are useful for physical modelling. A bicycle inner-tube with a puncture is useless — except as an example of a topological space, but a real rubber tube is by no means a uniform continuum. It is useful to be able to model the emergence of a realistic puncture. A toy version of this is to compare the punctured Hopf-link and the punctured unlink as objects in \(M={{\mathbb {R}}}^3\). They are connected in \(\textrm{FMot}_{M}\) but not in \(\textrm{Mot}_{M}{}\) — see Examples 3.62 and 5.5. (It is interesting to note that the question of connection is the same in the category as in the underlying magmoid.)
This leads us naturally to the question of the relationship between the different engines at fixed M. Localised to the ‘braid’ setting, motion groups and mapping classes have been related, at least implicitly, in the particular cases of the braid group and loop braid group [BB05, Dam17, Dah62]. The functor \({\textsf{F}}:\textrm{Mot}_{M}\rightarrow \textrm{MCG}_{M}\) generalises this. It yields immediate concrete applications: providing a route to using results about mapping class groups to inform about about motion (sub)groupoids.
The ‘braid group’ has several realisations, each with different flavours—see for example [BB05, Rol03, Bir75]. Each of the classical topological realisations consists of some ‘concrete’ elements, together with a composition and an equivalence [BB05, Bir69, Gol81, Dah62]. These constructions are not generally pairwise equivalent when considering the concrete elements. Bridges between the concrete elements in the different topological realisations can be illustrated using the left and middle images in Fig. 2. The middle picture may represent a motion, where the whole space is moving in the way prescribed by Fig. 1 and the induced movement of the points is marked. Further the picture may represent an element in \({\textbf{Top}}_{{\textbf{B}}}(N\times {{\mathbb {I}}},M)\), where N is two points and the image at each \(t\in {{\mathbb {I}}}\) drawn ascending up the page, this is Artin’s formulation of braids. Alternatively the picture may represent a monotonic embedding of two unit intervals in the cylinder, which, passing to the image, gives a concrete element of the tangle category (see e.g. [Kas12]); or a path in the configuration space of two points in the disk. Then a concrete element of the mapping class groupoid is the endpoint of the motion. Notice here that motions contain the most information: maps into the other settings ‘forget’ information.
Even from this simplest possible perspective, then, we see that we should begin by constructing the engine \(\textrm{Mot}_{-}\), since it is the one which keeps track of the most information. We then investigate in which cases it is possible to forget information whilst retaining the same algebraic structure. We will see that in general the ‘forgetting’ functors we construct are neither surjective, nor injective.
Generalisations of all the aforementioned constructions of braids to unknotted, unlinked, loops in 3 dimensions exist. There they lead again to isomorphic groups [Dam17, Dah62, BH13].
Yet another motivation for the study of motion groupoids is that we expect rich representation theory, as has already been found to be the case with motion groups. Firstly, in certain cases motion groups have the representation theoretically useful property that they can be finitely presented: a finite presentation of Artin’s braid group was given in [Art47], and Dahm gave a classification of the group of motions of a configuration of n unknotted, unlinked circles in \({{\mathbb {R}}}^3\) in terms of an isomorphism to the automorphism group of the free group with n generators [Dah62, Sec.III], which is known to have finite presentation [MKS04, p.131,Th.3.2]. A plethora of approaches to the study of the representation theory of the latter group are present in the literature, see [BWC07, KMRW17, QW21, BFMM19] for example. A motion group of a collection of Hopf links and trivial links in \({{\mathbb {R}}}^3\) is suggested to have a finite presentation in [DK19]. Similarly a presentation of a motion group of a ‘necklace’ in \({{\mathbb {R}}}^3\) is given in [BB16], and its representation theory studied in [BKMR19].
Having discussed the motivation for our construction we now introduce the content of the paper.
Firstly, for both the motion groupoid and the mapping class groupoid, we have a version which fixes a distinguished subset \(A\subset M\) pointwise, where \(A=\partial M\) for example. These are denoted \(\textrm{Mot}_{M}^A\) and \(\textrm{MCG}_{M}^A\). There are a few reasons for this considering this level of generality. For one thing it leads to interesting algebra; and for another it facilitates passage to various natural generalisations that are monoidal categories and/or canopolis or cubical algebras (whose main discussion we will postpone). This facility will also be necessary to find isomorphisms from the motion groupoid to the mapping class groupoid in the case \(M=D^n\).
In this work we will give several equivalent realisations of both motions and of the motion groupoid; each of the different realisations will have useful applications. In §3 we begin by defining motions and giving two different compositions of motions. Define a map \(\textbf{W}:\textrm{Flow}_{M}\times {{\mathcal {P}}}M \rightarrow {{\mathcal {P}}}(M\times {{\mathbb {I}}})\) by \(\textbf{W}(f,N) = \bigcup _{t \in [0,1]} f_t(N) \times \{t\}\). This is what we call the worldline of the corresponding motion. The \(*\) composition given above represents the physical picture; thinking of motions as a gradual deformation of space over time, the composition of two motions is the first followed by the other. This is made precise by Lemma 3.38, which says that the worldline of the \(*\) composition of two motions can be written in terms of a composition of the worldlines. The \(*\) composition is necessary to construct the functor \( \textbf{T}:\textrm{Mot}_{M}\rightarrow \textrm{FMot}_{M}\) in §5.3; as well as for functors into generalised tangle categories. The second is a pointwise composition \((g\cdot f)_t=g_t\cdot f_t\), which is introduced as a computational convenience as it simplifies a number of proofs. The compositions lead to distinct magmoids, although in the motion groupoid both compositions descend to the same well defined composition on equivalence classes.
Still in §3, we give our first construction of \(\textrm{Mot}_{M}\) (Theorem 3.32); the morphisms are equivalence classes of motions with the relation that \(f{\mathop {\sim }\limits ^{m}}g\in \textrm{Mt}_M^*(N,N')\) if \({\bar{f}}*g\) is path homotopic to an N-stationary motion – these are the motions which leave N fixed setwise for all \(t\in {{\mathbb {I}}}\). We prove that this leads to a groupoid by performing a two stage quotient, first identifying path equivalent motions, and then identifying each class that contains a stationary motion with the corresponding identity. We start with this particular equivalence relation as this is a direct generalisation of the relation used in Dahm’s motion groups [Dah62, Gol81], the construction we set out to generalise. There are also practical advantages, certain results are more straightforward to see with this relation; for example, Proposition 3.37 that motions with the same worldline are equivalent.
In § 3.7 we will present some key examples to demonstrate the richness of our construction. The unified treatment of objects discussed above leads to questions about skeletons (equivalent categories without extraneous isomorphisms [ML13, IV.2]), and about objects whose automorphism groups are related by canonical isomorphisms outside of the motion groupoid. Note that the existence of a homeomorphism between subspaces, or indeed a homeomorphism of the ambient space sending one subspace to the other is not enough to ensure that the underlying sets are connected by a morphism in the motion groupoid. In Sect. 3.7.1 we show that in \(\textrm{Mot}_{{{\mathbb {I}}}}\), the existence of morphisms in \(\textrm{Mot}_{{{\mathbb {I}}}}(N,N')\) depends only on the topology of N and \(N'\) if N and \(N'\) are compact subspaces in the interior of \({{\mathbb {I}}}\), but on details of the embeddings when they are non-compact manifolds. We also have Example 3.56 which shows that even for 1-dimensional manifolds, automorphism groups can be non-trivial. In § 3.7.3 we give examples relating automorphism groups \(\textrm{Mot}_{M}(N,N)\) and \(\textrm{Mot}_{M}(N',N')\) when N and \(N'\) are not connected in the motion groupoid.
In §3.8 we give two alternative realisations of motions from N to \(N'\) in M, as certain elements of \({\textbf{Top}}(M\times {{\mathbb {I}}}, M)\) and of \({\textbf{Top}}^h(M\times {{\mathbb {I}}},M\times {{\mathbb {I}}})\). The former connects to a direct generalisation of Artin braids [Art25, Art47]. We develop this further in §5. The latter suggests the existence of a map into a generalised tangle category, where concrete elements are embeddings \(N\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\), with conditions. These realisations also lead to some useful schematic representations of motions.
In Sect. 4, we discuss alternative ways to formulate the relation \({\mathop {\sim }\limits ^{m}}\). Firstly, in Theorem 4.6, we prove that \({\mathop {\sim }\limits ^{m}}\) defines the same relation on motions as the relation  given above. The relation
given above. The relation  is the same relation used to construct relative homotopy sets, thus facilitating the use of the long exact sequence of homotopy groups to investigate properties of the functor \({\textsf{F}}:\textrm{Mot}_{M}^A \rightarrow \textrm{MCG}_{M}^A\) in §7.
is the same relation used to construct relative homotopy sets, thus facilitating the use of the long exact sequence of homotopy groups to investigate properties of the functor \({\textsf{F}}:\textrm{Mot}_{M}^A \rightarrow \textrm{MCG}_{M}^A\) in §7.
As noted above, a flow f, together with \(N\subset M\), naturally gives rise to a subset \(\textbf{W}(f,N) \subset M\times {{\mathbb {I}}}\), the worldline of the corresponding motion. If N is a finite subset in the interior of \(D^2\), and f is a flow of \(D^2\), then \(\textbf{W}(f,N)\) is a tangle in \(D^2 \times {{\mathbb {I}}}\), and one such example is as shown on the middle image in Fig. 2. If \(N\subset \textrm{int}(D^2)\) is the union of a point and a line, and f the flow of \(D^2\) depicted in the left-hand-side of Fig. 2, then \(\textbf{W}(f,N)\) would look like the right-hand-side of Fig. 2. For the case of the motion of an unlink in \(D^3\), the worldline is a disjoint union of embedded tubes in \(D^3\times {{\mathbb {I}}}\). It should be observed that motions and worldlines are very different: the former are paths in the homeomorphism group of M, the latter are subsets of \(M\times {{\mathbb {I}}}\).
In Sect. 4.2 we prove that it is, in fact, possible to understand motion equivalence in terms of level preserving isotopies between worldlines (Theorem 4.18). This is a significant step towards proving the well-definedness, and potentially injectivity, of functors from motion groupoids into generalised tangle categories [BD95], and from our understanding this is the only such result in the literature. It also has applications to defining representations of motion groups, as explored in [MMTb].
Precisely, in Theorem 4.18, we prove that two motions and are motion equivalent if, and only if, their worldlines and are level preserving ambient isotopic subsets of \(M\times {{\mathbb {I}}}\), through an isotopy fixing \(M\times \{0\}\) and \(M\times \{1\}\). The proof relies on the above result that motions are equivalent if and only if they are relative path-equivalent, along with Proposition 3.37 that motions with the same worldline are equivalent.
Still in Sect. 4.2, we also define a further relation on \(\textrm{Flow}_{M}\times {{\mathcal {P}}}M \) (and hence on motions) by \((f,N)\sim (f',N')\) if \(\textbf{W}(f,N)=\textbf{W}(f',N')\) or if \(f,f'\) are path homotopic. Let \({\mathop {\sim }\limits ^{w}}\) be the equivalence closure of this relation. Using Theorem 4.18, we prove that \({\mathop {\sim }\limits ^{\omega }}\) defines the same relation on motions as \({\mathop {\sim }\limits ^{m}}\) (this is Theorem 4.22)
In Sect. 5 we construct, for a manifold M, the category \(\textrm{FMot}_{M}\). The morphisms in \(\textrm{FMot}_{M}\) are ‘fake motions’. We use this nomenclature since these are maps \(N\times {{\mathbb {I}}}\rightarrow M\) thus appear to specify a movement of N in M, although there does not always exist a motion \(M\times {{\mathbb {I}}}\rightarrow M\), which restricts to a given fake motion. We prove that there is a functor \(\textbf{T}:\textrm{FMot}_{M}^A\rightarrow \textrm{Mot}_{M}^A\) (Theorem 5.11). In Sect. 5.3 we restrict to the case that N is a finite set of points in the interior of a manifold. In this case we get that \(\textbf{T}\) restricts to an isomorphism on automorphism groups. This makes the connection with Artin’s presentation of the braid group [Art47], thus proving that there exists subgroupoids of \(\textrm{Mot}_{M}\) which have finite presentation. More generally \(\textbf{T}\) is an isomorphism of groupoids in the case of finite points (Theorem 5.21). For K a finite subset in the interior of a disk, the results in this section also rigorously prove isomorphisms \(\textrm{Mot}_{{{\mathbb {R}}}^2}(K,K)\cong \textrm{Mot}_{D^2}^{\partial D^2}(K,K)\cong \textrm{Mot}_{D^2{\setminus } \partial D^2}(K,K)\), explaining why these various settings are often used interchangeably in the literature.
In Theorems 6.4 and 6.10 we have the mapping class groupoid and its A-fixing version. These generalise the mapping class group of a submanifold N in a manifold M [Bir69] cf. for example [FM11, Iva02]. For \(C\subset D^3\) a subset consisting of unknotted, unlinked circles in the 3-disk, then \(\textrm{MCG}_{D^3}^{\partial D^3}(C,C)\) is the extended loop braid group as in [Dam17]. We also have some examples demonstrating the utility of results on homeomorphism spaces available in the literature.
In §7 we relate the motion groupoid and mapping class groupoid formalisms, giving the functor \({\textsf{F}}:\textrm{Mot}_{M}^A\rightarrow \textrm{MCG}_{M}^A\) in Theorem 7.1 and proving in Theorem 7.13 that this is an isomorphism if the space of A-fixing homeomorphisms of M is path connected and has trivial fundamental group. We also give examples to demonstrate the utility of the functor. In §7.3.1, we show that \(\textrm{Mot}_{D^m}^{\partial D^m}\cong \textrm{MCG}_{D^m}^{\partial D^m}\) for all integer m. The case \(m=2\) gives an isomorphism between two realisations of the braid group. We also show, in §7.3.2, that if we remove the condition that \(\partial D^m\) is fixed, we no longer have an isomorphism. In §7.3.3 and §7.3.4 we consider the (non-isomorphism) functor \({\textsf{F}}\) in the case \(M=S^1\) and \(M=S^2\). In each of these examples we rely heavily on known results on mapping class groups and spaces of homeomorphisms [Ham74].
To complete the introduction, we make a couple of comments on our technical choices.
In the current paper we do all constructions in the topological category, following [Dah62, Gol81]. We expect a construction in the smooth category to be possible, and this is certainly and interesting direction of future study. Various smooth motion group constructions exist in the literature, see [BWC07, QW21, Wat72].
For convenience we have formulated everything for ambient space M a manifold. However, the constructions in this paper will also lead to a theory of motion groupoids, fake motion groupoids and mapping class groupoids of spaces if the word “manifold” is substituted by “locally compact, locally connected, Hausdorff topological space” e.g. finite graphs, or locally finite CW-complexes, which are Hausdorff, locally connected and locally compact [FP90, Corollary 1.3.3, Proposition 1.5.10]. Note, however, that our results relating these groupoids in the manifold case may no longer hold in this generality.
1.1 Paper overview
In Sect. 2 we begin by introducing notation and recalling technology that will be useful in our construction. In Sect. 2.1 we recall the compact-open topology on spaces of continuous maps. We then give conditions under which the usual product-hom adjunction in the category of sets lifts to an adjunction in the category of topological spaces. In Sect. 2.3 we introduce magmoids and congruences on magmoids as a tool for constructing groupoids. In Sect. 2.5 we obtain the fundamental groupoid of a topological space X (Proposition 2.36) from the path magmoid. In Sect. 2.6 we give the construction of a groupoid of self-homeomorphisms \(\textrm{Homeo}_{M}\) corresponding to a manifold M, with object class the power set \({{\mathcal {P}}}M\) (Definition 2.39).
In Sect. 3 the first main theorem is Theorem 3.32, the construction of the motion groupoid \(\textrm{Mot}_{M}\) of a manifold M. Picking a single set in \({{\mathcal {P}}}(M)\) and looking at the group of automorphisms we get back the motion group. We also have Theorem 3.72 which says that motions N to \(N'\) in M are in correspondence with a certain subset of \({\textbf{TOP}}^h(M\times {{\mathbb {I}}}, M\times {{\mathbb {I}}})\). In Sect. 3.7 we have examples.
In Sect. 4.1 we have Theorem 4.6 which says that relative path-equivalence defines the same equivalence relation on motions as motion equivalence. We then have Theorems 4.17,4.18 and 4.22, which each prove various equivalence relations on worldlines of motions define the same relation as motion equivalence.
In Sect. 5 we have the construction of a groupoid of fake motions (Lemma 5.9), and the construction of the functor from \(\textbf{T}:\textrm{FMot}_{M}^A\rightarrow \textrm{Mot}_{M}^A\) (Theorem 5.11). There is also Theorem 5.17 which says that there is an isomorphism \(\textrm{Mot}_{M}^{\partial M}(K,K)\cong \textrm{FMot}_{M}^{\partial M}(K,K)\) where K is a finite set in the interior of the manifold, and Theorem 5.21 which says this extends to a groupoid isomorphism for the subgroupoids of all such K. Finally we have Theorem 5.22 which says that the same isomorphisms hold without fixing the boundary in \(\textrm{Mot}_{M}\).
In Sect. 6 we construct the mapping class groupoid of a manifold M (Theorem 6.4). Theorem 6.10 is a subset-fixing version.
In Sect. 7 we construct the functor \({\textsf{F}}:\textrm{Mot}_{M}^A\rightarrow \textrm{MCG}_{M}^A\) (Theorem 7.13). In Theorem 7.13 we prove that \({\textsf{F}}\) is an isomorphism if \(\pi _0({\textbf{TOP}}^h(M,M),{\textrm{id}}_M)\) and \(\pi _1({\textbf{TOP}}^h(M,M),{\textrm{id}}_M)\) are trivial. In Sect. 7.3 we give some examples demonstrating the utility of the functor.
Glossary | |
|---|---|
\({{\mathcal {P}}}M\) | The power set of a set M |
\({\textbf{Top}}\) | The category of topological spaces and continuous maps |
\({\textsf{Set}}\) | The category of sets and functions between sets |
\({\mathop {\sim }\limits ^{p}}\) | Indicates paths related by homotopy relative to end-points, see Definition 2.32 |
\([\gamma ]_{\text{ p }}\) | Equivalence class of a paths up to path-equivalence, see Definition 2.32 |
\(\tau ^{co}_{XY}\) | The compact-open topology on the set \({\textbf{Top}}(X,Y)\), see Definition 2.4 |
\({\textbf{Top}}^h(M,M)\) | The submonoid of \({\textbf{Top}}(M,M)\) containing homeomorphisms |
\({\textbf{TOP}}^h(M,M)\) | The set \({\textbf{Top}}^h(M,M)\) equipped with subspace topology from \(\tau ^{co}_{MM}\) |
\(\textrm{Homeo}_{M}^A\) | Groupoid with objects \({{\mathcal {P}}}M\) and morphisms homoeomorphisms, see Def. 2.39 |
| Notation for morphisms in \(\textrm{Homeo}_{M}^A\) |
\(\textrm{Flow}_{M}\) | Set of all flows in M, \(f \in {\textbf{Top}}^{}({{\mathbb {I}}},{\textbf{Top}}^h(M,M))\) with \(f_0 = {\textrm{id}}_M\), see Def. 3.1 |
Glossary | |
|---|---|
\({\textrm{Id}}_M\) | Flow in M which is the path \(f_t={\textrm{id}}_M\) for all t |
| A motion from N to \(N'\) in the specified manifold, see Definition 3.13 |
| Worldline of a motion |
\(\textrm{Mt}_{M}({N},{N'})\) | The set of all motions from N to \(N'\) in M |
\(\textbf{Mt}_M\) | The set of all motions in M |
\({\mathop {\sim }\limits ^{m}}\) | Indicates motions related by motion-equivalence, see Proposition 3.31 |
| Class of a motion |
\(\textrm{Mot}_{M}^A\) | Motion groupoid of a manifold M, fixing \(A\subset M\), see Theorems 3.32 and 3.49 |
| Indicates motions related by relative path-equivalence, see Definition 4.1 |
| Class of a motion |
\({\mathop {\sim }\limits ^{w}}\) | Equivalence relation on motions in terms of worldlines, see Definition 4.21 |
| Class of motions related by \({\mathop {\sim }\limits ^{w}}\), see Definition 4.21 |
\({\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\) | Set of fake motions from N to \(N'\) in a manifold M, see Definition 5.1 |
\({\mathop {\sim }\limits ^{fk}}\) | Indicates fake motions related by strong isotopy, see Definition 5.7 |
| Class of fake motions related by strong isotopy, see Lemma 5.9 |
\(\textrm{FMot}_{M}\) | Groupoid of strong isotopy classes of fake motions, see Lemma 5.9 |
\({\mathop {\sim }\limits ^{i}}\) | Indicates self-homeomorphisms related by isotopy, see Definition 6.1 |
| Class of self-homeomorphisms related by isotopy, see Lemma 6.2 |
\(\textrm{MCG}_{M}^A\) | Mapping class groupoid of a manifold M, fixing \(A\subset M\), see Theorems 6.4, 6.10 |
\({{\mathbb {I}}}\) | The space \([0,1]\subset {{\mathbb {R}}}\) with the subset topology |
\(D^n\) | The n-disk \(\{x\in {{\mathbb {R}}}^n\vert \,|x|\le 1 \}\subset {{\mathbb {R}}}^n\) with the subset topology |
\(S^n\) | The circle \(\{x\in {{\mathbb {R}}}^{n+1}\vert \,|x|= 1 \}\subset {{\mathbb {R}}}^{n+1}\) with the subset topology |
2 Preliminaries
In this section we recall concepts that we will need for our construction, and fix notation. First we have the compact-open topology on continuous maps, which leads to a product-hom adjunction in the category of topological spaces in Sect. 2.2. We then have magmoids, and groupoids defined in terms of magmoids in Sect. 2.3. Our first example here is the path magmoid of a topological space (Definition 2.14). In Sect. 2.4 we have congruences on magmoids, and on groupoids, which lead to quotient structures. Finally we give a construction of the fundamental groupoid of a topological space; as a quotient of the path magmoid.
2.1 The compact-open topology
Denote by \({\textbf{Top}}\) the category with topological spaces (spaces) as objects, continuous maps as morphisms and the usual composition. Thus we denote the set of morphisms from a space X to a space Y by \({\textbf{Top}}(X,Y)\). We assume familiarity with \({\textbf{Top}}\) (see e.g. Chapter 1 of [tD08]), thus with product spaces. We denote the categorical product of spaces X and Y by \(X\times Y\). We similarly assume familiarity with \({\textsf{Set}}\), the category of sets, functions and function composition.
To formalise ‘flows’ in a manifold, we will require a topology on the sets \({\textbf{Top}}(X,Y)\). For this we use the compact-open topology. Here we give the definition and give some results demonstrating its intuitive naturality (Proposition 2.7).
Definition 2.1
For X a set, \({{\mathcal {P}}}X\) denotes the power set.
Definition 2.2
Given a set X, and a subset Y of \({{\mathcal {P}}}X\) with \(\cup _{A \in Y} A=X\), we write \({\overline{Y}}\) for the topology closure of Y. Hence the open sets in the topological space \((X,{\overline{Y}})\) are arbitrary unions of finite intersections of elements in Y. We say that Y is a subbasis of \((X,\tau )\) if \({\overline{Y}} = \tau \). (NB: in general, \(\tau = {\overline{Y}}\) does not uniquely determine Y.)
Definition 2.3
A neighbourhood basis of \((X,\tau )\) at \(x\in X\) is a subset \(B\subseteq \tau \), whose members are called basic neighbourhoods of x, such that every neighbourhoodFootnote 1 of x contains an element of B.
Definition 2.4
Let \((X,\tau _X)\) and \((Y,\tau _Y)\) be topological spaces, then the compact-open topology \(\tau ^{co}_{XY}\) on \({\textbf{Top}}(X,Y)\) has subbasis
where
That is \(\tau ^{co}_{XY} = \overline{b_{XY}}\).Footnote 2
Proposition 2.5
Let Y be a space, and X be the space with a single point. Then the \(\tau ^{co}_{XY}\) is the same in the obvious sense as the topology on Y.
Proof
Maps from X to Y can be labelled by their image in Y. The only compact set K is the single point set X. The set \(B_{XY}(K,U)\) is the set of maps labelled by the elements of U. \(\quad \square \)
Proposition 2.6
Let Y be a space, and X be the space consisting of n points with discrete topology. Then \(\tau ^{co}_{XY}\) is the same in the obvious sense as the topology on \(Y^n=Y\times \ldots \times Y\).
Proof
Maps from X to Y are in bijection with tuples \((y_1,\dots ,y_n)\in Y^n\) where \(y_i\) is the image of \(x_i\in X\). All subsets K of X are compact and we have, using this bijection,
Hence elements of the subbasis of \(\tau ^{co}_{XY}\) are open sets in \(Y^n\).
Basis elements in the topology on \(Y^n\) are obtained from the compact open topology as follows. Let \(U^n\) be a basis open set in the topology on \(Y^n\). Then \(U^n\) is of the form \(U_1\times \ldots \times U_n\), with \(U_1,\dots , U_n\) open in Y. Now
and \(\cap _{i}B_{XY}(\{x_i\},U_i)=U^n\). \(\quad \square \)
In the case Y is a metric space we have an interpretation of the compact-open topology in terms of a metric on \({\textbf{Top}}(X,Y)\).
Proposition 2.7
(A.13 in [Hat02]) Let X be a compact space and Y a metric space with metric d. Then
-
(i)
the function
$$\begin{aligned} d'(f,g) \;:= \; \sup _{x \in X} d(f(x),g(x)) \end{aligned}$$is a metric on \({\textbf{Top}}(X,Y)\); and
-
(ii)
the compact open topology on \({\textbf{Top}}(X,Y)\) is the same as the one defined by the metric \(d'\).
Proof
See A.13 in [Hat02]. \(\quad \square \)
2.2 The space \({\textbf{TOP}}(X,Y)\) and the product-hom adjunction
In addition to its intuitive naturality, the compact-open topology allows us to find a partial lift of the classical product-hom adjunction in \({\textsf{Set}}\) to an adjunction in \({\textbf{Top}}\) (Theorem 2.10). We will make extensive use of this adjunction throughout this paper. First, in Theorem 3.72 to prove that motions in M to have an additional interpretation as homeomorphisms from \(M\times {{\mathbb {I}}}\) to \(M\times {{\mathbb {I}}}\). Then later in Sect. 4.2, to understand motion equivalence in terms of a relation on worldlines, and again in Lemma 6.5.
This adjunction holds subject to some conditions which are not too restrictive for us. In particular, the compact-open topology allows us to define a right-adjoint to the functor \(-\times Y:{\textbf{Top}}\rightarrow {\textbf{Top}}\) (see Lemma 2.8), when Y is a locally compact Hausdorff space. (The case \(Y=[0,1]\) was one of the examples given in the original reference on adjoint functors [Kan58, pp 294].)
In this section we also give some results regarding the continuity of the composition in \({\textbf{Top}}\) with respect to the compact open topology.
We will use capital \({\textbf{TOP}}(X,Y)\) to indicate the morphism set \({\textbf{Top}}(X,Y)\) considered as a space with the compact-open topology, so
Lemma 2.8
Fix a topological space Y. There exists a functor \(-\times Y:{\textbf{Top}}\rightarrow {\textbf{Top}}\) constructed as follows. A space X is sent to the product space \(X\times Y\). A continuous map \(f:X\rightarrow X'\) is sent to the map \(f\times {\textrm{id}}_Y :X\times Y\rightarrow X'\times Y\), \((x,y)\mapsto (f(x),y)\). We will refer to this as the product functor.
Proof
We first show that, for a map \(f:X\rightarrow X'\), \(f\times {\textrm{id}}_Y\) is a continuous map \(X \times Y\) to \(X'\times Y\). Let \(U'\times V\) be a basis open set in \(X'\times Y\). Then the preimage under \(f\times {\textrm{id}}_Y\) is \(f^{-1}(U')\times V\) which is open since f is continuous. It is clear that the product functor preserves the identity and respects the composition. \(\quad \square \)
Lemma 2.9
Fix a topological space Y. There exists a functor \({{\textbf{TOP}}( Y,-):}{\textbf{Top}}\rightarrow {\textbf{Top}}\) constructed as follows. A space Z is sent to the space \( {\textbf{TOP}}(Y,Z)\). A continuous map \(f:Z\rightarrow Z'\) is sent to \(f\circ -:{\textbf{TOP}}(Y,Z)\rightarrow {\textbf{TOP}}(Y,Z')\), \(g\mapsto f\circ g\). We will refer to this as the hom functor.
Proof
We first show that \(f\circ -\) is a continuous map. Open sets in the subbasis of \(\tau ^{co}_{YZ'}\) are of the form \(B_{YZ'}(K,U)\) for some \(K\subseteq Y\) a compact set and \(U\subseteq Z'\) an open set. The set \(f^{-1}(U)\) is open in Z since f is a continuous map. Hence \(B_{YZ}(K,f^{-1}(U))\) is an open set in \(\tau ^{co}_{YZ}\). We show that the inverse image of \(B_{YZ'}(K,U)\) under \(f\circ -\) is precisely \(B_{YZ}(K,f^{-1}(U))\). For any \(g\in B_{YZ}(K,f^{-1}(U))\) we have \(f\circ g\in B_{YZ'}(K,U)\). Conversely suppose \(h\in B_{YZ'}(K,U)\) can be written in the form \(f\circ g'\) for some \(g'\in {\textbf{TOP}}(Y,Z)\), then \(g'\in B_{YZ}(K,f^{-1}(U))\).
It is straightforward to see that \({\textbf{TOP}}(Y,-)\) preserves the identity and respects composition. \(\square \)
For a category \({{\mathcal {C}}}\), we will use \(\textrm{Hom}:{{\mathcal {C}}}^{op}\times {{\mathcal {C}}}\rightarrow {\textsf{Set}}\) to denote the usual bifunctor, see [ML13, pgs. 34,38]. (Note that by fixing first argument and topologising the image of objects, we get back the hom functor of Lemma 2.9.)
The following Lemma gives conditions under which the usual hom-tensor correspondence from \({\textsf{Set}}\) is well-defined in \({\textbf{Top}}\).
Lemma 2.10
Let Y be a locally compact Hausdorff topological space. The product functor \(-\times Y \) is left adjoint to the hom functor \({\textbf{TOP}}(Y,-)\). In particular, for objects \(X,Y,Z\in {\textbf{Top}}\), this gives a set map
that is a bijection, natural in the variables X and Z.Footnote 3
Proof
That we have a bijection of sets is proved in Proposition A.14 of [Hat02]. It remains to prove that this bijection is natural. Suppose we have continuous maps \(\alpha :X'\rightarrow X\) and \(\beta :Z\rightarrow Z'\), then we must show we have a commuting diagram of the form

Looking first at the left hand vertical arrow, a map \(f:X\rightarrow {\textbf{TOP}}(Y,Z)\) is sent to the map \(X'\rightarrow {\textbf{TOP}}(Y,Z')\), \(x'\mapsto \beta \circ f(\alpha (x'))\), and then to \((x',y)\mapsto (\beta \circ f(\alpha (x')))(y)\) in \({\textbf{Top}}(X'\times Y,Z')\). Going first along the top, a map f is sent to the map \( X\times Y \rightarrow Z\), \((x,y)\mapsto f(x)(y)\) and then to the map \(X'\times Y\rightarrow Z'\) defined by \((x',y) \mapsto (\beta \circ f(\alpha (x')))(y)\). \(\quad \square \)
For any space X then \({\textbf{Top}}(X,X)\) is a monoid, with identity the identity map. The subset of maps which are set bijections is a submonoid. Let \({\textbf{Top}}^h\) be the subcategory of \({\textbf{Top}}\) with the same objects as \({\textbf{Top}}\) and morphisms which are homeomorphisms. (Note that the indicated subset is in fact closed under composition.) Then \({\textbf{Top}}^h(X,X)\) is the group of homeomorphisms \(\mathfrak {f}:X \rightarrow X\). Denote by \({\textbf{TOP}}^h(X,X)\) the subspace of \({\textbf{TOP}}(X,X)\) with underlying set \({\textbf{Top}}^h(X,X)\).
In Sect. 3 we will be interested in formalising how certain paths in \({\textbf{TOP}}^h(M,M)\), where M is a manifold, induce ‘motions’ of subsets in M. We will introduce a ‘pointwise’ composition and inverse of such motions which requires that \({\textbf{TOP}}^h(M,M)\) is a topological group.
Theorem 2.11
[Are46, Thm.4]. If X is a locally connected, locally compact Hausdorff space then \({\textbf{TOP}}^h(X,X)\), is a topological group. (This means the composition \((\mathfrak {f},\mathfrak {g})\mapsto \mathfrak {g} \circ \mathfrak {f} \) and the map \(\mathfrak {f}\mapsto \mathfrak {f}^{-1}\) are both continuous.)
Proof
See Section A.1. \(\quad \square \)
Notice that if a space X satisfies the conditions of Theorem 2.11, then X also satisfies the conditions of Lemma 2.10.
In general, for fixed topological spaces X, Y and Z, the composition map \({\textbf{TOP}}(X,Y) \times {\textbf{TOP}}(Y,Z) \rightarrow {\textbf{TOP}}(X,Z)\) is continuous in each variable, despite the fact that it is not always continuous as a function of two variables ([Dug66, page 259, 2.1 and 2.2.]). We give the proof here, and will use this weaker result (in comparison to the previous lemma) where possible to emphasise where continuity of the composition map is really necessary for a given construction.
Lemma 2.12
Let Y be a space.
-
(I)
For any \(\mathfrak {g}\in {\textbf{TOP}}(X,Y)\), the map \(-\circ \mathfrak {g}:{\textbf{TOP}}(Y,Y)\rightarrow {\textbf{TOP}}(X,Y)\), \(\mathfrak {f}\mapsto \mathfrak {f}\circ \mathfrak {g}\) is continuous, and
-
(II)
for any \(\mathfrak {g}\in {\textbf{TOP}}(Y,Z)\), the map \(\mathfrak {g}\circ -:{\textbf{TOP}}(Y,Y)\rightarrow {\textbf{TOP}}(Y,Z)\), \(\mathfrak {f}\mapsto \mathfrak {g}\circ \mathfrak {f}\) is continuous.
Proof
(II) For a subbasis open set \(B_{XY}(K,U)\) (with notation as in Definition 2.4), with \(K\subseteq X\) compact and \(U\subseteq Y\) open, we have \(\mathfrak {f\circ g} \in B_{XY}(K,U)\iff \mathfrak {f}(\mathfrak {g}(K))\subseteq U \iff \mathfrak {f}\in B_{YY}(\mathfrak {g}(K),U)\), where the latter subset of the function space is open.
(I) For a subasis open set \(B_{YZ}(K,U)\) with \(K\subseteq Y\) compact and \(U\subseteq Y\) open, we have \(\mathfrak {g\circ f}\in B_{YZ}(K,U)\iff \mathfrak {g}(\mathfrak {f}(K))\subseteq U\iff \mathfrak {f}\in B_{YY}(K,\mathfrak {g}^{-1}(U))\), where the latter subset of the function space is open. \(\quad \square \)
2.3 Groupoids and magmoids
In this work constructions of groupoids are a recurrent theme. Such constructions will often start from something ‘concrete’ with a non-associative composition. Equivalence classes of these concrete things eventually become the morphisms of the constructed groupoid. So it will be useful to have a general machinery for studying such constructions. For example we can think of the underlying idea of a category as objects, morphisms between objects, and a composition which is not necessarily associative, or unital—a categorified magma, or ‘magmoid’. We can then study congruences on these magmoids, some of which will lead to groupoids.
Definition 2.13
A magmoid \({{{\textsf{M}}}}\) is a triple
consisting of
-
(I)
a collection \(Ob({{\textsf{M}}})\) of objects,
-
(II)
for each pair \(X,Y\in Ob({{\textsf{M}}})\) a set \({{\textsf{M}}}(X,Y)\) of morphisms from X to Y (we use \(f:X\rightarrow Y\) to indicate that f is a morphism from X to Y), and
-
(III)
for each triple \(X,Y,Z \in Ob({{\textsf{M}}})\) a composition
$$\begin{aligned} \Delta _{{\textsf{M}}}:{{\textsf{M}}}(X,Y)\times {{\textsf{M}}}(Y,Z)\rightarrow {{\textsf{M}}}(X,Z). \end{aligned}$$
Magmoids can be compared with cubical sets with composition, as defined in [BH81]. Quotients there lead to cubical n-groupoids.
For our example below we will need some notation.
Definition 2.14
Let X be a topological space. An element of \({\textbf{Top}}({{\mathbb {I}}},X)\) is called a path in X and \( {\textbf{TOP}}({{\mathbb {I}}},X)\) is called the path space of X.
Notation: Let \(\gamma \in {\textbf{Top}}({{\mathbb {I}}},X)\). We use \(\gamma _t\) for \(\gamma (t)\). We say \(\gamma \) is a path from x to \(x'\) when \(\gamma _0 = x\) and \(\gamma _1=x'\). For \(x,x'\in X\), let
Proposition 2.15
Let X be a topological space. For any \(x,x',x''\in X\), there exists a composition
(note the null composition symbol here) with
(Note the convention to choose distinguished point \(t=1/2\), we could have chosen any \(a \in (0,1)\).)
Proof
We have \(\gamma _1=\gamma '_0\) so Eq. (1) defines a continuous map. Notice \((\gamma '\gamma )_0=\gamma _0=x\) and \((\gamma '\gamma )_1=\gamma '_1=x''\). Hence \(\gamma '\gamma \in {{\mathfrak {P}}}X(x,x'')\). \(\quad \square \)
Remark 2.16
We find the above convention for ordering path composition to be convenient as we will later map paths to functions.
Definition 2.17
Let X be a topological space. From Proposition 2.15 we may define the path magmoid
Note that the magmoid \({{\mathfrak {P}}}X\) is neither associative nor unital.
Definition 2.18
Let \({{\textsf{M}}}\) and \({{\textsf{M}}}'\) be magmoids. A magmoid morphism \(F:{{\textsf{M}}}\rightarrow {{\textsf{M}}}'\) is a map sending each object \(X\in Ob({{\textsf{M}}})\) to an object \(F(X)\in Ob({{\textsf{M}}}')\) and each morphism \(f:X\rightarrow Y\) in \({{\textsf{M}}}\) to a morphism \(F(f):F(X)\rightarrow F(Y)\) in \({{\textsf{M}}}'\) such that for any morphisms \(f,g \in {{\textsf{M}}}\)
wherever \(\Delta _{{\textsf{M}}}(f,g)\) is defined.
Magmoid representation theory can be framed in terms of magmoid morphisms in a category of magmoids.
Proposition 2.19
For any set S of magmoids, there exists a small category with objects S and morphisms all magmoid morphisms between the elements of S.
The (partial) composition of magmoid morphisms sends a pair of magmoid morphisms \(F:{{\textsf{M}}}\rightarrow {{\textsf{M}}}'\) and \(F':{{\textsf{M}}}'\rightarrow {{\textsf{M}}}''\) to \(F'\circ F:{{\textsf{M}}}\rightarrow {{\textsf{M}}}''\) with
Proof
It is straightforward to check that \(F'\circ F\) is well defined and is a magmoid morphism. Associativity and identities follow from the properties of morphisms in \({\textsf{Set}}\). \(\square \)
2.4 Algebraic congruence and magmoid congruences
Definition 2.20
A congruence C on a magmoid \({{\textsf{M}}}\) consists of, for each pair \(X,Y\in Ob({{\textsf{M}}})\) an equivalence relation \(R_{X,Y}\) on \({{\textsf{M}}}(X,Y)\), such that \(f'\in [f]\), \(g'\in [g]\) implies \(\Delta _{{\textsf{M}}}(f',g')\in [\Delta _{{\textsf{M}}}(f,g)]\) where defined.
Example 2.21
Let X be a topological space. For each \(x,x'\in X\), define a relation on \({{\mathfrak {P}}}X(x,x')\) by \(\gamma \sim \gamma '\) if there exists \(f\in {\textbf{Top}}^h_{\partial {{\mathbb {I}}}}({{\mathbb {I}}},{{\mathbb {I}}})\) such that \(\gamma _t=\gamma '_{f(t)}\) for all \(t\in {{\mathbb {I}}}\). (Intuitively, \(\gamma '\) is a reparametrisation of \(\gamma \).) Then it can be shown that the family of relations \(({{\mathfrak {P}}}X(x,x'),\sim )\) is a congruence on \({{\mathfrak {P}}}X\).
Definition 2.22
Let \({{\textsf{M}}}=(Ob({{\textsf{M}}}),{{\textsf{M}}}(-,-),\Delta _{{{\textsf{M}}}})\) be a magmoid and C a congruence on \({{\textsf{M}}}\). The quotient magmoid of \({{\textsf{M}}}\) by C is \({{\textsf{M}}}/C=(Ob({{\textsf{M}}}),{{\textsf{M}}}(X,Y)/R_{X,Y},\Delta _{{{\textsf{M}}}/C})\) where for each triple \(X,Y,Z\in Ob({{\textsf{M}}}/C)\):
(That the composition is well defined follows directly from the definition of a congruence.)
In practice we will often use the notation for the composition in \({{\textsf{M}}}\) to denote also the composition in the quotient.
It follows directly from the definition of congruence that we have the following.
Lemma 2.23
Let \({{\textsf{M}}}\) be a magmoid and C a congruence on \({{\textsf{M}}}\). There is an induced magmoid morphism \({\tilde{C}} :{{\textsf{M}}}\rightarrow {{\textsf{M}}}/C\), called the quotient morphism, which is the identity on objects and which sends morphisms to their equivalence class under C. \(\quad \square \)
Definition 2.24
Let \({{\textsf{M}}}\) be a magmoid, C a congruence. If there exists a magmoid \({{\textsf{M}}}'\) and full, non-identity magmoid morphisms \(G:{{\textsf{M}}}\rightarrow {{\textsf{M}}}'\) and \(H:{{\textsf{M}}}' \rightarrow {{\textsf{M}}}/C\) such that \({\tilde{C}}=H\circ G\), we say that the congruence C has a factor.
The classical definition of a groupoid (see e.g. [Bro06, Ch. 6]) can be given as a magmoid plus extra structure. We give it here to fix notation. We will see shortly that congruences have some useful characterisations when considered on magmoids which are also groupoids.
Definition 2.25
A groupoid \({{{\mathcal {G}}}}\) is a tuple \({{\mathcal {G}}}=(Ob({{\mathcal {G}}}),{{\mathcal {G}}}(-,-),*_{{\mathcal {G}}},1_-,(-)\mapsto (-)^{-1})\) consisting of a magmoid \((Ob({{\mathcal {G}}}),{{\mathcal {G}}}(-,-),*_{{\mathcal {G}}})\) such that \(Ob({{\mathcal {G}}})\) is a set, and
-
(IV)
for each \(X\in Ob(X)\) a morphism \(1_X\in {{\mathcal {G}}}(X,X)\) called the identity;
-
(V)
for each pair \((X,Y)\in Ob({{\mathcal {G}}})\times Ob({{\mathcal {G}}})\) a function
$$\begin{aligned} (-)^{-1}:{{\mathcal {G}}}(X,Y)&\rightarrow {{\mathcal {G}}}(Y,X)\\ f&\mapsto f^{-1} \end{aligned}$$called the inverse assigning, or just inverse, function;
such that the following axioms are satisfied.
- \(({{\mathcal {G}}}1)\):
-
Identity law: for any morphism \(f:X \rightarrow Y\), we have \(1_Y*_{{\mathcal {G}}}f = f = f*_{{\mathcal {G}}}1_X\).
- \(({{\mathcal {G}}}2)\):
-
Associativity: for any triple of morphisms \( f:X\rightarrow Y\), \(g:Y \rightarrow Z\) and \(h:Z\rightarrow W\) we have \(h*_{{\mathcal {G}}}(g*_{{\mathcal {G}}}f)=(h*_{{\mathcal {G}}}g)*_{{\mathcal {G}}}f\).
- \(({{\mathcal {G}}}3)\):
-
Inverse: for any morphism \(f:X\rightarrow Y\), we have \(f^{-1}*_{{\mathcal {G}}}f=1_X\) and \(f*_{{\mathcal {G}}}f^{-1}=1_Y\).
We will sometimes replace − notation with generic symbols where convenient. Let \({{\mathcal {G}}}\) be a groupoid. By abuse of notation we will refer also to the underlying magmoid as \({{\mathcal {G}}}\).
Remark 2.26
Note that the identities and inverses of a groupoid \({{\mathcal {G}}}\) are uniquely determined from the underlying magmoid of \({{\mathcal {G}}}\).
Remark 2.27
Magmoid morphisms between groupoids automatically send identities to identities and inverses to inverses. So a functor of groupoids is simply a magmoid morphism between underlying magmoids. This is not true for categories, where preservation of identities does not follow automatically from the preservation of composition.
Proposition 2.28
Suppose \({{\mathcal {G}}}=(Ob({{\mathcal {G}}}),{{\mathcal {G}}}(-,-),*_G,1_,(-)^{-1})\) is a groupoid. Then for any congruence C on \({{\mathcal {G}}}\), there is a quotient groupoid \({{\mathcal {G}}}/C=(Ob({{\mathcal {G}}}),{{\mathcal {G}}}/C(-,-),*_{{{\mathcal {G}}}/C},[1_{-}],[f]\mapsto [f^{-1}])\).
Proof
\(({{\mathcal {G}}}1)\) For all \([f]:X\rightarrow Y\) we have
\(({{\mathcal {G}}}2)\) Let [f], [g], [h] be composable morphisms in \({{\mathcal {G}}}/C\). Then
\(({{\mathcal {G}}}3)\) Any \([f]\in {{\mathcal {G}}}/C(X,Y)\) has inverse \([f^{-1}]\) since
\(\square \)
As discussed in Sect. 3.5 below, we are interested in starting from a magmoid, which describes a physical system, and applying congruences until we arrive at a finitely generated category (hopefully without pushing the interesting physics into the kernel). Often we will find it convenient to do this by passing through a factor. When this factor is a groupoid \({{\mathcal {G}}}\) we can construct a congruence on \({{\mathcal {G}}}\) from a subgroupoid which is normal and thus obtain a quotient groupoid, mirroring quotienting groups by normal subgroups. We make this explicit here.
Everything in the remainder of this section can be found in Section 1.4.3 of [Bro99].
A subgroupoid \({{\mathcal {H}}}\) of groupoid \({{\mathcal {G}}}\) is said to be wide if \(Ob({{\mathcal {H}}})=Ob({{\mathcal {G}}})\).
Definition 2.29
Let \({{\mathcal {G}}}\) be a groupoid and \({{\mathcal {H}}}\) a wide subgroupoid. \(Ob({{\mathcal {H}}})=Ob({{\mathcal {G}}})\). Then \({{\mathcal {H}}}\) is said to be normal if for any morphism \(g:X\rightarrow Y\) in \({{\mathcal {G}}}\) and any \(h:Y\rightarrow Y\) in \({{\mathcal {H}}}\) we have \(g^{-1}*_{{\mathcal {G}}}h*_{{\mathcal {G}}}g:X\rightarrow X\) is in \({{\mathcal {H}}}\).
We say \({{\mathcal {H}}}\) is totally disconnected if for any \(X,Y\in Ob({{\mathcal {H}}})\) with \(X\ne Y\) we have \({{\mathcal {H}}}(X,Y)=\varnothing \).
Lemma 2.30
(See e.g. [Bro06, 8.3.1].) Let \({{\mathcal {G}}}\) be a groupoid and \({{\mathcal {H}}}\) a normal, totally disconnected subgroupoid. For each \(X,Y\in Ob({{\mathcal {G}}})\) and \(g,g'\in {{\mathcal {G}}}(X,Y)\) the relation \(g\sim g'\) if \(g'^{-1}*_{{{\mathcal {G}}}}g\in {{\mathcal {H}}}\), is an equivalence relation on \({{\mathcal {G}}}(X,Y)\). Moreover all such relations together form a congruence on \({{\mathcal {G}}}\).
We will denote this congruence also by \({{\mathcal {H}}}\), the meaning will be clear from context.\(\quad \square \)
Remark 2.31
Note that this is the weakest congruence such that all morphisms of the form \(h:X\rightarrow X\) in \({{\mathcal {H}}}\) become equivalent to the appropriate identity.
2.5 Interval \({{\mathbb {I}}}=[0,1]\), space \({\textbf{TOP}}({{\mathbb {I}}},X)\) and path-homotopy
In this section we spend some time focusing on the space \({\textbf{TOP}}({{\mathbb {I}}},X)\) of paths in X. We obtain the fundamental groupoid (Proposition 2.36) by quotienting the path magmoid by a congruence (Definition 2.17). Some careful constructions of the fundamental groupoid can be found in the literature, for example in [tD08] and [Bro06], although our magmoid approach is non-standard and we will use (more radical versions of) similar ideas repeatedly in later sections so we think this ‘warm up’ is worthwhile.
This also allows us to give a first example of the utility of the product-hom adjunction, Lemma 2.10; paths in the fundamental groupoid are equivalent if and only if there is a path between them in the space of paths (Lemma 2.34). Throughout the rest of this paper we will use path-equivalence alongside several other equivalence relations so we also introduce some careful notation here.
Definition 2.32
Let X be a topological space. Define a relation on \({{\mathfrak {P}}}X (x,x')\) as follows. Suppose we have paths \(\gamma ,\gamma '\in {{\mathfrak {P}}}X(x,x')\), then \(\gamma {\mathop {\sim }\limits ^{p}}\gamma '\) if there exists a continuous map \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow X\) such that
-
for all \(t\in {{\mathbb {I}}}\), \(H(t,0)=\gamma (t)\),
-
for all \(t\in {{\mathbb {I}}}\), \(H(t,1)=\gamma '(t)\), and
-
for all \(s\in {{\mathbb {I}}}\), \(H(0,s)=x\) and \(H(1,s)=x'\).
Notation: We call such an H a path-homotopy from \(\gamma \) to \(\gamma '\).
Proposition 2.33
Let X be a topological space. For each pair \(x,x'\in X\), \({\mathop {\sim }\limits ^{p}}\) is an equivalence relation on \({{\mathfrak {P}}}X(x,x')\).
Notation: If \(\gamma {\mathop {\sim }\limits ^{p}}\gamma '\) we say \(\gamma \) and \(\gamma '\) are path-equivalent . We use \([\gamma ]_{\text{ p }}\) for the path-equivalence class of \(\gamma \).
Proof
We show that \({\mathop {\sim }\limits ^{p}}\) is reflexive, symmetric and transitive. Let \(\gamma \in {{\mathfrak {P}}}X(x,x')\), \(\gamma '\in {{\mathfrak {P}}}X(x,x')\) and \(\gamma ''\in {{\mathfrak {P}}}X(x,x')\) be paths with \(\gamma {\mathop {\sim }\limits ^{p}}\gamma '\) and \(\gamma '{\mathop {\sim }\limits ^{p}}\gamma ''\).
The relation is reflexive since the function \(H(t,s)=\gamma _t\) is a path-homotopy from \(\gamma \) to \(\gamma \).
By assumption, there exists a path-homotopy, say \(H_{\gamma ,\gamma '}\), from \(\gamma \) to \(\gamma '\). The function \(H_{\gamma ',\gamma }(t,s)=H_{\gamma ,\gamma '}(t,1-s)\) is a path-homotopy from \(\gamma '\) to \(\gamma \), hence the relation is symmetric.
There also exists a path-homotopy, say \(H_{\gamma ',\gamma ''}\), from \(\gamma '\) to \(\gamma ''\). The function
is a path-homotopy from \(\gamma \) to \(\gamma ''\), so \({\mathop {\sim }\limits ^{p}}\) is transitive. \(\quad \square \)
Lemma 2.34
Let X be a topological space. Let \(\gamma ,\gamma '\in {{\mathfrak {P}}}X(x,x')\) be paths. Then \(\gamma {\mathop {\sim }\limits ^{p}}\gamma '\) if and only if there is a path \({\tilde{H}}:{{\mathbb {I}}}\rightarrow {\textbf{Top}}({{\mathbb {I}}},X)\) such that \({\tilde{H}}(0)=\gamma \), \({\tilde{H}}(1)=\gamma '\) and for all \(t\in {{\mathbb {I}}}\), \({\tilde{H}}(t)\in {{\mathfrak {P}}}X(x,x')\).
Proof
We have that \({{\mathbb {I}}}\) is a locally compact Hausdorff topological space so Lemma 2.10 gives that there is a bijection between continuous maps \({{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow X\) and continuous maps \({{\mathbb {I}}}\rightarrow {\textbf{TOP}}({{\mathbb {I}}},X)\). We obtain the appropriate conditions by looking at the image of a path homotopy under this bijection. \(\quad \square \)
Lemma 2.35
Let X be a topological space. The equivalence relations \(({{\mathfrak {P}}}X(x,x'),{\mathop {\sim }\limits ^{p}})\) for each pair \(x,x'\in X\) are a congruence on \({{\mathfrak {P}}}X\).
Proof
Suppose \(\gamma ,\gamma '\in {{\mathfrak {P}}}X(x,x')\) are path-equivalent and so there exists a path homotopy, say \(H_{\gamma ,\gamma '}\) from \(\gamma \) to \(\gamma '\). And suppose \(\delta ,\delta '\in {{\mathfrak {P}}}X(x',x'')\) are path-equivalent and so there exists a path homotopy, say \(H_{\delta ,\delta '}\) from \(\delta \) to \(\delta '\). Notice \(H_{\gamma ,\gamma '}(1,s) = H_{\delta ,\delta '}(0,s)=x'\) and so the function
is a homotopy from \(\delta \gamma \) to \(\delta '\gamma '\). \(\quad \square \)
Proposition 2.36
Let X be a topological space. There exists a groupoid
with \({{\mathfrak {P}}}X\) as in Definition 2.17. Here the identity morphism \([e_x]_{\text{ p }}\) at each object x is the path-equivalence class of the constant path \((e_x)_t=x\) for all \(t\in {{\mathbb {I}}}\). The inverse of a morphism \([\gamma ]_{\text{ p }}\) from x to \(x'\) is the path-equivalence class of \(\gamma ^{rev}_t=\gamma _{1-t}\).
We have obtained the fundamental groupoid of X.
Proof
(\({{\mathcal {G}}}1\)) Suppose \(\gamma \in {{\mathfrak {P}}}X(x,x')\), a suitable choice of path homotopy from \(e_x\gamma \) to \(\gamma \) is:
A choice for \(\gamma e_{x'}{\mathop {\sim }\limits ^{p}}\gamma \) can is given by splitting the segments at \(\frac{1}{2}-\frac{s}{2}\), and using the subscript \(\frac{t-\frac{1}{2}+\frac{s}{2}}{\frac{1}{2}+\frac{s}{2}}\).
(\({{\mathcal {G}}}2\)) The following function is a path homotopy \(\gamma ''(\gamma '\gamma )\) to \((\gamma ''\gamma ')\gamma \):
(\({{\mathcal {G}}}3\)) The following function is a homotopy \(\gamma ^{rev}\gamma \) to \(e_x\):
The same segments, with first and last term independent of s, and middle term \(\gamma _s\), defines a path homotopy \(\gamma \gamma ^{rev}{\mathop {\sim }\limits ^{p}}e_x\). \(\quad \square \)
Remark 2.37
Let X be a topological space and \(x\in X\) be a point, we have that \( \pi (X)(x,x) \) is the fundamental group based at \(x \in X\).
2.6 Action groupoid \(\textrm{Homeo}_{M}\) of the action of self-homeomorphisms on subsets
In this paper, manifold means a Hausdorff topological manifold, which in particular is locally compact and locally connected.
From here we will work always with M a manifold possibly with boundary. Then we have that \({\textbf{TOP}}^h(M,M)\) is a topological group (Theorem 2.11) and we can use the product-hom adjunction (Lemma 2.10).
Definition 2.38
Let P be a magma. A magma action of P on a set S is a map \(\alpha : P\times S \rightarrow S\) with \(q(ps)=(qp)s\) (denoting the composition in P of a pair (p, q) as qp, and the image \(\alpha (p,s)\) as ps). Given a magma action \(\alpha \), we can construct an action magmoid \(\varvec{\mu }_\alpha \), which is a triple consisting of objects S, morphisms which are triples \((p,s,p s) \in P \times S \times S\), and a partial composition \(((p,s,ps),(q,ps,qps))\mapsto (qp,s,qps)\).
If P additionally has the structure of a group with identity \(e\in P\), and \(\alpha \) additionally satisfies \(es=s\), then \(\varvec{\mu }_\alpha \) is a groupoid with \((p,s,ps)^{-1}=(p^{-1},ps,s)\), called the action groupoid.
For an action \(\alpha :P\times S\rightarrow S\), we will find it useful to keep track of both P and S in our notation for the action groupoid, so we denote \(\varvec{\mu }_\alpha \) as \( S/\!/_\alpha \, P. \)
Observe that since every magma (group) action on a set \(\alpha :P\times S\rightarrow S\) induces an action on the power set \({{\mathcal {P}}}S\), for every action there is a corresponding action magmoid (groupoid) of the action on \({{\mathcal {P}}}S\), which we denote \( {{\mathcal {P}}}S/\!/_\alpha \, P. \)
Let M be a manifold and \(A\subset M\) a subset. Recall the definition of \({\textbf{Top}}^{h}(M,M)\) from §2.2. Let \(A\subset X\) a subset and let \({\textbf{Top}}^h_A(M,M)\) denote the subset of \({\textbf{Top}}^h(M,M)\) of homeomorphisms which fix A pointwise.
Here we organise the elements of \({\textbf{Top}}^{h}_A(M,M)\) into a groupoid \(\textrm{Homeo}_{M}^A\) with objects \({{\mathcal {P}}}M\), constructed from an action on M. In general this category is too large to be an interesting object of study itself but it is a natural first step in the construction that follows.
Definition 2.39
The group \({\textbf{Top}}^h_A(M,M)\), of homeomorphisms fixing A pointwise, acts on the set M as \(\mathfrak {f}\triangleright m=\mathfrak {f}(m)\). We denote the action groupoid of the induced action on \({{\mathcal {P}}}M\) as
We will denote triples \((\mathfrak {f},N,\mathfrak {f}(N))\in \textrm{Homeo}_{M}^A(N,N')\) as  . In this notation, the identity at each object N is
. In this notation, the identity at each object N is  where \({\textrm{id}}_M\) denotes the identity homeomorphism, and, given a morphism
where \({\textrm{id}}_M\) denotes the identity homeomorphism, and, given a morphism  , the inverse is the morphism
, the inverse is the morphism  .
.
We will use just \(\textrm{Homeo}_{M}\) to denote \(\textrm{Homeo}_{M}^{\varnothing }\), so morphism sets are of the form \(\textrm{Homeo}_M(N,N')\).
Lemma 2.40
Let M be a manifold and \(A\subset M\) a subset. For any subsets \(N,N'\subset M\) we have
Proof
Since any  is a bijection, \(\mathfrak {f}(N)=N'\) if and only if \(\mathfrak {f}(M\setminus N)=M\setminus N'\).
is a bijection, \(\mathfrak {f}(N)=N'\) if and only if \(\mathfrak {f}(M\setminus N)=M\setminus N'\).
\(\square \)
Abusing notation, we will also use \(\textrm{Homeo}_{M}^A(N,N')\) to denote the set obtained by projecting to the first element of the triple. Then we have \({\textbf{Top}}^h(M,M)=\textrm{Homeo}_{M}(\varnothing ,\varnothing )=\textrm{Homeo}_{M}(M,M)\) and every \(\textrm{Homeo}_{M}^{A}(N,N')\subseteq {\textbf{Top}}^h(M,M)\). Notice each self-homeomorphism \(\mathfrak {f}\) of M will belong to many such \(\textrm{Homeo}_{M}^A(N,N')\).
Lemma 2.41
Let M be a manifold and \(A\subset M\) a subset. With the induced topology, each \(\textrm{Homeo}_{M}^A(N,N)\) becomes a topological subgroup of \({\textbf{TOP}}^h(M,M)\).
Proof
Note that any subgroup of a topological group is itself a topological group with the induced topology.
We check that \(\textrm{Homeo}_{M}^A(N,N)\subseteq {\textbf{TOP}}^h(M,M)\) is a subgroup. Suppose we are given self-homeomorphisms  and
and  , then \(\mathfrak {f}\circ \mathfrak {g} (N)= \mathfrak {f}(N)=N \) and for all \(a \in A\): \(\mathfrak {f}\circ \mathfrak {g} (a)= \mathfrak {f}(a)=a.\) So
, then \(\mathfrak {f}\circ \mathfrak {g} (N)= \mathfrak {f}(N)=N \) and for all \(a \in A\): \(\mathfrak {f}\circ \mathfrak {g} (a)= \mathfrak {f}(a)=a.\) So  is in \(\textrm{Homeo}_{M}^A(N,N)\). Similarly
is in \(\textrm{Homeo}_{M}^A(N,N)\). Similarly  is in \(\textrm{Homeo}_{M}^A(N,N)\). \(\quad \square \)
is in \(\textrm{Homeo}_{M}^A(N,N)\). \(\quad \square \)
Remark 2.42
There are various ways in which we could equip the subsets of M with extra structure. For example we could let N and \(N'\) be submanifolds of M equipped with an orientation and then consider homeomorphisms which preserve these orientations.
3 Motion Groupoid \(\textrm{Mot}_{M}^A\)
In this section we construct the motion groupoid associated to a pair of a manifold M and a pointwise fixed subset \(A\subset M\) (e.g. \(A=\partial M\) or \(A=\varnothing \)). The core topological ideas used in this section are present in [Gol81], and first appeared in [Dah62] (see also [Gol72]), which construct a group of classes of motions which return a subset N, in the interior of a manifold M, to its initial position.
We proceed by first defining flows in a manifold M, and giving two choices of composition, \(*\) and \(\cdot \). At this point there are no ‘objects’, one choice of composition gives a magma, the other a group. We obtain motions by considering an action of flows on M, and thus on \({{\mathcal {P}}}M\). The two compositions on flows lead to two action magmoids, each of which has object set \({{\mathcal {P}}}M\) and motions as morphisms, and one of which is also a groupoid.
The \(*\) composition is the intuitive composition where one motion is carried out, followed by another, similar to path composition. In addition it is only with this composition that we are able to interpret motion composition in terms of a composition of the wordlines of the motion (Lemma 3.38). This leads to it being a more useful setting to work with for examples. The \(\cdot \) composition is introduced as it will be more convenient for many proofs, Lemma 3.29 for example.
For physical/engineering purposes, it is often necessary to have something finitary, thus we add a congruence to our magmoids. We will find it most straightforward to construct this congruence in two stages, first quotienting by a congruence using path homotopy, under which these magmoids become the same groupoid. This groupoid has, in general, uncountable morphism sets, and thus we add a further equivalence. By quotienting by a normal subgroupoid of classes containing a set-stationary motion, we obtain the motion groupoid \(\textrm{Mot}_{M}\) (Theorem 3.32). The object set is the power set \({{\mathcal {P}}}M\) and the morphisms are equivalence classes of motions.
To make the notation more manageable we only give the full details of proofs when working in \(\textrm{Homeo}_{M}\). In Sect. 3.6 we also construct a version using \(\textrm{Homeo}_{M}^A\), i.e fixing a distinguished choice of subset \(A\subset M\). This leads to the motion groupoid \(\textrm{Mot}_{M}^A\).
In Sect. 3.7 we have some examples which frame some of the questions that our construction allows us to ask. For example we can think about skeletons of our motion groupoids, or equivalently which subsets of a manifold M are connected in the motion groupoid. Or we could instead look for subsets which are not connected by a morphism in the motion groupoid, but which do have isomorphic automorphism groups.
3.1 Flows: elements in \({\textbf{Top}}^{}({{\mathbb {I}}},{\textbf{TOP}}^h(M,M))\)
Here we define flows and introduce two compositions.
Definition 3.1
Fix a manifold M. A flow in M is a path in \({\textbf{TOP}}^h(M,M)\) starting at \({\textrm{id}}_M\). We define notation for the set of all flows in M,
Example 3.2
For any manifold M the path \(f_t = {\textrm{id}}_M\) for all t, is a flow. We will denote this flow \({\textrm{Id}}_M\).
Example 3.3
For \(M=S^1\) (the unit circle) we may parameterise by \(\theta \in {{\mathbb {R}}}/2\pi \) in the usual way. Consider the functions \(\tau _\phi : S^1 \rightarrow S^1\) (\(\phi \in {{\mathbb {R}}}\)) given by \(\theta \mapsto \theta +\phi \), and note that these are homeomorphisms. Then consider the path \(f_t = \tau _{t \pi }\) (‘half-twist’). This is a flow.
Lemma 3.4
Let S, R be manifolds and \(\psi :S\rightarrow R\) a homeomorphism. Then there exists a bijection \( \textrm{Flow}_{S} \rightarrow \textrm{Flow}_{R} \) denoted \(g \mapsto g^\psi \) where
Proof
That \(g^\psi :{{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(R,R)\) is a continuous map follows from Lemma 2.12. It is clear that \((g^\psi )_0={\textrm{id}}_R\). The inverse \(\textrm{Flow}_{R} \rightarrow \textrm{Flow}_{S}\) is given by \(f\mapsto f^{{(\psi ^{-1})}}\). \(\square \)
Lemma 3.5
Let M be a manifold. For any flow f in M, then \((f^{-1})_t=f_t^{-1}\) is a flow.
Proof
By Theorem 2.11 we have that \({\textbf{Top}}^h(M,M)\) is a topological group, so we have that the map \(g \in {\textbf{Top}}^h(M,M) \mapsto g^{-1} \in {\textbf{Top}}^h(M,M)\) is continuous. It follows that the composition \(t \mapsto f_t\mapsto f_t^{-1}\) is continuous. Notice also that \((f^{-1})_0={\textrm{id}}_M^{-1}={\textrm{id}}_M\). \(\square \)
Composition of flows
The usual non-associative ‘stack+shrink’ composition of paths in \({\textbf{Top}}({{\mathbb {I}}},X)\) (see (1) on p.1) is a partial composition, precisely gf is a path if the end of the path f is the start of the path g. Now suppose \(X={\textbf{TOP}}(Y,Y)\) for some space Y and \(f,g\in {\textbf{Top}}({{\mathbb {I}}},{\textbf{TOP}}(Y,Y))\). We can use the function composition in \({\textbf{TOP}}(Y,Y)\) to construct paths \(g_0\circ f_t\) and \(g_t\circ f_1\) which share an endpoint, and thus we can use the usual path composition on these modified paths.
Proposition 3.6
Let Y be a space. There exists a composition
where
Proof
It follows from Lemma 2.12 that \(g*f\) is continuous on each segment. We also have that the functions agree at \(t=1/2\), hence Eq. (2) defines an element in \({\textbf{Top}}({{\mathbb {I}}},{\textbf{TOP}}(Y,Y))\). \(\quad \square \)
Proposition 3.7
Let M be a manifold. There exists a composition
where
We denote the magma \((\textrm{Flow}_{M},*)\).
Proof
This is the restriction of the \(*\) function of Proposition 3.6 to \(\textrm{Flow}_{M}\) so we need only to check that \(g*f\in \textrm{Flow}_{M}\). We have \((g*f)_0=f_0={\textrm{id}}_M\) and for all \(t\in {{\mathbb {I}}}\), \((g*f)_t\) is a homeomorphism as it is the composition of two homeomorphisms. \(\quad \square \)
Note that the previous composition of flows does not require M a manifold. Given a manifold M, we can also define another ‘pointwise’ composition of paths in \(\textrm{Flow}_{M}\) which relies on the fact that \({\textbf{TOP}}^h(M,M)\) is a topological group.
Lemma 3.8
Let M be a manifold.
-
(I)
There is an associative composition
$$\begin{aligned} \cdot \;:\textrm{Flow}_{M}\times \textrm{Flow}_{M}&\rightarrow \textrm{Flow}_{M}\\ (f,g)&\mapsto g\cdot f \end{aligned}$$where \((g\cdot f)_t=g_t\circ f_t\).
-
(II)
There is a group \((\textrm{Flow}_{M}, \cdot )\), with identity \({\textrm{Id}}_M\) and inverse map \(f\mapsto f^{-1}\) with \(f^{-1}\) as defined in Lemma 3.5.
Proof
-
(I)
We first check that \(g\cdot f\) is a path. This can be seen by rewriting as
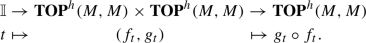
The map into the product is continuous because it is continuous on each projection, and the second map is continuous because \({\textbf{TOP}}^h(M,M)\) is a topological group, by Theorem 2.11. Notice also that \((g\cdot f)_0=g_0\circ f_0={\textrm{id}}_M\), so we have that \(g\cdot f\in \textrm{Flow}_{M}\). Associativity of the composition follows from the associativity of function composition in \({\textsf{Set}}\).
-
(II)
For all \(t\in {{\mathbb {I}}}\), \(({\textrm{Id}}_M\cdot f)_t={\textrm{id}}_M\circ f_t=f_t=f_t\circ {\textrm{id}}_M=(f\cdot {\textrm{Id}}_M)_t\) and \((f\cdot f^{-1})_t=f_t\circ f_t^{-1}= {\textrm{id}}_M=f_t^{-1}\circ f_t =(f^{-1}\cdot f)_t\). \(\quad \square \)
The following lemma says that, up to path-equivalence, both compositions are the same.
Lemma 3.9
Let M be a manifold and \(f,g\in \textrm{Flow}_{M}\). Then \(g*f \; {\mathop {\sim }\limits ^{p}}\; g\cdot f\).
Before the proof, let us fix some conventions. Flows are paths \(f:{{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) and then homotopies of paths are maps \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M) \). We will always think of the first copy of \({{\mathbb {I}}}\) in a homotopy as the one parameterising the flow, and will continue to use the parameter t. For the second copy of \({{\mathbb {I}}}\), which parameterises the homotopy, we will use s.
Proof
The following function is a suitable path homotopy to prove the path-equivalence
Notice \(H(t,0)=(g*f)_t\), \(H(t,1)=(g\cdot f)_t\) and for all \(s\in {{\mathbb {I}}}\) we have \(H(0,s)=g_0\circ f_0 ={\textrm{id}}_M\) and \(H(1,s)= g_1\circ f_1\). Note that continuity of each segment uses that \({\textbf{TOP}}^h(M,M)\) is a topological group by Theorem 2.11. \(\quad \square \)
Remark 3.10
There are other choices of compositions of flows which assign paths g and f to a path which is path-homotopic to \(g*f\) and \(g\cdot f\). For example
We can also generate from any flow f, a flow \({\bar{f}}\) which reverses the path. Intuitively \({\bar{f}}\) is obtained from f by first changing the direction of travel along the path, and then precomposing at each t with \(f_1^{-1}\) to force the reversed path to start at the identity.
Proposition 3.11
Let M be a manifold. There exists a set map
with
Proof
By Lemma 2.12, the composition with \(f_1^{-1}\) is continuous and so \({\bar{f}}\) is continuous. Also notice \({\bar{f}}_0=f_{1}\circ f_1^{-1}={\textrm{id}}_M\), and \({\bar{f}}_t\) is a composition of homeomorphisms, thus a homeomorphism. \(\quad \square \)
Remark 3.12
The operation \(f \mapsto {\bar{f}}\) is an involution, namely \(\bar{{\bar{f}}}=f\). Notice also that for a flow f, \({\bar{f}}*f=f^{rev}f\), with path composition as in (1) and \(f^{rev}\) as in Proposition 2.36. Thus we have already shown in the proof of Proposition 2.36 that \({\bar{f}}*f{\mathop {\sim }\limits ^{p}}{\textrm{Id}}_M\).
3.2 Motions: the action of flows on subsets
For a manifold M, there is a set map from \(\textrm{Flow}_{M}\times M\) to M defined by \((f,m)\mapsto f_1(m)\). This lifts to a magma action of \((\textrm{Flow}_{M}, *)\) on M, and a group action of \((\textrm{Flow}_{M}, \cdot )\) on M. Thus we can form the action magmoid and action groupoid respectively of these actions on \({{\mathcal {P}}}M\) (see Definition 2.38 and the following text).
A motion is a morphism in either of these magmoids, whose morphisms are, by construction, the same.
Definition 3.13
Fix a manifold M. A motion in M is a triple \((f,N,f_1(N))\) consisting of a flow \(f\in \textrm{Flow}_{M}{}\), a subset \(N\subseteq M\) and the image of N at the endpoint of f, namely \(f_1(N)\). (Note \(f_1(N)=N'\) if and only if \(f_1\in \textrm{Homeo}_M(N,N')\).)
Notation: We will denote such a triple by  where \(f_1(N)=N'\), and say it is a motion from N to \(N'\). For subsets \(N,N'\subseteq M\) we define
where \(f_1(N)=N'\), and say it is a motion from N to \(N'\). For subsets \(N,N'\subseteq M\) we define
A motion is uniquely determined by a pair of a flow f and a subset \(N\subseteq M\). This implies
where the union is over all pairs \(N,N'\subseteq M\).
As with \(\textrm{Homeo}_{M}\), where convenient we will also use \(\textrm{Mt}_{M}({N},{N'})\) to denote the set obtained by projecting to the first element of the triple. Then each \(f\in \textrm{Flow}_{M}\) will belong to many \(\textrm{Mt}_{M}({N},{N'})\).
The bar operation generates from any motion from N to \(N'\), a motion from \(N'\) to N.
Proposition 3.14
Let M be a manifold. For any subsets \(N,N'\subseteq M\) there is a set map

where \({\bar{f}}_t \;=\; f_{(1-t)}\circ f_1^{-1}\), as in Eq. (5).
Proof
Proposition 3.11 gives that \({\bar{f}}\) is a flow. Note that we have \({\bar{f}}_1(N')=N\), hence  . \(\quad \square \)
. \(\quad \square \)
Example 3.15
For a manifold M, a subset \(N\subseteq M\) and the flow \({\textrm{Id}}_M\) as in Example 3.2,  is a motion. We will call this the ‘trivial motion’ from N to N. Note that the flow \({\textrm{Id}}_M\) becomes a motion from N to N for any N, but not a motion from N to \(N'\) unless \(N=N'\).
is a motion. We will call this the ‘trivial motion’ from N to N. Note that the flow \({\textrm{Id}}_M\) becomes a motion from N to N for any N, but not a motion from N to \(N'\) unless \(N=N'\).
Example 3.16
The half-twist of \(S^1\) (see Example 3.3) becomes a motion in \(S^1\) from N to \(\tau _\pi (N)\) for any \(N\subseteq S^1\).
Remark 3.17
Suppose  is a motion in M, then N and \(N'\) are homeomorphic.
is a motion in M, then N and \(N'\) are homeomorphic.
Proposition 3.18
Let M be a manifold. There is a magma action \(*:(\textrm{Flow}_{M},*)\times M\rightarrow M\), \((f,m)\mapsto f_1(m)\). Hence we can construct the action magmoid (Definition 2.38) of the corresponding action on \({{\mathcal {P}}}M\)
Proof
For all \(m\in M\) and \(f,g\in \textrm{Flow}_{M}\), \((g*f)_1(m)= g_1\circ f_1 (m) =g_1(f_1(m))\). \(\square \)
In our notation, the composition in \(\textrm{Mt}_M^*\) is given by

where  with \(g*f\) as defined in Eq. (3).
with \(g*f\) as defined in Eq. (3).
Proposition 3.19
Let M be a manifold. There is a group action \(\cdot :(\textrm{Flow}_{M},\cdot )\times M\rightarrow M \), \((f,m)\mapsto f_1(m)\). Hence we can construct the action groupoid (Definition 2.38) of the corresponding action on \({{\mathcal {P}}}M\)
Proof
We have that for all \(m\in M\) and \(f,g\in \textrm{Flow}_{M}\), \((g\cdot f)_1(m)=g_1\circ f_1(m)=g_1(f_1(m))\) and \(({\textrm{Id}}_M)_1(m)={\textrm{id}}_M(m)=m\). \(\quad \square \)
In our notation the composition in \(\textrm{Mt}_M^{\;\cdot }\) is given by

where  and \((g\cdot f)_t=g_t\circ f_t\).
and \((g\cdot f)_t=g_t\circ f_t\).
Note that in the last three entries of the pentuple \(\textrm{Mt}_M\) we give only information about what happens to the group element in each morphism, as it is clear what should happen to the elements of \({{\mathcal {P}}}M\). We do this to keep notation readable and it will be common in our constructions.
3.3 Schematic for \({\textbf{TOP}}^h(M,M)\)
In Fig. 3 we represent the space \({\textbf{TOP}}^h(M,M)\) and elements of \({\textbf{Top}}({{\mathbb {I}}},{\textbf{TOP}}^h(M,M))\) schematically (i.e. on the page, which is to say, the plane) for arbitrary M. Figure 3 further gives, schematically, two examples of motions in M. Here \({\textbf{TOP}}^h(M,M)\) is represented as (a couple of disconnected) regions of the plane, so we have that the various \(\textrm{Homeo}_{M}(N,N')\)s are possibly intersecting subregions. The blue path (a) represents a motion from N to N. Notice this is a path starting and ending in the same shaded region of \(\textrm{Homeo}_{M}(N,N)\). This is possible since \(\textrm{Homeo}_{M}(N,N)\) must contain the identity. (Although \(\textrm{Homeo}_{M}(N,N)\) may also have path connected components which do not contain the identity, as pictured.) The red path (b) is a motion from N to \(N'\) where \(N\ne N'\).
Note a flow corresponds to precisely one path in \({\textbf{TOP}}^h(M,M)\), although many motions can have the same underlying flow, thus to make such a diagram convey a motion it is necessary to explicitly state the subsets in addition to the schematic representation of the path.
A schematic representation of \({\textbf{Top}}^h(M,M)\), for a fixed but arbitrary M, as a not-necessarily connected, not-necessarily simply-connected subset of \({{\mathbb {R}}}^2\). In practice we are only interested in the connected component of the point \({\textrm{id}}_M\). The blue line (a) is then a motion from N to N and the red line (b) a motion from N to \(N'\)
3.4 Path homotopy congruence on motion magmoids
Here we show that path-equivalence is a congruence on \(\textrm{Mt}_M^*\), and that the corresponding quotient magmoid is a groupoid. We then show the same equivalence is a congurence on \(\textrm{Mt}_M^{\;\cdot }\) and that the quotient magmoid is precisely the groupoid obtained from \(\textrm{Mt}_M^*\).
Notice that, since path homotopies fix the endpoints, for any motion  and any path-equivalence \(f{\mathop {\sim }\limits ^{p}}f'\),
and any path-equivalence \(f{\mathop {\sim }\limits ^{p}}f'\),  is a motion.
is a motion.
Lemma 3.20
Let M be a manifold.
-
(I)
For each pair \(N,N'\subseteq M\) of subsets the relation

is an equivalence relation on \(\textrm{Mt}_M(N,N')\) (see Definition 2.32 for the definition of \({\mathop {\sim }\limits ^{p}}\)).
-
(II)
The equivalence relations \((\textrm{Mt}_M(N,N'),\sim \,)\) for each pair \(N,N'\subseteq M\) are a congruence on \(\textrm{Mt}_M^{*}\).
Notation: By abuse of notation we will also use \({\mathop {\sim }\limits ^{p}}\) to denote this relation. We use  or \([f]_{\text{ p }}\) for the path-equivalence class of
or \([f]_{\text{ p }}\) for the path-equivalence class of  .
.
Proof
-
(I)
For any pair \(N,N'\), we have that \(\textrm{Mt}_M(N,N')\subset {\textbf{Top}}({{\mathbb {I}}},{\textbf{Top}}(M,M))\), thus the proof that path-homotopy is an equivalence relation on \({\textbf{Top}}({{\mathbb {I}}},{\textbf{Top}}(M,M))\) (Proposition 2.33) is sufficient.
-
(II)
Suppose we have pairs of equivalent motions
 and
and  . Then there exists a path homotopy, say \(H_f\) from f to \(f'\) and a path homotopy, say \(H_g\) from g to \(g'\). Notice that, since path homotopies fix the endpoints, for all \(s\in {{\mathbb {I}}}\) we have \(H_f(1,s)=f_1\). Thus the map $$\begin{aligned} H(t,s)={\left\{ \begin{array}{ll} H_f(2t,s) &{} 0\le t\le 1/2\\ H_g(2(t-1/2),s)\circ f_1 &{} 1/2 \le t\le 1 \end{array}\right. } \end{aligned}$$
. Then there exists a path homotopy, say \(H_f\) from f to \(f'\) and a path homotopy, say \(H_g\) from g to \(g'\). Notice that, since path homotopies fix the endpoints, for all \(s\in {{\mathbb {I}}}\) we have \(H_f(1,s)=f_1\). Thus the map $$\begin{aligned} H(t,s)={\left\{ \begin{array}{ll} H_f(2t,s) &{} 0\le t\le 1/2\\ H_g(2(t-1/2),s)\circ f_1 &{} 1/2 \le t\le 1 \end{array}\right. } \end{aligned}$$is a path homotopy \(g*f\) to \(g'*f'\). \(\quad \square \)
Lemma 3.21
Let M be a manifold. The pentuple
is a groupoid.
Proof
First notice that, by Lemma 3.20, \({\mathop {\sim }\limits ^{p}}\) is a congruence, hence there is a quotient magmoid \(({{\mathcal {P}}}M,\; \textrm{Mt}_M(N,N')/{\mathop {\sim }\limits ^{p}},\; *)\).
We have proved in Lemma 3.9 that \(g*f{\mathop {\sim }\limits ^{p}}g\cdot f\), and by Proposition 3.18\(\cdot \) is associative and unital with unit \({\textrm{Id}}_M\). This is sufficient to prove \(({{\mathcal {G}}}1)\) and \(({{\mathcal {G}}}2)\).
(\({{\mathcal {G}}}3\)) Since we are considering a different inverse to the inverse in the group \((\textrm{Flow}_{M},\cdot )\), we prove this directly. Note that for any morphism  ,
,  is well defined by Proposition 3.14. For any morphism
is well defined by Proposition 3.14. For any morphism  , the following function
, the following function
is a homotopy from \({\bar{f}}*f\) to \({\textrm{Id}}_M\). Observe that for each fixed s, the path \(H_{{\bar{f}}*f}(t,s)\) starts at the identity, follows f until \(f_{(1-s)}\), and then follows \(f_{(1-t)}\) back to \({\textrm{id}}_M\). \(\square \)
Remark 3.22
Note that \(\textrm{Mt}_M^*/{\mathop {\sim }\limits ^{p}}\) is the action groupoid \({{\mathcal {P}}}M/\!/_\triangleright \, \left( (\textrm{Flow}_{M},*)/{\mathop {\sim }\limits ^{p}}\right) \), where \([f]_{\text{ p }}\triangleright N=f_1(N)\). The proof of Lemma 3.21 is essentially a proof that \((\textrm{Flow}_{M},*)/{\mathop {\sim }\limits ^{p}}\) is a group. The downside of this approach is that motions are obscured, and since our motivation is to model particle trajectories which do not a priori include a choice of equivalence relation, we favour our approach.
Lemma 3.23
Let M be a manifold. (I) The relations \((\textrm{Mt}_M(N,N'),{\mathop {\sim }\limits ^{p}})\) for each \(N,N'\subseteq M\) are a congruence on \(\textrm{Mt}_M^\cdot \), thus we have a groupoid:
(II) We have that \(\textrm{Mt}_M^\cdot =\textrm{Mt}_M^{*}\).
Notation: We will now denote this groupoid by just \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\).
Proof
(I) By Lemma 3.9\(f\cdot g{\mathop {\sim }\limits ^{p}}f*g\) for all flows, hence that \({\mathop {\sim }\limits ^{p}}\) is a congruence follows from Lemma 3.20. By Proposition 3.19\(\textrm{Mt}_M^{\; \cdot }\) is a groupoid, thus, by Proposition 2.28, the quotient is also a groupoid.
(II) By construction the two categories have the same objects and morphisms. By Lemma 3.9 the composition is the same up to path-equivalence. Thus the underlying magmoids are the same. By uniqueness of inverses and identities, they are the same groupoid. \(\quad \square \)
Remark 3.24
Note in particular that Lemma 3.23 implies \({\bar{f}}{\mathop {\sim }\limits ^{p}}f^{-1}\).
The previous lemma allows us to work interchangeably with either choice of composition or inverse according to which simplifies each proof, this will be used throughout the paper.
Definition 3.25
We define the topological space \(D^2\), called the 2-disk, as \(\big \{x\in {{\mathbb {R}}}^2 \;\vert \; \; \vert x\vert \le 1\big \}\subset {{\mathbb {R}}}^2\) with the subset topology.
The groupoid \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\) typically has uncountable sets of morphisms. Morally this is because path-homotopy completely fixes endpoints, and thus there is still too much information being kept track of. To be more precise, let M be a manifold and \(N,N'\subseteq M\) be subsets. Given two motions  such that \(f_1\ne f_1'\), then their path-homotopy classes (which we recall are relative to end-points) are different, so
such that \(f_1\ne f_1'\), then their path-homotopy classes (which we recall are relative to end-points) are different, so  . In general there uncountably many choices of endpoints of homeomorphisms of M sending N to \(N'\).
. In general there uncountably many choices of endpoints of homeomorphisms of M sending N to \(N'\).
In particular, let \(M=D^2\) and \(N\subset \textrm{int}(D^2)\) be a finite set in the interior of \(D^2\). Fix an \(x\in \textrm{int}(D^2){\setminus } N\). For any \(y\in \textrm{int}(D^2){\setminus } N\) there is a motion  with \(f^{y}_1(x)=y\) and \(f^y_t(N)=N\) for all \(t\in {{\mathbb {I}}}\). (We are using the homogeneity of connected smooth manifolds discussed in [Mil65, §4], together with the fact that if M is connected, of dimension \(\ge 2\), then M minus a finite set of points is still connected.) Note that
with \(f^{y}_1(x)=y\) and \(f^y_t(N)=N\) for all \(t\in {{\mathbb {I}}}\). (We are using the homogeneity of connected smooth manifolds discussed in [Mil65, §4], together with the fact that if M is connected, of dimension \(\ge 2\), then M minus a finite set of points is still connected.) Note that  if \(y\ne y'\), as \(f^y_1(x)=y\) whereas \(f^{y'}_1(x)=y'\). There are uncountably many such \(f^y\), hence the set \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}(N,N)\) is uncountable.
if \(y\ne y'\), as \(f^y_1(x)=y\) whereas \(f^{y'}_1(x)=y'\). There are uncountably many such \(f^y\), hence the set \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}(N,N)\) is uncountable.
Both the braid groups and the loop braid groups have presentations with a finite number of generators, thus are not uncountable [Art47, Dam17]. In the next section we impose a further quotient that will identify the motions \(f^y\) and \(f^{y'}\).
3.5 The motion groupoid \(\textrm{Mot}_{M}\): congruence induced by set-stationary motions
Motivated by engineering/physical considerations, we aim to construct models where physical configurations are arranged into a countable/finitely-generated set of classes i.e. combinatorially. See [Fra13, Bai80, LM77, BFMM19] for examples of systems where the interesting physics is modelled by such structures. Accordingly, by imposing path equivalence, we have washed out some distinctions that do not affect the induced movement of our object subsets (without this our sets are certainly larger than combinatorial). However, for general subsets, so far, we are still only allowing motions to be equivalent if their underlying paths share the same end point, and these sets can still be very large. Dahm’s idea of ‘motion groups’ partially addresses this problem [Dah62]. Intuitively, the quotient used to construct a motion group can be thought of as de-emphasising the motion of the ambient space. (This point of view is made precise by Proposition 3.37 and Sect. 4.2.) Here we prove there is a lift of Dahm’s idea to the groupoid setting.
We start by defining N-stationary motions, motions  which leave N fixed setwise. We then show that there is a normal subgroupoid in \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\) whose morphisms are those classes containing an \(N\)-stationary motion for some \(N\in M\), hence this normal subgroupoid induces a congruence. This leads to the motion groupoid \(\textrm{Mot}_{M}\) in Theorem 3.32.
which leave N fixed setwise. We then show that there is a normal subgroupoid in \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\) whose morphisms are those classes containing an \(N\)-stationary motion for some \(N\in M\), hence this normal subgroupoid induces a congruence. This leads to the motion groupoid \(\textrm{Mot}_{M}\) in Theorem 3.32.
Definition 3.26
Let M be a manifold, and \(N\subseteq M\) a subset. A motion  in M is said to be N -stationary if \(f_t\in \textrm{Homeo}_{M}(N,N)\) (\(f_t(N)=N\)) for all \(t\in {{\mathbb {I}}}\). Define
in M is said to be N -stationary if \(f_t\in \textrm{Homeo}_{M}(N,N)\) (\(f_t(N)=N\)) for all \(t\in {{\mathbb {I}}}\). Define

Example 3.27
Let \(M=D^2\), the 2-disk and let \(N\subset M\) be a finite set of points. Then a motion  in M is \(N\)-stationary if, and only if, \(f_t(x)=x\), for all \(x\in N\) and \(t\in {{\mathbb {I}}}\). More generally this holds if N is a totally disconnected subspace of M, e.g. \({\mathbb {Q}}\) in \({\mathbb {R}}\).
in M is \(N\)-stationary if, and only if, \(f_t(x)=x\), for all \(x\in N\) and \(t\in {{\mathbb {I}}}\). More generally this holds if N is a totally disconnected subspace of M, e.g. \({\mathbb {Q}}\) in \({\mathbb {R}}\).
Example 3.28
Let \(M= D^2\). Consider \(D^2\) as a subset of \({{\mathbb {C}}}\). Let f in \({\textbf{TOP}}^h(D^2,D^2)\) be constructed as follows. Consider a continuous function \(g:[0,1] \rightarrow {{\mathbb {R}}}^-_0,\) such that \(g(0)=0\) and \(g(1)=0\), and with a single local minimum in \(x\in (0,1)\) with \(f(x)=-\pi \). Let \(f_t\) be the map \(z\mapsto z \exp (i g(|z|) t)\). Then sequential points on \(f\in \textrm{Flow}_{D^2}\) are represented by Fig. 1.
Now pick a subset \(N\subset D^2\) which is any circle centred on the centre of the disk, i.e. the set of all points a fixed distance from the centre using the metric induced from the complex plane. The motion  is \(N\)-stationary.
is \(N\)-stationary.
Lemma 3.29
Let M be a manifold and \(N,N'\subseteq M\) subsets. Let \(\overline{\textrm{SetStat}}_{M}(N,N)\) be the subset of \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}(N,N)\) of those classes that intersect \(\textrm{SetStat}_M(N,N)\). Let \(\overline{\textrm{SetStat}}_{M}(N,N') = \varnothing \) if \(N \ne N'\). There is a totally disconnected, normal, wide subgroupoid of \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\),
Note that

Proof
First we will show that the tuple \(\overline{\textrm{SetStat}}_{M}\) is a subgroupoid.
For each \(N\subseteq M\), the identity  is in \(\overline{\textrm{SetStat}}_{M}(N,N)\) as for all \(t\in {{\mathbb {I}}}\), \(({\textrm{Id}}_M)_t(N)={\textrm{id}}_M(N)=N\).
is in \(\overline{\textrm{SetStat}}_{M}(N,N)\) as for all \(t\in {{\mathbb {I}}}\), \(({\textrm{Id}}_M)_t(N)={\textrm{id}}_M(N)=N\).
For the existence of inverses, and for closure of composition, observe that there is nothing to show unless \(N=N'\). For each  , we may assume without loss of generality that
, we may assume without loss of generality that  is a \(N\)-stationary motion. Then the inverse
is a \(N\)-stationary motion. Then the inverse  is in \(\overline{\textrm{SetStat}}_{M}(N,N)\), since for all \(t\in {{\mathbb {I}}}\), \({\bar{x}}_t(N)=x_{1-t}\circ x_1^{-1}(N)=x_{1-t}(N)=N\).
is in \(\overline{\textrm{SetStat}}_{M}(N,N)\), since for all \(t\in {{\mathbb {I}}}\), \({\bar{x}}_t(N)=x_{1-t}\circ x_1^{-1}(N)=x_{1-t}(N)=N\).
Let  and
and  be in \(\overline{\textrm{SetStat}}_{M}(N,N)\), we may again assume without loss of generality, that
be in \(\overline{\textrm{SetStat}}_{M}(N,N)\), we may again assume without loss of generality, that  and
and  are \(N\)-stationary. For all \(t\in [0,1/2]\) we have that \((x'*x)_t(N)=x_t(N)=N\) and for \(t\in [1/2,1] \) that \((x'*x)_t(N)=x'_t\circ x_1(N)=x'_t(N)=N\). Thus composition closes, and so \(\overline{\textrm{SetStat}}_{M}\) is a groupoid.
are \(N\)-stationary. For all \(t\in [0,1/2]\) we have that \((x'*x)_t(N)=x_t(N)=N\) and for \(t\in [1/2,1] \) that \((x'*x)_t(N)=x'_t\circ x_1(N)=x'_t(N)=N\). Thus composition closes, and so \(\overline{\textrm{SetStat}}_{M}\) is a groupoid.
Observe now that \(\overline{\textrm{SetStat}}_{M}\) is totally disconnected and wide by construction.
Finally, we have that \(\overline{\textrm{SetStat}}_{M}\) is normal, since for any morphism  and for any
and for any  in \(\overline{\textrm{SetStat}}_{M}(N',N')\), with
in \(\overline{\textrm{SetStat}}_{M}(N',N')\), with  \(N'\)-stationary, the following function
\(N'\)-stationary, the following function
is a path homotopy from \(f^{-1}\cdot x \cdot f\) to the path \(t \mapsto f^{-1}_1\circ x_t \circ f_1 \in {\textbf{TOP}}^h(M,M)\), which is an \(N\)-stationary motion. \(\quad \square \)
Hence, by Lemma 2.30, we can form a quotient groupoid \((\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}})/\overline{\textrm{SetStat}}_{M}\). Precisely, morphisms  and
and  in \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\) are related in the quotient, denoted
in \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\) are related in the quotient, denoted

if  is in \(\overline{\textrm{SetStat}}_{M}(N,N)\). (Or equivalently if
is in \(\overline{\textrm{SetStat}}_{M}(N,N)\). (Or equivalently if  is in \(\overline{\textrm{SetStat}}_{M}(N,N)\).)
is in \(\overline{\textrm{SetStat}}_{M}(N,N)\).)
We give our first definition of the motion groupoid as a groupoid which is canonically isomorphic to \((\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}})/\overline{\textrm{SetStat}}_{M}\).
Proposition 3.30
Let M be a manifold. Let  be path-equivalent motions in M. Then
be path-equivalent motions in M. Then  is path-equivalent to an \(N\)-stationary motion.
is path-equivalent to an \(N\)-stationary motion.
Proof
We have  , hence, as \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\) is a groupoid (Lemma 3.21), thus with unique inverses,
, hence, as \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\) is a groupoid (Lemma 3.21), thus with unique inverses,  . This implies there is a path-homotopy H from \({\bar{g}}*f\) to \({\textrm{Id}}_M\), which is an \(N\)-stationary motion. \(\square \)
. This implies there is a path-homotopy H from \({\bar{g}}*f\) to \({\textrm{Id}}_M\), which is an \(N\)-stationary motion. \(\square \)
Proposition 3.31
For a manifold M and \(N,N' \subseteq M\), denote by \({\mathop {\sim }\limits ^{m}}\) (‘m’ for motion) the relation

on \(\textrm{Mt}_M(N,N')\). (I) This is an equivalence relation.
(II) There exists a canonical bijection \(\textrm{Mt}_M(N,N')/{\mathop {\sim }\limits ^{m}}\, \cong (\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}})/\overline{\textrm{SetStat}}_{M}\) sending  to the \({\mathop {\sim }\limits ^{\textrm{Stat}}}\) equivalence class of
to the \({\mathop {\sim }\limits ^{\textrm{Stat}}}\) equivalence class of  .
.
Notation: We call this motion-equivalence and denote by  the motion-equivalence class of
the motion-equivalence class of  .
.
Proof
First note the following general fact. Consider a set X, with an equivalence relation \(\sim _1\), and furthermore another equivalence relation \(\sim _2\) on \(X/\sim _1\). Then \(x\sim y\), if \([x]_{\sim _1} \sim _2 [y]_{\sim _1} \), is an equivalence relation on X. And moreover we have a bijection \(X/\sim \rightarrow {(X/\sim _1)}/\sim _2\) such that \([x]_\sim \mapsto {[[x]_{\sim _1}]}_{\sim _2}\).
Notice that another way to write \({\mathop {\sim }\limits ^{m}}\) is as

Further \({\mathop {\sim }\limits ^{p}}\) is an equivalence relation by Lemma 3.20, and \({\mathop {\sim }\limits ^{\textrm{Stat}}}\) is an equivalence relation, since it is the relation obtained from Lemma 2.30 applied to \(\overline{\textrm{SetStat}}_{M}\), which is normal by Lemma 3.29. Thus both results follow from the first paragraph. \(\quad \square \)
In the following theorem we continue our convention of only giving the first element of the triple corresponding to a motion in the tuple defining a groupoid, to keep the notation readable.
Thus \([f]_{\text{ m }}\) denotes, for some choice of N, and \(N'=f_1(N)\),  . We note however that the relation \({\mathop {\sim }\limits ^{m}}\) depends on the subsets.
. We note however that the relation \({\mathop {\sim }\limits ^{m}}\) depends on the subsets.
By Proposition 3.31 we have:
Theorem 3.32
Let M be a manifold. There is a groupoid
where
-
(I)
objects are subsets of M;
-
(II)
morphisms between subsets \(N,N'\) are motion-equivalence classes
 of motions, explicitly
of motions, explicitly 
if
 is path equivalent to an \(N\)-stationary motion;
is path equivalent to an \(N\)-stationary motion; -
(III)
composition of morphisms is given by

where
$$\begin{aligned} (g*f)_t = {\left\{ \begin{array}{ll} f_{2t} &{} 0\le t\le 1/2, \\ g_{2(t-1/2)}\circ f_1 &{} 1/2\le t \le 1; \end{array}\right. } \end{aligned}$$(7) -
(IV)
the identity at each object N is the motion-equivalence class of
 , \(({\textrm{Id}}_M)_t(m)=m\) for all \(m\in M\);
, \(({\textrm{Id}}_M)_t(m)=m\) for all \(m\in M\); -
(V)
the inverse for each morphism
 is the motion-equivalence class of
is the motion-equivalence class of  where \({\bar{f}}_t=f_{(1-t)}\circ f_1^{-1}\).
where \({\bar{f}}_t=f_{(1-t)}\circ f_1^{-1}\).
Moreover, we have a canonical isomorphism of groupoids:
\(\square \)
Remark 3.33
We have from Lemma 3.23 that \(\textrm{Mt}_M^{\dot{}}/{\mathop {\sim }\limits ^{p}}\) and \(\textrm{Mt}_M^{*}/{\mathop {\sim }\limits ^{p}}\) are the same groupoid. Thus in the statement of the theorem we could have chosen to define the composition in terms of \(\cdot \), or the inverse in terms of the pointwise inverse \((f^{-1})_t=f_t^{-1}\), or both. It follows that  if and only if
if and only if  is path-equivalent to an \(N\)-stationary motion.
is path-equivalent to an \(N\)-stationary motion.
Remark 3.34
The automorphism groups \(\textrm{Mot}_{M}(N,N)\), where \(N\subseteq M\) is a submanifold, are isomorphic to the motion groups constructed in [Dah62, Gol81], at least in the case when M is compact. We do not know the precise relation between our motion groups and those of loc cit when M is not compact, since the motion groups constructed by Dahm and Goldsmith only consider for homeomorphism of compact support, and furthermore all path-homotopies are required to only trace homeomorphisms of compact support. We settle that the two settings give the same result for the case of finite subsets contained in the interior of a manifold in Remark 5.25.
In the rest of this Section, now that we have our core construction, we collect some straightforward but useful properties of \(\textrm{Mot}_{M}\).
For certain choices of M and N, there exist subgroupoids of \(\textrm{Mot}_{M}\) which have finite presentation. We discuss this in Sect. 5.3.
Example 3.35
Let M be a manifold, then \(\textrm{Mot}_{M}(M,M)\) is trivial. This is because for any \(f\in \textrm{Flow}_{M}\),  is a motion, and it is M-stationary. Similarly \(\textrm{Mot}_{M}(\varnothing ,\varnothing )\cong \textrm{Mot}_{M}(M,M)\) is trivial.
is a motion, and it is M-stationary. Similarly \(\textrm{Mot}_{M}(\varnothing ,\varnothing )\cong \textrm{Mot}_{M}(M,M)\) is trivial.
Definition 3.36
The worldline of a motion  in a manifold M is
in a manifold M is

It follows directly from the definitions that an \(N\)-stationary motion is precisely a motion whose worldline is equal to \(N\times {{\mathbb {I}}}\).
The group case of the following result is effectively proved in [Dah62, pg.6].
Proposition 3.37
Let  be motions with the same worldline, so we have
be motions with the same worldline, so we have

Then  and
and  are motion equivalent.
are motion equivalent.
Proof
By using Lemma 3.23, there is a motion  and
and

The equality  means:
means:
In particular for each \(t \in [0,1]\), we have \(f_t(N)=g_t(N).\) This implies that for all \(t\in {{\mathbb {I}}}\), \((g^{-1}\cdot f )_t(N)=(g^{-1}_t ( f_t(N))= (g^{-1}_t(g_t(N))=g^{-1}_t\circ g_t(N)=N \). Thus \(g^{-1} \cdot f\) is N-stationary, and hence  is path-equivalent to an \(N\)-stationary motion. \(\square \)
is path-equivalent to an \(N\)-stationary motion. \(\square \)
In Sect. 4.2 we will prove a generalisation of Prop.3.37, fully describing motion equivalence in terms of a notion of isotopy of worldlines of motions.
The following lemma says that the \(*\) composition of motions descends to a composition of worldlines, the same is not true for the \(\cdot \) or the \(*'\) compositions of motions (Proposition 3.19 and Remark 3.10).
Lemma 3.38
Consider motions  and
and  , then
, then

where \(*\) composition is as in Eq. (3).
Proof
This follows from the definition of \(*\) in Proposition 3.7. \(\quad \square \)
Lemma 3.39
Let M and \(M'\) be manifolds such that there exists a homeomorphism \(\psi :M\rightarrow M'\). Then there is an isomorphism of categories
defined as follows. On objects \(N\subseteq M\), \(\Psi (N)=\psi (N)\). For a motion  in M, let \((\psi \circ f \circ \psi ^{-1})_t=\psi \circ f_t \circ \psi ^{-1}\). Then \(\Psi \) sends the equivalence class
in M, let \((\psi \circ f \circ \psi ^{-1})_t=\psi \circ f_t \circ \psi ^{-1}\). Then \(\Psi \) sends the equivalence class  to the equivalence class \([\psi \circ f \circ \psi ^{-1}:\psi (N)\rightarrow \psi (N')]_{\text{ m }} \).
to the equivalence class \([\psi \circ f \circ \psi ^{-1}:\psi (N)\rightarrow \psi (N')]_{\text{ m }} \).
Proof
We have from Lemma 3.4 that \(\psi \circ f \circ \psi ^{-1}\) is in \(\textrm{Flow}_{M'}\). Notice also that \((\psi \circ f \circ \psi ^{-1})_1(\psi (N))=\psi \circ f_1 \circ \psi ^{-1}(\psi (N))=\psi \circ f_1(N)=\psi (N')\).
We check \(\Psi \) is well defined. Suppose  and
and  are equivalent motions in M, so there is a path homotopy \(\bar{f'}*f\) to a path, say x, such that
are equivalent motions in M, so there is a path homotopy \(\bar{f'}*f\) to a path, say x, such that  is an \(N\)-stationary motion, let us call this H. It is straightforward to check that the function \((\psi \circ H\circ \psi ^{-1})(t,s)=\psi \circ H(t,s)\circ \psi ^{-1}\) is a homotopy making \(\overline{\Psi (f')}*\Psi (f)\) path-equivalent to
is an \(N\)-stationary motion, let us call this H. It is straightforward to check that the function \((\psi \circ H\circ \psi ^{-1})(t,s)=\psi \circ H(t,s)\circ \psi ^{-1}\) is a homotopy making \(\overline{\Psi (f')}*\Psi (f)\) path-equivalent to  which is a \(\psi (N)\)-stationary motion.
which is a \(\psi (N)\)-stationary motion.
We check \(\Psi \) preserves composition. Suppose  and
and  are motions, then \(\Psi (g\cdot f )_t=\psi \circ g_t\circ f_t \circ \psi ^{-1}=\psi \circ g_t\circ \psi ^{-1}\circ \psi \circ f_t \circ \psi ^{-1}=(\psi (g)\cdot \psi (f))_t\).
are motions, then \(\Psi (g\cdot f )_t=\psi \circ g_t\circ f_t \circ \psi ^{-1}=\psi \circ g_t\circ \psi ^{-1}\circ \psi \circ f_t \circ \psi ^{-1}=(\psi (g)\cdot \psi (f))_t\).
The inverse functor to \(\Psi \) is defined in the same way using the homeomorphism \(\psi ^{-1}:M'\rightarrow M\). \(\quad \square \)
Example 3.40
There exists a homeomorphism from \(D^2\setminus \partial D^2\) to \({{\mathbb {R}}}^2\), thus, by Lemma 3.39, there is an isomorphism \(\textrm{Mot}_{D^2\setminus \partial D^2}\cong \textrm{Mot}_{{{\mathbb {R}}}^2}\).
Corollary 3.41
Let M be a manifold and \(N,N'\subseteq M\) subsets such that there exists a homeomorphism \(\mathfrak {f}:M\rightarrow M\) with \(\mathfrak {f}(N)=N'\). Then there is a group isomorphism
Proof
Letting \(\psi =\mathfrak {f}\) in Lemma 3.39 gives the isomorphism. \(\quad \square \)
Example 3.42
It is folklore, and discussed for instance in [MV94], with roots in [Mil65, §4], that, if M has dimension \(\ge 2\), and is connected, then given any positive integer n, and a pair of n-tuples, \((x_1,\dots , x_n)\) and \((y_1,\dots , y_n)\), of points in the interior of M, there exists a homeomorphism \(f:M \rightarrow M\) such that \(f(x_i)=y_i\), for \(i=1,\dots , n\). This is not true in general if \(\dim (M)=1\), but, given that M is homeomorphicFootnote 4 to either \(S^1, [0,1)\), [0, 1] or \({{\mathbb {R}}}\), we can still prove that, if K and \(K'\) are finite subsets of the same cardinality in the interior of M, then there exists a homeomorphism of M sending K to \(K'\). From this it follows that, whenever M is connected and K is a finite subset of \(M\setminus \partial M\) the isomorphism type of \(\textrm{Mot}_{M}(K,K)\) depends only on the cardinality of K. This is proved in Lemma 5.26.
Lemma 3.43
Let M be a manifold. There is an involutive automorphism
which sends an object \(N\subseteq M\) to its complement \(M{\setminus } N\) and which sends a morphism  to
to  .
.
Proof
First notice that by Lemma 2.40, \(f_1\in \textrm{Homeo}_{M}(M{\setminus } N,M{\setminus } N')\). We also need to check this functor is well defined. Suppose  and
and  are motion-equivalent, so there is a path homotopy \(f'*f\) to a stationary motion. So then
are motion-equivalent, so there is a path homotopy \(f'*f\) to a stationary motion. So then  u sing the same homotopy. It is immediate from the definitions that composition is preserved. \(\quad \square \)
u sing the same homotopy. It is immediate from the definitions that composition is preserved. \(\quad \square \)
3.6 Pointwise A-fixing motion groupoid, \(\textrm{Mot}_{M}^A\)
So far we have avoided working with homeomorphisms which fix a distinguished subset to avoid overloading the notation and thus make the exposition clearer. Everything we have done so far in this section could have been done by working instead with paths in \({\textbf{TOP}}^h_A(M,M)\) for M a manifold and \(A\subset M\) a subset. Recall \(f\in {\textbf{TOP}}^h_{A}(M,M)\) is a self-homeomorphism with \(f(a)=a\) for all \(a \in A\). We have the following adjusted definitions.
Definition 3.44
Fix a manifold M and a subset \(A\subset M\). An A-fixing flow in M is a path in \({\textbf{TOP}}^h_{A}(M,M)\) starting at \({\textrm{id}}_M\). We define notation for the set of all A-fixing flows in M,
Definition 3.45
Let M be a manifold and \(A\subset M\) a subset. An A -fixing motion in M is a triple \((f,N,f_1(N))\) consisting of an A-fixing flow \(f\in \textrm{Flow}_{M}^A{}\), a subset \(N\subset M\) and the image of N at the endpoint of f, \(f_1(N)\).
Notation: We will denote such a triple by  where \(f_1(N)=N'\), and say it is an A-fixing motion from N to \(N'\). For subsets \(N,N'\subset M\) we define
where \(f_1(N)=N'\), and say it is an A-fixing motion from N to \(N'\). For subsets \(N,N'\subset M\) we define
In practice we will often be interested in the case \(A=\partial M\).
Example 3.46
All motions of \({{\mathbb {I}}}\) are \(\partial {{\mathbb {I}}}\)-fixing motions.
Example 3.47
The half-twist motions of \(S^1\), described in Example 3.16 are not A-fixing motions for any non-empty subset \(A\subset S^1\).
Example 3.48
Let f be the flow in \(D^2\) described in Example 3.28 (and represented in Fig. 1), then \(f:N\rightarrow N'\) a \(\partial D^2\)-fixing motion for any \(N,N'\subseteq D^2\).
We have the following version of the motion groupoid where morphisms are classes of A-fixing motions up to an equivalence of paths in \({\textbf{TOP}}_A^h(M,M)\).
Theorem 3.49
Let M be a manifold and \(A\subset M\) a subset. There is a groupoid
where A-fixing motions  and
and  are equivalent if \({\bar{g}}*f\) is path-equivalent to an A-fixing \(N\)-stationary motion as paths in \({\textbf{TOP}}_A^h(M,M)\).
are equivalent if \({\bar{g}}*f\) is path-equivalent to an A-fixing \(N\)-stationary motion as paths in \({\textbf{TOP}}_A^h(M,M)\).
Proof
Notice that if  are A-fixing motions then \({\bar{f}}\), \(f^{-1}\), \(g*f\) and \(g\cdot f\) are all A-fixing motions. All motions constructed in homotopies required for the proof of Theorem 3.32 and associated lemmas are A-fixing if the input paths are A-fixing. Thus all proofs work in exactly the same way for A-fixing motions. \(\quad \square \)
are A-fixing motions then \({\bar{f}}\), \(f^{-1}\), \(g*f\) and \(g\cdot f\) are all A-fixing motions. All motions constructed in homotopies required for the proof of Theorem 3.32 and associated lemmas are A-fixing if the input paths are A-fixing. Thus all proofs work in exactly the same way for A-fixing motions. \(\quad \square \)
Lemma 3.50
Let M and \(M'\) be manifolds such that there exists a homeomorphism \(\psi :M\rightarrow M'\). Then there is a isomorphism of categories
defined as in Lemma 3.39.
Proof
We can use the same proof as in Lemma 3.39 together with the fact that for any motion  , the path \((\psi \circ f\circ \psi ^{-1})_t=\psi \circ f_t\circ \psi ^{-1}\) fixes A pointwise. \(\quad \square \)
, the path \((\psi \circ f\circ \psi ^{-1})_t=\psi \circ f_t\circ \psi ^{-1}\) fixes A pointwise. \(\quad \square \)
Corollary 3.51
Let M be a manifold and \(A \subset M\) subset. Let \(N,N'\subset M\) be subsets such that there exists a homeomorphism \(\mathfrak {f}:M\rightarrow M\) with \(\mathfrak {f}(N)=N'\) and \(\mathfrak {f}(a)=a\) for all \(a\in A\). Then there is a group isomorphism
Proof
As for Corollary 3.41. \(\quad \square \)
Lemma 3.52
Let M be a manifold. There is an involutive automorphism
which sends and object \(N\subset M\) to it’s complement \(M{\setminus } N\) and which sends a morphism  to
to  .
.
Proof
This is the same as for Lemma 3.43. \(\quad \square \)
3.7 Examples
Here we will consider some examples which serve to illustrate some key aspects of the richness of the construction.
By Lemma 3.50 we have that if M and \(M'\) are homeomorphic manifolds, \(\textrm{Mot}_{M}\) and \(\textrm{Mot}_{M'}\) are isomorphic groupoids. Thus it is enough to consider one M for each homeomorphism class.
An interesting problem in each case is to give a characterisation of a skeleton. This is far from straightforward, even if we restrict to objects that are themselves manifolds. Note that subsets \(N,N'\subseteq M\) being homeomorphic submanifolds is not a sufficient condition to ensure an isomorphism connecting them in the motion groupoid. For example, let \(M={{\mathbb {I}}}^2\) and let \(N\subset \textrm{int}({{\mathbb {I}}}^2)\) be the circle of points a distance 1/4 from the point (1/2, 1/2). Let L be the point (1/2, 1/2), and \(L'\) the point (3/4, 3/4). Then \(N\cup L\) and \(N\cup L'\) are homeomorphic but \(\textrm{Mot}_{{{\mathbb {I}}}^2}(N\cup L,N\cup L')=\varnothing \). Sections 3.7.1 and 3.7.2 below discuss isomorphisms between objects in \(\textrm{Mot}_{{{\mathbb {I}}}}\) and \(\textrm{Mot}_{{{\mathbb {R}}}}\).
We can think of the skeleton question as looking for ‘inner’ isomorphisms, objects which are connected by an isomorphism in the motion groupoid. This perspective frames a comparison with ‘outer’ isomorphisms. By this we mean the phenomenon illustrated by the following question: for a manifold M, which subsets \(N,N'\subseteq M\) have a constructible group isomorphism \(\chi :\textrm{Mot}_{M}(N,N) \rightarrow \) \(\textrm{Mot}_{M}(N',N')\), but with \(\textrm{Mot}_{M}(N,N')\) empty? Such isomorphisms are potentially useful tools in the construction of specific motion (sub)groupoids. We give examples in Sect. 3.7.3.
Observe that even in a skeleton most objects are undefinable so it is a good exercise to restrict to a full subgroupoid of particular interest. Given a subset Q of the object class \({{\mathcal {P}}}M\) of \(\textrm{Mot}_{M}^{A}\), we write \(\textrm{Mot}_{M}^{A}|_{Q}\) for the corresponding full subgroupoid. For example, let M be \(S^3\), the 3-sphere, and Q the set of subsets which are homeomorphic, using the subset topology, to a disjoint union of copies of \(S^1\). Then finding the connected components of \(\textrm{Mot}_{S^3}|_{Q}\) is equivalent to classifying unoriented links up to isotopy. Note, however, that motion groupoids do not only bookkeep links, up to isotopy, but also the theory of possible ambient isotopies between links, up to motion equivalence. The latter has rich features, as indicated for instance by the case of an unlink in \(D^3\), whose automorphism group in \(\textrm{Mot}_{D^3}^{\partial D^3}\) gives the extended loop braid group, [Dam17]; see Definition 6.14 and Proposition 7.15 below. Given the fact that the components of the space of embeddings of \(S^1\) inside \(S^3\) typically have non-trivial fundamental group [Bud10], we expect that \(\textrm{Mot}_{S^3}(K,K)\), where K is a knot, will usually be non-trivial.
3.7.1 On \(\textrm{Mot}_{{{\mathbb {I}}}}\)
Proposition 3.53
Suppose \(N\subset {{\mathbb {I}}}\setminus \{0,1\}\) is a compact subset with a finite number of connected components, so N is a union of points and closed intervals. We can assign a word in \(\{ a,b \}\) to N as follows: each point in N is represented by an a and each interval by a b, ordered in the obvious way using the natural ordering on \({{\mathbb {I}}}\). Let \(N'\subset {{\mathbb {I}}}\setminus \{0,1\}\) be another compact subset with a finite number of connected components. Then \(|\textrm{Mot}_{{{\mathbb {I}}}}(N,N')|=1\) if the word assigned to N and \(N'\) is the same, otherwise \(\textrm{Mot}_{{{\mathbb {I}}}}(N,N')=\varnothing \).
Proof
(Sketch) It is possible to construct even a piecewise linear motion from N to \(N'\) if the word assigned to N and \(N'\) is the same. The result that all motions N to \(N'\) are equivalent follows from the intermediate value theorem. That \(\textrm{Mot}_{{{\mathbb {I}}}}(N,N')=\varnothing \) if the words assigned to N and \(N'\) are different follows from the fact that any orientation preserving homeomorphism of \({{\mathbb {I}}}\) is order preserving. \(\quad \square \)
Note homeomorphisms send boundary points to boundary points and interior points to interior points, so any continuous path of homeomorphisms \({{\mathbb {I}}}\rightarrow {{\mathbb {I}}}\) starting at the identity fixes the boundary points. Thus we can generalise the previous proposition to: for \(A,B\subset {{\mathbb {I}}}\) compact subsets with a finite number of connected components, we have \(|\textrm{Mot}_{{{\mathbb {I}}}}(A,B)|=1\) if and only if \(A\cap \{0,1\}=B\cap \{0,1\}\) and A and B give the same word. Otherwise \(\textrm{Mot}_{{{\mathbb {I}}}}(A,B)=\varnothing \).
If we consider non-compact subsets we must also pay attention to the embeddings.
Example 3.54
Suppose \(N=(1/4,1/2)\cup (1/2,3/4)\) and \(N'=(1/4,3/8)\cup (5/8,3/4)\), then we have \(\textrm{Mot}_{{{\mathbb {I}}}}(N,N')=\varnothing \).
The automorphism group \(\textrm{Mot}_{{{\mathbb {I}}}}(N,N)\) for \(N\subset {{\mathbb {I}}}\) with a finite number of connected components is always trivial. This changes dramatically if more complicated subsets of \({{\mathbb {I}}}\) are considered. We will prove in Proposition 7.18 that for \(M={{\mathbb {I}}}\) and \(N={{\mathbb {I}}}\cap {\mathbb {Q}}\), \(\textrm{Mot}_{{{\mathbb {I}}}}^{\partial {{\mathbb {I}}}}(N,N)\) is uncountably infinite.
3.7.2 On \(\textrm{Mot}_{{{\mathbb {R}}}}\)
Proposition 3.55
\(\textrm{Mot}_{{{\mathbb {R}}}}({\mathbb {Q}},{{\mathbb {Z}}})=\varnothing \).
Proof
This can be seen by observing that there is no homeomorphism \(\theta :{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\) sending \({\mathbb {Q}}\) to \({{\mathbb {Z}}}\), since homeomorphisms of \({{\mathbb {R}}}\) must map dense subsets to dense subsets.
\(\square \)
In contrast \(\textrm{Mot}_{{{\mathbb {R}}}}({\mathbb {Q}},{\mathbb {Q}})\) is uncountable. A proof follows the same ideas used in the proof of Theorem 6.7 together with Theorem 7.13 below.
Question: Let \(N\ne N'\) be countable dense subsets of \({{\mathbb {R}}}\). Then does this imply the existence of a motion  in \({{\mathbb {R}}}\)?
in \({{\mathbb {R}}}\)?
Example 3.56
Let \(M={{\mathbb {R}}}\). Then there is a group isomorphism \(\phi :({{\mathbb {Z}}},+) \xrightarrow {\cong }\textrm{Mot}_{{{\mathbb {R}}}}({{\mathbb {Z}}},{{\mathbb {Z}}}) \) such that, for \(n \in ({{\mathbb {Z}}},+)\), \(\phi (n)\) is the motion-equivalence class of the motion  such that \(f_t (x)= x+tn\).
such that \(f_t (x)= x+tn\).
3.7.3 Relating automorphism groups in \(\textrm{Mot}_{M}\)
To construct motion (sub)groupoids, it is useful to be able to obtain the automorphism group of an object in terms of the automorphism group of another object. If objects are connected in the motion groupoid then this is straightforward. Otherwise we may still be able to construct a canonical ‘outer’ isomorphism between automorphism groups, or we may be able to construct a group homomorphism. The following examples investigate this in various cases.
Example 3.57
In general, there will not exist a morphism in \(\textrm{Mot}_{M}(N,M{\setminus } N)\). However, by Lemma 2.40 we have a group isomorphism \(\textrm{Mot}_{M}(N,N)\cong \textrm{Mot}_{M}(M\setminus N,M\setminus N)\).
(Although we can construct specific cases for which \(\textrm{Mot}_{M}(N,M\setminus N)\ne \varnothing \). For example let \(M=S^1\), and  the half-twist motion as in Example 3.16—letting \(N=[0,\pi )\subset S^1\), we have that the motion-equivalence class is in \(\textrm{Mot}_{S^1}([0,\pi ),[\pi ,0))\).)
the half-twist motion as in Example 3.16—letting \(N=[0,\pi )\subset S^1\), we have that the motion-equivalence class is in \(\textrm{Mot}_{S^1}([0,\pi ),[\pi ,0))\).)
Proposition 3.58
Let M be a manifold, and let \(\textrm{cl}(- )\) denote the closure of a subset. (I) Let \(S,T\subseteq M\) be subsets. There is a well defined set map:
which sends a motion equivalence class  to the motion equivalence class
to the motion equivalence class  .
.
(II) Moreover, there is a functor \(\mathbf {\Gamma }^M:\textrm{Mot}_{M} \rightarrow \textrm{Mot}_{M}\) which is defined by \(N \mapsto \textrm{cl}(N)\) on objects, and on morphisms restricts to the map \(\Gamma ^M_{N,N'}:\textrm{Mot}_{M}(N,N') \rightarrow \textrm{Mot}_{M}\big (\textrm{cl}(N),\textrm{cl}(N')\big ).\)
It follows directly from (II) that when \(S=T\), the map \(\Gamma ^M_{S,S}\) is a group homomorphism. In this case, we denote the map by \(\Gamma ^M_{S}\).
Proof
-
(I)
Let \(h:M\rightarrow M\) be a homeomorphism such that \(T=h(S)\), then \(h\big (\textrm{cl}(S)\big )=\textrm{cl}(T)\). It follows that if f is a flow in M such that
 is a motion, then
is a motion, then  is a motion. It also follows that if \(S=T\), and
is a motion. It also follows that if \(S=T\), and  is S-stationary, then
is S-stationary, then 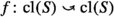 is also \(\textrm{cl}(S)\)-stationary.
is also \(\textrm{cl}(S)\)-stationary. -
(II)
That composition is preserved follows directly from the definition. \(\quad \square \)
This map is, in general, neither injective, nor surjective. Example 3.59 gives a case for which \(\Gamma ^M_{S,T}\) is not surjective, and Example 3.60 gives a case for which \(\Gamma ^M_{S,T}\) is not injective.
Example 3.59
Let \(M=D^2\) (here \(D^2 =\{x\in {{\mathbb {C}}}\vert \,|x|\le 1 \}\subset {{\mathbb {C}}}\)). Let \(N=[-a,a]\) be a closed interval in the real axis with \(0<a<1\), and let \(N'=(-a,a]\).
There is a path in \({\textbf{Top}}({{\mathbb {I}}},{\textbf{TOP}}^h(D^2,D^2))\), which we label \(\tau _{\pi }\), such that \(\tau _{\pi t}\) is a \(\pi t\) rotation of \(D^2\). Now \(\tau _{\pi }\) gives a motion from N to N, but not from \(N'\) to \(N'\). Any motion  must satisfy \(f_1(a)=a\).
must satisfy \(f_1(a)=a\).
An \(N\)-stationary motion  must satisfy, for all \(t\in {{\mathbb {I}}}\), \(s_t(a)=a\) and \(s_t(-a)=-a\), as there is no path in \(\textrm{Homeo}_{M}(N,N)\) starting at the identity and ending in a homeomorphism sending a to \(-a\). Suppose
must satisfy, for all \(t\in {{\mathbb {I}}}\), \(s_t(a)=a\) and \(s_t(-a)=-a\), as there is no path in \(\textrm{Homeo}_{M}(N,N)\) starting at the identity and ending in a homeomorphism sending a to \(-a\). Suppose  , then \({\bar{f}}*\tau _\pi {\mathop {\sim }\limits ^{p}}s\), where
, then \({\bar{f}}*\tau _\pi {\mathop {\sim }\limits ^{p}}s\), where  is some stationary motion. So we have \(({\bar{f}}*\tau _\pi )_1(a)=a\). We know \(\tau _{\pi 1}(a)=-a\), so this implies \({\bar{f}}_1(-a)=a\), and hence \(f_1(a)=-a\). So all \(f\in [\tau _\pi ]_{\text{ m }}\) satisfy \(f_1(a)=-a\). Hence \([\tau _\pi ]_{\text{ m }}\) has no preimage in \(\textrm{Mot}_{M}(N',N')\) under \(\Gamma ^{D^2}_{N'}\).
is some stationary motion. So we have \(({\bar{f}}*\tau _\pi )_1(a)=a\). We know \(\tau _{\pi 1}(a)=-a\), so this implies \({\bar{f}}_1(-a)=a\), and hence \(f_1(a)=-a\). So all \(f\in [\tau _\pi ]_{\text{ m }}\) satisfy \(f_1(a)=-a\). Hence \([\tau _\pi ]_{\text{ m }}\) has no preimage in \(\textrm{Mot}_{M}(N',N')\) under \(\Gamma ^{D^2}_{N'}\).
Notice that we do have a group isomorphism \(\Gamma ^{D^2}_{(-a,a)}:\textrm{Mot}_{D^2}((-a,a),(-a,a))\xrightarrow {\sim } \textrm{Mot}_{D^2}(N,N)\) (using the notation of Proposition 3.58). This can be shown by constructing an inverse, which is possible since a motion of a closed interval induces a motion of the open interval obtained by removing the boundary.
Example 3.60
As in the previous example, let \(M=D^2\) seen as a subset of \({{\mathbb {C}}}\). Let \(N=\{x\in {{\mathbb {C}}}\vert \; |x|=1/2 \}\) be a circle centred on the centre of the disk, and \(N'=N\setminus \{-1/2,1/2\}\), so \(N'=cl(N)\). Let \(\tau _{\pi }\) be the gradual rotation in \({\textbf{TOP}}^h(D^2,D^2)\), as constructed in Example 3.59. Then we have that  and
and  are motions.
are motions.
Notice that \(\tau _{\pi t}(N)=N\) for all \(t\in {{\mathbb {I}}}\), thus \(\tau _{\pi t}\) is a stationary motion, and  .
.
For \(N'\), \(\tau _{\pi t}(N')\ne N'\) unless \(t\in \{0,1\}\), thus we do not obtain a motion-equivalence between  and
and  in the same way. In fact
in the same way. In fact  is not path equivalent to any stationary motion. This is because \(({\textrm{Id}}_M*\tau _{\pi })_1(x)=y\), and there is no path in \(\textrm{Homeo}_{M}(N',N')\) starting at the identity and ending at a homeomorphism sending x to y. Thus \({\textrm{Id}}_M*\tau _\pi \) is not path equivalent to a stationary motion.
is not path equivalent to any stationary motion. This is because \(({\textrm{Id}}_M*\tau _{\pi })_1(x)=y\), and there is no path in \(\textrm{Homeo}_{M}(N',N')\) starting at the identity and ending at a homeomorphism sending x to y. Thus \({\textrm{Id}}_M*\tau _\pi \) is not path equivalent to a stationary motion.
Using the notation of Proposition 3.58, there is a map from \(\Gamma ^{D^2}_{N'}:\textrm{Mt}_M(N',N') \rightarrow \textrm{Mt}_M(N,N)\) sending a motion to the motion with the same underlying flow. By the previous paragraphs, this is not injective.
The following example shows that, in certain cases, we can keep track of the change to the automorphism group in a motion groupoid when a single point is removed from the subset being considered.
Example 3.61
Let \(M=S^1\) and \(N=S^1\setminus \{x\}\) where \(x\in S^1\) is any point. The group \(\textrm{Mot}_{S^1}(S^1,S^1)\) is trivial. The group \(\textrm{Mot}_{S^1}(S^1\setminus \{x\}, S^1\setminus \{x\})\cong {{\mathbb {Z}}}\), this follows from the fact that \(\textrm{Mot}_{S^1}(\{x\},\{x\})\cong {{\mathbb {Z}}}\) (Example 7.3.3) and Lemma 3.43.
An interesting question is to determine the kernel of the map \(\Gamma ^{D^2}_{{S^1{\setminus }\{x\}}}:\textrm{Mot}_{D^2}(S^1{\setminus }\{x\},S^1{\setminus }\{x\})\rightarrow \textrm{Mot}_{D^2}(S^1,S^1)\), where \(D^2\) is the 2-disk, \(S^1\) is a circle centred on the centre of the disk and x is any point in \(S^1\).
Example 3.62
Let \(N\subset {{\mathbb {I}}}^3\) a subset which is a Hopf link in the interior of \({{\mathbb {I}}}^3\). Let \(N'=N\setminus \{x\}\) where \(x\in N\) is any point. Then \(\textrm{Mot}_{{{\mathbb {I}}}^3}(N,N')=\varnothing \). There is a homomorphism \(\Gamma ^{{{\mathbb {I}}}^3}_{N'}:\textrm{Mot}_{{{\mathbb {I}}}^3}(N',N')\rightarrow \textrm{Mot}_{{{\mathbb {I}}}^3}(N,N)\). Again it would be interesting to characterise the kernel of this map.
Let \(K\subset {{\mathbb {I}}}^3\) be a subset with 2 unknotted unlinked connected components homeomorphic to \(S^1\), and let \(K'=K{\setminus } \{y\}\) where \(y\in K\) is any point. Then \(\textrm{Mot}_{M}(N,K)=\varnothing \), this can be seen by noticing that the fundamental group of the complement of N and K are different. It follows that \(\textrm{Mot}_{M}(N',K')=\varnothing \) since, if such a morphism were to exist, it would have image in \(\textrm{Mot}_{M}(N,K)\) under \(\Gamma _{N',K'}^{{{\mathbb {I}}}^3}\), contradicting the previous sentence.
Example 3.63
Let M be the torus \(T^2=S^1\times S^1\), and let \(N=S^1\times \{1\}.\) Let \(N'\) be the image of N under a Dehn twist about \(\{1\}\times S^1\). Then the curves N and \(N'\) are not isotopic so there is no path f in \({\textbf{TOP}}^h(T^2,T^2)\), starting in \({\textrm{id}}_{T^2}\) and with \(f_1(N)=N'\). However \(\textrm{Mot}_{T^2}(N,N)\cong \textrm{Mot}_{T^2}(N',N')\). This is just a case of Corollary 3.41.
For extended examples and first steps in representation theory see [MMTa].
3.8 Motions as maps from \(M\times {{\mathbb {I}}}\), schematics and movie representations
In this section we give two further equivalent ways to define motions in a manifold M, in terms of certain maps from \(M\times {{\mathbb {I}}}\). Equivalence Theorem 3.72 is significant because it indicates that we can connect to the embedded cobordism/generalised tangle picture of manifolds embedded in \(M\times {{\mathbb {I}}}\), as trailed in §1. (Note that the equivalences are still different so this does not immediately imply a functor between the two settings, this will be investigated further in Sect. 4.2.) The various definitions of motions lead us to some useful schematic representations, so we also discuss these below.
We now give an interpretation of flows, and hence motions in a manifold M as a subset of \({\textbf{Top}}(M\times {{\mathbb {I}}}, M)\).
Definition 3.64
Fix a manifold M. Let \(\textrm{Flow}_{M}^{mov}\subset {\textbf{Top}}(M\times {{\mathbb {I}}},M)\) denote the subset of elements \(g\in {\textbf{Top}}(M\times {{\mathbb {I}}},M)\) such that:
-
(I)
for all \(t\in {{\mathbb {I}}}\), \(m\mapsto g(m,t)\) is a homeomorphism \(M \rightarrow M\), and
-
(II)
for all \(m\in M\), \(g(m,0)=m\).
Let M be a manifold. Letting \(X={{\mathbb {I}}}\) and \(Y=Z=M\) in Lemma 2.10, and composing the bijection with a map flipping \({{\mathbb {I}}}\) and M in the product, gives a bijection which, by abuse of notation we label also as \(\Phi \):
Lemma 3.65
Let M be a manifold. The restriction of the map \(\Phi \) given before the lemma, yields a bijection
Proof
We have that \(\Phi \) is a bijection so we just need to check that \(\Phi (\textrm{Flow}_{M})\subseteq \textrm{Flow}_{M}^{mov}\) and that \(\Phi ^{-1}(\textrm{Flow}_{M}^{mov})\subseteq \textrm{Flow}_{M}\) where \(\Phi ^{-1}\) sends a map \(g:M\times {{\mathbb {I}}}\rightarrow M\) to the map \(t\mapsto (m\mapsto g(m,t))\).
Let \(f\in \textrm{Flow}_{M}\) be a flow. Then \(\Phi (f)|_{M\times \{t\}}=f_t\) which is a homeomorphism and \(\Phi (f)(m,0)=f_0(m)=m\). Hence \(\Phi (f)\in \textrm{Flow}_{M}^{mov}\).
Let \(g\in \textrm{Flow}_{M}^{mov}\). Then \(m\mapsto g(m,t)\) is a homeomorphism for all \(t\in {{\mathbb {I}}}\) and \(\Phi ^{-1}(g)(0)=(m\mapsto g(m,0))=id_M\). Hence \(\Phi ^{-1}(g)\in \textrm{Flow}_{M}\). \(\square \)
Let M be a manifold and \(g\in {\textbf{Top}}(M\times {{\mathbb {I}}}, M)\) be in \(\textrm{Flow}_{M}^{mov}\). Our first schematics are based on the ‘movie presentations’ of [CRS97]. A movie presentation of g consists of a number of pictures where each picture corresponds to a chosen value of t, ordered by \(t\in {{\mathbb {I}}}\). We may also add ‘grid line’ subsets in M—these help to show the homeomorphism at t of M. An example is given by Fig. 1. Here the grid lines are a polar grid at \(t=0\). By Lemma 3.65g corresponds to a motion and thus movie presentations can be considered as representations of motions. Movie presentations are used in [CRS97] for schematics representing the images of isotopies, and elements of \(\textrm{Flow}_{M}^{mov}\) are precisely isotopies.
Definition 3.66
Let M be a manifold and \(N,N'\subseteq M\). Let \(\textrm{Mt}_M^{mov}(N,N')\subseteq \textrm{Flow}_{M}^{mov}\) denote the subset of elements \(g\in \textrm{Flow}_{M}^{mov}\) such that \(g(N\times \{1\})=N'\).
Lemma 3.67
Let M be a manifold and \(N,N'\subset M\). The restriction of the map \(\Phi \) from Lemma 3.65 yields a bijection
Proof
Notice first that each \(\textrm{Mt}_M^{mov}(N,N')\) is a subset of \(\textrm{Flow}_{M}^{mov}\). We have from Lemma 3.65 that \(\Phi \) gives a bijection \(\textrm{Flow}_{M}\cong \textrm{Flow}_{M}^{mov}\) so we only need to check that \(\Phi (\textrm{Mt}_M(N,N ))\subseteq \textrm{Mt}_M^{mov}(N,N')\) and \(\Phi ^{-1}(\textrm{Mt}_M^{mov}(N,N ))\subseteq \textrm{Mt}_M(N,N')\).
Suppose  is a motion, then \(\Phi (f)(N\times \{1\})=f_1(N)=N'\). Suppose \(f'\in \textrm{Mt}_M^{mov}(N,N')\), then \(\Phi ^{-1}(f')_1(N)=f'(N\times \{1\})=N'\). \(\quad \square \)
is a motion, then \(\Phi (f)(N\times \{1\})=f_1(N)=N'\). Suppose \(f'\in \textrm{Mt}_M^{mov}(N,N')\), then \(\Phi ^{-1}(f')_1(N)=f'(N\times \{1\})=N'\). \(\quad \square \)
Using Lemma 3.67, we may add subsets to movie schematics. This can be seen in Fig. 2: the middle schematic shows a subset consisting of two points in the disk, and the right most a point and a line; the images of each subset at various ordered \(t\in {{\mathbb {I}}}\) are shown in each disk with t progressing up the page. Note that in this case we have not included grid lines. Roughly the homeomorphisms shown in Fig. 1 moves the subsets as shown in the first five disks.
Next we give our second interpretation of motions in a manifold M as a subset of \({\textbf{Top}}^h(M\times {{\mathbb {I}}}, M\times {{\mathbb {I}}})\).
Lemma 3.68
Fix a manifold M. Let \( \textrm{Flow}_{M}^{hom}\subset {\textbf{Top}}^h(M\times {{\mathbb {I}}},M\times {{\mathbb {I}}})\) denote the subset of homeomorphisms \(g\in {\textbf{Top}}^h(M\times {{\mathbb {I}}},M\times {{\mathbb {I}}})\) such that
-
(I)
\(g(m,0)=(m,0)\) for all \(m\in M\), and
-
(II)
\(g(M\times \{t\})=M\times \{t\}\) for all \(t\in {{\mathbb {I}}}\).
Remark 3.69
To prove the following we need both that \({\textbf{TOP}}^h(M,M)\) is a topological group and the product-hom adjunction of Lemma 2.10.Footnote 5
Lemma 3.70
Let M be a manifold. There is a bijection
Proof
We first check the \(\Theta \) is well defined. Let \(f\in \textrm{Flow}_{M}\). Then \(\Theta (f)\) is continuous since the projection onto the first coordinate of the map \((m,t)\mapsto (f_t(m),t)\) is \(\Phi (f)\) with \(\Phi \) as in Lemma 3.65, and the projection on the second coordinate is clearly continuous.
We also have \(\Theta (f)(m,0)=(f_0(m),0)=(m,0)\) and \(\Theta (f)(M\times \{t\})=f_t(M)\times \{t\}=M\times \{t\}\).
To complete the proof of well definedness, it remains only to check that \(\Theta (f)\) is a homeomorphism. The map \((m,t)\mapsto (f_t(m),t)\) has inverse \((m,t) \mapsto (f_t^{-1}(m),t)\). Let us see that the inverse is continuous. We have that f is a flow and so Lemma 3.5 gives that \(f^{-1}\) is a flow, specifically it is a continuous map \({{\mathbb {I}}}\rightarrow {\textbf{TOP}}(M,M)\). Hence \((m,t)\mapsto (f_t^{-1}(m),t)\), which is the image of \(f^{-1}\) under \(\Theta \), is continuous. Thus \(\Theta \) is a well defined homeomorphism.
We now show that \(\Theta \) is a bijection, by constructing an inverse. Consider the following map.
It is straightforward to check that for any \(f\in \textrm{Flow}_{M}\) we have \(\Theta ^{-1}\circ \Theta (f )=f\) and that for any \(g\in \textrm{Flow}_{M}^{hom}\) we have \(\Theta \circ \Theta ^{-1}(g)=g\). It remains to check that \(\Theta ^{-1}\) is well defined. Let \(g\in \textrm{Flow}_{M}^{hom}\). The map \(\Theta ^{-1}(g)\) is continuous as it is equal to \(\Phi ^{-1}(p_0\circ g)\), with \(\Phi \) as in Lemma 3.65.
We have \((\Theta ^{-1}(g))_0(m)=p_0\circ g(m,0)=m\) so \(\Theta ^{-1}(g)_0={\textrm{id}}_M\). For all \(t\in {{\mathbb {I}}}\) the restriction \(g|_{M\times \{t\}}\) is also a homeomorphism onto its image which, by (II) in the definition of \(\textrm{Flow}_{M}^{hom}\), is \(M\times \{t\}\). The projection \(p_0:M\times \{t\}\rightarrow M\) is an isomorphism. Hence for all \(t\in {{\mathbb {I}}}\), \(\Theta ^{-1}(g)_t= p_0\circ g|_{M\times \{t\}}\) is in \({\textbf{TOP}}^h(M,M)\). \(\quad \square \)
Flare schematic for the homeomorphism \({\textrm{Id}}_{{{\mathbb {I}}}\times {{\mathbb {I}}}}\) with \(F\subset {{\mathbb {I}}}\times {{\mathbb {I}}}\) the marked grid. This is also the image under \(\Theta \) of the constant path in \({\textbf{TOP}}^h({{\mathbb {I}}},{{\mathbb {I}}})\) starting at \({\textrm{id}}_{{{\mathbb {I}}}}\)
Flare line schematic for a non-identity self-homeomorphism of \({{\mathbb {I}}}\times {{\mathbb {I}}}\) in \(\textrm{Flow}_{M}^{hom}\). This homeomorphism restricts to the identity on the south, east and west but not the north part of the boundary. It is the image under \(\Theta \) of a path in \({\textbf{TOP}}^h({{\mathbb {I}}},{{\mathbb {I}}})\) starting at \({\textrm{id}}_{{{\mathbb {I}}}}\) (mapped to the southern edge) but not ending at \({\textrm{id}}_{{{\mathbb {I}}}}\)
We now introduce ‘flare schematic’ representations for individual flows (at least for M of low dimension). These are to be understood as follows. For a manifold M, a flare schematic represents a homeomorphism \(g:M\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\) in \(\textrm{Flow}_{M}^{hom}\), which by Lemma 3.70 represents a flow. To construct a flare schematic for g we proceed as follows. We first choose a subset \(F\subset M\times {{\mathbb {I}}}\) which is a 1-dimensional complex, i.e. the union of a set of (perhaps neatly) embedded real intervals—flare lines. The idea is to choose F such that the image of F under g reveals information about g. We note that this is only a useful exercise for sufficiently well behaved g, and in fact we consider only cases for which we have a one-size-fits-all F that is some regular array of lines. Finally we make a picture (i.e. a black-in-white-out representation of a projection onto the plane) of the subset F; together with a picture of the image g(F).
Our first examples are Figs. 4 and 5 where \(M={{\mathbb {I}}}\). The ambient space \({{\mathbb {I}}}\) is oriented horizontally left to right, and t in the second copy of \({{\mathbb {I}}}\) progresses up the page. We fix a choice of \(F\subset {{\mathbb {I}}}\) which is shown on the left hand side of both figures. The right hand figures represent the image of F under some homeomorphism in \(\textrm{Flow}_{M}^{hom}\). In Fig. 4 this is the identity morphism \({\textrm{id}}_{{{\mathbb {I}}}\times {{\mathbb {I}}}}\) and in Fig. 5 we have a non-identity homeomorphism.
Figures 6, 7, 8 and 9 show self-homeomorphisms of \(M\times {{\mathbb {I}}}\) in \(\textrm{Flow}_{M}^{hom}\) where \(M=S^1\). Again we choose a subset \(F\subset S^1\times {{\mathbb {I}}}\) which consists of the product of eight marked points in \(S^1\) with \({{\mathbb {I}}}\), together with ‘horizontal’ (in the sense of being orthogonal to \({{\mathbb {I}}}\)) lines. We have drawn \(-\times {{\mathbb {I}}}\) radially, thus marked points become radial lines, and horizontal lines will here become concentric circles. We note that in this case we vary the number of horizontal lines in F depending on each self-homeomorphism. These are by construction fixed setwise and thus are really only a guide to the eye.
We turn now to the paths themselves. The paths in \({\textbf{TOP}}(S^1,S^1)\) represented by Figs. 7 and 6 both end at a different self-homeomorphism to \({\textrm{id}}_{S^1} \). The paths represented by Figs. 8 and 9 instead both end at \({\textrm{id}}_{S^1}\).
The path in Fig. 8 is path homotopic to the constant path. The path in Fig. 9 is not.
Illustration of a path of self-homeomorphisms of the circle \(M = S^1\), realised as a homeomorphism \(M\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\). The circle is drawn together with eight marked points upon it, to reveal the space ‘moving’ under the path of self-homeomorphisms. In this case the \(-\times {{\mathbb {I}}}\) is drawn radially, outside-to-inside, rather than bottom-to-top on the page (so the drawing scale changes with radial distance; while the angular coordinate does not). The path in \({\textbf{Top}}^h(S^1, S^1)\) illustrated here does not end at the same homeomorphism in which it begins
Illustration of a path of self-homeomorphisms of the circle \(M = S^1\). Comparing with Fig. 8, both paths can be taken to start at \({\textrm{Id}}_{{\mathbb {I}}}\), and both finish at the same point
Definition 3.71
Let M be a manifold and \(N,N'\subseteq M\). Let \( \textrm{Mt}_M^{hom}(N,N') \subseteq \textrm{Flow}_{M}^{hom}\) denote the subset of homeomorphisms \(g\in \textrm{Flow}_{M}^{hom}\) such that \(g(N\times \{1\})=N'\times \{1\}\).
Theorem 3.72
Let M be a manifold and \(N,N'\subseteq M\). The restriction of \(\Theta \) as in Lemma 3.70 yields a bijection
Proof
Notice each \(\textrm{Mt}_M^{hom}(N,N')\) is a subset of \(\textrm{Flow}_{M}^{hom}\). Lemma 3.70 gives that \(\Theta \) yields a bijection \(\textrm{Flow}_{M}\cong \textrm{Flow}_{M}^{hom}\) hence we only need to check that \(\Theta (\textrm{Mt}_M(N,N'))\subseteq \textrm{Mt}_M^{hom}(N,N')\) and \(\Theta ^{-1}(\textrm{Mt}_M^{hom}(N,N'))\subseteq \textrm{Mt}_M(N,N')\).
If  is a motion, then \(\Theta (f)(N\times \{1\})=f_1(N)\times \{1\}=N'\times \{1\}\). Now suppose \(f':M\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\) is a homeomorphism with \(f'(N\times \{1\})=N'\times \{1\}\), then \(\Theta ^{-1} (f')_1(N)=p_0\circ f'(N\times \{1\})=p_0(N'\times \{1\})=N'\), so \(\Theta ^{-1}(f)\) is in \(\textrm{Mt}_M(N,N')\). \(\square \)
is a motion, then \(\Theta (f)(N\times \{1\})=f_1(N)\times \{1\}=N'\times \{1\}\). Now suppose \(f':M\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\) is a homeomorphism with \(f'(N\times \{1\})=N'\times \{1\}\), then \(\Theta ^{-1} (f')_1(N)=p_0\circ f'(N\times \{1\})=p_0(N'\times \{1\})=N'\), so \(\Theta ^{-1}(f)\) is in \(\textrm{Mt}_M(N,N')\). \(\square \)
Theorem 3.72 says that we can add subsets to flare schematics to obtain representations of motions. In Fig. 10 we have two more flare schematics corresponding to different motions in \({{\mathbb {I}}}\). Here we have omitted the image showing \(F\subset {{\mathbb {I}}}\times {{\mathbb {I}}}\) since it is the same as for Figs. 4 and 5. These schematics represent motions from various intervals, so we mark these intervals in addition to the flares. Notice that the motion represented in Fig. 10(b) is an \(N''\)-stationary motion.
Recall the from Definition 3.36 that  . The following proposition follows directly from the definition of \(\Theta :\textrm{Mt}_M(N,N')\rightarrow \textrm{Mt}_M^{hom}(N,N')\).
. The following proposition follows directly from the definition of \(\Theta :\textrm{Mt}_M(N,N')\rightarrow \textrm{Mt}_M^{hom}(N,N')\).
Proposition 3.73
For a motion  in a manifold M
in a manifold M

\(\square \)
Thus the image of the subsets progressing up the page in a flare schematic is the worldline of a motion. The worldline retains the information about the movement of the chosen subset, and forgets the information about the movement of the ambient space.
Flare schematic for motions (a) from N to \(N'\) and (b) from \(N''\) to \(N''\) in case \(M={{\mathbb {I}}}\), where \(N,N',N''\) are intervals in \({{\mathbb {I}}}\). The black represents the image of a regular grid subset of \({{\mathbb {I}}}\times {{\mathbb {I}}}\), and the grey shading represents the images of N and \(N'\), progressing up the page - the worldlines of the motions
In Fig. 11 we have an example of the \(*\) composition of motions in our flare schematic representation. Figure 11(a) simply shows the flare-schematics for two flows in a formal stack—note that this is not itself a flare-schematic for a motion, since the lines are not matched at the join. To turn this picture into a flare schematic, we must trace the images of the marked points along the bottom boundary in the top half of the schematic. This corresponds to composing with \(f_1\) in Eq. (3). In Fig. 11(b) we consider what happens when we move to motions. Lemma 3.38 gives that simply stacking (and shrinking) the flare schematics corresponding to composable motions will give a schematic with the correct worldline of the composition. Thus if we were to turn the right hand picture into a flare schematic, the bold line representing worldline will remain the same. We also have that given a formal stack of flare schematics for flows, choosing a subset along the bottom boundary and tracking it under the first flow determines a choice of subset in the second motion such that paths of self-homeomorphisms become composable motions.
A similar situation also applies to the construction of \(\bar{f}\). Suppose we have a flare schematic for a flow f and we turn it upside down (respectively inside-out in the \(S^1\) case) it is not a flare schematic of a motion, because \(f_{(1-t)}\) is not the identity at \(t=0\); but the composition with \(f_1^{-1}\) in \(\bar{f}\) ‘fixes’ this. However suppose now we add a subset and a worldline to f, then the naive ‘flip’ of the flare schematic gives the worldline of \(\bar{f}\).
Remark 3.74
If we take the definition of ambient isotopy given by, for example, [Kam02, Sec.0.3] in terms of maps \(M\times {{\mathbb {I}}}\) to \( M \times {{\mathbb {I}}}\), Definition 3.71 says precisely that \(g\in \textrm{Mt}_M^{hom}(N,N')\) is an ambient isotopy from N to \(N'\) in M. There are several other definitions of the term ‘ambient isotopy’ of subsets in the literature. The equivalences of \(\textrm{Mt}_M(N,N')\), \(\textrm{Mt}_M^{mov}(N,N')\) and \(\textrm{Mt}_M^{hom}(N,N')\) proved in Lemma 3.67 and Theorem 3.72 prove that the notions of ambient isotopy given by [Kam02] and the two notions of isotopy given by [CF63, Pg.8], in terms of maps from \(M\times {{\mathbb {I}}}\) to M and in terms of paths in \({\textbf{Top}}^h(M,M)\), are all equivalent. Thus we have that there exists a motion from N to \(N'\) in M if and only if N and \(N'\) are ambient isotopic. In particular knots K and \(K'\) in \(S^3\) are equivalent if and only if there is a motion in \(S^3\) from K to \(K'\).
4 Key Alternative Ways to Understand Motion Equivalence
In this section we give two alternative ways to understand motion equivalence. We give more details on each at the start of §4.1 and §4.2 below.
4.1 Relative path homotopy between motions
In this section we introduce the relation, relative path-homotopy on the sets \(\textrm{Mt}_M(N,N')\). We prove in Theorem 4.6 that this relation is the same as the relation \({\mathop {\sim }\limits ^{m}}\) constructed in the previous section.
Relative path-homotopy is the same equivalence relation used in the construction of the relative fundamental set \(\pi _1(X,Y,*)\) of a pointed pair of spaces. Thus it will allow us to use the relative homotopy long exact sequence to prove the relationship between motion groupoids and mapping class groupoids in Sect. 7. For X a space and f, g paths, recall the set of homotopies \({\textbf{Top}}({{\mathbb {I}}}^2, X)\!(\! f (\!\!\! ) g ) \). For M a manifold, f, g flows and \(N,N'\) subsets, let
Definition 4.1
Fix a manifold M. Define a relation on \(\textrm{Mt}_M(N,N')\) as follows. Let  if \({\textbf{Top}}({{\mathbb {I}}}^2,{\textbf{TOP}}^h(M,M))(f^{N'}_{N}\!g)\ne \varnothing \). This means that there exists a continuous map:
if \({\textbf{Top}}({{\mathbb {I}}}^2,{\textbf{TOP}}^h(M,M))(f^{N'}_{N}\!g)\ne \varnothing \). This means that there exists a continuous map:
such that:
-
for any fixed \(s\in {{\mathbb {I}}}\), \(t\mapsto H(t,s)\) is a motion from N to \(N'\), i.e. \(H(0,s)={\textrm{Id}}_M\) and \(H(1,s) \in \textrm{Homeo}_{M}(N,N')\), meaning that \(H(1,s)(N)=(N')\),
-
for all \(t\in {{\mathbb {I}}}\), \(H(t,0)=f_t\), and
-
for all \(t\in {{\mathbb {I}}}\), \(H(t,1)=g_t\).
Notation: We call such a map a relative path-homotopy, and the motions  and
and  are said to be relative path-homotopic.
are said to be relative path-homotopic.
Lemma 4.2
Fix a manifold M. For each pair \(N,N'\), the relation  is an equivalence relation on \(\textrm{Mt}_M(N,N')\).
is an equivalence relation on \(\textrm{Mt}_M(N,N')\).
Notation: We call  equivalence classes relative path-equivalence classes and use
equivalence classes relative path-equivalence classes and use  for the equivalence class of
for the equivalence class of  .
.
Figure 12 gives examples of relative path-homotopic, and non relative path-homotopic motions in our schema introduced in Fig. 3.
Let M be a manifold, and \(N,N'\subset M\) subsets. Here we use the same schema as in Fig. 3. For illustration we suppose \({\textbf{TOP}}^h(M,M)\) is a connected region of the plane homeomorphic to \(S^1\times {{\mathbb {I}}}\). The paths labelled (a), (b) and (c) represent motions from N to \(N'\) in M. There is a relative path-homotopy from (b) to (c), but not from (a) to (b) or to (c)
Proof
Let  ,
,  and
and  be motions. We can prove reflexivity by observing that the homotopy \(H(t,s)=f_t\) for all \(s\in {{\mathbb {I}}}\) is a relative path-homotopy from
be motions. We can prove reflexivity by observing that the homotopy \(H(t,s)=f_t\) for all \(s\in {{\mathbb {I}}}\) is a relative path-homotopy from  to itself.
to itself.
For symmetry let \(H_{f,g}\) be the relative path-homotopy from  to
to  . Then the function \(H_{g,f}(t,s)=H_{f,g}(t,1-s)\) is a relative path-homotopy from
. Then the function \(H_{g,f}(t,s)=H_{f,g}(t,1-s)\) is a relative path-homotopy from  to
to  .
.
For transitivity let \(H_{g,h}\) be the relative path-homotopy from  to
to  . Then
. Then
is a relative path-homotopy from  to
to  . \(\quad \square \)
. \(\quad \square \)
Recall the definition of path-equivalence from Definition 2.32 and also path-equivalence of motions, \({\mathop {\sim }\limits ^{p}}\), from Lemma 3.20.
Proposition 4.3
Let  be path-equivalent motions, then
be path-equivalent motions, then  .
.
Proof
A path-homotopy, H, from f to g has fixed endpoints, thus for fixed s, \(t\mapsto H(t,s)\) is a motion from N to \(N'\). Hence H is a relative path-homotopy from  to
to  . \(\quad \square \)
. \(\quad \square \)
Recall the construction of \(\textrm{Homeo}_{M}\) from §2.6. Morphisms in \(\textrm{Homeo}_{M}(N,N')\) are triples  , although it will often be useful to think of \(\textrm{Homeo}_{M}(N,N')\) as the projection to the first element of the triple, and further to topologise this as a subset of \({\textbf{TOP}}^h(M,M)\). The meaning will be clear from context.
, although it will often be useful to think of \(\textrm{Homeo}_{M}(N,N')\) as the projection to the first element of the triple, and further to topologise this as a subset of \({\textbf{TOP}}^h(M,M)\). The meaning will be clear from context.
Lemma 4.4
Suppose we have relative path-homotopic motions  , then
, then  .
.
Proof
Let H be a relative path-homotopy from  to
to  . We must show that
. We must show that  is path-equivalent to a stationary motion from N to N.
is path-equivalent to a stationary motion from N to N.
Notice first that \(s \mapsto H(1,1-s)\) is a path from \(f'_1\) to \(f_1\), which is in \(\textrm{Homeo}_M(N,N')\) for all s. We relabel this path as \(\gamma \). We define a path \({\tilde{\gamma }}\) by \({\tilde{\gamma }}_s=\gamma _s\circ f'^{-1}_1\), so  is a stationary motion with \({\tilde{\gamma }}_1=f_1\circ f'^{-1}_1\).
is a stationary motion with \({\tilde{\gamma }}_1=f_1\circ f'^{-1}_1\).
We can use H to construct a path-homotopy from f to the path composition \(\gamma f'\). For example, a suitable path-homotopy is:
For fixed \(s\in {{\mathbb {I}}}\), the path \(t \mapsto H_1(t,s)\) starts at the identity, traces the whole of the path \(t \mapsto H(t,s)\) followed by the part of the path \(\gamma \) starting from \(\gamma _{1-s}=H(1,s)\) and ending at \(\gamma _1\). Note that the path composition, \(\gamma f'\) is precisely the motion composition \({\tilde{\gamma }}*f'\), so \(f{\mathop {\sim }\limits ^{p}}{\tilde{\gamma }}*f'\).
By Lemma 3.20, path-equivalence is a congruence on the magmoid \(\textrm{Mt}_M^{*}\) (see Proposition 3.18), hence we have that \({\bar{f}}'*f\) is path-equivalent to \( {\bar{f}}'*({\tilde{\gamma }} * f')\).
Now recall that  is stationary. Therefore, using the normalcy of the subgroupoid \(\overline{\textrm{SetStat}}_{M}(N,N)\) of \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\), proved in Lemma 3.29, it follows that the motion
is stationary. Therefore, using the normalcy of the subgroupoid \(\overline{\textrm{SetStat}}_{M}(N,N)\) of \(\textrm{Mt}_M/{\mathop {\sim }\limits ^{p}}\), proved in Lemma 3.29, it follows that the motion  is path-equivalent to a stationary motion from N to N. Hence
is path-equivalent to a stationary motion from N to N. Hence  is path-equivalent to a stationary motion. \(\quad \square \)
is path-equivalent to a stationary motion. \(\quad \square \)
Lemma 4.5
Suppose we have motion-equivalent motions  . Then we have
. Then we have  .
.
Proof
We have from Theorem 3.32 that \(\textrm{Mot}_{M}\) is a groupoid. Hence it follows from the uniqueness of inverses that  implies
implies  . Thus there exists a path-homotopy, say H, from \(f'*{\bar{f}}\) to a stationary motion
. Thus there exists a path-homotopy, say H, from \(f'*{\bar{f}}\) to a stationary motion  .
.
We also have that  . To prove this we can use the following function:
. To prove this we can use the following function:
Notice that \(H_1(t,0)\) is the path f and \(H_1(t,1)\) is the path \( \gamma *f\). For any fixed \(s\in {{\mathbb {I}}}\), we have \(H_1(0,s)={\textrm{id}}_M\), and also:
Note that \(H_1\) is continuous as both functions agree when \(t=1-\frac{s}{2}\). Hence we have that \(H_1\) is a relative path-homotopy, proving that 
Using the associativity of \(\cdot \) (Proposition 3.19) together with Lemma 3.9, the fact that \(*\) and \(\cdot \) composition are the same up to path-equivalence, the fact that path-equivalence is a congruence on motions (Lemma 3.20), and that \({\bar{f}}*f{\mathop {\sim }\limits ^{p}}{\textrm{Id}}_M\) (Lemma 3.23), we have
so \(\gamma *f{\mathop {\sim }\limits ^{p}}f'\).
Since path-equivalence implies relative path-equivalence (Proposition 4.3), we have  , and hence we have
, and hence we have  . \(\square \)
. \(\square \)
All proofs in this section work in exactly the same way restricting to A-fixing motions, and defining A-fixing relative path-homotopies between A-fixing motions in the obvious way. Hence from Lemmas 4.4 and 4.5 we have:
Theorem 4.6
For a manifold M and an A-fixing motion  in M we have
in M we have

In particular, quotienting \(\textrm{Mt}_M^A\) by relative path-equivalence leads to the same groupoid as quotienting by motion-equivalence. \(\quad \square \)
Remark 4.7
Let M be a manifold. Combining Theorems 3.32 and 4.6 we hence can see that the motion groupoid \(\textrm{Mot}_{M}\) is such that given \(N,N'\subset M\) then \(\textrm{Mot}_{M}(N,N')\) is the set of relative path homotopy classes of motions  . The composition of
. The composition of  with
with  is
is  , which by Lemma 3.9 is the same as
, which by Lemma 3.9 is the same as  . In particular, indeed the compositions \(*\) and \(\cdot \) in the magmoids \(\textrm{Mt}_M^{\;\cdot }\) and \(\textrm{Mt}_M^{\;*}\) (the notation is as in §3.2) do descend to the quotient under
. In particular, indeed the compositions \(*\) and \(\cdot \) in the magmoids \(\textrm{Mt}_M^{\;\cdot }\) and \(\textrm{Mt}_M^{\;*}\) (the notation is as in §3.2) do descend to the quotient under  .
.
For instance, if  are relative path-homotopic via \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) and
are relative path-homotopic via \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) and  are relative path-homotopic via \(J:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\), then the functions \(K,K':{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) below are relative path-homotopies connecting
are relative path-homotopic via \(J:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\), then the functions \(K,K':{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) below are relative path-homotopies connecting  to
to  , and
, and  to
to  , respectively,
, respectively,
The same formulae also work in the A-fixing case.
Remark 4.8
Suppose that the motions  have the same worldline (Definition 3.36), then they are motion equivalent, by Proposition 3.37. By Theorem 4.6 it follows that
have the same worldline (Definition 3.36), then they are motion equivalent, by Proposition 3.37. By Theorem 4.6 it follows that  and
and  are relative path-homotopic. An explicit relative path-homotopy from
are relative path-homotopic. An explicit relative path-homotopy from  to
to  , is, for example, \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\), defined as:
, is, for example, \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\), defined as:
To see that H is a relative path-homotopy, note that if \(s \in I\) then \(g_s(N)=f_s(N)\). As above, the same formulae also work in the A-fixing case.
4.2 Level preserving isotopies between worldlines of motions
Recall from Definition 3.36 that the worldline of a motion  in M is
in M is

In Sect. 3.5 we had Proposition 3.37, which said that two motions represent the same morphism in the groupoid \(\textrm{Mot}_{M}\) if their worldlines are the same; cf. also Remark 4.8 just above. Here we prove that we can strengthen this result, by which we mean that we can formulate motion equivalence entirely in terms of a relation on worldlines of motions.
We begin by defining when two subsets of a space of the form \(M\times {{\mathbb {I}}}\) are level preserving ambient isotopic relative to some fixed subsets. The main result in this section is Theorem 4.18 which says that two motions are motion-equivalent if, and only if, their worldlines are level preserving ambient isotopic relative to \(M\times (\{0\}\cup \{1\})\), pointwise.
The following definitions of level preserving homeomorphism and level preserving isotopy can be found in [Wal68].
Definition 4.9
For a space M, a homeomorphism \(f:M\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\) is called level preserving if it is of the form \(f(m,t)=(p_0\circ f(m,t),t)\), where \(p_0\) is the projection to the first component of the product.
Definition 4.10
For a space M, a level preserving isotopy of \(M\times {{\mathbb {I}}}\) is an isotopy of \(M\times {{\mathbb {I}}}\) through level preserving maps. This means there exists a continuous map \( H:(M\times {{\mathbb {I}}})\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\), such that:
-
for each fixed \(s\in {{\mathbb {I}}}\), \((m,t)\mapsto H(m,t,s)\) is a level preserving homeomorphism from \(M\times {{\mathbb {I}}}\) to \(M\times {{\mathbb {I}}}\),
-
for all \(m\in M\) and \(t\in {{\mathbb {I}}}\), \(H(m,t,0)=(m,t)\).
Remark 4.11
Definition 4.10 says that a level preserving isotopy of \(M\times {{\mathbb {I}}}\) is an element of \(\textrm{Flow}_{M\times {{\mathbb {I}}}}^{mov}\) (Definition 3.64), and thus it is in canonical correspondence with a flow of \(M\times {{\mathbb {I}}}\). We will be using the existence of level preserving isotopies to construct an equivalence relation between subsets of \(M\times {{\mathbb {I}}}\), rather then keeping track of the isotopy itself. Therefore we use the term “isotopy”, rather than “flow”, since we feel it is unhelpful to conflate the two notions.
Definition 4.12
Let M be a space, and let \(E,P\subseteq M\times {{\mathbb {I}}}\) be fixed subsets. Two subsets \(K,L\subseteq M\times {{\mathbb {I}}}\) are level preserving ambient isotopic, relative to E setwise and P pointwise, if there is a level preserving isotopy of \(M\times {{\mathbb {I}}}\), such that:
-
\(H(K\times \{1\})=L\),
-
for all \(s\in {{\mathbb {I}}}\), \(H(E\times \{s\})=E\), and
-
for all \(p\in P\), and \(s\in {{\mathbb {I}}}\), \(H(p,s)=p\).
We will say that H is a level preserving isotopy, relative to E setwise and P pointwise, from, or connecting, K to L.
Lemma 4.13
For a space M, and subsets \(K,L \subset M\times {{\mathbb {I}}}\), \(K\sim L\) if there exists a level preserving isotopy \(M\times {{\mathbb {I}}}\) from K to L, relative to E setwise and P pointwise, is an equivalence relation on subsets of \(M\times {{\mathbb {I}}}\).
Proof
Let \(J,K,L\subseteq M\times {{\mathbb {I}}}\) be subsets, such that there are level preserving ambient isotopies relative to E setwise and P pointwise, \(H_1:(M\times {{\mathbb {I}}})\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\), from J to K, and \(H_2:(M\times {{\mathbb {I}}})\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\), from K to L. Reflexivity is proved by choosing the map \((m,t,s)\mapsto (m,t)\) which relates K to itself.
Let \(f:M\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\) be the inverse of the homeomorphism \((m,t) \mapsto H_1(m,t,1)\). The map \((m,t,s)\mapsto H_1(f(m,t),1-s)\) then relates K to J, so we have symmetry.
For transitivity, we may choose the map \((M\times {{\mathbb {I}}})\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\), \((m,t,s)\mapsto H_2(H_1(m,t,s),s)\), which relates J to L. \(\quad \square \)
Remark 4.14
By Remark 4.11 level preserving isotopies are flows, thus they can be composed as flows. In the previous proof, we essentially used the \(\cdot \) composition to prove transitivity, we could have also used \(*\) composition and used Lemma 2.12 to prove continuity, as opposed to Theorem 2.11. On the other hand, symmetry was proven by using the reverse of flows in Proposition 3.11.
Below we have two theorems proving that two a priori different equivalence relations on worldlines of motions, each defined using level preserving ambient isotopies, both induce the same equivalence relation on motions as motion equivalence.
Lemma 4.15
Let M be a manifold. Suppose we have motion equivalent motions  in M, and so, by Theorem 4.6, there exists a relative path homotopy, say \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\), from f to \(f'\). Then there exists a continuous map:
in M, and so, by Theorem 4.6, there exists a relative path homotopy, say \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\), from f to \(f'\). Then there exists a continuous map:
Moreover \({\hat{H}}\) is a level preserving ambient isotopy from the worldline  to the worldline
to the worldline  , relative to \(M\times \{0\}\) pointwise, and \(N'\times \{1\}\) setwise.
, relative to \(M\times \{0\}\) pointwise, and \(N'\times \{1\}\) setwise.
Proof
We first prove that \({\hat{H}}\) is continuous. Define a map \(H':{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) by \((t,s)\mapsto H(t,s)\circ f_t^{-1}\). This is continuous since, by Theorem 2.11, \({\textbf{TOP}}^h(M,M)\), with composition, is a topological group. Notice in particular, that for all \(t\in {{\mathbb {I}}}\), \(H'(t,0)={\textrm{id}}_M\). Using the bijection \(\Phi \), following from the product-hom adjunction (Lemma 2.10), with \(X={{\mathbb {I}}}\times {{\mathbb {I}}}\), \(Y=M\) and \(Z=M\), we have a continuous map \(\Phi (H'):M\times {{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow M\). The map \({\hat{H}}:M\times {{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\) is explicitly defined by:
which is continuous since each component is continuous.
From its construction, it is immediate that \({\hat{H}}:M\times {{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\) is a level preserving isotopy, and it follows directly from the definition of a relative path homotopy (Definition 4.1) that \({\hat{H}}\) fixes \(M\times \{0\}\) pointwise, and \(N'\times \{1\}\) setwise.
Now note that:

\(\square \)
Conversely we have the following.
Lemma 4.16
Let M be a manifold and let  be motions in M. Suppose that their worldlines
be motions in M. Suppose that their worldlines  and
and  are level preserving ambient isotopic, relative to \(M\times \{0\}\) pointwise and \(N'\times \{1\}\) setwise. Then
are level preserving ambient isotopic, relative to \(M\times \{0\}\) pointwise and \(N'\times \{1\}\) setwise. Then  .
.
Proof
There exists a level preserving isotopy, say \(H:M\times {{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\), from  to
to  , relative to \(M\times \{0\}\) pointwise and \(N'\times \{1\}\) setwise. We construct a motion
, relative to \(M\times \{0\}\) pointwise and \(N'\times \{1\}\) setwise. We construct a motion  , and a relative path homotopy \({\hat{H}}\) from
, and a relative path homotopy \({\hat{H}}\) from  to
to  , and then show that
, and then show that  . It follows (by Proposition 3.37) that the motions
. It follows (by Proposition 3.37) that the motions  and
and  are motion equivalent, and hence
are motion equivalent, and hence  .
.
There is a continuous map from \(M\times {{\mathbb {I}}}\times {{\mathbb {I}}}\) to M given by \((m,t,s)\mapsto p_0\big ( H(f_t(m),t,s)\big )\), where \(p_0\) is the projection to the first coordinate. Applying the bijection \(\Phi ^{-1}\), as in the proof of the product-hom adjunction (Lemma 2.10), we obtain a continuous map \({\hat{H}}:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\), defined by \((t,s)\mapsto \big (m\mapsto p_0 (H(f_t(m),t,s)) \big )\). Notice that \({\hat{H}}(t,0)=f_t\), because \(H(m,t,0)=(m,t)\).
Let \(g_t={\hat{H}}(t,1)\). Then by construction \(t \mapsto g_t\) is a path in \({\textbf{TOP}}^h(M,M)\), starting at \({\textrm{id}}_M\). (It starts at \({\textrm{id}}_M\) given that H is relative to \(M\times \{0\}\), pointwise.) Also
(Where we now used the fact that H is relative to \(N'\times \{1\}\), setwise.) So we have a motion  . Moreover, using again that \(H(N'\times \{1\} \times \{s\})=N'\times \{1\}\), for all \(s \in {{\mathbb {I}}}\), the function \({\hat{H}}\) is a relative path homotopy from
. Moreover, using again that \(H(N'\times \{1\} \times \{s\})=N'\times \{1\}\), for all \(s \in {{\mathbb {I}}}\), the function \({\hat{H}}\) is a relative path homotopy from  to
to  , and hence, using Theorem 4.6,
, and hence, using Theorem 4.6,  .
.
The worldline of g is the same as the worldline of \(f'\), since we have

\(\square \)
Theorem 4.17
Let M be a manifold. Let A be a subset of M. Two A-fixing motions  in M are motion equivalent if, and only if, their worldlines are level preserving ambient isotopic, relative to \((M\times \{0\})\cup (A\times {{\mathbb {I}}})\) pointwise, and \(N'\times \{1\}\) setwise.
in M are motion equivalent if, and only if, their worldlines are level preserving ambient isotopic, relative to \((M\times \{0\})\cup (A\times {{\mathbb {I}}})\) pointwise, and \(N'\times \{1\}\) setwise.
Proof
Lemma 4.15 gives that motion equivalence implies a level preserving ambient isotopy between the worldlines relative to \(M\times \{0\}\) pointwise, and \(N'\times \{1\}\) setwise. It is straightforward to check that \({\hat{H}}\), as in the previous proof, is relative to \(A\times {{\mathbb {I}}}\) pointwise if H fixes A.
Lemma 4.16 gives the reverse implication, and again it is straightforward to check that the constructed relative path homotopy is A-fixing if the level preserving isotopy H fixes \(A\times {{\mathbb {I}}}\). \(\quad \square \)
The previous result can be refined.
Theorem 4.18
Let M be a manifold. Let A be a subset of M. Two A-fixing motions  are motion equivalent if, and only if, their worldlines are level preserving ambient isotopic, relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\), pointwise.
are motion equivalent if, and only if, their worldlines are level preserving ambient isotopic, relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\), pointwise.
Proof
Suppose that the worldlines  and
and  are level preserving ambient isotopic, relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\), pointwise. Then, clearly, using the same isotopy, they are level preserving ambient isotopic, relative to \((M\times \{0\})\cup (A\times {{\mathbb {I}}})\), pointwise, and to \(N'\times \{1\}\), setwise. Using Theorem 4.17, we see that
are level preserving ambient isotopic, relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\), pointwise. Then, clearly, using the same isotopy, they are level preserving ambient isotopic, relative to \((M\times \{0\})\cup (A\times {{\mathbb {I}}})\), pointwise, and to \(N'\times \{1\}\), setwise. Using Theorem 4.17, we see that  .
.
Now suppose  . By Lemma 3.21, there is a path homotopy \(F:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) from f to \({\textrm{Id}}_M*f\). Since F is a path homotopy, it has fixed endpoints and so, for all \(s\in {{\mathbb {I}}}\), we have \(F(0,s)={\textrm{id}}_M\) and \(F(1,s)=f_1\). Therefore, \({\hat{F}}\), constructed as in Lemma 4.15:
. By Lemma 3.21, there is a path homotopy \(F:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) from f to \({\textrm{Id}}_M*f\). Since F is a path homotopy, it has fixed endpoints and so, for all \(s\in {{\mathbb {I}}}\), we have \(F(0,s)={\textrm{id}}_M\) and \(F(1,s)=f_1\). Therefore, \({\hat{F}}\), constructed as in Lemma 4.15:
is a level preserving ambient isotopy from  to
to  , which is relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\) pointwise. Similarly there is a path homotopy \(F'\) from \({\textrm{Id}}_M*f' \) to \(f'\). The same construction gives a level preserving ambient isotopy \(\hat{F'}\) from
, which is relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\) pointwise. Similarly there is a path homotopy \(F'\) from \({\textrm{Id}}_M*f' \) to \(f'\). The same construction gives a level preserving ambient isotopy \(\hat{F'}\) from  to
to  which is relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\) pointwise.
which is relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\) pointwise.
It remains to construct a level preserving ambient isotopy from  to
to  , which is relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\) pointwise. Since
, which is relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\) pointwise. Since  , there exists a relative path homotopy \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) from f to \(f'\). Thus there exists a level preserving isotopy \({\hat{H}}:M\times {{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\) from
, there exists a relative path homotopy \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) from f to \(f'\). Thus there exists a level preserving isotopy \({\hat{H}}:M\times {{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\) from  to
to  , relative to \((M\times \{0\})\cup (A\times {{\mathbb {I}}})\) pointwise and \(N'\times \{1\}\) setwise, constructed as in Lemma 4.15.
, relative to \((M\times \{0\})\cup (A\times {{\mathbb {I}}})\) pointwise and \(N'\times \{1\}\) setwise, constructed as in Lemma 4.15.
We now consider the function \({\hat{J}}:M\times {{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\), defined as:
Let us see that \({\hat{J}}\) is a level preserving isotopy of \(M\times {{\mathbb {I}}}\), relative to \(M\times \{0,1\}\), pointwise. By construction, it follows that, for each \(s\in {{\mathbb {I}}}\), we have a level preserving homeomorphism \(M\times {{\mathbb {I}}}\rightarrow M\times {{\mathbb {I}}}\), sending (m, t) to \({\hat{J}}(m,t,s)\), and also that \(J(m,t,0)=(m,t).\) That \({\hat{J}}\) is relative to \(M\times \{0\}\) pointwise, follows directly from the fact that \({\hat{H}}\) is so. Moreover for all \(m\in M\), \(s\in {{\mathbb {I}}}\), \({\hat{J}}(m,1,s)=(m,1)\) since \( {\hat{H}}(m,1,0)=(m,1)\). That \({\hat{J}}\) is relative to \(A\times {{\mathbb {I}}}\) pointwise follows directly from the fact that H fixes A.
We now show that \({\hat{J}}\) is a level preserving ambient isotopy from  to
to  . First notice that for all \(t\in [1/2,1]\) and \(s\in {{\mathbb {I}}}\), \({\hat{J}}(N'\times \{t\}\times \{s\})=N'\times \{t\}\), since \({\hat{H}}(N'\times \{1\}\times \{s\})=N'\times \{1\}\). We have
. First notice that for all \(t\in [1/2,1]\) and \(s\in {{\mathbb {I}}}\), \({\hat{J}}(N'\times \{t\}\times \{s\})=N'\times \{t\}\), since \({\hat{H}}(N'\times \{1\}\times \{s\})=N'\times \{1\}\). We have

\(\square \)
Remark 4.19
Suppose that  are motion equivalent, fixing A. In the proof of Theorem 4.18, we constructed a level preserving isotopy from
are motion equivalent, fixing A. In the proof of Theorem 4.18, we constructed a level preserving isotopy from  to
to  , relative to \(M\times \{0,1\} \cup A\times {{\mathbb {I}}}\), pointwise, by concatenating three level preserving isotopies.
, relative to \(M\times \{0,1\} \cup A\times {{\mathbb {I}}}\), pointwise, by concatenating three level preserving isotopies.
There are other ways to construct such a level preserving isotopy from  to
to  . Let us show another construction.
. Let us show another construction.
Since  are motion equivalent, fixing A, then
are motion equivalent, fixing A, then  is path-homotopic, in \({\textbf{TOP}}_A^h(M,M)\), see §3.6, to an N-stationary motion
is path-homotopic, in \({\textbf{TOP}}_A^h(M,M)\), see §3.6, to an N-stationary motion  , fixing A; we are using the notation in Lemma 3.8. (Recall also that \((f^{-1})_t=f_t^{-1}.\)) Applying Lemma 3.21, it follows that there exists a path-homotopy from
, fixing A; we are using the notation in Lemma 3.8. (Recall also that \((f^{-1})_t=f_t^{-1}.\)) Applying Lemma 3.21, it follows that there exists a path-homotopy from  to \(f\cdot \eta \cdot g^{-1}:N \rightarrow N\), fixing A. Call it \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_A(M,M).\) Then the function below is a level preserving isotopy from
to \(f\cdot \eta \cdot g^{-1}:N \rightarrow N\), fixing A. Call it \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_A(M,M).\) Then the function below is a level preserving isotopy from  to
to  , relative to \(M\times \{0,1\} \cup A\times {{\mathbb {I}}}\), pointwise:
, relative to \(M\times \{0,1\} \cup A\times {{\mathbb {I}}}\), pointwise:
The previous theorem allows us to give a proof of the (well-known) result that the automorphism group of a point in the motion groupoid \({{\mathbb {R}}}^n\) is trivial.
Example 4.20
Consider \(M=V\), where V is a finite dimensional space, with the unique Hausdorff topology that makes it a topological vector space. (In the case when \(V={{\mathbb {R}}}^n\), then this is just \({{\mathbb {R}}}^n\), with the usual topology.) Note that V is a manifold. Let \(v \in V\). Let us determine \(\textrm{Mot}_{V}(\{v\},\{v\})\).
Let  be any motion. Let us prove that f is motion equivalent to the identity motion
be any motion. Let us prove that f is motion equivalent to the identity motion  For each \(t \in [0,1]\), let \(v_t=v-f_t(v)\). Hence \(v_0=v_1=\textbf{0}\), the zero vector in V. Also the mapping \(t \in {{\mathbb {I}}}\mapsto v_t \in V\) is continuous. Consider the mapping
For each \(t \in [0,1]\), let \(v_t=v-f_t(v)\). Hence \(v_0=v_1=\textbf{0}\), the zero vector in V. Also the mapping \(t \in {{\mathbb {I}}}\mapsto v_t \in V\) is continuous. Consider the mapping
Then clearly H is a level preserving isotopy of \(V\times I\), which is relative to \(V\times \{0,1\}\), pointwise. Also clearly:

So, by Theorem 4.18,  is motion equivalent to the identity motion
is motion equivalent to the identity motion 
The same argument, with the obvious modifications, proves that that the full subcategory of \(\textrm{Mot}_{V}\), with objects the singletons has a unique arrow between each ordered pair of objects.
Definition 4.21
Let M be a manifold, A a subset of M, and \(N,N'\subseteq M\) be subsets. Define a relation on \(\textrm{Mt}_M(N,N')\) by  if
if  , or if \(f{\mathop {\sim }\limits ^{p}}f'\) (here \(f{\mathop {\sim }\limits ^{p}}f'\) means that f and \(f'\) are path-homotopic, as maps \({{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_A(M,M)\)). Let \({\mathop {\sim }\limits ^{w}}\) be the equivalence (i.e. transitive, symmetric and reflexive) closure of this relation. Denote the class of a motion
, or if \(f{\mathop {\sim }\limits ^{p}}f'\) (here \(f{\mathop {\sim }\limits ^{p}}f'\) means that f and \(f'\) are path-homotopic, as maps \({{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_A(M,M)\)). Let \({\mathop {\sim }\limits ^{w}}\) be the equivalence (i.e. transitive, symmetric and reflexive) closure of this relation. Denote the class of a motion  under this relation by
under this relation by 
Theorem 4.22
Let M be a manifold and \(N,N'\subseteq M\) be subsets, and  be an A-fixing motion for some \(A\subset M\). Then
be an A-fixing motion for some \(A\subset M\). Then

Proof
By Proposition 3.37, motions which have the same worldline are motion equivalent, and path equivalent motions are motion equivalent (Proposition 3.30). Each of these results works in the same way in the A-fixing case. Hence \({\mathop {\sim }\limits ^{w}}\) implies \({\mathop {\sim }\limits ^{m}}\).
Suppose two motions  are motion equivalent, fixing A. Then, by Theorem 4.18, there exists a level preserving ambient isotopy H relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\) from
are motion equivalent, fixing A. Then, by Theorem 4.18, there exists a level preserving ambient isotopy H relative to \((M\times (\{0,1\}))\cup (A\times {{\mathbb {I}}})\) from  to
to  From such an H, the map \({\hat{H}}:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) constructed as in the proof of Lemma 4.16 is a path homotopy from the motion f to a motion g, with
From such an H, the map \({\hat{H}}:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h(M,M)\) constructed as in the proof of Lemma 4.16 is a path homotopy from the motion f to a motion g, with  Thus \(f{\mathop {\sim }\limits ^{w}}g{\mathop {\sim }\limits ^{w}}f'\). \(\quad \square \)
Thus \(f{\mathop {\sim }\limits ^{w}}g{\mathop {\sim }\limits ^{w}}f'\). \(\quad \square \)
Remark 4.23
Note that the main idea of the second step of the proof of the previous theorem is that if  are motion equivalent, fixing A, then f is path-homotopic to g, where g has the same worldline as \(f'\). Again, there are multiple ways to construct such a path-homotopy. Alternatively to what we did in the proof, we can for instance use the following construction. We know that
are motion equivalent, fixing A, then f is path-homotopic to g, where g has the same worldline as \(f'\). Again, there are multiple ways to construct such a path-homotopy. Alternatively to what we did in the proof, we can for instance use the following construction. We know that  is path-homotopic to
is path-homotopic to  , N-stationary. So we have a path-homotopy \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_A(M,M)\) from
, N-stationary. So we have a path-homotopy \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_A(M,M)\) from  to
to  . Now note that the later motion has the same worldline as \(f'\).
. Now note that the later motion has the same worldline as \(f'\).
5 The Groupoid \(\textrm{FMot}_{M}^A\): Connections to Artin Braids
Recall from §1 that we define an engine as a construction that takes a manifold (possibly with a subset) as input and produces a power-set magmoid, and ultimately a groupoid, as output. More specifically we have in mind that the group obtained when the engine is restricted all the way down to fixed finite subsets of \({{\mathbb {R}}}^2\), is some version of the braid group. In this section we begin by giving an engine that, when restricted to fixed finite subsets of \({{\mathbb {R}}}^2\), coincides with the definition of Artin braids [Art47]. Our definition also generalises that of [Dah62, Sec.II], who defined braids similarly to Artin, albeit in general topological manifolds.
We call our morphisms here, prior to applying any equivalence, ‘fake motions’. The quotient of the magmoid of fake motions by strong isotopy is then a groupoid, \(\textrm{FMot}_{M}^A\) (where \(A\subseteq M\)). There is a ‘forgetful’ functor \(\textbf{T}:\textrm{Mot}_{M}^A \rightarrow \textrm{FMot}_{M}^A\).
In Sect. 5.3 we will restrict to the full subgroupoids of \(\textrm{Mot}_{M}^A\) and \(\textrm{FMot}_{M}^A\) with objects the set of finite subsets of a manifold. (Essentially treated by Dahm in the group case.) As we will see, the functor \(\textbf{T}\) will then restrict to an isomorphism between the full subgroupoids. Since for a finite subset \(K\subset {{\mathbb {R}}}^2\), \(\textrm{FMot}_{{{\mathbb {R}}}^2}(K,K)\) is isomorphic to the braid group on |K| strands, \({\textbf{B}}_{|K|}\), we can then use Artin’s presentation of braid groups [Art47] to prove that certain subgroupoids of our construction of motion groupoids have finite presentation.
In addition to relating them to classical constructions, in §5.1 we can also consider another overarching question: how should we think of these algebraic structures that we construct—how useful are they? This raises the interesting question of how to characterise magmoids generally—a hard problem because they are often very wild, and their representation theory is presently in its infancy. One of the simplest non-trivial questions we can ask, is how to parameterise the connected components of a given magmoid.
5.1 The magmoid \(\textrm{FMt}_{M}\) of fake motions and its connected components
Consider a manifold M and a subset \(N\subseteq M\) and define \({\textbf{Top}}_{{\textbf{B}}{}}(N\times {{\mathbb {I}}},M)\) to be the subset of elements \(f\in {\textbf{Top}}(N\times {{\mathbb {I}}},M)\) such that:
-
(I)
for each \(t\in {{\mathbb {I}}}\), the map from N to M given by \(n \mapsto f(n,t)\) is an embedding, and
-
(II)
for all \(n \in N\), \(f(n,0)=n\).
We note that, when N is a submanifold of M, a common name for an element of \({\textbf{Top}}_{{\textbf{B}}{}}(N\times {{\mathbb {I}}},M)\) is an isotopy of N inside M.
Definition 5.1
Let \(N,N'\subseteq M\). We say that \(f \in {\textbf{Top}}_{{\textbf{B}}{}}(N\times {{\mathbb {I}}},M)\) is a fake motion, from N to \(N'\), and we write  , if \(f(N,1)=N'\). Denote by \( {\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\subseteq {\textbf{Top}}_{{\textbf{B}}{}}(N\times {{\mathbb {I}}},M)\), the subset of fake motions from N to \(N'\). (Note here that \(N,N'\) are necessarily homeomorphic via \(f(-,1)\).)
, if \(f(N,1)=N'\). Denote by \( {\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\subseteq {\textbf{Top}}_{{\textbf{B}}{}}(N\times {{\mathbb {I}}},M)\), the subset of fake motions from N to \(N'\). (Note here that \(N,N'\) are necessarily homeomorphic via \(f(-,1)\).)
The reason for the nomenclature ‘fake motion’ of N in M is that it looks like f describes a reversible evolution of N over time, but there is no intrinsic guarantee that there is a deformation of M that will induce f. We return to this point shortly.
Lemma 5.2
Let M be a manifold. There is a partial composition of fake motions  that maps (f, g) to
that maps (f, g) to  , formally given by
, formally given by

Hence  is a magmoid of fake motions. We denote it \(\textrm{FMt}_{M}\).
is a magmoid of fake motions. We denote it \(\textrm{FMt}_{M}\).
Proof
Observe first that the second row of (8) gives a well-defined map in \( {\textsf{Set}}(N\times [1/2,1],M)\) by the matching middle \(N'\) of the domain of  . Furthermore, since \(g(f(n,1),0)=f(n,1)\), the segments agree at \(t=1/2\), hence
. Furthermore, since \(g(f(n,1),0)=f(n,1)\), the segments agree at \(t=1/2\), hence  is well-defined. Since
is well-defined. Since  is continuous when restricted to \(N\times [0,1/2]\) and \(N\times [1/2,1]\), closed subsets of \(N\times {{\mathbb {I}}}\), it follows that
is continuous when restricted to \(N\times [0,1/2]\) and \(N\times [1/2,1]\), closed subsets of \(N\times {{\mathbb {I}}}\), it follows that  is continuous.
is continuous.
It is immediate that the map  , such that
, such that  is an embedding, whenever \(t \in [0,1/2]\). If \(t \in [1/2,1]\), the map
is an embedding, whenever \(t \in [0,1/2]\). If \(t \in [1/2,1]\), the map  is an embedding as it is the composition of the homeomorphisms \(N \ni n \mapsto f(n,1) \in N'\) with the embedding \(N'\ni n' \mapsto g(n',2t-1) \in M\). Finally, \(g(f(N,1),1)=g(N',1)=N''\).
is an embedding as it is the composition of the homeomorphisms \(N \ni n \mapsto f(n,1) \in N'\) with the embedding \(N'\ni n' \mapsto g(n',2t-1) \in M\). Finally, \(g(f(N,1),1)=g(N',1)=N''\).
\(\square \)
We return now to the question of which objects are connected in \(\textrm{FMt}_{M}\). The following examples will be sufficient to intrigue the reader.
Example 5.3
Let \(x\in (0,1)\) be any point. There exists \(f\in {\textbf{Top}}_{{\textbf{B}}{}}(\{x\}\times {{\mathbb {I}}},[0,1])\), given by \(f(x,t)=x(1-t)\). So we have a fake motion  , sending an interior point in \({{\mathbb {I}}}\) to a boundary point.
, sending an interior point in \({{\mathbb {I}}}\) to a boundary point.
The following example gives a concrete way to write down the process, see e.g. [BZH13, page 2], of deforming any knot, here a string knot, continuously into an unknotted string knot, in a way that cannot in general be induced by a movement of space.
Example 5.4
Let \(M= [-1,1]\times {{\mathbb {R}}}^2\), with the topology induced by \({{\mathbb {R}}}^3\). We let \(g:[-1,1] \rightarrow M\) be an embedding (so equivalently, since \([-1,1]\) is compact, g is continuous and injective), such that \(g(-1)=(-1,0,0)\) and \(g(1)=(1,0,0)\). Also suppose that \(g\big ( (-1,1)\big ) \subset \textrm{int}(M)\). Let \(K=g([-1,1])\subset M\). Observe that K is a (possibly wild and also non-trivial) string knot. And then consider \(H:[-1,1] \times {{\mathbb {I}}}\rightarrow M\), defined as:
Define \(f:K \times {{\mathbb {I}}}\rightarrow M\) as \(f(k,t)=H(g^{-1}(k),t)\). We then have a fake motion from K to the trivial string knot \([-1,1] \times \{(0,0)\}\).
Example 5.5
Let \(M={{\mathbb {R}}}^2\), \(S^1=\{x\in {{\mathbb {R}}}^2 \,|\, |x|=1\}\) and \(y\in S^1\) be any point. Then it is straightforward to construct a fake motion  . Similarly, if \(H'\) is the Hopf link, with one point taken out of one of the components, then there exists a fake motion
. Similarly, if \(H'\) is the Hopf link, with one point taken out of one of the components, then there exists a fake motion  , where \(L'\) is the unlink, where we have taken a point out of one of the components.
, where \(L'\) is the unlink, where we have taken a point out of one of the components.
This leads us naturally back to the question of connection to the other structures introduced in this paper, and indeed to classical constructions. To address both of these, we proceed as follows.
Recall from Lemma 3.67 that there is a bijection \(\Phi :\textrm{Mt}_M(N,N')\rightarrow \textrm{Mt}_M^{mov}(N,N')\subset {\textbf{Top}}(M\times {{\mathbb {I}}},M)\) such that \(\Phi (f)(m,t)=f_t(m)\). Since motions are made from homeomorphisms of M, the restriction of \(\Phi (f)\) to \(N\times {{\mathbb {I}}}\) lies in \({\textbf{Top}}_{{\textbf{B}}{}}(N\times {{\mathbb {I}}},M)\). Thus there is a set map
given by \(T'(f)(n,t) = f_t (n)\).
An interesting question is to ask, for some manifold M and subsets N and \(N'\), which elements of \({\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\) have a preimage under \(T'\). Notice that no such preimage exists in Examples 5.3 and 5.5. Also, the fake motion f in Example 5.4 does not have a preimage under \(T'\) whenever K is a non-trivial string knot.
For fake motions of submanifolds, establishing a preimage amounts to establishing an isotopy extension property (to an ambient isotopy) in the context of topological manifolds. The Edwards-Kirby isotopy extension theorem for topological manifolds [EK71] is a powerful general result in this direction. A recent treatment of this result can be found in chapter 19, due to Arunima Ray, of [ACE+].
In the following result we can see that if a preimage of a fake motion exists then it will be unique under motion equivalence.
Lemma 5.6
Let  be motions in M. If
be motions in M. If  , then \(f{\mathop {\sim }\limits ^{m}}g\).
, then \(f{\mathop {\sim }\limits ^{m}}g\).
Proof
It follows directly from the definition of the worldline that  implies
implies  . By Proposition 3.37 motions with the same worldline are motion equivalent. \(\quad \square \)
. By Proposition 3.37 motions with the same worldline are motion equivalent. \(\quad \square \)
5.2 The groupoid \(\textrm{FMot}_{M}\) and the T-functor
Definition 5.7
For manifold M and subsets \(N,N'\subseteq M\), two fake motions \(f,f':N \times {{\mathbb {I}}}\rightarrow M\) in \({\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\) are said to be strongly isotopicFootnote 6 if there exists a homotopy \(H:(N \times {{\mathbb {I}}}) \times {{\mathbb {I}}}\rightarrow M\) from f to \(f'\) (i.e. \(H(n,t,0)=f(n,t)\) and \(H(n,t,1)=f'(n,t)\)) such that, for each \(s \in {{\mathbb {I}}}\), the map from \(N\times {{\mathbb {I}}}\) to M given by \((n,t) \mapsto H(n,t,s)\) is in \({\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\).
Notation: We write \(f{\mathop {\sim }\limits ^{fk}}f'\) to mean the fake motions f and \(f'\) are strongly isotopic.
Remark 5.8
Let M be a manifold, if \(N\subseteq M\) is locally compact, then, by the product-hom adjunction (Lemma 2.10), there is a one-to-one correspondence between fake motions of N in M and maps \(f:{{\mathbb {I}}}\rightarrow {\textbf{TOP}}(N,M)\) satisfying that \(f_0\) is the inclusion of N in M, and \(f_t:N \rightarrow M\) is always an embedding. However, note that, in general, a subset \(N\subseteq M\) need not be locally compact, so we do not know if this correspondence holds in general. In particular, we do not know whether there is a way to write the strong isotopy relation mirroring relative path-homotopy, as a map from \({{\mathbb {I}}}^2\), when N is not locally compact.
Lemma 5.9
Fix a manifold M. (I) The relations \({\mathop {\sim }\limits ^{fk}}\) on each \({\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\) is a congruence on \(\textrm{FMt}_{M}\). (II) The quotient is a groupoid. We denote it

We have used the notation \([f]_{\text{ fk }}\) or  to denote the strong isotopy equivalence class of a fake motion \(f\in {\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\). Note that in contrast with the motion case, the source and target of a fake motion are uniquely specified by \(f:N\times {{\mathbb {I}}}\rightarrow M\).
to denote the strong isotopy equivalence class of a fake motion \(f\in {\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\). Note that in contrast with the motion case, the source and target of a fake motion are uniquely specified by \(f:N\times {{\mathbb {I}}}\rightarrow M\).
Proof
(I). Suitable homotopies to prove that indeed isotopy between fake motions defines an equivalence relation follow similar constructions to those in the proofs of Proposition 2.33. In order to prove that the composition  of fake motions descends to the quotient, let \(f,f'\in {\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\), \(g,g'\in {\textbf{Top}}_{{\textbf{B}}{},M}[N',N'']\) with strong isotopies \(H_f\) from f to \(f'\) and \(H_g\) from g to \(g'\), then
of fake motions descends to the quotient, let \(f,f'\in {\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\), \(g,g'\in {\textbf{Top}}_{{\textbf{B}}{},M}[N',N'']\) with strong isotopies \(H_f\) from f to \(f'\) and \(H_g\) from g to \(g'\), then
is a strong isotopy from  to
to  . (Note that it may be that N is not closed in M. Since \(N\times [0,1/2]\) and \(N\times [1/2,1]\) are nevertheless closed in \(N\times [0,1]\), we can still apply the glue lemma to see that H is continuous.)
. (Note that it may be that N is not closed in M. Since \(N\times [0,1/2]\) and \(N\times [1/2,1]\) are nevertheless closed in \(N\times [0,1]\), we can still apply the glue lemma to see that H is continuous.)
(II) For \(N\subseteq M\), the identity on N is given by the strong isotopy class of \({\textrm{id}}_{{\textbf{B}},N}:N\times {{\mathbb {I}}}\rightarrow M\), \((n,t)\mapsto n\) (the identity fake motion). For a fake motion \(f\in {\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\), and fixed \(t\in [0,1]\), consider the map \(\sigma _{f}:N \rightarrow N'\) given by \(n\mapsto f(n,1)\). Note that \(\sigma _{f}\) is a homeomorphism. Define  as \((n',t)\mapsto f({\sigma _{f}^{-1}}(n'),1-t)\). Explicit homotopies proving the identity, associativity and inverse axioms follow a similar construction to those in the proof of Proposition 2.36. To illustrate the idea we give the homotopies which prove the inverse axiom. Thus the following function is a strong isotopy
as \((n',t)\mapsto f({\sigma _{f}^{-1}}(n'),1-t)\). Explicit homotopies proving the identity, associativity and inverse axioms follow a similar construction to those in the proof of Proposition 2.36. To illustrate the idea we give the homotopies which prove the inverse axiom. Thus the following function is a strong isotopy  to \({\textrm{id}}_{{\textbf{B}},{N}}\):
to \({\textrm{id}}_{{\textbf{B}},{N}}\):
Similarly
is a suitable strong isotopy from  to \({\textrm{id}}_{{\textbf{B}},{N'}}\). \(\quad \square \)
to \({\textrm{id}}_{{\textbf{B}},{N'}}\). \(\quad \square \)
As with the motion groupoid, we can construct a version of \(\textrm{FMot}_{M}\) which depends on a fixed choice of subset \(A\subset M\). Let M be a manifold M, and \(A\subset M\) a subset. Given \(N,N'\subseteq M\), a fake motion f, from N to \(N'\), relative to A, is by defined to be a fake motion \(f\in {\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\), such that furthermore:
-
(III)
If \(a \in N\cap A\), then \(f(a,t)=a\), for all t, and
-
(IV)
If \(a \in N {\setminus } A\), then \(f(t,a)\notin A\) for all t.
We let \({\textbf{Top}}_{{\textbf{B}}{},M}^A[N,N']\subset {\textbf{Top}}_{{\textbf{B}}{},M}[N,N']\) be the set of fake motions from N to \(N'\), relative to A. Note that the composition  restricts to fake-motions relative to A, thus there is a magmoid \(\textrm{FMt}_{M}^A\). If we restrict to strong isotopies H connecting \(f,f'\in {\textbf{Top}}_{{\textbf{B}}{},M}^A[N,N'] \), such that \(H( -,-,s)\) is always in \({\textbf{Top}}_{{\textbf{B}}{},M}^A[N,N']\) this a magmoid congruence on \(\textrm{FMt}_{M}^A\), called strong isotopy relative to A (also denoted \({\mathop {\sim }\limits ^{fk}}\)). We hence have a quotient groupoid, denoted \(\textrm{FMot}_{M}^A\).
restricts to fake-motions relative to A, thus there is a magmoid \(\textrm{FMt}_{M}^A\). If we restrict to strong isotopies H connecting \(f,f'\in {\textbf{Top}}_{{\textbf{B}}{},M}^A[N,N'] \), such that \(H( -,-,s)\) is always in \({\textbf{Top}}_{{\textbf{B}}{},M}^A[N,N']\) this a magmoid congruence on \(\textrm{FMt}_{M}^A\), called strong isotopy relative to A (also denoted \({\mathop {\sim }\limits ^{fk}}\)). We hence have a quotient groupoid, denoted \(\textrm{FMot}_{M}^A\).
Example 5.10
In Example 5.3, f is not a fake motion relative to \(\{0,1\}\). On the other hand, looking at Example 5.4, f is a fake motion relative to \( \{-1,1\} \times {{\mathbb {R}}}^2\).
Note that \(T'\) restricts to a set map \(\textrm{Mt}^A_{M}({N},{N'}) \rightarrow {\textbf{Top}}_{{\textbf{B}}{},M}^A[N,N']\), which we denote also by \(T'\). For a manifold M, and subset \(A\subset M\), the map \(T'\) extends to a functor from the motion groupoid to the groupoid of fake motions.
Theorem 5.11
Let M be a manifold, and \(A\subset M\) a subset. Given \(N,N'\subseteq M\), there is a well defined functor of groupoids,
which is the identity on objects, and sends  to
to  where \(T'(f)(n,t)= f_t(n)\). (Here \({\mathop {\sim }\limits ^{m}}\) denotes motion equivalence, fixing A and \({\mathop {\sim }\limits ^{fk}}\) denotes strong isotopy of fake motions, relative to A.)
where \(T'(f)(n,t)= f_t(n)\). (Here \({\mathop {\sim }\limits ^{m}}\) denotes motion equivalence, fixing A and \({\mathop {\sim }\limits ^{fk}}\) denotes strong isotopy of fake motions, relative to A.)
Proof
Suppose motions  fixing A, are motion equivalent, fixing A. Then, by Theorem 4.6, there exists a relative path-homotopy \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_A(M,M) \), from f to \(f'\). And then, by construction, the map \(H':( N\times {{\mathbb {I}}})\times {{\mathbb {I}}}\rightarrow M\) such that \(H'\big ((n,t),s\big )= H(t,s)(n) \) defines a strong isotopy, from \(T'(f)\) to \(T'(f')\), relative to A. Moreover, given motions
fixing A, are motion equivalent, fixing A. Then, by Theorem 4.6, there exists a relative path-homotopy \(H:{{\mathbb {I}}}\times {{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_A(M,M) \), from f to \(f'\). And then, by construction, the map \(H':( N\times {{\mathbb {I}}})\times {{\mathbb {I}}}\rightarrow M\) such that \(H'\big ((n,t),s\big )= H(t,s)(n) \) defines a strong isotopy, from \(T'(f)\) to \(T'(f')\), relative to A. Moreover, given motions  , fixing A, we have that
, fixing A, we have that  . The latter follows immediately from the conventions for the composition
. The latter follows immediately from the conventions for the composition  and \(*\) given in (8) and (3). From this it follows that \(T_A\) indeed preserves the compositions in \(\textrm{Mot}_{M}^A\) and \(\textrm{FMot}_{M}^A\). \(\quad \square \)
and \(*\) given in (8) and (3). From this it follows that \(T_A\) indeed preserves the compositions in \(\textrm{Mot}_{M}^A\) and \(\textrm{FMot}_{M}^A\). \(\quad \square \)
5.3 Motion groupoids and Artin braid group (oid)s
Armed with Theorem 4.6, we can now unpack our observation from Sect. 3.5 that at least certain non-trivial motion groups are finitely presented. (We will see in Proposition 7.18 that some are not.)
Our strategy here is simply to make contact with Artin’s proof that Artin’s braid group \(\textbf{B}_n\) (defined in (9) below) is presented by Artin’s presentation [Art47]. (The strategy is simple; the contact is not.)
Let M be a manifold and K be a finite subset of \(M{\setminus } \partial M\). We will define \({\textbf{B}}(M,K)\) as the group of morphisms from K to K in \(\textrm{FMot}_{M}^{\partial M}\). Then we prove that \(\textbf{T}\) restricts to a group isomorphism from \(\textrm{Mot}_{M}^{\partial M}(K,K)\) to \({\textbf{B}}(M,K)\) (Theorem 5.17). In particular we have an isomorphism when we further specialise to \(M={{\mathbb {R}}}^2\).
Of course a major point of our construction of motion groupoids, and fake motion groupoids, is that it coincides with Dahm’s construction when restricted to the group case, so in this final step we will be able essentially to follow Dahm’s version.
Definition 5.12
Suppose that M is a manifold and \(K\subset M\setminus \partial M\) a finite subset. An Artin braid of K in M is an element \(f\in {\textbf{Top}}_{{\textbf{B}}{},M}^{\partial M}[K,K]\).
It follows from Lemma 5.9 that Artin braids compose under  (defined in (8)), the composition descends to the quotient under strong isotopy, and moreover defines a group structure on the set of equivalence classes of Artin braids.
(defined in (8)), the composition descends to the quotient under strong isotopy, and moreover defines a group structure on the set of equivalence classes of Artin braids.
Definition 5.13
Let M be a manifold and \(K\subset M\setminus \partial M\) a finite subset. Denote by \({\textbf{B}}(M,K)\) the group \(\textrm{FMot}_{M}^{\partial M}(K,K)\) (\(\textrm{FMot}_{M}^{A}\) is defined in Lemma 5.9).
Remark 5.14
It follows directly from the definition that \(\textrm{FMot}_{M{\setminus } \partial M}(K,K)=\textrm{FMot}_{M}^{\partial M}(K,K)\).
Note that, by a similar argument as used in Example 3.42, if M is connected then the isomorphism type of \({\textbf{B}}(M,K)\) depends only on the cardinality of K. (Albeit up to non-canonical isomorphism.)
In case when \(M={{\mathbb {R}}}^2\), and \(K=K_n = \{ (0,1),(0,2),...,(0,n) \}\), we define
Then \(\textbf{B}_n\) coincides with the definition of the braid group on n-strands, arising from Artin’s construction in [Art47, Thm.5] (and in [Art25]).
Lemma 5.15
Let M be a manifold. Let n be a positive integer and \(K\subset M{\setminus \partial M}\) a finite subset with n elements. The formal map
that sends the motion equivalence class of a motion  to the strong isotopy class of the Artin braid \(X_f:K\times {{\mathbb {I}}}\rightarrow M\) of K in M, such that \((k,t) \mapsto f_t(k) \), is well-defined, and a group homomorphism.
to the strong isotopy class of the Artin braid \(X_f:K\times {{\mathbb {I}}}\rightarrow M\) of K in M, such that \((k,t) \mapsto f_t(k) \), is well-defined, and a group homomorphism.
Proof
This is a restriction of the functor given in Theorem 5.11. \(\quad \square \)
Remark 5.16
Note that the previous result holds when the boundary of the manifold M is not necessarily fixed, meaning that we have a homomorphism \(\textbf{T}:\textrm{Mot}_{M}(K,K)\rightarrow {\textbf{B}}(M,K),\) defined by using the same formulae as in the boundary-fixing setting. This follows from the fact that, given \(x \in \textrm{int}(M)\), then if \(f:M \rightarrow M \) is any homeomorphism we have that \(f(x) \in \textrm{int}(M)\).
The proof of the following theorem closely follows ideas present in [Dah62, Thm.II.1.2]. We note that our setup is not precisely the same as Dahm’s, who restricts to homeomorphisms with compact support and does not treat manifolds with boundary.
Theorem 5.17
Let M be a manifold. Let n be a positive integer and \(K\subset M{\setminus \partial M}\) a finite subset with n elements. The group homomorphism
given in Lemma 5.15 is a group isomorphism.
In particular we have \(\textrm{Mot}_{{{\mathbb {R}}}^2}(K,K)\cong \textbf{B}_n.\)
To prove Theorem 5.17 we will require some preliminary lemmas.
Recall that for M a topological manifold, possibly with non-empty boundary, the group of homeomorphisms \(M \rightarrow M\) fixing the boundary, with the compact-open topology, is denoted \({\textbf{TOP}}^h_{\partial M}(M,M)\). For the remainder of this section, we also put \(B^n=\{x \in {{\mathbb {R}}}^n\mid |x| \le 1\}\), \(OB^n=\{x \in {{\mathbb {R}}}^n\mid |x| < 1\}=B^n{\setminus } \partial B^n\) and \(S^n=\partial B^n\).
Lemma 5.18
Let n be a non-negative integer. There exists a continuous function:
such that, given any \(x,y\! \in \! OB^n\), we have \(F^n(x,y)(x)\!=\!y\), and moreover \(F^n(x,x):B^n\! \rightarrow \! B^n\) is the identity function.
There are several different ways to construct \(F^n\) with the given properties. We give such a construction in the following proof. See also [Mil65, §4] for a construction that can be done in the smooth setting.
Proof
Given \(x,w \in {{\mathbb {R}}}^n\) we put \((x,w]=\{x+t(w-x) \mid t \in (0,1]\}.\) Observe that for each \(x\in OB^n\), the union \( \{x\} \cup \bigcup _{w\in S^n} (x,w]\) gives a ‘radial’ partition of \(B^n\). Thus, for each \((x,y) \in OB^n \times OB^n \), there is an element \(F^n(x,y)\) in \({\textsf{Set}}(B^n, B^n)\), in fact a bijection, that sends the segment \([x,w]=\{tx +(1-t)w \mid t \in [0,1]\}\subset B^n\), linearly, to the segment [y, w], so that \(tx +(1-t)w \mapsto ty +(1-t)w.\) By construction, \(F^n({x,y}):B^n \rightarrow B^n\) is the identity when restricted to the boundary of \(B^n.\) Also \(F^n({x,y})(x)=y\) and \(F^n(y,x)\) is the inverse of \(F^n(x,y)\). This finishes our construction of \(F^n(x,y)\).
Let us give some detail as to why indeed we defined a continuous function \(F^n:OB^n \times OB^n \rightarrow {\textbf{TOP}}^h_{\partial B^n}(B^n,B^n)\). We use Lemma 2.10.
Note that \(F^n(0,y)(z)=y+z-y|z|.\) So \(F^n(0,y):B^n \rightarrow B^n\) is continuous, and since \(F^n(0,y)\) is a bijection, and \(B^n\) is compact, \(F^n(0,y)\) is a homeomorphism. Furthermore, the fact that \((y,z)\mapsto F^n(0,y)(z)\) is continuous, jointly in \(y \in OB^n\) and \(z \in B^n\), gives that we have a continuous function \(OB^n \ni y \mapsto F^n(0,y) \in {\textbf{TOP}}^h_{\partial B^n}(B^n,B^n)\), if the latter is given the compact-open topology. (By Lemma 2.10)
Since \({\textbf{TOP}}^h(B^n,B^n)\) is a topological group, Theorem 2.11, it follows that the map \(OB^n \ni x \mapsto F^n(x,0) \in {\textbf{TOP}}^h_{\partial B^n}(B^n,B^n)\) is continuous. (Where we note that \(F^n(x,0)\) is the inverse of \(F^n(0,x)\).) And then, again using that \({\textbf{TOP}}^h(B^n,B^n)\) is a topological group, it follows that the function
is continuous. Now note \(F^n(x,y)=F^n(0,y) \circ F^n(x,0)\). \(\quad \square \)
From here until the end of the proof of Theorem 5.17, we fix some choice of \(F^n:OB^n \times OB^n \rightarrow {\textbf{TOP}}^h_{\partial B^n }(B^n,B^n),\) satisfying the conditions of the previous lemma.
The following lemma is a special case of the isotopy extension theorem for topological manifolds. (As already mentioned, for that theorem see [EK71] and [ACE+, Chapter 19].)
Lemma 5.19
Let \(X:K \times {{\mathbb {I}}}\rightarrow M \setminus \partial M\) be an Artin braid of K in M, or more generally any element of \({\textbf{Top}}_{{\textbf{B}}{}}^{\partial M}(K\times {{\mathbb {I}}},M)\). There exists a continuous function \({\hat{X}} :{{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_{\partial M}(M,M)\), with \({\hat{X}}(0)={\textrm{id}}_M\), and such that if \(k\in K\) and \(t\in {{\mathbb {I}}}\) we have \({\hat{X}}(t)(k)=X(k,t)\).
Before we start the proof, note that the proof is quite simple in the case when \(M=B^n\) and \(|K|=1\). In this case, putting \(K=\{x_0\}\) and \(X(x_0,t)=x_t\), then \({\hat{X}}(t):=F^n(x_0,x_t)\) works. The proof of the result is strongly rooted in this idea.
Proof
Let \(n=\dim (M)\). For each \(t\in {{\mathbb {I}}}\) and \(k\in K\), we can find a subset \(U_k^t\subset M\setminus \partial M\), together with a homeomorphism \(f_k^t:U_k^t\rightarrow B^n\), such that \(X(k,t) \in \textrm{int}(U_k^t)\), and such that, moreover, for fixed t, all of the \(U_k^t\), \(k\in K\), are pairwise disjoint. The continuity of X implies that there exists \(\epsilon _t >0\) such that \(X(k,s) \in \textrm{int}(U_k^t)\), if \(|s-t|\le \epsilon _t\) for all \(k \in K\). (We have used the fact that the manifold is, by assumption, Hausdorff, and also that Artin braids take values only in the interior of M, by definition the set of points of M that have a neighbourhood homeomorphic to an open ball.)
The intervals \((t-\epsilon _t, t+\epsilon _t)\) form an open cover of \({{\mathbb {I}}}\). We then use the fact that \({{\mathbb {I}}}\) is compact, and the Lebesgue number lemma (see e.g. [Mun00]), to find a positive integer N and \(0=v_0< v_1< \dots < v_{N+1}=1,\) such that each interval \([v_i,v_{i+1}]\) is contained in an interval of the form \((t_i-\epsilon _{t_i}, t_i+\epsilon _{t_i})\), for some \(t_i\in [0,1]\).
For each \(i \in \{0,\dots ,N\}\), define \(Y_i:[v_{i},v_{i+1}] \rightarrow {\textbf{TOP}}^h_{\partial M}(M,M)\) asFootnote 7:
And finally \({\hat{X}}:{{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_{\partial M}(M,M)\), defined as:
has the required properties. \(\quad \square \)
Proof
(Of Theorem 5.17) The surjectivity of \( T:\textrm{Mot}_{M}^{\partial M}(K,K) \rightarrow {\textbf{B}}(M,K)\) follows directly from the above lemma.
Let us now prove the injectivity of TFootnote 8. For this we follow a similar technique to the proof of Lemma 5.19, with an extra dimension. Consider relative path-equivalent motions  , fixing \(\partial M\). Suppose that the geometric braids \(X_f,X_{f'}:K \times I \rightarrow M{\setminus } \partial M\) are strongly isotopic. Let \(H:(K\times I) \times I \rightarrow M{\setminus } \partial M \) be a strong isotopy connecting \(X_f\) and \(X_{f'}\). For each \((t,s)\in {{\mathbb {I}}}\times {{\mathbb {I}}}\), there exists pairwise disjoint subsets \(U^{(t,s)}_k\subset M {\setminus } \partial M\), \(k \in K\), together with homeomorphisms:
, fixing \(\partial M\). Suppose that the geometric braids \(X_f,X_{f'}:K \times I \rightarrow M{\setminus } \partial M\) are strongly isotopic. Let \(H:(K\times I) \times I \rightarrow M{\setminus } \partial M \) be a strong isotopy connecting \(X_f\) and \(X_{f'}\). For each \((t,s)\in {{\mathbb {I}}}\times {{\mathbb {I}}}\), there exists pairwise disjoint subsets \(U^{(t,s)}_k\subset M {\setminus } \partial M\), \(k \in K\), together with homeomorphisms:
and such that \(H(k,t,s) \in \textrm{int}(U^{(t,s)}_k).\) And again, using the continuity of H, there exists an open rectangle \(I_{t,s}\subset {{\mathbb {I}}}\times {{\mathbb {I}}}\), with \((t,s) \in I_{t,s}\), and such that \(H(k,t',s') \in \textrm{int}(U^{(t,s)}_k)\), for all \(k \in K\) and \((t',s')\in I_{t,s}\).
The \(I_{t,s}\) form an open cover of \({{\mathbb {I}}}\times {{\mathbb {I}}}\). By using the Lebesgue number theorem, there exists a positive integer N and \(0=m_0< m_1<\dots< m_{N}< m_{N+1}=1 \), such that each \([m_i,m_{i+1}]\times [m_j,m_{j+1}] \) is contained in some \(I_{t_i,s_j}\).
Given \(s \in [0,1]\), let \(X_s:K\times {{\mathbb {I}}}\rightarrow M{\setminus } \partial M\) be defined by \(X_s(k,t)=H(k,t,s)\).
For \(j\in \{0,1,\dots , N\}\), following the notation at the end of the proof of Lemma 5.19, if \(s \in [m_j,m_{j+1}]\), define \({\hat{X}}_s^j:{{\mathbb {I}}}\rightarrow {\textbf{TOP}}^h_{\partial M}(M,M) \) using Eq. (10), with \(X_s\) instead of X, and using the homeomorphisms below:
Then, by construction, the map \({{\mathbb {I}}}\times [m_j,m_{j+1}] \rightarrow {\textbf{TOP}}^h_{\partial M}(M,M)\) given by \((t,s) \mapsto {\hat{X}}_s^{j}(t)\) defines a relative path-homotopy from  to
to  , fixing \(\partial M\). (Albeit using the interval \([m_j,m_{j+1}]\) rather than [0, 1].) So
, fixing \(\partial M\). (Albeit using the interval \([m_j,m_{j+1}]\) rather than [0, 1].) So  , for each \(j\in {0,1,\dots , N}\). (Here and below,
, for each \(j\in {0,1,\dots , N}\). (Here and below,  means relative path-homotopy fixing \(\partial M\).)
means relative path-homotopy fixing \(\partial M\).)
Note that  and
and  are not necessarily the same motion: the lists of homeomorphisms,
are not necessarily the same motion: the lists of homeomorphisms,
and
may be different. However, by construction, the two motions  and
and  have the same worldline, which explicitly is
have the same worldline, which explicitly is
And therefore, using Theorem 4.6 combined with Proposition 3.37 (or equivalently Remark 4.8) we have:  .
.
Since the discussion holds for all \(j \in \{0,1,\dots , N\}\), by transitivity, we have that  .
.
To finish proving that  are relative path homotopic, fixing \(\partial M\), we now observe that the worldline of
are relative path homotopic, fixing \(\partial M\), we now observe that the worldline of  is the same as that of
is the same as that of  explicitly
explicitly
Analogously the worldline of  is the same as that of
is the same as that of  . So we can apply Remark 4.8 again to prove that
. So we can apply Remark 4.8 again to prove that  are relative path homotopic, fixing \(\partial M\). \(\quad \square \)
are relative path homotopic, fixing \(\partial M\). \(\quad \square \)
Remark 5.20
It follows from Theorem 5.17 together with the finite presentation of \(\textbf{B}_n\) in [Art47], that \(\textrm{Mot}_{{{\mathbb {R}}}^2}(K,K)\) is finitely generated.
Note that exactly the same argument as used in the proof of Theorem 5.17 will give the following result.
Theorem 5.21
Let M be a manifold. The groupoid map \({\textbf{T}} :\textrm{Mot}_{M}^{\partial M} \rightarrow \textrm{FMot}_{M}^{\partial M}\) restricts to an isomorphism between the respective full subgroupoids with objects the finite subsets of \(M\setminus \partial M\). \(\quad \square \)
Also, applying the same argument to the map from Remark 5.16 we also have:
Theorem 5.22
Let M be a manifold. We have an isomorphism between the full subgroupoids of \(\textrm{Mot}_{M}\) and \(\textrm{FMot}_{M}^{\partial M}\) with objects the finite subsets of \(M\setminus \partial M\). \(\quad \square \)
Remark 5.23
Let \(f:\textrm{Mot}_{{{\mathbb {R}}}^2}\rightarrow \textrm{Mot}_{D^2 \setminus \partial D^2}\) be a homeomorphism, and \(K=\{(0,1),(0,2),\dots ,(0,n)\}\). By Example 3.40, \(\textrm{Mot}_{{{\mathbb {R}}}^2}(K,K)\cong \textrm{Mot}_{D^2 {\setminus } \partial D^2}(f(K),f(K))\). Thus, by Theorem 5.17 there is an isomorphism \(\textbf{B}_n{}\cong {\textbf{B}}(D^2\setminus \partial D^2,f(K))\).
Remark 5.24
Let \(K\subset M\setminus \partial M\) be a finite subset. From Remark 5.14 we have that \({\textbf{B}}(M{\setminus } \partial M,K)\cong {\textbf{B}}(M,K)\), together with Theorem 5.17 this implies \(\textrm{Mot}_{M{\setminus } \partial M}(K,K)\cong \textrm{Mot}_{M}^{\partial M}(K,K)\), and with Theorem 5.22 we have \(\textrm{Mot}_{M}^{\partial M}(K,K)\cong \textrm{Mot}_{M}(K,K)\).
Remark 5.25
Notice that the proof of Theorem 5.17 works in exactly the same way if we had restricted to the subset of \({\textbf{TOP}}^h(M,M)\) of homeomorphisms with compact support in our construction of the motion groupoid, as is the set up in [Dah62]. Thus this implies in the Artin braid setting, the two constructions are isomorphic.
Finally in our discussion of the full subgroupoids of \(\textrm{Mot}_{M}\) and \(\textrm{FMot}_{M}\), with objects the finite subsets of \(M{\setminus } \partial M\), we have the following result.
Lemma 5.26
Let M be a connected manifold. Given a pair of finite subsets K and \(K'\) contained in the interior of M, of the same cardinality, then there exists a motion  of M. Moreover, we can suppose that the motion fixes the boundary M.
of M. Moreover, we can suppose that the motion fixes the boundary M.
Proof
(Sketch.) For the case \(\dim (M)=1\), note that M is homeomorphic to \(S^1, [0,1),[0,1]\) or \({{\mathbb {R}}}\). The proof in this case is left to the reader. Cf. Example 3.42, and also the maps constructed in Theorem 6.7 below.
So suppose that \(\dim (M)\ge 2\). Then M remains path-connected if a finite subset is taken out of M. Let \(K=\{x_1,\dots , x_n\}\) and \(K'=\{y_1,\dots , y_n\}\). We consider a path \(\gamma _1\) connecting \(x_1\) to \(y_1\), from which we can construct a fake motion \(X_1:\{x_1\} \times {{\mathbb {I}}}\rightarrow M\), sending \((x_1,t)\) to \(\gamma _1(t)\). So we have  . By Lemma 5.19, we hence have a motion
. By Lemma 5.19, we hence have a motion  extending \(X_1\), meaning that \(T'(f_1)=X_1\). We then consider a path \(\gamma _2\) from \(f_1^1(x_2)\) to \(y_2\) that avoids \(y_1\). This leads to a fake motion
extending \(X_1\), meaning that \(T'(f_1)=X_1\). We then consider a path \(\gamma _2\) from \(f_1^1(x_2)\) to \(y_2\) that avoids \(y_1\). This leads to a fake motion  , where \(y_1\) does not move. This can again be extended to a motion
, where \(y_1\) does not move. This can again be extended to a motion  , meaning that \(T'(f^2)=X_2\). This process can be continued. We consider a path \(\gamma _3\) from \(f_1^2\circ f_1^1(x_3)\) to \(y_3\) that avoids \(y_1\) and \(y_2\), from which we construct another fake motion
, meaning that \(T'(f^2)=X_2\). This process can be continued. We consider a path \(\gamma _3\) from \(f_1^2\circ f_1^1(x_3)\) to \(y_3\) that avoids \(y_1\) and \(y_2\), from which we construct another fake motion  that does not move either \(y_1\) or \(y_2\), and restricts to \(\gamma _3\) over \(\{f_1^2\circ f_1^1(x_3)\}\times {{\mathbb {I}}}\). We can lift \(X_3\) to another motion
that does not move either \(y_1\) or \(y_2\), and restricts to \(\gamma _3\) over \(\{f_1^2\circ f_1^1(x_3)\}\times {{\mathbb {I}}}\). We can lift \(X_3\) to another motion  . If we only have three points, in K and \(K'\), then a motion
. If we only have three points, in K and \(K'\), then a motion  can be \(f^3*f^2*f^1.\) It is clear how the induction can be completed. \(\quad \square \)
can be \(f^3*f^2*f^1.\) It is clear how the induction can be completed. \(\quad \square \)
It therefore follows that the full subgroupoid of the motion groupoid of a connected manifold M with objects the finite subsets of the interior has one connected component for each possible cardinality. The same holds for the fake motion groupoid.
6 Mapping Class Groupoid \(\textrm{MCG}_{M}^A\)
6.1 The mapping class groupoid \(\textrm{MCG}_{M}\)
In this section, we construct the mapping class groupoid \(\textrm{MCG}_{M}\) associated to a manifold M. We do this by constructing a congruence on \(\textrm{Homeo}_{M}\) (see Definition 2.39), so the morphisms in \(\textrm{MCG}_{M}\) are certain equivalence classes of self-homeomorphisms of M (together with a pair of subsets of M). Compare this with motions, which keep track of an entire path in \({\textbf{TOP}}^h(M,M)\).
As we will see, mapping class groupoids contain the classical mapping class groups.
Recall from Sect. 2.6 that for a manifold M and for subsets \(N,N'\subseteq M\), morphisms in \(\textrm{Homeo}_{M}(N,N')\) are triples denoted  where \(\mathfrak {f}\in {\textbf{Top}}^h(M,M)\) and \(\mathfrak {f}(N)=N'\). Where convenient, we also think of the elements of \(\textrm{Homeo}_{M}(N,N')\) as the projection to the first coordinate of each triple i.e. \(\mathfrak {f}\in {\textbf{Top}}^h(M,M)\) such that \(\mathfrak {f}(N)=N'\). From here we will also use \(\textrm{Homeo}_{M}(N,N')\) to denote the same set together with the subspace topology induced from \({\textbf{TOP}}^h(M,M)\).
where \(\mathfrak {f}\in {\textbf{Top}}^h(M,M)\) and \(\mathfrak {f}(N)=N'\). Where convenient, we also think of the elements of \(\textrm{Homeo}_{M}(N,N')\) as the projection to the first coordinate of each triple i.e. \(\mathfrak {f}\in {\textbf{Top}}^h(M,M)\) such that \(\mathfrak {f}(N)=N'\). From here we will also use \(\textrm{Homeo}_{M}(N,N')\) to denote the same set together with the subspace topology induced from \({\textbf{TOP}}^h(M,M)\).
Definition 6.1
Let M be a manifold and \(N,N'\subseteq M\). For any  and
and  in \(\textrm{Homeo}_{M}(N,N')\),
in \(\textrm{Homeo}_{M}(N,N')\),  is said to be isotopic to
is said to be isotopic to  , denoted by \({\mathop {\sim }\limits ^{i}}\), if there exists a continuous map:
, denoted by \({\mathop {\sim }\limits ^{i}}\), if there exists a continuous map:
such that
-
for all fixed \(s\in {{\mathbb {I}}}\), the map \(m\mapsto H(m,s)\) is in \(\textrm{Homeo}_M(N,N')\),
-
for all \(m\in M\), \(H(m,0) = \mathfrak {f}(m)\), and
-
for all \(m\in M\), \(H(m,1) = \mathfrak {g}(m)\).
We call such a map an isotopy from  to
to  .
.
More generally, let \(A\subset M\) be a subset, and  and
and  homeomorphisms in \(\textrm{Homeo}_{M}^A(N,N')\), then \(\mathfrak {f}\) and \(\mathfrak {g}\) are said to be A -fixing isotopic if an isotopy H from
homeomorphisms in \(\textrm{Homeo}_{M}^A(N,N')\), then \(\mathfrak {f}\) and \(\mathfrak {g}\) are said to be A -fixing isotopic if an isotopy H from  to
to  exists, satisfying moreover that for all \(a\in A\) and \(t \in {{\mathbb {I}}}\), \(H(a,t)=a\). We write:
exists, satisfying moreover that for all \(a\in A\) and \(t \in {{\mathbb {I}}}\), \(H(a,t)=a\). We write:  . Such a map \(H:M\times {{\mathbb {I}}}\rightarrow M\) is called an A-fixing isotopy.
. Such a map \(H:M\times {{\mathbb {I}}}\rightarrow M\) is called an A-fixing isotopy.
Lemma 6.2
Let M be a manifold. For all pairs \(N,N'\subseteq M\), the relation \({\mathop {\sim }\limits ^{i}}\) is an equivalence relation on \(\textrm{Homeo}_{M}(N,N')\).
Notation: We call this equivalence relation isotopy equivalence. We denote the equivalence class of  , up to isotopy equivalence, as
, up to isotopy equivalence, as  .
.
Proof
Let  ,
,  and
and  be in \(\textrm{Homeo}_{M}(N,N')\) with
be in \(\textrm{Homeo}_{M}(N,N')\) with  and
and  . Then there exists some isotopy, say \(H_{\mathfrak {f},\mathfrak {g}}\), from
. Then there exists some isotopy, say \(H_{\mathfrak {f},\mathfrak {g}}\), from  to
to  and an isotopy, say \(H_{\mathfrak {g},\mathfrak {h}}\), from
and an isotopy, say \(H_{\mathfrak {g},\mathfrak {h}}\), from  to
to  .
.
We first check reflexivity. The map \(H(m,s)=\mathfrak {f}(m)\) for all \(s\in {{\mathbb {I}}}\) is an isotopy from  to itself. For symmetry, \(H(m,s)=H_{\mathfrak {f},\mathfrak {g}}(m,1-s)\) is an isotopy from
to itself. For symmetry, \(H(m,s)=H_{\mathfrak {f},\mathfrak {g}}(m,1-s)\) is an isotopy from  to
to  . For transitivity,
. For transitivity,
is an isotopy from  to
to  . \(\quad \square \)
. \(\quad \square \)
Lemma 6.3
Let M be a manifold. The family of relations \((\textrm{Homeo}_{M}(N,N'),{\mathop {\sim }\limits ^{i}})\) for all pairs \(N,N'\subseteq M\) are a congruence on \(\textrm{Homeo}_{M}\).
Proof
We have that \({\mathop {\sim }\limits ^{i}}\) is an equivalence relation on each \(\textrm{Homeo}_{M}(N,N')\) from Lemma 6.2.
We check that the composition descends to a well defined composition on equivalence classes. Suppose there exists an isotopy, say \(H_{\mathfrak {f},\mathfrak {f'}}\), from  to
to  and another isotopy, say \(H_{\mathfrak {g},\mathfrak {g'}}\) from
and another isotopy, say \(H_{\mathfrak {g},\mathfrak {g'}}\) from  to
to  . Then:
. Then:
is an isotopy from  to
to  . Note that H is continuous since it is the composition of the continuous functions \(H_{\mathfrak {g},\mathfrak {g'}}\) and \((m,s) \in M\times {{\mathbb {I}}}\mapsto \left( H_{\mathfrak {g},\mathfrak {g'}}(m,s),s\right) \in M\times {{\mathbb {I}}}.\) \(\quad \square \)
. Note that H is continuous since it is the composition of the continuous functions \(H_{\mathfrak {g},\mathfrak {g'}}\) and \((m,s) \in M\times {{\mathbb {I}}}\mapsto \left( H_{\mathfrak {g},\mathfrak {g'}}(m,s),s\right) \in M\times {{\mathbb {I}}}.\) \(\quad \square \)
In the following theorem, as with Theorem 3.32, we drop the information about subsets in the tuple defining a groupoid, to keep the notation readable; so \([f:X \rightarrow Y]_{\text{ i }}\) is denoted \([f]_{\text{ i }}\). Again the subsets are essential to construct the relation \({\mathop {\sim }\limits ^{i}}\).
Theorem 6.4
Let M be a manifold. There is a groupoid
We call this the mapping class groupoid of M.
Proof
This is the quotient \(\textrm{Homeo}_{M}/{\mathop {\sim }\limits ^{i}}\). Lemma 6.3 gives that \({\mathop {\sim }\limits ^{i}}\) is a congruence and Proposition 2.28 gives that the quotient of a groupoid by a congruence is still a groupoid, with the given identity and inverse. \(\quad \square \)
Recall that, if X is a topological space, then the relation \(x\sim y\) if, and only if, x and y can be connected by a path in X, is an equivalence relation on (the underlying set of) X. We let \(\pi _0(X)\), the set of path-components of X, denote the quotient of the set X by this equivalence relation.
Lemma 6.5
Let M be a manifold. We have the following equality of sets
Proof
Using Theorem 2.10, a continuous map \(M\times {{\mathbb {I}}}\rightarrow M\) from  to
to  satisfying the conditions in Definition 6.1 corresponds to a path \({{\mathbb {I}}}\rightarrow \textrm{Homeo}_M(N,N')\) from \(\mathfrak {f}\) to \(\mathfrak {g}\), hence the equivalence relations on each side are the same. \(\square \)
satisfying the conditions in Definition 6.1 corresponds to a path \({{\mathbb {I}}}\rightarrow \textrm{Homeo}_M(N,N')\) from \(\mathfrak {f}\) to \(\mathfrak {g}\), hence the equivalence relations on each side are the same. \(\square \)
For an oriented compact manifold M, let \(\textrm{MCG}_{M}^{+}\subset \textrm{MCG}_{M}\) be the subgroupoid whose morphisms are only those equivalence classes containing an orientation preserving homeomorphism. Note that, if \(\mathfrak {f}\) is an orientation preserving, then so is every \(\mathfrak {g}\in [\mathfrak {f}]_{\text{ i }}\) [Hir76, Thm.1.6], and composition of orientation preserving maps is orientation preserving, thus \(\textrm{MCG}_{M}^{+}\) is indeed a subgroupoid.
Proposition 6.6
For an oriented compact manifold M without boundary, it follows directly from the definitions that the mapping class group of [KT08] is \(\textrm{MCG}_{M}^{+}(N,N)\) (cf. [Dam17, Bir69]). In the case M is a surface, \(\textrm{MCG}_{M}^{+}(\varnothing ,\varnothing )\) is the classical mapping class group, see e.g. [FM11]. \(\quad \square \)
Thus, to help understand specific mapping class groupoids, we can make use of results on mapping class (sub)groups e.g. in [Bir69, FM11, Ham74, HT80]. It is an interesting question as to the relationship between a connected groupoid and the groups it contains. The complement consists of morphism sets that are not groups, but they are (respectively left and right) G-sets for the the two different objects. Each morphism set \( \textrm{MCG}_{M}(N,N')\) is generated by the action of either group on any single element. But of course as soon as \(N \ne N'\) this set is not even pointed, so there is no analogue of the identity morphism.
The following proposition shows that, as with motion groupoids, automorphism groups in mapping class groupoids are only finitely generated for sufficiently tame choices of objects.
Theorem 6.7
Let \(M={{\mathbb {I}}}\) and \(N={{\mathbb {I}}}\cap {\mathbb {Q}}\). Then \(\textrm{MCG}_{{{\mathbb {I}}}}(N,N)\) is uncountably infinite.
Proof
We begin by constructing certain elements of \({\textbf{Top}}^h({{\mathbb {I}}},{{\mathbb {I}}})\). Choose points \(x,x'\in N\setminus \{0,1\}\), then there is a unique piecewise linear, orientation preserving map with precisely two linear segments sending x to \(x'\) and moreover this map sends N to itself. Denote this by \(\phi _{xx'}\). Let us fix the point x, then varying \(x'\) gives a countably infinite choice of maps \(\phi _{xx'}\). We prove by contradiction that all such \(\phi _{xx'}\) represent distinct equivalence classes in \(\textrm{MCG}_{{{\mathbb {I}}}}(N,N)\).
Let \(x,x',x''\in N\setminus \{0,1\}\) and suppose \(\phi _{xx'}:N\rightarrow N\) is isotopic to \(\phi _{xx''}:N\rightarrow N\) in \(\textrm{MCG}_{{{\mathbb {I}}}}(N,N)\). Then for all \(n\in N\) we have a path \(\phi _{xx'}(n)\) to \(\phi _{xx''}(n)\) in \({\mathbb {Q}}\), and hence a path \(\phi _{xx'}(x')\) to \(\phi _{xx''}(x'')\). But all paths \({{\mathbb {I}}}\rightarrow {\mathbb {Q}}\) are constant, which follows from the intermediate value theorem. Hence \(\phi _{xx'}=\phi _{xx''}\). Therefore any pair of distinct maps of the described form are not isotopic.
More generally a piecewise linear map can be defined as follows. Starting from \(t=0\), each segment is be defined by choosing an upper bound \(t\in \{0,1]\) and a gradient (which is bounded by condition that the map is well defined). Repeating with the condition that the upper bound must be distinct from the upper bound of the previous section until \(t=1\) is chosen, defines a map. Choosing rational gradients, and rational bounds is sufficient to ensure such a map sends N to itself. By the same argument as above distinct such maps are non isotopic. Allowing for an infinite number of segments, then the cardinality of maps that can be constructed this way is a countable product of countable sets, thus uncountable. (More precisely it has the cardinality of the continuum.) \(\quad \square \)
We now give some examples of automorphism groups in the mapping class groupoid which follow easily from classical results on homeomorphism spaces. We include proofs to set the scene for the next section.
Proposition 6.8
We have \( \textrm{MCG}_{S^1}(\varnothing ,\varnothing ) \cong {{\mathbb {Z}}}/ 2{{\mathbb {Z}}}. \)
Proof
It is proven in [Ham74, Theorem 1.1.2] that the space of orientation preserving homeomorphisms \(S^1 \rightarrow S^1\) is homotopic to \(S^1\), and in particular that it is path-connected. Since the identity map \(S^1 \rightarrow S^1\) is orientation preserving, the path-component of the identity in \({\textbf{TOP}}^h(S^1,S^1)\) is the set of orientation preserving homeomorphisms from \(S^1\) to itself.
Let \(\textrm{deg}:{\textbf{Top}}^h(S^1,S^1)\rightarrow \{\pm 1\}\) be the restriction of the degree map (see for example [Hat02, Sec.2.2]), thus \(\textrm{deg}(\mathfrak {f})=+1\) if \(\mathfrak {f}\) is orientation preserving and \(-1\) if \(\mathfrak {f}\) is orientation reversing. We show that \(\textrm{deg}\) descends to an isomorphism \(\pi _0(\textrm{Homeo}_{S^1}(\varnothing ,\varnothing ))\rightarrow \{\pm 1\}\cong {{\mathbb {Z}}}/2{{\mathbb {Z}}}\). If \(\mathfrak {f}\) and \(\mathfrak {g}\) are orientation reversing, then \(\mathfrak {f}\circ \mathfrak {g}^{-1}\) is orientation preserving, and hence can be connected by a path to \(\textrm{id}_{S^1}\). It follows that \(\mathfrak {f}\) and \(\mathfrak {g}\) can be connected by a path in \({\textbf{TOP}}^h(S^1,S^1)\). Moreover maps in the same path component must have the same degree, thus are either both orientation reversing, or both orientation preserving. \(\square \)
It is also known that the group of orientation preserving homeomorphisms of \(S^2\) and of \(S^3\) is path-connected, this follows from [Fis60, Thm.15]. In dimensions 2 and 3 a more recent discussion is in [ABD+20, Thm.3.1]. (The dimension 2 case is also present in [Ham74, Thm.1.2.2.].) Therefore the same argument as above gives:
Proposition 6.9
We have \( \textrm{MCG}_{S^2}(\varnothing ,\varnothing ) \cong {{\mathbb {Z}}}/ 2{{\mathbb {Z}}}\) and \(\textrm{MCG}_{S^3}(\varnothing ,\varnothing ) \cong {{\mathbb {Z}}}/ 2{{\mathbb {Z}}}\). \(\quad \square \)
6.2 Pointwise A-fixing mapping class groupoid, \(\textrm{MCG}_{M}^A\)
Here we discuss a version of the mapping class groupoid which fixes a distinguished subset.
Theorem 6.10
Let M be a manifold and \(A\subset M\) a subset. There is a groupoid
Proof
This is the quotient \(\textrm{Homeo}_{M}^A/{\mathop {\sim }\limits ^{i_A}}\). The proofs of Lemmas 6.2 and 6.3 proceed in the same way for A-fixing self-homeomorphisms. All constructed homotopies will be A-fixing for all \(s\in {{\mathbb {I}}}\). Proposition 2.28 gives that the quotient of a groupoid by a congruence is still a groupoid. \(\quad \square \)
We can now state an analogous version of Proposition 6.6 for manifolds with boundary.
Proposition 6.11
For an oriented manifold M with non empty boundary \(\partial M\), it follows from the definitions that the mapping class group of [KT08] is the automorphism group \(\textrm{MCG}_{M}^{\partial M}(N,N)\). (Note, when \(\partial M\) is non-empty, boundary fixing homeomorphisms are necessarily orientation preserving (cf. [Dam17, Bir69]). In the case M is a surface, and \(N=\varnothing \), \(\textrm{MCG}_{M}^{\partial M}(\varnothing ,\varnothing )\) is the classical mapping class group of e.g. [FM11]. \(\quad \square \)
By Proposition 6.11 we can follow the proof classical result [FM11, Lem.2.1] in the proof of the following proposition.
Proposition 6.12
The group \(\textrm{MCG}_{D^2}^{\partial D^2}(\varnothing ,\varnothing )\) is trivial.
Proof
This follows from the Alexander trick [Ale23], as we now recall. Suppose we have a homeomorphism \(\mathfrak {f}:D^2 \rightarrow D^2,\) that restricts to the identity on \(\partial D^2\). Define
Notice that \(f_0={\textrm{id}}_{D^2}\) and \(f_1=\mathfrak {f}\) and each \(f_t\) is continuous. Moreover:
is a continuous map. So we have constructed an isotopy from any boundary preserving self-homeomorphism of \(D^2\) to \({\textrm{id}}_{D^2}\). Also by construction H is \(\partial (D^2)\)-fixing. \(\quad \square \)
The same argument can be expanded to give a proof that the space of maps \(D^n \rightarrow D^n\) fixing the boundary is contractible; see [Ham74, Thm.1.1.3.2.].
Remark 6.13
The automorphism group \(\textrm{MCG}_{D^2}^{\partial D^2}(K,K)\) is finitely presented when K is a finite subset in the interior of \(D^2\). This follows from Theorem 7.16 below, along with the finite presentation of the braid group \(\textbf{B}_n\) given in [Art47].
Noting Proposition 6.11, the following definition is consistent with [Dam17, Def.2.5].
Definition 6.14
Let \(D^3\) be the 3-disk, and C a fixed choice of subset consisting of n disjoint unknotted, unlinked circles. Then the extended loop braid group may be defined as
Remark 6.15
In particular \(LB^{ext}_n=\textrm{MCG}_{D^3}^{\partial D^3}(C,C)\) has a finite presentation, given in [Dam17].
Adjusting the proof of Lemma 6.5 to consider paths in \(\textrm{Homeo}_{M}^A\) we have:
Lemma 6.16
Let M be a manifold. We have the following equality of sets
\(\square \)
7 Functor \({\textsf{F}}\) from \(\textrm{Mot}_{M}^A\) to \(\textrm{MCG}_{M}^A\)
Here we construct a functor \({\textsf{F}}:\textrm{Mot}_{M}^A \rightarrow \textrm{MCG}_{M}^A\), and prove this is an isomorphism of categories if \(\pi _1({\textbf{TOP}}^h(M,M),{\textrm{id}}_M)\) and \(\pi _0({\textbf{TOP}}^h(M,M))\) are trivial. Indeed we prove \({\textsf{F}}\) is full if and only if \(\pi _0({\textbf{TOP}}^h(M,M))\) is trivial, and that \({\textsf{F}}\) is faithful if \(\pi _1({\textbf{TOP}}^h(M,M),{\textrm{id}}_M)\) is trivial. (This will thus generalise, for example, the known equivalence between realisations of braid groups as mapping class groups and as motion groups [Dah62, Gol81, Bir69]; and similarly for loop braid groups [Dam17].)
Theorem 7.1
Let M be a manifold. There is a functor
which is the identity on objects, and on morphisms we have

Proof
We first check that \({\textsf{F}}\) is well defined. By Theorem 4.6 two motions  and
and  are motion-equivalent if, and only if, they are relative path-equivalent, i.e. we have a relative path-homotopy:
are motion-equivalent if, and only if, they are relative path-equivalent, i.e. we have a relative path-homotopy:
Then H(1, s) is a path \(f_1\) to \(f'_1\) such that for all \(s\in {{\mathbb {I}}}\), \(H(1,s)\in \textrm{Homeo}_M(N,N')\). Hence  and
and  are isotopic.
are isotopic.
We check \({\textsf{F}}\) preserves composition. For  and
and  in \(\textrm{Mot}_{M}\) we have:
in \(\textrm{Mot}_{M}\) we have:

\(\square \)
Lemma 7.2
Let M be a manifold. The functor
defined in Theorem 7.1 is full if and only if \(\pi _0({\textbf{TOP}}^h_A(M,M))\) is trivial.
Proof
Suppose \(\pi _0({\textbf{TOP}}_A^h(M,M))\) is trivial and let  . Then, since \({\textbf{TOP}}_A^h(M,M)\) is path connected, there exists a path \(f\in {\textbf{TOP}}^h_A(M,M)\) with \(f_0={\textrm{id}}_M\) and \(f_1=\mathfrak {f}\), and, since \(\mathfrak {f}(N)=N'\),
. Then, since \({\textbf{TOP}}_A^h(M,M)\) is path connected, there exists a path \(f\in {\textbf{TOP}}^h_A(M,M)\) with \(f_0={\textrm{id}}_M\) and \(f_1=\mathfrak {f}\), and, since \(\mathfrak {f}(N)=N'\),  is a motion. Hence
is a motion. Hence  .
.
Now suppose \(\pi _0({\textbf{TOP}}^h_A(M,M))\) is non-trivial. Let \(\mathfrak {f}\) be a self-homeomorphism in a path-component of \({\textbf{TOP}}^h_A(M,M)\) which does not contain \({\textrm{id}}_M\). Then  , and all representatives are in the same path-component. Hence there is no path f in \({\textbf{TOP}}^h_A(M,M)\), with \(f_0={\textrm{id}}_M\), and with
, and all representatives are in the same path-component. Hence there is no path f in \({\textbf{TOP}}^h_A(M,M)\), with \(f_0={\textrm{id}}_M\), and with  . \(\square \)
. \(\square \)
The following example shows that the functor \({\textsf{F}}\) may restrict to a surjection on some automorphism groups and not on others.
Example 7.3
Let \(M=S^3\). Recall from Lemma 6.5 that \(\textrm{MCG}_{M}(N,N')=\pi _0(\textrm{Homeo}_{M}(N,N'))\), where \(\textrm{Homeo}_{M}(N,N')\subseteq {\textbf{TOP}}^h(M,M)\) is given the subspace topology, and \(\textrm{Homeo}_M(\varnothing ,\varnothing )={\textbf{TOP}}^h(M,M)\). By Proposition 6.9\(\pi _0({\textbf{TOP}}^h(M,M))=\textrm{MCG}_{S^3}(\varnothing ,\varnothing ) \cong {{\mathbb {Z}}}/2{{\mathbb {Z}}}\), corresponding to an orientation preserving and orientation reversing component, and so by the previous lemma \({\textsf{F}}\) is not full.
Consider \(K\subset S^3\) a knot which is not isotopic to its mirror image. Then \(\textrm{MCG}_{S^3}(K,K)\) contains only orientation preserving self-homeomorphisms, which are therefore in the same connected component as the identity. Hence, by the first part of the proof of the previous lemma, the restriction \({\textsf{F}}:\textrm{Mot}_{S^3}(K,K)\rightarrow \textrm{MCG}_{S^3}(K,K)\) is full.
7.1 Applying the long exact sequence of relative homotopy groups
Here we prove that, for any fixed \(N\subseteq M\), the functor \({\textsf{F}}:\textrm{Mot}_{M}\rightarrow \textrm{MCG}_{M}\) restricts to a group isomorphism \(\textrm{F}:\textrm{Mot}_{M}(N,N)\xrightarrow {\sim } \textrm{MCG}_{M}(N,N)\) if \(\pi _1(\textrm{Homeo}_M(\varnothing ,\varnothing ),{\textrm{id}}_M)\) and \(\pi _0(\textrm{Homeo}_M(\varnothing ,\varnothing ))\) are both trivial (Lemma 7.11). For this we will need the homotopy long exact sequence of a pair. We briefly introduce this here, see [Hat02, Sec.4.1] or [May99, Ch.9] for further exposition.
In this section we work in the non A-fixing case to avoid overloading the notation. Everything proceeds in exactly the same way for the A-fixing case.
Definition 7.4
Let n be a positive integer. Let \({{\mathbb {I}}}^{n-1}\times \{1\}\) be the face of \({{\mathbb {I}}}^n\) with last coordinate 1, and let \(J^{n-1}\) be the closure of \(\partial {{\mathbb {I}}}^n\setminus ( {{\mathbb {I}}}^{n-1}\times \{1\})\), i.e. the union of all remaining faces of \({{\mathbb {I}}}^n\). So for instance, for \(n=1\), the triple \(({{\mathbb {I}}},\partial {{\mathbb {I}}}, J^0)\) is \(({{\mathbb {I}}}, \{0,1\}, \{0\})\).
Definition 7.5
Let X be a topological space, \(Y\subseteq X\) a subset and \(x_0\in Y\) a point. For fixed integer \(n\ge 1\) we define a relation on the set of continuous maps
as follows. We say \(\gamma \sim \gamma '\) if there exists \(H:{{\mathbb {I}}}^n\times {{\mathbb {I}}}\rightarrow X\) such that
-
for all \(s \in {{\mathbb {I}}}\), \(x\mapsto H(x,s)\) defines a map \(({{\mathbb {I}}}^n,\partial {{\mathbb {I}}}^n,J^{n-1})\rightarrow (X,Y,\{x_0\})\),
-
for all \(x\in {{\mathbb {I}}}^n\), \(H(x,0)=\gamma (x)\), and
-
for all \(x\in {{\mathbb {I}}}^n\), \(H(x,1)=\gamma '(x)\).
Proposition 7.6
For each n the relation described in Definition 7.5 is an equivalence relation.
Notation: We will call the set of equivalence classes of maps from \(({{\mathbb {I}}}^n,\partial {{\mathbb {I}}}^n,J^{n-1})\) to \((X,Y,\{x_0\})\) the \(n^{th}\) relative homotopy set and denote it \(\pi _n(X,Y,x_0)\).
Proof
We omit this proof. It is similar to Lemma 4.2. See also [Hat02, Sec.4.1]. \(\square \)
Recall that we also use \(\textrm{Homeo}_{M}(N,N')\) to denote the set together with the subspace topology from \({\textbf{TOP}}^h(M,M)\).
Lemma 7.7
Let M be a manifold and \(N\subseteq M\) a subset. Then as sets
Proof
This follows from Theorem 4.6, combined with the previous definition. \(\quad \square \)
Notation: The equivalence relation used to construct \(\pi _1(\textrm{Homeo}_M(\varnothing ,\varnothing ),\textrm{Homeo}_{M}(N,N),{\textrm{id}}_M)\) is precisely relative path-equivalence of motions  . We abuse notation, and use \([\gamma ]_{\text{ rp }}\) for the equivalence class of a continuous map \(\gamma \) in any relative homotopy set.
. We abuse notation, and use \([\gamma ]_{\text{ rp }}\) for the equivalence class of a continuous map \(\gamma \) in any relative homotopy set.
Lemma 7.8
(Cf. e.g. [Hat02, Sec.4.1]). Let X be a topological space, \(Y\subseteq X\) a subset and \(x_0\in Y\) a point. For \(n\ge 2\), given continuous maps \(\beta ,\gamma :({{\mathbb {I}}}^n,\partial {{\mathbb {I}}}^n,J^{n-1})\rightarrow (X,Y,\{x_0\}) \), define
Then there is a well-defined binary composition
Moreover the set \(\pi _n(X,A,x_0)\) becomes a group with \(+\). The identity is the equivalence class of the constant path \((t_1,\dots ,t_n)\mapsto x_0\). The inverse of \([\gamma ]_{\text{ rp }}\in \pi _n(X,Y,x_0)\) is the equivalence class of \((t_1,\dots ,t_n)\mapsto \gamma (1-t_1,\dots ,t_n)\). \(\square \)
For \(n=1\) there is not in general a sensible way to make \(\pi _1(X,Y,x_0)\) into a group. This is however possible when X is topological group, and Y is a subgroup. This is the case we will be interested in.
In the theorem below, given a continuous map \(\gamma :({{\mathbb {I}}}^n,\partial {{\mathbb {I}}}^n)\rightarrow (X,\{x_0\})\), of pairs, the set of maps \(\gamma ' :({{\mathbb {I}}}^n,\partial {{\mathbb {I}}}^n)\rightarrow (X,\{x_0\})\) homotopic to \(\gamma \), relative to \(\partial {{\mathbb {I}}}^n\) is denoted \([\gamma ]_{\text{ p }}\). For \(n=1\), this coincides with the conventions in Definition 2.32. Then for \(n\ge 1\), the group \(\pi _n(X,x_0)\) is the set of such homotopy classes, with the operation induced by \(+\) in (12). (We will continue to denote the operation in \(\pi _1(X,x_0)\) by the null symbol, since the group \(\pi _1(X,x_0)\) is not necessarily abelian).
For a space X, we use \(\pi _0(X,y)\), where \(y\in X\), to denote the set \(\pi _0(X)\), together with the path-component of y, so \(\pi _0(X,y)\) is a pointed set (a set together with an element of it). The set \( \pi _1(X,A,x_0)\) also naturally becomes a pointed set with distinguished element the homotopy class of the appropriate constant map to \(x_0\). In the last three stages of the exact sequence in Theorem 7.9 below, where group structures are not defined in general, exactness means that the image of a map is equal to the set of elements sent to the homotopy class of the constant map to \(\{x_0\}\) by the following map.
Theorem 7.9
(See for example [Hat02, Sec.4.1]). Let X be a space, \(Y\subseteq X\) a subset, \(x_0\in Y\) a point, and let the maps \(i:(Y,\{x_0\})\rightarrow (X,\{x_0\})\) and \(j:(X,\{x_0\},\{x_0\})\rightarrow (X,Y,\{x_0\})\) be the inclusions. Then we define
and
We also define a map which is the following restriction:
Note that for \(n=1\), we have
There is a long exact sequence:
\(\square \)
A version of the following long exact sequence appears in [Gol81, Prop.3.2]; there all homeomorphisms have compact support and in particular, the motion automorphism group is replaced by the motion group of [Gol81] (see Remark 3.34), keeping in mind also Propositions 6.6 and 6.11.
Lemma 7.10
Let M be a manifold and fix a subset \(N\subseteq M\). Then we have a long exact sequence
where all maps are group maps and \({\textsf{F}}\) is the appropriate restriction of the functor defined in Theorem 7.1.
Proof
We get the first part of the sequence by substituting into (13) \(X= \textrm{Homeo}_M(\varnothing ,\varnothing )\), \(Y=\textrm{Homeo}_{M}(N,N)\) and \(x_0={\textrm{id}}_M\). We have that as sets \(\textrm{MCG}_{M}(N,N)=\pi _0(\textrm{Homeo}_{M}(N,N))\) from Lemma 6.5, and in particular \(\textrm{MCG}_{M}(\varnothing ,\varnothing )=\pi _0(\textrm{Homeo}_M(\varnothing ,\varnothing ))\). From Lemma 7.7 we have \(\textrm{Mot}_{M}(N,N)=\pi _1(\textrm{Homeo}_M(\varnothing ,\varnothing ),\textrm{Homeo}_{M}(N,N),{\textrm{id}}_M)\) as sets. Notice also that, as a set map, \({\textsf{F}}:\textrm{Mot}_{M}(N,N)\rightarrow \textrm{MCG}_{M}(N,N)\) is precisely \(\partial ^1\). In the last few steps we have replaced pointed sets with groups that have the same underlying set, we show that the sequence is indeed an exact sequence of groups.
Note that each group identity is the distinguished object in the corresponding pointed set, hence exactness follows from the pointed set case, and we only need to check that each map is indeed a group homomorphism. We have that \({\textsf{F}}\) is a group map, as it is the restriction of a functor of groupoids. It remains to show that \(j_*^1\) and \(i_*^0\) become group maps. We check that \(j_*^1\) preserves composition. Let g and f be paths from \({\textrm{id}}_M\) to \({\textrm{id}}_M\) in \(\textrm{Homeo}_M(\varnothing ,\varnothing )\). Then gf, the concatenation of paths as in Proposition 2.15, is a well defined flow and it is precisely the flow \(g*f\) as \(f_1={\textrm{id}}_M\). Hence we have

The composition in \(\textrm{MCG}_{M}(N,N)\) is composition of homeomorphisms, hence the composition is the same in the source and target of \(i^0_*\), and \(i^0_*\) is an inclusion. Thus composition is preserved. \(\quad \square \)
Lemma 7.11
Suppose M is a manifold and fix a subset \(N\subseteq M\). Suppose
-
\(\pi _1(\textrm{Homeo}_M(\varnothing ,\varnothing ),{\textrm{id}}_M)\) is trivial, and
-
\(\textrm{MCG}_{M}(\varnothing ,\varnothing )=\pi _0(\textrm{Homeo}_M(\varnothing ,\varnothing ))=\pi _0({\textbf{TOP}}^h(M,M))\) is trivial.
Then there is a group isomorphism
Proof
Using the conditions of the lemma, the long exact sequence in Lemma 7.10 gives short exact sequence
\(\square \)
Remark 7.12
More generally (13) becomes an exact sequence of groups when X is a topological group, Y a subgroup and \(x_0=1_X\), which generalises the case treated in Lemma 7.10. This can be seen as follows. Using . to denote the composition in X, a pointwise composition in \(\pi _n(X,1_X)\) is defined as follows. The composition of a pair \(([\gamma ]_{\text{ p }},[\beta ]_{\text{ p }})\) is the class of \((t_1,\dots , t_n)\mapsto \gamma (t_1,\ldots , t_n).\beta (t_1,\ldots , t_n)\). That this is equivalent to the composition given by (12) follows from the same idea as in the proof of Lemma 3.9. The same composition gives a composition of paths in \(\pi _n(X,Y,1_X)\) for \(n\ge 1\), which again is the same as (12) for \(n\ge 2\). Composition in \(\pi _0(X)\) and \(\pi _0(Y)\) is given by the group composition. It is straightforward to check that all maps become group maps.
7.2 Isomorphisms \(\textrm{Mot}_{M}^A\) to \(\textrm{MCG}_{M}^A\)
Here we give conditions under which \(\textrm{Mot}_{M}^A\) and \(\textrm{MCG}_{M}^A\) are isomorphic categories.
Theorem 7.13
Let M be a manifold. If
-
\(\pi _1(\textrm{Homeo}_M(\varnothing ,\varnothing ),{\textrm{id}}_M)=\pi _1({\textbf{TOP}}^h(M,M),{\textrm{id}}_M)\) is trivial, and
-
\(\textrm{MCG}_{M}(\varnothing ,\varnothing )=\pi _0(\textrm{Homeo}_M(\varnothing ,\varnothing ))=\pi _0({\textbf{TOP}}^h(M,M))\) is trivial,
the functor
defined in Theorem 7.1 is an isomorphism of categories.
Proof
First note that by construction \({\textsf{F}}\) is the identity map on objects. Suppose \(\pi _1(\textrm{Homeo}_M(\varnothing ,\varnothing ),{\textrm{id}}_M)\) and \(\pi _0(\textrm{Homeo}_M(\varnothing ,\varnothing ))\) are trivial. We have from Lemma 7.2 that \({\textsf{F}}\) is full. We check \({\textsf{F}}\) is faithful. Let  and
and  be in \(\textrm{Mot}_{M}(N,N')\). If
be in \(\textrm{Mot}_{M}(N,N')\). If

then

By Lemma 7.11 this is true if and only if

which is equivalent to saying \({\textrm{Id}}_M*(\bar{f'}*f)\) is path-equivalent to a stationary motion, and hence that \(\bar{f'}*f\) is path-equivalent to the stationary motion (since \({\textrm{Id}}_M*(\bar{f'}*f){\mathop {\sim }\limits ^{p}}\bar{f'}*f\)). So we have  .
.
We have seen that \({\textsf{F}}:\textrm{Mot}_{M}\rightarrow \textrm{MCG}_{M}\) is such that, restricted to objects it is a bijection, and moreover proved that, given objects \(N,N' \in {{\mathcal {P}}}{M}\), then \({\textsf{F}}:\textrm{Mot}_{M}(N,N') \rightarrow \textrm{MCG}_{M}(N,N')\) is a bijection. Therefore \({\textsf{F}}\) is, by definition, an isomorphism of categories (see for example [ML13, Page 14]).
The proofs of the preceding lemmas and the theorem proceed in the same way for the A-fixing case. \(\quad \square \)
Remark 7.14
We note that for some manifolds M, we may have that \({\textsf{F}}\) is not an isomophism, but does restrict to an isomorphims on some full subgroupoid given by a particular choice of subsets of M. See Example 7.3.4 below.
7.3 Examples of \({\textsf{F}}:\textrm{Mot}_{M}^A\rightarrow \textrm{MCG}_{M}^A\)
Here we give examples of M for which \({\textsf{F}}\) is an isomorphism, and examples for which it is not. Even when we do not have a category isomorphism, the long exact sequence in (14) will often be useful to obtain results about motion groupoids from results about mapping class groupoids.
7.3.1 Example 1: the disk \(D^m\), fixing the boundary
Proposition 7.15
Let \(D^m\) be the m-dimensional disk. Then there is an isomorphism
with \({\textsf{F}}\) as in Theorem 7.1.
Proof
We proved in Proposition 6.12 that \(\textrm{MCG}_{D^2}^{\partial D^2}(\varnothing ,\varnothing )=\pi _0\big (\textrm{Homeo}_{D^2}^{\partial D^2}(\varnothing ,\varnothing )\big )\) is trivial. Also \(\textrm{Homeo}_{D^2}^{\partial D^2}(\varnothing ,\varnothing )\) is contractible, see e.g. Theorem 1.1.3.2 of [Ham74]. In fact, for all integer m, \(Homeo_{D^m}^{\partial D^m}(\varnothing ,\varnothing )\) contractible for all m. This follows from the Alexander Trick [Ale23]. Hence by Theorem 7.13 we have the result. \(\quad \square \)
One consequence of Proposition 7.15 is the following result, well-known via Proposition 6.11. A similar result can be found in [BB05, Thm.1], for instance, framed using instead groups of diffeomorphisms of \(D^2\) to formulate mapping class groups of \(D^2\).
Theorem 7.16
Let n be a positive integer. Let \(K\subset \textrm{int}(D^2)\) have cardinality n. Choose a homeomorphism \(f:{{\mathbb {R}}}^2\rightarrow \textrm{int}(D^2)\) and let \(K'\subset {{\mathbb {R}}}^2\) be such that \(f(K')=K\).
We have an isomorphism:
(Recall from §5.3 that \(\textbf{B}({{\mathbb {R}}}^2,K)\) is isomorphic, by construction, to the Artin braid group \(\textbf{B}_n\) on n strands, as formulated in [Art47].)
Proof
From Theorem 5.17 we have an isomorphism \(\textrm{Mot}_{{{\mathbb {R}}}^2}(K',K')\cong {\textbf{B}}({{\mathbb {R}}}^2,K')\). By Lemma 3.39 it follows that \(\textrm{Mot}_{\textrm{int}(D^2)}(K,K)\cong {\textbf{B}}({{\mathbb {R}}}^2,K')\), and with Remark 5.24 it follows that \(\textrm{Mot}_{D^2}^{\partial D^2}(K,K) \cong {\textbf{B}}({{\mathbb {R}}}^2,K')\). Combining with Proposition 7.15 we have the result. \(\quad \square \)
The following corollary is stated in [Dam17], and is essentially present in [Gol81] (see Proposition 3.2, Corollary 3.6 and Section 5), although the setting of the latter is \({{\mathbb {R}}}^3\) restricted to maps with compact support.
Corollary 7.17
Let \(D^3\) be the 3-disk, and C a fixed choice of subset consisting of n disjoint unknotted, unlinked circles. Then we have an isomorphism
(The group \(LB^{ext}_n\) was defined in Definition 6.14.) \(\quad \square \)
In particular notice that the previous corollary implies \(\textrm{Mot}_{D^3}^{\partial D^3}(C,C)\) is finitely generated, since the loop braid group has a finite presentation [Dam17, Prop.3.16].
Proposition 7.18
Let \(N={{\mathbb {I}}}\cap {\mathbb {Q}}\), then \(\textrm{Mot}_{{{\mathbb {I}}}}(N,N)\) is uncountably infinite.
Proof
It follows from Proposition 7.15 that we have an isomorphism
and, since all motions in \({{\mathbb {I}}}\) are boundary fixing, an isomorphism \( \textrm{Mot}_{{{\mathbb {I}}}}\rightarrow \textrm{MCG}_{{{\mathbb {I}}}}^{\partial {{\mathbb {I}}}} \). All mapping classes considered in Theorem 6.7 are boundary fixing, thus this isomorphism implies \(\textrm{Mot}_{{{\mathbb {I}}}}(N,N)\) uncountably infinite. \(\quad \square \)
7.3.2 Example 2: the disk \(D^2\), without fixing the boundary
In this section we consider the (non-isomorphism) functor
giving an explicit example of an motion contained in the kernel.
Let \(P_2\subset D^2\setminus \partial D^2 \) be a subset consisting of two points equidistant from and on a line through the centre of the disk. Let \(\tau _{\pi }\) be the path in  such that \((\tau _{\pi })_ t\) is a \(\pi t\) rotation of the disk. There is a motion
such that \((\tau _{\pi })_ t\) is a \(\pi t\) rotation of the disk. There is a motion  , and this motion represents a non-trivial equivalence class in \(\textrm{Mot}_{D^2}\). This can be seen by noting that there is no stationary motion which exchanges the points in \(P_2\). By a similar argument
, and this motion represents a non-trivial equivalence class in \(\textrm{Mot}_{D^2}\). This can be seen by noting that there is no stationary motion which exchanges the points in \(P_2\). By a similar argument  also represents a non trivial element of \(\textrm{MCG}_{D^2}\).
also represents a non trivial element of \(\textrm{MCG}_{D^2}\).
Now consider the motion  . It is intuitively clear this motion is non-trivial in \(\textrm{Mot}_{D^2}\) by considering its image as a homeomorphism \(D^2\times {{\mathbb {I}}}\rightarrow D^2\times {{\mathbb {I}}}\), see Fig. 13. A proof follows from the fact that the worldlines of the trajectory of the points in \(P_2\) transcribe a non-trivial braid. However its endpoint is a \(2\pi \) rotation, which is precisely \({\textrm{id}}_M\), hence represents
. It is intuitively clear this motion is non-trivial in \(\textrm{Mot}_{D^2}\) by considering its image as a homeomorphism \(D^2\times {{\mathbb {I}}}\rightarrow D^2\times {{\mathbb {I}}}\), see Fig. 13. A proof follows from the fact that the worldlines of the trajectory of the points in \(P_2\) transcribe a non-trivial braid. However its endpoint is a \(2\pi \) rotation, which is precisely \({\textrm{id}}_M\), hence represents  in \(\textrm{MCG}_{D^2}\).
in \(\textrm{MCG}_{D^2}\).
In fact, the map \({\textsf{F}}:\textrm{Mot}_{D^2}\rightarrow \textrm{MCG}_{D^2}\) is neither full nor faithful. The space \({\textbf{TOP}}^h(D^2,D^2)\) is homotopy equivalent to \(S^1\sqcup S^1\), where the first connected component corresponds to orientation preserving homeomorphisms and the second orientation reversing. That the space of orientation preserving homeomorphisms is homotopy equivalent to \(S^1\) follows from [Ham74, Sec.1.1]. We arrive at \(S^1\sqcup S^1\) following the same argument used in the proof of Proposition 6.8 (with the definition of degree map generalised to the disk), together with the fact that all path components of topological groups are homeomorphic. In particular we have from [Ham74] that \(\pi _1(\textrm{Homeo}_{D^2}(\varnothing ,\varnothing ),{\textrm{id}}_{D^2})={\mathbb {Z}}\) where the single generating element corresponds to the \(2\pi \) rotation. Also \(\pi _0(\textrm{Homeo}_{D^2}(\varnothing ,\varnothing ))={\mathbb {Z}}/2{\mathbb {Z}}\). The last steps of the exact sequence from Lemma 7.10 are:
7.3.3 Example 3: the circle \(S^1\)
The unit circle \(S^1\) provides another example for which we can explicitly construct elements of the non-trivial kernel of \({\textsf{F}}:\textrm{Mot}_{S^1} \rightarrow \textrm{MCG}_{S^1}\). Let \(P\subset S^1\) be a subset containing a single point in \(S^1\). Consider the flow f of \(S^1\), where \(f_t\) is a \(2\pi t\) rotation of the circle. There is a motion  , whose worldline is depicted figure 14.
, whose worldline is depicted figure 14.
Similarly to the construction for the disk, we then have:
Lemma 7.19
The morphism  in the motion groupoid \(\textrm{Mot}_{S^1}\) is non trivial, and moreover we have an exact sequence:
in the motion groupoid \(\textrm{Mot}_{S^1}\) is non trivial, and moreover we have an exact sequence:
In the proof of this lemma, we consider the homomorphism \(\textrm{Rot}:S^1 \rightarrow \textrm{Homeo}_{S^1}(\varnothing ,\varnothing )\), the topological space of homeomorphisms of \(S^1\), sending a point with coordinate \(\theta \) of \(S^1\) to a rotation of \(S^1\) along angle \(\theta \). Explicitly, seeing \(S^1\) as a subset of the complex plane, \(\textrm{Rot}\) is defined as:
This is an injective homomorphism, hence an embedding, since \(S^1\) is compact and \(\textrm{Homeo}_{S^1}(\varnothing ,\varnothing )\) is Hausdorff.
Proof
The last steps in the exact sequence in Lemma 7.10 are:
Now, the subspace of \(\textrm{Homeo}_{S^1}(P,P)\) containing orientation preserving maps is contractible (see §1.1.2 combined with Thm 1.1.1 [Ham74]). Also every point on a path in \(\textrm{Homeo}_{S^1}(P,P)\) starting at \({\textrm{id}}_M\) is an orientation preserving map (this is argued in the proof of Proposition 6.8). Hence \(\pi _1(\textrm{Homeo}_{S^1}(P,P),{{\textrm{id}}}_{S^1})\) is trivial, and also \({\textsf{F}}\) is the zero map, as the endpoint of a motion of \(S^1\) must be orientation preserving. Also from [Ham74, §1.1.2] we have that \(\textrm{Rot}(S^1)\) is a strong deformation retract of the path-component of \(\textrm{Homeo}_{S^1}(\varnothing ,\varnothing )\), containing the identity (i.e. the subgroup of orientation preserving homeomorphisms \(S^1 \rightarrow S^1\), as argued in Proposition 6.8). By Proposition 6.8, \( \textrm{MCG}_{S^1}(\varnothing ,\varnothing )={{\mathbb {Z}}}/ 2{{\mathbb {Z}}}\), hence the exact sequence becomes:
In particular, \(j^1_*:{{\mathbb {Z}}}\rightarrow \textrm{Mot}_{S^1}(P,P)\) is injective. That  is non trivial follows from the fact that it is, by construction, the image of the generator of \(\pi _1(\textrm{Rot}(S^1),{\textrm{id}}_{S^1}) \cong {{\mathbb {Z}}}\) arising (via \(\textrm{Rot}\)) from a positively oriented loop in \(S^1.\)
is non trivial follows from the fact that it is, by construction, the image of the generator of \(\pi _1(\textrm{Rot}(S^1),{\textrm{id}}_{S^1}) \cong {{\mathbb {Z}}}\) arising (via \(\textrm{Rot}\)) from a positively oriented loop in \(S^1.\)
Finally notice \(i_*^0\) is not the zero map as there is clearly an orientation reversing homeomorphism of \(S^1\) sending P to P. Hence the exact sequence in (16) becomes (15). In particular the motion-equivalence class of f is non-trivial in \(\textrm{Mot}_{S^1}(P,P)\); and its image in \(\textrm{MCG}_{S^1}(P,P)\) is trivial. \(\quad \square \)
Note that we can directly see that  , where the latter equality follows from the fact that a \(2 \pi \) rotation of \(S^1\) is the identity function. However we need the previous theorem to assert that f is non-trivial in \(\textrm{Mot}_{S^1}(P,P)\).
, where the latter equality follows from the fact that a \(2 \pi \) rotation of \(S^1\) is the identity function. However we need the previous theorem to assert that f is non-trivial in \(\textrm{Mot}_{S^1}(P,P)\).
7.3.4 Example 4: the 2-sphere \(S^2\)
The following example shows that \({\textsf{F}}\) can restrict to an isomorphism when considering certain subsets (and orientation preserving maps) but not others.
Let \(M=S^2\) and \(P_2\) be the subset containing 2 points in the sphere.
From Section 1.2 of [Ham74] we have the following,
So the exact sequence becomes
Also from [Ham74], the map \(\pi _1(\textrm{Homeo}_{S^2}(P_2,P_2),{\textrm{id}}_{S^2}) \rightarrow \pi _1(\textrm{Homeo}_{S^2}(\varnothing ,\varnothing ),{\textrm{id}}_{S^2})\) is surjective, with the non trivial element in \(\pi _1(\textrm{Homeo}_{S^2}(\varnothing ,\varnothing ),{\textrm{id}}_{S^2})\) represented by a path which maps \(t\in {{\mathbb {I}}}\) to a \(2\pi t\) rotation about some chosen axis. Hence the map \({{\mathbb {Z}}}/2{{\mathbb {Z}}}\rightarrow \textrm{Mot}_{S^2}(P_2,P_2)\) is the zero map, and the same rotation is trivial in \(\textrm{Mot}_{S^2}(P_2,P_2)\).
This can be seen directly by choosing the points to be antipodal, say the north and south pole. Now consider a \(2\pi \) rotation with axis through north and south pole. This is a path fixing both points, hence a stationary path which is equivalent to the identity.
Looking back at the exact sequence, we have that the map \(\textrm{Mot}_{S^2}(P_2,P_2)\rightarrow \textrm{MCG}_{S^2}(P_2,P_2)\) is injective. Combining the results of Hamstrom with the result on pg.52 of [FM11], we have that \(\textrm{MCG}_{S^2}(P_2,P_2)\cong {{\mathbb {Z}}}/2{{\mathbb {Z}}}\times {{\mathbb {Z}}}/2{{\mathbb {Z}}}\) where the non trivial element in the first copy of \({{\mathbb {Z}}}/2{{\mathbb {Z}}}\) is represented by a self-homeomorphism which swaps the points by an orientation preserving self-homeomorphism, and the non trivial element in the second component is represented by a self-homeomorphism swapping the two points with is orientation reversing. Hence a motion which swaps the two points represents a non trivial morphism in \(\textrm{Mot}_{S^2}(P_2,P_2)\).
Recall that \(\textrm{MCG}_{S^2}^{+}\) is the mapping class groupoid constructed using only orientation preserving homeomorphisms. Then we have a group isomorphism
Note this does not extend to a category isomorphism. Considering instead the subset consisting of three points the groups are non isomorphic. Intuitively we can see this by arguing that we cannot place three points on the sphere such that any \(2\pi \) rotation is a stationary motion. Arguing in a similar way to the preceding examples, a \(2\pi \) rotation of the sphere represents the identity morphism in the mapping class groupoid.
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
Our convention is that a neighbourhood of x is a subset of X containing an open set containing x.
There are two conventions for compact-open topology. The one written here (which is the classical one) and the one where we additionally impose that each K in the \(B_{XY}(K,U)\) be Hausdorff. For example, [May99, Chapter 5] takes the latter convention. This creates an a priori smaller set of open sets in the function space. However there will be no ambiguity issues in this paper as we will only be working with Hausdorff topological spaces.
There is in fact an adjustment of the compact open topology which, with an adjustment to the product, gives an adjunction without the need to restrict Y. See [Bro06, Sec.5.9] for more information.
Here we are assuming that M is not only Hausdorff, but also second countable.
Note we use the fact that M is a manifold, so that \({\textbf{TOP}}^h(M,M)\) is a topological group. An alternative proof of this result that holds if M is compact (and not necessarily a manifold) follows from the fact that any continuous bijection between compact Hausdorff spaces is a homeomorphism.
This nomenclature is borrowed from [Art47], where strong isotopies between braids are introduced.
Here note that, by the invariance of domain theorem, \(\textrm{int}(U_k^t)\) can be seen both as the interior of the set \(U_k^t\), in M, and as the interior of the manifold \(U_k^t\). This can be used to show that the function below is continuous, applying the pasting lemma to the closed subsets \(M{\setminus } \textrm{int}(U_k^t)\) and \(U_k^t\).
This is where the crucial fact that L can be chosen to be connected is used.
References
Aceto, P., Bregman, C., Davis, C.W., Park, J., Ray, A.: Isotopy and equivalence of knots in 3-manifolds (2020). arXiv:2007.05796
Ananthakrishna, G., Conway, A., Ergen, E., Floris, R., Galvin, D., Hobohm, C., Kirby, R., Kister, J., Kosanović, D., Christian, K., Lippert, F., Merz, A., Mezher, F., Niu, W., Nonino, I., Powell, M., Ray, A., Ruppik, B.M., Santoro, D., von Wunsch, M.: Topological manifolds. https://maths.dur.ac.uk/users/mark.a.powell/Topological-manifolds-lecture-notes-after-seminar.pdf
Alexander, J.W.: On the deformation of an n cell. Proc. Natl. Acad. Sci. USA 9(12), 406 (1923)
Arens, R.: Topologies for homeomorphism groups. Am. J. Math. 68(4), 593–610 (1946)
Artin, E.: Theorie der zöpfe. In: Abhandlungen aus dem mathematischen Seminar der Universität Hamburg, vol. 4, pp. 47–72. Springer (1925)
Artin, E.: Theory of braids. Ann. Math. 48, 101–126 (1947)
Bais, F.A.: Flux metamorphosis. Nucl. Phys. B 170(1), 32–43 (1980)
Birman, J.S., Brendle, T.E.: Braids: a survey. In: Menasco, W., Thistlethwaite, M. (eds.) Handbook of Knot Theory, pp. 19–103. Elsevier, Amsterdam (2005)
Bellingeri, P., Bodin, A.: The braid group of a necklace. Math. Z. 283(3), 995–1010 (2016)
Baez, J.C., Dolan, J.: Higher-dimensional algebra and topological quantum field theory. J. Math. Phys. 36(11), 6073–6105 (1995). https://doi.org/10.1063/1.531236
Bullivant, A., Faria Martins, J., Martin, P.: Representations of the loop braid group and Aharonov–Bohm like effects in discrete \((3+1)\)-dimensional higher gauge theory. Adv. Theor. Math. Phys. 23(7), 1685–1769 (2019). https://doi.org/10.4310/atmp.2019.v23.n7.a1
Brown, R., Higgins, P.J.: On the algebra of cubes. J. Pure Appl. Algebra 21, 233–260 (1981). https://doi.org/10.1016/0022-4049(81)90018-9
Brendle, T.E., Hatcher, A.: Configuration spaces of rings and wickets. Comment. Math. Helv. 88(1), 131–162 (2013)
Birman, J.S.: Mapping class groups and their relationship to braid groups. Commun. Pure Appl. Math. 22(2), 213–238 (1969)
Birman, J.S.: Braids, Links, and Mapping Class Groups. Based on Lecture Notes by James Cannon, vol. 82. Princeton University Press, Princeton (1975). https://doi.org/10.1515/9781400881420
Bullivant, A., Kimball, A., Martin, P., Rowell, E.C.: Representations of the necklace braid group: topological and combinatorial approaches. Commun. Math. Phys. (2019). https://doi.org/10.1007/s00220-019-03445-0
Brown, R.: Groupoids and crossed objects in algebraic topology. Homol. Homotopy Appl. 1(1), 1–78 (1999)
Brown, R.: Topology and groupoids. www.groupoids.org (2006)
Budney, R.: Topology of knot spaces in dimension 3. Proc. Lond. Math. Soc. (3) 101(2), 477–496 (2010). https://doi.org/10.1112/plms/pdp058
Baez, J.C., Wise, D.K., Crans, A.S.: Exotic statistics for strings in 4d BF theory. Adv. Theor. Math. Phys. 11(5), 707–749 (2007)
Burde, G., Zieschang, H., Heusener, M.: Knots. De Gruyter, Berlin (2013). https://doi.org/10.1515/9783110270785
Crowell, R., Fox, R.: Introduction to Knot Theory, p. 182. Ginn and Company, Boston (1963)
Carter, J.S., Rieger, J.H., Saito, M.: A combinatorial description of knotted surfaces and their isotopies. Adv. Math. 127(1), 1–51 (1997)
Dahm, D.M.: A generalization of braid theory. Ph.D. thesis, Princeton University, Mathematics (1962)
Damiani, C.: A journey through loop braid groups. Expo. Math. 35(3), 252–285 (2017)
Damiani, C., Kamada, S.: On the group of ring motions of an h-trivial link. Topol. Appl. 264, 51–65 (2019)
Dugundji, J.: Topology. Allyn and Bacon, Inc., Boston (1966)
Edwards, R.D., Kirby, R.C.: Deformations of spaces of imbeddings. Ann. Math. 2(93), 63–88 (1971). https://doi.org/10.2307/1970753
Fisher, G.M.: On the group of all homeomorphisms of a manifold. Trans. Am. Math. Soc. 97, 193–212 (1960). https://doi.org/10.2307/1993298
Farb, B., Margalit, D.: A Primer on Mapping Class Groups (pms-49). Princeton University Press, Princeton (2011)
Fritsch, R., Piccinini, R.A.: Cellular Structures in Topology, vol. 19. Cambridge University Press, Cambridge (1990)
Fradkin, E.: Field Theories of Condensed Matter Physics. Cambridge University Press, Cambridge (2013)
Goldsmith, D.L.: Motions of links in the 3-sphere. Ph.D. thesis, Princeton University, Mathematics (1972)
Goldsmith, D.L.: The theory of motion groups. Mich. Math. J. 28(1), 3–17 (1981)
Hamstrom, M.-E.: Homotopy in homeomorphism spaces, \( top \) and \( pl\). Bull. Am. Math. Soc. 80(2), 207–230 (1974)
Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge (2002)
Hirsch, M.W.: Differential Topology, vol. 33. Springer, Cham (1976). https://doi.org/10.1007/978-1-4684-9449-5
Hatcher, A., Thurston, W.: A presentation for the mapping class group of a closed orientable surface. Topology 19(3), 221–237 (1980)
Ivanov, N.V.: Mapping class groups. In: Daverman, R.J., Sher, R.B. (eds.) Handbook of Geometric Topology, pp. 523–633. North-Holland, Amsterdam (2002)
Kamada, S.: Braid and Knot Theory in Dimension Four, vol. 95. American Mathematical Society, Providence (2002)
Kan, D.M.: Adjoint functors. Trans. Am. Math. Soc. 87, 294–329 (1958)
Kassel, C.: Quantum Groups, vol. 155. Springer, Berlin (2012)
Kádár, Z., Martin, P., Rowell, E., Wang, Z.: Local representations of the loop braid group. Glasg. Math. J. 59(2), 359–378 (2017)
Kassel, C., Turaev, V.: Braid Groups. With the Graphical Assistance of Olivier Dodane, vol. 247. Springer, New York (2008). https://doi.org/10.1007/978-0-387-68548-9
Kupers, A.: Proving homological stability for homeomorphisms of manifolds. arxiv Algebraic Topology (2015). arXiv:1510.02456
Lees, J.A.: Immersions and surgeries of topological manifolds. Bull. Am. Math. Soc. 75, 529–534 (1969). https://doi.org/10.1090/S0002-9904-1969-12231-7
Leinaas, J.M., Myrheim, J.: On the theory of identical particles. Il Nuovo Cimento B (1971–1996) 37(1), 1–23 (1977)
May, J.P.: A Concise Course in Algebraic Topology. University of Chicago Press, Chicago (1999)
Milnor, J.W.: Topology from the Differentiable Viewpoint, p. 64. The University Press of Virginia, Charlottesville (1965)
Magnus, W., Karrass, A., Solitar, D.: Combinatorial Group Theory: Presentations of Groups in Terms of Generators and Relations. Couer Corporation, Chelmsford (2004)
Mac Lane, S.: Categories for the Working Mathematician, vol. 5. Springer, Berlin (2013)
Martins, J.F., Martin, P.P., Torzewska, F.: Motion groupoids: first steps in representation theory (in progress)
Martins, J.F., Martin, P.P., Torzewska, F.: Topological quantum field theories for homotopy cobordisms (in progress)
Munkres, J.: Topology, 2nd edn. Prentice Hall, Englewood Cliffs (2000)
Michor, P.W., Vizman, C.: \(n\)-transitivity of certain diffeomorphism groups. Acta Math. Univ. Comen. New Ser. 63(2), 221–225 (1994)
Picken, R.: Reflections on topological quantum field theory. Rep. Math. Phys. 40(2), 295–303 (1997)
Qiu, Y., Wang, Z.: Representations of motion groups of links via dimension reduction of TQFTs. Commun. Math. Phys. 382, 2071–2100 (2021)
Rolfsen, D.: New developments in the theory of Artin’s braid groups. Topol. Appl. 127(1–2), 77–90 (2003)
tom Dieck, T.: Algebraic Topology, vol. 8. European Mathematical Society, Helsinki (2008)
Waldhausen, F.: On irreducible 3-manifolds which are sufficiently large. Ann. Math. 87, 56–88 (1968)
Wattenberg, F.: Differentiable motions of unknotted, unlinked circles in 3-space. Math. Scand. 30(1), 107–135 (1972)
Acknowledgements
JFM and PM were partially funded by the Leverhulme trust research project Grant “RPG-2018-029: Emergent Physics From Lattice Models of Higher Gauge Theory”. FT was funded by a University of Leeds Ph.D. Scholarship and is now funded by EPSRC. FT thanks Carol Whitton; and PM thanks Paula Martin for useful conversations. We all thank Celeste Damiani and Martin Palmer-Anghel for comments, Arnaud Mortier for useful email discussions, and Hadeel Albeladi, Basmah Alsubhi and Manar Qadi for useful discussions. An initial version of this material was presented by FT in a series of LMS funded lectures available here https://media.ed.ac.uk/playlist/dedicated/51612401/1_dfxocmez/1_bm66fhc8, FT also thanks Simona Paoli for the invitation to give these lectures.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
JFM and PM were partially funded by the Leverhulme trust research project Grant “RPG-2018-029: Emergent Physics From Lattice Models of Higher Gauge Theory”, where this work was initiated. FT was funded by a University of Leeds Ph.D. Scholarship and is now funded by EPSRC. The authors have no relevant financial or non-financial interests to disclose.
Additional information
Communicated by C. Schweigert.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Appendix
A Appendix
1.1 A.1 Proof of Theorem 2.11
This section revisits the proof of Theorem 4 in [Are46] using our notation.
Recall that a space X is said to be locally compact if each \(x\in X\) has an open neighbourhood which is contained in a compact set. If X is Hausdorff, X is locally compact if and only if for each \(x \in X\) and open set \(U\subset X\) containing x, there exists an open set V containing x with \({\bar{V}}\) compact and \({\bar{V}}\subset U\) (where \({\bar{V}}\) is the closure of V) [Mun00, Thm 29.2].
Lemma A.1
Let X be a locally compact Hausdorff space. Let \(K\subset X\) be compact and \(U\subset X\) be open with \(K\subset U\). Then there exists an open set V with \(K\subset V\subset {\overline{V}}\subset U\), where \({\overline{V}}\) is compact.
Proof
Since X is locally compact Hausdorff, for every \(x\in K\) there is an open set \(V(x)\subset U\) with \(\overline{V(x)}\subset U\) compact. The set of all V(x) is a cover for K, and K is compact so there exists a finite subcover. Hence we have
for some finite set \(\{x_1,\dots x_n\}\subset K\). We can choose \(V=\bigcup _{i\in \{1,\dots ,n\}}{V(x_i)}\), noting that (since the union is finite) \({\overline{V}}=\bigcup _{i\in \{1,\dots ,n\}}\overline{V(x_i)}\), and hence \({\overline{V}}\) is compact, since it is a finite union of compact subsets. \(\quad \square \)
Lemma A.2
Let X be a locally compact Hausdorff space. Then the composition of homeomorphisms
is continuous.
Proof
Let \(B_{XX}(K,U)\) be an element of the subbasis of \(\tau ^{co}_{XX}\). Now suppose \(\mathfrak {h}\in B_{XX}(K,U)\) is in the image of \(\circ \), so \(\mathfrak {h}=\mathfrak {g}\circ \mathfrak {f}\) for some \(\mathfrak {g},\mathfrak {f}\in {\textbf{Top}}^h(X,X)\). We show that for all such \(\mathfrak {h}\), we can construct an open set in \(V\in {\textbf{Top}}^h(X,X) \times {\textbf{Top}}^h(X,X)\) with \((\mathfrak {f},\mathfrak {g})\in V\) and for all \((\mathfrak {f}',\mathfrak {g}')\in V\), \(\mathfrak {g}'\circ \mathfrak {f}'\in B_{XX}(K,U)\).
We have \(\mathfrak {g}(K)\subset \mathfrak {f}^{-1}(U)\), and so by Lemma A.1 there exists an open set W with \(\mathfrak {g}(K)\subset W\subset {\overline{W}}\subset f^{-1}(U)\), and \({\overline{W}}\) compact. Now \(B_{XX}(K,W)\times B_{XX}({\overline{W}},U)\) is an open set containing \((\mathfrak {f},\mathfrak {g})\) and for any \((\mathfrak {f}',\mathfrak {g}')\in B_{XX}(K,W)\times B_{XX}({\overline{W}},U)\), \(\mathfrak {g}\circ \mathfrak {f}\in B_{XX}(K,U)\). \(\quad \square \)
There is a more general version of the previous Lemma where the maps are not necessarily homeomorphisms, see Theorem 2.2 of [Dug66].
Lemma A.3
Let X be a locally connected, locally compact Hausdorff space. Then the sets \(B_{XX}(L,U)\) where L is compact, connected and has non empty interior, and U is open, form a subbasis for the compact open topology.
Proof
Again we follow the argument in [Are46]. Let \(\mathfrak {h}\in {\textbf{Top}}^h(X,X)\). We show that for any \(B_{XX}(K,U)\) containing \(\mathfrak {h}\) where K is compact and U is open, there exists a subset of \(B_{XX}(K,U)\) containing \(\mathfrak {h}\) of the form \(B_{XX}(L_1,U)\cap \dots \cap B_{XX}(L_n,U)\) where each \(L_i\) is compact, connected and has non empty interior.
Since \(\mathfrak {h}\) is continuous, for each \(x\in K\) we can find an open set V(x) containing x such that \(\mathfrak {h}(V(x))\subset U\). Since X is locally compact and Hausdorff, we can then find another \(V'(x)\), open in X, such that
with \(\overline{V'(x)}\) compact. Now since X is locally connected, there exists a connected open set \(V''(x)\) such that \(x \in V''(x)\subset {V'(x)}\). Also \(\overline{V''(x)}\) is compact, since \(\overline{V''(x)}\subset {\overline{V'(x)}}\) and closed subsets of compact spaces are compact. Furthermore \(\overline{V''(x)}\subset V(x)\), so \(\mathfrak {h}(\overline{V''(x)}) \subset U.\)
The \(V''(x)\) cover K and so there exists a finite subcover by \(V(x_i)\) for some finite set of \(x_i\in K\) with \(i\in \{1,\dots ,n\}\). Clearly:
\(\square \)
Lemma A.4
Let X be a locally connected, locally compact Hausdorff space. Then the inverse map
is continuous.
Proof
Throughout the proof, only, we will put \((-)^{-1}=T\). So \(T:{\textbf{TOP}}^h(X,X)\rightarrow {\textbf{TOP}}^h(X,X)\) is the function such that \(T(\mathfrak {h})=\mathfrak {h}^{-1}\).
By Lemma A.3, in order to prove that T is continuous, we only need to prove that the inverse images under T of sets of the form \(B_{XX}(L,U)\), with L compact, connected and with non-empty interior, and U open, are open in \({\textbf{TOP}}^h(X,X)\).
Let \(L\subset X\) be compact, connected, and with a non-empty interior. Let U be open in X. We show that for any \(\mathfrak {f}^{-1}\in B_{XX}(L,U)\), we can construct an open subset of \( {\textbf{TOP}}^h(X,X)\), containing \(\mathfrak {f}\), which is a subset of \(T^{-1}(B_{XX}(L,U))\).
Since \(\mathfrak {f}^{-1}\) is a homeomorphism, it sends compact subsets to compact subsets. So \(\mathfrak {f}^{-1}(L)\) is compact. Also \(\mathfrak {f}^{-1}(L) \subset U\), since \(\mathfrak {f}^{-1}\in B_{XX}(L,U)\).
Using Lemma A.1, we can choose an open set \(V\subset X\) such that \(f^{-1}(L)\subset V\subset {\overline{V}}\subset U\), with \({\overline{V}}\) compact, and then an open set \(W\subset X\) with \({\overline{V}}\subset W\subset {\overline{W}}\subset U\), with \({\overline{W}}\) compact. In full:
Therefore
We can also choose an \(x\in X\) such that \(\mathfrak {f}(x)\in int(L)\) (where int(L) is the interior of L). So there exists an open set (in \({\textbf{TOP}}^h(X,X)\)):
containing \(\mathfrak {f}\), which we denote \(U_0\). We claim that \(U_0 \in T^{-1}(B_{XX}(L,U)).\)
Let \(\mathfrak {h}\in U_0\). We have: \(\mathfrak {h}\left( (X{\setminus } V) \cap {\overline{W}}\right) \subset (X{\setminus } L) \cap \mathfrak {f}(U)\). Taking complements and reversing the inclusion we have
Now \(\mathfrak {h}(V)\) and \(\mathfrak {h}(X{\setminus } {\overline{W}})\) are disjoint open sets, and L is connected,Footnote 9 so either L is contained in \(\mathfrak {h}(V)\) or L is contained in \(\mathfrak {h}(X\setminus {\overline{W}})\), but not both. We claim that \(L\subset \mathfrak {h}(V)\).
Note that since \(\mathfrak {h} \in B_{XX}\left( \{x\},int(L)\right) \), we have \(\mathfrak {h}(x) \in int(L)\). Since \(\mathfrak {f}(x) \in int(L)\), by construction, we have \(x\in \mathfrak {f}^{-1}(int(L))\subset V.\) So \(\mathfrak {h}(x) \in \mathfrak {h}(V).\) So \(L\cap \mathfrak {h}(V) \ne \varnothing \). So \(L\subset \mathfrak {h}(V)\).
Since \(L\subset \mathfrak {h}(V)\), we have \(\mathfrak {h}^{-1}(L)\subset V\subset U\). Hence \(\mathfrak {h}^{-1}\in B_{XX}(L,U)\). \(\quad \square \)
Proof
(Of Theorem 2.11) In Lemma A.2 we prove that the composition is continuous if X is locally compact Hausdorff. In Lemma A.4 we prove that the inverse map is continuous. \(\quad \square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Torzewska, F., Faria Martins, J. & Martin, P.P. Motion Groupoids and Mapping Class Groupoids. Commun. Math. Phys. 402, 1621–1705 (2023). https://doi.org/10.1007/s00220-023-04755-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-023-04755-0










 , see Definition
, see Definition 
 up to motion-equivalence, see Proposition
up to motion-equivalence, see Proposition 

 up to relative path-equivalence, see Lemma
up to relative path-equivalence, see Lemma 


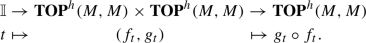


 and
and  . Then there exists a path homotopy, say
. Then there exists a path homotopy, say  of motions, explicitly
of motions, explicitly 
 is path equivalent to an
is path equivalent to an 
 ,
,  is the motion-equivalence class of
is the motion-equivalence class of  where
where  is a motion, then
is a motion, then  is a motion. It also follows that if
is a motion. It also follows that if  is S-stationary, then
is S-stationary, then 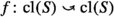 is also
is also 









 (see text), mapped into
(see text), mapped into 