Abstract
The KPZ fixed point is a 2d random field, conjectured to be the universal limiting fluctuation field for the height function of models in the KPZ universality class. Similarly, the periodic KPZ fixed point is a conjectured universal field for spatially periodic models. For both fields, their multi-point distributions in the space-time domain have been computed recently. We show that for the case of the narrow-wedge initial condition, these multi-point distributions can be expressed in terms of so-called integrable operators. We then consider a class of operators that include the ones arising from the KPZ and the periodic KPZ fixed points, and find that they are related to various matrix integrable differential equations such as coupled matrix mKdV equations, coupled matrix NLS equations with complex time, and matrix KP-II equations. When applied to the KPZ fixed points, our results extend previously known differential equations for one-point distributions and equal-time, multi-position distributions to multi-time, multi-position setup.


Similar content being viewed by others
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
The Airy\(_2\) process is often regarded as an evolution. The time in the Airy\(_2\) process corresponds to the position of the KPZ fixed point.
The condition \(\textsf {H}(u,u)=0\) is not strictly necessarily. We included it here to simplify technical details in the theory, especially when \(\Omega \) is a discrete set. This simplification is enough for our purposes regarding the (periodic) KPZ fixed points.
The usual KP-II equation is \( \partial _x \left( \partial _t w + 6w \partial _x w + \partial _{xxx} w \right) + 3\partial _{yy} w=0\) for a scalar function w. When \(m=1\), the x-derivative of Equation (2.14) becomes this equation if we set \(w(t,y,x)=2u(-4t,y,x)\).
The paper also obtained the result for general initial conditions.
In the paper [8], the roles of \(\textsf {r}\) and \(\textsf {p}\) are switched.
The published version of the system from [30] has a typo which was later fixed in the ArXiv version (arXiv:ArXiv:0302033v4, see Equations (1)–(3) and the last two displayed equations in page 3 therein). Our discussion here uses the latest Arxiv version.
The correspondence of terms between [26, Theorem 2.5] and here is \(\psi =\partial _{x}M\), \({\varvec{\Psi }}=M\), \(r=x\), and the variables \(y\) coincide.
We can also consider
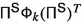 similar to (2.10). Then the discussions below still hold if we define the parameters \(x^{(i)}_\ell \), \(i=1, \cdots , |\textsf {S}|\), \(\ell =1, 2,3\) appropriately. For the convenience of presentation, we state results only when
similar to (2.10). Then the discussions below still hold if we define the parameters \(x^{(i)}_\ell \), \(i=1, \cdots , |\textsf {S}|\), \(\ell =1, 2,3\) appropriately. For the convenience of presentation, we state results only when 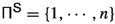 here.
here.To compute it, note, for example, that \(\partial ^3 u \partial ^{-2}= u \partial + 3 (\partial u) + 3(\partial ^2 u) \partial ^{-1} + (\partial ^3 u)\partial ^{-2}\) and \(\partial ^{-1} u \partial ^2=u\partial - (\partial u)+ (\partial ^2 u) \partial ^{-1}-\cdots \) from the product rule of derivatives, and thus, \((\partial ^3 u \partial ^{-1})_+= u \partial ^2+ 3 (\partial u) \partial \) and \((\partial ^{-1} u \partial ^2)+=u\partial - (\partial u)\) for any function u.
This equation is the special case when \(\alpha =0\) in equation (113) of [20]. The full Sato equations involve pseudo-differential operators parametrized by \(\alpha \in \mathbb {Z}^{n-1}\). The multi-component KP hierarchy may also involve infinitely many parameters \(x^{(i)}_\ell \), \(i\in \{1, \cdots , n\}\), \(\ell \in \{1, 2, \cdots \}\). Here we have the special case when \(\ell \in \{1,2, 3\}\).
In [23, Definition 2.25] the formulas \(Q_1(j)\) and \(Q_2(j)\) are used. Here, we use the function \(\textsf {Q}_{j}^\mathrm {(KPZ)}(z)=-Q_2(j) \chi _{\Omega _{1,j}}(z)+ Q_1(j) \chi _{\Omega _{2,j}}(z)\).
The factor \(\textsf {P}_j^\mathrm {(KPZ)}\) is not present in the kernels in [23, Equation (5) and Definition 2.4] This is because the \(L^2\) space is weighted. Here we use \(L^2(\textrm{d}z)\) space instead and include \(\textsf {P}_j^\mathrm {(KPZ)}\) as a part of the kernel.
References
Ablowitz, M.J., Clarkson, P.A.: Solitons, nonlinear evolution equations and inverse scattering, London Mathematical Society Lecture Note Series, vol. 149, Cambridge University Press, Cambridge, (1991). (MR1149378)
Adler, M., Cafasso, M., van Moerbeke, P.: Non-linear PDEs for gap probabilities in random matrices and KP theory. Phys. D 241(23–24), 2265–2284 (2012). (MR2998127)
Adler, M., van Moerbeke, P.: PDEs for the joint distributions of the Dyson, Airy and sine processes. Ann. Probab. 33(4), 1326–1361 (2005). (MR2150191 (2006g:60118))
Adler, M., van Moerbeke, P., Vanhaecke, P.: Moment matrices and multi-component KP, with applications to random matrix theory. Commun. Math. Phys. 286(1), 1–38 (2009). (MR2470922)
Baik, J.: KPZ limit theorems. arXiv:2206.14086
Baik, J., Liu, Z.: Fluctuations of TASEP on a ring in relaxation time scale. Commun. Pure Appl. Math. 71(4), 747–813 (2018). (MR3772401)
Baik, J., Liu, Z.: Multipoint distribution of periodic TASEP. J. Am. Math. Soc. 32(3), 609–674 (2019). (MR3981984)
Baik, J., Liu, Z., Silva, G.L.F.: Limiting one-point distribution of periodic TASEP. Ann. Inst. Henri Poincaré Probab. Stat. 58(1), 248–302 (2022). (MR4374678)
Bertola, M., Cafasso, M.: Riemann-Hilbert approach to multi-time processes: the Airy and the Pearcey cases. Phys. D 241(23–24), 2237–2245 (2012). (MR2998125)
Borodin, A.: Riemann–Hilbert problem and the discrete Bessel kernel. Int. Math. Res. Notices 9, 467–494 (2000). (MR1756945)
Dauvergne, D., Ortmann, J., Virág, B.: The directed landscape. arXiv:1812.00309
Deift, P.: Integrable operators, Differential operators and spectral theory, 1999, pp. 69-84. (MR1730504)
Fokas, A.S., Its, A.R., Kapaev, A. A., Yu, V.: Novokshenov, Painlevé transcendents, Mathematical Surveys and Monographs, vol. 128, American Mathematical Society, Providence, RI, 2006. The Riemann-Hilbert approach. (MR2264522)
Harnad, J., Balogh, F.: Tau functions and their applications, Cambridge Monographs on Mathematical Physics, Cambridge University Press, Cambridge (2021). (MR4411375)
Its, A.R., Izergin, A.G., Korepin, V.E., Slavnov, N.A.: Differential equations for quantum correlation functions. In: Proceedings of the Conference on Yang-Baxter Equations, Conformal Invariance and Integrability in Statistical Mechanics and Field Theory, 1990, pp. 1003–1037. (MR1064758)
Its, A.R.: The Riemann-Hilbert problem and integrable systems. Notices Am. Math. Soc. 50(11), 1389–1400 (2003). (MR2011605)
Johansson, K.: Two time distribution in Brownian directed percolation. Commun. Math. Phys. 351(2), 441–492 (2017). (MR3613511)
Johansson, K.: The two-time distribution in geometric last-passage percolation. Probab. Theory Relat. Fields 175(3–4), 849–895 (2019). (MR4026607)
Johansson, K., Rahman, M.: Multitime distribution in discrete polynuclear growth. Commun. Pure Appl. Math. 74(12), 2561–2627 (2021). (MR4373163)
V. G. Kac, J. W. van de Leur, The n-component KP hierarchy and representation theory, 2003, pp. 3245-3293. Integrability, topological solitons and beyond. (MR2006751)
Krajenbrink, A., Le Doussal, P.: Inverse scattering of the Zakharov-Shabat system solves the weak noise theory of the Kardar-Parisi-Zhang equation. Phys. Rev. Lett. 127(6), 8 (2021). (MR4312166)
Liao, Y.: Multi-point distribution of discrete time periodic TASEP. Probab. Theory Relat. Fields 182(3–4), 1053–1131 (2022). (MR4408510)
Liu, Z.: Multipoint distribution of TASEP. Ann. Probab. 50(4), 1255–1321 (2022). (MR4420420)
Matetski, K., Quastel, J., Remenik, D.: The KPZ fixed point. Acta Math. 227(1), 115–203 (2021). (MR4346267)
Prähofer, M., Spohn, H.: Scale invariance of the PNG droplet and the Airy process. J. Stat. Phys. 108(5–6), 1071–1106 (2002). (MR1933446)
Quastel, J., Remenik, D.: KP governs random growth off a 1-dimensional substrate, Forum Math. Pi 10 (2022), Paper No. e10, 26. (MR4413350)
Simon, B.: Trace ideals and their applications, Second, Mathematical Surveys and Monographs, vol. 120, American Mathematical Society, Providence, RI, 2005. (MR2154153) (2006f:47086)
Teo, L.P.: The multicomponent KP hierarchy: differential Fay identities and Lax equations. J. Phys. A 44(22), 225201 (2011)
Tracy, C.A., Widom, H.: Level-spacing distributions and the Airy kernel. Commun. Math. Phys. 159(1), 151–174 (1994). (MR1257246 (95e:82003))
Tracy, C.A., Widom, H.: A system of differential equations for the Airy process. Electron. Commun. Probab. 8, 93–98 (2003). (MR1987098)
Tracy, C.A., Widom, H.: Matrix kernels for the Gaussian orthogonal and symplectic ensembles. Ann. Inst. Fourier (Grenoble) 55(6), 2197–2207 (2005). (MR2187952 (2006j:82046))
Wang, D.: A PDE for the multi-time joint probability of the Airy process. Phys. D 238(8), 819–833 (2009). (MR2522977 (2010f:60020))
Acknowledgements
The work of Baik was supported in part by NSF grant DMS-1954790. Silva acknowledges his current support by São Paulo Research Foundation under grants # 2019/16062-1 and # 2020/02506-2, and by Brazilian National Council for Scientific and Technological Development (CNPq) under grant # 315256/2020-6. Prokhorov was supported by NSF MSPRF grant DMS-2103354, NSF grant DMS-1928930, and RSF grant 22-11-00070. The part of the work was done while Prokhorov was in residence at the Mathematical Sciences Research Institute in Berkeley, California, during the Fall 2021 semester.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest in the subject matter or materials discussed in this manuscript.
Additional information
Communicated by K. Johansson
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Baik, J., Prokhorov, A. & Silva, G.L.F. Differential Equations for the KPZ and Periodic KPZ Fixed Points. Commun. Math. Phys. 401, 1753–1806 (2023). https://doi.org/10.1007/s00220-023-04683-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-023-04683-z


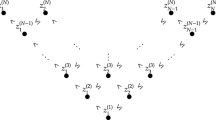

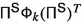 similar to (
similar to (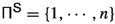 here.
here.