Abstract
On a closed manifold, consider the space of all Riemannian metrics for which \(-\Delta + kR\) is positive (nonnegative) definite, where \(k > 0\) and R is the scalar curvature. This spectral generalization of positive (nonnegative) scalar curvature arises naturally for different values of k in the study of scalar curvature via minimal hypersurfaces, the Yamabe problem, and Perelman’s Ricci flow with surgery. When \(k=1/2\), the space models apparent horizons in time-symmetric initial data to the Einstein equations. We study these spaces in unison and generalize Codá Marques’s path-connectedness theorem. Applying this with \(k=1/2\), we compute the Bartnik mass of 3-dimensional apparent horizons and the Bartnik–Bray mass of their outer-minimizing generalizations in all dimensions. Our methods also yield efficient constructions for the scalar-nonnegative fill-in problem.
Similar content being viewed by others
Notes
In the literature, they are sometimes referred to as having positive Yamabe invariant.
When M is not topologically PSC, the \({\mathscr {M}}^{>0}_{k}(M)\) in Theorem 1.2 are all empty (see Corollary C.2) and the \({\mathscr {M}}^{\ge 0}_{k}(M)\) consist of Ricci-flat metrics (see Lemma 2.1), so they are flat and isometrically covered by flat tori, and their space is understood (see [Kan06]).
We adopt the convention that the infimum of an empty set is \(\infty \).
See Remark 2.2 for more on differentiating \(t \mapsto \lambda _1(-\Delta _{g_t}: + \tfrac{1}{2} R_{g_t})\).
We are grateful to the anonymous referee for providing us with an abundance of references for this discussion and answering questions of ours.
Recall that this class is larger than the class of positive scalar curvature metrics on the boundary, which is the most commonly studied one.
Elements of \({\mathfrak {M}}(M)\) are called “canonical” metrics in [Mar12].
After normalizing by a constant, we can smoothly in t solve \(\Delta _{\sigma _t g^o_t} f_t = - \tfrac{1}{2} {{\,\textrm{Tr}\,}}_{\sigma _t g^o_t} \tfrac{d}{dt} (\sigma _t g^o_t)\) in view of (3.1) and elliptic regularity. Then, take \(X_t:= \nabla _{\sigma _t g^o_t} f_t\).
\(\hat{\varvec{M}}\) has a well-defined smooth structure; it is \(\hat{\varvec{g}}\) that has a “corner” in the sense of [Mia02].
For (3) we reparametrize so that \((1+\delta )^{4/(n-1)} \mapsto (1+\delta )\). This doesn’t affect (1), (2), (4), (5).
\(T_\delta \) may be a multiple cover of an underlying embedded hypersurface.
The gluing construction can be localized away from the boundary, or be applied to the double of our manifolds and then cut along the Schwarzschild horizons.
It is tempting to conjecture \({\mathfrak {m}}_B(M, g, H=0) \le \tfrac{1}{2} \sum _{i=1}^p (\sigma _n^{-1} {{\,\textrm{vol}\,}}_{g_i}(M_i))^{(n-1)/n}\) based on this bound and (6.3). We do not pursue this here.
References
Ammann, B., Dahl, M., Humbert, E.: Smooth Yamabe invariant and surgery. J. Differ. Geom. 94(1), 1–58 (2013)
Arnowitt, R., Deser, S., Misner, C.W.: Dynamical structure and definition of energy in general relativity. Phys. Rev. (2) 116, 1322–1330 (1959)
Arnowitt, R., Deser, S., Misner, C.W.: Canonical variables for general relativity. Phys. Rev. (2) 117, 1595–1602 (1960)
Ammann, B., Kröncke, K., Weiss, H., Witt, F.: Holonomy rigidity for Ricci-flat metrics. Math. Z. 291(1–2), 303–311 (2019)
Bär, C., Dahl, M.: Small eigenvalues of the conformal Laplacian. Geom. Funct. Anal. 13(3), 483–508 (2003)
Bär, C., Hanke, B.: Boundary conditions for scalar curvature, arXiv Mathematics e-prints (2020). arXiv:2012.09127 [math.DG]
Bär, C., Hanke, B.: Local flexibility for open partial differential relations. Commun. Pure Appl. Math. 75(6), 1377–1415 (2022)
Bamler, R.H., Kleiner, B.: Ricci flow and contractibility of spaces of metrics. arXiv Mathematics e-prints (2019). arXiv:1909.08710 [math.DG]
Bray, H.L., Lee, D.A.: On the Riemannian Penrose inequality in dimensions less than eight. Duke Math. J. 148(1), 81–106 (2009)
Brendle, S., Marques, F.C., Neves, A.: Deformations of the hemisphere that increase scalar curvature. Invent. Math. 185(1), 175–197 (2011)
Bray, H.L.: Proof of the Riemannian Penrose inequality using the positive mass theorem. J. Differ. Geom. 59(2), 177–267 (2001)
Brendle, S.: Convergence of the Yamabe flow for arbitrary initial energy. J. Differ. Geom. 69(2), 217–278 (2005)
Carr, R.: Construction of manifolds of positive scalar curvature. Trans. Am. Math. Soc. 307(1), 63–74 (1988)
Colding, T.H., Minicozzi II, W.P.: Estimates for the extinction time for the Ricci flow on certain 3-manifolds and a question of Perelman. J. Am. Math. Soc. 18(3), 561–569 (2005)
Chau, A., Martens, A.: Exterior Schwarzschild initial data for degenerate apparent horizons. arXiv Mathematics e-prints (2020). arXiv:2004.09060 [math.DG]
Chodosh, O., Mantoulidis, C.: Minimal surfaces and the Allen-Cahn equation on 3-manifolds: index, multiplicity, and curvature estimates. Ann. Math. (2) 191(1), 213–328 (2020)
Caffarelli, L., Nirenberg, L., Spruck, J.: The Dirichlet problem for nonlinear second-order elliptic equations. III. Functions of the eigenvalues of the Hessian. Acta Math. 155(3–4), 261–301 (1985)
Armando, J.: Cabrera Pacheco and Pengzi Miao, Higher dimensional black hole initial data with prescribed boundary metric. Math. Res. Lett. 25(3), 937–956 (2018)
Carlotto, A., Schoen, R.: Localizing solutions of the Einstein constraint equations. Invent. Math. 205(3), 559–615 (2016)
Dahl, M., Larsson, E.: Outermost apparent horizons diffeomorphic to unit normal bundles. Asian J. Math. 23(6), 1013–1040 (2019)
Dai, X., Wang, X., Wei, G.: On the stability of Riemannian manifold with parallel spinors. Invent. Math. 161(1), 151–176 (2005)
José, F.: Escobar, Conformal deformation of a Riemannian metric to a scalar flat metric with constant mean curvature on the boundary. Ann. Math. (2) 136(1), 1–50 (1992)
Galloway, G.J.: Rigidity of outermost MOTS: the initial data version. Gen. Relativ. Gravit. 50(3), Paper No. 32, 7 (2018)
Gaspar, P., Guaraco, M.A.M.: The Weyl law for the phase transition spectrum and density of limit interfaces. Geom. Funct. Anal. 29(2), 382–410 (2019)
Gromov, M., Lawson, H.B., Jr.: The classification of simply connected manifolds of positive scalar curvature. Ann. Math. (2) 111(3), 423–434 (1980)
Gromov, M., Lawson, H.B., Jr.: Spin and scalar curvature in the presence of a fundamental group. I. Ann. Math. (2) 111(2), 209–230 (1980)
Gromov, M., Lawson, H.B., Jr.: Positive scalar curvature and the Dirac operator on complete Riemannian manifolds. Inst. Hautes Études Sci. Publ. Math. (1983), (58), 83–196 (1984)
Gromov, M.: Metric inequalities with scalar curvature. Geom. Funct. Anal. 28(3), 645–726 (2018)
Gromov, M.: Scalar curvature of manifolds with boundaries: natural questions and artificial constructions. arXiv Mathematics e-prints (2018). arXiv:1811.04311 [math.DG]
Hamilton, R.S.: Three-manifolds with positive Ricci curvature. J. Differ. Geom. 17(2), 255–306 (1982)
Huisken, G., Ilmanen, T.: The inverse mean curvature flow and the Riemannian Penrose inequality. J. Differ. Geom. 59(3), 353–437 (2001)
Huisken, G., Sinestrari, C.: Convexity estimates for mean curvature flow and singularities of mean convex surfaces. Acta Math. 183(1), 45–70 (1999)
Irie, K., Marques, F.C., Neves, A.: Density of minimal hypersurfaces for generic metrics. Ann. Math. (2) 187(3), 963–972 (2018)
Jauregui, J.L.: Fill-ins of nonnegative scalar curvature, static metrics, and quasi-local mass. Pac. J. Math. 261(2), 417–444 (2013)
Jauregui, J.L., Miao, P., Tam, L.-F.: Extensions and fill-ins with non-negative scalar curvature. Class. Quant. Gravity 30(19), 195007, 12 (2013)
Kang, E.S.: Moduli spaces of 3-dimensional flat manifolds. J. Korean Math. Soc. 43(5), 1065–1080 (2006)
Kato, T.: Perturbation theory for linear operators. In: Classics in Mathematics. Springer, Berlin (1995), Reprint of the 1980 edition
Kazaras, D.: Desingularizing positive scalar curvature 4-manifolds. arXiv Mathematics e-prints (2019). arXiv:1905.05306 [math.DG]
Kazaras, D.: Personal communication (2021)
Kleiner, B., Lott, J.: Notes on Perelman’s papers. Geom. Topol. 12(5), 2587–2855 (2008)
Kotschwar, B.L.: Backwards uniqueness for the Ricci flow. Int. Math. Res. Not. IMRN (21), 4064–4097 (2010)
Li, J.-F.: Eigenvalues and energy functionals with monotonicity formulae under Ricci flow. Math. Ann. 338(4), 927–946 (2007)
Li, C., Mantoulidis, C.: Positive scalar curvature with skeleton singularities. Math. Ann. 374(1–2), 99–131 (2019)
Lohkamp, J.: Minimal smoothings of area minimizing cones. arXiv Mathematics e-prints (2018). arXiv:1810.03157 [math.DG]
Lee, D.A., Sormani, C.: Near-equality of the Penrose inequality for rotationally symmetric Riemannian manifolds. Ann. Henri Poincaré 13(7), 1537–1556 (2012)
Marques, F.C.: Deforming three-manifolds with positive scalar curvature. Ann. Math. (2) 176(2), 815–863 (2012)
Miao, P.: Positive mass theorem on manifolds admitting corners along a hypersurface. Adv. Theor. Math. Phys. 6(6), 1163–1182 (2002)
Milnor, J.: On spaces having the homotopy type of a \({\rm CW}\)-complex. Trans. Am. Math. Soc. 90, 272–280 (1959)
Mantoulidis, C., Miao, P.: Total mean curvature, scalar curvature, and a variational analog of Brown-York mass. Commun. Math. Phys. 352(2), 703–718 (2017)
Mantoulidis, C., Miao, P., Tam, L.-F.: Capacity, quasi-local mass, and singular fill-ins. J. Reine Angew. Math. 768, 55–92 (2020)
Marques, F.C., Neves, A., Song, A.: Equidistribution of minimal hypersurfaces for generic metrics. Invent. Math. 216(2), 421–443 (2019)
Mantoulidis, C., Schoen, R.: On the Bartnik mass of apparent horizons. Class. Quantum Gravity 32(20), 205002, 16 (2015)
Meeks, W., III., Simon, L., Yau, S.T.: Embedded minimal surfaces, exotic spheres, and manifolds with positive Ricci curvature. Ann. Math. (2) 116(3), 621–659 (1982)
Miao, P., Xie, N.: Bartnik mass via vacuum extensions. Int. J. Math. 30(13), 1940006, 11 (2019)
Pacheco, A.J.C., Cederbaum, C., Gehring, P., Diaz, A.P.: Constructing electrically charged Riemannian manifolds with minimal boundary, prescribed asymptotics, and controlled mass. arXiv Mathematics e-prints (2021). arXiv:2106.14703 [math.DG]
Perelman, G.: The entropy formula for the Ricci flow and its geometric applications. arXiv Mathematics e-prints (2002). arXiv:math/0211159
Perelman, G.: Finite extinction time for the solutions to the Ricci flow on certain three-manifolds. arXiv Mathematics e-prints (2003). arXiv:math/0307245
Perelman, G.: Ricci flow with surgery on three-manifolds. arXiv Mathematics e-prints (2003). arXiv:math/0303109
Petersen, P., Wylie, W.: Rigidity of gradient Ricci solitons. Pac. J. Math. 241(2), 329–345 (2009)
Schoen, R.M.: Variational theory for the total scalar curvature functional for Riemannian metrics and related topics, Topics in calculus of variations (Montecatini Terme, 1987), Lecture Notes in Mathematics, vol. 1365, Springer, Berlin, pp. 120–154 (1989)
Song, A.: Existence of infinitely many minimal hypersurfaces in closed manifolds. arXiv Mathematics e-prints (2018). arXiv:1806.08816 [math.DG]
Schoen, R., Simon, L.: Regularity of stable minimal hypersurfaces. Commun. Pure Appl. Math. 34(6), 741–797 (1981)
Stolz, S.: Simply connected manifolds of positive scalar curvature. Ann. Math. (2) 136(3), 511–540 (1992)
Schoen, R., Yau, S.T.: On the structure of manifolds with positive scalar curvature. Manuscr. Math. 28(1–3), 159–183 (1979)
Schoen, R., Yau, S.T.: Existence of incompressible minimal surfaces and the topology of three-dimensional manifolds with nonnegative scalar curvature. Ann. Math. (2) 110(1), 127–142 (1979)
Schoen, R., Yau, S.T.: On the proof of the positive mass conjecture in general relativity. Commun. Math. Phys. 65(1), 45–76 (1979)
Schoen, R., Yau, S.T.: The existence of a black hole due to condensation of matter. Commun. Math. Phys. 90(4), 575–579 (1983)
Schoen, R., Yau, S.-T.: Positive scalar curvature and minimal hypersurface singularities. arXiv Mathematics e-prints (2017). arXiv:1704.05490 [math.DG]
Wang, M.K.Y.: Preserving parallel spinors under metric deformations. Indiana Univ. Math. J. 40(3), 815–844 (1991)
White, B.: The topology of hypersurfaces moving by mean curvature. Commun. Anal. Geom. 3(1–2), 317–333 (1995)
White, B.: The size of the singular set in mean curvature flow of mean-convex sets. J. Am. Math. Soc. 13(3), 665–695 (2000)
White, B.: Which ambient spaces admit isoperimetric inequalities for submanifolds? J. Differ. Geom. 83(1), 213–228 (2009)
Witten, E.: A new proof of the positive energy theorem. Commun. Math. Phys. 80(3), 381–402 (1981)
Zhou, X.: On the multiplicity one conjecture in min-max theory. Ann. Math. (2) 192(3), 767–820 (2020)
Acknowledgements
This project began during “Geometry of Scalar Curvature,” a conference and summer school held in July 2019 in Italy and funded by the Deutsche Forschungsgemeinschaft (SPP 2026 “Geometry at Infinity”). We are grateful to the co-organizers. We also acknowledge Bernd Ammann, Renato Bettiol, Alessandro Carlotto, Otis Chodosh, Mattias Dahl, Demetre Kazaras, and Or Hershkovits for helpful discussions, and the anonymous referees for valuable comments. C.L. and C.M. were both supported by the NSF (DMS-2005287/2202343 and DMS-1905165/2050120/2147521). The authors have no financial or proprietary interests in any material discussed in this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Chrusciel.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Some Curvature Formulas
For the reader’s convenience, we collect some well-known curvature formulas from Riemannian geometry that play a crucial role for us.
First, suppose that \((M^n, g)\) is a Riemannian manifold with \(n = \dim M \ge 3\). If \(u > 0\) is smooth on M, then the conformal metric \({\overline{g}} = u^{4/(n-2)} g\) has (see [Esc92, (1.2)])
Additionally, if \(\Sigma \subset M\) is a two-sided hypersurface with unit normal \(\nu \), then the mean curvature scalar of \(H_\Sigma \) with \(\nu \) as an outward pointing normal (so, \(H_\Sigma = -{{\,\textrm{div}\,}}_\Sigma \nu \)) transforms as (see [Esc92, (1.4)], where mean curvatures are normalized with an \((n-1)^{-1}\) factor):
Next, the following slicing formulas for the curvature along normal foliations form the foundation for the deep relationship between \({\mathscr {M}}^{>0}_{1/2}(M)\), scalar curvature, and stable minimal hypersurfaces. They are well-known to experts and follow from elementary computations.
Lemma A.1
(Slicing formulas for curvature). Suppose that \(\varvec{M}\) is a smooth manifold, \(I \subset {\textbf{R}}\) is an interval, \((g_t)_{t \in I}\) is a smooth path of metrics on M, and \((u_t)\) is a smooth path of positive \(C^\infty (M)\) functions. On \(\varvec{N}:= M \times I\), consider the metric:
Then, for every \(x \in M\), \(t \in I\),
where \({{\,\mathrm{\mathbb {I}}\,}}_t(\cdot )\) and \(H_t(\cdot )\) are the second fundamental form and mean curvature scalar of \(M \times \{t\} \subset (\varvec{N}, \varvec{h})\) with \(\partial _t\) taken to be the outward pointing direction.
Proof
The formulas for \({{\,\mathrm{\mathbb {I}}\,}}_t\), \(H_t\) follow from the first variation formula, i.e., the interpretation of the second fundamental form and the mean curvature scalar as the rate of change of the metric and the volume form in the outward unit normal direction, \(u_t^{-1} \partial _t\). The formula for the scalar curvature follows from the second variation formula
and the twice-traced Gauss equation for \(M \times \{t\} \subset (\varvec{N}, \varvec{h})\)
multiply the former by \(2u_t^{-1}\) and subtract the latter. \(\square \)
Finally, we need the following formula for the mean curvature of graphs in case \(u_t \equiv 1\) for all t, i.e., in case we are working in Fermi coordinates:
Lemma A.2
(Mean curvature in Fermi coordinates). Assume the setting of Lemma A.1, with \(u_t \equiv 1\) for all t. Suppose that \(\Sigma := {{\,\textrm{graph}\,}}_M f \subset \varvec{N}\) for a smooth \(f: M \rightarrow I\). Then, the mean curvature scalar \(H_\Sigma \) of \(\Sigma \), with \(\partial _t\) as the outward pointing unit normal, equals:
Proof
See [CM20b, (A.13)]. \(\square \)
Appendix B. Round Normal Foliations
Seeing as to how we are concerned with the flexibility of PSC cobordances with mean-convex foliations throughout this paper, we dedicate this appendix to such cobordances of the simplest kind, namely:
where \(I \subset {\textbf{R}}\) is an interval, \(f: I \rightarrow (0, \infty )\) is a smooth function, and \(g_{{\textbf{S}}^n}\) indicates a round metric on a unit \({\textbf{S}}^n\). We call such metrics round normal foliations with unit speed.
By Lemma A.1, the second fundamental form and mean curvature of \({\textbf{S}}^n \times \{t\}\) (with the unit normal pointing to the right as the outward pointing normal) are:
and the ambient scalar curvature is
Thus, our cobordance is:
For the sake of the reader’s intuition, we point out that exact solutions of the equality case of (B.4) correspond to rotationally symmetric scalar-flat manifolds (i.e., Schwarzschild manifolds).
Lemma B.1
(Refined gluing lemma). Suppose that we have smooth functions \(f_i: [a_i, b_i] \rightarrow (0, \infty )\), \(i = 1\), 2, satisfying (B.4), (B.5). Assume, also, that \(f_1(b_1) < f_2(a_2)\).
Then, the following two statements are equivalent:
-
(1)
There exists a \(T > b_1 - a_2\) and a smooth function \(F: [a_1, T+b_2] \rightarrow (0, \infty )\) satisfying (B.4), (B.5), and
$$\begin{aligned} F = f_1 \text { on } [a_1, b_1] \text { and } F(T + \cdot ) = f_2 \text { on } [a_2, b_2]. \end{aligned}$$ -
(2)
The mean curvature of \({\textbf{S}}^n \times \{a_2\}\) in \(({\textbf{S}}^n \times [a_2, b_2], f_2^2 g_{{\textbf{S}}^n} + dt^2)\) is strictly less than the mean curvature of the sphere of radius \(f_2(a_2)\) in the unique Schwarzschild manifold containing \({\textbf{S}}^n \times \{b_1\}\) with its induced metric from \(({\textbf{S}}^n \times [a_2, b_2], f_1^2 g_{{\textbf{S}}^n} + dt^2)\).
Proof
Since we’re only interested in mean-convex foliations, i.e., solutions satisfying (B.5), we are allowed to change variables and treat f(t) as an independent variable \(x \in (0, \infty )\), and \(f'(t)\) as a dependent variable \(y(x) \in (0, \infty )\). This change of variables eliminates the need to determine T. Moreover, the chain rule gives:
This is a first order nonlinear differential inequality. Elementary ODE analysis shows that, for all \((x_0, y_0) \in (0, \infty ) \times (0, \infty )\), solutions \({\textbf{y}}(x)\) of the corresponding equation with \({\textbf{y}}(x_0) = y_0\) exist for all \(x \in [x_0, \infty )\) forward in time, and as long as \(x \not \rightarrow 0\), \(\infty \) backward in time, and are unique. We refer to such \({\textbf{y}}(x)\) as
Let us rewrite (1), (2) above in this formulation. Let \(y_i: [f_i(a_i), f_i(b_i)] \rightarrow (0, \infty )\), \(i=1\), 2, denote the reparametrizations of our \(f_i\). Then, (1) turns into:
-
(1’)
There exists a smooth extension \(Y: [f_1(a_1), f_2(b_2)] \rightarrow (0, \infty )\) of \(y_1\) and \(y_2\) that satisfies (B.6).
For (2), we note:
-
The mean curvature of \({\textbf{S}}^n \times \{a_2\}\) in \(({\textbf{S}}^n \times [a_2, b_2], f_2^2 g_{{\textbf{S}}^n} + dt^2)\) is \(n y_2(f_2(a_2)) / f_2(a_2)\) by (B.2).
-
If \({\textbf{y}}_1: [f_1(b_1), \infty ) \rightarrow (0, \infty )\) denotes the unique Schwarzschild solution through \((f_1(b_1), f_1'(b_1))\), then the mean curvature of the sphere of radius \(f_2(a_2)\) in this Schwarzschild solution is \(n {\textbf{y}}_1(f_2(a_2)) / f_2(a_2)\) by (B.2).
Therefore, (2) turns into:
-
(2’)
\(y_2(f_2(a_2)) < {\textbf{y}}_1(f_2(a_2))\).
The equivalence of (1’) and (2’) is now trivial. Indeed, the existence of Y in (1’) comes down to getting a smooth extension that always flows monotonically across the Schwarzschild solution flowlines. \(\square \)
Corollary B.2
(Bending and gluing Schwarzschild). Suppose that \(m_1 < m_2\) and \((\varvec{M}_{i}, \varvec{g}_{i})\), \(i = 1\), 2, are mass \(m_i\) exterior Schwarzschild manifolds. Suppose that \(\Sigma _i\), \(i = 1\), 2 are two round spheres (along the standard foliation) of radius \(\rho _i > 0\) and mean curvature \(h_i > 0\) with respect to the unit normal pointing to infinity. If \(\rho _1 < \rho _2\) and \(h_2\) is strictly less than the mean curvature of the mean-convex sphere of radius \(\rho _2\) that can be found inside \((\varvec{M}_{1}, \varvec{g}_{1})\), then there exists a smooth Riemannian manifold \((\widetilde{{\textbf{M}}}, \widetilde{{\textbf{g}}})\) with the following properties:
-
(1)
\((\widetilde{{\textbf{M}}}, \widetilde{{\textbf{g}}})\) contains an isometric copy of the mean-convex region bounded by \(\Sigma _1\) and the mean-concave region bounded by \(\Sigma _2\);
-
(2)
the interior region spanning the two regions above is of the form (B.1) and also satisfies (B.4), (B.5).
Additionally, recalling the inherent dependence \(h_i = h_i(m_i, \rho _i)\), we can also have:
-
(3)
If \(\rho _1\), \(\rho _2\) are held fixed and \(m_1\), \(m_2 \rightarrow m_\star \), then \((\widetilde{{\textbf{M}}}, \widetilde{{\textbf{g}}})\) converges in \(C^\infty \) to the mass \(m_\star \) exterior Schwarzschild manifold.
Proof
One can apply a small initial PSC bend to the region just past \(\Sigma _1 \subset (\varvec{M}_1, \varvec{g}_1)\) and the region just prior to \(\Sigma _2 \subset (\varvec{M}_2, \varvec{g}_2)\) (cf. [MS15, Lemma 2.3] for the 2-dimensional argument, which generalizes trivially now using (B.4) instead of the 2-dimensional formula). Since our inequalities on \(\rho _1\), \(\rho _2\),\(h_1\), \(h_2\) were strict, they are preserved for the boundaries of the slightly bent regions, which are then glued together using Lemma B.1. Conclusions (1) and (2) follow immediately from this construction. To see conclusion (3), it is perhaps fastest to revisit the proof of Lemma B.1. When \(m_1, m_2 \rightarrow m_\star \), our reduction shows
where \(y_2\), \({\textbf{y}}_1\) is as above, \(\rho _1 =: f_2(a_2)\), and \({\textbf{y}}_\star \) denotes the orbit line of the mass \(m_\star \) Schwarzschild solution through \((\rho _2, h_\star )\), where \(h_\star > 0\) is the mean curvature of our radius-\(\rho _2\) sphere inside \((\varvec{M}_\star , \varvec{g}_\star )\). Thus, we have convergence of the initial and terminal data of the Schwarzschild solution, and the result follows by the smooth dependence of ODE solutions on their data. \(\square \)
In the next lemma we deal with metrics of the form (B.1) that have strictly positive lower bounds on the scalar curvature.
Lemma B.3
(cf. [Mar12, Proposition 3.3], [Mar12, Lemma 6.2]). Suppose that \(\varvec{g}_0:= f_0(t)^2 g_{{\textbf{S}}^n} + dt^2 \in {\text {Met}}({\textbf{S}}^n \times [a,b])\) has \(R_{\varvec{g}_0} \ge \theta n(n-1)\), where the metric g is a unit round metric on \({\textbf{S}}^n\), \(n \ge 2\), and \(\theta \in [0,1]\). There exists a continuous extension of \(\varvec{g}_0\) to \([0,1] \ni \mu \mapsto \varvec{g}_\mu \in {\text {Met}}({\textbf{S}}^n \times [a,b])\), where each \(\varvec{g}_\mu \) is of the form \(f_\mu (t)^2 g_{{\textbf{S}}^n} + h_\mu (t)^2 dt^2\), and:
-
(1)
\(\varvec{g}_1 = g_{{\textbf{S}}^n} + dt^2\);
-
(2)
\(R_{\varvec{g}_\mu } > \theta n(n-1)\) on \({\textbf{S}}^n \times [a,b]\) for all \(\mu \in (0,1)\);
-
(3)
if \(f_0(t_0) = 1\), then \(f_\mu (t_0) = h_\mu (t_0) = 1\) for all \(\mu \in [0,1]\).
Proof
A key observation is that the conformal metric
modulo a reparametrization of the t coordinate.
Step 1 (\(\mu \in [0,\tfrac{1}{2}]\)). Define
Conclusion (3) is trivial. By (A.1), \(R_{\varvec{g}_\mu } \ge \theta n(n-1)\) is equivalent to
This inequality is an identity at \(\mu = 0\) by assumption, and is also true at \(\mu = \tfrac{1}{2}\) by (B.7) and \(\theta \in [0,1]\). For \(\mu \in (0, \tfrac{1}{2})\), we observe that the expression above is a concave function of \(\mu \in [0,\tfrac{1}{2}]\) since \(f_0 \le 1\). This implies conclusion (2) by calculus.
Step 2 (\(\mu \in (\tfrac{1}{2}, 1]\)). Define
By construction, \(\varvec{g}_\mu \) is continuous at \(\mu = \tfrac{1}{2}\), and as in (B.7), \(\varvec{g}_\mu \) is a standard product metric modulo a reparametrizatoin of the t coordinate. This readily implies conclusion (2), and conclusion (3) is trivial. \(\square \)
Appendix C. More Facts and Formulas Regarding \({\mathscr {M}}^{>0}_{k}\), \({\mathscr {M}}^{\ge 0}_{k}\)
The following lemma is well-known to experts in the Yamabe problem, and relates \({\mathcal {M}}^{>0}_k(M)\) (\({\mathcal {M}}^{\ge 0}_k(M)\)) to the question of existence of a metric of positive (nonnegative) scalar curvature on M.
Lemma C.1
(cf. [Sch89, Lemma 1.2]). Properties (1) and (2) below are equivalent for a closed connected Riemannian n-manifold (M, g), if \(n \ge 3\).
-
(1)
\(g \in {\mathscr {M}}^{>0}_{(n-2)/4(n-1)}(M)\) (\({\mathscr {M}}^{\ge 0}_{(n-2)/4(n-1)}(M)\));
-
(2)
there exists a metric \({\overline{g}}\) conformal to g with \(R_{{\overline{g}}} > 0\) (\(R_{{\overline{g}}} \ge 0\)).
If \(n = 2\), then property (1’) below implies (2’):
-
(1’)
\(g \in {\mathscr {M}}^{>0}_{k}(M)\) (\({\mathscr {M}}^{\ge 0}_{k}(M)\)) for any \(k \in (0, \infty )\);
-
(2’)
M is diffeomorphic to \({\textbf{S}}^2\) or \({\textbf{R}}{\textbf{P}}^2\) (or, additionally, \({\textbf{T}}^2\), \({\textbf{K}}^2\)).
Proof
We only treat \({\mathscr {M}}^{>0}_{k}(M)\); the case of \({\mathscr {M}}^{\ge 0}_{k}(M)\) is essentially similar. First consider \(n \ge 3\). For brevity, we write \(k=\tfrac{n-2}{4(n-1)}\).
(1) \(\implies \) (2). Let u be a positive first eigenfunction of \(-\Delta _g + k R_g\). Then \({\overline{g}} = u^{4/(n-2)} g\) has \(R_{{\overline{g}}} > 0\) by (A.1).
(2) \(\implies \) (1). Suppose that \({\overline{g}} \in [g]\) has \(R_{{\overline{g}}} > 0\). Then,
by (A.1). On the other hand, \([g] = [{\overline{g}}]\), so by (A.1) again,
Thus, \(g \in {\mathscr {M}}^{>0}_{k}(M)\) by the variational characterization of the first eigenvalue.
(1’) \(\implies \) (2’). By the variational characterization of the first eigenvalue,
Plugging in \(f \equiv 1\), it follows from Gauss–Bonnet that M is an \({\textbf{S}}^2\) or \({\textbf{R}}{\textbf{P}}^2\). \(\square \)
Corollary C.2
Let M be a closed n-manifold. The following are equivalent:
-
(1)
\({\mathscr {M}}^{>0}_{k}(M)\) (\({\mathscr {M}}^{\ge 0}_{k}(M)\)) is nonempty for all \(k \in [\tfrac{n-2}{4(n-1)}, \infty ) \cap (0, \infty )\);
-
(2)
\({\mathscr {M}}^{>0}_{k}(M)\) (\({\mathscr {M}}^{\ge 0}_{k}(M)\)) is nonempty for some \(k \in [\tfrac{n-2}{4(n-1)}, \infty ) \cap (0, \infty )\);
-
(3)
\({\mathscr {M}}^{>0}_{\infty }(M)\) (\({\mathscr {M}}^{\ge 0}_{\infty }(M)\)) is nonempty, i.e., M is topologically PSC (NNSC).
Proof
(1) \(\implies \) (2) is trivial.
(2) \(\implies \) (3) follows by applying (1.3) and Lemma C.1 to each component of M.
(3) \(\implies \) (1) also follows from (1.3). \(\square \)
The following problem seems interesting:
Problem C.3
Suppose that M is a closed n-manifold, and \(k \in (0, \infty ]\). Are \({\mathscr {M}}^{>0}_{k}(M)\), \({\mathscr {M}}^{>0}_{k} \big / {\text {Diff}}(M)\) connected when nonempty?
Here is what is known about this problem:
-
When \(n=2\), the answer is known to be yes for all \(k \in (0, \infty ]\). This follows from a crucial property of \(\lambda _1(-\Delta + kR)\) that was observed in [MS15, Proposition 1]. Since this reference only proves the result for \(k=\tfrac{1}{2}\), we show the general argument in Proposition C.4 below.
-
When \(n=3\), Theorems 1.3, 1.4 shows that the answer is yes for all \(k \in \{ \tfrac{1}{8} \} \cup [\tfrac{1}{4}, \infty ]\); when \(k=\infty \), this is due respectively to Bamler–Kleiner [BK19] (who proved a stronger result) and Codá Marques [Mar12]. We do not know what happens when \(k \in (0, \tfrac{1}{4}) {\setminus } \{ \tfrac{1}{8} \}\).
Proposition C.4
The following spaces are all smoothly path-connected:
-
\({\mathscr {M}}^{>0}_{k}({\textbf{S}}^2)\);
-
\({\mathscr {M}}^{\ge 0}_{k}({\textbf{S}}^2)\), and all path interiors can be taken in \({\mathscr {M}}^{>0}_{k}({\textbf{S}}^2)\);
Proof
The proof goes in three steps.
Step 1 (reduce to round metrics). Let \(g \in {\mathscr {M}}^{>0}_{k}({\textbf{S}}^2)\) (\({\mathscr {M}}^{\ge 0}_{k}({\textbf{S}}^2)\)). By uniformization, there exists a round metric \(g_0\) on \({\textbf{S}}^2\) and a smooth \(u: {\textbf{S}}^2 \rightarrow {\textbf{R}}\) such that \(g = e^{2u} g_0\). Define \([0,1] \ni t \mapsto g_t:= e^{2(tu + (1-t))} g_0 \in {\text {Met}}({\textbf{S}}^2)\), where \(g_1 = g\). We claim that \(g_t \in {\mathscr {M}}^{>0}_{k}({\textbf{S}}^2)\) for all \(t \in (0,1)\). Indeed, for any smooth test function \(f: {\textbf{S}}^2 \rightarrow {\textbf{R}}\), the 2-dimensional conformal invariance of Dirichlet energy, and
imply that
is linear in t. Since it is positive at \(t=0\) (\(g_0\) is round, so \(R_{g_0} > 0\)) and positive (nonnegative) at \(t=1\) (by assumption), it follows that the quantity is positive for all \(t \in (0,1)\), and all f. This completes the proof of the claim.
Step 2 (connectedness of moduli space). We have shown that all metrics in \({\mathscr {M}}^{>0}_{k}({\textbf{S}}^2)\) (\({\mathscr {M}}^{\ge 0}_{k}({\textbf{S}}^2)\)) can be continuously deformed to a round metric within \({\mathscr {M}}^{>0}_{k}({\textbf{S}}^2)\). On the other hand, by the classification of space forms, every round metric is of the form \(\varphi ^* A^2 g_\star \), where \(\varphi \in {\text {Diff}}({\textbf{S}}^2)\), \(A > 0\), and \(g_\star \) is the model round metric on the unit sphere in \({\textbf{R}}^3\). The second step follows by deforming A to \(A=1\) within the space of round metrics (a subset of \({\mathscr {M}}^{>0}_{k}({\textbf{S}}^2\))) by scaling.
Step 3 (connectedness of full space). It remains to deform \(\varphi ^* g_\star \) to \(g_\star \). By the path-connectedness of the space of orientation-preserving diffeomorphisms of \({\textbf{S}}^2\), we can deform \(\varphi \) to \(\pm {\text {Id}}\) within the space of round metrics (a subset of \({\mathscr {M}}^{>0}_{k}({\textbf{S}}^2\))). The result follows from the fact that \((-{\text {Id}})^* g_\star = g_\star \). \(\square \)
Remark C.5
The argument can be improved to showing that \({\mathscr {M}}^{>0}_{k}({\textbf{S}}^2)\), \({\mathscr {M}}^{\ge 0}_{k}({\textbf{S}}^2)\) are contractible. Compare to the proof of Theorem 1.4 which treats \(n=3\) and \(k=\tfrac{1}{8}\) as a consequence of Bamler–Kleiner’s breakthrough for \(k=\infty \) [BK19]. Their technique may extend to \(k \in [\tfrac{1}{4}, \infty )\). We do not pursue this.
Finally, a relationship to stable minimal hypersurfaces. If \((\varvec{N}, \varvec{h})\) is a Riemannian \((n+1)\)-manifold with \(R_{\varvec{h}} > 0\) and \(M \subset \varvec{N}\) is a two-sided closed stable minimal hypersurface in \(\varvec{N}\), then Schoen–Yau [SY79b] first observed that the second variation formula and the Gauss equation imply that \(\lambda _1(-\Delta _g + \tfrac{1}{2} R_g) > 0\) for the induced metric g on M, i.e., \(g \in {\mathscr {M}}^{>0}_{1/2}(M)\). Likewise, \(g \in {\mathscr {M}}^{\ge 0}_{1/2}(M)\) if \(R_{\varvec{h}} \ge 0\). While they did not explicitly formulate this observation in this manner at the time, they did explicitly consider this exact operator in [SY83], as did Gromov–Lawson in [GL83]. We summarize in the following:
Lemma C.6
The following are equivalent for closed Riemannian manifolds (M, g):
-
(1)
\(g \in {\mathscr {M}}^{>0}_{1/2}(M)\) (\({\mathscr {M}}^{\ge 0}_{1/2}(M)\));
-
(2)
g is the metric induced on M when M occurs as a two-sided stable minimal hypersurface in a manifold \((\varvec{N}, \varvec{h})\) with \(R_{\varvec{h}} > 0\) (\(R_{\varvec{h}} \ge 0\)).
Proof
(2) \(\implies \) (1) follows from the second variation formula.
(1) \(\implies \) (2) follows by letting \(f > 0\) be a first eigenfunction of the positive definite operator \(-\Delta _g + \tfrac{1}{2} R_g\) on M, and setting \((\varvec{N}, \varvec{h}):= (M \times {\textbf{S}}^1, g + f^2 dt^2)\). It is not hard to see that the slices \(\{ t = \text {const}\}\) are two-sided stable minimal hypersurfaces. \(\square \)
The following more subtle result is essentially contained in the proof of [Gal18, Theorem 3.1] but is not spelled out:
Lemma C.7
(cf [Gal18, Theorem 3.1]). Suppose that M is a closed two-sided minimal hypersurface in a manifold \((\varvec{N}, \varvec{h})\), with \(R_{\varvec{h}} \ge 0\), and that M is strictly area-minimizing on one side (either one) among small graphical perturbations. Then, the metric g induced on M satisfies \(g \in \overline{{\mathscr {M}}^{>0}_{1/2}(M)}\); the closure is in the usual \(C^\infty \) topology.
Proof
By Lemma C.6, it follows that \(g \in {\mathscr {M}}^{\ge 0}_{1/2}(M)\). Without loss of generality,
otherwise there is nothing to prove. By [Gal18, Lemma 2.3] (whose operator coincides with \(-\Delta _g + \tfrac{1}{2} R_g\) provided we take \(K \equiv 0\)), and restricting to the side of M on which it’s strictly minimizing, there exists a local foliation \(M \times [0, t_0)\) of \(\varvec{N}\) so that \(\varvec{h} = g_t + u_t^2 \, dt^2\) in these coordinates, and the mean curvature scalars \(H_t\) of \(M \times \{t\}\) with respect to the outward unit normal are all constant. Rearranging the slicing formula for scalar curvature, and using that \(R_{\varvec{h}}, H_t^2, |{{\,\mathrm{\mathbb {I}}\,}}_t|^2, u \ge 0\), yields:
Thus, \(\lambda _1(-\Delta _{g_t} + \tfrac{1}{2} R_{g_t}) \ge 0\) by the maximum principle whenever \(\tfrac{d}{dt} H_t \ge 0\), in which case the inequality is even strict unless \(\tfrac{d}{dt} H_t = 0\).
It remains to prove that there exist \(t_i \rightarrow 0\) with \([\tfrac{d}{dt} H_t]_{t=t_i} > 0\). Indeed, if this were false, then \(\tfrac{d}{dt} H_t \le 0\) for all \(t \in [0, t_1)\) for some \(t_1 \in (0, t_0)\). But \(H_0 = 0\) by assumption, so \(H_t \le 0\) for all \(t \in [0, t_1)\), contradicting that \(M \times \{0\}\) strictly minimizes area. This completes the proof. \(\square \)
Appendix D. Codimension \(\ge 3\) surgery in \({\mathscr {M}}^{>0}_{k}(M)\) by Bär–Dahl
Our proof relies on showing the Gromov–Lawson [GL80a, Theorem A] codimension \(\ge 3\) surgery (cf. Schoen–Yau’s slightly different [SY79a, Theorem 4]) maintains \({\mathscr {M}}^{>0}_{k}\), \(k \in (0, \infty )\), as it is known to maintain \({\mathscr {M}}^{>0}_{\infty }\). The following result follows from the proof of a rather general spectral approximation result by Bär–Dahl [BD03]. (We also refer the reader to [ADH13] for other interesting applications of such results.)
Proposition D.1
(cf. [BD03, Theorem 3.1]). Let \((M_1, g_1)\) and \((M_2, g_2)\) be closed n-dimensional Riemannian manifolds, \(n-3 \ge d \ge 0\), and \(\Sigma ^d\) be either a single point (\(d=0\)), or a d-dimensional sphere (\(1 \le d \le n-3\)). Fix k, \(\delta \in (0, \infty )\). For each \(i=1\), 2, assume that \(\Phi _i: \Sigma \rightarrow U_i\) is an embedding of \(\Sigma \) into a smooth open \(U_i \subset M_i\), and \(N_i: N(\Phi _i(\Sigma )): \Sigma \times {\textbf{R}}^{n-d}\) is a trivializing section of its normal bundle. Then, there exists a choice of connected-sum parameters for
where the connected sum is performed with the given trivializations \(N_1\), \(N_2\), as well as a diffeomorphism
of compact manifolds-with-boundary, for a smooth open \(U \subset M\) that is diffeomorphic to \(U_1 \#_\Sigma U_2\), such that the following hold:
-
(1)
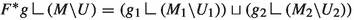 ;
; -
(2)
\(\min _U R_g \ge \min _{i=1,2} \min _{U_i} R_{g_i} - \delta \);
-
(3)
\(\lambda _1(-\Delta _g + kR_g) \ge \min _{i=1,2} \lambda _1(-\Delta _{g_i} + k R_{g_i}) - \delta \).
The parameters of the construction depend continuously on the underlying data, so it applies to continuous 1-parameter families of metrics. We summarize the result, which we only state for \(d=0\):
Corollary D.2
(cf. [Mar12, Proposition 6.1]). Let \(M_1\) and \(M_2\) be closed n-manifolds, \(n \ge 3\), k, \(\delta \in (0, \infty )\). For each \(i=1\), 2, suppose that we have the following continuous paths:
-
\([0, 1] \ni \mu \mapsto g_{i,\mu } \in {\text {Met}}(M_i)\);
-
\([0,1] \ni \mu \mapsto p_{i,\mu } \in U_i\) for a smooth open \(U_i \subset M_i\);
-
\([0,1] \ni \mu \mapsto \{ e^{(j)}_{i,\mu } \}_{j=1,\ldots ,n}\) for a \(g_i\)-orthonormal basis of \(T_{p_{i,\mu }} M_i\).
There exists a uniform (in \(\mu \)) choice of connected-sum parameters for
where the connected sum is performed with the given trivializations of \(T_{p_{i,\mu }} M_i\), so that \(\mu \mapsto g_\mu \) is continuous, and a diffeomorphism
of compact manifolds-with-boundary, for a smooth open \(U \subset M\) that is diffeomorphic to \(U_1 \# U_2\), such that the following hold for all \(\mu \in [0,1]\):
-
(1)
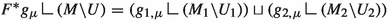 ;
; -
(2)
\(\min _{U} R_{g_\mu } \ge \min _{i=1,2} \min _{U_i} R_{g_{i,\mu }} - \delta \);
-
(3)
\(\lambda _1(-\Delta _{g_\mu } + k R_{g_\mu }) \ge \min _{i=1,2} \lambda _1(-\Delta _{g_{i,\mu }} + k R_{g_{i,\mu }}) - \delta \).
Appendix E. Some Results from Kleiner–Lott’s Notes
In this appendix we collect two results from [KL08, Section 93.12], where operators of the form \(-4 \Delta _g + V\) were studied.
Lemma E.1
(cf. [KL08, Lemma 93.16]). Let (M, g) be a closed n-dimensional Riemannian manifold. Suppose that \(X \subset M\) be a compact submanifold-with-boundary of the same dimension as M. If \(\psi \) denotes a first eigenfunction of \(-\Delta _g + kR_g\) on M, then:

for all \(\eta \in C^\infty _c(X {\setminus } \partial X)\). Here,  denotes the first Dirichlet eigenvalue of \(-\Delta _g + kR_g\) restricted to X.
denotes the first Dirichlet eigenvalue of \(-\Delta _g + kR_g\) restricted to X.
Proof
This follows by applying [KL08, Lemma 93.16] with \(4k R_g\) in place of V and rescaling by 2. \(\square \)
We will seek to control the right hand side of conclusion (2) above using the following coercivity (“Agmon-type”) estimate:
Lemma E.2
(cf. [KL08, Lemma 93.21]). With the notation of Lemma E.1, given a nonnegative smooth \(\phi : M \rightarrow {\textbf{R}}\), suppose that a smooth \(f: M \rightarrow {\textbf{R}}\) satisfies:
for some \(c > 0\), and \(\lambda := \lambda (-\Delta _g + kR_g)\). Then,
where the constant C depends only on c. The same holds true if f is only Lipschitz.
Proof
This follows by applying [KL08, Lemma 93.21] with \(4k R_g\) in place of V and 4c in place of c and rescaling by 2. \(\square \)
Appendix F. Mean Convex Foliation Refinement of Bär–Hanke Gluing
There are several important scalar curvature smoothing results in the literature; see, e.g., Gromov–Lawson [GL80b, Theorem 5.7], Miao [Mia02, Theorem 1], Brendle–Marques–Neves [BMN11, Theorem 5], Gromov [Gro18a, p. 705]). For our Bartnik mass computation, we will need a more refined smoothing theorem that respects the sign of both the scalar curvature and the mean curvature along foliations near the boundary.
We derive this from a recent beautiful construction of Bär–Hanke [BH20, BH22], whose work applies to other type of open partial relations as well, and even allows for the simultaneous treatment of families of metrics. For readers’ convenience and for the completeness of this paper, we include the results relevant to our specific purpose, as well as the modifications needed to ensure the mean curvature inequality in the interior, which was not handled in the original construction but nevertheless follows from it.
We introduce some necessary notation and definitions.
Given a Riemannian manifold-with-boundary \((\varvec{M},\varvec{g})\) with compact nonempty boundary \(M:= \partial \varvec{M}\), we write the metric in a tubular neighborhood \(\varvec{U}_M\) of M in Fermi coordinates (x, t) as follows:
Here \(g_t(x)\) is a smooth family of Riemannian metrics on M. Note that the vector field \(-\partial _t\) is the outward pointing unit normal to \(M_t\), the level surface of the distance function t. Throughout this appendix, we use \(\dot{g}_t\), \({\ddot{g}}_t\), etc. to denote t-derivatives of \(g_t\). The second fundamental form \({{\,\mathrm{\mathbb {I}}\,}}_t\) and mean curvature scalar \(H_t\) of the Fermi image of \(M \times \{t\}\) in \((\varvec{M}, \varvec{g})\), computed with \(-\partial _t\) as the outward pointing normal, equal
This follows from Lemma A.1 (see also [BH20, (14)]).
Definition F.1
(C-normal metrics, [BH20, Definition 21]). Let \(C\in {\textbf{R}}\). A Riemannian metric \(\varvec{g}\) is said to be C-normal if
in the notation of (F.1). In the notation of (F.2), \(g_1 = -2 {{\,\mathrm{\mathbb {I}}\,}}_0\).
Remark F.2
Two C-normal metrics glue together smoothly if and only if their \(g_0\), C coincide and their \({{\,\mathrm{\mathbb {I}}\,}}_0\) are additive inverses.
Theorem F.3
(cf. [BH20, Theorem 27]). Let \((\varvec{M}, \varvec{g})\) be a Riemannian manifold-with-compact-boundary \(M:= \partial \varvec{M}\), and that k is a symmetric 2-tensor on M with:
Fix \(\eta > 0\). There exists \(C_0 = C_0(\varvec{g}, \eta )\) such that, for every \(C \ge C_0\) and neighborhood \(\varvec{U}\) of M there is a tubular neighborhood \(\tilde{\varvec{U}} \subset \subset \varvec{U} \cap \varvec{U}_M\) of M and a metric \(\tilde{\varvec{g}}\) on \(\varvec{M}\) satisfying:
-
(1)
\(\tilde{\varvec{g}} \equiv \varvec{g}\) on \(\varvec{M} {\setminus } \tilde{\varvec{U}}\) and \(\Vert \tilde{\varvec{g}} - \varvec{g} \Vert _{C^0(\tilde{\varvec{U}}, \varvec{g})} \le \eta \);
-
(2)
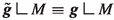 ;
; -
(3)
\({\tilde{{{\,\mathrm{\mathbb {I}}\,}}}}_0 \equiv - 2 k\) on M;
-
(4)
\(R_{\tilde{\varvec{g}}} \ge R_{\varvec{g}} - \eta \) on \(\tilde{\varvec{U}}\);
-
(5)
\({\tilde{H}}_t \ge {{\,\textrm{tr}\,}}_{g_0} k - \eta \) in Fermi coordinates on \(\tilde{\varvec{U}}\);
-
(6)
\(\tilde{\varvec{g}}\) is C-normal and \(\tilde{\varvec{g}} - \varvec{g}\) has no dt factors in Fermi coordinates on \(\tilde{\varvec{U}}\);
Above, \({\tilde{{{\,\mathrm{\mathbb {I}}\,}}}}_t\), \({\tilde{H}}_t\) are the second fundamental form and mean curvature scalar of the Fermi image of \(M \times \{t\}\) in \((\varvec{M}, \tilde{\varvec{g}})\) with respect to \(-\partial _t\) as the outward pointing normal.
Remark F.4
When two metrics near M differ by a tensor that has no dt factors, they have identical Fermi coordinates (x, t) relative the hypersurface M. Therefore, we will never need to specify whether we are computing Fermi coordinates, tubular neighborhoods, or distance-t level surfaces with respect to \(\varvec{g}\) or \(\tilde{\varvec{g}}\).
To prove Theorem F.3 we proceed in two steps:
-
Step 1: we initially deform \(\varvec{g}\) locally in a neighborhood of M to be C-normal without changing the induced second fundamental form (or metric) on M.
-
Step 2: we then deform this new C-normal metric to one whose second fundamental form on M equals k.
Proposition F.5
(Making a metric C-normal). Assume the same setup as above. There exists \(C_0 = C_0(\varvec{g}, \eta )\) such that, for every \(C \ge C_0\) and neighborhood \(\varvec{U}\) of M there is a tubular neighborhood \(\hat{\varvec{U}} \subset \subset \varvec{U} \cap \varvec{U}_M\) of M and a metric \(\hat{\varvec{g}}\) on \(\varvec{M}\) so that
-
(1)
\(\hat{\varvec{g}} \equiv \varvec{g}\) on \(\varvec{M} {\setminus } \hat{\varvec{U}}\) and \(\Vert \hat{\varvec{g}} - \varvec{g} \Vert _{C^1(\hat{\varvec{U}}, \varvec{g})} \le \eta \);
-
(2)
 ;
; -
(3)
\({\hat{{{\,\mathrm{\mathbb {I}}\,}}}}_0 \equiv {{\,\mathrm{\mathbb {I}}\,}}_0\) on M;
-
(4)
\(R_{\hat{\varvec{g}}} - R_{\varvec{g}} \ge - \eta \) on \(\hat{\varvec{U}}\);
-
(5)
\(\hat{\varvec{g}}\) is C-normal and \(\hat{\varvec{g}} - \varvec{g}\) has no dt factors in Fermi coordinates on \(\hat{\varvec{U}}\).
Above, \({\hat{{{\,\mathrm{\mathbb {I}}\,}}}}_0\) is the second fundamental form of the Fermi image of \(M \times \{t\}\) in \((\varvec{M}, \hat{\varvec{g}})\) with respect to \(-\partial _t\) as the outward pointing unit normal.
The deformation in this step is achieved by interpolation using a special cutoff function.
Lemma F.6
For any \(\delta \in (0,\tfrac{1}{4})\), \(\varepsilon \in (0,1)\), there exists a \(C^\infty \) function \(\tau _{\delta ,\varepsilon }:{\textbf{R}}\rightarrow {\textbf{R}}\) such that:
-
(1)
\(\tau _{\delta ,\varepsilon }=1\) when \(t\le \delta \varepsilon \).
-
(2)
\(\tau _{\delta ,\varepsilon }=0\) when \(t\ge \varepsilon \).
-
(3)
\(0\le \tau _{\delta ,\varepsilon }\le 1\) for \(t\in {\textbf{R}}\).
-
(4)
for every positive integer l, there is a constant \(C_l>0\) such that for all \(t>0\):
$$\begin{aligned} \left| \tau _{\delta ,\varepsilon }^{(l)}(t) \right| \le C_l \cdot t^{-l} \cdot |\log \delta |^{-1}. \end{aligned}$$
For the proof, see [BH22, Appendix A].
Proof of Proposition F.5
Write \(\varvec{g}(t,x)=dt^2+g_t(x)\) as in (F.1). Consider the Taylor expansion of the tensors \(g_t(x)\) in terms of t:
By Taylor’s theorem,
For \(C>0\) to be chosen later and \(s\in [0,1]\) consider the auxiliary metric
This metric is not the \(\hat{\varvec{g}}\) we will ultimately take, but will serve as a convenient comparison metric when we eventually define \(\hat{\varvec{g}}\). Note that, by construction, \({}^{(s)}\varvec{g}\) and \(\varvec{g}\) has the same first order terms in the Taylor expansion in t. Thus, by Lemma A.1, we have:
provided
Fix such a C. By compactness, there exists \(\varepsilon _0 \in (0, \varepsilon _M)\) such that
For \(\varepsilon \in [0,\varepsilon _0]\) small enough for the Fermi image \(\varvec{U}_\varepsilon \) of \(M \times [0,\varepsilon )\) to be contained in \(\varvec{U}\), and \(\delta >0\) to be chosen later, consider the metric
where \(\tau _{\delta ,\varepsilon }(t)\) is the function constructed in Lemma F.6. We claim \(\hat{\varvec{g}}\) has all the desired properties as long as we choose \(\delta >0\) small enough.
Properties (1.a), (2), (3), (6) are true by construction. It remains to check properties (1.b) and (4). Lemma F.6 and (F.4) imply:
as long as \(\varepsilon > 0\) is sufficiently small depending on \(\varvec{g}\), C, \(C_1\), \(\eta \). Thus (1.b) holds.
We finally check property (4). This is where we rely on the auxiliary family of metrics, \({}^{(s)}\varvec{g}\). Freeze a point in \(\varvec{U}_\varepsilon \), with Fermi coordinates (x, t), and set \(s:=\tau _{\delta ,\varepsilon }(t)\). We estimate the \(C^2\) norm of \(\hat{\varvec{g}} - {}^{(s)} \varvec{g}\) at (x, t) via Lemma F.6 and (F.4):
Note that the right hand side \(\rightarrow 0\) as \(\delta \rightarrow 0\), depending on \(\varvec{g}\), C, \(C_1\), \(C_2\). In particular, we may choose \(\delta > 0\) sufficiently small so that
Property (4) then follows from (F.5). \(\square \)
Let \((\varvec{M}, \hat{\varvec{g}})\) be the metric obtained in Proposition F.5 applied with \(\varepsilon \) and \(\eta \) small enough for property (5) to imply, for the mean curvature scalar \({\hat{H}}_t\) of the Fermi image of \(M \times \{t\}\) in \((\varvec{M}, \hat{\varvec{g}})\) with respect to \(-\partial _t\) as the outward pointing unit normal:
We may shrink \(\hat{\varvec{U}}\) to be the Fermi image of \(M \times [0,\varepsilon _1)\) in \(\varvec{M}\), where \(\varepsilon _1\) is an arbitrary constant in \((0,\delta \varepsilon )\) that will be fixed later. Note that:
where \({{\,\mathrm{\mathbb {I}}\,}}_0\) was the second fundamental form of \(M = \partial \varvec{M} \subset (\varvec{M}, \varvec{g})\) with respect to \(-\partial _t\) as an outward pointing unit normal.
Proposition F.7
(Interpolation in C-normal metrics). Assume the setup above. There exists \(C_0 = C_0(g_0, {{\,\mathrm{\mathbb {I}}\,}}_0, k)\) such that, for every \(C \ge C_0\) and neighborhood \(\varvec{U}' \subset \hat{\varvec{U}}\) of M, there is a tubular neighborhood \(\tilde{\varvec{U}} \subset \subset \varvec{U}'\) of M and a metric \(\tilde{\varvec{g}}\) on \(\varvec{M}\) satisfying:
-
(1)
\(\tilde{\varvec{g}} \equiv \hat{\varvec{g}}\) on \(\varvec{M} {\setminus } \tilde{\varvec{U}}\) and \(\Vert \tilde{\varvec{g}} - \hat{\varvec{g}} \Vert _{C^0(\tilde{\varvec{U}}, \varvec{g})} \le \eta \);
-
(2)
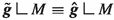 ;
; -
(3)
\({\tilde{{{\,\mathrm{\mathbb {I}}\,}}}}_0 \equiv k\) on M;
-
(4)
\(R_{\tilde{\varvec{g}}} \ge R_{\hat{\varvec{g}}} -\eta \) on \(\tilde{\varvec{U}}\);
-
(5)
\({\tilde{H}}_t \ge {{\,\textrm{tr}\,}}_{g_0} k - \eta \) on \(\tilde{\varvec{U}}\);
-
(6)
\(\tilde{\varvec{g}}\) is C-normal and \(\tilde{\varvec{g}} - \hat{\varvec{g}}\) has no dt factors on \(\tilde{\varvec{U}}\);
Above, \({\tilde{{{\,\mathrm{\mathbb {I}}\,}}}}_t\), \({\tilde{H}}_t\) are the second fundamental form and mean curvature scalar of the Fermi image of \(M \times \{t\}\) in \((\varvec{M}, \tilde{\varvec{g}})\) with respect to \(-\partial _t\) as the outward pointing normal.
Note that these propositions imply our theorems:
Proof of Theorem F.3
Follows from Propositions F.5, F.7 as explained. \(\square \)
Proposition F.7 essentially follows from the same proof of [BH20, Proposition 26]. We first take the same cutoff function as in [BH20, Lemma 25].
Lemma F.8
There exists a constant \(c_0>0\) such that for each \(\varepsilon _1\in (0,\tfrac{1}{2})\), there exists a smooth function \(\chi : [0,\infty )\rightarrow {\textbf{R}}\) such that:
-
(1)
\(\chi (t)=t\) for t near 0, \(\chi (t)=0\) for \(t\ge \sqrt{\varepsilon _1}\), and \(0\le \chi (t)\le \tfrac{1}{2} \varepsilon _1\) for all t.
-
(2)
\(|\chi '(t)|\le c_0\) and \(\chi '(t)\le 1\) for all t.
-
(3)
\(-\tfrac{2}{\varepsilon _1}\le \chi ''(t)\le 0\) for all \(t\in [0,\varepsilon _1]\) and \(|\chi ''(t)|\le c_0\) for all \(t\in [\sqrt{\varepsilon _1},\varepsilon _1]\).
Proof
Everything except the property \(\chi '\le 1\) was already proven in [BH20, Lemma 25]. The fact that \(\chi ' \le 1\) can be arranged follows from the construction of \(\chi \) as \(\varphi _\delta + \psi _\delta \) for smooth functions satisfying \(\varphi _\delta ' \le 1\) and \(\psi _\delta \) being able to be taken non-decreasing, so \(\psi _\delta ' \le 0\). \(\square \)
Proof of Proposition F.7
Consider the function \(\chi (t)\) constructed in Lemma F.8. We define the metric \(\tilde{\varvec{g}}\) so that
when \(t\le \sqrt{\varepsilon _1}\), and
when \(t\ge \sqrt{\varepsilon _1}\). The proof in [BH20, Proposition 26] verifies properties (1), (2), (3), (6) provided \(C>C_0(g_0, {{\,\mathrm{\mathbb {I}}\,}}_0, k)\) and \(\varepsilon _1 < \min \{\tfrac{1}{2}, \delta \varepsilon , C^{-2}\}\). Property (4) is verified as well in the course of the proof, except the authors’ statement doesn’t reflect it. It remains to verify property, (5). Write \(\tilde{\varvec{g}}(x,t) = dt^2 + {\tilde{g}}_t\) as in (F.1). Then
by (F.2). By [BH20, Lemma 24], as long as \(\varepsilon _1 < C^{-2}\), we have
where \(\lesssim \) denotes an inequality where the LHS is bounded by the RHS times a positive constant that only depends on \(g_0\), \({{\,\mathrm{\mathbb {I}}\,}}_0\), k, but no other data. We compute
When \(\chi '(t) \ge 0\), \({{\,\textrm{tr}\,}}_{g_0} k \le H_0\) and \(\chi '(t) \le 1\) from Lemma F.8 imply that
Otherwise, if \(\chi '(t) < 0\), we use \({{\,\textrm{tr}\,}}_{g_0} k \le H_0\) twice to obtain:
i.e., (F.9) holds once again. Property (5) then follows from (F.7), (F.8), (F.9) by choosing \(\varepsilon \) sufficiently small. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Li, C., Mantoulidis, C. Metrics with \(\lambda _1(-\Delta + k R) \ge 0\) and Flexibility in the Riemannian Penrose Inequality. Commun. Math. Phys. 401, 1831–1877 (2023). https://doi.org/10.1007/s00220-023-04679-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-023-04679-9



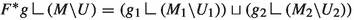 ;
;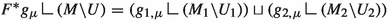 ;
;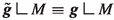 ;
; ;
;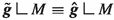 ;
;