Steady Euler Flows on ${\mathbb {R}}^3$ with Wild and Universal Dynamics

Abstract

Understanding complexity in fluid mechanics is a major problem that has attracted the attention of physicists and mathematicians during the last decades. Using the concept of renormalization in dynamics, we show the existence of a locally dense set ${\mathscr {G}}$ of stationary solutions to the Euler equations in ${\mathbb {R}}^3$ such that each vector field $X\in {\mathscr {G}}$ is universal in the sense that any area preserving diffeomorphism of the disk can be approximated (with arbitrary precision) by the Poincaré map of X at some transverse section. We remark that this universality is approximate but occurs at all scales. In particular, our results establish that a steady Euler flow may exhibit any conservative finite codimensional dynamical phenomenon; this includes the existence of horseshoes accumulated by elliptic islands, increasing union of horseshoes of Hausdorff dimension 3 or homoclinic tangencies of arbitrarily high multiplicity. The steady solutions we construct are Beltrami fields with sharp decay at infinity. To prove these results we introduce new perturbation methods in the context of Beltrami fields that allow us to import deep techniques from bifurcation theory: the Gonchenko-Shilnikov-Turaev universality theory and the Newhouse and Duarte theorems on the geometry of wild hyperbolic sets. These perturbation methods rely on two tools from linear PDEs: global approximation and Cauchy–Kovalevskaya theorems. These results imply a strong version of V.I. Arnold’s vision on the complexity of Beltrami fields in Euclidean space.

Appendices

Appendices

Proof of Proposition 3.7: Right Inverse of the Melnikov Operator

The aim of this appendix is to construct an inverse of the Melnikov operator for a vector field $X\in \Gamma ^\infty _\textrm{Leb}(U)$ displaying a strong heteroclinic link in U, for some open subset U of ${\mathbb {R}}^3$.

1.1 Displacement and Melnikov operators

The aim of this section is to introduce the definitions of displacement operator, Melnikov operator and explain their relation.

Let $\Sigma \subset {\mathbb {R}}^2$ and let $\Omega$ be the standard symplectic, smooth 2-form on $\Sigma \subset {\mathbb {R}}^2$. Let $f\in C^\infty (\Sigma ,{\mathbb {R}}^2)$ be a smooth, symplectic diffeomorphisms from $\Sigma$ onto its image. We assume that f displays two hyperbolic fixed point $p^+$, $p^-$ and a heteroclinic link L from $p^-$ to $p^+$. The displacement operator will describe the unfolding of L when we consider a perturbation of f.

Let ${\mathcal {N}}\subset C^\infty (\Sigma ,{\mathbb {R}}^2)$ be a neighborhood of 0. Assume that ${\mathcal {N}}$ is small enough such that, for every $\epsilon \in {\mathcal {N}}$, the diffeomorphism $f+\epsilon$ admits unique hyperbolic fixed points $p^\pm _\epsilon$ nearby $p^\pm$, called their hyperbolic continuations. Let $\ell :{\mathbb {R}}\rightarrow L$ be a smooth parametrization of the heteroclinic connection L such that

$$\begin{aligned} \lim _{t\rightarrow \pm \infty }\ell (t)=p^\pm \quad \text {and}\quad f(\ell (t))=\ell (t+1). \end{aligned}$$

Fix local unstable and local stable manifolds $W^u_{loc}(p^-;f)$ and $W^s_{loc}(p^+;f)$, of respectively $p^-$ and $p^+$, which both contain $\ell ([0,1])$.

For a fixed $\epsilon \in C^\infty (\Sigma ,{\mathbb {R}}^2)$ small, consider the smooth immersed submanifold $W^s_{loc}(p^+_\epsilon ; f+\epsilon )$. We can find a smooth diffeomorphism $\phi ^s_\epsilon :W^s_{loc}(p^+; f)\rightarrow W^s_{loc}(p^+_\epsilon ; f+\epsilon )$. Similarly, we find a smooth diffeomorphism $\phi ^u_\epsilon :W^u_{loc}(p^-; f)\rightarrow W^u_{loc}(p^-_\epsilon ; f+\epsilon )$. By Irwin’s proof [Irw72, Theorem 28] of the stable/unstable manifold theorem (which is based on the implicit function theorem), both $\phi ^s_\epsilon$ and $\phi ^u_\epsilon$ can be chosen so that they depend smoothly on $\epsilon$. Up to a smooth reparametrization, we can assume that

$$\begin{aligned} (f+\epsilon )\phi ^u_\epsilon (\ell (0))=\phi ^u_\epsilon (\ell (1))\qquad \text {and}\qquad (f+\epsilon )\phi ^s_\epsilon (\ell (0))=\phi ^s_\epsilon (\ell (1))\, . \end{aligned}$$

(B.1)

We define, for $t\in [0,1]$,⁸

$$\begin{aligned} \textrm{displ}(\epsilon )(t)=\Omega (\partial _t\ell (t),\phi ^u_\epsilon (\ell (t))-\phi ^s_\epsilon (\ell (t))). \end{aligned}$$

(B.2)

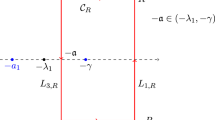
Roughly speaking, $\textrm{displ}(\epsilon )(t)$ is the algebraic distance, along an affine line passing through $\ell (t)$ and normal to L, between the perturbed local stable and unstable manifolds. See Fig. 6.

Fig. 6

The displacement function is the algebraic distance between perturbed local stable and unstable manifolds

By Eq. (B.1), $\phi ^u_\epsilon (\ell ([0,1]))$ and $\phi ^s_\epsilon (\ell ([0,1]))$ are fundamental domains. Then, the function $\textrm{displ}(\epsilon )$ vanishes if and only if $\phi ^s_\epsilon (\ell (t))= \phi ^u_\epsilon (\ell (t))$ for every $t\in [0,1]$. Thus, the heteroclinic link persists if and only if $\textrm{displ}(\epsilon )\equiv 0$.

Definition A.1

The displacement operator is the following map from a neighborhood ${\mathcal {N}}$ of 0 in $C^\infty (\Sigma ,{\mathbb {R}}^2)$:

$$\begin{aligned}{} & {} \textrm{displ}:{\mathcal {N}}\rightarrow C^\infty ([0,1],{\mathbb {R}}) \\{} & {} \quad \epsilon \mapsto \textrm{displ}(\epsilon ), \end{aligned}$$

where the function $\textrm{displ}(\epsilon )$ is defined in Eq. (B.2).

Remark A.2

The displacement operator is not uniquely defined: it depends on the parametrization $\ell$ of L and on the families $(\phi ^u_\epsilon )_\epsilon$ and $(\phi ^s_\epsilon )_\epsilon$.

We recall that $\phi ^s_\epsilon$ and $\phi ^u_\epsilon$ depend smoothly on $\epsilon$, so the following proposition holds.

Proposition A.3

The map $\textrm{displ}:{\mathcal {N}}\rightarrow C^\infty ([0,1],{\mathbb {R}})$ is smooth.

The distance between the perturbed stable and unstable manifolds can be studied through the so-called Melnikov functions. We present here the main definitions and properties and refer for detailed proofs to [LMRR08, DRR97, DRR96, GPB89]; the historical references are [Poi99] and [Mel63].

Definition A.4

Let $f\in C^\infty (\Sigma ,{\mathbb {R}}^2)$ be a symplectic diffeomorphism, which displays a heteroclinic link L, parametrized by $\ell :{\mathbb {R}}\rightarrow L$. The Melnikov function associated to a smooth family $r\mapsto \epsilon (r)\in C^\infty (\Sigma ,{\mathbb {R}}^2)$, with $\epsilon (0)=0$, is:

$$\begin{aligned} \begin{aligned} \mathcal {M}(\epsilon (s)):&\ {\mathbb {R}}\rightarrow {\mathbb {R}}\\ t\mapsto {\mathcal {M}}(\epsilon (s))(t ):=&\,\sum _{k\in {\mathbb {Z}}}\Omega \left( \partial _t\ell (t), (f^*)^k(\partial _r\epsilon (r)|_{r=0}\circ f^{-1})\circ \ell (t)\right) \, , \end{aligned} \end{aligned}$$

(B.3)

where $\partial _r\epsilon (r)|_{r=0}:=\lim _{r\rightarrow 0}\frac{\epsilon (r)}{r}$.

Remark A.5

In Eq. (B.3) the presence of $\partial _r\epsilon (r)|_{r=0}\circ f^{-1}$ is due to the fact that, for the given family $(f+\epsilon (r))_r$, it is the vector field $X=\partial _r\epsilon (r)|_{r=0}\circ f^{-1}$ which satisfies $\frac{d}{dr}(f+\epsilon (r))|_{r=0}=X\circ f$. See [LMRR08, Section 2].

Recall that f is symplectic and, since $f(\ell (t))=\ell (t+1)$, $\partial _t\ell (t)= Df^{-k}(\ell (t+k))\partial _t\ell (t+k)$. Thus, it holds

$$\begin{aligned} {\mathcal {M}}(\epsilon (s))(t)=\sum _{k\in {\mathbb {Z}}}\Omega \left( \partial _t\ell (t+k), \partial _s\epsilon |_{s=0}(\ell (t+k-1))\right) . \end{aligned}$$

(B.4)

Note that the Melnikov function belongs to the space $C^\infty ({\mathbb {R}}/{\mathbb {Z}},{\mathbb {R}})$ of smooth 1-periodic functions.

Definition A.6

Let f be a symplectic diffeomorphism in $C^\infty (\Sigma ,{\mathbb {R}}^2)$ displaying a heteroclinic link L, parametrized by $\ell :{\mathbb {R}}\rightarrow L$. The Melnikov operator is a linear and continuous map

$$\begin{aligned} {\mathcal {M}}:C^\infty (\Sigma ,{\mathbb {R}}^2)\ni \epsilon \mapsto {\mathcal {M}}(\epsilon )\in C^\infty ({\mathbb {R}}/{\mathbb {Z}},{\mathbb {R}})\, , \end{aligned}$$

where ${\mathcal {M}}(\epsilon )$ is the Melnikov function with respect to the smooth family $r\mapsto r\epsilon$.

Remark A.7

Observe that ${\mathcal {M}}(\epsilon )$ depends only on $\epsilon |_L$. Thus, we can define ${\mathcal {M}}(\epsilon )$ for $\epsilon \in C^\infty (L,{\mathbb {R}}^2)$.

Theorem A.8

(Poincaré-Melnikov, [Poi99]–[Mel63]) Let f be a symplectic diffeomorphism in $C^\infty (\Sigma ,{\mathbb {R}}^2)$, displaying a heteroclinic link L, parametrized by $\ell :{\mathbb {R}}\rightarrow L$. Then, the partial differential of the displacement operator at 0 is equal to the Melnikov operator at $\epsilon$, i.e.

$$\begin{aligned} D_0\textrm{displ}={\mathcal {M}}. \end{aligned}$$

(B.5)

Thus, for any $r\ge 1$, in the $C^r$-uniform norm it holds

$$\begin{aligned} \textrm{displ}(\epsilon )= \textrm{displ}(0)+ D_0\textrm{displ}(\epsilon )+O(\epsilon ^2)={\mathcal {M}}(\epsilon )+O(\epsilon ^2). \end{aligned}$$

For a detailed proof, we refer for example to [DRR97] and [GPB89].

1.2 Inverse Melnikov operator for flows in ${\mathbb {R}}^3$

Let U be an open subset of ${\mathbb {R}}^3$. Let $X\in \Gamma ^\infty _\textrm{Leb}(U)$ display a strong heteroclinic link $\Gamma \subset U$ between two saddle periodic orbits $\gamma ^\pm \subset U$. In particular, the closure of the link ${\bar{\Gamma }}$ is diffeomorphic to ${\mathbb {R}}/{\mathbb {Z}}\times [-1,1]$.

Let ${\bar{L}}$ be the closure of the half strong stable manifold of a point in $\gamma ^+$ in $\Gamma$. Let ${\hat{\Sigma }}\subset {\mathbb {R}}^3$ be a disk which contains ${\bar{L}}$ and that intersects transversally $\Gamma$. Up to reducing ${\hat{\Sigma }}$, it is transverse to the vector field X. Let $\Sigma \Subset {\hat{\Sigma }}$ be a neighborhood of L in ${\hat{\Sigma }}$ such that for every point $z \in \Sigma$, there exists $\tau (z)>0$ minimal such that the orbit of z intersect transersally ${\hat{\Sigma }}$ at time $\tau (z)$ at a point f(z). From the definition of strong heteroclinic link, the first return time $\tau |_{ \Sigma \cap \Gamma }$ is constant, in particular $\gamma ^+$ and $\gamma ^-$ have the same period. Indeed, since $\Sigma \cap \Gamma =L$ is a half strong stable manifold of a point in $\gamma ^+$, it is $T(\gamma ^+)$-periodic, where $T(\gamma ^+)$ denotes the period of $\gamma ^+$ (similarly, for a half strong unstable manifold of a point if $\gamma ^-$). The disks $\Sigma \subset {\hat{\Sigma }}$ are called Poincaré sections and f is called a Poincaré first return map. The maps f and $\tau$ are in, respectively, $C^\infty (\Sigma ,{\hat{\Sigma }})$ and $C^\infty (\Sigma ,{\mathbb {R}}^+)$. Moreover, it is standard that there exists a smooth symplectic form $\Omega$ in ${\hat{\Sigma }}$ which is invariant by the action of $f|_\Sigma$. By Darboux’s Theorem, we can identify $\Sigma$ with a disk of ${\mathbb {R}}^2$ so that $\Omega$ is the standard symplectic form.

Let $W\in \Gamma ^\infty _\textrm{Leb}(U)$ be a small perturbation of X: it induces a small perturbation $\epsilon \in C^\infty (\Sigma ,{\mathbb {R}}^2)$ of the Poincaré map f. So we can study the unfolding of $\Gamma$ using the tools of Melnikov operator for the heteroclinic link $L={\hat{\Sigma }}\cap \Gamma$ presented above.

Fix a parametrization $\ell :{\mathbb {R}}\rightarrow L$ of L, such that $\lim _{t\rightarrow \pm \infty }\ell (t)=p^\pm$, where $p^\pm :={\hat{\Sigma }}\cap \gamma ^\pm$, and $f(\ell (t))=\ell (t+1)$. Fix also $(\phi ^s_\epsilon )_\epsilon$ and $(\phi ^u_\epsilon )_\epsilon$ as in A.1. Let ${\mathcal {M}}$ be the Melnikov operator associated to this setting.

Definition A.9

The Melnikov operator is the following linear and continuous map from a neighborhood ${\mathcal {N}}$ of 0 in $\Gamma ^\infty _\textrm{Leb}(U)$

$$\begin{aligned} {\mathcal {M}}: {\mathcal {N}}\ni W\mapsto {\mathcal {M}}(W):={\mathcal {M}}(\epsilon )\in C^\infty ({\mathbb {R}}/{\mathbb {Z}},{\mathbb {R}})\, , \end{aligned}$$

where $\epsilon \in C^\infty (\Sigma ,{\mathbb {R}}^2)$ is the perturbation of the first return map f associated to the vector field W.

Remark A.10

Observe that, since ${\mathcal {M}}(\epsilon )$ depends only on $\epsilon |_L$ (see Remark A.7), and so on $W|_\Gamma$, the operator ${\mathcal {M}}$ can be defined for $W\in C^\infty (\Gamma ,{\mathbb {R}}^3)$.

The aim of this subsection is to give the proof of Proposition 3.7: such a proposition gives an inverse operator of the Melnikov one.

Proof of Proposition 3.7

We recall that $\Gamma$ is an invariant cylinder smoothly embedded in ${\mathbb {R}}^3$, and that $L\subset \Gamma$ is a line transverse to the flow whose return time is a constant $T>0$. As the statement is invariant by reparametrizing the flow, we can assume that $T=1$.

This defines a canonical diffeomorphism $\Gamma \rightarrow L\times {\mathbb {R}}/{\mathbb {Z}}$ which maps L to $L\times \{0\}$. Recall that $\ell :{\mathbb {R}}\rightarrow L$ is a parametrization of L such that $f\circ \ell (t)=\ell (t+1)$ for every $t\in {\mathbb {R}}$, where f is the first return map to $\Sigma$. Then using $\ell$, we identify $\Gamma$ to ${\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}$ and L to ${\mathbb {R}}\times \{0\}$:

$$\begin{aligned} \Gamma \equiv {\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}\quad \text {and}\quad L\equiv {\mathbb {R}}\times \{0\} \; , \end{aligned}$$

such that, with $p_2: \Gamma \rightarrow {\mathbb {R}}/{\mathbb {Z}}$ the second coordinate projection, the flow $(\Phi ^t_X)_{t\in {\mathbb {R}}}$ of X satisfies:

$$\begin{aligned} p_2\circ \Phi ^t_X(s,\theta )= \theta +t\ \mod 1\; , \quad \forall (s,\theta )\in {\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}\equiv \Gamma \, . \end{aligned}$$

Lemma A.11

There is a compactly supported function $\Psi \in C^\infty ({\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}},{\mathbb {R}}^+)$ such that:

$$\begin{aligned} \int _{\mathbb {R}}\Psi \circ \Phi ^t_X(s,0)dt=1\;, \quad \forall s\in {\mathbb {R}}. \end{aligned}$$

Proof

Let $\Psi _0\in C^\infty ({\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}},{\mathbb {R}}^+)$ be a smooth, compactly supported, non-negative function which is positive on $[\tfrac{1}{2}, \tfrac{3}{2}]\times \{0\}$. For every $(s,\theta )\in {\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}\equiv \Gamma$ define

$$\begin{aligned} C(s,\theta ):=\int _{\mathbb {R}}\Psi _0\circ \Phi ^t_X(s,\theta )dt\, . \end{aligned}$$

Note that every orbit intersects $[\tfrac{1}{2}, \tfrac{3}{2}]\times \{0\}$, so C is positive. Also the function C is $\Phi _V^t$-invariant and smooth. Actually, $C(s,\theta )$ is equal to some constant C, because $\Phi ^t_X|_{\Gamma }$ does not have any non trivial continuous first integral. Define then the function $\Psi \in C^\infty ({\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}, {\mathbb {R}}^+)$ as

$$\begin{aligned} (s,\theta )\in {\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}\mapsto \Psi (s,\theta ):=\dfrac{\Psi _0(s,\theta )}{C}\in {\mathbb {R}}^+\, . \end{aligned}$$

It is obvious that the mean of $\Psi$ along the orbits is one, as desired. $\square$

Note that for every $(s,\theta )\in {\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}$, the orbit of $(s,\theta )$ intersects L at a set $(\varphi (s,\theta )+{\mathbb {Z}})\times \{0\}$. This defines a $\Phi _X^t$-invariant map:

$$\begin{aligned} \varphi : {\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}\rightarrow {\mathbb {R}}/{\mathbb {Z}}. \end{aligned}$$

Note that for every $s,t\in {\mathbb {R}}$ it holds

$$\begin{aligned} \varphi \circ \Phi ^t_X(s,0)=s \mod 1\, . \end{aligned}$$

(B.6)

We recall that $\Sigma$ is a Poincaré section containing L and transverse to $\Gamma$ and that $\Omega$ denote an invariant symplectic form for the first return map f. Let $N:{\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}\equiv \Gamma \rightarrow {\mathbb {R}}^3$ be a vector field such that:

$$\begin{aligned} T\Gamma \oplus {\mathbb {R}}N= {\mathbb {R}}^3\quad \text {and}\quad \Omega (\partial _t \ell (s), N_\Sigma \circ \ell (s))= 1\quad \forall s\in {\mathbb {R}}\; , \end{aligned}$$

(B.7)

where $N_\Sigma$ denotes the projection of $N|_\Gamma$ into the section $\Sigma$.

Now for every $g\in C^\infty ({\mathbb {R}}/{\mathbb {Z}},{\mathbb {R}})$ we define the smooth vector field ${\mathcal {I}} (g)\in C^\infty ({\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}},{\mathbb {R}}^3)$ as:

$$\begin{aligned} {\mathcal {I}} (g):= (s , \theta )\in \Gamma \mapsto g\circ \varphi (s,\theta )\cdot \Psi (s,\theta )\cdot N(s, \theta )\in {\mathbb {R}}^3. \end{aligned}$$

(B.8)

We shall prove that the operator which associates to g the Melnikov function of ${\mathcal {I}} (g)$ is the identity. In order to do this, let us go back to the two dimensional setting. Let $\epsilon (g)\in C^\infty (\Sigma , {\mathbb {R}}^2)$ be the perturbation induced by the vector field $X+{\mathcal {I}}(g)$ on the first return map f. Consider the smooth family $r\mapsto \epsilon (rg)$. Then the partial derivative $\partial _r\epsilon |_{r=0}$ is:

$$\begin{aligned} \partial _r\epsilon (rg)|_{r=0}=\lim _{r\rightarrow 0} \frac{1}{r} \epsilon (r\cdot g) \, . \end{aligned}$$

Lemma A.12

For every $s\in {\mathbb {R}}$ it holds:

$$\begin{aligned} \Omega (\partial _t\ell (s+1), \partial _r\epsilon (rg)|_{r=0}\circ \ell (s))=g(s)\cdot \left( \int _0^{1}\Psi \circ \Phi ^t_X(s,0)dt\right) \, , \end{aligned}$$

where g is identified with a 1-periodic real function.

Proof

A flow-box coordinate neighborhood V of $\Gamma$ is diffeomorphic to $\Gamma \times (-1,1)$. This diffeomorphism induces an identification of V with ${\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}\times (-1,1)$ and can be chosen so that N is constantly equal to (0, 0, 1), $\Sigma \cap V$ is identified with ${\mathbb {R}}\times \{0\}\times {\mathbb {R}}$ and X has zero third component.

Let $X_g:= X+{{\mathcal {I}}}(g)$ and denote by $(\Phi _{X_g}^t)_{t\in {\mathbb {R}}}$ its flow. Let $\tau _g:\Sigma \rightarrow {\mathbb {R}}$ be the first return time on $\Sigma$ associated to $X_g$. In the coordinates given by the identification, we have:

$$\begin{aligned} X_g(s,t)= X(s,\theta )+(0,0, g\circ \varphi (s,\theta )\cdot \Psi (s,\theta ))\; ,\quad \forall (s,\theta )\in {\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}\; . \end{aligned}$$

Let $z=\ell (s)$ and express the perturbation $\epsilon (g)$ associated to ${\mathcal {I}} (g)$ as

$$\begin{aligned} \epsilon (g)(z)=\left( (f+\epsilon (g))(z)-z\right) -(f(z)-z)\,. \end{aligned}$$

In the coordinates of the tubular neighborhood of $\Gamma$ we have:

$$\begin{aligned} (0,\epsilon (g)(z))=\int _0^{\tau _g(z)}(X+{\mathcal {I}}(g))\circ \Phi ^t_{X+{\mathcal {I}}(g)}(z)dt-\int _0^{1}X\circ \Phi ^t_X(z)dt\, , \end{aligned}$$

where the coordinate 0 is the coordinate in ${\mathbb {R}}/{\mathbb {Z}}$ (we have changed the ordering of the coordinates for the ease of notation).

Hence for every $r\ge 1$:

$$\begin{aligned} (0,\epsilon (g)(z))={} & {} \int _1^{\tau _g(z)}X\circ \Phi ^t_{X}(z)dt+ \int _0^{1} {\mathcal {I}}(g) \circ \Phi ^t_{X}(z)dt+ \\ {}{} & {} \int _0^{1}\left( X\circ \Phi ^t_{X+{\mathcal {I}}(g)}(z)-X\circ \Phi ^t_X(z)\right) dt+ O(\Vert g\Vert ^2_{C^r})\, , \end{aligned}$$

where we have used that $\int _1^{\tau _g(z)}X\circ \Phi ^t_{X+{\mathcal {I}}(g)}(z) dt = \int _1^{\tau _g(z)} X\circ \Phi ^t_X(z)dt+ O(\Vert g\Vert ^2_{C^r})$. Since, with $p_3: {\mathbb {R}}\times {\mathbb {R}}/{\mathbb {Z}}\times (-1,1)\rightarrow (-1,1)$ the third coordinate projection, it holds $p_3(X)=0$ on the neighborhood V, the first and third terms have their third components null while the second term has its first and second components null. Thus, it holds:

$$\begin{aligned} p_3(0,\epsilon (g)(z))= p_3\left( \int _0^{1} {\mathcal {I}}(g) \circ \Phi ^t_{X}(z)dt\right) + O(\Vert g\Vert ^2_{C^r})\; . \end{aligned}$$

Now we plug Eq. (B.8) to obtain:

$$\begin{aligned} p_3(0,\epsilon (g)(z))= p_3\left( \int _0^{1} g\circ \varphi \circ \Phi ^t_{X}(z)\cdot \Psi \circ \Phi ^t_{X}(z)\cdot N \circ \Phi ^t_{X}(z)dt\right) + O(\Vert g\Vert ^2_{C^r})\; . \end{aligned}$$

Now we use that $p_3\circ N\equiv 1$ and that, from (B.7), $\Omega (\partial _t \ell (s+1) , \epsilon (g)\circ \ell (s))= p_3(0,\epsilon (g)(z))$, to obtain:

$$\begin{aligned} \Omega (\partial _t \ell (s+1), \epsilon (g) \circ \ell (s))= \int _0^{1} g\circ \varphi \circ \Phi ^t_{X}(z)\cdot \Psi \circ \Phi ^t_{X}(z)dt + O(\Vert g\Vert ^2_{C^r})\; . \end{aligned}$$

(B.9)

Using the invariance of $\varphi$ by the flow, we have $g\circ \varphi \circ \Phi ^t_{X}(z)= g\circ \ell (s)$ for every t. Using Eq.(B.9) with the perturbation $\epsilon (rg)$, taking its derivative with respect to r and evaluating at $r=0$ yield the sought equality. $\square$

The Melnikov function associated to ${\mathcal {I}}(g)$ is

$$\begin{aligned} {\mathcal {M}}({\mathcal {I}}(g))(s)={\mathcal {M}}(\epsilon (g))(s)=\sum _{k\in {\mathbb {Z}}}\Omega (\partial _t\ell (s+k),\partial _r\epsilon (rg)|_{r=0}(\ell (s+k-1))). \end{aligned}$$

By Lemma A.12, since the function g is 1-periodic and by Proposition A.11, we deduce that

$$\begin{aligned} {\mathcal {M}}({\mathcal {I}}(g))(s)=g(s)\cdot \sum _{k\in {\mathbb {Z}}} \left( \int _0^{1}\Psi \circ \Phi ^t_X(s+k,0)\,dt\right) \end{aligned}$$

and, since $\Phi ^t_X(s+k,0)=\Phi ^{t+k}_X(s,0)$ for every $k\in {\mathbb {Z}}$, we conclude that

$$\begin{aligned} {\mathcal {M}}({\mathcal {I}}(g))(s)= g(s)\cdot \int _{\mathbb {R}}\Psi \circ \Phi ^t_X(s,0) dt = g(s)\, . \end{aligned}$$

$\square$

Proof of Theorem 3.4: Cauchy–Kovalevskaya’s Theorem for Curl

1.1 Application of Cauchy–Kovalevskaya’s Theorem for curl

Let $\Sigma \subset {\mathbb {R}}^3$ be a bounded, oriented, analytic surface that can be analytically extended in a neighborhood. Given a vector field W on $\Sigma$, we can decompose it as follows:

$$\begin{aligned} W=W_T+(W\cdot N)N, \end{aligned}$$

where N is a unit normal to $\Sigma$, while $W_T$ is the component of W tangent to $\Sigma$. We refer to W as the Cauchy datum for the Cauchy–Kovalevskaya theorem. Denote as $g:=W\cdot N$ the normal component of the Cauchy datum.

We will be interested in W satisfying the following condition:

where $W^\flat _T$ is the 1-form dual to $W_T$, push-forwarded on $\Sigma$, and $\sigma$ is the area form on $\Sigma$ induced from the ambient space ${\mathbb {R}}^3$. The following generalizes Theorem 3.1 in [EPS12].

Theorem B.1

(Cauchy–Kovalevskaya’s Theorem for curl). Let $\Sigma \subset {\mathbb {R}}^3$ be a surface as above and let W be the analytic Cauchy datum in $C^\omega ({\bar{\Sigma }},{\mathbb {R}}^3)$. The equation

$$\begin{aligned} \textrm{curl }\, X&= X, \end{aligned}$$

(B.1)

$$\begin{aligned} X|_{\Sigma }&=W \end{aligned}$$

(B.2)

has a unique, analytic solution in a neighborhood $\Omega$ of $\Sigma$ if and only if W fulfills condition ($*$).

This theorem implies Theorem 3.4

Proof of Theorem 3.4

Let $\Gamma$ be an analytic surface in ${\mathbb {R}}^3$ whose closure ${\bar{\Gamma }}$ is diffeomorphic to ${\mathbb {I}}\times {\mathbb {R}}/{\mathbb {Z}}$. We are going to show that for every $g\in C^\omega ({\bar{\Gamma }},{\mathbb {R}})$, there exists a neighborhood $\Omega$ of ${\bar{\Gamma }}$ in ${\mathbb {R}}^3$ and a Beltrami field $X\in C^\omega (\Omega ,{\mathbb {R}}^3)$ such that the normal component to $\Gamma$ of $X|_\Gamma$ equals g. To be precise, with N a unit normal vector field on $\Gamma$, this means that $(X|_\Gamma )\cdot N= g$.

In order to show this, it suffices to observe that, given the normal component $g\in C^\omega ({\bar{\Gamma }},{\mathbb {R}})$ of a Cauchy datum on $\Gamma$, there are many Cauchy data W satisfying condition ($*$) and such that $W\cdot N=g$. Endow ${\bar{\Gamma }}\simeq {\mathbb {I}}\times {\mathbb {R}}/{\mathbb {Z}}$ with coordinates $(z,\theta )\in {\mathbb {I}}\times {\mathbb {R}}/{\mathbb {Z}}$ so that the area form $\sigma$ is $dz\wedge d\theta$. We are looking for a Cauchy datum W such that

$$\begin{aligned} d(W^\flat _T)=gdz\wedge d\theta . \end{aligned}$$

Defining

$$\begin{aligned} {\tilde{g}}(z,\theta ):=\int _{-1}^zg(s,\theta )ds, \end{aligned}$$

we set

$$\begin{aligned} W^\flat _T:={\tilde{g}}(z,\theta )d\theta . \end{aligned}$$

Thus, it clearly holds that $d(W^\flat _T)=g(z,\theta )dz\wedge d\theta$, that is W satisfies condition ($*$). By Theorem B.1 applied at $\Gamma$, we conclude that there exists a neighborhood $\Omega$ of $\Gamma$ in ${\mathbb {R}}^3$ and an Euclidean Beltrami field $X(g)\equiv X\in C^\omega (\Omega ,{\mathbb {R}}^3)$, defined as

$$\begin{aligned} X|_{\Gamma }:= gN+({{\tilde{g}}}(z,\theta )d\theta )^\#, \end{aligned}$$

whose normal component is g. $\square$

Remark B.2

Any other $W^\flat _T$ satisfying condition ($*$) is of the form ${\tilde{g}}(z,\theta )d\theta +\alpha$, where $\alpha$ is a closed 1-form on $\Sigma$. In the following, we will always choose $\alpha =0$, which implies the uniqueness of the Beltrami field with normal datum g.

Remark B.3

Let $g\in C^\omega ({\bar{\Sigma }},{\mathbb {R}})\mapsto X(g)\in C^\omega (\Omega ,{\mathbb {R}}^3)$ be the map that associates to every normal datum g the corresponding Beltrami field X(g) given by Corollary 3.4. Such a map is linear. Indeed, let $g_1,g_2$ be normal data and $c_1,c_2\in {\mathbb {R}}$. Then, for $i=1,2$, there exists a neighborhood $\Omega _i$ of $\Sigma$ and a Beltrami field $X^i:=X(g_i)\in C^\omega (\Omega _i,{\mathbb {R}}^3)$ such that

$$\begin{aligned} X^i|_{\Sigma }=W^i_T+g_iN \end{aligned}$$

where $W^i_T:=({\tilde{g}}_i(z,\theta )d\theta )^\#$. Thus, the Beltrami field $X(c_1 g_1+c_2 g_2)\in C^\omega (\Omega _1\cap \Omega _2,{\mathbb {R}}^3)$ satisfies

$$\begin{aligned}{} & {} X(c_1 g_1+c_2 g_2)|_{\Sigma }=:X=\\{} & {} \quad (c_1{\tilde{g}}_1(z,\theta )d\theta )^\#+(c_2{\tilde{g}}_2(z,\theta )d\theta )^\#+(c_1 g_1+c_2 g_2)N=(c_1 W^1_T+c_2 W^2_T) \\{} & {} \quad +(c_1 g_1+c_2 g_2)N= c_1(W^1_T+g_1N)+c_2(W^2_T+g_2N)=c_1 X^1+c_2 X^2. \end{aligned}$$

Since the equation $\textrm{curl }\, X=X$ is linear, by uniqueness (see Remark B.2) we have that X associated to the normal datum $c_1g_1+c_2g_2$ is

$$\begin{aligned} X=c_1 X^1|_{\Omega _1\cap \Omega _2}+c_2 X^2|_{\Omega _1\cap \Omega _2}. \end{aligned}$$

1.2 Proof of Theorem B.1

Let us first consider a toy model to understand Theorem B.1 and Condition ($*$), following [EPS20, Subsection 3.2]. Let us consider $\Sigma =\{x_3=0\}$ with coordinates $(x_1,x_2,x_3)$ in ${\mathbb {R}}^3$. Fix an analytic Cauchy datum

$$\begin{aligned} W=W_1(x_1,x_2)\partial _{x_1}+W_2(x_1,x_2)\partial _{x_2}+W_3(x_1,x_2)\partial _{x_3}. \end{aligned}$$

In coordinates, the Beltrami equation $\textrm{curl}\ X= X$ reads as

By the standard Cauchy-Kovaleskaya’s Theorem applied at $\Sigma =\{x_3=0\}$, there exists a unique analytic solution to this system in a neighborhood $\Omega$ of $\Sigma$, with Cauchy datum W.

Considering $\frac{\partial }{\partial x_1}$(B.4)$-\frac{\partial }{\partial x_2}$(B.3) and using (B.5), we obtain

$$\begin{aligned} \frac{\partial }{\partial x_3}\left( \frac{\partial X_2}{\partial x_1}-\frac{\partial X_1}{\partial x_2}- X_3\right) =0. \end{aligned}$$

Thus

$$\begin{aligned} \frac{\partial X_2}{\partial x_1}-\frac{\partial X_1}{\partial x_2}= X_3+f(x_1,x_2), \end{aligned}$$

(B.6)

in $\Omega$, for some analytic function f. Evaluating (B.6) at $\Sigma =\{x_3=0\}$, we obtain

$$\begin{aligned} \frac{\partial W_2}{\partial x_1}-\frac{\partial W_1}{\partial x_2}=W_3+f(x_1,x_2). \end{aligned}$$

The vector field $X=(X_1,X_2,X_3)$ is Beltrami in $\Omega$ if and only if the Cauchy datum satisfies the constraint

$$\begin{aligned} \frac{\partial W_2}{\partial x_1}-\frac{\partial W_1}{\partial x_2}=W_3. \end{aligned}$$

(B.7)

In terms of the dual 1-form $\beta :=W_1dx_1+W_2dx_2$, this is equivalent to

$$\begin{aligned} d\beta =W_3dx_1\wedge dx_2. \end{aligned}$$

(B.8)

We have to choose the tangent part $\beta$ of the Cauchy datum so that (B.8) is fullfilled. If $\Sigma$ is open, given $W_3$, this is always possible.

We now prove Theorem B.1, whose proof follows closely that of Theorem 3.1 in [EPS12]. Observe that Condition ($*$) reduces to the condition of [EPS12, Theorem 3.1] when $g=0$.

Proof of Proposition B.1

Let $\Sigma \subset {\mathbb {R}}^3$ be a bounded, oriented, analytic surface. Denote by

$$\begin{aligned} j_\Sigma :\Sigma \rightarrow {\mathbb {R}}^3 \end{aligned}$$

the analytic embedding of $\Sigma$ into ${\mathbb {R}}^3$. Let W be an analytic vector field defined on $\Sigma$. We will refer to it as Cauchy datum. We write W as

$$\begin{aligned} W=W_T+(W\cdot N) N, \end{aligned}$$

where N is the unit normal vector to $\Sigma$, while $W_T$ is the component of W tangent to $\Sigma$. Let $W^\flat$ be the dual 1-form of W, while $W_T^\flat$ denotes the dual 1-form of $W_T$. Let $g:=W\cdot N$. Recall that the vector field W satisfies Condition ($*$) if

$$\begin{aligned} d W_T^\flat =g\sigma , \end{aligned}$$

where here d is the exterior derivative on $\Sigma$ and $\sigma$ is the induced area-form on $\Sigma$.

Take local analytic coordinates in a neighborhood $\Omega$ of $\Sigma$:

$$\begin{aligned} (\rho ,\xi _1,\xi _2), \end{aligned}$$

where $\rho$ is the signed distance function from $\Sigma$: if $\Omega$ is narrow enough, then this function is analytic. In these coordinates, the Euclidean metric reads as:

$$\begin{aligned} ds^2=d\rho ^2+h_{ij}(\rho ,\xi _1,\xi _2)d\xi _id\xi _j, \end{aligned}$$

where the last expression has to be understood as sum for $i,j=1,2$. In the sequel, we will use such Einstein convention, i.e. repeated indices have to be understood as summed. Denote as $h^{ij}$ the inverse matrix of $h_{ij}$ and $|h|:=\textrm{det}(h_{ij})$ its determinant.

The Beltrami field X reads in these coordinates as

$$\begin{aligned} X=a(\rho ,\xi _1,\xi _2)\partial _{\rho }+b^i(\rho ,\xi _1,\xi _2)\partial _{\xi _i} \end{aligned}$$

for some functions $a(\rho ,\xi _1,\xi _2), b^1(\rho ,\xi _1,\xi _2),b^2(\rho ,\xi _1,\xi _2)$. The 1-form associated to X is so

$$\begin{aligned} \beta :=a(\rho ,\xi _1,\xi _2)d\rho +c_i(\rho ,\xi _1,\xi _2)d\xi _i, \end{aligned}$$

with $c_i:=h_{ij}b^j$. In terms of the 1-form $\beta$, the equation $\textrm{curl}\,X=X$ reads as

$$\begin{aligned} \star d\beta = \beta , \end{aligned}$$

(B.9)

where $\star$ denotes the Hodge star operator. In the coordinates $(\rho ,\xi _1,\xi _2)$, the term $\star d\beta$ has the form

$$\begin{aligned}{} & {} \star d\beta = \dfrac{1}{|h|^{1/2}}\left( \dfrac{\partial c_2}{\partial \xi _1}-\dfrac{\partial c_1}{\partial \xi _2} \right) d\rho +|h|^{1/2}h^{2i}\left( \dfrac{\partial a}{\partial \xi _i} -\dfrac{\partial c_i}{\partial \rho }\right) d\xi _1+|h|^{1/2}h^{1i}\left( \dfrac{\partial c_i}{\partial \rho }-\dfrac{\partial a}{\partial \xi _i} \right) d\xi _2. \end{aligned}$$

The equation $\star d\beta =\beta$ is then equivalent, in $(\rho ,\xi _1,\xi _2)$-coordinates, to:

We start by showing the necessity of Condition ($*$). The tangential component of X on $\Sigma$ is

$$\begin{aligned} X_T=b^i(0,\xi _1,\xi _2)\partial _{\xi _i}. \end{aligned}$$

Its dual 1-form is then $X_T^\flat =c_i(0,\xi _1,\xi _2)d\xi _i$.

Thus

$$\begin{aligned} d(c_i(0,\xi _1,\xi _2)d\xi _i)=\left( \dfrac{\partial c_2(0,\xi _1,\xi _2)}{\partial \xi _1}-\dfrac{\partial c_1(0,\xi _1,\xi _2)}{\partial \xi _2} \right) d\xi _1\wedge d\xi _2. \end{aligned}$$

On the other hand the area-form $\sigma$ on $\Sigma$ is, since $N=\partial _\rho$,

$$\begin{aligned} \sigma =|h|^{1/2}(0,\xi _1,\xi _2)d\xi _1\wedge d\xi _2. \end{aligned}$$

Evaluating then (B.10) at $\rho =0$, i.e. at $\Sigma$, we obtain

$$\begin{aligned} \dfrac{\partial c_2(0,\xi _1,\xi _2)}{\partial \xi _1}-\dfrac{\partial c_1(0,\xi _1,\xi _2)}{\partial \xi _2}=a(0,\xi _1,\xi _2)|h|^{1/2}(0,\xi _1,\xi _2), \end{aligned}$$

and, denoting $g:=a(0,\xi _1,\xi _2)$, we obtain Condition ($*$):

$$\begin{aligned} d(X_T^\flat )=g\sigma . \end{aligned}$$

We now show the sufficiency of Condition ($*$). Consider the auxiliary problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} (d+\delta )\psi =\star \psi \quad \text {in }\Omega \\ \psi |_\Sigma =W^\flat , \end{array}\right. } \end{aligned}$$

(A)

where $W^\flat$ is the dual 1-form of W, $\delta$ is the codifferential (i.e. for $\omega \in \Omega ^k$ it holds $\delta \omega =(-1)^{k}\star d\star \omega$), and, denoting as $\Omega ^k$ the space of k-forms, $\psi \in \Omega ^0\oplus \Omega ^1\oplus \Omega ^2\oplus \Omega ^3$. In particular, $\psi$ can be decomposed as $\psi ^0\oplus \psi ^1\oplus \psi ^2\oplus \psi ^3$, with $\psi ^k$ a k-form. The operator $d+\delta$ is a first order elliptic operator (notice that $(d+\delta )^2=d\delta +\delta d=\Delta$ is the Hodge Laplacian). So, by the standard Cauchy–Kovalevskaya’s Theorem (see [Tay11, Page 502, Proposition 4.2]), the Cauchy problem (A) has a unique analytic solution in $\Omega$, for some $\Omega$ narrow enough.

Lemma B.4

If W satisfies Condition ($*$), then $\delta \psi =0$ in $\Omega$.

Proof of Lemma B.4

In [EPS12, Section 4] the authors define a parity operator

$$\begin{aligned} Q:\Omega ^0\oplus \Omega ^1\oplus \Omega ^2\oplus \Omega ^3\rightarrow \Omega ^0\oplus \Omega ^1\oplus \Omega ^2\oplus \Omega ^3 \end{aligned}$$

as

$$\begin{aligned} Q\psi :=\psi ^0\oplus -\psi ^1\oplus \psi ^2\oplus -\psi ^3, \end{aligned}$$

where $\psi =\psi ^0\oplus \psi ^1\oplus \psi ^2\oplus \psi ^3$. First, since $\star d\star =-Q\delta$, applying $\star d$ at the equation (A) and since $\star \star =\textrm{Id}$, we notice that $\delta \psi$ satisfies the elliptic equation

$$\begin{aligned} (d+\delta )\delta \psi =-\star Q\delta \psi . \end{aligned}$$

Therefore, if we show that $\delta \psi |_\Sigma =0$, then $\delta \psi =0$ in $\Omega$ by uniqueness of the solution by the Cauchy–Kovalevskaya’s Theorem, since the operator $d+\delta$ is elliptic.

Our aim is then proving that $\delta \psi |_\Sigma =0$. Write $\psi$ as follows:

$$\begin{aligned} \psi =\Psi +d\rho \wedge {{\tilde{\Psi }}}, \end{aligned}$$

where $\Psi ,{{\tilde{\Psi }}}$ are forms in $\Omega ^0\oplus \Omega ^1\oplus \Omega ^2\oplus \Omega ^3$ such that $i_{\partial _\rho }\Psi =i_{\partial _\rho }{{\tilde{\Psi }}}=0$. Since $\psi |_\Sigma =W^\flat$, then

$$\begin{aligned} \Psi |_\Sigma =c_id\xi _i\quad \text {and}\quad {{\tilde{\Psi }}}|_\Sigma =g. \end{aligned}$$

From (A), it holds that

$$\begin{aligned} \delta \psi |_\Sigma =(\star \psi -d\psi )|_\Sigma . \end{aligned}$$

(B.13)

By the Cauchy condition, it holds that $\star \psi |_\Sigma =\star W^\flat |_\Sigma$. Using that $\star d\rho =|h|^{1/2}d\xi _1\wedge d\xi _2$, we deduce that

$$\begin{aligned} \star \psi |_\Sigma =\star W^\flat |_\Sigma =\star (gd\rho +c_1(0,\xi _1,\xi _2)d\xi _1+c_2(0,\xi _1,\xi _2)d\xi _2)= \end{aligned}$$

$$\begin{aligned} g|h|^{1/2}d\xi _1\wedge d\xi _2 +d\rho \wedge {{\tilde{\alpha }}}, \end{aligned}$$

(B.14)

for some 1-form ${{\tilde{\alpha }}}$. Denoting as ${\bar{d}}$ the exterior derivative only in the variables $\xi _1,\xi _2$, we have

$$\begin{aligned} d\psi ={\bar{d}}\Psi +d\rho \wedge \dfrac{\partial \Psi }{\partial \rho }-d\rho \wedge {\bar{d}}{{\tilde{\Psi }}}={\bar{d}}\Psi +d\rho \wedge \left( \dfrac{\partial \Psi }{\partial \rho }-{\bar{d}}{{\tilde{\Psi }}} \right) . \end{aligned}$$

Since $\Psi |_\Sigma =c_1(0,\xi _1,\xi _2)d\xi _1+c_2(0,\xi _1,\xi _2)d\xi _2$, it holds, using Condition ($*$),

$$\begin{aligned} {\bar{d}}\Psi |_\Sigma =g|h|^{1/2}d\xi _1\wedge d\xi _2. \end{aligned}$$

Consequently

$$\begin{aligned} d\psi |_\Sigma =g|h|^{1/2}d\xi _1\wedge d\xi _2+d\rho \wedge {\hat{\alpha }}, \end{aligned}$$

(B.15)

for some ${\hat{\alpha }}={\hat{\alpha ^{0}}}\oplus {\hat{\alpha ^{1}}}\oplus {\hat{\alpha ^{2}}}$ on $\Sigma$. Putting together (B.13), (B.14) and (B.15), we deduce that

$$\begin{aligned} \delta \psi |_\Sigma =d\rho \wedge {{\check{\alpha }}}, \end{aligned}$$

for some ${{\check{\alpha }}}={{\tilde{\alpha }}}-{\hat{\alpha }}={{\check{\alpha }}}^0\oplus {{\check{\alpha }}}^1\oplus {{\check{\alpha }}}^2$ on $\Sigma$. Noticing that $\psi |_\Sigma =W^\flat$ is a 1-form, we obtain:

• (i) Since $\delta \psi |_\Sigma =d\rho \wedge {{\check{\alpha }}}$ does not contain 0-forms, the components $\delta \psi ^0|_\Sigma$ and $\delta \psi ^1|_\Sigma$ are both zero;

• (ii) For $p=2,3$ we have

  $$\begin{aligned} \delta \psi ^p|_\Sigma =(-1)^p(\star d\star \psi ^p)|_\Sigma =(-1)^p\star (d\rho \wedge \beta )\end{aligned}$$

  for some form $\beta$. This comes from the fact that

  $$\begin{aligned} d(\star \psi ^2)|_\Sigma =d\rho \wedge \partial _\rho (\star \psi ^2)|_{\rho =0}+{\bar{d}}(\star \psi ^2)|_{\rho =0}, \end{aligned}$$

  but since $\psi ^2|_{\rho =0}=0$, then ${\bar{d}}(\star \psi ^2)|_{\rho =0}={\bar{d}}(\star \psi ^2|_{\rho =0})=0$. Similarly, since $\psi ^3|_\Sigma =0$, it holds that

  $$\begin{aligned} d(\star \psi ^3)|_\Sigma =d\rho \wedge \partial _\rho (\star \psi ^3)|_{\rho =0}. \end{aligned}$$

  Therefore, for $p=2,3$, $\delta \psi ^p|_\Sigma$ only contains elements with $d\xi _1$ and $d\xi _2$, for $p=2$, and only $d\xi _1\wedge d\xi _2$ for $p=3$.

The fact that $\delta \psi |_\Sigma$ does not contain the element $d\rho$ contradicts the expression $\delta \psi |_\Sigma =d\rho \wedge {{\check{\alpha }}}$ previously found, unless

$$\begin{aligned} \delta \psi |_\Sigma =0, \end{aligned}$$

as we wanted to prove. This complete the proof of Lemma B.4. $\square$

Going back to the problem (A), since $\delta \psi =0$ in $\Omega$, we have that

$$\begin{aligned} {\left\{ \begin{array}{ll} d\psi =\star \psi \quad \text {in }\Omega \\ \psi |_\Sigma =W^\flat \end{array}\right. } \end{aligned}$$

and, using the identity $\star (\star \psi )=\psi$, it holds

$$\begin{aligned} {\left\{ \begin{array}{ll} \star d\psi =\psi \quad \text {in }\Omega \\ \psi |_\Sigma =W^\flat . \end{array}\right. } \end{aligned}$$

Since $\star d$ maps 1-forms into 1-forms and $W^\flat$ is a 1-form, it holds $\psi ^0=\psi ^2=\psi ^3=0$. Hence

$$\begin{aligned} {\left\{ \begin{array}{ll} \star d\psi ^1=\psi ^1\quad \text {in }\Omega \\ \psi ^1|_\Sigma =W^\flat . \end{array}\right. } \end{aligned}$$

Taking the vector field X dual to $\psi ^1$, it satisfies then $\textrm{curl}\,X=X$ and the sufficiency follows. This concludes the proof of the sufficiency and so of Theorem B.1. $\square$

Disjoint Union of Compact Subsets with Connected Complement

The following result is used in the proof of Corollary 3.2. It is probably standard, but we include a proof for the sake of completeness.

Proposition C.1

Let $K_+$ and $K_-$ be two disjoint compact subsets of ${\mathbb {R}}^n$ with connected complement. Then $K=K_+\sqcup K_-$ has connected complement.

Proof

Since K is compact, it is clear that ${\mathbb {R}}^n\backslash K$ is connected if and only if ${\mathbb {S}}^n\backslash K$ is connected, where the n-sphere ${\mathbb {S}}^n$ is understood as the one-point compactification of ${\mathbb {R}}^n$. Alexander’s duality then implies [Mas78] that

$$\begin{aligned} {{\tilde{H}}}_0({\mathbb {S}}^n\backslash K;{\mathbb {Z}})={{\tilde{H}}}^{n-1}_{CE}(K;{\mathbb {Z}})\,, \end{aligned}$$

where ${{\tilde{H}}}_0({\mathbb {S}}^n\backslash K;{\mathbb {Z}})$ stands for the reduced singular homology of ${\mathbb {S}}^n\backslash K$ with integer coefficients (well defined because it is a manifold) and ${{\tilde{H}}}^{n-1}_{CE}(K;{\mathbb {Z}})$ denotes the reduced Čech cohomology, which is defined for any compact subset of ${\mathbb {R}}^n$. Now, since the reduced k-th cohomology group coincides with the cohomology group for $k\ge 1$ (this also holds for Čech cohomology, for which one can also write a long exact sequence [ES52]) and $K_+$ and $K_-$ are disjoint, we infer that

$$\begin{aligned} {{\tilde{H}}}^{n-1}_{CE}(K;{\mathbb {Z}})=H^{n-1}_{CE}(K;{\mathbb {Z}})=H^{n-1}_{CE}(K_+;{\mathbb {Z}})\oplus H^{n-1}_{CE}(K_-;{\mathbb {Z}})\,, \end{aligned}$$

where to write the last isomorphism we have used the standard Mayer-Vietoris sequence for Čech cohomology [Mil16]. Then, using again Alexander’s duality and that $H^{n-1}_{CE}(K_{\pm };{\mathbb {Z}})={{\tilde{H}}}^{n-1}_{CE}(K_{\pm };{\mathbb {Z}})$, we obtain that

$$\begin{aligned} H^{n-1}_{CE}(K_+;{\mathbb {Z}})\oplus H^{n-1}_{CE}(K_-;{\mathbb {Z}})={{\tilde{H}}}_0({\mathbb {S}}^n\backslash K_+;{\mathbb {Z}})\oplus {{\tilde{H}}}_0({\mathbb {S}}^n\backslash K_-;{\mathbb {Z}})=0 \end{aligned}$$

because ${\mathbb {S}}^n\backslash K_{\pm }$ are connected by assumption, and the 0-th reduced singular homology group of a manifold is trivial if and only if the manifold is connected. Putting all these computations together we finally conclude that

$$\begin{aligned} {{\tilde{H}}}_0({\mathbb {S}}^n\backslash K;{\mathbb {Z}})=0\,, \end{aligned}$$

so ${\mathbb {S}}^n\backslash K$ is connected, as we wanted to prove. $\square$