Skip to main content
SpringerLink
Log in

Projective Cones for Sequential Dispersing Billiards

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

We construct Birkhoff cones for dispersing billiards, which are contracted by the action of the transfer operator. This construction permits the study of statistical properties not only of regular dispersing billiards but also of sequential billiards (the billiard changes at each collision in a prescribed manner), open billiards (the dynamics exits some region or dies when hitting some obstacle) and many other examples. In particular, we include applications to chaotic scattering and the random Lorentz gas.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data Availibility

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Notes

  1. We do not claim that each such T is unique. It may be that \(T(Q) = T(Q')\) pointwise (consider a \(90^\circ \) rotation of a given configuration Q), yet for our purposes they will be considered distinct elements of \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\).

  2. The abstract set-up in [DZ2] also allows billiard tables with infinite horizon and those subjected to external forces, but we are not concerned with the most general case here.

  3. Indeed, the distance \(\mathbb {d}\) allows configurations to move from finite to infinite horizon (see [DZ2, Section 6.2]), but we will not need that here as we will restrict ourselves to finite horizon configurations.

  4. The parameter \(\gamma \in (0,1)\) is from the cone condition (4.8).

  5. Closed here means that for all \(f,g \in {\mathcal {C}}\) and sequence \(\{\alpha _n\}\subset {\mathbb {R}}\) such that \(\lim _{n\rightarrow \infty }\alpha _n=\alpha \) and \(g+\alpha _n f\in {\mathcal {C}}\) for all \(n\in {\mathbb {N}}\) we have \(g+\alpha f\in {\mathcal {C}}\cup \{0\}\).

  6. By independent of the cone parameters, we mean that we may first fix \(\chi < 1\), and then choose \(c,A,L, \delta \) satisfying the conditions of Sect. 5.3 so that the contraction by \(\chi \) is obtained for all choices of \(c' > c\), \(A'>A\), \(L'>L\) and \(\delta ' < \delta \) that satisfy those conditions. Note, however, that larger \(A'>A\) requires \(n_0\) to increase in size.

  7. Note that \(\sum _i |T_nW_i| \le |W|\) and \( \frac{|T_nW_i|}{|W_i|}\le |J_{W_i}T_n|_{C^0(W_i)}\).

  8. Note that, by [CM, Proposition 4.47], given two maximal homogeneous subcurves of \(T_n^{-1}W^k\) that are connected by a vertical segment disjoint from \({\mathcal {S}}_{n}^{{\mathbb {H}}}\), there must exist two piecewise smooth curves in \({\mathcal {S}}_{n}^{{\mathbb {H}}}\) that connect the boundaries of such two subcurves forming a rectangle that does not contain any element of \({\mathcal {S}}_{n}^{{\mathbb {H}}}\) in its interior. Thus \(U^2_{i,+}\) must be a connected subcurve.

  9. Notice that since we subdivide curves in \({\mathcal {G}}_n^\delta (W)\) according to length \(\delta \) and not \(\delta _0\), the estimate of Lemma 3.3(b) becomes \({{\bar{C}}}_0 \delta ^{-1} |W| + C_0 \theta _1^n \le 2 {{\bar{C}}}_0 + C_0 \theta _1^n\), since \(|W| \le 2\delta \).

  10. Since the \(U^k_j\) are vertically matched, the term on the right hand side of (5.8) proportional to \(C_s\) is absent here.

  11. The second inequality in (6.2) follows from (3.7).

  12. Recall from Sect. 2.1 that by Proposition 2.2, \({\mathcal {Q}}(Q_{\iota _j}, E_*; \kappa ) = \{ Q \in {\mathcal {Q}}(\frac{1}{2} \tau _*, \frac{1}{2} {\mathcal {K}}_*, E_*) : \mathbb {d}(Q, Q_{\iota _j}) < \kappa \}\).

  13. Although the stable/unstable directions in M vary, they always belong to the global stable/unstable cones defined in (H1) and so are uniformly transverse.

  14. The choice of \(\delta _0^4\) will be needed in Lemma 6.7.

  15. Recall that \({{\bar{C}}}_0\) is from Lemma 3.3.

  16. These Cantor rectangles \(R_i\) are maximal in the sense that they are the intersection of the maximal families of local invariant manifolds \({\mathfrak {S}}^{s/u}(D(R_i))\) that fully cross the solid rectangle \(D(R_i)\).

  17. Indeed, using Proposition 5.1 and choosing \(L \ge 60\), we can always choose \(\chi = \frac{8}{9}\), although this will affect the choice of \(N_{\mathcal {F}}\).

  18. Recall that \(n_*\) is defined in Lemma 6.6 while \(N(\delta )^-\) is defined in Eq. (6.4).

  19. A semi-norm \(\Vert \cdot \Vert \) is order preserving if \(-g\preceq f\preceq g\) implies \(\Vert f\Vert \le \Vert g\Vert \).

  20. [LSV, Lemma 2.2] is stated for order preserving norms but its proof holds verbatim for order preserving semi-norms, see [DKL1, Lemma D.4].

  21. According to (O1), \(W^k\) is divided into at most \(P_0\) pieces, and \(W^k \cap H^c\) comprises at most \(\frac{P_0}{2}+1\) of them. Each such piece can give rise to at most 2 unmatched pieces.

  22. Since \(I_{W^1_j} = I_{W^2_j}\), the term on the right side of (5.8) proportional to \(C_s\) is absent in this case.

  23. Since we have fixed the cone constants c, A, L, the number \({{\bar{n}}}_\delta \) depends on the constants appearing in (O\(1'\)) and (O2) as well as \(\mu _{\tiny {\text{ SRB }}}(H)\) and the choice of \(\delta \), from Lemma 8.6.

  24. \(N_{{\mathcal {F}}}'\) is number from Theorem 6.12 applied to the cone with larger constants \(c'', A'', L''\).

  25. Requiring \(\mu _{\tiny {\text{ SRB }}}(H) \le 1/2\) enables a uniform choice of \(n_\star \) for all \(H \in {\mathcal {H}}(P_0, C_t)\).

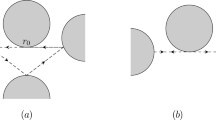
  26. Remember that the non-eclipsing condition is the requirement that the convex hull of any two obstacles does not intersect any other obstacle.

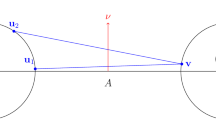
  27. Recall that \(\varphi \in [-\frac{\pi }{2},\frac{\pi }{2}]\) is the angle made by the post-collision velocity vector and the outward pointing normal to the boundary.

  28. This claim implies that the cone is Archimedean.

  29. Note that \(\mathring{{\mathcal {L}}}_{S}\) extends naturally to \(({\mathcal {C}}^1(M))'\) and therefore to \({\mathcal {C}}_\star \).

  30. If instead \(f \in {\mathcal {C}}_{c,A,L}(\delta )\), \(f \ge 0\) and \(\int f \, d\mu _{\tiny {\text{ SRB }}}=1\), then \(\Vert f \Vert _{C^1}\) can be dropped from the right hand side.

  31. The assumption that all obstacles are circular is not essential and can be relaxed by requiring that the obstacles at the corners are symmetric with respect to reflections as described in Sect. 8.4.

  32. Finite horizon requires \(r \ge \frac{1}{1+\sqrt{2}}\), yet our added condition that a particle cannot cross diagonally from, say, \({{\hat{R}}}_1\) to \({{\hat{R}}}_2\) without making a collision requires further that \(r \ge \frac{1}{3}\).

  33. The hole depends on the trajectory of x, which is different in different cells and hence depends on z, while the gates \({{\hat{R}}}_i\) are independent of z.

  34. By (mod 4*) we mean cyclic addition on 1, 2, 3, 4 rather than 0, 1, 2, 3.

  35. Since \(z_0 = (0,0)\), it is equivalent to specify \(z_1, \ldots z_n\) or \(w_{k_0}, \ldots w_{k_{n-1}}\) since \(w_{k_j}\) can be recovered as \(w_{k_j} = z_{j+1} - z_j\).

  36. Here in fact our operators are of the form \({\mathcal {L}}^n\mathbb {1}_H\) while in Proposition 8.7 they have the form \({\mathcal {L}}_n \mathbb {1}_{H^c}\) for some set H. Yet, this is immaterial since the boundaries of H and \(H^c\) in M are the same so that (O\(1'\)) and (O2), and in particular Lemma 8.6, apply equally well to both sets.

  37. Remark that [AL, Theorem 6.4] requires \(\mu _{\tiny {\text{ SRB }}}(G_i(z))\) to be the same for each i and z, independently of \(\omega \). This is precisely the case here since \(G_i(z)\) is defined as the projection of \({{\hat{R}}}_i\) under the inverse flow \(\Phi ^z_{-t}\), and Leb\(({{\hat{R}}}_i \times [0, 2\pi ))\) in the phase space of the flow is independent of i, while \(\mu _{\tiny {\text{ SRB }}}\) is the projection onto M of Lebesgue measure, which is invariant under the flow.

  38. The arguments in [AL, Section 6] are developed for expanding maps, but the relevant parts apply verbatim to the present context.

References

  1. Aimino, R., Liverani, C.: Deterministic walks in random environment. Ann. Probab. 48(5), 2212–2257 (2020)

    MathSciNet  MATH  Google Scholar 

  2. Atnip, J., Froyland, G., González-Tokman, C., Vaienti, S.: Thermodynamic formalism for random weighted covering systems. Commun. Math. Phys. 386(2), 819–902 (2021)

    ADS  MathSciNet  MATH  Google Scholar 

  3. Baladi, V.: Anisotropic Sobolev spaces and dynamical transfer operators: \({\cal{C} }^\infty \) foliations, algebraic and topological dynamics. In: Kolyada, S., Manin, Y., Ward, T. (eds.) Contemporary Mathematics, pp. 123–136. American Mathematical Society (2005)

  4. Baladi, V.: Dynamical Zeta Functions and Dynamical Determinants for Hyperbolic Maps, a Functional Approach, Results in Mathematics and Related Areas, 3rd Series, A Series of Modern Surveys in Mathematics, vol. 68, Springer, Ergebnisse (2018)

  5. Baladi, V., Demers, M.F.: On the measure of maximal entropy for finite horizon Sinai billiard maps. J. Am. Math. Soc. 33, 381–449 (2020)

    MathSciNet  MATH  Google Scholar 

  6. Baladi, V., Demers, M.F.: Thermodynamic formalism for dispersing billiards, preprint (2020)

  7. Baladi, V., Demers, M.F., Liverani, C.: Exponential decay of correlations for finite horizon Sinai billiard flows. Invent. Math. 211(1), 39–177 (2018)

    ADS  MathSciNet  MATH  Google Scholar 

  8. Baladi, V., Tsujii, M.: Anisotropic Hölder and Sobolev spaces for hyperbolic diffeomorphisms. Ann. Inst. Fourier. 57, 127–154 (2007)

    MathSciNet  MATH  Google Scholar 

  9. Balint, P., De Simoi, J., Kaloshin, V., Leguil, M.: Marked length spectrum, homoclinic orbits and the geometry of open dispersing billiards. Commun. Math. Phys. 374, 1531–1575 (2020)

    ADS  MathSciNet  MATH  Google Scholar 

  10. Birkhoff, G.: Extensions of Jentzsch’s theorem. Trans. Am. Math. Soc. 85, 219–227 (1957)

    MathSciNet  MATH  Google Scholar 

  11. Blank, M., Keller, G., Liverani, C.: Ruelle–Perron–Frobenius spectrum for Anosov maps. Nonlinearity 15(6), 1905–1973 (2002)

    ADS  MathSciNet  MATH  Google Scholar 

  12. Bunimovich, L., Sinai, Y.G., Chernov, N.: Markov partitions for two-dimensional hyperbolic billiards. Russ. Math. Surv. 45, 105–152 (1990)

    MathSciNet  MATH  Google Scholar 

  13. Chernov, N.: Advanced statistical properties of dispersing billiards. J. Stat. Phys. 122, 1061–1094 (2006)

    ADS  MathSciNet  MATH  Google Scholar 

  14. Chernov, N.: Sinai billiards under small external forces II. Ann. Henri Poincaré 9, 91–107 (2008)

    ADS  MathSciNet  MATH  Google Scholar 

  15. Chernov, N., Dolgopyat, D.: Brownian Brownian Motion—I, vol. 198, p. 927. Memoirs of American Mathematical Society (2009)

  16. Chernov, N., Markarian, R.: Chaotic Billiards, Mathematical Surveys and Monographs, vol. 127. American Mathematical Society (2006)

  17. Chernov, N., Zhang, H.-K.: On statistical properties of hyperbolic systems with singularities. J. Stat. Phys. 136, 615–642 (2009)

    ADS  MathSciNet  MATH  Google Scholar 

  18. Demers, M.F.: Escape rates and physical measures for the infinite horizon Lorentz gas with holes. Dyn. Syst. Int. J. 28(3), 393–422 (2013)

    MathSciNet  MATH  Google Scholar 

  19. Demers, M.F.: Dispersing billiards with small holes. In: Ergodic Theory, Open Dynamics and Coherent Structures, vol. 70, pp. 137–170. Springer Proceedings in Mathematics (2014)

  20. Demers, M.F., Liverani, C.: Stability of statistical properties in two-dimensional piecewise hyperbolic maps. Trans. Am. Math. Soc. 360(9), 4777–4814 (2008)

    MathSciNet  MATH  Google Scholar 

  21. Demers, M.F., Wright, P., Young, L.-S.: Escape rates and physically relevant measures for billiards with small holes. Commun. Math. Phys. 294(2), 353–388 (2010)

    ADS  MathSciNet  MATH  Google Scholar 

  22. Demers, M.F., Zhang, H.-K.: Spectral analysis of the transfer operator for the Lorentz gas. J. Mod. Dyn. 5(4), 665–709 (2011)

    MathSciNet  MATH  Google Scholar 

  23. Demers, M.F., Zhang, H.-K.: A functional analytic approach to perturbations of the Lorentz gas. Commun. Math. Phys. 324(3), 767–830 (2013)

    ADS  MathSciNet  MATH  Google Scholar 

  24. Demers, M.F., Zhang, H.-K.: Spectral analysis of hyperbolic systems with singularities. Nonlinearity 27, 379–433 (2014)

    ADS  MathSciNet  MATH  Google Scholar 

  25. Demers, M.F., Kiamari, N., Liverani, C.: Transfer operators in hyperbolic dynamics. An introduction. 33 Colloquio Brasilero de Matematica. Brazilian Mathematics Colloquiums series, Editora do IMPA, p 252 (2021). ISBN 978-65-89124-26-9

  26. De Simoi, J., Liverani, C.: Statistical properties of mostly contracting fast-slow partially hyperbolic systems. Invent. Math. 206(1), 147–227 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  27. De Simoi, J., Liverani, C.: Limit theorems for fast-slow partially hyperbolic systems. Invent. Math. 213(3), 811–1016 (2018)

    ADS  MathSciNet  MATH  Google Scholar 

  28. De Simoi, J., Liverani, C., Poquet, C., Volk, D.: Fast-slow partially hyperbolic systems versus Freidlin–Wentzell random systems. J. Stat. Phys. 166(3–4), 650–679 (2017)

    ADS  MathSciNet  MATH  Google Scholar 

  29. De Simoi, J., Kaloshin, V., Leguil, M.: Marked length spectral determination of analytic chaotic billiards with axial symmetries. Invent. Math. (to appear)

  30. Dobbs, N., Stenlund, M.: Quasistatic dynamical systems. Ergod. Theory Dyn. Syst. 37(8), 2556–2596 (2017)

    MathSciNet  MATH  Google Scholar 

  31. Dolgopyat, D.: Limit theorems for partially hyperbolic systems. Trans. Am. Math. Soc. 356(4), 1637–1689 (2004)

    MathSciNet  MATH  Google Scholar 

  32. Dolgopyat, D.: On differentiability of SRB states for partially hyperbolic systems. Invent. Math. 155(2), 389–449 (2004)

    ADS  MathSciNet  MATH  Google Scholar 

  33. Dolgopyat, D.: Averaging and invariant measures. Mosc. Math. J. 5(3), 537–576, 742 (2005)

  34. Dragičević, D., Froyland, G., González-Tokman, C., Vaienti, S.: A spectral approach for quenched limit theorems for random expanding systems. Commun. Math. Phys. 360(3), 1121–1187 (2018)

    ADS  MathSciNet  MATH  Google Scholar 

  35. Dragičević, D., Froyland, G., González-Tokman, C., Vaienti, S.: A spectral approach for quenched limit theorems for random hyperbolic dynamical systems. Trans. Am. Math. Soc. 373(1), 629–664 (2020)

    MathSciNet  MATH  Google Scholar 

  36. Fried, D.: The zeta functions of Ruelle and Selberg. I. Ann. Sci. École Norm. Sup. (4) 19(4), 491–517 (1986)

    MathSciNet  MATH  Google Scholar 

  37. Geiger, B., Ott, W.: Nonstationary open dynamical systems, arXiv:1808.05315v4 (2019)

  38. Gouëzel, S., Liverani, C.: Banach spaces adapted to Anosov systems. Ergod. Theorem Dyn. Syst. 26(1), 189–217 (2006)

    MathSciNet  MATH  Google Scholar 

  39. Gouëzel, S., Liverani, C.: Compact locally maximal hyperbolic sets for smooth maps: fine statistical properties. J. Differ. Geom. 79(3), 433–477 (2008)

    MathSciNet  MATH  Google Scholar 

  40. Keller, G., Liverani, C.: Stability of the spectrum for transfer operators. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 28(1), 141–152 (1999)

  41. Kitaev, A.Y.: Fredholm determinants for hyperbolic diffeomorphisms of finite smoothness. Nonlinearity 12, 141–179 (1999)

  42. Krylov, N.S.: Works on the foundations of statistical physics. Translated from the Russian by A. B. Migdal, Ya. G. Sinai and Yu. L. Zeeman. With a preface by A. S. Wightman. With a biography of Krylov by V. A. Fock. With an introductory article "The views of N. S. Krylov on the foundations of statistical physics” by Migdal and Fok. With a supplementary article "Development of Krylov’s ideas” by Sinai. Princeton Series in Physics. Princeton University Press, Princeton (1979)

  43. Lasota, A., Yorke, J.: On the existence of invariant measures for piecewise monotonic transformations. Trans. Am. Math. Soc. 186(1973), 481–488 (1974)

    MathSciNet  MATH  Google Scholar 

  44. Lenci, M.: Typicality of recurrence for Lorentz gases. Ergod. Theory Dyn. Syst. 26(3), 799–820 (2006)

    MathSciNet  MATH  Google Scholar 

  45. Liverani, C.: Decay of correlations. Ann. Math. 142, 239–301 (1995)

    MathSciNet  MATH  Google Scholar 

  46. Liverani, C.: Decay of correlations for piecewise expanding maps. J. Stat. Phys. 78(3–4), 1111–1129 (1995)

    ADS  MathSciNet  MATH  Google Scholar 

  47. Liverani, C., Saussol, B., Vaienti, S.: Conformal measure and decay of correlation for covering weighted systems. Ergod. Theory Dyn. Syst. 18(6), 1399–1420 (1998)

    MathSciNet  MATH  Google Scholar 

  48. Liverani, C., Maume-Deschamps, V.: Lasota–Yorke maps with holes: conditionally invariant probability measures and invariant probability measures on the survivor set. Ann. Inst. H. Poincaré Probab. Stat. 39(3), 385–412 (2003)

    ADS  MathSciNet  MATH  Google Scholar 

  49. Lopes, A., Markarian, R.: Open billiards: invariant and conditionally invariant probabilities on Cantor sets. SIAM J. Appl. Math. 56(2), 651–680 (1996)

    MathSciNet  MATH  Google Scholar 

  50. Mohapatra, A., Ott, W.: Memory loss for nonequilibrium open dynamical systems. Discrete Contin. Dyn. Syst. (Ser. A) 34(9), 3747–3759 (2014)

    MathSciNet  MATH  Google Scholar 

  51. Morita, T.: The symbolic representation of billiards without boundary condition. Trans. Am. Math. Soc. 325(2), 819–828 (1991)

    MathSciNet  MATH  Google Scholar 

  52. Morita, T.: Meromorphic extensions of a class of zeta functions for two-dimensional billiards without eclipse. Tohoku Math. J. (2) 59(2), 167–202 (2007)

    MathSciNet  MATH  Google Scholar 

  53. Ruelle, D., Sullivan, D.: Currents, flows and diffeomorphisms. Topology 14(4), 319–327 (1975)

    MathSciNet  MATH  Google Scholar 

  54. Ruelle, D.: Zeta-functions for expanding maps and Anosov flows. Invent. Math. 34, 231–242 (1976)

    ADS  MathSciNet  MATH  Google Scholar 

  55. Rugh, H.H.: Generalized Fredholm determinants and Selberg zeta functions for Axiom A dynamical systems. Ergod. Theorem Dyn. Syst. 16, 805–819 (1996)

    MathSciNet  MATH  Google Scholar 

  56. Sinai, Y.G.: Dynamical systems with elastic reflections. Ergodic properties of dispersing billiards. Russ. Math. Surv. 25, 137–189 (1970)

    MathSciNet  MATH  Google Scholar 

  57. Stoyanov, L.: Spectrum of the Ruelle operator and exponential decay of correlations for open billiard flows. Am. J. Math. 123(4), 715–759 (2001)

    MathSciNet  MATH  Google Scholar 

  58. Stenlund, M., Young, L.-S., Zhang, H.-K.: Dispersing billiards with moving scatterers. Commun. Math. Phys. 332(3), 909–955 (2013)

    ADS  MathSciNet  MATH  Google Scholar 

  59. Young, L.-S.: Statistical properties of dynamical systems with some hyperbolicity. Ann. Math. (2) 147(3), 585–650 (1998)

    MathSciNet  MATH  Google Scholar 

  60. Young, L.-S.: Recurrence times and rates of mixing. Israel J. Math. 110, 153–188 (1999)

    MathSciNet  MATH  Google Scholar 

  61. Zhang, H.-K.: Current in periodic Lorentz gases with twists. Commun. Math. Phys. 306, 747–776 (2011)

    ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the PRIN Grant “Regular and stochastic behavior in dynamical systems" (PRIN 2017S35EHN). C. Liverani acknowledges the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006. M. Demers was partially supported by NSF grants DMS 1800321 and DMS 2055070. C. Liverani is a member of the Editorial Board of Communications in Mathematical Physics.

Author information

Authors and Affiliations

  1. Department of Mathematics, Fairfield University, 06824, Fairfield, CT, USA

    Mark F. Demers

  2. Dipartimento di Matematica, Università di Roma II, Tor Vergata, 00133, Rome, Italy

    Carlangelo Liverani

  3. GNFM-INDAM, Rome, Italy

    Carlangelo Liverani

Authors
  1. Mark F. Demers
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Carlangelo Liverani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mark F. Demers.

Additional information

Communicated by S. Dyatlov.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

We thank Jochen Broecker, Tobias Kuna and especially Lea Oljaca for pointing out to us the possibility to prove Lemma 4.10. This work was supported by the PRIN Grant “Regular and stochastic behaviour in dynamical systems” (PRIN 2017S35EHN). C.L. acknowledges the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006. M.D. was partially supported by NSF grants DMS 1800321 and DMS 2055070.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Demers, M.F., Liverani, C. Projective Cones for Sequential Dispersing Billiards. Commun. Math. Phys. 401, 841–923 (2023). https://doi.org/10.1007/s00220-023-04657-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-023-04657-1

Search

Navigation