Random Splitting of Fluid Models: Unique Ergodicity and Convergence

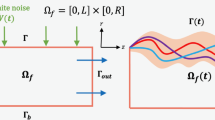
Abstract

We introduce a family of stochastic models motivated by the study of nonequilibrium steady states of fluid equations. These models decompose the deterministic dynamics of interest into fundamental building blocks, i.e., minimal vector fields preserving some fundamental aspects of the original dynamics. Randomness is injected by sequentially following each vector field for a random amount of time. We show under general conditions that these random dynamics possess a unique, ergodic invariant measure and converge almost surely to the original, deterministic model in the small noise limit. We apply our construction to the Lorenz-96 equations, often used in studies of chaos and data assimilation, and Galerkin approximations of the 2D Euler and Navier–Stokes equations. An interesting feature of the models developed is that they apply directly to the conservative dynamics and not just those with excitation and dissipation.

Appendices

Appendix A. Convergence Lemmas

1.1 A.1. Semigroups, norms, and bounds

In this subsection we elaborate on the semigroup framework of Sect. 4. The notation and results are used extensively in the proofs of Lemmas 4.2 and 4.6, which are given in Sects. A.2 and A.4, respectively.

Fix a $\mathcal {V}$-orbit $\mathcal {X}$. The $\mathcal {C}^2$ assumption implies the $V_k$, which act on functions f via $V_kf(x)=Df(x)V_k(x)$, are linear operators from $\mathcal {C}^2(\mathcal {X})$ to $\mathcal {C}^1(\mathcal {X})$ and from $\mathcal {C}^1(\mathcal {X})$ to $\mathcal {C}(\mathcal {X})$. It also implies the semigroups $\{S_t\}_{t\ge 0}$ and $\{\widetilde{S}^{(k)}_t\}_{t\ge 0}$ defined in (4.2) and (4.3) are linear operators on $\mathcal {C}^k(\mathcal {X})$ for $k\le 2$. Our aim now is to obtain bounds on norms of compositions of these random semigroups. For $i\le j$ define $\Phi ^{(i,j)}_{h\tau }:=\varphi ^{(j)}_{h\tau _j}\circ \cdots \circ \varphi ^{(i)}_{h\tau _i}$ and $\widetilde{S}^{(i,j)}_{h\tau }:=\widetilde{S}^{(i)}_{h\tau }\cdots \widetilde{S}^{(j)}_{h\tau }$. Note $\widetilde{S}^{(i,j)}_{h\tau }$ acts on functions f via

$$\begin{aligned} \widetilde{S}^{(i,j)}_{h\tau }f(x)&= f\left( \Phi ^{(i,j)}_{h\tau }(x)\right) = f\left( \varphi ^{(j)}_{h\tau _j}\circ \cdots \circ \varphi ^{(i)}_{h\tau _i}(x)\right) . \end{aligned}$$

So for any $f\in \mathcal {C}(\mathcal {X})$ with $\Vert f\Vert _\infty =1$, we have

$$\begin{aligned} \Vert \widetilde{S}^{(i,j)}_{h\tau }f\Vert _\infty&= \Vert f(\Phi ^{(i,j)}_{h\tau })\Vert _\infty = 1 \end{aligned}$$

and hence $\Vert \widetilde{S}^m_{h\tau }\Vert _{0\rightarrow 0}=1$. Next, let $\varphi =\varphi ^{(k)}$ for arbitrary k. Then

$$\begin{aligned} \varphi _t(x)&= x + \int _0^t V(\varphi _s(x)) ds \end{aligned}$$

and so

$$\begin{aligned} D\varphi _t(x)&= I + \int _0^t DV(\varphi _s(x))D\varphi _s(x) ds \end{aligned}$$

and

$$\begin{aligned} D^2\varphi _t(x)&= \int _0^t D^2V(\varphi _s(x))\left( D\varphi _s(x),D\varphi _s(x)\right) +DV(\varphi _s(x))D^2\varphi _s(x) ds. \end{aligned}$$

In particular, $\Vert D\varphi _t(x)\Vert \le 1 + C_*\int _0^t \Vert D\varphi _s(x)\Vert ds$ for all x in $\mathcal {X}$ and Grönwall’s inequality implies

$$\begin{aligned} \sup _{x\in \mathcal {X}}\Vert D\varphi _t(x)\Vert&\le e^{C_*t}, \end{aligned}$$

(A.1)

where here and throughout $C_*$ is the constant from (4.1) corresponding to $\mathcal {X}$. Similarly, since $\Vert D^2V\left( D\varphi ,D\varphi \right) \Vert \le \Vert D^2V\Vert \Vert D\varphi \Vert ^2\le C_*\Vert D\varphi \Vert ^2$,

$$\begin{aligned} \Vert D^2\varphi _t(x)\Vert \le C_*\int _0^t \Vert D\varphi _s(x)\Vert ^2+\Vert D^2\varphi _s(x)\Vert ds \le C_*te^{2C_*t}+C_*\int _0^t\Vert D^2\varphi _s(x)\Vert ds \end{aligned}$$

and Grönwall implies

$$\begin{aligned} \sup _{x\in \mathcal {X}}\Vert D^2\varphi _t(x)\Vert \le C_*te^{3C_*t}. \end{aligned}$$

(A.2)

Note (A.1) and (A.2) hold uniformly over all $\varphi ^{(k)}$. Thus, for $f\in C^1(\mathcal {X})$ with $\Vert f\Vert _1=1$,

$$\begin{aligned} \left\Vert D\left( \widetilde{S}^{(i,j)}_{h\tau }f\right) \right\Vert&= \left\Vert Df\left( \Phi ^{(i,j)}_{h\tau }\right) D\Phi ^{(i,j)}_{h\tau }\right\Vert \le \prod _{k=i}^{j} \Vert D\varphi ^{(k)}_{h\tau _k}\Vert \le e^{C_*h\sum _{k=i}^{j}\tau _k}, \end{aligned}$$

where the first inequality follows from submultiplicity and the second from (A.1). Similarly,

$$\begin{aligned} D^2\Phi ^{(i,j)}_{h\tau }&= \sum _{k=i}^j D\varphi ^{(j)}_{h\tau _j}\cdots D\varphi ^{(k+1)}_{h\tau _{k+1}}D^2\varphi ^{(k)}_{h\tau _k}\left( D\Phi ^{(i,k-1)}_{h\tau }, D\Phi ^{(i,k-1)}_{h\tau }\right) \end{aligned}$$

together with (A.1) and (A.2) gives

$$\begin{aligned} \left\Vert D^2\Phi ^{(i,j)}_{h\tau }\right\Vert&\le \sum _{k=i}^j \left\Vert D\varphi ^{(j)}_{h\tau _j}\right\Vert \cdots \left\Vert D\varphi ^{(k+1)}_{h\tau _{k+1}}\right\Vert \left\Vert D^2\varphi ^{(k)}\right\Vert \left\Vert D\Phi ^{(i,k-1)}_{h\tau }\right\Vert ^2 \\&\le C_*\sum _{k=i}^j h\tau _k e^{C_*h\sum _{k+1}^j\tau _\ell }e^{3C_*h\tau _k}e^{2C_*h\sum _1^{k-1}\tau _\ell } \le C_*he^{3C_*h\sum _{k=i}^j\tau _k}\sum _{k=i}^j \tau _k. \end{aligned}$$

Therefore

$$\begin{aligned} \left\Vert D^2\left( \widetilde{S}^{(i,j)}_{h\tau }f\right) \right\Vert&= \left\Vert D^2f\left( \Phi ^{(i,j)}_{h\tau }\right) \left( D\Phi ^{(i,j)}_{h\tau },D\Phi ^{(i,j)}_{h\tau }\right) +Df\left( \Phi ^{(i,j)}_{h\tau }\right) D^2\Phi ^{(i,j)}_{h\tau }\right\Vert \\&\le \left\Vert D\Phi ^{(i,j)}_{h\tau }\right\Vert ^2 + \left\Vert D^2\Phi ^{(i,j)}_{h\tau }\right\Vert \le e^{2C_*h\sum _{k=i}^{j}\tau _k} + \left\Vert D^2\Phi ^{(i,j)}_{h\tau }\right\Vert \\&\le e^{2C_*h\sum _{k=i}^{j}\tau _k} + C_*he^{3C_*h\sum _{k=i}^j\tau _k}\sum _{k=i}^j \tau _k \\&\le \left( 1+C_*h\sum _{k=i}^j\tau _k\right) e^{3C_*h\sum _{k=i}^j \tau _k}. \end{aligned}$$

The above computations prove

Lemma A.1

For any $h>0$ and $i\le j$, we have $\Vert \widetilde{S}^{(i,j)}_{h\tau }\Vert _{0\rightarrow 0}=1$ as well as

$$\begin{aligned} \left\Vert \widetilde{S}^{(i,j)}_{h\tau }\right\Vert _{1\rightarrow 1}\le e^{C_*h\sum _{k=i}^{j}\tau _k} \quad \text {and}\quad \left\Vert \widetilde{S}^{(i,j)}_{h\tau }\right\Vert _{2\rightarrow 2}\le \left( 1+C_*h\sum _{k=i}^j\tau _k\right) e^{3C_*h\sum _{k=i}^j \tau _k}. \end{aligned}$$

In particular, $\left\Vert \widetilde{S}^{(i,j)}_{h\tau }\right\Vert _{\ell \rightarrow \ell }\le \left( 1+C_*h\sum _{k=i}^j\tau _k\right) e^{3C_*h\sum _{k=i}^j \tau _k}$ for all $\ell \le 2$.

Note that under the $\mathcal {C}^2$ assumption $\widetilde{S}^{(i,j)}_{h\tau }$ can also be regarded as a linear operator from $\mathcal {C}^2( \mathcal {X})$ to $\mathcal {C}^1( \mathcal {X})$. So since $\{f\in \mathcal {C}^2(\mathcal {X}) : \Vert f\Vert _2=1\}$ is a subset of $\{f\in \mathcal {C}^1(\mathcal {X}) : \Vert f\Vert _1=1\}$, we have

$$\begin{aligned} \left\Vert \widetilde{S}^{(i,j)}_{h\tau }\right\Vert _{2\rightarrow 1}&= \sup _{\Vert f\Vert _2=1}\left\Vert \widetilde{S}^{(i,j)}_{h\tau }f\right\Vert _1 \le \sup _{\Vert f\Vert _1=1}\left\Vert \widetilde{S}^{(i,j)}_{h\tau }f\right\Vert _1 = \left\Vert \widetilde{S}^{(i,j)}_{h\tau }\right\Vert _{1\rightarrow 1} \le e^{C_*h\sum _{k=i}^{j}\tau _k}. \end{aligned}$$

(A.3)

We also have the following corollary of Lemma A.1.

Corollary A.2

Fix $i\le j$ and set $m:=j-i+1$. For all $\ell \le 2$ and polynomial $p:\mathbb {R}^m_+\rightarrow \mathbb {R}$ there exists $h_*>0$ such that for all $h<h_*$,

$$\begin{aligned} \mathbb {E}\Vert p(\tau _i,\dots ,\tau _j)\widetilde{S}^{(i,j)}_{h\tau }\Vert _{k\rightarrow k}&< \infty . \end{aligned}$$

(A.4)

Proof

Writing $t=(t_i,\dots ,t_j)$ and $dt=dt_i\cdots dt_j$, we have

$$\begin{aligned} \mathbb {E}\Vert p(\tau _i,\dots ,\tau _j)\widetilde{S}^{(i,j)}_{h\tau }\Vert _{\ell \rightarrow \ell }&= \int _{\mathbb {R}^m_+} |p(t)|\left\Vert \widetilde{S}^{(i,j)}_{ht}\right\Vert _{\ell \rightarrow \ell } e^{-\sum t_k} dt \\&\le \int _{\mathbb {R}^m_+} |p(t)|\left( 1+C_*h\sum _{k=i}^j t_k\right) e^{(3C_*h-1)\sum _{k=i}^j t_k} dt \end{aligned}$$

which is finite for all $h < h_*:=(3C_*)^{-1}$.$\square$

1.2 A.2. Proof of Lemma 4.2

We highlight the steps of the proof with italicized font.

Variation of constants. We begin by differentiating $\widetilde{S}_{h\tau }$ in h:

$$\begin{aligned} \partial _h\widetilde{S}_{h\tau }&= \sum _{k=1}^n \tau _k e^{h\tau _1}\cdots e^{h\tau _{k-1}}V_k e^{h\tau _k}\cdots e^{h\tau _n} = \sum _{k=1}^n \tau _k \widetilde{S}^{(1,k-1)}_{h\tau }V_k\widetilde{S}^{(k,n)}_{h\tau }. \end{aligned}$$

Next, commute $\widetilde{S}^{(1,k-1)}_{h\tau }$ and $V_k$ via $[\widetilde{S}^{(1,k-1)}_{h\tau }, V_k]:=\widetilde{S}^{(1,k-1)}_{h\tau }V_k-V_k\widetilde{S}^{(1,k-1)}_{h\tau }$ to get

$$\begin{aligned} \partial _h\widetilde{S}_{h\tau }&= \sum _{k=1}^n \tau _kV_k\widetilde{S}_{h\tau }+\sum _{k=1}^n \tau _k[\widetilde{S}^{(1,k-1)}_{h\tau }, V_k]\widetilde{S}^{(k,n)}_{h\tau } = V\widetilde{S}_{h\tau }+(V_\tau -V)\widetilde{S}_{h\tau }+E_{h\tau } \end{aligned}$$

where $V_\tau :=\sum _{k=1}^n \tau _kV_k$ and $E_{h\tau }:=\sum _{k=1}^n \tau _k[\widetilde{S}^{(1,k-1)}_{h\tau }, V_k]\widetilde{S}^{(k,n)}_{h\tau }$. So, by variation of constants,

$$\begin{aligned} \widetilde{S}_{h\tau }-S_h&= \int _0^h S_{h-r}(V_\tau -V)\widetilde{S}_{r\tau } dr+\int _0^hS_{h-r}E_{r\tau } dr. \end{aligned}$$

(A.5)

Call $S_{h-r}(V_\tau -V)\widetilde{S}_{r\tau }$ error term 1 and $S_{h-r}E_{r\tau }$ error term 2. These terms will be treated separately in what follows. First however, we invoke variation of constants again to get an expression for $[\widetilde{S}^{(1,k-1)}_{r\tau }, V_k]$ that will be used to control error term 2. Differentiating in r gives

$$\begin{aligned} \partial _r[\widetilde{S}^{(1,k-1)}_{r\tau }, V_k]&= \sum _{j=1}^{k-1}\tau _j[\widetilde{S}_{r\tau }^{(1,j-1)}V_j\widetilde{S}_{r\tau }^{(j,k-1)},V_k] \\&= \sum _{j=1}^{k-1}\tau _j\bigg ([V_j\widetilde{S}_{r\tau }^{(1,k-1)},V_k]+\big [[\widetilde{S}_{r\tau }^{(1,j-1)},V_j]\widetilde{S}_{r\tau }^{(j,k-1)},V_k\big ]\bigg ) \\&= \sum _{j=1}^{k-1} \tau _jV_j[\widetilde{S}_{r\tau }^{(1,k-1)},V_k] \\&\quad +\sum _{j=1}^{k-1} \tau _j\bigg ([V_j,V_k]\widetilde{S}_{r\tau }^{(1,k-1)}+\big [[\widetilde{S}_{r\tau }^{(1,j-1)}, V_j]\widetilde{S}_{r\tau }^{(j,k-1)},V_k\big ]\bigg ). \end{aligned}$$

The second equality follows from commuting $\widetilde{S}^{(1,j-1)}_{h\tau }$ and $V_j$ as before, and the third follows from the identity $[XY,Z]=X[Y,Z]+[X,Z]Y$. So, by variation of constants,

$$\begin{aligned}{}[\widetilde{S}_{r\tau }^{(1,k-1)},V_k]= & {} \sum _{j=1}^{k-1}\int _0^r\tau _j e^{(r-s)\sum _{j=1}^{k-1}\tau _jV_j}[V_j,V_k]\widetilde{S}^{(1,k-1)}_{s\tau }ds \nonumber \\{} & {} +\sum _{j=1}^{k-1}\int _0^r \tau _j e^{(r-s)\sum _{j=1}^{k-1}\tau _jV_j}\big [[\widetilde{S}^{(1,j-1)}_{s\tau },V_j]\widetilde{S}^{(j,k-1)}_{s\tau },V_k\big ]ds. \end{aligned}$$

(A.6)

Note $\Vert e^{(r-s)\sum _{j=1}^{k-1}\tau _jV_j}\Vert _{0\rightarrow 0}=1$. So, by Corollary A.2 the integrands above satisfy

$$\begin{aligned} \mathbb {E}\Vert \tau _j&e^{(r-s)\sum _{j=1}^{k-1}\tau _jV_j}[V_j,V_k]\widetilde{S}^{(1,k-1)}_{s\tau }\Vert _{2\rightarrow 0} \\&\quad \le \Vert [V_j,V_k]\Vert _{2\rightarrow 0}\mathbb {E}\Vert \tau _j\widetilde{S}^{(1,k-1)}_{s\tau }\Vert _{2\rightarrow 2} < C \end{aligned}$$

and

$$\begin{aligned}&\mathbb {E}\big \Vert \tau _j e^{(r-s)\sum _{j=1}^{k-1}\tau _jV_j}\big [[\widetilde{S}^{(1,j-1)}_{s\tau },V_j]\widetilde{S}^{(j,k-1)}_{s\tau },V_k\big ]\big \Vert _{2\rightarrow 0} \\&\quad \le \mathbb {E}\big \Vert \tau _j \big [[\widetilde{S}^{(1,j-1)}_{s\tau },V_j]\widetilde{S}^{(j,k-1)}_{s\tau },V_k\big ]\big \Vert _{2\rightarrow 0} < C \end{aligned}$$

for some C. Therefore

$$\begin{aligned} \mathbb {E}\Vert [\widetilde{S}_{r\tau }^{(1,k-1)},V_k]\Vert _{2\rightarrow 0}&\le 2\sum _{j=1}^{k-1}\int _0^r C ds \le Cr \end{aligned}$$

(A.7)

for some new constant C (we will often absorb arbitrary constants into existing ones).

Error term 1. Rewrite error term 1 as

$$\begin{aligned} S_{h-r}(V_\tau -V)\widetilde{S}_{r\tau }{} & {} =\sum _{k=1}^n (\tau _k-1)S_{h-r}V_k\widetilde{S}_{r\tau } \nonumber \\{} & {} = \sum _{k=1}^n (\tau _k-1)S_{h-r}V_k\widetilde{S}^{(1,k-1)}_{r\tau }\widetilde{S}^{(k+1,n)}_{r\tau }\nonumber \\{} & {} \quad +\sum _{k=1}^n (\tau _k-1)S_{h-r}V_k\widetilde{S}^{(1,k-1)}_{r\tau }(e^{r\tau _kV_k}-I)\widetilde{S}^{(k+1,n)}_{r\tau }\nonumber \\{} & {} =:\mathcal {A}_1+\mathcal {A}_2 \end{aligned}$$

(A.8)

where $\mathcal {A}_1$ and $\mathcal {A}_2$ are the first and second sums in the preceding expression. The second equality is obtained by adding and subtracting the identity I as follows:

$$\begin{aligned} \widetilde{S}_{r\tau }&= \widetilde{S}^{(1,k-1)}_{r\tau }\big (e^{r\tau _kV_k}-I+I\big )\widetilde{S}^{(k+1,n)}_{r\tau }\\&= \widetilde{S}^{(1,k-1)}_{r\tau }\widetilde{S}^{(k+1,n)}_{r\tau }+\widetilde{S}^{(1,k-1)}_{r\tau }(e^{r\tau _kV_k}-I)\widetilde{S}^{(k+1,n)}_{r\tau }. \end{aligned}$$

Notice $\widetilde{S}^{(1,k-1)}_{r\tau }\widetilde{S}^{(k+1,n)}_{r\tau }$ does not depend on $\tau _k$. So, since the $\tau _i$ are independent with mean 1,

$$\begin{aligned} \mathbb {E}(\mathcal {A}_1)&= \sum _{k=1}^n S_{t-r}V_k\mathbb {E}(\tau _k-1)\mathbb {E}\big (\widetilde{S}^{(1,k-1)}_{r\tau }\widetilde{S}^{(k+1,n)}_{r\tau }\big ) = 0. \end{aligned}$$

(A.9)

For the second sum, Taylor expanding $r\mapsto e^{r\tau _kV_k}$ about $r=0$ with remainder gives

$$\begin{aligned} e^{r\tau _kV_k}-I&= r\tau _kV_ke^{r_*\tau _kV_k} \end{aligned}$$

for some $r_*\in [0,r]$. Therefore

$$\begin{aligned} \mathcal {A}_2&= r\sum _{k=1}^n \tau _k(\tau _k-1)S_{h-r}V_k\widetilde{S}^{(1,k-1)}_{r\tau }V_ke^{r_*\tau _kV_k}\widetilde{S}^{(k+1,n)}_{r\tau } \end{aligned}$$

and by Lemma A.1 and Corollary A.2,

$$\begin{aligned} \Vert \mathbb {E}(\mathcal {A}_2)\Vert _{2\rightarrow 0}&\le Cr\sum _{k=1}^n \mathbb {E}\Vert \widetilde{S}^{(1,k-1)}_{r\tau }\Vert _{1\rightarrow 1}\mathbb {E}\Vert \tau _k(\tau _k-1)\widetilde{S}^{(k,n)}_{r\tau }\Vert _{2\rightarrow 2} \le Cr \end{aligned}$$

(A.10)

for some $C>0$. Combining Equations (A.8), (A.9), and (A.10) gives

$$\begin{aligned} \Vert \mathbb {E}(S_{h-r}(V_\tau -V)\widetilde{S}_{r\tau })\Vert _{2\rightarrow 0}&\le Cr. \end{aligned}$$

(A.11)

Error term 2. Recall error term 2 is $S_{h-r}E_{r\tau }:=\sum _{k=1}^n \tau _kS_{h-r}[\widetilde{S}^{(1,k-1)}_{r\tau }, V_k]\widetilde{S}^{(k,n)}_{r\tau }$. So, we have that

$$\begin{aligned} \Vert S_{h-r}E_{r\tau }\Vert _{2\rightarrow 0}&\le \sum _{k=1}^n \tau _k\Vert S_{h-r}\Vert _{0\rightarrow 0}\Vert [\widetilde{S}^{(1,k-1)}_{r\tau },V_k]\Vert _{2\rightarrow 0}\Vert \tau _k\widetilde{S}^{(k,n)}_{r\tau }\Vert _{2\rightarrow 2}\,. \end{aligned}$$

Note $[\widetilde{S}^{(1,k-1)}_{r\tau },V_k]$ is independent of $\tau _k$. So, by (A.7) Corollary A.2,

$$\begin{aligned} \Vert \mathbb {E}( S_{h-r}E_{r\tau })\Vert _{2\rightarrow 0}&\le Cr \end{aligned}$$

(A.12)

for some $C>0$.

Final step. Combining (A.5), (A.11), and (A.12) and absorbing constants into C, we have

$$\begin{aligned} \Vert P_h-S_h\Vert _{2\rightarrow 0}&= \Vert \mathbb {E}(\widetilde{S}_{h\tau }-S_h)\Vert _{2\rightarrow 0} \\&\le \int _0^h \Vert \mathbb {E}(S_{h-r}(V_\tau -V)\widetilde{S}_{r\tau })\Vert _{2\rightarrow 0} dr+\int _0^h\Vert \mathbb {E}(S_{h-r}E_{r\tau })\Vert _{2\rightarrow 0} dr \\&\le C\int _0^h r dr = \tfrac{1}{2}Ch^2. \end{aligned}$$

$\square$

1.3 A.3. Concentration of the sum of exponential random variables

The proof of Lemma 4.6 will itself use two lemmas.

Lemma A.3

Let $\{\tau _k\}_{k=1}^\infty$ be iid exponential with mean 1. For any $m\in \mathbb {N}$, $K>0$ and $\beta >1$,

$$\begin{aligned} \mathbb {P}\left( \sum _{k=1}^m\tau _k>Km^\beta \right)&\le 2^me^{-\frac{1}{2}Km^\beta }. \end{aligned}$$

(A.13)

Proof

Note if $\tau \sim \text {Exp}(1)$ then $\mathbb {E}(e^{\tau /2})=2$. So, by Markov’s inequality and independence,

$$\begin{aligned} \mathbb {P}\left( \sum _{k=1}^m\tau _k>Km^\beta \right)&= \mathbb {P}\left( e^{\frac{1}{2}\sum _{k=1}^m\tau _k}>e^{\frac{1}{2}Km^\beta }\right) \\&\le e^{-\frac{1}{2}Km^\beta }\left( \mathbb {E}\left[ e^{\frac{1}{2}\tau }\right] \right) ^m = 2^me^{-\frac{1}{2}Km^\beta }. \end{aligned}$$

$\square$

Lemma A.4

Let $\{\tau _k\}_{k=1}^\infty$ be iid exponential with mean 1. For any $m\in \mathbb {N}$ and $K\in (0,1)$,

$$\begin{aligned} \mathbb {P}\left( \bigg |\sum _{k=1}^m \tau _k-1\bigg |> Km\right)&< 2e^{-\frac{1}{2}K^2m}. \end{aligned}$$

(A.14)

Proof

Fix m. For any $\gamma \in (0,1)$,

$$\begin{aligned} \mathbb {P}\left( \bigg |\sum _{k=1}^m \tau _k-1\bigg |> Km\right)&= \mathbb {P}\left( \sum _{k=1}^m \tau _k> (1+K)m\right) +\mathbb {P}\left( -\sum _{k=1}^m \tau _k> -(1-K)m\right) \\&= \mathbb {P}\left( e^{\gamma \sum _{k=1}^m \tau _k}> e^{(1+K)\gamma m}\right) +\mathbb {P}\left( e^{-\gamma \sum _{k=1}^m \tau _k} > e^{-(1-K)\gamma m}\right) \\&\le e^{-(1+K)\gamma m}\left( \mathbb {E}\left[ e^{\gamma \tau }\right] \right) ^m + e^{(1-K)\gamma m}\left( \mathbb {E}\left[ e^{-\gamma \tau }\right] \right) ^m \\&= e^{-(1+K)\gamma m}\left( 1-\gamma \right) ^{-m} + e^{(1-K)\gamma m}\left( 1+\gamma \right) ^{-m} \\&= \exp \left( -\gamma m\left[ 1+K+\frac{\log (1-\gamma )}{\gamma }\right] \right) \\&\quad +\exp \left( \gamma m\left[ 1-K-\frac{\log (1+\gamma )}{\gamma }\right] \right) . \end{aligned}$$

The inequality is Markov’s inequality and the equality immediately after the inequality follows from independence together with $\mathbb {E}[\exp (\alpha \tau )]=(1-\alpha )^{-1}$ for any $\alpha \in (-1,1)$. The other steps are all algebraic manipulations. By Taylor’s theorem with remainder there exists $\gamma _1\in (-\gamma ,0)$ such that

$$\begin{aligned} \frac{1}{\gamma }\log (1-\gamma )&= -1-\frac{\gamma }{2(1-\gamma _1)^2} > -1-\frac{\gamma }{2}, \end{aligned}$$

where the inequality follows since $\gamma _1<0$. Therefore

$$\begin{aligned} \exp \left( -\gamma m\left[ 1+K+\frac{\log (1-\gamma )}{\gamma }\right] \right)&\le \exp \left( -\gamma m\left[ K-\frac{\gamma }{2}\right] \right) . \end{aligned}$$

Similarly,

$$\begin{aligned} \exp \left( \gamma m\left[ 1-K-\frac{\log (1+\gamma )}{\gamma }\right] \right)&\le \exp \left( -\gamma m\left[ K-\frac{\gamma }{2}\right] \right) . \end{aligned}$$

So combining with the first computation of this proof and taking $\gamma =K$ gives

$$\begin{aligned} \mathbb {P}\left( \bigg |\sum _{k=1}^m \tau _k-1\bigg |> Km\right)&\le 2\exp \left( -\gamma m\left[ K-\frac{\gamma }{2}\right] \right) = 2e^{-\frac{1}{2}K^2m}. \end{aligned}$$

$\square$

1.4 A.4. Proof of Lemma 4.6

Fix $t>0$. The argument is similar to that of Lemma 4.2.

Variation of constants. Fix $m\in \mathbb {N}$. Since $\widetilde{S}^m_{h\tau }=\exp (h\tau _1V_1)\cdots \exp (h\tau _{mn}V_{mn})$,

$$\begin{aligned} \partial _h\widetilde{S}^m_{h\tau }&= \sum _{k=1}^{mn} \tau _k\widetilde{S}^{(1,k-1)}_{h\tau }V_k\widetilde{S}^{(k,mn)}_{h\tau } = \sum _{k=1}^{mn} \tau _kV_k\widetilde{S}^m_{h\tau }+\tau _k[\widetilde{S}^{(1,k-1)}{h\tau }, V_k]\widetilde{S}^{(k,mn)}_{h\tau } \\&= mV\widetilde{S}^m_{h\tau }+\sum _{k=1}^{mn}(\tau _k-1)V_k\widetilde{S}^m_{h\tau }+\sum _{k=1}^{mn}\tau _k[\widetilde{S}^{(1,k-1)}_{h\tau }, V_k]\widetilde{S}^{(k,mn)}_{h\tau }, \end{aligned}$$

where the second equality is obtained by commuting $\widetilde{S}^{(1,k-1)}_{h\tau }$ and $V_k$, and the third by replacing $\tau _k$ with $\tau _k-1+1$. So, setting $E_{h\tau }^{(m)}:=\sum _{k=1}^{mn}\tau _k[\widetilde{S}^{(1,k-1)}_{h\tau }, V_k]\widetilde{S}^{(k,mn)}_{h\tau }$, variation of constants implies

$$\begin{aligned} \widetilde{S}^m_{h\tau }-S_{hm}&= \int _0^h S_{m(h-r)}\left( \sum _{k=1}^{mn}(\tau _k-1)V_k\right) \widetilde{S}^m_{r\tau } dr + \int _0^h S_{m(h-r)}E_{r\tau }^{(m)} dr. \end{aligned}$$

Therefore, since $\Vert S_{m(h-r)}\Vert _{0\rightarrow 0}=1$,

$$\begin{aligned} \Vert \widetilde{S}^m_{h\tau }-S_{hm}\Vert _{2\rightarrow 0}&\le \int _0^h \bigg \Vert \sum _{k=1}^{mn}(\tau _k-1)V_k\bigg \Vert _{1\rightarrow 0}\left\Vert \widetilde{S}^m_{r\tau }\right\Vert _{2\rightarrow 1} dr + \int _0^h \Vert E_{r\tau }^{(m)}\Vert _{2\rightarrow 0} dr. \end{aligned}$$

Let $I_1(h)$ and $I_2(h)$ denote the first and second integrals, respectively. Then for any $\varepsilon >0$,

$$\begin{aligned} \mathbb {P}\left( \Vert \widetilde{S}^m_{h\tau }-S_{hm}\Vert _{2\rightarrow 0}> \frac{\varepsilon }{m}\right)&\le \mathbb {P}\left( I_1(h)> \frac{\varepsilon }{2m}\right) +\mathbb {P}\left( I_2(h) > \frac{\varepsilon }{2m}\right) . \end{aligned}$$

(A.15)

We consider the two probabilities on the right, called the first and second probabilities, separately.

First probability. Note $\sum _{k=1}^{mn}(\tau _k-1)V_k=\sum _{k=1}^n\sum _{j=1}^m (\tau _j^{(k)}-1)V_k$ where $\tau ^{(k)}_j:=\tau _{(j-1)n+k}$. So

$$\begin{aligned} \bigg \Vert \sum _{k=1}^{mn}(\tau _k-1)V_k\bigg \Vert _{1\rightarrow 0}&\le C_*\sum _{k=1}^n\bigg |\sum _{j=1}^m \tau _j^{(k)}-1\bigg |, \end{aligned}$$

and together with Lemma A.1 and Equation (A.3),

$$\begin{aligned} I_1(h)&\le C_*\sum _{k=1}^n\bigg |\sum _{j=1}^m \tau _j^{(k)}-1\bigg |\int _0^h \prod _{k=1}^n e^{C_*r\sum _{j=1}^m \tau _j^{(k)}} dr\,. \end{aligned}$$

Therefore

$$\begin{aligned} \mathbb {P}\left( I_1(h)> \frac{\varepsilon }{2m}\right)&\le \mathbb {P}\left( C_*\sum _{k=1}^n\bigg |\sum _{j=1}^m \tau _j^{(k)}-1\bigg |\int _0^h \prod _{k=1}^n e^{C_*r\sum _{j=1}^m \tau _j^{(k)}} dr> \frac{\varepsilon }{2m}\right) \\&\le \sum _{k=1}^n\mathbb {P}\left( \bigg |\sum _{j=1}^m \tau _j^{(k)}-1\bigg |\int _0^h \prod _{k=1}^n e^{C_*r\sum _{j=1}^m \tau _j^{(k)}} dr > \frac{\varepsilon }{2C_*mn}\right) . \end{aligned}$$

The second inequality follows from a union bound together with the fact that for any nonnegative random variables $X_k$ and constant c, $\{\sum _{k=1}^n X_k>c\}\subseteq \cup _{k=1}^n \{X_k>c/n\}$. Set

$$\begin{aligned}&A(h) :=\bigcap _{k=1}^n\left\{ h\sum _{j=1}^m \tau _j^{(k)} \le \alpha \right\} \quad \text {and} \\&B_k(h):=\left\{ \bigg |\sum _{j=1}^m \tau _j^{(k)}-1\bigg |\int _0^h \prod _{k=1}^n e^{C_*r\sum _{j=1}^m \tau _j^{(k)}} dr > \frac{\varepsilon }{2C_*mn}\right\} \end{aligned}$$

for arbitrary $\alpha >0$ and note that

$$\begin{aligned} A(h)\cap B_k(h)&\subseteq \left\{ \bigg |\sum _{j=1}^m \tau _j^{(k)}-1\bigg |he^{C_*n\alpha } > \frac{\varepsilon }{2C_*mn}\right\} =:B(h). \end{aligned}$$

Therefore

$$\begin{aligned} \mathbb {P}\left( I_1(h) > \frac{\varepsilon }{m}\right)&\le \sum _{k=1}^n\mathbb {P}\left( B_k(h)\cap A(h)\right) +\mathbb {P}\left( B_k(h)\cap A(h)^c\right) \le n\big [\mathbb {P}\left( B(h)\right) +\mathbb {P}\left( A(h)^c\right) \big ]. \end{aligned}$$

Set $h=t/m^2$. By Lemma A.4 for all $\varepsilon >0$ such that $K:=\varepsilon (2C_*tn)^{-1}e^{-C_*n\alpha }<1$,

$$\begin{aligned} \mathbb {P}\left( B(h)\right)&= \mathbb {P}\left( \bigg |\sum _{j=1}^m \tau _j^{(k)}-1\bigg |> \frac{\varepsilon m}{2C_*tne^{C_*n\alpha }}\right) \le 2e^{-\frac{1}{2}K^2m}. \end{aligned}$$

And by Lemma A.3,

$$\begin{aligned} \mathbb {P}\left( A(h)^c\right)&= \mathbb {P}\left( \bigcup _{k=1}^n\left\{ \sum _{j=1}^m\tau _j^{(k)}> \frac{\alpha }{h}\right\} \right) \le n\mathbb {P}\left( \sum _{j=1}^m \tau _j > \frac{\alpha m^2}{t}\right) \le n2^me^{-\frac{1}{2}K'm^2} \end{aligned}$$

where $K':=\alpha /t$. Therefore

$$\begin{aligned} \mathbb {P}\left( I_1(h) > \frac{\varepsilon }{2m}\right)&\le 2e^{-\frac{1}{2}K^2m}+2^m ne^{-\frac{1}{2}K'm^2} \le 2^mCe^{-\frac{1}{2}Cm^2} \end{aligned}$$

(A.16)

for some positive constant C independent of m.

Second probability. Recall $E_{r\tau }^{(m)}:=\sum _{k=1}^{mn}\tau _k[\widetilde{S}^{(1,k-1)}_{r\tau }, V_k]\widetilde{S}^{(k,mn)}_{r\tau }$. Also, from Equation (A.6),

$$\begin{aligned}{}[\widetilde{S}_{r\tau }^{(1,k-1)},V_k]\widetilde{S}^{(k,mn)}_{r\tau }&= \sum _{j=1}^{k-1}\int _0^r\tau _j e^{(r-s)\sum _{j=1}^{k-1}\tau _jV_j}[V_j,V_k]\widetilde{S}^{(1,k-1)}_{s\tau }\widetilde{S}^{(k,mn)}_{r\tau }ds \\&\qquad +\sum _{j=1}^{k-1}\int _0^r \tau _j e^{(r-s)\sum _{j=1}^{k-1}\tau _jV_j}\big [[\widetilde{S}^{(1,j-1)}_{s\tau },V_j]\widetilde{S}^{(j,k-1)}_{s\tau },V_k\big ]\widetilde{S}^{(k,mn)}_{r\tau }ds. \end{aligned}$$

Lemma A.1 together with $\Vert [V_j,V_k]\Vert _{2\rightarrow 0} \le \Vert V_j\Vert _{1\rightarrow 0}\Vert V_k\Vert _{2\rightarrow 1}+\Vert V_k\Vert _{1\rightarrow 0}\Vert V_j\Vert _{2\rightarrow 1}\le 2C_*^2$ give

$$\begin{aligned} \left\Vert [V_j,V_k]\widetilde{S}^{(1,k-1)}_{s\tau }\widetilde{S}^{(k,mn)}_{r\tau }\right\Vert _{2\rightarrow 0}&\le 2C_*^2\left( 1+C_*r\sum _{j=1}^{mn}\tau _j\right) e^{3C_*r\sum _1^{mn}\tau _j}. \end{aligned}$$

Also,

$$\begin{aligned} \big [[\widetilde{S}^{(1,j-1)}_{s\tau },V_j]\widetilde{S}^{(j,k-1)}_{s\tau },V_k\big ]= & {} \widetilde{S}^{(1,j-1)}_{s\tau }V_j\widetilde{S}^{(j,k-1)}_{s\tau }V_k-V_k\widetilde{S}^{(1,j-1)}_{s\tau }V_j\widetilde{S}^{(j,k-1)}_{s\tau } \\{} & {} -V_j\widetilde{S}^{(1,k-1)}_{s\tau }V_k+V_kV_j\widetilde{S}^{(1,k-1)}_{s\tau } \end{aligned}$$

together with Lemma A.1 gives

$$\begin{aligned} \left\Vert \big [[\widetilde{S}^{(1,j-1)}_{s\tau },V_j]\widetilde{S}^{(j,k-1)}_{s\tau },V_k\big ]\widetilde{S}^{(k,mn)}_{r\tau }\right\Vert _{2\rightarrow 0}&\le 4C_*^2\left( 1+C_*r\sum _{j=1}^{mn}\tau _j\right) e^{3C_*r\sum _1^{mn}\tau _j}. \end{aligned}$$

Therefore for any $0\le r\le h$,

$$\begin{aligned} \left\Vert E_{r\tau }^{(m)}\right\Vert _{2\rightarrow 0}&\le \sum _{k=1}^{mn}\sum _{j=1}^{k-1}\tau _k\tau _j\int _0^r\left\Vert [V_j,V_k]\widetilde{S}^{(1,k-1)}_{s\tau }\widetilde{S}^{(k,mn)}_{r\tau }\right\Vert _{2\rightarrow 0} \\&\quad +\left\Vert \big [[\widetilde{S}^{(1,j-1)}_{s\tau },V_j]\widetilde{S}^{(j,k-1)}_{s\tau },V_k\big ]\widetilde{S}^{(k,mn)}_{r\tau }\right\Vert _{2\rightarrow 0} ds \\&\le 6C_*^2r\bigg (1+C_*r\sum _{\ell =1}^{mn}\tau _\ell \bigg )e^{3C_*r\sum _1^{mn}\tau _\ell }\sum _{k=1}^{mn}\sum _{j=1}^{k-1}\tau _k\tau _j \\&\le Ch\bigg (1+Ch\sum _{\ell =1}^{mn}\tau _\ell \bigg )e^{Ch\sum _1^{mn}\tau _\ell }\bigg (\sum _{k=1}^{mn}\tau _k\bigg )^2 \end{aligned}$$

for some $C>0$. So, we have that

$$\begin{aligned} I_2(h)&= \int _0^h\Vert E_{r\tau }^{(m)}\Vert _{2\rightarrow 0} dr \le Ch^2\bigg (1+Ch\sum _{\ell =1}^{mn}\tau _\ell \bigg )e^{Ch\sum _1^{mn}\tau _\ell }\bigg (\sum _{k=1}^{mn}\tau _k\bigg )^2\,. \end{aligned}$$

For arbitrary $\alpha >0$, set

$$\begin{aligned}&A(h) :=\left\{ h\sum _{k=1}^{mn}\tau _k\le \alpha \right\} \quad \text {and}\quad \\&B(h):=\left\{ Ch^2\bigg (1+Ch\sum _{\ell =1}^{mn}\tau _\ell \bigg )e^{Ch\sum _1^{mn}\tau _\ell }\bigg (\sum _{k=1}^{mn}\tau _k\bigg )^2 > \frac{\varepsilon }{2m}\right\} \,. \end{aligned}$$

Then taking $h=t/m^2$ as before,

$$\begin{aligned} \begin{aligned} \mathbb {P}\left( I_2(h)> \frac{\varepsilon }{2m}\right)&= \mathbb {P}\left( A(h)\cap B(h)\right) +\mathbb {P}\left( A(h)^c\cap B(h)\right) \\&\le \mathbb {P}\left( Ch^2\left( 1+C\alpha \right) e^{C\alpha }\bigg (\sum _{k=1}^{mn}\tau _k\bigg )^2> \frac{\varepsilon }{2m}\right) +\mathbb {P}\left( h\sum _{k=1}^{mn}\tau _k>\alpha \right) \\&= \mathbb {P}\left( \sum _{k=1}^{mn}\tau _k> Km^{\frac{3}{2}}\right) +\mathbb {P}\left( \sum _{k=1}^{mn}\tau _k>\frac{\alpha m^2}{t}\right) \\&\le n\left[ \mathbb {P}\left( \sum _{k=1}^m\tau _k> K'm^{\frac{3}{2}}\right) +\mathbb {P}\left( \sum _{k=1}^m\tau _k>\frac{\alpha m^2}{nt}\right) \right] \\&\le n\left( 2^me^{-\frac{1}{2}K'm^{3/2}}+2^me^{-\frac{1}{2}K''m^2}\right) \le 2^mC'e^{-\frac{1}{2}C'm^{3/2}} \end{aligned} \end{aligned}$$

(A.17)

for some $C'>0$ where $K=(\varepsilon (2t^2C(1+C\alpha )e^{C\alpha })^{-1})^{1/2}$, $K'=Kn^{-1}$, $K''=\alpha (nt)^{-1}$, and the second-to-last last inequality follows from Lemma A.3. Combining (A.15), (A.16), and (A.17) and taking $h=t/m^2$ we therefore have that for all $\varepsilon$ sufficiently small,

$$\begin{aligned} \mathbb {P}\left( \Vert \widetilde{S}^m_{t\tau /m^2}-S_{t/m}\Vert _{2\rightarrow 0} > \tfrac{\varepsilon }{m}\right)&\le 2^mC''e^{-\frac{1}{2}C''m^{3/2}} \end{aligned}$$

for some constant $C''>0$ independent of m. So, we have that

$$\begin{aligned} \sum _{m=1}^\infty \mathbb {P}\left( \Vert \widetilde{S}^m_{t\tau /m^2}-S_{t/m}\Vert _{2\rightarrow 0} > \tfrac{\varepsilon }{m}\right)&\le \sum _{m=1}^\infty 2^mC''e^{-\frac{1}{2}C''m^{3/2}} < \infty . \end{aligned}$$

$\square$

Appendix B. Controllability Lemmas

Combining the partial results obtained above we show the existence of transformations implementing the steps listed at the beginning of the section:

Lemma B.1

If $q^{(0)}$ in $\mathcal {Q}_0$ is nondegenerate, then there exists $M_1$ and a sequence of transition times and interaction triples $\{ \iota (m),\tau (m)\}_{m = 1}^{M_1}$ such that $\Phi _{\tau (M_1)}^{\iota (M_1)}\circ \dots \circ \Phi _{\tau (1)}^{\iota (1)} (q^{(0)}) = q^{(1)}$ as in (6.17).

Proof

If (6.17) is satisfied by $q^{(0)}$ we simply set $M_1 = 0$, $q^{(1)} = q^{(0)}$. If not, by nondegeneracy there exists a sequence of triples $\{\iota (m)\}_{m=1}^{M}$ with $\iota (m) = {\varvec{j}}(m){\varvec{k}}(m){\varvec{\ell }}(m)$ such that $\mathcal A_0 := \mathcal A(q^{(0)})$ and $\mathcal A_m = \mathcal A_{m-1} \oplus {\varvec{\ell }}(m)$ with $\{(0,1,+),(1,0,+),(j^*,-)\}\subset \mathcal A_{M}$. We notice that all steps of this procedure satisfy, upon possibly reordering the indices within each triple, either the conditions of Lemma 6.11 (b) or of Lemma 6.12, so we sequentially choose $\tau (m) = \tau _+^{\iota (m)}$ from those lemmas.

To activate coordinate $(1,1,-)$ – if this was not already done in the previous procedure – we start with component $b_{j^*} \ne 0$ for $|j^*|\ne 1$ and consider a nearest neighbors path $\{\ell (n)\}_{n=1}^{M'}$ in $\mathbb Z_N^2$ connecting $j^*$ to (1, 1) without performing any step on the axes. It is easy to see that such path can be realized through repeated application of Lemma 6.11 (b) by choosing for the n-th step the triples $\iota (n) = (0,1,+)(\ell (n),-)(\ell (n)\pm (0,1),-)$ or $\iota (n) = (1,0,+)(\ell (n),-)(\ell (n)\pm (1,0),-)$ for vertical and horizontal steps respectively.

Finally, coordinates $(1,0,-)$ and $(0,1,-)$ can be activated by applying Lemma 6.13 to the triples $(1,0,-)(0,1,+)(1,1,-)$ and $(1,0,+)(0,1,-)(1,1,-)$ respectively, while $(1,1,+)$ is activated by (b) by interchanging the type of modes $(1,1,-)$ and $(1,0,+)$ (or $(0,1,+)$) in $\iota (M')$ from the previous paragraph to $(1,1,+)$ and $(1,0,-)$ (or $(0,1,-)$).$\square$

Lemma B.2

Let $q^{(1)}$ be a nondegenerate point in $\mathcal {Q}_0$ satisfying (6.17). Then there exists $M_2$ and a sequence of interacting triples and transition times $\{\iota (m),\tau (m)\}_{m = 1}^{M_2}$ such that $\Phi _{\tau (M_2)}^{\iota (M_2)}\circ \dots \circ \Phi _{\tau (1)}^{\iota (1)} (q^{(1)}) = q^{(2)}$ is a nondegenerate point in $\mathcal {Q}_0$ satisfying (6.18) and (6.19).

Proof

In this part of the proof, we only consider interactions involving triples $\iota (m)$ of the form

$$\begin{aligned} \Big \{ (0,1)(l,h)(l,h\pm 1)\text { or } (1,0)(l,h)(l\pm 1,h) : |l|,|h|\le N,~|(l,h)|\ne 1 \Big \}\,. \end{aligned}$$

(B.1)

By Lemma 6.11 (a), if $|j|<|k|<|\ell |$ and $(0,1),(l,h) \in \mathcal A(q)$ there exists $\tau (m) = \tau _-^{\iota (m)}$ such that defining $\mathcal A_m = \mathcal A(\varphi ^{\iota (m)}_{\tau (m)}(q))$ we have $(l,h) \not \in \mathcal A_m$ and $(0,1) \in \mathcal A_m$ (and similarly for (1, 0)).¹⁰ Note that while a triple as above satisfies by assumption that $|j|<|k|<|\ell |$ and at least two of its coordinates are nonvanishing, it does not, in general, satisfy (6.24). However, assuming that q does not satisfy (6.24), by Lemma 6.12 and setting $\iota ' = (1,0)(0,1)(1,1)$, there exists $\tau ^{\iota '}$ such that $|q_{(1,0)}| \ne |(\Phi _{\tau ^{\iota '}}^{\iota '}(q))_{(1,0)}| >0$. Since none of the coordinates in $\mathbb Z_N^2\setminus \{(1,0)(0,1)(1,1)\}$ are affected by this operation, $(\Phi _{\tau ^{\iota '}}^{\iota '}(q))$ satisfies (6.24) and Lemma 6.11 can be applied to this state.

To conclude the proof we identify a sequence of triples $\iota (m) = (j(m),k(m),\ell (m))\in \mathcal I$ of the form (B.1) such that for $\mathcal A_0 = \mathcal A(q^{(1)}) \subseteq \mathbb Z_N^2\times \{+,-\}$

$$\begin{aligned}&(((\mathcal A_0 \ominus k(1)) \ominus k(2)) \ominus \dots ) \ominus k(M_2) \\&\quad = \{(1,0,\chi ),(0,1,\chi ), (1,1\chi ), (N,N\chi ), (-N,N\chi )\,, \chi \in \{+,-\}\}\,. \end{aligned}$$

A possible such sequence is given by triples of the form

$$\begin{aligned} \Big \{ (1,0,+)(l,h, \chi )(l+1,h,\chi )~ : ~ (l,h) \in \{(0,2),\dots , (0,N)\} \,,\chi \in \{+,-\}\Big \} \end{aligned}$$

to remove the vertical column of $\mathbb Z_N^2$ (which cannot interact with (0, 1)), followed by

$$\begin{aligned} \Big \{ \Big ((0,1,+)(l,h,\chi )(l,h+1,\chi )~:~ (l,h) \in \big \{(l,0),\dots , (l,N): |l| \in (1,\dots ,N-1) \big \}\setminus \{(1,1)\}\Big )\,,\chi \in \{+,-\}\Big \}\,, \end{aligned}$$

where importantly the set of transitions for each l is ordered. The above transformation zeroes all coefficients except those in the set $\{(1,1),(0,1),(1,0)\}\cup \{(l,N)~:~l \in (-N,\dots , N)\}$. We further remove the coefficients from $\{(l,N)~:~l \in (-N+1,\dots , N-1)\}$ by sequentially applying Lemma 6.11 to the ordered sequence of interacting triples

$$\begin{aligned} \Big ((1,0,+)(l,h,\chi )(l+1,h,\chi ) ~:~ (l,h) \in \{(0,N),\dots , (N-1,N)\,,\chi \in \{+,-\}\}\Big )\,,\end{aligned}$$

and then

$$\begin{aligned} \Big ((1,0,+)(l,h,\chi )(l-1,h,\chi )~:~ (l,h) \in \{(-1,N),\dots , (-N+1,N)\}\,,\chi \in \{+,-\}\Big )\,.\end{aligned}$$

It is easy to check that each transition in the above construction sequentially satisfies the assumptions of Lemma 6.11 (a), and that once a mode has been removed from $\mathcal A$ it will not interact again in this procedure. The fact that (6.19) holds follows from (6.17) and that in an interacting triple $\iota = {\varvec{j} \varvec{k} \varvec{\ell }}$ with $|j|<|k|<|l|$ both modes ${\varvec{j}}$ and ${\varvec{\ell }}$ are in $\mathcal A$ at the end of the interaction by $\tau _-^\iota$.$\square$

Lemma B.3

Let $q^{(2)}$ be a nondegenerate point in $\mathcal {Q}_0$ satisfying (6.18) and (6.19). Then there exists $M_3$ and a sequence of interacting triples and transition times $\{\iota (m),\tau (m)\}_{m = 1}^{M_3}$ such that $\Phi _{\tau (M_3)}^{\iota (M_3)}\circ \dots \circ \Phi _{\tau (1)}^{\iota (1)} (q^{(2)}) = q^{(3)}$ is a nondegenerate point in $\mathcal {Q}_0$ satisfying (6.20) and (6.21).

Since it may not be possible to “transfer” the content of e.g., mode $(-N,N)$ to $(-N+1,N)$ through one single interaction with mode (1, 0) – and therefore it won’t be possible to transfer the amplitude of mode $(-N,N)$ to (N, N) in one single “pass” – we proceed to prove that, through a sequence of interactions, we can transfer a finite and $q_{(-N,N)}$-independent amount of energy from mode $(-N,N)$ to (N, N). Therefore, the transfer of amplitude from mode $(-N,N)$ to (N, N) may be accomplished by repeating this sequence of interactions sufficiently many times.

The following corollary of Lemma 6.12 will be instrumental for the proof of Lemma B.3:

Corollary B.4

Let $q_{(1,1)}, b_{{(1,1)}} \ne 0$ then for any $q,q'$ with $q_{\varvec{j}}=q_{\varvec{j}}'$ for all $|j|>1$ there exist a sequence $\{\iota (m), \tau (m)\}_{m=1}^4$ such that $\Phi _{\tau (4)}^{\iota (4)} \circ \dots \circ \Phi _{\tau (1)}^{\iota (1)} (q) = q'$.

Proof of Lemma B.3

The desired result follows upon showing that for any $i \in \{-N,\dots ,N\}$, setting ${\varvec{\ell }}= (-i,N,\chi ), {\varvec{\ell }}' = {(i,N,\chi ')}$ for $\chi , \chi ' \in \{-,+\}$ there exists $M_{{\varvec{\ell }}, {\varvec{\ell }}'}$ and a sequence of triples and interaction times $\{\iota (m)$, $\tau (m)\}_{m = 1}^{M_{{\varvec{\ell }}, {\varvec{\ell }}'}}$ such that for any q satisfying $\bigcup _{|i'| < i}\{(i',N,+),{(i',N,-)}\} \cap \mathcal A(q) = \emptyset$ and $q' = \Phi _{\tau (M_{{\varvec{\ell }}, {\varvec{\ell }}'})}^{\iota (M_{{\varvec{\ell }}, {\varvec{\ell }}'})}\circ \dots \circ \Phi _{\tau (1)}^{\iota (1)}(q)$ we have

$$\begin{aligned} q_{\varvec{j}}' = {\left\{ \begin{array}{ll} q_{\varvec{j}}\qquad &{} \text {for } {\varvec{j}}\in \mathbb Z_N^2\setminus \{{\varvec{\ell }},{\varvec{\ell }}'\}\,,\\ 0&{}\text {for } {\varvec{j}}= {\varvec{\ell }}\text { if } {\varvec{\ell }}\ne {\varvec{\ell }}'\,,\end{array}\right. } \end{aligned}$$

(B.2)

and for ${\varvec{k}}\in \{{\varvec{\ell }}, {\varvec{\ell }}'\}$, $\text {sign}(q_{\varvec{k}}) = \text {sign}(q_{\varvec{k}}')$ holds if $q_{\varvec{k}}' \ne 0$ (recalling our choice of notation $\text {sign}(0)=+1$). Indeed, if $\text {sign}(b_{{(N,N)}})\ge 0$ we sequentially apply the above result to the pairs

$$\begin{aligned}({\varvec{\ell }},{\varvec{\ell }}') = ((N,N,+), (-N,N,+)), ((-N,N,+), (N,N,-)), ((-N,N,-), (N,N,-))\,.\end{aligned}$$

Otherwise, when $\text {sign}(b_{{(N,N)}})=-1$ we first apply the above result to ${\varvec{\ell }}={(N,N,-)}$, ${\varvec{\ell }}'={(-N,N,-)}$ and then proceed as in the previous case.

We prove the result above by induction on $i \in \{0,\dots ,N\}$. The proof for $i \le 0$ is analogous.

Base case ($i=0: (0,N,\chi )\rightarrow (0,N,\chi ')$): If ${\varvec{\ell }}= {\varvec{\ell }}'$ there is nothing to show. We proceed to consider the case ${\varvec{\ell }}= (0,N,+)$, ${\varvec{\ell }}'={(0,N,-)}$, as the converse follows by analogous arguments. In this case, for a sufficiently small $\varepsilon >0$ we consider the interactions $\iota = (1,0,+)(0,N,+)(1,N,+)$ and $\iota '= {(1,0,-)}{(0,N,-)}(1,N,+)$, running the corresponding flow maps by a small amount of time $\tau (\varepsilon )$, $\tau '(\varepsilon )$ such that $(\Phi _{\tau '(\varepsilon )}^{\iota '} \circ \Phi _{\tau (\varepsilon )}^\iota (q)_{{(0,N,-)}})^2 = b_{{(0,N)}}^2+\varepsilon$. We then apply Corollary B.4 to the coordinates $(1,0,+),{(1,0,-)}$ to return them in the initial configuration. Note that the existence of a uniform $\varepsilon >0$ such that the transitions above can be performed in a single pair of interactions (and therefore the finiteness of the total number of interactions required to perform the desired transformation) follows from the fact that $b_{{(0,N)}}$ is nondecreasing and the continuity of the dynamics together with Lemma 6.11.

Induction step ($i>0: (-i,N,\chi )\rightarrow (i,N,\chi ')$): We consider two possibilities for q: a) there exists $q''$ with $|a_{(1,0)}''| \in [|a_{(1,0)}|/2,|a_{(1,0)}| ]$, $q_{(-i,N,\chi )}''=0$ and for $\iota '' = (1,0,+)(-i+1,N,\chi )(-i,N,\chi )$

$$\begin{aligned} E_{\iota ''}(q)&= E_{\iota ''}(q''),\quad \mathcal E_{\iota ''}(q) = \mathcal E_{\iota ''}(q'')\,, \end{aligned}$$

or b) such $q''$ does not exist.

In case a) the state $q''$ can be reached by letting $\iota = (1,0,+)(-i+1,N,\chi )(-i,N,\chi )$ interact for a finite amount of time $\tau$ from Lemma 6.11 (c). Then, by the induction assumption there is a sequence of triples and interaction times allowing to reach a state $q'''$ with $q_{(-i+1,N,\chi )}''' = 0$, $q_{(i-1,N,\chi ')}''' = q_{(-i+1,N,\chi )}''$ and $q_{\varvec{j}}''' = q_{\varvec{j}}''$ for all other $j \in \mathbb Z_N^2$. The desired state can then be reached by application of Lemma 6.11 (a) to the triple $\iota = (1,0,+)(i-1,N,\chi ')(i,N,\chi ')$ . We proceed to check that the final state satisfies (B.2). Because modes $j \not \in \{(-i,N), \dots , (i,N), (1,0)\}$ did not interact in the procedure above for such ${\varvec{j}}$ we must have that $q_{\varvec{j}}= q_{\varvec{j}}'$. The fact that for $j \in \{(-i,N), \dots , (i-1,N)$ $q_{\varvec{j}}' = 0$ follows by construction and the induction assumption. It remains to check that $|a_{(1,0)}'| = |a_{(1,0)}|$. Since the only modes affected by the above transformation are $(-i,N,\chi ),(i,N\chi '),(1,0,+)$, this follows directly by conservation of energy and enstrophy:

$$\begin{aligned} (q_{(-i,N,\chi )})^2 + (q_{(i,N,\chi ')})^2 + ({q_{(1,0,+)}})^2&= (q_{(i,N,\chi ')}')^2 + (q_{(1,0,+)}')^2\,,\\ \frac{(q_{(-i,N,\chi )})^2}{N^2+i^2} + \frac{(q_{(i,N,\chi ')})^2}{N^2+i^2} + ({q_{(1,0,+)}})^2&= \frac{(q_{(-i,N,\chi )}')^2}{N^2+i^2} + (q_{(1,0,+)}')^2\,. \end{aligned}$$

In case b) we proceed to show that case a) can be reached with a finite number of interactions. More specifically if condition a) is not satisfied we let the triple $\iota '' = (-i,N,\chi )(-i+1,N, \chi )(1,0, +)$ for $\chi \in \{+,-\}$ interact as described by Lemma 6.11 for a time $\tau ''$ to reach a nondegenerate point $q''$ in $\mathcal {Q}_0$ with $q_{\varvec{j}}'' = q_{\varvec{j}}$ for ${\varvec{j}}\not \in \{(-i,N, \chi ),(-i+1,N,\chi ),(1,0,+)\}$, $a_{(1,0)}'' = a_{(1,0)}/2$ and $q_{(-i,N,\chi )}'',q_{(-i+1,N,\chi )}''$ satisfying the conservation laws

$$\begin{aligned} (q_{(-i,N, \chi )})^2 + ({q_{(1,0,+)}})^2&= (q_{(-i,N, \chi )}'')^2 + (q_{(-i+1,N,\chi )}'')^2 + (q_{(1,0,+)}/2)^2\,,\\ \frac{(q_{(-i,N, \chi )})^2}{N^2+i^2} + ({q_{(1,0,+)}})^2&= \frac{(q_{(-i,N,\chi )}'')^2}{N^2+i^2} +\frac{(q_{(-i+1,N,\chi )}'')^2}{N^2+(i-1)^2}+ (q_{(1,0,+)}/2)^2\,, \end{aligned}$$

so that $(q_{(-i,N,\chi )}'')^2 = (q_{(-i,N,\chi )})^2 - C_{N,i} (q_{(1,0)})^2$ for $C_{N,i} = \frac{3}{4} \frac{N^2+i^2}{i^2-(i-1)^2} ( N^2+(i-1)^2-1)$. We see that a positive, $q_{(1,0,+)}$-dependent amplitude is removed from $(q_{(-i,N,\chi )})^2$. Again applying the induction step and Lemma 6.11 (a) to transfer, respectively, the amplitude from ${(-i+1,N,\chi )}$ to ${(i-1,N, \chi ')}$ and from ${(i-1,N,\chi ')}$ to ${(i,N,\chi ')}$ we reach the state $q'$ with $q_{\varvec{j}}= q_{\varvec{j}}'$ for modes $j \not \in \{(-i,N), \dots , (i,N), (1,0)\}$ (since these modes either vanish in both cases or they did not interact). Further, by conservation of energy and enstrophy, we have that

$$\begin{aligned} (q_{(-i,N,\chi )})^2 + (q_{(i,N,\chi ')})^2+ ({q_{(1,0,+)}})^2&= (q_{(-i,N,\chi )}'')^2 + (q_{(i,N,\chi ')}'')^2 + (q_{(1,0,+)}'')^2\,,\\ \frac{(q_{(-i,N,\chi )})^2}{N^2+i^2} + \frac{(q_{(i,N,\chi ')})^2}{N^2+i^2} + ({q_{(1,0,+)}})^2&= \frac{(q_{(-i,N,\chi )}'')^2}{N^2+i^2} +\frac{(q_{(i,N,\chi ')}'')^2}{N^2+i^2}+ (q_{(1,0,+)}'')^2\,, \end{aligned}$$

so that $|q_{(1,0,+)}''| = |q_{(1,0,+)}|$. This shows that the amplitude $C_{N,i} (q_{(1,0,+)})^2$ subtracted to $q_{(-i,N,\chi )}$ is constant at each cycle, showing by boundedness of $q_{(-i,N,\chi )}$ that with a finite number of iterations as the one described above we can reach state a), concluding the proof.$\square$

Lemma B.5

Let $q^{(3)}$ be a nondegenerate point in $\mathcal {Q}_0$ satisfying (6.20) and (6.21). Then there exists $M_4$ and a sequence of interacting triples and transition times $\{\iota (m),\tau (m)\}_{m = 1}^{M_4}$ such that $\Phi _{\tau (M_4)}^{\iota (M_4)}\circ \dots \circ \Phi _{\tau (1)}^{\iota (1)} (q^{(3)}) = q^*$ is a nondegenerate point in $\mathcal {Q}_0$ satisfying (6.15).

Proof

We start the proof by applying Corollary B.4 to transform the state $q^{(3)}$ into $q = \Phi _{\tau (1)}(q^{(3)})$ satisfying $q_{\varvec{j}}^{(3)} = q_{\varvec{j}}$ for all $|j|>1$ and $a_{(0,1)}=b_{{(0,1)}}=b_{{(1,0})}=a_{(1,0)}>0$. Throughout this proof, we refer to states q such that $q_{(i,i',\chi )} = q_{(i',i,\chi )}$ for all $i,i' \in (0,\dots , N)$, $\chi \in \{+,-\}$ as symmetric.

We then proceed to transfer the amplitude from $a_{(1,1)}$ to $b_{(2,1)}, b_{(1,2)}$ by transforming q into another symmetric state $q'$ with ${(2,1,-)}, {(1,2,-)} \in \mathcal A(q')$ and $(1,1,+) \not \in \mathcal A(q')$. This can be done by letting triples $\iota (2) = {(1,0,-)}(1,1,+){(2,1,-)}\in \mathcal I$ and $\iota (3) = {(0,1,-)}(1,1,+){(1,2,-)}\in \mathcal I$ interact, and choosing the interaction times $\tau , \tau '(\tau )$ such that $\Phi _{\tau '(\tau )}^{\iota (3)}\circ \Phi _{\tau }^{\iota (2)}(q)_{(1,1 ,+)}=0$. Further, we note that the difference $b_{{(1,2)}}'-b_{{(2,1)}}'$ is negative for $\tau =0$, positive for $\tau '(\tau )=0$ and is continuous in $\tau$, so there must exist $\tau ^*$ such that $b_{{(1,2)}}'=b_{{(2,1)}}'$. To show that $q'$ is symmetric it only remains to show that $b_{{(1,0)}}' = b_{{(0,1)}}'$. This follows from the conservation laws:

$$\begin{aligned} B_{(1,0)(1,1)} \left( (b_{{(1,0)}}')^2-(b_{{(1,0)}})^2\right)&= B_{(2,1)(1,1)} (b_{{(2,1)}}')^2 = B_{(1,2)(1,1)} (b_{{(1,2)}}')^2\\&= B_{(0,1)(1,1)} \left( (b_{{(0,1)}}')^2-(b_{{(0,1)}})^2\right) \end{aligned}$$

where

$$\begin{aligned} B_{jk} :=\frac{1}{|j|^2} - \frac{1}{|k|^2}\,. \end{aligned}$$

Next, we let the triples $\iota (4) = (1,0,-)(0,1,+)(1,1,-)$ and $\iota (5) = (0,1,-)(1,0,+)(1,1,-)$ interact. By Lemma 6.12 there exists an interaction time such that the initial state $q'$ is mapped to $q''$ with $b_{{(1,0)}}'' = b_{{(0,1)}}'' = 0$ and $a_{{(1,0)}}'' = a_{{(0,1)}}'' > 0$, so that ${(1,0,-)}, {(0,1,-)}\not \in \mathcal A(q'')$.

We then proceed to transfer the amplitude from modes ${(1,2,-)}$ and ${(2,1,-)}$ to ${(2,2,-)}$. This is done letting triples $\iota (6) = (1,0,+){(1,2,-)}{(2,2,-)}$ and $\iota (7) = (0,1,+){(2,1,-)}{(2,2,-)}$ interact until the modes ${(2,1,-)},{(1,2,-)}$ are depleted, as proved in Lemma 6.11. The symmetry of the final state $q'''$ is again a consequence of the conservation laws:

$$\begin{aligned} B_{{(1,0)}{(2,2)}} \left( (a_{{(1,0)}}''')^2-(a_{{(1,0)}}'')^2\right)&= B_{{(2,1)}{(2,2)}} (b_{{(2,1)}}'')^2 = B_{{(1,2)}{(2,2)}} (b_{{(1,2)}}'')^2\\&= B_{{(0,1)}{(2,2)}} \left( (a_{{(0,1)}}''')^2-(a_{{(0,1)}}'')^2\right) \,. \end{aligned}$$

Summarizing, we have reached a symmetric state $q''' = \Phi _{\tau (7)}^{\iota (7)}\circ \dots \circ \Phi _{\tau (2)}^{\iota (2)}(q)$ with

$$\begin{aligned} \mathcal A(q''') = \{(1,0,+), (0,1,+), {(2,2,-)}, {(1,1,-)}, {(N,N,-)}\}\,. \end{aligned}$$

The desired result then follows immediately if we can show that we can transfer the amplitude of mode $(i-1,i-1,-)$ to $(i,i,-)$ for $i\in (2,\dots , N)$ while preserving the fact that $a_{(1,0)}' = a_{(0,1)}'$. We show this by considering, sequentially, the interaction triples

$$\begin{aligned}&\iota (4i) = (1,0,+)(i-1,i-1,-)(i,i-1,-)\,,\\&\iota (4i+1)=(0,1,+)(i-1,i-1,-)(i-1,i,-)\,,\\&\iota (4i+2)=(0,1,+)(i,i-1,-)(i,i,-)\,,\\&\iota (4i+3)=(1,0,+)(i-1,i,-)(i,i,-)\,. \end{aligned}$$

More specifically, we consider the family of endpoints

$$\begin{aligned} q''(t) = \Phi _{\tau _-^{\iota (4i+3)}}^{\iota (4i+3)}\circ \Phi _{\tau _-^{\iota (4i+2)}}^{\iota (4i+2)}\circ \Phi _{\tau _-^{\iota (4i+1)}}^{\iota (4i+1)}\circ \Phi _{t}^{\iota (4i)}(q')\,, \end{aligned}$$

where $\tau _-^{\iota }$ is defined in Lemma 6.11 (a). By construction, this sequence implies that $a_{(i-1,i-1)}''= a_{(i-1,i)}''= a_{(i,i-1)}''=0$ and $a_{(i,i)}''\ne 0$. It remains to prove that $a_{(1,0)}'' = a_{(0,1)}''$. As a composition of continuous functions, $q''(t)$ is continuous in t and therefore so is $\Delta q(t) = a_{(1,0)}''(t) - a_{(0,1)}''(t)$. Further, since by symmetry $a_{(1,0)}''(0) = a_{(0,1)}''(\tau _-^{\iota (4i)})$, we must have $\textrm{sign}( \Delta q(0)) = -\textrm{sign}(\Delta q(\tau _-^{\iota _1}))$. This implies the existence of $\tau (4i) \in [0,\tau _-^{\iota _1}]$ with $\Delta q(0)=0$, concluding the proof.$\square$