Topological Defects in Lattice Models and Affine Temperley–Lieb Algebra

Abstract

This paper is the first in a series where we attempt to define defects in critical lattice models that give rise to conformal field theory topological defects in the continuum limit. We focus mostly on models based on the Temperley–Lieb algebra, with future applications to restricted solid-on-solid (also called anyonic chains) models, as well as non-unitary models like percolation or self-avoiding walks. Our approach is essentially algebraic and focusses on the defects from two points of view: the “crossed channel" where the defect is seen as an operator acting on the Hilbert space of the models, and the “direct channel" where it corresponds to a modification of the basic Hamiltonian with some sort of impurity. Algebraic characterizations and constructions are proposed in both points of view. In the crossed channel, this leads us to new results about the center of the affine Temperley–Lieb algebra; in particular we find there a special basis with non-negative integer structure constants that are interpreted as fusion rules of defects. In the direct channel, meanwhile, this leads to the introduction of fusion products and fusion quotients, with interesting algebraic properties that allow to describe representations content of the lattice model with a defect, and to describe its spectrum.

Appendices

Proofs and Rigors

We collect in this appendix the proofs of certain technical results used in this work.

1.1 Topological defects with a higher spin

We show here how to obtain the expressions for topological defects with higher-spins given in Sect. 3.2, i.e.

$$\begin{aligned} Y_{j} = \textsf{U}_{2j} (Y/2). \end{aligned}$$

(147)

First we show that the result is independent of the choice of idempotent we make.

Let A be some finite dimensional $\mathbb {C}$-algebra, $\rho _{1}$, $\rho _{2}$ be two idempotents such that $A \rho _{1} \simeq A \rho _{2}$ as left A modules, and let F be any function defined on A such that for all $a,b \in A$, $F(ab) = F(ba)$ (in other words F is cyclic). We know that

$$\begin{aligned} \textsf{Hom}_{A}(A\rho _{1}, A \rho _{2}) \simeq \rho _{1}A\rho _{2}, \qquad \textsf{Hom}_{A}(A\rho _{2}, A \rho _{1}) \simeq \rho _{2}A\rho _{1}, \end{aligned}$$

(148)

where the isomorphism is obtained by right-multiplication. For instance,

$$\begin{aligned} (f: A\rho _{1} \rightarrow A\rho _{2}) \mapsto \rho _{1}f(\rho _{1}) \rho _{2}, \qquad \rho _{1}a\rho _{2} \mapsto (\underbrace{ b \rho _{1} \rightarrow b \rho _{1} a \rho _{2}}_{\in \textsf{Hom}_{A}(A\rho _{1}, A \rho _{2}) }). \end{aligned}$$

(149)

Because $A \rho _{1} \simeq A \rho _{2}$, it follows that there exists $a,b \in A$ such that $\rho _{1} a \rho _{2}$ gives the A-linear isomorphism $A \rho _{1} \rightarrow A \rho _{2}$ and $\rho _{2} b \rho _{1}$ gives the isomorphism $A\rho _{2} \rightarrow A\rho _{1}$. In particular, if $A \rho _{1}$ is irreducible this means that the compositions of the two isomorphisms applied to $\rho _1$ and $\rho _2$ are respectively $\rho _{1} a \rho _{2} b \rho _{1} = \alpha \rho _{1}$ and $\rho _{2} b \rho _{1} a \rho _{2} = \gamma \rho _{2}$ for some non-zero complex numbers $\alpha , \gamma$. However one quickly verifies that

$$\begin{aligned} \gamma ^{2} \rho _{2} = (\rho _{2}b \rho _1 a \rho _{2})^{2} = \rho _{2}b ( \rho _{1} a \rho _{2} b \rho _{1}) a \rho _{2} = \alpha \gamma \rho _{2}, \end{aligned}$$

so $\alpha = \gamma$ and we can thus choose a, b such that $\alpha = \gamma = 1$. Now by hypothesis the function F is cyclic and $\rho _{1}$ and $\rho _{2}$ are idempotents so

$$\begin{aligned} F(\rho _{1}) = F(\rho _{1} a \rho _{2} b \rho _{1}) = F(\rho _{2} b\rho _{1} a \rho _{2}) = F(\rho _{2}). \end{aligned}$$

(150)

Next, we remark that for any elements $a \in \textsf{TL}_{n}$, $b\in \textsf{TL}_{m}$, $Y^{n+m}(a \otimes ^{\textsf{TL}_{}} b) = Y^{n}(a)Y^{m}(b)$ where $\otimes ^{\textsf{TL}_{}}$ is the tensor product in the Temperley–Lieb category, obtained by joining diagrams side by side. For instance,

It follows in particular that for any idempotent $a\in \textsf{TL}_{n}$,

$$\begin{aligned} Y^{n+1}(a \otimes ^{\textsf{TL}_{}} \mathbb {I}_{\textsf{TL}_{1}}) = Y_{1/2} Y^{n}(a). \end{aligned}$$

(152)

Now if the idempotent a is such that $\textsf{TL}_{n}a \simeq \textsf{S}_{k/2}(n)$, one can show that there exists a decomposition of the idempotent $(a \otimes ^{\textsf{TL}_{}} \mathbb {I}_{\textsf{TL}_{1}}) = a_{-} + a_{+}$ in $\textsf{TL}_{n+1}$, where $a_{\pm }$ are orthogonal idempotents such that $\textsf{TL}_{n+1} a_{\pm } \simeq \textsf{S}_{(k \pm 1)/2}(n+1)$. This follows from the decomposition of the induced $\textsf{TL}_{n+1}$-module (see e.g. [12, 17]). We therefore have for generic values of $\mathfrak {q}$ the following relations:

$$\begin{aligned} Y_{(k+1)/2} = Y_{1/2}Y_{k/2} - Y_{(k-1)/2}, \qquad Y_{0} \equiv 1_{\textsf{aTL}_{n}}, \end{aligned}$$

(153)

which is the Chebyshev recurrence relation, giving (147).

1.2 The Jucys–Murphy elements

Here, we prove the identities (94) and (95) involving $C_{k}(n)$ and $\bar{C}_{k}(n)$ defined in (93). As the proofs for the identities involving Ms are identical to those involving the Js, we only prove the two identities involving $\bar{C}_{k}(n)$. The proof of this result relies on two key observations; the first is the identity

$$\begin{aligned}{}[i]_{k}(-\mathfrak {q})^{ \pm k} - [i-1]_{k} = (-\mathfrak {q})^{\pm k i}, \qquad i = 0, 1, \ldots . \end{aligned}$$

(154)

Furthermore, defining for $i = 1, \ldots , n-1$,

$$\begin{aligned} \bar{X}_{i+1}{} & {} \equiv (-\mathfrak {q})^{2} J_{i} + (-\mathfrak {q})^{-2} J_{i}^{-1},\end{aligned}$$

(155)

$$\begin{aligned} X_{i+1}{} & {} \equiv (-\mathfrak {q})^{2} M_{i} + (-\mathfrak {q})^{-2} M_{i}^{-1}, \end{aligned}$$

(156)

the second observation is that for all $i= 1, \ldots ,n -1$ we have the relations in $\textsf{aTL}_{n}(\mathfrak {q})$:

$$\begin{aligned} \bar{X}_{i+1}&= (-\mathfrak {q}) J_{i+1} + (-\mathfrak {q})^{-1} J_{i+1}^{-1} , \end{aligned}$$

(157)

$$\begin{aligned} X_{i+1}&= (-\mathfrak {q}) M_{i+1} + (-\mathfrak {q})^{-1} M_{i+1}^{-1} , \end{aligned}$$

(158)

$$\begin{aligned} Y&= (-\mathfrak {q})^{2} J_{n} + (-\mathfrak {q})^{-2} J_{n}^{-1} , \end{aligned}$$

(159)

$$\begin{aligned} \bar{Y}&= (-\mathfrak {q})^{2} M_{n} + (-\mathfrak {q})^{-2} M_{n}^{-1} . \end{aligned}$$

(160)

These can all be proven in the same way, by showing that both sides of these equality correspond to the same diagram. For instance

where we used the definition of the braids. Putting the two observations together gives the following relations, for all $i = 1, \ldots , n-1$,

where we used the fact that for all non-zero x

$$\begin{aligned} 2 \textsf{T}_{k}((x+x^{-1})/2) = x^{k} + x^{-k}. \end{aligned}$$

Then, it follows that

$$\begin{aligned} \bar{C}_{k}(n) + \bar{C}_{-k}(n)&= \sum _{i = 1}^{n}\left( ((-\mathfrak {q})^{i+1} J_{i})^{k} + ((-\mathfrak {q})^{i+1} J_{i})^{-k} \right) \\&= 2 [1]_{k} \textsf{T}_{k}(\bar{X}_{2}/2) + \sum _{i = 2}^{n}\left( ((-\mathfrak {q})^{i+1} J_{i})^{k} + ((-\mathfrak {q})^{i+1} J_{i})^{-k} \right) \\&= 2[2]_{k}\textsf{T}_{k}(\bar{X}_{3}/2) + \sum _{i = 3}^{n}\left( ((-\mathfrak {q})^{i+1} J_{i})^{k} + ((-\mathfrak {q})^{i+1} J_{i})^{-k} \right) \\&= 2[n]_{k} \textsf{T}_{k}(Y/2). \end{aligned}$$

Using very similar arguments, we have

$$\begin{aligned} ((-\mathfrak {q})^{i+1 - n} J_{i})^{k} + ((-\mathfrak {q})^{i+1-n} J_{i})^{-k}&= - [n-i]_{k}\left( ((-\mathfrak {q})^{2}J_{i})^{k} + ((-\mathfrak {q})^{2}J_{i})^{-k} \right) \\&\qquad + [n + 1 - i]_{k}\left( ((-\mathfrak {q})J_{i})^{k} + ((-\mathfrak {q})J_{i})^{-k} \right) \\&= 2[n + 1 - i]_{k} \textsf{T}_{k}(\bar{X}_{i}/2) - 2 [n-i]_{k} \textsf{T}_{k}(\bar{X}_{i+1}/2)\\ ((-\mathfrak {q})^{1} J_{n})^{k} + ((-\mathfrak {q})^{1} J_{n})^{-k}&= 2 \textsf{T}_{k}(\bar{X}_{n}/2), \end{aligned}$$

which give

$$\begin{aligned} (-\mathfrak {q})^{-n k }\bar{C}_{k}(n) + (-\mathfrak {q})^{n k }\bar{C}_{-k}(n)&= \sum _{i = 1}^{n}\left( ((-\mathfrak {q})^{i+1 - n} J_{i})^{k} + ((-\mathfrak {q})^{i+1- n} J_{i})^{-k} \right) \\&= 2[n+1-n]_{k} \textsf{T}_{k}(\bar{X}_{n}/2)\\&\quad + \sum _{i = 1}^{n-1}\left( ((-\mathfrak {q})^{i+1 - n} J_{i})^{k} + ((-\mathfrak {q})^{i+1- n} J_{i})^{-k} \right) \\&= 2 [n+1 - 1]_{k} \textsf{T}_{k}(\bar{X}_{1}/2) \equiv 2 [n]_{k} \textsf{T}_{k}(\bar{Y}/2), \end{aligned}$$

where we used the fact that $X_{1} \equiv \bar{Y}$ by definition.

1.3 Fusion with standard modules

We explain here how to compute the fusion product/quotient of standard modules. The final results from Propositions 4.1 and 4.3 rely on two key facts:

• 1. Fusions of the same type (u/o) are associative (see (126) and (127)), i.e. for any $\textsf{aTL}_{}$-module $\textsf{M}$, and $\textsf{TL}_{}$-modules $\textsf{V}_1$, $\textsf{V}_2$, we have isomorphisms

  $$\begin{aligned} \big ( \textsf{M} \times ^{u/o}_f \textsf{V}_1 \big )\times ^{u/o}_f \textsf{V}_2 \simeq \textsf{M} \times ^{u/o}_f \big ( \textsf{V}_1 \times _f \textsf{V}_2 \big ), \end{aligned}$$

  (162)
  $$\begin{aligned} \big ( \textsf{M} \div ^{u/o}_f \textsf{V}_1 \big ) \div ^{u/o}_f \textsf{V}_2 \simeq \textsf{M} \div ^{u/o}_f \big ( \textsf{V}_1 \times _f \textsf{V}_2 \big ). \end{aligned}$$

  (163)

• 2. For any $t \in \mathbb {N}$ and for generic $\mathfrak {q}$:

  $$\begin{aligned} \textsf{S}_{t/2}(n) \times _f \textsf{S}_{0}(2) \simeq \textsf{S}_{t/2}(n+2), \end{aligned}$$

  (164)
  $$\begin{aligned} \textsf{S}_{t/2}(n) \times _f \textsf{S}_{1/2}(1) \simeq \textsf{S}_{(t-1)/2}(n+1) \oplus \textsf{S}_{(t+1)/2}(n+1) , \end{aligned}$$

  (165)

  where it is understood that $\textsf{S}_{(-1)/2}(n+1) \equiv 0$.

Putting these two facts together, it follows that if we can compute the fusions of $\textsf{aTL}_{}$-modules with $\textsf{S}_{0}(2)$ and $\textsf{S}_{1}(1)$, fusions with $\textsf{S}_{t/2}(m)$, $t \ge 0, m \ge 1$ can be computed easily by recurrence. In this appendix, we thus present how these four necessary fusions are calculated.

1.3.1 $\textsf{W}_{k,z}(n+2) \div ^{u/o}_f \textsf{S}_{0}(2)$

Assuming that $\mathfrak {q}^{2} \ne -1$, the primitive idempotent corresponding to the projective module $\textsf{S}_{0}(2)$ is $\rho _{0} \equiv (\mathfrak {q}+\mathfrak {q}^{-1})^{-1} e_{1}$. According to our definition of the fusion quotient, we must consider the subspace $W_{0} \equiv \rho _{0}\textsf{W}_{k,z}(n+2)$ with the action of $\textsf{aTL}_{n}$ obtained from the morphism of algebras $\phi ^{u/o}_{n,2}$; however, in this case there is a map $\psi : \textsf{W}_{k,z}(n) \rightarrow W_{0}$ which consists in adding two positions linked with an arc on the right of every diagram in $\textsf{W}_{k,z}(n)$, for instance

One sees directly that this map defines a morphism of modules, and that the resulting sub-module of $W_{0}$ is the same for both types of fusion. Furthermore, any diagram in $\textsf{W}_{k,z}(n+2)$ is sent to one of the form $\psi (x)$ by the action of the idempotent $\rho _{0}$, so this morphism is surjective. Because the map $\psi$ is obviously injective as well, it must be an isomorphism and we thus get

$$\begin{aligned} \textsf{W}_{k,z}(n+2) \div ^{u/o}_{f} \textsf{S}_{0}(2) \simeq \textsf{W}_{k,z}(n), \end{aligned}$$

(167)

where it is understood that $k \le n/2$ because otherwise the $e_{n+1}$ would acts as zero on $\textsf{W}_{k,z}(n+2)$.

1.3.2 $\textsf{W}_{k,z}(n) \times _{f}^{u/o} \textsf{S}_{0}(2)$

Because both $\textsf{W}_{k,z}(n)$ and $\textsf{S}_{0}(2)$ are cyclic, so is their fusion product; in particular one can write $\textsf{W}_{k,z}(n) \times _{f}^{u/o} \textsf{S}_{0}(2) = \textsf{aTL}_{n+2}x$ with

We also recall our diagram notation for the fusion product: the diagram at the top is the element of $\textsf{aTL}_{n+2}$, the one on the bottom left corner is the element of $\textsf{W}_{k,z}(n)$, and the one on the bottom right corner is the element of $\textsf{S}_{0}(2)$. Note that closing together any of the through lines in the top diagram of x will yield the zero element, because it will be able to pass through the tensor product. It follows that this fusion product is isomorphic to a standard module of the form $\textsf{W}_{k,z'}(n+2)$ for some $z'$. Note also that because of the duality between the two types of fusion

$$\begin{aligned}{} & {} \text {Hom}_{\textsf{aTL}_{n+2}}\left( \textsf{W}_{k,z}(n) \times _{f}^{u/o} \textsf{S}_{0}(2), \textsf{W}_{k,z}(n+2)\right) \nonumber \\{} & {} \quad \simeq \text {Hom}_{\textsf{aTL}_{n}}\big (\textsf{W}_{k,z}(n) , \underbrace{\textsf{W}_{k,z}(n+2)\div _{f}^{u/o} \textsf{S}_{0}(2)}_{\simeq \textsf{W}_{k,z}(n)} \big ) \simeq \mathbb {C}, \end{aligned}$$

(169)

so we conclude that $z' = z$, and thus

$$\begin{aligned} \textsf{W}_{k,z}(n) \times _{f}^{u/o} \textsf{S}_{0}(2) \simeq \textsf{W}_{k,z}(n+2). \end{aligned}$$

(170)

1.3.3 $\textsf{W}_{k,z}(n+1) \div ^{u/o}_{f} \textsf{S}_{1/2}(1)$, ($k \ne 0$)

Both types of fusion are very similar so we focus on the u-type. The primitive idempotent corresponding to $\textsf{S}_{1/2}(1)$ is simply the identity so the fusion quotient is the full restriction of $\textsf{W}_{k,z}(n+1)$. There is then a map $\psi : \textsf{W}_{k-1/2,z'}(n) \rightarrow \textsf{W}_{k,z}(n+1)$ which consists in adding a single position on the right of every diagram in $\textsf{W}_{k-1/2,z'}(n)$ and adding a through line to it which passes under every other line. For instance,

One can see that this map (extended linearly) indeed defines an injective morphism of $\textsf{aTL}_{n}$ module if $z' = (-\mathfrak {q})^{1/2}z$; this condition on z can be seen by observing that

Next, consider the map $\phi : \textsf{W}_{k,z}(n+1) \rightarrow \textsf{W}_{k+1/2,z(-\mathfrak {q})^{-1/2}}(n+2)$, defined by $\phi = (\mathfrak {q}+\mathfrak {q}^{-1})^{-1}e_{n+1}\psi$. In other words we add an extra through line, going under all others, at the right of each diagram in $\textsf{W}_{k,z}(n+1)$ then multiply the result by the idempotent $(\mathfrak {q}+\mathfrak {q}^{-1})^{-1}e_{n+1}$. For instance, we get

Based on the previous results of this section, we recognize the the image of this map is $\textsf{W}_{k+1/2,z(-\mathfrak {q})^{-1/2}}(n+2) \div _{f}^{u} \textsf{S}_{0}(2) \simeq \textsf{W}_{k+1/2,z(-\mathfrak {q})^{-1/2}}(n)$. It can then be shown that this map (extended linearly) defines a surjective morphism of $\textsf{aTL}_{n}$ modules. Furthermore, one can see that the image of the first map $\psi$ is contained in the kernel of the second map $\phi$:

where we used the fact that diagrams with less than k/2 through lines are equivalent to the zero element in $\textsf{W}_{k,z}(n)$.

Finally, note that

$$\begin{aligned}{} & {} \textsf{Dim}(\textsf{W}_{k,z}(n+1) \div ^{u}_{f} \textsf{S}_{1}(1))\nonumber \\ {}{} & {} \quad = \underbrace{\textsf{Dim}(\textsf{W}_{k,z}(n+1))}_{\left( {\begin{array}{c}n+1\\ (n+1)/2 - k\end{array}}\right) } = \underbrace{\textsf{Dim}(\textsf{W}_{k-1/2,z'}(n))}_{\left( {\begin{array}{c}n\\ (n+1)/2 - k\end{array}}\right) } + \underbrace{\textsf{Dim}(\textsf{W}_{k+1/2,z''}(n))}_{\left( {\begin{array}{c}n\\ (n-1)/2 - k\end{array}}\right) }, \end{aligned}$$

(175)

so the image of $\psi$ is exactly the kernel of $\phi$. Since the eigenvalues of $\bar{Y}$ are different on $\textsf{W}_{k\pm 1/2,z(-\mathfrak {q})^{\mp 1/2}}(n)$, if z is generic, it follows that

$$\begin{aligned} \textsf{W}_{k,z}(n+1) \div ^{u}_{f} \textsf{S}_{1/2}(1) \simeq \textsf{W}_{k- 1/2,z(-\mathfrak {q})^{ 1/2}}(n) \oplus \textsf{W}_{k+ 1/2,z(-\mathfrak {q})^{- 1/2}}(n). \end{aligned}$$

(176)

What about when z is not generic? The eigenvalues of $\bar{Y}$ will be the same on the modules appearing in the previous direct sum if and only if $(-\mathfrak {q})^{2} = 1$ or $z^{2} = (-\mathfrak {q})^{k/2}$; one can verify directly that $\bar{Y}$ has a Jordan block when acting on the fusion quotient only in the later case. This can be seen by taking any $x \in \textsf{W}_{k,z}(n+1) \div ^{u}_{f} \textsf{S}_{1/2}(1)$ that is not in the kernel of $\phi$ and verifying that $(\bar{Y}- \lambda )x \ne 0$, where $\lambda$ is the eigenvalue of $\bar{Y}$ on $\textsf{W}_{k+1/2,z(-\mathfrak {q})^{-1/2}}(n)$. The modules appearing in the fusion quotient is then the indecomposable extension of two standard modules; while these are not yet classified, we shall show that they are indeed unique in our forthcoming work.

1.3.4 $\textsf{W}_{k,z}(n+1) \times ^{u/o}_{f} \textsf{S}_{1/2}(1)$, ($k \ne 0$)

Both types of fusion are very similar so we again focus on the u-type. Since standard modules are always cyclic, so is their fusion and $\textsf{W}_{k,z}(n) \times ^{u}_{f} \textsf{S}_{1/2}(1) = \textsf{aTL}_{n+1}x$ with

The module can be decomposed by defining diagrams

$$\begin{aligned} v_{+} = e_{2k+2}e_{2k+4} \ldots e_{n}, \qquad v_{-} = e_{2k}e_{2k+2}\ldots e_{n}. \end{aligned}$$

(178)

These were chosen such that

One verifies easily that $\textsf{aTL}_{n+1}v_{-}x$ is a sub-module: any diagram acting on $v_{-}x$ will either contract two (or more) through lines together or shuffle around the arcs on the bottom boundary. However, the former will be trivial because, for instance,

where we used the definition of the tensor product, and the definition of the standard modules. We thus conclude that $\textsf{aTL}_{n+1}v_{-}x$ is a sub module isomorphic to $\textsf{W}_{k-1/2 , z'} (n+1)$ for some $z'$, where the isomorphism is obtained by simply cutting off the top of the diagrams, i.e.

To find $z'$ we use the duality between the two fusion (125):

$$\begin{aligned}&\text {Hom}_{\textsf{aTL}_{n+1}}\left( \textsf{W}_{k,z}(n) \times _{f}^{u} \textsf{S}_{\frac{1}{2}}(1), \textsf{W}_{k-\frac{1}{2},z'}(n+1)\right) \\&\quad \simeq \text {Hom}_{\textsf{aTL}_{n}}\big (\textsf{W}_{k,z}(n) , \underbrace{\textsf{W}_{k-\frac{1}{2},z'}(n+1)\div _{f}^{u} \textsf{S}_{\frac{1}{2}}(1)}_{\simeq \textsf{W}_{k,z' (-\mathfrak {q})^{-1/2}}(n) \oplus \textsf{W}_{k-1,z' (-\mathfrak {q})^{1/2}}(n)}\!\!\!\big )\\&\quad \simeq \delta _{z, z' (-\mathfrak {q})^{-\frac{1}{2}}}\mathbb {C}, \end{aligned}$$

so it follows that $z' = z (-\mathfrak {q})^{1/2}$.

Note now that acting on $v_{+}x$ with some diagram a can do two things: it can shuffle the arcs on the bottom boundary, and it can close pairs of through lines. One can verify that closing the two rightmost through lines together will produce an element of the form $a v_{-}x$, and the same thing happens when closing the leftmost line with the rightmost one. To see this last assertion, observe that in $\textsf{W}_{k,z}$

it thus follows that

where we used the closed braid identity

Repeating the arguments leading to the identification of $\textsf{aTL}_{n+1}v_{-}x$, we finally obtain

$$\begin{aligned} (\textsf{W}_{k,z}(n) \times _{f}^{u} \textsf{S}_{1/2}(1))/(\textsf{aTL}_{n+1}v_{-}x)= & {} \textsf{aTL}_{n+1}(v_{+}x + \textsf{aTL}_{n+1}v_{-}x)\nonumber \\ {}\simeq & {} \textsf{W}_{k+1/2,z (-\mathfrak {q})^{-1/2}}(n+1). \end{aligned}$$

(185)

To complete the decomposition, we need to figure out if this quotient splits, i.e. if the fusion product is the direct sum of two standard modules, or if it’s their indecomposable extension. However, if z is generic then $\bar{Y}$ has distinct eigenvalues on $\textsf{W}_{k \pm 1/2, z (-\mathfrak {q})^{\mp 1/2}} (n+1)$ so the quotient must split, and thus

$$\begin{aligned} \textsf{W}_{k,z}(n) \times _{f}^{u} \textsf{S}_{1/2}(1) \simeq \textsf{W}_{k-1/2,z(-\mathfrak {q})^{1/2}}(n+1) \oplus \textsf{W}_{k+1/2,z(-\mathfrak {q})^{-1/2}}(n+1). \end{aligned}$$

(186)

If $z^{2} = (-\mathfrak {q})^{k}$ then the quotient does not split and the fusion product is then the indecomposable extension of the two standard modules appearing in the previous direct sum.

1.3.5 $\textsf{W}_{0,z}(n) \times ^{u}_{f} \textsf{S}_{{1/2}}(1)$

By the results in the previous sections and associativity of the fusion product (126), we know that

$$\begin{aligned} \textsf{W}_{0,z}(2m) \times ^{u}_{f} \textsf{S}_{1/2}(1)&\simeq (\textsf{W}_{0,z}(2) \times ^{u}_{f} \textsf{S}_{0}(2(m-1)))\times ^{u}_{f} \textsf{S}_{1/2}(1)\\&\simeq (\textsf{W}_{0,z}(2) \times ^{u}_{f} \textsf{S}_{1/2}(1))\times ^{u}_{f} \textsf{S}_{0}(2(m-1)), \end{aligned}$$

so we focus on the case $n=2$ and the other cases will follow directly from it. Using the same reasoning as in the $k\ne 0$ cases, we find that $\textsf{W}_{0,z}(2) \times ^{u}_{f} \textsf{S}_{1/2}(1) = \textsf{aTL}_{3}x$, with

Now acting on x with any diagram can only move around the arc at the bottom of x, so the fusion product is generated by elements of the form $u^{i}x$ for $i \in \mathbb {Z}$. However,

Since by construction $Y x = (z+z^{-1})x$, it follows that $(u^{3} - (-\mathfrak {q})^{-1/2}z)(u^{3} - (-\mathfrak {q})^{-1/2}z^{-1})x = 0$, and thus that the fusion product has dimension six. Furthermore, if $z^{2} \ne 1$ then $u^{3}$ must have the two eigenvalues $(-\mathfrak {q})^{-1/2}z^{\pm 1}$ so

$$\begin{aligned} \textsf{W}_{0,z}(2) \times ^{u}_{f} \textsf{S}_{1/2}(1) \simeq \textsf{W}_{1/2,(-\mathfrak {q})^{-1/2}z}(3) \oplus \textsf{W}_{1/2,(-\mathfrak {q})^{-1/2}z^{-1}}(3). \end{aligned}$$

(189)

Note that if $z^{2} = 1$ then the two standard modules $\textsf{W}_{1/2,(-\mathfrak {q})^{-1/2}z^{\pm 1}}(3)$ are isomorphic, and one can show that the fusion product is then the self-extension of $\textsf{W}_{1/2,(-\mathfrak {q})^{-1/2}z }(3)$.

1.3.6 $\textsf{W}_{0,z}(n+1) \div ^{u/o}_{f} \textsf{S}_{1/2}(1)$

Here again the two fusion types are similar so we focus only on the u-type. Here we must restrict to z generic right from the start; it is possible to present a unified proof for the z generic or not cases, but doing so requires more sophisticated tools which we haven’t introduced here. We thus start by noticing that

$$\begin{aligned}&\text {Hom}_{\textsf{aTL}_{n}} \big ( \textsf{W}_{k,z'}(n), \textsf{W}_{0,z}(n+1) \div ^{u}_{f} \textsf{S}_{1/2}(1)\big )\\ {}&\quad \simeq \text {Hom}_{\textsf{aTL}_{n+1}} \big ( \textsf{W}_{k,z'}(n) \times ^{u}_{f} \textsf{S}_{1/2}(1), \textsf{W}_{0,z}(n+1)\big )\\&\quad \simeq \delta _{k,1/2}(\delta _{z',(-\mathfrak {q})^{1/2} z^1}+\delta _{z',(-\mathfrak {q})^{1/2} z^{-1}}) \mathbb {C}, \end{aligned}$$

where we used the duality between the fusion product and the fusion quotient together with the formulas for the fusion product of standard modules obtained in the previous section. Furthermore, for generic values of z the standard modules $\textsf{W}_{1/2,(-\mathfrak {q})^{1/2}z^{\pm 1}}(n)$ are simple and non-isomorphic, so these morphisms must be injective. Finally, we have

$$\begin{aligned} \underbrace{\text {Dim}(\textsf{W}_{0,z}(n+1))}_{\left( {\begin{array}{c}n+1\\ (n+1)/2\end{array}}\right) } = 2 \underbrace{\text {Dim}(\textsf{W}_{1/2,z'}(n))}_{\left( {\begin{array}{c}n\\ (n-1)/2\end{array}}\right) }, \end{aligned}$$

(190)

and we thus conclude that

$$\begin{aligned} \textsf{W}_{0,z}(n+1)\div ^{u}_{f}\textsf{S}_{1/2}(1) \simeq \textsf{W}_{1/2,z(-\mathfrak {q})^{1/2}}(n) \oplus \textsf{W}_{1/2,z^{-1}(-\mathfrak {q})^{1/2}}(n). \end{aligned}$$

(191)

Comparison with the Other Fusion Types

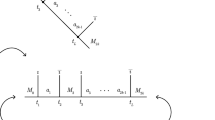
We discuss briefly how the defect operators—the hoop elements Y and $\bar{Y}$—introduced in this work behave with respect to the various previously defined fusion products, in particular the one introduced by Gainutdinov and Saleur in [13] and the one introduced by Belletête and Saint-Aubin [16].

1.1 The GS fusion

For this fusion, we endow $\textsf{aTL}_{n+m}$ (n, m positive integers) with the structure of a left $(\textsf{aTL}_{n},\textsf{aTL}_{m})$ module through the injection $\Phi \equiv \phi ^{u}_{n,m} \otimes \psi ^{o}_{m,n} : \textsf{aTL}_{n} \otimes \textsf{aTL}_{m} \rightarrow \textsf{aTL}_{n+m}$. In terms of diagrams, this corresponds to gluing the two cylinders on which $\textsf{aTL}_{n}$ and $\textsf{aTL}_{m}$ lives into a pair of pants; Fig. 7 illustrates how the hoop operators behave under this gluing.

Fig. 7

The behaviour of the hoop operators under the fusion product

Given an $\textsf{aTL}_{n}$-module U and an $\textsf{aTL}_{m}$-module V, their fusion is defined as

$$\begin{aligned} U \times _{GS} V \equiv \textsf{aTL}_{n+m} \otimes _{\textsf{aTL}_{n} \otimes \textsf{aTL}_{m}} U \otimes _{\mathbb {C}} V. \end{aligned}$$

(192)

Note that by construction (see Figs. 7a and 7b)

$$\begin{aligned} Y^{(n+m)} = \phi ^{u}_{n,m}(Y^{(n)}), \qquad \bar{Y}^{(n+m)} = \psi ^{o}_{m,n}(\bar{Y}^{(m)}), \end{aligned}$$

(193)

so that eigenvalues of the central elements Y, $\bar{Y}$ on $U \times _{GS} V$ are fully determined from their value on U and V, respectively. It follows in particular that this fusion product is not commutative in general. Furthermore, the construction also gives (see Fig. 7c)

$$\begin{aligned} \phi ^{u}_{n,m}(\bar{Y}^{(n)}) = \psi ^{o}_{m,n}(Y^{(m)}), \end{aligned}$$

(194)

which imposes severe constraints on the combinations of modules leading to non-trivial fusion products.

To illustrate just how restrictive equations (193) and (194) are, we compute the fusion of two standard modules $U \simeq \textsf{W}^{u}_{r,\delta }$, and $V \simeq \textsf{W}^{o}_{s,\mu }$. First, equation (194) imposes $\mu = \delta ^{\pm 1}$. Second, if the fusion product is non-zero then it must have at least one non-trivial simple quotient¹⁹ and, for generic values of $\mathfrak {q}$ and $\delta$, all of the simple modules of $\textsf{aTL}_{n}$ are isomorphic to standard modules $\textsf{W}^{o}_{k,\nu }$ for some integer k and $\nu \in \mathbb {C}^{*}$. Combining this observation with equation (193) gives the conditions

$$\begin{aligned} \nu = (\delta (-\mathfrak {q})^{2r})^{\pm 1}, \qquad \text { and } \qquad \nu = (\mu (-\mathfrak {q})^{-2s})^{ \pm 1}(-\mathfrak {q})^{2k}, \end{aligned}$$

(195)

where all the ± are independent. In the generic cases where $\delta ^{2}$ is not an integer power of $(-\mathfrak {q})$, and $\mathfrak {q}$ is not a root of unity, this leaves the possibilities:

$$\begin{aligned} k = (r + \epsilon s), \qquad \delta = \mu ^{\epsilon }, \end{aligned}$$

(196)

or, using a more usual notation

$$\begin{aligned} \textsf{W}_{r,z}(n) \times _{GS} \textsf{W}_{s,w}(m) \simeq {\left\{ \begin{array}{ll} a_{+} \textsf{W}_{r+s,z (-\mathfrak {q})^{-s}}(n) &{} \text { if } z = w (-\mathfrak {q})^{r + s}\\ a_{-} \textsf{W}_{r-s,z (-\mathfrak {q})^{s}}(n) &{} \text { if } z = w^{-1} (-\mathfrak {q})^{r - s}\\ 0 &{} \text {otherwise} \end{array}\right. }, \end{aligned}$$

(197)

where $a_{\pm }$ are (unknown) non-negative integers (because each module could appear multiple times) and it is understood that if $s>r$, $\textsf{W}_{r-s,z (-\mathfrak {q})^{s}}(n) \equiv \textsf{W}_{s-r, z^{-1} (-\mathfrak {q})^{-s}}(n)$. It therefore simply remains to find the value of $a_{\pm }$; more extensive calculations [13] yields $a_{\pm } = 1$.

1.2 The BSA fusion

For this fusion, we endow $\textsf{aTL}_{n+m}$ (n, m positive integers) with the structure of a left $(\textsf{TL}_{n},\textsf{TL}_{m})$ module through the injection $\Phi \equiv \phi ^{u}_{n,m} \otimes \psi ^{o}_{m,n} : \textsf{TL}_{n} \otimes \textsf{TL}_{m} \rightarrow \textsf{aTL}_{n+m}$, where we identified the regular algebras with their images inside the affine algebra. In terms of diagrams, this corresponds to taking the two strips on which the regular algebras live and stitching them into a cylinder, introducing no particular relations for the hoop operators. Given U, V a $\textsf{TL}_{n}$ and a $\textsf{TL}_{m}$ module, respectively, their fusion is defined as

$$\begin{aligned} U \times _{BSA} V \equiv \textsf{aTL}_{n+m} \otimes _{\textsf{TL}_{n} \otimes \textsf{TL}_{m}} U \otimes _{\mathbb {C}} V. \end{aligned}$$

(198)

Note that because no relations were introduced for the hoop operators, the fusion of any non-zero module is always infinite dimensional. For the particular case of standard modules (and $\mathfrak {q}$ generic), one finds [16]

$$\begin{aligned} \textsf{S}_{r} \times _{BSA} \textsf{S}_{s} \simeq \bigoplus _{k = |r-s|}^{r+s} \textsf{P}_{k}, \end{aligned}$$

(199)

where the $\textsf{P}_{k}$ are the projective indecomposable modules of the affine Temperley–Lieb algebra. The algebraic structure of these modules is quite complicated and described in some details in [16]. We simply mention that there is a family of inclusions $\textsf{P}_{k} \subset \textsf{P}_{k+2} \subset \textsf{P}_{k+4} \subset \ldots$ that is such that $\textsf{P}_{k}/\textsf{P}_{k-2}$ is an indecomposable submodule of the direct product of the standard modules $\textsf{W}_{k,z}$ for all non-zero z. In other (more heuristic) words, $\textsf{P}_{k}$ is an indecomposable collage of all $\textsf{W}_{r,z}$ with $r \le k$, $z \in \mathbb {C}^{*}$.

C Alternative Proof of the Relations (114)–(115)

We first establish the branching rules from $\textsf{aTL}_{n_1+n_2}$ to $\textsf{aTL}_{n_1} \otimes \textsf{TL}_{n_2}$, by an adaptation of the working of [14] that dealt with the case of $\textsf{aTL}_{n_1} \otimes \textsf{aTL}_{n_2}$. The algebras $\textsf{aTL}_{n_1}$ and $\textsf{TL}_{n_2}$ can be embedded into $\textsf{aTL}_{n}$ on $n = n_1 + n_2$ sites, by defining the periodic generator $e_0^{(1)}$ and the shift operator $u^{(1)}$ for the first subalgebra by braid translation in $\textsf{aTL}_{n}$ (see [14]), while all other generators simply carry over.

Using the techniques of [14], and in particular the operator $\tau _j^{(1)}$ defined there, we then find the branching rules (actually, one has just to restrict the second tensor factor in branching rules of [14] to the subalgebra $\textsf{TL}_{n_2}\subset \textsf{aTL}_{n_2}$)

$$\begin{aligned} \textsf{W}_{j,z}(n)|_{\textsf{aTL}_{n_1} \otimes \textsf{TL}_{n_2}} \cong \bigoplus _{j_1,j_2} \textsf{W}_{j_1,z_1}(n_1) \otimes \left( \bigoplus _{k \ge j_2} \textsf{S}_{k}(n_2) \right) \,, \end{aligned}$$

(200)

with the following values of the momenta:

• For $j = j_1 + j_2$ and any values of $j_1,j_2$: $z_1 = (i \sqrt{\mathfrak {q}})^{-2 j_2} z^{+1}$.

• For $j = j_1 - j_2$ and either $j=0$ or $j_2 > 0$: $z_1 = (i \sqrt{\mathfrak {q}})^{+2 j_2} z^{+1}$.

• For $j = j_2 - j_1$ and either $j=0$ or $j_1 > 0$: $z_1 = (i \sqrt{\mathfrak {q}})^{+2 j_2} z^{-1}$.

Notice that this closely parallels the main result of [14], the only difference being that the right tensorands $\textsf{W}_{j_2,z_2}$ there have been repaced by $\bigoplus _{k \ge j_2} \textsf{S}_{k}$, which is exactly the restriction of $\textsf{W}_{j_2,z_2}$ to the subalgebra $\textsf{TL}_{n_2}\subset \textsf{aTL}_{n_2}$. In particular, these modules have the same dimensions.

We can now read off the corresponding fusion rules by Frobenius reciprocity:

$$\begin{aligned}{} & {} \text {Hom}_{\textsf{aTL}_{n + m}}\big ( \textsf{W}_{k,w}(n) \times _{f} \textsf{S}_{j}(m), \textsf{W}_{j,z}(n+m) \big )\\ {}{} & {} \quad \simeq \text {Hom}_{\textsf{aTL}_{n} \otimes \textsf{TL}_{m}}\big ( \textsf{W}_{k,w}(n) \otimes \textsf{S}_{j}(m), \textsf{W}_{j,z}(n+m) \big ), \end{aligned}$$

where on the right side of the equation $\textsf{W}_{j,z}(n+m)$ is seen as a $\textsf{aTL}_{n} \otimes \textsf{TL}_{m}$-module, i.e. is identified with the branching rules (200). If $\mathfrak {q}$ and z are generic, the standard modules $\textsf{W}_{j,z}(n+m)$ are simple, so the dimension of this homomorphism group is the number of copies of the standard module appearing as direct summands of the fusion product.²⁰ There is however a slight subtlety in computing these dimensions, which is conveniently illustrated in the example $(n_1,n_2,n) = (2,4,6)$. The branching rules read in this case

$$\begin{aligned} \textsf{W}_{0,z}(6)= & {} \textsf{W}_{0,z}(2) \otimes \big (\textsf{S}_{2}(4) \oplus \textsf{S}_{1}(4) \oplus \textsf{S}_{0}(4)\big ) \oplus \nonumber \\{} & {} \textsf{W}_{1,(i \sqrt{\mathfrak {q}})^2 z}(2) \otimes \big (\textsf{S}_{2}(4) \oplus \textsf{S}_{1}(4)\big ) \oplus \textsf{W}_{1,\frac{(i \sqrt{\mathfrak {q}})^2}{z}}(2) \otimes \big (\textsf{S}_{2}(4) \oplus \textsf{S}_{1}(4)\big ) \,, \nonumber \\ \textsf{W}_{1,z}(6)= & {} \textsf{W}_{0,\frac{z}{(i \sqrt{\mathfrak {q}})^2}}(2) \otimes \big (\textsf{S}_{2}(4) \oplus \textsf{S}_{1}(4)\big ) \oplus \nonumber \\{} & {} \textsf{W}_{1,z}(2) \otimes \big (\textsf{S}_{2}(4) \oplus \textsf{S}_{1}(4) \oplus \textsf{S}_{0}(4)\big ) \oplus \textsf{W}_{1,\frac{(i \sqrt{\mathfrak {q}})^4}{z}}(2) \otimes \textsf{S}_{2}(4) \,, \nonumber \\ \textsf{W}_{2,z}(6)= & {} \textsf{W}_{0,\frac{z}{(i \sqrt{\mathfrak {q}})^4}}(2) \otimes \textsf{S}_{2}(4) \oplus \textsf{W}_{1,\frac{z}{(i \sqrt{\mathfrak {q}})^2}}(2) \otimes \big (\textsf{S}_{2}(4) \oplus \textsf{S}_{1}(4)\big ) \nonumber \\ \textsf{W}_{3,z}(6)= & {} \textsf{W}_{1,\frac{z}{(i \sqrt{\mathfrak {q}})^4}}(2) \otimes \textsf{S}_{2}(4) \,. \end{aligned}$$

(201)

At first sight it appears that one would have fusion rules like

$$\begin{aligned} \textsf{W}_{0,z} \times _{f}\textsf{S}_{1}= & {} \textsf{W}_{0,z} \oplus \textsf{W}_{1,(-\mathfrak {q})z} \,,\nonumber \\ \textsf{W}_{0,z} \times _{f}\textsf{S}_{2}= & {} \textsf{W}_{0,z} \oplus \textsf{W}_{1,(-\mathfrak {q})z} \oplus \textsf{W}_{2,(-\mathfrak {q})^2 z} \,. \end{aligned}$$

(202)

This is however not quite correct. Indeed, we should be careful when the left tensorand in the fusion product is $\textsf{W}_{0,z}$, since we have to take into account the isomorphism $\textsf{W}_{0,z} \simeq \textsf{W}_{0,z^{-1}}$. Therefore the corresponding terms in the branching rules (201) can also be written

$$\begin{aligned} \textsf{W}_{1,z}(6)= & {} \textsf{W}_{0,\frac{(i \sqrt{\mathfrak {q}})^2}{z}}(2) \otimes \big (\textsf{S}_{2}(4) \oplus \textsf{S}_{1}(4)\big ) \oplus \ldots \,, \nonumber \\ \textsf{W}_{2,z}(6)= & {} \textsf{W}_{0,\frac{(i \sqrt{\mathfrak {q}})^4}{z}}(2) \otimes \textsf{S}_{2}(4) \oplus \ldots \,. \end{aligned}$$

(203)

This implies that we have a few extra terms, and (202) should be corrected into

$$\begin{aligned} \textsf{W}_{0,z} \times _{f}\textsf{S}_{1}= & {} \textsf{W}_{0,z} \oplus \textsf{W}_{1,(-\mathfrak {q})z} \oplus \textsf{W}_{1,(-\mathfrak {q}) z^{-1}} \,, \\ \textsf{W}_{0,z} \times _{f}\textsf{S}_{2}= & {} \textsf{W}_{0,z} \oplus \textsf{W}_{1,(-\mathfrak {q})z} \oplus \textsf{W}_{2,(-\mathfrak {q})^2 z} \oplus \textsf{W}_{1,(-\mathfrak {q}) z^{-1}} \oplus \textsf{W}_{2,(-\mathfrak {q})^2 z^{-1}} \,. \end{aligned}$$

Taking into account this subtlety, the general result comes out as

$$\begin{aligned} \textsf{W}_{j_1,z} \times _{f}\textsf{S}_{j_2} = \bigoplus _{j=\textrm{max}(j_1-j_2,j_{12}^\star )}^{j_1+j_2} \textsf{W}_{j,(-\mathfrak {q})^{j-j_1} z} \oplus \bigoplus _{j=j_{21}^\star }^{j_2-j_1} \textsf{W}_{j,(-\mathfrak {q})^{j+j_1} z^{-1}} \,, \end{aligned}$$

(204)

where we have defined $j_{12}^\star = (j_1 - j_2) \text{ mod } 1$, and $j_{21}^\star = (j_2 - j_1) \text{ mod } 1$. After some amount of rewriting, this can be shown to lead to (114)–(115) in the main text, as claimed.

D Finding the Basis in (105) to (107)

We explain here how we arrived at the basis of $\textsf{W}_{1/2,z}(3) \times ^{o}_{f} \textsf{S}_{1/2}(1) = \textsf{aTL}_{4}x$ shown in Sect. 4.1. The general procedure can be used to find bases of the fusion product of arbitrary standard modules, but the calculations quickly become very difficult to track when the size of the modules increases.

Recall that since $\textsf{W}_{1/2,z}(3)$ and $\textsf{S}_{1/2}(1)$ are both cyclic, so is their fusion, and we can thus write $\textsf{W}_{1/2,z}(3) \times ^{o}_{f} \textsf{S}_{1/2}(1) = \textsf{aTL}_{4}y$ with

To start, observe that

It thus follows that $e_2e_1 y = y$, and thus, when looking for a basis of $\textsf{W}_{1/2,z}(3) \times ^{o}_{f} \textsf{S}_{1/2}(1)$, we can restrict our search to elements of the form ay where $a \in \textsf{aTL}_{4}$ is a sum of diagrams with at most 2 through lines (lines connecting the top and bottom of the diagram), and such that $a e_1 = \beta a$ (since $a y = a e_2 e_1 y$).

Furthermore, one also has

and since

it follows that

$$\begin{aligned} z y = \left( (-\mathfrak {q})^{-1/2}u e_1 + (-\mathfrak {q})^{1/2} u e_1e_3 \right) y. \end{aligned}$$

(209)

Let’s consider then $M_0$, the submodule of $\textsf{W}_{1/2,z}(3) \times ^{o}_{f} \textsf{S}_{1/2}(1)$ generated by elements of the form ay, where a is a diagram with no through lines, no closed loop wrapping around the cylinder,²¹ and such that $ae_1 = \beta a$. We find 12 such diagrams:

However, we then have

where we used the closed braid identity

Using equation (209), it follows that

Applying the same reasoning to the other diagrams in (211), one concludes that $M_0$ is generated entirely by elements of the form ay with a one of the diagrams in (210). Furthermore, these elements are clearly linearly independent since the bottom side of the diagrams in (210) are all identical, and any relation of the form $a y = a b y$ for some $b \in \textsf{aTL}_{4}$ cannot affect the top side of the diagram a, since it acts on its bottom (provided that a has no through line, which is the case here). We thus conclude that this set of elements spans $M_0$.

We now consider $\bar{M}_{2}$, the subspace of $\textsf{W}_{1/2,z}(3) \times ^{o}_{f} \textsf{S}_{1/2}(1)$ generated by elements of the form ay, where a is a diagram with exactly two through lines, and such that $ae_1 = \beta a$. Such diagrams are all those which can be written in the form $u^{k} e_{j_m} e_{j_{m-1}} \ldots e_{j_{0}}$, where $k \in \mathbb {Z}$ and $\lbrace j_{i} \rbrace$ is a set of $m \in \mathbb {N}$ consecutive integers such that $j_0 = 1$.

However, from (209),

$$\begin{aligned} e_1 y&= z^{-1}e_1\left( (-\mathfrak {q})^{-1/2}u e_1 + (-\mathfrak {q})^{1/2} u e_1e_3 \right) y, \end{aligned}$$

(215)

$$\begin{aligned}&= z^{-1}(-\mathfrak {q})^{-1/2} u e_4 e_1 y + a_0y, \end{aligned}$$

(216)

where $a_0$ is a diagram with zero through lines (so $a_0y \in M_0$). It thus follows that

$$\begin{aligned} u^{-1} e_1 y = w^{-1} e_4e_1 y + b_1 y, \end{aligned}$$

(217)

where $w = z(-\mathfrak {q})^{1/2}$ and $b_1$ is a diagram with no through lines. Repeating this argument, we find

$$\begin{aligned} u^{-2} e_1 y = w^{-2} e_3 e_4 e_1 y + b_2 y, \end{aligned}$$

(218)

$$\begin{aligned} u^{-3} e_1 y = w^{-3} e_2 e_3 e_4 e_1 y + b_3 y, \end{aligned}$$

(219)

$$\begin{aligned} u^{-4} e_1 y = w^{-4} e_1 e_2 e_3 e_4 e_1 y + b_4 y, \end{aligned}$$

(220)

where $b_j$, $j = 1, \ldots , 4$ are diagrams with no through lines. Note that from the algebra relations (2) one has $e_1 e_2 e_3 = u^2 e_3$, so that

$$\begin{aligned} u^{-4} e_1 y&= w^{-4} u^2 e_3 e_4 e_1 y + b_4 y, \end{aligned}$$

(221)

$$\begin{aligned}&= w^{-2} e_1 y + b_4 y - w^{-2} b_2 y. \end{aligned}$$

(222)

It follows that $M_{2}$, the quotient of $\textsf{W}_{1/2,z}(3) \times ^{o}_{f} \textsf{S}_{1/2}(1)$ by the submodule $M_0$, is spanned by the set of equivalence classes $\lbrace u^{-k} e_1 ( y + M_0)| k = 0,1,2,3 \rbrace .$

We thus conclude that a basis of $\textsf{W}_{1/2,z}(3) \times ^{o}_{f} \textsf{S}_{1/2}(1)$ can be chosen as $\lbrace a_i y| i = 5, \ldots , 10 \rbrace \cup \lbrace u^{-k} e_1 y| k = 0, \ldots , 3 \rbrace$, where the diagrams $a_i$ are given in equation (210). Note that it is often more convenient to work with the set $e_1y, e_2e_1y, \ldots$ instead of $e_1 y, u^{-1} e_1 y, \ldots$ as the resulting diagrams are easier to draw.