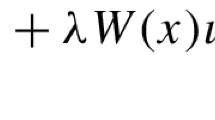Sharp Resolvent Estimate for the Damped-Wave Baouendi–Grushin Operator and Applications

Abstract

In this article we study the semiclassical resolvent estimate for the non-selfadjoint Baouendi–Grushin operator on the two-dimensional torus ${\mathbb {T}}^2={\mathbb {R}}^2/(2\pi {\mathbb {Z}})^2$ with Hölder dampings. The operator is subelliptic degenerating along the vertical direction at $x=0$. We exhibit three different situations: (i) the damping region verifies the geometric control condition with respect to both the non-degenerate Hamiltonian flow and the vertical subelliptic flow; (ii) the undamped region contains a horizontal strip; (iii) the undamped part is a horizontal line. In all of these situations, we obtain sharp resolvent estimates. Consequently, we prove the optimal energy decay rate for the associated damped waved equations. For (i) and (iii), our results are in sharp contrast to the Laplace resolvent since the optimal bound is governed by the quasimodes in the subelliptic regime. While for (ii), the optimality is governed by the quasimodes in the elliptic regime, and the optimal energy decay rate is the same as for the classical damped wave equation on ${\mathbb {T}}^2$. Our analysis contains the study of adapted two-microlocal semiclassical measures, construction of quasimodes and refined Birkhoff normal-form reductions in different regions of the phase-space. Of independent interest, we also obtain the propagation theorem for semiclassical measures of quasimodes microlocalized in the subelliptic regime.

Appendices

Appendix A: Special Symbol Classes and Quantizations

In this section, we will collect some special symbolic calculus needed in Sect. 3. First, let us recall that a symbol ${\textbf{a}}\in S^{\rho ,\delta }({\mathbb {R}}^d)$ is a smooth function on ${\mathbb {R}}_{z,\zeta }^{2d}$ such that

$$\begin{aligned} |\partial _z^{\alpha }\partial _{\zeta }^{\beta }{\textbf{a}}(z,\zeta )|\le C_{\alpha ,\beta }(1+|\zeta |)^{\rho |\alpha |-\delta |\beta |},\;\forall \alpha ,\beta \in {\textbf{N}}^{d}. \end{aligned}$$

For a symbol ${\textbf{a}}$, we define the Weyl quantization $\textrm{Op}_{1,{\mathbb {R}}^d}^w({\textbf{a}})$ via the formula

$$\begin{aligned} \textrm{Op}_{1,{\mathbb {R}}^d}^\textrm{w}({\textbf{a}})f(z):=\frac{1}{(2\pi )^d}\iint _{{\mathbb {R}}^{2d}}{\textbf{a}}\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }f(z')d\zeta dz', \end{aligned}$$

(6.13)

for any Schwartz function $f\in {\mathcal {S}}({\mathbb {R}}^d)$. When $z=(x,y)\in {\mathbb {R}}^{2m},\zeta =(\xi ,\eta )\in {\mathbb {R}}^{2m}$, we denote by ${\text {Op}}_{1}^{\textrm{w},(x,\xi )}({\textbf{a}}),{\text {Op}}_1^{\textrm{w},(y,\eta )}({\textbf{a}})$ the partial quantization of ${\textbf{a}}$ with respect to $(x,\xi )$ and $(y,\eta )$ variables, respectively. Note that we can write

$$\begin{aligned} \textrm{Op}_1^{\textrm{w}}({\textbf{a}})=\textrm{Op}_{1}^{\textrm{w},(y,\eta )}({\text {Op}}_{1}^{\textrm{w},(x,\xi )}({\textbf{a}})). \end{aligned}$$

This means that we quantize the ${\mathcal {L}}(L^2({\mathbb {R}}_x^n))$-valued symbol $\textrm{Op}_1^{\textrm{w},(x,\xi )}({\textbf{a}})={\textbf{a}}^{\textrm{w}}(x,D_x;y,\eta )$ with domain $(y,\eta )\in {\mathbb {R}}^{2n}$.

Recall the following version of the Calderon–Vaillancourt theorem for $S^{0,0}$ symbols:

Proposition A.1

[30, Theorem 2]. Let ${\textbf{a}}\in S^{0,0}({\mathbb {R}}^{d})$. Then

$$\begin{aligned} \Vert {\text {Op}}_{1,{\mathbb {R}}^d}^\textrm{w}({\textbf{a}})\Vert _{{\mathcal {L}}(L^2({\mathbb {R}}^d))}\le C_0\sum _{|\alpha |+|\beta |\le 2d}\sup _{{\mathbb {R}}^{2d}}|\partial _z^{\alpha }\partial _{\zeta }^{\beta }{\textbf{a}}(z,\zeta )|, \end{aligned}$$

where $C_0>0$ is a uniform constant.

By rescaling $u(z)\mapsto {\widetilde{u}}({\widetilde{z}}):=h^{\frac{d}{4}}u(h^{\frac{1}{2}}{\widetilde{z}})$, we obtain that

$$\begin{aligned} \textrm{Op}_{h,{\mathbb {R}}^d}^{\textrm{w}}({\textbf{a}})u(z)=h^{-\frac{d}{4}}\textrm{Op}_{1,{\mathbb {R}}^d}^{\textrm{w}}({\textbf{a}}_{h}({\widetilde{z}},\zeta )){\widetilde{u}}({\widetilde{z}}), \end{aligned}$$

where ${\textbf{a}}_h({\widetilde{z}},{\widetilde{\zeta }})={\textbf{a}}(h^{\frac{1}{2}}{\widetilde{z}},h^{\frac{1}{2}}{\widetilde{\zeta }})$. Consequently, we have

Corollary A.2

(Theorem 5.1, [46]). Suppose that ${\textbf{a}}\in S^{0,0}({\mathbb {R}}^d)$. Then

$$\begin{aligned} \Vert \textrm{Op}_{h,{\mathbb {R}}^d}^{\textrm{w}}({\textbf{a}})\Vert _{{\mathcal {L}}(L^2)}\le C_0\sup _{{\mathbb {R}}^{2d}}|a(z,\zeta )|+O(h^{\frac{1}{2}}), \end{aligned}$$

where $C_0$ is an absolute constant.

1.1 A.1 Explicit quantization on $M_0={\mathbb {R}}_x\times {\mathbb {T}}_y$

In this subsection, we follow the procedure of Chapter 5, Section 3 of [46] to define quantization for partially periodic symbols. Denote by $\iota : L^2(M_0)\rightarrow {\mathcal {S}}'({\mathbb {R}}^2)$ the identification of a function in $L^2(M_0)$ as a tempered distribution in ${\mathcal {S}}'({\mathbb {R}}^2)$. In coordinate, we can write

$$\begin{aligned} (\iota f)(x,y)=\sum _{k\in {\mathbb {Z}}}f(x,y-2\pi k){\textbf{1}}_{{\mathbb {T}}_y}(y-2\pi k), \end{aligned}$$

where ${\textbf{1}}_{{\mathbb {T}}_y}$ stands for the restriction to the fundamental domain $(-\pi ,\pi )$ of ${\mathbb {T}}_y$. Denote by ${\mathcal {S}}_{\text {per}}'({\mathbb {R}}^2)$ the subspace of partially $2\pi$-periodic distributions (in y variable) which is the image of $\iota$. Note that

$$\begin{aligned} (\iota \circ {\textbf{1}}_{{\mathbb {T}}_y})|_{{\mathcal {S}}_{\text {per}}'}=\textrm{Id},\; \text { on } {\mathcal {S}}_{\textrm{per}}'. \end{aligned}$$

(A.1)

Symbols ${\textbf{a}}$ on $T^*M_0$ can be identified as partially periodic symbols on $T^*{\mathbb {R}}^2$, namely ${\textbf{a}}\in C^{\infty }({\mathbb {R}}^4)$, bounded as well as its derivatives and satisfying

$$\begin{aligned} {\textbf{a}}(x,y,\xi ,\eta )={\textbf{a}}(x,y+2k\pi ,\xi ,\eta ),\quad \forall k\in {\mathbb {Z}},\; \forall (x,y,\xi ,\eta ). \end{aligned}$$

The quantization $\textrm{Op}_1^\textrm{w}(\cdot )$ on $M_0$ is naturally defined by

$$\begin{aligned} \textrm{Op}_1^\textrm{w}(\cdot )={\textbf{1}}_{{\mathbb {T}}_y}\textrm{Op}_{1,{\mathbb {R}}^2}^\textrm{w}\iota , \end{aligned}$$

(A.2)

where the notation ${\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}$ is to emphasize the quantization is on ${\mathbb {R}}^2$, given by the formula (A.1).

The quantization formula (A.3) can be expanded explicitly as

$$\begin{aligned} \textrm{Op}_1^\textrm{w}({\textbf{a}})u(x,y)=\sum _{k\in {\mathbb {Z}}}{\textbf{A}}_ku(x,y), \end{aligned}$$

(A.3)

where

$$\begin{aligned} {\textbf{A}}_ku(x,y):= & {} \frac{1}{(2\pi )^2}\int _{{\mathbb {R}}^2}\int _{{\mathbb {R}}\times {\mathbb {T}}}{\textbf{a}}\big (\frac{x+x'}{2},\frac{y+y'}{2},\xi ,\eta \big )\textrm{e}^{i(x-x')\xi +i(y-y'+2\pi k)\eta }\\{} & {} u(x',y')dx'dy'd\xi d\eta , \end{aligned}$$

or equivalently,

$$\begin{aligned} {\textbf{A}}_ku(x,y)={\textbf{1}}_{{\mathbb {T}}_y}\tau _{-2\pi k}\textrm{Op}_{1,{\mathbb {R}}^2}^{\textrm{w}}({\textbf{a}}){\textbf{1}}_{{\mathbb {T}}_y}, \end{aligned}$$

(A.4)

where $\tau _{y_0}f(x,y)=f(x,y-y_0)$ is the translation operator. If there exist $\sigma \ge 0$, $M\ge 2$ such that some h-dependent family of symbols ${\textbf{a}}_h$ satisfies additionally $|\partial _{\eta }^{m}{\textbf{a}}_h|\lesssim h^{m\sigma }$ for any $m\le M$ (the situation of $\sigma >0$ appears when considering the semiclassical quantization), then in $\textrm{Op}_1^\textrm{w}({\textbf{a}}_h)$ we may only consider the contribution ${\textbf{A}}_{k}$ for $|k|\le 1$. Indeed, for $|k|\ge 2$, we have, for any $y,y'\in {\mathbb {T}}$, $|y-y'+2\pi k|\ge (|k|-1)2\pi$. By writing $\textrm{e}^{i(y-y'+2\pi k)}$ as $\frac{\partial _{\eta }^m(\textrm{e}^{i(y-y'+2\pi k)} )}{(i(y-y'+2\pi k))^m }$ and using integration by parts, we deduce that

$$\begin{aligned}\Vert {\textbf{A}}_k\Vert _{{\mathcal {L}}(L^2(M_0))}=O(h^{m\sigma }\langle k\rangle ^{-m}).\end{aligned}$$

Consequently, we have the following version of the Calderon–Vaillancourt theorem:

Corollary A.3

(Calderon–Vaillancourt). There exists $C_0>0$, such that for all $a\in C^{\infty }(T^*M_0)$,

$$\begin{aligned} \Vert {\text {Op}}_1^\textrm{w}(a)\Vert _{{\mathcal {L}}(L^2(M_0))}\le C_0\sum _{|\alpha |\le 4}\sup _{T^*M_0}|\partial ^{\alpha }a|. \end{aligned}$$

1.2 A.2 Special symbol classes associated to the second microlocalization

Definition A.4

Assume that $h,\epsilon ,R$ are sequences of parameters¹³ satisfying the following asymptotic:

$$\begin{aligned} h\rightarrow 0,\;\epsilon \rightarrow 0,\;R\rightarrow \infty ,\; \frac{h}{\epsilon }\rightarrow 0. \end{aligned}$$

(A.5)

The $(h,\epsilon ,R)$ parameter-dependent symbol class ${\textbf{S}}_{1,1;1^-,0}^0({\mathbb {R}}^6)$ consists of families of smooth functions ${\textbf{a}}(x,x_1,y,y_1,\xi ,\eta ;h,\epsilon ,R)$, satisfying the following hypotheses:

• (i) There exists $K>0$ such that uniformly in parameters $h,\epsilon ,R$, ${\textbf{a}}(x,x_1,y,y_1,\xi ,\eta ;h,\epsilon ,R)\equiv 0$ when

  $$\begin{aligned} \sqrt{(x+x_1)^2+(y+y_1)^2}> K\quad \text {or}\quad \sqrt{\xi ^2+\eta ^2}> Kh^{-1}. \end{aligned}$$

• (ii) For any $k,k_1,m,m_1,l,j$, there exists $C_{k,k_1,m,m_1,l,j}>0$, such that for all $h,\epsilon ,R$, the following estimate holds

  $$\begin{aligned} \sup _{{\mathbb {R}}^6}|\partial _x^k\partial _{x_1}^{k_1}\partial _y^m\partial _{y_1}^{m_1}\partial _{\xi }^l\partial _{\eta }^j{\textbf{a}}|\le C_{k,k_1,m,m_1,l,j}\cdot \big (\frac{\epsilon }{h}\big )^{k+k_1}\cdot h^{l+j}. \end{aligned}$$

  (A.6)

Similarly, ${\textbf{a}}={\textbf{a}}(x,y,\xi ,\eta ;h,\epsilon ,R)$ belongs to ${\textbf{S}}_{1,1;1^-,0}^0({\mathbb {R}}^4)$ if the analogue of the hypotheses $\mathrm {(i)},\mathrm {(ii)}$ hold without variables $x_1,y_1$.

When there is no risk of confusing, we will not display the dependence in $h,\epsilon ,R$ explicitly for symbols in ${\textbf{S}}_{1,1;1^-,0}^0$. Moreover, when the symbol ${\textbf{a}}\in {\textbf{S}}_{1,1;1^-,0}^0({\mathbb {R}}^4)$ is $2\pi$-periodic in y variable, we denote by ${\textbf{a}}\in {\textbf{S}}_{1,1;1^-,0}^0(T^*M_0)$. We have the following $L^2$ boundedness property for the quantization of this class of symbols:

Proposition A.5

Assume that ${\textbf{a}}\in {\textbf{S}}_{1,1;1^-,0}^0({\mathbb {R}}^6)$ and let $T_{{\textbf{a}}}$ be the linear operator on ${\mathcal {S}}'({\mathbb {R}}^2)$ with the Schwartz kernel

$$\begin{aligned} K_{{\textbf{a}}}(x,x_1,y,y_1)=\frac{1}{(2\pi )^2}\iint _{{\mathbb {R}}^2}{\textbf{a}}(x,x_1,y,y_1,\xi ,\eta )\textrm{e}^{i(x-x_1)\xi +i(y-y_1)\eta }d\xi d\eta , \end{aligned}$$

where $x,x_1,y,y_1\in {\mathbb {R}}$. Then $T_{{\textbf{a}}}\in {\mathcal {L}}(L^2({\mathbb {R}}^2))$ uniformly in $h,\epsilon$ and R obeying the asymptotic (A.6). More precisely,

$$\begin{aligned}{} & {} \Vert T_{{\textbf{a}}}\Vert _{{\mathcal {L}}(L^2({\mathbb {R}}^2))}\\{} & {} \quad \le C_0\sup _{{\mathbb {R}}^6}|{\textbf{a}}|+C_{{\textbf{a}}}\big (\epsilon ^{\frac{1}{2}}+h^{\frac{1}{2}}\big ), \end{aligned}$$

where the first constant $C_0$ is independent of ${\textbf{a}}$. Consequently, if ${\textbf{a}}\in {\textbf{S}}_{1,1;1^-,0}^0({\mathbb {R}}^4)$ and is $2\pi$-periodic in y, then

$$\begin{aligned} \Vert \textrm{Op}_1^\textrm{w}({\textbf{a}})\Vert _{{\mathcal {L}}(L^2(M_0))}\le C_0\sup _{{\mathbb {R}}^4}|{\textbf{a}}|+C_{{\textbf{a}}}\big (\epsilon ^{\frac{1}{2}}+h^{\frac{1}{2}}\big ). \end{aligned}$$

Proof

Consider the scalings $x=\frac{h}{\epsilon ^{1/2}}X, y=h^{1/2}Y$ and $\xi =\frac{\epsilon ^{1/2}}{h}\Xi , \eta =h^{-1/2}\Theta$ and for $f,g\in L^2({\mathbb {R}}^2)$, we denote by

$$\begin{aligned}f(x,y)=\frac{\epsilon ^{1/4}}{h^{3/4}}F(X,Y),\quad g(x,y)=\frac{\epsilon ^{1/4}}{h^{3/4}}G(X,Y). \end{aligned}$$

Note that we have $\Vert f\Vert _{L^2({\mathbb {R}}^2)}=\Vert F\Vert _{L^2({\mathbb {R}}^2)}$ and $\Vert g\Vert _{L^2({\mathbb {R}}^2)}=\Vert G\Vert _{L^2({\mathbb {R}}^2)}$. Direct computation yields

$$\begin{aligned} \langle T_{{\textbf{a}}}f,g\rangle _{L^2({\mathbb {R}}^2)}=\langle T_{\widetilde{{\textbf{a}}}}F,G\rangle _{L^2({\mathbb {R}}^2)}, \end{aligned}$$

where

$$\begin{aligned} \widetilde{{\textbf{a}}}(X,X_1,Y,Y_1,\Xi ,\Theta )={\textbf{a}}\left( \frac{h}{\epsilon ^{1/2}}X,\frac{h}{\epsilon ^{1/2}}X_1,h^{1/2}Y,h^{1/2}Y_1,\frac{\epsilon ^{1/2}}{h}\Xi ,h^{-1/2}\Theta \right) \end{aligned}$$

with $X_1=\frac{\epsilon ^{1/2}}{h}x_1, Y_1=h^{-1/2}y_1$. By the assumption on ${\textbf{a}}$, we verify that

$$\begin{aligned} \sup _{{\mathbb {R}}^6}|\partial _{X}^{k}\partial _{X_1}^{k_1}\partial _Y^{m}\partial _{Y_1}^{m_1}\partial _{\Xi }^{l}\partial _{\Theta }^{j}\widetilde{{\textbf{a}}}|\lesssim _{{\textbf{a}}} \epsilon ^{\frac{k+k_1+l}{2}}h^{\frac{m+m_1+j}{2}}. \end{aligned}$$

(A.7)

Then by a variant version of the Calderón–Vaillancourt theorem (Theorem 2.8.1 of [42]), we deduce that $T_{\widetilde{{\textbf{a}}}}$ are uniformly bounded on $L^2({\mathbb {R}}^2)$. This means that

$$\begin{aligned} |\langle T_{{\textbf{a}}}f,g\rangle _{L^2({\mathbb {R}}^2)}|&=|\langle T_{\widetilde{{\textbf{a}}}}F,G\rangle _{L^2({\mathbb {R}}^2)}| \le \Big (C_0\sup _{{\mathbb {R}}^6}|{\textbf{a}}|+C_{\alpha }\sum _{1\le |\alpha |\le N_0 }\sup _{{\mathbb {R}}^6}|\partial ^{\alpha }\widetilde{{\textbf{a}}}|\Big ) \Vert f\Vert _{L^2}\Vert g\Vert _{L^2}, \end{aligned}$$

where the first constant $C_0$ does not depend on ${\textbf{a}}$. By (A.8) and duality, we obtain the desired bound for $\Vert T_{{\textbf{a}}}\Vert _{{\mathcal {L}}(L^2({\mathbb {R}}^2))}$. For ${\textbf{a}}\in {\textbf{S}}_{1,1;1^-,0}^0({\mathbb {R}}^4)$, $2\pi$-periodic in y, the extension to ${\text {Op}}_1^\textrm{w}({\textbf{a}})$ on $L^2(M_0)$ follows simply from the decomposition (A.4) and (A.5). The proof of Proposition A.5 is now complete. $\square$

Next, we need the following Lemma to derive a G$\mathring{\textrm{a}}$rding type inequality for symbols in ${\textbf{S}}_{1,1;1^-,0}^0$:

Lemma A.6

Let ${\textbf{a}},{\textbf{b}}\in {\textbf{S}}_{1,1;1^-,0}^0(T^*M_0)$. Then there exists $C_1>0$, such that uniformly in $h,\epsilon ,R$ satisfying the asymptotic (A.6),

$$\begin{aligned} \Vert {\text {Op}}_1^\textrm{w}({\textbf{a}}{\textbf{b}})-{\text {Op}}_1^\textrm{w}({\textbf{a}}){\text {Op}}_1^\textrm{w}({\textbf{b}}) \Vert _{{\mathcal {L}}(L^2(M_0))}\le C_1(h+\epsilon ). \end{aligned}$$

Proof

We first prove the estimate for ${\textbf{a}},{\textbf{b}}\in {\textbf{S}}_{1,1;1^-,0}^0({\mathbb {R}}^4)$. Recall that

$$\begin{aligned} \textrm{Op}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{a}})\textrm{Op}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{b}})=\textrm{Op}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{c}}), \end{aligned}$$

with

$$\begin{aligned} {\textbf{c}}(z,\zeta )=\frac{1}{\pi ^4}\int _{{\mathbb {R}}^8}\textrm{e}^ {-2i\sigma (z_1,\zeta _1;z_2,\zeta _2)}{\textbf{a}}(z+z_1,\zeta +\zeta _1){\textbf{b}}(z+z_2,\zeta +\zeta _2)dz_1dz_2 d\zeta _1 d\zeta _2, \end{aligned}$$

where

$$\begin{aligned} \sigma (z_1,\zeta _1;z_2,\zeta _2)=\zeta _1\cdot z_2-z_1\cdot \zeta _2. \end{aligned}$$

With $X=(z,\zeta ), X_j=(z_j,\zeta _j)\in {\mathbb {R}}^4$, $j=1,2$, $Z=(X_1,X_2)\in {\mathbb {R}}^8$, we can write

$$\begin{aligned} {\textbf{c}}(X)=\frac{1}{\pi ^4}\int _{{\mathbb {R}}^8}\textrm{e}^{i\langle QZ,Z\rangle }{\mathcal {A}}(X,Z)dZ, \end{aligned}$$

where ${\mathcal {A}}(X,Z)={\textbf{a}}(X+X_1){\textbf{b}}(X+X_2)$, and

$$\begin{aligned} Q=\left( \begin{matrix} 0 &{}0 &{}0 &{}-\textrm{Id}_2\\ 0 &{}0 &{}\textrm{Id}_2 &{}0\\ 0 &{}\textrm{Id}_2 &{}0 &{}0\\ -\textrm{Id}_2 &{}0 &{}0 &{}0 \end{matrix} \right) . \end{aligned}$$

Note that $Q^{-1}=Q$ and $\langle QZ,Z\rangle =-2\sigma (X_1,X_2)$. Direct computation yields

$$\begin{aligned} {\textbf{c}}(X)-{\textbf{a}}(X){\textbf{b}}(X)=-\frac{1}{i\pi ^4}\int _0^1tdt\int _{{\mathbb {R}}^8}\textrm{e}^{i\langle QZ,Z\rangle }({\mathcal {D}}_Z{\mathcal {A}})(X,tZ)dZ, \end{aligned}$$

(A.8)

where ${\mathcal {D}}_Z=D_{\zeta _1}\cdot D_{z_2}-D_{z_1}\cdot D_{\zeta _2}$. Indeed, since¹⁴

$$\begin{aligned} \frac{1}{\pi ^4}\int _{{\mathbb {R}}^8}\textrm{e}^{i\langle QZ,Z\rangle }dZ=1, \end{aligned}$$

by Taylor expansion

$$\begin{aligned} {\mathcal {A}}(X,Z)={\mathcal {A}}(X,0)+\int _0^1Z\cdot (\nabla _Z{\mathcal {A}})(X,tZ)dZ \end{aligned}$$

and the simple observation that $Z=\frac{Q^{-1}}{2i}\nabla _Z(\textrm{e}^{i\langle QZ,Z\rangle })$, we have

$$\begin{aligned} {\textbf{c}}(X)-{\textbf{a}}(X){\textbf{b}}(X)&={\mathcal {A}}(X,Z)-{\mathcal {A}}(X,0)\\&=\frac{1}{\pi ^4}\int _0^1dt\int _{{\mathbb {R}}^8}\frac{1}{2i}\nabla _Z(\textrm{e}^{i\langle QZ,Z\rangle })\cdot (Q^{-1}\nabla _Z{\mathcal {A}})(X,tZ)dZ\\&=-\frac{1}{2i\pi ^4}\int _0^1tdt\int _{{\mathbb {R}}^8}\textrm{e}^{i\langle QZ,Z\rangle } (\nabla _Z\cdot (Q^{-1}\nabla _Z){\mathcal {A}})(X,tZ)dZ. \end{aligned}$$

Noting that $Q^{-1}=-Q$ and $\nabla _Z\cdot Q\nabla _Z=-2{\mathcal {D}}_Z$, we obtain (A.9).

Note that ${\mathcal {D}}_Z{\mathcal {A}}(X,tZ)$ is a linear combination of the terms

$$\begin{aligned} \epsilon \cdot \widetilde{{\textbf{a}}}(X+tX_1)\widetilde{{\textbf{b}}}(X+tX_2), \end{aligned}$$

with $\widetilde{{\textbf{a}}},\widetilde{{\textbf{b}}}\in {\textbf{S}}_{1,1;1^-,0}^0({\mathbb {R}}^4)$. It suffices to show that for $t\in (0,1]$,

$$\begin{aligned} {\textbf{d}}_t(X):=\int _{{\mathbb {R}}^8}\textrm{e}^{i\langle QZ,Z\rangle }\widetilde{{\textbf{a}}}(X+tX_1)\widetilde{{\textbf{b}}}(X+tX_2)dX_1dX_2\in {\textbf{S}}^0_{1,1;1^-,0}. \end{aligned}$$

Since the derivatives on $z,\zeta$ will fall on $\widetilde{{\textbf{a}}},\widetilde{{\textbf{b}}}$, by definition of the symbol class, we only need to show that

$$\begin{aligned} |{\textbf{d}}_t(X)|\lesssim 1, \end{aligned}$$

(A.9)

uniformly in $h,\epsilon ,R$ and $t\in (0,1]$. Denote by

$$\begin{aligned} \widetilde{{\mathcal {F}}}\widetilde{{\textbf{a}}}(z,\theta ):=\int _{{\mathbb {R}}^4}\widetilde{{\textbf{a}}}(z,\zeta )\textrm{e}^{-i\zeta \cdot \theta }d\zeta , \quad \widetilde{{\mathcal {F}}}\widetilde{{\textbf{b}}}(z,\theta ):=\int _{{\mathbb {R}}^4}\widetilde{{\textbf{b}}}(z,\zeta )\textrm{e}^{-i\zeta \cdot \theta }d\zeta \end{aligned}$$

the partial Fourier transform, then we have

$$\begin{aligned} {\textbf{d}}_t(z,\zeta )=\int _{{\mathbb {R}}^4}\textrm{e}^{-2i(z_1-z_2)\cdot \zeta }(\widetilde{{\mathcal {F}}}\widetilde{{\textbf{a}}})(z+t^2z_1,2z_2) (\widetilde{{\mathcal {F}}}\widetilde{{\textbf{b}}})(z+t^2z_2,-2z_1)dz_1 dz_2. \end{aligned}$$

Since $\widetilde{{\textbf{a}}},\widetilde{{\textbf{b}}}\in {\textbf{S}}_{1,1;1^-,0}^0$, it follows from the integration by part that

$$\begin{aligned} |\widetilde{{\mathcal {F}}}\widetilde{{\textbf{a}}}(z,\theta )|\lesssim _N\frac{h^{N}}{|\theta |^N},\quad |\widetilde{{\mathcal {F}}}\widetilde{{\textbf{b}}}(z,\theta )|\lesssim _N\frac{h^{N}}{|\theta |^N} \end{aligned}$$

for all $N\ge 1$ and $|\theta |\ge 1$. This leads to (A.10). Once we have established (A.10), applying Proposition A.5, we obtain that

$$\begin{aligned} \Vert \textrm{Op}_{1,{\mathbb {R}}^2}^{\textrm{w}}(\textbf{ab})-\textrm{Op}_{1,{\mathbb {R}}^2}^{\textrm{w}}({\textbf{a}})\textrm{Op}_{1,{\mathbb {R}}^2}^{\textrm{w}}({\textbf{b}})\Vert _{{\mathcal {L}}(L^2)}\le C(h+\epsilon ). \end{aligned}$$

(A.10)

Next we extend the above estimate to symbols that are $2\pi$- periodic in y. Take $f,g\in L^2(M_0)$, we have

$$\begin{aligned}&\big \langle \big ({\text {Op}}_1^\textrm{w}({\textbf{a}}{\textbf{b}})-{\text {Op}}_1^\textrm{w}({\textbf{a}}){\text {Op}}_1^\textrm{w}({\textbf{b}}) \big )f,g \big \rangle _{L^2(M_0)}\\&\quad =\big \langle \big ({\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{a}}{\textbf{b}})-{\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{a}}){\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{b}})\big )\iota f, {\textbf{1}}_{{\mathbb {T}}_y}\iota g \big \rangle _{L^2({\mathbb {R}}^2)}, \end{aligned}$$

where we used (A.2). By self-adjointness, the above quantity equals to

$$\begin{aligned} \big \langle \iota f, \big ({\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{a}}{\textbf{b}})-{\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{b}}){\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{a}})\big ){\textbf{1}}_{{\mathbb {T}}_y}\iota g \big \rangle _{L^2({\mathbb {R}}^2)}. \end{aligned}$$

Recall that $\iota =\sum _{k\in {\mathbb {Z}}}\tau _{2\pi k}({\textbf{1}}_{{\mathbb {T}}_y}\cdot )$, from the discussion below (A.5), we have for all $|k|\ge 2$,

$$\begin{aligned}{} & {} \big \langle \tau _{-2\pi k}({\textbf{1}}_{{\mathbb {T}}_y}f), \big ({\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{a}}{\textbf{b}})-{\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{b}}){\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{a}})\big ){\textbf{1}}_{{\mathbb {T}}_y}\iota g \big \rangle _{L^2({\mathbb {R}}^2)}\\{} & {} \quad =O(h^{\infty }\langle k\rangle ^{-\infty })\Vert f\Vert _{L^2(M_0)}\Vert g\Vert _{L^2(M_0)}. \end{aligned}$$

When $|k|\le 1$, by (A.11),

$$\begin{aligned}{} & {} \big \langle \tau _{-2\pi k}({\textbf{1}}_{{\mathbb {T}}_y}f), \big ({\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{a}}{\textbf{b}})-{\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{b}}){\text {Op}}_{1,{\mathbb {R}}^2}^\textrm{w}({\textbf{a}})\big ){\textbf{1}}_{{\mathbb {T}}_y}\iota g \big \rangle _{L^2({\mathbb {R}}^2)}\\{} & {} \quad =C(h+\epsilon )\Vert f\Vert _{L^2(M_0)}\Vert g\Vert _{L^2(M_0)}. \end{aligned}$$

Adding up all $k\in {\mathbb {Z}}$, we obtain that

$$\begin{aligned} \Vert \textrm{Op}_{1}^{\textrm{w}}(\textbf{ab})-\textrm{Op}_{1}^{\textrm{w}}({\textbf{a}})\textrm{Op}_{1,{\mathbb {R}}^2}^{\textrm{w}}({\textbf{b}})\Vert _{{\mathcal {L}}(L^2)}\le C(h+\epsilon ). \end{aligned}$$

By duality, the desired result then follows and we complete the proof of Lemma A.6. $\square$

Consequently, we have:

Corollary A.7

Let ${\textbf{a}}\in {\textbf{S}}_{1,1;1^-,0}^0(T^*M_0)$, then there exists $C_1>0$, such that

$$\begin{aligned} \big \langle {\text {Op}}_1^{\textrm{w}}({\textbf{a}}^2)f,f\big \rangle _{L^2(M_0)}\ge -C_1(h+\epsilon )\Vert f\Vert _{L^2(M_0)}^2. \end{aligned}$$

Appendix B: Exact Computations for Commutators

In this part, we collect some computations for commutators needed in Sect. 3. Below, all computations will be done only for operators acting on $L^2({\mathbb {R}}^2)$, since all the commutators are of the form $[P,{\text {Op}}_1^\textrm{w}(q)]$, with some differential operator P and a symbol q that is periodic in y, thanks to the identification (A.3). First we prove the commutator formula below, used to prove the propagation theorem for the scalar-valued second semiclassical microlocal measure:

Lemma B.1

Let $q(z,\zeta )\in {\mathcal {S}}({\mathbb {R}}^4)$. We have the following formula

$$\begin{aligned}{}[-h^2\Delta _G,{\text {Op}}_1^{\textrm{w}}(q)]&=\frac{h^2}{i}{\text {Op}}_1^\textrm{w}(2\xi \partial _xq+2V(x)\eta \partial _yq-2x\eta ^2\partial _{\xi }q)+\frac{h^2}{2i}{\text {Op}}_1^{\textrm{w}}(x\partial _y^2\partial _{\xi }q)\nonumber \\&\quad +\frac{h^2}{i}{\text {Op}}_1^\textrm{w}\big (V_1'(x)(\frac{1}{4}\partial _y^2\partial _{\xi }q-\eta ^2\partial _{\xi }q) \big )\nonumber \\&\quad -\frac{h^2}{24i}{\text {Op}}_1^\textrm{w}\big (V_1'''(x)(\frac{1}{4}\partial _y^2\partial _{\xi }^3q-\eta ^2\partial _{\xi }^3q) \big )-{\mathcal {R}}_h(q), \end{aligned}$$

(A.11)

where $V_1(x)=V(x)-x^2=O(x^3)$ and the operator ${\mathcal {R}}_h(q)$ has the Schwartz kernel

$$\begin{aligned} {\mathcal {K}}_q(z,z')= & {} \frac{h^2}{(2\pi )^2}\int _{{\mathbb {R}}^2}\big [{\widetilde{V}}_1(x,x')(\frac{1}{4}\partial _y^2\partial _{\xi }^4q-\eta ^2\partial _{\xi }^4q)\big (\frac{z+z'}{2},\zeta \big )\\{} & {} +{\widetilde{V}}_2(x,x')\frac{\eta }{i}(\partial _y\partial _{\xi }^2q)\big (\frac{z+z'}{2},\zeta \big )\big ]e^{i(z-z')\cdot \zeta }d\zeta , \end{aligned}$$

with

$$\begin{aligned} {\widetilde{V}}_1(x,x')=\frac{1}{16}\int _{-1}^1dt\int _0^tdt_1\int _0^{t_1}dt_2\int _0^{t_2}V_1^{(4)}\big (\frac{x+x'}{2}+t\frac{x-x'}{2}\big )dt_3 \end{aligned}$$

and

$$\begin{aligned} {\widetilde{V}}_2(x,x')=\frac{1}{4}\int _0^1dt\int _{-t}^tV''\big (\frac{x+x'}{2}+t_1\frac{x-x'}{2}\big )dt_1. \end{aligned}$$

Remark .1

In our applications of the formula, apart from the first operator on the right hand side, the others are all viewed as remainders.

Proof

The proof follows from a direct computation. Write

$$\begin{aligned}{}[-h^2\Delta _G,{\text {Op}}_1^{\textrm{w}}(q)] =[h^2D_x^2,{\text {Op}}_1^{\textrm{w}}(q)]+V(x)[h^2D_y^2,{\text {Op}}_1^{\textrm{w}}(q)]+[V(x),{\text {Op}}_1^{\textrm{w}}(q)]h^2D_y^2, \end{aligned}$$

we have for any $f\in {\mathcal {S}}({\mathbb {R}}^2)$,

$$\begin{aligned}&[-h^2\Delta _G,\textrm{Op}_1^{\textrm{w}}(q)]f(z) \\&\quad =-ih^2\textrm{Op}_1^\textrm{w}(2\xi \partial _xq)f-ih^2\textrm{Op}_1^{\textrm{w}}(2V(x)\eta \partial _yq)f\\&\quad \quad -\frac{ih^2}{(2\pi )^2}\iint _{{\mathbb {R}}^4}\big (V(x)-V\big (\frac{x+x'}{2}\big )\big )2\eta (\partial _yq) \big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }f(z')dz'd\zeta \\&\quad \quad -\frac{h^2}{(2\pi )^2}\iint _{{\mathbb {R}}^4}(V(x)-V(x'))[\frac{1}{4}\partial _y^2q-i\eta \partial _yq-\eta ^2q] \big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }f(z')dz'd\zeta . \end{aligned}$$

After arrangement, we have

$$\begin{aligned}{}[-h^2\Delta _G,{\text {Op}}_1^{\textrm{w}}(q)] s=\frac{h^2}{i}{\text {Op}}_1^\textrm{w}(2\xi \partial _xq+2V(x)\eta \partial _yq)-{\mathcal {T}}_1-{\mathcal {T}}_2, \end{aligned}$$

where ${\mathcal {T}}_1,{\mathcal {T}}_2$ have Schwartz kernels

$$\begin{aligned}&{\mathcal {K}}_1(z,z')=\frac{h^2}{(2\pi )^2}\int _{{\mathbb {R}}^2}\big (V(x)-V(x')\big )\big [\frac{1}{4}\partial _y^2q-\eta ^2q \big ]\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta ,\\&{\mathcal {K}}_2(z,z')=\frac{ih^2}{(2\pi )^2}\int _{{\mathbb {R}}^2}\big [V(x)+V(x')-2V\big (\frac{x+x'}{2}\big )\big ]\eta (\partial _yq)\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta . \end{aligned}$$

Since $V(x)=x^2+V_1(x)$, $V_1(x)=O(|x|^3)$, we have

$$\begin{aligned} {\mathcal {T}}_1f(z)&=\frac{h^2}{(2\pi )^2}\iint _{{\mathbb {R}}^4}[(x+x')(x-x')+V_1(x)-V_1(x')][\frac{1}{4}\partial _y^2q-\eta ^2q]\\&\qquad \big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }f(z')dz'd\zeta \\&\quad = ih^2\textrm{Op}_1^\textrm{w}(2x\cdot (\frac{1}{4}\partial _y^2\partial _{\xi }q-\eta ^2\partial _{\xi }q))f\\&\qquad + \frac{ih^2}{(2\pi )^2}\iint _{{\mathbb {R}}^4}\Big (\int _{-1}^1\frac{1}{2}V_1'\big (\frac{x+x'}{2}+t\frac{x-x'}{2}\big )dt\Big )\\&\qquad [\frac{1}{4}\partial _y^2\partial _{\xi }q-\eta ^2\partial _{\xi }q]\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }f(z')dz'd\zeta . \end{aligned}$$

We can further write

$$\begin{aligned}&\frac{1}{2}\int _{-1}^1V_1'\big (\frac{x+x'}{2}+t\frac{x-x'}{2}\big )dt\\&\quad =V_1'\big (\frac{x+x'}{2}\big )+\frac{(x-x')^2}{24}V_1'''\big (\frac{x+x'}{2}\big )\\&\qquad + \frac{(x-x')^3}{16}\int _{-1}^1dt\int _0^{t}dt_1\int _{0}^{t_1}dt_2\int _{0}^{t_2}V_1^{(4)}\big (\frac{x+x'}{2}+t\frac{x-x'}{2}\big )dt_3, \end{aligned}$$

hence

$$\begin{aligned} {\mathcal {T}}_1f= & {} ih^2{\text {Op}}_1^\textrm{w}\big ((2x+V_1'(x))(\frac{1}{4}\partial _y^2\partial _{\xi }q-\eta ^2\partial _{\xi }q)\big )\\{} & {} -\frac{ih^2}{24}{\text {Op}}_1^\textrm{w}\big (V_1'''(x)(\frac{1}{4}\partial _y^2\partial _{\xi }^3q-\eta ^2\partial _{\xi }^3q)\big )+{\mathcal {R}}_1, \end{aligned}$$

where ${\mathcal {R}}_1$ has the Schwartz kernel

$$\begin{aligned} {\mathcal {K}}_{{\mathcal {R}}_1}(z,z')&=\frac{h^2}{(2\pi )^2}\int _{{\mathbb {R}}^2} \Big (\frac{1}{16}\int _{-1}^1dt\int _0^tdt_1\int _0^{t_1}dt_2\int _0^{t_2}V_1^{(4)}\big (\frac{x+x'}{2}+t\frac{x-x'}{2}\big )dt_3 \Big )\\&\times (\frac{1}{4}\partial _y^2\partial _{\xi }^4q-\eta ^2\partial _{\xi }^4q)\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta . \end{aligned}$$

For ${\mathcal {T}}_2$, by Taylor expansion and integration by part, we can write its kernel as

$$\begin{aligned} {\mathcal {K}}_2(z,z')=\frac{h^2}{4i(2\pi )^2}\int _{{\mathbb {R}}^2}\Big (\int _0^1dt\int _{-t}^tV''\big (\frac{x+x'}{2}+t_1\frac{x-x'}{2}\big )dt_1\Big )\\ \eta (\partial _y\partial _{\xi }^2q)\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta , \end{aligned}$$

which is part of the remainder. We complete the proof of Lemma B.1. $\square$

The following formula will be used to prove the propagation formula for the operator-valued second semiclassical microlocal measures:

Lemma B.2

Let $q(z,\zeta )\in {\mathcal {S}}({\mathbb {R}}^4)$. We have the following formula

$$\begin{aligned}&[-\partial _x^2-V(hx)h^2\partial _y^2,{\text {Op}}_1^\textrm{w}(q)]\\&= {\text {Op}}_1^{\textrm{w},(y,\eta )}\big (\big [-\partial _x^2+x^2h^4\eta ^2,{\text {Op}}_1^{\textrm{w},(x,\xi )}(q)\big ]_{L^2({\mathbb {R}}_x)}\big )\\&\quad + {\text {Op}}_1^{\textrm{w},(y,\eta )}\big (\big [(V(hx)-h^2x^2)h^2\eta ^2,{\text {Op}}_1^{\textrm{w},(x,\xi )}(q) \big ]_{L^2({\mathbb {R}}_x)}\big )\\&\quad + \frac{h^2}{i}{\text {Op}}_1^{\textrm{w}}(2V(hx)\eta \partial _yq)+\frac{h^3}{4i}{\text {Op}}_1^\textrm{w}\big (V'(hx)\partial _y^2\partial _{\xi }q) +{\mathcal {R}}_q, \end{aligned}$$

where the operator ${\mathcal {R}}_q$ has the Schwartz kernel

$$\begin{aligned} {\mathcal {K}}_q(z,z')= & {} \frac{h^4}{(2\pi )^2}\int _{{\mathbb {R}}^2}\big [{\widetilde{V}}_3(hx,hx')\frac{1}{4}\partial _y^2\partial _{\xi }^2q\big (\frac{z+z'}{2},\zeta \big )\\{} & {} +i{\widetilde{V}}_4(hx,hx')\eta \partial _y\partial _{\xi }^2q\big (\frac{z+z'}{2},\zeta \big ) \big ]\textrm{e}^{i(z-z')\cdot \zeta }d\zeta , \end{aligned}$$

where

$$\begin{aligned} {\widetilde{V}}_3(hx,hx')=\frac{1}{4}\int _{-1}^1dt\int _0^tV''\big (h\frac{x+x'}{2}+t_1h\frac{x-x'}{2}\big )dt_1, \end{aligned}$$

and

$$\begin{aligned} {\widetilde{V}}_4(hx,hx')=\frac{1}{4}\int _0^1dt\int _{-t}^{t}V''\big (h\frac{x+x'}{2}+t_1h\frac{x-x'}{2}\big )dt_1. \end{aligned}$$

Proof

The proof follows from a direct computation. We write

$$\begin{aligned}{}[D_x^2+V(hx)h^2D_y^2,{\text {Op}}_1^\textrm{w}(q)]&=[D_x^2,{\text {Op}}_1^\textrm{w}(q)]+V(hx)[h^2D_y^2,{\text {Op}}_1^\textrm{w}(q)]\\&\quad +[V(hx),{\text {Op}}_1^\textrm{w}(q)]h^2D_y^2. \end{aligned}$$

We observe that

$$\begin{aligned}{} & {} [D_x^2,{\text {Op}}_1^\textrm{w}(q)]={\text {Op}}_1^{\textrm{w},(y,\eta )}([D_x^2,{\text {Op}}_1^{\textrm{w},(x,\xi )}(q)]_{L^2({\mathbb {R}}_x)}),\\{} & {} V(hx)[h^2D_y^2,{\text {Op}}_1^{\textrm{w}}(q)]=\frac{h^2}{i}V(hx){\text {Op}}_1^\textrm{w}(2\eta \partial _yq),\end{aligned}$$

and the third operator $[V(hx),{\text {Op}}_1^\textrm{w}(q)]h^2D_y^2$ has the Schwartz kernel

$$\begin{aligned} \frac{h^2}{(2\pi )^2}\int _{{\mathbb {R}}^2}(V(hx)-V(hx'))[\frac{1}{4}D_y^2q-\eta D_yq+\eta ^2q]\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta . \end{aligned}$$

Since $\frac{h^2}{(2\pi )^2}\int _{{\mathbb {R}}^2}(V(hx)-V(hx'))\eta ^2q\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta$ is the Schwartz kernel of the operator

$$\begin{aligned} {\text {Op}}_1^{\textrm{w},(y,\eta )}([V(hx)h^2\eta ^2,{\text {Op}}_1^{\textrm{w},(x,\xi )}(q)]_{L^2({\mathbb {R}}_x)}), \end{aligned}$$

we get

$$\begin{aligned}{}[D_x^2+V(hx)h^2D_y^2,{\text {Op}}_1^{\textrm{w}}(q)]=&{\text {Op}}_1^{\textrm{w},(y,\eta )}\big ([D_x^2+V(hx)h^2\eta ^2,{\text {Op}}_1^{\textrm{w},(x,\xi )}(q) ]_{L^2({\mathbb {R}}_x)}\big )\nonumber \\&\quad +\frac{h^2}{i}{\text {Op}}_1^{\textrm{w}}(2V(hx)\eta \partial _yq)\nonumber \\&\quad +{\mathcal {T}}, \end{aligned}$$

(B.1)

where the operator ${\mathcal {T}}$ has the Schwartz kernel

$$\begin{aligned} {\mathcal {K}}_{{\mathcal {T}}}(z,z')=&\frac{h^2}{(2\pi )^2}\int _{{\mathbb {R}}^2}(V(hx)-V(hx'))[\frac{1}{4}D_y^2q-\eta D_yq]\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta \\&+\frac{h^2}{(2\pi )^2}\int _{{\mathbb {R}}^2}\big (V(hx)-V\big (h\frac{x+x'}{2}\big )\big )\frac{2}{i}\eta (\partial _yq)\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta , \end{aligned}$$

or equivalently,

$$\begin{aligned} {\mathcal {K}}_{{\mathcal {T}}}(z,z')=&\underbrace{\frac{h^2}{(2\pi )^2}\int _{{\mathbb {R}}^2}(V(hx)-V(hx'))\frac{1}{4}(D_y^2q)\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta }_{{\mathcal {K}}_{{\mathcal {T}}}^{(1)}(z,z') }\\&+\underbrace{\frac{h^2}{(2\pi )^2}\int _{{\mathbb {R}}^2}\big [V(hx)+V(hx')-2V\big (h\frac{x+x'}{2}\big ) \big ]\eta (D_yq)\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta }_{{\mathcal {K}}_{{\mathcal {T}}}^{(2)}(z,z') }. \end{aligned}$$

By Taylor expansion and doing the integration by part, we can further write

$$\begin{aligned} {\mathcal {K}}_{{\mathcal {T}}}^{(1)}(z,z')&=-\frac{h^3}{(2\pi )^2}\int _{{\mathbb {R}}^2}V'\big (h\frac{x+x'}{2}\big )\frac{1}{4}(D_y^2D_{\xi }q)\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta \\&\quad +\frac{h^4}{(2\pi )^2}\int _{{\mathbb {R}}^2}\Big (\frac{1}{4}\int _{-1}^1dt\int _{0}^tV''\big (h\frac{x+x'}{2}+t_1h\frac{x-x'}{2} \big )dt_1\Big )\\&\qquad \frac{1}{4}(D_y^2D_{\xi }^2)q\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta , \end{aligned}$$

and

$$\begin{aligned} {\mathcal {K}}_{{\mathcal {T}}}^{(2)}&:=\frac{h^4}{(2\pi )^2}\int _{{\mathbb {R}}^2}\Big (\frac{1}{4}\int _0^1dt\int _{-t}^{t}V''\big (h\frac{x+x'}{2}+t_1h\frac{x-x'}{2}\big )dt_1\Big )\eta \\&\quad \cdot (D_yD_{\xi }^2q)\big (\frac{z+z'}{2},\zeta \big )\textrm{e}^{i(z-z')\cdot \zeta }d\zeta . \end{aligned}$$

By organizing terms, we complete the proof of Lemma B.2. $\square$

To end this section, we collect an elementary averaging Lemma for the one-dimensional harmonic oscillator:

Lemma B.3

Denote by $H_0=D_x^2+x^2$ is the harmonic oscillator and ${\mathcal {U}}(t)=\textrm{e}^{itH_0}$ is the associated propagator, then for any $k\in {\mathbb {N}}$,

$$\begin{aligned}&\int _0^{2\pi }{\mathcal {U}}(t)^*x^{2k-1}{\mathcal {U}}(t)dt=0, \end{aligned}$$

(B.2)

$$\begin{aligned}&\int _0^{2\pi }{\mathcal {U}}(t)^*x^{2}{\mathcal {U}}(t)dt= \frac{1}{2}(D_x^2+x^2). \end{aligned}$$

(B.3)

Proof

Consider the ladder operators ${\mathcal {L}}_{\pm }:=x\mp iD_x$. These operators have properties:

$$\begin{aligned}{}[{\mathcal {L}}_+,{\mathcal {L}}_-]=-2,\quad {\mathcal {L}}_+{\mathcal {L}}_-=H_0-1,\quad {\mathcal {L}}_-{\mathcal {L}}_+=H_0+1 \end{aligned}$$

and ${\mathcal {L}}_+:{\mathcal {H}}_n\mapsto {\mathcal {H}}_{n+1}$ while ${\mathcal {L}}_-:{\mathcal {H}}_n\rightarrow {\mathcal {H}}_{n-1}$, where ${\mathcal {H}}_n$ is the eigenspace of $H_0$ associated with the eigenvalue $2n+1$. Let $\Pi _n: L^2({\mathbb {R}})\rightarrow {\mathcal {H}}_n$ be the orthogonal projection. From this, we deduce that the averaging $\int _0^{2\pi }{\mathcal {U}}(t)^*(\cdots ){\mathcal {U}}(t)dt$ for a monomial composed of ${\mathcal {L}}_{\pm }$ is non-zero if and only if the number of ${\mathcal {L}}_+$ equals the number of ${\mathcal {L}}_-$. Since $x=\frac{1}{2}({\mathcal {L}}_++{\mathcal {L}}_-)$, each monomial in the expansion of $x^{2k-1}$ has different numbers of ${\mathcal {L}}_+,{\mathcal {L}}_-$, thus (B.3) holds. The second identity (B.4) follows from the explicit expansion of $x^2=\frac{1}{4}(2H_0+{\mathcal {L}}_+^2+{\mathcal {L}}_-^2)$. $\square$

Appendix C: Subelliptic a Priori Estimates

Lemma C.1

There exists $C_0>0$ such that for all $u\in H_G^2({\mathbb {T}}^2)$,

$$\begin{aligned} \Vert \Delta _Gu\Vert _{L^2}\le \Vert u\Vert _{{\dot{H}}_G^2}\le C_0\Vert \Delta _G u\Vert _{L^2}+C_0\Vert u\Vert _{L^2}. \end{aligned}$$

Proof

The inequality $\Vert \Delta _G u \Vert _{L^2}\le \Vert u\Vert _{{\dot{H}}_G^2}$ follows trivially by the triangle inequality, hence it suffices to prove the other. Let $\chi$ be a bump function which is equal to 1 near 0. We decompose $u=v+w$, with

$$\begin{aligned}\quad v(x)=(1-\chi (x))u(x),\quad w(x)=\chi (x)u(x). \end{aligned}$$

Since $(-\Delta _Gu,u)=\Vert \nabla _Gu\Vert _{L^2}^2$, we deduce that for test functions $\varphi =1-\chi (x)$ or $\chi (x)$,

$$\begin{aligned} \Vert \Delta _G(\varphi u)\Vert _{L^2}\lesssim _{\varphi } \Vert \Delta _G u\Vert _{L^2}+\Vert u\Vert _{L^2}. \end{aligned}$$

Therefore, it suffices to show that

$$\begin{aligned} \Vert v\Vert _{{\dot{H}}_G^2}\lesssim \Vert \Delta _Gv\Vert _{L^2}+\Vert v\Vert _{L^2},\; \Vert w\Vert _{{\dot{H}}_G^2}\lesssim \Vert \Delta _Gw\Vert _{L^2}+\Vert w\Vert _{L^2}. \end{aligned}$$

Note that $\Delta _G$ is elliptic on supp$(1-\chi )\subset {\mathbb {T}}^2{\setminus }\{x=0\}$, from the support property of v, we deduce that

$$\begin{aligned}\Vert v\Vert _{{\dot{H}}_G^2}\lesssim \Vert \Delta _G v\Vert _{L^2}+\Vert v\Vert _{L^2}.\end{aligned}$$

To estimate $\Vert w\Vert _{{\dot{H}}_G^2}$, we expand w as Fourier series in y, i.e. $w=\sum _{n\in {\mathbb {Z}}}w_n(x)\textrm{e}^{iny}$. It suffices to show that uniformly in n,

$$\begin{aligned}&\Vert |n|V^{1/2}(x)\partial _xw_n\Vert _{L_x^2}+\Vert \partial _x|n|V^{1/2}(x)w_n\Vert _{L_x^2}+ \Vert \partial _x^2w_n\Vert _{L_x^2}+\Vert n^2V(x)w_n\Vert _{L_x^2}\nonumber \\&\quad \le C_0\Vert {\mathcal {L}}_nw_n\Vert _{L_x^2}+\Vert w_n\Vert _{L_x^2} \end{aligned}$$

(B.4)

where ${\mathcal {L}}_n=-\partial _x^2+n^2V(x)$ and $w_n$ are supported on supp$(\chi )$. The estimate is trivial when $n=0$, so below we assume that $n\ne 0$, and without loss of generality, we assume that $n>0$. Set $f_n={\mathcal {L}}_nw_n$ and consider the change of variable $z=n^{\frac{1}{2}}x$ and ${\widetilde{w}}_n(z)=w_n(x), {\widetilde{f}}_n(z)=f_n(x)$, we have

$$\begin{aligned} \widetilde{{\mathcal {L}}}_n {\widetilde{w}}_n={\widetilde{g}}_n:=n^{-1}{\widetilde{f}}_n, \end{aligned}$$

where $\widetilde{{\mathcal {L}}}_n=-\partial _z^2+nW\big (\frac{z}{\sqrt{n}}\big )^2$. By rescaling, it suffices to show that

$$\begin{aligned}&\sqrt{n}\big \Vert \partial _zW\big (\frac{z}{\sqrt{n}}\big ){\widetilde{w}}_n\big \Vert _{L_z^2}+ \sqrt{n}\big \Vert W\big (\frac{z}{\sqrt{n}}\big )\partial _z{\widetilde{w}}_n\big \Vert _{L_z^2}+ \Vert \partial _z^2{\widetilde{w}}_n\Vert _{L_z^2}+n\big \Vert W\big (\frac{z}{\sqrt{n}}\big )^2{\widetilde{w}}_n\big \Vert _{L_z^2}\nonumber \\&\quad \lesssim \Vert {\widetilde{g}}_n\Vert _{L_z^2}+\Vert {\widetilde{w}}_n\Vert _{L_z^2}. \end{aligned}$$

(C.1)

Having in mind that $\sqrt{n}W\big (\frac{z}{\sqrt{n}}\big )\approx z$, the desired estimate is nothing but the a priori estimate for the elliptic equation $(-\partial _z^2+z^2){\widetilde{w}}={\widetilde{g}}$.

We expand

$$\begin{aligned} \Vert {\widetilde{g}}_n\Vert _{L_z^2}^2= \Vert \widetilde{{\mathcal {L}}}_n{\widetilde{w}}_n\Vert _{L_z^2}^2=\Vert \partial _z^2{\widetilde{w}}_n\Vert _{L_z^2}^2+\big \Vert nW\big (\frac{z}{\sqrt{n}}\big )^2{\widetilde{w}}_n\big \Vert _{L_z^2}^2-2n{\text {Re}}\big (\partial _z^2{\widetilde{w}}_n,W\big (\frac{z}{\sqrt{n}}\big )^2{\widetilde{w}}_n\big )_{L_z^2}. \end{aligned}$$

(C.2)

Integration by part yields

$$\begin{aligned} -2n{\text {Re}}\big (\partial _z^2{\widetilde{w}}_n,W\big (\frac{z}{\sqrt{n}}\big )^2{\widetilde{w}}_n\big )_{L_z^2}&=2\big \Vert \sqrt{n}W\big (\frac{z}{\sqrt{n}}\big )\partial _z{\widetilde{w}}_n\big \Vert _{L_z^2}^2\\&\quad +2{\text {Re}}\big (\partial _z{\widetilde{w}}_n,\big [\partial _z,nW\big (\frac{z}{\sqrt{n}}\big )^2\big ]{\widetilde{w}}_n\big )_{L_z^2}. \end{aligned}$$

Note that the second term containing the commutator can be bounded from below by

$$\begin{aligned} -4\big \Vert \sqrt{n}W\big (\frac{z}{\sqrt{n}}\big )\partial _z{\widetilde{w}}_n\big \Vert _{L_z^2}\big \Vert W'\big (\frac{z}{\sqrt{n}}\big ){\widetilde{w}}_n\big \Vert _{L_z^2}\ge -C\big \Vert \sqrt{n}W\big (\frac{z}{\sqrt{n}}\big )\partial _z{\widetilde{w}}_n\big \Vert _{L_z^2}\Vert {\widetilde{w}}_n\Vert _{L_z^2}. \end{aligned}$$

Plugging into (C.3) and using Young’s inequality $AB\le \epsilon A^2+\frac{4}{\epsilon }B^2$, we deduce that

$$\begin{aligned} \Vert {\widetilde{g}}_n\Vert _{L_z^2}^2\ge \Vert \partial _z^2{\widetilde{w}}_n\Vert _{L_z^2}^2 +\big \Vert nW\big (\frac{z}{\sqrt{n}}\big ){\widetilde{w}}_n\big \Vert _{L_z^2}^2+\big \Vert \sqrt{n}W\big (\frac{z}{\sqrt{n}}\big )\partial _z{\widetilde{w}}_n\big \Vert _{L_z^2}^2-C'\Vert {\widetilde{w}}_n\Vert _{L_z^2}^2. \end{aligned}$$

Since

$$\begin{aligned} \sqrt{n}\big \Vert \partial _zW\big (\frac{z}{\sqrt{n}}\big ){\widetilde{w}}_n\big \Vert _{L_z^2}\le + \sqrt{n}\big \Vert W\big (\frac{z}{\sqrt{n}}\big )\partial _z{\widetilde{w}}_n\big \Vert _{L_z^2}+C\Vert {\widetilde{w}}_n\Vert _{L_z^2}, \end{aligned}$$

this implies (C.2). The proof of Lemma C.1 is complete.

$\square$

Appendix D: Equivalence to the Semiclassical Resolvent Estimate

Let us recall the classical theorem of Borichev–Tomilov:

Proposition D.1

[14] The following statements are equivalent:

$$\begin{aligned}&(a) \quad \big \Vert (i\lambda -\dot{{\mathcal {A}}})^{-1}\big \Vert _{{\mathcal {L}}(\dot{{\mathscr {H}}})}\le C|\lambda |^{\frac{1}{\alpha }} \quad \text { for all }\lambda \in {\mathbb {R}}, \quad |\lambda |\ge 1;\\&(b) \quad \Vert \textrm{e}^{t \dot{{\mathcal {A}}}} \dot{{\mathcal {A}}}^{-1} \Vert _{{\mathcal {L}}(\dot{{\mathscr {H}}})} = O(t^{-\alpha }). \end{aligned}$$

Denoting $\Pi _0$ the spectral projector of ${\mathcal {A}}$ on $\ker {\mathcal {A}}$, since $\textrm{e}^{t {\mathcal {A}}} = \textrm{e}^{t \dot{{\mathcal {A}}}} (\textrm{Id}- \Pi _0) + \Pi _0$, we have, if (a) or (b) hold true, that the semigroup $\textrm{e}^{t {\mathcal {A}}}$ is stable at rate $t^{-\alpha }$. In what follows, ${\mathcal {A}}$ is given by (1.3), associated to the damping b.

Lemma D.2

For sufficiently small $h>0$, the following resolvent estimates are equivalent:

$$\begin{aligned}&\mathrm {(a)}\quad \Vert (ih^{-1}-{\mathcal {A}})^{-1}\Vert _{{\mathcal {L}}(H_G^1\times L^2)}\le C_1 h^{-\alpha };\\&\mathrm {(b)}\quad \Vert (-h^2\Delta _G-1\pm ihb)^{-1}\Vert _{{\mathcal {L}}(L^2)}\le C_2h^{-\alpha -1}. \end{aligned}$$

Proof

Essentially, the proof is given in [2]. For the sake of completeness, we provide the proof here. Denote by $U=(u,v)^t$ and $F=(f,g)^t$, then $(ih^{-1}-{\mathcal {A}})U=F$ is equivalent to

$$\begin{aligned} u=-ih(v+f),\quad (-h^2\Delta _G-1+ihb)v=ihg+h^2\Delta _Gf. \end{aligned}$$

The implication (a)$\implies$ (b) follows from making a special choice $(f,g)=(0,g)\in H_G^1\times L^2$.

To prove (b) $\implies$ (a), we first claim that:

• (i) $\Vert (-h^2\Delta _G-1+ihb)^{-1}\Vert _{L^2\rightarrow H_G^1}\lesssim h^{-\alpha -2}$;

• (ii) $\Vert (-h^2\Delta _G-1+ihb)^{-1}\Vert _{H_G^{-1}\rightarrow L^2}\lesssim h^{-\alpha -2}$.

Indeed, assume that

$$\begin{aligned} (-h^2\Delta _G-1+ihb)w=r, \end{aligned}$$

from the energy identity

$$\begin{aligned} \Vert h\nabla _G w\Vert _{L^2}^2-\Vert w\Vert _{L^2}^2={\text {Re}}(r,w)_{L^2}, \end{aligned}$$

we deduce that

$$\begin{aligned} \Vert h\nabla _G w\Vert _{L^2}\lesssim \Vert w\Vert _{L^2}+\Vert r\Vert _{L^2}^{1/2}\Vert w\Vert _{L^2}^{1/2}. \end{aligned}$$

The hypothesis (b) implies that $\Vert w\Vert _{L^2}\lesssim h^{-\alpha -1}\Vert r\Vert _{L^2}$, hence $\Vert w\Vert _{H_G^1}\lesssim h^{-\alpha -2}\Vert r\Vert _{L^2}$, and this verifies (i). Note that the argument above is also valid for $(-h^2\Delta _G-1-ihb(y))^{-1}$, which is the adjoint of $(-h^2\Delta _G-1+ihb(y))^{-1}$. By duality, we obtain (ii).

Finally, from (b) and (ii),

$$\begin{aligned} \Vert v\Vert _{L^2}\lesssim h^{-\alpha -1}\Vert hg\Vert _{L^2}+h^{-\alpha -2}\Vert h^2\Delta _G f\Vert _{H_G^{-1}}\lesssim h^{-\alpha }\Vert (f,g)\Vert _{H_G^1\times L^2}. \end{aligned}$$

(C.3)

From the energy identity

$$\begin{aligned} \Vert h\nabla _G v\Vert _{L^2}^2-\Vert v\Vert _{L^2}^2={\text {Re}}\langle ihg+h^2\Delta _Gf,v\rangle _{H_G^{-1},H_G^1}, \end{aligned}$$

hence

$$\begin{aligned} h^2\Vert v\Vert _{H_G^1}^2\lesssim \Vert v\Vert _{L^2}^2+\Vert ihg+h^2\Delta _G f\Vert _{H_G^{-1}}\Vert v\Vert _{H_G^1}. \end{aligned}$$

Consequently,

$$\begin{aligned} h\Vert v\Vert _{H_G^1}\lesssim h^{-\alpha }\Vert (f,g)\Vert _{H_G^1\times L^2},\end{aligned}$$

thanks to (D.1). Finally, from $u=-ihv-ihf$, we deduce that $\Vert u\Vert _{H_G^1}\lesssim h^{-\alpha }\Vert (f,g)\Vert _{H_G^1\times L^2}$. This completes the proof of Lemma D.2 .

$\square$

Appendix E: Averaging Method in Finite Dimension

In this part of Appendix, we prove the following well-known finite-dimensional averaging lemma, used in Sect. 5:

Lemma E.1

Let $D \in {\mathbb {R}}^{n \times n}$ be a diagonal matrix with entries $\lambda _1< \cdots < \lambda _n$. Let $A_j \in \mathbb {{\mathbb {R}}}^{n\times n}$ for $j= 1, \ldots , N$ be self-adjoint matrices. Then for all $N\in {\mathbb {N}}$, there exist diagonal matrices $D_j\in {\mathbb {R}}^{n\times n}$ for all $j=1,\ldots , N$, such that for any sufficiently small $\epsilon$, there is a unitary matrix ${\mathfrak {U}}_N(\epsilon ) \in {\mathbb {C}}^{n\times n}$, close to the identity, such that

$$\begin{aligned} {\mathfrak {U}}_N \Big ( D + \sum _{j=1}^N \epsilon ^j A_j \Big ) {\mathfrak {U}}_N^* = D + \sum _{j=1}^N \epsilon ^j D_j + O(\epsilon ^{N+1}). \end{aligned}$$

Proof

Write ${\mathfrak {U}}_1 = \textrm{e}^{i \epsilon F_1}$ with $F_1 \in {\mathbb {R}}^{n\times n}$ to be chosen. Then, Taylor expansion gives

$$\begin{aligned} {\mathfrak {U}}_1 \Big ( D + \sum _{j=1}^N \epsilon ^j A_j \Big ) {\mathfrak {U}}_1^*&= D + i \epsilon [F_1, D] + \epsilon A_1\\&\qquad + (i\epsilon )^2 \int _0^1 (1-s) e^{i s \epsilon F_1}[F_1, [F_1,D]] e^{-is \epsilon F_1} ds \\&\qquad + i \epsilon ^2 \int _0^1 e^{is \epsilon F_1} [F_1, A_1] e^{- i s \epsilon F_1} ds+O(\epsilon ^3). \end{aligned}$$

We choose $F_1$ and $D_1$ so that

$$\begin{aligned} i [D,F_1] = A_1 - D_1. \end{aligned}$$

This is possible since the eigenvalues of D are distinct, by taking

$$\begin{aligned} (F_1)_{j_1 j_2} := \frac{1 - \delta _{j_1 j_2}}{i(\lambda _{j_1} - \lambda _{j_2})} (A_1)_{j_1 j_2}; \quad (D_1)_{j_1 j_2} := \delta _{j_1 j_2} (A_1)_{j_1j_2}, \end{aligned}$$

(D.1)

where $\delta _{j_1 j_2}$ denotes the Kronocker delta. Then we obtain:

$$\begin{aligned} {\mathfrak {U}}_1 \left( D + \sum _{j=1}^N \epsilon ^j A_j \right) {\mathfrak {U}}_1^*&= D + \epsilon D_1 + i \epsilon ^2 \int _0^1 e^{i s \epsilon F_1} [F_1, s A_1 + (1-s) D_1] e^{- is \epsilon F_1} ds\\&\quad +O(\epsilon ^3) \\&= D + \epsilon D_1 + O(\epsilon ^2). \nonumber \end{aligned}$$

(E.1)

Iterating this procedure, we obtain the claim by defining ${\mathfrak {U}}_N := \textrm{e}^{ i \epsilon ^N F_n} \cdots \textrm{e}^{i \epsilon F_1}$ for suitable self-adjoint matrices $F_1, \ldots , F_N$ and diagonal matrices $D_1, \ldots , D_N$. $\square$

Appendix F: Some Black-Box Lemma

We collect some known 1D resolvent estimates as black boxes. All will be used in Sect. 4, when reducing the resolvent estimate to the one-dimensional setting. The first estimate is now well-known as the geometric control estimate:

Lemma F.1

[23] Let $I\subset {\mathbb {T}}$ be a non-empty open set. Then there exists $C=C_I>0$, such that for any $v\in L^2({\mathbb {T}})$, $f_1\in L^2({\mathbb {T}}), f_2\in H^{-1}({\mathbb {T}})$, $\lambda \ge 1$, if

$$\begin{aligned} (-\partial _x^2-\lambda ^2)v=f_1+f_2, \end{aligned}$$

we have

$$\begin{aligned} \Vert v\Vert _{L^2({\mathbb {T}})}\le \frac{C}{\lambda }\Vert f_1\Vert _{L^2({\mathbb {T}})}+C\Vert f_2\Vert _{H^{-1}({\mathbb {T}})}+C\Vert v\Vert _{L^2(I)}. \end{aligned}$$

This result can be deduced from the one-dimensional uniform stabilization for the wave equation in [23]. The passage from the uniform stabilization to the resolvent estimate can be also found in Proposition 4.2 and “Appendix A” of [15], or the proof of Proposition 1.4 of [21].

The second estimate follows from the sharp resolvent estimate for the damped-wave operator on ${\mathbb {T}}^2$ with rectangular-shaped damping:

Lemma F.2

[24, Formula (6)]. There exists $h_0>0$, $C>0$ such that for all $0<h<h_0$, $E\in {\mathbb {R}}$, for any solution v of

$$\begin{aligned} -h^2\partial _y^2v-Ev+ihb_2(y)v=f, \end{aligned}$$

we have

$$\begin{aligned} \Vert v\Vert _{L^2({\mathbb {T}})}\le Ch^{-2-\frac{1}{\nu +2}}\Vert f\Vert _{L^2({\mathbb {T}})}. \end{aligned}$$

The third estimate is the almost sharp resolvent estimate for the damped-wave operator on ${\mathbb {T}}^2$, proved in [2] and (essentially) revisited in [45]:

Lemma F.3

[2, Theorem 2.6]. There exists $h_0>0$, $C>0$ and $\delta _0=\delta _0(\sigma )$ such that for all $0<h<h_0$, for any solution v of

$$\begin{aligned} -h^2\Delta v-v+ihb_1(y)v=f, \end{aligned}$$

we have

$$\begin{aligned} \Vert v\Vert _{L^2({\mathbb {T}}^2)}\le Ch^{-2-\delta _0}\Vert f\Vert _{L^2({\mathbb {T}}^2)}. \end{aligned}$$

The last estimate is a special case of the sharp resolvent estimate for the damped-wave operator on ${\mathbb {T}}^2$ for the narrowly undamped situation:

Lemma F.4

[34, Theorem 1.8]. There exists $h_0>0$, $C>0$, such that for all $0<h<h_0$, for any solution v of

$$\begin{aligned} -h^2\Delta v-v+ihb_3(y)v=f, \end{aligned}$$

we have

$$\begin{aligned} \Vert v\Vert _{L^2({\mathbb {T}}^2)}\le Ch^{-2+\frac{2}{\nu +2}}\Vert f\Vert _{L^2({\mathbb {T}}^2)}. \end{aligned}$$

We used also intensively a commutator estimate for Lipschitz functions:

Lemma F.5

Assume that $\kappa \in W^{1,\infty }({\mathbb {R}}^d)$ and $a\in S^0({\mathbb {R}}^{2d})$, then

$$\begin{aligned} \Vert [{\text {Op}}_h^{\textrm{w}}(a),\kappa ] \Vert _{{\mathcal {L}}(L^2({\mathbb {R}}^d))}\le Ch. \end{aligned}$$

The proof of this Lemma is standard and can be found, for example, in Corollary (A.2) of [?]. The proof there applies to Weyl quantization as well. In various places of this article, we apply Lemma F.5 to deduce that $[b^{1/2},{\text {Op}}_h^{\textrm{w}}(a)]=O_{{\mathcal {L}}(L^2)}(h)$ and $[b^{1/2},[b^{1/2},{\text {Op}}_h^{\textrm{w}}(a)]]=O_{{\mathcal {L}}(L^2)}(h^2)$, thanks to the hypothesis (1.5).