Abstract
Bit threads are curves in holographic spacetimes that manifest boundary entanglement, and are represented mathematically by continuum analogues of network flows or multiflows. Subject to a density bound, the maximum number of threads connecting a boundary region to its complement computes the Ryu–Takayanagi entropy. When considering several regions at the same time, for example in proving entropy inequalities, there are various inequivalent density bounds that can be imposed. We investigate for which choices of bound a given set of boundary regions can be “locked”, in other words can have their entropies computed by a single thread configuration. We show that under the most stringent bound, which requires the threads to be locally parallel, non-crossing regions can in general be locked, but crossing regions cannot, where two regions are said to cross if they partially overlap and do not cover the entire boundary. We also show that, under a certain less stringent density bound, a crossing pair can be locked, and conjecture that any set of regions not containing a pairwise crossing triple can be locked, analogously to the situation for networks.









Similar content being viewed by others
Notes
In this paper we restrict ourselves to the domain of validity of the RT formula in the form (1.1), namely holographic field theories in a limit where the dual is governed by classical Einstein gravity, in a static or time-reflection-invariant state. Relaxing each of these limitations leads to very interesting questions about both entropy inequalities and bit threads; however, we will not venture to address those questions here.
We use \(A,B,\ldots \) to represent non-empty, non-overlapping boundary regions, which we refer as elementary regions. More generally, a region is an elementary region or union thereof (where AB denotes \(A\cup B\), etc.). We do not impose any restrictions on the dimension or topology of the bulk or on the topology of the boundary regions. Formal definitions will be given in Sect. 2.1.
Such a set-up was used in [25] for computing a quantity called holographic multipartite entanglement of purification.
We are implicitly assuming that the dual state is pure, so that \(\mathcal {M}\) is not bounded by any horizons; to our knowledge, any holographic mixed state (such as a thermal state) can be purified holographically, so this assumption comes without loss of generality. One can also consider “internal” boundaries that are not part of the conformal boundary where the field theory lives, such as confining walls and end-of-the-world branes. To avoid cluttering the discussion, we will not consider such internal boundaries here; however, they can easily be included simply by not allowing threads to end on them. See [19] for a discussion of how to include such boundaries in the dualization and max flow-min cut theorem.
This notation is borrowed from [5]. However, note that, in contrast to that reference, the \(A_i\) cover all of \(\partial {\mathcal {M}}\); we do not include a “purifying” region O.
We permit closed threads purely as a matter of mathematical convenience, allowing us to pass more easily between the thread and flow languages. (Indeed, much of the power of the flow language derives from the fact that it involves only local constraints, using which one cannot rule out closed flow lines.) In the holographic setting, they do not (as far as we know) correspond to any form of entanglement. Mathematically, for the purposes of locking, our main interest in this paper, they play no role and can always be deleted.
Restoring units, the density is required to be less than or equal to \(1/4G_{\mathrm{N}}\). Since the threads are 1-dimensional, the density has units of length\(^{1-d}\).
As discussed in [18], we can define a thread configuration mathematically as a set of unoriented curves equipped with a measure, allowing us to “count” the number passing through a surface or connecting one boundary region to another. However, in this paper we will not aim for mathematical precision in our discussion of threads.
At first sight, the condition \(\nu _c(V)\le 1\) may appear stronger than (2.15), since the former forbids bundles from overlapping, whereas the latter merely forces them to be parallel. However, since distinct bundles start and/or end on distinct boundary regions, in order to overlap they must be non-parallel somewhere.
We are slightly abusing the term “norm”, since \(\nu _c\) does not obey the homogeneity property usually required of a norm.
There is also the trivial notational difference that in [18] the fields \(\vec {v}_{ij}\) were also defined for \(i\ge j\), but with the constraint \(\vec {v}_{ji}=-\vec {v}_{ij}\).
We can fix the ambiguity in the direction of the component flows by forcing the flow lines of \(\vec {v}_{ij}\) to go from \(A_i\) to \(A_j\). This would be accomplished by adding to the definition of a multiflow the further constraint \({\hat{n}}\cdot \vec {v}_{ij}\ge 0\) on \(A_i\). This essentially amounts to fixing a gauge ambiguity and would not change anything in the main substance of the paper. It would lead to the following changes to the material in the rest of this section: It would guarantee that (2.28) is obeyed; eliminate the possibility of threads connecting \(A_i\) to itself, requiring us to delete such threads in the procedure below (2.28) to convert a flow to a multiflow; make (2.19), as applied to (2.31), a necessary (in addition to sufficient) condition for the multiflow V to lock \(A_I\); and change the constraints (2.42) for the dual program to \(\psi _{ij}\ge N_{ij}\) on \(A_i\), \(\psi _{ij}\le 0\) on \(A_j\). It would leave unchanged the dual program in the second form (2.48).
Specifically, suppose \(m_{IJ}:=m(A_I)\cap m(A_J)\ne \emptyset \) for some \(I\ne J\). By the nesting property of homology regions, for every K on the path \(p_{IJ}\) on G connecting I and J, \(m(A_K)\supset m_{IJ}\), except \(K=[n]\). We introduce an infinitesimal gap between \(m(A_K)\) and \(m(A_L)\) for the distinct pair of vertices K, L on \(p_{IJ}\) if (1) \(K\leftarrow J\ne [n]\), in which case the gap is included in \(r(A_M)\) for all \(M\supseteq L\); or (2) \(K\leftarrow [n]\rightarrow L\), in which case the gap is only included in \(r(A_{[n]})=\mathcal {M}\).
It may seem tempting to try to untangle more than two flows at once, accelerating us towards our eventual \(\nu _c\)-compliant solution. However, there is in general no way to combine three or more flows into a composite flow while conserving the flux out of all \(A_I\). In fact, the very simple case of three primitive boundary regions (each its own composite region) and three component flows provides a counterexample, which will be left as an exercise to the reader.
This argument was pointed out to us by V. Hubeny.
On the other hand, they would not necessarily obey the \(\nu _v\) bound, for example if at some point \(\vec {v}_{1,2}\) are orthogonal unit vectors. This is thus the step where the \(\nu _a\) bound demonstrates its advantage over the \(\nu _v\) bound.
The theorem can also be proven without using Lemma 6.2. A similar calculation to (6.12), but without assuming that \(\vec {v}_{AC}^+\) and \(\vec {v}_{BD}^-\) vanish, shows that
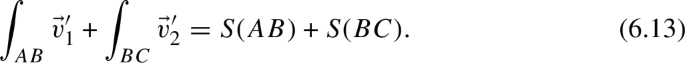
Combined with the inequalities \(\int _{AB}\vec {v}_1'\le S(AB)\), \(\int _{BC}\vec {v}_2' \le S(BC)\), (6.13) shows that both inequalities are saturated, hence AB and BC are locked.
An integral network \(\mathcal {N}\) is essentially equivalent to a network \(\mathcal {N}'\) based on a multigraph with unit capacities, where for every edge e with capacity c(e) in \(\mathcal {N}\) there are c(e) edges connecting the same pair of vertices in \(\mathcal {N}'\). An integral path set on \(\mathcal {N}\) is then equivalent to a pairwise edge-disjoint path set on \(\mathcal {N}'\). (See below for the definition of a path set.) This equivalent language is commonly used in the network flow literature.
There are locking theorems with additional conditions on the network interior that are able to surpass the three-cross-free “ceiling”. One example, mentioned in [26], states that if the network is planar with all its terminals on the exterior, and terminal sets in \(\mathcal {I}\) consist only of contiguous spans of the network perimeter, then \(\mathcal {I}\) can be locked.
We leave the proofs of this and other statements in this subsection to the reader.
The component flows may overlap on \(\mathcal {M}\) in this construction, so the result is not necessarily a \(\nu _c\)-multiflow. A \(\nu _c\)-multiflow can be produced by going to higher dimensions as follows: Map each vertex of \(\mathcal {N}\) to a 3-sphere; for each edge e sew the appropriate 3-spheres along a 2-sphere of area w(e); decompose the 2-sphere into non-overlapping regions of area \(|\vec {v}_{\mathcal {N}ij}(e)|\) for all \(i<j\); set \(\vec {v}_{\mathcal {M}ij}\) equal to the unit normal vector on its respective region; and extend the \(\vec {v}_{\mathcal {M}ij}\)s to the rest of \(\mathcal {M}\) to divergenceless vector fields obeying the \(\nu _c\) norm bound. The reason it is necessary to go to higher dimensions for this construction is that, on 2-spheres, the component flows (or threads) may be topologically forced to cross each other.
References
Ryu, S., Takayanagi, T.: Holographic derivation of entanglement entropy from AdS/CFT. Phys. Rev. Lett. 96, 181602 (2006). arXiv:0603001 [hep-th]
Headrick, M., Takayanagi, T.: A Holographic proof of the strong subadditivity of entanglement entropy. Phys. Rev. D 76, 106013 (2007). arXiv:0704.3719
Headrick, M.: General properties of holographic entanglement entropy. JHEP 03, 085 (2014). arXiv:1312.6717
Hayden, P., Headrick, M., Maloney, A.: Holographic mutual information is monogamous. Phys. Rev. D 87(4), 046003 (2013). arXiv:1107.2940
Bao, N., Nezami, S., Ooguri, H., Stoica, B., Sully, J., Walter, M.: The holographic entropy cone. JHEP 09, 130 (2015). arXiv:1505.07839
Czech, B., Dong, X.: Holographic entropy cone with time dependence in two dimensions. JHEP 10, 177 (2019). arXiv:1905.03787
Brown, E., Bao, N.: Non-linear Holographic Entanglement Entropy Inequalities for Single Boundary 2D CFT. arXiv:1508.05441
Bao, N., Cao, C., Walter, M., Wang, Z.: Holographic entropy inequalities and gapped phases of matter. JHEP 09, 203 (2015). arXiv:1507.05650
Bao, N., Blitz, S., Stoica, B.: Holographic Entropy Cone Measures. arXiv:1701.03498
Bao, N., Mezei, M.: On the Entropy Cone for Large Regions at Late Times. arXiv:1811.00019
Hubeny, V.E., Rangamani, M., Rota, M.: Holographic entropy relations. Fortsch. Phys. 66(11–12), 1800067 (2018). arXiv:1808.07871
Hubeny, V.E., Rangamani, M., Rota, M.: The holographic entropy arrangement. Fortsch. Phys. 67(4), 1900011 (2019). arXiv:1812.08133
He, T., Headrick, M., Hubeny, V.E.: Holographic entropy relations repackaged. JHEP 10, 118 (2019). arXiv:1905.06985
Caginalp, R.J.: Holographic entropy cone in AdS-Vaidya spacetimes. Phys. Rev. D 101(2), 026010 (2020). arXiv:1905.00544
Hernández Cuenca, S.: Holographic entropy cone for five regions. Phys. Rev. D 100(2), 026004 (2019). arXiv:1903.09148
He, T., Hubeny, V.E., Rangamani, M.: Superbalance of holographic entropy inequalities. JHEP 07, 245 (2020). arXiv:2002.04558
Freedman, M., Headrick, M.: Bit threads and holographic entanglement. Commun. Math. Phys. 352(1), 407–438 (2017). arXiv:1604.00354
Cui, S.X., Hayden, P., He, T., Headrick, M., Stoica, B., Walter, M.: Bit threads and holographic monogamy. Commun. Math. Phys. (2019) arXiv:1808.05234
Headrick, M., Hubeny, V.E.: Riemannian and Lorentzian flow-cut theorems. Class. Quant. Grav. 35(10), 10 (2018). arXiv:1710.09516
Nezami, S., Walter, M.: Multipartite Entanglement in Stabilizer Tensor Networks. arXiv:1608.02595
Akers, C., Rath, P.: Entanglement Wedge Cross Sections Require Tripartite Entanglement. arXiv:1911.07852
Hubeny, V.E.: Bulk locality and cooperative flows. JHEP 12, 068 (2018). arXiv:1808.05313
Agon, C.A., de Boer, J., Pedraza, J.F.: Geometric aspects of holographic bit threads. JHEP 05, 075 (2019). arXiv:1811.08879
Karzanov, A., Lomonosov, M.: Flow systems in undirected networks. In: Larichev, O.I. (ed.) Mathematical Programming, pp. 59–66. Institute for System Studies, Moscow (1978) (in Russian)
Harper, J., Headrick, M.: Bit threads and holographic entanglement of purification. JHEP 08, 101 (2019). arXiv:1906.05970
Frank, A., Karzanov, A., Sebo, A.: On integer multiflow maximization. SIAM J. Discrete Math. 10, 158–170 (1997)
Hirai, H.: A note on multiflow locking theorem. J. Oper. Res. Soc. Jpn. 53(2), 149–156 (2010)
Karzanov, A., Pevzner, P.: A complete description of the class of cut-nondetermined maximum multicommodity flow problems. In: Combinatorial Methods for Flow Problems, 3rd edn, pp. 70–81. Institute for System Studies, Moscow (1979) (in Russian)
Acknowledgements
The work of Headrick and Herman is supported in part by the Simons Foundation through It from Qubit: Simons Collaboration on Quantum Fields, Gravity, and Information and in part by the Department of Energy, Office of High-Energy Physics, through Award DE-SC0009987. We would like to thank Veronika Hubeny for very useful conversations and comments on the draft, and John Wilmes for help with the numerical optimization. Headrick would also like to thank the Kavli Institute for Theoretical Physics for hospitality while this work was completed; KITP is supported in part by the National Science Foundation under Grant No. NSF PHY-1748958.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A. Multiflows on Networks
A. Multiflows on Networks
Much of the work in this paper is inspired by the well-established theory of multiflows on networks and the question of to what extent that theory carries over to multiflows on manifolds. In this appendix we discuss some aspects of multiflows on networks and their relation to multiflows on manifolds. We begin in “Appendix A.1” by reviewing basic definitions of networks and path sets, as well as the standard network locking theorem, Theorem A.1, which says that a three-cross-free terminal subset can be locked. In “Appendix A.2”, we explain the importance of the three-cross-free condition by proving what is essentially a converse result. Theorem A.1 involves integral networks and integral paths sets, and its proof is correspondingly discrete and combinatorial in nature. In “Appendix A.3”, we give an alternative description of multiflows in terms of vector fields, analogous to multiflows on manifolds, and in “Appendix A.4” we use that desciption to prove Theorem A.7, which is a network analogue of Theorem 6.1. While this is essentially a special case of Theorem A.1, as far as we know the method of proof is new. Finally, in “Appendix A.5”, we explain how to map a manifold to a network and vice versa, and correspondingly map multiflows from one to the other.
More detailed information on multiflows on networks can be found in [27] and references therein.
1.1 A.1 Basic definitions and theorems
A network \(\mathcal {N}\) consists of a graph (V, E) with vertex set V and edge set E, a subset \(T\subseteq V\) of its vertices called terminals, and perhaps some extra data such as a positive real- or integer-valued capacity (or weight) c(e) associated to each edge \(e\in E\). Various types of graphs are considered in the literature: directed or undirected graphs; simple graphs (with at most one edge connecting any pair of distinct vertices and no edge connecting a vertex to itself) or multigraphs (with any number of edges connecting a given pair of distinct vertices or a vertex to itself); finite or infinite graphs; etc. To focus the discussion, we will consider only finite, undirected, simple graphs, with real or integral capacities. A network will be assumed to have real capacities unless specified as an “integral network”.Footnote 20
We will use x, y to denote general vertices and i, j to denote terminals, and take \(T=[n]:=\{1,\ldots ,n\}\). Given a subset \(I\subseteq T\) of terminals, we write \({\bar{I}}:=T{\setminus } I\). An I-cut is a set of edges \(C\subseteq E\) such that in the graph \((V,E{\setminus } C)\) there is no path connecting I and \({\bar{I}}\). In the analogy between networks and manifolds, the terminal set is the analogue of the boundary of the manifold, each terminal is the analogue of an elementary region \(A_i\), and an I-cut is the analogue of a bulk surface homologous to \(A_I\). The min cut function S(I) is the minimum total capacity of any I-cut:
The analogue of a “thread configuration” is a set \(\mathcal {P}\) of (unoriented simple) paths, each of which connects distinct terminals, together with a positive weight \(w_P\) for each path \(P\in \mathcal {P}\), satisfying the capacity constraint:
Such a weighted path set is sometimes called a “multiflow” in the literature on network flows, but we will reserve the term for a set of vector fields, defined in “Appendix A.3” and analogous to a multiflow on a manifold used in the main text. We will use the term path set to mean a weighted path set obeying (A.2), and integral path set for one with integer weights.
Given a path set \(\mathcal {P}\), we will denote the total weight of paths connecting disjoint terminal sets I, J by \(N_{I:J}\):
In particular, the number connecting I and \({\bar{I}}\) is bounded above by S(I):
The network max flow-min cut theorem says that this inequality is tight:
We say that \(\mathcal {P}\) locks I if it achieves the maximum. Menger’s theorem says further that, on an integral network, I can be locked by an integral path set.
Given a family \(\mathcal {I}\subseteq 2^T\) of terminal sets, we say that \(\mathcal {P}\) locks \(\mathcal {I}\) if it locks I for all \(I\in \mathcal {I}\). The network locking theorem of Karzanov-Lamonosov gives sufficient conditions for \(\mathcal {I}\) to be lockable by an integral path set.
Theorem A.1
(Network locking [24, 26]). Let \(\mathcal {N}\) be an inner-Eulerian network, and \(\mathcal {I}\) a family of subsets of T without a pairwise-crossing triple. Then there exists an integral path set that locks \(\mathcal {I}\).
An inner-Eulerian network is an integral network such that, for every interior (i.e. non-terminal) vertex \(x\in V{\setminus } T\), the total capacity of the incident edges is even. To see why this condition is needed, consider the simplest non-trivial integral network that is not inner-Eulerian, namely the star graph with 3 external vertices A, B, C and unit capacities. Locking the set \(\mathcal {I}=\{A,B,C\}\) requires paths of weight 1/2 connecting every pair of external vertices. A refined proof of theorem A.1 is given in [26], and will not be repeated here.
The following corollaries follow simply by multiplying all the capacities of \(\mathcal {N}\) by 2 (for Corollary A.2) or twice their lowest common denominator (for Corollary A.3), which makes the network inner-Eulerian, and then dividing the weights in the resulting locking path set by the same factor.
Corollary A.2
Let \(\mathcal {N}\) be an integral network, and \(\mathcal {I}\) a family of subsets of T without a pairwise-crossing triple. Then there exists a path set with half-integer weights that locks \(\mathcal {I}\).
(The above star graph is an example of Corollary A.2.)
Corollary A.3
Let \(\mathcal {N}\) be a network with rational capacities, and \(\mathcal {I}\) a family of subsets of T without a pairwise-crossing triple. Then there exists a path set with rational weights that locks \(\mathcal {I}\).
It seems reasonable to expect, by approximating the capacities more and more closely by rationals, that Corollary A.3 holds with “rational” replaced by “real”; however, we have neither seen this statement in the literature nor proved it.
1.2 A.2 Network locking failure
The three-cross-free condition in Theorem A.1 and its corollaries is in fact necessary if one wants lockability of \(\mathcal {I}\) to be guaranteed without putting further restrictions on the network, as shown by the following theorem:Footnote 21
Theorem A.4
(Network locking failure). Let n be an integer \(\ge 4\), and \(\mathcal {I}\supseteq \{I,J,K\}\) a family of subsets of [n] such that I, J, K are pairwise crossing. Then there exists an inner-Eulerian integral network \(\mathcal {N}\) with terminal set \(T=[n]\) on which \(\mathcal {I}\) cannot be locked by any path set.
(Note that we do not require the path set to be integral, so the theorem is a bit stronger than the converse to Theorem A.1.) Theorem A.4 was proven in [28], which is in Russian. We are not aware of a proof in English, so we provide one here.
Visual representation of the regions defined in (A.6)
Proof
We will classify the different types of three-crossing, and for each type find a network on which \(\{I,J,K\}\) cannot be locked.
We decompose [n] into the following eight subsets (see Fig. 10):
H is the subset of terminals not in I, J, or K, and will be referred to as the purification set. In order for I, J, K to cross pairwise, we need all of the following sets to be non-empty:
To avoid double-counting equivalent cases under complementation, we will assume that H is non-empty. This automatically satisfies the requirement that GH, DH, and FH are non-empty, and we are left with the other nine. We can visually represent these constraints with the following graph, in which the nodes are labeled \(A,\ldots ,G\) and two terminal sets \(X,Y\in \{A,\ldots , G\}\) are adjacent if their union XY must be non-empty:

For each edge in the above graph, at least one of the incident vertices must be a non-empty terminal set. There are three distinct minimal cases which satisfy this requirement. Vertices in red are non-empty in their respective cases. All instances of three-crossing are reducible to at least one of these cases:

As it turns out, cases 1 and 3 are not distinct. In case 3, if we replace I, J, K with their complements \(\bar{I}\), \(\bar{J}\), \(\bar{K}\) (making A the new purification set), and then set the old purification set H to the empty set, we are left with exactly case 1. This leaves only cases 1 and 2.
In case 1, B, C, E, H are all non-empty; let \(b,c,e,h\in [n]\) be elements of the respective subsets. Then \(I\supseteq \{b,c\}\), \(J\supseteq \{b,e\}\), \(K\supseteq \{ c,e\}\). It is a straightforward to show that, on the following graph with terminals b, c, e, h and unit capacities on all edges, the set \(\{bc,ce,be\}\) cannot be locked:

Adding the elements of \([n]{\setminus }\{b,c,e,h\}\) as isolated terminals, the result is a network with terminal set [n] in which \(\{I,J,K\}\), and therefore \(\mathcal {I}\), cannot be locked.
In case 2, A, B, C, F, G, H are non-empty; again let a, b, c, f, g, h be elements. Then \(I\supseteq \{ a,b,c\}\), \(J\supseteq \{ a,b,f\}\), \(K\supseteq \{ a,c,g\}\). By the same reasoning, \(\mathcal {I}\) is not lockable on the following graph:

\(\square \)
1.3 A.3 Flows, multiflows, and path sets
In this subsection, we will define the notions of flows and multiflows on networks in terms of vector fields, by analogy with those concepts on manifolds. We will then show that they can be converted to and from path sets and each other.
First, we associate to each edge \(e=\{x,y\}\in E\) a one-dimensional vector space with an inner product—the “tangent space”. In this tangent space, we label vectors on one side of 0 as being directed from x to y and on the other side from y to x. We denote the unit vector from x to y by \({\hat{n}}(x,y)\). A vector field \(\vec v\) associates a vector \(\vec v(e)\) to each edge e. Given a vector field, the net flux out of a vertex x is defined as
\(\Phi \) is a linear map from vector fields to real functions on the vertex set V. We also write the total flux out of a set of terminals \(I\subseteq T\) as \(\Phi [\vec v](I)\):
A flow is a vector field \(\vec v\) satisfying the capacity constraint
and the divergenceless constraint
The flux of a flow out of a terminal set I cannot exceed its min cut:
The flow version of the max flow-min cut theorem says that this bound is tight:
This is equivalent to the path-set version of the theorem (A.5) by converting between flows and path sets, as discussed below. We say \(\vec v\) locks I if it achieves the maximum.
A multiflow is a set of flows \(V=(\vec v_{ij})_{i<j}\) obeying the joint capacity condition
and the no-flux condition for \(\vec v_{kl}\) on i:
Together with the divergenceless condition, (A.15) implies
Given a multiflow, any constant (e-independent) linear combination of the component flows with coefficients between \(-1\) and 1 is a flow:
We say that a multiflow locks a set I of terminals if the flow
locks I. As in the continuum, the advantage of multiflows is that they allow us to keep track not just of the total flux out of a given set of terminals but of how much flux is flowing from one terminal to another.
It was indicated in (A.17) that the component flows of a multiflow can be combined to obtain a single flow. Conversely, as we will show, a flow can be decomposed into a multiflow. We will do this by first writing the flow as a path set and then sorting the paths by their endpoints.
We first define an (integral) oriented path set \({\tilde{\mathcal {P}}}\) as a set of paths P, each of which has a positive (integer) weight \(w_P\) and an orientation \({\hat{n}}_P(e)\), which is a unit vector on each edge \(e\in P\), obeying the capacity constraint (A.2). We allow oriented path sets to include not only paths connecting distinct terminals but also loops. This is merely a technical convenience, as it makes the correspondence to flows closer and simplifies some formulas. An oriented path set \({\tilde{\mathcal {P}}}\) can be converted to a path set \(\mathcal {P}\) by dropping the orientations and deleting any loops; this preserves any integrality and locking properties of \({\tilde{\mathcal {P}}}\).
An oriented path set \({\tilde{\mathcal {P}}}\) can be converted to a flow \(\vec {v}\):
Similarly, to write \({\tilde{\mathcal {P}}}\) as a multiflow we assign the paths connecting distinct terminals \(i<j\) to the component flow \(\vec {v}_{ij}\), and the loops to any component flow.
The converse decomposition is given by the following lemma, which we prove below:
Lemma A.5
Let \(\mathcal {N}\) be a network and \(\vec {v}\) a flow on \(\mathcal {N}\). Then there exists an oriented path set \({\tilde{\mathcal {P}}}\) such that (A.19) holds and the orientations \({\hat{n}}_P(e)\) are equal for all \(e\in E\) and \(P\in \mathcal {P}\) containing e, implying
Furthermore, if \(\vec {v}\) is integral then there exists such a \({\tilde{\mathcal {P}}}\) that is integral.
By separating the paths according to their endpoints, and converting the paths with endpoints \(i<j\) into the component flow \(\vec {v}_{ij}\), we obtain a multiflow:
Corollary A.6
Given a flow \(\vec v\) on a network \(\mathcal {N}\), there exists a multiflow V such that
and, for all \(e\in E\), all non-zero \(\vec v_{ij}(e)\) have the same direction, implying
Proof of Lemma A.5
We proceed iteratively, building up \({\tilde{\mathcal {P}}}\) step by step. It will be seen that if \(\vec {v}\) is integral then the resulting \({\tilde{\mathcal {P}}}\) is also integral.
Let \(\vec v^{(0)}:=\vec v\). For \(m\ge 0\), if \(\vec {v}^{(m)}\ne 0\), we define an oriented weighted path \(P_m\) and a new flow \(\vec {v}^{(m+1)}\). If \(\vec v^{(m)}=0\), we stop the procedure, and set \({\tilde{\mathcal {P}}}:=\{P_{m'}\}_{0\le m'<m}\).
Given \(\vec {v}^{(m)}\), we find an oriented path \(P_m\)—either a loop or a path connecting distinct terminals—such that on every edge \(e\in P_m\), \(\vec v^{(m)}(e)\) is non-zero and is in the same direction as \(P_m\). To construct \(P_m\), first choose an edge \(e_0=\{x_0,x_1\}\) where \(\vec v^{(m)}(e_0)\ne 0\); assume without loss of generality that \(\vec v^{(m)}(e_0)\) is directed from \(x_0\) to \(x_1\). If \(x_1\) is in the interior, then there exists an edge \(e_1=\{x_1,x_2\}\) such that \(\vec v^{(m)}(e_1)\) is non-zero and directed from \(x_1\) to \(x_2\). Continue extending the path in this way until it either reaches a terminal or meets a vertex already on the path: \(x_{s_1}=x_{s_2}\), \(s_1<s_2\). In the latter case let \(P_m\) be the loop from \(s_1\) to \(s_2\); drop the part of the path up to \(s_1\). In the former case, continue the path “backward” from \(x_0\); again, until it either reaches a terminal or a vertex already on the path. Again, in the latter case retain only the loop. This defines \(P_m\).
The weight of \(P_m\) is fixed as follows,
and the new flow \(\vec {v}^{(m+1)}\) is defined by reducing the flow along \(P_m\) by \(w_{P_m}\):
This is still a flow, since the divergenceless constraint is still obeyed, as is the capacity constraint: \(|\vec v^{(m+1)}(e)|\le |\vec v^{(m)}(e)|\le c(e)\) for all \(e\in E\). Furthermore, the flow has been zeroed out on the edge \(e_{\mathrm{min}}\) where the minimum in (A.23) is achieved: \(\vec v^{(m)}(e_{\mathrm{min}})\ne 0\) but \(\vec v^{(m+1)}(e_{\mathrm{min}})=0\). Hence, if we repeat this procedure, given that the graph is finite, it will end with the vanishing flow in a finite number of steps. Finally, on any edge e where \(\vec v^{(m)}(e)=0\), \(\vec v^{(m+1)}(e)=0\), and on any edge e where \(\vec v^{(m)}(e)\ne 0\), \(\vec v^{(m+1)}(e)\) either vanishes or is in the same direction as \(\vec v^{(m)}(e)\). In other words, the flow direction is never reversed by the update. Hence \({\hat{n}}_{P_m}(e)\) is the same for all \(P_m\) containing e. \(\square \)
1.4 A.4 Crossing-pair locking theorem
In this subsection we use flows and multiflows to prove the following theorem. The proof follows closely that of Theorem 6.1.
Theorem A.7
(Network crossing-pair locking). Let \(\mathcal {N}\) be a network and \(I,J\subset T\) terminal sets that cross. Then there exists a path set that locks \(\{I,J\}\). Furthermore, if \(\mathcal {N}\) is integral then there exists a path set with half-integral weights that locks \(\{I,J\}\).
The first part of this theorem is a special case of Corollary A.3, or more precisely its conjectured real version, while the second part is a special case of Corollary A.2.
Proof
For clarity we consider the case where there are only four terminals, which we denote A, B, C, D, and we wish to lock \(\{AB,BC\}\). This is without loss of generality. Given crossing sets of terminals I, J on \(\mathcal {N}\), we can make a new network \(\mathcal {N}'\) by adding a new terminal A attached with edges of infinite capacity to the terminals in \(I{\setminus } J\), and convert the latter into interior vertices; similarly with B and \(I\cap J\); C and \(J{\setminus }{\setminus } I\); and D and \(\overline{I\cup J}\). A path set on \(\mathcal {N}'\) that locks \(\{AB,BC\}\) defines a path set on \(\mathcal {N}\) that locks \(\{I,J\}\).
We now proceed to the proof. We start with max flows \(\vec v_{1,2}\) for AB, BC respectively:
We would like to combine these into a single multiflow, while preserving the fluxes on AB and BC. We could use Corollary A.6 to decompose each of \(\vec v_1\) and \(\vec v_2\) into a multiflow. The problem is that these two multiflows are not necessarily compatible with each other; we cannot necessarily combine them while obeying the joint capacity constraint (A.14).
Therefore we will use a trick. We combine them into flows \(\vec v^\pm \):
Obviously this reshuffling does not lose any information about the original flows. However, unlike the original flows, \(\vec v^\pm \) are compatible with each other, i.e. they obey a joint capacity constraint:
for every edge. (A.27) follows from the fact that the left-hand side equals the maximum of \(|\vec v_1(e)|\) and \(|\vec v_2(e)|\). Since they are compatible, when we convert each into a multiflow, we can combine them into a single multiflow, in a way that preserves the relevant fluxes.
We thus use Corollary A.6 to convert each flow \(\vec v^\pm \) into a multiflow \(\{\vec v^\pm _{ij}\}\). Each of these obeys (A.22), that is
for all \(e\in E\). Combining this with (A.27), we have
This implies that an arbitrary linear combination of \(\{\vec v^+_{ij}\}\) and \(\{\vec v^-_{ij}\}\) of the form
with (e-independent) coefficients \(\xi ^\pm _{ij}\in [-1,1]\), obeys the joint capacity constraint, as well as the other conditions in the definition of a multiflow. We choose the following combinations:
We now show that the multiflow (A.31) locks AB and BC. From (A.31) we define the following flows:
We now calculate the total flux of \(\vec v_1'\) out of AB:
A similar calculation shows that
Finally, given that
(A.33), (A.34) imply that both bounds must be saturated, i.e. \(\vec v_1'\) locks AB and \(\vec v_2'\) locks BC. Each component of the multiflow (A.31) can be converted using Lemma A.5 into a path set, the union of which locks AB, BC.
If \(\mathcal {N}\) is integral, then by Menger’s theorem \(\vec {v}_{1,2}\) can be chosen to be integral. \(\vec {v}^\pm \) are then half-integral, and therefore so is the multiflow (A.31) and the resulting path set.\(\square \)
Network obtained by dessication of flat unit square with sides A, B, C, D. (More precisely, the square with padding added to separate each boundary region from its respective minimal surface; e.g. a disk of radius \(1/\sqrt{2}\) with boundary circle divided into equal arcs.) The capacity of each edge is shown in black. Also shown (in color) is a multiflow that locks both AB and BC. The multiflow has only two non-zero components, \(\vec v_{AC}\) (red) and \(\vec v_{BD}\) (blue)
1.5 A.5 Relation between network and manifold multiflows
Multiflows on networks and on manifolds are closely related, since either one can be converted into the other. Given a Riemannian manifold with boundary \(\mathcal {M}\) and boundary decomposition \(\{A_1,\ldots ,A_n\}\), we can define a network \(\mathcal {N}\) with terminal set [n] such that the respective min cut functions \(S_\mathcal {M}\), \(S_{\mathcal {N}}\) agree:
The construction, described in [5] and sometimes called “dessication”, proceeds by cutting \(\mathcal {M}\) up along the minimal surfaces \(m(A_I)\) for all possible composite regions \(A_I\). Each resulting bulk region, or cell, is mapped to a vertex of the network, which is labelled a terminal if the region is bounded by an \(A_i\). If two cells are adjacent then the corresponding vertices are joined by an edge, with capacity given by the area of their shared boundary. Under this construction, the minimal cut in \(\mathcal {N}\) for any \(I\subseteq [n]\) lifts to the minimal surface \(m(A_I)\) in \(\mathcal {M}\). The dessication of the flat unit square studied in Sect. 5 is shown in Fig. 11.
A flow \(\vec {v}_\mathcal {M}\) on \(\mathcal {M}\) can be mapped to a flow \(\vec {v}_\mathcal {N}\) on the dessication of \(\mathcal {M}\) by setting \(\vec {v}_\mathcal {N}(e)\) on a given edge e to the flux of \(\vec {v}_\mathcal {M}\) over the corresponding surface in \(\mathcal {M}\). This guarantees that, for any terminal set \(I\subseteq [n]\),
in particular, \(\vec {v}_\mathcal {N}\) locks I if and only if \(\vec {v}_\mathcal {M}\) locks \(A_I\). Similarly, a \(\nu _a\)-, \(\nu _v\)-, or \(\nu _c\)-multiflow on \(\mathcal {M}\) can be mapped to a multiflow on \(\mathcal {N}\), preserving the fluxes of all component flows. Figure 11 shows the multiflow obtained in this way from the \(\nu _a\)-multiflow on the unit square that locks AB and BC, discussed in Sect. 6 (in which \(\vec {v}_{AC}\) is a constant horizontal vector field with norm \(1/\sqrt{2}\) and \(\vec {v}_{BD}\) is a constant vertical vector field with the same norm).
In the other direction, a network \(\mathcal {N}\) can be “hydrated” to form a manifold \(\mathcal {M}\) and boundary decomposition \(\{A_i\}\) such that (A.36) is again satisfied. One such construction is as follows. Each internal vertex of \(\mathcal {N}\) is mapped to a very large sphere (of radius much larger than \(\max _{e\in E}w(e)\)), and each terminal \(i\in [n]\) to a very large hemisphere whose boundary is labelled \(A_i\). If \(\mathcal {N}\) contains an edge \(e=\{x,y\}\), then the (hemi)spheres corresponding to vertices x, y are sewn together along a circle of circumference w(e), with different circles well separated on each sphere. Again, under this construction the minimal surface \(m(A_I)\) in \(\mathcal {M}\) corresponds to the minimal cut in \(\mathcal {N}\) for the terminal subset I.Footnote 22 Note that dessication and hydration are not inverse operations, in the sense that the dessication of the hydration of a network \(\mathcal {N}\) does not necessarily equal \(\mathcal {N}\) (a simple counterexample being a graph with one terminal and one internal vertex; after hydration and dessication, the internal vertex is lost).
Under hydration, a flow \(\vec {v}_\mathcal {N}\) can be lifted to a flow \(\vec {v}_\mathcal {M}\), while preserving fluxes, by setting \(\vec {v}_\mathcal {M}\) on the sewing circle corresponding to an edge e equal to \(|\vec {v}_\mathcal {N}(e)|\) times the unit normal on the circle (with the obvious orientation); the fact that the spheres are large and the sewing circles well-separated guarantees that \(\vec {v}_\mathcal {M}\) can be extended between the circles while being divergenceless and obeying the norm bound. Similarly, a multiflow on \(\mathcal {N}\) can be lifted to a \(\nu _v\)- or \(\nu _a\)-multiflow on \(\mathcal {M}\).Footnote 23 An implication is that Theorem A.4 (network locking failure) can be lifted directly to manifolds:
Corollary A.8
Let n be an integer \(\ge 4\) and \(\mathcal {I}\subseteq 2^{[n]}\) a family of terminal sets containing a pairwise crossing triple. Then there exists a manifold \(\mathcal {M}\) and boundary decomposition \(\{A_1,\ldots ,A_n\}\) such that \(\mathcal {I}\) cannot be locked by a \(\nu _a\)-multiflow (and therefore cannot be locked by a \(\nu _c\)- or \(\nu _v\)-multiflow).
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Headrick, M., Held, J. & Herman, J. Crossing Versus Locking: Bit Threads and Continuum Multiflows. Commun. Math. Phys. 396, 265–313 (2022). https://doi.org/10.1007/s00220-022-04476-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-022-04476-w