Asymptotic Freeness of Layerwise Jacobians Caused by Invariance of Multilayer Perceptron: The Haar Orthogonal Case

Abstract

Free Probability Theory (FPT) provides rich knowledge for handling mathematical difficulties caused by random matrices appearing in research related to deep neural networks (DNNs), such as the dynamical isometry, Fisher information matrix, and training dynamics. FPT suits these researches because the DNN’s parameter-Jacobian and input-Jacobian are polynomials of layerwise Jacobians. However, the critical assumption of asymptotic freeness of the layerwise Jacobian has not been proven mathematically so far. The asymptotic freeness assumption plays a fundamental role when propagating spectral distributions through the layers. Haar distributed orthogonal matrices are essential for achieving dynamical isometry. In this work, we prove asymptotic freeness of layerwise Jacobians of multilayer perceptron (MLP) in this case. A key to the proof is an invariance of the MLP. Considering the orthogonal matrices that fix the hidden units in each layer, we replace each layer’s parameter matrix with itself multiplied by the orthogonal matrix, and then the MLP does not change. Furthermore, if the original weights are Haar orthogonal, the Jacobian is also unchanged by this replacement. Lastly, we can replace each weight with a Haar orthogonal random matrix independent of the Jacobian of the activation function using this key fact.

1 Introduction

Free Probability Theory (FPT) provides essential insight when handling mathematical difficulties caused by random matrices that appear in deep neural networks (DNNs) [6, 7, 18]. The DNNs have been successfully used to achieve empirically high performance in various machine learning tasks [5, 12]. However, their understanding at a theoretical level is limited, and their success relies heavily on heuristic search settings such as architecture and hyperparameters. To understand and improve the training of DNNs, researchers have developed several theories to investigate, for example, the vanishing/exploding gradient problem [22], the shape of the loss landscape [10, 19], and the global convergence of training and generalization [8]. The nonlinearity of activation functions, the depth of DNN, and the lack of commutation of random matrices result in significant mathematical challenges. In this respect, FPT, invented by Voiculescu [25,26,27], is well suited for this kind of analysis.

FPT essentially appears in the analysis of the dynamical isometry [17, 18]. It is well known that reducing the training error in very deep models is difficult without carefully preventing the gradient’s vanishing/exploding. Naive settings (i.e., activation function and initialization) cause vanishing/exploding gradients, as long as the network is relatively deep. The dynamical isometry [18, 21] was proposed to solve this problem. The dynamical isometry can facilitate training by setting the input-output Jacobian’s singular values to be one, where the input-output Jacobian is the Jacobian matrix of the DNN at a given input. Experiments have shown that with initial values and models satisfying dynamical isometry, very deep models can be trained without gradient vanishing/exploding; [18, 23, 29] have found that DNNs achieve approximately dynamical isometry over random orthogonal weights, but they do not do so over random Gaussian weights. For the sake of the prospect of the theory, let J be the Jacobian of the multilayer perceptron (MLP), which is the fundamental model of DNNs. The Jacobian J is given by the product of layerwise Jacobians:

$$\begin{aligned} J = D_L W_L \dots D_1 W_1, \end{aligned}$$

where each $W_\ell$ is $\ell$-th weight matrix, each $D_\ell$ is Jacobian of $\ell$-th activation function, and L is the number of layers. Under an assumption of asymptotic freeness, the limit spectral distribution is given by [18].

To examine the training dynamics of MLP achieving the dynamical isometry, [7] introduced a spectral analysis of the Fisher information matrix per sample of MLP. The Fisher information matrix (FIM) has been a fundamental quantity for such theoretical understandings. The FIM describes the local metric of the loss surface concerning the KL-divergence function [1]. The neural tangent kernel [8], which has the same eigenvalue spectrum except for trivial zero as FIM, also describes the learning dynamics of DNNs when the dimension of the last layer is relatively smaller than the hidden layer. In particular, the FIM’s eigenvalue spectrum describes the efficiency of optimization methods. For instance, the maximum eigenvalue determines an appropriate size of the learning rate of the first-order gradient method for convergence [10, 13, 28]. Despite its importance in neural networks, the FIM spectrum has been the object of only very little study from a theoretical perspective. The reason is that it was limited to random matrix theory for shallow networks [19] or mean-field theory for eigenvalue bounds, which may be loose in general [9]. Thus, [7] focused on the FIM per sample and found an alternative approach applicable to DNNs. The FIM per sample is equal to $J_\theta ^\top J_\theta$, where $J_\theta$ is the parameter Jacobian. Also, the eigenvalues of the FIM per sample are equal to the eigenvalues of the $H_L$ defined recursively as follows, except for the trivial zero eigenvalues and normalization:

$$\begin{aligned} H_{\ell +1 } = {\hat{q}}_{\ell }I + W_{\ell +1} D_{\ell }H_{\ell }D_{\ell }W_{\ell +1}^\top , \ \ell =1, \dots , L-1, \end{aligned}$$

where I is the identity matrix, and ${\hat{q}}_\ell$ is the empirical variance of $\ell$-th hidden unit. Under an asymptotic freeness assumption, [7] gave some limit spectral distributions of $H_L$.

The asymptotic freeness assumptions have a critical role in these researches [7, 18] to obtain the propagation of spectral distributions through the layers. However, the proof of the asymptotic freeness was not completed. In the present work, we prove the asymptotic freeness of layerwise Jacobian of multilayer perceptrons with Haar orthogonal weights.

1.1 Main results

Our results are as follows. Firstly, the following $L+1$ tuple of families are asymptotically free almost surely (see Theorem 4.1):

$$\begin{aligned} ((W_1, W_1^*),\dots , (W_L,W_L^*) , (D_1, \dots , D_L) ). \end{aligned}$$

Secondly, for each $\ell =1, \dots , L-1$, the following pair is almost surely asymptotically free (see Proposition 4.2):

$$\begin{aligned} W_{\ell +1} J_\ell J_\ell ^* W_{\ell +1} , D_\ell ^2. \end{aligned}$$

The asymptotic freeness is at the heart of the spectral analysis of the Jacobian. Lastly, for each $\ell =1, \dots , L-1$, the following pair is almost surely asymptotically free (see Proposition 4.3):

$$\begin{aligned} H_\ell , D_\ell ^2. \end{aligned}$$

The asymptotic freeness of the pair is the key to the analysis of the conditional Fisher information matrix.

The fact that each parameter matrix $W_\ell$ contains elements correlated with the activation’s Jacobian matrix $D_\ell$ is a hurdle towards showing asymptotic freeness. Therefore, among the components of $W_\ell$, we move the elements that appear in $D_\ell$ to the N-th row or column. This is achieved by changing the basis of $W_\ell$. The orthogonal matrix (3.2) that defines the change of basis can be realized so that each hidden layer is fixed, and as a result, the MLP does not change. Then, the dependency between $W_\ell$ and $D_\ell$ is only in the N-th row or column, so it can be ignored by taking the limit of $N \rightarrow \infty$. From this result, we can say that $(W_\ell , W_\ell ^\top )$ and $D_\ell$ are asymptotically free for each $\ell$. However, this is still not enough to prove the asymptotical freeness between families $(W_\ell , W_\ell ^\top )_{\ell =1, \dots , L}$ and $(D_\ell )_{\ell =1, \dots , L}$. Therefore, we complete the proof of the asymptotic freeness by additionally considering another change of basis (3.3) that rotates the $N-1 \times N-1$ submatrix of each $W_\ell$ by independent Haar orthogonal matrices. A key of the desired asymptotic freeness is the invariance of MLP described in Lemma 3.1. The invariance follows from a structural property of MLP and an invariance property of Haar orthogonal random matrices. The invariance of MLP helps us apply the asymptotical freeness of Haar orthogonal random matrices [2] to our situation.

1.2 Related works

The asymptotic freeness is weaker than the assumption of the forward-backward independence that research of dynamical isometry assumed [10, 17, 18]. Although studies of mean-field theory [4, 12, 21] succeeded in explaining many experimental deep learning results, they use an artificial assumption (gradient independence [30]), which is not rigorously true. Asymptotic freeness is weaker than this artificial assumption. Our work clarifies that asymptotic free independence is just the right property that is useful and strictly valid for analysis.

Several works prove or treat the asymptotic freeness with Gaussian initialization [6, 16, 30, 31]. However, asymptotic freeness was not proven for the orthogonal initialization. As dynamical isometry can be achieved under orthogonal initialization but cannot be done under Gaussian initialization [18], proof of the asymptotic freeness in orthogonal initialization is essential. Since our proof makes crucial use of the properties of Haar distributed random matrices, the proof is clear because we only need to aim to replace the weights with Haar orthogonal, which is independent of the other Jacobians. While [6] restricting the activation function to ReLU, our proof covers a comprehensive class of activation functions, including smooth functions.

1.3 Organization of the paper

Section 2 is devoted to preliminaries. It contains settings of MLP and notations about random matrices, spectral distribution, and free probability theory. Section 3 consists of two keys to prove main results. A key is the invariance of MLP, and the other is to cut off a dimension. Section 4 is devoted to proving the main results on the asymptotic freeness. In Sect. 5, we show applications of the asymptotic freeness to spectral analysis of random matrices, which appear in the theory of dynamical isometry and training dynamics of DNNs. Section 6 is devoted to the discussion and future works.

2 Preliminaries

2.1 Setting of MLP

We consider multilayer perceptron settings, as usual in the studies of FIM [10, 19] and dynamical isometry [7, 18, 21]. Fix $L,N \in {\mathbb {N}}$. We consider an L-layer multilayer perceptron as a parametrized map $f=(f_\theta \mid \theta =(W_1, \dots , W_L) )$ with weight matrices $W_1, W_2, \dots , W_L \in M_N({\mathbb {R}})$ as follows. Firstly, consider functions $\varphi ^1, \dots \varphi ^{L-1}$ on ${\mathbb {R}}$. Besides, we assume that $\varphi ^\ell$ is continuous and differentiable except for finite points. Secondly, for a single input $x \in {\mathbb {R}}^N$ we set $x^0=x$. In addition, for $\ell =1, \dots , L$, set inductively

$$\begin{aligned} h^\ell = W_\ell x^{\ell -1} + b^\ell , \ \ x^\ell = \varphi ^\ell (h^\ell ), \end{aligned}$$

where $\varphi ^\ell$ acts on ${\mathbb {R}}^N$ as the entrywise operation. Here, we set $b^\ell = 0$ to simplify the analysis, according to the setting of [18, 19].

Write $f_\theta (x) = x^L$. Denote by $D_\ell$ the Jacobian of the activation $\varphi ^\ell$ given by

$$\begin{aligned} D_\ell = \frac{\partial x^\ell }{\partial h^\ell } = {{\,\mathrm{\textrm{diag}}\,}}( (\varphi ^\ell )^\prime (h^\ell _1), \dots , (\varphi ^\ell )^\prime (h^{\ell }_N)). \end{aligned}$$

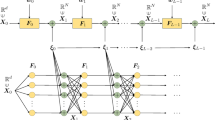
Lastly, we assume that each $W_\ell$ ($\ell =1, \dots , L$) be independent Haar orthogonal random matrices and further consider the following condition (d1), ..., (d4) on distributions. In Fig. 1, we visualize the dependency of the random variables.

Fig. 1

A graphical model of random matrices and random vectors drawn by the following rules (i–iii). (i) A node’s boundary is drawn as a square or a rectangle if it contains a square random matrix; otherwise, it is drawn as a circle. (ii) For each node, its parent node is a source node of a directed arrow. A node is measurable concerning the $\sigma$-algebra generated by all parent nodes. (iii) The nodes which have no parent node are independent

• (d1) For each $N \in {\mathbb {N}}$, the input vector $x^0$ is ${\mathbb {R}}^N$-valued random variable such that there is $r > 0$ with

  $$\begin{aligned} \lim _{N \rightarrow \infty }||x^0||_2/\sqrt{N} = r \end{aligned}$$

  almost surely.

• (d2) Each weight matrix $W_\ell$ ($\ell =1, \dots , L$) satisfies

  $$\begin{aligned} W_\ell = \sigma _{w,\ell } O_\ell , \end{aligned}$$

  where $O_\ell ~(\ell =1,\dots , L)$ are independent orthogonal matrices distributed with the Haar probability measure and $\sigma _{w,\ell } > 0$.

• (d3) For fixed N, the family

  $$\begin{aligned} (x^0, W_1, \dots , W_L) \end{aligned}$$

  is independent.

Let us define $r_\ell > 0$ and $q_\ell > 0$ by the following recurrence relations:

$$\begin{aligned} r_0&= r,\\ (r_\ell )^2&= {\mathbb {E}}_{h \sim {{\,\mathrm{{\mathcal {N}}}\,}}(0, q_\ell )} \left[ \varphi _\ell \left( h \right) ^2 \right] \ (l=1, \dots , L),\\ q_\ell&= (\sigma _{w,\ell })^2 (r_{\ell -1})^2 \ (l=1, \dots , L). \end{aligned}$$

The inequality $r_\ell < \infty$ holds by the assumption (a2) of activation functions.

We further assume that each activation function satisfies the following conditions (a1), ..., (a5).

• (a1) It is a continuous function on ${\mathbb {R}}$ and is not the identically zero function.

• (a2) For any $q >0$,

  $$\begin{aligned} \int _{\mathbb {R}}\varphi ^\ell (x)^2 \exp (-x^2/q)dx < \infty . \end{aligned}$$

• (a3) It is differentiable almost everywhere concerning Lebesgue measure. We denote by $(\varphi ^\ell )^\prime$ the derivative defined almost everywhere.

• (a4) The derivative $(\varphi ^\ell )^\prime$ is continuous almost everywhere concerning the Lebesgue measure.

• (a5) The derivative $(\varphi ^\ell )^\prime$ is bounded.

Example 2.1

(Activation Functions) The following activation functions are used [7, 17, 18] to satisfy the above conditions.

• 1. (Rectified linear unit)

  $$\begin{aligned} \textrm{ReLU}(x) = {\left\{ \begin{array}{ll} x ; &{}x \ge 0,\\ 0 ; &{}x < 0. \end{array}\right. } \end{aligned}$$

• 2. (Shifted ReLU)

  $$\begin{aligned}\text {shifted-ReLU}_\alpha (x) = {\left\{ \begin{array}{ll} x ;&{} x \ge \alpha ,\\ \alpha ;&{} x < \alpha . \end{array}\right. } \end{aligned}$$

• 3. (Hard hyperbolic tangent)

  $$\begin{aligned} \text {htanh}(x) = {\left\{ \begin{array}{ll} -1 ;&{} x \le -1,\\ x ;&{} -1< x < 1,\\ 1 ;&{} 1 \le x. \end{array}\right. } \end{aligned}$$

• 4. (Hyperbolic tangent)

  $$\begin{aligned} \tanh (x) = \frac{e^x- e^{-x}}{e^x+e^{-x}}. \end{aligned}$$

• 5. (Sigmoid function)

  $$\begin{aligned} \sigma (x) = \frac{1}{e^{-x}+1}. \end{aligned}$$

• 6. (Smoothed ReLU)

  $$\begin{aligned} \textrm{SiLU}(x) = x \sigma (x). \end{aligned}$$

• 7. (Error function)

  $$\begin{aligned} \text {erf}(x) = \frac{2}{\sqrt{\pi }}\int ^x_0 e^{-t^2}dt. \end{aligned}$$

2.2 Basic notations

Linear Algebra We denote by $M_N({\mathbb {K}})$ the algebra of $N \times N$ matrices with entries in a field ${\mathbb {K}}$. Write unnormalized and normalized traces of $A \in M_N({\mathbb {K}})$ as follows:

$$\begin{aligned} {{\,\mathrm{\textrm{Tr}}\,}}(A)&= \sum _{i=1}^N A_{ii},\\ {{\,\mathrm{\textrm{tr}}\,}}(A)&= \frac{1}{N}{{\,\mathrm{\textrm{Tr}}\,}}(A). \end{aligned}$$

In this work, a random matrix is a $M_N(\mathbb {R})$ valued Borel measurable map from a fixed probability space for an $N \in {\mathbb {N}}$. We denote by ${{\textbf{O}}}_{\textbf{N}}$ the group of $N \times N$ orthogonal matrices. It is well-known that ${{\textbf{O}}}_{\textbf{N}}$ is equipped with a unique left and right translation invariant probability measure, called the Haar probability measure.

Spectral Distribution Recall that the spectral distribution $\mu$ of a linear operator A is a probability distribution $\mu$ on ${\mathbb {R}}$ such that ${{\,\mathrm{\textrm{tr}}\,}}(A^m) = \int t^m\mu (dt)$ for any $m \in {\mathbb {N}}$, where ${{\,\mathrm{\textrm{tr}}\,}}$ is the normalized trace. If A is an $N \times N$ symmetric matrix with $N \in {\mathbb {N}}$, its spectral distribution is given by $N^{-1}\sum _{n=1}^N \delta _{\lambda _n}$, where $\lambda _n (n=1, \dots , N)$ are eigenvalues of A, and $\delta _\lambda$ is the discrete probability distribution whose support is $\{\lambda \} \subset {\mathbb {R}}$.

Joint Distribution of All Entries For random matrices $X_1, \dots ,X_L, Y_1, \dots , Y_L$ and random vectors $x_1, \dots , x_L, y_1, \dots , y_L$, we write

$$\begin{aligned} (X_1, \dots , X_L, x_1, \dots , x_L) \sim ^\textrm{entries}(Y_1, \dots , Y_L, y_1, \dots , y_L) \end{aligned}$$

if the joint distributions of all entries of corresponding matrices and vectors in the families match.

2.3 Asymptotic freeness

In this section, we summarize required topics of random matrices and free probability theory. We start with the following definition. We omit the definition of a C$^*$-algebra, and for complete details, we refer to [14].

Definition 2.2

A noncommutative $C^*$-probability space (NCPS, for short) is a pair $(\mathfrak {A},\tau )$ of a unital C$^*$-algebra $\mathfrak {A}$ and a faithful tracial state $\tau$ on $\mathfrak {A}$, which are defined as follows. A linear map $\tau$ on $\mathfrak {A}$ is said to be a $tracial state$ on $\mathfrak {A}$ if the following four conditions are satisfied.

• 1. $\tau (1) =1$.

• 2. $\tau (a^*) = \overline{\tau (a)} \ (a \in \mathfrak {A})$.

• 3. $\tau (a^*a) \ge 0 \ (a \in \mathfrak {A})$.

• 4. $\tau (ab) = \tau (ba) \ (a,b \in \mathfrak {A})$.

In addition, we say that $\tau$ is faithful if $\tau (a^*a)=0$ implies $a=0$.

For $N \in {\mathbb {N}}$, the pair of the algebra $M_N({\mathbb {C}})$ of $N \times N$ matrices of complex entries and the normalized trace ${{\,\mathrm{\textrm{tr}}\,}}$ is an NCPS. Consider the algebra of $M_N({\mathbb {R}})$ of $N \times N$ matrices of real entries and the normalized trace ${{\,\mathrm{\textrm{tr}}\,}}$. The pair itself is not an NCPS in the sense of Definition 2.2 since it is not ${\mathbb {C}}$-linear space. However, $M_N({\mathbb {C}})$ contains $M_N({\mathbb {R}})$ and preserves $*$ by setting, for $A \in M_N({\mathbb {R}})$:

$$\begin{aligned} A^* = A^\top . \end{aligned}$$

Also, the inclusion $M_N({\mathbb {R}}) \subset M_N({\mathbb {C}})$ preserves the trace. Therefore, we consider the joint distributions of matrices in $M_N({\mathbb {R}})$ as that of elements in the NCPS $(M_N({\mathbb {C}}), {{\,\mathrm{\textrm{tr}}\,}})$.

Definition 2.3

(Joint Distribution in NCPS). Let $a_1, \dots , a_k \in \mathfrak {A}$ and let ${\mathbb {C}}\langle X_1, \dots , X_k \rangle$ be the free algebra of non-commutative polynomials on ${\mathbb {C}}$ generated by k indeterminates $X_1, \dots , X_k$. Then the joint distirubtion of the k-tuple $(a_1, \dots , a_k)$ is the linear form $\mu _{a_1, \dots , a_k} : {\mathbb {C}}\langle X_1, \dots , X_k \rangle \rightarrow {\mathbb {C}}$ defined by

$$\begin{aligned} \mu _{a_1, \dots , a_k} ( P ) = \tau (P(a_1, \dots , a_k)), \end{aligned}$$

where $P \in {\mathbb {C}}\langle X_1, \dots , X_k \rangle$.

Definition 2.4

Let $a_1, \dots , a_k \in \mathfrak {A}$. Let $A_1(N), \dots , A_k(N)$ $( N \in {\mathbb {N}})$ be sequences of $N \times N$ matrices. Then we say that they converge in distribution to $(a_1, \dots , a_k)$ if

$$\begin{aligned} \lim _{N \rightarrow \infty }{{\,\mathrm{\textrm{tr}}\,}}\left( P \left( A_1 (N), \dots , A_k(N) \right) \right) = \tau \left( P \left( a_1, \dots , a_k\right) \right) \end{aligned}$$

for any $P \in {\mathbb {C}}\langle X_1, \dots , X_k \rangle$.

Definition 2.5

(Freeness). Let $(\mathfrak {A}, \tau )$ be a NCPS. Let $\mathfrak {A}_1, \dots , \mathfrak {A}_k$ be subalgebras having the same unit as $\mathfrak {A}$. They are said to be free if the following holds: for any $n \in {\mathbb {N}}$, any sequence $j_1, \dots , j_n \in [k]$, and any $a_i \in \mathfrak {A}_{j_i}$ ($i=1, \dots , k$) with

$$\begin{aligned}&\tau \left( a_i\right) = 0 \ (i=1, \dots , n),\\&j_1 \ne j_2, j_2 \ne j_3, \dots , j_{n-1} \ne j_n, \end{aligned}$$

the following holds true:

$$\begin{aligned} \tau \left( a_{j_1} a_{j_2} \dots a_{j_n} \right) = 0. \end{aligned}$$

Besides, elements in $\mathfrak {A}$ are said to be free iff the unital subalgebras that they generate are free.

The example below is basically a reformulation of freeness, and follows from [27].

Example 2.6

Let $w_1,w_2, \dots , w_L \in \mathfrak {A}$ and $d_1, \dots , d_L \in \mathfrak {A}$. Then the families $(w_1,w_1^*), (w_2,w_2^*), \dots , (w_L, w_L^*), (d_1, \dots , d_L)$ are free if and only if the following $L+1$ unital subalgebras of $\mathfrak {A}$ are free:

$$\begin{aligned}&\{ P( w_1, w_1^*) \mid P \in {\mathbb {C}}\langle X, Y \rangle \}, \dots ,\{ P( w_L, w_L^*) \mid P \in {\mathbb {C}}\langle X, Y \rangle \}, \\&\{ Q(d_1, \dots , d_L) \mid Q \in {\mathbb {C}}\langle X_1, \dots , X_L \rangle \}. \end{aligned}$$

Let us now introduce asymptotic freeness of random matrices with compact support limit spectral distributions. Since we consider a family of a finite number of random matrices, we restrict it to a finite index set. Note that the finite index is not required for a general definition of freeness.

Definition 2.7

(Asymptotic Freeness of Random Matrices). Consider a nonempty finite index set I, a family $A_i(N)$ of $N \times N$ random matrices where $N \in {\mathbb {N}}$. Given a partition $\{I_1, \dots , I_k\}$ of I, consider a sequence of k-tuples

$$\begin{aligned} \left( A_i \left( N \right) \mid i \in I_1 \right) , \dots , \left( A_i \left( N \right) \mid i \in I_k \right) . \end{aligned}$$

It is then said to be almost surely asymptotically free as $N \rightarrow \infty$ if the following two conditions are satisfied.

• 1. There exist a family $(a_i)_{i \in I}$ of elements in $\mathfrak {A}$ such that the following k tuple is free:

  $$\begin{aligned} (a_i \mid i \in I_1) , \dots , (a_i \mid i \in I_k ) . \end{aligned}$$

• 2. For every $P \in {\mathbb {C}}\langle X_1, \dots , X_{|I|} \rangle$,

  $$\begin{aligned} \lim _{N \rightarrow \infty }{{\,\mathrm{\textrm{tr}}\,}}\left( P \left( A_1(N), \dots , A_{|I|}(N) \right) \right) = \tau \left( P \left( a_1 ,\dots , a_{|I|} \right) \right) , \end{aligned}$$

  almost surely, where |I| is the number of elements of I.

2.4 Haar distributed orthogonal random matrices

We introduce asymptotic freeness of Haar distributed orthogonal random matrices.

Proposition 2.8

Let $L,L' \in {\mathbb {N}}$. For any $N \in {\mathbb {N}}$, let $V_1(N), \dots , V_{L}(N)$ be independent ${{\textbf{O}}}_{\textbf{N}}$ Haar random matrices, and $A_1(N), \dots , A_{L'}(N)$ be symmetric random matrices, which have the almost-sure-limit joint distribution. Assume that all entries of $(V_\ell (N))_{\ell =1}^{L}$ are independent of that of $(A_1(N), \dots , A_{L'}(N))$, for each N. Then the families

$$\begin{aligned} ( V_1(N), V_1(N)^\top ), \dots , (V_{L}(N), V_{L}(N)^\top ), (A_1(N), \dots , A_{L'}(N)). \end{aligned}$$

are asymptotically free as $N \rightarrow \infty$.

Proof

This is a particular case of [2, Theorem 5.2]. $\square$

The following proposition is a direct consequence of Proposition 2.8.

Proposition 2.9

For $N \in N$, let A(N) and B(N) be $N \times N$ symmetric random matrices, and let V(N) be a $N \times N$ Haar-distributed orthogonal random matrix. Assume that

• 1. The random matrix V(N) is independent of A(N), B(N) for every $N \in {\mathbb {N}}$.

• 2. The spectral distribution of A(N) (resp. B(N)) converges in distribution to a compactly supported probability measure $\mu$ (resp. $\nu$), almost surely.

Then the following pair is asymptotically free as $N \rightarrow \infty$,

$$\begin{aligned} A(N), V(N)B(N)V(N)^\top , \end{aligned}$$

almost surely.

Proof

Instead of proving that $A(N), V(N)B(N)V(N)^\top$ are asymptotically free, we will prove that $U(N)A(N)U(N)^\top , U(N)V(N)B(N)V(N)^\top U(N)^\top$ for any orthogonal matrix U(N), and in particular, for an independent Haar distributed orthogonal matrix. This is equivalent because a global conjugation by U(N) does not affect the joint distribution. In turn, since U(N), U(N)V(N) has the same distribution as U(N), V(N) thanks to the Haar property, it is enough to prove that $U(N)A(N)U(N)^\top , V(N)B(N)V(N)^\top$ is asymptotically free as as $N \rightarrow \infty$. Let us replace A(N) by ${{\tilde{A}}}(N)$ where ${{\tilde{A}}}(N)$ is diagonal, and has the same eigenvalues as A(N), arranged in non-increasing order, and likewise, we construct ${{\tilde{B}}}(N)$ from B(N). It is clear that

$$\begin{aligned} U(N)A(N)U(N)^\top , V(N)B(N)V(N)^\top \end{aligned}$$

and

$$\begin{aligned} U(N){{\tilde{A}}}(N)U(N)^\top , V(N){{\tilde{B}}}(N)V(N)^\top \end{aligned}$$

have the same distribution. In addition, ${{\tilde{B}}}(N), {{\tilde{A}}}(N)$ have a joint distribution by construction, therefore we can apply Proposition 2.8. $\square$

Note that we do not require independence between A(N) and B(N) in Proposition 2.9. Here we recall the following result, which is a direct consequence of the translation invariance of Haar random matrices.

Lemma 2.10

Fix $N \in {\mathbb {N}}$. Let $V_1, \dots , V_L$ be independent ${{\textbf{O}}}_{\textbf{N}}$ Haar random matrices. Let $T_1, \dots , T_L$ be ${{\textbf{O}}}_{\textbf{N}}$ valued random matrices. Let $S_1, \dots , S_L$ be ${{\textbf{O}}}_{\textbf{N}}$ valued random matrices. Let $A_1, \dots , A_L$ be $N \times N$ random matrices. Assume that all entries of $(V_\ell )_{\ell =1}^L$ are independent of

$$\begin{aligned} (T_1, \dots , T_L, S_1, \dots , S_L, A_1, \dots , A_L). \end{aligned}$$

Then,

$$\begin{aligned} (T_1 V_1 S_1, \dots , T_L V_L S_L, A_1, \dots , A_L) \sim ^\textrm{entries}( V_1, \dots , V_L, A_1, \dots , A_L). \end{aligned}$$

Proof

For the readers’ convenience, we include a proof. The characteristic function of $(T_1 V_1 S_1, \dots , T_L V_L S_L, A_1, \dots , A_L)$ is given by

$$\begin{aligned} {\mathbb {E}}\left[ \exp \left[ -i {{\,\mathrm{\textrm{Tr}}\,}}\left( \sum _{\ell =1}^L X_\ell ^\top T_\ell V_\ell S_\ell + Y_\ell ^\top A_\ell \right) \right] \right] , \end{aligned}$$

(2.1)

where $X_1, \dots , X_L \in M_N({\mathbb {R}})$ and $Y_1, \dots , Y_L \in M_N({\mathbb {R}})$. By using conditional expectation, (2.1) is equal to

$$\begin{aligned} {\mathbb {E}}\left[ {\mathbb {E}}\left[ \exp \left[ -i {{\,\mathrm{\textrm{Tr}}\,}}\left( \sum _{\ell =1}^L X_\ell ^\top T_\ell V_\ell S_\ell \right) \mid T_\ell , S_\ell , A_\ell \left( \ell =1, \dots , L\right) \right] \exp \left[ -i {{\,\mathrm{\textrm{Tr}}\,}}\left( Y_\ell ^\top A_\ell \right) \right] \right] \right] . \end{aligned}$$

(2.2)

By the property of the Haar measure and the independence, the conditional expectation contained in (2.2) is equal to

$$\begin{aligned} {\mathbb {E}}\left[ \exp \left[ -i {{\,\mathrm{\textrm{Tr}}\,}}\left( \sum _{\ell =1}^L X_\ell ^\top V_\ell \right) \right] \mid T_\ell , S_\ell , A_\ell \left( \ell =1, \dots , L\right) \right] . \end{aligned}$$

Thus the assertion holds. $\square$

2.5 Forward propagation through MLP

2.5.1 Action of Haar orthogonal matrices

Firstly we consider action of Haar orthogonal to a random vector with finite second moment. For N-dimensional random vector $x=(x_1, \dots , x_N)$, we denote its empirical distribution by

$$\begin{aligned} \nu _x := \frac{1}{N}\sum _{n=1}^N \delta _{x_n}, \end{aligned}$$

where $\delta _x$ is the delta probability measure at the point $x \in {\mathbb {R}}$.

Let u(N) be a random vector uniformly distributed on the $N-1$ dimensional unit sphere. It is known that for any fixed $k \in {\mathbb {N}}$, the joint distribution of $\sqrt{N}u(N)_1, \dots , \sqrt{N}u(N)_k$ converges to the standard normal distribution on ${\mathbb {R}}^k$ as $N \rightarrow \infty$ [24]. In the course of Lemma’s proof below, we prove the convergence of the empirical distribution $\nu _{\sqrt{N}u(N)}$ since it is easier than proving the convergence in joint distribution. We prove it with the moments of the empirical distribution. Here, for any probability distribution $\mu$ and $k \in {\mathbb {N}}$, we write $\mu$’s k-th moment by $m_k(\mu )$.

Lemma 2.11

Let $(\Omega , {\mathcal {F}}, {\mathbb {P}})$ be a probability space and x(N) be a ${\mathbb {R}}^N$ valued random variable for each $N\in {\mathbb {N}}$. Assume that there exists $r > 0$ such that

$$\begin{aligned} \sqrt{ \frac{1}{N} \sum _{n=1}^N \left( x(N)_n \right) ^2 } \rightarrow r \end{aligned}$$

as $N \rightarrow \infty$ almost surely. Let O(N) be a Haar distributed N-dimensional orthogonal matrix. Set

$$\begin{aligned} h(N) = O(N) x(N). \end{aligned}$$

Furthermore we assume that x(N) and O(N) are independent. Then

$$\begin{aligned} \nu _{h(N)} \implies {{\,\mathrm{{\mathcal {N}}}\,}}(0, r^2) \end{aligned}$$

as $N \rightarrow \infty$ almost surely.

Proof

Let $e_1=(1, 0, \dots , 0) \in {\mathbb {R}}^N$. Then there is an orthogonal random matrix U such that $x(N) = ||x(N)||_2 Ue_1$, where $|| \cdot ||_2$ is the Euclid norm. Write $r(N) := ||x(N)||_2/\sqrt{N}$ and u(N) be unit vector uniformly distributed on the unit sphere, independent of r(N). Since O(N) is a Haar orthogonal and since O(N) and U are independent, it holds that $O(N)U \sim ^{dist.} O(N)$. Then

$$\begin{aligned} h(N) = O(N)x(N) = (||x(N)||_2/\sqrt{N} )( \sqrt{N}O(N)U e_1) \sim ^{dist.} r(N) (\sqrt{N}u(N)). \end{aligned}$$

Firstly, by the assumption,

$$\begin{aligned} r(N) = \sqrt{ \frac{1}{N}\sum _{n=1}^N x(N)_n^2 }\rightarrow r \text { as} N \rightarrow \infty , \text {almost surely.} \end{aligned}$$

Secondly, let $(Z_i)_{i=1}^\infty$ be i.i.d. standard Gaussian random variables. Then

$$\begin{aligned} u(N) \sim ^{dist.} \left( \frac{Z_n}{ \sqrt{ \sum _{n=1}^N Z_n^2 } } \right) _{n=1}^N. \end{aligned}$$

For $k \in {\mathbb {N}}$,

$$\begin{aligned} m_k(\nu _{\sqrt{N}u(N)})&= \frac{1}{N}\sum _{n=1}^{N}N^{k/2}u(N)_n^k = \frac{ N^{-1}\sum _{n=1}^N Z_n^k }{[N^{-1} \sum _{n=1}^N Z_n^2 ]^{k/2} }\\&\rightarrow \frac{m_k( {{\,\mathrm{{\mathcal {N}}}\,}}(0,1) )}{m_2( {{\,\mathrm{{\mathcal {N}}}\,}}(0,1) )^{k/2} } = m_k( {{\,\mathrm{{\mathcal {N}}}\,}}(0,1) ) \text {as} N \rightarrow \infty , \text {a.s.} \end{aligned}$$

Now convergence in moments to Gaussian distribution implies convergence in law. Therefore,

$$\begin{aligned} \nu _{\sqrt{N}u(N)} \implies {{\,\mathrm{{\mathcal {N}}}\,}}(0, 1), \end{aligned}$$

almost surely. This completes the proof. $\square$

Note that we do not assume that entries of x(N) are independent.

Lemma 2.12

Let g be a measurable function and set

$$\begin{aligned} N_g=\{x \in {\mathbb {R}}\mid g \text {\ is discontinuous at } x \}. \end{aligned}$$

Let $Z \sim {{\,\mathrm{{\mathcal {N}}}\,}}(0,1)$. Assume that ${\mathbb {P}}(Z \in N_g) = 0$. Then under the setting of Lemma 2.11, it holds that

$$\begin{aligned} \nu _{g(h(N) ) } \implies g(Z) \end{aligned}$$

as $N \rightarrow \infty$ almost surely.

Proof

Let $F = \{\omega \in \Omega \mid \nu _{g(h(N)(\omega )) } \implies g(Z) \text { as } N \rightarrow \infty \}$. By Lemma 2.11, $P(F) = 0$. Fix $\omega \in \Omega \setminus F$. For $N \in {\mathbb {N}}$, let $X_N$ be a real random variable on the probability space with

$$\begin{aligned} X_N \sim \nu _{h(N)(\omega )}. \end{aligned}$$

By the assumption, we have ${\mathbb {P}}( Z \in N_g ) = 0$. Then the continuous mapping theorem (see [3, Theorem 3.2.4]) implies that

$$\begin{aligned} g(X_N) \Rightarrow g(Z). \end{aligned}$$

Thus for any bounded continuous function $\psi$,

$$\begin{aligned} \int \psi (t) \nu _{g\circ h(N)(\omega )}( dt) = \frac{1}{N}\sum _{i=n}^N \psi \circ g\left( h(n)\left( \omega \right) \right) = {\mathbb {E}}[ \psi \circ g(X_N) ] \rightarrow {\mathbb {E}}[\psi \circ g(Z)]. \end{aligned}$$

Hence $\nu _{g(h(N)(\omega ))} \implies g(Z)$. Since we took arbitrary $\omega \in \Omega \setminus F$ and ${\mathbb {P}}(\Omega \setminus F) = 1$, the assertion follows. $\square$

2.5.2 Convergence of empirical distribution

Furthermore, for any measurable function g on ${\mathbb {R}}$ and probability measure $\mu$, we denote by $g_*(\mu )$ the push-forward of $\mu$. That is, if a real random variable X is distributed with $\mu$, then $g_*(\mu )$ is the distribution of g(X).

Proposition 2.13

For all $\ell =1, \dots , L$, it holds that

• 1. $\nu _{h^\ell } \Rightarrow {{\,\mathrm{{\mathcal {N}}}\,}}(0, q_\ell ),$

• 2. $\nu _{\varphi ^\ell (h^\ell )} \Rightarrow \varphi ^{\ell }_*({{\,\mathrm{{\mathcal {N}}}\,}}(0, q_\ell )),$

• 3. $\nu _{(\varphi ^\ell )^\prime (h^\ell )} \Rightarrow (\varphi ^\ell )^\prime _{*}({{\,\mathrm{{\mathcal {N}}}\,}}(0, q_\ell )),$

as $N \rightarrow \infty$ almost surely.

Proof

on $\ell$. Let $\ell =1$. Then $q_1 = \sigma _{w,1}^2 r^2 + \sigma _{b,1}^2$. By Lemma 2.11, (1) follows. Since $\varphi ^1$ is continuous (2) follows by Lemma 2.12. Since $(\varphi ^1)^\prime$ is continuous almost everywhere by the assumption (a4), (3) follows by Lemma 2.11. Now we have $||x^1||_2/\sqrt{N} = \sqrt{m_2(\nu _{\varphi ^1(h^1)})} \Rightarrow \sqrt{ m_2(\varphi ^1_*({{\,\mathrm{{\mathcal {N}}}\,}}(0,q_1))) }= r_1$. The same conclusion can be drawn for the rest of induction. $\square$

Corollary 2.14

For each $\ell =1, \dots , L$, $D_\ell$ has the compactly supported limit spectral distribution $(\varphi ^\ell )^\prime _{*}({{\,\mathrm{{\mathcal {N}}}\,}}(0, q_\ell ))$ as $N \rightarrow \infty$.

Proof

The assertion follows directly from (3) and (a5). $\square$

3 Key to Asymptotic Freeness

Here we introduce key lemmas to prove the asymptotic freeness. A key lemma is about an invariance of MLP, and the other one is about a property of cutting off matrices.

3.1 Notations

We prepare notations related to the change of basis to cut off entries in $W_\ell$, which are correlated with $D_\ell$.

For $N \in {\mathbb {N}}$, fix a standard complete orthonormal basis $(e_1, \dots , e_N)$ of ${\mathbb {R}}^N$. Firstly, set ${\hat{n}} = \min \{ n =1, \dots , N \mid \langle x^\ell , e_n \rangle \ne 0\}$. Since $x^\ell$ is non-zero almost surely, ${\hat{n}}$ is defined almost surely. Then the following family is a basis of ${\mathbb {R}}^N$:

$$\begin{aligned} (e_1, \dots , e_{{\hat{n}} - 1}, e_{{\hat{n}} + 1}, \dots , e_N, x^\ell /||x^\ell ||_2), \end{aligned}$$

(3.1)

where $||\cdot ||_2$ is the Euclidian norm. Secondly, we apply the Gram-Schmidt orthogonalization to the basis (3.1) in reverse order, starting with $x^\ell /||x^\ell ||_2$, to construct an orthonormal basis $(f_1, \dots , f_N)$ with $f_N=x^\ell /||x^\ell ||_2$. Thirdly, let $Y_\ell$ be the orthogonal matrix determined by the following change of orthonormal basis:

$$\begin{aligned} Y_\ell f_n = e_n \ (n=1, \dots , N). \end{aligned}$$

(3.2)

Then $Y_\ell$ satisfies the following conditions.

• 1. $Y_\ell$ is $x^{\ell }$-measurable.

• 2. $Y_\ell x^\ell = ||x^\ell ||_2 e_N$.

Lastly, let $V_0, \dots , V_{L-1}$ be independent Haar distributed $N-1 \times N-1$ orthogonal random matrices such that all entries of them are independent of that of $(x^0, W_1, \dots , W_L)$. Set

$$\begin{aligned} U_\ell = Y_\ell ^\top \begin{pmatrix} V_\ell &{} 0 \\ 0 &{} 1 \end{pmatrix} Y_\ell . \end{aligned}$$

(3.3)

Then

$$\begin{aligned} U_\ell x^\ell = Y_\ell ^\top ||x^\ell ||_2 e_N = x^\ell . \end{aligned}$$

Each $V_{\ell }$ is the $N-1 \times N-1$ random matrix which determines the action of $U_{\ell }$ on the orthogonal complement of ${\mathbb {R}}x^{\ell }$. Further, for any $\ell =0, \dots , L-1$, all entries of $(U_0, \dots , U_{\ell -1})$ are independent from that of $(W_\ell , \dots , W_L)$ since each $U_{\ell }$ is $\mathcal {G}(x^\ell , V^\ell )$-measurable, where $\mathcal {G}(x^\ell , V^\ell )$ is the $\sigma$-algebra generated by $x^\ell$ and $V^\ell$. We have completed the construction of the $U_\ell$. Figure 2 visualizes a dependency of the random variables that appeared in the above discussion.

Fig. 2

A graphical model of random variables in a specific case using $V_\ell$ for $U_\ell$. See Fig. 1 for the graph’s drawing rule. The node of $W_\ell , \dots , W_L$ is an isolated node in the graph

In addition, let P(N) be the $N \times N$ diagonal matrix given by

$$\begin{aligned} P(N) = \textrm{diag}(1,1,\dots , 1, 0). \end{aligned}$$

(3.4)

If there is no confusion, we omit the index N and simply write it P. The matrix P(N) is an orthogonal projection onto an $N-1$ dimenstional subspace.

3.2 Invariance of MLP

Since Haar random matrices’ invariance leads to asymptotic freeness (Proposition 2.8), it is essential to investigate the network’s invariance. The following invariance is the key to the main theorem. Note that the Haar property of $V_\ell$ is not necessary to construct $U_\ell$ in Lemma 3.1, but the property is used in the proof of Theorem 4.1.

Lemma 3.1

Under the setting of Sect. 2.1, let $U_\ell$ be arbitrary ${{\textbf{O}}}_{\textbf{N}}$ valued random matrix satisfying

$$\begin{aligned} U_\ell x^\ell = x^\ell . \end{aligned}$$

(3.5)

for each $\ell =0,1, \dots , L-1$. Further assume that all entries of $(U_0, \dots , U_{\ell -1})$ are independent from that of $(W_\ell , \dots , W_L)$ for each $\ell =0,1,\dots , L-1$. Then the following holds:

$$\begin{aligned} (W_1U_0, \dots , W_LU_{L-1}, h^1, \dots , h^L) \sim ^\textrm{entries}(W_1, \dots , W_L, h^1, \dots , h^L). \end{aligned}$$

(3.6)

Proof of Lemma 3.1

Let $U_0, \dots , U_{L-1}$ be arbitrary random matrices satisfing conditions in Lemma 3.1. We prove the corresponding characteristic functions of the joint distributions in (3.6) match.

Fix $T_1, \dots , T_L \in M_N({\mathbb {R}})$ and $\xi _1, \dots , \xi _L \in {\mathbb {R}}^N$. For each $\ell = 1, \dots , L$, define a map $\psi _\ell$ by

$$\begin{aligned} \psi _\ell (x,W) = \exp \left[ -i {{\,\mathrm{\textrm{Tr}}\,}}(T_\ell ^\top W) -i \langle \xi _\ell , Wx\rangle \right] , \end{aligned}$$

where $W \in M_N({\mathbb {R}})$ and $x \in {\mathbb {R}}^N$. Write

$$\begin{aligned} \alpha _\ell&= \psi _\ell (x_{\ell -1}, W_\ell ), \end{aligned}$$

(3.7)

$$\begin{aligned} \beta _\ell&= \psi _\ell (x_{\ell -1}, W_\ell U_{\ell -1}). \end{aligned}$$

(3.8)

By (3.5) and by $W_\ell x^{\ell -1} = h^\ell$, the values of characteristic functions of the joint distributions at the point $(T_1, \dots , T_L, \xi _1, \dots \xi _L)$ is given by ${\mathbb {E}}[\beta _1 \dots \beta _L]$ and ${\mathbb {E}}[\alpha _1 \dots \alpha _L]$, respectively. Now we only need to show

$$\begin{aligned} {\mathbb {E}}[\beta _1 \dots \beta _L] = {\mathbb {E}}[\alpha _1 \dots \alpha _L]. \end{aligned}$$

(3.9)

Firstly, we claim that the following holds: for each $\ell =1, \dots , L$,

$$\begin{aligned} {\mathbb {E}}[\beta _\ell \alpha _{\ell +1} \dots \alpha _L | x^{\ell -1}] = {\mathbb {E}}[\alpha _\ell \alpha _{\ell +1} \dots \alpha _L | x^{\ell -1}]. \end{aligned}$$

(3.10)

To show (3.10), fix $\ell$ and write for a random variable x,

$$\begin{aligned} \mathcal {J}(x) = {\mathbb {E}}[\alpha _{\ell +1} \dots \alpha _L | x]. \end{aligned}$$

By the tower property of conditional expectations, we have

$$\begin{aligned} {\mathbb {E}}[\beta _\ell \alpha _{\ell +1} \dots \alpha _L | x^{\ell -1}]= {\mathbb {E}}[\beta _\ell \mathcal {J}(x^{\ell }) | x^{\ell -1}]&= {\mathbb {E}}[{\mathbb {E}}[\beta _\ell \mathcal {J}(x^{\ell }) | x^{\ell -1}, U_{\ell -1}] | x^{\ell -1} ]. \end{aligned}$$

(3.11)

Let $\mu$ be the Haar measure. Then by the invariance of the Haar measure, we have

$$\begin{aligned} {\mathbb {E}}[\beta _\ell \mathcal {J}(x^{\ell }) | x^{\ell -1}, U_{\ell -1}]&= \int \psi _\ell (x^{\ell -1}, W U_{\ell -1}) \mathcal {J}(\phi _\ell (W U_{\ell -1} x^{\ell -1})) \mu (dW)\\&=\int \psi _\ell (x^{\ell -1}, W) \mathcal {J}(\phi _\ell (W x^{\ell -1})) \mu (dW) \\&=\int \alpha _\ell \mathcal {J}(x^\ell ) \mu (dW)\\&= {\mathbb {E}}[\alpha _\ell {\mathbb {E}}[ \alpha _{\ell +1 } \dots \alpha _L | x^\ell ] | x^{\ell -1}]\\&= {\mathbb {E}}[\alpha _\ell \alpha _{\ell +1 } \dots \alpha _L | x^{\ell -1}]. \end{aligned}$$

In particular, ${\mathbb {E}}[\beta _\ell \mathcal {J}(x^{\ell }) | x^{\ell -1}, U_{\ell -1}]$ is $x^{\ell -1}$-measurable. By (3.11), we have (3.10).

Secondly, we claim that for each $\ell =2, \dots , L$,

$$\begin{aligned} {\mathbb {E}}[ \beta _1 \dots \beta _{\ell -1}\beta _\ell \alpha _{\ell +1} \dots \alpha _L] = {\mathbb {E}}[\beta _1 \dots \beta _{\ell -1} \alpha _\ell \alpha _{\ell +1}\dots \alpha _L]. \end{aligned}$$

(3.12)

Denote by $\mathcal {G}$ the $\sigma$-algebra generated by $(x_0, W_1, \dots , W_{\ell -1}, U_0, \dots , U_{\ell -2})$. By definition, $\beta _1, \dots , \beta _{\ell -1}$ are $\mathcal {G}$-measurable. Therefore,

$$\begin{aligned} {\mathbb {E}}[\beta _1 \dots \beta _{\ell -1}\beta _\ell \alpha _{\ell +1} \dots \alpha _L]&= {\mathbb {E}}[\beta _1 \dots \beta _{\ell -1} {\mathbb {E}}[\beta _\ell \alpha _{\ell +1}\dots \alpha _L | \mathcal {G} ] ] . \end{aligned}$$

Now we have

$$\begin{aligned} {\mathbb {E}}[\beta _\ell \alpha _{\ell +1}\dots \alpha _L | \mathcal {G}]&= {\mathbb {E}}[\beta _\ell \alpha _{\ell +1}\dots \alpha _L | x^{\ell -1} ],\\ {\mathbb {E}}[\alpha _\ell \alpha _{\ell +1}\dots \alpha _L | \mathcal {G}]&= {\mathbb {E}}[\alpha _\ell \alpha _{\ell +1}\dots \alpha _L | x^{\ell -1} ], \end{aligned}$$

since the generators of $\mathcal {G}$ needed to determine $\beta _\ell , \alpha _\ell , \alpha _{\ell +1}, \dots \alpha _L$ are coupled into $x^{\ell -1}$. Therefore, by (3.10), we have

$$\begin{aligned} {\mathbb {E}}[\beta _1 \dots \beta _{\ell -1} {\mathbb {E}}[\beta _\ell \alpha _{\ell +1}\dots \alpha _L | \mathcal {G} ] ]&= {\mathbb {E}}[\beta _1 \dots \beta _{\ell -1} {\mathbb {E}}[\alpha _\ell \alpha _{\ell +1} \dots \alpha _L | \mathcal {G}] ]\\&={\mathbb {E}}[\beta _1 \dots \beta _{\ell -1} \alpha _\ell \alpha _{\ell +1} \dots \alpha _L ]. \end{aligned}$$

Therefore, we have proven (3.12).

Lastly, by applying (3.12) iteratively, we have

$$\begin{aligned} {\mathbb {E}}[ \beta _1 \beta _2 \dots \beta _L] = {\mathbb {E}}[ \beta _1 \alpha _2 \dots \alpha _L]. \end{aligned}$$

By (3.10),

$$\begin{aligned} {\mathbb {E}}[ \beta _1 \alpha _2 \dots \alpha _L] = {\mathbb {E}}[{\mathbb {E}}[\beta _1 \alpha _2 \dots \alpha _L | x^0 ] ]= {\mathbb {E}}[ {\mathbb {E}}[\alpha _1 \alpha _2 \dots \alpha _L | x^0] ] = {\mathbb {E}}[\alpha _1 \alpha _2 \dots \alpha _L ]. \end{aligned}$$

We have completed the proof of (3.9).

Here we visualize the dependency of the random variables in Fig. 3 in the case of the specific $(U_{\ell })_{\ell =0}^{L-1}$ in (3.3) constructed with $(V_\ell )_{\ell =0}^{L-1}$. Note that we do not use the specific construction in the proof of Lemma 3.1.

Fig. 3

A graphical model of random variables for computing characteristic functions in a specific case using $V_\ell$ for constructing $U_\ell$. See (3.7) and (3.8) for the definition of $\alpha _\ell$ and $\beta _\ell$. See Fig. 1 for the graph’s drawing rule

3.3 Matrix size cutoff

The invariance described in Lemma 2.10 fixes the vector $x^{\ell -1}$, and there are no restrictions on the remaining $N-1$ dimensional space $P(N) {\mathbb {R}}^N$. We call P(N)AP(N) the cutoff of any $N\times N$ matrix A. This section quantifies that cutting off the fixed space causes no significant effect when taking the large-dimensional limit.

For $p \ge 1$, we denote by $||X||_p$ the $L^p$-norm of $X \in M_N({\mathbb {R}})$ defined by

$$\begin{aligned} || X ||_p= ({{\,\mathrm{\textrm{tr}}\,}}|X|^p )^{1/p} = \left[ {{\,\mathrm{\textrm{tr}}\,}}\left[ \left( \sqrt{X^\top X}\right) ^p\right] \right] ^{1/p}. \end{aligned}$$

Recall that the following non-commutative Hölder’s inequality holds:

$$\begin{aligned} || XY ||_r \le || X ||_p || Y ||_q, \end{aligned}$$

(3.13)

for any $r,p,q \ge 1$ with $1/r = 1/p + 1/q$.

Lemma 3.2

Fix $n \in {\mathbb {N}}$. Let $X_1(N), \dots , X_n(N)$ be $N \times N$ random matrices for each $N \in {\mathbb {N}}$. Assume that there is a constant $C > 0$ satisfying almost surely

$$\begin{aligned} \sup _{N \in {\mathbb {N}}} \sup _{j=1, \dots , n}{||X_j(N)||_n } \le C. \end{aligned}$$

Let P(N) be the orthogonal projection defined in (3.4). Then we have almost surely

$$\begin{aligned} |{{\,\mathrm{\textrm{tr}}\,}}[P(N)X_1(N)P(N) \dots P(N)X_n(N)P(N)] - {{\,\mathrm{\textrm{tr}}\,}}[X_1(N) \dots X_n(N)] | \le \frac{nC^n}{N^n}. \end{aligned}$$

(3.14)

In particular, the left-hand side of (3.14) goes to 0 as $N \rightarrow \infty$ almost surely.

Proof

We omit the index N if there is no confusion. Set

$$\begin{aligned} T = \sum _{j=0}^{n-1} PX_1 \cdots PX_{k-j-1}( P-1 )X_{n-j} X_{n-j+1} \cdots X_n. \end{aligned}$$

Then the left-hand side of (3.14) is equal to $|{{\,\mathrm{\textrm{tr}}\,}}T|$. By the Hölder’s inequality (3.13),

$$\begin{aligned} |{{\,\mathrm{\textrm{tr}}\,}}T| \le ||T||_1 \le \sum _{j=0}^{n-1} ||P||_n^{n-j-1} ||X_1||_n \cdots ||X_n||_n || P -1 ||_n. \end{aligned}$$

Now

$$\begin{aligned} || P -1 ||_n = (\frac{1^n}{N})^{1/n} = \frac{1}{N^{1/n}}. \end{aligned}$$

Then by the assumption, we have $|{{\,\mathrm{\textrm{tr}}\,}}T| \le nC^n/N^{1/n}$ almost surely. $\square$

By Lemma 3.2, the cutoff P(N)XP(N) approximate X in the sence of polynomials. Next, we check that an orthogonal matrix approximates the cutoff of any orthogonal matrix.

Lemma 3.3

Let $N\in {\mathbb {N}}$ and $N \ge 2$. For any ${{\textbf{O}}}_{\textbf{N}}$ valued random matrix W, there is W-measurable ${{\textbf{O}}}_{\mathbf {N-1}}$ valued random matrix $\grave{W}$ satisfying

$$\begin{aligned} || PWP - \begin{pmatrix} \grave{W} &{} 0 \\ 0 &{} 0 \end{pmatrix} ||_p \le \frac{1}{(N-1)^{1/p}}, \end{aligned}$$

for any $p \in {\mathbb {N}}$ almost surely

Proof

Consider the singular value decomposition $(U_1, D, U_2)$ of PWP in the $N-1$ dimensional subspace $P {\mathbb {R}}^N$, where $U_1, U_2$ belong to ${{\textbf{O}}}_{\mathbf {N-1}}$, $D={{\,\mathrm{\textrm{diag}}\,}}(\lambda _1, \dots , \lambda _{N-1})$, and $\lambda _1 \ge \dots \ge \lambda _{N-1}$ are singular values of PWP except for the trivial singular value zero. Now

$$\begin{aligned} PWP = \begin{pmatrix} U_1 D U_2 &{} 0 \\ 0 &{} 0 \end{pmatrix}. \end{aligned}$$

Set

$$\begin{aligned} \grave{W} = U_1 U_2. \end{aligned}$$

Now $\grave{W}$ is W-measurable since $U_1$ and $U_2$ are determined by the singular value decomposition. We claim that $\grave{W}$ is the desired random matrix.

We only need to show that ${{\,\mathrm{\textrm{Tr}}\,}}[ (1-D)^p ]\le 1$, where ${{\,\mathrm{\textrm{Tr}}\,}}$ is the unnormalized trace. Write

$$\begin{aligned} R = P - (PWP)^\top PWP = PW^\top (1-P)WP. \end{aligned}$$

Then ${{\,\mathrm{\textrm{rank}}\,}}R \le 1$ and ${{\,\mathrm{\textrm{Tr}}\,}}R \le ||WPW^\top || {{\,\mathrm{\textrm{Tr}}\,}}(1-P) \le 1$. Therefore, R’s nontrivial singular value belongs to [0, 1]. We write it $\lambda$. Then $(PWP)^\top PW = P - R$ has nontrivial eigenvalue $1 - \lambda$ and eigenvalue 1 of multiplicity $N-2$. Therefore,

$$\begin{aligned} D^2 = {{\,\mathrm{\textrm{diag}}\,}}(1, \dots , 1, 1- \lambda ). \end{aligned}$$

Thus ${{\,\mathrm{\textrm{Tr}}\,}}[(1-D)^p] = (1 - \sqrt{1-\lambda })^p \le 1$. We have completed the proof. $\square$

4 Asymptotic Freeness of Layerwise Jacobians

This section contains some of our main results. The first one is the most general form, but it relies on the existence of the limit joint moments of $(D_\ell )_\ell$. The second one is required for the analysis of the dynamical isometry. The last one is needed for the analysis of the Fisher information matrix. The second and the third ones do not assume the existence of the limit joint moments of $(D_\ell )_\ell$.

We use the notations in Sect. 3.1. In the sequel, for each $\ell , N \in {\mathbb {N}}$, each $Y_\ell$ is the $x^\ell$-measurable and ${{\textbf{O}}}_{\textbf{N}}$ valued random matrix described in (3.2). It is $x^\ell$-measurable and satisfies $Y_\ell x^\ell = || x^\ell ||_2 e_N$, where $e_N$ is the N-th vector of the standard basis of ${\mathbb {R}}^N$. Recall that $V_0, \dots , V_{L-1}$ are independent ${{\textbf{O}}}_{\mathbf {N-1}}$ valued Haar random matrices such that all entries of them are independent of that of $(x^0, W_1, \dots , W_L)$. In addition,

$$\begin{aligned} U_\ell = Y_\ell ^\top \begin{pmatrix} V_\ell &{} 0 \\ 0 &{} 1 \end{pmatrix} Y_\ell \end{aligned}$$

and $U_\ell x^\ell = x^\ell$. Further, for any $\ell =0, \dots , \ell -1$, all entries of $(U_0, \dots , U_{\ell -1})$ are independent from that of $(W_\ell , \dots , W_L)$. Thus by Lemma 3.1,

$$\begin{aligned} (W_1 U_0, \dots , W_L U_{L-1}, D_1, \dots , D_L) \sim ^\textrm{entries}(W_1, \dots , W_L, D_1, \dots , D_L). \end{aligned}$$

In addition, for any $n \in {\mathbb {N}}$ and almost surely we have

$$\begin{aligned} \max _{\ell =1, \dots , L} \sup _{n \in {\mathbb {N}}}||D_\ell ||_n < \infty , \end{aligned}$$

(4.1)

since each $D_\ell$ has the limit spectral distribution by Corollary 2.14.

We are now prepared to prove our main theorem.

Theorem 4.1

Assume that $(D_1, \dots , D_L)$ has the limit joint distribution almost surely. Then the families $(W_1,W_1^\top ), \dots ( W_L, W_L^\top )$, and $(D_1, \dots , D_L)$ are asymptotically free as $N \rightarrow \infty$ almost surely.

Proof

Without loss of generality, we may assume that $\sigma _{w,1}, \dots , \sigma _{w,L}=1$. Set

$$\begin{aligned} Q_\ell = P W_\ell P Y_{\ell -1}^\top P \begin{pmatrix}V_{\ell -1} &{} 0\\ 0 &{} 1\end{pmatrix}P Y_{\ell -1} P. \end{aligned}$$

for each $\ell =1, \dots ,L$, where $P=P(N)$ is defined in (3.4). By Lemma 3.2 and (4.1), we only need to show the asymptotic freeness of the families

$$\begin{aligned} (Q_\ell , Q_\ell ^\top )_{\ell =1}^L, (PD_1P,\dots , PD_LP), \end{aligned}$$

Now

$$\begin{aligned} P \begin{pmatrix}V_{\ell -1} &{} 0\\ 0 &{} 1\end{pmatrix} P = \begin{pmatrix}V_{\ell -1} &{} 0\\ 0 &{} 0\end{pmatrix}. \end{aligned}$$

In addition, let $\grave{D}_\ell$ be the $N-1 \times N-1$ matrix determined by

$$\begin{aligned} PD_\ell P = \begin{pmatrix} \grave{D}_\ell &{} 0 \\ 0 &{} 0 \end{pmatrix}. \end{aligned}$$

(4.2)

By Lemma 3.3, there are ${{\textbf{O}}}_{\mathbf {N-1}}$ valued random matrices $\grave{W}_\ell$ and $\grave{Y}_{\ell -1}$ satisfying

$$\begin{aligned} || P W_\ell P - \begin{pmatrix} \grave{W}_\ell &{} 0 \\ 0 &{} 0 \end{pmatrix} ||_n&\le \frac{1}{(N-1)^{1/n}},\nonumber \\ || P Y_\ell P - \begin{pmatrix} \grave{Y}_\ell &{} 0 \\ 0 &{} 0 \end{pmatrix} ||_n&\le \frac{1}{(N-1)^{1/n}}, \end{aligned}$$

(4.3)

for any $n \in {\mathbb {N}}$. Therefore, we only need to show asymptotic freeness of the following $L+1$ families:

$$\begin{aligned} \left( \grave{W}_\ell \grave{Y}_{\ell -1}^\top V_{\ell -1} \grave{Y}_{\ell -1}, \left( \grave{W}_\ell \grave{Y}_{\ell -1}^\top V_{\ell -1} \grave{Y}_{\ell -1}\right) ^\top \right) _{\ell =1}^L, \left( \grave{D_1},\dots , \grave{D}_L\right) . \end{aligned}$$

(4.4)

Now all entries of Haar random matrices $(V_\ell )_\ell$ are independent of those of $(\grave{W}_\ell , \grave{Y}_{\ell -1}, \grave{D}_\ell )_\ell$. Thus by Lemma 2.10 and Proposition 2.8, the asymptotic freeness of (4.4) holds as $N \rightarrow \infty$ almost surely. We have completed the proof. $\square$

The following result is useful in the study of dynamical isometry and spectral analysis of Jacobian of DNNs. It follows directly from Theorem 4.1 if we assume the existence of the limit joint moments of $(D_\ell )_{\ell =1}^L$. Note that the following result does not assume the existence of the limit joint moments.

Proposition 4.2

For each $\ell =1,\dots , L-1$, let $J_\ell$ be the Jacobian of $\ell$-th layer, that is,

$$\begin{aligned} J_\ell = D_\ell W_\ell \dots D_1 W_1. \end{aligned}$$

Then $J_\ell J_\ell ^\top$ has the limit spectral distribution and the pair

$$\begin{aligned} W_{\ell +1}J_\ell J_\ell ^\top W_{\ell +1}^\top , D_{\ell +1}^2 \end{aligned}$$

is asymptotically free as $N \rightarrow \infty$ almost surely.

Proof

Without loss of generality, we may assume $\sigma _{w,1}, \dots , \sigma _{w,L}=1$. We proceed by induction over $\ell$.

Let $\ell =1$. Then $J_1J_1^\top = D_1^2$ has the limit spectral distribution by Proposition 2.13. By Lemma 3.2 and (4.1), we only need to show that the asymptotically freeness of the pair

$$\begin{aligned} PW_2 P Y_{1}^\top P \begin{pmatrix}V_1 &{} 0 \\ 0 &{} 1 \end{pmatrix} P D_1^2 P \begin{pmatrix}V_1^\top &{} 0 \\ 0 &{} 1 \end{pmatrix} P Y_1 P W_2^\top P, PD_2^2P, \end{aligned}$$

By Lemma 3.3, there are $\grave{W}_2 \in {{\textbf{O}}}_{\mathbf {N-1}}$ and $\grave{Y}_{1} \in {{\textbf{O}}}_{\mathbf {N-1}}$ which approximate $P W_2 P$ and $PY_1 P$ in the sence of (4.3). Let $\grave{D}_2$ be the $N-1 \times N-1$ random matrix given by (4.2). Then, we only need to show the asymptotical freeness of the following pair:

$$\begin{aligned} \grave{W}_2 \grave{Y}_{1}^\top V_1 \grave{D}_1^2 V_1^\top Y_1 \grave{W}_2^\top , \grave{D}_2^2. \end{aligned}$$

By the independence and Lemma 2.10, the asymptotic freeness holds almost surely.

Next, fix $\ell \in [1, L-1]$ and assume that the limit spectral distribution of $J_\ell J_\ell ^\top$ exists and the asymptotic freeness holds for the $\ell$. Now

$$\begin{aligned} J_{\ell +1}J_{\ell +1}^\top = D_{\ell +1}W_{\ell +1}(J_\ell J_\ell ^\top ) W_{\ell +1}^\top D_{\ell +1}. \end{aligned}$$

By the asymptotic freeness for the case $\ell$, $J_{\ell +1}J_{\ell +1}^\top$ has the limit spctral distribution. There exists $\grave{J}_\ell \in M_{N-1}({\mathbb {R}})$ so that

$$\begin{aligned} P J_\ell P = \begin{pmatrix} \grave{J}_\ell &{} 0 \\ 0 &{} 0 \end{pmatrix}. \end{aligned}$$

Then for the case of $\ell +1$, by the same argument as above, we only need to show the asymptotic freeness of

$$\begin{aligned} \grave{W}_{\ell +2} \grave{Y}_{\ell +1}^\top V_{\ell +1} \grave{J}_{\ell +1} \grave{J}^\top _{\ell +1} V_{\ell +1}^\top Y_{\ell +1} \grave{W}_{\ell +2}^\top , \grave{D}_{\ell +2}^2. \end{aligned}$$

Now, all enties of $V_{\ell +1}$ are independent from those of $(\grave{J}_{\ell +1}, \grave{W}_{\ell +1}, \grave{Y}_{\ell +1}, \grave{D}_{\ell +2})$. By the independence and Lemma 2.10, we only need to show the asymptotic freeness of

$$\begin{aligned} V_{\ell +1} \grave{J}_{\ell +1} \grave{J}_{\ell +1}^\top V_{\ell +1}^\top , \grave{D}_{\ell +2}^2. \end{aligned}$$

The asymptotic freeness of the pair follows from Proposition 2.9. The assertion follows by induction. $\square$

Next, we treat a conditional Fisher information matrix $H_L$ of the MLP. (See Sect. 5.2.)

Proposition 4.3

Define $H_\ell$ inductively by $H_1 = I_N$ and

$$\begin{aligned} H_{\ell +1 } = {\hat{q}}_{\ell }I + W_{\ell +1} D_{\ell }H_{\ell }D_{\ell }W_{\ell +1}^\top , \end{aligned}$$

(4.5)

where ${\hat{q}}_{\ell } = \sum _{j=1}^N (x^{\ell }_j)^2 / N$ and $\ell =1,\dots , L-1$. Then for each $\ell = 1,2, \dots , L$, $H_\ell$ has a limit spectral distribution and the pair

$$\begin{aligned} H_\ell , D_\ell \end{aligned}$$

is asymptotically free as $N \rightarrow \infty$, almost surely.

Proof

We proceed by induction over $\ell$. The case $\ell =1$ is trivial. Assume that the assertion holds for an $\ell \ge 1$ and consider the case $\ell +1$. Then by (4.5) and the assumption of induction, $H_{\ell +1}$ has the limit spectral distribution. Let $\grave{H}_{\ell +1}$ be the $N-1 \times N-1$ matrix determined by

$$\begin{aligned} P H_{\ell } P = \begin{pmatrix} \grave{H}_{\ell } &{} 0 \\ 0 &{} 0 \end{pmatrix}. \end{aligned}$$

By the same arguments as above, we only need to prove the asymptotic freeness of the following pair:

$$\begin{aligned} \grave{W}_{\ell +1} \grave{Y}_\ell V_\ell \grave{Y}_\ell ^\top \grave{D}_\ell \grave{H}_\ell \grave{ D}_\ell (W_{\ell +1}\grave{Y}_\ell V_\ell \grave{Y}_\ell ^\top )^\top , \grave{D}_{\ell +1}. \end{aligned}$$

By Lemma 2.10, considering the joint distributions of all entries, we only need to show the asymptotic freeness of the following pair:

$$\begin{aligned} V_\ell \grave{D}_\ell \grave{H}_\ell \grave{ D}_\ell V_\ell ^\top , \grave{D}_{\ell +1}. \end{aligned}$$

By the assumption, $\grave{D}_\ell \grave{H}_\ell \grave{ D}_\ell$ has the limit spectral distribution. Then by Proposition 2.9, the assertion holds for $\ell +1$. The assertion follows by induction. $\square$

5 Applications

Let $\nu _\ell$ be the limit spectral distribution of $D_\ell ^2$ for each $\ell$ given by Corollary 2.14. We introduce applications of the main results.

5.1 Jacobian and dynamical isometry

Let J be the Jacobian of the network with respect to the input vector. In [17, 18, 21], a DNN is said to achieve dynamical isometry if J acts as a near isometry, up to some overall global O(1) scaling, on a subspace of as high a dimension as possible. Calling ${{\tilde{H}}}$ such a subspace, the $||(J^\top J)_{|\tilde{H}}-Id_{{{\tilde{H}}}}||_2=o(\sqrt{dim {{\tilde{H}}}})$. Note that in [17, 18, 21], a rigorous definition is not given, and that many variants of this definition are likely to be acceptable for the theory. In their theory, they take firstly the wide limit $N \rightarrow \infty$. To examine the dynamical isometry as the wide limit $N \rightarrow \infty$ and the deep limit $L \rightarrow \infty$, [7, 17, 18] consider S-transform of the spectral distribution. (See [20, 26] for the definition of S-transform).

Now

$$\begin{aligned} J = J_L= D_L W_L \dots D_1 W_1. \end{aligned}$$

Recall that the existence of the limit spectral distribution of each $J_\ell$ $(\ell =1, \dots , L)$ is supported by Proposition 4.2. In addition, recall that $\nu _\ell$ is the limit spectral distribution of $D_\ell ^2$ as $d \rightarrow \infty$ for each $\ell$.

Corollary 5.1

Let $\xi _\ell$ be the limit spectral distribution as $N \rightarrow \infty$ of $J_\ell J_\ell ^\top$. Then for each $\ell =1, \dots , L$, it holds that

$$\begin{aligned} S_{\xi _\ell }(z) = \frac{1}{\sigma _{w,1}^2 \dots \sigma _{w,\ell }^2} S_{\nu _1}(z) \cdots S_{\nu _\ell }(z). \end{aligned}$$

(5.1)

Proof

Consider the case $\ell =1$. Then $J_1 J_1^\top = D_1 W_1 W_1^\top D_1= \sigma _{w,1}^2 D_1^2$. Then $S_{\xi _\ell }(z) = \sigma _{w,1}^{-2} S_{\nu _1}(z)$.

Assume that (5.1) holds for an $\ell \ge 1$. Consider the case $\ell +1$. By Proposition 4.2, $W_{\ell +1}^\top W_{\ell +1} = \sigma _{w, \ell +1}^2 I$ and the tracial condition,

$$\begin{aligned} S_{\xi _{\ell +1}}(z) = \frac{1}{\sigma _{w,\ell +1}^2} S_{\xi _{\ell }}(z) S_{\nu _{\ell +1}}(z). \end{aligned}$$

The assertion holds by induction. $\square$

Corollary 5.1 is a resolution of an unproven result in [18], and it enables us to compute the deep limit $S_{\xi _L}(z)$ as $L \rightarrow \infty$.

5.2 Fisher information matrix and training dynamics

We focus on the the Fisher information matrix (FIM) for supervised learning with a mean squared error (MSE) loss [9, 15, 19]. Let us summarize its definition and basic properties. Given $x \in {\mathbb {R}}^N$ and parameters $\theta =(W_1, \dots , W_\ell )$, we consider a Gaussian probability model

$$\begin{aligned} p_\theta (y | x) = \frac{1}{\sqrt{2\pi }}\exp \left( - {\mathcal {L}}\left( f_\theta (x) -y\right) \right) \ (y \in {\mathbb {R}}^N). \end{aligned}$$

Now, the normalized MSE loss ${\mathcal {L}}$ is given by ${\mathcal {L}}(u) = ||u||_2^2/2N$, for $u \in {\mathbb {R}}^N$, and $||\cdot ||_2$ is the Euclidean norm. In addition, consider a probability density function p(x) and a joint density $p_\theta (x,y) = p_\theta (y|x)p(x)$. Then, the FIM is defined by

$$\begin{aligned} {\mathcal {I}}(\theta ) = \int [\nabla _\theta \log p_\theta (x,y )^\top \nabla _\theta \log p_\theta (x,y)] p_\theta (x,y)dxdy, \end{aligned}$$

which is an $LN^2 \times LN^2$ matrix. As it is known in information geometry [1], the FIM works as a degenerate metric on the parameter space: the Kullback–Leibler divergence between the statistical model and itself perturbed by an infinitesimal shift $d\theta$ is given by $D_{\textrm{KL}}(p_\theta || p_{\theta + d\theta }) = d\theta ^\top {\mathcal {I}}(\theta ) d\theta .$ More intuitive understanding is that we can write the Hessian of the loss as

$$\begin{aligned} \left( \frac{\partial }{\partial \theta }\right) ^2{\mathbb {E}}_{x,y}[{\mathcal {L}}(f_\theta (x) - y)] = {\mathcal {I}}(\theta ) + {\mathbb {E}}_{x,y}[ (f_\theta (x) -y )^\top \left( \frac{\partial }{\partial \theta } \right) ^2 f_\theta (x) ]. \end{aligned}$$

Hence the FIM also characterizes the local geometry of the loss surface around a global minimum with a zero training error. In addition, we regard p(x) as an empirical distribution of input samples and then the FIM is usually referred to as the empirical FIM [9, 11, 19].

The conditional FIM is used [7] for the analysis of training dynamics of DNNs achieving dynamical isometry. Now, we denote by $\mathcal {I}(\theta | x)$ the conditional FIM (or FIM per sample) given a single input x defined by

$$\begin{aligned} \mathcal {I}(\theta | x) = \int [\nabla _\theta \log p_\theta (y | x)^\top \nabla _\theta \log p_\theta (y | x)] p_\theta (y|x)dy. \end{aligned}$$

Clearly, $\int \mathcal {I}(\theta | x) p(x)dx = {\mathcal {I}}(\theta )$. Since $p_\theta (y|x)$ is Gaussian, we have

$$\begin{aligned} \mathcal {I}(\theta | x) = \frac{1}{N}J_\theta ^\top J_\theta . \end{aligned}$$

Now, in order to ignore ${\mathcal {I}}(\theta |x)$’s trivial eigenvalue zero, consider a dual of $\mathcal {I}(\theta |x)$ given by

$$\begin{aligned} {\mathcal {J}}(x,\theta ) = \frac{1}{N} J_\theta J_\theta ^\top , \end{aligned}$$

which is an $N \times N$ matrix. Except for trivial zero eigenvalues, ${\mathcal {I}}(\theta |x)$ and ${\mathcal {J}}(x,\theta )$ share the same eigenvalues as follows:

$$\begin{aligned} \mu _{I(\theta |x)} = \frac{LN^2 -N }{LN^2} \delta _0 + \frac{1}{L} \mu _{{\mathcal {J}}(x, \theta )}, \end{aligned}$$

where $\mu _A$ is the spectral distribution for a matrix A. Now, for simplicity, consider the case bias parameters are zero. Then it holds that

$$\begin{aligned} {\mathcal {J}}(x,\theta ) = D_L H_L D_L, \end{aligned}$$

where

$$\begin{aligned} H_L&= \sum _{\ell =1}^L {\hat{q}}_{\ell -1}\delta _{L \rightarrow \ell } \delta _{L \rightarrow \ell }^\top ,\\ {\hat{q}}_\ell&= ||x^\ell ||_2^2/N,\\ \delta _{L \rightarrow \ell }&= \frac{\partial h^L}{\partial h^\ell }. \end{aligned}$$

Since $\delta _{L \rightarrow \ell } = W_LD_{L-1} \delta _{L-1 \rightarrow \ell }$ $(\ell < L)$, it holds that

$$\begin{aligned} H_{\ell +1 } = {\hat{q}}_{\ell }I + W_{\ell +1} D_{\ell }H_{\ell }D_{\ell }W_{\ell +1}^\top , \end{aligned}$$

where I is the identity matrix. Recall that $\nu _\ell$ is the limit spectral distribution of $D_\ell ^2$ as $d \rightarrow \infty$ for each $\ell$.

Corollary 5.2

Let $\mu _{\ell }$ be the limit spectral distribution as $N \rightarrow \infty$ of $H_\ell$ ($\ell =1, \dots , L$). Set $q_\ell = \lim _{N \rightarrow \infty }{\hat{q}}_{\ell }$. Then for each $\ell =1, \dots , L$ it holds that

$$\begin{aligned} \mu _{\ell +1} = (q_\ell + \sigma _{\ell +1}^2 \cdot )_* (\mu _\ell \boxtimes \nu _\ell ), \end{aligned}$$

(5.2)

where $f_*\mu$ is the pushforward of a measure $\mu$ by a measurable map f.

Proof

The assertion directly follows from Proposition 4.3 and by induction. $\square$

[7] uses the recursive equation (5.2) to compute the maximum value of the limit spectrum of $H_L$.

6 Discussion

We have proved the asymptotic freeness of MLPs with Haar orthogonal initialization by focusing on the invariance of the MLP. [6] shows the asymptotic freeness of MLP with Gaussian initialization and ReLU activation. The proof relies on the observation that each ReLU’s derivative can be replaced with independent Bernoulli from weight matrices. On the contrary, our proof builds on the observation that weight matrices are replaced with independent random matrices from activations’ Jacobians based on Haar orthogonal random matrices’ invariance. In addition, [30, 31] proves the asymptotic freeness of MLP with Gaussian initialization, which relies on Gaussianity. Since our proof relies on the orthogonal invariance of weight matrices, our proof covers and generalizes the GOE case.

It is straightforward to extend our results including Theorem 4.1 to MLPs with Haar unitary weights since the proof basely relies on the invariance of weight matrices (see Lemma 3.1) and the cut off (see Lemma 3.3). We expect that our theorem can be extended to Haar permutation weights since Haar distributed random permutation matrices and independent random matrices are asymptotic free [2]. Moreover, we expect that it is possible to extend the principal results and cover MLPs with orthogonal/unitary/permutation invariant random weights since each proof is based on the invariance of MLP.

The neural tangent kernel theory [8] describes the learning dynamics of DNNs when the dimension of the last layer is relatively smaller than the hidden layers. In our analysis, we do not consider such a case and instead consider the case where the last layer has the same order dimension as the hidden layers.