Abstract
We show that every unitarizable fusion category, and more generally every semisimple \(\textrm{C}^*\)-tensor category, admits a unique unitary structure. Our proof is based on a categorified polar decomposition theorem for monoidal equivalences between such categories. We prove analogous results for unitarizable braided fusion categories and module categories.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A unitary fusion category is a fusion category over the complex numbers with a positive \(*\)-structure. Such unitary structures naturally arise in many applications and constructions of fusion categories, most notably in the context of operator algebras, subfactor theory, and the mathematical physics of unitary (or reflection positive) conformal and topological quantum field theories. Not every fusion category admits a unitary structure; the Yang-Lee category [10, Ex 8.18.7, Ex 9.4.6] is a famous example of a non-unitary fusion category. Conversely, a fusion category could, in principle, have more than one unitary structure. Especially in light of the recent powerful operator algebraic classification techniques of unitary fusion categories [1, 6, 7, 18, 19], the question of uniqueness of unitary structure has become a significant open problem [11,12,13, 17]. (The explicit statement of Theorem 1 appears as Question 2.8 in [17].) A partial answer for weakly group theoretical fusion categories was obtained in [13].
In this paper, we completely address the general question and prove that every unitarizableFootnote 1 fusion category, and more generally every semisimple \(\textrm{C}^*\)-tensor category, admits a unique unitary structure. We also extend our techniques to unitarizable braided fusion categories and unitarizable module categories.
1.1 Unitary fusion categories
Theorem 1
Every monoidal equivalence between unitary fusion categories is monoidally naturally isomorphic to a unitary monoidal equivalence.
In particular, any unitarizable fusion category admits a unique unitary structure (up to unitary monoidal equivalence).
Theorem 1 is proven in Sect. 2.1. It essentially follows from a categorification of polar decomposition (Corollary 2.4): Every monoidal equivalence between semisimple \(\textrm{C}^*\)-categories (with possibly infinitely many simple objects) can be factored as a unitary monoidal equivalence followed by a ‘positive monoidal auto-equivalence’ (see Definition 2.1). In particular, every semisimple \(\textrm{C}^*\)-tensor category admits a unique \(*\)-structure. If \(\mathcal D\) is a unitary fusion category, it moreover follows from the finiteness of its group of monoidal auto-equivalences that every positive monoidal auto-equivalence of \(\mathcal D\) is trivial (Proposition 2.6), leading to Theorem 1.
When preparing this manuscript, we became aware of an alternative, independent proof of Theorem 1 by Carpi, Ciamprone and Pinzari (to appear [4]) using the framework of weak quasi Hopf algebras.
Natural isomorphisms between unitary monoidal equivalences behave analogously.
Theorem 2
Let  be unitary monoidal equivalences between unitary fusion categories. Then, every monoidal natural isomorphism
be unitary monoidal equivalences between unitary fusion categories. Then, every monoidal natural isomorphism  is unitary.
is unitary.
Theorem 2 is proven in Sect. 2.3. It is again a consequence of polar decomposition: Every monoidal natural isomorphism factors into a unitary monoidal natural isomorphism followed by a positive monoidal natural automorphism. It follows from the finiteness of the universal grading group of \(\mathcal D\) that there are no non-trivial positive monoidal natural automorphisms.
Adopting notation from [9], Theorems 1 and 2 show that the 2-groupoid \(\underline{\textrm{Eq}}\) of unitarizable fusion categories, monoidal equivalences and monoidal natural isomorphisms is equivalent to the 2-groupoid \(\underline{\textrm{Eq}}^\dagger \) of unitary fusion categories, unitary monoidal equivalences and unitary monoidal natural isomorphisms.
Corollary 3
The forgetful 2-functor  is an equivalence.
is an equivalence.
In a certain sense, the existence of a unitary structure on a fusion category \(\mathcal C\) may therefore be thought of as a property of \(\mathcal C\) (‘unitarizability’), rather than as additional structure.
Remark 4
Since the group of monoidal auto-equivalences of a multifusion category is finite [8, Thm 2.31], Theorem 1 immediately generalizes to multifusion categories. However, Theorem 2 does not hold for multifusion categories: There can be non-trivial positive (and hence non-unitary) monoidal natural transformations between unitary monoidal equivalences of unitary multifusion categories (see e.g. [23]).
1.2 Unitary braided fusion categories
The constructions in the proof of Theorem 1 are compatible with braidings, allowing us to extend our results to unitary braided fusion categories.
Theorem 5
Every braided monoidal equivalence  between unitary braided fusion categories is monoidally naturally isomorphic to a unitary braided monoidal equivalence.
between unitary braided fusion categories is monoidally naturally isomorphic to a unitary braided monoidal equivalence.
Theorem 5 is proven in Sect. 2.4.
By a result of Galindo [12, Thm 3.2], any braiding on a unitary fusion category is unitary. Combining this with Theorem 5 shows that there is a unique unitary braided structure on any braided unitarizable fusion categoryFootnote 2.
Corollary 6
Every braided unitarizable fusion category admits a unique unitary braided structure (up to unitary braided monoidal equivalence).
Together with Theorem 2, Theorem 5 shows that the 2-groupoid \(\underline{\textrm{EqBr}}\) of braided unitarizable fusion categories, braided monoidal equivalences and monoidal natural isomorphisms is equivalent to the 2-groupoid \(\underline{\textrm{EqBr}}^\dagger \) of unitary braided fusion categories, unitary braided monoidal equivalences and unitary natural isomorphisms.
Corollary 7
The forgetful 2-functor  is an equivalence.
is an equivalence.
1.3 Unitary module categories
The proof of Theorem 1 translates almost directly into a proof of uniqueness of the unitary structure on a unitarizable module category.
Theorem 8
Every module equivalence  between unitary module categories over unitary fusion categories \(\mathcal C\) and \(\mathcal D\) is naturally isomorphic, as a module functor, to a unitary module equivalence.
between unitary module categories over unitary fusion categories \(\mathcal C\) and \(\mathcal D\) is naturally isomorphic, as a module functor, to a unitary module equivalence.
Theorem 8 is proven in Section 2.5. Its proof is completely analogous to the proof of Theorem 1, replacing finiteness of the group of monoidal auto-equivalences with finiteness of the group of module auto-equivalences. Again, uniqueness of the unitary structure on a unitarizable module categoryFootnote 3 is an immediate corollary.
Corollary 9
Every unitarizable module category of a unitary fusion category admits a unique unitary structure (up to unitary module equivalence).
Remark 10
The category of \(*\)-module functors between two given unitary module categories is a finitely semisimple \(\textrm{C}^*\)-category. Hence, any module natural isomorphism  between unitary module equivalences may be factored into a unitary module natural isomorphism followed by a positive module natural isomorphism. However, there is no analogous statement to Theorem 2; there are non-trivial positive module natural isomorphisms.
between unitary module equivalences may be factored into a unitary module natural isomorphism followed by a positive module natural isomorphism. However, there is no analogous statement to Theorem 2; there are non-trivial positive module natural isomorphisms.
Remark 11
Similar to Corollaries 3 and 7, it would be interesting to compare the algebraic Brauer–Picard 2-groupoidFootnote 4\(\underline{\textrm{BrPic}}\) of unitarizable fusion categories, invertible bimodule categories, and natural isomorphism classes of bimodule equivalences with its unitary counterpart \(\underline{\textrm{BrPic}}^\dagger \) and prove that the forgetful 2-functor  is an equivalence. In fact, by Corollary 7 and the fact that the unitary Drinfeld center \(\mathcal Z^\dagger (\mathcal C)\) of a unitary fusion category equals [12, Prop 3.1] its ordinary Drinfeld center \(\mathcal Z(\mathcal C)\), this would be a direct consequence of the widely expected (but to our knowledge still unproven) unitary version of the equivalence
is an equivalence. In fact, by Corollary 7 and the fact that the unitary Drinfeld center \(\mathcal Z^\dagger (\mathcal C)\) of a unitary fusion category equals [12, Prop 3.1] its ordinary Drinfeld center \(\mathcal Z(\mathcal C)\), this would be a direct consequence of the widely expected (but to our knowledge still unproven) unitary version of the equivalence  constructed in [9, Thm 1.1]. (A unitary version of this functor may be extracted from [21, Section 6], however to our knowledge it remains unproven that it is an equivalence.)
constructed in [9, Thm 1.1]. (A unitary version of this functor may be extracted from [21, Section 6], however to our knowledge it remains unproven that it is an equivalence.)
Remark 11 provides very strong evidence that every invertible finitely semisimple bimodule category between unitary fusion categories is unitarizable and hence admits a unique unitary structure. Indeed, note that Theorems 1, 2, 5 and 8 may all be understood as asserting ‘unitarizability’ of various invertible morphisms. For non-invertible morphisms—such as non-invertible bimodule categories—the situation is far less clear.
Question 12
Does every finitely semisimple module category over a unitary fusion category admit a (by Corollary 9 necessarily unique) unitary structure?
1.4 A cohomological perspective
Our results can be understood as a generalization of the fact that for a finite group G, the homomorphism  induced from the inclusion \(U(1) \hookrightarrow \mathbb C^\times \) is an isomorphism. Indeed, our proof mirrors the following elementary proof of this fact: Let \(\omega (g_1,\ldots , g_n)\) denote a \(\mathbb C^\times \)-valued n-cocycle. Taking absolute values of the n-cocycle equation shows that \(|\omega (g_1,\ldots , g_n)|\) and \(u(g_1,\ldots , g_n):= \omega (g_1,\ldots , g_n)/|\omega (g_1,\ldots , g_n)|\) are n-cocycles in \(H^n(G,\mathbb R_{>0})\) and \(H^n(G,U(1))\), respectively, and that \(\omega (g_1,\ldots , g_n) = u(g_1,\ldots , g_n) |\omega (g_1,\ldots , g_n)|\). Moreover, it follows from finiteness of G that \(H^n(G, \mathbb R_{>0})\) is zero, and hence that the positive n-cocycle \(|\omega (g_1,\ldots ,g_n)|\) is cohomologous to the trivial cocycle. Therefore, \(\omega \) is cohomologous to u.
induced from the inclusion \(U(1) \hookrightarrow \mathbb C^\times \) is an isomorphism. Indeed, our proof mirrors the following elementary proof of this fact: Let \(\omega (g_1,\ldots , g_n)\) denote a \(\mathbb C^\times \)-valued n-cocycle. Taking absolute values of the n-cocycle equation shows that \(|\omega (g_1,\ldots , g_n)|\) and \(u(g_1,\ldots , g_n):= \omega (g_1,\ldots , g_n)/|\omega (g_1,\ldots , g_n)|\) are n-cocycles in \(H^n(G,\mathbb R_{>0})\) and \(H^n(G,U(1))\), respectively, and that \(\omega (g_1,\ldots , g_n) = u(g_1,\ldots , g_n) |\omega (g_1,\ldots , g_n)|\). Moreover, it follows from finiteness of G that \(H^n(G, \mathbb R_{>0})\) is zero, and hence that the positive n-cocycle \(|\omega (g_1,\ldots ,g_n)|\) is cohomologous to the trivial cocycle. Therefore, \(\omega \) is cohomologous to u.
Our proofs of Theorems 1 and 2 proceed analogously, replacing the factorization \(\omega = u |\omega |\) by a polar decomposition and deducing triviality of the positive part from the finiteness of the group of monoidal auto-equivalences and the universal grading group, respectively.
More precisely, given a unitary fusion category \(\mathcal C\), Theorem 1 is a direct consequence of the vanishing of the group \(h^2(\mathcal C, \mathbb R_{>0})\) of (natural isomorphism classes of) monoidal auto-equivalences of \(\mathcal C\) with underlying identity functor and positive coherence natural isomorphism (see Proposition 2.6). Similarly, Theorem 2 is a direct consequence of the vanishing of the group \(h^1(\mathcal C, \mathbb R_{>0})\) of positive monoidal natural automorphisms of the identity monoidal equivalence  (see Proposition 2.8). The appearance of these groups is no coincidence: If \(\mathcal C\) is the category of G-graded vector spaces, then \(h^1(\mathcal C, \mathbb R_{>0})\) and \(h^2(\mathcal C, \mathbb R_{>0})\) are precisely the group cohomology groups \(H^1(G, \mathbb R_{>0})\) and \(H^2(G, \mathbb R_{>0})\). In general, there is no obvious cohomology theory \(h^n\) of fusion categories specializing to \(h^1\) and \(h^2\) at \(n=1,2\), but the prominent appearance of these groups nevertheless raises the question of whether our proofs are elementary versions of a more elegant cohomological result.
(see Proposition 2.8). The appearance of these groups is no coincidence: If \(\mathcal C\) is the category of G-graded vector spaces, then \(h^1(\mathcal C, \mathbb R_{>0})\) and \(h^2(\mathcal C, \mathbb R_{>0})\) are precisely the group cohomology groups \(H^1(G, \mathbb R_{>0})\) and \(H^2(G, \mathbb R_{>0})\). In general, there is no obvious cohomology theory \(h^n\) of fusion categories specializing to \(h^1\) and \(h^2\) at \(n=1,2\), but the prominent appearance of these groups nevertheless raises the question of whether our proofs are elementary versions of a more elegant cohomological result.
1.5 Generalizing to semisimple \(\textrm{C}^*\)-categories and beyond
In Corollary 2.4, we prove a polar decomposition theorem for semisimple \(\textrm{C}^*\)-tensor categories (with possibly infinitely many simple objects): Every monoidal equivalence between semisimple \(\textrm{C}^*\)-tensor categories is monoidally naturally isomorphic to the composite of a unitary monoidal equivalence followed by a positive monoidal auto-equivalence. In particular, any semisimple \(\textrm{C}^*\)-tensor category admits a unique \(\textrm{C}^*\)-structure (even though there might be non-trivial positive monoidal auto-equivalences, see Remark 2.5). In fact, we expect Corollary 2.4 to be more generally true for arbitrary \(\textrm{W}^*\)-tensor categories. By Theorem 2.2, this would follow from a positive answer to the following question:
Question 13
Is every equivalence  between \(\textrm{W}^*\)-categories naturally isomorphic to a \(*\)-equivalence?
between \(\textrm{W}^*\)-categories naturally isomorphic to a \(*\)-equivalence?
Note that a positive answer to this question may be understood as a generalization of a theorem of Okayasu [22] that any (not necessarily \(*\)-preserving) isomorphism  of \(\textrm{W}^*\)-algebras is of the form
of \(\textrm{W}^*\)-algebras is of the form  , where
, where  is a \(*\)-isomorphism and \(\eta \) is a positive invertible element of B.
is a \(*\)-isomorphism and \(\eta \) is a positive invertible element of B.
1.6 Monoidal 2-categories
Most of the material in this paper was developed using the framework and graphical calculus of the monoidal 2-category \(\textrm{2Hilb}\) [2]. However, to keep our presentation as elementary and accessible as possible, we present all proofs in terms of standard 1-categorical machinery, completely omitting the use of higher category theory.
For the interested reader, we demonstrate in Sect. 3 how some of the more subtle applications of naturality in the proof of Theorem 2.2 arise from simple isotopies in the graphical calculus. Section 3 is purely expositional and is not necessary for the technical developments of our results.
2 Preliminaries
2.1 \(*\)-categories
In the following, a linear category is a category enriched in the category \(\textrm{Vect}_{\mathbb C}\) of \(\mathbb C\)-vector spaces and linear maps, and a linear functor is a \(\textrm{Vect}_{\mathbb C}\)-enriched functor.
A \(*\)-category is a linear category equipped with a \(*\)-structure, a \(\mathbb C\)-antilinear, involutive, identity-on-objects functor  . A morphism
. A morphism  in a \(*\)-category is unitary if \(u^* u = \textrm{id}_A\) and \(u u^* = \textrm{id}_B\). An endomorphism
in a \(*\)-category is unitary if \(u^* u = \textrm{id}_A\) and \(u u^* = \textrm{id}_B\). An endomorphism  is positive if there is some morphism
is positive if there is some morphism  such that \(p= g^* g\). A \(*\)-functor
such that \(p= g^* g\). A \(*\)-functor  between \(*\)-categories is a linear functor F such that \(F(f^*) = F(f)^*\) for all morphisms f. The category of \(*\)-functors and natural transformations between two \(*\)-categories is itself a \(*\)-category: For a natural transformation
between \(*\)-categories is a linear functor F such that \(F(f^*) = F(f)^*\) for all morphisms f. The category of \(*\)-functors and natural transformations between two \(*\)-categories is itself a \(*\)-category: For a natural transformation  , we define
, we define  to be the natural transformation with components \((\eta ^*)_A:= \eta _A^*\). In particular, this gives rise to notions of positive and unitary natural transformations. A \(*\)-equivalence
to be the natural transformation with components \((\eta ^*)_A:= \eta _A^*\). In particular, this gives rise to notions of positive and unitary natural transformations. A \(*\)-equivalence  between \(*\)-categories is a \(*\)-functor F such that there exists a \(*\)-functor
between \(*\)-categories is a \(*\)-functor F such that there exists a \(*\)-functor  for which \(F\circ G\) and \(G\circ F\) are unitarily naturally isomorphic to the respective identity functors.
for which \(F\circ G\) and \(G\circ F\) are unitarily naturally isomorphic to the respective identity functors.
A \(\textrm{C}^*\)-category [14] is a \(*\)-category fulfilling the following two additional properties:
-
(a)
For every morphism
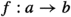 , there exists a morphism
, there exists a morphism 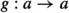 such that \(f^*f = g^*g\);
such that \(f^*f = g^*g\); -
(b)
The following expression defines a complete norm on the Hom-spaces
$$\begin{aligned} \Vert f\Vert =\sup \{|\lambda |~|~\lambda \in {\mathbb {C}}, \text { s.t.} f^*f-\lambda \cdot \textrm{id}\text { is not invertible}\} \end{aligned}$$such that \(\Vert fg\Vert \le \Vert f\Vert \Vert g\Vert \) and \(\Vert f^*f\Vert = \Vert f\Vert ^2\).
A \(\textrm{W}^*\)-category [14] is a \(\textrm{C}^*\)-category with the additional property that every Banach space \({{\,\textrm{Hom}\,}}(a,b)\) has a predual.
We emphasize that being a \(\textrm{C}^*\)-category, or a \(\textrm{W}^*\)-category, is a property of a \(*\)-category, and not additional structure. The standard example of a \(\textrm{W}^*\)-category is the category \(\textrm{Hilb}\) of finite-dimensional Hilbert spaces and linear maps. A natural transformation  between \(*\)-functors
between \(*\)-functors  between \(\textrm{C}^*\)-categories is bounded if \(\sup _{c \in \textrm{ob} \mathcal C}\Vert \eta _c\Vert < \infty \). The category of \(*\)-functors and bounded natural transformations between two \(\textrm{C}^*\)-categories again forms a \(\textrm{C}^*\)-category.
between \(\textrm{C}^*\)-categories is bounded if \(\sup _{c \in \textrm{ob} \mathcal C}\Vert \eta _c\Vert < \infty \). The category of \(*\)-functors and bounded natural transformations between two \(\textrm{C}^*\)-categories again forms a \(\textrm{C}^*\)-category.
An object x in a \(\textrm{C}^*\)-category is simple if \({{\,\textrm{End}\,}}(x)\cong {\mathbb {C}}\). A \(\textrm{C}^*\)-category is semisimple if it has finite direct sums and every object is a finite direct sum of simple objects. In particular, a semisimple \(\textrm{C}^*\)-category has finite-dimensional morphism spaces (and is hence a \(\textrm{W}^*\)-category). Equivalently, a semisimple \(\textrm{C}^*\)-category is a \(*\)-category that is equivalent, as a \(*\)-category, to a direct sum of copies of \(\textrm{Hilb}\).
2.2 \(\textrm{C}^*\)-tensor categories, \(\textrm{W}^*\)-tensor categories and unitary fusion categories
A \(*\)-monoidal category is a linear monoidal category equipped with a \(*\)-structure such that all monoidal coherence isomorphisms are unitary and such that \((f\otimes g)^*= f^*\otimes g^*\) for all morphisms f, g. The latter condition may equivalently be expressed as stating that the tensor product functor  is a \(*\)-functor. A \(\textrm{C}^*\)-tensor category (or a \(\textrm{W}^*\)-tensor category) is a \(*\)-monoidal category whose underlying \(*\)-category is a \(\textrm{C}^*\)-category (or a \(\textrm{W}^*\)-category).
is a \(*\)-functor. A \(\textrm{C}^*\)-tensor category (or a \(\textrm{W}^*\)-tensor category) is a \(*\)-monoidal category whose underlying \(*\)-category is a \(\textrm{C}^*\)-category (or a \(\textrm{W}^*\)-category).
A monoidal category is rigid if every object has a right and a left dual. A unitary multifusion category is a rigid semisimple \(\textrm{C}^*\)-tensor category with a finite number of simple objects. A unitary fusion category is a unitary multifusion category with simple monoidal unit.
Recall [10, Def 2.4.1] that a monoidal functor  between monoidal categories may be defined as a pair (F, f) of a functor
between monoidal categories may be defined as a pair (F, f) of a functor  with the property that \(F(I_{\mathcal C})\) is isomorphic to \(I_{\mathcal D}\), together with a natural isomorphism
with the property that \(F(I_{\mathcal C})\) is isomorphic to \(I_{\mathcal D}\), together with a natural isomorphism  fulfilling the usual coherence condition. In the following, we always denote a monoidal functor by a blackboard-bold letter \(\mathbb F\) and its underlying functor F and natural isomorphism f by the corresponding upper and lower case letter. A monoidal equivalence is a monoidal functor
fulfilling the usual coherence condition. In the following, we always denote a monoidal functor by a blackboard-bold letter \(\mathbb F\) and its underlying functor F and natural isomorphism f by the corresponding upper and lower case letter. A monoidal equivalence is a monoidal functor  for which
for which  is an equivalence of categories.
is an equivalence of categories.
A monoidal natural isomorphism  between monoidal equivalences is a natural isomorphism
between monoidal equivalences is a natural isomorphism  fulfilling \(g_{c,c'} \eta _{c\otimes c'} = (\eta _c\otimes \eta _{c'}) f_{c,c'}\).
fulfilling \(g_{c,c'} \eta _{c\otimes c'} = (\eta _c\otimes \eta _{c'}) f_{c,c'}\).
A unitary monoidal equivalence between \(*\)-monoidal categories is a monoidal equivalence \(\mathbb F=(F,f)\) whose underlying functor F is a \(*\)-equivalence for which \(F(I_{\mathcal C})\) is unitarily natural isomorphic to \(I_{\mathcal D}\) and whose underlying natural isomorphism f is unitary.
A unitary braided fusion category is a unitary fusion category equipped with a unitary braiding. A unitary braided monoidal equivalence between unitary braided fusion categories is a unitary monoidal equivalence  such that \( f_{a',a}F(\sigma ^\mathcal {A}_{a,a'})=\sigma ^\mathcal B_{F(a), F(a')}f_{a,a'}\), where
such that \( f_{a',a}F(\sigma ^\mathcal {A}_{a,a'})=\sigma ^\mathcal B_{F(a), F(a')}f_{a,a'}\), where  and
and  denote the braidings of \(\mathcal {A}\) and \(\mathcal B\), respectively.
denote the braidings of \(\mathcal {A}\) and \(\mathcal B\), respectively.
2.3 Unitary module categories
A module category \({}_{\mathcal C}\mathcal M= (\mathcal M, {-\vartriangleright -},\mu ^\mathcal M)\) over a monoidal category \(\mathcal C\) is a category \(\mathcal M\) equipped with a functor  with the property that
with the property that  is an autoequivalence, and a natural isomorphism
is an autoequivalence, and a natural isomorphism  fulfilling the usual coherence condition [10, Def 7.1.1]. A module functor
fulfilling the usual coherence condition [10, Def 7.1.1]. A module functor  between module categories is a pair of a functor
between module categories is a pair of a functor  and a natural isomorphism
and a natural isomorphism  fulfilling the usual coherence conditions [10, Def 7.2.1]. A module equivalence is a module functor
fulfilling the usual coherence conditions [10, Def 7.2.1]. A module equivalence is a module functor  for which
for which  is an equivalence of categories.
is an equivalence of categories.
A unitary module category \({}_{\mathcal C}\mathcal M=(\mathcal M, {-\vartriangleright -}, \mu ^\mathcal M)\) over a unitary fusion category \(\mathcal C\) is a module category for which \(\mathcal M\) is a semisimple \(\textrm{C}^*\)-category with a finite number of simple objects, for which  is a \(*\)-functor with the property that
is a \(*\)-functor with the property that  is a \(*\)-equivalence,Footnote 5 and for which the natural isomorphism \(\mu ^\mathcal M_{c,c',m}\) is unitary. A unitary module equivalence is a module equivalence
is a \(*\)-equivalence,Footnote 5 and for which the natural isomorphism \(\mu ^\mathcal M_{c,c',m}\) is unitary. A unitary module equivalence is a module equivalence  between unitary module categories for which f is unitary and F is a \(*\)-equivalence.
between unitary module categories for which f is unitary and F is a \(*\)-equivalence.
2.4 Polar decomposition
Every \(\textrm{W}^*\)-category admits a notion of polar decomposition [14, Cor 2.7]. Here, we will only make use of the following special case: Every positive morphism  in a \(\textrm{W}^*\)-category has a unique positive square root; that is, there exists a unique positive morphism
in a \(\textrm{W}^*\)-category has a unique positive square root; that is, there exists a unique positive morphism  such that \(\sqrt{p}^2 = p\).
such that \(\sqrt{p}^2 = p\).
This immediately gives rise to the following polar decomposition of invertible morphisms in a \(\textrm{W}^*\)-category: If  is an invertible morphism, then f is the composite of the unitary morphism
is an invertible morphism, then f is the composite of the unitary morphism  followed by the positive morphism
followed by the positive morphism  . We will make frequent use of the following direct consequence of polar decomposition.
. We will make frequent use of the following direct consequence of polar decomposition.
Proposition 1.1
Let \(\mathcal C\) be a \(\textrm{W}^*\)-category. Let v and w be unitary morphisms and x and y be morphisms in \(\mathcal C\) fulfilling \(xv = w y\) (where the types of v, w, x, y are such that this equation makes sense). Then, \(|x| w =w |y| \), where |x| and |y| are the unique positive square roots of \(x x^*\) and \( yy^*\).
Proof
Taking the adjoint of \(xv = wy\) and using unitarity of v and w, it follows that \(x^* w = v y^*\) and in particular that \(xx^* w = w y y^*\) or equivalently \(|x|^2 = w |y|^2 w^*\). By uniqueness of the positive square root of positive morphisms, it follows that \(|x| = w|y| w^*\). \(\square \)
Even though the \(*\)-category of \(*\)-functors and (possibly unbounded) natural transformations between two \(\textrm{W}^*\)-categories is not a \(\textrm{W}^*\)-category, we can nevertheless polar decompose unbounded natural transformations.
Proposition 1.2
A natural endomorphism  of a \(*\)-functor between \(\textrm{C}^*\)-categories is positive if and only if it is componentwise positive. Such a positive natural transformation admits a unique positive square root with components \((\sqrt{\eta })_c = \sqrt{\eta _c}\).
of a \(*\)-functor between \(\textrm{C}^*\)-categories is positive if and only if it is componentwise positive. Such a positive natural transformation admits a unique positive square root with components \((\sqrt{\eta })_c = \sqrt{\eta _c}\).
Proof
By definition, a natural transformation  is positive if there is a natural transformation
is positive if there is a natural transformation  such that \(\eta = \epsilon ^* \epsilon \). In particular, every positive natural transformation is componentwise so. Conversely, suppose that
such that \(\eta = \epsilon ^* \epsilon \). In particular, every positive natural transformation is componentwise so. Conversely, suppose that  is componentwise positive. Then, for every object c of \(\mathcal C\), the morphism
is componentwise positive. Then, for every object c of \(\mathcal C\), the morphism  admits a unique positive square root
admits a unique positive square root  . Note that given a morphism
. Note that given a morphism  and positive morphisms
and positive morphisms  and
and  in a \(\textrm{C}^*\)-category such that \(q\alpha = \alpha p\), then \(\sqrt{q} \alpha = \alpha \sqrt{p}\). Using the linking algebras M(a, b) developed in [14], this follows for example from the analogous statement for \(\textrm{C}^*\)-algebras. In particular, the morphisms
in a \(\textrm{C}^*\)-category such that \(q\alpha = \alpha p\), then \(\sqrt{q} \alpha = \alpha \sqrt{p}\). Using the linking algebras M(a, b) developed in [14], this follows for example from the analogous statement for \(\textrm{C}^*\)-algebras. In particular, the morphisms  assemble into a natural transformation. \(\square \)
assemble into a natural transformation. \(\square \)
Corollary 1.3
Every (possibly unbounded) natural isomorphism  of \(*\)-functors between \(\textrm{W}^*\)-categories admits a polar decomposition into a unitary (and hence bounded) natural transformation
of \(*\)-functors between \(\textrm{W}^*\)-categories admits a polar decomposition into a unitary (and hence bounded) natural transformation  followed by a positive (and possibly unbounded) natural transformation
followed by a positive (and possibly unbounded) natural transformation  .
.
Proof
By definition, \(\eta \eta ^*\) is positive and invertible and hence, following Proposition 1.2, admits a unique positive invertible square root \(p=\sqrt{\eta \eta ^*}\). A direct computation shows that \(u=\sqrt{\eta \eta ^*}^{-1} \eta \) is unitary. \(\square \)
3 On the Uniqueness of Unitary Structure
3.1 Categorified polar decomposition
In this section, we prove a polar decomposition theorem for monoidal equivalence between \(\textrm{W}^*\)-categories.
Definition 2.1
Let \(\mathcal D\) be a \(\textrm{C}^*\)-tensor category. We say that a monoidal auto-equivalence  is positive if it is monoidally naturally isomorphic to a monoidal auto-equivalence \((\textrm{id}_{\mathcal D}, p)\) whose underlying functor is the identity functor and whose coherence natural isomorphism
is positive if it is monoidally naturally isomorphic to a monoidal auto-equivalence \((\textrm{id}_{\mathcal D}, p)\) whose underlying functor is the identity functor and whose coherence natural isomorphism  is positive.
is positive.
Theorem 2.2
Let  be a monoidal equivalence between \(\textrm{W}^*\)-categories whose underlying functor F is naturally isomorphic to a \(*\)-equivalence. Then, \(\mathbb F\) is monoidally naturally isomorphic to the composite of a unitary monoidal equivalence
be a monoidal equivalence between \(\textrm{W}^*\)-categories whose underlying functor F is naturally isomorphic to a \(*\)-equivalence. Then, \(\mathbb F\) is monoidally naturally isomorphic to the composite of a unitary monoidal equivalence  followed by a positive monoidal auto-equivalence
followed by a positive monoidal auto-equivalence  .
.
Proof
We may assume that  is a monoidal equivalence whose underlying functor F is a \(*\)-equivalence. Polar decomposition (cf. Corollary 1.3) of the natural isomorphism
is a monoidal equivalence whose underlying functor F is a \(*\)-equivalence. Polar decomposition (cf. Corollary 1.3) of the natural isomorphism  results in a unitary natural isomorphism
results in a unitary natural isomorphism  followed by a positive natural automorphism
followed by a positive natural automorphism
(i.e. a natural automorphism of the functor  ). Since F is a \(*\)-equivalence, there is a positive natural automorphism
). Since F is a \(*\)-equivalence, there is a positive natural automorphism  such that \(q_{c,c'} = p_{F(c), F(c')}\). (Explicitly, p is defined as \(p_{d,d'} := q_{F^{-1}(d), F^{-1}(d')}\) where
such that \(q_{c,c'} = p_{F(c), F(c')}\). (Explicitly, p is defined as \(p_{d,d'} := q_{F^{-1}(d), F^{-1}(d')}\) where  is a \(*\)-inverse of F.) Note that this is the only step in the proof where we use the crucial fact that \(\mathbb F\) is an equivalence rather than an arbitrary monoidal functor.
is a \(*\)-inverse of F.) Note that this is the only step in the proof where we use the crucial fact that \(\mathbb F\) is an equivalence rather than an arbitrary monoidal functor.
We first show that \((\textrm{id}_{\mathcal D}, p)\) is a monoidal equivalence. In terms of the composites

the coherence equation for \(\mathbb F\) can be written as
where  and
and  are the associator unitary natural isomorphisms of \(\mathcal C\) and \(\mathcal D\), respectively.
are the associator unitary natural isomorphisms of \(\mathcal C\) and \(\mathcal D\), respectively.
It follows from naturality of p that
and hence that \(f^R_{c,c',c''}\) can be expressed as the composite
where \(u^R\) and \(p^R\) are defined as follows:

Similarly, it follows from positivity of p and naturality of its square root \(\sqrt{p}\) that the composite \(p^R\) is equal to the composite \(g^* g\), where g is defined as follows

and hence is positive. In particular, \(p_{F(c),F(c'),F(c'')}^R\) is the unique positive square root of \(f^R_{c,c',c''}(f^R_{c,c',c''})^*\). Defining \(u^L\) and \(p^L\) analogously and applying Proposition 1.1 to Eq. (2) implies that
Since F is a \(*\)-equivalence, this is equivalent to the coherence equation for \((\textrm{id}_{\mathcal D}, p)\).
By definition (F, u) can be written as the composite of the monoidal equivalence  followed by
followed by  and is hence also a monoidal equivalence. \(\square \)
and is hence also a monoidal equivalence. \(\square \)
It follows from the following well-known observation [13, Rem 2.7] [23, Rem 3.4], that the assumptions of Theorem 2.2 are automatically satisfied for semisimple \(\textrm{C}^*\)-categories.
Proposition 2.3
Every linear functor between semisimple \(\textrm{C}^*\)-categories is naturally isomorphic to a \(*\)-functor, which is uniquely determined up to unitary natural isomorphism. Moreover, a \(*\)-functor is an equivalence if and only if it is a \(*\)-equivalence.
Proof
Let \(\textrm{Irr}(\mathcal C)\) and \(\textrm{Irr}(\mathcal D)\) be sets of representing simple objects of \(\mathcal C\) and \(\mathcal D\), respectively. Any linear functor  is completely determined up to natural isomorphism by the (finite) dimensions of the vector spaces \({{\,\textrm{Hom}\,}}_{\mathcal D}(d,Fc)\) for \(c\in \textrm{Irr}(\mathcal C)\) and \(d\in \textrm{Irr}(\mathcal D)\) and is in particular naturally isomorphic to the \(*\)-functor \({\widetilde{F}}\) determined by the same data. It follows from polar decomposition of natural transformations (Corollary 1.3) that the \(*\)-functor \({\widetilde{F}}\) is uniquely determined up to unitary natural isomorphism. Together with polar decomposition, this implies that every \(*\)-functor which is an equivalence is a \(*\)-equivalence. \(\square \)
is completely determined up to natural isomorphism by the (finite) dimensions of the vector spaces \({{\,\textrm{Hom}\,}}_{\mathcal D}(d,Fc)\) for \(c\in \textrm{Irr}(\mathcal C)\) and \(d\in \textrm{Irr}(\mathcal D)\) and is in particular naturally isomorphic to the \(*\)-functor \({\widetilde{F}}\) determined by the same data. It follows from polar decomposition of natural transformations (Corollary 1.3) that the \(*\)-functor \({\widetilde{F}}\) is uniquely determined up to unitary natural isomorphism. Together with polar decomposition, this implies that every \(*\)-functor which is an equivalence is a \(*\)-equivalence. \(\square \)
Combining Theorem 2.2 with Proposition 2.3, we obtain the following polar decomposition theorem for semisimple \(\textrm{C}^*\)-categories.
Corollary 2.4
Every monoidal equivalence between semisimple \(\textrm{C}^*\)-categories  is monoidally naturally isomorphic to the composite of a unitary monoidal equivalence followed by a positive monoidal auto-equivalence.
is monoidally naturally isomorphic to the composite of a unitary monoidal equivalence followed by a positive monoidal auto-equivalence.
In particular, every semisimple \(\textrm{C}^*\)-tensor category has a unique \(\textrm{C}^*\)-structure, that is, if \(\mathcal C\) and \(\mathcal D\) are semisimple \(\textrm{C}^*\)-tensor categories and if there is a monoidal equivalence between \(\mathcal C\) and \(\mathcal D\), then there is a unitary monoidal equivalence.
Remark 2.5
In contrast to unitary fusion categories (Proposition 2.6), semisimple \(\textrm{C}^*\)-tensor categories with infinitely many simple objects can admit non-trivial positive monoidal auto-equivalences. For example, for a (discrete, possibly infinite) group G let \(\textrm{Hilb}_G\) be the category of G-graded finite-dimensional Hilbert spaces. The group of monoidal natural isomorphism classes of positive monoidal auto-equivalences of \(\textrm{Hilb}_G\) is isomorphic to \(H^2(G, {\mathbb {R}}_{> 0})\) and may therefore be non-trivial. In particular, the first part of Theorem 1 is not true for such categories.
3.2 Unitary fusion categories
For the rest of the paper, we restrict attention to unitary fusion categories. Theorem 1 follows from the fact that every positive monoidal auto-equivalence of a unitary fusion category is trivial.
Proposition 2.6
Every positive monoidal auto-equivalence  of a unitary fusion category \(\mathcal C\) is monoidally naturally isomorphic to the identity monoidal equivalence.
of a unitary fusion category \(\mathcal C\) is monoidally naturally isomorphic to the identity monoidal equivalence.
Proof
By definition, every positive monoidal equivalence is naturally isomorphic to a monoidal equivalence \(\mathbb P= (\textrm{id}_{\mathcal C}, p)\) where  is positive. It follows from [8, Thm 2.31] that the group \(\textrm{Eq}(\mathcal C)\) of monoidal autoequivalences of \(\mathcal C\) up to natural isomorphisms is finite. In particular, there is a natural number n such that \(\mathbb P^n = (\textrm{id}_{\mathcal C}, p^n)\) is naturally isomorphic to the identity monoidal equivalence. In other words, there is a natural isomorphism
is positive. It follows from [8, Thm 2.31] that the group \(\textrm{Eq}(\mathcal C)\) of monoidal autoequivalences of \(\mathcal C\) up to natural isomorphisms is finite. In particular, there is a natural number n such that \(\mathbb P^n = (\textrm{id}_{\mathcal C}, p^n)\) is naturally isomorphic to the identity monoidal equivalence. In other words, there is a natural isomorphism  such that \(p_{c,c'}^n = \eta _{c\otimes c'}^{-1} (\eta _{c}\otimes \eta _{c'})\). Since p is self-adjoint, it follows from repeated use of naturality of \(\eta \) that
such that \(p_{c,c'}^n = \eta _{c\otimes c'}^{-1} (\eta _{c}\otimes \eta _{c'})\). Since p is self-adjoint, it follows from repeated use of naturality of \(\eta \) that
where \(\mu = \eta ^\dagger \eta \) is positive. Denote the unique positive 2nth root of \(\mu \) by  and note that \(\epsilon \) is invertible. It follows from uniqueness of 2nth roots that \(p_{c,c'} = \epsilon _{c\otimes c'}^{-1}(\epsilon _c \otimes \epsilon _{c'})\) , and hence that \((\textrm{id}_{\mathcal C}, p)\) is monoidally naturally isomorphic to \((\textrm{id}_{\mathcal C}, \textrm{id}_{-\otimes -})\). \(\square \)
and note that \(\epsilon \) is invertible. It follows from uniqueness of 2nth roots that \(p_{c,c'} = \epsilon _{c\otimes c'}^{-1}(\epsilon _c \otimes \epsilon _{c'})\) , and hence that \((\textrm{id}_{\mathcal C}, p)\) is monoidally naturally isomorphic to \((\textrm{id}_{\mathcal C}, \textrm{id}_{-\otimes -})\). \(\square \)
Theorem 1 follows as a direct consequence of Corollary 2.4 and 2.6.
3.3 Unitary monoidal natural isomorphisms
In this section, we show that every monoidal natural isomorphism between unitary monoidal equivalences is automatically unitary. The proof is completely analogous to the proof of Theorem 1: First, we decompose the monoidal natural isomorphism into a unitary monoidal natural isomorphism followed by a positive monoidal natural isomorphism, and then we use a finiteness argument to show that there is no non-trivial positive monoidal natural isomorphism.
Proposition 2.7
Let  be unitary monoidal equivalences between unitary fusion categories. Then, every monoidal natural isomorphism
be unitary monoidal equivalences between unitary fusion categories. Then, every monoidal natural isomorphism  is the composite of a unitary monoidal natural isomorphism
is the composite of a unitary monoidal natural isomorphism  followed by a positive monoidal natural automorphism
followed by a positive monoidal natural automorphism  .
.
Proof
The natural isomorphism  factors as a unitary natural isomorphism
factors as a unitary natural isomorphism  followed by a positive natural isomorphism
followed by a positive natural isomorphism  . Applying Proposition 1.1 to the coherence equation
. Applying Proposition 1.1 to the coherence equation
proves
and hence that  is a monoidal natural automorphism.
is a monoidal natural automorphism.
By definition, the unitary natural isomorphism  can be written as the composite
can be written as the composite  of monoidal natural isomorphisms and is therefore also a monoidal natural isomorphism. \(\square \)
of monoidal natural isomorphisms and is therefore also a monoidal natural isomorphism. \(\square \)
Proposition 2.8
Let  be a unitary monoidal equivalence between unitary fusion categories. Every positive monoidal natural automorphism
be a unitary monoidal equivalence between unitary fusion categories. Every positive monoidal natural automorphism  equals the identity.
equals the identity.
Proof
Since F is a \(*\)-equivalence, every positive natural isomorphism  is of the form \(F\circ p\), where
is of the form \(F\circ p\), where  is a positive natural isomorphism. It follows from naturality of f that the monoidality equation for \(\eta = F\circ p\) may be rewritten as follows:
is a positive natural isomorphism. It follows from naturality of f that the monoidality equation for \(\eta = F\circ p\) may be rewritten as follows:
Invertibility of f and the fact that F is an equivalence imply that \(p_{c\otimes c'} = p_{c} \otimes p_{c'}\), and hence that p is a positive monoidal natural automorphism of the identity unitary monoidal equivalence  . It is shown in [23, Lem 3.19] that the group \(\textrm{Aut}^+(\textrm{id}_{\mathcal C})\) of positive monoidal natural automorphisms of the identity is isomorphic to the group of group homomorphisms \({{\,\textrm{Hom}\,}}(\mathcal U_{\mathcal C}, \mathbb R_{>0})\) from the universal grading group [10, Def 4.14.2] of \(\mathcal C\) to \(\mathbb R_{>0}\). Since \(\mathcal C\) is a unitary fusion category, the group \(\mathcal U_{\mathcal C}\) is finite and \({{\,\textrm{Hom}\,}}(\mathcal U_{\mathcal C}, \mathbb R_{>0})\) is trivial. \(\square \)
. It is shown in [23, Lem 3.19] that the group \(\textrm{Aut}^+(\textrm{id}_{\mathcal C})\) of positive monoidal natural automorphisms of the identity is isomorphic to the group of group homomorphisms \({{\,\textrm{Hom}\,}}(\mathcal U_{\mathcal C}, \mathbb R_{>0})\) from the universal grading group [10, Def 4.14.2] of \(\mathcal C\) to \(\mathbb R_{>0}\). Since \(\mathcal C\) is a unitary fusion category, the group \(\mathcal U_{\mathcal C}\) is finite and \({{\,\textrm{Hom}\,}}(\mathcal U_{\mathcal C}, \mathbb R_{>0})\) is trivial. \(\square \)
Theorem 2 is a direct consequence of Propositions 2.7 and 2.8.
Remark 2.9
If \(\mathcal C\) is a unitary multifusion category, the group \({{\,\textrm{Hom}\,}}(\mathcal U_{\mathcal C}, \mathbb R_{>0})\) is non-trivial if \(\mathcal C\) has more than one summand. In this case, there are non-trivial positive monoidal natural isomorphisms between unitary monoidal equivalences. In particular, Proposition 2.8 and therefore also Theorem 2 and Corollary 3 do not hold for general multifusion categories.
3.4 Unitary braided fusion categories
Turning our attention to braided monoidal categories, we now show that Theorem 5 immediately follows from the proof of Theorem 1.
Proof of Theorem 5
By Proposition 2.3, every braided monoidal equivalence between unitary braided fusion categories is naturally isomorphic to a braided monoidal equivalence  whose underlying functor F is a dagger equivalence. Following the proof of Theorem 2.2, we factor \(\mathbb F\) into a unitary monoidal equivalence
whose underlying functor F is a dagger equivalence. Following the proof of Theorem 2.2, we factor \(\mathbb F\) into a unitary monoidal equivalence  followed by a positive monoidal auto-equivalence
followed by a positive monoidal auto-equivalence  , and show that \((\textrm{id}_{\mathcal B}, p)\) is in fact a braided monoidal auto-equivalence. Indeed, applying Proposition 1.1 to the compatibility condition
, and show that \((\textrm{id}_{\mathcal B}, p)\) is in fact a braided monoidal auto-equivalence. Indeed, applying Proposition 1.1 to the compatibility condition
shows that
and hence that \((\textrm{id}_{\mathcal B}, p)\) is a braided monoidal auto-equivalence. By definition, (F, u) is the composite of  followed by
followed by  and is hence also a braided monoidal equivalence. The theorem then follows from Proposition 2.6 and the fact that \((\textrm{id}_{\mathcal B}, p)\) is monoidally naturally isomorphic to the identity. \(\square \)
and is hence also a braided monoidal equivalence. The theorem then follows from Proposition 2.6 and the fact that \((\textrm{id}_{\mathcal B}, p)\) is monoidally naturally isomorphic to the identity. \(\square \)
3.5 Unitary module categories
The proof of Theorem 8 is completely analogous to the proof of Theorem 1; we will first show that every module equivalence factors into a unitary module equivalence followed by a positive module equivalence, and then show that every positive module equivalence is trivial. The proofs of Propositions 2.11 and 2.12 are completely analogous to the proofs of Theorem 2.2 and Proposition 2.6. For the reader’s convenience, we spell them out again, following the wording of Theorem 2.2 and Proposition 2.6 as closely as possible.
Definition 2.10
Let \({}_{\mathcal C}\mathcal M\) be a unitary module category over a unitary fusion category. We say that a module auto-equivalence  is positive if it is naturally isomorphic, as a module functor, to a module functor \((\textrm{id}_{\mathcal M}, p)\) whose underlying functor is the identity functor and whose coherence natural isomorphism
is positive if it is naturally isomorphic, as a module functor, to a module functor \((\textrm{id}_{\mathcal M}, p)\) whose underlying functor is the identity functor and whose coherence natural isomorphism  is positive.
is positive.
Proposition 2.11
Every module equivalence  between unitary module categories over a unitary fusion category \(\mathcal C\) is naturally isomorphic, as a module functor, to the composite of a unitary module equivalence followed by a positive module auto-equivalence.
between unitary module categories over a unitary fusion category \(\mathcal C\) is naturally isomorphic, as a module functor, to the composite of a unitary module equivalence followed by a positive module auto-equivalence.
Proof
By Proposition 2.3, every module equivalence  is naturally isomorphic to a module equivalence (F, f) whose underlying functor F is a \(*\)-functor. Polar decomposition of the natural isomorphism
is naturally isomorphic to a module equivalence (F, f) whose underlying functor F is a \(*\)-functor. Polar decomposition of the natural isomorphism  results in a unitary natural isomorphism
results in a unitary natural isomorphism  followed by a positive natural isomorphism
followed by a positive natural isomorphism  . Since F is a \(*\)-equivalence, there is a positive natural isomorphism
. Since F is a \(*\)-equivalence, there is a positive natural isomorphism  such that \(q_{c,m} = p_{c, F(m)}\).
such that \(q_{c,m} = p_{c, F(m)}\).
We first show that \((\textrm{id}_{\mathcal N}, p)\) is a module equivalence. In terms of the composite

the coherence equation [10, Eq (7.6)] for \(\mathbb F\) can be written as follows:
where  and
and  are the coherence isomorphisms of \(\mathcal M\) and \(\mathcal N\), respectively.
are the coherence isomorphisms of \(\mathcal M\) and \(\mathcal N\), respectively.
As in the proof of Theorem 2.2, it follows from naturality of p that \(f^R_{c,c',m}\) can be expressed as the composite
where \(u^R\) and \(p^R\) are defined as follows:

Again as in the proof of Theorem 2.2, it follows from positivity of p and naturality of its square root \(\sqrt{p}\) that the composite \(p^R\) is positive. In particular, \(p_{c,c',F(m)}^R\) is the unique positive square root of \(f^R_{c,c',m}(f^R_{c,c',m})^\dagger \). Applying Proposition 1.1 to Eq. (5) implies that
Since F is a \(*\)-equivalence, this is equivalent to the coherence equation for \((\textrm{id}_{\mathcal N}, p)\). Compatibility with the unitors [10, Eq (7.7)] \(l_m: I_{\mathcal C} \vartriangleright m \cong m\) follows analogously.
By definition (F, u) can be written as the composite of the module equivalence  followed by
followed by  and is hence also a module equivalence. \(\square \)
and is hence also a module equivalence. \(\square \)
Proposition 2.12
Every positive module auto-equivalence  of a unitary module category \({}_\mathcal C\mathcal M\) is naturally isomorphic, as a module functor, to the identity module equivalence.
of a unitary module category \({}_\mathcal C\mathcal M\) is naturally isomorphic, as a module functor, to the identity module equivalence.
Proof
By definition, every positive module equivalence is naturally isomorphic to a module equivalence \(\mathbb P= (\textrm{id}_{\mathcal M}, p)\) where  is positive. The group \(\textrm{Aut}_{\mathcal C}(\mathcal M)\) of module auto-equivalences
is positive. The group \(\textrm{Aut}_{\mathcal C}(\mathcal M)\) of module auto-equivalences  up to module natural isomorphisms is finite. (This can for example be seen by noting that the monoidal category \({{\,\textrm{End}\,}}_{\mathcal C}(\mathcal M)\) of module endofunctors is a multifusion category, and that \(\textrm{Aut}_{\mathcal C}(\mathcal M)\) is the group of invertible objects in this multifusion category.) In particular, there is a natural number n such that \(\mathbb P^n = (\textrm{id}_{\mathcal M}, p^n)\) is naturally isomorphic to the identity module functor. In other words, there is a natural isomorphism
up to module natural isomorphisms is finite. (This can for example be seen by noting that the monoidal category \({{\,\textrm{End}\,}}_{\mathcal C}(\mathcal M)\) of module endofunctors is a multifusion category, and that \(\textrm{Aut}_{\mathcal C}(\mathcal M)\) is the group of invertible objects in this multifusion category.) In particular, there is a natural number n such that \(\mathbb P^n = (\textrm{id}_{\mathcal M}, p^n)\) is naturally isomorphic to the identity module functor. In other words, there is a natural isomorphism  such that \(p_{c,m}^n =\eta _{c\vartriangleright m}^{-1} ( c \vartriangleright \eta _m)\). Since p is self-adjoint, it follows from repeated use of naturality of \(\eta \) that \(p^{2n}_{c,m} = \mu _{c\vartriangleright m}^{-1}(c\vartriangleright \mu _m)\) where \(\mu = \eta ^\dagger \eta \) is positive. Denote the unique positive 2nth root of \(\mu \) by
such that \(p_{c,m}^n =\eta _{c\vartriangleright m}^{-1} ( c \vartriangleright \eta _m)\). Since p is self-adjoint, it follows from repeated use of naturality of \(\eta \) that \(p^{2n}_{c,m} = \mu _{c\vartriangleright m}^{-1}(c\vartriangleright \mu _m)\) where \(\mu = \eta ^\dagger \eta \) is positive. Denote the unique positive 2nth root of \(\mu \) by  and note that \(\epsilon \) is invertible. It follows from uniqueness of 2nth roots that \(p_{c,m} = \epsilon _{c\vartriangleright m}^{-1}(c \vartriangleright \epsilon _{m})\) , and hence that \((\textrm{id}_{\mathcal M}, p)\) is naturally isomorphic, as a module functor to \((\textrm{id}_{\mathcal M}, \textrm{id}_{-\vartriangleright -})\). \(\square \)
and note that \(\epsilon \) is invertible. It follows from uniqueness of 2nth roots that \(p_{c,m} = \epsilon _{c\vartriangleright m}^{-1}(c \vartriangleright \epsilon _{m})\) , and hence that \((\textrm{id}_{\mathcal M}, p)\) is naturally isomorphic, as a module functor to \((\textrm{id}_{\mathcal M}, \textrm{id}_{-\vartriangleright -})\). \(\square \)
Theorem 8 is a direct consequence of Propositions 2.11 and 2.12.
4 A Monoidal 2-Categorical Perspective
Most of the proofs in this paper were developed using the graphical calculus of the monoidal dagger 2-category \(\textrm{2Hilb}\) of finitely semisimple \(\textrm{C}^*\)-categories, \(*\)-functors and natural transformations. (This monoidal 2-category is equivalent to Baez’s 2-category of ‘finite-dimensional 2-Hilbert spaces’ [2] and is a unitary version of Kapranov and Voevodsky’s 2-category of ‘finite-dimensional 2-vector spaces [20].) Many of the more subtle applications of naturality in the proofs of Theorem 2.2 and Proposition 2.6 become transparent once expressed in this graphical calculus. To give a flavour of such arguments, we sketch the relevant parts of the proof of Theorem 2.2 (in the case that both \(\mathcal C\) and \(\mathcal D\) are unitary fusion categories) in this language. The following section is purely expositional and not relevant to the mathematical developments of Sects. 1 and 2.
Proposition 2.3 shows that all structural data in question—the monoidal category \(\mathcal C\) with tensor product  and associator
and associator  , as well as the monoidal equivalence \(\mathbb F= (F,f)\) with underlying \(*\)-functor
, as well as the monoidal equivalence \(\mathbb F= (F,f)\) with underlying \(*\)-functor  and natural isomorphism
and natural isomorphism  —are given by objects, 1- and 2-morphisms of \(\textrm{2Hilb}\). As a monoidal 2-category, \(\textrm{2Hilb}\) admits a graphical calculus of surface diagramsFootnote 6 in 3-space [3]. We draw 1-morphism composition from right to left, 2-morphism composition from bottom to top, and depict the monoidal structure by layering surfaces behind one another, with the convention that tensor product occurs from back to front: that is, in a diagram for \(A \boxtimes B\), the surface labeled A appears in front of the surface labeled B (see [5, Sec 2.1.2] for a more careful description of our conventions).
—are given by objects, 1- and 2-morphisms of \(\textrm{2Hilb}\). As a monoidal 2-category, \(\textrm{2Hilb}\) admits a graphical calculus of surface diagramsFootnote 6 in 3-space [3]. We draw 1-morphism composition from right to left, 2-morphism composition from bottom to top, and depict the monoidal structure by layering surfaces behind one another, with the convention that tensor product occurs from back to front: that is, in a diagram for \(A \boxtimes B\), the surface labeled A appears in front of the surface labeled B (see [5, Sec 2.1.2] for a more careful description of our conventions).
For example, the associator \(\alpha \) of a unitary fusion category is depicted as follows:

Here, the thick gray wires denote the 1-morphism \(m_{\mathcal C}\), and the central black node denotes the 2-isomorphism \(\alpha \). (The thin gray bounding wires simply indicate the extent of the picture.) For clarity, we have also explicitly depicted the source and target of \(\alpha \); that source and target appear in the surface diagram as the bottom and top horizontal slices, respectively. Note that we will often omit labels on regions, wires, and nodes, when it is clear from context what those labels should be. The coherence natural isomorphism f of a monoidal equivalence  is depicted as follows:
is depicted as follows:

The proof of Theorem 2.2 begins by polarly decomposing the natural isomorphism f into a unitary natural isomorphism  followed by a positive natural isomorphism
followed by a positive natural isomorphism  , depicted as follows:
, depicted as follows:

Next, we use naturality of p to re-expresses the composite \(f^R\), defined in Eq. (1), as the composite of Eq. (3). Graphically, this corresponds to the following simple isotopy:

In particular, the composites \(p^R\) and \(u^R\) of Eq. (4) are depicted as follows:

Unitarity of \(u^R\) and positivity of \(p^R\) evidently follow from unitarity of u and positivity of p, proving that \(f^R = p^R u^R\) is the unique polar decomposition of \(f^R\), which in turn allows us to conclude the proof of Theorem 2.2 by applying Proposition 1.1.
Notes
A unitarizable fusion category is a fusion category which admits a compatible positive \(*\)-structure.
A braided unitarizable fusion category is a braided fusion category whose underlying fusion category is unitarizable.
A unitarizable module category over a unitary fusion category \(\mathcal C\) is a finitely semisimple module category over \(\mathcal C\) which admits a compatible positive dagger structure.
By Remark 10, there are non-unitary module natural isomorphisms. Hence, we may only hope for an equivalence between the 2-truncations \(\underline{\textrm{BrPic}}\) and \(\underline{\textrm{BrPic}}^\dagger \) of the algebraic and unitary Brauer–Picard 3-groupoids \({\underline{\underline{\textrm{BrPic}}}}\) and \({\underline{\underline{\textrm{BrPic}}}}^\dagger \).
By Proposition 2.3, this condition is automatically satisfied.
References
Afzaly, N., Penneys, D., Morrison, S.: The classification of subfactors with index at most \(5\frac{1}{4}\). To appear in the Memoirs of the American Mathematical Society. arXiv:1509.00038 (2015)
Baez, J.C.: Higher-dimensional algebra. II. \(2\)-Hilbert spaces. Adv. Math. 127(2), 125–189 (1997). arXiv:q-alg/9609018
Barrett, J.W., Meusburger, C., Schaumann, G.: Gray categories with duals and their diagrams. arXiv:1211.0529v3 (2012)
Carpi, S., Ciamprone, S., Pinzari, C.: Weak quasi Hopf algebras, \(C^*\)-tensor categories and conformal field theory. To appear. Talk slides available at https://www.dima.unige.it/aqft/cortona/slides/Carpi.pdf and https://drive.google.com/file/d/1i_VI3r-3kyrdrrlecZg-JeUOpaMGBqMB/view
Douglas, C.L., Reutter, D.J.: Fusion 2-categories and a state-sum invariant for 4-manifolds. arXiv:1812.11933 (2018)
Evans, D.E., Gannon, T.: The exoticness and realisability of twisted Haagerup-Izumi modular data. Commun. Math. Phys. 307(2), 463–512 (2011). arXiv:1006.1326
Evans, D.E., Gannon, T.: Near-group fusion categories and their doubles. Adv. Math. 255, 586–640 (2014). arXiv:1208.1500
Etingof, P., Nikshych, D., Ostrik, V.: On fusion categories. Ann. Math. 162(2), 581–642 (2005). arXiv:math/0203060
Etingof, P., Nikshych, D., Ostrik, V.: Fusion categories and homotopy theory. Quantum Topol. 1(3), 209–273 (2010). With an appendix by Ehud Meir
Etingof, P., Gelaki, S., Nikshych, D., Ostrik, V.: Tensor Categories. American Mathematical Society. Available online at http://www.math.mit.edu/~etingof/egnobookfinal.pdf (2015)
Galindo, C.: Mathoverflow question: unitary structures on fusion categories. https://mathoverflow.net/questions/131546 (2013)
Galindo, C.: On braided and ribbon unitary fusion categories. Can. Math. Bull. 57(3), 506–510 (2014). arXiv:1209.2022
Galindo, C., Hong, S.-M., Rowell, E.C.: Generalized and quasi-localizations of braid group representations. Int. Math. Res. Not. IMRN 3, 693–731 (2013). arXiv:1105.5048
Ghez, P., Lima, R., Roberts, J.E.: \(W^\ast \)-categories. Pac. J. Math. 120(1), 79–109 (1985)
Gurski, M.N.: An algebraic theory of tricategories. ProQuest LLC, Ann Arbor, MI, Ph.D. Thesis–The University of Chicago (2006)
Guthmann, P.: The tricategory of formal composites and its strictification. PhD thesis, Friedrich-Alexander Universität Erlangen-Nürnberg. arXiv:1903.05777 (2018)
Henriques, A., Penneys, D.: Bicommutant categories from fusion categories. Selecta Math. (N.S.) 23(3), 1669–1708 (2017). arXiv:1511.05226
Izumi, M.: A Cuntz algebra approach to the classification of near-group categories. In Proceedings of the 2014 Maui and 2015 Qinhuangdao conferences in Honour of Vaughan F. R. Jones’ 60th birthday, vol. 46 of Proc. Centre Math. Appl. Austral. Nat. Univ., pp. 222–343. Austral. Nat. Univ., Canberra. arXiv:1512.04288 (2017)
Jones, V.F.R., Morrison, S., Snyder, N.: The classification of subfactors of index at most 5. Bull. Am. Math. Soc. (N.S.) 51(2), 277–327 (2014). arXiv:1304.6141
Kapranov, M., Voevodsky, V.: 2-categories and Zamolodchikov tetrahedra equations. Proc. Sympos. Pure Math 56(2), 177–259 (1994)
Neshveyev, S., Yamashita, M.: Drinfeld center and representation theory for monoidal categories. Commun. Math. Phys. 345(1), 385–434 (2016). arXiv:1501.07390
Okayasu, T.: A structure theorem of automorphisms of von Neumann algebras. Tohoku Math. J. 2(20), 199–206 (1968)
Penneys, D.: Unitary dual functors for unitary multitensor categories. arXiv:1808.00323 (2018)
Acknowledgements
I am grateful to André Henriques and David Penneys for many helpful comments and suggestions on an early version of this manuscript, and to Makoto Yamashita for pointing out that the proof of Theorem 2.2 also applies to semisimple \(\textrm{C}^*\)-categories with infinitely many simple objects. I also thank the anonymous referees for their comments and suggestions. I am grateful for the financial support of the Clarendon Fund and the Oxford-Google DeepMind Scholarship and the hospitality of the University of Oxford where most of this work was carried out. Open Access funding enabled and organized by Projekt DEAL.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Y. Kawahigashi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Reutter, D. Uniqueness of Unitary Structure for Unitarizable Fusion Categories. Commun. Math. Phys. 397, 37–52 (2023). https://doi.org/10.1007/s00220-022-04425-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-022-04425-7



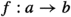 , there exists a morphism
, there exists a morphism 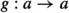 such that
such that