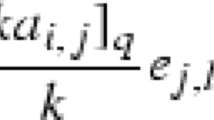On the Harish-Chandra Homomorphism for Quantum Superalgebras

Abstract

In this paper, we introduce the Harish-Chandra homomorphism for the quantum superalgebra $\mathrm {U}_q({\mathfrak {g}})$ associated with a simple basic Lie superalgebra ${\mathfrak {g}}$ and give an explicit description of its image. We use it to prove that the center of $\mathrm {U}_q({\mathfrak {g}})$ is isomorphic to a subring of the ring $J({\mathfrak {g}})$ of exponential super-invariants in the sense of Sergeev and Veselov, establishing a Harish-Chandra type theorem for $\mathrm {U}_q({\mathfrak {g}})$. As a byproduct, we obtain a basis of the center of $\mathrm {U}_q({\mathfrak {g}})$ with the aid of quasi-R-matrix.

Appendices

Appendix A. Dynkin Diagrams in Distinguished Root Systems

The Dynkin diagrams in the distinguished root systems of a simple basic Lie superalgebra of type A-G are listed below, where r is the number of nodes and s is the element of $\tau$. Note that the form of Dynkin diagrams in the distinguished root systems is quite uniform in the literature.

$\boxed {A(m,n) ~{\mathbf{case }}:}$ Let ${\mathfrak {h}}^*$ be a vector space spanned by $\{\varepsilon _i-\varepsilon _{i+1},\varepsilon _{m+1}-\delta _1 ,\delta _j-\delta _{j+1}| 1\leqslant i\leqslant m, 1\leqslant j\leqslant n \}$ satisfies

$$\begin{aligned} (\varepsilon _1+\ldots +\varepsilon _{m+1})-(\delta _1+\ldots +\delta _{n+1})=0. \end{aligned}$$

We equip the dual ${\mathfrak {h}}^*$ with a bilinear form $(\cdot ,\cdot )$ such that

$$\begin{aligned} (\varepsilon _i, \varepsilon _j)=\delta _{ij},\quad (\varepsilon _i,\delta _j)=(\delta _j, \varepsilon _i)=0, \quad (\delta _i, \delta _j)=-\delta _{ij}\quad \text {for all possible}~i,j. \end{aligned}$$

The distinguished fundamental system $\Pi =\{\alpha _1,\ \ldots ,\ \alpha _{m+n+1}\}$ is given by

$$\begin{aligned} \{\varepsilon _1-\varepsilon _2, \ \ldots ,\ \varepsilon _m,-\varepsilon _{m+1}, \ \varepsilon _{m+1}-\delta _1, \ \delta _1-\delta _2,\ \ldots ,\ \delta _{n}-\delta _{n+1}\}. \end{aligned}$$

The Dynkin diagram associated with $\Pi$ is depicted as follows:

In this case $r=m+n+1$, $s=m+1$. The distinguished positive system $\Phi ^+=\Phi _{{\bar{0}}}^+\cup \Phi _{{\bar{1}}}^+$ corresponding to the distinguished Borel subalgebra for A(m, n) is

$$\begin{aligned}&\{\varepsilon _i-\varepsilon _j, \delta _k-\delta _l| 1\leqslant i<j\leqslant m+1, 1\leqslant k<l\leqslant n+1\}\\&\quad \cup \{\varepsilon _i-\delta _j| 1\leqslant i\leqslant m+1, 1\leqslant j\leqslant n+1\}. \end{aligned}$$

The Weyl group $W\cong {\mathfrak {S}}_{m+1}\times {\mathfrak {S}}_{n+1}$.

$\boxed {B(m,n) ~\mathbf{case: }}$ Let ${\mathfrak {h}}^*$ be a vector space with basis $\{\varepsilon _i, \delta _j| 1\leqslant i\leqslant m, 1\leqslant j\leqslant n\}$. We equip the dual ${\mathfrak {h}}^*$ with a bilinear form $(\cdot ,\cdot )$ such that

$$\begin{aligned} (\varepsilon _i, \varepsilon _j)=\delta _{ij},\quad (\varepsilon _i,\delta _j)=(\delta _j, \varepsilon _i)=0, (\delta _i, \delta _j)=-\delta _{ij}\quad \text {for all possible}~i,j. \end{aligned}$$

The distinguished fundamental system $\Pi =\{\alpha _1,\ \ldots ,\ \alpha _{m+n}\}$ is given by

$$\begin{aligned} \{\delta _1-\delta _2, \ \ldots ,\ \delta _{n-1}-\delta _{n},\ \delta _{n}-\varepsilon _1, \varepsilon _{1}-\varepsilon _2,\ \ldots ,\ \varepsilon _{m-1}-\varepsilon _{m}, \ \varepsilon _m\}. \end{aligned}$$

The Dynkin diagram associated with $\Pi$ is depicted as follows:

In this case $r=m+n$, $s=n+1$. The distinguished positive system $\Phi ^+=\Phi ^+_{{\bar{0}}}\cup \Phi _{{\bar{1}}}^+$ corresponding to the distinguished Borel subalgebra is

$$\begin{aligned} \{\delta _{i}\pm \delta _j,\ 2\delta _p,\ \varepsilon _k\pm \varepsilon _l, \ \varepsilon _q\}\cup \{\delta _p\pm \varepsilon _q,\ \delta _p\}, \end{aligned}$$

where $1\leqslant i<j\leqslant n, 1\leqslant k<l\leqslant m, 1\leqslant p\leqslant n, 1\leqslant q\leqslant m$. The Weyl group $W\cong ({\mathfrak {S}}_{n}\ltimes {\mathbb {Z}}_2^n)\times ({\mathfrak {S}}_{m}\ltimes {\mathbb {Z}}_2^m)$.

$\boxed {B(0,n) ~\mathbf{case: }}$ Let ${\mathfrak {h}}^*$ be a vector space with basis $\{\delta _i|1\leqslant i\leqslant n \}$. We equip the dual ${\mathfrak {h}}^*$ with a bilinear form $(\cdot ,\cdot )$ such that

$$\begin{aligned} (\delta _i, \delta _j)=-\delta _{ij}\quad \text {for all possible}~i,j. \end{aligned}$$

The distinguished fundamental system $\Pi =\{\alpha _1,\ \ldots ,\ \alpha _{n}\}$ is given by

$$\begin{aligned} \{\delta _1-\delta _2, \ \ldots ,\ \delta _{n-1}-\delta _{n},\ \delta _{n}\}. \end{aligned}$$

The Dynkin diagram associated with $\Pi$ is depicted as follows:

In this case, $r=s=n$. The distinguished positive system $\Phi ^+=\Phi ^+_{{\bar{0}}}\cup \Phi _{{\bar{1}}}^+$ corresponding to the distinguished Borel subalgebra is

$$\begin{aligned} \{\delta _{i}\pm \delta _j,\ 2\delta _p|1\leqslant i<j\leqslant n, 1\leqslant p\leqslant n\}\cup \{\delta _p|1\leqslant p\leqslant n\}. \end{aligned}$$

The Weyl group $W\cong ({\mathfrak {S}}_{n}\ltimes {\mathbb {Z}}_2^n)$.

$\boxed {C(n+1) ~\mathbf{case: }}$ Let ${\mathfrak {h}}^*$ be a vector space with basis $\{\varepsilon ,\delta _i|1\leqslant i\leqslant n \}$. We equip the dual ${\mathfrak {h}}^*$ with a bilinear form $(\cdot ,\cdot )$ such that

$$\begin{aligned} (\varepsilon ,\varepsilon )=1,\quad (\varepsilon ,\delta _i)=(\delta _i, \varepsilon )=0,\quad (\delta _i, \delta _j)=-\delta _{ij}\quad \text {for all possible}~i,j. \end{aligned}$$

The distinguished fundamental system $\Pi =\{\alpha _1,\ \ldots ,\ \alpha _{n+1}\}$ is given by

$$\begin{aligned} \{\varepsilon -\delta _1,\delta _1-\delta _2, \ \ldots ,\ \delta _{n-1}-\delta _{n},\ 2\delta _{n}\}. \end{aligned}$$

The Dynkin diagram associated with $\Pi$ is depicted as follows:

In this case $r=n+1,s=1$. The distinguished positive system $\Phi ^+=\Phi ^+_{{\bar{0}}}\cup \Phi _{{\bar{1}}}^+$ corresponding to the distinguished Borel subalgebra is

$$\begin{aligned} \{\delta _{i}\pm \delta _j,\ 2\delta _p|1\leqslant i<j\leqslant n, 1\leqslant p\leqslant n\}\cup \{\varepsilon \pm \delta _p|1\leqslant p\leqslant n\}. \end{aligned}$$

The Weyl group $W\cong ({\mathfrak {S}}_{n}\ltimes {\mathbb {Z}}_2^n)$.

$\boxed {D(m,n) ~\mathbf{case: }}$ Let ${\mathfrak {h}}^*$ be a vector space with basis $\{\varepsilon _i, \delta _j| 1\leqslant i\leqslant m, 1\leqslant j\leqslant n\}$. We equip the dual ${\mathfrak {h}}^*$ with a bilinear form $(\cdot ,\cdot )$ such that

$$\begin{aligned} (\varepsilon _i, \varepsilon _j)=\delta _{ij},\quad (\varepsilon _i,\delta _j)=(\delta _j, \varepsilon _i)=0, \quad (\delta _i, \delta _j)=-\delta _{ij}\quad \text {for all possible}~i,j. \end{aligned}$$

The distinguished fundamental system $\Pi =\{\alpha _1,\ \ldots ,\ \alpha _{m+n}\}$ is given by

$$\begin{aligned} \{\delta _1-\delta _2, \ \ldots ,\ \delta _{n-1}-\delta _{n},\ \delta _{n}-\varepsilon _1, \varepsilon _{1}-\varepsilon _2,\ \ldots ,\ \varepsilon _{m-1}-\varepsilon _{m}, \ \varepsilon _{m-1}+\varepsilon _m\}. \end{aligned}$$

The Dynkin diagram associated with $\Pi$ is depicted as follows:

In this case $r=m+n$, $s=n+1$. The distinguished positive system $\Phi ^+=\Phi ^+_{{\bar{0}}}\cap \Phi _{{\bar{1}}}^+$ corresponding to the distinguished Borel subalgebra is

$$\begin{aligned} \{\delta _{i}\pm \delta _j,\ 2\delta _p,\ \varepsilon _k\pm \varepsilon _l, \}\cup \{\delta _p\pm \varepsilon _q\}, \end{aligned}$$

where $1\leqslant i<j\leqslant n, 1\leqslant k<l\leqslant m, 1\leqslant p\leqslant n, 1\leqslant q\leqslant m$. The Weyl group $W\cong ({\mathfrak {S}}_{n}\ltimes {\mathbb {Z}}_2^n)\times ({\mathfrak {S}}_{m}\ltimes {\mathbb {Z}}_2^{m-1} )$.

$\boxed {D(2,1;\alpha ) ~\mathbf{case }:}$ Let ${\mathfrak {h}}^*$ be a vector space with basis $\{\varepsilon _1, \varepsilon _2,\varepsilon _3\}$. We equip the dual ${\mathfrak {h}}^*$ with a bilinear form $(\cdot ,\cdot )$ with

$$\begin{aligned} (\varepsilon _1, \varepsilon _1)= & {} -(1+\alpha ),\quad (\varepsilon _2, \varepsilon _2)=1, \quad (\varepsilon _3, \varepsilon _3)=\alpha \quad \text {and}\\ (\varepsilon _i,\varepsilon _j)= & {} 0\quad \text {for all}~\quad 1\leqslant i\ne j\leqslant 3. \end{aligned}$$

The distinguished fundamental system

$$\begin{aligned} \Pi =\{\alpha _1=\varepsilon _1+\varepsilon _2+\varepsilon _3, \alpha _2=-2\varepsilon _2, \alpha _3=-2\varepsilon _3\}. \end{aligned}$$

The Dynkin diagram associated with $\Pi$ is depicted as follows:

In this case $r=3$, $s=1$. The distinguished positive system $\Phi ^+=\Phi ^+_{{\bar{0}}}\cap \Phi _{{\bar{1}}}^+$ corresponding to the distinguished Borel subalgebra is

$$\begin{aligned} \Phi ^+_{{{\bar{0}}}}=\{2\varepsilon _1,-2\varepsilon _2,-2\varepsilon _3\}, \quad \Phi ^+_{{{\bar{1}}}}=\{\varepsilon _1\pm \varepsilon _2\pm \varepsilon _3\}. \end{aligned}$$

The Weyl group $W\cong {\mathbb {Z}}_2^3$.

$\boxed {F(4) ~{\mathbf{case }}:}$ Let ${\mathfrak {h}}^*$ be a vector space with basis $\{\delta , \varepsilon _1, \varepsilon _2, \varepsilon _3\}$.We equip the dual ${\mathfrak {h}}^*$ with a bilinear form $(\cdot ,\cdot )$ such that

$$\begin{aligned} (\delta , \delta )=-3,\quad (\varepsilon _i,\delta )=(\delta , \varepsilon _i)=0, \quad (\varepsilon _i, \varepsilon _j)=\delta _{ij}\quad \text {for all}~i . \end{aligned}$$

The distinguished fundamental system

$$\begin{aligned} \Pi =\left\{ \alpha _1=\frac{1}{2}(\delta -\varepsilon _1-\varepsilon _2-\varepsilon _3), \quad \alpha _2=\varepsilon _3, \quad \alpha _3=\varepsilon _2-\varepsilon _3, \quad \alpha _4=\varepsilon _1-\varepsilon _2\right\} . \end{aligned}$$

The Dynkin diagram associated with $\Pi$ is depicted as follows:

In this case $r=4$, $s=1$. The distinguished positive system $\Phi ^+=\Phi ^+_{{\bar{0}}}\cap \Phi _{{\bar{1}}}^+$ corresponding to the distinguished Borel subalgebra is

$$\begin{aligned} \{ \delta ,\ \varepsilon _p,\ \varepsilon _i\pm \varepsilon _j |1\leqslant i<j\leqslant 3,1\leqslant p\leqslant 3\}\cup \left\{ \frac{1}{2}(\delta \pm \varepsilon _1\pm \varepsilon _2\pm \varepsilon _3)\right\} , \end{aligned}$$

The Weyl group $W={\mathbb {Z}}_2\times ({\mathfrak {S}}_3\ltimes {\mathbb {Z}}_2^3)$.

$\boxed {G(3) ~\mathbf{case }:}$ Let ${\mathfrak {h}}^*$ be a vector space with basis $\{\delta , \varepsilon _1, \varepsilon _2\}$ and $\varepsilon _3=-\varepsilon _1-\varepsilon _2$. We equip the dual ${\mathfrak {h}}^*$ with a bilinear form $(\cdot ,\cdot )$ such that

$$\begin{aligned} (\delta , \delta )=-(\varepsilon _i, \varepsilon _i)=-2,\quad (\varepsilon _i,\delta )=(\delta , \varepsilon _i)=0, \quad (\varepsilon _i, \varepsilon _j)=-1,\quad \text {for all}~1\leqslant i\ne j\leqslant 3. \end{aligned}$$

The distinguished fundamental system

$$\begin{aligned} \Pi =\{\alpha _1=\delta +\varepsilon _3, \alpha _2=\varepsilon _1, \alpha _3=\varepsilon _2-\varepsilon _1\}. \end{aligned}$$

The Dynkin diagram associated with $\Pi$ is depicted as follows:

In this case $r=3$, $s=1$. The distinguished positive system $\Phi ^+=\Phi ^+_{{\bar{0}}}\cap \Phi _{{\bar{1}}}^+$ corresponding to the distinguished Borel subalgebra is

$$\begin{aligned} \{ 2\delta ,\ \varepsilon _1,\ \varepsilon _2,\ \varepsilon _2\pm \varepsilon _1,\ \varepsilon _1-\varepsilon _3,\ \varepsilon _2-\varepsilon _3 \}\cup \{\delta ,\ \delta \pm \varepsilon _i|i=1,2,3\}, \end{aligned}$$

The Weyl group $W={\mathbb {Z}}_2\times D_6$, where $D_6$ is the dihedral group of order 12.

Appendix B. Explicit Description of the Rings $J_{\mathrm {ev}}({\mathfrak {g}})$

Now we give the explicit description of the rings $J_{\mathrm {ev}}({\mathfrak {g}})$ for quantum superalgebras, which is inspired by Sergeev and Veselov’s description for Lie superalgebras [42, Sects. 7, 8]. Let $x_i={\mathbb {K}}_{-\varepsilon _i/2}$ and $y_j={\mathbb {K}}_{-\delta _j/2}$ formally. First we need to review the rings $J({\mathfrak {g}})$ for ${\mathfrak {g}}$ is of type A. Let

$$\begin{aligned} P_0=\bigg \{ \mathop {\sum }\limits _{i=1}^{m+1}a_i\varepsilon _i +\mathop {\sum }\limits _{j=1}^{n+1}b_j\delta _j\bigg | a_i,b_j \in {\mathbb {C}}~\text {and}~a_i-a_{i+1},b_j-b_{j+1}\in {\mathbb {Z}}, ~ \forall i,j \bigg \}\bigg /{\mathbb {C}}\gamma \end{aligned}$$

be the weights of $\mathfrak {sl}_{m+1|n+1}$, where $\gamma =\varepsilon _1+\cdots +\varepsilon _{m+1}-\delta _1-\cdots -\delta _{n+1}$ and $x_i=e^{\varepsilon _i}, y_j=e^{\delta _j}$ for all possible i, j be the elements of the group ring of ${\mathbb {C}}[P_0]$. For convenience, we set ${\mathbb {C}}[x^{\pm },y^{\pm }]={\mathbb {C}}[x_1^{\pm 1},\cdots ,x_{m+1}^{\pm 1},y_1^{\pm 1},\cdots ,y_{n+1}^{\pm 1}],~ {\mathbb {Z}}[x^{\pm },y^{\pm }]={\mathbb {Z}}[x_1^{\pm 1},\cdots ,x_{m+1}^{\pm 1},y_1^{\pm 1},\cdots ,y_{n+1}^{\pm 1}]$ and then for $(m,n)\ne (1,1)$

$$\begin{aligned} J(\mathfrak {sl}_{m+1|n+1})&=\left\{ f\in {\mathbb {Z}}[P_0]^W \left| y_j\frac{\partial f}{\partial y_j}+x_i\frac{\partial f}{\partial x_i}\in (x_i-y_j) \right. \right\} \\&=\mathop {\bigoplus }\limits _{a\in {\mathbb {C}}/{\mathbb {Z}} }J(\mathfrak {sl}_{m+1|n+1})_{a}, \end{aligned}$$

where

$$\begin{aligned} J(\mathfrak {sl}_{m+1|n+1})_{a}=(x_1\cdots x_{m+1})^a \mathop {\prod }\limits _{i,p}\left( 1-\frac{x_i}{y_p}\right) {\mathbb {Z}}[x^{\pm 1},y^{\pm 1}]_0^{{\mathfrak {S}}_{m+1}\times {\mathfrak {S}}_{n+1}} \end{aligned}$$

if $a\notin {\mathbb {Z}}$;

$$\begin{aligned} J(\mathfrak {sl}_{m+1|n+1})_0=\left\{ f\in {\mathbb {Z}}[x^{\pm 1}, y^{\pm 1}]_0^{{\mathfrak {S}}_{m+1}\times {\mathfrak {S}}_{n+1} }\left| x_i\frac{\partial f}{\partial x_i}+y_j\frac{\partial f}{\partial y_j}\in (x_i-y_j) \right. \right\} \end{aligned}$$

and ${\mathbb {Z}}[x^{\pm 1},y^{\pm 1}]_0^{{\mathfrak {S}}_{m+1}\times {\mathfrak {S}}_{n+1}}$ is the quotient of the ring ${\mathbb {Z}}[x^{\pm 1},y^{\pm 1}]^{{\mathfrak {S}}_{m+1}\times {\mathfrak {S}}_{n+1}}$ by the ideal generated by $x_1\cdots x_{m+1}-y_1\cdots y_{n+1}$.

$J(A(n,n))=\mathop {\oplus }\limits _{i=0}^{n}J(A(n,n))_i$ for $n\ne 1$, where for $i\ne 0$

$$\begin{aligned} J(A(n,n))_i=\bigg \{ f=(x_1\cdots x_{n+1})^{\frac{i}{n+1}}\mathop {\prod }\limits _{j,p}^{n+1}\left( 1-\frac{x_j}{y_p}\right) g\bigg | g\in {\mathbb {Z}}[x^{\pm 1},y^{\pm 1}]_0^{{\mathfrak {S}}_{n+1}\times {\mathfrak {S}}_{n+1}},~ \mathrm {deg}~g=-i \bigg \} \end{aligned}$$

and $J(A(n,n))_0$ is the subring of $J(\mathfrak {sl}_{n+1|n+1})_0$ consisting of elements of degree 0.

$J(A(1,1))=\{c+(u-v)^2g |c\in {\mathbb {Z}}, g\in {\mathbb {Z}}[u,v] \}$ where $u=\left( \frac{x_1}{x_2}\right) ^{\frac{1}{2}}+\left( \frac{x_2}{x_1}\right) ^{\frac{1}{2}},~ v=\left( \frac{y_1}{y_2}\right) ^{\frac{1}{2}}+\left( \frac{y_2}{y_1}\right) ^{\frac{1}{2}}$.

$\boxed {A(m,n), m\ne n ~\mathbf{case: }}$ Define

$$\begin{aligned} J^{m|n}=\left\{ f\in {\mathbb {Z}}[x^{\pm 1}, y^{\pm 1}]^{{\mathfrak {S}}_{m+1}\times {\mathfrak {S}}_{n+1}}\left| x_i\frac{\partial f}{\partial x_i}+ y_j\frac{\partial f}{\partial y_j}\in (x_i-y_j)\right. \right\} \end{aligned}$$

and

$$\begin{aligned} J^{m|n}_{k}=\left\{ \left. f\in J^{m|n}\right| \mathrm {deg}~f=k \right\} . \end{aligned}$$

Thus, $J^{m|n}=\bigoplus \limits _{k\in {\mathbb {Z}}}J^{m|n}_{k}$.

For any element $\lambda \in {\mathfrak {h}}^*$, we write $\lambda =\mathop {\sum }\limits _{i=1}^{m+1}a_i\varepsilon _i+\mathop {\sum }\limits _{j=1}^{n+1}b_j\delta _j$, then we have

$$\begin{aligned}&{\mathbb {Z}}\Phi =\bigg \{ \lambda \in {\mathfrak {h}}^* \bigg | a_i,b_j\in {\mathbb {Z}},~\forall i,j \text { and } \mathop {\sum }\limits _{i=1}^{m+1}a_i+\mathop {\sum }\limits _{j=1}^{n+1}b_j=0 \bigg \}, \end{aligned}$$

and

$$\begin{aligned} \Lambda&=\bigg \{ \lambda \in {\mathfrak {h}}^* \bigg | a_i,b_j\in {\mathbb {Q}},~ a_i-a_{i+1},b_j-b_{j+1}\in {\mathbb {Z}}, ~\forall i\leqslant m,j\leqslant n \\&\qquad \text {and}~ \mathop {\sum }\limits _{i=1}^{m+1}a_i+\mathop {\sum }\limits _{j=1}^{n+1}b_j=0 \bigg \}. \end{aligned}$$

By direct computation, we know that

$$\begin{aligned} 2\Lambda \cap {\mathbb {Z}}\Phi ={\left\{ \begin{array}{ll} 2{\mathbb {Z}}\Phi +{\mathbb {Z}}\left( \mathop {\sum }\limits _{i=1}^{m+1}(-1)^{i+1}\varepsilon _i+\mathop {\sum }\limits _{j=1}^{n+1}(-1)^j\delta _j\right) , &{} \quad \text { if } m=2k,n=2l,\\ 2{\mathbb {Z}}\Phi +{\mathbb {Z}}\mathop {\sum }\limits _{j=1}^{n+1}(-1)^j\delta _j, &{}\quad \text { if } m=2k,n=2l+1,\\ 2{\mathbb {Z}}\Phi +{\mathbb {Z}}\mathop {\sum }\limits _{i=1}^{m+1}(-1)^{i+1}\varepsilon _i, &{} \quad \text { if } m=2k+1,n=2l,\\ 2{\mathbb {Z}}\Phi +{\mathbb {Z}}\mathop {\sum }\limits _{i=1}^{m+1}(-1)^{i+1}\varepsilon _i+{\mathbb {Z}}\mathop {\sum }\limits _{j=1}^{n+1}(-1)^j\delta _j, &{} \quad \text { if } m=2k+1,n=2l+1, \end{array}\right. } \end{aligned}$$

for some non-negative integers k, l. Then the algebra

$$\begin{aligned} J_{\mathrm {ev}}({\mathfrak {g}})={\left\{ \begin{array}{ll} J^{m|n}_0\oplus \mathop {\prod }\limits _{i}x_i^{\frac{1}{2}}\mathop {\prod }\limits _{j}y_j^{\frac{1}{2}}J^{m|n}_{-(k+l+1)},&{} \quad \text {if} ~m=2k,n=2l,\\ J^{m|n}_0\oplus \mathop {\prod }\limits _{j}y_j^{\frac{1}{2}}J^{m|n}_{-(l+1)},&{}\quad \text {if} ~m=2k,n=2l+1,\\ J^{m|n}_0\oplus \mathop {\prod }\limits _{i}x_i^{\frac{1}{2}}J^{m|n}_{-(k+1)}, &{}\quad \text {if} ~m=2k+1,n=2l,\\ J^{m|n}_0\oplus \mathop {\prod }\limits _{i}x_i^{\frac{1}{2}}J^{m|n}_{-(k+1)}\oplus \mathop {\prod }\limits _{j}y_j^{\frac{1}{2}}J^{m|n}_{-(l+1)}\oplus \mathop {\prod }\limits _{i}x_i^{\frac{1}{2}}\mathop {\prod }\limits _{j}y_j^{\frac{1}{2}}J^{m|n}_{-(k+l+2)}, &{}\quad \text {if} ~m=2k+1,n=2l+1. \end{array}\right. } \end{aligned}$$

for some non-negative integers k, l. So it can be viewed as a subalgebra of $J({\mathfrak {g}})$ by $\iota :J_{\mathrm {ev}}({\mathfrak {g}})\rightarrow J({\mathfrak {g}})$ with ${\mathbb {K}}_i\mapsto e^{-\alpha _i/2}$ and its image is coincide with $\mathrm {Sch}(K_{\mathrm {ev}}({\mathfrak {g}}))$.

$\boxed {A(n,n)~~ (n\ne 1)~\mathbf{case: }}$ In this case, we set

$$\begin{aligned} J(n)_0&=\left\{ f\in {\mathbb {Z}}[x^{\pm 1}, y^{\pm 1}]_{0,0}^{{\mathfrak {S}}_{n+1}\times {\mathfrak {S}}_{n+1}}\left| x_i\frac{\partial f}{\partial x_i}+ y_j\frac{\partial f}{\partial y_j}\in (x_i-y_j) \right. \right\} \end{aligned}$$

where ${\mathbb {Z}}[x^{\pm 1},y^{\pm 1}]_{0,0}$ is the quotient of the ring ${\mathbb {Z}}[x^{\pm 1},y^{\pm 1}]$ with degree 0 by the ideal $I=\left\langle \frac{x_1\cdots x_{n+1}}{y_1\cdots y_{n+1}}-1\right\rangle$. Then we have

$$\begin{aligned} J_{\mathrm {ev}}({\mathfrak {g}})={\left\{ \begin{array}{ll} J(n)_0 &{}\quad \text {if} ~ n ~\text { is even},\\ J(n)_0\oplus \bigg \{\overrightarrow{x}^{\frac{1}{2}} \mathop {\prod }\limits _{j,p}\left( 1-\frac{x_j}{y_p}\right) g +I\bigg |g\in {\mathbb {Z}}[x^{\pm 1},y^{\pm 1}]^{W},~\mathrm {deg} ~g=-\frac{n+1}{2}\bigg \} &{}\quad \text {if} ~ n ~\text { is odd}, \end{array}\right. } \end{aligned}$$

where $\overrightarrow{x}=x_1x_2\cdots x_{n+1}$ and $W={\mathfrak {S}}_{n+1}\times {\mathfrak {S}}_{n+1}$. It can be viewed as a subalgebra by $\iota :J_{\mathrm {ev}}({\mathfrak {g}})\rightarrow J({\mathfrak {g}})$ with ${\mathbb {K}}_i\mapsto e^{-\alpha _i/2}$ and its image is coincide with $\mathrm {Sch}(K_{\mathrm {ev}}({\mathfrak {g}}))$.

$\boxed {A(1,1) ~\mathbf{case: }}$ We have $J_{\mathrm {ev}}(A(1,1))=\left\{ c+(u-v)g\left| g\in {\mathbb {Z}}[u,v]\right. \right\}$ where $u=\left( \frac{x_1}{x_2}\right) ^{\frac{1}{2}}+\left( \frac{x_2}{x_1}\right) ^{\frac{1}{2}},~ v=\left( \frac{y_1}{y_2}\right) ^{\frac{1}{2}}+\left( \frac{y_2}{y_1}\right) ^{\frac{1}{2}}$. And $u-v={\mathbb {K}}_{1}+{\mathbb {K}}^{-1}_{1}-{\mathbb {K}}_{3}-{\mathbb {K}}_{3}^{-1}\in J_{\mathrm {ev}}(A(1,1))$, but $u-v\notin J(A(1,1))$.

$\boxed {B(m,n), m, n>0 ~\mathbf{case: }}$ We set $\lambda =\mathop {\sum }\limits _{i=1}^{m}\lambda _i\varepsilon _i+\mathop {\sum }\limits _{j=1}^{n} \mu _j\delta _j\in {\mathfrak {h}}^*$, then in this case

$$\begin{aligned}&{\mathbb {Z}}\Phi =\left\{ \lambda \in {\mathfrak {h}}^*\left| \lambda _i, \mu _j\in {\mathbb {Z}}, ~\forall i,j \right. \right\} ~\text { and }\\&\Lambda =\left\{ \lambda \in {\mathfrak {h}}^*\left| \mu _j\in {\mathbb {Z}},~\forall j \text { and all }\lambda _i\in {\mathbb {Z}} \text { or all } \lambda _i\in {\mathbb {Z}}+\frac{1}{2} \right. \right\} . \end{aligned}$$

So $2\Lambda \cap {\mathbb {Z}}\Phi =2\Lambda$. Let $u_i=x_i+x_i^{-1}$ and $v_j=y_j+y_j^{-1}$ for all possible i, j, then we have $J_{\mathrm {ev}}({\mathfrak {g}})=J({\mathfrak {g}})_0\oplus J({\mathfrak {g}})_{1/2}$, where

$$\begin{aligned} J({\mathfrak {g}})_0=\left\{ f\in {\mathbb {Z}}[u_1,\cdots ,u_m,v_1,\cdots ,v_n]^{{\mathfrak {S}}_m\times {\mathfrak {S}}_n}\left| u_i\frac{\partial f}{\partial u_i}+v_j\frac{\partial f}{\partial v_j}\in (u_i-v_j) \right. \right\} , \end{aligned}$$

and

$$\begin{aligned} J({\mathfrak {g}})_{1/2}=\bigg \{ \prod \limits _{i=1}^m(x_i^{1/2}+x_i^{-1/2})\mathop {\prod }\limits _{i=1}^m\prod \limits _{j=1}^n(u_i-v_j)g \bigg |g\in {\mathbb {Z}}[u_1,\cdots ,u_m,v_1,\cdots ,v_n]^{{\mathfrak {S}}_m\times {\mathfrak {S}}_n} \bigg \}. \end{aligned}$$

$\boxed {B(0,n) ~\mathbf{case: }}$ In this case $\Lambda ={\mathbb {Z}}\Phi =\Big \{\mathop {\sum }\limits _{j=1}^{n} \mu _j\delta _j\Big |\mu _j\in {\mathbb {Z}},~\forall j \Big \},$ so $2\Lambda \cap {\mathbb {Z}}\Phi =2\Lambda$ and this algebra $J_{\mathrm {ev}}({\mathfrak {g}})={\mathbb {Z}}[v_1,v_2,\cdots ,v_n]^{{\mathfrak {S}}_n}$, where the notation $v_i$ are the same as above.

$\boxed {C(n+1) ~\mathbf{case: }}$ In this case

$$\begin{aligned}&\Lambda =\bigg \{ \lambda \varepsilon +\mathop {\sum }\limits _{j=1}^{n} \mu _j\delta _j\bigg |\lambda \in {\mathbb {C}},\mu _j\in {\mathbb {Z}},~\forall j \bigg \} \end{aligned}$$

and

$$\begin{aligned}&{\mathbb {Z}}\Phi =\bigg \{ \lambda \varepsilon +\mathop {\sum }\limits _{j=1}^{n} \mu _j\delta _j\bigg |\lambda ,\mu _j\in {\mathbb {Z}},~\forall j ~\text {and}~ \lambda +\mathop {\sum }\limits _{j=1}^{n} \mu _j ~\text {is even} \bigg \}. \end{aligned}$$

So $2\Lambda \cap {\mathbb {Z}}\Phi =\Big \{ \lambda \varepsilon +\mathop {\sum }\limits _{j=1}^{n} \mu _j\delta _j\Big |\lambda ,\mu _j\in 2{\mathbb {Z}},~\forall j \Big \}$ and the algebra

$\boxed {D(m,n), m>1,n>0 ~\mathbf{case: }}$ Let $\lambda =\mathop {\sum }\limits _{i=1}^{m}\lambda _i\varepsilon _i+\mathop {\sum }\limits _{j=1}^{n} \mu _j\delta _j\in {\mathfrak {h}}^*$ and $u_i, v_j$ are as above, then

$$\begin{aligned}&\Lambda =\left\{ \lambda \in {\mathfrak {h}}^*\left| \mu _j\in {\mathbb {Z}},~\forall j \text { and all } \lambda _i\in {\mathbb {Z}} ~\text {or all}~ \lambda _i\in {\mathbb {Z}}+\frac{1}{2} \right. \right\} \end{aligned}$$

and

$$\begin{aligned}&{\mathbb {Z}}\Phi =\bigg \{ \lambda \in {\mathfrak {h}}^*\bigg |\lambda _i,\mu _j\in {\mathbb {Z}},~\forall i,j ~\text {and}~ \mathop {\sum }\limits _{i=1}^{m}\lambda _i+\mathop {\sum }\limits _{j=1}^{n} \mu _j ~\text {is even} \bigg \}. \end{aligned}$$

So

$$\begin{aligned} 2\Lambda \cap {\mathbb {Z}}\Phi ={\left\{ \begin{array}{ll} 2{\mathbb {Z}}\Phi +{\mathbb {Z}}\left( \mathop {\sum }\limits _{i=1}^n \varepsilon _i\right) +2{\mathbb {Z}}\varepsilon _n, &{}\quad \text {if }m=2k,\\ 2{\mathbb {Z}}\Phi +2{\mathbb {Z}}\varepsilon _n, &{}\quad \text {if }m=2k+1, \end{array}\right. } \end{aligned}$$

for some positive integer k. Thus the algebra $J_{\mathrm {ev}}({\mathfrak {g}})$ is, respectively, equal to $J({\mathfrak {g}})_0\oplus J({\mathfrak {g}})_{1/2}$ for $m=2k$ and $J({\mathfrak {g}})_0$ for $m=2k+1$, where

$$\begin{aligned} J({\mathfrak {g}})_0=\left\{ f\in {\mathbb {Z}}[x^{\pm 1}_1,\cdots ,x^{\pm 1}_m,y^{\pm 1}_1,\cdots ,y^{\pm 1}_n]^{W}\left| x_i\frac{\partial f}{\partial x_i}+y_j\frac{\partial f}{\partial y_j}\in (x_i-y_j) \right. \right\} , \end{aligned}$$

and

$$\begin{aligned} J({\mathfrak {g}})_{1/2}=\bigg \{ \mathop {\prod }\limits _{i,j}(u_i-v_j)\Big ((x_1x_2\cdots x_m)^{1/2}{\mathbb {Z}}[x^{\pm 1}_1,\cdots ,x^{\pm 1}_m,y^{\pm 1}_1,\cdots ,y^{\pm 1}_n]\Big )^W \bigg \}. \end{aligned}$$

$\boxed {D(2,1,\alpha ) ~\mathbf{case: }}$ In this case,

$$\begin{aligned} \Lambda =\bigg \{ \mathop {\sum }\limits _{i=1}^3\lambda _i\varepsilon _i\bigg | \lambda _i\in {\mathbb {Z}}, ~\forall i \bigg \},\text { and } {\mathbb {Z}}\Phi =\bigg \{ \mathop {\sum }\limits _{i=1}^3\lambda _i\varepsilon _i\bigg | \lambda _i\in {\mathbb {Z}} ~\text {and}~\lambda _i-\lambda _j\in 2{\mathbb {Z}}, ~\forall i,j \bigg \}. \end{aligned}$$

So $2\Lambda \cap {\mathbb {Z}}\Phi =2\Lambda$. Thus the algebra

$$\begin{aligned} J_{\mathrm {ev}}({\mathfrak {g}})={\left\{ \begin{array}{ll} \big \{c+\Delta h | c\in {\mathbb {Z}},h\in {\mathbb {Z}}[u_1,u_2,u_3] \big \},&{}\quad \text { if } \alpha \text { is not rational}, \\ \big \{g(w_{\alpha })+\Delta h| g\in {\mathbb {Z}}[\omega ],h\in {\mathbb {Z}}[u_1,u_2,u_3] \big \}, &{}\quad \text { if }\alpha =p/q \text { with } p\in {\mathbb {Z}},q\in {\mathbb {N}}, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \Delta =u_1^2+u_2^2+u_3^2-u_1u_2u_3-4,~ u_i=x_i+x_i^{-1}, \text { for }i=1,2,3, \end{aligned}$$

and

$$\begin{aligned} \omega _{\alpha }=(x_1+x_1^{-1}-x_2x_3-x_2^{-1}x_3^{-1}) \frac{(x_2^p-x_2^{-p})(x_3^{q}-x_3^{-q})}{(x_2-x_2^{-1}) (x_3-x_3^{-1})}+x_2^px_3^{-q}+x_2^{-p}x_3^q. \end{aligned}$$

$\boxed {F(4) ~\mathbf{case: }}$ In this case,

$$\begin{aligned}&\Lambda =\bigg \{ \mu \delta +\mathop {\sum }\limits _{i=1}^3\lambda _i \varepsilon _i\bigg |\text {all}~\lambda _i\in {\mathbb {Z}} ~\text {or}~\text {all}~\lambda _i\in {\mathbb {Z}}+\frac{1}{2} ,~ 2\mu \in {\mathbb {Z}} \bigg \}, \end{aligned}$$

and

$$\begin{aligned}&{\mathbb {Z}}\Phi =\bigg \{ \mu \delta +\mathop {\sum }\limits _{i=1}^3 \lambda _i\varepsilon _i\bigg |\text {all}~\lambda _i,~\mu \in {\mathbb {Z}} ~\text {or}~\text {all}~\lambda _i,~\mu \in {\mathbb {Z}}+\frac{1}{2} \bigg \}. \end{aligned}$$

So $2\Lambda \cap {\mathbb {Z}}\Phi =2\Lambda$, and the algebra

$$\begin{aligned} J_{\mathrm {ev}}({\mathfrak {g}})=\Big \{ g(\omega _1,\omega _2)+\Delta h\Big | h\in {\mathbb {Z}}[x_1^{\pm 2},x_2^{\pm 2},x_3^{\pm 2},(x_1x_2x_3)^{\pm 1},y^{\pm 1}]^W, ~g\in {\mathbb {Z}}[\omega _1,\omega _2] \Big \}, \end{aligned}$$

where

$$\begin{aligned} \Delta =\left( y+y^{-1}-x_1x_2x_3-x_1^{-1}x_2^{-1}x_3^{-1}\right) \mathop {\prod }\limits _{i=1}^3\left( y+y^{-1}-\frac{x_1x_2x_3}{x_i ^2}-\frac{x_i^2}{x_1x_2x_3}\right) , \end{aligned}$$

and

$$\begin{aligned} \omega _k&=\mathop {\sum }\limits _{1\leqslant i<j\leqslant 3}\left( x^{2k}_i+x^{-2k}_i+\frac{1}{2}\right) \left( x^{2k}_j +x^{-2k}_j+\frac{1}{2}\right) \\&\quad -\frac{3}{4}+y^{2k}+y^{-2k}-(y^k+y^{-k}) \mathop {\prod }\limits _{i=1}^3\left( x_i^k+x_i^{-k}\right) \end{aligned}$$

with $k=1,2$, and $W={\mathbb {Z}}_2\times ({\mathfrak {S}}_3\ltimes {\mathbb {Z}}_2^3)$.

$\boxed {G(3) ~\mathbf{case: }}$ In this case, $\Lambda ={\mathbb {Z}}\Phi =\big \{ \lambda _1\varepsilon _1+\lambda _2\varepsilon _2+\mu \delta |\lambda _1,\lambda _2,\mu \in {\mathbb {Z}} \big \}$. So $2\Lambda \cap {\mathbb {Z}}\Phi =2\Lambda$, and the algebra

$$\begin{aligned} J_{\mathrm {ev}}({\mathfrak {g}})=\bigg \{g(\omega ) +\mathop {\prod }\limits _{i=1}^3(v-u_i)h\bigg |h\in {\mathbb {Z}} [v,u_1,u_2,u_3]^{{\mathfrak {S}}_3},~g\in {\mathbb {Z}}[\omega ] \bigg \}, \end{aligned}$$

where

$$\begin{aligned} \omega =v^2-v(u_1+u_2+u_3+1)+u_1u_2+u_1u_3+u_2u_3. \end{aligned}$$

and the notations $u_i, v$ are the same as above.