Abstract
We establish a surface order large deviation estimate for the magnetisation of low temperature \(\phi ^4_3\). As a byproduct, we obtain a decay of spectral gap for its Glauber dynamics given by the \(\phi ^4_3\) singular stochastic PDE. Our main technical contributions are contour bounds for \(\phi ^4_3\), which extends 2D results by Glimm et al. (Commun Math Phys 45(3):203–216, 1975). We adapt an argument by Bodineau et al. (J Math Phys 41(3):1033–1098, 2000) to use these contour bounds to study phase segregation. The main challenge to obtain the contour bounds is to handle the ultraviolet divergences of \(\phi ^4_3\) whilst preserving the structure of the low temperature potential. To do this, we build on the variational approach to ultraviolet stability for \(\phi ^4_3\) developed recently by Barashkov and Gubinelli (Duke Math. J. 169(17):3339–3415, 2020).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We study the behaviour of the average magnetisation
for fields \(\phi \) distributed according to the measure \({\nu _{\beta ,N}}\) with formal density
in the infinite volume limit \(N \rightarrow \infty \). Above, \({\mathbb {T}}_N= ({\mathbb {R}}/N{\mathbb {Z}})^3\) is the 3D torus of sidelength \(N \in {\mathbb {N}}\), \(\prod _{x\in {\mathbb {T}}_N}d\phi (x)\) is the (non-existent) Lebesgue measure on fields \(\phi :{\mathbb {T}}_N\rightarrow {\mathbb {R}}\), \(\beta > 0\) is the inverse temperature, and \({\mathcal {V}}_\beta : {\mathbb {R}}\rightarrow {\mathbb {R}}\) is the symmetric double-well potential given by \({\mathcal {V}}_\beta (a) = \frac{1}{\beta }(a^2-\beta )^2\) for \(a \in {\mathbb {R}}\).
\({\nu _{\beta ,N}}\) is a finite volume approximation of a \(\phi ^4_3\) Euclidean quantum field theory [Gli68, GJ73, FO76]. Its construction, first in finite volumes and later in infinite volume, was a major achievement of the constructive field theory programme in the ’60s-’70s: Glimm and Jaffe made the first breakthrough in [GJ73] and many results followed [Fel74, MS77, BCG+80, BFS83, BDH95, MW17, GH18, BG19]. The model in 2D was constructed earlier by Nelson [Nel66]. In higher dimensions there are triviality results: in dimensions \(\geqslant 5\) these are due to Aizenman and Fröhlich [Aiz82, Frö82], whereas the 4D case was only recently done by Aizenman and Duminil-Copin [ADC20]. By now it is also well-known that the \(\phi ^4_3\) model has significance in statistical mechanics since it arises as a continuum limit of Ising-type models near criticality [SG73, CMP95, HI18].
It is natural to define \({\nu _{\beta ,N}}\) using a density with respect to the centred Gaussian measure \(\mu _N\) with covariance \((-\Delta )^{-1}\), where \(\Delta \) is the Laplacian on \({\mathbb {T}}_N\) (see Remark 1.1 for how we deal with the issue of constant fields/the zeroeth Fourier mode). However, in 2D and higher \(\mu _N\) is not supported on a space of functions and samples need to be interpreted as Schwartz distributions. This is a serious problem because there is no canonical interpretation of products of distributions, meaning that the nonlinearity \(\int _{{\mathbb {T}}_N}{\mathcal {V}}_\beta (\phi (x)) dx\) is not well-defined on the support of \(\mu _N\). If one introduces an ultraviolet (small-scale) cutoff \(K>0\) on the field to regularise it, then one sees that the nonlinearities \({\mathcal {V}}_\beta (\phi _K)\) fail to converge as the cutoff is removed—there are divergences. The strength of these divergences grow as the dimension grows: they are only logarithmic in the cutoff in 2D, whereas they are polynomial in the cutoff in 3D. In addition, \({\nu _{\beta ,N}}\) and \(\mu _N\) are mutually singular [BG20] in 3D, which produces technical difficulties that are not present in 2D.
Renormalisation is required in order to kill these divergences. This is done by looking at the cutoff measures and subtracting the corresponding counter-term \(\int _{{\mathbb {T}}_N}\delta m^2(K) \phi ^2_K\) where \(\phi _K\) is the field cutoff at spatial scales less than \(\frac{1}{K}\) and the renormalisation constant \(\delta m^2(K) = \frac{C_1}{\beta } K - \frac{C_2}{\beta ^2} \log K\) for specific constants \(C_1, C_2 > 0\) (see Sect. 2). If these constants are appropriately chosen (i.e. by perturbation theory), then a non-Gaussian limiting measure is obtained as \(K \rightarrow \infty \). This construction yields a one-parameter family of measures \({\nu _{\beta ,N}}={\nu _{\beta ,N}}(\delta m^2)\) corresponding to bounded shifts of \(\delta m^2(K)\).
Remark 1.1
For technical reasons, we work with a massive Gaussian free field as our reference measure. We do this by introducing a mass \(\eta > 0\) into the covariance. This resolves the issue of the constant fields/zeroeth Fourier mode degeneracy. In order to stay consistent with (1.1), we subtract \(\int _{{\mathbb {T}}_N}\frac{\eta }{2} \phi ^2 dx\) from \({\mathcal {V}}_\beta (\phi )\).
Once we have chosen \(\eta \), it is convenient to fix \(\delta m^2\) by writing the renormalisation constants in terms of expectations with respect to \(\mu _N(\eta )\). The particular choice of \(\eta \) is inessential since one can show that changing \(\eta \) corresponds to a bounded shift of \(\delta m^2\) that is \(O\Big (\frac{1}{\beta }\Big )\) as \(\beta \rightarrow \infty \).
The large-scale behaviour of \({\nu _{\beta ,N}}\) depends heavily on \(\beta \) as \(N \rightarrow \infty \). To see why, note that \(a \mapsto {\mathcal {V}}_\beta (a)\) has minima at \(a = \pm {\sqrt{\beta }}\) with a potential barrier at \(a=0\) of height \(\beta \), so the minima become widely separated by a steep barrier as \(\beta \rightarrow \infty \). Consequently, \({\nu _{\beta ,N}}\) resembles an Ising model on \({\mathbb {T}}_N\) with spins at \(\pm {\sqrt{\beta }}\) (i.e. at inverse temperature \(\beta > 0\)) for large \(\beta \). Glimm et al. [GJS75] exploited this similarity and proved phase transition for \(\nu _\beta \), the infinite volume analogue of \({\nu _{\beta ,N}}\), in 2D using a sophisticated modification of the classical Peierls’ argument for the low temperature Ising model [Pei36, Gri64, Dob65]. See also [GJS76a, GJS76b]. Their proof relies on contour bounds for \({\nu _{\beta ,N}}\) in 2D that hold in the limit \(N \rightarrow \infty \). Their techniques fail in the significantly harder case of 3D. However, phase transition for \(\nu _\beta \) in 3D was established by Fröhlich, Simon, and Spencer [FSS76] using a different argument based heavily on reflection positivity. Whilst this argument is more general (it applies, for example, to some models with continuous symmetry), it is less quantitative than the Peierls’ theory of [GJS75]. Specifically, it is not clear how to use it to control large deviations of the (finite volume) average magnetisation \({\mathfrak {m}}_N\).
Although phase coexistence for \(\nu _\beta \) has been established, little is known of this regime in comparison to the low temperature Ising model. In the latter model, the study of phase segregation at low temperatures in large but finite volumes was initiated by Minlos and Sinai [MS67, MS68], culminating in the famous Wulff constructions: due to Dobrushin, Kotecký, and Shlosman in 2D [DKS89, DKS92], with simplifications due to Pfister [Pfi91] and results up to the critical point by Ioffe and Schonmann [IS98]; and Bodineau [Bod99] in 3D, see also results up to the critical point by Cerf and Pisztora [CP00] and the bibliographical review in [BIV00, Section 1.3.4]. We are interested in a weaker form of phase segregation: surface order large deviation estimates for the average magnetisation \({\mathfrak {m}}_N\). For the Ising model, this was first established in 2D by Schonmann [Sch87] and later extended up to the critical point by Chayes, Chayes, and Schonmann [CCS87]; in 3D this was first established by Pisztora [Pis96]. These results should be contrasted with the volume order large deviations established for \({\mathfrak {m}}_N\) in the high temperature regime where there is no phase coexistence [CF86, Ell85, FO88, Oll88].
Our main result is a surface order upper bound on large deviations for the average magnetisation under \({\nu _{\beta ,N}}\).
Theorem 1.2
Let \(\eta > 0\) and \({\nu _{\beta ,N}}= {\nu _{\beta ,N}}(\eta )\) as in Remark 1.1. For any \(\zeta \in (0,1)\), there exists \(\beta _0 = \beta _0(\zeta ,\eta ) > 0\), \(C=C(\zeta , \eta )>0\), and \(N_0 = N_0(\zeta ) \geqslant 4\) such that the following estimate holds: for any \(\beta > \beta _0\) and any \(N > N_0\) dyadic,
Proof
See Sect. 3.5. \(\quad \square \)
The condition that N is a sufficiently large dyadic in Theorem 1.2 comes from Proposition 3.8 (we also need that N is divisible by 4 to apply the chessboard estimates of Proposition 6.5). Our analysis can be simplified to prove Theorem 1.2 in 2D with \(N^2\) replaced by N in (1.2).
Our main technical contributions are contour bounds for \({\nu _{\beta ,N}}\). As a result, the Peierls’ argument of [GJS75] is extended to 3D, thereby giving a second proof of phase transition for \(\phi ^4_3\). The main difficulty is to handle the ultraviolet divergences of \({\nu _{\beta ,N}}\) whilst preserving the structure of the low temperature potential. We do this by building on the variational approach to showing ultraviolet stability for \(\phi ^4_3\) recently developed by Barashkov and Gubinelli [BG19]. Our insight is to separate scales within the corresponding stochastic control problem through a coarse-graining into an effective Hamiltonian and remainder. The effective Hamiltonian captures the macroscopic description of the system and is treated using techniques adapted from [GJS76b]. The remainder contains the ultraviolet divergences and these are killed using the renormalisation techniques of [BG19].
Our next contribution is to adapt arguments used by Bodineau, Velenik, and Ioffe [BIV00], in the context of equilibrium crystal shapes of discrete spin models, to study phase segregation for \(\phi ^4_3\). In particular, we adapt them to handle a block-averaged model with unbounded spins. Technically, this requires control over large fields.
1.1 Application to the dynamical \(\phi ^4_3\) model
The Glauber dynamics of \({\nu _{\beta ,N}}\) is given by the singular stochastic PDE
where \(\Phi \in S'({\mathbb {R}}_+\times {\mathbb {T}}_N)\) is a space-time Schwartz distribution, \(\phi _0 \in {\mathcal {C}}^{-\frac{1}{2} -\kappa }({\mathbb {T}}_N)\), the infinite constant indicates renormalisation (see Remark 6.16), and \(\xi \) is space-time white noise on \({\mathbb {T}}_N\). The well-posedness of this equation, known as the dynamical \(\phi ^4_3\) model, has been a major breakthrough in stochastic analysis in recent years [Hai14, Hai16, GIP15, CC18, Kup16, MW17, GH19, MW18].
In finite volumes the solution is a Markov process and its associated semigroup \(({\mathcal {P}}_t^{\beta ,N})_{t \geqslant 0}\) is reversible and exponentially ergodic with respect to its unique invariant measure \({\nu _{\beta ,N}}\) [HM18a, HS19, ZZ18a]. As a consequence, there exists a spectral gap \(\lambda _{\beta ,N}>0\) given by the optimal constant in the inequality:
for suitable \(F \in L^2({\nu _{\beta ,N}})\). \(\lambda _{\beta ,N}^{-1}\) is called the relaxation time and measures the rate of convergence of variances to equilibrium. An implication of Theorem 1.2 is the exponential explosion of relaxation times in the infinite volume limit provided \(\beta \) is sufficiently large.
Corollary 1.3
Let \(\eta > 0\) and \({\nu _{\beta ,N}}= {\nu _{\beta ,N}}(\eta )\) as in Remark 1.1. Then, there exists \(\beta _0=\beta _0(\eta )>0\), \(C=C(\beta _0,\eta )\), and \(N_0 \geqslant 4\) such that, for any \(\beta > \beta _0\) and \(N > N_0\) dyadic,
Proof
See Sect. 7. \(\quad \square \)
Corollary 1.3 is the first step towards establishing phase transition for the relaxation times of the Glauber dynamics of \(\phi ^4\) in 2D and 3D. This phenomenon has been well-studied for the Glauber dynamics of the 2D Ising model, where a relatively complete picture has been established (in higher dimensions it is less complete). The relaxation times for the Ising dynamics on the 2D torus of sidelength N undergo the following trichotomy as \(N \rightarrow \infty \): in the high temperature regime, they are uniformly bounded in N [AH87, MO94]; in the low temperature regime, they are exponential in N [Sch87, CCS87, Tho89, MO94, CGMS96]; at criticality, they are polynomial in N [Hol91, LS12]. It would be interesting to see whether the relaxation times for the dynamical \(\phi ^4\) model undergo such a trichotomy.
1.2 Paper organisation
In Sect. 2 we introduce the renormalised, ultraviolet cutoff measures \(\nu _{\beta ,N,K}\) that converge weakly to \({\nu _{\beta ,N}}\) as the cutoff is removed. In Sect. 3 we carry out the statistical mechanics part of the proof of Theorem 1.2. In particular, conditional on the moment bounds in Proposition 3.6, we develop contour bounds for \({\nu _{\beta ,N}}\). These contour bounds allow us to adapt techniques in [BIV00], which were developed in the context of discrete spin systems, to deal with \({\nu _{\beta ,N}}\).
In Sect. 4 we lay the foundation to proving Proposition 3.6 by introducing the Boué–Dupuis formalism for analysing the free energy of \({\nu _{\beta ,N}}\) as in [BG19]. We then use a low temperature expansion and coarse-graining argument within the Boué–Dupuis formalism in Sect. 5 to establish Proposition 5.1 which contains the key analytic input to proving Proposition 3.6.
In Sect. 6, we use the chessboard estimates of Proposition 6.5 to upgrade the bounds of Proposition 5.1 to those of Proposition 3.6. Chessboard estimates follow from the well-known fact that \({\nu _{\beta ,N}}\) is reflection positive. We give an independent proof of this fact by using stability results for the dynamics (1.3) to show that lattice and Fourier regularisations of \({\nu _{\beta ,N}}\) converge to the same limit. Then, in Sect. 7, we prove Corollary 1.3 showing that the spectral gaps for the dynamics decay in the infinite volume limit provided \(\beta \) is sufficiently large.
We collect basic notations and analytic tools that we use throughout the paper in “Appendix A”.
2 The Model
In the following, we use notation and standard tools introduced in “Appendix A”.
Let \(\eta > 0\). Denote by \(\mu _N = \mu _N(\eta )\) the centred Gaussian measure with covariance \((-\Delta + \eta )^{-1}\) and expectation \({\mathbb {E}}_N\). Above, \(\Delta \) is the Laplacian on \({\mathbb {T}}_N\). As pointed out in Remark 1.1, the choice of \(\eta \) is inessential. We consider it fixed unless stated otherwise and we do not make \(\eta \)-dependence explicit in the notation.
Fix \(\beta > 0\). Let \({\mathcal {V}}_\beta :{\mathbb {R}}\rightarrow {\mathbb {R}}\) be given by
\({\mathcal {V}}_\beta \) is a symmetric double well potential with minima at \(a = \pm {\sqrt{\beta }}\) and a potential barrier at \(a=0\) of height \(\beta \).
Fix \(\rho \in C^\infty _c({\mathbb {R}}^3;[0,1])\) rotationally symmetric; decreasing; and satisfying \(\rho (x)=1\) for \(|x| \in [0,c_\rho )\), where \(c_\rho >0\). See Lemma 4.6 for why the last condition is important. Note that many of our estimates rely on the choice of \(\rho \), but we omit explicit reference to this.
For every \(K>0\), let \(\rho _K\) be the Fourier multiplier on \({\mathbb {T}}_N\) with symbol \(\rho _K(\cdot ) = \rho (\frac{\cdot }{K})\). For \(\phi \sim \mu _N\), we denote \(\phi _K = \rho _K \phi \). Note that \(\phi _K\) is smooth. Let

where \(\langle \cdot \rangle = \sqrt{\eta + 4\pi ^2|\cdot |}\). Note that  as \(K \rightarrow \infty \). The first four Wick powers of \(\phi _K\) are given by the generalised Hermite polynomials:
as \(K \rightarrow \infty \). The first four Wick powers of \(\phi _K\) are given by the generalised Hermite polynomials:

We define the Wick renormalised potential by linearity:
Let \(\nu _{\beta ,N,K}\) be the probability measure with density
Above, \({\mathcal {H}}_{\beta ,N,K}\) is the renormalised Hamiltonian
where \(\gamma _K\) and \(\delta _K\) are additional renormalisation constants given by (5.25) and (5.26), respectively, and \({\mathscr {Z}}_{\beta ,N,K} = {\mathbb {E}}_N e^{-{\mathcal {H}}_{\beta ,N,K}(\phi _K)}\) is the partition function.
Proposition 2.1
For every \(\beta > 0\) and \(N \in {\mathbb {N}}\), the measures \(\nu _{\beta ,N,K}\) converge weakly to a non-Gaussian measure \({\nu _{\beta ,N}}\) on \(S'({\mathbb {T}}_N)\) as \(K \rightarrow \infty \). In addition, \({\mathscr {Z}}_{\beta ,N,K} \rightarrow {\mathscr {Z}}_{\beta ,N}\) as \(K \rightarrow \infty \) and satisfies the following estimate: there exists \(C=C(\beta ,\eta ) > 0\) such that
Proof
Proposition 2.1 is a variant of the classical ultraviolet stability for \(\phi ^4_3\) first established in [GJ73]. Our precise formulation, i.e. the choice of \(\gamma _\bullet \) and \(\delta _\bullet \), is taken from [BG19, Theorem 1]. \(\quad \square \)
We write \(\langle \cdot \rangle _{\beta ,N}\) and \(\langle \cdot \rangle _{\beta ,N,K}\) for expectations with respect to \({\nu _{\beta ,N}}\) and \(\nu _{\beta ,N,K}\), respectively.
Remark 2.2
The constants  are, respectively, Wick renormalisation, (second order) mass renormalisation, and energy renormalisation constants. They all depend on \(\eta \) and N. \(\delta _K\) additionally depends on \(\beta \) and is needed for the convergence of \({\mathscr {Z}}_{\beta ,N,K}\) as \(K \rightarrow \infty \), but drops out of the definition of the cutoff measures (2.2).
are, respectively, Wick renormalisation, (second order) mass renormalisation, and energy renormalisation constants. They all depend on \(\eta \) and N. \(\delta _K\) additionally depends on \(\beta \) and is needed for the convergence of \({\mathscr {Z}}_{\beta ,N,K}\) as \(K \rightarrow \infty \), but drops out of the definition of the cutoff measures (2.2).
Remark 2.3
In 2D a scaling argument [GJS76c] allows one to work with the measure with density proportional to
where \({\tilde{\mu }}_N\) is the Gaussian measure with covariance \((-\Delta + {\sqrt{\beta }}^{-1})^{-1}\), i.e. a \(\beta \)-dependent mass. This measure is significantly easier to work with due to the degenerate mass when \(\beta \) is large. In particular, it is easier to obtain contour bounds which, although suboptimal from the point of view of \(\beta \)-dependence, are sufficient for the Peierls’ argument in [GJS75] and for the analogue of our argument in Sect. 3 carried out in 2D. In 3D one cannot work with such a measure.
3 Surface Order Large Deviation Estimate
In this section we carry out the statistical mechanics part of the proof of Theorem 1.2. Recall that for large \(\beta \), the the minima of potential \({\mathcal {V}}_\beta \) at \(\pm {\sqrt{\beta }}\) are widely separated by a steep potential barrier of height \(\beta \), so formally \({\nu _{\beta ,N}}\) resembles an Ising model at inverse temperature \(\beta \). We use this intuition to prove contour bounds for \({\nu _{\beta ,N}}\) (see Proposition 3.2) conditional on certain moment bounds (see Proposition 3.6). The contour bounds are then used to adapt arguments from [BIV00] to prove Theorem 1.2.
3.1 Block averaging
Let \(e_1, e_2, e_3\) be the standard basis for \({\mathbb {R}}^3\). We identify \({\mathbb {T}}_N\) with the set
Define
We call elements of \({{\mathbb {B}}_N}\) blocks. For any \(B \subset {{\mathbb {B}}_N}\), we overload notation and write  . Hence, \(|B| = \int _B 1 dx\) is the number of blocks in B. In addition, we identify any \(f \in {\mathbb {R}}^{{\mathbb {B}}_N}\) with the piecewise continuous function on \({\mathbb {T}}_N\) given by
. Hence, \(|B| = \int _B 1 dx\) is the number of blocks in B. In addition, we identify any \(f \in {\mathbb {R}}^{{\mathbb {B}}_N}\) with the piecewise continuous function on \({\mathbb {T}}_N\) given by  for
for  .
.
Let \(\phi \sim {\nu _{\beta ,N}}\). For any  , let
, let  . Here, the integral is interpreted as the duality pairing between \(\phi \) (a distribution) and the indicator function
. Here, the integral is interpreted as the duality pairing between \(\phi \) (a distribution) and the indicator function  (a test function); we use this convention throughout. We let
(a test function); we use this convention throughout. We let  denote the block averaged field obtained from \(\phi \).
denote the block averaged field obtained from \(\phi \).
Remark 3.1
Testing \(\phi \) against  , which is not smooth, yields a well-defined random variable on the support of \({\nu _{\beta ,N}}\). Indeed, \(\phi \) belongs almost surely to \(L^\infty \)-based Besov spaces of regularity s for every \(s < -\frac{1}{2}\) (see Appendix A for a review of Besov spaces and see Sect. 4 for the almost sure regularity of \(\phi \)). On the other hand, indicator functions of blocks belong to \(L^1\)-based Besov spaces of regularity s for every \(s < 1\) or, more generally, \(L^p\)-based Besov spaces of regularity s for every \(s < \frac{1}{p}\) (see, for example, Lemma 1.1 in [FR12]). This is sufficient to test \(\phi \) against indicator functions of blocks (using e.g. Proposition A.1). We also give an alternative proof using a type of Itô isometry in Proposition 5.23.
, which is not smooth, yields a well-defined random variable on the support of \({\nu _{\beta ,N}}\). Indeed, \(\phi \) belongs almost surely to \(L^\infty \)-based Besov spaces of regularity s for every \(s < -\frac{1}{2}\) (see Appendix A for a review of Besov spaces and see Sect. 4 for the almost sure regularity of \(\phi \)). On the other hand, indicator functions of blocks belong to \(L^1\)-based Besov spaces of regularity s for every \(s < 1\) or, more generally, \(L^p\)-based Besov spaces of regularity s for every \(s < \frac{1}{p}\) (see, for example, Lemma 1.1 in [FR12]). This is sufficient to test \(\phi \) against indicator functions of blocks (using e.g. Proposition A.1). We also give an alternative proof using a type of Itô isometry in Proposition 5.23.
3.2 Phase labels
We define a map \({\phi }\in {\mathbb {R}}^{{\mathbb {B}}_N}\mapsto \sigma \in \{-{\sqrt{\beta }}, 0, {\sqrt{\beta }}\}^{{\mathbb {B}}_N}\) called a phase label. A basic function of \(\sigma \) is to identify whether the averages  take values around the well at \(+{\sqrt{\beta }}\), the well at \(-{\sqrt{\beta }}\), or neither. We quantify this to a given precision \(\delta \in (0,1)\), which is taken to be fixed in what follows.
take values around the well at \(+{\sqrt{\beta }}\), the well at \(-{\sqrt{\beta }}\), or neither. We quantify this to a given precision \(\delta \in (0,1)\), which is taken to be fixed in what follows.
-
We say that
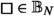 is plus (resp. minus) valued if
is plus (resp. minus) valued if 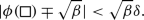
The set of plus (resp. minus) valued blocks is denoted \({\mathcal {P}}\) (resp. \({\mathcal {M}}\)).
-
The set of neutral blocks is defined as \({\mathcal {N}}= {{\mathbb {B}}_N}{\setminus } ({\mathcal {P}}\cup {\mathcal {M}})\).
Each block in \({{\mathbb {B}}_N}\) contains a midpoint. Given two distinct blocks in \({{\mathbb {B}}_N}\), we say that they are nearest-neighbours if their midpoints are of distance 1. They are \(*\)-neighbours if either they are nearest-neighbours or if their midpoints are of distance \(\sqrt{3}\). For any  , the \(*\)-connected ball centred at
, the \(*\)-connected ball centred at  is the set
is the set  consisting of
consisting of  and its \(*\)-neighbours. It contains exactly 27 blocks.
and its \(*\)-neighbours. It contains exactly 27 blocks.
-
We say that
 is plus good if every
is plus good if every  is plus valued. The set of plus good blocks is denoted \({\mathcal {P}}_G\).
is plus valued. The set of plus good blocks is denoted \({\mathcal {P}}_G\). -
We say that
 is minus good if every
is minus good if every  is minus valued. The set of minus good blocks is denoted \({\mathcal {M}}_G\).
is minus valued. The set of minus good blocks is denoted \({\mathcal {M}}_G\). -
The set of bad blocks is defined as \({\mathcal {B}}= {{\mathbb {B}}_N}{\setminus } ({\mathcal {P}}_G \cup {\mathcal {M}}_G)\).
Define the phase label \(\sigma \) associated to \({\phi }\) of precision \(\delta > 0\) by

The following proposition can be thought of as an extension of the contour bounds developed for \(\phi ^4\) in 2D [GJS75, Theorem 1.2] to 3D.
Proposition 3.2
Let \(\sigma \) be a phase label of precision \(\delta \in (0,1)\). Then, there exists \(\beta _0=\beta _0(\delta , \eta ) > 0\) and \(C_P=C_P(\delta , \eta ) > 0\) such that, for \(\beta > \beta _0\), the following holds for any \(N \in 4{\mathbb {N}}\): for any set of blocks \(B\subset {{\mathbb {B}}_N}\),

Proof
See Sect. 3.3.1. The main estimates required in the proof are given in Proposition 3.6, which extends [GJS75, Theorem 1.3] to 3D and improves the \(\beta \)-dependence. Assuming this, we then prove Proposition 3.2 in the spirit of the proof of [GJS75, Theorem 1.2]. \(\quad \square \)
3.3 Penalising bad blocks
Given a phase label, we partition the set of bad blocks \({\mathcal {B}}\) into two types.
-
Frustrated blocks are blocks
 such that
such that 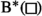 contains a neutral block. We denote the set of frustrated blocks \({\mathcal {B}}_F\).
contains a neutral block. We denote the set of frustrated blocks \({\mathcal {B}}_F\). -
Interface block are blocks
 such that
such that  contains no neutral blocks, but there exists at least one pair of nearest-neighbours
contains no neutral blocks, but there exists at least one pair of nearest-neighbours  such that
such that  but
but  . We denote the set of interface blocks \({\mathcal {B}}_I\).
. We denote the set of interface blocks \({\mathcal {B}}_I\).
For any  and any nearest-neighbours
and any nearest-neighbours  , define:
, define:

Remark 3.3
Note that testing \(:\phi ^2:\) against  yields a well-defined random variable on the support of \({\nu _{\beta ,N}}\). We give a proof of this fact in Proposition 5.24.
yields a well-defined random variable on the support of \({\nu _{\beta ,N}}\). We give a proof of this fact in Proposition 5.24.
We write  for the set of unordered pairs of nearest-neighbour blocks
for the set of unordered pairs of nearest-neighbour blocks  in \({{\mathbb {B}}_N}\) such that
in \({{\mathbb {B}}_N}\) such that  . There are 54 elements in this set.
. There are 54 elements in this set.
Lemma 3.4
Let \(N \in {\mathbb {N}}\) and fix a phase label of precision \(\delta \in (0,1)\). Then, for every  ,
,


where \(C_\delta = \min \Big ( \frac{\delta }{2}, 2-2\delta \Big ) > 0\).
Frustrated blocks are penalised by the potential \({\mathcal {V}}_\beta \) whereas interface blocks are penalised by the gradient term in the Gaussian measure. Lemma 3.4 formalises this through use of the random variables \(Q_1, Q_2\) and \(Q_3\), which (up to trivial modifications) were introduced in [GJS75]. \(Q_1\) penalises frustrated blocks. \(Q_2\) is an error term coming from the fact that the potential is written in terms of \(\phi \) rather than \({\phi }\). \(Q_3\) penalises interface blocks.
Proof of Lemma 3.4
For any  ,
,

where in the penultimate line we have used that \(\delta ^2 \leqslant \delta \).
By the definition of \({\mathcal {B}}_F\),

Using (3.5) applied to  in (3.6) yields (3.3).
in (3.6) yields (3.3).
(3.4) is established by the following estimates: by the definition of \({\mathcal {B}}_I\),

\(\square \)
In order to use Lemma 3.4 to prove Proposition 3.2, we want to control expectations of \(\cosh Q_1, \cosh Q_2\) and \(\cosh Q_3\) by the exponentially small (in \({\sqrt{\beta }}\)) prefactor in (3.3) and (3.4). Moreover, we want to control these expectations over a set of blocks as opposed to just single blocks.
Let \(B_1, B_2 \subset {{\mathbb {B}}_N}\) and let \(B_3\) be any set of unordered pairs of nearest-neighbours in \({{\mathbb {B}}_N}\). Define

Remark 3.5
Although the random variable  does depend on the ordering of
does depend on the ordering of  and
and  ,
,  does not.
does not.
Proposition 3.6
For every \(a_0 > 0\), there exist \(\beta _0 = \beta _0(a_0,\eta )>0\) and \(C_Q = C_Q(a_0,\beta _0,\eta )>0\) such that the following holds uniformly for all \(\beta > \beta _0\), \(a_1,a_2,a_3 \in {\mathbb {R}}\) such that \(|a_i| \leqslant a_0\), and \(N \in 4{\mathbb {N}}\): let \(B_1, B_2 \subset {{\mathbb {B}}_N}\) and \(B_3\) a set of unordered pairs of nearest-neighbour blocks in \({{\mathbb {B}}_N}\). Then,
where \(|B_3|\) is given by the number of pairs in \(B_3\).
Proof
Proposition 3.6 is established in Sect. 6.3, but its proof takes up most of this article. The overall strategy is as follows: the crucial first step is to obtain upper and lower bounds on the free energy \(-\log {\mathscr {Z}}_{\beta ,N}\) that are uniform in \(\beta \) and extensive in the volume, \(N^3\). We then build on this analysis to obtain upper bounds on expectations of the form \(\langle \exp Q \rangle _{\beta ,N}\) that are uniform in \(\beta \) and extensive in \(N^3\). Here, Q is a placeholder for random variables that are derived from the \(Q_i\)’s, but that are supported on the whole of \({\mathbb {T}}_N\) rather than arbitrary unions of blocks. This is all done in Sect. 5, where the key results are Propositions 5.3 and 5.1 , within the framework developed in Sect. 4.
The next step in the proof is to use the chessboard estimates of Proposition 6.5 (which requires \(N \in 4{\mathbb {N}}\)) to bound the lefthand side of (3.8) in terms of \(|B_1|+|B_2|+|B_3|\) products of expectations of the form \(\langle \exp Q \rangle _{\beta ,N}^\frac{1}{N^3}\). Applying the results of Sect. 5 then completes the proof. \(\quad \square \)
Key features of the estimate (3.8) used in the proof of Proposition 3.2 are that it is uniform in \(\beta \) and extensive in the support of the \(Q_i\)’s.
3.3.1 Proof of the Proposition 3.2 assuming Proposition 3.6
We first show that we can reduce to the case where B contains no \(*\)-neighbours, which simplifies the combinatorics later on. Identify \({{\mathbb {B}}_N}\) with a subset of \({\mathbb {Z}}^3\). For every \(e_l \in \{-1,0,1\}^3\), let \({\mathbb {Z}}^3_l = e_l + (3 {\mathbb {Z}})^3\). There are 27 such sub-lattices which we order according to \(l \in \{1,\dots ,27\}\). Note that \({\mathbb {Z}}^3 = \bigcup _{l=1}^{27} {\mathbb {Z}}^3_l\). Let \({\mathbb {B}}_N^l = {{\mathbb {B}}_N}\cap {\mathbb {Z}}^3_l\). Each \(*\)-connected ball in \({{\mathbb {B}}_N}\) contains at most one block from each of these \({\mathbb {B}}_N^l\).
Assume that (3.1) has been established for sets with no \(*\)-neighbours with constant \(C_P'\). Then, by Hölder’s inequality,

thereby establishing (3.1) with \(C_P = \frac{C_P'}{27}\).
Now assume that B contains no \(*\)-neighbours. Fix any \(A \subset B\). Let  and let
and let  . By our assumption, A contains no \(*\)-neighbours. Hence, for any
. By our assumption, A contains no \(*\)-neighbours. Hence, for any  there exists a unique
there exists a unique  such that
such that  ; we define the root of
; we define the root of  to be
to be  . Similarly, for any
. Similarly, for any  there exists a unique
there exists a unique  such that
such that  ; we define the root of
; we define the root of  to be
to be  . Note that the definition of root is A-dependent in both cases.
. Note that the definition of root is A-dependent in both cases.
By Lemma 3.4, there exists \(C_\delta \) such that

where the last sum is over all \(A_1, A_2 \subset \mathrm {B}^*(A)\) and \(A_3 \subset \mathrm {B}^*_{\mathrm {nn}}(B {\setminus } A)\) such that: no two blocks in \(A_1 \cup A_2\) share a root, and no two pairs of blocks in \(A_3\) share a root; and, \(|A_1| + |A_2| = |A|\) and \(|A_3| = |B {\setminus } A|\). We note that there are \((2 \cdot 27)^{|A|}=54^{|A|}\) possible \(A_1\) and \(A_2\), and \(54^{|B {\setminus } A|}\) possible \(A_3\).
By Proposition 3.6, there exists \(C_Q\) such that, after taking expectations in (3.10) and using that \(|A| + |B {\setminus } A| = |B|\), we obtain

Thus, choosing
yields (3.1) with \(C_P= \frac{C_\delta }{2}\). This completes the proof.
3.4 Exchanging the block averaged field for the phase label
We now show that Propositions 3.2 and 3.6 allow one to reduce the problem of analysing the block averaged field to that of analysing the phase label. The main difficulty here is dealing with large fields, i.e. those \({\phi }\) for which \(\int _{{\mathcal {B}}} |{\phi }|\) is large.
Proposition 3.7
Let \(\delta , \delta ' \in (0,1)\) satisfy \(\delta ' \leqslant \frac{\delta }{2}\). Then, there exists \(\beta _0 = \beta _0(\delta ,\eta )>0\), \(C=C(\delta , \beta _0, \eta )>0\) and \(N_0=N_0(\delta )>0\) such that, for all \(\beta > \beta _0\) and \(N \in 4{\mathbb {N}}\) with \(N>N_0\),
where \(\sigma \) is the phase label of precision \(\delta ' \leqslant \frac{\delta }{2}\).
Proof
Observe that
By Proposition 3.2, there exists \(\beta _0>0\) and \(C_P>0\) such that, for \({\sqrt{\beta }}> \max \Big (\sqrt{\beta _0}, \frac{16 \log 2}{C_P\delta } \Big ) \),
Now consider the first term on the right hand side of (3.12). We decompose one step further:
where
We show that \(T_1 = \emptyset \) and that
for some constant \(C=C(\delta )>0\) and for \(\beta \) sufficiently large. Combining these estimates with (3.13) completes the proof.
First, we treat \(T_1\). On good blocks \(|\phi _i - \sigma |\) is bounded by the \({\sqrt{\beta }}\) multiplied by the precision of the phase label (\(\delta ' \leqslant \frac{\delta }{2}\) in this instance) and \(\sigma = 0\) on bad blocks. Therefore, on the set \(\Big \{ \int _{{\mathcal {B}}} |{\phi }| dx \leqslant \frac{\delta }{2} {\sqrt{\beta }}N^3\Big \}\), we have:
which shows that the first condition in \(T_1\) is inconsistent with the second, so \(T_1 = \emptyset \).
We turn our attention to \(T_2\). Fix \(B \subset {{\mathbb {B}}_N}\). By Chebyschev’s inequality, Young’s inequality, and Proposition 3.6, there exists \(\beta _0>0\) and \(C_Q>0\) such that, for \(\beta > \beta _0\),

Therefore,
Taking
yields (3.14) with \(C=\frac{3\delta }{16}\). \(\quad \square \)
3.5 Proof of the main result
Adapting an argument from [Bod02], we reduce the proof of Theorem 1.2 to bounding the probability that \({\phi }\) is far from \(\pm {\sqrt{\beta }}\)-valued functions on \({{\mathbb {B}}_N}\) whose boundary (between regions of opposite spins) is of certain fixed area. Proposition 3.7 then allows us to go from analysing \({\phi }\) to the phase label, for which we use existing results from [BIV00].
For any \(B \subset {{\mathbb {B}}_N}\), let \(\partial B\) denotes its boundary, which is given by the union of faces of blocks in B. Let \(|\partial B| = \int _{\partial B} 1 ds(x)\), where ds(x) is the 2D Hausdorff measure (normalised so that faces have unit area). Thus, \(|\partial B|\) is the number of faces in \(\partial B\).
For any \(a > 0\), let \(C_a\) be the set of functions \(f \in \{ \pm 1\}^{{\mathbb {B}}_N}\) such that \(|\partial \{ f = +1\}|\leqslant aN^2\). For any \(\delta > 0\), let \({\mathfrak {B}}(C_a,\delta )\) be the set of integrable functions g on \({\mathbb {T}}_N\) such that there exists \(f \in C_a\) that satisfies \(\int _{{\mathbb {T}}_N}|g-f| dx \leqslant \delta N^3\).
Proposition 3.8
Let \(\delta , \delta ' \in (0,1)\) satisfy \(\delta ' \leqslant \delta \). Then, there exists \(\beta _0 = \beta _0(\delta ,\eta )>0\) and \(C=C(\delta ,\beta _0,\eta )>0\) such that, for all \(\beta > \beta _0\), the following estimate holds: for all \(a>0\), there exists \(N_0 = N_0(a,\delta ) \geqslant 4\) such that, for all \(N > N_0\) dyadic,
where \(\sigma \) is the phase label of precision \(\delta '\).
Proof
See [BIV00, Theorem 2.2.1] where Proposition 3.8 is proven for a more general class of phase labels that satisfy a Peierls’ type estimate such as the one in Proposition 3.2. We give a self-contained proof for our setting in Sect. 3.6. \(\quad \square \)
The following lemma is our main geometric tool. It is a weak form of the isoperimetric inequality on \({\mathbb {T}}_N\), although it can be reformulated in arbitrary dimension. Its proof is a standard application of Sobolev’s inequality and we include it for the reader’s convenience.
Lemma 3.9
There exists \(C_I>0\) such that the following estimate holds for every \(N \in {\mathbb {N}}\):
for every \(f \in \{\pm 1 \}^{{\mathbb {B}}_N}\).
Proof
Let \(\theta \in C^\infty _c({\mathbb {R}}^3)\) be rotationally symmetric with \(\int _{{\mathbb {R}}^3} \theta dx = 1\). By Sobolev’s inequality, there exists C such that, for every \(\varepsilon \),
where \(f_\varepsilon = f *\varepsilon ^{-3} \theta ( \varepsilon ^{-1} \cdot )\) and \(c_\varepsilon = \frac{1}{N^3} \int _{{\mathbb {T}}_N}f_\varepsilon dx\). Note that C is independent of N by scaling.
Letting \(\varepsilon \rightarrow 0\) in the left hand side of (3.16), we obtain
where \(c = \frac{ |\{ f = 1 \}| - |\{ f = -1 \}|}{N^3}\). Note that \(c\in [-1,1]\).
Without loss of generality, assume \(c\geqslant 0\). This implies that \(|\{ f = 1 \}| \geqslant \{ f = -1 \}|\). Then, evaluating the integral on the righthand side of (3.17), we find that
where we have used that the function
has minimum at \(c=0\) on the interval [0, 1].
For the term on the right hand side of (3.16), using duality we obtain
where \(|\cdot |_\infty \) denotes the supremum norm on \(C^\infty ({\mathbb {T}}_N,{\mathbb {R}}^3)\).
For any such \({\mathbf {g}}\), using integration by parts and commuting the convolution with differentiation,
where the \({\mathbf {g}}_\varepsilon \) is interpreted as convolving each component of \({\mathbf {g}}\) with \(\varepsilon ^{-3} \theta (\varepsilon ^{-1}\cdot )\) separately.
Hence, by the divergence theorem, Young’s inequality for convolutions, and using the supremum norm bound on \({\mathbf {g}}\),
where \({\hat{n}}\) denotes the unit normal to \(\partial \{ f = 1 \}\) pointing into \(\{ f = -1\}\).
Inserting (3.21) in (3.19) implies that, for any \(\varepsilon \),
Thus, by inserting (3.22), (3.17) and (3.18) into (3.16), we obtain
\(\square \)
Proof (Proof of Theorem 1.2)
Let \(\zeta \in (0,1)\). Choose \(a>0\) and \(\delta \in (0,1)\) such that
where \(C_I\) is the same constant as in Lemma 3.9. We first show that
Assume \(\frac{1}{{\sqrt{\beta }}} {\phi }\in {\mathfrak {B}}(C_a,\delta ).\) Then, there exists \(f \in C_a\) such that
This implies
from which we deduce, together with Lemma 3.9,
Since \(f \in C_a\), we obtain
by (3.23).
Hence,
Taking complements establishes (3.24).
Now let \(\sigma \) be the phase label of precision \(\frac{\delta }{2}\). Note that
Applying Proposition 3.7, Proposition 3.8, and using (3.24) finishes the proof. \(\quad \square \)
3.6 Proof of Proposition 3.8
For any \(B \subset {{\mathbb {B}}_N}\), let \(\partial ^* B\) be the set of blocks in B with \(*\)-neighbours in \({\mathbb {T}}_N{\setminus } B\). Note that this is not the same as \(\partial B\), which was defined earlier. Let \({\mathcal {D}}\) be the set of \(*\)-connected components of \(\partial ^* ({\mathbb {T}}_N{\setminus } {\mathcal {M}}_G)\). We call this the set of defects. Necessarily, any \(\Gamma \in {\mathcal {D}}\) satisfies \(\Gamma \subset {\mathcal {B}}\).
Fix \(\gamma \in (0, 1)\). Let \({\mathcal {D}}^\gamma \subset {\mathcal {D}}\) be the set of \(\Gamma \in {\mathcal {D}}\) such that \(|\Gamma | \leqslant 6 N^\gamma \). The elements of \({\mathcal {D}}^\gamma \) are called \(\gamma \)-small defects and the elements of \({\mathcal {D}}{\setminus } {\mathcal {D}}^\gamma \) are called \(\gamma \)-large defects.
Take any \(\Gamma \in {\mathcal {D}}^\gamma \). Recall that we identify \(\Gamma \) with the subset of \({\mathbb {T}}_N\) given by the union of blocks in \(\Gamma \). Write \(\mathrm {Cl}(\Gamma )\) for its closure in \({\mathbb {T}}_N\). The condition \(\gamma < 1\) ensures that, provided N is taken sufficiently large depending on \(\gamma \), any \(\Gamma \in {\mathcal {D}}^\gamma \) is contained in a (translate of a) sphere of radius \(\frac{N}{4}\) in \({\mathbb {T}}_N\). Let \(\mathrm {Ext}(\Gamma )\) be the unique connected component of \({\mathbb {T}}_N{\setminus } \mathrm {Cl}(\Gamma )\) that intersects with the complement of this sphere. Let \(\mathrm {Int}(\Gamma ) = {\mathbb {T}}_N{\setminus } \mathrm {Ext}(\Gamma )\). We identify \(\mathrm {Ext}(\Gamma )\) and \(\mathrm {Int}(\Gamma )\) with their representations as subsets of \({{\mathbb {B}}_N}\). Note that \(\Gamma \subset \mathrm {Int}(\Gamma )\) and generically the inclusion strict, e.g. when \(\Gamma \) encloses a region.
Let \({\mathcal {D}}^{\gamma ,\max }\) be the set of \(\Gamma \in {\mathcal {D}}^{\gamma }\) such that \(\Gamma \bigcap \mathrm {Int}({\tilde{\Gamma }}) = \emptyset \) for any \({\tilde{\Gamma }} \in {\mathcal {D}}^\gamma {\setminus } \{ \Gamma \}\). In other words, \({\mathcal {D}}^{\gamma ,\max }\) is the set of \(\gamma \)-small defects that are not contained in the interior of any other \(\gamma \)-small defects, and we call these maximal \(\gamma \)-small defects.
We define two events, one corresponds to the total surface area of \(\gamma \)-large defects being small and the other corresponding to the total volume contained within maximal \(\gamma \)-small defects being small. Let
We now show that for \(\phi \in S_1 \cap S_2 \cap \{|{\mathcal {B}}| < \frac{\delta }{2} N^3\}\), we have \(\frac{1}{{\sqrt{\beta }}}\sigma \in {\mathfrak {B}}(C_a,\delta )\).
We obtain a \(\pm {\sqrt{\beta }}\)-valued spin configuration from \(\sigma \) by erasing all \(\gamma \)-small defects in two steps: First, we reset the values on bad blocks to \({\sqrt{\beta }}\). Define \(\sigma _1 \in \{ \pm {\sqrt{\beta }}\}^{{\mathbb {B}}_N}\) by  if
if  , otherwise
, otherwise  . Second, define \(\sigma _2\in \{\pm {\sqrt{\beta }}\}^{{\mathbb {B}}_N}\) as follows: Given
. Second, define \(\sigma _2\in \{\pm {\sqrt{\beta }}\}^{{\mathbb {B}}_N}\) as follows: Given  for some \(\Gamma \in {\mathcal {D}}^{\gamma ,\max }\), let
for some \(\Gamma \in {\mathcal {D}}^{\gamma ,\max }\), let  , where
, where  is any block in \(\mathrm {Ext}(\Gamma )\) that is \(*\)-neighbours with a block in \(\Gamma \). Note that the second step is well-defined since the first step ensures that every block in \(\mathrm {Ext}(\Gamma )\) that is \(*\)-neighbours with \(\Gamma \) has the same value. See Figure 1 for an example of this procedure.
is any block in \(\mathrm {Ext}(\Gamma )\) that is \(*\)-neighbours with a block in \(\Gamma \). Note that the second step is well-defined since the first step ensures that every block in \(\mathrm {Ext}(\Gamma )\) that is \(*\)-neighbours with \(\Gamma \) has the same value. See Figure 1 for an example of this procedure.
From the definition of \(S_1\) and using that the factor 6 in the definition of \(\gamma \)-small defects accounts for the discrepancy between \(|\partial \cdot |\) and \(|\partial ^*\cdot |\),
yielding \(\frac{1}{{\sqrt{\beta }}}\sigma _2 \in C_a\). Then, from the definition of \(S_2\) and using the smallness assumption on the number of bad blocks,
which establishes that \(\frac{1}{{\sqrt{\beta }}}\sigma \in {\mathfrak {B}}(C_a,\delta )\).
We deduce that the event \(\Big \{ \frac{1}{{\sqrt{\beta }}}\sigma \not \in {\mathfrak {B}}(C_a,\delta ) \Big \}\) necessarily implies one of three things: either there are many bad blocks; or, the total surface area of \(\gamma \)-large defects is large; or, the density of \(\gamma \)-small defects is high. That is,
Proposition 3.2 gives control on the first event. The other two are controlled by the following lemmas.
Lemma 3.10
Let \(\gamma ,\delta \in (0,1)\). Then, there exists \(\beta _0=\beta _0(\gamma ,\delta ,\eta )>0\) and \(C=C(\gamma ,\delta ,\beta _0,\eta )>0\) such that, for all \(\beta > \beta _0\), the following holds: for any \(a > 0\), there exists \(N_0 = N_0(\gamma ,a)>0\) such that, for any \(N \in 4{\mathbb {N}}\) with \(N > N_0\),
where the underlying phase label is of precision \(\delta \).
Proof
We give a proof based on arguments from [DKS92, Theorem 6.1] in Sect. 3.6.1. \(\quad \square \)
Lemma 3.11
Let \(\gamma ,\delta ,\delta ' \in (0,1)\). Then, there exists \(\beta _0=\beta _0(\gamma ,\delta ,\delta ',\eta )>0\), \(C=C(\gamma ,\delta , \delta ',\beta _0,\eta )>0\) and \(N_0=N_0(\gamma , \delta ) \geqslant 4\) such that, for all \(\beta > \beta _0\) and \(N > N_0\) dyadic,
where the underlying phase label is of precision \(\delta '\).
Proof
See [BIV00, Section 5.1.3] for a proof in a more general setting. We give an alternative proof in Sect. 3.6.2 that avoids the use of techniques from percolation theory. \(\quad \square \)
As in (3.13), by Proposition 3.2 there exists \(C_P > 0\) such that
provided \({\sqrt{\beta }}> \frac{4\log 2}{\delta C_P}\).
Therefore, from (3.25), (3.26), Lemma 3.10 and Lemma 3.11, there exists \(C>0\) such that
Taking \(\gamma < \frac{1}{3}\) and N sufficiently large completes the proof. All that remains is to show Lemmas 3.10 and 3.11.
3.6.1 Proof of Lemma 3.10
By a union bound
where\(\{ \Gamma _i \}\) refers to a non-empty set of distinct \(*\)-connected subsets of \({{\mathbb {B}}_N}\).
By Proposition 3.2 there exists \(C_P\) such that, for any \(\{ \Gamma _i \}\),

Inserting this into (3.27) and using the trivial estimate \(\sum |\Gamma _i| \geqslant \frac{1}{2} aN^2 + \frac{1}{2} \sum |\Gamma _i|\),
Summing first over the number of elements in \(\{ \Gamma _i \}\) and then the number of \(*\)-connected regions containing a fixed number of blocks,
provided \({\sqrt{\beta }}> \max \Big ( \frac{4\log 27}{C_P}, \frac{4\log 2}{C_P} \Big ) = \frac{4 \log 27}{C_P} \) (note that the condition arises so that \(e^{-\frac{C_P}{4} {\sqrt{\beta }}} < \frac{1}{2}\), so that the geometric series with this rate is bounded by 1).
For any \(\gamma > 0\), the final series in (3.29) is summable provided \(N^\gamma > \log N\) and \({\sqrt{\beta }}> \frac{24}{C_P}\), thereby finishing the proof.
3.6.2 Proof of Lemma 3.11
Choose \( 2 N^\gamma \leqslant K \leqslant 4 N^\gamma \) such that K divides N. Such a choice is possible since we take N to be a sufficiently large dyadic. Let

Elements of \({\mathbb {B}}_N^K\) are called K-blocks.
We say that two distinct K-blocks are \(*_K\)-neighbours if their corresponding midpoints are of distance at most \(K\sqrt{3}\). We define the \(*_K\)-connected ball around  to be the set containing itself and its \(*_K\)-neighbours. As in the proof of Proposition 3.2, we can decompose \({\mathbb {B}}_N^K = \bigcup _{l=1}^{27} {\mathbb {B}}_N^{K,l}\) such that any \(*_K\)-connected ball in \({\mathbb {B}}_N^K\) contains exactly one K-block from each element of the decomposition.
to be the set containing itself and its \(*_K\)-neighbours. As in the proof of Proposition 3.2, we can decompose \({\mathbb {B}}_N^K = \bigcup _{l=1}^{27} {\mathbb {B}}_N^{K,l}\) such that any \(*_K\)-connected ball in \({\mathbb {B}}_N^K\) contains exactly one K-block from each element of the decomposition.
For each  , distinguish the unit block
, distinguish the unit block  . For every \(h \in \{0,\dots ,K-1\}^3\), let \(\tau _h\) be the translation map on \({{\mathbb {B}}_N}\) induced from the translation map on \({\mathbb {T}}_N\). We identify
. For every \(h \in \{0,\dots ,K-1\}^3\), let \(\tau _h\) be the translation map on \({{\mathbb {B}}_N}\) induced from the translation map on \({\mathbb {T}}_N\). We identify  . Denote the set of distinguished unit blocks in \({\mathbb {B}}_N^K\) (respectively, \({\mathbb {B}}_N^{K,l}\)) as \({\mathbb {U}}{\mathbb {B}}_N^K\) (respectively, \({\mathbb {U}}{\mathbb {B}}_N^{K,l}\)).
. Denote the set of distinguished unit blocks in \({\mathbb {B}}_N^K\) (respectively, \({\mathbb {B}}_N^{K,l}\)) as \({\mathbb {U}}{\mathbb {B}}_N^K\) (respectively, \({\mathbb {U}}{\mathbb {B}}_N^{K,l}\)).
By our choice of K, \(\mathrm {Int}(\Gamma )\) is entirely contained in a translation of a K-block for any \(\Gamma \in {\mathcal {D}}^\gamma \). As a result, \(\mathrm {Int}(\Gamma )\) intersects at most one K-block in \({\mathbb {B}}_N^{K,l}\) for any fixed l.
Using the correspondence between K-blocks and unit blocks described above, we have

Hence,

where the maximum is over \(h \in \{0,\dots ,K-1\}^3\) and \(1\leqslant l \leqslant 27\).
Let \(E_k\) be the event that precisely k indicator functions appearing on the right hand side of (3.30) are nonzero. In other words, \(E_k\) is the event that there are k distinct defects of size at most \(N^\gamma \) such that the k distinct  , where
, where  , are contained in their interiors.
, are contained in their interiors.
Given a block there are \(27 \cdot 26^{n-1}\) possible defects of size n that contain this block. Thus, by Proposition 3.2, there exists \(C_P\) such that
provided e.g. \({\sqrt{\beta }}> \max \Big ( \frac{4\log 27}{C_P}, \frac{2\log 2}{C_P} \Big ) = \frac{4\log 27}{C_P}\). This estimate is uniform over the choice of h and l.
By a union bound on (3.30), using (3.31), and that \(2N^\gamma \leqslant K \leqslant 4N^\gamma \),
provided \(\gamma \log N < N^{3-3\gamma }\) and \({\sqrt{\beta }}> \frac{81 \cdot 32 + 4\log 2}{\delta C_P}\). Taking logarithms and dividing by \(N^2\) completes the proof.
4 Boué–Dupuis Formalism for \(\phi ^4_3\)
In this section we introduce the underlying framework that we build on to analyse expectations of certain random variables under \({\nu _{\beta ,N}}\), as required in the proof of Proposition 3.6. This framework was originally developed in [BG19] to show ultraviolet stability for \(\phi ^4_3\) and identify its Laplace transform.
In particular, we want to obtain estimates on expectations of the form \(\langle e^{Q_K} \rangle _{\beta ,N,K}\), where \(Q_K\) are random variables that converge (in an appropriate sense) to some random variable Q of interest. We always work with a fixed ultraviolet cutoff K and establish estimates on \(\langle e^{Q_K} \rangle _{\beta ,N,K}\) that are uniform in K: this requires handling of ultraviolet divergences. The first observation is that we can represent such expectations as a ratio of Gaussian expectations:
where we recall \({\mathbb {E}}_N\) denotes expectation with respect to \(\mu _N\) and \({\mathscr {Z}}_{\beta ,N,K} = {\mathbb {E}}_N e^{-{\mathcal {H}}_{\beta ,N,K}(\phi _K)}\) is the partition function.
We then introduce an auxiliary time variable that continuously varies the ultraviolet cutoff between 0 and K, and use it to represent these Gaussian expectations in terms of expectations of functionals of finite dimensional Brownian motions. This allows us to use the Boué–Dupuis variational formula given in Proposition 4.7 to write these expectations in terms of a stochastic control problem. Hence, the problem of obtaining bounds is translated into choosing appropriate controls. An insight made in [BG19] is that one can use methods developed in the context of singular stochastic PDEs, specifically the paracontrolled calculus approach of [GIP15], within the control problem to kill ultraviolet divergences.
Remark 4.1
In the following, we make use of tools in Appendices A and A concerning Besov spaces and paracontrolled calculus. In addition, for the rest of Sects. 4 and 5 , we consider \(N \in {\mathbb {N}}\) fixed and drop it from notation when clear.
4.1 Construction of the stochastic objects
Fix \(\kappa _0 > 0\) sufficiently small. We equip \(\Omega = C({\mathbb {R}}_+; {\mathcal {C}}^{-\frac{3}{2} -\kappa _0})\) with its Borel \(\sigma \)-algebra. Denote by \({\mathbb {P}}\) the probability measure on \(\Omega \) under which the coordinate process \(X_{\bullet }=(X_k)_{k \geqslant 0}\) is an \(L^2\) cylindrical Brownian motion. We write \({\mathbb {E}}\) to denote expectation with respect to \({\mathbb {P}}\). We consider the filtered probability space \((\Omega , {\mathcal {A}}, ({\mathcal {A}}_k)_{k \geqslant 0},{\mathbb {P}})\), where \({\mathcal {A}}\) is the \({\mathbb {P}}\)-completion of the Borel \(\sigma \)-algebra on \(\Omega \), and \(({\mathcal {A}}_k)_{k \geqslant 0}\) is the natural filtration induced by X and augmented with \({\mathbb {P}}\)-null sets of \({\mathcal {A}}\).
Given \(n \in (N^{-1}{\mathbb {Z}})^3\), define the process \(B^n_\bullet \) by \(B^n_k = \frac{1}{N^\frac{3}{2}} \int _{{\mathbb {T}}_N}X_k e_{-n} dx\), where \(e_n(x) = e^{2\pi i n \cdot x}\) and we recall that the integral denotes duality pairing between distributions and test functions. Then, \(\{B^n_\bullet : n \in (N^{-1}{\mathbb {Z}})^3\}\) is a set of complex Brownian motions defined on \((\Omega , {\mathcal {A}}, ({\mathcal {A}}_k)_{k \geqslant 0},{\mathbb {P}})\), independent except for the constraint \(\overline{B_k^n} = B_k^{-n}\). Moreover,
where \({\mathbb {P}}\)-almost surely the sum converges in \({\mathcal {C}}^{-\frac{3}{2} - \kappa _0}\).
Let \({\mathcal {J}}_k\) be the Fourier multiplier with symbol
where \(\rho _k\) is the ultraviolet cutoff defined in Sect. 2 and we recall \(\langle \cdot \rangle = \sqrt{\eta + 4\pi ^2|\cdot |^2}\). \({\mathcal {J}}_k\) arises from a continuous decomposition of the covariance of the pushforward measure \(\mu _N\) under \(\rho _k\):
where \({\mathcal {F}}\) denotes the Fourier transform and \({\mathcal {F}}^{-1}\) denotes its inverse (see “Appendix A”). Note that the function \(\partial _k \rho _k^2\) has decay of order \(\langle k \rangle ^{-\frac{1}{2}}\) and the corresponding multiplier is supported frequencies satisfying \(|n| \in (c_\rho k, C_\rho k)\) for some \(c_\rho < C_\rho \). Thus, we may think of \({\mathcal {J}}_k\) as having the same regularising properties as the multiplier  ; precise statements are given in Proposition A.9.
; precise statements are given in Proposition A.9.
Define the process  by
by

 is a centred Gaussian process with covariance:
is a centred Gaussian process with covariance:

for any \(f,g \in L^2\). Thus, the law of  is the law of \(\rho _k \phi \) where \(\phi \sim \mu _N\). As with other processes in the following, we simply write
is the law of \(\rho _k \phi \) where \(\phi \sim \mu _N\). As with other processes in the following, we simply write  .
.
4.1.1 Renormalised multilinear functions of the free field
The second, third, and fourth Wick powers of  are the space-stationary stochastic processes
are the space-stationary stochastic processes  defined by:
defined by:

where we recall from Sect. 2 that  . Note that
. Note that  , and
, and  are equal in law to \(:\phi _k^2:, :\phi _k^3:\), and \(:\phi _k^4:\), respectively.
are equal in law to \(:\phi _k^2:, :\phi _k^3:\), and \(:\phi _k^4:\), respectively.
The Wick powers of  can be expressed as iterated integrals using Itô’s formula (see [Nua06, Section 1.1.2]). We only need the iterated integral representation
can be expressed as iterated integrals using Itô’s formula (see [Nua06, Section 1.1.2]). We only need the iterated integral representation  :
:

where we have used the convention that sums over frequencies \(n_i\) range over \((N^{-1}{\mathbb {Z}})^3\).
We define additional space-stationary stochastic processes  by
by

We make two observations: first, a straightforward calculation shows that  diverges in variance as \(k \rightarrow \infty \). However, due to the presence of \({\mathcal {J}}_k\),
diverges in variance as \(k \rightarrow \infty \). However, due to the presence of \({\mathcal {J}}_k\),  can be made sense of as \(k \rightarrow \infty \). See Lemma 4.6.
can be made sense of as \(k \rightarrow \infty \). See Lemma 4.6.
Second,  ,
,  , and
, and  are renormalised resonant products of
are renormalised resonant products of  ,
,  , and
, and  , respectively. The latter products are classically divergent in the limit \(k \rightarrow \infty \). We refer to Remark 4.2 for an explanation of why the resonant product is used.
, respectively. The latter products are classically divergent in the limit \(k \rightarrow \infty \). We refer to Remark 4.2 for an explanation of why the resonant product is used.
Remark 4.2
Let \(f \in {\mathcal {C}}^{s_1}\) and \(g \in {\mathcal {C}}^{s_2}\) for \(s_1< 0 < s_2\). Bony’s decomposition states that, if the product exists,  and is of regularity \(s_1\) (see Appendix A). Since paraproducts are always well-defined (see Proposition A.5), the resonant product contains all of the difficulty in defining the product. However, the resonant product gives regularity information of order \(s_1 + s_2\) (see Proposition A.6), which is strictly stronger than the regularity information of the product: i.e. the bound on
and is of regularity \(s_1\) (see Appendix A). Since paraproducts are always well-defined (see Proposition A.5), the resonant product contains all of the difficulty in defining the product. However, the resonant product gives regularity information of order \(s_1 + s_2\) (see Proposition A.6), which is strictly stronger than the regularity information of the product: i.e. the bound on  is strictly stronger than the bound on \(\Vert fg \Vert _{{\mathcal {C}}^{s_1}}\). This is the key property that makes paracontrolled calculus useful in this context [GIP15].
is strictly stronger than the bound on \(\Vert fg \Vert _{{\mathcal {C}}^{s_1}}\). This is the key property that makes paracontrolled calculus useful in this context [GIP15].
The required renormalisations of  and
and  are related to the usual “sunset” diagram appearing in the perturbation theory for \(\phi ^4_3\),
are related to the usual “sunset” diagram appearing in the perturbation theory for \(\phi ^4_3\),

See [Fel74, Theorem 1]. We emphasise that  depends on \(\eta , N\) and k.
depends on \(\eta , N\) and k.
By the fundamental theorem of calculus, the Leibniz rule, and symmetry,

Thus, the renormalisations of  and
and  are given by
are given by  and
and  , respectively.
, respectively.
Remark 4.3
It is straightforward to verify that there exists \(C=C(\eta )>0\) such that

Let  . We refer to the coordinates of \(\Xi \) as diagrams. The following proposition gives control over arbitrarily high moments of diagrams in Besov spaces.
. We refer to the coordinates of \(\Xi \) as diagrams. The following proposition gives control over arbitrarily high moments of diagrams in Besov spaces.
Proposition 4.4
For any \(p,p' \in [1,\infty )\), \(q \in [1,\infty ]\), and \(\kappa > 0\) sufficiently small, there exists \(C=C(p,p',q,\kappa ,\eta )>0\) such that

Proof
See [BG19, Lemma 24]. \(\quad \square \)
Remark 4.5
The constant on the righthand side of (4.5) is independent of N because our Besov spaces are defined with respect to normalised Lebesgue measure  (see Appendix A). For \(p=\infty \), bounds that are uniform in N do not hold. Indeed, for \(L^\infty \)-based norms, there is in general no chance of controlling space-stationary processes uniformly in the volume. Thus, we cannot work in Besov-Hölder spaces.
(see Appendix A). For \(p=\infty \), bounds that are uniform in N do not hold. Indeed, for \(L^\infty \)-based norms, there is in general no chance of controlling space-stationary processes uniformly in the volume. Thus, we cannot work in Besov-Hölder spaces.
We prove the bound in (4.5) for  since it illustrates the role of \({\mathcal {J}}_k\), is used later in the proof of Proposition 5.23, and gives the reader a flavour of how to prove the bounds on the other diagrams.
since it illustrates the role of \({\mathcal {J}}_k\), is used later in the proof of Proposition 5.23, and gives the reader a flavour of how to prove the bounds on the other diagrams.
Lemma 4.6
There exists \(C=C(\eta )>0\) such that, for any \(n \in (N^{-1}{\mathbb {Z}})^3\),

As a consequence, for every \(p \in [1,\infty )\) and \(s < \frac{1}{2}\), there exists \(C=C(p,s,\eta )>0\) such that

Proof
Inserting (4.3) in the definition of  and switching the order of integration,
and switching the order of integration,

Therefore, by Itô’s formula,

where we have performed the \(k_2\) and \(k_3\) integrations, and used that \(|\rho _k| \leqslant 1\).
Recall that \(\partial _{k'} \rho _{k'}^2\) is supported on frequencies \(| n | \in (c_\rho k', C_\rho k')\). Hence, for any \(\kappa > 0\),
where \(\lesssim \) means \(\leqslant \) up to a constant depending only on \(\eta \), \(c_\rho \) and \(C_\rho \); the last inequality uses standard bounds on discrete convolutions contained in Lemma A.12; and we have used that the double convolution produces a volume factor of \(N^6\). Note that, as said in Sect. 2, we omit the dependence on \(c_\rho \) and \(C_\rho \) in the final bound.
By Fubini’s theorem, Nelson’s hypercontractivity estimate [Nel73] (or the related Burkholder-Davis-Gundy inequality [RY13, Theorem 4.1]), and space-stationarity

where \(\Delta _j\) is the j-th Littlewood-Paley block defined in Appendix A and we recall  .
.
We overload notation and also write \(\Delta _j\) to mean its corresponding Fourier multiplier. Then, by space-stationarity, for any \(j \geqslant -1\),

Inserting (4.10) into (4.9) we obtain

which converges provided \(s < \frac{1}{2}\), thus finishing the proof. \(\quad \square \)
4.2 The Boué–Dupuis formula
Fix an ultraviolet cutoff K. Recall that we are interested in Gaussian expectations of the form
where \({\mathcal {H}}(\phi _K) = {\mathcal {H}}_{\beta ,N,K}(\phi _K) + Q_K(\phi _K)\).
We may represent such expectations on \((\Omega , {\mathcal {A}}, ({\mathcal {A}}_k)_{k \geqslant 0}, {\mathbb {P}})\):

The key point is that the righthand side of (4.11) is written in terms of a measurable functional of Brownian motions. This allows us to exploit continuous time martingale techniques, crucially Girsanov’s theorem [RY13, Theorems 1.4 and 1.7], to reformulate (4.11) as a stochastic control problem.
Let \({\mathbb {H}}\) be the set of processes \(v_\bullet \) that are \({\mathbb {P}}\)-almost surely in \(L^2({\mathbb {R}}_+;L^2({\mathbb {T}}_N))\) and progressively measurable with respect to \(({\mathcal {A}}_k)_{k \geqslant 0}\). We call this the space of drifts. For any \(v \in {\mathbb {H}}\), let \(V_\bullet \) be the process defined by
For our purposes, it is sufficient to consider the subspace of drifts \({\mathbb {H}}_K \subset {\mathbb {H}}\) consisting of \(v \in {\mathbb {H}}\) such that \(v_k = 0\) for \(k > K\).
We also work with the subset of bounded drifts \({\mathbb {H}}_{b,K} \subset {\mathbb {H}}_K\), defined as follows: for every \(M \in {\mathbb {N}}\), let \({\mathbb {H}}_{b,M,K}\) be the set of \(v \in {\mathbb {H}}_K\) such that
\({\mathbb {P}}\)-almost surely. Set \({\mathbb {H}}_{b,K} = \bigcup _{M \in {\mathbb {N}}} {\mathbb {H}}_{b,M,K}\).
The following proposition is the main tool of this section.
Proposition 4.7
Let \(N \in {\mathbb {N}}\) and \({\mathcal {H}}:C^\infty ({\mathbb {T}}_N) \rightarrow {\mathbb {R}}\) be measurable and bounded. Then, for any \(K > 0\),

where the infimum can be taken over v in \({\mathbb {H}}_K\) or \({\mathbb {H}}_{b,K}\).
Proof
(4.13) was first established by Boué and Dupuis [BD98], but we use the version in [BD19, Theorem 8.3], adapted to our setting. \(\quad \square \)
We cannot directly apply Proposition 4.7 for the case \({\mathcal {H}}= {\mathcal {H}}_{\beta ,N,K} + Q_K\) because it is not bounded. To circumvent this technicality, we introduce a total energy cutoff \(E \in {\mathbb {N}}\). Since K is taken fixed, \({\mathcal {H}}_{\beta ,N,K} + Q_K\) is bounded from below. Hence, by dominated convergence
We apply Proposition 4.7 to \({\mathcal {H}}= \big ({\mathcal {H}}_{\beta ,N,K} + Q_K\big ) \wedge E\). For the lower bound on the corresponding variational problem, we establish estimates that are uniform over \(v \in {\mathbb {H}}_{b,K}\). For the upper bound, we establish estimates for a specific choice of \(v \in {\mathbb {H}}_K\) which is constructed via a fixed point argument. All estimates that we establish are independent of E. Hence, using (4.14) and the representation (4.11), they carry over to \({\mathbb {E}}_N e^{-{\mathcal {H}}_{\beta ,N,K}(\phi _K) + Q_K(\phi _K)}\). We suppress mention of E unless absolutely necessary.
Remark 4.8
The assumption that \({\mathcal {H}}\) is bounded allows the infimum in (4.13) to be interchanged between \({\mathbb {H}}_K\) and \({\mathbb {H}}_{b,K}\). The use of \({\mathbb {H}}_{b,K}\) allows one to overcome subtle stochastic analysis issues that arise later on: specifically, justifying certain stochastic integrals appearing in Lemmas 5.15 and 5.17 are martingales and not just local martingales. See Lemma 5.14. The additional boundedness condition is important in the lower bound on the variational problem as the only other a priori information that we have on v there is that \({\mathbb {E}}\int _0^K\int _{{\mathbb {T}}_N}v_k^2 dx dk < \infty \), which alone is insufficient. On the other hand, the candidate optimiser for the upper bound is constructed in \({\mathbb {H}}_K\), but it has sufficient moments to guarantee the aforementioned stochastic integrals in Lemma 5.14 are martingales. See Lemma 5.22.
Remark 4.9
A version of the Boué–Dupuis formula for \({\mathcal {H}}\) measurable and satisfying certain integrability conditions is given in [Üst14, Theorem 7]. These integrability conditions are broad enough to cover the cases that we are interested in, and it is required in [BG19] to identify the Laplace transform of \(\phi ^4_3\). However, it is not clear to us that the infimum in the corresponding variational formula can be taken over \({\mathbb {H}}_{b,K}\). Therefore, it seems that the stochastic analysis issues discussed in Remark 4.8 cannot be resolved directly using this version without requiring some post-processing (e.g. via a dominated convergence argument with a total energy cutoff as above).
4.2.1 Relationship with the Gibbs variational principle
Given a drift \(v \in {\mathbb {H}}_K\), we define the measure \({\mathbb {Q}}\) whose Radon-Nikodym derivative with respect to \({\mathbb {P}}\) is given by the following stochastic exponential:
Let \({\mathbb {H}}_{c,K}\) be the set of \(v \in {\mathbb {H}}_K\) such that its associated measure defined in (4.15) is a probability measure, i.e. the expectation of the stochastic integral is 1. Then, by Girsanov’s theorem [RY13, Theorems 1.4 and 1.7 in Chapter VIII] it follows that the process \(X_\bullet \) is a semi-martingale under \({\mathbb {Q}}\) with decomposition:
where \(X^v_\bullet \) is an \(L^2\) cylindrical Brownian motion with respect to \({\mathbb {Q}}\). This induces the decomposition

where  .
.
Lemma 4.10
Let \(N \in {\mathbb {N}}\) and \({\mathcal {H}}:C^\infty ({\mathbb {T}}_N) \rightarrow {\mathbb {R}}\) be measurable and bounded from below. Then, for any \(K > 0\),

where \({\mathbb {E}}_{\mathbb {Q}}\) denotes expectation with respect to \({\mathbb {Q}}\).
Proof
(4.17) is a well-known representation of the classical Gibbs variational principle [DE11, Proposition 4.5.1]. Indeed, one can verify that \(R({\mathbb {Q}}\Vert {\mathbb {P}}) = {\mathbb {E}}_{{\mathbb {Q}}} \Big [ \int _0^\infty \int _{{\mathbb {T}}_N}v_k^2 dx dk\Big ]\), where \(R({\mathbb {Q}}\Vert {\mathbb {P}}) = {\mathbb {E}}_{{\mathbb {Q}}} \log \frac{d{\mathbb {Q}}}{d{\mathbb {P}}}\) is the relative entropy of \({\mathbb {Q}}\) with respect to \({\mathbb {P}}\). A full proof in our setting is given in [GOTW18, Proposition 4.4]. \(\quad \square \)
Proposition 4.7 has several upshots over Lemma 4.10. The most important for us is that drifts can be taken over a Banach space, thus allowing candidate optimisers to be constructed using fixed point arguments via contraction mapping. In addition, the underlying probability space is fixed (i.e. with respect to the canonical measure \({\mathbb {P}}\)), although this is a purely aesthetic advantage in our case. The cost of these upshots is that the minimum in (4.17) is replaced by an infimum in (4.13), and more rigid conditions on \({\mathcal {H}}\) are required. We refer to [BD19, Section 8.1.1] or [BG19, Remark 1] for further discussion.
With the connection with the Gibbs variational principle in mind, we call \({\mathcal {H}}(V_K)\) the drift (potential) energy and we call \(\int _0^K\int _{{\mathbb {T}}_N}v_k^2 dx dk\) the drift entropy.
4.2.2 Regularity of the drift
In our analysis we use intermediate scales between 0 and K. As we explain in Sect. 5.1, this means that we require control over the process \(V_\bullet \) in terms of the drift energy and drift entropy terms in (4.13).
The drift entropy allows a control of \(V_\bullet \) in \(L^2\)-based topologies.
Lemma 4.11
For every \(v \in L^2({\mathbb {R}}_+;L^2({\mathbb {T}}_N))\) and \(K > 0\),

Proof
(4.18) is a straightforward consequence definition of \({\mathcal {J}}_k\), see [BG19, Lemma 2]. \(\quad \square \)
To control the homogeneity in our estimates, we also require bounds on \(\Vert V_\bullet \Vert _{L^4}^4\). This is a problem: for our specific choices of \({\mathcal {H}}\), the drift energy allows a control in \(L^4\)-based topologies at the endpoint \(V_K\). It is in general impossible to control the history of the path by the endpoint (for example, consider an oscillating process \(V_\bullet \) with \(V_K = 0\)). We follow [BG19] to sidestep this issue.
Let \({\tilde{\rho }} \in C^\infty _c({\mathbb {R}}_+;{\mathbb {R}}_+)\) be non-increasing such that
and let \({\tilde{\rho }}_k(\cdot ) = {\tilde{\rho }}(\frac{\cdot }{k})\) for every \(k>0\).
Define the process \(V^\flat _\bullet \) by
Note that \({\mathcal {F}}(V_k^\flat )(n) = {\mathcal {F}}(V_k)(n)\) if \(|n| \leqslant \frac{c_\rho }{2}\). Thus, \(V^\flat _\bullet \) and \(V_\bullet \) have the same low frequency/large-scale behaviour (hence the notation).
The two processes differ on higher frequencies/small-scales. Indeed, as a Fourier multiplier, \({\tilde{\rho }}_k {\mathcal {J}}_k = 0\) for \(k' > k\). Hence, for any \(k \leqslant K\),
This is sufficient for our purposes because \({\tilde{\rho }}_k\) is an \(L^p\) multiplier for \(p \in (1,\infty )\), and hence the associated operator is \(L^p\) bounded for \(p \in (1,\infty )\).
Lemma 4.12
For any \(p \in (1,\infty )\), there exists \(C=C(p,\eta )>0\) such that, for every \(v \in L^2({\mathbb {R}}_+;L^2({\mathbb {T}}_N))\),
Moreover, for any \(s,s' \in {\mathbb {R}}\), \(p \in (1,\infty )\), \(q \in [1,\infty ]\), there exists \(C=C(s,s',p,q,\eta )\) such that, for every \(v \in L^2({\mathbb {R}}_+;L^2({\mathbb {T}}_N))\),
Proof
(4.19) and (4.20) are a consequence of the preceding discussion together with the observation that \(\partial _k V_k^\flat \) is supported on an annulus in Fourier space and, subsequently, applying Bernstein’s inequality (A.6). See [BG19, Lemma 20]. \(\quad \square \)
5 Estimates on Q-Random Variables
The main results of this section are upper bounds on expectations of certain random variables, derived from \(Q_1,Q_2,\) and \(Q_3\) defined in (3.2), that are uniform in \(\beta \) and extensive in \(N^3\).
Proposition 5.1
For every \(a_0 > 0\), there exist \(\beta _0 = \beta _0(a_0,\eta ) \geqslant 1\) and \(C_Q = C_Q(a_0, \beta _0, \eta )>0\) such that the following estimates hold: for all \(\beta > \beta _0\) and \(a \in {\mathbb {R}}\) satisfying \(|a| \leqslant a_0\),

In addition,

where B is any set of unordered pairs of nearest-neighbour blocks that partitions \({{\mathbb {B}}_N}\).
Proof
See Sect. 5.9. \(\quad \square \)
Proposition 5.1 is used in Sect. 6.3, together with the chessboard estimates of Proposition 6.5, to prove Proposition 3.6. Indeed, chessboard estimates allow us to obtain estimates on expectations of random variables, derived from the \(Q_i\), that are extensive in their support from estimates that are extensive in \(N^3\). Note that the latter are significantly easier to obtain than the former since these random variables may be supported on arbitrary unions of blocks.
Remark 5.2
For the remainder of this section, we assume \(\eta < \frac{1}{392 C_P}\) where \(C_P\) is the Poincaré constant on unit blocks (see Proposition A.11). This is for convenience in the analysis of Sects. 5.8.1 and 5.9 (see also Lemma 5.21). Whilst this may appear to fix the specific choice of renormalisation constants \(\delta m^2\), we can always shift into this regime by absorbing a finite part of \(\delta m^2\) into \({\mathcal {V}}_\beta \).
Most of the difficulties in the proof of Proposition 5.1 are contained in obtaining the following upper and lower bounds on the free energy \(-\log {\mathscr {Z}}_{\beta ,N}\) that are uniform in \(\beta \).
Proposition 5.3
There exists \(C=C(\eta )>0\) such that, for all \(\beta \geqslant 1\),
and
Proof
See Sects. 5.8.1 and 5.8.2 for a proof of (5.1) and (5.2), respectively. These proofs rely on Sects. 5.2–5.7, and the overall strategy is sketched in Sect. 5.1. \(\quad \square \)
Remark 5.4
In [BG19] estimates on \(-\log {\mathscr {Z}}_{\beta ,N,K}\) are obtained that are uniform in \(K > 0\) and extensive in \(N^3\). However, one can show that these estimates are \(O(\beta )\) as \(\beta \rightarrow \infty \). This is insufficient for our purposes (compare with the uniform in \(\beta \) estimates required to prove Proposition 3.2).
5.1 Strategy to prove Proposition 5.3
The lower bound on \(-\log {\mathscr {Z}}_{\beta ,N,K}\), given by (5.1), is the harder bound to establish in Proposition 5.3. Our approach builds on the analysis of [BG19] by incorporating a low temperature expansion inspired by [GJS76a, GJS76b]. This is explained in more detail in Sect. 5.1.1.
On the other hand, we establish the upper bound on \(-\log {\mathscr {Z}}_{\beta ,N,K}\), given by (5.2), by a more straightforward modification of the analysis in [BG19]. See Sect. 5.8.2.
We now motivate our approach to establishing (5.1) by first isolating the the difficulty in obtaining \(\beta \)-independent bounds when using [BG19] straight out of the box. The starting point is to apply Proposition 4.7 with \({\mathcal {H}}= {\mathcal {H}}_{\beta ,N,K}\), together with a total energy cutoff that we refrain from making explicit (see Remark 4.8 and the discussion that precedes it), to represent \(-\log {\mathscr {Z}}_{\beta ,N,K}\) as a stochastic control problem.
For every \(v \in {\mathbb {H}}_{b,K}\), define

Ultraviolet divergences occur in the expansion of  since the integrals
since the integrals  and
and  appear and cannot be bounded uniformly in K:
appear and cannot be bounded uniformly in K:
-
For the first integral, there are difficulties in even interpreting
 as a random distribution in the limit \(K \rightarrow \infty \). Indeed, the variance of
as a random distribution in the limit \(K \rightarrow \infty \). Indeed, the variance of  tested against a smooth function diverges as the cutoff is removed.
tested against a smooth function diverges as the cutoff is removed. -
On the other hand, one can show that
 does converge as \(K \rightarrow \infty \) to a random distribution of Besov-Hölder regularity \(-1-\kappa \) for any \(\kappa > 0\) (see Proposition 4.4). However, this regularity is insufficient to obtain bounds on the second integral uniform on K . Indeed, \(V_K\) can be bounded in at most \(H^1\) uniformly in K (see Lemma 4.11), and hence we cannot test
does converge as \(K \rightarrow \infty \) to a random distribution of Besov-Hölder regularity \(-1-\kappa \) for any \(\kappa > 0\) (see Proposition 4.4). However, this regularity is insufficient to obtain bounds on the second integral uniform on K . Indeed, \(V_K\) can be bounded in at most \(H^1\) uniformly in K (see Lemma 4.11), and hence we cannot test  against \(V_K\) (or \(V_K^2\)) in the limit \(K \rightarrow \infty \).
against \(V_K\) (or \(V_K^2\)) in the limit \(K \rightarrow \infty \).
This is where the need for renormalisation beyond Wick ordering appears.
To implement this, we follow [BG19] and postulate that the small-scale behaviour of the drift v is governed by explicit renormalised polynomials of  through the change of variables:
through the change of variables:

where the remainder term \(r=r(v)\) is defined by (5.3). Since \(v \in {\mathbb {H}}_K \supset {\mathbb {H}}_{b,K}\), we have that \(r \in {\mathbb {H}}_K\) and, hence, has finite drift entropy; however, note that \(r \not \in {\mathbb {H}}_{b,K}\). The optimisation problem is then changed from optimising over \(v \in {\mathbb {H}}_{b,K}\) to optimising over \(r(v) \in {\mathbb {H}}_K\).
The change of variables (5.3) means that the drift entropy of any v now contains terms that are divergent as \(K \rightarrow \infty \). One uses Itô’s formula to decompose the divergent integrals identified above into intermediate scales, and then uses these divergent terms in the drift entropy to mostly cancel them. Using the renormalisation counterterms beyond Wick ordering (i.e. the terms involving \(\gamma _K\) and \(\delta _K\)), the remaining divergences can be written in terms of well-defined integrals involving the diagrams  defined in Sect. 4.1.1.
defined in Sect. 4.1.1.
One can then establish that, for every \(\varepsilon >0\), there exists \(C=C(\varepsilon ,\beta ,\eta )>0\) such that, for every \(v \in {\mathbb {H}}_{b,K}\),
where
The quadratic term in \(G_K(v)\) allows one to control the \(H^{\frac{1}{2} -\kappa }\) norm of \(V_K\) for any \(\kappa > 0\), uniformly in K (see Proposition 5.9). These derivatives on \(V_K\) appear when analysing terms in \(\Psi _K(v)\) involving Wick powers of  tested against (powers of) \(V_K\). However, some of these integrals have quadratic or cubic dependence on the drift, thus the quadratic term in \(G_K(v)\) is insufficient to control the homogeneity in these estimates; instead, this achieved by using the quartic term in \(G_K(v)\). Note that the good sign of the quartic term in the \({\mathcal {H}}_{\beta ,N,K}\) ensures that \(G_K(v)\) is indeed non-negative.
tested against (powers of) \(V_K\). However, some of these integrals have quadratic or cubic dependence on the drift, thus the quadratic term in \(G_K(v)\) is insufficient to control the homogeneity in these estimates; instead, this achieved by using the quartic term in \(G_K(v)\). Note that the good sign of the quartic term in the \({\mathcal {H}}_{\beta ,N,K}\) ensures that \(G_K(v)\) is indeed non-negative.
Using the representation (4.11) on \({\mathbb {E}}_N e^{-{\mathcal {H}}_{\beta ,N,K}(\phi _K)}\) and applying Proposition 4.7, one obtains \(-\log {\mathscr {Z}}_{\beta ,N,K} \geqslant - CN^3\) from (5.4) and the positivity of \(G_K(v)\).
As pointed out in Remark 5.4, this argument gives \(C=O(\beta )\) for \(\beta \) large and this is insufficient for our purposes. The suboptimality in \(\beta \)-dependence comes from the treatment of the integral
in  . The choice of \(G_K(v)\) in the preceding discussion is not appropriate in light of (5.5) since the term \(\int _{{\mathbb {T}}_N}V_K^4 dx\) destroys the structure of the non-convex potential \(\int _{{\mathbb {T}}_N}{\mathcal {V}}_\beta (V_K) dx\). On the other hand, replacing \(\frac{1}{\beta }\int _{{\mathbb {T}}_N}V_K^4 dx\) with the whole integral (5.5) in \(G_K(v)\) does not work. This is because (5.5) does not admit a \(\beta \)-independent lower bound.
. The choice of \(G_K(v)\) in the preceding discussion is not appropriate in light of (5.5) since the term \(\int _{{\mathbb {T}}_N}V_K^4 dx\) destroys the structure of the non-convex potential \(\int _{{\mathbb {T}}_N}{\mathcal {V}}_\beta (V_K) dx\). On the other hand, replacing \(\frac{1}{\beta }\int _{{\mathbb {T}}_N}V_K^4 dx\) with the whole integral (5.5) in \(G_K(v)\) does not work. This is because (5.5) does not admit a \(\beta \)-independent lower bound.
5.1.1 Fixing \(\beta \) dependence via a low temperature expansion
We expand (5.5) as two terms
The first integral in (5.6) is non-negative so we use it as a stability/good term for the deterministic analysis, i.e. replacing \(G_K(v)\) by
This requires a comparison of \(L^p\) norms of \(V_K\) for \(p \leqslant 4\) on the one hand, and \(\int _{{\mathbb {T}}_N}{\mathcal {V}}_\beta (V_K) dx\) on the other. Due to the non-convexity of \({\mathcal {V}}_\beta \), this produces factors of \(\beta \); these have to be beaten by the good (i.e. negative) powers of \(\beta \) appearing in  . We state the required bounds in the following lemma.
. We state the required bounds in the following lemma.
Lemma 5.5
For any \(p\in [1,4]\), there exists \(C=C(p) > 0\) such that, for all \(a \in {\mathbb {R}}\),
Hence, for any \(f \in C^\infty ({\mathbb {T}}_N)\),

where we recall  .
.
Proof
(5.8) follows from a straightforward computation. (5.9) follows from using (5.8) and Jensen’s inequality. \(\quad \square \)
The difficulty lies in bounding the second integral in (5.6) uniformly in \(\beta \). In 2D an analogous problem was overcome in [GJS76a, GJS76b] in the context of a low temperature expansion for \(\Phi ^4_2\). Those techniques rely crucially on the logarithmic ultraviolet divergences in 2D, and the mutual absolute continuity between \(\Phi ^4_2\) and its underlying Gaussian measure. Thus, they do not extend to 3D. However, we use the underlying strategy of that low temperature expansion in our approach.
We write \({\mathscr {Z}}_{\beta ,N,K}\) as a sum of \(2^{N^3}\) terms, where each term is a modified partition function that enforces the block averaged field to be either positive or negative on blocks. For each term in the expansion, we change variables and shift the field on blocks to \(\pm {\sqrt{\beta }}\) so that the new mean of the field is small. We then apply Proposition 4.7 to each of these \(2^{N^3}\) terms.
We separate the scales in the variational problem by coarse-graining the resulting Hamiltonian. Large scales are captured by an effective Hamiltonian, which is of a similar form to the second integral in (5.6). We treat this using methods inspired by [GJS76b, Theorem 3.1.1]: the expansion and translation allow us to obtain a \(\beta \)-independent bound on the effective Hamiltonian with an error term that depends only on the difference between the field and its block averages (the fluctuation field). The fluctuation field can be treated using the massless part of the underlying Gaussian measure (compare with [GJS76b, Proposition 2.3.2]).
The remainder term contains all the small-scale/ultraviolet divergences and we renormalise them using the pathwise approach of [BG19] explained above. Patching the scales together requires uniform in \(\beta \) estimates on the error terms from the renormalisation procedure using an analogue of the stability term (5.7) that incorporates the translation, and Lemma 5.5.
5.2 Expansion and translation by macroscopic phase profiles
Let \(\chi _+,\chi _-:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be defined as
They satisfy
and hence

for any  .
.
For any \(K>0\), we expand

where we recall  .
.
We fix \(\sigma \) in what follows and sometimes suppress it from notation. Let \(h = {\sqrt{\beta }}\sigma \). We then have

We translate the Gaussian fields so that their new mean is approximately h. The translation we use is related to the classical magnetism, or response to the external field \(\eta h\), used in the 2D setting [GJS76a] and given by \(\eta (-\Delta +\eta )^{-1} h\).
Lemma 5.6
For every \(K>0\), let \(h_K = \rho _K h\). Define \({\tilde{g}}_K = \eta (-\Delta + \eta )^{-1} h_K\) and \(g_K = \rho _K {\tilde{g}}_K\). Then, there exists \(C=C(\eta )\) such that
where \(| \cdot |_{\infty }\) denotes the supremum norm. Moreover,
Finally, let
where \({\tilde{\rho }}_k\) is as in Sect. 4.2.2. Then, for any \(s,s' \in {\mathbb {R}}\), \(p \in (1,\infty )\) and \(q \in [1,\infty ]\), there exists \(C_1=C_1(\eta ,s,p,q)\) and \(C_2=C_2(\eta ,s,s',p,q)\) such that
and
Proof
The estimate (5.11) follows from the fact that \(\eta (-\Delta + \eta )^{-1}\) and \(\nabla \eta (-\Delta + \eta )^{-1}\) are \(L^\infty \) bounded operators. This is because the (\(\eta \)-dependent) Bessel potential and its first derivatives are absolutely integrable on \({\mathbb {R}}^3\). Hence, by applying Young’s inequality for convolutions one obtains the \(L^\infty \) boundedness. The uniformity of the estimate over \(\sigma \) follows from \(\Vert \sigma \Vert _{L^\infty }=1\) for every \(\sigma \in {{\mathbb {B}}_N}\). The other estimates follow from standard results about smooth multipliers, the observation that \(g_k^\flat = {\tilde{\rho }}_k g_K\) for any \(K \geqslant k\), and Lemma 4.12. \(\quad \square \)
Remark 5.7
Note that \(g_K\) is given by the covariance operator of \(\mu _N\) applied to \(\eta h\). Moreover, note that \(g_K \ne {\tilde{g}}_K\) since \(\rho _K^2 \ne \rho _K\), i.e. the Fourier cutoff is not sharp.
By the Cameron-Martin theorem the density of \(\mu _N\) under the translation \(\phi = \psi + {\tilde{g}}_K\) transforms as
Hence,
where

and
By integration by parts, the self-adjointness of \(\rho _K\), and the definition of \({\tilde{g}}_K\)
Thus, \(F^\sigma _{\beta ,N,K}(\psi )\) is independent of \(\psi \) and non-negative.
Remark 5.8
Let \(g = \eta (-\Delta + \eta )^{-1} h\). Then,
The second integrand on the righthand side of (5.16) penalises the discontinuities of \(\sigma \). Indeed, \(e^{-\int _{{\mathbb {T}}_N}\frac{1}{2} |\nabla g|^2 dx}\) is approximately equal to \(e^{-C{\sqrt{\beta }}|\partial \sigma |}\), where \(\partial \sigma \) denotes the surfaces of discontinuity of \(\sigma \), \(|\partial \sigma |\) denotes the area of these surfaces, and \(C>0\) is an inessential constant. Thus, for \(\beta \) sufficiently large, \({\mathscr {Z}}_{\beta ,N}\) is approximately equal to
where \(\Gamma _i\) are the connected components of \(\partial \sigma \) (called contours). It would be interesting to further develop this contour representation for \({\nu _{\beta ,N}}\) (compare with the 2D expansions of [GJS76a, GJS76b]).
5.3 Coarse-graining of the Hamiltonian
We apply Proposition 4.7 to  . For every \(v \in {\mathbb {H}}_{b,K}\), define
. For every \(v \in {\mathbb {H}}_{b,K}\), define

Let  , where
, where  . We split the Hamiltonian as
. We split the Hamiltonian as

where

is an effective Hamiltonian introduced to capture macroscopic scales of the system. The quantity \({\mathcal {R}}_K\) is then determined by (5.18) and is explicitly given by

All analysis/cancellation of ultraviolet divergences occurs within the sum of \({\mathcal {R}}_K\) and the drift entropy, see (5.27). Finally, the last term in (5.18) is a stability term which is key for our non-perturbative analysis, namely it allows us to obtain estimates that are uniform in the drift.
The key point is that we coarse-grain the field by block averaging  , the most singular term. This allows us to preserve the structure of the low temperature potential \({\mathcal {V}}_\beta \) on macroscopic scales (captured in \({\mathcal {H}}_K^\mathrm {eff}(Z_K)\)), which is crucial to obtaining estimates independent of \(\beta \) on the free energy.
, the most singular term. This allows us to preserve the structure of the low temperature potential \({\mathcal {V}}_\beta \) on macroscopic scales (captured in \({\mathcal {H}}_K^\mathrm {eff}(Z_K)\)), which is crucial to obtaining estimates independent of \(\beta \) on the free energy.
5.4 Killing divergences
5.4.1 Changing drift variables
For any \(v \in {\mathbb {H}}_{b,K}\), define \(r=r(v) \in {\mathbb {H}}_{K}\) by

In our analysis it is convenient to use an intermediate change of variables for the drift. Define \(u=u(v) \in {\mathbb {H}}_K\) by

Inserting (5.19) and (5.20) into the definition of the integrated drift, \(V_k = \int _0^k {\mathcal {J}}_{k'} v_{k'} dk'\), we obtain

where \(R_k = \int _0^k {\mathcal {J}}_{k'} r_{k'} dk'\) and \(U_k = \int _0^k {\mathcal {J}}_{k'} u_{k'} dk'\).
The following proposition contains useful estimates estimates on \(U_K\) and \(V_K\).
Proposition 5.9
For any \(\varepsilon > 0\) and \(\kappa > 0\) sufficiently small, there exists \(C=C(\varepsilon ,\kappa ,\eta ) > 0\) such that, for all \(\beta > 1\),


where we recall  ; and \(N^\Xi _K\) is a positive random variable on \(\Omega \) that is \({\mathbb {P}}\)-almost surely given by a finite linear combination of powers of (finite integrability) Besov and Lebesgue norms of the diagrams
; and \(N^\Xi _K\) is a positive random variable on \(\Omega \) that is \({\mathbb {P}}\)-almost surely given by a finite linear combination of powers of (finite integrability) Besov and Lebesgue norms of the diagrams  on the interval [0, K].
on the interval [0, K].
Proof
See Sect. 5.6.1. \(\quad \square \)
Remark 5.10
As a consequence of Proposition 4.4, the random variable \(N^\Xi _K\) satisfies the following estimate: there exists \(C = C(\eta )>0\) such that
In the following we denote by \(N^\Xi _K\) any positive random variable on \(\Omega \) that satisfies (5.24). In practice it is always \({\mathbb {P}}\)-almost surely given by a finite linear combination of powers of (finite integrability) Besov norms of the diagrams in \(\Xi \) on [0, K]. Note that \(N^\Xi _K\) includes constants of the form \(C=C(\eta )>0\).
5.4.2 The main small-scale estimates
In the following we write \(\approx \) to mean equal up to a term with expectation 0 under \({\mathbb {P}}\).
Proposition 5.11
Let \(\beta > 0\). For every \(K>0\), define

where  is defined in (4.4), and
is defined in (4.4), and

Then, for every \(v \in {\mathbb {H}}_{b,K}\),
where

Moreover, the following estimate holds: for any \(\varepsilon >0\), there exists \(C=C(\varepsilon , \eta )>0\) such that, for all \(\beta > 1\),
where \(N^\Xi _K\) is as in Remark 5.10.
Proof
We establish (5.27) in Sect. 5.5 by arguing as in [BG19, Lemma 5]. The remainder estimates (5.28) are then established in Sect. 5.6. \(\quad \square \)
Remark 5.12
The terms \({\mathcal {R}}^i_K\) are ordered according to their occurrence when isolating divergences for the readers’ convenience. For the estimates, however, it is more convenient to order them according to difficulty. Define
where

and let \({\mathcal {R}}^b_K = \sum _{i=1}^4 {\mathcal {R}}^i_K - {\mathcal {R}}^a_K\).
\({\mathcal {R}}^a_K\) contains the most difficult terms to bound, either due to analytic considerations or \(\beta \)-dependence; \({\mathcal {R}}^b_K\) contains the terms that follow almost immediately from [BG19, Lemmas 18-23].
Remark 5.13
The products  and
and  appearing above are classically ill-defined in the limit \(K \rightarrow \infty \). However, (probabilistic) estimates on the resonant product
appearing above are classically ill-defined in the limit \(K \rightarrow \infty \). However, (probabilistic) estimates on the resonant product  uniform in K are obtained in Proposition 4.4. Hence, the first product can be analysed using a paraproduct decompositions (A.7). The second product is less straightforward and requires a double paraproduct decomposition (see [BG19, Lemma 21 and Proposition 6] and [CC18, Proposition 2.22]).
uniform in K are obtained in Proposition 4.4. Hence, the first product can be analysed using a paraproduct decompositions (A.7). The second product is less straightforward and requires a double paraproduct decomposition (see [BG19, Lemma 21 and Proposition 6] and [CC18, Proposition 2.22]).
5.5 Proof of (5.27): Isolating and cancelling divergences
Using that  and
and  all have expectation zero,
all have expectation zero,

Hence, by reordering terms,

Ignoring the renormalisation counterterms (i.e. those involving \(\gamma _K\) and \(\delta _K\)), the divergences in (5.29) are contained in the integrals  and
and  . In order to kill these divergences, we use changes of variables in the drift entropy to mostly cancel them; the remaining divergences are killed by the renormalisation counterterms. We renormalise the leading order divergences, ie. those polynomial in K, in Sect. 5.5.1. The divergences that are logarithmic in K are renormalised in Sect. 5.5.2.
. In order to kill these divergences, we use changes of variables in the drift entropy to mostly cancel them; the remaining divergences are killed by the renormalisation counterterms. We renormalise the leading order divergences, ie. those polynomial in K, in Sect. 5.5.1. The divergences that are logarithmic in K are renormalised in Sect. 5.5.2.
In order to use the drift entropy to cancel divergences, we decompose certain (spatial) integrals across ultraviolet scales \(k \in [0,K]\) using Itô’s formula. Error terms are produced that are stochastic integrals with respect to martingales (specifically, with respect to  and
and  ). The following lemma allows us to argue that these stochastic integrals are \(\approx 0\).
). The following lemma allows us to argue that these stochastic integrals are \(\approx 0\).
Lemma 5.14
For any \(v \in {\mathbb {H}}_{b,K}\), the stochastic integrals

and

are martingales. We recall that, above, \(\Delta _i\) denotes the i-th Littlewood-Paley block.
Proof
In this proof, for any continuous local martingale \(Z_\bullet \), we write  for the corresponding quadratic variation process. Moreover, for any Z-adapted process \(Y_\bullet \), we write \( \int _0^KY_k \cdot dZ_k\) to denote the stochastic integral \(\int _{{\mathbb {T}}_N}\int _0^KY_k dZ_k dx\).
for the corresponding quadratic variation process. Moreover, for any Z-adapted process \(Y_\bullet \), we write \( \int _0^KY_k \cdot dZ_k\) to denote the stochastic integral \(\int _{{\mathbb {T}}_N}\int _0^KY_k dZ_k dx\).
We begin with two observations: first, let \(v \in {\mathbb {H}}_{b,M,K}\) for some \(M > 0\), i.e. those \(v \in {\mathbb {H}}_{b,K}\) satisfying (4.18). Then, by Sobolev embedding, there exists \(C=C(M,N,K,\eta )>0\) such that
\({\mathbb {P}}\)-almost surely.
Second, recalling the iterated integral representation of the Wick powers  and
and  (see e.g. (4.3)), one can show
(see e.g. (4.3)), one can show  and
and  . Thus, we can write the stochastic integrals (5.30) and (5.31) in terms of stochastic integrals with respect to
. Thus, we can write the stochastic integrals (5.30) and (5.31) in terms of stochastic integrals with respect to  . It suffices to show that their quadratic variations are finite in expectation.
. It suffices to show that their quadratic variations are finite in expectation.
Using that  and by Young’s inequality,
and by Young’s inequality,

Hence, (5.30) is a martingale.
Now consider (5.31). By (5.21),

where

Arguing as for (5.30), one can show  .
.
By Young’s inequality and using that Littlewood-Paley blocks and the \(\flat \) operator are \(L^p\) multipliers, we have

thus establishing that (5.31) is a martingale. \(\quad \square \)
5.5.1 Energy renormalisation
In the next lemma, we cancel the leading order divergence using the change of variables (5.20) in the drift entropy. The error term does not depend on the drift and is divergent in expectation (as \(K \rightarrow \infty \)); it is cancelled by one part of the energy renormalisation \(\delta _K\) (see (5.26)).
Lemma 5.15

Proof
By Itô’s formula, Lemma 5.14, and the self-adjointness of \({\mathcal {J}}_k\),

Hence, by (5.20),

\(\square \)
As a consequence of (5.20), the remaining (non-counterterm) integrals in (5.29) acquire additional divergences that are independent of the drift. We isolate them in the next lemma; they are also renormalised by parts of the energy renormalisation (see (5.26)).
Lemma 5.16

and

Proof
By (5.21),

Above we have used Wick’s theorem and the fact that  is Wick ordered to conclude
is Wick ordered to conclude  .
.
Similarly, 
 . Hence, by (5.21)
. Hence, by (5.21)

Combining (5.34) and (5.35) establishes (5.32).
By (5.21),

where we have used that  and, by Wick’s theorem,
and, by Wick’s theorem,  . This establishes (5.33). \(\quad \square \)
. This establishes (5.33). \(\quad \square \)
The divergences encountered in Lemmas 5.15 and 5.16 that are independent of the drift are killed by the energy renormalisation \(\delta _K\) since, by definition,

5.5.2 Mass renormalisation
The integrals on the righthand side of (5.33) that involve the drift cannot be bounded uniformly as \(K \rightarrow \infty \). We isolate divergences using a paraproduct decomposition and expand the drift entropy using (5.19) to mostly cancel them. This is done in Lemma 5.17. The remaining divergences are then killed in Lemma 5.18 using the mass renormalisation.
Lemma 5.17

Proof
We write

Thus, using (5.21) and a paraproduct decomposition on the most singular products,

All except the first two integrals are absorbed into \({\mathcal {R}}_K^3\).
For the first integral, we use the (drift-dependent) change of variables (5.19) in the drift entropy of u to mostly cancel the divergence. Due to the paraproduct term, using Itô’s formula to decompose into scales requires us to control \(V_k + g_k\) for \(k < K\). In order to be able to do this, we replace \(V_K + g_K\) by \(V_K^\flat + g_K^\flat \) first. Then, applying Itô’s formula, Lemma 5.14, and using the self-adjointness of \({\mathcal {J}}_k\),


Combining (5.38), (5.39), and (5.40) yields (5.37). \(\quad \square \)
We now cancel the divergences in the last two terms of (5.37) using the mass renormalisation.
Lemma 5.18

Proof
By the definition of  (see Sect. 4.1.1),
(see Sect. 4.1.1),

where we have used that, by Wick’s theorem,  .
.
To renormalise the second integral in (5.41), we need to rewrite the remaining counterterm in terms of \(V_K^\flat \):
Using Itô’s formula on the first integral of the right hand side of (5.43),
By the definition of  (see Sect. 4.1.1),
(see Sect. 4.1.1),

Hence, combining (5.42), (5.43), and (5.44) establishes (5.41). \(\quad \square \)
Proof of (5.27)
Lemmas 5.15, 5.16, 5.17, and 5.18 , together with (5.36), establish (5.27). \(\quad \square \)
5.6 Proof of (5.28): Estimates on remainder terms
Recall the definition of \({\mathcal {R}}^a_K\), which contains the most difficult terms to bound, and \({\mathcal {R}}^b_K\) from Remark 5.12.
Proposition 5.19
For any \(\varepsilon > 0\), there exists \(C=C(\varepsilon ,\eta )>0\) such that, for all \(\beta > 1\),
Proof
The estimates (5.45), (5.46), and (5.47) are established in Sects. 5.6.2, 5.6.3, and 5.6.4 respectively. (5.46) and (5.47) are established by a relatively straightforward combination of techniques in [BG19, Lemmas 18-23] together with Lemmas 5.5 and 5.6 . On the other hand, the terms with cubic dependence in the drift (5.45) require a slightly more involved analysis.
Note that, since our norms on functions/distributions were defined using  instead of dx to track N dependence, in the proof we rewrite the integrals above in terms of
instead of dx to track N dependence, in the proof we rewrite the integrals above in terms of  by dividing both sides by \(N^3\). \(\quad \square \)
by dividing both sides by \(N^3\). \(\quad \square \)
Proposition 5.20
For any \(\varepsilon > 0\), there exists \(C=C(\varepsilon ,\eta )>0\) such that, for all \(\beta > 1\),
Proof
Follows from a direct combination of arguments in [BG19, Lemmas 18-23] with Lemmas 5.5 and 5.6 . We omit it. \(\quad \square \)
Proof of (5.28)
Since \(\sum _{i=1}^4 {\mathcal {R}}_K^i = {\mathcal {R}}^a_K + {\mathcal {R}}^b_K\), Propositions 5.19 and 5.20 establish (5.28). \(\quad \square \)
The proofs of Propositions 5.19 and 5.20 rely heavily on bounds on the drift established in Proposition 5.9, so we prove this first in the next subsection. Throughout the remainder of this section, we use the notation \(a \lesssim b\) to mean \(a \leqslant Cb\) for some \(C=C(\varepsilon ,\eta )\), and we also allow for this constant to depend on other inessential parameters (i.e. not \(\beta \), N, or K).
5.6.1 Proof of Proposition 5.9
First, note that (5.23) is a direct consequence of (5.22) along with (5.21) and bounds contained in Proposition 4.4.
We now prove (5.22). Fix any \(k' \in [0,K]\). As a consequence of (5.21),

By Minkowski’s integral inequality, Bernstein’s inequality (A.6), the multiplier estimate on \({\mathcal {J}}_k\) (A.13), the paraproduct estimate (A.8), and the \(\flat \)-estimates (4.19),

Hence, by Cauchy–Schwarz with respect to the finite measure \(\frac{dk}{\langle k \rangle ^{1+\kappa }}\), the potential bound (5.9), and Young’s inequality,

For the remaining term in (5.48), note that by the trivial embedding \(H^1 \hookrightarrow H^{1-\kappa }\) and the bound (4.18) applied to \(R_{k'}\),

Inserting (5.49) and (5.50) into (5.48) establishes (5.22).
5.6.2 Proof of (5.45)
We start with the first integral in \({\mathcal {R}}^{a,1}_K\). Fix \(\kappa > 0\) and let q be such that \((1+\kappa )^{-1} + q^{-1} = 1\). Then, by Young’s inequality (and remembering \(\beta > 1\)),

Adding and subtracting \(g_K\) into the second term on the righthand side and using the pointwise potential bound (5.8),

where we recall that \(|\cdot |_\infty \) is the supremum norm.
By the bounds on \(g_K\) (5.11) and \(V_K\) (5.23), taking \(\kappa <1\) yields

Above, we recall that \(N^\Xi _K\) can contain constants \(C=C(\eta )>0\).
For the remaining term on the righthand side of (5.52), we reorganise terms and iterate the preceding argument:

provided that \(\kappa < \frac{1}{4}\).
We now estimate the second integral in \({\mathcal {R}}^{a,1}_K\). Let \({\tilde{\kappa }} > 0\) be sufficiently small. Let q be such that \(\frac{3-{\tilde{\kappa }}}{4(1+{\tilde{\kappa }})(1-{\tilde{\kappa }})} + \frac{1}{q} = 1\). Moreover, let \(\theta = \frac{2{\tilde{\kappa }}(1-{\tilde{\kappa }})}{(1+{\tilde{\kappa }}) (1-2{\tilde{\kappa }})}\). By duality (A.1), the fractional Leibniz rule (A.2) and interpolation (A.4),

By the change of variables (5.21) in reverse, reorganising terms, Young’s inequality, the bound on \(U_K\) (5.22), and using \(\varepsilon < 1\),

For the last term on the righthand side of (5.56), we iterate the potential bound (5.8) and bound on \(g_K\) (5.11) as in the estimate of (5.52):

where in the penultimate line we used Young’s inequality and in the last line we have used (5.23).
Combining (5.51), (5.53), (5.54), (5.56), and (5.57) establishes (5.45).
5.6.3 Proof of (5.46)
For any \(\theta \in (0,1)\) let \(\frac{1}{p} = \frac{\theta }{4} + \frac{1-\theta }{2}\) and let \(\frac{1}{p'} = 1- \frac{1}{p}\). Then, by duality (A.1), the paraproduct estimate (A.8), the Bernstein-type bounds on the derivatives of the drift (4.20), and bounds on the \(\partial _k g_k^\flat \) (5.14),

where in the last inequality we have reordered terms.
Then,

where in the first line we have used Bernstein’s inequality (A.5); in the second line we have used interpolation (A.4); in the penultimate line we used Young’s inequality; and in the last line we have used the bounds on \(V_K\) (5.23), \(U_k\) (5.22), together with the potential bound (5.9).
In order to bound the second integrand in \({\mathcal {R}}^{a,2}_K\), we use Fubini’s theorem, the Cauchy–Schwarz inequality, the bounds on \(V_k^\flat \) (4.19) and \(\partial _k V_K^\flat \) (4.20), and the bounds on \(g_K\) (5.11) to obtain

where in the last inequality we have used the observation made in Remark 4.3 that \(|\gamma _k|\lesssim \log \langle k \rangle \).
Thus, by Young’s inequality (applied to each term after expanding the sum), the potential bound (5.9), and the bound on \(V_K\) (5.23),

Combining (5.59) and (5.61) yields (5.46).
5.6.4 Proof of (5.47)
We write \({\mathcal {R}}^{a,3}_K = I_1 + I_2 + I_3\), where

Let \(\theta \in (0,1)\) be sufficiently small and let \(\frac{1}{p} = \frac{\theta }{4} + \frac{1-\theta }{2}\), \(\frac{1}{q} = \frac{1-\theta }{2}\) and \(\frac{1}{p'} = \frac{1}{2}-\frac{1}{p}\), \(\frac{1}{q'} = \frac{1}{2} - \frac{1}{q}\). Then,

where the first inequality is by duality (A.1); the second inequality is by the commutator estimate (A.14) and the triangle inequality; and the third inequality is by the multiplier estimate (A.13) and the paraproduct estimate (A.8).
Thus,

where the first inequality is by Bernstein’s inequality (A.5); and the second inequality is by the \(\flat \)-bounds applied to \(V_k^\flat + g_k^\flat \) (4.19), interpolation (A.4), and the trivial bound \(\Vert V_K + g_K \Vert _{B^{4\kappa \theta }_{4,\infty }} \lesssim \Vert V_K+g_K\Vert _{L^4}\).
By applying Young’s inequality, the potential bound (5.9), and the bound on \(V_K\) (5.23), we have

Now consider \(I_2\). Using the commutator estimate (A.10) with  , \(g = V_k^\flat + g_k^\flat \) and
, \(g = V_k^\flat + g_k^\flat \) and  , followed by the paraproduct estimate (A.8), we obtain
, followed by the paraproduct estimate (A.8), we obtain

By applying Young’s inequality, the potential bound (5.9), and the a priori bound on \(V_K\) (5.23),

where the final inequality uses the multiplier estimate (A.13), the \(\flat \)-bounds applied to \(V_K+g_K\) (4.19), and Bernstein’s inequality (A.6).
For \(I_3\), we apply duality (A.1), the commutator estimate (A.11) with  and \(g=V_k^\flat + g_k^\flat \), followed by the \(\flat \)-bounds applied to \(V_K+g_K\) (4.19), to obtain
and \(g=V_k^\flat + g_k^\flat \), followed by the \(\flat \)-bounds applied to \(V_K+g_K\) (4.19), to obtain

where in the last line we have used Young’s inequality, the potential bound (5.9), and the bound on \(V_K\) (5.23) as in (5.66).
Using that \({\mathcal {R}}^{a,3}_K = I_1 + I_2 + I_3\), the estimates (5.64), (5.66), and (5.67) establish (5.47).
5.7 A lower bound on the effective Hamiltonian
The following lemma, based on [GJS76b, Theorem 3.1.1], gives a \(\beta \)-independent lower bound on \({\mathcal {H}}^{\mathrm{eff}}_K(Z_K)\) in terms of the \(L^2\)-norm of the fluctuation field \(Z_K^\perp = Z_K - Z_K\), where we recall  and
and  for
for  . This is useful for us because the latter can be bounded in a \(\beta \)-independent way (see Sect. 5.8.1).
. This is useful for us because the latter can be bounded in a \(\beta \)-independent way (see Sect. 5.8.1).
Lemma 5.21
There exists \(C>0\) such that, for any \(\zeta > 0\) and \(K \in (0,\infty )\),
provided \(\eta < \min \Big ( \frac{1}{32}, \frac{2\zeta }{49} \Big )\).
Proof
First, we write

Fix  . Without loss of generality, assume \(\sigma (x) = 1\) and, hence, \(h(x) = {\sqrt{\beta }}\). Define
. Without loss of generality, assume \(\sigma (x) = 1\) and, hence, \(h(x) = {\sqrt{\beta }}\). Define
In order to show (5.68), it suffices to show that, for some \(C > 0\),
The fundamental observation is that \(Z_K(x) \mapsto \frac{1}{2}{\mathcal {V}}_\beta (Z_K(x))\) can be approximated from below near the minimum at \(Z_K(x) = {\sqrt{\beta }}\) by the quadratic \(Z_K(x) \mapsto \frac{\eta }{2} (Z_K(x)-{\sqrt{\beta }})^2\) provided \(\eta \) is taken sufficiently small. Indeed, we have
which is non-negative provided \(|Z_K(x) + {\sqrt{\beta }}| \geqslant \sqrt{\eta \beta }\). Thus, this approximation is valid except for the region near the opposite potential well satisfying \((-1-\sqrt{\eta }){\sqrt{\beta }}< Z_K(x) < (-1+\sqrt{\eta }){\sqrt{\beta }}\) (see Figure 2). When \(Z_K(x)\) sits in this region, we split \(Z_K(x) = Z_K(x) + Z_K^\perp (x)\) and observe that:
-
either the deviation to the opposite well is caused by \(Z_K(x)\), which is penalised by the logarithm in I(x);
-
or, the deviation is caused by \(Z_K^\perp (x)\), which produces the integral involving \(Z_K^\perp \) in (5.68).
Motivated by these observations, we split the analysis of I(x) into two cases. First we treat the case \(Z_K(x) \in {\mathbb {R}}{\setminus }\Big ( -\frac{4{\sqrt{\beta }}}{3}, -\frac{2{\sqrt{\beta }}}{3} \Big )\). Under this condition, we have
provided that \(\eta \leqslant \frac{1}{9}\). Since \(\chi _+(\cdot ) \leqslant 1\), \(-\log \chi _+(\cdot ) \geqslant 0\). It follows that \(I(x) \geqslant 0\).
Now let \(Z_K(x) \in \Big ( -\frac{4{\sqrt{\beta }}}{3}, -\frac{2{\sqrt{\beta }}}{3} \Big )\). Necessarily, either \(Z_K(x) \leqslant - \frac{{\sqrt{\beta }}}{3}\) or \(Z_K^\perp (x) \leqslant - \frac{{\sqrt{\beta }}}{3}\).
We first assume that \(Z_K(x) \leqslant - \frac{{\sqrt{\beta }}}{3}\). By standard bounds on the Gaussian error function (see e.g. [GJS76b, Lemma 2.6.1]), for any \(\theta \in (0,1)\) there exists \(C=C(\theta )>0\) such that

Applying this with \(\theta \in (\frac{1}{2}, 1)\) and that, by our assumption, \(Z_K(x) - {\sqrt{\beta }}> 4Z_K(x)\),

provided \(\eta < \min \Big ( \zeta , \frac{1}{32} \Big )\).
Finally, assume that \(Z_K^\perp (x) < - \frac{{\sqrt{\beta }}}{3}\). Since \(Z_K(x) - {\sqrt{\beta }}\in \Big ( -\frac{7{\sqrt{\beta }}}{3}, -\frac{-5{\sqrt{\beta }}}{3} \Big )\), we have
provided that \(\eta \leqslant \frac{2\zeta }{49}\). \(\quad \square \)
5.8 Proof of Proposition 5.3
5.8.1 Proof of the lower bound on the free energy (5.1)
We derive bounds uniform in \(\sigma \) for each term in the expansion (5.10). Since there are \(2^{N^3}\) terms, this is sufficient to establish (5.1). Fix \(\sigma \in \{\pm 1\}^{{\mathbb {B}}_N}\).
Recall
Let \(C_P > 0\) be the sharpest constant in the Poincaré inequality (A.15) on unit boxes. Note that \(C_P\) is independent of N. Fix \(\zeta < \frac{1}{8C_P}\) and let \(\varepsilon = 1-8C_P\zeta > 0\). By Proposition 5.11 and Lemma 5.21 there exists \(C=C(\zeta ,\eta )>0\) such that, for every \(v \in {\mathbb {H}}_{b,K}\),

provided \(\eta< \frac{2\zeta }{49} < \frac{1}{196 C_P}\).
Note that for any \(f \in L^2\), \(\int _{{\mathbb {T}}_N}(f^\perp )^2 dx \leqslant \int _{{\mathbb {T}}_N}f^2 dx\). Therefore, using the inequality \((a_1 + a_2 + a_3 + a_4)^2 \leqslant 4(a_1^2 + a_2^2 + a_3^2 + a_4^2)\) and that \(Z_K^\perp (x) = (V_K+g_K)^\perp (x)\), we have

Arguing as in (5.49),

By the Poincaré inequality (A.15) on unit boxes,

where in the last inequality we used that \(\int _{{\mathbb {T}}_N}|\nabla R_K|^2 dx \leqslant \Vert R_K\Vert _{H^1}^2\) and Lemma 4.11 (applied to \(R_K\)).
Similarly, by the Poincaré inequality (A.15) and the (trivial) bound \(\Vert \nabla g_K\Vert _{L^2}^2 \leqslant \Vert \nabla {\tilde{g}}_K \Vert _{L^2}^2\) (5.12),
Then, recalling that \(\beta > 1\),
from which, by Proposition 4.7, we obtain
Inserting this into (5.70) and using that \(F_{\beta ,N,K}^\sigma \geqslant \frac{1}{2} \int _{{\mathbb {T}}_N}|\nabla {\tilde{g}}_K|^2 dx\) (see (5.15)) yields:
which establishes (5.1).
5.8.2 Proof of the upper bound on the free energy (5.2)
We (globally) translate the field to one of the minima of \({\mathcal {V}}_\beta \): this kills the constant \(\beta \) term. Thus, under the translation \(\phi = \psi + {\sqrt{\beta }}\),
where
and
We apply the Proposition 4.7 to \({\mathscr {Z}}_{\beta ,N,K}\) with the infimum taken over \({\mathbb {H}}_K\). In order to obtain an upper bound, we choose a particular drift in the corresponding stochastic control problem (4.13). Following [BG19], we seek a drift that satisfies sufficient moment/integrability conditions with estimates that are extensive in \(N^3\), as formalised in Lemma 5.22 below. Such a drift is constructed using a fixed point argument, hence the need to work in the Banach space \({\mathbb {H}}_K\) as opposed to \({\mathbb {H}}_{b,K}\).
Lemma 5.22
There exist processes  and
and  satisfying
satisfying  and a unique fixed point \({\check{v}} \in {\mathbb {H}}_K\) of the equation
and a unique fixed point \({\check{v}} \in {\mathbb {H}}_K\) of the equation

where \({\check{V}}_K = \int _0^K{\mathcal {J}}_k {\check{v}}_k dk\), such that the following estimate holds: for all \(p \in [1,\infty )\), there exists \(C=C(p,\eta )>0\) such that, for all \(\beta > 1\),
where  .
.
Proof
See [BG19, Lemma 6]. Note that the key difficulty lies in obtaining the right N dependence in (5.72). Due to the paraproduct in the definition of (5.71), one can show that this requires finding a decomposition of  such that
such that  has Besov-Hölder norm that is uniformly bounded in \(N^3\) (see Proposition A.5). Such a bound is not true for
has Besov-Hölder norm that is uniformly bounded in \(N^3\) (see Proposition A.5). Such a bound is not true for  (see Remark 4.5). This is overcome by defining
(see Remark 4.5). This is overcome by defining  to be a random truncation of the Fourier series of
to be a random truncation of the Fourier series of  , where the location of the truncation is chosen to depend on the Besov-Hölder norm of
, where the location of the truncation is chosen to depend on the Besov-Hölder norm of  . \(\quad \square \)
. \(\quad \square \)
For \(v \in {\mathbb {H}}_K\), let

and define \({\mathcal {R}}_K^+\) by
We observe
Thus, unlike the lower bound, the negative mass \(-\frac{\eta }{2} \int _{{\mathbb {T}}_N}V_K^2 dx\) can be ignored in bounding the upper bound on the free energy.
Now fix \({\check{v}}\) as in (5.71). Arguing as in Proposition 5.11, there exists \({\tilde{{\mathcal {R}}}}^+_K\) such that
and \({\tilde{{\mathcal {R}}}}_K^+\) satisfies the following estimate: for every \(\varepsilon > 0\), there exists \(C=C(\varepsilon ,\eta ) > 0\) such that, for all \(\beta > 1\),
Above, we have used that the moment conditions (5.72) are sufficient for conclusions of Lemma 5.14 to apply to \({\check{v}}\).
Thus, by (5.73), (5.74), and (5.75),
By Young’s inequality, \(\frac{1}{\beta }a^4 + \frac{4}{{\sqrt{\beta }}}a^3 + 4a^2 \leqslant 3a^4 + 6a^2 \leqslant 9a^4 + 9\) for all \(\beta > 1\) and \(a \in {\mathbb {R}}\). Thus,
Inserting this into (5.76) and using the moment estimates on the drift (5.72) yields
Hence, by Proposition 4.7,
thereby establishing (5.2).
5.9 Proof of Proposition 5.1
We begin with two propositions, the first of which is a type of Itô isometry for fields under \({\nu _{\beta ,N}}\) and the second of characterises functions against which the Wick square field can be tested against. Together, they imply that the random variables in Proposition 5.1 are integrable and that these expectations can be approximated using the cutoff measures \(\nu _{\beta ,N,K}\). Recall also Remarks 3.1 and 3.3 .
Proposition 5.23
Let \(f \in H^{-1+\delta }\) for some \(\delta > 0\). For every \(K \in (0,\infty )\), let \(\phi ^{(K)} \sim \nu _{\beta ,N,K}\) and \(\phi \sim {\nu _{\beta ,N}}\).
The random variables \(\{ \int _{{\mathbb {T}}_N}\phi ^{(K)} f dx \}_{K > 0}\) converge weakly as \(K \rightarrow \infty \) to a random variable
Moreover, for every \(c> 0\),
Proof
Let \(\{ f_n \}_{n \in {\mathbb {N}}} \subset C^\infty ({\mathbb {T}}_N)\) such that \(f_n \rightarrow f\) in \(H^{-1+\delta }\). We first show that \(\{ \phi (f_n) \}\) is Cauchy in \(L^2({\nu _{\beta ,N}})\).
Let \(\varepsilon > 0\). Choose \(n_0\) such that, for all \(n,m > n_0\), \(\Vert f_n - f_m \Vert _{H^{-1+\delta }} < \frac{\varepsilon }{N^3}\).
Fix \(n,m > n_0\) and let \(\delta f = f_n - f_m\). Then,
By Proposition 5.3, there exists \(C=C(\eta )>0\) such that
We apply Proposition 4.7 to the expectation on the righthand side (with total energy cutoff suppressed, see Remark 4.8 and the paragraph that precedes it).
For \(v \in {\mathbb {H}}_{b,K}\), define

Expanding out the second term (and ignoring the prefactor \(\frac{1}{\varepsilon }\) for the moment), we obtain:

Consider the first integral in (5.78). By Parseval’s theorem, the Fourier coefficients of  (see (4.2)), and Itô’s isometry,
(see (4.2)), and Itô’s isometry,

where sums are taken over frequencies \(n_i \in (N^{-1}{\mathbb {Z}})^3\). Above, the N dependency in the last inequality is due to our Sobolev spaces being defined with respect to normalised Lebesgue measure  .
.
For the second term in (5.78), by Parseval’s theorem, Itô’s isometry, and the Fourier coefficients of  (see (4.6)), we obtain
(see (4.6)), we obtain

For the final term in (5.78), by duality (A.1)
Therefore, using that \(\Vert \delta f \Vert _{H^{1-\delta }}^2 \leqslant \frac{\varepsilon ^2}{N^6}\), the estimates (5.79), (5.80), and (5.81) yield:

Using arguments in Sect. 5.8.1, it is straightforward to show that there exists \(C=C(\eta ,\beta )>0\) such that, for \(\varepsilon \) sufficiently small,
for every \(v \in {\mathbb {H}}_{b,K}\) (note that \(\beta \) dependence is not important here).
Inserting this into Proposition 4.7 gives
Taking expectations in (5.77) and using (5.83) finishes the proof that \(\{ \phi (f_n) \}\) is Cauchy in \(L^2({\nu _{\beta ,N}})\).
Similar arguments can be used to show exponential integrability of the limiting random variable, \(\phi (f)\) and that,
We now show that \(\phi ^{(K)}(f)\) converges weakly to \(\phi (f)\) as \(K \rightarrow \infty \). Let \(G : {\mathbb {R}}\rightarrow {\mathbb {R}}\) be bounded and Lipschitz with Lipschitz constant \(|G|_{\mathrm{Lip}}\), and let \(\varepsilon > 0\). Choose n sufficiently large so that
and
Then,
The first term on the righthand side goes to zero as \(K \rightarrow \infty \) since \(f_n \in C^\infty \). Thus,
Since \(\varepsilon \) is arbitrary, we have shown that \(\phi ^{(K)}(f)\) converges weakly to \(\phi (f)\). \(\quad \square \)
Proposition 5.24
Let \(f \in B^s_{\frac{4}{3},1} \cap L^{2}\) for some \(s > \frac{1}{2}\). For every \(K \in (0,\infty )\), let \(\phi ^{(K)} \sim \nu _{\beta ,N,K}\) and \(\phi \sim {\nu _{\beta ,N}}\).
The random variables \(\{ \int _{{\mathbb {T}}_N}:(\phi ^{(K)})^2: f dx \}_{K>0}\) converge weakly as \(K \rightarrow \infty \) to a random variable
Moreover, for \(c > 0\),
Proof
The proof of Proposition 5.24 follows the same strategy as the proof of Proposition 5.23, so we do not give all the details. The only real key difference is the analytic bounds required in the stochastic control problem. Indeed, these require one to tune the integrability assumptions on f in order to get the required estimates.
It is not too difficult to see that the term we need to control is the integral

Strictly speaking, we need to control the above integral with f replaced by \(\delta f = f_n - f_m\), where \(\{ f_n \}_{n \in {\mathbb {N}}}\subset C^\infty ({\mathbb {T}}_N)\) such that \(f_n \rightarrow f\) in \(B^s_{\frac{3}{4}, 1} \cap L^2\), but the analytic bounds are the same.
Note that  . Moreover by Young’s inequality and the additional integrability assumption \(f \in L^2\), for any \(\varepsilon > 0\) we have
. Moreover by Young’s inequality and the additional integrability assumption \(f \in L^2\), for any \(\varepsilon > 0\) we have
which can be estimated as in the proof of Proposition 5.23. Thus, we only need to estimate the second integral in (5.84). Note that the product  is a well-defined distribution from a regularity perspective as \(K \rightarrow \infty \) since \(f \in B^{s}_{\frac{4}{3},1}\) for \(s > \frac{1}{2}\). The difficulty in obtaining the required estimates comes from integrability issues.
is a well-defined distribution from a regularity perspective as \(K \rightarrow \infty \) since \(f \in B^{s}_{\frac{4}{3},1}\) for \(s > \frac{1}{2}\). The difficulty in obtaining the required estimates comes from integrability issues.
We split the integral into three terms by using the paraproduct decomposition  . The integral associated to
. The integral associated to  is straightforward to estimate, so we focus on the first two terms. Since \(f \in L^2\) and
is straightforward to estimate, so we focus on the first two terms. Since \(f \in L^2\) and  , by the paraproduct estimate A.8 we have
, by the paraproduct estimate A.8 we have  . Thus, the integral
. Thus, the integral  can be treated similarly as in the proof of Proposition 5.23. Note that, in this proposition the use of Hölder-Besov norms is fine because we are not concerned with issues of N dependency. Moreover, note that if we just used that \(f \in B^s_{\frac{4}{3},1}\) the resulting integrability of
can be treated similarly as in the proof of Proposition 5.23. Note that, in this proposition the use of Hölder-Besov norms is fine because we are not concerned with issues of N dependency. Moreover, note that if we just used that \(f \in B^s_{\frac{4}{3},1}\) the resulting integrability of  is not sufficient to justify testing against \(V_K\), which can be bounded in \(L^2\)-based Sobolev spaces. For the final integral, by the resonant product estimate (A.9) we have
is not sufficient to justify testing against \(V_K\), which can be bounded in \(L^2\)-based Sobolev spaces. For the final integral, by the resonant product estimate (A.9) we have  . Hence, we can use Young’s inequality to estimate
. Hence, we can use Young’s inequality to estimate  and then argue similarly as in the proof of Proposition 5.23. \(\quad \square \)
and then argue similarly as in the proof of Proposition 5.23. \(\quad \square \)
Without loss of generality, we assume \(a_0 = a = 1\) in Proposition 5.1 and we split its proof into Lemmas 5.25, 5.26, and 5.27 .
Lemma 5.25
There exists \(\beta _0 > 1\) and \(C_Q > 0\) such that, for any \(\beta > \beta _0\),

Proof
For any \(K \in (0,\infty )\), define
where
Then, by Propositions 5.24 and 5.3 , there exists \(C=C(\eta )>0\) such that

where
Therefore, we have reduced the problem to proving Proposition 5.3 for the potential \({\mathcal {V}}_\beta ^{Q_1}\) instead of \({\mathcal {V}}_\beta \). The proof follows essentially word for word after two observations: first, the same \(\gamma _K\) and \(\delta _K\) works for both \({\mathcal {V}}_\beta \) and \({\mathcal {V}}_\beta ^{Q_1}\) since the quartic term is unchanged. Second, since \(\sqrt{\beta + \frac{{\sqrt{\beta }}}{2}} = {\sqrt{\beta }}+ o({\sqrt{\beta }})\) as \(\beta \rightarrow \infty \), the treatment of \(\beta \)-dependence of the estimates in Sect. 5.6 is exactly the same. \(\quad \square \)
Lemma 5.26
There exists \(\beta _0 > 1\) and \(C_Q > 0\) such that, for any \(\beta > \beta _0\),

Proof
By Propositions 5.23, 5.24, and 5.3 , there exists \(C=C(\eta )>0\) such that, for \(\beta \) sufficiently large,

where

As in Sect. 5.2, we perform the expansion
where \(F_{\beta ,N,K}^\sigma \) is defined in (5.15) and

Fix \(\sigma \in \{\pm 1\}^{{\mathbb {B}}_N}\). For \(v \in {\mathbb {H}}_{b,K}\), define

where \(\Psi _K=\Psi _K^\sigma \) is defined in (5.17).
We estimate second term in (5.87). First, note that

By a standard Gaussian covariance calculation, there exists \(C=C(\eta )>0\) such that

For the other term, by the Cauchy–Schwarz inequality followed by bounds on the potential (5.8) and \(g_K\) (5.11), the following estimate holds: for any \(\zeta > 0\),

where \(C_P > 0\) is the Poincaré constant on unit boxes (A.15).
We now estimate the third term in (5.87). Since  ,
,

For the first integral on the righthand side of (5.88), by change of variables (5.21), and the paraproduct decomposition (A.7), we have

Note that  and
and  can be respectively bounded uniformly in \( {\mathcal {C}}^{-\frac{1}{2} - \kappa }\) and \({\mathcal {C}}^{-2\kappa }\) by using the paraproduct estimate (A.8) and a mild modification for the second term. Moreover, by Proposition 4.4,
can be respectively bounded uniformly in \( {\mathcal {C}}^{-\frac{1}{2} - \kappa }\) and \({\mathcal {C}}^{-2\kappa }\) by using the paraproduct estimate (A.8) and a mild modification for the second term. Moreover, by Proposition 4.4,  can be bounded uniformly in \({\mathcal {C}}^{-2\kappa }\). Hence, by (5.88), Proposition 4.4, duality (A.1), the potential bounds (5.8), and the bounds on \(U_K\) (5.22), for any \(\varepsilon > 0\) there exists \(C=C(\varepsilon ,\eta )>0\) such that
can be bounded uniformly in \({\mathcal {C}}^{-2\kappa }\). Hence, by (5.88), Proposition 4.4, duality (A.1), the potential bounds (5.8), and the bounds on \(U_K\) (5.22), for any \(\varepsilon > 0\) there exists \(C=C(\varepsilon ,\eta )>0\) such that

For the second integral on the righthand side of (5.88), again by (5.8) and (5.11), there exists an inessential constant \(C>0\) such that
Arguing as in Sect. 5.8.1 and taking into account the calculations above, the following estimate holds: let \(\zeta < \frac{1}{8C_P}\) and \(\varepsilon = 1-8C_P\zeta > 0\) as in Sect. 5.8.1. Then, provided \(\eta < \frac{1}{196C_P}\) and \(\beta > 1\),
Hence, by Proposition 4.7 applied with the Hamiltonian \({\mathcal {H}}_{\beta ,N,K}^{Q_2,\sigma }(\phi _K)\) with total energy cutoff suppressed (see Remark 4.8),
This estimate is uniform in \(\sigma \), thus summing over the \(2^{N^3}\) terms in the expansion (5.86) yields (5.85). \(\quad \square \)
Lemma 5.27
There exists \(\beta _0 > 1\) and \(C_Q > 0\) such that, for any \(\beta > \beta _0\),

where B is a set of unordered pairs of nearest-neighbour blocks that partitions \({{\mathbb {B}}_N}\).
Proof
By Propositions 5.23 and 5.3 there exists \(C=C(\eta )>0\) such that, for \(\beta \) sufficiently large,

where

We expand
where \(F_{\beta ,N,K}^\sigma \) is defined in (5.15) and

Fix \(\sigma \in \{\pm 1\}^{{\mathbb {B}}_N}\). For \(v \in {\mathbb {H}}_{b,K}\), define

where \(\Psi _K(v) = \Psi _K^\sigma (v)\) is defined in (5.17).
A standard Gaussian calculation yields  for some constant \(C=C(\eta )>0\). Hence, by the triangle inequality, Proposition 4.4 and the Cauchy–Schwarz inequality,
for some constant \(C=C(\eta )>0\). Hence, by the triangle inequality, Proposition 4.4 and the Cauchy–Schwarz inequality,

The integral with the paraproduct can be estimated as in (5.49) to establish: for any \(\zeta > 0\),

where \(C_P>0\) is the Poincaré constant on unit blocks (A.15).
We now estimate the remaining integral. Assume without loss of generality that  . Then, by the triangle inequality and the fundamental theorem of calculus,
. Then, by the triangle inequality and the fundamental theorem of calculus,

Hence, by the Cauchy–Schwarz inequality, the bound on the drift (4.18) and the bound on \(\nabla g_K\) (5.12), we have the following estimate: for any \(\zeta > 0\),

Thus, by arguing as in Sect. 5.8.1, one can show the following estimate: let \(\zeta < \frac{1}{16C_P}\) and \(\varepsilon = 1 - 8\zeta C_P > 0\). Then, provided \(\eta < \frac{1}{392 C_P}\) and \(\beta > 1\),
Applying Proposition 4.7 with Hamiltonian \({\mathcal {H}}_{\beta ,N,K}^{Q_3,\sigma }(\phi _K)\), with total energy cutoff suppressed (see Remark 4.8), yields
This estimate is uniform over all \(2^{N^3}\) choices of \(\sigma \), hence establishing (5.89). \(\quad \square \)
6 Chessboard Estimates
In this section we prove Proposition 3.6 using the chessboard estimates of Proposition 6.5 and the estimates obtained in Sect. 5. In addition, we establish that \({\nu _{\beta ,N}}\) is reflection positive.
6.1 Reflection positivity of \({\nu _{\beta ,N}}\)
We begin by defining reflection positivity for general measures on spaces of distributions following [Shl86] and [GJ87].
For any \(a \in \{0, \dots , N-1\}\) and \(\{i,j,k\} = \{ 1,2,3 \}\), let
where \(x = x_i e_i + x_j e_j + x_k e_j \in {\mathbb {T}}_N\) and addition is understood modulo N. Define
Note that for any \(x \in \Pi _{a,i}\), \(x_i = a \text { or } a+\frac{N}{2}\). We say that \({\mathcal {R}}_{\Pi _{a,i}}\) is the reflection map across the hyperplane \(\Pi _{a,i}\).
Fix such a hyperplane \(\Pi \). It separates \({\mathbb {T}}_N= {\mathbb {T}}_N^+ \sqcup \Pi \sqcup {\mathbb {T}}_N^-\) such that \({\mathbb {T}}_N^+ = {\mathcal {R}}_\Pi {\mathbb {T}}_N^-\). For any \(f \in C^\infty ({\mathbb {T}}_N)\), we say f is \({\mathbb {T}}_N^+\)-measurable if \(\text {supp} f \subset {\mathbb {T}}_N^+\). The reflection of f in \(\Pi \) is defined pointwise by \({\mathcal {R}}_\Pi f(x) = f({\mathcal {R}}_\Pi x)\). For any \(\phi \in S'({\mathbb {T}}_N)\), we say that \(\phi \) is \({\mathbb {T}}_N^+\)-measurable if, for any \(f \in C^\infty ({\mathbb {T}}_N)\) such that \(\mathrm{supp} f \subset ({{\mathbb {T}}_N^+})^c\), \(\phi (f) = 0\), where \(\phi (f)\) denotes the duality pairing between \(S'({\mathbb {T}}_N)\) and \(C^\infty ({\mathbb {T}}_N)\). For any such \(\phi \), we define \({\mathcal {R}}_\Pi \phi \) pointwise by \({\mathcal {R}}_\Pi \phi (f) = \phi ({\mathcal {R}}_\Pi f)\).
Let \(\nu \) be a probability measure on \(S'({\mathbb {T}}_N)\). We say that \(F \in L^2(\nu )\) is \({\mathbb {T}}_N^+\)-measurable if it is measurable with respect to the \(\sigma \)-algebra generated by the set of \(\phi \in S'({\mathbb {T}}_N)\) that are \({\mathbb {T}}_N^+\)-measurable. For any such F, we define \({\mathcal {R}}_\Pi F\) pointwise by \({\mathcal {R}}_\Pi F(\phi ) = F({\mathcal {R}}_\Pi \phi )\).
The measure \(\nu \) on \(S'({\mathbb {T}}_N)\) is called reflection positive if, for any hyperplane \(\Pi \) of the form (6.1),
for all \(F \in L^2(\nu )\) that are \({\mathbb {T}}_N^+\)-measurable.
Proposition 6.1
The measure \({\nu _{\beta ,N}}\) is reflection positive.
6.1.1 Proof of Proposition 6.1
In general, Fourier approximations to \({\nu _{\beta ,N}}\) (such as \(\nu _{\beta ,N,K}\)) are not reflection positive. Instead, we prove Proposition 6.1 by considering lattice approximations to \({\nu _{\beta ,N}}\) for which reflection positivity is straightforward to show.
Let \({\mathbb {T}}_N^{\varepsilon } = (\varepsilon {\mathbb {Z}}/ N {\mathbb {Z}})^3\) be the discrete torus of sidelength N and lattice spacing \(\varepsilon > 0\). In order to use discrete Fourier analysis, we assume that \(\varepsilon ^{-1} \in {\mathbb {N}}\). Note that any hyperplane \(\Pi \) of the form (6.1) is a subset of \({\mathbb {T}}_N^\varepsilon \).
For any \(\varphi \in ({\mathbb {R}})^{{\mathbb {T}}_N^\varepsilon }\), define the lattice Laplacian
Let \({\tilde{\mu }}_{N,\varepsilon }\) be the Gaussian measure on \({\mathbb {R}}^{{\mathbb {T}}_N^\varepsilon }\) with density
where \(d{\phi }(x)\) is Lebesgue measure.
A natural lattice approximation to \({\nu _{\beta ,N}}\) is given by the probability measure \({\tilde{\nu }}_{\beta ,N,\varepsilon }\) with density proportional to
where
where \(\frac{1}{2} \delta m^2(\varepsilon ,\eta )\) is a renormalisation constant that diverges as \(\varepsilon \rightarrow 0\) (see Proposition 6.19). Note two things: first, the renormalisation constant is chosen dependent on \(\eta \) for technical convenience. Second, no energy renormalisation is included since we are only interested in convergence of measures.
Remark 6.2
By embedding \({\mathbb {R}}^{{\mathbb {T}}_N^\varepsilon }\) into \(S'({\mathbb {T}}_N)\), we can define reflection positivity for lattice measures. We choose this embedding so that the pushforward of \({\tilde{\nu }}_{\beta ,N,\varepsilon }\) is automatically reflection positive, but other choices are possible.
For any \(\varphi \in {\mathbb {R}}^{{\mathbb {T}}_N^\varepsilon }\), we write \(\mathrm {ext}^\varepsilon \varphi \) for its unique extension to a trigonometric polynomial on \({\mathbb {T}}_N\) of degree less than \(\varepsilon ^{-1}\) that coincides with \(\varphi \) on lattice points (i.e. in \({\mathbb {T}}_N^\varepsilon \)). Precisely,
where the sum ranges over all \(n=(a_1,a_2,a_3) \in (N^{-1}{\mathbb {Z}})^3\) such that \(|a_i| \leqslant \varepsilon ^{-1}\), and we recall \(e_n(x) = e^{2\pi i n \cdot x}\).
Lemma 6.3
Let \(\varepsilon > 0\) such that \(\varepsilon ^{-1} \in {\mathbb {N}}\). Denote by \(\mathrm {ext}^\varepsilon _* {\tilde{\nu }}_{\beta ,N,\varepsilon }\) the pushforward of \({\tilde{\nu }}_{\beta ,N,\varepsilon }\) by the map \(\mathrm {ext}^\varepsilon \). Then, the measure \(\mathrm {ext}^\varepsilon _* {\tilde{\nu }}_{\beta ,N,\varepsilon }\) is reflection positive.
Proof
Fix a hyperplane \(\Pi \) of the form (6.1) and recall that \(\Pi \) separates \({\mathbb {T}}_N={\mathbb {T}}_N^+ \sqcup \Pi \sqcup {\mathbb {T}}_N^-\). Write \({\mathbb {T}}_{N,\varepsilon }^+ = {\mathbb {T}}_N^+ \cap {\mathbb {T}}_N^\varepsilon \).
Since the measure \({\tilde{\nu }}_{\beta ,N,\varepsilon }\) is reflection positive on the lattice by [Shl86, Theorem 2.1], the following estimate holds: let \(F^\varepsilon \in L^2({\tilde{\nu }}_{\beta ,N,\varepsilon })\) be \({\mathbb {T}}_{N,\varepsilon }^+\)-measurable - i.e. \(F^\varepsilon (\varphi )\) depends only on \(\varphi (x)\) for \(x \in {\mathbb {T}}_{N,\varepsilon }^+\). Then,
Let \(F \in L^2(\mathrm {ext}^\varepsilon _*{\tilde{\nu }}_{\beta ,N,\varepsilon })\) be \({\mathbb {T}}_N^+\)-measurable. Then, \(F \circ \mathrm {ext}^\varepsilon \in L^2({\tilde{\nu }}_{\beta ,N,\varepsilon })\) is \({\mathbb {T}}_{N,\varepsilon }^+\)-measurable. Using that \(\mathrm {ext}^\varepsilon \) and \({\mathcal {R}}_\Pi \) (the reflection across \(\Pi \)) commute,
where the last inequality is by (6.2). Hence, \(\mathrm {ext}^\varepsilon _*{\tilde{\nu }}_{\beta ,N,\varepsilon }\) is reflection positive. \(\quad \square \)
Proposition 6.4
There exist constants \(\frac{1}{2} \delta m^2(\bullet ,\eta )\) such that \(\mathrm {ext}^\varepsilon _*\nu _{\beta ,N,\varepsilon } \rightarrow {\nu _{\beta ,N}}\) weakly as \(\varepsilon \rightarrow \infty \).
Proof
The existence of a weak limit of \(\mathrm {ext}^\varepsilon _*{\tilde{\nu }}_{\beta ,N,\varepsilon }\) as \(\varepsilon \rightarrow 0\) was first established in [Par75]. The fact the lattice approximations and the Fourier approximations (i.e. \(\nu _{\beta ,N,K}\)) yield the same limit as the cutoff is removed is not straightforward in 3D because of the mutual singularity of \({\nu _{\beta ,N}}\) and \(\mu _N\) [BG20]. Previous approaches have relied on Borel summation techniques to show that the correlation functions agree with (resummed) perturbation theory [MS77].
In Sect. 6.4 we give an alternative proof using stochastic quantisation techniques. The key idea is to view \({\nu _{\beta ,N}}\) as the unique invariant measure for a singular stochastic PDE with a local solution theory that is robust under different approximations. This allows us to show directly that \(\mathrm {ext}^\varepsilon _*{\tilde{\nu }}_{\beta ,N,\varepsilon }\) converges weakly to \({\nu _{\beta ,N}}\) and avoids the use of Borel summation and perturbation theory. The strategy is explained in further detail at the beginning of that section. \(\quad \square \)
Proof of Proposition 6.1 assuming Proposition 6.4
Proposition 6.1 is a direct consequence of Lemma 6.3 and Proposition 6.4 since reflection positivity is preserved under weak limits. \(\quad \square \)
6.2 Chessboard estimates for \({\nu _{\beta ,N}}\)
Let \(B \subset {{\mathbb {B}}_N}\) be either a unit block or a pair of nearest-neighbour blocks. Recall the natural identification of B with the subset of \({\mathbb {T}}_N\) given by the union of blocks in B. \({\mathbb {T}}_N\) can be written as a disjoint union of translates of B. Let \({\mathbb {B}}_N^B\) be the set of these translates; its elements are also identified with subsets of \({\mathbb {T}}_N\). Note that if  , then \({\mathbb {B}}_N^B = {{\mathbb {B}}_N}\).
, then \({\mathbb {B}}_N^B = {{\mathbb {B}}_N}\).
We say that \(f \in C^\infty ({\mathbb {T}}_N)\) is B-measurable if \(\text {supp} f \subset B\) and \(\text {supp} f \cap \partial B = \emptyset \). We say that \(\phi \in S'({\mathbb {T}}_N)\) is B-measurable if \(\phi (f) = 0\) for every \(f \in C^\infty ({\mathbb {T}}_N)\) unless f is B-measurable. We say that \(F \in L^2({\nu _{\beta ,N}})\) is B-measurable if it is measurable with respect to the \(\sigma \)-algebra generated by \(\phi \in S'({\mathbb {T}}_N)\) that are B-measurable.
Proposition 6.5
Let \(N \in 4{\mathbb {N}}\). Let \(\{ F_{{\tilde{B}}} : {\tilde{B}} \in {\mathbb {B}}_N^B \}\) be a given set of \(L^2({\nu _{\beta ,N}})\)-functions such that each \(F_{{\tilde{B}}}\) is \({\tilde{B}}\)-measurable.
Fix \({\tilde{B}} \in {\mathbb {B}}_N^B\) and define an associated set of \(L^2({\nu _{\beta ,N}})\)-functions \(\{ F_{{\tilde{B}}, B'} : B' \in {\mathbb {B}}_N^B \}\) by the conditions: \(F_{{\tilde{B}}, {\tilde{B}}} = F_{{\tilde{B}}}\); and, for any \(B', B'' \in {\mathbb {B}}_N^B\) such that \(B'\) and \(B''\) share a common face,
where \(\Pi \) is the unique hyperplane of the form (6.1) containing the shared face between \(B'\) and \(B''\).
Then,
Proof
This is a consequence of the reflection positivity of \({\nu _{\beta ,N}}\). The condition \(N \in 4{\mathbb {N}}\) guarantees \(F_{{\tilde{B}}, B'}\) is well-defined. See [Shl86, Theorem 2.2]. \(\quad \square \)
6.3 Proof of Proposition 3.6
In order to be able to apply Proposition 6.5 to the random variables \(Q_i\) of Proposition 3.6, we need the following lemma.
Lemma 6.6
Let \(N \in {\mathbb {N}}\) and \(\beta > 0\). Then, for any  ,
,  is
is  -measurable.
-measurable.
In addition, for any nearest neighbours  ,
,  is
is  -measurable.
-measurable.
Proof
The fact that  follows from estimates obtained in Proposition 5.23. The
follows from estimates obtained in Proposition 5.23. The  and
and  measurability of these observables comes from taking approximations to indicators which are supported on blocks (e.g. using some appropriate regularisation of the distance function) and estimates obtained in Proposition 5.23. \(\quad \square \)
measurability of these observables comes from taking approximations to indicators which are supported on blocks (e.g. using some appropriate regularisation of the distance function) and estimates obtained in Proposition 5.23. \(\quad \square \)
Proof of Proposition 3.6
Let \(B_1, B_2 \subset {{\mathbb {B}}_N}\) and \(B_3\) be a set of unordered pairs of nearest neighbour blocks in \({{\mathbb {B}}_N}\). Then,

where \(\cosh Q_i(B_i)\) is defined in (3.7) and the sum is over all partitions \(B_1^+ \sqcup B_1^- = B_1\) and \(B_2^+\sqcup B_2^- = B_2\).
It suffices to prove that there exists \({\tilde{C}}_Q>0\) such that, for any \(B_1^\pm , B_2^\pm \) and \(B_3\) as above,

Then, taking expectations in (6.3) and using (6.4)

which yields Proposition 3.6 with \(C_Q = {\tilde{C}}_Q\).
To prove (6.4), first fix \(B_1^\pm \) and \(B_2^\pm \). Then, by Hölder’s inequality,

Let \(i=1,2\). Without loss of generality, we use Proposition 6.5 to estimate

Define  if
if  and 1 otherwise. For each
and 1 otherwise. For each  , we generate the family of functions
, we generate the family of functions  as in Proposition 6.5. Note that for
as in Proposition 6.5. Note that for  such that
such that  and
and  are nearest-neighbours,
are nearest-neighbours,

where \({\mathcal {R}}\) is the reflection across the unique hyperplane containing the shared face of  and
and  . Thus, we have
. Thus, we have  for every
for every  and
and  . If
. If  , we have
, we have  for every
for every  .
.
Lemma 6.6 ensures that  is
is  -measurable for every
-measurable for every  . Hence, by Proposition 6.5, we obtain
. Hence, by Proposition 6.5, we obtain

Therefore, by Proposition 5.1, there exists \(C_Q'>0\) such that, for all \(\beta \) sufficiently large,

For the remaining term involving \(Q_3\), partition \(B_3 = \bigcup _{k=1}^6 B_3^{(k)}\) such that each \(B_3^{(k)}\) is a set of disjoint pairs of nearest neighbour blocks, all with same orientation. Then, by Hölder’s inequality,

Assuming that we have established that there exists \(C_Q'>0\) such that

for every \(k \in \{1,\dots ,6\}\), then (6.7) yields

Hence, without loss of generality, we may assume \(B_3\) is a set of disjoint pairs of nearest neighbour blocks, all of the same orientation.
Define  for any
for any  and 1 otherwise. Note that for any two pairs of nearest-neighbour blocks,
and 1 otherwise. Note that for any two pairs of nearest-neighbour blocks,  ,
,

where \({\mathcal {R}}\) is the reflection across the unique hyperplane containing the shared face of  . Thus, for any
. Thus, for any  and \(B\), we have
and \(B\), we have  . If \(B \not \in B_3\), then we have \(F_{B,B'}=1\) for all \(B' \in {\mathbb {B}}_N^B\).
. If \(B \not \in B_3\), then we have \(F_{B,B'}=1\) for all \(B' \in {\mathbb {B}}_N^B\).
Lemma 6.6 ensures that  is
is  -measurable. Thus, applying Propositions 6.5 and 5.1 , there exists \(C_Q'>0\) such that, for all \(\beta \) sufficiently large,
-measurable. Thus, applying Propositions 6.5 and 5.1 , there exists \(C_Q'>0\) such that, for all \(\beta \) sufficiently large,

Inserting (6.6) and (6.8) into (6.5), and taking into account (6.7), yields (6.4) with \({\tilde{C}}_Q = \frac{C_Q'}{15}\), thereby finishing the proof. \(\quad \square \)
6.4 Equivalence of the lattice and Fourier cutoffs
This section is devoted to a proof of Proposition 6.4 using stochastic quantisation techniques. In Sect. 6.4.1, we give a rigorous interpretation to (1.3) via the change of variables (6.14). Subsequently, in Sect. 6.4.2, we establish that \({\nu _{\beta ,N}}\) is the unique invariant measure of (1.3), see Proposition 6.18. In Sect. 6.4.3, we first establish that local solutions of spectral Galerkin and lattice approximations to (1.3) converge to the same limit (see Propositions 6.13 and 6.19 ); these approximations admit unique invariant measures given by \(\nu _{\beta ,N,K}\) and \({\tilde{\nu }}_{\beta ,N,\varepsilon }\), respectively. Then, using the global existence of solutions and uniqueness of the invariant measure of (1.3), we show that both of these measures converge to \({\nu _{\beta ,N}}\) as the cutoffs are removed.
6.4.1 Giving a meaning to (1.3)
Let \(\xi \) be space-time white noise on \({\mathbb {T}}_N\) defined on a probability space  . This means that \(\xi \) is a Gaussian random distribution on \(\Omega \) satisfying
. This means that \(\xi \) is a Gaussian random distribution on \(\Omega \) satisfying

where \(\Phi ,\Psi \in C^\infty ({\mathbb {R}}_+\times {\mathbb {T}}_N)\) and  denotes expectation with respect to
denotes expectation with respect to  . We use the colour blue here to distinguish between the space random processes defined in Sect. 4 and the space-time random processes that we consider here.
. We use the colour blue here to distinguish between the space random processes defined in Sect. 4 and the space-time random processes that we consider here.
We interpret (1.3) as the limit of renormalised approximations. For every \(K \in (0,\infty )\), the Glauber dynamics of \(\nu _{\beta ,N,K}\) is given by the stochastic PDE

Above, \(\rho _K\) is as in Sect. 2 and we recall \(\rho _K^2 \ne \rho _K\);  is defined in (2.1); and
is defined in (2.1); and  , where
, where  is defined in (4.4).
is defined in (4.4).
Remark 6.7
Recall that the Glauber dynamics for the measure \(\nu \) with formal density \(d\nu (\phi ) \propto e^{-{\mathcal {H}}(\phi )}\prod _{x\in {\mathbb {T}}_N} d\phi (x)\) is given by the (overdamped) Langevin equation
where \(\partial _\phi {\mathcal {H}}\) denotes the functional derivative of \({\mathcal {H}}\).
For fixed K, the (almost sure) global existence and uniqueness of mild solutions to (6.9) is standard (see e.g. [DPZ88, Section III]). Moreover, \(\nu _{\beta ,N,K}\) is its unique invariant measure (see [Zab89, Theorem 2]). The approximations (6.9), which we call spectral Galerkin approximations, are natural in our context since \({\nu _{\beta ,N}}\) is constructed as the weak limit of \(\nu _{\beta ,N,K}\) as \(K \rightarrow \infty \).
The difficulty in obtaining a local well-posedness theory that is stable in the limit \(K \rightarrow \infty \) lies in the roughness of the white noise \(\xi \). The key idea is to exploit that the small-scale behaviour of solutions to (6.9) is governed by the Ornstein-Uhlenbeck process

This allows us to obtain an expansion of \(\Phi _K\) in terms of explicit (renormalised) multilinear functions of  , which give a more detailed description of the small-scale behaviour of \(\Phi _K\), plus a more regular remainder term. Given the regularities of these explicit stochastic terms, the local solution theory then follows from deterministic arguments.
, which give a more detailed description of the small-scale behaviour of \(\Phi _K\), plus a more regular remainder term. Given the regularities of these explicit stochastic terms, the local solution theory then follows from deterministic arguments.
Remark 6.8
We are only concerned with the limit \(K \rightarrow \infty \) in (6.9). We do not try to make sense of the joint \(K,N \rightarrow \infty \) limit.
We use the paracontrolled distribution approach of [MW17], which is modification of the framework of [CC18] (both influenced by the seminal work of [GIP15]). In this approach, the expansion of \(\Phi _K\) is given by an ansatz, see (6.10), that has similarities to the change of variables encountered in Sect. 5.4.1. See Remark 6.10. There are also related approaches via regularity structures [Hai14, Hai16, MW18] and renormalisation group [Kup16], but we do not discuss them further.
For every \(K \in (0,\infty )\), define

We recall that the colour blue is used to distinguish between the above space-time diagrams and the space diagrams of Sect. 4.1.1.
For any \(T>0\), the vector  is space-time stationary and almost surely an element of the Banach space
is space-time stationary and almost surely an element of the Banach space
where the norm on \({\mathcal {X}}_T\) is given by the maximum of the norms on the components. Above, for any \(s \in {\mathbb {R}}\), \(C([0,T];{\mathcal {C}}^s)\) consists of continuous functions \(\Phi :[0,T] \rightarrow {\mathcal {C}}^s\) and is a Banach space under the norm \(\sup _{t\in [0,T]}\Vert \cdot \Vert _{{\mathcal {C}}^s}\). In addition, for any \(\alpha \in (0,1)\), \(C^\alpha ([0,T];{\mathcal {C}}^s)\) consists of \(\alpha \)-Hölder continuous functions \(\Phi : [0,T] \rightarrow {\mathcal {C}}^s\) and is a Banach space under the norm \(\Vert \cdot \Vert _{C([0,T];{\mathcal {C}}^s)} + | \cdot |_{\alpha , T}\) where
Proposition 6.9
There exists a stochastic process  such that, for every \(T > 0\),
such that, for every \(T > 0\),  almost surely and
almost surely and

Proof
The proof follows from [CC18, Section 4] (see also [MWX17] and [Hai14, Section 10]). The only subtlety is to check that the renormalisation constants  and
and  , which were determined by the field theory \({\nu _{\beta ,N}}\), are sufficient to renormalise the space-time diagrams appearing in the analysis of the SPDE. Precisely, it suffices to show
, which were determined by the field theory \({\nu _{\beta ,N}}\), are sufficient to renormalise the space-time diagrams appearing in the analysis of the SPDE. Precisely, it suffices to show  and
and  for every \((t,x) \in {\mathbb {R}}_+\times {\mathbb {T}}_N\).
for every \((t,x) \in {\mathbb {R}}_+\times {\mathbb {T}}_N\).
There exists a set of complex Brownian motions \(\{ W^n(\bullet ) \}_{n \in (N^{-1}{\mathbb {Z}})^3}\) defined on  , independent modulo the condition \(W^n(\bullet ) = \overline{W^{-n}(\bullet )}\), such that
, independent modulo the condition \(W^n(\bullet ) = \overline{W^{-n}(\bullet )}\), such that
for every \(\phi \in L^2({\mathbb {R}}\times {\mathbb {T}}_N)\).
For \(t \geqslant 0\) and \(n \in (N^{-1}{\mathbb {Z}})^3\), let \(H(t,n) = e^{-t \langle n \rangle ^2}\) be the (spatial) Fourier transform of the heat kernel associated to \((\partial _t - \Delta + \eta )\). For any \(K>0\), define \(H_K(t,n) = \rho _K (n) H(t,n)\). We extend both kernels to \(t \in {\mathbb {R}}\) by setting \(H(t,\cdot ) = H_K(t,\cdot ) = 0\) for any \(t < 0\). Then

By Parseval’s theorem and Itô’s isometry,

for all \((t,x) \in {\mathbb {R}}_+\times {\mathbb {T}}_N\). With this observation the convergence of  ,
,  and
and  follows from mild adaptations of [CC18, Section 4].
follows from mild adaptations of [CC18, Section 4].
For the remaining two diagrams, one can show from arguments in [CC18, Section 4] that

converge to well-defined space-time distributions.
Writing

we have, by Parseval’s theorem and Itô’s isometry,

By symmetry,

thereby completing the proof. \(\quad \square \)
We return now to the solution theory for (1.3)/(6.9). Fix \(K \in (0,\infty )\). Using the change of variables

we say that \(\Phi _K\) is a mild solution of (6.9) with initial data \(\phi _0 \in {\mathcal {C}}^{-\frac{1}{2}-\kappa }\) if \((\Upsilon _K, \Theta _K)\) is a mild solution to the system of equations

where

with initial data  .
.
We split  ,
,

where  and
and  are commutator terms defined through the manipulations
are commutator terms defined through the manipulations

The precise choice of the splitting of  into \(\Upsilon _K\) and \(\Theta _K\) is explained in detail in [MW17, Introduction]. For our purposes, it suffices to note that \(\Upsilon _K\) captures the small-scale behaviour of this difference. On the other hand, \(\Theta _K\) captures the large-scale behaviour: the term \(G_K^2\) contains a cubic damping term in \(\Theta _K\) (i.e. with a good sign). Finally, we note that there is a redundancy in the specification of initial condition: any choice such that
into \(\Upsilon _K\) and \(\Theta _K\) is explained in detail in [MW17, Introduction]. For our purposes, it suffices to note that \(\Upsilon _K\) captures the small-scale behaviour of this difference. On the other hand, \(\Theta _K\) captures the large-scale behaviour: the term \(G_K^2\) contains a cubic damping term in \(\Theta _K\) (i.e. with a good sign). Finally, we note that there is a redundancy in the specification of initial condition: any choice such that  is sufficient. Our choice is informed by Remark 1.3 in [MW17].
is sufficient. Our choice is informed by Remark 1.3 in [MW17].
Remark 6.10
Rewriting (6.10) as

we note the similarity between the change of variables for the stochastic PDE given above and for the field theory in (5.21).
Formally taking \(K \rightarrow \infty \) in (6.11) leads us to the following system:

where

and \(G^{1,a}\) and \(G^{1,b}\) are commutator terms defined analogously as in (6.12).
For every \(T>0\), define the Banach space
equipped with the norm
Remark 6.11
The choice of exponents in function spaces in \({\mathcal {Y}}_T\), as well as the choice of exponents in the blow-up at \(t=0\) in \(\Vert \cdot \Vert _{{\mathcal {Y}}_T}\), corresponds to the one made in [MW17]. It is arbitrary to an extent: it depends on the choice of initial condition, which must have Besov-Hölder regularity strictly better than \(-\frac{2}{3}\).
The local well-posedness of (6.13) follows from entirely deterministic arguments, so we state it with  replaced by any deterministic
replaced by any deterministic  .
.
Proposition 6.12
Let  for any \(T_0>0\), and let \((\Upsilon _0,\Theta _0) \in {\mathcal {C}}^{-\frac{3}{5}}\times {\mathcal {C}}^{-\frac{3}{5}}\). Then, there exists
for any \(T_0>0\), and let \((\Upsilon _0,\Theta _0) \in {\mathcal {C}}^{-\frac{3}{5}}\times {\mathcal {C}}^{-\frac{3}{5}}\). Then, there exists  such that there is a unique mild solution \((\Upsilon , \Theta ) \in {\mathcal {Y}}_T\) to (6.13) with initial data \((\Upsilon _0,\Theta _0)\).
such that there is a unique mild solution \((\Upsilon , \Theta ) \in {\mathcal {Y}}_T\) to (6.13) with initial data \((\Upsilon _0,\Theta _0)\).
In addition, let  such that
such that  for some \(R>0\), and let \((\Upsilon _0^1,\Theta _0^1),(\Upsilon _0^2,\Theta _0^2) \in {\mathcal {C}}^{-\frac{3}{5}} \times {\mathcal {C}}^{-\frac{3}{5}}\). Let the respective solutions to (6.13) be \((\Upsilon ^1,\Theta ^1) \in {\mathcal {Y}}_{T_1}\) and \((\Upsilon ^2,\Theta ^2) \in {\mathcal {Y}}_{T_2}\) and define \(T=\min (T_1,T_2)\). Then there exists \(C=C(R)>0\) such that
for some \(R>0\), and let \((\Upsilon _0^1,\Theta _0^1),(\Upsilon _0^2,\Theta _0^2) \in {\mathcal {C}}^{-\frac{3}{5}} \times {\mathcal {C}}^{-\frac{3}{5}}\). Let the respective solutions to (6.13) be \((\Upsilon ^1,\Theta ^1) \in {\mathcal {Y}}_{T_1}\) and \((\Upsilon ^2,\Theta ^2) \in {\mathcal {Y}}_{T_2}\) and define \(T=\min (T_1,T_2)\). Then there exists \(C=C(R)>0\) such that

Proof
Proposition 6.12 is proven in Theorem 2.1 [MW17] (see also Theorem 3.1 [CC18]) by showing that the mild solution map

is a contraction in the ball
provided that T is taken sufficiently small and M is taken sufficiently large (both depending on the norm of the initial data and of  ). \(\quad \square \)
). \(\quad \square \)
We say that \(\Phi \in C([0,T];{\mathcal {C}}^{-\frac{1}{2}-\kappa })\) is a mild solution to (1.3) with initial data \(\phi _0 \in {\mathcal {C}}^{-\frac{1}{2}-\kappa }\) if

where \((\Upsilon ,\Theta ) \in {\mathcal {Y}}_T\) is a solution to (6.13) with  as in Proposition 6.9 and initial data
as in Proposition 6.9 and initial data  .
.
Proposition 6.13
For any \(\phi _0 \in {\mathcal {C}}^{-\frac{1}{2}-\kappa }\), let \(\Phi \in C([0,T];{\mathcal {C}}^{-\frac{1}{2}-\kappa })\) be the unique solution of (1.3) with initial data \(\phi _0\) up to time \(T>0\). In addition, for any \(K \in (0,\infty )\), let \(\Phi _K \in C({\mathbb {R}}_+;{\mathcal {C}}^{-\frac{1}{2}-\kappa })\) be the unique global solution of (6.9) with initial data \(\rho _K\phi _0\).
Then,

Proof
It suffices to show convergence of \((\Upsilon _K,\Theta _K)\) to \((\Upsilon ,\Theta )\) as \(K \rightarrow \infty \). This follows from Proposition 6.9 and mild adaptations of arguments in [MW17, Section 2]. \(\quad \square \)
Proposition 6.13 implies that \(\Phi _K \rightarrow \Phi \) in probability in \(C([0,T];{\mathcal {C}}^{-\frac{1}{2}-\kappa })\). Local-in-time convergence is not sufficient for our purposes.
The following proposition establishing global well-posedness of (1.3).
Proposition 6.14
For every \(\phi _0 \in {\mathcal {C}}^{-\frac{1}{2}-\kappa }\) let \(\Phi \in C([0,T^*);{\mathcal {C}}^{-\frac{1}{2}-\kappa })\) be the unique solution to (1.3) with initial condition \(\phi _0\) and where \(T^*>0\) is the maximal time of existence. Then \(T^* = \infty \) almost surely.
Proof
Proposition 6.14 is a consequence of a strong a priori bound on solutions to (6.13) established in [MW17, Theorem 1.1]. \(\quad \square \)
An immediate corollary of Proposition 6.14 is a global-in-time convergence result sufficient for our purposes.
Corollary 6.15
For every \(\phi _0 \in {\mathcal {C}}^{-\frac{1}{2}-\kappa }\), let \(\Phi \in C({\mathbb {R}}_+;{\mathcal {C}}^{-\frac{1}{2}-\kappa })\) be the unique global solution to (1.3) with initial condition \(\phi _0\). For every \(K \in (0,\infty )\), let \(\Phi _K \in C({\mathbb {R}}_+;{\mathcal {C}}^{-\frac{1}{2}-\kappa })\) be the unique global solution to (6.9) with initial condition \(\rho _K \phi _0\).
For every \(T>0\),

Remark 6.16
The infinite constant in (1.3) represents the renormalisation constants of the approximating equation (6.9) going to infinity as \(K \rightarrow \infty \). Note that there is a one-parameter family of distinct nontrivial “solutions” to (1.3) corresponding to taking finite shifts of the renormalisation constants. However, the use of  in the change of variables (6.14) fixes the precise solution.
in the change of variables (6.14) fixes the precise solution.
6.4.2 \({\nu _{\beta ,N}}\) is the unique invariant measure of (6.14)
Denote by \(B_b({\mathcal {C}}^{-\frac{1}{2} -\kappa })\) the set of bounded measurable functions on \({\mathcal {C}}^{-\frac{1}{2} -\kappa }\) and by \(C_b({\mathcal {C}}^{-\frac{1}{2} - \kappa }) \subset B_b({\mathcal {C}}^{-\frac{1}{2}-\kappa })\) the set of bounded continuous functions on \({\mathcal {C}}^{-\frac{1}{2} - \kappa }\).
Let \(\Phi (\cdot ;\cdot )\) be the solution map to (1.3): for \(\phi _0 \in {\mathcal {C}}^{-\frac{1}{2} - \kappa }\) and \(t \in {\mathbb {R}}_+\), \(\Phi (t;\phi _0)\) is the solution at time t to (1.3) with initial condition \(\phi _0\). For every \(t>0\), define \({\mathcal {P}}^{\beta ,N}_t:B_b({\mathcal {C}}^{-\frac{1}{2}-\kappa }) \rightarrow B_b({\mathcal {C}}^{-\frac{1}{2}-\kappa })\) by

for \(F \in B_b({\mathcal {C}}^{-\frac{1}{2} - \kappa })\), \(\phi _0 \in {\mathcal {C}}^{-\frac{1}{2}-\kappa }\), and \(t \in {\mathbb {R}}_+\).
Proposition 6.17
The solution \(\Phi \) to (1.3) is a Markov process and its transition semigroup \(({\mathcal {P}}^{\beta ,N}_t)_{t\geqslant 0}\) satisfies the strong Feller property, i.e. \({\mathcal {P}}_t:B_b({\mathcal {C}}^{-\frac{1}{2}-\kappa }) \rightarrow C_b({\mathcal {C}}^{-\frac{1}{2}-\kappa })\).
Proof
See [HM18b, Theorem 3.2]. \(\quad \square \)
Proposition 6.18
The measure \({\nu _{\beta ,N}}\) is the unique invariant measure of (1.3).
Proof
By Proposition 2.1 the measures \(\nu _{\beta ,N,K}\) converge weakly to \({\nu _{\beta ,N}}\) as \(K \rightarrow \infty \). Hence, by Skorokhod’s representation theorem [Bil08, Theorem 25.6] we can assume that there exists a sequence of random variables \(\{\phi _K\}_{K \in {\mathbb {N}}} \subset {\mathcal {C}}^{-\frac{1}{2} - \kappa }\) defined on the probability space  , independent of the white noise \(\xi \), such that \(\phi _K \sim \nu _{\beta ,N,K}\) and \(\phi _K\) converges almost surely to a random variable \(\phi \sim {\nu _{\beta ,N}}\).
, independent of the white noise \(\xi \), such that \(\phi _K \sim \nu _{\beta ,N,K}\) and \(\phi _K\) converges almost surely to a random variable \(\phi \sim {\nu _{\beta ,N}}\).
For every \(K \in (0,\infty )\), recall that the unique invariant measure of (6.9) is \(\nu _{\beta ,N,K}\). Let \(\Phi _K\) denote the solution to (6.9) with random initial data \(\phi _K\). Hence, \(\Phi _K(t) \sim \nu _{\beta ,N,K}\) for all \(t \in {\mathbb {R}}_+\).
Denote by \(\Phi \) the solution to (1.3) with initial condition \(\phi \). By Proposition 6.14, \(\Phi _K(t)\) converges in distribution to \(\Phi (t)\) for every \(t \in {\mathbb {R}}\), which implies \(\Phi (t) \sim {\nu _{\beta ,N}}\). Thus, \({\nu _{\beta ,N}}\) is an invariant measure of (1.3). As a consequence of the strong Feller property in Proposition 6.17, we obtain that \({\nu _{\beta ,N}}\) is the unique invariant measure of (1.3). \(\quad \square \)
6.4.3 Proof of Proposition 6.4
The Glauber dynamics of \({\tilde{\nu }}_{\beta ,N,\varepsilon }\) is given by the system of SDEs
where \({\tilde{\Phi }} : {\mathbb {R}}_+\times {\mathbb {T}}_N^\varepsilon \rightarrow {\mathbb {R}}\), \(\varphi \in {\mathbb {R}}^{{\mathbb {T}}_N^\varepsilon }\), and \(\xi _\varepsilon \) is the lattice discretisation of \(\xi \) given by

Note that the integral above means duality pairing between \(\xi (t,\cdot )\) and  .
.
For each \(\varepsilon > 0\), the global existence and uniqueness of (6.15), as well as the fact that \({\tilde{\nu }}_{\beta ,N,\varepsilon }\) is its unique invariant measure, is well-known.
The following proposition establishes a global-in-time convergence result for solutions of (6.15) to solutions of (1.3).
Proposition 6.19
For every \(\varepsilon > 0\), denote by \({\tilde{\Phi }}^\varepsilon \) the unique global solution to (6.15) with initial data \(\varphi _{\varepsilon } \in {\mathbb {R}}^{{\mathbb {T}}_N^\varepsilon }\). In addition, denote by \(\Phi \) the unique global solution to (1.3) with initial data \(\phi \in {\mathcal {C}}^{-\frac{1}{2}-\kappa }\).
Then, there exists a choice of constants \(\delta m^2(\varepsilon ,\eta ) \rightarrow \infty \) as \(\varepsilon \rightarrow 0\) such that, for every \(T > 0\),

provided that
almost surely.
Proof
See [ZZ18b, Theorem 1.1] or [HM18a, Theorem 1.1]. \(\quad \square \)
The next proposition establishes that the lattice measures are tight.
Proposition 6.20
Let \(\delta m^2(\bullet ,\eta )\) be as in Proposition 6.19. Then, \(\mathrm {ext}^\varepsilon _*{\tilde{\nu }}_{\beta ,N,\varepsilon }\) converges weakly to a measure \(\nu \) as \(\varepsilon \rightarrow 0\).
Proof
See [Par75, BFS83, GH18]. \(\quad \square \)
Proof of Proposition 6.4
For every \(\varepsilon >0\), let \(\varphi _\varepsilon \sim {\tilde{\nu }}_{\beta ,N,\varepsilon }\) be a random variable on  and independent of the white noise \(\xi \). By Proposition 6.20 and in light of Skorokhod’s representation theorem [Bil08, Theorem 25.6], we may assume that \(\mathrm {ext}^\varepsilon \varphi _\varepsilon \) converges almost surely to \(\phi \sim \nu \) as \(\varepsilon \rightarrow 0\). Reflection positivity is preserved by weak limits hence, by Lemma 6.3, \(\nu \) is reflection positive.
and independent of the white noise \(\xi \). By Proposition 6.20 and in light of Skorokhod’s representation theorem [Bil08, Theorem 25.6], we may assume that \(\mathrm {ext}^\varepsilon \varphi _\varepsilon \) converges almost surely to \(\phi \sim \nu \) as \(\varepsilon \rightarrow 0\). Reflection positivity is preserved by weak limits hence, by Lemma 6.3, \(\nu \) is reflection positive.
Denote by \({\tilde{\Phi }}^\varepsilon \) the solution to (6.15) with initial data \(\varphi _\varepsilon \). Since \({\tilde{\nu }}_{\beta ,N,\varepsilon }\) is the invariant measure of (6.15), \({\tilde{\Phi }}^\varepsilon (t) \sim {\tilde{\nu }}_{\beta ,N,\varepsilon }\) for every \(t \in {\mathbb {R}}_+\).
Denote by \(\Phi \) the (global-in-time) solution to (1.3) with initial data \(\phi \). For every \(t>0\), \(\mathrm {ext}^\varepsilon {\tilde{\Phi }}^\varepsilon (t) \rightarrow \Phi (t)\) in distribution as \(\varepsilon \rightarrow 0\) as a consequence of Proposition 6.19. Hence, \(\Phi (t) \sim \nu \) for every \(t > 0\). Thus, \(\nu \) is an invariant measure of (1.3). By Proposition 6.17 the invariant measure of (1.3) is unique. Therefore, \(\nu = {\nu _{\beta ,N}}\). \(\quad \square \)
7 Decay of Spectral Gap
Proof of Corollary 1.3
The Markov semigroup \(({\mathcal {P}}_t^{\beta ,N})_{t \geqslant 0}\) associated to (1.3) is reversible with respect to \({\nu _{\beta ,N}}\) (see [HM18a, Corollary 1.3] or [ZZ18a, Lemma 4.2]). Thus, one can express \(\lambda _{\beta ,N}\) as the sharpest constant in the Poincaré inequality
where \({\mathcal {E}}_{\beta ,N}\) is the associated Dirichlet form with domain \(D({\mathcal {E}}_{\beta ,N}) \subset L^2({\nu _{\beta ,N}})\). See [ZZ18a, Corollary 1.5].
The proof of Corollary 1.3 amounts to choosing the right test function in (7.1) and then using the explicit expression for \({\mathcal {E}}_{\beta ,N}\) for sufficiently nice functions due to [ZZ18a, Theorem 1.2].
Let \(\mathrm {Cyl}\) be the set of \(F \in L^2({\nu _{\beta ,N}})\) of the form
where \(m \in {\mathbb {N}}\), \(f \in C^1_b({\mathbb {R}}^m)\), \(l_1,\dots ,l_m\) are real trigonometric polynomials, and \(l_i(\cdot )\) denotes the (\(L^2\)) duality pairing between \(l_i\) and elements in \({\mathcal {C}}^{-\frac{1}{2}-\kappa }\). For any \(F \in \mathrm {Cyl}\), let \(\partial _{l_i} F\) denote the Gâteaux derivative of F in direction \(l_i\). Let \(\nabla F: {\mathcal {C}}^{-\frac{1}{2} -\kappa } \rightarrow {\mathbb {R}}\) be the unique function such that \(\partial _{l_i} F(\phi ) = \int _{{\mathbb {T}}_N}\nabla F(\phi ) l_i dx\) for every \(\phi \in {\mathcal {C}}^{-\frac{1}{2} - \kappa }\). In other words, \(\nabla F\) is the representation of the Gâteaux derivative with respect to the \(L^2\) inner product. Then, for any \(F,G \in \mathrm {Cyl}\),
Now we choose a test function in \(\mathrm{Cyl}\) to insert into (7.1). Take any \(\zeta \in (0,1)\) and \(m \in [0, (1-\zeta ){\sqrt{\beta }})\). Let \(\chi _m:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be a smooth, non-decreasing odd function such that \(\chi _m(a) = -1\) for \(a \leqslant -m\) and \(\chi _m(a) = 1\) for \(a \geqslant m\). Define
Then, \(F \in \mathrm {Cyl}\) and \(\langle F \rangle _{\beta ,N}= 0\). Moreover, its Fréchet derivative DF is supported on the set \(\{ {\mathfrak {m}}_N \in [-m,m] \}\).
Thus, inserting F into (7.1), we obtain
For any \(g \in L^2({\mathbb {T}}_N)\) and \(\varepsilon > 0\), by the linearity of \({\mathfrak {m}}_N\) and the Cauchy–Schwarz inequality,
where \(\chi _m'\) is the derivative of \(\chi _m\) and \(|\cdot |_\infty \) denotes the supremum norm. Note that this estimate is uniform over \(\phi \in {\mathcal {C}}^{-\frac{1}{2} -}\). Then, by duality and the definition of \(\nabla F\),
For the other term in (7.2), using that \(F^2\) is identically 1 on \(\{ |{\mathfrak {m}}_N| \geqslant m \}\),

We insert (7.3) and (7.4) into (7.2) to give
By Theorem 1.2, there exists \(C=C(\zeta ,\eta )>0\) and \(\beta _0 = \beta _0(\zeta ,\eta ) > 0\) such that, for all \(\beta > \beta _0\),
from which (1.4) follows. \(\quad \square \)
References
Aizenman, M., Duminil-Copin, H.: Marginal triviality of the scaling limits of critical 4d Ising and \(\varphi ^4\). Ann. of Math. (2) 194(1), 163–235 (2021
Aizenman, M., Holley, R.: Rapid convergence to equilibrium of stochastic Ising models in the Dobrushin-Shlosman regime. In: Percolation Theory and Ergodic Theory of Infinite Particle Systems, pp. 1–11. Springer, Berlin (1987)
Aizenman, M.: Geometric analysis of \(\varphi ^4\) fields and Ising models. Parts I and II. Commun. Math. Phys. 86(1), 1–48 (1982)
Bahouri, H., Chemin, J.-Y., Danchin, R.: Fourier Analysis and Nonlinear Partial Differential Equations, vol. 343. Springer, Berlin (2011)
Benfatto, G., Cassandro, M., Gallavotti, G., Nicolo, F., Olivieri, E., Presutti, E., Scacciatelli, E.: Ultraviolet stability in Euclidean scalar field theories. Commun. Math. Phys. 71(2), 95–130 (1980)
Boué, M., Dupuis, P.: A variational representation for certain functionals of Brownian motion. Ann. Probab. 26(4), 1641–1659 (1998)
Budhiraja, A., Dupuis, P.: Analysis and Approximation of Rare Events: Representations and Weak Convergence Methods, vol. 94. Springer, Berlin (2019)
Brydges, D., Dimock, J., Hurd, T.: The short distance behavior of \((\varphi )^4_3\). Commun. Math. Phys. 172(1), 143–186 (1995)
Brydges, D.C., Fröhlich, J., Sokal, A.D.: A new proof of the existence and nontriviality of the continuum \(\phi ^4_2\) and \(\phi ^4_3\) quantum field theories. Commun. Math. Phys. 91(2), 141–186 (1983)
Barashkov, N., Gubinelli, M.: A variational method for. Duke Math. J. 169(17), 3339–3415 (2020)
Barashkov, N., Gubinelli, M.: The \(\phi ^4_3\) measure via Girsanov’s theorem. arXiv preprint arXiv:2004.01513
Billingsley, P.: Probability and Measure. Wiley, New York (2008)
Bodineau, T., Ioffe, D., Velenik, Y.: Rigorous probabilistic analysis of equilibrium crystal shapes. J. Math. Phys. 41(3), 1033–1098 (2000)
Brezis, H., Mironescu, P.: Gagliardo–Nirenberg inequalities and non-inequalities: the full story. In: Annales de l’Institut Henri Poincaré C, Analyse non linéaire, vol. 35, pp. 1355–1376. Elsevier, New York (2018)
Bodineau, T.: The Wulff construction in three and more dimensions. Commun. Math. Phys. 207(1), 197–229 (1999)
Bodineau, T.: Phase coexistence for the Kac-Ising models. In: In and Out of Equilibrium, pp. 75–111. Springer, Berlin (2002)
Catellier, R., Chouk, K.: Paracontrolled distributions and the 3-dimensional stochastic quantization equation. Ann. Probab. 46(5), 2621–2679 (2018)
Chayes, J., Chayes, L., Schonmann, R.H.: Exponential decay of connectivities in the two-dimensional Ising model. J. Stat. Phys. 49(3–4), 433–445 (1987)
Comets, F., Fortet, R.: Grandes déviations pour des champs de Gibbs sur \({\mathbb{Z}}^{d}\). Comptes rendus de l’Académie des sciences. Série 1, Mathématique 303(11), 511–513 (1986)
Cesi, F., Guadagni, G., Martinelli, F., Schonmann, R.: On the two-dimensional stochastic Ising model in the phase coexistence region near the critical point. J. Stat. Phys. 85(1–2), 55–102 (1996)
Cassandro, M., Marra, R., Presutti, E.: Corrections to the critical temperature in 2d Ising systems with Kac potentials. J. Stat. Phys. 78(3–4), 1131–1138 (1995)
Cerf, R., Pisztora, Á.: On the Wulff crystal in the Ising model. Ann. Probab. 947–1017
Dupuis, P., Ellis, R.S.: A Weak Convergence Approach to the Theory of Large Deviations, vol. 902. Wiley, New York (2011)
Dobrushin, R.L., Kotecký, R., Shlosman, S.B.: Equilibrium crystal shapes—a microscopic proof of the Wulff construction. In: Stochastic Methods in Mathematics and Physics (Karpacz, 1988), pp. 221–229. World Sci. Publ., Teaneck (1989)
Dobrushin, R., Kotecký, R., Shlosman, S.: Wulff construction: a global shape from local interaction. Translations of Mathematical Monographs, vol. 104. American Mathematical Society, Providence (1992)
Dobrushin, R.L.: Existence of a phase transition in two-dimensional and three-dimensional Ising models. Theory Probab. Appl. 10(2), 193–213 (1965)
Da Prato, G., Zabczyk, J.: A note on semilinear stochastic equations. Differ. Integral Equ. 1(2), 143–155 (1988)
Ellis, R.S.: Entropy, Large Deviations, and Statistical Mechanics. Springer, Berlin (1985)
Feldman, J.: The \(\lambda \phi ^4_3\) field theory in a finite volume. Commun. Math. Phys. 37(2), 93–120 (1974)
Feldman, J.S., Osterwalder, K.: The Wightman axioms and the mass gap for weakly coupled \((\Phi ^{4})_{3}\) quantum field theories. Ann. Phys. 97(1), 80–135 (1976)
Föllmer, H., Ort, M.: Large deviations and surface entropy for Markov-fields. Astérisque 157–58, 173–190 (1988)
Faraco, D., Rogers, K.M.: The Sobolev norm of characteristic functions with applications to the Calderón inverse problem. Q. J. Math. 64(1), 133–147 (2012)
Fröhlich, J.: On the triviality of \(\lambda \phi ^4_d\) theories and the approach to the critical point in d (-)\(>\) 4 dimensions. Nucl. Phys. B 200(2), 281–296 (1982)
Fröhlich, J., Simon, B., Spencer, T.: Infrared bounds, phase transitions and continuous symmetry breaking. Commun. Math. Phys. 50(1), 79–95 (1976)
Gubinelli, M., Hofmanová, M.: A PDE construction of the Euclidean \(\phi ^4_3\) quantum field theory. arXiv preprint arXiv:1810.01700
Gubinelli, M., Hofmanová, M.: Global solutions to elliptic and parabolic \({\Phi }^4\) models in Euclidean space. Commun. Math. Phys. 368(3), 1201–1266 (2019)
Gubinelli, M., Imkeller, P., Perkowski, N.: Paracontrolled distributions and singular PDEs. In: Forum of Mathematics, Pi, vol. 3. Cambridge University Press, Cambridge (2015)
Glimm, J., Jaffe, A.: Positivity of the \(\varphi ^4_3\) Hamiltonian. Fortschr. Phys. 21(7), 327–376 (1973)
Glimm, J., Jaffe, A.: Quantum Physics: A Functional Integral Point of View, 2nd edn. Springer, New York (1987)
Glimm, J., Jaffe, A., Spencer, T.: Phase transitions for \(\phi _{2}^{4}\) quantum fields. Commun. Math. Phys. 45(3), 203–216 (1975)
Glimm, J., Jaffe, A., Spencer, T.: A convergent expansion about mean field theory. I. The expansion. Ann. Phys. 101(2), 610–630 (1976)
Glimm, J., Jaffe, A., Spencer, T.: A convergent expansion about mean field theory. II. Convergence of the expansion. Ann. Phys. 101(2), 631–669 (1976)
Glimm, J., Jaffe, A., Spencer, T.: Existence of phase transitions for \(\phi ^{4}_{2}\) quantum fields. In Les méthodes mathématiques de la théorie quantique des champs (Colloq. Internat. CNRS, No. 248, Marseille, 1975), pp. 175–184 (1976)
Glimm, J.: Boson fields with the :\(\phi ^4\): interaction in three dimensions. Commun. Math. Phys. 10(1), 1–47 (1968)
Gunaratnam, T.S., Oh, T., Tzvetkov, N., Weber, H.: Quasi-invariant Gaussian measures for the nonlinear wave equation in three dimensions. arXiv preprint arXiv:1808.03158
Griffiths, R.B.: Peierls proof of spontaneous magnetization in a two-dimensional Ising ferromagnet. Phys. Rev. 136(2A), A437 (1964)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (2015)
Gubinelli, M., Ugurcan, B., Zachhuber, I.: Semilinear evolution equations for the Anderson Hamiltonian in two and three dimensions. Stochast. Partial Differ. Equ. Anal. Comput. 8(1), 82–149 (2020)
Hairer, M.: A theory of regularity structures. Invent. Math. 198(2), 269–504 (2014)
Hairer, M.: Regularity structures and the dynamical \({\Phi }^4_3\) model, current developments in mathematics 2014. Int. Press, Somerville, pp. 1–49
Hairer, M., Iberti, M.: Tightness of the Ising-Kac model on the two-dimensional torus. J. Stat. Phys. 171(4), 632–655 (2018)
Hairer, M., Matetski, K.: Discretisations of rough stochastic PDEs. Ann. Probab. 46(3), 1651–1709 (2018)
Hairer, M., Mattingly, J.: The strong Feller property for singular stochastic PDEs. In: Annales de l’Institut Henri Poincaré, Probabilités et Statistiques, vol. 54, pp. 1314–1340. Institut Henri Poincaré, (2018)
Holley, R.: On the asymptotics of the spin-spin autocorrelation function in stochastic Ising models near the critical temperature. In: Spatial Stochastic Processes, pp. 89–104. Springer, Berlin (1991)
Hairer, M., Schönbauer, P.: The support of singular stochastic PDEs. arXiv preprint arXiv:1909.05526
Ioffe, D., Schonmann, R.H.: Dobrushin-Koteckỳ-Shlosman theorem up to the critical temperature. Commun. Math. Phys. 199(1), 117–167 (1998)
Kupiainen, A.: Renormalization group and stochastic PDEs. In: Annales Henri Poincaré, vol. 17, pp. 497–535. Springer, Berlin (2016)
Lubetzky, E., Sly, A.: Critical Ising on the square lattice mixes in polynomial time. Commun. Math. Phys. 313(3), 815–836 (2012)
Martinelli, F., Olivieri, E.: Approach to equilibrium of Glauber dynamics in the one phase region. I. The attractive case. Commun. Math. Phys. 161(3), 447–486 (1994)
Minlos, R.A., Sinai, Y.G.: The phenomenon of “phase separation” at low temperatures in some lattice models of a gas. I. Math. USSR-Sbornik 2(3), 335 (1967)
Minlos, R.A., Sinai, Y.G.: The phenomenon of “separation of phases” at low temperatures in certain lattice models of a gas. II. Trudy Moskovskogo Matematicheskogo Obshchestva 19, 113–178 (1968)
Magnen, J., Sénéor, R.: Phase space cell expansion and Borel summability for the Euclidean \(\varphi ^4_3\) theory. Commun. Math. Phys. 56(3), 237–276 (1977)
Mourrat, J.-C., Weber, H.: The dynamic \(\Phi ^4_3\) model comes down from infinity. Commun. Math. Phys. 356(3), 673–753 (2017)
Moinat, A., Weber, H.: Space-time localisation for the dynamic \({\Phi }^4_3\) model. arXiv preprint arXiv:1811.05764
Mourrat, J.-C., Weber, H., Xu, W.: Construction of \(\Phi ^4_3\) diagrams for pedestrians. In: From particle systems to partial differential equations, vol. 209 of Springer Proc. Math. Stat., pp. 1–46. Springer, Cham (2017)
Nelson, E.: A quartic interaction in two dimensions. In: Mathematical Theory of Elementary Particles, Proc. Conf., Dedham, Mass., 1965, pp. 69–73. MIT Press, Cambridge (1966)
Nelson, E.: The free Markoff field. J. Funct. Anal. 12, 211–227 (1973)
Nualart, D.: The Malliavin Calculus and Related Topics, vol. 1995. Springer, Berlin (2006)
Olla, S.: Large deviations for Gibbs random fields. Probab. Theory Relat. Fields 77(3), 343–357 (1988)
Park, Y.M.: Lattice approximation of the \((\lambda \varphi ^4- \mu \varphi )_3\) field theory in a finite volume. J. Math. Phys. 16(5), 1065–1075 (1975)
Peierls, R.: On Ising’s model of ferromagnetism. In: Mathematical Proceedings of the Cambridge Philosophical Society, vol. 32, pp. 477–481. Cambridge University Press, Cambridge (1936)
Pfister, C.-E.: Large deviations and phase separation in the two-dimensional Ising model. Helv. Phys. Acta 64, 953–1054 (1991)
Pisztora, A.: Surface order large deviations for Ising, Potts and percolation models. Probab. Theory Relat. Fields 104(4), 427–466 (1996)
Revuz, D., Yor, M.: Continuous Martingales and Brownian Motion, vol. 293. Springer, Berlin (2013)
Schonmann, R.H.: Second order large deviation estimates for ferromagnetic systems in the phase coexistence region. Commun. Math. Phys. 112(3), 409–422 (1987)
Simon, B., Griffiths, R.B.: The \((\varphi ^4)_2\) field theory as a classical Ising model. Commun. Math. Phys. 33(2), 145–164 (1973)
Shlosman, S.B.: The method of reflection positivity in the mathematical theory of first-order phase transitions. Russ. Math. Surv. 41, 83–134 (1986)
Thomas, L.E.: Bound on the mass gap for finite volume stochastic Ising models at low temperature. Commun. Math. Phys. 126(1), 1–11 (1989)
Üstünel, A.S.: Variational calculation of Laplace transforms via entropy on Wiener space and applications. J. Funct. Anal. 267(8), 3058–3083 (2014)
Zabczyk, J.: Symmetric solutions of semilinear stochastic equations. In: Stochastic Partial Differential Equations and Applications II, pp. 237–256. Springer, Berlin (1989)
Zhu, R., Zhu, X.: Dirichlet form associated with the \(\phi ^4_3\) model. Electron. J. Probab. 23
Zhu, R., Zhu, X.: Lattice approximation to the dynamical \(\phi ^4_3\) model. Ann. Probab. 46(1), 397–455 (2018)
Acknowledgements
We thank Roman Kotecký for inspiring discussions throughout all stages of this project. We thank Nikolay Barashkov for useful discussions regarding the variational approach to ultraviolet stability for \(\phi ^4_3\). We thank Martin Hairer for a particularly useful discussion. AC and TSG thank the Hausdorff Research Institute for Mathematics for the hospitality and support during the Fall 2019 junior trimester programme Randomness, PDEs and Nonlinear Fluctuations. AC, TSG, and HW thank the Isaac Newton Institute for Mathematical Sciences for hospitality and support during the Fall 2018 programme Scaling limits, rough paths, quantum field theory, which was supported by EPSRC Grant No. EP/R014604/1. AC was supported by the Leverhulme Trust via an Early Career Fellowship, ECF-2017-226. TSG was supported by EPSRC as part of the Statistical Applied Mathematics CDT at the University of Bath (SAMBa), Grant No. EP/L015684/1. HW was supported by the Royal Society through the University Research Fellowship UF140187 and by the Leverhulme Trust through a Philip Leverhulme Prize.
Funding
Open access funding provided by University of Geneva.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by S. Chatterjee
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A Analytic Notation and Toolbox
Appendix A Analytic Notation and Toolbox
1.1 A. 1 Basic function spaces on the torus
Let \({\mathbb {T}}_N= ({\mathbb {R}}/ N{\mathbb {Z}})^3\) be the 3D torus of sidelength \(N \in {\mathbb {N}}\). Denote by \(C^\infty ({\mathbb {T}}_N)\) the space of smooth functions on \({\mathbb {T}}_N\) and by \(S'({\mathbb {T}}_N)\) the space of distributions. For \(\phi \in S'({\mathbb {T}}_N)\) and \(f \in C^\infty ({\mathbb {T}}_N)\), we write \(\int _{{\mathbb {T}}_N}\phi f dx\) to denote their duality pairing. For any \(p \in [1,\infty ]\), let  denote the Lebesgue space with respect to the normalised Lebesgue measure
denote the Lebesgue space with respect to the normalised Lebesgue measure  .
.
Let \({\mathcal {F}}\) denote the Fourier transform, i.e. for any \(f \in C^\infty ({\mathbb {T}}_N)\) and \(n \in (N^{-1}{\mathbb {Z}})^3\),
where \(e_n(x) = e^{2\pi i n \cdot x }\).
For any \(\rho : {\mathbb {R}}^3 \rightarrow {\mathbb {R}}\), let \(T_\rho \) be the Fourier multiplier with symbol \(\rho (\cdot )\) defined on smooth functions via
When clear from context, we simply write \(\rho f\) instead of \(T_\rho f\).
For \(s \in {\mathbb {R}}\), the inhomogeneous Sobolev space \(H^s\) is the completion of \(f \in C^\infty \) with respect to the norm
where \(\langle \cdot \rangle = \sqrt{ \eta + 4\pi ^2 | \cdot |^2}\) for a fixed \(\eta > 0\) (see Sect. 2). The norms depend on \(\eta \) but they are equivalent for different choices.
1.2 A.2 Besov Spaces
In this section, we introduce Besov spaces on \({\mathbb {T}}_N\) and give some useful estimates. All of the results can be found in [BCD11, Section 2.7] stated for Besov spaces on \({\mathbb {R}}^3\), but can be adapted to \({\mathbb {T}}_N\).
Let B(x, r) denote the ball centred at \(x \in {\mathbb {R}}^3\) of radius \(r > 0\) and let A denote the annulus \(B(0, \frac{4}{3}) {\setminus } B(0, \frac{3}{8})\). Let \({\tilde{\Delta }}, \Delta \in C^\infty _c({\mathbb {R}}^3;[0,1])\) be radially symmetric and satisfy
-
\(\mathrm {supp} {\tilde{\chi }} \subset B(0, \frac{4}{3})\) and \(\mathrm {supp} \chi \subset A\);
-
\(\sum _{k \geqslant -1} \chi _k = 1\), where \(\chi _{-1} = {\tilde{\chi }}\) and \(\chi _k(\cdot ) = \chi (2^{-k}\cdot )\) for \(k \in {\mathbb {N}}\cup \{0\}\).
Identify \(\Delta _k\) with its Fourier multiplier.
\(\{ \Delta _k \}_{k \in {\mathbb {N}}\cup \{-1\}}\) are called Littlewood-Paley projectors. For \(f \in C^\infty ({\mathbb {T}}_N)\), we have
For \(k \geqslant 0\), \(\Delta _k f\) contains the frequencies of f order \(2^k\). \(\Delta _{-1}\) contains all the low frequencies (i.e. of size less than order 1).
For \(s \in {\mathbb {R}}\), \(p,q \in [1,\infty ]\), we define the Besov spaces \(B^s_{p,q}({\mathbb {T}}_N)\) to be the completion of \(C^\infty ({\mathbb {T}}_N)\) with respect to the norm
where \(l^q\) is the usual space of q-summable sequences, interpreted as a supremum when \(q=\infty \). Note that these spaces are separable. Besov-Hölder spaces are denoted \(B^s_{\infty ,\infty }({\mathbb {T}}_N) = {\mathcal {C}}^{s}({\mathbb {T}}_N)\) and are a strict subset of the usual Hölder spaces (which are not separable) for \(s \in {\mathbb {R}}_+ {\setminus } {\mathbb {N}}\). Moreover, the \(B^s_{2,2}({\mathbb {T}}_N) = H^s({\mathbb {T}}_N)\) and their norms are equivalent.
Proposition A.1
(Duality). Let \(s \in {\mathbb {R}}\) and \(p_1,p_2,q_1,q_2 \in [1,\infty ]\) such that \(\frac{1}{p_1} + \frac{1}{p_2} = \frac{1}{q_1} + \frac{1}{q_2} = 1\). Then,

for \(f,g \in C^\infty ({\mathbb {T}}_N)\).
Proof
See [GOTW18, Lemma 2.1]. \(\quad \square \)
Proposition A.2
(Fractional Leibniz estimate). Let \(s \in {\mathbb {R}}\), \(p,p_1,p_2,p_3,p_4,q \in [1,\infty ]\) satisfy \(\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2} = \frac{1}{p_3} + \frac{1}{p_4}\). Then, there exists \(C=C(s,p_1,p_2,p_3,p_4,q,\eta ) > 0\) such that
for \(f,g \in C^\infty ({\mathbb {T}}_N)\).
Proof
See [GOTW18, Lemma 2.1]. \(\quad \square \)
Proposition A.3
(Interpolation). Let \(s,s_1,s_2 \in {\mathbb {R}}\) such that \(s_1< s < s_2\), \(p,p_1,p_2,q,q_1,q_2 \in [1,\infty ]\) and \(\theta \in (0,1)\) satisfy
Then, there exists \(C=C(s,s_1,s_2,p,p_1,p_2,q,q_1,q_2,\theta ,\eta ) > 0\) such that
for \(f \in C^\infty ({\mathbb {T}}_N)\).
Proof
See [BM18, Proposition 5.7]. \(\quad \square \)
Proposition A.4
(Bernstein’s inequality). For \(R > 0\), denote \(B_f(R) = \{ n \in (N^{-1}{\mathbb {Z}})^3 : |n| \leqslant R \}\). Let \(s_1, s_2 \in {\mathbb {R}}\) such that \(s_1 < s_2\), \(p,q \in [1,\infty ]\). Then, there exists \(C=C(s_2,s_2,p,q,\eta )>0\) such that
for \(f,g \in C^\infty ({\mathbb {T}}_N)\) such that \(\mathrm {supp} ({\mathcal {F}}f) \subset B_f(R)\) and \(\mathrm {supp} ({\mathcal {F}}g) \subset (N^{-1}{\mathbb {Z}})^3 {\setminus } B_f(R)\).
Proof
See [BCD11, Lemma 2.1] for a proof on \({\mathbb {R}}^3\). \(\quad \square \)
1.3 A.3 Paracontrolled calculus
Let \(f,g \in C^\infty ({\mathbb {T}}_N)\). Define the paraproduct

and the resonant product

Then,

Proposition A.5
(Paraproduct estimates). Let \(s \in {\mathbb {R}}\) and \(p,p_1,p_2,q \in [1,\infty ]\) be such that \(\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2}\). Then, there exists \(C=C(s,p,p_1,p_2,q,\eta )>0\) such that

for \(f,g \in C^\infty ({\mathbb {T}}_N)\).
Proof
See [BCD11, Theorem 2.82] for a proof on \({\mathbb {R}}^3\). \(\quad \square \)
Proposition A.6
(Resonant product estimate). Let \(s_1,s_2 \in {\mathbb {R}}\) such that \(s=s_1 + s_2 > 0\). Let \(p,p_1,p_2,q \in [1,\infty ]\) satisfy \(\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2}\). Then, there exists \(C=C(s_1,s_2,p,p_1,p_2,q,\eta ) > 0\) such that

for \(f,g \in C^\infty ({\mathbb {T}}_N)\).
Proof
See [BCD11, Theorem 2.85] for a proof on \({\mathbb {R}}^3\). \(\quad \square \)
We now state some useful commutator estimates.
Proposition A.7
Let \(s_1, s_3 \in {\mathbb {R}}\), \(s_2 \in (0,1)\) such that \(s_1 + s_3 < 0\) and \(s_1 + s_2 + s_3 = 0\). Moreover, let \(p,p_1,p_2,q_1,q_2 \in [1,\infty ]\) satisfy \(\frac{1}{p} + \frac{1}{p_1} + \frac{1}{p_2} = 1\) and \(\frac{1}{q_1} + \frac{1}{q_2} = 1\). Then, there exists \(C=C(s_1,s_2,s_3,p,p_1,p_2,q_1,q_2,\eta )>0\) such that

for \(f,g,h \in C^\infty ({\mathbb {T}}_N)\).
Proof
This is a modification of [GUZ20, Lemma A.6]. See [BG19, Proposition 7]. \(\quad \square \)
Proposition A.8
Let \(s_1,s_3 \in {\mathbb {R}}\), \(s_2 \in (0,1)\) such that \(s_1+s_3 < 0\) but \(s_1+s_2+s_3 > 0\). Morover, let \(p,p_1,p_2,p_3 \in [1,\infty ]\) satisfy \(\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2} + \frac{1}{p_3}\). Then, there exists \(C=C(s_1,s_2,s_3,p,p_1,p_2,\eta )>0\) such that

for \(f,g,h \in C^\infty ({\mathbb {T}}_N)\).
Proof
This is a modification of [GIP15, Lemma 2.4]. See [BG19, Proposition 6]. \(\quad \square \)
1.4 A.4 Analytic Properties of \({\mathcal {J}}_k\)
The family of operators \(\{ {\mathcal {J}}_k \}_{k \geqslant 0}\) defined in Sect. 4.1 satisfies the following estimate: for every multi-index \(\alpha \in {\mathbb {N}}^3\), there exists \(C=C(\alpha ,\eta )\) such that
Proposition A.9
Let \(s \in {\mathbb {R}}\), \(p,q\in [1,\infty ]\). Then, there exists \(C=C(s,p,q)>0\) such that
for every \(f \in C^\infty ({\mathbb {T}}_N)\)
Proof
This follows from (A.12) and [BCD11, Proposition 2.78]. \(\quad \square \)
We now state another useful commutator estimate.
Proposition A.10
Let \(s_1 \in {\mathbb {R}}\), \(s_2 \in (0,1)\), \(p,p_1,p_2,q,q_1,q_2 \in [1,\infty ]\) such that \(\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2}\) and \(\frac{1}{q} = \frac{1}{q_1} + \frac{1}{q_2}\). Then, for any \(\kappa > 0\), there exists \(C=C(s_1,s_2,p,p_1,p_2, q, \kappa , \eta )>0\) such that

for \(f,g \in C^\infty ({\mathbb {T}}_N)\).
Proof
This follows from (A.12) and [BCD11, Lemma 2.99]. \(\quad \square \)
1.5 A.5 Poincaré Inequality on Blocks
Proposition A.11
There exists \(C_P > 0\) such that, for any \(N \in {\mathbb {N}}\) and  a unit block, the following estimate holds for all \(f \in C^\infty ({\mathbb {T}}_N)\):
a unit block, the following estimate holds for all \(f \in C^\infty ({\mathbb {T}}_N)\):

where  .
.
Proof
See [GT15, (7.45)]. \(\quad \square \)
1.6 A.6 Bounds on Discrete Convolutions
Lemma A.12
Let \(d \geqslant 1\) and \(\alpha , \beta \in {\mathbb {R}}\) satisfy
Then, there exists \(C=C(d,\alpha ,\beta )>0\) such that, uniformly over \(n \in (N^{-1}{\mathbb {Z}})^d\),
Proof
Follows from [MWX17, Lemma 4.1] and by keeping track of N dependence.
\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chandra, A., Gunaratnam, T.S. & Weber, H. Phase Transitions for \(\phi ^4_3\). Commun. Math. Phys. 392, 691–782 (2022). https://doi.org/10.1007/s00220-022-04353-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-022-04353-6




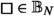 is plus (resp. minus) valued if
is plus (resp. minus) valued if 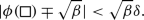
 is plus good if every
is plus good if every  is plus valued. The set of plus good blocks is denoted
is plus valued. The set of plus good blocks is denoted  is minus good if every
is minus good if every  is minus valued. The set of minus good blocks is denoted
is minus valued. The set of minus good blocks is denoted  such that
such that  contains a neutral block. We denote the set of frustrated blocks
contains a neutral block. We denote the set of frustrated blocks  such that
such that  contains no neutral blocks, but there exists at least one pair of nearest-neighbours
contains no neutral blocks, but there exists at least one pair of nearest-neighbours  such that
such that  but
but  . We denote the set of interface blocks
. We denote the set of interface blocks 
 as a random distribution in the limit
as a random distribution in the limit  tested against a smooth function diverges as the cutoff is removed.
tested against a smooth function diverges as the cutoff is removed. does converge as
does converge as  against
against 