Abstract
Three decades ago, Inozemtsev discovered an isotropic long-range spin chain with elliptic pair potential that interpolates between the Heisenberg and Haldane–Shastry spin chains while admitting an exact solution throughout, based on a connection with the elliptic quantum Calogero–Sutherland model. Though Inozemtsev’s spin chain is widely believed to be quantum integrable, the underlying algebraic reason for its exact solvability is not yet well understood. As a step in this direction we refine Inozemtsev’s ‘extended coordinate Bethe ansatz’ and clarify various aspects of the model’s exact spectrum and its limits. We identify quasimomenta in terms of which the M-particle energy is close to being (functionally) additive, as one would expect from the limiting models. This moreover makes it possible to rewrite the energy and Bethe-ansatz equations on the elliptic curve, turning the spectral problem into a rational problem as might be expected for an isotropic spin chain. We treat the \(M=2\) particle sector and its limits in detail. We identify an S-matrix that is independent of positions despite the more complicated form of the extended coordinate Bethe ansatz. We show that the Bethe-ansatz equations reduce to those of Heisenberg in one limit and give rise to the ‘motifs’ of Haldane–Shastry in the other limit. We show that, as the interpolation parameter changes, the ‘scattering states’ from Heisenberg become Yangian highest-weight states for Haldane–Shastry, while bound states become (\({{\mathfrak {sl}}}_2\)-highest weight versions of) affine descendants of the magnons from \(M=1\). We are able to treat this at the level of the wave function and quasimomenta. For bound states we find an equation that, for given Bethe integers, relates the ‘critical’ values of the spin-chain length and the interpolation parameter for which the two complex quasimomenta collide; it reduces to the known equation for the ‘critical length’ in the limit of the Heisenberg spin chain. We also elaborate on Inozemtsev’s proof of the completeness for \(M=2\) by passing to the elliptic curve. Our review of the two-particle sectors of the Heisenberg and Haldane–Shastry spin chains may be of independent interest.













Similar content being viewed by others
Notes
Note that the existence of a family of commuting Hamiltonians does not follow from Inozemtsev’s quantum Lax pair (L, M), as the entries of L and M are operators that do not commute. Moreover, the remedy proposed in [UHW92, SS93] cannot be applied here because the sum condition \(\sum _k M_{ik} = 0\) is not satisfied.
The above Hamiltonians are ferromagnetic: the potentials are positive (for real arguments) while \(1-P\) is a positive operator, yielding energies \(\ge 0\), with the ferromagnetic (pseudo)vacuum \(|\!\!\uparrow \cdots \!\!\uparrow \rangle \) at zero energy. Importantly, this choice of overall sign will yield a relative sign in the expression (3.28) for the energy of \(H_\text {s}\), and eventually give energies that are elliptic in the sense of Sects. 4.5.5 and 5. Indeed, in (3.28) the dispersion \(\varepsilon _\text {s}\), see (3.7), inherits the sign of \(H_\text {s}\) while the potential part \({\widetilde{U}}\) originates from the elliptic Calogero–Sutherland (eCS) operator (3.25), which should be a positive operator. Only with the relative signs as in (3.28) a shift of the energy in \(\varphi \) (Sect. 4.5.5) or any \(t_\alpha \) (Sect. 5) is proportional to the eCS Bethe-ansatz equations, vanishing on shell.
Note the prefactor in \(\theta _b'(z) = (\pi /\omega _b)\,\vartheta '(\pi \,z/\omega _b|\tau _b)\), where \(\tau _b\) is the nome from (2.6).
We will prove positivity of the dispersion in Footnote 13 on p. p. 18.
Our equation differs in the prefactor of \(\eta _2\) from (59) in [Ino03]: we find that it is independent of L.
We will review these exact wave functions in Sect. 4.4.1 for \(M=2\). In short: the HS wave function is the square of the Vandermonde polynomial times (a special case of) a Jack polynomial, where the variables are ‘evaluated’ at roots of unity that represent the coordinates of the magnons on the chain. This has one similarity with (3.14) that is worth pointing out: Jack polynomials are naturally constructed by symmetrising so-called nonsymmetric Jack polynomials. We plan to pursue this line of thought in future work.
An argument for the passage from (3.17) to (3.18) goes as follows. Thinking of \({\varvec{n}}\) in the extended domain as fixed let us view \(\Psi _{\tilde{{\varvec{p}}},{\varvec{p}}}\) as a function of \({\varvec{r}} \,{:}{=}\,\, {\varvec{p}} - \tilde{{\varvec{p}}}\). As long as \({\varvec{n}}\) has all entries distinct there exists an \(1\le m^* \le M\) for which \(n_{m^{\!*}}\) is the (strict) largest among \({\varvec{n}}\). For \(1\le m \le M\) consider the limit \(r_m \rightarrow -\mathrm {i}\, \infty \). On both sides of (3.17) the terms for w for which \(w(m) = m^*\) then dominate all others. However, the additional exponential factor on the left-hand side contains \(r_m = p_m - {\tilde{p}}_m\) too if \(w(m)=1\). Provided \(\Psi _{\tilde{{\varvec{p}}},{\varvec{p}}}({\varvec{n}}) \ne 0\) the only way that (3.17) can hold in this limit is when \(-{\tilde{p}}_m + \varphi _m/L\) grows like \(r_m\), i.e. (3.18) must hold asymptotically. Since we want all functions to depend meromorphically on all parameters this extend from a neighbourhood of infinity to the whole complex plane.
In fact, solutions will either have a simple pole or a double zero, corresponding to the two solutions \(\beta =2\) and \(\beta =-1\) of \(\beta \,(\beta -1)=2\), respectively. We will briefly get back to this in Sect. 4.1.1.
Note that
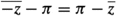 holds for
holds for 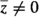 . The value at
. The value at 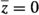 , a pole of \({\rho }^{\vee }_1\), is not determined by the limit.
, a pole of \({\rho }^{\vee }_1\), is not determined by the limit.This relation, which can be understood as a consequence of the ‘trace identities’ expressing the Heisenberg Hamiltonians as logarithmic derivatives of the transfer matrix, breaks down away from the Heisenberg limit. Indeed, numerical evaluation of \(\mathrm {d}\,p/\mathrm {d}\,{\tilde{p}}\,|_{{\tilde{p}} = \lambda _\text {n}(p)} = -\coth \kappa \, ((\bar{\rho }^{\vee }_1)^{-1})'(\bar{\rho }^{\vee }_1(p))\) differs from \(\varepsilon _\text {n}(p)\) for finite \(\kappa \). (This is clear in the HS limit, where \({\tilde{p}}=(p-\pi )/2\) if \(p\in [0,2\pi ]\) so \(\mathrm {d}\,p/\mathrm {d}\,{\tilde{p}} = 2\) is constant.)
Note that \(\bar{F}^{\vee }_1{}'(p) = \bar{\rho }^{\vee }_1{}'(p) \, c(p)\) for \(c(p) \,{:}{=}\,\, \bar{\rho }^{\vee }_1{}''(p)/\bar{\rho }^{\vee }_1{}'(p) +2\, \bar{\rho }^{\vee }_1(p)\). Thus \(\bar{F}^{\vee }_1{}'(p)\) vanishes if c(p) does. The function \(c'(p)\) is elliptic of order two and thus has no more than two zeroes on \([0,2\pi )\). By Rolle’s theorem, this implies that c(p) has at most three zeroes in this interval. Since \(\bar{\rho }^{\vee }_1{}'(p)\) is nonzero on \([0,2\pi )\) this implies \(\bar{F}^{\vee }_1{}'(p)\) has at most three zeroes on \([0,2\pi )\), of which two are at \(p=0\) and \(p=\pi \). Since \(\bar{F}^{\vee }_1{}'(p) = - \bar{F}^{\vee }_1{}'(2 \pi - p)\) we see that if there were a third zero \(p^*\) then there would be another at \(2 \pi - p^*\), yielding a contradiction. So \({\bar{F}}_1{}'(p)\) has precisely two zeroes. Since \(\bar{F}^{\vee }_1\) vanishes at \(p=0\) and \(p=2\pi \) and \(\bar{F}^{\vee }_1 (p) = \bar{F}^{\vee }_1(\pi -p)\) the above implies that \(\bar{F}^{\vee }_1\) does not have any further zeroes and is therefore either nonnegative or nonpositive. Since \(\bar{F}^{\vee }_1(\pi ) <0\) it follows that it is nonpositive, proving that the dispersion (3.38) is nonnegative.
These functions are symmetric, \(\chi _b(t,z) = \chi _b(z,t)\), and doubly (quasi)periodic, \(\chi _b(z+\omega _b,t) = \chi _b(z,t)\) and \(\chi _b(z+\omega _a,t) = \mathrm {e}^{(-1)^b \, 2\,\pi \mathrm {i}\,t/\omega _b} \,\chi _b(z,t)\) for \(a\ne b\). See also Footnote 3 on p. 6. These are the unique meromorphic functions of z regular on \({\mathbb {C}}{\setminus }{\mathbb {L}}\) with a simple pole with residue one at the origin and the aforementioned double (quasi)periodicity. Note that [Ino03] uses \(\chi _1(z,t) = \mathrm {e}^{-2\,\kappa \, z\,t/L} \, \chi _2(z,t)\), therein denoted by \(-{\tilde{\sigma }}_z(-t)\). We will work with \(\chi _2\), whose quasiperiods fit with (3.15) to yield the relation (3.33) with the eCS momenta \({\tilde{p}}_m\).
Compared to [Ino90] the shift in our quasimomenta \(p_m\) leads to a simpler energy, built directly from the dispersion relation at the quasimomenta and the eCS potential energy \({\tilde{U}}\).
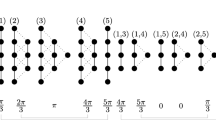
A priori the \(I_m\) single out a interval of length \(2\pi \) at the corresponding \(I_\text {tot}\). We observe that the uniqueness holds for \(\varphi \in [0,2\pi )\), with the actual root lying in \((0,\pi )\). This is natural from the structure illustrated in Fig. 5 and readily verified numerically for all roots in this class for \(L\le 30\). For the extra real roots present for \(L\ge 22\) (see below) uniqueness only holds in the smaller interval \((0,\pi )\) just below the trivial root.
The parity self-conjugate cases \({\varvec{I}} = (i,L-i)\), with \(1\le i \le \lfloor L/2\rfloor -1\), admit explicit roots: \(\varphi = 2\pi i/(L-1)\).
This bound-state curve follows from \(p_{1,2} = p_\text {tot}/2 {\mp } \mathrm {i}\log [\cos (p_\text {tot}/2)]\), the exact solution for \(L\rightarrow \infty \).
In fact there is a whole one-parameter family of physically equivalent roots at \(\mathrm {i}\,\infty \). For definiteness take \(I_1 = \lfloor L/4 \rfloor \), \(I_2 = \lceil L/4 \rceil \). The Bethe equations (4.12) are solved by \(p_1 = u + \mathrm {i}v\), \(p_2 = \pi - p_1\) (allowed by the reality of \(p_\text {tot},E\)) and \(\varphi = L \,u - 2\pi \lfloor L/4\rfloor + \mathrm {i}\,L\, v\). When \(v \rightarrow \infty \) the constraint (4.26) is obeyed for any value of \(u \in {\mathbb {R}}/2\pi {\mathbb {Z}}\). The choices \(u = \pi /2\) and \(u = -\pi /2 \equiv 3\pi /2\) are preferred in that \(p_2=p_1^* \,\mathrm {mod}\,2\pi \) and \({\mathrm {Re}}\varphi \in [0,\pi ]\) is small (if we switch to \(I_1 = \lfloor 3L/4 \rfloor \), \(I_2 = \lceil 3L/4 \rceil \) for \(u = 3\pi /2\)), as for all other roots.
As the pole in (4.33) signals, the naive value of the energy (4.33) via \({\varvec{p}}\) is incorrect. Regularise \(\lambda _{1,2} = \pm \mathrm {i}/2 - \epsilon \) so that \(\epsilon \rightarrow 0^+ \, (0^-)\) gives \(p_1 \rightarrow \pi /2 + \mathrm {i}\,\infty \) (\(p_1 \rightarrow 3\pi /2 + \mathrm {i}\,\infty \)) and \(p_2 = p_1^*\), yielding the correct value \(E = 2\). (More generally the \(p_m\) from Footnote 21 arise as \(\epsilon \rightarrow \mathrm {e}^{\mathrm {i}(u-\pi /2)}\,0^+\) with \(u \in [-\pi ,\pi )\).) The S-matrix (4.27) is still singular. Following [AV85] keep \(\lambda _1 = \mathrm {i}/2 - \epsilon \) but take \(\lambda _2 = -\mathrm {i}/2 - \epsilon - 2\,\mathrm {i}\, (\mathrm {i}\,\epsilon )^L\). This doesn’t affect the limits of \({\varvec{p}},E\) yet allows the wave function to be renormalised: \(\epsilon ^{(L-2)/2} \, \Psi _{{\varvec{p}}}(n_1,n_2) \rightarrow \pm [(-1)^{n_2}\,\delta _{n_2,n_1+1} - \delta _{n_1,1}\,\delta _{n_2,L}]\) as \(\epsilon \rightarrow 0\) for \(1\le n_1 < n_2\le L\), with sign depending on L and the direction from which \(\epsilon \) approaches zero.
If we ignore that \({\varvec{I}}\) might first occur as the parity-conjugate of some lower \({\varvec{I}}'\), any such root starts out as exceptional, \(\varphi = \pi + \mathrm {i}\,\infty \), at \(L=2\,n\).
This first occurs at \(L=9\), for \({\varvec{I}}=(1,3)\) and its parity conjugate \({\varvec{I}}'=(6,8)\), with \(\varphi |_{\kappa =3/2} \approx 2.02\) vs \(\varphi |_{\kappa =\infty } \approx 2.00\). If one looks closely it is visible for the left-most pair of zeroes, with \({\varvec{I}} = (1,3)\), in Fig. 5.
Let us make contact with Footnote 21. For Inozemtsev \(v = {\mathrm {Im}}p_1 = \kappa \) ensures that the imaginary part of (4.23) is zero, after which the real part of the constraint requires \(u \in \{0,\pi /2,\pi ,3\pi /2\}\). As \(\kappa \rightarrow \infty \) the constraint flattens out, vanishing identically to give rise to the one-parameter family of exceptional roots from Footnote 21. As we argued there \(u \in \{\pi /2, 3\pi /2\}\) are preferred for Heisenberg. Inozemtsev requires \(u\in \{0,\pi \}\), corresponding to ‘macroscopic’ \({\mathrm {Re}}\varphi \sim L/2\). See the end of Sect. 4.3.2 for a way to understand this shift of u.
We thank István M. Szécsényi for a suggestion that led to the following approach.
Note that the critical equation does not single out this choice, as, by \(2\pi \)-periodicity, it only depends on \(I_1+I_2\). Numerics confirm that colliding momenta occur only for choices of the \(I_m\) that correspond to Heisenberg bound states; the roots for scattering states only vary in a small real interval, never getting near any trivial roots.
More precisely, \(L_\text {cr,r}^{(n)}\) is the largest real root of (4.39). Just like for (4.40) there are further roots L with \(0<L \lesssim n\). In the Heisenberg limit these ‘unphysical’ roots disappear when we take square roots: \(\cot [\pi \,n/2L] = -\sqrt{L-1}\) accounts for all unphysical roots, while \(L_\text {cr}^{(n)}\) is the unique positive solution to \(\cot [\pi \,n/2L] = \sqrt{L-1}\), which is equivalent to (4.36). We have not been able to obtain the elliptic version of the latter equation.
For example, at \(\kappa =1\) the first few values are \(L_\text {cr,i}^{(2)} \approx 6.9\), \(L_\text {cr,i}^{(4)} \approx 13.7\), \(L_\text {cr,i}^{(6)} \approx 21.6\), \(L_\text {cr,i}^{(8)} \approx 27.5\), \(L_\text {cr,i}^{(10)} \approx 34.4\).
At \(\kappa =1\) the first few values are \(L_\text {cr,i}^{(3)} \approx 10.3\), \(L_\text {cr,i}^{(5)} \approx 17.2\), \(L_\text {cr,i}^{(7)} \approx 24.1\), \(L_\text {cr,i}^{(9)} \approx 30.9\) versus \(L_\text {cr,r}^{(3)} \approx 23.2\), \(L_\text {cr,r}^{(5)} \approx 62.9\), \(L_\text {cr,r}^{(7)} \approx 122.1\), \(L_\text {cr,r}^{(9)} \approx 201.1\). Compare the latter with the values for \(\kappa =\infty \) given below (4.36).
See [Kla15] for another perspective: one can understand the existence of these two types of bound states from the non-injectivity of \(\bar{\rho }^{\vee }_1(z)\) (\(=\phi (z)/(2\mathrm {i}\kappa )\) therein).
Note that these are not just the \(I_m\): in order to follow a given solution to the bae (at fixed \(p_\text {tot}\)) in a meaningful way as L increases one has to increase the \(I_m\) in the appropriate way, cf. the end of Sect. 4.3.3.
To the best of our knowledge, Haldane’s equation (4.49) does not arise from requiring (L-periodicity for) a Bethe ansatz—the HS wave functions are manifestly L-periodic, see (4.51)—but is of bae form and, by construction, has the desired solutions. Note that Haldane [Hal91b] works with (distinct, chosen in ascending order) quantum numbers \(I''_m \,{:}{=}\,\, I'_m + (M-1)/2 - (m-1) \in \{(M+1)/2,(M+1)/2 + 1, \dots , L-(M+1)/2\}\). Here the shift over \((M-1)/2\) absorbs the constant in (4.49).
The first equality hinges on the evaluation: split the sum on the right-hand side of the first line into two, one sum for each summand, and use \(\sum _{k(\ne n)}^L \mathrm {ev}[ (z_n + z_k)/(z_n - z_k)] = 0\), valid for any \(n \in \{1,\dots \,,L\}\).
Namely, let \(x \,{:}{=}\,\, L\,p_1/2\pi \). We may take \(p_1 \in [0,2\pi )\) so \(x \in [0,L)\), and \(\lfloor x/L\rfloor = 0\). There are two cases to consider. If \(x\le I_\text {tot}\) then \(\lfloor (I_\text {tot}-x)/L\rfloor = 0\) and (4.64) vanishes if \(\lfloor x\rfloor = (I_\text {tot} -1)/2\), i.e. \(2\,x \in [I_\text {tot} - 1, I_\text {tot} + 1)\). Both \(p_m\) then lie in the interval of length \(2\pi /L\) around the first trivial root from (4.24). In case \(x>I_\text {tot}\) (possible when \(I_1+I_2>L\)) instead \(\lfloor (I_\text {tot}-x)/L\rfloor = -1\) and we obtain \(\lfloor x\rfloor = (I_\text {tot} + L -1)/2\). This time both \(p_m\) lie in the interval around the second trivial root from (4.24). The latter case is shown in Fig. 5.
We have reformulated Inozemtsev’s original statement for the lattice \(\hat{\,\,{\mathbb {L}}}^{\vee }\) and fixed a slight inconsistency that we discuss in more detail in Appendix D.3.
It is remarkable that even though the elliptic wave functions have a simple pole at coinciding arguments, see (3.16) and (4.9), in the Haldane–Shastry limit the pole disappears: the numerator becomes (the evaluation of) an antisymmetric polynomial that is divisible by the denominator, see (4.63). Upon evaluation the result is equal to a polynomial with a double zero rather than a simple pole, see (4.55).
Another way to compute this sum can be found in [FG14].
This slightly extends the definition of what Inozemtsev denotes by T in the equation below (23c) in [Ino95].
One can show this by noting that the complex conjugate \(\rho _2(\gamma _\text {r} +\mathrm {i}\, \gamma _\text {i})^* = \rho _2 (\gamma _\text {r} - \mathrm {i}\, \gamma _\text {i})\), thus the only way this term is real is when \(\rho _2 (\gamma _\text {r} - \mathrm {i}\, \gamma _\text {i}) = \rho _2 (\gamma _\text {r} + \mathrm {i}\, \gamma _\text {i})\), which only happens if \(\mathrm {i}\, \gamma _\text {i} = L \omega /2\).
References
Abramowitz, M., Stegun, I.A.: Handbook of mathematical functions with formulas, graphs, and mathematical tables. US Government printing office 55 (1948)
Avdeev, L.V., Vladimirov, A.A.: On exceptional solutions of the Bethe ansatz equations. Theor. Math. Phys. 69, 1071 (1985)
Bernard, D.: An introduction to Yangian symmetries. Int. J. Mod. Phys. B7, 3517 (1993). arXiv:hep-th/9211133
Bethe, H.: Zur Theorie der Metalle. Z. Phys. 71(3–4), 205–226 (1931). (see also the English translation by T.C. Dorlas (2009))
Bernard, D., Gaudin, M., Haldane, F.D.M., Pasquier, V.: Yang–Baxter equation in long-range interacting systems. J. Phys. A Math. Gen. 26(20), 5219 (1993)
Berntson, B.K., Klabbers, R., Langmann, E.: Multi-solitons of the half-waves map equation and Calogero–Moser spin–pole dynamics. J. Phys. A Math. Theor. 53, 505702 (2020)
Bernard, D., Pasquier, V., Serban, D.: A one dimensional ideal gas of spinons, or some exact results on the XXX spin chain with long range interaction. In: Quantum Field Theory and String Theory, pp. 11– 22 (1995)
Calogero, F.: Exactly solvable one-dimensional many-body problems. Lett. Nuov. Cim. (1971–1985) 13(11), 411–416 (1975)
Caux, J.-S.: The Bethe ansatz. Part II. Eigenstates and thermodynamics of Heisenberg spin chains; primer on the algebraic Bethe ansatz (unpublised) (2018)
Chalykh, O.A., Veselov, A.P.: Commutative rings of partial differential operators and Lie algebras. Commun. Math. Phys. 126, 597–611 (1990)
Dittrich, J., Inozemtsev, V.I.: The commutativity of integrals of motion for quantum spin chains and elliptic functions identities. Reg. Chaot. Dyn. 13(1), 19–26 (2008). arXiv:0711.1973
Dittrich, J., Inozemtsev, V.I.: On the second-neighbour correlator in 1D XXX quantum antiferromagnetic spin chain. J. Phys. A Math. Gen. 30(18), L623 (1997)
Dittrich, J., Inozemtsev, V.I.: On the two-magnon bound states for the quantum Heisenberg chain with variable range exchange. Mod. Phys. Lett. B 11(11), 453–459 (1997). arXiv:solv-int/9612008
Olver, F.W.J., Olde Daalhuis, A.B., Lozier, D.W., Schneider, B.I., Boisvert, R.F., Clark, C.W., Miller, B.R., Saunders, B.V., Cohl, H.S., McClain, M.A. (eds.) NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/, http://dlmf.nist.gov/. Release 1.0.28 of 2020-09-15
De La Rosa Gomez, A., MacKay, N., Regelskis, V.: How to fold a spin chain: integrable boundaries of the Heisenberg XXX and Inozemtsev hyperbolic models. Phys. Lett. A 381, 1340–1348 (2017). arXiv:1610.01523
Deguchi, T., Ranjan Giri, P.: Exact quantum numbers of collapsed and non-collapsed two-string solutions in the spin-1/2 Heisenberg spin chain. J. Phys. A 49(17), 174001 (2016). arXiv:1509.00108
Drinfel’d, V.G.: Degenerate affine Hecke algebras and Yangians. Funct. Anal. Appl. 20(1), 58–60 (1986)
Essler, F.H.L., Korepin, V.E., Schoutens, K.: Fine structure of the Bethe ansatz for the spin-1/2 Heisenberg XXX model. J. Phys. A Math. Gen. 25(15), 4115–4126 (1992)
Faddeev, L.D.: How algebraic Bethe ansatz works for integrable model (1995)
Finkel, F., González-López, A.: A new perspective on the integrability of Inozemtsev’s elliptic spin chain. Ann. Phys. 351, 797–827 (2014)
Finkel, F., González-López, A.: Yangian-invariant spin models and Fibonacci numbers. Ann. Phys. 361, 520–547 (2015). arXiv:1501.05223
Felder, G., Varchenko, A.: Integral representation of solutions of the elliptic Knizhnik–Zamolodchikov–Bernard equations. Int. Math. Res. Notices 1995, 221–233 (1995). arXiv:hep-th/9502165
Gaudin, M.: La fonction d’onde de Bethe, Masson, (1983), English transl.: The Bethe wavefunction (Caux, J.-S., transl.). Cambridge University Press (2014)
Haldane, F.D.M.: Exact Jastrow–Gutzwiller resonating-valence-bond ground state of the spin-\(1/2\) antiferromagnetic Heisenberg chain with \(1/r^2\) exchange. Phys. Rev. Lett. 60(7), 635 (1988)
Haldane, F.D.M.: "Fractional statistics" in arbitrary dimensions: a generalization of the Pauli principle. Phys. Rev. Lett. 67, 937–940 (1991)
Haldane, F.D.M.: "Spinon gas" description of the \(S=1/2\) Heisenberg chain with inverse-square exchange: exact spectrum and thermodynamics. Phys. Rev. Lett. 66, 1529–1532 (1991)
Haldane, F.D.M.: Physics of the ideal semion gas: spinons and quantum symmetries of the integrable Haldane–Shastry spin chain. In: Correlation Effects in Low-Dimensional Electron Systems (1994)
Heisenberg, W.: Zur Theorie der Ferromagnetismus. Z. Phys. 49, 619–636 (1928)
Ha, Z.N.C., Haldane, F.D.M.: Squeezed strings and Yangian symmetry of the Heisenberg chain with long-range interaction. Phys. Rev. B 47(19), 12459 (1993)
Haldane, F.D.M., Ha, Z.N.C., Talstra, J.C., Bernard, D., Pasquier, V.: Yangian symmetry of integrable quantum chains with long-range interactions and a new description of states in conformal field theory. Phys. Rev. Lett. 69, 2021–2025 (1992)
Inozemtsev, V.I., Dorfel, B.-D.: Ground-state energy corrections for antiferromagnetic \(s=1/2\) chains with short-range interaction. J. Phys. A Math. Gen. 26(19), L999 (1993)
Inozemtsev, V.I.: Bethe-ansatz equations for quantum Heisenberg chains with elliptic exchange. Reg. Chaot. Dyn. 5(3), 243 (2000). arXiv:math-ph/9911022
Inozemtsev, V.I.: Integrable Heisenberg–Van Vleck chains with variable range exchange. Phys. Part. Nucl. 34, 166–193 (2003). arXiv:hep-th/0201001, [Fiz. Elem. Chast. Atom. Yadra 34, 332 (2003)]
Inozemtsev, V.I.: On the connection between the one-dimensional \(s=1/2\) Heisenberg chain and Haldane–Shastry model. J. Stat. Phys. 59(5–6), 1143–1155 (1990)
Inozemtsev, V.I.: The extended Bethe Ansatz for infinite \(s=1/2\) quantum spin chains with non-nearest-neighbor interaction. Commun. Math. Phys. 148(2), 359–376 (1992)
Inozemtsev, V.I.: The Hermite-like description of two-magnon states of 1d quantum \(s = 1/2\) chains with elliptic exchange is complete. Lett. Math. Phys. 28(2), 281–286 (1993)
Inozemtsev, V.I.: On the spectrum of \(s=1/2\) XXX Heisenberg chain with elliptic exchange. J. Phys. A Math. Gen. 28(16), L439–L445 (1995). arXiv:cond-mat/9504096
Inozemtsev, V.I.: Invariants of linear combinations of transpositions. Lett. Math. Phys. 36(1), 55–63 (1996)
Inozemtsev, V.I.: Solution to three-magnon problem for s= 1/2 periodic quantum spin chains with elliptic exchange. J. Math. Phys. 37(1), 147–159 (1996)
Klabbers, R.: Inozemtsev’s elliptic spin chains asymptotic Bethe ansatz and thermodynamics. Master’s Thesis (2015)
Klabbers, R.: Thermodynamics of Inozemtsev’s elliptic spin chain. Nucl. Phys. B 907, 77–106 (2016). arXiv:1602.05133
Karbach, M., Müller, G.: Introduction to the Bethe ansatz I. Comp. Phys. 11 (1997). arXiv:cond-mat/9809162
Lamers, J.: A pedagogical introduction to quantum integrability, with a view towards theoretical high-energy physics. PoS. Modave 2014, 001 (2014). arXiv:1501.06805
Lamé, G.: Mémoire sur les surfaces isothermes dans les corps solides homogènes en équilibre de température. Impr, Royale (1834)
Lamers, J.: Resurrecting the partially isotropic Haldane-Shastry model. Phys. Rev. B. 97, 214416 (2018). arXiv:1801.05728
Langmann, E.: Anyons and the elliptic Calogero–Sutherland model. Lett. Math. Phys. 54(4), 279–289 (2000)
Lamers, J., Pasquier, V., Serban, D.: Spin-Ruijsenaars, q-deformed Haldane–Shastry and Macdonald polynomials (2020)
Macdonald, I.G.: Symmetric Functions and Hall Polynomials, 2nd edn. Oxford University Press, Oxford (1995)
Maier, R.S.: Lamé polynomials, hyperelliptic reductions and Lamé band structure. Philos. Trans. R. Soc. A 366, 1115–1153 (2007). arXiv:math-ph/0309005
Olshanetsky, M., Perelomov, A.: Quantum integrable systems related to Lie algebras. Phys. Rep. 94(6), 313–404 (1983)
Polychronakos, A.P.: Lattice integrable systems of Haldane–Shastry type. Phys. Rev. Lett. 70, 2329–2331 (1993). arXiv:hep-th/9210109
Serban, D.: Unpublished notes (2021)
Shastry, B.S.: Exact solution of an \(s=1/2\) Heisenberg antiferromagnetic chain with long-ranged interactions. Phys. Rev. Lett. 60(7), 639 (1988)
Serban, D., Staudacher, M.: Planar \(N=4\) gauge theory and the Inozemtsev long range spin chain. JHEP 06, 001 (2004). arXiv:hep-th/0401057
Shastry, B.S., Sutherland, B.: Super lax pairs and infinite symmetries in the 1/\({ r }^{2}\) system. Phys. Rev. Lett. 70, 4029–4033 (1993). https://doi.org/10.1103/PhysRevLett.70.4029
Stanley, R.P.: Some combinatorial properties of Jack symmetric functions. Adv. Math. 77, 76–115 (1989)
Sutherland, B.: Beautiful Models: 70 Years of Exactly Solved Quantum Many-Body Problems. World Scientific Publishing Company, Singapore (2004)
Sutherland, B.: Exact ground-state wave function for a one-dimensional plasma. Phys. Rev. Lett. 34(17), 1083 (1975)
Talstra, J.C., Haldane, F.D.M.: Integrals of motion of the Haldane-Shastry model. J. Phys. A Math. Gen. 28, 2369 (1995). arXiv:cond-mat/9411065
Thouless, D.J.: Long-range order in one-dimensional Ising systems. Phys. Rev. 187(2), 732 (1969)
Uglov, D.: The trigonometric counterpart of the Haldane–Shastry model (1995). arXiv:hep-th/9508145
Ujino, H., Hikami, K., Wadati, M.: Integrability of the quantum Calogero–Moser model. J. Phys. Soc. Japan 61(10), 3425–3427 (1992). https://doi.org/10.1143/JPSJ.61.3425
Whittaker, E.T., Watson, G.N.: A Course of Modern Analysis: An Introduction to the General Theory of Infinite Series and of Analytic Functions, with an Account of the Principal Transcendental Functions. Cambridge University Press, Cambridge (1902)
Acknowledgements
The work of RK was supported by the grant “Exact Results in Gauge and String Theories” from the Knut and Alice Wallenberg foundation (KAW). JL acknowledges the Australian Research Council Centre of Excellence for Mathematical and Statistical Frontiers (acems) for financial support. We are indebted to G. Arutyunov for motivating us to study the Inozemtsev spin chain back when we were MSc students. We are grateful to J. Brödel, J.-S. Caux, A. Kaderli, E. Langmann, D. Serban, I. M. Szécsényi and V. Pasquier for their interest and stimulating discussions. We thank the organisers of Elliptic integrable systems, special functions and quantum field theory (Nordita, 2019) and Baxter 2020: Frontiers in Integrability (ANU Canberra, 2020) for opportunities to present part of this work. We thank the referees for their feedback on the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H-T.Yau.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Notation Compared with the Literature
In this work we have made some changes with respect to Inozemtsev’s extended Bethe ansatz, see Sect. 3.2. To facilitate comparison with the literature we have summarised the notation used for important quantities here and in the literature in Table 4. When applicable the relation to our notation is indicated in square brackets; for example, the \({\varvec{p}}\) of [Ino95] coincides with our \(\widetilde{{\varvec{p}}} - {\varvec{\varphi }}\).
Appendix B. Elliptic Functions
In this work we make use of six sets of Weierstrass elliptic functions associated to six different lattices depending on the spin chain length \(L \in {\mathbb {N}}\) and the interpolation parameter \(\kappa \in {\mathbb {R}}_+\) setting \(\omega = \mathrm {i}\pi /\kappa \). The six lattices can be divided into three ‘coordinate lattices’ along with three (reciprocal) ‘momentum lattices’ that differ by a rescaling by \(-2\pi /\omega \) (see Sect. 3.4). The Hamiltonian and wave function are defined on the coordinate lattice \({\mathbb {L}}\) with periods \((\omega _1,\omega _2) = (L,\omega )\). The elliptic sums discussed in Appendix C are naturally defined on the lattice \(\bar{\,\,{\mathbb {L}}}\) with periods \(({\bar{\omega }}_1,{\bar{\omega }}_2) = (1,\omega )\), whereas the coordinate-version \(\gamma \) of the scattering phase \(\varphi \) in e.g. (4.4) behaves most naturally on the lattice \(\hat{\,\, {\mathbb {L}}}\) with periods \(({\hat{\omega }}_1,{\hat{\omega }}_2) = ( L, L\,\omega )\), which appears in Appendix D.3–D.4. The momentum analogues are decorated with a ‘\({}^\vee \)’. The lattices \({\mathbb {L}}^{\!\vee }\) with periods \((\omega _1^\vee ,\omega _2^\vee ) \,{:}{=}\,\, (2\pi , -2\pi L /\omega )\) and \(\bar{\,\,{\mathbb {L}}}^{\!\vee }\) with \(({\bar{\omega }}_1^\vee ,{\bar{\omega }}_2^\vee ) \,{:}{=}\,\, (2\pi , -2\pi /\omega )\) are discussed at length in Sect. 3.4, providing the natural setting for expressions involving the quasimomenta. The lattice \(\hat{\,\,{\mathbb {L}}}^{\vee }\) with periods \((\hat{\omega }^{\vee }_1,\hat{\omega }^{\vee }_2) \,{:}{=}\,\, (2\pi L, -2\pi L/\omega )\) is the natural choice for the scattering phase \(\varphi \) and therefore the lattice that defines the elliptic curve on which the spectral problem gets rationalised in Sect. 4.5.
Now we turn to the associated elliptic functions. Useful references are [OOL+, AS48, WW02].
1.1 B.1. Weierstrass functions
The Weierstrass elliptic function with periods \((\omega _1,\omega _2)\) is
where the asterisk indicates that the term with \(j=k=0\) is to be omitted from the sum. This (even) function is related to the other two (odd) Weierstrass functions by
These two functions are doubly quasiperiodic with quasiperiods \((\omega _1,\omega _2)\). Denote (twice) the values of \(\zeta \) at half its quasiperiods by
These constants obey the Legendre relation
Then the (arithmetic) quasiperiodicity of \(\zeta \) reads \(\zeta (z+\omega _b)=\zeta (z) + \eta _b\) for \(b=1,2\), while \(\sigma \) is doubly (geometric) quasiperiodic, \(\sigma (z+\omega _b) = {-}\mathrm {e}^{(z+\omega _b/2)\,\eta _b }\,\sigma (z)\).
We make frequent use of the functions
These functions are odd, \(\rho _b(-z) = -\rho _b(z)\), periodic in one direction, \(\rho _b(z+\omega _b) = \rho _b(z)\), and (arithmetically) quasiperiodic in the other, \(\rho _b(z+\omega _a) = \rho _b(z) + (-1)^a\, 2\pi \mathrm {i}/\omega _a\) for \(a\ne b\). Due to the Legendre relation they differ by \(\rho _2(z) - \rho _1(z) = (2\pi \mathrm {i})/(L\,\omega )\,z\).
We will need the doubling formulae, valid as long as \(u,v,u+v \notin {\mathbb {L}}\):
where, to make the structure of the equations more clear, we write
1.2 B.2. Jacobi theta functions
The odd Jacobi theta function \(\vartheta \) is defined as
It is double quasiperiodic, \(\vartheta (z +\pi | \tau ) = -\vartheta (z | \tau ) \) and \(\vartheta (z + \pi \,\tau | \tau ) = - q^{-1} \, \mathrm {e}^{-2\mathrm {i}z} \, \vartheta (z | \tau )\), and entire with a simple zero at the origin and its lattice shifts. We will use two variants of this function, which we denote by
and are related by \(\theta _1(z) = \mathrm {i}\, (\mathrm {i}\, L/\omega )^{1/2} \, \mathrm {e}^{-\mathrm {i}\pi \,z^2/(L\omega )} \, \theta _2(z) = \mathrm {i}\, (L \, \kappa /\pi )^{1/2} \, \mathrm {e}^{-\kappa \, z^2/L} \, \theta _2(z)\). These functions inherit the double quasiperiodicy in the form \(\theta _b(z+\omega _b) = -\theta _b(z)\) along with \(\theta _1(z+\omega ) = -\mathrm {e}^{-2\, \pi \mathrm {i}z/L -\pi \mathrm {i}\, \omega /L} \theta _1(z)\) and \(\theta _2(z+L) = -\mathrm {e}^{2\, \pi \mathrm {i}z/\omega +\pi \mathrm {i}\, L/\omega } \theta _2(z)\). In particular these functions are closely related to Weierstrass \(\sigma \). We have
Notice that (B.4) naturally arises as
This is a close cousin of the Jacobi zeta function. Its derivative
appears in Sect. 2.2 as the pair potential (for \(b=2\)). That is, the Weierstrass elliptic functions \(\wp : \zeta : \sigma \) have Jacobi counterparts \(V_{\text {s}} : \rho _2 : \theta _2\) (along with a version for \(b=1\)). Let us stress once more that, despite their subscripts, both of (B.7) are versions of the odd Jacobi theta function (B.6).
Appendix C. Inozemtsev’s Trick for Computing Elliptic Sums
To compute the sums that appear in various places of the analysis of Inozemtsev’s spin chain we often use the fact that two elliptic functions with the same pole structure must be equal up to a constant, as stipulated by Louiville’s theorem. This allows us to find simple explicit quasiperiodic functions for complicated object of which we only know its poles and quasiperiodicity properties. This trick was used repeatedly by Inozemtsev [Ino90, Ino92, Ino95].
Consider an analytic function W that is doubly (quasi)periodic on the lattice \(\bar{\,\,{\mathbb {L}}} = {\mathbb {Z}} \oplus \omega \, {\mathbb {Z}}\),
where we assume \(\delta \ne 0\) to ensure W is not doubly periodic, and whose only pole in the fundamental parallelogram occurs at \(z=0\), with Laurent expansion
For us the real periodicity of W is typically true only on-shell, i.e. by virtue of the Bethe-ansatz equations (3.18). In order to rewrite W in terms of known elliptic functions we first engineer an elliptic function with first and second order poles at \(z=0\). This goes as follows. The second-order pole is taken care of by \({\bar{\wp }}(z)\), which is doubly periodic. For the first-order pole we use \({\bar{\zeta }}(z)\), which has the right expansion, but does not have the correct double quasiperiodicity properties. To remedy this we subtract another zeta function with argument shifted by some \(s \ne 0\) to be determined:
So far our ansatz therefore is
which has the right double quasiperiodicity, but has a spurious pole at \(z=-s\). To remove this spurious pole we multiply the ansatz by \({\bar{\sigma }}(z+s)\), and divide by \({\bar{\sigma }}(z-s)\) to compensate for the z-dependent behaviour under \(z \mapsto z+\omega _b\),
However, this prefactor introduces another spurious pole at \(z=s\); to compensate for this we add a zero at that point by subtracting the value of (C.3) at \(z=s\):
To finish we note that the first factor has two quasiperiods, but only one quasiperiodicity parameter to tune. Multiplying the ansatz with the simplest doubly quasiperiodic, \(\mathrm {e}^{q \, z}\), we arrive at the Weierstrass form of our function W:
This is the general form of a doubly quasiperiodic function with second and first-order poles at the origin. The parameters q and s are fixed by (C.1), yielding the system of linear equations
with unique solution
The final step is to determine the residues A, B. To this end we expand (C.4) at \(z=0\),
which matches (C.2) provided
Putting everything together we conclude that the function W can be written as
supplemented by (C.5).
Note that we did not discuss the possibility that the above expression for W is off by a constant, since the quasiperiodicity (rather than periodicity) demands that such a constant is zero. This means in particular that we can express \(c_0\), the zeroth order term in the Laurent expansion (C.2) of W in terms of the other expansion coefficients along with s and q:
This will prove to be very useful for the computation of various sums, which we will now discuss in turn.
1.1 C.1. Dispersion
Since there are some subtleties in the evaluation of the sums in (3.6) needed to find the dispersion relation we include a detailed computation here. This also serves as a warm-up for the general-M case in Appendix C.3. We wish to compute the sums
We will start with the p-dependent sum, which is a variant of a sum computed in [Ino90]. Following Inozemtsev let us consider the function
The presence of the exponential can be exploited: it makes W doubly quasiperiodic,
iff \(\mathrm {e}^{\mathrm {i}\, L \, p} = 1\), which is required by the periodicity of the one-particle wave function anyway. Therefore W can be expressed in the Weierstrass form (C.7) with the choices (C.5) with \(\delta = p \, \omega \) for the two parameters s and q:
including the now important restriction that we must have \(s\ne 0\) to ensure W is only quasiperiodic and not periodic. Since W has only a second order pole at zero with residue \(c_{-2} = 1\) we can use (C.8) to find that
which by computing the zeroth-order term of the sum directly is seen to equal the sum
we are after. Plugging in s and q and using the doubling formulae for \({\bar{\wp }}\) and \({\bar{\zeta }}\) we conclude
This equality only holds when \(p = 2\pi I/L\) with \(I \in {\mathbb {Z}}_L\) quantised by the periodicity condition,Footnote 39 and moreover \(s\ne 0\), which implies \(I \ne 0 \text { mod } L\).
It remains to compute the sum with \(p=0\), which we also use to get the elliptic M-particle difference equation (3.13).Footnote 40 To this end we analyse the function
which is obviously doubly periodic with periods \((1,\omega )\) and has a double pole at the origin. This means that
with C a constant. By performing the Laurent expansion we see that C equals the sum we are after. We can find an expression for C by analysing \(W(z) - {\bar{\wp }}(z)\): as long as we pick \(\tau \) such that we do not pass any poles we have
Differentiation with respect to \(\tau \) shows that this expression, and in fact each pair of \(\zeta \)s, is constant. This allows us to choose \(\tau \) as we like. Sending \(\tau \rightarrow 0\) (or to \(-n\) for the summands) we find
We conclude that
1.2 C.2. Highest-weight sum
In order to prove the highest-weight property of the \(M=2\) eigenfunctions we need to compute the sum
To compute it we first introduce the function
which, due to the periodicity properties of \(\chi _2\) has the following periodicity properties:
where the first equation is only true on-shell, i.e. as long as \(p_1\) and \(\gamma \) satisfy (4.12). Further inspection shows that W has only one pole in the fundamental parallelogram, of first order. This means that we can again postulate that W is of the form (C.7), where we can now choose \(w_ {-2} = 0\) and find the parameters q and s from the quasiperiods (for which we must assume that \(p_1 \ne 0\)). To continue we first note that at \(z=0\) W expands as
Using the relation between the Laurent coefficients given in (C.8) we straightforwardly find
1.3 C.3. M-particle sums
Recall the short-hand \({\varvec{r}} \,{:}{=}\,\, {\varvec{p}} - \tilde{{\varvec{p}}}\). We wish to compute the sum
defined in (3.21). Finding an explicit expression for this sum is the main task in order to analyse the difference equation and follows the strategy of Inozemtsev [Ino95].
We view \({\varvec{n}}\) as fixed and introduce the function
which obeys the periodicity conditions
using the Bethe-ansatz equations (3.18). Its only pole in the fundamental parallellogram occurs at zero with Laurent expansion matching (C.2). Therefore \(W_m\) can be expressed as (C.7) with q and s determined by (C.5) with \(\delta = p_m \, \omega \). Because of this we know that we can express the constant term \(c_0\) of \(W_m\) as in (C.8), which we will here sometimes abbreviate as \(c_0 = Y_m \, c_{-2} + X_m \, c_{-1}\). On the other hand we can directly evaluate the Laurent coefficients \(c_{-2}\), \(c_{-1}\) and \(c_0\) by performing the relevant residue integrals, see below. Recall that \({\widetilde{\Phi }}_{{\tilde{p}}}({\varvec{n}})\) denotes the numerator from (3.16) and abbreviate \({\widetilde{\Phi }}_{\tilde{{\varvec{p}}},{\varvec{p}}}({\varvec{n}}) \,{:}{=}\,\, {\widetilde{\Phi }}_{{\tilde{p}}}({\varvec{n}}) \, \mathrm {e}^{\mathrm {i}{\varvec{r}} \cdot {\varvec{n}}}\). Then we claim that
where
By equating this expression for \(c_0\) with the expression (C.8) containing \(c_{-2}\) and \(c_{-1}\) we find an expression for \(\Sigma _m({\varvec{n}})\), which can be plugged into the M-particle difference equation (3.20).
Using the definition (C.22) we can compute the Laurent coefficients of \(W_m\) directly.
Computing \(c_{-2}\). To find \(c_{-2}\) we only need to consider the second-order poles in the sum, which is relatively easy. Since we assumed that the summands in the ansatz have no second-order poles they can only occur in the \(\wp \) function and restricted to the \((1,\omega )\) lattice the only relevant one occurs when \(n'=n_m\). Thus we find
Computing \(c_{-1}\). Things already get a little more interesting when we consider the first order poles, as there are many more of those. Nevertheless, let us start noting that there is also a contribution coming from the second-order pole at \(n'=n_m\), yielding \(\partial _{n_m} {\widetilde{\Psi }}_{{\tilde{{\varvec{p}}}},{\varvec{r}}}\). Further contributions from this pole combined with possible zeroes that compensate are impossible, since such a zero would mean that the entire eigenfunction is zero. Therefore all further contributions come from the first order poles in the eigenfunctions in the summands with \(n'\ne n_{m}\). So let us set \(n'=n_{m'}\) with \(m'\ne m\), so that the summand reads
As the pole comes from \(1/\Delta \) we can set \(z=0\) everywhere else in the expression, yielding
If \(m'<m\) the residue is
where we noted the minus sign explicitly coming from the minus in front of the z that gives the pole and introduced extra factors of \(\sigma \) to simplify the products. Namely, we see that the first product is basically \(\Delta (n_1,\ldots ,n_M)\). So we find
Repeating the same argument for \(m'>m\) one finds the same result, the lack of a minus sign being compensated for by the oddness of the separate \(\sigma \) function. This expression is the same as that obtained by Inozemtsev in [Ino95] up to a factor \(\wp (n_m-n_{m'})\). So we finally have
where we defineFootnote 41
Computing \(c_0\). Of course now comes the most important coefficient, the one that contains the sum we are actually after. It has three contributions: the direct contribution from setting \(z=0\) is exactly \(\Sigma _m({\varvec{n}})\). The contribution from the second order pole is also straightforward, as it is simply \(\partial _{n_m}^2 {\widetilde{\Psi }}_{{\varvec{r}}}/2\). The contribution coming from the first order poles at \(n'=n_{m'}\) is the most complicated, as it requires us to differentiate
with respect to z before setting it to zero. Doing this yields
In this way we obtain (C.24).
Appendix D. Further Proofs
1.1 D.1. A simplification
Before we can plug (C.24) into the M-particle difference equation (3.20) let us consider the action of the permutation \(w \in S_M\) on the coordinates in \(\Sigma ({\varvec{n}}_w)\). In the first line of (C.24) we can simply replace \({\varvec{n}} \rightarrow {\varvec{n}}_w\), while in the second line the antisymmetry of the Vandermonde factor, \(\Delta ({\varvec{n}}_w) = \mathrm {sgn}(w) \, \Delta ({\varvec{n}})\), yields a total antisymmetrisation. This allows the summands in that line to be simplified in pairs (whence the factor 1/2 in front) with permutations differing by the transposition \((m,m') \in S_M\). Indeed, define
Then it follows that
where \(\tau \,{:}{=}\,\, (m m')\) is a transposition. By noting that
we can drastically simplify
Plugging (C.24) with \({\varvec{n}} \rightarrow {\varvec{n}}_w\) into the M-particle difference equation (3.20) yields a left-hand side containing the sum (D.2). Using (D.4) we obtain (3.22).
1.2 D.2. Derivatives of the numerator
By assuming that \({\widetilde{\Psi }}_{\tilde{{\varvec{p}}}}\) is an eigenfunction of the eCS Hamiltonian at \(\beta =2\) we can deduce further information about its numerator \({\widetilde{\Phi }}_{\tilde{{\varvec{p}}}} = \Delta \, {\widetilde{\Psi }}_{\tilde{{\varvec{p}}}}\), see (3.16), from the eCS eigenvalue equation. Carefully cancelling the denominator \(\Delta \) we find
This looks slightly different than equation (62b) in [Ino03] but luckily we can draw the same conclusions: the left-hand side of this equation is analytic, as every pole from \(\wp \) gets cancelled by one from the square of \(\zeta \) functions. Since the right-hand side has \(\zeta \) functions as well (and therefore poles), we see that it must be true that
to ensure the analyticity of the right-hand side.
1.3 D.3. Trivial symmetry map
In this appendix we try to give some more explanation to one of the central tools Inozemtsev used in [Ino93] to perform his version of the counting of the \(M=2\) solutions as we have done in Sect. 4.5.4, because it turns out to be a nice piece of Weierstrass analysis that can be applicable in other situations. In order to facilitate comparison with Inozemtsev’s work we will work on the lattice \(\hat{\,\,{\mathbb {L}}}\) with periods \((L, L\,\omega )\), which is the coordinate version of the lattice \(\hat{\, {\mathbb {L}}}^{\vee }\) defined in (4.68).
Let us first define the map \({\hat{R}}_x\) on the fundamental parallelogram of \(\hat{\,\,{\mathbb {L}}}\) by requiring it to satisfy \(x_{{\hat{R}}_x(\gamma )} = x_{\gamma }\), i.e. \(\gamma \) and \({\hat{R}}_x(\gamma )\) belong to the same solution of (4.78). Here \(\gamma \) relates to \(\varphi \) as in (4.10). Note that there is a unique \(\gamma ' \ne \gamma \) inside the fundamental parallelogram with the same image under \(\wp \) since the latter is a second-order elliptic function, implying the map \({\hat{R}}_x\) is indeed well-defined.
More precisely, let \(\gamma \) be in the fundamental parallelogram and
We can find this \(\gamma '\) by congruence:
which tells us that the second solution is
i.e. we can define the map \({\hat{R}}_x\) by
It is not so hard to work out what the modulo means in practice and derive a formula for \({\hat{R}}_x(\gamma )\). By assumption \(0\le {\mathrm {Re}}\gamma < L\) and \(0\le {\mathrm {Im}}\,\gamma \le L |\omega |\). First we consider the real part of \(\gamma '\). If \(\gamma \) is purely imaginary then so is \(\gamma '\) and we do not have to adjust the real part, while if \({\mathrm {Re}}\gamma \) is positive then \({\mathrm {Re}}(I_\text {tot} \, \omega -\gamma )<0\) so we should add L to land in the fundamental parallelogram. In total, then, the real shift can be written as \(L \, \mathrm {sgn}({\mathrm {Re}}\gamma )\), with the convention that \(\mathrm {sgn}\,0 = 0\). To determine the imaginary shift there are three cases to consider. If \(I_\text {tot} \, {\mathrm {Im}}\omega - {\mathrm {Im}}\gamma \) is positive we do not have to do anything, while if it is negative we can add \(L\,\omega \) to land in the fundamental parallelogram, and when
then \(\gamma ' = -{\mathrm {Re}}\gamma \) is real. This means only the real shift by L is necessary in order for the solution to be in the fundamental parallelogram. We therefore find that
where \(\theta \) is the Heaviside step function satisfying \(\theta (0) = 0\).
This expression looks a lot like the equation for \(\gamma _0'\) below (14) in [Ino93], with the only difference sitting in the final term. Before exploring this difference in more details, let us first note that the map \({\hat{R}}_x\) has a nice geometric meaning. Indeed, \(\gamma ' = {\hat{R}}_x(\gamma )\) is the unique second solution to \(x_{\gamma '} = x_\gamma \), which has \(y_{{\hat{R}}_x(\gamma )} = -y_{\gamma }\). Therefore \({\hat{R}}_x\) maps a point \((x_{\gamma }, y_{\gamma })\) on the elliptic curve to the point \((x_{\gamma }, - y_{\gamma })\): it is nothing but a reflection in the x-axis.
To investigate the difference between \({\hat{R}}_x\) and the expression for \(\gamma _0'\) in [Ino93], let us first note that on the set of solutions to the constraints the maps are nearly identical, with the only difference occurring when (D.9) holds. However, solutions like this are extremely rare: consider such a solution \(\gamma = \gamma _\text {r} + I_\text {tot} \, \omega \) where \(\gamma _\text {r} \in [0,L]\). Plugging in this form into the constraint yields
where we used the periodicity of \(\rho _2\) to omit the shift by \(I_\text {tot} \, \omega \) in the first term. Now note that \(\rho _2\) and \({\bar{\rho }}_2\) are analytic functions away from poles (i.e. meromorphic) and that there is only one term here that will generate a non-trivial imaginary part as long as \(I_\text {tot} \not \cong 0 \) mod L/2.Footnote 42
Thus this can happen only if \(I_\text {tot} = 0,L/2\), but \(I_\text {tot} = 0\) yields the trivial solution \(\gamma = L/2\). Choosing \(I_\text {tot} = L/2\) yields a unique non-trivial solution with \(\gamma _\text {r} = L/2\), i.e. \(\gamma = L/2 + L\omega /2\). This is not a trivial root: the two-particle wave function is nonzero for this \(\gamma \). Now we see that \({\hat{R}}_x(L/2 + L\omega /2) = L/2\), while \(\gamma '_0 = L/2 + L\omega /2\). So both expressions send this solution to a solution in the fundamental domain, but in the case discussed in [Ino93] we have \(\gamma '_0 = \gamma _0\).
Let us finally note that this analysis can be performed on any of the lattices. For our purposes the lattice \(\hat{\,{\mathbb {L}}}^{\vee }\), in terms of \(\varphi \), is most convenient. Following the preceding steps one readily finds that on that lattice the action of the reflection \(\hat{R}^{\vee }_x\) is given by
1.4 D.4. Trivial roots are nonphysical
In Sect. 4 we simplified (4.75) by discarding the four simple explicit solutions (4.24). Let us show that this is allowed by analysing these trivial solutions. First, all the trivial solutions of (4.75) can be identified with the solutions toFootnote 43
which on the elliptic curve is easy to see: checking that all our trivial solutions satisfy the above equation is straightforward, so let us consider the converse. If \(x_{{\hat{R}}_x(\gamma )} = x_{\gamma } \in {\mathbb {C}}\), then we have \(y_{{\hat{R}}_x(\gamma )} = -y_{\gamma }\), so in particular if \({\hat{R}}_x(\gamma ) = \gamma \) we find \(y_{\gamma } = -y_{\gamma }\), i.e. \(y_{\gamma } = 0\). This yields the last three trivial solutions listed in (4.24). The fourth trivial root at \(\gamma = I_\text {tot} \, \omega /2\) is slightly more subtle: for this value \(x_\gamma \) and \(y_\gamma \) diverge, i.e. \(x_\gamma \notin {\mathbb {C}}\). This implies we cannot follow the approach above as there is only one point for which \(x_\gamma \) diverges in the fundamental parallelogram. Moreover, we technically have not proven the validity of (D.8) for such \(\gamma \). Nevertheless, by the previous we see that if \(x_{{\hat{R}}_x(\gamma )} = x_\gamma \notin {\mathbb {C}}\) it must be that \(\gamma \) lies at a pole, which can only be \(\gamma = I_\text {tot} \, \omega /2\). Thus we see that the set of trivial solutions is in one-to-one correspondence with the solutions to (D.13).
Now we would like to furthermore demonstrate that the two-particle wave function corresponding to a trivial root vanishes. On the lattice \(\hat{\,{\mathbb {L}}}^{\vee }\) the roots in question are
which on the corresponding coordinate lattice \(\hat{\,\,{\mathbb {L}}}\) yields
The \(M=2\) wave function can be written in terms of \(\gamma \) as
where we have omitted irrelevant regular non-vanishing factors. The overall factor is finite as long as \(\gamma \) does not lie on the lattice. The mechanism for vanishing is the same for all four roots: we check that at these roots the two occurring sigma functions are the same by applying the quasi-periodicity rule we defined just below (B.3b) as often as necessary. The easiest one is the root \(\gamma = I_\text {tot} \, \omega /2\): by applying the quasi-periodicity rule \(I_\text {tot}\) times we obtain
thus we can rewrite the first factor in the brackets of (D.15) as
This directly implies that the wave function vanishes as long as \(I_\text {tot}\) is odd. Note that the possible pole occurring due the first factor in (D.15) is avoided due to this requirement on \(I_\text {tot}\) as well.
Performing a similar analysis on \(\gamma = (I_\text {tot}\, \omega + L)/2\) shows that we can rewrite the first term in the brackets of (D.15) as
thus in this case the wave function vanishes without any restrictions.
The third and fourth root require another repeated application of the quasi-periodicity rule: for the third root (which is parity-dual to the first one) we find after another L applications that
and when evaluated at the third root in (D.14) the first term in the brackets of the \(M=2\) wave function becomes
which when evaluated for integer \(\delta n\) vanishes against the second factor in the brackets of (D.15) as long as \(L+I_\text {tot}\) is odd, which is exactly what is necessary to avoid the pole coming from the overall factor.
Finally, for the fourth root \(\gamma = [(I_\text {tot}+L) \, \omega +L]/2\) we can follow the approach of its parity-dual, the second root, and rewrite the first term to cancel the second term without any restrictions on L and \(I_\text {tot}\).
Thus we see that the wave function vanishes precisely when these roots also occur as solutions to the constraint (4.75) and can thus safely be removed from this equation to ultimately yield the constraint (4.78). It would be interesting to see this analysis for higher M as it could reveal what would be suitable coordinates for the spectral problem in those sectors.
Rights and permissions
About this article
Cite this article
Klabbers, R., Lamers, J. How Coordinate Bethe Ansatz Works for Inozemtsev Model. Commun. Math. Phys. 390, 827–905 (2022). https://doi.org/10.1007/s00220-021-04281-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04281-x




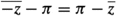 holds for
holds for 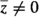 . The value at
. The value at 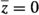 , a pole of
, a pole of