Stationary Flows for Compressible Viscous Fluid in a Perturbed Half-Space

Abstract

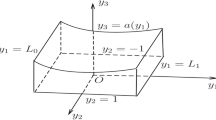
We consider the compressible Navier–Stokes equation in a perturbed half-space with an outflow boundary condition as well as the supersonic condition. For a half-space, it is known that a certain planar stationary solution exists and it is time-asymptotically stable. The planar stationary solution is independent of the tangential directions and its velocities of the tangential directions are zero. In this paper, we show the unique existence of stationary solutions for the perturbed half-space. The feature of our work is that our stationary solution depends on all directions and has multidirectional flow. Furthermore, we prove the asymptotic stability of this stationary solution.

Appendices

A General Inequalities

We discuss some basic inequalities and estimates that are frequently used throughout the paper. The following lemmas cover the case $M\equiv 0$, that is, $\Omega ={\mathbb {R}}^3_+$.

Lemma A.1

(Hardy’s inequality). Let $\alpha >0$. For $f \in H^1(\Omega )$, it holds that

$$\begin{aligned} \int _{\Omega } e^{-\alpha x_1}|f(x)|^2 \, d x \lesssim \Vert \nabla f\Vert ^2 + \Vert {f(M(\cdot ),\cdot )}\Vert _{L^2({\mathbb {R}}^2)}^2. \end{aligned}$$

(A.1)

Proof

This can be proved in the same way as in [8]. $\quad \square$

Lemma A.2

(Sobolev’s inequalities). For $f \in H^1(\Omega )$ and $g \in H^2(\Omega )$, it holds that

$$\begin{aligned} \Vert f\Vert _{L^p(\Omega )}&\lesssim \Vert f\Vert _{H^1(\Omega )}, \quad 2\le p <6, \end{aligned}$$

(A.2)

$$\begin{aligned} \Vert f\Vert _{L^6(\Omega )}&\lesssim \Vert \nabla f\Vert _{L^2(\Omega )}, \end{aligned}$$

(A.3)

$$\begin{aligned} \Vert g\Vert _{L^\infty (\Omega )}&\lesssim \Vert g\Vert _{H^2(\Omega )}. \end{aligned}$$

(A.4)

Proof

It is straightforward to show (A.2) and (A.4). We show only (A.3). Let us introduce a standard extension operator E from $H^1(\Omega )$ to $H^1({\mathbb {R}}^3)$ with

$$\begin{aligned} Eh(x)=h(x) \quad \text {for } x\in \Omega , \quad \Vert Eh\Vert _{H^1(\mathbb R^3)} \lesssim \Vert h\Vert _{H^1(\Omega )}, \quad \Vert \nabla Eh\Vert _{L^{2}({\mathbb {R}}^3)} \lesssim \Vert \nabla h\Vert _{L^{2}(\Omega )}. \end{aligned}$$

Furthermore, we know that for ${\tilde{f}} \in H^{1}({\mathbb {R}}^3)$,

$$\begin{aligned} \Vert {\tilde{f}}\Vert _{L^6({\mathbb {R}}^3)} \lesssim \Vert \nabla {\tilde{f}}\Vert _{L^2({\mathbb {R}}^3)}. \end{aligned}$$

Then putting ${\tilde{f}}=Ef$ gives

$$\begin{aligned} \Vert Ef\Vert _{L^6({\mathbb {R}}^3)} \lesssim \Vert \nabla Ef\Vert _{L^2({\mathbb {R}}^3)} \lesssim \Vert \nabla f\Vert _{L^2(\Omega )}, \end{aligned}$$

where we have used the properties of the extension operator in deriving the last inequality. This together with $\Vert f\Vert _{L^6 (\Omega )} \le \Vert Ef\Vert _{L^6({\mathbb {R}}^3)}$ gives (A.3). $\quad \square$

Lemma A.3

(Gagliardo–Nirenberg inequality). Let $k=2,3,4 \cdots$. For $f \in H^{k} (\Omega )$, there holds that

$$\begin{aligned} \Vert f\Vert _{H^{k-1}(\Omega )} \lesssim \Vert f\Vert _{H^{k}(\Omega )}^{1-1/k}\Vert f\Vert _{L^2(\Omega )}^{1/k}. \end{aligned}$$

(A.5)

Proof

This can be shown in much the same way as in Sobolev’s inequality. $\quad \square$

Lemma A.4

(Commutator estimate). Let $k=0,1,2,\ldots$. For $f, g, \nabla f \in H^{k} (\Omega ) \cap L^\infty (\Omega )$, we have

$$\begin{aligned} \Vert [\nabla ^{k+1},f]g\Vert _{L^2(\Omega )}\lesssim & {} \Vert \nabla f\Vert _{L^\infty (\Omega )}\Vert g\Vert _{H^{k}(\Omega )}+\Vert \nabla f\Vert _{H^{k}(\Omega )}\Vert g\Vert _{L^\infty (\Omega )} , \end{aligned}$$

(A.6)

$$\begin{aligned} \Vert [\nabla ^{k+1},\nabla M]g\Vert _{L^2(\Omega )}\lesssim & {} \Vert g\Vert _{H^{k}(\Omega )}. \end{aligned}$$

(A.7)

Proof

Lemma 4.9 in [14] claims that for ${\tilde{f}}, {\tilde{g}}, \nabla {\tilde{f}} \in H^{k}({\mathbb {R}}^3) \cap L^\infty (\mathbb R^3)$,

$$\begin{aligned} \Vert [\nabla ^{k+1},{\tilde{f}}]{\tilde{g}} \Vert _{L^2({\mathbb {R}}^3)} \lesssim \Vert \nabla {\tilde{f}}\Vert _{L^\infty (\mathbb R^3)}\Vert {\tilde{g}}\Vert _{H^{k}({\mathbb {R}}^3)}+\Vert \nabla {\tilde{f}}\Vert _{H^{k}({\mathbb {R}}^3)}\Vert {\tilde{g}}\Vert _{L^\infty (\mathbb R^3)}. \end{aligned}$$

Then one can show (A.6) in a similar way as in the proof of Sobolev’s inequality. Furthermore, (A.7) can be shown by direct expansion and Sobolev’s inequality. $\quad \square$

Lemma A.5

(Cattabriga estimate). Consider the following Stokes system

$$\begin{aligned} {\bar{\rho }} \mathop {\mathrm{div}}u = h , \quad - {\hat{\mu }} \Delta u + {\hat{p}} \nabla p = g , \quad u|_{\partial \Omega } =0, \quad \ \lim _{|x| \rightarrow \infty }u =0 \end{aligned}$$

with ${\bar{\rho }}$, ${\hat{\mu }}$, ${\hat{p}}$ being constants. For $k= 0, 1, \cdots , 4$ and $(h,g)\in H^{k+1}(\Omega )\times H^{k}(\Omega )$, if $(u,p) \in H^{k+2}(\Omega )\times H^{k+1}(\Omega )$ is a solution to the Stokes system, then it holds that

$$\begin{aligned} \Vert \nabla ^{k+2} u \Vert _{L^2(\Omega )}^2 + \Vert \nabla ^{k+1} p \Vert _{L^2(\Omega )}^2 \le C_0 (\Vert h \Vert ^2_{H^{k+1}(\Omega )} + \Vert g \Vert ^2_{H^k(\Omega )} + \Vert \nabla u \Vert _{L^2(\Omega )}^2), \end{aligned}$$

(A.8)

where $C_0=C_0(\Omega )$ is a positive constant depending on $\Omega$. Furthermore, there exists a positive constant $\kappa$ such that if $\Vert M\Vert _{H^{9}({\mathbb {R}}^2)} \le \kappa$, then (A.8) holds with $C_0$ independent of $\Omega$.

Proof

We may assume that ${\bar{\rho }}={\hat{\mu }}={\hat{p}}=1$ without loss of generality. Indeed, suitable change of variables enables us to have this. Let us also set

$$\begin{aligned} \Omega _{R'}:=\Omega \cap B(0,R') \quad \text {for any } R'>1 \end{aligned}$$

and then take a bounded domain $\tilde{\Omega }_{R'}$ whose boundary is $C^2$ such that

$$\begin{aligned} \Omega _{R'} \subset \tilde{\Omega }_{R'} \subset \Omega . \end{aligned}$$

For any $\phi \in C_0^\infty (\tilde{\Omega }_{R'})$, define $\phi _{\tilde{\Omega }_{R'}}$ by

$$\begin{aligned} \phi _{\tilde{\Omega }_{R'}}(x) := \phi (x)-|\tilde{\Omega }_{R'}|^{-1}\int _{\tilde{\Omega }_{R'}} \phi (x) \,dx \end{aligned}$$

and $\psi$ by solving the following problem:

$$\begin{aligned} \Delta \psi = \phi _{\tilde{\Omega }_{R'}} \quad \text {in } \tilde{\Omega }_{R'}, \quad \nabla \psi \cdot {n}|_{\tilde{\Omega }_{R'}}=0, \quad \int _{\tilde{\Omega }_{R'}} \psi \,dx=0, \end{aligned}$$

where n is the unit outer normal vector on $\tilde{\Omega }_{R'}$. The paper [1, Section 15] ensures that $\psi$ is well-defined, and that the following estimate holds:

$$\begin{aligned} \Vert \psi \Vert _{H^2(\tilde{\Omega }_{R'})} \lesssim _{\tilde{\Omega }_{R'}} \Vert \phi \Vert _{L^2(\tilde{\Omega }_{R'})}. \end{aligned}$$

(A.9)

From now on we show the Cattabriga estimate for $k=0$. Let us first show that

$$\begin{aligned} \Vert p_{\tilde{\Omega }_{R'}}\Vert _{L^2(\tilde{\Omega }_{R'})} \lesssim _{{R'}} (\epsilon \Vert \nabla ^2 u\Vert _{L^2(\Omega )}+C(\epsilon ) \Vert \nabla u\Vert _{L^2(\Omega )}+\Vert g\Vert _{L^2(\Omega )}), \quad R'>1, \quad \epsilon \in (0,1),\nonumber \\ \end{aligned}$$

(A.10)

where $p_{\tilde{\Omega }_{R'}}:=p-|\tilde{\Omega }_{R'}|^{-1}\int _{\tilde{\Omega }_{R'}} p\,dx$. We observe from $\int _{\tilde{\Omega }_{R'}} p_{\tilde{\Omega }_{R'}}\,dx=0$ and the definition of $\psi$ that

$$\begin{aligned}&\int _{\tilde{\Omega }_{R'}} p_{\tilde{\Omega }_{R'}} \phi \,dx \\&\quad =\int _{\tilde{\Omega }_{R'}} p_{\tilde{\Omega }_{R'}} \phi _{\tilde{\Omega }_{R'}} \,dx =\int _{\tilde{\Omega }_{R'}} p_{\tilde{\Omega }_{R'}} \Delta \psi \,dx\\&\quad =-\int _{\tilde{\Omega }_{R'}} (\nabla p) \cdot (\nabla \psi ) \,dx =-\int _{\tilde{\Omega }_{R'}} (\Delta u +g) \cdot (\nabla \psi ) \,dx \\&\quad =-\sum _{j=1}^3\left\{ \int _{\partial \tilde{\Omega }_{R'}} (\partial _j \psi )\{(\nabla u_j)\cdot {n}\} \,dS\right. \\&\left. \qquad -\int _{\tilde{\Omega }_{R'}} (\nabla u_j) \cdot (\nabla \partial _j \psi ) \,dx \right\} -\int _{\tilde{\Omega }_{R'}} g \cdot (\nabla \psi ) \,dx. \end{aligned}$$

Then estimating the right hand side by (A.9) leads to

$$\begin{aligned}&\int _{\tilde{\Omega }_{R'}} p_{\tilde{\Omega }_{R'}} \phi \,dx \\&\quad \lesssim (\epsilon \Vert \nabla ^2 u\Vert _{L^2(\Omega )} + C(\epsilon )\Vert \nabla u\Vert _{L^2(\Omega )})\Vert \psi \Vert _{H^2(\tilde{\Omega }_{R'})} \\&\qquad +\Vert \nabla u\Vert _{L^2(\Omega )}\Vert \psi \Vert _{H^2(\tilde{\Omega }_{R'})}+\Vert g\Vert _{L^2(\Omega )}\Vert \psi \Vert _{H^2(\tilde{\Omega }_{R'})} \\&\quad \lesssim _{\tilde{\Omega }_{R'}} (\epsilon \Vert \nabla ^2 u\Vert _{L^2(\Omega )} + C(\epsilon )\Vert \nabla u\Vert _{L^2(\Omega )}+\Vert g\Vert _{L^2(\Omega )})\Vert \phi \Vert _{L^2(\tilde{\Omega }_{R'})}. \end{aligned}$$

From the arbitrariness of $\phi \in C_0^\infty (\tilde{\Omega }_{R'})$, we conclude (A.10).

We next show that

$$\begin{aligned} \Vert \nabla ^2 u\Vert _{L^2(\Omega _R)}+\Vert \nabla p\Vert _{L^2(\Omega _R)}\lesssim & {} _{\Omega _R} \Vert h\Vert _{H^1(\Omega )}+\Vert g\Vert _{L^2(\Omega )}\nonumber \\&+ \epsilon \Vert \nabla ^2 u\Vert _{L^2(\Omega )} + C(\epsilon )\Vert \nabla u\Vert _{L^2(\Omega )}, \quad R>1,\nonumber \\ \end{aligned}$$

(A.11)

Noting that $\nabla p = \nabla p_{\tilde{\Omega }_{4R}}$, we have

$$\begin{aligned} \mathop {\mathrm{div}}u = h , \quad -\Delta u + \nabla ( p_{\tilde{\Omega }_{4R}} )= g , \quad u|_{\partial \Omega } =0 , \quad \lim _{|x| \rightarrow \infty } u =0. \end{aligned}$$

Applying Theorem IV.5.1 (see also Exercise IV.5.2) in [3] to the above problem, we have

$$\begin{aligned} \Vert \nabla ^2 u\Vert _{L^2(\Omega _R)}+\Vert \nabla p\Vert _{L^2(\Omega _R)}&\lesssim _{\Omega _R} \Vert h\Vert _{H^1(\Omega )} + \Vert g\Vert _{L^2(\Omega )} + \Vert u\Vert _{H^1(\Omega _{2R})} + \Vert p_{\tilde{\Omega }_{4R}}\Vert _{L^2(\Omega _{2R})} \\&\lesssim _{\Omega _R} \Vert h\Vert _{H^1(\Omega )} + \Vert g\Vert _{L^2(\Omega )} + \epsilon \Vert \nabla ^2 u\Vert _{L^2(\Omega )} + C_\epsilon \Vert \nabla u\Vert _{L^2(\Omega )}, \end{aligned}$$

where we have also used the Hölder inequality, (A.3), and (A.10) in deriving the last inequality. Hence, we conclude (A.11).

We complete the Cattabriga estimate for $k=0$ by deriving an estimate over the domain $\Omega \backslash \Omega _R$. To do this, we use the cut-off function $\chi _R(\cdot )=\chi (|\cdot |/R) \in C^\infty _0$, where $R>0$ and

$$\begin{aligned} \chi (s):= \left\{ \begin{array}{ll} 1 &{} \quad \text {if } s\le 1, \\ 0 &{} \quad \text {if } s\ge 2. \end{array}\right. \end{aligned}$$

(A.12)

Let us set

$$\begin{aligned} M_{R/8}(x'):=(1-\chi _{R/8}(x'))M(x'). \end{aligned}$$

For any $\delta \in (0,1)$, there exists $R_0=R_0(\delta )>1$ such that if $R/8>R_0$, then

$$\begin{aligned} \Vert M_{R/8}\Vert _{W^{1,\infty }({\mathbb {R}}^2)} < \delta , \quad M_{R/8}(x')=M(x') \ \ \text {for } (x,x') \in \Omega \backslash \Omega _{R/3}. \end{aligned}$$

(A.13)

We show that

$$\begin{aligned}&\Vert \nabla ^2 u\Vert _{L^2(\Omega \backslash \Omega _R)}+\Vert \nabla p\Vert _{L^2(\Omega \backslash \Omega _R)} \nonumber \\&\quad \lesssim _{\Omega _R}\Vert h\Vert _{H^1(\Omega )}+\Vert g\Vert _{L^2(\Omega )}+ \epsilon \Vert \nabla ^2 u\Vert _{L^2(\Omega )} + C_\epsilon \Vert \nabla u\Vert _{L^2(\Omega )}, \quad R> R_0(\delta _0),\nonumber \\ \end{aligned}$$

(A.14)

where $\delta _0$ is a constant to be determined later. Multiplying the Stokes equation by the cut-off function $(1-\chi _{R/2}(x))$ and using the zero extension of $(1-\chi _{R/2}) u$ and $(1-\chi _{R/2}) p_{\tilde{\Omega }_{4R}}$ on $\Omega '_{R/8}:=\{x_1>M_{R/8}(x')\}$, we see that

$$\begin{aligned} \mathop {\mathrm{div}}((1-\chi _{R/2}) u)= & {} h^*, \quad -\Delta ((1-\chi _{R/2}) u) + \nabla ( (1-\chi _{R/2}) p_{\tilde{\Omega }_{4R}} ) = g^* \quad \text {in } \Omega '_{R/8}, \\ (1-\chi _{R/2})u|_{\partial \Omega '_{R/8}}= & {} 0, \quad \lim _{|x| \rightarrow \infty } (1-\chi _{R/2}) u =0, \end{aligned}$$

where

$$\begin{aligned} h^* (x)&:= (1-\chi _{R/2}) h + (\nabla \chi _{R/2})\cdot u, \\ g^* (x)&:= (1-\chi _{R/2}) g -(\Delta \chi _{R/2}) u-\nabla u \nabla \chi _{R/2} + p_{\tilde{\Omega }_{4R}} \nabla \chi _{R/2}. \end{aligned}$$

Furthermore, using the change of variables

$$\begin{aligned} x_1 = y_1 + M_{R/8}(y_2, y_3), \quad x_2 = y_2, \quad x_3 = y_3, \end{aligned}$$

we have the problem

$$\begin{aligned} {\mathop {\mathrm{div}}}_y ((1-\chi _{R/2}) u)= & {} h^* + \{\partial _{y_1} ((1-\chi _{R/2}) u)\}\cdot \nabla _y M_{R/8}, \\&-\Delta _y ((1-\chi _{R/2}) u) + \nabla _y( (1-\chi _{R/2}) p_{\tilde{\Omega }_{4R}} ) \\= & {} g^* \!+ \sum _{j=2}^3\!\left[ ((\partial _{y_j}M_{R/8})\partial _{y_1}-\partial _{y_j})\{(\partial _{y_j}M_{R/8})\partial _{y_1} ((1-\chi _{R/2}) u)\}\right. \\&\left. -(\partial _{y_j}M_{R/8})\{\partial _{y_1y_j} ((1-\chi _{R/2}) u)\} \!\right] \\&+ \{\partial _{y_1} ((1-\chi _{R/2}) p_{\tilde{\Omega }_{4R}})\}\nabla _y M_{R/8} \quad \text {in } \mathbb R_+^3, \\ (1-\chi _{R/2})u|_{\partial {\mathbb {R}}_+^3}= & {} 0, \quad \lim _{|y| \rightarrow \infty } (1-\chi _{R/2}) u =0. \end{aligned}$$

Applying Theorem IV.3.2 in [3] with (A.13) to the above problem, we have

$$\begin{aligned}&\Vert \nabla ^2 ((1-\chi _{R/2}) u)\Vert _{L^2({\mathbb {R}}_+^3)} +\Vert \nabla ((1-\chi _{R/2}) p_{\tilde{\Omega }_{4R}})\Vert _{L^2({\mathbb {R}}_+^3)} \\&\quad \lesssim \delta \Vert \nabla ^2 ((1-\chi _{R/2}) u)\Vert _{L^2(\mathbb R_+^3)}+\delta \Vert \nabla ((1-\chi _{R/2}) p_{\tilde{\Omega }_{4R}})\Vert _{L^2({\mathbb {R}}_+^3)} \\&\qquad + \Vert h^*\Vert _{H^1({\mathrm{supp}}(1-\chi _{R/2}))} + \Vert g^*\Vert _{L^2({\mathrm{supp}}(1-\chi _{R/2}))} +\Vert u\Vert _{L^2({\mathrm{supp}}\nabla \chi _{R/2})}+\Vert \nabla u\Vert _{L^2({\mathrm{supp}}(1-\chi _{R/2}))}. \end{aligned}$$

Let us now take $\delta _0$ so small that

$$\begin{aligned}&\Vert \nabla ^2 ((1-\chi _{R/2}) u)\Vert _{L^2({\mathbb {R}}_+^3)} +\Vert \nabla ((1-\chi _{R/2}) p_{\tilde{\Omega }_{4R}})\Vert _{L^2({\mathbb {R}}_+^3)} \\&\quad \lesssim \Vert h^*\Vert _{H^1({\mathrm{supp}}(1-\chi _{R/2}))} + \Vert g^*\Vert _{L^2({\mathrm{supp}}(1-\chi _{R/2}))} +\Vert u\Vert _{L^2({\mathrm{supp}}\nabla \chi _{R/2})}+\Vert \nabla u\Vert _{L^2({\mathrm{supp}}(1-\chi _{R/2}))}. \end{aligned}$$

Then changing the coordinate $y \in {\mathbb {R}}_+^3$ to the coordinate $x \in \Omega _{R/8}'$ and noting that ${\mathrm{supp}}(1-\chi _{R/2}) \subset \Omega$ and $(1-\chi _{R/2})(x)=1$ hold for $x \in \Omega \backslash \Omega _{R} \subset \Omega _{R/8}'$, we have

$$\begin{aligned}&\Vert \nabla ^2 u\Vert _{L^2(\Omega \backslash \Omega _R)}+\Vert \nabla p\Vert _{L^2(\Omega \backslash \Omega _R)} \lesssim _{\Omega } \Vert h^*\Vert _{H^1(\Omega )} + \Vert g^*\Vert _{L^2(\Omega )}+ \Vert u\Vert _{L^2({\mathrm{supp}}\nabla \chi _{R/2})}+\Vert \nabla u\Vert _{L^2(\Omega )}. \end{aligned}$$

Then estimating the right hand side by (A.3), (A.10), and Poincaré inequality, we obtain

$$\begin{aligned} \Vert \nabla ^2 u\Vert _{L^2(\Omega \backslash \Omega _R)}+\Vert \nabla p\Vert _{L^2(\Omega \backslash \Omega _R)}&\lesssim _{\Omega } \Vert h\Vert _{H^1(\Omega )} \\&\quad + \Vert g\Vert _{L^2(\Omega )}+ \Vert (u,p_{\tilde{\Omega }_{4R}})\Vert _{L^2({\mathrm{supp}}\nabla \chi _{R/2})}+\Vert \nabla u\Vert _{L^2(\Omega )} \\&\lesssim _{\Omega } \Vert h\Vert _{H^1(\Omega )} + \Vert g\Vert _{L^2(\Omega )} + \epsilon \Vert \nabla ^2 u\Vert _{L^2(\Omega )} + C_\epsilon \Vert \nabla u\Vert _{L^2(\Omega )}. \end{aligned}$$

Hence, we conclude (A.14).

From (A.11) and (A.14), we have (A.8) with $k=0$ by taking $\epsilon$ small enough. Furthermore, one can show inductively for the case $k=1, 2$ with the aid of Theorem IV.3.2 and Theorem IV.5.1 in [3] which discusses the estimate of higher order derivatives.

We next discuss the case $\Vert M\Vert _{H^{9}({\mathbb {R}}^2)}\ll 1$. Using (3.37), we have the following problem:

$$\begin{aligned} {\mathop {\mathrm{div}}}_y u= & {} h + \partial _{y_1}u\cdot \nabla _y M, \\&-\Delta _y u + \nabla _y p =g + \sum _{j=2}^3\left[ \{(\partial _{y_j}M)\partial _{y_1}-\partial _{y_j}\}\{(\partial _{y_j}M)\partial _{y_1}u\} -(\partial _{y_j}M)\partial _{y_1y_j} u \right] \\&+ \partial _{y_1} p \nabla _y M \quad \text {in } {\mathbb {R}}_+^3, \\ u|_{\partial {\mathbb {R}}_+^3}= & {} 0 , \quad \lim _{|y| \rightarrow \infty } u =0 . \end{aligned}$$

Applying Theorem IV.3.2 in [3] with $\Vert M\Vert _{H^{9}(\mathbb R^2)} \le \kappa$ to the above problem, we have

$$\begin{aligned}&\Vert \nabla ^2 u\Vert _{L^2({\mathbb {R}}_+^3)} +\Vert \nabla p \Vert _{L^2(\mathbb R_+^3)} \\&\quad \lesssim \kappa \Vert \nabla ^2 u\Vert _{L^2({\mathbb {R}}_+^3)}+\kappa \Vert \nabla p \Vert _{L^2({\mathbb {R}}_+^3)} + \Vert h\Vert _{H^1({\mathbb {R}}_+^3)} + \Vert g\Vert _{L^2({\mathbb {R}}_+^3)} +\Vert \nabla u\Vert _{L^2({\mathbb {R}}_+^3)}. \end{aligned}$$

Let us take $\kappa$ so small that

$$\begin{aligned}&\Vert \nabla ^2 u\Vert _{L^2({\mathbb {R}}_+^3)} +\Vert \nabla p \Vert _{L^2(\mathbb R_+^3)} \lesssim \Vert h\Vert _{H^1({\mathbb {R}}_+^3)} + \Vert g\Vert _{L^2(\mathbb R_+^3)} +\Vert \nabla u\Vert _{L^2({\mathbb {R}}_+^3)}. \end{aligned}$$

Then changing the coordinate $y \in {\mathbb {R}}_+^3$ to the coordinate $x \in \Omega$ we conclude that

$$\begin{aligned} \Vert \nabla ^2 u\Vert _{L^2(\Omega )}+\Vert \nabla p\Vert _{L^2(\Omega )} \lesssim \Vert h\Vert _{H^1(\Omega )} + \Vert g\Vert _{L^2(\Omega )} + \Vert \nabla u\Vert _{L^2(\Omega )}. \end{aligned}$$

Furthermore, one can show inductively for the case $k=1, 2$ with aid of Theorem IV.5.1 in [3] which discusses the estimate of higher order derivatives. $\quad \square$

Lemma A.6

(Elliptic estimate). Consider the following elliptic system

$$\begin{aligned} \begin{aligned} - {\hat{\mu }} \Delta u - {\hat{\nu }} \nabla \mathop {\mathrm{div}}u = f, \quad u|_{\partial \Omega } =0 , \quad \lim _{|x| \rightarrow \infty } u =0 . \end{aligned} \end{aligned}$$

with ${\hat{\mu }}$ and ${\hat{\nu }}$ being positive constants. For $k= 0,1,2$ and $f \in H^{k}(\Omega )$, if $u \in H^{k+2}(\Omega )$ is a solution to the elliptic system, then it holds that

$$\begin{aligned} \Vert \nabla ^{k+2} u \Vert _{L^2(\Omega )} \lesssim \Vert f \Vert _{H^{k}(\Omega )} + \Vert u \Vert _{L^2(\Omega )} . \end{aligned}$$

(A.15)

Proof

This can be shown in much the same way as Theorems 4 and 5 in Section 6.3 in [2]. $\quad \square$

B Initial Data

We find a certain initial data $\Phi _0^{\#}$ which satisfies the compatibility conditions (2.3).

Lemma B.1

There exists $\psi _0^{\#}\in H^5(\Omega )$ such that $\Phi _0^{\#}=(0,\psi _0^{\#})$ satisfies (2.3) and $\Vert \Phi _0^{\#}\Vert _{L^{2}_{\mathrm{e},\beta }}+\Vert \Phi _0^{\#}\Vert _{H^5} \lesssim \delta$.

Proof

Note that problem (2.1) over $\Omega$ is equivalent to problem (3.44) over ${{\mathbb {R}}^3_+}$. To complete the proof, let us consider problem (3.44). It suffices to find the data ${\hat{\Phi }}_0^{\#}(y)=(0,\chi (y_1){\hat{\psi }}_0(y))\in H^5({{\mathbb {R}}^3_+})$ of which ${\hat{\psi }}_0$ satisfies

$$\begin{aligned}&{\hat{\psi }}_0|_{y_1=0} = 0, \end{aligned}$$

(B.1a)

$$\begin{aligned}&\left\{ {\hat{\rho }}_0 ({\hat{u}}_0 \cdot {\hat{\nabla }}) {\hat{\psi }}_0 - {\hat{L}} {\hat{\psi }}_0 - ({\hat{g}}+{\hat{G}})|_{t=0} \right\} |_{y_1 = 0} = 0, \end{aligned}$$

(B.1b)

$$\begin{aligned}&\left[ \partial _t\left\{ {\hat{\rho }} ({\hat{u}} \cdot {\hat{\nabla }}) {\hat{\psi }} - {\hat{L}} {\hat{\psi }} + p'({\hat{\rho }}) {\hat{\nabla }} {\hat{\varphi }} - {\hat{g}} \right\} |_{t=0}\right] _{y_1 = 0} = 0, \end{aligned}$$

(B.1c)

$$\begin{aligned}&\Vert {\hat{\psi }}_0\Vert _{H^5} \lesssim \delta , \end{aligned}$$

(B.1d)

where the cut-off function $\chi$ is defined in (A.12). Indeed, we see from the first three conditions that $\Phi _0^{\#} :={\hat{\Phi }}_0^{\#} ({\hat{\Gamma }}(x))$ satisfies (2.3a). The last condition implies $\Vert \Phi _0^{\#}\Vert _{L^{2}_{\mathrm{e},\beta }}+\Vert \Phi _0^{\#}\Vert _{H^5} \lesssim \delta$.

We will apply an extension theorem [4, Theorem 2.5.7]. To do so, let us first fix the boundary values of the zeroth, first, and third derivatives with respect to $y_1$ of ${\hat{\psi }}_0$ as

$$\begin{aligned} {\hat{\psi }}_0|_{y_1=0} = (\partial _{y_1}{\hat{\psi }}_0)|_{y_1=0} = (\partial _{y_1}^3{\hat{\psi }}_0)|_{y_1=0} = 0. \end{aligned}$$

(B.2)

Next we determine the boundary value of $\partial _{y_1}^2{\hat{\psi }}_0$ from the compatibility condition of order 2. Using (B.2), we simplify (B.1b) as

$$\begin{aligned} \left\{ - {\mathscr {A}}\partial _{y_1}^2{\hat{\psi }}_0 - {\hat{G}} \right\} |_{y_1 = 0}= & {} 0, \nonumber \\ {\mathscr {A}}(y_2,y_3):= & {} \mu _1(1+|\nabla M|^2)I+ (\mu _1+\mu _2){\mathscr {B}}, \nonumber \\ {\mathscr {B}}(y_2,y_3):= & {} \begin{bmatrix} 1 &{} -M_{y_2} &{} -M_{y_3} \\ -M_{y_2} &{} (M_{y_2})^2 &{} M_{y_2}M_{y_3} \\ -M_{y_3} &{} M_{y_2}M_{y_3} &{} (M_{y_3})^2 \end{bmatrix}. \end{aligned}$$

(B.3)

Since $\mathcal A$ is nonsingular, we see from (B.3) that the boundary value of $\partial _{y_1}^2{\hat{\psi }}_0$ must be

$$\begin{aligned} (\partial _{y_1}^2{\hat{\psi }}_0)|_{y_1 = 0} = ({\mathscr {A}}^{-1} {{\hat{G}}}) |_{y_1 = 0}. \end{aligned}$$

(B.4)

Now let us determine the boundary value of $\partial _{y_1}^4{\hat{\psi }}_0$. Using ${\hat{\varphi }}_t|_{t=0, \, y_1 = 0}=0$ which comes from (3.44a) and (B.2), we simplify (B.1c) as

$$\begin{aligned} \left[ \left\{ {\hat{\rho }}_0 \{u_b\cdot \nabla (x_1-M) \}\partial _{y_1} {\hat{\psi }}_{t} - {\mathscr {A}} \partial _{y_1}^2 {\hat{\psi }}_t + p'({\hat{\rho }}_0) {\hat{\nabla }} {\hat{\varphi }}_t \right\} |_{t=0}\right] _{y_1 = 0} = 0. \end{aligned}$$

(B.5)

We compute necessary conditions for $({\hat{\nabla }}{\hat{\varphi }}_t)|_{t=0,\,y_1=0}$, $(\partial _{y_1}{\hat{\psi }}_t)|_{t=0,\,y_1=0}$, and $(\partial _{y_1}^2{\hat{\psi }}_t)|_{t=0,\,y_1=0}$. Applying ${\hat{\nabla }}$ to (3.44a) gives

$$\begin{aligned} ({\hat{\nabla }}{\hat{\varphi }}_t)|_{t=0,\,y_1=0} =( {\hat{\nabla }} {\hat{F}}-{\hat{\rho }}_0 {\mathscr {B}} \partial _{y_1}^2 {\hat{\psi }}_0) |_{y_1 = 0} = ( {\hat{\nabla }} {\hat{F}} + {\hat{\rho }}_0 {\mathscr {B}} {\mathscr {A}}^{-1} {{\hat{G}}}) |_{y_1 = 0}. \end{aligned}$$

Furthermore, applying $\partial _{y_1}$ to (3.44b) leads to

$$\begin{aligned} (\partial _{y_1}{\hat{\psi }}_t)|_{t=0,\,y_1=0}&=\left[ -\{u_b\cdot \nabla (x_1-M) \} \partial _{y_1}^2 {\hat{\psi }}_0 +{\hat{\rho }}_0^{-1} {\hat{L}}\partial _{y_1}{\hat{\psi }}_0 +{\hat{\rho }}_0^{-1} \partial _{y_1}{\hat{G}}\right] |_{y_1 = 0}. \end{aligned}$$

Apply $\partial _{y_1}^2$ to (3.44b) and use (B.2) and $(\tilde{\rho } {\tilde{u}}_1)_{y_1}=0$ to obtain

$$\begin{aligned}&(\partial _{y_1}^2{\hat{\psi }}_t)|_{t=0,\,y_1=0} -({\hat{\rho }}_0^{-1}{\mathscr {A}}\partial _{y_1}^4{\hat{\psi }}_0)|_{y_1 = 0} \\&\quad =\biggl \{-\sum _{i=2}^3 u_{bi}\partial _{y_i}\partial _{y_1}^2{\hat{\psi }}_0 -2{\hat{\rho }}_0^{-1}\{ \partial _{y_1} ({\hat{\rho }}_0 {\hat{U}}) \cdot \nabla (x_1-M) \} \partial _{y_1}^2 {\hat{\psi }}_0 \\&\qquad +{\hat{\rho }}_0^{-1} ({\hat{L}}-{\mathscr {A}}\partial _{y_1}^2)\partial _{y_1}^2{\hat{\psi }}_0 +{\hat{\rho }}_0^{-1} \partial _{y_1}^2({\hat{g}}+{\hat{G}})\biggr \}\biggr |_{y_1 = 0}. \end{aligned}$$

Note that ${\hat{L}}-{\mathscr {A}}\partial _{y_1}^2$ does not have the second derivative operator $\partial _{y_1}^2$. Plugging these into (B.5), we see that the boundary value of $\partial _{y_1}^4{\hat{\psi }}_0$ must be

$$\begin{aligned}&(\partial _{y_1}^4{\hat{\psi }}_0)|_{y_1 = 0} \nonumber \\&\quad =({\mathscr {A}}^{-1})^2\biggl [ {\hat{\rho }}_0 p'({\hat{\rho }}_0) ( {\hat{\nabla }} {\hat{F}} +{\hat{\rho }}_0 {\mathscr {B}} {\mathscr {A}}^{-1} {{\hat{G}}}) |_{y_1 = 0} \nonumber \\&\qquad \left. +{\hat{\rho }}_0 \{u_b\cdot \nabla (x_1-M) \} \big [ -{\hat{\rho }}_0\{u_b\cdot \nabla (x_1-M) \}\partial _{y_1}^2 {\hat{\psi }}_0 +{\hat{L}}\partial _{y_1}{\hat{\psi }}_0 +\partial _{y_1}{\hat{G}} \big ] \right\} |_{y_1 = 0} \nonumber \\&\qquad +{\mathscr {A}}\biggl \{\sum _{i=2}^3 {\hat{\rho }}_0u_{bi}\partial _{y_i}\partial _{y_1}^2{\hat{\psi }}_0 +2\{ \partial _{y_1} ({\hat{\rho }}_0 {\hat{U}}) \cdot \nabla (x_1-M) \} \partial _{y_1}^2 {\hat{\psi }}_0 \nonumber \\&\qquad -({\hat{L}}-{\mathscr {A}}\partial _{y_1}^2)\partial _{y_1}^2{\hat{\psi }}_0 -\partial _{y_1}^2({\hat{g}}+{\hat{G}})\biggr \}\biggr |_{y_1=0} \biggr ]. \end{aligned}$$

(B.6)

We notice that the right hand side can be expressed by a linear combination of ${\hat{F}}$, ${\hat{G}}$ and their derivatives with some coefficients given by the smooth functions ${\hat{\rho }}_0(=\tilde{\rho })$, $u_b$, ${\mathscr {A}}$, ${\mathscr {B}}$, ${\mathscr {A}}^{-1}$, $\nabla M$, $\nabla ^2 M$, $\partial _{y_1}({\hat{\rho }}_0 {\hat{U}})$ if we write explicitly $\partial _{y_1} {\hat{\psi }}_0|_{y_1 = 0}$, $\partial _{y_1}^2 {\hat{\psi }}_0|_{y_1 = 0}$, and $\partial _{y_1}^3 {\hat{\psi }}_0|_{y_1 = 0}$ by using (B.2) and (B.4).

Using an extension theorem [4, Theorem 2.5.7] with (B.2), (B.4), and (B.6), we have a function ${\hat{\psi }}_0$ satisfies (B.1). Indeed, the first three lines in (B.1) obviously follow from the above computations of the compatibility conditions. The last line in (B.1) can be also obtained by using the fact that all derivatives with respect to $y_1$ of ${\hat{\psi }}_0$ are linear combinations of ${\hat{F}}$, ${\hat{G}}$ and their derivatives whose $L^2$ norms are bounded by $C \delta$. The proof is complete. $\quad \square$

C The Equation of the Energy Form

In this section, we derive the equations of the energy form i.e. (3.9) and (5.6). Let us first treat (3.9). A direct computation yields

$$\begin{aligned} (\rho {\mathscr {E}})_t + \mathop {\mathrm{div}}(\rho u {\mathscr {E}}) = {\mathscr {E}}\{\rho _t + \mathop {\mathrm{div}}(\rho u) \} + I_1 + I_2 +I_3, \end{aligned}$$

(C.1)

where

$$\begin{aligned} I_{1}= & {} \rho \psi \cdot \psi _t + \rho u \cdot (\nabla \psi ) \psi , \quad I_{2} = \frac{p(\rho ) -p(\tilde{\rho })}{\rho ^2} (\rho \rho _t + \rho u \cdot \nabla \rho ), \\ I_{3}= & {} -\int ^\rho _{\tilde{\rho }} \frac{d\eta }{\eta ^2} p'(\tilde{\rho }) \nabla \tilde{\rho }\cdot \rho u. \end{aligned}$$

Note that the first term on the right hand side is zero owing to (1.1a). Let us rewrite terms $I_{1}$, $I_{2}$, and $I_{3}$ as follows. Use (2.1b) and recall the definition of g to obtain

$$\begin{aligned} \begin{aligned} I_1&= L \psi \cdot \psi - \nabla (p(\rho ) - p(\tilde{\rho })) \cdot \psi - \rho (\psi \cdot \nabla ) ({\tilde{u}}+U) \cdot \psi \\&\quad - \varphi (({\tilde{u}}+U) \cdot \nabla ) ({\tilde{u}}+U) \cdot \psi + G \cdot \psi . \\ \end{aligned} \end{aligned}$$

Notice that

$$\begin{aligned} L \psi \cdot \psi = \mathop {\mathrm{div}}B_{1}+ \mu _1 |\nabla \psi |^{2} + (\mu _1 + \mu _2) (\mathop {\mathrm{div}}\psi )^{2}. \end{aligned}$$

Using (1.1a), we arrive at

$$\begin{aligned} \begin{aligned} I_2&= - (p(\rho ) - p(\tilde{\rho }) ) \mathop {\mathrm{div}}u \\&= -(p(\rho ) - p(\tilde{\rho }) ) \mathop {\mathrm{div}}({\tilde{u}} +U ) - \mathop {\mathrm{div}}\{ (p(\rho ) - p(\tilde{\rho }) ) \psi \} + \nabla (p(\rho ) - p(\tilde{\rho }) ) \cdot \psi . \\ \end{aligned} \end{aligned}$$

Furthermore, it is seen that

$$\begin{aligned} \begin{aligned} I_3&= - p'(\tilde{\rho }) \varphi \frac{\nabla \tilde{\rho }}{\tilde{\rho }} \cdot (\psi + {\tilde{u}} + U) = - p'(\tilde{\rho }) \varphi \frac{\nabla \tilde{\rho }}{\tilde{\rho }} \cdot (\psi + U) + p'(\tilde{\rho }) \varphi \mathop {\mathrm{div}}{\tilde{u}}, \\ \end{aligned} \end{aligned}$$

where we have also used $\mathop {\mathrm{div}}(\tilde{\rho }{\tilde{u}})=0$ coming from (1.5a) in deriving the last inequality. On the other hand, using (1.5b), we derive

$$\begin{aligned}&\varphi \left\{ ({\tilde{u}} \cdot \nabla ) {\tilde{u}} + p'(\tilde{\rho })\frac{\nabla \tilde{\rho }}{\tilde{\rho }} \right\} \cdot \psi \\&\quad = \frac{\varphi }{\tilde{\rho }} L {\tilde{u}} \cdot \psi { -\frac{\varphi }{\tilde{\rho }} (\mu _{1} {\tilde{u}}_{1}'' |\nabla M|^{2} - \mu _{1} {\tilde{u}}_{1}' \Delta M)\psi _{1} -{\varphi } \left( \mu _{1} \frac{{\tilde{u}}_{1}''}{\tilde{\rho }} -{\tilde{u}}_{1}{\tilde{u}}_{1}' \right) \nabla M \cdot \psi } . \end{aligned}$$

Plugging the results above into (C.1), we conclude (3.9). One can also have (5.6) just by replacing $(\tilde{\rho },{\tilde{u}},U,G,\nabla {\tilde{M}})$ by $(\rho ^{s},u^{s},0,0,0)$ in the above computation.