Abstract
We consider the multicomponent Smoluchowski coagulation equation under non-equilibrium conditions induced either by a source term or via a constant flux constraint. We prove that the corresponding stationary non-equilibrium solutions have a universal localization property. More precisely, we show that these solutions asymptotically localize into a direction determined by the source or by a flux constraint: the ratio between monomers of a given type to the total number of monomers in the cluster becomes ever closer to a predetermined ratio as the cluster size is increased. The assumptions on the coagulation kernel are quite general, with isotropic power law bounds. The proof relies on a particular measure concentration estimate and on the control of asymptotic scaling of the solutions which is allowed by previously derived estimates on the mass current observable of the system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many processes of particle formation in the atmosphere are due to the aggregation of gas molecules into small molecular clusters which grow by colliding with additional gas molecules and with each other (cf. [10, 11]). The aggregation process of gas molecules to form larger clusters is usually described using the so-called General Dynamic Equation (cf. [3]). This model includes in particular effects like cluster–cluster reaction as well as cluster–gas reaction. It also allows for source terms for small clusters, to take into account physically relevant source processes such as molecules produced in reactions of vegetation to sunlight.
In many situations of interest the particle clusters are made of aggregates of different types of coagulating molecular types, called monomers. Keeping track of the composition of the clusters, instead only of the total number of particles in them, can be important for the applications. For instance, atmospheric coagulation involves chemically distinct monomer types such as sulfuric acid and ammonia or dimethylamine molecules which are bases (for an example about the resulting effects on the composition of small clusters we refer to the numerical study in [10]).
An important common feature of these multicomponent models is that, in the absence of source terms and gelation, they conserve the total mass of each monomer type. Each of these conservation laws is then naturally associated with a current observable, corresponding to the flux of the monomer type towards arbitrarily large cluster sizes. The main motivation for the present work is to develop understanding of the asymptotic, large time and cluster size, properties of the solutions of these equations, both with and without source terms. We consider here only cases which have a source term or a non-zero constant flux of particles from small to large cluster sizes, and call these non-equilibrium solutions. We also ignore the effect of fragmentation, as motivated later.
Following a common approach in such analysis of asymptotic large-scale properties, the first step is to understand what happens to stationary, i.e., time-independent, solutions to the equations. In a related work [5], we have already extended the analysis from the one-component case in [4], and we have shown that a natural class of coagulation kernels can be easily partitioned into two subclasses depending on whether a stationary solution exists or not. Here we continue the analysis of stationary solutions in the class of kernels which can have a stationary non-equilibrium solution. Although not necessarily unique, we will prove that these solutions share a somewhat surprising common feature which we call asymptotic localization: for large clusters, the solutions will become completely localized in one direction. The direction is determined by the source or flux constraint. Roughly summarized, if one is interested in the monomer composition of a typical large cluster, the ratio of the number of monomers in that cluster will be the same as in the total induced flux, with small corrections which vanish with increasing cluster size. (More detailed definitions and discussion will be given Sect. 1.2).
At the first sight, it might appear that this localization is a feature produced by the strong perturbation associated with the constant input of monomers into the system. Instead, we conjecture that the localization is a fairly universal feature of the related time-dependent solutions, even without influx of particles. Indeed, preliminary results on particular example cases support this conjecture, and we expect to report on more general analysis soon in [6].
To formulate the problem mathematically, we label the clusters by \(\alpha =\left( \alpha _{1},\alpha _{2},\ldots ,\right. \)\(\left. \alpha _{d}\right) \in {\mathbb {N}}_{0}^{d}\), where d denotes the number of monomer types and \(\alpha _j\) the number of monomers of the type j in the corresponding cluster. The relevant version of the General Dynamic Equation which includes coagulation, fragmentation, and monomer injection is then
where \(\left| \alpha \right| \) denotes the \(\ell ^{1}\) norm of \(\alpha \), namely
Moreover, we will assume that in (1.1) we have \(\alpha \ne O=\left( 0,0,\ldots ,0\right) \).
The coefficients \(K_{\alpha ,\beta }\) describe the coagulation rate between clusters with compositions \(\alpha \) and \(\beta \), and the coefficients \(\Gamma _{\alpha ,\beta }\) describe the fragmentation rate of clusters of composition \(\alpha \) into two clusters, one with composition \(\beta \) and the other with \(\left( \alpha -\beta \right) \). Suppose that \(\alpha =\left( \alpha _{1},\alpha _{2},\ldots ,\alpha _{d}\right) \) and \(\beta =\left( \beta _{1},\beta _{2},\ldots ,\beta _{d}\right) .\) We use the notation \(\beta <\alpha \) to indicate that \(\beta _{k}\le \alpha _{k}\) for all \(k=1,2,\ldots ,d\), and in addition \(\alpha \ne \beta .\) We denote as \(s_{\beta }\) the source of monomers characterized by the composition \(\beta .\) In (1.1), we have only allowed source terms with \(\left| \beta \right| =1\) which correspond to injecting clusters containing only one monomer, although of any of the d possible types. We will relax this condition in the results to allow for source terms \(s_{\beta }\) which are supported on a finite set of values \(\beta \).
The coefficients \(K_{\alpha ,\beta }\) yield the coagulation rate between clusters \(\alpha \) and \(\beta \) to produce clusters \(\left( \alpha +\beta \right) .\) The form of these coefficients depends on the specific mechanism which is responsible for the aggregation of the clusters. These coefficients have been computed using kinetic models under different assumptions on the particle sizes and the processes describing the motion of the clusters. Various choices of the coagulation kernel have been described in the literature, see e.g. the textbook [3].
We will continue to work under the same class of coagulation kernels as in our previous work on multicomponent coagulation [5]. The precise conditions are collected in Sect. 1.1. In particular, the results proven here will apply to the so called diffusive coagulation or Brownian kernel
where \(C>0\) is a constant depending on the process producing the diffusion, assuming that the volume scales linearly with the number of monomers in the cluster, i.e., if
The inequalities (1.4) hold, for instance, if we suppose \(V\left( \alpha \right) =\sum _{j=1}^{d}\alpha _{j}v_{j}\) where \(v_{j}>0\) for each \(j=1,2,\ldots ,d.\)
In this paper, we will ignore the fragmentation terms in (1.1), and set \(\Gamma _{\alpha ,\beta }=0.\) The rationale for this, as discussed in [4], is that in the situations we are interested, the formation of larger particles is energetically favourable and therefore only the coagulation of clusters must be taken into account. This yields the following evolution problem
We are interested in the steady states of (1.5) as well as in the steady states of the continuous version of (1.5) which is given by
where given \(x=\left( x_{1},x_{2},\ldots ,x_{d}\right) ,\) \(y=\left( y_{1} ,y_{2},\ldots ,y_{d}\right) \) we recall the previously introduced comparison notation: \(x<y\) whenever \(x\le y\) componentwise, and \(x\ne y\). In particular,
Most of the mathematical analysis of coagulation equations has been made for one-component systems, i.e., with \(d=1\). On the other hand, there are only a few papers addressing the problem of the coagulation equations with injection terms like \(\sum _{\left| \beta \right| =1}s_{\beta }\delta _{\alpha ,\beta }\) or \(\eta .\) This issue has been discussed in [4] and we refer to that paper for additional references on earlier related works.
1.1 Coagulation kernel assumptions
We will restrict our attention to the class of coagulation kernels satisfying the following inequalities
where p, \(\gamma \in {{\mathbb {R}}}\) are some given parameters, \(0<c_{1}\le c_{2}<\infty \), and we define
Note that then \(\Phi \left( s\right) =\Phi \left( 1-s\right) \) for all \(0<s<1\), and thus the above bounds are symmetric under the exchanges \(\alpha \leftrightarrow \beta \) and \(x\leftrightarrow y\). We stress that even though the bound functions are isotropic, i.e., invariant under permutation of components, the kernels need not to be that. It would be interesting to explore whether localization still holds for strongly non-isotropic kernels.
The existence of steady states to the problems (1.5), (1.6) has been considered in [5]. It is proven there that in the multicomponent case and under the assumptions (1.7)–(1.9), there exists a stationary solution to (1.5), (1.6) if and only if
In particular, since for \(\gamma +2p\ge 1\) there are no stationary solutions, we can leave those parameter values out of consideration here. (Further discussion about the physical significance and qualitative explanation for the non-existence of stationary solutions for \(\gamma +2p\ge 1\) can be found in [5].)
It is now straightforward to check that for the diffusive kernel in (1.3) and assuming (1.4) is valid, the assumptions are satisfied after choosing \(\gamma =0\) and \(p=\frac{1}{3}\). Thus the inequality (1.10) then holds, and there exists at least one stationary solution.
1.2 Asymptotic localization
The main result of this paper is a property of the steady states to (1.5), (1.6) which is specific to the multicomponent coagulation system, i.e., occurs only if \(d>1.\) This property, called here localization, consists in the fact that the mass in the stationary solutions to (1.5), (1.6) concentrates for large values of the cluster size \(\left| \alpha \right| \) or \(\left| x\right| \) along a specific direction of the cone \({{\mathbb {R}}}^{d}_{+}\). More precisely, we can find some relative width of the strip, \(\zeta >1\), such that if \(\left\{ n_{\alpha }\right\} _{\alpha \in {\mathbb {N}}_{0} ^{d}\setminus \left\{ O\right\} }\) or f are solutions to (1.5) or (1.6), respectively, there exists a vector \(\theta \in {\mathbb {R}}_{+}^{d}\) satisfying \(\left| \theta \right| =1\) such that for any \(\varepsilon >0\) the following inequalities hold (respectively for \(\left\{ n_{\alpha }\right\} _{\alpha }\) or f)
In fact, the direction \(\theta \) can be uniquely determined from the source term, \(s_{\beta }\) or \(\eta \), in the sense that \(\theta _j\) will agree with the total relative injection rate of monomers of type j. Thus the flux of monomers towards large cluster sizes occurs via clusters with essentially fixed relative monomer compositions. Let us remark that (1.11) is a non-equilibrium property which cannot be derived from a variational principle such as by minimization of the free energy or any other thermodynamic potential. On the contrary, the localization property emerges as a consequence of the coagulation dynamics. We also point out that for systems of the form (1.5), (1.6) the detailed balance property fails.
Asymptotic localization appears to be a very generic feature of multicomponent coagulation, including time-dependent problems. This has been shown to occur for the constant kernel \(K=1\) and the additive kernel \(K=x+y\) for the discrete coagulation equation in [9], using the fact that for these kernels the solutions to (1.5) can be obtained explicitly by means of the generating function method. In a forthcoming paper [6], a similar localization property will be shown for mass conserving solutions of the coagulation equation (i.e. with \(\eta =0\) or \(s_{\beta }=0\)), asymptotically for long times.
1.3 Main notations and structure
In this paper we will denote the non-negative real numbers and integers by \({\mathbb {R}}_{+}:={[}0,\infty {)} \) and \({{\mathbb {N}}}_0:= \{0,1,2,\ldots \}\), respectively. We also use a subindex “\(*\)” to denote restriction of real-component vectors x to those which satisfy \(x>0\), i.e., for which \(x_i>0\) for some i. In particular, we denote \({{\mathbb {R}}}_*:={{\mathbb {R}}}_+\setminus \{0\}\), \({{\mathbb {R}}}^d_*:={{\mathbb {R}}}_+^d\setminus \{O\}\) and \({{\mathbb {N}}}^d_*:={{\mathbb {N}}}_0^d\setminus \{O\}\).
Assuming that X is a locally compact Hausdorff space, for example \(X={{\mathbb {R}}}^d_*\), we denote with \(C_{c}\left( X\right) \) the space of compactly supported continuous functions from X to \({{\mathbb {C}}}\), and let \(C_0(X)\) denote its completion in the standard sup-norm. Moreover, we will denote as \({\mathscr {M}}_{+}(X)\) the collection of non-negative Radon measures on X, not necessarily bounded, and as \({\mathscr {M}}_{+,b}(X)\) its subset consisting of bounded measures. We recall that \( {\mathscr {M}}_{+}(X) \) can be identified with the space of positive linear functionals on \(C_{c}(X)\) via Riesz–Markov–Kakutani Theorem.
We will use indistinctly \(\eta (x) dx\) and \(\eta (dx)\) to denote elements of the above measure spaces. The notation \(\eta ( dx) \) will be preferred when performing integrations or when we want to emphasize that the measure might not be absolutely continuous with respect to the Lebesgue measure. In addition, “dx” will often be dropped from the first notation, typically when the measure eventually turns out to be absolutely continuous. We will also borrow a convenient notation from physics to denote “Dirac \(\delta \)”-measures: if X is locally compact Hausdorff space and \(x_0\in X\), we denote the bounded positive Radon measure defined by the functional \(\Lambda _{x_0}[f]=f(x_0)\), \(f\in C_{c}(X)\), by “\(\delta (x-x_0)\mathrm{d}x\)”.
We also use the notation \({\mathbb {1}}_{\{P\}}\) to denote the generic characteristic function of a condition P: \({\mathbb {1}}_{\{P\}}=1\) if the condition P is true, and otherwise \({\mathbb {1}}_{\{P\}}=0\).
The plan of the paper is the following. In Sect. 2 we introduce the definitions of stationary injection solutions (continuous and discrete) and constant flux solutions that are considered in this paper and we recall the existence results which have been obtained in [5]. Section 3 contains the main results on mass localization in stationary solutions. The proofs are presented in Sects. 5 and 6 and they use some technical results that are collected in Sect. 4.
2 Classes of Steady State Solutions
2.1 Stationary injection solutions
The stationary solutions of (1.5), (1.6) are described respectively by the equations
We will assume that the sources \(s_{\beta }\) and \(\eta \) are compactly supported. For examples of how to relax the assumptions about the source, we refer to a recent paper [8] where compact support is not required assuming that the solution f is absolutely continuous with respect to the Lebesgue measure.
Definition 2.1
Let \(\eta \in {\mathscr {M}}_{+,b}\left( {\mathbb {R}}_{*}^{d}\right) \) with support contained in the set  for some \(L>1.\) Suppose that K is continuous and it satisfies (1.8), (1.9). We will say that \(f\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*} ^{d}\right) \) is a stationary injection solution to (2.2) if f is supported in
for some \(L>1.\) Suppose that K is continuous and it satisfies (1.8), (1.9). We will say that \(f\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*} ^{d}\right) \) is a stationary injection solution to (2.2) if f is supported in  and satisfies
and satisfies
as well as the identity
for any test function \(\varphi \in C^{1}_c\left( {{{{\mathbb {R}}}}_{*}^{d}}\right) \).
For the definition, we recall the notation \({{\mathbb {R}}}^d_*:={{\mathbb {R}}}^d_{+}\setminus \{O\}\) and that we use the \(\ell _1\)-norm in \({{\mathbb {R}}}^d_*\), i.e., \(|x|=\sum _j |x_j|\).
In order to define stationary injection solutions for the discrete Eq. (2.1) we use the fact that the solutions of (2.1) can be thought as solutions f of (2.2) where f is supported at the elements of \({\mathbb {N}}_{*}^{d}={{\mathbb {N}}}_0^d\setminus \{O\}\). More precisely, suppose that the sequence \(\left\{ n_{\alpha }\right\} _{\alpha \in {\mathbb {N}}_{*}^{d}}\) is a solution of (2.1) and assume that there is \(L>1\) such that \(s_\alpha =0\) whenever \(|\alpha |>L\). We define
as well as
Then \(\eta \) satisfies the assumptions of Definition 2.1 with the same parameter L.
With these identifications in mind, we can then define a solution of (2.1) as follows:
Definition 2.2
Suppose that \(\left\{ s_{\alpha }\right\} _{\alpha \in {\mathbb {N}}_{*}^{d} }\) is a non-negative sequence supported in a finite collection of values \(\alpha .\) We say that a sequence \(\left\{ n_{\alpha }\right\} _{\alpha \in {\mathbb {N}}_{*}^{d} }\), with \(n_{\alpha }\ge 0\) for \(\alpha \in {\mathbb {N}}_{*}^{d}\), is a stationary injection solution of (2.1) if
and the measure \(f\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*}^{d}\right) \) defined by means of (2.4) is a solution of (2.2) in the sense of Definition 2.1.
Note that the assumptions made about \(n_\alpha \) guarantee that the associated measure f is supported in  and satisfies (2.1).
and satisfies (2.1).
Next we state the existence of stationary injection solutions to (2.2) and (2.1) for kernels K with \(\gamma +2p<1.\) This result has been proved in [5] and it is a natural extension from one- to multi-component systems of the result contained in [4].
Theorem 2.3
Suppose that K is a continuous symmetric function that satisfies (1.8), (1.9) with \(\gamma +2p<1.\) We have the following results:
-
(i)
Suppose that \(\eta \in {\mathscr {M}}_{+,b}\left( {\mathbb {R}}_{*}^{d}\right) \) is supported inside the set
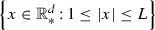 for some \(L>1\). Then, there exists a stationary injection solution \(f\in {\mathscr {M}} _{+}\left( {\mathbb {R}}_{*}^{d}\right) \) to (2.2) in the sense of Definition 2.1.
for some \(L>1\). Then, there exists a stationary injection solution \(f\in {\mathscr {M}} _{+}\left( {\mathbb {R}}_{*}^{d}\right) \) to (2.2) in the sense of Definition 2.1. -
(ii)
Suppose that K is symmetric and satisfies (1.7), (1.9) with \(\gamma +2p<1.\) Let \(\left\{ s_{\alpha }\right\} _{\alpha \in {\mathbb {N}}_{*}^{d} }\) be a non-negative sequence supported on a finite number of values \(\alpha .\) Then, there exists a stationary injection solution \(\left\{ n_{\alpha }\right\} _{\alpha \in {\mathbb {N}}_{*}^{d} }\) to (2.1) in the sense of Definition 2.2.
Remark 2.4
Let us point out that no uniqueness of the solutions is claimed in Theorems 2.3, 2.3. The issue of uniqueness of stationary injection solutions is an interesting open problem. Moreover, we remark that restrictions for the values of \(\gamma \) an p in Theorem 2.3 are not only sufficient to have stationary injection solutions, but they are also necessary. Indeed, for values of \(\gamma \) an p such that \(\gamma +2p\ge 1\) it is possible to prove that no such solutions exist (cf. [5]).
2.2 Change to \((r,\theta )\)-variables
The definition of constant flux solution presented in the next section, as well as the main results of this paper are more conveniently written in the coordinates \(\left( r,\theta \right) \) with \(r=|x|>0\) and \(\theta = \frac{1}{|x|}x\in \Delta ^{d-1}\) for \(x\in {{\mathbb {R}}}^d_*\), where \(\Delta ^{d-1}\) denotes the simplex
We use the variables \(\theta _{1},\theta _{2},\ldots ,\theta _{d-1}\) to parametrize the simplex and set then \( \theta _{d}=1-\sum _{j=1}^{d-1}\theta _{j}. \) Thus, the change of variables is \(x\rightarrow \left( r,\theta _{1},\theta _{2},\ldots ,\theta _{d-1}\right) \). This map is a bijection from \({{\mathbb {R}}}^d_*\) to \({{\mathbb {R}}}_*\times \Delta ^{d-1} \) and the inverse map \({{\mathbb {R}}}_*\times \Delta ^{d-1} \rightarrow {{\mathbb {R}}}^d_* \) is defined by \(x=r\theta ,\ r>0,\ \theta \in \Delta ^{d-1}\).
We now rewrite Eq. (2.2) using this change of variables. For further details we refer to [5]. Computing the determinant of the Jacobian of the mapping \(\left( r,\theta \right) \rightarrow x,\) we obtain
Rewriting \(d\theta _{1}d\theta _{2}\ldots d\theta _{d-1}\) in terms of the area element of the simplex, denoted by \(d\tau \left( \theta \right) \), yields \(d\tau \left( \theta \right) =\sqrt{d}\, d\theta _{1}d\theta _{2}\ldots d\theta _{d-1}\) and
Here we used the formula \(d\tau \left( \theta \right) =\sqrt{1+\left( \nabla _{\theta }h\right) ^{2} }d\theta _{1}d\theta _{2}\ldots d\theta _{d-1}\) with \(\theta _{d}=h\left( \theta _{1},\theta _{2},\right. \)\(\left. \ldots ,\theta _{d-1}\right) := 1-\sum _{j=1}^{d-1}\theta _{j} .\)
Suppose that \(x=r\theta \) and \(y=\rho \sigma .\) We define the kernel function in these new variables by
and replace the measure f by the measure \(F\in {\mathscr {M}}_+({{\mathbb {R}}}_*\times \Delta ^{d-1})\) which is uniquely fixed by the requirement that
for all test functions \(\psi \in C_c({{\mathbb {R}}}_*\times \Delta ^{d-1})\). The normalization with the Jacobian is made to guarantee that, if f is absolutely continuous, then the respective density functions transform as expected.
Then, we obtain that (2.3) is equivalent to
for all \(j=1,2,\ldots ,d\) and \(\psi \in C_c({{\mathbb {R}}}_*\times \Delta ^{d-1})\) and using \(\varphi (x) = \psi (r,\theta )\) and \(\varphi (y) = \psi (\rho ,\sigma )\).
Note that the change of measure in (2.7) from f to F should be understood via the Riesz–Markov–Kakutani Theorem applied to the linear functional
Clearly, if \(F(r,\theta )dr d\tau (\theta )\) denotes the unique non-negative Radon measure associated with this functional, then F satifies also (2.7). Note also that if f satisfies the assumptions in Definition 2.1, we also have that the support of F lies in \([1,\infty )\times \Delta ^{d-1}\) and F satisfies
2.3 Constant flux solutions
Finally, let us detail also the definition of the constant flux solutions associated to the Eq. (2.2) with \(\eta =0\), i.e., to the equation
Definition 2.5
Suppose that K is continuous and it satisfies (1.8), (1.9). We say that \(f\in {\mathscr {M}}\left( {\mathbb {R}}_{*}^{d}\right) \) is a stationary solution of (2.9) if

is satisfied and (2.3) holds with \(\eta =0\), for every test function \(\varphi \in C^{1}_c\left( {{{{\mathbb {R}}}}_{*}^{d}}\right) \).
We then define the total flux across the surface \(\left\{ \left| x\right| =R\right\} \) as the vector-valued function \(A(R)\in {{\mathbb {R}}}_+^d\), \(R>0\), defined by
where the function G is defined as in (2.6) and the measure F using (2.7), as explained above. We say that f is a non-trivial constant flux solution of (2.9) if it is a stationary solution and there is \(J_0>O\) such that \(A(R)=J_0\) for all \(R>0\).
Remark 2.6
The flux (2.10) is obtained by considering in (2.8) the test function \(\psi (r,\theta )=r\chi _\delta (r)\), with \(\chi _\delta (r) \in C_c^\infty ({{\mathbb {R}}}_*)\) such that \(\chi _\delta (r) \in [0,1]\), \(\chi _\delta (r)=1\) for \(r \in [1,z]\) and \(\chi _\delta (r)=0\) for \(r \ge z+\delta \) and computing the limit when \(\delta \rightarrow 0\) following similar arguments as in the proof of Lemma 2.7 in [4]. We refer to [5] for the details of the computations. Note that in the one-component equation the fluxes being constant implies that f is a solution to the coagulation equation. The same is not true in the multicomponent equation, which justifies the need to assume (2.3).
Remark 2.7
Assume that the kernel K is continuous and homogeneous with homogeneity \(\gamma \). If K satisfies (1.8), (1.9) with \(\gamma +2p<1\), then one can show (cf. [5]) that a family of constant flux solutions of (2.9) is given by the following weighted Dirac \(\delta \)-measures
where \(\theta _{0}\in \Delta ^{d-1}\) is fixed but arbitrary.
3 Main Result
The main result of this paper is a rigorous proof of the so-called localization in the above described stationary solutions. It turns out that all solutions to (2.1), (2.2) concentrate along a straight line as \(\left| x\right| \) or \(\left| \alpha \right| \) tend to infinity respectively.
Theorem 3.1
Suppose that K is a continuous symmetric function that satisfies (1.8), (1.9) with \(\gamma +2p<1.\) Suppose that \(\eta \in {\mathscr {M}}_{+,b}\left( {\mathbb {R}}_{*}^{d}\right) \) is supported inside the set  for some \(L>1\) and \(\eta \ne 0\). Let \(f\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*}^{d}\right) \) be a stationary injection solution of (2.2) in the sense of Definition 2.1 and let F be defined by means of (2.7). Then, there exists \(b \in (0,1)\) and a function \(\delta :{\mathbb {R}}_{*}\rightarrow {\mathbb {R}}_{+}\) with \(\lim _{R\rightarrow \infty }\delta \left( R\right) =0\) such that
for some \(L>1\) and \(\eta \ne 0\). Let \(f\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*}^{d}\right) \) be a stationary injection solution of (2.2) in the sense of Definition 2.1 and let F be defined by means of (2.7). Then, there exists \(b \in (0,1)\) and a function \(\delta :{\mathbb {R}}_{*}\rightarrow {\mathbb {R}}_{+}\) with \(\lim _{R\rightarrow \infty }\delta \left( R\right) =0\) such that
where
Notice that Theorem 3.1 implies that any stationary injection solution to (2.2) concentrates for large values of \(\left| x\right| \) along the direction \(x=\left| x\right| \theta _{0}.\) A similar result holds for the discrete problem, since the solutions to (2.1) are solutions to (2.2) supported in the points with integer coordinates \({\mathbb {N}}_{*}^{d} .\) Although the following result is a Corollary of Theorem 3.1, we have preferred to formulate it separately due to the fact that the discrete coagulation equations have an independent interest in many applications in aerosol science. It is worth to remark that an analogue of the solution (2.11) does not exist for the discrete Smoluchowski coagulation equation.
Theorem 3.2
Suppose that K is symmetric and satisfies (1.7), (1.9) with \(\gamma +2p<1.\) Let \(\left\{ s_{\alpha }\right\} _{\alpha \in {\mathbb {N}}_{*}^{d}}\) be a nonnegative sequence supported on a finite number of values \(\alpha \), and assume the sequence is not identically zero. Suppose that \(\left\{ n_{\alpha }\right\} _{\alpha \in {\mathbb {N}}_{*}^{d} }\) is a stationary injection solution to (2.1) in the sense of Definition 2.2. Then, there exists \(b \in (0,1)\) and a function \(\delta :{\mathbb {R}}_{*}\rightarrow {\mathbb {R}}_{+}\) with \(\lim _{R\rightarrow \infty }\delta \left( R\right) =0\) such that
where
We will prove also that all constant flux solutions to (2.9) are supported along a half-line \(\left\{ x=r\theta _{0}:r>0\right\} \) and their analysis can be reduced to the constant flux solutions in the one-component case \(d=1.\) More precisely we have:
Theorem 3.3
Suppose that K is a continuous symmetric function that satisfies (1.8), (1.9) with \(\gamma +2p<1\). Suppose that \(f\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*}^{d}\right) \) is a constant flux solution to (2.9) in the sense of Definition 2.5 with total flux \(J_0 > O\). We define F as in (2.7) and G as in (2.6). Then,
where \(\theta _0 = J_0/|J_0| \in \Delta ^{d-1}\) and \(H\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*}\right) \) is a constant flux solution for the one-component coagulation equation with the kernel \({\tilde{K}}\left( r,\rho \right) =G\left( r,\rho ;\theta _{0},\theta _{0}\right) .\)
Remark 3.4
We observe that we did not require the kernel K to be homogeneous for the asymptotic localization of stationary injection solutions (Theorems 3.1, 3.2) nor to prove the complete localization of constant flux solutions in Theorem 3.3. Notice that, if the kernel K is homogeneous, there are constant flux solutions to (2.9) with \(H\left( r\right) =r^{-\frac{\gamma +3}{2}}\) (cf. (2.11)). However, we cannot expect all the constant flux solutions to the one-dimensional coagulation equation to be power-law solutions, even for homogeneous kernels. Indeed, there are one-dimensional coagulation kernels for which there exist constant flux solutions which are not power laws (cf. [7]).
The proofs (cf. Sects. 5 and 6 ) rely on growth bounds for the stationary injection and constant flux solutions given in Proposition 4.3 below which has been proven in [5]. The bounds are used to derive estimates for an appropriate family in R of probability measures in \(\theta \) as defined in (5.6) in Sect. 5. These measures are then shown to converge weakly to the Dirac \(\delta (\theta -\theta _0)\) as \(R\rightarrow \infty \) by using a measure concentration estimate (cf. Lemma 4.7). In the case of constant flux solutions \(F(r,\theta )\) we further show that the mass is concentrated not only asymptotically but for all r by using similar estimates.
4 Technical Tools
In this section we collect some results that will be used later in the proofs of Theorems 3.1, 3.2, and 3.3 . Some statements are taken from [4] and [5].
4.1 Reduction of the problem to \(p=0\)
The kernels K satisfying (1.7)–(1.9) can be characterized by the two parameters \(\gamma , p\). Using a suitable change of variable, we can transform the stationary solutions with kernels K into stationary solutions with new kernels \({\tilde{K}}\) with parameters \({\tilde{\gamma }}=\gamma +2p\) and \({\tilde{p}}=0\).
This follows from an idea introduced in [2] (see also [1])Footnote 1. The idea is based on the observation that f is a stationary injection solution (resp. constant flux solution) associated to the kernel K if and only if \(h :=\left| x\right| ^{-p}f\) is a stationary injection solution (resp. constant flux solution) associated with the kernel \({{\tilde{K}}}\) defined by
This new kernel \({{\tilde{K}}}\) satisfies (1.8) after replacing \(\gamma \) by \(\tilde{\gamma }=\gamma +2p\) and p by \({\tilde{p}}=0\), i.e., \({{\tilde{K}}}\) satisfies
We then have the following Lemma (cf. [5]).
Lemma 4.1
Let \(\eta \in {\mathscr {M}}_{+,b}\left( {\mathbb {R}}_{*}^{d}\right) \) be supported inside the set  for some \(L>1\). Suppose that K is continuous and it satisfies (1.8), (1.9). The Radon measure \(f\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*}^{d}\right) \) is a stationary injection solution to (2.2) in the sense of Definition 2.1 (resp. a constant flux solution to (2.9) in the sense of Definition 2.5) if and only if the Radon measure \(h\left( x\right) =\frac{f\left( x\right) }{\left| x\right| ^{p}}\) is a stationary injection solution to (2.2) (resp. a constant flux solution to (2.9)) with the kernel \({\tilde{K}}\) defined in (4.1). The kernel \({\tilde{K}}\) satisfies (4.2).
for some \(L>1\). Suppose that K is continuous and it satisfies (1.8), (1.9). The Radon measure \(f\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*}^{d}\right) \) is a stationary injection solution to (2.2) in the sense of Definition 2.1 (resp. a constant flux solution to (2.9) in the sense of Definition 2.5) if and only if the Radon measure \(h\left( x\right) =\frac{f\left( x\right) }{\left| x\right| ^{p}}\) is a stationary injection solution to (2.2) (resp. a constant flux solution to (2.9)) with the kernel \({\tilde{K}}\) defined in (4.1). The kernel \({\tilde{K}}\) satisfies (4.2).
4.2 A technical lemma
The following lemma allows to transform estimates of averaged integrals into estimates in the whole line. This lemma is a particular case of Lemma 2.10 (items 2 and 3) in [4].
Lemma 4.2
Suppose \(a>0, R \in [a,\infty ]\) and \(b,r \in (0,1)\) are such that \(a \le rR \). Define the interval \(I=[a,R]\) if \(R<\infty \), or \(I = [a,\infty )\) if \(R=\infty \). Consider some \(f \in \mathscr {M_+}({{\mathbb {R}}}_*)\) and \(\varphi \in C({{\mathbb {R}}}_*)\), with \(\varphi \ge 0\). If there is a polynomial function \(g(x) = c_0x^q\) with \(c_0\ge 0\) and \(q \in {{\mathbb {R}}}\) such that \(g \in L^1(I)\) and
then there is a constant \(C>0\) which depends only on r, b and q such that
4.3 Growth bounds
We now recall some relevant growth bounds, obtained in [5], which are valid for any stationary injection solution of the continuous (2.2) and discrete (2.1) equations, as well as for any constant flux solution.
Proposition 4.3
Suppose that K is a continuous symmetric function satisfying (1.8), (1.9) with \(\gamma +2p<1.\) Suppose that \(\eta \in {\mathscr {M}}_{+,b}\left( {\mathbb {R}}_{*}^{d}\right) \) is supported inside the set  for some \(L>1\) and let \(\vert J_{0}\vert \) denote the total mass injection rate, where \(J_{0} =\int _{{\mathbb {R}}_{*}^{d}} x\eta \left( dx\right) \in {{\mathbb {R}}}^d_*\).
for some \(L>1\) and let \(\vert J_{0}\vert \) denote the total mass injection rate, where \(J_{0} =\int _{{\mathbb {R}}_{*}^{d}} x\eta \left( dx\right) \in {{\mathbb {R}}}^d_*\).
Consider a stationary injection solution \(f\in {\mathscr {M}} _{+}\left( {\mathbb {R}}_{*}^{d}\right) \) to (2.2) in the sense of Definition 2.1. Then there exist positive constants \(C_{1},\ C_{2}\) and \(b\in \left( 0,1\right) \) depending only on \(\gamma ,\ p,\ d\) and the constants \(c_{1},c_{2}\) in (1.8) such that with \(\xi = \frac{L}{b}\) it holds
Alternatively, suppose that f is a nontrivial constant flux solution as in Definition 2.5 with flux \(J_0\). Then there exist positive constants \(C_{1},\ C_{2}\) and \(b\in \left( 0,1\right) \) depending only on \(\gamma ,\ p,\ d\) and the constants \(c_{1},c_{2}\) in (1.8) such that (4.3) and (4.4) hold with \(\xi = 0\).
Remark 4.4
Notice that \(\vert J_{0}\vert \) is the total injection rate, i.e., it includes all of the possible monomer types.
Remark 4.5
We observe that for \(\gamma > -1\), Proposition 4.3 and Lemma 4.2 imply that the number of clusters associated to the stationary injection solutions \(\int _{{{\mathbb {R}}}_{*}} f(dx)\) is finite and the following integral estimates hold:
where \(\vert J_{0}\vert = \int _{{{\mathbb {R}}}^d_{*}} \vert x \vert \eta (dx)\) and \(0< C_{1} \le C_{2} \).
Remark 4.6
It is possible to obtain similar lower estimates for stationary injection solutions \(\left\{ n_{\alpha }\right\} _{\alpha \in {\mathbb {N}}_{*}^{d} }\) to the discrete problem (2.1). More precisely, we have (cf. [5])
where the constants \(c_{1},c_{2},C_{1}, C_{2}\) and \(b\in \left( 0,1\right) \) are as in Proposition 4.3 and the total injection rate of monomers is given by \(\vert J_{0}\vert =\sum _{\alpha }\left| \alpha \right| s_{\alpha }.\)
4.4 A measure concentration lemma
The following Lemma states that given any probability measure \(\lambda \) on the unit simplex either a quadratic functional acting on the space of measures \(\lambda \) is large, or there exists a set with small diameter containing most of the mass of the measure \(\lambda \).
Lemma 4.7
There is a constant \(C_d>0\) which depends only on the dimension \(d\ge 1\) and for which the following alternative holds.
Suppose a Borel probability measure \(\lambda \in {\mathscr {M}}_{+,b}\left( \Delta ^{d-1}\right) \) and parameters \(\varepsilon ,\delta \in (0,1)\) are given. Then at least one of the following alternatives is true:
-
(i)
There exists a measurable set \(A\subset \Delta ^{d-1}\) with \({{\,\mathrm{diam}\,}}\left( A\right) \le \varepsilon \) such that \(\int _{A}\lambda (d\theta )> 1-\delta \).
-
(ii)
\(\int _{\Delta ^{d-1}}\lambda \left( d\theta \right) \int _{\Delta ^{d-1} }\lambda \left( d\sigma \right) \left\| \theta -\sigma \right\| ^{2} \ge C_d \delta \varepsilon ^{d+1}\) where \(\left\| \cdot \right\| \) denotes the Euclidean distance in \({{\mathbb {R}}}^d\) given by \(\left\| \theta \right\| ^{2}=\sum _{j=1}^{d}\left( \theta _{j}\right) ^{2}.\)
Proof
If \(d=1\), we have \(\Delta ^{d-1}=\{1\}\) so \({{\,\mathrm{diam}\,}}(\Delta ^{d-1})=0\). Thus alternative (i) holds in this case always, with the choice \(A=\Delta ^{d-1}\). We may set \(C_1=1\), although it will never be used.
Let us then suppose \(d\ge 2\) and that the case (i) is not true. It suffices to prove that we can define \(C_d>0\), depending only on d, such that case (ii) holds.
Given \(x\in \Delta ^{d-1}\), let us consider its following \({{\mathbb {R}}}^d\)-metric neighbourhood: define

and denote its \(\lambda \)-measure by
For clarity, we drop \(\varepsilon \) from the notation in the following, we recall that it is fixed. Then \({{\,\mathrm{diam}\,}}(A(x))\le \varepsilon \), so we can conclude from the assumption that \(m(x)\le 1-\delta \).
Let us then consider the expectation in item (ii), and estimate it from below as follows, using generic characteristic functions:
Now for any \(x\in {{\mathbb {R}}}^d\), by the triangle inequality, assuming \(\Vert \theta -x\Vert \ge \frac{\varepsilon }{2}\) and \(\Vert x-\sigma \Vert < \frac{\varepsilon }{4}\) implies \(\Vert \theta -\sigma \Vert \ge \frac{\varepsilon }{4}\). Therefore,
Thus we obtain the following lower bound, valid for any \(x\in \Delta ^{d-1}\),
Here \({\mathbb {1}}_{\{\Vert \theta -x\Vert \ge \frac{\varepsilon }{2}\}} =1-{\mathbb {1}}_{\{\Vert \theta -x\Vert <\frac{\varepsilon }{2}\}}\), and thus \(\int _{\Delta ^{d-1}}\lambda \left( d\theta \right) {\mathbb {1}}_{\{\Vert \theta -x\Vert \ge \frac{\varepsilon }{2}\}}=1-m(x)\ge \delta \). We conclude that
We now integrate the previous inequality over the measure \(d\tau (x)\). Denoting \(c_d := \int _{\Delta ^{d-1}}d\tau (x)\) and using Fubini’s Theorem, we thus obtain a lower bound
We claim that there is a uniform lower bound \(C_d>0\) which depends only on d and such that, for any \(\sigma \in \Delta ^{d-1}\),
Since \(\lambda \) is a probability measure, we may then conclude that
and thus item (ii) holds for this constant \(C_d\) which satisfies the requirements of the Lemma.
It only remains to prove (4.5). The proof relies on the following geometrical argument. We consider the volume of the intersection of the simplex with d-balls centered at \(\sigma \). The worst case scenario occurs at the extreme corner points of the simplex. However, since d is fixed and finite, even the cones associated with the corner points have a finite volume fraction of the ball, hence they have the same scaling as the radius goes to zero. This implies that \(\int _{\Delta ^{d-1}}d\tau (x) {\mathbb {1}}_{\{\Vert x-\sigma \Vert < \frac{\varepsilon }{4}\}} \ge c'_d \varepsilon ^{d-1}\) using some \(c'_d>0\) and for all \(\varepsilon \in (0,1)\), and this estimate may be used to complete the proof of (4.5).
For the detailed proof, let us parametrize the simplex using the coordinate system introduced in Sect. 2.2: for \(\theta \in \Delta ^{d-1}\) denote \({\hat{\theta }}=\left( \theta _1,\ldots ,\theta _{d-1}\right) \in {{\mathbb {R}}}_+^{d-1}\), and note that then \(|{{\hat{\theta }}}|\le 1\) and \(\theta _d=1-|{\hat{\theta }}|\). Using the Schwarz inequality, we find \(\Vert \theta -\sigma \Vert ^2\le d\Vert {{\hat{\theta }}}-{{\hat{\sigma }}}\Vert ^2\), and thus \({\mathbb {1}}_{\{\Vert \theta -\sigma \Vert< \frac{\varepsilon }{4}\}} \ge {\mathbb {1}}_{\{\Vert {{\hat{\theta }}}-{{\hat{\sigma }}}\Vert < \frac{\varepsilon }{4\sqrt{d}}\}}\). Therefore, denoting \(\varepsilon ':= \frac{\varepsilon }{4\sqrt{d}}>0\),
where we have made a change of variables to \(y=\frac{1}{\varepsilon '}\left( {{\hat{\theta }}}-{\hat{\sigma }}\right) \). Now if \(|{{\hat{\sigma }}}|\le 1-\varepsilon '\sqrt{d}=1-\frac{\varepsilon }{4}\), the remaining integrand is one on the set  , and hence its value may be bounded from below by an only d-dependent strictly positive constant. Otherwise, there has to be some \(j'\) such that \({\hat{\sigma }}_{j'}\ge \frac{1}{2d}\) and then \(\frac{{\hat{\sigma }}_{j'}}{\varepsilon '}\ge \frac{2}{\sqrt{d}}\). Now for y such that \(\Vert y\Vert <1\), \(-\frac{2}{\sqrt{d}}\le y_{j'}\le -\frac{1}{\sqrt{d}}\) and \(0\le y_j \le \frac{1}{d\sqrt{d}}\) for \(j\ne j'\), all the conditions in the characteristic functions are satisfied, and thus the integrand is then one. Again the integral over this non-empty set results in a lower bound by an only d-dependent strictly positive constant. This proves (4.5) and completes the proof of the Lemma. \(\quad \square \)
, and hence its value may be bounded from below by an only d-dependent strictly positive constant. Otherwise, there has to be some \(j'\) such that \({\hat{\sigma }}_{j'}\ge \frac{1}{2d}\) and then \(\frac{{\hat{\sigma }}_{j'}}{\varepsilon '}\ge \frac{2}{\sqrt{d}}\). Now for y such that \(\Vert y\Vert <1\), \(-\frac{2}{\sqrt{d}}\le y_{j'}\le -\frac{1}{\sqrt{d}}\) and \(0\le y_j \le \frac{1}{d\sqrt{d}}\) for \(j\ne j'\), all the conditions in the characteristic functions are satisfied, and thus the integrand is then one. Again the integral over this non-empty set results in a lower bound by an only d-dependent strictly positive constant. This proves (4.5) and completes the proof of the Lemma. \(\quad \square \)
5 Localization Properties of the Stationary Injection Solutions for the Continuous and Discrete Coagulation Equations
We prove here Theorems 3.1 and 3.2 . Given that the solutions to the discrete problem (2.1) can be thought of as solutions to the continuous model (2.2) it will be sufficient to prove the localization results in the case of the continuous Eq. (2.2).
We can argue as in Sect. 4.1 in order to reduce the localization in stationary injection solutions to the case in which the kernels K satisfy (1.8), (1.9) with \(p = 0, \gamma < 1\). We formulate this result precisely.
Lemma 5.1
Suppose that K and \(\eta \) are as in the statement of Theorem 3.1. Let \(f\in {\mathscr {M}}_{+}\left( {\mathbb {R}}_{*}^{d}\right) \) be a stationary injection solution of (2.2) in the sense of Definition 2.1 and let F be defined by means of (2.7). Define \(h\left( x\right) =\frac{f\left( x\right) }{\left| x\right| ^{p}}.\) Then h is a stationary injection solution with the kernel \({\tilde{K}}\) in (4.1) which satisfies (4.2). Let \(H\left( r,\theta \right) \) be obtained from \(h\left( x\right) \) as F is obtained from f. Then, there exists \(b \in (0,1)\) and a function \(\delta :{\mathbb {R}}_{*}\rightarrow {\mathbb {R}}_{+}\) satisfying \(\lim _{R\rightarrow \infty }\delta \left( R\right) =0\) and such that (3.1) holds for some \(\theta _{0}\in \Delta ^{d-1}\) if and only if
Proof
First, note that (3.1) is equivalent to
Using that \(H\left( r,\theta \right) dr d\tau \left( \theta \right) =r^{-p} F\left( r,\theta \right) d r d\tau \left( \theta \right) \) we obtain
and
If we assume that (5.2) holds, and then use these two inequalities, we find that
from which (5.1) follows. The opposite direction is proven via similar estimates, and the rest of the Lemma is a matter of comparison of definitions. \(\quad \square \)
We now prove Theorem 3.1.
Proof of Theorem 3.1
Due to Lemma 5.1 it is enough to prove the result for \(p=0,\ \gamma <1.\) For convenience, we rewrite here the weak formulation (2.8), which is valid for any function \(\psi \in C_{c}^1\left( {{\mathbb {R}}}_* \times \Delta ^{d-1}\right) \)
where \(\varphi (x) = \psi (\theta ,r)\) and the source \(\eta \) is supported in the set  for some \(L>1\). In order to obtain estimates for the measure F we consider in (5.3) test functions \(\psi \left( r,\theta ;R\right) =r\phi _{R}\left( r\right) \left\| \theta \right\| ^{2}\) with \(\left\| \theta \right\| ^{2}=\sum _{j=1}^{d}\left( \theta _{j}\right) ^{2}\) and \(R\ge L\). Here, \(\phi _R\in C^\infty _c({{\mathbb {R}}}_*)\) is chosen as a bump function: it is monotone increasing on (0, 1] and monotone decreasing on \([1,\infty )\). We also assume that \(\phi _{R}\left( r\right) =1\) for \(1\le r\le R,\) and \(\phi _{R}\left( r\right) =0\) for \(r\ge 2R\).
for some \(L>1\). In order to obtain estimates for the measure F we consider in (5.3) test functions \(\psi \left( r,\theta ;R\right) =r\phi _{R}\left( r\right) \left\| \theta \right\| ^{2}\) with \(\left\| \theta \right\| ^{2}=\sum _{j=1}^{d}\left( \theta _{j}\right) ^{2}\) and \(R\ge L\). Here, \(\phi _R\in C^\infty _c({{\mathbb {R}}}_*)\) is chosen as a bump function: it is monotone increasing on (0, 1] and monotone decreasing on \([1,\infty )\). We also assume that \(\phi _{R}\left( r\right) =1\) for \(1\le r\le R,\) and \(\phi _{R}\left( r\right) =0\) for \(r\ge 2R\).
Then,
We next assume \(r,\rho \ge 1\), and note that then \(\phi _{R}\left( r\right) \ge \phi _{R}\left( r+\rho \right) \) and \(\phi _{R}\left( \rho \right) \ge \phi _{R}\left( r+\rho \right) \). This yields an upper bound
Then, for \(R\ge L\), we obtain from (5.3)
where \(J_0:= \int _{{{\mathbb {R}}_{*}^{d}}} x \eta \left( dx\right) \in {{\mathbb {R}}}^d_*\) is the mass injection rate vector and the last equality is obtained by taking into account that the injection solutions do not have any support on values with \(|x|<1\).
Since \({\mathbb {1}}_{\{1\le r+\rho \le R\}}\le \phi _{R}\left( r+\rho \right) \), the bound in (5.4) remains valid after we replace \(\phi _{R}\) with this characteristic function. The new function, however, is pointwise monotone increasing in R, approaching 1 pointwise as \(R\rightarrow \infty \), so we may apply monotone dominated convergence Theorem to take the limit \(R\rightarrow \infty \) inside the integral. This yields
where \(K_0:=2 d |J_0|>0\). Using now the lower estimate in (1.8), (1.9) with \(p=0\), as well as (2.6), we obtain
For the rest of the proof, let us recall Proposition 4.3, and let \(b\in (0,1)\) and \(C_1,C_2>0\) be some choice of constants for which the Proposition holds. We record the following bounds implied by Proposition 4.3 and Lemma 4.2: If \(q<\frac{\gamma +1}{2}\) and \(R\ge L\), we have
where the lower bound is obtained by restricting the integral into \(r\in [R,b^{-1} R]\). The constants depend on q and b, as well as on \(\gamma ,\ p\) and d. In particular, for any fixed \(R\ge L\) the value of the integral belongs to \((0,\infty )\), and we may define the Radon probability measures \(\lambda (\theta ;R)d\tau \left( \theta \right) \in {\mathscr {M}}_{+,b}\left( \Delta ^{d-1}\right) \) via the formula
Let Z(R) denote the value of the integral in the denominator, for which we have bounds
To apply the measure concentration estimate, let us then consider the function
Using Fubini’s Theorem, we can rewrite the definition as
Here, \(r^\gamma \rho ^\gamma = r \rho (r+\rho )^{\gamma -1} (r^{-1}+ \rho ^{-1})^{1-\gamma }\le r \rho (r+\rho )^{\gamma -1} (2/R)^{1-\gamma }\). Therefore, by (5.7),
Hence, there is a constant \(C'>0\) such that
The finite bound in (5.5) now allows to use the dominated convergence Theorem to conclude that
We can then apply Lemma 4.7 as follows, with \(C_d\) denoting the constant in the Lemma. We first choose \(R_0\ge L,\frac{2}{C_d}\) so that \(V(R)< \frac{C_d}{2}\) for all \(R\ge R_0\), which is possible due to (5.9). Given \(R\ge R_0\), we choose \(\delta (R)\) and \(\varepsilon (R)\) so that the alternative (ii) fails. To this end, let us pick an arbitrary function \(\varepsilon _0:{{\mathbb {R}}}_*\rightarrow {{\mathbb {R}}}_*\) which satisfies \(\varepsilon _0(R)\le \frac{1}{R}\) for all \(R>0\), and then define for \(R\ge R_0\)
so that always \(C_d\delta (R)\varepsilon (R)^{d+1}=V(R)+\varepsilon _0(R)>V(R)\) and \(\delta (R)=\varepsilon (R)\in (0,1)\), with \(\varepsilon (R)\rightarrow 0\) as \(R\rightarrow \infty \). Then Lemma 4.7 implies that for each \(R\ge R_0\) there exists \(\sigma _{0}\left( R\right) \in \Delta ^{d-1}\) for which
Then, the compactness of \(\Delta ^{d-1}\) implies that for every sequence \(\left\{ R_{n}\right\} _{n\in {\mathbb {N}}}\) with \(\lim _{n\rightarrow \infty }R_{n}=\infty ,\) there exists a subsequence \(\left\{ R_{n_{k}}\right\} _{k\in {\mathbb {N}}}\) and \(\theta _{0}\in \Delta ^{d-1}\) such that \({\bar{\sigma }}_k:=\sigma _0(R_{n_k})\rightarrow \theta _0\) in \({{\mathbb {R}}}^d\) and, hence,
where the convergence takes place in the weak topology of measures. The Dirac \(\delta \)-measure above is defined with respect to \(d\tau \left( \theta \right) \), for instance, \(\int _{\Delta ^{d-1}}d\tau \left( \theta \right) \delta \left( \theta -\theta _{0}\right) = 1\) even if \(\theta _0\) is on the boundary of \(\Delta ^{d-1}\).
In principle, \(\theta _0\) depends on the chosen subsequence \(\{R_{n_{k}}\}\). We prove now that this is not the case and characterize \(\theta _{0}.\) We plug into the weak formulation (5.3) the test functions \(\psi _j\left( r,\theta \right) =r\phi _{R}\left( r\right) \theta _j\), \(j=1,2,\ldots ,d\), where \(\phi _R\) satisfies all earlier conditions. In addition, we now require that there is \(c>0\) such that \(0\ge \phi '_R(r)\ge -\frac{c}{R}\) for \(r\ge 1\), so that \(0\le \phi _R(r)-\phi _R(r+\rho )\le \frac{c}{R} \rho \) for all \(r,\rho \ge 1\). A function satisfying all the requirements can be constructed for instance by taking a smooth non-increasing function \(g_1\) for which \(g_1(r)=1\) for \(r\le 1\), \(g_1(r)=0\), \(r\ge 2\), and then defining \(\phi _R(r)=(1-g_1(2 r)) g_1(r/R)\).
Then, using a vector notation,
Plugging this identity into (5.3) and using a symmetrization argument to exchange the variables \(\left( r,\theta \right) \longleftrightarrow \left( \rho ,\sigma \right) \) we obtain
where we assume that \(R>L\) and \(J_0\) is the injection rate vector, as defined above.
We then expand using \(\theta =\theta _0 + \theta - \theta _0\), and denote
We also note that
as seen by summing over the components in (5.12), since \(\theta \in \Delta ^{d-1}\). Therefore, for all \(R>L\),
We claim that there is a sequence \(R'_k> L\) such that \(\omega (R'_k)\rightarrow 0\) in \({{\mathbb {R}}}^d\) as \(k\rightarrow \infty \). This implies
as claimed in the Theorem. In particular, the value does not then depend on the choice of the subsequence \((R_{n_k})\) above. Therefore, \(\sigma (R)\rightarrow \theta _0\) as \(R\rightarrow \infty \), and we can then replace (5.11) by \(\lambda \left( \theta ;R\right) \rightharpoonup \delta \left( \theta -\theta _{0}\right) \) as \(R\rightarrow \infty \).
Thus it only remains to construct the sequence \(R'_k>L\), \(k\in {{\mathbb {N}}}_+\), such that \(\omega (R'_k)\rightarrow 0\) as \(k\rightarrow \infty \). We do this by showing that \(\lim _{\delta \rightarrow 0}\limsup _{k\rightarrow \infty }\Vert \omega (R_{n_k} \delta ^{-2})\Vert =0\) where \(\delta \in \left( 0,\frac{1}{4}\right] \) since then a diagonal construction allows finding suitable \(R'_k\).
We start from (5.13) after choosing arbitrary k and \(\delta \in \left( 0,\frac{1}{4}\right] \) and setting \(R=R_{n_k} \delta ^{-2}>L\). For \(r,\rho \ge 1\), we have \(0\le \phi _R(r)-\phi _{R}(r+\rho )\le \min \left( 1,\frac{c}{R} \rho \right) \), by assumption. In addition, the difference is zero, if \(r\ge 2 R\) or \(r+\rho \le R\). Therefore, the integration region may be restricted to

We now split the region into three parts \(\Omega _i\), \(i=1,2,3\), analogously to what was used in the proof of Proposition 6.3 in [4]: We set

and then define
so that \(\omega (R) = \sum _{i=1}^3 I_i\).
In the region \(\Omega _1\) we use the trivial bound \(\left[ \phi _{R}\left( r\right) -\phi _{R}\left( r+\rho \right) \right] \Vert \theta -\theta _0\Vert \le 2\) in the integrand, as well as the estimate \(G\left( r,\rho ;\theta ,\sigma \right) \le c_2 (r+\rho )^\gamma \). By adapting the proof of the corresponding estimate in Lemma 6.1 in [4] applied to the measure \( \int _{\Delta ^{d-1}}d\tau \left( \theta \right) r^{d-1} F\left( r,\theta \right) \) with the kernel \( (r+\rho )^\gamma \), we may conclude that \(\sup _{R} \Vert I_1(\delta ,R) \Vert \rightarrow 0\) as \(\delta \rightarrow 0\).
In the region \(\Omega _3\) we use the upper bound \(\left[ \phi _{R}\left( r\right) -\phi _{R}\left( r+\rho \right) \right] \Vert \theta -\theta _0\Vert \le 2 c \rho /R\). Moreover, using that \(\Omega _3 \subset [ 1,\delta R] \times [ R/2 , 2R]\) as well as the upper bound of the kernel in (1.8), (1.9) with \(p=0\), and recalling (2.6), we obtain the bound
where in the second inequality we have applied Lemma 4.2 with \(q=1-\frac{\gamma +3}{2}\). Also this bound is independent of R and goes to zero as \(\delta \rightarrow 0\).
It remains to estimate \(I_2\). Now on \(\Omega _2\) we have \((r+\rho )^\gamma \le 3^{|\gamma |}\delta ^{-|\gamma |}\rho ^\gamma \), and also \(\Omega _2 \subset [\delta ^2 R,2 R]\times [\delta R,\infty )\). Therefore, we obtain an estimate
By our choice of \(R, \delta \), we have here \(\delta ^2 R=R_{n_k}\). Therefore,
which goes to zero as \(k\rightarrow \infty \), by construction.
Collecting the estimates of \(I_i\) together, we find \(\lim _{\delta \rightarrow 0}\limsup _{k\rightarrow \infty }\Vert \omega (R_{n_k} \delta ^{-2})\Vert =0\) which completes the proof of \(\lim _{R\rightarrow \infty }\sigma _0(R)= \theta _0\). Hence, also
and by Chebyshev-type estimate then
To conclude the proof of the Theorem, let us show that this result implies the claim in the Theorem, if we choose there \(\delta (R)=\sqrt{d}\,v(R)\). We have
where the constant C depends only on b, d and \(\gamma \). Employing Proposition 4.3 and (5.7), we find that the first factor on the right hand side is uniformly bounded in R, and thus the right hand side goes to zero as \(R\rightarrow \infty \). Thus (3.1), (3.2) hold. This concludes the proof of Theorem 3.1. \(\quad \square \)
Remark 5.2
We notice that, in principle, the value of \(\theta _0\) can be at the boundary of \(\Delta ^{d-1}\).
We now prove Theorem 3.2 for the discrete coagulation equation.
Proof of Theorem 3.2
It is an easy consequence of Theorem 3.1 using the fact that \(f\left( \cdot \right) =\sum _{\alpha }n_{\alpha }\delta \left( \cdot -\alpha \right) \) and \(\eta \left( \cdot \right) =\sum _{\alpha }s_{\alpha }\delta \left( \cdot -\alpha \right) \) satisfy all the assumptions in Theorem 3.1. Then (3.3) is just a consequence of (3.1). \(\quad \square \)
6 Localization Properties of the Constant Flux Solutions
We now prove Theorem 3.3. The assumptions and some of the details of the proof are very similar to the earlier cases, and then they will not be repeated here.
Proof of Theorem 3.3
Due to Lemma 4.1 it is enough to prove the result for \(\gamma <1,\ p=0.\) We consider the weak formulation (5.3) (with \(\eta =0\)), namely
We now choose continuous test functions \(\psi \left( r,\theta \right) =r\phi _{R_{1},R_{2}}\left( r\right) \left\| \theta \right\| ^{2}\) where we require that \(0<R_{1}<R_{2}\) and we construct \(\phi _{R_{1},R_{2} }\left( r\right) \) as
where the functions \(\phi _{R}\) are defined by
Then each \(\phi _{R}\) is Lipschitz continuous and decreasing, and \(\phi _{R_{1},R_{2}}\) are compactly supported. Although \(\phi _{R}\) is not continuously differentiable, and hence strictly speaking not an allowed test function, a standard approximation argument shows that, nevertheless, Eq. (6.1) holds also for this choice. Alternatively, one may use below the smooth bump function \(\phi _{R}\) constructed after (5.11), although some of the constants in the upper bounds would need to be increased then.
For this choice of test functions we obtain
Plugging this into (6.1) and using also the symmetrization \(\left( r,\theta \right) \longleftrightarrow \left( \rho ,\sigma \right) \) we obtain
where
and
Using (6.2) we can then write (6.3) as
where
Note that, since the functions \(\phi _{R}\) are decreasing, we have \(j_{R}\ge 0\). Moreover, given that \(\phi _{R_{1},R_{2}}\ge 0\) then \(D_{\frac{R_{1}}{2},R_{2}}\ge 0\). Hence,
We next show that the integrals \(j_{R}\) for any \(R> 0\) are bounded by \(C\left| J_0\right| \) where \(J_0\) is the vector flux appearing in the definition of constant flux solution (cf. Definition 2.5) and C is independent on R. More precisely, we claim that
To prove this we notice that the integrand in the definition of \(j_{R}\) can be non-zero only if \(r\le 2R\), \(r+\rho >R\). Furthermore, since \(\phi _{R}(r)-\phi _{R}(r+\rho )\le \frac{\rho }{R}\) and \(\phi _{R}(r)\le 1 \) we have
Then, using (6.5) we obtain
where we set \(W(r,\rho ;\theta ,\sigma )=G\left( r,\rho ;\theta ,\sigma \right) F\left( r,\theta \right) F\left( \rho ,\sigma \right) \). Using Definition 2.5 we have
Hence, thanks to (2.10), we arrive at
where for notational convenience we drop the arguments in \( {\mathbb {1}}_{\{r \le \xi < r+\rho \}}(\xi , r,\rho )\). This implies
We now want to prove that in the integrand of (6.12)
With this aim we consider separately the cases \(\rho \le r\) and \(\rho >r\). If \(\rho \le r\), \(r\le 2R\), and \(\rho +r \ge \frac{R}{2}\), we have \(r\ge \frac{R}{4}\) and \(\rho +r \le 4R\). Then
Suppose now that \(\rho > r\), \(r\le 2R\), and \(\rho +r \ge \frac{R}{2}\). Then
where \(\psi \left( y_1,y_2\right) = \min \left\{ (y_1+y_2),4\right\} -\max \left\{ y_1,\frac{1}{4}\right\} \). It turns out that
This inequality follows considering separately the regions \(U_j\cap V_k\cap \{y_1\le y_2 \}\) for \(j=1,2\), \(k=1,2\) with
Therefore, (6.13) follows. Combining (6.9) with (6.12) and (6.13) we obtain (6.8). We now use the inequality (6.8) which, together with (6.7), yields
By monotone convergence, this result implies also that
Our next goal is to use the above convergent integral to prove a dominated convergence argument similar to what was used in the proof of Theorem 3.1.
First, let us recall that by Proposition 4.3, if we set
then we may follow the same argument as in the proof of Theorem 3.1 and find constants such that (5.7) holds for all \(R>0\). In particular, we may define the probability measures \(\lambda (\theta ;R)\) as in (5.6) for all \(R>0\). Using Lemma 4.7, we may then conclude via the same argument, now relying on (6.14), that with \(\theta _0:= J_0/|J_0|\) we have
For the constant flux solution it is also possible to consider the limit \(R\rightarrow 0\) for the probability distribution
For this limit, we replaced the power \(\gamma \) with 1 since now, whenever \(0<r,\rho \le R\), we have \(r \rho (r+\rho )^{\gamma -1}\ge r\rho (2R)^{\gamma -1}\), and on the other hand applying Lemma 4.2 and Proposition 4.3 we find constants \(C'_1\) and \(C'_2\) such that for all \(R>0\)
Following analogous steps as in the first limit case, it follows that
where \(\theta _0\) is the same constant vector as in the first case.
It only remains to show that the Dirac mass occurs not only for \(R\rightarrow 0\) or \(R\rightarrow \infty ,\) but also for arbitrary values of R. If \(0<R_1<R_2\), we can use the test function \(\psi \left( r,\theta \right) =r\phi _{R_{1},R_{2}}\left( r\right) \) to obtain \({\tilde{j}}_{\frac{R_1}{2}}={\tilde{j}}_{R_2}\) where
Then, using (6.15), (6.18) together with (6.14), we may conclude that \(j_{R}-\Vert \theta _0\Vert ^2 {\tilde{j}}_{R}\rightarrow 0\) both when \(R\rightarrow 0\) and when \(R\rightarrow \infty \); note that for any \(\theta \in \Delta ^{d-1}\) we have \(|\Vert \theta \Vert ^2-\Vert \theta _0\Vert ^2| \le 2|\Vert \theta \Vert -\Vert \theta _0\Vert |\le 2 \Vert \theta -\theta _0\Vert \). Thus, using the dissipation formula (6.4), we obtain that \(D_{\frac{R_{1}}{2},R_{2}}\rightarrow 0\) as \(R_1\rightarrow 0\), \(R_2\rightarrow \infty \). This implies that \(D_{0,\infty }=0\), and this is possible only if there is a measure \({\tilde{H}}(r)\) such that
It is readily seen that, since F solves the coagulation Eq. (6.1), we can write \({\tilde{H}}\left( r\right) \) as \(\frac{H\left( r\right) }{r^{d-1}}\) where H is a constant flux solution with the kernel \(G\left( r,\rho ,\theta _{0},\theta _{0}\right) \) and the result follows. \(\quad \square \)
References
Banasiak, J., Lamb, W., Laurencot, P.: Analytic Methods for Coagulation-Fragmentation Models. CRC Press, Boca Raton (2019)
Degond, P., Liu, J., Pego, R.L.: Coagulation-fragmentation model for animal group-size statistics. J. Nonlinear Sci. 27, 379–424 (2017)
Friedlander, S.K.: Smoke, Dust, and Haze. Oxford University Press, Oxford (2000)
Ferreira, M.A., Lukkarinen, J., Nota, A., Velázquez, J.J.L.: Stationary non-equilibrium solutions for coagulation systems. Arch. Ration. Mech. Anal. (2021). https://doi.org/10.1007/s00205-021-01623-w
Ferreira, M.A., Lukkarinen, J., Nota, A., Velázquez, J.J.L.: Multicomponent coagulation systems: existence and non-existence of stationary non-equilibrium solutions (2021). arXiv:2103.12763
Ferreira, M.A., Lukkarinen, J., Nota, A., Velázquez, J.J.L.: Asymptotic localization in multicomponent time-dependent coagulation equations. In preparation (2021)
Ferreira, M.A., Lukkarinen, J., Nota, A., Velázquez, J.J.L.: Existence of non-power law constant flux solutions for the Smoluchowski coagulation equation. In preparation (2021)
Laurencot, P.: Stationary solutions to Smoluchowski’s coagulation equation with source. North-W. Eur. J. Math. 6, 137–164 (2020)
Krapivsky, P.I., Ben-Naim, E.: Aggregation with multiple conservation laws. Phys. Rev. E 53(1), 291–298 (1996)
Olenius, T., Kupiainen-Määttä, O., Ortega, I.K., Kurtén, T., Vehkamäki, H.: Free energy barrier in the growth of sulfuric acid-ammonia and sulfuric acid-dimethylamine clusters. J. Chem. Phys. 139, 084312 (2013)
Vehkamäki, H., Riipinen, I.: Thermodynamics and kinetics of atmospheric aerosol particle formation and growth. Chem. Soc. Rev. 41(15), 5160 (2012)
Acknowledgements
The authors gratefully acknowledge the support of the Hausdorff Research Institute for Mathematics (Bonn), through the Junior Trimester Program on Kinetic Theory, of the CRC 1060 The mathematics of emergent effects at the University of Bonn funded through the German Science Foundation (DFG), of the Atmospheric Mathematics (AtMath) collaboration of the Faculty of Science of University of Helsinki, of the ERC Advanced Grant 741487 as well as of the Academy of Finland via the Centre of Excellence in Analysis and Dynamics Research (Project No. 307333). The funders had no role in study design, analysis, decision to publish, or preparation of the manuscript. Funding Open access funding provided by Università degli Studi dell’Aquila within the CRUI-CARE Agreement.
Funding
Open access funding provided by Universitá degli Studi dell’Aquila within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by C. Mouhot.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferreira, M.A., Lukkarinen, J., Nota, A. et al. Localization in Stationary Non-equilibrium Solutions for Multicomponent Coagulation Systems. Commun. Math. Phys. 388, 479–506 (2021). https://doi.org/10.1007/s00220-021-04201-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04201-z



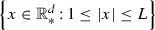 for some
for some