Abstract
Let G be a connected semi-simple Lie group with torsion-free fundamental group. We show that the twisted equivariant KK-theory \(KK_{\bullet }^{G}(G/K, \tau _G^G)\) of G has a ring structure induced from the renowned ring structure of the twisted equivariant K-theory \(K^{\bullet }_{K}(K, \tau _K^K)\) of a maximal compact subgroup K. We give a geometric description of representatives in \(KK_{\bullet }^{G}(G/K, \tau _G^G)\) in terms of equivalence classes of certain equivariant correspondences and obtain an optimal set of generators of this ring. We also establish various properties of this ring under some additional hypotheses on G and give an application to the quantization of q-Hamiltonian G-spaces in an appendix. We also suggest conjectures regarding the relation to positive energy representations of LG that are induced from certain unitary representations of G in the noncompact case.
Similar content being viewed by others
References
Abels, H.: Parallelizability of proper actions, global K-slices and maximal compact subgroups. Math. Ann. 212, 1–19 (1974)
Alekseev, A., Malkin, A., Meinrenken, E.: Lie group valued moment maps. J. Differ. Geom. 48(3), 445–95 (1998)
Baum, P., Connes, A., Higson, N.: Classifying space for proper actions and K-theory of group C*-algebras. C*-algebras: 1943–1993. Contemp. Math. 167, 240–291 (1994)
Bochnak, J., Coste, M., Roy, M.-F.: Real Algebraic Geometry, Ergeb. Math. Grenzgeb. (3), vol. 36, Springer (1998)
Belkale, P.: Quantum generalization of the Horn conjecture. J. Am. Math. Soc. 21(2), 365–408 (2008)
Brodzki, J., Mathai, V., Rosenberg, J., Szabo, R.: Non-commutative correspondences, duality and D-branes in bivariant K-theory. Adv. Theor. Math. Phys. 13(2), 497–552 (2009)
Chabert, J., Echterhoff, S., Nest, S.R.: The Connes–Kasparov conjecture for almost connected groups and for linear p-adic groups. Publ. Math. Inst. Hautes Etudes Sci. 97, 239–278 (2003)
Clare, P., Crisp, T., Higson, N.: Parabolic induction and restriction via \(C^*\)-algebras and Hilbert \(C^*\)-modules. Compos. Math. 152(6), 1286–1318 (2016)
Connes, A., Skandalis, G.: The longitudinal index theorem for foliations. Publ. Res. Inst. Math. Sci. 20(6), 1139–1183 (1984)
Echterhoff, S., Emerson, H., Kim, H.: KK-theoretic duality for proper twisted actions (English summary). Math. Ann. 340(4), 839–873 (2008)
Emerson, H., Meyer, R.: Bivariant K-theory via correspondences. Adv. Math. 225(5), 2883–2919 (2010)
Freed, D.S., Hopkins, M.J., Teleman, C.: Twisted equivariant \(K\)-theory with complex coefficients. J. Topol. 1, 16–44 (2008)
Freed, D.S., Hopkins, M.J., Teleman, C.: Consistent Orientation of Moduli Spaces, in The Many Facets of Geometry, 395th edn, p. 419. Oxford University Press, Oxford (2010)
Freed, D.S., Hopkins, M.J., Teleman, C.: Loop groups and twisted K-theory I. J. Topol. 4(4), 737–798 (2011)
Freed, D.S., Hopkins, M.J., Teleman, C.: Loop groups and twisted K-theory III. Ann. Math. (2) 174(2), 947–1007 (2011)
Higson, N., Kasparov, G.: E-theory and KK-theory for groups which act properly and isometrically on Hilbert space. Invent. Math. 144(1), 23–74 (2001)
Hochs, P.: Quantisation commutes with reduction for cocompact Hamiltonian group actions. Ph.D. thesis, Radboud University, Nijmegen (2008)
Kasparov, G.G.: Equivariant KK-theory and the Novikov conjecture. Invent. Math. 91, 147–201 (1988)
Kirchberg, E., Wassermann, S.: Permanence properties of \(C^*\)-exact groups. Doc. Math. 4, 513–558 (1999)
Knapp, A.W.: Representation Theory of Semisimple Groups. Princeton Landmarks in Mathematics. Princeton University Press (2001)
Luck, W., Oliver, B.: The completion theorem in K-theory for proper actions of a discrete group. Topology 40(3), 585–616 (2001)
Meinrenken, E.: On the quantization of conjugacy classes. L’Enseignement Mathematique 55, 33–75 (2009)
Meinrenken, E.: Twisted K-homology and group-valued moment maps. Int. Math. Res. Not. 20, 4563–4618 (2012)
Meyer, R., Nest, R.: The Baum–Connes conjecture via localization of categories. J. Topol. 45(2), 209–259 (2006)
Packer, J.: Transformation group \(C*\)-algebras: a selective survey. Contemp. Math. 17, 183–217 (1994)
Penington, M., Plymen, R.: The Dirac operator and the principal series for complex semisimple Lie groups. J. Funct. Anal. 53(3), 269–286 (1983)
Phillips, C.N.: Equivariant K-Theory for Proper Actions and C*-Algebras. Index Theory of Elliptic Operators, Foliations, and Operator Algebras, Contemporary Mathematics, vol. 70, pp. 175–204. American Mathematical Society, Providence (1988)
Phillips, C.N.: Equivariant K-theory for proper actions. II. Some Cases in Which Finite-Dimensional Bundles Suffice. Index Theory of Elliptic Operators, Foliations, and Operator Algebras, Contemporary Mathematics, vol. 70, pp. 205–227. American Mathematical Society, Providence (1988)
Segal, G.B.: Loop groups, talk review. https://people.mpim-bonn.mpg.de/zagier/files/doi/10.1007/BFb0084581/chapter08.pdf
Wang, B.-L.: Geometric cycles, index theory and twisted K-homology. J. Noncommut. Geom. 2(4), 497–552 (2008)
Wassermann, A.: Une démonstration de la conjecture de Connes-Kasparov pour les groupes de Lie connexes reductifs. C. R. Acad. Sci. Paris 304, 559–562 (1987)
Wei, Z.: Baum–Connes conjecture, flag varieties and representations of semisimple Lie groups. Dissertation, The University of Pennsylvania (2013)
Weinstein, A.: Poisson geometry of discrete series orbits, and momentum convexity for noncompact group actions. Lett. Math. Phys. 56, 17–30 (2001)
Witten, E.: The Verlinde algebra and the cohomology of the Grassmannian. arXiv:hep-th/9312104
Acknowledgements
The authors thank Jonathan Rosenberg, James Humphreys and a member of MathOverflow (username: Dap) for their advice on finding a suitable cover as in Proposition 2.1, and the anonymous referee for critical comments and in particular pointing out a mistake in an earlier draft of the paper. VM thanks the participants of the conference,Quantization in symplectic geometry, Cologne, July 15 - 19, 2019, for feedback on his talk over there. Both authors acknowledge support from the Australian Research Council through the Discovery Project grant DP150100008. Varghese Mathai thanks the Australian Research Council for support via the Australian Laureate Fellowship FL170100020.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H-T. Yau.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. K-Theory of Reduced Group \(C^*\)-Algebras
In this appendix, we let G be a real reductive linear Lie group. We would like to give a brief review of the results in [33] and [8] on the K-theory of \(C_r^*G\), which reflects the tempered representations of G. The classification of the latter by parabolic induction can be found in [20]. We also give an explicit description of the map \(K_K^\bullet (K, \tau _K^K)\rightarrow K_\bullet (\Gamma _0(\tau _G^G)\rtimes G)\) in terms of weights when G is a complex semisimple linear Lie group, based on the commutative diagram and the description of the ordinary Connes–Kasparov map in terms of weights.
Given a Cartan decomposition \({\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}\) and a Cartan subalgebra \({\mathfrak {h}}\) of \({\mathfrak {g}}\), we define the following
-
(1)
\({\mathfrak {a}}:={\mathfrak {h}}\cap {\mathfrak {p}}\),
-
(2)
\(A:=\)the analytic subgroup of G with Lie algebra \({\mathfrak {a}}\).
-
(3)
\({\mathfrak {m}}:=\)the orthogonal complement of \({\mathfrak {a}}\) in \(Z_{\mathfrak {g}}({\mathfrak {a}})\).
-
(4)
\(M_0:=\)the analytic subgroup of G with Lie algebra \({\mathfrak {m}}\), and
-
(5)
\(M=Z_K({\mathfrak {a}})M_0\).
Using the abelian Lie subalgebra \({\mathfrak {a}}\) one can define a root space decomposition of \({\mathfrak {g}}\):
With a choice of positive roots, let
and N the analytic subgroup of G with Lie algebra \({\mathfrak {n}}\).
Definition A.1
The cuspidal parabolic subgroup of G associated to \({\mathfrak {h}}\) and \(\Delta _{{\mathfrak {a}}^*}^+\) is defined to be \(P:=MAN\).
Let T be a maximal torus of K. Note that \({\mathfrak {t}}\cap {\mathfrak {m}}\) is a Cartan subalgebra of \({\mathfrak {m}}\) and so M admits discrete series or limits of discrete series.
Theorem A.2
([20], Theorem 14.76) Every irreducible tempered representation \(\pi \) of G can be obtained by induction from a cuspidal parabolic subgroup \(P=MAN\) as \(\pi _{\sigma , \nu }:=\text {Ind}_P^G(\sigma \otimes e^{i\nu }\otimes 1)\) where \(\sigma \in {\widehat{M}}_{\text {ds}}\) or a limit of discrete series, and \(\nu \in {\mathfrak {a}}^*\).
Definition A.3
Let \(W:=N_K({\mathfrak {a}})/Z_K({\mathfrak {a}})\).
Since \(N_K({\mathfrak {a}})<N_K(M)\), W also acts on M by conjugation and thus also on \({\widehat{M}}_\text {ds}\). Let \(W_\sigma :=\{w\in W| w\sigma =\sigma \}\). Let the unitary intertwining operator
be defined as in [20, Theorem 7.22].
Definition A.4
One can write \(W_\sigma =W'_\sigma \rtimes R_\sigma \) for some elementary abelian 2-subgroup \(R_\sigma \).
Theorem A.5
Let G be a real reductive linear Lie group.
-
(1)
[8, Proposition 6.7] Let \({\mathcal {E}}_\sigma \rightarrow {\mathfrak {a}}^*\) be the G-Hilbert space bundle whose fiber at \(\nu \) is \(\text {Ind}_P^G(\sigma \otimes e^{i\nu }\otimes 1)\). Then we have the isomorphism
$$\begin{aligned}C_r^*G\cong \bigoplus _{[P]}\bigoplus _{[\sigma ]\in {\widehat{M}}_\text {ds}/W}\Gamma _0({\mathcal {K}}({\mathcal {E}}_\sigma ))^{W_\sigma }\end{aligned}$$where the first sum is taken over conjugacy classes of cuspidal parabolic subgroups P and the second over representatives of W-orbits of discrete series representations. The isomorphism is realized by the map
$$\begin{aligned}f\mapsto \int _G f(g)\pi _{\sigma , \nu }(g)dg\text { at }\nu .\end{aligned}$$ -
(2)
[33] The above \(C^*\)-algebras are Morita equivalent to
$$\begin{aligned}\bigoplus _{[P]}\bigoplus _{[\sigma ]\in {\widehat{M}}_\text {ds}/W}C_0({\mathfrak {a}}^*/W'_\sigma )\rtimes R_\sigma .\end{aligned}$$We have that
$$\begin{aligned}K_{\text {dim }G/K}(C_r^*G)\cong \bigoplus _{[P]}\bigoplus _{\begin{array}{c} [\sigma ]\in {\widehat{M}}_\text {ds}/W\\ W'_\sigma =1 \end{array}}{\mathbb {Z}}\end{aligned}$$and \(K_{\text {dim }G/K+1}(C_r^*(G))=0\). Moreover, the Connes–Kasparov Conjecture is true, i.e. the Dirac induction map
$$\begin{aligned}R(K)\rightarrow K_\bullet (C_r^*G)\end{aligned}$$is an isomorphism.
The Connes–Kasparov conjecture asserts that the Dirac induction

with  acting on the space of sections \(L^2(G/K, G\times _K(S\otimes V_\mu ))\), is an isomorphism. Here S is a K-representation induced by the homomorphism \(K\rightarrow \text {Spin}({\mathfrak {p}})\) which is a lifting of the adjoint representation \(K\rightarrow SO({\mathfrak {p}})\), followed by the the spin representation \(\text {Spin}({\mathfrak {p}})\rightarrow \text {End}(S)\). The Connes–Kasparov conjecture is proved in [33] in the case of connected real reductive linear Lie groups.
acting on the space of sections \(L^2(G/K, G\times _K(S\otimes V_\mu ))\), is an isomorphism. Here S is a K-representation induced by the homomorphism \(K\rightarrow \text {Spin}({\mathfrak {p}})\) which is a lifting of the adjoint representation \(K\rightarrow SO({\mathfrak {p}})\), followed by the the spin representation \(\text {Spin}({\mathfrak {p}})\rightarrow \text {End}(S)\). The Connes–Kasparov conjecture is proved in [33] in the case of connected real reductive linear Lie groups.
Example A.6
([26]) When G is a complex connected semisimple Lie group, there is only one conjugacy class of cuspidal parabolic subgroups, and we can take M to be a maximal torus of K, \({\mathfrak {a}}=i{\mathfrak {m}}\), and W the Weyl group of K. By [26, Proposition 4.1], \(C_r^*G\) is Morita equivalent to \(C_0({\widehat{M}}\times {\mathfrak {a}}^*/W)\) which indeed is Morita equivalent to
by Theorem A.5 (A.5) (here \(R_\sigma =1\) for all \(\sigma \)). The summand \(C_0({\mathfrak {a}}^*/W_\sigma )\) contributes a copy of \({\mathbb {Z}}\) to \(K_\bullet (C_r^*G)\) if and only if \(W_\sigma =1\), i.e. \(\sigma \) is a regular weight. By fixing a set of dominant weights \(\Lambda ^*_+(K)\) in \({\widehat{M}}\) and picking from \(\Lambda _+^*(K)\) representatives of the W-orbits of \({\widehat{M}}\), we see that those \(\sigma \) is of the form \(\sigma =\mu +\rho \) for \(\mu \) a dominant weight and \(\rho \) the half sum of the positive roots of K. We may view \(K_\bullet (C_r^*G)\) as the free abelian group generated by regular dominant weights. By [26, Section 5], one can decompose \(L^2(G/K, G\times _K(S\otimes V_\mu ))\cong L^2(G, G\times (S\otimes V_\mu ))^K\) as
viewed as a Hilbert space bundle over \({\widehat{M}}\times {\mathfrak {a}}^*/W\), where \({\mathcal {H}}_{\sigma , \nu }\) is the underlying Hilbert space for \(\pi _{\sigma , \nu }\). Then  acts as \(\text {Id}\otimes \varphi (\sigma , \nu , \mu )\) for some \(\varphi (\sigma , \nu , \mu )\in \text {End}(({\mathcal {H}}_{\sigma , \nu }\otimes S\otimes V_\mu )^K)\). We then have that
acts as \(\text {Id}\otimes \varphi (\sigma , \nu , \mu )\) for some \(\varphi (\sigma , \nu , \mu )\in \text {End}(({\mathcal {H}}_{\sigma , \nu }\otimes S\otimes V_\mu )^K)\). We then have that
-
(1)
If \(\mu +\rho -\sigma \) is in the positive Weyl chamber and not 0, then \(\varphi (\sigma , \nu , \mu )\) is invertible for all \(\nu \in {\mathfrak {a}}^*\).
-
(2)
If \(\mu +\rho -\sigma \) is not in the positive Weyl chamber, then \(({\mathcal {H}}_{\sigma , \nu }\otimes S\otimes V_\mu )^K=0\).
-
(3)
If \(\mu +\rho =\sigma \) then \(\varphi (\sigma , \nu , \mu )\) acts by Clifford multiplication by \(\nu \).
Hence  can be thought of as the complex of vector bundles over \(\{\mu +\rho \}\times {\mathfrak {a}}^*\)
can be thought of as the complex of vector bundles over \(\{\mu +\rho \}\times {\mathfrak {a}}^*\)
whose K-theory class is the Bott element \(\beta _{\mu +\rho }\) of the summand \(K_\bullet (C_0({\mathfrak {a}}^*/W_{\mu +\rho }))\cong K_\bullet (C_0({\mathfrak {a}}^*))\) of \(K_\bullet (C_r^*G)\). In short, the Dirac induction map is given by \(\rho \)-shift, i.e.
From the commutative diagram (2), we can see that \(K_\bullet (\Gamma _0(\tau _G^G)\rtimes G)\) is isomorphic to the free abelian group generated by the set of regular level k weights \(\Lambda ^*_{k, \text {reg}}(K)\). The map
then sends the class of positive energy representation \(W_\mu \) with the lowest weight \(\mu \in \Lambda ^*_{k-\textsf {h}^\vee }(K)\) to the generator of \(K_\bullet (\Gamma _0(\tau _G^G)\rtimes G)\) labelled by \(\mu +\rho \in \Lambda _{k, \text {reg}}^*(K)\).
The Freed–Hopkins–Teleman Theorem, Theorem A.5 and the commutative diagram (2) inspire the following conjecture.
Conjecture A.7
-
(1)
The K-group \(K_\bullet (\Gamma _0(\tau _G^G)\rtimes G)\) reflects the tempered, positive energy representations of LG in a suitable sense.
-
(2)
The map \(q: K_K^\bullet (K, \tau _K^K)\rightarrow K_\bullet (\Gamma _0(\tau _G^G)\rtimes G)\) is given by the Dirac induction
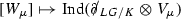 for \(\mu \in \Lambda ^*_{k-\textsf {h}^\vee }(K)\).
for \(\mu \in \Lambda ^*_{k-\textsf {h}^\vee }(K)\).
Appendix B. Quantization of q-Hamiltonian G-Spaces
q-Hamiltonian manifolds, which are defined in [2] and equipped with Lie group-valued moment maps as opposed to ordinary moment maps which take values in dual of Lie algebras, can be thought of as the ‘exponentiated’ version of ordinary Hamiltonian manifolds, and gives rise to finite dimensional construction of moduli spaces of Riemann surfaces. In [22, 23], quantization of q-Hamiltonian manifolds with Hamiltonian action by compact Lie groups is defined as pushforward of twisted K-theory fundamental class of the manifold along the group-valued moment map. In this appendix, we will construct q-Hamiltonian G-manifolds, where G is noncompact acting properly and cocompactly, from q-Hamiltonian K-manifolds, where K is a maximal compact subgroup of G, by means of induction and cross-section, following [2, 17] and define their quantization in terms of twisted G-equivariant KK-theory, which we show is a finite dimensional Frobenius ring, hence associated to a TQFT.
Definition B.1
We say \(g\in G\) is strongly stable if its centralizer \(G_g\) is compact. Let \({\mathcal {D}}\) be the set of strongly stable elements in G.
Remark B.2
In [33], strongly stable elements refer to those in the Lie algebra \({\mathfrak {g}}\) with compact centralizers.
By adapting [33, Corollary 2.4, Propositions 2.6 and 2.8], we have the following.
Proposition B.3
-
(1)
\({\mathcal {D}}\) is an open set of G.
-
(2)
\({\mathcal {D}}\) is non-empty if and only if \(\text {rk }G=\text {rk }K\).
-
(3)
Let \({\mathcal {D}}\) be non-empty and T a maximal torus of K (so T is a compact Cartan subgroup of G). If \({\mathcal {F}}:=\{\xi \in {\mathfrak {t}}| \alpha (\xi )\ne 2k\pi i\text { for }k\in {\mathbb {Z}}\text { and }\alpha \text { a noncompact root}\}\), then \({\mathcal {D}}=\text {Ad}_g\text {exp}({\mathcal {F}})\).
Proposition B.4
Let \(\langle , \rangle _{\mathfrak {g}}\) be the normalized Killing form on \({\mathfrak {g}}\) such that its restriction to \({\mathfrak {k}}\) is the basic inner product of \({\mathfrak {k}}\), and \(\eta _G=\frac{1}{12}\langle \theta ^L, [\theta ^L, \theta ^L]\rangle _{\mathfrak {g}}\). Let \(\mu _{G/K, k_0}: G/K\rightarrow G\) be the map
for some \(k_0\in K\) and \(\omega _{G/K, k_0}\) the 2-form on G/K defined by
Here \(X_\xi \) is the vector field on G/K induced by the infinitesimal action by \(\xi \) through left translation. Then \((G/K, \omega _{G/K, k_0}, \mu _{G/K, k_0})\) is a q-Hamiltonian G-manifold. If we further assume that \(k_0\in {\mathcal {D}}\cap K\), then \(\mu _{G/K, k_0}\) is a proper map and its image, the conjugacy class containing \(k_0\), is acted properly upon by G through conjugation.
Proof
This is just a straightforward adaptation of [2, Proposition 3.1] on conjugacy classes of K as an example of q-Hamiltonian K-spaces. \(\quad \square \)
Let \(k_0\in K\) and \({\mathfrak {p}}={\mathfrak {k}}^\perp \) with respect to \(\langle , \rangle _{\mathfrak {g}}\) so that \({\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}\) is the Cartan decomposition of \({\mathfrak {g}}\). Then \({\mathfrak {p}}\) and G/K are K-equivariantly diffeomorphic through the map
In this way, \(\omega _{G/K, k_0}\in \Omega ^2(G/K)\) corresponds to the 2-form \(\omega _{{\mathfrak {p}}, k_0}\in \Omega ^2({\mathfrak {p}})\) defined by
The moment map \(\mu _{G/K, k_0}\) corresponds to
Thus \(({\mathfrak {p}}, \omega _{{\mathfrak {p}}, k_0}, \mu _{{\mathfrak {p}}, k_0})\) is a q-Hamiltonian G-space.
Proposition B.5
Let N be a K-manifold, and M the induction of N, i.e. the quotient
with the G-action \(h\cdot [g, n]=[hg, n]\). Then
-
(1)
The map
$$\begin{aligned} s: {\mathfrak {p}}\times N&\rightarrow M\\ (\xi , n)&\mapsto [\text {exp}(\xi ), n] \end{aligned}$$is a K-equivariant diffeomorphism.
-
(2)
\(T_{[e_G, n]}M\) can be identified with \(T_nN\oplus {\mathfrak {p}}\). Under this identification, \(\xi \in {\mathfrak {p}}\) corresponds to \((X_\xi )_{[e_G, n]}\in T_{[e_G, N]}M\).
Proof
It is easy to check that, if for \(g\in G\), its Cartan decomposition is \(g=\text {exp}(\xi )k\) for \(\xi \in {\mathfrak {p}}\), \(k\in K\), then the map
is smooth, K-equivariant and the inverse of s. This proves (1). (2) follows from (1). \(\quad \square \)
Proposition B.6
-
(1)
Let \((N, \omega _N, \mu _N)\) be a q-Hamiltonian K-manifold. On the induction M of N, define the 2-form \(\omega _M\) by requiring that it be G-invariant and
$$\begin{aligned}(\omega _M)_{[e_G, n]}(v+\xi , w+\zeta )=\omega _N(v, w)+\frac{1}{2}(\langle \text {Ad}_{\mu _N(n)}\xi , \zeta \rangle _{\mathfrak {g}}-\langle \xi , \text {Ad}_{\mu _N(n)}\zeta \rangle _{\mathfrak {g}})\end{aligned}$$(Here we use the identification of tangent spaces as in Proposition B.5 (2)). Also define
$$\begin{aligned} \mu _M: M&\rightarrow G\\ [g, n]&\mapsto \text {Ad}_g{\mu _N(n)}. \end{aligned}$$Then \((M, \omega _M, \mu _M)\) is a q-Hamiltonian G-manifold.
-
(2)
If we further assume that G and K be of equal rank such that \(\text {Im }\mu _N\subseteq {\mathcal {D}}\cap K\), then G acts on M properly.
Remark B.7
The construction of the q-Hamiltonian G-manifold \((M, \omega _M, \mu _M)\) is inspired by the similar construction of Hamiltonian structure on M from that on N in [17, §12.2].
Proof
It suffices to check that \((M, \omega _M, \mu _M)\) satisfies the three conditions in the definition of q-Hamiltonian spaces ([2, Definition 2.2]).
-
(1)
\(d\omega _M=-\mu _M^*\eta _G\). As both \(\omega _M\) and \(\eta _G\) are G-invariant, and N as the submanifold of M through the embedding
$$\begin{aligned} i: N&\rightarrow M\\ n&\mapsto [e_G, n] \end{aligned}$$is a slice of M, it suffices to check that the equation holds on \(T_{[e_G, n]}M\cong T_nN\oplus {\mathfrak {p}}\) for \(n\in N\). Note that
$$\begin{aligned} i^*d\omega _M&=di^*\omega _M\\&=d\omega _N\\&=-\mu _N^*\eta _G\\&=-(\mu _M\circ i)^*\eta _G\\&=-i^*\mu _M^*\eta _G \end{aligned}$$Thus the equation holds when restricted to \(T_n N\). Next, \({\mathfrak {p}}\subseteq T_{[e_G, n]}M\) and \(\omega _M\) restricted to it can be identified naturally with \(({\mathfrak {p}}, \omega _{{\mathfrak {p}}, \mu _N(n)}, \mu _{{\mathfrak {p}}, \mu _N(n)})\), and the equation restricted to \({\mathfrak {p}}\) is equivalent to, under this identification, \(d\omega _{{\mathfrak {p}}, \mu _N(n)}=-\mu _{{\mathfrak {p}}, \mu _N(n)}^*\eta _G\), which is true as we have shown that \(({\mathfrak {p}}, \omega _{{\mathfrak {p}}, \mu _N(n)}, \mu _{{\mathfrak {p}}, \mu _N(n)})\) is a q-Hamiltonian G-manifold.
-
2.
\(\displaystyle \iota _{X_\xi }\omega _M=\frac{1}{2}\mu _M^*\langle \theta ^L+\theta ^R, \xi \rangle _{\mathfrak {g}}\). Again, by G-invariance of \(\omega _M\), \(X_\xi \) and \(\displaystyle \frac{1}{2}\mu _M^*\langle \theta ^L+\theta ^R, \xi \rangle _{\mathfrak {g}}\), it suffices to show that the equation holds on \(T_{[e_G, n]}M\cong T_nN\oplus {\mathfrak {p}}\). If \(\alpha \in {\mathfrak {g}}\) and \(\alpha =\xi +\eta \) for \(\xi \in {\mathfrak {p}}\) and \(\eta \in {\mathfrak {k}}\), then \(X_\alpha =X_\xi +X_\eta \) by the Baker-Campbell-Hausdorff formula. Besides, under the identification \(T_{[e_G, n]}M\cong T_nN\oplus {\mathfrak {p}}\), we have \((X_\xi )_{[e_G, n]}\in T_{[e_G, n]}M\) corresponds to \(\xi \in {\mathfrak {p}}\) and \((X_\eta )_{[e_G, n]}\in T_n N\). We then have
$$\begin{aligned} (\iota _{X_\alpha }\omega _M)_{[e_G, n]}(w+\zeta )&=(\omega _M)_{[e_G, n]}(X_\eta +\xi , w+\zeta )\\&=(\omega _N)_n(X_\eta , w)+\frac{1}{2}(\langle \text {Ad}_{\mu _N(n)}\xi , \zeta \rangle _{\mathfrak {g}}-\langle \xi , \text {Ad}_{\mu _N(n)}\zeta \rangle _{\mathfrak {g}})\\&=\frac{1}{2}\mu _N^*(\theta ^L+\theta ^R, \eta )(w)+\frac{1}{2}(\theta ^L+\theta ^R, \xi ) (\zeta )\\&\quad (\text {by } [2, \text { Proposition 3.1}])\\&=\frac{1}{2}\mu _M^*(\theta ^L+\theta ^R, \xi )(w+\zeta )\\&(\text {As }(\mu _{M*})_{[e_G, n]}(w+\zeta )\\&=(\mu _{N*})_n(w)+\zeta \text { because }\mu _M([e_G, n])=\mu _N(n)) \end{aligned}$$ -
(3)
\(\text {ker}(\omega _M)_{[g, n]}=\{X_\xi | \xi \in \text {ker}(\text {Ad}_{\mu _M([g, n])}+1)\}\). It suffices to prove the equation for \(g=e_G\) because both sides of the equations are G-invariant: that the LHS is G-invariant is due to the G-invariance of \(\omega _M\). For the G-invariance of the RHS, note that \(g\cdot (X_\xi )_{[e_G, n]}=(X_{\text {Ad}_g\xi })_{[g, n]}\) and \(\xi \in \text {ker}(\text {Ad}_{\mu _M([e_G, n])}+1)\) if and only if \(\text {Ad}_g\xi \in \text {ker}(\text {Ad}_{\mu _M([g, n])}+1)\) by the G-equivariance of \(\mu _M\). Now for \(v\in T_nN\) and \(\xi \in {\mathfrak {p}}\), \(v+\xi \in \text {ker}(\omega _M)_{[e_G, n]}\) if and only if
-
(a)
\(v\in \text {ker}(\omega _N)_n\), i.e. \(v=(X_\eta )_n\) for some \(\eta \in {\mathfrak {k}}\) such that \(\eta \in \text {ker}(\text {Ad}_{\mu _N(n)}+1)_{\mathfrak {k}}\), and
-
(b)
\(X_\xi \in \text {ker}(\omega _{{\mathfrak {p}}, \mu _N(n)})\), i.e. \(\xi \in \text {ker}(\text {Ad}_{\mu _N(n)}+1)_{\mathfrak {g}}\) (or equivalently \(\xi \in \text {ker}(\text {Ad}_{\mu _N(n)}+1)_{\mathfrak {p}}\) as \(\xi \in {\mathfrak {p}}\)).
Moreover, \(v+X_\xi =X_\eta +X_\xi =X_{\eta +\xi }\) and \(\eta +\xi \in \text {ker}(\text {Ad}_{\mu _N(n)}+1)_{\mathfrak {g}}\). This completes the proof of the equation.
-
(a)
The second part of the proposition follows by adapting the proof of [17, Lemma 6.12]. \(\quad \square \)
One can also construct a q-Hamiltonian K-manifold from a q-Hamiltonian G-manifold by means of taking the so-called q-Hamiltonian cross-section, defined to be \(N:=\mu _M^{-1}(K)\). The following proposition, which asserts that induction and taking cross-section are reverse to each other, is straightforward (cf. [17, §12.4]).
Proposition B.8
Let G and K have the same rank, \((M, \omega _M, \mu _M)\) be a q-Hamiltonian G-manifold with proper G-action and \(\text {Im}\mu _M\in {\mathcal {D}}\). Suppose the map \(\mu _M: M\rightarrow G\) composed with the quotient map \(G\rightarrow G/K\) has \(e_GK\) as a regular value. Define the q-Hamiltonian cross-section \(N:=\mu _M^{-1}(K)\) and let \(i: N\rightarrow M\) be the embedding. Then \((N, i^*\omega _M, \mu _M\circ i)\) is a q-Hamiltonian K-manifold.
Let M be a q-Hamiltonian proper, cocompact G-manifold. By Abel’s global slice theorem [1], M is G-equivariantly diffeomorphic to \(G\times _K N\), therefore there is a projection map \(b: M \rightarrow G/K\). Since there is a canonical twisted G-\({\text {spin}^c}\) structure on M, there is also a morphism \(f: M \rightarrow (G, \tau ^G_G)\) which is the G-valued moment map (denoted earlier by \(\mu _M\)),
Definition B.9
The quantization of M, \({\mathcal {Q}}(M)\), is defined to be the equivalence class of the correspondence,

where \(\xi = G\times _K TN\). That is, \({\mathcal {Q}}(M) \in KK^G(G/K, (G, \tau _G^G))\).
Define \({{\mathcal {D}}}_\mu = G\times _K {{\mathcal {C}}}_\mu \), on which G acts by left translation on the first factor and trivially on the second factor. Here \(\mu \in \Lambda ^*_{k-\textsf {h}^\vee }(K)\) is a level \(k-\textsf {h}^\vee \) weight and \({\mathcal {C}}_\mu \) the conjugacy class in K containing \(\text {exp}\left( \frac{B^\sharp (\mu )}{k-\textsf {h}^\vee }\right) \). Note that \({{\mathcal {D}}}_\mu \) has a proper G-action and is also G-cocompact.
In fact, we show in Proposition B.6 that \({{\mathcal {D}}}_\mu \) is a q-Hamiltonian G-space with these properties. Then there is a natural projection map \(b: {{\mathcal {D}}}_\mu \longrightarrow G/K\). There is also a natural twisted G-\({\text {spin}^c}\) map \(f: {{\mathcal {D}}}_\mu \longrightarrow G\) defined by, \([g, c] \longrightarrow gcg^{-1}\), which is the G-valued moment map (denoted earlier by \(\mu _{{{\mathcal {D}}}_\mu }\)), .

where \(\xi _\mu = G\times _K T{{\mathcal {C}}}_\mu \), are correspondences.
Theorem B.10
The correspondences (9) for \(\mu \in \Lambda _{k-\textsf {h}^\vee }(K)\) are all the generators of \(KK^G(G/K, (G, \tau _G^G)),\) that is,
forms a complete set of generators.
Recall that \({\mathcal {I}}_K\) denotes the Verlinde ideal for \((K, \tau ^K_K)\), and that
Recall also that \({\mathcal {I}}_G = \text {D-Ind} ({\mathcal {I}}_K)\) is defined to be the Verlinde ideal for G, in which case
showing that \(KK^G_\bullet (G/K, (G, \tau _G^G))\) is a Verlinde ring.
Now \( K_0(C^*_rG)\) is a ring by Dirac induction, so this gives an alternate description of the ring structure of \(KK^G_\bullet (G/K, (G, \tau _G^G))=K_*(C^*_rG)/{\mathcal {I}}_G\) which has the following properties.
-
(1)
\(K_*(C^*_rG)/{\mathcal {I}}_G\) is a unital ring with involution.
-
(2)
\(K_*(C^*_rG)/{\mathcal {I}}_G\) has a finite \({\mathbb {Z}}\)-basis, \(K_*(C^*_rG)/{\mathcal {I}}_G= {\mathbb {Z}}[Q]\) where Q are the level \((k-h^\vee )\)-weights in the compact case, and in the non-compact case they can be viewed as those Harishchandra parameters that are in the image of the level \((k-h^\vee )\)-weights under the Dirac induction isomorphism (see also Example A.6). They are generated by a certain subset of discrete series of M where M appears in the decomposition \(P = MAN\) (see Definition A.1).
-
(3)
\(K_*(C^*_rG)/{\mathcal {I}}_G\) has a trace map, \( {\text {tr}}:K_*(C^*_rG)/{\mathcal {I}}_G \longrightarrow {\mathbb {Z}}\), defined as the coefficient of the unit in \(K_*(C^*_rG)/{\mathcal {I}}_G\).
Therefore \(K_*(C^*_rG)/{\mathcal {I}}_G\) is a finite dimensional Frobenius ring, hence it is associated to a TQFT.
Rights and permissions
About this article
Cite this article
Fok, CK., Mathai, V. The Ring Structure of Twisted Equivariant KK-Theory for Noncompact Lie Groups. Commun. Math. Phys. 385, 633–666 (2021). https://doi.org/10.1007/s00220-021-04131-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04131-w



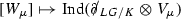 for
for