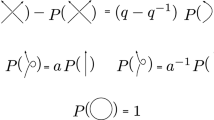Abstract
The recently conjectured knots-quivers correspondence (Kucharski et al. in Phys Rev D 96(12):121902, 2017. arXiv:1707.02991, Adv Theor Math Phys 23(7):1849–1902, 2019. arXiv:1707.04017) relates gauge theoretic invariants of a knot K in the 3-sphere to the representation theory of a quiver \(Q_{K}\) associated to the knot. In this paper we provide geometric and physical contexts for this conjecture within the framework of Ooguri-Vafa large N duality (Ooguri and Vafa in Nucl Phys B 577:419–438, 2000), that relates knot invariants to counts of holomorphic curves with boundary on \(L_{K}\), the conormal Lagrangian of the knot in the resolved conifold, and corresponding M-theory considerations. From the physics side, we show that the quiver encodes a 3d \({\mathcal {N}}=2\) theory \(T[Q_{K}]\) whose low energy dynamics arises on the worldvolume of an M5 brane wrapping the knot conormal and we match the (K-theoretic) vortex partition function of this theory with the motivic generating series of \(Q_{K}\). From the geometry side, we argue that the spectrum of (generalized) holomorphic curves on \(L_{K}\) is generated by a finite set of basic disks. These disks correspond to the nodes of the quiver \(Q_{K}\) and the linking of their boundaries to the quiver arrows. We extend this basic dictionary further and propose a detailed map between quiver data and topological and geometric properties of the basic disks that again leads to matching partition functions. We also study generalizations of A-polynomials associated to \(Q_{K}\) and (doubly) refined version of LMOV invariants (Ooguri and Vafa 2000; Labastida and Marino in Commun Math Phys 217(2):423–449, 2001. arXiv:hep-th/0004196; Labastida et al. in JHEP 11:007, 2000. arXiv:hep-th/0010102; Aganagic and Vafa in Large N duality, mirror symmetry, and a Q-deformed A-polynomial for knots. arXiv:1204.4709; Fuji et al. in Nucl Phys B 867:506–546, 2013. arXiv:1205.1515).





Similar content being viewed by others
References
Ooguri, H., Vafa, C.: Knot invariants and topological strings. Nucl. Phys. B 577, 419–438 (2000). arXiv:hep-th/9912123
Witten, E.: Chern–Simons gauge theory as a string theory. Prog. Math. 133, 637–678 (1995). arXiv:hep-th/9207094
Kucharski, P., Reineke, M., Stosic, M., Sulkowski, P.: BPS states, knots and quivers. Phys. Rev. D 96(12), 121902 (2017). arXiv:1707.02991
Kucharski, P., Reineke, M., Stosic, M., Sulkowski, P.: Knots-quivers correspondence. Adv. Theor. Math. Phys. 23(7), 1849–1902 (2019). arXiv:1707.04017
Kucharski, P., Sulkowski, P.: BPS counting for knots and combinatorics on words. JHEP 11, 120 (2016). arXiv:1608.06600
Luo, W., Zhu, S.: Integrality structures in topological strings I: framed unknot. arXiv:1611.06506
Zhu, S.: Topological strings, quiver varieties and Rogers–Ramanujan identities. Ramanujan J. 48(2), 399–421 (2019). arXiv:1707.00831
Aganagic, M., Ekholm, T., Ng, L., Vafa, C.: Topological strings, D-model, and knot contact homology. Adv. Theor. Math. Phys. 18(4), 827–956 (2014). arXiv:1304.5778
Ekholm, T., Shende, V.: Skeins on branes, arXiv:1901.08027
Dimofte, T., Gukov, S., Hollands, L.: Vortex counting and Lagrangian 3-manifolds. Lett. Math. Phys. 98, 225–287 (2011). arXiv:1006.0977
Terashima, Y., Yamazaki, M.: SL(2, R) Chern–Simons, Liouville, and gauge theory on duality walls. JHEP 08, 135 (2011). arXiv:1103.5748
Dimofte, T., Gaiotto, D., Gukov, S.: Gauge theories labelled by three-manifolds. Commun. Math. Phys. 325, 367–419 (2014). arXiv:1108.4389
Yagi, J.: 3d TQFT from 6d SCFT. JHEP 08, 017 (2013). arXiv:1305.0291
Lee, S., Yamazaki, M.: 3d Chern–Simons theory from M5-branes. JHEP 12, 035 (2013). arXiv:1305.2429
Cordova, C., Jafferis, D.L.: Complex Chern–Simons from M5-branes on the squashed three-sphere. JHEP 11, 119 (2017). arXiv:1305.2891
Fuji, H., Gukov, S., Sulkowski, P.: Super-A-polynomial for knots and BPS states. Nucl. Phys. B 867, 506–546 (2013). arXiv:1205.1515
Dunfield, N.M., Gukov, S., Rasmussen, J.: The superpolynomial for knot homologies. Exp. Math. 15(2), 129–159 (2006). arXiv:math/0505662
Hwang, C., Yi, P., Yoshida, Y.: Fundamental vortices, wall-crossing, and particle-vortex duality. JHEP 05, 099 (2017). arXiv:1703.00213
Denef, F.: Quantum quivers and Hall/hole halos. JHEP 10, 023 (2002). arXiv:hep-th/0206072
Alim, M., Cecotti, S., Cordova, C., Espahbodi, S., Rastogi, A., Vafa, C.: \(\cal{N} = 2\) quantum field theories and their BPS quivers. Adv. Theor. Math. Phys. 18(1), 27–127 (2014). arXiv:1112.3984
Gabella, M., Longhi, P., Park, C.Y., Yamazaki, M.: BPS graphs: from spectral networks to BPS quivers. JHEP 07, 032 (2017). arXiv:1704.04204
Ekholm, T., Ng, L.: Higher genus knot contact homology and recursion for colored HOMFLY-PT polynomials. arXiv:1803.04011
Iacovino, V.: Open Gromov–Witten theory on Calabi–Yau three-folds I. arXiv:0907.5225
Iacovino, V.: Open Gromov–Witten theory on Calabi–Yau three-folds II, arXiv:0908.0393
Iacovino, V.: Frame ambiguity in open Gromov–Witten invariants. arXiv:1003.4684
Okounkov, A., Pandharipande, R.: Hodge integrals and invariants of the unknot. Geom. Topol. 8, 675–699 (2004)
Katz, S., Liu, C.-C.M.: Enumerative geometry of stable maps with Lagrangian boundary conditions and multiple covers of the disc. Adv. Theor. Math. Phys. 5(1), 1–49 (2001)
Freyd, P., Yetter, D., Hoste, J., Lickorish, W.B.R., Millett, K., Ocneanu, A.: A new polynomial invariant of knots and links. Bull. Am. Math. Soc. (N.S.) 12(2), 239–246 (1985)
Przytycki, J., Traczyk, P.: Invariants of links of Conway type. Kobe J. Math. 4, 115–139 (1987)
Witten, E.: Quantum field theory and the Jones polynomial. Commun. Math. Phys. 121(3), 351–399 (1989)
Labastida, J.M.F., Marino, M.: Polynomial invariants for torus knots and topological strings. Commun. Math. Phys. 217(2), 423–449 (2001). arXiv:hep-th/0004196
Labastida, J.M.F., Marino, M., Vafa, C.: Knots, links and branes at large \(N\). JHEP 11, 007 (2000). arXiv:hep-th/0010102
Kirillov, A.: Quiver representations and quiver varieties. Graduate Studies in Mathematics. American Mathematical Society (2016)
Kontsevich, M., Soibelman, Y.: Stability structures, motivic Donaldson–Thomas invariants and cluster transformations. arXiv:0811.2435
Kontsevich, M., Soibelman, Y.: Cohomological Hall algebra, exponential Hodge structures and motivic Donaldson–Thomas invariants. Commun. Num. Theor. Phys. 5, 231–352 (2011). arXiv:1006.2706
Meinhardt, S., Reineke, M.: Donaldson–Thomas invariants versus intersection cohomology of quiver moduli. arXiv:1411.4062
Franzen, H., Reineke, M.: Semi-stable Chow–Hall algebras of quivers and quantized Donaldson-Thomas invariants. arXiv:1512.03748
Efimov, A.I.: Cohomological Hall algebra of a symmetric quiver. Compos. Math. 148(4), 1133–1146 (2012). arXiv:1103.2736
Stosic, M., Wedrich, P.: Rational links and DT invariants of quivers. Int. Math. Res. Notices, rny289 (2019) arXiv:1711.03333
Panfil, M., Sulkowski, P., Stosic, M.: Donaldson–Thomas invariants, torus knots, and lattice paths. Phys. Rev. D 98(2), 026022 (2018). arXiv:1802.04573
Sulkowski, P., Panfil, M.: Topological strings, strips and quivers. JHEP 01, 124 (2019). arXiv:1811.03556
Gopakumar, R., Vafa, C.: M-theory and topological strings—I. arXiv:hep-th/9809187
Gopakumar, R., Vafa, C.: M-theory and topological strings—II. arXiv:hep-th/9812127
Douglas, M.R., Moore, G.W.: D-branes, quivers, and ALE instantons. arXiv:hep-th/9603167
Fiol, B., Marino, M.: BPS states and algebras from quivers. JHEP 07, 031 (2000). arXiv:hep-th/0006189
Alim, M., Cecotti, S., Cordova, C., Espahbodi, S., Rastogi, A., Vafa, C.: BPS quivers and spectra of complete N=2 quantum field theories. Commun. Math. Phys. 323, 1185–1227 (2013). arXiv:1109.4941
Gopakumar, R., Vafa, C.: On the gauge theory/geometry correspondence. Adv. Theor. Math. Phys. 3, 1415–1443 (1999). arXiv:hep-th/9811131
Aganagic, M., Vafa, C.: Mirror symmetry, D-branes and counting holomorphic discs. arXiv:hep-th/0012041
Aganagic, M., Klemm, A., Vafa, C.: Disk instantons, mirror symmetry and the duality web. Z. Naturforsch. A 57, 1–28 (2002). arXiv:hep-th/0105045
Shadchin, S.: On F-term contribution to effective action. JHEP 08, 052 (2007). arXiv:hep-th/0611278
Witten, E., Olive, D.I.: Supersymmetry algebras that include topological charges. Phys. Lett. 78B, 97–101 (1978)
Hori, K., Kim, H., Yi, P.: Witten index and wall crossing. JHEP 01, 124 (2015). arXiv:1407.2567
Khovanov, M.: A categorification of the Jones polynomial. Duke Math. J. 101, 359–426 (2000). arXiv:math/9908171
Khovanov, M., Rozansky, L.: Matrix factorizations and link homology. Fund. Math. 199, 1–91 (2008). arXiv:math/0401268
Khovanov, M., Rozansky, L.: Matrix factorizations and link homology II. Geom. Topol. 12, 1387–1425 (2008). arXiv:math/0505056
Gukov, S., Nawata, S., Saberi, I., Stosic, M., Sulkowski, P.: Sequencing BPS spectra. JHEP 03, 004 (2016). arXiv:1512.07883
Gukov, S., Stosic, M.: Homological algebra of knots and BPS states. Proc. Symp. Pure Math. 85, 125–172 (2012). arXiv:1112.0030. [Geom. Topol. Monographs 18 (2012) 309]
Gorsky, E., Gukov, S., Stosic, M.: Quadruply-graded colored homology of knots. arXiv:1304.3481
Aganagic, M., Vafa, C.: Large N duality, mirror symmetry, and a Q-deformed A-polynomial for knots. arXiv:1204.4709
Garoufalidis, S., Lauda, A.D., Le, T.T.Q.: The colored HOMFLY-PT polynomial is \(q\)-holonomic. Duke Math. J. 167(3), 397–447 (2018). arXiv:1604.08502
Fuji, H., Gukov, S., Sulkowski, P., Stosic, M.: 3d analogs of Argyres–Douglas theories and knot homologies. JHEP 01, 175 (2013). arXiv:1209.1416
Ng, L.: Framed knot contact homology. Duke Math. J. 141(2), 365–406 (2008). arXiv:math/0407071
Ng, L.: Combinatorial knot contact homology and transverse knots. Adv. Math. 227(6), 2189–2219 (2011). arXiv:1010.0451
Garoufalidis, S., Kucharski, P., Sulkowski, P.: Knots, BPS states, and algebraic curves. Commun. Math. Phys. 346(1), 75–113 (2016). arXiv:1504.06327
Chung, H.-J., Dimofte, T., Gukov, S., Sulkowski, P.: 3d–3d correspondence revisited. JHEP 04, 140 (2016). arXiv:1405.3663
Ng, L.: A topological introduction to knot contact homology. arXiv:1210.4803
Dadda, A., Davis, A.C., Di Vecchia, P., Salomonson, P.: An effective action for the supersymmetric CP \(^{n-1}\) model. Nuclear Phys. B 222, 45–70 (1983)
Witten, E.: Phases of N=2 theories in two-dimensions. Nucl. Phys. B 403, 159–222 (1993). arXiv:hep-th/9301042 [AMS/IP Stud. Adv. Math. 1 (1996) 143–211]
Hanany, A., Hori, K.: Branes and N=2 theories in two-dimensions. Nucl. Phys. B 513, 119–174 (1998). arXiv:hep-th/9707192
Hori, K., Vafa, C.: Mirror symmetry. arXiv:hep-th/0002222
Dimofte, T., Gukov, S.: Chern–Simons theory and S-duality. JHEP 05, 109 (2013). arXiv:1106.4550
Lawrence, A.E., Nekrasov, N.: Instanton sums and five-dimensional gauge theories. Nucl. Phys. B 513, 239–265 (1998). arXiv:hep-th/9706025
Gaiotto, D., Moore, G.W., Neitzke, A.: Four-dimensional wall-crossing via three-dimensional field theory. Commun. Math. Phys. 299, 163–224 (2010). arXiv:0807.4723
Aharony, O., Hanany, A., Intriligator, K.A., Seiberg, N., Strassler, M.J.: Aspects of N=2 supersymmetric gauge theories in three-dimensions. Nucl. Phys. B 499, 67–99 (1997). arXiv:hep-th/9703110
Smolinski, P.: From Topological Strings to Quantum Invariants of Knots and Quivers. Master’s thesis, University of Warsaw (2017)
Aganagic, M., Shakirov, S.: Refined Chern–Simons theory and topological string. arXiv:1210.2733
Beem, C., Dimofte, T., Pasquetti, S.: Holomorphic blocks in three dimensions. JHEP 12, 177 (2014). arXiv:1211.1986
Hwang, C., Kim, H.-C., Park, J.: Factorization of the 3d superconformal index. JHEP 08, 018 (2014). arXiv:1211.6023
Bullimore, M., Dimofte, T., Gaiotto, D., Hilburn, J., Kim, H.-C.: Vortices and Vermas, arXiv:1609.04406
Gadde, A., Gukov, S., Putrov, P.: Walls, lines, and spectral dualities in 3d gauge theories. JHEP 05, 047 (2014). arXiv:1302.0015
Gukov, S.: Gauge theory and knot homologies. Fortsch. Phys. 55, 473–490 (2007). arXiv:0706.2369
Gukov, S., Schwarz, A., Vafa, C.: Khovanov–Rozansky homology and topological strings. Lett. Math. Phys. 74, 53–74 (2005). arXiv:hep-th/0412243
Wedrich, P.: Exponential growth of colored HOMFLY-PT homology. Adv. Math. 353, 471–525 (2019). arXiv:1602.02769
Kameyama, M., Nawata, S.: Refined large N duality for knots. arXiv:1703.05408
Gross, M., Pandharipande, R.: Quivers, curves, and the tropical vertex. arXiv:0909.5153
Galakhov, D., Longhi, P., Mainiero, T., Moore, G.W., Neitzke, A.: Wild wall crossing and BPS giants. JHEP 11, 046 (2013). arXiv:1305.5454
Seiberg, N., Witten, E.: Monopoles, duality and chiral symmetry breaking in N=2 supersymmetric QCD. Nucl. Phys. B 431, 484–550 (1994). arXiv:hep-th/9408099
Witten, E.: Solutions of four-dimensional field theories via M theory. Nucl. Phys. B 500, 3–42 (1997). arXiv:hep-th/9703166
Gaiotto, D., Moore, G.W., Neitzke, A.: Wall-crossing, Hitchin systems, and the WKB approximation. arXiv:0907.3987
Gaiotto, D., Moore, G.W., Neitzke, A.: Spectral networks. Annales Henri Poincare 14, 1643–1731 (2013). arXiv:1204.4824
Acknowledgements
We would like to thank Sergei Gukov, Hélder Larraguível, Fabrizio Nieri, Miłosz Panfil, Du Pei, Ingmar Saberi, Marko Stošić, Piotr Sułkowski, and Paul Wedrich for insightful discussions. We are also grateful to the organizers of the conferences “6th International Workshop on Combinatorics of Moduli Spaces, Cluster Algebras, and Topological Recursion” at Steklov Mathematical Institute, and “Quantum Fields, knots, and strings" at the University of Warsaw, where the results of this paper were presented. Parts of the paper is based upon work supported by the National Science Foundation under Grant No. DMS-1440140 while the authors T.E. and P.K. were in residence at the Mathematical Sciences Research Institute in Berkeley, California, during the 2018 spring semester. P.L. thanks Aarhus QGM, the Aspen Center for Physics, ENS Paris, Caltech, The University of California at Berkeley, and Trinity College Dublin for hospitality during completion of this work. The work of T.E. is supported by the Knut and Alice Wallenberg Foundation and the Swedish Reserach Council. P.K. acknowledges support from the Knut and Alice Wallenberg Foundation. The work of P.L. is supported by the NCCR SwissMAP, funded by the Swiss National Science Foundation. P.L. also acknowledges support from grants “Geometry and Physics”and “Exact Results in Gauge and String Theories” from the Knut and Alice Wallenberg Foundation during part of this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H. T. Yau.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Cross-Check of \(\mathbf {t}\) Refinement
Cross-Check of \(\mathbf {t}\) Refinement
In order to compare refined LMOV invariants for trefoil obtained in Sect. 5.2 with [64] we have to adjust conventions and take care about some subtleties.
Authors of [64] use the convention of \(t_{r}\) refinement with \(-a^{2}t^{3}\) instead of \(-a^{2}t\) in the q-Pochhammer. Moreover, in section 4.7 concerning refined classical LMOV invariants they consider “super-A-polynomials as T-deformation and a-deformation of bottom A-polynomials (that arise for \(a=0\) and \(T=1\)), where \(t=-T^{2}\)”, which is equivalent to rescaling of \(N_{r}^{3_{1}}(a,q,t)\) by the overall a factor in such a way that it starts from 1. Therefore, the refined LMOV generating function for the fundamental representation should be transformed as follows
In order to see 1 clearly, we rescaled also the q power, which however does not matter due to the semiclassical limit. It will also hide the q-shift between definitions of denominators of \(N_{r}(a,q,t)\) (we have \(1-q^{2}\), they have \(q-q^{-1}\)), however the sign difference will stay. In consequence
Finally, authors of [64] put \(t=-T^{2}\) and then rescale \(a\rightarrow a^{1/2},\ T\rightarrow T^{1/2}\) to reduce the volume of Table 10 in the reference, which contains classical refined LMOV invariants. Unfortunately the last rescaling is not explicitly stated, for which the common author of the two papers apologizes. They consider only terms up to power 5, so summing up
which is exactly equal to \(\sum _{i,j}\tilde{b}_{1,i,j}a^{i}T^{j}\) from [64, Table 10] (\(\tilde{b}_{r,i,j}\) denotes classical refined LMOV invariants in representation r corresponding to power i of a and power j of T).
We can repeat above steps for \(r=2,3,4\) to obtain
which again matches results from [64, Table 10] perfectly.
Rights and permissions
About this article
Cite this article
Ekholm, T., Kucharski, P. & Longhi, P. Physics and Geometry of Knots-Quivers Correspondence. Commun. Math. Phys. 379, 361–415 (2020). https://doi.org/10.1007/s00220-020-03840-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-020-03840-y