Abstract
We develop a renormalisation group approach to deriving the asymptotics of the spectral gap of the generator of Glauber type dynamics of spin systems with strong correlations (at and near a critical point). In our approach, we derive a spectral gap inequality for the measure recursively in terms of spectral gap inequalities for a sequence of renormalised measures. We apply our method to hierarchical versions of the 4-dimensional n-component \(|\varphi |^4\) model at the critical point and its approach from the high temperature side, and of the 2-dimensional Sine-Gordon and the Discrete Gaussian models in the rough phase (Kosterlitz–Thouless phase). For these models, we show that the spectral gap decays polynomially like the spectral gap of the dynamics of a free field (with a logarithmic correction for the \(|\varphi |^4\) model), the scaling limit of these models in equilibrium.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Main Results
1.1 Introduction
Spin systems in equilibrium have been studied by a variety of methods which led to a very complete mathematical description of the physical phenomena occurring in the different regimes of the phase diagrams. This includes in particular a good understanding of the critical phenomena in a wide range of models. Much less is known about the Glauber dynamics of spin systems. For sufficiently high temperatures, it is well understood that the dynamics relaxes exponentially fast towards the equilibrium measure. For the Ising model, the much more difficult question of fast relaxation in the entire uniqueness regime was addressed in [22, 46, 50, 51]. In the phase transition regime, at least for scalar spins, the dynamical behaviour is governed by the interface motion and the relaxation becomes much slower. In particular, the relaxation time diverges as the system size increases, but the dynamical scaling depends strongly on the choice of the boundary conditions. We refer to [49] for a review, as well as to [21, 44] for more recent results. In the vicinity of the critical point, strong correlations develop and as a consequence the dynamic evolution slows down but is no longer driven by phase separation. Even though the critical dynamical behaviour has been well investigated in physics [36], mathematical results are scarce. The only cases for which polynomial lower bounds on the relaxation or mixing times are known are the two-dimensional Ising model [45], exactly at the critical point, the Ising model on a tree [27], both without sharp exponent, and the mean-field Ising model which is fully understood [26, 42].
The goal of this paper is to investigate the dynamical relaxation of hierarchical models near and at the critical point by deriving the scaling of the spectral gap in terms of the temperature (or the equivalent parameter of the model) and the system size.
Since their introduction by Dyson [28] and the pioneering work of Bleher–Sinai [11], hierarchical models have been a stepping stone to develop renormalisation group arguments. At equilibrium, sharp results on the critical behaviour of a large class of models have typically been obtained first in a hierarchical framework and then later been extended to the Euclidean lattice. For the equilibrium problem, the hierarchical framework results in a significant technical simplification, but the results and methods have turned out to be surprisingly parallel to the case of the Euclidean lattice \(\mathbb {Z}^d\). This point of view is discussed in detail in [9], to which we also refer for an overview of results and references. Building on the results for the hierarchical set-up for the equilibrium problem, we derive recursive relations on the spectral gap after one renormalisation step. This enables us to obtain sharp asymptotic behaviour of the spectral gap for large size Sine-Gordon model in the rough phase (Kosterlitz–Thouless phase) and for the \(|\varphi |^4\) model in the vicinity of the critical point. The scaling coincides in both cases with the one of the hierarchical free field dynamics (with a logarithmic corrections for the \(|\varphi |^4\) model) which describes the equilibrium scaling limit of these models. Renormalisation procedures have already been used to analyze spectral gaps for Glauber dynamics, see e.g., [49], but the renormalisation scheme used in this paper is different and allows to keep sharp control from one scale to the next.
After recalling the definitions of the hierarchical models and presenting the results of this paper in Sect. 1.4, we implement, in Sect. 2, the induction procedure to control the spectral gap after one renormalisation step. We believe that our method could be extended beyond the hierarchical models, thus the induction is described in a general framework under some assumptions which can then be checked for each microscopic models. This is completed in Sect. 3 for the hierarchical \(|\varphi |^4\) model, and in Sect. 4 for the hierarchical Sine-Gordon and the Discrete Gaussian models. Proving these assumptions requires establishing stronger control on the renormalised Hamiltonians in the large field region than needed when studying the renormalisation at equilibrium (convexity instead of probabilistic bounds). Such convexity for large fields is the main challenge to extend the method of this paper beyond hierarchical models.
1.2 Spectral gap
Let \(\Lambda \) be a finite set and M be a symmetric matrix of spin couplings acting on \(\mathbb {R}^\Lambda \). We consider possibly vector-valued spin configurations \(\varphi = (\varphi _x^i)_{x\in \Lambda , i=1,\dots , n} \in \mathbb {R}^{n\Lambda } = \{ \varphi : \Lambda \rightarrow \mathbb {R}^n\}\), with action of the form
for some potential \(V: \mathbb {R}^n\rightarrow \mathbb {R}\), where \((\cdot ,\cdot )\) is the standard inner product on \(\mathbb {R}^{n\Lambda }\). In the vector-valued case \(n>1\), we assume that V is O(n)-invariant and that M acts by \((M\varphi )_x^i = (M\varphi ^i)_x\) for \(i=1,\dots , n\) and \(x\in \Lambda \). The associated probability measure \(\mu \) has expectation
The (continuous) Glauber dynamics associated with H is given by the system of stochastic differential equations
where the \(B_x\) are independent n-dimensional standard Brownian motions. (The continuous Glauber dynamics is also referred to as overdamped Langevin dynamics; to keep the terminology concise we use the term Glauber dynamics in the continuous as well as in the discrete case.) By construction, the measure \(\mu \) defined in (1.2) is invariant with respect to this dynamics. Its relaxation time scale is controlled by the inverse of the spectral gap of the generator of the Glauber dynamics (see, for example, [2, Proposition 2.1]). By definition, the spectral gap is the largest constant \(\gamma \) such that, for all functions \(F: \mathbb {R}^{n\Lambda } \rightarrow \mathbb {R}\) with bounded derivative,
Our goal in this paper is to determine the order of the spectral gap \(\gamma \) for specific choices of M and V, when the size of the domain \(\Lambda \) diverges. For statistical mechanics, the setting of primary interest is a finite domain of a lattice or a torus \(\Lambda = \Lambda _N \subset \mathbb {Z}^d\) whose size tends to infinity, and a short-range spin coupling matrix M, such as the discrete Laplace operator \(-\Delta \) on \(\Lambda \). The discrete Laplace operator has a nontrivial kernel. This degeneracy must be removed through boundary conditions or an external field (mass term). For example, for a cube of side length D with Dirichlet boundary conditions, the smallest eigenvalue is of order \(D^{-2}\). In the hierarchical set-up that we consider, we impose an external field instead of boundary conditions whose size is such that the smallest eigenvalue is at least of order \(D^{-2}\).
For \(V=0\), or more generally for quadratic potentials which can be absorbed in the definition of M, the spectral gap \(\gamma \) of the generator of the Langevin dynamics is equal to the minimal eigenvalue of M (assuming that it is positive) by explicit diagonalisation of (1.3). More generally, for V any strictly convex potential satisfying \(V''(\varphi ) \geqslant c > 0\) uniformly in \(\varphi \), the Bakry–Emery criterion [3] implies that
where \(\lambda \) is the smallest eigenvalue of M. Under these conditions, \(\mu \) actually satisfies a logarithmic Sobolev inequality with the same constant. In particular, under these assumptions, the dynamics relaxes quickly, in time of order 1.
The situation is much more subtle when the potential V is non-convex. Indeed, as the potential becomes sufficiently non-convex, the static measure \(\mu \) typically undergoes phase transitions. In fact for unbounded spin systems on a lattice, the relaxation of the Glauber dynamics has been controlled only in the uniqueness regime under some assumptions on the decay of correlations [12, 13, 39, 41, 53] (see also [52] for conservative dynamics). By considering hierarchical models, we are able to show that the spectral gap decays polynomially in the vicinity of a phase transition. The idea is to decompose the measure into renormalised fields such that at each scale, conditioned on a block spin field, the renormalised potential remains strictly convex. By induction, we then obtain a recursion on the spectral gaps of the renormalised measures.
Before stating the results, we first turn to the definition of the hierarchical models.
1.3 Hierarchical Laplacian
The Gaussian free field (GFF) on a finite approximation to \(\mathbb {Z}^d\) is a Gaussian field whose covariance is the Green function of the Laplace operator. The Green function has decay \(|x|^{-(d-2)}\) in dimensions \(d\geqslant 3\) and has asymptotic behaviour \(-\log |x|\) in dimension \(d=2\). The hierarchical Laplace operator is an approximation to the Euclidean one in the sense that its Green function has comparable long-distance behaviour, but simpler short-distance structure. The study of hierarchical models has a long history in statistical mechanics going back to [11, 28]; recent studies and uses of hierarchical models include [1, 10, 15, 35, 54] and references.
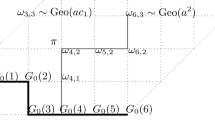
There is some flexibility in the choice of the hierarchical field; the precise choice is not significant. Let \(\Lambda = \Lambda _N\) be a cube of side length \(L^N\) in \(\mathbb {Z}^d\), \(d \geqslant 1\), for some fixed integer \(L>1\) and N eventually chosen large. For scale \(0\leqslant j \leqslant N\), we decompose \(\Lambda \) as the union of disjoint blocks of side lengths \(L^j\) denoted \(B \in {\mathcal {B}}_j\); see Fig. 1. In particular, \({\mathcal {B}}_0 = \Lambda \) and the unique block in \({\mathcal {B}}_N\) is \(\Lambda _N\) itself. The blocks have the structure of a K-ary tree with \(K=L^d\), height N and the leaves are indexed by the sites \(x \in \Lambda _N\).
For scale j and \(x\in \Lambda \), let \(B_{j}(x)\) be the block in \({\mathcal {B}}_j\) containing x. As in [9, Chapter 4], define the block averaging operators, which are the projections
Let \(P_j = Q_{j-1}-Q_{j}\). Then \(P_1, \dots , P_N, Q_N\) are orthogonal projections on \(\mathbb {R}^\Lambda \) with disjoint ranges whose direct sum is the full space. An operator on \(\mathbb {R}^\Lambda \) is hierarchical if it is diagonal with respect to this decomposition. To obtain a hierarchical Green function with the scaling of the Green function of the usual Laplace operator, we choose the hierarchical Laplace operator on \(\Lambda \) to be
Like the usual Laplacian on the discrete torus, this choice of hierarchical Laplacian annihilates the constant functions. The definition implies that the Green function of the hierarchical Laplacian has comparable long distance behaviour to that of the nearest-neighbour Laplacian: for \(|x-y|^{-1} \ll m\),
where \(|x-y|\) is the Euclidean distance and \(\sigma = 1-L^{-2}\) is a constant independent of N, and \(A \asymp B\) denotes that A / B and B / A are bounded by N-independent constants. On the other hand, the hierarchical Laplacian has coarser small distance behaviour than the lattice Laplacian. For a more detailed introduction to the hierarchical Laplacian, as well as discussion of its relation to the lattice Laplacian, see [9, Chapters 3–4].
1.4 Models and results
In Sect. 2, we are going to develop a quite general multiscale strategy to estimate the spectral gap of (critical) spin systems by using a renormalisation group approach. We will then apply this method to the n-component \(|\varphi |^4\) model and the Sine-Gordon model as well as the degenerate case of the Discrete Gaussian model. These models correspond to choices of the potential V defined now. In the setting of the hierarchical spin coupling, we study the critical region of the \(|\varphi |^4\) model and the rough phase of the Sine-Gordon and Discrete Gaussian models. These are both settings for which the renormalisation group method is well developed for the equilibrium case, and we use this as input.
1.4.1 Ginzburg–Landau–Wilson \(|\varphi |^4\) model
The n-component \(|\varphi |^4\) model is defined by the double-well potential (if \(n=1\)), respectively Mexican hat shaped potential (if \(n\geqslant 2\)),
Our interest is in the case \(\nu <0\), when this potential is non-convex. The \(|\varphi |^4\) model is a prototype for a spin model with O(n) symmetry. The spatial dimension \(d=4\) is critical for this model (see, e.g., [9]). The following theorem quantifies the decay of the spectral gap in the four-dimensional hierarchical \(|\varphi |^4\) model when approaching the critical point from the high temperature side.
Theorem 1.1
Let \(\gamma _N(g,\nu ,n)\) be the spectral gap of the hierarchical n-component \(|\varphi |^4\) model on \(\Lambda _N\) with dimension \(d=4\) (as defined above). Let \(L \geqslant L_0\), and let \(g>0\) be sufficiently small. There exists \(\nu _c = \nu _c(g,n) = -C(n+2)g + O(g^2)\) and a constant \(\delta \geqslant 1\) (independent of n) such that for \(t_0 \geqslant t \geqslant cL^{-2N}\), where \(t_0\) is a small constant,
provided that N is sufficiently large. In particular, \(t\geqslant cL^{-2N}\) is allowed to depend on N.
The proof is postponed to Sect. 3. The same proof also implies easily that for \(t \geqslant t_0\) the gap is of order 1, but since we are interested in the more delicate approach of the critical point, we omit the details. Together with this, Theorem 1.1 implies that for the \(|\varphi |^4\) model, the spectral gap is of order 1 in the high temperature phase, \(\nu > \nu _c\) independently of N, and as the critical point is approached the spectral gap scales like that of the free field, with a logarithmic correction. We expect that \(\gamma \sim Ct(-\log t)^{-z}\) for a universal critical exponent \(z = z(n) \geqslant \frac{n+2}{n+8}\), which our method does not determine (see also [36]). The upper bound follows easily from the estimates derived at equilibrium in [9, Theorem 4.2.1] and we also use the renormalisation group flow constructed in [9] as input to prove the lower bound (see also [33]). References for the renormalisation group analysis of the \(|\varphi |^4\) model on \(\mathbb {Z}^4\), with different approaches, include [31, 34, 37, 38] and [5,6,7,8, 17,18,19,20].
1.4.2 Sine-Gordon model
The Sine-Gordon model is defined by a \(2\pi \)-periodic potential and coupling matrix proportional to the inverse temperature \(\beta \), i.e.,
The corresponding energy \(H(\varphi )\) in (1.1) is invariant under  for any \(n \in \mathbb {Z}\), where
for any \(n \in \mathbb {Z}\), where  denotes the constant function on \(\Lambda \) with
denotes the constant function on \(\Lambda \) with  for all \(x\in \Lambda \). To break this non-compact symmetry, we add the external field and consider
for all \(x\in \Lambda \). To break this non-compact symmetry, we add the external field and consider
As previously, we are interested in the large volume limit \(|\Lambda |\uparrow \infty \); to avoid some uninteresting technicalities, we will make the convenient choice \(\varepsilon =\beta L^{-2N}\). If V was, e.g., the double well potential \(V(\varphi ) = \varphi ^4-\varphi ^2\) instead of a periodic potential as above, then the corresponding measure has a uniform spectral gap for any \(\beta >0\) sufficiently small (see, e.g., [4]). The following theorem shows that this is not the case for periodic potentials: the spectral gap decreases to 0. Thus that the resulting models are critical, in the sense of slow decay of correlations, is also reflected in their dynamics.
For the statement of the theorem, denote by \({\hat{V}}(q) = (2\pi )^{-1} \int _{-\pi }^\pi e^{iq\varphi } V(\varphi ) \, d\varphi \) the Fourier coefficient of the \(2\pi \)-periodic function V, and let \(\sigma = 1-L^{-2}\) be the constant in (1.9) with dimension \(d=2\).
Theorem 1.2
Let \(\gamma _N(\beta ,V)\) be the spectral gap of the hierarchical Sine-Gordon model on \(\Lambda _N\) with dimension \(d=2\) (as defined above). Assume \(\sum _{q\in \mathbb {Z}\setminus \{0\}} (1+q^2) |{\hat{V}}(q)|\) is small enough. Let \(0< \beta < \sigma /(4\log L)\) and let \(\varepsilon = \beta L^{-2N}\). There are \(\kappa \in (0,1)\) and \(c>0\) such that the spectral gap scales as
provided that N is sufficiently large.
The Sine-Gordon model is dual to a Coulomb gas model (see, e.g., [16, 32]). Under this duality, the inverse temperature of the Coulomb gas model is proportional to the temperature \(1/\beta \) of the Sine-Gordon model. We here primarily view the Sine-Gordon model as a spin model, rather than as a description of the Coulomb gas, and therefore choose \(\beta \) instead of \(1/\beta \) in (1.12). Note that the usual normalisation of the logarithm in (1.9) is \(c_N - \frac{1}{2\pi } \log |x| + O(1)\) for the Laplace operator on \(\mathbb {Z}^2\). For this normalisation of the hierarchical Laplace operator, the hierarchical critical inverse temperature becomes \(1/\beta = 8\pi \). This is only approximately true in the Euclidean model because of a field-strength (stiffness) renormalisation which is not present in the hierarchical model. For the critical inverse temperature \(\beta = \sigma /(4\log L)\), we expect that \(\gamma \sim C L^{-2N} N^{-z}\) for a universal critical exponent \(z>0\). For the presence of logarithmic corrections to the free field scaling in the static case, see [30]. Our theorem uses the set-up for the renormalisation group for this model of [16] (see also [48]). References for the Sine-Gordon model on \(\mathbb {Z}^2\) include [32] and [23,24,25, 29, 30, 47].
1.4.3 Discrete Gaussian model
We conclude this section with a discrete model which is closely linked to the Sine-Gordon model. The Discrete Gaussian model is an integer-valued field with expectation given by
Note that by rescaling \(\beta \) and \(\varepsilon \) by \((2\pi )^2\), this definition is equivalent to the one in which the model takes values in \(\mathbb {Z}\) rather than \(2\pi \mathbb {Z}\). The normalisation by \(2\pi \) is convenient for our proof. The model formally takes the form of a degenerate Sine-Gordon model in which \(e^{-V(\varphi )}\) is replaced by a sum of \(\delta \)-functions. As the spins take integer values, we now consider a discrete Glauber dynamics for the Discrete Gaussian model with Dirichlet form
where \(\sigma ^{x\pm }\) is obtained from \(\sigma \in (2\pi \mathbb {Z})^\Lambda \) by increasing/decreasing the entry at \(x\in \Lambda \) by \(2\pi \). Thus the corresponding spectral gap of this dynamics is the smallest constant \(\gamma \) such that, for all functions \(F: (2\pi \mathbb {Z})^\Lambda \rightarrow \mathbb {R}\) with finite variance,
The following theorem is related to Theorem 1.2. It shows that the spectral gap of the Discrete Gaussian model scales like the one of the GFF.
Theorem 1.3
Let \(\gamma _N(\beta )\) be the spectral gap of the hierarchical Discrete Gaussian model on \(\Lambda _N\) in dimension \(d=2\) (as defined above). For \(\beta >0\) sufficiently small and \(\varepsilon = \beta L^{-2N}\), there are \(\kappa \in (0,1)\) and \(c>0\) such that
provided that N is sufficiently large.
2 Induction on Renormalised Brascamp–Lieb Inequalities
The Brascamp–Lieb inequality is a generalisation of the spectral gap inequality. We here say that a measure \(\mu \) on a finite-dimensional vector space X with inner product \((\cdot ,\cdot )\) satisfies a Brascamp–Lieb inequality with quadratic form \(D :X \rightarrow X\) if for all smooth functions F,
In particular, if the quadratic form satisfies \(D \leqslant \mathrm {id}/ \lambda \) for some \(\lambda >0\), then \(\mu \) satisfies a spectral gap inequality with constant \(\lambda \). In this section, we construct inductive bounds on Brascamp–Lieb inequalities between renormalised versions of a spin system. From these we deduce in particular an induction on the spectral gap. In the remainder of this paper, we will verify the generic assumptions made in this section in the specific cases of the hierarchical \(|\varphi |^4\) and the Sine-Gordon models.
2.1 Hierarchical decomposition
While the results of this section are somewhat more general, in the remainder of this paper we will apply them to hierarchical models. We therefore recall their structure which can be helpful to keep in mind throughout this section. From Sect. 1.3, first recall the orthogonal projections \(P_1, \dots , P_N, Q_N\) whose ranges span \(\mathbb {R}^\Lambda \), and the hierarchical Laplacian \(\Delta _H\) [see (1.7)]. By spectral calculus, for any \(m^2 > 0\), its Green function can be written as
Using the definition \(P_j = Q_{j-1}-Q_j\) to express the right-hand side of the last equation in terms of the block averaging operators \(Q_j\), we can alternatively write
where
The above spin coupling matrices generalise directly to the O(n)-invariant vector-valued case, in which all operators act separately on each component, and we use the same notation in this case. Thus the Laplacian and the covariances act on the space \(X_0 = \mathbb {R}^{n\Lambda }\).
The covariances \(C_j\) are degenerate and it is convenient to introduce the subspaces of \(X_0=\mathbb {R}^{n\Lambda }\) on which they are supported. Thus define \(X_j\) to be the image of \(C_j\), i.e.,
and, for \(S \subset \Lambda \),
Then the Gaussian field \(\zeta = \{\zeta _x\}_{x\in \Lambda }\) with values in \(X_j\) and covariance \(C_j\) can be realised as
where \(\{ \zeta _B \}_{B \in {\mathcal {B}}_j}\) are independent Gaussian variables in \(\mathbb {R}^n\) with variance \( \frac{\lambda _j}{|B_{j}(x)|}= L^{-dj} \lambda _j\).
In general, one can identify \(\varphi \in X_j\) with \(\{\varphi _B\}_{B\in {\mathcal {B}}_j}\). In the following, we are going to consider functions defined only on the subspaces \(X_j\). Let F be such a function of class \(C^2\) written as
Then F can be extended as a smooth function on the whole of \(\mathbb {R}^{n\Lambda }\) by setting, for example,
For such F, we will consider the gradient and the Hessian of F only in the directions spanned by  so that we set
so that we set
As the gradient and the Hessian are projected only in the directions spanned by  , their restrictions on \(X_j\) are independent of the way F has been extended in \(\mathbb {R}^{n\Lambda }\).
, their restrictions on \(X_j\) are independent of the way F has been extended in \(\mathbb {R}^{n\Lambda }\).
2.2 Renormalised measure
Let \(X_0=\mathbb {R}^{n\Lambda }\) with the standard inner product \((\cdot ,\cdot )\). From now on, we consider a Gaussian measure on \(X_0\) whose covariance \(C_{\geqslant 0}\) has a decomposition \(C_{\geqslant 0}=C_0 + \cdots + C_N\), with the \(C_i\) symmetric and positive semi-definite. We then consider the class of probability measures \(\mu \) with expectation
for some potential \(V_0\). In particular, the models introduced in Sect. 1 are in this class, with
and the decomposition (2.3). Given such a decomposition \(C_0+ \cdots +C_N\) and the potential \(V_0\), we define the renormalised potentials \(V_j\) inductively by
where the expectation applies to \(\zeta \). (This definition includes \(j=N\), but throughout this section we will only use \(j<N\).) The associated renormalised measure \(\mu _j\) is then defined by the expectation
As is the case for the hierarchical decomposition, the covariances \(C_j\) are permitted to be degenerate and we denote by \(X_j\) the subspaces of \(X_0\) on which they are supported, i.e., \(X_j\) is the image of \(C_j\) [see (2.6) for the hierarchical decomposition].
2.3 One step of renormalisation
For the remainder of the section, we fix a scale \(j \in \{0,1,\dots , N\}\), and consider a single renormalisation group step from scale j to scale \(j+1\) when \(j<N\), and a final estimate when \(j=N\). To simplify the notation, we usually omit the scale index j and write \(+\) in place of \(j+1\). In particular, we write \(C=C_j\), \(V=V_j\), \(\mu = \mu _{j}\), \(\mu _{+} = \mu _{j+1}\), and so on. Let \(X = X_j \subseteq X_0\) be the image of C and denote by Q the orthogonal projection from \(X_0\) onto X. We need the following assumptions.
For \(j<N\), in the assumptions below, \(D_+=D_{j+1}\) is the matrix associated with a quadratic form for a Brascamp–Lieb inequality for the measure \(\mu _+\) [see (2.19)], and we set \(D_{N+1}=0\). Throughout the paper, inequalities between operators and matrices are interpreted in the sense of quadratic forms.
A1. Non-convexity of potential There is a constant \(\varepsilon = \varepsilon _j < 1\) such that uniformly in \(\varphi \in X\),
A2. Coupling of scales The images of C and \(C_+\) contain all directions on which \(D_+\) is nontrivial, more precisely
A3. Symmetry For all \(\varphi \in X\),
where \([A,B] = AB-BA\) denotes the commutator.
The most significant assumption is (2.16), which will be seen to ensure that the fluctuation field measure given the block spin field is uniformly strictly convex. The more technical assumptions (2.17) and (2.18) are very convenient (and obvious in the hierarchical setting (2.3)) but seem less fundamental. We use (2.16) in Lemma 2.7 and (2.60), (2.17) in (2.56), and (2.18) in (2.59).
Under the above assumptions, we relate the Brascamp–Lieb inequality for \(\mu _+\) to that for \(\mu \).
Theorem 2.1
Fix \(j< N\), and assume (A1)–(A3) and that \(\mu _+\) satisfies the Brascamp–Lieb inequality
Then \(\mu \) satisfies a Brascamp–Lieb inequality (2.1) with
For \(j=N\), assume only that (A1) holds. Then \(\mu \) satisfies a Brascamp–Lieb inequality (2.1) with
Iterating this theorem starting from \(j=N\) gives the Brascamp–Lieb inequality for the original measure \(\mu _{0}\) as follows. In particular, the spectral gap of \(\mu _0\) is bounded by the inverse of the largest eigenvalue of the matrix \(D_0\).
Corollary 2.2
Assume that, for \(j=0,\dots , N\), the sequence of renormalised measures \((\mu _{j})\) satisfies Assumptions (A1)-(A3) where \(\varepsilon = \varepsilon _j\). Then \(\mu _0\) satisfies a Brascamp–Lieb inequality with
Proof
By backward induction starting from \(j=N\), we will prove that the renormalised measures \(\mu _j\) satisfy the Brascamp–Lieb inequality
and
The claim (2.22) is then the case \(j=0\). To start the induction, we apply (2.21) which gives (2.23) for \(j=N\). To advance the induction, suppose \(0 \leqslant j < N\) is such that the inductive assumption (2.23) holds with j replaced by \(j+1\). This means that (2.19) holds for j and Assumptions (A1)–(A3) also hold by assumption of the corollary. Theorem 2.1 and the inductive assumption imply that \(\mu _j\) satisfies the Brascamp–Lieb inequality with
This advances the inductive assumption, i.e., (2.23) holds for j. \(\square \)
Corollary 2.3
Under the assumptions of the previous corollary, the measure \(\mu _0\) satisfies a spectral gap inequality with inverse spectral gap less than the largest eigenvalue of the matrix \(D_0\).
Proof
The claim is immediate from the definitions of the Brascamp–Lieb and the spectral gap inequalities. Indeed, if \(1/\lambda \) is the largest eigenvalue of \(D_0\) then
as claimed. \(\square \)
In Sects. 3 and 4, Assumptions (A1)–(A3) will be checked for the different hierarchical models in order to derive the scaling of the spectral gap from the previous corollary.
Remark 2.4
More generally, in the assumption \(D_+ = D_+(\varphi )\) and \(\varepsilon =\varepsilon (\varphi )\) could depend on \(\varphi \in X\), with \(\varepsilon \) uniformly bounded by 1. The conclusion (2.20) is then replaced by
However, this strengthened inequality may be difficult to use. To improve the readability, we therefore do not carry the additional arguments for \(D_+\) and \(\varepsilon \) through the proof.
2.4 Proof of Theorem 2.1
We write the renormalised field at scale j as \(\zeta +\varphi \) where \(\varphi \in X_+\) is the block spin field at the next scale \(j+1\) and \(\zeta \in X\) is the fluctuation field at scale j. More precisely, recall that
where \(C = C_j\) and \(\zeta \) denotes the corresponding random field, where \(C_>\) stands for the covariance \(C_{j+1} + C_{j+2} + \cdots C_N\) and \(\varphi \) denotes the corresponding random field, where \(C_{\geqslant } = C + C_>\), and where \(\mathbb {E}_C\) denotes the expectation of a Gaussian measure with covariance C.
Define the expectation conditioned on the block spin field \(\varphi \) in \(X_+\) by
where we will often use the notation \(\mathbb {E}_{\mu _\varphi }\) for the conditional measure \(\mathbb {E}_{\mu }(\cdot |\varphi )\) to make the notation more concise. Then, using (2.15),
where \(Z_{j+1}\) is a normalising constant.
To prove Theorem 2.1, we write using the conditional expectation,
with
In the remainder of this section, we will bound each term separately thanks to the following lemmas.
Lemma 2.5
Assume (A1). Then for any function F with gradient in \(L^2(\mu )\), one has
Lemma 2.6
Assume (A1)–(A3) and that \(\mu _+\) satisfies the Brascamp–Lieb inequality (2.19). Then for any function F with gradient in \(L^2(\mu )\), one has
Proof of Theorem 2.1
For \(j<N\), the proof is immediate by combining the decomposition (2.31) and the previous two lemmas. For \(j=N\), the claim follows directly from Lemma 2.5 only. \(\square \)
2.4.1 Proof of Lemma 2.5
From now on, we freeze the block spin field \(\varphi \in X_+\). Then the conditional measure \(\mu _\varphi = \mu ( \,\cdot \, |\varphi )\) is a probability measure on the space X, the image of C [see (2.6) in the hierarchical case]. As a subspace of the Euclidean vector space \(X_0\), the space X has an induced inner product which we also denote by \((\cdot ,\cdot )\), and an induced surface measure, which is equivalent to the Lebesgue measure of the dimension of X. The measure \(\mu _\varphi \) has density proportional to \(e^{-H_\varphi (\zeta )}\) with respect to this measure given by
(By definition of the subspace X we can regard C as an invertible symmetric operator \(X \rightarrow X\).) For a function \(F: X_0 \rightarrow \mathbb {R}\) and \(\varphi \in X_0\), the function \(F_\varphi : X \rightarrow \mathbb {R}\) is defined by \(F_\varphi (\zeta ) = F(\varphi +\zeta )\).
Lemma 2.7
Assume (A1). Then for all \(\varphi \in X_+\), the conditional measure \(\mu _\varphi \) satisfies the Brascamp–Lieb inequality
Proof
As a consequence of Assumption (2.16) and of the definition of the space X, the Hamiltonian \(H_\varphi \) associated with \(\mu _\varphi \) is strictly convex on X, with
where we used that C is invertible on X and that \(QC = CQ= C\). The Brascamp–Lieb inequality (A.4) implies the inequality. \(\square \)
Proof of Lemma 2.5
The term \({{\mathbb {A}}} _1\) is a variance under the conditional measure \(\mu _\varphi \). By Lemma 2.7, the measure satisfies the Brascamp–Lieb inequality (2.37). Therefore
In the last equality we used that \(CQ=C\) by definition of Q as the orthogonal projection onto the image of C so that \(\nabla _X\) can be replaced by \(\nabla \). \(\square \)
2.4.2 Proof of Lemma 2.6
The second term \({{\mathbb {A}}} _2\) in (2.32) is a variance under \(\mu _{+}\):
Using Assumption (2.19) that the measure \(\mu _{+}\) satisfies a Brascamp–Lieb inequality, we have
where \(\nabla _{X_+}\) applies to the variable \(\varphi \) and \(\Vert f\Vert _2^2 = \sum _{x\in \Lambda } |f_x|^2\).
We first state a technical lemma.
Lemma 2.8
Assume (A3). For \({\dot{\varphi }} \in X_+\),
Proof
The derivative applies only on the block spin field \(\varphi \). We write \(\nabla _\varphi \) for \(\nabla _{X_+}\) with respect to the variable \(\varphi \) and \(\nabla _\zeta \) for \(\nabla _{X}\) with respect to the variable \(\zeta \). Using the notation (2.36),
where in the last term we used that, since \({\dot{\varphi }} \in X_+\),
By integration by parts, we get also that
Using this relation and (2.18), we get that for any \(\zeta \in X\),
and therefore
The last equality applied to \(F=1\) implies that (as an identity between elements of \(X_+\))
Thus (2.42) becomes
as claimed. \(\square \)
Lemma 2.9
Assume (A1)–(A3). Then for \(\varphi \) in \(X_+\),
Applying the expectation \(\mathbb {E}_{\mu _+}( \cdot )\) on both sides and substituting the result into (2.40), this completes Lemma 2.6.
Proof of Lemma 2.9
The block spin field \(\varphi \in X_+\) is fixed and in the proof we study the measure \(\mu _\varphi \) on the subspace X. We define \(L_\varphi \) to be the self-adjoint generator of the Glauber dynamics for the conditional measure \(\mu _\varphi \) on X, i.e.,
see also Appendix A. Moreover, we define the Witten Laplacian \({\mathcal {L}}_\varphi \) on \(L^2(\mu _\varphi ) \otimes X\) by
Using the Helffer–Sjöstrand representation (Theorem A.1), one can rewrite the correlations (2.41) under the conditional measure in terms of the operator \({\mathcal {L}}_\varphi \) as
This is an identity in \(X_+\) which can be rewritten by using the projection \(Q_+\) as
Composing by \(D_+^{1/2}\) and using that \(D_+ = D_+ Q_+\) by (2.17), we deduce that
where the operator \(M_\varphi \) is defined as
Since \(D_+\) commutes with C and with \({\mathcal {L}}_\varphi C\) by (2.18), the operator \(M_\varphi \) acts on \(L^2(\mu _\varphi ) \otimes X\) and is self-adjoint. From (2.54) and the Cauchy-Schwarz inequality, we finally obtain
where \(\Vert f\Vert _2^2 = (f,f)\) and \(\nabla _{X_+}\) applies to \(\varphi \) and \(\nabla _X\) applies to \(\zeta \). In the following, we will show that the operator \(M_\varphi \) obeys the following form inequality on \(L^2(\mu _\varphi )\otimes X\):
which then concludes the proof of the lemma. Recall that the operator \({\mathcal {L}}_\varphi \) is defined by
Under Assumption (2.18), we can write
Using that \(L_\varphi \) and C are positive operators, using Assumption (2.16), it follows that as operators on \(L^2(\mu _\varphi ) \otimes X\),
Finally, using that \(D_+=D_+Q\) by Assumption (2.17), and using (2.18), it follows that \(M_\varphi \) satisfies the desired form bound
This completes the proof. \(\square \)
3 Hierarchical \(|\varphi |^4\) Model
In this section, we apply Corollaries 2.2 and 2.3 to the hierarchical \(|\varphi |^4\) model. Throughout this section, the dimension is fixed to be \(d=4\). Nevertheless, we sometimes write d to emphasise that a factor 4 arises from the dimension \(d=4\) rather than from the exponent of \(|\varphi |^4\).
3.1 Renormalisation group flow
For \(m^2>0\) (to be determined in Theorem 3.1 as a function of g and \(\nu \)), we decompose
as in (2.3), and define the renormalised potential with respect to this decomposition as in (2.14),
Note in particular that the sequence of renormalised potentials depends on the choice of \(m^2\), and that \(C_j \leqslant \vartheta _j^2 L^{2j} Q_j\) where we define \(\vartheta _j = 2^{-(j-j_m)_+}\). As a consequence of the hierarchical structure, the renormalised potential can be written as
where \(V_j(B,\varphi )\) is a function of \(\varphi \) that depends only on the restriction \(\varphi |_B\) for any block \(B \in {\mathcal {B}}_j\).
We always restrict the domain of the functions \(V_j(B)\) to the space \(X_j(B) \cong \mathbb {R}^n\) of fields that are constant on B. Explicitly, for a block \(B \in {\mathcal {B}}\), denote by \(i_B: \mathbb {R}^n \rightarrow \mathbb {R}^{nB}\) the linear map that sends \(\varphi \in \mathbb {R}^n\) to the constant field \(\varphi : B \rightarrow \mathbb {R}^n\) with \(\varphi _x = \varphi \) at every \(x \in B\). Then \(V_j(B) \circ i_B\) is a function of a single variable in \(\mathbb {R}^n\) induced by \(V_j(B)\). In particular using (2.10) one can view \(V_j(B)\) as a function in \(\mathbb {R}^{nB}\), so that for any \({{\dot{\varphi }}} \in X_j(B)\) taking the constant value \({{\dot{\varphi }}}_B \in \mathbb {R}^n\),
If there is a constant \(s >0\) such that
then using that \(({\dot{\varphi }},{\dot{\varphi }}) =|{\dot{\varphi }}_B|^2|B|\), we deduce
With the notation (2.11), the inequalities (3.5) and \(C_j \leqslant \vartheta _j^2 L^{2j} Q_j\), it follows that
Thus, in the hierarchical model, Assumption (A1) in (2.16) with \(\varepsilon _j = s \vartheta _j^2 L^{2j}\) follows from (3.5). In the rest of this section, we therefore reduce to the study of the function \(V_j(B) \circ i_B\) in \(\mathbb {R}^n\).
The renormalisation group for the \(|\varphi |^4\) model provides precise estimates on the renormalised potential \(V_j\) when the field \(\varphi \) is not too large. The following theorem about the renormalisation group flow is proved in [9]. Note that \(V_j\) in (3.2) is the full renormalised potential (the logarithm of the density with respect to the Gaussian reference measure), not its leading contribution as in [9]. We will denote the latter instead by \({\hat{V}}_j\) as it plays a less central role in the arguments of this paper. It is determined by the coupling constants \((g_j,\nu _j) \in \mathbb {R}^2\) through
where \(\alpha _j = \alpha _j(m^2) = O(L^{2j}L^{-(j-j_m)_+})\) is an explicit (j-dependent) constant and \(j_m = \lfloor {\log _L m^{-1}} \rfloor \) is the mass scale. We stress the fact that if the field is constant on B then
so that in the following we will often consider the effective potential normalised by the factor 1 / |B| [see also (3.5)].
For the statement of the theorem, define the fluctuation field scale\(\ell _j\) and the large field scale\(h_j\) by
Finally, we define \({\mathcal {F}}_j\) by \(F \in {\mathcal {F}}_j\) if for any \(B\in {\mathcal {B}}_j\) there is a function \(\varphi \in \mathbb {R}^{n\Lambda } \mapsto F(B,\varphi )\) that (i) depends only on the average of \(\varphi \) over the block B; (ii) the function \(F(B) \circ i_B\) is the same for any block B; and (iii) the function F(B) is invariant under rotations, i.e., \(F(\varphi ,B) = F(T\varphi ,B)\) for any \(T \in O(n)\) acting on \(\varphi \in \mathbb {R}^{n\Lambda }\) by \((T\varphi )_x = T\varphi _x\); see [9, Definition 5.1.5].
Theorem 3.1
Let \(L \geqslant L_0\). For any \(g>0\) small enough, there exists \(\nu _c(g) = -C(n+2)g + O(g^2)\) such that for \(\nu > \nu _c(g)+cL^{-2N}\), there exists \(m^2 > 0\), a sequence of coupling constants \((g_j,\nu _j, u_j) \subset \mathbb {R}^3\), and \({\hat{K}}_j \in {\mathcal {F}}_j\) such that the following are true.
- 1.
The full renormalised potential \(V_j\) defined by (3.2) satisfies: for all \(\varphi \) that are constant on B,
$$\begin{aligned} e^{-V_j(B,\varphi )} = e^{-u_j|B|}(e^{-{\hat{V}}_j(B,\varphi )}(1+{\hat{W}}_j(B,\varphi )) + {\hat{K}}_j(B,\varphi )). \end{aligned}$$(3.11) - 2.
The sequence \((g_j,\nu _j)\) of coupling constants satisfies \((g_0,\nu _0)=(g,\nu -m^2)\), and
$$\begin{aligned} g_{j+1} = g_j - \beta _j g_j^2 + O(2^{-(j-j_m)_+}g_j^3), \qquad 0 \geqslant L^{2j}\nu _j = O(2^{-(j-j_m)_+}g_j), \end{aligned}$$(3.12)where \(\beta _j = \beta _0^0(1+m^2L^{2j})^{-2}\) for an absolute constant \(\beta _0^0>0\) and \(j_m = \lfloor {\log _Lm^{-1}} \rfloor \).
- 3.
The functions \({\hat{K}}_j\) satisfy \({\hat{K}}_0=0\) and
$$\begin{aligned} \sup _{\varphi \in \mathbb {R}^n} \max _{0\leqslant \alpha \leqslant 3} h_j^{\alpha } |\nabla ^\alpha ({\hat{K}}_j(B) \circ i_B)(\varphi )|&= O(2^{-(j-j_m)_+}g_j^{3/4}), \end{aligned}$$(3.13)$$\begin{aligned} \max _{0\leqslant \alpha \leqslant 3} \ell _j^{\alpha } |\nabla ^\alpha ({\hat{K}}_j(B) \circ i_B)(0)|&= O(2^{-(j-j_m)_+}g_j^{3}), \end{aligned}$$(3.14)where \(\ell _j = L^{-j}\) and \(h_j = L^{-j} g_j^{-1/4}\).
- 4.
The relation between \(t = \nu - \nu _c(g) >0\) and \(m^2>0\) satisfies, as \(t \downarrow 0\),
$$\begin{aligned} m^2 \sim C_g t(\log t^{-1})^{-(n+2)/(n+8)}. \end{aligned}$$(3.15)
In the above theorem and everywhere else, the error terms \(O(\cdot )\) are uniform in the scale j. The theorem is mainly proved and explained in [9]. For our application to the analysis of the spectral gap of the Glauber dynamics, it is however more convenient to use a slightly different organisation than that used in [9]. It is here better to use the decomposition (2.3) instead of (2.2) (used in [9]). We translate between the conventions in [9] and those used in the statement of Theorem 3.1 in Appendix B and also give precise references there.
We remark that the normalising constants \(u_j\) are unimportant for our purposes, and that the recursion (3.12) implies that, as \(m^2 \downarrow 0\),
see [9, Proposition 6.1.3].
A variant of the theorem implies the following asymptotic behaviour of the susceptibility as the critical point is approached.
Corollary 3.2
Let \(F= \sum _x\varphi _x^{1}\). Then for \(t = \nu -\nu _c \geqslant c L^{-2 N}\),
with o(1) tending to 0 as \(L^{2N}m^2 \rightarrow \infty \), and \({{\,\mathrm{Var}\,}}_\mu \) denotes the variance under the full \(|\varphi |^4\) measure as in (1.2).
Indeed, the corollary is [9, Theorem 5.2.1 and (6.2.17)], noting that \({{\,\mathrm{Var}\,}}_\mu (F)/|\Lambda _N|\) is the finite volume susceptibility studied there. The corollary provides the upper bound in Theorem 1.1 since, with F as defined in the corollary,
and \(\gamma _N(g,\nu _c(g)) \leqslant {{\,\mathrm{Var}\,}}_\mu (F)/\mathbb {E}_\mu (\nabla F,\nabla F)\) for any F by definition of the spectral gap.
3.2 Small field region
The bounds of Theorem 3.1 are effective for small fields \(|\varphi | \leqslant h_j\). For such fields \(\varphi \), the approximate effective potential \({\hat{V}}_j(\varphi )\) is a good approximation to \(V_j(\varphi )\). Indeed, then \(e^{{\hat{V}}_j(B,\varphi )} = e^{O(1)}\) and
Recall the abbreviation \(\vartheta _j= 2^{-(j-j_m)_+}\) where \(j_m = \lfloor \log _L m^{-1} \rfloor \) is the mass scale. By (3.12) and (3.13) and the definition of \({\hat{W}}\), uniformly in \(\varphi \in \mathbb {R}^n\) with \(|\varphi | \leqslant h_j\),
and the remainder satisfies an analogous estimate. In particular, by (3.19),
where \(\mathrm {id}_{n}\) is the identity matrix acting on the single-spin space \(\mathbb {R}^n\). The first term on the right-hand side can be computed explicitly from (3.8), which implies that as quadratic forms,
where \(|B| =L^{dj}\), and where we used that the \(n\times n\) matrix \((\varphi ^k\varphi ^l)_{k,l}\) has eigenvalues 0 and \(|\varphi |^2 \geqslant 0\). Combining (3.22) with (3.23) and (3.24), we find that
Using that \(\alpha _j g_j|\varphi |^2 = O(g_j^{1/2})\) for \(|\varphi | \leqslant h_j\) (since \(\alpha _j = O(L^{2j})\)), in summary, we have obtained the following corollary of Theorem 3.1.
Corollary 3.3
Suppose that \(V_0\) satisfies the conditions of Theorem 3.1. Then for all scales \(j\in \mathbb {N}\) and all \(\varphi \in \mathbb {R}^n\) with \(|\varphi |\leqslant h_j\), the effective potential satisfies the quadratic form bounds
with \(0 \leqslant -\nu _j = O(\vartheta _jL^{-2j}g_j)\), and furthermore
3.3 Large field region
Using the small field estimates as input, we are going to prove the following estimate for the large field region.
Theorem 3.4
Assume the conditions of Theorem 3.1, in particular that \(g>0\) is sufficiently small and that \(\nu > \nu _c(g) + cL^{-2N}\). Then for all \(j \in \mathbb {N}\) and all \(B \in {\mathcal {B}}_j\), the effective potential satisfies
where the constants \(\varepsilon _j\) satisfy \(\varepsilon _{j+1} = {\bar{\varepsilon }}_j - O(\vartheta _j^2{\bar{\varepsilon }}_{j}^2)\) and \(\varepsilon _0= \frac{1}{5} g_0^{1/2}\) where \({\bar{\varepsilon }}_j = \varepsilon _j \wedge \frac{1}{5} g_j^{1/2}\).
To prove Theorem 1.1, we will only use the conclusion \(\varepsilon _j \geqslant 0\) from Theorem 3.4. However, in order to prove Theorem 3.4, it is convenient that the \(\varepsilon _j\) do not become too small. The elementary proof of the following estimate is given in Appendix B.
Lemma 3.5
The sequence \((\varepsilon _j)\) defined in Theorem 3.4 satisfies \(\varepsilon _j \geqslant c g_j\) for all \(j\in \mathbb {N}\).
We will prove Theorem 3.4 by induction in j. For \(j=0\), the estimate (3.28) can be checked directly from (3.23) and \(\nu \geqslant \nu _c(g) = -O(g)\), which imply that
From the inductive assumption and Corollary 3.3, we can get the following bounds.
Lemma 3.6
Assume that (3.28) holds for some \(j\in \mathbb {N}\) and that \(\varepsilon _j \leqslant \frac{1}{4} g_j^{1/2} - O(g_j)\). Then
Proof
For \(|\varphi | \geqslant h_j\), the estimate (3.30) follows directly from the assumption (3.28) and the trivial bound \(L^2\varepsilon _j \geqslant \varepsilon _j\). Next we consider the case \(\frac{1}{2} h_{j+1} \leqslant |\varphi | \leqslant h_j\). By definition,
Therefore (3.26) implies
Similarly, using Corollary 3.3 for the small fields and the inductive assumption for the large fields, we have for all \(\varphi \) that
which implies (3.31). This completes the proof of Lemma 3.6. \(\square \)
The following proposition now advances the induction and thus proves Theorem 3.4.
Proposition 3.7
Assume (3.30) and (3.31) with \(j<N\). For \(\varphi \in \mathbb {R}^n\) with \(|\varphi | \geqslant h_{j+1}\) and \(B_+ \in {\mathcal {B}}_{j+1}\),
The proposition will be proved in the remainder of this section. Since the scale j will be fixed we usually drop the j and write \(+\) instead of \(j+1\). To set-up notation, we fix a block \(B_+ \in {\mathcal {B}}_{+}\) and write \(V(B_+) = \sum _{B \in {\mathcal {B}}_j(B_+)} V(B)\). By the hierarchical structure, \({{\,\mathrm{Hess}\,}}V(B_+)\) is a block diagonal matrix indexed by the blocks \(B \in {\mathcal {B}}(B_+)\), and we will always restrict the domain to \(X_j(B_+)\), the space of fields constant inside the small blocks B. On this domain, \(V(B_+)\) can be identified with a function of \(L^d\) vector-valued variables while \(V_+(B_+)\) has domain \(X_{+}(B_+)\) and can be identified with a function of a single vector-valued variable. The covariance operator C and the projection Q operate naturally on \(X(B_+)=X_j(B_+)\) and can be identified with diagonal matrices indexed by blocks \(B \in {\mathcal {B}}(B_+)\); in particular, they are invertible on \(X(B_+)\). By the definition of \(V_+\) in (3.2), together with the hierarchical structure of C, it follows that
where (recall that here C denotes the restriction of C to \(X(B_+)\))
By differentiating (3.36) we obtain, for \({\dot{\varphi }} \in X_+(B_+)\),
where \(\langle \cdot \rangle _{H_\varphi }\) denotes the expectation of the probability measure with density \(e^{-H_\varphi }\) on \(X(B_+)\), and \(\nabla \) is the gradient in \(X(B_+)\), i.e., with respect to fields that are constants on scale-j blocks in \(B_+\).
To estimate the right-hand side of the last equation, we need some information on the typical value of the fluctuation field \(\zeta \) under the expectation \(\langle \cdot \rangle _{H_\varphi }\). By assumption of the proposition, the bound (3.31) holds, and together with the definition of \(C = C_j\) in particular,
as an operator on \(X(B_+)\), i.e., \(\zeta \) is a constant on every \(B \in {\mathcal {B}}(B_+)\). Therefore, uniformly in \(\zeta \),
For any \(\varphi \), the action \(H_\varphi \) is therefore strictly convex on \(X(B_+)\) and, in particular, it has a unique minimiser in this space. We denote this minimiser by \(\zeta ^0\). It satisfies the Euler–Lagrange equation
Here recall the definition \(V(B_+) = \sum _{B\in {\mathcal {B}}(B_+)} V(B)\), and hence that \(\nabla V(B_+)\) is a vector of blocks indexed by \(B \in {\mathcal {B}}(B_+)\), on which the covariance operator C acts diagonally.
Further recall that \(\varphi \) is constant on \(B_+\). By symmetry and uniqueness of the minimiser, we see that \(\zeta ^0\) has to be constant not only in each small block B, but in each \(B_+\), i.e., \(\zeta ^0 \in X_{+}(B_+)\). In the following lemma, the block \(B_+\) is fixed and \(\varphi \) and \(\zeta ^0\) are both in \(X_{+}(B_+)\) so that we may identify them with variables in \(\mathbb {R}^n\).
Lemma 3.8
Let \(|\varphi |\geqslant h_+\). Then \(|\varphi +\zeta ^0| \geqslant h_+(1 - O(g^{1/2}))\).
Proof
As discussed above, we regard \(\nabla V\) and \(C\nabla V\) both as block vectors indexed by \(B \in {\mathcal {B}}(B_+)\). For \(\varphi '\) constant on \(B_+\), the blocks of \(\nabla V(B_+,\varphi ')\) are equal and C acts by multiplying each of these blocks by the same constant \(O(\vartheta ^2 L^{2j})\). Hence \(C\nabla V(B_+,\varphi ')\) is a block vector with all blocks equal to \(O(\vartheta ^2 L^{2j})\nabla V(B,\varphi ')\) where B is any of the block in \({\mathcal {B}}(B_+)\). We denote by \(|C\nabla V(B_+,\varphi ')|_\infty \) the value in any of these blocks. Now (3.27) implies that, for \(\varphi '\) constant on \(B_+\) with \(|\varphi '|\leqslant h_+\),
To prove the claim, we may assume that \(|\varphi +\zeta ^0| \leqslant h_+\) since otherwise the claim holds trivially. Then \(|\zeta ^0| \leqslant M = O(\vartheta ^2 g^{1/2} h_+)\) by (3.41) and (3.42). We conclude from this that \(|\varphi +\zeta ^0| > h_+\) or \(|\zeta ^0| = O(\vartheta ^2 g^{1/2}h_+)\). Thus \(|\varphi +\zeta ^0| \geqslant h_+ \wedge (|\varphi |-O(\vartheta ^2 g^{1/2}h_+)) \geqslant h_+(1- O(\vartheta ^2 g^{1/2}))\). \(\square \)
In the following lemma, \(\zeta \in X(B_+)\) is the fluctuation field under the measure with expectation \(\langle \cdot \rangle _{H_\varphi }\). Thus \(\zeta \) is constant in any small block B, but unlike the minimiser \(\zeta ^0\) the field \(\zeta \) is not constant in \(B_+\).
Lemma 3.9
For any \(t \geqslant 1\), with \(\ell = L^{-j}\) as in (3.10),
Proof
By changing variables, it suffices to study the measure with action \(H(\zeta ) = H_\varphi (\zeta +\zeta ^0)\), whose unique minimiser is \(\zeta =0\), and clearly H has the same Hessian as \(H_\varphi \). From the information that the minimiser of H is 0, we obtain a bound on the random variable \(\zeta \) as follows. Using that \({{\,\mathrm{Hess}\,}}H \geqslant \frac{1}{2} C^{-1}\) as quadratic forms and that \(C_{xx} \leqslant \vartheta ^2\ell ^2\) for all \(x\in \Lambda \) by definition, the Brascamp–Lieb inequality (A.5) for the measure \(\langle \cdot \rangle _H\) with density proportional to \(e^{-H}\) implies
By Markov’s inequality therefore
To estimate the mean \(\langle \zeta \rangle _H\), we integrate by parts to get
where the integral is over \(X(B_+)\) and \(\nabla \) is the gradient on \(X(B_+)\), and where we used that, by (3.40),
Since \(\mathbb {E}(\zeta ,\zeta ) = | B_+| \langle \zeta _x^2 \rangle _H\) by symmetry, therefore
Finally, combining (3.45) and (3.48)
which is the claim. \(\square \)
Next we use the following estimate on \({{\,\mathrm{Hess}\,}}V_+(B_+)\).
Lemma 3.10
Let \(\varphi , {\dot{\varphi }} \in X_{+}(B_+)\). Then
where \({{\,\mathrm{Hess}\,}}V_+(B_+)\) is taken in \(X_+(B_+)\) and \({{\,\mathrm{Hess}\,}}V(B_+)\) is taken in \(X(B_+)\).
Note that \({{\,\mathrm{Hess}\,}}V(B_+,\varphi +\zeta )\) are both diagonal matrices indexed by \(B \in {\mathcal {B}}_+\), with constant entries on each block B. In fact, C is proportional to the identity matrix on \(X(B_+)\).
Proof
We freeze the block spin field \(\varphi \in X_{+}(B_+)\) and recall that the fluctuation field \(\zeta \in X(B_+)\) is distributed with expectation \(\langle \cdot \rangle _{H_\varphi }\). We abbreviate \({{\,\mathrm{Hess}\,}}V = {{\,\mathrm{Hess}\,}}V(\varphi +\zeta ) = {{\,\mathrm{Hess}\,}}V(B_+,\varphi +\zeta )\) throughout the proof. Applying the Brascamp–Lieb inequality (A.4) to the measure \(\langle \cdot \rangle _{H_\varphi }\) gives
Inserting this into (3.38), the above can be written as
Since \({{\,\mathrm{Hess}\,}}V\) and C are both (block) diagonal matrices, the term inside the expectation can be written as
This completes the proof. \(\square \)
For \(\varphi \in X(B_+)\), let \(\Lambda (\varphi )\) be the largest constant such that \(L^{2(j+1)} {{\,\mathrm{Hess}\,}}V(B_+,\varphi ) \geqslant \Lambda (\varphi )\) as quadratic forms on \(X(B_+)\). From (3.39) it follows that \(\Lambda (\varphi ) \geqslant -\frac{1}{2}\) uniformly in \(\varphi \in X(B_+)\). Then (3.50) implies that for \({\dot{\varphi }} \in X_{+}(B_+)\),
where the second inequality uses that \(t/(1+a t)\) is increasing in \(t>-1/a\) and that \(C \leqslant \vartheta ^2 L^{2j}Q\).
The next lemma completes the proof of Proposition 3.7.
Lemma 3.11
For \(\varphi \in X_{+}(B_+)\) with \(|\varphi | \geqslant h_+\), we have
Proof
On the event \(\min _x |\varphi +\zeta _x| \geqslant \frac{1}{2} h_+\) we have \(\Lambda (\varphi +\zeta ) \geqslant \varepsilon >0\) by (3.30), and since \(t/(1+at)\) is increasing for \(t > 0\) therefore
By Lemma 3.9, the probability that \(|\zeta _x-\zeta ^0| \geqslant \frac{1}{4} h_+\) is bounded by \(2e^{-(h_+/(12\vartheta \ell ))^2/4} \leqslant 2e^{-c \, (\vartheta g)^{-1/2}}\) for any point \(x\in B_+\) (since \(\vartheta \leqslant 1\)). Using that \(\zeta \) is constant on the small blocks B and taking a union bound over the \(L^d\) blocks \(B \in {\mathcal {B}}(B_+)\) we get that \(\max _x |\zeta _x-\zeta ^0| \geqslant \frac{1}{4} h_+\) with probability at most \(2L^d e^{-c (\vartheta g)^{-1/2}}\). Since \(|\varphi +\zeta ^0| \geqslant h_+(1-O(g^{1/2})) \geqslant \frac{3}{4} h_+\) by Lemma 3.8, together with the assumption \(|\varphi | \geqslant h_+\), we conclude that \(\min _x|\varphi +\zeta _x| \geqslant \frac{1}{2} h_+\) with probability at least \(1-2L^d e^{-c(\vartheta g)^{-1/2}}\). Thus (3.56) holds with at least this probability.
On the event that (3.56) does not hold, we still have the bound \(\Lambda (\varphi +\zeta ) \geqslant -\frac{1}{2}\) by (3.39). Thus the contribution of this event to the expectation (3.55) is bounded by \(-O(L^d e^{-c \, (\vartheta g)^{-1/2}}) = -O(\vartheta ^2\varepsilon ^4)\), where we used that \(\varepsilon _j \geqslant c \vartheta _j g_j\) by Lemma 3.5. In summary,
This implies the claim. \(\square \)
3.4 Proof of Theorem 1.1
We now use Corollary 3.3 and Theorem 3.4 to verify the assumptions of Corollaries 2.2–2.3 and in doing so deduce Theorem 1.1. By (2.3), the covariances in the decomposition of \((-\Delta _H+m^2)^{-1}\) are given by
We recall that \(\vartheta _j = 2^{(j-j_m)_+}\). Corollary 3.3 implies
The right-hand side is less than 0 by Theorem 3.1. Thus, by Theorem 3.4, the same estimate holds for \(|\varphi |\geqslant h_j\) and therefore for all \(\varphi \). In summary, and since the above estimates hold for all blocks, and using (3.7),
Thus Assumption (A1) holds with
Lemma 3.12
There exists a constant \(\delta >0\) such that for all \(j \in \mathbb {N}\),
The elementary proof requires some notation from [9]; we therefore postpone it to Appendix B.
Proof of Theorem 1.1
We apply Corollary 2.2. By (3.60), Assumption (A1) holds for all \(j\leqslant N\), and Assumptions (A2) and (A3) follow automatically from the hierarchical structure. Therefore, by (2.22), the \(|\varphi |^4\) measure satisfies a Brascamp–Lieb inequality with quadratic form
We abbreviate \(\gamma =(n+2)/(n+8)\). Using \(g_j^{-1} = O(g_{j_m}^{-1})\) which holds by (3.16), and using (3.62),
We then use that \(g_{j_m}^{-1}= O(\log m^{-1})\) by (3.16), to show that (3.64) is a logarithmic correction of order \((- \log m)^{\delta \gamma }\). Thus the dominant contribution in (3.63) is given by
where we recall that \(m^2 \sim Ct (-\log t)^{-\gamma }\) as \(t \downarrow 0\) by (3.15). In summary, we conclude that \(D_0\) is bounded as a quadratic form from above by
Replacing by \(1+\delta \) by \(\delta \), this implies the lower bound for the spectral gap claimed in (1.11). The upper bound for the spectral gap follows immediately from (3.17). \(\square \)
4 Hierarchical Sine-Gordon and Discrete Gaussian Models
In this section, we apply Corollaries 2.2 and 2.3 to the hierarchical versions of the Sine-Gordon and the Discrete Gaussian models. This boils down to checking that Assumption (A1) is satisfied along the renormalisation group flow of both models. Throughout this section \(d=2\).
4.1 Proof of Theorem 1.2
We start by defining the renormalisation group for the hierarchical Sine-Gordon model, essentially in the set-up of [16, Chapter 3]. By definition, with \(\varepsilon =\beta L^{-2N}\), the Sine-Gordon model has energy
where the potential \(V_0\) is even and \(2\pi \)-periodic. We decompose the covariance of the Gaussian part as
with
Relative to this decomposition, the renormalised potential is defined as in Sect. 2.2. Due to the hierarchical structure of this decomposition, the renormalised potential takes the form
where \(V_j(B,\varphi )\) only depends on \(\varphi |_B\). As in Sect. 3.1, we restrict the domain of \(V_j(B)\) to \(X_j(B)\), i.e., the constant fields on B. The final potential obtained as \(V_{N+1}\) in (2.14) will instead be denoted by \(V_{N,N}\) since it is indexed by the final block \(\Lambda \in {\mathcal {B}}_N\), i.e., \(V_{N,N}(\varphi ) = V_{N,N}(\Lambda _N,\varphi )\), and \(\varphi \) can be seen as an external field. Then each \(V_j(B)\) can be identified with a \(2\pi \)-periodic function on \(\mathbb {R}\) (and analogously for \(V_{N,N}\)). For any such function \(F: S^1 \rightarrow \mathbb {R}\), we use the norm
where our convention for the Fourier coefficients of F is \({\hat{F}}(q) = (2\pi )^{-1} \int _0^{2\pi } F(\varphi ) e^{iq\varphi } \, d\varphi \). We write
for an arbitrary \(B \in {\mathcal {B}}_j\) (the definition is independent of B). Except for the weight w(q), the norm (4.5) is the one used in [16, 48].
Proposition 4.1
Let \(j<N\). Assume that \(\Vert V_j- {\hat{V}}_j(0)\Vert \) is sufficiently small. Then the renormalised potential satisfies
Moreover, for the last step \(j=N\),
The derivation of this proposition is postponed to Sect. 4.2. We now state consequences of this proposition and prove Theorem 1.2 using these.
Corollary 4.2
For every \(\beta < \sigma /(4\log L)\) and \(\kappa< L^{2} e^{-\sigma /2\beta } < 1\), for all \(V_0-{\hat{V}}_0\) sufficiently small,
and
Proof
Fix \(\eta >0\) small and set \(\kappa = L^2 e^{-(1-\eta )\sigma /2\beta } < 1\). The bound (4.7) implies that for \(\Vert V_0-{\hat{V}}_0(0)\Vert \) sufficiently small depending on \(\eta ,\beta ,\eta \),
Then (4.9) follows by iterating this bound, and (4.10) follows from this and (4.8). \(\square \)
Corollary 4.3
Let \(\beta < \sigma /(4 \log L)\) and let \(\varepsilon = \beta L^{-2N}\). Then the variance of \(F = \sum _{x \in \Lambda _N} \varphi _x\) under the Gibbs measure \(\mu \) defined in (1.2) is given by
Proof
Throughout the following proof, we denote by \(C = (-\beta \Delta _H+\varepsilon Q_N)^{-1}\) the full covariance of the hierarchical Gaussian free field. By completion of the square, and using that  ,
,

With \(F(\varphi ) = \sum _x \varphi _x\), we get by translating the measure by  that
that

By Corollary 4.2 and the fact that the norm controls the second derivatives,
where \(V_{N,N}''\) is the second derivative of the function \(V_{N,N}(\Lambda _N) \circ i_{\Lambda _N}: \mathbb {R}\rightarrow \mathbb {R}\). Finally, and using that  as well as that \(\varepsilon = \beta L^{-2N}\),
as well as that \(\varepsilon = \beta L^{-2N}\),
This completes the proof. \(\square \)
Proof of Theorem 1.2
We start by proving the lower bound on the spectral gap by applying Corollary 2.2. Thanks to the hierarchical structure, the spins are constant in the blocks at any given scale j, and Assumptions (A2) and (A3) always hold. Assumption (A1) follows from Corollary 4.2 which implies that for \(j \leqslant N\)
This implies the bound (3.5) with
The equivalent of (3.7) is
Therefore Assumption (A1) in (2.16) holds with \(\varepsilon _j = s L^{2j} = \kappa ^j \Vert V_0-{\hat{V}}_0(0)\Vert \). With \(\delta _j\) defined as in (2.22), it follows that
Applying Corollary 2.2, we get that the measure \(\mu \) satisfies a Brascamp–Lieb inequality with matrix
This implies immediately the asserted lower bound on the spectral gap, i.e., \(\gamma _N \geqslant c\varepsilon \).
Finally, the upper bound on the spectral gap follows readily from Corollary 4.3. Choosing as test function \(F = \sum _{x \in \Lambda _N} \varphi _x\), we have \({{\mathbb {E}}} _\mu (\nabla F, \nabla F) = |\Lambda _N|\) and (4.12) implies
This completes the proof. \(\square \)
4.2 Proof of Proposition 4.1
The proof of Proposition 4.1 follows as in [16, Chapter 3], with small modifications. Throughout Sect. 4.2, the full covariance matrix \((-\beta \Delta _H+\varepsilon Q_N)^{-1}\) does not play a role and we write \(C = C_j\) for a fixed scale j. More generally, we drop the scale index j and write \(+\) in place of \(j+1\). We write \(B_+\) for a fixed block in \({\mathcal {B}}_+\) and B for the blocks in \({\mathcal {B}}(B_+)\).
We need the following properties of the norm (4.5). Since \(w(p+q) \leqslant w(p)w(q)\), i.e.,
the norm (4.5) satisfies the product property
As a consequence, for any \(F: S^1 \rightarrow \mathbb {R}\) with \(\Vert F\Vert \) small enough,
Lemma 4.4
For \(F:S^1 \rightarrow \mathbb {R}\) with \({\hat{F}}(0) = 0\) and \(\Vert F\Vert <\infty \), and for \(x\in \Lambda \),
Proof
By (2.3), under the expectation \(\mathbb {E}_C\), each \(\zeta _x\) is a Gaussian random variable with variance \(\sigma /\beta \). Therefore
This gives
Since by assumption \({\hat{F}}(0) = 0\), we obtain
as claimed. \(\square \)
Proof of Proposition 4.1
We may assume that \({\hat{V}}(0)=0\). We fix \(B_+ \in {\mathcal {B}}_+\) and use B for the blocks in \({\mathcal {B}}(B_+)\). By definition of the hierarchical model, the Gaussian field \(\zeta \) with covariance \(C=C_j\) is constant in any block \(B \in {\mathcal {B}}_j\) and we thus write \(\zeta _B\) for \(\zeta _x\) with \(x\in B\). We then start from
where \(X\subset B_+\) denotes that X is a union of blocks \(B\in {\mathcal {B}}(B_+)\). The term with \(|X|=0\) is simply 1. By (4.27) and (4.25), the terms with \(|X|=1\) are bounded by
By (4.27), using that the \(\zeta _B\) are independent for different blocks B and the product property of the norm, the terms with \(|X|>1\) give
In summary, for \(\Vert V\Vert \) small enough, we get
Finally, by (4.26),
as needed. \(\square \)
4.3 Proof of Theorem 1.3
We will now reduce the result for the Discrete Gaussian model to that for the Sine-Gordon model. For this, we carry out an initial renormalisation group step by hand, resulting in an effective Sine-Gordon potential for the Discrete Gaussian model. This strategy for the Discrete Gaussian model (and more general models) goes back to [32].
First, recall that the covariance of the hierarchical GFF can be written as
where \(C_0 = \frac{1}{\beta } Q_0\) and where \(Q_0\) is simply the identity matrix on \(\mathbb {R}^\Lambda \). Therefore, by the convolution property of Gaussian measures,
where \(A \propto B\) denotes that A / B is independent of \(\sigma \), and where the Gaussian expectation applies to the field \(\varphi \). We define the effective single-site potential \(V(\psi )\) for \(\psi \in \mathbb {R}\) by
The potential V is \(2\pi \)-periodic as in the Sine-Gordon model. This is where the \(2\pi \)-periodicity of the Discrete Gaussian Model is convenient. For \(\psi \in \mathbb {R}\), we also define a probability measure \(\mu _\psi \) on \(2\pi \mathbb {Z}\) by
For \(\varphi \in \mathbb {R}^\Lambda \), we further set \(\mu _\varphi = \prod _{x\in \Lambda } \mu _{\varphi _x}\) with \(\mu _{\varphi _x}\) as in (4.39) with \(\psi =\varphi _x\). With this notation, in summary, we have the representation
Denote by \(\mu _r(d\varphi )\) the probability measure on \(\mathbb {R}^\Lambda \) of the Sine-Gordon model with potential \(V(\varphi )\) defined by (4.38) with \(C_{\geqslant 0}\) replaced by \(C_{\geqslant 1}\).
In the next two lemmas, we verify that V satisfies the conditions of Theorem 1.2 provided \(\beta \) is sufficiently small, and that the probability measure \(\mu _\psi \) satisfies a spectral gap inequality on \(2\pi \mathbb {Z}\), with constant uniform in \(\psi \). It is clear from the definition (4.38) that V is \(2\pi \)-periodic.
Lemma 4.5
For \(\beta >0\) small enough, V is smooth with \(\Vert V-{\hat{V}}(0)\Vert =O(e^{-1/(2\beta )})\).
Proof
The function \(F = e^{-V}\) is \(2\pi \)-periodic, and subtracting a constant from V, we can normalise F such that \({\hat{F}}(0)=1\). Note that subtraction of a constant does not change \(V-{\hat{V}}(0)\). The Fourier coefficients of F are then given by
where the constant C and the last equality are due to the normalisation \({\hat{F}}(0)=1\). It follows that
By (4.26), it then also follows that
Since \(\Vert V-{\hat{V}}(0)\Vert \leqslant \Vert V\Vert \), this clearly implies the claim. \(\square \)
Corollary 4.6
For \(\beta >0\) sufficiently small, the measure \(\mu _r\) has inverse spectral gap \(O(1/\varepsilon )\).
Proof
The proof is essentially the same as that of Theorem 1.2. The only difference compared to Theorem 1.2 is that we replaced \(C_{\geqslant 0}\) by \(C_{\geqslant 1}\) which does not change the conclusion. For small \(\beta \), the assumption on V is satisfied thanks to Lemma 4.5. \(\square \)
The following lemma can be proved, e.g., using the path method for spectral gap inequalities; we postpone the elementary proof to Appendix C.
Lemma 4.7
For any \(\beta >0\), there exists a constant \(C_\beta \) such that the measure \(\mu _\psi \) on \(2\pi \mathbb {Z}\) has a spectral gap uniformly in \(\psi \in \mathbb {R}\),
With the above ingredients, the proof can now be completed as follows.
Proof of Theorem 1.3
We start with the proof of the lower bound on the spectral gap. By (4.41), the variance of a function \(F: (2\pi \mathbb {Z})^\Lambda \rightarrow \mathbb {R}\) under the Discrete Gaussian measure can be written as
By Corollary 4.6, the measure \(\mu _r\) has an inverse spectral gap bounded by \(O(1/\varepsilon )\). By Lemma 4.7 and the tensorisation principle for spectral gaps, the product measure \(\mu _\varphi = \prod _{x\in \Lambda } \mu _{\varphi _x}\) has a spectral gap uniformly bounded by \(C_\beta \). It follows that
where the Dirichlet form introduced in (1.16) has been denoted by
We also set
Then the second term on the right-hand side is bounded as follows. Since with respect to the measure \(\mu _\varphi \) for fixed \(\varphi \), the \(\sigma _x\) are independent, we have
where we used the following inequality, which follows from \({{\,\mathrm{Var}\,}}_{\mu _{\varphi _x}}(\sigma _x) \leqslant C_\beta \) and (4.45):
Using that \({{\mathbb {D}}} (F) = \sum _{x\in \Lambda } \mathbb {E}_{\mu _r}({{\mathbb {D}}} _{x,\mu _\varphi }(F))\), in summary, we conclude that
and therefore that the inverse spectral gap obeys \(1/\gamma = O(1/\varepsilon )\).
For the matching upper bound on the spectral gap, we use the test function \(F = \sum _{x\in \Lambda } \sigma _x\), analogously to the Sine-Gordon case. For any \(\psi \in \mathbb {R}\) and \(t \in \mathbb {R}\),
Let \(u = \sum _{y} [C_{\geqslant 1}]_{xy}\) (which is independent of x). It follows that
Since \(\sum _y [C_0]_{xy} = [C_0]_{xx}=1/\beta \), note that
As in the proof of Corollary 4.3, it follows that
Since \({{\mathbb {D}}} (F) = |\Lambda _N|\), this completes the proof of \(\gamma \leqslant \varepsilon (1+O(\kappa ^N))\) and therefore the proof of the theorem. \(\square \)
References
Abdesselam, A., Chandra, A., Guadagni, G.: Rigorous quantum field theory functional integrals over the p-adics I: anomalous dimensions. Preprint arXiv:1302.5971
Bakry, D.: Functional inequalities for Markov semigroups. In: Probability Measures on Groups: Recent Directions and Trends. Tata Institute of Fundamental Research, Mumbai, pp. 91–147 (2006)
Bakry, D., Émery, M.: Diffusions hypercontractives. In: Séminaire de probabilités, XIX, 1983/84, volume 1123 of Lecture Notes in Mathematics. Springer, Berlin, pp. 177–206 (1985)
Bauerschmidt, R., Bodineau, T.: A very simple proof of the LSI for high temperature spin systems. J. Funct. Anal. 276(8), 2582–2588 (2019)
Bauerschmidt, R., Brydges, D.C., Slade, G.: Scaling limits and critical behaviour of the 4-dimensional \(n\)-component \(\vert \phi \vert ^4\) spin model. J. Stat. Phys. 157(4–5), 692–742 (2014)
Bauerschmidt, R., Brydges, D.C., Slade, G.: Critical two-point function of the 4-dimensional weakly self-avoiding walk. Commun. Math. Phys. 338(1), 169–193 (2015)
Bauerschmidt, R., Brydges, D.C., Slade, G.: Logarithmic correction for the susceptibility of the 4-dimensional weakly self-avoiding walk: a renormalisation group analysis. Commun. Math. Phys. 337(2), 817–877 (2015)
Bauerschmidt, R., Brydges, D.C., Slade, G.: A renormalisation group method. III. Perturbative analysis. J. Stat. Phys. 159(3), 492–529 (2015)
Bauerschmidt, R., Brydges, D.C., Slade, G.: Introduction to a Renormalisation Group Method. Lecture Notes in Mathematics. Springer, to appear. Preprint http://www.statslab.cam.ac.uk/~rb812/
Benfatto, G., Gallavotti, G., Jauslin, I.: Kondo effect in a fermionic hierarchical model. J. Stat. Phys. 161(5), 1203–1230 (2015)
Bleher, P.M., Sinai, J.G.: Investigation of the critical point in models of the type of Dyson’s hierarchical models. Commun. Math. Phys. 33(1), 23–42 (1973)
Bodineau, T., Helffer, B.: The log-Sobolev inequality for unbounded spin systems. J. Funct. Anal. 166(1), 168–178 (1999)
Bodineau, T., Helffer, B.: Correlations, spectral gap and log-Sobolev inequalities for unbounded spins systems. In: Differential Equations and Mathematical Physics (Birmingham, AL, 1999), volume 16 of AMS/IP Studies in Advanced Mathematics. American Mathematical Society, Providence, RI, pp. 51–66 (2000)
Brascamp, H.J., Lieb, E.H.: On extensions of the Brunn–Minkowski and Prékopa–Leindler theorems, including inequalities for log concave functions, and with an application to the diffusion equation. J. Funct. Anal. 22(4), 366–389 (1976)
Brydges, D., Evans, S.N., Imbrie, J.Z.: Self-avoiding walk on a hierarchical lattice in four dimensions. Ann. Probab. 20(1), 82–124 (1992)
Brydges, D.C.: Lectures on the renormalisation group. In: Statistical Mechanics, volume 16 of IAS/Park City Mathematical Series. American Mathematical Society, Providence, RI, pp. 7–93 (2009)
Brydges, D.C., Slade, G.: A renormalisation group method. I. Gaussian integration and normed algebras. J. Stat. Phys. 159(3), 421–460 (2015)
Brydges, D.C., Slade, G.: A renormalisation group method. II. Approximation by local polynomials. J. Stat. Phys. 159(3), 461–491 (2015)
Brydges, D.C., Slade, G.: A renormalisation group method. IV. Stability analysis. J. Stat. Phys. 159(3), 530–588 (2015)
Brydges, D.C., Slade, G.: A renormalisation group method. V. A single renormalisation group step. J. Stat. Phys. 159(3), 589–667 (2015)
Caputo, P., Martinelli, F., Simenhaus, F., Toninelli, F.L.: “Zero” temperature stochastic 3D Ising model and dimer covering fluctuations: a first step towards interface mean curvature motion. Commun. Pure Appl. Math. 64(6), 778–831 (2011)
Crawford, N., De Roeck, W.: Stability of the uniqueness regime for ferromagnetic Glauber dynamics under don-reversible perturbations. Ann. Henri Poincaré 19(9), 2651–2671 (2018)
Dimock, J., Hurd, T.R.: A renormalization group analysis of the Kosterlitz–Thouless phase. Commun. Math. Phys. 137(2), 263–287 (1991)
Dimock, J., Hurd, T.R.: Construction of the two-dimensional sine-Gordon model for \(\beta < 8\pi \). Commun. Math. Phys. 156(3), 547–580 (1993)
Dimock, J., Hurd, T.R.: Sine-Gordon revisited. Ann. Henri Poincaré 1(3), 499–541 (2000)
Ding, J., Lubetzky, E., Peres, Y.: The mixing time evolution of Glauber dynamics for the mean-field Ising model. Commun. Math. Phys. 289(2), 725–764 (2009)
Ding, J., Lubetzky, E., Peres, Y.: Mixing time of critical Ising model on trees is polynomial in the height. Commun. Math. Phys. 295(1), 161–207 (2010)
Dyson, F.J.: Existence of a phase-transition in a one-dimensional Ising ferromagnet. Commun. Math. Phys. 12(2), 91–107 (1969)
Falco, P.: Kosterlitz–Thouless transition line for the two dimensional Coulomb gas. Commun. Math. Phys. 312(2), 559–609 (2012)
Falco, P.: Critical exponents of the two dimensional Coulomb gas at the Berezinskii–Kosterlitz–Thouless transition (2013). Preprint arXiv:1311.2237
Feldman, J., Magnen, J., Rivasseau, V., Sénéor, R.: Construction and Borel summability of infrared \(\Phi ^{4}\_{4}\) by a phase space expansion. Commun. Math. Phys. 109(3), 437–480 (1987)
Fröhlich, J., Spencer, T.: The Kosterlitz–Thouless transition in two-dimensional abelian spin systems and the Coulomb gas. Commun. Math. Phys. 81(4), 527–602 (1981)
Gawędzki, K., Kupiainen, A.: Triviality of \(\varphi ^{4}\_{4}\) and all that in a hierarchical model approximation. J. Stat. Phys. 29(4), 683–698 (1982)
Gawędzki, K., Kupiainen, A.: Massless lattice \(\varphi ^{4}\_{4}\) theory: rigorous control of a renormalizable asymptotically free model. Commun. Math. Phys. 99(2), 197–252 (1985)
Gawędzki, K., Kupiainen, A.: Asymptotic freedom beyond perturbation theory. Phénomènes critiques. systèmes aléatoires, théories de jauge, Part I, II (Les Houches, 1984), pp. 185–292. North-Holland, Amsterdam (1986)
Halperin, B., Hohenberg, P.: Theory of dynamical critical phenomena. Rev. Mod. Phys. 49, 435–479 (1977)
Hara, T.: A rigorous control of logarithmic corrections in four-dimensional \(\phi ^4\) spin systems. I. Trajectory of effective Hamiltonians. J. Stat. Phys. 47(1–2), 57–98 (1987)
Hara, T., Tasaki, H.: A rigorous control of logarithmic corrections in four-dimensional \(\phi ^4\) spin systems. II. Critical behavior of susceptibility and correlation length. J. Stat. Phys. 47(1–2), 99–121 (1987)
Helffer, B.: Semiclassical analysis, Witten Laplacians, and statistical mechanics, volume 1 of Series in Partial Differential Equations and Applications. World Scientific Publishing Co., Inc, River Edge, NJ (2002)
Helffer, B., Sjöstrand, J.: On the correlation for Kac-like models in the convex case. J. Stat. Phys. 74(1–2), 349–409 (1994)
Ledoux, M.: Logarithmic Sobolev inequalities for unbounded spin systems revisited. In: Séminaire de Probabilités, XXXV, volume 1755 of Lecture Notes in Mathematics. Springer, Berlin, pp. 167–194 (2001)
Levin, D.A., Luczak, M.J., Peres, Y.: Glauber dynamics for the mean-field Ising model: cut-off, critical power law, and metastability. Probab. Theory Relat. Fields 146(1–2), 223–265 (2010)
Levin, D.A., Peres, Y., Wilmer, E.L.: Markov chains and mixing times. American Mathematical Society, Providence, RI. With a chapter by James G. Propp and David B. Wilson (2009)
Lubetzky, E., Martinelli, F., Sly, A., Toninelli, F.L.: Quasi-polynomial mixing of the 2D stochastic Ising model with “plus” boundary up to criticality. JEMS 15(2), 339–386 (2013)
Lubetzky, E., Sly, A.: Critical Ising on the square lattice mixes in polynomial time. Commun. Math. Phys. 313(3), 815–836 (2012)
Lubetzky, E., Sly, A.: Information percolation and cutoff for the stochastic Ising model. J. Am. Math. Soc. 29(3), 729–774 (2016)
Marchetti, D.H.U., Klein, A., Perez, J.F.: Power-law falloff in the Kosterlitz–Thouless phase of a two-dimensional lattice Coulomb gas. J. Stat. Phys. 60(1–2), 137–166 (1990)
Marchetti, D.H.U., Perez, J.F.: The Kosterlitz–Thouless phase transition in two-dimensional hierarchical Coulomb gases. J. Stat. Phys. 55(1–2), 141–156 (1989)
Martinelli, F.: Lectures on Glauber dynamics for discrete spin models. In: Lectures on Probability Theory and Statistics (Saint-Flour, 1997), volume 1717 of Lecture Notes in Mathematics. Springer, Berlin, pp. 93–191 (1999)
Martinelli, F., Olivieri, E.: Approach to equilibrium of Glauber dynamics in the one phase region. I. The attractive case. Commun. Math. Phys. 161(3), 447–486 (1994)
Martinelli, F., Olivieri, E.: Approach to equilibrium of Glauber dynamics in the one phase region. II. The general case. Commun. Math. Phys. 161(3), 487–514 (1994)
Menz, G., Otto, F.: Uniform logarithmic Sobolev inequalities for conservative spin systems with super-quadratic single-site potential. Ann. Probab. 41(3B), 2182–2224 (2013)
Yoshida, N.: The log-Sobolev inequality for weakly coupled lattice fields. Probab. Theory Relat. Fields 115(1), 1–40 (1999)
Zeitouni, O.: Branching random walks and Gaussian fields. In: Probability and Statistical Physics in St. Petersburg, volume 91 of Proceedings of Symposia in Pure Mathematics. American Mathematical Society, Providence, RI, pp. 437–471 (2016)
Acknowledgements
We warmly thank Tom Spencer for his contributions to this paper; his input has been crucial. We also thank David Brydges and Gordon Slade for a number of important discussions and for careful reading and many helpful comments on a preliminary version of this paper. Figure 1 is taken from [9]. We acknowledge the support of ANR-15-CE40-0020-01 grant LSD.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. Salmhofer.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Estimates for Log-Concave Measures
Let X be a finite-dimensional vector space with inner product \((\cdot ,\cdot )\) and Lebesgue measure m. Choosing an orthonormal basis, we may identify X with \(\mathbb {R}^k\) for some k. Using this identification or the inner product structure directly, the gradient, Laplacian, and Hessian of a function \(F: X \rightarrow \mathbb {R}\) are defined. Assume that \(H: X \rightarrow \mathbb {R}\) satisfies \({{\,\mathrm{Hess}\,}}H > c \mathrm {id}\) uniformly for a constant \(c>0\). Let \(\mu \) be the probability measure on X with density proportional to \(e^{-H}\) with respect to m. Let L be the (positive) self-adjoint generator of the Langevin dynamics leaving \(\mu \) invariant, i.e., for smooth \(F: X \rightarrow \mathbb {R}\),
where \(\nabla \) and \(\Delta \) are the gradient and Laplacian on X.
In Sects. 2 and 3, we make use of the Helffer–Sjöstrand representation and the Brascamp–Lieb inequality. Define the operator \({\mathcal {L}}\) (Witten Laplacian) on \(D \otimes X \subset L^2(\mu ) \otimes X\) by
where \(D \subset L^2(\mu )\) is the domain on which the operator L is self-adjoint. Then one has the Helffer–Sjöstrand representation [40] (see also [39]) for the covariance of two random variables \(F,G: X \rightarrow \mathbb {R}\).
Theorem A.1
(Helffer–Sjöstrand representation). For sufficiently smooth \(F,G: X \rightarrow \mathbb {R}\),
In particular, one can easily obtain the Brascamp–Lieb inequality [14] from this representation.
Theorem A.2
(Brascamp–Lieb inequality). For sufficiently nice \(F: X \rightarrow R\),
In particular, if \({{\,\mathrm{Hess}\,}}H(\varphi ) \geqslant Q\) uniformly in \(\varphi \in X\), then for any \(f\in X\),
Proof of Theorem 3.1 and of Lemmas 3.5 and 3.12
In this appendix, we translate the results from [9] to assume the form stated in Theorem 3.1, and we prove two elementary lemmas for the sequences \((\varepsilon _j)\) and \((\mu _j)\).
Proof of Theorem 3.1
First, since our constants are allowed to depend on L and since we are only considering derivatives of finite order, the constants \(\ell _0\) and \(k_0\) that appear in the definitions of the versions of \(\ell _j\) and \(h_j\) in [9] are insignificant for our estimates here and we therefore drop them.
The critical point \(\nu _c = \nu _c(g)\) is chosen as in [9, Theorem 4.2.1]. Moreover, given \(t = \nu -\nu _c(g) > 0\) and \(g=g_0>0\) small, the mass parameter \(m^2>0\) and \(\nu _0= \nu -m^2\) are determined as in the proof of [9, Theorem 4.2.1]. In [9], the renormalisation group flow is defined in terms of the decomposition of \((-\Delta _H+m^2)^{-1}\) in terms of the orthogonal projections \(P_j\) as in (2.2), namely as
where we here write \({\tilde{C}}_j = {\tilde{\lambda }}_j P_j\) for the covariances denoted by \(C_j\) in [9] to distinguish them from the covariances \(C_j = \lambda _jQ_j\) that we primarily use in this paper. In terms of these, we also have
To translate between the two decompositions, note that \(\sum _{j=0}^k \lambda _j Q_j =\sum _{j=1}^k {\tilde{\lambda }}_j P_j + {\tilde{\lambda }}_{j+1} Q_j\), i.e.,
In [9, Theorem 6.2.1], it is shown that there is a sequence \(({\tilde{g}}_j,{\tilde{\nu }}_j,{\tilde{u}}_j)\) and a sequence of functions \({\tilde{K}}_j\), with \({\tilde{g}}_0 = g_0 = g\), \({\tilde{\nu }}_0 = \nu _0\), \({\tilde{u}}_0=0\) and \({\tilde{K}}_0=0\), and with estimates as stated in that proposition, such that
where again we use tildes to refer to the quantities as defined in [9]. Therefore, using the relation between the two decompositions \((C_j)\) and \(({\tilde{C}}_j)\), our effective potential \(V_j\) as defined in (3.2) in terms of the decomposition \((C_j)\) is given by
Differently from the usual renormalisation group steps, the expectation on the right-hand side does not involve any reblocking, i.e., the size of the blocks is the same on both sides of the equality. This is the same situation as in the last renormalisation group step in [9, Proposition 6.2.2]. In [9], the last renormalisation group step is only applied at the last scale, but we can here apply it at any scale. More precisely, by [9, Proposition 6.2.2 and Remark 10.7.2] with the covariance \({\hat{C}}\) replaced by \({\hat{C}} = {\tilde{\lambda }}_{j+1} Q_j\) and the scale N replaced by j, we obtain
as in (3.11). Moreover, the bounds on the \(T_\infty (h)\)-norm and the \(T_0(\ell )\)-norm of \({\hat{K}}\) stated in [9, Proposition 6.2.2 and Remark 10.7.2] directly translate directly to the estimates (3.13) and (3.14).
Finally, (3.15) is a consequence of [9, Corollary 6.2.2], together with the definition of \(\nu _c(g)\) below [9, (6.2.24)] and [9, Theorem 4.2.1] for the asymptotics of \(m^2 = 1/\chi \). \(\square \)
Finally, we prove the elementary estimates for the sequences \(\varepsilon _j\) and \(\mu _j\) stated in Lemmas 3.5 and 3.12.
Proof of Lemma 3.5
By decreasing \(\varepsilon _j\) to \(\frac{1}{5} g_j^{1/2}\) if necessary, we can assume that \(\varepsilon _{j+1} = \varepsilon _j - \gamma _j\varepsilon _j^2\) with \(\gamma _j=O(\vartheta _j^2)\). To obtain a lower bound on the sequence \((\varepsilon _j)\), we may also increase the \(\gamma _j\) and assume that \(\gamma _j = \gamma \vartheta _j^2\) for some \(\gamma =O(1)\). The solution to this recursion behaves as
This follows, e.g., from [9, Proposition 6.1.3 and (6.1.9)]. Likewise, the sequence \(g_j\) obeys
Therefore
as needed. \(\square \)
Proof of Lemma 3.12
We recall the definition \(\vartheta _j= 2^{-(j-j_m)_+}\) and set \(\mu _j = L^{2j} \nu _j\). By [9, Proposition 8.3.1], the sequence \(\mu _j\) satisfies \(\mu _j= O(\vartheta _j g_j)\) and
where \(\eta _j=O(1)\). Let \(\eta _{\geqslant j} = \sum _{k=j}^\infty L^{-2(k-j)} \eta _k\) and \({\hat{\mu }}_j = \mu _j+\eta _{\geqslant j}g_j\). Then \({\hat{\mu }}_j = O(g_j)\) and
Iterating this equation together with the boundedness of \({\hat{\mu }}_j\) implies
We will repeatedly use that (see for example [9, Exercise 6.1.4])
Hence
We now bound the sum on the last right-hand side. By definition and rearranging sums,
The last sum can be rearranged and bounded as
By [9, (5.3.10) and (5.3.7)], there exists a constant \(\delta \) independent of n such that \((1-L^{-2})^{-1}\eta _l \leqslant \delta \frac{n+2}{n+8} \beta _l\). Therefore
where the last inequality again follows from [9, Exercise 6.1.4]. This concludes the proof of the first inequality in (3.62). The second inequality is immediate from \(\mu _j = O(\vartheta _j g_j)\) and [9, Exercise 6.1.4]. \(\square \)
Spectral Gap Inequality for Single-Spin Discrete Gaussian Measure
In this appendix, we prove Lemma 4.7. Thus we prove that for any \(\beta >0\), there exists a constant \(C_\beta \) such that the measure \(\mu _\psi \) on \(\mathbb {Z}\) defined in (4.39) has a spectral gap uniformly in \(\psi \in \mathbb {R}\),
Proof
It is enough to consider \(\psi \in [0, 2\pi ]\). To simplify notation, we assume in this proof that \( \mu _\psi \) is supported on \(\mathbb {Z}\) up to rescaling n by a factor \(2 \pi \), i.e.,
We are going to apply the path method to evaluate the gap [43]. Thus we write
where we used the Cauchy–Schwarz inequality in the last inequality and Fubini to change the order of the summations. The Dirichlet form in (4.45) can be rewritten as
Thus we deduce from (C.3) that
For \(i \geqslant 0\), the maximum can be bounded by
where we used that \(c_\beta = \sum _n \mu _\psi (n) |n|\) is a constant. From (C.2), we see that the following bound holds uniformly in \(\psi \in [0, 2 \pi ]\):
Together, the previous two inequalities imply that the maximum over \(i\geqslant 0\) in (C.5) is bounded. The case \( i<0\) can be controlled in the same way. This completes the proof of Lemma 4.7. \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bauerschmidt, R., Bodineau, T. Spectral Gap Critical Exponent for Glauber Dynamics of Hierarchical Spin Models. Commun. Math. Phys. 373, 1167–1206 (2020). https://doi.org/10.1007/s00220-019-03553-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-019-03553-x