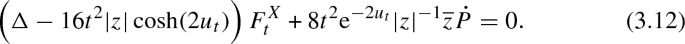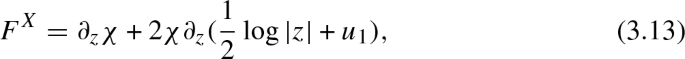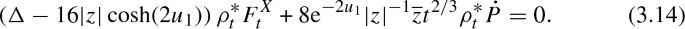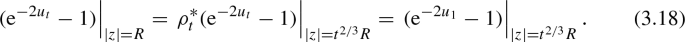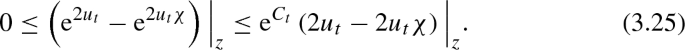Skip to main content
SpringerLink
Log in

Exponential Decay for the Asymptotic Geometry of the Hitchin Metric

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

We consider Hitchin’s hyperkähler metric \(g_{L^2}\) on the SU(n)-Hitchin moduli space over a compact Riemann surface. We prove that the difference between the metric \(g_{L^2}\) and a simpler “semiflat” hyperkähler metric \(g_{\mathrm {sf}}\) is exponentially-decaying along generic rays in the Hitchin moduli space, as conjectured by Gaiotto–Moore–Neitzke.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. For SU(2), we take \(({\overline{\partial }}_E, \varphi )\) in any non-degenerate fiber. For SU(n), the genericity condition is defined in Definition 4.1.

  2. Here, the compatibility condition is \(F_{D({\overline{\partial }}_{{{\,\mathrm{Det}\,}}E}, h_{{{\,\mathrm{Det}\,}}E})}=0\).

  3. The hyperkähler metric \(g_{L^2}\) on \({\mathcal {M}}\) determines and is completely determined by a twisted fiber-wise holomorphic symplectic structure on the twistor space \({\mathcal {Z}}={\mathcal {M}}\times {{\mathbb {C}}}{{\mathbb {P}}}^1\). The integral relation is actually formulated in terms of certain “holomorphic Darboux coordinates” \({\mathcal {X}}_\gamma \) on the twistor space \({\mathcal {Z}}={\mathcal {M}}\times {{\mathbb {C}}}{{\mathbb {P}}}^1\)

  4. In the SU(2) case, \(\Gamma _b=H^{\mathrm {odd}}_1(\Sigma _b, {\mathbb {Z}})\), the sublattice of \(H_1(\Sigma _b,{\mathbb {Z}})\) which is odd under the exchange of the two sheets of \(\Sigma \). For SU(n), \(\Gamma _b = H_1(\Sigma _b, {\mathbb {Z}})_{\sigma }\), a sublattice defined in (2.36).

  5. The function \(K_0(x)\) solves the modified Bessel differential equation \(x^2 y''(x) + x y'(x) - x^2 y(x) =0\) on \((0, \infty )\). Within the two-dimensional family of solutions, the function \(K_0(x)\) is determined (up to multiplication by constant) by the property that \(\lim _{x \rightarrow \infty } K_0(x)=0\). It is defined by the integral \(K_0(x) = \int _0^\infty \frac{\cos (xt)}{\sqrt{t^2+1}} \mathrm {d}t\).

  6. Let \(\Gamma \rightarrow {\mathcal {B}}'\) be the lattice bundle with fiber \(\Gamma _b\). Then, \(\Omega : \Gamma \rightarrow {\mathbb {Z}}\). Given a section \(\gamma \) of \(\Gamma \rightarrow {\mathcal {B}}'\), the function \(\Omega (\gamma ; \; \cdot \;): {\mathcal {B}}' \rightarrow {\mathbb {Z}}\) is typically not continuous. The value jumps at real-codimension-1 walls in \({\mathcal {B}}'\) and satisfies the Kontsevich–Soibelman wall-crossing formula.

  7. This special Kähler metric is not unique; we have the freedom to rescale it by a constant.

  8. The statement \(\nabla ^{GM}_{{\dot{b}}} \lambda = {{\dot{\tau }}}\) appears in [HHP10, Proposition 8.2], where \(\nabla ^{GM}\) is the Gauss–Manin connection.

  9. Given a Higgs bundle \(({\overline{\partial }}_E, \varphi )\), let \({\mathcal {L}}\rightarrow \Sigma _b\) be the associated spectral data. To see the difficulty in passing from \(({\dot{\eta }}, {\dot{\varphi }})\) to \({\dot{\xi }}\), note that the holomorphic line bundle \({\mathcal {L}}\) arises from \(({\overline{\partial }}_E, \varphi )\) as follows: the underlying complex line bundle \(L \subset \pi ^*E\) is the eigenline bundle of the tautological eigenvalue of \(\pi ^* \varphi \) acting on \(\pi ^*E \rightarrow \Sigma _b\). The holomorphic structure on \({\mathcal {L}}=(L, {\overline{\partial }}_L)\) is from the holomorphic structure of the ambient holomorphic bundle \(\pi ^*{{\mathcal {E}}}\rightarrow \Sigma _b\). Now, given a deformation \(({\dot{\eta }}, {\dot{\varphi }})\) note that the section \(L_\epsilon \subset \pi ^*E\) moves in the family \(\varphi +\epsilon {\dot{\varphi }}\), consequently, we first need to identify \(L_\epsilon \) with a common fixed complex line bundle L. We can avoid this in the case where \({\dot{\varphi }}=0\). In this case, the deformation \({\dot{\xi }}\) is given in terms of \({\dot{\eta }}\) by \(\pi ^*{\dot{\eta }} \cdot s = {\dot{\xi }} s\), where \(\pi ^*{\dot{\eta }}\) is locally a (0, 1)-form valued in \({{\mathfrak {s}}}{{\mathfrak {l}}}(n,{\mathbb {C}})\) acting by matrix multiplication on any section s of L, while \({\dot{\xi }}\) is locally a (0, 1)-form acting by scalar multiplication on s.

  10. The Gauss–Manin connection is considerably more general. Consider a family of algebraic varieties \({\mathcal {X}} \rightarrow {\mathcal {B}}\) where the fibers \(\pi ^{-1}(b)=X_b\) are all diffeomorphic. Fixing \(k \in {\mathbb {N}}\), the associated deRham cohomology groups \(H^k_{dR}(X_b)\) are all isomorphic. The Gauss–Manin connection is a connection on the vector bundle \({\mathcal {H}} \rightarrow {\mathcal {B}}\) whose fiber over b is \({\mathcal {H}}_b=H^k_{dR}(X_b)\). As such, the Gauss–Manin connection allows us to identify nearby fibers of \({\mathcal {H}}\).

    For the SU(n)-Hitchin moduli space, the relevant family of varieties is the family of spectral curves \(\Sigma _b\) and the relevant cohomology groups are \({\mathcal {H}}_b=H^{0,1}(\Sigma _b)_\sigma \), since \(T \mathrm {Prym}(\Sigma _b) \simeq H^0(\Sigma _b, K_{\Sigma _b})_\sigma ^* \simeq H^{0,1}(\Sigma _b)_\sigma \). We view \({\mathcal {M}}' \simeq {\mathcal {H}}/\Gamma \) where \(\Gamma \) is a local system with fiber \(\Gamma _b\).

  11. The fact that \({{\dot{\nu }}}^X_t\) satisfies the complex variation equation reduces to the fact that

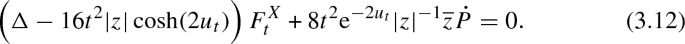
    figure a

    We can reduce this to the case \(t=1\) which appears in [DN19, Eq. 10.15] in which the deformation associated to \({\dot{P}}\) is

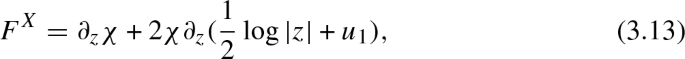
    figure b

    Define \(\rho _t(z) =t^{-2/3} z\). One can check that \(\rho _t^* u_t = u_1\). Because of this, by pulling back the expression (3.12) by \(\rho _t\) and dividing by \(t^{4/3}\), we get

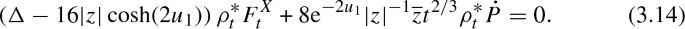
    figure c

    Thus the function \(F_t^X\) in (3.13) is defined so that \(\rho _t^* F^X_t\) solves the complex variation for the deformation \(t^{2/3} \rho _t^*{\dot{P}}\).

  12. This is because

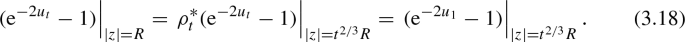
    figure d

  13. For a fixed value of t, once we know that

    figure e

    we immediately get that that for all \(z \in {{\mathbb {D}}}\)

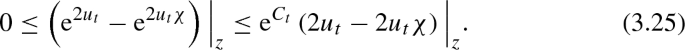
    figure f

    This is because the slope of any secant line of the function \({\mathrm e}^x\) valued on \([0,C_t]\) is less than the slope of the tangent line to \({\mathrm e}^x\) at \(x=C_t\).

  14. To prove this, Mazzeo–Swoboda–Weiss–Witt use their earlier work describing the family of harmonic metrics. In [MSWW16], they prove that \(h_t(w_1,w_2)= h_t^\mathrm {app}({\mathrm e}^{-\kappa _t} w_1, {\mathrm e}^{-\kappa _t} w_2)\) for \(h_0\)-hermitian \(\kappa _t\) satisfying \(\Vert \kappa _t\Vert _{H^2\left( i {{\mathfrak {s}}}{{\mathfrak {u}}}(E)\right) } \le C {\mathrm e}^{-\delta t}\). (This formulation in terms of the hermitian metrics appears in [Fre18], but Mazzeo–Swoboda–Weiss–Witt’s \(h_0\)-unitary formulation is equivalent to it.)

References

  1. Douady, A., Hubbard, J.: On the density of Strebel differentials. Inventiones Math. 30, 175–179 (1975)

    Article  ADS  MathSciNet  Google Scholar 

  2. Donaldson, S., Kronheimer, P.: The Geometry of Four-Manifolds. Oxford University Press, Oxford (1990)

    MATH  Google Scholar 

  3. Dumas, D., Neitzke, A.: Asymptotics of Hitchin’s metric on the Hitchin section. Commun. Math. Phys. 367(1), 127–150 (2019). arXiv:1802.07200

    Article  ADS  MathSciNet  Google Scholar 

  4. Fredrickson, L., Neitzke, A.: From \(S^{1}\)-fixed points to \({\cal{W}}\)-algebra representations, (2017). arXiv:1709.06142

  5. Freed, D.: Special Kähler manifolds. Commun. Math. Phys 203(1), 31–52 (1999). arXiv:hep-th/9712042

    Article  ADS  Google Scholar 

  6. Fredrickson, L.: Generic ends of the moduli space of \(SL(n,{\mathbb{C}})\)-Higgs bundles, (2018) arXiv:1810.01556

  7. Gaiotto, D., Moore, G.W., Neitzke, A.: Wall-crossing, Hitchin systems, and the WKB approximation. Adv. Math. 237, (2009). arXiv:0907.3987

  8. Gaiotto, D., Moore, G.W., Neitzke, A.: Four-dimensional wall-crossing via three-dimensional field theory. Commun. Math. Phys. 299, 163–224 (2010). arXiv:0807.4723

    Article  ADS  MathSciNet  Google Scholar 

  9. Hertling, C., Hoevenaars, L., Posthuma, H.: Frobenius manifolds, projective special geometry and Hitchin systems. J. Reine Angew. Math. 649, 117–165 (2010). arXiv:0905.3304

    MathSciNet  MATH  Google Scholar 

  10. Hubbard, J., Masur, H.: Quadratic differentials and foliations. Acta Math. 142, 221–274 (1979)

    Article  MathSciNet  Google Scholar 

  11. Jost, J.: Compact Riemann Surfaces. Springer, Berlin (2006)

    Book  Google Scholar 

  12. Joyce, D., Song, Y.: A theory of generalized Donaldson–Thomas invariants, arXiv:0810.5645

  13. Kontsevich, M., Soibelman, Y.: Stability structures, motivic Donaldson-Thomas invariants and cluster transformations, (2008). arXiv:0811.2435

  14. Mazzeo, R., Swoboda, J., Weiss, H., Witt, F.: Ends of the moduli space of Higgs bundles. Duke Math. J. 165(12), 2227–2271 (2016). arXiv:1405.5765

    Article  MathSciNet  Google Scholar 

  15. Mazzeo, R., Swoboda, J., Weiss, H., Witt, F.: Asymptotic geometry of the Hitchin metric. Commun. Math. Phys. 367(1), 151–191 (2019). arXiv:1709.03433

    Article  ADS  MathSciNet  Google Scholar 

  16. Neitzke, A.: Notes on a new construction of hyperkähler metrics, (2013). arXiv:1308.2198

  17. Neitzke, A.: Metric on the moduli space of Higgs bundles, (2018). https://www.ma.utexas.edu/users/neitzke/expos/higgs-metric.pdf

Download references

Acknowledgements

The author thanks Rafe Mazzeo, Andy Neitzke, Hartmut Weiss, and Ákos Nagy for helpful discussions related to this work, and Georgios Kydonakis for his comments on an earlier version. The author also thanks the anonymous referee for helpful comments.

Author information

Authors and Affiliations

  1. Department of Mathematics, Stanford University, Stanford, USA

    Laura Fredrickson

Authors
  1. Laura Fredrickson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Laura Fredrickson.

Additional information

Communicated by N. Nekrasov.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fredrickson, L. Exponential Decay for the Asymptotic Geometry of the Hitchin Metric. Commun. Math. Phys. 375, 1393–1426 (2020). https://doi.org/10.1007/s00220-019-03547-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-019-03547-9

Search

Navigation