Abstract
For a \(C^\infty \) map f on a compact manifold M we prove that for a Lebesgue randomly picked point x there is an empirical measure from x with entropy larger than or equal to the top Lyapunov exponent of \(\Lambda \, df:\Lambda \,TM\circlearrowleft \) at x. This contrasts with the well-known Ruelle inequality. As a consequence we give some refinement of Tsujii’s work [23] relating physical and Sinai-Ruelle-Bowen measures.
Similar content being viewed by others
Notes
The example given in the “Appendix” is on the interval. Following the same approach we build in a forthcoming work [7] such counter-examples of surface diffeomorphisms.
By \(\bigcup _{i\in I}A_i\Supset B \) we mean that \(\bigcup _{i\in I}A_i\supset B \) and \(A_i\cap B\ne \emptyset \) for all \(i\in I\).
Of course we only reparametrize in this a way the subset \(\sigma (\alpha [0,1]^k)\). But one can reparametrize similarly \(\sigma (C_\alpha )\) for any subcube \(C_\alpha \) of \([0,1]^k\) of size \(\alpha \) and we only need \(\lceil \alpha ^{-1}\rceil ^{d}\) such subcubes to cover \([0,1]^k\).
The \(C^r\) norm of a \(C^r\) smooth interval map f is the maximum over \(k=0,\ldots ,r\) of the supremum norms \(\Vert f^{(k)}\Vert _\infty \).
References
Bareira, L., Pesin, Y.: Nonuniform hyperbolicity: dynamics of systems with nonzero Lyapunov exponents. Encyclopedia Math. Its Appl. 115 (2007)
Boyle, M., Downarowicz, T.: The entropy theory of symbolic extension. Invent. Math. 156(1), 119–161 (2004)
Bonatti, C., Diaz, L., Viana, M.: Dynamics Beyond Uniform Hyperbolicity. A Global Geometric and Probabilistic Perspective. Encyclopaedia of Mathematical Sciences, 102. Mathematical Physics, III. Springer, Berlin (2005)
Bowen, R.: Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms, Vol. 470. Springer Lecture Notes in Math (1975)
Burguet, D.: Symbolic extensions in intermediate smoothness on surfaces. Ann. Sci. Éc. Norm. Supér. (4) 45(2), 337–362 (2012)
Burguet, D.: Periodic expansiveness of surface diffeomorphisms and applications. J.E.M.S. (to appear)
Burguet, D.: A \(C^r\) surface diffeomorphism with a physical atomic measure whose basin contains a positive Lebesgue subset of points with positive Lyapunov exponent, in preparation
Catsigeras, E., Enrich, H.: SRB-like measures for C0 dynamics. Bull. Pol. Acad. Sci. Math. 59(2), 151–164 (2011)
Catsigeras, E., Cerminara, M., Enrich, H.: The Pesin entropy formula for diffeomorphisms with dominated splitting. Ergodic Theory Dyn. Syst. 35(3), 737–761 (2015)
Gromov, M.: Entropy, homology and semi-algebraic geometry. Seminaire Bourbaki 663 (1986)
Kozlovski, O.: An integral formula for topological entropy of \(C^{infty}\) maps. Ergodic Theory Dyn. Syst. 18(2), 405–424 (1998)
Ledrappier, F., Young, L.-S.: The metric entropy of diffeomorphisms. I. Characterization of measures satisfying Pesin’s entropy formula. Ann. Math. (2) 122(3), 509–539 (1985)
Young, L.-S.: What are SRB measures, and which dynamical systems have them? J. Stat. Phys. 108(5–6), 733–754 (2002)
Misiurewicz, M.: A short proof of the variational principle for \(\mathbb{Z}^d\) actions. Asterisque 40, 147–158 (1976)
Newhouse, S.: Continuity properties of entropy. Ann. Math. 129, 215–235 (1989)
Oseledets, V.I.: A multiplicative ergodic theorem: Lyapunov characteristic numbers for dynamical systems. Trans. Moscow Math. Soc. 19, 197–231 (1968)
Ott, W., Yorke, J.A.: When Lyapunov exponents fail to exist. Phys. Rev. E (3) 78(5) (2008)
Pesin, Y.: Lyapunov characteristic exponent and smooth ergodic theory. Russian Math. Surv. 32(4), 55–114 (1977)
Qian, M., Zhu, S.: SRB measures and Pesin’s entropy formula for endomorphisms. Trans. Am. Math. Soc. 354(4), 1453–1471 (2002)
Ruelle, D.: A measure associated with Axiom A attractors. Am. J. Math. 98, 619–654 (1976)
Ruelle, D.: An inequality for the entropy of differentiable maps. Bol. Soc. Brasil. Mat. 9(1), 83–87 (1978)
Sinai, Ya.G.: Gibbs measure in ergodic theory. Russian Math. Surv. 27 21–69 (1972)
Tsujii, M.: Regular point for ergodic Sinai measures I. Transactions of the American Mathematical Society 328(2) (1991)
Young, L.S.: Entropy of continuous flows on compact 2-manifolds. Topology 16(4), 469–471 (1977)
Yomdin, Y.: \(C^k\) resolution of semialgebraic mappings. Israel J. Math. 57(3), 301–317 (1987)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Liverani
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Counter-Example for \(C^r\) Interval Maps for Any Finite r
For any positive integer r we give an example of a \(C^r\) (but not \(C^{r+1}\)) interval map \(h:[0,3/2]\circlearrowleft \) such that for x in a positive Lebesgue measure set the following properties hold:
- (1)
the empirical measures \((\mu _n^x)_n\) are converging to the Dirac measure at a fixed point (therefore with zero entropy),
- (2)
the Lyapunov exponent at x satisfies \(\chi (x)=\frac{\log \Vert h'\Vert _\infty }{r}>0\).
Consequently the Main Theorem does not hold true in finite smoothness.
Step 1 Let \(\lambda >1\). We first consider a \(C^r\) (even \(C^\infty \)) interval map \(f:[0,3/2]\circlearrowleft \) with the following properties
\(f(0)=f(1)=0\),
f has a tangency of order r at 1, i.e. \(f^{(k)}(1)=0\) for \(k=1,\ldots ,r\),
f is affine with a slope equal to \(\lambda =\Vert f'\Vert _{\infty }\) on the interval \([0, 1/\lambda ]\).
Step 2 After a small \(C^\infty \) perturbation of f around 1 we may build a new map g such that for some \(n_0\) and \(n\ge n_0\), \(g^k(1-1/n)\) lies in \([0, 1/\lambda ]\) for \(k=1,\ldots ,r^n-1\) and \(g^{r^{n}}(1-1/n)=1-1/n+1\). Indeed these conditions require \(g(1-1/n)=(1-1/n+1)\lambda ^{-r^n+1}=o(1/n^r)\), so that one can choose g arbitrarily \(C^\infty \) closed to f by taking \(n_0\) large enough. For the interval map g, the empirical measures at \(1-1/n\) are converging to the Dirac measure at the fixed point 0. We may also assume g is constant on \(J_n:=[1-1/n, 1-1/n-1/2n^2]\) for \(n\ge n_0\).
Step 3 We lastly modify g on \(J_n\), \(n\ge n_0\) such that the resulting map h satisfies the desired properties. Let us first introduce an auxiliary family of functions \((f_p)_{p\in \mathbb {N}}\). For any p we define \(f_p\) as the tent map \(x\mapsto \max (x,1-x)\) on \([1/p,1/2-1/p]\cup [1/2+1/p,1-1/p]\). We extend it into a \(C^r\) smooth interval map in such a way \(f_p\) vanishes and admits a tangency of order r at the points 0, 1 / 2 and 1. Finally we extend \(f_p\) periodically on the whole real axis. The intervals \([1/p,1/2-1/p]+k\) and \( [1/2+1/p,1-1/p]+k\) for \(k\in \mathbb {Z}\) are called the affine branches of \(f_p\). Observe that the \(C^r\) normFootnote 4 of \(f_p\) may be chosen of order \(p^{r}\). Then we let h be \(x\mapsto \alpha _nf_{n^2}\left( (x-1+1/n) 2n^2N_n\right) +g(1-1/n)\) on \(J_n\) where \(\alpha _n\in \mathbb {R}^+\) and \(N_n\in \mathbb {N}\) are chosen such that
for each affine branch \(I_n\) in \(J_n\),
$$\begin{aligned} h^{k}(I_n)\subset [0,1/\lambda ]\quad \text {for }k=1,\ldots ,r^n-1 \end{aligned}$$and
$$\begin{aligned} h^{r^{n}}(I_n)=J_{n+1}, \end{aligned}$$the \(C^r\) norm of h on \(J_n\) goes to zero with n.
The first and second conditions are respectively fulfilled whenever
and
Conclusion Let \(E_n=\bigcup _{I_n}I_n\) be the union of affine branches in \(J_n\) and let \(E=E_{n_0}\cap h^{-r^{n_0}}E_{n_0+1} \cap h^{-r^{n_0}-r^{n_0+1}}E_{n_0+2}\cap \cdots \) be the subset of points in \(J_{n_0}\) visiting successively the sets \(E_n\), \(n\ge n_0\). Clearly E is contained in the basin of the Dirac measure at 0. To conclude it remains to see that E has positive Lebesgue measure and that \(\chi (x)\ge \frac{\log \lambda }{r}\) for any x in E. The set E is an affine dynamically defined Cantor set where we remove a proportion of \(4/n^2\) at the nth step. Therefore \(\mathop {{\mathrm {Leb}}}(E)=\mathop {{\mathrm {Leb}}}(E_{n_0})\prod _{n>n_0}(1-4/n^2)>0\). Finally as \(\log |h'|\) is equal on \(I_n\) to \( \log (\alpha _n4n^2N_n)\sim \frac{r-1}{r}\log \alpha _n\sim -r^{n-1}(r-1)\log \lambda \), the Lyapunov exponent at any \(x\in E\) is given by
Observe that any point in E is not recurrent.
Appendix B. Essential Range of \(x\mapsto p\omega (x)\)
We recall here the definition of the essential range of a Borel map with respect to a Borel measure. Finally we relate the set of physical-like measures of a topological system (M, f) with the essential range of \(M\ni x\mapsto p\omega (x)\).
We consider two metric spaces X and Y with Y separable. Let m be a Borel measure on X and \(\phi :X\rightarrow Y\) be a Borel map.
Definition 1
With the above notations the essential range \(\overline{\mathop {{\mathrm {Im}}}}_m(\phi )\) of \(\phi \) with respect to m is the complement of \(\{y\in Y, \ \exists U \text { open with }y\in U \text { and }m(\phi ^{-1}U)=0\}\).
The set \(\overline{\mathop {{\mathrm {Im}}}}_m(\phi )\) is a closed subset of Y and for m-almost every x the point \(\phi (x)\) belongs to \(\overline{\mathop {{\mathrm {Im}}}}_m(\phi )\). Moreover it is the smallest set satisfying these properties.
Lemma 8
Let (M, f) be a topological system. The map \(p\omega : x\mapsto p\omega (x)\) from M to \(\mathcal {KM}(M)\) is Borel.
Proof
As the set \(\mathcal {KM}(M)\) is separable, it is enough to show \(p\omega ^{-1}(B)\) is a Borel subset of M for any closed ball B of \(\mathcal {KM}(M)\). Let B be the closed ball of radius \(\epsilon \) centered at \(K\in \mathcal {KM}(M)\), i.e. the set of compact subsets \(K'\) of M with \(K'\subset K_{\epsilon }\) and \(K\subset K'_\epsilon \) where \(K_\epsilon \) and \(K'_\epsilon \) denote respectively the closed \(\epsilon \)-neighborhoods of K and \(K'\). Firstly observe that \(\{x\in M, \ p\omega (x)\subset K_{\epsilon }\}\) is closed. Then for a fixed sequence \((k_n)_{n\in \mathbb {N}}\) dense in K the following properties are equivalent:
The functions \(x\mapsto \mathfrak {d} (k_n,\mu _x^p)\) being continuous we conclude that \(p\omega ^{-1}(B)\) is a Borel set. \(\square \)
Lemma 9
The set \(\mathcal {PL}(m)\) of physical-like measures is the union of all \(K\in \overline{\mathop {{\mathrm {Im}}}}_m(p\omega )\).
Proof
Firstly, the set \(\overline{\mathop {{\mathrm {Im}}}}_m(p\omega )\) being a compact subset of \(\mathcal {KM}(M)\), the set \(\bigcup _{K\in \overline{\mathop {{\mathrm {Im}}}}_m(p\omega )}K\) is a compact subset of M. Therefore, from the definitions we get \(\mathcal {PL}(m)\subset \bigcup _{K\in \overline{\mathop {{\mathrm {Im}}}}_m(p\omega )}K\). We argue by contradiction to prove the converse inclusion. Assume there is \(K\in \overline{\mathop {{\mathrm {Im}}}}_m(p\omega )\) such that K is not contained in \(\mathcal {PL}(m)\). Then this also holds for any \(K'\) close enough to K. Therefore there exists an open neighborhood U of K such that \(p\omega ^{-1}(U)\) has positive m-measure and for all x in this set \(p\omega (x)\) is not contained in \(\mathcal {PL}(m)\). It is impossible by definition of \(\mathcal {PL}(m)\). \(\quad \square \)
Rights and permissions
About this article
Cite this article
Burguet, D. Entropy of Physical Measures for \(C^\infty \) Dynamical Systems. Commun. Math. Phys. 375, 1201–1222 (2020). https://doi.org/10.1007/s00220-019-03516-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-019-03516-2



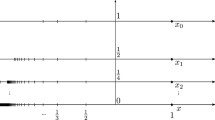

 The arrows and points in blue represent the orbit of
The arrows and points in blue represent the orbit of 