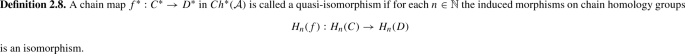Skip to main content
SpringerLink
Log in

Categorical Webs and S-Duality in 4d \({\mathcal {N}}\) = 2 QFT

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

We review the categorical approach to the BPS sector of a 4d \(\mathcal {N}=2\) QFT, clarifying many tricky issues and presenting a few novel results. To a given \(\mathcal {N}=2\) QFT one associates several triangulated categories: they describe various kinds of BPS objects from different physical viewpoints (e.g. IR versus UV). These diverse categories are related by a web of exact functors expressing physical relations between the various objects/pictures. A basic theme of this review is the emphasis on the full web of categories, rather than on what we can learn from a single description. A second general theme is viewing the cluster category as a sort of ‘categorification’ of ’t Hooft’s theory of quantum phases for a 4d non-Abelian gauge theory. The S-duality group is best described as the auto-equivalences of the full web of categories. This viewpoint leads to a combinatorial algorithm to search for S-dualities of the given \(\mathcal {N}=2\) theory. If the ranks of the gauge and flavor groups are not too big, the algorithm may be effectively run on a laptop. This viewpoint also leads to a clearer view of 3d mirror symmetry. For class \(\mathcal {S}\) theories, all the relevant triangulated categories may also be constructed in terms of geometric objects on the Gaiotto curve, and we present the dictionary between triangulated categories and the WKB approach of GMN. We also review how the VEV’s of UV line operators are related to cluster characters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Notes

  1. Although we do not make explicitly such a claim in this particular paper, we do expect that supersymmetric quantum field theories have an associated triangulated category because most (possibly all) supersymmetric quantum systems may be geometrically engineered from string/F-/M-theory. In this case, all BPS objects arise from BPS branes in the string/F-/M-theory geometry. These branes are classified by triangulated categories such as derived categories of coherent sheaves or the derived Fukaya category. This property is inherited by the BPS objects of the engineered QFT after decoupling gravity. Moreover all “reasonable” operations we may perform on the QFT (such as gauging, decoupling, RG-flow, etc.) will preserve the “triangulated category” property, even if they change the details of the categories involved. We are not aware of any exception to this “rule”. “Morally” we like to think of the categorification of the BPS sector as the ultimate version of Seiberg’s principle of the power of holomorphicity; holomorphic structures lead to triangulated categories (the derived category of analytic coherent sheaves) but triangulated categories are more general and flexible than holomorphic structures. However, in the present paper we do not make any strong statement in this regard and confine ourselves to the special case of \(\mathcal {N} = 2\) QFT with the BPS-quiver property, where the the required triangulated categories may be constructed explicitly.

  2. The index a take values in some index set I.

  3. References to previous work are provided in the appropriate sections of the paper.

  4. See Sect. 2 for precise definitions. Informally, a triangulated category is k-CY iff it behaves as the derived category of coherent sheaves, \(D^b\,\mathsf {coh}\,\mathcal {M}_k\), on a Calabi–Yau k-fold \(\mathcal {M}_k\).

  5. This is slightly imprecise. Properly speaking, the line operators correspond to the generic objects on the irreducible components of the moduli spaces of isoclasses of objects of \(\mathcal {C}(\Gamma )\).

  6. By “gauge group” we actually mean the quotient group of the full gauge group that acts effectively on the UV degrees of freedom. See Sect. 3.2.1 for more details.

  7. The subtleties in the definition are immaterial when the QFT is UV superconformal (as contrasted to asymptotically-free) and all chiral operators have integral dimensions.

  8. In facts, the cluster Grothendieck group \(K_0(\mathcal {C}(\Gamma ))\) should contain even more detailed informations on the flavor. For instance, in SU(2) gauge theory with \(N_f\) flavors the states of even magnetic charge are in tensor representations of the flavor \(SO(2N_f)\) while states of odd magnetic charge are in spinorial representation of \(\mathrm {Spin}(2N_f)\); \(K_0(\mathcal {C}(\Gamma ))\) should know the correlation between the parity of the magnetic charge and \(SO(2N_f)\) vs. \(\mathrm {Spin}(2N_f)\) flavor symmetries (and it does).

  9. For the precise definition of \(\mathrm {Auteq}\,D^b\Gamma \), see Sect. 5. \(\mathrm {Aut}(Q)\) is the group of automorphisms of the quiver Q modulo the subgroup which fixes all nodes.

  10. In all our physical applications k will be the (algebraically closed) field of complex numbers \(\mathbb {C}\).

  11. Let \(\mathcal {A}\) be an abelian category and write \(Ch^*(\mathcal {A})\) for its category of chain complexes.

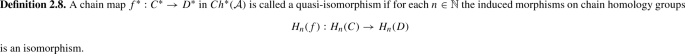
    figure a

  12. In terms of the corresponding SQM system, the process of replacing the pair (Q, W) by its reduced part \((Q_\text {red.},W_\text {red.})\) corresponds to integrate away the massive Higgs bifundamentals.

  13. The completion is taken with respect to the I-adic topology, where I is the ideal of the path algebra generated by all arrows of the quiver.

  14. See [72] for more details.

  15. More generally, we say that a triangulated category is \(\ell \)-CY (for \(\ell \in \mathbb {N}\)) iff we have the bifunctorial isomorphism \(D\mathrm {Hom}(X,Y)\cong \mathrm {Hom}(Y,X[\ell ])\).

  16. In the triangulated category \(\mathcal {T}\), a set of objects \(S_i \in \mathcal {T}\) is a generating set if all objects of \(\mathcal {T}\) can be obtained from the generating set via an iterated cone construction.

  17. If (Q, W) is Jacobi-finite (as in our applications), \(\mathsf {nil}\,J(Q, W)\equiv \mathsf {mod}\, J(Q, W)\).

  18. Here and below, given a (collection of) object(s) \(\mathcal {O}\) of a linear category \(\mathfrak {L}\), by \(\mathsf {add}\,\mathcal {O}\) we mean the additive closure of\(\mathcal {O}\)in\(\mathfrak {L}\), that is, the full subcategory over the direct summands of finite direct sums of copies of \(\mathcal {O}\).

  19. Its objects are those M’s with \(\mathrm {Hom}(S_k, M) = 0\). It is a full subcategory of \(\mathcal {A}\).

  20. See Definition 2.18.

  21. The main references for these categorical facts are [46, 84]. We recall the definition of Verdier quotient of triangulated categories:

    figure b

  22. See Definition 2.18.

  23. See Definition 2.18.

  24. In the elliptic type we are restricted to the four types \(D_4\), \(E_6\), \(E_7\) and \(E_8\), corresponding to the four tubular weighted projective lines [58, 79, 81]. Elliptic \(D_4\) is SU(2) with \(N_f=4\) [24].

  25. In our conventions, \(p_i=1\) means the empty matter system, while \(p_i=2\) is a free quark doublet.

  26. For a review of the category of coherent sheaves on weighted projective lines and corresponding cluster categories from a physicist prospective, see [32].

  27. In general, the conserved quantum numbers take value in the numeric Grothendieck group \(K_0(\mathfrak {T})_\text {num}\). For the categories we consider in this paper, the Grothendieck group is a finitely generated Abelian group and the two groups coincide.

  28. Note that this image is invariant under quiver mutation.

  29. \(\mathcal {F}(p)\) is linear, Hom-finite, and 2-CY. However, it is not necessarily a generalized cluster category since it may or may not have a tilting object. The prime examples of such a category without a tilting object are the cluster tubes, see [15, 16]. Sometimes the term ‘cluster categories’ is extended also to such categories.

  30. If \([X]\in K_0(\mathcal {A})\) is the class of \(X\in \mathcal {A}\), we write simply Z(X) for Z([X]).

  31. See below Definition 2.23 of semistability of objects in an abelian category.

  32. The half-BPS lines are also parametrized by an angle \(\vartheta \) which specifies which susy subalgebra leaves them invariant. We suppress \(\vartheta \) from the notation.

  33. As always, \(\varvec{\mu }\) denotes the group of roots of unity. The name ‘Weil pairing’ is due to its analogy with the Weil pairing in the torsion group of a polarized Abelian variety which arises in exactly the same way.

  34. For the corresponding discussion in 2d, see [22].

  35. When the UV fixed point SCFT is non degenerated, the operator \(\mathbb {M}\) is semisimple, and its conjugacy class is encoded in its spectrum, that is, the spectrum of dimensions of chiral operators \(\Delta \mod 1\).

  36. In Eq. (33) we use the notations of [23]: the product is over the BPS stable states of charge \(\lambda \in \Lambda \) and spin \(s_\lambda \) taken in the clockwise order in their phase \(\arg Z_u(\lambda )\); \(\psi (z;q)=\prod _{n\ge 0}(1-q^{n+1/2}z)^{-1}\) is the quantum dilogarithm, and the \(X_\lambda \) are quantum torus operators, i.e. they satisfy the algebra \(X_\lambda X_{\lambda ^\prime }=q^{\langle \lambda ,\lambda ^\prime \rangle /2} X_{\lambda +\lambda ^\prime }\) with \(\langle -,-\rangle \) the Dirac pairing.

  37. As contrasted with ‘antiparticles’ whose charges belong to \(-\Lambda _+\).

  38. From now on the ground field k is taken to be \(\mathbb {C}\).

  39. \(\mathbb {H}\) denotes the upper half-plane \(\mathbb {H}{:}{=}\{z\in \mathbb {C}\,|\,\mathrm {Im}\,z>0\}\).

  40. The Cartan generator of \(SU(2)_R\) acting on a BPS particle described by a (p, q)-harmonic form on \(M_\lambda \) is \((p-q)\); however, it is conjectured that only trivial representations of \(SU(2)_R\) appear [38, 56].

  41. Since the shift by [1] acts on the BPS states as PCT, it is quite natural to identify the BPS states associated to stable objects differing by even shifts.

  42. Of course, \(\mathsf {A}^\vee \cong \mathsf {A}\); however it is natural to distinguish the group and its dual.

  43. For the relation of this fact with the Y-systems, see [30].

  44. However we often write simply \(\mathbb {X}\) instead of \(\mathbb {X}(p_1,\dots ,p_s)\) leaving the weights implicit.

  45. Or, more generally, to several Argyres–Douglas systems of type D.

  46. Notice that \(\deg \mathcal {K}=0\) does not mean that \(\mathcal {K}\) is trivial but only that it is a torsion sheaf in the sense that \(\mathcal {K}^m\cong \mathcal {O}\) for some integer m.

  47. Indeed, for \(N_f\le 3\), the triangulated category \(D^b\mathsf {coh}\,\mathbb {X}\) admits \(\mathsf {mod}\,\mathbb {C}\hat{\mathfrak {g}}\) as the core of a \(\varvec{t}\)-structure (here \(\hat{\mathfrak {g}}\) is an acyclic affine quiver in the mutation class of the model [24]; see also Example 5.2.

  48. In the paper there are two levels of discussion of these issues: ‘abstract’ and ‘concrete’. The abstract definition of the category \(\mathfrak {Per}\,\Gamma \), valid for all \(\mathcal {N} = 2\) QFT which admit a quiver with potential, is rather implicit and its physical interpretation is hard to pinpoint in all details from that abstract characterization. At this very abstract level we limit to present a general picture and to state some natural expectations. The discussion at the concrete level exploits the fact that there are classes of \(\mathcal {N} = 2\) theories, such as class \(\mathcal {S}\), where an explicit (and convenient) realization of the category \(\mathfrak {Per}\,\Gamma \) is known; the explicit form may be used to check the general expectations and also to refine them (in fact, our proposed interpretation arises as a straightforward generalization of what is true in the class \(\mathcal {S}\) case, which is well known in the literature (see e.g. [56]) and reviewed in Sect. 7.7 of the paper in full detail. At the abstract level, the very definition of the cluster category through the ‘exact sequence’ of triangulated categories

    $$\begin{aligned} D^b\Gamma \rightarrow \mathfrak {Per}\,\Gamma \rightarrow C(\Gamma ) \end{aligned}$$

    which says that \(\mathfrak {Per}\,\Gamma \) is the extension of the category describing BPS UV lines \(C(\Gamma )\) and the one describing BPS particles \(D^b\Gamma \) strongly suggests that \(\mathfrak {Per}\,\Gamma \)—if it has any physical meaning—should describe BPS configurations with combine lines and particles, or more precisely, lines in the IR in a specific vacuum which gets polarized by the line which is then screened by particles. The precise meaning of this “moral” statement becomes clear when we have a concrete model of the category \(\mathfrak {Per}\,\Gamma \) as in class \(\mathcal {S}\). This concrete instance (discussed in all detail) clarifies the picture and motivates the general claim. We stress that the generic phrase of the kind “the such and such BPS objects are described by the such and such triangular category” does not mean that the triangulated category yields by itself a full description of the BPS objects: this is very rarely the case. Typically a full description requires extra data besides the category, and in particular a stability condition on the category. The need of endowing \(\mathfrak {Per}\,\Gamma \) with the datum of a stability condition is obvious from the explicit example of class \(\mathcal {S}\); however, to the best of our knowledge a general notion of stability suitable for categories of the form \(\mathfrak {Per}\,\Gamma \) is not worked out in the math literature; on this level we limit ourselves to stating a few basic properties we expect such a stability condition should enjoy on the base of the class \(\mathcal {S}\) example.

  49. We point out here that we do not require a Lagrangian description: of course, when a Lagrangian is available, the abstract definition of the S-duality group leads to a finite extension of the standard S-duality group by some irrelevant finite groups. Although we do not need a Lagrangian, the BPS quiver property is necessary to build up all the categories needed.

  50. The simplest example of such a negligible equivalence is the case of pure SU(2) whose quiver is the Kronecker quiver, \(\mathsf {Kr}= \bullet \rightrightarrows \bullet \). The stable representations associated to the W boson are the simples in the homogeneous tube which form a \(\mathbb {P}^1\) family (i.e. \(M_\text {W boson}\equiv \mathbb {P}^1\)) since the W boson belongs to a vector superfield. Then a negligible auto-equivalence is just a projective automorphism of \(\mathbb {P}^1\).

  51. We first recall that the Auslander–Reiten quiver of a cluster-tilted algebra always has a unique component containing local slices, which coincides with the whole Auslander–Reiten quiver whenever the cluster-tilted algebra is representation-finite. This component is called the transjective component and an indecomposable module lying in it is called a transjective module.

  52. See https://webusers.imj-prg.fr/~bernhard.keller/quivermutation/.

  53. Physically this is obvious. Mathematically, consider e.g. the shift shift \(\theta \rightarrow \theta -4\pi +N_f\pi \) in SU(2) with \(N_f\) flavors. It corresponds to the auto-equivalence \(\mathcal {A}\mapsto \mathcal {A}[1]\), which acts trivially on the 1-periodic subcategory.

  54. Notice that there is no periodic sub-category associated to the quark sector; this is related to the absence of conserved flavor currents in this model.

  55. In particular, \(\mathrm {coker}\,B=\varvec{Z}(G)^\vee \oplus \varvec{Z}(G)\) is the correct ’t Hooft group for pure SYM.

  56. In facts, there is a systematic procedure, called gentling in ref. [31] which allow to reduce the general class \(\mathcal {S}[A_1]\) model to one having a gente Jacobian algebra.

  57. When \(g=0\), the theory is defined only if \(b\ge 1\) or \(b=0\) and \(p\ge 3\); in case \(p=0\), \(b=1\) we require \(k\ge 4\); when \(g=1\) we need \(p+b\ge 1\). Except for the case \(p=0\), \(b=1\), corresponding to Argyres–Douglas of type A, m in Eq. (53) is \(\ge 0\). \(m=0\) only for Argyres–Douglas of type D [29].

  58. Argyres–Douglas of type \(D_1\) is the empty theory and the one of type \(D_2\) a fundamental quark doublet.

  59. This formula holds under the condition \(\dim \mathcal {M}_{g,p+b}=3g-3+p+b\ge 0\).

  60. Here the asymptotically-free gauge couplings are counted as IR deformations.

  61. As written, these equations hold even if the condition in footnote 59 is not satisfied. Notice that we count also the dimensions of the internal Coulomb branches of the matter Argyres–Douglas systems.

  62. We call marked/decorated points in \(\Sigma \) the pre-images of marked/decorated points on C.

  63. Compare Eqs. (6.26)–(6.28) in ref. [24].

  64. These are the objects in the perfect derived category \(\mathfrak {Per}\,\Gamma \).

  65. Traditionally, they are defined by composing a sequence of elementary operations on conformal blocks, each corresponding to a map between spaces of conformal blocks which may differ in the number or type of insertions. Roughly speaking, one inserts an identity operator into the original conformal block, splits into two conjugate chiral operators \(\phi _a\) and \(\bar{\phi }_a\), transports \(\phi _a\) along \(\gamma \) and then fuses the operators \(\phi _a\) and \(\bar{\phi }_a\) back to the identity channel.

  66. A boundary arc is the part of a boundary component between two adjacent marked points.

  67. This is slightly imprecise since, in presence of regular punctures W contains free parameters [80]. The statement in the text refers to the full family of allowed W’s.

  68. A simple arc does not have self intersections.

  69. A closed arc starts and ends in \(\Delta \).

  70. The figure is taken from [89].

  71. CA = closed arc, OA = open arc.

  72. If \(B^\prime \) does not exist, then \(X(B^\prime )=1.\)

  73. Recall that a module N is a submodule of M iff there exists an injective map \(N \rightarrow M\).

  74. \(\mathrm {Gr}_e(FM){:}{=}\{N \subset FM\; |\; \dim N =e\}\), i.e. it is the space of subrepresentations of M with fixed dimension e.

  75. The vertices are the \(T_i\) and the arrows \(j \rightarrow i\) correspond to \(\mathrm {Hom}_{\mathcal {C}}(T_i,T_j).\)

  76. Id est \(Y_i=\prod _jx_j^{B_{ij}}.\)

References

  1. Aharony, O., Seiberg, N., Tachikawa, Y.: Reading between the lines of four-dimensional gauge theories. J. High Energy Phys. 2013(8), 115 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alday, L.F.: Wilson loops in supersymmetric gauge theories. Lecture Notes, CERN Winter School on Supergravity, Strings, and Gauge Theory (2012)

  3. Alday, L.F., Gaiotto, D., Gukov, S., Tachikawa, Y., Verlinde, H.: Loop and surface operators in gauge theory and Liouville modular geometry. J. High Energy Phys. 1, 1–50 (2010)

    MathSciNet  MATH  Google Scholar 

  4. Alim, M., Cecotti, S., Córdova, C., Espahbodi, S., Rastogi, A., Vafa, C.: BPS quivers and spectra of complete \(\text{ N }=2\) quantum field theories. Commun. Math. Phys. 323(3), 1185–1227 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. Alim, M., Cecotti, S., Cordova, C., Espahbodi, S., Rastogi, A., Vafa, C.: \(\text{ N }=2\) quantum field theories and their BPS quivers. Adv. Theor. Math. Phys. 18(1), 27–127 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Amiot, C.: Cluster categories for algebras of global dimension 2 and quivers with potential. In Annales de l’Institut Fourier 59, 2525 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Amiot, C.: On generalized cluster categories. Representations of algebras and related topics, pp. 1–53 (2011)

  8. Aspinwall, P.S., et al.: Dirichlet Branes and Mirror Symmetry. American Mathematical Society, Providence (2009)

    MATH  Google Scholar 

  9. Aspinwall, P.S., Fidkowski, L.M.: Superpotentials for quiver gauge theories. J. High Energy Phys. 2006(10), 047 (2006)

    Article  MathSciNet  Google Scholar 

  10. Assem, I., Brüstle, T., Charbonneau Jodoin, G., Plamondon, P.-G.: Gentle algebras arising from surface triangulations. Algebra Number Theory 4(2), 201–229 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Assem, I., Dupont, G.: Modules over cluster-tilted algebras determined by their dimension vectors. Commun. Algebra 41(12), 4711–4721 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  12. Assem, I., Dupont, G., Schiffler, R., Smith, D.: Friezes, strings and cluster variables. Glasg. Math. J. 54(01), 27–60 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  13. Assem, I., Schiffler, R., Shramchenko, V.: Cluster automorphisms. Proc. Lond. Math. Soc. 104(6), 1271–1302 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. Assem, I., Skowronski, A., Simson, D.: Elements of the Representation Theory of Associative Algebras: Volume 1: Techniques of Representation Theory, vol. 65. Cambridge University Press, Cambridge (2006)

    Book  MATH  Google Scholar 

  15. Barot, M., Kussin, D., Lenzing, H.: The Grothendieck group of a cluster category. J. Pure Appl. Algebra 212(1), 33–46 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Barot, M., Kussin, D., Lenzing, H.: The cluster category of a canonical algebra. Trans. Am. Math. Soc. 362(8), 4313–4330 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  17. Bridgeland, T.: Stability conditions on triangulated categories. Ann. Math. 166, 317–345 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  18. Bridgeland, T., Smith, I.: Quadratic differentials as stability conditions. Publications mathématiques de l’IHÉS 121(1), 155–278 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  19. Brüstle, T., Zhang, J.: On the cluster category of a marked surface without punctures. Algebra Number Theory 5(4), 529–566 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  20. Burban, I., Iyama, O., Keller, B., Reiten, I.: Cluster tilting for one-dimensional hypersurface singularities. Adv. Math. 217(6), 2443–2484 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  21. Caorsi, M., Cecotti, S.: Homological S-duality in 4d \(\text{ N }=2\) QFTs. (2016) arXiv preprint arXiv:1612.08065

  22. Cecotti, S., Vafa, C.: 2d Wall-crossing, R-twisting, and a supersymmetric index. arXiv:1002.3638 [hep-th]

  23. Cecotti, S., Neitzke, A., Vafa, C.: R-twisting and 4d/2d correspondences. (2010) arXiv preprint arXiv:1006.3435

  24. Cecotti, S., Vafa, C.: Classification of complete \(\text{ N }=2\) supersymmetric theories in 4 dimensions. Surveys in differential geometry 18 (2013). arXiv:1103.5832 [hep-th]

  25. Cecotti, S., Cordova, C., Vafa, C.: Braids, walls, and mirrors. arXiv:1110.2115 [hep-th]

  26. Cecotti, S., Del Zotto, M.: 4d \(\text{ N }=2\) gauge theories and quivers: the non-simply laced case. J. High Energy Phys. 1210, 190 (2012). arXiv:1207.7205 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. Cecotti, S.: The quiver approach to the BPS spectrum of a 4d \(\text{ N }=2\) gauge theory. Proc. Symp. Pure Math. 90, 3 (2015). arXiv:1212.3431 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  28. Cecotti, S.: Categorical Tinkertoys for \(\text{ N }=2\) gauge theories. Int. J. Mod. Phys. A 28, 1330006 (2013). arXiv:1203.6734 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Cecotti, S., Del Zotto, M., Giacomelli, S.: More on the \(\text{ N }=2\) superconformal systems of type \(D_p(G)\). J. High Energy Phys. 1304, 153 (2013). arXiv:1303.3149 [hep-th]

    Article  ADS  MATH  MathSciNet  Google Scholar 

  30. Cecotti, S., Del Zotto, M.: \(Y\)-systems, \(Q\)-systems, and 4D \(\cal{N}=2\) supersymmetric QFT. J. Phys. A 47(47), 474001 (2014). arXiv:1403.7613 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  31. Cecotti, S., Del Zotto, M.: Galois covers of \(\cal{N}=2\) BPS spectra and quantum monodromy. Adv. Theor. Math. Phys. 20, 1227 (2016). arXiv:1503.07485 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  32. Cecotti, S., Del Zotto, M.: Higher S-dualities and Shephard–Todd groups. J. High Energy Phys. 1509, 035 (2015). arXiv:1507.01799 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  33. Cecotti, S., Del Zotto, M.: to appear

  34. Chen, J., Lin, Y., Ruan, S.: Tilting objects in the stable category of vector bundles on a weighted projective line of type (2, 2, 2, 2; \(\lambda \)). J. Algebra 397, 570–588 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  35. Córdova, C., Neitzke, A.: Line defects, tropicalization, and multi-centered quiver quantum mechanics. (2013) arXiv preprint arXiv:1308.6829

  36. Dehy, R., Keller, B.: On the Combinatorics of rigid objects in 2-Calabi–Yau categories. International Mathematics Research Notices 2008 (2008)

  37. Del Zotto, M.: Four-dimensional \(\text{ N }=2\) superconformal quantum field theories and BPS-quivers. PhD thesis, Scuola Internazionale Superiore di Studi Avanzati (2013)

  38. Del Zotto, M., Sen, A.: About the absence of exotics and the Coulomb branch formula. (2014) arXiv preprint arXiv:1409.5442

  39. Denef, F.: Quantum quivers and Hall/hole halos. J. High Energy Phys. 0210, 023 (2002). arXiv:hep-th/0206072

    Article  ADS  MathSciNet  Google Scholar 

  40. Derksen, H., Weyman, J., Zelevinsky, A.: Quivers with potentials and their representations I: mutations. Sel. Math. New Ser. 14(1), 59–119 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  41. Di Francesco, P., Kedem, R.: Q-systems, heaps, paths and cluster positivity. Commun. Math. Phys. 293, 727802 (2009). arXiv:0811.3027 [math.CO]

    MathSciNet  Google Scholar 

  42. Di Francesco, P., Kedem, R.: Q-systems as cluster algebras II: Cartan matrix of finite type and the polynomial property. Lett. Math. Phys. 89, 183 (2009). https://doi.org/10.1007/s11005-009-0354-z. arXiv:0803.0362 [math.RT]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  43. Dimofte, T.: Duality domain walls in class \(\cal{S}[A_1]\). Proc. Symp. Pure Math. 88, 271 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  44. Dimofte, T., Gaiotto, D., van der Veen, R.: RG domain walls and hybrid triangulations. Adv. Theor. Math. Phys. 19, 137 (2015). arXiv:1304.6721 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  45. Dominguez, S., Geiss, C.: A Caldero–Chapoton formula for generalized cluster categories. J. Algebra 399, 887–893 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  46. Drinfeld, V.: DG quotients of DG categories. J. Algebra 272(2), 643–691 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  47. Drukker, N., Morrison, D.R., Okuda, T.: Loop operators and S-duality from curves on Riemann surfaces. J. High Energy Phys. 2009(09), 031 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  48. Dupont, G.: Generic variables in acyclic cluster algebras. J. Pure Appl. Algebra 215(4), 628–641 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  49. Farb, B., Margalit, D.: A Primer on Mapping Class Groups. Princeton University Press, Princeton (2012)

    MATH  Google Scholar 

  50. Fock, V., Goncharov, A.: Cluster ensembles, quantization and the dilogarithm. arXiv preprint arXiv:math.AG/0311245

  51. Fock, V., Goncharov, A.: Dual Teichmuller and lamination spaces. 2005 arXiv preprint arXiv:math/0510312

  52. Fomin, S., Shapiro, M., Thurston, D.: Cluster algebras and triangulated surfaces. Part I: cluster complexes. Acta Math. 201(1), 83–146 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  53. Fomin, S., Zelevinsky, A.: Cluster algebras I: foundations. J. Am. Math. Soc. 15(2), 497–529 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  54. Gaiotto, D.: \(\text{ N }=2\) dualities. J. High Energy Phys. 2012(8), 1–58 (2012)

    Article  MathSciNet  Google Scholar 

  55. Gaiotto, D., Moore, G.W., Neitzke, A.: Wall-crossing, Hitchin systems, and the WKB approximation. Adv. Math. 234, 239–403 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  56. Gaiotto, D., Moore, G.W., Neitzke, A.: Framed BPS states. Adv. Theor. Math. Phys. 17(2), 241–397 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  57. Gaiotto, D.: Open Verlinde line operators. (2014) arXiv preprint arXiv:1404.0332

  58. Geigle, W., Lenzing, H.: A Class of Weighted Projective Lines Arising in Representation Theory of Finite Dimensional Algebras. Lecture Notes in Mathematics, pp. 265–297. Springer, Berlin (1987)

    MATH  Google Scholar 

  59. Ginzburg, V.: Calabi–Yau algebras. (2006) arXiv preprint arXiv:math/0612139

  60. Goncharov, A.B.: Ideal webs, moduli spaces of local systems, and 3d Calabi–Yau categories. (2016) arXiv preprint arXiv:1607.05228

  61. Griffiths, P., Harris, J.: Principles of Algebraic Geometry. Wiley, Hoboken (1994)

    Book  MATH  Google Scholar 

  62. Hooft, G.: On the phase transition towards permanent quark confinement. Nucl. Phys. B 138(1), 1–25 (1978)

    Article  ADS  MathSciNet  Google Scholar 

  63. Hooft, G.: A property of electric and magnetic flux in non-Abelian gauge theories. Nucl. Phys. B 153, 141–160 (1979)

    Article  ADS  MathSciNet  Google Scholar 

  64. Hooft, G.: Confinement and topology in non-abelian gauge theories. Acta Phys. Austriaca Suppl. 22, 531–586 (1980)

    Google Scholar 

  65. Hooft, G.’t.: Which topological features of a gauge theory can be responsible for permanent confinement? Recent developments in gauge theories. In: Proceedings of the NATO Advanced Study Institute on recent developments in gauge theories, held in Cargèse, Corsica, August 26–September 8, 1979, pp 117–133 (1980)

  66. Iyama, O., Yoshino, Y.: Mutation in triangulated categories and rigid Cohen–Macaulay modules. Invent. Math. 172(1), 117–168 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  67. Kapustin, A., Kreuzer, M., Schlesinger, K.-G.: Homological Mirror Symmetry: New Developments and Perspectives, vol. 757. Springer, Berlin (2008)

    MATH  Google Scholar 

  68. Keller, B.: On triangulated orbit categories. Doc. Math 10(551–581), 21–56 (2005)

    MathSciNet  MATH  Google Scholar 

  69. Kedem, R.: Q-systems as cluster algebras. J. Phys. A: Math. Theor. 41, 194011 (2008) arXiv:0712.2695 [math.RT]

  70. Keller, B.: On differential graded categories. (2006) arXiv preprint arXiv:math/0601185

  71. Keller, B.: Derived Categories and Tilting. London Mathematical Society Lecture Note Series, p. 49. Cambridge University Press, Cambridge (2007)

    Google Scholar 

  72. Keller, B.: On cluster theory and quantum dilogarithm identities. In: Skowronski, A., Yamagata, K. (eds.) Representations of Algebras and Related Topics, EMS Series of Congress Reports, European Mathematical Society, pp. 85–11 (2011)

  73. Keller, B., Reiten, I.: Cluster-tilted algebras are Gorenstein and stably Calabi–Yau. Adv. Math. 211(1), 123–151 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  74. Keller, B., Van den Bergh, M.: Deformed Calabi–Yau completions. Journal für die reine und angewandte Mathematik (Crelles Journal) 2011(654), 125–180 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  75. Keller, B., Yang, D.: Derived equivalences from mutations of quivers with potential. Adv. Math. 226(3), 2118–2168 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  76. Kontsevich, M.: Homological algebra of mirror symmetry. (1994) arXiv preprint arXiv:alg-geom/9411018

  77. Kontsevich, M., Soibelman, Y.: Stability structures, motivic Donaldson–Thomas invariants and cluster transformations. arXiv:0811.2435 [math.AG]

  78. Kontsevich, M., Soibelman, Y.: Wall-crossing structures in Donaldson–Thomas invariants, integrable systems and mirror symmetry. In: Castano-Bernard, R., Catanese, F., Kontsevich, M., Pantev, T., Soibelman, Y., Zharkov, I. (eds.) Homological Mirror Symmetry and Tropical Geometry, pp. 197–308. Springer, Berlin (2014)

    Chapter  MATH  Google Scholar 

  79. Kussin, D., Lenzing, H., Meltzer, H.: Triangle singularities, ADE-chains, and weighted projective lines. Adv. Math. 237, 194–251 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  80. Labardini-Fragoso, D.: Quivers with potentials associated to triangulated surfaces. Proc. Lond. Math. Soc. 98(3), 797–839 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  81. Lenzing, H.: Hereditary categories. In: Angeleri Hügel, L., Happel, D., Krause, H. (eds.) Handbook of Tilting Theory. London Mathematical Society Lecture Note Series, vol. 332, pp. 105–146. Cambridge University Press, Cambridge (2007)

    Chapter  Google Scholar 

  82. Miyachi, J.-I., Yekutieli, A.: Derived Picard groups of finite dimensional hereditary algebras. arXiv:math/9904006

  83. Musiker, G., Schiffler, R., Williams, L.: Bases for cluster algebras from surfaces. Compos. Math. 149(02), 217–263 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  84. Neeman, A.: Triangulated Categories. (AM-148), vol. 148. Princeton University Press, Princeton (2014)

    Google Scholar 

  85. Newman, M.: Integral Matrices. Academic Press, New York (1972)

    MATH  Google Scholar 

  86. Palu, Y.: Cluster characters for 2-Calabi–Yau triangulated categories. Annales de l’institut Fourier 58, 2221–2248 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  87. Palu, Y.: Grothendieck group and generalized mutation rule for 2-Calabi–Yau triangulated categories. J. Pure Appl. Algebra 213(7), 1438–1449 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  88. Plamondon, P.-G.: Cluster algebras via cluster categories with infinite-dimensional morphism spaces. Compos. Math. 147(06), 1921–1954 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  89. Qiu, Y.: Decorated marked surfaces: spherical twists versus braid twists. Math. Ann. 365(1–2), 595–633 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  90. Qiu, Y., Zhou, Y.: Cluster categories for marked surfaces: punctured case. (2013) arXiv preprint arXiv:1311.0010

  91. Qiu, Y., Zhou, Y.: Decorated marked surfaces II: intersection numbers and dimensions of Homs. (2014) arXiv preprint arXiv:1411.4003

  92. Reiten, I.: Tilting theory and cluster algebras. (2010) arXiv preprint arXiv:1012.6014

  93. Segal, E.D.: All autoequivalences are spherical twists. (2016) arXiv preprint arXiv:1603.06717

  94. Seiberg, N.: Electric-magnetic duality in supersymmetric non-Abelian gauge theories. Nucl. Phys. B 435(1–2), 129–146 (1995)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  95. Seiberg, N., Witten, E.: Monopoles, duality and chiral symmetry breaking in \(\text{ N }=2\) supersymmetric QCD. Nucl. Phys. B 431(3), 484–550 (1994)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  96. Seidel, P., Thomas, R.: Braid group actions on derived categories of coherent sheaves. Duke Math. J. 108(1), 37–108 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  97. Shapere, A.D., Vafa, C.: BPS structure of Argyres–Douglas superconformal theories. (1999) arXiv preprint arXiv:hep-th/9910182

  98. Terashima, Y., Yamazaki, M.: SL(2, R) Chern–Simons, Liouville, and gauge theory on duality walls. JHEP 1108, 135 (2011). arXiv:1103.5748 [hep-th]

    Article  ADS  MATH  Google Scholar 

  99. Witten, E.: Dyons of charge \(e \theta /2 \pi \). Phys. Lett. 86B, 283 (1979)

    Article  ADS  Google Scholar 

  100. Xie, D.: Network, Cluster coordinates and \(\text{ N }=2\) theory I. (2012) arXiv preprint arXiv:1203.4573

Download references

Acknowledgements

We would like to sincerely thank the anonymous referee for pointing out many mistakes and typos: his/her comments definitely improved the quality of our manuscript. We have benefit from discussions with Michele Del Zotto, Dirk Kussin, and Pierre-Guy Plamondon. SC thanks the Simons Center for Geometry and Physics, where this work was completed, for hospitality.

Author information

Authors and Affiliations

  1. SISSA, Via Bonomea 265, 34100, Trieste, Italy

    Matteo Caorsi & Sergio Cecotti

Authors
  1. Matteo Caorsi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sergio Cecotti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Matteo Caorsi.

Additional information

Communicated by C. Schweigert

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

A Code for Cluster Characters

This is a short Mathematica code that computes the \(L_c\) polynomials of Sect. 8.2.1. Up to an overall normalization factor, the \(L_c\) polynomials are the cluster characters. The algorithm follows precisely the procedure described in Sect. 8.2.1.

figure r

B Code for Cluster Automorphisms

This short Mathematica script is useful to find generators and relations for the automorphisms of the cluster exchange graph. The formulas used to implement the mutations for the exchange matrix \(B_{ij}\) and the dimension vectors \(d_l\) (where l is an index that runs over the nodes) are the following:

$$\begin{aligned} \mu _k(B)_{ij}&={\left\{ \begin{array}{ll} - B_{ij}, &{} i=k \ \text {or }j=k\\ B_{ij}+\max [-B_{ik},0]\,B_{kj}+B_{ik}\,\max [B_{kj},0] &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$
(73)
$$\begin{aligned} \mu _k(d)_{l}&=\left\{ \begin{array}{lr} d_{l}, &{} l\ne k\\ -d_{k}+\max \Big [\sum _i\max \big [B_{ik},0\big ]d_{i},\sum _i\max \big [-B_{ik},0\big ]d_i\Big ] &{} l=k \end{array} \right. \end{aligned}$$
(74)

The procedure of this script is explained in Sect. 6.

figure s

C Weyl Group of \(E_6\)

With this short Mathematica script, we explicitly construct the Weyl group of \(E_6\) over the basis of simple roots.

figure t

We directly checked that the longest elements has length 36, that the order of the Weyl group is

$$\begin{aligned} 51840=2^7 3^45 \end{aligned}$$

and the order of each element belongs to this set:

$$\begin{aligned} \{1,3,2,5,4,6,12,8,10,9\}. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Caorsi, M., Cecotti, S. Categorical Webs and S-Duality in 4d \({\mathcal {N}}\) = 2 QFT. Commun. Math. Phys. 368, 885–984 (2019). https://doi.org/10.1007/s00220-019-03461-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-019-03461-0

Search

Navigation