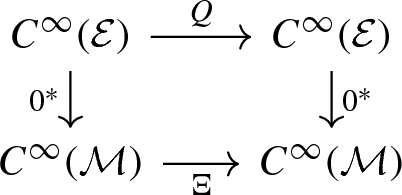Shifted Derived Poisson Manifolds Associated with Lie Pairs

Abstract

We study the shifted analogue of the “Lie–Poisson” construction for $L_\infty$ algebroids and we prove that any $L_\infty$ algebroid naturally gives rise to shifted derived Poisson manifolds. We also investigate derived Poisson structures from a purely algebraic perspective and, in particular, we establish a homotopy transfer theorem for derived Poisson algebras. As an application, we prove that, given a Lie pair (L, A), the space $\hbox {tot}\Omega ^{\bullet }_A(\Lambda ^\bullet (L/A))$ admits a degree $(+1)$ derived Poisson algebra structure with the wedge product as associative multiplication and the Chevalley–Eilenberg differential $d_A^{\hbox {Bott}}:\Omega ^{\bullet }_A(\Lambda ^\bullet (L/A))\rightarrow \Omega ^{\bullet +1}_A(\Lambda ^\bullet (L/A))$ as unary $L_\infty$ bracket. This degree $(+1)$ derived Poisson algebra structure on $\hbox {tot}\Omega ^{\bullet }_A(\Lambda ^\bullet (L/A))$ is unique up to an isomorphism having the identity map as first Taylor coefficient. Consequently, the Chevalley–Eilenberg hypercohomology ${\mathbb {H}}({{\,\mathrm{tot}\,}}\Omega ^{\bullet }_A(\Lambda ^\bullet (L/A)),d_A^{\hbox {Bott}})$ admits a canonical Gerstenhaber algebra structure.

Appendices

Appendix A. $L_\infty$ Algebroids and dg Manifolds

We recall some standard notions and results which we used throughout the paper. We mainly follow the conventions of Bruce [8], Voronov [55], and Lada–Markl [28].

The following proposition reveals a close relation between $L_\infty$ algebroids and dg manifolds. See [8, 25].

Proposition A.1

Let ${\mathcal {L}}\rightarrow \mathcal {M}$ be a vector bundle of ${\mathbb {Z}}$-graded manifolds. Then ${\mathcal {L}}$ is an $L_\infty$ algebroid if and only if ${\mathcal {L}}[1]$ is a dg manifold whose homological vector field Q is tangent to the zero section $0:\mathcal {M}\hookrightarrow {\mathcal {L}}[1]$.

The rest of the section is devoted to the proof of this proposition, where the set-up was used in the paper. We first start with the following

Lemma A.2

Let ${\mathcal {L}}\rightarrow \mathcal {M}$ be a vector bundle of ${\mathbb {Z}}$-graded manifolds, and let k be a fixed integer. An $L_\infty$ algebroid structure on ${\mathcal {L}}\rightarrow \mathcal {M}$ is equivalent to an $L_\infty$ algebra structure on the ${\mathbb {K}}$-vector space $\Gamma ({\mathcal {L}})\oplus C^{\infty }(\mathcal {M})[k]$ with structure maps

$$\begin{aligned} {\bar{\lambda }}_l: \Lambda ^l\big (\Gamma ({\mathcal {L}})\oplus C^{\infty }(\mathcal {M})[k]\big ) \rightarrow \big (\Gamma ({\mathcal {L}})\oplus C^{\infty }(\mathcal {M})[k]\big )[2-l] \end{aligned}$$

satisfying the Leibniz rule

$$\begin{aligned} {\bar{\lambda }}_l({w_1,w_2, \ldots ,w_{l-1},fw_l})&= {\bar{\lambda }}_l({w_1,w_2, \ldots ,w_{l-1}, f})w_l \nonumber \\&\quad +(-1)^{(l+\left| w_1\right| +\cdots +\left| w_{l-1}\right| ) \left| f\right| } f {\bar{\lambda }}_l({w_1,w_2, \ldots ,w_{l-1},w_l}) , \end{aligned}$$

(34)

for all $w_1, \ldots ,w_l\in \Gamma ({\mathcal {L}})\oplus C^{\infty }(\mathcal {M})[k]$, and $f\in C^{\infty }(\mathcal {M})$, and the following conditions:

• (1) $\Gamma ({\mathcal {L}})$ is an $L_\infty$ subalgebra of $\Gamma ({\mathcal {L}})\oplus C^{\infty }(\mathcal {M})[k]$;

• (2) $C^{\infty }(\mathcal {M})[k]$ is an $L_\infty$ ideal of $\Gamma ({\mathcal {L}})\oplus C^{\infty }(\mathcal {M})[k]$, i.e. ${\bar{\lambda }}_l(w_1,w_2, \ldots ,w_l)\in C^{\infty }(\mathcal {M})[k]$ if at least one of the arguments $w_1,w_2,\dots ,w_l$ is in $C^{\infty }(\mathcal {M})[k]$; and

• (3) $C^{\infty }(\mathcal {M})[k]$ is abelian, i.e. ${\bar{\lambda }}_l(w_1,w_2, \ldots ,w_l)=0$ if at least two of the arguments $w_1,w_2,\dots ,w_l$ are in $C^{\infty }(\mathcal {M})[k]$.

Proof

Assume that ${\mathcal {L}}$ is an $L_\infty$ algebroid with multi-brackets $(\lambda _l)_{l\geqslant 1}$ and multi-anchor maps $(\rho _l)_{l\geqslant 0}$ as in Definition 3.6. Define a sequence $({\bar{\lambda }}_l)_{l\geqslant 1}$ of ${\mathbb {K}}$-multilinear maps

$$\begin{aligned} {\bar{\lambda }}_l: \Lambda ^l\big (\Gamma ({\mathcal {L}})\oplus C^{\infty }(\mathcal {M})[k]\big ) \rightarrow \big (\Gamma ({\mathcal {L}})\oplus C^{\infty }(\mathcal {M})[k]\big )[2-l] \end{aligned}$$

by the following relations:

• ${\bar{\lambda }}_l(x_1, \ldots ,x_l)=0$ if at least two of the arguments $x_1,\dots ,x_l$ are in $C^{\infty }(\mathcal {M})[k]$;

• ${\bar{\lambda }}_l(a_1, \ldots ,a_l)=\lambda _l(a_1, \ldots ,a_l)$, for all $a_1, \ldots ,a_l\in \Gamma ({\mathcal {L}})$; and

• ${\bar{\lambda }}_{l+1}(a_1, \ldots ,a_l,f)=\rho _{l}(a_1, \ldots ,a_l)f$, for all $a_1, \ldots ,a_l\in \Gamma ({\mathcal {L}})$ and $f\in C^{\infty }(\mathcal {M})[k]$.

It is straightforward to verify that $({\bar{\lambda }}_l)_{l\geqslant 1}$ satisfy all the required properties.

The converse can be proved by going backwards. $\quad \square$

Given a vector bundle $\mathcal {E}\xrightarrow {\pi }\mathcal {M}$ of ${\mathbb {Z}}$-graded manifolds, consider the graded Lie algebra $\mathscr {D}^{\leqslant 1}(\mathcal {E})$ of first-order differential operators on $\mathcal {E}$. Namely, $\mathscr {D}^{\leqslant 1}(\mathcal {E})$ consists of those operators on the algebra $C^\infty (\mathcal {E})$ that are the sum of a derivation and the multiplication by an element of $C^\infty (\mathcal {E})$. Indeed, $\mathscr {D}^{\leqslant 1}(\mathcal {E})$ can be identified to $\mathscr {X}(\mathcal {E})\oplus C^\infty (\mathcal {E})$ in a canonical way. Since $C^\infty (\mathcal {E}) \cong \Gamma ({\hat{S}}(\mathcal {E}^\vee ))$, the contraction operator ${\iota }_{s}$ by a section $s\in \Gamma (\mathcal {E})$ defines a derivation of $C^\infty (\mathcal {E})$, i.e. a vector field on $\mathcal {E}$. The inclusion $\Gamma (\mathcal {E})\oplus C^\infty (\mathcal {M})\hookrightarrow \mathscr {X}(\mathcal {E})\oplus C^\infty (\mathcal {E})$ sending $s+f$ to ${\iota }_{s}+\pi ^*(f)$ identifies $\Gamma (\mathcal {E})\oplus C^\infty (\mathcal {M})$ with an abelian Lie subalgebra of $\mathscr {D}^{\leqslant 1}(\mathcal {E})$. We proceed to define a projection $P: \mathscr {D}^{\leqslant 1}(\mathcal {E})\twoheadrightarrow \Gamma (\mathcal {E})\oplus C^\infty (\mathcal {M})$. Given a vector field $X\in \mathscr {X}(\mathcal {E})$, consider the composition

$$\begin{aligned} \Gamma (\mathcal {E}^\vee )\hookrightarrow \Gamma ({\hat{S}}(\mathcal {E}^\vee ))\cong C^\infty (\mathcal {E})\xrightarrow {X}C^\infty (\mathcal {E})\xrightarrow {0^*}C^\infty (\mathcal {M}) , \end{aligned}$$

where $0^*$ denotes the pullback of functions through the zero section $0:\mathcal {M}\rightarrow \mathcal {E}$ of the vector bundle. The vector bundle $\mathcal {E}$ can be canonically identified with the normal bundle of the zero section inside $\mathcal {E}$. Therefore, there exists a unique $X^\uparrow \in \Gamma (\mathcal {E})$ such that $\left\langle \xi ,X^\uparrow \right\rangle = 0^*\big (X(\xi )\big )$, for all $\xi \in \Gamma (\mathcal {E}^\vee )$. Define $P: \mathscr {D}^{\leqslant 1}(\mathcal {E})\twoheadrightarrow \Gamma (\mathcal {E})\oplus C^\infty (\mathcal {M})$ by $P(X+f)=X^\uparrow +0^*(f)$, for all $X\in \mathscr {X}(\mathcal {E})$ and $f\in C^\infty (\mathcal {E})$. Note that the projection operator P satisfies

$$\begin{aligned} P\big (\left[ x,y\right] \big ) = P\big (\left[ P(x),y\right] +\left[ x,P(y)\right] \big ), \quad \forall x,y\in \mathscr {D}^{\leqslant 1}(\mathcal {E}). \end{aligned}$$

(35)

The following lemma is easily verified, and is left to the reader.

Lemma A.3

For any $Q\in \mathscr {X}(\mathcal {E})$, the following assertions are equivalent.

• (1) The vector field Q is tangent to the zero section of $\mathcal {E}\xrightarrow {\pi }\mathcal {M}$.

• (2) There exists a unique vector field $\Xi$ on $\mathcal {M}$ such that the diagram

  

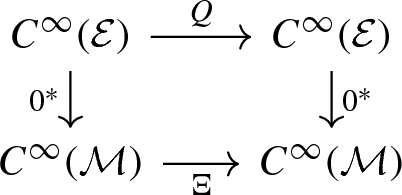
  commutes.

• (3) The ideal $\ker (0^*)$ of $C^\infty (\mathcal {E})$ is Q-stable.

• (4) $Q\in \ker ( P).$

Proof of Proposition A.1

Consider the vector bundle $\mathcal {E}\xrightarrow {\pi }\mathcal {M}$ of ${\mathbb {Z}}$-graded manifolds, where $\mathcal {E}={\mathcal {L}}[1]$. Assume that Q is a homological vector field on ${\mathcal {L}}[1]$ tangent to the zero section of ${\mathcal {L}}[1]\xrightarrow {\pi }\mathcal {M}$. According to Lemma A.3, we have $Q\in \ker (P)$.

The graded Lie algebra ${\mathfrak {A}}=\mathscr {D}^{\leqslant 1}({\mathcal {L}}[1])$, its abelian Lie subalgebra ${\mathfrak {a}}=\Gamma ({\mathcal {L}}[1])\oplus C^\infty (\mathcal {M})$, the projection $P:{\mathfrak {A}}\rightarrow {\mathfrak {a}}$ of $\mathscr {D}^{\leqslant 1}({\mathcal {L}}[1])$ onto $\Gamma ({\mathcal {L}}[1])\oplus C^\infty (\mathcal {M})$, and together with the vector field $Q\in \ker (P)$ constitute an $L_\infty [1]$ algebra Voronov data [55, Theorem 1 and Corollary 1]. The multi-brackets $(\mu _l)_{l\geqslant 1}$ are given by a sequence of derived brackets:

$$\begin{aligned} \mu _l(z_1,z_2, \ldots ,z_l) = P \big (\left[ \left[ \left[ \left[ Q,z_1\right] ,z_2\right] ,\cdots \right] ,z_l\right] \big ) ,\end{aligned}$$

(36)

for all $z_1,z_2,\dots ,z_l\in \Gamma ({\mathcal {L}}[1])\oplus C^\infty (\mathcal {M})$.

Applying the décalage isomorphism, we obtain an $L_\infty$ algebra on $\Gamma ({\mathcal {L}})\oplus C^\infty (\mathcal {M})[-1]$ with multi-brackets $({\bar{\lambda }}_l)_{l\geqslant 1}$. The multi-brackets $(\mu _l)_{l\geqslant 1}$ and $({\bar{\lambda }}_l)_{l\geqslant 1}$ are related as follows:

$$\begin{aligned} {\bar{\lambda }}_l(w_1,w_2, \ldots ,w_l) =(-1)^{\star } \mu _l(w_1,w_2, \ldots ,w_l) , \end{aligned}$$

where $\star =(l-1)\left| w_{ 1}\right| +(l-2)\left| w_{2}\right| +\cdots +\left| w_{ {l-1}}\right|$ for all homogeneous $w_1,w_2,\dots ,w_l\in \Gamma ({\mathcal {L}})\oplus C^\infty (\mathcal {M})[-1]$.

It is straightforward to verify that the $L_\infty$ algebra structure $({\bar{\lambda }}_l)_{l\geqslant 1}$ on $\Gamma ({\mathcal {L}})\oplus C^\infty (\mathcal {M})[-1]$ satisfies the four conditions listed in Lemma A.2. Therefore, ${\mathcal {L}}\rightarrow \mathcal {M}$ is an $L_\infty$ algebroid. Its multi-anchor maps $\rho _l: \Lambda ^l {{\mathcal {L}}}\rightarrow T_\mathcal {M}$ (with $l\geqslant 0$) and multi-brackets $\lambda _l: \Lambda ^l\Gamma ({\mathcal {L}})\rightarrow \Gamma ({\mathcal {L}})$ (with $l\geqslant 1$) are defined by the relations:

$$\begin{aligned} \rho _l(a_1,a_2, \ldots ,a_l) f= (-1)^{\flat } 0^*\big ( \left[ \left[ \left[ \left[ Q,{\iota }_{a_1}\right] ,{\iota }_{a_2}\right] ,\cdots \right] ,{\iota }_{a_l}\right] (\pi ^* f) \big ), \end{aligned}$$

(37)

where $\flat =l\left| a_{ 1}\right| +(l-1)\left| a_{2}\right| +\cdots +\left| a_{ {l}}\right|$ and

$$\begin{aligned} \left\langle \lambda _l(a_1,a_2, \ldots ,a_l),\xi \right\rangle = (-1)^{\sharp } 0^*\big ( \left[ \left[ \left[ \left[ Q,{\iota }_{a_1}\right] ,{\iota }_{a_2}\right] ,\cdots \right] ,{\iota }_{a_l}\right] (\xi ) \big ) \end{aligned}$$

(38)

where $\sharp =(l-1)\left| a_{ 1}\right| +(l-2)\left| a_{2}\right| +\cdots +\left| a_{ {l-1}}\right|$ for all $\xi \in \Gamma ({\mathcal {L}}^\vee ),a_1,a_2,\dots ,a_l\in \Gamma ({\mathcal {L}})$ and $f\in C^\infty (\mathcal {M})$.

Conversely, given an $L_\infty$ algebroid ${\mathcal {L}}\rightarrow \mathcal {M}$ with multi-anchors $(\rho _l)_{l\geqslant 0}$ and multi-brackets $(\lambda _l)_{l\geqslant 1}$, one can recover the corresponding homological vector field Q on ${\mathcal {L}}[1]$ satisfying the desired properties.

The algebra $C^\infty ({\mathcal {L}}[1])$ admits the direct product decomposition

$$\begin{aligned} C^\infty ({\mathcal {L}}[1]) = \prod _{k=0}^\infty \Gamma (S^k({\mathcal {L}}^\vee [-1])) . \end{aligned}$$

We will refer to $\Gamma (S^k({\mathcal {L}}^\vee [-1]))$ as the weight k component of $C^\infty ({\mathcal {L}}[1])$. Note that $\pi ^* C^\infty (\mathcal {M})$ (the component of weight 0) and $\Gamma ({\mathcal {L}}^\vee [-1])$ (the component of weight 1) generate the associative algebra $C^\infty ({\mathcal {L}}[1])$. A vector field Q on ${\mathcal {L}}[1]$ is necessarily of the form $Q=\sum _{l=-1}^\infty D_l$, where $D_l$ is a derivation on $C^\infty ({\mathcal {L}}[1])$ of weight l:

$$\begin{aligned} D_l: \Gamma ({{S}}^{k}({\mathcal {L}}^\vee [-1]))\rightarrow \Gamma ({{S}}^{k+l}({\mathcal {L}}^\vee [-1])), \qquad \forall k . \end{aligned}$$

Since Q is tangent to $\mathcal {M}$, i.e. we want $Q\in \ker ( P)$, its weight $(-1)$ component $D_{-1}$ must vanish. Choose a local coordinate chart $(x^j)_{j\in J}$ on $\mathcal {M}$; a local frame $(s_k)_{k\in K}$ for ${\mathcal {L}}[1]$; and the dual local frame $(\xi ^k)_{k\in K}$ for ${\mathcal {L}}^\vee [-1]$, the derivation $D_l$ can be written as

$$\begin{aligned} D_l= & {} \frac{1}{l!}\sum _{j\in J} \xi ^{i_l}\cdots \xi ^{i_{2}}\xi ^{i_1} \pi ^*({\tilde{Q}}^j_{i_1,i_2, \ldots ,i_l}) \frac{\partial }{\partial x^j}\\&+ \frac{1}{(l+1)!}\sum _{k\in K} \xi ^{i_l}\cdots \xi ^{i_1}\xi ^{i_0} \pi ^*(Q^k_{i_0,i_1, \ldots ,i_l}) \frac{\partial }{\partial \xi ^k} , \end{aligned}$$

where

$$\begin{aligned} {\tilde{Q}}^j_{i_1,i_2, \ldots ,i_l} = (-1)^{\diamond } \rho _l(s_{i_1},s_{i_2}, \ldots ,s_{i_l}) x_j \end{aligned}$$

with $\diamond =(l-1)\left| s_{i_1}\right| +(l-2)\left| s_{i_2}\right| +\cdots +\left| s_{i_{l-1}}\right|$, and

$$\begin{aligned} Q^k_{i_0,i_1, \ldots ,i_l} = (-1)^{\dag } \left\langle \lambda _{l+1}(s_{i_0},s_{i_1}, \ldots ,s_{i_l}),\xi ^k\right\rangle \end{aligned}$$

with $\dag =(l+1)\left| s_{i_0}\right| +l\left| s_{i_1}\right| +\cdots +\left| s_{i_{l}}\right|$. One checks that $D_l$, and therefore Q, is well defined. In summary, the multi-anchors and multi-brackets of the $L_\infty$ algebroid ${\mathcal {L}}\rightarrow \mathcal {M}$ determine through Eqs. (37) and (38) a vector field Q of degree $+1$ on ${\mathcal {L}}[1]$, which is tangent to the zero section $\mathcal {M}$.

The $L_\infty [1]$ algebra structure $(\mu _l)_{l\geqslant 1}$ on $\Gamma ({\mathcal {L}}[1])\oplus C^\infty (\mathcal {M})$ determined by the $L_\infty$ algebroid ${\mathcal {L}}\rightarrow \mathcal {M}$ as per Lemma A.2 is related to the vector field Q through Eq. (36). It follows from the generalized Jacobi identity, Eq. (36), and repetitive use of Eq. (35) that

$$\begin{aligned} 0 = \sum _{p+r=l+1}(\mu _p\circ \mu _r)(z_1, \ldots ,z_l) = P \big (\left[ \left[ \left[ \left[ \left[ Q,Q\right] ,z_1\right] ,z_2\right] ,\cdots \right] ,z_l\right] \big ) , \end{aligned}$$

for all $z_1,z_2,\dots ,z_l\in \Gamma ({\mathcal {L}}[1])\oplus C^\infty (\mathcal {M})$. Therefore $\left[ Q,Q\right] =0$, i.e. Q is a homological vector field. $\quad \square$

Appendix B. Shifted Poisson Algebras

Definition B.1

A degree k Poisson algebra is a ${\mathbb {Z}}$-graded commutative associative algebra ${\mathfrak {R}}$ with a degree k Poisson bracket, denoted by $[-,-]$ (i.e. $[{\mathfrak {R}}^i,{\mathfrak {R}}^j]\subset {\mathfrak {R}}^{i+j+k}$), satisfying

• (1) $[a,b]=-(-1)^{ \left| a\right| ^{[k]} \left| b\right| ^{[k]} }[b,a]$,

• (2) $[a,[b,c]]=[[a,b],c]+(-1)^{ \left| a\right| ^{[k]} \left| b\right| ^{[k]}}[b,[a,c]]$,

• (3) $[a,bc]=[a,b]c+(-1)^{ \left| a\right| ^{[k]}\left| b\right| }b[a,c]$,

for all homogeneous elements $a,b,c\in {\mathfrak {R}}$.

Note that Conditions (1) and (2) are equivalent to that ${\mathfrak {R}}[-k]$ is a ${\mathbb {Z}}$-graded Lie algebra, while (3) means that the Lie bracket is a biderivation.

Also note that degree 0 Poisson algebras are usual Poisson algebras while degree $(+1)$ Poisson algebras are Gerstenhaber algebras. In the meantime, one can obtain a degree k Poisson algebra from a graded Lie algebra as indicated in the following

Proposition B.2

Let $\mathfrak {g}$ be a graded Lie algebra. Then the symmetric product $S(\mathfrak {g}[k])$ (similarly ${\hat{S}} (\mathfrak {g}[k])$) admits a unique degree k Poisson algebra structure which extends the original Lie bracket on $\mathfrak {g}$.

Appendix C. Shifted Polyvector Fields

Let $\mathcal {M}$ be a ${\mathbb {Z}}$-graded manifold. A degree l vector field $X\in \mathscr {X}(\mathcal {M})$ is a derivation $C^{\infty }(\mathcal {M})\xrightarrow {X}C^{\infty }(\mathcal {M})$ of degree l. The degree of X is denoted by $\left| X\right| =l$.

The commutator in $\mathscr {X}(\mathcal {M})$ is standard:

$$\begin{aligned}{}[X,Y]=X\circ Y-(-1)^{\left| X\right| \left| Y\right| }Y\circ X , \end{aligned}$$

for all homogeneous $X,Y\in \mathscr {X}(\mathcal {M})$. It is obvious that $\mathscr {X}(\mathcal {M})$ is a left $C^{\infty }(\mathcal {M})$-module, and the pair $(\mathscr {X}(\mathcal {M}),C^{\infty }(\mathcal {M}))$ forms a ${\mathbb {Z}}$-graded Lie–Rinehart algebra.

Let $n\in {\mathbb {Z}}$ be a fixed integer. Following Pridham [39, 40], let $\mathscr {X}^0_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)=C^{\infty }(\mathcal {M})$, and for each $m\geqslant 1$,

$$\begin{aligned} \mathscr {X}^{m}_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n) ={S}^m_{C^{\infty }(\mathcal {M})}\bigl (\Gamma (\mathcal {M}; T_\mathcal {M}[n+1]\bigr ) . \end{aligned}$$

Elements in $\mathscr {X}^{m}_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$ are called n-shifted m-polyvector fields on $\mathcal {M}$. Then the space

$$\begin{aligned} \mathscr {X}^{\bullet }_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n) =\bigoplus _{m\geqslant 0}\mathscr {X}^{m}_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n) \end{aligned}$$

is called the n-shifted Schouten–Nijenhuis algebra of $\mathcal {M}$. Its completion is denoted by ${\hat{\mathscr {X}}}^\bullet _{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$. It is simple to see that

$$\begin{aligned} {\hat{\mathscr {X}}}^\bullet _{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)\cong C^{\infty }(T^\vee _\mathcal {M}[-n-1]) , \end{aligned}$$

the space of functions on the $(-n-1)$-shifted cotangent bundle $T^\vee _\mathcal {M}$.

Since $T_\mathcal {M}$ is a Lie algebroid, $T^\vee _\mathcal {M}$ is a canonical Poisson manifold, which is in fact symplectic. According to Proposition 3.8, we have the following

Lemma C.1

The space $\mathscr {X}^{\bullet }_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$ admits a degree $(n+1)$ Poisson algebra structure, similarly ${\hat{\mathscr {X}}}^\bullet _{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$.

This degree $(n+1)$ Poisson bracket is also known as the n-shifted Schouten–Nijenhuis bracket. When $n=0$, the space of 0-shifted polyvector fields $\mathscr {X}^{\bullet }_{{{\,\mathrm{poly}\,}}}(\mathcal {M},0)$, coincides with the usual Schouten–Nijenhuis algebra on $\mathcal {M}$, which is simply denoted by $\mathscr {X}^\bullet _{{{\,\mathrm{poly}\,}}}(\mathcal {M})$. When $n=-1$, the space of $(-1)$-shifted polyvector fields $\mathscr {X}^{\bullet }_{{{\,\mathrm{poly}\,}}}(\mathcal {M},-1)$ is the Poisson algebra $\text{ Pol }({T^\vee _\mathcal {M}})$. Its completion ${\hat{\mathscr {X}}}^\bullet _{{{\,\mathrm{poly}\,}}}(\mathcal {M},-1)\cong C^{\infty }(T^\vee _\mathcal {M})$.

Any element in $\mathscr {X}^{m}_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$ is a finite sum of homogeneous elements of the form:

$$\begin{aligned} \Pi ={\bar{X}}_1\odot {\bar{X}}_2\odot \cdots \odot {\bar{X}}_m , \end{aligned}$$

where $X_i\in \mathscr {X}(\mathcal {M})$, and ${\bar{X}}_i\in \mathscr {X}(\mathcal {M})[n+1]$ denotes the corresponding element with shifted degree. The number $\left| \Pi \right| =\left| X_1\right| +\cdots +\left| X_m\right|$ is called the pure degree of X, whereas m is called the weight. By

$$\begin{aligned} \parallel \Pi \parallel _{n}=\left| \Pi \right| -m(n+1) , \end{aligned}$$

we denote the total degree of $\Pi$. The following lemma provides an alternative description of shifted polyvector fields.

Lemma C.2

A homogeneous n-shifted m-polyvector field of pure degree p is equivalent to an m-ary operation

$$\begin{aligned} \Pi : {(C^{\infty }(\mathcal {M}))}^{\otimes m}\rightarrow C^{\infty }(\mathcal {M}) \end{aligned}$$

on $C^{\infty }(\mathcal {M})$ satisfying the following properties:

• 1) $\Pi$ is symmetric multilinear on $C^{\infty }(\mathcal {M})[-n-1]$:

  $$\begin{aligned}&\Pi (f_1, \ldots ,f_{i-1},f_i,f_{i+1},f_{i+2}, \ldots ,f_m) \\&~~\quad = (-1)^{\left| {f}_i\right| ^{[n+1]}\left| {f}_{i+1}\right| ^{[n+1]}}\Pi (f_1, \ldots ,f_{i-1}, f_{i+1},f_{i},f_{i+1}, \ldots ,f_m) ;\end{aligned}$$

• 2) $\Pi$ is a (multi-) derivation of degree p:

  $$\begin{aligned}&\Pi (f_1, \ldots ,f_{m-1},f_mf'_m)\\&~\quad = \Pi (f_1, \ldots ,f_{m-1},f_m)f'_m +(-1)^{(p+\left| f_1\right| +\cdots +\left| f_{m-1}\right| )\left| f_m\right| } f_m\Pi (f_1, \ldots ,f_{m-1},f'_m) . \end{aligned}$$

The proof is omitted as it is completely analogous to the usual unshifted polyvector fields on ordinary smooth manifolds.

Finally, we need a technical lemma for an explicit formula describing the $(n+1)$-shifted Poisson bracket in $\mathscr {X}^{\bullet }_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$. For any $\Pi \in \mathscr {X}^p_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$ and $\Lambda \in \mathscr {X}^q_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$, let $\Pi \circ \Lambda$ be the $(p+q-1)$-ary operation $({C^{\infty }({\mathcal {M}})})^{\otimes {p+q-1}}\rightarrow C^{\infty }({\mathcal {M}})$ given by

$$\begin{aligned}&(\Pi \circ \Lambda )(f_1, \ldots ,f_{p+q-1}) \\&\quad = \sum _{\sigma \in \mathrm {Sh}(p,q-1)}{\epsilon ^{[n+1]}}(\sigma ) \Pi (\Lambda (f_{\sigma (1)}, \ldots ,f_{\sigma (q)}),f_{\sigma (q+1)}, \ldots ,f_{\sigma (p+q-1)}). \end{aligned}$$

Here ${\epsilon }^{[n+1]}(\sigma )$ denotes the Koszul sign with respect to the shifted degrees $\left| {f}_1\right| ^{[n+1]}$, $\cdots$, $\left| {f}_{p+q}\right| ^{[n+1]}$.

Lemma C.3

For any $\Pi \in \mathscr {X}^{p}_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$ and $\Lambda \in \mathscr {X}^{q}_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$, the degree $(n+1)$ Poisson bracket $[\Pi ,\Lambda ]$ in $\mathscr {X}^{\bullet }_{{{\,\mathrm{poly}\,}}}(\mathcal {M},n)$ as in Lemma C.1 coincides with the graded commutator:

$$\begin{aligned}{}[\Pi ,\Lambda ]=\Pi \circ \Lambda -(-1)^{(\parallel \Pi \parallel _{n}+n+1)(\parallel \Lambda \parallel _{n}+n+1)}\Lambda \circ \Pi . \end{aligned}$$