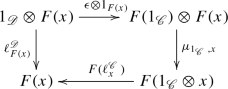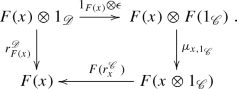Abstract
In the framework of Atiyah’s axioms of topological quantum field theory with unitarity, we give a direct proof of the fact that symmetry protected topological phases without Hall effects are classified by cobordism invariants. We first show that the partition functions of those theories are cobordism invariants after a tuning of the Euler term. Conversely, for a given cobordism invariant, we construct a unitary topological field theory whose partition function is given by the cobordism invariant, assuming that a certain bordism group is finitely generated. Two theories having the same cobordism invariant partition functions are isomorphic.














Similar content being viewed by others
References
Kapustin, A.: Symmetry protected topological phases, anomalies, and cobordisms: beyond group cohomology. arXiv:1403.1467
Kapustin, A., Thorngren, R., Turzillo, A., Wang, Z.: Fermionic symmetry protected topological phases and cobordisms. JHEP 12, 052 (2015). arXiv:1406.7329
Freed, D.S., Hopkins, M.J.: Reflection positivity and invertible topological phases. arXiv:1604.06527
Hasan, M.Z., Kane, C.L.: Topological insulators. Rev. Mod. Phys. 82, 3045 (2010). arXiv:1002.3895
Qi, X.L., Zhang, S.C.: Topological insulators and superconductors. Rev. Mod. Phys. 83(4), 1057–1110 (2011)
Freed, D.S., Moore, G.W.: Setting the quantum integrand of M-theory. Commun. Math. Phys. 263, 89–132 (2006). hep-th/0409135
Ryu, S., Moore, J.E., Ludwig, A.W.W.: Electromagnetic and gravitational responses and anomalies in topological insulators and superconductors. Phys. Rev. B 85, 045104 (2012). arXiv:1010.0936
Wen, X.-G.: Classifying gauge anomalies through symmetry-protected trivial orders and classifying gravitational anomalies through topological orders. Phys. Rev. D88(4), 045013 (2013). arXiv:1303.1803
Kapustin, A., Thorngren, R.: Anomalies of discrete symmetries in various dimensions and group cohomology. arXiv:1404.3230
Freed, D.S.: Anomalies and invertible field theories. Proc. Symp. Pure Math. 88, 25–46 (2014). arXiv:1404.7224
Wang, J.C., Gu, Z.-C., Wen, X.-G.: Field theory representation of gauge-gravity symmetry-protected topological invariants, group cohomology and beyond. Phys. Rev. Lett. 114(3), 031601 (2015). arXiv:1405.7689
Hsieh, C.-T., Cho, G.Y., Ryu, S.: Global anomalies on the surface of fermionic symmetry-protected topological phases in (3+1) dimensions. Phys. Rev. B93(7), 075135 (2016). arXiv:1503.01411
Witten, E.: Fermion path integrals and topological phases. Rev. Mod. Phys. 88(3), 035001 (2016). arXiv:1508.04715
Witten, E.: The “parity” anomaly on an unorientable manifold. Phys. Rev. B94(19), 195150 (2016). arXiv:1605.02391
Guo, M., Putrov, P., Wang, J.: Time reversal, SU(N) Yang-Mills and cobordisms: interacting topological superconductors/insulators and quantum spin liquids in 3+1D. arXiv:1711.11587
Atiyah, M.F., Patodi, V.K., Singer, I.M.: Spectral asymmetry and riemannian geometry 1. Math. Proc. Camb. Philos. Soc. 77, 43 (1975)
Dai, X-z, Freed, D.S.: eta invariants and determinant lines. J. Math. Phys. 35, 5155–5194 (1994), [hep-th/9405012]. [Erratum: J. Math. Phys.42,2343(2001)]
Yonekura, K.: Dai-freed theorem and topological phases of matter. JHEP 09, 022 (2016). arXiv:1607.01873
Fukaya, H., Onogi, T., Yamaguchi, S.: Atiyah-Patodi-Singer index from the domain-wall fermion Dirac operator. Phys. Rev. D96(12), 125004 (2017). arXiv:1710.03379
Chen, X., Gu, Z.-C., Liu, Z.-X., Wen, X.-G.: Symmetry protected topological orders and the group cohomology of their symmetry group. Phys. Rev. B87(15), 155114 (2013). arXiv:1106.4772
Gu, Z.-C., Wen, X.-G.: Symmetry-protected topological orders for interacting fermions: fermionic topological nonlinear ? models and a special group supercohomology theory. Phys. Rev. B90(11), 115141 (2014). arXiv:1201.2648
Wang, Q.-R., Gu, Z.-C.: Towards a complete classification of fermionic symmetry protected topological phases in 3D and a general group supercohomology theory. Phys. Rev. X8(1), 011055 (2018). arXiv:1703.10937
Kitaev, A.: On the classification of short-range entangled states. Talk at Simons Center. http://scgp.stonybrook.edu/archives/16180
Gaiotto, D., Johnson-Freyd, T.: Symmetry protected topological phases and generalized cohomology. arXiv:1712.07950
Xiong, Z.: Minimalist approach to the classification of symmetry protected topological phases. arXiv:1701.00004
Freed, D.S.: Short-range entanglement and invertible field theories. arXiv:1406.7278
Freed, D.S., Komargodski, Z., Seiberg, N.: The sum over topological sectors and \(\theta \) in the 2+1-dimensional \(\mathbb{CP}^{1}\,\sigma \)-Model. arXiv:1707.05448
Baez, J .C., Dolan, J.: Higher dimensional algebra and topological quantum field theory. J. Math. Phys. 36, 6073–6105 (1995). [q-alg/9503002]
Lurie, J.: On the classification of topological field theories. arXiv:0905.0465
Schommer-Pries, C.: Invertible topological field theories. arXiv:1712.08029
Fidkowski, L., Chen, X., Vishwanath, A.: Non-abelian topological order on the surface of a 3D topological superconductor from an exactly solved model. Phys. Rev. X3(4), 041016 (2013). arXiv:1305.5851
Wang, C., Senthil, T.: Interacting fermionic topological insulators/superconductors in three dimensions. Phys. Rev. B89(19), 195124 (2014). arXiv:1401.1142. [Erratum: Phys. Rev.B91,no.23,239902(2015)]
Metlitski, M.A., Fidkowski, L., Chen, X., Vishwanath, A.: Interaction effects on 3D topological superconductors: surface topological order from vortex condensation, the 16 fold way and fermionic Kramers doublets. arXiv:1406.3032
Morimoto, T., Furusaki, A., Mudry, C.: Breakdown of the topological classification \(\mathbb{Z}\) for gapped phases of noninteracting fermions by quartic interactions. Phys. Rev. B92(12), 125104 (2015). arXiv:1505.06341
Tachikawa, Y., Yonekura, K.: Gauge interactions and topological phases of matter. PTEP 2016(9), 093B07 (2016). arXiv:1604.06184
Witten, E.: Three lectures on topological phases of matter. Riv. Nuovo Cim. 39(7), 313–370 (2016). arXiv:1510.07698
Gaiotto, D., Kapustin, A., Seiberg, N., Willett, B.: Generalized global symmetries. JHEP 02, 172 (2015). arXiv:1412.5148
Thorngren, R.: Topological terms and phases of sigma models. arXiv:1710.02545
Kapustin, A., Thorngren, R.: Higher symmetry and gapped phases of gauge theories. arXiv:1309.4721
Tachikawa, Y.: On gauging finite subgroups. arXiv:1712.09542
Córdova, C., Dumitrescu, T.T., Intriligator, K.: Exploring 2-group global symmetries. arXiv:1802.04790
Benini, F., Córdova, C., Hsin, P.-S.: On 2-group global symmetries and their anomalies. arXiv:1803.09336
Seiberg, N., Tachikawa, Y., Yonekura, K.: Anomalies of duality groups and extended conformal manifolds. arXiv:1803.07366
Freed, D.S.: The cobordism hypothesis. arXiv:1210.5100
Atiyah, M.: Topological quantum field theories. Inst. Hautes Etudes Sci. Publ. Math. 68, 175–186 (1989)
Baez, J.C.: Some definitions everyone should know. http://math.ucr.edu/home/baez/qg-fall2004/definitions.pdf
Milnor, J.: Lectures on the h-cobordism theorem. Princeton University Press, Princeton (1965)
Acknowledgements
The author would like to thank Y. Tachikawa and E. Witten for helpful comments, and K. Hori, C.-T. Hsieh, and Y. Tachikawa for discussions on related topics. The work of KY is supported in part by the WPI Research Center Initiative (MEXT, Japan), and also supported by JSPS KAKENHI Grant-in-Aid (Wakate-B), No.17K14265.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by X. Yin
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Some Categorical Notions
A Some Categorical Notions
For completeness, here we reproduce the definitions of symmetric monoidal categories, functors and natural transformations summarized in [46]. We denote categories by \({\mathscr {C}},{\mathscr {D}},\ldots \), functories by \(F,G,\ldots \), and natural transformations by \(\eta ,\ldots \). The definitions of ordinary categories, functors and natural transformations are explained very briefly in Sect. 2.4.
Symmetric monoidal category. First we define symmetric monoidal category.
Definition A.1
A monoidal category is a category equipped with
-
a functor \(\otimes : {\mathscr {C}}\times {\mathscr {C}}\rightarrow {\mathscr {C}}\) called the tensor product,
-
an object \(1 \in \mathrm{obj}({\mathscr {C}})\) called the unit object,
-
a natural isomorphism \(a_{x,y,z}\) (\(x,y,z \in \mathrm{obj}({\mathscr {C}})\)) called the associator
$$\begin{aligned} a_{x,y,z}: (x \otimes y) \otimes z \rightarrow x \otimes (y \otimes z) \end{aligned}$$(A.1)satisfying the pentagon equation
 (A.2)
(A.2) -
natural isomorphisms \(\ell _x\) and \(r_x\) called the left and right unit laws,
$$\begin{aligned} \ell _x : 1 \otimes x \rightarrow x, \qquad r_x: x \otimes 1 \rightarrow x \end{aligned}$$(A.3)satisfying the triangle equations
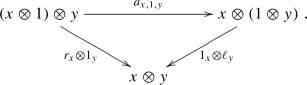 (A.4)
(A.4)
Roughly speaking, the pentagon equation means that “multiplications can be done in any order”, or “any ways to go from \((( w \otimes x) \otimes y) \otimes z\) to \(w \otimes ( x \otimes ( y \otimes z )) \) are the same”. The triangle equation means that “any ways to eliminate the unit 1 are the same”.
Definition A.2
A braided monoidal category is a monoidal category with a natural isomorphism \(b_{x,y}\) called the braiding,
satisfying the hexagon equations


Roughly speaking, the first hexagon equation above means that “moving x all at once from the left to the right of \(y \otimes z\) is the same as moving x step by step by first going through y and then z.” The second hexagon equation means a similar thing for z.
Definition A.3
A symmetric monoidal category is a braided monoidal category such that the braiding satisfies \(b_{y,x} b_{x,y} = 1_{x \otimes y}\).
Symmetric monoidal functor. Let us next consider functors between monoidal categories. In the following, if an expression like e.g. \(a^{\mathscr {D}}_{x,y,z}\) appears with a superscript or subscript \({\mathscr {D}}\), that means (in this particular case) “the associator in the category \({\mathscr {D}}\)”. The same remark applies to subscripts/superscripts of other quantities.
Definition A.4
A monoidal functor F between monoidal categories \({\mathscr {C}}\) and \({\mathscr {D}}\) is a functor with
-
a natural transformation
$$\begin{aligned} \mu _{x,y}: F(x) \otimes F(y) \rightarrow F(x \otimes y) \end{aligned}$$(A.8)satisfying the associativity
 (A.9)
(A.9) -
an isomorphism
$$\begin{aligned} \epsilon : 1_{{\mathscr {D}}} \rightarrow F(1_{\mathscr {C}}) \end{aligned}$$(A.10)satisfying
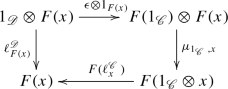 (A.11)
(A.11)and
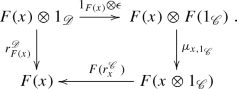 (A.12)
(A.12)
Roughly speaking, these equations mean that “the associator \(a_{x,y,z}\) and the left, right unit laws \(\ell _x\), \(r_x\) can be used before or after the application of the functor, giving the same result”.
Definition A.5
A braided monoidal functor between braided monoidal categories is a monoidal functor with the additional condition that

Again, this roughly means that “the braiding can be used before or after the functor”.
Definition A.6
A symmetric monoidal functor between symmetric monoidal categories is a braided monoidal functor without extra conditions.
Symmetric monoidal natural transformation.Finally, we describe natural transformations.
Definition A.7
A monoidal natural transformation \(\eta \) between monoidal functors F and G is a natural transformation such that the following diagram commutes:


Definition A.8
A braided (reps. symmetric) monoidal natural transformation between braided (reps. symmetric) monoidal functors is a monoidal natural transformation, without extra conditions.
Involution. For completeness, we also describe the notion of involution following [3].
Definition A.9
An involution on a category \({\mathscr {C}}\) is a pair \((\beta , \xi )\) of a functor \(\beta : {\mathscr {C}}\rightarrow {\mathscr {C}}\) and a natural isomorphism \(\xi : \mathrm{id}_{\mathscr {C}}\rightarrow \beta ^2\) such that \(\beta ( \xi _x) = \xi _{\beta (x)}\) as morphisms \(\beta (x) \rightarrow \beta ^3(x)\).
Roughly speaking, the involution functor \(\beta \) “squares to the identity functor”.
Definition A.10
Let \(\beta _{\mathscr {C}}\) and \(\beta _{\mathscr {D}}\) be involutions of categories \({\mathscr {C}}\) and \({\mathscr {D}}\). A functor \(F : {\mathscr {C}}\rightarrow {\mathscr {D}}\) is equivariant under the involution pair \((\beta _{\mathscr {C}}, \beta _{\mathscr {D}})\) if there is a natural isomorphism \(\phi : F \beta _{\mathscr {C}}\Rightarrow \beta _{\mathscr {D}}F\) such that the following diagram commutes:

Roughly speaking, this means that “the involution \(\beta \) and the functor F commutes with each other in the way consistent with the fact that the involution squires to the identity”.
The corresponding notions in symmetric monoidal categories can also be defined by using symmetric monoidal functors and symmetric monoidal natural isomorphisms.
Rights and permissions
About this article
Cite this article
Yonekura, K. On the Cobordism Classification of Symmetry Protected Topological Phases. Commun. Math. Phys. 368, 1121–1173 (2019). https://doi.org/10.1007/s00220-019-03439-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-019-03439-y