Skip to main content
SpringerLink
Log in

Critical Elastic Coefficient of Liquid Crystals and Hysteresis

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

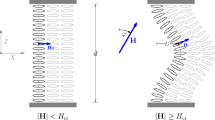
P. G. de Gennes predicted the analogies between the effect of the elastic coefficients to liquid crystals and the effect of applied magnetic fields to superconductors, and predicted that all elastic coefficients diverge to infinity at smectic-C to nematic transition. One would expect quantitative comparison in the analogies. In the case of equal elastic coefficients (K 1 = K 2 = K 3 = K), we define the critical value K c of the elastic coefficients and make comparison of it with the upper critical magnetic field H C 3 for type II superconductors. We classify the smectic liquid crystals into subcritical, critical and supercritical cases according to the Ginzburg-Landau parameter κ, the wave number q and the boundary value of the director at the surface. We show that in the subcritical case the liquid crystal does not undergo phase transition; and in the supercritical case both phase transition and hysteresis occur. The prediction of de Gennes is true in the critical case where μ π (u 0, q) = κ 2 and K c =  + ∞.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Brezis H., Coron J.-M. and Lieb E. (1986). Harmonic maps with defects. Commun. Math. Phys. 107: 649–705

    Article  ADS  MathSciNet  MATH  Google Scholar 

  2. Bauman P., Calderer M., Liu C. and Phillips D. (2002). The phase transition between chiral nematic and smectic A * liquid crystals. Arch. Rat. Mech. Anal. 165: 161–186

    Article  MathSciNet  MATH  Google Scholar 

  3. Bolley C. and Helffer B. (1993). An application of semi-classical analysis to the asymptotic study of the supercooling field of a superconducting material. Ann. Inst. Henri Poincaré, Physique Théorique 58: 189–233

    MathSciNet  MATH  Google Scholar 

  4. Bates P. and Pan X.-B. (2007). Nucleation of Instability of the Meissner State of three-Dimensional Superconductors. Commun. Math. Phys. 276(3): 571–610

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. Calderer M.C. (2001). Studies of layering and chirality of smectic A * liquid crystals. Math. Computer Modelling, 34: 1273–1288

    Article  MathSciNet  MATH  Google Scholar 

  6. Chapman S.J. (1995). Superheating fields of type II superconductors. SIAM J. Appl. Math. 55: 1233–1258

    Article  MathSciNet  MATH  Google Scholar 

  7. Caffarelli L.A., Kohn R. and Nirenberg L. (1984). First order interpolation inequalities with weights. Compositio Math. 53(3): 259–275

    MathSciNet  MATH  Google Scholar 

  8. Gennes P.G. (1972). An analogy between superconductors and smectics A. Solid State Commun. 10: 753–756

    Article  ADS  Google Scholar 

  9. Gennes P.G. (1973). Some remarks on the polymorphism of smectics. Molecular Crystals and Liquid Crystals 21: 49–76

    Article  Google Scholar 

  10. Prost J. and Gennes P.G. (1993). The Physics of Liquid Crystals. Second edition. Oxford Science Publications, Oxford

    Google Scholar 

  11. Du Y.H. and Pan X.-B. (2005). Multiple states and hysteresis for type I superconductors. J. Math. Phys. 46(7): Article no. 073301

    Article  ADS  MathSciNet  Google Scholar 

  12. Fournais S. and Helffer B. (2006). On the third critical field in Ginzburg-Landau theory. Commun. Math. Phys. 266: 153–196

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Ginzburg, V., Landau , L.: On the theory of superconductivity. In: Collected Papers, New York: Gordon and Breach, 1967, pp. 546–568

  14. Gilbarg D. and Trudinger N.S. (1983). Elliptic Partial Differential Equations of Second Order. Second edition. Springer, Berlin

    Google Scholar 

  15. Goodby J. and Waugh M. (1989). Characterization of a new helical smectic liquid-crystal. Nature 337(6206): 449–452

    Article  ADS  Google Scholar 

  16. Goodby J. and Waugh M. (1989). A new molecular ordering in helical liquid-crystals. J. Amer. Chem. Soc. 111(21): 8119–8125

    Article  Google Scholar 

  17. Helffer B. (1988). Semi-classical Analysis for the Schrödinger Operator and Applications. Lecture Notes in Mathematics 1336. Springer-Verlag, Berlin

    Google Scholar 

  18. Hardt R., Kinderlehrer D. and Lin F.H. (1986). Existence and partial regularity of static liquid crystal configurations. Commun. Math. Phys. 105: 547–570

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. Hardt R., Kinderlehrer D. and Lin F.H. (1988). Stable defects of minimizers of constrained variational principles. Ann. Inst. H. Poincasé Anal. Nonlineaire 5: 297–322

    MathSciNet  MATH  Google Scholar 

  20. Hardy, G.H., Littlewood, J.E., Pólya, G. (1952): Inequalities. Second edition, Cambridge: Cambridge University Press

    Google Scholar 

  21. Joo S.Y. and Phillips D. (2007). The phase transitions from chiral nematic toward smectic liquid crystals. Commun. Math. Phys. 269: 367–399

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. Lin F.H. and Liu C. (2001). Static and dynamic theories of liquid crystals. J. Partial Diff. Eqs. 14: 289–330

    MathSciNet  Google Scholar 

  23. Lu K. and Pan X.-B. (1999). Estimates of the upper critical field for the Ginzburg-Landau equations of superconductivity. Physica D 127(1–2): 73–104

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Lu K. and Pan X.-B. (2000). Surface nucleation of superconductivity in 3-dimension. J. Diff. Eqs. 168: 386–452

    Article  MathSciNet  MATH  Google Scholar 

  25. Pan X.-B. (2003). Landau-de Gennes model of liquid crystals and critical wave number. Commun. Math. Phys. 239: 343–382

    Article  ADS  MATH  Google Scholar 

  26. Pan X.-B. (2006). Landau-de Gennes model of liquid crystals with small Ginzburg-Landau parameter. SIAM J. Math. Anal. 37: 1616–1648

    Article  MathSciNet  MATH  Google Scholar 

  27. Pan, X.-B.: Analogies between superconductors and liquid crystals: nucleation and critical fields. Advanced Studies in Pure Math., Japan Math. Soc., to appear

  28. Pan, X.-B.: Phase transitions of liquid crystals with abnormal elastic coefficients. In preparation

  29. Pan X.-B. and Kwek K. (2002). On a problem related to vortex nucleation of superconductivity. J. Diff. Eqs. 182: 141–168

    Article  MathSciNet  MATH  Google Scholar 

  30. Renn S. and Lubensky T. (1988). Abrikosov dislocation lattice in a model of the cholesteric–to–smectic-A transition. Phys. Rev. A 8(4): 2132–2147

    Google Scholar 

  31. Rudin W. (2004). Real and Complex Analysis. McGraw-Hill, New York

    Google Scholar 

  32. Saint-James D. and de Gennes P.G. (1963). Onset of superconductivity in decreasing fields. Phys. Lett. 6(5): 306–308

    ADS  Google Scholar 

  33. Schoen, R., Uhlenbeck, K.: A regularity theory for harmonic maps. J. Diff. Geom. 17, 307–335 (1982). Correction in J. Diff. Geom. 18, 329 (1983)

    Google Scholar 

  34. Schoen R. and Uhlenbeck K. (1983). Boundary regularity and the Dirichlet problem for harmonic maps. J. Diff. Geom. 17: 253–268

    MathSciNet  Google Scholar 

  35. Uhlenbeck K. (1972). Eigenfunctions of Laplace operators. Bull. Amer. Math. Soc. 78: 1073–1076

    Article  MathSciNet  MATH  Google Scholar 

  36. Uhlenbeck K. (1976). Generic properties of eigenfunctions. Amer. J. Math. 98(4): 1059–1078

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, East China Normal University, Shanghai, 200062, People’s Republic of China

    Xing-Bin Pan

Authors
  1. Xing-Bin Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xing-Bin Pan.

Additional information

Communicated by H. Spohn

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pan, XB. Critical Elastic Coefficient of Liquid Crystals and Hysteresis. Commun. Math. Phys. 280, 77–121 (2008). https://doi.org/10.1007/s00220-008-0413-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-008-0413-9

Keywords

Search

Navigation