Abstract
We consider L1→L∞ estimates for the time evolution of Hamiltonians H=−Δ+V in dimensions d=1 and d=3 with bound  We require decay of the potentials but no regularity. In d=1 the decay assumption is ∫(1+|x|)|V(x)|dx<∞, whereas in d=3 it is |V(x)|≤C(1+|x|)−3−.
We require decay of the potentials but no regularity. In d=1 the decay assumption is ∫(1+|x|)|V(x)|dx<∞, whereas in d=3 it is |V(x)|≤C(1+|x|)−3−.
Similar content being viewed by others
References
Agmon, S.: Spectral properties of Schrödinger operators and scattering theory. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 2(2), 151–218 (1975)
Artbazar, G., Yajima, K.: The Lp-continuity of wave operators for one dimensional Schrödinger operators. J. Math. Sci. Univ. Tokyo 7(2), 221–240 (2000)
Deift, P., Trubowitz, E.: Inverse scattering on the line. Comm. Pure Appl. Math. XXXII, 121–251 (1979)
Jensen, A.: Spectral properties of Schrödinger operators and time-decay of the wave functions results in L2(Rm), m≥ 5. Duke Math. J. 47(1), 57–80 (1980)
Jensen, A.: Spectral properties of Schrödinger operators and time-decay of the wave functions. Results in L2(R4). J. Math. Anal. Appl. 101(2), 397–422 (1984)
Jensen, A., Kato, T.: Spectral properties of Schrödinger operators and time-decay of the wave functions. Duke Math. J. 46(3), 583–611 (1979)
Jensen, A., Nenciu, G.: A unified approach to resolvent expansions at thresholds. Rev. Math. Phys. 13(6), 717–754 (2001)
Journé, J.-L., Soffer, A., Sogge, C.D.: Decay estimates for Schrödinger operators. Comm. Pure Appl. Math. 44(5), 573–604 (1991)
Kato, T.: Wave operators and similarity for some non-selfadjoint operators. Math. Ann. 162, 258–279 (1965/1966)
Katznelson, Y.: An introduction to harmonic analysis. New York: Dover, 1968
Rauch, J.: Local decay of scattering solutions to Schrödinger’s equation. Commun. Math. Phys. 61(2), 149–168 (1978)
Reed, M., Simon, B.: Methods of modern mathematical physics. IV. Analysis of operators. New York-London: Academic Press [Harcourt Brace Jovanovich, Publishers], 1978
Rodnianski, I., Schlag, W.: Time decay for solutions of Schrödinger equations with rough and time-dependent potentials. Invent. Math. 155, 451–513 (2004)
Schlop, W.: Dispersive estimates for Schrödinger operators in dimension two, preprint 2004, to appear in Comm. Math. Phys.
Weder, R.:
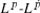 estimates for the Schrödinger equation on the line and inverse scattering for the nonlinear Schrödinger equation with a potential. J. Funct. Anal. 170(1), 37–68 (2000)
estimates for the Schrödinger equation on the line and inverse scattering for the nonlinear Schrödinger equation with a potential. J. Funct. Anal. 170(1), 37–68 (2000)Weder, R.: The Wk,p-continuity of the Schrödinger wave operators on the line. Commun. Math. Phys. 208(2), 507–520 (1999)
Yajima, K.: The Wk,p-continuity of wave operators for Schrödinger operators. J. Math. Soc. Japan 47(3), 551–581 (1995)
Yajima, K.: Lp-boundedness of wave operators for two-dimensional Schrödinger operators. Commun. Math. Phys. 208(1), 125–152 (1999)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by B. Simon
Supported by the NSF grant DMS-0070538 and a Sloan fellowship.
Rights and permissions
About this article
Cite this article
Goldberg, M., Schlag, W. Dispersive Estimates for Schrödinger Operators in Dimensions One and Three. Commun. Math. Phys. 251, 157–178 (2004). https://doi.org/10.1007/s00220-004-1140-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-004-1140-5



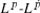 estimates for the Schrödinger equation on the line and inverse scattering for the nonlinear Schrödinger equation with a potential. J. Funct. Anal. 170(1), 37–68 (2000)
estimates for the Schrödinger equation on the line and inverse scattering for the nonlinear Schrödinger equation with a potential. J. Funct. Anal. 170(1), 37–68 (2000)