Introduction

Zinc isotopes can be fractionated by a number of chemical, biological, and physical processes. This characteristic provides the opportunity to investigate the bio-inorganic chemistry and cycling of this micronutrient element in the environment [1–3].

Over the past 10 years, efforts have been underway to use “non-traditional” naturally occurring isotopes in geochemical and cosmochemical studies whereby much information has been gained as to the magnitude of, and the processes that govern, Zn isotope fractionation [1, 2, 4–20]. This research has initiated an interest in applying Zn naturally occurring isotope studies at a biological level to understand mechanisms of uptake [21–24] and to gain insights into how organisms are involved with nutrient cycling in the wider environment [10, 16, 25].

Essential for such studies are precise and accurate Zn isotope analyses applicable to a wide variety of samples. High-precision isotope measurements by MC-ICPMS are, however, easily affected by matrix problems, which can produce inaccuracies [5, 6, 13, 26]. The adoption of a double-spike (DS) methodology for stable isotope analyses can overcome many of the most prevalent analytical problems. In particular, it enables a robust and precise correction for the instrumental mass bias and corrects for laboratory-induced isotope fractionations that may accompany incomplete element recovery during sample preparation. Despite these advantages, little attention has been given to the DS technique [5, 11].

The aim of this investigation was to develop a DS protocol for the accurate and precise determination of Zn isotope ratios and to provide confidence in the chosen spike combination. The performance of the DS technique was evaluated using a number of in-house and international standard reference materials. Following this, bulk soil from the Rothamsted farm (UK) and soil leachates were analyzed to characterize the Zn isotope pool available to plants in a natural setting. The results are discussed in relation to the soil’s history. This work forms part of ongoing efforts to investigate the Zn isotope geochemistry in the soil–plant environment [16, 21, 22, 24].

Experimental

Analytical facilities and reagents

Sample preparation was carried out in Class 10 laminar flow benches within the class 1,000 clean room facility of the Imperial College MAGIC Laboratories. Mineral acids except for HF were purified from Analar grade by sub-boiling distillation in quartz stills. Distilled HF (~28 M Ultrapure grade) and H2O2 (~30% v/v Aristar grade) were purchased from VWR. For the anion exchange chromatography, 7 M HCl was made by mixing sub-boiled (~6 M) and Merck Suprapur (~9 M) HCl. All other acid dilutions used >18.2 MΩ cm−1 grade H2O from a Millipore purification system.

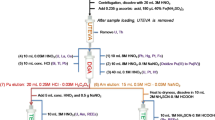
Sample digestion and Zn separation

Samples used in this study include two reference materials certified for elemental composition, blend ore BCR 027, previously analyzed by Chapman et al. [6], and the rye grass standard BCR 281. Also analyzed was a basalt from the East Pacific Rise (sample SO 40 31D from the Natural History Museum, London) and soil, obtained from the plow layer (0–20 cm) of an arable field on the Rothamsted farm, southeast England.

The rye grass standard BCR 281 digestion used a CEM Microwave Accelerated Reaction System MARS-X, with 100-ml XP-1500 Teflon vessels. To approximately 0.35 g of plant material were added 5 ml 9 M HNO3, 3 ml 30% H2O2, and 0.6 ml 28 M HF. The mixture was ramped to 210 °C and 250 psi and held for 90 min. Soil samples (50 mg) were digested using the same protocol. Soil leaches were used as a technique to estimate the composition of the Zn pool available to the plants [21, 27]. To this end, 30 ml 0.1 M HCl was added to 0.3 g of air-dried soil, and the resulting suspension was stirred continuously for 48 h at 25 °C. The suspension was centrifuged, and the supernatant was collected. The basalt sample (100 mg) was dissolved in 5 ml 28 M HF and 2 ml 15 M HNO3 at 120 °C on a hotplate for 48 h. The Zn blend ore BCR-027 (100 mg) was dissolved in 4 ml 15 M HNO3 and 1 ml 6 M HCl at 120 °C on a hotplate for 48 h.

After digestion, samples were evaporated to dryness, and the residue was dissolved in ~1 ml 7 M HCl with 0.05 ml 30% H2O2 added to prevent reduction of ferric Fe. The solutions were dried again and redissolved in 2.5 ml 7 M HCl containing 0.001% H2O2 by volume. These solutions were split into three aliquots: (1) 0.5 ml for preliminary Zn concentration measurements, (2) 1 ml for anion exchange chromatography to purify Zn for isotopic analysis, and (3) 1 ml for archive. The 0.5-ml aliquots for concentration measurement were first diluted to 3.5 ml and made up to 1 M HCl. These solutions were analyzed for Zn concentrations by inductively coupled plasma atomic emission spectroscopy (ICP-AES on a Vista PRO (Varian, Inc.) at the EMMA Laboratories of the Natural History Museum, London. The concentration data were used to ensure that an optimal amount of Zn DS was added to the sample solution prior to anion exchange chromatography.

The separation of Zn from matrix utilized Bio-Rad Poly-Prep columns that were filled with 2 ml of AG MP-1 100–200 mesh anion exchange resin. The resin was conditioned with 7 M HCl (10 ml) and successively washed with 0.08 M HNO3 (10 ml), H2O (10 ml), 0.08 M HNO3 (10 ml) and H2O (10 ml). This was followed by re-conditioning with 7 M HCl–0.001% H2O2 (7 ml) and loading of the samples (1 ml solution in 7 M HCl–0.001% H2O2). The majority of matrix elements were first eluted using 30 ml 7 M HCl–0.001% H2O2, followed by elution of Fe in 17 ml 2 M HCl (for separate isotope analysis). If Fe was not collected then all matrix elements were removed with 17 ml 2 M HCl. Finally, Zn was eluted from the columns with 12 ml 0.1 M HCl. The resin was then washed with 10 ml 0.5 M HNO3, after which it could be used again for further separations.

The Zn fraction was dried down, dissolved in 0.2 ml 15 M HNO3, and dried again to drive off residual HCl. Finally, 1 ml 0.1 M HNO3 was added and the samples refluxed for >2 h to ensure complete dissolution. The solutions were then ready to be analyzed with the Nu Plasma MC-ICPMS.

For the plant samples that were digested using a microwave oven, the total procedural Zn blank from dissolution and the ion exchange separation was 60 ± 15 ng, which represents ~1% of the total Zn for the samples with the lowest concentrations. For the rock samples that were dissolved in the clean room on a hotplate, the procedural Zn blank was lower than 20 ng, which is small considering that these samples contained at least 5 μg Zn. The effect of these blank contributions on the final isotopic results was essentially negligible when compared to the measurement uncertainty, and no correction was therefore applied.

Mass spectrometry and double spike

Double-spike design

Zinc has five stable isotopes, 64Zn (48.63%), 66Zn (27.90%), 67Zn (4.10%), 68Zn (18.75%), and 70Zn (0.62%), four of which are needed to implement a DS approach for stable isotope analysis. Numerical methods, adapted from Galer [28], were used to identify spike compositions that provide near-optimal (~90o) intersection angles between the mass fractionation vectors of spiked and unspiked samples, as well as minimal error magnification factors over a wide range of spike-sample ratios. These calculations demonstrate that a Zn DS enriched in 64Zn and 67Zn with a molar ratio of 64Zn/67Zn ≈ 2.5 provides the most favorable results if the equations are solved in 64Zn/67Zn–66Zn/67Zn–68Zn/67Zn isotope space. The calculations also indicate that this DS is ideally used with a molar fraction of spike derived to total Zn of between 0.5 and 0.6. This yields molar ratios 64Zn/66Zn/67Zn/68Zn for the sample spike mixture of about 5.2:1.4:1.5:1. These differ from those of the 64Zn–67Zn DS techniques of Bermin et al. [5] and John et al. [11] that are best used at molar ratios of 4.5:1.4:1.8:1 and 4.2:1.3:1.6:1, respectively.

Recently, Rudge et al. [29] published a thorough evaluation of possible double spikes for all elements with at least four naturally occurring isotopes. They identified the most suitable compositions using error propagation techniques on all possible spike combinations. We used the MATLAB codes made available by Rudge et al. [29] to compare the characteristics of our Zn DS with other favorable compositions. A number of factors made the inclusion of 70Zn difficult. These were (1) difficulties in expanding the measurable mass range in terms of instrumental mass dispersion, (2) the high cost of purified 70Zn, and (3) the spectral interference 54Fe16O+ and 70Ge+. With all other parameters remaining at default values, the methods of Rudge et al. [29] indicate that the optimal composition of a 64Zn–67Zn DS is 64Zn/67Zn = 4.88, which differs from the composition chosen for this study (64Zn/67Zn ≈ 2.51); however, the effect on error propagation and the range of optimal spike sample ratios is small (Fig. 1). Further calculations indicate that two other spike combinations (a 66Zn–67Zn and a 66Zn–68Zn DS) may be superior to a 64Zn–67Zn DS considering the error propagated on the natural fractionation factor (α). However, the maximum possible error reduction is only about 25% (Fig. 1). This and the results obtained in this study thus suggest that a suitable and robust DS composition was chosen for the Zn isotope measurements.

Fig. 1
figure 1

Results obtained from the evaluation of four favorable Zn double-spike compositions with the MATLAB error minimization code of Rudge et al. [29]. The curves denote the uncertainty in the natural fractionation factor α as a function of the proportion of double spike in the spike sample mixture. The results indicate that the double spike used in the present study (with 64Zn/67Zn = 2.51) can be used over a wide range of spike sample ratios and yields only marginally less precise results than alternative compositions

Full size image

The Zn DS was prepared as a mixture of two concentrated spike solutions that are enriched in 64Zn and 67Zn, respectively. 21.3 mg of 64Zn metal (99.30% purity; Isoflex Corp., USA) and 10.9 mg 67Zn (89.60% purity; Oak Ridge National Laboratory, USA) were each separately dissolved in 2 M HNO3. The Zn concentrations of the solutions were determined by reverse isotope dilution mass spectrometry to plan the preparation of the final DS solution. Suitable volumes of the individual spikes were then mixed to obtain a DS solution, which was characterized by 64Zn/67Zn ≈ 2.5 (Table 1) and a total Zn concentration of 5.1 μg g−1.

Table 1 Average Zn isotope compositions determined for London Zn and the Zn double spike
Full size table

The isotopic composition of the DS was determined by repeated MC-ICPMS analyses conducted during three separate analytical sessions over a period of six months. These measurements were carried out relative to a standard solution of natural Zn, hereafter named “London Zn,” which was prepared in our laboratory from a Zn wire of 99.9985% purity (Alfa Aesar, Puratronic grade). The Zn wire was first leached with 0.1 M HNO3, washed with water and ethanol, and then dissolved in 2 M HNO3.

The isotopic analyses of the spike used external normalization to Cu and the exponential law for mass bias correction:

$$ {R_{\rm{Zn}}} = {r_{\rm{Zn}}}{\left( {\frac{{66}}{{64}}} \right)^f} $$
(1)

where R Zn and r Zn denote the “true” and measured 66Zn/64Zn ratios, respectively, and the number is the atomic mass of the relevant isotope (integer values shown for simplicity). The fractionation factor f is given by:

$$ f = \frac{{\ln \left( {\frac{{{R_{\rm{Cu}}}}}{{{r_{\rm{Cu}}}}}} \right)}}{{\ln \left( {\frac{{65}}{{63}}} \right)}} $$
(2)

where R Cu is a presumed 65Cu/63Cu ratio for the copper dopant and r Cu is the measured ratio.

The 65Cu/63Cu ratio applied as R Cu in Eq. 2 was optimized for each measurement session from interspersed analyses of the London Zn solution doped with Cu. Re-calculation of the 65Cu/63Cu ratio was necessary in order to account for changes in the mass bias behavior between Zn and Cu on the day (this effect is further discussed in section Double-spike sample analysis protocol). A 65Cu/63Cu ratio was chosen, such that mass bias correction relative to 65Cu/63Cu and internal normalization relative to the reference ratio of 66Zn/64Zn = 0.565023 (from Rosman [30]) produced identical results for 64Zn/67Zn, 66Zn/67Zn, and 68Zn/67Zn. The optimized 65Cu/63Cu ratio was then used for the mass bias correction of the pure Zn DS solution (Table 1). This procedure implies that the isotope ratios of the DS were determined relative to the “normal” Zn isotope composition and relative to the reference ratio of 66Zn/64Zn of 0.565023. The Zn concentrations of the standard and spike solutions were accurately matched for these measurements and potential matrix effects due to different acid concentrations were avoided by drying down and re-dissolving suitable aliquots of the concentrated Zn DS and London Zn stock solutions in 0.1 M HNO3 prior to analysis. Thus, the mass bias behavior of Cu isotopes between standard and spike analyses remained identical, and a correction on the Zn isotope ratios could be made. This technique is analogous to that used by Siebert et al. [31] in calculating the Mo spike isotope composition by doping with Pd and by Weiss et al. [32] in calculating the Tl spike isotope composition during Pb isotope measurements using MC-ICPMS.

Double-spike measurement protocol

All isotopic measurements were performed with a Nu Plasma MC-ICPMS instrument, connected to a DSN-100 (Nu Instruments) desolvating sample introduction system that was operated with a CETAC Aspire nebulizer. The collector configuration is given in Table 2. Four Zn isotopes and 62Ni were measured simultaneously with the Faraday cups, all equipped with 1011 Ω resistors. The ion beam of 62Ni was monitored to correct for the isobaric interference on 64Zn from 64Ni.

Table 2 Nu Plasma collector configuration, natural isotope abundances for relevant elements, and typical ion beam intensities encountered in measurements conducted with optimal spike sample ratios
Full size table

The data acquisition sequence comprised 60 integrations of 5 s, in blocks of 20. Prior to each block, the baseline signals were monitored for 15 s, while the ion beam was deflected by the electrostatic analyzer; these data were subsequently subtracted from the measured ion beam intensities. This approach ignores any residual (memory) signals from previously analyzed sample or standard solutions. Tests showed that a further correction was not necessary because the memory signals contributed less than 0.4% to the ion beam intensities that were employed for isotopic measurements in this study. Each analysis was followed by a washout, whereby the sample introduction system was flushed with 0.1 M HNO3 for 100 s.

A complete sample analysis, excluding washout, required about 6 min and consumed ~500 μl sample solution. The instrumental sensitivity for Zn was usually 70 to 80 V/ppm. Analyses using an 8 V ion beam for 64Zn (Table 2) therefore required ~50 ng of natural Zn.

Double-spike data reduction

The Zn isotope data collected during the mass spectrometric analyses represent the “raw” Zn isotope compositions of the spike-sample mixtures. These data were processed to calculate the “true” mass-bias-corrected isotope compositions of the unspiked-samples. The DS data reduction was performed off-line, using a previously described iterative method [31]. The procedure applies a geometric approach to solve the DS equations in three-dimensional isotope space defined by isotope ratios with a common denominator [33]. It is particularly suitable for the accurate reduction of data collected by MC-ICPMS because it does not make the simplifying assumption that the instrumental mass bias can be described by a linear law. This assumption has been used for some measurements by thermal ionization mass spectrometry [28]; however, the mass bias of MC-ICPMS is at least an order of magnitude larger. Therefore, an iterative procedure is used, which accounts for the curved trajectories that are obtained, when mass discrimination is described using the exponential law [31].

Zn isotope notation

The Zn isotope data are reported relative to an isotope standard using the δ notation:

$$ \delta {\text{x}}/{\text{y}} = {\left( {\frac{{R_{{{\text{sample}}}} }} {{R_{{{\text{standard}}}} }} - 1} \right)} \times 10^{3} $$
(3)

where R sample and R standard denote the xZn/yZn isotope ratio of the sample and standard, respectively, and where x and y denote the isotope masses. In this study, Zn isotope ratios are generally quoted as δ66/64Zn values, which are abbreviated as δ66Zn.

Standard sample bracketing protocol

A standard sample bracketing (SSB) method was used for analyses of matrix-free Zn standard solutions to obtain additional and precise isotope data that were used to evaluate the DS technique. The SSB approach assumes that any temporal drift in mass bias between bracketing standards is predictable and approximates to a linear interpolation. This requires the mass bias to change smoothly during the course of a measurement session, without significant jumps between adjacent analyses. The sample and standard measurements by SSB comprised 20 integrations of 5 s each, in one block. The procedures employed for baseline and interference corrections remained identical to the DS protocol, as did the collector setup (Table 2). Results were obtained by inserting the “raw” average 66Zn/64Zn (or 67Zn/64Zn, 68Zn/64Zn) ratios for each sample into Equation 3, along with the mean result determined for the two bracketing standards.

Results and discussion

Double-spike sample analysis protocol

The London Zn standard was used as the in-house “zero-delta” reference material during this study. Repeated measurements of solution mixtures, prepared from Zn DS and London Zn with a near-optimal molar proportion of spike-derived relative to total Zn (approximately 0.55), were carried out during each analytical session. These mixtures commonly exhibited small deviations from δ66Zn = 0, in line with observations of previous studies using double spikes in conjunction with MC-ICPMS [5, 34, 35]. These small but significant variations (<1‰) appear to reflect changes in the instrumental mass bias, which produce fractionation patterns that deviate from exponential law behavior [36]. The generalized power law can be employed to accurately describe complex mass bias characteristics, but the exponential law was nonetheless implemented in this study because this approach is (1) more straightforward and (2) has been shown to provide accurate and precise stable isotope data if a simple empirical correction is employed to correct for this offset [34].

The offset corrections were performed by referencing the sample data of a measurement session to the mean isotopic composition determined from repeated analyses of a Zn DS–London Zn mixture:

$$ {\delta^{{66}}}{\hbox{Z}}{{\hbox{n}}_{{\rm{sample}}({\rm{true}})}}^= {\delta^{{66}}}{\hbox{Z}}{{\hbox{n}}_{{\rm{sample}}({\rm{measured}})}}-{\hbox{Z}}{{\hbox{n}}_{{\rm{London}}({\rm{measured}})}} $$
(4)

Over time periods of minutes to several (2–5) hours, the Zn DS–London Zn mixtures displayed isotope compositions that were essentially constant within the measurement precision (Fig. 2a). Small isotopic variations were seen on some days over periods of about 10–20 h (Fig. 2b). Contamination of the system was carefully monitored and could not account for the variation. When present, such trends were usually gradual and could be approximated by a linear interpolation for the correction of the data. For the results shown in Fig. 2b, the application of such a correction improved the precision of the repeated London Zn analyses from ±0.08 to ±0.04‰ (2SD) for δ66Zn.

Fig. 2
figure 2

The Zn isotope data (δ66Zn values) determined for London Zn–DS mixtures vs. time of data acquisition for two measurement sessions that had duration of a 3 h and b 23 h. In b, the measured δ66Zn values (filled symbols) are corrected for both the absolute offset and the drift in mass bias behavior (open symbols). This improves the precision of the dataset to ±0.04‰ (2 SD, open symbols)

Full size image

Bermin et al. [5] accounted for the small day-to-day deviations of the “zero-delta” standard using daily measurements of the natural Zn isotope composition for a natural standard, and applying this composition in the DS data reduction routine for samples analyzed on the same day. This approach, however, suffers from the drawback that the natural Zn isotope composition must be re-determined if there are larger drifts in mass bias behavior during the course of longer measurement sessions (e.g., Fig. 2b).

Each sample was measured four times during an analytical session, and these analyses yielded precisions (2SD) for δ66Zn of between ±0.06‰ and ±0.15‰, depending on instrument stability (Table 3). The average uncertainty of sample measurements was similar to the external precision (2SD) obtained for multiple analyses of a London Zn solution conducted during the same time interval. (NB: Uncertainties given in the text are always specific to the measurement made; average uncertainties are not used.)

Table 3 Zn isotope data acquired during this study
Full size table

A number of analyses were performed to ascertain that the DS technique could be used for accurate determination of Zn isotope compositions over a sensibly large range of spike sample ratios (Fig. 3). The Zn isotope compositions of Zn DS–London Zn mixtures with variable proportions of Zn DS were analyzed relative to a mixture with a DS-derived Zn proportion of P ≈ 0.55 (Fig. 3). The results demonstrate that the DS methodology yields accurate results when the DS contributes about 40% to 70% of the total Zn present in DS sample mixtures. At higher and lower proportions, the precision and accuracy of the data appear to deteriorate. The preliminary ICP-AES Zn concentration measurements allowed all samples to be spiked and analyzed with near-optimal proportion of DS-derived Zn (P ≈ 0.55).

Fig. 3
figure 3

The Zn isotope data obtained for various London Zn–Zn double-spike mixtures. The molar proportion of spike-derived Zn vs. total Zn varied between 0.2 and 1. The results are reported relative to data acquired at optimal proportion (0.55). The error bars denote the internal precision (±2SE) of the analyses

Full size image

Analysis of single-element standards

Comparisons of old and new in-house standards

Previous Zn isotope work in our laboratory used an “Imperial Zn” solution prepared from Alfa Aesar Puratronic Zn wire as the in-house reference material [9, 37]. The isotope composition of Imperial Zn was calibrated relative to the Johnson Matthey (JMC) Zn standard solution (batch 3-0749L) of the École Normale Supérieure Lyon Earth Science Laboratory (denoted “Lyon Zn” hereafter), thereby allowing inter-laboratory comparison. Numerous measurements performed using an Isoprobe MC-ICPMS over the last three years yielded δ66Zn = −0.06 ± 0.05‰ for Lyon Zn relative to Imperial Zn.

The newly prepared London Zn solution will be used as the in-house Zn isotope standard from this point forward, and several measurements were therefore made to calibrate the Zn isotope composition of London Zn relative to both Lyon Zn and Imperial Zn (Table 3). DS and SSB analyses reveal that the isotopic composition of Imperial Zn is identical to London Zn within analytical uncertainty. Most importantly, analyses of London Zn relative to Lyon Zn yielded δ66ZnLyon = 0.08 ± 0.04‰ using the DS protocol. This value is identical to data acquired during the course of this study by SSB on the Nu Plasma MC-ICPMS (Table 3) and demonstrates that the DS method is able to provide accurate Zn isotope data for pure Zn standard solutions. All samples were measured relative to London Zn, but to facilitate inter-laboratory comparison, the results were then recalculated and reported relative to Lyon Zn in Table 3.

Highly fractionated industrial single-element solution

Of particular interest are the results for the Spec-pure single-element solution with highly fractionated Zn. The DS protocol yielded δ66ZnLyon = −7.07 ‰ (±0.08, 2SD; ±0.02, 2SE; n = 11), while SSB protocols yielded δ66ZnLyon = −7.96 ‰ (±0.07, 2SD; ±0.03, 2SE, n = 6, Table 3). Each average value is based on multiple (between three and six) analyses of n separate stock solution aliquots. The number of measurements that were carried out for the Spec-pure Zn solution justifies the use of a 2SE error envelope to characterize the uncertainty of averages. Figure 4a shows the DS and the SSB data in three isotope diagrams of δ67Zn vs. δ66Zn and δ68Zn vs. δ64Zn. The results obtained for Spec-pure Zn by SSB and the DS approach are significantly different at the 95% confidence level. The DS protocol inherently forces all points to lie on an exponential mass-dependent fractionation curve, while the SSB analyses produced three independent Zn isotope ratios.

Fig. 4
figure 4

The Zn isotope compositions (open symbols for δ67Zn vs. δ66Zn; closed symbols for δ68Zn vs. δ66Zn) obtained by DS and by standard sample bracketing (SSB) for a Spec-pure Zn and b Lyon Zn. For Lyon Zn, only SSB results are shown for clarity (results by the DS methodology are shown in Table 3). The mean results of multiple analyses are shown. The error bars denote the ±2SE uncertainty limits (see text for details). Panel c presents a compilation of Zn isotope data from this study (Spec-pure), previous work on Romil Zn, and another pure Zn standard solutions with highly fractionated isotope compositions (JMC LMTG-10K Zn; Sonke et al. [40]). Note that the data of all three Zn standards appear to plot below the kinetic isotope fractionation line. The kinetic and equilibrium fractionation curves were calculated with Eq. 5 using β = 1.490 (kinetic) and 1.479 (equilibrium) for δ67Zn vs. δ66Zn and β = 1.971 (kinetic) and 1.942 (equilibrium) for δ68Zn vs. δ66Zn

Full size image

Theoretical mass-dependent fractionation lines for equilibrium and kinetic systems diverge as the magnitude of fractionation increases (Fig. 4). These fractionation lines are defined by the following equation:

$$ {\delta^{{\rm{x}}/{64}}} = [{(\frac{{{\delta^{{\rm{x}}/{64}}}}}{{{{10}^3}}})^\beta } - 1] \times {10^3} $$
(5)

Here, x and y represent the isotopes of mass m x and m y , and β is given by [ln(m y /m 64)]/[ln(m x /m 64)] for kinetic or (1/m 64 − 1/m y )/(1/m 64 − 1/m x ) for equilibrium systems [38].

The Spec-pure Zn isotope data (δ68Zn) obtained by SSB lie off the mass-dependent fractionation curves that describe equilibrium and kinetic isotope fractionation, or any intermediate mass bias relationship (Fig. 4a). Possible reasons include (1) spectral interferences on one or more isotopes during the analyses, (2) mass-independent isotope effects, or (3) complicated isotope fractionation processes characterized by multiple stages with different β values, which may have occurred during the production and purification of the Spec-pure Zn sample.

Spectral interferences are not responsible for the offset of the Spec-pure Zn SSB data seen in Fig. 4a. This is demonstrated by (1) the observation that only the Spec-pure but not the Lyon Zn data plot off the fractionation lines (Fig. 4a, b), while (2) elements that can form interfering species, such as Mg, Al, Ti, V, Cr, and Ba, are present at similar insignificant levels in the solutions of Spec-pure Zn, London Zn, Lyon Zn, and the Zn DS (measured using an ion counter on the Nu Plasma MC-ICPMS, data not shown). Mass-independent isotope effects related to nuclear volume are also unlikely to cause the offset because such effects are essentially insignificant for the first row d-block metals [39].

It is more likely that Spec-pure Zn was affected by multiple, and possibly repetitive, isotope fractionation processes that occurred during isolation and purification of the Zn metal. This conclusion is supported by close inspection of data for other highly fractionated Zn solutions analyzed in various laboratories with different instruments (Fig. 4c). Values for Romil Zn measured by standard sample bracketing on the Isoprobe at Imperial College (Table 3) and the results of Sonke et al. [40], for the most fractionated Zn standard measured to date (JMC LMTG-10k), also cluster below the kinetic mass fractionation curve. Furthermore, similar results were obtained for Cd metal that was the fractionated residue of Cd evaporation into vacuum [41].

The unusual isotopic characteristics of the Spec-pure Zn sample can be explained if two processes, such as evaporation and condensation, with slightly different β values (see Eq. 5) affected the Zn isotope composition during the production and purification. As an example, if we assume that (1) evaporation and condensation are characterized by β values of 1.95 and 1.97, respectively, and (2) that condensation and evaporation involve a +1‰ and −1‰ shift in δ66Zn, respectively. Hence, the overall shift in δ66Zn is 0, but the resulting net change for δ68Zn is about −0.02‰. The offset observed for Spec-pure Zn from the kinetic mass-dependent line is approximately 0.09 ‰ (δ68Zn), which can be readily produced by multiple evaporation/condensation cycles.

Stable isotope data acquired by the DS procedure cannot detect such effects because the data reduction assumes that the natural isotope fractionation is adequately described by a single kinetic mass fractionation curve, which connects sample and starting material (Siebert et al. [31]). Our finding implies that a subtle breakdown of the DS data reduction technique occurs, when it is applied to large isotopic fractionations, which are produced by multiple processes with different mass fractionation characteristics (β values).

Sample analysis: reproducibility and accuracy

The Zn isotope data obtained for geological and biological reference materials are summarized in Table 3. Four separate aliquots from the BCR-027 Zn blend digest were purified and analyzed over the course of three separate analytical sessions. The average δ66ZnLyon of these four measurements is +0.25 ± 0.06‰ (2SD), and this agrees well with the value of δ66ZnLyon = +0.33 ± 0.07‰ (2SD) obtained by Chapman et al. [6] for the same sample using SSB.

The basalt SO 40 31D from the East Pacific Rise was measured during a single analytical session and yielded δ66ZnLyon = +0.29 ± 0.07‰ (2SD). This value is within the range of Zn isotope compositions reported for other basalt samples (0.26–0.58‰; summarized by Cloquet et al. [2]).

Seven analyses of the ryegrass BCR 281 conducted on three separate analytical sessions gave a mean result of +0.40 ± 0.09‰ (2SD) for δ66ZnLyon. A slightly heavier average value of +0.71 ± 0.17‰ (2SD) was reported by Peel et al. [42] for the same material. Isotopic heterogeneity in the plant standard could be the reason for the difference. We expect the DS method to provide the most reliable Zn isotope measurements for plant material, given the reproducibility and accuracy of the data demonstrated here.

The Zn isotope composition of the Rothamsted soil: bulk sample and acid leachates

A standard method for the determination of the Zn pool available to rice plants is the extraction of Zn from the soil by leaching with 0.1 M HCl [27]. We used this method to investigate the isotopic composition of the Zn reservoir accessible to plants. The acid extracts Zn adsorbed on soil surfaces, such as amorphous Fe oxides, and organically bound Zn. For the Rothamsted soil, the Zn isotope composition of the leach fraction was on average ~0.2 ‰ heavier (δ66Zn) compared to the bulk soil (Table 3). In previous studies, enrichment of heavy Zn isotopes due to the long-term deposition of anthropogenic atmospheric Zn has been reported [18, 40]. The atmospheric deposition of Zn was linked to increases in the soil Zn content and other metals at Rothamsted UK from at least the beginning of twentieth century [43, 44]. The control plot (no additions of any fertilizers) of Rothamsted’s Broadbalk continuous wheat experiment showed an increase of 40% in the total Zn content between 1,865 and 2,000 µg g-1 [43]. Our results thus suggest that the Zn deposited by atmospheric pollution mainly remains loosely bound and is released in the 0.1 M HCl leach fraction, giving rise to the heavier isotopic signature observed in the acid leachate (Table 3).

A further interesting observation is made when evaluating mass balance calculations based on the soil fractions. Bulk soil and leach fractions of the Rothamsted soil have concentrations of ~105 and 26 μg g−1, respectively. Combining these data with the Zn isotope data (Table 3) in a mass balance calculation yields an undissolved soil fraction (after leaching) that possesses a δ66ZnLyon of ~0.28 ‰. This value agrees with the δ66Zn values reported for basalts both here and in previous studies [2, 6].

Conclusions

A Zn DS technique was developed for isotope analysis of a range of samples with the aim to overcome the instrumental mass bias problems, which are associated with the different sample matrices and can cause inaccuracies. Relative to previous Zn double-spike methods, this technique makes significant improvements regarding both ease of measurement and the precisions obtained. Single-element standards and various natural samples were analyzed to test the method. Results obtained from DS measurements of industrial Zn standard solutions were all consistent, within uncertainty (±0.05‰ to 0.10‰ for δ66Zn; 2SD), with data obtained in this and previous studies using alternative methods of mass bias correction. Further analyses of the BCR 027 Blend Ore reference material and a basalt sample from the East Pacific Rise yielded data that confirm previously reported values. Results from several digests of the BCR 281 ryegrass standard yielded δ66ZnLyon = 0.40 ± 0.09‰ (2SD, n = 7). Taken together, these results validate the new DS methodology, as the technique yields precise and accurate Zn isotope ratio results.

The highly fractionated Spec-pure Zn standard solution, however, yielded a small but significant difference between results obtained by the DS and SSB measurement protocols. The Zn isotope composition determined by SSB falls below the theoretical kinetic mass-dependent fractionation line (δ66ZnLyon = −7.06 ± 0.07 ‰), and this is probably due to repetitive fractionation events that occurred during purification of Spec-pure Zn. The slightly different DS result (δ66ZnLyon = −7.17 ± 0.08 ‰) for this sample is therefore most likely an analytical artifact of the DS data reduction routine because the latter assumes that the isotope fractionation is generated by a one-step process, which induces only kinetic isotope effects. Caution is therefore required if the DS procedure is applied to samples, which are strongly fractionated due to overprinting by multiple fractionation events.

The DS methodology was applied to estimate the isotopic pool of Zn available to plants from a soil. Mild acid leaching was used to extract the likely pool of bioavailable Zn, which was found to have an isotope composition 0.2‰ heavier than the bulk soil. Given the history of the soil, we suggest that the slightly heavier composition in the leachate originates from deposited atmospheric pollution.