Abstract
Anharmonic effects due to the shape of the molecular potential energy surface far from the equilibrium geometry are major responsible for the deviations of the actual frequencies of vibration from the harmonic estimates. However, anharmonic effects are not the solely responsible for this. Quantum nuclear effects also play a prominent role in theoretical vibrational spectroscopy as they contribute to drive away the molecular vibrational frequencies from their harmonic counterpart. The consequence of this is that anharmonicity and quantum effects may be difficult to separate spectroscopically and get often confused. In this work we show that anharmonicity can be detected by means of classical simulations, while quantum nuclear effects need to be identified by means of an approach originating from either the time independent or the time dependent Schroedinger equation of quantum mechanics. We show that classical methods are sensitive to the temperature or energy conditions under which they are undertaken. This leads to wrong frequency estimates, when dealing with few-Kelvin experiments, if one performs simulations simply matching the experimental temperature. Conversely, quantum approaches are not affected by this issue and they provide more and better information.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Vibrational spectroscopy is one of the main fields of investigation in modern molecular physics and theoretical chemistry [1]. Dealing with molecular vibrations requires both high level electronic structure theories and accurate approaches able to describe the nuclear motion. From the point of view of the electronic structure it is clear that coarse grained methods are not suitable and the most refined theories in quantum chemistry should be adopted. The computational burden gets even larger when one considers theories to describe the vibrational motion of the nuclei: This can be done at a classical or quantum mechanical level, using time-independent or time-dependent methods. For this reason different kinds of approximations have been introduced according to the complexity of the molecular system to study.
Probably the easiest way to provide an assessment of the vibrational behavior of a molecule is by means of the harmonic approximation: One optimizes the molecular geometry, calculates the mass-scaled matrix of second derivatives (Hessian) at the equilibrium geometry, and finally diagonalize it. For a nonlinear molecule 6 eigenvalues, related to translations and rigid rotations, are found to be 0 and the square roots of the remaining \(3N-6\) eigenvalues provide the harmonic frequencies of vibration. The corresponding eigenvectors define what are known as the normal modes of vibration.
This procedure involves only electronic structure calculations at a particular molecular geometry and therefore it is based on a very local investigation of the potential energy surface (PES). Actually, molecular PESs can be very complicated and they clearly deviate from the parabolic (harmonic) approximation as soon as the molecule moves away from the equilibrium geometry. In other words, PESs are anharmonic and this feature is reflected by the vibrational spectrum of the molecular system under investigation. The immediate consequence is that harmonic estimates are often off the mark and more refined methods are needed to take anharmonicity into account. Anharmonicity indeed influences both frequencies of vibration and intensities of absorption. When the harmonic approximation is employed for both frequencies and intensities the calculation is termed a double-harmonic approximation. This kind of approximation is the one that commonly commercial electronic structure software perform. Anyway, for the goals of this work we can focus just on anharmonicity and quantum effects related to the vibrational frequencies.
One ad hoc attempt to account for anharmonic frequencies consists in scaling the harmonic frequencies by a constant factor dependent on the level of electronic theory and basis set employed [2]. However, there are more elaborated and refined theories able to account for anharmonic effects. For instance, classical molecular dynamics (MD) simulations have been often adopted to determine the molecular frequencies of vibration. In this kind of approach the simulated trajectory is employed in the mathematical formalism of the Fourier transformed velocity–velocity autocorrelation function. The issue which emerges is that the frequency estimates are temperature dependent, and not always carrying out the simulation at the temperature of the reference experiment provides an accurate result. This is particularly true when the experiment is performed at very low temperature as we demonstrate in this work. Another approach able to include anharmonic effects is represented by quasi-classical trajectory (QCT) molecular dynamics. In this case a trajectory is started with harmonically quantized energy for the initial conditions and then the Fourier transform of the velocity–velocity autocorrelation function is evaluated the same way as in classical molecular dynamics. The approach is more suitable than classical MD when the experiment is undertaken at very low temperature (a few K), but still there is a dependence of the results on the trajectory energy.
Moving to quantum mechanics and spectroscopy, a number of methods have been developed. These have been developed within either a time-dependent or time-independent framework. To provide a short but not exhaustive list we mention approaches like discrete variabile representation (DVR) [3], vibrational self-consistent field (VSCF) [4], and second-order vibrational perturbation theory (VPT2) [5] as examples of time-independent methods. In the realm of time-dependent approaches lie instead the multi configuration time dependent Hartree (MCTDH) method [6], semiclassical (SC) dynamics theories [7,8,9,10,11,12,13,14], and other path integral-related methods, like centroid or ring polymer molecular dynamics [15, 16]. Similarly to classical methods, all these quantum approaches can detect the anharmonicity effects related to the potential energy surface, but differently from their classical counterparts they are able to describe also quantum effects.
Quantum effects play a fundamental role in molecular vibrational spectroscopy. One of them is the zero-point energy. This is a purely quantum mechanical quantity which can be estimated by neither experiments nor classical theoretical approaches. The presence of the zero-point energy poses also a challenge to quantum dynamical methods (i.e., those developed in a time-dependent framework). In fact these methods may suffer from zero-point energy leakage [17,18,19,20], while time-independent approaches do not have this issue. However, time-independent methods experience exponential scaling of computational memory with the number of degrees of freedom, an issue not affecting the trajectory-based time-dependent approaches.
As anticipated, experiments cannot provide an estimate of the zero-point energy, but there are other quantum effects clearly present in experimental spectra. Among them, combination bands provide a quantum fingerprint of even complex molecular systems and a representative example is given, for instance, by water clusters [21, 22] or adsorbed molecules on titania [23,24,25]. Combination bands are due to transitions associated to the simultaneous excitation of two or more modes. Another difference between a classical and a quantum spectroscopy simulation is that in a classical simulation spectroscopic features are found at integer multiples of the frequencies of vibration (these frequencies are known as higher harmonics and sometimes improperly called classical overtones), while in the quantum world anharmonic overtones, which reflect the changing spacing between energy levels due to the anharmonicity of the potential, are present. Tunneling is another quantum effect which influences spectroscopy [26,27,28,29,30]. For systems presenting a double well the tunnel effect splits the energy levels and the effect on the vibrational spectrum is that a doublet is present instead of a single peak. This feature is obviously present in experiments but cannot be reproduced with a classical simulation. Finally, quantum mechanics anticipates the possibility of quantum interference, a purely quantum effect which may affect the quantum frequencies of vibration.
Another difference between the classical and quantum description of spectroscopy lies in the dependence of the vibrational frequencies on the temperature. In the classical world, the frequencies of vibration are in general a continous function of the energy of the system, i.e., \(\omega =\omega (E)\), and so they are a function of temperature. The quantum picture is described instead by the Schroedinger equation, and in the Schroedinger equation there is no temperature. In few words, the discrete Hamiltonian eigenvalues do not depend on temperature, and so the transition energy gaps between them. This means that quantum mechanically vibrational frequencies are temperature independent. Consequently, a quantum approach should be able to describe quantum effects and also achieve some sort of convergence in the calculation of vibrational frequencies, which makes the method energy or temperature independent. This may look counterintuitive because experience shows that experimental spectra are temperature dependent. However, the reason is that it is the intensity of absorption which varies with temperature, not the frequency which is related to the energy gap between two states. This is because the temperature influences the population of the quantum energy levels and therefore affects the intensity of the quantum transitions (the theoretical counterpart of experimental spectroscopic signals).
The field of theoretical vibrational spectroscopy is currently very active. Machine learning approaches are being adopted to try to describe IR and Raman experiments [31] and also new methods are being developed. For instance, in a recent paper, Chen and Yang introduced the constrained nuclear-electronic orbital molecular dynamics (C-NEO MD) technique to evaluate the vibrational features of a few model systems [32]. In that paper the authors claim they demonstrate the ability of their technique to detect quantum effects in vibrational spectroscopy. Thanks to the transparent review process a debate between the authors and one anonymous referee is available, in which the referee argues that not all systems presented in the paper are suitable to draw the conclusion that C-NEO MD is a method able to detect quantum effects because the authors might be confusing anharmonicity for quantum effects.
In the current paper we would like to give evidence that anharmonic and quantum effects, which may appear to be closely intertwined because they are both responsible for the deviations of the actual frequencies of vibration of a molecule from their harmonic estimates, are actually a molecular tale of two cities. In one case (anharmonic effects) a classical investigation properly undertaken is sufficient, in the other case (quantum effects) proper quantum approaches must be employed. Therefore, newly proposed methods for quantum theoretical spectroscopy should be tested against zero-point energy evaluations or on systems that clearly display quantum spectroscopical features. Furthermore, quantum methods must derive from the Schroedinger equation (either in its time-independent or time-dependent version) and provide frequency estimates which are independent of energy or temperature.
The outline of the paper is as follows. Section 2 is dedicated to the theoretical description of the methods employed in this paper. Section 3 shows the results of the application of the chosen methods to a simple molecule: Formaldehyde (\(\hbox {H}_{2}\hbox {CO}\)). Furthermore, a rather complex system (protonated glycine tagged with hydrogen molecules) displaying a clear quantum effect, which we already presented in a previous paper, is here reproposed to better demonstrate the conclusions of this work. The paper ends with a summary and some conclusions.
2 Theoretical methods
In this Section we provide a brief overview of the theoretical methods employed in the simulations presented in Sect. 3. The reader interested in having more details may find them in the references cited along this section. We already described the well-known harmonic approximation in Sect. 1, so the first methods we illustrate are those employed for the classical simulations.
Our classical MD and QCT runs differ in the way the dynamics is performed but they both rely on the mathematical formalism of the Fourier-transformed velocity–velocity autocorrelation function. The initial distributions of velocities for the MD simulations are obtained from the Maxwell–Boltzmann distribution. Then, a thermalization run at the desired temperature is performed by means of a stochastic velocity rescaling algorithm applied to an evolution of 200000 a.u. [33] followed by a production run 30000 a.u. long in an NVE ensemble (i.e., in a microcanonical ensemble where the number of particles, volume and total energy are held fixed). The production dynamics is used to collect the data necessary for calculating the vibrational frequencies [34]. QCT simulations start the trajectories at a target and harmonically quantized energy [35]. The starting configuration of all trajectories is chosen to be the equilibrium geometry, while initial atomic linear momenta are extracted from a Husimi distribution and then rescaled in a way that the total energy matches the target one, i.e., the harmonic zero point energy or a multiple of it. QCT trajectories are evolved in an NVE ensemble for a total time of 25000 a.u. For both MD and QCT a 4th order symplectic algorithm is adopted for evolving the trajectories [36].
For the Fourier transform of the velocity–velocity autocorrelation function we employ its time averaged version [37, 38]
where j indicates the mode under consideration, \({p}_\text {j}\) is the linear momentum associated to mode j, and T is the total trajectory evolution time. The phase space integration is evaluated in a Monte Carlo way: For all temperatures and energies investigated we generate 6000 trajectories starting from a distribution of initial conditions and average the time-dependent integrand over the trajectories.
Another technique employed in this work is known as adiabatic switching (AS) [39,40,41,42,43,44,45]. The starting point of adiabatic switching is the classical Hamiltonian of a set of \(N_\textrm{vib}\) uncoupled harmonic oscillators (\(H_{0}\)) to obtain a harmonic quantization of the initial energy. In this aspect AS resembles QCT but, differently from the QCT runs, in which trajectories are evolved in the NVE ensemble according to the classical molecular Hamiltonian, in AS the actual classical molecular Hamiltonian (H) is very slowly switched on. In formulae
where \(H^\textrm{AS}(t)\) is the AS Hamiltonian and \(f_\textrm{S}\) is a switching function, for which several expressions have been proposed and adopted in the literature. Here, we choose one of them we already employed in our previous works with adiabatic switching [46,47,48]
\(T_\textrm{AS}\) is the total time of the adiabatic switching evolution. We choose \(T_{AS}=200{,}000\) a.u. AS is based on the adiabatic theorem which states that if one starts with a quantized model system (a set of harmonic oscillators) and switches on very slowly the molecular Hamiltonian (ideally taking an infinite amount of time), then the initial quantization is preserved also for the molecular system [49]. Looking at the final total energy provides an estimate of the quantized energy levels and therefore of the frequencies of vibration. The theorem is valid when the density of states is low, i.e., for the ground state (zero-point energy) and the first excited states, i.e., for determining the fundamental frequencies of vibration. Therefore, by means of adiabatic switching one can employ a classical dynamics to get a limited amount of approximate quantum information. For this reason AS is sometimes labeled as a semiclassical approach. However, we point out that AS is not derived from the Schroedinger equation and it is based on Newton’s laws of motion.
We also employ a proper semiclassical approach, i.e., a method derived from the time-dependent Schroedinger equation by approximating Feynman’s quantum propagator by means of a stationary phase approximation. This approach is known as the semiclassical initial value representation (SCIVR) [50]. Likewise adiabatic switching, SCIVR is able to get quantum estimates starting from classical trajectories. However, SCIVR is applicable to the whole range of energies, it accounts for quantum interference, anharmonic overtones, Fermi resonances, and can provide nuclear eigenfunctions [38, 51,52,53,54]. All these features make SCIVR a time-dependent quantum approximate method for calculating vibrational frequencies. Similarly to the case of QCT simulations, we use SCIVR in its time averaged version (TA SCIVR) for application to \(\hbox {H}_{2}\hbox {CO}\) [38, 51], while another version of it, the divide-and-conquer semiclassical initial value representation (DC SCIVR) is employed in the study of \(\hbox {H}_{2}\)-tagged protonated glycine [55, 56]. In this work we rely on the TA-SCIVR working formula
where I(E) is the density of vibrational states which displays peaks centered at the eigenenergies of the molecular vibrational Hamiltonian. The quantum frequencies of vibration are obtained by difference between the eigenenergies. The phase-space integral is treated in a Monte Carlo way upon evolution of a Husimi distribution of trajectories centered at the equilibrium geometry and at the zero-point energy. \(S_{t}(\textbf{p}_{0},\textbf{q}_{0})\) is the classical action along the trajectory started at \((\textbf{p}_{0},\textbf{q}_{0})\), \(\phi _{t}(\textbf{p}_{0},\textbf{q}_{0})\) is the phase of the Herman Kluk prefactor, \(|\) \(\textbf{p}_{t},\textbf{q}_{t}\rangle\) is a coherent state evolved for a time t, and \(|\chi \rangle\) is an arbitrary quantum reference state which can be chosen to enhance selectively specific spectroscopic signals. To this end, \(|\chi \rangle\) is commonly selected to be an appropriate combination of coherent states [12, 57]. This choice also facilitates calculations because the projection of a coherent state onto the configuration space is of Gaussian form
with \(\Gamma\) being the width matrix that we choose to be diagonal with elements equal to the harmonic frequencies of vibration. As for the classical action the usual definition stands
and the phase of the Herman–Kluk prefactor is
The Herman–Kluk prefactor (and its phase) depends on the monodromy matrix elements. The monodromy matrix, also known as the stability matrix, is a \(2N_{\hbox {vib}}\times 2N_{\hbox {vib}}\) matrix of elements \(\partial \textbf{i}/\partial \textbf{j}_{0}\,i,j=p,q\), which can be used to pinpoint classical chaotic trajectories. The determinant of the monodromy matrix should equal 1 along the whole trajectory but, in practice and in presence of a chaotic trajectory, numerical instability leads to a large deviation from 1. In this work we discard a trajectory when the deviation is larger than 1%.
Furthermore, we employ a particular version of TA SCIVR known as the adiabatically switched semiclassical initial value representation (AS SCIVR) [46,47,48]. It is made of a preliminary part in which an adiabatic switch run is performed followed by a TA-SCIVR simulation. In this kind of approach the starting conditions of the TA-SCIVR simulation correspond to the exit conditions of the AS procedure. This is more accurate than using a Husimi distribution. Indeed, AS SCIVR provides better resolved spectroscopic signals, it is characterized by a much lower trajectory rejection rate, and it allows one to perform full-dimensional simulations of larger systems.
AS SCIVR is used in this work for formaldehyde, while, as anticipated, for the \(\hbox {H}_{2}\)-tagged protonated glycine we employed DC SCIVR in a previous work [58]. The divide-and-conquer method adopts Eq. 4 upon projection (indicated by the ~ symbol) on appropriate \(N_\textrm{S}\)-dimensional subspaces
This is an approach which is used for large dimensional systems to be able to get a sensible spectroscopic signal. We have developed several methods to determine the best subspace partition, going from an analysis of the off-diagonal elements of the Hessian matrices to an evolutionary algorithm which uses a fitness function based on Liouville’s theorem [22, 59, 60]. Furthermore, while the kinetic part of the vibrational Hamiltonian is separable, the potential energy is not directly projectable onto subspace and a specific projection formula for the potential energy has been formulated and validated. The interested reader can find more details about this in Ref. [55].
So far we have described approaches based on a distribution of trajectories, but it is actually possible to perform simulations based on tailored single trajectories. We do that in the QCT case by exciting the mode of vibration associated with the highest fundamental frequency of formaldehyde (\(\nu _{6}\)). We also use a single trajectory in the application of DC SCIVR to the tagged protonated glycine spectrum. In the semiclassical case the single-trajectory approach is also known as multiple coherent semiclassical initial value representation (MC SCIVR) [12, 57, 61]. In MC SCIVR one specializes a single trajectory according to the spectral feature to be identified. The method provides an accurate approximation as demonstrated by several studies and by the fact that with a single semiclassical trajectory it is in principle possible to get the exact eigenvalues (and eigenfunctions) of the vibrational Hamiltonian provided the trajectory is run at the exact (but unknown) eigenenergy [62]. Based on this approach, we repropose the single DC-SCIVR calculation we performed for \(\hbox {H}_{2}\)-tagged protonated glycine [58].
3 Results and discussion
We choose the \(\hbox {H}_{2}\hbox {CO}\) molecule as an example of a system where anharmonicity is present. To show this we report in Table 1 a comparison between the quantum mechanical and harmonic fundamental frequencies of vibration of this molecule. We employ an analytical PES for \(\hbox {H}_{2}\hbox {CO}\) constructed by Martin et al. at CCSD(T) level of theory [63]. On this PES time-independent, full-dimensional quantum mechanical calculations were performed by Carter et al. [64] From the data reported, it is clear that the quantum frequencies of vibration are substantially shifted with respect to harmonic estimates, and, as anticipated, being the results at the quantum mechanical level, there is no need to specify what temperature these data are referred to.
We now present the results of the classical simulations. We perform both MD and QCT runs. The MD simulations, carried out in the NVT ensemble (i.e., in a canonical ensemble where the number of particles, volume and temperature are held fixed), are performed at different temperatures, while the QCT ones, carried out in the NVE ensemble, are undertaken at different values of the total energy.
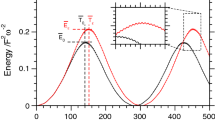
To start off we focus on the highest fundamental frequency, labeled \(\nu _{6}\), because it is the frequency presenting the largest shift (\(-154\,\text {cm}^{-1}\)). The normal mode associated to it, mode 6, is related to the C\(\hbox {H}_{2}\) asymmetric stretch. From Fig. 1 it is evident that the estimated frequency is changing with the temperature or energy employed. More precisely, when MD is performed at very low temperature (10 K) or QCT is undertaken at an energy which is just 5% of the harmonic zero-point energy, the simulations return a frequency value which is basically the harmonic one. The reason for this is that at such low temperature or energy the classical trajectory can sample only a region of the PES close to the equilibrium position. In this region the parabolic (harmonic) approximation to the PES is valid and a frequency value close to the harmonic one is obtained. Remarkably, for the same reason, the MD simulation at room temperature (300 K) fails badly in estimating the frequency of vibration.
Moving to higher energies (or temperature) we first notice that when the energy equals the harmonic ZPE, then the frequency estimate gets closer to the quantum mechanical benchmark (it is about 30 \(\hbox {cm}^{-1}\) away). Secondly and remarkably, the \(\nu _{6}\) exc. and 1.5 ZPE simulations are characterized by about the same energy (just a few wavenumbers difference) but while the \(\nu _{6}\) exc. trajectory is on the mark, the 1.5 ZPE trajectory is clearly underestimating the QM frequency. This is a demonstration that not only the total energy (temperature) of the trajectory but also the way it is distributed in the molecule may affect the outcome of a classical simulation. The fact that with the \(\nu _{6}\) exc. trajectory a classical method like QCT is able to reproduce the quantum frequency demonstrates that there are no sizeable quantum effects in play and anharmonicity can be detected by means of classical approaches. Finally, we notice that for the trajectories run at high energy or temperature some spectroscopic features appear above 3000 \(\hbox {cm}^{-1}\). Those are the higher harmonics associated to lower-frequency modes, in particular mode 3 and mode 4. It is not surprising that their intensity is quite high because we are not simulating dipole (IR) spectra, so intensities in Fig. 1 are not related to the actual absorption intensities but to the recurrence of trajectories in the phase space.
Then, we move to apply adiabatic switching to the case of \(\nu _{6}\) of formaldehyde. The AS estimate of this vibrational frequency can be obtained by running an AS simulation for the ground state to determine the AS zero-point energy, and another AS simulation to determine the energy level associate to a quantum of excitation in the C\(\hbox {H}_{2}\) asymmetric stretch. We find an anharmonic ZPE of 5764 \(\hbox {cm}^{-1}\) and the energy level associated to mode 6 to be at 8614 \(\hbox {cm}^{-1}\). This is depicted in Fig. 2 and leads to an estimate of \(\nu _{6}=2850\) \(\hbox {cm}^{-1}\), which is only 8 \(\hbox {cm}^{-1}\) off the quantum mechanical result.
Figure 2 shows that all trajectories are initially given the same harmonic energy corresponding to a quantum of harmonic excitation in the C\(\hbox {H}_{2}\) asymmetric stretch. During the AS simulation the true molecular Hamiltonian is slowly switched on and this changes the energy of the trajectories. Eventually the trajectories provide a distribution of final energies, which is peaked at 8614 \(\hbox {cm}^{-1}\). We notice that in Fig. 2, for graphical clarity, only six trajectories are reported, while the Gaussian envelope of the final energies is representative of the whole 6000 trajectories run.
Before moving to the semiclassical (quantum) results, we collect all data for formaldehyde obtained by means of the classical simulations. These are reported in Figs. 3 and 4 for all six modes of vibrations.
It is interesting to notice that MD and QCT simulations provide spectroscopic signals which are wider than the AS ones. This is a direct result of the fact that AS runs tend to preserve the initial quantization, while MD and QCT suffer from coupling with other vibrational modes and rotations. One effect of the coupling is visible in Fig. 3 relatively to mode 3: The QCT simulation presents a peak at higher frequencies which is due to the coupling to mode 4. Furthermore, both MD and QCT simulations of the C\(\hbox {H}_{2}\) asymmetric stretch in Fig. 4 are characterized by a structure at lower frequency due to the coupling to the C\(\hbox {H}_{2}\) symmetric stretch.
It is clear that all methods are able to account for the anharmonicity of the formaldehyde PES with adiabatic switching and tailored single-trajectory QCT giving the best estimates. Also, classical spectra, as expected, present only the spectroscopic features related to the fundamental frequencies of vibration and some higher harmonic overtones. In Table 2 we report values obtained with the classical simulations and compare them with the harmonic and quantum mechanical results. For QCT we report the results obtained running the trajectories at \(E=\hbox {ZPE}\), while for MD we provide results for the trajectories thermalized at \(T=1405\) K. This temperature is the thermal equivalent of the zero-point energy according to the equipartition theorem.
From Table 2 we notice that QCT and MD values for simulations run at similar energies are very close to each other, another clue at the dependence of classical results on the involved energy. Furthermore, they provide good estimates of the frequency of vibration when anharmonicity is low, while they are off the mark for the higher frequency modes where anharmonicity is more evident. We anticipated that, for instance, we need to run a tailored single-trajectory QCT simulation to get the correct \(v_{6}\) frequency. AS provides very good estimates for all modes. Therefore, overall, classical methods are able to fully describe the anharmonicity of the fundamental frequencies of the formaldehyde molecule.
It is now possible to move to our quantum results obtained in semiclassical approximation by means of AS SCIVR. There are two ways, which are relevant for the present work, in which quantum spectroscopical effects can show up: One is by means of a peculiar quantum shift from harmonic estimates not reproducible by classical simulations; the other one is the presence in the quantum spectrum of additional features with respect to the classical counterpart. The former is not the case of \(\hbox {H}_{2}\hbox {CO}\) since appropriate classical simulations provide estimates which are very close to the quantum mechanical benchmark. As for the latter aspect we report in Fig. 5 the outcome of our AS-SCIVR simulation for \(\hbox {H}_{2}\hbox {CO}\). To perform the AS-SCIVR calculation we employ 50,000 a.u. long trajectories, characterized by initial harmonic ZPE quantization, for the preliminary adiabatic switching part, followed by 50,000 a.u. long trajectories for the semiclassical part. We set the threshold for trajectory rejection at the very strict value of \(10^{-6}\) with the result that about 500 trajectories are retained for the simulation. This number of trajectories is sufficient for AS SCIVR to simulate a very detailed spectrum.
It is immediate to notice that the AS-SCIVR spectrum presents many more features than the classical one. The reason is that AS SCIVR is able to point out quantum features. One example is given by the combination bands, which are mixed excitations of several modes (see for instance the energy levels associated to 1\(_{1}\)2\(_{1}\) and 1\(_{1}\)3\(_{1}\) and many others). This also demonstrates that AS SCIVR goes beyond a simple AS approach. In fact AS SCIVR works properly in energy regions where the density of states is high. Furthermore, being part of the family of semiclassical dynamics methods AS SCIVR is also able to provide eigenfunctions, which cannot be obtained with simple AS.
As anticipated, our simulation has been performed starting from harmonic ZPE energy quantization. This is the best condition to evaluate the ZPE (5768 \(\hbox {cm}^{-1}\)), but a more accurate estimate of frequencies is obtained by employing different AS-SCIVR runs for the several energy levels starting each simulation from the appropriate harmonic energy quantization. Results are reported in Table 3, from which another quantum spectroscopic feature can be appreciated: AS-SCIVR overtones are anharmonic if compared to twice the corresponding fundamental frequency (this is evident for \(\nu _{4}^{2}\) compared to \(\nu _{4}\)), whereas in classical simulations one finds higher harmonics at integer multiples of the frequencies of vibration. Finally, we notice that AS SCIVR returns a very low MAE even when overtones are taken into consideration.
We have demonstrated that some spectroscopic features can be detected only when a quantum approach, even in an approximate way, is undertaken. However, so far the demonstration has not involved the fundamental frequencies of vibration, which are the most relevant ones in an experimental spectrum. We showed indeed that a tailored QCT simulation is able to accurately identify even the most anharmonic (\(\nu _{6}\)) of the six vibrational frequencies of formaldehyde. However, as anticipated, quantum spectroscopic effects may show up as deviations from classical spectra and this is true also for the fundamental frequencies. To demonstrate this, we recall one of our previous papers about the investigation of the spectrum of protonated glycine tagged with 3 hydrogen molecules [58]. In Fig. 6 experimental data and simulations for this supramolecular system are reported.

Reproduced from Ref. [58] with permission from the Royal Society of Chemistry
Scaled harmonic (a), experimental (b), QCT (c), and DC-SCIVR spectra of \((\hbox {GlyH}+\hbox {3H}_{2})^{+}\)
Experiments and simulations describe the OH and NH stretches. As expected, the harmonic estimates are far off the mark even employing a scaling factor (0.96) and this is particularly true for the much red shifted \(\hbox {NH}_\text {a}\) signal, which is due to the NH stretch involved in an intramolecular hydrogen bond. For the simulations we employed an ab initio on-the-fly dynamics at DFT-B3LYP level of theory and aug-cc-pVDZ basis set. Such a type of dynamics is needed because there is no analytical PES available for the system. Therefore both QCT and semiclassical (DC-SCIVR) simulations were performed using exactly the same single trajectory. The outcome clearly points out a quantum effect associated to the \(\hbox {NH}_{a}\) stretch with a shift between the QCT and semiclassical signals of about 200 \(\hbox {cm}^{-1}\).
4 Summary and conclusions
An interesting question in theoretical vibrational spectroscopy concerns the possibility to identify anharmonicity and quantum effects and distinguish between them in a spectrum. In this work we have presented different types of theoretical approaches to the vibrational spectroscopy of two very different systems: the isolated formaldehyde molecule, and the isolated protonated glycine tagged with three hydrogen molecules. We were interested in studying the frequencies of vibration because both anharmonicity and quantum effects imply a shift in the spectrum from the harmonic value. We found out that in these two systems anharmonicity and quantum effects show up in different ways.
Our findings are that, on the one hand, anharmonicity, which is related to the PES, can be correctly assessed by means of both classical and quantum approaches. On the other hand, quantum effects do need a quantum method to be detected. We have demonstrated this for formaldehyde by means of the identification of additional spectral features like combination bands and anharmonic overtones, and for the \(\hbox {H}_{2}\)-tagged protonated glycine through reproduction of the \(\hbox {NH}_{a}\) shift due to intramolecular hydrogen bonding. The latter is an example of quantum effect which could not be detected using QCT but that was found using DC SCIVR.
Based on this evidence our conclusions are twofold. First of all, appropriate simulations provide one with a way to distinguish between anharmonicity and quantum effects. Secondly, recalling the title of the paper, things are not always as they seem. Not necessarily a shift with respect to the harmonic estimates is related to a quantum effect. For this reason to confirm the effectiveness of a new method in theoretical vibrational spectroscopy one should test it against systems known to present quantum effects like a double well potential, which is characterized by a tunneling splitting, or the \(\hbox {H}_{2}\)-tagged protonated glycine.
Going back to the work by Chen and Yang mentioned in the Introduction [32] we agree with the anonymous referee that a Morse oscillator is not a good system to prove the ability of a new method to detect quantum effects on the basis of a shift with respect to the harmonic estimate of the fundamental frequency. In this paper, we demonstrated that even a molecular system like formaldehyde is characterized by spectral shifts due uniquely to anharmonicity. However, we believe that the study of a quartic double well proposed by Chen and Yang is a valid example that could prove, upon further investigation, the effectiveness of C-NEO MD in getting quantum spectroscopic effects.
As a final note, we spend a few words on the relative computational costs of the methods here presented. The computationally cheaper approach is QCT, which requires only to run the distribution of trajectories. Classical MD is more expensive because of the thermalization run. This takes about 8 times the production run, the latter being comparable to a QCT simulation. AS is more cpu intensive than the previous two methods because it is based on the evolution of a different distribution of trajectories for each normal mode. Finally AS SCIVR is the computationally most expensive among the methods we have employed. This is mainly due to the necessity to calculate Hessian matrices along the trajectories. The computational burden of AS and AS SCIVR increases with the size of the system under investigation.
References
Bowman JM (2022) Vibrational dynamics of molecules. World Scientific, Singapore
Merrick Jeffrey P, Damian M, Leo R (2007) An evaluation of harmonic vibrational frequency scale factors. J Phys Chem A 111(45):11683–11700
Colbert DT, Miller WH (1992) A novel discrete variable representation for quantum mechanical reactive scattering via the S-matrix Kohn method. J Chem Phys 96(3):1982–1991
Bowman JM, Carter S, Huang X (2003) MULTIMODE: a code to calculate rovibrational energies of polyatomic molecules. Int Rev Phys Chem 22(3):533–549
Vincenzo B, Malgorzata B, Julien B, Monika B-P, Ivan C, Pawel P (2011) Toward anharmonic computations of vibrational spectra for large molecular systems. Int J Quantum Chem 112(9):2185–2200
Meyer H-D, Manthe U, Cederbaum LS (1990) The multi-configurational time-dependent Hartree approach. Chem Phys Lett 165(1):73–78
Heller EJ (1981) The semiclassical way to molecular spectroscopy. Acc Chem Res 14(12):368–375
Miller WH (2001) The semiclassical initial value representation: a potentially practical way for adding quantum effects to classical molecular dynamics simulations. J Phys Chem A 105(13):2942–2955
Shalashilin DV, Child MS (2001) Multidimensional quantum propagation with the help of coupled coherent states. J Chem Phys 115(12):5367–5375
Pollak E, Miret-Artés S (2004) Thawed semiclassical IVR propagators. J Phys A 37(41):9669
Grossmann F (2006) A semiclassical hybrid approach to many particle quantum dynamics. J Chem Phys 125(1):014111
Ceotto M, Atahan S, Tantardini GF, Aspuru-Guzik A (2009) Multiple coherent states for first-principles semiclassical initial value representation molecular dynamics. J Chem Phys 130(23):234113
Zambrano E, Šulc M, Vaníček J (2013) Improving the accuracy and efficiency of time-resolved electronic spectra calculations: cellular dephasing representation with a prefactor. J Chem Phys 139(5):054109
Church MS, Hele TJH, Ezra GS, Ananth N (2018) Nonadiabatic semiclassical dynamics in the mixed quantum-classical initial value representation. J Chem Phys 148(10):102326
Cao J, Voth GA (1994) The formulation of quantum statistical mechanics based on the Feynman path centroid density. I. Equilibrium properties. J Chem Phys 100(7):5093–5105
Habershon S, Manolopoulos DE, Markland TE, Miller TF III (2013) Ring-polymer molecular dynamics: quantum effects in chemical dynamics from classical trajectories in an extended phase space. Annu Rev Phys Chem 64:387–413
Da-hong L, Hase WL (1988) Classical mechanics of intramolecular vibrational energy flow in benzene. IV. Models with reduced dimensionality. J Chem Phys 89:6723–6735
Miller WH, Hase WL, Darling CL (1989) A simple model for correcting the zero point energy problem in classical trajectory simulations of polyatomic molecules. J Chem Phys 91(5):2863–2868
Czakó G, Kaledin AL, Bowman JM (2010) A practical method to avoid zero-point leak in molecular dynamics calculations: application to the water dimer. J Chem Phys 132(16):164103
Buchholz M, Fallacara E, Gottwald F, Ceotto M, Grossmann F, Ivanov SD (2018) Herman–Kluk propagator is free from zero-point energy leakage. Chem Phys 515:231–235
Rognoni A, Conte R, Ceotto M (2021) How many water molecules are needed to solvate one? Chem Sci 12:2060–2064
Gandolfi M, Rognoni A, Aieta C, Conte R, Ceotto M (2020) Machine learning for vibrational spectroscopy via divide-and-conquer semiclassical initial value representation molecular dynamics with application to n-methylacetamide. J Chem Phys 153(20):204104
Cazzaniga M, Micciarelli M, Moriggi F, Mahmoud A, Gabas F, Ceotto M (2020) Anharmonic calculations of vibrational spectra for molecular adsorbates: a divide-and-conquer semiclassical molecular dynamics approach. J Chem Phys 152(10):104104
Cazzaniga M, Micciarelli M, Gabas F, Finocchi F, Ceotto M (2022) Quantum anharmonic calculations of vibrational spectra for water adsorbed on titania anatase (101) surface: dissociative versus molecular adsorption. J Phys Chem C 126(29):12060–12073
Mino L, Cazzaniga M, Moriggi F, Ceotto M (2022) Elucidating NOx surface chemistry at the anatase (101) surface in TiO2 nanoparticles. J Phys Chem C 127(1):437–449
Tucker C Jr, Miller WH (1986) Reaction surface description of intramolecular hydrogen atom transfer in malonaldehyde. J Chem Phys 84(8):4364–4370
Conte R, Aspuru-Guzik A, Ceotto M (2013) Reproducing deep tunneling splittings, resonances, and quantum frequencies in vibrational spectra from a handful of direct ab initio semiclassical trajectories. J Phys Chem Lett 4(20):3407–3412
Wehrle M, Oberli S, Vaníček J (2015) On-the-fly ab initio semiclassical dynamics of floppy molecules: absorption and photoelectron spectra of ammonia. J Phys Chem A 119(22):5685–5690
Richardson JO, Pérez C, Lobsiger S, Reid AA, Temelso B, Shields GC, Kisiel Z, Wales DJ, Pate BH, Althorpe SC (2016) Concerted hydrogen-bond breaking by quantum tunneling in the water hexamer prism. Science 351(6279):1310–1313
Chen Q, Conte R, Houston PL, Bowman JM (2021) Full-dimensional potential energy surface for acetylacetone and tunneling splittings. Phys Chem Chem Phys 23:7758–7767
Schienbein P (2023) Spectroscopy from machine learning by accurately representing the atomic polar tensor. J Chem Theory Comput 19(3):705–712
Chen Z, Yang Y (2023) Incorporating nuclear quantum effects in molecular dynamics with a constrained minimized energy surface. J Phys Chem Lett 14:279–286
Bussi G, Donadio D, Parrinello M (2007) Canonical sampling through velocity rescaling. J Chem Phys 126(1):014101
Galimberti DR, Milani A, Tommasini M, Castiglioni C, Gaigeot M-P (2017) Combining static and dynamical approaches for infrared spectra calculations of gas phase molecules and clusters. J Chem Theory Comput 13(8):3802–3813
Bonnet L, Rayez JC (1997) Quasiclassical trajectory method for molecular scattering processes: necessity of a weighted binning approach. Chem Phys Lett 277(1–3):183–190
Brewer ML, Hulme JS, Manolopoulos DE (1997) Semiclassical dynamics in up to 15 coupled vibrational degrees of freedom. J Chem Phys 106(12):4832–4839
Rognoni A, Conte R, Ceotto M (2021) Caldeira–Leggett model vs ab initio potential: a vibrational spectroscopy test of water solvation. J Chem Phys 154(9):094106
Kaledin AL, Miller WH (2003) Time averaging the semiclassical initial value representation for the calculation of vibrational energy levels. J Chem Phys 118(16):7174–7182
Skodje RT, Borondo F, Reinhardt WP (1985) The semiclassical quantization of nonseparable systems using the method of adiabatic switching. J Chem Phys 82(10):4611–4632
Johnson BR (1987) Semiclassical vibrational eigenvalues of h+3, d+3, and t+3 by the adiabatic switching method. J Chem Phys 86(3):1445–1450
Sun Q, Bowman JM, Gazdy B (1988) Application of adiabatic switching to vibrational energies of three-dimensional HCO, H2O, and H2CO. J Chem Phys 89(5):3124–3130
Saini S, Zakrzewski J, Taylor HS (1988) Semiclassical quantization via adiabatic switching. II. Choice of tori and initial conditions for multidimensional systems. Phys Rev A 38:3900–3908
Bose A, Makri N (2015) Wigner phase space distribution via classical adiabatic switching. J Chem Phys 143(11):114114
Chen Q, Bowman JM (2016) Revisiting adiabatic switching for initial conditions in quasi-classical trajectory calculations: application to CH4. J Phys Chem A 120:4988–4993
Nagy T, Lendvay G (2017) Adiabatic switching extended to prepare semiclassically quantized rotational-vibrational initial states for quasiclassical trajectory calculations. J Phys Chem Lett 8(18):4621–4626
Conte R, Parma L, Aieta C, Rognoni A, Ceotto M (2019) Improved semiclassical dynamics through adiabatic switching trajectory sampling. J Chem Phys 151(21):214107
Botti G, Ceotto M, Conte R (2021) On-the-fly adiabatically switched semiclassical initial value representation molecular dynamics for vibrational spectroscopy of biomolecules. J Chem Phys 155(23):234102
Botti G, Aieta C, Conte R (2022) The complex vibrational spectrum of proline explained through the adiabatically switched semiclassical initial value representation. J Chem Phys 156(16):164303
Landau LD, Lifshitz EM (1982) Mechanics. Elsevier, Amsterdam
Miller WH, George TF (1972) Semiclassical theory of electronic transitions in low energy atomic and molecular collisions involving several nuclear degrees of freedom. J Chem Phys 56(11):5637–5652
Kaledin AL, Miller WH (2003) Time averaging the semiclassical initial value representation for the calculation of vibrational energy levels. II. Application to H2CO, NH3, CH4, CH2D2. J Chem Phys 119(6):3078–3084
Micciarelli M, Conte R, Suarez J, Ceotto M (2018) Anharmonic vibrational eigenfunctions and infrared spectra from semiclassical molecular dynamics. J Chem Phys 149(6):064115
Micciarelli M, Gabas F, Conte R, Ceotto M (2019) An effective semiclassical approach to IR spectroscopy. J Chem Phys 150(18):184113
Aieta C, Bertaina G, Micciarelli M, Ceotto M (2020) Representing molecular ground and excited vibrational eigenstates with nuclear densities obtained from semiclassical initial value representation molecular dynamics. J Chem Phys 153(21):214117
Ceotto M, Di Liberto G, Conte R (2017) Semiclassical “divide-and-conquer’’ method for spectroscopic calculations of high dimensional molecular systems. Phys Rev Lett 119(1):010401
Di Liberto G, Conte R, Ceotto M (2018) “Divide and conquer’’ semiclassical molecular dynamics: a practical method for spectroscopic calculations of high dimensional molecular systems. J Chem Phys 148(1):014307
Ceotto M, Dell’Angelo D, Tantardini GF (2010) Multiple coherent states semiclassical initial value representation spectra calculations of lateral interactions for CO on Cu (100). J Chem Phys 133(5):054701
Gabas F, Di Liberto G, Conte R, Ceotto M (2018) Protonated glycine supramolecular systems: the need for quantum dynamics. Chem Sci 9:7894–7901
Conte R, Gabas F, Botti G, Zhuang Y, Ceotto M (2019) Semiclassical vibrational spectroscopy with Hessian databases. J Chem Phys 150(24):244118
Gandolfi M, Ceotto M (2021) Unsupervised machine learning neural gas algorithm for accurate evaluations of the Hessian matrix in molecular dynamics. J Chem Theory Comput 17(11):6733–6746
Schwaab G, Pérez R, de Tudela D, Mani NP, Roy TK, Gabas F, Conte R, Caballero LD, Ceotto M, Marx D et al (2022) Zwitter ionization of glycine at outer space conditions due to microhydration by six water molecules. Phys Rev Lett 128(3):033001
De Leon N, Heller EJ (1983) Semiclassical quantization and extraction of eigenfunctions using arbitrary trajectories. J Chem Phys 78:4005–4017
Martin JML, Lee TJ, Taylor PR (1993) An accurate ab initio quartic force field for formaldehyde and its isotopomers. J Mol Spectr 160(1):105–116
Carter S, Pinnavaia N, Handy NC (1995) The vibrations of formaldehyde. Chem Phys Lett 240(5):400–408
Acknowledgements
All the authors are grateful to Maurizio Persico, the father of the Italian semiclassical community and to whom this paper is dedicated, for his pioneering works that have been of inspiration for all of us. R.C. warmly thanks Maurizio Persico also for his classes and teaching in theoretical photochemistry and quantum chemistry at Università di Pisa. All authors thank the ERC for funding under project ERC POC SEMISOFT (Grant No. 101081361) and project ERC CoG SEMICOMPLEX (Grant No. 647107).
Funding
Open access funding provided by Università degli Studi di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Conte, R., Aieta, C., Botti, G. et al. Anharmonicity and quantum nuclear effects in theoretical vibrational spectroscopy: a molecular tale of two cities. Theor Chem Acc 142, 53 (2023). https://doi.org/10.1007/s00214-023-02993-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00214-023-02993-y