1 Introduction

Transition metal ions fall in between group 1 and group 2 metal cations, which form mainly ionic bonds, and the p-block elements of the periodic table, which form bonds of more covalent character. In the frame of classical force fields used to model biological macromolecules, the former group is described exclusively with non-bonded parameters (charge and Lennard–Jones vdW parameters), whereas elements from the p-block of the periodic table, e.g., C, N, O, P, S, Se, are treated with bonded parameters (explicit covalent bonds). Thus, it is, perhaps, not surprising that some authors describe transition metal ions with the non-bonded model, whereas others with the bonded counterpart. Each of these approaches has its pros (as well as cons), e.g., the non-bonded model allows for dynamic change of coordination number, whereas the bonded model offers a good control over geometry of the first coordination sphere of the metals. Within the bonded model for transition metal ions one needs to determine force constants and reference values for metal–ligand bonds and all valence angles formed by the metal ion. Dihedral potential is usually not fitted and left to be zero. To derive these bond and angle parameters one resorts to quantum chemistry, as typically there is not enough available experimental data for the (often unique) composition of the ion first coordination shell. Here, we are presenting our efforts to find the best set of force field parameters to describe the geometry of the Fe(II) cofactor present in the active site of ectoine synthase (EctC). Experimental data strongly indicate that the Fe(II) ion plays a central role in catalytic activity of EctC [1, 2], thus we aim to obtain as precise description of the metal site as possible by testing three parameterization methods for bonded approach: the projected Hessian method proposed by Seminario [3]⁠, Hessian-based methods developed and implemented within the ParmHess program by R. Wang et al. [4, 5]⁠ and the energy-based method implemented within the ParamFit program by Betz and Walker [6]⁠. Over the years, thorough surveys of the metal site parameterization methods have been published. In 2011, Hu and Ryde analyzed five different approaches (both bonded and non-bonded) for MM parameters derivation while applying them to zinc metalloproteins for testing purposes [7]. They concluded, that before attempting the parameterization procedure, it is crucial to determine the future use of the parameters, as their performance will heavily depend on the nature of the metal-binding site, for example, they recommend using Norrby-Lijefors automated method for the catalytically important ions [7, 8]. In 2017, Li and Merz published a comprehensive review of the metal site parameterization methods [9]. Their goal was to cover the current state of the art in one paper in order to facilitate the decision-making over which approach to choose, without testing the performance of the methods in proteins. Our goal is somewhat similar to the work of Hu and Ryde, but in this case, we are focusing only on the bonded approaches, keeping in mind that the Fe(II) ion takes part in the enzymatic reaction and we need a good description of its coordination sphere for further work. Here, we try to find the method that will provide the best compromise between energetic and geometric accuracy. All of the methods tested here are discussed in the 2017 review [9], but here we apply them to perform parameterization and then we validate the performance of the resulting parameter sets.

The cupin-type protein EctC is one of four enzymes that are involved in the ectoine biosynthesis pathway, which is found mostly in bacterial but also archaeal species [2, 10]⁠. Ectoine is a small molecule osmolyte and cell-protective agent preventing macromolecules from dehydration during osmotic stress [1, 11]⁠. It is formed from N-γ-acetyl-L-2,4-diaminobutyric acid (N-γ-ADABA) by cyclo-condensation and water elimination catalyzed by EctC (Fig. 1). Recent work by Czech et al. reveals not only the presence of the metal-binding motifs in EctC amino acid sequence, but also points out that iron ion most likely plays an important role during enzymatic catalysis [1]⁠. When compared to the amino acid sequences identified as metal-coordinating motifs in other cupin-type proteins, the one found in the EctC sequence deviates from the consensus patterns in a unique way (Table 1). In the first motif, two usually conserved histidines are missing and only the metal-binding glutamate (Glu57) is conserved, while the second motif contains two metal-binding residues instead of one: tyrosine (Tyr84) replaces a canonical histidine and an additional histidine (His92) is present. To check the importance of these iron-binding residues for EctC enzymatic activity, they were individually replaced by alanine via site-directed mutagenesis, and the results showed a substantial reduction in enzymatic activity: A drop of 94,6%, 87.3% and 84.9% with respect to the activity of the WT form was observed for the E57A, H92A and Y84A mutants, respectively. Furthermore, the study indicated that the substrate-binding site is in close proximity to the iron and a direct N-γ-ADABA-iron interaction, via the carbonyl oxygen, was proposed. It is also interesting that no good quality crystals were obtained in the absence of iron, indicating a stabilizing effect of the metal on structural integrity [1]⁠.

Fig. 1
figure 1

Simplified reaction scheme of cyclo-condensation of N-γ-ADABA to ectoine, catalyzed by EctC in the presence of Fe2+

Full size image
Table 1 Metal-coordinating consensus motifs established for cupin-type proteins vs EctC metal-binding motifs
Full size table

The crystal structure of Paenibacillus lautus ectoine synthase with substrate and Fe2+ ion bound (PDB code: 5ONN) was our starting point for the parametrization procedure. Although the overall resolution of the crystal structure is high (1.4 Å), the bond lengths found in the first coordination sphere of the iron are significantly longer than expected (2.8–2.9 vs. ~ 2.0 Å) [12]⁠. In this structure occupation for Fe is only 0.38 and the B-factor for this atom is larger than for its nearest protein atoms (23.9 vs. 16.75–18.85 Å2), which might be the reason why this fragment of the structure is less reliable. Hence, the force field parameters, whose derivation is detailed beneath, will not only help us gain insights into the dynamic behavior of the EctC active site, but they will also aid in further refinement of the metal cofactor geometry, both of which are desirable, as the structure captured in this crystal is most likely not catalytically competent.

The rest of this article is organized as follows. First, models and quantum chemistry methods used to infer the spin of the ground state and to derive reference energy and geometry data are described, then methods used to derive force field bonded parameters are presented, followed by description of the MD protocol and metrics used to assess the performance of derived parameter sets. In the Results and discussion section, we first present quantum chemistry data for plausible spin states of the cofactor, and shortly present QM (ADMP) trajectories. Then, the major part of the manuscript is devoted to the derived parameter sets and their performance in reproducing stationary and dynamic geometries as well as energies. The report finishes with concise conclusions.

2 Computational models and methods

2.1 Models

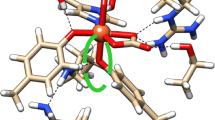
Because of the unclear ionization state of Tyr84, which coordinates Fe2+, two types of models were considered in this study; one with Tyr84 phenolic group ionized to a tyrosinate, hereafter called model 1 and model s1, and a second with a protonated Tyr84 phenolic group, hereafter called model 2 and model s2 (s stands for ‘small’) (see Fig. 2 and S1). Primary models, i.e., model 1 and model 2, were full optimized in vacuum with no geometrical constraints, whereas models s1 and s2 were constructed from the optimized structures of model 1 and 2, respectively, by trimming the model, substituting terminal unsaturated atoms with H and manual adjustment of lengths for thus introduced H–X bonds.

Fig. 2
figure 2

Fe2+ cofactor of ectoine synthase with bound N-γ-ADABA in the crystal structure (a) and its parts selected for the models used in this study: primary model 1 (b) and the minimal model s1 used for some post-HF calculations (c). Red letters show amber atom types of the key atoms; X → H denotes that a given atom is replaced by hydrogen in the model. Model 2 and model s2 differ from model 1 and s1 only by the presence of a proton bound to the phenolic oxygen of Tyr84 (see Fig. S1)

Full size image

2.2 Quantum chemistry methods

2.2.1 DFT

B3LYP-D3 [13, 14]⁠ combined with the Def2TZVP basis set [15]⁠ was used to obtain optimal geometries of the models and their electronic energy for three possible spin-states: singlet (low spin-state), triplet (intermediate spin-state) and quintet (high spin-state). As for model 1 and model 2, the singlet state was computed to lie very high in energy, 44.3 and 36.7 kcal/mol higher than the quintet ground state, respectively; therefore, the singlet state was not further considered. Single point energy computations were also done for the quintet and triplet states with the use of CAM-B3LYP-D3 [16]⁠ and MN15 [17]⁠ functionals combined with the Def2TZVP basis set. Computations were done with Gaussian 16 rev C.01 using default convergence criteria [18]⁠.

2.2.2 ADMP

Atom-centered Density Matrix Propagation (ADMP) method is a Car-Parinello method that allows for time-efficient calculations of ab initio molecular dynamics trajectories [19,20,21,22]⁠. Here, we used the ADMP method at the UB3LYP-D3/Def2SVP level. The starting geometry was the optimal structure with iron in a quintet spin-state, obtained at the UB3LYP-D3/Def2SVP level, the initial nuclear kinetic energy was set at the 0.43250 Hartree level, which is the oscillation energy obtained from the frequency calculations. 30 000 frames with default 0.1 fs time step were collected (3 ps), velocity scaling thermostat was used throughout the simulation (IOp(1/80) = 1000000)), with temperature checked and scaled every 10 steps (IOp(1/81 = 10)). The temperature of the thermostat was set at 300 K (IOp(1/82 = 300)).

2.2.3 ONIOM

ONIOM(ROCCSD(T):UB3LYP-D3) computations were successfully performed only for model 1, as despite many attempts, the CCSD calculations did not converge for model 2 in the quintet state. The ONIOM model was partitioned into layers as shown in Fig. 2 i.e., the CCSD(T) calculations were done for model 1 s, whereas DFT calculations for model 1 and model 1 s. For CCSD(T), restricted open shell (RO) formalizm was used and the basis set combined cc-pVTZ basis for Fe, N and O, and cc-pVDZ for C and H atoms. FreezeNobleGasCore option was used to correlate only the valence electrons. For the UB3LYP-D3 calculations, Def2TZVP basis set was used and the D3 correction with the Becke-Johnson damping.

2.2.4 DLPNO-UCCSD(T)

DLPNO-UCCSD(T) is an approximation to the canonical UCCSD(T) method that treats electronic correlations as local phenomena [23,24,25,26]⁠. Thanks to its much more favorable scaling with the system size it could be applied directly to model 1 and model 2. The basis set used combined the cc-pwCVQZ basis for Fe and cc-pVTZ for all other atoms of the system. AutoAux option was used to generate an auxiliary basis set. As the basis used for Fe justifies it, 3 s and 3p electrons of Fe were included in the correlated calculations. The calculations were performed in two variants, first with ROHF orbitals, and second with UB3LYP orbitals. For all other settings, default values were used. The calculations were performed with ORCA 4.0.0 [27].

2.2.5 NEVPT2

NEVPT2 (n-electron valence state perturbation theory) is a multireference perturbation (second order) method build on top of a CASSCF wave function [28,29,30,31]⁠, which is very well suited for calculations of excitation energies [32]. Here, we have used its strongly contracted (SC) variant to calculate the quintet-triplet adiabatic energy difference using 6 electrons in 10 orbitals (3d + 4d) active space. The basis set used was the same as in the DLPNO-UCCSD(T) calculations, i.e., cc-pwCVQZ basis for Fe and cc-pVTZ for all other atoms. All electrons were correlated at the NEVPT2 stage. The calculations were performed with ORCA 4.0.0 [27].

2.3 Methods used to fit bonded force field parameters for the cofactor

2.3.1 Seminario

The Seminario method allows for direct evaluation of bond and angle force constants from the Hessian matrix and it can be viewed as a projection method from cartesian to internal coordinates [3]⁠. The Hessian was computed at the B3LYP-D3/Def2TZVP level using Gaussian 16, whereas force constants of bonds and angles involving Fe were obtained from it with the use of the XYZViewer program, in which the Seminario method is implemented. Parameter sets derived with this method are labeled “Sem'' throughout the manuscript.

2.3.2 ParmHess

The Hessian computed with a quantum chemistry method includes all components of interatomic interactions (bonded, vdW, electrostatic), whereas when deriving force field parameters, one tries to determine individual terms separately. Hence, if one uses within the amber force field bond and angle force constants derived with the Seminario method together with atomic partial charges and atomic vdW (Lennard–Jones) parameters, a potential problem of double-counting of non-bonded interactions arises. To address this issue Wang et. al. developed three Hessian-based methods, whereby before the fitting of MM-based Hessian to the QM counterpart, the non-bonded contributions to the MM Hessian are subtracted from the QM one. The free methods, implemented in the ParmHess program, differ in the details of the fitting procedure and are called: partial Hessian fitting (PHF), full Hessian fitting (FHF) and internal Hessian fitting (IHF) [4, 5]⁠. Here, we have used ParmHess to derive force constants for bonds and angles involving Fe. The same QM Hessian as used with the Seminario methods was employed here (B3LYP-D3/Def2TZVP). For our system, only the PHF method gave satisfactory results, i.e., no negative force constant, hence only these parameters are presented and discussed beneath.

2.3.3 Katachi amendment

The bonded force constants derived from any Hessian-based method, be it Seminario or PHF/FHF/IHF, are usually combined with reference bond lengths and angle values taken directly from the QM-optimized geometry. For systems with soft bonds where non-bonded interactions (mainly electrostatic) are significant, this procedure often leads to significant deviations between QM- and MM-optimized geometries. This problem can be solved with the Katachi amendment procedure proposed by Wang et al., whereby bond and angle reference values (req, Θeq) are iteratively changed until the MM-optimized geometry reproduces bond and angle values from the QM structure [5]⁠. The Katachi procedure was used here with 100 iterations limit and it was applied to Seminario, PHF and ParamFit derived sets of parameters. Thus, obtained parameter sets are labeled with the “_K” suffix.

2.3.4 Paramfit

Paramfit program, which is part of the AmberTools package [33], fits the bonded force field parameters using a set of geometries for which it tries to minimize differences between MM and QM energies by using the least square method [6]⁠. To obtain a representative set of geometries that would allow reliable fitting of bond and angle parameters involving Fe, we used the following procedure. First, around 150 evenly spaced snapshots from the ADMP trajectory (151 for model 1 and 149 for model 2) were selected and subjected to constrained minimization at the B3LYP-D3/def2SVP level with all bond lengths and valence angles involving Fe constrained to the values as in the given snapshot. The purpose of this minimization is to reduce the noise in the data due to energy changes caused by variation of internal coordinates for which the parameters are not going to be fitted. For the minimized structures, single point QM energy values were computed at the B3LYP-D3/def2TZVP level, and these values were used for fitting. QM input preparation and parameter fitting were done with the paramfit program. During the fitting procedure, one first needs to calculate the K constant, which is an intrinsic discrepancy between QM and MM energies: EMM − EQM + K = 0. Then, the K value is used as one of input options for actual parameters fitting. Parameter sets derived with this method are labeled “Param'' throughout the manuscript. Sets with a few manually adjusted parameters are labeled “Param_t” (tuned) throughout the manuscript.

Paramfit was also used, with the same QM reference data points, to test how well different parameter sets reproduce QM energy variations with the geometry changes around the Fe(II) ion.

2.3.5 Tuning paramfit parameters

In the case of model 1, param force constants for 2 bonds and 3 angles with MD averages most deviating from the reference ADMP values were iteratively changed and newly obtained MD averages were used to test if the modified set gave better or worse description of dynamics of the cofactor. Five iterations gave a parameter set, labeled as param_t, which yielded satisfactory results. In the case of the model 2, param_t parameters were obtained by substituting parameters (both K and Θeq) describing only one angle, namely O2–Fe–O, which showed the biggest deviation from the ADMP averages with those taken from the first seminario_katachi run. This adjustment improved rather poor initial paramfit-based geometries, both minimized and MD averages.

2.3.6 Non-bonded force field parameters

Lennard–Jones parameters used for Fe2+ (R* = 1.456 Å, ε = 0.013 kcal/mol) were taken from the UFF force field [34]⁠. Atomic partial charges were fitted with the RESP program, which is part of the AmberTools package. For model 1 and model 2, electrostatic potential was calculated at the B3LYP-D3/def2TZVP level and it was used to fit RESP atomic charges, which were used in MM optimization and MD simulations in vacuum for model 1 and model 2. To derive atomic charges for whole residues coordinated to Fe2+, another, larger model, which includes parts of the protein backbone, was optimized at the B3LYP-D3/def2SVP level with constrained coordinates of the backbone heavy atoms (see Fig. S2). For this large model electrostatic potential was then computed at the UHF/6-31G(d) level, which is consistent with the ff14SB amber protein force field, and it was used for RESP fitting. In the latter charges on CA, HA, N and C atoms of the backbones of Tyr, His and Glu and all atoms of NGA that were not part of model 1 or model 2 were fitted, whereas charges on all other atoms were kept fixed to their values taken either from the previous RESP fit for model 1 or model 2 (core region) or ff14SB force field (for backbone atoms of Tyr, His and Glu). Thus fitted charges for model 1 sum to the following residue values: Fe (0.9719), His (0.0788), Glu ( − 0.6368), Tyr( − 0.6185), NGA ( − 0.7955), whereas for model 2 their totals are: Fe (0.9719), His (0.2195), Glu ( − 0.5391), Tyr(0.094), NGA ( − 0.7955).

2.4 Classical MD simulations

The classical MD simulations were performed for model 1 and model 2 in vacuum and also for the EctC-NGA complex in explicit water under periodic boundary conditions. In vacuum, simulations were done with sander program, which is part of the AmberTools package [33], using Langevin dynamics, T = 300 K, time step of 0.5 fs, total simulation time was 25 ps and snapshots were saved every 20 steps (2500 snapshot in total). To prepare the EctC system for simulations, the protein was placed in a cuboid filled with TIP3P water with the cuboid faces at least 10 Å from the protein surface in each direction. To neutralize the charge of the system and also mimic the ionic strength of physiological conditions (I = 0.15 M), 33 Na+ and 23 Cl− ions were added to the system. The system was subsequently minimized and then heated from 0 to 300 K during 50 ps NV Langevin dynamics. The next step was 0.5 ns NPT (T = 300 K, p = 1 bar) density equilibration dynamics. During these two initial MD runs, coordinates of the protein were restrained with 1 kcal/molÅ2 force constant to their values in the minimized structure. Subsequently, 100 ns NPT (T = 300 K, p = 1 bar) dynamics was simulated with no restraints. The time step was 2 fs and the SHAKE algorithm was used to constraint bond lengths and valence angles involving hydrogen atoms. Snapshots were saved every 5000 steps (every 10 ps; 10 000 snapshots in total). Simulations were done with the use of sander and parmed programs [33]⁠.

2.5 Metrics used to validate FF parameter sets

In order to perform quality assessment of a given set of tested parameters, several different metrics were used.

  1. (1)

    Discrepancy between bond lengths [Å] and valence angles [°] involving Fe between MM and DFT optimized geometries. Furthermore, mean absolute error and max signed error were calculated separately for bonds and angles.

  2. (2)

    Discrepancy between mean values of bond lengths [Å] and angles [°] that involve iron ion between the ADMP and MM MD trajectories. Furthermore, mean absolute error and max signed error were calculated separately for bonds and angles.

  3. (3)

    Dissimilarity index (DQF) computed for bond or angle histograms, which is based on a quadratic form (QF) [35]⁠. Before computing the value of DQF, the histograms were normalized to 1 and one of them was shifted, so that the mean values of the two compared histograms are the same. This shift guarantees that the DQF measures dissimilarity between the shape of the two histograms. The value of DQF for a pair of histograms h and f, where h and f are vectors with bin counts, was calculated using the formula: (DQF)2 = (h-f)TA(h-f). The similarity matrix elements were computed as: Aij = 1 − |i-j|/dmax, where dmax is the maximum distance (in number of bins) between bins of the two compared histograms. For bond lengths, the bin width was 0.02 Å, whereas for angles the bin width was 1°. Procedures to compute DQF for bond and angle histograms were implemented as Octave scripts (see Code availability) [36]⁠.

  4. (4)

    Correlation between QM and MM energy values calculated for the set of ~ 150 relaxed geometries generated from the ADMP trajectory as described above. R2 coefficient was computed with paramfit for all sets of tested FF parameters.

3 Results and discussion

3.1 Geometry of the cofactor

Overall geometry of the cofactor optimized in vacuum at the DFT level (in the quintet ground state) resembles the geometry from the crystal structure (PDB: 5ONN), the coordination geometry remains tetrahedral (cf. Figures 2 and  3), but the bond lengths are significantly shorter (see Table 2).

Fig. 3
figure 3

Optimized (B3LYP-D3/def2-TZVP) structure of model 1 (left) and model 2 (right) in the quintet ground state

Full size image
Table 2 Fe–X bond lengths [Å] for the Fe(II) cofactor
Full size table

3.2 Spin state energetics probed with DFT and post-HF methods

In order to investigate the spin states energy ladder of the cofactor, we have optimized model 1 and model 2 in three spin states: quintet (S = 2), triplet (S = 1) and closed-shell singlet (S = 0). Since the singlet state was computed to lie very high in energy relative to the quintet, i.e., 44.28 and 36.66 kcal/mol for model 1 and 2, respectively, only quintet and triplet spin states were considered further. Using the B3LYP-D3/def2TZVP optimized geometries, single point energy values were computed for quintet and triplet with a range of DFT and post-HF methods (Table 3). All of the methods used predicted the quintet to be the ground state and the quintet—triplet adiabatic energy difference ranged from 14.4 to 35.9 kcal/mol. This energy difference is sufficiently large to justify focusing only on the quintet state when deriving FF parameters for the cofactor. Interestingly, DFT methods consistently give a smaller energy gap compared to post-HF methods. Moreover, protonation of the tyrosine ligand lowers the gap by 3–7 kcal/mol according to post-HF methods and the MN15 functional, whereas B3LYP-D3 and CAM-B3LYP-D3 predict much smaller decrease, by 0.1—0.2 kcal/mol.

Table 3 Relative energies [kcal/mol] computed for lowest lying spin-states of the Fe(II) cofactor
Full size table

3.3 Dynamics of the cofactor probed with the ADMP method

The 300 K ADMP trajectories obtained for model 1 and 2 provide valuable insights into the dynamics and plasticity of the cofactor (for movies of these trajectories, see Supporting Information). Analysis of ADMP trajectories reveals that both bidentate and monodentate binding modes of Glu57 are present throughout the simulated time span. Classifying snapshots with two Fe–O bonds < 2.2 Å as bidentate and snapshots with at least one Fe–O bond > 2.4 Å as monodentate, for model 1 51% of frames were assigned to the monodentate category while only 9% to the bidentate one. For model 2 both values are 24%. Therefore, we can conclude that for model 1 bidentate mode is present in a small minority of structures, whereas for model 2, the situation is more even. Since the Fe-liganding oxygen atom of Glu57 exchanged several times with its neighboring carboxylic oxygen during the simulated time span, atomic labels in the obtained ADMP trajectories were re-ordered to give the same label (and number) to the oxygen atom of Glu57 that is closest to Fe throughout the whole trajectory. This relabeling enabled straightforward preparation of geometries for MM calculations (where explicit bonds between bonded atoms need to be specified) and also for direct comparison of histograms for bonds and angles generated for ADMP and MM trajectories. Histograms were generated for all bonds and angles involving Fe, and they are shown in Figs. 4, 5 and 6 for model 1 (for histograms for model 2, see Fig. S4, S5 and S6). Average bond lengths and angles are gathered for model 1 in Table 4, where they are compared to averages calculated for MM MD trajectories (for data for model 2 see Tab. S3).

Fig. 4
figure 4

Histograms for Fe–X bonds computed for ADMP trajectory for model 1

Full size image
Fig. 5
figure 5

Histogram for Fe – O2’(OE1) distances computed for ADMP trajectory for model 1

Full size image
Fig. 6
figure 6

Histograms for Fe–X–Y and X-Fe-Y valence angles computed for ADMP trajectory for model 1

Full size image
Table 4 Averaged bond length [Å] and valence angle [°] for model 1 derived from MD simulations in vacuum at 300 K performed at a specified level of theory
Full size table

Analysis of bond-length histograms (Fig. 4) reveals that they are notably narrower for Fe-NB (His) and Fe-OH (Tyr) compared to those for Fe-O2 (Glu) and Fe–O (N- γ-ADABA), which suggests stronger bonds for the former group. Indeed, this finds confirmation in values of bond force constants (vide infra). The histogram for the ‘non-bonded’ second oxygen atom of Glu (Fig. 5) has a very asymmetric shape, which reflects multiple stable positions this atom can reach. Histograms for angles (Fig. 6) are all very broad suggesting low force constants; those for Fe–X–Y angles seem on average more symmetric than those for X-Fe-Y angles. The shape of the histograms for (NB)NE2-Fe-O2 and OH-Fe-NE2(NB) suggests that these angles might have two preferred optimal ranges.

3.4 Amber force field parameters and their performance in vacuum

Force field parameters for bonds and angles involving Fe, derived with each method tested here, are gathered in Table 5 and they are also presented graphically on Figs. S7, S8 and S11, S13 (for data for model 2, see Tab. S1 and Fig. S7, S8, S12, S14). A quick survey of the values presented in Table 5 reveals that both force constants and reference values can differ very significantly between the FF sets.

Table 5 Derived amber force field bonded parameters for model 1
Full size table

These bonded parameters for the Fe2+ ion and its surrounding were combined with RESP atomic charges and standard ff14SB amber force field parameters (for bonded and non-bonded terms involving other atoms) and applied to model 1 and model 2. Molecular mechanics geometry minimization was carried out with Gaussian 16, whereas a short (6 ps) T = 300 K MD simulation in vacuum was done with the sander program. Equilibrium bond lengths and valence angle values are gathered in Table 6 (for data for model 2, see Tab. S2), whereas average values from trajectories are reported in Tables 4, 7 (Tab. S3 for model 2).

Table 6 Bond length [Å] and valence angle [°] for model 1 optimized in vacuum at a specified level of theory
Full size table
Table 7 MAE and MaxE values calculated for energy values [kcal/mol]
Full size table

Concerning stationary geometries, Sem_K and PHF_K produced the best geometries for model 1 and model 2, respectively, as measured by RMSD computed for the 1st shell of Fe ion. Consistently, these parameter sets also gave lowest values of errors for bond lengths and valence angles involving Fe. Analysis of the error values shows that Sem_K and PHF_K perform rather similarly and in both cases application of the Katachi amendment brings about a very significant improvement of the stationary geometry. On the other hand, application of the Katachi method to the Param set of parameters improves stationary geometry either only slightly (model 1) or not at all (model 2). The original Param sets of parameters yielded a rather poor geometry, i.e., 1st shell RMSD of 0.556 and 0.985 Å, bond MaxE of −0.240 and −0.209 Å and angle MaxE of −57.60° and −69.77°, for model 1 and model 2, respectively. However, manual adjustment of a few parameters for bonds and/or angles most deviating from the reference structure, gave us the Param_t sets that yielded an acceptable (in our subjective view) stationary geometry.

Focusing on the average bond and angle values sampled during 300 K MD simulations (Table 4 and S3, as well Fig. S10 and S17, S18), performance of Sem_K, PHF_K and Param_t sets is very similar, whereas an analysis of quadratic form distance (DQF) between bond and angle histograms (see Tab. S4, S5) suggests that Param_t sets are marginally better than the other sets (superposition of ADMP and Sem_K/Param_t original histograms is shown in Fig. S32—S41).

Finally, focusing on how well a given parameter set can reproduce QM energy values for a set of ca. 150 geometries, one can infer already from the R2 values reported in Table 7 and S3 that Param and Param_t sets are significantly better performing than any Hessian-based set. Analysis of correlation plots and energy residues, presented in Fig. S21-S27, clearly shows that only the Param and Param_t sets give good correspondence between QM and MM energies with energy residues of reasonable magnitudes (up to 10–15 kcal/mol). In contrast, the MM-QM energy differences obtained from the other parameter sets can reach values in the range 60–150 kcal/mol, which means that if one uses these sets for MD simulations, some regions of configurational space will be much less frequently probed than they should.

3.5 Testing the parameters for the cofactor within the protein

Four test simulations were also performed for the whole EctC protein complexed with the substrate. Both protonation states of Tyr84 were considered, which corresponds to model 1 and model 2, and for each of them two parameter sets were employed: Sem_K and Param_t. Apart from Tyr84, the rest of tyrosines were in charge-neutral, whereas all lysines and arginines were in their cationic forms. Histidine residues were neutral, with protonated δ-nitrogen (His55, His89, His92) or ε-nitrogen (His5, His116, His136), while acidic amino acids (Glu, Asp) were all ionized. The protonation states of all amino acid residues were based on the results of the propKa3.1 program for pH 7.0 [37, 38]. We generated 100 ns-long trajectories with typical settings for a protein in explicit solvent MD run (e.g., 2 fs time step, SHAKE algorithm used for hydrogen atoms) to serve as tests if these parameter sets cause any instabilities during the simulations or not. All four runs went smoothly, RMSD calculated for the whole main chain reached plateaus at around 3.9, and 4.8 Å for model 1 with Param_t and Sem_K sets, respectively, and 4.4, 4.7 Å for model 2 with Param_t and Sem_K sets. When the mobile and unstructured C-terminal fragment (aa: 126–138) was excluded, the RMSD values reached plateau at: 1.9 and 2.5 Å for model 1 with Param_t and Sem_K sets, respectively, 2.3 and 2.5 Å for model 2 with Param_t and Sem_K sets, respectively. Detailed results of MD simulations will be published elsewhere, but here we want to mention that the choice of the parameter set representing the metal cofactor seems to have non-negligible impact on the conformational freedom of the N-γ-ADABA substrate. More specifically, we observed how many snapshots of MD simulations yielded distances of less than 3.5 Å between the amino nitrogen and carbonyl carbon of N-γ-ADABA, which may be assumed as a limit for enabling the cyclisation reaction of EctC. Defining these situations provisionally as “near attack conformations'' (NAC), we observed 88 and 17 NAC snapshots out of 10 000 for model 1, using the Sem_K and Param_t sets, respectively. For model 2, 2 (Sem_K) and 4 (Param_t) NAC snapshots were observed. It remains open if this difference is statistically significant, yet we consider it as a warning that meaningful modeling of the reaction can only be achieved with an appropriate parametrization of the Fe cofactor.

4 Conclusions

The results presented above show that very accurate minimum energy geometries could be obtained with force constants derived from Hessian (Seminario or PHF methods) when combined with reference bond length and valence angle values refined with the Katachi amendment (Sem_K and PHF_K sets). Unfortunately, such parameter sets do not allow for accurate reproduction of energy variation with geometrical changes brought about by thermal fluctuations (T = 300 K), as for these sets MM-QM energy differences can be as high as 150 kcal/mol. On the other hand, parameters derived from the energy fitting procedure (Paramfit) gave much, much better performance in terms of energy, yet stationary geometry and, to a lesser extent, average dynamics geometry are less accurate. As for Param sets only a limited number of bonds and/or angles showed large discrepancies from the reference values, manual adjustment of a few parameters gave us Param_t sets that are still very good in terms of energy and they well reproduce averaged bond lengths and angle values as well as their distributions (histograms). Most likely the procedure of amendment of Param sets can be automated via adding geometry terms to the minimized penalty function, as previously demonstrated by Norrby and Liljefors [8]⁠, yet this requires code development, optimization of weights for different terms and validation of the method. Hence, for the moment we are of the opinion that the Param_t sets derived here offer the best compromise between energy and geometry accuracy, and they will be used in our ongoing computational studies on structure and function of EctC.