Abstract
Fewest-switches surface hopping (FSSH) is employed in order to investigate the nonadiabatic excited-state dynamics of thiophene and related compounds and hence to establish a connection between the electronic system, the critical points in configuration space and the deactivation dynamics. The potential-energy surfaces of the studied molecules were calculated with complete active space self-consistent field and time-dependent density-functional theory. They are analyzed thoroughly to locate and optimize minimum-energy conical intersections, which are essential to the dynamics of the system. The influence of decoherence on the dynamics is examined by employing different decoherence schemes. We find that irrespective of the employed decoherence algorithm, the population dynamics of thiophene give results which are sound with the expectations grounded on the analysis of the potential-energy surface. A more detailed look at single trajectories as well as on the excited-state lifetimes, however, reveals a substantial dependence on how decoherence is accounted for. In order to connect these findings, we describe how ensemble averaging cures some of the overcoherence problems of uncorrected FSSH. Eventually, we identify carbon–sulfur bond cleavage as a common feature accompanying electronic transitions between different states in the simulations of all thiophene-related compounds studied in this work, which is of interest due to their relevance in organic photovoltaics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Chemistry is known to be at the boundary of both the applicability of classical models and the necessity of quantum mechanical concepts. On the one side, theories that are at least partially based on assumptions from classical mechanics like transition-state theory (TST) [1, 2] and classical collision theory [3, 4] can accurately predict reaction rates in certain parameter regimes, but on the other side are usually insufficient to give a general description of chemical reactions, particularly when quantum-nuclear effects such as zero-point energy, quantum tunneling [5] or nonadiabaticity [6] play an important role [7,8,9,10]. For the case of TST, it was realized early by Wigner that it is not possible to reintroduce these quantum effects in a simple way after making the classical assumption along the reaction coordinate [8], because all degrees of freedom are coupled together [9, 10].
Hence, finding a way to describe a continuous quantum-to-classical transition in chemical dynamics is highly desirable in order to treat systems computationally as efficient as possible but also with the necessary accuracy. The concept of quantum decoherence is a promising approach to accomplish this transition [11,12,13,14]. It comprises the consideration of molecules as open quantum systems interacting with their environment. The correct treatment of the quantum-to-classical transition is essential for gaining a deeper understanding of chemical dynamics and in particular for introducing new well-grounded semiclassical approximations.
One of the most popular methods for simulating nonadiabatic dynamics is Tully’s fewest-switches surface-hopping (FSSH) algorithm [15]. While it can be remotely connected to the quantum-classical Liouville equation [16], it lacks such a solid theoretical foundation. One of the major deficiencies of FSSH is the absence of decoherence, widely known as overcoherence problem. In the seminal work of Schwartz et al. [17] the authors address this issue by deriving a decoherence rate based on a frozen-Gaussian approximation of the nuclei. Their central expression suggests that decoherence is caused by the differences in nuclear forces on the various potential-energy surfaces, which drive the different parts of the nuclear wavepacket apart.
Since then, various correction schemes have been proposed by numerous authors in order to rectify the problem of overcoherence in FSSH [18,19,20,21,22]. However, as the variety of different approaches suggests, there is no general way to correctly implement decoherence in the FSSH algorithm, because the problem originates from the fundamental idea of using an ensemble of independent trajectories in order to approximate the time evolution of the nuclear wavepacket. The absence of coupling between the different trajectories entails that the bifurcation of the wavepacket cannot be described adequately, because different trajectories within the ensemble have no information about when in time they should maintain or lose phase relations (coherences) with each other. The utilization of independent trajectories, however, is in fact one of the main strengths of the FSSH technique with respect to computational costs and parallelization enabling it to be applied even to large molecular, biological and condensed-phase systems [23,24,25]. Hence, the correction schemes retain the independent-trajectory picture, so as to preserve the computational strengths of the algorithm.
Many of the proposed decoherence correction schemes are yet to be extensively examined comparatively for molecular chemical problems for which FSSH is most relevant due to its computational efficiency. Previous tests on model systems have already shown that the (approximately) correct description of decoherence in FSSH is essential to obtain accurate results for reaction dynamics and rates, though different decoherence algorithms lead to different outcomes [26].
The effect of decoherence on the dynamics and the transition rates that derive from it is usually far from trivial. The rate of a transition process depends in an intricate way on the coupling of the electronic system to the environment, in our case to the classical nuclei. Although in the case of very strong coupling to the environment the rate is expected to decrease as this corresponds to the well-known quantum Zeno effect [27], for intermediate coupling the rate can even increase with respect to the uncoupled case, which is then called an anti-Zeno effect [12, 28]. Hence, decoherence can cause the rate of a transition process both to speed up or slow down.
Therefore, the aim of this work is to clarify the influence of different decoherence correction schemes on the results of FSSH simulations for chemically relevant systems, while also emphasizing the importance of correctly describing such effects.
For this purpose, we employ uncorrected, coherent FSSH, the widely used energy-based correction by Granucci and Persico [18], and the augmented-FSSH (AFSSH) algorithm by Subotnik et al. [29, 30] to explore the excited-states dynamics of thiophene and related systems. The electronic-structure calculations were performed using the complete active space self-consistent field (CASSCF) method and linear-response time-dependent density-functional theory (TDDFT).
Since the interpretability of FSSH results hinges on an in-detail knowledge of the pivotal features of the potential-energy surfaces (PESs), critical points on and between the different surfaces were optimized and proven to be essential for correctly describing the dynamics.
Eventually, the overall objective is to get a coherent picture which encompasses the potential-energy surfaces, the dynamics taking place on them and the role of quantum decoherence. Due to their relevance in organic photovoltaics, extensive literature on thiophene-based materials [31,32,33,34,35] is available, which was used to constantly test our results.
A comprehensive understanding of the deactivation pathway and excited-state lifetimes for these thiophene-based materials including effects of decoherence is therefore not only of fundamental scientific interest, but also plays a key role in explaining and maybe even predicting the success of promising materials in different fields of application.
2 Computational methods
For performing the dynamics simulations, state-averaged CASSCF calculations of thiophene were realized using the OpenMolcas program [36] with the cc-pVDZ basis set [37] including three singlet and triplet states, respectively (SA(\(3S+3T\))-CASSCF). In addition, the Columbus program [38,39,40], utilizing the Dalton program for calculating atomic orbital integrals [41], was used to carry out the static calculations and optimizations [42, 43]. These calculations were performed using three singlet states (SA(3S)-CASSCF) in conjunction with the 6-\(31\text {G}^*\) basis set [44], which led to the values given in Tables 1 and 2.
For all CASSCF calculations, an active space composed of ten electrons in nine orbitals was employed. The active orbitals are shown in Fig. 1. Five valence \(\pi\) and \(\pi ^*\) orbitals were included to correctly describe the aromaticity of the thiophene molecule, while two pairs of \(\sigma\) and \(\sigma ^*\) orbitals were needed to accurately describe the C–S bond cleavage occurring during the dynamics
The long-range corrected \(\omega\)B97XD exchange-correlation functional as implemented in the Gaussian09 program suite [45] with a 6-\(31\text {G}^*\) basis set was employed for the calculation of the electronic states using linear-response TDDFT. Here, we followed the recommendation of Barbatti et al. [34] for thiophene-based systems.
The molecular-dynamics simulations were performed using the SHARC ab initio dynamics package version 2.0 [46, 47] within the diagonal representation and including spin–orbit couplings in the CASSCF calculations. For each of the CASSCF and TDDFT calculations, 500 and 200 initial conditions, respectively, were generated based on a Wigner distribution, computed from harmonic vibrational frequencies for the optimized ground-state equilibrium geometry. The number of trajectories starting in each of the excited states was chosen stochastically, based on the excitation energies and oscillator strengths associated with the respective excited states at each initial geometry.
The classical nuclear degrees of freedom were propagated using the velocity-Verlet algorithm with a time step of \({0.5}\hbox { fs}\), while the time step for evolving the quantum system was chosen as \({0.02}\hbox { fs}\). For analyzing the influence of the decoherence-correction scheme on the trajectories, the following methods were applied: (1) standard (coherent) FSSH (in the diagonal representation) as implemented in the SHARC program package [47], (2) the energy-based correction by Granucci and Persico [18] with a parameter of \(\alpha = 0.1 \, \text {a.u.}\), and (3) the augmented-FSSH (AFSSH) algorithm by Subotnik et al. [29].
The energy-based decoherence algorithm is motivated by the idea that close to a point of (near) degeneracy between the currently active state (labeled by j), on which the trajectory travels, and an inactive state (labeled by i) coherent superpositions between the states will emerge and hops are expected. After leaving this area of strong coupling, however, the forces on different potential-energy surfaces will most definitely drive the populations in different directions which should lead to a rapid decay of the previously built-up coherences. In order to understand how the decoherence corrections take effect, we have to make a quick detour into the basics of the surface hopping algorithm. In the surface-hopping framework, the total electronic wavefunction \(\Psi (t,r;R(t))\) at time t along a single classical trajectory R(t) is expanded in a basis of (adiabatic) wavefunctions \(\{\psi _k\}\)
where r are the electronic coordinates. Plugging this expansion into the time-dependent Schrödinger equation leads equations of motions for the wavefunction coefficients \(c_k(t)\), or equivalently the elements of the electronic density matrix \(\rho _{kl}(t) = c^{*}_k(t) c_l(t)\) [15]. Introducing decoherence is hence synonymous to changing these equations of motions. In particular, the algorithm of Granucci and Persico [18] consists in damping the wavefunction coefficients belonging to the inactive states by an exponential factor which is mainly determined by the energy difference to the active state while the coefficient of the active state is renormalized accordingly at each time stepFootnote 1:
Here, \(E_\text {kin}\) is the nuclear kinetic energy, \(E_i\) and \(E_j\) are the potential energies of the respective states, \(\alpha\) is a free parameter, and \(\Delta t\) is the time step for evolving the quantum system.
In contrast, in AFSSH an additional set of variables, called moments of classical position and momenta, is propagated for every inactive state. Solving the equations of motions for these moments essentially means to integrate the force difference between the different adiabatic states. As opposed to the decoherence method of Persico and Granucci, where the central object of the decoherence rate is the energy difference between the states, in AFSSH the difference in forces is the pivotal quantity. This is in accordance with the decoherence rate in Ref. [17] and well-grounded in the mapping between FSSH and quantum-classical Liouville equation [48]. The propagation of these auxiliary variables provides the active trajectory at least with partial information about trajectories on the other states and therefore about when different parts of the wavepacket decohere. Following the derivation in Refs. [29, 30, 49] one obtains a parameter-free decoherence rate.
Due to the inability of linear-response TDDFT to correctly describe nonadiabatic couplings involving the ground state [50, 51], no couplings to the ground state were computed in the optimization. Instead, the trajectories were terminated in the ground state when the energy gap between \(S_1\) and \(S_0\) reached a value smaller than \({0.1}\hbox { eV}\), so as to obtain a realistic estimate of the deactivation time to the ground state and to prevent unphysical behavior arising after a trajectory’s passage through a conical intersection between an excited state and the ground state. The populations were corrected accordingly. An approximate optimization scheme implemented in the ORCA program [52] without explicit calculation of nonadiabatic coupling vectors [53, 54] was employed for optimization and comparison of the minimum-energy conical intersections. The optimization was facilitated by the SHARC utility programs with parameters \(\sigma = 3.5\) and \(\alpha = {0.02}\hbox {E}_{\hbox {h}}\). In this way, it was possible to optimize conical intersections between excited states using TDDFT. The fits of the state populations were performed with the program Maxima [55], in combination with the SHARC utility programs.
3 Results and discussion
From the generated initial conditions, excitation spectra can be obtained from the excitation energies and oscillator strengths associated with each geometry. Figure 2 shows the resulting spectra calculated with CASSCF and TDDFT. Although the excitations lie within a similar energy range, the CASSCF spectrum clearly shows a double band, which is present also in the experimental gas-phase spectrum [56]. With TDDFT, this double band is not resolved. However, both spectra illustrate the importance of including both low-lying excited singlet states when simulating the low-band excitations of thiophene.
As mentioned above, critical points on and between different potential-energy surfaces have to be optimized and analyzed, before the dynamics reliably can be interpreted and discussed. The CASSCF and TDDFT results are compared to more sophisticated but also more computationally expensive methods in Table 1. Therein, the energies of the three lowest singlet states are displayed for different geometries, such as local minima and minimum-energy conical intersections. Comparing the results of the calculations, we find the calculated energies to agree relatively well for the different methods at the considered geometries. The average deviation lies between 0.5 and \({1.0}\hbox {eV}\). The DFT ground-state energy in the \(S_1^{\text {a}}\) minimum geometry alone deviates more significantly.
However, the energies in the remaining structures correspond well to CASSCF and reference values. Even the \(S_2/S_1\) conical intersection is well described by TDDFT using the approximate optimization scheme described in Sect. 2. As a single substantial difference, the dihedral angle given in Table 2 indicates that the corresponding molecular structure is not entirely planar, which is in contrast to the CASSCF results. The structural data given in Table 2 further confirm the similarity between CASSCF and TDDFT results. Only the \(S_1/S_0\) conical intersection and the \(S^{b}_1\) minimum structures cannot be described adequately by a single-reference method such as linear-response TDDFT, due to the multiconfigurational characteristics of the underlying ground state.
In summary, the accuracy of the CASSCF calculations with the selected active space makes the method well suited to describe the photochemical deactivation process of thiophene on a qualitatively correct level. On the other hand, TDDFT constitutes a computationally more efficient method, which is appropriate for describing the dynamics between the excited states. Based on these observations, we believe TDDFT to be a good approximation to the excited-states dynamics of the chosen thiophene molecule, but also of other, larger thiophene-based systems.
It has been suggested that the transition between two of the singlet states, generally being mediated by a conical intersection, is accompanied by the cleavage of a carbon–sulfur bond [32, 34, 35]. In order to attain a better understanding of the connection between the electronic and nuclear systems, the gradients and nonadiabatic coupling vectors (NACs) were analyzed during the conical-intersection optimization (using the Columbus program). Both involved potential-energy surfaces in the branching space, which is spanned by the corresponding NAC vector \(\mathbf {h}\) and energy gradient difference vector \(\mathbf {g}\), were plotted close to the minimum-energy conical intersection. The potential-energy surfaces are approximated linearly by
whereby the parameters \(\sigma _x\), \(\sigma _y\), \(\delta _{gh}\) and \(\Delta _{gh}\) describe the pitch, inclination and ellipticity of the cone and \(x \propto g\), \(y \propto h\). The corresponding data are given in Table SI.1. The resulting plots as well as the corresponding molecular structures are depicted in Fig. 3.
The \(S_2/S_1\) conical intersection has a steep gradient, with an only marginally tilted double-cone shape. Additionally, its underlying molecular structure is located relatively close to the Franck–Condon region. Both facts suggest that a fast transition to the \(S_1\) state occurs following an initial excitation to the \(S_2\) state. Moreover, in the molecular structure a substantial C–S bond elongation is clearly visible. In the structure corresponding to the \(S_1/S_0\) conical intersection, this elongation is even more pronounced and leads to cleavage of the C–S bond. However, the \(S_1/S_0\) conical intersection is strongly tilted and has a smaller slope than ConI \(S_2/S_1\). Furthermore, its corresponding molecular structure is located farther away from the Franck–Condon region and can only be reached by overcoming a small barrier from the \(S^{b}_1\) minimum [32]. Thus, a population transfer through the \(S_1/S_0\) conical intersection is expected to be slower than through the one connecting the states \(S_2\) and \(S_1\) [59].
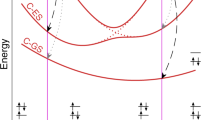
Potential energy profile along a single, characteristic trajectory (using the energy-based Granucci decoherence correction) initiated from the \(S_2\) state. Energies are given relative to the ground-state minimum. For illustration, structures at crucial points are depicted as insets together with the time at which they occur
The following analysis of the thiophene dynamics is based on the CASSCF simulations which give a qualitatively correct description of the dynamics through both conical intersections. Whenever we discuss TDDFT-based results in the following, we will state so explicitly.
Figure 4 shows the potential-energy profile of the involved singlet states for a selected trajectory, together with snapshots of the respective thiophene structures. It is apparent that a structure similar to the \(S_2\) minimum geometry is reached shortly after initial excitation. The first hop to the \(S_1\) state appears at \(t= {28}\,\hbox {fs}\) at a structure close to that of the \(S_2/S_1\) conical intersection. Shortly after, at \(t = {53}\,\hbox {fs}\) the C–S bond has broken and the structure strongly resembles the one of the \(S^{b}_1\) minimum shown in Fig. SI.3. By overcoming a small barrier the molecule hits the \(S_1/S_0\) conical intersection [32], and a transition to the ground state follows. The potential energy remains relatively high over the course of the whole trajectory. This implies that the closed-ring ground-state minimum is not reached within the simulation time. Instead, new bonds are constantly being formed and broken resulting in intermediary three- and four-membered rings as well as in open-chain structures.
Statistical analysis of the time dependence of the C–S bond length in the trajectory ensemble of the AFSSH simulation. The color code indicates the number of trajectories that exhibit a bond in the respective length interval at a given time. In 80% of the trajectories at \({300}\,\hbox {fs}\) one of the original C–S bonds of thiophene is longer than \({2.79}{\AA }\) and therefore more than 56% longer than the ground-state equilibrium distance
For a statistical analysis of the ensemble evolution, Fig. 5 depicts the C–S bond lengths as function of simulation time for our set of independent trajectories. It turns out that bond cleavage as a result of electronic transitions in thiophene is not only an occasional feature of some trajectories, but occurs in the majority of the simulations. While the C–S bond length is close to its equilibrium value at the beginning of all trajectories, large elongations are observed in most simulations at later times. Using the AFSSH simulation from Fig. 5 as an example, at \({300}\,\hbox {fs}\) more than 80% of the trajectories exhibit one C–S bond that is elongated by more than 55% of its value in the ground-state minimum. We conclude that the C–S bond cleavage and transitions in the electronic system are strongly connected within the excited-state dynamics of thiophene. The residual trajectories without C–S bond cleavage either do not reach the ground state within simulation time (e.g. due to intersystem crossings) or undertake different, less pronounced deactivation pathways such as ring puckering [34, 35]. Compared to similar studies of thiophene [35], we find a higher ratio of trajectories which exhibit a transition to the ground state accompanied by C–S bond cleavage. This difference is likely to be rooted in the fact that, as compared to previous CASSCF studies, we also include the second excited singlet state in our simulations. As recognized in the TDDFT study of thiophene by Fazzi et al. [34] and in accordance with the computed spectra in Fig. 2, this state cannot be ignored when the photoexcitation of thiophene is sought to be described appropriately. Therefore, the trajectories we sampled possess on average a higher initial energy which enables them to quickly explore different areas of configuration space and also reach the \(S_1/S_0\) ConI though it is not in immediate vicinity of the Franck–Condon region. Moreover, the small barrier separating the \(S_1^\text {b}\) minimum and \(S_1/S_0\) ConI [32] can be facilely overcome hence promoting the deactivation via bond cleavage.
As a result of this analysis, a clear connection has been observed between the structural and the electronic systems. Moreover, the evolution of the molecular structure for the ensemble of trajectories has been examined with a focus on the statistical behavior of the C–S bond length.
We will now turn to the exploration of the ensemble’s electronic population dynamics. These are shown in Fig. 6 for three different FSSH variations, using the same initial conditions. Due to the high potential energy associated with the molecular structure after excitation, the molecular intermediates break and form new bonds before reaching the ground-state minimum. It is vital to a correct description of these processes that the molecular orbitals corresponding to these bonds are contained within the active space, otherwise the calculations would most likely fail. This is particularly important for describing transitions to and time evolution in the ground state, due to the high kinetic energy of the system after the electronic transition. As a consequence, the calculated transition rates to the ground state would be too small, because only stable trajectories are considered. However, transitions back from the ground state to the excited states are unlikely, especially for the decoherence-corrected methods, because the respective couplings vanish on short timescales. Thus, we include trajectories that terminated after reaching the ground state, due to failure to converge the electronic structure, into the calculation of the ground-state population from the time they reached the ground state onwards until the end of the simulation. Although this approach is less justified for the coherent FSSH method, as we will discuss in the following, it can help to correct the ensemble population for some of the overcoherence errors.
Ensemble populations given by the ratio of trajectories propagated on the respective electronic state at a given time for coherent (C) and augmented (A) FSSH as well as for FSSH with the energy-based decoherence correction of Granucci and Persico (G). Although also three triplet states have been included into the simulation, their populations are not shown here as intersystem crossing takes place on a longer timescale (see Table 3) and hence plays a subdominant role
Although all of the methods produce similar results in Fig. 6 at first glance, the populations obtained with the energy-based correction of Granucci exhibit a more pronounced population transfer between \(S_2\) and \(S_1\), as well as between \(S_1\) and \(S_0\) than for the other two methods. This corresponds to an anti-Zeno effect, where the transition rate is enhanced as compared to the coherent FSSH results, because the decoherence correction leads to a quick decrease of the electronic coupling between the states after reaching a strong-coupling region and hence inhibits transitions back to the initial state or other weakly coupled states. Coherent FSSH and AFSSH mainly differ in the description of the \(S_2\) population: while it practically vanishes in the force-based corrected AFSSH scheme after 200 fs, the \(S_2\) population calculated with the fully coherent FSSH method remains on a higher level also at long times and shows persistent oscillations.
The calculated time-dependent populations can be fitted to a system of elementary reactions. Based on the hops occurring during the first \({300}\,\hbox {fs}\), the proposed deactivation mechanism, illustrated in Fig. SI.4, incorporates the transition from \(S_2\) to \(S_1\) with the corresponding deactivation time \(\tau _{21}\). Potential subsequent reactions could include the population transfers to the ground state (\(S_0\)) or to one of the triplet states with deactivation times \(\tau _{10}\) and \(\tau _{\text {ISC}}\), respectively. The resulting lifetimes are shown in Table 3 for the different FSSH variations and a set of TDDFT-based AFSSH simulations.
In a few cases, Table 3 reveals significant deviations between the lifetime values calculated with different methods. This indicates a substantial dependence of the ensemble’s electronic populations—and the whole dynamics—on the incorporation of decoherence. Thus, lifetimes obtained from surface-hopping simulations are a rather “fragile” quantity. Substantial dependencies of the calculated lifetimes on the inclusion of triplet states [35] or on the electronic structure method [34] are well-known and have been studied already. The fundamental difference with the dependence on the decoherence implementation is, however, that decoherence is a ubiquitous phenomenon in every nonadiabatic multi-state simulation, no matter how simple the potential-energy surfaces or how low the number of relevant states might be. Apart from that, it is not currently clear how to evaluate the influence of decoherence as well as decide which algorithm is appropriate for each particular problem [60]. Rather than being just a tool to partially restore internal consistency [18] within the surface-hopping framework, an approximately correct treatment of decoherence is essential for making reliable predictions.
In Table 3, nonetheless, all methods show the \(\tau _{21}\) value to be significantly smaller than the respective \(\tau _{10}\) lifetime. This confirms the predictions based on the shape of the two conical intersections. The fully coherent FSSH method exhibits the largest \(\tau _{10}\) lifetime with a comparable intersystem crossing lifetime \(\tau _{\text {ISC}}\). This can be explained by the fact that this method has the highest transition probability from the \(S_0\) ground state to \(S_1\) and triplet states due to the lack of decoherence. In comparison, the results obtained with the energy-based Granucci correction, which tends to be overly incoherent [26], exhibit a large difference between the smallest \(\tau _{10}\) and largest \(\tau _{\text {ISC}}\) lifetime values out of all CASSCF-based methods. The approximation, described in the computational methods section, for obtaining a \(\tau _{10}\) lifetime with TDDFT should generally lead to overly rapid decay rates to the ground state, as no transitions back to excited states are possible. Yet, the resulting total lifetime of \({101.6}\,\hbox {fs}\) is closest to the experimental value of approximately \({105}\,\hbox {fs}\) [61], which reflects the fragility of the surface-hopping lifetimes. Thus, in this article the discussion solely focuses on qualitative arguments.
Top: magnitudes of the wave function coefficients corresponding to the considered singlet states for one selected trajectory simulated with three different FSSH variations. The simulations were started from the same initial conditions. Bottom: magnitudes of the nondiagonal elements of the electronic density matrix corresponding to the coherence between the singlet states for the same trajectory. For reasons of clarity, coefficients of the triplet states are not shown as they do not play a decisive role in the selected trajectories
In order to obtain a better understanding of how different decoherence mechanisms affect the electronic populations, it is worth taking a closer look at the evolution of the electronic system in a single trajectory. For this purpose, we picked out a single trajectory from the ensemble simulations with all three FSSH schemes, that was started from identical initial conditions. The magnitudes of the wave function coefficients as a function of time along this trajectory are depicted in the top panels of Fig. 7, while the corresponding magnitudes of the nondiagonal elements of the electronic density matrix, which correspond to the coupling and coherence between the various states, are shown in the lower panels. As opposed to the ensemble populations, the displayed graphs look considerably distinct for the different FSSH variations.
Although the stochastic nature of surface hopping makes it sometimes difficult to compare results for single trajectories, even when started from the same initial conditions, the features we choose to discuss are easily compared for all of the trajectories of the respective FSSH method. As shown in Fig. 7a, the results obtained with Granucci’s decoherence scheme confirm the pronounced incoherent character of the energy-based correction. For the most part of the chosen trajectory, the electronic system is dominated by a single electronic state. Since here we chose the same trajectory to study the coupling between the states as we did to examine the evolution of the molecular structure in Fig. 4, we can directly identify which points on the potential energy surfaces the different coupling regions correspond to. Therefore, starting from the \(S_2\) state the trajectory reaches the \(S_2/S_1\) conical intersection, which coincides with a strong coupling region, at about \(t=\) \({25}\,\hbox {fs}\), as can be seen in Fig. 7d. Accordingly, the electronic system enters a region with significant coherent superposition between the two excited singlet states. Shortly after at \(t={55}\,\hbox {fs}\), the traversing of the \(S_1/S_0\) conical intersection causes the electronic system to be in a superposition of all three singlet states. This region of coherent coupling, however, is very localized both in space and time. Therefore, shortly after the transition to the ground state (at \(t=\) \({60}\,\hbox {fs}\)), the electronic system is almost exclusively dominated by the \(S_0\) state, except for a second coupling region at \({270}\,\hbox {fs}\). As expected, this is consistent with reaching the adiabatic, incoherent limit.
On the contrary, both the coherent and the augmented FSSH algorithms show much more delocalized couplings and thus more prolonged periods for which the system is in a coherent superposition of multiple electronic states, as shown in Figs. 7b, c, e, f. The general similarity between these two methods is consistent with the incorporation of a lower bound for the decoherence rate immanent in AFSSH [30]. Coherences in AFSSH are therefore not as strongly damped as in the energy-based decoherence algorithm.
The main difference between the two methods, however, can also clearly be seen in the corresponding panels of Fig. 7. While the electronic system propagated with AFSSH also reaches the incoherent limit, wherein the only significant contribution to the dynamics at large simulation times comes from \(S_0\), the electronic system of the trajectory propagated with standard FSSH remains in a superposition of multiple electronic states for the whole simulation, even though multiple hops to the ground state occur. Thus, the transition probabilities for coherent, uncorrected FSSH remain on a constantly high level leading to multiple hops between almost all of the included potential-energy surfaces. This results in a highly complex, overly coherent superposition of electronic states, which is in accordance with previously observed persistent oscillations of ensemble populations, as well as the large \(\tau _{10}\) lifetime and the comparatively small value of \(\tau _{\text {ISC}}\).
The similarity between the ensemble populations for the three different methods arises through averaging over the ensemble of trajectories. This key feature of surface hopping is the decisive factor for its broad success in spite of severe shortcomings such as the lack of decoherence. Hence, it is desirable to use an alternative way to quantify the effect of ensemble averaging on the results. In addition, defining (de-)coherence via the nondiagonal elements of the reduced density matrix inherently carries a basis dependence. In order to obtain a basis-independent quantity, the purity of the ensemble density matrix is defined as the trace of the ensemble averaged electronic density matrix squared, \({{\,\mathrm{Tr}\,}}\{\rho ^2\}\), whose evolution during the simulation is illustrated in Fig. 8.Footnote 2
As can be seen from Fig. 8, the qualitative evolution of the purity is very similar between the different methods. From the very beginning of the simulation, the initial purity is already smaller than 1, because the simulations comprise trajectories starting both in the \(S_2\) and \(S_1\) states. The maximum in the purity that occurs at around \({25}\,\hbox {fs}\) with all methods originates from the quick transition from \(S_2\) to \(S_1\) and is consistent with the corresponding lifetimes in Table 3. As a consequence, most of the trajectories are situated in the \(S_1\) state at this time. It might seem unexpected that the fully coherent FSSH algorithm exhibits the smallest value of the purity among the different methods at \({300}\,\hbox {fs}\). This is because the here defined purity is mostly a measure of the dissipation of the electronic population among the various electronic states. Due to the previously mentioned, constantly high transition probabilities to other states in the coherent FSSH method, the population is widely distributed among different states, resulting in the small purity value at \({300}\,\hbox {fs}\) compared to the other two methods. Moreover, this explains why the results on the ensemble level are relatively similar to those obtained with the decoherence-corrected algorithms, although the evolution of the electronic system within the single trajectories significantly differs [62].
The different curve shape obtained with AFSSH at early times is caused by the fact that only trajectories which are stable for at least \({300}\,\hbox {fs}\) are taken into account for the calculation of the purity. The number of stable trajectories, especially the ones started in \(S_2\), was significantly higher for AFSSH than for the other two methods, as can be seen from Table SI.2. Before reaching the maximum, the AFSSH purity exhibits a kink showing that here the intermediary accumulation of trajectories in the \(S_1\) state is preceded by an initial delocalization of the population into other states. This process is likely to be driven by the high-energy trajectories which explore different areas of configuration space more rapidly and are therefore also more likely to become unstable.
Despite the rather different number of stable trajectories in the simulations with the energy- and force-based decoherence correction, both methods reach practically the same purity value toward the end of the simulation. This further confirms that, in contrast to the fully coherent FSSH, both decoherence-corrected methods reach the incoherent limit with the majority of the electronic population in the ground state as expected.
In general, the extent of decoherence is expected to rise with an increasing number of nuclear degrees of freedom [63, 64]. The increasing dimensionality of the system raises the likelihood of forces on different potential-energy surfaces to drive the electronic populations in different directions, which leads to rapid decoherence. At the same time, we need to bear in mind that many systems studied by surface hopping are molecules relevant, e.g., in organic photovoltaics. Thus, they often possess an extended \(\pi\) electron system. By increasing the size of the \(\pi\) system, the number of low-lying excited states which are energetically close together grows as well, meaning that coherent superpositions can still play an important role. This can be seen from the TDDFT-based simulation results of oligothiophenes (up to four rings) and two further thiophene-based compounds shown in the supporting information, where both standard and augmented FSSH show again relatively similar results for the ensemble populations over the first \({300}\,\hbox {fs}\). Although the number of trajectories we ran for these systems are not sufficient to make reliable statistical statements about their decay dynamics, the breaking of C–S bonds accompanying electronic transitions is clearly an essential feature for all of the investigated molecules. Whether this is a practically relevant degradation mechanism for materials based on these compounds or whether, e.g., a substrate can prevent this deactivation pathway remains to be investigated in more detail.
4 Conclusions and outlook
Based on the analysis of the photochemical decay process of the thiophene molecule following a low-band excitation, the role of decoherence for the excited-state dynamics has been studied and evaluated in detail. Thus, a clear connection between the accessibility of conical intersections, the accompanying carbon–sulfur bond cleavage and the treatment of decoherence has been drawn. Similar to other recent studies [60, 65], we addressed the influence of different implementations of decoherence within the surface-hopping framework on the dynamics of molecular systems, which are to a large extent only tested for low-dimensional model problems. It has been shown that different treatments of decoherence produce significantly different decay rates and lead to considerable deviations in the evolution of the electronic system for individual trajectories. Consequently, implementation of decoherence is not only a tool to approximately realize internal consistency, but is a crucial factor to make the surface-hopping simulations more meaningful and consistent with what is observed in experiment, especially for longer simulation times.
Furthermore, it has been shown that the effect of a decoherence correction on the population dynamics is in general not easily predictable, because various factors pertaining to electronic and nuclear systems have to be taken into account. Depending on the coupling strength between the electronic system and the nuclear bath state-to-state transitions can be both sped up or slowed down compared to the uncorrected algorithm leading to the occurrence of Zeno and anti-Zeno effects. Due to the inability of surface hopping to correctly describe decoherence on the ensemble level, as a result of the use of independent trajectories, FSSH simulations might not be the best choice to test the characteristics of decoherence for a special problem [66]. However, during the last few years different methods have emerged which are similar to surface hopping, but address the problem of decoherence on the ensemble level [67, 68]. Overall, our results indicate that if one strives for an accurate description of the dynamics, it is not only necessary to thoroughly study the potential-energy surfaces, but also to examine how exactly decoherence takes effect.
From the FSSH variations considered here, the Granucci correction is expected to work well for strongly incoherent dynamics, where coupling and coherence appear very localized and are damped shortly after. However, due to the ad hoc character of the approximation, which is essentially only based on the energy difference between the different states, it is not clear whether the method is able to correctly describe branching ratios and the dependence of the dynamics on the size of the nuclear system. In contrast, the dimensionality of the system directly enters into the AFSSH algorithm, which is based on the difference of forces on the various potential-energy surfaces. Also considering the performance in model problems, AFSSH should be preferred for systems with pronounced coherent character.
Despite the sensitive dependence of the population dynamics for single trajectories on decoherence, it was possible to catch the main features of the thiophene dynamics with all three FSSH variations, due to the effect of ensemble averaging, which has been characterized by defining the purity of the ensemble density matrix. Thus, the main differences between the AFSSH and standard FSSH algorithms are only expected to be significant for longer simulations, where the correct asymptotics play an important role.
Finally, the TDDFT simulations of oligothiophenes and other thiophene-based systems relevant for organic photovoltaics showed an intrinsic connection between electronic-state transitions and the elongation and cleavage of a C–S bond, as has also been observed in previous results for bithiophene [69]. The phenomenon occurred at hopping geometries of all investigated molecules without exception. Hence, although not explicitly optimized, the structures at the respective minimum-energy conical intersections are very likely to exhibit an elongated or broken C–S bond just as in thiophene itself. Therefore, transitions in the electronic system seem to be induced very locally, which could be associated with the exciton self-localization mechanism in these systems [34]. Another possibly interesting prospect is to study whether this is a relevant degradation pathway in the devices based on these materials or if, for instance, the substrate is altering the decay pathway. Therefore, this is again a question for which environment-induced dissipation and decoherence must be considered.
Notes
Note that in comparison with Ref. [18] an additional factor of \(\tfrac{1}{2}\) occurs in the exponent in Eq. 2a. This is because the formula in Ref. [18] should be applied to populations (as the authors mention in Ref. [19]). When applied to wavefunction coefficients, an additional factor of \(\tfrac{1}{2}\) has to be added [47].
The elements of the electronic density matrix of a single trajectory labeled by the index \(\lambda\) consist of products of wavefunction coefficients \(\rho ^\lambda _{kl} = c^{\lambda *}_{k} c^{\lambda }_l\). The electronic density matrices of all N trajectories are then averaged over the ensemble to obtain \(\rho = \frac{1}{N}\sum _\lambda \rho ^\lambda\) at every time step.
References
Eyring H, Polanyi M, Z. Phys. Chem. 227(9-11) (1931). https://doi.org/10.1524/zpch.2013.9023
Eyring H (1935) J. Chem. Phys. 3(2):107. https://doi.org/10.1063/1.1749604
Trautz M (1916) Z. anorg. allg. Chem. 96(1):1. https://doi.org/10.1002/zaac.19160960102
Lewis W C M (1918) J. Chem. Soc., Trans. 113(0):471. https://doi.org/10.1039/ct9181300471
Orville-Thomas W (1981) J. Mol. Struct. 74(2):356. https://doi.org/10.1016/0022-2860(81)80048-8
Chandler D Electron transfer in water and other polar environments, how it happens (World Scientific, Singapore, 1998), chap. 2, p. 25. Quantum Dynamics in Condensed Phase Simulations
Wigner E (1932) Phys. Rev. 40(5):749. https://doi.org/10.1103/physrev.40.749
Wigner E (1938) Trans. Faraday Soc. 34:29. https://doi.org/10.1039/tf9383400029
Miller WH (1993) Acc. Chem. Res. 26(4):174. https://doi.org/10.1021/ar00028a007
Richardson JO (2018) CHIMIA 72(5):309. https://doi.org/10.2533/chimia.2018.309
Zeh HD (1970) Found. Phys 1(1):69. https://doi.org/10.1007/bf00708656
Joos E, Zeh HD, Kiefer C, Giulini D, Kupsch J, Stamatescu IO (2003) Decoherence and the Appearance of a Classical World in Quantum Theory (Springer. Berlin Heidelberg. https://doi.org/10.1007/978-3-662-05328-7
Zurek WH (2003) Rev. Mod. Phys. 75(3):715. https://doi.org/10.1103/revmodphys.75.715
de la Lande A, Řezáč J, Lévy B, Sanders BC, Salahub DR (2011) J. Am. Chem. Soc. 133(11):3883. https://doi.org/10.1021/ja107950m
Tully JC (1990) J. Chem. Phys. 93(2):1061. https://doi.org/10.1063/1.459170
Subotnik JE, Ouyang W, Landry BR (2013) J. Chem. Phys. 139(21):214107. https://doi.org/10.1063/1.4829856
Schwartz BJ, Bittner ER, Prezhdo OV, Rossky PJ (1996) J. Chem. Phys. 104(15):5942. https://doi.org/10.1063/1.471326
Granucci G, Persico M (2007) J. Chem. Phys. 126(13):134114. https://doi.org/10.1063/1.2715585
Granucci G, Persico M, Zoccante A (2010) J. Chem. Phys. 133(13):134111. https://doi.org/10.1063/1.3489004
Subotnik JE, Jain A, Landry B, Petit A, Ouyang W, Bellonzi N (2016) Annu. Rev. Phys. Chem. 67(1):387. https://doi.org/10.1146/annurev-physchem-040215-112245
Jain A, Subotnik JE (2015) J. Phys. Chem. Lett. 6(23):4809. https://doi.org/10.1021/acs.jpclett.5b02148
Jaeger HM, Fischer S, Prezhdo OV (2012) J. Chem. Phys. 137(22):22A545. https://doi.org/10.1063/1.4757100
Blumberger J (2015) Chem. Rev. 115(20):11191. https://doi.org/10.1021/acs.chemrev.5b00298
Long R, Liu J, Prezhdo OV (2016) J. Am. Chem. Soc. 138(11):3884. https://doi.org/10.1021/jacs.6b00645
Giannini S, Carof A, Ellis M, Yang H, Ziogos OG, Ghosh S, Blumberger J (2019) Nat. Commun. 10:1. https://doi.org/10.1038/s41467-019-11775-9
Falk MJ, Landry BR, Subotnik JE (2014) J. Phys. Chem. B 118(28):8108. https://doi.org/10.1021/jp5011346
Misra B, Sudarshan ECG (1977) J. Math. Phys. 18(4):756. https://doi.org/10.1063/1.523304
Fischer MC, Gutiérrez-Medina B, Raizen MG (2001) Phys. Rev. Lett. 87:4. https://doi.org/10.1103/physrevlett.87.040402
Jain A, Alguire E, Subotnik JE (2016) J. Chem. Theory Comput. 12(11):5256. https://doi.org/10.1021/acs.jctc.6b00673
Subotnik JE, Shenvi N (2011) J. Chem. Phys. 134(2):024105. https://doi.org/10.1063/1.3506779
Wu XF, Zheng X, Wang HG, Zhao YY, Guan X, Phillips DL, Chen X, Fang W (2010) J. Chem. Phys. 133(13):134507. https://doi.org/10.1063/1.3480361
Cui G, Fang W (2011) J. Phys. Chem. A 115(42):11544. https://doi.org/10.1021/jp206893n
Salzmann S, Kleinschmidt M, Tatchen J, Weinkauf R, Marian CM (2008) Phys. Chem. Chem. Phys. 10(3):380. https://doi.org/10.1039/b710380h
Fazzi D, Barbatti M, Thiel W (2015) Phys. Chem. Chem. Phys. 17(12):7787. https://doi.org/10.1039/c5cp00019j
Schnappinger T, Kölle P, Marazzi M, Monari A, González L, de Vivie-Riedle R (2017) Phys. Chem. Chem. Phys. 19(37):25662. https://doi.org/10.1039/c7cp05061e
Aquilante F, Autschbach J, Carlson RK, Chibotaru LF, Delcey MG, Vico LD, Galván IF, Ferré N, Frutos LM, Gagliardi L, Garavelli M, Giussani A, Hoyer CE, Manni GL, Lischka H, Ma D, Malmqvist PÅ, Müller T, Nenov A, Olivucci M, Pedersen TB, Peng D, Plasser F, Pritchard B, Reiher M, Rivalta I, Schapiro I, Segarra-Martí J, Stenrup M, Truhlar DG, Ungur L, Valentini A, Vancoillie S, Veryazov V, Vysotskiy VP, Weingart O, Zapata F, Lindh R (2015) J. Comput. Chem. 37(5):506. https://doi.org/10.1002/jcc.24221
Dunning TH (1989) J. Chem. Phys. 90(2):1007. https://doi.org/10.1063/1.456153
Lischka H et al. (2017) Columbus, an ab initio electronic structure program, release 7.0. https://www.univie.ac.at/columbus/
Lischka H, Müller T, Szalay PG, Shavitt I, Pitzer RM, Shepard R (2011) Wiley Interdiscip. Rev. Comput. Mol. Sci. 1(2):191. https://doi.org/10.1002/wcms.25
Lischka H, Shepard R, Pitzer RM, Shavitt I, Dallos M, Müler T, Szalay PG, Seth M, Kedziora GS, Yabushita S, Zhang Z (2001) Phys. Chem. Chem. Phys. 3(5):664. https://doi.org/10.1039/b008063m
Aidas K, Angeli C, Bak KL, Bakken V, Bast R, Boman L, Christiansen O, Cimiraglia R, Coriani S, Dahle P, Dalskov EK, Ekström U, Enevoldsen T, Eriksen JJ, Ettenhuber P, Fernández B, Ferrighi L, Fliegl H, Frediani L, Hald K, Halkier A, Hättig C, Heiberg H, Helgaker T, Hennum AC, Hettema H, Hjertenaes E, Høst S, Høyvik IM, Iozzi MF, Jansík B, Jensen HJA, Jonsson D, Jørgensen P, Kauczor J, Kirpekar S, Kjaergaard T, Klopper W, Knecht S, Kobayashi R, Koch H, Kongsted J, Krapp A, Kristensen K, Ligabue A, Lutnaes OB, Melo JI, Mikkelsen KV, Myhre RH, Neiss C, Nielsen CB, Norman P, Olsen J, Olsen JMH, Osted A, Packer MJ, Pawlowski F, Pedersen TB, Provasi PF, Reine S, Rinkevicius Z, Ruden TA, Ruud K, Rybkin VV, Sałek P, Samson CCM, de Merás AS, Saue T, Sauer SPA, Schimmelpfennig B, Sneskov K, Steindal AH, Sylvester-Hvid KO, Taylor PR, Teale AM, Tellgren EI, Tew DP, Thorvaldsen AJ, Thøgersen L, Vahtras O, Watson MA, Wilson DJD, Ziolkowski M, Ågren H (2013) Wiley Interdiscip. Rev. Comput. Mol. Sci. 4(3):269. https://doi.org/10.1002/wcms.1172
Fogarasi G, Zhou X, Taylor PW, Pulay P (1992) J. Am. Chem. Soc. 114(21):8191. https://doi.org/10.1021/ja00047a032
Császár P, Pulay P (1984) J. Mol. Struct. 114:31. https://doi.org/10.1016/s0022-2860(84)87198-7
Ditchfield R, Hehre WJ, Pople JA (1971) J. Chem. Phys. 54(2):724. https://doi.org/10.1063/1.1674902
M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, G. Scalmani, V. Barone, G.A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A.V. Marenich, J. Bloino, B.G. Janesko, R. Gomperts, B. Mennucci, H.P. Hratchian, J.V. Ortiz, A.F. Izmaylov, J.L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V.G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J.A. Montgomery, Jr., J.E. Peralta, F. Ogliaro, M.J. Bearpark, J.J. Heyd, E.N. Brothers, K.N. Kudin, V.N. Staroverov, T.A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A.P. Rendell, J.C. Burant, S.S. Iyengar, J. Tomasi, M. Cossi, J.M. Millam, M. Klene, C. Adamo, R. Cammi, J.W. Ochterski, R.L. Martin, K. Morokuma, O. Farkas, J.B. Foresman, D.J. Fox. Gaussian 09 Revision A.02 (2009). Gaussian Inc. Wallingford CT
Richter M, Marquetand P, González-Vázquez J, Sola I, Gonzáez L (2011) J. Chem. Theory Comput. 7(5):1253. https://doi.org/10.1021/ct1007394
Mai S, Richter M, Heindl M, Menger M.F.S.J, Atkins A., Ruckenbauer M, Plasser F, Oppel M, Marquetand P, González L (2018) Sharc2.0: Surface hopping including arbitrary couplings — program package for non-adiabatic dynamics. sharc-md.org
Jain A, Herman MF, Ouyang W, Subotnik JE (2015) J. Chem. Phys. 143(13):134106. https://doi.org/10.1063/1.4930548
Landry BR, Subotnik JE (2012) J. Chem. Phys. 137(22):22A513. https://doi.org/10.1063/1.4733675
Levine BG, Ko C, Quenneville J, MartÍnez TJ (2006) Mol. Phys. 104(5–7):1039. https://doi.org/10.1080/00268970500417762
Gozem S, Melaccio F, Valentini A, Filatov M, Huix-Rotllant M, Ferré N, Frutos LM, Angeli C, Krylov AI, Granovsky AA, Lindh R, Olivucci M (2014) J. Chem. Theory Comput. 10(8):3074. https://doi.org/10.1021/ct500154k
Neese F (2011) Wiley Interdiscip. Rev. Comput. Mol. Sci. 2(1):73. https://doi.org/10.1002/wcms.81
Bearpark MJ, Robb MA, Schlegel HB (1994) Chem. Phys. Lett. 223(3):269. https://doi.org/10.1016/0009-2614(94)00433-1
Levine BG, Coe JD, Martínez TJ (2008) J. Phys. Chem. B 112(2):405. https://doi.org/10.1021/jp0761618
Maxima. Maxima, a computer algebra system. version 5.42.1. http://maxima.sourceforge.net/ (30.11.2018)
Holland DMP, Trofimov AB, Seddon EA, Gromov EV, Korona T, de Oliveira N, Archer LE, Joyeux D, Nahon L (2014) Phys. Chem. Chem. Phys. 16(39):21629. https://doi.org/10.1039/c4cp02420f
Kölle P, Schnappinger T, de Vivie-Riedle R (2016) Phys. Chem. Chem. Phys. 18(11):7903. https://doi.org/10.1039/c5cp07634j
Stenrup M (2012) Chem. Phys. 397:18. https://doi.org/10.1016/j.chemphys.2011.12.004
Matsika S, Krause P (2011) Annu. Rev. Phys. Chem. 62(1):621. https://doi.org/10.1146/annurev-physchem-032210-103450
Plasser F, Mai S, Fumanal M, Gindensperger E, Daniel C, González L (2019) J. Chem. Theory Comput. 15(9):5031. https://doi.org/10.1021/acs.jctc.9b00525
Weinkauf R, Lehr L, Schlag EW, Salzmann S, Marian CM (2008) Phys. Chem. Chem. Phys. 10(3):393. https://doi.org/10.1039/b710381f
Subotnik JE, Shenvi N (2011) J. Chem. Phys. 134(24):244114. https://doi.org/10.1063/1.3603448
Gu B, Franco I (2017) J. Phys. Chem. Lett. 8(17):4289. https://doi.org/10.1021/acs.jpclett.7b01817
Gu B, Franco I (2018) J. Phys. Chem. Lett. 9(4):773. https://doi.org/10.1021/acs.jpclett.7b03322
Xie W, Sapunar M, Došlić N, Sala M, Domcke W (2019) J. Chem. Phys. 150(15):154119. https://doi.org/10.1063/1.5084961
Mignolet B, Curchod BFE (2019) J. Phys. Chem. A 123(16):3582. https://doi.org/10.1021/acs.jpca.9b00940
Martens CC (2016) J. Phys. Chem. Lett. 7(13):2610. https://doi.org/10.1021/acs.jpclett.6b01186
Min SK, Agostini F, Tavernelli I, Gross EKU (2017) J. Phys. Chem. Lett. 8(13):3048. https://doi.org/10.1021/acs.jpclett.7b01249
Prlj A, Curchod BFE, Corminboeuf C (2015) Phys. Chem. Chem. Phys. 17(22):14719. https://doi.org/10.1039/c5cp01429h
Acknowledgements
The authors acknowledge financial support from Deutsche Forschungsgemeinschaft (DFG) for M-ERA.NET project ICENAP as well as user support and granted computational time from the Zentrum für Informationsdienste und Hochleistungsrechnen (ZIH) in Dresden for project QDSIM and TRANSPHEMAT. The authors wish Fernand Spiegelman many years of fruitful scientific activity in good health.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Published as part of the special collection of articles “Festschrift in honor of Fernand Spiegelmann”.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Heller, E.R., Joswig, JO. & Seifert, G. Exploring the effects of quantum decoherence on the excited-state dynamics of molecular systems. Theor Chem Acc 140, 42 (2021). https://doi.org/10.1007/s00214-021-02741-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00214-021-02741-0