1 Introduction

The interactions between atomic or molecular species and metal surfaces are fundamental to surface chemistry [1], and the field of modern theoretical surface science provides an opportunity to investigate adsorbates and surface structures on the microscopic scale. The insight gained at this scale has useful applications in industrial technologies, including the search for more efficient catalysts [2]. There are numerous reviews and articles which deal with adsorption of small molecules and radicals on metal surfaces, from both experimental and theoretical studies [3,4,5,6,7,8,9,10,11].

A complete mechanistic study of surface reactions requires the identification of the elementary processes, including the reaction intermediates. Hydrocarbon synthesis from carbon monoxide and hydrogen (synthesis gas which is often referred to as syngas) is probably the most important source for manufacturing fuels and chemicals from non-petroleum-based sources [12]. Fischer–Tropsch synthesis (FTS) converts the syngas into high molecular weight hydrocarbons, which can subsequently be transformed into high-quality chemicals and ultraclean fuels [13, 14]. Various mechanisms have been proposed for the hydrocarbon chain initiation and growth steps [15]. One is the carbide mechanism, where CO dissociation precedes hydrogenation of the chemisorbed carbon atom to form CHx monomers that initiate the growth of hydrocarbon chains [16]. Hence, the dissociation of the surface-adsorbed CO molecule is an important step in the Fischer–Tropsch reaction [15].

Formyl (CHO) is also an important intermediate in hydrocarbon synthesis, FTS and hydrocarbon combustion [17, 18]. In contrast to hydrocarbon synthesis, the catalytic combustion of hydrocarbons is a very important technology for efficient energy production [19]. The main reaction pathway of catalytic combustion of hydrocarbons is the reaction between methylidyne (CH) and oxygen (O) to form formyl (CHO) [20]. This CHO species subsequently decomposes to yield adsorbed carbon monoxide and hydrogen (CHO → CO + H) [18].

Gomes et al. [20] studied adsorption of the formyl species on Cu, Au and Pt (111) surfaces using density functional theory (DFT) and where the metals are modelled as clusters. They found that the adsorption energy of formyl on the Au surface is very small (− 0.54 eV) and characteristic of a physisorbed species, whereas the interaction between CHO and the Pt surface is very strong (with an adsorption energy of − 2.61 eV). The calculated CHO adsorption energy on the Cu surface is approximately − 1.45 eV.

Inderwildi et al. [21] used DFT with the PW91 functional to study the mechanisms of hydrocarbon synthesis and combustion on noble metals. They suggested that CHO is an essential intermediate species in both synthesis and combustion reactions, and that these reactions have very similar mechanisms but in opposite directions, irrespective of the metal used to catalyze the reactions. Zhao et al. [22] also used DFT with the PW91 functional to explore the role of CHO in syngas conversion to hydrocarbons and its dependence on the Co and Rh catalyst surfaces. They found that the activation energy for insertion of CHO into CHx (x = 1–3) is the same, or even lower, than CO insertion or the formation of a C–C bond by combining two C atoms. The mechanism of dry reforming of methane on a Ni catalyst was studied by Zhu et al. [23] using DFT with the PW91 functional. This reaction includes the formation and decomposition of CHO. They showed that oxidation determines the overall reaction rates for both C and CH oxidation pathways.

Mahmood et al. [24] used DFT with the PW91 functional to study CO adsorption on several low and high Miller index surfaces of Cu. They showed that the adsorption energy increases as the coordination number of the adsorption site decreases from 9 to 6, in qualitative agreement with experimental observations. They also found a large decrease in the adsorption energy with increased surface coverage. The synthesis of formaldehyde and methanol from CO and H2 on a Ni(111) catalyst was investigated by Remediakis et al. [25] using DFT based on the RPBE functional. They showed that when CO and H are adsorbed on Ni(111) surfaces, CO hydrogenation is favoured over CO dissociation or desorption since it has the lowest activation energy. Further hydrogenation leads to the formation of formaldehyde (CH2O), methoxy (CH3O) and, finally, methanol (CH3OH).

Despite the developments in theoretical modelling combined with improved computer hardware, it is still computationally expensive to calculate reaction and activation energies of industrially relevant processes. It is therefore of interest to be able to predict relevant energies using, for example, descriptor-based approaches. The existence of linear relations between the adsorption, reaction and activation energies is the basis of many of these approaches [26]. For example, it was recently established that the activation energy varies linearly with the reaction energy for dissociative chemisorption of a number of molecules on a wide range of metal surfaces [27,28,29]. The Brønsted–Evans–Polanyi (BEP) relationship is an empirical observation that, for an elementary reaction, there is a linear relationship between the kinetics (activation barriers) and the thermodynamics (reaction energies). Similarly, the transition state scaling (TSS) relationship proposes a linear relation between the transition state energy and the initial (reactant) or final (product) state energy [30]. Fajin et al. [31] studied the generalized BEP relationships and descriptors for O–H bond cleavage of organic molecules on transition metal surfaces. They found that there is a linear relationship between the O–H bond breaking activation energy of RO–H compounds (R = organic moiety) on catalytic transition metal systems and the adsorption energy of the products. Consequently, the product’s adsorption energy is a good descriptor for the activation barrier for the breaking RO–H bond on transition metal surfaces. Pederson et al. [32] used DFT with the RPBE functional to study scaling properties of adsorption energies for hydrogen-containing molecules on transition metal surfaces. Their database provided a linear scaling relation connecting the adsorption energy of molecules such as CHx, NHx, SHx and OHx to the C, N, S and O adsorption energies, respectively, on transition metal surfaces. BEP relationships have also been validated for C–O and C–C bond dissociation during methanol decomposition and for ethylene dehydrogenation and hydrogenation on different Pd overlayer surfaces [33].

In this contribution, systematic and comparative DFT calculations have been performed to obtain the adsorption, reaction and activation energies of hydrocarbon synthesis

  1. 1.
    $$ {\text{CO }} \to {\text{ C}} + {\text{O}} $$
  2. 2.
    $$ {\text{CO}} + {\text{H }} \to {\text{CHO}} $$
  3. 3.
    $$ {\text{CHO}} \to {\text{CH}} + {\text{O}} $$

on Ag, Au, Al, Cu, Rh, Pt and Pd face-centred-cubic (111) surfaces. These surfaces were chosen because they have been used in numerous experimental and computational efforts [34,35,36,37,38]. The same methods were used to study hydrocarbon combustion on these surfaces. The splitting of CH (CH → C + H) has been studied by us previously [39], and those data are complemented in the present contribution by studying the following two combustion reactions.

  1. 4.
    $$ {\text{CH}} + {\text{O }} \to {\text{CHO}} $$
  2. 5.
    $$ {\text{CHO}} \to {\text{CO}} + {\text{H}} $$

The calculated energies are used to test the validity of the BEP and TSS relationships for these reactions on these metal surfaces. Since these relationships are seen to be valid for most of the reactions studied here, they are used to predict the energetics of these reactions on three new metal surfaces (Ni face-centred-cubic (111), Co hexagonal-closed-packed (111) and Fe body-centred-cubic (111) surfaces). The predicted values were compared to the same energies calculated from DFT, using the same models and methods that were used for the original surfaces. To the best of our knowledge this is the first time that the same models and methods are used for all of the above reactions and surfaces to investigate the mechanism of catalytic synthesis and combustion of hydrocarbons and to test the validity of the BEP and TSS relationships.

2 Computational methods and models

The Vienna ab initio simulation package (VASP) [40,41,42,43,44,45], using spin-polarized density functional theory, was used to obtain the results presented here. The exchange–correlation was treated within the generalized-gradient approximation (GGA) using the revised Perdew–Burke–Ernzerhof (RPBE) functional [27, 30, 32, 46, 47]. The interactions between valence electrons and ion cores were described using the projector-augmented wave method (PAW) [48,49,50]. The Kohn–Sham orbitals were expanded in a plane-wave basis set using a kinetic energy cut-off of 400 eV [13], and a 4 × 4 × 1 Monkhorst–Pack grid of k-points [51] was used for the numerical integration in reciprocal space. A 0.1 eV Fermi smearing was used for the density of states calculations, and the convergence criteria for the geometry optimizations, which used a conjugate-gradient algorithm (CG), were 10−3 eV Å−1 for the forces acting on the ions and 10−5 eV for the total energy [23]. Also, a dense 41 × 41 × 1 k-point grid was used for the density of state calculations.

The parameters used in this work have been used in previous, successful calculations of similar catalytic reactions [17, 52, 53]. In addition, calculations made both here and in our previous work [39] confirm that the trends presented here are converged with respect to all important parameters, such as the size of the unit cell, the energy cut-off and the k-point mesh.

The metal (111) surfaces were constructed using a three-layer slab with a 2 × 2 unit cell and periodic boundary conditions in two directions (xy plane) to model a semi-infinite crystal surface. The ionic positions in the uppermost two layers and the adsorbates [54] were allowed to relax, while those in the bottom layer of the slab were fixed to maintain the crystal structure of the bulk. A 10-Å vacuum region was placed between the slabs (in the z direction) to ensure that the adsorbates do not interact with the neighbouring slab. Similar models have been used in previous studies of comparable systems [53].

The transition states were identified using the climbing image-nudged elastic band (CI-NEB) method [55, 56]. In this method, the lowest energy configurations of reactants and products were used as the initial and final states, and six images were created between these geometries using a linear interpolation [57]. A − 5.0-eV Å−2 spring force constant between images was used to relax all of the images until the maximum force acting on each ion was less than 0.1 eV Å−1.

The vibrational frequencies of the reactants, transition states and products were calculated using ionic displacements of 0.01 Å and by diagonalizing the resulting Hessian matrix. Only the ionic positions of the adsorbates were displaced for these calculations. These frequencies were used to calculate the zero point vibrational energies (ZPVEs) and vibrational partition functions, as well as to confirm that the stationary structures were minimum energy structures (zero imaginary frequencies) or transition states (one imaginary frequency). The normal mode with the imaginary frequency was also analysed to ensure that this vibrational mode connected the reactants with the products.

The adsorption energies (Eads) of the reactants and products were calculated as Eads = E(slab+adsorbate) − (Eadsorbate + Eslab) where E(slab+adsorbate) is the total energy of the slab-adsorbate(s) system, Eadsorbate is the total energy of the isolated geometry optimized adsorbate(s) in vacuum, and Eslab is the total energy of the slab [58, 59]. All energies were ZPVE-corrected.

The rate constants (k) were estimated from transition state theory [60] using

$$ k = \left( {\frac{{k_{\text{B}} T}}{h}} \right)\left( {\frac{{q^{\# } }}{q}} \right)e^{{\frac{{ - E_{\text{a}} }}{{k_{\text{B}} {\text{T}}}}}} $$
(1)

where kB is Boltzmann’s constant, T is the absolute temperature, h is Planck’s constant, and Ea is the ZPVE-corrected activation energy. q and q# are the partition functions for the reactants and transition state, respectively. The partition functions were calculated assuming harmonic vibrations.

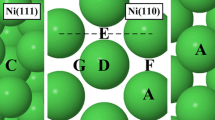
There are four high symmetry adsorption sites on all surfaces studied here (shown in Panel a of Fig. 1) except Fe (111) (shown in Panel b of Fig. 1). The hcp hollow site (where the central metal atom is in the second surface layer) is labelled A, the top site is above the uppermost metal surface atom and is labelled B, the bridge site between two neighbouring atoms is labelled C, and the fcc hollow site (where the central atom is in the third surface layer) is labelled D. There are five high symmetry adsorption sites on the Fe (111) surface. These are the top site labelled B, a short bridge site labelled E, a long bridge site labelled F, a pseudo-threefold hollow site labelled G and rectangular fourfold hollow site labelled H.

Fig. 1
figure 1

Adsorption sites on the a Ag, Au, Al, Cu, Rh, Pt, Pd, Ni and Co (111) surfaces and b Fe (111) surface. A is an hcp site; B is a top site; C is a bridge site; D is a fcc site; E is a short bridge site; F is a long bridge site; G is a pseudo-threefold hollow site, and H is a rectangular fourfold hollow site

Full size image

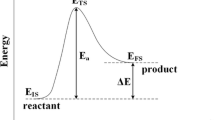
Geometry optimizations were performed by placing the adsorbate, with different initial orientations, on each of the adsorption sites shown in Fig. 1 and subsequently optimizing the system to yield the lowest ZPVE-corrected energy structure. The site that yielded the lowest energy was the preferred adsorption site. The preferred sites, energies and geometries of co-adsorbed adsorbates were obtained by placing the adsorbates in the same periodic cell and in their lowest energy sites identified from the geometry optimisations of the individual adsorbates [52]. The reaction energies (ΔE) are the difference between product (final state) and reactant (initial state) energies (ΔE = EFS − EIS), and the activation energies (Ea) are the difference between transition state and initial state energies (Ea = ETS − EIS).

3 Results and discussion

3.1 Adsorption energies of reactants and products

The ZPVE-corrected adsorption energies, Eads, for CH, C and H have been previously calculated by us using the same methods and models that are used in the present study [39]. Eads, for the remaining species involved in the hydrocarbon synthesis and combustion reactions studied here, are presented in Table 1. Previously obtained computed and experimental data are shown for the sake of comparison. Details of the adsorption sites and geometries of the reactants, transition states and products are given in Tables S1–S3 in the supporting information.

Table 1 ZPVE-corrected adsorption and co-adsorption energies (eV) of all species involved in the hydrocarbon synthesis and combustion reactions. The references for the previously published data are given in the footnote to the table
Full size table

The calculated CHO adsorption energies on these surfaces decrease in the order Ag  > Cu  > Au  > Al  > Pd  > Rh > Pt. The highest adsorption energy (weakest adsorption) is on the Ag(111) surface and is − 0.52 eV, compared to − 2.14 eV on Pt (111). The preferred adsorption site for CHO is the top site for all surfaces except for Al, Rh and Pd where it is the fcc site for Al and bridge site for Rh and Pd. Similar trends in adsorption energies are reported in previous studies. For example, the CHO adsorption energies in the study by Lin et al. [35] decrease in the order Cu  > Au  > Ag  > Pd  > Rh > Pt, which, except for Ag, is in agreement with the trend seen in the present work. They found lower adsorption energies for CHO on all surfaces, and this difference is probably due to the fact that they used different super cell size, adsorption sites and exchange–correlation functional.

The calculated adsorption energies for CO vary from 0.16 eV on Au(111) to − 1.50 eV on Pt(111) and decrease (become more negative) in the order Au  > Ag  > Al  > Cu  > Rh  > Pd > Pt. The most stable adsorption site for CO is the fcc site for all surfaces except for Ag, Au and Al, where it is the top site for Ag and Al and the bridge site for Au. The trends in the calculated energies of CO adsorption are similar to those seen in previous studies. For example, the CO adsorption energies obtained by Hammer et al. [7] decreased in the order Ag > Au >  Al > Cu > Pd > Pt, which is similar to the trend seen in the present work.

The calculated O adsorption energies decrease in the order Au  > Ag  > Pt > Pd  > Cu  > Rh  > Al. The weakest adsorption is − 2.40 eV on the Au (111) surface compared to − 6.79 eV on the Al (111) surface. The preferred adsorption site for atomic oxygen is the fcc site for all surfaces. The O adsorption energies in a previous study by Liao et al. follow the same trend as that discussed in the present work (Au  > Ag  > Pd  > Pt  > Cu  > Rh) except for Pd and Pt, which are very similar in the present study (− 3.68 eV on Pt and − 3.69 eV on Pd). The atomic oxygen adsorption energies reported by Liao et al. are more negative than those reported in this study, and the difference is probably due to the fact that they used different super cell size, adsorption sites and exchange–correlation functional.

The calculated (C + O) co-adsorption energies decrease in the order Ag  > Au  > Cu  > Pt  > Pd  > Rh > Al. The weakest adsorption is − 4.99 eV on the Ag (111) surface compared to − 11.99 eV on the Al (111). Co-adsorption data for these species, as well as those discussed below, have not been reported previously, and hence comparison with other studies is not possible.

For (CO + H) co-adsorption on these surfaces, Eads range from − 1.55 eV on Ag (111) to − 3.86 eV on Pt (111) and decrease in the order Ag  > Au  > Al  > Cu  > Rh  > Pd > Pt. The co-adsorption energy is therefore highest on the Ag (111) surface, which was also seen for the CH, C and H adsorbates.

The calculated (CH + O) co-adsorption energies range from − 5.28 eV on the Ag (111) surface to − 12.32 eV on the Al (111) and decrease in the order Ag  > Au  > Cu  > Pd  > Pt > Rh  > Al.

The weakest adsorption is on the Ag (111) surface for all species, except for the CO and O species, where it is on the Au (111) surface. In contrast, the strongest adsorption is on the Pt (111) surface for all species except for the CH, O, C + O and CH + O species, where it is on the Rh (111) for the CH species and on the Al (111) for the O, C + O and CH + O species. Co-adsorption data for the products of CO and CHO splitting have not been reported previously, and hence, comparison with other studies is not possible.

4 Reaction and activation energies

4.1 Catalytic hydrocarbon synthesis

The reaction energies, activation barriers and rate constants at 600 K, which is typical for industrial low-temperature catalytic reactions of hydrocarbons [64,65,66], for hydrocarbon synthesis are shown in Table 2.

Table 2 Reaction and activation energies (eV) and reaction rate constants at 600 K (s−1) for the hydrocarbon synthesis reactions. The energies are ZPVE-corrected. Reaction and activation energies for these reactions have not previously been reported
Full size table

The results in Table 2 show that the reaction energies for dissociation of CO decrease in the order Ag  > Au  > Cu  > Pt  > Pd  > Rh  > Al. The reaction is endothermic on all surfaces except for the Al (111) surface, where it is exothermic with a reaction energy − 0.87 eV.

The calculated activation energies for dissociation of CO decrease in the order Ag  > Au  > Pd  > Cu  > Rh  > Pt > Al, which is similar to the order for the reaction energies. The highest activation energy for CO splitting, obtained on the Ag (111) surface, was 6.05 eV, compared to 2.01 eV on Al (111).

The reaction rate constants for the CO dissociation are strongly influenced by the different metal surfaces, and at 600 K, they decrease from 1.93 × 106 s−1 on Al (111) to 1.99 × 10−39 s−1 on Ag (111). Thus, Al is the most active catalyst for CO splitting at 600 K. The trend in rate constants follows the opposite trend to the activation energies, with a higher activation energy leading to a lower rate constant.

The reaction energies for CO hydrogenation decrease in the order Pd  > Rh  > Pt  > Cu  > Ag  > Au  > Al. The reaction on the Ag, Cu, Rh, Pt and Pd (111) surfaces is endothermic, while it is exothermic on the Au and Al(111) surfaces with reaction energies of − 0.21 eV and − 0.74 eV, respectively.

The activation energy for this reaction ranges from 1.32 eV on Rh (111) to 0.29 eV on Al (111) and decreases in the order Rh > Pd  > Pt  > Cu  > Au  > Ag > Al. The calculated reaction rate constants decrease in the opposite order to the activation energies. Thus, Rh and Pd are the least active catalysts and Al (111) is the most active catalyst for CO hydrogenation at 600 K.

The reaction energy of formyl dissociation to CH and O decreases in the order of Ag  > Au  > Cu  > Pd  > Pt  > Rh  > Al. This reaction follows the same order as CO dissociation, except for Pd and Pt. The reaction is endothermic on all surfaces except for the Al (111) surface, where it is exothermic with a reaction energy of − 2.12 eV.

The calculated activation energies for dissociation of CHO to CH and O decrease in the order Au  > Ag  > Pt  > Pd  > Cu > Rh  > Al. The highest activation energy obtained on the Au (111) surface was 3.88 eV, compared to 0.42 eV on Al (111). The reaction rate constant ranges from 9.46 × 108 s−1 on Al (111) to 4.07 × 10−22 s−1 on Au (111). Similarly to the two reactions discussed above, the trend in rate constants follows the opposite trend to the activation energies, with a higher activation energy leading to a lower rate constant. Al (111) is the most active catalyst for dissociation of CHO to CH and O.

For all three reactions studied here, the lowest reaction energy is on the Al (111) surface and the highest reaction energy is on Ag (111), except for the CO hydrogenation where it is on Pd (111). The trends of the reaction energies for the CO → C + O and CHO → CH + O reactions are the same except for Pd and Pt. The smallest activation energy, and consequently the highest reaction rate constant, is on Al (111) surface for all synthesis reactions. Al (111) is therefore the most active catalyst for all three reactions.

Figure 2 shows the geometries of the reactants, transition states and products of the species that are discussed with reference to Table 2. Data for the CH → C + H reaction is not shown here since it has been presented elsewhere [39].

Fig. 2
figure 2

Top and side views of the optimized structures for the initial, transition and final states for the a CO → C + O, b CO + H → CHO and c CHO → CH + O reactions

Full size image

4.1.1 Catalytic hydrocarbon combustion

The reaction and activation energies for the hydrocarbon combustion reactions studied here, as well as the reaction rate constants at 600 K, are listed in Table 3 together with results of previous studies when available.

Table 3 Reaction and activation energies (eV) and reaction rate constants at 600 K (s−1) for the hydrocarbon combustion reactions. The energies are ZPVE-corrected
Full size table

The reaction energies for CHO dissociation to CO and H decrease in the order Al  > Au  > Ag  > Cu  > Pt  > Rh  > Pd. The highest reaction energy, obtained on the Al (111) surface, was 0.64 eV, compared to − 1.16 eV on Pd (111). The reaction on the Ag, Cu, Rh, Pt and Pd (111) is exothermic, while it is endothermic on the Au and Al (111) surfaces. Similar reaction energies are reported in the previous studies by Inderwildi et al. [21]. They found exothermic reaction energies on the Rh (111), Pt (111) and Pd (111) surfaces of − 1.33 eV, − 0.89 eV and − 1.16 eV compared to − 0.95 eV, − 0.89 eV and − 1.16 eV obtained here, respectively.

The activation energy for this reaction decreases in the order Al  > Au  > Ag  > Rh  > Pt  > Pd > Cu. It ranges from 0.93 eV on the Al (111) surface to 0.13 eV on the Cu (111) surface. The calculated activation energies are comparable with most of the previous results. Inderwildi et al. [21] reported activation energies of 0.30, 0.57 and 0.36 eV for the Rh, Pt and Pd (111) surfaces, respectively, compared to 0.37, 0.28 and 0.14 eV in this work. As discussed above, these differences may be due to difference in the functionals and system sizes used in the studies.

The reaction rate constants at 600 K decrease from 3.02 × 1012 s−1 on Pd (111) to 1.03 × 105 s−1 on Al (111) and decrease in the order Pd  > Ag  > Rh  > Pt  > Cu > Au  > Al. Pd (111) is the most active catalyst for CHO dissociation.

The results in Table 3 show that the reaction energies for oxidation of CH decrease in the order Al  > Rh  > Pt  > Pd  > Cu  > Au  > Ag. The lowest reaction energy for CH oxidation, obtained on the Ag (111) surface, was − 3.73 eV, compared to 2.12 eV on Al (111). This reaction is exothermic on the all surfaces except for Al, where it is endothermic. Inderwildi et al. [21] obtained reaction energies of − 0.14 eV, − 1.18 eV and − 1.38 eV on the Rh (111), Pt (111) and Pd (111) surfaces, respectively, which are similar to the values obtained in this work of − 0.24 eV, − 1.50 eV and − 1.61 eV. As discussed above, these differences may be due to differences in the system sizes and functionals used in the studies.

The calculated activation energies for CH oxidation decrease in the order Al  > Rh  > Pt  > Pd  > Au  > Cu  > Ag. The highest activation energy for CH oxidation, obtained on the Al (111) surface, was 2.53 eV, compared to 0.04 eV on Ag (111) surface. The results presented here are in agreement with those obtained previously. For example, Inderwildi et al. [21] reported activation energies of 1.15, 1.12 and 0.78 eV for the Rh, Pt and Pd (111) surfaces, respectively. These can be compared to 1.37, 0.98 and 0.79 eV obtained in this work. Some activation energies reported by Inderwildi et al. are higher than those reported in this study, and the difference is probably due to the fact that they used different super cell size, adsorption sites and exchange–correlation functional.

The reaction rate constant at 600 K ranges from 3.83 × 1012 s−1 on Ag (111) to 4.17 × 10−9 on Al (111) and decreases in the order Ag  > Cu  > Au  > Pd  > Pt  > Rh > Al. The trend in rate constants follows the opposite trend to the activation energies, with a higher activation energy leading to a lower rate constant. Ag (111) is the most active catalyst for CH oxidation.

The highest reaction energy is obtained on the Al (111) surface for both combustion reactions. As for the synthesis reactions discussed before, the trend in rate constants for the combustion reactions follows the opposite trend to the activation energies, with a higher activation energy leading to a lower rate constant, except for CHO → CO + H reaction.

4.2 Brønsted–Evans–Polanyi (BEP) and transition state scaling (TSS) relationships

According to the BEP relationship, the activation energy of a chemical reaction is linearly proportional to its reaction energy [67], and according to the TSS relationship the transition state energy is linearly proportional to the final state or initial state energy. Figure 3 shows these correlations for the hydrocarbon synthesis and combustion reactions on the metal surfaces listed in Tables 1, 2, 3. This figure reveals that the synthesis reactions support the BEP relationship with R2 values of 0.83, 0.88 and 0.94 for CO dissociation, CO hydrogenation and formyl dissociation to CH + O, respectively. The BEP relationships are also valid for the combustion reactions. The activation energies for CH oxidation and formyl dissociation to CO + H are linearly proportional to the reaction energies with R2 values of 0.89 and 0.88, respectively. As shown previously [39], the activation energy for the CH splitting combustion reaction is linearly proportional to the reaction energy with and R2 of 0.94.

Fig. 3
figure 3

(A) BEP and (B) TSS relationships for the a CO → C + O, b CO + H → CHO, c CHO → CH + O, d CH + O → CHO and e CHO → CO + H reactions on the metallic surfaces listed in Table 1

Full size image

The TSS relationship is excellent with an R2 value of 1 for all synthesis and combustion reactions.

The validity of the BEP and TSS relationships was also tested by using the equations shown in Fig. 3 to predict the activation energies from the reaction energies (BEP) and the transition state energies from the initial state energies (TSS) for three new metal surfaces. These were the Ni (face-centred-cubic (111)), Co (hexagonal-closed-packed (111)) and Fe (body-centred-cubic (111)) surfaces. The predictions were for all synthesis and combustion reactions studied here. The predicted values were subsequently compared with the values calculated using the methods and models described in Sect. 2. The DFT data are shown in Tables S1–S3 in the supporting information, and the initial, transition and final state structures are illustrated in Fig. 4.

Fig. 4
figure 4

Optimized structures for the initial, transition and final states for the synthesis reactions on the Ni, Co and Fe (111) surfaces

Full size image

The activation and transition state energies predicted by the BEP and TSS relationships, as well as those determined from DFT calculations, are shown in Table 4. It can be seen that the activation energies predicted by the BEP relationships for the Ni, Co and Fe (111) surfaces are similar to the DFT values. Also, as shown before [39], the activation energies predicted by the BEP relationship for the CH → C + H combustion reaction on the Ni, Co and Fe surfaces are 1.20, 1.08 and 0.83 eV, respectively, which can be compared to the explicit DFT energies of 1.23, 1.08 and 0.79 eV. Similarly, the transition state energies predicted by the TSS relationship for this reaction are − 69.70, − 87.93 and − 92.45 eV on the Ni, Co and Fe surfaces, respectively, which can be compared to the explicit DFT energies of − 69.98, − 87.88 and − 92.57 eV, respectively. The average difference between the BEP-predicted Ea for all six synthesis and combustion reactions and the DFT-calculated Ea is 17.65%, with the best agreement for CH → C + H reaction on the Co surface with an error of 0.15% and the worst for the CHO → CO + H reaction on Co with an error of 89.47%.

Table 4 BEP-predicted Ea, TSS-predicted ETS and the corresponding energies explicitly calculated from DFT using the methods described in Sect. 2. All energies are in eV
Full size table

There is only a 0.39% average difference between TSS-predicted ETS and the DFT-calculated ETS. The best agreement is for the CO + H → CHO reaction on the Co surface with error of 0.02% and the worst for the CHO → CH + O reaction on Ni with an error of 1.13%.

The R2 values obtained for the BEP and TSS relationships (Fig. 3) and the average differences between the DFT-calculated values and the BEP- or TSS-predicted values, show that the TSS relationship appears to be a better predictor than the BEP relationship. Moreover, the TSS relationship may be preferred since the structure of either the final or initial state, and not both, is sufficient for estimating the activation barrier.

It may be noted that the BEP and TSS relationships were derived from DFT data obtained for the reactions on the surfaces of diamagnetic metals (Ag, Au, Al, Cu, Rh, Pt and Pd) and that they are used to test the resulting predictions for reactions on the surfaces of paramagnetic metals. The different magnetisms of these metals were taken into account in the calculations (by using ISPIN = 1 for the diamagnetic metals and ISPIN = 2 for the paramagnetic metals). In spite of this difference between the sampling and test groups, the predictions are very good. One can therefore expect the predictions made for other diamagnetic metals would be at least as good as the results presented here.

4.3 Analysis of trends in the adsorption and activation energies

The d-band centre, which demonstrates the ability to eject an electron from the d-band of the metal to the adsorbate, is obtained from the distribution of the surface electronic energy levels [68, 69]. It is calculated from the projected density of states (PDOS) of the d-orbitals and can be used to measure the proximity of the d-electrons to the Fermi level. It is a common way to try to understand trends in adsorption and activation energies of different metal surfaces. The projected density of states was calculated for the upper atomic layer of the metal surfaces studied here, and the results are given in Fig. S1 in supporting information. According to this figure, the adsorption energies would expect to decrease in the order Au  > Ag  > Cu  > Pd  > Pt  > Rh. This is different to the ordering of the adsorption and activation energies of reactant, product and the transition states given above and hence does not explain the trends seen in this work. For example, the activation energies for the CH + O → CHO reaction decrease in the order Al  > Rh  > Pt  > Pd  > Au  > Cu  > Ag. Similar results are reported in previous studies. For example, Fajin et al. [68] reported that the d-band model cannot be used to understand the origin of the BEP relationship of water dissociation on different metal surfaces.

Another way to explain trends in adsorption and activation energies is the coordination number of the metal surface atoms. It is argued that adsorbates typically bind more strongly to surfaces with low coordination numbers [70,71,72]. Since the coordination numbers for all (111) surfaces studied here are identical, this is not able to explain the trends seen in the present work.

5 Conclusions

The thermodynamic and catalytic activity of Ag, Au, Al, Cu, Rh, Pt and Pd (111) metal surfaces for hydrocarbon synthesis and combustion has been examined using DFT calculations based on the RPBE functional. The results have been used to test the validity of the BEP and TSS relationships for these reactions on these metal surfaces. The BEP relationship appears to be an adequate indicator for the synthesis reactions with R2 values of 0.83, 0.88 and 0.94 for CO dissociation, CO hydrogenation and CHO dissociation to CH + O. In addition to the CH → C + H combustion reaction, which has been studied previously [39], the BEP relationship also appears to be valid for the CH + O → CHO and CHO → CO + H combustion reactions with R2 values of 0.89 and 0.88, respectively. It was also found that the TSS relationship is an excellent indicator with an R2 value of 1 for all synthesis and combustion reactions.

The BEP and TSS relationships were subsequently used to estimate the energetics of the synthesis and combustion reactions on Ni, Co and Fe (111) surfaces. As expected, the energies predicted by the TSS relationship are more accurate (closer to the DFT calculations) than those predicted by the BEP relationship. In fact, there is only a 0.39% average difference between TSS-predicted transition state and the DFT-calculated values, where this average is over all synthesis and combustion reactions and all three metal surfaces. This indicates that the TSS relationship can be used to predict transition state energetics for these reactions on these surfaces without doing the time-consuming transition state DFT calculations.