1 Introduction

Chemical reactions are traditionally known to be catalysed in nature by protein enzymes, but in the early 80s it was discovered that natural RNA molecules, named as ribozymes, present catalytic activity [1, 2]. According to their size, these natural ribozymes can be divided into three families: small self-cleaving RNAs (less than 200 nucleotides), medium-sized self-splicing introns and larger catalytic ribonuclear protein (RNP) complexes [3]. Some authors assemble the two last families in the same one [4]. The class of small ribozymes includes the hammerhead [5], hairpin [6], hepatitis delta virus (HDV) [7], Varkud satellite (VS) [8], glmS [9], twister [10], twister sister [11], pistol [11] and hatchet [11]. The reaction that is catalysed by these ribozymes is the site-specific self-cleavage of the RNA phosphodiester backbone, as well as the reverse ligation process.

As observed in Scheme 1 the reaction can be considered to take place through an SN2 mechanism, and four basic aspects have been proposed as key factors in the catalysis: (1) the geometric constrain favouring the linearity between the nucleophile, the phosphorous and the leaving group (angle O2′–P–O5′); (2) the activation of the nucleophile by abstracting the proton from the O2′; (3) the facilitation of the departure of the leaving group by protonation of O5′; and (4) the stabilization of the transition state (TS) [12].

Scheme 1
scheme 1

Chemical mechanism of the self-cleavage nucleolytic ribozymes

Full size image

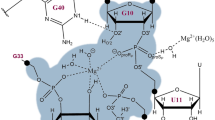
It has been proposed that different ribozymes employ different agents to activate the nucleophile and the leaving group. Thus, experimental studies and theoretical calculations have suggested that the nucleophile is activated in the HDV ribozyme through a divalent cation located in the active site, which can be partially hydrated, and would serve either as a Lewis acid, a Brønsted base or both [13, 14]. In the case of the hammerhead, experimental and computational studies suggest that an adenine (A38) and a guanine (G8) have an important role in the catalytic mechanism, the later acting as an acid (“AH” in Scheme 1) whose hydroxyl O2′ is activated by the presence of a Mg2+ cation [15, 16]. In the rest of small ribozymes, Mg2+ cation does not play a chemical but only structural role. The activation of the nucleophile and leaving groups, if occurred, has been proposed to take place through nucleosides located in the active site as general acid or base catalysts (“AH” and “B” in Scheme 1).

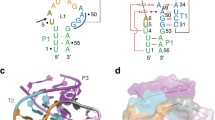
In 2014, a new class of small ribozyme has been revealed using bioinformatic techniques by Breaker and co-workers, termed as “twister” because its conserved secondary structure resembles the Egyptian hieroglyph “twisted flax” (see Fig. 1) [10]. From the analysis of the genoma, twister RNAs have been suggested to be similar to hammerhead in size and structural complexity, and their self-cleavage rate constants are also similar. Nevertheless, its overall structure is distinct from all the other known small ribozymes, as recently confirmed by X-ray diffraction studies [17,18,19,20]. As stated by Patel, Kreutz, Micura and co-workers [20], the analysis of these crystal structures reveals a common double-pseudoknot overall architecture but with noticeable differences in residues and divalent cation alignments in the active sites. Thus, while in the X-ray structure of Oryza sativa twister ribozyme the O2′–P–O5′ angle is far from 180° (offline orientation, with an angle ca. 83°) with a fully base-paired stem P1, in the env22 twister structure an in-line orientation is observed with this angle being closer to 180° (ca. 148°) and oriented at the cleavage step A1-U-1, with a Mg2+ interacting with the scissile phosphate [21]. Obviously, the structure from Oryza sativa is not a reactive structure but, as suggested by Lilley and co-workers, this particular conformation could be an artefact of crystallization and possibly result of the use of a deoxyribonucleotide to prevent cleavage [17]. Based on molecular modelling simulations, the authors observed that rotation of U-1 towards A34 brought the nucleobase to the expected position underneath G33 with the O2′ atom presenting the required in-line orientation for the nucleophilic attack. Based on restrained molecular dynamics (MD) simulations, Gaines and York explored different conformational states of U-1 in Oryza sativa twister ribozyme and confirmed the existence of the two previously described conformations, termed as extruded and stacked [22].

Fig. 1
figure 1

a Representation of the crystal structure of the twister ribozyme (PDB code 4OJI). b Schematic representation of the secondary structure with indication of the self-cleavage site between A7 and U6 nucleotides

Full size image

Recent kinetic studies of the pH dependence of the rate constant on the wild-type Oryza sativa and several mutants suggested that G33 must be the base activating the nucleophile (“B” in Scheme 1) [17], while A1 must be acting as a general acid capable of donating a proton to the oxyanion leaving group (“AH” in Scheme 1) [23]. Moreover, the structures also support the role of G33 in stabilizing the negative charge developed on the phosphate group in the TS through the interaction between the exocyclic NH2 group and the non-bridging oxygen atoms of the phosphate. Surprisingly, atomic mutagenesis of the nitrogen atoms of the A1 nucleobase has established that the pH dependence of the cleavage reaction arises in part from the protonation state of the N3 ring nitrogen of that adenine, and not of the N1 atom, that usually is the acid position [23]. The standard pKa value of N3 of adenine in solution is 1.5, and consequently, a dramatic shift must be suffered in order to be protonated at physiological conditions. Lilley and co-workers suggested that the origin of this shift must be found in the local environment, since the six-membered ring of A1 lies between three phosphate groups [23]. This pKa shift was predicted by Gaines and York from computational simulations that rendered a variation of the pKa at the N3 position of A1 towards neutrality by approximately five units [22].

Molecular dynamics simulations have been carried out by Hammes-Schiffer and co-workers to elucidate the self-cleavage mechanism and structural properties of the env22 twister ribozyme [24]. One of the two Mg2+ ions located in the active site interacting with the non-bridging oxygen atoms of the scissile phosphate and a water molecule could stabilize the TS, and the activated water molecule could play the role of general acid. Furthermore, a Na+ located between A1(N3) and A1(O5′) could stabilize the negative charge developed during the reaction. It was observed that these ions retained their position during the molecular dynamics simulations. Thus, a relatively rigid network of hydrogen bonding, electrostatic and π-stacking interactions around the self-cleavage site was then proposed as being important in either the stabilization of the geometry and catalysis. The study of Hammes-Schiffer and co-workers [24], published just after the work of Gaines and York [22], suggested a quite different mechanism for the Oryza sativa and env22 twister ribozymes.

The purpose of the present paper, based on MD simulations performed with quantum mechanics/molecular mechanics (QM/MM) potentials, is to study the reactivity of the Oryza sativa twister ribozyme by means of a different mechanism previously proposed in the hairpin ribozyme [25,26,27]. In particular, an intramolecular mechanism without participation of acid and bases species has been termed as baseline mechanism (see Scheme 2) [25, 26]. In this mechanism, the proton from O2′ is transferred to O5′ leaving group through a non-bridging oxygen atom [25,26,27]. This mechanism is explored both in aqueous solution and in the active site of the Oryza sativa twister ribozyme using QM/MM techniques with the purpose of establishing the origin of catalysis in this ribozyme.

Scheme 2
scheme 2

Chemical mechanism of the nucleolytic ribozyme through a baseline mechanism

Full size image

2 Computational methods

The computational study of the site-specific self-cleavage reaction of the RNA phosphodiester backbone in terms of free energies presents two problems. First, as previously demonstrated by Mulholland and Otyepka for the catalytic mechanism of a hairpin ribozyme, the use of semiempirical methods to describe the QM region in multiscale schemes can predict reaction pathways significantly different than the ones obtained at more accurate level using more expensive methods [28]. The second computational problem is related to the amount of internal coordinates associated with the chemical reaction. The reaction involves, at least, six bond forming and breaking processes. Then, a complete exploration of multidimensional free energy surfaces based on, for instance, umbrella sampling (US) methods, is not viable. Consequently, in this work the exploration of the free energy profile has been carried out by means of free energy perturbation (FEP) methods. These methods imply the sampling of the environment (usually the MM region) along a previously traced IRC from TS located at QM/MM level. Keeping in mind that the sampling is performed along the IRC, the free energy profile is obtained along a realistic reaction coordinate. Nevertheless, a possible limitation of the technique is that, since there is no sampling on the chemical system, the result could be biased by the fact that just one TS structure is used. In our case, since the QM subset of atoms, or chemical system, cannot present significant different conformations, this limitation is not expected to be dramatic. Moreover, the use of FEP methods has the advantage that the QM geometries along the reaction path can be obtained from IRC that can be traced at high level of theory. The M06-2X hybrid functional developed by Truhlar’s group [29, 30] with the standard 6-31+G(d,p) basis set has been selected to treat the QM subset of atoms. The rest of the system (RNA, water molecules and counterions) was described using the AMBER [31] and TIP3P [32] force fields, as implemented in the fDYNAMO library [33, 34]. Therefore, the QM wave function is polarized by the charges of the MM subset of atoms.

The coordinates of the initial structure of the twister ribozyme from Oryza sativa were chosen from the X-ray structures deposited in the PDB with code 4OJI [17]. This X-ray structure contains 5 Mg2+ cations, but none of them located in the cleavage site. Then, the RNA was solvated in a truncated octahedral box by adding 10 Å buffer of water molecules around RNA system (the resulting systems were of 85 × 105 × 92 Å3). A total of 43 Na+ counterions were required to electrostatically balance the system which were placed into optimal electrostatic positions around the protein. The coordinates of the hydrogen atoms were added using the AMBER tools, considering the standard pKa values of the titratable residues. After properly modified, water molecules with an oxygen atom lying within 2.8 Å of any heavy atom of the RNA were removed. The resulting QM/MM system consisted of 19 atoms in the QM region and 36135 atoms in the MM region.

To saturate the valence of the QM/MM frontier atoms, three link atoms were placed: (1) between the A76 sugar ring of P site and the subsequent phosphate group, (2) between the same sugar ring and the adenine and (3) in the A76 sugar ring of A site (see Scheme 3). Cut-offs for non-bonding interactions were applied using a switching force scheme, within a range radius from 14.5 to 16 Å. All atoms included in a radius of 20 Å from active centre were free to move during optimizations and dynamics (7274 atoms). In order to equilibrate the model, a MD simulation of the system in the NVT ensemble was ran during 5 ns at a temperature of 300 K, using the Langevin–Verlet algorithm with a time step of 1 fs. Optimization of the TSs structures for the reaction mechanisms has been done at the M06-2X/MM level following an iterative micro–macro procedure [35].

Scheme 3
scheme 3

Schematic representation of the active site of the twister ribozyme from Oryza sativa. Atoms in the blue region are treated quantum mechanically. QM link atoms are depicted as black dots

Full size image

Additionally, in order to compare the enzymatic reaction with the uncatalysed process in water solution, the same QM atoms (including the corresponding link atoms) were placed in a pre-equilibrated cubic box of 50 Å of lattice. The removal of the overlapping waters led to a model composed by 22 QM atoms and 4156 mobile TIP3P water molecules, which was studied with the same methodology as the ribozyme.

The configurations for which the free energy differences were estimated using the FEP methodology correspond to those structures obtained along the IRC calculation and are thus characterized by a single s coordinate:

$$ s_{i} = s_{i - 1} + \left[ {\sum\limits_{j \in QM} {m_{j} \left( {\left( {x_{j,i} - x_{j,i - 1} } \right)^{2} + \left( {y_{j,i} - y_{j,i - 1} } \right)^{2} + \left( {z_{j,i} - z_{j,i - 1} } \right)^{2} } \right)} } \right]^{1/2} $$
(1)

where x j,i , y j,i and z j,i are the coordinates of the ith structure belonging to the IRC traced from the transition state structure (x j0, y j0 and z j0 coordinates) and m j are the masses of the atoms. Within this treatment the free energy relative to the reactant can be expressed as a function of the s coordinate as:

$$ \Delta G_{\text{FEP}} \left( {s^{R} - s^{j} } \right) = \left( {E_{\text{QM}}^{0} \left( {s^{j} } \right) - E_{\text{QM}}^{0} \left( {s^{R} } \right)} \right) + \left( {{\text{ZPE}}\left( {s^{j} } \right) - {\text{ZPE}}\left( {s^{R} } \right)} \right) - k_{\text{B}} T\mathop \sum \limits_{i = R}^{i = j - 1} {\text{lnexp}}\left( { - \frac{{E_{{{\text{QM}}/{\text{MM}}}} \left( {s^{i + 1} } \right) - E_{{{\text{QM}}/{\text{MM}}}} \left( {s^{i} } \right)}}{{k_{\text{B}} T}}} \right)_{{{\text{MM}},i}} $$
(2)

where \( E_{QM}^{0} \) is the gas-phase energy of the QM subsystem computed at M06-2X level, k B is the Boltzmann constant, and T is the temperature. The QM/MM interaction contribution to the free energy difference between two different values of s is obtained by averaging the QM/MM interaction energy (including the polarization energy) over all the MM coordinates of the system obtained during the MD simulation carried out for the ith window. Then, the coordinates of the QM atoms are those corresponding to the si and si+1 structures along the IRC. The MDs for the FEP calculation were performed at 300 K, using the NVT ensemble. Ten picoseconds of relaxation and 20 ps of production, with a time step of 1 fs, were run in each window. The total amount of windows required to generate the full free energy path was 77 for the ribozyme and 107 for water.

Kinetic isotope effects (KIEs) have been computed for isotopic substitutions of key atoms, for the transition states and the reactant complexes, localized at the levels of theory described above. The free energy of a state, G i , can be expressed as a function of the internal energy U i , and the total partition function Q i containing the thermal contribution of the vibrations to the molecular free energy with the zero-point vibrational energy, ZPEi, considered as a separate term:

$$ G_{i} = U_{i} - RTlnQ_{i} + {\text{ZPE}}_{i} . $$
(3)

In Eq. 3, the six lowest frequency modes of the transition state and the reactant structures correspond to very low-frequency librational motions [36] that have been projected out. Then, from Eq. (3) and using transition state theory, the ratio between the rate constants corresponding to the light atom “L” and the heavier isotope “H” can be computed as:

$$ {\text{KIE}} = \frac{{\left( {\frac{{Q_{TS} }}{{Q_{R} }}} \right)_{L} }}{{\left( {\frac{{Q_{TS} }}{{Q_{R} }}} \right)_{H} }}e^{{ - \frac{1}{RT}\left( {\Delta {\text{ZPE}}_{L} - \Delta {\text{ZPE}}_{H} } \right)}} . $$
(4)

In Eq. (4), the total partition function, Q, was computed as the product of the translational, rotational and vibrational partition functions for the isotopologs in reactants and TS in the active site of the open- and closed-loop conformation monomers. The Born–Oppenheimer, rigid rotor and harmonic oscillator approximations were considered to independently compute the different contributions. Keeping in mind that involved states, reactants and TS are in a condensed media (the active site of a protein), contribution of translation and rotation to KIEs are negligible. Nevertheless, the full 3 N × 3 N Hessians have been subjected to a projection procedure to eliminate translational and rotational modes, which transforms them into almost zero frequencies, as previously described [37]. Thus, it has been assumed that the 3 N–6 vibrational degrees of freedom are separable from the six translational and rotational degrees of freedom of the substrate.

3 Results and discussion

The first step of our computational study was to check whether the X-ray structure was the most adequate starting structure to study the baseline mechanism of the site-specific self-cleavage of the RNA phosphodiester backbone by the twister ribozyme from Oryza sativa. Thus, 5 ns of unconstrained classical MD simulations was carried out from the conformation directly derived from the X-ray structure (after properly setting up the model, as described in previous section) and from a conformation prepared by keeping the O5′–P–O2′ angle at 145° (a value taken from env22 X-ray structure). The population analysis of the structures generated along the MD simulations is shown in Fig. 2. As can be observed, the alignment of O2′–P–O5′ atoms remains around the initial values in both MD trajectories, indicating that both conformations are stable during the 5-ns unbiased MD simulations. Keeping in mind the reaction under study, as depicted in Scheme 1, this result indicates that the X-ray structure that presents an outline conformation would not necessarily be the reactive conformation for the reaction to proceed (the average value of the angle during the unbiased MD simulation was around 90°). On the contrary, the MD simulation started from a conformation with a O2′–P–O5′ angle of 145° remains in an in-line conformation during the whole simulation. Figure 2 also shows how the O2′–P–O5′ angle appears to be associated with the O2′–P distance. Thus, those conformations with a more favourable O2′–P–O5′ angle for the nucleophilic attack (the in-line conformations) also show shorter distances between the attacking O2′ atom and the P atom.

Fig. 2
figure 2

Population of structures generated along 5 ns of classical AMBER/TIP3P molecular dynamic simulations displayed as a function the O2′–P–O5′ angle (in degrees) and the O2′–P interatomic distance (in Å). Results obtained for the twister ribozyme from Oryza sativa at 300 K

Full size image

These conclusions can be complemented with the analysis of the time evolution of the distance between the HO2′ and the OP1 atoms, and the O2′–P–O5′ angle (see Figure S1 in Supporting Information). The in-line conformation presents an adequate geometry for the direct transfer of the H2′ proton from the O2′ atom to the OP1 atom (the HO2′–OP1 interatomic distance is ca 1.9 Å along the simulation).

Two representative geometries of the in-line and outline conformations are shown in Fig. 3. According to the in-line conformation shown in the right panel of Fig. 3, an eventual baseline mechanism could take place through TS involving the O2′ attack to the P atom, concomitant with the H2′ proton transfer to the OP1. Then, from the putative intermediate the products of the reaction would be reached by the HO2′ transfer to O5′ and the P–O5′ bond breaking. A detailed representation of the full baseline reaction mechanism is shown in Scheme 4. According to the proposed substrate-assisted mechanism, the reaction would take place in two steps through an intermediate involving two different conformations just differing in the value of the O5′–P–OP1–HO2′ dihedral angle. The interconversion between the two conformations on this intermediate would not require overcoming a noticeable free energy barrier at 300 K.

Fig. 3
figure 3

Representation of the outline (left panel) and the in-line (right panel) conformations obtained from the last structures generated in the 5 ns of classical AMBER/TIP3P molecular dynamic simulations for the twister ribozyme from Oryza sativa at 300 K

Full size image
Scheme 4
scheme 4

Proposed baseline mechanism of the nucleolytic ribozyme self-cleaving reaction

Full size image

In order to confirm whether the proposed reaction mechanism is feasible in the twister ribozyme starting from outline or in-line conformations, the corresponding potential energy surfaces (PESs) have been generated. In addition, the reaction has been studied considering both OP1 and OP2 oxygen atoms as the possible acceptors of the HO2′ proton transferred from O2′ in the in-line conformation. Nevertheless, the study of the reaction from the outline conformation involving OP2 as the HO2′ acceptor atom generated odd conformations when forcing the proton transfer and approaching O2′ to the P atom. Since these high-energy conformations were not in the nucleolytic ribozyme self-cleaving reaction path, only the reaction path involving OP1 was obtained for this initial outline conformation. The obtained relative potential energies are listed in Table 1. The energy barrier obtained for the first step of the outline conformation is significantly high, 57.6 kcal mol−1, which is not an unexpected result considering that, apart from presenting a non-favourable distance and orientation of the O2′ atom with respect to the P and the O5′ atoms, the O2′–H2′ hydroxyl group is oriented towards the O3′ atom, thus preventing the transfer to the OP1 atom or, hypothetically, to the OP2 atom. The much lower relative potential energies for the in-line conformation indicate that the nucleolytic ribozyme self-cleaving reaction pathway must take place from this conformation. In addition, the energy required to reach the TS of the rate-limiting step (TS2) is more than 10 kcal mol−1 higher when the reaction takes place through the OP2 than when OP1 is the HO2′ proton acceptor (36.4 and 26.3 kcal mol−1, respectively). Consequently, the much more computationally demanding free energy profiles were computed just for the mechanism starting from the in-line conformation of reactants and using the OP1 atom as the HO2′ proton shuttle.

Table 1 Relative potential energies of the different states appearing along the baseline mechanisms obtained at M06-2X/AMBER/TIP3P level in the ribozyme for the in-line and outline conformations, involving OP1 and OP2 atoms as proton shuttles
Full size table

The resulting free energy profiles for the baseline mechanism in aqueous solution and in the twister ribozyme from Oryza sativa, as described in Computational Methods section, are shown in Fig. 4, and the geometry of the QM subset of atoms of the five states involved in the mechanism is presented in Fig. 5. The free energy differences between these states and the reactants states are listed in Table 2.

Fig. 4
figure 4

Schematic representation of the QM/MM free energy profiles for the substrate-assisted mechanism in twister ribozyme from Oryza sativa obtained from the M06-2X/AMBER/TIP3P FEPs in the ribozyme and in aqueous solution after adding the quantum vibrational corrections. Relative free energies with respect to reactants in the ribozyme system (in kcal mol−1) are displayed in the red arrows

Full size image
Fig. 5
figure 5

Detail of the structures of the QM subsystem, optimized at M06-2X/AMBER/TIP3P along the different states located in the substrate-assisted mechanism in twister ribozyme from Oryza sativa. Key distances are reported in Å

Full size image
Table 2 Free energy differences with reactants obtained from the M06-2X/AMBER/TIP3P FEPs in the ribozyme and in aqueous solution, before and after adding the zero-point vibrational energy (ZPVE)
Full size table

The free energy profiles presented in Fig. 4 confirm that the mechanism of the nucleolytic self-cleavage of RNA proposed in Scheme 4 can take place in a stepwise manner through a stable intermediate. Interestingly, the free energy profile in the enzyme is almost coincident with the profile obtained in solution. The rate-limiting step corresponds to the second step involving the HO2′ transfer from OP1 to O5′ and the P–O5′ bond breaking. The quantum vibrational corrections diminish the activation free energy barrier of this step, TS2, by 2.7 and 2.9 kcal mol−1 in the ribozyme and in water, respectively. Thus, the rate-limiting activation free energy is 29.1 kcal mol−1 in both environments, suggesting no catalytic effect if the reaction would proceed in the ribozyme by means of this substrate-assisted mechanism. The reaction is endergonic in both media, although the product state is slightly more stabilized in solution than in the ribozyme (the reaction free energies are 7.6 and 2.3 kcal mol−1 in the ribozyme and in water, respectively).

Analysis of the selected interatomic distances along the reaction path reported in Table 3 shows how, despite that the energetics are almost coincident, the reaction in solution and in the ribozyme cannot be considered as completely equivalent from the geometrical point of view. Important differences can be detected in the distances related to O2′ in TS1. Thus, the O2′–P forming bond is in a much earlier stage of the reaction in solution than in the ribozyme (O2′–P distance equal to 2.35 and 2.18 Å, respectively). Another interesting observation is noticed when comparing the two conformations of the intermediate. It is perceptible that INT and INT’ conformers differ not only in the distances related to the HO2′ (O2′–HO2′ and HO2′–O5′, as commented above) but also in the O2–P distance. As observed, this distance is slightly larger in INT than in INT’ (0.14 and 0.22 Å in solution and in the ribozyme, respectively) indicating that this bond is not completely formed until arriving at the INT’ intermediate. In general, shorter interatomic distances are detected in the stationary structures located in solution than in the ribozyme.

Table 3 Interatomic distances between key atoms on the different states appearing along the baseline mechanisms obtained at M06-2X/AMBER/TIP3P level (a) in the twister Oryza sativa ribozyme and (b) in aqueous solution
Full size table

The evolution of the atomic charge on key atoms along the reaction, as shown in Table 4, confirms that, from the electronic point of view, the substrate-assisted mechanism in the active site of the ribozyme is similar to the process in aqueous solution. The charge on the O5′ leaving atom reaches the most negative value at TS2 in both media (−0.917 and −0.866 a.u. in the ribozyme and in aqueous solution, respectively), while the O2′ nucleophilic atom reaches the most negative value at TS1 also in both media (−1.095 and −0.994 a.u. in the ribozyme and in aqueous solution, respectively). It is interesting to note that, although no noticeable differences of energy were observed between the two conformations of the intermediate, the atomic charges on the key atoms in INT and INT’ are substantially different. In particular, the atomic charges on INT are closer to those measured in TS1, while the values of INT’ are closer to the atomic distribution found for TS2.

Table 4 Atomic charges of key atoms obtained with the CHELPG method at M06-2X/6-31 + G(d,p)//AMBER level for the reaction in the (a) twister Oryza sativa ribozyme and (b) in aqueous solution, for the baseline mechanism starting from the in-line conformation of reactants
Full size table

The activation free energy of the rate-limiting step in aqueous solution is in agreement with the values reported by Glennon and Warshel [38] that combine experimental data of Wolfenden et al. [39] and computational values for the transesterification reactions. The proposal that the process takes place by a stepwise mechanism controlled by the second transition state can be supported by KIEs calculations. The primary 18O KIEs in solution, listed in Table 5, indicate a slightly normal KIE of nucleophilic O2′ of 1.010 and a high normal value of 1.041 for the O5′ leaving group when computed from the rate-limiting TS2. The value of the O5′ leaving group is in good agreement with experimental 18O KIE (1.039–1.001, depending on the model reaction and pH) and with computational studies based on QM calculations on a simplified ribose 3′-ethylphosphate model (1.046 for the leaving 18O KIEs) [40]. Regarding the effect of the substitution of the nucleophile O2′ oxygen atom, Gu et al. reported values in the range 0.998–0.981 [40]. It is important to stress that the precise values of the 18O KIEs strongly depend on the nature of the leaving groups present in the phosphodiester, which explain the variability observed in the aforementioned results.

Table 5 18O KIEs computed at M06-2X/6-31 + G(d,p)//AMBER level from TS1 and TS2 for the self-cleaving nucleolytic catalysed by the twister Oryza sativa ribozyme and in aqueous solution
Full size table

Our results for the 18O KIEs for the O2′ and O5′ substitutions in the ribozyme are 0.994 and 1.046, respectively, which are in good agreement with the experiments by Gu et al. [40]. These authors reported 18O KIE values of 0.994 ± 0.002 for the substitution of the nucleophile O2′ and 1.014 ± 0.003 for the substitution of the leaving O5′, and with their previous QM results of 0.998 and 1.026, respectively [40].

The normal 18O KIE value for the substitution of O2′ in solution reflects the slightly differences detected in the geometries, as presented above. As observed, shorter interatomic distances involving the O2′ are detected in the TS2 located in the ribozyme than in solution, rendering slightly inverse 18O KIEs for the O2′ substitution in the ribozyme (0.994) and slightly normal in solution (1.010).

Finally, considering the values of the 18O KIE computed from the TS1, we can assert that a hypothetical mechanism kinetically controlled by the nucleophilic attack of O2′ to the P atom, concomitant with the HO2′ proton transfer to OP1, can be discarded.

4 Conclusions

The molecular mechanism for the cleavage of the RNA phosphodiester backbone has been studied in aqueous solution and catalysed by a twister ribozyme from Oryza sativa. In particular, the present paper shows the results of exploring the baseline or substrate-assisted mechanism by means of QM/MM MD simulations where the QM subset of atoms is described by a DFT functional (M06-2X). An initial equilibration of the ribozyme system was carried out by means of unbiased MD simulations with two different starting conformations of the reacting system: an outline conformation where the angle between the O2′–P forming bond and the P–O5′ breaking bond is equal to the values presented in the X-ray structure of the Oryza sativa twister ribozyme, and an in-line conformation where this angle was initially forced to be 145°, which is the value taken from the X-ray structure of the env22 ribozyme. Both conformations revealed to be stable during the MD trajectories but, keeping in mind the reaction under examination, it appears that the crystal structure of Oryza sativa is not a reactive conformation for the mechanism analysed in this work. This result justifies the need of performing MD simulations before starting the study of a chemical reaction in condensed media.

The reaction was studied by generating the corresponding PES from in-line and outline reactants state conformations and exploring the possibility of the two oxygen atoms of the phosphate group, OP1 and OP2, acting as the atoms involved in the transfer of the HO2′ atom. The potential energy barriers clearly indicate that the most favourable reaction mechanism would be the one starting from the in-line conformation and involving the OP1 atom as proton shuttle. Then, the free energy profile was computed at M06-2X/AMBER/TIP3P level by means of FEP methods only for this mechanistic route. The full free energy profile was also explored in solution, and the results confirmed that the proposed reaction mechanism takes place, in both media, through a stepwise mechanism kinetically controlled by the second step. The rate-limiting TS involves the P–O5′ breaking bond concomitant with the proton transfer from the OP1 atom to the leaving O5′ atom. The fact that the free energy profiles in the enzyme and in solution are almost coincident, rendering a rate-limiting activation free energy of 29.1 kcal mol−1, suggests no catalytic effect of the Oryza sativa twister ribozyme, if the reaction proceeds through a baseline substrate-assisted mechanism.

Warshel and co-workers, in a comparative study of the peptide bond formation reaction in water and catalysed by the ribosome [41], already pointed out that catalytic effects cannot be attributed to substrate-assisted mechanisms. Nevertheless, calculation of 18O KIEs for the substitution of the nucleophile and leaving oxygen atoms (O2′ and O5′) in solution and in the ribozyme gives a high normal KIE value of 1.04 for the isotopic substitution on O5′ position when computed for rate-limiting TS (TS2), which is in excellent agreement with previous experiments and calculations by Gu et al. [40].

All in all, our results suggest that the ribozyme-catalysed reaction should take place by a different mechanism whereby different species belonging to the active site of the ribozyme could act as the HO2′ proton acceptor and the proton donor to the O5′ leaving oxygen atom (B and AH species in Scheme 1). In other words, catalysis must come from the role of alternative acid–base species not available in aqueous solution. Nevertheless, on the basis of the agreement between our predicted 18O KIEs and the experimental data, the rate-limiting step of the cleavage of the RNA phosphodiester backbone catalysed by the twister ribozyme from Oryza sativa must be associated with the P–O5′ bond cleavage.