1 Introduction

Iron-sulphide minerals in aqueous environment are of considerable interest in geochemistry. Due to its relevance to areas ranging from acid mine drainage [1, 2] to a prominent theory on the origin of life [3], the interface between pyrite (FeS\(_2\)), the most common sulphide mineral, and water has attracted considerable experimental [4, 5] and theoretical attention [6–10].

Like pyrite [11], mackinawite (FeS) is an exceptional scavenger for heavy metals in water [12, 13], while the similarity between its structural unit [14] and reactive biological clusters [15] has suggested that FeS structures could have catalysed the formation of the first prebiotic molecules in deep sea hydrothermal vents [16, 17]. However, contrary to FeS\(_2\), the interface between water and FeS has not been widely investigated [18, 19], in part because of the lack of force field parameters for the system.

In previous work, we have derived a force field, based on pairwise interactions, for molecular mechanics (MM) simulations of mackinawite [20]. In this model, each interaction can be written as a function of the interatomic distances \(r_{ij}\):

$$\begin{aligned} U_{ij} = A \exp \left( -\frac{r_{ij}}{\rho } \right) - \frac{C}{r_{ij}^6} + \frac{q_i q_j}{r_{ij}}, \end{aligned}$$
(1)

where A, \(\rho\), and C are the coefficients of Buckingham potentials, and \(q_i\) the electrostatic charges of the atoms. In addition, to take into account polarisability effects, each sulphur atom is represented by a core and a massless shell (S–S\(_\text {shell}\)), which interact through a harmonic potential [21]:

$$\begin{aligned} U_{ij} = \frac{1}{2} k_s r_{ij}^2, \end{aligned}$$
(2)

where \(k_\text {s}\) is the shell force constant, and \(r_{ij}\) the core–shell distance. The parameters, reported in Table 1, have highlighted the stability of the (001) surface compared to all other surfaces, in agreement with ab initio calculations [22] and experimental findings [23].

Table 1 Force field parameters for FeS from reference [20]
Full size table

Here, we expand the FeS interatomic potential model to include its interaction with water, the latter described by the popular SPC/Fw model [24]. In order to achieve this, we first refined the existing FeS interatomic potentials, followed by the derivation of the missing FeS–H\(_2\)O parameters, by fitting with two-body interactions the ab initio intermolecular energies between the FeS molecule (FeS\(_\text {mol}\)) and H\(_2\)O. Finally, we validated the force field against density functional theory (DFT) calculations of water on the low-index surfaces of FeS and DFT-based molecular dynamics (MD) of intercalated water. In both cases, our model reproduced the ab initio findings. The force field is therefore suitable to model bulk mackinawite and its surfaces in an aqueous environment.

2 Methods

2.1 Molecular dynamics

MD simulations of bulk mackinawite were carried out in the NPT ensemble with the semi-anisotropic constraint, as implemented in DL_POLY_4 [25]. We have employed the Nosé–Hoover algorithm [26], with target temperature and pressure of 300 K and 1 atm. The thermostat and barostat had a relaxation time of 0.1 ps. The \(6 \times 6 \times 5\) simulation supercells, containing 180 tetragonal Fe\(_2\)S\(_2\) units, were equilibrated for 2 ns, and the data were collected during the following 1-ns run. The time step corresponded to 0.5 fs. The Smoothed Particle Mesh Ewald was used to calculate the long-range electrostatics [27], with a precision of \(10^{-6}\). The real space part of the electrostatics calculations had a cut-off of 9.0 Å. Following the adiabatic method proposed by Mitchell et al. [28], shells were assigned a mass of 0.1 Da.

MD simulations of water confined in FeS sheets were carried out in the NVT ensemble, with a target temperature of 500 K. The system was equilibrated for 500 ps, and the data were collected during the following 500 ps. The time step corresponded to 0.5 fs. A precision of \(10^{-6}\) was used in the Smoothed Particle Mesh Ewald. A cut-off of 8.3 Å was used for the real space part of the electrostatics calculations and the Van der Waals potentials. In the adiabatic method, a mass of 0.1 Da was given to the shells.

2.2 Ab initio interaction energies

We have employed Gaussian 09 [29] to derive the ab initio interaction energies, at the MP2 level of theory, between the atom pair FeS\(_\text {mol}\) (in its lowest energy quintet spin multiplicity) and H\(_2\)O. The geometries of the two molecules corresponded to those at equilibrium in their respective force fields (Fe–S \(=1.893\) Å, O–H \(=1.012\) Å, H–O–H \(=113.24^\circ\)). The basis set chosen was the AUG-cc-pVTZ [30], particularly suitable for post-Hartee–Fock methods. Counterpoise corrections were taken into account to avoid basis set superposition effects [31]. A total of 41 reference energies were collected in both profiles.

2.3 Fitting procedure

We have used GULP 4.2 [32, 33] to fit the interatomic interactions between FeS and H\(_2\)O to the energy surfaces derived ab initio. In GULP, the fitting procedure is carried out by varying the parameters, so as to minimise the “sum of squares” of the differences between the classical and ab initio reference energies. In order to take into account the presence of the shell, we have adopted the simultaneous fitting scheme, where the shell coordinates are also treated as fitting parameters.

2.4 Geometry optimisations

DFT optimisations were performed with VASP 5.3 [34, 35], taking into account the Van der Waals correction as implemented in the DFT-D2 method of Grimme [36]. As in our previous works [22, 37], FeS was modelled in the non-magnetic state. We have employed the PBE functional [38], together with the projector augmented wave method to model the core–electron interaction [39]. Specifically, we have treated explicitly the 4s, 3d, and 3p electrons of Fe, the 3s and 3p of S, the 2s and 2p of O, and the 1s of H. The plane wave cut-off was 500 eV, and bulk and surface calculations were performed with, respectively, \(13 \times 13 \times 13\) and \(3 \times 3 \times 1\) Monkhorst–Pack grids [40].

MM optimisations with the force field presented in this work have been carried out with GULP 4.2, with an accuracy of \(10^{-8}\) in the Ewald summation.

In both approaches, we have employed a \(1 \times 1 \times 1\) bulk unit cell (one Fe\(_2\)S\(_2\) unit) to derive the lattice parameters, and subsequently we have used the relaxed bulk structures to construct \(3 \times 3 \times 4\) surface unit cells. In the surface calculations, a vacuum spacing of around 15 Å was introduced to avoid spurious interactions between replica atoms.

3 Results

3.1 Refining the existing FeS force field

The FeS force field already in the literature had thus far only been employed to derive properties of the crystal at zero temperature [20]. However, it is also important that thermal properties are reproduced correctly. Unfortunately, we noted that the existing force field, when employed in MD, does not maintain the correct tetrahedral geometry of the iron atoms. After a few ps of dynamics, one of the four bonds of each FeS\(_4\) tetrahedron is lost, leaving the iron in a trigonal-planar coordination. In order to effectively solve this issue, we have added a three-body term between the S–Fe–S angles:

$$\begin{aligned} U_{ijk} = \frac{1}{2} k_\text {tb} \left( \theta _{ijk} - \theta _0\right) ^2, \end{aligned}$$
(3)

where \(\theta _0\) is the tetrahedral S–Fe–S angle, and \(k_\text {tb}\) the associated force constant. We have adopted for \(k_\text {tb}\) a convenient value of 3.0 eV rad\(^{-2}\) (cut-off 3.0 Å), which we have validated in Sect. 3.2. From here on, and throughout the paper, we will always refer to the refined FeS force field described in this subsection (Table 1) and not to the previous potential parameters.

3.2 Thermal behaviour of mackinawite

First, we have applied the force field in MD simulations in the NPT ensemble with the semi-anisotropic constraint to study the thermal behaviour of mackinawite. Under ambient conditions, we obtain for the lattice constants a and c the values of 3.680 and 5.045, respectively, which are in very good agreement with the experimental values (3.674 and 5.033 [41]). The average Fe–Fe and Fe–S distances during the MD simulation correspond to 2.606 and 2.259 Å, which again match the experimental values (2.598 and 2.256 [41]).

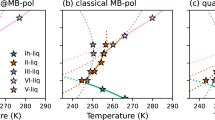
We illustrate in Fig. 1 the dependence of the lattice parameters on the temperature, as predicted by our force field. Following the approach by Lennie et al. [42], who have used X-ray diffraction to estimate the linear expansion coefficients of mackinawite in the temperature range 293–453 K, we have fitted the data with a linear function and used its slope to derive the coefficients:

$$\begin{aligned} \alpha _a = \frac{1}{a_0} \frac{\partial a}{\partial T}, \end{aligned}$$
(4)

and

$$\begin{aligned} \alpha _c = \frac{1}{c_0} \frac{\partial c}{\partial T}, \end{aligned}$$
(5)

where \(a_0\) and \(c_0\) are the reference lattice parameters at 300 K. The resulting \(\alpha _a = 8.1 \times 10^{-6}\) K\(^{-1}\) and \(\alpha _c = 25.1 \times 10^{-6}\) K\(^{-1}\) are comparable to the experimental findings of \(13.6 \times 10^{-6}\) and \(29.8 \times 10^{-6}\) K\(^{-1}\), respectively. Our force field correctly predicts \(\alpha _c\) to be larger than \(\alpha _a\), which causes an elongation in the direction of the c-axis with increasing temperature. The anisotropy can be explained by considering that the sheets of mackinawite are held together by Van der Waals interactions. Their separation is energetically more favourable than stretching the crystal along the a-axis. The structural information and the thermal expansion coefficients of mackinawite are summarised in Table 2. For comparison, we have also listed the experimental and DFT results, although the latter do not include temperature and are effectively at 0 K.

Fig. 1
figure 1

Lattice constants of mackinawite with respect to the temperature (\(p=1\) bar). The fitted lines are also shown

Full size image
Table 2 Bulk properties of FeS
Full size table
Fig. 2
figure 2

Different relative orientations between H\(_2\)O and FeS\(_\text {mol}\). The intermolecular interactions were scanned along the z-axis. Colour code: Fe pink, S yellow, O red, H white

Full size image

3.3 Derivation of the mineral–water parameters

Next, we have derived the parameters describing the mineral/water interface. These were obtained by fitting interatomic potentials to ab initio interaction energies between H\(_2\)O and FeS\(_\text {mol}\), and the latter intended to be a minimal model of the atoms at the FeS surface. A similar approach has been adopted to develop H\(_2\)O–CO\(_2\) pairwise potentials to simulate the deposition of CO\(_2\) layers on water ice surfaces [43]. In this work, we have focused on two different FeS\(_\text {mol}\)–H\(_2\)O orientations. In the first (Fig. 2, left), the water molecule is forced to keep a tetrahedral angle (109.47\(^\circ\)) with FeS\(_\text {mol}\), as we expect to happen for surface orientations exposing Fe atoms. In the second (Fig. 2, right), the water molecule is moved along an ideal O–H\(\cdots\)S hydrogen bond of 180\(^\circ\). As our goal was to design a force field for the FeS/H\(_2\)O interface which was compatible both with the existing FeS parameters described in Sect. 3.1, and the SPC/Fw water model [24], during the fitting procedure, we have constrained all the original charges, together with the shell force constant. In addition, for consistency with the FeS force field, we have modelled the Fe–O and S\(_\text {shell}\)–O intermolecular interactions with Buckingham contributions. However, we have introduced a Lennard-Jones 12-10 term for the S\(_\text {shell}\)–H pair, which reproduced the surface profiles better than a Buckingham potential. The pairwise terms of the FeS\(_\text {mol}\)–H\(_2\)O energy are then given by:

$$\begin{aligned} \begin{aligned} U_{ij}&= A \exp \left( -\frac{r_{ij}}{\rho } \right) - \frac{C}{r_{ij}^6}\\&\quad+ \varepsilon \left[ 5 \left( \frac{\sigma }{r_{ij}} \right) ^{12} - 6 \left( \frac{\sigma }{r_{ij}} \right) ^{10} \right] + \frac{q_i q_j}{r_{ij}},\\ \end{aligned} \end{aligned}$$
(6)

where the additional parameters with respect to Eq. 1, \(\varepsilon\) and \(\sigma\), are, respectively, the strength and the equilibrium distance of the Lennard-Jones 12-10 potential.

We present the ab initio interaction energies in Fig. 3, together with the respective fitted points. Both profiles are attractive, with the binding energy for the Fe–O interaction stronger than the S–H. Despite the presence of the attracive Lennard-Jones 12-10 term, the strength of the S–H interaction energy around the minimum is underestimated by approximately 0.1 eV. One way to improve the agreement may be to release the constraint on the FeS\(_\text {mol}\) charges and/or the shell force constant, a route which however we have not pursued here. The parameters which best reproduce the dissociation paths are listed in Table 3.

Fig. 3
figure 3

Ab initio and fitted interaction energies for the FeS\(_\text {mol}\)–H\(_2\)O orientations shown in Fig. 2

Full size image
Table 3 Force field parameters for the FeS–water interaction
Full size table

3.4 Adsorption of water

We have tested the interatomic potentials derived in Sect. 3.3 by investigating the adsorption energies and structures of undissociated water on three different orientations of FeS, namely the dominant (001), and the minor (100) and (011) surfaces [20]. Below, we show a comparison between the results obtained by our force field with those obtained ab initio by DFT.

We have evaluated the adsorption energy per water molecule, \(E_\text {a}\), according to

$$\begin{aligned} E_\text {a} = \frac{E_\text {surf+wat} - E_\text {surf} - n E_\text {wat}}{n}, \end{aligned}$$
(7)

where \(E_\text {surf+wat}\) is the energy of the cell with adsorbed n water molecules, while \(E_\text {surf}\) and \(E_\text {wat}\) are the energy of the cell with only the surface or an isolated water molecule, respectively.

3.4.1 Mackinawite (001) surface

Isolated molecule The (001) is the most stable mackinawite surface [20]. Here, according to DFT, a water molecule can only be physisorbed, forming two hydrogen bonds with two S atoms. These can belong to the same row along [100] (Fig. 4, top) or to two adjacent rows (Fig. 4, bottom). The two configurations are isoenergetic, with a binding energy of \(-0.17\) eV. This value less negative than the interaction energy of two water molecules (\(-0.22\) eV [44]) is typical of water physisorption on hydrophobic surfaces [10, 45, 46].

Fig. 4
figure 4

Top and side view of the structures of isolated water on the mackinawite (001) surface forming two hydrogen bonds with two S atoms belonging to the same (top) or adjacent (bottom) rows along [100]. Colour code: Fe pink, S yellow, O red, H white

Full size image

When optimised by MM, both the adsorption modes converge towards the first arrangement (Fig. 4, top), with a binding energy of \(-0.15\) eV. The key adsorption parameters of an isolated water molecule on the mackinawite (001) surface are summarised in Table 4.

Table 4 Adsorption energies and main distances of an isolated H\(_2\)O molecule on the mackinawite (001) surface
Full size table

Increased coverage Next, we have considered the adsorption of water at increased coverage. We are not concerned here with identifying the exact amount of molecules to model a monolayer nor with finding the global minimum. Instead, we would like to test the capability of the force field to reproduce a DFT local minimum at increased coverage. Accordingly, we have chosen to load the surface with 12 H\(_2\)O molecules (corresponding to a water coverage of 9.9 H\(_2\)O nm\(^{-2}\)).

The structure optimised by DFT consists of a pattern of cyclic pentamers interacting weakly with the surface (Fig. 5, left). The stability of five-membered rings resembling those found in the gas phase [47] has also been reported by Zhang et al. for water physisorption on a different substrate [46]. When the DFT configuration is subsequently re-optimised by MM, the water–water and water–surface interactions cooperate to preserve the hydrogen bond network (Fig. 5, right).

Fig. 5
figure 5

Top view of the DFT (left) and MM (right) structures at increased water coverage on the mackinawite (001) surface. Colour code: Fe pink, S yellow, O red, H white

Full size image

DFT and MM give adsorption energies per water molecule which are very close (Table 5) and more negative than the isolated molecule adsorption, reflecting the fact that water–water interactions are stronger than water–surface binding, and that the water layer is stabilised by intermolecular hydrogen bonds. This weak interaction with the surface can be appreciated especially from Fig. 6, which shows the local density of states (LDOS) of the S atoms in the topmost surface plane, with and without the adsorbed water layer. No important changes in the LDOS are observed, in line with a weak water–surface interaction.

Table 5 Adsorption energies per molecule at increased water coverage on the mackinawite (001) surface
Full size table
Fig. 6
figure 6

Local density of states of the S atoms in the topmost plane of the (001) surface of mackinawite with and without the adsorbed water layer

Full size image

3.4.2 Mackinawite (100) and (011) surfaces

Next, we have investigated the single molecule adsorption on the (100) and (011) faces of mackinawite. Our intent, here, is to show that the force field introduced is transferable among the low-index surfaces of mackinawite. For this reason, it is worth mentioning that on both the mackinawite (100) and (011) surfaces, the most stable structures obtained by DFT and MM describe the same minimum.

The (100) surface is the most reactive towards water, providing the most negative adsorption energy among the three surfaces studied here (\(-1.02\) eV). On this face, the water oxygen binds to a topmost Fe, while two hydrogen bonds with two S atoms of the adjacent sheet are formed (Fig. 7, top). The strength of the adsorption and the geometric parameters is reproduced very accurately by our force field (Table 6).

Fig. 7
figure 7

Top and side view of the structures of isolated water on the mackinawite (100) (top) and (011) (bottom) surfaces. Colour code: Fe pink, S yellow, O red, H white

Full size image

Similarly, on the (011) termination, the water molecule is adsorbed on top of a Fe atom (Fig. 7, bottom). However, here, the interaction is less strong (\(-0.81\) eV), due to the absence of additional hydrogen bonds. The predicted binding energy is within the typical force field expectations, while the agreement with the Fe–O distance calculated by DFT remains quantitative (Table 7).

Table 6 Adsorption energies and main distances of an isolated H\(_2\)O molecule on the mackinawite (100) surface
Full size table
Table 7 Adsorption energies and main distances of an isolated H\(_2\)O molecule on the mackinawite (011) surface
Full size table
Fig. 8
figure 8

The unit cell of system A employed in our MD simulations

Full size image

3.5 Water intercalated between FeS sheets

Finally, we have tested the transferability of the force field to the aqueous phase, under typical hydrothermal vent conditions. In particular, we have investigated the properties of thin films of water inside FeS sheets and validated our force field against the ab initio MD results, based on DFT, by Wittekindt and Marx [18]. In their “system A”, one of the two FeS interlayer distances of a \(4 \times 4 \times 2\) bulk unit cell was expanded to 11.70 Å. In order to reproduce a pressure of 20 MPa, at a temperature of 500 K, the resulting cavity between the 64 FeS units was filled with 49 water molecules. In our classical approach, however, we have used a larger unit cell, consisting of 256 FeS units and 196 water molecules (Fig. 8). Both Fe planes were kept fixed during the dynamics.

Fig. 9
figure 9

Density profiles of water (normalised to 1) along the direction normal to the surface. The origin of the z coordinate corresponds to the central plane of system A. \(^a\)From reference [18]

Full size image

Figure 9 compares the MM and DFT density profiles of water. In our MM simulation, two layers of water are formed, clearly distinguishable by the maxima at positions \(\pm 1.6\) Å. In between them, the density is very low, shown by a minimum in correspondence with the central plane of the cell. This structural behaviour of water reproduces that found by ab initio MD [18], both qualitatively and quantitatively.

Fig. 10
figure 10

Distribution of the number of hydrogen bonds formed per water molecule. \(^a\)From reference [18]

Full size image

The distribution of the number of hydrogen bonds formed per water molecule is reported in Fig. 10. As a criterion for hydrogen bonding, we have adopted a O–O distance smaller than 3.5 Å and a O–H–O angle larger than 150\(^\circ\) [48]. The average of the distribution is 1.98 hydrogen bonds per water molecule, very close to the ab initio value of 1.96. The maximum is at two hydrogen bonds, but with a significant fraction of water molecules having one or three. The fraction of molecules with zero or four hydrogen bonds is less than 0.1. These features are all present in the ab initio distribution [18], as shown in Fig. 10.

4 Conclusions

We have introduced a force field for the description of the mackinawite/water interface, which can be reliably used in MD simulations involving aqueous mackinawite.

The addition of a simple three-body term to the existing interatomic potential model for mackinawite was sufficient to avoid the emergence of trigonal-planar coordinated irons during MD, while reproducing well the structural properties and thermal behaviour of mackinawite. In order to derive the missing interaction parameters between the mineral and water, we have fitted two ab initio interaction energy curves between a single H\(_2\)O molecule and FeS\(_\text {mol}\) by a sum of pairwise potentials. As shown by the parallel DFT investigation of water adsorption on the low-index mackinawite faces, the resulting force field reliably predicts the energetics and the geometries of the most stable configurations on defect-free mineral surfaces, which lends support to our procedure. Further validation is provided by the description of thin films of water within FeS sheets, where the structural properties at extreme thermodynamic conditions agree quantitatively with the ab initio data in the literature.

One limitation of our approach is the lack of parameters for dissociated water, which is consistent with the SPC/Fw model. While on the dominant (001) surface this is justified by the finding that DFT predicts water to be only physisorbed, dissociative adsorption may play a role on the minority faces, although spontaneous dissociation was not observed by DFT. We intend to include an investigation on water dissociation in a future work.