1 Introduction

Time Dependent Density Functional Theory (TDDFT) became nowadays a standard tool to study excited states of molecular systems owing to its relatively low computational cost and availability in popular quantum-chemistry software. Increasing popularity of the method results in vast amount of TDDFT calculations reported in literature accompanied by a large number of works focused on the assessment of performance of different functionals.

It is well known from experiments that electronic spectra of molecular systems may be greatly influenced by the solvent. Proper accounting for the solvent effects is therefore important for correct prediction of spectral properties from quantum-chemical calculations. Two extreme approaches to solvent modeling in TDDFT may be considered: modeling the solvent in an implicit way in a model of an effective continuous solvent (e.g. commonly used Polarizable Continuum Model, PCM [1, 2]) or, at the other end, using explicit solvent molecules in computations (some recent examples of this method are [3, 4]). The latter approach is computationally expensive and therefore used quite often in combination with implicit models, e.g. in [5]. A less demanding method is based on semiempirical calculations of electronic transitions with explicit solvent modeled via Molecular Dynamics or Monte Carlo methodology [6, 7].

Most TDDFT calculations have been performed for individual molecules or molecular ions; ion complexation processes and their effects on spectral properties are much less commonly studied. Examples of the TDDFT methodology applied in studies of complexation induced shifts in absorption or luminescence spectra of organic molecules include complexation of flavonoids with iron or copper [8, 9], complexation of organic dyes with Mg2+ [10] or divalent metal ions [11] and Li+ or Mg2+ interactions with ketocyanine dyes [12].

Electronic spectra of ketocyanine dyes are influenced by the dye interaction with the solvent (e.g. acetonitrile, ACN). Substantial shifts in absorption or fluorescence spectra are observed when the dye molecule is complexed by a metal cation [13–15]. Such dyes are examples of the systems sensitive to changes in their microenvironment in solution, and therefore are well suited for theoretical studies of dye interactions with ions and with the solvent.

Recently, a TDDFT study of a ketocyanine dye complexation with Li+ or Mg2+ has been presented [12]. Reasonable values of spectral shifts have been obtained from TDDFT/PCM calculations employing hybrid functionals with Lee–Yang–Parr correlation. It has been also shown that accounting for the solvent is crucial for correct reproduction of spectral properties.

Calculations of Ref. [12] used equilibrium geometries of complexes and the implicit model of effective solvent (acetonitrile modeled via PCM). In this paper we would like to address the question how the transition energies are related to the microenvironment of the complex. In particular we would like to see how the results of explicit solvent modeling evolve with increasing number of solvent molecules and how they compare with the results obtained for implicit solvent. We will also try to investigate to which extent the differences in the arrangement of ions and solvent acetonitrile molecules around the dye molecule affect the absorption spectrum. We will use Molecular Dynamics (MD) to generate series of atomistic geometries of the ketocyanine dye and neighboring ions and acetonitrile molecules. Next, based on MD results, TDDFT calculations will be performed for an increasing number of explicit solvent molecules in the system.

2 Calculations

2.1 Molecular Dynamics simulations

Molecular Dynamics simulations were employed to prepare molecular structures of a dye molecule in acetonitrile solution of lithium or magnesium perchlorate. In this paper we used the ketocyanine dye studied theoretically in [12] (labeled as dye-A in experimental work [14])—shown in Fig. 1. Tinker 4.2 package [16] was used for all Molecular Mechanics and Molecular Dynamics calculations. MM3(2000) force field parameterization was adopted for most bonds, angles, dihedral angles and Buckingham-type van der Waals interactions. Minor adjustments were applied to selected bonded parameters in order to improve the agreement of the MM-optimized geometry of the dye molecule to the geometry optimized in B3LYP/6-31G** quantum-chemical calculations. Partial charges for the dye molecule were assigned using Merz-Kollman fit to the electrostatic potential calculated at the B3LYP/6-31G** level. This procedure yielded the charges −0.485e on oxygen and 0.435e on neighboring carbon atom. Partial charge of −0.22e on N atom was equal to the net charge on nitrogen and three neighboring carbon atoms. To simplify the parameterization all remaining charge needed to ensure the electroneutrality of the dye molecule was distributed equally on all C atoms (except the carbon atom bounded to oxygen) which yielded –0.015e as the partial charge per carbon atom.

Fig. 1
figure 1

Chemical formula of the ketocyanine dye studied in this work

Full size image

As a simple check of the parameterization for the dye molecule geometry of the dye was optimized using MM and the resulting structure was then used in the TDDFT B3LYP/6-31G** calculations. The energy of 366 nm obtained for the lowest observable singlet transition compares well with the value of 367 nm found in [12] for the geometry optimized in B3LYP/6-31G** calculations.

Force field parameters for acetonitrile (also MM3-based) were adopted from a recent work [17]. Van der Waals radii for Li+ and Mg2+ were decreased from the MM3 values (to 1.70 and 1.85 Å, respectively) to achieve better reproduction of Me-O distances obtained in MD simulations compared to the structures of dye-cation complexes calculated in [12] at B3LYP/6-31G** level. According to the B3LYP/6-31G** geometry optimization of perchlorate anion followed by the fit of partial charges, the Cl–O bond length was set to 1.50 Å and the partial charges on Cl and O atoms were 0.788e and −0.447e, respectively.

Model systems used in MD consisted of a single dye molecule solvated in 1000 acetonitrile molecules. Systems modeling electrolyte solutions contained additionally 10 Li+ or Mg2+ ions with charge-neutralizing number of perchlorate anions. Cation concentration was therefore 10−2 M in accord with salt concentration used in experiments [14]. MD simulations were performed using periodic boundary conditions in the NVT ensemble at 300K with the density of the system fixed at 0.786 g/cm3 (corresponding to pure acetonitrile). Cutoff of 9 Å was used for all non-bonded interactions. After 100–200 ps of equilibration snapshots of the system were collected every 0.1 ps for 300 ps.

In Fig. 2 the distance between the oxygen atom of the dye molecule and the nearest cation is displayed. Owing to its positive charge 2e, the Mg2+ ion is attracted to the oxygen (bearing negative partial charge) and remains close (up to 2.2 Å) to the O atom. The average Mg2+–O distance is about 1.80 Å, close to the value of 1.81 Å obtained in [12] for dye-Mg2+ complex optimized in PCM calculations. Smaller charge of the lithium cation reduces the electrostatic attraction and the ion can move further from the O atom as readily seen in Fig. 2 (for some parts of the trajectory complete dissociation of the complex was observed; these frames are however of lesser interest as they correspond to free dye molecule). Mean Li+–O distance amounts to 1.85 Å and is larger than the Mg2+–O distance. Smaller radius of the Li+ ion allows for closer contact and therefore minimal ion-oxygen distances for lithium are about 0.05 Å smaller than in the Mg2+ case, which again agrees with the structure of Li+-dye complex found in [12] from the DFT(PCM)/6-31G** calculations.

Fig. 2
figure 2

Distance between the metal ion and the oxygen atom of the dye molecule during the MD simulation

Full size image

The mean value of the C–N–C–C dihedral angle averaged over the trajectory collected for the dye molecule is −35.5°, i.e. slightly smaller than the optimum values obtained from DFT(PCM)/6-31G** calculations in [12].

2.2 TDDFT calculations

MD simulations described above served as a source of atomistic structures used in the TDDFT calculations. For each system about 100 frames selected from the whole trajectory were analyzed. Geometries of the dye molecule and neighboring acetonitrile molecules and ions were extracted from the MD data. Specified number (between 0 and 50) of ACN molecules closest to the dye was selected, with the dye-ACN distance defined as the shortest distance between atoms from the two molecules. For dye-ion complexes always the cation closest to the O atom was included, other ions were chosen based on the requested total number of ions or on the distance limit.

Gaussian 03 [18] was used for all quantum-chemical calculations in this work. As the performance of hybrid functionals with LYP correlation in the TDDFT calculations reported in [12] was among the best, the B3LYP functional was used to calculate excitation energies within the TDDFT methodology. The number of the excited states requested in the TDDFT calculations depended on the system, typically for free dye and dye-Li+ complex 10 states were calculated, for dye-Mg2+ complex the number of states was increased to 20. For each series of structures simulated absorption spectrum was obtained as a superposition of Gaussian peaks with σ = 250 cm−1 and heights corresponding to the transition intensities placed at transition energies.

3 Results

3.1 Dependence of the spectrum on the basis set

TDDFT calculations with explicit solvent molecules are computationally expensive, therefore we are restricted to small basis sets. To estimate how the calculated transition energies depend on the basis set we performed series of calculations for dye and its complexes with Li+ or Mg2+ solvated in 0, 5, 10 or 15 ACN molecules using 3-21G or 6-31G** basis sets. Each series consisted of about 100 structures. Only one cation nearest to the O atom from the dye molecule and no perchlorate anions were included in the cluster.

Resulting simulated spectra are displayed in Fig. 3 for free dye and dye-Li+ complex, for clarity only data for 0 or 15 solvent molecules are presented. With increasing basis set maxima in the absorption spectra shift to lower energies. The shift is practically independent on the number of acetonitrile molecules included in the cluster. Apart from the change in the transition energies there were no substantial differences between results obtained for the two basis sets. For 15 ACN molecules we tested also the possibility of using different basis sets for the solvent and the dye or its complex. As readily seen from Fig. 3, the transition energy depends mainly on the basis set used for the description of the dye-cation complex; changes in the basis set used for acetonitrile result merely in tiny additional shifts. This suggests that the basis set dependence in the TDDFT results obtained for explicitly solvated dye is governed by the “flexibility” of the dye molecule or the complex responsible for observed transitions; a slight increase of the polarizability of the solvent with increasing basis set leads to only small decrease of the transition energy.

Fig. 3
figure 3

Dependence of the transition energies obtained from TD B3LYP calculation on the basis set. Symbol code: basis set used for the dye: # of ACN molecules/basis set used for acetonitrile; 3G and 6G stand for 3-21G and 6-31G**, respectively

Full size image

We can therefore conclude that the choice of the basis set will not affect changes in the spectra resulting from the increase of the number of solvent molecules. Although the increase of the basis lowers the transition energies, the differences between spectra obtained for different amount of explicit solvent will remain unaffected. While small basis set is inadequate to compare the absolute values of the transition energies with the experiment, it allows for the comparison of the spectral shifts (which are of our primary interest in this work) at reduced computational cost. As our goal in this paper was to study the solvent effect and not to reproduce the experimentally measured transition energies we sacrificed the agreement of calculated energies to the experiment in favor of the possibility to study larger systems and we decided to use small 3-21G basis in most calculations, except in the study of the effect of perchlorate counterion (Cf. Sect. 3.3).

3.2 Evolution of the spectra with increasing number of solvent molecules

To examine changes in the absorption spectra upon increasing number of explicit acetonitrile molecules series of TDDFT calculations for ketocyanine dye and its complexes were performed for 0, 5, 10, 15, 25 and 50 ACN molecules in the aggregate.

Typically, the lowest observable transition calculated for the dye molecule without surrounding ACN molecules is the second transition with dominant contribution of the HOMO → LUMO excitation. With increasing number of solvent molecules the lowest intense transition is still of HOMO → LUMO parentage but more often it becomes the first calculated transition (about 60% samples for 50 ACN molecules). This is consistent with the findings of [12] showing that for isolated dye molecule the second transition is observable in vacuum, while in PCM calculations the first transition carries the intensity; in both cases it is of HOMO → LUMO origin.

The lowest intense transition for the dye-Li+ complex without solvating ACN molecules usually is of HOMO → LUMO parentage (although in few samples it has HOMO → LUMO+1 origin) and appears as the second transition (in about 70% cases). In TDDFT vacuum calculations for the equilibrium geometry of the Li+ complex [12] the first transition (with dominant HOMO → LUMO contribution) carried the intensity. This shows that the structural disorder present in current calculations changes the sequence of transitions and in some cases also the parentage of the observable transition. When the number of acetonitrile molecules increases, the intense transition more likely becomes the lowest transition. In the structures with 50 ACN molecules it is almost always the first transition and originates from the HOMO → LUMO excitation in agreement with the TDDFT/PCM results for the optimized complex [12].

TDDFT calculations for the dye-Mg2+ complexes suffer from the problems of “spurious” low-energy transitions with small intensity. In the B3LYP calculations for the equilibrium structure of the complex [12] the observable transition was the 4th transition in vacuum calculations and the 2nd in the PCM solvent, in both cases the dominant contribution was from the HOMO → LUMO+1 excitation. In present calculations without solvent molecules (0 ACN data) the observable transition originates from the HOMO → LUMO+1 excitation and in most cases it is the 6th transition. Distortion of the complex leads therefore to the increase in the number of spurious states. This problem becomes even more prominent in the structures with 5 or 10 ACN molecules. More low-lying spurious states appear and the intensity-carrying state is located somewhere between 10th and 20th state. Spurious states below observable transition start to disappear in systems with more explicit solvent molecules and simultaneously the parentage of the intense transition changes. In the systems with 50 ACN molecules the transition with large oscillator strength is the first transition and originates from the HOMO → LUMO excitation (more than 90% samples).

This analysis suggests that for the isolated dye molecule (without solvating acetonitrile molecules) the distortion of the molecule from the equilibrium geometry may change the sequence of transitions predicted by TDDFT calculations. Results of the solvation with explicit solvent molecules show that with increasing number of ACN molecules the observable transition becomes the lowest predicted transition and always originates from the HOMO → LUMO excitation. This agrees with the prediction of implicit solvent model (PCM) for free dye and dye-Li+ complex, but differs from the PCM results for dye-Mg2+ system [12].

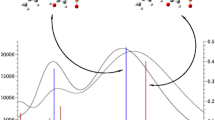
Absorption spectra averaged over series of samples and their evolution with increasing number of ACN molecules are shown in Fig. 4. For comparison predictions of the TDDFT B3LYP/3-21G calculations for equilibrium geometries obtained in [12] at the 6-31G** level are marked by vertical lines. All spectra show some structure resulting from different energies of the observable transition for different geometries. This structure would be probably in some cases averaged out if the sufficiently long series of samples were used in calculations.

Fig. 4
figure 4

Evolution of absorption spectra with the number of explicit solvent molecules. Vertical lines mark the transition energies from TD B3LYP/3-21G calculations for geometries optimized at the B3LYP/6-31G** level. Insets: dependence of the transition energy on the M–O distance for 0 (dark symbols) and 50 (bright symbols) ACN molecules

Full size image

Solvation of the dye molecule shifts the absorption maximum to lower energies. This shift saturates fast with the number of acetonitrile molecules and the center of gravity of the band practically does not change position for more than 15 ACN molecules. Predicted gas-to-solvent shift is in the same direction as calculated for equilibrium geometries using PCM approach. Value of the shift obtained in explicit solvent model is significantly reduced with respect to the PCM results. To some extent this is a consequence of the fact that the absorption maximum calculated for 0 ACN molecules for the geometries of the dye extracted from MD results is red-shifted from the position of the vacuum transition obtained for optimized geometry.

The picture is more complicated for dye complexes with metal ions. For both cations the absorption maximum shifts to higher energies with increasing number of solvating molecules. Complexation of the dye molecule with a cation leads to large red-shift of the transition energy with respect to free dye. Transition energy in the solvent results from the balance of two factors. First, solvation decreases the HOMO-LUMO gap in the dye [12], therefore decreases the observed transition energy as seen for the dye molecule (Fig. 4a). On the other hand, the solvent reduces the electric field of the ion (and therefore the perturbation experienced by the dye) which should shift the transition energies towards vacuum values. In the explicit solvation approach the latter effect prevails for both cations and in the solvent we observe the blue-shift with respect to vacuum. In the implicit solvation approach for the dye-Li+ complex the net effect of the balance is different and a small red-shift in the PCM model is observed (Fig. 4b). It should be, however, noted that the results obtained in this work for dye-cation complexes without the solvent (0 ACN) should not be compared in principle to the results of vacuum calculations for equilibrium geometries, because in the latter case the position of the ion was optimized in vacuum while in this work “vaccum” dye-ion geometries are taken from the MD simulations and the position of the ion corresponds to the complex in solution. Nevertheless, it is clear that the gas-to-solvent shifts obtained from explicit solvent model are larger than calculated within PCM approach and for dye-Li+ complex even the sign is different between explicit and implicit model.

It is evident from Fig. 4 that in the explicit solvation model the absorption band of the dye-cation complex shifts to higher energies when more solvent molecules are included in calculations. Such shifts are larger than the difference between “vacuum” and PCM results obtained for equilibrium geometries. This reflects the sensitivity of the transition energy to the structure of the complex, a feature which can not be fully modeled in continuous solvation models. In particular for the Li+ complex the direction of the solvent shift can be easily determined in contrast to the PCM data where the effect is small, probably due to cancellation of two opposite trends as described above.

A rather weak correlation is observed between the transition energy for dye-ion complex and the distance between the ion and the oxygen atom from the dye molecule (Cf. insets in Fig. 4). The energy increases slightly with increasing Me–O distance, the effect is better visible for complexes without solvating ACN molecules and weakens with increasing solvation—for 50 ACNs the correlation almost vanishes. No particular relation between structural parameters of the complex and the presence of two maxima in dye-Li+ results with 0 ACN was found.

Using the data displayed in Fig. 4 the centers of gravity for the simulated absorption band were calculated. Corresponding values for the systems with 50 ACN molecules are 26,910, 26,020 and 24,430 cm−1 for the dye, dye-Li+ and dye-Mg2+, respectively. The complexation-induced red-shifts are therefore about 890 cm−1 for Li+ and 2,480 cm−1 for Mg2+. These values compare reasonably well with the shifts of about 700 and 1,700 cm−1 for lithium and magnesium ions, respectively, estimated in [12] from the experimental data [14]. With more explicit acetonitrile molecules used in the TDDFT calculations the bands for dye-cation complexes will shift to higher energies, reducing therefore the shifts and even further improving the agreement to the experimental values.

3.3 Effect of the perchlorate counterion

The results of explicit solvation presented in preceding sections were obtained for solvated complexes containing only one metal cation and no perchlorate counterions. It would be therefore interesting to check the effect of inclusion of other ions. The dye-Li+ system was chosen to investigate this effect, because of the prospect of less time-consuming calculations owing to less problems with spurious transitions compared to dye-Mg2+ systems.

Several (about 90) configurations were selected from the MD results in a way that there was at least one perchlorate ion present (in addition to the cation or cations) within the distance from the dye to the farthest of the 50 acetonitrile molecules solvating the complex. Three series of calculations were then performed: one including all ions found within the above-specified distance, second in which one Li+ ion (closest to O atom) and one perchlorate anion closest to the dye were used and third, including only one lithium cation. The third series served as a reference to the dye-Li+ with 50 ACN data from Sect. 3.2. From all samples used in this part of calculations about 35% contained 1 Li+ and 1 ClO4 − ion, about 25% included 2 Li+ and 1 ClO4 −, 20% contained 2 Li+ and 2 ClO4 − ions and in about 10% samples there were 3 cations and 2 anions; the rest of the samples contained other number of ions.

Presence of more ions in addition to acetonitrile molecules increases the problems with spurious states and with the convergence in the TDDFT calculations to such extent that in many cases it was not possible to obtain satisfactory convergence within the 3-21G basis set. According to Sect. 3.1 the most important for the transition energies is the basis set used for the dye, therefore in this study of the multiple-ion effect the 6-31G** basis was applied to the description of the dye molecule and 3-21G basis was used for the acetonitrile molecules. Even then for some systems it was necessary to calculate tens of states in TDDFT in order to locate the first transition with non-zero intensity.

The results are summarized in Fig. 5. The absorption band for 1 cation—1 anion systems is shifted to lower energies with respect to the reference spectrum for 1 cation. This may look surprising at the first glimpse, because one might expect that the counterion would partially cancel the field of the Li+ reducing the complexation-induced shift and therefore moving the transition to higher energies. Inspection of the results reveals, however, that the effect should be opposite—as the Li+ ion is coordinated to the dye molecule (oxygen atom) it has no closely located counterion. The ClO4 − anion closest to the dye is therefore quite likely to be found at the other end of the dye molecule, and the molecule is between the ions. This obviously strengthens the electric field acting on the molecule and increases the spectral shift.

Fig. 5
figure 5

Effect of the perchlorate ion for the absorption spectrum calculated for dye-Li+ complex solvated in 50 acetonitrile molecules. The three lines correspond to the results obtained when all ions, 1 cation and 1 anion or only one cation (reference data) were included in the TDDFT calculations

Full size image

When all ions within certain distance to the dye molecule are included in the TDDFT calculations the absorption shifts to higher energies with respect to the systems with ion pair. Simultaneously, the additional maxima on the main band are decreasing. It seems that in many-ions case the cancellation of electric fields of individual ions takes place at least in a substantial part of the samples and as a result the band shifts towards the spectrum obtained for a single Li+ ion.

It follows from the comparison of single-cation and many-ion spectra in Fig. 5 that inclusion of multiple ions in TDDFT results in blue-shift of the absorption band. Because of insufficient averaging and split maxima in the spectra it is difficult to give precisely the value of this shift but according to Fig. 5 1,000–2,000 cm−1 may be a rough estimate for dye-Li+ complex. This is an overestimated size of the effect as our test set of structures was artificially constructed in such a way that it contains only samples with multiple ions close to the dye molecule. In the whole MD trajectory percentage of such samples is much lower and therefore the spectral shift resulting from multiple-ion configurations is supposed to be smaller.

4 Summary

We have presented a model study of the effect of explicit solvation for absorption spectra of a ketocyanine dye and its complexes with lithium and magnesium ions. Molecular Dynamics simulations were employed to prepare series of molecular structures of the dye and dye-ion complexes solvated with increasing number of explicit acetonitrile molecules. These structures were subsequently used as input data in TDDFT calculations of transition energies.

Calculations of this kind allowed us to investigate the effect of structural disorder in the solute–solvent system. Apart observing the expectable broadening of the spectra and the distribution of transition energies arising from different dye—solvent configurations we were able to check how fast the changes in the spectrum saturate with the number of solvent molecules and to analyze the relationship between structural parameters of the complex and the calculated transition energies. Even the structural disorder alone in the isolated dye molecule with no solvent molecules shifts the maximum of the absorption band from the value obtained in the vacuum calculations for the equilibrium geometry.

As described in Sect. 3.2 explicit modeling of the solvent increased the number of “spurious” low-energy transitions with small intensity encountered for small numbers of acetonitrile molecules. This was observed especially for the dye-Mg2+ system. The results tended to stabilize when more than 15–20 molecules were included in calculations.

For all systems: dye, dye-Li+ and dye-Mg2+ the data for 25 and 50 ACN molecules suggest that the lowest observable transition in the solvent is the first calculated transition, originating from the HOMO → LUMO excitation. This assignment is different than in the implicit solvent model (PCM) where the intense transition in the dye-Mg2+ complex was the second transition of the HOMO → LUMO+1 parentage. Explicit solvent model could therefore lead to different sequence of transitions and to their different origin compared to the PCM approach.

Although estimating of the transition energies in the bulk solvent from the explicit solvation results might require extrapolation of the data because of limitations of computationally feasible system size, the trend itself is well pronounced. We showed that for the dye molecule a red-shift in the solvent is observed; its value saturates fast with the number of solvent molecules. For both complexes with metal ions, explicit solvation results in a blue-shift of the absorption maximum. Much slower saturation of the effect for dye-ion complexes is presumably related to the long-range nature of the perturbation induced by the electric field of the cation.

Explicit modeling of the dye-ions-solvent system allowed us to check the effect of the perchlorate counterion and of the presence of multiple ions in the vicinity of the dye molecule. The effect of the first ClO4 − anion (closest to the dye) is a substantial shift of the absorption maximum to lower energies. The effect of including multiple ions in calculations is smaller because of averaging of their electric field, nevertheless we showed that the net effect is the red-shift of the spectrum.

We can conclude that the TDDFT calculations with explicit solvent molecules can provide additional insight to the implicit solvent approach. Although they are not much helpful in obtaining accurate transition energies because of the limitations of the basis set size, they are well suited to study the shifts induced by structural changes in the system. This approach may be particularly useful for systems containing ions which may relatively easy change their positions.