Abstract
A density functional investigation into differently substituted silylenes with respect to the first step in the addition to white phosphorus is presented. The investigations include dispersion corrections in the density functional treatment. They become sizable for the transition state geometries for the silylenes as they become increasingly substituted by bulky groups. Hence, dispersion corrections are essential for a quantum chemical treatment of real molecules using density functional theory. The different singlet–triplet energy separations of differently substituted silylenes were also investigated and compared with calculated activation barriers for the first step in the addition reaction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Professor Hinze made seminal contributions in his early work on electronegativity [1], a valuable basis for further developments in electronic structure theory [2]. His scientific interests spanned a broad range of physics and chemistry, and he always exhibited a strong empathy for students. I am pleased to be able to contribute the present scientific work in memory of this prominent scientist and teacher.
The degradation of white phosphorus (P4), although known for more than a century [3–6], has so far escaped a clear mechanistic understanding. Experimental studies in the 1980s [7–9] reveal that the degradation process is strongly dependent on a diverse set of conditions: the choice of the nucleophile, the ratio of the nucleophile with respect to P4, etc. A more clear-cut understanding of these reactions comes from the systematic investigation into metal fragments involved in white phosphorus degradation [10–12], as well as, more recently, by reactions with carbenes [13, 14] and, in one report, on silylene addition to white phosphorus [15]. Detailed experimental reaction studies are also known for phosphenium cations [16, 17].
The reaction of the silylene I with P4 proceeds in two steps (Scheme 1). In the first step, the silylene inserts into the PP-bond with the formation of a bicyclobutane species II, which can be isolated and structurally characterized [15]. A second silylene can be added with concomitant final product formation of III. Both processes were recently characterized by density functional calculations [18]. These studies confirm the two-step mechanism, but at the same time reveal the electrophilic nature of the silylene in the P4 attack (Scheme 2).
For the reaction to form II, an electrophilic transition state structure IIa is adopted with a simultaneous stretching of one PP-bond of the tetrahedron. Furthermore, a second P4 can stabilize the transition state structure, forming a trigonal bipyramid, IIb. Under product formation, this second P4 is freed again; thus, it can participate in the white phosphorus degradation in an autocatalytic cycle [18].
Most noticeably, white phosphorus degradation with silylenes has been demonstrated by only a single representative example capable [15]. This prompts me to investigate this aspect more closely and to search for other silylenes having low-energy barriers for the insertion reaction. While the principal findings regarding the reaction mechanism of a silylene addition to P4 are outlined in part 1 of my study [18], in the present work, a further analysis of substituent effects is described. I report here density functional calculations on the following two aspects of silylene addition to white phosphorus: (a) variation of the silylene ranging from species with small to large singlet–triplet energy separations and (b) the effect of substituents on the energy barrier for the reaction. It will be shown that large substituents, which in general are required for kinetic stabilization of silylenes, cause considerable steric crowding, with concomitant sizable dispersion energies in the transition state structures. Hence, an adequate description for these reactions requires density functional treatments with dispersion corrections. At this point, the approach is restricted to the consideration of the first step in the reaction, i.e. from the educt to II. A proof that the second step in the reaction from II to III follows the same reaction path has previously been given in the first part of my studies on this problem [18].
This paper is organized as follows: In the first part, a selected variety of silylenes is discussed. In the second part, the corresponding energy barriers for the first step of the addition reaction are evaluated for the various silylenes.
2 Theoretical section
All calculations were performed with the Turbomole-6.0 [19] set of programs. Throughout, density functional theory was employed. The structures of the molecules were optimized with the PBE (Perdew, Burke, Ernzerhof) functional [20] using the triple-ζ basis set of Ahlrichs et al. [21]. This level of theory is denoted here by PBE/TZVP. In addition, we utilized this functional with further corrections for the dispersion energies. These were performed according to the approach of Grimme et al. [22]. This computational level is denoted as PBE-D/TZVP. The vibrational calculations were carried out using analytical derivatives. All transition states and energy minima have been characterized according to their vibrational frequencies.
3 Results and discussion
3.1 Silylenes
Silylenes became intensely studied during the last two decades and are nicely summarized in a recent review [23]. The species taken into consideration in the present study are shown in Scheme 3.
Of these species, 2 and 5 have yet to be described experimentally. On the one hand, silylene 6, which has no nitrogen stabilization of the electron-deficient center, appears to be only marginally stable in the reported experiments [24]. On the other hand, 3 (R = t-butyl) has been characterized as indefinitely stable [23].
One characteristic aspect of these electron-deficient compounds is the singlet–triplet energy separation. When this is large, then the silylene is expected to be stable, but at the same time it is reluctant to react. The adiabatic energy differences between the singlet and triplet lowest in energy were evaluated with the PBE density functional, both with and without dispersion corrections. Computational details are outlined in the Theoretical Section of this publication.
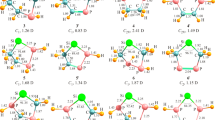
The silylene 1 with a 6-membered ring was characterized with different types of substitution patterns, with methyl or silyl groups attached at either the exocyclic double bond, 1b and 1c, or the nitrogen atoms, 1d and 1e. The silylenes 1f and 1g refer to the cases with phenyl or 2,6-dimethyl-phenyl substitution at the nitrogen positions. Finally, the species 1h corresponds to the experimentally characterized structure, with 2,6-diisopropyl-phenyl (R = Ph2) substitution at the nitrogens [25]. In accord with the experiment, 1h bears an additional methyl group at C(3) of the ylium structure. We also consider bulky substituted silylenes with terphenyl substituents, 1i, and silylenes having t-butyl, 6c, or trimethylsilyl, 6d, substitution. The terphenyl-substituted silylene, 1i, has not previously been reported. Plots of the computed equilibrium structures for the sterically encumbered structures in their energy lowest singlet states are shown in Fig. 1.
In 1f, the phenyl substituents tend to π-overlap with the 6-membered ring. Substitution with alkyl groups, as in 1g and 1i (a = CH3, b = CH2), brings these, however, into an almost perpendicular orientation. In 1h, the iso-propyl groups are oriented in such a way that the methyl groups become trans to the 6-membered ring, and the hydrogen at the α-C is aligned over the C–N axis. In 1f to 1i, the 6-membered ring is almost planar, but such is not the case in 6c and 6d. There the five-membered ring is strongly puckered and the CSiC angle in 6c is less acute (95.7°) than in 6d (91.9°). This parallels the smaller S-T energy separation in the former compared to the latter (see Table 1). An evaluation of the S-T energy separations for these latter two silylenes without dispersion corrections (PBE level) was not attempted.
The calculated energy separations between the lowest singlet and triplet electronic states (S-T) span a wide range (see Table 1). Alkyl substitution (6c, 6b) reveals small energy differences, as is known from previous investigations [26], while the 5-membered silylenes show large S-T energy separations. That result agrees with findings for the corresponding carbon analogues [27].
A peculiar effect results from silyl substitution at the exocyclic double bond, i.e. in 1b vs. 1c. The largest S-T separation is computed for R = H and R′ = SiH3. In conformity with a population analysis, the singlet structure of 1 is stabilized by admixture of an ionic limiting structure shown by the resonance structure 1cb (Scheme 4).
By contrast, phenyl substitution, i.e. in 1f to 1i, reduces the S-T energy separation with respect to the parent compound 1a. The smallest energy separation is predicted for 1i, which refers to R = a terphenyl substituent. The species 3 and 4 are summarized as stable species [23]; the S-T energy separations are large but less than in the corresponding carbon analogues [27]. Silylene 5 is experimentally unknown and can best be compared with the monoamino-substituted carbon analogue [28], while silylene 6 is known for its fleeting existence [24]. For comparison, we have included in our considerations the parent silylene SiH2. The resulting S-T energy separation (PBE-D/TZVP) is 16.0 kcal/mol in favor of the singlet ground state, thus giving rough agreement with the best available calculations on this species (21.0 kcal/mol) [29], based on a MCSCF calculation with subsequent MRCI energy correction.
One further aspect should be discussed here. The S-T separations were calculated at the two computational levels, (a) with (PBE-D) and (b) without (PBE) inclusion of dispersion effects in the density functional treatment. The values in Table 2 are collected for both levels. The difference in dispersion effects between singlet and triplet structures appears negligibly small, albeit triplet structures tend to have larger valence angles at the silicon center, when compared with the corresponding singlet geometries. This aspect becomes more important, since dispersion energy corrections to the density functional treatment may change considerably during the reaction (vide infra).
3.2 Reaction barriers
As outlined in part I of these studies [18], the molecular orbitals of white phosphorus, 8b, can be related to the molecular orbitals of a simple phosphine, 8a. Local orbitals of a PH3 unit can be used to construct the full set of molecular orbitals for the P4 tetrahedron with Td symmetry [30]. Based on these symmetry considerations, both electrophilic (El) and nucleophilic (Nu) approach to the tetrahedron are feasible, either at the corners (i, k) or at the edge (j) of the tetrahedron. A schematic sketch is shown in Scheme 5.
Since the silylene behaves as an electrophilic species with respect to P4 [18], interaction can only occur according to (i) or (j). The former refers to π-complex formation, in which one lone pair at P4 combines with the empty p-orbital at the silylene. The calculations reveal that such an interaction is fairly small (≤2 kcal/mol) for the investigated silylenes [18] and does not cause any considerable reorganization of the P4 moiety. The reaction path to insertion of the silylene into one PP-bond of the tetrahedron follows according to (j). The transition state structures are anticipated in IIa and IIb [18].
The stationary points for the overall reactions toward II, the first insertion step of the overall path, are sketched in Scheme 6.
As in the S-T investigations, a selected variety of silylenes was chosen. Quantum chemical calculations were then performed at a density functional level with dispersion corrections (PBE-D). The results of these investigations are collected in Table 2.
The energy barriers E 1 are computed as the sum of the energies from the educt side (P4 plus silylene) minus the energy of the transition state structure. Table 2 also summarizes the changes in the dispersion energy corrections, ΔE disp, from the educt side to the transition state.
The stronger steric demand of the substituents in the transition state structure of 1h is depicted in Fig. 2.
The nitrogens in TS-1h are pyramidalized, with the consequence that the iso-propyl substituents tend to bend toward each other. They thus increase the steric hindrance, and dispersion corrections in the transition state structure come to the fore.
In general, the energy of the density functional is given by the following ansatz (1).
Emean is the energy resulting from the density functional treatment, and Edisp is the dispersion energy. The dispersion energy is not an observable quantity: it is a correction to the density functional. The magnitude of Edisp is negligibly small for the silylenes with “small” substituents, but it becomes sizable for the very bulky 1h. On the one hand, the dispersion-corrected energy barrier for the overall reaction of 1g compared with 1h increases only slightly, which can be attributed to the increase in the van der Waals interaction in the transition state structure. On the other hand, density functional calculations without dispersion corrections predict a sizable increase in the energy barrier from 1f to 1h. For the latter, a PBE/TZVP calculation of the reaction path predicts a barrier of 29 kcal/mol, too large for reasonable agreement with experiment. The reaction occurs under mild conditions [15], which indicates a much lower barrier for the insertion.
The lowest energy barrier is predicted for 5, a hitherto experimentally unknown silylene. As has been shown in carbene chemistry [14], such species may become more stable by steric protection with bulky substituents. The largest energy barrier results for 3 (and to a lesser extent for 4), which also shows large S-T energy separations (Table 1).
4 Conclusions
Our investigations can be summarized as follows:
-
(1)
A variety of silylenes, studied by density functional calculations at PBE/TZVP and PBE-D/TZVP level, present singlet–triplet energy separations that depend on the stabilization of the electron-deficient silicon center by electron-donating substituents. The 6-membered ring system is intermediate, it possesses S-T energy separations between 45 and 50 kcal/mol. The 5-membered ring systems (“Arduengo type” compounds) exhibit larger S-T differences; hence, an insertion into P4 becomes less favorable. At the same time, they are well characterized as isolable entities. An attainable target is 2. Based on the S-T estimate, it should be isolable if substituted with bulky substituents. By contrast, the terphenyl-substituted 1i reveals a lower S-T energy difference.
-
(2)
The energy barrier for insertion has been studied here only for the first step of the overall reaction (see Scheme 1). Based on the previous study [18] (part I), the second step proceeds similarly to the first step and findings for the second step appear likely to apply equally to the first step. While the present calculations did not account for participation of a second P4 in the addition process, such a process seems less likely for sterically encumbered silylenes such as 1h, due to steric congestion in the transition state structure.
-
(3)
The density functional computations reveal an important aspect regarding the overall calculations of transition state barriers using these methods. The advantage of density functional calculations is that they can nowadays be performed easily for bulky structures. In general, these are needed for the synthesis of unstable structures in main group chemistry, in order to protect kinetically highly reactive centers, e.g. that of a silylene. Such calculations need to account for alterations in steric congestion as the transition state forms. As this study illustrates, changes in the dispersion energy corrections in going from the educt to the transition state may become sizable, which may be a non-negligible quantity in the density functional treatment. Finally, the importance of dispersion forces in the equilibria of silylenes with disilenes has been recently stressed in a combined experimental and theoretical study [31]. Hence, similar effects on the reactions of “real” molecules of chemical interest in main group chemistry are to be anticipated.
References
Hinze J, Jaffe HH (1962) J Am Chem Soc 84:540
Bergmann D, Hinze J (1996) Angew Chem Intern Ed 35:150
Michaelis A, Pitsch M (1899) Ber. Dt. Chem. Ges. 32:337
Lehmann H-A, Grossmann G (1980) Pure Appl Chem 52:905
Burgess CH, Chapman DL (1901) J Chem Soc Trans 79:1235
Maier L (1971) Fortschr Chem Forsch 19:1
Fritz G, Haerer J (1983) Z Anorg Allg Chem 504:23
Schmidpeter A, Burget G, Zwascha F, Sheldrick WS (1985) Z Anorg Allg Chem 527:17
Baudler M, Faber W (1980) Chem Ber 113:3394
Perruzini M, Gonsalvi L, Romerosa A (2005) Chem Soc Rev 34:1038
Scherer OJ (1999) Acc Chem Res 32:751
Biegerl A, Brunner E, Groger C, Scheer M (2007) Chem A Europ J 13:9270
Masuda JD, Schoeller WW, Donnadieu B, Bertrand G (2007) Angew Chem Intern Ed 46:7052
Masuda JD, Schoeller WW, Donnadieu B, Bertrand G (2007) J Am Chem Soc 129:14180
Xiong Y, Yao S, Brym M, Driess M (2007) Angew Chem Intern Ed 46:4511
Weigand JJ, Holthausen M, Fröhlich R (2009) Angew Chem Intern Ed 48:295
Krossing I, Raabe I (2001) Angew Chem Intern Ed 40:4406
Schoeller WW (2009) Phys Chem Chem Phys 11:5273
Ahlrichs R, Bär M, Häser M, Horn H, Kölmel C (1989) Chem Phys Lett 162:165
Perdew JP, Burke K, Ernzerhof M (1996) Phys Rev Lett 77:3865
Schäfer A, Huber C, Ahlrichs R (1994) J Chem Phys 100:5829
Grimme S (2006) J Comput Chem 27:1787
Haaf M, Schmedake TS, West R (2000) Acc Chem Res 33:704
Kira M, Ishida S, Iwamoto T, Kabuto C (1999) J Am Chem Soc 121:9722
Driess M, Yao S, Brym M, van Wuellen C (2006) Angew Chem Intern Ed 45:6730
Olah J, Veszpremi T (2003) J Organomet Chem 686:112
Dixon DA, Arduengo AJ III (1991) J Phys Chem 95:4180
Lavallo V, Canac Y, Präsang C, Donnadieu B, Bertrand G (2005) Angew Chem Intern Ed 44:5705
Balasubramanian K, McLean AD (1986) J Chem Phys 85:5117
Schmidtke HH (1968) Theor Chim Acta 9:199
Jutzi P, Mix A, Neumann B, Rummel B, Schoeller WW, Stammler H-G, Rozhenko AB (2009) J Am Chem Soc 131:12137
Acknowledgments
The author thanks the University of California of Riverside for financial support, Dr. Thorsten Tönsing (University of Bielefeld) for computational help and Prof. Thomas Morton (University of California at Riverside) for prolific discussions.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to the memory of Professor Jürgen Hinze and published as part of the Hinze Memorial Issue.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Schoeller, W.W. Dispersion-corrected energy barriers for silylene addition to white phosphorus, a density functional investigation into substituent effects. Theor Chem Acc 127, 223–229 (2010). https://doi.org/10.1007/s00214-010-0750-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00214-010-0750-6