1 Introduction

The light sensitivity of the rhodopsin protein family is due to the retinal chromophore, a protonated Schiff base (PSB) which undergoes photoisomerisation on absorption of a photon. In the human protein rhodopsin, the 11-cis isomer of retinal is isomerised to the all-trans form [1], while in bacteriorhodopsin, all-trans retinal is isomerised to the 13-cis form [2, 3]. The reaction in both directions is extremely efficient and occurs over a sub-picosecond timescale.

Model retinal systems have been extensively used to elucidate the reaction. The minimal model is the penta-3,5-dieniminium cation C5H6NH +2 , or PSB3, with a conjugated π-system of three double bonds. Robb and co-workers have shown that at the ab initio CASSCF level the S1 minimum energy path (MEP) to the ground state is barrierless and leads to a conical intersection between the S0 and S1 energy surfaces [4]. CASSCF dynamics calculations on PSB3 are characterised by a sub-picosecond isomerisation with a high quantum yield [5, 6].

At the higher CASPT2 level of theory, Page and Olivucci [7] have shown that the PSB3 S1 potential energy surface is qualitatively different from CASSCF, with only a single planar cis CASPT2 minimum compared to two for CASSCF. However, CASPT2 gradient calculations are computationally too expensive to scale up to the full protein system. Instead, mixed methods have been used, with single-point CASPT2 energies calculated at geometries from a lower level of theory, such as CASSCF. At the CASPT2//CASSCF level, the PSB3 S1 photoisomerisation coordinate contains a small (2.5 kcal mol−1) barrier [8], indicating that CASSCF alone is insufficient to properly describe the path of the reaction.

Single-point CASPT2 calculations can also be used to study the retinal chromophore, including interactions with the protein binding pocket, with geometries provided by lower level methods [9–11]. CASPT2//CASSCF has further been used to calculate the excitation energies [12] and absorption spectra [13, 14] of retinal in the full protein environment using a combined quantum mechanical/molecular mechanical (QM/MM) description. The conical intersection of rhodopsin has also been characterised using this technique [15]. However, mixed methods such as CASPT2//CASSCF are still too costly for non-adiabatic dynamics calculations. An approximate method using scaled-CASSCF has been investigated [16], but again only a limited number of trajectories can be calculated.

It is therefore of great interest to see whether lower cost methods can give results of a similar accuracy on retinal models with a view to calculations in the full protein environment. Semiempirical approaches are promising in this regard [17]. The OM2 semiempirical Hamiltonian [18, 19] with GUGA configuration interaction [20] is of particular interest because it has already been shown to give accurate absorption energies for bacteriorhodopsin [21] and to predict the spectral shift between bacteriorhodopsin and sensory rhodopsin II [22].

In this study we compare the OM2/GUGA-CI description of the PSB3 retinal model with CASSCF and CASPT2 results. In Sect. 2 the details of the computational methods are given, including in particular the various methods considered for selecting the GUGA-CI active space. In Sect. 3, the semiempirical and ab initio methods are compared for optimising critical points on the PSB3 potential energy surface. The semiempirical S1 MEPs are mapped to determine whether a barrier exists to the isomerisation reaction, and surface-hopping dynamics calculations are carried out to determine the S1 lifetime and quantum yield of the isomerisation. Ab initio CASSCF and CASPT2 S1 potential energy surface scans are also discussed. Section 4 presents our conclusions about the validity of the semiempirical methods considered.

2 Computational methods

Except for the surface-hopping dynamics runs, all calculations were carried out within the ChemShell environment [23] using the DL-FIND optimiser module [24]. In work to be detailed in a forthcoming article, DL-FIND was extended to include the conical intersection optimisation algorithms previously implemented in the MNDO semiempirical package [25].

2.1 Ab initio calculations

Reference ab initio calculations for PSB3 were obtained at the CASSCF and CASPT2 levels. Analytic energies and gradients were provided by the MOLPRO package [26]. In order to make the results available to the optimiser, the ChemShell interface to MOLPRO was extended to cover CAS calculations (both single and multiple state).

Following Page and Olivucci [7], we have used the 6-31G(d) basis set. In our calculations cartesian basis functions were employed. Again following Ref. [7], the active space was selected to include the six π-valence molecular orbitals. C s symmetry was enforced for the planar optimisations.

For the single state optimisations, conventional (non state-averaged) CASSCF and CASPT2 calculations were performed. For the conical intersection optimisations the calculations were state-averaged between the S0 and S1 states, with an equal weighting given to both. Multi-state multi-reference CASPT2 (MS-MR-CASPT2) was used, with no level shift applied.

The optimised geometries of the cis form of PSB3 can be compared directly with the results of Ref. [7]. A detailed comparison is available in the electronic supplementary material. To summarise, the CASSCF results are in very good agreement with the geometries given in the supplementary material of Ref. [7], with errors for bond lengths and angles within 0.001 Å and 0.1°, respectively. Larger deviations are seen for the CASPT2 results, with some errors of the order of 0.01 Å/1.0°. We attribute these discrepancies to the different implementation of CASPT2 gradients used in Ref. [7], namely numerical gradients derived from MOLCAS energies.

2.2 Semiempirical calculations

All semiempirical calculations used the OM2 Hamiltonian with GUGA configuration interaction. Energies and gradients were provided by MNDO [27]. The SCF calculations were performed using either the restricted Hartree–Fock (RHF) or restricted open-shell Hartree–Fock (ROHF) formalism, with the latter corresponding to a singlet excited state. In both cases three reference configurations were used for the configuration interaction procedure, corresponding to the closed shell ground state and to single and double HOMO–LUMO excitations. This ensured that the RHF calculations correctly described the S1 state and the ROHF calculations correctly described the S0 state. All single and double excitations within the active space from these references were included in the calculations.

The active space for OM2/GUGA-CI calculations is typically chosen to be equivalent to those used in CASSCF calculations, because these are assumed to give the largest contribution to the correlation energy. Therefore we would like to select the six molecular orbitals that make up the conjugated π system. However, these MOs have to be deduced from the output of the SCF calculation at any given geometry.

For planar PSB3 they are straightforward to identify, and this can be done automatically in MNDO. In this procedure, the MO eigenvectors are used to calculate the total p-orbital population for each MO along the vector perpendicular to the plane of the molecule. The MOs with p populations above a certain threshold (default: 0.4) are classified as π MOs. These MOs are included in the active space, counting outwards from the HOMO and LUMO, until the user-specified active space size is reached.

This procedure is not practical for excited state calculations of PSB3, where the molecule is only planar at the ground state minimum. In previous excited state calculations of retinal models (e.g. Ref. [25]), an ‘orbital tracking’ procedure was used instead. In this method, the π MOs are first identified by inspection at the starting geometry. At each subsequent geometry, the eigenvectors of every MO are compared (by dot product) to those of the previous geometry. The most similar MOs then form the new active space.

There are two problems with applying this approach to PSB3. First, if an optimisation is started at a distorted geometry, it is not always clear from inspection which orbitals correspond to the planar π orbitals. Second, as the molecule twists around its central bond, the orbitals with π character can mix with those of σ character, which causes the orbital tracking procedure to break down. Orbital tracking only works for PSB3 if the starting geometry has roughly the same torsion angle as the endpoint.

To overcome these difficulties, a new procedure was developed for selecting the active space in conjugated π systems. It is an extension of the method described above for planar systems. At the beginning of the calculation, the conjugated chain is identified. By default, this includes all atoms with p-type basis functions, but for more complicated systems it can be restricted to a user-specified list of atoms. Then, for any given geometry, a plane is determined for each atom in the chain based on the positions of its two nearest neighbours in the chain. These planes therefore follow the twists and turns of the conjugated chain. As before, the total p-population for each MO is calculated along the vectors perpendicular to these planes, and the MOs with the greatest π character identified. Figure 1 illustrates this method for two MOs identified as having π character at a point of conical intersection. For the special case of a planar molecule, the new method is equivalent to the original.

Fig. 1
figure 1

Two molecular orbitals identified as having π character at a point of conical intersection. The arrows indicate the vectors along which the p-population is calculated

Full size image

This new approach solves both the problems of the orbital tracking method: there is no longer any need to identify the active orbitals by inspection at the beginning of the calculation, and the selection of the active space is dependent only on the current geometry. The active space selection will still be ambiguous at points where active and inactive orbitals mix, but this is reduced to a localised problem and no longer causes the whole calculation to break down. The main restriction of the new approach is that it is limited to conjugated π-systems, although it could potentially be extended to include other easily-identifiable orbital types (e.g. n orbitals).

By using this method, it becomes possible to carry out OM2/GUGA-CI dynamics calculations of retinal models using an active space larger than the minimal size. However, the problem of inactive/active orbital mixing still has to be contended with. When mixing occurs (i.e. when the eigenvalues of the active and inactive orbitals become close and the π-population is split between them), large, unphysical gradients may result. As this problem is localised, its only effect on geometry optimisations is to hinder convergence (assuming no mixing occurs at the target geometry). For dynamics calculations the problem is more serious, as the unphysical gradient will affect the course of the trajectory.

We have therefore considered another method which adds extra previously inactive orbitals into the active space. The MNDO program was modified to allow the size of the active space to vary. All MOs with p populations above the threshold of 0.4 formed the basis of the active space. Following this, neighbouring inactive orbitals were also included in the active space if the eigenvalue difference between them was lower than 0.1 eV.

To illustrate the effect of this change, Fig. 2 shows part of a ground state PSB3 trajectory for the fixed-sized active space method (denoted AS6). The gradients have then been recalculated along the same trajectory for the variable-sized active space method (denoted AS+). The gradient ‘spikes’ have been removed. Note, however, that the thresholds we have used are somewhat arbitrary, so some gradient artefacts remain on the trajectory.

Fig. 2
figure 2

Gradient norms along a section of a ground state PSB3 trajectory calculated using the AS6 method with a timestep of 0.1 fs. Gradients for the AS+ method have been recalculated along the same trajectory

Full size image

The downside of the AS+ approach is that inclusion of extra orbitals into the active space necessarily introduces discontinuities into the energy. Large energy discontinuities can occur for AS6 due to inactive/active orbital mixing, but these are rarer. It is therefore appropriate to use AS+ only when the local accuracy of the gradient is considered more important than the local continuity of energy.

A third method, AS2, has also been considered. This uses a minimal active space with two orbitals, for which no special active space selection procedure is necessary. In total six methods have been investigated, with each of the active space approaches tested with RHF and ROHF orbitals.

3 Results and discussion

3.1 Geometry optimisations

Cartesian coordinates for all geometry optimisations are available in the electronic supplementary material. In this section AS+ results are not quoted as they are identical to the AS6 results to the level of precision given. In some cases extra orbitals are added to the active space at the minimum, but the change in the energy is not significant (<0.001 eV). This demonstrates that the AS+ method does not distort the most important points on the PSB3 potential energy surfaces.

Optimised bond lengths and angles for the cis S0 minimum are given in Table 1. There is little variation in the semiempirical results, with all methods in good agreement with CASPT2. The AS2 methods perform at least as well as AS6, and there is little difference between RHF and ROHF. Very similar results are found for the trans S0 minimum (Table 2).

Table 1 Ab initio and semiempirical optimised geometrical parameters at the PSB3 cis S0 minimum
Full size table
Table 2 Ab initio and semiempirical optimised geometrical parameters at the PSB3 trans S0 minimum
Full size table

For the cis planar S1 minimum (Table 3), there are two CASSCF minima but only a single CASPT2 minimum was found, in agreement with the findings of Ref. [7]. The first CASSCF minimum is characterised by a long central C=C bond (third line of Table 3), whereas in the second the central bond is much shorter and the bond length alternation (BLA) pattern of the C–C bonds is reversed. The CASPT2 minimum lies between these extremes. In the semiempirical case, two minima were found for RHF/AS2, of a similar nature to those of CASSCF. All the other methods converged to a single minimum. Only ROHF/AS2 gives the same BLA as CASPT2, although the absolute values of the bond lengths are considerably different. Of the AS6/AS+ methods, RHF is closer to CASPT2 than ROHF.

Table 3 Ab initio and semiempirical optimised geometrical parameters at the PSB3 cis planar S1 minima
Full size table

Only one CASSCF minimum could be located for the trans planar S1 minimum (Table 4). It is clearly not similar to the CASPT2 minimum however, with a long central C=C bond and BLA pattern reminiscent of the first cis CASSCF minimum. Again, two minima were found for RHF/AS2, of a similar nature to the cis minima. RHF/AS6 has the wrong BLA with absolute bond lengths considerably in error compared to CASPT2. The ROHF methods perform better, with ROHF/AS2 closer to CASPT2 for the central three bond lengths and ROHF/AS6 closer for the outer bonds.

Table 4 Ab initio and semiempirical optimised geometrical parameters at the PSB3 trans planar S1 minima
Full size table

Results for the S0/S1 minimum energy crossing point (MECP) are presented in Table 5. Due to numerical instabilities in the region of the conical intersection, it was not possible to obtain reliable interstate coupling gradients for CASSCF at the time of the study, and CASPT2 interstate coupling gradients are not implemented in MOLPRO. Therefore for both methods a penalty function approach [25, 28] was used to optimise the MECP, which does not require the interstate coupling gradient. By its nature the penalty function method does not converge exactly to the true minimum MECP, but the difference is insignificant for this analysis. For the semiempirical methods the interstate coupling gradient is available and so the more efficient Lagrange–Newton method was used [25, 29].

Table 5 Ab initio and semiempirical optimised geometrical parameters at the PSB3 S0/S1 minimum energy crossing point
Full size table

The CASSCF and CASPT2 MECPs are quite similar, with the same BLA and similar bond lengths and angles. The results for the semiempirical methods are much more varied. For RHF/AS2, no MECP could be located. For RHF/AS6 and RHF/AS+, the MECP point features a large torsion around the C=C–C–N single bond (141.7°). This is an artefact: in all the RHF cases there is an avoided crossing in the region where the true MECP should lie. We cannot therefore expect to obtain realistic dynamics results from the RHF methods and they will not be considered further. The ROHF methods perform better, with both AS2 and AS6/AS+ giving qualitatively correct MECP geometries compared to CASPT2. However only AS6/AS+ gives the same BLA pattern as CASPT2.

The relative energies for the various points on the potential energy surfaces are given in Table 6, along with cis and trans vertical excitation energies and energy differences between the planar S1 minima and the MECPs. ROHF/AS2 and CASSCF have similar excitation energies. However, the difference between the planar S1 minimum and the MECP is significantly larger for ROHF/AS2, which means the slope between the two points is greater and we therefore might expect the ROHF/AS2 lifetime to be shorter than CASSCF. For ROHF/AS6 and ROHF/AS+, the excitation energies are similar to CASPT2 (over 1 eV lower than CASSCF), and the difference in energy to the MECP is also lower than either of the ab initio methods, so we can expect these lifetimes to be longer than for CASSCF. Note that this analysis assumes that all the energy paths are barrierless, as a barrier on the S1 surface will strongly affect the lifetime of the S1 state. To investigate whether this is the case, MEP calculations are required.

Table 6 Energies and selected energy differences on the PSB3 S0 and S1 potential energy surfaces
Full size table

3.2 Excited state minimum energy paths

Minimum energy paths were calculated using the climbing image nudged elastic band (NEB) method [30, 31] as implemented in DL-FIND. The cis and trans paths were refined separately, with the MECP and appropriate planar S1 minimum serving as fixed end points to the paths. Ten images were optimised between the endpoints.

The results for the three ROHF methods are shown in Fig. 3. For ROHF/AS2, no barrier was found on either the cis or trans S1 MEP. The AS2 MEP is much steeper than the AS6/AS+ MEPs due to the higher AS2 vertical excitation energies for both cis and trans forms.

Fig. 3
figure 3

PSB3 minimum energy paths between the cis and trans planar S1 minima and the S0/S1 MECP for the ROHF/AS2, ROHF/AS6 and ROHF/AS+ methods. Energies (in eV) are plotted relative to the MECP

Full size image

For ROHF/AS6 and ROHF/AS+, the MEPs are essentially identical within the error due to the convergence criteria. In both cases there are small barriers on both the cis and trans MEPs. To determine their precise heights, the transition states were fully optimised using the dimer method in DL-FIND [32]. The barrier heights relative to the respective S1 planar minima were for the cis form 0.036 eV for both methods and for the trans form 0.039 eV for ROHF/AS6 and 0.037 eV for ROHF/AS+. The AS+ cis barrier is very slightly higher than AS6, as the cis planar S1 minimum is stabilised by an additional orbital in the active space. In contrast, the AS+ trans barrier is slightly lower than the AS6 barrier because the AS+ transition state is stabilised by an additional orbital in the active space. As both methods give almost identical barriers, it is apparent that these are true barriers and not an artefact of the orbital selection procedure.

The results can be compared with the ab initio CASSCF(6,9)/6-31G* MEP from the cis isomer to the MECP in Ref. [4], which was determined by steepest descent from the Franck–Condon point using mass-weighted cartesian coordinates. The initial relaxation results in stretching of all the formal double bonds, i.e. movement towards the two CASSCF planar S1 minima. The barrierless steepest descent path then continues to an MECP with a central double bond torsion of 76.8°. Note that this end point cannot be compared directly to the present NEB paths because the latter have an endpoint fixed at the MECP.

A CASPT2//CASSCF energy profile for the cis isomer starting from the Franck–Condon point is also available [8]. A state-averaged (6,6) CASSCF wave function was used with the 6-31G* basis set. For this method a barrier is observed, in agreement with ROHF/AS6 and ROHF/AS+, but with a somewhat larger height of 2.5 kcal mol−1 (0.11 eV).

Energy paths for SA-2-CASSCF(6,6), MR-CIS(4,5) and MR-CISD(4,5) with the 6-31G* basis set are given in Ref. [33] (Fig. 3) for both the cis and trans MEPs. All three methods are barrierless for the path from the planar trans minimum to the MECP, but both MR-CI methods appear to have very small barriers on the cis path. These results should not be over-interpreted, however, because the paths are calculated by linear interpolation and are therefore only a first approximation to the true MEPs.

The results indicate that the ROHF/AS2 photoisomerisation is likely to proceed much faster than either AS6 or AS+, due to both the larger vertical excitation energy and the barrierless path.

3.3 Surface-hopping dynamics

Semiempirical surface-hopping dynamics calculations were performed using the non-adiabatic dynamics module implemented in MNDO [34]. Six sets of trajectories were run to compare the ROHF methods starting from the cis and trans isomers.

Initial geometries were sampled from ground state Born–Oppenheimer dynamics runs. An equilibration run was carried out first, starting from the appropriate ground state minimum. An initial instantaneous temperature of 300 K was set, and the trajectory propagated for 1 ps with a time step of 0.1 fs. Velocity scaling was used to equilibrate the system to 300 K. It was applied every 100 steps with a maximum allowed energy change of 1.0 kcal mol−1.

Following the equilibration run, a production run was carried out. Again the trajectory was propagated for 1 ps with a time step of 0.1 fs. Velocity scaling was applied again to prevent the possibility of discontinuities in the system energy pushing the system away from its equilibrium temperature. In the case of AS6 several preliminary dynamics runs had to be discarded due to discontinuities too large to be controlled by the scaling procedure.

In each case 200 snapshots were taken at random from the production run. A snapshot consists of both the geometry and the atom velocities at the chosen timestep. For each snapshot a single point calculation was performed to obtain the excitation energy, ΔE 10, and oscillator strengths, f 10, for the S1 excitation (only excitations to the S1 state were considered, as this is considered to be the only state relevant to PSB photodynamics [35]). Following Ref. [36], a stochastic algorithm was used to determine whether a surface-hopping run should be started from a given snapshot on the basis of the normalised transition probability

$$ P_{10} = {\frac{f_{10}/\Updelta E^{2}_{10}}{\max(f_{10}/\Updelta E^{2}_{10})}} $$
(1)

where the denominator is the maximum value of all computed f 10/ΔE 2 10 ratios.

For each snapshot a random number between 0 and 1 is generated, and if the number is lower than P 10 then a surface-hopping trajectory is started from the snapshot’s geometry and initial velocities. The surface hopping method of Tully (fewest switches algorithm) was used [37, 38]. In all cases a timestep of dt =  0.05 fs was used for propagation of the nuclear degrees of freedom, with quantum amplitudes propagated using a unitary propagator with a time step \(\hbox{d}t^{\prime}=\hbox{d}t/200\). The ROHF/AS2 trajectories were propagated for 250 fs, compared to 1 ps for AS6 and AS+.

The fractional populations of the S1 state for the cis case are given in Fig. 4a. As expected, the AS2 trajectories return to the ground state much more rapidly than AS6 or AS+. The AS2 photodynamics is characterised by a delay period followed by exponential decay of the occupation of the S1 state. The best fit line is of the form

$$ f(t) = \hbox{e}^{-(t-\tau_{\rm d})/\tau_{1}} $$
(2)
Fig. 4
figure 4

Average occupation of the S1 state of PSB3 over time starting from a the cis isomer and b the trans isomer for the ROHF/AS2, ROHF/AS6 and ROHF/AS+ methods. Exponential/bi-exponential best fit lines are also plotted

Full size image

The fitting parameters are given in Table 7. The total S1 lifetime, defined as the time for the fraction of trajectories occupying the S1 state to drop to 1/e, is τd + τ1 = 63.7 fs. Just over half of the trajectories resulted in formation of the trans product, giving a quantum yield for the photoisomerisation of 0.51.

Table 7 Exponential/bi-exponential fitting parameters and quantum yield calculations for the cis and trans PSB3 photoisomerisation reactions using the ROHF/AS2, ROHF/AS6 and ROHF/AS+ methods
Full size table

The decay of the S1 population for ROHF/AS6 is clearly much slower than for AS2. Assuming that the curve is exponential, the total lifetime is over 1 ps. The quantum yield is also dramatically lower, another indication of the barrier to torsional motion.

The AS+ decay is intermediate between AS2 and AS6, but is also characterised by a more complex curve that cannot be fitted to a simple exponential decay. This is in line with the findings of Olivucci et al. [39], who used wavepacket dynamics on a simple analytic potential to show that the presence of even a small excited-state barrier (0.6 kcal mol−1) has a drastic effect on retinal model dynamics, introducing multi-exponential decay. The additional slow exponential component corresponds to trajectories that have oscillated around the planar S1 minimum due to the barrier to torsion. The S1 decay for AS+ can be fitted to a bi-exponential curve of the form

$$ f(t) = A \hbox{e}^{-(t-\tau_{\rm d})/\tau_{1}} + (1-A) \hbox{e}^{-(t-\tau_{\rm d})/\tau_{2}} $$
(3)

Although the bi-exponential decay curve is not strictly comparable with simple exponential decay, we can use a nominal S1 lifetime (again defined as the time taken for the fractional occupation to drop to 1/e) as an indication of the initial relative speed of the photodynamics. This is 305.4 fs, significantly slower than AS2 but much faster than AS6. The fraction of trajectories belonging to the fast exponential component, A, is 0.63. The quantum yield is also intermediate between AS2 and AS6. We can therefore think of the decay behaviour of the AS6 dynamics as being similar to the slow component of the AS+ dynamics.

The results for the trans form of PSB3 are given in Fig. 4b. The ROHF/AS2 curve is again of a simple exponential form, but the total lifetime is longer at 110.8 fs and the quantum yield much lower. There is no obvious explanation for these results as the MEPs are virtually symmetrical around the conical intersection point. It is presumably related to more subtle aspects of the energy surfaces which are not captured by the MEPs.

Unlike the cis form, the trans AS6 decay curve clearly has two exponential components. The S1 lifetime is also much lower at 613.9 fs. Roughly one third of the trajectories follow the fast exponential decay component. This is also reflected in the quantum yield which has risen to 0.25.

The trans population decay for AS+ is of a similar nature to AS6 but slower overall, again in contrast to the cis results. The quantum yield is also similar to AS6.

The dynamics results clearly highlight the difference between the barrierless S1 surface of ROHF/AS2, leading to simple exponential decay, and the torsional barrier of ROHF/AS6 and ROHF/AS+, leading to bi-exponential decay. There is however no straightforward answer to the question of how the change from ROHF/AS6 to ROHF/AS+ affects the PSB3 dynamics. As the level of inactive/active orbital mixing at any given point is inherently unpredictable, it is perhaps not surprising that the resulting gradient spikes lead to unpredictable changes in the results. Unlike with the optimisation calculations, there may also be a statistical effect present. Although a relatively large number of trajectories have been used in this study, the active space effects and more complex dynamics may require an even larger number to average out completely, which could explain some of the difference between AS6 and AS+.

Ab initio surface-hopping dynamics results for PSB3 are available in Refs. [5, 6, 36, 40]. In Refs. [5, 6], SA-2-CASSCF(6,6)/6-31G* dynamics is studied starting from the cis and trans isomers. The reactions are started with initial velocities sampled using the ground state vibrational modes at 0 K. 70 trajectories were calculated for the cis dynamics and 66 for trans. The photoisomerisation reaction in both cases is found to be fast and efficient, with 55% of the trajectories showing decay within 80 fs for the cis form. It is not reported whether the decay is of a simple exponential form, although this is what we would expect as the MEP is barrierless [4]. The cis lifetime is almost as short as that of the present ROHF/AS2 results, in line with our expectations. The authors state that similar results are found for the trans form. The quantum yield for both directions was found to be 0.81, much higher than any of the results obtained with OM2/GUGA-CI. This could be due to the different initial conditions, because the initial geometries and velocities in this study were generated from a 300 K dynamics run and so are likely to be more varied than those generated at 0 K from the harmonic vibrational modes. This in turn means that more of the configuration space will be sampled and so conical intersection regions will be found at lower torsional angles, leading preferentially to a return to the reactant isomer. It is also notable that the quantum yield for the AS6 and AS+ results is roughly proportional to the proportion of trajectories that decay via the fast component of the reaction, so a barrier on the S1 surface appears to favour a return to the reactant after decay to the ground state.

SA-2-CASSCF(6,6)/6-31G* calculations are also available in Ref. [36] for dynamics starting from the trans form. 30 trajectories were calculated with initial conditions again sampled using vibrational modes. The decay process is shown to be a simple delayed exponential decay, with τd = 47.5 fs and τ1 =  82.5 fs, giving a total lifetime of 130 fs. This is similar to our ROHF/AS2 results, reflecting the similarity of the MEPs of the two methods. The calculation was repeated for 90 trajectories in Ref. [40], with a lifetime of 98 fs reported, although in this case the exponential fit does not include the 22% of trajectories that did not decay within 200 fs, thereby lowering the lifetime. Barbatti et al. [40] report a quantum yield for the trans dynamics of 0.52, again higher than our ROHF results which are in the range 0.25–0.27.

In Ref. [40], results using the same method starting from the cis form are also available. 150 trajectories were run, and a lifetime of 109 fs was found (again eliminating 15% of the trajectories that failed to hop). This lifetime is significantly slower than that found for ROHF/AS2, but faster than for ROHF/AS+. The quantum yield is 0.65, rather lower than in Ref. [5]. This is possibly because the results are not converged in Ref. [5] due to the lower number of trajectories run, or possibly because of differences in the initial sampling or surface hopping algorithms.

In Refs. [33, 36], MR-CIS(4,5)/3-21G results are available for the trans form. 50 trajectories were run in Ref. [36] and 100 in Ref. [33], with reported lifetimes of 149 and 96 fs, respectively. This suggests that the value is not converged when only 50 trajectories are run. In both cases the decay is of a simple delayed exponential form, which agrees with the barrierless MEPs shown in Fig. 3 of Ref. [33].

Higher level results for the cis form are not to our knowledge available. However, it is notable that the MR-CIS and MR-CISD paths differ qualitatively for the 6-31G* basis set compared to the 3-21G basis set (as shown in Fig. 3 of Refs. [33] and [40]). A very small barrier or energy plateau is observed for 6-31G* which would presumably affect the dynamics results. This is not the case for the trans form, where no barrier is observed for either basis set.

3.4 Ab initio excited state surface scans

Although it was not feasible to run CASPT2 surface hopping dynamics calculations in this study, a first step towards understanding the dynamics can be made by examining the CASPT2 S1 potential energy surface. If the path from the planar S1 minimum to the MECP is barrierless, the dynamics will resemble the simple exponential decay of CASSCF or ROHF/AS2. If there is a barrier, we can expect the dynamics to resemble ROHF/AS6 and AS+. CASPT2 energies calculated along the CASSCF MEP do find a barrier [8], but this result does not prove that a barrier is present along the true CASPT2 path.

For technical reasons the nudged-elastic band method in DL-FIND is currently incompatible with CAS methods. However, the NEB paths for the OM2/GUGA-CI methods are qualitatively all very similar, in that the reaction coordinate is essentially the torsion angle of the central double bond, while the two parts of the system either side of the central bond remain close to planar. Therefore it should be possible to determine whether there is a barrier on the ab initio S1 surfaces using a simple PES scan around the region of the planar S1 minimum.

As a first step PES scans were performed using the OM2/GUGA-CI method to check that they were in agreement with the NEB results. Six torsional restraints were used. The major restraint was on the central C–C=C–C double bond, with a force constant of 10.0 Hartree/rad2. There were five further constraints, including the H–C=C–H torsion of the central double bond, and two pairs of torsions for the C–C bonds adjacent to the central double bond. The latter four torsions were fixed to 180°, as all the OM2/GUGA-CI NEB results gave torsional values of roughly 180° along the MEP. If these restraints were not included, the scan tended to break down as it reached strangely distorted geometries that did not correspond to the true MEP. Only a small force was needed for the five further restraints (force constant of 0.1 Hartree/rad2), which allowed the torsions to relax away from 180° to some extent.

The restraints are simple penalty functions, and the restraint energy increases as the system moves away from planarity. For very small barriers this gives a significant contribution to the height of the barrier, so the restraint energies were subtracted again to obtain the final energies.

The PES scans were calculated at 5° intervals from 0° to 35° for cis and from 180° to 145° for trans. For both sets of scans, the OM2/GUGA-CI results were quantitatively in agreement with the NEB results. The ROHF/AS2 path was again found to be barrierless, and the ROHF/AS6 and ROHF/AS+ paths again had barriers, of a similar height to the NEB result (approximately 0.01 eV higher in all cases). The small increase in the barrier heights can be explained by the fact that the PES scan is only an approximation to the true MEP.

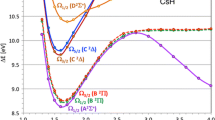
The same procedure was then repeated for CASSCF and CASPT2 using the 6-31G(d) basis set. For the cis form of CASSCF, two scans were run starting from the two CASSCF minima. The cis results are shown in Fig. 5a. The scan for CASSCF minimum 1 is characterised by a smooth barrierless descent, similar to ROHF/AS2. The scan for CASSCF minimum 2, however, features a barrier, but collapses to the same path as minimum 1 at a torsional angle of 15°. This suggests that the path via minimum 1 is favoured during dynamics, leading to the observed single exponential decay.

Fig. 5
figure 5

Constrained S1 potential energy surface scans for a the cis isomer and b the trans isomer of PSB3 using CASSCF and CASPT2. Energies (in eV) are plotted relative to the trans S0 minimum

Full size image

For CASPT2, the PES features an energy plateau from 0° to 25°. The sudden drop in energy at 30° is accompanied by a substantial change in the geometry of the system, with the central C=C bond length rising from 1.432 Å at 25° to 1.514 Å at 30°. This change is not seen for the CASSCF minimum 1 curve because the central C=C bond is already long in the planar form (1.524 Å).

Results for the trans form are given in Fig. 5b. Again for CASSCF the S1 curve is smooth and barrierless, much like ROHF/AS2. For CASPT2, an energy plateau is observed from 180° to 160°. There is an extremely small barrier with a maximum at 160°, but this is well within the margin of error of the PES scan procedure. A downward turn in the energy then begins at 155° accompanied by an increase in the central C=C bond length from 1.421 Å at 160° to 1.512 Å at 155°. Again this is not seen in the CASSCF scan because the planar form already has a long central bond length (1.519 Å).

The CASPT2 S1 cis and trans surfaces are therefore quite different to those of CASSCF and they would be expected to give different dynamics, possibly with bi-exponential decay. However, unlike ROHF/AS6 and AS+, there is no explicit barrier, and so the effect on the dynamics can be expected to be less dramatic than for those methods.

There is experimental evidence that the excited-state decay of the full retinal chromophore, both in solution [41] and in the protein environment [42–44], is multi-exponential. The results in solution have been shown to arise from a barrier on the excited-state surface [41]. It remains to be seen whether the OM2/GUGA-CI method can model this dynamics accurately, but the results for PSB3 suggest that this approach is promising.

4 Conclusions

This study has shown that the semiempirical OM2/GUGA-CI description of the PSB3 potential energy surfaces and excited state dynamics is acutely sensitive to both the choice of molecular orbitals (closed-shell or restricted open-shell) and active space. Methods using RHF orbitals have been found to give a qualitatively incorrect description of the MECP and so cannot be expected to give meaningful dynamics results. The ROHF methods perform better. The minimal ROHF/AS2 method gives results that are similar to CASSCF(6,6)/6-31G*, including similar vertical excitation energies, a barrierless MEP and single delayed exponential decay dynamics with a broadly similar lifetime. However, CASSCF is not an ideal reference, in particular for vertical excitation energies which are much lower for CASPT2/6-31G*. ROHF/AS6 and ROHF/AS+ are much closer to CASPT2 for vertical excitation energies. The MEPs for both these methods feature barriers on the S1 surface, leading to multi-exponential dynamics with a fast sub-picosecond component (similar to AS2) and a slower picosecond component. Significant barriers are not found on the corresponding CASPT2 surfaces, although the CASPT2 path was found to have an energy plateau extending over a wide range of torsional angles. This may lead to multi-exponential dynamics, although the effect is unlikely to be as pronounced as that seen for ROHF/AS6 and ROHF/AS+.