Abstract
Rationale
Even in elementary cognitive tasks, alcohol consumption results in both cognitive and motor impairments (e.g., Schweizer and Vogel-Sprott, Exp Clin Psychopharmacol 16: 240–250, 2008).
Objectives
The purpose of this study is to quantify the latent psychological processes that underlie the alcohol-induced decrement in observed performance.
Methods
In a double-blind experiment, we administered three different amounts of alcohol to participants on different days: a placebo dose (0 g/l), a moderate dose (0.5 g/l), and a high dose (1 g/l). Following this, participants performed a “moving dots” perceptual discrimination task. We analyzed the data using the drift diffusion model. Model parameters drift rate, boundary separation, and non-decision time allow a decomposition of the alcohol effect in terms of their respective cognitive components, that is, rate of information processing, response caution, and non-decision processes (e.g., stimulus encoding, motor processes).
Results
We found that alcohol intoxication causes higher mean RTs and lower response accuracies. The diffusion model decomposition showed that alcohol intoxication caused a decrease in drift rate and an increase in non-decision time.
Conclusions
In a simple perceptual discrimination task, even a moderate dose of alcohol decreased the rate of information processing and negatively affected the non-decision component. However, alcohol consumption left response caution largely intact.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Alcohol intoxication is well known to decrease performance in response time (RT) tasks (e.g., Schweizer and Vogel-Sprott, 2008). For instance, alcohol intoxication leads to higher mean RT and lower accuracy in tasks that involve response inhibition (e.g., Mulvihill et al. 1997; Easdon and Vogel-Sprott 2000; Fillmore et al. 2005; Marczinski and Fillmore 2005; Schweizer et al. 2006), response mapping (e.g., Schweizer et al. 2004), selective attention (e.g., Fillmore et al. 2000), working memory (e.g., Grattan-Miscio and Vogel-Sprott 2005), simulated driving (e.g., Burian et al. 2002), and learning (e.g., Schweizer et al. 2006).
Aside from the large body of research on the effects of alcohol on tasks involving RT, effects of alcohol intoxication on psychological processes have also been amply documented. In the context of research on alcohol intoxication, psychological processes can be usefully subdivided in cognitive processes and motor processes. With respect to the former, research has shown that alcohol intoxication impairs cognitive processing (e.g., Fillmore and van Selst 2002; Fillmore 2004). Examples include acute drops in evoked potentials in visual systems associated with the processing of motion (Neill et al. 1990), impairments in sensory processing in general (e.g., Lewis et al. 1969; MacArthur and Sekuler 1982; Hindmarch et al. 1991), decreases in memory (Maylor and Rabbitt 1987a; Saults et al. 2007), and impairments in performance monitoring (Ridderinkhof et al. 2002).
In addition to the negative effects on cognitive processes, research has also demonstrated debilitating effects of alcohol intoxication on motor processes (e.g., Drew et al. 1958; Guppy 1994; Volkow et al. 1990; Hindmarch 1980; Maylor and Rabbitt 1987b; Abroms et al. 2003; Marczinski and Fillmore 2005). Moreover, Hernandez et al. (2006) and Hernandez et al. (2007) showed that the adverse effects of alcohol intoxication on motor performance are apparent at a higher alcohol dose than the adverse effects of alcohol intoxication on cognitive performance.
Despite all this work, to date no precise quantitative account exists of the interplay between cognitive and motor processes on the performance in RT tasks after alcohol consumption. For instance, does the increase in mean RT after alcohol consumption signify a drop in information processing, a more cautious response strategy, slower motor processes, or a combination of the previous factors? And to what extent, and at which alcohol doses, do each of these psychological processes deteriorate?
One way to quantify the underlying processes that determine performance on a task is by using a cognitive process model. Cognitive process models propose concrete mechanisms that drive observed behavior; therefore, a cognitive process model is a means to translate what is observed but relatively uninformative to what is unobserved and relatively informative. An example of such a successful cognitive process model is the diffusion model for response times and accuracy (Ratcliff 1978; van Ravenzwaaij and Oberauer 2009). The diffusion model allows for a decomposition of RT data into its constituent components, such as the rate of information processing, response caution, and time needed for stimulus encoding and motor processes (i.e., response execution).
In this study, we investigate the effects of alcohol on RT performance from the perspective of the diffusion model. Specifically, we administered three different doses of alcohol to 18 psychology students in a double-blind design. We will then assess the effect of alcohol on RT and accuracy in the moving dots task, a perceptual decision-making task that is often used in neuroscience (e.g., Newsome et al. 1989; Gold and Shadlen 2007). In the moving dots task, participants have to determine whether a cloud of dots appears to move to the left or to the right. While a small proportion of the dots move coherently, a larger proportion moves randomly. We will analyze the data with the diffusion model and explore at what dose and to what extent both cognitive and non-decision processes are affected by alcohol.
The diffusion model
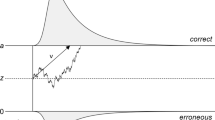
In the diffusion model for speeded two-choice tasks (Ratcliff 1978; Wagenmakers 2009; van Ravenzwaaij and Oberauer 2009), stimulus processing is conceptualized as the accumulation of noisy evidence over time. A response is initiated when the accumulated evidence reaches a predefined threshold (Fig. 1).
The diffusion model and its parameters. Evidence accumulation begins at z, proceeds over time guided by drift rate v, and halts when either the upper or the lower boundary is reached, the distance between which is boundary separation a. Observed RT is an additive combination of the time during which evidence is accumulated and the non-decision time T er. Note that non-decision time consists of stimulus encoding (prior to the decision process) and response execution (after the decision process)
The model applies to tasks in which the participant has to decide quickly between two alternatives. For instance, in the moving dots task, participants have to decide whether a cloud of dots appears to move to the left or to the right. The RTs in this task generally do not exceed 1.0 or 1.5 s.
The four key components of the diffusion model are (1) the rate of information processing, quantified by drift rate v; (2) response caution, quantified by boundary separation a; (3) a priori bias, quantified by starting point z; and (4) non-decision time, quantified by T er.
The model assumes that the decision process starts at z, after which information is accumulated with a signal-to-noise ratio that is governed by mean drift rate v. Values of v near zero produce long RTs and high error rates. Boundary separation a determines the speed–accuracy tradeoff; lowering a leads to faster RTs at the cost of a higher error rate. For the simple diffusion model, z is fixed to .5a. Together, these parameters generate a distribution of decision times DT. The observed RT, however, also consists of non-decision time T er, which in part can be subdivided in stimulus encoding (prior to the decision process) and motor execution (after the decision process). The model assumes that T er simply shifts the distribution of DT, such that RT = DT + T er (Luce 1986). The full model includes parameters that specify across-trial variability in drift rate, η, starting point, s z, and non-decision time, s t, (e.g., Ratcliff and Tuerlinckx 2002). For the remainder of this paper, we will be working with the simple “EZ” diffusion model that uses the mean and variance of the RT and the error rate to calculate v, a, and T er (Wagenmakers et al. 2007).Footnote 1
The main advantages of a diffusion model analysis are twofold. First, the model takes into account entire RT distributions, both for correct and incorrect responses. Second, the model allows researchers to decompose observed RTs and error rates into latent psychological processes.
The diffusion model has been successfully applied to a wide range of experimental paradigms, including perceptual discrimination, letter identification, lexical decision, recognition memory, implicit association, and signal detection (e.g., Ratcliff 1978; Ratcliff et al. 2004a, b; Klauer et al. 2007; Wagenmakers et al. 2008; van Ravenzwaaij et al. 2011; Ratcliff et al. 2010).
Recently, the diffusion model has also been used in more clinical settings. For instance, research on the effects of sleep deprivation by Ratcliff and van Dongen (2009) showed that following sleep deprivation, information processing is negatively affected (evident in a decrease in drift rate), and people respond somewhat more cautiously (evident in a slight increase in boundary separation), presumably in an attempt to compensate for the lower rate of information processing. In a study on the effects of incorrect responses on people with different trait levels of anxiety by White et al. (2010), it was concluded that following an error, high-anxiety people respond more cautiously (evident in an increase in boundary separation), whereas low-anxiety people did not. Recently, work has been done to map diffusion model estimates on neurological correlates, such as neural firing rates of monkeys (Ratcliff et al. 2007) and EEG components of humans (Philiastides et al. 2006).
While the detrimental effects of alcohol on observed data from perceptual discrimination are known, a precise quantification of the interplay of these underlying processes is as yet unknown. For this particular experiment, multiple hypotheses could be entertained. One possibility is that alcohol only affects the cognitive component, indicated by a decrease in the information processing parameter drift rate. Alternatively, alcohol could negatively affect the motor component, indicated by a decrease in the non-decision time parameter. Hernandez et al. (2007) showed that alcohol intake affects cognitive processes at lower doses, but motor processes at higher doses. A decrease in boundary separation (i.e., response caution) with alcohol intake would also be possible as alcohol intake is known to increase risk taking (e.g., Burian et al. 2002). Of course, any combination of these effects is possible.
Method
Participants
Eighteen male students from the University of Amsterdam, aged 18 to 25, participated in all three conditions in exchange for a monetary reward of 80 euros. Participants were screened for health problems, alcohol and drug abuse.Footnote 2
Materials
The amount of alcohol administered to participants was based on Widmark’s Formula:
where BAC is the blood alcohol concentration (in grams per liter), A is the weight of the alcohol consumed since the commencement of drinking (in grams), W is the weight of the person (in kilograms), r is the alcohol distribution ratio (in liters per kilogram), which is on average 0.68 for men, t is the amount of hours elapsed since the commencement of drinking, and ζ is the decay factor (Watson et al. 1981). Each participant returned to the lab for three different sessions. In three sessions, the participant was assigned to one of three conditions (counterbalanced and double blind): the placebo condition (0 g/l BAC), the moderate condition (0.5 g/l BAC), and the high condition (1 g/l BAC). This led to six possible orders of administration, with three participants per order.
Pilot work showed ζ to be approximately 0.15. We administered vodka that contains 37.5% alcohol. An amount of vodka of 100 ml contained 37.5 ml of alcohol, which is approximately 30 g. Thus, each participant was required to drink an amount of vodka (in milliliters) equal to 1.28 times their body weight (in kilograms) in the moderate condition and double that amount in the high condition. For example, a man weighing 70 kg would be required to drink 90 ml of vodka in the tipsy condition and 180 ml of vodka in the drunk condition.
Participants were required to drink two 0.4-l milkshake cups of fluid. Both cups consisted of half the amount of vodka the participant had to consume, then filled up with multifruit juice. On top of all these, six drops of mint oil was added, as earlier tests had shown this to mask both the taste and the scent of the alcohol.
Procedure
The whole experiment was administered by two experimenters. Experimenter #1 would supervise the entire session, while experimenter #2 prepared the alcoholic drinks and administered the breathalyzer measurements. Each participant started the experiment at 3 p.m. Upon entering, the participant was welcomed by experimenter #1. If it was the participant’s first session, the participant received a general instruction about the procedure and signed an informed consent form. Then, the participant was asked whether he had drank alcohol the night before, whether he had a light lunch, and whether he had consumed any tea, coffee, or cola earlier that day (the required answers were no, yes, no). Next, experimenter #2 entered to administer the first breathalyzer measurement to the participant. If the BAC read 0 (which it invariably did), the participant was given his first milkshake cup by experimenter #2, who then left. To finish the first cup, the participant was allowed 15 min, after which the second cup was brought in. The participant was allowed 30 min to finish the second cup. After finishing the two cups, the participant received a glass of water and was required to wait for another 20 min for the alcohol to take its full effect. During the consumption of the alcoholic beverages and the following 20 min, the participant could choose to watch either a Lion King DVD or a David Attenborough DVD. After this, experimenter #1 momentarily left and experimenter #2 administered a second breathalyzer measurement. The participant then completed the moving dots task (25 to 45 min after alcohol consumption). Subsequently, experimenter #1 momentarily left and experimenter #2 administered a third breathalyzer measurement. Participants then completed a task designed to measure risk taking: the Balloon Analogue Risk Task, or BART, the results of which are published elsewhere (van Ravenzwaaij et al. 2011). Finally, a last breathalyzer measure (experimenter #2) and an unrelated task (experimenter #1) were administered. Upon completion of the experiment, the participant was delivered home by taxi.
Task
The task was administered on a 17-in. screen (resolution, 1,280 × 1,024 pixels). Participants were seated approximately 80 cm from the screen. In each of the three sessions, a moving dots task was administered with two blocks of 200 trials each. On every trial, the stimulus consisted of 120 dots, 40 of which moved coherently and 80 of which moved randomly. After each 50-ms frame, the 40 coherently moving dots moved 1 pixel in the target direction. The other 80 dots were relocated randomly. On the subsequent frame, each dot might switch roles, with the constraint that there were always 40 dots moving coherently between a given set of frames. This setup elicits the impressions of the cloud of dots moving systematically in one direction, even though the cloud remains centered. Each dot consisted of 3 pixels, the entire cloud of dots was 250 pixels. Pixels were uniformly distributed over this pixel range.
Participants indicated their response by pressing one of two buttons with their left or right index finger. Prior to each stimulus, a fixation cross was displayed for an interval chosen at random out of 500, 800, 1,000 or 1,200 ms. Subsequent to fixation, participants had 1,500 ms to view the stimulus and give a response. The stimulus disappeared as soon as a response was made. If, for a given trial, the participant’s response was slower than 1,000 ms, participants saw the message “too slow” at the end of the trial. The moving dots task took approximately 20 min.
Results
The mean number of days between sessions for participants was 11.1 (SD = 8.6); participants never had two sessions on adjoining days. Prior to administration of the moving dots task, breathalyzer measurements showed a mean reading of 0 (SD = 0), 0.32 (SD = 0.10), and 0.91 g/l (SD = 0.16) BAC for the placebo, moderate, and high conditions, respectively. Directly after administration of the moving dots task, breathalyzer measurements showed a mean reading of 0 (SD = 0), 0.28 (SD = 0.09), and 0.88 g/l (SD = 0.13) BAC for the placebo, moderate, and high conditions, respectively. In the next two subsections, we will first present the behavioral results (mean RT and accuracy) and then the modeling results.
Behavioral results
For each participant, we excluded all RTs below 275 ms as these were unlikely to be non-guessing responses. This led to the exclusion of 0.5% of all RTs. Figure 2 shows the within-subject effects for mean RT and accuracy. For the presented post hoc analyses, we report Bayesian posterior probabilities in addition to conventional p values. When we assume, for fairness, that the null hypothesis and the alternative hypothesis are equally plausible a priori, a default Bayesian t test (Rouder et al. 2009) allows one to determine the posterior plausibility of the null hypothesis and the alternative hypothesis. We denote the posterior probability for the null hypothesis as p Bayes H0. When, for example, p Bayes H0 = .9, this means that the plausibility for the null hypothesis has increased from .5 to .9. Posterior probabilities avoid the problems that plague p values, allow one to directly quantify evidence in favor of the null hypothesis, and arguably relate more closely to what researchers want to know (e.g., Wagenmakers 2007).
For mean RT, a higher alcohol dose led to higher mean RTs, with mean RTs of 440, 465, and 476 for the placebo, the moderate, and the high condition, respectively (F(2,28) = 11.82, p < .001). A paired t test revealed that the increase from placebo to moderate (t(17) = 2.48, p < .05, p Bayes H0 = .31) and the increase from placebo to high (t(17) = 4.70, p < .001, p Bayes H0 = .01) were significant, although only the latter contrast was convincing according to the Bayesian t test. Mean RTs were lower for later sessions, with mean RTs of 479, 448, and 454 for sessions 1, 2, and 3, respectively (F(2,28) = 9.34, p < .001), indicating a practice effect. A paired t test revealed that only the decrease from session 1 to session 2 (t(17) = 3.99, p < .001, p Bayes H0 = .03) was significant.
For response accuracy, a higher alcohol dose led to more errors, with accuracies of 96.3%, 95.7%, and 94.3% for the placebo, the moderate, and the high condition, respectively (F(2,28) = 6.47, p < .01). A paired t test revealed that the difference between moderate and high (t(17) = 2.27, p < .05, p Bayes H0 = .39) and the difference between placebo and high (t(17) = 3.63, p < .01, p Bayes H0 = .05) were significant, although only the latter contrast was convincing according to the Bayesian t test. No significant training effect on accuracy could be established.
In sum, we found that alcohol increased mean RT from 440 to 476 ms. from placebo to high, which is a normal mean RT effect for these alcohol doses (e.g., MacArthur and Sekuler 1982). We also found that alcohol decreased accuracy up to 2% for the high dose.
While informative, these results do not tell us what underlying psychological processes are responsible for the drop in performance. In order to answer this question, we now turn to the diffusion model analyses.
Diffusion model results
In order to fit the diffusion model to the data, we used a range of fitting routines, including DMAT (Vandekerckhove and Tuerlinckx 2007), fast-dm (Voss and Voss 2007, 2008), and a Bayesian diffusion model (Vandekerckhove et al. 2011). Ultimately, it turned out that the simple “EZ” algorithm (Wagenmakers et al. 2007; for applications, see e.g., Schmiedek et al. 2007; Schmiedek et al. 2009; Kamienkowski et al. 2011) provided the best fitting diffusion parameters. The EZ algorithm takes as input RT mean, RT variance, and percentage correct, and computes from these the three key diffusion model parameters drift rate v, boundary separation a, and non-decision time T er. The EZ diffusion model parameters are computed such that the error rate is described perfectly. EZ calculates diffusion model parameters for each participant and each condition separately. Effects on the diffusion model parameters are displayed in Fig. 3.
The top panels of the figure show within-subject effects of alcohol dose, and the bottom panels show within-subject effects of session. The left panels display alcohol and training effects on the drift rate parameter v. For drift rate, a higher alcohol dose led to a lower rate of information processing (F(2,28) = 13.08, p < .001). A paired t test revealed that the decrease from moderate to high (t(17) = 2.66, p < .05, p Bayes H0 = .19) and the decrease from placebo to high (t(17) = 4.96, p < .001, p Bayes H0 < .001) were significant. Information processing was higher for later sessions (F(2,28) = 8.08, p < .01), indicating a practice effect. A paired t test revealed that the increase from session 1 to session 2 (t(17) = 2.78, p < .05, p Bayes H0 = .16) and the increase from session 1 to session 3 (t(17) = 2.66, p < .05, p Bayes H0 = .19) were significant.
The middle panels display alcohol and training effects on the boundary separation parameter a. For boundary separation, no alcohol effect could be established. Also, participants did not respond more or less cautiously in later session.
The right panels display alcohol and training effects on the non-decision time parameter T er. For non-decision time, a higher alcohol dose led to slower non-decision processes (F(2,28) = 10.61, p < .001). A paired t test revealed that the increase from moderate to high (t(17) = 3.52, p < .01, p Bayes H0 = .04) and the increase from placebo to high (t(17) = 3.90, p < .01, p Bayes H0 = .01) were significant. The 19 ms increase in T er accounts for about 54% of the effect of alcohol on RT from the placebo to the high condition. No training effect on non-decision time could be established.
In sum, the increase in RT and the lower accuracy for higher alcohol doses seem to be caused by a decreased rate of information processing, reflected by lower values of the drift rate parameter. In addition to the effect of information processing, the higher RTs are likely to be caused by a slowdown of motor processes, reflected by an increase in the non-decision time parameter.
Model predictives
In cognitive modeling, model fit can be assessed by means of model predictives. Model predictives are simulated data generated from the cognitive model, based on the parameter estimates for the real data. If the generated data closely resemble the real empirical data, then the model fit is deemed adequate (e.g., Gelman and Hill 2007).
For this experiment, we used the diffusion model parameter estimates of v, a, and T er for each participant and each condition separately to generate 10,000 RT trials each. We then calculated the 0.1, 0.3, 0.5, 0.7, and 0.9 RT quantiles for both the real data set and the simulated data set and compared these. The real and simulated RT quantiles can be compared in Fig. 4.
Figure 4 shows a quantile probability plot (e.g., Ratcliff 2002), where the left-hand side represents error RTs for the five quantiles, and the right-hand side represents correct RTs for those same quantiles. The outermost points represent the placebo condition, the ones next to them represent the moderate condition, and the innermost points represent the high condition. The black symbols in the figure show the empirical data, and the gray dots are the simulated data that were generated using the best-fitting parameter estimates.
For response accuracy, the correspondence between the empirical data and the synthetic data can be judged by the horizontal disparity between the data points and the model points. Figure 4 shows that the diffusion model captures the error rate very well, as is expected from the EZ transformation rules. The right part of Fig. 4 shows that the correct RTs of the empirical data and the synthetic data are very close to each other (e.g., the vertical disparity is small), indicating that the diffusion model describes the data well.
The model fit for the error RTs is much worse than the fit for the correct RTs. This is not surprising as participants had an average error rate of less than 5%, meaning that five quantiles had to be computed from fewer than 20 observations per participant. The relatively large statistical uncertainty about the error RT quantiles partly explains the relatively poor correspondence between the real and the simulated data for the error responses (see also e.g., Ratcliff et al. 2004b, 2010). Another reason for the misfit is that the EZ algorithm predicts that error RTs are just as fast as correct RTs; in the data, error RTs appear to be systematically faster. This aspect of the data can be captured by variability in the starting point of information accumulation (see e.g., Ratcliff and Rouder 1998); however, with a low 5% error rate the inclusion of extra parameters turned out to be problematic, and for more complicated models, predictive performance suffered. It is of note that for 95% of the RT data, the model fit is very good. The only information the EZ algorithm receives about the RT distribution is its variance, and Fig. 4 shows that the model nonetheless captures the shape of the entire RT distribution.
Concluding comments
In this study, we decomposed the alcohol-induced performance decrement into meaningful psychological processes. This was achieved by fitting the diffusion model on RT data from the moving dots task, administered to participants on three separate occasions. The three test moments differed in the amount of alcohol participants had consumed prior to the start of the experiment.
The results showed that participants slowed down 36 ms from a sober state to a state in which participants have a blood alcohol concentration of 1 g/l. Their error rate also increased by 2%. Consistent with the behavioral findings of Fillmore and van Selst (2002) and Fillmore (2004), our diffusion model analysis revealed that the relatively poor performance following alcohol intake is partly caused by a lower drift rate, signifying a decrease in the rate of information processing. Furthermore, we replicated the often-found deterioration of motor behavior following alcohol intake (e.g., Drew et al. 1958), which in our diffusion model corresponded to an alcohol-induced increase in non-decision time. Our results are also consistent with the finding by Hernandez et al. (2006) and Hernandez et al. (2007) that the negative effects of alcohol on motor processes manifest itself at a higher alcohol dose than the negative effects on cognitive performance.
The novelty of our study lies in the diffusion model analysis of the data, which allowed for a precise quantification of the contribution of both the cognitive and the non-decisional aspects of decision making on the performance following alcohol intake. In this study, we found that the non-decision component accounted for approximately 54% of the alcohol-induced RT increase, whereas the remaining 46% was accounted for by a decrease in the rate of information processing.
One may wonder whether alcohol always affects drift rate and non-decision time without affecting boundary separation (i.e., the response caution parameter). It stands to reason that this is not the case; in certain situations, people might realize that they are negatively affected by alcohol and correspondingly adjust their boundary separation. Of course, this might also happen when people incorrectly assume they are under influence of alcohol.
Without a detailed examination of RT distributions, both for correct and error responses, it is impossible to assess separately the effects of alcohol on the rate of information processing, response caution, and non-decision processes. This study highlights an important advantage of cognitive modeling. Instead of just detecting a decrease in performance, cognitive modeling allows a researcher to directly relate performance decrements to their constituent cognitive components.
Notes
The simple, or EZ, diffusion model is particularly suitable for sparse data with up to 400 observations per participant. Estimating the full diffusion model for this number of trials causes numerical instability.
We only tested men in order to preclude confounding effects due to the menstrual cycle (e.g., Linnoila et al. 1980).
References
Abroms BD, Fillmore MT, Marczinski CA (2003) Alcohol-induced impairment of behavioral control: effects on the alteration and suppression of prepotent responses. J Stud Alcohol 64:687–696
Burian SE, Liguori A, Robinson JH (2002) Effects of alcohol on risk-taking during simulated driving. Hum Psychopharmacol 17:141–150
Drew GC, Colquhoun WP, Long HA (1958) Effects of small doses of alcohol on a skill resembling driving. Br Med J 2:993–999
Easdon C, Vogel-Sprott M (2000) Alcohol and behavioral control: impaired response inhibition and flexibility in social drinkers. Exp Clin Psychopharmacol 8:387–394
Fillmore MT (2004) Environmental dependence of behavioral control mechanisms: effects of alcohol and information processing demands. Exp Clin Psychopharmacol 12:216–223
Fillmore MT, van Selst M (2002) Constraints on information processing under alcohol in the context of response execution and response suppression. Exp Clin Psychopharmacol 10:417–424
Fillmore MT, Dixon MJ, Schweizer TA (2000) Alcohol affects processing of ignored stimuli in a negative priming paradigm. J Stud Alcohol 61:571–578
Fillmore MT, Marczinski CA, Bowman AM (2005) Acute tolerance to alcohol effects on inhibitory and activational mechanisms of behavioral control. J Stud Alcohol 66:663–672
Gelman A, Hill J (2007) Data analysis using regression and multilevel/hierarchical models. Cambridge University Press, Cambridge
Gold JI, Shadlen MN (2007) The neural basis of decision making. Annu Rev Neurosci 30:535–574
Grattan-Miscio KE, Vogel-Sprott M (2005) Effects of alcohol and performance incentives on immediate working memory. Psychopharmacology 181:188–196
Guppy A (1994) At what blood alcohol concentration should drink–driving be illegal. Br Med J 308:1055–1056
Hernandez OH, Vogel-Sprott M, Huchin-Ramirez TC, Ake-Estrada F (2006) Acute dose of alcohol affects cognitive components of reaction time to an omitted stimulus: differences among sensory systems. Psychopharmacology 184:75–81
Hernandez OH, Vogel-Sprott M, Ke-Aznar VI (2007) Alcohol impairs the cognitive component of reaction time to an omitted stimulus: a replication and an extension. J Stud Alcohol Drugs 68:276–281
Hindmarch I (1980) Psychomotor function and psychoactive drugs. Br J Clin Pharmacol 10:189–209
Hindmarch I, Kerr JS, Sherwood N (1991) The effects of alcohol and other drugs on psychomotor performance and cognitive function. Alcohol Alcohol 26:71–79
Kamienkowski JE, Pashler H, Dehaene S, Sigman M (2011) Effects of practice on task architecture: combined evidence from interference experiments and random-walk models of decision making. Cognition 119:81–95
Klauer KC, Voss A, Schmitz F, Teige-Mocigemba S (2007) Process components of the implicit association test: a diffusion-model analysis. J Pers Soc Psychol 93:353–368
Lewis EG, Dustman RE, Beck EC (1969) The effect of alcohol on sensory phenomena and cognitive and motor tasks. Q J Stud Alcohol 30:618–633
Linnoila M, Erwin CW, Ramm D, Cleveland WP, Brendle A (1980) Effects of alcohol on psychomotor performance of women: interaction with menstrual cycle. Alcohol Clin Exp Res 4:302–305
Luce RD (1986) Response times. Oxford University Press, New York
MacArthur RD, Sekuler R (1982) Alcohol and motion perception. Percept Psychophys 31:502–505
Marczinski CA, Fillmore MT (2005) Compensating for alcohol-induced impairment of control: effects on inhibition and activation of behavior. Psychopharmacology 181:337–346
Maylor EA, Rabbitt PMA (1987a) Effect of alcohol on rate of forgetting. Psychopharmacology 91:230–235
Maylor EA, Rabbitt PMA (1987b) Effects of practice and alcohol on performance of a perceptual-motor task. Q J Exp Psychol 39:777–795
Mulvihill LE, Skilling TA, Vogel-Sprott M (1997) Alcohol and the ability to inhibit behavior in men and women. J Stud Alcohol 58:600–605
Neill RA, Delahunty AM, Fenelon B (1990) Discrimination of motion in depth trajectory following acute alcohol ingestion. Biol Psychol 31:1–22
Newsome WT, Britten KH, Movshon JA (1989) Neuronal correlates of a perceptual decision. Nature 341:52–54
Philiastides MG, Ratcliff R, Sajda P (2006) Neural representation of task difficulty and decision-making during perceptual categorization: a timing diagram. J Neurosci 26:8965–8975
Ratcliff R (1978) A theory of memory retrieval. Psychol Rev 85:59–108
Ratcliff R (2002) A diffusion model account of response time and accuracy in a brightness discrimination task: fitting real data and failing to fit fake but plausible data. Psychon Bull Rev 9:278–291
Ratcliff R, Rouder JN (1998) Modeling response times for two-choice decisions. Psychol Sci 9:347–356
Ratcliff R, Tuerlinckx F (2002) Estimating parameters of the diffusion model: approaches to dealing with contaminant reaction times and parameter variability. Psychon Bull Rev 9:438–481
Ratcliff R, van Dongen HPA (2009) Sleep deprivation affects multiple distinct cognitive processes. Psychon Bull Rev 16:742–751
Ratcliff R, Gomez P, McKoon G (2004a) Diffusion model account of lexical decision. Psychol Rev 111:159–182
Ratcliff R, Thapar A, McKoon G (2004b) A diffusion model analysis of the effects of aging on recognition memory. J Mem Lang 50:408–424
Ratcliff R, Hasegawa YT, Hasegawa YP, Smith PL, Segraves MA (2007) Dual diffusion model for single-cell recording data from the superior colliculus in a brightness-discrimination task. J Neurophysiol 97:1756–1774
Ratcliff R, Thapar A, McKoon G (2010) Individual differences, aging, and IQ in two-choice tasks. Cogn Psychol 60:127–157
Ridderinkhof KR, de Vlugt Y, Bramlage A, Spaan M, Elton M, Snel J, Band GPH (2002) Alcohol consumption impairs detection of performance errors in mediofrontal cortex. Science 298:2209–2211
Rouder JN, Speckman PL, Sun D, Morey RD, Iverson G (2009) Bayesian t-tests for accepting and rejecting the null hypothesis. Psychon Bull Rev 16:225–237
Saults JS, Cowan N, Sher KJ, Moreno MV (2007) Differential effects of alcohol on working memory: distinguishing multiple processes. Exp Clin Psychopharmacol 15:576–587
Schmiedek F, Oberauer K, Wilhelm O, Süß H-M, Wittmann WW (2007) Individual differences in components of reaction time distributions and their relations to working memory and intelligence. J Exp Psychol Gen 136:414–429
Schmiedek F, Lövdén M, Lindenberger U (2009) On the relation of mean reaction time and intraindividual reaction time variability. Psychol Aging 24:841–857
Schweizer TA, Vogel-Sprott M (2008) Alcohol-impaired speed and accuracy of cognitive functions: a review of acute tolerance and recovery of cognitive performance. Exp Clin Psychopharmacol 16:240–250
Schweizer TA, Jolicoeur P, Vogel-Sprott M, Dixon MJ (2004) Fast, but error-prone, responses during acute alcohol intoxication: effects of stimulus-response mapping complexity. Alcohol Clin Exp Res 28:643–649
Schweizer TA, Vogel-Sprott M, Danckert J, Roy EA, Skakum A, Broderick CE (2006) Neuropsychological profile of acute alcohol intoxication during ascending and descending blood alcohol concentrations. Neuropsychopharmacology 31:1301–1309
van Ravenzwaaij D, Oberauer K (2009) How to use the diffusion model: parameter recovery of three methods: EZ, fast-dm, and DMAT. J Math Psychol 53:463–473
van Ravenzwaaij D, Dutilh G, Wagenmakers E-J (2011a) Cognitive model decomposition of the BART: assessment and application. J Math Psychol 55:94–105
van Ravenzwaaij D, van der Maas HLJ, Wagenmakers E-J (2011b) Does the name-race implicit association test measure racial prejudice? Exp Psychol 58(4):271–277
Vandekerckhove J, Tuerlinckx F (2007) Fitting the Ratcliff diffusion model to experimental data. Psychon Bull Rev 14:1011–1026
Vandekerckhove J, Tuerlinckx F, Lee MD (2011) Hierarchical diffusion models for two-choice response times. Psychol Meth 16(1):44–62
Volkow ND, Hitzemann R, Wolf AP, Logan J, Fowler JS, Christman D, Dewey SL, Schyler D, Burr G, Vitkun S, Hirschowitz J (1990) Acute effects of ethanol on regional brain glucose metabolism and transport. Psychiatry Res: Neuroimaging 35:39–48
Voss A, Voss J (2007) Fast–dm: a free program for efficient diffusion model analysis. Behav Res Methods 39:767–775
Voss A, Voss J (2008) A fast numerical algorithm for the estimation of diffusion model parameters. J Math Psychol 52:1–9
Wagenmakers E-J (2007) A practical solution to the pervasive problems of p-values. Psychon Bull Rev 14:779–804
Wagenmakers E-J (2009) Methodological and empirical developments for the Ratcliff diffusion model of response times and accuracy. Eur J Cogn Psychol 21:641–671
Wagenmakers E-J, van der Maas HL, Grasman RPPP (2007) An EZ-diffusion model for response time and accuracy. Psychon Bull Rev 14:3–22
Wagenmakers E-J, Ratcliff R, Gomez P, McKoon G (2008) A diffusion model account of criterion shifts in the lexical decision task. J Mem Lang 58:140–159
Watson PE, Watson ID, Batt RD (1981) Prediction of blood alcohol concentrations in human subjects. J Stud Alcohol 42:547–556
White C, Ratcliff R, Vasey MW, McKoon G (2010) Using diffusion models to understand clinical disorders. J Math Psychol 54:39–52
Acknowledgment
This research was supported by a Vidi grant (grant number 452-06-009) from the Dutch Organization for Scientific Research (NWO).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
van Ravenzwaaij, D., Dutilh, G. & Wagenmakers, EJ. A diffusion model decomposition of the effects of alcohol on perceptual decision making. Psychopharmacology 219, 1017–1025 (2012). https://doi.org/10.1007/s00213-011-2435-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00213-011-2435-9