Introduction

It has long been suspected that the nucleus accumbens core (AcbC) plays a pivotal role in the control of operant behaviour by reinforcers. Early evidence appeared to support the suggestion that the AcbC and its dopaminergic afferents mediate the reinforcing value of both ‘natural’ rewards and drugs of abuse (see Wise 1981; Koob 1992). However, recent evidence indicates that the role of the AcbC in reinforcement may be less straightforward than was originally thought. For example, the deleterious effect of destroying the AcbC or its dopaminergic afferents on food-motivated responding has been found to depend critically on the response cost associated with obtaining a reinforcer, leading to the suggestion that the AcbC may play a particular role in regulating the voluntary expenditure of effort (see Salamone et al. 2002, 2007).

Another aspect of motivated behaviour in which the AcbC appears to play an important role is the control of behaviour by delayed reinforcers (see Cardinal et al. 2003; Schultz 2006). Cardinal et al. (2001) examined the effect of lesions of the AcbC on rats’ choices between small immediately available reinforcers and larger delayed reinforcers. AcbC-lesioned rats showed reduced preference for the larger delayed reward, leading Cardinal et al. (2001, 2003) to propose that destruction of the AcbC increased the rate of ‘delay discounting’ (i.e. the degradation of reinforcer value as a function of delay to reinforcement: Ainslie 1975; Mazur 1987, 1997). Although Cardinal et al.’s (2001) findings did not exclude the possibility that the lesion reduced the relative incentive value of the larger reinforcer (see Cardinal et al. 2003), the results of a recent experiment by Bezzina et al (2007) provided support for Cardinal et al.’s proposal. Bezzina et al.’s (2007) experiment was based on a mathematical model of inter-temporal choice that provides separate indices of delay discounting and instantaneous reinforcer value (Ho et al. 1999); their results suggested that destruction of the AcbC altered the delay discounting parameter, without affecting the instantaneous values of food reinforcers.

The aim of the present experiment was to provide further evidence relevant to the question of whether destruction of the AcbC alters instantaneous reinforcer value, using a progressive ratio schedule of food reinforcement (Hodos 1961; Hodos and Kalman 1963). In this schedule, the number of responses required to earn a reinforcer (the response/reinforcer ratio) increases progressively with successive reinforcers. The traditional measure of performance on this schedule is the ratio at which responding ceases for some pre-defined period (the ‘breakpoint’: Hodos 1961; Baron et al. 1992; Stafford and Branch 1998), or alternatively the highest ratio completed within a time-limited experimental session (Aberman et al. 1998; Hamill et al. 1999; Ho et al. 2003; Weatherley et al. 2003). The popularity of the progressive ratio schedule in behavioural pharmacology is no doubt related to the widely accepted interpretation of the breakpoint or highest completed ratio as an index of the subject’s motivational state (Ferguson and Paule 1997; Barr and Philips 1999; Bowman and Brown 1998), or the incentive value of the reinforcer (Hodos 1961; Cheeta et al. 1995), an interpretation that is supported by reports that the breakpoint is sensitive to changes in deprivation level and reinforcer size (Skjoldager et al. 1993; Ferguson and Paule 1997; Sclafani and Ackroff 2003). There are, however, significant problems with the use of the breakpoint as an index of motivation or reinforcer value, including the sensitivity of this parameter to ‘non-motivational’ manipulations such as changes in the response requirement (Stewart 1975; Skjoldager et al. 1993; Aberman et al. 1998) and the ratio step size (Stafford and Branch 1998). Fortunately, this problem may be circumvented by the application of a quantitative model of ratio-schedule performance (Killeen 1994, 1998), which takes into account the response rate in each component ratio of the schedule. This model is derived from a general theory of schedule-controlled behaviour, the mathematical principles of reinforcement (MPR: Killeen 1994), which is founded on fundamental postulates relating to the incentive value of reinforcers and the efficiency with which particular reinforcement schedules couple operant responses to reinforcers. In the case of fixed-ratio schedules, in which N responses are required for each reinforcer delivery, response rate, R, is predicted by

$$R = \frac{\zeta }{\delta } - \frac{N}{a},\;where\;\zeta = 1 - \left( {1 - \beta } \right)^N ;a,\delta > 0;0 < \beta < 1.$$
(1)

The parameter β (currency) represents the extent to which the strengthening effect of the reinforcer is focussed on the most recent response, δ (response time) is the reciprocal of the maximum response rate, and a (specific activation) is the time for which a reinforcer is able to activate behaviour (Fig. 1). The last of these parameters, a, provides an index of reinforcer efficacy or ‘value’ (Killeen 1994; Killeen and Sitomer 2003; Reilly 2003). The link between the concepts of behavioural activation and incentive value arises from Killeen’s (1982, 1985) observation that behaviour is activated by reinforcers (incentives) in proportion to the rate of reinforcement; in Killeen’s (1994) model, a specifies the duration of activation induced by a single reinforcer delivery. According to MPR, the characteristic shapes of the response rate functions generated by different schedules of reinforcement derive from biological constraints on responding (specified as the minimum response time, δ) and the efficiency with which the schedule couples reinforcers to the measured behaviour (reflected in ζ, and hence also in β). Consistent with the interpretation of a as an index of reinforcer value, it has been demonstrated that this parameter is sensitive to manipulation of reinforcer size and quality (Bizo and Killeen 1997; Reilly 2003). Reilly (2003) has recently recommended the use of a to construct a quantitative scale of reinforcer value. Although Equation 1 was originally proposed as a model of fixed-ratio performance (Killeen 1994), it also provides a good description of performance on progressive-ratio schedules, and has been used to evaluate the effects of centrally acting drugs (Mobini et al. 2000; Reilly 2003; Ho et al. 2003; Zhang et al. 2005a, b) and cerebral lesions (Kheramin et al. 2005) on reinforcer efficacy.

Fig. 1
figure 1

Fit of Equation 1 to data obtained from one rat responding on the progressive-ratio schedule, illustrating the derivation of the parameters. Ordinate: response rate; abscissa: response/reinforcer ratio (N). Points are mean overall response rates, averaged across ten sessions; the curve is defined by Equation 1 (parameter values: see inset). The (projected) point of intersection of the function with the ordinate is at R = 1/δ; the slope of the descending limb of the function is −1/a. Note that the data-point represented by the open symbol was excluded from the function-fitting (see text)

Full size image

Materials and methods

The experiment was carried out in accordance with UK Home Office regulations governing experiments on living animals.

Subjects

Thirty experimentally naive female Wistar rats approximately 4 months old and weighing 250–300 g at the start of the experiment were used. They were housed under a constant cycle of 12 h light and 12 h darkness (light on 0600–1800 hours), and were maintained at 80% of their initial free-feeding body weights throughout the experiment by providing a limited amount of standard rodent diet after each experimental session. Tap water was freely available in the home cages.

Surgery

The rats received either lesions of the AcbC (n = 16) or sham lesions (n = 14). Anaesthesia was induced with isoflurane (4% in oxygen), and the rat positioned in a stereotaxic apparatus (David Kopf), with the upper incisor bar set 3.3 mm below the inter-aural line. Anaesthesia was maintained with 2% isoflurane in oxygen during surgery. A small hole was drilled in the skull over each hemisphere for microinjection of quinolinic acid into the AcbC. The following coordinates (mm, measured from bregma) were used to locate the AcbC: AP +1.2, L  ± 1.8, V -7.1 (mm, measured from bregma: Paxinos and Watson 1998). Injections were given via a 0.3-mm diameter cannula connected by a polyethylene tube to a 10-μl Hamilton syringe. In the case of the lesioned group, the cannula tip was slowly lowered to the position of each site and 0.5 μl of a 0.1 M solution of quinolinic acid (2,3-pyridinedicarboxylic acid) in phosphate-buffered 0.9% NaCl (pH 7.0) was injected at a rate of 0.1 μ1 per 15 s. The cannula was left in its position for 3 min after completion of the injection in each site. In the case of the sham-lesioned group, the procedure was identical, except that the vehicle alone was injected.

Apparatus

The rats were trained in custom built operant conditioning chambers of internal dimensions 20 × 23 × 22.5 cm. One wall of the chamber contained a recess into which a motor-operated dispenser could deliver 45-mg food pellets. An aperture was situated 5 cm above and 2.5 cm to the left of the recess; a motor-operated retractable lever could be inserted into the chamber through this aperture. The lever could be depressed by a force of approximately 0.2 N. The chamber was enclosed in a sound-attenuating chest; masking noise was provided by a rotary fan. An Acorn 5000 microcomputer and interface unit (Paul Fray), programmed in ARACHNID BASIC and located in an adjoining room, controlled the schedules and recorded the behavioural data.

Behavioural training

Two weeks after surgery, the food deprivation regimen was introduced and the rats were gradually reduced to 80% of their free-feeding body weights. Then they were trained to press the lever for a food pellet reinforcer (45 mg), and were exposed to a fixed-ratio one schedule for 3 days, followed by a fixed-ratio five schedule for 3 days. Thereafter, they underwent daily training sessions under the progressive-ratio schedule. The progressive-ratio schedule was based on the following exponential progression: 1, 2, 4, 6, 9, 12, 15, 20, 25, 32, 40, 50, ..., derived from the formula \(\left[ {\left( {5 \times e^{0.2n} } \right) - 5} \right]\), rounded to the nearest integer, where n is the position in the sequence of ratios (Roberts and Richardson 1992). Sessions took place at the same time each day during the light phase of the daily cycle (between 0800 and 1400 hours) 7 days a week. At the start of each session, the lever was inserted into the chamber; the session was terminated by withdrawal of the lever 50 min later. The experiment consisted of three phases: in phase 1 (90 sessions), the reinforcer was a single 45-mg food pellet, in phase 2 (30 sessions), it was 2 pellets, and in phase 3 (30 sessions), it was again one pellet.

Histology

At the end of the behavioural experiment, the rats were deeply anaesthetised with sodium pentobarbitone, and perfused transcardially with 0.9% sodium chloride, followed by 10% formol saline. The brains were removed from the skull and fixed in formol saline for 1 week. Coronal sections (40-μm) were taken through the nucleus accumbens region using a freezing microtome.

Cresyl violet staining

The procedure was similar to that described by Kheramin et al. (2002). Alternate sections were mounted on chrome-gelatine-coated slides and air dried, hydrated by successive immersion in 95, 70 and 50% ethanol, stained in 0.25% cresyl violet for 2 min at room temperature, dehydrated by successive immersion in 50, 70, 95, and 100% ethanol and xylene, and mounted with DPX.

Immunocytochemistry

In the other sections, neurone-specific nuclear protein (NeuN) was labelled as described by Jongen-Relo and Feldon (2002). Our protocol has been described by Bezzina et al. (2007). Briefly, freshly sliced sections were rinsed in 0.1 M phosphate buffered saline (PBS) and placed in 0.5% H2O2 in PBS for 30 min. After twice rinsing in PBS, they were placed for 1 h in a blocking solution [10% normal horse serum (Vector Laboratories, Peterborough, UK), 1% bovine serum albumin (BSA, Sigma-Aldrich, Gillingham, UK) and 0.3% Triton X-100 (Sigma-Aldrich) in PBS]. They were incubated for 48 h at 4°C with the primary antibody [monoclonal mouse anti-NeuN serum (1:5,000, Chemicon, Chandlers Ford, UK) in 1% normal horse serum, 1% BSA and 0.3% Triton X-100 in PBS], washed twice in PBS, and incubated for 2 h at room temperature in biotinylated horse antimouse serum (Vector Laboratories; 1:1,000 in 1% BSA and 0.3% Triton X-100 in PBS). After further rinsing in PBS, they were placed for 2 h in avidin–biotin–horseradish peroxidase complex (1:200, ABC-Elite, Vector Laboratories) in PBS. After two further rinses in PBS, they were placed in a chromagen solution [0.05% diaminobenzidine (Sigma-Aldrich) and 0.01% H2O2 (Sigma-Aldrich)] for 5 min. The reaction was observed visually and stopped by rinsing in PBS. The sections were floated on to chrome-gelatine-coated slides and mounted with DPX.

An investigator who was blind to the behavioural results performed the microscopic examination. Drawings of the area of the lesions were superimposed on the appropriate coronal sections in the stereotaxic atlas of Paxinos and Watson (1998).

Data analysis

One rat from the AcbC-lesioned group died during the course of the experiment, leaving 15 rats in the AcbC-lesioned group and 14 rats in the sham-lesioned group.

Except where indicated otherwise below, data derived from the last ten sessions of each phase of the experiment were used in the statistical analyses. Because the number of ratios completed within a session under a progressive-ratio schedule differs among individual subjects, analyses of variance of the raw data included only those ratios that were completed by at least 75% of the rats in each group in each phase of the experiment (ratios up to and including 77), missing values being filled using the value obtained in the highest ratio completed by the subject in question. The quantitative analysis was not subject to this limitation because Eq. 1 was fitted to the data from individual subjects.

Highest completed ratio and peak response rate

The breakpoint was defined as the last ratio to be completed before 5 min elapsed without any responding (Hodos 1961; Hodos and Kalman 1963). In most cases, this was identical to the highest ratio completed in the session. However, in some cases, the breakpoint criterion was not met within the 50-min session. Therefore, the highest completed ratio, rather than breakpoint, was adopted as the performance measure for analysis. The highest completed ratio and the peak (overall) response rate were analysed by two-factor analyses of variance (group × phase); in the case of a significant group × phase interaction, between-group comparisons were made in each phase using Student’s t test.

Overall response rate was calculated for each ratio using the total time taken to complete the ratio, including the post-reinforcement pause, measured from the end of the preceding reinforcer delivery until the emission of the last response of the ratio (Bizo and Killeen 1997). The first ratio (a single response) and any ratios that had not been completed at the end of the session were excluded from the analysis. The data were analysed by three-factor analysis of variance (group × phase × ratio), with repeated measures on the second and third factors.

Post-reinforcement pause and run-time

The total time taken to complete each ratio was fractionated into the post-reinforcement pause (time from the end of the preceding reinforcer delivery until the first response of the ratio) and the run-time (time from the first response until the final response of the ratio). These data were analysed by three-factor analyses of variance (group × phase × ratio), with repeated measures on the second and third factors.

Running rate

Running rate, calculated by dividing the number of responses by the run-time (Bizo and Killeen 1997), was analysed by three-factor analysis of variance (group × phase × ratio), with repeated measures on the second and third factors.

Quantitative analysis

Equation 1 was fitted to the overall response rate data obtained from each rat using an iterative least-squares method (SigmaPlot, Version 8.0), and the estimated values of the parameters β, δ and a were derived; goodness of fit was expressed as r 2, the proportion of the data variance accounted for by the equation. In agreement with previous findings (Mobini et al. 2000; Ho et al. 2003; Zhang et al. 2005a, b), examination of the data revealed that Eq. 1 provided a good description of the response rate data at low and intermediate ratios; however, the low response rates generated under highest ratios did not conform to the equation. Therefore, the equation was fitted to each rat’s data after exclusion of these low rates using the operational criterion described by Mobini et al. (2000) (see Fig. 1); a fit was accepted when the predicted response rates for all the surviving data points had positive values (see also Ho et al. 2003). An initial analysis was carried out to assess the change of the parameter values during successive blocks of ten training sessions during phase 1, using two-factor analyses of variance (group × session block). Then, as with the other performance measures (see above), the estimates of each parameter were compared across phases using the data obtained from the final ten sessions of each phase using two-factor analyses of variance (group × phase) with repeated measures on the second factor, followed, if appropriate, by multiple comparisons within each phase, as described above.

A significance criterion of P < 0.05 was adopted in all statistical analyses.

Results

Behavioural data

Highest completed ratio

The group mean highest completed ratios (±SEM) in the three phases of the experiment are shown in Table 1. The data were significantly skewed, and therefore a logarithmic transformation was applied before carrying out the analysis of variance. The analysis of variance revealed a significant main effect of group [F(1,27) = 5.8, P < 0.05], reflecting the attainment of higher ratios by the sham-lesioned group than by the AcbC-lesioned group; the effect of phase was also significant [F(2,54) = 4.3, P < 0.05], reflecting the tendency for higher ratios to be achieved in phase 2, when the reinforcer consisted of two pellets, than in phases 1 and 3, when it consisted of a single pellet; the group × phase interaction was not statistically significant [F < 1].

Table 1 Highest completed ratios and peak response rates (mean ± SEM) of the AcbC-lesioned and sham-lesioned groups on three phases of the experiment
Full size table

Peak response rate

Peak response rates are shown in Table 1. The main effect of group was significant [F(1,27) = 7.4, P < 0.05], reflecting higher peak rates in the sham-lesioned than the AcbC-lesioned group; the effect of phase was also significant [F(2,54) = 22.9, P < 0.01], reflecting the tendency for peak rate to be lower in phase 2 than in phases 1 and 3; the group × phase interaction was not statistically significant [F(2,54) = 2.2, NS].

Overall response rate

Figure 2 shows the group mean overall response rates in each phase of the experiment; the curves are the functions defined by equation 1 (see below). Response rates tended to be lower in the AcbC-lesioned group than in the sham-lesioned group. Analysis of variance revealed significant main effects of group [F(1,27) = 8.7, P < 0.01], phase [F(2,54) = 20.1, P < 0.001] and ratio [F(12,324) = 11.9, P < 0.001]. There were significant group × phase [F(2,54) = 3.7, P < 0.05], phase × ratio [F(24,648) = 12.2, P < 0.001] and group × phase × ratio [F(24,648) = 3.1, P < 0.001] interactions; the group × ratio interaction was not significant [F(12,324) = 1.3, NS].

Fig. 2
figure 2

Overall response rates under the progressive-ratio schedule during the final 10 sessions of each phase of the experiment. Ordinate: response rate (responses minute−1); abscissa: response/reinforcer ratio. Points are group mean data from the sham-lesioned (open circles) and AcbC-lesioned (filled circles) groups. The curves are fits of Equation 1 to the data. See text for details of analysis

Full size image

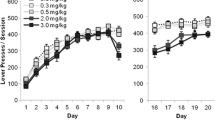
Post-reinforcement pause

The upper panels of Fig. 3 show the relationship between post-reinforcement pause and the ratio requirement in the three phases of the experiment. Analysis of variance revealed a significant main effect of ratio [F(12,324) = 16.2, P < 0.001] and a significant group × ratio interaction [F(12,324) = 2.3, P < 0.01], reflecting the steeper increase in post-reinforcement pause in the AcbC-lesioned group. Neither the main effect of phase [F(2,54) = 1.8, NS] nor any of the other interaction terms [Fs < 1] was statistically significant. In both groups, the proportion of the total inter-reinforcement interval taken up by the post-reinforcement pause declined from about 70% at the lowest ratio values to about 30% at the highest ratio values; the decline was somewhat steeper in phase 2 than in phases 1 and 3. Analysis of variance revealed significant main effects of phase [F(2,54) = 6.8, P < 0.01] and ratio [F(12,324) = 65.5, P < 0.001] and a significant phase × ratio interaction [F(24,648) = 3.8, P < 0.001]; neither the main effect of group [F < 1] nor any of the interactions involving the group factor [Fs < 1.7, NS] was statistically significant.

Fig. 3
figure 3

Performance in successive ratios of the progressive-ratio schedule during the final 10 sessions of each phase of the experiment. Upper panels. Post-reinforcement pause: ordinate, pause duration (s). Middle panels. Run-time (inter-reinforcement interval after subtraction of the post-reinforcement pause): ordinate, run-time (s). C. Lower panels. Running response rate (response rate during the ‘run-time’): ordinate: running rate (responses minute−1). Other conventions are as in Fig. 2

Full size image

Run-time

The middle panels of Fig. 3 show that run-times were consistently longer in the AcbC-lesioned group than in the sham-lesioned group, the between group difference increasing as a function of ratio size. Analysis of variance revealed significant main effects of group [F(1,27) = 9.5, P < 0.01] and ratio [F(12,324) = 34.6, P < 0.001], and a significant group  × ratio interaction [F(12,324) = 2.8, P < 0.01]; neither the main effect of phase nor any of the other interactions was statistically significant [Fs < 1.1, NS].

Running response rate

The lower panels of Fig. 3 show the running response rate data. Running response rate declined monotonically as a function of ratio in both groups, the AcbC-lesioned rats displaying consistently lower running response rates than the sham-lesioned rats. These findings are reflected in the results of the analysis of variance: there were significant main effects of group [F(1,27) = 52.1, P < 0.001] and ratio [F(12,324) = 35.8, P < 0.001], but not of phase [F(2,54) = 2.2, NS], and none of the interactions was statistically significant [Fs < 1.8, NS].

Quantitative analysis: parameters of Eq. 1

Equation 1 was fitted to the overall response-rate data obtained from the individual rats in each group. The group mean estimated values (±SEM) of the parameters in successive ten-session blocks in phase 1 are shown in Fig. 4. Specific activation (a). The AcbC-lesioned group showed higher values of a than the sham-lesioned group during the initial stages of training (Fig. 4, upper graph). The value of a declined in the AcbC-lesioned group and gradually increased in the sham-lesioned group; in the final 30 sessions similar values were seen in the two groups. Analysis of variance confirmed these trends: the main effects of group [F(1,27) = 2.1, NS] and session block [F < 1] were not significant, but there was a significant group × block interaction [F(8,216) = 5.0, P < 0.001]. Response time (δ). The AcbC-lesioned group’s value of this parameter declined during training, although it remained consistently higher than that of the sham-lesioned group throughout phase 1. There were significant main effects of group [F(1,27) = 10.2, P < 0.01] and session block [F(8,216) = 9.2, P < 0.001]; the interaction was also significant [F(8,216) = 2.3, P < 0.05]. Currency parameter (β). In both groups, the value of β declined progressively during the 90 sessions of phase 1, and did not attain stability by the end of the phase. There was no significant main effect of group [F < 1]; the main effect of session block [F(8,216) = 9.2, P < 0.001] and the group × block interaction [F(8,216) = 2.7, P < 0.05] were significant.

Fig. 4
figure 4

Parameters of Equation 1 obtained during successive 10-session blocks of Phase 1: Upper panel. ‘specific activation’ parameter, a (s). Middle panel. ‘response time’ parameter; δ (s). Lower panel. ‘currency’ parameter, β. Points are group mean data ±SEM. Other conventions as in Fig. 2

Full size image

The values of the parameters derived in the final ten sessions of each phase are shown in Table 2. Specific activation (a). Analysis of variance showed a significant effect of phase [F(2,54) = 10.6, P < 0.001], reflecting the increase in the value of this parameter when the reinforcer size was increased from one pellet to two. However, there was no significant effect of group [F < 1] and no significant interaction [F(2,54) = 2.0, NS]. Response time (δ) was significantly higher in the AcbC-lesioned group than in the sham-lesioned group [F(1,27) = 4.3, P < 0.05], indicating a lower maximum response rate in the AcbC-lesioned group. δ was significantly higher in phase 2 than in phases 1 and 3 [F(2,54) = 6.7, P < 0.01], but there was no significant group × phase interaction [F < 1]. The currency parameter (β) showed no significant main effect of group [F < 1]; however, the main effect of phase [F(2,54) = 12.3, P < 0.001] and the group × phase interaction [F(2,54) = 7.1, P < 0.01] were significant. Analysis of the simple effects of phase in each group showed that in the sham-lesioned group, β was significantly lower in phase 2 than in the other phases [F(2,26) = 15.6, (F(2,28) = 1.5, P > 0.2]; there was no significant effect of phase in the case of the AcbC-lesioned group [F < 1].

Table 2 Estimated parameters of Equation 1, goodness of fit (r 2) and numbers of data points excluded from the function-fitting (mean ± S.E.M.) of the AcbC-lesioned and sham-lesioned groups on three phases of the experiment (see text for explanation)
Full size table

Histology

Bilateral lesions were found to be accurately placed in all 15 rats that had received injections of quinolinic acid. Coronal sections showed ventricular dilatation and atrophy in the ventral striatal area. The NeuN labelled sections showed that there was extensive neuronal loss in the area of the AcbC of all lesioned animals, with some neuronal loss in the ventral and medial portions of the caudate-putamen in some animals; the shell region of the nucleus accumbens was essentially spared. Examples of cresyl violet stained and NeuN labelled sections are shown in Fig. 5, and the extent of the lesions is summarized in Fig. 6.

Fig. 5
figure 5

Sample photomicrographs showing coronal sections of the brains of a sham-lesioned rat (panels a nand c) and a AcbC-lesioned rat (panels b and d). Left-hand panels: sections stained with cresyl violet; right-hand panels: sections stained for NeuN. LV, lateral ventricle; CPu, caudate-putamen; AcbC, nucleus accumbens core; AcbS, nucleus accumbens shell; aca, anterior commisure. Note ventricular dilatation, neuronal loss and atrophy of the AcbC in the lesioned brain

Full size image
Fig. 6
figure 6

Diagram of the approximate area of destruction of the AcbC in the lesioned group. Drawings were made from the microscopic sections, and were superimposed on the relevant pages from Paxinos and Watson’s (1998) stereotaxic atlas. The black area represents the smallest, and the stippled area the largest extent of the lesion

Full size image

Discussion

Injection of quinolinic acid produced a substantial lesion of the AcbC, similar to that seen in previous experiments using this protocol (e.g. Bowman and Brown 1998; Cardinal et al. 2001; Bezzina et al. 2007). The lesions were mainly restricted to the AcbC. Some additional damage was inflicted on the ventral and medial portions of the caudate-putamen in some rats. However, the mesial shell region of the nucleus accumbens was spared.

Performance on the progressive ratio schedule

The performance of both groups on the progressive ratio schedule was similar to that reported previously (e.g. Bizo and Killeen 1997; Baron and Derenne 2000; Mobini et al. 2000; Ho et al. 2003; Kheramin et al. 2005; Zhang et al. 2005a, b). Overall response rate was bitonically related to ratio size, initially rising to a peak and then declining as a function of increasing ratio size. Post-reinforcement pause and run-time increased monotonically, and running response rate declined monotonically, as a function of ratio size. The increase in reinforcer size from one food pellet to two during phase 2 resulted in a significant increase in the highest completed ratio, consistent with previous reports (Skjoldager et al. 1993; Sclafani and Ackroff 2003).

Extended training under the progressive ratio schedule resulted in good conformity of the overall response rates to Equation 1, the values of the parameters obtained for the sham-lesioned group in the final ten-session block of phase 1 being similar to those obtained for intact rats in previous experiments (Mobini et al. 2000; Ho et al. 2003; Kheramin et al. 2005; Zhang et al. 2005a, b). In phase 2, when the reinforcer size was increased from one food pellet to two, there was a significant increase in the ‘specific activation’ parameter, a. This is consistent with the predictions of MPR, according to which a reflects the value of an individual reinforcer, and with previous findings both with pigeons (Bizo and Killeen 1997) and with rats (Bizo et al. 2001).

The ‘response time’ parameter, δ, was somewhat higher in phase 2 than in the other phases, reflecting the lower peak response rates seen under the two-pellet condition. This effect, which has been noted previously in ratio schedules (Bizo et al. 2001), may reflect a greater contribution of post-prandial behaviour to post-reinforcement pauses in the case of the larger reinforcer.

The ‘currency’ parameter, β, was lower under the two-pellet condition than under the one-pellet condition (at least in the case of the sham-lesioned group); this is consistent with previous findings with variable-ratio schedules (Bizo et al. 2001). Since, in MPR, β encapsulates the coupling of responses to reinforcers (Killeen 1994), the result suggests that the larger reinforcer was able to exert control over longer sequences of responses than the smaller reinforcer (see below for further discussion).

Effect of the AcbC lesion on performance on the progressive ratio schedule

The main aim of this experiment was to use the progressive ratio schedule to address the question of whether destruction of the AcbC would reduce the instantaneous value of a food reinforcer. The finding that the highest completed ratio, which has traditionally been viewed as an index of reinforcer efficacy (see above), was significantly lower in the AcbC-lesioned group than in the sham-lesioned group appears, at first glance, to be in agreement with this notion. However, as discussed earlier, the highest completed ratio or breakpoint may be influenced by ‘motoric’ as well as ‘motivational’ factors (Stewart 1975; Skjoldager et al. 1993; Aberman et al. 1998; Stafford and Branch 1998), and the quantitative analysis based on Eq. 1 suggests that this was probably the case in this experiment. Parameter a, which is believed to express reinforcer value, was not affected by the lesion, whereas δ, which expresses the minimum response time, was significantly greater in the AcbC-lesioned group than in the sham-lesioned group.

This experiment is not the first to examine the effect of AcbC lesions on progressive ratio schedule performance. Bowman and Brown (1998) reported that excitotoxic lesions of the AcbC resulted in an increase in the breakpoint, in contrast to the reduction of the highest completed ratio seen in this experiment. A possible resolution of this discrepancy is suggested by the data shown in Fig. 4. In the initial stages of training, the AcbC-lesioned rats showed higher values of a than the sham-lesioned rats. This pattern persisted for more than 50 sessions; however, while the sham-lesioned group showed a gradual increase in a, there was a marked decline in the AcbC-lesioned group’s value of this parameter, with the result that by the time stability was reached, after approximately 70 sessions of training, there was no significant difference between the two groups. The duration of training in Bowman and Brown’s (1998) experiment was considerably shorter than in the present experiment, and it is likely, therefore, that the value of a would have been higher in the AcbC-lesioned group than in the sham-lesioned group in Bowman and Brown’s experiment. This would be expected to produce a higher breakpoint in the lesioned group, given that these authors allowed responding to persist for up to four hours in each session. The long period of training that was needed in order to attain stability of a in this experiment is consistent with our previous experience with this schedule (Kheramin et al. 2005; Zhang et al. 2005a, b). It is not clear why the AcbC-lesioned rats showed such a high value of a initially. However, it is likely that the progressive reduction of a required active suppression of responding in response to the increasing response cost imposed by the progressive-ratio schedule. The AcbC-lesioned rats may have been slow to adapt to this aspect of the schedule due to deficient inhibitory regulation of responding (Reading and Dunnett 1995; Bowman and Brown 1998).

The higher value of δ seen in the AcbC-lesioned rats persisted through all three phases of the experiment. This is partly explicable in terms of the longer post-reinforcement pauses seen in this group, suggesting that the AcbC-lesioned rats may have had difficulty in initiating trains of responses. However, the AcbC-lesioned rats also displayed lower running response rates than the sham-lesioned group, suggesting that the lesion may have had a deleterious effect on motor performance.

The AcbC lesion had a more complex effect on the ‘currency parameter’, β. β declined steadily in both groups, and did not fully stabilize even after 90 sessions of training in phase 1. The increase in reinforcer size during phase 2 produced a significant reduction in the value of β in the sham-lesioned rats, which fully reversed when the original reinforcer size was reinstated. However, the value of β was impervious to the effects of manipulating reinforcer size in the AcbC-lesioned group. Changes in the value of β are reflected in the slope of the rising phase of the response rate function. The different effects of reinforcer size on this parameter in the two groups probably underlies the significant three-way interaction term in the analysis of variance of the overall response rates (see above). The interpretation of this finding is a matter for conjecture at this time; however, a modification of Eq. 1 suggested by Bizo et al. (2001) may offer some clues. In Killeen’s (1994) original model, the relation between response-reinforcer coupling in ratio schedules (ζ) and the currency parameter β (see Eq. 1) is based on the assumption that reinforcer delivery produces complete ‘erasure’ of the organism’s short-term memory for recent responses. However, in Bizo et al.’s (2001) modification of the model, the degree of erasure produced by a reinforcer varies as a direct function of its size. This is reflected in the degree of coupling, and hence in the empirical value of β when Eq. 1 is fitted to overall response rates. The empirical values of β derived for the sham-lesioned group are consistent with this suggestion, since β was higher in the one-pellet condition than in the two-pellet condition, which implies a greater degree of erasure produced by the larger reinforcer. The lack of effect of reinforcer size on β in the AcbC-lesioned group suggests that although the lesion did not alter the incentive values of the reinforcers (as indicated by the lack of effect on a), it may have altered the relationship between reinforcer size and the strength of coupling between responses and reinforcers. The implications of the effect of the lesion on β for behaviour in other paradigms remain to be explored. There is evidence that lesions of the AcbC can impede instrumental learning (Cardinal and Cheung 2005; De Leonibus et al. 2005). The present results raise the possibility that this learning impairment may reflect defective response-reinforcer coupling. Since the lesion’s effect on β depended upon the reinforcer size, it would be of some interest in future experiments to examine whether the AcbC lesion-induced impairment of instrumental learning may also be influenced by reinforcer size.

Implications for the role of the AcbC in inter-temporal choice

The mechanisms whereby lesions of the AcbC disrupt inter-temporal choice behaviour is controversial (Cardinal et al. 2001; Acheson et al. 2006; Bezzina et al. 2007). Since inter-temporal choice paradigms entail choice between reinforcers that differ with respect to both size and delay, it is often unclear whether an intervention has altered the rate of delay-discounting, the incentive values of the reinforcers, or both (see Ho et al. 1999; Cardinal et al. 2003). In an attempt to overcome this difficulty, Bezzina et al. (2007) adopted a null-equation approach based on a mathematical model of inter-temporal choice (Ho et al. 1999). By determining the indifference delay to the larger of two reinforcers corresponding to a range of delays to the smaller reinforcer, a linear indifference function was constructed, which yielded separate indices of the rate of delay discounting and the relative incentive values of the two reinforcers (for a full explanation, see Ho et al. 1999). Destruction of the AcbC selectively altered the intercept of the indifference function, consistent with an effect on the rate of delay discounting without any concomitant effect on instantaneous reinforcer value (Bezzina et al. 2007). The present results offer support for Bezzina et al.’s (2007) contention that the AcbC lesion did not alter instantaneous reinforcer value, using an operant paradigm, the progressive ratio schedule, that does not entail choice between reinforcers or delay of reinforcement.

The conclusion that the AcbC lesion did not affect instantaneous reinforcer value is based on the failure of the lesion to affect the activation parameter a. Although we cannot totally exclude the possibility that the lack of effect on a reflects a Type-II error, we think it unlikely that this is the case. Firstly, a was sensitive to changes in reinforcer size, consistent with previous reports (Bizo and Killeen 1997; Bizo et al. 2001). Secondly, a has been found to be sensitive to other neuropharmacological interventions. Thus, destruction of the orbital prefrontal cortex significantly altered this parameter (Kheramin et al. 2005), consistent with evidence from an inter-temporal choice experiment indicating that this lesion altered instantaneous reinforcer value (Kheramin et al. 2002).

Conclusions

Excitotoxic lesions of the AcbC altered performance in the progressive ratio schedule, reducing overall and running response rates and prolonging post-reinforcement pauses. The quantitative analysis of response rates based on Killeen’s (1994) MPR model indicated that the lesion did not reduce the incentive value of the food reinforcers (a). However, it did increase the minimum response time (δ) and may also have altered the strength of response-reinforcer coupling (β). The results are consistent with a growing body of evidence that the AcbC and its dopaminergic afferents are not paramount in determining the instantaneous values of reinforcers, but may play an important role in other aspects of reward-motivated behaviour, including sensitivity to effort requirement (Salamone 2002, 2007) and the delay-dependent degradation of reinforcer value (Cardinal et al. 2001, 2003; Bezzina et al. 2007).