The pressure-wired Stokes element: a mesh-robust version of the Scott–Vogelius element

Abstract

The Scott–Vogelius finite element pair for the numerical discretization of the stationary Stokes equation in 2D is a popular element which is based on a continuous velocity approximation of polynomial order k and a discontinuous pressure approximation of order $k-1$. It employs a “singular distance” (measured by some geometric mesh quantity $\Theta \left( \textbf{z}\right) \ge 0$ for triangle vertices $\textbf{z}$) and imposes a local side condition on the pressure space associated to vertices $\textbf{z}$ with $\Theta \left( \textbf{z}\right) =0$. The method is inf-sup stable for any fixed regular triangulation and $k\ge 4$. However, the inf-sup constant deteriorates if the triangulation contains nearly singular vertices $0<\Theta \left( \textbf{z}\right) \ll 1$. In this paper, we introduce a very simple parameter-dependent modification of the Scott–Vogelius element with a mesh-robust inf-sup constant. To this end, we provide sharp two-sided bounds for the inf-sup constant with an optimal dependence on the “singular distance”. We characterise the critical pressures to guarantee that the effect on the divergence-free condition for the discrete velocity is negligibly small, for which we provide numerical evidence.

1 Introduction

In this paper we consider the numerical solution of the stationary Stokes equation in a bounded two-dimensional polygonal Lipschitz domain by a conforming Galerkin finite element method.

Motivation The intuitive choice for a Stokes element $\left( \textbf{S}_{k}\left( \mathcal {T}\right) ,\mathbb {P}_{k-1}\left( \mathcal {T} \right) \right)$, where $\textbf{S}_{k}\left( \mathcal {T}\right)$ denotes the space of continuous velocity fields with local polynomial degree k over a given triangulation $\mathcal {T}$ and $\mathbb {P}_{k-1}\left( \mathcal {T}\right)$ the discontinuous pressures space of degree $k-1$, is in general not inf-sup stable (see, e.g., [1] and [2, Chap. 7] for quadrilateral meshes). A careful analysis [1, 3] of the range of the divergence operator reveals that the dimension of the image ${\text {div}}(\textbf{S}_{k}( \mathcal {T}))\subset \mathbb {P}_{k-1}(\mathcal {T})$ reduces by one linear constraint for every singular vertex. For $k\ge 4$, this results in the inf-sup stable Scott–Vogelius [3] pair $(\textbf{S}_{k}( \mathcal {T}),{\text {div}}(\textbf{S}_{k}(\mathcal {T})))$ on families of shape-regular meshes [4] that naturally computes fully divergence-free velocity approximations. However the Scott–Vogelius element, as described in [1, 3, 4], has two major drawbacks.

• 1. The inf-sup constant is not robust with respect to small perturbations of the mesh when a singular vertex becomes nearly singular, measured through the geometric quantity $\Theta _{\min }:= {\min }\left\{ \left. \Theta \left( \textbf{z}\right) \; \right| \; \Theta \left( \textbf{z} \right) > 0\right\}$. Here $\Theta \left( \textbf{z}\right)$ is a measure of the singular distance of a vertex $\textbf{z}$ from a proper singular situation. $\Theta _{\min }$ strongly affects the stability of the discretization, the size of the discretization error, as well as the condition number of the resulting algebraic linear system.

• 2. In order to implement the method, the condition: “Is a mesh point, say $\textbf{z}$, a singular vertex?” cannot be realized in floating point arithmetics and has to be replaced by a threshold condition for “nearly singular vertices” of the form “$\Theta \left( \textbf{z}\right) \le \varepsilon$”. Through this threshold condition, it is possible that the constraints are imposed on nearly singular vertices, i.e. for ${0}<\Theta \left( \textbf{z}\right) \le \varepsilon$ and the discrete velocity looses the divergence-free property as a consequence. To the best of our knowledge, this effect has not been analyzed in the literature and we will estimate the influence of $\varepsilon >0$ to the divergence-free property of the discrete velocity in Sect. 5.

In [5, Rem. 2], two mesh modification strategies are sketched as a remedy of (1): (i) nearly singular vertices are moved so that they become properly singular; (ii) triangles which contain a nearly singular vertex are refined. Both strategies require the finite element code to have control on the mesh generator. However, in many engineering finite element codes the mesh design is separated from the discretization and hence, interactive refinement features are not available. In addition fast solvers in computational fluid dynamics sometimes make use of a very regular mesh structure (e.g., C-meshes for the modelling of airfoils) and then local mesh refinement is not compatible.

In this paper, we propose a simpler strategy where a modification of the mesh is avoided. We introduce a parameter dependent modification to the standard Scott–Vogelius pair, the pressure-wired Stokes element, and prove that the inf-sup constant is independent of $\Theta _{\min }$, the mesh width, the polynomial degree but depends only on the shape-regularity of the mesh.

Main contributions The construction of our modification employs a geometric quantity $\Theta \left( \textbf{z}\right) \ge 0$ which measures the singular distance of the vertex $\textbf{z}$ in the mesh from a singular configuration. For some arbitrary (in general small) control parameter $0\le \eta$, the pressure space is reduced by the same constraint as in the Scott–Vogelius FEM for every vertex with singular distance $\Theta (\textbf{z})\le \eta$, which we call nearly singular . Since the constraints involve the alternating sum of pressure values over all triangles that encircle a nearly singular vertex (similar to a wire that is loosely woven around the tips of all triangles sharing a common vertex) we call the new element the pressure-wired Stokes element. We prove that the inf-sup constant of this element scales as $\Theta _{\min }(\eta ):=\min \{\Theta (\textbf{z})\ |\ \Theta (\textbf{z}) >\eta \}$ with equivalence constants independent of the mesh width and the polynomial degree (depending on the mesh only through the shape-regularity constant). The lower bound on the inf-sup constant by $\Theta _{\min }(\eta )$ employs results from [5, Sections 4 & 5] and implies the discrete stability of the numerical scheme, whereas the novel upper bound follows from an explicit characterisation of the critical pressures. We can therefore choose the threshold $\eta$ for our generalization of the Scott–Vogelius element such that the resulting pressure-wired Stokes element is inf-sup stable (with $\eta <\Theta _{\min }(\eta )$) independent of the mesh size, the polynomial degree, and any (nearly) singular vertex. These improvements come at some cost: in general we cannot expect divergence-free velocity approximations as for the standard Scott–Vogelius pair. We investigate the dependence of the $L^{2}$ norm of the divergence of the velocity approximation $\textbf{u}_{\textbf{S}}$ in the pressure-wired Stokes element and establish an estimate of the form $\left\| {\text {div}} \textbf{u}_{\textbf{S}}\right\| _{L^{2}\left( \Omega \right) }\le C\eta$ with $C>0$ being independent of the mesh width and the polynomial degree. We emphasize that this estimate does not require any regularity of the Stokes solution. Numerical experiments will be reported in Sect. 6 and show that the constant C is very small for the considered examples.

Literature overview The Scott–Vogelius pair for triangulations of two-dimensional domains (see [1, 3]) is inf-sup stable for $k\ge 4$, while the inf-sup constant deteriorates for nearly singular vertices. This problem can be attenuated by using special mesh-refinement strategies, e.g., Alfeld splits that are also known as barycentric refinements and provide inf-sup stability already for $k\ge 2$ in two dimensions [6] and $k\ge 3$ in three dimensions [7]. In three dimensions, inf-sup stability and a full characterisation of the divergence ${\text {div}}\textbf{S}_{k}(\mathcal {T})$ is not known on general meshes, see [8] and references therein. Our pressure-wired Stokes element places few additional constraints on the pressure space and acquires robust inf-sup stability on arbitrary shape-regular grids—the proof for the estimate of the inf-sup constant is based on the theory developed in [1, 3,4,5, 9, 10]. An alternative approach constitutes the enrichment of the velocity space, e.g., in [11] with Raviart-Thomas bubble functions leading to a divergence-free velocity approximation in $H({\text {div}})$. Conforming alternatives to the Scott–Vogelius element are the Mini element [12], the (modified) Taylor–Hood element [2, Chap. 3, §7], the Bernardi-Raugel element [9], and the element by Falk-Neilan [13] to mention some but few of them. We note that there exist further possibilities to obtain a stable discretization of the Stokes equation; one is the use of non-conforming schemes and/or modifications of the discrete equation by adding stabilizing terms. We do not go into details here but refer to the monographs and overviews [14,15,16] instead. For a discussion on the divergence-free condition and pressure-robustness, we refer to [17].

Further contributions and outline After introducing the Stokes problem on the continuous as well as on the discrete level and the relevant notation in Sect. 2, we define the conforming pressure-wired Stokes element in Sect. 3. The first main result in Sect. 4 establishes the discrete inf-sup condition for this new element with a lower bound on the inf-sup constant that is independent of h, k, and (nearly) critical points. The second main result controls the $L^{2}$ norm of the divergence of the discrete velocity in Sect. 5 and verifies its negligibility for small $\eta \ll 1$ in practice. In fact, the $L^{2}$ norm tends to zero (at least) linearly in $\eta$ without imposing any regularity assumption on the continuous problem. The involved constants are again independent of h, k, and $\Theta _{\min }$ but possibly depend on the mesh via its shape-regularity constant. For this analysis, we identify the critical pressure functions which are also the key for a sharp upper bound on the inf-sup constant in Sect. 5.3 implying the sharpness of the lower bound from Sect. 4. We report on numerical evidence on optimal convergence rates in Sect. 6, both as an h-version with regular mesh refinement and as a k-version that successively increases the polynomial degree. While this new element is technically not divergence-free, our benchmarks suggest that the discrete divergence is near machine-precision already on coarse meshes and for moderate parameters $\eta >0$.

2 The Stokes problem and its numerical discretization

Let $\Omega \subset \mathbb {R}^{2}$ denote a bounded polygonal Lipschitz domain with boundary $\partial \Omega$. We consider the numerical solution of the Stokes equation

$$\begin{aligned} \begin{array}{lll} -\Delta \textbf{u}+\nabla p &{} =\textbf{f} &{} \text {in }\Omega , \\ {\text {div}}\textbf{u} &{} =0 &{} \text {in }\Omega \end{array} \end{aligned}$$

with homogeneous Dirichlet boundary conditions for the velocity and the usual normalisation condition for the pressure

$$\begin{aligned} \textbf{u}=\textbf{0}\quad \text {on }\partial \Omega \quad \text {and } \int _{\Omega }p=0. \end{aligned}$$

Throughout this paper, standard notation for Lebesgue and Sobolev spaces applies. All function spaces are considered over the field of real numbers. The space $H_{0}^{1}\left( \Omega \right)$ is the closure of the space of smooth functions with compact support in $\Omega$ with respect to the $H^{1}\left( \Omega \right)$ norm. Its dual space is denoted by $H^{-1}\left( \Omega \right) :=H_{0}^{1}\left( \Omega \right) ^{\prime }$. The scalar product and norm in $L^{2}\left( \Omega \right)$ read

$$\begin{aligned} \left( u,v\right) _{L^{2}\left( \Omega \right) }:=\int _{\Omega }uv\quad \text {and}\quad \left\| u\right\| _{L^{2}\left( \Omega \right) }:=\left( u,u\right) _{L^{2}\left( \Omega \right) }^{1/2}\qquad \text {in } L^{2}\left( \Omega \right) . \end{aligned}$$

Vector-valued and $2\times 2$ tensor-valued analogues of the function spaces are denoted by bold and blackboard bold letters, e.g., $\textbf{H}^{s}\left( \Omega \right) =\left( H^{s}\left( \Omega \right) \right) ^{2}$ and $\mathbb { H}^{s}\left( \Omega \right) =\left( H^{s}\left( \Omega \right) \right) ^{2\times 2}$ and analogously for other quantities.

Notation 1

For vectors $\textbf{v},\textbf{w}\in \mathbb {R}^{2}$, the Euclidean scalar product $\left\langle \textbf{v},\textbf{w} \right\rangle :=\sum _{j=1}^{2}v_{j}w_{j}$ induces the Euclidean norm $\left\| \textbf{v}\right\| :=\left\langle \textbf{v},\textbf{v} \right\rangle ^{1/2}$. We denote the area of a subset $M\subset \mathbb R^2$ by $\left| M\right|$ and write $[ \textbf{v}|\textbf{w}]$ for the $2\times 2$ matrix with column vectors $\textbf{v},\textbf{w}{\in \mathbb R^2}$.

The $\textbf{L}^{2}\left( \Omega \right)$ scalar product and norm for vector-valued functions are

$$\begin{aligned} \left( \textbf{u},\textbf{v}\right) _{\textbf{L}^{2}\left( \Omega \right) }:=\int _{\Omega }\left\langle \textbf{u},\textbf{v}\right\rangle \quad \text { and }\left\| \textbf{u}\right\| _{\textbf{L}^{2}\left( \Omega \right) }:=\left( \textbf{u},\textbf{u}\right) _{\textbf{L} ^{2}\left( \Omega \right) }^{1/2}. \end{aligned}$$

In a similar fashion, we define for $\textbf{G},\textbf{H}\in \mathbb {L} ^{2}\left( \Omega \right)$ the scalar product and norm by

$$\begin{aligned} \left( \textbf{G},\textbf{H}\right) _{\mathbb {L}^{2}\left( \Omega \right) }:=\int _{\Omega }\left\langle \textbf{G},\textbf{H}\right\rangle \quad \text { and }\left\| \textbf{G}\right\| _{\mathbb {L}^{2}\left( \Omega \right) }:=\left( \textbf{G},\textbf{G}\right) _{\mathbb {L} ^{2}\left( \Omega \right) }^{1/2}, \end{aligned}$$

where $\left\langle \textbf{G},\textbf{H}\right\rangle =\sum _{i,j=1}^{2}G_{i,j}H_{i,j}$. Finally, let $L_{0}^{2}\left( \Omega \right) :=\left\{ u\in L^{2}\left( \Omega \right) :\int _{\Omega }u=0\right\}$. We introduce the bilinear forms $a:\textbf{H} ^{1}\left( \Omega \right) \times \textbf{H}^{1}\left( \Omega \right) \rightarrow \mathbb {R}$ and $b: \textbf{H}^{1}\left( \Omega \right) \times L^2 \left( \Omega \right) \rightarrow \mathbb {R}$ by

$$\begin{aligned} \begin{array}{ccc} a\left( \textbf{u},\textbf{v}\right) :=\left( \nabla \textbf{u},\nabla \textbf{v}\right) _{\mathbb {L}^{2}\left( \Omega \right) }&\text { and }&b \left( \textbf{u},p\right) = \left( {\text {div}} \textbf{u}, p\right) _{L^2\left( \Omega \right) }, \end{array} \end{aligned}$$

(1)

where $\nabla \textbf{u}$ and $\nabla \textbf{v}$ denote the gradients of $\textbf{u}$ and $\textbf{v}$. Given $\textbf{F}\in \textbf{H} ^{-1}\left( \Omega \right)$, the variational form of the stationary Stokes problem seeks $\left( \textbf{u},p\right) \in \textbf{H}_{0}^{1}\left( \Omega \right) \times L_{0}^{2}\left( \Omega \right)$ such that

$$\begin{aligned} \begin{array}{lll} a\left( \textbf{u},\textbf{v}\right) -b\left( \textbf{v},p\right) &{} =\textbf{ F}\left( \textbf{v}\right) &{} \forall \textbf{v}\in \textbf{H}_{0}^{1}\left( \Omega \right) , \\ b \left( \textbf{u},q\right) &{} =0 &{} \forall q\in L_{0}^{2}\left( \Omega \right) . \end{array} \end{aligned}$$

(2)

The inf-sup condition guarantees well-posedness of (2), cf. [18] for details. In this paper, we consider a conforming Galerkin discretization of (2) by a pair $\left( \textbf{S},M\right)$ of finite dimensional subspaces of the continuous solution spaces $\left( \textbf{H}_{0}^{1}\left( \Omega \right) ,L_{0}^{2}\left( \Omega \right) \right)$. For any given $\textbf{F}\in \textbf{H}^{-1}\left( \Omega \right)$, the weak formulation yields $\left( \textbf{u}_{\textbf{S}},p_{M}\right) \in \textbf{S}\times M\;$such that

$$\begin{aligned} \begin{array}{lll} a\left( \textbf{u}_{\textbf{S}},\textbf{v}\right) -b\left( \textbf{v},p_{M}\right) &{} =\textbf{F}\left( \textbf{v}\right) &{} \forall \textbf{v} \in \textbf{S}, \\ b\left( \textbf{u}_{\textbf{S}},q\right) &{} =0 &{} \forall q\in M. \end{array} \end{aligned}$$

(3)

It is well known that the bilinear form $a\left( \cdot ,\cdot \right)$ is symmetric, continuous, and coercive so that problem (3) is well-posed if the bilinear form $b\left( \cdot ,\cdot \right)$ satisfies the inf-sup condition.

Definition 1

Let $\textbf{S}$ and M be finite-dimensional subspaces of $\textbf{H} _{0}^{1}\left( \Omega \right)$ and $L_{0}^{2}\left( \Omega \right)$. The pair $\left( \textbf{S},M\right)$ is inf-sup stable if the inf-sup constant $\beta \left( \textbf{S},M\right)$ is positive, i.e.,

$$\begin{aligned} \beta \left( \textbf{S},M\right) := \inf _{q\in M\backslash \left\{ 0\right\} }\sup _{\textbf{v}\in \textbf{S} \backslash \left\{ \textbf{0}\right\} }\frac{\left( q,{\text {div}} \textbf{v}\right) _{L^{2}\left( \Omega \right) }}{\left\| \textbf{v} \right\| _{\textbf{H}^{1}\left( \Omega \right) }\left\| q\right\| _{L^{2}\left( \Omega \right) }} >0. \end{aligned}$$

(4)

Fig. 1

Reference triangle (left) and physical triangle (right)

3 The pressure-wired Stokes element

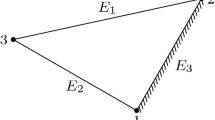
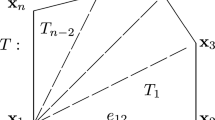
Throughout this paper, $\mathcal {T}$ denotes a conforming triangulation of the bounded polygonal Lipschitz domain $\Omega \subset \mathbb {R}^{2}$ into closed triangles: the intersection of two different triangles is either empty, a common edge, or a common point. The set of edges in $\mathcal {T}$ is denoted by $\mathcal {E}\left( \mathcal {T} \right)$, comprised of boundary edges $\mathcal {E}_{\partial \Omega }\left( \mathcal {T}\right) :=\left\{ E\in \mathcal {E}\left( \mathcal {T}\right) :E\subset \partial \Omega \right\}$ and interior edges $\mathcal {E}_{\Omega }\left( \mathcal {T}\right) :=\mathcal {E}\left( \mathcal {T}\right) \backslash \mathcal {E}_{\partial \Omega }\left( \mathcal {T}\right)$. For any edge $E\in \mathcal {E}(\mathcal {T})$, we fix a unit normal vector $\textbf{n}_{E}$ with the convention that for boundary edges $E\in \mathcal {E}_{\partial \Omega }, \ \textbf{n}_{E}$ points to the exterior of $\Omega$. The set of vertices in $\mathcal {T}$ is denoted by $\mathcal {V}\left( \mathcal {T}\right)$ while the subset of boundary vertices is $\mathcal {V}_{\partial \Omega }\left( \mathcal {T}\right) :=\left\{ \textbf{z}\in \mathcal {V}\left( \mathcal {T} \right) :\textbf{z}\in \partial \Omega \right\}$. The interior vertices form the set $\mathcal {V}_{\Omega }\left( \mathcal {T}\right) :=\mathcal {V} \left( \mathcal {T}\right) \backslash \mathcal {V}_{\partial \Omega }\left( \mathcal {T}\right)$. For a triangle $K\in \mathcal {T}$ with diameter $h_K:= {\text {diam}}K$, the set of its vertices is denoted by $\mathcal {V}\left( K\right)$ (cf. Fig. 1). For $\textbf{z}\in \mathcal {V} \left( \mathcal {T}\right)$, we consider the local element vertex patch

$$\begin{aligned} \begin{array}{ll} \mathcal {T}_{ \textbf{z}}:=\left\{ K\in \mathcal {T}\mid \textbf{z}\in K\right\}&\text { and }\omega _{\textbf{z}}:=\bigcup \limits _{K\in \mathcal {T}_{\textbf{z} }}K \end{array} \end{aligned}$$

(5)

with the local mesh width $h_{\textbf{z}}:=\max \left\{ h_{K}:K\in \mathcal {T}_{\textbf{z}}\right\}$. For any vertex $\textbf{z}\in \mathcal {V}\left( \mathcal {T}\right)$, we fix a counterclockwise numbering of the $N_{\textbf{z}}:=\left| \mathcal {T}_{ \textbf{z}}\right|$ triangles in

$$\begin{aligned} \mathcal {T}_{\textbf{z}}=\left\{ \left. K_{j} \; \right| \; 1\le j\le N_{\textbf{z}}\right\} \quad \text {and set }\mathcal {E}_{\textbf{z}}:=\left\{ E\in \mathcal {E} \left( \mathcal {T}\right) :\textbf{z}\text { is an endpoint of }E\right\} . \end{aligned}$$

(6)

Fig. 2

Singular configuration (top) and generic configuration (bottom) of a vertex patch for an interior vertex $\textbf{z}\in \mathcal {V} _{\Omega }(\mathcal {T})$ with $N_{\textbf{z}}=4$ (resp. boundery vertex $\textbf{z}\in \mathcal {V}_{\partial \Omega }(\mathcal {T})$ with $N_{\textbf{z}}=1,2,3$) triangles

In Fig. 2, $\mathcal {T}_{\textbf{z}}$ is shown for four important configurations. The shape-regularity constant

$$\begin{aligned} \gamma _{\mathcal {T}}:=\max _{K\in \mathcal {T}}\frac{h_{K}}{\rho _{K}} \end{aligned}$$

(7)

relates the local mesh width $h_{K}{=}{\text {diam}}K$ with the diameter $\rho _{K}$ of the largest inscribed ball in an element $K\in \mathcal {T}$. The global mesh width is given by $h_{\mathcal {T}}:=\max \left\{ h_{K}:K\in \mathcal {T}\right\}$.

Remark 1

The shape-regularity implies the existence of some $\phi _{\mathcal {T}}>0$ exclusively depending on $\gamma _{\mathcal {T}}$ such that every triangle angle in $\mathcal {T}$ is bounded from below by $\phi _{\mathcal {T}}$. In turn, every triangle angle in $\mathcal {T}$ is bounded from above by $\pi -2\phi _{\mathcal {T}}$.

Let $\mathbb {P} _{k}(K)$ denote the space of polynomials up to degree $k\in \mathbb {N}_{0}$ on $K\in \mathcal {T}$ and define

$$\begin{aligned} \begin{aligned} \mathbb {P}_{k}\left( \mathcal {T}\right)&:=\left\{ q\in L^{2}\left( \Omega \right) \mid \forall K\in \mathcal {T}:\left. q\right| _{\overset{\circ }{K}}\in \mathbb {P}_{k}\left( \overset{\circ }{K}\right) \right\} ,\\ \mathbb {P}_{k,0}\left( \mathcal {T}\right)&:=\left\{ q\in \mathbb {P}_{k}\left( \mathcal {T}\right) \mid \int _{\Omega }q=0\right\} \equiv \mathbb P_k({\mathcal {T}})\cap L^2_0(\Omega ),\\ S_{k}\left( \mathcal {T}\right)&:=\mathbb {P}_{k}\left( \mathcal {T}\right) \cap H^{1}(\Omega ),\\ S_{k,0}\left( \mathcal {T}\right)&:=S_{k}\left( \mathcal {T} \right) \cap H_{0}^{1}\left( \Omega \right) . \end{aligned} \end{aligned}$$

(8)

The vector-valued spaces are $\textbf{S}_{k}\left( \mathcal {T}\right) :=S_{k}\left( \mathcal {T}\right) ^{2}$ and $\textbf{S}_{k,0}\left( \mathcal {T }\right) :=S_{k,0}\left( \mathcal {T}\right) ^{2}$. It is well known that the most intuitive Stokes element $\left( \textbf{S}_{k,0}\left( \mathcal {T} \right) ,\mathbb {P}_{k-1,0}\left( \mathcal {T}\right) \right)$ is in general unstable. The analysis in [1, 3] for $k\ge 4$ relates the instability of $\left( \textbf{S}_{k,0}\left( \mathcal {T}\right) ,\mathbb {P}_{k-1,0}\left( \mathcal {T}\right) \right)$ to critical or singular points of the mesh $\mathcal {T}$. The set of $\eta$-critical points $\mathcal {C}_{\mathcal {T}}\left( \eta \right)$ for the control parameter $\eta \ge 0$ recovers the definition of the classical critical points $\mathcal {C}_{\mathcal {T}}(0)$ (introduced in [1, R.1, R.2] and called singular vertices in [1]) for $\eta =0$.

Definition 2

The local measure of singularity $\Theta \left( \textbf{ z}\right)$ at $\textbf{z}\in \mathcal {V}(\mathcal {T})$ is given by

$$\begin{aligned} \Theta \left( \textbf{z}\right) :={\left\{ \begin{array}{ll} \max \left\{ \left. \left| \sin \left( \theta _{i}+\theta _{i+1}\right) \right| \; \right| \; 1 \le i \le N_{\textbf{z}} \right\} &{} \text {if}\,\,\textbf{z}\in \mathcal {V}_{\Omega }\left( \mathcal {T} \right) ,\\ \max \left\{ \left. \left| \sin \left( \theta _{i}+\theta _{i+1}\right) \right| \; \right| \; 1 \le i \le N_{\textbf{z}} -1\right\} &{} \text {if }\textbf{z}\in \mathcal {V}_{\partial \Omega }({\mathcal {T}})\wedge N_{\textbf{z}}>1,\\ 0 &{} \text {if }\mathbf {z\in }\mathcal {V}_{\partial \Omega }({\mathcal {T}})\wedge N_{\textbf{z}}=1, \end{array}\right. } \end{aligned}$$

(9)

where the angles $\theta _{j}$ in $\mathcal {T}_{z}$ are numbered counterclockwise from $1\le j\le N_{\textbf{z}}$ (see (6)) and cyclic numbering is applied, i.e. $\theta _{N_{\textbf{z}}}+1=\theta _{1}$. For $\eta \ge 0$, the vertex $\textbf{z}\in \mathcal {V}\left( \mathcal {T} \right)$ is an $\eta$-critical vertex if $\Theta \left( \textbf{z} \right) \le \eta$. The set of all $\eta$-critical vertices is given by

$$\begin{aligned} \mathcal {C}_{\mathcal {T}}\left( \eta \right) :=\left\{ \textbf{z}\in \mathcal {V}\left( \mathcal {T}\right) \mid \Theta \left( \textbf{z}\right) \le \eta \right\} . \end{aligned}$$

For a vertex $\textbf{z}\in \mathcal {V}\left( \mathcal {T}\right)$, the functional $A_{\mathcal {T},\textbf{z}}:\mathbb {P}_{k}\left( \mathcal {T} \right) \rightarrow \mathbb {R}$ alternates counterclockwise through the numbered triangles $K_{\ell }$, $1\le \ell \le N_{\textbf{z}}$, in the patch $\mathcal {T}_{\textbf{z}}$ and is given by

$$\begin{aligned} A_{\mathcal {T},\textbf{z}}\left( q\right) :=\sum _{\ell =1}^{N_{\textbf{z}}}\left( -1\right) ^{\ell }\left( \left. q\right| _{K_{\ell }}\right) \left( \textbf{z}\right) . \end{aligned}$$

(10)

From Definition (9) it follows that for any $\eta \ge 1$ we have $\mathcal {C}_{\mathcal {T}}\left( \eta \right) =\mathcal {V}\left( \mathcal {T}\right)$ and the assumption $\eta \in \left[ 0,1\right]$ throughout this paper is not an actual restriction. The first row in Fig. 2 displays all four singular mesh configurations (i.e., $\Theta (\textbf{z})=0$) that occur when all edges of the vertex patch $\mathcal {T}(\textbf{z})$ lie on two straight lines. It follows from [10] that for moderately small $\eta {<\eta _0}$, the only possible $\eta$-critical mesh configurations are perturbations of those four situations and illustrated in the second row of Fig. 2.

Lemma 1

[10, Lem. 2.13] There exists a constant $\eta _{0}>0$ only depending on the shape-regularity of the mesh and on $\Omega$ such that $\Theta (\textbf{z})\le \eta _{0}$ for $\textbf{z}\in \mathcal {V}(\mathcal {T})$ implies

• 1. if $\textbf{z}\in \mathcal {V}_{\Omega }(\mathcal {T})$ is an interior vertex, then $N_{\textbf{z}}=4$,

• 2. if $\textbf{z}\in \mathcal {V}_{\partial \Omega }(\mathcal {T})$ is a boundary vertex, then $N_{\textbf{z}}\le 3$.

$\square$

The pressure space of the pressure-wired Stokes element is obtained by requiring the condition $A_{\mathcal {T}, \textbf{z}}\left( q\right) =0$ for all $\eta$-critical points.

Definition 3

For $\eta \ge 0$, the subspace $M_{\eta ,k-1}\left( \mathcal {T} \right) \subset \mathbb {P}_{k-1,0}\left( \mathcal {T} \right)$ of the pressure space is given by

$$\begin{aligned} M_{\eta ,k-1}\left( \mathcal {T}\right) :=\left\{ q\in \mathbb {P} _{k-1,0}\left( \mathcal {T}\right) \mid \forall \textbf{z}\in \mathcal {C} _{\mathcal {T}}\left( \eta \right) :A_{\mathcal {T},\textbf{z}}\left( q\right) =0\right\} . \end{aligned}$$

(11)

The pressure-wired Stokes element is given by $\left( \textbf{S} _{k,0}\left( \mathcal {T}\right) ,M_{\eta ,k-1}\left( \mathcal {T}\right) \right)$.

Note that for the choice $\eta = 0$, $M_{0,k-1}\left( \mathcal {T}\right)$ is the pressure space introduced by Vogelius [1] and Scott–Vogelius [3] and the following inclusions hold: for $0\le \eta \le \eta ^{\prime }$

$$\begin{aligned} M_{\eta ^{\prime },k-1}\left( \mathcal {T}\right) \subset M_{\eta ,k-1}\left( \mathcal {T}\right) \subset M_{0,k-1}\left( \mathcal {T}\right) =Q_{h}^{k-1} \end{aligned}$$

(12)

(with the pressure space $Q_{h}^{k-1}$ in [4, p. 517]). The existence of a continuous right-inverse of the divergence operator ${\text {div}}: \textbf{S}_{k,0}(\mathcal {T})\rightarrow M_{0,k-1}(\mathcal {T})$ was proved in [1] and [3, Thm. 5.1].

Proposition 1

(Scott–Vogelius) Let $k\ge 4$. For any $q\in M_{0,k-1}\left( \mathcal {T} \right)$ there exists some $\textbf{v}\in \textbf{S}_{k,0}\left( \mathcal {T}\right)$ such that

$$\begin{aligned} {\text {div}}\textbf{v}=q\mathbf {\quad }\text {and }\left\| \textbf{v}\right\| _{\textbf{H}^{1}\left( \Omega \right) }\le C\left\| q\right\| _{L^{2}\left( \Omega \right) }. \end{aligned}$$

The constant C is independent of $h_{\mathcal {T}}$ and only depends on the domain $\Omega$, the shape-regularity of the mesh, the polynomial degree k, and on:

$$\begin{aligned} \Theta _{\min }:=\min _{\textbf{z}\in \mathcal {V}\left( \mathcal {T}\right) \backslash \mathcal {C}_{\mathcal {T}}\left( 0\right) }\Theta \left( \textbf{z}\right) . \end{aligned}$$

(13)

It follows from [4, Thm. 1] that the inf-sup constant of the Scott–Vogelius element $\left( \textbf{S} _{k,0}\left( \mathcal {T}\right) ,M_{0,k-1}\left( \mathcal {T}\right) \right)$ can be bounded from below by $\beta \left( \textbf{S}_{k,0}\left( \mathcal {T} \right) ,M_{0,k-1}\left( \mathcal {T}\right) \right) \ge \Theta _{\min }c\left( \gamma _{\mathcal {T}},k\right)$, where $c\left( \gamma _{\mathcal {T }},k\right) >0$ depends on the shape regularity constant $\gamma _{\mathcal {T }}$ and the polynomial degree k. The dependence on k has been analysed in a series of papers starting from [1, Lem. 2.5] with the final result in [5, Theorem 5.1], which states that

$$\begin{aligned} \beta \left( \textbf{S}_{k,0}\left( \mathcal {T}\right) ,M_{0,k-1}\left( \mathcal {T}\right) \right) \ge \Theta _{\min }c\left( \gamma _{\mathcal {T} }\right) >0 \end{aligned}$$

is independent of the polynomial degree k. However, the estimate is non-robust with respect to small perturbations of critical configurations $0\ne \Theta \left( \textbf{z}\right) \ll 1$. Our notion of $\eta$-critical points can be regarded as a robust generalization and we will analyse the consequences in this paper. In the next section, we prove for the pressure-wired Stokes element and $\Theta _{\min }(\eta )$ (with $\Theta _{\min }(\eta )\ge \max \{\eta , \Theta _{\min }\}$) introduced below that

$$\begin{aligned} \beta \left( \textbf{S}_{k,0}\left( \mathcal {T}\right) ,M_{\eta ,k-1}\left( \mathcal {T}\right) \right) \ge {\Theta _{\min }(\eta )} c\left( \gamma _{\mathcal {T}}\right) >0 \end{aligned}$$

by modifying the arguments in [5, Sections 4 & 5] and investigate the effect on the divergence-free property of the discrete velocity in Sect. 5.

4 Inf-sup stability of the pressure-wired Stokes element

In this section we prove that the inf-sup constant for the pressure-wired Stokes element allows for a lower bound that is independent of the mesh width and the polynomial degree k, and we examine the dependence on the modified geometric quantity

$$\begin{aligned} \Theta _{\min }(\eta ):=\min _{\textbf{z}\in \mathcal {V}\left( \mathcal {T}\right) \backslash \mathcal {C}_{\mathcal {T}}\left( \eta \right) }\Theta \left( \textbf{z}\right) \equiv \min \{\Theta (\textbf{z})\ |\ \textbf{z}\in \mathcal {V}(\mathcal {T})\text { with } \Theta (\textbf{z}) > \eta \} \end{aligned}$$

(14)

with the convention $\Theta _{\min }(\eta )=1$ if $\mathcal {V}(\mathcal {T})\setminus \mathcal {C}_{\mathcal {T}}(\eta )=\emptyset$. Note that $\Theta _{\min }(\eta )\ge \max \{\eta , \Theta _{\min }\}$ provided $0\le \eta \le 1$.

Theorem 2

(inf-sup stability) For any $k\ge 4$, the inf-sup constant (4) satisfies

$$\begin{aligned} \beta \left( \textbf{S}_{k,0}\left( \mathcal {T}\right) ,M_{\eta ,k-1}\left( \mathcal {T}\right) \right) \ge c{\, \Theta _{\min }(\eta )}. \end{aligned}$$

(15)

The constant $c>0$ exclusively depends on the shape-regularity of the mesh and on $\Omega$. In particular, c is independent of the mesh width $h_{\mathcal {T}}$, the polynomial degree k, and $\eta$.

Remark 4 verifies that the lower bound in (15) is qualitatively sharp. By choosing $\eta =0$ we obtain the original Scott–Vogelius element with a k-robust inf-sup constant (see [5, Theorem 5.1]). Due to (12), [5, Theorem 5.1] immediately yields that the pressure-wired Stokes element is also inf-sup stable and the inf-sup constant $\beta \left( \textbf{S}_{k,0}\left( \mathcal {T}\right) ,M_{\eta ,k-1}\left( \mathcal {T}\right) \right)$ is also independent of the polynomial degree k and the mesh width $h_{\mathcal {T}}$. However, in order to obtain the bounds as described in Theorem 2, we have to modify the arguments in [5, Sections 4 & 5]. The goal of these modifications is to prove that there exists a right-inverse $\Pi _{\eta ,k}:M_{\eta ,k-1}\left( \mathcal {T}\right) \rightarrow \textbf{S} _{k,0}\left( \mathcal {T}\right)$ for the divergence operator ${\text {div}} \left( \cdot \right)$. This is expressed in the following Lemma.

Lemma 2

Given any $k\ge 4$, there exists a linear operator $\Pi _{\eta ,k}:M_{\eta ,k-1}\left( \mathcal {T}\right) \rightarrow \textbf{S}_{k,0}\left( \mathcal {T}\right)$ such that, for any $q\in M_{\eta ,k-1}\left( \mathcal {T}\right)$,

$$\begin{aligned} {\text {div}}\Pi _{\eta ,k} q&= q \qquad \text {and}\qquad \left\| \Pi _{\eta ,k}q\right\| _{\textbf{H}^{1}\left( \Omega \right) } \le {C\,\Theta _{\min }(\eta )^{-1}}\left\| q\right\| _{L^{2}\left( \Omega \right) }. \end{aligned}$$

(16)

The constant $C > 0$ exclusively depends on the shape-regularity of the mesh and on $\Omega$.

In order to prove this lemma, we modify [5, Lemma 4.2 and 4.5] to take the parameter $\eta$ into account; its formulation uses the following notation. Enumerate the elements in $\mathcal { T}_{\textbf{z}}$ counterclockwise by $K_{i}$ for $1\le i\le N_{\textbf{z}}$ such that the edges in $\mathcal {E}_{\textbf{z}}$ are given by $E_{i}=K_{i-1}\cap K_{i}$, employing cyclic numbering convention, meaning $K_{0}=K_{N_{\textbf{z} }}$ and $K_{N_{\textbf{z}}+1}=K_{1}$. For $1\le i\le N_{\textbf{z}}$, $\theta _{i}$ denotes the angle at $\textbf{z}$ in $K_{i}$. The vectors $\textbf{t}_{i}$ and $\textbf{n}_{i}$ denote the unit tangent vector and the unit normal vector of the edge $E_{i}$ pointing away from $\textbf{z}$ and into $K_{i}$ respectively.

Lemma 3

[5, Lemma 4.2 and 4.5] Given any $k\ge 4$, then for all $\textbf{z} \in \mathcal {V} \left( \mathcal {T}\right)$ and $q \in M_{\eta ,k-1} \left( \mathcal {T}\right)$, there exists a solution $\left( \tilde{\textbf{d}}_{E_i}^{\textbf{z}}\right) _{i=1}^{N_{\textbf{z}}} \subseteq \mathbb {R}^2$ of the system

$$\begin{aligned} \left. q \right| _{K_i} \left( \textbf{z}\right) \sin \theta _i = \left\langle \tilde{\textbf{d}}_{E_i}^{\textbf{z}}, \textbf{n}_{i+1} \right\rangle - \left\langle \tilde{\textbf{d}}_{E_{i+1}}^{\textbf{z}}, \textbf{n}_i \right\rangle \qquad \forall 1 \le i \le N_{\textbf{z}}, \end{aligned}$$

(17)

that satisfies

$$\begin{aligned} \sum _{i=1}^{N_{\textbf{z}}} \left\| \tilde{\textbf{d}}_{E_i}^{\textbf{z}} \right\| ^2 \le C \sum _{i=1}^{N_{\textbf{z}}} \left. q \right| _{K_i} \left( \textbf{z}\right) {^2} \times {\left\{ \begin{array}{ll} {\Theta _{\min }(\eta )}^{-{2}}, &{} \text {if } \; \textbf{z} \notin {\mathcal {C}_{\mathcal {T}} \left( \eta \right) }, \\ 1, &{} \text {if } \; \textbf{z} \in {\mathcal {C}_{\mathcal {T}} \left( \eta \right) }, \end{array}\right. } \end{aligned}$$

(18)

where $C>0$ solely depends on the shape-regularity of $\mathcal {T}$.

Proof

Let us first consider $\textbf{z} \notin \mathcal {C}_{\mathcal {T}} \left( \eta \right)$. If $\textbf{z} \in \mathcal {V}_{\Omega } \left( \mathcal {T}\right)$, then by [5, Lemma 4.2] we know that there exists $\left( \textbf{d}_{E_i}^{\textbf{z}}\right) _{i=1}^{N_{\textbf{z}}} \subseteq \mathbb {R}^2$ satisfying (17) and

$$\begin{aligned} \sum _{i=1}^{N_{\textbf{z}}} \left\| \textbf{d}_{E_i}^{\textbf{z}} \right\| ^2 \le 2\left( 1 + \frac{N_{\textbf{z}}}{\xi \left( \textbf{z}\right) } \right) ^2 \sum _{i=1}^{N_{\textbf{z}}} \left. q \right| _{K_i} \left( \textbf{z}\right) ^2, \end{aligned}$$

where $\xi \left( \textbf{z}\right) : = \sum _{i=1}^{N_{\textbf{z}}} \left| \sin \left( \theta _i + \theta _{i+1}\right) \right|$ employing cyclic numbering convention. We observe that from the definition of $\xi$ and $\textbf{z} \notin \mathcal {C}_{\mathcal {T}} \left( \eta \right)$, it follows that

$$\begin{aligned} {\Theta _{\min }(\eta )}\le \Theta \left( \textbf{z}\right) \le \xi \left( \textbf{z}\right) . \end{aligned}$$

Since the maximal possible number $N_{\textbf{z}}$ of triangles around a vertex $\textbf{z}\in \mathcal {V}(\mathcal {T})$ only depends on the shape-regularity, we conclude that

$$\begin{aligned} \sum _{i=1}^{N_{\textbf{z}}} \left\| \textbf{d}_{E_i}^{\textbf{z}} \right\| ^2 \le C\,{\Theta _{\min }(\eta )^{-2}}\sum _{i=1}^{N_{\textbf{z}}} \left. q \right| _{K_i} \left( \textbf{z}\right) ^2, \end{aligned}$$

for some constant $C > 0$ solely depending on the shape-regularity of $\mathcal {T}$. If $\textbf{z} \in \mathcal {V}_{\partial \Omega } \left( \mathcal {T}\right)$ we repeat the arguments presented above on the set of vectors $\left( \textbf{d}_{E_i}^{\textbf{z}}\right) _{i=1}^{N_{\textbf{z}}}$ given by [5, Lemma 4.5 (1)] and therefore by setting $\tilde{\textbf{d}}_{E_i}^{\textbf{z}}:= \textbf{d}_{E_i}^{\textbf{z}}$ as described above, we have proven (17) and (18) for non-$\eta$-critical vertices. Let us now consider $\textbf{z} \in \mathcal {C}_{\mathcal {T}} \left( \eta \right)$ and we first assume $\textbf{z} \in \mathcal {V}_{\Omega } \left( \mathcal {T}\right)$. We choose $\tilde{\textbf{d}}_{E_i}^{\textbf{z}} = \delta _i \textbf{t}_i$ and some elementary computation transforms (17) into

$$\begin{aligned} \left. q \right| _{K_i} \left( \textbf{z}\right)&= \delta _i + \delta _{i+1} \qquad \forall 1 \le i \le N_{\textbf{z}} , \end{aligned}$$

(19)

employing cyclic notation convention (cf. [5, (4.8)]). Set $\delta _1:= 0$ and $\delta _{i+1}:= \sum _{j=1}^{i} \left( -1\right) ^{i-j} \left. q \right| _{K_j} \left( \textbf{z}\right)$ for all $1 \le i \le N_{\textbf{z}}-1$. For $i=1$, (19) is trivially satisfied and for $2 \le i \le N_{\textbf{z}}-1$, we compute

$$\begin{aligned} \delta _i + \delta _{i+1}&= \sum _{j=1}^{i-1} \left( -1\right) ^{i-1-j} \left. q \right| _{K_j} \left( \textbf{z}\right) + \sum _{j=1}^{i} = \left( -1\right) ^{i-j} \left. q \right| _{K_j} \left( \textbf{z}\right) \\&= \sum _{j=1}^{i-1} \left( -1\right) ^{i-1 -j} \left. q \right| _{K_j} \left( \textbf{z}\right) + \left( -1\right) ^{i-j} \left. q \right| _{K_j} \left( \textbf{z}\right) + \left. q \right| _{K_i} \left( \textbf{z}\right) = \left. q \right| _{K_i} \left( \textbf{z}\right) . \end{aligned}$$

For $i = N_{\textbf{z}}$ we have by assumption that $A_{\mathcal {T}, \textbf{z}} \left( q\right) = 0$ and conclude after rearranging the terms that $\delta _{N_{\textbf{z}}} = \left. q \right| _{K_{N_{\textbf{z}}}} \left( \textbf{z}\right)$. Since the $\tilde{\textbf{d}}_{E_i}^{\textbf{z}}$ are the same as in [5, Lemma 4.3] we obtain

$$\begin{aligned} \sum _{i=1}^{N_{\textbf{z}}} \left\| \tilde{\textbf{d}}_{E_i}^{\textbf{z}} \right\| ^2 \le C \sum _{i=1}^{N_{\textbf{z}}} \left. q \right| _{K_i} \left( \textbf{z}\right) ^2 \end{aligned}$$

for some constant $C>0$ solely depending on the shape-regularity of the mesh. If $\textbf{z} \in \mathcal {V}_{\partial \Omega } \left( \mathcal {T}\right)$ holds, the same construction as in [5, Lemma 4.3] and $A_{\mathcal {T}, \textbf{z}} \left( q\right) = 0$ verify (17) and (18) also for the $\eta$-critical vertices. $\square$

Proof of Lemma 2

Let $q \in M_{\eta ,k-1} \left( \mathcal {T}\right)$ be given. Taking the functions $\phi _{E,k}^{\textbf{z}}$ from [5, Lem. B.1] we set

$$\begin{aligned} \Psi _{h,k}:= \sum _{\begin{array}{c} \textbf{z} \in \mathcal {V}\left( \mathcal {T}\right) \\ E \in \mathcal {E}\left( \mathcal {E}\right) \end{array}} \textbf{d}_E^{\textbf{z}} \phi _{E,k}^{\textbf{z}}, \end{aligned}$$

where $\textbf{d}_E^{\textbf{z}}$ is taken as in Lemma 3. Mimicking the arguments in [5, Sec. 5] (with $\Psi _{h,k}$ replaced by $\Psi _{h,p}$ therein) in combination with Lemma 3, we obtain that there exists a vector field $\textbf{u}_q \in \textbf{S}_{k,0} \left( \mathcal {T}\right)$ satisfying ${\text {div}} \textbf{u}_q = q$ and

$$\begin{aligned} \left\| \textbf{u}_q \right\| _{\textbf{H}^{1}\left( \Omega \right) } \le C \max \left\{ 1,{\Theta _{\min }(\eta )}^{-1}\right\} \left\| q \right\| _{L^{2}\left( \Omega \right) }\le C\,{\Theta _{\min }(\eta )}^{-1} \left\| q \right\| _{L^{2}\left( \Omega \right) } \end{aligned}$$

with $1\le {\Theta _{\min }(\eta )}^{-1}$ by definition in the last step. The constant $C>0$ is independent of the polynomial degree k, the mesh width $h_{\mathcal {T}}$, and the parameter $\eta$ and exclusively depending on the shape-regularity of the mesh, and the domain $\Omega$. Therefore by setting $\Pi _{\eta ,k}q:= \textbf{u}_q$ we have proven our statement. $\square$

Proof of Theorem 2

For the estimate of the inf-sup constant we compute

$$\begin{aligned} \inf _{\begin{array}{c} q\in M_{\eta ,k-1}\left( \mathcal {T}\right) \\ p \ne 0 \end{array}}\sup _{\begin{array}{c} \textbf{v}\in \textbf{S}_{k,0} \left( \mathcal {T}\right) \\ \textbf{v} \ne \textbf{0} \end{array}}\frac{\left( q,{\text {div}}\textbf{v}\right) _{L^{2}\left( \Omega \right) }}{\left\| \textbf{v}\right\| _{\textbf{H}^{1}\left( \Omega \right) }\left\| q\right\| _{L^{2}\left( \Omega \right) }}&\overset{\text {Lem. }~3}{\ge }\inf _{\begin{array}{c} q\in M_{\eta ,k-1}\left( \mathcal {T}\right) \\ q \ne 0 \end{array}}\frac{\left( q,{\text {div}}\Pi _{\eta ,k}q \right) _{L^{2}\left( \Omega \right) } }{\left\| \Pi _{\eta ,k}q \right\| _{\textbf{H}^{1}\left( \Omega \right) }\left\| q\right\| _{L^{2}\left( \Omega \right) }} \\&\ge c\,{\Theta _{\min }(\eta )} , \end{aligned}$$

where c only depends on the shape-regularity of the mesh and on $\Omega$. $\square$

Main properties of a “good” Stokes element are the inf-sup stability, the approximation properties of the velocity and pressure space, and the divergence-free condition for the velocity solution. We end this section by a remark on the approximation properties while the next section is devoted to the analysis of the smallness of the divergence.

Remark 2

(Approximation properties) Since the velocity space is the standard conforming finite element space, the approximation properties are standard. For the pressure space we start with an observation for $q\in M_{\eta ,k-1}(\mathcal {T})$ where $0\le \eta \le \eta _0$ with $\eta _0$ from Lemma 1. Suppose $\textbf{z}\in \mathcal {V}_{\partial \Omega }(\mathcal {T})\cap \mathcal {C}_{\mathcal {T}}(\eta )$ is an $\eta$-critical boundary vertex with $N_{\textbf{z}}$ odd (type 2 or 4 in Fig. 2), $A_{\mathcal {T},\textbf{z}}(q)=0$ reveals the following implication

$$\begin{aligned} q\text { continuous in }\textbf{z}\Longrightarrow q(\textbf{z})=0. \end{aligned}$$

Since the exact pressure does not vanish at theses points in general, we cannot expect a good approximation property of $M_{\eta ,k-1}(\mathcal {T})$ in neighborhoods of such vertices that can only occur at corners of the domain $\Omega$ by Lemma 1. This is a drawback for both, the original Scott–Vogelius element and the pressure-wired Stokes element. In [19], we present a strategy to modify the pressure space in these vertices such that standard approximation properties hold while the discrete inf-sup stability is preserved.

5 Divergence estimate of the discrete velocity

The Scott–Vogelius pair $\left( \textbf{S}_{k,0}\left( \mathcal {T}\right) ,M_{0,k-1}\left( \mathcal {T}\right) \right)$ is inf-sup stable for $k\ge 4$ but sensitive with respect to nearly singular vertex configurations, where $0 < \Theta \left( \textbf{z}\right) \ll 1$ for some $\textbf{z} \in \mathcal {V} \left( \mathcal {T}\right)$. The corresponding discrete solution is divergence free. Since our $\eta$-dependent pressure space $M_{\eta ,k-1}\left( \mathcal {T}\right)$ is a proper subspace of the image of the divergence operator ${\text {div}}:\textbf{S}_{k,0}(\mathcal {T})\rightarrow M_{0,k-1}\left( \mathcal {T}\right)$ in general, we cannot expect the discrete velocity solution to be pointwise divergence-free. However, since $\lim _{\eta \rightarrow 0} M_{\eta ,k-1} \left( \mathcal {T}\right) = M_{0,k-1} \left( \mathcal {T}\right)$, we may expect $\left\| {\text {div}}\textbf{u}_{\textbf{S}}\right\| _{L^{2}\left( \Omega \right) }$ to be small. The main result of this section establishes an estimate of the divergence which tends to zero as $\eta \rightarrow 0$ without any regularity assumption on the continuous Stokes problem.

Consider the open subset

$$\begin{aligned} \Omega (\eta ):=\bigcup _{\textbf{z}\in \mathcal {C}_{\mathcal {T}}(\eta )}{\text {int}}(\omega _{\textbf{z}})\subset \Omega , \end{aligned}$$

(20)

where ${\text {int}}(\omega _{\textbf{z}})$ denotes the interior of the closed vertex patch $\omega _{\textbf{z}}$ from (5).

Theorem 3

(Velocity control) Let $k\ge 4$ and $0\le \eta <\eta _{0}$ be given with $\eta _{0}>0$ as in Lemma 1. Let $(\textbf{u}, p)$ denote the solution to (2) for $\textbf{F}\in \textbf{H}^{-1}(\Omega )$. Then the discrete solution $\left( \textbf{u}_{\textbf{S}},p_{M}\right)$ to (3) in $\left( \textbf{S}_{k,0}\left( \mathcal {T}\right) ,M_{\eta ,k-1} \left( \mathcal {T}\right) \right)$ satisfies

$$\begin{aligned} \left\| \nabla (\textbf{u}-\textbf{u}_\textbf{S})\right\| _{\mathbb {L}^{2}\left( \Omega \right) }&\le C \phantom {\eta }\min _{\begin{array}{c} \textbf{v}_\textbf{S}\in \textbf{S}_{k,0}(\mathcal {T})\\ {\text {div}}\textbf{v}_\textbf{S} = 0 \end{array}}\left\| \nabla (\textbf{u}-\textbf{v}_\textbf{S})\right\| _{\mathbb {L}^{2}\left( \Omega \right) } + \eta \phantom {^2}\hspace{-.4em}\min _{q_M\in M_{\eta ,k-1}(\mathcal {T})}\Vert p - q_M\Vert _{L^2({\Omega (\eta )})},\\ \left\| {\text {div}}\textbf{u}_\textbf{S}\right\| _{{L}^{2}\left( \Omega \right) }&\le C\eta \min _{\begin{array}{c} \textbf{v}_\textbf{S}\in \textbf{S}_{k,0}(\mathcal {T})\\ {\text {div}}\textbf{v}_\textbf{S} = 0 \end{array}}\left\| \nabla (\textbf{u}-\textbf{v}_\textbf{S})\right\| _{\mathbb {L}^{2}\left( \Omega \right) } + \eta ^2\hspace{-.4em}\min _{q_M\in M_{\eta ,k-1}(\mathcal {T})}\Vert p - q_M\Vert _{L^2({\Omega (\eta )})}. \end{aligned}$$

If $\mathcal {T}$ does not have $\eta$-critical boundary vertices $\textbf{z}\in \mathcal {C}_{\mathcal {T}}(\eta )\cap \mathcal {V}_{\partial \Omega }(\mathcal {T})$ with $N_{\textbf{z}}$ odd (type 2 or 4 in Fig. 2), then ${\text {div}}u_{\textbf{S}}\equiv 0$ in $\Omega \setminus \Omega (\eta )$. The constant $C > 0$ depends solely on the shape regularity of $\mathcal {T}$ and on the domain $\Omega$. In particular C is independent of the mesh width $h_{\mathcal {T}}$, the polynomial degree k, the geometric quantity $\Theta _{\min }$ and the control parameter $\eta$.

A key ingredient in the proof of Theorem 3 is the following control of the divergence. Define the space

$$\begin{aligned} \textbf{S}_{\eta ,k,0}(\mathcal {T}):=\left\{ \left. \textbf{v}_{\textbf{S}}\in \textbf{S}_{k,0}\left( \mathcal {T}\right) \ \right| \ A_{\mathcal {T},\textbf{z}}\left( {\text {div}} \textbf{v}_{\textbf{S}}\right) =0\;\text { for all }\textbf{z}\in \mathcal {C}_{\mathcal {T} }\left( \eta \right) \right\} . \end{aligned}$$

For a function $v\in L^2(\Omega )$ and a subspace $U\subset L^2(\Omega )$, $v\perp U$ abbreviates the $L^2$ orthogonality onto U, i.e., $\left( v,u\right) _{L^2\left( \Omega \right) } = 0$ for all $u \in U$. The same notation applies for vector-valued functions $\textbf{v}\in \textbf{L}^2(\Omega )$.

Lemma 4

(Divergence control) Let $k\ge 4$ and $0\le \eta <\eta _{0}$ be given with $\eta _{0}>0$ as in Lemma 1. For any $\textbf{v}_\textbf{S}\in \textbf{S}_{k,0}(\mathcal {T})$ with ${\text {div}}\textbf{v}_\textbf{S} \perp M_{\eta ,k-1}(\mathcal {T})$, there exists $C_{\textbf{S}}\in \mathbb R$ with

• (a) $\displaystyle {\text {div}}\textbf{v}_{\textbf{S}}|_{\Omega {\setminus }\overline{\Omega (\eta )}} \equiv C_{\textbf{S}}\quad \text {and}\quad \left\| {\text {div}}\textbf{v}_{\textbf{S}}-C_{\textbf{S}}\right\| _{L^{2}\left( \Omega (\eta )\right) }\le \sqrt{16/7}\left\| {\text {div}}\textbf{v}_{\textbf{S}}\right\| _{L^{2}\left( \Omega (\eta )\right) }$,

• (b) $\displaystyle \left\| {\text {div}}\textbf{v}_{\textbf{S}}\right\| _{L^{2}\left( \Omega \right) } \le \left\| {\text {div}}\textbf{v}_{\textbf{S}}-C_{\textbf{S}}\right\| _{L^{2}\left( \Omega (\eta )\right) } \le C_{{\text {div}}}\eta \min _{\textbf{w}_{\textbf{S}}\in \textbf{S}_{\eta ,k,0}\left( \mathcal {T}\right) }\left\| \nabla \left( \textbf{v}_{\textbf{S}}-\textbf{w}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega (\eta )\right) }$.

If $\mathcal {T}$ does not contain $\eta$-critical boundary vertices $\textbf{z}\in \mathcal {C}_{\mathcal {T}}(\eta )\cap \mathcal {V}_{\partial \Omega }(\mathcal {T})$ with $N_{\textbf{z}}$ odd, then $C_{\textbf{S}}=0$. The constant $C_{{\text {div}}}>0$ exclusively depends on the shape regularity of $\mathcal {T}$.

Proof of Theorem 3

The discrete formulation (3) imposes that the discrete velocity $\textbf{u}_{\textbf{S}}$ satisfies ${\text {div}}\textbf{u}_\textbf{S}\perp M_{\eta ,k-1}(\mathcal {T})$. Consider an arbitrary $\textbf{v}_\textbf{S}\in \textbf{S}_{k,0}(\mathcal {T})$ with ${\text {div}}\textbf{v}_\textbf{S}=0$ and observe $\textbf{v}_\textbf{S}\in \textbf{S}_{\eta ,k,0}(\mathcal {T})$ by definition. The weak formulation (2) and the discrete formulation (3) for the test function $\textbf{e}_\textbf{S}:=\textbf{u}_{\textbf{S}}-\textbf{v}_{\textbf{S}} \in \textbf{S}_{k,0}(\mathcal {T})$ satisfy

$$\begin{aligned} a(\textbf{u}-\textbf{u}_\textbf{S}, \textbf{e}_\textbf{S}) = b(\textbf{e}_\textbf{S}, p-p_M)=b(\textbf{u}_\textbf{S}, p-q_M) \qquad \forall q_M \in M_{\eta ,k-1}(\mathcal {T}) \end{aligned}$$

with ${\text {div}}\textbf{e}_\textbf{S}={\text {div}}\textbf{u}_\textbf{S}\perp M_{\eta ,k-1}(\mathcal {T})$ in the last step. Let $q_M\in M_{\eta ,k-1}(\mathcal {T})$ be arbitrary. Lemma 4 provides ${\text {div}}\textbf{u}_{\textbf{S}}|_{\Omega {\setminus }\overline{\Omega (\eta )}}\equiv C_{\textbf{S}}\in \mathbb R$ and $C_{\textbf{S}}\perp p-q_M\in L^2_0(\Omega )$ reveals

$$\begin{aligned} b(\textbf{u}_{\textbf{S}}, p-q_{M})=\left( {\text {div}}\textbf{u}_{\textbf{S}}-C_{\textbf{S}},p-q_M\right) _{L^2(\Omega (\eta ))}. \end{aligned}$$

The previous two displayed equalities and a Cauchy inequality provide

$$\begin{aligned} \Vert \nabla ( \textbf{u}_{\textbf{S}}&-\textbf{v}_{\textbf{S}}) \Vert _{\mathbb {L}^{2}\left( \Omega \right) }^2 = a \left( \textbf{u}_{\textbf{S}} - \textbf{v}_{\textbf{S}}, \textbf{e}_{\textbf{S}}\right) = a(\textbf{u}-{\textbf{v}}_\textbf{S}, \textbf{e}_\textbf{S}) - a(\textbf{u}-\textbf{u}_\textbf{S}, \textbf{e}_\textbf{S})\\&\le \left\| \nabla \left( \textbf{u}-\textbf{v}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega \right) } \left\| \nabla \textbf{e}_{\textbf{S}} \right\| _{\mathbb {L}^{2}\left( \Omega \right) } +\Vert p-q_M\Vert _{L^2({\Omega (\eta )})}\Vert {\text {div}}\textbf{u}_\textbf{S}{-C_{\textbf{S}}}\Vert _{L^2({\Omega (\eta )})}. \end{aligned}$$

Lemma 4 reveals $\left\| \nabla \left( \textbf{u}_{\textbf{S}}-\textbf{v}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega \right) }\le \left\| \nabla \left( \textbf{u}-\textbf{v}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega \right) } +C_{{\text {div}}}\eta \Vert p-q_M\Vert _{L^2({\Omega (\eta )})}$. This, $\left\| \nabla \left( \textbf{u}-\textbf{u}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega \right) }\le \left\| \nabla \left( \textbf{u}-\textbf{v}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega \right) }+ \left\| \nabla \left( \textbf{u}_{\textbf{S}}-\textbf{v}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega \right) }$ from a triangle inequality, and Lemma 4 lead to

$$\begin{aligned} \left\| \nabla \left( \textbf{u}-\textbf{u}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega \right) }\le 2\left\| \nabla \left( \textbf{u}-\textbf{v}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega \right) } +C_{{\text {div}}}\eta \Vert p-q_M\Vert _{L^2({\Omega (\eta )})},\\ \left\| {\text {div}}\textbf{u}_{\textbf{S}}\right\| _{L^{2}\left( \Omega \right) }\le C_{{\text {div}}}\eta \left\| \nabla \left( \textbf{u}-\textbf{v}_{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega \right) } +C_{{\text {div}}}^2\eta ^2\Vert p-q_M\Vert _{L^2({\Omega (\eta )})}. \end{aligned}$$

Since $\textbf{v}_\textbf{S}$ and $q_M$ are arbitrary, this concludes the proof. $\square$

One remark precedes the preparation and proof of Lemma 4 in Sects. 5.1–5.2.

Remark 3

(localized pressure-robustness) The presence of $\eta$-critical but non-singular vertices implies that the discrete pressure space $M_{\eta ,k-1}(\mathcal {T})\subsetneq M_{0,k-1}(\mathcal {T})={\text {div}}\textbf{S}_{k,0}(\mathcal {T})$ is a strict subset of the discrete divergence characterised in [1, 3].

Thus, full pressure-robustness [17] cannot be expected in general and the velocity error may depend on the pressure. However, Theorem 3 guarantees that this pollution effect appears only locally around the $\eta$-critical vertices and is at most linear in $\eta$; the velocity approximation is independent of the pressure restricted to $\Omega \setminus \overline{\Omega (\eta )}$.

5.1 Analysis for $\eta$-critical vertices

This subsection analyses the divergence of piecewise smooth and globally continuous functions on the vertex patch $\mathcal {T} _{\textbf{z}}$ of an $\eta$-critical vertex $\textbf{z}\in C_{\mathcal {T} }\left( \eta \right)$.

Fig. 3

Setting of Lemma 5

Lemma 5

Consider four directions $\textbf{t}_{1},\dots ,\textbf{t}_{4} \in \mathbb {R}^{2}\backslash \left\{ \textbf{0}\right\}$ and some functions $\textbf{v}_{1},\dots ,\textbf{v}_{4}\in \textbf{C}^{1}\left( U\left( \textbf{z}\right) \right)$ defined in some neighborhood $U\left( \textbf{z}\right)$ of $\textbf{z}\in \mathbb {R}^{2}$ as in Fig. 3. Let $\theta _{j}$ denote the (signed) angles counted counterclockwise between $\textbf{t}_{j}$ and $\textbf{t}_{j+1}$ for $j=1,\dots ,4$ (with cyclic notation). If the Gâteaux derivatives $\partial _{\textbf{t}_{j}}(\textbf{v}_{j-1} -\textbf{v}_{j})$ vanish at $\textbf{z}$ for all $j=1,\dots ,4$ then

$$\begin{aligned} \mu \left| \sin \theta _{1}\right| \left| \sum _{j=1}^{4}\left( -1\right) ^{j}{\text {div}}\textbf{v}_{j}\left( \textbf{z}\right) \right| \le \sqrt{8}\Theta \sum _{j=1}^{4}\left\| \nabla \textbf{v} _{j} \left( \textbf{z}\right) \right\| \end{aligned}$$

(21)

with $\mu :=\min \left\{ \left| \sin \theta _{2}\right| ,\left| \sin \theta _{4}\right| \right\}$ and $\Theta :=\max \left\{ \left| \sin \left( \theta _{1}+\theta _{2}\right) \right| ,\left| \sin \left( \theta _{2}+\theta _{3}\right) \right| \right\}$.

The proof of this lemma requires two intermediate results. Recall the definition of the condition number

$$\begin{aligned} {\text {cond}}_{2}\left( \textbf{M}\right) :=\left\| \textbf{M}^{-1}\right\| _{2}\left\| \textbf{M}\right\| _{2} \end{aligned}$$

of a regular matrix $\textbf{M}\in \mathbb {R}^{2\times 2}$ with the induced Euclidean norm given by $\left\| \textbf{M}\right\| _{2}:=\sup _{\textbf{x} \in \mathbb {R}^{2}\backslash \left\{ \textbf{0}\right\} }\left\| \textbf{Mx}\right\| /\left\| \textbf{x}\right\|$.

Proposition 4

Given two vectors $\textbf{t}_{1},\textbf{t}_{2} \in \mathbb {R}^{2}$ of unit length $\left\| \textbf{t}_{1}\right\| =\left\| \textbf{t}_{2}\right\| =1$, set $\textbf{M}:={\left[ \textbf{t}_{1}|\textbf{t}_{2}\right] } \in \mathbb {R}^{2\times 2}$ (cf. Notation 1). Let $\theta$ be the angle between $\textbf{t}_{1}$ and $\textbf{t}_{2}$, i.e., $\cos \theta =\left\langle \textbf{t}_{1},\textbf{t} _{2}\right\rangle$. Then

$$\begin{aligned} {\text {cond}}_{2}\left( \textbf{M}\right) \le \frac{2}{\left| \sin \theta \right| }. \end{aligned}$$

Proof

Recall the characterisation of the spectral norm $\left\| \textbf{M}\right\| _{2}^{}=\sigma _\textrm{max}({\textbf{M}})$ as the maximal singular value of the matrix ${\textbf{M}}$ from linear algebra. A direct computation reveals the eigenvalues $1\pm \cos \theta$ and the corresponding eigenfunctions $\left( \pm 1;1\right) \in \mathbb {R}^{2}$ of

$$\begin{aligned} \textbf{M}^{\top }\textbf{M}= \begin{pmatrix} 1 &{} \cos \theta \\ \cos \theta &{} 1 \end{pmatrix}. \end{aligned}$$

Suppose $1-\cos \theta \le 1+\cos \theta$ (otherwise replace $\theta$ by $\pi +\theta$ and observe $\left| \sin \theta \right| =\left| \sin \left( \theta +\pi \right) \right|$). Then, the estimate for the condition number of $\textbf{M}$ follows from

$$\begin{aligned} {\text {cond}}_{2}\left( \textbf{M}\right) =\sqrt{\frac{1+\cos \theta }{1-\cos \theta }}=\sqrt{\frac{(1+\cos \theta )^{2}}{1-\cos ^{2}\theta }}\le \frac{2}{|\sin (\theta )|}. \end{aligned}$$

$\square$

The second intermediate result for the proof of Lemma 5 is an algebraic identity for the rotation of vectors in 2D. Define the rotation matrix

$$\begin{aligned} \textbf{R}\left( \theta \right) := \begin{pmatrix} \cos \theta &{} -\sin \theta \\ \sin \theta &{} \cos \theta \end{pmatrix} = \begin{pmatrix} {\text {Re}} &{} -{\text {Im}}\\ {\text {Im}} &{} {\text {Re}} \end{pmatrix} {\text {e}}^{{\text {i}}\theta }. \end{aligned}$$

(22)

Proposition 5

(Rotation identity) Any $\alpha ,\beta ,\gamma \in \mathbb {R}$ satisfies

$$\begin{aligned} \sin \left( \alpha -\beta \right) \textbf{R}\left( \gamma \right) =\sin \left( \gamma -\beta \right) \textbf{R}\left( \alpha \right) +\sin \left( \alpha -\gamma \right) \textbf{R}\left( \beta \right) . \end{aligned}$$

Proof

The real ${\text {Re}}$ and imaginary ${\text {Im}}$ parts are $\mathbb {R}$-linear and it is enough to verify

$$\begin{aligned} \sin \left( \alpha -\beta \right) {\text {e}}^{{\text {i}} \gamma }=\sin \left( \gamma -\beta \right) {\text {e}} ^{{\text {i}}\alpha }+\sin (\alpha -\gamma ){\text {e}} ^{{\text {i}}\beta }. \end{aligned}$$

(23)

Indeed, a direct computation with the identity $2 \! {\text {i}}\sin \theta ={\text {e}}^{{\text {i}}\theta }-{\text {e}} ^{-{\text {i}}\theta }$ for $\theta \in \mathbb {R}$ shows

$$\begin{aligned} 2 \! {\text {i}}\sin \left( \gamma -\beta \right) {\text {e}} ^{{\text {i}}\alpha }&=\left( {\text {e}} ^{{\text {i}}\left( \gamma -\beta \right) }-{\text {e}} ^{{\text {i}}\left( \beta -\gamma \right) }\right) {\text {e}}^{{\text {i}}\alpha }={\text {e}} ^{{\text {i}}\gamma }{\text {e}} ^{{\text {i}}\left( \alpha -\beta \right) }-{\text {e}} ^{{\text {i}}\beta }{\text {e}} ^{{\text {i}}\left( \alpha -\gamma \right) },\\ 2 \! {\text {i}}\sin \left( \alpha -\gamma \right) {\text {e}} ^{{\text {i}}\beta }&=\left( {\text {e}} ^{{\text {i}}\left( \alpha -\gamma \right) }-{\text {e}} ^{{\text {i}}\left( \gamma -\alpha \right) }\right) {\text {e}}^{{\text {i}}\beta }={\text {e}} ^{{\text {i}}\alpha }{\text {e}} ^{{\text {i}}\left( \beta -\gamma \right) }-{\text {e}} ^{{\text {i}}\gamma }{\text {e}} ^{{\text {i}}\left( \beta -\alpha \right) }. \end{aligned}$$

The sum of these terms and ${\text {e}}^{{\text {i}} \beta }{\text {e}}^{{\text {i}}\left( \alpha -\gamma \right) }={\text {e}}^{{\text {i}}\alpha }{\text {e}} ^{{\text {i}}\left( \beta -\gamma \right) }$ lead to the identity (23). This and (22) conclude the proof. $\square$

Proof of Lemma 5

Assume $\sin \theta _{1}\ne 0$, otherwise the left-hand side of (21) is zero and there is nothing to prove. Step 1 (preparations): Rescale the directions to unit length $\left\| \textbf{t}_{1}\right\| =\dots =\left\| \textbf{t}_{4}\right\| =1$ and let $\textbf{M}:={[\textbf{t} _{1}|\textbf{t}_{2}]}\in \mathbb {R}^{2\times 2}$ be the matrix with columns $\textbf{t}_{1}$ and $\textbf{t}_{2}$. It is well known that the Piola transform preserves the divergence of a function. Indeed, the transformed function $\widehat{\textbf{v}}:=\textbf{M}^{-1}\textbf{v}\circ \mathbf {\Phi }$ with $\mathbf {\Phi }({\hat{\textbf{x}}}):={\textbf{M}}{\hat{\textbf{x}}}+\textbf{z}$ satisfies $\left( {\text {div}}\textbf{v}\right) \circ \mathbf {\Phi } ={\text {div}}\widehat{\textbf{v}}$ and the componentwise Gâteaux derivatives satisfy

$$\begin{aligned} \partial _{\tilde{\textbf{t}}_{j}}\left( \widehat{\textbf{v}}_{j-1} -\widehat{\textbf{v}}_{j}\right) \left( \textbf{0}\right) =0\quad \text {for }j=1,\dots ,4 \end{aligned}$$

(24)

in the directions ${\tilde{\textbf{t}}}_{j}:=\textbf{M}^{-1}\textbf{t}_{j}$ by assumption. Note that ${\tilde{\textbf{t}}}_{1} =\textbf{e}_{1}$ and ${\tilde{\textbf{t}}} _{2}=\textbf{e}_{2}$ are the canonical unit vectors in $\mathbb {R}^{2}$ so that $\partial _{1}=\partial _{{\tilde{\textbf{t}}}_{1}}$ and $\partial _{2}=\partial _{{\tilde{\textbf{t}}}_{2}}$ hold. We denote the components of $\widehat{\textbf{v}}_{j}$ by $\left( \widehat{v}_{j}^{1},\widehat{v}_{j} ^{2}\right)$. Following the proof of [4, Lem. 2] we conclude that the sum in the left-hand side of (21) equals

$$\begin{aligned} \sum _{j=1}^{4}(-1)^{j}&\left( {\text {div}}\textbf{v}_{j}\right) \left( \textbf{z}\right) =\sum _{j=1}^{4}(-1)^{j}\left( {\text {div}} \widehat{\textbf{v}}_{j}\right) \left( \textbf{0}\right) =\sum _{j=1} ^{4}\left( -1\right) ^{j}\left( \partial _{1}\widehat{v}_{j}^{1} +\partial _{2}\widehat{v}_{j}^{2}\right) \left( \textbf{0}\right) \nonumber \\&=\partial _1 \! \left( \widehat{v}_{4}^{1}-\widehat{v}_{1}^{1}\right) \left( \textbf{0}\right) +\partial _{1} \! \left( \widehat{v}_{2}^{1} -\widehat{v}_{3}^{1}\right) \left( \textbf{0}\right) +\partial _{2} \! \left( \widehat{v}_{2}^{2}-\widehat{v}_{1}^{2}\right) \left( \textbf{0}\right) +\partial _{2} \! \left( \widehat{v}_{4}^{2}-\widehat{v}_{3}^{2}\right) \left( \textbf{0}\right) \nonumber \\&=\partial _{1} \! \left( \widehat{v}_{2}^{1}-\widehat{v}_{3}^{1}\right) \left( \textbf{0}\right) +\partial _{2} \! \left( \widehat{v}_{4}^{2} -\widehat{v}_{3}^{2}\right) \left( \textbf{0}\right) \end{aligned}$$

(25)

with (24) in the last step. The other terms might not vanish but (24) leads to a bound in terms of the full gradient $\nabla (\widehat{v}_{2}^{1}-\widehat{v}_{3}^{1})$ and $\nabla (\widehat{v}_{4}^{2} -\widehat{v}_{3}^{2})$ at $\textbf{0}$.

Step 2 (bounds by the full gradient): The directions $\textbf{t}_{j}=\textbf{R}\left( \theta _{1} +\dots +\theta _{j-1}\right) \textbf{t}_{1}$ are rotations of $\textbf{t}_{1}$ by the angles $\theta _{j}$ satisfying $\cos \theta _{j}=\left\langle \textbf{t}_{j},\textbf{t}_{j+1}\right\rangle$ for $j=1,\dots ,4$. The application of Proposition 5 for the rotation of $\textbf{t} _{1}$ first with $\alpha \leftarrow \theta _{1}+\theta _{2}$, $\beta \leftarrow 0$, $\gamma \leftarrow \theta _{1}$ and second with $\alpha \leftarrow \theta _{1} +\theta _{2}+\theta _{3}=2\pi -\theta _{4}$, $\beta \leftarrow \theta _{1}$, $\gamma \leftarrow 0$ leads to

$$\begin{aligned} \sin \left( \theta _{1}+\theta _{2}\right) \,\textbf{t}_{2}&=\sin \left( \theta _{1}\right) \textbf{t}_{3}+\sin \left( \theta _{2}\right) \,\textbf{t}_{1},\\ \sin \left( \theta _{2}+\theta _{3}\right) \,\textbf{t}_{1}&=\sin \left( -\theta _{1}\right) \,\textbf{t}_{4}+\sin \left( 2\pi -\theta _{4}\right) \,\textbf{t}_{2}. \end{aligned}$$

This, (24) with ${\tilde{\textbf{t}}}_{j}=\textbf{e}_{j}$ for $j=1,2$, and the anti-symmetry of the sine result in

$$\begin{aligned} \begin{array}{l} \left| \sin \left( \theta _{2}\right) \,\partial _{1} \! \left( \widehat{v} _{2}^{1}-\widehat{v}_{3}^{1}\right) \right| =\left| \sin \left( \theta _{1}+\theta _{2}\right) \,\partial _{2} \! \left( \widehat{v}_{2} ^{1}-\widehat{v}_{3}^{1}\right) \right| \le \left\| \sin \left( \theta _{1}+\theta _{2}\right) \,\nabla \! \left( \widehat{v}_{2}^{1} -\widehat{v}_{3}^{1}\right) \right\| ,\\ \left| \sin \left( \theta _{4}\right) \,\partial _{2} \! \left( \widehat{v} _{3}^{2}-\widehat{v}_{4}^{2}\right) \right| =\left| \sin \left( \theta _{2}+\theta _{3}\right) \,\partial _{1} \! \left( \widehat{v}_{3} ^{2}-\widehat{v}_{4}^{2}\right) \right| \le \left\| \sin \left( \theta _{2}+\theta _{3}\right) \,\nabla \! \left( \widehat{v}_{3}^{2} -\widehat{v}_{4}^{2}\right) \right\| \end{array} \end{aligned}$$

(26)

at $\textbf{0}=\mathbf {\Phi }^{-1}($ $\textbf{z})$. Introduce the shorthand

$$\begin{aligned} \mu :=\min \left\{ \left| \sin \left( \theta _{2}\right) \right| ,\left| \sin \left( \theta _{4}\right) \right| \right\} \quad \text {and }\Theta :=\max \left\{ \left| \sin \left( \theta _{1}+\theta _{2}\right) \right| ,\left| \sin \left( \theta _{2} +\theta _{3}\right) \right| \right\} . \end{aligned}$$

The combination of (25) and (26) provide

$$\begin{aligned} \mu \left| \sum _{j=1}^{4}(-1)^{j}\left( {\text {div}}\textbf{v} _{j}\right) (\textbf{z})\right|&\le \Theta \left( \left\| \nabla \left( \widehat{v}_{2}^{1}-\widehat{v}_{3}^{1}\right) \right\| +\left\| \nabla \left( \widehat{v}_{3}^{2}-\widehat{v}_{4}^{2}\right) \right\| \right) \left( \textbf{0}\right) \\&\le \sqrt{2}\Theta \sum _{j=1}^{4}\left\| \nabla \widehat{\textbf{v}}_{j}\right\| \left( \textbf{0}\right) \end{aligned}$$

with a triangle inequality and $\left\| \nabla \widehat{\textbf{v}}_{3} ^{1}\right\| +\left\| \nabla \widehat{\textbf{v}}_{3}^{2}\right\| \le \sqrt{2}\left\| \nabla \widehat{\textbf{v}}_{3}\right\|$ in the last step.

Step 3 (finish of the proof): Recall the assumption $\sin \theta _{1}\ne 0$. This, the chain rule for derivatives $D\widehat{\textbf{v}}_{j}=\textbf{M}^{-1}\left( \left( D\textbf{v}_{j}\right) \circ \mathbf {\Phi }\right) \textbf{M}$, and the Cauchy–Schwarz inequality imply $\left\| \nabla \widehat{\textbf{v}} _{j}\right\| \left( \textbf{0}\right) \le \left\| \textbf{M} ^{-1}\right\| _{2}\left\| \textbf{M}\right\| _{2}\left\| \nabla \textbf{v}_{j}\right\| \left( \textbf{z}\right)$ for $j=1,\dots ,4$. Since ${\text {cond}}_{2}\left( \textbf{M}\right) =\left\| \textbf{M}^{-1}\right\| _{2}\left\| \textbf{M}\right\| _{2} \le 2/\left| \sin \theta _{1}\right|$ from Proposition 4, this concludes the proof. $\square$

Lemma 5 allows for an important generalisation of the known result, e.g., [4, Lem. 2], that $A_{\mathcal {T},\textbf{z}}\left( {\text {div}}\textbf{v}\right) =0$ vanishes for continuous piecewise polynomials $\textbf{v}\in \textbf{S}_{k,0}\left( \mathcal {T} _{\textbf{z}}\right)$.

Corollary 1

Let $k\ge 0$ and recall $\eta _{0}>0$ from Lemma 1. Any vertex $\textbf{z}\in \mathcal {V}\left( \mathcal {T}\right)$ with $\Theta (\textbf{z})<\eta _0$ satisfies

$$\begin{aligned} \left| A_{\mathcal {T},\textbf{z}}\left( {\text {div}}\textbf{v}\right) \right| \le C_{{{\text {shape}}}}h_{\textbf{z}} ^{-1}k^{2}{\Theta (\textbf{z})}\left\| \nabla \textbf{v}\right\| _{\mathbb {L}^{2}\left( \omega _{\textbf{z}}\right) }\text { for all }\textbf{v}\in \textbf{S} _{k,0}\left( \mathcal {T}\right) . \end{aligned}$$

The constant $C_{{{\text {shape}}}}>0$ exclusively depends on the shape-regularity.

Proof

For $\textbf{z}\in \mathcal {V}\left( \mathcal {T} \right)$, recall the fixed counterclockwise numbering (6) of the triangles in $\mathcal {T}_{\textbf{z}}$ so that $\mathcal {T}_{\textbf{z}}=\left\{ K_{j}:1\le j\le N_{\textbf{z}}\right\}$ for $N_{\textbf{z}}:=\left| \mathcal {T}_{\textbf{z}}\right|$ as in Fig. 2. First we consider the case of an interior vertex $\textbf{z}\in \mathcal {V}_{\Omega }\left( \mathcal {T} \right)$ with $N_{\textbf{z}}=4$ from Lemma 1(a). Since $\textbf{v}\in \textbf{S}_{k,0}\left( \mathcal {T}\right)$ is globally continuous, the jump $\left[ \textbf{v}\right] _{E_{j}}=0$ vanishes along the common edge $E_{j}:=\partial K_{j-1} \cap \partial K_{j}$ and, as a consequence, $\partial _{\textbf{t}_{j}}( \left. \textbf{v}\right| _{K_{j-1}}-\left. \textbf{v}\right| _{K_{j}}) \left( \textbf{z}\right) =\textbf{0}$. Thus, Lemma 5 applies to $\textbf{v}_{j}:=\left. \textbf{v} \right| _{K_{j}}$ for $j=1,\dots ,4$ and shows

$$\begin{aligned} \mu \left( \sin \theta _{1}\right) \left| A_{\mathcal {T},\textbf{z}}\left( {\text {div}}\textbf{v}\right) \right| \le \sqrt{8}\Theta \sum _{K\in \mathcal {T}_{\textbf{z}}}\left\| \nabla \textbf{v} \vert _{K} \left( \textbf{z}\right) \right\| . \end{aligned}$$

The k-explicit inverse inequality [20, Thm. 4.76] and a scaling argument imply that there is a constant $\widetilde{C} _{{{\text {shape}}}}>0$ exclusively depending on the shape-regularity of $\mathcal {T}$ with

$$\begin{aligned} \left\| \nabla \textbf{v}\vert _{K}\left( \textbf{z}\right) \right\| \le \left\| \nabla \textbf{v}\right\| _{\mathbb {L} ^{\infty }\left( K\right) }\le \widetilde{C}_{{{\text {shape}}}}h_{\textbf{z} }^{-1}k^{2}\left\| \nabla \textbf{v}\right\| _{\mathbb {L}^{2}\left( K\right) } \quad \forall K\in \mathcal {T}_{\textbf{z}}. \end{aligned}$$

Since $\Theta ($ $\textbf{z})=\Theta$ holds and the minimal angle property implies $\sin \phi _{\mathcal {T}}\le \sin \theta _{1}$, this, the definition of $\mu$ with $\sin \phi _{\mathcal {T}}\le \mu$ in Lemma 5, and $\sum _{K\in \mathcal {T}_{\textbf{z}} }\left\| \nabla \textbf{v}\right\| _{\mathbb {L}^{2}(K)}\le 2\left\| \nabla \textbf{v}\right\| _{\mathbb {L}^{2}\left( \omega _{\textbf{z} }\right) }$ from a Cauchy inequality conclude the proof with $C_{{{\text {shape}}}}:=\sqrt{32}\left( \sin \phi _{\mathcal {T}}\right) ^{-2}\widetilde{C}_{{\text {shape}}}$. The case of a boundary vertex $\textbf{z}\in \mathcal {V}_{\partial \Omega }\left( \mathcal {T}\right)$ with $N_{\textbf{z}}\le 3$ from Lemma 1(b) can be transformed to the first case. One extends the “open” boundary patch $\mathcal {T}_{\textbf{z}}$ to a closed patch by defining shape regular triangles $K_{j}$, $N+1\le j\le 4$, such that the extended patch $\widetilde{\mathcal {T}}_{\textbf{z}}:=\mathcal {T}_{\textbf{z}}\cup \left\{ K_{j}:N+1\le j\le 4\right\}$ satisfies: a) $\widetilde{\mathcal {T} }_{\textbf{z}}$ a closed patch, i.e., $\textbf{z}$ is a vertex of $K_{j}$, $1\le j\le 4$ and the intersection $K_{j-1}\cap K_{j}$ is a common edge, b) $\textbf{z}$ is a $\eta$-critical vertex in $\widetilde{\mathcal {T} }_{\textbf{z}}$. The function $\textbf{v}\in \textbf{S}_{k,0}\left( \mathcal {T}\right)$ then extends to the full patch ${\textstyle \bigcup _{N+1\le j\le 4}} K_{j}$ by $\textbf{0}$ and the proof of the first case carries over. $\square$

5.2 Proof of Lemma 4

The last ingredient for the proof of Lemma 4 concerns the explicit characterisation of the functions in $M_{0,k-1}(\mathcal {T})$ that are $L^{2}$ orthogonal to $M_{\eta ,k-1}\left( \mathcal {T}\right)$. Recall the fixed counter-clockwise numbering (6) of $\mathcal {T}_\textbf{z}$ and let $\lambda _{K_j,\textbf{z}}$ denote the barycentric coordinate associated to $\textbf{z}$ on $K_j\in {\mathcal {T}}_\textbf{z}$.

Definition 4

For $\textbf{z}\in \mathcal {V}\left( \mathcal {T}\right)$, the function $b_{k,\textbf{z} }\in \mathbb {P}_{k}\left( \mathcal {T}_{\textbf{z}}\right)$ is given by

$$\begin{aligned} b_{k,\textbf{z}}:=\sum _{j=1}^{N_{\textbf{z}}}\frac{\left( -1\right) ^{j{+k}} }{\left| K_{j}\right| }P_{k}^{\left( 0,2\right) }\left( 1-2\lambda _{K_{j},\textbf{z}}\right) \chi _{K_{j}}. \end{aligned}$$

(27)

The polynomials $P_{k}^{\left( 0,2\right) }\left( 1-2\lambda _{K,\textbf{z}}\right) \in \mathbb P_k(K)$ have been introduced in [21] to characterize the orthogonal complement of ${\text {div}}(\textbf{S}_{k+1,0}(\mathcal {T}))$ in $\mathbb P_{k,0}(\mathcal {T})$ on certain macro elements, see also [10, 22, 23].

Lemma 6

Set $\zeta _{k}:=\left( {\begin{array}{c}k+2\\ 2\end{array}}\right)$ for $k\ge 1$ and let $\textbf{z}\in \mathcal {V}\left( \mathcal {T}\right)$.

• 1. The function $b_{k,\textbf{z}}\in \mathbb {P}_{k}\left( \mathcal {T} _{\textbf{z}}\right)$ from (27) satisfies, for all $1\le j\le N_{\textbf{z}}$, that

  $$\begin{aligned} \left. b_{k,\textbf{z}}\right| _{K_{j}}\left( \textbf{y}\right) =\frac{\left( -1\right) ^{j}}{\left| K_{j}\right| }\times \left\{ \begin{array}{ll} \zeta _{k} &{}\text {if } \textbf{y}=\textbf{z},\\ {(-1)^k} &{}\text {else} \end{array} \right.{} & {} \forall \textbf{y}\in \mathcal {V}(K_j). \end{aligned}$$

  (28)

• 2. The following integral relations hold on the triangle $K_j\in \mathcal {T}_{\textbf{z}}$:

  $$\begin{aligned} \left( b_{k,\textbf{z}},1\right) _{L^{2}\left( K_{j}\right) }&=\left( -1\right) ^{j}\zeta _{k}^{-1},{} & {} \end{aligned}$$

  (29)
  $$\begin{aligned} \left( b_{k,\textbf{z}},q\right) _{L^{2}\left( K_{j}\right) }&=q\left( \textbf{z}\right) \left( b_{k,\textbf{z}},1\right) _{L^{2}\left( K_{j}\right) }&\forall q&\in \mathbb {P}_{k}(K_{j}). \end{aligned}$$

  (30)

• 3. The function $\zeta _{k}b_{k,\textbf{z}}$ is the Riesz representation of $A_{\mathcal {T},\textbf{z}}$ in $\mathbb P_k(\mathcal {T}_{\textbf{z}})$, i.e.,

  $$\begin{aligned} \zeta _{k}\left( b_{k,\textbf{z}},q\right) _{L^{2}\left( \omega _{\textbf{z}}\right) }&= A_{\mathcal {T} ,\textbf{z}}\left( q\right)&\forall q&\in \mathbb P_{k}(\mathcal {T}_{\textbf{z}}). \end{aligned}$$

  (31)

  In partiular, $b_{k,\textbf{z}}$ is $L^{2}( \omega _{\textbf{z}})$ orthogonal to all $q\!\in \!\mathbb {P}_{k}(\mathcal {T}_{\textbf{z}})$ with $A_{\mathcal {T},\textbf{z}}( q) \!=\!0$.

• 4. For $k\ge 2$, the set $\{1\}\cup \{ b_{k,\textbf{z}}\}_{\textbf{z}\in \mathcal {V}(\mathcal {T})}$ is linearly independent and

  $$\begin{aligned} {\frac{3}{4}\Bigg \Vert \sum ^{}_{\textbf{z}\in \mathcal {V}(K)} c_\textbf{z}b_{k,\textbf{z}} \Bigg \Vert _{L^2(K)}^2}\hspace{-1em}\le |K|^{-1}\sum ^{}_{\textbf{z}\in \mathcal {V}(K)} c_\textbf{z}^2\le \frac{12}{7} {\text {min}}_{C\in \mathbb R}\Bigg \Vert \sum ^{}_{\textbf{z}\in \mathcal {V}(K)} c_\textbf{z}b_{k,\textbf{z}} - C\Bigg \Vert _{L^2(K)}^2 \end{aligned}$$

  (32)

  for any $K\in \mathcal {T}$ and $c_\textbf{z}\in \mathbb R$.

Proof

From [22, (3.14), (3.2)] it follows that the function $b_{j}:=P_{k}^{\left( 0,2\right) }\left( 1-2\lambda _{K_{j},\textbf{z} }\right)$ is orthogonal to any function $q\in \mathbb {P}_{k}(K_{j})$ with $q\left( \textbf{z}\right) =0$ and fulfils

$$\begin{aligned} b_{j}\left( \textbf{z}\right) =P_{k}^{(0,2)}\left( -1\right) =\left( -1\right) ^{k}\zeta _{k},\quad b_{j}\left( \textbf{y}\right) =P_{k}^{\left( 0,2\right) }\left( 1\right) =1\quad \forall \textbf{y} \in \mathcal {V}\left( K_{j}\right) \backslash \left\{ \textbf{z}\right\} . \end{aligned}$$

(33)

The integral of $b_{j}$ over the triangle $K_j$ can be evaluated explicitly as

$$\begin{aligned} \left( b_{j},1\right) _{L^{2}\left( K_{j}\right) }&=\int _{K_{j}}P_{k}^{\left( 0,2\right) }\left( 1-2\lambda _{K_{j},\textbf{z}}\right) =2\left| K_{j}\right| \int _{0}^{1}\int _{0}^{1-x_{1}}P_{k}^{\left( 0,2\right) }\left( 1-2x_{1}\right) d x_{2} d x_{1}\nonumber \\&=2\left| K_{j}\right| \int _{0}^{1}\!\!\left( 1-x_{1}\right) P_{k}^{\left( 0,2\right) }( 1-2x_{1}) d x_{1} \nonumber \\ {}&\overset{t=1-2x_{1}}{=}\frac{|K_j|}{2} \int _{-1}^{1}\!\!\left( t+1\right) P_{k}^{\left( 0,2\right) }( t) d t\nonumber \\&\overset{\text {[22, Lem. C.1]}}{=}\left( -1\right) ^{k}\left| K_{j}\right| /\zeta _{k}. \end{aligned}$$

(34)

This implies (29). The $L^{2}$ orthogonality $\left( b_{j},q-q\left( \textbf{z}\right) \right) _{L^{2}\left( K_{j}\right) }=0$ shows

$$\begin{aligned} 0<\left( b_{j},b_{j}\right) _{L^{2}\left( K_{j}\right) }=b_{j}\left( \textbf{z}\right) \;\left( b_{j},1\right) _{L^{2}\left( K_{j}\right) }\overset{(33), (34)}{=}\left| K_{j}\right| \qquad \forall q\in \mathbb {P}_{k}\left( K_{j}\right) . \end{aligned}$$

In turn, (30) follows from

$$\begin{aligned} \left( b_{k,\textbf{z}},q\right) _{L^{2}\left( K_{j}\right) }=\left( b_{k,\textbf{z}},q-q\left( \textbf{z}\right) \right) _{L^{2}\left( K_{j}\right) }+\left( b_{k,\textbf{z}},q\left( \textbf{z}\right) \right) _{L^{2}\left( K_{j}\right) }=q\left( \textbf{z}\right) \left( b_{k,\textbf{z}},1\right) _{L^{2}\left( K_{j}\right) }. \end{aligned}$$

The definition of $\left. b_{k,\textbf{z}}\right| _{K_{j}}=\left( -1\right) ^{j{+k}}\left| K_{j}\right| ^{-1}b_{j}$ in $K_{j}\in \mathcal {T}_{\textbf{z}}$ reveals

$$\begin{aligned} \left( b_{k,\textbf{z}},q\right) _{L^{2}\left( \omega _{\textbf{z}}\right) }&=\sum _{j=1}^{N_{\textbf{z}}}\left. q\right| _{K_{j}}\left( \textbf{z}\right) \frac{\left( -1\right) ^{j{+k}}}{\left| K_{j}\right| }\left( b_{j},1\right) _{L^{2}\left( K_{j}\right) } \overset{(34)}{=} \zeta _{k}^{-1}A_{\mathcal {T} ,\textbf{z}}\left( q\right) \end{aligned}$$

for any $q\in \mathbb {P}_{k}(\mathcal {T}_{\textbf{z}})$. This is (31) and implies the orthogonality $\left( b_{k,\textbf{z}},q\right) _{L^{2}(\omega _{\textbf{z} })} = 0$ for any $q\in \mathbb {P}_{k}\left( \mathcal {T}_{\textbf{z}}\right)$ with $A_{\mathcal {T},\textbf{z}}\left( q\right) =0$. Given coefficients $c_\textbf{z}\in \mathbb R$ for $\textbf{z}\in \mathcal {V}(K),K\in \mathcal {T}$, set $q:=\sum ^{}_{\textbf{z}\in \mathcal {V}(K)} c_\textbf{z}b_{k,\textbf{z}}$. The minimum in (32) is obtained for the integral mean $q_K=|K|^{-1} (q,1)_{L^2(K)}$, i.e.,

$$\begin{aligned} {\text {min}}_{C\in \mathbb R}\Vert q&- C\Vert _{L^2(K)}^2= \Vert q-q_K\Vert _{L^2(K)}^2=\Vert q\Vert _{L^2(K)}^2-\Vert q_K\Vert _{L^2(K)}^2=\sum ^{}_{\textbf{z},\textbf{y}\in \mathcal {V}(K)} c_\textbf{z}c_\textbf{y}M_{\textbf{z},\textbf{y}} \end{aligned}$$

with $M_{\textbf{z},\textbf{y}}:=(b_{k,\textbf{z}},b_{k,\textbf{y}})_{L^2(K)}-|K|^{-1} (b_{k,\textbf{z}},1)_{L^2(K)}(b_{k,\textbf{y}},1)_{L^2(K)}$. Since $\Vert b_{k,\textbf{z}}\Vert _{L^2(K)}^2=|K|^{-1}$ and $|(b_{k,\textbf{z}},b_{k,\textbf{y}})_{L^2(K)}|=\zeta _k^{-1}|K|^{-1}$ from (28) to (30) for $\textbf{z}\ne \textbf{y}\in \mathcal {V}(K)$, (29) shows that the diagonal and offdiagonal elements of the symmetric diagonally dominant $3\times 3$ matrix $M:=(M_{\textbf{z},\textbf{y}})_{\textbf{z},\textbf{y}\in \mathcal {V}(K)}\in \mathbb R^{3\times 3}$ are controlled by

$$\begin{aligned} M_{\textbf{z},\textbf{z}}=|K|^{-1}(1-\zeta _k^{-2})=:m{} & {} |M_{\textbf{z},\textbf{y}}|\le |K|^{-1}(\zeta _k^{-1}+\zeta _k^{-2})=:r \end{aligned}$$

$\textbf{z}\ne \textbf{y}\in \mathcal {V}(K)$. This and the Gerschgorin circle theorem [24, Thm. 7.2.1] prove that (all and in particular) the lowest eigenvalue $\lambda _\textrm{min}$ of M is bounded from below by $m-2r\ge 7|K|^{-1}/12$ for $k\ge 2$. Analog arguments control the maximal eigenvalue $\lambda _{\max }\le |K|^{-1}(1+2\zeta _k^{-1})\le |K|^{-1}4/3$ for $k\ge 2$ of $N\in \mathbb R^{3\times 3}$ with $N_{\textbf{z},\textbf{y}}:=(b_{k,\textbf{z}},b_{k,\textbf{y}})_{L^2(K)}$. Hence, the min-max theorem implies (32) and the linear independence follows from the support property, ${\text {supp}}b_{k,{\textbf{z}}}=\omega _{{\textbf{z}}}$. This concludes the proof. $\square$

Now we have all the ingredients for the proof of the key Lemma 4 of this section.

Proof of Lemma 4:

This proof is split into 3 steps.

Step 1 (characterisation of the divergence): Note that ${\text {div}}\textbf{v}_{\textbf{S}}\in \mathbb P_{k-1,0}\left( \mathcal {T} \right)$ has integral mean zero from $\textbf{v}_{\textbf{S}}\in \textbf{S}_{k,0}({\mathcal {T}})$. The $L^{2}$ orthogonality ${\text {div}}\textbf{v}_{\textbf{S}}\perp M_{\eta ,k-1}\left( \mathcal {T}\right)$ implies

$$\begin{aligned} {\text {div}}\textbf{v}_{\textbf{S}}\in M_{\eta ,k-1}\left( \mathcal {T}\right) ^{\perp }:=\left\{ p\in \mathbb P_{k-1}\left( \mathcal {T} \right) | \left( p,q\right) _{L^{2}\left( \Omega \right) }=0\text { for all }q\in M_{\eta ,k-1}\left( \mathcal {T}\right) \right\} . \end{aligned}$$

It follows from Lemma 6(4) that ${\text {span}}\{1,b_{k-1,\textbf{z}}\,\ \textbf{z}\in C_{\mathcal {T}}\left( \eta \right) \}$ is the orthogonal complement of $M_{\eta ,k-1}\left( \mathcal {T}\right)$ in $\mathbb {P}_{k-1} \left( \mathcal {T}\right)$. This guarantees the existence of coefficients $c_{\textbf{z}}\in \mathbb {R}$ for $\textbf{z}\in \mathcal {C}_{{\mathcal {T}}}\left( \eta \right)$ and $C_{\textbf{S}}\in \mathbb R$ such that

$$\begin{aligned} {\text {div}}\textbf{v}_{\textbf{S}}=\sum _{\textbf{z}\in \mathcal {C}_{\mathcal T} \left( \eta \right) }c_{\textbf{z}} b_{k-1,\textbf{z}} +C_{\textbf{S}}. \end{aligned}$$

(35)

Recall the open subset $\Omega (\eta )\subset \Omega$ from (20).

Since ${\text {supp}}b_{k-1,\textbf{z}}=\omega _{\textbf{z}}\subset \overline{\Omega (\eta )}$ from Definition 4, (35) verifies ${\text {div}} \textbf{v}_{\textbf{S}}|_{\Omega {\setminus }\overline{\Omega (\eta )}}\equiv C_{\textbf{S}}$. For any $K\in \mathcal {T}$, Lemma 6(4) provides

$$\begin{aligned} \Vert {\text {div}}\textbf{v}_{\textbf{S}}-C_{\textbf{S}}\Vert _{L^2(K)}=\left\| \sum ^{}_{\textbf{z}\in \mathcal {C}_{\mathcal {T}}(\eta )} c_{\textbf{z}}b_{k-1,\textbf{z}}\right\| _{L^2(K)}\le \sqrt{16/7}\Vert {\text {div}}\textbf{v}_{\textbf{S}}\Vert _{L^2(K)}. \end{aligned}$$

The integral mean is the best-approximation onto constants and vanishes for ${\text {div}}\textbf{v}_{\textbf{S}}$ so that this and ${\text {div}}\textbf{v}_{\textbf{S}}|_{\Omega {\setminus }\overline{\Omega (\eta )}}\equiv C_{\textbf{S}}$ verify

$$\begin{aligned} \Vert {\text {div}}\textbf{v}_{\textbf{S}}\Vert _{L^2(\Omega )}&=\min _{C\in \mathbb R}\Vert {\text {div}}\textbf{v}_{\textbf{S}}\!-\!C\Vert _{L^2(\Omega )}\nonumber \\&\le \Vert {\text {div}}\textbf{v}_{\textbf{S}} -C_{\textbf{S}}\Vert _{L^2(\Omega (\eta ))} \le \sqrt{16/7}\Vert {\text {div}}\textbf{v}_{\textbf{S}}\Vert _{L^2(\Omega (\eta ))}. \end{aligned}$$

(36)

Lemma 1(a) and $\eta \le \eta _0$ guarantee $N_{\textbf{z}}=4$ for any interior $\eta$-critical vertex $\textbf{z}\in \mathcal {C}_{\mathcal {T}}(\eta )\cap \mathcal {V}_{\Omega }(\mathcal {T})$. If $\mathcal {T}$ does not contain $\eta$-critical boundary vertices $\textbf{z}\in \mathcal {C}_{\mathcal {T}}(\eta )\cap \mathcal {V}_{\partial \Omega }(\mathcal {T})$ with $N_{\textbf{z}}$ odd, the integral mean of $b_{k-1,\textbf{z}}$ vanishes for all $\textbf{z}\in \mathcal {C}_{\mathcal {T}}(\eta )$ by (29) and

$$\begin{aligned} |\Omega |\,C_{\textbf{S}}=\int _\Omega {\text {div}}\textbf{v}_{\textbf{S}}- \sum ^{}_{\textbf{z}\in \mathcal {C}_{\mathcal {T}}(\eta )} c_{\textbf{z}}\int _\Omega b_{k-1,\textbf{z}} = 0. \end{aligned}$$

Step 2 (preparations): Let $K_{\textbf{z}}\in \mathcal {T}_{\textbf{z}}$ denote any fixed triangle in the vertex patch of $\textbf{z}\in \mathcal {C}_{\mathcal {T}}(\eta )$. The orthogonality of ${\text {div}}{\textbf{v}}_\textbf{S}$ onto $C_{\textbf{S}}\in \mathbb R$, (35), and Lemma 6(3) provide

$$\begin{aligned} \left\| {\text {div}}\textbf{v}_{\textbf{S}}\right\| _{L^{2}\left( \Omega \right) }^{2}&=\sum _{\textbf{z}\in C_{\mathcal {T}}( \eta ) }\left( c_{\textbf{z}}b_{k-1,\textbf{z} },{\text {div}}\textbf{v}_{\textbf{S}}\right) _{L^{2}\left( \omega _{\textbf{z}}\right) }{\overset{(31)}{=}{\zeta _{k-1}^{-1}}\sum _{\textbf{z}\in C_{\mathcal {T}}( \eta ) }c_{\textbf{z}}\,A_{\mathcal {T},\textbf{z}}\left( {\text {div}} \textbf{v}_{\textbf{S}}\right) }\nonumber \\&{\le \zeta _{k-1}^{-1}\sqrt{\sum _{\textbf{z}\in \mathcal C_{\mathcal {T}}\left( \eta \right) }\left| K_{\textbf{z}}\right| \left( A_{\mathcal {T},\textbf{z}}\left( {\text {div}}\textbf{v}_{\textbf{S}}\right) \right) ^{2}}\sqrt{\sum _{\textbf{z}\in C_\mathcal {T}(\eta ) }\left| K_{\textbf{z}}\right| ^{-1}c_\textbf{z}^2}} \end{aligned}$$

(37)

with a Cauchy inequality in $\ell ^2$ in the last step. Lemma 6(4) controls the last term by

$$\begin{aligned} \sum _{\textbf{z}\in C_\mathcal {T}(\eta ) }\left| K_{\textbf{z}}\right| ^{-1}c_\textbf{z}^2\le \sum ^{}_{K\in \mathcal {T}} \sum ^{}_{\textbf{z}\in \mathcal {V}(K)\cap \mathcal {C}_{\mathcal {T}}(\eta )} |K|^{-1}c_{\textbf{z}}^2\le 12/7\Vert {\text {div}}\textbf{v}_{\textbf{S}}\Vert _{L^2(\Omega (\eta ))}^2. \end{aligned}$$

(38)

Fig. 4

Perturbation ${\mathcal {T}}_\varepsilon$ (blue) of the criss-cross triangulation $\mathcal {T}_0$ (gray) of the square

Step 3 (divergence control): Let $\textbf{w}_\textbf{S}\in {{\textbf{S}}_{\eta ,k,0}}(\mathcal T){\subset \textbf{S}_{k,0}(\mathcal {T})}$ be arbitrary and recall $\left| K\right| \le h_{\textbf{z}}^{2}$ for all $K\in \mathcal {T}_\textbf{z}$ by definition. Since $A_{\mathcal {T},\textbf{z}}\left( {\text {div}}\textbf{w}_{\textbf{S}}\right)$ vanishes and $\Theta \left( \textbf{z}\right) \le \eta$ for every $\textbf{z}\in {\mathcal {C}}_{\mathcal {T}}\left( \eta \right)$, (37 ‘38) and Corollary 1 applied to $\textbf{v}_{\textbf{S}}-\textbf{w}_{\textbf{S}}\in \textbf{S}_{k,0}\left( \mathcal {T}\right)$ imply

$$\begin{aligned} \left\| {\text {div}}\textbf{v}_{\textbf{S}}\right\| _{L^{2}\left( \Omega \right) }&\le \sqrt{12/7}\zeta _{k-1}^{-1}\sqrt{\sum _{\textbf{z}\in \mathcal C_{\mathcal {T} }\left( \eta \right) }h_{\textbf{z}}^{2}\left( A_{\mathcal {T},\textbf{z}}\left( {\text {div}}\textbf{v}_{\textbf{S}}-{\text {div}}\textbf{w} _{\textbf{S}}\right) \right) ^{2}}\\&\le \sqrt{12/7}\,{C_{{\text {shape}}}}\zeta _{k-1}^{-1}k^{2} \sqrt{\sum _{\textbf{z}\in {\mathcal {C}}_{\mathcal {T}}\left( \eta \right) }\Theta \left( \textbf{z}\right) ^{2}\left\| \nabla \left( \textbf{u}_{\textbf{S}}-\textbf{w}_{\textbf{S} }\right) \right\| _{\mathbb {L}^{2}\left( \omega _{\textbf{z}}\right) }^{2}}. \end{aligned}$$

Hence, the finite overlap of the vertex patches and $\Theta (\textbf{z})\le \eta$ result in

$$\begin{aligned} \Vert {\text {div}}\textbf{v}_{\textbf{S}}\Vert _{L^2(\Omega )} \le \sqrt{36/7}\,{C_{{\text {shape}}}}\zeta _{k-1}^{-1}k^{2}\eta \left\| \nabla \left( \textbf{u}_{\textbf{S}}-\textbf{w} _{\textbf{S}}\right) \right\| _{\mathbb {L}^{2}\left( \Omega (\eta )\right) }. \end{aligned}$$

Since $\textbf{w}_{\textbf{S}}\in {{\textbf{S}}_{\eta ,k,0}}(\mathcal T)$ was arbitrary, this, (36), and $\zeta _{k-1}^{-1}k^2=2k/(k+1)\le 2$ conclude the proof. $\square$

5.3 Upper bound on the inf-sup constant

The characterisation of the spurious pressures in Lemma 6 and the analysis for $\eta$-critical vertices in Sect. 5.1 imply an upper bound on the discrete inf-sup constant (4) for the pressure-wired Stokes element. Recall $\Theta _{\min }(\eta )$ from (14).

Theorem 6

Let $k\ge 3$ and $0\le \eta <\eta _0$ with $\eta _0$ from Lemma 1 be given. If the mesh contains a vertex $\textbf{z}\in \mathcal {V}(\mathcal {T})$ with $\eta<\Theta (\textbf{z})<\eta _0$, then the inf-sup constant (4) satisfies

$$\begin{aligned} \beta \left( \textbf{S}_{k,0}\left( \mathcal {T}\right) ,M_{\eta ,k-1}\left( \mathcal {T}\right) \right) \le C\,\Theta _{\min }(\eta ). \end{aligned}$$

The constant $C>0$ exclusively depends on the shape-regularity of the mesh.

Proof

Consider a vertex $\textbf{z}\in \mathcal {V}(\mathcal {T})$ minimizing $\Theta (\textbf{z})=\Theta _{\min }(\eta )$ together with $b_{k-1,\textbf{z}}\in \mathbb P_{k-1}(\mathcal {T}_{\textbf{z}})$ from Lemma 6. (Observe $b_{k-1,\textbf{z}}\not \in M_{\eta ,k-1}(\mathcal {T})$ if $\mathcal {V}(\mathcal {T}(\textbf{z}))\cap \mathcal {C}_{\mathcal {T}}(\eta )\ne \emptyset$.) Recall from Lemma 6(4) that ${\text {span}}\{1,b_{k-1,\textbf{y}}| \textbf{y}\in C_{\mathcal {T}}\left( \eta \right) \}$ is the orthogonal complement of $M_{\eta ,k-1}\left( \mathcal {T}\right)$ in $\mathbb {P}_{k-1} \left( \mathcal {T}\right)$. This guarantees the existence of coefficients $c_{\textbf{y}}\in \mathbb {R}$ for all $\textbf{y}\in \mathcal {C}_{{\mathcal {T}}}\left( \eta \right)$ and $C_{\textbf{z}}\in \mathbb R$ with

$$\begin{aligned} \phi _{\textbf{z}}:=b_{k-1,\textbf{z}}+ \sum _{\textbf{y}\in \mathcal {C}_{{\mathcal {T}}} \left( \eta \right) }c_{\textbf{y}} b_{k-1,\textbf{y}} +C_{\textbf{z}}\in M_{\eta ,k-1}(\mathcal {T}). \end{aligned}$$

(39)

Observe that the assumption in Theorem 6 guarantees the existence of such a $\textbf{z}\in \mathcal {V}({\mathcal {T}})$ and $\Theta (\textbf{z})<\eta _0$ so that Corollary 1 is applicable. This enables the verification of

$$\begin{aligned} \sup _{\textbf{v}_{\textbf{S}}\in \textbf{S}_{k,0}(\mathcal {T})}\frac{(\phi _{\textbf{z}}, {\text {div}}(\textbf{v}_\textbf{S}))_{L^2(\Omega )}}{\Vert \textbf{v}_{\textbf{S}}\Vert _{\textbf{H}^1(\Omega )}\Vert \phi _{\textbf{z}}\Vert _{L^2(\Omega )}}\le C \Theta _{\min }(\eta ) \end{aligned}$$

(40)

in the following. Since the inf-sup constant $\beta \left( \textbf{S}_{k,0}\left( \mathcal {T}\right) , M_{\eta ,k-1}\left( \mathcal {T}\right) \right)$ is by definition smaller than the left-hand side of (40), this implies the claim.

To prove (40), let $\textbf{v}_{\textbf{S}}\in \textbf{S}_{k,0}(\mathcal {T})$ be arbitrary. Define $\mathcal {C}_{\mathcal {T}}^+(\eta ):=\mathcal {C}_{\mathcal {T}}(\eta )\cup \{\textbf{z}\}$ and set $c_{\textbf{z}}:=1$. Since $\zeta _{k-1}b_{k-1,\textbf{y}}$ is the Riesz representation of $A_{\mathcal {T},\textbf{y}}$ in $\mathbb P_{k-1}(\mathcal {T})$ for all $\textbf{y}\in \mathcal {V}(\mathcal {T})$ by Lemma 6(3), the orthogonality of ${\text {div}}(\textbf{v}_\textbf{S})$ onto $C_{\textbf{z}}\in \mathbb R$ and (39) reveal

$$\begin{aligned} (\phi _{\textbf{z}}, {\text {div}}(\textbf{v}_\textbf{S}))_{L^2(\Omega )}&= \zeta _{k-1}^{-1}A_{\mathcal {T},\textbf{z}}({\text {div}}(\textbf{v}_\textbf{S})) + \zeta _{k-1}^{-1}\sum ^{}_{\textbf{y}\in \mathcal {C}_{\mathcal {T}}(\eta )}c_{\textbf{y}} A_{\mathcal {T},\textbf{y}}({\text {div}}(\textbf{v}_\textbf{S}))\\&\le C_{\textrm{shape}}\zeta _{k-1}^{-1}k^2 \sqrt{\sum _{\textbf{y}\in \mathcal {C}_{\mathcal {T}}^+(\eta )} h_{\textbf{y}}^{-2}c_{\textbf{y}}^2} \sqrt{\sum _{\textbf{y}\in \mathcal {C}_{\mathcal {T}}^+(\eta )} \Theta (\textbf{y})^2\Vert \nabla \textbf{v}_{\textbf{S}}\Vert _{\mathbb L^2(\omega _{\textbf{z}})}^2} \end{aligned}$$

with Corollary 1 and a Cauchy inequality in $\ell ^2$ in the last step. Lemma 6(4) (applicable since $k\ge 3$), $h_{\textbf{y}}^{-2}\le |K_{\textbf{y}}|^{-1}$ by definition, and (39) lead as in (38) to the upper bound $12/7\Vert \phi _{\textbf{z}}\Vert _{L^2(\Omega )}^2$ for the first sum in the previously displayed inequality. The finite overlap of the vertex patches and $\Theta (\textbf{y})\le \Theta (\textbf{z})=\Theta _{\min }(\eta )$ for all $\textbf{y}\in \mathcal {C}_{\mathcal {T}}^+(\eta )$ control the second sum by

$$\begin{aligned} \sum _{\textbf{y}\in \mathcal {C}_{\mathcal {T}}^+(\eta )} \Theta (\textbf{y})^2\Vert \nabla \textbf{v}_{\textbf{S}}\Vert _{\mathbb L^2(\omega _{\textbf{z}})}^2 \le 3\Theta _{\min }(\eta )^2\Vert \nabla \textbf{v}_{\textbf{S}}\Vert _{\mathbb L^2(\Omega )}^2. \end{aligned}$$

The combination of the previous arguments with $\zeta _{k-1}^{-1}k^2=2k/(k+1)\le 2$ reads

$$\begin{aligned} (\phi _{\textbf{z}}, {\text {div}}(\textbf{v}_\textbf{S}))_{L^2(\Omega )} \le \sqrt{144/7}\, C_{\textrm{shape}}\Theta _{\min }(\eta )\Vert \nabla \textbf{v}_{\textbf{S}}\Vert _{\mathbb L^2(\Omega )}\Vert \phi _{\textbf{z}}\Vert _{L^2(\Omega )}. \end{aligned}$$

Since $\textbf{v}_{\textbf{S}}\in \textbf{S}_{k,0}(\mathcal {T})$ was arbitrary and $\Vert \nabla \textbf{v}_{\textbf{S}}\Vert _{\mathbb L^2(\Omega )}\le \Vert \textbf{v}_{\textbf{S}}\Vert _{\textbf{H}^1(\Omega )}$, this verifies (40) for $C:=\sqrt{144/7}\,C_{\textrm{shape}}\Theta _{\min }(\eta )$ and concludes the proof. $\square$

Remark 4

(Equivalence) Theorems 2 and 6 reveal that the inf-sup constant

$$\begin{aligned} \beta \left( \textbf{S}_{k,0}\left( \mathcal {T}\right) ,M_{\eta ,k-1}\left( \mathcal {T}\right) \right) \approx \Theta _{\min }(\eta ) \end{aligned}$$

is equivalent to the measure of singularity $\Theta _{\min }(\eta )$ with equivalence constants hidden in “$\approx$” that are independent of the mesh-size and the polynomial degree $k\ge 4$. In particular, the dependence on $\Theta _{\min }(\eta )$ in Theorem 2 is sharp.

6 Numerical experiments

In this section we report on numerical experiments of the convergence rates for the pressure-wired Stokes elements and investigate the dependence of $\left\| {\text {div}}\textbf{u}_{\textbf{S}}\right\| _{L^{2}\left( \Omega \right) }$ on $\eta$ and the number of degrees of freedom.

We comment on a straightforward implementation with a direct LU solver and Lagrange multipliers for the pressure constraints. For the original Scott–Vogelius element and nearly singular vertices the condition number of the algebraic system becomes very large. As a consequence all input errors and variational crimes are amplified by the bad conditioning. The treatment of the ill-conditioning in the presence of few nearly singular vertices by more robust solvers, e.g, of Krylov type, lies beyond the scope of this paper with its focus on the pressure-wired Stokes element.

Analytical solution on the unit square. The difference to the classical Scott–Vogelius element stems from the different treatment of near-singular vertices only. Therefore we focus our benchmark on the criss-cross triangulation $\mathcal {T}_{\varepsilon }$ of the unit square $\Omega :=(0,1)^2$ with interior vertex $\textbf{z}_{\varepsilon }:=(1/2+\varepsilon ;1/2)$ perturbed by some $0<\varepsilon <1/2$ shown in Fig. 4. For $\varepsilon \ll 1$, this triangulation locally models a critical mesh configuration with $0<\Theta (\textbf{z}_\varepsilon )\ll 1$ where in finite arithmetic the classical Scott–Vogelius FEM becomes unstable. Consider the exact smooth solution

$$\begin{aligned} \textbf{u}\left( \textbf{x}\right) =\begin{pmatrix} \phantom {-}\sin ^{2}\left( \pi x_{1}\right) \sin \left( \pi x_{2}\right) \cos \left( \pi x_{2}\right) \\ -\sin ^{2}\left( \pi x_{2}\right) \sin \left( \pi x_{1}\right) \cos \left( \pi x_{1}\right) \end{pmatrix} ,{} & {} \hspace{-.5em}p\left( \textbf{x}\right) =10^{6}{\text {e}}^{-\left( x_{1} -0.3\right) ^{-2}-\left( x_{2}-32/500\right) ^{-2}}\hspace{-.4em}+C, \end{aligned}$$

to the Stokes problem with body force $\textbf{F}\equiv \textbf{f}:=-\Delta \textbf{u} +\nabla p\in \textbf{C}^{\infty }\left( \Omega \right)$. The velocity is pointwise divergence-free as it is the vector curl of $\sin ^{2}\left( \pi x_{1}\right) \sin ^2\left( \pi x_{2}\right)$ and C is chosen such that the pressure $p\in L^2_0(\Omega )$ has zero integral mean.

Optimal convergence of the h-method This benchmark considers uniform red-refinement of the initial mesh ${\mathcal {T}}_\varepsilon$ that subdivides each element into four congruent children by joining the edge midpoints. This refinement strategy does not introduce new near-singular vertices in the refinement and $\Theta (\textbf{z}_\varepsilon )$ remains constant throughout the refinement. We consider $\varepsilon =0.01,0.0001,10^{-6},10^{-8}$ that corresponds to $\Theta (\textbf{z}_{\varepsilon }) \approx 2\varepsilon$. Figure 5 displays the total error $\Vert \nabla (\textbf{u}-\textbf{u}_\textbf{S})\Vert _{\mathbb L^2(\Omega )} + \Vert p-p_M\Vert _{L^2(\Omega )}$ and the $L^2$ norm of the discrete divergence $\Vert {\text {div}}\textbf{u}_\textbf{S}\Vert _{L^2(\Omega )}$ when $\textbf{z}_\varepsilon \not \in \mathcal {C}_\mathcal {T}(\eta )$ is treated as non-singular or as singular $\textbf{z}_\varepsilon \in \mathcal {C}_\mathcal {T}(\eta )$ vertex. In the first case, our pressure-wired Stokes FEM is identical to the classical Scott–Vogelius FEM. We observe that for low polynomial degrees k and perturbations $\Theta (\textbf{z}_{\varepsilon })>10^{-6}$, both variants converge optimally. However, for small perturbations $\Theta (\textbf{z}_{\varepsilon })<10^{-6}$ (dotted), the solution to the classical Scott–Vogelius FEM is polluted by the high condition number of the algebraic system and only our modification that treats $\textbf{z}_\varepsilon \in \mathcal {C}_\mathcal {T}(\eta )$ as $\eta$-critical converges at all and with optimal rate. The divergence of the classical Scott–Vogelius FEM vanishes up to rounding errors except for a similar pollution effect for $\Theta (\textbf{z}_\varepsilon )<10^{-6}$. We also observe that the $L^2$ norm of the divergence for the pressure-wired Stokes FEM is very small compared to the total error and also significantly smaller than the velocity error $\Vert \nabla (\textbf{u}-\textbf{u}_\textbf{S})\Vert _{\mathbb L^2(\Omega )}$ (undisplayed) by a factor of $\Theta (\textbf{z}_{\varepsilon })$.

Fig. 5

Convergence history of the total error (left) and of the divergence (right) with $\textbf{z}_\varepsilon$ treated as $\eta$-critical $\textbf{z}_\varepsilon \in \mathcal C_\mathcal {T}(\eta )$ or non-singular $\textbf{z}_\varepsilon \not \in {\mathcal {C}}_\mathcal {T}(\eta )$ vertex for the h-method

Exponential convergence of the k-method This benchmark monitors the behaviour of the k-method that successively increases the polynomial degree k. The convergence history of the total error in Fig. 6 displays the same pollution effect for small perturbations $0<\varepsilon \ll 1$ or higher polynomial degree k when $\textbf{z}_\varepsilon$ is treated as a non-singular vertex. All other graphs overlay and, in particular, the pressure-wired Stokes FEM converges exponentially. For the discrete divergence, we observe the same convergence up to a certain threshold when accumulated rounding errors dominate. We remark that a sophisticated choice of bases, e.g., from [25], could improve this threshold. However, this does not affect the high condition number caused by the singular mesh configuration that produces the pollution effect for the Scott–Vogelius FEM.

Fig. 6

Convergence history of the discretisation error (left) and $\Vert {\text {div}}\, \textbf{u}_{\textbf{S}}\Vert$ (right) with $\textbf{z}_\varepsilon$ treated as nearly singular $\textbf{z}_\varepsilon \in \mathcal {C}_{\mathcal {T}}(\eta )$ or non-singular $\textbf{z}_\varepsilon \not \in \mathcal {C}_{\mathcal {T}}(\eta )$ vertex for the k-method